ЭЛЕКТРОСТАТИКА И ПОСТОЯННЫЙ ТОК
%PDF-1.6 % 1 0 obj > endobj 6 0 obj /CreationDate (D:20110602100030+03’00’) /Creator (Acrobat PDFMaker 9.0 for Word) /ModDate (D:20110602104751+03’00’) /Producer (Acrobat Distiller 9.0.0 \(Windows\)) /Title >> endobj 2 0 obj > stream 2011-06-02T10:47:51+03:002011-06-02T10:00:30+03:002011-06-02T10:47:51+03:00Acrobat PDFMaker 9.0 for Wordapplication/pdf
0.0 (Windows)2011-06-02T09:59:11+03:002011-06-02T09:59:02+03:00Acrobat PDFMaker 9.0 for Word2011-06-02T09:59:11+03:00application/pdf
0.0 (Windows)2011-06-02T09:59:46+03:002011-06-02T09:59:45+03:00Acrobat PDFMaker 9.0 for Word2011-06-02T09:59:46+03:00application/pdfНапряжённость электрического поля — это… Что такое Напряжённость электрического поля?
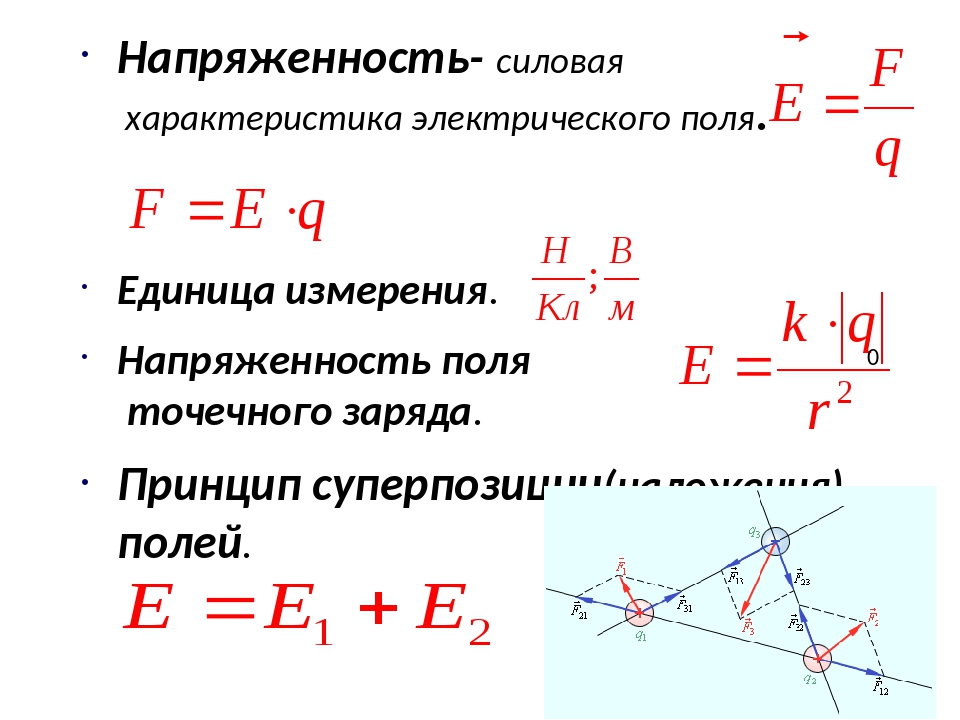
Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на неподвижный[1]пробный заряд, помещенный в данную точку поля, к величине этого заряда :
- .
Из этого определения видно, почему напряженность электрического поля иногда называется силовой характеристикой электрического поля (действительно, всё отличие от вектора силы, действующей на заряженную частицу, только в постоянном[2] множителе).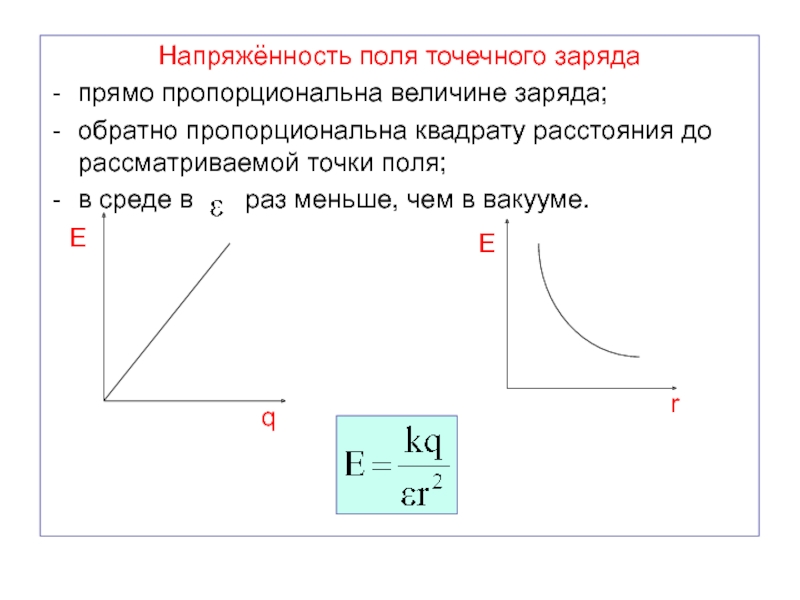
В каждой точке пространства в данный момент времени существует свое значение вектора (вообще говоря — разное[3] в разных точках пространства), таким образом, — это векторное поле. Формально это выражается в записи
представляющей напряженность электрического поля как функцию пространственных координат (и времени, т.к. может меняться со временем). Это поле вместе с полем вектора магнитной индукции представляет собой электромагнитное поле[4], и законы, которым оно подчиняется, есть предмет электродинамики.
Напряжённость электрического поля в СИ измеряется в вольтах на метр [В/м] или в ньютонах на кулон.
Напряжённость электрического поля в классической электродинамике
Из сказанного выше ясно, что напряженность электрического поля — одна из основных фундаментальных величин классической электродинамики. В этой области физики можно назвать сопоставимыми с ней по значению только вектор магнитной индукции (вместе с вектором напряженности электрического поля образующий тензор электромагнитного поля) и электрический заряд.
С некоторой точки зрения столь же важными представляются потенциалы электромагнитного поля (образующие вместе единый электромагнитный потенциал).
Приведем краткий обзор основных контекстов классической электродинамики в отношении напряженности электрического поля.
Сила, с которой действует электромагнитное поле на заряженные частицы
Полная сила, с которой электромагнитное поле (включающее вообще говоря электрическую и магнитную составляющие) действует на заряженную частицу, выражается формулой силы Лоренца:
где q — электрический заряд частицы, — ее скорость, — вектор магнитной индукции (основная характеристика магнитного поля), косым крестом обозначено векторное произведение. Формула приведена в единицах СИ.
Как видим, эта формула полностью согласуется с определением напряженности электрического поля, данном в начале статьи, но является более общей, т.к. включает в себя также действие на заряженную частицу (если та движется) со стороны магнитного поля.
В этой формуле частица предполагается точечной. Однако эта формула позволяет рассчитать и силы, действующие со стороны электромагнитного поля на тела любой формы с любым распределением зарядов и токов — надо только воспользоваться обычным для физики приемом разбиения сложного тела на маленькие (математически — бесконечно маленькие) части, каждая из которых может считаться точечной и таким образом входящей в область применимости формулы.
Остальные формулы, применяемые для расчета электромагнитных сил (такие, как, например, формула силы Ампера) можно считать следствиями[5] фундаментальной формулы силы Лоренца, частными случаями ее применения итп.
Однако для того, чтобы эта формула была применена (даже в самых простых случаях, таких, как расчет силы взаимодействия двух точечных зарядов), необходимо знать (уметь рассчитывать) и чему посвящены следующие параграфы.
Уравнения Максвелла
Достаточным вместе с формулой силы Лоренца теоретическим фундаментом классической электродинамики являются уравнения электромагнитного поля, называемые уравнениями Максвелла.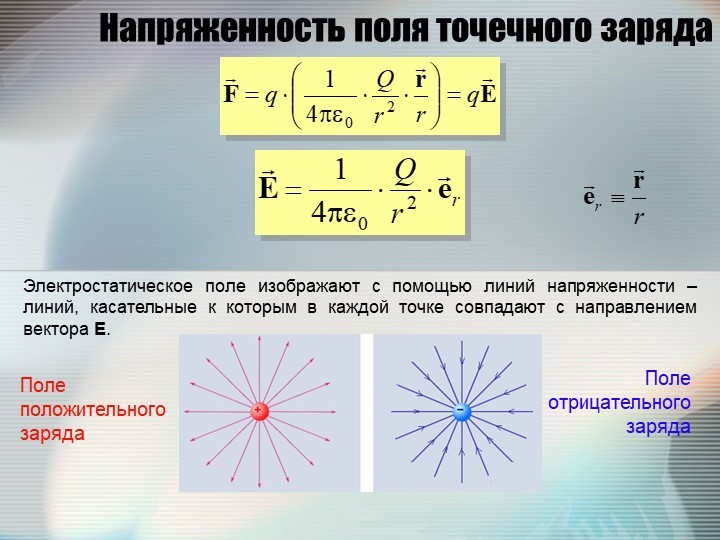
Их стандартная традиционная форма представляет собой четыре уравнения, в три из которых входит вектор напряженности электрического поля:
Здесь — плотность заряда, — плотность тока, — универсальные константы (уравнения здесь записаны в единицах СИ).
Здесь приведена наиболее фундаментальная и простая форма уравнений Максвелла — так называемые «уравнения для вакуума» (хотя, вопреки названию, они вполне применимы и для описания поведения электромагнитного поля в среде). Подробно о других формах записи уравнений Максвелла — см. основную статью.
Этих четырех уравнений вместе с пятым — уравнением силы Лоренца — в принципе достаточно, чтобы полностью описать классическую (то есть не квантовую) электродинамику, то есть они представляют ее полные законы. Для решения конкретных реальных задач с их помощью необходимы еще уравнения движения «материальных частиц» (в классической механике это законы Ньютона), а также зачастую дополнительная информация о конкретных свойствах физических тел и сред, участвующих в рассмотрении (их упругости, электропроводности, поляризуемости итд итп), а также о других силах, участвующих в задаче (например, о гравитации), однако вся эта информация уже не входит в рамки электродинамики как таковой, хотя и оказывается зачастую необходимой для построения замкнутой системы уравнений, позволяющих решить ту или иную конкретную задачу в целом.
«Материальные уравнения»
Такими дополнительными формулами или уравнениями (обычно не точными, а приближенными, зачастую всего лишь эмпирическими), которые не входят непосредственно в область электродинамики, но поневоле используются в ней ради решения конкретных практических задач, называемыми «материальными уравнениями», являются, в частности:
- Закон Ома,
- Закон поляризации
- в разных случаях многие другие формулы и соотношения.
Связь с потенциалами
Связь напряженности электрического поля с потенциалами в общем случае такова:
где — скалярный и векторный потенциалы. Приведем здесь для полноты картины и соответствующее выражение для вектора магнитной индукции:
В частном случае стационарных (не меняющихся со временем) полей, первое уравнение упрощается до:
Это выражение для связи электростатического поля с электростатическим потенциалом.
Электростатика
Важным с практической и с теоретической точек зрения частным случаем в электродинамике является тот случай, когда заряженные тела неподвижны (например, если исследуется состояние равновесия) или скорость их движения достаточно мала чтобы можно было приближенно воспользоваться теми способами расчета, которые справедливы для неподвижных тел.
Этим частным случаем занимается раздел электродинамики, называемый электростатикой.
Как мы уже заметили выше, напряженность электрического поля в этом случае выражается через скалярный потенциал как
или
то есть электростатическое поле оказывается потенциальным полем. ( в этом случае — случае электростатики — принято называть электростатическим потенциалом).
- Также и обратно
Уравнения поля (уравнения Максвелла) при этом также сильно упрощаются (уравнения с магнитным полем можно исключить, а в уравнение с дивергенцией можно подставить ) и сводятся к уравнению Пуассона:
а в областях, свободных от заряженных частиц — к уравнению Лапласа:
Учитывая линейность этих уравнений, а следовательно применимость к ним принципа суперпозиции, достаточно найти поле одного точечного единичного заряда, чтобы потом найти потенциал или напряженность поля, создаваемого любым распределением зарядов (суммируя решения для точечного заряда).
Теорема Гаусса
Очень полезной в электростатике оказывается теорема Гаусса, содержание которой сводится к интегральной форме единственного нетривиального для электростатики уравнения Максвелла:
где интегрирование производится по любой замкнутой поверхности S (вычисляя поток через эту поверхность), Q — полный (суммарный) заряд внутри этой поверхности.
Эта теорема дает крайне простой и удобный способ расчета напряженности электрического поля в случае, когда источники имеют достаточно высокую симметрию, а именно сферическую, цилиндрическую или зеркальную+трансляционную. В частности, таким способом легко находится поле точечного заряда, сферы, цилиндра, плоскости.
Напряжённость электрического поля точечного заряда
В единицах СИ
Для точечного заряда в электростатике верен закона Кулона
или
- .
- .
Исторически закон Кулона был открыт первым, хотя с теоретической точки зрения уравнения Максвелла более фундаментальны.
С этой точки зрения он является их следствием. Получить этот результат проще всего исходя из теоремы Гаусса, учитывая сферическую симметрию задачи: выбрать поверхность S в виде сферы с центром в точечном заряде, учесть, что направление будет очевидно радиальным, а модуль этого вектора одинаков везде на выбранной сфере (так что E можно вынести за знак интеграла), и тогда, учитывая формулу для площади сферы радиуса r: , имеем:
откуда сразу получаем ответ для E.
Ответ для получается тогда интегрированием E:
Для системы СГС
Формулы и их вывод аналогичны, отличие от СИ лишь в константах.
Напряженность электрического поля произвольного распределения зарядов
По принципу суперпозиции для напряженности поля совокупности дискретных источников имеем:
где каждое
Подставив, получаем:
Для непрерывного распределения аналогично:
где V — область пространства, где расположены заряды (ненулевая плотность заряда), или всё пространство, — радиус-вектор точки, для которой считаем , — радиус-вектор источника, пробегающий все точки области V при интегрировании, dV — элемент объема.
Можно подставить x,y,z вместо , вместо , вместо dV.
Системы единиц
В системе СГС напряжённость электрического поля измеряется в СГСЭ единицах, в системе СИ — в ньютонах на кулон или в вольтах на метр (русское В/м, международное V/m).
Литература
Примечания
- ↑ На движущийся заряд действует также магнитное поле, если, конечно, оно имеется (не равно нулю), поэтому в определение напряженности электрического поля вносится условие неподвижности пробного заряда; при условии гарантированного отсутствия магнитного поля неподвижность пробного заряда перестает быть обязательной, однако требование отсутствия магнитного поля в общем случае невозможно (а возможно только в частных классах задач).
- ↑ Для любой частицы ее электрический заряд постоянен. Измениться он может только если от частицы что-то заряженное отделится или если к ней что-то заряженное присоединится.
- ↑ Хотя иногда его значения могут оказываться и одинаковыми в разных точках пространства; если одинаков всюду в пространстве (или какой-то области пространства), говорят об однородном электрическом поле — это всего лишь частный случай электрического поля, хотя и наиболее простой; притом что в реальности электрическое поле может быть однородным лишь приближенно, то есть различия в разных точках пространства есть, но иногда они небольшие и ими можно пренебречь в рамках некоторого приближения.
- ↑ Электромагнитное поле может быть выражено и по-другому, например через электромагнитный потенциал или в несколько иной математической записи (прячущей вектор напряженности электрического поля вместе с вектором магнитной индукции внутрь тензора электромагнитного поля), однако все эти способы записи тесно связаны между собой, таким образом, утверждение о том, что поле — одна из основных составляющих электромагнитного поля не утрачивает смысла.
- ↑ Хотя исторически многие из них были открыты раньше.
См. также
13.8. Примеры применения теоремы Гаусса
1. Напряженность электростатического поля, создаваемого равномерно заряженной сферической поверхностью.
Пусть сферическая поверхность радиуса R (рис. 13.7) несет на себе равномерно распределенный заряд q, т.е. поверхностная плотность заряда в любой точке сферы будет одинакова.
Заключим нашу сферическую поверхность в симметричную поверхность S с радиусом r>R.
Поток вектора напряженности через поверхность S будет равенПо теореме Гаусса
Следовательно
(13.8) Сравнивая это соотношение с формулой для напряженности поля точечного заряда, можно прийти к выводу, что напряженность поля вне заряженной сферы такова, как если бы весь заряд сферы был сосредоточен в ее центре.
Для точек, находящихся на поверхности заряженной сферы радиуса R, по аналогии с вышеприведенным уравнением, можно написать
(13.9) Проведем через точку В, находящуюся внутри заряженной сферической поверхности, сферу S радиусом г<R. Внутри сферы S зарядов нет, т.к. все они расположены на внешней сферической поверхности, т.е. Следовательно, по теореме Гаусса, и напряженность электростатического поля внутри полой равномерно заряженной сферы будет равна нулю.
Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис. 13.8.
Поток вектора напряженности через поверхность S будет равен
Зависимость напряженности поля заряженной сферы от расстояния r приведена на рис. 13.8.2. Электростатическое поле шара.
Пусть имеем шар радиуса R, равномерно заряженный с объемной плотностью .
В любой точке А, лежащей вне шара на расстоянии r от его центра (r>R), его поле аналогично полю точечного заряда , расположенного в центре шара. Тогда вне шара
| (13.10) |
а на его поверхности (r=R)
| (13.11) |
В точке В, лежащей внутри шара на расстояний r от его центра (r>R), поле определяется лишь зарядом , заключенным внутри сферы радиусом r. Поток вектора напряженности через эту сферу равен
с другой стороны, в соответствии с теоремой Гаусса
Из сопоставления последних выражений следует
(13. 12) |
где- диэлектрическая проницаемость внутри шара. Зависимость напряженности поля, создаваемого заряженной сферой, от расстояния до центра шара приведена на (рис.13.10)
3. Напряженность поля равномерно заряженной бесконечной прямолинейной нити (или цилиндра).
Предположим, что полая цилиндрическая поверхность радиуса R заряжена с постоянной линейной плотностью .
Проведем коаксиальную цилиндрическую поверхность радиуса Поток вектора напряженности через эту поверхность
По теореме Гаусса
Из последних двух выражений определяем напряженность поля, создаваемого равномерно заряженной нитью:
| (13.13) |
4. Напряженность поля, создаваемого, бесконечной равномерно заряженной плоскостью.
Пусть плоскость имеет бесконечную протяженность и заряд на единицу площади равен σ. Из законов симметрии следует, что поле направлено всюду перпендикулярно плоскости, и если не существует никаких других внешних зарядов, то поля по обе стороны плоскости должны быть одинаковы.
Ограничим часть заряженной плоскости воображаемым цилиндрическим ящиком, таким образом, чтобы ящик рассекался пополам и его образующие были перпендикулярны, а два основания, имеющие площадь S каждое, параллельны заряженной плоскости (рис 1.10).
Суммарный поток вектора; напряженности равен вектору , умноженному на площадь S первого основания, плюс поток вектора через противоположное основание. Поток напряженности через боковую поверхность цилиндра равен нулю, т.к. линии напряженности их не пересекают. Таким образом, С другой стороны по теореме Гаусса
Следовательно
но тогда напряженность поля бесконечной равномерно заряженной плоскости будет равна
| (13.14) |
В это выражение не входят координаты, следовательно электростатическое поле будет однородным, а напряженность его в любой точке поля одинакова.
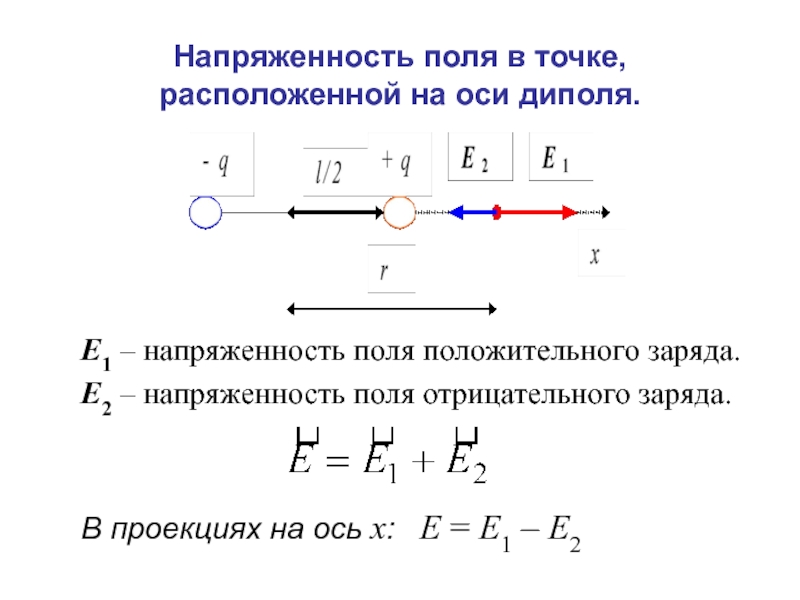
5. Напряженность поля, создаваемого двумя бесконечными параллельными плоскостями, заряженными разноименно с одинаковыми плотностями.
Как видно из рисунка 13.13, напряженность поля между двумя бесконечными параллельными плоскостями, имеющими поверхностные плотности зарядов и , равны сумме напряженностей полей, создаваемых пластинами, т.е.
Таким образом,
| (13.15) |
Вне пластины векторы от каждой из них направлены в противоположные стороны и взаимно уничтожаются. Поэтому напряженность поля в пространстве, окружающем пластины, будет равна нулю Е=0.
Ускорение заряда электрическим полем. Методические материалы
Цифровой ресурс может использоваться для обучения в рамках программы средней школы (базового и профильного уровней).
Компьютерная модель–задача. Пользователю предлагаются пять пар изображений, содержащих информацию о движении заряженных частиц и электрических полях. Требуется установить соответствие между электрическим полем и ускорением, которое поле может сообщить заряду.
Краткая теория
Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к значению этого заряда:
Напряженность электрического поля – векторная физическая величина. Направление вектора в каждой точке пространства совпадает с направлением силы, действующей на положительный пробный заряд.
Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.
Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности.
Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряженностей электрических полей, создаваемых в той же точке зарядами в отдельности:
Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции.
В соответствии с законом Кулона напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:
Это поле называется кулоновским. В кулоновском поле направление вектора зависит от знака заряда Q: если Q > 0, то вектор направлен по радиусу от заряда, если Q < 0, то вектор направлен к заряду.
В предлагаемой задаче для расчета напряженности можно применить формулу напряженность поля в конденсаторах:
Здесь U – напряжение между обкладками конденсатора, d – расстояние между обкладками.
Сила, с которой поле действует на заряд, вычисляется по формуле F = Eq. При этом согласно второму закону Ньютона получаем выражение для напряженности поля при известных заряде, массе и ускорении: E = ma / q.
Работа с моделью
Для решения задачи требуется рассчитать для каждой из пяти изображенных систем напряженность в указанных точках и расположить схемы, соответствующие системам, в порядке возрастания напряженности. Зная напряженность каждого изображенного поля, можно для четырех зарядов посчитать напряженность поля по массе, ускорению и значению заряда и определить, какое из приведенных полей сообщает данное ускорение, для пятого заряда поле можно определить методом исключения.
Пользователь имеет возможность перемещать с помощью курсора мышки рисунки в соответствующие позиции. При нажатии на кнопку анализируется результат, после чего можно либо обновить экран для нового решения, либо посмотреть правильное решение данного задания.
Рекомендации по применению модели
Данная модель может быть применена в качестве интерактивной задачи на уроках повторения, решения задач в 10 классе по теме «Напряженность электрического поля», «Движение заряженной частицы в электростатическом поле».
Пример планирования урока с использованием модели
Тема «Напряженность электрического поля. Решение задач»
Цель урока: повторить понятие напряженности электрического поля; второго закона Ньютона; отработать решение задач.
|
|||||||||||||||||||||
|
Таблица 1. |
Примеры вопросов и заданий
| 1. |
Две частицы массой m каждая с одинаковыми электрическими зарядами q находились в вакууме на расстоянии r в состоянии покоя друг относительно друга. Какой будет максимальная скорость относительного движения частиц при их удалении друг от друга под действием электростатических сил отталкивания при отсутствии других сил? |
Как рассчитать напряженность электрического поля при точечной зарядке
Этапы расчета напряженности электрического поля на точечном заряде
Шаг 1: Определите абсолютное значение количества заряда.
Шаг 2: Определите величину силы.
Шаг 3: Найдите силу электрического поля, разделив величину силы на абсолютное значение количества заряда.
Словарь и формулы для расчета напряженности электрического поля при точечном заряде
Электрическое поле: Электрическое поле — это поле, окружающее электрический заряд или группу зарядов.
Это векторное поле, имеющее как величину, так и направление, которое можно определить по его влиянию на испытательный заряд, помещенный в поле. Если мы поместим небольшой положительный тестовый заряд {eq} \ text {q} {/ eq} в электрическом поле и измерьте электростатическую силу {eq} \ vec {F} {/ eq}, действующее на тестовый заряд, электрическое поле в этой точке равно: $$ \ vec {E} = \ frac {\ vec {F}} {\ text {q}} $$
Напряженность или величину электрического поля можно найти, разделив величину силы на абсолютное значение заряда.{6} \: N / C} {/ экв}.
Получите доступ к тысячам практических вопросов и объяснений!точечных зарядов — AP Physics 2
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Где самая сильная напряженность электрического поля? — MVOrganizing
Где напряженность электрического поля самая сильная?
Напряженность электрического поля наибольшая в местах наибольшего сближения линий, а наименьшая — в местах наибольшего расстояния между линиями.
От чего зависит напряженность электрического поля?
Напряженность электрического поля зависит от заряда источника, а не от испытательного заряда. Касательная к силовой линии указывает направление электрического поля в этой точке. Там, где силовые линии расположены близко друг к другу, электрическое поле сильнее, чем там, где они дальше друг от друга.
Что такое нормальная напряженность электрического поля?
Напряженность электрического поля обычно варьируется от 10 до 150 вольт на метр под линиями распределения электроэнергии и от 5 до 100 вольт на метр внутри домов и на рабочих местах.Сила магнитного поля обычно измеряется в единицах гаусс или миллигаусс и изменяется в зависимости от силы тока, проходящего через проводник.
Какое электрическое поле находится на расстоянии 4 м от заряда 4 Кл?
= 0,04 м. ∴ E = 8,99 × 10⁶ N / C. Следовательно, напряженность электрического поля составляет 8,99 × 10⁶ N / C. Надеюсь, это поможет.
По какой формуле рассчитывается электрическое поле?
величина электрического поля (E), создаваемого точечным зарядом с зарядом величины Q, в точке на расстоянии r от точечного заряда, задается уравнением E = kQ / r2, где k — постоянная со значением 8.
99 x 109 Н м2 / C2.
Какова формула электрического поля для бесконечного заряженного листа?
E = ρ / 2ϵ0 aN, где aN — единичный вектор, нормальный к листу.
Постоянна ли напряженность электрического поля?
Если скорость изменения потенциала с расстоянием постоянна, то напряженность электрического поля постоянна. Электрическое поле связано с концепцией силы: оно описывает силу на единицу заряда. Если потенциал постоянный, то наклон потенциала равен нулю, что означает, что электрическое поле равно нулю.
Каково выражение для напряженности электрического поля на расстоянии?
Расстояние точки P от заряда + q в точке B равно BP = r — a. Расстояние точки P от заряда –q в точке A равно AP = r + a. Пусть E1 и E2 — напряженности электрического поля в точке P, обусловленные зарядами + q и –q соответственно.
Напряженность и напряженность электрического поля одинаковы?
То есть единица напряженности электрического поля — Ньютон / Кулон.
Напряженность электрического поля имеет направление и, следовательно, является векторной величиной.Интенсивность означает величину или количество. Напряженность поля аналогично означает величину напряженности поля.
Как расстояние влияет на напряженность магнитного поля?
Магнитная сила подчиняется закону обратных квадратов с расстоянием. Если расстояние между двумя магнитами увеличится вдвое, магнитная сила между ними упадет до четверти исходного значения. (F / 4) Если расстояние между двумя магнитами уменьшить вдвое, магнитная сила между ними увеличится в четыре раза по сравнению с исходным значением.
Как рассчитать напряженность магнитного поля на расстоянии?
Уравнение простое и красивое: в основном это I = 1 / d2, где d — расстояние (или I = 1 / r2 на фотографии, где r — расстояние), а I — интенсивность. Часто предполагается, что напряженность магнитного поля также подчиняется закону обратных квадратов.
Как сила магнитного поля изменяется с увеличением расстояния от стержневого магнита?
— Магнитное поле становится слабее по мере удаления от магнита.
Моделирование показывает это, затемняя иглы по ходу движения. Когда магнит будет максимально сильным, измените его полярность, используя экранную кнопку «Перевернуть полярность» на панели управления. Когда компас касается стержневого магнита в его средней точке.
Какая связь между магнитным полем и расстоянием?
Магнитное поле провода уменьшается по мере удаления от провода. Вместо того, чтобы поле было пропорционально обратному квадрату расстояния, как электрическое поле точечного заряда, магнитное поле обратно пропорционально расстоянию от провода.
Какая связь между силой магнитного поля и положением?
В соответствии с законом Био – Савара напряженность магнитного поля обратно пропорциональна расстоянию от проводника с током. В этом примечании к приложению мы будем использовать ту же концепцию в приложении определения положения.
Все ли магнитные поля имеют одинаковую силу?
Влияет ли размер магнита на его силу? Короткий ответ — да, но только потому, что размер магнита означает, что существует пропорционально больше доменов, которые могут выравниваться и создавать более сильное магнитное поле, чем меньший кусок того же материала.
Как сделать магнит более мощным?
Если вам удастся найти очень сильный магнит, несколько раз потрите им ослабленный магнит. Сильный магнит перестроит магнитные домены внутри ослабленного магнита [источник: Luminaltech]. Укладка магнитов Один из способов сделать слабые магниты сильнее — сложить их вместе.
Напряженность гравитационного поля — Викиверситет
Это уменьшает силу до силы тяжести, действующей на единицу массы.Есть еще одно определение, в котором напряженность поля находится по пространственным и временным производным потенциалов гравитационного поля или по компонентам гравитационного тензора. [1]
Поскольку гравитационное поле является полем, его напряженность Γ {\ displaystyle ~ \ mathbf {\ Gamma}} от времени и координаты точки в пространстве, где измеряется напряженность поля:
- Γ = Γ (x, y, z, t). {\ Displaystyle ~ \ mathbf {\ Gamma} = \ mathbf {\ Gamma} (x, y, z, t).}
Напряженность гравитационного поля Γ {\ displaystyle ~ \ mathbf {\ Gamma}} и гравитационное торсионное поле Ω {\ displaystyle ~ \ mathbf {\ Omega}} описывают гравитационное поле в лоренц-инвариантной теории гравитации и подчиняются уравнениям гравитации типа Максвелла.
В общей теории относительности напряженность гравитационного поля называется напряженностью гравитоэлектрического поля, а торсионное поле соответствует гравитомагнитному полю. В пределе слабого гравитационного поля указанные величины входят в уравнения гравитоэлектромагнетизма.
Напряженность гравитационного поля в международной системе единиц измеряется в метрах на секунду в квадрате [м / с 2 ] или в Ньютонах на килограмм [Н / кг].
Напряженность гравитационного поля в лоренц-инвариантной теории гравитации [редактировать | править источник]
Если мы запишем соотношения лоренц-инвариантной теории гравитации (ЛИТГ) в терминах 4-векторов и тензоров, мы обнаружим, что вектор напряженности гравитационного поля и вектор торсионного поля составляют гравитационный тензор и являются частью гравитационный тензор энергии-импульса и лагранжиана для отдельной частицы в гравитационном поле, а также скалярный и векторный потенциалы гравитационного поля образуют гравитационный четырехпотенциал.
{2}}} \ mathbf {H},}
где cg {\ displaystyle ~ c_ {g}} — это скорость распространения гравитационного эффекта (скорость гравитации), G {\ displaystyle ~ G} — гравитационная постоянная.
Гравитационная сила [править | править источник]
Полная сила, с которой гравитационное поле действует на пробную частицу, выражается следующей формулой:
- F знак равно M (Γ + V × Ω), {\ Displaystyle ~ \ mathbf {F} = M \ left (\ mathbf {\ Gamma} + \ mathbf {V} \ times \ mathbf {\ Omega} \ right) ,}
где: M {\ displaystyle ~ M} — масса частицы, V {\ displaystyle ~ \ mathbf {V}} — скорость частицы, Ω {\ displaystyle ~ \ mathbf {\ Omega}} — вектор гравитационного торсионного поля.
В этой формуле первый член силы пропорционален силе гравитационного поля, а второй член силы зависит от скорости частицы и от торсионного поля, действующего на частицу. Предполагается, что Γ {\ displaystyle ~ \ mathbf {\ Gamma}} и Ω {\ displaystyle ~ \ mathbf {\ Omega}} — это напряженность и торсионное поле от внешнего гравитационного поля, усредненные по объему частицы, и собственным полем частицы можно пренебречь из-за его малости.
Для расчета суммарной силы, действующей на протяженное тело, в пределах которой сила и кручение гравитационного поля изменяются в значительном масштабе, выполняем разбиение тела на мелкие части и для каждой части вычисляем их силу и силу. затем произведите векторное суммирование всех этих сил.
Плотность вектора силы f {\ displaystyle ~ \ mathbf {f}}, понимаемая как гравитационная сила, действующая на единицу движущегося объема, является частью пространственно-подобного компонента 4-вектора плотности гравитационной силы. (см. четыре силы).{2}}}}} — фактор Лоренца, ρ0 {\ displaystyle ~ \ rho _ {0}} — плотность массы в сопутствующей системе отсчета.
Формула показывает, что произведение Γ⋅J {\ displaystyle ~ \ mathbf {\ Gamma} \ cdot \ mathbf {J}} равно мощности работы, совершаемой гравитационной силой на единицу объема, а торсионное поле равно не входит в этот товар и не выполняет работы по этому поводу.
Уравнения Хевисайда [править | править источник]
Лоренц-ковариантные уравнения гравитации в инерциальных системах отсчета можно найти в работах Оливера Хевисайда.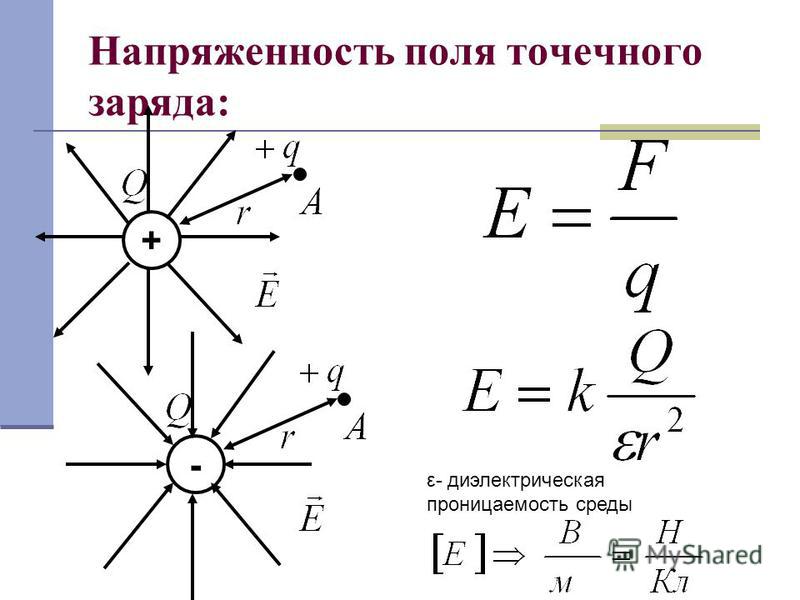
{2}}} \ left (-4 \ pi G \ mathbf {J} + {\ frac {\ partial \ mathbf {\ Gamma}} {\ partial t}} \ right),}
где: J = ρV {\ displaystyle ~ \ mathbf {J} = \ rho \ mathbf {V}} — массовая плотность тока, ρ = γρ0 {\ displaystyle ~ \ rho = \ gamma \ rho _ {0} } — плотность движущейся массы, V {\ displaystyle ~ \ mathbf {V}} — скорость потока массы, создающего гравитационное поле и кручение.
Эти четыре уравнения полностью описывают гравитационное поле для случаев, когда поле недостаточно велико, чтобы влиять на распространение электромагнитных волн, их скорость и частоту. В этих уравнениях источниками гравитационного поля являются плотность массы и массовые токи, а формула гравитационной силы, в свою очередь, показывает, как поле действует на материю.
Если гравитационное поле имеет большие размеры, его влияние на электромагнитные процессы приводит к гравитационному красному смещению, замедлению времени, отклонению движения электромагнитных волн вблизи источников гравитационного поля и другим эффектам.
Поскольку измерения времени и пространства производятся с помощью электромагнитных волн, то в гравитационном поле размеры тела наблюдателя могут быть меньше, а скорость времени может замедлиться. Подобные эффекты учитываются путем введения метрики пространства-времени, которая зависит от координат и времени. Поэтому в случае сильного гравитационного поля вместо приведенных выше уравнений используются более общие уравнения ковариантной теории гравитации или уравнения общей теории относительности, в которых присутствует метрический тензор.{2}}} \ nabla \ times \ mathbf {J}.}
Наличие волновых уравнений предполагает, что сила и кручение гравитационного поля в любой точке могут быть найдены как суммы (интегралы) набора отдельных простые волны, вносящие свой вклад в общее поле, где каждый вклад следует рассчитывать с учетом запаздывания воздействия источников поля из-за ограниченной скорости гравитационного распространения.
Третье уравнение Хевисайда приводит к возможности гравитационной индукции, когда изменяющееся во времени торсионное поле, проходящее через какой-либо контур, или изменение площади контура при постоянном торсионном поле, создают круговую напряженность гравитационного поля по окружности этого контура.
.
Потенциалы гравитационного поля [править | править источник]
Напряженность гравитационного поля может быть выражена через скалярный потенциал ψ {\ displaystyle ~ \ psi}, а также через векторный потенциал гравитационного поля D {\ displaystyle ~ \ mathbf {D}} следующим образом:
- Γ = −∇ψ − ∂D∂t. {\ Displaystyle ~ \ mathbf {\ Gamma} = — \ nabla \ psi — {\ frac {\ partial \ mathbf {D}} {\ partial t}}.}
Торсионное поле зависит только от векторного потенциала, так как:
- Ом = ∇ × D.{\ displaystyle ~ \ mathbf {\ Omega} = \ nabla \ times \ mathbf {D}.}
Гравистатика [править | править источник]
Самым простым случаем изучения свойств гравитации является случай взаимодействия неподвижных или движущихся с малой скоростью тел. В гравитациях векторный потенциал D {\ displaystyle ~ \ mathbf {D}} гравитационного поля не учитывается из-за отсутствия или малости поступательного или вращательного движения масс, создающих поле, потому что D {\ displaystyle ~ \ mathbf {D} } пропорционален скорости масс.
В результате уменьшается и торсионное поле, которое рассчитывается как ротор векторного потенциала. В этом приближении мы можем написать:
- Γ = −∇ψ, {\ displaystyle ~ \ mathbf {\ Gamma} = — \ nabla \ psi,}
где ψ {\ displaystyle ~ \ psi} называется гравитационным потенциалом, чтобы подчеркнуть статический случай гравитационное поле. В гравитатах напряженность гравитационного поля — это потенциальное векторное поле, то есть поле, которое зависит только от градиента некоторой функции, в данном случае скалярного потенциала.
При условии, что в рассматриваемой системе нет массовых токов и, следовательно, J = 0, {\ displaystyle ~ \ mathbf {J} = 0,} напряженность гравитационного поля не зависит от времени, векторный потенциал D {\ displaystyle ~ \ mathbf {D}} и торсионное поле Ω {\ displaystyle ~ \ mathbf {\ Omega}} равны нулю, в уравнениях Хевисайда остается только одно уравнение:
- ∇⋅Γ = −4πGρ0. (1) {\ displaystyle ~ \ nabla \ cdot \ mathbf {\ Gamma} = -4 \ pi G \ rho _ {0}. \ Qquad \ qquad (1)}
\ Qquad \ qquad (1)}Если в (1) мы используем соотношение Γ = −∇ψ, {\ displaystyle ~ \ mathbf {\ Gamma} = — \ nabla \ psi,}, то мы получим уравнение, которое имеет форму уравнения Пуассона:
- Δψ = 4πGρ0.{\ displaystyle ~ \ Delta \ psi = 4 \ pi G \ rho _ {0}.}
За пределами тел плотность массы в состоянии покоя равна нулю, ρ0 = 0, {\ displaystyle ~ \ rho _ {0} = 0,} и уравнение для гравистатического потенциала становится уравнением Лапласа:
- Δψ = 0. {\ Displaystyle ~ \ Delta \ psi = 0.}
Уравнения Пуассона и Лапласа справедливы как для потенциала точечной частицы, так и для суммы потенциалов набора частиц, что составляет можно использовать принцип суперпозиции для вычисления полного потенциала и напряженности общего гравитационного поля в любой точке системы.Однако из модернизированной теории гравитации Лесажа следует, что в сильных полях принцип суперпозиции нарушается из-за экспоненциальной зависимости потоков гравитонов в веществе от пройденного расстояния.
[4]
Применение теоремы о расходимости [править | править источник]
Уравнение (1) может быть проинтегрировано по произвольному объему пространства, а затем мы можем применить теорему о дивергенции, которая заменяет интеграл от дивергенции вектор-функции по определенному объему интегралом от потока этой вектор-функции по замкнутой поверхности. вокруг заданного объема:
- ∮SΓ⋅dS = −4πGM, {\ displaystyle ~ \ oint \ limits _ {S} \ mathbf {\ Gamma} \ cdot d \ mathbf {S} = -4 \ pi GM,}
где M { \ displaystyle ~ M} — это общая масса вещества внутри поверхности.{2}}}.}
Эта формула остается в силе независимо от радиуса тела сферической формы, пока этот радиус не превышает R {\ displaystyle ~ R}, то есть когда напряженность поля Γ {\ displaystyle ~ \ Gamma} ищется вне тела. Для точечной частицы с массой M {\ displaystyle ~ M} мы можем предположить, что расстояние R {\ displaystyle ~ R} измеряется из этой статьи.
В случае применения теоремы о расходимости к сферической поверхности внутри тела со сферически-симметричным расположением массы из теоремы следует, что напряженность гравитационного поля внутри тела зависит только от массы тела M (r) { \ displaystyle ~ M (r)} внутри сферической поверхности с радиусом r {\ displaystyle ~ r}:
- Γ = −GM (r) r2. {3} \ rho _ {0}} {3}}}, что дает для напряженности поля:
- Γ = −4πGρ0r3. {\ Displaystyle ~ \ Gamma = — {\ frac {4 \ pi G \ rho _ {0} r} {3}}.}
В центре сферы, где r = 0, {\ displaystyle ~ r = 0,} напряженность поля равна нулю, а радиус r = a {\ displaystyle ~ r = a}, где a {\ displaystyle ~ a} — радиус сферы, сила достигает максимальной амплитуды.
Классическая теория гравитации [править | править источник]
Выражение для напряженности гравитационного поля точечной частицы также может быть получено из закона Ньютона для гравитационной силы, действующей на пробную частицу с массой m {\ displaystyle ~ m}.{2}}},}
{3} \ rho _ {0}} {3}}}, что дает для напряженности поля:где: R {\ displaystyle ~ R} — радиус-вектор от центра тела до точки в пространстве, где определяется напряженность гравитационного поля Γ {\ displaystyle ~ \ Gamma}. , а знак минус указывает, что сила F {\ displaystyle ~ F} и напряженность поля направлены противоположно радиус-вектору R {\ displaystyle ~ R}.
В классической теории скалярный потенциал гравитационного поля вне сферического тела равен:
- ψ = −GMR. {2}}} = \ Gamma,}
{2}}} = \ Gamma,}т.е. сила гравитационного поля равна по количеству (и размеру) ускорению свободного падения g {\ displaystyle ~ g} пробной частицы в этом поле.
- ↑ Федосин С.Г. Электромагнитные и гравитационные картины мира. Апейрон, 2007, т. 14, № 4, С. 385 — 413.
- ↑ Федосин С.Г. Физика и философия подобия: от преонов до метагалактиков, Пермь: Стиль-МГ, 1999, ISBN 5-8131-0012-1. 544 стр., Табл.66, Илл.93, Библ.377 исх.
- ↑ Оливер Хевисайд. Гравитационная и электромагнитная аналогия, часть I, Электрик, 31, 281-282 (1893).
- ↑ Федосин С.Г. Модель гравитационного взаимодействия в концепции гравитонов. Журнал векторной теории относительности, март 2009 г., т. 4, No. 1, P.1 — 24.
Точка P находится в середине прямоугольника. Какова напряженность электрического поля в P? Спасибо!
Поскольку четыре заряда являются точечными, уравнение для поля, обусловленного каждым отдельным зарядом, часто записывается как
# E = (kQ) / r ^ 2 # где # k = 9xx10 ^ 9 (Нм ^ 2) / C ^ 2 #
Теперь мы должны вычислить поле в P, которое связано с каждым зарядом отдельно, и, наконец, сложить эти вклады вместе (как векторы).
7 N / C # в положительном направлении # x #.
Эпизод 402: Поля, силовые линии и напряженность поля
Гравитационное поле
Земля и космос | Силы и движение
Эпизод 402: Поля, силовые линии и напряженность поля
Урок для 16-19
- Время активности 60 минут
- Уровень Передовой
Этот эпизод знакомит с понятием «силовое поле» и знакомит с тем, как мы можем схематически представить такое поле с помощью силовых линий.Фактическая напряженность поля в точке пространства определяется напряженностью поля.
Краткое содержание урока
- Обсуждение: Поля и линии поля (10 минут)
- Обсуждение: Напряженность поля, г (10 минут)
- Рабочие примеры: Напряженность поля (20 минут)
- Упражнение с электронными таблицами: анализ данных миссии «Аполлон-11» (20 минут)
Обсуждение: Поля и линии полей
Когда вы берете в руки какой-либо предмет, например ручку, между вами и ручкой возникает прямой контакт.Этот прямой контакт оказывает давление на перо, заставляя его двигаться таким же образом. Однако ручка также имеет вес из-за ее присутствия в гравитационном поле Земли. Как проявляется эта сила, даже если между Землей и пером нет прямого контакта? На перо действует сила со стороны Земли, потому что перо находится в гравитационном поле Земли . Мы можем определить поле, создаваемое телом, как область окружающего его пространства, где другие тела будут ощущать силу из-за него.
Насколько сильно гравитационное поле? (Гравитационная сила бесконечна по радиусу действия, хотя на больших расстояниях она становится очень слабой, поскольку это закон обратных квадратов. Таким образом, гравитационное поле, создаваемое телом, также бесконечно.)
Мы не можем увидеть или коснуться этого поля, но мы можем попытаться смоделировать его, используя силовых линий или силовых линий . На диаграмме силовых линий направление силовой линии в точке дает направление силы притяжения, которое будет ощущаться небольшой массой, помещенной там.Относительная плотность силовых линий на диаграмме указывает на напряженность поля. (Сравните это с более знакомыми моделями магнитного поля.)
Таким образом, для сферической массы, такой как Земля, мы имели бы следующую диаграмму:
Силовые линии направлены радиально внутрь, потому что в любой точке поля Земли тело ощущает силу, направленную к центру Земли. Силовые линии становятся более разбросанными по мере увеличения расстояния от Земли, что указывает на уменьшение напряженности поля.
Обратите внимание, что поле действительно трехмерное, но, конечно, на бумаге мы можем взять его только двумерный срез. Это радиальное поле или сферическое поле .
Вблизи поверхности Земли силовые линии выглядят так:
Они направлены вниз (направление, в котором тело, находящееся у поверхности Земли, будет ощущать гравитационную силу), и они параллельны и равноудалены, что указывает на то, что поле является постоянным или однородным .
Несколько важных замечаний:
- Линии поля не начинаются и не заканчиваются на пустом месте (хотя на диаграммах они должны где-то останавливаться!).Они заканчиваются массой и уходят в бесконечность.
- Линии поля никогда не пересекаются. (Если бы они это сделали, то объект, помещенный в точку пересечения, почувствовал бы силы более чем в одном направлении. Эти силы можно было бы преобразовать в одно направление — истинное направление там линии поля.)
(Понятия поля и силовых линий будут использоваться снова, когда мы посмотрим на электрические поля и магнитные поля).
Обсуждение: Напряженность гравитационного поля,
гКак вы уже видели, вы притягиваете Землю с той же силой, что и она.Однако ваше гравитационное поле по своей природе намного, намного слабее, чем у Земли. Чтобы попытаться понять внутреннюю силу гравитационного поля тела, нам нужно определить напряженность поля в точке поля.
Мы определяем напряженность поля в точке поля тела как гравитационную силу, действующую на объект, помещенный в этой точке, на килограмм массы объекта. Другими словами, это просто число в ньютонах силы притяжения, действующей на килограмм массы объекта.Поскольку сила притяжения — это просто то, что мы называем весом, мы можем записать это как:
г = Ш м
, где W — вес в ньютонах. Таким образом, г имеет единицы N кг -1 .
Мы можем использовать это определение, чтобы получить уравнение для g , используя закон всемирного тяготения Ньютона.
Сила притяжения массы M (вызывающей поле) на массу m на расстоянии r прочь просто G M m r 2 .Таким образом, сила притяжения на кг массы объекта (масса м ) составляет G M м м r 2 .
Таким образом, г = G M r 2 .
Это дает выражение для напряженности поля на расстоянии r от (точечной или сферической) массы M .
Несколько замечаний:
- Напряженность гравитационного поля в точке поля не зависит от размещенной там массы — это свойство поля.Таким образом, два объекта разной массы, помещенные в одну и ту же точку поля, будут испытывать одинаковую напряженность поля, но будут ощущать разные гравитационные силы.
- В некоторых текстах в этом уравнении присутствует знак минус, поэтому оно читается как g = — G M r 2 ; это из более правильного, но не входящего в учебный план, векторного уравнения для g.
Величину напряженности поля лучше рассчитать, используя g = G M r 2 и тогда направление задается тем фактом, что гравитация всегда притягивает (т.е. поле всегда действует навстречу гравитирующему телу).Примеры работ: Напряженность поля
Расчеты с учетом напряженности поля.
Эпизод 402: 1 Напряженность поля — лист учеников (Word, 31 КБ)
Таблица упражнений
Здесь студенты могут попробовать проанализировать данные миссии «Аполлон-11».
Эпизод 402-2: Анализ данных полета Аполлона 11 на Луну (Word, 29 КБ)
Эпизод 402-3: Данные миссии Аполлон-11 (Word, 85 КБ)
Величина и направление электрического поля — проблемы и решения
1.Рассчитайте величину и направление электрического поля в точке A, расположенной на расстоянии 5 см от точечного заряда Q = +10 мкКл.
k = 9 x 10 9 Нм 2 C −2 , 1 мкКл = 10 −6 C)
Известный:
Электрический заряд (Q) = +10 мкКл = +10 x 10 -6 C
Расстояние между точкой A и точечным зарядом Q (r A ) = 5 см = 0,05 м = 5 x 10 -2 м
k = 9 x 10 9 Нм 2 C −2
Разыскивается: Величина и направление электрического поля в точке A
Решение:
Направление электрического поля в точке A:
Электрический заряд положительный, следовательно, направление электрического поля от электрического заряда и точек A.
2. Рассчитайте величину и направление электрического поля в точке P, расположенной на расстоянии 10 см от точечного заряда Q = -20 мкКл. k = 9 x 10 9 Нм 2 C −2 , 1 мкКл = 10 −6 C.
Известный:
Электрический заряд (q) = -20 мкКл = -20 x 10 -6 C
Расстояние между точкой P и электрическим зарядом (r P ) = 10 см = 0,1 м = 1 x 10 -1 м
k = 9 x 10 9 Нм 2 C −2
Разыскивается: Величина и направление электрического поля в точке P
Решение:
Направление электрического поля в точке A:
Электрический заряд отрицательный, отсюда и направление электрического поля к электрическому заряду.
3. Два точечных заряда разделены расстоянием 40 см. Каковы величина и направление электрического поля в точке P между двумя зарядами, то есть в 20 см от точки A?
Известный:
Заряд A (q A ) = -2 мкКл = -2 x 10 -6 C
Заряд B (q B ) = +4 мкКл = +4 x 10 -6 C
Расстояние между зарядом A и точкой P (r AP ) = 20 см = 0,2 м = 2 x 10 -1 м
Расстояние между зарядом B и точкой P (r BP ) = 20 см = 0.2 м = 2 x 10 -1 м
Разыскивается: Величина и направление электрического поля в точке P.
Решение:
Заряд A отрицательный, поэтому направление электрического поля указывает на Q A (влево).
Заряд B положительный, так что направление электрического поля указывает от Q B (налево).
Полное электрическое поле в точке A:
E = E A + E B
E = (4.5 х 10 5 ) + (9 х 10 5 )
E = 13,5 x 10 5 N / C
Направление электрического поля указывает на Q A (слева).
4. Величина электрического поля равна нулю при…
.Заряд A положительный, а заряд B положительный, так что величина электрического поля равна нулю в точке P между обоими зарядами.
Известно:
Заряд A (q A ) = +20 мкКл = +20 x 10 −6 C
Заряд B (q B ) = +40 мкКл = +40 x 10 −6 C
k = 9 x 10 9 Нм 2 C −2
Расстояние между зарядом A и зарядом B = 20 см
Заряд между зарядом A и точкой P (r AP ) = a
Расстояние между зарядом B и точкой P (r BP ) = 20 — a
Разыскивается: Величина электрического поля равна нулю и находится в….
Решение:
Величина электрического поля, создаваемого зарядом A в точке P
Заряд A положительный, так что направление электрического поля направлено от заряда A (вправо).
Величина электрического поля, создаваемого зарядом B в точке P:
Заряд B положительный, так что направление электрического поля указывает от заряда B (влево).
Полное электрическое поле в точке P = 0:
Мы используем формулу корней квадратного уравнения, чтобы определить a.
Величина электрического поля равна нулю на расстоянии 8 см от заряда A или 12 см от заряда B.
5. Как видно из рисунка ниже, где находится точка P, чтобы электрическое поле в точке P было равно нулю? (k = 9 x 10 9 Нм 2 C −2 , 1 мкКл = 10 −6 C)
Решение
Для расчета напряженности электрического поля в точке P предполагается, что в точке P имеется положительный испытательный заряд.
Q 1 положительно, а Q 2 отрицательно, поэтому точка P должна быть справа от Q 2 или слева от Q 1 . Если точка P находится слева от Q 1 ; электрическое поле, создаваемое Q 1 в точке P, находится слева (от Q 1 ), а электрическое поле, создаваемое Q 2 в точке P справа (по направлению к Q 1 ). Направление электрического поля противоположно, так что два электрических поля устраняют друг друга, так что напряженность электрического поля в точке P равна нулю.
Известно:
Q 1 = +9 мкC = +9 x 10 −6 C
Q 2 = -4 мкКл = -4 x 10 −6 ° С
k = 9 x 10 9 Нм 2 C −2
Расстояние между зарядом 1 и зарядом 2 = 3 см
Расстояние между Q 1 и точкой P (r 1P ) = a
Расстояние между Q 2 и точкой P (r 2P ) = 3 + a
Разыскивается: местоположение точки P так, чтобы электрическое поле в точке P было равно нулю
Решение:
Точка P находится слева от Q 1 .
Электрическое поле, создаваемое Q 1 в точке P:
Тестовый заряд положительный, а Q 1 положительный, так что направление электрического поля влево.
Электрическое поле, создаваемое Q 2 в точке P:
Тестовый заряд положительный, а Q 2 отрицательный, так что направление электрического поля направлено вправо.
Чистое электрическое поле в точке A:
Используйте формулу корней квадратного уравнения, чтобы определить a:
а = -1.25, b = -13,5, c = -20,25
Расстояние между Q 2 и точкой P (r 2P ) = 3 + a = 3 — 1,8 = 1,2 см.
Точка P находится на 1,2 см справа от Q 1 .
.