Импедансная технология
Импедансная технология используется для измерения Величина, указывающая, как много воды содержится в газе
или в жидкости. Для количественного выражения влажности
используются различные единицы
Принцип действия импедансной технологии
Датчик состоит из трёх слоёв, размещённых на керамической подложке: пористого проводящего, активного адсорбирующего и ещё одного проводящего. Слои очень тонкие, порядка 1 мкм. Система представляет собой крошечный конденсатор.
Газ, содержащий молекулы воды, свободно проникает сквозь проводящий слой в адсорбирующий. Молекулы воды обладают высоким дипольным моментом, поэтому их присутствие в адсорбирующем слое изменяет диэлектрическую проницаемость среды между обкладками конденсатора, что в свою очередь определяет емкость конденсатора и  импеданс системы. Датчик В процессе эксплуатации значения некоторых переменных, от которых зависит работа анализатора, изменяются. Калибровкой
называется процесс коррекции значений этих переменных,
необходимый для обеспечения достоверности показаний.калибруют, занося в память прибора кривую зависимости импеданса системы от влажности газа. При измерениях электроника преобразует значение импеданса в выходной сигнал и линеаризует его.
импеданс системы. Датчик В процессе эксплуатации значения некоторых переменных, от которых зависит работа анализатора, изменяются. Калибровкой
называется процесс коррекции значений этих переменных,
необходимый для обеспечения достоверности показаний.калибруют, занося в память прибора кривую зависимости импеданса системы от влажности газа. При измерениях электроника преобразует значение импеданса в выходной сигнал и линеаризует его.
Приборы, основанные на импедансной технологии, рассчитаны на рабочее давление в несколько сотен
Приборам необходима периодическая Совокупность процедур, необходимых для подтверждения
соответствия конкретного прибора паспортным данным. В случае
успешного прохождения выдается свидетельство о поверке; в противном случае выдается извещение о непригодности прибора к использованию. Выполняется только аккредитованными
организациями.
Выполняется только аккредитованными
организациями.
Электрический импеданс — это… Что такое Электрический импеданс?
Электри́ческий импеда́нс (комплексное сопротивление, полное сопротивление) — комплексное сопротивление двухполюсника для гармонического сигнала. Это понятие ввёл физик и математик О. Хевисайд в 1886 году.[1][2]
Аналогия с сопротивлением
В отличие от резистора, электрическое сопротивление которого характеризует соотношение напряжения к току на нём, попытка применения термина электрическое сопротивление к реактивным элементам (катушка индуктивности и конденсатор) приводит к тому, что сопротивление идеальной катушки индуктивности стремится к нулю, а сопротивление идеального конденсатора — к бесконечности.
Сопротивление правильно описывает свойства катушки и конденсатора только на постоянном токе. В случае же переменного тока свойства реактивных элементов существенно иные: напряжение на катушке индуктивности и ток через конденсатор не равны нулю. Такое поведение сопротивлением уже не описывается, поскольку сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов тока и напряжения.
Такое поведение сопротивлением уже не описывается, поскольку сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов тока и напряжения.
Было бы удобно иметь некоторую характеристику и для реактивных элементов, которая бы при любых условиях связывала ток и напряжение на них подобно сопротивлению. Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при гармонических воздействиях на них. В этом случае ток и напряжение оказываются связаны некоей стабильной константой (подобной в некотором смысле сопротивлению), которая и получила название
Определение
Импедансом называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник.
| (1) |
Здесь
Исторически сложилось, что обозначение импеданса, комплексных амплитуд и других комплекснозначных функций частоты записывают как , а не . Такое обозначение показывает, что мы имеем дело с комплексными представлениями гармонических функций вида . Кроме того, над символом, обозначающим комплексный сигнал или комплексный импеданс, обычно ставят «домик» или точку: чтобы отличать от соответствующих действительных (некомплексных) величин.
Физический смысл
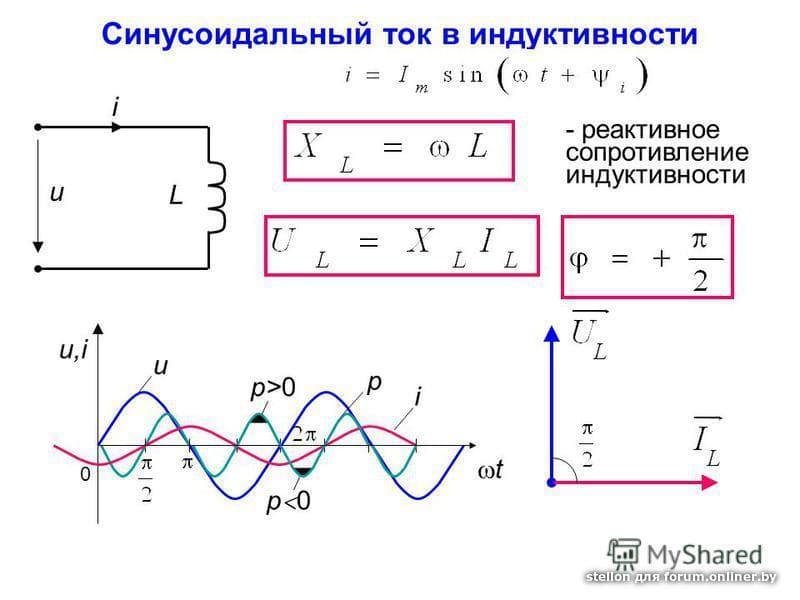
Навстречу нарастающему току генератора, идет ток самоиндукции катушки. Вот это противодействие тока самоиндукции катушки нарастающему току генератора, и называется индуктивным сопротивлением.На преодоление этого противодействия затрачивается часть энергии переменного тока генератора. Вся эта часть энергии полностью превращается в энергию магнитного поля катушки. Когда ток генератора будет убывать, магнитное поле катушки, также, будет убывать, пресекая катушку и индуктируя в цепи ток самоиндукции. Теперь ток самоиндукции будет идти в одном направлении с убывающим током генератора. Таким образом вся энергия затраченная током генератора на преодоление противодействия тока самоиндукции катушки полностью вернулась в цепь в виде энергии электрического тока. Поэтому индуктивное сопротивление является реактивным, т. е. не вызывающим безвозвратных потерь энергии.
Вся эта часть энергии полностью превращается в энергию магнитного поля катушки. Когда ток генератора будет убывать, магнитное поле катушки, также, будет убывать, пресекая катушку и индуктируя в цепи ток самоиндукции. Теперь ток самоиндукции будет идти в одном направлении с убывающим током генератора. Таким образом вся энергия затраченная током генератора на преодоление противодействия тока самоиндукции катушки полностью вернулась в цепь в виде энергии электрического тока. Поэтому индуктивное сопротивление является реактивным, т. е. не вызывающим безвозвратных потерь энергии.
Алгебраическая форма
Если рассматривать комплексный импеданс как комплексное число в алгебраической форме, то действительная часть соответствует активному сопротивлению, а мнимая — реактивному. То есть двухполюсник с импедансом можно рассматривать как последовательно соединенные резистор с сопротивлением и чисто реактивный элемент с импедансом
Рассмотрение действительной части полезно при расчёте мощности, выделяемой в двухполюснике, поскольку мощность выделяется только на активном сопротивлении.
Тригонометрическая форма
Если рассматривать импеданс как комплексное число в тригонометрической форме, то модуль соответствует отношению амплитуд напряжения и тока (сдвиг фаз не учитывается), а аргумент — сдвигу фазы между током и напряжением, то есть на сколько ток отстаёт от напряжения.
Ограничения
Понятие импеданса применимо, если при приложении к двухполюснику гармонического напряжения, ток, вызванный этим напряжением, также гармонический той же частоты. Для этого необходимо и достаточно, чтобы двухполюсник был линейным и его свойства не менялись со временем. Если это условие не выполнено, то импеданс не может быть найден по следующей причине: невозможно получить выражение для импеданса,
- Однако и для линейных двухполюсников (для которых зависимость от времени сокращается) импеданс всё же зависит от частоты (за исключением случая когда двухполюсник сводится к схеме из одних резисторов и импеданс оказывается действительной величиной).

Практически это означает, что импеданс может быть вычислен для любого двухполюсника, состоящего из резисторов, катушек индуктивности и конденсаторов, то есть из линейных пассивных элементов. Также импеданс хорошо применим для активных цепей, линейных в широком диапазоне входных сигналов (например, цепи на основе операционных усилителей). Для цепей, импеданс которых не может быть найден в силу указанного выше ограничения, бывает полезным найти импеданс в малосигнальном приближении для конкретной рабочей точки. Для этого необходимо перейти к эквивалентной схеме и искать импеданс для нее.
Вычисление импеданса
Идеальные элементы
Резистор
Для резистора импеданс всегда равен его сопротивлению
| (2) |
Конденсатор
Ток и напряжение для конденсатора связаны соотношением:
| (3) |
Отсюда следует, что при напряжении
| (4) |
ток, текущий через конденсатор, будет равен:
| (5) |
После подстановки (4) и (5) в (1) получаем:
| (6) |
Катушка индуктивности
Аналогичное рассмотрение для катушки индуктивности приводит к результату:
| (7) |
Общий случай
Для произвольного двухполюсника, состоящего из элементов с известным импедансом, нет необходимости производить приведенные выше вычисления с целью нахождения импеданса.
| (8) |
Экспериментальное измерение импеданса
Импеданс реальных элементов может быть измерен специальными приборами: измерителем RLC или анализатором импеданса. Эти приборы позволяют производить измерения в широком диапазоне частот и при различных напряжениях смещения.
Применение импеданса
Введение импеданса позволяет описывать поведение двухполюсника с реактивными свойствами при воздействии на него гармонического сигнала. Кроме того, в случае негармонического сигнала импеданс применяется столь же успешно. Для этого сигнал раскладывается на спектральные компоненты при помощи ряда Фурье или преобразования Фурье и рассматривается воздействие каждой спектральной компоненты. Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал.
Вследствие линейности двухполюсника сумма откликов на спектральные компоненты равна отклику на исходный негармонический сигнал.
См. также
Примечания
- ↑ Science, p. 18, 1888
- ↑ Oliver Heaviside. The Electrician. P. 212; 23 July 1886 reprinted as Electrical Papers, p64, AMS Bookstore, ISBN 0-8218-3465-7
Литература
- Л. А. Бессонов. Теоретические основы электротехники. — 9-е изд. — М.: Высшая школа, 1996.
- Графов Б.М., Укше Е.А. Электрохимические цепи переменного тока. — М.: Наука, 1983.
2200mkf — 25v (Низький імпеданс) CapXon KF 13*25, 105°C конденсатор електролітичний, цена 10.37 грн
2200mkf — 25v (Низкий импеданс) CapXon (KF 13*25), 105°CИзображения служат только для ознакомления
См. спецификации продукта
Максимальная рабочая температура: 105°C
Производитель: CapXon
Серия: KF
Тип: Конденсатор электролитический низкий импеданс
· срок службы больше, чем у стандартных конденсаторов;
· максимальный импеданс задается на частоте 100 кГц и остается неизменным в диапазоне температур +20…-10°С;
· пульсирующий ток определяется на частоте 100 кГц;
· повышенная температурная стабильность (температурный коэффициент импеданса).
Конденсаторы с низким ESR одного и того же номинала могут монтироваться в корпуса различных размеров.
Для лучшего понимания того, что же представляют собой конденсаторы с низким ESR и каковы их характеристики, необходимо сначала понять, что же значит низкое ESR и как оно влияет на рабочие характеристики схемы.
Эквивалентная схема конденсатора содержит четыре основных элемента, причем значения трех – импеданса конденсатора (Z), эквивалентного последовательного сопротивления (ESR), эквивалентной последовательной индуктивности (ESL) – зависят от частоты. Значение Rp зависит от постоянного тока. Рассмотрим лишь зависящие от частоты характеристики конденсатора – ESL, ESR и Z.
ESL – сумма индуктивностей всех индуктивных элементов конденсатора. ESL = 2PIЧfЧL, где f – рабочая частота и L – индуктивность.
ESR, подобно ESL, – сумма всех резистивных элементов конденсатора. ESR = DF/(2PIЧfЧC)ЧХс, где DF – коэффициент рассеяния,
f – частота, С – емкость и Хс – емкостное сопротивление,
. ..
..
Z – импеданс конденсатора. Z = Ц(ESR)2 + (ESL – Xc)2.
Срок службы конденсатора в зависимости от температуры
| Температура | время работы | при 24 ч эксплуатации | при 8 ч эксплуатации |
| при 50оС | 60,000 часов | 7 лет | 20 лет |
| при 30оС | 200,000 часов | 30 лет | 86 лет |
CapXon предлагает алюминиевые электролитические низкоимпедансные конденсаторы с низким ESR на рабочую температуру до 105°C серий KF срок службы которых достигает 5 тыс. ч при температуре 105°C .
Импеданс и его влияние в акустической системе
Сам столкнулся с этой темой давно, но разобраться решил, когда начал серьёзно заниматься акустическими измерениями. Немного покапал в инете, немного пообщался с друзьями и в конце концов нарисовалась данная статья, которая надеюсь поможет в нашем непростом деле.
Импеданс – это комплексное (полное) сопротивление двухполюсника для гармонического сигнала, которое имеет активную и реактивную составляющие. Обычно импеданс акустических систем равен 4, 6 или 8 Ом. Импедансом так же называется отношение комплексной амплитуды напряжения гармонического сигнала, прикладываемого к двухполюснику, к комплексной амплитуде тока, протекающего через двухполюсник.
Пример импеданса акустической системы:
В отличие от резистора, электрическое сопротивление которого характеризует соотношение напряжения к току на нём, попытка применения термина электрическое сопротивление к реактивным элементам (катушка индуктивности и конденсатор) приводит к тому, что сопротивление идеальной катушки индуктивности стремится к нулю, а сопротивление идеального конденсатора — к бесконечности.
Сопротивление правильно описывает свойства катушки и конденсатора только на постоянном токе. В случае же переменного тока свойства реактивных элементов существенно иные: напряжение на катушке индуктивности и ток через конденсатор не равны нулю. Такое поведение сопротивлением уже не описывается, поскольку сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов тока и напряжения.
Такое поведение сопротивлением уже не описывается, поскольку сопротивление предполагает постоянное, не зависящее от времени соотношение тока и напряжения, то есть отсутствие фазовых сдвигов тока и напряжения.
Было бы удобно иметь некоторую характеристику и для реактивных элементов, которая бы при любых условиях связывала ток и напряжение на них подобно сопротивлению. Такую характеристику можно ввести, если рассмотреть свойства реактивных элементов при гармонических воздействиях на них. В этом случае ток и напряжение оказываются связаны некой стабильной константой (подобной в некотором смысле сопротивлению), которая и получила название электрический импеданс (или просто импеданс). При рассмотрении импеданса используется комплексное представление гармонических сигналов, поскольку именно оно позволяет одновременно учитывать и амплитудные, и фазовые характеристики сигналов и систем.
В целом величина полного электрического сопротивления (импеданса) акустической системы ни о чем, связанном с качеством звучания того или иного изделия, покупателю не скажет. Производителем указывается этот параметр лишь, чтобы сопротивление учитывали при подключении акустической системы к усилителю. Если значение сопротивления колонки ниже, чем рекомендуемое значение нагрузки усилителя, в звучании могут присутствовать искажения или сработает защита от короткого замыкания; если выше, то звук будет значительно тише, нежели с рекомендуемым сопротивлением.
Производителем указывается этот параметр лишь, чтобы сопротивление учитывали при подключении акустической системы к усилителю. Если значение сопротивления колонки ниже, чем рекомендуемое значение нагрузки усилителя, в звучании могут присутствовать искажения или сработает защита от короткого замыкания; если выше, то звук будет значительно тише, нежели с рекомендуемым сопротивлением.
Если представить акустическую систему, как четырёхполюсник к входным клеммам которого подключен генератор сигналов, то в зависимости от частоты подаваемого сигнала и состава вашего фильтра + излучатель, импеданс будет изменяться. Изменение носит нелинейный характер и может быть в одной области частот ёмкостным, а в другой – индуктивным. Чем сложнее выполнен фильтр в вашей акустической системе, тем больше изменений в импедансе.
Сопротивление акустической системы зависит от частоты. Но при использовании усилителя с обратной связью по току – ИТУН (источник тока управляемый напряжением) или полу-ИТУН (в народе широко известен такой усилитель, как например MF1), такой показатель, как зависимость от частоты, сама собой отпадает. Потому что уже нет зависимости от сопротивления на разных частотах, а это значит что ток, проходящий через катушку, уже не так изменяется. Он и работает только от того, что ток не превышает определённых значений. Но добавлю, что ИТУН и MF1 (полу-ИТУН) это не одно и то же, так как в ИТУНе есть только обратная связь по току, а в MF1 – комбинированная связь по току и по напряжению. Поэтому MF1 можно назвать «полу-ИТУН», так как он сочетает в себе комбинированную обратную связь.
Потому что уже нет зависимости от сопротивления на разных частотах, а это значит что ток, проходящий через катушку, уже не так изменяется. Он и работает только от того, что ток не превышает определённых значений. Но добавлю, что ИТУН и MF1 (полу-ИТУН) это не одно и то же, так как в ИТУНе есть только обратная связь по току, а в MF1 – комбинированная связь по току и по напряжению. Поэтому MF1 можно назвать «полу-ИТУН», так как он сочетает в себе комбинированную обратную связь.
Хочу обратить внимание на то, что ИТУН имеет небольшой подъём на высоких частотах, а связано это как раз с тем, что ток который проходит через катушку ВЧ динамика уже не «проваливается» и динамик играет как бы ровнее. Точно такой же эффект (поднятие высоких частот) присутствует и в MF1 всё по той же причине, а вот на НЧ уже сказывается меньше, таким образом, MF1 более универсален в плане АС и комплексной нагрузки, относительно чистого ИТУНа.
А в случае с ИНУН (источник напряжения управляемый напряжением), которые и являются подавляющее большинство усилителей, может в момент низкого сопротивления создать такой ток, который выведет из строя выходной каскад вследствие перегрузки по току. В другом случае, если сопротивление будет слишком высоким, то будет провал в этой части АЧХ, что вместе с пиком (который возникает от низкого сопротивления) дадут большие искажения, причем в несколько раз.
В другом случае, если сопротивление будет слишком высоким, то будет провал в этой части АЧХ, что вместе с пиком (который возникает от низкого сопротивления) дадут большие искажения, причем в несколько раз.
Еще раз памятка тем, кто хочет создать самодельные АС или что-то доработать. Как минимум, для получения удовлетворительного результата, нужно иметь под рукой комплекс для этих измерений и хотя бы немного знаний в электротехнике.
Вывод. При создании, доработке или переделки акустических систем, отдельное внимание нужно уделять импедансу. Измерять его можно с помощью компьютера, несложной коробочке-приставки и такой программы, например как LspLab, ну или как при замере параметров ТС, но в этом случае нужно иметь калиброванный (20 – 20000 Гц) милливольтметр. А также для уверенности использовать усилитель с обратной связью по току – ИТУН или полу-ИТУН, которым является всеми любимый и известный MF1 от Linkor.
Особую благодарность хочу сделать DTSу, в помощи по написанию статьи и решению некоторых нюансов. Ну а так как обычно, статью подготовил LDS, которая специально написана для сайта ldsound.ru.
Ну а так как обычно, статью подготовил LDS, которая специально написана для сайта ldsound.ru.
2013
волшебные свойства загадочных баночек / Хабр
Было ли лучшее время для энтузиастов и любителей Hi-Fi, чем конец 1970-х и начало 1980-х годов? С одной стороны, так много всего происходило с развитием цифрового аудио, а с другой — наблюдался рост субъективизма. Внезапно проигрыватели и усилители стали оценивать не по уровню детонации, выходной мощности и гармоническим искажениям, а по их звучанию! И можно было даже всерьёз говорить о звучании кабелей. В этой новой атмосфере всё, что когда-то считалось само собой разумеющимся в области Hi-Fi, стало кандидатом на переоценку.
Пристальному изучению подверглось и влияние на звук пассивных электронных компонентов — резисторов, индуктивностей и конденсаторов. В особенности, конденсаторов. Знающие люди начали обсуждать такие явления как эквивалентное последовательное сопротивление (ESR) и диэлектрическое поглощение.
Сегодня мы нечасто слышим об этой теме, но не потому, что проблема была исчерпана. Скорее всего, разработчики нынче уделяют столь же пристальное внимание используемым пассивным компонентам, как и схемам, в которых они применяются, так что общественный фурор несколько стих.
Азы
В простейшем виде конденсатор состоит из двух металлических пластин, разделённых воздухом (или, ещё лучше, вакуумом) и схематично изображён на рис. 1. Поскольку между пластинами нет проводящего пути, конденсатор блокирует постоянный ток (например, от батареи). При этом конденсатор, напротив, пропускает сигналы переменного тока — как раз такие как звуковые волны.
Рис. 1. Компоненты, из которых состоит конденсатор — две проводящие пластины, разделённые слоем диэлектрика.Проверенное решение
Мы нечасто сталкиваемся с воздушными конденсаторами, но если вы заглядывали внутрь старого лампового радиоприемника и видели элемент, отвечающий за настройку, который состоит из чередующихся металлических пластин, это как раз воздушный конденсатор переменной ёмкости. В большинстве конденсаторов, с которыми мы сталкиваемся в аудиотехнике и прочей электронике, в качестве изолирующего материала (диэлектрика), разделяющего пластины, не используется воздух, поскольку он имеет низкую диэлектрическую постоянную (1,0), а это означает, что воздушные конденсаторы большой емкости слишком громоздкие, чтобы быть практичными. По этой причине используются, в основном, твёрдые диэлектрики, с более высокими диэлектрическими свойствами, в том числе из керамики и различных видов пластмасс (например, ПВХ с диэлектрической проницаемостью 4,0). Именно здесь история становится особенно интересной, поскольку для всех этих диэлектриков характерны те или иные компромиссы в плане влияния на звук, в то время как воздух практически идеален.
В большинстве конденсаторов, с которыми мы сталкиваемся в аудиотехнике и прочей электронике, в качестве изолирующего материала (диэлектрика), разделяющего пластины, не используется воздух, поскольку он имеет низкую диэлектрическую постоянную (1,0), а это означает, что воздушные конденсаторы большой емкости слишком громоздкие, чтобы быть практичными. По этой причине используются, в основном, твёрдые диэлектрики, с более высокими диэлектрическими свойствами, в том числе из керамики и различных видов пластмасс (например, ПВХ с диэлектрической проницаемостью 4,0). Именно здесь история становится особенно интересной, поскольку для всех этих диэлектриков характерны те или иные компромиссы в плане влияния на звук, в то время как воздух практически идеален.
Простые фильтры
Для начала, узнаем побольше о том, как ведут себя конденсаторы и для чего они используются. Конденсаторы блокируют постоянный ток и пропускают переменный, однако они не пропускают переменный ток с разной частотой одинаково. Это объясняется тем, что конденсаторы обладают реактивным сопротивлением, которое снижается с увеличением частоты (к слову, катушки индуктивности тоже обладают реактивным сопротивлением, которое, наоборот, увеличивается с ростом частоты).
Это объясняется тем, что конденсаторы обладают реактивным сопротивлением, которое снижается с увеличением частоты (к слову, катушки индуктивности тоже обладают реактивным сопротивлением, которое, наоборот, увеличивается с ростом частоты).
Таким образом, конденсаторы пропускают высокочастотные сигналы легче, чем низкочастотные, что делает их крайне полезными в частотно-селективных цепях (то есть, в фильтрах), а также для устранения нежелательных сигналов (например, гул или шум с шины питания постоянного напряжения).
Простые фильтры верхних и нижних частот показаны на рис.2. В фильтре верхних частот (рис. 2а) последовательно включенный конденсатор подключен к шунтирующему резистору. В фильтре нижних частот (рис. 2b) конденсатор и резистор меняются местами.
Рис. 2. RC-фильтр первого порядка верхних (2a) и нижних (2b) частот.Итак, конденсаторы зачастую используются для объединения цепей, отделения нежелательного шума в цепях постоянного напряжения и в частотно-селективных цепях (фильтрах). Поскольку конденсаторы накапливают электрический заряд, большие из них также применяются в качестве резервуаров в источниках питания переменного и постоянного тока. На рис. 3 показан типовой источник питания, включающий в себя понижающий трансформатор (он понижает напряжение сети), мостовой выпрямитель (который преобразует переменный ток из трансформатора в импульсный постоянный ток) и пару конденсаторов-резервуаров (сглаживающих пульсации после выпрямления переменного тока).
Поскольку конденсаторы накапливают электрический заряд, большие из них также применяются в качестве резервуаров в источниках питания переменного и постоянного тока. На рис. 3 показан типовой источник питания, включающий в себя понижающий трансформатор (он понижает напряжение сети), мостовой выпрямитель (который преобразует переменный ток из трансформатора в импульсный постоянный ток) и пару конденсаторов-резервуаров (сглаживающих пульсации после выпрямления переменного тока).
Подобные схемы встречаются во многих твердотельных аудиокомпонентах. Аналогичные решения используются и в ламповом оборудовании, но из-за высоких напряжений, требуемых для работы ламп, трансформатор здесь обычно повышает напряжение сети.
Ёмкость резервуарных конденсаторов, используемых в транзисторных усилителях мощности, может достигать 50 000 мкФ и более, тогда как в других случаях в схеме могут использоваться конденсаторы емкостью 1 НФ (одна тысячная микрофарада) или даже меньше. Таким образом, очевидно, что некоторые типы конденсаторов лучше подходят под определённые задачи, чем другие.
Таким образом, очевидно, что некоторые типы конденсаторов лучше подходят под определённые задачи, чем другие.
Важное уточнение
Как правило, самые большие резервуарные конденсаторы являются электролитическими, ведь они обеспечивают высокую ёмкость в сравнительно небольшом объёме. Такие конденсаторы содержат электролит (жидкость или гель), который химически реагирует с металлической фольгой внутри банки, образуя слой диэлектрика. Подобные электролитические конденсаторы, а также некоторые другие — например, танталовые, называются полярными, а несоблюдение полярности подключения может привести к их выходу из строя.
Другая разновидность — неполярные конденсаторы, которые можно подключать без учёта полярности. Подобные электролиты иногда использовались в пассивных кроссоверах акустических систем, однако такая практика сегодня устарела, поскольку плёночные конденсаторы справляются с этой задачей лучше, хоть и занимают больше места.
Конденсаторы также могут иметь различное расположение выводов — аксиальное (осевое) или радиальное. Преимущество радиальных электролитов заключается в том, что они занимают меньше площади на плате, однако их минус — в том, что они увеличивают её высоту. В больших электролитических конденсаторах обычно отказываются от выводов под пайку — в пользу винтовых клемм.
Преимущество радиальных электролитов заключается в том, что они занимают меньше площади на плате, однако их минус — в том, что они увеличивают её высоту. В больших электролитических конденсаторах обычно отказываются от выводов под пайку — в пользу винтовых клемм.
Что скрывают конденсаторы
Настоящие конденсаторы, как и настоящие политики, ведут себя не идеально, и именно здесь кроется причина их влияния на качество звука. Во-первых, на практике ни один конденсатор не является только ёмкостью — он также имеет индуктивность и сопротивление. На принципиальной схеме конденсатор обычно обозначается одним из символов на рис. 4 (все они визуально отсылают к двум разделенным пластинам), однако в реальности он представляет собой что-то вроде схемы, представленной на рис. 5. Резистор обозначенный на рисунке как ESR (эквивалентное последовательное сопротивление) может быть не постоянным — сопротивление может зависеть от частоты. В случае с электролитическими конденсаторами, ESR обычно уменьшается с частотой.
Одним из последствий того, что у конденсаторов есть индуктивность (ESL или эквивалентная последовательная индуктивность на рис. 6), является то, что они, по сути, являются электрически резонансными. Если проанализировать импеданс конденсатора в зависимости от частоты, он не будет продолжать уменьшаться с ростом частоты. На рис. 6 показано, что импеданс достигает минимума (эквивалентного значению ESR) на резонансной частоте, а затем, по мере увеличения частоты, он снова начинает расти из-за ESL.
Рис. 5. Схематичный эквивалент реального конденсатора демонстрирует паразитное сопротивление (ESR) и индуктивность (ESL)Рис. 6. Паразитная индуктивность приводит к тому, что у конденсаторы имеют электрический резонанс, иногда — в пределах слышимого диапазона частот.У больших электролитических конденсаторов частоты электрического резонанса обычно находятся в пределах звукового диапазона. У небольших конденсаторов частоты электрического резонанса могут превышать 1 МГц. Для увеличения частоты электрического резонанса для заданной емкости следует уменьшить ESL — последовательную индуктивность.
Для увеличения частоты электрического резонанса для заданной емкости следует уменьшить ESL — последовательную индуктивность.
Для достижения этой цели, при разработке электролитических конденсаторов, где такая проблема стоит наиболее остро, применяются различные методы. Например, в конденсаторах DNM T-Network для снижения индуктивности используются специальные Т-образные соединения из фольги — таким образом, их резонансная частота более чем в два раза выше по сравнению со стандартной конструкцией (от 28 кГц до 75 кГц — в примере, который приводит компания DNM на своём веб-сайте).
ESR оказывает потенциально благотворное влияние на демпфирование электрического резонанса конденсатора, однако, в отличие от индуктивности или ёмкости, сопротивление генерирует тепло в то время, когда через конденсатор проходит ток. В больших ёмкостных конденсаторах, где проходящие через них токи велики, этот эффект внутреннего нагрева ограничивает безопасные условия эксплуатации. Тем не менее, электролитические конденсаторы лучше всего работают именно тёплыми.
Микрофонный эффект
Не секрет, что ламповое оборудование чувствительно к вибрации. Внутри вакуумированной стеклянной оболочки лампы находятся тонкие металлические электроды, расстояние между которыми влияет на работу лампы. Таким образом, если встряхнуть лампу достаточно сильно, это отразится на её электрической мощности — эффект, который называют «микрофонным», поскольку лампа в таком случае ведёт себя подобно микрофону.
Твердотельная электроника меньше подвержена этому эффекту, однако приведём в пример некий крайний случай: разработчики первых систем управления двигателем в гоночных автомобилях вскоре научились не прикреплять электронные блоки к двигателю, либо использовать хорошую изоляцию, иначе вибрации от двигателя могли нарушить её работу. Уровни вибрации, которые испытывает Hi-Fi оборудование при повседневном использовании, гораздо ниже, однако некоторые производители, среди которых, например, Naim Audio, по-прежнему прилагают большие усилия, чтобы свести к минимуму вероятное воздействие микрофонного эффекта.
Способность конденсатора накапливать заряд (его ёмкость) пропорциональна площади пластин и обратно пропорциональна расстоянию между ними, а «пластины» обычно представляют собой тонкую фольгу с тонкими слоями диэлектрика между ними. Это приводит к тому, что конденсаторы подвержены воздействию микрофонного эффекта, поскольку из-за вибрации расстояние между пластинами и, следовательно, значение ёмкости может меняться.
Таким образом, физические свойства материалов, из которых изготовлен конденсатор, могут быть столь же важны, как и электрические параметры. Но что ещё интереснее, вибрация извне не является необходимым условием для того, чтобы конденсаторы страдали от её воздействия, ведь силы, формируемые напряжениями и токами внутри самого конденсатора, также могут вызывать механические резонансы. Из-за этого эффекта можно даже услышать, как некоторые конденсаторы издают звук, когда через них проходит сигнал. В кроссовере акустической системы, где уровни вибраций, напряжения и токи высоки, присутствует «идеальный шторм» факторов, которые делают выбор подходящего конденсатора особенно важной задачей.
Ключевые слова
Проблема микрофонного эффекта и механических резонансов конденсаторов активно обсуждалась на протяжении многих лет, однако исследований по этому вопросу было достаточно мало. Во всяком случае, мало опубликованных исследований. Но те, что существуют, подтверждают мнение, что данный эффект может оказывать заметное влияние качества звучания.
К тому же, в некоторых случаях конденсаторы могут приводить к необычайно высоким уровням гармонических и интермодуляционных искажений. Понимание того, как и почему это происходит, позволяет разработчикам сосредоточить свои усилия на доработке электронной схемы и тщательном выборе электронных компонентов — таким образом, чтобы это принесло наибольшую пользу.
Не секрет, что при смене логических состояний у большинства цифровых устройств возникает большой бросок тока, который следует сразу за фронтом тактового сигнала (рис. 1). Например, схеме, работающей на частоте 100 МГц и потребляющей в среднем около 4 А, реально может потребоваться 20 А
тока в течение первых нескольких наносекунд тактовой последовательности. | Очевидно, что питание этой схемы от 20-амперного источника увеличит размеры и стоимость изделия. Менее очевидно, что паразитные последовательные индуктивности соединительных проводов, проводников печатной платы и выводов компонентов могут сделать невозможным быструю ответную реакцию мощного источника питания на мгновенные изменения тока. С другой стороны, недостаточная нагрузочная способность источника будет приводить к возникновению нестабильных падений напряжений на шинах питания и земли. Это явление обычно проявляется как высокочастотный шум. | Применение развязывающих конденсаторов позволяет распределить рабочий ток между потребителями, используя
низкоимпедансные (т.е. низкоиндуктивные для токов ВЧ) пути прохождения тока. Практически это означает, что развязывающие
конденсаторы непосредственно обслуживают цифровые компоненты, в то время как источник питания занимается их перезарядом. Использование конденсаторов в качестве элементов развязки требует понимания основ их работы. На рисунке 2а показан идеальный конденсатор — емкость для накопления и хранения заряда и для освобождения от него. На рисунке 3 приведена частотная зависимость импеданса идеального конденсатора — монотонное уменьшение значения при увеличении частоты. Поскольку основной шум цифровых систем является высокочастотным шумом (>50 МГц), уменьшение импеданса на высоких частотах хорошо соответствует задаче развязки цепей питания. К сожалению, поведение реального конденсатора не такое простое; его модель показана на рисунке 2б. Физическое
устройство реального конденсатора включает в себя эквивалентное последовательное сопротивление (ESR) и эквивалентную
последовательную индуктивность (ESL). К тому же, реальный конденсатор обладает сопротивлением утечки. Низшая точка импедансной зависимости известна как частота собственного резонанса. Разработчики часто пытаются подобрать конденсаторы с собственной резонансной частотой, находящейся близко от рабочей частоты системы. Однако, параметры реальных конденсаторов делают этот подбор нецелесообразным при тактовой частоте, превышающей 100 МГц. Важное правило, которое следует помнить: развязывающие конденсаторы допустимо использовать на частотах более низких, чем частота их собственного резонанса, до тех пор, пока их импеданс на этих частотах остается достаточно низким. | Падение напряжения на эквивалентном последовательном сопротивлении конденсатора пропорционально протекающему
через него току. Поскольку важным является поддержание питающего напряжения стабильным, желательным является использование
в цепях развязки конденсаторов с малым ESR (т.
Конденсаторы с материалом I типа в качестве диэлектрика не ухудшают свои характеристики от времени и воздействия
температуры, но малое значение диэлектрической постоянной делает их использование в качестве компонентов развязки неэффективным. В таблице 1 показаны типичные значения ESL для различных типов корпусов конденсаторов. Типоразмер является
определяющим элементом эквивалентной последовательной индуктивности — обычно конденсатор меньшего размера обладает меньшим
значением ESL при таком же значении емкости. В общем случае, правильной стратегией является поиск конденсатора с наибольшей емкостью при наименьших габаритных размерах (это верно лишь с точки зрения ESL, но не всегда правильно с точки зрения другого важнейшего параметра конденсаторов — диэлектрической абсорбции — прим. переводчика). Однако при таком выборе необходимо быть внимательным. Высота корпуса конденсатора в достаточно значительной мере оказывает влияние на ESL. Для перекрывающихся диапазонов ESL в таблице 1 возможен выбор корпуса с меньшим посадочным местом на печатной плате. Однако значение ESL может оказаться большим. Поэтому при выборе типа конденсатора необходимо руководствоваться параметрами производителя для определения лучшего компромиссного варианта. | При разводке компонентов и цепей основным препятствием хорошей развязки является индуктивность. С весьма грубыми
приближениями можно считать, что индуктивность трассы с волновым сопротивлением 50 Ом на материале FR-4 будет составлять около
9 пГн на каждые 0,025 мм длины. Индуктивность пропорциональна длине, поэтому важно минимизировать длину проводника между выводами компонента и развязывающего конденсатора. Индуктивность обратно пропорциональна ширине трассы, поэтому широкие проводники более предпочтительны, чем узкие. | Помните, что путь тока всегда представляет собой петлю, и эта петля должна быть минимизирована. Уменьшение расстояния между выводом питания компонента и выводом конденсатора может и не уменьшить общую индуктивность. Как правильно расположить конденсатор? Ближе к выводу питания компонента? Или ближе к выводу земли? Или посередине между этими выводами? Некоторые источники рекомендуют располагать конденсатор вблизи от вывода, наиболее удаленного от полигона питания или земли. | Хорошая разводка чрезвычайно важна для эффективной работы цепей развязки. На рисунке 5 показано несколько методов размещения и подключения конденсатора развязки. Для упрощения на схемах показаны лишь выводы конденсатора и вывод питания активного компонента. Соединению между выводом конденсатора и общим выводом питания компонента также должно быть уделено значительное внимание. На рисунке 5A показана наиболее часто встречающаяся конфигурация разводки. Вывод питания компонента подключен
коротким проводником к шине питания во внутреннем слое через переходное отверстие. Конденсатор развязки, расположенный на другой
стороне платы, подключен к этому же переходному отверстию. Если конденсатор расположен на расстоянии 50 мил (1,27 мм) от вывода компонента, то добавляемая индуктивность в лучшем случае составит около 0,9 нГн. При более удаленном размещении конденсатора от активного компонента проводники будут более длинными, а паразитная индуктиность будет иметь большее значение. | Вариант B представляет собой значительное улучшение варианта A с размещением конденсатора развязки и активного компонента на одной стороне печатной платы. Конденсатор подключен после паразитной индуктивности переходного отверстия. При достаточно коротких проводниках схема развязки вносит дополнительно менее 1 нГн паразитной индуктивности. Вариант D представляет собой развитие варианта A — для уменьшения собственной индуктивности и увеличения распределенной
емкости проводники сделаны шире, что также улучшает характеристики цепи развязки. Вариант E — модификация варианта B с более широкими проводниками и более хорошими характеристиками. На первый взгляд кажется, что вариант C совершенно не подходит для разводки цепей развязки, поскольку нет проводников, напрямую подключающих активный компонент к конденсатору развязки; фактически они оба подключены через отверстия к полигонам питания и земли, которые расположены во внутренних слоях. При четырех отверстиях к цепям развязки добавится минимум 2 нГн паразитной индуктивности. Однако, очень широкие проводники питания и земли практически не будут добавлять индуктивности при не очень большой длине. Такой вариант разводки пригоден, когда конденсатор развязки не может быть размещен достаточно близко к активному компоненту. Вариант F — улучшение варианта C добавлением дополнительных параллельных отверстий. Такое добавление приводит к уменьшению
паразитной индуктивности переходных отверстий в два раза, позволяет улучшить качественные характеристики схемы и должно использоваться
всякий раз, когда позволяет место. | Поскольку емкости при параллельном соединении суммируются, а результирующая индуктивность уменьшается, то параллельное соединение двух небольших конденсаторов с одинаковыми значениями емкости может привести к качественному выигрышу, по сравнению с применением одного большого конденсатора. Конечным результатом будет такая же емкость развязки и меньшая паразитная эквивалентная последовательная индуктивность. На практике обычно избегают использования конденсаторов с разными значениями емкостей для создания локальной развязки. Составные конденсаторы с разными емкостями обладают частотной зависимостью импеданса, складывающейся из частотных зависимостей импедансов отдельных конденсаторов. Пример показан на рисунке 6. Конденсатор емкостью 47 нФ используется для развязки низких частот, а конденсатор емкостью 150 пФ — для высоких.
На первый взгляд, можно предположить, что параллельное соединение этих конденсаторов позволит улучшить импедансную характеристику. | К сожалению, это не так. Такое соединение может породить существенные проблемы на частотах, находящихся между собственными резонансными частотами конденсаторов. На рисунке 7 видно, что комбинация двух конденсаторов создает антирезонансный пик (а, следовательно, повышенное сопротивление) на суммарной частотной характеристике. Источник данной проблемы легко определяется при рассмотрении эквивалентной схемы, показанной на рисунке 8. Результатом соединения паразитных компонентов конденсаторов является классический резонансный контур. Тем не менее, составные конденсаторы, используемые в качестве элементов развязки, достаточно широко используются в прецизионных схемах. В этом случае, к выбору конденсаторов необходимо подходить с большой тщательностью, моделируя схемы, включающие все паразитные компоненты. |
rf — Что такое импеданс?
На вопрос «что такое импеданс», я хотел бы отметить, что импеданс — это широкая концепция физики в целом, электрическим импедансом которой является только один пример.
Чтобы понять, что это значит и как это работает, часто проще рассмотреть механический импеданс. Подумайте о попытке толкнуть тяжелую кушетку по полу. Вы применяете определенное усилие, а кушетка скользит с определенной скоростью, в зависимости от того, насколько сильно вы нажимаете, вес кушетки, тип поверхности пола, тип ног, которые есть на диване, и так далее. Для этой ситуации можно определить механический импеданс, который дает соотношение между тем, насколько сильно вы нажимаете и как быстро проходит кушетка.
Это на самом деле очень похоже на электрическую цепь постоянного тока, где вы применяете определенное напряжение на цепи, и ток течет с определенной скоростью через него.
В случае как кушетки, так и схемы ответ на ваш вход может быть простым и довольно линейным: резистор, который подчиняется закону Ома, где его электрический импеданс — это просто сопротивление, а на кушетке могут быть фрикционные ползунки которые позволяют ему двигаться со скоростью, пропорциональной вашей силе. *
*
Схемы и механические системы также могут быть нелинейными. Если ваша схема состоит из переменного напряжения, расположенного поперек резистора последовательно с диодом, ток будет почти нулевым, пока вы не превысите прямое напряжение диода, и в этот момент ток начнет протекать через резистор в соответствии с сигналом Ом закон. Аналогично, диван, сидящий на полу, обычно имеет некоторую степень статического трения: он не начнет двигаться, пока вы не нажмете с определенной силой. Ни в механической, ни в электрической системе нет единого линейного импеданса, который можно определить. Скорее, лучшее, что вы можете сделать, — это отдельно определить импедансы в разных условиях. (Реальный мир намного больше похож на этот.)
Даже когда вещи очень четкие и линейные, важно отметить, что импеданс просто описывает отношение — он не описывает пределы для системы, и это не «плохо». Вы можете определенно получить столько тока /скорости, сколько хотите (в идеальной системе), добавив больше напряжения /толчка.
Механические системы также могут дать довольно хорошее ощущение полного сопротивления. Представьте, что вы едете на велосипеде. С каждым полупериодом педалей вы нажимаете налево, нажимаете вправо. Вы также можете представить педали с одной ногой и носком клипа, так что вы нажимаете и тянете с каждым циклом педали. Это во многом напоминает применение переменного напряжения в цепи: вы нажимаете и тянете поочередно, циклически, на определенной частоте.
Если частота достаточно медленная — например, когда вы остановились на велосипеде, проблема нажатия на педали — это просто проблема «постоянного тока», например, нажатие дивана. Однако, когда вы ускоряетесь, все может действовать по-другому.
Теперь предположим, что вы едете на велосипеде с определенной скоростью, а ваш велосипед — с тремя скоростями с низким, средним и высоким передаточным числом. Среда чувствует себя естественной, на передачу очень сложно применить достаточную силу, чтобы иметь какое-либо значение, и на малой передаче вы просто вращаете педали, не передавая какую-либо энергию колесам. Это вопрос соответствия импеданса , где вы можете только эффективно передавать мощность на колеса, когда они оказывают определенное физическое сопротивление вашей ноге — не слишком много, не слишком мало. Соответствующее электрическое явление также очень распространено; вам нужны линии согласованного импеданса для эффективной передачи мощности радиочастоты от точки A до точки B, и в любое время, когда вы соединяете две линии передачи вместе, на интерфейсе будет какая-то потеря.
Это вопрос соответствия импеданса , где вы можете только эффективно передавать мощность на колеса, когда они оказывают определенное физическое сопротивление вашей ноге — не слишком много, не слишком мало. Соответствующее электрическое явление также очень распространено; вам нужны линии согласованного импеданса для эффективной передачи мощности радиочастоты от точки A до точки B, и в любое время, когда вы соединяете две линии передачи вместе, на интерфейсе будет какая-то потеря.
Сопротивление, которое педали обеспечивают на ваших ногах, пропорционально тому, как сильно вы нажимаете, что наиболее близко относится к простому сопротивлению — особенно при низких скоростях. Даже в цепях переменного тока резистор ведет себя как резистор (до определенной точки).
Однако, в отличие от резистора, импеданс велосипеда зависит от частоты. Предположим, что вы положили свой велосипед на высокую передачу, начиная с остановки. Это может быть труднее начать very . Но, как только вы начнете, импеданс, представленный педалями, снизится по мере того, как вы ускоряетесь, и как только вы пойдете очень быстро, вы обнаружите, что педали не имеют слишком большого сопротивления, чтобы поглощать силу у ваших ног.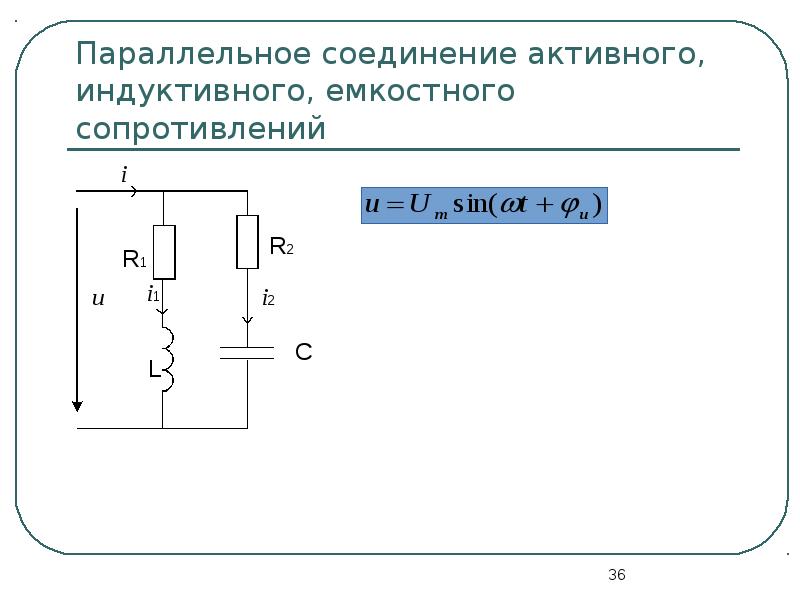 Таким образом, на самом деле существует частотно-зависимый импеданс (a реактивное сопротивление ), которое начинается высоко и становится ниже, когда вы направляетесь на более высокую частоту.
Таким образом, на самом деле существует частотно-зависимый импеданс (a реактивное сопротивление ), которое начинается высоко и становится ниже, когда вы направляетесь на более высокую частоту.
Это очень похоже на поведение конденсатора, и довольно хорошая модель для механического импеданса велосипеда будет резистором параллельно с конденсатором.
При dc (нулевая скорость) вы просто видите высокое постоянное сопротивление как ваш импеданс. По мере увеличения частоты педалей импеданс конденсатора становится ниже, чем сопротивление резистора, и позволяет течению течь таким образом.
Есть, конечно, различные другиеэлектрические компоненты и их механические аналоги **, но это обсуждение должно дать вам некоторую первоначальную интуицию по общей концепции, чтобы оставаться заземленной (каламбур), когда вы узнаете о математических аспектах того, что может порой казаться очень абстрактным предметом.
* Слово для придирчивости: закон Ома никогда не бывает точным для реального устройства, а силы трения реального мира никогда не дают скорости, точно пропорциональной силе. Однако «довольно линейный» легко. Я стараюсь быть все учебным и прочим здесь. Сократите мне слабину.
** Например, индуктор — это что-то вроде подпружиненного ролика на вашем колесе, который добавляет сопротивление, когда вы достигаете более высокой частоты).
Импеданс конденсатора — Емкостное реактивное сопротивление
Импеданс конденсатора (емкостное реактивное сопротивление) является мерой сопротивления изменению электрического тока в этом компоненте. В общих чертах можно резюмировать, что конденсатор пропускает сигналы высоких частот и блокирует сигналы низких частот. (включая сигналы 0 Гц)
Формула импеданса конденсатора (емкостного реактивного сопротивления): Z = 1 / jCw
где:
- Z: полное сопротивление в омах
- j: оператор для мнимого числа.(мнимая единица)
- C: значение емкости конденсатора в фарадах (C)
- w: равно 2π.f, где буква f представляет частоту сигнала, подаваемого на конденсатор. (Единица частоты — Герцы).
Импеданс — Емкостное реактивное сопротивление
Обычно конденсаторы используются в цепях с частотой сигналов, отличной от нуля (0 Гц).
Из формулы импеданса конденсатора видно, что импеданс обратно пропорционален частоте.Это означает, что если частота равна нулю (0 Гц), импеданс бесконечен.
Теперь, если импеданс бесконечен, напряжение на выводах конденсатора является разомкнутой цепью, и ток через конденсатор не течет. Ток = 0.
Полное сопротивление имеет общую формулу: Z = V / I (действующее значение напряжения / действующее значение тока). Эта формула похожа на закон Ома, который применяется к резисторам, но в данном случае он используется для сигналов переменного тока.
Оператор «j».
Причина, по которой этот оператор используется в электронике, заключается в том, что существует разность фаз между напряжением и током в конденсаторе.Эта разность фаз составляет 90 ° или π / 2, а ток опережает напряжение на 90 °. (90 градусов). Частота напряжения и тока в конденсаторе одинакова.
Разность фаз между напряжением и током в конденсаторе
Оператор «j» не используется с резистором, поскольку нет разности фаз между напряжением и током. Другими словами, напряжение и ток в резисторе синфазны.
Вт (угловая частота).
Значение w напрямую зависит от f (частоты) и измеряется в радианах / сек.(w = 2.π.f)
Например, для частоты 300 Гц, w = 2.π.f = 2 x (3,1416) x 300 = 1884,96 рад / сек.
Как рассчитать импеданс катушки индуктивности?
Для расчета импеданса (емкостного реактивного сопротивления) конденсатора используется формула Z = 1 / wC.
Пример 1:
Получите полное сопротивление конденсатора 10 мкФ при 300 Гц.
Z = 1 / (2 x π x 300 Гц x 10 мкФ) = 1 / (2 x (3,1416) x 300 x 0,000010) = 53,05 Ом
Пример 2:
Получите сопротивление конденсатора 10 мкФ при 50 Гц.
Z = 1 / (2 x π x 50 Гц x 10 мкФ) = 1 / (2 x (3,1416) x 50 x 0,000010) = 318,31 Ом.
Из двух предыдущих примеров, где емкость конденсатора одинакова (10 мкФ), видно, что сопротивление ниже для более высоких частот. В общих чертах можно резюмировать, что конденсаторы пропускают высокочастотные сигналы (есть низкий импеданс) и блокируют низкочастотные сигналы (есть высокий импеданс).
Пример 3:
Получите полное сопротивление конденсатора 4700 мкФ при 120 Гц.
Z = 1 / (2 x π x 120 Гц x 4700 мкФ) = 1 / (2 x (3,1416) x 120 x 0,004700) = 0,2822 Ом.
Примечание: Xc = емкостное реактивное сопротивление
Импеданс конденсатора — Как обсудить
Импеданс конденсатора
Как рассчитать импеданс конденсатора? Калькулятор импеданса конденсатора . Калькулятор импеданса емкости вычисляет импеданс конденсатора на основе емкости конденсатора C и частоты f сигнала, проходящего через конденсатор, по формуле XC = 1 / (2πfC).
В чем разница между сопротивлением и емкостью?
Емкость возникает из-за электрического поля тока. Емкость сопротивляется изменениям напряжения. Импеданс — это чистое сопротивление цепи при протекании тока. Здесь w — угловая частота источника питания, L — собственная индуктивность, а C — емкость.
Как рассчитать импеданс?
Импеданс устройства можно рассчитать, приложив синусоидальное напряжение к устройству последовательно с резистором и измерив напряжение на резисторе и на устройстве.Выполняя это измерение путем дискретизации частот подаваемого сигнала, получают фазу и амплитуду импеданса.
Как рассчитать конденсатор?
Чтобы рассчитать общую общую емкость нескольких конденсаторов, подключенных таким образом, сложите отдельные емкости по следующей формуле: Ctotal = C1 + C2 + C3 и так далее. Пример: Рассчитайте общую емкость этих трех конденсаторов, соединенных параллельно.
Как определить емкость неизвестного конденсатора?
Чтобы определить неизвестную емкость с помощью осциллографа, последовательно подключают источник постоянного тока, такой как батарея 9 В, известный резистор, переключатель и конденсатор.К клеммам конденсатора подключаются щуп осциллографа и заземляющий провод. Вам также понадобится короткая перемычка для конденсаторного моста.
Что такое идеальный конденсатор?
Идеальный конденсатор — это чисто реактивное устройство, которое, в отличие от резистора, выделяющего много тепла, не имеет абсолютно никакого эффекта сопротивления (поглотителя энергии). Намного проще сконструировать и изготовить конденсатор с низким внутренним последовательным сопротивлением, чем с катушкой индуктивности.
Какое уравнение для импеданса?
Импеданс (Z) передает сопротивление компонентов как постоянному, так и переменному току и выражается в виде комплексного числа Z = R + jX.В этом случае импеданс идеального резистора равен его сопротивлению, действительная часть импеданса — это сопротивление, а мнимая часть равна нулю.
Импеданс и сопротивление — это одно и то же?
Импеданс (Z) равен сопротивлению (R). И полное сопротивление, и сопротивление зависят от тока в цепи. Они оба почти одинаковы, но сопротивление указано для промежуточного контура. Резистор противодействует постоянному току в цепи постоянного тока.
В чем разница между измерением импеданса и емкости
В случае резистора импеданс равен значению сопротивления постоянному току. В случае конденсаторов и катушек индуктивности реактивное сопротивление является мнимым числом и называется емкостным реактивным сопротивлением или индуктивным реактивным сопротивлением. Емкостное реактивное сопротивление. омега ω — частота контура в радианах / с.
В чем разница между импедансом и емкостью в переменном токе?
Сопротивление, которое представляет собой силу тока в цепи переменного тока, обусловленную сопротивлением, емкостью и индуктивностью, называется импедансом.Сопротивление возникает в цепях переменного и постоянного тока, в то время как полное сопротивление возникает только в цепях переменного тока.
Как вы измеряете импеданс?
Метод 2 из 2: Точное измерение Купите прибор для измерения синусоидальной волны. Импеданс динамика зависит от частоты, поэтому вам нужен инструмент, который может излучать синусоидальную волну. Подключите инструмент ко входу вашего усилителя. См. Этикетку на усилителе зажигания или справочную информацию о среднеквадратичной мощности. Установите усилитель на низкое напряжение. Выберите сопротивление для интенсивного использования.
Какое уравнение для полного импеданса?
Расчет импеданса и полного тока. Есть две стратегии расчета импеданса и полного тока. Вы можете сначала рассчитать общий импеданс всех отдельных резисторов, подключенных параллельно (Total Z = 1 / (1 / ZR + 1 / ZL + 1 / ZC), а затем рассчитать общий ток, разделив напряжение источника на полное сопротивление. ( I = E / Z).
Как рассчитывается импеданс трансформаторов в процентах?
Например, если трансформатор 2400/240 вольт имеет измеренное импедансное напряжение 72 вольт на высоковольтных обмотках, полное сопротивление (Z) выражается в процентах: Z% = (импедансное напряжение / номинальное напряжение) x 100%. Z = (72/2400) * 100 = 3 процента.
Как рассчитать параллельное сопротивление?
При расчете общего сопротивления параллельной цепи возьмите каждое отдельное сопротивление и разделите его на (не на) единицу. Затем сложите все сопротивления, разделенные на единицу, и разделите это число на единицу. Для диаграммы в верхней части статьи формула выглядит следующим образом. 1 Rt (импеданс) = 1 ÷ R1 + 1 ÷ R2 + 1 ÷ R3.
Что означает импеданс трансформатора?
Импеданс трансформатора — это импеданс переменного тока.Это можно рассчитать для каждой обмотки. Однако относительно простой тест обеспечивает простой способ измерения эквивалентного импеданса трансформатора без отключения импеданса обмоток.
Как импеданс влияет на трансформатор?
Процент импеданса трансформатора имеет большое влияние на уровни неисправности системы. Определяет максимальное значение тока, протекающего в условиях неисправности. Определяет максимальное значение тока, протекающего в условиях неисправности.
Как они могут рассчитать сопротивление трансформатора?
Сопротивление обмоток трансформатора можно измерить вольт-амперным методом. В этом методе измерения сопротивления обмотки к обмотке прикладывают испытательный ток и измеряют соответствующее падение напряжения на обмотке. Применяя простой закон Ома R x = VI, вы можете легко определить значение сопротивления.
Как определить емкость конденсатора?
Параметры конденсатора могут быть определены по-разному в зависимости от типа конденсатора, например, электролитический, дисковый, из алюминиевой фольги и т. Д.Эти методы включают значение или число, напечатанное на корпусе конденсатора, или цветовую кодировку конденсатора.
В какой емкости измеряется емкость конденсатора?
Емкость измеряется в единицах, называемых фарадами (сокращенно F). Определение фарада обманчиво простое. Определение фарада обманчиво простое. Конденсатор емкостью в одну фараду поддерживает напряжение на пластинах ровно один вольт при нагрузке током ровно один ампер в секунду.
Как определить конденсатор?
Типы керамических конденсаторов обычно имеют трехзначный код, напечатанный на их корпусе, чтобы определить значение их емкости в пикофарадах. Как правило, первые две цифры указывают номинал конденсатора, а третья цифра — количество добавляемых нулей.
Как рассчитать конденсатор в физике
Энергия, запасенная в конденсаторе, может быть выражена тремя способами: Ecap = QV2 = CV22 = Q22C E cap = QV 2 = CV 2 2 = Q 2 2 C, где Q — заряд , V — напряжение, C — конденсатор.. Энергия выражается в джоулях для заряда в кулонах, напряжения в вольтах и емкости в фарадах.
Как рассчитать емкость конденсатора?
Чтобы рассчитать общую общую емкость нескольких конденсаторов, подключенных таким образом, сложите отдельные емкости по следующей формуле: Ctotal = C1 + C2 + C3 и так далее. Пример: Рассчитайте общую емкость этих трех конденсаторов, соединенных параллельно. Итого C = C1 + C2 + C3.
Как рассчитать заряд конденсатора?
Калькулятор заряда конденсатора рассчитывает заряд конденсатора емкости C и напряжения V по формуле Q = CV.Пользователь просто вводит два параметра, емкость C и напряжение V, и результирующая нагрузка рассчитывается автоматически.
Как рассчитать размер необходимого конденсатора?
- Отсоедините электрическую изоляцию от воздушного конденсатора или теплового насоса. Откройте электрическую коробку и снимите автоматический выключатель.
- Найдите и откройте дверцу доступа к воздушному конденсатору или тепловому насосу. Выверните винты, которыми крепится панель.
- Проверьте этикетку конденсатора на предмет диапазона напряжения и ватт.
Как найти напряжение на конденсаторе?
Однако в цепи последовательного конденсатора напряжение на каждом отдельном конденсаторе отличается. Вы можете легко найти напряжение на каждом отдельном конденсаторе, используя формулу C = Q / V. Емкость и заряд каждого отдельного конденсатора известны. Итак, вам нужно найти неизвестное напряжение.
Как рассчитать температуру конденсатора
Теплогенерирующие свойства конденсаторов.Чтобы измерить теплогенерирующие свойства конденсатора, температура конденсатора должна быть измерена в условиях, которые сводят к минимуму рассеивание тепла с поверхности из-за конвекции и излучения, а также рассеивание тепла из-за передачи тепла через шаблон.
Как температура влияет на электростатическую емкость?
Электростатическая емкость конденсаторов обычно зависит от рабочей температуры. Конденсаторы имеют хорошие температурные характеристики при небольшом диапазоне отклонения или плохие температурные характеристики при большом диапазоне отклонения.
Как можно предсказать емкость конденсатора?
Используя правильные формулы, можно точно предсказать емкость конденсатора, зная площадь пластин, расстояние между ними и относительную диэлектрическую проницаемость диэлектрической проницаемости материала между двумя пластинами.
Как рассчитывается энергия, запасенная в конденсаторе?
Энергия, запасенная в конденсаторе, равна работе, необходимой для стимулирования заряда на конденсаторе.Если в какой-то момент напряжение равно v и этому напряжению передается небольшой заряд δq, то проделанная работа равна v δq. Следовательно, вся проделанная работа и, следовательно, энергия хранится в конденсаторе: W = ∫ Q V d Q.
Как рассчитать размер конденсатора
К счастью, есть три способа определить размер конденсатора компрессора. Обратитесь к руководству по эксплуатации вашего кондиционера, чтобы убедиться, что указан правильный размер конденсатора. Если нет, позвоните производителю и спросите, какой размер им нужен.Умножьте ток полной нагрузки на 2650. Разделите это число на напряжение питания.
Как рассчитать массу конденсатора
Чтобы рассчитать ток через конденсатор с помощью онлайн-калькулятора, проверьте свой калькулятор тока конденсатора. Если напряжение постоянное, это постоянный ток, и ток заряжается (23 секунды в зависимости от сопротивления и емкости).
Как рассчитывается полупериод сглаживающего конденсатора?
Пояснение: Рассчитайте сглаживающий конденсатор.Ток потребления \\ (\\ mathbf {I} \\) схемы можно рассчитать по закону Ома. Высокая потребляемая мощность потребителя значительно увеличивает требуемую емкость конденсатора. Полупериод \\ (\\ mathbf {\\ Delta t} \\) можно рассчитать по частоте напряжения.
Как определяется напряжение пульсации в сглаживающем конденсаторе?
Пульсации напряжения (факторы при расчете пульсаций напряжения) представляют собой пульсации остаточного напряжения. Тип потребителя определяет допустимое падение напряжения.Чем больше падает пульсация напряжения, тем больше должен быть сглаживающий конденсатор.
Как сглаживающий конденсатор используется в электросети?
Сглаживающий конденсатор снижает остаточную пульсацию от ранее выпрямленного напряжения. В этой статье описывается, как работает сглаживающий конденсатор. В дополнение к формуле расчета в Интернете вы также найдете удобный калькулятор размера конденсатора. Электросеть Германии подает синусоидальное переменное напряжение с частотой 50 Гц.2 \). Давайте рассмотрим пример, чтобы лучше понять, как рассчитывается энергия, запасенная в конденсаторе.
Как рассчитать напряжение конденсатора?
Формула, которая вычисляет напряжение конденсатора на основе этих входных данных, следующая: V = 1 / C∫Idt, где V — напряжение на конденсаторе, C — емкость, а I — ток, протекающий через конденсатор. Часто встречается расширенная формула V = V + 1 / C∫Idt.
Какая общая энергия хранится в конденсаторе?
Полная энергия, запасенная в конденсаторе (выраженная в джоулях), равна общей работе, проделанной для создания электрического поля из незаряженного состояния.это емкость. Эта потенциальная энергия остается в конденсаторе до тех пор, пока заряд не будет снят.
Какой ток на конденсаторе?
Ток через конденсатор равен емкости конденсатора, умноженной на производную (или изменение) напряжения на конденсаторе. По мере увеличения напряжения на конденсаторе увеличивается ток.
Как рассчитать формулу конденсатора
Формула для расчета емкости конденсатора: C (мкФ) = (P (W) x η x 1000) / (V (V) x V (V) xf) Посмотрите на формулу , необходимое значение емкости прямо пропорционально мощности двигателя.Следовательно, с увеличением размера двигателя увеличивается и мощность.
Какова формула тока конденсатора?
Формула для расчета тока конденсатора: I = Cdv / dt, где I — ток, протекающий через конденсатор, C — емкость конденсатора, а dv / dt — производная напряжения на конденсаторе. Эта формула показывает, что ток прямо пропорционален производной напряжения.
Какое реактивное сопротивление формула конденсатора?
В калькуляторе емкостного реактивного сопротивления для расчета емкостного реактивного сопротивления используется емкостное реактивное сопротивление = 1 / (угловая скорость * емкость).Формула для емкостного реактивного сопротивления определяется как величина, обратная произведению угловой скорости и емкости цепи. емкость и обозначается символом Xc.
Расчет импеданса конденсатора
Формула для расчета емкостного реактивного сопротивления или импеданса конденсатора: емкость. где: XC = емкостное реактивное сопротивление, измеренное в омах.
Что приводит к выходу конденсатора из строя?
Скачки напряжения также могут вызвать выход конденсатора из строя.Очевидно, что молния во время летней грозы может перегрузить и сжечь вашу электрическую систему отопления, вентиляции и кондиционирования воздуха. Кроме того, более низкие пики могут со временем повредить конденсаторы.
В чем разница между конденсатором и батареей?
Основное различие между батареей и конденсатором заключается в том, что батарея накапливает заряд в виде химической энергии и преобразует его в электрическую энергию, в то время как конденсатор сохраняет заряд в виде электростатического поля.
Для чего нужен конденсатор?
Конденсаторы используются для точного измерения уровня топлива в самолетах, поскольку топливо покрывает более нескольких пластин, емкость контура увеличивается.Гибкий пластинчатый конденсатор можно использовать для измерения напряжения, давления или веса.
Сопротивление конденсатора уравнение
Формула для расчета емкостного реактивного сопротивления или импеданса конденсатора — это емкость. где: XC = емкостное реактивное сопротивление, измеренное в омах.
Какая частотная характеристика конденсатора?
Конденсатор имеет частотную характеристику 1 / RC (частота, при которой конденсатор начинает реагировать, начинает проводить).И время, необходимое для достижения этой частоты, равно RC. Напряжение или ток конденсатора зависит от частоты или времени.
Импеданс индуктивности
Импеданс индуктивности (также называемый индуктивностью или индуктивным реактивным сопротивлением) является мерой его сопротивления изменению электрического тока в этой части. В общем, можно резюмировать, что катушка пропускает низкочастотные сигналы (включая сигналы Hz) и блокирует высокочастотные сигналы.
Какая формула для индуктора?
Формула, которая вычисляет ток катушки индуктивности на основе этих входных данных, следующая: I = 1 / L∫Vdt, где I равно току через катушку индуктивности, L равно индуктивности катушки индуктивности, а V равно напряжению на катушке.Часто встречается расширенная формула I = I0 + 1 / L∫Vdt.
Как называется сопротивление индуктора?
Другими словами, электрическое сопротивление индуктора, когда оно используется в цепи переменного тока, называется индуктивным реактивным сопротивлением. Индуктивное реактивное сопротивление, обозначаемое XL, — это свойство цепи переменного тока, которое сопротивляется изменению тока.
Что такое индуктивное сопротивление?
Импеданс индуктивности, также известный как индуктивное реактивное сопротивление, является общим термином для сопротивления постоянному току (DC) и переменному току (AC) для индуктора.
Как найти импеданс конденсатора
Импеданс идеального конденсатора по величине равен его реактивному сопротивлению, но эти два значения не равны. Реактивное сопротивление выражается простым числом в единицах Ом, а полное сопротивление конденсатора — это реактивное сопротивление, умноженное на j ,, Z = jX.
Какое уравнение для емкости?
Емкость конденсатора — это способность конденсатора накапливать один электрический заряд на единицу напряжения на своих пластинах конденсатора.Емкость определяется делением электрического заряда на напряжение по формуле C = Q / V.
Что такое измерение емкости?
Измерение емкости. Мера взаимосвязи между зарядом, индуцированным в проводнике, и изменением потенциала по отношению к соседнему проводнику, которое индуцирует заряд.
Калькулятор импеданса конденсатора
Калькулятор импеданса конденсатора Калькулятор импеданса конденсатора вычисляет импеданс конденсатора на основе емкости конденсатора C и частоты f сигнала, проходящего через конденсатор, по формуле XC = 1 / (2πfC).
Как увеличить емкость конденсатора?
Увеличить емкость конденсатора можно тремя способами: за счет увеличения обкладок. Уменьшение расстояния между плитами. Сделайте диэлектрик таким же хорошим, как и изолятор.
Частота и сопротивление конденсатора
Частота и сопротивление. Импеданс конденсаторов и катушек индуктивности в цепи зависит от частоты электрического сигнала. Импеданс катушки прямо пропорционален частоте, а импеданс конденсатора обратно пропорционален частоте.
Какая связь между емкостью и частотой?
Емкостная емкость зависит от частоты. Перед точкой резонанса емкость уменьшается с увеличением частоты. После точки резонанса емкость увеличивается с частотой. Взаимосвязь кривой фактически относится к взаимосвязи между керамической емкостью и частотой, то есть взаимосвязью между Z (= ESR + jwLj / wC) и частотой.
Увеличивается ли емкость с частотой?
По мере увеличения частоты конденсатор вызывает прохождение большего заряда через пластины в течение определенного периода времени, вызывая прохождение большего тока через конденсатор, что, очевидно, снижает внутреннее сопротивление конденсатора.
Фазоры и импедансы
Что вы всегда хотели знать о
ФАЗОРЫ И ИМПЕДАНСЫ
но спросить боялись
Мы узнали, что напряжение на индуктор пропорционален производной по времени тока через индуктор и напряжение на конденсаторе пропорционально интегралу тока через конденсатор. В результате при наличии катушек индуктивности и / или конденсаторов ток Кирхгофа и законы напряжения выражаются в форме дифференциальных уравнений даже в простейшие случаи.В случае переходного процесса или произвольной зависимости напряжения от времени или источников тока, анализ схемы включает решение обыкновенных дифференциальных уравнений.
Однако есть один очень важный частный случай, когда дифференциальные уравнения можно заменить комплексным анализом. Это случай переменные токи и напряжения, используемые для промышленного и бытового применения повсюду мир. В этом случае токи и напряжения синусоидальные функции времени.Синусоидальную функцию всегда можно представить в виде
V (t) = V p cos (w t + q v )
для напряжений и
i (t) = i p cos (w t + q i ) для токов, где t — время, V p и i p — пиковые значения напряжения и тока соответственно q v и q i — начальные фазы напряжения и тока, соответственно, а w — угловая частота сигналов генерируется источниками напряжения и / или тока.
По определению, любое комплексное число Z равно представлен как
Z = Re {Z} + j Im {Z} (прямоугольная форма),
или
Z = M (cos a + j sin a) (полярная форма)
где j = sqrt (-1), Re {Z} — действительная часть, а Im {Z} — мнимая часть. комплексного числа Z, M — его величина, a — угол между действительной осью и вектором, ведущим из начала координат в точку в комплексе плоскость, определяющая данное комплексное число.Согласно теореме Эйлера комплекс экспоненциальная функция определяется как
ехр (j a) = cos a + j sin a
Отсюда следует, что полярная форма любого комплексного числа может быть представлен как
Z = M ехр (j a)
и наши функции можно переписать как действительные части комплексных чисел:
V (t) = Re {V p exp [j (w t + q v )]}
и
i (t) = Re {i p exp [j (w t + q i )]}
Давайте еще раз перепишем наши функции:
V (t) = Re {V p exp (jq v ) exp (jwt)} = Re { V exp (jw t)}
и
i (t) = Re {i p exp (jq i ) exp (jwt)} = Re { i exp (jw t)}
где
V = V p exp (jq v )
и
i = i p exp (jq и )
— это векторы напряжения и тока соответственно.В фазоры — комплексные числа. Их миссия — помочь нам найти реальные функции V (t) и Это). В самом деле, если мы знаем векторы, все, что нам нужно сделать, это умножить их на exp (jwt), а затем взять действительную часть полученного комплексного числа.
Обратите внимание, что векторы не зависят от времени. Следовательно, если мы дифференцировать V (t) и i (t) по времени, результат будет просто
dV / dt = Re {jw V exp (jw t)}
и
di / dt = Re {jw i exp (jw t)},
и.е., в комплексной области дифференцирование по времени имеет вид заменено умножением на jw. В результате наши дифференциальные уравнения становятся простыми алгебраическими уравнениями, подобными тем, которые мы имеем когда мы имеем дело с резистивными цепями. Единственная разница в том, что все напряжения и токи теперь являются векторами, а все сопротивления, емкости и индуктивности заменены с их комплексными сопротивлениями Z R, Z L, и Z C, соответственно, где
Z R = R
Z L = jwL
Z C = 1 / (jwC) = -j / (wC)
Импеданс резистора — это просто его сопротивление (действительное значение), но импедансы конденсатора или катушки индуктивности являются мнимыми.Пока сопротивляется, емкости и индуктивности имеют постоянные значения, импедансы зависят от частоты. Единица измерения сопротивления — Ом.
Анализ цепей в сложной области такой же, как и для чисто резистивные цепи, но мы должны иметь дело с фазорами и импедансами. Когда у нас есть элементы в серии, их импедансы складываются для получения эквивалентного импеданса. Для параллельного элементы, обратные импедансы добавляются, чтобы обеспечить обратную величину эквивалентное сопротивление.Все методы, изученные для резистивных цепей, могут быть применены в сложный домен. После нахождения векторных токов и напряжений умножаем их на exp (jwt), а затем возьмем действительную часть полученного комплексное число, которое является нашей реальной функцией во временной области.
Некоторым ученикам все это кажется довольно абстрактным. Через некоторое время Однако на практике вы найдете этот метод простым и удобным. Рассмотрим простой пример. Источник обеспечивает напряжение V (t) = 100 cos (500 t) в последовательной цепи RLC (R = 100 Ом, L = 1 Гн, C = конденсатор 5 мкФ).Какой ток в этом схема? Попробуйте решить проблему самостоятельно, а затем сравните свое решение с тот, который следует здесь.
Вектор напряжения В = 100 В. Полное сопротивление
Z = 100 + j 500 * 1 — j / (500 * 5 * 10 -6 ) = 100 + j (500-400) = 100 (1 + j) Ом.
Находим текущий вектор как i = V / Z = 100 / [100 (1 + j)] = (1 — j) / [(1 + j) (1 — j)] = (1 — j) / 2 = [sqrt (2) / 2] exp (- jp / 4) A
Ответ: i (t) = Re {0.707 ехр (-jp / 4 + j500t)} = 0,707 cos (500t — p / 4) A
Если бы вы могли решить эту проблему самостоятельно, вы поняли основную идею о фазорах и импедансах. Поздравляю!
Наконец, мы должны подчеркнуть, что этот мощный подход можно использовать только для синусоидальных токов и напряжений. Если зависимость от времени является произвольной функцией время, мы должны иметь дело с дифференциальными уравнениями!
Пожалуйста, отправьте мне отзыв об этом руководстве. Что вы думаете об этом? Любые вопросы?
.
Ридли Инжиниринг | — Измерения конденсаторов
В нескольких прошлых статьях мы исследовали некоторые сложные характеристики силового магнетизма импульсного источника питания. В этой статье мы рассмотрим еще один важный пассивный компонент источника питания — конденсатор. Часто это компонент, который рассматривается как простая деталь, не требующая особого внимания.
Конденсаторы блока питания
На рисунке 1 показан простой понижающий преобразователь.Учитывая современные интегрированные контроллеры, задача разработчика, по-видимому, очень проста — все, что нам нужно сделать, это выбрать индуктор и два конденсатора, и работа будет выполнена. Выбор катушек индуктивности может быть очень сложным, и теперь мы увидим, что конденсаторы тоже могут быть проблематичными.
Рис. 1. Понижающий преобразователь с критически важными компонентами конденсатора. Импеданс выходного конденсатора определяет средне- и высокочастотный отклик преобразователя с использованием режима напряжения, тока или любой другой формы управления, включая цифровой.
Меня часто просят провести анализ наихудшего случая подобных схем импульсных источников питания для компаний. Первый шаг этого процесса обычно заключается в том, что компания присылает мне схемы, списки деталей и спецификации компонентов. Прежде чем продолжить, я всегда должен запрашивать рабочие физические образцы блоков питания для тестирования на стенде. К тревоге людей, не знакомых с источниками питания, большая часть анализа наихудшего случая зависит от измерений, существующих конструкций, в сочетании с задокументированными вариантами технических данных, которые изменят конструкцию.
Листы технических данных компонентов редко бывают адекватными для правильной характеристики деталей, а для всестороннего анализа требуется информация, которую производители не могут предоставить. Дополнительные измерения необходимы для магнетизма, а также необходимы дополнительные измерения для конденсаторов.
Измерение низкоомного конденсатора
Простой фиксированный тестер RLC с единственной частотой измерения не подходит для определения характеристик конденсаторов для использования в современном импульсном источнике питания.Конденсаторы необходимо измерять в широком диапазоне частот, чтобы полностью охарактеризовать их поведение.
Рисунок 2: Схема измерения для конденсаторов с низким сопротивлением
На рисунке 2 показано, как проводить измерения конденсаторов с низким сопротивлением с помощью анализатора частотной характеристики [1]. Правильный выбор чувствительного резистора и правильная ВЧ-схема тестовых цепей позволят вам измерять импеданс до 1 мОм с помощью этой испытательной установки. Хотя многие тестеры компонентов будут рассматривать только одну частоту или узкий диапазон частот, рекомендуется прокручивать частоту, чтобы увидеть импеданс тестируемого компонента, от 10 Гц до как минимум 10 МГц.
Измерение электролитического конденсатора
Электролитические конденсаторы по-прежнему являются предпочтительным компонентом большинства коммерческих недорогих источников питания. Они также широко используются в автомобильной промышленности, где могут быть экстремальные температуры.
Электролиты относительно легко измерить, поскольку они имеют относительно высокое эквивалентное последовательное сопротивление. Но важно варьировать температуру конденсатора, чтобы увидеть ее влияние на характеристики.
Рисунок 3: Измерение импеданса электролитического конденсатора 10 мкФ при двух разных температурах
На рис. 3 показано изменение импеданса конденсатора для электролита 10 мкФ.Показаны две кривые: красный график — для конденсатора при 25 градусах, а синий — для -55 градусов по Цельсию. Обратите внимание на большое разделение кривых. Это связано с известным эффектом замерзания электролита в конденсаторе. Выполнив это измерение самостоятельно, вы обнаружите, что СОЭ продолжает расти по мере того, как температура падает все ниже и ниже нуля градусов. Вряд ли вы найдете полный набор данных, который вам нужен именно для вашей части.
Рисунок 4: Емкость электролитического конденсатора 10 мкФ при двух разных температурах
На рис. 4 показана мнимая составляющая импеданса, извлеченная для отображения эквивалентной емкости конденсатора.Видны два изменения емкости: одно — слабая зависимость от частоты, а второе — зависимость от температуры.
или холодный конденсатор на синей кривой, очевидное существенное падение емкости за пределами нескольких кГц не является действительно значительным, поскольку на импеданс устройства преобладает эквивалентное последовательное сопротивление (ESR) на этих частотах.
Рисунок 5: Эквивалентное последовательное сопротивление электролитического конденсатора 10 мкФ при двух разных температурах
ESR определяется путем измерения действительной части импеданса, показанного на Рисунке 3, изображенном на Рисунке 5.На низких частотах оба сопротивления имеют высокие значения, но это всегда сомнительное измерение — мы пытаемся извлечь очень маленькую реальную составляющую из вектора импеданса, который в основном является реактивным.
Показано, что за пределами нескольких кГц интересующее нас значение ESR зависит как от частоты, так и от температуры. Обратите внимание, что ESR холодного конденсатора составляет около 12 Ом, а теплого конденсатора — около 0,5 Ом. Разница больше, чем 20: 1!
Многие конструкторы, работающие в широком диапазоне температур, будут держаться подальше от электролитов по этой и другим причинам.Однако в некоторых случаях они необходимы с экономической точки зрения, и контур управления должен учитывать изменения, которые будут происходить с температурой. Это может стать серьезной проблемой при проектировании контура управления. Это, безусловно, можно сделать, особенно при использовании управления текущим режимом, но полоса пропускания контура часто сильно снижается.
Электролитические свойства также будут существенно изменяться при старении, особенно при повышенной температуре. Это еще одна важная тема, которая выходит за рамки данной статьи, но вы должны проверить срок службы и температуру работы в источнике питания, чтобы убедиться, что электролитические соединения не выйдут из строя.
Измерение многослойного керамического конденсатора
Источники питания в точке нагрузки и материнские платы широко используют многослойные керамические конденсаторы в качестве альтернативы электролитическим. Достижения в конструкторских технологиях сделали доступными конденсаторы очень большой емкости с чрезвычайно низким ESR в очень маленьких корпусах. Это важно для преобразователей точки нагрузки, где пространство на плате ограничено.
Я редко вижу, чтобы должная осмотрительность проводилась при рассмотрении характеристик выходных конденсаторов MLC.Несмотря на то, что они не страдают от резких температурных сдвигов ESR электролитов, MLC одинаково сложны по своим характеристикам.
Рис. 6. Измерение многослойного керамического конденсатора 10 мкФ при разных уровнях тестового сигнала и с переменным смещением постоянного тока
На рис. 6 показано значение емкости небольшого 0805 MLC с номинальным напряжением 6,3 В и номинальным значением 10 мкФ. Красная верхняя кривая показывает, что емкость конденсатора составляет 10,7 мкФ при 100 Гц. Обратите внимание на значительную частотную зависимость от 10 Гц до 10 кГц.
Это изменение с частотой связано с тем, что емкость MLC является функцией приложенного переменного напряжения [2]. В испытательной установке, показанной на Рисунке 2, от анализатора частотной характеристики подается постоянный источник 1 В. На низких частотах все напряжение появляется на конденсаторе, но с увеличением частоты мощность конденсатора уменьшается. MLC показывают увеличение емкости с увеличением уровня возбуждения.
Зеленая кривая показывает, как эта частотная зависимость устраняется с помощью небольшого управляющего сигнала всего 50 мВ.Обратите внимание, что номинальная емкость конденсатора 10 мкФ теперь составляет всего 7,9 мкФ.
MLCтакже сильно зависят от приложенного постоянного напряжения. Синяя кривая на рисунке 6 показывает, как значение емкости падает до 3,5 мкФ при смещении 5 В постоянного тока и до 2,5 мкФ при смещении 6,3 В постоянного тока. Если вы подтолкнете конденсатор к номинальному напряжению, у вас не останется много емкости в этом конкретном примере. Мой опыт работы с MLC показывает, что в любом случае подталкивать их близко к их рейтингу нецелесообразно из соображений надежности.
Все различные диэлектрики, используемые для MLC, будут иметь разные характеристики. На веб-сайте AVX есть много полезной информации, и вам предлагается прочитать как можно больше, чтобы глубже понять эту тему. У MLC есть дополнительная зависимость от температуры и времени жизни, которую мы здесь не будем рассматривать.
Хотя вы не можете найти много информации, всегда полезно провести измерения самостоятельно на скамейке. Варианты MLC настолько запутаны, что часто бывает трудно быть уверенным в том, как именно будет вести себя ваш компонент, если вы не измеряете его самостоятельно.Кроме того, большинство представленных кривых являются типичными характеристиками, а многие характеристики наихудшего случая настолько экстремальны, что вы не можете учесть их все в практической конструкции.
Сводка
Конденсаторычасто упускаются из виду как источник изменений в источниках питания, но они не попадают в эту ловушку. У всех типов конденсаторов источника питания есть свои особые наборы проблем, которые вы должны полностью понять, если собираетесь строить рекомендуемые преобразователи.
Всегда проводите измерения силовых конденсаторов на этапе разработки.И, как катушки индуктивности и сердечники для магнетиков, не следует слепо делать замену от одного производителя или диэлектрика к другому без надлежащей характеристики новой детали. Не все поставщики хорошо справляются с предоставлением полных данных — будьте готовы сделать это сами.
Конденсаторная муфтадля минимального импеданса | 2018-01-02
Хорошо известно, что монтажный контур конденсатора имеет основную долю паразитной индуктивности [1]. Практичный конденсатор, установленный на печатной плате, имеет связанную с ним паразитную индуктивность (L).Его эквивалентная схема представляет собой последовательную цепь RLC, где R представляет потери, связанные с конденсатором (C). Он имеет заданную выше собственную (последовательную) резонансную частоту, которая действует как индуктивность. Другими важными факторами паразитной индуктивности являются ESL и индуктивность рассеяния плоскости.
Монтажная петля образована двумя переходными отверстиями, соединяющими конденсатор с плоскостями заземления питания. Конденсатор малого форм-фактора уменьшает эту площадь и помогает минимизировать паразитную индуктивность. Более близкие плоскости питания и земли уменьшают индуктивность распространения плоскости.
Геометрия для отрицательного коэффициента связи
Если два конденсатора включены параллельно, мы можем создать отрицательный коэффициент связи для уменьшения паразитной индуктивности. Это показано на рисунке 1. Точки A и E находятся в одной плоскости, а точки B и F — в одной плоскости. Предположим, что плоскости силовой и заземленной разделены тонким диэлектриком толщиной (2-3 мил).
На рисунке 1 (b) показано геометрическое соединение для отрицательного коэффициента связи (M и k отрицательны).Когда присутствуют плоскости питания и земли, эта геометрия может быть достигнута путем изменения местоположений; B и E находятся в одной плоскости, а A и F — в одной плоскости.
На рисунке 2 показана эквивалентная схема подключения двух конденсаторов параллельно. Записывая для него уравнения,
Идентичные конденсаторы
Для больших значений w уравнение. 2 становится классическим уравнением связанных параллельных катушек индуктивности.
где знаки + и — указывают на положительную и отрицательную связь.Для одинаковых площадей контура (L1 = L2 = L) индуктивность определяется выражением,
. Эксперименты проводятся с двумя керамическими дисковыми конденсаторами номиналом C1 = C2 = 4,7 нФ. Измерение конденсаторным измерителем дает их значение 4,30 нФ. Провода нарезаны и изготовлены из изолированной медной проволоки SWG 21 (диаметр = 0,813 мм). Из проводов сделайте петлю площадью 1,5 см _ 0,5 см. В качестве измерительного прибора используется векторный анализатор цепей (ВАЦ) Rohde & Schwarz. Измеренные параметры рассеяния преобразуются в значения импеданса.ВАЦ задается следующими значениями: ширина полосы разрешения (RBW) = 10 Гц; количество баллов = 1000; и мощность = -15 дБм. Две петли держат на расстоянии 1 мм (край к краю). Коэффициент связи между контурами (k = M / L) рассчитан равным 0,4, где L — 17,6 нГн, а M — 6,97 нГн [2]. Результаты моделирования и экспериментов показаны на рис. 4 (а) и рис. 4 (б) соответственно. На частоте 100 МГц индуктивность в 2,5 раза (8 дБ) меньше, чем для случая положительной связи.
Пока здесь нет сюрпризов.Как насчет случая, когда значения двух конденсаторов различаются?
Неидентичные конденсаторы
Когда номиналы конденсаторов разные, параллельная комбинация дает антирезонансные пики, как показано на рисунке 5. Антирезонансный пик ниже для случая с положительной связью. Предполагается, что конденсаторы имеют примерно одинаковую монтажную индуктивность и сопоставимы по размерам. Эксперименты проводятся для тех же значений, что и в предыдущем эксперименте, за исключением того, что один конденсатор заменен на 390 пФ.Измерение с помощью измерителя емкости дает для этого конденсатора 380 пФ. Экспериментальные результаты (рис. 5 (б)) показывают, что пик антирезонанса ниже для случая с положительной связью в 3,2 раза. Когда оба конденсатора становятся индуктивными, эквивалентная индуктивность ниже для случая отрицательной связи.
Резюме
Отрицательный коэффициент связи дает больший антирезонансный пик по сравнению с положительным коэффициентом связи, даже если эквивалентная индуктивность ниже.Множественные антирезонансные пики способны генерировать волны-убийцы [7, 8], и их подавление становится все более важным. Для схем с низким уровнем шума резонанс в распределительной сети (PDN) является важной проблемой проектирования и должен быть подавлен!
Как насчет допуска двух одинаковых керамических конденсаторов, соединенных параллельно? «Это зависит» от типа конденсаторов, определяющих вариации емкости. Построение ур. (2) с наихудшими значениями даст ответ. Авторы оставляют это на усмотрение любопытного читателя!
Ссылки
[1] Roy, T., Смит, Л. и Примак, Дж .: «ESR и ESL керамического конденсатора, применяемые для развязки», IEEE 7th Top. Встретиться. Избрать. Выполнять. Электрон. Packag., 1998, стр. 213-216.
[2] Пол, К.Р .: «Эффективность нескольких разделительных конденсаторов», IEEE Trans. Электромагнит. Compat., 1992, 34, (2), стр. 130-133.
[3] Дэвис А.К .: «Влияние магнитной связи между монтажными контурами двух параллельных конденсаторов на антирезонанс», IET Sci. Измер. Tech., 2016, 10, (8), с. 889-899.
[4] Дэвис, А.К., Гунасекаран М.К .: «Микропроцессорное шумоподавление с помощью переключаемых суперконденсаторов», Электрон. Письма, 2014, 51, (1), стр. 92-94.
[5] Новак И., Паннала С. и Миллер Дж. Р .: «Обзор некоторых вариантов создания байпасных конденсаторов с низкой добротностью и управляемым ESR», IEEE 13th Top. Встретиться. Избрать. Выполнять. Электрон. Packag., 2004, стр. 55-58.
[6] Дэвис А.К .: «Влияние резистивной петли с магнитной связью на антирезонанс», Электрон. Письма, 2016, 52, (13), с. 1162 — 1164.
[7] Стив Сэндлер: «Решения на основе целевого импеданса для PDN могут не обеспечивать реалистичную оценку», доступно https://www.edn.com/design/test-and-measurement/4413192/Target-impedance-based -solutions-for-PDN-may-not-обеспечить-реалистичную-оценку
[8] Эрик Богатин, Иштван Новак, Стив Сэндлер, Ларри Смит, Брэд Брим и Стив Вейр: «Целевое сопротивление и случайные волны», доступно http://www.electrical-integrity.com/Paper_download_files/DC16_TargetImpedanceRogueWaves-panel.pdf
Импеданс конденсатора
ГЛАВА 4
4.3 Полное сопротивление конденсатора
Импеданс конденсатора определяется выражением
где,
f = частота
C = емкость конденсатора,
Xc = Импеданс конденсатора
В области целостности сигнала используются развязывающие конденсаторы для обеспечения пути с низким импедансом для сигналов переменного тока между плоскостями питания и земли.Что мы подразумеваем под обеспечением пути переменного тока с низким сопротивлением между источником питания и землей? Мы хотим, чтобы в системе распределения электроэнергии не было шума. Нам нужен только сигнал постоянного тока над ним. Если какой-то шум каким-то образом попадает на шину питания, тогда у нас должно быть устройство, которое заставит этот сигнал переменного тока течь на землю через это устройство, вместо того, чтобы попадать к другим компонентам на шине питания. Конденсатор — такое устройство.
При низкой частоте или для сигналов постоянного тока конденсатор кажется открытым для низкой частоты или сигнала постоянного тока.Конденсатор здесь не работает. Если бы наш силовой сигнал был бы чистым сигналом постоянного тока при всех условиях постоянного тока, не было бы использования разделительных конденсаторов. Все они должны быть удалены. Однако на практике существует ряд источников шума, которые проникают в шину питания. В таком случае между этими источниками шума и землей, образованной этими конденсаторами, будет низкий импеданс. Это приводит к заземлению источника шума конденсаторами.
4.3 Емкость в тракте прохождения сигнала
В то время как емкость между сигналом питания и заземлением полезна, емкость между трактом высокоскоростного сигнала чаще всего искажает сигнал.Эта емкость может быть образована переходным отверстием, толстой дорожкой на краю разъема карты, контактной площадкой SMD, контактной площадкой BGA или контрольной точкой.
Предыдущий — Конденсатор с параллельными пластинами
Импеданс конденсатора — надежная схема
В этой статье Short and Sweet мы кратко рассмотрим, как работают конденсаторы, и выведем формулу для импеданса конденсатора, используя формулу Эйлера для комплексных экспонент.Этот пост представляет собой перефразированный отрывок из SWE Lesson 1.2 .
Конденсатор хранит заряд в форме электрического поля или электрического поля. В своей базовой конфигурации это пара параллельных пластин с изоляционным материалом (или воздухом, или вакуумом) между ними, называемым диэлектриком . Когда на пластины подается напряжение, на пластинах накапливаются заряды противоположной полярности и возникает электрическое поле.
Рассмотрим следующую схему, состоящую из батареи, резистора, конденсатора и переключателя, который позволяет конденсатору заряжаться и разряжаться.
Предположим, что конденсатор изначально разряжен (не имеет электрического поля), а затем переключатель перемещается, чтобы подключить батарею к конденсатору. Отрицательные заряды текут от батареи на нижнюю пластину конденсатора, и они притягивают положительные заряды к верхней пластине. Эти положительные заряды можно рассматривать как отрицательные заряды (электроны), которые были перемещены, когда они покинули верхнюю пластину и вернулись в батарею. Таким образом образуется цепь, и на пластине возникает электрическое поле.
Когда конденсатор заряжается (или разряжается), идет заряд, а это означает, что есть ток. Вы можете подумать, что это означает, что ток проходит через конденсатор , но это не так (по крайней мере, не для «идеального» конденсатора). Заряды перемещаются на пластины (или от них), но не поперек них. По этой причине ток, связанный с конденсатором, часто называют током смещения .
Конденсатор может удерживать определенное количество заряда, величина которого пропорциональна напряжению, приложенному к пластинам.Константа пропорциональности называется емкостью , а уравнение заряда можно записать как:
\ (Q = CV \)
Поскольку ток является производной заряда по времени, мы можем вывести формулу для тока смещения:
\ (\ Displaystyle I (t) = \ frac {{d {Q (t)}}} {{dt}} = C \ frac {{dV (t)}} {{dt}} \)
Теперь у нас есть зависимость между напряжением и током конденсатора. Если мы возьмем их соотношение, мы можем получить полное сопротивление конденсатора .Уравнение происходит прямо из закона Ома:
\ (\ Displaystyle Z = V / I \)
Мы сформулировали уравнение в общем, где каждая переменная является сложной. Здесь Z — это импеданс, и, как правило, это функция от частоты. Мы рассматриваем V и I как функции частоты, и, сделав эти переменные комплексными, а не простыми действительными числами, мы можем изящно представить эту частотную зависимость.
В случае конденсатора давайте посмотрим, куда нас ведет закон Ома.Начнем с временной области. Предположим, что V задано. Тогда, поскольку мы знаем, как I связывает V через формулу тока конденсатора, мы можем написать:
\ (\ displaystyle Z = \ frac {V} {{C \ frac {{dV}} {{dt}}}} \)
Из страны времени в страну частот
Как связать это дифференциальное уравнение, находящееся во временной области, с частотной областью? Что ж, вот уловка: предположим, мы думаем о нашем напряжении как о синусоидальном (нет, не самоубийственном, а sin-u-soid-al).То есть это какая-то синусоидальная или косинусная волна. Давайте станем еще более безумными и представим напряжение как комплексную синусоиду , имеющую как мнимую, так и действительную части.
А зачем нам это делать? Что ж, давным-давно была открыта особая формула, которая связывает комплексные экспоненты со сложными синусоидами, а представление синусоид в виде экспонент позволяет использовать удобные компактные обозначения. {{j \ theta}}} = А \ соз \ theta + jA \ sin \ theta \)
Может показаться немного странным, особенно с показателем степени комплексности экспоненты, но, возможно, цифра справа поможет в вашем понимании, поскольку она показывает геометрию в комплексной плоскости.{{j \ omega t}}}}}}} = \ frac {1} {{j \ omega C}} \)
Передаточная функция RC-фильтра
Что мы можем сделать с формулой импеданса конденсатора? Во-первых, мы можем вывести передаточную функцию для RC-фильтра нижних частот. Вот схема:
Из уравнения для делителей напряжения можно записать:
\ (\ Displaystyle \ frac {{Vc}} {{Vi}} = \ frac {{{{Z} _ {c}}}} {{R + {{Z} _ {c}}}} = \ frac {{1 / (j \ omega C)}} {{R + 1 / (j \ omega C)}} \ times \ frac {{j \ omega C}} {{j \ omega C}} = \ frac { 1} {{j \ omega RC + 1}} \)
где \ ({Z} _ {c} \) — полное сопротивление конденсатора.{{-1}}} \ left ({\ frac {1} {{\ omega RC}}} \ right) \)
На графике Боде мы получаем классическую форму фильтра нижних частот, здесь для схемы с R = 159,2 Ом, C = 1 нФ:
Конденсатор — отношение напряжений
Мы можем использовать комплексную экспоненциальную формулу и по-другому, что касается импеданса конденсатора. Мы можем видеть, как напряжение и ток меняются относительно друг друга. Вы увидите, что для напряжения синусоиды ток конденсатора будет косинусоидальной.
Чтобы вывести это, мы обратим внимание на следующий факт: мнимая часть комплексной экспоненты представляет собой синусоидальную волну.{2}} \ sin (\ omega t))] = Im [\ omega CA (j \ cos (\ omega t) — \ sin (\ omega t)] \)
\ (\ displaystyle Im [{{I} _ {c}} (t)] = \ omega CAcos (\ omega t) \)
Сравнивая результаты по напряжению и току, мы приходим к интересному факту: для заданного синусоидального напряжения амплитуды A ток представляет собой косинусоидальную волну амплитуды \ (\ omega CA \).
Предположим, что A = 1V, \ (\ omega = 1 \, \, {{rad}} / {S} \; \) и C = 1 F. Ниже показаны графики обеих форм сигналов. Вы увидите, что напряжение конденсатора отстает от тока , или, другими словами, ток конденсатора опережает напряжение :
.Удивительно, на что способна небольшая математика, особенно когда она включает сложные экспоненты.


 (Причина возникновения больших токов при смене логических
состояний рассмотрена в статье Б. Картера «Техника разводки
печатных плат» — прим. переводчика.)
(Причина возникновения больших токов при смене логических
состояний рассмотрена в статье Б. Картера «Техника разводки
печатных плат» — прим. переводчика.) Ключом к созданию работоспособной и удачной схемы развязки является правильный выбор применяемых конденсаторов и
правильная разводка цепей их подключения.
Ключом к созданию работоспособной и удачной схемы развязки является правильный выбор применяемых конденсаторов и
правильная разводка цепей их подключения.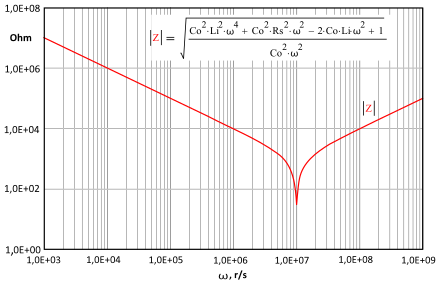 Сумма этих паразитных
эффектов приводит к изменению характера частотной зависимости импеданса (рис. 3).
Сумма этих паразитных
эффектов приводит к изменению характера частотной зависимости импеданса (рис. 3). е. с меньшим, чем 200 мОм). Эквивалентная последовательная индуктивность определяет
скорость реагирования конденсатора на изменения тока — конденсаторы с более низким значением ESL будут реагировать более быстро
на изменения протекающего тока, что очень важно для цепей высокочастотной развязки. Несмотря на то, что, как параметр, ESR более
широко описан и изучен, ESL, наверное, более важен. Все конденсаторы для поверхностного монтажа, приведенные в таблице 1,
обладают достаточно низкими значениями ESL.
е. с меньшим, чем 200 мОм). Эквивалентная последовательная индуктивность определяет
скорость реагирования конденсатора на изменения тока — конденсаторы с более низким значением ESL будут реагировать более быстро
на изменения протекающего тока, что очень важно для цепей высокочастотной развязки. Несмотря на то, что, как параметр, ESR более
широко описан и изучен, ESL, наверное, более важен. Все конденсаторы для поверхностного монтажа, приведенные в таблице 1,
обладают достаточно низкими значениями ESL. Конденсаторы с материалом II типа (т.е. X7R) являются более лучшим выбором из-за хорошей долговременной стабильности (10% потерь
в течение 10 лет), температурных характеристик и высокого значения диэлектрической постоянной. Материал III типа обладает наивысшим
значением диэлектрической постоянной и плохими температурными показателями (от 50 до 75% потерь при работе на предельных
температурах) и плохой долговременной стабильностью (20% потерь в течение 10 лет). Среди популярных диэлектриков многослойная керамика
и синтетика обладают небольшими эквивалентными последовательными индуктивностью и сопротивлением. Керамические конденсаторы
более легко доставаемы. Танталовые конденсаторы часто используются как общие элементы развязки по низкой частоте, однако они не
подходят для локальной развязки.
Конденсаторы с материалом II типа (т.е. X7R) являются более лучшим выбором из-за хорошей долговременной стабильности (10% потерь
в течение 10 лет), температурных характеристик и высокого значения диэлектрической постоянной. Материал III типа обладает наивысшим
значением диэлектрической постоянной и плохими температурными показателями (от 50 до 75% потерь при работе на предельных
температурах) и плохой долговременной стабильностью (20% потерь в течение 10 лет). Среди популярных диэлектриков многослойная керамика
и синтетика обладают небольшими эквивалентными последовательными индуктивностью и сопротивлением. Керамические конденсаторы
более легко доставаемы. Танталовые конденсаторы часто используются как общие элементы развязки по низкой частоте, однако они не
подходят для локальной развязки.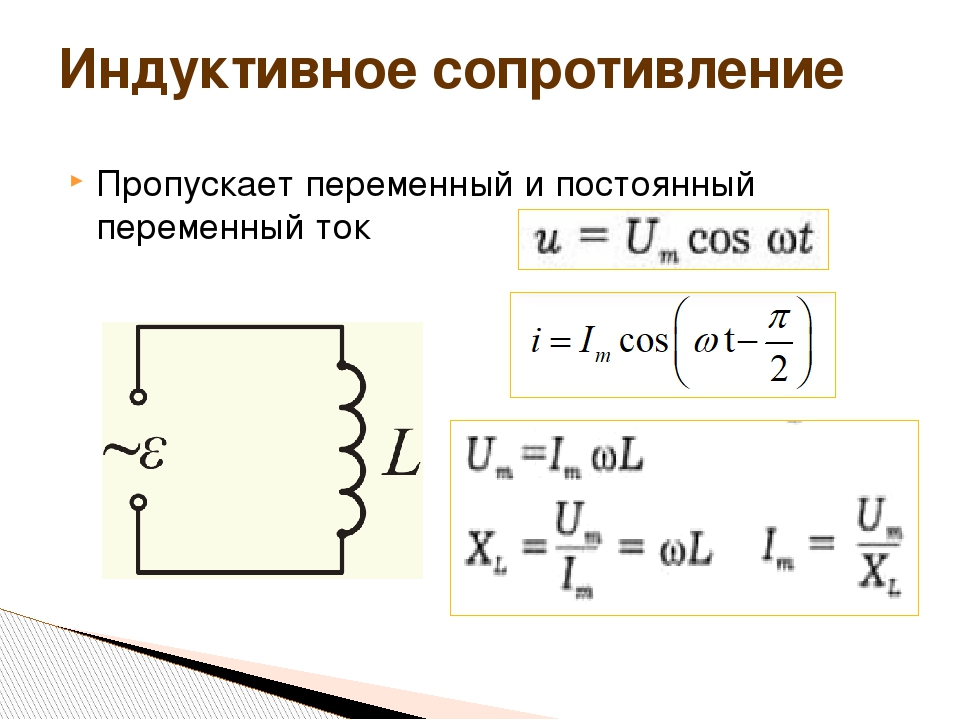 Конденсаторы с большими значениями ESL не годятся для использования в качестве элементов
развязки.
Конденсаторы с большими значениями ESL не годятся для использования в качестве элементов
развязки. Индуктивность одиночного переходного отверстия примерно равняется 500 пГн и зависит от
геометрической конфигурации.
Индуктивность одиночного переходного отверстия примерно равняется 500 пГн и зависит от
геометрической конфигурации.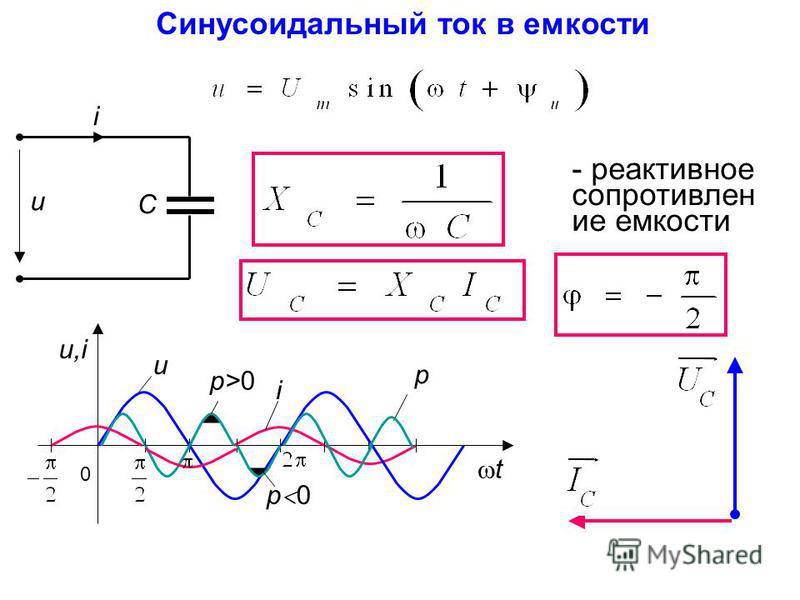 Как видно из таблицы 1, конденсаторы со
значением эффективной последовательной индуктивности менее 1 нГн вполне доступны. Добавление всего лишь 2 нГн утроит значение
ESL конденсатора. Рисунок 4 демонстрирует изменение частоты собственного резонанса и увеличение интегрального реактивного
сопротивления при добавлении индуктивности проводника в 2 нГн к собственной индуктивности (0,8 нГн) конденсатора емкостью
4,7 нФ.
Как видно из таблицы 1, конденсаторы со
значением эффективной последовательной индуктивности менее 1 нГн вполне доступны. Добавление всего лишь 2 нГн утроит значение
ESL конденсатора. Рисунок 4 демонстрирует изменение частоты собственного резонанса и увеличение интегрального реактивного
сопротивления при добавлении индуктивности проводника в 2 нГн к собственной индуктивности (0,8 нГн) конденсатора емкостью
4,7 нФ.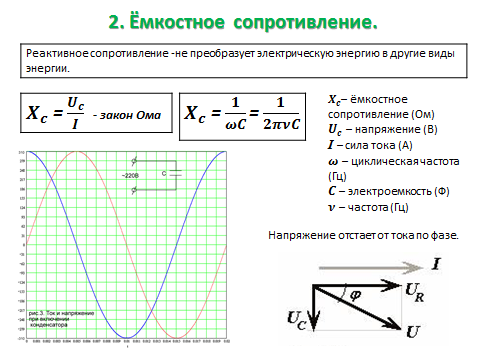 Несмотря на то, что такой подход часто обусловливается простотой разводки,
он позволяет эффективно работать цепям развязки и экономит пространство разводки. Два одиночных отверстия добавят в цепь развязки
около 1 нГн паразитной индуктивности.
Несмотря на то, что такой подход часто обусловливается простотой разводки,
он позволяет эффективно работать цепям развязки и экономит пространство разводки. Два одиночных отверстия добавят в цепь развязки
около 1 нГн паразитной индуктивности.