Электростатический потенциал — Википедия с видео // WIKI 2

У этого термина существуют и другие значения, см. Потенциал.

Электростатический потенциа́л — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию, которой обладает единичный положительный пробный заряд, помещённый в данную точку поля. Единицей измерения потенциала в Международной системе единиц (СИ) является вольт (русское обозначение: В; международное: V), 1 В = 1 Дж/Кл (подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

φ = W p q p . {\displaystyle \varphi ={\frac {W_{p}}{q_{p}}}.}

Напряжённость электростатического поля E {\displaystyle \mathbf {E} } и потенциал φ {\displaystyle \varphi } связаны соотношением^[1]

∫ A B E ⋅ d l = φ ( A ) − φ ( B ) , {\displaystyle \int \limits _{A}^{B}\mathbf {E} \cdot \mathbf {dl} =\varphi (A)-\varphi (B),}

или обратно^[2]:

E = − ∇ φ . {\displaystyle \mathbf {E} =-\nabla \varphi .}

Здесь ∇ {\displaystyle \nabla }  — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля ∇ ⋅ E = ρ ε 0 {\displaystyle \mathbf {\nabla } \cdot \mathbf {E} ={\rho \over \varepsilon _{0}}} , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона в вакууме. В единицах системы СИ:

∇ 2 φ = − ρ ε 0 , {\displaystyle {\nabla }^{2}\varphi =-{\rho \over \varepsilon _{0}},}

где φ {\displaystyle \varphi }  — электростатический потенциал (в вольтах), ρ {\displaystyle \rho }  — объёмная плотность заряда (в кулонах на кубический метр), а ε 0 {\displaystyle \varepsilon _{0}}  — электрическая постоянная (в фарадах на метр).

Энциклопедичный YouTube

• 1/5

  Просмотров:

  2 129

  3 649

  28 280

  6 546

  10 614

• ✪ Электрический потенциал — определение и решение простых задач.

• ✪ 3.1.5 Потенциал электростатического поля

• ✪ Урок 229. Работа электрического поля. Потенциал. Электрическое напряжение

• ✪ Потенциал заряженного проводника

• ✪ Урок 230. Простейшие задачи на электрический потенциал

Содержание

Неоднозначность определения потенциала

Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов, которая определяется как:

φ 1 − φ 2 = A f q ∗ 1 → 2 q ∗ , {\displaystyle \varphi _{1}-\varphi _{2}={\frac {A_{f}^{q^{*}1\to 2}}{q^{*}}},}

где:

φ 1 {\displaystyle \varphi _{1}}  — потенциал в точке 1,

φ 2 {\displaystyle \varphi _{2}}  — потенциал в точке 2,

A f q ∗ 1 → 2 {\displaystyle A_{f}^{q^{*}1\to 2}}  — работа, совершаемая полем при переносе пробного заряда q ∗ {\displaystyle q^{*}} из точки 1 в точку 2.

При этом считается, что все остальные заряды при такой операции «заморожены» — то есть неподвижны во время этого перемещения (имеется в виду вообще говоря скорее воображаемое, а не реальное перемещение, хотя в случае, если остальные заряды действительно закреплены — или пробный заряд исчезающе мал по величине — чтобы не вносить заметного возмущения в положения других — и переносится достаточно быстро, чтобы остальные заряды не успели заметно переместиться за это время, формула оказывается верной и для вполне реальной работы при реальном перемещении).

Впрочем, иногда для снятия неоднозначности используют какие-нибудь «естественные» условия. Например, часто потенциал определяют таким образом, чтобы он был равен нулю на бесконечности для любого точечного заряда — и тогда для любой конечной системы зарядов выполнится на бесконечности это же условие, а над произволом выбора константы можно не задумываться (конечно, можно было бы выбрать вместо нуля любое другое число, но ноль — «проще»).

Единицы измерения

В СИ за единицу разности потенциалов принимают вольт (В).

Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1 В = 1 Дж/Кл (L²MT⁻³I⁻¹).

В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг.

Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ.

Использование термина

Широко используемые термины напряжение и электрический потенциал имеют несколько иной смысл, хотя нередко используются неточно как синонимы электростатического потенциала. В отсутствие меняющихся магнитных полей напряжение равно разности потенциалов.

Кулоновский потенциал

Иногда термин

кулоновский потенциал используется просто для обозначения электростатического потенциала как полный синоним. Однако можно сказать, что в целом эти термины несколько различаются по оттенку и преимущественной области применения.

Также под кулоновским могут понимать потенциал любой природы (то есть не обязательно электрический), который при точечном или сферически симметричном источнике имеет зависимость от расстояния 1 r {\displaystyle {\frac {1}{r}}} (например, гравитационный потенциал в теории тяготения Ньютона, хотя последний чаще всё же называют ньютоновским, так как он был изучен в целом раньше), особенно если надо как-то обозначить весь этот класс потенциалов в отличие от потенциалов с другими зависимостями от расстояния.

Формула электростатического потенциала (кулоновского потенциала) точечного заряда в вакууме:

φ = k q r , {\displaystyle \varphi =k{\frac {q}{r}},}

где k {\displaystyle k} обозначен коэффициент, зависящий от системы единиц измерения — например, в СИ:

k = 1 4 π ε 0 {\displaystyle k={\frac {1}{4\pi \varepsilon _{0}}}} = 9·10⁹ В·м/Кл,

q {\displaystyle q}  — величина заряда, r {\displaystyle r}  — расстояние от заряда-источника до точки, для которой рассчитывается потенциал.

• Можно показать, что эта формула верна не только для точечных зарядов, но и для любого сферически симметричного заряда конечного размера, например, равномерно заряженного шара, правда, только в свободном от заряда пространстве — то есть, например, над поверхностью шара, а не внутри его.
• Кулоновский потенциал в приведенном выше виде используется в формуле кулоновской потенциальной энергии (потенциальной энергии взаимодействия системы электростатически взаимодействующих зарядов):

  W = ∑ i < j k q i q j r i j = 1 2 ∑ i ≠ j k q i q j r i j . {\displaystyle W=\sum _{i<j}k{\frac {q_{i}q_{j}}{r_{ij}}}={\frac {1}{2}}\sum _{i\neq j}k{\frac {q_{i}q_{j}}{r_{ij}}}.}

В электродинамике

Когда присутствуют изменяющиеся во времени магнитные поля (что справедливо, при изменяющихся во времени электрических полей и наоборот), то невозможно описать электрическое поле в терминах скалярного потенциала V, поскольку электрическое поле больше не является консервативным: циркуляция ∫ C E ⋅ d ℓ {\displaystyle \textstyle \int _{C}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}} зависит от пути, потому что ∇ × E ≠ 0 {\displaystyle \mathbf {\nabla } \times \mathbf {E} \neq \mathbf {0} } (см. Закон индукции Фарадея).

Вместо этого всё ещё можно определить скалярный потенциал, дополнив его магнитным векторным потенциалом A. В частности,

А определен так чтобы

B = ∇ × A , {\displaystyle \mathbf {B} =\mathbf {\nabla } \times \mathbf {A} ,\,}

где B — магнитное поле. Поскольку дивергенция магнитного поля всегда равно нулю из-за отсутствия магнитных монополей, то A всегда существует. Учитывая это, величина

F = E + ∂ A ∂ t {\displaystyle \mathbf {F} =\mathbf {E} +{\frac {\partial \mathbf {A} }{\partial t}}}

является консервативным полем по закону Фарадея, и поэтому можно написать

E = − ∇ V − ∂ A ∂ t , {\displaystyle \mathbf {E} =-\mathbf {\nabla } V-{\frac {\partial \mathbf {A} }{\partial t}},\,}

где

V — скалярный потенциал, определённый консервативным полем F.

Электростатический потенциал — это частный случай этого определения, где A не зависит от времени. С другой стороны, для изменяющихся во времени полей,

− ∫ a b E ⋅ d ℓ ≠ V ( b ) − V ( a ) , {\displaystyle -\int _{a}^{b}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}\neq V_{(b)}-V_{(a)},\,}

в отличие от электростатики.

См. также

Примечания

Эта страница в последний раз была отредактирована 29 мая 2020 в 23:46.

«Разность потенциалов в чем измеряется?» – Яндекс.Кью

Этот вопрос, как капуста, его раскрываешь-раскрываешь, а до «фундаментальной» кочерыжки всё ещё далеко. Хоть вопрос, видимо, касается этой самой кочерыжки, придётся всё же попробовать одолеть всю капусту.

На самый поверхностный взгляд природа тока кажется простой: ток — это когда заряженные частицы движутся. (Если частица не движется, то тока нет, есть только электрическое поле.) Пытаясь постичь природу тока, и не зная из чего состоит ток, выбрали для тока направление, соответствующее направлению движения положительных частиц. Позже оказалось, что неотличимый, точно такой же по действию ток получается при движении отрицательных частиц в противоположном направлении. Эта симметрия является примечательной деталью природы тока.

В зависимости от того, где движутся частицы природа тока тоже различна. Отличается сам текущий материал:

• В металлах есть свободные электроны;
• В металлических и керамических сверхпроводниках — тоже электроны;
• В жидкостях — ионы, которые образуются при протекании химических реакций или при воздействии приложенного электрического поля;
• В газах — снова ионы, а также электроны;
• А вот в полупроводниках электроны несвободны и могут двигаться «эстафетно». Т.е. двигаться может не электрон, а как бы место, где его нет — «дырка». Такая проводимость называется дырочной. На спайках разных полупроводников природа такого тока рождает эффекты, делающие возможной всю нашу радиоэлектронику.
  У тока две меры: сила тока и плотность тока. Между током зарядов и током, например, воды в шланге больше различий, чем сходства. Но такой взгляд на ток вполне продуктивен, для понимания природы последнего. Ток в проводнике это векторное поле скоростей частиц (если это частицы с одинаковым зарядом). Но мы обычно для описания тока не учитываем эти детали. Мы усредняем этот ток.

Если мы возьмём одну только частицу (естественно заряженную и движущуюся), то ток равный произведению заряда и мгновенной  скорости в конкретный момент времени существует ровно там, где находится эта частица. Помните, как было в песне дуэта Иваси «Пора по пиву»: «…если климат тяжёл и враждебен астрал, если поезд ушёл и все рельсы ЗА-БРАЛ…» 🙂

И вот мы пришли к той кочерыжке, которую упоминали вначале. Почему частица имеет заряд (с движением вроде всё ясно, а что же такое заряд)? Наиболее фундаментальные частицы (вот теперь уж точно 🙂 вроде бы неделимые) несущие заряд — это электроны, позитроны (антиэлектроны) и кварки. Отдельно взятый кварк вытащить и исследовать невозможно из-за конфайнмента, с электроном вроде проще, но тоже пока не очень-то ясно. На данный момент видно, что ток квантуется: не наблюдается зарядов меньше заряда электрона (кварки наблюдаются только в виде адронов с совокупным зарядом таким же или нулевым). Электрическое поле отдельно от заряженной частицы может существовать только в связке с магнитным полем, как электромагнитная волна, квантом которой является фотон. Возможно, какие-то интерпретации природы электрического заряда лежат в сфере квантовой физики. Например, предсказанное ею и обнаруженное сравнительно недавно поле Хиггса (есть бозон — есть и поле) объясняет массу ряда частиц, а масса — это мера того, как частица откликается на гравитационное поле. Может быть и с зарядом, как с мерой отклика на электрическое поле, обнаружится какая-то похожая история. Почему есть масса и почему есть заряд — это в чём-то родственные вопросы.

Многое известно о природе электрического тока, но самое главное пока нет.

Электростатический потенциал — это… Что такое Электростатический потенциал?

У этого термина существуют и другие значения, см. Потенциал.

Электростатический потенциа́л (см. также кулоновский потенциал) — скалярная энергетическая характеристика электростатического поля, характеризующая потенциальную энергию поля, которой обладает единичный заряд, помещённый в данную точку поля. Единицей измерения потенциала является, таким образом, единица измерения работы, деленная на единицу измерения заряда (для любой системы единиц; подробнее о единицах измерения — см. ниже).

Электростатический потенциал — специальный термин для возможной замены общего термина электродинамики скалярный потенциал в частном случае электростатики (исторически электростатический потенциал появился первым, а скалярный потенциал электродинамики — его обобщение). Употребление термина электростатический потенциал определяет собой наличие именно электростатического контекста. Если такой контекст уже очевиден, часто говорят просто о потенциале без уточняющих прилагательных.

Электростатический потенциал равен отношению потенциальной энергии взаимодействия заряда с полем к величине этого заряда:

Напряжённость электростатического поля и потенциал связаны соотношением^[1]

или обратно^[2]:

Здесь  — оператор набла, то есть в правой части равенства стоит минус градиент потенциала — вектор с компонентами, равными частным производным от потенциала по соответствующим (прямоугольным) декартовым координатам, взятый с противоположным знаком.

Воспользовавшись этим соотношением и теоремой Гаусса для напряжённости поля , легко увидеть, что электростатический потенциал удовлетворяет уравнению Пуассона. В единицах системы СИ:

где  — электростатический потенциал (в вольтах),  — объёмная плотность заряда (в кулонах на кубический метр), а  — диэлектрическая проницаемость вакуума (в фарадах на метр).

Неоднозначность определения потенциала

Поскольку потенциал (как и потенциальная энергия) может быть определён с точностью до произвольной постоянной (и все величины, которые можно измерить, а именно напряженности поля, силы, работы — не изменятся, если мы выберем эту постоянную так или по-другому), непосредственный физический смысл (по крайней мере, пока речь не идет о квантовых эффектах) имеет не сам потенциал, а разность потенциалов, которая определяется как:

где:  — потенциал в точке 1,  — потенциал в точке 2,  — работа, совершаемая полем при переносе пробного заряда из точки 1 в точку 2. При этом считается, что все остальные заряды при такой операции «заморожены» — то есть неподвижны во время этого перемещения (имеется в виду вообще говоря скорее воображаемое, а не реальное перемещение, хотя в случае, если остальные заряды действительно закреплены — или пробный заряд исчезающе мал по величине — чтобы не вносить заметного возмущения в положнения других — и переносится достаточно быстро, чтобы остальные заряды не успели заметно переместиться за это время, формула оказывается верной и для вполне реальной работы при реальном перемещении).

Впрочем, иногда для снятия неоднозначности используют какие-нибудь «естественные» условия. Например, часто потенциал определяют таким образом, чтобы он был равен нулю на бесконечности для любого точечного заряда — и тогда для любой конечной системы зарядов выполнится на бесконечности это же условие, а над произволом выбора константы можно не задумываться (конечно, можно было бы выбрать вместо нуля любое другое число, но ноль — «проще»).

Единицы измерения

В СИ за единицу разности потенциалов принимают вольт (В). Разность потенциалов между двумя точками поля равна одному вольту, если для перемещения между ними заряда в один кулон нужно совершить работу в один джоуль: 1В = 1 Дж/Кл (L²MT⁻³I⁻¹). В СГС единица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной одна единица заряда СГСЭ нужно совершить работу в один эрг. Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ

Использование термина

Широко используемые термины напряжение и электрический потенциал имеют несколько иной смысл, хотя нередко используются неточно как синонимы электростатического потенциала.

Кулоновский потенциал

Иногда термин кулоновский потенциал используется просто для обозначения электростатического потенциала, как полный синоним. Однако можно сказать, что в целом эти термины несколько различаются по оттенку и преимущественной области применения.

Чаще всего под кулоновским потенциалом имеют в виду электростатический потенциал одного точечного заряда (или нескольких точечных зарядов, полученный сложением кулоновского потенциала каждого из них). Зачастую даже в случае, когда имеется в виду потенциал, созданный непрерывно распределенными зарядами, если его называют кулоновским, это может подразумевать, что он выражен (или может быть выражен) всё же в виде суммы (интеграла) пусть и бесконечного числа элементов, на которые разбит заряженный объем, но всё же потенциал каждого рассчитан как потенциал точечного заряда. Однако, поскольку электростатический потенциал в принципе может быть выражен таким образом практически всегда (подробнее см. чуть ниже), то разграничение терминов всё же достаточно размывается.

Также под кулоновским могут понимать потенциал любой природы (то есть не обязательно электрический), который при точечном или сферически симметричном источнике имеет зависимость от расстояния 1/r (например, гравитационный потенциал в теории тяготения Ньютона, хотя последний чаще всё же называют ньютоновским, так как он был изучен в целом раньше), особенно если надо как-то обозначить весь этот класс потенциалов в отличие от потенциалов с другими зависимостями от расстояния.

Формула электростатического потенциала (кулоновского потенциала) точечного заряда:

(где K обозначен коэффициент, зависящий от системы единиц измерения — например в СИ K = 1/(4πε₀), q — величина заряда, r — расстояние от заряда-источника до точки, для которой рассчитывается потенциал).

• Можно показать, что эта формула верна не только для точечных зарядов, но и для любого сферически симметричного заряда конечного размера, например, равномерно заряженного шара, правда, только в свободном от заряда пространстве — то есть например над поверхностью шара, а не внутри его.
• Кулоновский потенциал в виде приведенной выше формулы используется в формуле кулоновской потенциальной энергии (потенциальной энергии взаимодействия системы электростатически взаимодействующих зарядов):

См. также

Примечания

потенциальная энергия, потенциал поля, эквипотенциальные поверхности

В статье расскажем про потенциальную энергию и потенциал поля Е, узнаете что такое линии напряженности электрического поля и эквипотенциальные поверхности, а так же про потенциальный градиент.

Потенциальная энергия U нагрузки в поле E и потенциал поля V E

Энергетический подход очень эффективен при описании электрических явлений, поскольку можно определить потенциальную энергию U заряда в электрическом поле. Рассмотрим электрическое поле между двумя параллельными пластинами, на которых есть нагрузки одинаковой величины, но с противоположными знаками. Размер плит велик по сравнению с расстоянием между ними, и, таким образом, в большинстве областей поле между ними можно рассматривать как однородное. Небольшой положительный точечный заряд +q имеет наибольшую потенциальную энергию U, когда он находится в точке на поверхности положительного электрода, как на чертеже.

Это означает, что в этот момент заряд +q обладает наибольшей способностью выполнять работу при его возврате к отрицательному электроду. Нам нужно дать эту энергию заряда U, выполняя работу по переносу этого заряда с отрицательного на положительный электрод. Работа выполняется против силы электростатического отталкивания F = Q*E . В разделе dl мы сделаем работу dW равной:

или

Работа по переносу заряда +q между двумя электродами, то есть потенциальной энергии U этого заряда на положительном электроде, равна:

Поскольку электрическое поле является потенциальным полем, работа по переносу заряда из точки а в точку b не зависит от формы пути нагрузки между этими точками.

Ранее мы определяли напряженность электрического поля, как силу, действующую на единицу нагрузку. Аналогичным образом мы определяем электрический потенциал V или просто потенциал как отношение потенциальной энергии, которую заряд q имеет в электрическом поле, к величине заряда. Следовательно, если любой заряд q имеет потенциальную энергию U в некоторой точке поля, то потенциал поля V в этой точке равен:

В общем случае, когда поле E не является однородным, мы должны написать общее соотношение, которое также верно и для однородного поля:

Теперь мы можем выразить напряженность поля E, уменьшив потенциал dV на участке dl:

Когда направление сдвига dl не параллельно направлению поля E, тогда общее соотношение между обсуждаемыми значениями будет получено путем записи его в векторной форме. Тогда падение dV-потенциала будет скалярным произведением, и в общем случае неоднородного поля приращения dU и dV равны:

Разность потенциалов V_ab между точками А и В на рисунке выше, даже если поле было неоднородным, получим интегрированием:

Линии напряженности электрического поля и эквипотенциальные поверхности

Назовем линии E-поля дорожками тест-положительных зарядов, движущимися под действием этого поля. Поверхности, где электрический потенциал имеет одинаковое значение, называются эквипотенциальными поверхностями. Линии поля E (зеленые) всегда перпендикулярны эквипотенциальным поверхностям (красные). На рисунке ниже показано окружение точки нагрузки.

Распределение линий E (зеленые), перпендикулярных эквипотенциальным поверхностям (красные), окруженным диполем, можно представить следующим образом:

Поверхность металла всегда является эквипотенциальной поверхностью. Таким образом, когда нагрузки в состоянии покоя распределяются по поверхности металла, электрическое поле непосредственно над поверхностью металла должно быть перпендикулярно его поверхности в каждой точке.

Потенциальный градиент и поле E

Поскольку, как мы показали выше, интенсивность поля E связана с уменьшением потенциала dV и расстояния dl, на котором это уменьшение происходит с помощью формулы:

Этот вектор напряженности поля E может быть определен непосредственно как градиент потенциала:

Полученная связь между вектором поля E и градиентом потенциала:

Как мы помним из свойств векторных функций, градиент скалярной функции (в данном случае потенциал V) равен размеру вектора E. Компоненты этого вектора выражаются частными производными (уменьшаются по x, y и z)

Если поле E является постоянным и однородным, то градиент потенциала также является постоянным, и теперь очень простым и удобным правилом для определения разности потенциалов V (напряжения) в этом поле является отношение, которое напрямую вытекает из соотношения между E и градиентом потенциала:

где расстояние l отсчитывается вдоль поля. Это правило зависит от изменения напряжения, показанного вольтметром, если мы плавно изменим положение его клемм, касаясь провода сопротивления, по которому течет ток. Напряжение, определяемое по этому правилу, называется шаговым напряжением. Название «шаговое напряжение» возникает из-за риска поражения электрическим током, когда мы предпринимаем длинные шаги (например, бегаем), а удар молнии рядом с нами ударит о землю. Ступенчатое напряжение опасно для скота, остающегося на поляне во время шторма.

Только разность потенциалов может быть измерена в эксперименте. Единица измерения электрического потенциала и разности потенциалов составляет 1 вольт (1 В = 1 Дж / 1 С).

11. В каких единицах измеряется электрический потенциал?

Ответ:

12. Что называется электрической силовой линией?

Ответ:

13. Как определить работу по переносу заряда из одной точки электрического поля в дрyгyю?

Ответ:

14. Определите потенциал точки электрического поля, в кото­рую из бесконечности внесен заряд q = 3· 10-6 К, если при этом силами поля совершена работа А = 6 . 10-6 Дж.

Дано:

Найти:

Решение:

Ответ:

15. Потенциал электрического поля в точке а составляет 60 в, а в точке б — 76 в. Заряд в 6 к перенесен из точки а в точку б. Какая при этом совершена работа?

Дано:

Найти:

Решение:

Ответ:

16. Вычислите напряженность двух различных электрически полей, действующих на заряд q = 0,004 К с силой F 1 = 0,08 Н и F2 = 0,012 Н.

Дано:

Н

айти:

Решение:

Ответ:

17. Заряд величиной в 0,3 К помещен в однородное электрическое поле, которое действует на него с силой в 4,5 Н. Каков напряженность однородного электрического поля?

Дано:

Найти:

Решение:

Ответ:

18. Электрический заряд величиной 2· 10-6 находится в вакууме. Какова напряженность электрического поля на расстоянии 20 см от заряда?

Дано:

Найти:

Р

ешение:

Ответ:

19. На шелковых нитках висят два медных шара. Потенциал первого шара ₁ = — 18 В, потенциал второго шара ₂ = + 32 В Определите напряжение U₂₁ между вторым и первым шарами.

Дано:

Найти:

Решение:

Ответ:

1.3. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ

Ответьте па вопросы:

20. От чего зависит емкость конденсатора?

Ответ:

21. Как влияет диэлектрик на емкость конденсаторов?

Ответ:

22. В каком случае необходимо применять последовательное соединение конденсаторов?

Ответ:

23. Заполните таблицу:

0,0015 Ф	33 мкФ	0,047 мкФ	100 пФ	6,8нФ	820 пФ
?мкФ	?Ф	?пФ	?мкФ	?пФ	?нФ

24. Определите общую емкость соединения конденсаторов, схема которых приведена на рис. 3, если все конденсаторы имеют ем­кость по 5 мкФ.

Дано:

Найти:

Решение:

Ответ:

С1 С2

С3 С4

Рис. 3

Электрический потенциал — Простая английская Википедия, бесплатная энциклопедия

Электрический потенциал — электрическая потенциальная энергия (ЭПЭ) на единицу заряда. (Единица энергии — джоуль, а единица заряда — кулон.) Электрический потенциал показывает, какой будет электрическая потенциальная энергия заряженного объекта на каждый кулон заряда, который он имеет, или сколько джоулей энергии будет приходиться на кулон. Единица измерения электрического потенциала, джоуль на кулон, названа вольт в память об Алессандро Вольта.Один вольт равен одному джоулю на кулон.

Хорошая аналогия — вода в мельничном пруду. Вода в пруду обладает потенциальной гравитационной энергией из-за того, насколько высоко она находится над уровнем моря. Когда вода падает, она теряет энергию. На холмах может быть пруд со 100 литрами воды и 1000 джоулей энергии в пруду, поэтому на литр приходится 10 джоулей энергии. В другом пруду может быть 100 литров воды, но при этом только 500 джоулей энергии, потому что пруд находится в нижней долине.В этом пруду 5 джоулей на литр. Точно так же у нас может быть 100 кулонов заряда с 1000 джоулей электрической потенциальной энергии, хранящейся где-то, может быть, в электрической цепи. Электрический потенциал составит 10 джоулей энергии на кулон. В другом месте, может быть, в другом месте той же электрической цепи, может быть электрический потенциал 5 джоулей на кулон.

Точно так же, как масса падает из места, где у нее более высокая потенциальная энергия, из самолета или другого места во Вселенной, на землю или другое место во Вселенной, где она имеет более низкую потенциальную энергию, то же самое происходит и с зарядами.Заряды всегда идут туда, где у них более низкий электрический потенциал или потенциал. Это движение также называется «падением». Группа зарядов или заряженный объект упадет с места с электрическим потенциалом 10 джоулей на кулон до места с электрическим потенциалом 5 джоулей на кулон или из места с электрический потенциал 10 вольт на единицу с электрическим потенциалом 5 В. Если на объекте имеется 20 кулонов заряда, он упадет из-за наличия электрической потенциальной энергии (EPE) 200 джоулей (20 cx (10 Дж / c) = 200 джоулей) в месте с электрическим потенциалом 10 вольт до электрической потенциальной энергии 100 джоулей (20 cx (5 Дж / c) = 100 джоулей) в месте с электрическим потенциалом 5 вольт.

Хотя эта концепция также применима к гравитации, мы ее не используем. Почти всегда полезнее думать и использовать полную гравитационную потенциальную энергию, GPE, объекта, а не использовать GPE на килограмм. В электричестве очень часто более полезно использовать электрический потенциал, EPE на заряд, вместо использования полной электрической потенциальной энергии.

Электрический потенциал — это не то же самое, что электрическая потенциальная энергия. Это электрическая потенциальная энергия на единицу заряда. Электрический потенциал — это не то же самое, что разность электрических потенциалов.Разность электрических потенциалов также называется напряжением (см. Страницу напряжения).

Обратите внимание, что вольт и напряжение — это разные вещи. Вольт — это единица измерения, с помощью которой мы что-то измеряем. И электрический потенциал, и напряжение — это то, что мы измеряем, и вольт является единицей измерения для обоих. Да, немного запутано, но так оно и есть. Обозначение единицы вольта записывается как В (9 В или 9 В). Когда напряжение используется в формуле, символом напряжения является строчная буква v.(например, напряжение = ток x сопротивление или v = ir). Это отличает разницу между вольтами (V) и напряжением (v), когда существует только однобуквенный символ. Инженеры-электрики используют символ «e» для обозначения напряжения (например, e = ir), чтобы более четко различать разницу.

,

Электрический потенциал | физика | Британника

Электрический потенциал, объем работы, необходимо, чтобы переместить единичный заряд от опорной точки к определенной точке против электрического поля. Обычно точкой отсчета является Земля, хотя можно использовать любую точку, не подверженную влиянию заряда электрического поля.

Подробнее по этой теме

Электромагнетизм: электрические поля и силы

Еще одно полезное поле — электрический потенциал.Он обеспечивает альтернативу электрическому полю в задачах электростатики. Потенциал …

На диаграмме показаны силы, действующие на положительный заряд q , расположенный между двумя пластинами, A и B, электрического поля E . Электрическая сила F , прикладываемая полем к положительному заряду, равна F = qE; , чтобы переместить заряд от пластины A к пластине B, тогда должна быть приложена равная и противоположная сила ( F ′ = — qE ).Работа W, , проделанная при перемещении положительного заряда на расстояние d , составляет W = F ′ d = — qEd.

электрический потенциал Силы, действующие на заряд q между двумя пластинами, A и B, между которыми существует электрическое поле E . Электрическая сила F , прикладываемая полем к положительному заряду, равна F = qE . Чтобы переместить заряд от пластины A к пластине B, необходимо приложить равную и противоположную силу ( F ′ = — qE ).Электрический потенциал, то есть работа W , совершенная при перемещении положительного заряда на расстояние d , составляет W = F ′ d = — qEd. Encyclopædia Britannica, Inc.

Потенциальная энергия положительного заряда увеличивается, когда он движется против электрического поля, и уменьшается, когда он движется вместе с электрическим полем; обратное верно для отрицательного заряда. Если единичный заряд не пересекает изменяющееся магнитное поле, его потенциал в любой данной точке не зависит от пройденного пути.

Хотя концепция электрического потенциала полезна для понимания электрических явлений, можно измерить только разницу в потенциальной энергии. Если электрическое поле определяется как сила, приходящаяся на единицу заряда, то по аналогии электрический потенциал можно рассматривать как потенциальную энергию на единицу заряда. Следовательно, работа, выполняемая при перемещении единичного заряда из одной точки в другую (например, в пределах электрической цепи), равна разнице потенциальных энергий в каждой точке. В Международной системе единиц (СИ) электрический потенциал выражается в джоулях на кулон (т.е.е., вольт), а разность потенциальной энергии измеряется вольтметром.

Получите эксклюзивный доступ к контенту нашего 1768 First Edition с подпиской. Подпишитесь сегодня ,

Что такое электрический потенциал и разность потенциалов? Определение и их единицы

Определение : Электрический потенциал определяется как способность заряженного тела выполнять работу. Когда тело заряжено, либо к нему подводятся электрические электроны, либо они удаляются от него. В обоих случаях работа сделана. Эта работа сохраняется в теле в виде электрического потенциала. Таким образом, тело может совершать работу, оказывая силу притяжения или отталкивания другим заряженным частицам.

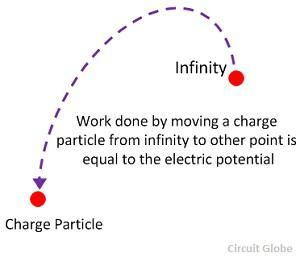
Способность заряженного тела выполнять работу определяет электрический потенциал на нем. Мера электрического потенциала — это работа, совершаемая для зарядки тела величиной в один кулон, то есть

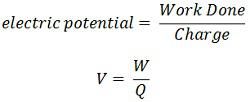
Единицы: Поскольку проделанная работа измеряется в джоулях, а заряд — в кулонах , единицей электрического потенциала является джоуль / кулон, единицей электрического потенциала является джоулей / кулон, или вольт.

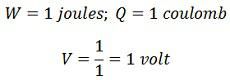
Следовательно, считается, что тело имеет электрический потенциал в 1 вольт, если один джоуль работы затрачивается на заряд тела до одного кулона.

Разница электрических потенциалов

Разность электрических потенциалов определяется как количество работы, выполняемой для переноса единичного заряда из одной точки в другую в электрическом поле. Другими словами, разность потенциалов определяется как разность электрических потенциалов двух заряженных тел.

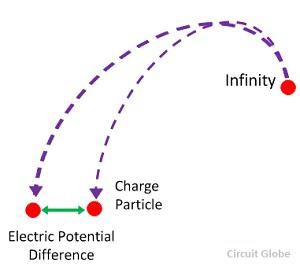
Когда одно тело заряжено до другого электрического потенциала по сравнению с другим заряженным телом, два тела имеют разность потенциалов.Оба тела находятся в напряжении и напряжении и пытаются достичь минимального потенциала

.

Единица : Единица разности потенциалов вольт .

,

Электрический потенциал и разность электрических потенциалов (напряжение)

В этой лекции мы узнаем об электрическом потенциале и разнице электрических потенциалов, которая также известна как напряжение.

Вы можете посмотреть следующее видео или прочитать письменное руководство под видео.

В предыдущей лекции мы говорили об электрической потенциальной энергии, которая зависит от заряда объекта, находящегося в электрическом поле. Теперь мы собираемся узнать об электрическом потенциале, который зависит только от положения объекта.

Электрический потенциал (или просто потенциал) — это просто мера электрической потенциальной энергии на единицу заряда.

Формула электрического потенциала

Это основное уравнение для расчета электрического потенциала, которое показывает, что электрический потенциал V равен электрической потенциальной энергии U, деленной на заряд q, который будет помещен в точку на некотором расстоянии от основного заряда.

Электрическая потенциальная энергия U равна кулоновской постоянной k, умноженной на заряд, который создает большой потенциал Q, умноженный на заряд, который будет помещен в точку, находящуюся на некотором расстоянии от основного заряда small q, и деленное на это расстояние r.

Чтобы вычислить электрический потенциал, нам просто нужно разделить потенциальную энергию на малую q.

Мы можем заметить, что маленький q появляется дважды в уравнении, поэтому мы можем его сократить.

Теперь у нас есть это простое уравнение.

Уравнение показывает, что потенциал прямо пропорционален величине заряда Q — по мере увеличения заряда потенциал увеличивается, и наоборот, по мере уменьшения заряда потенциал уменьшается.

С другой стороны, обратно пропорционально расстоянию r , потому что по мере удаления от заряда потенциал будет уменьшаться, а по мере приближения к заряду потенциал будет увеличиваться до увеличение.

Наконец, мы получили бы количество электрической потенциальной энергии, которое в этот момент будет иметь каждая единица заряда.

Связано: Закон Кулона

Единица электрического потенциала

Теперь вернемся к основному уравнению.

Мы знаем, что электрическая потенциальная энергия измеряется в Джоулях, а единицей заряда является кулон. Итак, единица измерения электрического потенциала — Джоули на кулон, или одним словом Вольт.

Точечный заряд равен +2 мкКл, и мы хотим найти электрический потенциал на расстоянии 15 см (0,15 м) от этого заряда.

Теперь мы можем использовать это уравнение для вычисления электрического потенциала.

Мы получили положительный электрический потенциал +1.2 × 10 ⁵ В.

В случае отрицательного заряда, скажем, -2 мкКл, электрический потенциал в этой же точке будет -1,2 × 10 ⁵ В. Мы получили бы то же самое. значение, но со знаком минус.

Давайте взглянем на этот график электрического потенциала. Ось X показывает расстояние от заряда, а ось Y показывает электрический потенциал в определенной точке.

Здесь у нас положительный заряд, а потенциал вокруг положительного заряда всегда положительный. По мере того, как вы удаляетесь от заряда, по мере того, как расстояние от заряда увеличивается, потенциал становится менее положительным и уменьшается все ближе и ближе к нулю.

С другой стороны, у нас отрицательный заряд, а потенциал вокруг отрицательного заряда всегда отрицательный. По мере того, как вы удаляетесь от заряда, по мере того, как расстояние от заряда увеличивается, потенциал становится менее отрицательным и фактически увеличивается, также приближаясь к нулю.

Если вы находитесь бесконечно далеко от заряда, потенциал будет равен нулю как для положительных, так и для отрицательных зарядов.

Связано: Что такое электрический заряд и как работает электричество

Теперь мы можем перейти к разнице электрических потенциалов или напряжению.

По определению, разность электрических потенциалов или напряжение — это разность электрических потенциалов между конечным и начальным положением, когда над зарядом выполняется работа по изменению его потенциальной энергии.

Теперь давайте рассмотрим пример, который поможет нам легко понять термин «напряжение».

У нас есть положительный заряд + 1,6 × 10 ^-19 С. Это основной заряд, создающий потенциал.

Первый круг — это первый энергетический уровень, на расстоянии 2,5 × 10 ^-11 м от заряда. Второй круг — это второй энергетический уровень, на расстоянии 4,2 × 10 ^-12 м от заряда.

Чтобы найти разность электрических потенциалов или напряжение, нам нужно найти потенциал в точке A и потенциал в точке B.

Потенциал в точке A, которая является первым уровнем энергии, будет 57,6 В.

Потенциал в точке B, которая находится на большем расстоянии, будет 34,2 В. .

Сначала мы собираемся вычислить напряжение по мере движения от A к B, а затем от B к A.

В первом случае A — это наш начальный потенциал, а B — наш конечный потенциал. , Итак, разность потенциалов будет окончательной минус начальный потенциал, или 34.2–57,6 = -23,4 В. Мы получили отрицательный потенциал, что означает, что при переходе от A к B потенциал уменьшается.

Во втором случае B — это наш начальный потенциал, а A — наш конечный потенциал. Итак, разность потенциалов будет 57,6-34,2 = + 23,4 В. У нас есть положительный потенциал, или когда мы идем от B к A, потенциал увеличивается.

Что это значит?

По мере продвижения от A к B электрический потенциал уменьшается из-за того, что у нас есть положительный основной заряд, а его линии электрического поля направлены наружу.Если мы поместим положительный тестовый заряд на первый энергетический уровень, электрическая потенциальная энергия будет больше. Точечный заряд будет отталкивать пробный заряд, потому что плотность силовых линий электрического поля намного сильнее. В B плотность силовых линий электрического поля слабее, а электрическая потенциальная энергия меньше.

Вот и все, что касается электрического потенциала и разности электрических потенциалов. Надеюсь, это было полезно, и вы узнали что-то новое.

.