Удельное электрическое сопротивление стали — таблицы при различных температурах
Представлены таблицы значений удельного электрического сопротивления сталей различных типов и марок в зависимости от температуры — в диапазоне от 0 до 1350°С.
В общем случае, удельное сопротивление определяется только составом вещества и его температурой, оно численно равно полному сопротивлению изотропного проводника, имеющего длину 1 м и площадь поперечного сечения 1 м2.
Удельное электрическое сопротивление стали существенно зависит от состава и температуры. При повышении температуры этого металла увеличивается частота и амплитуда колебаний атомов кристаллической решетки, что создает дополнительное сопротивление прохождению электрического тока через толщу сплава. Поэтому, с ростом температуры сопротивление стали увеличивается.
Изменение состава стали и процента содержания в ней легирующих добавок значительно сказывается на величине электросопротивления.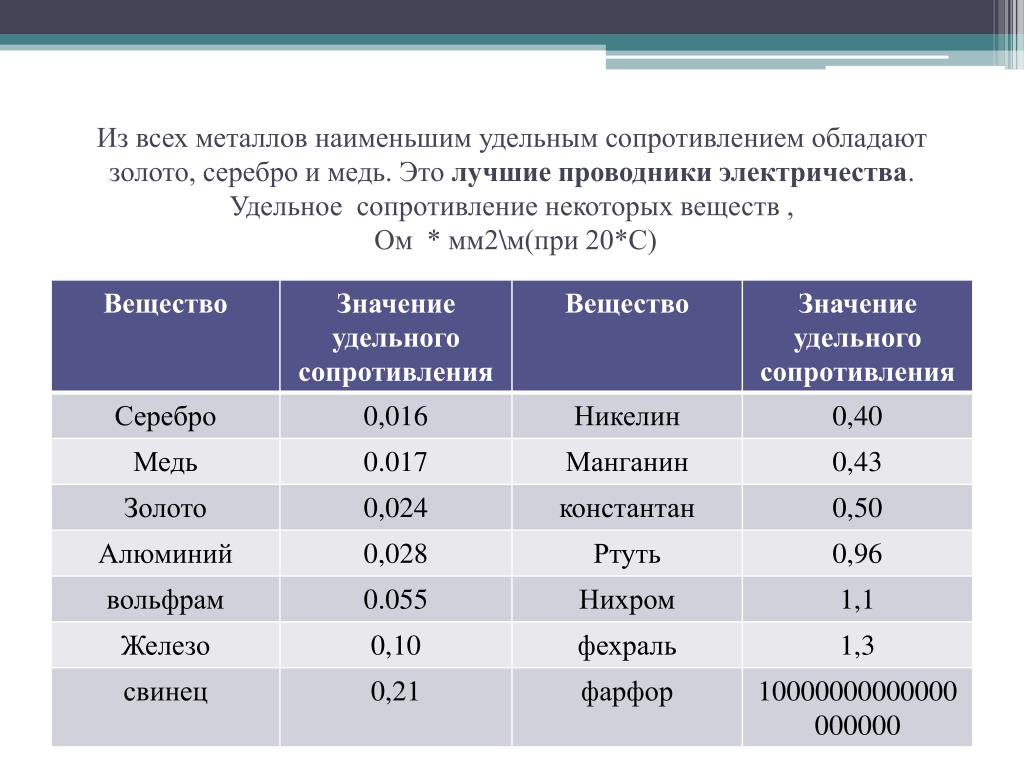
Углеродистые стали
Углеродистые стали при комнатной температуре, как уже было сказано, имеют низкое удельное электросопротивление за счет высокого содержания железа. При 20°С значение их удельного сопротивления находится в диапазоне от 13·10-8 (для стали 08КП) до 20·10-8 Ом·м (для У12).
При нагревании до температур более 1000°С способность углеродистых сталей проводить электрический ток сильно снижается. Величина сопротивления возрастает на порядок и может достигать значения 130·10-8 Ом·м.
| Температура, °С | Сталь 08КП | Сталь 08 | Сталь 20 | Сталь 40 | Сталь У8 | Сталь У12 |
|---|---|---|---|---|---|---|
| 0 | 12 | 13,2 | 15,9 | 16 | 17 | 18,4 |
| 20 | 13 | 14,2 | 16,9 | 17,1 | 18 | 19,6 |
| 50 | 14,7 | 15,9 | 18,7 | 18,9 | 19,8 | 21,6 |
| 100 | 17,8 | 19 | 21,9 | 22,1 | 23,2 | 25,2 |
| 150 | 21,3 | 22,4 | 25,4 | 25,7 | 26,8 | 29 |
| 200 | 25,2 | 26,3 | 29,2 | 29,6 | 30,8 | 33,3 |
| 250 | 29,5 | 30,5 | 33,4 | 33,9 | 35,1 | 37,9 |
| 300 | 34,1 | 35,2 | 38,1 | 38,7 | 39,8 | 43 |
| 350 | 39,3 | 40,2 | 43,2 | 43,8 | 45 | 48,3 |
| 400 | 44,8 | 45,8 | 48,7 | 49,3 | 50,5 | 54 |
| 450 | 50,9 | 51,8 | 54,6 | 55,3 | 56,5 | 60 |
| 500 | 57,5 | 58,4 | 60,1 | 61,9 | 62,8 | 66,5 |
| 550 | 64,8 | 65,7 | 68,2 | 68,9 | 69,9 | 73,4 |
| 600 | 72,5 | 73,4 | 75,8 | 76,6 | 77,2 | 80,2 |
| 650 | 80,7 | 81,6 | 83,7 | 84,4 | 85,2 | 87,8 |
| 700 | 89,8 | 90,5 | 92,5 | 93,2 | 93,5 | 96,4 |
| 750 | 100,3 | 101,1 | 105 | 107,9 | 110,5 | 113 |
| 800 | 107,3 | 108,1 | 109,4 | 111,1 | 112,9 | 115 |
| 850 | 110,4 | 111,1 | 111,8 | 113,1 | 114,8 | 117,6 |
| 900 | 112,4 | 113 | 113,6 | 114,9 | 116,4 | 119,6 |
| 950 | 114,2 | 114,8 | 115,2 | 116,6 | 117,8 | 121,2 |
| 1000 | 116 | 116,5 | 116,7 | 117,9 | 119,1 | 122,6 |
| 1050 | 117,5 | 117,9 | 118,1 | 119,3 | 120,4 | 123,8 |
| 1100 | 118,9 | 119,3 | 119,4 | 120,7 | 121,4 | 124,9 |
| 1150 | 120,3 | 120,7 | 120,7 | 122 | 122,3 | 126 |
| 1200 | 121,7 | 122 | 121,9 | 123 | 123,1 | 127,1 |
| 1250 | 123 | 123,3 | 122,9 | 124 | 123,8 | 128,2 |
| 1300 | 124,1 | 124,4 | 123,9 | — | 124,6 | 128,7 |
| 1350 | 125,2 | 125,3 | 125,1 | — | 125 | 129,5 |
Низколегированные стали
Низколегированные стали способны чуть более сильно сопротивляться прохождению электричества, чем углеродистые.
Следует отметить марки стали этого типа, которые наиболее плохо проводят электрический ток — это 18Х2Н4ВА и 50С2Г. Однако при высоких температурах, способность проводить электрический ток у сталей, приведенных в таблице, практически не различается.
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 | 1300 |
|---|---|---|---|---|---|---|---|---|
| 15ХФ | — | 42,1 | 60,6 | 83,3 | — | — | — | |
| 30Х | 21 | 25,9 | 41,7 | 63,6 | 93,4 | 114,5 | 120,5 | 125,1 |
| 12ХН2 | 33 | 36 | 52 | 67 | — | 112 | — | — |
| 12ХН3 | 29,6 | — | — | 67 | — | 116 | — | — |
| 20ХН3 | 24 | 29 | 46 | 66 | — | 123 | — | — |
| 30ХН3 | 26,8 | 31,7 | 46,9 | 68,1 | 98,1 | 114,8 | 120,1 | 124,6 |
| 20ХН4Ф | 36 | 41 | 56 | 72 | 102 | 118 | — | — |
| 18Х2Н4ВА | 41 | 44 | 58 | 73 | 97 | 115 | — | — |
| 30Г2 | 20,8 | 25,9 | 42,1 | 64,5 | 94,6 | 114,3 | 120,2 | 125 |
| 12МХ | 24,6 | 27,4 | 40,6 | 59,8 | — | — | — | — |
| 40Х3М | — | 33,1 | 48,2 | 69,5 | 96,2 | — | — | — |
| 20Х3ФВМ | — | 39,8 | 54,4 | 74,3 | 98,2 | — | — | — |
| 50С2Г | 42,9 | 47 | 60,1 | 78,8 | 105,7 | 119,7 | 124,9 | 128,9 |
| 30Н3 | 27,1 | 32 | 47 | 67,9 | 99,2 | 114,9 | 120,4 | 124,8 |
Высоколегированные стали
Высоколегированные стали имеют удельное электрическое сопротивление в несколько раз выше чем углеродистые и низколегированные. По данным таблицы видно, что при температуре 20°С его величина составляет (30…86)·10-8 Ом·м.
По данным таблицы видно, что при температуре 20°С его величина составляет (30…86)·10-8 Ом·м.
При температуре 1300°С сопротивление высоко- и низко- легированных сталей становится почти одинаковым и не превышает 131·10
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 | 1300 |
|---|---|---|---|---|---|---|---|---|
| Г13 | 68,3 | 75,6 | 93,1 | 95,2 | 114,7 | 123,8 | 127 | 130,8 |
| Г20Х12Ф | 72,3 | 79,2 | 91,2 | 101,5 | 109,2 | — | — | — |
| Г21Х15Т | — | 82,4 | 95,6 | 104,5 | 119,2 | — | — | |
| Х13Н13К10 | — | 90 | 100,8 | 109,6 | 115,4 | 119,6 | — | — |
| Х19Н10К47 | — | 90,5 | 98,6 | 105,2 | 110,8 | — | — | — |
| Р18 | 41,9 | 47,2 | 62,7 | 81,5 | 103,7 | 117,3 | 123,6 | 128,1 |
| ЭХ12 | 31 | 36 | 53 | 75 | 97 | 119 | — | — |
| 40Х10С2М (ЭИ107) | 86 | 91 | 101 | 112 | 122 | — | — | — |
Хромистые нержавеющие стали
Хромистые нержавеющие стали имеют высокую концентрацию атомов хрома, что увеличивает их удельное сопротивление — электропроводность такой нержавеющей стали не высока. При обычных температурах ее сопротивление составляет (50…60)·10-8 Ом·м.
При обычных температурах ее сопротивление составляет (50…60)·10-8 Ом·м.
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 | 1300 |
|---|---|---|---|---|---|---|---|---|
| Х13 | 50,6 | 58,4 | 76,9 | 93,8 | 110,3 | 115 | 119 | 125,3 |
| 2Х13 | 58,8 | 65,3 | 80 | 95,2 | 110,2 | — | — | — |
| 3Х13 | 52,2 | 59,5 | 76,9 | 93,5 | 109,9 | 114,6 | 120,9 | 125 |
| 4Х13 | 59,1 | 64,6 | 78,8 | 94 | 108 | — | — | — |
Хромоникелевые аустенитные стали
Хромоникелевые аустенитные стали также являются нержавеющими, но за счет добавки никеля имеют удельное сопротивление почти в полтора раза выше, чем у хромистых — оно достигает величины (70…90)·10-8 Ом·м.
| Марка стали | 20 | 100 | 300 | 500 | 700 | 900 | 1100 |
|---|---|---|---|---|---|---|---|
| 12Х18Н9 | — | 74,3 | 89,1 | 100,1 | 109,4 | 114 | — |
| 12Х18Н9Т | 72,3 | 79,2 | 91,2 | 101,5 | 109,2 | — | — |
| 17Х18Н9 | 72 | 73,5 | 92,5 | 103 | 111,5 | 118,5 | — |
| Х18Н11Б | — | 84,6 | 97,6 | 107,8 | 115 | — | — |
| Х18Н9В | 71 | 77,6 | 91,6 | 102,6 | 111,1 | 117,1 | 122 |
| 4Х14НВ2М (ЭИ69) | 81,5 | 87,5 | 100 | 110 | 117,5 | — | — |
| 1Х14Н14В2М (ЭИ257) | — | 82,4 | 95,6 | 104,5 | 112 | 119,2 | — |
| 1х14Н18М3Т | — | 89 | 100 | 107,5 | 115 | — | — |
| 36Х18Н25С2 (ЭЯ3С) | — | 98,5 | 105,5 | 110 | 117,5 | — | — |
| Х13Н25М2В2 | — | 103 | 112,1 | 118,1 | 121 | — | — |
| Х7Н25 (ЭИ25) | — | — | 109 | 115 | 121 | 127 | — |
| Х2Н35 (ЭИ36) | 87,5 | 92,5 | 103 | 110 | 116 | 120,5 | — |
| Н28 | 84,2 | 89,1 | 99,6 | 107,7 | 114,2 | 118,4 | 122,5 |
Жаропрочные и жаростойкие стали
По своим электропроводящим свойствам жаропрочные и жаростойкие стали близки к хромоникелевым.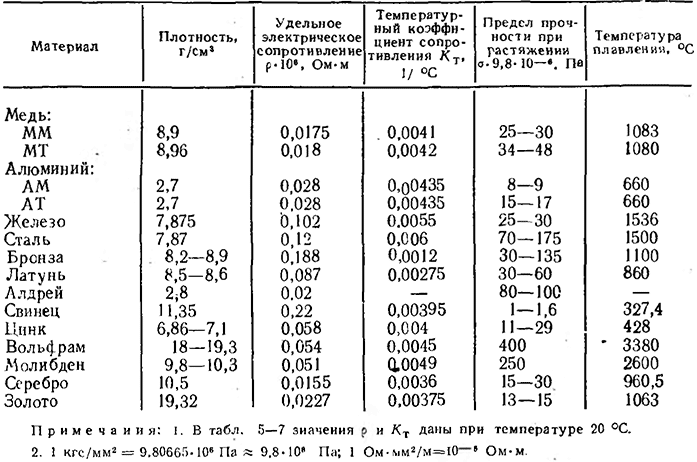 Высокое содержание в этих сплавах хрома и никеля не позволяет им проводить электрический ток, подобно обычным углеродистым с высокой концентрацией железа.
Высокое содержание в этих сплавах хрома и никеля не позволяет им проводить электрический ток, подобно обычным углеродистым с высокой концентрацией железа.
Значительное удельное электросопротивление и высокая рабочая температура таких сталей делают возможным их применение в качестве рабочих элементов электрических нагревателей. В частности, сталь 20Х23Н18 по своему сопротивлению и жаростойкости в некоторых случаях способна заменить такой популярный сплав для нагревателей, как нихром Х20Н80.
| Температура, °С | 15Х25Т (ЭИ439) | 15Х28 (ЭИ349) | 40Х9С2 (ЭСХ8) | Х25С3Н (ЭИ261) | 20Х23Н18 (ЭИ 417) | Х20Н35 |
|---|---|---|---|---|---|---|
| 0 | — | — | — | — | — | 106 |
| 20 | — | — | 75 | 80 | — | — |
| 100 | — | — | — | — | 97 | — |
| 200 | — | — | — | — | 98 | 113 |
| 400 | 102 | — | — | — | 105 | 120 |
| 600 | 113 | — | — | — | 115 | 124 |
| 800 | — | 122 | — | — | 121 | 128 |
| 900 | — | — | — | — | 123 | — |
| 1000 | — | 127 | — | — | — | 132 |
Источники:
- Казанцев Е.
 И. Промышленные печи. Справочное руководство для расчетов и проектирования.
И. Промышленные печи. Справочное руководство для расчетов и проектирования. - Физические величины. Справочник. Под ред. И. С. Григорьева, Е. З. Мейлихова. — М.: Энергоатомиздат, 1991. — 1232 с.
Сопротивление меди и стали. Удельное сопротивление железа, алюминия, меди и других металлов
- активное — или омическое, резистивное, — происходящее от затрат электроэнергии на нагревание проводника (металла) при прохождении в нем электрического тока, и
- реактивное — емкостное или индуктивное, — которое происходит от неизбежных потерь на создание всякими изменениями тока, проходящего через проводник электрических полей, то и удельное сопротивление проводника бывает двух разновидностей:
Удельное сопротивление железа, алюминия и других проводников
Передача электроэнергии на дальние расстояния требует заботиться о минимизации потерь, происходящих от преодоления током сопротивления проводников, составляющих электрическую линию. Разумеется, это не значит, что подобные потери, происходящие уже конкретно в цепях и устройствах потребления, не играют роли.
Поэтому важно знать параметры всех используемых элементов и материалов. И не только электрические, но и механические. И иметь в распоряжении какие-то удобные справочные материалы, позволяющие сравнивать характеристики разных материалов и выбирать для проектирования и работы именно то, что будет оптимальным в конкретной ситуации. В линиях передачи энергии, где задачей ставится наиболее продуктивно, то есть с высоким КПД, довести энергию до потребителя, учитывается как экономика потерь, так и механика самих линий. От механики — то есть устройства и расположения проводников, изоляторов, опор, повышающих/понижающих трансформаторов, веса и прочности всех конструкций, включая провода, растянутые на больших расстояниях, а также от выбранных для выполнения каждого элемента конструкции материалов, зависит и конечная экономическая эффективность линии, ее работы и затрат на эксплуатацию. Кроме того, в линиях, передающих электроэнергию, более высоки требования на обеспечение безопасности как самих линий, так и всего окружающего, где они проходят. А это добавляет затрат как на обеспечение проводки электроэнергии, так и на дополнительный запас прочности всех конструкций.
В линиях передачи энергии, где задачей ставится наиболее продуктивно, то есть с высоким КПД, довести энергию до потребителя, учитывается как экономика потерь, так и механика самих линий. От механики — то есть устройства и расположения проводников, изоляторов, опор, повышающих/понижающих трансформаторов, веса и прочности всех конструкций, включая провода, растянутые на больших расстояниях, а также от выбранных для выполнения каждого элемента конструкции материалов, зависит и конечная экономическая эффективность линии, ее работы и затрат на эксплуатацию. Кроме того, в линиях, передающих электроэнергию, более высоки требования на обеспечение безопасности как самих линий, так и всего окружающего, где они проходят. А это добавляет затрат как на обеспечение проводки электроэнергии, так и на дополнительный запас прочности всех конструкций.
Для сравнения данные обычно приводятся к единому, сопоставимому виду. Зачастую к таким характеристикам добавляется эпитет «удельный», а сами значения рассматриваются на неких унифицированных по физическим параметрам эталонах. Например, удельное электрическое сопротивление — это сопротивление (ом) проводника, выполненного из какого-то металла (меди, алюминия, стали, вольфрама, золота), имеющего единичную длину и единичное сечение в используемой системе единиц измерения (обычно в СИ). Кроме того, оговаривается температура, так как при нагревании сопротивление проводников может вести себя по-разному. За основу берутся нормальные средние условия эксплуатации — при 20 градусах Цельсия. А там, где важны свойства при изменении параметров среды (температуры, давления), вводятся коэффициенты и составляются дополнительные таблицы и графики зависимостей.
Например, удельное электрическое сопротивление — это сопротивление (ом) проводника, выполненного из какого-то металла (меди, алюминия, стали, вольфрама, золота), имеющего единичную длину и единичное сечение в используемой системе единиц измерения (обычно в СИ). Кроме того, оговаривается температура, так как при нагревании сопротивление проводников может вести себя по-разному. За основу берутся нормальные средние условия эксплуатации — при 20 градусах Цельсия. А там, где важны свойства при изменении параметров среды (температуры, давления), вводятся коэффициенты и составляются дополнительные таблицы и графики зависимостей.
Виды удельного сопротивления
Так как сопротивление бывает:
- Удельное электрическое сопротивление постоянному току (имеющее резистивный характер) и
- Удельное электрическое сопротивление переменному току (имеющее реактивный характер).

Здесь удельное сопротивление 2 типа является величиной комплексной, оно состоит из двух компонент ТП — активной и реактивной, так как резистивное сопротивление существует всегда при прохождении тока, независимо от его характера, а реактивное бывает только при любом изменении тока в цепях. В цепях постоянного тока реактивное сопротивление возникает только при переходных процессах, которые связаны с включением тока (изменение тока от 0 до номинала) или выключением (перепад от номинала до 0). И их учитывают обычно только при проектировании защиты от перегрузок.
В цепях же переменного тока явления, связанные с реактивными сопротивлениями, гораздо более многообразны. Они зависят не только от собственно прохождения тока через некоторое сечение, но и от формы проводника, причем зависимость не является линейной.
Дело в том, что переменный ток наводит электрическое поле как вокруг проводника, по которому протекает, так и в самом проводнике. И от этого поля возникают вихревые токи, которые дают эффект «выталкивания» собственно основного движения зарядов, из глубины всего сечения проводника на его поверхность, так называемый «скин-эффект» (от skin — кожа). Получается, вихревые токи как бы «воруют» у проводника его сечение. Ток течет в некотором слое, близком к поверхности, остальная толщина проводника остается неиспользуемой, она не уменьшает его сопротивление, и увеличивать толщину проводников просто нет смысла. Особенно на больших частотах. Поэтому для переменного тока измеряют сопротивления в таких сечениях проводников, где все его сечение можно считать приповерхностным. Такой провод называется тонким, его толщина равна удвоенной глубине этого поверхностного слоя, куда вихревые токи и вытесняют текущий в проводнике полезный основной ток.
Получается, вихревые токи как бы «воруют» у проводника его сечение. Ток течет в некотором слое, близком к поверхности, остальная толщина проводника остается неиспользуемой, она не уменьшает его сопротивление, и увеличивать толщину проводников просто нет смысла. Особенно на больших частотах. Поэтому для переменного тока измеряют сопротивления в таких сечениях проводников, где все его сечение можно считать приповерхностным. Такой провод называется тонким, его толщина равна удвоенной глубине этого поверхностного слоя, куда вихревые токи и вытесняют текущий в проводнике полезный основной ток.
Разумеется, уменьшением толщины круглых в сечении проводов не исчерпывается эффективное проведение переменного тока. Проводник можно утончить, но при этом сделать его плоским в виде ленты, тогда сечение будет выше, чем у круглого провода, соответственно, и сопротивление ниже. Кроме того, простое увеличение площади поверхности даст эффект увеличения эффективного сечения. Того же можно добиться, используя многожильный провод вместо одножильного, к тому же, многожилка по гибкости превосходит одножилку, что часто тоже бывает ценно. С другой стороны, принимая во внимание скин-эффект в проводах, можно сделать провода композитными, выполнив сердцевину из металла, обладающего хорошими прочностными характеристиками, например, стали, но невысокими электрическими. При этом поверх стали делается алюминиевая оплетка, имеющая меньшее удельное сопротивление.
С другой стороны, принимая во внимание скин-эффект в проводах, можно сделать провода композитными, выполнив сердцевину из металла, обладающего хорошими прочностными характеристиками, например, стали, но невысокими электрическими. При этом поверх стали делается алюминиевая оплетка, имеющая меньшее удельное сопротивление.
Кроме скин-эффекта на протекание переменного тока в проводниках влияет возбуждение вихревых токов в окружающих проводниках. Такие токи называются токами наводки, и они наводятся как в металлах, не играющих роль проводки (несущие элементы конструкций), так и в проводах всего проводящего комплекса — играющих роль проводов других фаз, нулевых, заземляющих.
Все перечисленные явления встречаются во всех конструкциях, связанных с электричеством, это еще более усиливает важность иметь в своем распоряжении сводные справочные сведения по самым разным материалам.
Удельное сопротивление для проводников измеряется очень чувствительными и точными приборами, так как для проводки и выбираются металлы, имеющие самое низкое сопротивление -порядка ом *10-6 на метр длины и кв.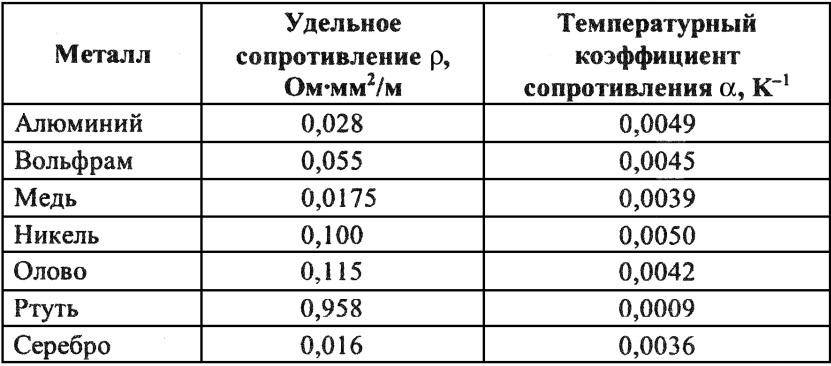 мм. сечения. Для измерения же удельного сопротивления изоляции нужны приборы, наоборот, имеющие диапазоны очень больших значений сопротивления — обычно это мегомы. Понятно, что проводники обязаны хорошо проводить, а изоляторы хорошо изолировать.
мм. сечения. Для измерения же удельного сопротивления изоляции нужны приборы, наоборот, имеющие диапазоны очень больших значений сопротивления — обычно это мегомы. Понятно, что проводники обязаны хорошо проводить, а изоляторы хорошо изолировать.
Таблица
Железо как проводник в электротехнике
Железо — самый распространенный в природе и технике металл (после водорода, который металлом тоже является). Он и самый дешевый, и имеет прекрасные прочностные характеристики, поэтому применяется повсюду как основа прочности различных конструкций.
В электротехнике в качестве проводника железо используется в виде стальных гибких проводов там, где нужна физическая прочность и гибкость, а нужное сопротивление может быть достигнуто за счет соответствующего сечения.
Имея таблицу удельных сопротивлений различных металлов и сплавов, можно посчитать сечения проводов, выполненных из разных проводников.
В качестве примера попробуем найти электрически эквивалентное сечение проводников из разных материалов: проволоки медной, вольфрамовой, никелиновой и железной. За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
Нам нужно, чтобы на длине в 1 м сопротивление провода из всех этих металлов равнялось сопротивлению исходной. Сопротивление алюминия на 1 м длины и 2,5 мм сечения будет равно
, где R – сопротивление, ρ – удельное сопротивление металла из таблицы, S – площадь сечения, L – длина.Подставив исходные значения, получим сопротивление метрового куска провода алюминия в омах.
После этого разрешим формулу относительно S
, будем подставлять значения из таблицы и получать площади сечений для разных металлов.Так как удельное сопротивление в таблице измерено на проводе длиной в 1 м, в микроомах на 1 мм2 сечения, то у нас и получилось оно в микроомах. Чтобы получить его в омах, нужно умножить значение на 10-6. Но число ом с 6 нулями после запятой нам получать совсем не обязательно, так как конечный результат все равно находим в мм2.
Как видим, сопротивление железа достаточно большое, проволока получается толстая.
Но существуют материалы, у которых оно еще больше, например, никелин или константан.
Похожие статьи:
domelectrik.ru
Таблица удельного электрического сопротивления металлов и сплавов в электротехнике
Главная > у >
Удельное сопротивление металлов.
Удельное сопротивление сплавов.
Значения даны при температуре t = 20° C. Сопротивления сплавов зависят от их точного состава. comments powered by HyperCommentstab.wikimassa.org
Удельное электрическое сопротивление | Мир сварки
Удельное электрическое сопротивление материалов
Удельное электрическое сопротивление (удельное сопротивление) — способность вещества препятствовать прохождению электрического тока.
Единица измерения (СИ) — Ом·м; также измеряется в Ом·см и Ом·мм2/м.
| Металлы | ||
| Алюминий | 20 | 0,028·10-6 |
| Бериллий | 20 | 0,036·10-6 |
| Бронза фосфористая | 20 | 0,08·10-6 |
| Ванадий | 20 | 0,196·10-6 |
| Вольфрам | 20 | 0,055·10-6 |
| Гафний | 20 | 0,322·10-6 |
| Дюралюминий | 20 | 0,034·10-6 |
| Железо | 20 | 0,097·10-6 |
| Золото | 20 | 0,024·10-6 |
| Иридий | 20 | 0,063·10-6 |
| Кадмий | 20 | 0,076·10-6 |
| Калий | 20 | 0,066·10-6 |
| Кальций | 20 | 0,046·10-6 |
| Кобальт | 20 | 0,097·10-6 |
| Кремний | 27 | 0,58·10-4 |
| Латунь | 20 | 0,075·10-6 |
| Магний | 20 | 0,045·10-6 |
| Марганец | 20 | 0,050·10-6 |
| Медь | 20 | 0,017·10-6 |
| Магний | 20 | 0,054·10-6 |
| Молибден | 20 | 0,057·10-6 |
| Натрий | 20 | 0,047·10-6 |
| Никель | 20 | 0,073·10-6 |
| Ниобий | 20 | 0,152·10-6 |
| Олово | 20 | 0,113·10-6 |
| Палладий | 20 | 0,107·10-6 |
| Платина | 20 | 0,110·10-6 |
| Родий | 20 | 0,047·10-6 |
| Ртуть | 20 | 0,958·10-6 |
| Свинец | 20 | 0,221·10-6 |
| Серебро | 20 | 0,016·10-6 |
| Сталь | 20 | 0,12·10-6 |
| Тантал | 20 | 0,146·10-6 |
| Титан | 20 | 0,54·10-6 |
| Хром | 20 | 0,131·10-6 |
| Цинк | 20 | 0,061·10-6 |
| Цирконий | 20 | 0,45·10-6 |
| Чугун | 20 | 0,65·10-6 |
| Пластмассы | ||
| Гетинакс | 20 | 109–1012 |
| Капрон | 20 | 1010–1011 |
| Лавсан | 20 | 1014–1016 |
| Органическое стекло | 20 | 1011–1013 |
| Пенопласт | 20 | 1011 |
| Поливинилхлорид | 20 | 1010–1012 |
| Полистирол | 20 | 1013–1015 |
| Полиэтилен | 20 | 1015 |
| Стеклотекстолит | 20 | 1011–1012 |
| Текстолит | 20 | 107–1010 |
| Целлулоид | 20 | 109 |
| Эбонит | 20 | 1012–1014 |
| Резины | ||
| Резина | 20 | 1011–1012 |
| Жидкости | ||
| Масло трансформаторное | 20 | 1010–1013 |
| Газы | ||
| Воздух | 0 | 1015–1018 |
| Дерево | ||
| Древесина сухая | 20 | 109–1010 |
| Минералы | ||
| Кварц | 230 | 109 |
| Слюда | 20 | 1011–1015 |
| Различные материалы | ||
| Стекло | 20 | 109–1013 |
ЛИТЕРАТУРА
- Альфа и омега.
 Краткий справочник / Таллин: Принтэст, 1991 – 448 с.
Краткий справочник / Таллин: Принтэст, 1991 – 448 с. - Справочник по элементарной физике / Н.Н. Кошкин, М.Г. Ширкевич. М., Наука. 1976. 256 с.
- Справочник по сварке цветных металлов / С.М. Гуревич. Киев.: Наукова думка. 1990. 512 с.
weldworld.ru
Удельное сопротивление металлов, электролитов и веществ (Таблица)
Удельное сопротивление металлов и изоляторов
В справочной таблице даны значения удельного сопротивления р некоторых металлов и изоляторов при температуре 18-20° С, выраженные в ом·см. Величина р для металлов в сильной степени зависит от примесей, в таблице даны значения р для химически чистых металлов, для изоляторов даны приближенно. Металлы и изоляторы расположены в таблице в порядке возрастающих значений р.
Таблица удельное сопротивление металлов
Чистые металлы | 104 ρ (ом·см) | Чистые металлы | 104 ρ (ом·см) |
Алюминий | |||
Дюралюминий | |||
Платинит 2) | |||
Аргентан | |||
Марганец | |||
Манганин | |||
Вольфрам | Константан | ||
Молибден | Сплав Вуда 3) | ||
Сплав Розе 4) | |||
Палладий | Фехраль 6) | ||
Таблица удельное сопротивление изоляторов
Изоляторы | Изоляторы | ||
Дерево сухое | |||
Целлулоид | |||
Канифоль | |||
Гетинакс | Кварц _|_ оси | ||
Стекло натр | Полистирол | ||
Стекло пирекс | |||
Кварц || оси | |||
Кварц плавленый |
Удельное сопротивление чистых металлов при низких температурах
В таблице даны значения удельного сопротивления (в ом·см) некоторых чистых металлов при низких температурах (0°С).
Отношение сопротивлении Rt/Rq чистых металлов при температуре Т °К и 273° К.
В справочной таблице дано отношение Rt/Rq сопротивлений чистых металлов при температуре Т °К и 273° К.
Чистые металлы | ||
Алюминий | ||
Вольфрам | ||
Молибден | ||
Удельное сопротивление электролитов
В таблице даны значения удельного сопротивления электролитов в ом·см при температуре 18° С. Концентрация растворов с дана в процентах, которые определяют число граммов безводной соли или кислоты в 100 г раствора.
Концентрация растворов с дана в процентах, которые определяют число граммов безводной соли или кислоты в 100 г раствора.
Источник информации: КРАТКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ СПРАВОЧНИК/ Том 1, — М.: 1960.
infotables.ru
Удельное электрическое сопротивление — сталь
Cтраница 1
Удельное электрическое сопротивление стали возрастает с ростом температуры, причем наибольшие изменения наблюдаются при нагреве до температуры точки Кюри. После точки Кюри величина удельного электросопротивления изменяется незначительно и при температурах выше 1000 С практически остается постоянной.
Ввиду большого удельного электрического сопротивления стали эти iuKii создают НсОольшое замедление в спадании потока. В контакторах на 100 а время отпадания составляет 0 07 сек, а в контакторах 600 а-0 23 сек. В связи с особыми требованиями, предъявляемыми к контакторам серии КМВ, которые предназначены для включения и отключения электромагнитов приводов масляных выключателей, электромагнитный механизм у этих контакторов допускает регулировку напряжения срабатывания и напряжения отпускания за счет регулировки силы возвратной пружины и специальной отрывной пружины. Контакторы типа КМВ должны работать при глубокой посадке напряжения. Поэтому минимальное напряжение срабатывания у этих контакторов может спускаться до 65 % UH. Такое низкое напряжение срабатывания приводит к тому, что при номинальном напряжении через обмотку протекает ток, приводящий к повышенному нагреву катушки.
Контакторы типа КМВ должны работать при глубокой посадке напряжения. Поэтому минимальное напряжение срабатывания у этих контакторов может спускаться до 65 % UH. Такое низкое напряжение срабатывания приводит к тому, что при номинальном напряжении через обмотку протекает ток, приводящий к повышенному нагреву катушки.
Присадка кремния увеличивает удельное электрическое сопротивление стали почти пропорционально содержанию кремния и этим способствует уменьшению потерь на вихревые токи, возникающие в стали при ее работе в переменном магнитном поле.
Присадка кремния увеличивает удельное электрическое сопротивление стали, что способствует уменьшению потерь на вихревые токи, но одновременно кремний ухудшает механические свойства стали, делает ее хрупкой.
Ом — мм2 / м — удельное электрическое сопротивление стали.
Для уменьшения вихревых токов применяются сердечники, выполненные из сортов стали с повышенным удельным электрическим сопротивлением стали, содержащие 0 5 — 4 8 % кремния.
Для этого на массивный ротор из оптимального сплава СМ-19 был надет тонкий экран из магнитно-мягкой стали. Удельное электрическое сопротивление стали мало отличается от удельного сопротивления сплава, а цг стали примерно на порядок выше. Толщина экрана выбрана по глубине проникновения зубцовых гармоник первого порядка и равна йэ 0 8 мм. Для сравнения приведены добавочные потери, Вт, при базовом короткозамкнутом роторе и двухслойном роторе с массивным цилиндром из сплава СМ-19 и с медными торцевыми кольцами.
Основным магнитопроводящим материалом является листовая легированная электротехническая сталь, содержащая от 2 до 5 % кремния. Присадка кремния увеличивает удельное электрическое сопротивление стали, в результате чего уменьшаются потери на вихревые токи, сталь становится устойчивой к окислению и старению, но делается более хрупкой. В последние годы широко используется холоднокатаная текстурованная сталь с более высокими магнитными свойствами в направлении проката. Для уменьшения потерь от вихревых токов сердечник магнитопровода выполняется в виде пакета, собранного из листов штампованной стали.
Электротехническая сталь является низкоуглеродистой сталью. Для улучшения магнитных характеристик в нее вводят кремний, который вызывает повышение удельного электрического сопротивления стали. Это приводит к уменьшению потерь на вихревые токи.
После механической обработки магнитопровод отжигают. Так как в создании замедления участвуют вихревые токи в стали, следует ориентироваться на величину удельного электрического сопротивления стали порядка Рс (Ю-15) 10 — 6 ом см. В притянутом положении якоря магнитная система достаточно сильно насыщена, поэтому начальная индукция в различных магнитных системах колеблется в очень незначительных пределах и составляет для стали марки Э Вн1 6 — 1 7 гл. Указанное значение индукции поддерживает напряженность поля в стали порядка Ян.
Для изготовления магнитных систем (магнитопроводов) трансформаторов применяются специальные тонколистовые электротехнические стали, имеющие повышенное (до 5 %) содержание кремния. Кремний способствует обезуглероживанию стали, что приводит к увеличению магнитной проницаемости, снижает потери на гистерезис и увеличивает ее удельное электрическое сопротивление.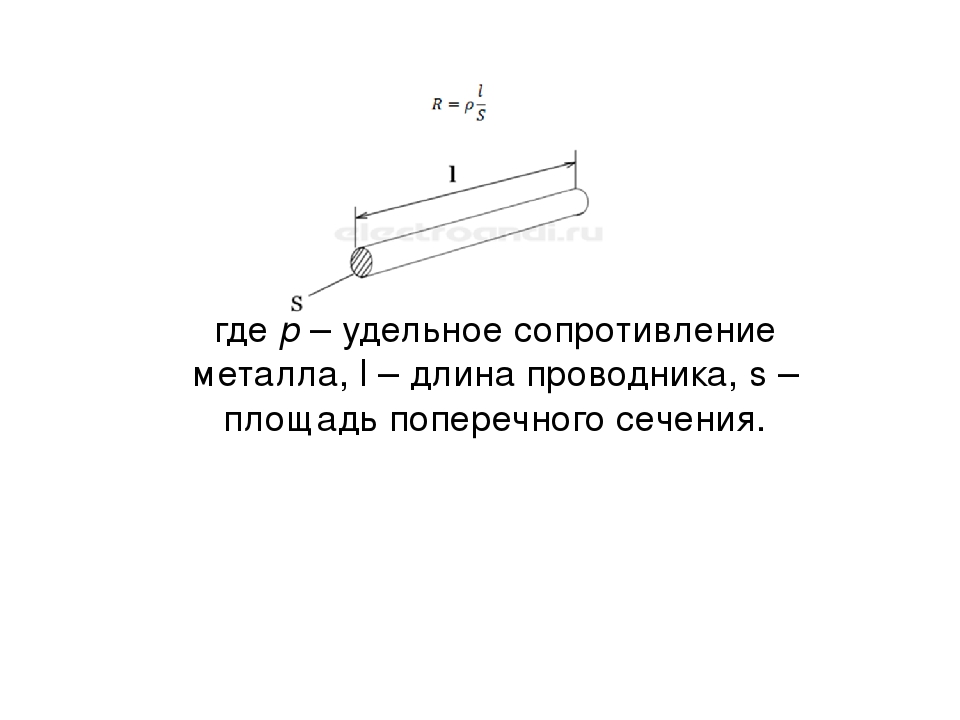 Увеличение удельного электрического сопротивления стали позволяет уменьшить потери в ней от вихревых токов. Кроме того, кремний ослабляет старение стали (увеличение потерь в стали с течением времени), уменьшает ее магнитострикцию (изменение формы и размеров тела при намагничивании) и, следовательно, шум трансформаторов. В то же время наличие кремния в стали приводит к повышению ее хрупкости и затрудняет ее механическую обработку.
Увеличение удельного электрического сопротивления стали позволяет уменьшить потери в ней от вихревых токов. Кроме того, кремний ослабляет старение стали (увеличение потерь в стали с течением времени), уменьшает ее магнитострикцию (изменение формы и размеров тела при намагничивании) и, следовательно, шум трансформаторов. В то же время наличие кремния в стали приводит к повышению ее хрупкости и затрудняет ее механическую обработку.
Страницы: 1 2
www.ngpedia.ru
Удельное сопротивление | Викитроника вики
Удельное сопротивление — характеристика материала, определяющая его способность проводить электрический ток. Определяется как отношение электрического поля к плотности тока. В общем случае является тензором, однако для большинства материалов, не проявляющих анизотропных свойств, принимается скалярной величиной.
Обозначение — ρ
$ \vec E = \rho \vec j, $
$ \vec E $ — напряжённость электрического поля, $ \vec j $ — плотность тока.
Единица измерения СИ — ом-метр (ом·м, Ω·m).
Сопротивление цилиндра или призмы (между торцами) из материала длиной l, и сечением S по удельному сопротивлению определяется следующим образом:
$ R = \frac{\rho l}{S}. $
В технике применяется определение удельного сопротивления, как сопротивление проводника единичного сечения и единичной длины.
Удельное сопротивление некоторых материалов, используемых в электротехнике Править
| серебро | 1,59·10⁻⁸ | 4,10·10⁻³ |
| медь | 1,67·10⁻⁸ | 4,33·10⁻³ |
| золото | 2,35·10⁻⁸ | 3,98·10⁻³ |
| алюминий | 2,65·10⁻⁸ | 4,29·10⁻³ |
| вольфрам | 5,65·10⁻⁸ | 4,83·10⁻³ |
| латунь | 6,5·10⁻⁸ | 1,5·10⁻³ |
| никель | 6,84·10⁻⁸ | 6,75·10⁻³ |
| железо (α) | 9,7·10⁻⁸ | 6,57·10⁻³ |
| олово серое | 1,01·10⁻⁷ | 4,63·10⁻³ |
| платина | 1,06·10⁻⁷ | 6,75·10⁻³ |
| олово белое | 1,1·10⁻⁷ | 4,63·10⁻³ |
| сталь | 1,6·10⁻⁷ | 3,3·10⁻³ |
| свинец | 2,06·10⁻⁷ | 4,22·10⁻³ |
| дюралюминий | 4,0·10⁻⁷ | 2,8·10⁻³ |
| манганин | 4,3·10⁻⁷ | ±2·10⁻⁵ |
| константан | 5,0·10⁻⁷ | ±3·10⁻⁵ |
| ртуть | 9,84·10⁻⁷ | 9,9·10⁻⁴ |
| нихром 80/20 | 1,05·10⁻⁶ | 1,8·10⁻⁴ |
| канталь А1 | 1,45·10⁻⁶ | 3·10⁻⁵ |
| углерод (алмаз, графит) | 1,3·10⁻⁵ | |
| германий | 4,6·10⁻¹ | |
| кремний | 6,4·10² | |
| этанол | 3·10³ | |
| вода, дистиллированная | 5·10³ | |
| эбонит | 10⁸ | |
| бумага твёрдая | 10¹⁰ | |
| трансформаторное масло | 10¹¹ | |
| стекло обычное | 5·10¹¹ | |
| поливинил | 10¹² | |
| фарфор | 10¹² | |
| древесина | 10¹² | |
| ПТФЭ (тефлон) | >10¹³ | |
| резина | 5·10¹³ | |
| стекло кварцевое | 10¹⁴ | |
| бумага вощёная | 10¹⁴ | |
| полистирол | >10¹⁴ | |
| слюда | 5·10¹⁴ | |
| парафин | 10¹⁵ | |
| полиэтилен | 3·10¹⁵ | |
| акриловая смола | 10¹⁹ |
ru. electronics.wikia.com
electronics.wikia.com
Удельное электрическое сопротивление | формула, объемное, таблица
Удельное электрическое сопротивление является физической величиной, которая показывает, в какой степени материал может сопротивляться прохождению через него электрического тока. Некоторые люди могут перепутать данную характеристику с обыкновенным электрическим сопротивлением. Несмотря на схожесть понятий, разница между ними заключается в том, что удельное касается веществ, а второй термин относится исключительно к проводникам и зависит от материала их изготовления.
Обратной величиной данного материала является удельная электрическая проводимость. Чем выше этот параметр, тем лучше проходит ток по веществу. Соответственно, чем выше сопротивление, тем больше потерь предвидится на выходе.
Формула расчета и величина измерения
Рассматривая, в чем измеряется удельное электрическое сопротивление, также можно проследить связь с не удельным, так как для обозначения параметра используются единицы Ом·м. Сама величина обозначается как ρ. С таким значением можно определять сопротивление вещества в конкретном случае, исходя из его размеров. Эта единица измерения соответствует системе СИ, но могут встречаться и другие варианты. В технике периодически можно увидеть устаревшее обозначение Ом·мм2/м. Для перевода из этой системы в международного не потребуется использовать сложные формулы, так как 1 Ом·мм2/м равняется 10-6 Ом·м.
Сама величина обозначается как ρ. С таким значением можно определять сопротивление вещества в конкретном случае, исходя из его размеров. Эта единица измерения соответствует системе СИ, но могут встречаться и другие варианты. В технике периодически можно увидеть устаревшее обозначение Ом·мм2/м. Для перевода из этой системы в международного не потребуется использовать сложные формулы, так как 1 Ом·мм2/м равняется 10-6 Ом·м.
Формула удельного электрического сопротивления выглядит следующим образом:
R= (ρ·l)/S, где:
- R – сопротивление проводника;
- Ρ – удельное сопротивление материал;
- l – длина проводника;
- S – сечение проводника.
Зависимость от температуры
Удельное электрическое сопротивление зависит от температуры. Но все группы веществ проявляют себя по-разному при ее изменении. Это необходимо учитывать при расчете проводов, которые будут работать в определенных условиях. К примеру, на улице, где значения температуры зависят от времени года, необходимые материалы с меньшей подверженностью изменениям в диапазоне от -30 до +30 градусов Цельсия.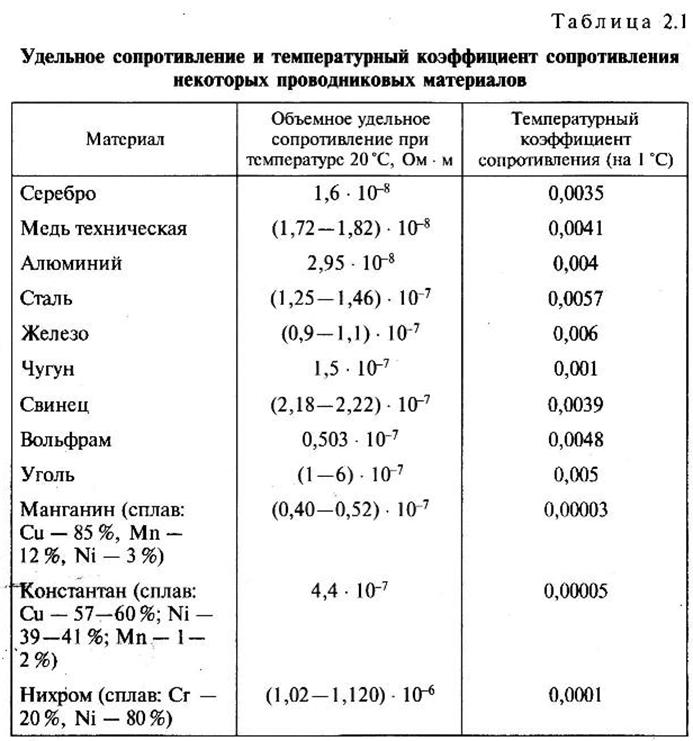 Если же планируется применение в технике, которая будет работать в одних и тех же условиях, то здесь также нужно оптимизировать проводку под конкретные параметры. Материал всегда подбирается с учетом эксплуатации.
Если же планируется применение в технике, которая будет работать в одних и тех же условиях, то здесь также нужно оптимизировать проводку под конкретные параметры. Материал всегда подбирается с учетом эксплуатации.
В номинальной таблице удельное электрическое сопротивление берется при температуре 0 градусов Цельсия. Повышение показателей данного параметра при нагреве материала обусловлено тем, что интенсивность передвижения атомов в веществе начинает возрастать. Носители электрических зарядов хаотично рассеиваются во всех направлениях, что приводит к созданию препятствий при передвижении частиц. Величина электрического потока снижается.
При уменьшении температуры условия прохождения тока становятся лучше. При достижении определенной температуры, которая для каждого металла будет отличаться, появляется сверхпроводимость, при которой рассматриваемая характеристика почти достигает нуля.
Отличия в параметрах порой достигают очень больших значений. Те материалы, которые обладают высокими показателями, могут использовать в качестве изоляторов. Они помогают защищать проводку от замыкания и ненамеренного контакта с человеком. Некоторые вещества вообще не применимы для электротехники, если у них высокое значение этого параметра. Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы. Здесь приведены значения некоторых веществ с высокими показателями.
Они помогают защищать проводку от замыкания и ненамеренного контакта с человеком. Некоторые вещества вообще не применимы для электротехники, если у них высокое значение этого параметра. Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы. Здесь приведены значения некоторых веществ с высокими показателями.
| Материалы с высоким удельным сопротивлением | ρ (Ом·м) |
| Бакелит | 1016 |
| Бензол | 1015…1016 |
| Бумага | 1015 |
| Вода дистиллированная | 104 |
| Вода морская | 0.3 |
| Дерево сухое | 1012 |
| Земля влажная | 102 |
| Кварцевое стекло | 1016 |
| Керосин | 1011 |
| Мрамор | 108 |
| Парафин | 1015 |
| Парафиновое масло | 1014 |
| Плексиглас | 1013 |
| Полистирол | 1016 |
| Полихлорвинил | 1013 |
| Полиэтилен | 1012 |
| Силиконовое масло | 1013 |
| Слюда | 1014 |
| Стекло | 1011 |
| Трансформаторное масло | 1010 |
| Фарфор | 1014 |
| Шифер | 1014 |
| Эбонит | 1016 |
| Янтарь | 1018 |
Более активно в электротехнике применяются вещества с низкими показателями. Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
| Материалы с низким удельным сопротивлением | ρ (Ом·м) |
| Алюминий | 2.7·10-8 |
| Вольфрам | 5.5·10-8 |
| Графит | 8.0·10-6 |
| Железо | 1.0·10-7 |
| Золото | 2.2·10-8 |
| Иридий | 4.74·10-8 |
| Константан | 5.0·10-7 |
| Литая сталь | 1.3·10-7 |
| Магний | 4.4·10-8 |
| Манганин | 4.3·10-7 |
| Медь | 1.72·10-8 |
| Молибден | 5.4·10-8 |
| Нейзильбер | 3.3·10-7 |
| Никель | 8.7·10-8 |
| Нихром | 1.12·10-6 |
| Олово | 1. 2·10-7 2·10-7 |
| Платина | 1.07·10-7 |
| Ртуть | 9.6·10-7 |
| Свинец | 2.08·10-7 |
| Серебро | 1.6·10-8 |
| Серый чугун | 1.0·10-6 |
| Угольные щетки | 4.0·10-5 |
| Цинк | 5.9·10-8 |
| Никелин | 0,4·10-6 |
Удельное объемное электрическое сопротивление
Данный параметр характеризует возможность пропускать ток через объем вещества. Для измерения необходимо приложить потенциал напряжения с разных сторон материала, изделие из которого будет включено в электрическую цепь. На него подается ток с номинальными параметрами. После прохождения измеряются данные на выходе.
Использование в электротехнике
Изменение параметра при разных температурах широко применяется в электротехнике. Наиболее простым примером является лампа накаливания, где используется нихромовая нить. При нагревании она начинает светиться.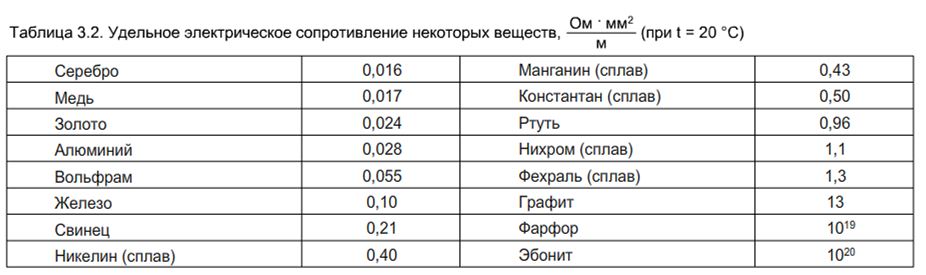 При прохождении через нее тока она начинает нагреваться. С ростом нагрева возрастает и сопротивление. Соответственно, ограничивается первоначальный ток, который нужен был для получения освещения. Нихромовая спираль, используя тот же принцип, может стать регулятором на различных аппаратах.
При прохождении через нее тока она начинает нагреваться. С ростом нагрева возрастает и сопротивление. Соответственно, ограничивается первоначальный ток, который нужен был для получения освещения. Нихромовая спираль, используя тот же принцип, может стать регулятором на различных аппаратах.
Широкое применение коснулось и благородных металлов, которые обладают подходящими характеристиками для электротехники. Для ответственных схем, которым требуется быстродействие, подбираются серебряные контакты. Они обладают высокой стоимостью, но с учетом относительно небольшого количества материалов их применение вполне оправданно. Медь уступает серебру по проводимости, но обладает более доступной ценой, благодаря чему ее чаще используют для создания проводов.
В условиях, где можно использовать предельно низкие температуры, применяются сверхпроводники. Для комнатной температуры и уличной эксплуатации они не всегда уместны, так как при повышении температуры их проводимость начнет падать, поэтому для таких условий лидерами остаются алюминий, медь и серебро.
На практике учитывается много параметров и этот является одним из наиболее важных. Все расчеты проводятся еще на стадии проектирования, для чего и используются справочные материалы.
Удельное сопротивление металлов является мерой их свойства противодействовать прохождению электрического тока. Эта величина выражается в Ом-метр (Ом⋅м). Символ, обозначающий удельное сопротивление, является греческая буква ρ (ро). Высокое удельное сопротивление означает, что материал плохо проводит электрический заряд.
Удельное сопротивление
Удельное электрическое сопротивление определяется как отношение между напряженностью электрического поля внутри металла к плотности тока в нем:
где:
ρ — удельное сопротивление металла (Ом⋅м),
Е — напряженность электрического поля (В/м),
J — величина плотности электрического тока в металле (А/м2)
Если напряженность электрического поля (Е) в металле очень большая, а плотность тока (J) очень маленькая, это означает, что металл имеет высокое удельное сопротивление.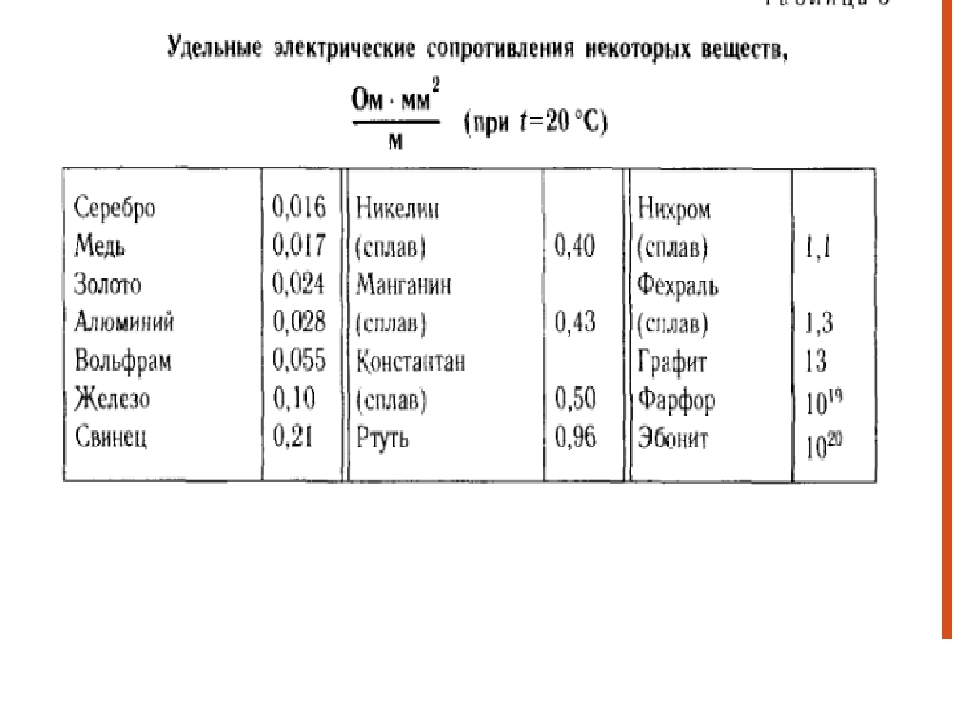
Обратной величиной удельного сопротивления является удельная электропроводность, указывающая, насколько хорошо материал проводит электрический ток:
σ — проводимость материала, выраженная в сименс на метр (См/м).
Электрическое сопротивление
Электрическое сопротивление, одно из составляющих , выражается в омах (Ом). Следует заметить, что электрическое сопротивление и удельное сопротивление — это не одно и то же. Удельное сопротивление является свойством материала, в то время как электрическое сопротивление — это свойство объекта.
Электрическое сопротивление резистора определяется сочетанием формы и удельным сопротивлением материала, из которого он сделан.
Например, проволочный , изготовленный из длинной и тонкой проволоки имеет большее сопротивление, нежели резистор, сделанный из короткой и толстой проволоки того же металла.
В тоже время проволочный резистор, изготовленный из материала с высоким удельным сопротивлением, обладает большим электрическим сопротивлением, чем резистор, сделанный из материала с низким удельным сопротивлением. И все это не смотря на то, что оба резистора сделаны из проволоки одинаковой длины и диаметра.
И все это не смотря на то, что оба резистора сделаны из проволоки одинаковой длины и диаметра.
В качестве наглядности можно провести аналогию с гидравлической системой, где вода прокачивается через трубы.
- Чем длиннее и тоньше труба, тем больше будет оказано сопротивление воде.
- Труба, заполненная песком, будет больше оказывать сопротивление воде, нежели труба без песка
Сопротивление провода
Величина сопротивления провода зависит от трех параметров: удельного сопротивления металла, длины и диаметра самого провода. Формула для расчета сопротивления провода:
Где:
R — сопротивление провода (Ом)
ρ — удельное сопротивление металла (Ом.m)
L — длина провода (м)
А — площадь поперечного сечения провода (м2)
В качестве примера рассмотрим проволочный резистор из нихрома с удельным сопротивлением 1.10×10-6 Ом.м. Проволока имеет длину 1500 мм и диаметр 0,5 мм. На основе этих трех параметров рассчитаем сопротивление провода из нихрома:
R=1,1*10 -6 *(1,5/0,000000196) = 8,4 Ом
Нихром и константан часто используют в качестве материала для сопротивлений. Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.
Ниже в таблице вы можете посмотреть удельное сопротивление некоторых наиболее часто используемых металлов.
Поверхностное сопротивление
Величина поверхностного сопротивления рассчитывается таким же образом, как и сопротивление провода. В данном случае площадь сечения можно представить в виде произведения w и t:
Для некоторых материалов, таких как тонкие пленки, соотношение между удельным сопротивлением и толщиной пленки называется поверхностное сопротивление слоя RS:
где RS измеряется в омах. При данном расчете толщина пленки должна быть постоянной.
Часто производители резисторов для увеличения сопротивления вырезают в пленке дорожки, чтобы увеличить путь для электрического тока.
Свойства резистивных материалов
Удельное сопротивление металла зависит от температуры. Их значения приводится, как правило, для комнатной температуры (20°С). Изменение удельного сопротивления в результате изменения температуры характеризуется температурным коэффициентом.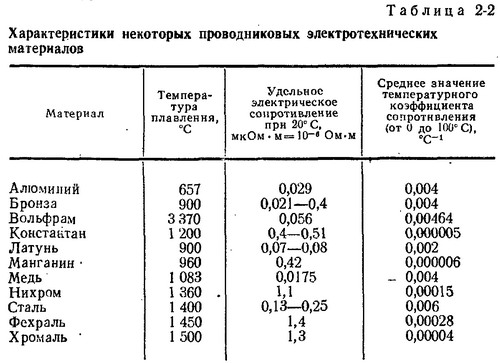
Например, в термисторах (терморезисторах) это свойство используется для измерения температуры. С другой стороны, в точной электронике, это довольно нежелательный эффект.
Металлопленочные резисторы имеют отличные свойства температурной стабильности. Это достигается не только за счет низкого удельного сопротивления материала, но и за счет механической конструкции самого резистора.
Много различных материалов и сплавов используются в производстве резисторов. Нихром (сплав никеля и хрома), из-за его высокого удельного сопротивления и устойчивости к окислению при высоких температурах, часто используют в качестве материала для изготовления проволочных резисторов. Недостатком его является то, что его невозможно паять. Константан, еще один популярный материал, легко паяется и имеет более низкий температурный коэффициент.
Электрическое сопротивление — физическая величина, которая показывает, какое препятствие создается току при его прохождении по проводнику . Единицами измерения служат Омы, в честь Георга Ома. В своем законе он вывел формулу для нахождения сопротивления, которая приведена ниже.
Единицами измерения служат Омы, в честь Георга Ома. В своем законе он вывел формулу для нахождения сопротивления, которая приведена ниже.
Рассмотрим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а хаотично перемещаются между узлами решетки. Из квантовой физики известно, что движение электронов в металле это распространение электромагнитной волны в твердом теле. То есть электрон в проводнике движется со скоростью света (практически), и доказано, что он проявляет свойства не только как частица, но еще и как волна. А сопротивление металла возникает в результате рассеяния электромагнитных волн (то есть электронов) на тепловых колебаниях решетки и её дефектах. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при постоянном токе , благодаря закону Джоуля-Ленца – Q=I 2 Rt. Как видите чем больше сопротивление, тем больше энергии выделяется.
Эту энергию можно вычислить при постоянном токе , благодаря закону Джоуля-Ленца – Q=I 2 Rt. Как видите чем больше сопротивление, тем больше энергии выделяется.
Удельное сопротивление
Существует такое важное понятие как удельное сопротивление, это тоже самое сопротивление, только в единице длины. У каждого металла оно свое, например у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м. Это значит, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а такой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а рассчитать сопротивление всего проводника можно по формуле
где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.
Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)
Вещество | p , Ом*мм 2 /2 | α,10 -3 1/K |
Алюминий | 0. | |
Вольфрам | 0.055 | |
Железо | 0.098 | |
Золото | 0.023 | |
Латунь | 0.025-0.06 | |
Манганин | 0.42-0.48 | 0,002-0,05 |
Медь | 0.0175 | |
Никель | ||
Константан | 0.44-0.52 | 0.02 |
Нихром | 0. | |
Серебро | 0.016 | |
Цинк | 0.059 |
Кроме удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуть позже.
Зависимость удельного сопротивления от деформаций
При холодной обработке металлов давлением, металл испытывает пластическую деформацию. При пластической деформации кристаллическая решетка искажается, количество дефектов становится больше. С увеличением дефектов кристаллической решетки, сопротивление течению электронов по проводнику растет, следовательно, удельное сопротивление металла увеличивается. К примеру, проволоку изготавливают методом протяжки, это значит, что металл испытывает пластическую деформацию, в результате чего, удельное сопротивление растет. На практике для уменьшения сопротивления применяют рекристаллизационный отжиг, это сложный технологический процесс, после которого кристаллическая решетка как бы, “расправляется” и количество дефектов уменьшается, следовательно, и сопротивление металла тоже.
При растяжении или сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды тепловых колебаний узлов кристаллической решетки увеличиваются, следовательно, электроны испытывают большие затруднения, и в связи с этим, увеличивается удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды тепловых колебаний узлов уменьшаются, следовательно, электронам проще двигаться, и удельное сопротивление уменьшается.
Влияние температуры на удельное сопротивление
Как мы уже выяснили выше, причиной сопротивления в металле являются узлы кристаллической решетки и их колебания. Так вот, при увеличении температуры, тепловые колебания узлов увеличиваются, а значит, удельное сопротивление также увеличивается. Существует такая величина как температурный коэффициент сопротивления (ТКС), который показывает насколько увеличивается, или уменьшается удельное сопротивление металла при нагреве или охлаждении. Например, температурный коэффициент меди при 20 градусах по цельсию равен 4. 1 · 10 − 3 1/градус. Это означает что при нагреве, к примеру, медной проволоки на 1 градус цельсия, её удельное сопротивление увеличится на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле
1 · 10 − 3 1/градус. Это означает что при нагреве, к примеру, медной проволоки на 1 градус цельсия, её удельное сопротивление увеличится на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле
где r это удельное сопротивление после нагрева, r 0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t 2 – температура до нагрева, t 1 — температура после нагрева.
Подставив наши значения, мы получим: r=0,0175*(1+0.0041*(154-20))=0,0271 Ом*мм 2 /м. Как видите наш брусок из меди длиной 1 м и площадью поперечного сечения 1 мм 2 , после нагрева до 154 градусов, имел бы сопротивление, как у такого же бруска, только из алюминия и при температуре равной 20 градусов цельсия.
Свойство изменения сопротивления при изменении температуры, используется в термометрах сопротивления. Эти приборы могут измерять температуру основываясь на показаниях сопротивления. У термометров сопротивления высокая точность измерений, но малые диапазоны температур.
На практике, свойства проводников препятствовать прохождению тока используются очень широко. Примером может служить лампа накаливания, где нить из вольфрама, нагревается за счет высокого сопротивления металла, большой длины и узкого сечения. Или любой нагревательный прибор, где спираль разогревается благодаря высокому сопротивлению. В электротехнике, элемент главным свойством которого является сопротивление, называется – резистор . Резистор применяется практически в любой электрической схеме.
Уде́льное электри́ческое сопротивле́ние , или просто удельное сопротивление вещества — физическая величина, характеризующая способность вещества препятствовать прохождению электрического тока .
Удельное сопротивление обозначается греческой буквой ρ
. Величина, обратная удельному сопротивлению, называется удельной проводимостью (удельной электропроводностью). В отличие от электрического сопротивления , являющегося свойством проводника и зависящего от его материала, формы и размеров, удельное электрическое сопротивление является свойством только вещества .
Электрическое сопротивление однородного проводника с удельным сопротивлением ρ , длиной l и площадью поперечного сечения S может быть рассчитано по формуле R = ρ ⋅ l S {\displaystyle R={\frac {\rho \cdot l}{S}}} (при этом предполагается, что ни площадь, ни форма поперечного сечения не меняются вдоль проводника). Соответственно, для ρ выполняется ρ = R ⋅ S l . {\displaystyle \rho ={\frac {R\cdot S}{l}}.}
Из последней формулы следует: физический смысл удельного сопротивления вещества заключается в том, что оно представляет собой сопротивление изготовленного из этого вещества однородного проводника единичной длины и с единичной площадью поперечного сечения.
Энциклопедичный YouTube
1 / 5
Единица измерения удельного сопротивления в Международной системе единиц (СИ) — Ом · . Из соотношения ρ = R ⋅ S l {\displaystyle \rho ={\frac {R\cdot S}{l}}} следует, что единица измерения удельного сопротивления в системе СИ равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 м² , изготовленный из этого вещества, имеет сопротивление, равное 1 Ом .
 Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м
и площадью поперечного сечения 1 м²
.
Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м
и площадью поперечного сечения 1 м²
.В технике также применяется устаревшая внесистемная единица Ом·мм²/м, равная 10 −6 от 1 Ом·м . Данная единица равна такому удельному сопротивлению вещества, при котором однородный проводник длиной 1 м с площадью поперечного сечения 1 мм² , изготовленный из этого вещества, имеет сопротивление, равное 1 Ом . Соответственно, удельное сопротивление какого-либо вещества, выраженное в этих единицах, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м и площадью поперечного сечения 1 мм² .
Обобщение понятия удельного сопротивления
Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E → (r →) {\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J → (r →) {\displaystyle {\vec {J}}({\vec {r}})} в данной точке r → {\displaystyle {\vec {r}}} .
 {3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}
{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}В анизотропном, но однородном веществе тензор ρ i j {\displaystyle \rho _{ij}} от координат не зависит.
Тензор ρ i j {\displaystyle \rho _{ij}} симметричен , то есть для любых i {\displaystyle i} и j {\displaystyle j} выполняется ρ i j = ρ j i {\displaystyle \rho _{ij}=\rho _{ji}} .
Как и для всякого симметричного тензора, для ρ i j {\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρ i j {\displaystyle \rho _{ij}} становится диагональной , то есть приобретает вид, при котором из девяти компонент ρ i j {\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ 11 {\displaystyle \rho _{11}} , ρ 22 {\displaystyle \rho _{22}} и ρ 33 {\displaystyle \rho _{33}} . В этом случае, обозначив ρ i i {\displaystyle \rho _{ii}} как , вместо предыдущей формулы получаем более простую
E i = ρ i J i . {3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}Из этого равенства и приведённого ранее соотношения для E i (r →) {\displaystyle E_{i}({\vec {r}})} следует, что тензор удельного сопротивления является обратным тензору удельной проводимости. С учётом этого для компонент тензора удельного сопротивления выполняется:
ρ 11 = 1 det (σ) [ σ 22 σ 33 − σ 23 σ 32 ] , {\displaystyle \rho _{11}={\frac {1}{\det(\sigma)}}[\sigma _{22}\sigma _{33}-\sigma _{23}\sigma _{32}],} ρ 12 = 1 det (σ) [ σ 33 σ 12 − σ 13 σ 32 ] , {\displaystyle \rho _{12}={\frac {1}{\det(\sigma)}}[\sigma _{33}\sigma _{12}-\sigma _{13}\sigma _{32}],}где det (σ) {\displaystyle \det(\sigma)} — определитель матрицы , составленной из компонент тензора σ i j {\displaystyle \sigma _{ij}} . Остальные компоненты тензора удельного сопротивления получаются из приведённых уравнений в результате циклической перестановки индексов 1 , 2 и 3 .
Удельное электрическое сопротивление некоторых веществ
Металлические монокристаллы
В таблице приведены главные значения тензора удельного сопротивления монокристаллов при температуре 20 °C .

Кристалл ρ 1 =ρ 2 , 10 −8 Ом·м ρ 3 , 10 −8 Ом·м Олово 9,9 14,3 Висмут 109 138 Кадмий 6,8 8,3 Цинк 5,91 6,13 - Константан (58,8 Cu, 40 Ni, 1,2 Mn)
- Манганин (85 Cu, 12 Mn, 3 Ni)
- Нейзильбер (65 Cu, 20 Zn, 15 Ni)
- Никелин (54 Cu, 20 Zn, 26 Ni)
- Нихром (67,5 Ni, 15 Cr, 16 Fe, 1,5 Mn)
- Реонат (84Cu, 12Mn, 4 Zn)
- Фехраль (80 Fe, 14 Cr, 6 Al)
Удельное сопротивление нихрома
Каждое тело, через которое пропускается электрический ток, автоматически оказывает ему определенное сопротивление. Свойство проводника противостоять электрическому току принято называть электрическим сопротивлением.
Рассмотрим электронную теорию данного явления. При движении по проводнику свободные электроны постоянно встречают на своем пути другие электроны и атомы.
 Взаимодействуя с ними, свободный электрон теряет часть своего заряда. Таким образом, электроны сталкиваются с сопротивлением со стороны материала проводника. Каждое тело имеет свою атомную структуру, которая оказывает электрическому току разное сопротивление. Единицей сопротивления принято считать Ом. Обозначается сопротивление материалов — R или r.
Взаимодействуя с ними, свободный электрон теряет часть своего заряда. Таким образом, электроны сталкиваются с сопротивлением со стороны материала проводника. Каждое тело имеет свою атомную структуру, которая оказывает электрическому току разное сопротивление. Единицей сопротивления принято считать Ом. Обозначается сопротивление материалов — R или r.Чем меньше сопротивление проводника, тем легче электрическому току пройти через это тело. И наоборот: чем выше сопротивление, тем хуже тело проводит электрический ток.
Сопротивление каждого отдельно взятого проводника зависит от свойств материала, из которого он изготовлен. Для точной характеристики электрического сопротивления того или иного материала было введено понятие — удельное сопротивление (нихрома, алюминия и т. д.). Удельным считается сопротивление проводника длиной до 1 м, сечение которого — 1 кв. мм. Этот показатель обозначается буквой p. Каждый материал, использующийся в производстве проводника, обладает своим удельным сопротивлением.
 Для примера рассмотрим удельное сопротивление нихрома и фехрали (более 3 мм):
Для примера рассмотрим удельное сопротивление нихрома и фехрали (более 3 мм):- Х15Н60 — 1.13 Ом*мм/м
- Х23Ю5Т — 1.39 Ом*мм/м
- Х20Н80 — 1.12 Ом*мм/м
- ХН70Ю — 1.30 Ом*мм/м
- ХН20ЮС — 1.02 Ом*мм/м
Удельное сопротивление нихрома, фехрали указывает на основную сферу их применения: изготовление аппаратов теплового действия, бытовых приборов и электронагревательных элементов промышленных печей.
Поскольку нихром и фехраль преимущественно используются в производстве нагревательных элементов, то самая распространенная продукция — нихромовая нить, лента, полоса Х15Н60 и Х20Н80, а также фехралевая проволока Х23Ю5Т.
Зависимость удельного сопротивления чистого металла от температуры
Зависимость удельного сопротивления чистого металла от температуры [c.193]На рис. 7.6, а схематически показана кривая зависимости удельного сопротивления чистых металлов от температуры, достаточно хорошо подтверждаемая экспериментально (рис.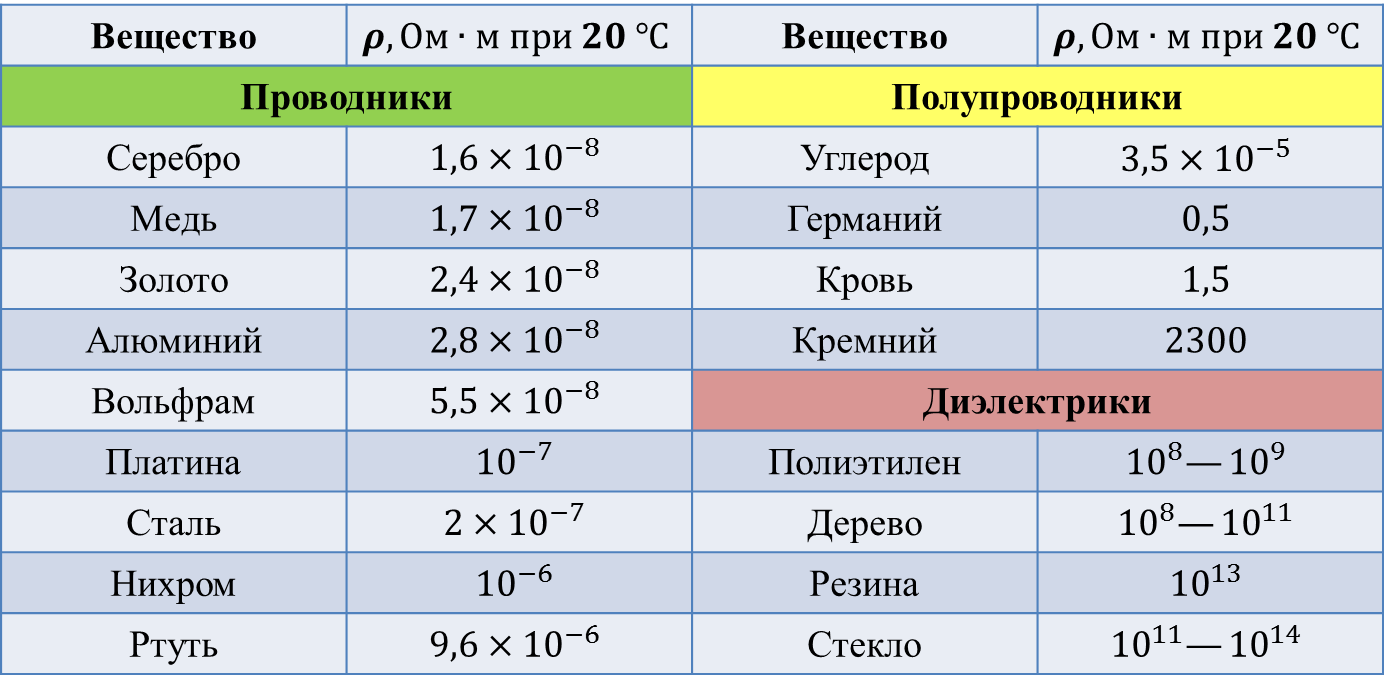 7.6, б).
[c.188]
7.6, б).
[c.188]
Зависимость удельного сопротивления чистых металлов от температуры не может быть удовлетворительно объяснена в рамках классической электронной теории электропроводности. В современной квантовой теории электропроводности металлов доказывается, что при всех температурах, кроме абсолютного нуля, свободные электроны испытывают такие взаимодействия с узлами кристаллической решетки металла, что среднее время Т свободного пробега электронов в области средних температур обратно пропорционально абсолютной температуре Т металла [c.220]
Никель и железо. Никель и железо обладают значительно более высоким температурным коэфициентом сопротивления, чем все прочие металлы 6,28 10″1 град и л= 6,4-10 . град). Кроме того, эти металлы обладают довольно высоким удельным сопротивлением, равным приблизительно 0,1—0,13 ом-мм /м. Однако возможность использования никеля и железа для изготовления термометров сопротивления ограничена в силу присущих этим металлам существенных недостатков. Получение никеля и железа в чистом виде затруднительно, а поэтому низка воспроизводимость их свойств. Далее, зависимость сопротивления этих металлов от температуры выражается к,ривыми, которые не могут быть записаны в виде простых эмпирических формул. Наконец, никель и, особенно железо чрезвычайно легко окисляются. Железные Термопары в СССР не изготовляются соверщенно. Никелевые термометры используются для технических измерений температуры в пределах до 250°. Однако щирокого распространения эти термометры до настоящего времени не нашли.
[c.77]
Получение никеля и железа в чистом виде затруднительно, а поэтому низка воспроизводимость их свойств. Далее, зависимость сопротивления этих металлов от температуры выражается к,ривыми, которые не могут быть записаны в виде простых эмпирических формул. Наконец, никель и, особенно железо чрезвычайно легко окисляются. Железные Термопары в СССР не изготовляются соверщенно. Никелевые термометры используются для технических измерений температуры в пределах до 250°. Однако щирокого распространения эти термометры до настоящего времени не нашли.
[c.77]
Электросопротивление алюминия высокой чистоты (99,99 %) при температуре 20 °С составляет 2,6548-10 Ом-м (0,0265 МКОМ М). В интервале температур 273—300 К температурная зависимость электрического сопротивления чистого алюминия почти линейна при постоянном коэффициенте 1,15-10 Ом-м-К . Электрическая проводимость алюминия в значительной степени зависит от чистоты металла, причем влияние различных примесей на электрическое сопротивление зависит не только от концентрации данной примеси, но и от ее нахождения в твердом растворе или вне его. Наиболее сильно повышают сопротивление алюминия примеси хрома, лития, марганца, магния, титана и ванадия [5]. Удельное электросопротивление р (мкОм м) отожженной алюминиевой проволоки в зависимости от содержания примесей (%) можно приближенно определить по следующей формуле [9]
[c.12]
Наиболее сильно повышают сопротивление алюминия примеси хрома, лития, марганца, магния, титана и ванадия [5]. Удельное электросопротивление р (мкОм м) отожженной алюминиевой проволоки в зависимости от содержания примесей (%) можно приближенно определить по следующей формуле [9]
[c.12]
Для определения результирующих потоков излучения необходимо располагать данными по коэффициентам излучения. Коэффициент излучения является сложной функцией, зависящей от природы излучающего тела, его температуры, состояния поверхности, а для металлов — от степени окисления этой поверхности. Для чистых металлов с полированными поверхностями коэффициент излучения имеет низкие значения. Так, при температуре 100 °С коэффициент излучения по отношению к его величине для абсолютно черного тела не превышает 0,1. Металлы характеризуются высокой отражательной способностью, так как из-за большой электропроводности луч проникает лишь на небольшую глубину.
 Для чистых металлов коэффициент излучения может быть найден теоретическим путем. Относительный коэффициент (степень черноты) полного нормального излучения для них связан с удельным электрическим сопротивлением рэ зависимостью
[c.385]
Для чистых металлов коэффициент излучения может быть найден теоретическим путем. Относительный коэффициент (степень черноты) полного нормального излучения для них связан с удельным электрическим сопротивлением рэ зависимостью
[c.385]Наряду с малым удельным сопротивлением чистые металлы обладают хорошей пластичностью, т. е. могут вытягиваться в тонкую проволоку (до диаметра 0,01 мм), ленты (до толщины 0,01 мм) и прокатываться в фольгу толщиной менее 0,01 мм. Сплавы металлов обладают меньшей пластичностью по сравнению с чистыми металлами, они более упруги и имеют большую механическую прочность. Характерной особенностью всех металлических проводниковых, материалов является их электронная электропроводность. Удельное сопротивление всех металлических проводников увеличивается с ростом температуры и в зависимости от температурного коэффициента сопротивления, а также в результате механической обработки, вызывающей остаточную деформацию в металле. К холодной обработке (прокатка, волочение) приходится прибегать для получения проводниковых изделий с повышенным пределом прочности при разрыве, например при изготовлении проводов воздушных линий, троллейных проводов и т. д. Чтобы вернуть деформированным металлическ , проводникам прежнюю величину удельного сопротивления, их подвергают термической обработке — отжигу без доступа кислорода.
[c.225]
д. Чтобы вернуть деформированным металлическ , проводникам прежнюю величину удельного сопротивления, их подвергают термической обработке — отжигу без доступа кислорода.
[c.225]
Прежде чем перейти к подробному обсуждению зависимости удельного сопротивления металлов и полупроводников от температуры, коснемся особенностей поведения концентрированных сплавов. Введение значительного количества примесных атомов в твердый раствор приводит к искажению кристаллической решетки. Вследствие этого появляется дополнительный вклад в рассеяние. Его величина почти не зависит от температуры и может во много раз превышать долю электрон-фонон-ного рассеяния в чистом металле. Изменение остаточного удельного сопротивления неупорядоченного сплава Си—Аи в зави- [c.191]
Теоретические соображения. Интересно обсудить возможный механизм частичной сверхпроводимости проволоки из фосфористой бронзы. Кеезом [25] и Бэббит и Мендельсон [45] предположили, что явление частичной сверхпроводимости обусловливается наличием большого количества сверхпроводящих включений в виде чистого металла или сверхпроводящего сплава, растворенного в фосфористой бронзе.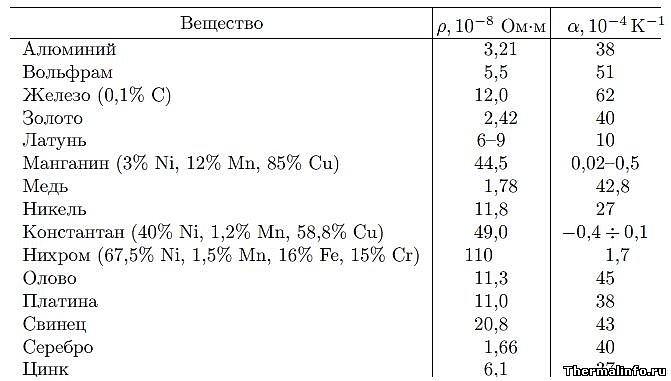 Кроме того, они предположили, что эти включения имеют форму тонких игл, образовавшихся при протяжке и расположенных параллельно оси проволоки. Однако эти авторы дают различную интерпретацию линейной зависимости удельного сопротивления от температуры. Кеезом полагал, что благодаря очень малым и случайно распределенным размерам игл сверхпроводящие переходы в них беспорядочно распределены по всему температурному интервалу. По мере понижения температуры все большее и большее число игл становится сверхпроводящим и, таким образом, уменьшается сопротивление проволоки. Бэббит и Мендельсон, напротив, предположили, что иглы образуют цепи, и так как один и тот же ток проходит через все иглы, составляющие одну цепь, то более тонкие иглы становятся сверхпроводниками при более низких температурах, чем более толстые. Этим можно объяснить незначительный наклон кривой зависимости удельного электросопротивления от температуры.
[c.205]
Кроме того, они предположили, что эти включения имеют форму тонких игл, образовавшихся при протяжке и расположенных параллельно оси проволоки. Однако эти авторы дают различную интерпретацию линейной зависимости удельного сопротивления от температуры. Кеезом полагал, что благодаря очень малым и случайно распределенным размерам игл сверхпроводящие переходы в них беспорядочно распределены по всему температурному интервалу. По мере понижения температуры все большее и большее число игл становится сверхпроводящим и, таким образом, уменьшается сопротивление проволоки. Бэббит и Мендельсон, напротив, предположили, что иглы образуют цепи, и так как один и тот же ток проходит через все иглы, составляющие одну цепь, то более тонкие иглы становятся сверхпроводниками при более низких температурах, чем более толстые. Этим можно объяснить незначительный наклон кривой зависимости удельного электросопротивления от температуры.
[c.205]
Простая модель электронного газа, созданная Друде в 1900 г.
 , успещно предсказала законы Ома и Видемана — Франца. Однако она не объяснила зависимость электропроводности от температуры, а также магнитные свойства и малую величину электронной теплоемкости по сравнению с классическим значением 3/ . В настоящее время ясно, почему удельное сопротивление особо чистых металлов падает от типичного для комнатных температур значения 10 мкОм см до значения менее 10 з мкОм -см при температуре жидкого гелия в то время как удельное сопротивление концентрированного сплава падает всего в два раза в том же диапазоне температур. Поведение полупроводников также хорошо понято удельное сопротивление экспоненциально возрастает при уменьшении температуры, и при очень низких температурах чистые полупроводники становятся хорошими диэлектриками. Добавка в образец полупроводника небольшого количества примесей чаще всего существенно уменьшает удельное сопротивление (в противоположность чистым металлам, в которых наличие примесей ведет к увеличению удельного сопротивления).
, успещно предсказала законы Ома и Видемана — Франца. Однако она не объяснила зависимость электропроводности от температуры, а также магнитные свойства и малую величину электронной теплоемкости по сравнению с классическим значением 3/ . В настоящее время ясно, почему удельное сопротивление особо чистых металлов падает от типичного для комнатных температур значения 10 мкОм см до значения менее 10 з мкОм -см при температуре жидкого гелия в то время как удельное сопротивление концентрированного сплава падает всего в два раза в том же диапазоне температур. Поведение полупроводников также хорошо понято удельное сопротивление экспоненциально возрастает при уменьшении температуры, и при очень низких температурах чистые полупроводники становятся хорошими диэлектриками. Добавка в образец полупроводника небольшого количества примесей чаще всего существенно уменьшает удельное сопротивление (в противоположность чистым металлам, в которых наличие примесей ведет к увеличению удельного сопротивления). [c.187]
[c.187]
|
Реостат изготовлен из железной проволоки (удельное сопротивление железа равно 0,098 Ом·мм²/м)
Под каким углом по вертикали падают солнечные лучи на спокойную поверхность озера, если отбитые лучи образуют вдвое больший угол с поверхностью воды?
Тело массой м=2кг движется вдоль оси о. на графике представлена временная зависимость координаты тела х(т)
на графике представлена временная зависимость координаты тела х(т)
Помогите пожалуйста!! 1.Даны уравнения движения двух тел: x1 = -5 + 0,5t и x2 = 8 + 2,5t. Определите начальные координаты тел, скорости тел, а также м … есто и время их встречи. 2.Зависимость от времени координаты точки, движущейся вдоль оси x, имеет вид: x = 4 + 3t – t2. Опишите характер движения. Каковы начальная скорость и ускорение? Запишите уравнение для проекции скорости. 3.Какие из приведенных зависимостей описывают равномерное движение? 1) v = 6– 3t; 2) s = 2t2; 3) v = 6; 4) s = 2t; 5) s = 2t + 3.
одинаковы ли объем и состав молекул одного и того же вещества
3. Даны уравнения движения двух тел: x1 = -2 + 0,25t и x2 = 3 + 1,5t. Определите начальные координаты тел, скорости тел, а также место и время их встр … ечи. 4. Автомобиль начал двигаться с постоянным ускорением 0,2 м/с2. За какое время она достигнет скорости 72 км/ч?
2. Зависимость от времени координаты точки, движущейся вдоль оси x, имеет вид: x = 4 – 5t + 2t2. Опишите характер движения. Каковы начальная скорость
… и ускорение? Запишите уравнение для проекции скорости.
Опишите характер движения. Каковы начальная скорость
… и ускорение? Запишите уравнение для проекции скорости.
1. Какие из приведенных зависимостей описывают равномерное движение? 1) s = 2t + 3; 2) s = 3t; 3) s = 6t2; 4) v = 11; 5) v = 2 – 3t.
4. Какое количество энергии требуется для обращения воды массой 150 г в пар при температуре 100 °С?
упражнения 11 и 11дпожалуйста помогите ❤️❤️❤️❤️❤️❤️❤️ПРОШУ ПОЖАЛУЙСТА ❤️
1. Налейте в калориметр воду массой 100 г комнатной температуры. Измерьте температуру воды – tl =______________
2. Нагрейте цилиндр в сосуде с горячей
… водой. Измерьте её температуру (эта температура и будет начальной температурой цилиндра) – t2=_____________________________
3. Опустите цилиндр в калориметр с холодной водой. Измерьте температуру нагревшейся от цилиндра воды – t = _____________________
Результаты измерений запишите в таблицу.
Масса воды в
калориметре
m, кг
Начальная
температура
воды, t1 ,оС
Масса
цилиндра
т2, кг
Начальная
температура
цилиндра t2 ,оС
Общая
температура
воды и цилиндра t, оС
Вычисления:
Количество теплоты, полученное водой при нагревании:
Ql = Своды mводы (t — tl)
Количество теплоты Q2, отданное металлическим цилиндром:
Q2 = Сцил. mцил. (t2 — t)
т. к. Ql = Q2 , то Своды mводы (t — tl) = Сцил.mцил. (t2 — t).
Сцил=Сводыmводыt−t1mцил.t2−t=
Сравните полученный результат с табличным значением (табл. № 1 в учебнике) и сделайте вывод.
Вывод: __________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
mцил. (t2 — t)
т. к. Ql = Q2 , то Своды mводы (t — tl) = Сцил.mцил. (t2 — t).
Сцил=Сводыmводыt−t1mцил.t2−t=
Сравните полученный результат с табличным значением (табл. № 1 в учебнике) и сделайте вывод.
Вывод: __________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
________________________________________________________________
Магнетит как проводник — Справочник химика 21
К типичным проводникам принадлежат тягучие минералы, обладающие металлическим блеском медь (р = 15-10 Ом-м), серебро (16-10-в Ом-м). Удельное сопротивление несколько выше для ковких минералов, халькозина (1,1-10 Ом-м), галенита (3-10-е Ом-м). Все сульфиды характеризуются более низким сопротивлением по сравнению с кислородными соединениями и являются типичными полупроводниками. Минералы— кислородные соединения с металлическим блеском — отличаются более высоким удельным электросопротивлением по сравнению с сульфидами, но и для них р металлическим блеском имеют р[c.120]
Минералы— кислородные соединения с металлическим блеском — отличаются более высоким удельным электросопротивлением по сравнению с сульфидами, но и для них р металлическим блеском имеют р[c.120]
Гранулированный магнетит с добавкой 4,5% окиси алюминия и 5,3% азотнокислого калия (соответствующих 2,5% окиси калия) нагревают до плавления между двумя охлаждаемыми водой электродами один из этих электродов соединяют с третьим электродом, посредством которого производят нагревание до температуры, при которой магнетит становится проводником расплавленный продукт после восстановления смесью азота с водородом при 500° испытывают на каталитическую активность поверхностный слой катализатора значительно беднее закисью железа, чем внутренняя масса, состоящая главным образом из окиси железа могут быть приготовлены сплавы, содержащие до 50% окиси алюминия Железо [c.46]
В статье обсуждаются проблемы приклеивания выводов проводников, контактов, контактных колец на гетинакс, использования клеев в системах магнето, приклеивания стеклянных пластин на металлические пли пластмассовые корпуса, на которые также приклеена токопроводящая фольга из меди или алюминия и т. д. Описывается воз.можность приготовления токопроводящих клеев из эпоксидных смол путем смешения эпоксидной смолы с мелким порошком серебра. Указано, что при горячем отверждении. механические свойства клеевого шва выше, чем при холодно.м отверждении. [c.903]
д. Описывается воз.можность приготовления токопроводящих клеев из эпоксидных смол путем смешения эпоксидной смолы с мелким порошком серебра. Указано, что при горячем отверждении. механические свойства клеевого шва выше, чем при холодно.м отверждении. [c.903]
В мокрые периоды элемент железо раствор сернокислого закисного железа гидрат окиси железа будет восстанавливать гидрат окиси железа (ржавчину) до магнетита, который в дальнейшем в сухие периоды снова окисляется до гидрата окиси железа. Таким образом, все большее и большее количество железа превраш,ается в рыхлую ржавчину на участках, где присутствует сернокислая закись железа, чем и объясняется быстрое отслаивание лака. Для протекания электрохимической реакции необходима соль, увеличивающая электропроводность воды. Нет сомнения в том, что металлическое железо может реагировать химически с нижним слоем окисной ржавчины и образовывать магнетит, но на дальнейшее преобразование сказывается то обстоятельство, что магнетит — электронный проводник, а раствор сернокислой закиси железа — ионный проводник. Это позволяет гидроокиси трехвалентного железа способствовать за счет катодной реакции. переходу железа в раствор и превращению в магнетит до тех пор, пока вся ржавчина не перейдет в черный магнетит. Другие соли (хлориды и т. п.) могут, несомненно, реагировать таким же путем, объясняя тем самым тот факт (стр. 464), что ржавчина, содержащая следы хлоридов, стимулирует последующее ржавление, тогда как чистая ржавчина не обладает таким свойством. Этот механизм невозможен для цинка, чем и объясняется тот факт, что цинк в условиях полного или частичного погружения в солевые растворы корродирует с большей скоростью, чем железо, тогда как в атмосферных условиях с меньшей скоростью, чем железо, за исключением случаев, когда среда очень кислая (например в ж.-д. туннелях). [c.447]
Это позволяет гидроокиси трехвалентного железа способствовать за счет катодной реакции. переходу железа в раствор и превращению в магнетит до тех пор, пока вся ржавчина не перейдет в черный магнетит. Другие соли (хлориды и т. п.) могут, несомненно, реагировать таким же путем, объясняя тем самым тот факт (стр. 464), что ржавчина, содержащая следы хлоридов, стимулирует последующее ржавление, тогда как чистая ржавчина не обладает таким свойством. Этот механизм невозможен для цинка, чем и объясняется тот факт, что цинк в условиях полного или частичного погружения в солевые растворы корродирует с большей скоростью, чем железо, тогда как в атмосферных условиях с меньшей скоростью, чем железо, за исключением случаев, когда среда очень кислая (например в ж.-д. туннелях). [c.447]
Остановимся на возможности использования магнетита в качестве проводника. При обсуждении параметра индукционной катушки мы выбрали для удельного сопротивления проводящего материала значение 50 Ом см это довольно большая величина для обычного материала биологического происхождения.
 Поскольку магнетит обнаружен у самых разных животных, мы пересчитали наши результаты для случая проводника с удельным сопротивлением магнетита, т. е. 5 -10 Ом-см, и пришли к выводу, что если бы катушка была сделана из материала с проводимостью магнетита, то ее размеры были бы на порядок меньше, чем указано выше. Однако существование магнетитовой петли с размерами в несколько десятых долей миллиметра представляется нам менее вероятным, чем существование системы, описанной выше, особенно если учесть условие (7) для объема необходимый объем магнетита оказывается на порядок больше, чем обнаружено у животных. [c.303]
Поскольку магнетит обнаружен у самых разных животных, мы пересчитали наши результаты для случая проводника с удельным сопротивлением магнетита, т. е. 5 -10 Ом-см, и пришли к выводу, что если бы катушка была сделана из материала с проводимостью магнетита, то ее размеры были бы на порядок меньше, чем указано выше. Однако существование магнетитовой петли с размерами в несколько десятых долей миллиметра представляется нам менее вероятным, чем существование системы, описанной выше, особенно если учесть условие (7) для объема необходимый объем магнетита оказывается на порядок больше, чем обнаружено у животных. [c.303] Электрическое обогащеине (электрическая сепарация) основано на различии в электрич. св-вах (электрич. проводимости, диэлектрич. проницаемости, способности заряжаться при трении и т. д.) компонентов ископаемого сырья. Воздействие на него электрич. поля, создаваемого в сепараторе электродами с высокой разностью потенциалов, обусловливает неодинаковые электрич.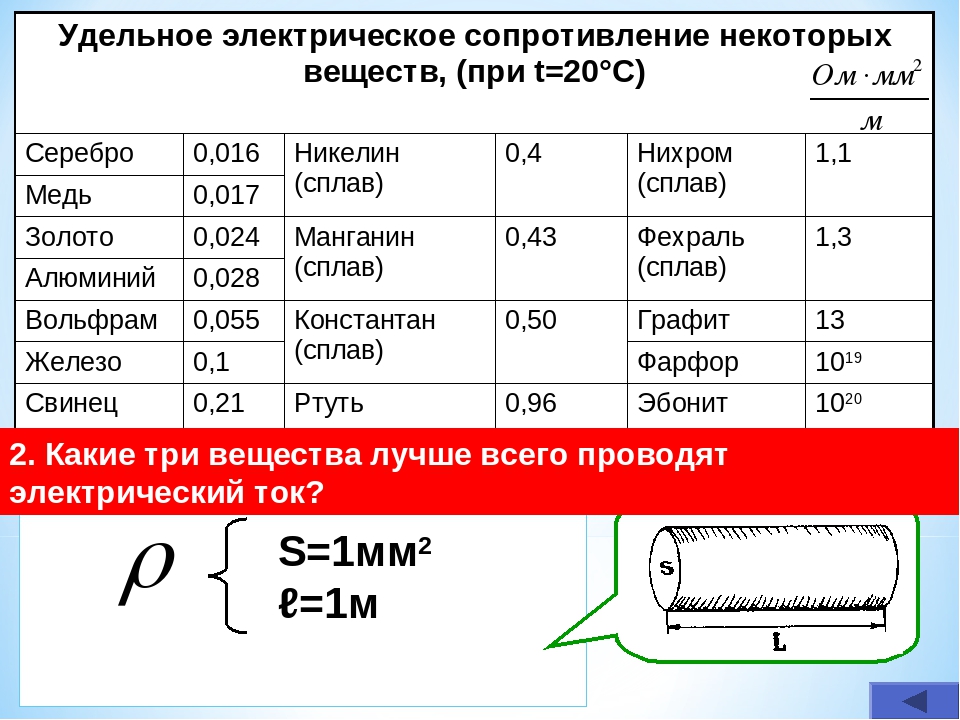 заряды минер, частиц и их разделение. При сепарации по электрич. проводимости хорошо проводящие электрич. ток частицы получают одноименный заряд, соприкасаясь с электродом, и отталкиваются от него остальные частицы практически не заряжаются. О. по электрич. проводимости осуществляется успешно (рис. 5), если компоненты минер, смеси значительно отличаются один от другого этим св-вом. Напр., проводники (антрацит, галенит, магнетит и др.) хорошо отделяются от полупроводников (боксит, касситерит, сфалерит и др.) и непроводников (алмаз, апатит, кварц и др.). [c.321]
заряды минер, частиц и их разделение. При сепарации по электрич. проводимости хорошо проводящие электрич. ток частицы получают одноименный заряд, соприкасаясь с электродом, и отталкиваются от него остальные частицы практически не заряжаются. О. по электрич. проводимости осуществляется успешно (рис. 5), если компоненты минер, смеси значительно отличаются один от другого этим св-вом. Напр., проводники (антрацит, галенит, магнетит и др.) хорошо отделяются от полупроводников (боксит, касситерит, сфалерит и др.) и непроводников (алмаз, апатит, кварц и др.). [c.321]
Магнитная сепарация коллективного гравитационного концентрата (снльномагнитная фракция железо, магнетит, пирротин, магнитная платина средне-магнитная фракция вольфрамит, гематит, гранаты, ильменит, колумбит, лимонит, турмалин, ферберит слабомагнитная фракция моиацит, светлые гранаты, турмалины, пироксены, эпидот, хромит) Электростатическая репарация (проводники вольфрамит, рутил, хромит, танталит, ильменит непроводники гранат, циркон, монацит, ксенотим) [c.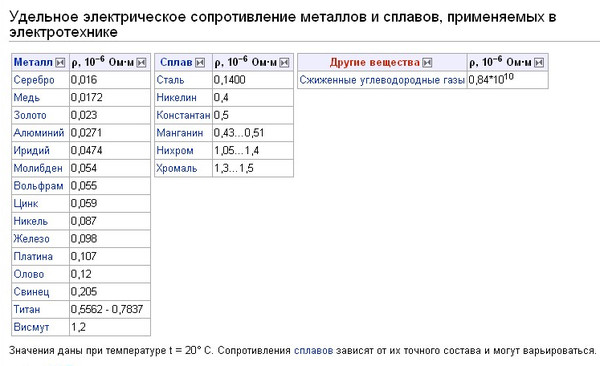 117]
117]
Магнетит К эквимолярному раство- Кубическая струк- Изометрические кристал- Проводник ру ГеЗО и Ге2(3 04)з тура (типа шпинели) лы или сферолиты черного добавляют N3 Он до pH 12 цвета Ферромаг- нетик [c.183]
Для того чтобы соединение, не проводящее электрического тока, стало электропроводным, достаточно незначительного отклонения состава от стехиометрического. Даже самые устойчивые окиси, такие, как окись алюминия А Оз, при высоких температурах становятся полупроводниками. Электропроводность таких полупроводников меняется в зависимости от парциального давления кислорода, с которым они находятся в равновесии. Особый случай представляет магнетит Рез04, в котором ионы Ре и Ре » в соотнощении 2 1 распределены в пустотах плотной решетки ионов О » (шпинельная решетка). Поэтому магнетит является почти таким же хорошим проводником электрического тока, как и металл. МП3О4 и N 304 хуже проводят электрический ток, так как имеют другое кристаллическое строение.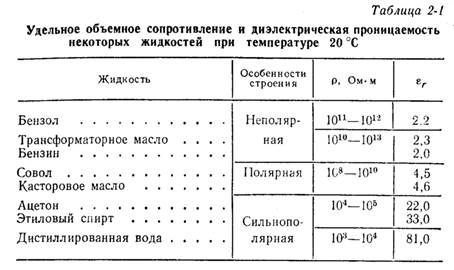 [c.670]
[c.670]
Удельное электрическое сопротивление проводника. Что такое удельное сопротивление проводника
При замыкании электрической цепи, на зажимах которой имеется разность потенциалов, возникает электрический ток. Свободные электроны под влиянием электрических сил поля перемещаются вдоль проводника. В своем движении электроны наталкиваются на атомы проводника и отдают им запас своей кинетической энергии. Скорость движения электронов непрерывно изменяется: при столкновении электронов с атомами, молекулами и другими электронами она уменьшается, потом под действием электрического поля увеличивается и снова уменьшается при новом столкновении. В результате этого в проводнике устанавливается равномерное движение потока электронов со скоростью нескольких долей сантиметра в секунду. Следовательно, электроны, проходя по проводнику, всегда встречают с его стороны сопротивление своему движению. При прохождении электрического тока через проводник последний нагревается.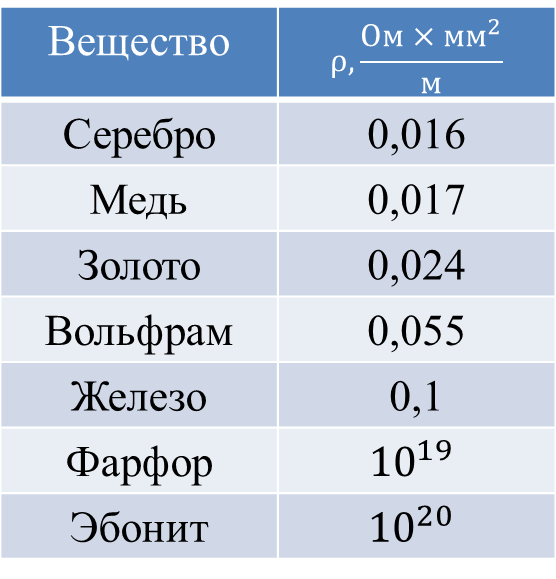
Электрическое сопротивление
Электрическим сопротивлением проводника, которое обозначается латинской буквой r , называется свойство тела или среды превращать электрическую энергию в тепловую при прохождении по нему электрического тока.
На схемах электрическое сопротивление обозначается так, как показано на рисунке 1, а .
Переменное электрическое сопротивление, служащее для изменения тока в цепи, называется реостатом . На схемах реостаты обозначаются как показано на рисунке 1, б . В общем виде реостат изготовляется из проволоки того или иного сопротивления, намотанной на изолирующем основании. Ползунок или рычаг реостата ставится в определенное положение, в результате чего в цепь вводится нужное сопротивление.
Длинный проводник малого поперечного сечения создает току большое сопротивление. Короткие проводники большого поперечного сечения оказывают току малое сопротивление.
Если взять два проводника из разного материала, но одинаковой длины и сечения, то проводники будут проводить ток по-разному. Это показывает, что сопротивление проводника зависит от материала самого проводника.
Это показывает, что сопротивление проводника зависит от материала самого проводника.
Температура проводника также оказывает влияние на его сопротивление. С повышением температуры сопротивление металлов увеличивается, а сопротивление жидкостей и угля уменьшается. Только некоторые специальные металлические сплавы (манганин, констаитан, никелин и другие) с увеличением температуры своего сопротивления почти не меняют.
Итак, мы видим, что электрическое сопротивление проводника зависит от: 1) длины проводника, 2) поперечного сечения проводника, 3) материала проводника, 4) температуры проводника.
За единицу сопротивления принят один Ом. Ом часто обозначается греческой прописной буквой Ω (омега). Поэтому вместо того чтобы писать «Сопротивление проводника равно 15 Ом», можно написать просто: r = 15 Ω.
1 000 Ом называется 1 килоом (1кОм, или 1кΩ),
1 000 000 Ом называется 1 мегаом (1мгОм, или 1МΩ).
При сравнении сопротивления проводников из различных материалов необходимо брать для каждого образца определенную длину и сечение. Тогда мы сможем судить о том, какой материал лучше или хуже проводит электрический ток.
Тогда мы сможем судить о том, какой материал лучше или хуже проводит электрический ток.
Видео 1. Сопротивление проводников
Удельное электрическое сопротивление
Сопротивление в омах проводника длиной 1 м, сечением 1 мм² называется удельным сопротивлением и обозначается греческой буквой ρ (ро).
В таблице 1 даны удельные сопротивления некоторых проводников.
Таблица 1
Удельные сопротивления различных проводников
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм² обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом.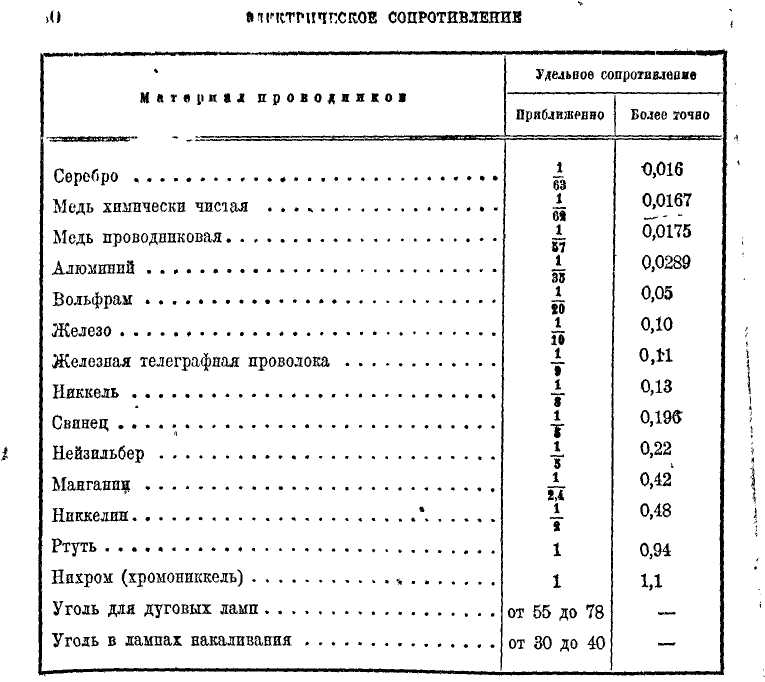 Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r – сопротивление проводника в омах; ρ – удельное сопротивление проводника; l – длина проводника в м; S – сечение проводника в мм².
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм².
Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм².
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм². Определить необходимую длину проволоки.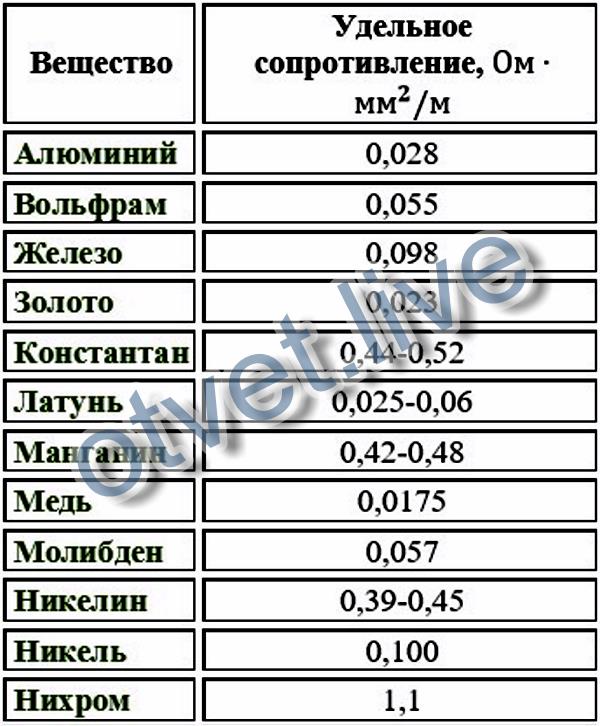
Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5. Проволока сечением 0,5 мм² и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом.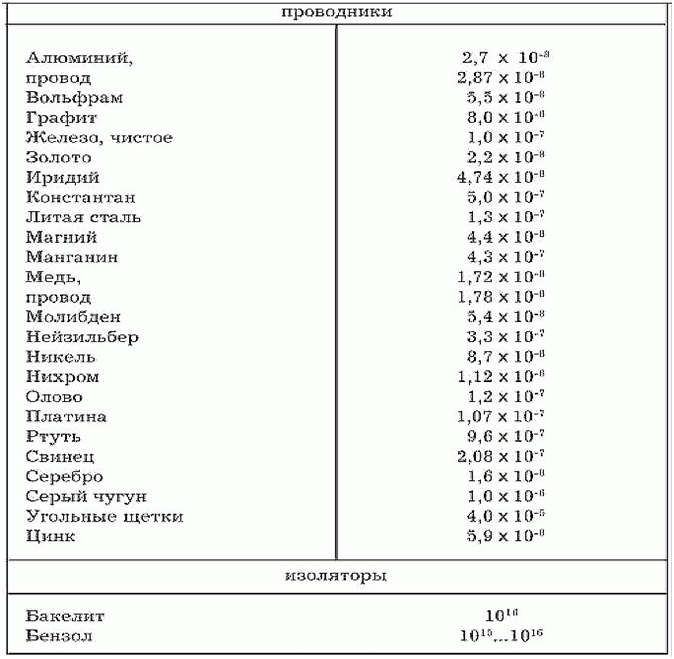 Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, называется температурным коэффициентом сопротивления и обозначается буквой α.
Если при температуре t 0 сопротивление проводника равно r 0 , а при температуре t равно r t , то температурный коэффициент сопротивления
Примечание.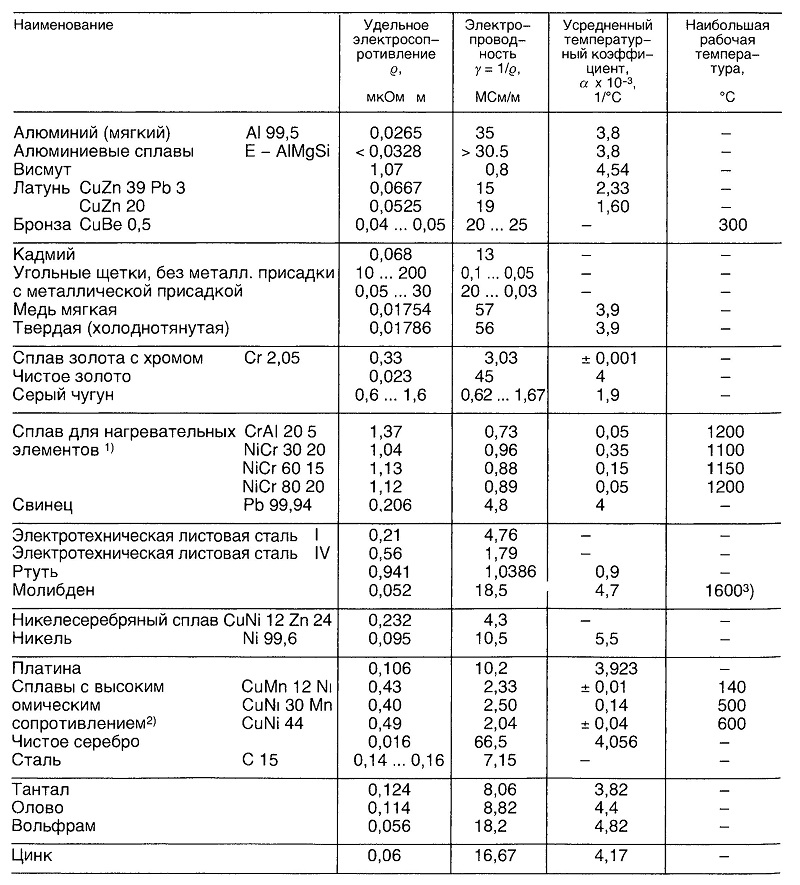 Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Таблица 2
Значения температурного коэффициента для некоторых металлов
Из формулы температурного коэффициента сопротивления определим r t :
r t = r 0 .
Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
r t = r 0 = 100 (1 + 0,0066 × 200) = 232 Ом.
Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.
Электрическая проводимость
До сих пор мы рассматривали сопротивление проводника как препятствие, которое оказывает проводник электрическому току. Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.
Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.
Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем большей проводимостью он обладает, тем легче току пройти по проводнику. Поэтому сопротивление и проводимость проводника есть величины обратные.
Из математики известно, что число, обратное 5, есть 1/5 и, наоборот, число, обратное 1/7, есть 7. Следовательно, если сопротивление проводника обозначается буквой r , то проводимость определяется как 1/r . Обычно проводимость обозначается буквой g.
Электрическая проводимость измеряется в (1/Ом) или в сименсах.
Пример 8. Сопротивление проводника равно 20 Ом. Определить его проводимость.
Если r = 20 Ом, то
Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определить его сопротивление,
Определить его сопротивление,
Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)
- активное — или омическое, резистивное, — происходящее от затрат электроэнергии на нагревание проводника (металла) при прохождении в нем электрического тока, и
- реактивное — емкостное или индуктивное, — которое происходит от неизбежных потерь на создание всякими изменениями тока, проходящего через проводник электрических полей, то и удельное сопротивление проводника бывает двух разновидностей:
Удельное сопротивление железа, алюминия и других проводников
Передача электроэнергии на дальние расстояния требует заботиться о минимизации потерь, происходящих от преодоления током сопротивления проводников, составляющих электрическую линию. Разумеется, это не значит, что подобные потери, происходящие уже конкретно в цепях и устройствах потребления, не играют роли.
Поэтому важно знать параметры всех используемых элементов и материалов. И не только электрические, но и механические. И иметь в распоряжении какие-то удобные справочные материалы, позволяющие сравнивать характеристики разных материалов и выбирать для проектирования и работы именно то, что будет оптимальным в конкретной ситуации.В линиях передачи энергии, где задачей ставится наиболее продуктивно, то есть с высоким КПД, довести энергию до потребителя, учитывается как экономика потерь, так и механика самих линий.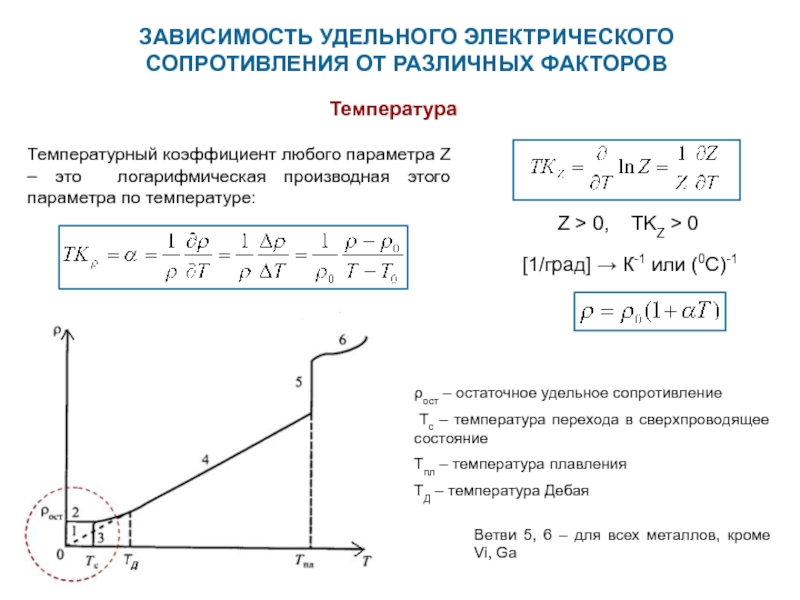 От механики — то есть устройства и расположения проводников, изоляторов, опор, повышающих/понижающих трансформаторов, веса и прочности всех конструкций, включая провода, растянутые на больших расстояниях, а также от выбранных для выполнения каждого элемента конструкции материалов, зависит и конечная экономическая эффективность линии, ее работы и затрат на эксплуатацию. Кроме того, в линиях, передающих электроэнергию, более высоки требования на обеспечение безопасности как самих линий, так и всего окружающего, где они проходят. А это добавляет затрат как на обеспечение проводки электроэнергии, так и на дополнительный запас прочности всех конструкций.
От механики — то есть устройства и расположения проводников, изоляторов, опор, повышающих/понижающих трансформаторов, веса и прочности всех конструкций, включая провода, растянутые на больших расстояниях, а также от выбранных для выполнения каждого элемента конструкции материалов, зависит и конечная экономическая эффективность линии, ее работы и затрат на эксплуатацию. Кроме того, в линиях, передающих электроэнергию, более высоки требования на обеспечение безопасности как самих линий, так и всего окружающего, где они проходят. А это добавляет затрат как на обеспечение проводки электроэнергии, так и на дополнительный запас прочности всех конструкций.
Для сравнения данные обычно приводятся к единому, сопоставимому виду. Зачастую к таким характеристикам добавляется эпитет «удельный», а сами значения рассматриваются на неких унифицированных по физическим параметрам эталонах. Например, удельное электрическое сопротивление — это сопротивление (ом) проводника, выполненного из какого-то металла (меди, алюминия, стали, вольфрама, золота), имеющего единичную длину и единичное сечение в используемой системе единиц измерения (обычно в СИ). Кроме того, оговаривается температура, так как при нагревании сопротивление проводников может вести себя по-разному. За основу берутся нормальные средние условия эксплуатации — при 20 градусах Цельсия. А там, где важны свойства при изменении параметров среды (температуры, давления), вводятся коэффициенты и составляются дополнительные таблицы и графики зависимостей.
Кроме того, оговаривается температура, так как при нагревании сопротивление проводников может вести себя по-разному. За основу берутся нормальные средние условия эксплуатации — при 20 градусах Цельсия. А там, где важны свойства при изменении параметров среды (температуры, давления), вводятся коэффициенты и составляются дополнительные таблицы и графики зависимостей.
Виды удельного сопротивления
Так как сопротивление бывает:
- Удельное электрическое сопротивление постоянному току (имеющее резистивный характер) и
- Удельное электрическое сопротивление переменному току (имеющее реактивный характер).

Здесь удельное сопротивление 2 типа является величиной комплексной, оно состоит из двух компонент ТП — активной и реактивной, так как резистивное сопротивление существует всегда при прохождении тока, независимо от его характера, а реактивное бывает только при любом изменении тока в цепях. В цепях постоянного тока реактивное сопротивление возникает только при переходных процессах, которые связаны с включением тока (изменение тока от 0 до номинала) или выключением (перепад от номинала до 0). И их учитывают обычно только при проектировании защиты от перегрузок.
В цепях же переменного тока явления, связанные с реактивными сопротивлениями, гораздо более многообразны. Они зависят не только от собственно прохождения тока через некоторое сечение, но и от формы проводника, причем зависимость не является линейной.
Дело в том, что переменный ток наводит электрическое поле как вокруг проводника, по которому протекает, так и в самом проводнике. И от этого поля возникают вихревые токи, которые дают эффект «выталкивания» собственно основного движения зарядов, из глубины всего сечения проводника на его поверхность, так называемый «скин-эффект» (от skin — кожа).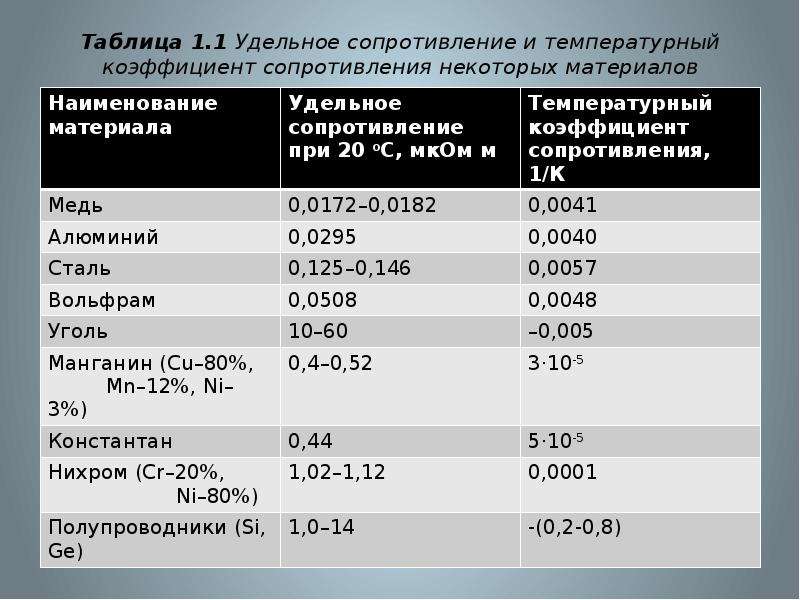 Получается, вихревые токи как бы «воруют» у проводника его сечение. Ток течет в некотором слое, близком к поверхности, остальная толщина проводника остается неиспользуемой, она не уменьшает его сопротивление, и увеличивать толщину проводников просто нет смысла. Особенно на больших частотах. Поэтому для переменного тока измеряют сопротивления в таких сечениях проводников, где все его сечение можно считать приповерхностным. Такой провод называется тонким, его толщина равна удвоенной глубине этого поверхностного слоя, куда вихревые токи и вытесняют текущий в проводнике полезный основной ток.
Получается, вихревые токи как бы «воруют» у проводника его сечение. Ток течет в некотором слое, близком к поверхности, остальная толщина проводника остается неиспользуемой, она не уменьшает его сопротивление, и увеличивать толщину проводников просто нет смысла. Особенно на больших частотах. Поэтому для переменного тока измеряют сопротивления в таких сечениях проводников, где все его сечение можно считать приповерхностным. Такой провод называется тонким, его толщина равна удвоенной глубине этого поверхностного слоя, куда вихревые токи и вытесняют текущий в проводнике полезный основной ток.
Разумеется, уменьшением толщины круглых в сечении проводов не исчерпывается эффективное проведение переменного тока. Проводник можно утончить, но при этом сделать его плоским в виде ленты, тогда сечение будет выше, чем у круглого провода, соответственно, и сопротивление ниже. Кроме того, простое увеличение площади поверхности даст эффект увеличения эффективного сечения. Того же можно добиться, используя многожильный провод вместо одножильного, к тому же, многожилка по гибкости превосходит одножилку, что часто тоже бывает ценно. С другой стороны, принимая во внимание скин-эффект в проводах, можно сделать провода композитными, выполнив сердцевину из металла, обладающего хорошими прочностными характеристиками, например, стали, но невысокими электрическими. При этом поверх стали делается алюминиевая оплетка, имеющая меньшее удельное сопротивление.
С другой стороны, принимая во внимание скин-эффект в проводах, можно сделать провода композитными, выполнив сердцевину из металла, обладающего хорошими прочностными характеристиками, например, стали, но невысокими электрическими. При этом поверх стали делается алюминиевая оплетка, имеющая меньшее удельное сопротивление.
Кроме скин-эффекта на протекание переменного тока в проводниках влияет возбуждение вихревых токов в окружающих проводниках. Такие токи называются токами наводки, и они наводятся как в металлах, не играющих роль проводки (несущие элементы конструкций), так и в проводах всего проводящего комплекса — играющих роль проводов других фаз, нулевых, заземляющих.
Все перечисленные явления встречаются во всех конструкциях, связанных с электричеством, это еще более усиливает важность иметь в своем распоряжении сводные справочные сведения по самым разным материалам.
Удельное сопротивление для проводников измеряется очень чувствительными и точными приборами, так как для проводки и выбираются металлы, имеющие самое низкое сопротивление -порядка ом *10-6 на метр длины и кв.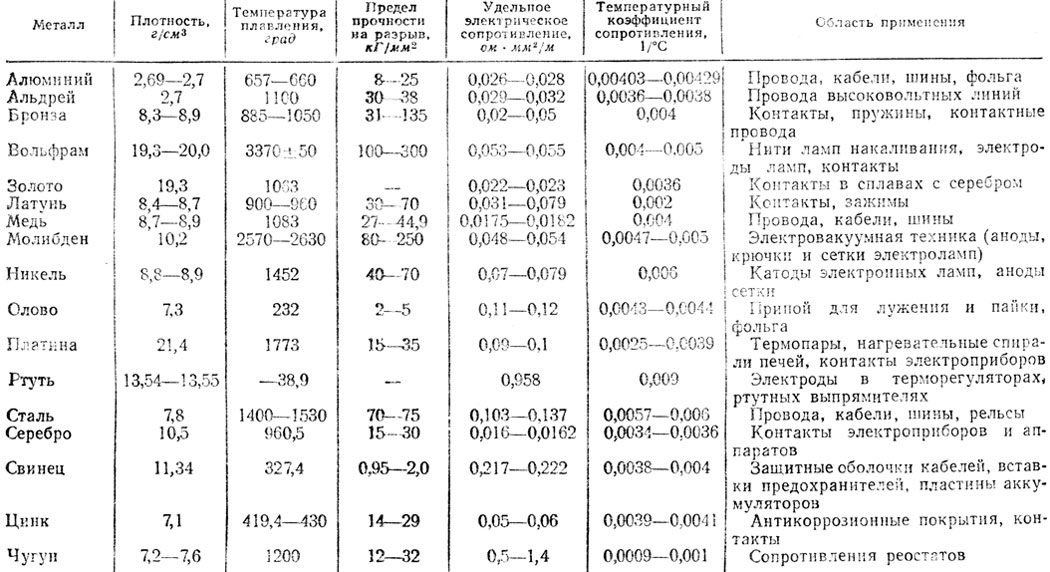 мм. сечения. Для измерения же удельного сопротивления изоляции нужны приборы, наоборот, имеющие диапазоны очень больших значений сопротивления — обычно это мегомы. Понятно, что проводники обязаны хорошо проводить, а изоляторы хорошо изолировать.
мм. сечения. Для измерения же удельного сопротивления изоляции нужны приборы, наоборот, имеющие диапазоны очень больших значений сопротивления — обычно это мегомы. Понятно, что проводники обязаны хорошо проводить, а изоляторы хорошо изолировать.
Таблица
Железо как проводник в электротехнике
Железо — самый распространенный в природе и технике металл (после водорода, который металлом тоже является). Он и самый дешевый, и имеет прекрасные прочностные характеристики, поэтому применяется повсюду как основа прочности различных конструкций.
В электротехнике в качестве проводника железо используется в виде стальных гибких проводов там, где нужна физическая прочность и гибкость, а нужное сопротивление может быть достигнуто за счет соответствующего сечения.
Имея таблицу удельных сопротивлений различных металлов и сплавов, можно посчитать сечения проводов, выполненных из разных проводников.
В качестве примера попробуем найти электрически эквивалентное сечение проводников из разных материалов: проволоки медной, вольфрамовой, никелиновой и железной. За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
Нам нужно, чтобы на длине в 1 м сопротивление провода из всех этих металлов равнялось сопротивлению исходной. Сопротивление алюминия на 1 м длины и 2,5 мм сечения будет равно
, где R – сопротивление, ρ – удельное сопротивление металла из таблицы, S – площадь сечения, L – длина.Подставив исходные значения, получим сопротивление метрового куска провода алюминия в омах.
После этого разрешим формулу относительно S
, будем подставлять значения из таблицы и получать площади сечений для разных металлов.Так как удельное сопротивление в таблице измерено на проводе длиной в 1 м, в микроомах на 1 мм2 сечения, то у нас и получилось оно в микроомах. Чтобы получить его в омах, нужно умножить значение на 10-6. Но число ом с 6 нулями после запятой нам получать совсем не обязательно, так как конечный результат все равно находим в мм2.
Как видим, сопротивление железа достаточно большое, проволока получается толстая.
Но существуют материалы, у которых оно еще больше, например, никелин или константан.
Похожие статьи:
domelectrik.ru
Таблица удельного электрического сопротивления металлов и сплавов в электротехнике
Главная > у >
Удельное сопротивление металлов.
Удельное сопротивление сплавов.
Значения даны при температуре t = 20° C. Сопротивления сплавов зависят от их точного состава. comments powered by HyperCommentstab.wikimassa.org
Удельное электрическое сопротивление | Мир сварки
Удельное электрическое сопротивление материалов
Удельное электрическое сопротивление (удельное сопротивление) — способность вещества препятствовать прохождению электрического тока.
Единица измерения (СИ) — Ом·м; также измеряется в Ом·см и Ом·мм2/м.
| Металлы | ||
| Алюминий | 20 | 0,028·10-6 |
| Бериллий | 20 | 0,036·10-6 |
| Бронза фосфористая | 20 | 0,08·10-6 |
| Ванадий | 20 | 0,196·10-6 |
| Вольфрам | 20 | 0,055·10-6 |
| Гафний | 20 | 0,322·10-6 |
| Дюралюминий | 20 | 0,034·10-6 |
| Железо | 20 | 0,097·10-6 |
| Золото | 20 | 0,024·10-6 |
| Иридий | 20 | 0,063·10-6 |
| Кадмий | 20 | 0,076·10-6 |
| Калий | 20 | 0,066·10-6 |
| Кальций | 20 | 0,046·10-6 |
| Кобальт | 20 | 0,097·10-6 |
| Кремний | 27 | 0,58·10-4 |
| Латунь | 20 | 0,075·10-6 |
| Магний | 20 | 0,045·10-6 |
| Марганец | 20 | 0,050·10-6 |
| Медь | 20 | 0,017·10-6 |
| Магний | 20 | 0,054·10-6 |
| Молибден | 20 | 0,057·10-6 |
| Натрий | 20 | 0,047·10-6 |
| Никель | 20 | 0,073·10-6 |
| Ниобий | 20 | 0,152·10-6 |
| Олово | 20 | 0,113·10-6 |
| Палладий | 20 | 0,107·10-6 |
| Платина | 20 | 0,110·10-6 |
| Родий | 20 | 0,047·10-6 |
| Ртуть | 20 | 0,958·10-6 |
| Свинец | 20 | 0,221·10-6 |
| Серебро | 20 | 0,016·10-6 |
| Сталь | 20 | 0,12·10-6 |
| Тантал | 20 | 0,146·10-6 |
| Титан | 20 | 0,54·10-6 |
| Хром | 20 | 0,131·10-6 |
| Цинк | 20 | 0,061·10-6 |
| Цирконий | 20 | 0,45·10-6 |
| Чугун | 20 | 0,65·10-6 |
| Пластмассы | ||
| Гетинакс | 20 | 109–1012 |
| Капрон | 20 | 1010–1011 |
| Лавсан | 20 | 1014–1016 |
| Органическое стекло | 20 | 1011–1013 |
| Пенопласт | 20 | 1011 |
| Поливинилхлорид | 20 | 1010–1012 |
| Полистирол | 20 | 1013–1015 |
| Полиэтилен | 20 | 1015 |
| Стеклотекстолит | 20 | 1011–1012 |
| Текстолит | 20 | 107–1010 |
| Целлулоид | 20 | 109 |
| Эбонит | 20 | 1012–1014 |
| Резины | ||
| Резина | 20 | 1011–1012 |
| Жидкости | ||
| Масло трансформаторное | 20 | 1010–1013 |
| Газы | ||
| Воздух | 0 | 1015–1018 |
| Дерево | ||
| Древесина сухая | 20 | 109–1010 |
| Минералы | ||
| Кварц | 230 | 109 |
| Слюда | 20 | 1011–1015 |
| Различные материалы | ||
| Стекло | 20 | 109–1013 |
ЛИТЕРАТУРА
- Альфа и омега.
 Краткий справочник / Таллин: Принтэст, 1991 – 448 с.
Краткий справочник / Таллин: Принтэст, 1991 – 448 с. - Справочник по элементарной физике / Н.Н. Кошкин, М.Г. Ширкевич. М., Наука. 1976. 256 с.
- Справочник по сварке цветных металлов / С.М. Гуревич. Киев.: Наукова думка. 1990. 512 с.
weldworld.ru
Удельное сопротивление металлов, электролитов и веществ (Таблица)
Удельное сопротивление металлов и изоляторов
В справочной таблице даны значения удельного сопротивления р некоторых металлов и изоляторов при температуре 18-20° С, выраженные в ом·см. Величина р для металлов в сильной степени зависит от примесей, в таблице даны значения р для химически чистых металлов, для изоляторов даны приближенно. Металлы и изоляторы расположены в таблице в порядке возрастающих значений р.
Таблица удельное сопротивление металлов
Чистые металлы | 104 ρ (ом·см) | Чистые металлы | 104 ρ (ом·см) |
Алюминий | |||
Дюралюминий | |||
Платинит 2) | |||
Аргентан | |||
Марганец | |||
Манганин | |||
Вольфрам | Константан | ||
Молибден | Сплав Вуда 3) | ||
Сплав Розе 4) | |||
Палладий | Фехраль 6) | ||
Таблица удельное сопротивление изоляторов
Изоляторы | Изоляторы | ||
Дерево сухое | |||
Целлулоид | |||
Канифоль | |||
Гетинакс | Кварц _|_ оси | ||
Стекло натр | Полистирол | ||
Стекло пирекс | |||
Кварц || оси | |||
Кварц плавленый |
Удельное сопротивление чистых металлов при низких температурах
В таблице даны значения удельного сопротивления (в ом·см) некоторых чистых металлов при низких температурах (0°С).
Отношение сопротивлении Rt/Rq чистых металлов при температуре Т °К и 273° К.
В справочной таблице дано отношение Rt/Rq сопротивлений чистых металлов при температуре Т °К и 273° К.
Чистые металлы | ||
Алюминий | ||
Вольфрам | ||
Молибден | ||
Удельное сопротивление электролитов
В таблице даны значения удельного сопротивления электролитов в ом·см при температуре 18° С. Концентрация растворов с дана в процентах, которые определяют число граммов безводной соли или кислоты в 100 г раствора.
Концентрация растворов с дана в процентах, которые определяют число граммов безводной соли или кислоты в 100 г раствора.
Источник информации: КРАТКИЙ ФИЗИКО-ТЕХНИЧЕСКИЙ СПРАВОЧНИК/ Том 1, — М.: 1960.
infotables.ru
Удельное электрическое сопротивление — сталь
Cтраница 1
Удельное электрическое сопротивление стали возрастает с ростом температуры, причем наибольшие изменения наблюдаются при нагреве до температуры точки Кюри. После точки Кюри величина удельного электросопротивления изменяется незначительно и при температурах выше 1000 С практически остается постоянной.
Ввиду большого удельного электрического сопротивления стали эти iuKii создают НсОольшое замедление в спадании потока. В контакторах на 100 а время отпадания составляет 0 07 сек, а в контакторах 600 а-0 23 сек. В связи с особыми требованиями, предъявляемыми к контакторам серии КМВ, которые предназначены для включения и отключения электромагнитов приводов масляных выключателей, электромагнитный механизм у этих контакторов допускает регулировку напряжения срабатывания и напряжения отпускания за счет регулировки силы возвратной пружины и специальной отрывной пружины. Контакторы типа КМВ должны работать при глубокой посадке напряжения. Поэтому минимальное напряжение срабатывания у этих контакторов может спускаться до 65 % UH. Такое низкое напряжение срабатывания приводит к тому, что при номинальном напряжении через обмотку протекает ток, приводящий к повышенному нагреву катушки.
Контакторы типа КМВ должны работать при глубокой посадке напряжения. Поэтому минимальное напряжение срабатывания у этих контакторов может спускаться до 65 % UH. Такое низкое напряжение срабатывания приводит к тому, что при номинальном напряжении через обмотку протекает ток, приводящий к повышенному нагреву катушки.
Присадка кремния увеличивает удельное электрическое сопротивление стали почти пропорционально содержанию кремния и этим способствует уменьшению потерь на вихревые токи, возникающие в стали при ее работе в переменном магнитном поле.
Присадка кремния увеличивает удельное электрическое сопротивление стали, что способствует уменьшению потерь на вихревые токи, но одновременно кремний ухудшает механические свойства стали, делает ее хрупкой.
Ом — мм2 / м — удельное электрическое сопротивление стали.
Для уменьшения вихревых токов применяются сердечники, выполненные из сортов стали с повышенным удельным электрическим сопротивлением стали, содержащие 0 5 — 4 8 % кремния.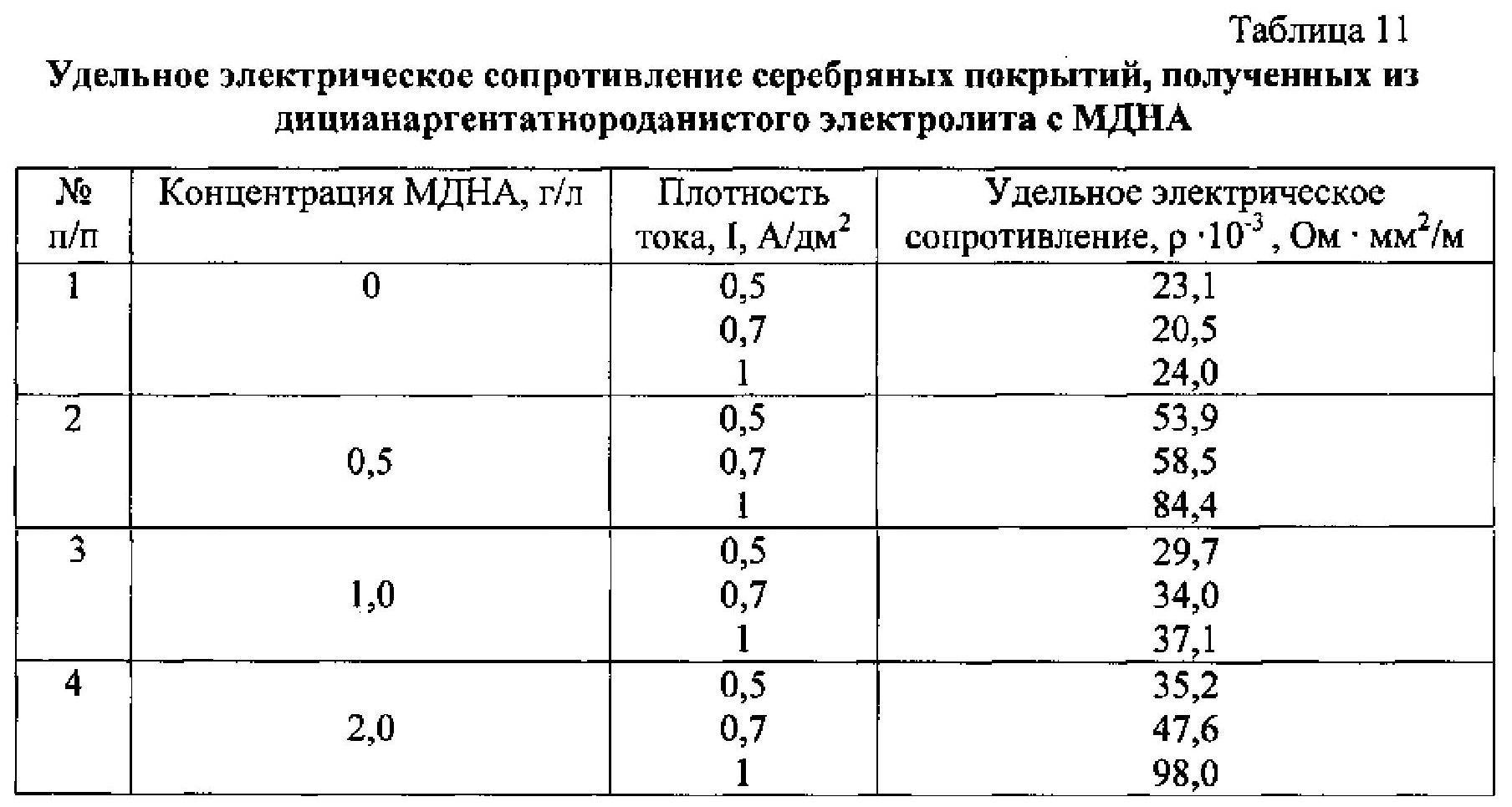
Для этого на массивный ротор из оптимального сплава СМ-19 был надет тонкий экран из магнитно-мягкой стали. Удельное электрическое сопротивление стали мало отличается от удельного сопротивления сплава, а цг стали примерно на порядок выше. Толщина экрана выбрана по глубине проникновения зубцовых гармоник первого порядка и равна йэ 0 8 мм. Для сравнения приведены добавочные потери, Вт, при базовом короткозамкнутом роторе и двухслойном роторе с массивным цилиндром из сплава СМ-19 и с медными торцевыми кольцами.
Основным магнитопроводящим материалом является листовая легированная электротехническая сталь, содержащая от 2 до 5 % кремния. Присадка кремния увеличивает удельное электрическое сопротивление стали, в результате чего уменьшаются потери на вихревые токи, сталь становится устойчивой к окислению и старению, но делается более хрупкой. В последние годы широко используется холоднокатаная текстурованная сталь с более высокими магнитными свойствами в направлении проката. Для уменьшения потерь от вихревых токов сердечник магнитопровода выполняется в виде пакета, собранного из листов штампованной стали.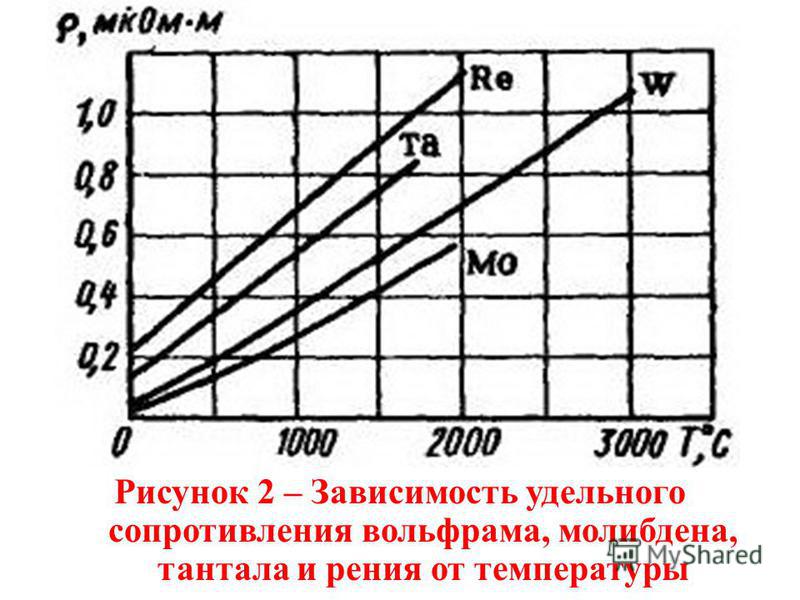
Электротехническая сталь является низкоуглеродистой сталью. Для улучшения магнитных характеристик в нее вводят кремний, который вызывает повышение удельного электрического сопротивления стали. Это приводит к уменьшению потерь на вихревые токи.
После механической обработки магнитопровод отжигают. Так как в создании замедления участвуют вихревые токи в стали, следует ориентироваться на величину удельного электрического сопротивления стали порядка Рс (Ю-15) 10 — 6 ом см. В притянутом положении якоря магнитная система достаточно сильно насыщена, поэтому начальная индукция в различных магнитных системах колеблется в очень незначительных пределах и составляет для стали марки Э Вн1 6 — 1 7 гл. Указанное значение индукции поддерживает напряженность поля в стали порядка Ян.
Для изготовления магнитных систем (магнитопроводов) трансформаторов применяются специальные тонколистовые электротехнические стали, имеющие повышенное (до 5 %) содержание кремния. Кремний способствует обезуглероживанию стали, что приводит к увеличению магнитной проницаемости, снижает потери на гистерезис и увеличивает ее удельное электрическое сопротивление. Увеличение удельного электрического сопротивления стали позволяет уменьшить потери в ней от вихревых токов. Кроме того, кремний ослабляет старение стали (увеличение потерь в стали с течением времени), уменьшает ее магнитострикцию (изменение формы и размеров тела при намагничивании) и, следовательно, шум трансформаторов. В то же время наличие кремния в стали приводит к повышению ее хрупкости и затрудняет ее механическую обработку.
Увеличение удельного электрического сопротивления стали позволяет уменьшить потери в ней от вихревых токов. Кроме того, кремний ослабляет старение стали (увеличение потерь в стали с течением времени), уменьшает ее магнитострикцию (изменение формы и размеров тела при намагничивании) и, следовательно, шум трансформаторов. В то же время наличие кремния в стали приводит к повышению ее хрупкости и затрудняет ее механическую обработку.
Страницы: 1 2
www.ngpedia.ru
Удельное сопротивление | Викитроника вики
Удельное сопротивление — характеристика материала, определяющая его способность проводить электрический ток. Определяется как отношение электрического поля к плотности тока. В общем случае является тензором, однако для большинства материалов, не проявляющих анизотропных свойств, принимается скалярной величиной.
Обозначение — ρ
$ \vec E = \rho \vec j, $
$ \vec E $ — напряжённость электрического поля, $ \vec j $ — плотность тока.
Единица измерения СИ — ом-метр (ом·м, Ω·m).
Сопротивление цилиндра или призмы (между торцами) из материала длиной l, и сечением S по удельному сопротивлению определяется следующим образом:
$ R = \frac{\rho l}{S}. $
В технике применяется определение удельного сопротивления, как сопротивление проводника единичного сечения и единичной длины.
Удельное сопротивление некоторых материалов, используемых в электротехнике Править
| серебро | 1,59·10⁻⁸ | 4,10·10⁻³ |
| медь | 1,67·10⁻⁸ | 4,33·10⁻³ |
| золото | 2,35·10⁻⁸ | 3,98·10⁻³ |
| алюминий | 2,65·10⁻⁸ | 4,29·10⁻³ |
| вольфрам | 5,65·10⁻⁸ | 4,83·10⁻³ |
| латунь | 6,5·10⁻⁸ | 1,5·10⁻³ |
| никель | 6,84·10⁻⁸ | 6,75·10⁻³ |
| железо (α) | 9,7·10⁻⁸ | 6,57·10⁻³ |
| олово серое | 1,01·10⁻⁷ | 4,63·10⁻³ |
| платина | 1,06·10⁻⁷ | 6,75·10⁻³ |
| олово белое | 1,1·10⁻⁷ | 4,63·10⁻³ |
| сталь | 1,6·10⁻⁷ | 3,3·10⁻³ |
| свинец | 2,06·10⁻⁷ | 4,22·10⁻³ |
| дюралюминий | 4,0·10⁻⁷ | 2,8·10⁻³ |
| манганин | 4,3·10⁻⁷ | ±2·10⁻⁵ |
| константан | 5,0·10⁻⁷ | ±3·10⁻⁵ |
| ртуть | 9,84·10⁻⁷ | 9,9·10⁻⁴ |
| нихром 80/20 | 1,05·10⁻⁶ | 1,8·10⁻⁴ |
| канталь А1 | 1,45·10⁻⁶ | 3·10⁻⁵ |
| углерод (алмаз, графит) | 1,3·10⁻⁵ | |
| германий | 4,6·10⁻¹ | |
| кремний | 6,4·10² | |
| этанол | 3·10³ | |
| вода, дистиллированная | 5·10³ | |
| эбонит | 10⁸ | |
| бумага твёрдая | 10¹⁰ | |
| трансформаторное масло | 10¹¹ | |
| стекло обычное | 5·10¹¹ | |
| поливинил | 10¹² | |
| фарфор | 10¹² | |
| древесина | 10¹² | |
| ПТФЭ (тефлон) | >10¹³ | |
| резина | 5·10¹³ | |
| стекло кварцевое | 10¹⁴ | |
| бумага вощёная | 10¹⁴ | |
| полистирол | >10¹⁴ | |
| слюда | 5·10¹⁴ | |
| парафин | 10¹⁵ | |
| полиэтилен | 3·10¹⁵ | |
| акриловая смола | 10¹⁹ |
ru.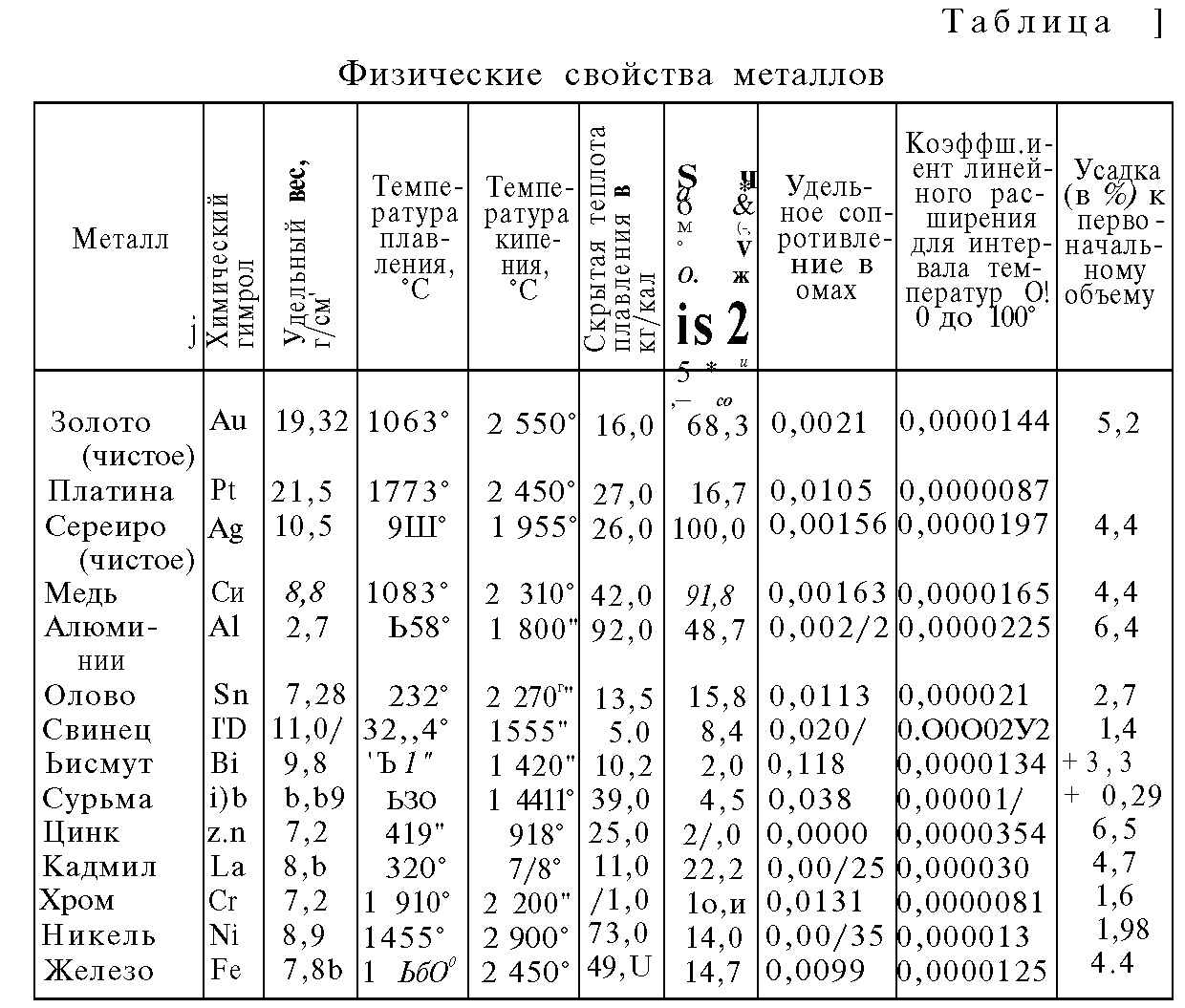 electronics.wikia.com
electronics.wikia.com
Удельное электрическое сопротивление | формула, объемное, таблица
Удельное электрическое сопротивление является физической величиной, которая показывает, в какой степени материал может сопротивляться прохождению через него электрического тока. Некоторые люди могут перепутать данную характеристику с обыкновенным электрическим сопротивлением. Несмотря на схожесть понятий, разница между ними заключается в том, что удельное касается веществ, а второй термин относится исключительно к проводникам и зависит от материала их изготовления.
Обратной величиной данного материала является удельная электрическая проводимость. Чем выше этот параметр, тем лучше проходит ток по веществу. Соответственно, чем выше сопротивление, тем больше потерь предвидится на выходе.
Формула расчета и величина измерения
Рассматривая, в чем измеряется удельное электрическое сопротивление, также можно проследить связь с не удельным, так как для обозначения параметра используются единицы Ом·м. Сама величина обозначается как ρ. С таким значением можно определять сопротивление вещества в конкретном случае, исходя из его размеров. Эта единица измерения соответствует системе СИ, но могут встречаться и другие варианты. В технике периодически можно увидеть устаревшее обозначение Ом·мм2/м. Для перевода из этой системы в международного не потребуется использовать сложные формулы, так как 1 Ом·мм2/м равняется 10-6 Ом·м.
Сама величина обозначается как ρ. С таким значением можно определять сопротивление вещества в конкретном случае, исходя из его размеров. Эта единица измерения соответствует системе СИ, но могут встречаться и другие варианты. В технике периодически можно увидеть устаревшее обозначение Ом·мм2/м. Для перевода из этой системы в международного не потребуется использовать сложные формулы, так как 1 Ом·мм2/м равняется 10-6 Ом·м.
Формула удельного электрического сопротивления выглядит следующим образом:
R= (ρ·l)/S, где:
- R – сопротивление проводника;
- Ρ – удельное сопротивление материал;
- l – длина проводника;
- S – сечение проводника.
Зависимость от температуры
Удельное электрическое сопротивление зависит от температуры. Но все группы веществ проявляют себя по-разному при ее изменении. Это необходимо учитывать при расчете проводов, которые будут работать в определенных условиях. К примеру, на улице, где значения температуры зависят от времени года, необходимые материалы с меньшей подверженностью изменениям в диапазоне от -30 до +30 градусов Цельсия. Если же планируется применение в технике, которая будет работать в одних и тех же условиях, то здесь также нужно оптимизировать проводку под конкретные параметры. Материал всегда подбирается с учетом эксплуатации.
Если же планируется применение в технике, которая будет работать в одних и тех же условиях, то здесь также нужно оптимизировать проводку под конкретные параметры. Материал всегда подбирается с учетом эксплуатации.
В номинальной таблице удельное электрическое сопротивление берется при температуре 0 градусов Цельсия. Повышение показателей данного параметра при нагреве материала обусловлено тем, что интенсивность передвижения атомов в веществе начинает возрастать. Носители электрических зарядов хаотично рассеиваются во всех направлениях, что приводит к созданию препятствий при передвижении частиц. Величина электрического потока снижается.
При уменьшении температуры условия прохождения тока становятся лучше. При достижении определенной температуры, которая для каждого металла будет отличаться, появляется сверхпроводимость, при которой рассматриваемая характеристика почти достигает нуля.
Отличия в параметрах порой достигают очень больших значений. Те материалы, которые обладают высокими показателями, могут использовать в качестве изоляторов. Они помогают защищать проводку от замыкания и ненамеренного контакта с человеком. Некоторые вещества вообще не применимы для электротехники, если у них высокое значение этого параметра. Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы. Здесь приведены значения некоторых веществ с высокими показателями.
Они помогают защищать проводку от замыкания и ненамеренного контакта с человеком. Некоторые вещества вообще не применимы для электротехники, если у них высокое значение этого параметра. Этому могут мешать другие свойства. Например, удельная электрическая проводимость воды не будет иметь большого значения для данный сферы. Здесь приведены значения некоторых веществ с высокими показателями.
| Материалы с высоким удельным сопротивлением | ρ (Ом·м) |
| Бакелит | 1016 |
| Бензол | 1015…1016 |
| Бумага | 1015 |
| Вода дистиллированная | 104 |
| Вода морская | 0.3 |
| Дерево сухое | 1012 |
| Земля влажная | 102 |
| Кварцевое стекло | 1016 |
| Керосин | 1011 |
| Мрамор | 108 |
| Парафин | 1015 |
| Парафиновое масло | 1014 |
| Плексиглас | 1013 |
| Полистирол | 1016 |
| Полихлорвинил | 1013 |
| Полиэтилен | 1012 |
| Силиконовое масло | 1013 |
| Слюда | 1014 |
| Стекло | 1011 |
| Трансформаторное масло | 1010 |
| Фарфор | 1014 |
| Шифер | 1014 |
| Эбонит | 1016 |
| Янтарь | 1018 |
Более активно в электротехнике применяются вещества с низкими показателями.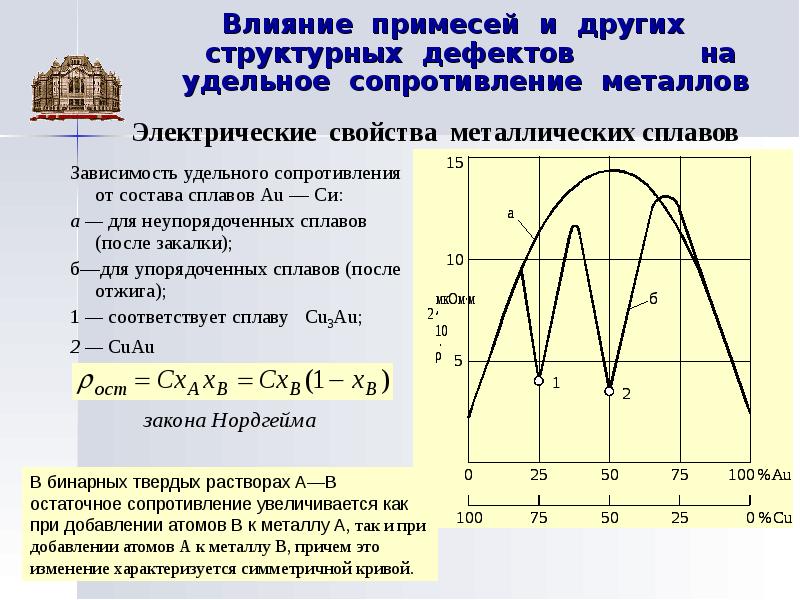 Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
Зачастую это металлы, которые служат проводниками. В них также наблюдается много различий. Чтобы узнать удельное электрическое сопротивление меди или других материалов, стоит посмотреть в справочную таблицу.
| Материалы с низким удельным сопротивлением | ρ (Ом·м) |
| Алюминий | 2.7·10-8 |
| Вольфрам | 5.5·10-8 |
| Графит | 8.0·10-6 |
| Железо | 1.0·10-7 |
| Золото | 2.2·10-8 |
| Иридий | 4.74·10-8 |
| Константан | 5.0·10-7 |
| Литая сталь | 1.3·10-7 |
| Магний | 4.4·10-8 |
| Манганин | 4.3·10-7 |
| Медь | 1.72·10-8 |
| Молибден | 5.4·10-8 |
| Нейзильбер | 3.3·10-7 |
| Никель | 8.7·10-8 |
| Нихром | 1.12·10-6 |
| Олово | 1. 2·10-7 2·10-7 |
| Платина | 1.07·10-7 |
| Ртуть | 9.6·10-7 |
| Свинец | 2.08·10-7 |
| Серебро | 1.6·10-8 |
| Серый чугун | 1.0·10-6 |
| Угольные щетки | 4.0·10-5 |
| Цинк | 5.9·10-8 |
| Никелин | 0,4·10-6 |
Удельное объемное электрическое сопротивление
Данный параметр характеризует возможность пропускать ток через объем вещества. Для измерения необходимо приложить потенциал напряжения с разных сторон материала, изделие из которого будет включено в электрическую цепь. На него подается ток с номинальными параметрами. После прохождения измеряются данные на выходе.
Использование в электротехнике
Изменение параметра при разных температурах широко применяется в электротехнике. Наиболее простым примером является лампа накаливания, где используется нихромовая нить. При нагревании она начинает светиться. При прохождении через нее тока она начинает нагреваться. С ростом нагрева возрастает и сопротивление. Соответственно, ограничивается первоначальный ток, который нужен был для получения освещения. Нихромовая спираль, используя тот же принцип, может стать регулятором на различных аппаратах.
Широкое применение коснулось и благородных металлов, которые обладают подходящими характеристиками для электротехники. Для ответственных схем, которым требуется быстродействие, подбираются серебряные контакты. Они обладают высокой стоимостью, но с учетом относительно небольшого количества материалов их применение вполне оправданно. Медь уступает серебру по проводимости, но обладает более доступной ценой, благодаря чему ее чаще используют для создания проводов.
В условиях, где можно использовать предельно низкие температуры, применяются сверхпроводники. Для комнатной температуры и уличной эксплуатации они не всегда уместны, так как при повышении температуры их проводимость начнет падать, поэтому для таких условий лидерами остаются алюминий, медь и серебро.
На практике учитывается много параметров и этот является одним из наиболее важных. Все расчеты проводятся еще на стадии проектирования, для чего и используются справочные материалы.
Каждое вещество способно проводить ток в разной степени, на эту величину влияет сопротивление материала. Обозначается удельное сопротивление меди, алюминия, стали и любого другого элемента буквой греческого алфавита ρ. Эта величина не зависит от таких характеристик проводника, как размеры, форма и физическое состояние, обычное же электросопротивление учитывает эти параметры. Измеряется удельное сопротивление в Омах, умноженных на мм² и разделенных на метр.
Категории и их описание
Любой материал способен проявлять два типа сопротивления в зависимости от подаваемого на него электричества. Ток бывает переменным или постоянным, что значительно влияет на технические показатели вещества. Так, существуют такие сопротивления:
- Омическое. Проявляется под воздействием постоянного тока. Характеризует трение, которое создается движением электрически заряженных частиц в проводнике.
- Активное. Определяется по такому же принципу, но создается уже под действием переменного тока.
В связи с этим определений удельной величины тоже два. Для постоянного тока она равна сопротивлению, которое оказывает единица длины проводящего материала единичной фиксированной площади сечения. Потенциальное электрополе воздействует на все проводники, а также полупроводники и растворы, способные проводить ионы. Эта величина определяет проводящие свойства самого материала. Форма проводника и его размеры не учитываются, поэтому ее можно назвать базовой в электротехнике и материаловедении.
При условии прохождения переменного тока удельная величина рассчитывается с учетом толщины проводящего материала. Здесь уже происходит воздействие не только потенциального, но и вихревого тока, кроме того, принимается во внимание частота электрических полей. Удельное сопротивление этого типа больше, чем при постоянном токе, поскольку здесь идет учет положительной величины сопротивления вихревому полю. Также эта величина зависит от формы и размеров самого проводника. Именно эти параметры и определяют характер вихревого движения заряженных частиц.
Переменный ток вызывает в проводниках определенные электромагнитные явления. Они очень важны для электротехнических характеристик проводящего материала:
- Скин-эффект характеризуется ослаблением электромагнитного поля тем больше, чем дальше оно проникает в среду проводника. Это явление также носит название поверхностного эффекта.
- Эффект близости снижает плотность тока благодаря близости соседних проводов и их влиянию.
Эти эффекты являются очень важными при расчете оптимальной толщины проводника, так как при использовании провода, у которого радиус больше глубины проникновения тока в материал, остальная его масса останется незадействованной, а следовательно, такой подход будет неэффективным. В соответствии с проведенными расчетами эффективный диаметр проводящего материала в некоторых ситуациях будет следующим:
- для тока в 50 Гц — 2,8 мм;
- 400 Гц — 1 мм;
- 40 кГц — 0,1 мм.
Ввиду этого для высокочастотных токов активно применяется использование плоских многожильных кабелей, состоящих из множества тонких проводов.
Характеристики металлов
Удельные показатели металлических проводников содержатся в специальных таблицах. По этим данным можно производить необходимые дальнейшие расчеты. Пример такой таблицы удельных сопротивлений можно увидеть на изображении.
На таблице видно, что наибольшей проводимостью обладает серебро — это идеальный проводник среди всех существующих металлов и сплавов. Если рассчитать, сколько потребуется провода из этого материала для получения сопротивления в 1 Ом, то выйдет 62,5 м. Проволоки из железа для такой же величины понадобится целых 7,7 м.
Какими бы замечательными свойствами ни обладало серебро, оно является слишком дорогим материалом для массового использования в электросетях, поэтому широкое применение в быту и промышленности нашла медь. По величине удельного показателя она стоит на втором месте после серебра, а по распространенности и простоте добычи намного лучше его. Медь обладает и другими преимуществами, позволившими ей стать самым распространенным проводником. К ним относятся:
Для применения в электротехнике используют рафинированную медь, которая после плавки из сульфидной руды проходит процессы обжигания и дутья, а далее обязательно подвергается электролитической очистке. После такой обработки можно получить материал очень высокого качества (марки М1 и М0), который будет содержать от 0,1 до 0,05% примесей. Важным нюансом является присутствие кислорода в крайне малых количествах, так как он негативно влияет на механические характеристики меди.
Часто этот металл заменяют более дешевыми материалами — алюминием и железом, а также различными бронзами (сплавами с кремнием, бериллием, магнием, оловом, кадмием, хромом и фосфором). Такие составы обладают более высокой прочностью по сравнению с чистой медью, хотя и меньшей проводимостью.
Преимущества алюминия
Хоть алюминий обладает большим сопротивлением и более хрупок, его широкое использование объясняется тем, что он не настолько дефицитен, как медь, а следовательно, стоит дешевле. Удельное сопротивление алюминия составляет 0,028, а его низкая плотность обеспечивает ему вес в 3,5 раза меньше, чем медь.
Для электрических работ применяют очищенный алюминий марки А1, содержащий не более 0,5% примесей. Более высокую марку АВ00 используют для изготовления электролитических конденсаторов, электродов и алюминиевой фольги. Содержание примесей в этом алюминии составляет не более 0,03%. Существует и чистый металл АВ0000 , включающий не более 0,004% добавок. Имеют значение и сами примеси: никель, кремний и цинк незначительно влияют на проводимость алюминия, а содержание в этом металле меди, серебра и магния дает ощутимый эффект. Наиболее сильно уменьшают проводимость таллий и марганец.
Алюминий отличается хорошими антикоррозийными свойствами. При контакте с воздухом он покрывается тонкой пленкой окиси, которая и защищает его от дальнейшего разрушения. Для улучшения механических характеристик металл сплавляют с другими элементами.
Показатели стали и железа
Удельное сопротивление железа по сравнению с медью и алюминием имеет очень высокие показатели, однако благодаря доступности, прочности и устойчивости к деформациям материал широко используют в электротехническом производстве.
Хоть железо и сталь, удельное сопротивление которой еще выше, имеют существенные недостатки, изготовители проводникового материала нашли методы их компенсирования. В частности, низкую стойкость к коррозии преодолевают путем покрытия стальной проволоки цинком или медью.
Свойства натрия
Металлический натрий также очень перспективен в проводниковом производстве. По показателям сопротивления он значительно превышает медь, однако имеет плотность в 9 раз меньше, чем у неё. Это позволяет использовать материал в изготовлении сверхлёгких проводов.
Металлический натрий очень мягкий и совершенно неустойчив к любого рода деформационным воздействиям, что делает его использование проблемным — провод из этого металла должен быть покрыт очень прочной оболочкой с крайне малой гибкостью. Оболочка должна быть герметичной, так как натрий проявляет сильную химическую активность в самых нейтральных условиях. Он моментально окисляется на воздухе и демонстрирует бурную реакцию с водой, в том числе и с содержащейся в воздухе.
Еще одним плюсом использования натрия является его доступность. Его можно получить в процессе электролиза расплавленного хлористого натрия, которого в мире существует неограниченное количество. Другие металлы в этом плане явно проигрывают.
Чтобы рассчитать показатели конкретного проводника, необходимо произведение удельного числа и длины проволоки разделить на площадь ее сечения. В результате получится значение сопротивления в Омах. Например, чтобы определить, чему равно сопротивление 200 м проволоки из железа с номинальным сечением 5 мм², нужно 0,13 умножить на 200 и разделить полученный результат на 5. Ответ — 5,2 Ом.
Правила и особенности вычисления
Для измерения сопротивления металлических сред пользуются микроомметрами. Сегодня их выпускают в цифровом варианте, поэтому проведенные с их помощью измерения отличаются точностью. Объяснить ее можно тем, что металлы обладают высоким уровнем проводимости и имеют крайне маленькое сопротивление. Для примера, нижний порог измерительных приборов имеет значение 10 -7 Ом.
С помощью микроомметров можно быстро определить, насколько качественен контакт и какое сопротивление проявляют обмотки генераторов, электродвигателей и трансформаторов, а также электрические шины. Можно вычислить присутствие включений другого металла в слитке. Например, вольфрамовый кусок, покрытый позолотой, показывает вдвое меньшую проводимость, чем полностью золотой. Тем же способом можно определить внутренние дефекты и полости в проводнике.
Формула удельного сопротивления выглядит следующим образом: ρ = Ом · мм 2 /м . Словами ее можно описать как сопротивление 1 метра проводника , имеющего площадь сечения 1 мм². Температура подразумевается стандартная — 20 °C.
Влияние температуры на измерение
Нагревание или охлаждение некоторых проводников оказывает значительное влияние на показатели измерительных приборов. В качестве примера можно привести следующий опыт: необходимо подключить к аккумулятору спирально намотанную проволоку и подключить в цепь амперметр.
Чем сильнее нагревается проводник, тем меньше становятся показания прибора. Сила тока имеет обратно пропорциональную зависимость от сопротивления. Следовательно, можно сделать вывод, что в результате нагрева проводимость металла уменьшается. В большей или меньшей степени так ведут себя все металлы, однако изменения проводимости у некоторых сплавов практически не наблюдается.
Примечательно, что жидкие проводники и некоторые твердые неметаллы имеют тенденцию уменьшать свое сопротивление с повышением температуры. Но и эту способность металлов ученые обратили себе на пользу. Зная температурный коэффициент сопротивления (α) при нагреве некоторых материалов, можно определять внешнюю температуру. Например, проволоку из платины, размещенную на каркасе из слюды, помещают в печь, после чего проводят измерение сопротивления. В зависимости от того, насколько оно изменилось, делают вывод о температуре в печи. Такая конструкция называется термометром сопротивления.
Если при температуре t 0 сопротивление проводника равно r 0, а при температуре t равно rt , то температурный коэффициент сопротивления равен
Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200 °C).
Поэтому важно знать параметры всех используемых элементов и материалов. И не только электрические, но и механические. И иметь в распоряжении какие-то удобные справочные материалы, позволяющие сравнивать характеристики разных материалов и выбирать для проектирования и работы именно то, что будет оптимальным в конкретной ситуации.
В линиях передачи энергии, где задачей ставится наиболее продуктивно, то есть с высоким КПД, довести энергию до потребителя, учитывается как экономика потерь, так и механика самих линий. От механики — то есть устройства и расположения проводников, изоляторов, опор, повышающих/понижающих трансформаторов, веса и прочности всех конструкций, включая провода, растянутые на больших расстояниях, а также от выбранных для выполнения каждого элемента конструкции материалов, зависит и конечная экономическая эффективность линии, ее работы и затрат на эксплуатацию. Кроме того, в линиях, передающих электроэнергию, более высоки требования на обеспечение безопасности как самих линий, так и всего окружающего, где они проходят. А это добавляет затрат как на обеспечение проводки электроэнергии, так и на дополнительный запас прочности всех конструкций.
Для сравнения данные обычно приводятся к единому, сопоставимому виду. Зачастую к таким характеристикам добавляется эпитет «удельный», а сами значения рассматриваются на неких унифицированных по физическим параметрам эталонах. Например, удельное электрическое сопротивление — это сопротивление (ом) проводника, выполненного из какого-то металла (меди, алюминия, стали, вольфрама, золота), имеющего единичную длину и единичное сечение в используемой системе единиц измерения (обычно в СИ). Кроме того, оговаривается температура, так как при нагревании сопротивление проводников может вести себя по-разному. За основу берутся нормальные средние условия эксплуатации — при 20 градусах Цельсия. А там, где важны свойства при изменении параметров среды (температуры, давления), вводятся коэффициенты и составляются дополнительные таблицы и графики зависимостей.
Виды удельного сопротивления
Так как сопротивление бывает:
- активное — или омическое, резистивное, — происходящее от затрат электроэнергии на нагревание проводника (металла) при прохождении в нем электрического тока, и
- реактивное — емкостное или индуктивное, — которое происходит от неизбежных потерь на создание всякими изменениями тока, проходящего через проводник электрических полей, то и удельное сопротивление проводника бывает двух разновидностей:
- Удельное электрическое сопротивление постоянному току (имеющее резистивный характер) и
- Удельное электрическое сопротивление переменному току (имеющее реактивный характер).
Здесь удельное сопротивление 2 типа является величиной комплексной, оно состоит из двух компонент ТП — активной и реактивной, так как резистивное сопротивление существует всегда при прохождении тока, независимо от его характера, а реактивное бывает только при любом изменении тока в цепях. В цепях постоянного тока реактивное сопротивление возникает только при переходных процессах, которые связаны с включением тока (изменение тока от 0 до номинала) или выключением (перепад от номинала до 0). И их учитывают обычно только при проектировании защиты от перегрузок.
В цепях же переменного тока явления, связанные с реактивными сопротивлениями, гораздо более многообразны. Они зависят не только от собственно прохождения тока через некоторое сечение, но и от формы проводника, причем зависимость не является линейной.
Дело в том, что переменный ток наводит электрическое поле как вокруг проводника, по которому протекает, так и в самом проводнике. И от этого поля возникают вихревые токи, которые дают эффект «выталкивания» собственно основного движения зарядов, из глубины всего сечения проводника на его поверхность, так называемый «скин-эффект» (от skin — кожа). Получается, вихревые токи как бы «воруют» у проводника его сечение. Ток течет в некотором слое, близком к поверхности, остальная толщина проводника остается неиспользуемой, она не уменьшает его сопротивление, и увеличивать толщину проводников просто нет смысла. Особенно на больших частотах. Поэтому для переменного тока измеряют сопротивления в таких сечениях проводников, где все его сечение можно считать приповерхностным. Такой провод называется тонким, его толщина равна удвоенной глубине этого поверхностного слоя, куда вихревые токи и вытесняют текущий в проводнике полезный основной ток.
Разумеется, уменьшением толщины круглых в сечении проводов не исчерпывается эффективное проведение переменного тока. Проводник можно утончить, но при этом сделать его плоским в виде ленты, тогда сечение будет выше, чем у круглого провода, соответственно, и сопротивление ниже. Кроме того, простое увеличение площади поверхности даст эффект увеличения эффективного сечения. Того же можно добиться, используя многожильный провод вместо одножильного, к тому же, многожилка по гибкости превосходит одножилку, что часто тоже бывает ценно. С другой стороны, принимая во внимание скин-эффект в проводах, можно сделать провода композитными, выполнив сердцевину из металла, обладающего хорошими прочностными характеристиками, например, стали, но невысокими электрическими. При этом поверх стали делается алюминиевая оплетка, имеющая меньшее удельное сопротивление.
Кроме скин-эффекта на протекание переменного тока в проводниках влияет возбуждение вихревых токов в окружающих проводниках. Такие токи называются токами наводки, и они наводятся как в металлах, не играющих роль проводки (несущие элементы конструкций), так и в проводах всего проводящего комплекса — играющих роль проводов других фаз, нулевых, заземляющих.
Все перечисленные явления встречаются во всех конструкциях, связанных с электричеством, это еще более усиливает важность иметь в своем распоряжении сводные справочные сведения по самым разным материалам.
Удельное сопротивление для проводников измеряется очень чувствительными и точными приборами, так как для проводки и выбираются металлы, имеющие самое низкое сопротивление -порядка ом *10 -6 на метр длины и кв. мм. сечения. Для измерения же удельного сопротивления изоляции нужны приборы, наоборот, имеющие диапазоны очень больших значений сопротивления — обычно это мегомы. Понятно, что проводники обязаны хорошо проводить, а изоляторы хорошо изолировать.
Таблица
Таблица удельных сопротивлений проводников (металлов и сплавов) | ||||
Материал провод-ника | Состав (для сплавов) | Удельное сопротивление ρ мом × мм 2 / м | ||
медь, цинк, олово, никель, свинец, марганец, железо и др. | ||||
Алюминий | ||||
Вольфрам | ||||
Молибден | ||||
медь, олово, алюминий, кремний, бериллий, свинец и др. (кроме цинка) | ||||
железо, углерод | ||||
медь, никель, цинк | ||||
Манганин | медь, никель, марганец | |||
Константан | медь, никель, алюминий | |||
никель, хром, железо, марганец | ||||
железо, хром, алюминий, кремний, марганец | ||||
Железо как проводник в электротехнике
Железо — самый распространенный в природе и технике металл (после водорода, который металлом тоже является). Он и самый дешевый, и имеет прекрасные прочностные характеристики, поэтому применяется повсюду как основа прочности различных конструкций.
В электротехнике в качестве проводника железо используется в виде стальных гибких проводов там, где нужна физическая прочность и гибкость, а нужное сопротивление может быть достигнуто за счет соответствующего сечения.
Имея таблицу удельных сопротивлений различных металлов и сплавов, можно посчитать сечения проводов, выполненных из разных проводников.
В качестве примера попробуем найти электрически эквивалентное сечение проводников из разных материалов: проволоки медной, вольфрамовой, никелиновой и железной. За исходную возьмем проволоку алюминиевую сечением 2,5 мм.
Нам нужно, чтобы на длине в 1 м сопротивление провода из всех этих металлов равнялось сопротивлению исходной. Сопротивление алюминия на 1 м длины и 2,5 мм сечения будет равно
Где R – сопротивление, ρ – удельное сопротивление металла из таблицы, S – площадь сечения, L – длина.
Подставив исходные значения, получим сопротивление метрового куска провода алюминия в омах.
После этого разрешим формулу относительно S
Будем подставлять значения из таблицы и получать площади сечений для разных металлов.
Так как удельное сопротивление в таблице измерено на проводе длиной в 1 м, в микроомах на 1 мм 2 сечения, то у нас и получилось оно в микроомах. Чтобы получить его в омах, нужно умножить значение на 10 -6 . Но число ом с 6 нулями после запятой нам получать совсем не обязательно, так как конечный результат все равно находим в мм 2 .
Как видим, сопротивление железа достаточно большое, проволока получается толстая.
Но существуют материалы, у которых оно еще больше, например, никелин или константан.
Электрический ток возникает в результате замыкания цепи с разностью потенциалов на зажимах. Силы поля воздействуют на свободные электроны и они перемещаются по проводнику. В процессе этого путешествия, электроны встречаются с атомами и передают им часть своей накопившейся энергии. В результате этого их скорость уменьшается. Но, из-за воздействия электрического поля, она снова набирает обороты. Таким образом, электроны постоянно испытывают на себе сопротивление, именно поэтому электрический ток нагревается.
Свойство вещества, превращать электроэнергию в тепло во время воздействия тока, и является электрическим сопротивлением и обозначается, как R, его измерительной единицей является Ом. Величина сопротивления зависит, главным образом от способности различных материалов проводить ток.
Впервые, о сопротивляемости заявил немецкий исследователь Г. Ом.
Для того, чтобы узнать зависимость силы тока от сопротивления, известный физик провел множество экспериментов. Для опытов он использовал различные проводники и получал различные показатели.
Первое, что определил Г. Ом — это то, что удельное сопротивление зависит от длинны проводника. То есть, если увеличивалась длинна проводника, сопротивление тоже увеличивалось. В результате, эта связь была определена, как прямо пропорциональная.
Вторая зависимость — это площадь поперечного сечения. Её можно было определить путем поперечного среза проводника. Площадь той фигуры, что образовалась на срезе и есть площадь поперечного сечения. Здесь связь получилась обратно пропорциональная. То есть чем больше была площадь поперечного сечения, тем меньше становилось сопротивление проводника.
И третья, важная величина, от которой зависит сопротивление, это материал. В результате того, что Ом использовал в опытах различные материалы, он обнаружил различные свойства сопротивляемости. Все эти опыты и показатели были сведены в таблицу из которой видно, различное значение удельной сопротивляемости у различных веществ.
Известно, что самые лучшие проводники — металлы. А какие из металлов лучшие проводники? В таблице показано, что наименьшей сопротивляемостью обладают медь и серебро. Медь используется чаще из-за меньшей стоимости, а серебро применяют в наиболее важных и ответственных приборах.
Вещества с высоким удельным сопротивлением в таблице, плохо проводят электрический ток, а значит могут быть прекрасными изоляционными материалами. Вещества обладающие этим свойством в наибольшей степени, это фарфор и эбонит.
Вообще, удельное электрическое сопротивление является очень важным фактором, ведь, определив его показатель, мы можем узнать из какого вещества сделан проводник. Для этого необходимо измерить площадь сечения, узнать силу тока с помощью вольтметра и амперметра, а также измерить напряжение. Таким образом мы узнаем значение удельного сопротивления и, с помощью таблицы легко выйдем на вещество. Получается, что удельное сопротивление — это в роде отпечатков пальцев вещества. Кроме этого, удельное сопротивление важно при планировании длинных электрических цепей: нам необходимо знать этот показатель, чтобы соблюдать баланс между длинной и площадью.
Есть формула, определяющая, что сопротивление равно 1 ОМ, если при напряжении 1В, его сила тока равняется 1А. То есть, сопротивление единичной площади и единичной длинны, сделанного из определенного вещества и есть удельное сопротивление.
Надо отметить также, что показатель удельного сопротивления напрямую зависит от частоты вещества. То есть от того имеет ли он примеси. Та, добавление всего одного процента марганца увеличивает сопротивляемость самого проводящего вещества — меди, в три раза.
Эта таблица демонстрирует величину удельного электрического сопротивления некоторых веществ.
Материалы с высокой проводимостью
Медь
Как мы уже говорили медь чаще всего применяется в качестве проводника. Это объясняется не только её низкой сопротивляемостью. Медь имеет такие преимущества, как высокая прочность, стойкость к коррозии, легкость в использовании и хорошая обрабатываемость. Хорошими марками меди считается М0 и М1. В них количество примесей не превышает 0,1%.
Высокая стоимость металла и его преобладающая в последнее время дефицитность побуждает производителей применять в качестве проводника алюминий. Также, используются сплавы меди с различными металлами.
Алюминий
Этот металл значительно легче меди, но алюминий обладает большими значениями теплоемкости и температуры плавления. В связи с этим для того, что довести его до расплавленного состояния требуется больше энергии, чем меди. Тем не менее нужно учитывать факт дефицитности меди.
В производстве электротехнических изделий применяется, как правило, алюминий марки А1. Он содержит не более 0,5% примесей. А металл наивысшей частоты — это алюминий марки АВ0000.
Железо
Дешевизна и доступность железа омрачается его высокой удельной сопротивляемостью. Кроме того, она быстро подвергается коррозии. По этой причине стальные проводники часто покрывают цинком. Широко используется так называемый биметалл — это сталь покрытая для защиты медью.
Натрий
Натрий, тоже доступный и перспективный материал, но его сопротивляемость почти в три раза больше меди. Кроме того, металлический натрий обладает высокой химической активностью, что обязывает покрывать такой проводник герметичной защитой. Она же должна защищать проводник от механических повреждений, так как натрий очень мягкий и достаточно непрочный материал.
Сверхпроводимость
В таблице ниже, указано удельное сопротивление веществ при температуре 20 градусов. Указание температуры неслучайно, ведь удельное сопротивление напрямую зависит от этого показателя. Это объясняется тем, что при нагревании, повышается и скорость атомов, а значит вероятность встречи их с электронами тоже увеличится.
Интересно, что происходит с сопротивляемостью в условиях охлаждения. Впервые поведение атомов при очень низких температурах заметил Г. Камерлинг-Оннес в 1911 году. Он охладил ртутную проволоку до 4К и обнаружил падение её сопротивляемости до нуля. Изменение показателя удельной сопротивляемости у некоторых сплавов и металлов в условиях низкой температуры, физик назвал сверхпроводимостью.
Сверхпроводники переходят в состояние сверхпроводимости при охлаждении, и, при этом их оптические и структурные характеристики не меняются. Главное открытие состоит в том, что электрические и магнитные свойства металлов в сверхпроводящем состоянии сильно отличаются от их же свойств в обычном состоянии, а также от свойств других металлов, которые при понижении температуры не могут переходить в это состояние.
Применение сверхпроводников осуществляется, главным образом, в получении сверхсильного магнитного поля, сила которого достигает 107 А/м. Также разрабатываются системы сверхпроводящих линий электропередач.
Похожие материалы.
Рекомендуем также
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в cookie-файлах может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Удельное электрическое сопротивление и теплопроводность жидких сплавов Fe при высоких значениях P и T, а также тепловой поток в ядре Земли
Abstract
Магнитное поле Земли поддерживается за счет магнитогидродинамической конвекции внутри металлического жидкого ядра. В термически адвекционном ядре доля тепла, доступного для движения геодинамо, уменьшается за счет тепла, проводимого вдоль геотермы ядра, которое сильно зависит от теплопроводности жидкого железа и его сплавов с кандидатами на легкие элементы.Теплопроводность ядра Земли очень плохо ограничена, текущие оценки основаны на наборе масштабных соотношений, которые ранее не тестировались при высоких давлениях. Мы выполняем расчеты электронной структуры из первых принципов для определения теплопроводности и электросопротивления для жидких сплавов Fe, Fe – Si и Fe – O. Расчетное удельное сопротивление очень хорошо согласуется с существующими измерениями ударного сжатия и показывает сильную зависимость от концентрации и типа легких элементов. Теплопроводность при давлении и температуре, характерных для ядра Земли, выше, чем предыдущие экстраполяции.Кондуктивный тепловой поток вблизи границы ядро-мантия сравним с оценками полного теплового потока от ядра, но уменьшается с глубиной, так что тепловой поток будет ограничиваться большей глубиной в отсутствие внутреннего ядра.
Генерация магнитного поля Земли напрямую связана с тепловой эволюцией жидкого внешнего ядра, охлаждение которого модулируется тепловым потоком из ядра в основание мантии (1⇓⇓⇓⇓ – 6). В простом ядре с тепловым приводом, например, при отсутствии кристаллизующегося внутреннего ядра и связанного с ним выделения скрытого тепла и химической плавучести, тепло, переносимое за счет теплопроводности, недоступно для движения геодинамо.Знание его относительного вклада в перенос тепла в ядре, следовательно, имеет решающее значение для понимания долгосрочной стабильности магнитного поля Земли, которое присутствовало еще 3,45 миллиарда лет назад (7), когда ядро, вероятно, было слишком горячим для твердое внутреннее ядро для кристаллизации (1, 4).
Существующие оценки теплопроводности ( k el ) и удельного электрического сопротивления ( ρ el ) внешнего ядра Земли основаны на экстраполяциях (8, 9) измерений удельного сопротивления в ударно сжатых Fe и Fe– Сплавы Si (10⇓ – 12) до температуры и давления в сердцевине.Эти экстраполяции предполагают прямую пропорциональность удельного электрического сопротивления температуре, его неизменность вдоль и поперек ликвидуса Fe и соблюдение закона Видемана-Франца, который связывает электрическое сопротивление и теплопроводность для металлов через число Лоренца (13) λ 0 = k el ρ el / T = 2,44 × 10 -8 WΩ / K 2 . Нет данных для Fe-сплавов других кандидатов в легкие элементы, которые были предложены для объяснения наблюдаемого сейсмически дефицита плотности ядра Земли по сравнению с чистым Fe (14).Предыдущие исследования электронных транспортных свойств Fe при высоком давлении (15⇓⇓ – 18) при высоком давлении ограничивались низкими температурами. Очевидно, что существует потребность в прямом определении удельного электрического сопротивления и теплопроводности феррометаллических жидкостей при давлениях и температурах, характерных для внешнего ядра Земли.
Мы вычисляем k el и ρ el для Fe, Fe 7 Si, Fe 3 Si, Fe 7 O и Fe 3 O жидких сплавов (6.7, 14,3 мас.% Si; 3,9, 8,7 мас.% O) из первых принципов, используя теорию функционала плотности и функционал Мермина для определения конечной температурной равновесной плотности заряда и электронной структуры (19⇓ – 21). Моделирование из первых принципов молекулярной динамики (FPMD) выполняется в каноническом ансамбле для температур 2 000–8 000 K и объемов, соответствующих давлениям 0–360 ГПа. Свойства электронного переноса впоследствии вычисляются для серии некоррелированных снимков из моделирования FPMD с использованием уравнения Кубо – Гринвуда (22, 23) (см. методы ), которое выражает электронные коэффициенты Онзагера L ij непосредственно в члены математических ожиданий электронного оператора скорости (24).
Расчетные удельные сопротивления для чистой жидкости Fe (рис. 1) хорошо согласуются с измерениями ударного сжатия Киллера (10) и точки самого низкого давления Bi et al. (11), при давлениях, где температуры Гюгонио (25) сравнимы с таковыми в наших расчетах. Аналогично, значения для жидкости Fe 3 Si согласуются с ударными измерениями Матасова (12) для того же состава. Измерения ударного сжатия при более низком давлении проводятся при все более низких температурах; измерение 18 ГПа Киллера (10) при 320 К и хорошо согласуется со статическими измерениями при комнатной температуре в ГПУ Fe (17, 18), что добавляет уверенности данным удельного сопротивления ударному сжатию и нашим результатам.В свете большого разброса результатов Bi et al. (11), и серьезное расхождение между данными Bi et al. (11) и Киллер (10) выше 120 ГПа, мы считаем, что сравнение наших результатов с измерениями Киллера (10) более уместно. Расчетное удельное сопротивление при низком давлении для чистого жидкого Fe несколько меньше экспериментальных значений (26, 27), однако расчетная теплопроводность при атмосферном давлении хорошо согласуется с экспериментальными оценками для жидкого Fe при температурах выше плавления (1810 K) (28).
Рис. 1.Расчетное удельное электрическое сопротивление ( ρ el ), теплопроводность ( k el ) и соответствующие числа Лоренца ( λ ). Сплошные линии (верхний ряд) и пунктирные линии (средний и нижний ряды) показывают модели Блоха – Грюнайзена жидкости Fe; горизонтальная пунктирная линия указывает значение числа Лоренца, ожидаемое с помощью соотношения Видемана – Франца (W-F). Для сравнения показаны температуры Гюгонио (25) для выбранных точек данных ударного сжатия [K71 (10), M77 (12), B02 (11)].Другие экспериментальные данные (см. Текст): R83 (17), B61 (18), T71 (28), S89 (27), V80 (26).
При сравнении с измерениями удельного сопротивления ударному сжатию мы предполагаем, что удельное сопротивление жидкой и твердой металлических фаз одинаково, что, как известно, имеет место для Fe при низком давлении (26, 27). В нашем сравнении теплопроводностей мы также предполагаем, что электронный вклад в перенос тепла намного больше, чем за счет переноса только фононами. В жидком Fe при атмосферном давлении последнее оценивается примерно в 3 Вт / м · К (8), что намного меньше экспериментальной полной проводимости, равной 40.3 Вт / м · К (28).
В отличие от предыдущих предположений для ядра Земли (8, 9), мы находим, что справедливость соотношения Видемана – Франца сильно зависит от температуры и состава. При температурах ядра вычисленные числа Лоренца для жидкостей Fe и Fe – Si находятся в диапазоне 2,2–2,4 · 10 -8 Вт · Ом / К 2 ; легирование жидкого Fe с O приводит к заметному уменьшению λ со значениями всего 1,8 · 10 -8 WΩ / K 2 для жидкости Fe 3 O при высоком давлении и температуре.Это отклонение от соотношения Видемана – Франца предполагает, что рассеяние электронов в жидких сплавах Fe – O является сильно неупругим, что приводит к нарушению простой картины времени релаксации электронной миграции.
Мы обнаружили, что удельное электрическое сопротивление изменяется линейно с температурой, что согласуется с предсказанием уравнения Блоха – Грюнайзена для систем, в которых электроны в основном рассеиваются фононами. Однако ρ el не прямо пропорционально T (рис.2), как предполагается при часто используемых экстраполяциях экспериментальных измерений на условия активной зоны (8, 9). Дополняя формализм Блоха – Грюнайзена (29), мы строим описания моделей для k el и ρ el в зависимости от объема и температуры для различных рассматриваемых жидких фаз (таблица 1; см. методы ). . Комбинируя эти модели с уравнением состояния для проводящих жидкостей давление-объем-температура (30), мы получаем значения ρ el и k el вдоль набора возможных адиабатических тепловых профилей для ядра Земли, полученных из диапазон температур плавления Fe (25, 31, 32).
Рис. 2.Температурная зависимость электросопротивления для чистого жидкого Fe при 136 ГПа, определенная с использованием модели в Таблице 1 (сплошная красная линия), очень хорошо согласуется с измерением удельного сопротивления Киллера (10) при том же давлении. Стейси и Андерсон (8) использовали ? el ∝ T (пунктирная линия) при экстраполяции этого измерения на температуры ядра вблизи границы ядро-мантия. Заштрихованная область указывает диапазон T вблизи границы ядро – мантия из диапазона использованных возможных адиабат (см. Текст).
Таблица 1. Параметры моделиk el и ρ el для уравнения. 5
Наши значения k el для внешнего ядра заметно выше, чем предыдущие экстраполяции [Рис. 3; 30–60 Вт / м · К (8, 9)], что отражает неверную температурную зависимость удельного сопротивления, принятую в более ранних исследованиях (рис. 2). Как следствие, наш прогнозируемый кондуктивный тепловой поток в верхней части ядра составляет 14-20 ТВт, что больше, чем 5-15 ТВт полного теплового потока через границу ядро-мантия, полученного из внутриплитного вулканизма (5).Более низкий тепловой поток в верхней части сердечника потребует меньшего размера k el , который может быть получен за счет большей концентрации легких элементов в этой области. Действительно, аномальная доля легких элементов в верхней части ядра была предложена на основе динамических соображений (33) и подтверждена сейсмическими наблюдениями (34). Однако, поскольку такая концентрация легких элементов, вероятно, является результатом кристаллизации внутреннего ядра и связанной с ним химической плавучести, трудности, создаваемые большим теплопроводным потоком тепла, остаются, особенно в отсутствие кристаллизующегося внутреннего ядра.
Рис. 3. Удельное электрическое сопротивление( Верх, ) и ( Среднее ) электронная теплопроводность для различных составов, рассматриваемых в этом исследовании, оцененные с использованием моделей в Таблице 1 по ряду возможных основных адиабат (см. Текст). ( Bottom ) Соответствующие значения теплового потока, рассчитанные как 4 πr 2 k el ∇ T , где r — радиус, по сравнению с геофизическими оценками теплового потока на границе ядра и мантии (CMB) (5).
Модельный кондуктивный тепловой поток быстро уменьшается с глубиной в активной зоне, в первую очередь из-за сферической геометрии. За исключением возможных эффектов радиогенного нагрева и скрытого тепла, выделяемого при кристаллизации внутреннего ядра, сохранение энергии требует, чтобы общий тепловой поток оставался постоянным по всей активной зоне. Следовательно, доля общего теплового потока, переносимого посредством конвекции, будет увеличиваться с глубиной, что позволяет предположить, что поток, вызванный тепловым воздействием, будет происходить в основном в более глубокой части жидкого ядра.
Методы
Моделирование из первых принципов.
Метод, используемый для расчета свойств электронного транспорта, аналогичен методу исх. 22 и 23. Молекулярная динамика Борна – Оппенгеймера (FPMD) выполняется с использованием кода VASP (35). Чтобы проверить эффекты конечного размера, мы рассматриваем размеры системы из 64, 128, 144 и 192 атомов (см. Ниже). Обменно-корреляционный потенциал представлен в приближении обобщенного градиента (GGA-PBE) (36) с валентными электронами, представленными в виде плоских волн с порогом отсечки 300 эВ в формализме проекционной расширенной волны (PAW) (37, 38).Зона Бриллюэна отбирается только в точке Γ. Моделирование выполняется в ансамбле NVT для объемов V / V X = 1,0, 0,7, 0,65 и 0,6, где V X = 7,121 см 3 / моль атома и температуры 2000, 3000, 4000, 6000 и 8000 K, и покрывают не менее 20 пс времени моделирования. Среднеквадратичное смещение, зависящее от времени, используется для проверки того, действительно ли системы находятся в жидком состоянии.
Из каждой фазовой траектории, сгенерированной FPMD, мы извлекаем моментальные снимки атомной конфигурации каждые 1000 фс (т. Е. 20 на точку P — T ), для которых мы вычисляем удельное электрическое сопротивление ( ρ el ) и теплопроводность. ( к эл ). Все функции автокорреляции скорости (39) для наших симуляций затухают в пределах 250 фс, что указывает на то, что временное разделение в 1000 фс достаточно для того, чтобы отдельные снимки не коррелировали. Таким образом получают репрезентативную выборку структуры жидкости в каждой точке P — T .
Электронные транспортные свойства ρ el и k el вычисляются с использованием уравнения Кубо – Гринвуда, реализованного в коде Abinit (22, 40). Уравнение, которое следует из автокорреляционной функции электронного тока через формализм линейного отклика Кубо, имеет вид [1] [2] [3] In Eqs. 1 — 3 ϵ F — энергия Ферми; ψ k , ϵ k и f ( ϵ k ) — волновая функция, собственное значение и ферми-дираковское заполнение собственного состояния k , соответственно; — оператор скорости; и V ячейка — объем ячейки моделирования.Для данного снимка самосогласованная электронная релаксация выполняется для электронной температуры, равной ионной температуре, с помощью функционала Мермина (21). ψ k и ϵ k представлены собственными функциями Кона – Шэма и собственными значениями для каждого данного снимка, а вычисляются из градиента гамильтониана,.
Ячейки из 144 атомов для Fe и 128 атомов для сплавов Fe – Si и Fe – O используются в производственных циклах; тестовое моделирование со 192 атомами при В / В X = 0.6 и 1,0 для T = 8000 K дали коэффициенты переноса в пределах 1% от значений, определенных для меньших систем. Чтобы избежать перекрытия зарядов ядра в расчетах линейного отклика при высоких степенях сжатия, мы построили атомные потенциалы GGA-PAW с малыми радиусами отсечки (0,9 Å для Fe и Si, 0,53 Å для O) (36, 41). Установлено, что отсечка базисной волны в 400 эВ дает конвергентные коэффициенты электронного переноса. Производственные циклы отбирают зону Бриллюэна только в Γ-точке.Этот выбор подходит для больших ячеек моделирования, где край зоны Бриллюэна эффективно загибается в центр. Испытательные значения, рассчитанные с использованием 2 × 2 × 2 сетки Monkhorst – Pack k (42) при В / В X = 0,6 и 1,0 для T = 8000 K, изменяются не более более 5% от единичных результатов k баллов.
Следует отметить, что уравнение Кубо – Гринвуда определяет электронные транспортные свойства непосредственно из самосогласованной электронной структуры в рамках приближения Борна – Оппенгеймера.Ионное и электронное рассеяние неявно учитываются в расчетах, но электрон-фононная связь не описывается. Таким образом, этот подход хорошо подходит для характеристики коэффициентов электронного переноса при высоких температурах, особенно в жидких металлах.
Благодарности
Мы благодарим Анри Самуэля за полезные обсуждения. Эта работа стала возможной благодаря поддержке Deutsche Forschungsgemeinschaft по контракту KO3958 / 2-1 в рамках целевой программы «Планетарный магнетизм». Вычислительное оборудование было предоставлено Суперкомпьютерным центром им. Лейбница Баварской академии наук и гуманитарных наук.
Сноски
Вклад авторов: N.d.K. и Г.С.-Н. спланированное исследование; N.d.K. и В.В. проведенное исследование; N.d.K. проанализированные данные; и N.d.K. и Г.С.-Н. написал газету.
Авторы заявляют об отсутствии конфликта интересов.
Эта статья представляет собой прямое представление PNAS.
Доступно бесплатно в Интернете через опцию открытого доступа PNAS.
(PDF) Насыщение удельного электрического сопротивления твердого железа в условиях ядра Земли
Стр. 5 из 6
Поццо и Альфе SpringerPlus (2016) 5: 256
Эксперименты DAC под высоким давлением на Fe и Fe сплавах.Включив эффект насыщения
в экстраполяцию измеренного удельного электрического сопротивления к высоким температурам, они
нашли значения удельного сопротивления около 0,4, 0,5, 0,5 и 0,4
—
при 101 ГПа / 2010K,
135 ГПа / 3750K (CMB), 208GPa / 5220K и 330GPa / 4971K (ICB) соответственно. Эти результаты
были недавно подтверждены Ohta etal. (2014, 2015), которые выполнили измерения электричества
и теплопроводности железа при давлениях и температурах до
до 4500K с использованием нагреваемой лазером ячейки с алмазными наковальнями и явно наблюдали насыщение
. эффект.Эти новые экспериментальные результаты предполагают меньшие удельные сопротивления, чем обычные оценки, и согласуются со значениями, приведенными в этой работе.
Выводы
Мы расширили наши недавние расчеты удельного сопротивления чистого твердого железа, выполненные
в условиях ядра Земли (Поццо и др., 2014), на более низкие температуры, чтобы исследовать температурное поведение сопротивления
. Наши результаты показывают, что удельное сопротивление
начинает насыщаться при высоких температурах, и подтверждают анализ, включенный в недавнюю экспериментальную работу
(Gomi et al.2013; Ohta etal. 2014, 2015).
Вклад авторов
DA разработал исследование, MP выполнил расчеты ab-initio. Депутат и DA написали газету. Оба автора прочитали и утвердили окончательную рукопись
.
Сведения об авторе
1 Департамент наук о Земле и Центр Томаса Янга @ UCL, University College London, Gower Street, Lon-
don WC1E 6BT, United Kingdom. 2 Департамент физики и астрономии и Лондонский центр нанотехнологий,
Университетский колледж Лондона, Гауэр-стрит, Лондон, WC1E 6BT, Соединенное Королевство.
Благодарности
Работа М. П. была поддержана грантами NERC под номерами NE / H02462X / 1 и NE / M000990 / 1. Расчеты были выполнены на сервисе ARCHER в Великобритании.
. Авторы благодарят К. Хиросе и Дж. У. Хернлунда за плодотворные обсуждения.
Конкурирующие интересы
Авторы заявляют, что у них нет конкурирующих интересов.
Получено: 14 сентября 2015 г. Принято: 15 февраля 2016 г.
Ссылки
Alfè D (1999) Ab initio молекулярная динамика, простой алгоритм экстраполяции заряда.Comput Phys Commun
118: 31–33
Альфе Д., Поццо М., Десьярле М.П. (2012) Удельное электрическое сопротивление решетки магнитного ОЦК-железа на основе расчетов из первых принципов.
Phys Rev B 85: 024102-4
Andersen HC (1980) Моделирование молекулярной динамики при постоянном давлении и / или температуре. J Chem Phys
72: 2384–2393
Bi Y, Tan H, Jing F (2002) Электропроводность железа при ударном сжатии до 200 ГПа. J Phys Condens Matter
14: 10849–10854
Blöchl PE (1994) Метод расширенных волн для проектора.Phys Rev B 50: 17953–17979
Buett BA, King EM, Matsui H (2014) Физическая интерпретация стохастических моделей колебаний в поле земного диполя
. Geophys J Int 198: 597–608
Бюетт Б.А., Мацуи Х. (2015) Спектр мощности для геомагнитного дипольного момента. Earth Planet Sci Lett 411: 20–26
Дэвис К., Поццо М., Губбинс Д., Альфе Д. (2015) Ограничения свойств материала на динамику и эволюцию ядра
Земли. Nat Geosci 8: 678–685
de Koker N, Steinle-Neumann G, Vlček V (2012) Удельное электрическое сопротивление и теплопроводность жидких сплавов Fe при высоких значениях P
и T, а также тепловой поток в ядре Земли.Proc Natl Acad Sci 109: 4070–4073
Desjarlais MP, Kress JD, Collins LA (2002) Электропроводность для теплой, плотной алюминиевой плазмы и жидкостей. Phys Rev
E 66: 025401–4
Glasbrenner JK, Pujari BS, Belashchenko KD (2014) Отклонения от правила Маттиссена и влияние насыщения удельным сопротивлением в
Gd и Fe из первых принципов. Phys Rev B 89: 174408–10
Gomi H, Ohta K, Hirose K, Labrosse S, Caracas R, Vestraete MJ, Hernlund JW (2013) Высокая проводимость железа и
тепловая эволюция ядра Земли.Phys Earth Planet Int 224: 88–103
Измерения удельного электрического сопротивления и вязкости сплавов железа под давлением с помощью синхротронной рентгеновской радиографии на месте сплавы под давлением с использованием синхротронной рентгеновской радиографии «,
аннотация =» Мы разработали экспериментальную установку нового типа, использующую многопозиционный пресс большого объема и предназначенную для одновременного измерения структурно-чувствительных теплофизических свойств (дифракция, удельное электрическое сопротивление, вязкость).Эта возможность использования нескольких зондов была проверена на сплавах железа при давлении 2 ГПа и температуре до 1750 К. Фазовые переходы, обнаруженные с помощью дифрактограммы рентгеновских лучей, явно связаны с изменениями в электрическом отклике образцов. В жидкостях Fe-S измерения вязкости в расплавленном состоянии показывают увеличение вязкости с увеличением количества легирующего агента. Наблюдается корреляция между удельным сопротивлением и вязкостью по нашим данным и предыдущим работам. Эта возможность измерения с помощью нескольких датчиков улучшает обнаружение преобразований твердого тела и переходов твердое тело-расплав, связывает структурные и электрические свойства геоматериалов и позволяет ограничивать подвижность расплавов с помощью данных вязкости.Эта новая установка продвигает исследования распределения и подвижности расплава в условиях, относящихся к внутренним планетам. «,
keywords =» Множественная наковальня, рентгеновское излучение, импедансная спектроскопия, сплавы железа, вязкость «,
author =» A. Поммье и К. Лейненвебер, Х. Пиротт, Т. Ю и Ю. Ван «,
note =» Информация о финансировании: Это исследование, включая покупку импедансного спектрометра, финансировалось грантом NSF-CAREER EAR 1750746, предоставленным AP . AP и KL также выражают признательность за финансовую поддержку со стороны суб-премии NSF-COMPRES IV EOID.Использование проекта сборки ячеек COMPRES также поддерживалось COMPRES в рамках Соглашения о сотрудничестве NSF EAR 1661511. Мы благодарим Пин-Ченг Чен за техническую помощь в проведении некоторых экспериментов. AP благодарит Чарльза Лешера за возможность изучить технику вискозиметрии с падающими сферами и Джонатана Содерса за его помощь в разработке блока электрического переключателя температуры APS. Эта работа была выполнена в GeoSoilEnviroCARS (Чикагский университет, сектор 13), Advanced Photon Source (APS), Аргоннская национальная лаборатория.GeoSoilEnviroCARS поддерживается Национальным научным фондом — наук о Земле (EAR — 1634415) и Министерством энергетики — геонаук (DE-FG02-94ER14466). В этом исследовании использовались ресурсы Advanced Photon Source, Научно-исследовательского центра Министерства энергетики США (DOE), используемого для Управления науки Министерства энергетики Аргоннской национальной лабораторией по контракту № DE-AC02-06Ch21357. Мы благодарим двух анонимных рецензентов за их вдумчивые комментарии и Стефана Клотца за его редакторскую работу. Авторские права издателя: {\ textcopyright} 2020 Informa UK Limited, торговая марка Taylor & Francis Group.»,
год =» 2021 «,
doi =» 10.1080 / 08957959.2020.1865343 «,
язык =» Английский (США) «,
объем =» 41 «,
страниц =» 1—13 «,
journal =» Исследование высокого давления «,
issn =» 0895-7959 «,
publisher =» Taylor and Francis Ltd. «,
number =» 1 «,
}
Индуцированное гамма-излучением изменения удельного сопротивления железа
Приложение
На основе линейной зависимости между N д и T плотина на рис. {{T_ {dam}}} {dT_ {dam}} $$
(3)
$$ N_ {d} = k \ left ({T_ {dam} — E_ {d}} \ right) $$
(4)
\ (\ frac {{N_ {d}}} {n} = k \ left ({\ frac {{T_ {dam}}} {n} — \ frac {{E_ {d}}} {n}} \ справа) \) можно использовать для расчетов на падающую частицу.Плотность смещенных атомов может быть записана как
$$ n_ {d} = \ frac {{N_ {d}}} {V} = k \ frac {{\ left ({T_ {dam} — E_ {d }} \ right)}} {V} $$
(5)
$$ V = \ frac {{N_ {d}}} {{n_ {d}}} $$
(6)
Предполагая, что n d примерно постоянное, неупорядоченный объем можно записать как,
$$ dV = \ left ({\ frac {1} {{n_ {d}}}} \ right) dN_ {d} $ $
Из уравнения.(6),
$$ \ frac {dV} {V} = \ frac {{dN_ {d}}} {{N_ {d}}} $$
(7)
Следовательно, используя уравнение. (2) можно написать
$$ \ frac {dV} {V} = \ frac {k} {{N_ {d}}} dT_ {dam} $$
(8)
При объяснении сопротивления Бринкман [26] связал его с неупорядоченным объемом. После этого мы можем написать, что
$$ \ frac {{\ rho — \ rho_ {0}}} {{\ rho_ {D} — \ rho_ {0}}} = \ frac {dV} {V} $$
(9)
, где \ (\ rho_ {0} \) и \ (\ rho_ {D} \) соответствуют удельному сопротивлению исходного и сильно разупорядоченного состояния образца соответственно.
В ситуации отсутствия данных удельного сопротивления \ (\ rho_ {D} \) мы присвоили \ (\ rho_ {D} = x \ rho_ {0} \). Здесь параметр x ≥ 0 соответствует неупорядоченному состоянию облучаемого материала и также зависит от спектра. Например, dV = 0 соответствует \ (\ rho = \ rho_ {0} \), а dV = V соответствует \ (\ rho_ {D} = \ rho \). В этом смысле более высокие значения x могут привести к более интересным результатам. Таким образом, соотношение (9) можно записать как,
$$ \ frac {d \ rho} {{\ left ({x \ rho_ {0} — \ rho_ {0}} \ right)}} = \ frac { dV} {V} $$
(10)
Подставляя выражение для \ (\ frac {dV} {V} \) из уравнения.(8) изменение удельного сопротивления можно аппроксимировать следующим соотношением:
$$ d \ rho = \ left ({x \ rho_ {0} — \ rho_ {0}} \ right) \ left ({\ frac { k} {{N_ {d}}}} \ right) dT_ {dam} $$
$$ d \ rho = \ rho_ {0} \ left ({x — 1} \ right) \ left ({\ frac {k} {{N_ {d}}}} \ right) dT_ {dam} $$
(11)
, где « k » и « x » зависят от спектра. Таким образом, существует составная независимая переменная \ (\ frac {{dT_ {dam}}} {{N_ {d}}} \), от которой удельное сопротивление зависит линейно.
В случае одного спектра излучения, такого как гамма-спектр Co 60 , \ (k = \ frac {{d N_ {d}}} {{d T_ {dam}}} \), поэтому уравнение. (11) можно записать как,
$$ \ left ({\ rho — \ rho_ {0}} \ right) = \ rho_ {0} \ left ({x — 1} \ right) \ ln N_ {d } $$
(12)
или существует линейная зависимость между \ (\ rho \) и \ (\ ln N_ {d} \),
$$ \ rho = \ rho_ {0} + {\ text {Z}} \ ln N_ {d} $$
(13)
где \ (Z = \ left ({{\ text {x}} — 1} \ right) \ rho_ {0} \).Взяв данные из Таблицы 2 на следующем рисунке 4, нормированное удельное сопротивление, \ (\ rho / \ rho_ {0} \) было построено как функция ( x — 1) ln N д , и видно, что нормированное удельное сопротивление линейно увеличивается с ( x — 1) ln N д .
Рис. 4Измеренное нормированное удельное сопротивление, построенное как функция ( x — 1) ln N д
Переключатель сопротивления показывает роль магнетизма в сверхпроводниках на основе железа — ScienceDaily
Физики из Университета им.Лаборатория Эймса Министерства энергетики США обнаружила неожиданные изменения удельного электрического сопротивления в сверхпроводниках на основе железа. Открытия, опубликованные в Nature Communications , предлагают дополнительные доказательства того, что магнетизм и сверхпроводимость тесно связаны в этом классе новых сверхпроводников.
«Мы обнаружили, что направления наименьшего и наибольшего удельного сопротивления внутри проводящих слоев в значительной степени зависят от состава соединений, и в некоторых композициях они меняют знак, или, другими словами, электрический ток легче течет в том направлении, которое было «Изначально сложнее», — сказал ученый факультета «Лаборатории Эймса» Руслан Прозоров.«Это изменение можно объяснить только в том случае, если лежащее в основе магнитное поведение тесно связано со сверхпроводимостью».
Понимание основ физики сверхпроводимости на основе железа однажды может позволить использовать их в сверхэффективных энергетических технологиях.
Эрик Бломберг, научный сотрудник лаборатории Эймса, возглавил исследование под руководством Прозорова и ученого из лаборатории Эймса Макария Танатара. Команда исследовала удельное сопротивление в соединениях бария, железа и арсенида с различными химическими замещениями, что позволило получить
исследует электронные свойства во всем режиме сосуществования магнетизма и сверхпроводимости.
В обычных сверхпроводниках магнетизм и сверхпроводимость не сосуществуют, и одно подавляет другое. Напротив, некоторые сверхпроводники на основе железа демонстрируют значительное перекрытие между магнетизмом и сверхпроводимостью, что позволяет проводить уникальные измерения их свойств в области сосуществования.
«Но есть осложнение», — сказал Прозоров, который также является профессором факультета физики и астрономии Университета штата Айова. «В области сосуществования кристаллическая структура кристаллов арсенида бария-железа такова, что кристалл расщепляется на структурные домены (также известные как структурные двойники), что затрудняет изучение направленных электронных свойств.
Чтобы устранить структурные домены, команда разработала метод физического разделения монокристаллов. Образец подвешен на проволочках в кронштейне в форме подковы, который можно растягивать механически. Затем этот блок помещается в небольшой криостат с жидким гелием для достижения температур, при которых сосуществуют магнетизм и сверхпроводимость. Поляризационная оптическая микроскопия используется для различения различных структурных доменов, чтобы убедиться, что образцы находятся в детвинованном (без фрагментированных доменов) состоянии.Затем измеряется удельное электрическое сопротивление.
Бломберг и его коллеги изучили серию образцов, охватывающих точный диапазон композиций, предоставленных Хай-Ху Веном из Нанкинского университета.
«В данном случае химические замещения фактически отнимали электроны от соединения или добавляли электроны к соединению», — сказал Бломберг, который скоро получит докторскую степень по физике конденсированных сред в Университете штата Айова. «И по мере того, как вы убираете электроны, в определенный момент направление, в котором электричеству было труднее течь, становится направлением, в котором ему было легче течь.«
Теоретические предсказания, сделанные физиками Йоргом Шмалианом и Рафаэлем Фернандесом (оба бывшие ученые Лаборатории Эймса), а также Игорем Мазином и Мишель Йоханнес из морской исследовательской лаборатории, полностью совпадают с экспериментальными выводами.
История Источник:
Материалы предоставлены DOE / Ames Laboratory . Примечание. Содержимое можно редактировать по стилю и длине.
Реле сопротивления — окно в роль магнетизма в сверхпроводниках на основе железа
Изображение структурных доменов в кристалле арсенида железа, бария, типа сверхпроводника, полученное при микроскопии в поляризованном свете.Физики из лаборатории Эймса Министерства энергетики США обнаружили неожиданные изменения удельного сопротивления в кристаллах, легированных калием, которые предполагают тесную связь между магнетизмом и сверхпроводимостью в сверхпроводниках на основе железа. Предоставлено: лаборатория Эймса Департамента энергетики США.(Phys.org) — Физики из лаборатории Эймса Министерства энергетики США обнаружили неожиданные изменения удельного электрического сопротивления в сверхпроводниках на основе железа. Открытия, опубликованные в Nature Communications , предлагают дополнительные доказательства того, что магнетизм и сверхпроводимость тесно связаны в этом классе новых сверхпроводников.
«Мы обнаружили, что направления наименьшего и наибольшего удельного сопротивления внутри проводящих слоев в значительной степени зависят от состава соединений, и в некоторых композициях они меняют знак, или, другими словами, электрический ток течет легче в направлении, которое «Изначально было сложнее», — сказал научный сотрудник лаборатории Эймса Руслан Прозоров. «Это изменение можно объяснить только в том случае, если лежащее в основе магнитное поведение тесно связано со сверхпроводимостью.«
Понимание основ физики сверхпроводимости на основе железа однажды может позволить использовать их в сверхэффективных энергетических технологиях.
Эрик Бломберг, научный сотрудник лаборатории Эймса, возглавил исследование под руководством Прозорова и ученого из лаборатории Эймса Макария Танатара. Команда исследовала удельное сопротивление в соединениях бария-железа-арсенида с различными химическими замещениями, что позволило исследовать электронные свойства на протяжении всего режима, в котором сосуществуют магнетизм и сверхпроводимость.
В обычных сверхпроводниках магнетизм и сверхпроводимость не сосуществуют, и одно подавляет другое. Напротив, некоторые сверхпроводники на основе железа демонстрируют значительное перекрытие между магнетизмом и сверхпроводимостью, что позволяет проводить уникальные измерения их свойств в области сосуществования.
«Но есть осложнение», — сказал Прозоров, который также является профессором факультета физики и астрономии Университета штата Айова. «В области сосуществования кристаллическая структура кристаллов арсенида бария-железа такова, что кристалл расщепляется на структурные домены (также известные как структурные двойники), что затрудняет изучение направленных электронных свойств.
(слева направо) Эрик Бломберг, Макарий Танатар и Руслан Прозоров.Чтобы устранить структурные домены, команда разработала метод физического разделения монокристаллов. Образец подвешен на проволочках в кронштейне в форме подковы, который можно растягивать механически. Затем этот блок помещается в небольшой криостат с жидким гелием для достижения температур, при которых сосуществуют магнетизм и сверхпроводимость. Поляризационная оптическая микроскопия используется для различения различных структурных доменов, чтобы убедиться, что образцы находятся в детвинованном (без фрагментированных доменов) состоянии.Затем измеряется удельное электрическое сопротивление.
Бломберг и его коллеги изучили серию образцов, охватывающих точный диапазон композиций, предоставленных Хай-Ху Веном из Нанкинского университета.
«В данном случае химические замещения фактически отнимали электроны от соединения или добавляли электроны к соединению», — сказал Бломберг, который скоро получит докторскую степень по физике конденсированных сред в Университете штата Айова.«И по мере того, как вы убираете электроны, в определенный момент направление, в котором электричеству было труднее течь, становится направлением, в котором ему было легче течь».
Теоретические предсказания, сделанные физиками Йоргом Шмалианом и Рафаэлем Фернандесом (оба бывшие ученые Лаборатории Эймса), а также Игорем Мазином и Мишель Йоханнес из морской исследовательской лаборатории, полностью совпадают с экспериментальными выводами.
Раскрывая тайны экзотических сверхпроводников
Доп. Информация: www.nature.com/ncomms/journal/… full / ncomms2933.html Предоставлено Лаборатория Эймса
Ссылка : Переключатель сопротивления — окно в роль магнетизма в сверхпроводниках на основе железа (2013, 5 июня) получено 10 ноября 2021 г. с https: // физ.org / news / 2013-06-resistivity-window-role-magnetism-iron-based.html
Этот документ защищен авторским правом.

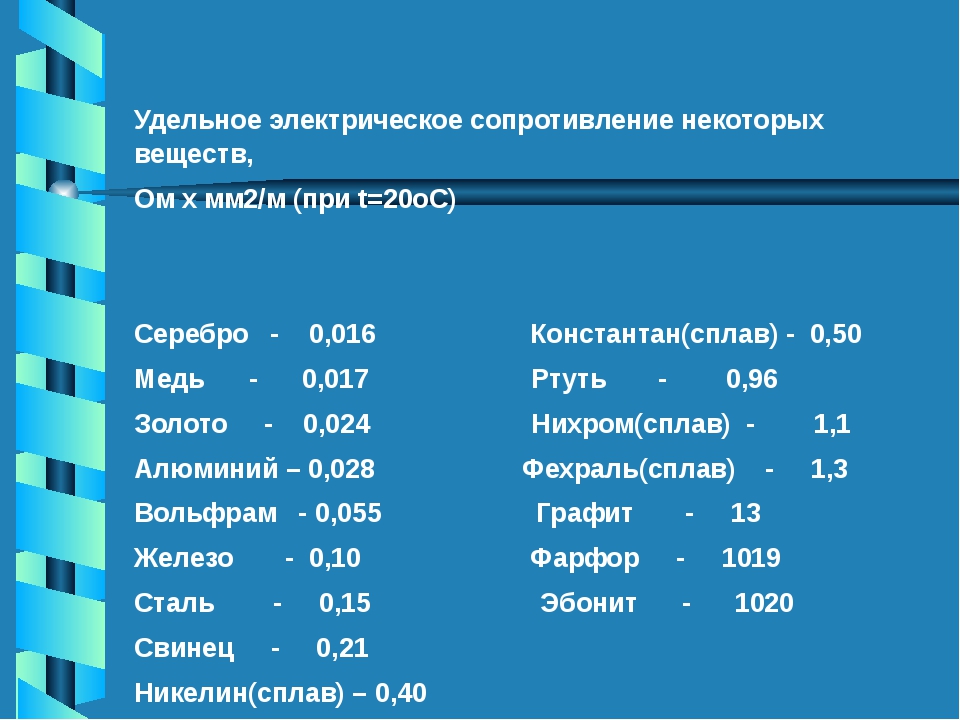 И. Промышленные печи. Справочное руководство для расчетов и проектирования.
И. Промышленные печи. Справочное руководство для расчетов и проектирования.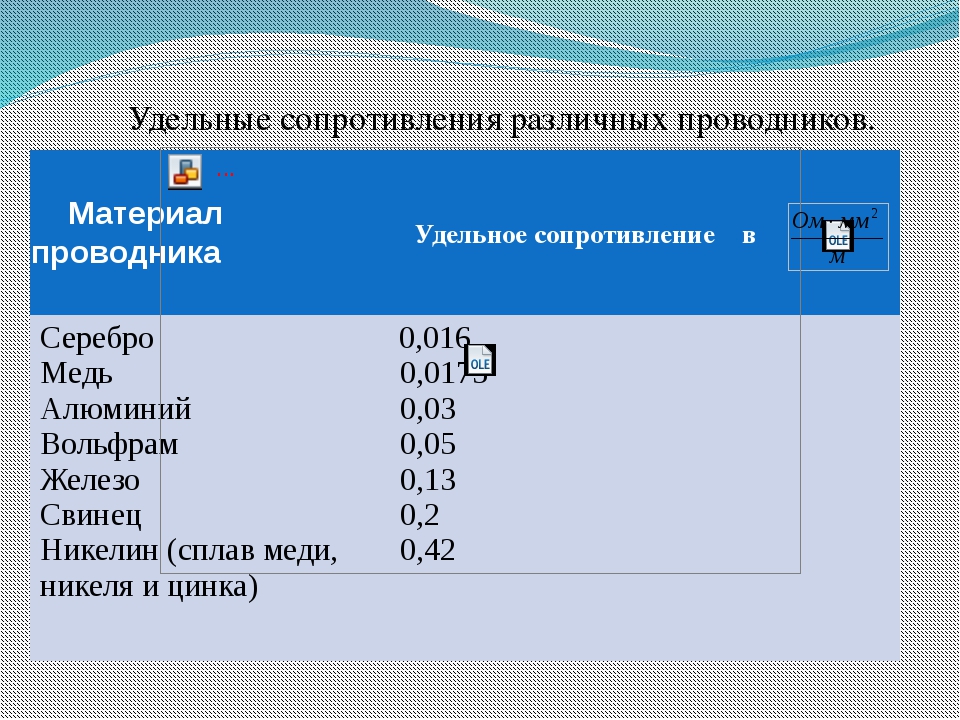
 Краткий справочник / Таллин: Принтэст, 1991 – 448 с.
Краткий справочник / Таллин: Принтэст, 1991 – 448 с.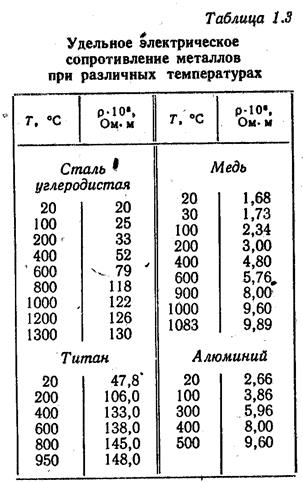 0271
0271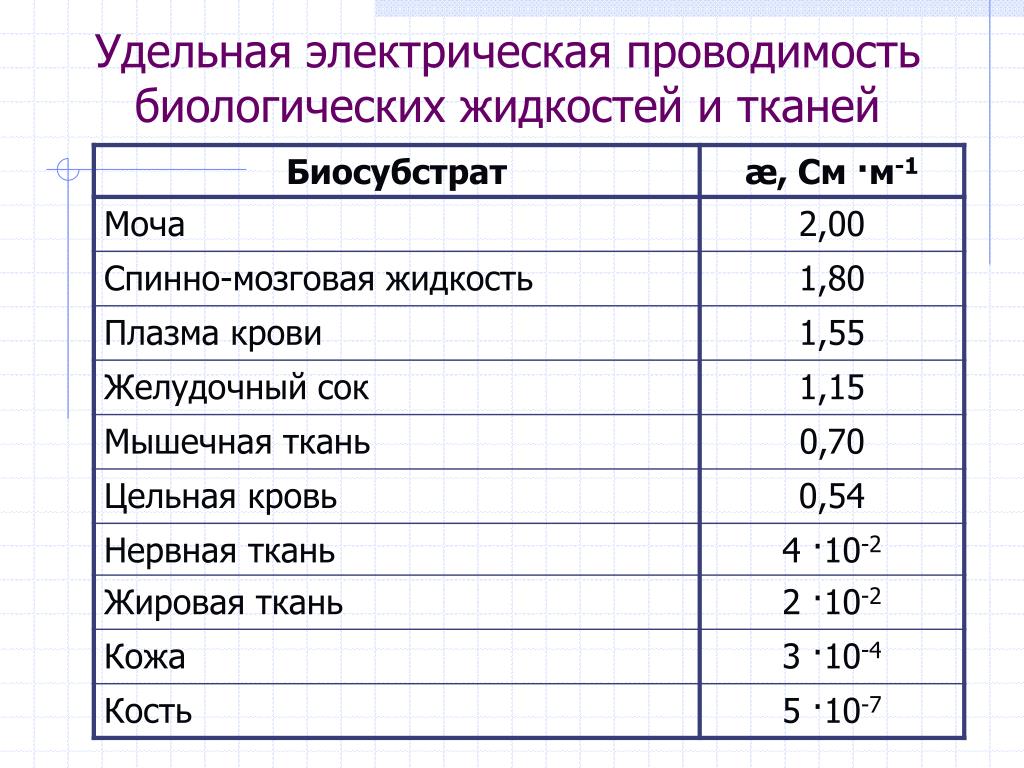 15
15 Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м
и площадью поперечного сечения 1 м²
.
Соответственно, удельное сопротивление произвольного вещества, выраженное в единицах СИ, численно равно сопротивлению участка электрической цепи, выполненного из данного вещества, длиной 1 м
и площадью поперечного сечения 1 м²
. {3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}
{3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).} {3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
{3}\sigma _{ij}({\vec {r}})E_{j}({\vec {r}}).}
 Взаимодействуя с ними, свободный электрон теряет часть своего заряда. Таким образом, электроны сталкиваются с сопротивлением со стороны материала проводника. Каждое тело имеет свою атомную структуру, которая оказывает электрическому току разное сопротивление. Единицей сопротивления принято считать Ом. Обозначается сопротивление материалов — R или r.
Взаимодействуя с ними, свободный электрон теряет часть своего заряда. Таким образом, электроны сталкиваются с сопротивлением со стороны материала проводника. Каждое тело имеет свою атомную структуру, которая оказывает электрическому току разное сопротивление. Единицей сопротивления принято считать Ом. Обозначается сопротивление материалов — R или r.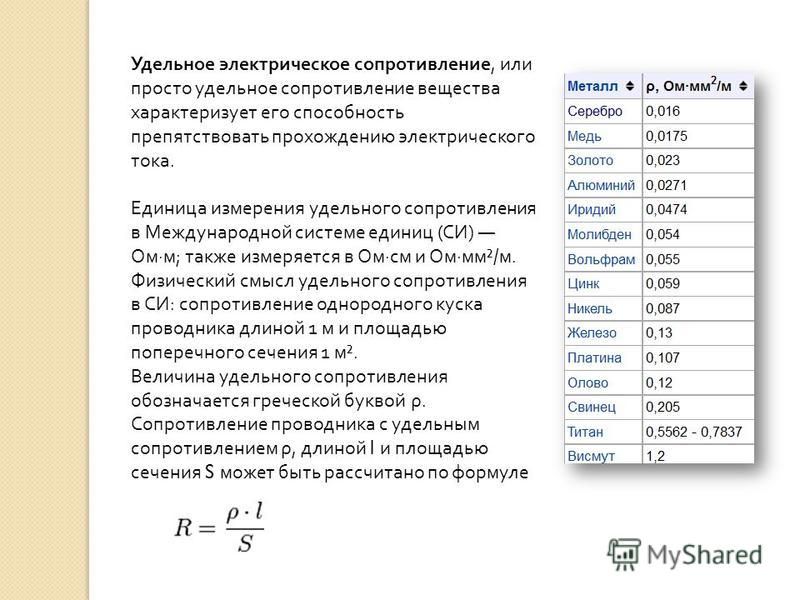 Для примера рассмотрим удельное сопротивление нихрома и фехрали (более 3 мм):
Для примера рассмотрим удельное сопротивление нихрома и фехрали (более 3 мм):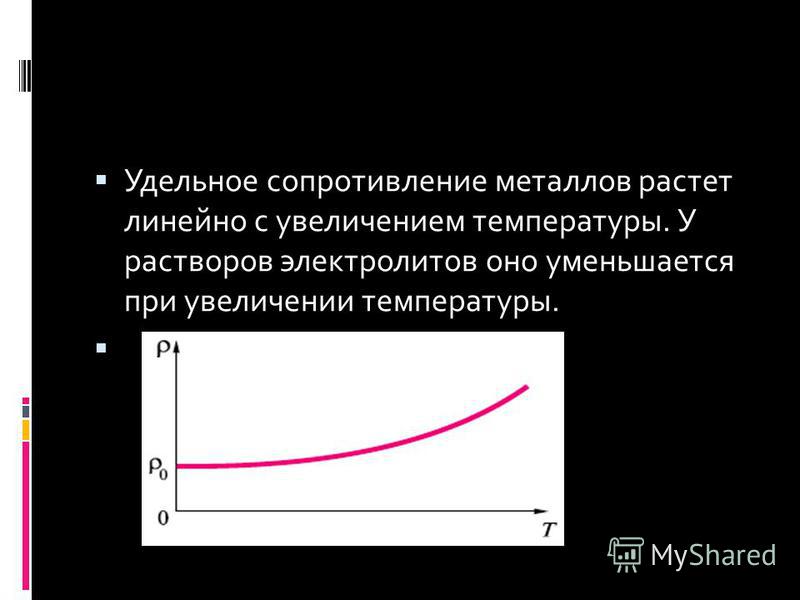 024
024
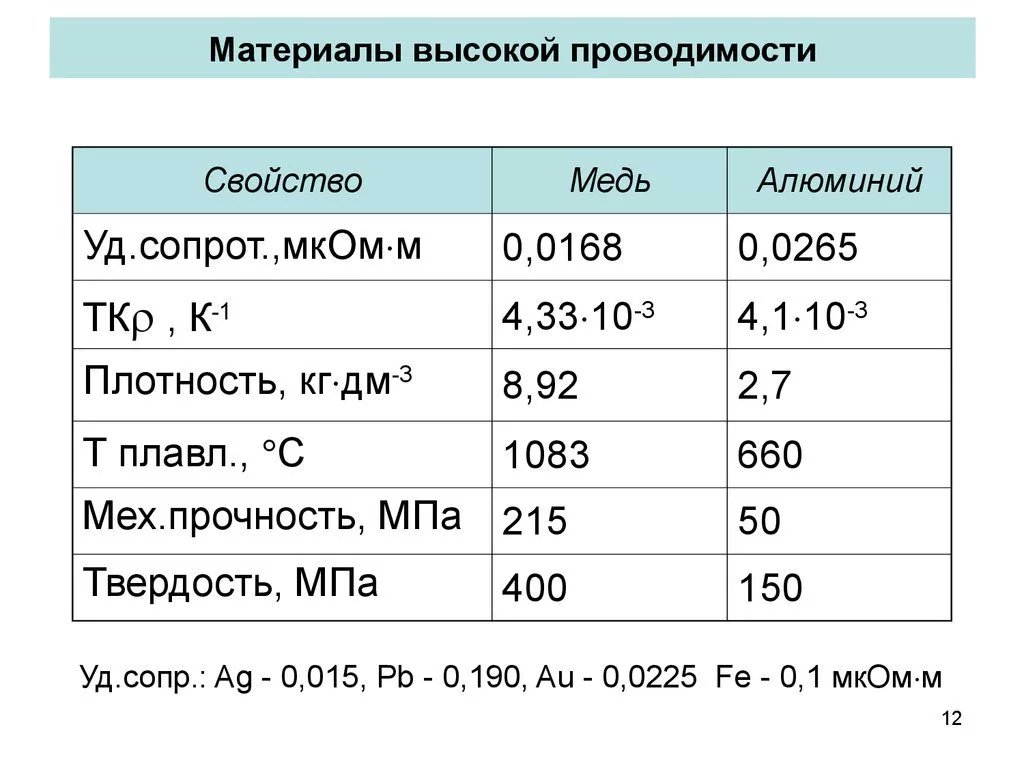 Краткий справочник / Таллин: Принтэст, 1991 – 448 с.
Краткий справочник / Таллин: Принтэст, 1991 – 448 с.