Напряжение, как его понизить и повысить

Электрическое напряжение между точками A и B электрической цепи или электрического поля — физическая величина, значение которой равно работе эффективного электрического поля (включающего сторонние поля), совершаемой при переносе единичного пробного электрического заряда из точки A в точку B.

Напряжение и сила тока — две основных величины в электричестве. Кроме них выделяют и ряд других величин: заряд, напряженность магнитного поля, напряженность электрического поля, магнитная индукция и другие. Практикующему электрику или электронщику в повседневной работе чаще всего приходится оперировать именно напряжением и током — Вольтами и Амперами. В этой статье мы расскажем именно о напряжении, о том, что это такое и как с ним работать.

Определение физической величины

Напряжение это разность потенциалов между двумя точками, характеризует выполненную работу электрического поля по переносу заряда из первой точки во вторую.

Измеряется напряжение в Вольтах. Значит, напряжение может присутствовать только между двумя точками пространства. Следовательно, измерить напряжение в одной точке нельзя.

Потенциал обозначается буквой «Ф», а напряжение буквой «U». Если выразить через разность потенциалов, напряжение равно:

U=Ф1-Ф2

Если выразить через работу, тогда:

U=A/q,

где A — работа, q — заряд.

Измерение напряжения

Напряжение измеряется с помощью вольтметра. Щупы вольтметра подключают на две точки напряжение, между которыми нас интересует, или на выводы детали, падение напряжения на которой мы хотим измерить. При этом любое подключение к схеме может влиять на её работу. Это значит, что при добавлении параллельно элементу какой-либо нагрузки ток в цепи изменить и напряжение на элементе измениться по закону Ома.

Вывод:

Вольтметр должен обладать максимально высоким входным сопротивлением, чтобы при его подключении итоговое сопротивление на измеряемом участке оставалось практически неизменным. Сопротивление вольтметра должно стремиться к бесконечности, и чем оно больше, тем большая достоверность показаний.

На точность измерений (класс точности) влияет целый ряд параметров. Для стрелочных приборов – это и точность градуировки измерительной шкалы, конструктивные особенности подвеса стрелки, качество и целостность электромагнитной катушки, состояние возвратных пружин, точность подбора шунта и прочее.

Для цифровых приборов — в основном точность подбора резисторов в измерительном делителе напряжения, разрядность АЦП (чем больше, тем точнее), качество измерительных щупов.

Для измерения постоянного напряжения с помощью цифрового прибора (например, мультиметра), как правило, не имеет значения правильность подключения щупов к измеряемой цепи. Если вы подключите положительный щуп к точке с более отрицательным потенциалом, чем у точки, к которой подключен отрицательный щуп — то на дисплее перед результатом измерения появится знак «–».

А вот если вы меряете стрелочным прибором нужно быть внимательным, При неправильном подсоединении щупов стрелка начнет отклоняться в сторону нуля, упрется в ограничитель. При измерении напряжений близких к пределу измерений или больше она может заклинить или погнуться, после чего о точности и дальнейшей работе этого прибора говорить не приходится.

Для большинства измерений в быту и в электронике на любительском уровне достаточно и вольтметра встроенного в мультиметры типа DT-830 и подобных.

Чем больше измеряемые значения — тем ниже требования к точности, ведь если вы измеряете доли вольта и у вас погрешность в 0.1В — это существенно исказит картину, а если вы измеряете сотни или тысяч вольт, то погрешность и в 5 вольт не сыграет существенной роли.

Что делать если напряжение не подходит для питания нагрузки

Для питания каждого конкретного устройства или аппарата нужно подать напряжение определенной величины, но случается, так что имеющийся у вас источник питания не подходит и выдает низкое или слишком высокое напряжение. Решается эта проблема разными способами, в зависимости от требуемой мощности, напряжения и силы тока.

Как понизить напряжение сопротивлением?

Сопротивление ограничивает ток и при его протекании падает напряжение на сопротивление (токоограничивающий резистор). Такой способ позволяет понизить напряжение для питания маломощных устройств с токами потребления в десятки, максимум сотни миллиампер.

Примером такого питания можно выделить включение светодиода в сеть постоянного тока 12 (например, бортовая сеть автомобиля до 14.7 Вольт). Тогда, если светодиод рассчитан на питание от 3.3 В, током в 20 мА, нужен резистор R:

R=(14.7-3.3)/0.02)= 570 Ом

Но резисторы отличаются по максимальной рассеиваемой мощности:

P=(14.7-3.3)*0.02=0.228 Вт

Ближайший по номиналу в большую сторону — резистор на 0.25 Вт.

Именно рассеиваемая мощность и накладывает ограничение на такой способ питания, обычно мощность резисторов не превышает 5-10 Вт. Получается, что если нужно погасить большое напряжение или запитать таким образом нагрузку мощнее, придется ставить несколько резисторов т.

к. мощности одного не хватит и ее можно распределить между несколькими.

Способ снижения напряжения резистором работает и в цепях постоянного тока и в цепях переменного тока.

Недостаток — выходное напряжение ничем нестабилизировано и при увеличении и снижении тока оно изменяется пропорционально номиналу резистора.

Как понизить переменное напряжение дросселем или конденсатором?

Если речь вести только о переменном токе, то можно использовать реактивное сопротивление. Реактивное сопротивление есть только в цепях переменного тока, это связно с особенностями накопления энергии в конденсаторах и катушках индуктивности и законами коммутации.

Дроссель и конденсатор в переменном токе могут быть использованы в роли балластного сопротивления.

Реактивное сопротивление дросселя (и любого индуктивного элемента) зависит от частоты переменного тока (для бытовой электросети 50 Гц) и индуктивности, оно рассчитывается по формуле:

где ω – угловая частота в рад/с, L-индуктивность, 2пи – необходимо для перевода угловой частоты в обычную, f – частота напряжения в Гц.

Реактивное сопротивление конденсатора зависит от его емкости (чем меньше С, тем больше сопротивление) и частоты тока в цепи (чем больше частота, тем меньше сопротивление). Его можно рассчитать так:

Пример использования индуктивного сопротивление — это питание люминесцентных ламп освещения, ДРЛ ламп и ДНаТ. Дроссель ограничивает ток через лампу, в ЛЛ и ДНаТ лампах он используется в паре со стартером или импульсным зажигающем устройством (пусковое реле) для формирования всплеска высокого напряжения включающего лампу. Это связано с природой и принципом работы таких светильников.

А конденсатор используют для питания маломощных устройств, его устанавливают последовательно с питаемой цепью. Такой блок питания называется «бестрансфоматорный блок питания с балластным (гасящим) конденсатором».

Очень часто встречают в качестве ограничителя тока заряда аккумуляторов (например, свинцовых) в носимых фонарях и маломощных радиоприемниках. Недостатки такой схемы очевидны — нет контроля уровня заряда аккумулятора, их выкипание, недозаряд, нестабильность напряжения.

Как понизить и стабилизировать напряжение постоянного тока

Чтобы добиться стабильного выходного напряжения можно использовать параметрические и линейные стабилизаторы. Часто их делают на отечественных микросхемах типа КРЕН или зарубежных типа L78xx, L79xx.

Линейный преобразователь LM317 позволяет стабилизировать любое значение напряжения, он регулируемый до 37В, вы можете сделать простейший регулируемый блок питания на его основе.

Если нужно незначительно снизить напряжение и стабилизировать его описанные ИМС не подойдут. Чтобы они работали должна быть разница порядка 2В и более. Для этого созданы LDO(low dropout)-стабилизаторы. Их отличие заключается в том, что для стабилизации выходного напряжение нужно, чтобы входное его превышало на величину от 1В. Пример такого стабилизатора AMS1117, выпускается в версиях от 1.2 до 5В, чаще всего используют версии на 5 и 3.3В, например в платах Arduino и многом другом.

Конструкция всех вышеописанных линейных понижающих стабилизаторов последовательного типа имеет существенный недостаток – низкий КПД.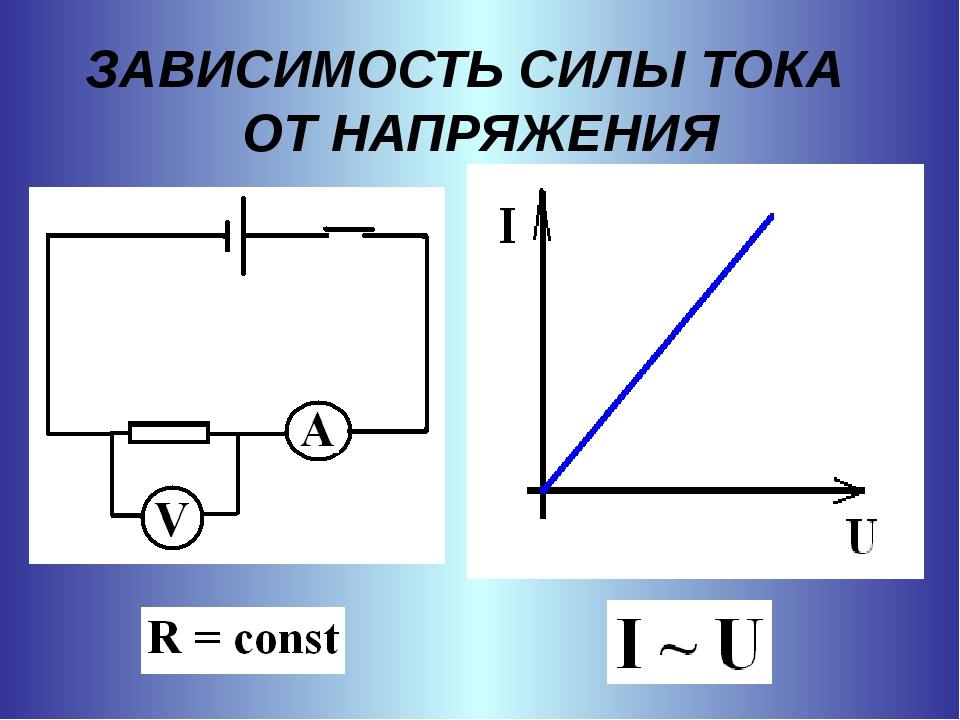 Чем больше разница между входным и выходным напряжением – тем он ниже. Он просто «сжигает» лишнее напряжение, переводя его в тепло, а потери энергии равны:

Pпотерь = (Uвх-Uвых)*I

Компания AMTECH выпускает ШИМ аналоги преобразователей типа L78xx, они работают по принципу широтно-импульсной модуляции и их КПД равен всегда более 90%.

Они просто включают и выключают напряжение с частотой до 300 кГц (пульсации минимальны). А действующее напряжение стабилизируется на нужном уровне. А схема включения аналогичная линейным аналогам.

Как повысить постоянное напряжение?

Для повышения напряжения производят импульсные преобразователи напряжения. Они могут быть включены и по схеме повышения (boost), и понижения (buck), и по повышающе-понижающей (buck-boost) схеме. Давайте рассмотрим несколько представителей:

1. Плата на базе микросхемы XL6009

2. Плата на базе LM2577, работает на повышение и понижение выходного напряжения.

3. Плата преобразователь на FP6291, подходит для сборки 5 V источника питания, например powerbank. С помощью корректировке номиналов резисторов может перестраиваться на другие напряжения, как и любые другие подобные преобразователь – нужно корректировать цепи обратной связи.

4. Плата на базе MT3608

Здесь всё подписано на плате – площадки для пайки входного – IN и выходного – OUT напряжения. Платы могут иметь регулировку выходного напряжения, а в некоторых случая и ограничения тока, что позволяет сделать простой и эффективный лабораторный блок питания. Большинство преобразователей, как линейных, так и импульсных имеют защиту от КЗ.

Как повысить переменное напряжение?

Для корректировки переменного напряжения используют два основных способа:

1. Автотрансформатор;

2. Трансформатор.

Автотрансформатор – это дроссель с одной обмоткой. Обмотка имеет отвод от определенного количества витков, так подключаясь между одним из концов обмотки и отводом, на концах обмотки вы получаете повышенное напряжение во столько раз, во сколько соотносится общее количество витков и количество витков до отвода.

Промышленностью выпускаются ЛАТРы – лабораторные автотрансформаторы, специальные электромеханические устройства для регулировки напряжения. Очень широко применение они нашли в разработке электронных устройств и ремонте источников питания. Регулировка достигается за счет скользящего щеточного контакта, к которому подключается питаемое устройство.

Недостатком таких устройств является отсутствие гальванической развязки. Это значит, что на выходных клеммах может запросто оказаться высокое напряжение, отсюда опасность поражения электрическим током.

Трансформатор – это классический способ изменения величины напряжения. Здесь есть гальваническая развязка от сети, что повышает безопасность таких установок. Величина напряжения на вторичной обмотке зависит от напряжений на первичной обмотки и коэффициента трансформации.

Uвт=Uперв*Kтр

Kтр=N1/N2

Отдельный вид – это импульсные трансформаторы. Они работают на высоких частотах в десятки и сотни кГц. Используются в подавляющем большинстве импульсных блоках питания, например:

— Зарядное устройство вашего смартфона;

— Блок питания ноутбука;

— Блок питания компьютера.

За счет работы на большой частоте снижаются массогабаритные показатели, они в разы меньше чем у сетевых (50/60 Гц) трансформаторов, количество витков на обмотках и, как следствие, цена. Переход на импульсные блоки питания позволил уменьшить габариты и вес всей современной электроники, снизить её потребление за счет увеличения кпд (в импульсных схемах 70-98%).

В магазинах часто встречаются электронные траснформаторы, на их вход подаётся сетевое напряжение 220В, а на выходе например 12 В переменное высокочастотное, для использования в нагрузке которая питается от постоянного тока нужно дополнительно устанавливать на выход диодный мост из высокоскоростных диодов.

Внутри находится импульсный трансформатор, транзисторные ключи, драйвер, или автогенераторная схема, как изображена ниже.

Достоинства – простота схемы, гальваническая развязка и малые размеры.

Недостатки – большинство моделей, что встречаются в продаже, имеют обратную связь по току, это значит что без нагрузки с минимальной мощностью (указано в спецификациях конкретного прибора) он просто не включится. Отдельные экземпляры оборудованы уже ОС по напряжению и работают на холостом ходу без проблем.

Используются чаще всего для питания 12В галогенных ламп, например точечные светильники подвесного потолка.

Заключение

Мы рассмотрели базовые сведения о напряжении, его измерении, а также регулировки. Современная элементная база и ассортимент готовых блоков и преобразователей позволяет реализовывать любые источники питания с необходимыми выходными характеристиками. Подробнее о каждом из способов можно написать отдельную статью, в пределах этой я постарался уместить базовые сведения, необходимые для быстрого подбора удобного для вас решения.

Ранее ЭлектроВести писали о топе-5 самых безумных батарей будущего

По материалам: electrik. info.

 

Что такое сила натяжения?

Как и любую силу, поверхностное натяжение можно измерить, и учёные придумали множество способов это сделать. Самый простой из них — измерение высоты подъёма смачивающих жидкостей в капиллярах: чем выше поднялся столбик, тем больше сила натяжения. Метод достаточно точен и теоретически выверен, но не является единственным.

Для следующего способа измерения понадобится сталагмометр — стеклянный пузырёк известного объёма, имеющий точно калиброванный капилляр для истечения жидкости. Число вытекающих капель и значение плотности жидкости позволяют при помощи специальной формулы определить поверхностное натяжение с погрешностью всего в 1%. Полное научное название этого способа — сталагмометрический метод или метод счёта капель.

Классикой стали два необычных способа расчёта силы σ, названные в честь своих изобретателей — Дю Нуи, Падди и Вильгельми. Суть метода Дю Нуи — в измерении усилия, необходимого для отрыва кольца от поверхности жидкости. При подъёме кольца жидкость стремится стечь с него, что приводит к постепенному утончению плёнки и отрыву измерительного приспособления. Созданы даже специальные приборы для подобных измерений — тензиометры, максимально упростившие исследовательские ­процедуры.

Если вместо кольца в тензиометре взять пластину, то получится уже новый метод Вильгельми, отличающийся меньшей точностью, но не требующий знания плотности жидкости.

Очередной вариацией тензиометрических способов выступает метод ­Падди — в нём нет ни кольца, ни пластины, а есть цилиндр, отрывая который от поверхности жидкости, определяется величина «сигма».

Но некоторые жидкости имеют столь малое поверхностное натяжение, что вышеописанные методы им не подходят. И тогда на помощь придёт метод вращающейся капли. Для этого капля исследуемой жидкости помещается в стеклянную трубку с другой, более тяжёлой жидкой субстанцией. Далее трубку начинают вращать вдоль своей продольной оси, капля лёгкой жидкости вытягивается вдоль оси, принимая форму цилиндра. Измерив радиус этого своеобразного вращающегося цилиндра, можно узнать даже самые минимальные значения поверхностного натяжения жидкости. 

Силы, деформации, напряжения и связь между ними

Силы, деформации, напряжения и связь между ними

Категория:

Деформации при сварке

Силы, деформации, напряжения и связь между ними

Прочностью металла называют способность его сопротивляться разрушению под действием сил.

Силы подразделяют на внешние и внутренние. Внешние силы создаются от постоянной нагрузки: вес изделия, давление газа в сосуде, предварительное натяжение элемента, например, арматурного стержня в железобетоне и от временной нагрузки: вес снега на крыше здания, ветер, создающий нагрузку на стену сооружения, сейсмические воздействия и др.

Рис. 1. Изменение длины стержня при возрастании нагрузки: Р, Р1 — силы, действующие на стержень

Рис. 2. Диаграмма растяжения стали: (Уу— предел упругости, <гт— предел текучести, бв — временное сопротивление растяжению

Внутренние силы возникают от изменения температуры изделия при эксплуатации, изменения структуры металла под действием внешней нагрузки или при сварке, или от действия тех и других. В расчетах на прочность внутреннюю силу часто называют усилием.

Внешние нагрузки бывают статическими (постоянными в процессе эксплуатации изделия), динамическими (переменными по величине и направлению) и ударными. Динамические знакопеременные нагрузки называются также вибрационными. Внутренние силы носят изменяющийся характер.

Деформацией называется изменение формы и размеров тела под действием внешней или внутренней силы. Допустим, что к концам стержня длиной L (рис. 1) приложены силы, возрастающие от Р до Р\, растягивающие его.

При растяжении стержня постоянного сечения величина деформации определяется действующей силой. Чем больше сила, тем больше вызываемая ей деформация.

Напряжением называют силу, отнесенную к единице площади ррперечного сечения тела. Сила измеряется в кгс, площадь в мм2 или см2,, а напряжение в кгс/мм2, кгс/см2.

Различают напряжения растяжения, сжатия, изгиба, кручения и среза.

Деформации могут быть упругие и пластические. Если форма и размеры тела восстанавливаются после прекращения действия силы, то такая деформация будет упругой. Для образца из низкоуглеродистой стали, в котором действует постоянно возрастающее напряжение, деформация в виде относительного удлинения 6% остается упругой до тех пор, пока сила не превысит некоторый предел, называемый пределом упругости. Точкой С на диаграмме отмечена сила (или напряжение), при которой появляется деформация, остающаяся” после снятия нагрузки,— пластическая деформация. Эту точку называют пределом текучести ат.

Упругая деформация по величине весьма незначительна. Для низкоуглеродистых сталей она не превышает 0,2%. Следовательно, любое усилие, вызывающее относительное удлинение менее 0,2’%, приводит лишь к упругой деформации, которая сразу же исчезает при прекращении действия приложенного усилия.

Пластическая деформация сильно увеличивается, если напряжение превышает предел упругости. Например, если напряжение в детали из стали СтЗ превысит предел упругости на 1 кгс/мм2, относительное удлинение возрастет с 0,2 до 2%.

При повышении температуры стали предел упругости и предел текучести понижаются, следовательно, пластическая деформация возникает при меньших напряжениях или усилиях, чем в холодном металле (рис. 3). Из рисунка видно, что предел текучести при температуре 0 °С, равный 25 кгс/мм2, при температуре 400 °С понижается до 15 кгс/мм2, а при 600 °С до 6 кгс/мм2. При темпе ратуре выше 600 °С предел-текучести становится настолько малым что достаточно совсем небольшого усилия для возникновения остаточной деформации.

Рис. 3. Влияние температуры на величину предела текучести стали

Реклама:

Читать далее:

Возникновение напряжении и деформаций при сварке

Статьи по теме:

Влияние частоты, напряжения и силы тока на человека. Поражение электрическим током. Таблица поражающего действия силы тока для сети 220/380В 50Гц и пояснения.

	Навигация по справочнику TehTab.ru:  главная страница  / / Техническая информация / / Справочник инженера / / Физика и химия человека. Данные о среднем инженере / инженере-даме или будущем инженере. Механика и гидравлика инженеров. Расход энергии инженерами. Тепловые параметры инженеров. Инженеры и звук. Электрические параметры инженеров. Оптика инженеров.  / / Влияние частоты, напряжения и силы тока на человека. Поражение электрическим током. Таблица поражающего действия силы тока для сети 220/380В 50Гц и пояснения. Влияние частоты, напряжения и силы тока на человека. Поражение электрическим током. Таблица поражающего действия силы тока для сети 220/380В 50Гц и пояснения. Убивает ток (людей с кардиостимуляторами и т.п.- не только ток). Любой ощутимый ток проходящий через Вас в течение достаточно длительного времени убьет Вас. Поэтому сперва приведем примерные времена допустимого воздействия электрического тока в зависимости от напряжения на человека (по ГОСТ 12.1.038-82 ССБТ «Предельно допустимые величины напряжений и токов. Электробезопасность»): Допустимое время действия, сек длительно До 30 1 0,5 0,2 0,1 Величина тока, мА. 1 6 50 100 250 500 Величина напряжения, В. 6 36 50 100 250 500 Теперь небольшие пояснения: ощутимый ток — ток, вызывающий при прохождении через организм ощутимые раздражения неотпускающий ток — ток, вызывающий при прохождении через человека непреодолимые судорожные сокращения мышц руки, в которой зажат проводник (самому разжать руки невозможно) фибрилляционный ток — ток, вызывающий при прохождении через организм фибрилляцию сердца (мышцы сокращаются разрозненно и нескоординированно, вследствие чего сердце теряет способность совершать согласованные сокращения) Поражающее воздействие постоянного (DC) и переменного (AC) тока в зависимости от напряжения. Напряжение < 500 В поражения постоянным током меньше, чем переменным той же величины, якобы напряжение 120 В постоянного тока при одинаковых условиях эквивалентно по опасности напряжению 40 В переменного тока промышленной частоты (50Гц) Напряжение > 500 В различий в воздействии постоянного и переменного токов практически не наблюдаются Влияние частоты на поражающее воздействие переменного тока (для диапазона напряжений 0-500В) 50 Гц — промышленная частота в РФ самыми неблагоприятными для человека являются токи промышленной частоты. 50 Гц — 0 Гц с уменьшением частоты значения силы неотпускающего тока возрастает. При частоте, равной нулю (постоянный ток ), они становятся больше примерно в три раза значений для 50 Гц 50 Гц -100 Гц значения фибрилляционного тока при этих частотах равны. 200 Гц фибрилляционный ток возрастает примерно в 2 раза по сравнению с диапазоном 50-100 Гц 400 Гц фибрилляционный ток возрастает примерно в 3,5 раза по сравнению с диапазоном 50-100 Гц Таблица поражающего действия силы тока для сети 220/380В 50Гц и пояснения. Значение силы тока, мА Характер воздействия Общее название для воздействия тока Переменный ток 50 Гц Постоянный ток 0,6-1,6 Начало ощущения — слабый зуд, пощипывание кожи под электродами Не ощущается неощущаемые токи (0,6 – 1,6мА) 2-4 Ощущение тока распространяется и на запястье руки, слегка сводит руку Не ощущается ощущаемые токи (3мА) 5-7 Болевые ощущения усиливаются во всей кисти руки, сопровождаются судорогами; слабые боли ощущаются во всей руке, вплоть до предплечья. Руки, как правило, можно оторвать от электродов Начало ощущения. Впечатление нагрева кожи под электродом отпускающие токи (6мА) 8-10 Сильные боли и судороги во всей руке, включая предплечье. Руки трудно, но в большинстве случаев еще можно оторвать от электродов Усиление ощущения нагрева   10-15 Едва переносимые боли во всей руке. Во многих случаях руки невозможно оторвать от электродов. С увеличением продолжительности протекание тока боли усиливаются Еще большее усиление ощущения нагрева как под электродами, так и в прилегающих областях кожи неотпускающие токи (10-15мА) 20-25 Руки парализуются мгновенно, оторваться от электродов невозможно. Сильные боли, дыхание затруднено Еще большее усиление ощущения нагрева кожи, возникновение ощущения внутреннего нагрева. Незначительные сокращения мышц рук   25-50 Очень сильная боль в руках и груди. Дыхание крайне затруднено. При длительном токе может наступить паралич дыхания или ослабление деятельности сердца с потерей сознания Ощущение сильного нагрева, боли и судороги в руках. При отрыве рук от электродов возникают едва переносимые боли в результате судорожного сокращения мышц удушающие токи (25-50мА) 50-80 Дыхание парализуется через несколько секунд, нарушается работа сердца. При длительном протекании тока может наступить фибрилляция сердца Ощущение очень сильного поверхностного и внутреннего нагрева, сильные боли во всей руке и в области груди. Затруднение дыхания. Руки невозможно оторвать от электродов из-за сильных болей при нарушении контакта   100 Фибрилляция сердца через 2-3 с; еще через несколько секунд — паралич сердца Паралич дыхания при длительном протекании тока фибрилляционные токи (100-200мА) 300 То же действие за меньшее время Фибрилляция сердца через 2-3 с; еще через несколько секунд — паралич дыхания   более 5000 (5А) Дыхание парализуется немедленно — через доли секунды. Фибрилляция сердца, как правило, не наступает; возможна временная остановка сердца в период протекания тока. При длительном протекании тока (несколько секунд) тяжелые ожоги, разрушения тканей тепловые воздействия (5А и выше)
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.
TehTab.ru Реклама, сотрудничество: [email protected]	Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями.

Зависимость силы тока от напряжения

Различные действия тока, такие, как нагревание проводника, магнитные и химические действия, зависят от силы тока. Изменяя силу тока в цепи, можно регулировать эти действия. Но чтобы управлять током в цепи, надо знать, от чего зависит сила тока в ней.

Мы знаем, что электрический ток в цепи — это упорядоченное движение заряженных частиц в электрическом поле. Чем сильнее действие электрического поля на эти частицы, тем, очевидно, и больше сила тока в цепи.

Но действие поля характеризуется физической величиной — напряжением. Поэтому можно предположить, что сила тока зависит от напряжения. Эту зависимость можно установить на опыте.

На рисунке 256, а изображена электрическая цепь, состоящая из источника тока — аккумулятора, амперметра, спирали из никелиновой проволоки, ключа и параллельно присоединенного к спирали вольтметра. На рисунке 256, б показана схема этой цепи.

Замыкают цепь и отмечают показания приборов. Затем присоединяют к первому аккумулятору второй такой же аккумулятор и снова замыкают цепь. Напряжение на спирали при этом увеличится вдвое, и амперметр покажет вдвое большую силу тока. При трех аккумуляторах напряжение на спирали увеличивается втрое, во столько же раз увеличивается сила тока.

Таким образом, опыт показывает, что, во сколько раз увеличивается напряжение, приложенное к одному и тому же проводнику, во столько же раз увеличивается сила тока в нем. Другими словами, сила тока в проводнике прямо пропорциональна напряжению на концах проводника.

На рисунке 257 показан график зависимости силы тока в проводнике от напряжения между его концами. На этом графике в условно выбранном масштабе отложены по горизонтальной оси напряжение в вольтах, а по вертикальной — сила тока в амперах.

Вопросы. 1. Как зависит сила тока в проводнике от напряжения на концах проводника? 2. Как на опыте показать зависимость силы тока от напряжения? 3. Какой вид имеет график зависимости силы тона от напряжения?

Упражнения. 1. При напряжении на концах участка цепи, равном 2 В, сила тока в проводнике 0,4 А. Каким должно быть напряжение, чтобы в том же проводнике сила тока была 0,8 А? 2. При напряжении на концах проводника 2 В сила тона в проводнике 0,5 А. Какой будет сила тока в проводнике, если напряжение на его концах увеличится до 4 В? если напряжение на его концах уменьшится до 1 В?

Формула и определение электрического напряжения в цепи в физике

В современном быту, строительстве и других сферах жизни человека огромную роль играет энергия, которая необходима для приведения в движение различных механизмов, производственных станков и инструментов. Электрическое напряжение, или как его принято называть в народе ток, занимает первое место среди ресурсов снабжения, поэтому человек во многом зависит от бесперебойной подачи электричества правильного номинала. В данной статье рассмотрено определение электрического напряжения, его формула, а также, от чего зависит и на что влияет данный показатель.

Электрическое напряжение

Что такое напряжение

Электрическое напряжение – это работа, которая необходима для подачи заряда электрическим полем от поставщика до потребляемого прибора по проводам или без них. Проще говоря, это величина силы, потраченной для доставки определенного заряда тока по проводнику от одного конца на другой. Без напряжения не будет перемещения заряженных частиц, а, следовательно, ток не будет поступать к потребителю, номинальная величина в цепи будет равна нулю.

Электрическим током заряжены все элементы и предметы, которые окружают человека, разница лишь в величине напряжения – у некоторых вещей данный показатель минимален и фактически не заметен, у других – наличие тока более выражено. За долгие годы исследований ученые изобрели множество приборов, которые способны вырабатывать электрический ток различного напряжения и силы, начиная от малогабаритных и заканчивая крупными электростанциями, питающими целые города. Электрическое напряжение напрямую связано с силой тока: чем выше напряжение, тем выше будет величина силы тока.

Для более точного понимания определения напряжения тока необходимо разобраться в физике образования электричества в целом. Откуда берется электрический ток?

Все предметы и вещества состоят из атомов с положительным зарядом, число которых равно числу вращающихся вокруг них отрицательно заряженных частиц. Проще говоря, количество электронов равно количеству нейтронов. Чтобы возникло напряжение в сети, из ядра извлекаются некоторые электроны, возникает разряжение, и оставшиеся частицы пытаются восполнить пробел путем притяжения электронов снаружи, возникает положительный заряд. Если же добавить электроны в атом, возникнет переизбыток, и образуется отрицательное энергетическое поле.

В результате такого взаимодействия возникают положительный и отрицательный потенциалы, и чем больше контакта у этих элементов, тем выше сила и напряжение электрического тока. При соединении указанных потенциалов образуется энергетическое поле, которое увеличивается при повышении количества заряженных атомов внутри себя.

Формула для вычисления напряжения тока выглядит следующим образом:

U=A/q, где:

• U – это само напряжение,
• A – работа, необходимая для перемещения заряда,
• Q – отрезок расстояния, на которое перемещается заряженный атом.

Формула напряжения

Таким образом, можно сделать вывод, что сила тока на протяжении всей цепи будет одинаковой, а напряжение на каждом из участков будет разным, в зависимости от нагрузки на данный отрезок. Как известно, энергия не возникает из ниоткуда и не пропадает в неизвестном направлении, поэтому при повышении напряжения на определенном участке провода избыточный ток выражается в тепловой нагрузке, проще говоря, материал, из которого изготовлен проводник, начинает греться.

Влияние температуры проводника на сопротивление

От чего зависит напряжение

Существует три основных фактора, влияющих на норматив напряжения электрических токов, среди которых:

1. Материал, из которого выполнен проводник. Для решения определенных задач существуют различные типы проводов, чаще всего можно встретить медные или алюминиевые изделия различного сечения и наружной оболочки. Наружная обмотка таких проводов бывает также из множества материалов, защитных и декоративных, например, ПВХ пленка или резиновая защита. Такая обработка позволяет использовать проводку в любых условиях, в том числе для организации наружного освещения;
2. Температуры использования проводника;
3. Уровня сопротивления электрического тока на данном участке. Данная величина зависит от свойств проводимости кабеля или иного предмета, подключенного к сети, и способности к беспрепятственному пропуску атомов через себя. Существуют материалы с нулевым сопротивлением или полностью диэлектрические, то есть не способные проводить электрический ток любого напряжения.

Ток и его напряжение напрямую зависят друг от друга, поэтому и их обозначения одинаковы. Напряжение тока измеряется в Вольтах и обозначается буквой В. Вольт выражается в разности положительного и отрицательного потенциалов на двух удаленных от друг друга точках поля, силы которого совершают усилия, равные одному Дж, при доставке заряда от одного отрезка к конечному. Номинал единицы заряда равен одному Кл, таким образом, обозначение 220 Вольт включает в себя понятие, что данная сеть способна потратить энергию в 220 Дж для транспортировки зарядов от входной точки до потребителя, это и называется электрическим напряжением в сети.

Виды напряжения электрического тока

Синусоида постоянного и переменного тока

Что такое электрическое напряжение, описывается в учебниках по физике, там же приводится его классификация на основании временного промежутка подачи энергии. По данному признаку напряжение бывает:

1. Постоянное – это когда на одном конце проводника ток и электрическое напряжение положительные, а на другом – отрицательные, и их значение направлено в одну сторону. Чаще всего такая система встречается в автономных батареях слабой и средней мощности;

Важно! Случайная или умышленная замена полярностей может привести к выходу из строя прибора, а также короткому замыканию при соединении нескольких элементов, осуществлять это нужно последовательно, стыкуя минусовый контакт к плюсовому. Синусоида при постоянном токе будет ровной без рывков и волн.

2. Переменный ток и электрическое напряжение отличаются от постоянных тем, что у них может быть несколько направлений, например, при частой замене потенциалов полярностей или их перемещении возникает обратное движение заряда, частота данного действия и будет показателем переменного тока. Чаще всего данную систему используют для транспортировки электричества по проводнику на большие расстояния, так как потери тока минимальны, следовательно, и напряжение не уменьшается. Также переменный ток используется в трехфазных двигателях и при доставке постоянного тока на трансформатор для его последующего разделения. Синусоида переменного тока выглядит неровной, волнообразной, с множественными скачками. Существуют формула и механизмы, которые используются для преобразования переменного тока в постоянный, это возможно при наличии конденсаторов и диодного моста.

Между фазами переменного тока также существуют свои показатели, в данном случае напряжение равно 380В, по количеству разности потенциалов в трехфазной сети. В сети напряженностью 220В всего два провода: один – с несущей фазой, второй – с нулем, также для безопасности добавляется кабель заземления. В трехфазной сети имеется четыре жилы, и один дополнительный заземляющий провод, в сумме напряжение всех трех фаз составляет 380В.

Меры предосторожности

Ток и электрическое напряжение являются источником повышенной опасности, поэтому при работе и эксплуатации данного типа энергии необходимо соблюдать нормы и правила безопасности, не допускать аварийных ситуаций и обеспечить все приборы автоматической системой отключения питания.

Запрещается работать с проводкой, находящейся под напряжением, или без устройства для заземления. В случае возникновения короткого замыкания необходимо отключить все приборы от сети и предотвратить возгорание обмотки двигателя или кабеля.

Видео

Оцените статью:

Список параметров напряжения и силы электрического тока

В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока

Значения переменного напряжения (тока)

Далее для определенности будем говорить о параметрах напряжения, хотя они справедливы и для токов.

• Мгновенное значение — значение сигнала в определённый момент времени, функцией которого является (      ).

Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой осциллограф.

• Пиковое (амплитудное) значение — наибольшее мгновенное значение напряжения или силы тока за период

Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.

• Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата сигнала.

Среднеквадратичные значения являются самыми распространёнными, т. к. они наиболее удобны для практических расчётов, когда говорят просто о напряжении или силе тока, то по умолчанию имеются в виду именно их среднеквадратичные значения. В среднеквадратичных значениях проградуированы показывающие устройства всех вольтметров и амперметров переменного тока, однако, большинство приборов дают правильные показания для этих значений только при форме тока близкой к синусоидальной, некритичны к форме сигнала только приборы с термопреобразователем, специальным квадратичным детектором или квадратичным АЦП. Квадрат среднеквадратичного значения напряжения численно равен средней мощности, рассеиваемой на сопротивлении 1Ом.

• Среднее значение — постоянная составляющая напряжения или силы тока

На практике используется редко Геометрически это разность площадей под и над осью времени.

• Средневыпрямленное значение — среднее значение модуля сигнала

На практике используется редко, однако большинство измерительных приборов переменного тока (те, в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям. Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

Коэффициенты пересчёта значений

• Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению

• Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока)

Параметры постоянного тока

• Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени

• Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
  • Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
  • Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)

Литература и документация

Литература

Нормативно-техническая документация

Ссылки

См. также

Нормальные, растягивающие и другие примеры сил

Пример 1. Вес на уклоне, двумерная задача

Рассмотрим лыжника на склоне, показанном на рисунке 2. Ее масса, включая снаряжение, составляет 60,0 кг. а) Каково ее ускорение, если трение незначительно? б) Каково ее ускорение, если известно, что трение составляет 45,0 Н?

Рис. 2. Поскольку движение и трение параллельны склону, наиболее удобно проецировать все силы в систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева от лыжника). N перпендикулярно склону, а f параллельно склону, но w имеет компоненты вдоль обеих осей, а именно w _⊥ и [латекс] \ textbf {w} _ {\ parallel} [ /латекс]. N равно по величине w _⊥ , так что нет движения, перпендикулярного наклону, но f меньше w∥, так что есть ускорение вниз по склону (вдоль параллельной оси).

Стратегия

Это двумерная задача, поскольку силы, действующие на лыжника (интересующая система), не параллельны.Подход, который мы использовали в двумерной кинематике, также здесь очень хорошо работает. Выберите удобную систему координат и спроецируйте векторы на ее оси, создав , две , связанные, , одну -мерную задачу, которую нужно решить. Самая удобная система координат для движения по наклонной поверхности — это та, в которой одна координата параллельна склону, а другая — перпендикулярна склону. (Помните, что движения по взаимно перпендикулярным осям независимы.) Мы используем символы ⊥ и ∥ для обозначения перпендикуляра и параллельности соответственно.Такой выбор осей упрощает этот тип проблемы, потому что нет движения, перпендикулярного уклону, и потому что трение всегда параллельно поверхности между двумя объектами. Единственными внешними силами, действующими на систему, являются вес лыжника, трение и поддержка склона, обозначенные соответственно w , f и N на рисунке 2. N всегда перпендикулярно склону, а f параллельно ему. Но w не находится в направлении ни одной из осей, и поэтому первый шаг, который мы делаем, — проецируем его на компоненты вдоль выбранных осей, определяя w _∥ как составляющую веса, параллельную наклону, и w _⊥ компонент веса, перпендикулярный уклону. {\ circ}) — f} {m} [/ latex].{2} [/ латекс]

, что соответствует ускорению, параллельному наклону, при противоположном трении 45,0 Н.

Обсуждение

Поскольку трение всегда противодействует движению между поверхностями, ускорение меньше при трении, чем при его отсутствии. Фактически, общий результат заключается в том, что если трение на уклоне незначительно, то ускорение вниз по уклону составляет a = g sin θ , независимо от массы .Это связано с ранее обсуждавшимся фактом, что все объекты падают с одинаковым ускорением при отсутствии сопротивления воздуха. Точно так же все объекты, независимо от массы, скользят по склону без трения с одинаковым ускорением (если угол одинаков).

Определение силы натяжения, формула, примеры и закон движения Ньютона

Сила — это действие, которое заставляет свободный объект с конечной массой ускоряться относительно неускоряющейся системы отсчета.

Сила может быть разделена на два типа, а именно: Контактная сила и Бесконтактная сила.

Контактные силы — это силы, требующие контакта с другим объектом. Все механические силы — это силы контакта. Контактные силы можно разделить на следующие типы: мышечная сила, сила трения, нормальная сила, приложенная сила, сила натяжения, сила пружины и сила сопротивления воздуха.

Точно так же бесконтактные силы могут проявляться без какого-либо контакта с каким-либо объектом. Они делятся на гравитационную, магнитную и электростатическую.

Теперь рассмотрим подробное описание Силы натяжения, которая является контактной силой.

Сила натяжения Определение:

Сила натяжения — это сила, которая передается через кабель, канат, проволоку или струну, когда они натягиваются силами, действующими с противоположных концов. Он направлен по длине кабеля и одинаково натягивает предметы на противоположных концах провода.

Натяжение можно также описать как пару сил действие-противодействие, действующих на каждом конце упомянутых элементов. Напряжение могло быть противоположным сжатию.

Каждый физический объект, который находится в контакте, применяет некоторую силу друг к другу.Этим контактным силам будут присвоены имена в зависимости от типа объектов. Если одной из сил, действующих на объект, является трос, цепь или веревка, это называется натяжением.

Кабели и канаты могут использоваться для приложения силы, поскольку они могут эффективно передавать силу на определенное расстояние. Натяжение — это тянущая сила, поскольку канаты не могут толкать эффективно. При толкании веревкой веревка провисает и теряет натяжение, которое позволяло ей тянуть ее в исходном месте.

Формула натяжения:

Натяжение равно массе объекта × ускорение свободного падения для подвешенных объектов, находящихся в равновесии.

T = мг

T = натяжение, Н, кг-м / с²

m = масса, кг

g = сила тяжести,

Чему равна сила натяжения?

Система имеет постоянную скорость и равновесие, потому что натяжение троса / струны, тянущего вверх объект, равно силе веса, т.е.е. мг. где m — масса, а g — ускорение, вызванное силой тяжести, притягивающей объект.

Работает ли натяжение?

Очень просто, что натяжение никогда не возникает само по себе. Натяжение должно быть приложено к системе, и натяжение всегда является тянущим усилием, поэтому оно тянет с обоих концов, независимо от того, насколько сложна система, что делает сеть нулевой. Напряжение не действует само по себе, а только передается.

Почему важна сила натяжения?

Все находящиеся в контакте физические объекты могут оказывать друг на друга силу.Важно отметить, что натяжение — это тянущая сила, поскольку веревки просто не могут толкать эффективно. Попытка толкнуть веревку приводит к тому, что веревка провисает и теряет натяжение, которое изначально позволяло ей тянуть.

Почему в безмассовой струне постоянное натяжение?

Понятие натяжения струны может быть трудным для понимания, потому что струна удлиненная и нежесткая, так что натяжение существует по всей струне, а не в одной точке.

Зависит ли натяжение от массы?

Если груз подвешен к кабелю или проводу за фиксированную точку, провод или кабель будут находиться под натяжением, пропорциональным массе объекта.Проволока находится под натяжением, пропорциональным силе вытягивания.

Сила натяжения и законы Ньютона:

Окончательное применение закона Ньютона касается напряжения. Напряжение обычно возникает при использовании тросов, тросов для передачи силы. Рассмотрим блок, который тянут за веревку. Человек, тянущий за один конец веревки, не контактирует с блоком на другом конце и не может приложить прямую силу к блоку. Итак, на веревку действует сила, которая передает усилие на блок.Сила, которую испытывает блок от веревки, называется силой натяжения.

Классическая механика имеет дело с безмассовыми веревками или тросами. Если трос или веревка безмассовые, то они отлично передают силу от одного конца к другому. Например, если человек тянет безмассовую веревку с силой 30 Н, то блок также будет испытывать силу только 30 Н.

Важным свойством безмассовой веревки должно быть то, что общая сила на веревке всегда должна быть равна нулю.Чтобы доказать это, мы смотрим на второй закон Ньютона. Если результирующая сила действует на безмассовую веревку, это вызовет бесконечное ускорение A = F / m, а масса веревки равна нулю.

Ситуация, упомянутая выше, физически невозможна, и, следовательно, безмассовый канат никогда не сможет испытать результирующую силу.

Таким образом, на всю безмассовую веревку будут действовать две равные и противоположные силы натяжения. В случае, если человек тянет блок с помощью веревки / струны, веревка испытывает натяжение в одном направлении из-за тяги и натяжение в другом направлении из-за реактивной силы блока.

Натяжение и шкивы:

Динамика одиночной веревки довольно проста и легка, поскольку она передает приложенную силу. Но когда вместо канатов используются шкивы, возникают сложности. В динамическом смысле шкивы изменяют направление троса и не изменяют величину сил, действующих на трос.

На приведенной выше диаграмме показан небольшой блок слева, который поднимается большим блоком справа.Обратите внимание на силы T и -T на рисунке. Даже когда используются шкивы, канат должен испытывать две равные и противоположные силы натяжения. На рисунке выше веревка действительно испытывает две силы в одном направлении, что делает ситуацию невозможной.

Наличие шкива меняет ситуацию, делая его физически устойчивым.

Когда появляются трос и шкив, полезно определять направление не в терминах вверх и вниз, а в терминах формы веревки.В приведенной выше ситуации мы можем определить положительное направление веревки, как указывающее вверх с левой стороны и направленное вниз с правой стороны шкива. Когда направление определяется указанным выше способом, веревка действительно испытывает две равные и противоположные силы.

Если струна изгибается вокруг одного или нескольких шкивов, она будет иметь постоянное натяжение по всей длине в ситуации, когда шкивы не имеют трения и массы.

Натяжение в одном измерении:

Натяжение в одномерной струне является скалярной величиной.Это неотрицательно. Нулевое натяжение слабое / слабое. Канат или струна имеют длину одного измерения, но не имеют массы и имеют нулевое поперечное сечение. Если в канате / струне нет изгибов, которые возникают при колебаниях и шкивах, то натяжение будет постоянным вдоль струны, равным величине сил, приложенных концом струны.

Согласно третьему закону Ньютона, это силы, прилагаемые к концам веревки или веревки объектами, к которым эти концы прикреплены.Вибрирующая струна будет вибрировать с набором частот, который зависит от натяжения струн. Эти частоты могут быть получены из закона движения Ньютона.

Натяжение в трех измерениях:

Натяжение также используется для описания силы, прилагаемой к концам трехмерного непрерывного материала, такого как ферма и стержни. Такие стержни при растяжении удлиняются. Величина удлинения и нагрузка вызовут разрушение, и оба будут зависеть от силы, приходящейся на площадь поперечного сечения, а не только от силы, поэтому напряжение = осевая сила / площадь поперечного сечения.Напряжение — это матрица 3 × 3. Это называется тензором.

Направление натяжения:

Направление натяжения — это тяга, получившая название натяжение. Таким образом, натяжение будет направлено от массы в направлении струны / веревки. В случае подвешенной массы струна тянет ее вверх, поэтому струна / веревка оказывает на массу верхнее усилие, и натяжение будет происходить с верхней стороны.

Концы струны или другого объекта, передающего натяжение, будут прикладывать силы к объектам, к которым привязана струна, в направлении стержня / струны в точке присоединения.Силы, возникающие из-за натяжения, называются пассивными силами. У объектов, удерживаемых струнами / стержнями, есть два шанса: либо ускорение равно нулю, и система, следовательно, находится в равновесии, либо есть ускорение, и в системе присутствует результирующая сила.

Система будет находиться в равновесии, когда сумма всех сил равна нулю.

∑ F = 0

Система под действием чистой силы:

Система имеет результирующую силу, когда на нее действует неуравновешенная сила; я.е. сумма всех сил не равна нулю. Ускорение и чистая сила всегда существуют вместе.

∑ F ≠ 0.

Силы натяжения — Nexus Wiki

Твердое вещество (и, в меньшей степени, жидкости) имеет тенденцию удерживаться вместе, даже если вы попытаетесь разорвать его на части. Феноменологически мы пришли к примеру, когда кусок твердого вещества реагирует на растяжение растяжением (пружина). Гибкие твердые тела, такие как, например, струны, можно использовать для передачи сил от одного объекта к другому.Например, мы могли бы привязать веревку к крюку на коробке и потянуть за нее, чтобы потянуть коробку, ожидая, что веревка передаст силу, которую мы прилагаем к веревке, на коробку. Чтобы увидеть, как это работает, давайте посмотрим на диаграмму свободного тела для строки.

Если мы потянем за один конец веревки, и веревка прикреплена к коробке, коробка будет удерживать веревку в натянутом состоянии, потянув за другой конец. Если струна не меняет свою скорость, мы знаем из 2-го закона Ньютона, что результирующая сила, действующая на струну, должна быть равна 0, поэтому натяжение на любом конце струны будет одинаковым.

Чтобы понять, что происходит внутри строки, давайте рассмотрим простую модель строки: цепочку. (На самом деле, нить состоит из намотанных друг на друга волокон, действующих друг на друга за счет трения, но цепочка дает более простую картину и качественно верна.)

Простая модель натяжения: Цепь

Чтобы увидеть, как это работает, давайте рассмотрим простую модель связанных кусочков материи — звенья цепи, натянутые парой рук (не показаны), тянущей в противоположных направлениях — как схематично показано с несколькими звеньями на рисунке ниже. .

Если цепь находится в состоянии покоя, то каждое звено должно ощущать результирующую силу, равную 0. Рассмотрим схему свободного тела звеньев 1, 2 и 3. Руки тянут цепь влево и вправо с силой величиной T

Чередуя использование N2 и N3, мы можем изучить все силы на каждом звене цепи.

• Сила, с которой левая рука тянет вправо на L1, по определению равна T.
• Поскольку L1 не движется (и не ускоряется), по N2 T _{2 → 1} должно быть равно и противоположно T _{LH → 1} , поэтому L1 одинаково тянется в обоих направлениях с силой T.
• Переходим к звену 2, поскольку T _{2 → 1} и T _{1 → 2} являются одним и тем же типом силы и имеют обратные индексы, они представляют собой пары N3. Значит, они тоже имеют одинаковую величину.
• Поскольку L2 не движется (и не ускоряется), по N2 T _{3 → 2} должно быть равно и противоположно T _{1 -> 2} , поэтому L2 одинаково тянется в обоих направлениях с силой T.
• Переход к звену 3, так как T _{3 → 2} и T _{2 → 3} являются одним и тем же типом силы и имеют обратные индексы, это пары N3.Значит, они тоже имеют одинаковую величину.

Таким образом мы можем спуститься по цепи, чередуя N2 (силы, действующие на конкретное звено) и N3 (силы, которые два звена действуют друг на друга), чтобы увидеть, что каждое звено в цепи тянется в обоих направлениях за счет та же сила, T, что приложена к концам. Таким образом сила на одном конце передается по цепи.

Если мы рассмотрим струну (волокно) и ее внутреннюю часть, как показано на рисунке ниже, мы увидим, что верен тот же аргумент.Таким образом, каждая часть струны натягивается одинаково и противоположно одной и той же силой.

Векторные и скалярные напряжения

Мы говорили о «напряжении» как о силе, исходящей от объекта наружу. Но в случае тетивы или цепи, несмотря на равные и противоположные силы натяжения, важная вещь о натянутой струне или цепи состоит в том, что каждая ее часть, , тянется в противоположных направлениях, с той же силой. Для внутренних частей струны или цепи нет чистой силы, но есть своего рода «внутренняя ненаправленная сила».«Поскольку у него нет направления, это на самом деле не сила, но, тем не менее, это нечто значительное. Представьте, что ваши руки тянутся в двух противоположных направлениях. Даже если вы никуда не идете, вы об этом знаете!

К сожалению, традиционно используется одно и то же слово — натяжение — для обозначения равной внутренней тяги в противоположных направлениях. Когда вы читаете слово «напряжение», будьте осторожны, чтобы увидеть, имеется в виду сила с направлением или это «внутреннее» напряжение без направления.Поскольку величина без направления называется скаляром , в отличие от величины с направлением наподобие силы — вектором , эти понятия можно отличить, назвав их «скалярное натяжение» и «векторное натяжение», но, увы , это не стандартная практика.

Безмассовые струны

Если наша струна или цепь НЕ находятся в состоянии покоя или движутся с постоянной скоростью, тогда они должны удовлетворять закону Ньютона 2 ^и : ее ускорение должно возникать в результате ощущения неуравновешенной силы.НО, поскольку мы часто будем соединять наши струны с объектами, которые намного массивнее, чем они есть, разница в векторных напряжениях, необходимых для ускорения струны, обычно намного меньше, чем натяжение, необходимое для ускорения объекта, к которому она прикреплена. В результате мы обычно игнорируем массу струн, которые мы используем для передачи сил. Когда это сойдет с рук, мы поговорим об использовании «безмассовых струн».

В случае, если масса струны мала и ею можно пренебречь (по сравнению с другими массами в задаче), натяжения на обоих концах струны должны быть одинаковыми.{net} / m $, если масса очень мала, вам понадобится только небольшая чистая сила для создания большого ускорения.)

Джо Редиш 26.09.11

Сила натяжения — Определение | примеры | формула — DewWool

Ездовые собаки, тянущие сани, используя натяжение тросов

В физике натяжение — это сила, возникающая в струне, веревке или канате, когда они растягиваются под действием силы. Напряжение прилагается по длине провода / кабеля, но в направлении, противоположном приложенной к нему силе.Напряжение также иногда называют напряжением, натянутостью или напряжением. Давайте посмотрим на формулы, примеры силы напряжения в нашей повседневной жизни.

Сила натяжения — это тип контактной силы, так как она может возникать только при контакте между кабелем и объектом. Эта сила в основном тянет, но никогда не толкает. Нажатие на кабель снижает натяжение, а при натяжении — увеличивает натяжение.

Натяжение равное и противоположное для идеального каната с нулевой массой.Предположим, что на тросе висит груз весом 50 Н, тогда натяжение троса будет 50 Н в направлении вверх. Натяжение уравновешивает вес объекта. Напряжение противоположно силам сжатия.

В чем преимущество силы натяжения?

Натяжение позволяет передавать силу на большие расстояния. Предположим, мы хотим вытащить ведро, которое находится глубоко в колодце, и мы не можем туда спуститься физически. Натяжение веревки позволяет нам передавать нашу силу через веревку, чтобы поднять объект.

Единица силы натяжения

Напряжение — это вид силы. Итак, единицей измерения напряжения в системе СИ будет ньютон. Он также может быть выражен в других единицах силы, таких как дин, фунтал и т. Д. Вы можете прочитать наш блог о единицах силы для получения дополнительной информации.

Примеры силы натяжения Для подъема тяжелых материалов используются прочные тросы. Они могут выдерживать высокое усилие натяжения без разрушения.
Изображение Military_Material с сайта Pixabay

• Собаки тянут сани.Сила собак может быть эффективно передана на упряжку.
• Натяжение троса можно использовать для забора воды из колодцев через шкивы.
• Кабели от вертолетов используются для спасательных операций, подъема людей или тяжелого оборудования.
• Натяжение тросов используется для лазания по скалам или преодоления пересеченной местности.
• В лифтах используются тросы, которые могут выдерживать высокие силы натяжения.
• Сеть кабелей используется для удержания больших мостов. Такие конструкции называются подвесными мостами.Мост Золотые ворота в Сан-Франциско является примером подвесного моста.
• Во время перетягивания каната в канате возникает натяжение.

Формула силы натяжения

Нет специальной формулы для натяжения. Напряжение всегда равно и противоположно приложенной к нему силе (идеальный случай).

Скалолазы используют веревки для лазания по каменистой местности для поддержки и защиты от любого падения. Изображение Pexels с сайта Pixabay

Рассмотрим этот пример скалолазания.Натяжение веревки равно силе, действующей на нее человеком. Сила, прилагаемая человеком, равна его весу. Следовательно, натяжение в этом случае будет иметь вес = m * g в направлении вверх.

Шкив использует натяжение канатов для передачи силы.
Изображение billcosmos с сайта Pixabay

Давайте посмотрим на другой пример. Шкивы используются для подъема тяжелых предметов. Натяжение веревки передает нашу силу, приложенную в нисходящем или горизонтальном направлении, чтобы поднять объект в восходящем направлении.

Сила натяжения тросов лифта при разных сценариях.

Давайте теперь на примере кабелей, участвующих в движении лифта. Величина натяжения тросов различна в разных состояниях движения. Это связано с тем, что это зависит от того, движется ли лифт против силы тяжести или движется в направлении силы тяжести.

• Когда лифт остановлен, натяжение троса равно m * g.
• Когда лифт движется вверх против силы тяжести, натяжение равно m (g + a)
• Когда лифт движется вниз под действием силы тяжести, натяжение равно m (ga)

Значение максимального натяжение троса ограничивает его вес.Поэтому количество людей, которым разрешено находиться в лифте, ограничено.

Значение натяжения положительное или отрицательное?

Напряжение всегда положительное. Если значение натяжения отрицательное, это означает, что струна находится в состоянии сжатия. Значение будет положительным для любой силы, тянущей веревку. И значение будет отрицательным для любой сжимающей силы.

См. Также:

Напряжение (физика): определение, формула, как найти (с диаграммами и примерами)

Обновлено 28 декабря 2020 г.

Автор: Эми Дусто

Несмотря на название, физика напряжения не должна вызывать головную боль у студентов-физиков.Этот общий тип силы встречается в любом реальном приложении, где веревка или канатоподобный объект натягивается.

Физическое определение натяжения

Натяжение — это сила контакта, передаваемая через веревку, струну, проволоку или что-то подобное, когда силы на противоположных концах действуют на нее.

Например, качели шины, свисающие с дерева, вызывают натяжение веревки, удерживающей ее на ветке. Тяга нижней части веревки происходит под действием силы тяжести, а тяга вверх — от ветви, сопротивляющейся рывку веревки.

Сила натяжения действует по всей длине веревки и одинаково действует на объекты на обоих концах — шину и ветку. На шине сила натяжения направлена ​​вверх (поскольку натяжение троса удерживает шину вверх), а на ветви сила натяжения направлена ​​вниз (натянутый трос тянет вниз по ветви).

Как найти силу натяжения

Чтобы найти силу натяжения на объекте, нарисуйте диаграмму свободного тела, чтобы увидеть, где эта сила должна применяться (везде, где натягивается веревка или веревка).Затем найдите чистую силу , чтобы определить ее количественно.

Обратите внимание, что натяжение — это только тянущее усилие . Нажатие на один конец провисшей веревки не вызывает натяжения. Следовательно, сила натяжения на диаграмме свободного тела всегда должна быть нарисована в том направлении, в котором струна натягивает объект.

В сценарии качания шины, как упоминалось ранее, если шина все еще — то есть не ускоряется вверх или вниз — должна быть чистая сила , равная нулю .Поскольку на шину действуют только две силы, сила тяжести и натяжение, действующие в противоположных направлениях, эти две силы должны быть равны.

Математически: F _г = F _т , где F _г — сила тяжести, а F _т — сила натяжения. , как в ньютонах.

Напомним, что сила тяжести F _g равна массе объекта, умноженной на ускорение свободного падения g .Итак, F _г = мг = F _т .

Для шины массой 10 кг сила натяжения, таким образом, будет F _т = 10 кг × 9,8 м / с ² = 98 Н.

В том же сценарии, где веревка соединяется с ветвью дерева также нулевая чистая сила . Однако на этом конце каната сила натяжения на диаграмме свободного тела направлена ​​ вниз . Однако величина силы натяжения такая же: 98 Н .

Отсюда следует, что вверх контактная сила, которую ветвь прикладывает к веревке, должна быть такой же, как сила натяжения вниз, которая была такой же, как сила тяжести, действующая на шину вниз: 98 Н.

Сила натяжения в шкивных системах

Обычная категория физических проблем, связанных с натяжением, связана с шкивной системой . Шкив — это круглое устройство, которое вращается, чтобы выпустить веревку или веревку.

Обычно в школьных задачах по физике шкивы трактуются как безмассовые и не имеющие трения, хотя в реальном мире это не так.Масса веревки обычно также игнорируется.

Пример шкива

Предположим, что груз на столе соединен веревкой, которая изгибается на 90 градусов над шкивом на краю стола и соединяется с подвешенным грузом. Предположим, что вес на столе равен 8 Н, а вес подвесного блока справа 5 Н. Каково ускорение обоих блоков?

Чтобы решить эту проблему, нарисуйте отдельные диаграммы свободного тела для каждого блока. Затем найдите чистую силу на каждом блоке и используйте второй закон Ньютона ( F _net = ma ), чтобы связать это с ускорением.(Примечание: нижние индексы «1» и «2» ниже для «левого» и «правого» соответственно.)

Нормальная сила и сила тяжести (вес) блока уравновешены, поэтому результирующая сила равна все от напряжения, направленного вправо.

F_ {net, 1} = F_ {t1} = m_1a

Справа, натяжение тянет блок вверх, а сила тяжести тянет его вниз, поэтому чистая сила должна быть разницей между ними.

F_ {net, 2} = F_ {t2} -m_2g = -m_2a

Обратите внимание, что отрицательные значения в предыдущем уравнении означают, что вниз является отрицательным в этой системе отсчета и что окончательное ускорение блока (чистая сила) направлена ​​вниз.2

Сила натяжения в двух измерениях

Рассмотрим подвесную стойку для кастрюль. Стойку весом 30 кг удерживают две веревки, каждая под углом 15 градусов от углов стойки.

Чтобы определить натяжение любой веревки, необходимо уравновесить чистую силу в обоих направлениях x и y.

Начните со схемы свободного тела подставки для кастрюль.

Из трех сил, действующих на стойку, известна сила тяжести, и она должна быть одинаково уравновешена в вертикальном направлении обоими вертикальными составляющими сил натяжения.

F_g = mg = F_ {T1, y} + F_ {T2, y}

и потому что F _{T 1, y} = F _{T2, y} :

30 \ times 9,8 = 2 F_ {T1, y} \ подразумевает F_ {T1, y} = 147 \ text {N}

Другими словами, каждая веревка воздействует вверх на стойку для подвесных горшков с силой 147 Н.

Чтобы получить отсюда общую силу натяжения в каждой веревке, используйте тригонометрию.

Тригонометрическое соотношение синуса связывает y-компонент, угол и неизвестную диагональную силу натяжения веревки с обеих сторон.Решение для натяжения слева:

\ sin {15} = \ frac {147} {F_ {T1}} \ подразумевает F_ {T1} = \ frac {147} {\ sin {15}} = 568 \ text {N}

Эта величина будет такой же и с правой стороны, хотя направление силы натяжения другое.

Как насчет горизонтальных сил, которые оказывает каждая веревка?

Тригонометрическая связь тангенса связывает неизвестную компоненту x с известной компонентой y и углом. Решение для x-компоненты:

\ tan {15} = \ frac {147} {F_ {T1, x}} \ подразумевает F_ {T1, x} = \ frac {147} {\ tan {15}} = 548.6 \ text {N}

Поскольку горизонтальные силы также уравновешены, это должна быть сила, действующая на веревку справа в противоположном направлении.

ньютоновская механика — Есть ли общее правило для определения направления силы натяжения?

Натяжение — это внутренняя сила в теле, таком как веревка, которая сопротивляется любой попытке разорвать веревку. Просто напряжение возникает из-за межмолекулярных взаимодействий, и если бы его не было, веревки развалились бы в тот момент, когда вы их потянули.

Теперь необходимо различать внутренние и внешние силы для тела. Внешние силы — это силы, которые действуют на тело из-за других тел, например трение и гравитация. Когда вы смотрите на тело в целом, легко увидеть влияние силы на тело. Внешние силы позволяют большей части тела ускоряться при условии, что никакие другие внешние силы не нейтрализуют их (равновесие). Например: тело, на которое действует сила тяжести Земли:

Внутренние силы тела разные.Внутренние силы существуют внутри тела, и эффекты внутренних сил не могут напрямую взаимодействовать с чем-либо внешним по отношению к телу. Другими словами, внутренние силы — это силы, которые одна часть тела вызывает на другую часть того же тела (см. Ниже). Следовательно, не так ясно видеть «направление» таких сил. Внутренние силы не приводят к массовому ускорению, а вместо этого вызывают деформацию тела (например, растяжение пружины или изгиб линейки). Вот диаграмма, показывающая внутренние силы, действующие на блок:

Ну, вы не можете увидеть ничего очевидного снаружи, но это не потому, что внутренней силы не существует.Это потому, что если бы вы взяли все внутренние силы, присутствующие в теле, они бы в сумме равнялись нулю. Это результат 3-го закона Ньютона. Вместо этого лучший способ визуализировать внутренние силы в теле — это сделать воображаемый разрез через тело и посмотреть, как силы действуют на разрезанную поверхность. Это лучше продемонстрировано ниже на диаграмме, где веревка разрывается:

Рассматривая воображаемый разрез, вы смотрите на две половинки и обеспечиваете равновесие (если вся веревка подчиняется равновесию, то же самое должно происходить с любым произвольным отрезком веревки).Поступая таким образом, вы обнаруживаете, что для достижения равновесия одна половина должна воздействовать на другую половину, и наоборот по 3-му закону Ньютона. Эти особые силы являются внутренними, поскольку они вызваны действием одной части веревки на другую часть той же веревки. Эти внутренние силы действуют на границах раздела воображаемого разреза и в данном случае известны как натяжение. Точнее, натяжение в том месте веревки, где сделан воображаемый разрез. Обратите внимание, что вы можете определить направление натяжения, если посмотрите на одну половину веревки, но, поскольку натяжения возникают в паре, нет очевидного направления натяжения в этой точке веревки для всей веревки.

Рассматривая ваш пример, давайте сделаем несколько разрезов, чтобы увидеть силы натяжения в канате:

В приведенную выше диаграмму включены только силы, действующие на / в тросе, на коробке или на подвешенном грузе.

Короче говоря, внутренние силы, такие как натяжение в определенной точке веревки, на самом деле не имеют четкого направления, поскольку они возникают попарно.

границ | Колебания силы тяги и натяжения в растущих аксонах

1. Введение

Рост и движение клеток — это по своей сути механический процесс, включающий модуляцию внутриклеточных и внеклеточных сил, но на удивление мало известно о роли динамических сил в росте и наведении аксонов (Franze et al., 2013). Аксоны находятся под напряжением во время роста, и напряжение активно регулируется in vivo (Rajagopalan et al., 2010), и темпы роста могут модулироваться с помощью приложенных извне сил (rev. Suter and Miller, 2011). Также было показано, что изменения напряжения влияют на транспорт везикул и формирование синапсов (Ahmed and Saif, 2014). Во время разрастания напряжение связано с растягивающими напряжениями, создаваемыми силовыми участками адгезии между конусом роста и внеклеточным матриксом (ЕСМ).Недавно мы показали, что картирование этих стрессов обеспечивает динамическое считывание напряжения нейритов, а также подробную картину сложной картины стрессов, генерируемых во время роста (Koch et al., 2012). Сходные результаты были получены при исследовании нейронов мешочных клеток с аплизией (Hyland et al., 2014).

Как суммировано ниже в разделе «Предпосылки», флуктуирующие силы в аксоне и конусе роста включают согласованную активность разнообразного набора компонентов цитоскелета и моторных белков.Сборка и разборка структур, связывающих цитоскелет с субстратом, и генерация активных сил по своей сути является случайным процессом. Клетка должна управлять этими случайными колебаниями, чтобы обеспечить устойчивый рост, и регулировать те же процессы по мере необходимости, чтобы производить изменения, такие как поворот конуса роста в ответ на управляющие сигналы. Сами по себе колебания могут дать ключ к разгадке механизма оркестровки. В этой рукописи мы исследуем несколько взаимосвязанных аспектов флуктуаций силы, выявленных с помощью микроскопии силы тяги: устойчивые модели напряжений, которые лежат в основе сложных тяговых напряжений, создаваемых конусом роста, распределение локальных пиков напряжения в течение жизни и динамика флуктуаций натяжения аксонов. .Взятые вместе, эти результаты подтверждают модель динамики силы, в которой двигательная активность в аксоне и конусе роста постоянно генерирует сократительное напряжение, а наблюдаемые колебания происходят в основном из стохастической сборки и разборки спаек в конусе роста.

2. Справочная информация

Рост и руководство аксонов контролируется сложным взаимодействием полимеризации актина, ретроградного потока актина и полимеризации микротрубочек (rev. Dent et al., 2011; Gomez and Letourneau, 2013; Liu and Dwyer, 2014).Полимеризация актина генерирует ламеллиподиальные выступы и филоподиальный рост на переднем крае конуса роста, а сайты адгезии связывают цитоскелет актина с ECM. Этот процесс катализируется управляющими сигналами и стимулирующими рост лигандами, которые запускают передачу сигналов, которая локально модулирует полимеризацию актина (обзор Suter and Miller, 2011; Gomez and Letourneau, 2013). Спайки, также называемые фокальными или точечными контактами, действуют как «сцепление», которое при включении вызывает уменьшение ретроградного потока, питаемого миозином-II, что может способствовать протрузии мембраны и вторжению микротрубочек в периферическую зону конуса роста (Chan and Odde , 2008; Gomez, Letourneau, 2013).Таким образом, локальные напряжения, создаваемые конусом роста, обеспечивают прямое динамическое считывание сцепления (Chan and Odde, 2008; Koch et al., 2012; Toriyama et al., 2013; Hyland et al., 2014).

Создавая стрессы через связи ECM, клетки могут ощущать жесткость окружающей их среды, и в настоящее время имеются обширные доказательства того, что механика клеточной среды играет решающую роль в широком диапазоне нормальных и патологических биологических процессов и что нейронная реакция на ригидность играет роль как в нормальном развитии (Tyler, 2012; Franze, 2013), так и в эффективности имплантатов, предназначенных для восстановления после травм нервной системы (Minev et al., 2015). Головной и спинной мозг чрезвычайно мягкие (Franze et al., 2013), поэтому жесткие стеклянные подложки, используемые в большинстве исследований in vitro , особенно плохо отражают среду in vivo . Рост нейронов и ветвление дендритов модулируются жесткостью субстрата (обзор у Franze et al., 2013), и были идентифицированы некоторые из механочувствительных путей (Previtera et al., 2010; Kilinc et al., 2014), но картина остается в основном неполный.

Мы показали, что отрастание нейритов DRG оптимально на субстратах с промежуточной жесткостью, в то время как отростки нейронов гиппокампа нечувствительны к жесткости, и что эта разница в чувствительности коррелирует с различиями в силах тяги, создаваемых адгезией (Koch et al., 2012). Спайки, вызывающие стресс, обеспечивают критическую механическую связь между конусом роста и внеклеточным матриксом и, таким образом, играют центральную роль в определении жесткости, генерации напряжения и модуляции динамики цитоскелета во время роста нейритов и управления ими. Производство тяговых стрессов представляет собой одну из центральных мишеней богато сложных биохимических сигнальных путей, связанных с подвижностью и наведением (Dent et al., 2011), и, наоборот, генерация стресса вызывает отчетливую передачу сигналов от белков адгезии (Kuo, 2013).Таким образом, колебания напряжения представляют собой неоценимое средство измерения жесткости и подвижности конуса роста.

3. Материалы и методы

3.1. Культура клеток

Все эксперименты на животных в этом исследовании проводились в соответствии с рекомендациями Институционального комитета по уходу и использованию животных (IACUC) Джорджтаунского университета с использованием протокола, одобренного IACUC. Ганглии спинных корней (DRG) получали из поясничной области крысят P0-P1, подвергали их обрезке, промывали в среде Игла, модифицированной Дульбекко (DMEM), и ферментативно расщепляли в течение 20 мин в 3 мл 0.25% трипсина / 10 мкг / мл ДНКазы / Ca ²⁺ и Mg ²⁺ -свободный сбалансированный солевой раствор Хэнкса (HBSS). Реакцию останавливали добавлением равного объема фетальной бычьей сыворотки (FBS) с последующим добавлением DMEM до конечного объема 15 мл. Затем ганглии диссоциировали титрованием с помощью отполированной огнем пипетки Пастера. Затем клетки осаждали, ресуспендировали в 5 мл DMEM и пропускали через сетчатый фильтр для клеток 100 мкм. Сетчатый фильтр для клеток дважды промывали 5 мл DMEM, и клеточную суспензию объединяли, осаждали, дважды промывали в DMEM и ресуспендировали в нейробазальной среде (Life Technologies, Grand Island, NY).Клетки культивировали в нейробазальной среде с 2% B27, 5% лошадиной сывороткой, 100 ед. / Мл пенициллина, 100 мг / мл стрептомицина, 0,5 мкг / мл фунгизона и 10 мМ HEPES вместе с добавлением 2 нМ фактора роста нервов. Клетки высевали при относительно низкой плотности 1 × 10 ⁴ клеток / чашку и инкубировали при 37 ° С и 5% CO ² атмосфере. Количество клеток глии поддерживали на очень низком уровне за счет тщательной обрезки во время процесса препарирования и посева с низкой плотностью. Кроме того, для наблюдений были выбраны отдельные нейроны / ростовые конусы, чтобы избежать вмешательства со стороны глиальных клеток или других нейронов.Жизнеспособность клеток на предметном столике микроскопа обеспечивалась с помощью камеры для живых клеток (Tokai Hit, Сидзуока-Кен, Япония), оснащенной нагревателем объектива, который контролировал температуру и pH.

3.2. Подложки из полиакриламидного гидрогеля

Гидрогели полиакриламида (ПАК) были приготовлены в соответствии с опубликованными процедурами (Pelham and Wang, 1997; Sabass et al., 2008) с некоторыми модификациями. Вкратце, чашки со стеклянным дном диаметром 20 мм (MatTek, Ashland, MA) протирали 0,1 н. NaOH и силанизировали 3-аминопропилтриметоксисиланом (Sigma-Aldrich, St.Луис, Миссури). Чашки тщательно мыли и поверхность стекла обрабатывали в течение 30 минут 0,5% -ным глутаральдегидом с последующей последней промывкой. После этого 18-миллиметровые покровные стекла были покрыты Sigmacote (Sigma-Aldrich) для получения неклейких верхних покровных стекол. Акриламид и бис-акриламид (Bio-Rad Laboratories, Ричмонд, Калифорния) смешивали в растворе PBS до конечного объема 1 мл при соответствующих концентрациях для достижения желаемой жесткости геля. Для измерения силы тяги раствор FluoSphere bead (0.2 мкм, 660 нм; Invitrogen) добавляли в количестве 5% по объему. Конечный раствор дегазировали в течение 15 мин и помещали на лед на 5 мин. Полимеризацию инициировали добавлением 10 мкл свежеприготовленного персульфата аммония (10% раствор в / об; Sigma-Aldrich) и 3 мкл N, N, N, N -тетраметилэтилендиамина (TEMED; AcorsOrganics, Morris Plains, NJ). Сразу после инициирования 5 мкл раствора PAA было нанесено пипеткой на покровное стекло для чашки MatTek, и неклейкое верхнее покровное стекло было быстро помещено на каплю геля и осторожно прижато.Чашку переворачивали для облегчения оседания флуоресцентных шариков на верхней поверхности геля. Через 30 мин гель погружали в воду на 10 мин, а затем под водой осторожно удаляли верхние покровные стекла. Перед обработкой поверхности гели оставляли набухать в dH ² O в течение 1-2 ч. Гели покрывали 2 мкг / см ² [5 мкл 1 мг / мл CellTak (BD BioSciences) в 200 мкл dH ² O] при 20-минутной инкубации при комнатной температуре, а затем мкг / см ² (5 мкл 1 мг / мл ламинина в 200 мкл PBS) инкубация ламинина в течение 2 ч при 37 ° C.Перед посевом клеток гели инкубировали в среде для культивирования клеток в течение минимум 2 ч при 37 ° C. Предыдущие исследования не показали существенной разницы в адсорбции ламинина на гелях разной жесткости (Georges et al., 2006; Kostic et al. , 2007). Жесткость характеризовали во время полимеризации с помощью реологических измерений, проводимых на объемном реометре с контролируемым напряжением (Anton Paar KG, Грац, Австрия) с колебательным сдвигом 1 Гц при 1% деформации в течение 30 мин. Модуль Юнга, используемый при расчете тягового напряжения, был определен из модуля накопления меры G ‘как E = 2G’ (1 + ν) с использованием коэффициента Пуассона ν, равного 0.45 (Frey et al., 2007).

3.3. Обработка изображений и силовая микроскопия

гидрогелей PAA получали, как описано выше, и смещения флуоресцентных шариков на поверхности геля отслеживали, чтобы определить тяговые напряжения, создаваемые конусами роста. (Обзор этой техники см. В Style et al., 2014). В частности, флуоресцентные изображения шариков и изображения клеток в светлом поле записывали в виде временных рядов 3D-суммирования в течение 1-2 часов с временным разрешением 1-5 минут на конфокальном лазерном сканирующем микроскопе Leica TCS SP5 (Leica, Deerfield, IL), оборудованном. с водоиммерсионным объективом 63x при z шагов по 0.3–0,5 мкм. Срезы изображений каждой стопки были подвергнуты медианной фильтрации для уменьшения шума, а затем каждая стопка была уменьшена до двухмерного изображения с помощью проекции максимальной интенсивности. Полученные изображения были скорректированы смещением путем обнаружения сдвига каждого изображения относительно первого изображения. Сдвиг вычислялся в каждой угловой области (1/5 × 1/5 изображения) от пика взаимной корреляции, а медиана четырех значений использовалась для коррекции дрейфа. Эталонное изображение, представляющее конфигурацию с нулевым напряжением, было вычислено из медианы временного хода интенсивности в каждом пикселе.Смещения гранул между изображениями и эталонным изображением были обнаружены на двумерной сетке 0,75 мкм с использованием взаимной корреляции. Соответствующее поле деформации было получено методом 2D гауссовой интерполяции. Мы рассчитали поле тягового напряжения из поля деформации для каждого изображения во временном ряду, реализовав алгоритм на основе преобразования Фурье с использованием функции Буссинеска Грина, представленной Sabass et al. (2008).

Чтобы свести к минимуму Z-дрейф, данные с высоким временным разрешением были получены как 2D-изображения только после минимального времени уравновешивания системы, равного 1 часу, с чашкой для образцов на столике микроскопа.Данные записывались с временными интервалами 1 или 2 с с ручной коррекцией Z-фокуса каждые несколько минут, когда это необходимо для корректировки любого остаточного Z-дрейфа.

3.4. Анализ силы тяги конуса роста

Каждый рассматриваемый набор данных состоял из набора из N наблюдений или изображений, разделенных по времени Δ t . Для каждого изображения в наборе данных мы вычислили порог относительного напряжения S _порог

Порог (n) = 3 Шум (n), (1)

, где мы определили стресс-шум, S _noise , как среднее значение максимальных напряжений, извлеченных из четырех угловых областей карты растягивающих напряжений, связанной с наблюдением n .Мы наложили пороговое значение S _{пороговое значение} ( n ) на каждую соответствующую карту растягивающего напряжения, что привело как минимум к одной сохранившейся области напряжения. Затем мы нарисовали выпуклый корпус, определяемый пиками напряжения карты пороговых напряжений тяги, которую в целом можно понимать как многоугольник, определяемый наименьшим периметром, полностью охватывающий все оставшиеся области напряжений. Мы определили приблизительное «местоположение» конуса роста, вычислив центроид (геометрический центр) получившейся выпуклой оболочки (рис. 1).Результирующий набор векторов положения R = {r → 1, r → 2,… r → n,… r → N − 1, r → N} описывает траекторию конуса роста на временном интервале набора данных (рисунок 2). . Мы определили вектор v → n

v → n = r → n + 1 − r → nΔt, (2)

как скорость конуса роста, что дает мгновенное направление движения конуса роста во время наблюдения n .

Рис. 1. Метод определения положения конуса роста . Серый контур показывает общую форму конуса роста.Пунктирная линия показывает выпуклую оболочку карты пороговой силы тяги, а красный кружок показывает расположение центроида выпуклой оболочки, используемой для определения местоположения конуса роста. Масштабная линейка представляет 10 мкм.

Рис. 2. Пример траектории роста DRG с конусом . Красные кружки показывают рассчитанные положения конуса роста на основе изображений, сделанных с интервалом 180 с. Конус роста перемещается слева направо от изображения.Конечное положение DRG и поле тягового напряжения, как показано на рисунке 1. Красные кружки внутри белого прямоугольника указывают положения конуса роста, использованные на рисунке 3. Масштабная полоса представляет 10 мкм.

Чтобы исследовать природу генерирования силы тяги с «точки зрения» конуса роста, мы независимо повернули карту силы тяги каждого изображения вокруг центра тяжести выпуклой оболочки, чтобы сориентировать скорость конуса роста вдоль отрицательной оси x (рис. 3). . Это включало вращение каждой карты силы тяги на положительный угол, разделяющий вектор скорости и отрицательную ось x, которую мы выбрали в качестве положительного направления движения для любого произвольного конуса роста.После вращения карты силы тяги были обрезаны и повторно дискретизированы соответствующим образом, чтобы сохранить исходный масштаб и разрешение предварительно повернутого изображения. После вращения полученные карты силы тяги для каждого набора данных были добавлены вместе, чтобы создать усредненную картину пространственного распределения сил тяги, генерируемых в инерциальной системе отсчета конуса роста за период времени набора данных (рисунок 4).

Рисунок 3. Вращение системы координат поля напряжений (слева) в системе отсчета конуса роста (справа) .Пунктирная белая граница показывает выпуклую оболочку карты пороговых напряжений тяги, на основании которой было рассчитано положение конуса роста. Красные и белые круги представляют положения конусов роста в предыдущие и текущие моменты времени соответственно (в этом примере из белого поля на Рисунке 1). Пурпурная стрелка указывает направление движения конуса роста между этими временными точками. Панель справа создается путем поворота поля напряжений слева на угол (серая стрелка) вокруг текущего центроида (белый круг) таким образом, чтобы направление движения размещалось вдоль отрицательной оси x.Эта процедура превращает систему отсчета лаборатории в систему отсчета или перспективу конуса роста. Масштабная линейка представляет 5 мкм.

Рис. 4. Среднее пространственное распределение тяговых сил, оказываемых конусом роста, показанным на рис. 1, в течение всего периода сбора данных в системе отсчета конуса роста . Конус роста перемещается влево вдоль показанной горизонтальной оси. Фиолетовая стрелка, расположенная в начале координат, указывает направление результирующей силы.Черные кружки указывают местоположения максимумов напряжений в положительной и отрицательной y-плоскостях, а белые стрелки показывают соответствующее направление и относительную величину этих напряжений. Масштабная линейка представляет 5 мкм.

Природа и морфология конусов роста часто были очень динамичными. В частности, положение и направление движения, полученные из функции пространственного распределения тяговых сил (описанного выше), могут сильно различаться в небольших временных масштабах по сравнению с направленным изменением траектории аксона, характеризуемым в более крупных временных рамках.Таким образом, в краткосрочной перспективе мгновенное смещение привело к большим изменениям по сравнению с долгосрочным поведением конуса роста, поэтому мы наложили дискретную функцию сглаживания с подвижным окном на R для каждого набора данных. Размер окна был определен как функция Δ t , чтобы учесть различия во временном разрешении наблюдений в наборах данных, рассматриваемых для этого анализа. Дальнейшая мера была принята для учета периодов, когда конус роста «останавливался» или прекращал движение вперед.Если скалярное произведение вектора скорости и его преемника было меньше нуля, эти временные точки были исключены из рассмотрения из-за того, что наш анализ был сосредоточен только на общем поступательном движении аксона и конуса роста. Явно, если для любых последовательных временных точек n , n +1,

v → n · v → n + 1 <0, (3)

карты силы тяги, связанные с этими временными точками, не были включены в наш анализ для этого конкретного набора данных.

Отслеживание пиков напряжения выполнялось с использованием программного обеспечения для отслеживания частиц Imaris (Bitplane, Цюрих).Пики напряжения первоначально обнаруживались и отслеживались автоматически с использованием алгоритма обнаружения роста области, где пик A в одном кадре был связан с пиком B в следующем кадре, если расстояние между A и B было достаточно маленьким и если B был самым близким к A всех пиков, обнаруженных во втором кадре. Затем треки вручную проверялись и редактировались для каждого набора данных, чтобы учесть ошибки из-за алгоритмических ограничений (Дополнительное видео 1).

Мы рассчитали автокорреляцию,

R (τ) = <[(F (t) −μ) (F (t + τ) −μ)]> σ2,

для временного ряда чистой силы для каждого набора данных с высоким разрешением, где τ — временное разделение, σ — стандартное отклонение временного ряда, μ — среднее значение временного ряда, и каждая сумма за все время составляет т. .Мы учли время запаздывания или временное разделение, τ до 480 с, и нормализовали результат для каждого набора данных по его среднему значению (рисунок 7).

Мы также рассчитали среднеквадратичное смещение чистой силы,

MSD (τ) = <[F (t + τ) −F (t)] 2>,

для каждого набора данных с высоким разрешением, где τ было временным разделением, и каждая сумма за все время составляет t . Мы рассмотрели значения от τ до 900 (с), половину продолжительности захвата длин наборов данных, и нормализовали результат для каждого набора данных по его среднему значению (рис. 8).

Код расчета и анализа тягового усилия, используемый в описанных выше методах, можно найти по адресу https://github.com/rjpolackwich/gctf.

4. Результаты

4.1. Определение поля среднего напряжения конуса роста

Ранее мы сообщали, что стрессы конуса роста для развивающихся DRG нейритов крыс демонстрируют сложные пространственно-временные паттерны, при этом максимальные напряжения обычно возникают в периферической области между центральной зоной, близкой к шейке аксона, и филопдией на дистальном конце аксона (Koch и другие., 2012). В любой конкретный момент моментальный снимок этого поля напряжений выглядит совершенно неупорядоченным, хотя пиковые напряжения обычно направлены в центральную зону, а интегральная результирующая сила параллельна аксону, как того требует баланс сил.

Чтобы определить среднее поведение, вызванное колеблющимся полем напряжений, мы разработали алгоритм для определения положения конусов роста непосредственно из поля напряжений. Мы заметили, что, поскольку тяговые напряжения равномерно распределяются вокруг конуса роста DRG, они обеспечивают «след», который надежно охватывает центр конуса роста.Как описано в разделе 3 и показано на рисунке 1, мы использовали центр выпуклой оболочки этого отпечатка для алгоритмического извлечения положений конуса роста из каждой карты напряжений. Сравнение с контурами клеток на изображениях, сделанных одновременно с микроскопией силы тяги, подтвердило, что положение, определенное этим методом, обеспечивает разумную оценку середины конуса роста (дополнительное видео 2).

Используя полученную серию положений конуса роста (рисунок 2), мы преобразовали каждое поле напряжений в систему координат, зафиксированную на продвигающемся конусе роста (рисунок 3), как описано в разделе 3.Усреднение полей напряжений из всего временного ряда для продвигающегося конуса роста дало удивительно четкую и последовательную симметричную картину, один из примеров которой показан на рисунке 4. Поле среднего напряжения имеет сильные максимумы по сторонам конуса роста, направленные внутрь. к шейке конуса роста. Этот паттерн напоминает «силовые диполи», наблюдаемые в изолированных клетках (Mandal et al., 2014; Tanimoto and Sano, 2014), но с остаточной несбалансированной чистой силой, указывающей на напряжение аксонов.Мы выполнили этот анализ на 10 наборах данных траекторий DRG в диапазоне относительно мягких (150–400 Па) полиакриламидных подложек, снятых с интервалами времени от 120 до 180 с. Мы обнаружили, что изображения средней силы тяги были одинаковыми для всех изученных жесткости подложки (дополнительный рисунок 1).

4.2. Пиковое время жизни при локализованном напряжении

Напряжения тяги возникают из-за динамических несущих нагрузок адгезий, которые образуются и рассеиваются в слишком короткие сроки, чтобы их можно было измерить с низким временным разрешением данных, описанных выше и сообщенных в Koch et al.(2012). Поэтому мы выполнили серию измерений тягового усилия с гораздо более высоким временным разрешением, с изображением каждые 2 секунды. Эта процедура требовала почти непрерывного освещения клеток, в результате чего многие нейриты втягивались в ответ, но мы смогли записать 5 наборов данных для постоянно продвигающихся конусов роста. Для этих наборов данных можно четко определить рост и падение локализованных максимумов тягового напряжения (см. Раздел 3 и дополнительное видео 1).

На рис. 5 показана гистограмма времени жизни пиков напряжения, извлеченная из всех пяти наборов данных.Имеется большое количество очень короткоживущих пиков, за которыми следует промежуточный режим, который хорошо описывается распределением Пуассона (экспоненциальный спад), характеризующийся временем затухания 38 с (рис.5, вставка), за которым следует длительный хвост очень долгоживущих пиков. Длина траекторий (1800 с) достаточно велика, чтобы на статистику в области экспоненциального затухания существенно влияло конечное время наблюдения.

Рисунок 5. Гистограмма времени жизни стрессовых пиков .Большинство пиков напряжения имеют короткую продолжительность, некоторые — большую, а время жизни пиков около 30–150 с хорошо согласуется с экспоненциальным распределением (красная кривая). Очень короткие (<15 с) и очень долгоживущие (> 600 с) пики стресса не показаны на гистограмме. Вставка: лог-линейный график значений гистограммы от t = 30 до t = 150 с, с аппроксимацией методом наименьших квадратов (красная линия) с наклоном 1/38 с, что указывает на то, что большая часть пикового срока службы напряжения соответствует распределение Пуассона с временем затухания около 38 с.

4.3. Колебания натяжения нейрита

Карты растяжения обеспечивают прямое динамическое считывание напряжения нейритов. Как сообщается в Koch et al. (2012), натяжение нейритов DRG варьирует в умеренном диапазоне и не зависит от жесткости субстрата в доступном диапазоне (см. Supplementary Figure S6B в Koch et al., 2012). Высокое временное разрешение проанализированных здесь данных дает гораздо более подробную картину динамики натяжения. Временные ряды для всех 5 ячеек показаны на рисунке 6.Напряжение, по-видимому, изменяется случайным образом в коротких временных масштабах, хотя изменение от одного изображения к другому обычно невелико, что указывает на то, что шум измерения не вносит значительного вклада в колебания (каждая карта напряжений вычисляется независимо).

Рис. 6. Зависимость натяжения нетто от времени для каждого конуса роста, используемого для анализа колебаний . Размер флуктуации больше среднего, что приводит к отрицательной автокорреляции в течение длительного времени (рисунок 7).

Временную шкалу колебаний натяжения можно определить количественно путем вычисления автокорреляционной функции, показанной на рисунке 7.Этот стандартный анализ стохастических сигналов показывает степень, в которой изменения напряжения в один момент времени коррелируют с изменениями в более позднее время. Корреляция в очень короткие промежутки времени близка к единице, что указывает на небольшие колебания от одного изображения к другому, как указано выше. Однако корреляции затухают относительно быстро, с начальным быстрым падением, за которым следует область от 10 до 80 с, которая хорошо описывается экспоненциальным затуханием со временем затухания 95 с, что указывает на то, что флуктуации натяжения за время, намного большее, чем это в основном некоррелированы.Это время затухания чуть более чем в два раза превышает время затухания для экспоненциальной области распределения времени жизни пика напряжения (рис. 5).

Рис. 7. Автокорреляция нормализованной чистой силы . Колебания натяжения (результирующая сила) показаны для каждого набора данных (цветные линии) до времени запаздывания 500 с. Черная линия представляет среднее значение по ансамблю. Колебания от одного изображения к другому невелики, однако корреляции затухают относительно быстро, с начальным быстрым падением, за которым следует примерно экспоненциальный спад от 10 до 80 с со временем затухания 95 с, что указывает на то, что колебания натяжения на больших временах уменьшаются. в основном некоррелированы.Это время затухания чуть более чем в два раза превышает время затухания для экспоненциальной области распределения времени жизни пика напряжения (рис. 5).

В то время как кратковременная динамика колебаний напряжения кажется стохастической, напряжение не может расти неограниченно. Общее тяговое напряжение, создаваемое поперек конуса роста, почти постоянно (Koch et al., 2012), что может быть связано с относительно постоянным общим размером конуса роста. Влияние этого ограничения на колебания натяжения можно увидеть в росте среднего квадрата смещения (СКО) с течением времени, как показано на Рисунке 8.Этот анализ, часто используемый для траекторий диффундирующих частиц, описывает среднюю разницу между значениями натяжения, разделенными временем τ. СКО быстро растет в короткие промежутки времени, как и следовало ожидать из-за стохастических флуктуаций, обнаруженных в автокорреляционной функции. Однако через ~ 400 с МСД выходит на насыщение, указывая на то, что диапазон колебаний ограничен. Кривые MSD на Рисунке 8 нормализованы к среднему натяжению, и тот факт, что насыщение происходит при значении, превышающем единицу, является следствием больших колебаний натяжения относительно среднего значения (Рисунок 6).Таким образом, общая форма кривой MSD соответствует диффузионному движению в ограниченной области, но кривизна намного сильнее, чем при нормальной диффузии. Фактически, от 2 до 200 с MSD растет примерно как τ ^3/7 , по сравнению с показателем, равным единице для нормальной диффузии. Однако, учитывая значительную наблюдаемую межклеточную изменчивость, потребуется значительно больше данных, прежде чем можно будет сделать сильные количественные выводы о средней статистике популяции.

Рисунок 8.Нормированное среднеквадратичное смещение колебаний чистой силы . Цветные линии представляют отдельные МСД, а черная линия показывает среднее значение всех пяти. Каждый набор данных был нормализован по его среднему значению. MSD ограничен (как и ожидалось, потому что чистая сила конуса роста ограничена) и растет субдиффузионно с кажущимся показателем примерно 3/7.

5. Обсуждение

Мы показали, что существует четкий, устойчивый паттерн, лежащий в основе сложной пространственно-временной динамики тяговых напряжений, генерируемых конусами роста продвигающихся аксонов DRG крыс.Эта картина напоминает силовые диполи, наблюдаемые в изолированных подвижных клетках, которые обычно возникают из-за эффектов миозиновых моторов, генерирующих напряжение в актиновых стрессовых волокнах, закрепленных в местах адгезии на противоположных сторонах клетки (Mandal et al., 2014; Tanimoto and Sano , 2014). Однако, в отличие от изолированных клеток, растягивающие напряжения внутри конуса роста не уравновешиваются, а вместо этого имеют результирующую силу, равную напряжению в аксоне. Похожая ситуация наблюдается в гораздо более крупных конусах роста нейронов мешочных клеток аплизии , но со значительно уменьшенными временными вариациями (Hyland et al., 2014). С другой стороны, гораздо меньшие конусы роста аксонов гиппокампа крысы создают прерывистые, локализованные тяговые напряжения, которые всегда параллельны аксону. Одно прямое объяснение этого диапазона поведения состоит в том, что размер конуса роста определяет количество независимо колеблющихся участков адгезии, которые присутствуют в конусе роста в любой момент. Если есть только один, напряжение может возникнуть только между этим участком и аксоном. Когда есть несколько сайтов, напряжение может возникать как между сайтами адгезии, так и между адгезиями и аксоном.Для больших конусов роста количество участков адгезии может быть достаточно большим, чтобы относительные колебания были относительно небольшими, а характер напряжения напрямую связан с относительно постоянным распределением участков адгезии.

Используя измерения тягового напряжения с очень высоким временным разрешением, мы смогли охарактеризовать срок службы отдельных участков тягового напряжения. Мы обнаружили, что существует большое количество очень короткоживущих узлов и примерно такое же количество, которые распределены по распределению Пуассона с характерным временем затухания 38 с.Это примерно соответствует временной шкале, указанной для пиков растягивающего напряжения в конусах роста аплизии , (Hyland et al., 2014) и для участков адгезии конусов роста (Woo and Gomez, 2006), хотя значительно больше, чем временная шкала ~ 10 с. сообщили о колебаниях протрузивной активности на переднем крае конуса роста (Betz et al., 2007). Кроме того, некоторые конусы роста также обнаруживают очень долгоживущие сайты адгезии, которые трансформируются по мере продвижения, создавая большое напряжение аксонов.

Измерения с высоким временным разрешением показывают заметные колебания результирующей силы, отражающей натяжение аксона. Насколько нам известно, это первое сообщение об этом явлении. Автокорреляция колебаний предполагает лежащий в основе стохастический компонент, который изменяется в масштабе времени в десятки секунд, но что напряжение не колеблется слишком далеко от своего долгосрочного среднего значения. Наиболее вероятным источником колебаний натяжения является образование и разрушение спаек, о чем говорилось выше.Сходство временных шкал между временем жизни локальных максимумов напряжения и общими колебаниями напряжения подтверждает эту простую картину. Однако колебания в генерации активного напряжения в аксоне также могут играть роль.

Зрелые аксоны, в которых больше нет конуса роста, обнаруживают напряжение покоя, и их реакция на возмущения может быть смоделирована с помощью активного сокращения и вязкоупругой релаксации (Bernal et al., 2010). Недавние результаты измерений силы на буксируемых аксонах согласуются с сократительными силами, исходящими как от задней части конуса роста, так и от самого аксона, а также с вязкой диссипацией из потока компонентов цитоскелета (O’Toole et al., 2015). Таким образом, разумная минимальная модель, объединяющая эти результаты, будет включать в себя генерацию активной силы в аксоне и основании конуса роста, а также в самом конусе роста (для генерации дипольного компонента силы, а также компонента, параллельного конусу роста). аксон), причем колебания возникают исключительно из-за динамики адгезии. На этой картине миозин-зависимая сократимость, необходимая для генерации тягового стресса (Koch et al., 2012), вызывает по существу постоянное сократительное напряжение (и примерно постоянную скорость ретроградного потока актина в конусе роста) и критическую динамику. — это спайки и их связь с цитоскелтоном конуса роста.Стохастическая динамика адгезии может обеспечить механизм для исследования жесткости субстрата и, таким образом, обеспечить механическое управление (дуротаксис) и может быть чувствительно модулирована во время химического управления (хемотаксис).

Представленная здесь работа ограничена небольшим количеством конусов роста и теми, которые неуклонно продвигаются вперед. Будущие исследования должны включать более широкий спектр поведенческих моделей, в частности паузу, поворот и ветвление, поскольку они необходимы для понимания управления аксонами и созревания нейронов.Кроме того, необходимы измерения тягового усилия с высоким временным разрешением на других типах нейронных клеток, чтобы определить, можно ли применить представленное изображение к нейронам с небольшими конусами роста, демонстрирующими очень прерывистое напряжение, как это видно на нейронах гиппокампа крысы (Koch et al., 2012 ), а также с большими конусами роста, показывающими почти постоянное натяжение, как это наблюдается у aplysia конусов роста (Hyland et al., 2014). Наконец, необходимы экспериментальные манипуляции с компонентами цитоскелета, чтобы осветить лежащие в основе механизмы генерации силы внутри конуса роста и его роль в росте и управлении аксонами.

Авторские взносы

JP выполнил анализ данных, представленных в рукописи, DK выполнил все эксперименты и начальный анализ, RM помогал на всех этапах проекта, а HG и JU контролировали работу. JP, RM и JU создали рукопись при участии DK и HG.

Заявление о конфликте интересов

Авторы заявляют, что исследование проводилось при отсутствии каких-либо коммерческих или финансовых отношений, которые могут быть истолкованы как потенциальный конфликт интересов.

Благодарности

Эта работа была поддержана грантом 1R01NS064250-01 (JU) Национального института неврологических расстройств и инсульта и Программой интрамуральных исследований Национального института сердца, легких и крови (HG).

Дополнительные материалы

Дополнительные материалы к этой статье можно найти в Интернете по адресу: https://www.frontiersin.org/article/10.3389/fncel.2015.00417

Дополнительный рисунок 1. Распределение среднего пространственного тягового усилия, оказываемого 9 различными конусами роста, как показано на рисунке 4 .Мы наблюдали постоянную картину «силового диполя» во всем диапазоне жесткости подложки. Каждая метка относится к значению модуля Юнга подложки (в паскалях). Масштабные линейки соответствуют 5 микронам.

Дополнительное видео 1. Пример результатов автоматического отслеживания пиков . Расположение выявленных пиков напряжения отмечено красными сферами. Очевидные разрывы траекторий пиков напряжения были скорректированы вручную после автоматического отслеживания для учета алгоритмических ошибок.

Дополнительное видео 2.Отслеживание конуса роста с течением времени . Конус роста отслеживают с использованием метода выпуклого центроида холма при растяжении, как описано в разделе «Методы для флуоресцентно меченного аксона» (трансфекция актин-GFP, как описано в Koch et al., 2012).

Список литературы

Бернал Р., Мело Ф. и Пулларкат П. (2010). Сила перетаскивания как инструмент для проверки активной механической реакции нейритов PC12. Biophys. J. 98, 515–523. DOI: 10.1016 / j.bpj.2009.10.024

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Бец, Т., Кох, Д., Штурманн, Б., Эрлихер, А., и Кас, Дж. (2007). Статистический анализ роста нейронов: динамика краев и влияние сфокусированного лазера на подвижность конуса роста. New J. Phys. 9, 426–426. DOI: 10.1088 / 1367-2630 / 9/11/426

CrossRef Полный текст | Google Scholar

Дент, Э. У., Гуптон, С. Л., и Гертлер, Ф. Б. (2011). Цитоскелет конуса роста в росте и управлении аксонами. Cold Spring Harb. Перспектива. Биол. 3: а001800. DOI: 10.1101 / cshperspect.a001800

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Фрей, М., Энглер, А., Дишер, Д., Ли, Дж. И Ван, Ю. (2007). Микроскопические методы измерения эластичности гелевых субстратов для клеточных культур: микросферы, микроинденторы и атомно-силовая микроскопия. Methods Cell Biol. 83, 47–65. DOI: 10.1016 / S0091-679X (07) 83003-2

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Джордж, П., Миллер, В., Мини, Д., Сойер, Э., и Джанми, П. (2006). Матрицы с податливостью, сравнимой с податливостью ткани мозга, отбирают рост нейронов, а не глии в смешанных кортикальных культурах. Biophys. J. 90, 3012–3018. DOI: 10.1529 / biophysj.105.073114

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Хайланд, К., Мерц, А. Ф., Форшер, П., и Дюфрен, Э. (2014). Динамические силы периферической тяги уравновешивают стабильное напряжение нейритов в регенерирующих нейронах клеток мешка аплизии. Sci.Отчет 4: 4961. DOI: 10.1038 / srep04961

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Килинч, Д., Бласиак, А., О’Махони, Дж. Дж., И Ли, Г. У. (2014). Низкий пиконьютон аксонов ЦНС против диффундирующих и связанных с поверхностью репеллентов требует ингибирования путей, связанных с моторными белками. Sci. Отчет 4: 7128. DOI: 10.1038 / srep07128

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Кох, Д., Рософф, В. Дж., Цзян, Дж., Геллер, Х. М., и Урбах, Дж. С. (2012). Сила на периферии: биомеханика конуса роста и реакция жесткости субстрата в нейронах периферической и центральной нервной системы. Biophys. J. 102, 452–460. DOI: 10.1016 / j.bpj.2011.12.025

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Костич, А., Сап, Дж., И Шитц, М. (2007). RPTPalpha необходим для зависимого от жесткости ингибирования расширения и дифференцировки нейронов гиппокампа. J. Cell Sci. 120, 3895–904. DOI: 10.1242 / jcs.009852

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Мандал, К., Ван, И., Витиелло, Э., Орельяна, Л. А. К., и Балланд, М. (2014). Поведение клеточного диполя, выявленное субклеточной геометрией ECM. Нат. Commun. 5: 5749. DOI: 10.1038 / ncomms6749

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Минев И. Р., Мусиенко П., Хирш А., Барро К., Венгер Н., Морауд Э. М. и др.(2015). Электронная dura mater для долгосрочных мультимодальных нейронных интерфейсов -SM. Наука 347, 159–163. DOI: 10.1126 / science.1260318

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Пелхэм, Р. Дж., И Ван, Ю. (1997). Передвижение клеток и фокальные адгезии регулируются гибкостью субстрата. Proc. Natl. Акад. Sci. США 94, 13661–13665. DOI: 10.1073 / pnas.94.25.13661

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Превитера, М.Л., Лангхаммер, К. Г., Ланграна, Н. А., и Файрстейн, Б. Л. (2010). Регуляция ветвления дендритов жесткостью субстрата опосредуется рецепторами глутамата. Ann. Биомед. Англ. 38, 3733–3743. DOI: 10.1007 / s10439-010-0112-5

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Сабасс Б., Гардель М., Уотерман К. и Шварц У. (2008). Микроскопия тягового усилия высокого разрешения, основанная на экспериментальных и вычислительных достижениях. Biophys. J. 94, 207–220.DOI: 10.1529 / biophysj.107.113670

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Style, R. W., Boltyanskiy, R., German, G. K., Hyland, C., MacMinn, C. W., Mertz, A. F., et al. (2014). Тяговая силовая микроскопия в физике и биологии. Мягкое вещество 10, 4047. doi: 10.1039 / c4sm00264d

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Танимото, Х., Сано, М. (2014). Простое соотношение силы и движения для мигрирующих клеток, выявленное с помощью мультипольного анализа тягового напряжения. Biophys. J. 106, 16–25. DOI: 10.1016 / j.bpj.2013.10.041

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Торияма М., Кодзава С., Сакумура Ю. и Инагаки Н. (2013). Преобразование сигнала в силы для разрастания аксонов через Pak1-опосредованное фосфорилирование Shootin1. Curr. Биол. 23, 529–534. DOI: 10.1016 / j.cub.2013.02.017

PubMed Аннотация | CrossRef Полный текст | Google Scholar

Ву, С.

No related posts.