⇐ ПредыдущаяСтр 2 из 4Следующая ⇒
| Дано: | Решение: |
| С1,2=0,8 (пос) С1,2=5 (пар) мкФ | Сэк = = 0,8 (пос.) Сэк =С1+С2=5 (парал) С1,2 = 0,8×5 С2 = (5-С2)=4 -5с2+4=0 С1=4; С2=1 С1=1; С2=4 |
| Найти: | |
| С — ? | |
| Ответ: |
1.3.9. Определите, какой заряд способны накопить конденсаторы, включенные по схеме, показанной на рисунке, если U = 350 В, а емкости всех конденсаторов равны между собой и составляют 0,5 мкФ.
| Дано: | Решение: |
| U = 350 В С=0,5мкФ =0,5×10-6Ф | С=0,5мкФ×0,125мкФ+0,5мкФ=1,125мкФ |
| Найти: | |
| Q — ? | |
| Ответ: | 1,125мкФ |
Определите, какую энергию способны накопить конденсаторы, включенные по схеме, приведенной на рисунке в задаче 1.3.9.
| Дано: | Решение: |
| U = 350 В С=1,125*10-6 | 6.89 ДЖ |
| Найти: | |
| W — ? | |
| Ответ: | 6,89дж |
Глава 2 Электрические цепи постоянного тока
Сопротивление и проводимость проводников
От чего зависит сопротивление проводника?
Ответ: сопротивление зависит от площади сечения, материала и длины проводника.
Заполните таблицу.
| 10 МОм | 470 Ом | 0,33 МОм | 47 кОм | 4700 Ом | 1,5 кОм |
| 1*10 7Ом | 0,47кОм | 330кОм | 4,7×10-2Мом | 4,7×10-3Мом | 1500Ом |
2.1.3. Определите сопротивление стальной проволоки длиной 200 м и площадью сечения 5 мм2.
| Дано: | Решение: |
| L= 200м S =5мм2 P=1,3×10-7 | =5,20Ом |
| Найти: | |
| R -? | |
| Ответ: | 5,20 ом |
2.1.4. Для радиоприемника необходимо намотать сопротивление 30 Ом из никелиновой проволоки площадью сечения 0, 21 мм
| Дано: | Решение: |
| R-300м S-0.21мм2 q-0.42 | =15 м |
| Найти: | |
| T — ? | |
| Ответ: | 15 м |
Определите площадь сечения нихромовой проволоки длиной 20 м, если сопротивление ее равно 25 Ом.
| Дано: | Решение: |
| Q=1.1 t-20 r-250 | |
| Найти: | |
| S — ? | |
| Ответ: | 0,88 мм2 |
2.1.6. Проволока площадью сечения 0,5 мм2 и длиной 40 м имеет сопротивление 16Ом. Определите материал, из которого она изготовлена.
| Дано: | Решение: |
| R=16 Ом S=0.5 мм2 T=40 М | =0.2 По таблицы удаленых сопротив. Находим, что таким сопротивлением обладает свинец. |
| Найти: | |
| Q — ? | |
| Ответ: | 0.2 свинец |
В каких единицах системы СИ измеряется электрическая проводимость?
Ответ: Сименс (См)
Определите проводимость проводников, если их сопротивления равны 5 Ом, 1кОм, 125 кОм, 1 МОм.
2.1.9. Медный стальной провода имеют одинаковые диаметр и длину. Какой из них сильнее нагревается при одной и той же силе тока? (Выберите правильный ответ)
А) медный
Б) стальной
В) оба провода нагреются одинаково.
Зависит ли сопротивление катушки, изготовленной из медного провода, от величины приложенного к ней напряжения?
Ответ: нет независит.
Во сколько раз увеличится сопротивление линии, если медный провод заменить стальным таких же длины и поперечного сечения?
Ответ: сопротивление увеличится в 7-8 раз
Как измениться проводимость проводника, если его длину и диаметр увеличили в два раза?
Ответ: не изменится
Как определить длину мотка медной проволоки, не разматывая его?
Ответ: V=ST; T ; V=
2.1.14. Сверхпроводники – это материал, электрического сопротивления которого при понижении температуры до некоторой величины Тс понижается до ООМ.
Как зависит от длины кабеля электрическое сопротивление его жилы и сопротивление изоляции?
Ответ: Прямо пропорционально. Чем она длиннее, тем оно больше,
2.1.16. Провод состоит из одной стальной (ρ = 0,2410 Ом . м) и шести алюминиевых (ρ = 0,291 Ом . м) проволок диаметром 4,8 мм каждая. Определите сопротивление провода при температуре 20 0С.
| Дано: | Решение: |
| D1=4.8мм=0.0048м
T=200C
q1=0,2410 Ом
q | R= R=0.241 |
| Найти: | |
| R -? | |
| Ответ: `0.241 |
2.1.17. Обмотка трансформатора, изготовлена из медного провода, в нерабочем состоянии при температуре 150С имела сопротивление R1 =2 Ом. В ходе работы сопротивление ее стало R2 = 2,48 Ом. Определите температуру обмотки в рабочем состоянии, зная, что температурный коэффициент меди α = 0,004.
| Дано: | Решение: |
| R1 =2 Ом
R | r2=r1[l + a ( t2-t1) ] — t1 t2= |
| Найти: | |
| T — ? | |
| Ответ: | 45℃ |
Закон Ома
Напишите формулы закона Ома для участка и полной цепи.
I = I =
Между какими величинами закон Ома для участка цепи устанавливает зависимость?
Ответ: напряжение, сопротивление, сила тока.
Заполните таблицу.
| 0,15 А | 25 мА | 140 мкА | 0,02 А | 1,7А | 420 мкА |
| 150 мА | 2,5×104 мкА | 0.00014А | 20 мА | 1700000мкА | 0.42 мА |
Заполните таблицу.
| 0,2 В | 15 кВ | 0,03 MB | 25 мВ | 1200 мкВ | 220 В |
| 200 мВ | 15000 В | 30кВ | 25000мкВ | 0.0012 В | 0.22 КВ |
Ответ: увеличиться в 2 раза
2.2.6 Электрическая лампочка включена в сеть напряжением 220 В. Какой ток будет проходить через лампочку, если сопротивление ее нити 240 Ом?
| Дано: | Решение: |
| U-220 В R-240 Ом | I= =0.91 A |
| Найти: | |
| I — ? | |
| Ответ: | 0.91A |
Рекомендуемые страницы:
r = 0,5 мм = 0,0005 м
σ = 73 мН/м = 73*10⁻³ Н/м
Высота поднятия жидкости в капилляре определяется по формуле:
h = 2*σ / (ρ*g*r)
ρ = 1000 кг/м³ — плотность воды
g = 9,8 м/с² — ускорение свободного падения
Имеем:
h = 2*73*10⁻³ / (1000*9,8*0,0005) ≈ 0,030 м или 30 мм
Ответ: Высота поднятия воды в капилляре равна 30 миллиметрам
Плотность золота — 19,3 г/см^3. Плотность свинца — 11,35 г/см^3.
Масса = объём умножить плотность (m=V/r)
Масса слитка золота равна объёмом 1см3 равна 19,3г
Масса слитка свинца того же объёма = 11,35г.
19,3г-11,35г=7,95г.
7,95 приблизительно равно 8 грамм
Ответ: а)8 грамм; на 8г масса тела из золота больше массы тела из свинца.
T=2Пsqr(LC)=6.28*sqr(3.2*10^-9 ф* 9,6*10^-6 Гн=6,28*5,5*3,1*10^(-8) что приблизительно равно 1,07*10^(-6) c
Imax=UmaxCW=UmaxC(2П/Т)=12В*3,2*10^(-9)*(6.28/1.07*10^(-6) что приблизительно =0,2 А
Дальше 2 варианта у меня. пиши какой больше нарвится
1)I=Imax/sqr(2)=(приблизительно)0,14А
P=I^(2)R=0.0196 A * 0.66 Ом=(приблизительно) 0,013 Вт
2)P=UI=12В*0,2А=2,4 Вт
Теория
угол отклонения тонким клином с показателем преломления n размещенным в воздухе равен (n-1)*alpha
(смотри вложение 1)
представим задание из условия как три тонких клина
— боковые жидкостные клинья с углом у вершины alpha/2 и коэффициентом n
— центральный клин с углом у вершины alpha и коэффициентом nс
вершины у клиньев направлены в разные стороны, поэтому водяные дают вклад в отклонение в противоположном направлении
в итоге получаем δ=α*(nc-n)
(смотри вложение 2)
Элементы цепи могут быть подключены двумя способами:
- последовательно
- параллельно
Проиллюстрируем данные подключения на примере двух конденсаторов (рис. 1).
- последовательное соединение конденсаторов
Рис. 1. Последовательное соединение конденсаторов
Логическая зарядка конденсаторов происходит как показано на рис.1. Приходя из цепи, электрон останавливается на левой обкладке (пластине) конденсатора. При этом, благодаря своему электрическому полю (электризация через влияние), он выбивает другой электрон с правой обкладки, уходящий дальше в цепь (рис. 1.1). Этот образовавшийся электрон приходит на левую обкладку следующего конденсатора, соединённого последовательно. И всё повторяется снова. Таким образом, в результате «прохождения» через последовательную цепь конденсаторов «одного» электрона, мы получаем заряженную систему с одинаковыми по значению зарядами на каждом из конденсаторов (рис. 1.2).
Кроме того, напряжение на последовательно соединённой батареи конденсаторов есть сумма напряжений на каждом из элементов (аналог последовательного сопротивления проводников).
Рис. 2. Последовательное соединение конденсаторов
Часть задач школьной физики касается поиска общей электроёмкости участка цепи, логика такого поиска: найти такую электроёмкость, которым можно заменить цепь, чтобы параметры напряжения и заряда остались неизменными (рис. 2). Пусть заряд на обоих конденсаторах — (помним, что они одинаковы), электроёмкости — , и соответствующие напряжения — и .
Учитывая определение электроёмкости:
(1)
Тогда:
(2)
(3)
(4)
Памятуя о том, что конденсаторы соединены последовательно, получаем:
(5)
Тогда:
(6)
Или в общем виде:
(7)
- где
- — электроёмкость последовательно соединённых конденсаторов,
- — сумма обратных емкостей.
Для цепи из двух последовательных соединений:
(8)
- параллельное соединение конденсаторов
Рис. 3. Параллельное соединение конденсаторов
Параллельное подключение конденсаторов представлено на рисунке 3. При внесении электрона в систему, у него есть выбор: пойти на верхний или нижний конденсатор. При большом количестве электронов заполнение обкладок конденсатора происходит прямо пропорционально электроёмкости конденсаторов.
Рис. 4. Параллельное соединение конденсаторов. Поиск полной электроёмкости
Опять попробуем решить задачу по поиску полной ёмкости конденсаторов (рис. 4). Помним, что при параллельном подключении напряжения на элементах одинаковы, тогда:
(9)
(10)
(11)
С учётом того, что , получим:
(12)
Сокращаем:
(13)
Или в общем виде:
(14)
- где
- — электроёмкость параллельно соединённых конденсаторов,
- — сумма электроёмкостей последовательно соединённой цепи.
Вывод: в задачах, в которых присутствует цепь, необходимо рассмотреть, какое конкретно соединение рассматривается, а потом использовать соответствующую логику рассуждений:
- для последовательного соединения
- для параллельного соединения
Поделиться ссылкой:
Эквивалентная ёмкость конденсаторов
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
| Альтернативное отображение |
Последовательное соединение
Написав бот, расчета размерностей Система единиц измерения онлайн теперь начнем осваивать такую многогранную и сложную область как электротехника.
И первое, что нам пригодится, это расчет эквивалентных характеристик основных электрических элементов( ёмкость, индуктивность, сопротивление).
Хотелось бы напомнить, что ёмкости некоторых типовых конструкций мы уже умеем рассчитывать Ёмкость конденсатора онлайн
Сами по себе формулы очень просты, но нюанс состоит в том, как нам точно посчитать ёмкость двух последовательно соединенных конденсаторов если один из конденсаторов имеет ёмкость 10 пФ, а второй 250нФ. Размерность показывает что они различаются в 1000 раз. Можно конечно все перевести в абсолютные значения, но это при большом количестве конденсаторов способствует возникновению ошибок.
Итак, последовательное соединение конденсаторов имеет следующий вид
И формула расчета эквивалентной ёмкости выглядит так
Паралельное СОЕДИНЕНИЕ
Последовательное соединение нескольних конденсаторов выглядит так, как показано на рисунке
А формула становится до безобразия простой и наглядной
Синтаксис
Он очень прост
calc_e список емкостей с размерностями через запятую.
В ответе мы получим эквививалентное значение ёмкости при последовательном и паралельных соединениях.
Важное замечание: размерности нужно писать на русском языке. Для пользователей сайта, не знающих русский язык, можем по запросу добавить обработку англоязычных наименований приставок и размерностей. Это не сложно.
Примеры
Рассчитать ёмкость трех конденсаторов следующих номиналов: 10 пФ, 0.2нФ и 344мФ
В запросе так и пишем calc_e 10пФ,0.2нФ,344мФ
Ответ не заставит себя долго ждать и выглядит вот так
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
|
9.5238095235459пикофарад |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
|
344.00000021милифарад |
| Альтернативное отображение |
Удачи в расчетах!
- Эквивалентное сопротивление онлайн >>
Соединение конденсаторов — Знаешь как
 При отсутствии конденсатора нужной емкости или на нужное номинальное напряжение его можно заменить несколькими конденсаторами с другими параметрами.
При отсутствии конденсатора нужной емкости или на нужное номинальное напряжение его можно заменить несколькими конденсаторами с другими параметрами.
Конденсаторы соединяются последовательно, параллельно или смешано.
При последовательном соединении (рис. 4-5) на электродах всех конденсаторов будут одинаковые по величине заряды, так как от источника энергии заряды поступают только на внешние электроды, а на внутренних электродах они получаются только за счет разделения зарядов, ранее нейтрализовавших друг друга.
Рис. 4-5. Последовательное соединение конденсаторов
Обозначив заряд каждого из электродов конденсатора через Q, можно написать:
U1 = Q/C1 и U2 = Q/C2
таким образом, при различных значениях емкостей напряжения на них будут различны.
Выражая напряжение на зажимах цепи
U = U1 + U2
через отношение зарядов к емкостям конденсаторов, получим:
Q : C = (Q : C1) + (Q : C2)
или, сокращая на Q, напишем:
1 : C = (1 :C1) + (1 : C2)
откуда обща я или эквивалентная емкость двух последовательно соединенных конденсаторов
C = (C1C2) : (C1 + C2)
При параллельном соединении конденсаторов (рис. 4-6) напряжения на всех конденсаторах одинаковы, а заряды в общем случае имеют разные значения

Рис. 4-6. Параллельное соединение конденсаторов.
Заряд, полученный всеми параллельно соединенными конденсаторами, равен сумме зарядов отдельных конденсаторов, т. е.
Q = Q1 + Q2
откуда общая или эквивалентная емкость
C = Q/U = (Q1 + Q2)/U = C1 + C2
т. е. равна сумме емкостей отдельных конденсаторов.
При другом числе последовательно или параллельно соединенных конденсаторов, пользуясь формулами , нетрудно определить эквивалентные емкости.
Пример 4-1. Определить общую или эквивалентную емкость двух конденсаторов при последовательном и параллельном соединении их: С1 — 1 мкф; С2 = 3 мкф.
Эквивалентная емкость при последовательном соединении конденсаторов
С = (С1С2) : (C1 + C2) = (1 • 3) : 1 + 3 = 0,75 мкф
Эквивалентная емкость при параллельном соединении конденсаторов
C = C1 + C2 = 1+ 3 = 4 мкф.
Статья на тему Соединение конденсаторов
Лекция № 4
Тема 1. 2. Электрические цепи постоянного тока. Электрические измерения
План
Последовательное, параллельное и смешанное соединение конденсаторов
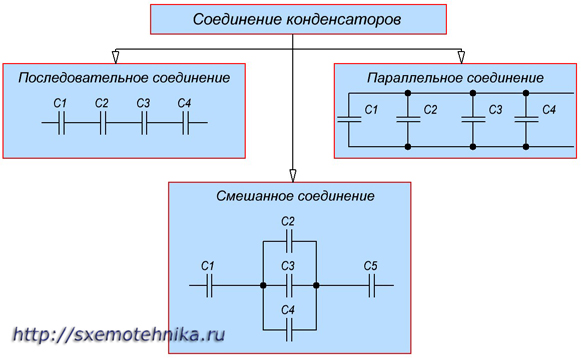
1. В электрических цепях применяются различные способы соединения конденсаторов. Соединение конденсаторов может производиться: после -довательно, параллельно и последовательно-параллельно (последнее иногда называют смешанное соединение конденсаторов). Существующие виды соединения конденсаторов показаны на рисунке 1.
Если группа конденсаторов включена в цепь таким образом, что к точкам включения непосредственно присоединены пластины всех конденсаторов, то такое соединение называется параллельным соединением конденсаторов (рисунок 2.).
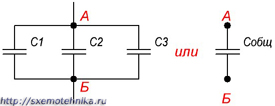
Рисунок 2. Параллельное соединение конденсаторов.
При заряде группы конденсаторов, соединенных параллельно, между пластинами всех конденсаторов будет одна и та же разность потенциалов, так как все они заряжаются от одного и того же источника тока. Общее же количество электричества на всех конденсаторах будет равно сумме количеств электричества, помещающихся на каждом из конденсаторов, так как заряд каждого их конденсаторов происходит независимо от заряда других конденсаторов данной группы. Исходя из этого, всю систему параллельно соединенных конденсаторов можно рассматривать как один эквивалентный (равноценный) конденсатор. Тогда общая емкость конденсаторов при параллельном соединении равна сумме емкостей всех соединенных конденсаторов.
Обозначим суммарную емкость соединенных в батарею конденсаторов буквой Собщ, емкость первого конденсатора С1 емкость второго С2 и емкость третьего С3. Тогда для параллельного соединения конденсаторов будет справедлива следующая формула:
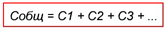
Последний знак + и многоточие указывают на то, что этой формулой можно пользоваться при четырех, пяти и вообще при любом числе конденсаторов.
Если же соединение конденсаторов в батарею производится в виде цепочки и к точкам включения в цепь непосредственно присоединены пластины только первого и последнего конденсаторов, то такое соединение конденсаторов называется последовательным (рисунок 3).
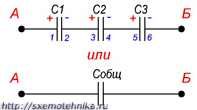
Рисунок 2. Последовательное соединение конденсаторов.
При последовательном соединении все конденсаторы заряжаются одинаковым количеством электричества, так как непосредственно от источника тока заряжаются только крайние пластины (1 и 6), а остальные пластины (2, 3, 4 и 5) заряжаются через влияние. При этом заряд пластины 2 будет равен по величине и противоположен по знаку заряду пластины 1, заряд пластины 3 будет равен по величине и противоположен по знаку заряду пластины 2 и т. д.
Напряжения на различных конденсаторах будут, вообще говоря, различными, так как для заряда одним и тем же количеством электричества конденсаторов различной емкости всегда требуются различные напряжения. Чем меньше емкость конденсатора, тем большее напряжение необходимо для того, чтобы зарядить этот конденсатор требуемым количеством электричества, и наоборот.
Таким образом, при заряде группы конденсаторов, соединенных последовательно, на конденсаторах малой емкости напряжения будут больше, а на конденсаторах большой емкости — меньше.
Аналогично предыдущему случаю можно рассматривать всю группу конденсаторов, соединенных последовательно, как один эквивалентный конденсатор, между пластинами которого существует напряжение, равное сумме напряжений на всех конденсаторах группы, а заряд которого равен заряду любого из конденсаторов группы.
Возьмем самый маленький конденсатор в группе. На нем должно быть самое большое напряжение. Но напряжение на этом конденсаторе составляет только часть общего напряжения, существующего на всей группе конденсаторов. Напряжение на всей группе больше напряжения на конденсаторе, имеющем самую малую емкость. А отсюда непосредственно следует, что общая емкость группы конденсаторов, соединенных последовательно, меньше емкости самого малого конденсатора в группе.
Для вычисления общей емкости при последовательном соединении конденсаторов удобнее всего пользоваться следующей формулой:

Для частного случая двух последовательно соединенных конденсаторов формула для вычисления их общей емкости будет иметь вид:
Последовательно-параллельным соединением конденса-торов называется цепь имеющая в своем составе участки, как с параллельным, так и с последовательным соединением конденсаторов.
На рисунке 4 приведен пример участка цепи со смешанным соединением конденсаторов.
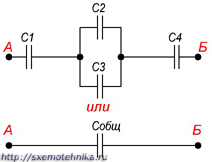
Рисунок 4. Последовательно-параллельное соединение конденсаторов.
При расчете общей емкости такого участка цепи с последовательно-параллельным соединением конденсаторов этот участок разбивают на простейшие участки, состоящие только из групп с последовательным или параллельным соединением конденсаторов. Дальше алгоритм расчета имеет вид:
1. Определяют эквивалентную емкость участков с последовательным соединением конденсаторов.
2. Если эти участки содержат последовательно соединенные конденсаторы, то сначала вычисляют их емкость.
3. После расчета эквивалентных емкостей конденсаторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных конденсаторов.
4. Рассчитывают емкость полученной схемы.
Один из примеров расчета емкости при смешанном соединении конденсаторов приведен на рисунке 5.
Вопросы для самопроверки:
Перечислить классификацию конденсаторов.
Объяснить, чему равна энергия заряженного конденсатора.
Перечислить способы соединения конденсаторов применяются в электрических цепях.
Обьяснить, какой способ соединения конденсаторов наз. параллельным?
Определить, чему равна суммарная емкость конденсаторов при параллельном соединении.
Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-пареллельным (смешанным).
Если провести аналогию между соединением конденсаторов и соединением резисторов , то стоит отметить, что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений:
Формула Cобщ при параллельном соединении конденсаторов = формула Rобщ при последовательном соединении резисторов.
Формула Cобщ при последовательном соединении конденсаторов = формула Rобщ при параллельном соединении резисторов.
- Cобщ — общая емкость
- Rобщ — общее сопротивление
Параллельное соединение конденсаторов
Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов.
При параллельном соединении формируется один большой конденсатор с площадью обкладок, равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо пропорциональна площади обкладок, общая емкость Собщ при параллельном соединении равняется сумме емкостей всех конденсаторов в цепи.
Параллельное соединение конденсаторов
Напряжение при параллельном соединении
На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит, потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение). Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения.
Падение напряжения при параллельном соединении
Ток при параллельном соединении
Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:
- ic — ток конденсатора
- C — Емкость конденсатора
- ΔVC/Δt – Скорость изменения напряжения
При параллельном соединении через каждый конденсатор потечет одельный ток, в зависимости от емкости конденсатора:
Ток при параллельном соединении
Последовательное соединение конденсаторов
Последовательное соединение конденсаторов – это соединение двух или более конденсаторов в форме цепи, в которой каждый отдельный конденсатор соединяется с другим отдельным конденсатором только в одной точке.
Последовательное соединение конденсаторов
Ток при последовательном соединении
Ток (iC), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения:
Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора.
Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд:
Посмотрим на последовательную цепь из трех конденсаторов на рисунке выше. Правая обкладка первого конденсатора С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3. Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи.
В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится.
При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.
Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи.
Площадь и расстояние между обкладками при последовательном соединении
Падение напряжения и общая емкость при последовательном соединении
На каждый отдельный конденсатор в последовательной цепи падает разное напряжение. Поскольку емкость обратно пропрциональна напряжению (С = Q/V), то чем меньше емкость конденсатора, тем большее напряжение на него упадет.
Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов:
Падение напряжения при последовательном соединении
Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3.
Следовательно:
Разделив все выражение на Qобщ мы получим уравнение для общей емкости при последовательном соединении:
Из данного уравнения можно легко вывести формулу общей емкости для любого частного случая последовательного соединения.
Например, общая емкость для трех конденсаторов:
Общая емкость для двух конденсаторов:
Смешанное соединение конденсаторов
Если в цепи есть и последовательное и параллельное соединение, то такую цепь называют смешанной или последовательно-параллельной. Тем не менее, смешанное соединение может иметь как последовательный, так и параллельный характер.
Смешанное соединение конденсаторов
Общая емкость смешанного соединения конденсаторов
Чтобы посчитать общую емкость смешанного соединения конденсаторов, следуют такому же алгоритму, как и при расчете общего сопротивления смешанного соединения резисторов.
- Цепь разбивают на участки с только пареллельным или только последовательным соединением
- Вычисляют общую емкость для каждого отдельного участка.
- Вычисляют общую емкость для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 2:
Преобразование смешанного соединения в параллельное
Зачем все это нужно?
Вполне справедливым может оказаться вопрос, для чего надо соединять конденсаторы последовательно, если общая емкость будет меньше? Скорее всего, первым что приходит в голову — это чтобы получить новый эквивалентный конденсатор с меньшей емкостью. Но в производстве микросхем вряд ли будут делать подобное, поскольку, во -первых, обычно нужно экономить место на печатной плате, а во-вторых, нет смысла тратить деньги на два компонента или больше, если можно купить один с требуемой емкостью.
Но если в параллельном или последовательном соединении конденсаторов еще есть хоть какая-то логика, то кому вообще нужно смешанное?
Дело в том, что емкостью, то есть способностью накапливать электрический заряд, обладает любое тело в природе, даже человеческое. Если мы говорим о электрической цепи, то все ее элементы на практике обладают емкостью, и их можно представить как конденсаторы. Часто такую емкость еще называют паразитической, потому как она создает разного рода помехи.
Например, у нас есть какая-то электронная цепь с множеством различных компонентов, которая принимает сигнал, обрабатывает его определенным образом и выдает на выход результат. Известно, что время задержки сигнала, в основном, зависит от паразитической емкости электронных компонентов схемы. Поскольку должно пройти время зарядки паразитической емкости, прежде чем она начнет пропускать сигнал. Если мы хотим узнать время задержки, нужно посчитать общую емкость всех компонентов, конвертировав их в цепь из конденсаторов.
% PDF-1.4 % 3194 0 объектов> endobj Xref 3194 95 0000000016 00000 n 0000003618 00000 n 0000003886 00000 n 0000004263 00000 n 0000004597 00000 n 0000004735 00000 n 0000004873 00000 n 0000005011 00000 n 0000005147 00000 n 0000005285 00000 n 0000005423 00000 n 0000005561 00000 n 0000005699 00000 n 0000005837 00000 n 0000005975 00000 n 0000006113 00000 n 0000006251 00000 n 0000006388 00000 n 0000006526 00000 n 0000006664 00000 n 0000006802 00000 n 0000006940 00000 n 0000007078 00000 n 0000007216 00000 n 0000007354 00000 n 0000007492 00000 n 0000007630 00000 n 0000007767 00000 n 0000007904 00000 n 0000008042 00000 n 0000008180 00000 n 0000008318 00000 n 0000008455 00000 n 0000008592 00000 n 0000008728 00000 n 0000008864 00000 n 0000009001 00000 n 0000009138 00000 n 0000009276 00000 n 0000009414 00000 n 0000009921 00000 n 0000010554 00000 n 0000010929 00000 n 0000010967 00000 n 0000011208 00000 n 0000011455 00000 n 0000011533 00000 n 0000011756 00000 n 0000012408 00000 n 0000012979 00000 n 0000013574 00000 n 0000014162 00000 n 0000014745 00000 n 0000015384 00000 n 0000015526 00000 n 0000015572 00000 n 0000016136 00000 n 0000016788 00000 n 0000019459 00000 n 0000019513 00000 n 0000019567 00000 n 0000019621 00000 n 0000019675 00000 n 0000019729 00000 n 0000019783 00000 n 0000019837 00000 n 0000019891 00000 n 0000019945 00000 n 0000019999 00000 n 0000020053 00000 n 0000020107 00000 n 0000020161 00000 n 0000020215 00000 n 0000020269 00000 n 0000020323 00000 n 0000020377 00000 n 0000020432 00000 n 0000020487 00000 n 0000020542 00000 n 0000020597 00000 n 0000020652 00000 n 0000020707 00000 n 0000020762 00000 n 0000020817 00000 n 0000020872 00000 n 0000020927 00000 n 0000020982 00000 n 0000021037 00000 n 0000021092 00000 n 0000021147 00000 n 0000021202 00000 n 0000021257 00000 n 0000021312 00000 n 0000003381 00000 n 0000002245 00000 n прицеп ] >> startxref 0 %% EOF 3288 0 объект> поток х ڼ U] ЛТ> vԪ «ч; I8 (Qď ܒ RMJ # I ْ bZuDj! $ 0L $ E {x @> LS5yuU {| 9 ‘
.Страница не найдена | MIT
Перейти к содержанию ↓- образование
- Исследовательская работа
- новаторство
- Прием + помощь
- Студенческая жизнь
- Новости
- Alumni
- О MIT
- Больше ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Alumni
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Посмотреть больше результатов
Предложения или отзывы?
,Страница не найдена | MIT
Перейти к содержанию ↓- образование
- Исследовательская работа
- новаторство
- Прием + помощь
- Студенческая жизнь
- Новости
- Alumni
- О MIT
- Больше ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Alumni
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Посмотреть больше результатов
Предложения или отзывы?
,Какова роль конденсатора в цепи переменного и постоянного тока?
Очень короткими словами (подробное описание и публикация ниже)
Роль конденсатора в цепях переменного тока:
В цепи переменного тока конденсатор меняет свои заряды по мере изменения тока и создает запаздывающее напряжение (другими словами, конденсатор обеспечивает опережающий ток в цепях и сетях переменного тока)
Роль конденсатора в цепях постоянного тока:
В цепи постоянного тока конденсатор, однажды заряженный от приложенного напряжения, действует как размыкающий переключатель.

 Какова роль конденсатора в цепи переменного и постоянного тока?
Какова роль конденсатора в цепи переменного и постоянного тока?Давайте объясним подробно, но сначала мы вернемся к основам конденсатора, чтобы обсудить этот вопрос.
Что такое конденсатор?
Конденсатор представляет собой двухполюсное электрическое устройство, используемое для хранения электрической энергии в виде электрического поля между двумя пластинами. Он также известен как конденсатор, и единицей измерения его емкости является Фарад «F», где Фарад — это большая единица емкости, поэтому в настоящее время они используют микрофарады (мкФ) или нанофарады (нФ).
Конденсатор похож на батарею, поскольку оба хранят электрическую энергию. Конденсатор — намного более простое устройство, которое не может производить новые электроны, но сохраняет их. Внутри конденсатора клеммы соединены с двумя металлическими пластинами, разделенными диэлектрическим материалом (таким как вощеная бумага, слюда и керамика), которые разделяют пластины и позволяют им удерживать противоположные электрические заряды, поддерживая электрическое поле.
Конденсаторы могут быть полезны для накопления заряда и быстрого разряда в нагрузке.Проще говоря, конденсатор также работает как небольшая перезаряжаемая батарея. Электрический эквивалентный символ различных типов конденсаторов приведен ниже: 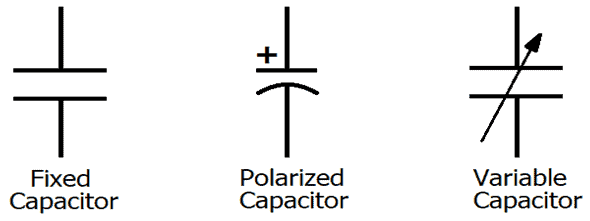

Теперь мы знаем концепцию зарядки конденсатора и его структуру, но, , знаете ли вы, что такое емкость? емкость — это способность конденсатора сохранять заряд в нем. Есть несколько факторов, которые влияют на емкость.
- Площадь пластины
- Разрыв между пластинами
- Диэлектрическая проницаемость изоляционного материала
Похожие сообщения:
Конденсатор имеет широкий спектр применений в электронике , таких как накопление энергии, кондиционирование, коррекция коэффициента мощности, Осцилляторы и фильтрация.
В этом уроке мы объясним вам, как вы можете использовать конденсатор в электронной схеме. Существует три способа подключения конденсатора в электронную цепь: конденсатор
- в серии
- параллельно в конденсаторе
- конденсатор в цепях переменного тока
- конденсатор в цепях постоянного тока
Похожие сообщения: Конденсаторы MCQ с пояснительными ответами
Как работает конденсатор?
Работа и сборка конденсатора
Всякий раз, когда на его клеммы подается напряжение (также известный как зарядка конденсатора), ток начинает течь и продолжает распространяться до тех пор, пока напряжение не станет отрицательным и положительным (Анод и Катодные) пластины становятся равными напряжению источника (Applied Voltage).Эти две пластины разделены диэлектрическим материалом (таким как слюда, бумага, стекло и т. Д., Которые являются изоляторами), который используется для увеличения емкости конденсатора.
Когда мы подключаем заряженный конденсатор через небольшую нагрузку, он начинает подавать напряжение (накопленную энергию) на эту нагрузку, пока конденсатор не разрядится полностью.
Конденсатор имеет различные формы, и его значение измеряется в Фарадах (F). Конденсаторы используются в системах переменного и постоянного тока (мы обсудим это ниже).
Емкость (C):
Емкость — это количество электрического заряда, перемещаемого в конденсаторе (конденсаторе), когда один источник напряжения вольт подключен к его клемме.
Математически,
Уравнение емкости:
C = Q / V
Где,
- C = Емкость в Фарадах (F)
- Q = Электрическая зарядка в Coul V = напряжение в вольтах
Мы не будем вдаваться в подробности, потому что наша основная цель этого обсуждения — объяснить роль и применение / использование конденсаторов в системах переменного и постоянного тока.Чтобы понять эту базовую концепцию, мы должны понимать основные типы конденсаторов, относящиеся к нашей теме (поскольку существует много типов конденсаторов, и мы обсудим последние типы конденсаторов в другом посте, поскольку он не связан с вопросом).
Похожие сообщения:
Конденсаторы в серии
Как подключить конденсаторы в серии?
Последовательно, ни один конденсатор не подключен напрямую к источнику. Чтобы соединить их последовательно, необходимо соединить их последовательно, как показано на рисунке ниже, 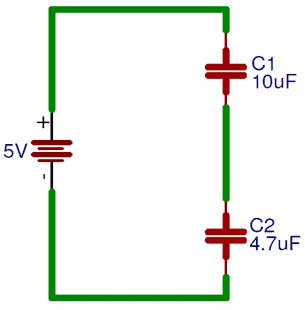

При последовательном подключении конденсаторов общая емкость уменьшается.Следовательно, соединение последовательно, поэтому ток через конденсаторы будет одинаковым. Кроме того, заряд, накопленный пластиной конденсатора, будет таким же, потому что он исходит от пластины соседнего конденсатора.
Следовательно,
I T = I 1 + I 2 + I 3 +… + I n
и
Q T 901 = + Q 2 + Q 3 +… + Q n
Теперь, чтобы найти значение емкости вышеуказанной цепи, мы применим закон напряжения Кирхгофа (KVL), тогда у нас будет
V T = V C1 + V C2 + V C3
Как мы знаем, Q = CV
И V = Q / C
Итак,
(Q / C T ) = (Q / C 1 ) + (Q / C 2 ) + (Q / C 3 )
Следовательно,
1 / C T = (1 / C 1 ) + (1 / C 2 ) + (1 / C 3 )
Для n th №.конденсатора, соединенного последовательно,
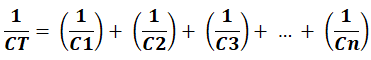
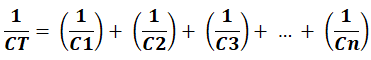
Для двух последовательно соединенных конденсаторов формула будет
C T = (C1 x C2) / (C1 + C2)
Теперь вы можете найти Емкость вышеуказанной цепи, используя формулу,
Здесь, C1 = 10 мкФ и C2 = 4,7 мкФ
Итак, C T = (10 x 4,7) / (10 + 4,7)
C T = 47 / 14,7
C T = 3.19 мкФ
Параллельно конденсаторы
Как подключить конденсаторы параллельно?
Параллельно каждый конденсатор напрямую подключен к источнику, как вы можете видеть на рисунке ниже, 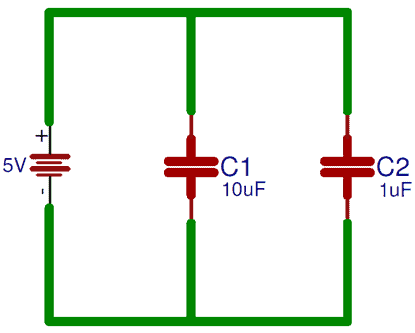

При параллельном подключении конденсаторов общая емкость равна сумме всех емкостей конденсатора.Поскольку верхняя и нижняя пластины всех конденсаторов соединены вместе, благодаря этому площадь пластины также увеличивается.
Общий ток в параллельной цепи будет равен току на каждом конденсаторе.
Применяя закон Кирхгофа,
I T = I 1 + I 2 + I 3
Теперь ток через конденсатор выражается как,
I = C (dV / dt)
Итак, 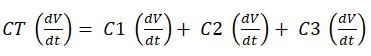
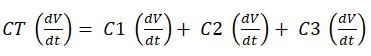
Решая вышеприведенное уравнение
C T = C 1 + C 2 + C 3
А, для n th нет.конденсатора, подключенного последовательно,
C T = C 1 + C 2 + C 3 +… + C n
Теперь вы можете найти емкость цепи по: используя приведенную выше формулу,
Здесь C 1 = 10 мкФ и C 2 = 1 мкФ
Итак, C T = 10 мкФ + 1 мкФ
C T = 11 мкФ
Похожие сообщения:
Полярный и неполярный конденсатор
Неполярный конденсатор: (Используется как в системах переменного, так и постоянного тока)
Конденсаторы неполярного типа могут использоваться как в системах переменного, так и постоянного тока.Они могут быть подключены к источнику питания в любом направлении, и их емкость не влияет на изменение полярности.
Polar Capacitor: (Используется только в цепях и системах постоянного тока)
Этот тип конденсаторов чувствителен к их полярности и может использоваться только в системах и сетях постоянного тока. Полярные конденсаторы не работают в системе переменного тока из-за изменения полярности после каждого полупериода питания переменного тока.

 Типы конденсаторов: полярные и неполярные конденсаторы с символами
Типы конденсаторов: полярные и неполярные конденсаторы с символамиРоль конденсаторов в цепях переменного тока
Конденсатор имеет множество применений в системах переменного тока, и мы обсудим несколько вариантов использования конденсаторов в сетях переменного тока ниже.
Бестрансформаторный источник питания:
Конденсаторы используются в бестрансформаторных источниках питания. В таких цепях конденсатор соединен последовательно с нагрузкой, потому что мы знаем, что конденсатор и катушка индуктивности в чистом виде не потребляют энергию. Они просто принимают мощность в одном цикле и передают ее в другом цикле нагрузке. В этом случае он используется для снижения напряжения с меньшими потерями энергии.
Асинхронные двигатели с разделенной фазой:
Конденсаторы также используются в асинхронном двигателе для разделения однофазного источника питания на двухфазный источник для создания вращающегося магнитного поля в роторе для захвата этого поля.Этот тип конденсатора в основном используется в бытовых водяных насосах, вентиляторах, кондиционерах и многих устройствах, для работы которых требуется как минимум две фазы.
Коррекция и улучшение коэффициента мощности:
Существует множество преимуществ улучшения коэффициента мощности. В трехфазных энергосистемах конденсаторная батарея используется для подачи реактивной мощности на нагрузку и, следовательно, для повышения коэффициента мощности системы. Конденсаторная батарея устанавливается после точного расчета. По сути, он выдает реактивную мощность, которая ранее поступала от энергосистемы, следовательно, он уменьшает потери и повышает эффективность системы.
Конденсаторы в цепях переменного тока
Как подключить конденсаторы в цепях переменного тока?
В цепи постоянного тока конденсатор заряжается медленно, пока зарядное напряжение конденсатора не станет равным напряжению питания. Кроме того, в этом состоянии конденсатор не позволяет току проходить через него после того, как он полностью зарядится. 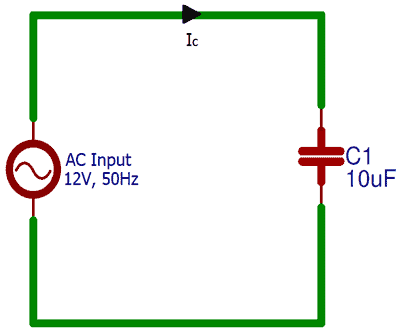

И, когда вы подключаете конденсатор к источнику переменного тока, он заряжается и разряжается непрерывно, из-за постоянного изменения уровней напряжения.Емкость в цепях переменного тока зависит от частоты подаваемого входного напряжения. Кроме того, если вы видите фазовую диаграмму идеальной конденсаторной цепи переменного тока, вы можете заметить, что ток опережает напряжение на 90⁰. 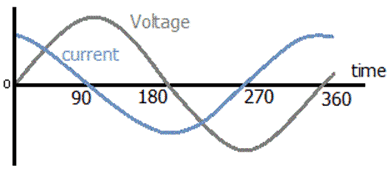

В цепи конденсатора переменного тока ток прямо пропорционален скорости изменения подаваемого входного напряжения, которая может быть выражена как
I = dQ / dt
I = C (dV / dt)
Теперь мы рассчитаем емкостное реактивное сопротивление в цепи переменного тока .
Как мы знаем, I = dQ / dt и Q = CV
А, входное переменное напряжение в вышеуказанной цепи будет выражаться как,
В = V м Sin вес
Итак, m = d (CV m Sin wt ) / dt
I m = C * V m Cos wt * w (после дифференциации)
I m = wC V m Sin (wt + π / 2)
At, w = 0, Sin (wt + π / 2) = 1
Следовательно,
I m = wCV m
V m / I м = 1 / wC (где, w = 2πf и V м / I м = X c )
Емкостная реактивность (X c ) = 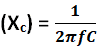
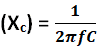
Теперь, до рассчитать емкостное реактивное сопротивление вышеуказанной цепи,
Xc = 1 / 2π (50) (10)
Xc = 3183.09 Ω
Похожие сообщения: В чем разница между батареей и конденсатором?
Роль конденсаторов в цепях постоянного тока
Кондиционирование питания:
В системах постоянного тока конденсатор используется в качестве фильтра (в основном). Его наиболее распространенное использование — преобразование переменного тока в постоянный источник питания при выпрямлении (например, мостовой выпрямитель). Когда мощность переменного тока преобразуется в флуктуирующую (с пульсациями, т.е. не в устойчивом состоянии с помощью выпрямительных цепей), мощность постоянного тока (пульсирующий постоянный ток), чтобы сгладить и отфильтровать эти пульсации и флуктуации, используется полярный конденсатор постоянного тока.Его значение рассчитывается точно и зависит от напряжения системы и требуемого тока нагрузки.
Разъединяющий конденсатор:
Разъединяющий конденсатор используется, где мы должны разъединить две электронные схемы. Другими словами, шум, создаваемый одной цепью, основан на развязывающем конденсаторе, и это не влияет на работу другой цепи.
Соединительный конденсатор:
Как мы знаем, конденсатор блокирует постоянный ток и пропускает через него переменный ток (мы обсудим его на следующем занятии, как это происходит).Таким образом, он используется для разделения сигналов переменного и постоянного тока (также используется в цепях фильтра для той же цели). Его значение рассчитывается таким образом, что его реактивное сопротивление минимизируется на основе частоты, которую мы хотим пройти через него. Соединительный конденсатор также используется в фильтрах (схемах удаления пульсаций, таких как RC-фильтры) для разделения сигнала переменного и постоянного тока и удаляет пульсации из пульсирующего напряжения питания постоянного тока для преобразования его в чистое напряжение переменного тока после выпрямления.
Вы также можете прочитать:
.