Плоский конденсатор. Электризация. Электроёмкость, напряжённость конденсатора формулы

Рис. 1. Заряженный проводник

Представим себе отрицательно заряженный кусок проводника (рис. 1.1). Проводник в целом должен быть электронейтральным, т.е. его заряженность обеспечивается дополнительными электронами, которые помещены на проводник. Данный заряженный проводник организует вокруг себя электрические поле, напряженностью

. Добавим ещё один проводник (рис. 1.2). Во втором проводнике, из-за электрического поля первого проводника, происходит электризация через влияние — появление разделённого электрического заряда. Данный процесс проистекает из воздействия внешнего электрического поля (поле первого проводника) на свободные электроны внутри второго проводника, смещая их против направления поля (по закону Кулона). Тогда, в части, ближайшей к первому проводнику, остаётся несбалансированный положительный заряд (т.к. второй проводник изначально электронейтрален). Таким образом, мы получили систему, состоящую из двух заряженных разным по модулю, но одинаковым по значению зарядом. Такую систему и назовём конденсатором.

Рис. 2. Плоский конденсатор

Простейшим конденсатором, рассматриваемым в школе, является плоский конденсатор. Плоским конденсатором называется система из двух пластин, площадью 

, помещённых на близком расстоянии () друг от друга (рис. 2). Пластины (обкладки конденсатора) заряжены одинаковым по модулю и различным по знаку зарядами ( и ). Между пластинами конденсатора чаще всего воздух (с диэлектрической проницаемостью ), тогда такой конденсатор называется воздушным.  В случае заполнения пространства между обкладками конденсатора неким диэлектриком свойства конденсатора меняются и описываются диэлектрической проницаемостью данной среды ().

Нами были уже введены два параметра для плоского конденсатора:

(1)

(2)

• где
  • — заряд конденсатора.

Вывод: в принципе, конденсатором можно считать любые разнозаряженные тела, поднесённые близко друг к другу. Плоский конденсатор — это уже вполне определённая система, параметры которой достаточно просто рассчитать (1) и (2).

Поделиться ссылкой:

Электрическая емкость. Конденсаторы. Емкость конденсатора.

Электрическая емкость. Конденсаторы.
Емкость уединенного проводника. Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен:  , где e — диэлектрическая проницаемость окружающей среды.  Следовательно:  эта величина не зависит ни от заряда, ни от потенциала и определяется только размерами шара (радиусом) и диэлектрической проницаемостью среды. Этот вывод справедлив для проводника любой формы.
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу: .
Емкость определяется геометрической формой, размерами проводника и свойствами среды (от материала проводника не зависит). Чем больше емкость проводника, тем меньше меняется потенциал при изменении заряда.	Емкость шара в СИ:   —
Единицы емкости. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл. Емкостью 1Ф  обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Емкость Земли  700 мкФ Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется.	1 мкФ=10-6Ф 1нФ=10-9Ф 1пФ=10-12Ф
Конденсаторы (condensare — сгущение) . Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы — лейденская банка (Мушенбрук, сер. XVII в.).
Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.  Проводники наз.  обкладками  конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то  под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок.
На рисунке — плоский и сферический конденсаторы. Поле плоского конденсатора почти все сосредоточено внутри (у идеального — все). Усферического — все поле сосредоточено между обкладками.
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: .
При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды — конденсатор заряжается. Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними.
Емкость плоского конденсатора. , т. о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика.
Емкость сферического конденсатора . Если зазор между обкладками мал по сравнению с радиусами, то формула переходит в формулу емкости плоского конденсатора.
Виды конденсаторов
При подключении электролитического конденсатора необходимо соблюдать полярность.
Назначение конденсаторов Накапливать на короткое время заряд или энергию для быстрого изменения потенциала. Не пропускать постоянный ток. В радиотехнике: колебательный контур, выпрямитель. Фотовспышка.

Плоский конденсатор формулы. Коэффициент электростатической емкости. Конденсаторы. Емкость конденсаторов различной геометрической конфигурации

Конденса́тор (от лат. condensare — «уплотнять», «сгущать», или от от лат. condensatio

— «накопление») — двухполюсник с определённым или переменным значением ёмкости и малой проводимостью; устройство для накопления заряда и энергии электрического поля.

Конденсатор является пассивным электронным компонентом. В простейшем варианте конструкция состоит из двух электродов в форме пластин (называемыхобкладками ), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок (см. рис.). Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами (из-за намотки).

Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончаниипереходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.

В методе гидравлических аналогийконденсатор — это гибкая мембрана, вставленная в трубу. Анимация демонстрирует мембрану, которая растягивается и сокращается под действием потока воды, что аналогично заряду и разряду конденсатора под действием электрического тока.

С точки зрения метода комплексных амплитуд конденсатор обладает комплексным импедансом

,

Где j — мнимая единица, ω — циклическая частота (рад/с ) протекающего синусоидального тока, f — частота в Гц , C — ёмкость конденсатора (фарад ). Отсюда также следует, что реактивное сопротивление конденсатора равно: . Для постоянного тока частота равна нулю, следовательно, реактивное сопротивление конденсатора бесконечно (в идеальном случае).

Резонансная частота конденсатора равна

При f > f p конденсатор в цепи переменного тока ведёт себя как катушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах

f , на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2-3 раза ниже резонансной.

Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора:

где U — напряжение (разность потенциалов), до которого заряжен конденсатор, а q — электрический заряд.

Обозначение конденсаторов на схемах. В России условные графические обозначения конденсаторов на схемах должны соответствовать ГОСТ 2.

728-74 ] либо международному стандарту IEEE 315-1975:

На электрических принципиальных схемах номинальная ёмкость конденсаторов обычно указывается в микрофарадах (1 мкФ = 1·10 6 пФ = 1·10 −6 Ф) и пикофарадах, но нередко и в нанофарадах (1 нФ = 1·10 −9 Ф). При ёмкости не более 0,01 мкФ, ёмкость конденсатора указывают в пикофарадах, при этом допустимо не указывать единицу измерения, то есть постфикс «пФ» опускают. При обозначении номинала ёмкости в других единицах указывают единицу измерения. Для электролитических конденсаторов, а также для высоковольтных конденсаторов на схемах, после обозначения номинала ёмкости, указывают их максимальное рабочее напряжение в вольтах (В) или киловольтах (кВ). Например так: «10 мкФ x 10 В». Для переменных конденсаторов указывают диапазон изменения ёмкости, например так: «10 — 180». В настоящее время изготавливаются конденсаторы с номинальными ёмкостями из десятично логарифмических рядов значений Е3, Е6, Е12, Е24, то есть на одну декаду приходится 3, 6, 12, 24 значения, так, чтобы значения с соответствующим допуском (разбросом) перекрывали всю декаду.

Характеристики конденсаторов

Основные параметры Ёмкость Основной характеристикой конденсатора является его ёмкость , характеризующая способность конденсатора накапливать электрический заряд. В обозначении конденсатора фигурирует значение номинальной ёмкости, в то время как реальная ёмкость может значительно меняться в зависимости от многих факторов. Реальная ёмкость конденсатора определяет его электрические свойства. Так, по определению ёмкости, заряд на обкладке пропорционален напряжению между обкладками (

q = CU ). Типичные значения ёмкости конденсаторов составляют от единиц пикофарад до тысяч микрофарад. Однако существуют конденсаторы (ионисторы) с ёмкостью до десятков фарад.

Ёмкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположена на расстоянии d друг от друга, в системе СИ выражается формулой: , где — диэлектрическая проницаемость среды, заполняющая пространство между пластинами (в вакууме равна единице), — электрическая постоянная, численно равная8,854187817·10 −12 Ф/м. Эта формула справедлива, лишь когда d намного меньше линейных размеров пластин.

Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.

Если у всех параллельно соединённых конденсаторов расстояние между обкладками и свойства диэлектрика одинаковы, то эти конденсаторы можно представить как один большой конденсатор, разделённый на фрагменты меньшей площади.

При последовательном соединении конденсаторов заряды всех конденсаторов одинаковы, так как от источника питания они поступают только на внешние электроды, а на внутренних электродах они получаются только за счёт разделения зарядов, ранее нейтрализовавших друг друга. Общая ёмкость батареи последовательно соединённых конденсаторов равна

Или

Эта ёмкость всегда меньше минимальной ёмкости конденсатора, входящего в батарею. Однако при последовательном соединении уменьшается возможность пробоя конденсаторов, так как на каждый конденсатор приходится лишь часть разницы потенциалов источника напряжения.

Если площадь обкладок всех конденсаторов, соединённых последовательно, одинакова, то эти конденсаторы можно представить в виде одного большого конденсатора, между обкладками которого находится стопка из пластин диэлектрика всех составляющих его конденсаторов.

Удельная ёмкость Конденсаторы также характеризуются удельной ёмкостью — отношением ёмкости к объёму (или массе) диэлектрика. Максимальное значение удельной ёмкости достигается при минимальной толщине диэлектрика, однако при этом уменьшается его напряжение пробоя.

Плотность энергии Плотность энергии электролитического конденсатора зависит от конструктивного исполнения. Максимальная плотность достигается у больших конденсаторов, где масса корпуса невелика по сравнению с массой обкладок и электролита.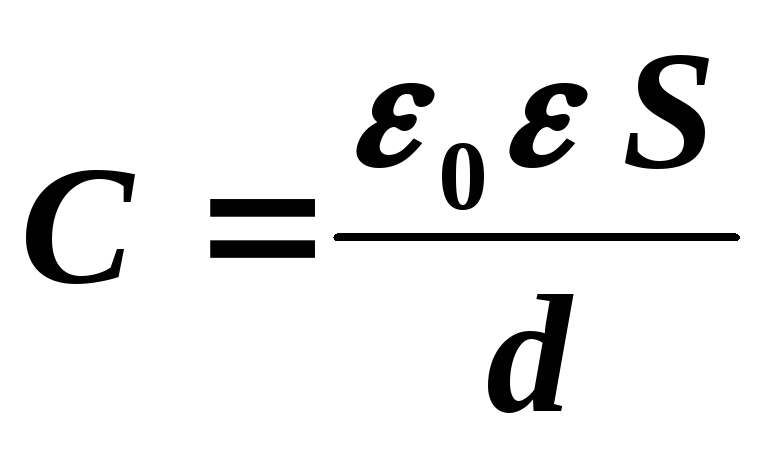 Например, у конденсатора EPCOS B4345 с ёмкостью 12 000 мкФ, максимально допустимым напряжением 450 В и массой 1,9 кг плотность энергии при максимальном напряжении составляет 639 Дж/кг или 845 Дж/л. Особенно важен этот параметр при использовании конденсатора в качестве накопителя энергии, с последующим мгновенным её высвобождением, например, в пушке Гаусса.

Взаимная электроемкость. Конденсаторы. Пусть вблизи заряженного проводника А нахо­дятся незаряженные проводни­ки или диэлектрики. Под действием поля проводника А в телах 1 и 2 возни­кают индуцированные (если 1 и 2 проводники) или свя­занные (если диэлектрики) заряды, причем ближе к А будут располагаться заряды противоположного знака (рис.1.25). Индуцированные (или связанные) заряды соз­дают свое поле противоположного на­правления, чем ослабляют поле проводника А, уменьшая его потенциал и увеличи­вая его электроемкость.

На практике существует потребность в устройствах, которые при относитель­но небольшом потенциале накапливали (конденсировали) бы на себе заметные по вели­чине заряды. В основу таких устройств, называемых конденсаторами, поло­жен факт, что емкость проводника возрастает при приближении к нему других тел. Простейший плоский конденсатор состоит из двух близко расположенных про­водников, заряженных равными по величине и противоположными по знаку заряда­ми. Образующие данную систему проводники называются обкладка­ми.

Для того, чтобы поле, создаваемое заряженны­ми обкладками, было полностью сосредоточено внутри конденсатора, обкладки должны быть в виде двух близко рас­положенных пластин, или коаксиаль­ных цилиндров, или концентрических сфер. Со­ответ­ственно конденсаторы называются плоскими, цилиндрическими или сфериче­скими.

Разность потенциалов между обкладками пропорциональна абсолютной вели­чине заряда обкладки. Поэтому отношение есть величина постоянная для конкретного кон­денсатора. Она обозначается С и называется взаимной электроемкостью провод­ников или емкостью конденсатора.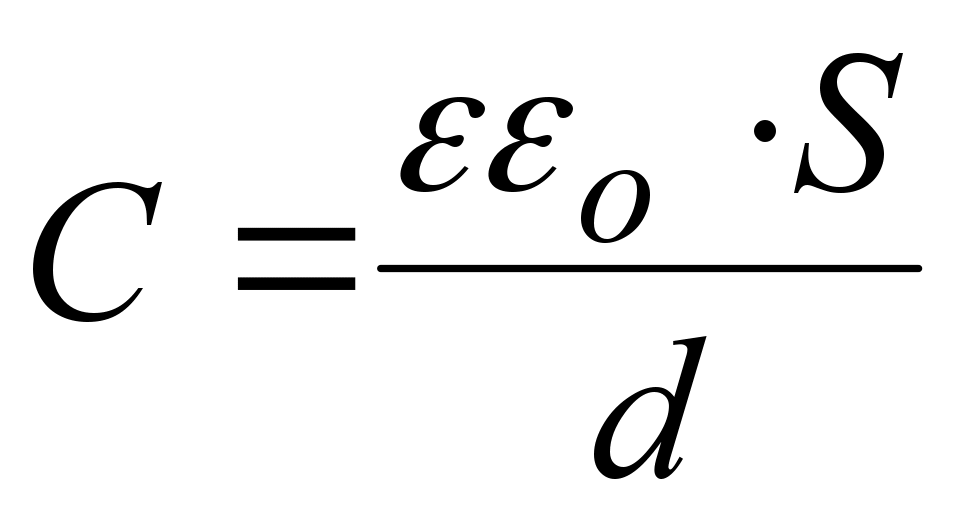 Емкость конденсатора численно равна заряду, который нужно перенести с одной обкладки конденсатора на другую, чтобы изме­нить разность их потенциалов на единицу.

Разность потенциалов плоского конденсатора равна , где поверхностная плотность заряда обкладки.

S — площадь обкладки конденса­тора.. Отсюда емкость плоского конденсатора . Из этой формулы следует, что С плоского конденсатора зави­сит от его геометрических размеров, т.е. от S и d, и диэлектри­ческой проницаемости диэлектрика, заполняющего межплоско­стное пространство. Применение в качестве прослойки сегнетоэлектриков значительно увеличива­ет емкость конденсатора, т.к. e у них достигает очень больших значений. В очень сильных полях (порядка Е пр »10 7 В/м) происходит разруше­ние диэлектрика или «пробой», он перестает быть изо­ля­тором и становится проводником. Это «пробивное напряжение» зависит от формы обкладок, свойств диэлектрика и его толщины..

Для получения устройств различной электроемкости конденсаторы соединяют парал­лельно и после­довательно.

Плоский конденсатор состоит из двух параллельных пластин, разделённых небольшим зазором шириной , заполненным однородным диэлектриком.

Нам известно, что поле между двумя разноимённо заряженными пластинами с одинаковой по величине поверхностной плотностью равно, где,S– площадь каждой пластины. Напряжение между обкладками:

Используя определение емкости конденсатора, получаем:

Отметим, что полученная формула является приближенной, так как выведена без учета искажения поля у краев пластин. Расчет по этой формуле дает завышенное значение ёмкости и тем точнее, чем меньше зазор по сравнению с линейными размерами пластин.

Ёмкость сферического конденсатора.

Сферический конденсатор представляет собой систему двух концентрических сфер с радиусами и. Электрическое поле между обкладками сферического конденсатора согласно теореме Гаусса определяется зарядом внутренней сферы. Напряжение между обкладками равно:

.

Для ёмкости сферического конденсатора получаем:

Это формула точная.

Если , полученная формула переходит в выражение для ёмкости плоского конденсатора.

Ёмкость цилиндрического конденсатора.

Цилиндрический конденсатор составляет систему двух коаксиальных цилиндров с радиусами и, длиной.

Рассуждая аналогично выводу ёмкости сферического конденсатора, получаем:

..

Полученная формула является приближенной и при малом зазоре переходит в формулу емкости плоского конденсатора.

Соединение конденсаторов.

В практике для получения необходимых значений емкости используют соединения конденсаторов: а) последовательное, б) параллельное, в) смешанное (см. рисунок).

Ёмкость последовательного соединения конденсаторов.

Заряды последовательно соединенных конденсаторов равны , а напряжение на батарее. Из определения емкости следует:

Если , то(ёмкость последовательного соединения меньше наименьшей ёмкости в последовательном соединении).

Для последовательно соединенных конденсаторов емкость вычисляется по формуле:

Ёмкость параллельного соединения конденсаторов.

Заряд батареи равен сумме зарядов:

а напряжение . По определению емкости получаем:

Для параллельно соединенных конденсаторов:.

В случае одинаковых конденсаторов: .

Оценить емкость батареи (см. рисунок) .

Используя свойство бесконечности можно представить цепь в виде соединения (см. рисунок).

Для расчета ёмкости батареи получаем:

Откуда: , так как, то.

Лекция 7.

Диэлектрики в электрическом поле.

Диэлектриками (изоляторами) называют вещества, не проводящие постоянного электрического тока. Это означает, что в диэлектриках отсутствуют «свободные» заряды, способные перемещаться на значительные расстояния.

Диэлектрики состоят либо из нейтральных молекул, либо из ионов, находящихся в узлах кристаллической решетки. Сами же молекулы могут быть полярными инеполярными. Полярные молекулы обладают дипольным моментом, у неполярных молекул дипольный момент равен нулю.

Поляризация.

В электрическом поле диэлектрики поляризуются. Это явление связано с появлением в объеме и на поверхности диэлектрика «связанных » зарядов. При этом конечный объем диэлектрика приобретает дипольный момент. Механизм поляризации связан с конкретным строением диэлектрика. Если диэлектрик состоит из неполярных молекул, то в пределах каждой молекулы происходит смещение зарядов – положительных по полю, отрицательных против поля, т.е. молекулы, приобретают дипольный момент. У диэлектрика с полярными молекулами в отсутствии внешнего электрического поля их дипольные моменты ориентированы хаотично.

Под действием электрического поля диполи ориентируются преимущественно в направлении поля. Рассмотрим подробнее этот механизм (см. рисунок). Пара сил исоздает вращательный момент равный, где- дипольный момент молекулы. Этот момент стремится ориентировать диполь вдоль поля. В ионных кристаллах под действием электрического поля все положительные ионы смещаются по полю, отрицательные – против поля. Отметим, что смещение зарядов очень малы даже по сравнению с размерами молекул. Это связано с тем, что напряженность внешнего электрического поля обычно много меньше напряженности внутренних электрических полей в молекулах.

Отметим, что существуют диэлектрики, поляризованные даже при отсутствии внешнего поля (электреты, сегнетоэлектрики). Мы остановимся на рассмотрении только однородных диэлектриков, в которых отсутствует остаточная поляризация, а объемный и «связанный» заряд всегда равен нулю .

Рассмотрим уединенный проводник , т.е. проводник, который удален от других проводников, тел и зарядов. Его потенциал прямо пропорционален заряду проводника. Из опыта следует, что разные проводники, будучи одинаково заряженными, принимают различные потенциалы. Поэтому для уединенного проводника можно записать

Величину (8.11.1.)

называют электроемкостью (или просто емкостью ) уединенного проводника.

Емкость уединенного проводника определяется зарядом, сообщение которого проводнику изменяет его потенциал на единицу.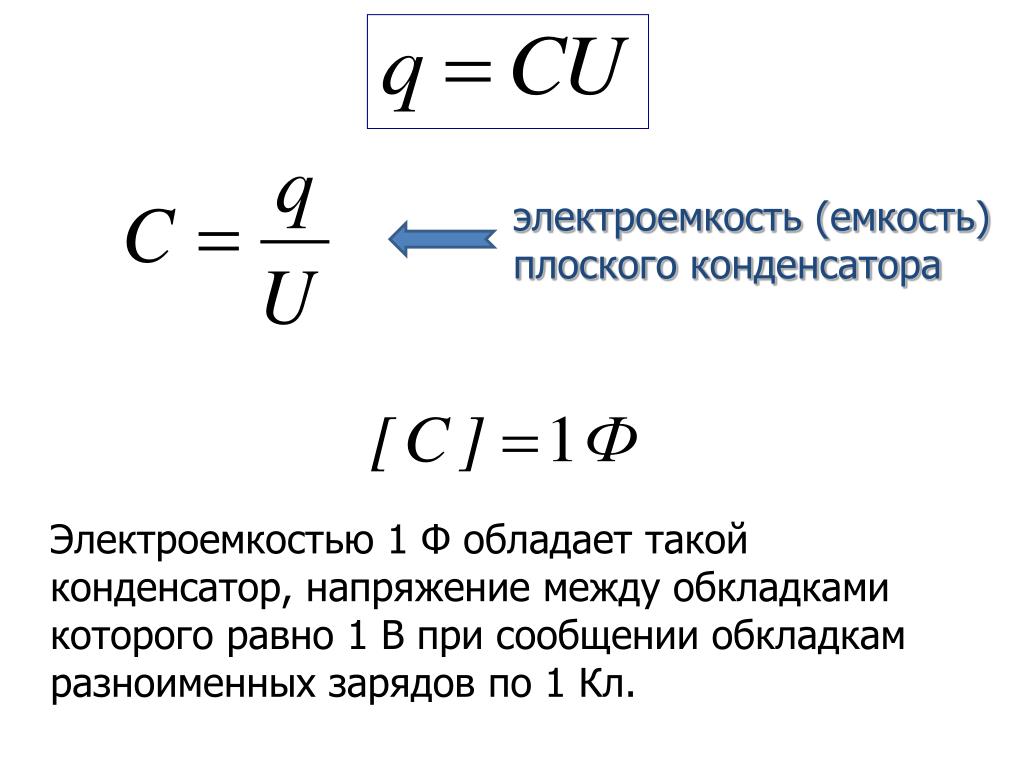

Емкость проводника зависит от его размеров и формы, но не зависит от материала, агрегатного состояния, формы и размеров полостей внутри проводника. Это связано с тем, что избыточные заряды распределяются на внешней поверхности проводника. Емкость не зависит также ни от заряда проводника, ни от его потенциала.

Единица измерения электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда в 1 Кл.

Согласно формуле , потенциал уединенного шара радиуса R, находящегося в однородной среде с диэлектрической проницаемостью , равен

Используя формулу (8.11.1.), получим, что емкость шара

Для того чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов.

Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду q будут заряды противоположного знака. Эти заряды, естественно, ослабляют поле, создаваемое зарядом q, т.е. понижают потенциал проводника, что приводит (см.(8.11.1.)) к повышению его электроемкости.

Конденсатор — устройство, состоящее из двух проводников (обкладок), разделенных диэлектриком.

На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.

Емкость конденсатора — это физическая величина, равная отношению заряда q одной из обкладок, к разности потенциалов () между его обкладками:

Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +q и -q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. Его можно рассчитать, используя формулы (8.3.7) и (8.11.4.). При наличии диэлектрика между обкладками разность потенциалов между ними:

где — диэлектрическая проницаемость.

Тогда из формулы (8.11.4.), заменяя q= , с учетом (8.11.5.) получим выражение для емкости плоского конденсатора:

Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиальных цилиндров с радиусами и ( > ), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Разность потенциалов между обкладками вычислим по формуле для поля равномерно заряженного бесконечного цилиндра с линейной плотностью (l — длина обкладок). С учетом наличия диэлектрика между обкладкамиПодставив (8.11.9.) в (8.11.4.), получим

т.е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.

Электроёмкость плоского конденсатора | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Плоским конденсатором обычно называ­ют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Про­стота конструкции такого конденсатора по­зволяет сравнительно просто рассчитывать его электроемкость и получать значения, совпадающие с результатами эксперимента.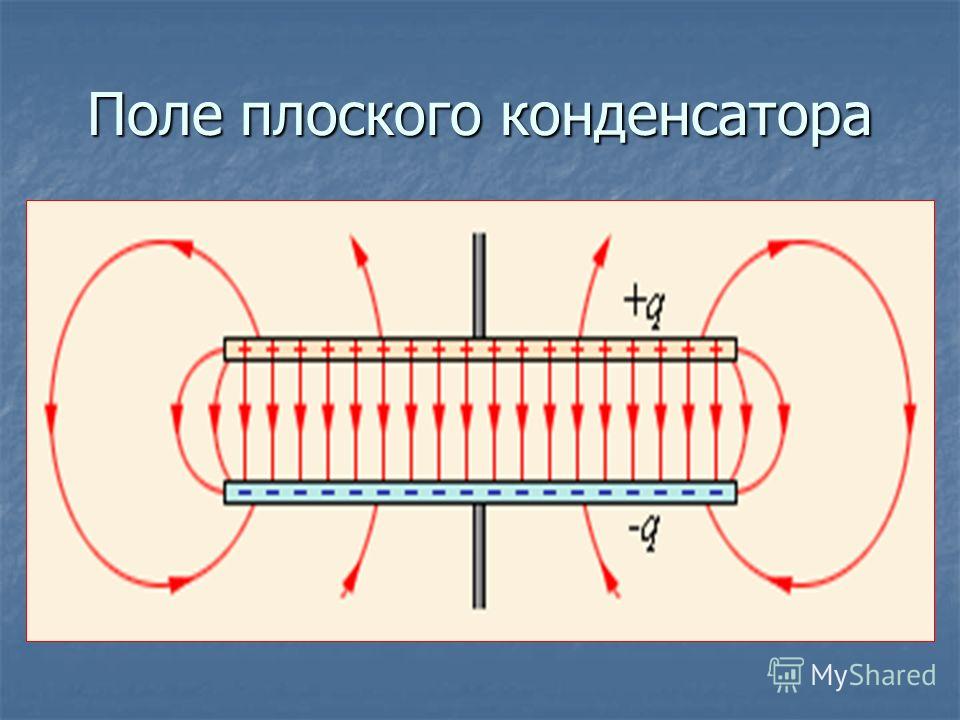

Рис. 4.71. Плоский конденсатор на элект­рометре

Укрепим две металлические пластины на изоляционных подставках и соединим с электрометром так, что одна из пластин будет присоединена к стержню электромет­ра, а вторая — к его металлическому кор­пусу (рис. 4.71). При таком соединении электрометр будет измерять разность по­тенциалов между пластинами, которые об­разуют плоский конденсатор из двух пла­стин. Проводя исследования, необходимо пом­нить, что

при постоянном значении заряда пластин уменьшение разности потенциалов свидетельствует об увеличении электроем­кости конденсатора, и наоборот.

Сообщим пластинам разноименные заря­ды и отметим отклонение стрелки электро­метра. Приближая пластины друг к другу (уменьшая расстояние между ними), заме­тим уменьшение разности потенциалов. Та­ким образом, при уменьшении расстояния между пластинами конденсатора его элект­роемкость увеличивается. При увеличении расстояния показания стрелки электрометра увеличиваются, что является свидетельст­вом уменьшения электроемкости.

Электроемкость плоского конденсатора об­ратно пропорциональна расстоянию между его обкладками.

C ~ 1 / d,

где d — расстояние между обкладками.

Рис. 4.72. График зависимости емкости плоского конденсатора от расстояния между пластинами

Рис. 4.73. При расчетах емкости плоских конденсаторов учитывают площадь пере­крытия пластин

Эту зависимость можно изобразить гра­фиком обратной пропорциональной зависи­мости (рис. 4.72).

Будем смещать пластины одну относи­тельно другой в параллельных плоскостях, не изменяя расстояния между ними.

При этом площадь перекрытия пластин будет уменьшаться (рис. 4.73). Увеличение разности потенциалов, отмеченное электрометром, будет свидетельствовать об умень­шении электроемкости.

Увеличение площади перекрытия пластан приведет к увеличению емкости.

Электроемкость плоского конденсатора про­порциональна площади пластин, которые пере­крываются.

C ~ S,

где S — площадь пластин.

Рис. 4.74. График зависимости емкости плоского конденсатора от площади его пластин

Эту зависимость можно представить гра­фиком прямой пропорциональной зависи­мости (рис. 4.74). 

Возвратив пластины в начальное поло­жение, внесем в пространство между ними плоский диэлектрик. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увели­чении электроемкости конденсатора. Если между пластинами поместить другой диэлек­трик, то изменение электроемкости будет иным.

Электроемкость плоского конденсатора за­висит от диэлектрической проницаемости ди­электрика.

C ~ ε,

где ε — диэлектрическая проницаемость ди­электрика. Материал с сайта http://worldofschool.ru

Рис. 4.75. График зависимости емкости плоского конденсатора от диэлектри­ческой проницаемости диэлектрика

Такая зависимость показана на графике рис. 4.75.

Результаты опытов можно обобщить в ви­де формулы ёмкости плоского конденсатора:

C = εε₀S / d,

где S — площадь пластины; d — расстояние между ними; ε — диэлектрическая прони­цаемость диэлектрика; ε₀ — электрическая постоянная.

Конденсаторы, которые состоят из двух пластин, в практике применяются очень редко. Как правило, конденсаторы имеют много пластин, соединенных между собой по определенной схеме.

На этой странице материал по темам:

• График электроемкости плоского конденсатора от площади его пластин

• Простые задачи энергия плоского конденсатора скачать

• При збільшенні площі перекриття пластин конденсатора , що буде з електроємністю

• Самостоятельная работа по теме электроемкость плоского конденсатора

• При увеличении площади перекрывания пластин заряд на обкладках конденсатора

Вопросы по этому материалу:

• Какое строение плоского конденсатора?

• По изменению какой величины в опыте можно делать заключение об изменении электроемкости?

• В какой последовательности проводится опыт, в котором устанавли­валась зависимость электроемкости конденсатора от его параметров?

• Как зависит электроемкость плоского конденсатора от активной площади пластин?

• Как зависит электроемкость плоского конденсатора от расстояния между пластинами?

• Как влияет диэлектрик на электроемкость конденсатора?

Формула для расчета электроемкости плоского конденсатора

Для заряженного тела или заряженной системы вводят параметр, характеризующий способность тела накапливать заряд, — электроёмкость. Стандартное обозначение — , единица измерения — = Ф (Фарад). Электроёмкость численно равна отношению заряда тела/системы к потенциалу этого тела/системы. Для неизменной системы данный параметр является постоянным.

Рассчитаем в качестве примера электроёмкость шара радиуса .

Исходя из рассмотренного ранее потенциала шара:

(2)

• — диэлектрическая проницаемость среды (параметр, характеризующий способность среды проводить электрическое поле). Данный параметр является табличным.
• — электрическая постоянная ( Ф/м),
• — заряд шара,
• — радиус шара.

Подставим (2) в (1):

(3)

Формула (3) представляет собой математический способ нахождения электроёмкости проводящего шара.

Ещё одной системой, в которой можно достаточно просто рассчитать электроёмкость, является плоский конденсатор. Для расчёта электроёмкости такой системы воспользуемся (1), знаниями о связи напряжённости электростатического поля и потенциала электростатического поля (4) и напряжённостью электростатического поля между двумя параллельными пластинами (5).

• — напряжённость электростатического поля,
• — расстояние между взаимодействующими телами.

(5)

• — заряд пластины (обкладки конденсатора),
• — площадь пластин конденсатора.

(6)

Выражение (6) является соотношением для поиска электроёмкости плоского конденсатора.

Вывод: Таким образом, задачи на поиск электроёмкости системы сводятся или к определению электроёмкости (1), или к рассмотрению конкретной системы: шар (3), плоский конденсатор (6).

Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.

Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:

C = q φ 1 – φ 2 = q U .

Значением φ 1 – φ 2 = U обозначают разность потенциалов, называемую напряжением, то есть U . По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.

Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.

Плоский конденсатор

Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1 .

Формула для расчета электроемкости записывается как

C = ε ε 0 S d , где S является площадью обкладки, d – расстоянием между ними, ε – диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.

При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется d i , вычисление диэлектрической проницаемости этого слоя ε i выполняется, исходя из формулы:

C = ε 0 S d 1 ε 1 + d 2 ε 2 + . . . + d N ε N .

Сферический конденсатор

Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.

Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2 . Емкость рассчитывается по формуле:

C = 4 π ε ε 0 R 1 R 2 R 2 – R 1 , где R 1 и R 2 являются радиусами обкладок.

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равняется:

C = 2 πεε 0 l ln R 2 R 1 , где l – высота цилиндров, R 1 и R 2 – радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3 .

Важной характеристикой конденсаторов считается пробивное напряжение – напряжение, при котором происходит электрический разряд через слой диэлектрика.

U m a x находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.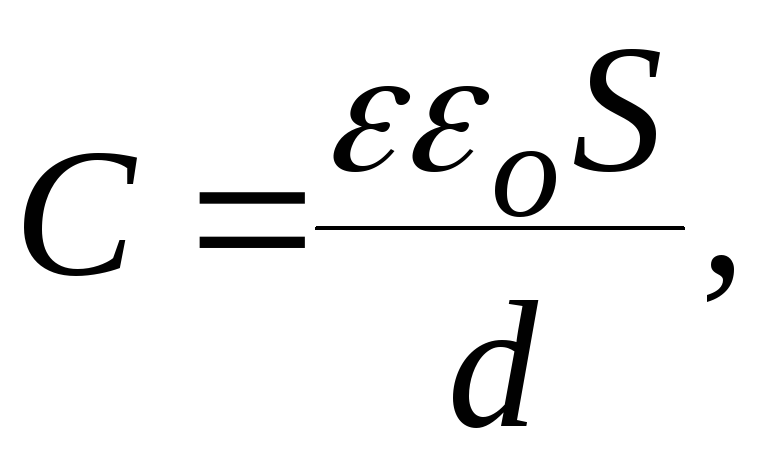

Электроемкость плоского конденсатора. Формулы

Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы C i , где C i – это емкость конденсатора с номером i :

При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:

Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 с м 2 с расстоянием между ними 1 м м . Пространство между обкладками находится в вакууме.

Решение

Чтобы рассчитать электроемкость конденсатора, применяется формула:

ε = 1 , ε 0 = 8 , 85 · 10 – 12 Ф м ; S = 1 с м 2 = 10 – 4 м 2 ; d = 1 м м = 10 – 3 м .

Подставим числовые выражения и вычислим:

C = 8 , 85 · 10 – 12 · 10 – 4 10 – 3 = 8 , 85 · 10 – 13 ( Ф ) .

Ответ: C ≈ 0 , 9 п Ф .

Найти напряженность электростатического поля у сферического конденсатора на расстоянии x = 1 с м = 10 – 2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R 1 = 1 с м = 10 – 2 м , внешнем – R 2 = 3 с м = 3 · 10 – 2 м . Значение напряжения – 10 3 В .

Решение

Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:

E = 1 4 π ε ε 0 q r 2 , где q обозначают заряд внутренней сферы, r = R 1 + x – расстояние от центра сферы.

Нахождение заряда предполагает применение определения емкости конденсатора С:

Для сферического конденсатора предусмотрена формула вида

C = 4 π ε ε 0 R 1 R 2 R 2 – R 1 с радиусами обкладок R 1 и R 2 .

Производим подстановку выражений для получения искомой напряженности:

E = 1 4 πεε 0 U ( x + R 1 ) 2 4 πεε 0 R 1 R 2 R 2 – R 1 = U ( x + R 1 ) 2 R 1 R 2 R 2 – R 1 .

Данные представлены в системе С И , поэтому достаточно заменить буквы числовыми выражениями:

E = 10 3 ( 1 + 1 ) 2 · 10 – 4 · 10 – 2 · 3 · 10 – 2 3 · 10 – 2 – 10 – 2 = 3 · 10 – 1 8 · 10 – 6 = 3 , 45 · 10 4 В м .

Ответ: E = 3 , 45 · 10 4 В м .

Что такое электроемкость проводников

Если у нас есть два проводника, изолированных друг от друга, которым мы сообщаем некоторые заряды (обозначим их соответственно q 1 и q 2 ), то между ними возникнет определенная разность потенциалов. Ее величина будет зависеть от формы проводников, а также от исходных величин зарядов. Обозначим такую разность Δ φ . Если мы говорим о разности, возникающей в электрическом поле между двумя точками, то ее обычно обозначают U .

В рамках темы данной статьи нам больше всего интересна такая разность потенциалов между проводниками, когда их заряды противоположны по знаку, но равны друг другу по модулю. В таком случае мы можем ввести новое понятие – электрическая емкость (электроемкость).

Электрической емкостью системы, состоящей из двух проводников, называется отношение заряда одного проводника ( q ) к разности потенциалов между этими двумя проводниками.

В виде формулы это записывается так: C = q ∆ φ = q U .

Для измерения электрической емкости применяется единица, называемая фарад. Она обозначается буквой Ф .

Конфигурации и размеры проводников, а также свойства диэлектрика определяют величину электроемкости заданной системы. Наибольший интерес для нас представляют проводники особой формы, называемые конденсаторами.

Конденсатор – это проводник, конфигурация которого позволяет локализовать (сосредотачивать) электрическое поле в одной выделенной части пространства. Проводники, составляющие конденсатор, называются обкладками.

Если мы возьмем две плоские пластины из проводящего материала, расположим их на небольшом расстоянии друг от друга и проложим между ними слой диэлектрика, то мы получим простейший конденсатор, называемый плоским. При его работе электрическое поле будет располагаться преимущественно в промежутке между пластинами, но небольшая часть этого поля будет рассеиваться вокруг них.

Часть электрического поля вблизи конденсатора называется полем рассеяния.

Иногда в задачах мы можем не учитывать его и работать только с той частью электрического поля, которое расположено между обкладками. Однако пренебрегать полем рассеяния допустимо далеко не всегда, поскольку это может привести к ошибочным расчетам из-за нарушения потенциального характера электрического поля.

Рисунок 1 . 6 . 1 . Электрическое поле в плоском конденсаторе.

Рисунок 1 . 6 . 2 . Электрическое поле конденсатора без учета поля рассеяния, не обладающее потенциальностью.

Модуль напряженности электрического поля, которое создает каждая обкладка в плоском конденсаторе, выражается соотношением следующего вида:

Исходя из принципа суперпозиции, можно утверждать, что напряженность E → поля, которое создают обе пластины конденсатора, будет равна сумме напряженностей E + → и E – → полей каждой пластины, то есть E → = E + → + E – → .

Векторы напряженностей обеих пластин во внутренней части конденсатора будут параллельны друг другу. Значит, мы можем выразить модуль напряженности их суммарного поля в виде формулы E = 2 E 1 = σ ε 0 .

Как рассчитать электроемкость конденсатора

Вне пластин векторы напряженности будут направлены в противоположные друг от друга стороны, значит, E будет равно нулю. Если мы обозначим заряд каждой обкладки как q , а ее площадь как S , то соотношение q S даст нам представление о поверхностной плотности. Умножив E на расстояние между обкладками ( d ) , мы получим разность потенциалов между пластинами в однородном электрическом поле. Теперь возьмем оба этих соотношения и выведем из них формулу, по которой может быть рассчитана электрическая емкость конденсатора.

C = q ∆ φ = σ · S E · d = ε 0 S d .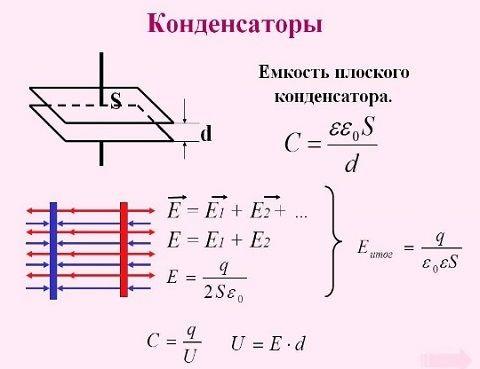

Электрическая емкость плоского конденсатора – величина, обратно пропорциональная расстоянию между обкладками и прямо пропорциональная их площади.

Заполнение пространства между проводниками диэлектрическим материалом может увеличить электроемкость плоского конденсатора в число раз, кратное undefined.

Введем обозначение емкости в виде буквы С и запишем это в виде формулы:

Данная формула называется формулой электроемкости плоского конденсатора.

Конденсаторы бывают не только плоскими. Возможны и другие конфигурации, также обладающие специфическими свойствами.

Сферическим конденсатором называется система из 2 -х концентрических сфер, сделанных из проводящего материала, радиусы которых равны R 1 и R 2 соответственно.

Цилиндрическим конденсатором называется системы из двух проводников цилиндрической формы, длина которых равна L , а радиусы R 1 и R 2 .

Обозначим проницаемость диэлектрического материала как ε и запишем формулы, по которым можно найти электрическую емкость конденсаторов:

• C = 4 πε 0 ε R 1 R 2 R 2 – R 1 (сферический конденсатор),
• C = 2 π ε 0 ε L ln R 2 R 1 (цилиндрический конденсатор).

Как рассчитать электроемкость батареи конденсаторов

Если мы соединим несколько проводников между собой, то мы получим конструкцию, называемую батареей.

Способы соединения могут быть разными. Если соединение будет параллельным, то напряжение всех конденсаторов в системе будет одинаково: U 1 = U 2 = U , а заряды можно найти по формулам q 1 = С 1 U и q 2 = C 2 U . При таком соединении вся система может считаться одним конденсатором, электроемкость которого равна C , заряд – q = q 1 + q 2 , а напряжение – U . В виде формулы это выглядит так:

С = q 1 + q 2 U или C = C 1 + C 2

Если в батарее конденсаторов элементы соединены параллельно, то для нахождения общей электроемкости нам нужно сложить емкости ее отдельных элементов.

Рисунок 1 . 6 . 3 . Конденсаторы, соединенные параллельно. C = C 1 + C 2

Рисунок 1 . 6 . 4 . Конденсаторы, соединенные последовательно: 1 C = 1 C 1 + 1 C 2

Если же батарея состоит из двух последовательно соединенных конденсаторов, то заряды обоих будут одинаковы: q 1 = q 2 = q . Найти их напряжения можно так: U 1 = q C 1 и U 2 = q C 2 . Такую систему тоже можно считать одним конденсатором, заряд которого равен q , а напряжение U = U 1 + U 2 .

C = q U 1 + U 2 или 1 C = 1 C 1 + 1 C 2

Если конденсаторы в батарее соединены последовательно, то для нахождения общей электроемкости нам нужно сложить величины, обратные емкостям каждого из них.

Справедливость обеих формул, приведенных выше, не зависит от количества конденсаторов в батарее.

Рисунок 1 . 6 . 5 . Смоделированное электрическое поле плоского конденсатора.

By : admin

Электроемкость проводника — Технарь

Плоский конденсатор, площадь каждой пластины которого 6,20*10^-3 м², заполнен слюдой с относительной диэлектрической проницаемостью, равной 6. Расстояние между пластинами 2,00 мм. Определить:

1. электроемкость конденсатора;
2. разность потенциалов на пластинах конденсатора;
3. напряженность поля в нем;
4. силу взаимного притяжения пластин, если заряд на каждой из них равен 4,00*10^-8 Кл.

Дано: S=6,20*10^-3 м² — площадь одной пластины, d=2,00*10^-3 м — расстояние между пластинами, ԑ=6 — относительная диэлектрическая проницаемость слюды, q=4,00*10^-8 Кл—заряд на одной пластине, ԑ₀=8,85*10^-12 Ф/м— электрическая постоянная.

Найти: 1) С — электроемкость конденсатора; 2) U — разность потенциалов на пластинах; 3) E — напряженность поля в конденсаторе; 4) F — силу взаимного притяжения пластин.

Решение. Электроемкость конденсатора определим по формуле емкости плоского конденсатора:

С=ԑ₀ԑS/d

Зная заряд q и емкость С, определим разность потенциалов на пластинах конденсатора:

U=q/C=qd/ԑԑ₀S.

Напряженность поля внутри конденсатора и разность потенциалов на его пластинах связаны зависимостью:

E=U/d=q/ԑԑ₀S.

Так как поле между пластинами получается в результате наложения двух полей (от обеих пластин), напряженность поля одной пластины Е₁=Е/2. Сила, с которой каждая из пластин притягивает другую:

F=E₁q=Eq/2

Используя числовые данные из условия задачи и записанные формулы, определим искомые величины:

Ответ. Электроемкость конденсатора 1,65*10^-10Ф; разность потенциалов на пластинах 242В; напряженность поля в конденсаторе 1,21*10⁵ В/м; сила взаимного притяжения пластин 2,42*10^-3 Н.

Напряженность поля между пластинами конденсатора формула

Автор На чтение 12 мин. Опубликовано 12.12.2019

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.

Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W_эл = CU 2 /2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U_c = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I_зар = Е/R_i, поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: I_ут = U/R_d, где I_ут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а R_d – сопротивление изоляции.

Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.

В чем измеряется емкость конденсатора

Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.

Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.

Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.

Формула энергии конденсатора

С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.

В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.

Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.

Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W_эл = CU 2 /2.

Формула заряда конденсатора

Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U_c = E.

Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.

В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).

Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I_зар = Е/R_i, поскольку к сопротивлению Ri приложена вся ЭДС генератора.

Формула тока утечки конденсатора

Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.

Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.

Основная формула для расчета выглядит следующим образом: I_ут = U/R_d, где I_ут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а R_d – сопротивление изоляции.

Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.

Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:

C = q φ 1 – φ 2 = q U .

Значением φ 1 – φ 2 = U обозначают разность потенциалов, называемую напряжением, то есть U . По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.

Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.

Плоский конденсатор

Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1 .

Формула для расчета электроемкости записывается как

C = ε ε 0 S d , где S является площадью обкладки, d – расстоянием между ними, ε – диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.

При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется d i , вычисление диэлектрической проницаемости этого слоя ε i выполняется, исходя из формулы:

C = ε 0 S d 1 ε 1 + d 2 ε 2 + . . . + d N ε N .

Сферический конденсатор

Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.

Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2 . Емкость рассчитывается по формуле:

C = 4 π ε ε 0 R 1 R 2 R 2 – R 1 , где R 1 и R 2 являются радиусами обкладок.

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равняется:

C = 2 πεε 0 l ln R 2 R 1 , где l – высота цилиндров, R 1 и R 2 – радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3 .

Важной характеристикой конденсаторов считается пробивное напряжение – напряжение, при котором происходит электрический разряд через слой диэлектрика.

U m a x находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Электроемкость плоского конденсатора. Формулы

Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы C i , где C i – это емкость конденсатора с номером i :

При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:

Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 с м 2 с расстоянием между ними 1 м м . Пространство между обкладками находится в вакууме.

Решение

Чтобы рассчитать электроемкость конденсатора, применяется формула:

ε = 1 , ε 0 = 8 , 85 · 10 – 12 Ф м ; S = 1 с м 2 = 10 – 4 м 2 ; d = 1 м м = 10 – 3 м .

Подставим числовые выражения и вычислим:

C = 8 , 85 · 10 – 12 · 10 – 4 10 – 3 = 8 , 85 · 10 – 13 ( Ф ) .

Ответ: C ≈ 0 , 9 п Ф .

Найти напряженность электростатического поля у сферического конденсатора на расстоянии x = 1 с м = 10 – 2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R 1 = 1 с м = 10 – 2 м , внешнем – R 2 = 3 с м = 3 · 10 – 2 м . Значение напряжения – 10 3 В .

Решение

Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:

E = 1 4 π ε ε 0 q r 2 , где q обозначают заряд внутренней сферы, r = R 1 + x – расстояние от центра сферы.

Нахождение заряда предполагает применение определения емкости конденсатора С:

Для сферического конденсатора предусмотрена формула вида

C = 4 π ε ε 0 R 1 R 2 R 2 – R 1 с радиусами обкладок R 1 и R 2 .

Производим подстановку выражений для получения искомой напряженности:

E = 1 4 πεε 0 U ( x + R 1 ) 2 4 πεε 0 R 1 R 2 R 2 – R 1 = U ( x + R 1 ) 2 R 1 R 2 R 2 – R 1 .

Данные представлены в системе С И , поэтому достаточно заменить буквы числовыми выражениями:

E = 10 3 ( 1 + 1 ) 2 · 10 – 4 · 10 – 2 · 3 · 10 – 2 3 · 10 – 2 – 10 – 2 = 3 · 10 – 1 8 · 10 – 6 = 3 , 45 · 10 4 В м .

Ответ: E = 3 , 45 · 10 4 В м .

Конденсаторы и диэлектрики | Физика II

Цели обучения

К концу этого раздела вы сможете:

• Опишите действие конденсатора и определите емкость.
• Объясните, что такое конденсаторы с параллельными пластинами и их емкости.
• Обсудите процесс увеличения емкости диэлектрика.
• Определите емкость при заданном заряде и напряжении.

Конденсатор — это устройство, используемое для хранения электрического заряда.Конденсаторы имеют разные применения: от фильтрации статического электричества при радиоприеме до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как показано на рисунке 1. (В большинстве случаев между двумя пластинами используется изолятор для обеспечения разделения — см. Обсуждение диэлектриков ниже). Клеммы батареи подключены к первоначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, + Q и — Q , разделены на его две пластины.Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд Q .

Рис. 1. Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них есть разделенные заряды + Q и — Q на своих двух половинах. (а) Конденсатор с параллельными пластинами. (b) Скрученный конденсатор с изоляционным материалом между двумя проводящими листами.

Конденсатор

Конденсатор — это устройство, используемое для хранения электрического заряда.

Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Количество заряда

Q конденсатор может хранить

Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.

Рис. 2. Линии электрического поля в этом конденсаторе с параллельными пластинами, как всегда, начинаются с положительных зарядов и заканчиваются отрицательными.Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.

Система, состоящая из двух идентичных параллельных проводящих пластин, разделенных расстоянием, как на рисунке 2, называется конденсатором с параллельными пластинами . Легко увидеть взаимосвязь между напряжением и накопленным зарядом для конденсатора с параллельными пластинами, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поля будет больше. линии, если есть больше заряда.(Рисование одной силовой линии для каждого заряда — это только удобство. Мы можем нарисовать много силовых линий для каждого заряда, но их общее количество пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна Ом. .

Поле пропорционально начислению:

E ∝ Q ,

, где символ ∝ означает «пропорционально». Из обсуждения электрического потенциала в однородном электрическом поле мы знаем, что напряжение на параллельных пластинах равно

.

V = Ed .

Таким образом, V ∝ E . Отсюда следует, что V ∝ Q , и, наоборот,

Q ∝ V .

В целом это верно: чем больше напряжение, приложенное к любому конденсатору, тем больше в нем хранится заряд.

Различные конденсаторы будут накапливать разное количество заряда для одного и того же приложенного напряжения, в зависимости от их физических характеристик. Мы определяем их емкость C так, чтобы заряд Q , хранящийся в конденсаторе, был пропорционален C .Заряд, накопленный в конденсаторе, равен

.

Q = CV .

Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора C и напряжение В . Переставляя уравнение, мы видим, что емкость C — это количество заряда, сохраненного на вольт, или

.

[латекс] C = \ frac {Q} {V} \\ [/ latex].

Емкость

Емкость C — это количество хранимого заряда на вольт, или

[латекс] C = \ frac {Q} {V} \\ [/ latex]

Единица измерения емкости — фарад (Ф), названная в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или

.

[латекс] 1 \ text {F} = \ frac {1 \ text {C}} {1 \ text {V}} \\ [/ latex].

Конденсатор емкостью 1 фарад может хранить 1 кулон (очень большое количество заряда) при подаче всего 1 вольт. Таким образом, одна фарада — это очень большая емкость. Типичный диапазон конденсаторов составляет от долей пикофарада (1 пФ = 10 ⁻¹² Ф) до миллифарадов (1 мФ = 10 ⁻³ Ф).

На рисунке 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.

Рисунок 3. Некоторые типичные конденсаторы. Размер и значение емкости не обязательно связаны. (Источник: Windell Oskay)

Конденсатор с параллельными пластинами

Рис. 4. Конденсатор с параллельными пластинами, разделенные пластинами на расстояние d. Каждая пластина имеет площадь A.

Конденсатор с параллельными пластинами, показанный на рисунке 4, имеет две идентичные проводящие пластины, каждая из которых имеет площадь поверхности A, , разделенных расстоянием d (без материала между пластинами).Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость зависит от A и d , рассмотрев характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, в отличие от зарядов притягиваются, и сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут расходиться больше. Таким образом, C должен быть больше для большего A .Точно так же, чем ближе пластины расположены друг к другу, тем сильнее на них притяжение противоположных зарядов. Значит, C должно быть больше для меньшего d .

Можно показать, что для конденсатора с параллельными пластинами есть только два фактора ( A, и d ), которые влияют на его емкость C . Емкость конденсатора с параллельными пластинами в форме уравнения равна

.

[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].

Емкость параллельного пластинчатого конденсатора

[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex]

A — это площадь одной пластины в квадратных метрах, а d — это расстояние между пластинами в метрах.Константа ε ₀ — диэлектрическая проницаемость свободного пространства; его числовое значение в единицах СИ составляет ε ₀ = 8,85 × 10 ⁻¹² Ф / м. Единицы измерения Ф / м эквивалентны C ² / Н · м ² . Небольшое числовое значение ε ₀ связано с большим размером фарада. Конденсатор с параллельными пластинами должен иметь большую площадь, чтобы его емкость приближалась к фарадам. (Обратите внимание, что приведенное выше уравнение действительно, когда параллельные пластины разделены воздухом или свободным пространством.Когда между пластинами помещается другой материал, уравнение изменяется, как обсуждается ниже.)

Пример 1. Емкость и заряд в параллельном пластинчатом конденсаторе

1. Какова емкость конденсатора с параллельными пластинами, каждая из которых имеет площадь 1,00 м ² , разделенных расстоянием 1,00 мм?
2. Какой заряд сохраняется в этом конденсаторе, если к нему приложено напряжение 3,00 × 10 ³ В?

Стратегия

Определение емкости C представляет собой прямое приложение уравнения [латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].{-9} \ text {F} = 8.85 \ text {nF} \ end {array} \\ [/ latex]

Обсуждение части 1

Это небольшое значение емкости указывает на то, насколько сложно изготовить устройство с большой емкостью. Помогают специальные методы, например, использование тонких пленок очень большой площади, расположенных близко друг к другу.

Решение для Части 2

Заряд любого конденсатора определяется уравнением Q = CV . Ввод известных значений в это уравнение дает

[латекс] \ begin {array} {lll} Q & = & CV = \ left (8.{3} \ text {V} \ right) \\\ text {} & = & 26.6 \ mu \ text {C} \ end {array} \\ [/ latex]

Обсуждение части 2

Этот заряд лишь немного больше, чем у обычного статического электричества. Поскольку воздух разрывается при примерно 3,00 × 10 ⁶ В / м, на этом конденсаторе не может быть накоплено больше заряда за счет увеличения напряжения.

Другой интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам выборочно входить и выходить из клетки.Существует разность потенциалов на мембране около –70 мВ. {6} \ text {V / m} \\ [/ latex]

Этого электрического поля достаточно, чтобы вызвать пробой в воздухе.

Диэлектрик

Предыдущий пример подчеркивает сложность сохранения большого количества заряда в конденсаторах. Если d сделать меньше, чтобы получить большую емкость, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс] E = \ frac {V} {d} \\ [/ latex]). Важным решением этой проблемы является размещение изоляционного материала, называемого диэлектриком , между пластинами конденсатора и обеспечение минимально возможного размера d .Мало того, что меньший d увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем сломаться.

Есть еще одно преимущество использования диэлектрика в конденсаторе. В зависимости от используемого материала емкость больше, чем заданная уравнением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], на коэффициент κ , называемый диэлектрическая проницаемость . Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex] (конденсатор с параллельными пластинами с диэлектриком).

Значения диэлектрической проницаемости κ для различных материалов приведены в таблице 1. Обратите внимание, что κ для вакуума равно 1, поэтому приведенное выше уравнение справедливо и в этом случае. Если использовать диэлектрик, например, поместив тефлон между пластинами конденсатора в примере 1, то емкость будет больше в κ раз, что для тефлона составляет 2,1.

Эксперимент на вынос: создание конденсатора

Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут из алюминиевой фольги, а разделитель (диэлектрик) между ними — из бумаги.

Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC
Материал	Диэлектрическая проницаемость κ	Электрическая прочность (В / м)
Вакуум	1,00000	–
Воздух	1.00059	3 × 10 6
Бакелит	4,9	24 × 10 6
Плавленый кварц	3.78	8 × 10 6
Неопреновый каучук	6,7	12 × 10 6
Нейлон	3,4	14 × 10 6
Бумага	3,7	16 × 10 6
Полистирол	2,56	24 × 10 6
Стекло Pyrex	5,6	14 × 10 6
Кремниевое масло	2.5	15 × 10 6
титанат стронция	233	8 × 10 6
Тефлон	2,1	60 × 10 6
Вода	80	–

Обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, действуют так же, как конденсаторы с вакуумом между пластинами , за исключением , что воздух может стать проводящим, если напряженность электрического поля становится равной. слишком большой.(Напомним, что [латекс] E = \ frac {V} {d} \\ [/ latex] для конденсатора с параллельными пластинами.) В таблице 1 также показаны максимальные напряженности электрического поля в В / м, которые называются диэлектрической прочностью , для нескольких материалов. Это поля, над которыми материал начинает разрушаться и проводить. 6 \ text {V / m} \ right) \ left ( 1.{-3} \ text {m} \ right) \\\ text {} & = & 3000 \ text {V} \ end {array} \\ [/ latex]

Однако предел для расстояния в 1,00 мм, заполненного тефлоном, составляет 60 000 В, поскольку диэлектрическая прочность тефлона составляет 60 × 10 ⁶ В / м. Таким образом, тот же конденсатор, заполненный тефлоном, имеет большую емкость и может подвергаться гораздо большему напряжению. Используя емкость, которую мы рассчитали в приведенном выше примере для конденсатора с параллельными пластинами, заполненного воздухом, мы обнаружили, что конденсатор с тефлоновым заполнением может хранить максимальный заряд

[латекс] \ begin {array} {lll} Q & = & CV \\\ text {} & = & \ kappa {C} _ {\ text {air}} V \\\ text {} & = & (2.4 \ text {V}) \\\ text {} & = & 1.1 \ text {mC} \ end {array} \\ [/ latex]

Это в 42 раза больше заряда того же конденсатора, заполненного воздухом.

Диэлектрическая прочность

Максимальная напряженность электрического поля, при превышении которой изолирующий материал начинает разрушаться и становится проводником, называется его диэлектрической прочностью.

Микроскопически, как диэлектрик увеличивает емкость? За это отвечает поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость κ .Вода, например, представляет собой полярную молекулу , потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды обуславливает ее относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации лучше всего объясняется характеристиками кулоновской силы. На рис. 5 схематично показано разделение зарядов в молекулах диэлектрического материала, помещенных между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень сильна, поскольку они находятся очень близко друг к другу.Это притягивает больше заряда к пластинам, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии d друг от друга.

Рис. 5. (a) Молекулы изоляционного материала между пластинами конденсатора поляризованы заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда к пластине, увеличивая ее емкость. (б) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к уменьшению напряжения между пластинами при одинаковом заряде.Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.

Другой способ понять, как диэлектрик увеличивает емкость, — это рассмотреть его влияние на электрическое поле внутри конденсатора. На рисунке 5 (b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются зарядами в диэлектрике, их меньше, идущих от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, даже если бы на пластинах был одинаковый заряд.Напряжение между пластинами составляет В, = Ед, , поэтому оно тоже снижается за счет диэлектрика. Таким образом есть меньшее напряжение В, для того же заряда Q ; поскольку [латекс] C = \ frac {Q} {V} \\ [/ latex], емкость C больше.

Диэлектрическая постоянная обычно определяется как [латекс] \ kappa = \ frac {E_0} {E} \\ [/ latex], или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале, и в конечном итоге связанных с поляризуемостью материала.

Великие и малые вещи: субмикроскопическое происхождение поляризации

Поляризация — это разделение зарядов внутри атома или молекулы. Как уже отмечалось, планетарная модель атома описывает его как имеющее положительное ядро, вращающееся вокруг отрицательных электронов, аналогично планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в других местах, например, в атомной физике. Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рисунке 6.

Рис. 6. Художественное представление о поляризованном атоме. Орбиты электронов вокруг ядра слегка смещены внешними зарядами (показаны в преувеличении). Получающееся разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что непохожий заряд теперь ближе к внешним зарядам, вызывая поляризацию.

В атомной физике мы обнаружим, что орбиты электронов более правильно рассматривать как электронные облака с плотностью облака, связанной с вероятностью обнаружения электрона в этом месте (в отличие от определенных положений и путей движения планет на их орбитах). вокруг Солнца).Это облако сдвигается кулоновской силой, так что в среднем атом имеет разделенный заряд. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.

Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому они называются полярными молекулами. На рисунке 7 показано разделение зарядов в молекуле воды, которая имеет два атома водорода и один атом кислорода (H ₂ O).Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды больше сконцентрированы вокруг более заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец — слегка положительным. Внутреннее разделение зарядов в полярных молекулах облегчает их выравнивание с внешними полями и зарядами. Следовательно, полярные молекулы обладают более сильными поляризационными эффектами и имеют более высокие диэлектрические проницаемости.Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды собирают ионы гораздо эффективнее, потому что у них есть электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как было показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.

Рис. 7. Художественная концепция молекулы воды. Существует внутреннее разделение зарядов, поэтому вода — полярная молекула.Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда около двух ядер водорода. (Обратите внимание, что схема справа является приблизительной иллюстрацией распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.)

Исследования PhET: лаборатория конденсаторов

Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость.Измените напряжение и посмотрите, как на пластинах образовались заряды. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.

Щелкните, чтобы загрузить симуляцию. Запускать на Java.

Сводка раздела

• Конденсатор — это устройство для накопления заряда.
• Количество заряда Q , которое может хранить конденсатор, зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.
• Емкость C, — это количество заряда, накопленного на вольт, или [латекс] C = \ frac {Q} {V} \\ [/ latex].
• Емкость конденсатора с параллельными пластинами составляет [латекс] C = {\ epsilon} _ {0} \ frac {A} {d} \\ [/ latex], когда пластины разделены воздухом или свободным пространством. [latex] {\ epsilon} _ {\ text {0}} [/ latex] называется диэлектрической проницаемостью свободного пространства.
• Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], где κ — диэлектрик. константа материала.
• Максимальная напряженность электрического поля, при превышении которой изолирующий материал начинает разрушаться и становится проводником, называется электрической прочностью.

Концептуальные вопросы

1. Зависит ли емкость устройства от приложенного напряжения? А как насчет хранящегося в нем заряда?
2. Используйте характеристики кулоновской силы, чтобы объяснить, почему емкость должна быть пропорциональна площади пластины конденсатора. Аналогичным образом объясните, почему емкость должна быть обратно пропорциональна расстоянию между пластинами.
3. Объясните причину, по которой диэлектрический материал увеличивает емкость по сравнению с тем, что было бы с воздухом между пластинами конденсатора.Какова независимая причина того, что диэлектрический материал также позволяет приложить большее напряжение к конденсатору? (Таким образом, диэлектрик увеличивает C и допускает более В .)
4. Как полярный характер молекул воды помогает объяснить относительно большую диэлектрическую проницаемость воды? (См. Рисунок 7.)
5. Искры возникают между пластинами заполненного воздухом конденсатора при более низком напряжении, когда воздух влажный, чем когда сухой. Объясните почему, учитывая полярный характер молекул воды.
6. Вода имеет большую диэлектрическую проницаемость, но редко используется в конденсаторах. Объяснить, почему.
7. Мембраны в живых клетках, включая клетки человека, характеризуются разделением заряда через мембрану. Таким образом, мембраны представляют собой заряженные конденсаторы, важные функции которых связаны с разностью потенциалов на мембране. Требуется ли энергия для разделения этих зарядов в живых мембранах, и если да, то является ли ее источником метаболизм пищевой энергии или каким-либо другим источником?

Рисунок 8.Полупроницаемая мембрана клетки имеет разную концентрацию ионов внутри и снаружи. Диффузия перемещает ионы K ⁺ (калий) и Cl ^— (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Это приводит к слою положительного заряда снаружи, слою отрицательного заряда внутри и, следовательно, к напряжению на клеточной мембране. Мембрана обычно непроницаема для Na ⁺ (ионы натрия).

Задачи и упражнения

1. Какой заряд сохраняется в конденсаторе 180 мкФ, когда к нему приложено 120 В?
2. Найдите накопленный заряд, когда 5.50 В подается на конденсатор емкостью 8,00 пФ.
3. Какой заряд хранится в конденсаторе в Примере 1?
4. Рассчитайте напряжение, приложенное к конденсатору 2,00 мкФ, когда он имеет заряд 3,10 мкКл.
5. Какое напряжение необходимо подать на конденсатор емкостью 8,00 нФ для накопления заряда 0,160 мкКл?
6. Какая емкость необходима для хранения заряда 3,00 мкКл при напряжении 120 В?
7. Какая емкость терминала большого генератора Ван-де-Граафа, учитывая, что он хранит 8?00 мкКл заряда при напряжении 12,0 МВ?
8. Найдите емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 5,00 м ² , разделенных слоем тефлона 0,100 мм.
9. (a) Какова емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 1,50 м ² , разделенных 0,0200 мм неопреновой резины? (b) Какой заряд он держит, когда к нему приложено 9,00 В?
10. Интегрированные концепции. Шутник подает 450 В на 80.Конденсатор 0 мкФ, а затем бросает его ничего не подозревающей жертве. Палец пострадавшего обгорел от разряда конденсатора через 0,200 г мяса. Какое повышение температуры мяса? Разумно ли предполагать отсутствие изменения фазы?
11. Необоснованные результаты. (a) Конденсатор с параллельными пластинами имеет площадь пластин 4,00 м ² , разделенных нейлоном толщиной 0,0100 мм, и накапливает 0,170 Кл заряда. Какое приложенное напряжение? б) Что неразумного в этом результате? (c) Какие допущения являются ответственными или противоречивыми?

Глоссарий

конденсатор: устройство, накапливающее электрический заряд

емкость: количество заряда на единицу вольт

диэлектрик: изоляционный материал

диэлектрическая прочность: максимальное электрическое поле, выше которого изоляционный материал начинает разрушаться и проводить

Конденсатор с параллельными пластинами: две идентичные проводящие пластины, разделенные расстоянием

полярная молекула: молекула с внутренним разделением заряда

Избранные решения проблем и упражнения

1.21,6 мК

3. 80.0 мС

5. 20,0 кВ

7. 667 пФ

9. (а) 4,4 мкФ; (б) 4.0 × 10 ⁻⁵ C

11. (а) 14,2 кВ; (b) Напряжение неоправданно велико, более чем в 100 раз больше напряжения пробоя нейлона; (c) Предполагаемый заряд неоправданно велик и не может храниться в конденсаторе таких размеров.

Сделайте конденсатор из того, что у вас уже есть (принцип работы + расчеты): 10 шагов

Итак, мы подсчитали.00000000000440 фарадов
, и мы нашли 0,0000000000000173 фарадов при тестировании.
Это разница в 0,0000000000000267 фарадов.
К сожалению, вычисленное нами число немного отличается от найденного. Почему это могло быть так?

1) Окантовка: в идеальном мире конденсатор должен иметь электрическое поле только между двумя панелями. Однако это не всегда так, и поэтому, когда поле конденсатора выходит за пределы двух полей, инженеры называют это окантовкой.

2) Несовершенное измерение размеров / несовершенное измерение: При измерении мы предположили, что пластины представляют собой идеальные прямоугольники. Однако это было не так, и это могло привести к тому, что результат был отвергнут.

3) Неправильная диэлектрическая проницаемость: я взял диэлектрическую проницаемость Lexan с их веб-сайта. Однако не все пластмассы одинаковы — даже если они одного типа и могут быть изготовлены на одной фабрике в один и тот же день, они будут иметь разную диэлектрическую проницаемость.

4) Еще одна вещь, о которой следует помнить, это то, что алюминиевая лента держалась с помощью клея. Как сказал пользователь jmwells: «[Клей обычно является латексной основой, это может отбросить ваши расчеты на 10%»

Как бы то ни было, в разных конденсаторах проблема здесь явно окаймляющая. Я знаю это, потому что есть кое-что, что я не учел при создании конденсатора. В отношении этих вещей существует инженерное эмпирическое правило: если отношение к наименьшей длине и расстояние между двумя пластинами меньше пятидесяти, то будет окантовка.Если он выше, окантовка все равно будет, но она будет достаточно маленькой, и ее можно будет игнорировать.

Чтобы уменьшить бахрому, мне следовало сделать так, чтобы соотношение было больше пятидесяти. Кроме того, разрезание конденсатора на круг может помочь, так как таким образом вы получите меньше края и большую площадь.

Несмотря на это, я очень доволен тем, что снизился всего на 0,0000000000000267 фарадов, особенно при выполнении такой работы снижение на 10% считается фантастически хорошим результатом, если только это не точный продукт.

электростатика — Емкость однозарядной пластины?

Ответ Тома совершенно правильный, но я хотел добавить к нему некоторые детали.

Во-первых, почему ваша логика не работает? Ответ заключается в том, что известная формула емкости двух параллельных пластин основана на приближении, согласно которому электрическое поле между двумя пластинами полностью однородно. В таком случае имеем $ E = V / d $ и $ E = Q / \ epsilon_0 A $; Приравнивая два выражения друг к другу и решая для $ C = Q / V $, получаем знакомую формулу для емкости пары параллельных пластин.

Однако, если мы возьмем две пластины и начнем их раздвигать, то в какой-то момент наши приближения об электрическом поле потерпят неудачу; электрическое поле больше не будет однородным и определенно не будет связано с зарядом на пластинах вышеупомянутым образом. Обычно это приближение действительно начинает терпеть неудачу, когда размер $ d $ становится значительной частью размера пластин; как только это произойдет, формула параллельных пластин будет плохим приближением.Другими словами, известная формула емкости параллельных пластин была получена в предположении, что $ d \ ll \ sqrt {A} $, и поэтому вы не можете принять его предел как $ d \ to \ infty $ и все же ожидать это держать.

Итак, представьте, что два диска перемещаются на огромное расстояние друг от друга. В какой-то момент они окажутся достаточно далеко друг от друга, чтобы больше не «чувствовать» друг друга, и в этот момент каждая пластина будет действовать как независимый заряженный проводник, одиноко сидящий в космосе. Но между каждым проводником и бесконечностью все еще будет существовать разность потенциалов, и в этот момент мы можем определить емкость этого одиночного проводника и другого «электрода на бесконечности».Поскольку мы обычно определяем $ V = 0 $ на бесконечности, нам просто нужно вычислить потенциал проводника, когда он несет заряд $ Q $, и снова взять отношение $ Q / V $. Это процесс, описанный @tom в своем ответе.

Теперь для проводника произвольной формы у вас возникнут проблемы с получением точного результата для $ C $. @tom создал сферу, что является простейшим результатом. Однако оказывается, что это можно сделать и для бесконечно тонкого проводящего диска! Для этого мы рассматриваем диск как предел эллипсоида, когда одна из главных осей стремится к нулю.2}} $$ где $ s $ — расстояние от центра, $ Q $ — полный заряд диска, а $ R $ — его радиус. Тогда мы можем довольно легко найти потенциал на диске; просто разделите диск на концентрические кольца, вычислите потенциал в центре каждого из них и проинтегрируйте. Результат после некоторой математики: $$ V = \ frac {Q} {8 \ epsilon_0 R} $$ и поэтому мы имеем $ C = Q / V = ​​8 \ epsilon_0 R $.

Конденсатор

Конденсатор — это устройство, используемое для хранения электрической энергии.

Пластины конденсатора заряжены, и между ними существует электрическое поле.Конденсатор разрядится, если пластины соединить вместе через резистор.

Заряд конденсатора

Заряд конденсатора можно выразить как

Q = I t (1)

, где

Q = заряд конденсатора (кулон, Кл, мкКл)

I = ток (А)

t = время (с)

Количество заряда (количество электронов) измеряется в кулонах — C — , где

1 кулон = 6.24 10 ¹⁸ электронов

Наименьший существующий заряд — это заряд, переносимый электроном, равный -1,602 10 ^-19 кулонов .

Пример — количество переданной электроэнергии

Если ток 5 А протекает в течение 2 минут, количество электроэнергии — кулонов — можно рассчитать как

Q = (5 А) (2 мин. ) (60 с / мин)

= 600 C

или, в электронах:

(600 C) ( 6.24 10 ¹⁸ электронов / C)

= 3,744 10 ²¹ электронов

Напряженность электрического поля (диэлектрическая прочность)

Если две заряженные пластины разделены изолирующей средой — диэлектрик — напряженность электрического поля (градиент потенциала) между двумя пластинами может быть выражена как

E = U / d (2)

, где

E = напряженность электрического поля (вольт / м)

U = электрический потенциал (вольт)

d = толщина диэлектрика, расстояние между пластинами (м)

Пример — напряженность электрического поля

Напряжение между двумя пластинами составляет 230 В, и расстояние между ними. их 5 мм .Напряженность электрического поля может быть рассчитана как

E = (230 В) / ((5 мм) (10 ^-3 м / мм))

= 46000 вольт / м

= 46 кВ / м

Плотность электрического потока

Плотность электрического потока — это соотношение между зарядом конденсатора и площадью поверхности обкладок конденсатора:

D = Q / A (3)

, где

D = плотность электрического потока (кулон / м ² )

A = площадь поверхности конденсатора (м ² )

Заряд и приложенное напряжение

Заряд в конденсаторе пропорционален приложенное напряжение и может быть выражено как

Q = CU (4)

, где

C = константа пропорциональности или емкость (фарад, Ф, 90 027 мкФ )

Емкость

Из (4) емкость можно выразить как

C = Q / U (5)

Один фарад определяется как емкость конденсатора, когда существует разность потенциалов на пластинах в один вольт при удерживании заряда в один кулон.

Обычно используется мкФ (10 ^-6 F) .

Пример — Напряжение на конденсаторе

Конденсатор 5 мкФ заряжен током 10 мКл . Напряжение на конденсаторе можно рассчитать, изменив (4) на

U = Q / C

= (10 мКл) (10 ^-3 Кл / мКл) / ((5 мкФ) ( 10 ^-6 Ф / мкФ)

= 2000 В

= 2 кВ

Абсолютная диэлектрическая проницаемость

Отношение плотности электрического потока к электрическому полю называется абсолютной диэлектрической проницаемостью — ε — диэлектрическая проницаемость и может быть выражена как

ε = D / E (6)

где

ε = абсолютная диэлектрическая проницаемость (Ф / м)

Абсолютная диэлектрическая проницаемость свободного пространства или вакуума — также называемая электрической постоянной — ε ₀ — это 8.85 10 ^-12 Ф / м .

Относительная диэлектрическая проницаемость

Относительная диэлектрическая проницаемость — также называемая диэлектрической проницаемостью ε _r — это отношение между плотностью потока поля в реальном диэлектрике — ε — и плотностью потока поля в абсолютном вакуум — ε ₀ .

ε _r = ε / ε ₀ (7a)

Фактическая диэлектрическая проницаемость может быть рассчитана путем преобразования (7a) в

ε = ε _r ε ₀ ( 7b)

Параллельный пластинчатый конденсатор

Емкость пластинчатого конденсатора — как показано на рисунке выше — пропорциональна площади А пластины.Емкость может быть выражена как

C = ε _r ε ₀ A / d (8)

, где

A = площадь пластины (м ² )

d = толщина диэлектрика, расстояние между пластинами (м)

Для пластинчатого конденсатора с несколькими пластинами емкость можно выразить как

C = ε _r ε ₀ A (n — 1) / d (8b)

, где

n = количество пластин

Пример — емкость пластинчатого конденсатора

Емкость пластинчатого конденсатора площадью 5 см ² , 10 пластин и расстояние 0.1 мм между пластинами — с керамическим диэлектриком с относительной диэлектрической проницаемостью 30 между пластинами — можно рассчитать как

C = ( 8,85 10 ^-12 Ф / м ) _{(30) (5 см ² ) (10 ^-4 м ² / см ² ) (10-1) / ((0,1 мм) (10 ^-3 м / мм))}

= 11 10 ^{— 9} F

= 11 пФ

Типичные обычно используемые конденсаторы

Типичные конденсаторы —

• конденсаторы переменного воздуха
• конденсаторы слюдяные
• бумажные конденсаторы
• керамические конденсаторы
9000 пластмассовые конденсаторы пластиковые 9000 конденсаторы
• конденсаторы электролитические

5.23: Конденсатор с тонкими параллельными пластинами

Давайте теперь определим емкость конденсатора общего типа, известного как конденсатор с тонкими параллельными пластинами , показанный на рисунке \ (\ PageIndex {1} \). Этот конденсатор состоит из двух плоских пластин, каждая из которых имеет площадь \ (A \), разделенную расстоянием \ (d \). Чтобы облегчить обсуждение, поместим начало системы координат в центр нижней пластины с осью \ (+ z \), направленной к верхней пластине так, чтобы верхняя пластина лежала в плоскости \ (z = + d \ ) самолет.

Рис. \ (\ PageIndex {1} \): Тонкопараллельный пластинчатый конденсатор

Ниже мы найдем емкость, предполагая определенный заряд на одной пластине, используя граничное условие для плотности электрического потока \ ({\ bf D} \), чтобы связать эту плотность заряда с внутренним электрическим полем, а затем интегрировать по электрическому полю между пластинами, чтобы получить разность потенциалов. Тогда емкость — это отношение предполагаемого заряда к результирующей разности потенциалов.

Основная трудность в этом подходе — нахождение электрического поля.Чтобы понять проблему, сначала представьте, что если бы площадь пластин была бесконечной, то электрическое поле было бы очень простым; он начнется с положительно заряженной пластины и продолжится в перпендикулярном направлении к отрицательно заряженной пластине (раздел 5.19). Кроме того, поле между пластинами везде будет постоянным. Это очевидно из одной только симметрии. Однако, когда площадь пластины конечна, мы ожидаем появления окаймляющего поля . «Поле окаймления» — это просто термин, применяемый к неоднородному полю, которое появляется у края пластин.Поле в этой области неоднородно, потому что граничные условия на за пределами (обращенных наружу) поверхностей пластин имеют существенное влияние в этой области. Однако в центральной области конденсатора поле мало отличается от поля, которое существует в случае бесконечной площади пластины.

В любом конденсаторе с параллельными пластинами, имеющем конечную площадь пластин, некоторая часть энергии будет накапливаться приблизительно однородным полем центральной области, а остальная часть будет накапливаться в окаймляющем поле.Мы можем сделать последний незначительным по сравнению с первым, сделав конденсатор очень «тонким» в том смысле, что наименьший идентифицируемый размер пластины намного больше, чем \ (d \). При этом условии мы можем получить хорошее приближение емкости, просто пренебрегая окаймляющим полем, поскольку там сохраняется незначительная часть энергии.

Наложение «тонкого» условия приводит к трем дополнительным упрощениям. Во-первых, можно предположить, что распределение поверхностного заряда приблизительно равномерно по пластине, что значительно упрощает анализ.Во-вторых, не имеет значения форма тарелок; они могут быть круглыми, квадратными, треугольными и т. д. При вычислении емкости в «тонком» случае важна только площадь пластины \ (A \). В-третьих, толщина каждой из пластин становится неактуальной.

Теперь мы готовы определить емкость тонкого конденсатора с параллельными пластинами. Вот шаги:

1. Предположим, что на верхней пластине имеется полный положительный заряд \ (Q _ + \).
2. Используя условие «тонкости», мы предполагаем, что плотность заряда на пластинах однородна.2 \)).
3. Из граничного условия на нижней поверхности верхней пластины \ ({\ bf D} \) на этой поверхности будет \ (- \ hat {\ bf z} \ rho_ {s, +} \).
4. Полный заряд на нижней пластине, \ (Q _- \), должен быть равен и противоположен полному заряду на верхней пластине; то есть \ (Q _- = — Q _ + \). Точно так же поверхностная плотность заряда на верхней поверхности нижней пластины \ (\ rho_ {s, -} \) должна быть \ (- \ rho_ {s, +} \).
5. Из граничного условия на верхней поверхности нижней пластины (Раздел 5.18), \ ({\ bf D} \) на этой поверхности есть \ (+ \ hat {\ bf z} \ rho_ {s, -} \). Поскольку \ (+ \ hat {\ bf z} \ rho_ {s, -} = — \ hat {\ bf z} \ rho_ {s, +} \), \ ({\ bf D} \) на лицевых сторонах пластин равно.
6. Снова применяя условие «тонкости», мы предполагаем, что \ ({\ bf D} \) между пластинами имеет примерно такую ​​же структуру, как если бы площадь пластины была бесконечной. Следовательно, мы вправе предположить, что \ ({\ bf D} \ приблизительно- \ hat {\ bf z} \ rho_ {s, +} \) везде между пластинами. (Вы также можете увидеть, что это очевидно из определения \ ({\ bf D} \) как плотности потока электрического заряда (Раздел 2.{d} \ left (- \ hat {\ mathbf {z}} \ frac {\ rho_ {s, +}} {\ epsilon} \ right) \ cdot (\ hat {\ mathbf {z}} dz) \\
   & = + \ frac {\ rho_ {s, +} d} {\ epsilon}
   \ end {align}
7. Наконец, \ [C = \ frac {Q _ +} {V} = \ frac {\ rho_ {s, +} ~ A} {\ rho_ {s, +} ~ d / \ epsilon} = \ frac {\ epsilon A} {d} \]

Обобщение: \ [\ boxed {C \ приблизительно \ frac {\ epsilon A} {d}} \ label {m0070_eTPPC} \]

Емкость конденсатора с параллельными пластинами, расстояние между пластинами которого намного меньше размера пластины, определяется уравнением \ ref {m0070_eTPPC}.2 \) разделенное на m дает F. Также стоит отметить влияние различных параметров:

Емкость увеличивается пропорционально диэлектрической проницаемости и площади пластины и уменьшается пропорционально расстоянию между пластинами.

Пример \ (\ PageIndex {1} \): Емкость печатной платы

Печатные платы

обычно включают в себя «заземляющую пластину», которая служит точкой отсчета напряжения для платы, и по крайней мере одну «пластину питания», которая используется для распределения напряжения питания постоянного тока (см. «Дополнительная информация» в конце эта секция).Эти плоскости разделены диэлектрическим материалом, и полученная структура демонстрирует емкость. Эту емкость можно рассматривать как эквивалентный дискретный конденсатор, подключенный параллельно источнику питания. Стоимость этого эквивалентного конденсатора может быть либо незначительной, значительной и полезной, либо значительной и вредной. Итак, полезно знать значение этого эквивалентного конденсатора.

Для обычных печатных плат толщина диэлектрика составляет около 1,6 мм, а относительная диэлектрическая проницаемость материала составляет около 4.2 \) и \ (d \ cong 1,6 \) мм. Используя уравнение \ ref {m0070_eTPPC}, значение эквивалентного конденсатора составляет \ (62,3 \) пФ.

Авторы и авторство

Дополнительное чтение:

Емкость двух параллельных пластин

Емкость двух параллельных пластин

Емкость из двух параллельных пластин

Самый распространенный Конденсатор состоит из двух параллельных пластин. Емкость конденсатор с параллельными пластинами зависит от площади пластин А и их разделение d .По мнению Гаусса закон, электрическое поле между двумя пластинами:

Поскольку емкость определяется тем, что емкость:

Таким образом, вы получите максимум емкость, когда пластины большие и близко друг к другу. Большой емкость означает, что конденсатор хранит большое количество обвинять.

Если диэлектрик материал вставлен между пластинами, микроскопический диполь моменты материала будут экранировать заряды на пластинах и изменить отношение.Материалы имеют проницаемость e, который задается относительной величиной проницаемость k, e = ke ₀ . Таким образом, емкость дается по:

Все материалы имеют относительную проницаемость k больше единицы, поэтому емкость можно увеличить, вставив диэлектрик. Иногда k равно называется диэлектрической проницаемостью материала. В электрическое поле вызывает некоторую часть диполей в материала, чтобы ориентироваться вдоль E-поля, в отличие от обычная случайная ориентация.Фактически это выглядит так, как если бы отрицательный заряд выстраивается напротив положительной пластины, и положительный заряд против отрицательной пластины. На рисунке к справа синий материал — это диэлектрик.

---

Примеры Конденсаторы главная Список лекций

Часть 7: Емкость и конденсаторы

7.1 Электрический заряд и электрические поля

Рассмотрим пару плоских проводящих пластин, расположенных параллельно друг другу (как на рисунке 7.1) и разделены изолятором, который может быть просто воздухом. Каждая пластина, как электрический проводник, будет содержать большое количество подвижных отрицательно заряженных электронов. Если пластины подключены к источнику постоянного тока, отрицательные электроны будут притягиваться от верхней пластины к положительному полюсу источника питания, но для каждого электрона, который это делает, другой должен покинуть отрицательный полюс источника питания и перейти к нижней пластине. Верхняя пластина станет положительно заряженной из-за нехватки электронов, тогда как избыток электронов на нижней пластине даст ей отрицательный заряд.Разница в полярности заряда между пластинами означает, что между ними существует разность потенциалов (PD), и поток электронов исчезает и прекращается, когда PD между пластинами совпадает с напряжением питания. Как только это произошло, источник питания больше не может подавать достаточно энергии для удаления электронов с верхней пластины или проталкивания электронов на нижнюю пластину, и пластины называют «заряженными».

Рисунок 7.1: Система заряженных пластин

Между двумя заряженными пластинами существует электрическое поле.Подобно магнитному полю, электрическое поле нельзя увидеть, но его можно описать в терминах заряженной частицы, движущейся сквозь него. Также, как и магнитные поля, электрические поля представляются как линий электрического потока .

Рисунок 7.2: Электрическое поле между двумя заряженными пластинами.

Если пластины отсоединить от источника питания и соединить вместе через резистор, электроны потекут от отрицательно заряженной пластины к положительно заряженной пластине. Этот ток исчезнет, ​​поскольку заряды на пластинах уменьшатся.По мере прохождения тока он выделяется в виде тепла, поэтому видно, что энергия накапливается в заряженном конденсаторе.

Заряд, накопленный в электрическом поле, можно измерить в кулонах (Кл), то есть ток, протекающий для зарядки пластин, умноженный на время, в течение которого происходит течение. Однако следует отметить, что при постоянном напряжении питания ток будет уменьшаться по мере увеличения заряда на пластинах, так что пластины не заряжаются постоянным током. На практике общий заряд, который может накапливаться параллельными пластинами, зависит от площади пластины, расстояния между пластинами, частичного разряда между ними и природы изоляционного материала, который их разделяет.

7,2 Емкость

Для любой системы параллельных пластин отношение количества накопленного заряда к частичному разряду между пластинами является постоянным. Эта постоянная называется емкостью , (C), а система накопительных пластин называется конденсатором (иногда ошибочно называют конденсатор ). Условное обозначение цепи конденсатора показано на рисунке 7.3.

Рисунок 7.3: Условное обозначение цепи конденсатора.

Единицей измерения емкости является фарад (Ф) и:

где:
C = емкость (F)
Q = накопленный заряд в емкости (C)
U = PD между пластинами конденсатора (В)

Поскольку в Части 1 мы отметили, что Q = I t, мы можем сказать, что:

где:
I = средний зарядный ток конденсатора (C)
t = время, в течение которого проходит зарядный ток (с)

Конденсатор имеет емкость в одну фараду, если он может хранить один кулон, когда частичный разряд между его пластинами составляет один вольт.Однако, поскольку на практике один фарад оказывается довольно большим значением емкости, большинство емкостей указывается в микрофарадах (мкФ), что равно 1 × 10 ^-6 F.

Обратите внимание, что если к конденсатору подключено постоянное напряжение, конденсатор будет заряжаться до тех пор, пока частичный разряд на нем не станет таким же, как напряжение питания. Он будет оставаться заряженным до тех пор, пока не будет обеспечен путь для прохождения тока между пластинами. Однако, если конденсатор подключен к источнику переменного тока, где направление тока постоянно меняется, он будет постоянно заряжаться и разряжаться.

7.3 Пробой диэлектрика и диэлектрическая проницаемость

Изоляционный материал, который занимает пространство между пластинами конденсатора, называется диэлектриком . Изоляционные материалы обычно не проводят электричество, потому что в них нет свободных электронов, которые могли бы течь как ток. Однако, если изоляторы подвергаются достаточно сильному электрическому полю, электроны могут вырываться, а изолирующие свойства теряются в процессе, называемом пробой диэлектрика .Это явление может быть очень серьезным при нарушении изоляции кабеля.

Напряженность электрического поля может быть выражена через частичные разряды, приложенные к изолятору определенной толщины, это значение называется средним градиентом потенциала и обычно измеряется в киловольтах на миллиметр (кВ / мм). Градиент потенциала, при котором изолятор выходит из строя, называется его диэлектрической прочностью , и его можно использовать как меру того, насколько хорош изолятор. В таблице 7.1 указана электрическая прочность нескольких изоляторов.

Пример

Бумажный пропитанный конденсатор силового конденсатора с параллельными пластинами имеет толщину 0,5 мм и электрическую прочность 5 кВ / мм. Если соответствующий конденсатор имеет приложенное частичное напряжение 1,8 кВ, каков средний градиент потенциала в бумаге? При каком приложенном напряжении можно ожидать выхода конденсатора из строя?

Таблица 7.1: Электрическая прочность некоторых распространенных изоляторов.

Материал	Диэлектрическая прочность (кВ / мм)	Приложения
Воздух	3	Общий
Бакелит	20-25	Вилки, оборудование и т. Д.
Битум	14	Коробки уплотнительные кабельные
Стекло	50-120	Изоляторы воздушные
Слюда	40–150	Коммутаторы, горячие элементы, конденсаторы
Миканит	30	Машины
Пропитанная бумага	4-10	Кабели силовые, конденсаторы
Парафиновый воск	8	конденсаторы
Фарфор	9-10	Держатели предохранителей, изоляторы ВЛ

Диэлектрические материалы также можно охарактеризовать с точки зрения их относительной диэлектрической проницаемости (ε _r ).Абсолютная диэлектрическая проницаемость материала определяется как отношение заряда на единицу площади на поверхности этого материала к напряженности создаваемого электрического поля. Относительная диэлектрическая проницаемость определяется как отношение емкости конденсатора с рассматриваемым материалом между пластинами к емкости того же конденсатора с вакуумом между пластинами. Это отношение также равно диэлектрической проницаемости диэлектрика диэлектрической проницаемости свободного пространства (т.е.е. вакуум). Таким образом:

где:
ε _r = относительная диэлектрическая проницаемость диэлектрического материала, без единиц
C = емкость конденсатора с рассматриваемым материалом (F)
C ₀ = емкость того же конденсатора с вакуумом между пластина (F)
ε = абсолютная диэлектрическая проницаемость материала (Ф / м)
ε ₀ = диэлектрическая проницаемость свободного пространства (Ф / м)

Обратите внимание, что диэлектрическая проницаемость свободного пространства является константой, равной 8,85 × 10 ^-12 Ф / м (или C ² / Нм ² ), и что по определению относительная диэлектрическая проницаемость вакуума равна 1.Также обратите внимание, что диэлектрическая проницаемость (ε) очень похожа по концепции и названию на проницаемость (μ) магнитных материалов, однако их не следует путать. Таблица 7.2 содержит относительную проницаемость некоторых распространенных диэлектрических материалов.

Таблица 7.2: Относительная проницаемость некоторых распространенных диэлектрических материалов.

Материал диэлектрика	Относительная диэлектрическая проницаемость (ε r )
Воздух	1
Бакелит	4.5-5,5
Стекло	5-10
Микра	3-7
Пропитанная бумага	2
Полистирол	2,5
Фарфор	6-7

7,4 Конденсаторы параллельно и последовательно

Рассмотрим три конденсатора, включенных параллельно, как показано на рисунке 7.4, каждый из них будет иметь одинаковое напряжение (В) на каждом, а общий заряд (Q _T ) будет суммой отдельных зарядов.Следовательно:

Рисунок 7.4: Три конденсатора параллельно.

Но Q = CV, и если C _T — эквивалентная емкость трех конденсаторов:

Следовательно:

Теперь рассмотрим три последовательно соединенных конденсатора, как показано на рисунке 7.5. Напряжение питания распределяется между тремя конденсаторами, и, поскольку через каждый конденсатор будет протекать одинаковый зарядный ток, каждый из них получит одинаковый заряд за одно и то же время. Таким образом:

Рисунок 7.5: Три конденсатора последовательно.

Но U = Q / C, поэтому, если C _T — эквивалентное значение трех последовательно соединенных конденсаторов:

Следовательно:

Пример

Рассчитайте эквивалентную емкость конденсаторов 5 мкФ, 10 мкФ и 30 мкФ, соединенных последовательно.

Эти конденсаторы подключены к источнику питания 240 В постоянного тока. Рассчитайте заряд каждого конденсатора и разность потенциалов на каждом из них.

Общий накопленный заряд:

Поскольку конденсаторы соединены последовательно, заряд каждого из них равен общему заряду, т.е.е. 720 мкКл.

Части разряда через конденсатор 5 мкФ:

Частичные разряды на конденсаторе 10 мкФ:

ЧР через конденсатор 30 мкФ:

Чек: 144 + 72 + 24 = 240В

Обратите внимание, что конденсатор с наименьшим значением имеет наибольшее напряжение на нем, и если конденсаторы аналогичной конструкции, все они должны быть рассчитаны на максимальное напряжение. По этой причине конденсаторы не часто подключают последовательно, если они не идентичны.

7,5 Емкость параллельного конденсатора

Емкость конденсатора с параллельными пластинами зависит от:

• Площадь пластины (A в м ² ), так что C α A
• Расстояние между пластинами (d в м ² ), так что C α 1/ d
• Абсолютная диэлектрическая проницаемость диэлектрика (ε в Ф / м), так что C α ε
• Количество пластин (N), конденсаторы могут быть сконструированы из ряда соединяющихся пластин (рисунок 7.6), так что C α (N-1).

Объединение вышеперечисленных факторов дает:

На самом деле используется абсолютная диэлектрическая проницаемость диэлектрика, и поскольку ε = ε _r ε ₀ , уравнение принимает следующий вид:

Рисунок 7.6: Конденсатор с чередующимися пластинами, содержащий 11 обкладок, дефектно 10 конденсаторов, включенных параллельно.

7,6 Энергия, накопленная в конденсаторе

Подобно индукторам, которые накапливают энергию в магнитном поле, конденсаторы накапливают энергию в электрическом поле.Однако, в отличие от катушек индуктивности, конденсаторы могут сохранять энергию, накопленную после отключения питания, хотя со временем она рассеивается. Энергия, запасенная в конденсаторе, может быть выражена как:

Количество энергии, хранящейся в большинстве конденсаторов, невелико, тем не менее, этого достаточно, чтобы вызвать у человека электрошок. Хотя заряд и, следовательно, энергия со временем улетучатся, разрядный резистор обычно подключается к клеммам конденсатора. Такой резистор должен иметь достаточно высокое значение, чтобы предотвратить протекание через него заметных токов от источника заряда, но достаточно низкое, чтобы разрядить конденсатор за разумное время.Типичное значение — 10 МОм.

7.7 Кривые роста и спада

Как упоминалось в разделе 7.1, ток зарядки двух параллельных пластин не является постоянным, а затухает по мере нарастания заряда и увеличения частичных разрядов на выводах конденсаторов. Рассмотрим схему на рис. 7.7, где конденсатор подключен последовательно с резистором к источнику постоянного тока с ЭДС E вольт. Мгновенные частичные разряды на конденсаторе (то есть частичные разряды в любой момент времени, t ) обозначаются как v , мгновенный ток, протекающий через конденсатор, составляет i , а мгновенный заряд на конденсаторе составляет q .

Рисунок 7.7: Цепь заряда и разряда конденсатора.

Если конденсатор изначально не заряжен, когда переключатель находится в положении 1, начальный ток (I ₀ ) будет равен I ₀ = V / R.

No related posts.