Механическая мощность формула и определение. Мощность — физическая величина, формула мощности
Если вам нужно единицы измерения мощности привести в одну систему, вам пригодится наш перевод мощности – конвертер онлайн. А ниже вы сможете почитать, в чем измеряется мощность.
Мощность — физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени.
В чем измеряется мощность?
Единицы измерения мощности, которые известны каждому школьнику и являются принятыми в международном сообществе – ватты. Названы так в честь ученого Дж. Уатта. Обозначаются латинской W или вт.
1 Ватт – единица измерения мощности, при которой за секунду происходит работа, равная 1 джоулю. Ватт равен мощности тока, сила которого 1 ампер, а напряжение – 1 вольт. В технике, как правило, применяются мегаватты и киловатты. 1 киловатт равен 1000 ватт.
Измеряется мощность и в эрг в секунду. 1 эрг в сек. Равен 10 в минус седьмой степени ватт. Соответственно, 1 ватт равен 10 в седьмой степени эрг/сек.
Соответственно, 1 ватт равен 10 в седьмой степени эрг/сек.
А еще единицей измерения мощности считается внесистемная «лошадиная сила». Она была введена в оборот еще в восемнадцатом веке и продолжает до сих пор применяться в автомобилестроении. Обозначается она так:
- Л.С. (в русском),
- HP (в английском).
- PS (в немецком),
- CV (во французском).
При переводе мощности помните, что в рунете существует невообразимая путаница при конверте лошадиных сил в ватты. В России, странах СНГ и некоторых других государствах 1 л.с. равняется 735, 5 ватт. В Англии и Америке 1 hp равняется 745, 7 ватт.
Здравствуйте! Для вычисления физической величины, называемой мощностью, пользуются формулой, где физическую величину — работу делят на время, за которое эта работа производилась.
Выглядит она так:
P, W, N=A/t, (Вт=Дж/с).
В зависимости от учебников и разделов физики, мощность в формуле может обозначаться буквами P, W или N.
Чаще всего мощность применяется, в таких разделах физики и науки, как механика, электродинамика и электротехника. В каждом случае, мощность имеет свою формулу для вычисления. Для переменного и постоянного тока она тоже различна. Для измерения мощности используют ваттметры.
Теперь вы знаете, что мощность измеряется в ваттах. По-английски ватт — watt, международное обозначение — W, русское сокращение — Вт. Это важно запомнить, потому что во всех бытовых приборах есть такой параметр.
Мощность — скалярная величина, она не вектор, в отличие от силы, которая может иметь направление. В механике, общий вид формулы мощности можно записать так:
P=F*s/t, где F=А*s,
v=s/t,
Р=F*v.
Из формул видно, как мы вместо А подставляем силу F умноженную на путь s. В итоге мощность в механике, можно записать, как силу умноженную на скорость. К примеру, автомобиль имея определенную мощность, вынужден снижать скорость при движении в гору, так как это требует большей силы.
Средняя мощность человека принята за 70-80 Вт. Мощность автомобилей, самолетов, кораблей, ракет и промышленных установок, часто, измеряют в лошадиных силах. Лошадиные силы применяли еще задолго до внедрения ватт. Одна лошадиная сила равна 745,7Вт. Причем в России принято что л. с. равна 735,5 Вт.
Если вас вдруг случайно спросят через 20 лет в интервью среди прохожих о мощности, а вы запомнили, что мощность — это отношение работы А, совершенной в единицу времени t. Если сможете так сказать, приятно удивите толпу. Ведь в этом определении, главное запомнить, что делитель здесь работа А, а делимое время t. В итоге, имея работу и время, и разделив первое на второе, мы получим долгожданную мощность.
При выборе в магазинах, важно обращать внимание на мощность прибора. Чем мощнее чайник, тем быстрее он погреет воду. Мощность кондиционера определяет, какой величины пространство он сможет охлаждать без экстремальной нагрузки на двигатель. Чем больше мощность электроприбора, тем больше тока он потребляет, тем больше электроэнергии потратит, тем больше будет плата за электричество.
В общем случае электрическая мощность определяется формулой:
W=I*U,
где I — сила тока, U-напряжение
Иногда даже ее так и измеряют в вольт-амперах, записывая, как В*А. В вольт-амперах меряют полную мощность, а чтобы вычислить активную мощность нужно полную мощность умножить на коэффициент полезного действия(КПД) прибора, тогда получим активную мощность в ваттах.
Часто такие приборы, как кондиционер, холодильник, утюг работают циклически, включаясь и отключаясь от термостата, и их средняя мощность за общее время работы может быть небольшой.
В цепях переменного тока, помимо понятия мгновенной мощности, совпадающей с общефизической, существуют активная, реактивная и полная мощности. Полная мощность равна сумме активной и реактивной мощностей.
Для измерения мощности используют электронные приборы — Ваттметры. Единица измерения Ватт, получила свое название в честь изобретателя усовершенствованной паровой машины, которая произвела революцию среди энергетических установок того времени.
Мощность электрического тока
04 Апреля 2017
5856
Привет друзья, продолжаем!
Часто, в быту используется понятие мощность источника питания, мощность потребления бытовых приборов и прочих электрических устройств. Особенно, это многим хорошо знакомо по обычной лампочке (лампа накаливания). Эти лампочки отличаются друг от друга мощностью (50 Вт, 100 Вт, 150 Вт и т. д.) и соответственно освещением.
Для того, чтобы разобраться с мощностью источника питания или потребляемого устройства, мы разберем, что такое — мощность электрического тока.
Мощность электрического тока
Мощность электрического тока — это отношение произведенной им работы ко времени в течение которого совершена работа.
Давайте, теперь разберем это определение. Соберем простую электрическую цепь.
наведите или кликните мышкой, для анимации
Как нам уже известно, по цепи за единицу времени протекают определенное количество заряженных частиц — это показатель силы тока, также расходуется сила для движения частиц — это напряжение тока, но помимо этого при движении совершается «работа».
Вот тут необходимо обратить внимание, «работа» в данном случае может быть разной. В проводнике — это нагревание, то есть электрическая энергия перешла в тепловую. В потребляемых устройствах, то есть в нагрузке — это может быть освещение, нагревание, вращение двигателей и т.д.
Исходя из определения мощности тока, запишем формулу: P = W/t
P — мощность электрического тока (Вт)
W — работа электрического тока (Дж)
t — время протекания тока (с)
Единица измерения мощности Ватт (Вт), 1 Вт это совершение «работы» в 1 джоуль за 1 секунду времени.
Ну эта формула, не совсем нам интересна. Нам нужно понять, как связана мощность с известными нам величинами — силой тока, напряжением тока и сопротивлением нагрузки.
Таким образом, чем больше напряжение и сила тока в цепи, тем больше мощность тока. Я думаю это понятно, так как при большом токе, через поперечное сечение проводника и нагрузки, проходит больше частиц, тем самым совершатся больше «работы». Так же с напряжением, больше силы для движения частиц, больше совершается «работа.
Так же, можно вывести разные формулы:
для определения мощности тока через напряжение и сопротивление
для определения мощности тока через ток и сопротивление
Разобрали, что такое мощность электрического тока. Для того, чтобы еще было понятнее рекомендую ознакомиться следующей статьей. В которой подытожим раздел основы радиотехники.
Мгновенная мощность формула механика. Мощность: определение и формула
Для того, чтобы перетащить 10 мешков картошки с огорода, расположенного в паре километров от дома, вам потребуется целый день носиться с ведром туда-обратно. Если вы возьмете тележку, рассчитанную на один мешок, то справитесь за два-три часа.
Ну а если закинуть все мешки в телегу, запряженную лошадью, то через полчаса ваш урожай благополучно перекочует в ваш погреб. В чем разница? Разница в быстроте выполнения работы.
Формула расчета мощности
И в таком случае, формула расчета мощности принимает следующий вид: мощность= работа/время, или
N=A/t,
где N — мощность,
A — работа,
t — время.
Единицей мощности является ватт (1 Вт). 1 Вт — это такая мощность, при которой за 1 секунду совершается работа в 1 джоуль. Единица эта названа в честь английского изобретателя Дж. Уатта, который построил первую паровую машину. Любопытно, что сам Уатт пользовался другой единицей мощности — лошадиная сила, и формулу мощности в физике в том виде, в котором мы ее знаем сегодня, ввели позже. Измерение мощности в лошадиных силах используют и сегодня, например, когда говорят о мощности легкового автомобиля или грузовика. Одна лошадиная сила равна примерно 735,5 Вт.
Применение мощности в физике
Мощность является важнейшей характеристикой любого двигателя. Различные двигатели развивают совершенно разную мощность. Это могут быть как сотые доли киловатта, например, двигатель электробритвы, так и миллионы киловатт, например, двигатель ракеты-носителя космического корабля. При различной нагрузке двигатель автомобиля вырабатывает разную мощность , чтобы продолжать движение с одинаковой скоростью. Например, при увеличении массы груза, вес машины увеличивается, соответственно, возрастает сила трения о поверхность дороги, и для поддержания такой же скорости, как и без груза, двигатель должен будет совершать большую работу. Соответственно, возрастет вырабатываемая двигателем мощность. Двигатель будет потреблять больше топлива. Это хорошо известно всем шоферам. Однако, на большой скорости свою немалую роль играет и инерция движущегося транспортного средства, которая тем больше, чем больше его масса. Опытные водители грузовиков находят оптимальное сочетание скорости с потребляемым бензином, чтобы машина сжигала меньше топлива.
Например, при увеличении массы груза, вес машины увеличивается, соответственно, возрастает сила трения о поверхность дороги, и для поддержания такой же скорости, как и без груза, двигатель должен будет совершать большую работу. Соответственно, возрастет вырабатываемая двигателем мощность. Двигатель будет потреблять больше топлива. Это хорошо известно всем шоферам. Однако, на большой скорости свою немалую роль играет и инерция движущегося транспортного средства, которая тем больше, чем больше его масса. Опытные водители грузовиков находят оптимальное сочетание скорости с потребляемым бензином, чтобы машина сжигала меньше топлива.
Выполняемой за некоторый промежуток времени, к этому промежутку времени.
Эффективная мощность , мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу. Различают полезную, полную и номинальную Э. м. двигателя. Полезной называют Э. м. двигателя за вычетом затрат мощности на приведение в действие вспомогательных агрегатов или механизмов, необходимых для его работы, но имеющих отдельный привод (не от двигателя непосредственно). Полная Э. м. — мощность двигателя без вычета указанных затрат. Номинальная Э. м., или просто номинальная мощность, — Э. м., гарантированная заводом-изготовителем для определённых условий работы. В зависимости от типа и назначения двигателя устанавливаются Э. м., регламентируемые стандартами или техническими условиями (например, наибольшая мощность судового реверсивного двигателя при определённой частоте вращения коленчатого вала в случае заднего хода судна — так называемая мощность заднего хода, наибольшая мощность авиационного двигателя при минимальном удельном расходе топлива — так называемая крейсерская мощность и т. п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.
Полная Э. м. — мощность двигателя без вычета указанных затрат. Номинальная Э. м., или просто номинальная мощность, — Э. м., гарантированная заводом-изготовителем для определённых условий работы. В зависимости от типа и назначения двигателя устанавливаются Э. м., регламентируемые стандартами или техническими условиями (например, наибольшая мощность судового реверсивного двигателя при определённой частоте вращения коленчатого вала в случае заднего хода судна — так называемая мощность заднего хода, наибольшая мощность авиационного двигателя при минимальном удельном расходе топлива — так называемая крейсерская мощность и т. п.). Э. м. зависит от форсирования (интенсификации) рабочего процесса, размеров и механического кпд двигателя.
Единицы измерения
Другой распространённой единицей измерения мощности является лошадиная сила .
| Единицы | Вт | кВт | МВт | кгс·м/с | эрг/с | л. с. с. |
|---|---|---|---|---|---|---|
| 1 ватт | 1 | 10 -3 | 10 -6 | 0,102 | 10 7 | 1,36·10 -3 |
| 1 киловатт | 10 3 | 1 | 10 -3 | 102 | 10 10 | 1,36 |
| 1 мегаватт | 10 6 | 10 3 | 1 | 102·10 3 | 10 13 | 1,36·10 3 |
| 1 килограмм-сила-метр в секунду | 9,81 | 9,81·10 -3 | 9,81·10 -6 | 1 | 9,81·10 7 | 1,33·10 -2 |
| 1 эрг в секунду | 10 -7 | 10 -10 | 10 -13 | 1,02·10 -8 | 1 | 1,36·10 -10 |
| 1 лошадиная сила | 735,5 | 735,5·10 -3 | 735,5·10 -6 | 75 | 7,355·10 9 | 1 |
Мощность в механике
Если на движущееся тело действует сила , то эта сила совершает работу. Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
Мощность в этом случае равна скалярному произведению вектора силы на вектор скорости, с которой движется тело:
M — момент, — угловая скорость, — число пи , n — частота вращения (об/мин).
Электрическая мощность
Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.
S — Полная мощность, ВА
P — Активная мощность, Вт
Q — Реактивная мощность, ВАр
Приборы для измерения мощности
Примечания
См. также
Ссылки
- Влияние формы электрического тока на его действие. Журнал «Радио», номер 6, 1999 г.
Wikimedia Foundation . 2010 .
Смотреть что такое «Мощность (физика)» в других словарях:
Наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, св ва и строение материи и законы её движения. Понятия Ф. и её законы лежат в основе всего естествознания. Ф. относится к точным наукам и изучает количеств … Физическая энциклопедия
Ф. относится к точным наукам и изучает количеств … Физическая энциклопедия
Примеры разнообразных физических явлений Физика (от др. греч. φύσις … Википедия
I. Предмет и структура физики Ф. – наука, изучающая простейшие и вместе с тем наиболее общие закономерности явлений природы, свойства и строение материи и законы её движения. Поэтому понятия Ф. и сё законы лежат в основе всего… … Большая советская энциклопедия
Физика высоких плотностей энергий (англ. High Energy Density Physics, HED Physics) раздел физики на стыке физики конденсированного состояния и физики плазмы, занимающийся изучением систем, имеющих высокую плотность энергии. Под высокой … Википедия
Электрическая мощность физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Содержание 1 Мгновенная электрическая мощность … Википедия
Электрическая мощность физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Содержание 1 Мгновенная электрическая мощность 2 Мощность постоянного тока … Википедия
Содержание 1 Мгновенная электрическая мощность 2 Мощность постоянного тока … Википедия
У этого термина существуют и другие значения, см. Интенсивность. Интенсивность Размерность MT−3 Единицы измерения СИ Вт/м² … Википедия
Ваттметр (ватт + гр. μετρεω измеряю) измерительный прибор, предназначенный для определения мощности электрического тока или электромагнитного сигнала. Содержание 1 Классификация 2 Ваттметры низкой частоты и постоянного тока … Википедия
Ваттметр (ватт + гр. μετρεω измеряю) измерительный прибор, предназначенный для определения мощности электрического тока или электромагнитного сигнала. Содержание 1 Классификация 2 Ваттметры низкой частоты и постоянного тока … Википедия
Книги
- Физика. 7 класс. Дидактические материалы к учебнику А. В. Перышкина. Вертикаль. ФГОС , Марон Абрам Евсеевич, Марон Евгений Абрамович. Данное пособие включает тренировочные задания, тесты для самоконтроля, самостоятельные работы, контрольные работы и примеры решения типовых задач.
 Всего в предлагаемом комплекте дидактических…
Всего в предлагаемом комплекте дидактических…
Каждое тело, совершающее движение, можно охарактеризовать работой. Иными словами, она характеризует действие сил.
Работа определяется как:
Произведение модуля силы и пути пройденного телом, умноженное на косинус угла между направлением силы и движения.
Работа измеряется в Джоулях:
1 [Дж] = = [кг* м2/c2]
К примеру, тело A под действием силы в 5 Н, прошло 10 м. Определить работу совершенную телом.
Так как направление движения и действия силы совпадают, то угол между вектором силы и вектором перемещения будет равен 0°. Формула упроститься, потому что косинус угла в 0° равен 1.
Подставляя исходные параметры в формулу, находим:
A= 15 Дж.
Рассмотрим другой пример, тело массой 2 кг, двигаясь с ускорением 6 м/ с2, прошло 10 м. Определить работу проделанную телом, если оно двигалось по наклоненной плоскости вверх под углом 60°.
Для начала, вычислим какую силу нужно приложить, что бы сообщить телу ускорение 6 м/ с2.
F = 2 кг * 6 м/ с2 = 12 H.
Под действием силы 12H, тело прошло 10 м. Работу можно вычислить по уже известной формуле:
Где, а равно 30°. Подставляя исходные данные в формулу получаем:
A= 103, 2 Дж.
Мощность
Множество машин механизмов выполняют одну и ту же работу за различный промежуток времени. Для их сравнения вводится понятие мощности.
Мощность – это величина, показывающая объем работы выполненный за единицу времени.
Мощность измеряется в Ватт, в честь Шотландского инженера Джеймса Ватта.
1 [Ватт] = 1 [Дж/c].
К примеру, большой кран поднял груз весом 10 т на высоту 30 м за 1 мин. Маленький кран на эту же высоту за 1 мин поднял 2 т кирпича. Сравнить мощности кранов.
Определим работу выполняемую кранами. Груз поднимается на 30м, при этом преодолевая силу тяжести, поэтому сила, затрачиваемая на поднятие груза, будет равна силе взаимодействия Земли и груза(F = m * g). А работа – произведению сил на расстояние пройденное грузами, то есть на высоту.
Для большого крана A1 = 10 000 кг * 30 м * 10 м / с2 = 3 000 000 Дж, а для маленького A2 = 2 000 кг * 30 м * 10 м / с2 = 600 000 Дж.
Мощность можно вычислить, разделив работу на время. Оба крана подняли груз за 1 мин (60 сек).
Отсюда:
N1 = 3 000 000 Дж/60 c = 50 000 Вт = 50 кВт.
N2 = 600 000 Дж/ 60 c = 10 000 Вт = 10 к Вт.
Из выше приведенных данных наглядно видно, что первый кран в 5 раз мощнее второго.
Здравствуйте! Для вычисления физической величины, называемой мощностью, пользуются формулой, где физическую величину — работу делят на время, за которое эта работа производилась.
Выглядит она так:
P, W, N=A/t, (Вт=Дж/с).
В зависимости от учебников и разделов физики, мощность в формуле может обозначаться буквами P, W или N.
Чаще всего мощность применяется, в таких разделах физики и науки, как механика, электродинамика и электротехника. В каждом случае, мощность имеет свою формулу для вычисления. Для переменного и постоянного тока она тоже различна. Для измерения мощности используют ваттметры.
Для переменного и постоянного тока она тоже различна. Для измерения мощности используют ваттметры.
Теперь вы знаете, что мощность измеряется в ваттах. По-английски ватт — watt, международное обозначение — W, русское сокращение — Вт. Это важно запомнить, потому что во всех бытовых приборах есть такой параметр.
Мощность — скалярная величина, она не вектор, в отличие от силы, которая может иметь направление. В механике, общий вид формулы мощности можно записать так:
P=F*s/t, где F=А*s,
Из формул видно, как мы вместо А подставляем силу F умноженную на путь s. В итоге мощность в механике, можно записать, как силу умноженную на скорость. К примеру, автомобиль имея определенную мощность, вынужден снижать скорость при движении в гору, так как это требует большей силы.
Средняя мощность человека принята за 70-80 Вт. Мощность автомобилей, самолетов, кораблей, ракет и промышленных установок, часто, измеряют в лошадиных сил ах. Лошадиные силы применяли еще задолго до внедрения ватт. Одна лошадиная сила равна 745,7Вт. Причем в России принято что л. с. равна 735,5 Вт.
Лошадиные силы применяли еще задолго до внедрения ватт. Одна лошадиная сила равна 745,7Вт. Причем в России принято что л. с. равна 735,5 Вт.
Если вас вдруг случайно спросят через 20 лет в интервью среди прохожих о мощности, а вы запомнили, что мощность — это отношение работы А, совершенной в единицу времени t. Если сможете так сказать, приятно удивите толпу. Ведь в этом определении, главное запомнить, что делитель здесь работа А, а делимое время t. В итоге, имея работу и время, и разделив первое на второе, мы получим долгожданную мощность.
При выборе в магазинах, важно обращать внимание на мощность прибора. Чем мощнее чайник, тем быстрее он погреет воду. Мощность кондиционера определяет, какой величины пространство он сможет охлаждать без экстремальной нагрузки на двигатель. Чем больше мощность электроприбора, тем больше тока он потребляет, тем больше электроэнергии потратит, тем больше будет плата за электричество.
В общем случае электрическая мощность определяется формулой:
где I — сила тока, U-напряжение
Иногда даже ее так и измеряют в вольт-амперах, записывая, как В*А. В вольт-амперах меряют полную мощность, а чтобы вычислить активную мощность нужно полную мощность умножить на коэффициент полезного действия(КПД) прибора, тогда получим активную мощность в ваттах.
В вольт-амперах меряют полную мощность, а чтобы вычислить активную мощность нужно полную мощность умножить на коэффициент полезного действия(КПД) прибора, тогда получим активную мощность в ваттах.
Часто такие приборы, как кондиционер, холодильник, утюг работают циклически, включаясь и отключаясь от термостата, и их средняя мощность за общее время работы может быть небольшой.
В цепях переменного тока , помимо понятия мгновенной мощности, совпадающей с общефизической, существуют активная, реактивная и полная мощности. Полная мощность равна сумме активной и реактивной мощностей.
Для измерения мощности используют электронные приборы — Ваттметры. Единица измерения Ватт, получила свое название в честь изобретателя усовершенствованной паровой машины, которая произвела революцию среди энергетических установок того времени. Благодаря этому изобретению развитие индустриального общества ускорилось, появились поезда, пароходы, заводы, использующие силу паровой машины для передвижения и производства изделий.
Все мы много раз сталкивались с понятием мощности. Например, разные автомобили характеризуются разной мощностью двигателя. Также, электроприборы могут иметь различную мощность , даже если они имеют одинаковое предназначение.
Мощность — это физическая величина , характеризующая скорость работы.
Соответственно, механическая мощность — это физическая величина, характеризующая скорость механической работы:
Т. е. мощность — это работа в единицу времени.
Мощность в системе СИ измеряется в ваттах: [N ] = [Вт].
1 Вт — это работа в 1 Дж, совершенная за 1 с.
Существуют и другие единицы измерения мощности, например, такие, как лошадиная сила:
Именно в лошадиных силах чаще всего измеряется мощность двигателя автомобилей.
Давайте вернемся к формуле для мощности: Формула, по которой вычисляется работа, нам известна: Поэтому мы можем преобразовать выражение для мощности:
Тогда в формуле у нас образуется отношение модуля
перемещения к промежутку времени. Это, как вы знаете, скорость:
Это, как вы знаете, скорость:
Только обратите внимание, что в получившейся формуле мы используем модуль скорости, поскольку на время мы поделили не само перемещение, а его модуль. Итак, мощность равна произведению модуля силы, модуля скорости и косинуса угла между их направлениями.
Это вполне логично: скажем, мощность поршня можно повысить за счет увеличения силы его действия. Прикладывая бо́льшую силу, он будет совершать больше работы за то же время, то есть увеличит мощность. Но даже если оставить силу постоянной, и заставить поршень двигаться быстрее, он, несомненно, увеличит работу, совершаемую в единицу времени. Следовательно, увеличится мощность.
Примеры решения задач.
Задача 1. Мощность мотоцикла равна 80 л.с. Двигаясь по горизонтальному участку, мотоциклист развивает скорость равную 150 км\ч. При этом, двигатель работает на 75% от своей максимальной мощности. Определите силу трения, действующую на мотоцикл.
Задача 2. Истребитель,
под действием постоянной силы тяги, направленной под углом 45° к горизонту,
разгоняется от 150 м/с до 570 м/с. При этом, вертикальная и горизонтальная
скорость истребителя увеличиваются на одинаковое значение в каждый момент
времени. Масса истребителя равна 20 т. Если истребитель разгонялся в течение
одной минуты, то какова мощность его двигателя?
Истребитель,
под действием постоянной силы тяги, направленной под углом 45° к горизонту,
разгоняется от 150 м/с до 570 м/с. При этом, вертикальная и горизонтальная
скорость истребителя увеличиваются на одинаковое значение в каждый момент
времени. Масса истребителя равна 20 т. Если истребитель разгонялся в течение
одной минуты, то какова мощность его двигателя?
Если вам нужно единицы измерения мощности привести в одну систему, вам пригодится наш перевод мощности – конвертер онлайн. А ниже вы сможете почитать, в чем измеряется мощность.
Формула мощности электрического тока
При создании новой проводки часто возникает необходимость рассчитать мощность электроприборов, находящихся в одной комнате или на одной линии. У многих людей с этим возникают проблемы. В этой статье мы разберем, какая формула мощности электрического тока используется для подсчета и как правильно ей пользоваться.
Введение
Подсчет мощности силы тока потребления необходим для того, чтобы правильно рассчитать сечение проводов, купить автоматы и защитить систему от перегрузок и возгорания. Расчет общей суммы также поможет владельцу правильно выбрать стабилизатор на вход в квартиру. Неверные расчеты могут привести к серьезным последствиям, поэтому внимательно отнеситесь к информации, описанной в нашей статье.
Расчет общей суммы также поможет владельцу правильно выбрать стабилизатор на вход в квартиру. Неверные расчеты могут привести к серьезным последствиям, поэтому внимательно отнеситесь к информации, описанной в нашей статье.
Рассчитываем силу тока
В работающей сети силу тока можно легко узнать при помощи мультиметра, переключив его в режим амперметра. Но этот вариант подходит только в том случае, если все уже работает. Мы же пытаемся сделать расчет согласно проекту, поэтому хитрость с амперметром нам не подходит.
Для чего нужно знать силу тока? Для правильного выбора сечения кабеля и автомата. Считается она по формуле I=P/(U×cosφ), где I – это сила тока, P – мощность прибора, U – напряжение в сети. Представленная выше формула справедлива для однофазной сети. Для трехфазной используется I=P/(1,73×U×cosφ). Косинус Фи в нашем случае показывает коэффициент мощности.
Пример: на одной линии висит холодильник мощностью 150 Вт, микроволновка (800 Вт), электрочайник (1300 Вт) и блендер (1500 Вт).
Все это включено одновременно. Находим действующую силу тока: I=(150+800+1300+1500)/220*0.95=17.94 Ампера. Для подобной нагрузки необходим кабель на 2.5 мм2 и автомат на 25 Ампер.
Как найти мощность устройств, работающих на одной линии? Нужно сложить все паспортные данные на этих потребителей. Косинус Фи принят за 0,95, что является наиболее приближенным к реальности, хотя в некоторых случаях его принимают за 1.
Если в сеть подключаются “жирные” потребители, такие как бойлер, духовой шкаф, электрокотел или электрический твердый пол, то разумнее использовать коэффициент фи на уровне 0,8. Соответственно, для одной фазы считается напряжение на 220 вольт, для трех фаз – 380 вольт.
Немного теории
Теперь давайте рассмотрим действующую формулу электрической мощности. Прежде всего разберем, что это вообще такое. Мощностью называют скорость, с которой энергия перетекает из одного вида в другой, преобразуется или потребляется. Она измеряется в ваттах. Ток силой в один ампер обладает мощностью в один ватт при имеющейся разности потенциалов в один ватт.
Ток силой в один ампер обладает мощностью в один ватт при имеющейся разности потенциалов в один ватт.
Для подсчета используется формула P = I*U. Этот показатель показывает, сколько “кушает” прибор при работе.
Внимание: существуют различные виды мощности. Их необходимо отличать, чтобы правильно собрать проводку и рассчитать нормативы для закупки кабелей и автоматов.
Виды
Существует два основных типа показателей:
- Номинальная. Та, которую устройство потребялет за единицу времени. Для холодильника это 150 ватт, для микроволновки, в зависимости от настроек – 600-800 ватт, для лампочки 65 или 99 ватт и пр.
- Стартовая. Формула расчета мощности этого типа не отличается от классической, несмотря на то, что стартовая может превышать на порядок номинальную. К примеру, тот же холодильник в момент старта потребляет до 2 кВт энергии, необходимой на запуск двигателя и всех систем.

Главное, что нужно знать о стартовой мощности – она временная и краткосрочная, но ее нужно обязательно учитывать при создании проводки. Обычно для этого делается запас. К примеру, кабель на 2,5 квадрата выдерживает до 4,5 кВт и на него ставится автомат на 25А. Поэтому, если у вас суммарный коэффициент по линии доходит до 4 или 4.3, то лучше не рисковать и поставить дополнительную линию, чем в один прекрасный момент ваша проводка просто сгорит.
Зная, чему равна мощность электрического тока для каждого устройства, находящегося на линии, выделите те, которые вполне могут работать одновременно. Почитайте о технических характеристиках своих устройств, после чего сложите мощность всех подключенных. Затем добавьте к получившемуся числу 30% на всякие тяги и помехи – вот это и станет запасом для стартовых неприятностей.
Как определить мощность электродвигателя без бирки? Формула
Общепромышленные асинхронные электродвигатели имеют срок службы и подлежат периодичной замене, ремонту. Дефекты электрической части, замыкание, обрывы, износ подшипников, перемотка, нарушение центровки, сырая обмотка. При отсутствии паспорта, бирки на двигателе возникает вопрос: как узнать мощность электродвигателя без таблички или технических характеристик?
Дефекты электрической части, замыкание, обрывы, износ подшипников, перемотка, нарушение центровки, сырая обмотка. При отсутствии паспорта, бирки на двигателе возникает вопрос: как узнать мощность электродвигателя без таблички или технических характеристик?
Параметры для определения мощности электродвигателя:
Определение мощности двигателя по диаметру вала и длине
Простейшие способы определения мощности и марки двигателя – габаритные размеры – вал или крепежные отверстия. В таблице указаны длины и диаметры валов (D1) и длина (L1) для каждой модели асинхронного промышленного трехфазного мотора. Габариты электродвигателей АИР:
| Мощность, (Р) кВт | 3000 об/мин | 1500 об/мин | 1000 об/мин | 750 об/мин | ||||
| D1, мм | L1, мм | D1, мм | L1, мм | >D1, мм | L1, мм | D1, мм | L1, мм | |
| 1,5 | 22 | 50 | 22 | 50 | 24 | 50 | 28 | 60 |
| 2,2 | 24 | 28 | 60 | 32 | 80 | |||
| 3 | 24 | 32 | 80 | |||||
| 4 | 28 | 60 | 28 | 60 | 38 | |||
| 5,5 | 32 | 80 | 38 | |||||
| 7,5 | 32 | 80 | 38 | 48 | 110 | |||
| 11 | 38 | 48 | 110 | |||||
| 15 | 42 | 110 | 48 | 110 | 55 | |||
| 18,5 | 55 | 60 | 140 | |||||
| 22 | 48 | 55 | 60 | >140 | ||||
| 30 | 65 | |||||||
| 37 | 55 | >60 | 140 | 65 | 75 | |||
| 45 | 75 | 75 | ||||||
| 55 | 65 | 80 | 170 | |||||
| 75 | 65 | 140 | 75 | 80 | 170 | |||
| 90 | 90 | |||||||
| 110 | 70 | 80 | 170 | 90 | ||||
| 132 | 100 | 210 | ||||||
| 160 | 75 | 90 | 100 | 210 | ||||
| 200 | ||||||||
| 250 | 85 | 170 | 100 | 210 | ||||
| 315 | — | — | ||||||
Расчет мощности электродвигателя по габаритам и крепежным размерам
Таблица подбора мощности двигателя по крепежным отверстиям на лапах (L10 и B10):
|
Р, кВт |
3000 об. |
1500 об. |
1000 об. |
750 об. |
||||
|
L10, мм |
B10, мм |
L10, мм |
B10, мм |
L10, мм |
B10, мм |
L10, мм |
B10, мм |
|
|
1,5 |
100 |
125 |
100 |
125 |
125 |
140 |
140 |
160 |
|
2,2 |
125 |
140 |
140 |
160 |
190 |
|||
|
3 |
125 |
140 |
112 |
160 |
190 |
|||
|
4 |
112 |
160 |
140 |
216 |
||||
|
5,5 |
140 |
190 |
216 |
178 |
||||
|
7,5 |
190 |
216 |
178 |
254 |
||||
|
11 |
178 |
216 |
178 |
254 |
210 |
|||
|
15 |
254 |
254 |
210 |
241 |
279 |
|||
|
18,5 |
210 |
210 |
241 |
279 |
267 |
318 |
||
|
22 |
203 |
279 |
203 |
279 |
267 |
318 |
310 |
|
|
30 |
241 |
241 |
310 |
311 |
356 |
|||
|
37 |
267 |
318 |
267 |
318 |
311 |
356 |
406 |
|
|
45 |
310 |
310 |
406 |
349 |
||||
|
75 |
311 |
406 |
311 |
406 |
368 |
457 |
419 |
457 |
|
90 |
349 |
349 |
419 |
406 |
508 |
|||
|
110 |
368 |
457 |
368 |
457 |
406 |
508 |
547 |
|
|
132 |
419 |
419 |
457 |
610 |
355 |
|||
|
160 |
406 |
508 |
406 |
508 |
610 |
355 |
||
|
200 |
457 |
457 |
560 |
610 |
||||
|
250 |
610 |
355 |
610 |
355 |
560 |
610 |
||
|
315 |
630/800 |
686/630 |
— |
— |
||||
Подбор габарита двигателя с фланцем
Востребованные маркировки трехфазных асинхронных электродвигателей АИР: АИР63А2, АИР71А2, АИР80В4, АИР90L2, АИР100S2, АИР132М2, АИР180М6, АИР200L2, АИР250S4
Таблица для подбора мощности электродвигателя асинхронного по диаметру фланца (D20) и диаметру крепежных отверстий фланца (D22)
|
Мощность электродвигателя P, кВт |
3000 об. |
1500 об. |
1000 об. |
750 об. |
||||
|
D20, мм |
D22, мм |
D20, мм |
D22, мм |
D20, мм |
D22, мм |
D20, мм |
D22, мм |
|
|
1,5 |
165 |
11 |
165 |
11 |
215 |
14 |
215 |
14 |
|
2,2 |
215 |
14 |
265 |
|||||
|
3 |
215 |
14 |
365 |
|||||
|
4 |
265 |
300 |
19 |
|||||
|
5,5 |
265 |
300 |
19 |
|||||
|
7,5 |
265 |
300 |
19 |
|||||
|
11 |
300 |
19 |
||||||
|
15 |
350 |
|||||||
|
18,5 |
350 |
400 |
||||||
|
22 |
350 |
350 |
400 |
|||||
|
30 |
500 |
|||||||
|
37 |
400 |
400 |
500 |
|||||
|
45 |
400 |
|||||||
|
55 |
500 |
500 |
550 |
24 |
||||
|
75 |
500 |
550 |
24 |
|||||
|
90 |
500 |
28 |
||||||
|
110 |
550 |
24 |
550 |
24 |
28 |
|||
|
132 |
550 |
680 |
||||||
|
160 |
550 |
28 |
28 |
680 |
||||
|
200 |
550 |
740 |
24 |
|||||
|
250 |
680 |
680 |
740 |
24 |
— |
|||
|
315 |
680 |
— |
||||||
Как определить мощность электродвигателя мультиметром
Измерение тока, напряжения, сопротивления, проверка обрывов выполняется мультиметром. Электродвигатель подключают к сети питания, замеряя напряжение. Амперметром поочередно замеряют ток в цепи каждой из обмоток статора. Производится проверка резисторов, диодов, конденсаторов, транзисторов.
Сумму потребляемых токов умножают на фиксированное напряжение. Полученное число – мощность электродвигателя в ваттах.
- Р — мощность электродвигателя
- U — напряжение
- Iа — токи первой фазы
- Iв — токи второй фазы
- Iс — токи третьей фазы
Как проверить мощность электродвигателя по току холостого хода
Проверить мощность двигателя по току холостого хода можно с помощью таблицы.
|
Р двигателя, кВт |
Ток холостого хода (% от номинального) |
||||
|
Обороты двигателя, об/мин |
|||||
|
600 |
750 |
1000 |
1500 |
3000 |
|
|
0,75-1,5 |
85 |
80 |
75 |
70 |
50 |
|
1,5-5,5 |
80 |
75 |
70 |
65 |
45 |
|
5,5-11 |
75 |
70 |
65 |
60 |
40 |
|
15-22,5 |
70 |
65 |
60 |
55 |
30 |
|
22,5-55 |
65 |
60 |
55 |
50 |
20 |
|
55-110 |
55 |
50 |
45 |
40 |
20 |
Как рассчитать мощность трехфазного двигателя по сопротивлению обмоток
Соединение звездой. Измеряем сопротивление между выводами (1-2, 2-3, 3-1). Делим на 2 – получаем сопротивление одной обмотки. Мощность одной обмотки рассчитывается так: P=(220V*220V)/R. Цифру умножаем на 3 (количество обмоток) – получаем мощность двигателя.
Соединение треугольником. Измеряем сопротивление в начале и в конце каждой обмотки. По той же формуле определяем мощность и умножаем на 6.
Статья о схемах подключения электродвигателей к сети. Инструкция подключения трехфазного асинхронного электродвигателя к сети 220/380, 380/660 Вольт.
Нет возможности определить самостоятельно
Если Вы не уверены, рекомендуем доверить определение мощности электродвигателя или подбор профессионалам. Это сэкономит Ваше время и позволит избежать досадных ошибок в эксплуатации оборудования. Купить электродвигатель у «Слобожанского завода» — это профессиональный подбор или капитальный и текущий ремонт и перемотка электродвигателей любых типов.
Определение мощности главных механизмов проектируемого судна. Адмиралтейский коэффициент
Рассмотрены различные способы определения мощности главных механизмов проектируемого судна по двухкомпонентным формулам и сделан сравнительный анализ полученных результатов.Введение. В процессе проектирования судов маловероятна возможность точного соблюдения геометрического подобия формы проектируемого судна и судна-прототипа, так как форма судов определяется не только из условий ходкости, но и из целого ряда других требований (остойчивости, вместимости, прочности, маневренных качеств и т.д.). Соблюдение их для проектируемого судна может находиться в противоречии с геометрическим подобием формы. Кроме того, большую трудность представляет и сам выбор прототипа для формы обводов проектируемого судна даже в том случае, если ограничиться только критерием ходкости судна. От правильного выбора мощности и типа двигателя судна существенно зависят все эксплуатационные качества: скорость, устойчивость на курсе, поворотливость и другие характеристики. Мощность энергетической установки (ЭУ) судна зависит от скорости его движения, сопротивления среды и потерь мощности в системе «корпус — двигатель — движитель».
На практике в начале проектирования принято связывать мощность ЭУ со скоростью и водоизмещением, это связано с ограниченностью информации о судне. Такая ограниченность снижает точность получаемых значений, что в последствии необходимо подтверждать модельными испытаниями.
На сегодняшний день разными авторами предложены различные двухкомпонентные формулы для расчета мощности ЭУ судна. В данной работе будет рассмотрен ряд зависимостей и точность полученных по ним результатов.
Постановка задачи. Оценка степени точности определения мощности по двухкомпонентным формулам на ранних стадиях проектирования.
Изложение основного материала. При определении мощности главных механизмов в первом приближении, когда еще неизвестны размерения проектируемого судна, обычно используются различные двухкомпонентные формулы, например:
определяемый по данным близких судов-прототипов, либо по статистическим данным.
В работе [1] В.В. Ашик рассматривает ряд формул двухкомпонентного типа. Наиболее широкое распространение на практике получила формула так называемых адмиралтейских коэффициентов,
Обрабатывая статистические данные по морским транспортным судам, английский инженер Эйр (Ayre) предложил формулу с меньшим влиянием водоизмещения судна на мощность, понизив показатель m = 0,67 до величины m = 0,64, в виде:
В.И. Афанасьев [1] предложил формулу:
Таблица 1 — Значения коэффициентов Сmn для различных типоразмеров морских судов
В.В. Давыдов [1], обрабатывал данные мощности транспортных судов, и предложил следующую аналитическую зависимость,где еще больше снижено влияние водоизмещения судна на мощность, но сохранено достаточно высокое значение параметра n = 3,25.
Аналогичная формула была предложена Энсли:
Как показало исследование большой группы транспортных судов (порядка 1000 единиц), построенных во второй половине XX века (после 1950 г.), выполненное под руководством В.В. Ашика [1], наиболее точные результаты дала формула:
использованием вышеуказанных вариантов формулы (1), предложенных разными авторами различных стран и в разное время.
Пример. Определить мощность главных механизмов универсального сухогруза, имеющего водоизмещение D = 19600 т и скорость хода Vs = 20,5 уз. В качестве судна-прототипа примем универсальный сухогруз «Капитан Кушнаренко», имеющий водоизмещение D0 = 22040 т; скорость хода Vs0 = 19,2 уз и мощность главных механизмов N0 = 10010 кВт.
Таблица 2 — Определение мощности главных механизмов универсального сухогруза
Из данных таблицы 2 следует, что мощность главных механизмов универсального сухогруза, определенная по указанным формулам, имеет практически одинаковую величину. Максимальные расхождения составляют ошибку:что вполне допустимо для первого приближения.
Выводы:
1. Рассмотренные формулы определения мощности главных механизмов проектируемых судов в первом приближении, предложенные разными авторами различных стран и в разное время, равнозначно могут использоваться в практических расчетах;
2. Наибольшее распространение в практике проектирования нашли: формула адмиралтейских коэффициентов и формула В.В. Ашика, определяющая Сmn с точностью Сmn = 27,2 ± 2,7.
Библиографический список
1. Ашик В.В. Проектирование судов / В.В. Ашик. —2-е изд., перераб. и доп. — Л.: Судостроение, 1985. — 318 с.
Способы определения мощности тока
Нагрузка в электрической цепи характеризуется силой тока, измерение тока в амперах. Силу тока иногда приходится измерять для проверки допустимой величины нагрузки на кабель. Для прокладки электрической линии применяются кабели разного сечения. Если кабель работает с нагрузкой выше допустимой величины, то он нагревается, а изоляция постепенно разрушается. В результате это приводит к короткому замыканию и замене кабеля.
Измерение тока рекомендуется делать в следующих случаях:
- После прокладки нового кабеля необходимо измерить проходящий через него ток при всех работающих электрических устройствах.
- Если к старой электропроводке подключена дополнительная нагрузка, то также следует проверить величину тока, которая не должна превышать допустимые пределы.
- При нагрузке, равной верхнему допустимому пределу, проверяется соответствие тока, протекающего через электрические автоматы. Его величина не должна превышать номинальное значение рабочего тока автоматов. В противном случае автоматический выключатель обесточит сеть из-за перегрузки.
- Измерение тока также необходимо для определения режимов эксплуатации электрических устройств. Измерение токовой нагрузки электродвигателей выполняется не только для проверки их работоспособности, но и для выявления превышения нагрузки выше допустимой, которая может возникнуть из-за большого механического усилия при работе устройства.
- Если измерить ток в цепи работающего обогревателя, то он покажет исправность нагревательных элементов.
- Работоспособность теплого пола в квартире также проверяется измерением тока.
Кроме силы тока, существует понятие мощности тока. Этот параметр определяет работу тока, выполненную в единицу времени. Мощность тока равна отношению выполненной работы к промежутку времени, за которое эта работа была выполнена. Обозначают буквой «Р» и измеряют в ваттах.
Мощность рассчитывается путем перемножения напряжения сети на силу тока, потребляемого подключенными электрическими устройствами: Р = U х I. Обычно на электроприборах указывают потребляемую мощность, с помощью которой можно определить ток. Если ваш телевизор имеет мощность 140 Вт, то для определения тока делим эту величину на 220 В, в результате получаем 0,64 ампера. Это значение максимального тока, на практике ток может быть меньше при снижении яркости экрана или других изменениях настроек.
Измерение тока приборамиДля определения потребления электрической энергии с учетом эксплуатации потребителей в разных режимах, необходимы электрические измерительные приборы, способные выполнить измерение параметров тока.
- Амперметр. Для измерения величины тока в цепи используют специальные приборы, называемые амперметрами. Они включаются в измеряемую цепь по последовательной схеме. Внутреннее сопротивление амперметра очень мало, поэтому он не влияет на параметры работы цепи.Шкала амперметра может быть размечена в амперах или других долях ампера: микроамперах, миллиамперах и т.д. Существует несколько видов амперметров: электронные, механические и т.д.
- Мультиметр является электронным измерительным прибором, способным измерить различные параметры электрической цепи (сопротивление, напряжение, обрыв проводника, пригодность батарейки и т.д.), в том числе и силу тока. Существуют два вида мультиметров: цифровой и аналоговый. В мультиметре имеются различные настройки измерений.
Порядок измерения силы тока мультиметром:
- Выяснить, какой интервал измерения вашего мультиметра. Каждый прибор рассчитан на измерение тока в некотором интервале, который должен соответствовать измеряемой электрической цепи. Наибольший допустимый ток измерения должен быть указан в инструкции.
- Выбрать соответствующий режим измерений. Многие мультиметры способны работать в разных режимах, и измерять разные величины. Для замеров силы тока нужно переключиться на соответствующий режим, учитывая вид тока (постоянный или переменный).
- Установить на приборе необходимый интервал измерений. Лучше установить верхний предел силы тока несколько выше предполагаемой величины. Снизить этот предел можно в любое время. Зато будет гарантия, что вы не выведете прибор из строя.
- Вставить измерительные штекеры проводов в гнезда. В комплекте прибора имеются два провода со щупами и разъемами. Гнезда должны быть отмечены на приборе или изображены в паспорте.
- Для начала измерения необходимо подключить мультиметр в цепь. При этом следует соблюдать правила безопасности и не касаться токоведущих частей незащищенными частями тела. Нельзя проводить измерения во влажной среде, так как влага проводит электрический ток. На руки следует надеть резиновые перчатки. Чтобы разорвать цепь для проведения измерений, следует разрезать проводник и зачистить изоляцию на обоих концах. Затем подсоединить щупы мультиметра к зачищенным концам провода и убедиться в хорошем контакте.
- Включить питание цепи и зафиксировать показания прибора. В случае необходимости откорректировать верхний предел измерений.
- Отключить питание цепи и отсоединить мультиметр.
- Измерительные клещи. Если необходимо произвести измерение тока без разрыва электрической цепи, то измерительные клещи будут отличным вариантом для выполнения этой задачи. Этот прибор выпускают нескольких видов, и разной конструкции. Некоторые модели могут измерять и другие параметры цепи. Пользоваться измерительными токовыми клещами очень удобно.
Для измерения силы тока в электрической цепи, необходимо один вывод амперметра или другого прибора, способного измерять силу тока, подключить к положительной клемме источника тока или блока питания, а другой вывод к проводу потребителя. После этого можно измерять силу тока.
При измерениях необходимо соблюдать аккуратность, так как при размыкании действующей электрической цепи может возникнуть электрическая дуга.
Для измерения силы тока электрических устройств, подключаемых непосредственно к розетке или кабелю бытовой сети, измерительный прибор настраивается на режим переменного тока с завышенной верхней границей. Затем измерительный прибор подключают в разрыв провода фазы.
Все работы по подключению и отключению допускается производить только в обесточенной цепи. После всех подключений можно подавать питание и измерять силу тока. При этом нельзя касаться оголенных токоведущих частей, во избежание поражения электрическим током. Такие методы измерения неудобны и создают определенную опасность.
Значительно удобнее проводить измерения токоизмерительными клещами, которые могут выполнять все функции мультиметра, в зависимости от исполнения прибора. Работать такими клещами очень просто. Необходимо настроить режим измерения постоянного или переменного тока, развести усы и охватить ими фазный провод. Затем нужно проконтролировать плотность прилегания усов между собой и измерить ток. Для правильных показаний необходимо охватывать усами только фазный провод. Если охватить сразу два провода, то измерения не получится.
Токоизмерительные клещи служат только для замеров параметров переменного тока. Если их использовать для измерения постоянного тока, то усы сожмутся с большой силой, и раздвинуть их можно будет только, отключив питание.
Источник: electrosam.ru
Методы измерения мощности в электрических цепях
Очень часто при проектировании электрических схем радиолюбители сталкиваются с проблемой измерения мощности, которую потребляют радиокомпоненты. Специалисты в метрологической сфере рекомендуют два метода, позволяющих вычислить и грамотно рассчитать ее значение. В этом случае нужно разобрать подробнее физический смысл величины, а также ее составляющих, от которых она зависит.
Общие сведения
При проектировании устройств нужно уметь правильно рассчитывать мощность электроэнергии электрооборудованием. Это необходимо, прежде всего, для долговечной работы устройства. Если изделие работает на износ, то оно способно выйти из строя сразу или в течение некоторого времени.
Такой вариант считается недопустимым, поскольку существуют виды техники, которые должны работать без отказов (аппарат искусственного дыхания, контроль уровня метана в шахте и так далее), так как от этого зависит человеческая жизнь. К основным характеристикам электрической энергии относятся следующие: мощность, сила тока, напряжение (разность потенциалов) и электропроводимость (сопротивление) материалов.
Мощность потребителя
Мощность не следует путать с электрической энергией. Единицей измерения первой является ватт (Вт), название которой произошло от фамилии известного физика Джеймса Уатта. Физическим смыслом 1 Вт является расход электрической энергии за единицу времени, равной 1 секунде (1 Вт = расход 1 джоуля за 1 секунду). Существуют производные единицы измерения: милливатт (1 мВт = 0,001 Вт), киловатт (1 кВт = 1000 Вт), мегаватт (1 МВт = 1000 кВт = 1000000 Вт), гигаватт (1 ГВт = 1000 МВт = 1000000 кВт = 1000000000 Вт) и так далее. Для измерения электрической энергии применяются специальные счетчики, а ее единицей измерения является Вт*ч.
Ватт можно связать с некоторыми физическими величинами: 1 Вт = 1 Дж/с = (1 кг * sqr (м)) / (c * sqr ©) = 1 Н * м / с = 746 л.(18) электронов.
Ток в научной интерпретации классифицируется на постоянный и переменный. Первый вид не изменяет своего направления за единицу времени, но его амплитудные значения могут изменяться. Направление и амплитуда переменного тока изменяется по определенному закону (синусоидальный и несинусоидальный). Основным параметром считается его частота. Определяется тип переменного тока с помощью осциллографа.
Электрическое напряжение
Из курса физики известно, что каждое вещество состоит из атомов, которые обладают нейтральным зарядом. Они состоят из субатомных частиц. К ним относятся следующие: протоны, электроны и нейтроны. Первые имеют положительный заряд, вторые — отрицательный, а третьи — не заряжены вообще.
Суммарный заряд протонов компенсирует заряд всех электронов. Однако под действием внешних сил это равенство нарушается, и электрон «вырывается» из атома, который уже обладает положительным зарядом. Он притягивает электрон с соседнего атома, и процесс повторяется до тех пор, пока энергия не будет минимальной (меньше энергии «вырывания» электрона).
При межатомном взаимодействии образуется электромагнитное поле с отрицательной или положительной составляющими. Разность между двумя точками противоположных по знаку составляющих называется электрическим напряжением. Работа электромагнитного поля по перемещению точечного электрического заряда из точки А в точку В называется разностью потенциалов. Физический смысл напряжения (U): разность потенциалов в 1 В между двумя точечными зарядами в 1 Кл, на перемещение которых тратится энергия электромагнитного поля, равная 1 Дж.
Единицей измерения является вольт (В). Определить значение разности потенциалов можно с помощью вольтметра, который подключается параллельно. Производными единицами измерения считаются следующие: 1 мВ = 0,001 В, 1 кВ = 1000 В, 1 МВ = 1000 кВ = 1000000 В и так далее.
Сопротивление электрической цепи
Электропроводимость материала зависит от нескольких факторов: электронной конфигурации, типа вещества, геометрических параметров и температуры. Сведения об электронной конфигурации вещества можно получить из периодической таблицы Д. И. Менделеева. Согласно этой информации вещества бывают:
- Проводниками.
- Полупроводниками.
- Диэлектриками.
К первой группе следует отнести все металлы, электролиты (растворы, проводящие ток) и ионизированные газы. Носителями электрического заряда в металлах являются электроны. В растворах их роль выполняют ионы, которые бывают положительными (анионы) и отрицательными (катионы). Свободными носителями заряженных частиц в газах считаются свободные электроны и положительно заряженные ионы.
Полупроводники проводят электричество только при определенных условиях. Например, при воздействии на него внешних сил. Под их действием кулоновские связи электрона с ядром уменьшаются. При этом отрицательно заряженная частица «вырывается». На ее месте образуется «дырка», обладающая положительным зарядом. Она притягивает соседний электрон, вырывая его с атома. В результате этого осуществляется движение электронов и дырок. Изоляторы или диэлектрики вообще не проводят электричество. К ним относятся материалы без свободных носителей заряда, а также инертные газы.
В проводниках при повышении температурных показателей происходит рост величины сопротивления. При этом происходит разрушение и искажение кристаллической решетки. Заряженные частицы сталкиваются (взаимодействуют) с атомами и другими частицами материала. В результате их движение замедляется, но потом снова возобновляется под действием электромагнитного поля. Процесс этого «взаимодействия» называется электрической проводимостью вещества. Однако в полупроводниках при повышении температуры эта величина уменьшается. К геометрии материалов следует отнести следующие: длину и площадь поперечного сечения.
Сопротивление измеряется в Омах (Ом) при помощи омметра, который подсоединяется параллельно к участку цепи или радиодетали. Существуют производные единицы измерения: 1 кОм = 1000 Ом, 1 МОм = 1000 кОм = 1000000 Ом.
Методы измерения
Мощность можно определить двумя способами: косвенным и прямым. В первом случае это делается при помощи амперметра и вольтметра, а также осциллографа. Измеряются значения напряжения и тока, а затем по формулам вычисляется мощность. Этот способ имеет один недостаток: величина мощности получается с некоторой погрешностью.
При использовании прямого метода используется специальный прибор-измеритель. Он называется ваттметром и показывает мгновенное значение мощности. У каждого из способов есть свои достоинства и недостатки. Какой из методов наиболее оптимален, определяет сам радиолюбитель. Если проектируется какое-либо изделие, которое отличается надежностью, то следует применять прямой метод. В других случаях рекомендуется воспользоваться косвенным методом.
Косвенный способ
Мощность в цепях постоянного и переменного токов определяется различными способами. Для каждого случая существуют свои законы и формулы. Однако мощность можно не рассчитывать, поскольку она указана на электрооборудовании. Расчет применяется только при проектировании устройств.
Для цепей постоянного тока нужно воспользоваться формулой: P = U * I. Ее можно вывести из закона Ома для участка или полной цепи. Если рассматривается полная цепь, то формула принимает другой вид с учетом ЭДС (е): P = e * I. Основные соотношения для расчета:
- Для участка электрической цепи: P = I * I * R = U * U / R.
- Для полной цепи, в которой подключен электродвигатель или выполняется зарядка аккумулятора (потребление): P = I * e = I * e — sqr (I) * Rвн = I * (e — (I * Rвн)).
- В цепи присутствует генератор или гальванический элемент (отдача): P = I * (e + (I * Rвн)).
Эти соотношения невозможно применять для цепей переменного тока, поскольку он подчиняется другим физическим законам. При измерении мощности в цепях переменного тока следует учитывать ее составляющие (активная, реактивная и полная). Если в цепи присутствует только резистор, то мощность считается активной. При наличии емкости или индуктивности — реактивной. Полная — сумма активной и реактивной составляющих.
Для вычисления первого типа физической величины применяется формула такого вида: Ра = I * U * cos (a). Значения тока и напряжения являются среднеквадратичными, а cos (a) — косинус угла между ними. Для определения реактивной мощности нужно воспользоваться следующей формулой: Qр = I * U * sin (a). Если нагрузка в цепи является индуктивной, то значение будет больше 0. В противном случае — меньше 0. Полная мощность Р определяется по следующему соотношению: P = Pa + Qp.
Прямое определение величины
Для определения значения мощности в цепях переменного и постоянного тока применяются ваттметры. В них используются электродинамические или ферроидальные механизмы. Приборы с электродинамическим механизмом выпускаются в виде переносных приборов. Они обладают высоким классом точности. Измерители мощности рекомендуется применять при выполнении точных расчетов для цепей постоянного и переменного тока с частотой до 5 кГц.
Ферродинамические приборы изготавливаются в виде электронных узлов, которые вставляются в измерительные стенды или щитовые. Основное их назначение — контроль приблизительных параметров потребления мощности электрооборудованием. Они обладают низким классом точности и применяются для измерения значений мощности переменного тока. При постоянном токе погрешность увеличивается, поскольку это обусловлено искажением петли гистерезиса ферромагнитных сердечников.
По диапазону частот приборы можно разделить на две группы: низкочастотные и радиочастотные. Ваттметры низких частот применяются в сетях промышленного питания переменного тока. Радиочастотный тип рекомендуется применять для точных измерений при проектировании различной техники. Они делятся на две категории по мощности:
Первый вид подключается в разрыв линии, а второй — в ее конец в качестве нагрузки согласования. Кроме того, приборы для измерения мощности бывают аналоговыми и цифровыми.
При измерении мощности на высоких частотах применяются электронные и термоэлектронные ваттметры. Главным узлом считается микроконтроллер и преобразователь активной мощности. Последний преобразовывает переменный ток в постоянный. После этого происходит перемножение в микроконтроллере силы тока и напряжения. Результатом является сигнал на выходе, который зависит от I и U.
Ваттметр состоит из двух катушек. Первая из них подключается последовательно в цепь нагрузки, а другая (подвижная с резистором) — параллельно. В цифровых моделях роль катушек выполняют датчики тока и напряжения. Прибор имеет две пары зажимов. Одна пара применяется для последовательной цепи, а другая — для параллельной. Для правильного включения ваттметра выполняется обозначение * одной из двух пар зажимов.
Таким образом, для измерения мощности электрического тока применяются два метода. Первый из них является косвенным, а второй — прямым. Последний рекомендуется применять при проектировании сложной техники.
Источник: proagregat.com
Измерение электрической мощности и энергии
Довольно часто возникает необходимость измерять мощность, потребляемую из сети, или же генерируемую в сеть. Это необходимо для учета потребляемой или генерируемой энергии, а также для обеспечения нормальной работы энергосистемы (избежание перегрузок). Измерять мощность можно несколькими способами – прямым и косвенным. При прямом измерении применяют ваттметр, а при косвенном амперметр и вольтметр.
Измерение мощности в цепи постоянного тока
Из-за отсутствия реактивной и активной составляющей в цепях постоянного тока для измерения мощности ваттметр применяют очень редко. Как правило, величину потребляемой или отдаваемой энергии измеряют косвенным методом, с помощью последовательно включенного амперметра измеряют ток I в цепи, а с помощью параллельно подключенного вольтметра измеряют напряжение U нагрузки. После чего применив простую формулу P=UI и получают значение мощности.
Чтоб уменьшить погрешность измерений из-за влияний внутренних сопротивлений устройств, приборы могут подключать по различным схемам, а именно при относительно малом сопротивлении нагрузки R применяют такую схему включения:
А при большом значении R такую схему:
Измерение мощности в однофазных цепях переменного тока
Главным отличием цепей переменного тока от сетей постоянного тока, пожалуй, заключается в том, что в переменном напряжении существует несколько мощностей – полная, активная и реактивная . Полную измеряют зачастую тем же косвенным методом с помощью амперметра и вольтметра и значение ее равно S=UI.
Замер же активной P=UIcosφ и реактивной Q=UIsinφ производится прямым методом, с помощью ваттметра. Для измерения ваттметр в цепь подключают по следующей схеме:
Где токовую обмотку необходимо подключить последовательно с нагрузкой Rн, и, соответственно, обмотку напряжения параллельно нагрузке.
Замер реактивной мощности в однофазных сетях не производится. Такие опыты зачастую ставятся только в лабораториях, где ваттметры включают по специальным схемам.
Измерение мощности в трехфазных цепях переменного тока
Как и в однофазных сетях, так же и в трехфазных полную энергию сети можно измерять косвенным методом, то есть с помощью вольтметра и амперметра по схемам показанным выше. Если нагрузка трехфазной цепи будет симметричной, то можно применить такую формулу:
Uл – напряжение линейное, I- фазный ток.
Если же фазная нагрузка не симметрична, то производят суммирование мощностей каждой из фаз:
При измерении активной энергии в четырехпроводной цепи при использовании трех ваттметров, как показано ниже:
Общей энергией потребляемой из сети будет сумма показаний ваттметров:
Не меньшее распространение получил и метод измерения двумя ваттметрами (применим только для трехпроводных цепей):
Сумму их показаний можно выразить следующим выражением:
При симметричной нагрузке применима такая же формула как и для полной энергии:
Где φ – сдвиг между током и напряжением (угол фазового сдвига).
Измерение реактивной составляющей производят по той же схеме (смотри рисунок в)) и в этом случае она будет равна разности алгебраической между показателями приборов:
Если сеть не симметрична, то для измерения реактивной составляющей применяют два или три ваттметра, которые подключают по различным схемам.
Процесс измерения активной и реактивной мощности
Счетчиками индукционными или электронными производят измерения активной мощности цепи переменного напряжения. Они подключаются по тем же схемам что и ваттметры. Учет реактивной энергии в однофазных потребителей в нашей стране не ведется. Ее учет производят в трехфазных цепях крупных промышленных предприятий, потребляющих большие объемы электроэнергии. Счетчики активной энергии имеют маркировку СА, реактивной СР. Также широкое применение получают электронные счетчики электроэнергии.
Источник: elenergi.ru
Особенности переменного тока
Мощность — то, что характеризует скорость передачи с преобразованием электроэнергии. Какие есть нормы мощности в сети переменного тока и виды, что такое активная и реактивная мощность? Об этом и другом далее.
Нормы мощности в сети переменного тока
Напряжение и мощность — то, что нужно знать каждому человеку, живущему в квартире или частном доме. Стандартное напряжение сети переменного тока в квартире и частном доме выражается в количестве 220 и 380 ватт. Что касается определения количественной меры силы электрической энергии, необходимо сложить электрический ток с напряжением или же измерить необходимый показатель ваттметром. При этом чтобы сделать измерения последним аппаратом, нужно использовать щупы и специальные программы.
Мощность переменного тока определяется соотношением величины тока со временем, которая производит работу за определенное время. Обычный пользователь использует мощностный показатель, передаваемый ему поставщиком электрической энергии. Как правило, он равен 5-12 киловатт. Этих цифр хватает, чтобы обеспечить работоспособность необходимого бытового электрооборудования.
Этот показатель зависит от того, какие внешние условия поступления энергии в дом, какие поставлены ограничительные токовые устройства (автоматы или полуавтоматы), регулирующие момент поступления мощностных емкостей к потребительскому источнику. Это совершается на разных уровнях, от бытового электрощита до центрального устройства электрического распределения.
Характеристики
Переменный ток течет по цепи и меняет свое направление с величиной. Создает магнитное поле. Поэтому его нередко называют периодическим синусоидальным переменным электротоком. Согласно закону кривой линии, величина его меняется через конкретный промежуток времени. Поэтому он называется синусоидным. Имеет свои параметры. Из важных стоит указать период с частотой, амплитудой и мгновенным значением.
Период — это то время, на протяжении которого происходит изменение электротока, а затем оно повторяется вновь. Частота — период течение за секунду. Измеряется в герцах, килогерцах и миллигерцах.
Амплитуда — токовое максимальное значение с напряжением и эффективностью протекания на протяжении полного периода. Мгновенное значение — переменный ток или напряжение, возникающее за конкретное время.
Виды мощностей
Мощностью называется измеряемая физическая величина, которая равна скорости изменения с преобразованием, передачей или потреблением системной энергии. Согласно более узкому понятию, это показатель, который равен отношению затраченного времени на работы к самому периоду, который тратится на работу. Обозначается в механике символом N. В электротехнической науке используется буква P. Нередко можно увидеть также символ W, от слова ватт.
Мощность переменного тока -это произведение силы тока с напряжением и косинусом сдвига фаз. При этом беспрепятственно можно посчитать только активную и реактивную разновидность. Узнать полное мощностное значение можно через векторную зависимость этих показателей и площади.
Активная мощность
Активной называется полезная сила, определяющая процесс прямого преобразования электроэнергии в необходимый вид силы. В каждом электроприборе преобразовывается она по-своему. К примеру, в лампочке получается свет с теплом, в утюге — тепло, а в электрическом двигателе — механическая энергия. Соответственно, показывает КПД устройства.
Реактивная мощность
Реактивной называется та, которая определяется при помощи электромагнитного поля. Образуется при работе электроприборов. Обратите внимание! Это вредная и паразитная мощностная характеристика, которая определяется тем, каков характер нагрузки. Для лампочки она равняется нулю, а для электродвигателя она может быть равна большим значением.
Разница между величинами в том, что активно действующая мощностная характеристика показывает КПД устройств, а реактивная является передачей этого КПД. Разница также наблюдается в определении, символе, формуле и значимости.
Обратите внимание! Что касается значения, то вторая нужна лишь для того, чтобы управлять создавшимся напряжением от первой величины и преодолевать мощностные колебания. Обе измеряются в ваттах и имеют большое значение в электромагнитном излучении, механической форме генератора или акустической волне. Активно применяются в промышленности.
Полная мощность
Полная — это сумма активной с реактивной мощностью. Равна сетевому мощностному показателю. Это произведение напряжения с током в момент игнорирования фазы угла между ними. Вся рассеиваемая с поглощаемой и возвращаемой энергией — это полная энергия.
Это произведение напряжения и тока, единица измерения которого это ватт, перемноженный на ампер. При активности цепи, полная равняется активной. Если речь идет об индуктивной или емкостной схеме, то полная больше, чем активная.
Комплексная мощность
Это сумма всех мощностных показателей фаз источника электроэнергии. Это комплексный показатель, модуль которого равняется полному мощностному показателю электроцепи. Аргументом является фазовый сдвиг между электротоком с сетевым напряжением. Может быть выражена уравнением, где суммарный мощностный показатель, который генерируют источники электроэнергии, равен суммарному мощностному показателю, который потребляется в электроцепи.
Обратите внимание! Вычисляется посредством использования соответствующей формулы. Так, необходимо комплексное напряжение перемножить на комплексны ток или же удвоенное значение комплексного тока перемножить на импеданс. Также можно удвоенное значение комплексного напряжения поделить на удвоенное значение импеданса.
Как узнать какая мощность в цепи переменного тока
Стоит указать, что это величина, которая прямо связывается с иными показателями. К примеру, она находится в прямой зависимости от времени, силы, скорости, вектора силы и скорости, модуля силы и скорости, момента силы и частоты вращения. Часто в формулах во время вычисления электромощности используется также число Пи с показателем сопротивления, мгновенным током, напряжением на конкретном участке электрической сети, активной, полной и реактивной силой. Непосредственно участник вычисления это амплитуда, угловая скорость и начальная сила тока с напряжением.
В однофазной цепи
Понять, какой мощностный показатель есть в однофазной цепи переменного тока, можно при помощи применения трансформатора тока. Для этого необходимо воспользоваться ваттметром, который включен через токовый трансформатор. Показания следует перемножить на трансформаторный коэффициент тока. В момент измерения мощности в высоком напряжении трансформатор тока необходим, чтобы заизолировать ваттметр и обеспечить безопасность пользователя. Параллельна цепь включается не непосредственным способом, а благодаря трансформатору напряжения. Вторичные обмотки с корпусами измерительных трансформаторных установок необходимо заземлять во избежание случайного изоляционного повреждения и попадания высокого напряжения на приборы.
Обратите внимание! Для определения параметров в сети необходимо амперметр перемножить на трансформаторный коэффициент тока, а цифры, полученные вольтметром, перемножить на трансформаторный коэффициент напряжения.
В трехфазной цепи
В цепи переменного тока мощностный показатель в трехфазной цепи определить можно, перемножив ток на напряжение. Поскольку это непостоянный электроток, он зависит от времени и других параметров, поэтому необходимо использовать другие проверенные схемы. Так, можно использовать ваттметр.
Измерение должно быть проведено только в одной фазе и по формуле умножено на три. Этот способ экономит приборы и уменьшает габариты измерения. Применяется для высокой точности измерения каждой фазы. В случае несимметричной нагрузки, нужно использовать соответствующую схему подключения ваттметра. Это более точный способ, но требует наличие трех ваттметров.
Обратите внимание! Если цепь не предусматривает наличие нулевого проводника, нужна также соответствующая схема.
Стоит указать, что сегодня измерить можно необходимые показатели не только аналоговым, но и цифровым прибором. Отличие второго в уменьшенных размерах и легкости. Кроме того, цифровые агрегаты способы осуществлять фиксацию тока с напряжением, косинусом сети и другим. Это позволяет на дистанции осуществлять отслеживание различных величин и передавать предупреждения, если есть отклонение. Это удобно, поскольку не нужно измерять ток с напряжением, а потом, используя формулы, все досконально просчитывать.
В целом, мощность — это величина, основное предназначение которой показывать силу работы конкретного прибора и во многих случаях скорость деятельности, взаимодействуя с ним. Она бывает механической, электрической, гидравлической и для постоянного с переменным током. Измеряется по международной системе в ваттах и киловаттах.
Источник: rusenergetics.ru
ИЗМЕРЕНИЕ МОЩНОСТИ В ЦЕПЯХ ПОСТОЯННОГО ТОКА
Измерение мощности постоянного тока, определяемой формулой
где U и І — соответственно напряжение тока и ток, производится либо косвенным методом — по показаниям вольтметра и амперметра, либо прямым методом — по показаниям ваттметра.
Сущность косвенного метода измерения мощности заключается в измерении с помощью вольтметра и амперметра напряжения U и тока І цепи и последующем вычислении в соответствии с выражением (2). На рис. 1 приведены две возможные схемы включения вольтметра и амперметра в цепь при измерении мощности, потребляемой нагрузкой RH, Для схемы 1,а мощность, потребляемая схемой, равна:
где ІН и ІВ — токи, протекающие соответственно через нагрузку и вольтметр; РН и РВ — мощность, потребляемая соответственно нагрузкой и вольтметром.
Таким образом, для данной схемы включения рассчитанное значение мощности Р будет больше действительного значения мощности, потребляемой нагрузкой РН, на величину РВ= UIB. При этом погрешность определения мощности, потребляемой нагрузкой, будет тем меньше, чем меньше ток ІВ по сравнению с ІН, т. е. чем больше входное сопротивление вольтметра (RВ).
Потребляемая схемой (рис. 1, б) мощность равна:
т. е. определяемая расчетом мощность будет больше действительной мощности нагрузки PH на величину потери мощности в амперметре Pa=IHRа. Погрешность определения потребляемой нагрузкой мощности будет тем меньше, чем меньше сопротивление амперметра по сравнению с сопротивлением нагрузки.
Анализ показывает, что погрешность измерения мощности будет минимальной при включении измерительных приборов по схеме, приведенной на рис. 1,а, если выполняется условие
(3)
При включении приборов по схеме, показанной на рис. 1, б, погрешность измерения будет минимальной при условии
(4)
При точных измерениях упомянутую погрешность можно учесть, если известно сопротивление измерительных приборов.
Для известного сопротивления нагрузки RH потребляемая им мощность Ра определяется путем измерения тока Iн, протекающего через него, или падения напряжения на нем Un. Расчет мощности производится в соответствии с выражениями:
Рассмотренные методы определения мощности, потребляемой нагрузкой, применяются и при измерении мощности генераторов постоянного тока.
Измерение мощности в цепи постоянного тока прямым методом в основном производится с помощью ваттметров электродинамической системы.
Измерительный механизм ваттметра электродинамической системы, состоящей из неподвижной и расположенной внутри нее подвижной катушек, включается в цепь постоянного тока по схеме, приведенной на рис. 2. Неподвижная (токовая) катушка включается последовательно с нагрузкой, а подвижная — параллельно нагрузке. Добавочное сопротивление Rд, включаемое последовательно с подвижной катушкой, предназначено для расширения предела измерения прибора по напряжению. В результате взаимодействия магнитных полей катушек создается вращающий момент:
где I1 и I2 — токи, протекающие соответственно через неподвижную и подвижную катушку; f (α) — функция, учитывающая изменение вращающего момента в зависимости от угла поворота а подвижной катушки (обусловлена изменением взаимной индукции между катушками).
Противодействующий момент создается токопроводящими пружинами подвижной катушки
где W — удельный противодействующий момент пружин.
| Рис. 2 | При равенстве вращающего и противодействующего моментов подвижная катушка повернется на некоторый угол а, определяемый из выражения Так как то |
Здесь R2 — сопротивление подвижной катушки; — постоянная величина; Р = IHU — мощность, потребляемая нагрузкой.
Для того чтобы шкала прибора была равномерной, необходимо обеспечить постоянство функции f (α). Это достигается путем соответствующего выбора размеров и формы катушек и их начального взаимного положения.
При включении ваттметра в цепь постоянного тока необходимо соблюдать полярность соединения катушек. Для этого два из четырех зажимов прибора, соответствующих «началу» подвижной и неподвижной катушек, обозначаются звездочками (*) или знаком плюс (+). Эти зажимы должны быть подключены к положительному полюсу источника питания (к генератору — генераторные зажимы), а не к нагрузке.
На рис. 3 приведены две схемы включения ваттметра в цепь постоянного тока. При включении прибора по схеме, показанной на рис. 3, а, на подвижную катушку подается напряжение источника питания UИ которое больше напряжения на сопротивлении нагрузки Uна величину падения напряжения на неподвижной катушке, т. е. показание ваттметра будет больше действительного значения мощности нагрузки. При этом погрешность измерения мощности будет тем меньше, чем меньше сопротивление токовой катушки по сравнению с сопротивлением нагрузки. При включении прибора по схеме, показанной на рис. 3, б, ток, протекающий через нагрузку, будет меньше тока в токовой катушке на величину тока, протекающего через подвижную катушку, т. е. показание прибора будет больше действительного значения мощности, потребляемой нагрузкой. Погрешность измерения мощности, потребляемой нагрузкой, при этом будет тем меньше, чем больше сопротивление подвижной катушки с последовательно включенным добавочным сопротивлением Rд сопротивления нагрузки Rн.
Как при косвенном, так и при прямом методе измерения мощности результат измерения отличается от действительного значения потребляемой мощности нагрузкой на некоторую систематическую погрешность. Величина систематической погрешности определяется схемой включения ваттметра и сопротивлением его катушек.
Погрешность измерения мощности при включении ваттметра по схеме, показанной на рис. 3, а, будет минимальной, если выполняется условие (3), причем в этом случае за Ra принимается сопротивление неподвижной катушки, а за RB — сопротивление подвижной катушки с последовательно включенным добавочным сопротивлением Rд. При включении ваттметра по схеме (рис. 3, б) погрешность будет минимальной при выполнении условия (4).
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Только сон приблежает студента к концу лекции. А чужой храп его отдаляет. 8776 — | 7506 — или читать все.
Источник: studopedia.ru
Блестящая вики по математике и науке
Пусть N = {1,2,3, ⋯} \ mathbb {N} = \ {1, 2, 3, \ cdots \} N = {1,2,3, ⋯} обозначает множество натуральных чисел.
Бесконечное множество AAA называется счетно бесконечным (или счетным ), если оно имеет ту же мощность, что и N \ mathbb {N} N. Другими словами, существует биекция A → NA \ to \ mathbb {N} A → N.
Бесконечное множество AAA называется несчетно бесконечным (или несчетным ), если оно равно , а не .Другими словами, не существует биекции A → NA \ to \ mathbb {N} A → N.
Эти определения предполагают, что даже среди класса бесконечных множеств существуют различные «размеры бесконечности». В смысле мощности счетно бесконечные множества «меньше», чем несчетно бесконечные множества. Конечно, конечные множества «меньше», чем любые бесконечные множества, но различие между счетными и несчетными дает также способ сравнения размеров бесконечных множеств. Ниже приведены несколько примеров счетных и несчетных множеств.
Пусть Z = {…, −2, −1,0,1,2,…} \ mathbb {Z} = \ {\ ldots, -2, -1, 0, 1, 2, \ ldots \} Z = { …, −2, −1,0,1,2,…} обозначают множество целых чисел. Является ли Z \ mathbb {Z} Z счетным или несчетным?
Рассмотрим следующую карту из N → Z: \ mathbb {N} \ в \ mathbb {Z}: N → Z:
{1,2,3,4,5,6,7,8,9,…} ↦ {0,1, −1,2, −2,3, −3,4, −4,…}. \ {1, 2, 3, 4, 5, 6, 7, 8,9, \ ldots \} \ mapsto \ {0,1, -1,2, -2,3, -3,4, -4, \ ldots \}. {1,2,3,4,5,6,7,8,9,…} ↦ {0,1, −1,2, −2,3, −3,4, −4,… }.
Каждому целому числу соответствует некоторое натуральное число, и никакое целое число не отображается дважды.Таким образом, это биекция. Мы заключаем, что Z \ mathbb {Z} Z счетно. □ _ \ квадрат □
SSS конечно SSS счетно бесконечен SSS бесконечно бесконеченПусть Q \ mathbb {Q} Q обозначает множество рациональных чисел. Можно ли считать Q \ mathbb {Q} Q или нет?
Отображение из N → Q \ mathbb {N} \ в \ mathbb {Q} N → Q может быть описано просто списком рациональных чисел. Если этот список содержит каждое рациональное число хотя бы один раз, мы можем удалить повторы, чтобы получить биекцию N → Q \ mathbb {N} \ to \ mathbb {Q} N → Q.
Для рационального числа ab \ frac abba (в младших терминах) вызовите ∣a∣ + ∣b∣ | a | + | b | ∣a∣ + ∣b∣ его высота .Рациональных чисел каждой высоты конечное число. Следовательно, если мы перечислим все рациональные числа высоты 1, затем рациональные числа высоты 2, затем рациональные числа высоты 3 и т. Д., Мы получим желаемый список рациональных чисел.
Таким образом, мы заключаем, что Q \ mathbb {Q} Q счетно. □ _ \ квадрат □
Число α∈R \ alpha \ in \ mathbb {R} α∈R называется алгебраическим , если существует многочлен p (x) p (x) p (x) с рациональными коэффициентами такой, что p (α) = 0p (\ альфа) = 0p (α) = 0.
Пусть S⊂RS \ subset \ mathbb {R} S⊂R обозначает множество алгебраических чисел. Что из следующего верно в отношении S? S? S?
SSS конечно SSS счетно бесконечен SSS бесконечно бесконеченРассмотрим интервал [0,1] [0,1] [0,1]. Является ли набор [0,1] [0,1] [0,1] счетным или несчетным?
Согласно знаменитому диагональному аргументу Кантора , оказывается, что [0,1] [0,1] [0,1] несчетное число. Его аргумент — умное доказательство от противного.
Предположим, что [0,1] [0,1] [0,1] счетно, так что мы можем написать [0,1] = {a1, a2, a3,…} [0,1] = \ {a_1, a_2, a_3, \ ldots \} [0,1] = {a1, a2, a3,…}, где каждый ai∈ [0,1] a_i \ in [0,1] ai ∈ [0, 1].Для каждого aia_iai запишите (одно из) его двоичное представление (я):
ai = 0.di1di2di3… 2, a_i = {0.d_ {i1} d_ {i2} d_ {i3} \ ldots} _ {2}, ai = 0.di1 di2 di3… 2, где каждое di∈ {0,1} d_i \ in \ {0,1 \} di ∈ {0,1}.
Для каждого iii положим ei = 1 − diie_i = 1-d_ {ii} ei = 1 − dii, так что ei = 0e_i = 0ei = 0, если dii = 1d_ {ii} = 1dii = 1 и ei = 1e_i = 1ei = 1, если dii = 0d_ {ii} = 0dii = 0. Теперь построим число x∈ [0,1] x \ in [0,1] x∈ [0,1], записав его двоичное представление:
x = 0.e1e2e3… 2.x = {0.\ text {th} i с двоичной цифрой, мы знаем, что x ≠ aix \ neq a_ix = ai для всех i∈Ni \ in \ mathbb {N} i∈N.
Но это означает, что xxx отсутствует в списке {a1, a2, a3,…} \ {a_1, a_2, a_3, \ ldots \} {a1, a2, a3,…}, даже если x∈ [0 , 1] x \ in [0,1] x∈ [0,1]. Таким образом, список не включает все элементы множества [0,1] [0,1] [0,1], что противоречит нашему предположению о счетности! □ _ \ квадрат □
Пусть SSS обозначает множество непрерывных функций f: [0,1] → Rf: [0,1] \ to \ mathbb {R} f: [0,1] → R.
Что из следующего верно относительно S? S? S?
Мощность | Конечные множества | Бесконечные наборы
Здесь нам нужно поговорить о мощности набора, что в основном является размером набора. Мощность множества обозначается $ | A | $. Сначала обсудим мощность для конечных множеств и потом поговорим о бесконечных множествах.
Рассмотрим набор $ A $. Если $ A $ имеет только конечное число элементов, его мощность равна просто количество элементов в $ A $.Например, если $ A = \ {2,4,6,8,10 \} $, то $ | A | = 5 $. Перед обсуждением бесконечных множеств, что является основным обсуждением в этом разделе, мы хотели бы поговорить об очень Полезное правило: принцип включения-исключения . Для двух конечных множеств $ A $ и $ B $ имеем $$ | A \ чашка B | = | A | + | B | — | A \ cap B |. $$ Чтобы убедиться в этом, обратите внимание, что когда мы складываем $ | A | $ и $ | B | $, мы дважды подсчитываем элементы в $ | A \ cap B | $, таким образом, вычитая его из $ | A | + | B | $, мы получаем количество элементов в $ | A \ cup B | $, (можно см. рисунок 1.n \ left | A_i \ right | — \ sum_ {i \> \> \> \> \> \> + \ sum_ {i
Пример
В группе,
- есть люди за 10 долларов в белых рубашках и за 8 долларов за людей в красных рубашках;
- $ 4 $ у людей черные туфли и белые рубашки;
- $ 3 $ у людей черные туфли и красные рубашки;
- человек. Общее количество людей в белых или красных рубашках или черных туфлях составляет 21 доллар.
- Решение
Пусть $ W $, $ R $ и $ B $ будут количеством людей в белых рубашках, красных рубашках и черных туфлях. соответственно.Затем, вот краткое изложение доступной информации: $$ | W | = 10 $$ $$ | R | = 8 $$ $$ | W \ cap B | = 4 $$ $$ | R \ cap B | = 3 $$ $$ | W \ чашка B \ чашка R | = 21. $$ Также разумно предположить, что $ W $ и $ R $ не пересекаются, $ | W \ cap R | = 0 $. Таким образом, применяя принцип включения-исключения получаем
$ | W \ чашка R \ чашка B | $$ = 21 $ $ = | W | + | R | + | B | — | W \ cap R | — | W \ cap B | — | R \ cap B | + | W \ cap R \ cap B | $ $ = 10 + 8 + | B | -0-4-3 + 0 $.
Таким образом $$ | B | = 10. $$Обратите внимание, что другой способ решить эту проблему — использовать диаграмму Венна, как показано на рисунке 1.11.
Рис.1.11 — Диаграмма включения-исключения Венна.
Бесконечные наборы:
Что, если $ A $ — бесконечное множество? Оказывается, нам нужно различать два типа бесконечных множеств: где один тип значительно «крупнее» другого.В частности, один вид называется счетным , в то время как другой называется бесчисленное . Такие множества, как $ \ mathbb {N} $ и $ \ mathbb {Z} $, называются счетными, но «большие» наборы, такие как $ \ mathbb {R} $, называются несчетными. Разница между двумя типами заключается в что вы можете перечислить элементы счетного множества $ A $, т.е. вы можете написать $ A = \ {a_1, a_2, \ cdots \} $, но вы не можете перечислить элементы в бесчисленном множестве. Например, вы можете написать
- $ \ mathbb {N} = \ {1,2,3, \ cdots \} $,
- $ \ mathbb {Z} = \ {0,1, -1,2, -2,3, -3, \ cdots \} $.
Тот факт, что вы можете перечислить элементы счетно бесконечного набора, означает, что набор может быть сопоставлен один к одному. соответствие с натуральными числами $ \ mathbb {N} $. С другой стороны, вы не можете перечислить элементы в $ \ mathbb {R} $, так что это бесчисленное множество. Если быть точным, вот определение.
ОпределениеНабор $ A $ называется счетным, если выполняется одно из следующих утверждений.
- , если это конечное множество, $ \ mid A \ mid
- его можно поставить во взаимно однозначное соответствие с натуральными числами $ \ mathbb {N} $, в которых В этом случае множество называется счетно бесконечным. Набор называется несчетным, если он не счетный.
Вот простой совет, чтобы решить, является ли набор счетным или нет. Что касается прикладной вероятности обеспокоен, этого руководства должно быть достаточно для большинства случаев.
- $ \ mathbb {N}, \ mathbb {Z}, \ mathbb {Q} $ и любые их подмножества счетны.
- Любой набор, содержащий интервал на действительной прямой, такой как $ [a, b], (a, b], [a, b), $ или $ (a, b) $, где $ a
Приведенного выше правила обычно достаточно для целей данной книги.Однако, чтобы аргументировать Более конкретно, здесь мы приводим некоторые полезные результаты, которые помогают нам доказать, является ли множество счетным или нет. Если доказательства вас меньше интересуют, вы можете их пропустить.
Теорема
Любое подмножество счетного множества счетно.
Любое надмножество бесчисленного множества неисчислимо.
Интуиция, лежащая в основе этой теоремы, такова: если множество счетно, то любое «меньшее» множество также должно быть счетным, поэтому подмножество счетного множества также должно быть счетным.Предоставлять доказательство, мы можем рассуждать следующим образом.
Пусть $ A $ счетное множество и $ B \ subset A $. Если $ A $ — конечное множество, то $ | B | \ leq | A |
Вторую часть теоремы можно доказать с помощью первой части. Предположим, что $ B $ несчетное число. Если $ B \ subset A $ и $ A $ счетно, то по первой части теоремы $ B $ также является счетным множество, противоречие.
Теорема
Если $ A_1, A_2, \ cdots $ — это список счетных множеств, то множество $ \ bigcup_ {i} A_i = A_1 \ cup A_2 \ cup A_3 \ cdots $ также счетно.
ДоказательствоДостаточно создать список элементов в $ \ bigcup_ {i} A_i $. Поскольку каждый $ A_i $ счетен, мы можем перечислите его элементы: $ A_i = \ {a_ {i1}, a_ {i2}, \ cdots \} $. Таким образом, мы имеем
- $ A_1 = \ {a_ {11}, a_ {12}, \ cdots \} $,
- $ A_2 = \ {a_ {21}, a_ {22}, \ cdots \} $,
- $ A_3 = \ {a_ {31}, a_ {32}, \ cdots \} $,
- …
Мы смогли создать список, содержащий все элементы в $ \ bigcup_ {i} A_i $, так что это множество счетно.
Теорема
Если $ A $ и $ B $ счетны, то $ A \ times B $ также счетно.
ДоказательствоДоказательство этой теоремы очень похоже на предыдущую теорему.Поскольку $ A $ и $ B $ являются счетно, мы можем написать $$ A = \ {a_1, a_2, a_3, \ cdots \}, $$ $$ B = \ {b_1, b_2, b_3, \ cdots \}. $$ Теперь мы создаем список, содержащий все элементы в $ A \ times B = \ {(a_i, b_j) | i, j = 1,2,3, \ cdots \} $. Идея точно такая же, как и раньше. На рис. 1.13 показан один из возможных вариантов заказа.
Рис.1.13 — Порядок составления списка.Приведенные выше аргументы можно повторить для любого набора $ C $ в виде $$ C = \ bigcup_i \ bigcup_j \ {a_ {ij} \}, $$ где индексы $ i $ и $ j $ принадлежат некоторым счетным множествам.Таким образом, любое множество в этой форме счетно. Например, следствием этого является счетность множества рациональных чисел $ \ mathbb {Q} $. Это потому, что мы можем написать $$ \ mathbb {Q} = \ bigcup_ {i \ in \ mathbb {Z}} \ bigcup_ {j \ in \ mathbb {N}} \ {\ frac {i} {j} \}. $$
Приведенные выше теоремы подтверждают, что такие множества, как $ \ mathbb {N}, \ mathbb {Z}, \ mathbb {Q} $ и их подмножества счетны. Однако, как мы упоминали, интервалы в $ \ mathbb {R} $ неисчислимы. Таким образом, вы никогда не сможете предоставить список в виде $ \ {a_1, a_2, a_3, \ cdots \} $, содержащий все элементы, скажем, в $ [0,1] $.Этот факт можно доказать с помощью так называемого диагонального аргумента, и мы опускаем доказательство здесь, поскольку оно не является важным для остальной части книги.
Математика для гуманитарных наук
Часто нас интересует количество элементов в наборе или подмножестве. Это называется мощностью множества.
Мощность
Количество элементов в наборе — это мощность этого набора.
Мощность набора A часто обозначается как | A | или n ( A )
Пример 12
Пусть A = {1, 2, 3, 4, 5, 6} и B = {2, 4, 6, 8}.
Какая мощность у B ? A B , A ⋂ B ?
Мощность элемента B равна 4, так как в наборе 4 элемента.
Мощность элемента A ⋃ B равна 7, поскольку A ⋃ B = {1, 2, 3, 4, 5, 6, 8}, который содержит 7 элементов.
Количество элементов A ⋂ B равно 3, поскольку A ⋂ B = {2, 4, 6}, которое содержит 3 элемента.
Пример 13
Какова мощность числа P = набор английских названий месяцев в году?
Количество элементов этого набора равно 12, поскольку в году 12 месяцев.
Иногда нас может интересовать мощность объединения или пересечения множеств, но мы не знаем фактических элементов каждого набора. Это обычное дело в геодезии.
Пример 14
В опросе 200 человек спрашивают «Какой напиток вы пьете утром» и предлагают варианты выбора:
- Только чай
- Только кофе
- И кофе, и чай
Предположим, 20 сообщают только чай, 80 сообщают только кофе, 40 сообщают и то, и другое.Сколько людей пьют чай по утрам? Сколько людей не пьют ни чая, ни кофе?
На этот вопрос проще всего ответить, создав диаграмму Венна. Мы видим, что людей, пьющих чай, можно найти, добавив тех, кто пьет только чай, к тем, кто пьет и то, и другое: 60 человек.
Мы также можем видеть, что те, кто не пьет, не входят ни в одну из трех других групп, поэтому мы можем подсчитать их, вычтя из мощности универсального набора 200.
200-20-80-40 = 60 человек, которые не пьют.
Пример 15
В ходе опроса спрашивается: Какие онлайн-сервисы вы использовали за последний месяц:
- Твиттер
- Использовали оба
Результаты показывают, что 40% опрошенных использовали Twitter, 70% использовали Facebook и 20% использовали оба. Сколько людей не использовали ни Twitter, ни Facebook?
Пусть T будет набором всех людей, которые использовали Twitter, а F будет набором всех людей, которые использовали Facebook.Обратите внимание, что, хотя мощность F составляет 70%, а мощность T составляет 40%, мощность F ⋃ T не просто 70% + 40%, так как это учитывает тех, кто использует оба услуги дважды. Чтобы найти мощность F ⋃ T , мы можем сложить мощность F и мощность T , а затем вычесть те, которые находятся в пересечении, которые мы посчитали дважды. В символах,
n ( F ⋃ T ) = n ( F ) + n ( T ) — n ( F ⋂ T )
n ( F ⋃ T ) = 70% + 40% — 20% = 90%
Теперь, чтобы узнать, сколько людей не использовали ни одну из служб, мы ищем мощность ( F ⋃ T ) c .Поскольку универсальный набор содержит 100% людей и мощность F ⋃ T = 90%, мощность ( F ⋃ T ) c должна равняться остальным 10%.
Предыдущий пример проиллюстрировал два важных свойства
Свойства мощности
n ( A ⋃ B ) = n ( A ) + n ( B ) — n ( A ⋂ B )
n ( Ac ) = n ( U ) — n ( A )
Обратите внимание, что первое свойство также можно записать в эквивалентной форме, решив мощность пересечения:
n ( A ⋂ B ) = n ( A ) + n ( B ) — n ( A ⋃ B )
Пример 16
Было опрошено пятьдесят студентов, и их спросили, будут ли они проходить курс социальных наук (SS), гуманитарных наук (HM) или естественных наук (NS) в следующем квартале.
21 проходили курс SS 26 проходили курс HM
19 проходили курс NS 9 проходили курс SS и HM
7 принимали SS и 10 NS принимали HM и NS
3 принимали все три 7 не принимали
Сколько студентов проходят только курс SS?
Может быть полезно взглянуть на диаграмму Венна.
Из приведенных данных мы знаем, что существует
3 студента в районе e и
7 студентов в районе ч .
Поскольку 7 студентов проходили курсы SS и NS, мы знаем, что n ( d ) + n ( e ) = 7. Поскольку мы знаем, что в регионе 3 3 студента, должно быть
7 — 3 = 4 студента в районе d .
Аналогичным образом, поскольку есть 10 студентов, изучающих HM и NS, включая регионы e и f , должно быть
10 — 3 = 7 студентов в районе f .
Поскольку 9 студентов изучали SS и HM, должно быть 9 — 3 = 6 студентов в регионе b .
Итак, мы знаем, что 21 студент проходил курс SS. Сюда входят студенты из регионов a, b, d, и e . Поскольку мы знаем количество студентов во всех регионах, кроме a , мы можем определить, что 21 — 6 — 4 — 3 = 8 студентов находятся в регионе a .
8 студентов проходят только курс SS.
Попробовать 4
Было опрошено сто пятьдесят человек, и их спросили, верят ли они в НЛО, призраков и снежного человека.
43 верили в НЛО 44 верили в призраков
25 верили в снежного человека 10 верили в НЛО и привидений
8 верили в призраков, а снежный человек 5 верили в НЛО и снежного человека
2 верили во все три
Сколько опрошенных верили хотя бы в одно из этих утверждений?
Попробовать сейчас Ответы
1.Есть несколько ответов: Множество всех нечетных чисел меньше 10. Множество всех нечетных чисел. Набор всех целых чисел. Набор всех действительных чисел.
2. A ⋃ C = {красный, оранжевый, желтый, зеленый, сине-фиолетовый}
Bc ⋂ A = {зеленый, синий}
3. A ⋃ B ⋂ CC
4. Начав с пересечения всех трех кругов, мы выходим наружу. Поскольку 10 человек верят в НЛО и Призраков, а двое верят во все три, остается 8 человек, которые верят только в НЛО и Призраков.Мы прорабатываем свой выход, заполняя все регионы. Как только у нас получится, мы можем сложить все эти регионы, получив 91 человека в объединении всех трех наборов. Остается 150 — 91 = 59 тех, кто ни во что не верит.
Теория множеств — мощности и множества | Хесус Наджера
С основными обозначениями и операциями, очищенными в первой и второй статьях этой серии, мы построили фундаментальное понимание теории множеств. Эта третья статья дополняет эти знания, анализируя наиболее важное свойство любого набора: — общее количество уникальных элементов, которые он содержит.
Также известное как мощность , количество отдельных элементов в наборе обеспечивает исходную точку перехода для дальнейшего, более богатого анализа данного набора. Во-первых, количество элементов — это первое обнаруженное нами уникальное свойство, которое позволяет нам объективно сравнивать различные типы множеств — проверять, существует ли взаимное соответствие (причудливый термин для функции с небольшими квалификаторами ) от одного набора к другому. Другая форма приложения, а также тема для оставшейся части этой части, количество элементов предоставляет окно для всех возможных подмножеств, которые существуют в данном наборе. Что буквально переводится на повседневные проблемы распределения решений, такие как составление бюджета похода за продуктами или балансирование портфеля.
Первоначально опубликовано на https://www.setzeus.com/В примере слева (вверху на мобильном устройстве) изображены пять отдельных наборов с их соответствующей мощностью справа. Как видно, символ количества элементов набора напоминает символ абсолютного значения — переменную, зажатую между двумя вертикальными линиями. Примеры ясны, за исключением, возможно, последней строки, которая подчеркивает тот факт, что только уникальных элементов в наборе вносят вклад в мощность.
Помните подмножества из предыдущей статьи? Оказывается, мощность некоторого набора A и количество возможных подмножеств набора A имеют увлекательную взаимосвязь. Подробно ниже, количество подмножеств, которые могут быть построены из некоторого подмножества, увеличивается с порядком мощности на предсказуемую величину:
# возможных подмножеств в C = | C | ²
Мы пройдемся по пример ниже. Однако сначала давайте поразмышляем над интуитивно понятной формулой, приведенной выше.Представьте количество элементов как общее количество «слотов», которые представляет набор. При построении некоторого подмножества решение Boolean (да / нет) принимается для каждого возможного «слота». Это означает, что каждый уникальный элемент, добавленный к набору (то есть увеличение количества элементов на единицу), увеличивает количество возможных подмножеств в два раза. Как программист или ученый-компьютерщик, вы могли бы оценить эту логику немного больше, когда поймете, что все подмножества данного набора могут быть вычислены с использованием таблицы чисто двоичных чисел.
Прежде чем мы выведем все подмножества для приведенного выше примера набора C , я хотел бы ввести один последний термин — набор мощности . с прописной буквой S , за которой следует скобка, содержащая исходный набор S (C) , набор мощности представляет собой набор всех подмножеств C, включая пустой / нулевой набор & само множество C. В таблице ниже показан набор мощности S (C) со всеми изменяющимися перестановками возможных подмножеств для набора C , содержащихся в одном большом наборе.
Из соображений форматирования я исключил запятые между наборами ***Чем полезен набор мощности? Что ж, вы, вероятно, использовали интуицию, лежащую в основе силовых наборов, несколько раз, даже не подозревая об этом. Каждый раз, когда вы выбираете подмножество элементов из большего набора, вы выбираете элемент набора мощности. Например, ребенок просматривает кондитерскую с 5 долларами — какой элемент набора мощности из всех доступных конфет она выберет? Или для более технических специалистов, как инженеры-программисты, вы можете запросить всех возможных пользователей базы данных , у которых также есть свойство X & Y — — другой пример, где одно подмножество выбрано из всех возможных подмножеств.
Теперь мы понимаем количество элементов множества, почему они важны и их отношение к множеству степеней. Итак, давайте вернемся на мгновение назад, чтобы рассмотреть то, что мы замалчивали в самом начале этой статьи: , что именно определяет эквивалентность в теории множеств?
Возможно, два набора с одинаковой мощностью имеют какое-то общее свойство, но на этом сходство заканчивается — что, если в одном из наборов есть элемент, повторяющийся несколько раз? Что, если два набора имеют одинаковое количество элементов и ? Нельзя отрицать, что они в какой-то степени «равны», но даже в этом сценарии остается возможностей для дифференциации, поскольку в каждом наборе разные элементы могут повторяться одинаковое количество раз.Дело в том, что концепция эквивалентности в теории множеств немного чужда по сравнению с другими разделами математики. Для установления эквивалентности в этом мире требуется его собственное введение и язык. В последней статье этой серии представлены концепции эквивалентности, а также ее основные свойства, такие как инъективные, биективные и сюръективные функции.
, первоначально опубликовано на
https://www.setzeus.com/
Количество элементов набора
Определение
Рассмотрим множество \ (A.\) Если \ (A \) содержит ровно \ (n \) элементов, где \ (n \ ge 0, \), то мы говорим, что множество \ (A \) конечно и его мощность равна количеству элементов \ (n. \) Мощность множества \ (A \) обозначается \ (\ left | A \ right |. \). Например,
\ [A = \ left \ {{1,2,3,4,5} \ right \}, \ Rightarrow \ left | А \ право | = 5. \]
Напомним, что мы считаем только различные элементы, поэтому \ (\ left | {\ left \ {{1,2,1,4,2} \ right \}} \ right | = 3. \)
Мощность пустого множества равна нулю:
\ [{\ left | \ varnothing \ right | = 0.} \]
Понятие мощности можно обобщить на бесконечные множества.
Два бесконечных множества \ (A \) и \ (B \) имеют одинаковую мощность (то есть \ (\ left | A \ right | = \ left | B \ right | \)), если существует биекция \ ( От A \ до B. \) Это определение, основанное на взаимно однозначности, также применимо к конечным множествам. Биекция между конечными множествами \ (A \) и \ (B \) будет существовать тогда и только тогда, когда \ (\ left | A \ right | = \ left | B \ right | = n. \)
Если биекция не существует из \ (A \) в \ (B, \), то множества имеют неравные мощности, то есть \ (\ left | A \ right | \ ne \ left | B \ right |.\)
Если множества \ (A \) и \ (B \) имеют одинаковую мощность, они называются равными. В этом случае мы пишем \ (A \ sim B. \) Формально
\ [A \ sim B \; \ text {iff} \; \ left | А \ право | = \ left | B \ right |. \]
Эквивалентность — это отношение эквивалентности в семействе множеств. Класс эквивалентности множества \ (A \) при этом отношении содержит все множества с одинаковой мощностью \ (\ left | A \ right |. \)
Примеры равных множеств
Наборы \ (\ mathbb {N} \) и \ (\ mathbb {O} \)
Отображение \ (f: \ mathbb {N} \ to \ mathbb {O} \) между множеством натуральных чисел \ (\ mathbb {N} \) и множеством нечетных натуральных чисел \ (\ mathbb {O} = \ left \ {{1,3,5,7,9, \ ldots} \ right \} \) определяется функцией \ (f \ left (n \ right) = 2n — 1, \), где \ ( п \ в \ mathbb {N}.\) Эта функция биективна. Следовательно, оба набора \ (\ mathbb {N} \) и \ (\ mathbb {O} \) имеют одинаковую мощность: \ (\ left | \ mathbb {N} \ right | = \ left | \ mathbb {O} \ справа |. \)
Два конечных интервала
Пусть \ (\ left ({a, b} \ right) \) и \ (\ left ({c, d} \ right) \) два открытых конечных интервала на вещественной оси. Покажем, что любые интервалы \ (\ left ({a, b} \ right) \) и \ (\ left ({c, d} \ right) \) имеют одинаковую мощность.
Отображение из \ (\ left ({a, b} \ right) \) и \ (\ left ({c, d} \ right) \) задается функцией
\ [f (x) = c + \ frac {{d — c}} {{b — a}} \ left ({x — a} \ right) = y, \]
, где \ (x \ in \ left ({a, b} \ right) \) и \ (y \ in \ left ({c, d} \ right).
Проверить сопоставление конечных точек:
\ [f \ left (a \ right) = c + \ frac {{d — c}} {{b — a}} \ left ({a — a} \ right) = c + 0 = c, \]
\ [\ require {cancel} f \ left (b \ right) = c + \ frac {{d — c}} {\ cancel {b — a}} \ cancel {\ left ({b — a} \ right )} = \ cancel {c} + d — \ cancel {c} = d. \]
Докажите, что функция \ (f \) инъективна. Противоположное утверждение: \ (f \ left ({{x_1}} \ right) = f \ left ({{x_2}} \ right) \) для \ ({x_1} \ ne {x_2}. \). Если это так, тогда у нас есть
\ [f \ left ({{x_1}} \ right) = f \ left ({{x_2}} \ right), \; \; \ Rightarrow c + \ frac {{d — c}} {{b — a}} \ left ({{x_1} — a} \ right) = c + \ frac {{d — c}} {{b — a }} \ left ({{x_2} — a} \ right), \; \; \ Rightarrow \ frac {{d — c}} {{b — a}} \ left ({{x_1} — a} \ right) = \ frac {{d — c}} {{b — a}} \ left ({{x_2} — a} \ right), \; \; \ Rightarrow {x_1} — a = {x_2} — a, \; \; \ Rightarrow {x_1} = {x_2}.\]
Получили противоречие. Следовательно, функция \ (f \) инъективна.
Убедитесь, что \ (f \) сюръективен. Возьмите число \ (y \) из домена \ (\ left ({c, d} \ right) \) и найдите прообраз \ (x: \)
\ [y = c + \ frac {{d — c}} {{b — a}} \ left ({x — a} \ right), \; \; \ Rightarrow \ frac {{d — c}} {{b — a}} \ left ({x — a} \ right) = y — c, \; \; \ Rightarrow x — a = \ frac {{b — a}} {{d — c}} \ left ({y — c} \ right), \; \; \ Rightarrow x = a + \ frac {{b — a}} {{d — c}} \ left ({y — c} \ right).\]
Прообраз \ (x \) лежит в области \ (\ left ({a, b} \ right) \) и
\ [f \ left (x \ right) = f \ left ({a + \ frac {{b — a}} {{d — c}} \ left ({y — c} \ right)} \ right) = c + \ frac {{d — c}} {{b — a}} \ left ({\ cancel {a} + \ frac {{b — a}} {{d — c}} \ left ({y — c} \ right) — \ cancel {a}} \ right) = c + \ frac {\ cancel {d — c}} {\ cancel {b — a}} \ cdot \ frac {\ cancel {b — a }} {\ cancel {d — c}} \ left ({y — c} \ right) = \ cancel {c} + y — \ cancel {c} = y. \]
Мы видим, что функция \ (f \) сюръективна.Поскольку \ (f \) и инъективно, и сюръективно, оно биективно. Следовательно, интервалы \ (\ left ({a, b} \ right) \) и \ (\ left ({c, d} \ right) \) равнозначны.
Наборы \ (\ mathbb {N} \) и \ (\ mathbb {Z} \)
Этот канонический пример показывает, что множества \ (\ mathbb {N} \) и \ (\ mathbb {Z} \) равны. Чтобы доказать это, нам нужно найти биективную функцию из \ (\ mathbb {N} \) в \ (\ mathbb {Z} \) (или из \ (\ mathbb {Z} \) в \ (\ mathbb {N } \)).
Расположим все числа \ (z \ in \ mathbb {Z} \) в следующем порядке:
\ [0, — 1,1, — 2,2, — 3,3, — 4,4, \ ldots \]
Теперь пронумеруем эту последовательность натуральными числами \ (1,2,3,4,5, \ ldots \).В результате мы получаем отображение из \ (\ mathbb {Z} \) в \ (\ mathbb {N} \), которое описывается функцией
\ [n = f \ left (z \ right) = \ left \ {{\ begin {array} {* {20} {l}} {2z + 1,} & {\ text {if} \; z \ ge 0} \\ {2 \ left | z \ right |,} & {\ text {if} \; z \ lt 0} \ end {array}} \ right .. \]
Функция \ (f \) инъективна, потому что \ (f \ left ({{z_1}} \ right) \ ne f \ left ({{z_2}} \ right) \) всякий раз, когда \ ({z_1} \ ne { z_2}. \) Это также сюръективно, потому что для любого натурального числа \ (n \ in \ mathbb {N}, \) существует целое число \ (z \ in \ mathbb {Z} \) такое, что \ (n = е \ влево (г \ вправо).\) Следовательно, функция \ (f \) биективна, что означает, что оба множества \ (\ mathbb {N} \) и \ (\ mathbb {Z} \) равны:
\ [\ left | \ mathbb {N} \ right | = \ left | \ mathbb {Z} \ right |. \]
Мощность множеств \ (\ mathbb {N} \) и \ (\ mathbb {R} \)
Интересно сравнить мощности двух бесконечных множеств: \ (\ mathbb {N} \) и \ (\ mathbb {R}. \). Оказывается, \ (\ left | \ mathbb {N} \ right | \ ne \ left | \ mathbb {R} \ right |. \) Это было доказано Георгом Кантором в \ (1891 \), который показал, что существуют бесконечные множества, которые не имеют биективного отображения на множество натуральных чисел \ ( \ mathbb {N}.\) Это доказательство известно как диагональный аргумент Кантора.
Рассмотрим произвольную функцию \ (f: \ mathbb {N} \ to \ mathbb {R}. \) Предположим, что функция имеет следующие значения \ (f \ left (n \ right) \) для первых нескольких записей \ ( п: \)
Рис. 1.Теперь мы построим диагональ, которая покрывает десятичный знак \ (n \ text {th} \) в \ (f \ left (n \ right) \) для каждого \ (n \ in \ mathbb {N}). \) Эта диагональ помогает нам найти число \ (b \) в кодомене \ (\ mathbb {R} \), которое не соответствует никакому значению \ (f \ left (n \ right).\)
Возьмите первое число \ (\ color {# 006699} {f \ left (1 \ right)} = 0. \ color {# f40b37} {5} 8109205 \) и измените \ (1 \ text {st} \) значение десятичного разряда в другое значение, например \ (\ color {# f40b37} {5} \ to \ color {blue} {9}. \) Аналогичным образом возьмите второе число \ (\ color {# 006699} {f \ left (2 \ right)} = 5.3 \ color {# f40b37} {0} 159257 \) и измените десятичный знак \ (2 \ text {nd} \): \ (\ color {# f40b37} {0} \ в \ color {blue} {6}. \) Продолжайте этот процесс для всех \ (n \ in \ mathbb {N}. \) числа \ (b = 0. \ color {blue} {96 \ ldots} \) будет состоять из измененных значений в каждой ячейке диагонали.Ясно, что \ (f \ left (n \ right) \ ne b \) для любого \ (n \ in \ mathbb {N}. \). Это означает, что функция \ (f \) не сюръективна. Следовательно, нет биекции от \ (\ mathbb {N} \) к \ (\ mathbb {R}. \), Поэтому
\ [\ left | \ mathbb {N} \ right | \ ne \ left | \ mathbb {R} \ right |. \]
См. Решенные проблемы на странице 2.
Что такое мощность? — Определение с сайта WhatIs.com
КСм. Также целое число, натуральное число, рациональное число и действительное число.
Термин мощность относится к количеству кардинальных (основных) членов в наборе. Мощность может быть конечной (целое неотрицательное число) или бесконечной. Например, количество людей в США составляет приблизительно 270 000 000 человек; мощность множества целых чисел счетно бесконечна.
В таблицах количество строк (или кортежей) называется мощностью. На практике таблицы всегда имеют положительное целое число элементов. Причина этого проста: таблицы без строк или с отрицательным числом строк не могут существовать.Теоретически, однако, могут существовать таблицы со счетно бесконечной мощностью. Примером может служить таблица умножения неотрицательных целых чисел, в которой подразумеваются записи для всех возможных значений:
| 0 | 1 | 2 | 3 | .. |
| 1 | 1 | 2 | 3 | .. |
| 2 | 2 | 4 | 6 | .. |
| 3 | 3 | 6 | 9 | .. |
| : | : | : | : |
Концепция мощности представляет интерес для теоретиков множеств, потому что она использовалась для демонстрации того, что одни бесконечные множества больше других. Мощность набора действительных чисел больше, чем мощность набора целых чисел, даже если оба набора бесконечны.Мощность набора целых чисел называется aleph-null или aleph-naught; мощность множества действительных чисел называется алеф-единицей.
Одна из величайших загадок математики заключается в вопросе: «Какова мощность множества точек на геометрической прямой?» Обычно предполагается, что это алеф-он; считается, что набор точек на линии взаимно однозначно соответствует набору действительных чисел. Это отнюдь не тривиальное предположение, и оно стало известно как гипотеза континуума.
Последний раз обновлялся в сентябре 2005 г.
Что такое количество элементов в базе данных?
В базах данных много жаргона, и мощность — одно из тех слов, о которых опытные люди склонны забывать, что они когда-то не знали. Но если вы этого не знаете — а чтобы по-настоящему освоиться с кардинальностью требуется время, — это очень сбивает с толку, когда администратор баз данных просто помещает его в середину предложения, не замедляясь! Не бойся: я тебя поймал, как говорится.Количество элементов в базах данных означает две вещи. Для наших целей одно имеет гораздо большее значение, чем другое. Давайте сначала сделаем простой, а затем перейдем к тому, который важен для производительности запроса. Определение количества элементов, которое имеет большое значение для производительности запроса, — это количество элементов данных . Все дело в том, сколько различных значений содержится в столбце. Первое значение количества элементов — это когда вы проектируете базу данных — то, что называется моделированием данных. В этом смысле кардинальность означает, является ли отношение взаимно-однозначным, много-к-одним или много-ко-многим.Итак, вы действительно говорите о мощности отношения , . Официальное определение Cardinality, не связанное с базами данных, является математическим: количество значений в наборе. Применительно к базам данных значение немного иное: — количество различных значений в столбце таблицы по отношению к количеству строк в таблице . Повторяющиеся значения в столбце не учитываются. Однако мы обычно не говорим о мощности числа как о числе , . Чаще всего говорят просто о «высокой» и «низкой» мощности.Множество различных значений — это высокая мощность; много повторяющихся значений — это низкая мощность. Изобразите таблицу описания продукта в базе данных электронной коммерции: Столбец ProductID будет иметь большое количество элементов, потому что он, вероятно, является первичным ключом этой таблицы, поэтому он полностью уникален. Если в таблице тысяча строк, будет тысяча различных значений ProductID . Столбец Категория будет иметь много повторений и будет иметь низкую или среднюю мощность: может быть, 50 или 100 различных значений категории . Имя , вероятно, имеет большое количество элементов, если только в этой таблице нет большего, чем кажется на первый взгляд (например, несколько строк для разных цветов продукта и других вариантов). Количество элементов сильно влияет на производительность, поскольку влияет на план выполнения запроса.
 Всего в предлагаемом комплекте дидактических…
Всего в предлагаемом комплекте дидактических…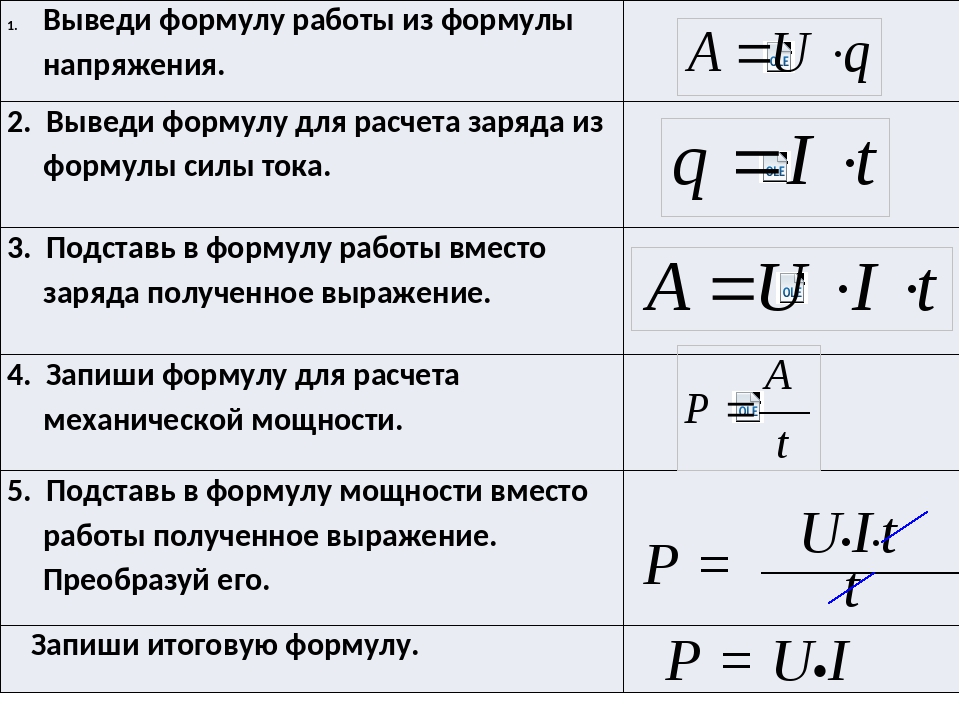 Все это включено одновременно. Находим действующую силу тока: I=(150+800+1300+1500)/220*0.95=17.94 Ампера. Для подобной нагрузки необходим кабель на 2.5 мм2 и автомат на 25 Ампер.
Все это включено одновременно. Находим действующую силу тока: I=(150+800+1300+1500)/220*0.95=17.94 Ампера. Для подобной нагрузки необходим кабель на 2.5 мм2 и автомат на 25 Ампер.
