Все формулы по магнетизму физика. Основные формулы по физике

Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с самого начала – дело не самое быстрое, а у нас на счету каждая минута.

Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.

Магнетизм: определение

Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.

Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.

Магнитная индукция

Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.

Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.

Магнитная индукция – это силовая векторная характеристика магнитного поля.

Она обозначается буквой B и измеряется в

Тесла (Тл ) . По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.

Кстати, вы найдете много интересных фактов на эту тему в нашей статье про .

Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.

Для определения направления вектора магнитной индукции существует правило правой руки . Приготовьтесь задействовать абстрактное и пространственное мышление!

Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.

Сила Ампера

Представим, что есть магнитное поле с индукцией B . Если мы поместим в него проводник длиной l , по которому течет ток силой I , то поле будет действовать на проводник с силой:

Это и есть сила Ампера . Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.

Сила Лоренца

Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца . Здесь важно отметить слово

«движущийся» , так на неподвижные заряды магнитное поле не действует.

Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v , а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:

Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.

Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:

Взаимодействие токов

Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.

В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:

Мю

– магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.

Во втором случае магнитная индукция в центре кругового витка с током равна:

Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. – это катушка, то есть множество круговых витков с током.

Пусть их количество – N , а длина самого соленоилда – l . Тогда поле внутри соленоида вычисляется по формуле:

Кстати! Для наших читателей сейчас действует скидка 10% на

Магнитный поток и ЭДС

Если магнитная индукция – векторная характеристика магнитного поля, то

магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф .

S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В .

При изменении магнитного потока через контур в контуре индуцируется ЭДС , равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила , вы можете почитать в еще одной нашей статье.

По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.

Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:

L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн) . На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:

Формула для ЭДС самоиндукции:

Энергия магнитного поля

Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током

I и индуктивностью L равна:

Объемная плотность энергии поля:

Конечно, это не все основные формулы раздела физики « электричество и магнетизм» , однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в

Электричество и магнетизм формулы.

Закон Кулона

1. закон Кулона

2 .

напряженность электрического поля

3. модуль напряженности поля точечного заряда

4 . принцип суперпозиции

5. -вектор электрического момента диполя – дипольный момент

6.

2. Теорема Гаусса

7

8.

9. теорема Гаусса

10. теорема Гаусса

11.

12. — дивергенция поля

13

Потенциал электростатического поля

14. -работа сил электростатического поля по перемещению пробного заряда q в электрическом поле точечного заряда Q

15. — интегральный признак потенциальности электростатического поля

16. — приращение потенциала электростатического поля

17 . — убыль потенциала электростатического поля

18 . — нормировка потенциала (выбор начала отсчета)

19 . — принцип суперпозиции для

20. — квазистатическая работа сил поля при перемещении

по произвольному пути из т. 1 в т.2

21. — локальное соотношение между и

22. — потенциал точечного заряда

23. — потенциал диполя

24. — дифференциальный оператор Гамильтона («набла») в полярной системе координат

25 . — оператор Лапласа или лапласиан

26. — уравнение Лапласа

27. — уравнение Пуассона

4. Энергия в электростатике.

28. — энергия электростатического взаимодействия зарядов друг с другом

29 . — полная электростатическая энергия заряженного тела

30. — объемная плотность энергии (энергия, локализованная в единичном объеме)

31. — энергия взаимодействия точечного диполя с внешним полем

5. Проводники электростатике

32. — поле вблизи поверхности проводника

33. — электроемкость уединенного проводника

34. — емкость плоского конденсатора

35 . — емкость сферического конденсатора, образованного сферическими проводящими поверхностями радиусов а и b

36 . — энергия конденсатора

6. Электростатическое поле в диэлектриках

37. , — диэлектрическая восприимчивость вещества

38. — поляризованность (электрический дипольный момент единицы объема вещества)

39. — связь между напряженностью и поляризованностью

40 . теорема Гаусса для вектора в интегральной форме

41. — теорема Гаусса для вектора в дифференциальной форме

42. — граничные условия для вектора

43. — теорема Гаусса для вектора в диэлектриках

44 . — электрическое смещение

45. — интегральная и локальная теорема Гаусса для вектора

46. — граничные условия для вектора , где – поверхностная плотность сторонних зарядов

47. — связь и для изотропных сред

Постоянный ток

48. — сила тока

49 . — заряд, проходящий через сечение проводника

50. — уравнение непрерывности (закон сохранения заряда)

51. — уравнение непрерывности в дифференциальной форме

52 . — разность потенциалов для проводника, в котором не действуют сторонние силы, отождествляется с падением напряжения

53. — закон Ома

54. — закон Джоуля -Ленца

55. — сопротивление провода из однородного материала одинаковой толщины

56. — закон Ома в дифференциальной форме

57 . — величина, обратная удельному сопротивлению называется удельной электрической проводимостью

58 . — закон Джоуля –Ленца в дифференциальной форме

59. -интегральная форма закона Ома с учетом поля сторонних сил для участка цепи, содержащего ЭДС.

60 . — первый закон Кирхгофа. Алгебраическая сумма сил токов для каждого узла в разветвленной цепи равна нулю.

61. -второй закон Кирхгофа. Сумма напряжений вдоль любого замкнутого контура цепи равна алгебраической сумме ЭДС, действующих в этом контуре.

62 . — удельная тепловая мощность тока в неоднородной проводящей среде

Закон Био-Савара

63 . — сила Лоренца

64 . — если в некоторой системе отсчета электромагнитное поле является электрическим

(т.е. ), то в другой системе отсчета , движущейся относительно К со скоростью , компоненты электромагнитного поля отличны от нуля и связаны соотношением 64

65 . — если в некоторой системе отсчета электрически заряженное тело имеет скорость , то электрическая и магнитная компоненты электромагнитного поля, создаваемого его зарядом, связаны в этой системе отсчета соотношением

66 . — если в некоторой системе отсчета электромагнитное поле является магнитным (), то в любой другой системе отсчета, движущейся со скоростью относительно первой, компоненты и электромагнитного поля отличны от нуля и связаны соотношением

67. — индукция магнитного поля движущегося заряда

68 . — магнитная постоянная

6.

2. Теорема Гаусса

7 . — поток поля через произвольную поверхность

8. — принцип аддитивности потоков

9. теорема Гаусса

10. теорема Гаусса

11. — дифференциальный оператор Гамильтона («набла»)в декартовой системе координат

12. — дивергенция поля

13 . локальная (дифференциальная) теорема Гаусса

Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый магнитным полем . Следовательно, электрический ток, представляющий собой упорядоченное движение зарядов, тоже создает магнитное поле. Как и электрическое поле, магнитное поле не ограничено в пространстве, распространяется очень быстро, но все же с конечной скоростью. Его можно обнаружить только по действию на движущиеся заряженные тела (и, как следствие, токи).

Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B магнитной индукции. В системе единиц СИ за единицу магнитной индукции принят 1 Тесла (Тл). Если в магнитное поле с индукцией B поместить проводник длиной l с током I , то на него будет действовать сила, называемая силой Ампера , которая вычисляется по формуле:

где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику.

Для определения направления силы Ампера обычно используют правило «Левой руки» : если расположить левую руку так, чтобы линии индукции входили в ладонь, а вытянутые пальцы были направлены вдоль тока, то отведенный большой палец укажет направление силы Ампера, действующей на проводник (см. рисунок).

Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.

Момент сил, действующих на рамку с током

Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю. Если поменять направление тока, то силы Ампера поменяют своё направление, и рамка будет не сжиматься, а растягиваться. Если линии магнитной индукции лежат в плоскости рамки, то возникает вращательный момент сил Ампера. Вращательный момент сил Ампера равен:

где: S — площадь рамки, α — угол между нормалью к рамке и вектором магнитной индукции (нормаль — вектор, перпендикулярный плоскости рамки), N – количество витков, B – индукция магнитного поля, I – сила тока в рамке.

Сила Лоренца

Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I , находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца . Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B , двигающуюся со скоростью v , вычисляется по следующей формуле:

Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на положительно заряженную частицу, так же, как и направление силы Ампера, может быть найдено по правилу левой руки или по правилу буравчика (как и сила Ампера). Вектор магнитной индукции нужно мысленно воткнуть в ладонь левой руки, четыре сомкнутых пальца направить по скорости движения заряженной частицы, а отогнутый большой палец покажет направление силы Лоренца. Если частица имеет отрицательный заряд, то направление силы Лоренца, найденное по правилу левой руки, надо будет заменить на противоположное.

Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает . Поэтому модуль вектора скорости при движении частицы не изменяется. Если заряженная частица движется в однородном магнитном поле под действием силы Лоренца, а ее скорость лежит в плоскости, перпендикулярной вектору индукции магнитного поля, то частица будет двигаться по окружности, радиус которой можно вычислить по следующей формуле:

Сила Лоренца в этом случае играет роль центростремительной силы. Период обращения частицы в однородном магнитном поле равен:

Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R .

Теория о магнитном поле

Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I 1 и I 2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:

где: μ 0 – постоянная величина, которую называют магнитной постоянной . Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:

μ 0 = 4π ·10 –7 H/A 2 ≈ 1,26·10 –6 H/A 2 .

Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:

где: μ – магнитная проницаемость вещества (об этом чуть ниже). Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:

Силовыми линиями магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй — на юг. Отсюда название полюсов: северный (N ) и южный (S ). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N ) и южный (красным цветом или буквой S ). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом. Даже если магнит разломать, то у каждой части будет по два разных полюса.

Вектор магнитной индукции

Вектор магнитной индукции — векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику. Обозначается В , единица измерения — 1 Тесла. 1 Тл — очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.

Вектор магнитной индукции направлен по касательной к силовым линиям, т.е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.

Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:

В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки» : если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:

В случае прямого тока линии магнитной индукции — окружности, плоскости которых перпендикулярны току. Вектора магнитной индукции направлены по касательной к окружности.

Соленоид — намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):

Линии магнитного поля имеют вид замкнутых линий — это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.

Магнитные свойства вещества

Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ , для которой верно следующее:

Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики — кислород, платина, магний — несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков — железо, никель, кобальт — μ >> 1. Например, у железа μ ≈ 25000.

Магнитный поток. Электромагнитная индукция

Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:

где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре. Единица магнитного потока в системе СИ называется Вебером (Вб).

Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции ε инд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:

Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.

1. Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
2. Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.

При решении задач важно сразу определить за счет чего меняется магнитный поток. Возможно три варианта:

1. Меняется магнитное поле.
2. Меняется площадь контура.
3. Меняется ориентация рамки относительно поля.

При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S , вращающемся с угловой скоростью ω в магнитном поле с индукцией В :

Движение проводника в магнитном поле

При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:

где: α — угол, который измеряется между направлением скорости и вектора магнитной индукции. В неподвижных частях контура ЭДС не возникает.

Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω , то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:

Индуктивность.

Самоиндукция. Энергия магнитного поля

Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ , пронизывающий контур или катушку с током, пропорционален силе тока I :

Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).

Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:

где: n — концентрация витков на единицу длины катушки:

ЭДС самоиндукции , возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:

Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия W м магнитного поля катушки с индуктивностью L , создаваемого током I , может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI ):

Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):

Правило Ленца

Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.

На этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.

Выучить все формулы и законы в физике, и формулы и методы в математике . На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.

Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.

Успешное, старательное и ответственное выполнение этих трех пунктов позволит Вам показать на ЦТ отличный результат, максимальный из того на что Вы способны.

Нашли ошибку?

Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на почту. Написать об ошибке можно также в социальной сети (). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.

Сессия приближается, и пора нам переходить от теории к практике. На выходных мы сели и подумали о том, что многим студентам было бы неплохо иметь под рукой подборку основных физических формул. Сухие формулы с объяснением: кратко, лаконично, ничего лишнего. Очень полезная штука при решении задач, знаете ли. Да и на экзамене, когда из головы может «выскочить» именно то, что накануне было жесточайше вызубрено, такая подборка сослужит отличную службу.

Больше всего задач обычно задают по трем самым популярным разделам физики. Это механика , термодинамика и молекулярная физика , электричество . Их и возьмем!

Основные формулы по физике динамика, кинематика, статика

Начнем с самого простого. Старое-доброе любимое прямолинейное и равномерное движение.

Формулы кинематики:

Конечно, не будем забывать про движение по кругу, и затем перейдем к динамике и законам Ньютона.

После динамики самое время рассмотреть условия равновесия тел и жидкостей, т.е. статику и гидростатику

Теперь приведем основные формулы по теме «Работа и энергия». Куда же нам без них!

Основные формулы молекулярной физики и термодинамики

Закончим раздел механики формулами по колебаниям и волнам и перейдем к молекулярной физике и термодинамике.

Коэффициент полезного действия, закон Гей-Люссака, уравнение Клапейрона-Менделеева — все эти милые сердцу формулы собраны ниже.

Кстати! Для всех наших читателей сейчас действует скидка 10% на .

Основные формулы по физике: электричество

Пора переходить к электричеству, хоть его и любят меньше термодинамики. Начинаем с электростатики.

И, под барабанную дробь, заканчиваем формулами для закона Ома, электромагнитной индукции и электромагнитных колебаний.

На этом все. Конечно, можно было бы привести еще целую гору формул, но это ни к чему. Когда формул становится слишком много, можно легко запутаться, а там и вовсе расплавить мозг. Надеемся, наша шпаргалка основных формул по физике поможет решать любимые задачи быстрее и эффективнее. А если хотите уточнить что-то или не нашли нужной формулы: спросите у экспертов студенческого сервиса . Наши авторы держат в голове сотни формул и щелкают задачи, как орешки. Обращайтесь, и вскоре любая задача будет вам «по зубам».

основные формулы, законы и правила

Магнитное поле — это форма материи, окружающей движущиеся электрические заряды. Магнитное поле окружает проводники с током.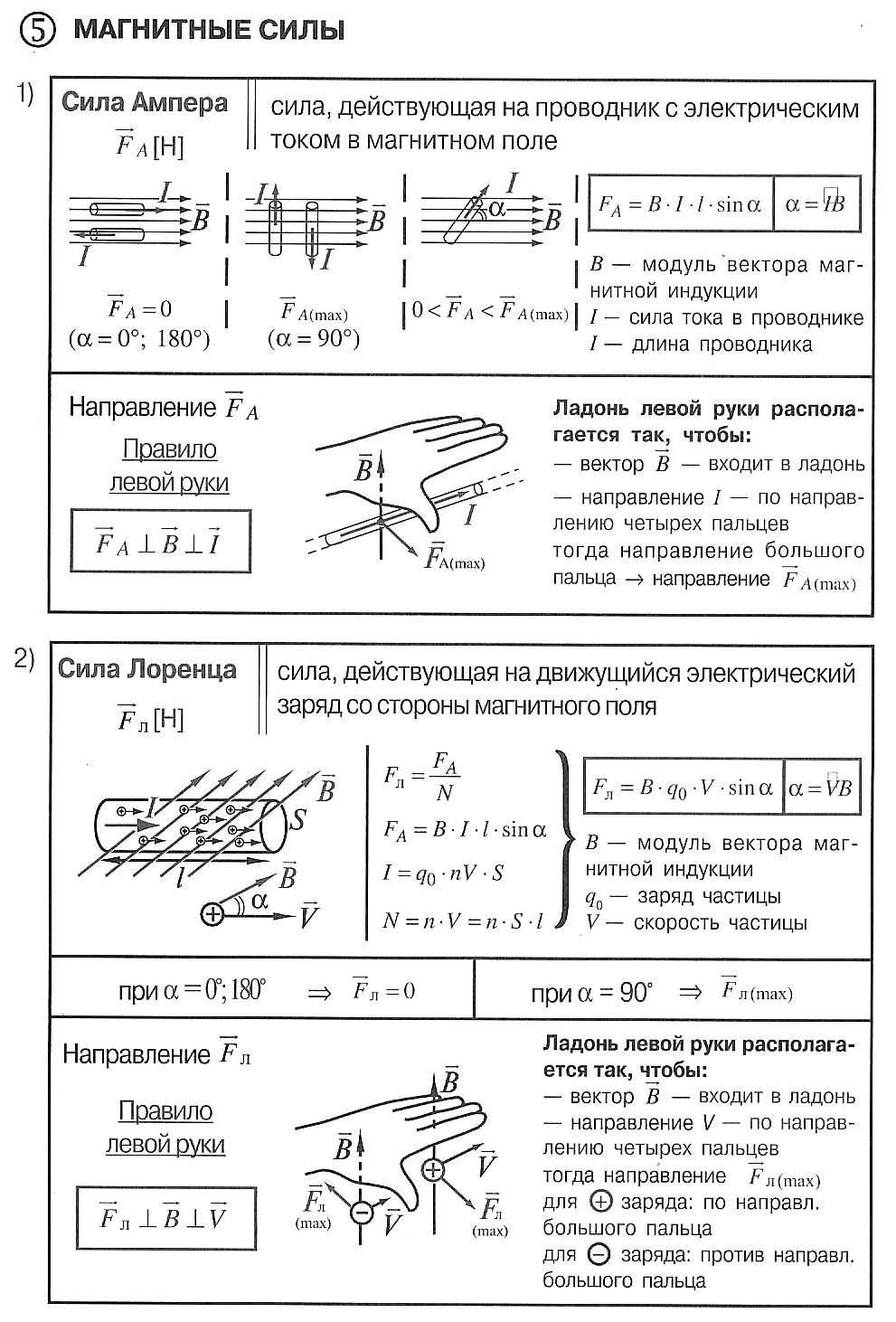

Силовой характеристикой магнитного поля является магнитная индукция.

Магнитная индукция — это величина, равная отношению максимального момента силы, вращающей контур с током в магнитном поле, к силе тока в этом контуре и его площади:

Другое определение магнитной индукции: магнитная индукция — это величина, равная отношению максимальной силы, действующей на проводник с током в магнитном поле, к силе тока в нем и длине этого проводника в магнитном поле:

Магнитная индукция — векторная величина. Вектор магнитной индукции совпадает по направлению с положительной нормалью к плоскости контура. За

направление положительной нормали п принято направление поступательного движения правого винта (буравчика), когда его головка вращается по току в контуре (рис. 208).

Правым винтом может служить ваша правая рука. Если свернуть четыре пальца правой руки в направлении тока в контуре, то большой палец, отставленный на 90°, покажет направление положительной нормали и вектора магнитной индукции.

Единица магнитной индукции в СИ — тесла (Тл).

Магнитное поле изображают графически с помощью магнитных силовых линий или линий вектора магнитной индукции.

В природе не существует магнитных зарядов, поэтому линии вектора магнитной индукции всегда замкнуты.

Магнитное поле является вихревым, в отличие от потенциального электростатического поля, линии которого всегда разомкнуты, т. к. начинаются и оканчиваются на электрических зарядах. Линии вектора магнитной индукции охватывают проводники с током. Линии вектора магнитной индукции поля прямого тока представляют собой концентрические окружности с центром на проводнике с током (рис. 209). Их направление можно определить с помощью правого винта (или с помощью вашей правой руки: если большой палец правой руки направить по направлению тока в проводнике, то четыре загнутых пальца покажут направление линии магнитной индукции). По мере удаления от проводника с током индукция магнитного поля этого тока уменьшается.

Магнитное поле, в каждой точке которого вектор магнитной индукции одинаков, называется однородным. Линии магнитной индукции однородного поля представляют собой прямые, расположенные на одинаковом расстоянии друг от друга. Чем гуще они располагаются, тем больше магнитная индукция.

Примером однородного магнитного поля является магнитное поле внутри длинного соленоида — катушки с током (рис. 210).

Линии магнитной индукции выходят из северного полюса N и входят в его южный полюс S.

Магнитное поле полосового магнита (рис. 211) наибольшее на его полюсах, а в центре его магнитная индукция равна нулю.

Если в однородное поле внести контур с током, расположив его плоскость параллельно линиям магнитной индукции, то на стороны контура, перпендикулярным линиям магнитной индукции, будет действовать пара сил Ампера, которая создаст максимальный вращающий момент сил , равный произведению индукции магнитного поля, силы тока в ней и ее площади:

Если плоскость контура расположена под углом к линиям вектора индукции однородного магнитного поля, то момент сил определяет формула

Здесь — угол между вектором индукции магнитного поля и нормалью к плоскости рамки.

Момент сил, вращающих контур с током в однородном магнитном поле, равен произведению индукции этого поля, силы тока в контуре, площади контура и синуса угла между векторами магнитной индукции и нормали к плоскости контура.

Если плоскость контура перпендикулярна линиям вектора магнитной индукции, то вращающий момент сил равен 0, а силы Ампера действуют в плоскости контура, деформируя его.

Направление силы Ампера можно определить по правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в ладонь, а четыре вытянутых пальца направить по току в проводнике, то большой палец, отставленный на 90 , покажет направление силы Ампера, действующей на этот проводник в данном магнитном поле (рис. 212).

Если проводник с током расположить параллельно магнитным линиям, то сила Ампера на него действовать не будет.

Сила Ампера

Величину силы Ампера определяет закон Ампера: сила F, действующая на проводник с током в однородном магнитном поле, равна произведению магнитной индукции этого поля В, силы тока в проводнике I, длины проводника в магнитном поле I и синуса угла а между направлением магнитного поля и направлением тока в проводнике:

Сила, с которой магнитное поле действует на движущийся в нем заряд, называется силой Лоренца.

Сила Лоренца

Сила Лоренца действующая на заряд q, движущийся в однородном магнитном поле, равна произведению индукции этого поля В на заряд, на скорость его движения v и на синус угла между направлением магнитного поля и направлением движения заряда

Определить направление силы Лоренца можно тоже по правилу левой руки: если ладонь левой руки расположить так, чтобы магнитные линии входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления движения отрицательного заряда), то большой палец, отставленный на 90″, покажет направление силы Лоренца.

Заряженная частица, влетевшая в однородное магнитное поле перпендикулярно его магнитным линиям, движется равномерно по окружности, охватывающей магнитные линии.

При этом сила Лоренца направлена по радиусу к центру окружности.

На рис. 213 положительно заряженная частица с зарядом q, влетевшая в направлении, показанном вектором v в однородное магнитное поле индукцией В, направленном за чертеж, движется вокруг магнитных линий против часовой стрелки.

Если заряженная частица влетает в магнитное поле под углом к магнитным линиям, то она станет двигаться по винтовой линии (рис. 214), вращаясь по окружности с линейной скоростью, равной нормальной составляющей вектора скорости usin а, и одновременно перемещаясь

равномерно вдоль линий вектора индукции магнитного поля с тангенциальной составляющей vcos а вектора скорости .

Расстояние х, которое она пролетит вдоль магнитной линии за один оборот, называется шагом винта. Поскольку вдоль магнитной линии частица движется с постоянной скоростью и, то шаг винта равен

Здесь Т — период, т.е. время одного оборота частицы вокруг магнитных линий.

Сила Лоренца всегда перпендикулярна вектору скорости и, следовательно, вектору перемещения заряда, поэтому она работы перемещения заряда в магнитном поле не совершает, вследствие чего кинетическая энергия заряда, движущегося в магнитном поле под действием силы Лоренца, не изменяется.

Если заряженная частица движется одновременно в электрическом и магнитном полях (т. е. в электромагнитном поле), то на нее действует обобщенная сила Лоренца, равная векторной сумме силы Лоренца, действующей на нее со стороны магнитного поля, и силы Кулона, действующей со стороны электрического поля.

Пусть в однородном магнитном поле индукцией находится некоторая площадка S (рис. 215).

Магнитный поток Ф, создаваемый однородным магнитным полем сквозь некоторую площадку, равен произведению индукции этого магнитного поля В на величину площадки S и на косинус угла а между вектором магнитной индукции и нормалью к площадке.

Если площадка S расположена перпендикулярно магнитным линиям однородного поля, то магнитный поток, пересекающий ее, максимален:

Если площадка S расположена параллельно магнитным линиям, то они ее не пересекают, поэтому магнитный поток через площадку в этом случае равен нулю.

Магнитный поток

Магнитный поток — скалярная алгебраическая величина, т. е. он может быть положителен и отрицателен, поскольку косинус угла может быть больше и меньше нуля.

Если магнитный поток пересекает замкнутую поверхность (представьте ее в виде надутого воздушного шарика), то, поскольку все магнитные линии непрерывны и замыкаются сами на себя, число входящих в эту поверхность магнитных линий, создающих отрицательный поток, будет равно числу выходящих магнитных линий, создающих численно такой же по модулю, но положительный поток. Поэтому полный поток вектора магнитной индукции сквозь замкнутую поверхность равен нулю. Это важное свойство магнитного поля свидетельствует об отсутствии в природе магнитных зарядов и вихревом характере магнитного поля.

Единица магнитного потока в СИ — вебер (Вб).

Когда магнитный поток сквозь площадь, ограниченную проводящим контуром, изменяется, в этом контуре возникает индукционный ток.

Правило Ленца: индукционный ток всегда направлен так, что своим магнитным полем он противодействует изменению магнитного потока, вызвавшего этот ток.

Обратимся к рис. 216, а). Когда магнитный поток сквозь контур, создаваемый внешним по отношению к контуру магнитным полем индукцией , нарастает , индукционный ток в контуре направлен так, что его магнитное поле индукцией (на рис. 216, а) оно изображено штриховыми стрелками), антинаправлено внешнему магнитному полю, противодействуя увеличению магнитного потока. Отметим, что направление тока связано с направлением своего магнитного поля правилом правого винта — буравчика. Когда же магнитный поток, создаваемый внешним магнитным полем индукцией убывает (рис. 216, б), индукционный ток в контуре изменяет свое направление на противоположное и при этом его магнитное поле оказывается сонаправленным с внешним полем . Теперь магнитное поле индукционного тока противодействует убыли магнитного потока, создаваемого внешним магнитным полем сквозь контур, поддерживая его.

Явление возникновения индукционного тока в контуре при изменении магнитного потока, пересекающего этот контур, называется электромагнитной индукцией. По закону Ома сила индукционного тока прямо пропорциональна ЭДС индукции и обратно пропорциональна сопротивлению контура В:

Закон Фарадея

Закон Фарадея для электромагнитной индукции: ЭДС электромагнитной индукции, возникающая в контуре при всяком изменении магнитного потока, пересекающего этот контур, равна скорости изменения магнитного потока, взятой со знаком минус,

Здесь — ЭДС индукции в контуре, — скорость изменения магнитного потока, пересекающего контур, N — число витков в контуре (безразмерное).

Эта формула справедлива, когда магнитный поток изменяется монотонно, т.е. когда за равные промежутки времени он изменяется на одинаковую величину и ЭДС индукции постоянна. Если же магнитный поток изменяется произвольно, то увеличиваясь, то уменьшаясь, что бывает при вращении контура в магнитном поле, то пользоваться этой формулой для определения мгновенного значения ЭДС индукции нельзя, по ней можно определить только среднее значение ЭДС индукции.

При произвольном изменении магнитного потока сквозь контур ЭДС индукции равна первой производной магнитного потока по времени, взятой со знаком минус:

Здесь — первая производная магнитного потока по времени.

Знак минус в этих формулах объясняется правилом Ленца.

Если контур, пересекаемый переменным магнитным потоком, содержит не один, а N витков, то ЭДС индукции в нем будет в N раз больше, чем в одном витке. При этом предыдущие формулы примут вид:

ЭДС индукции, возникающая в проводнике, движущемся поступательно в однородном магнитном поле под углом к магнитным линиям, равна произведению индукции этого поля на скорость проводника, на его длину в этом поле и на синус угла между вектором индукции магнитного и вектором скорости проводника:

ЭДС индукции , возникающая в контуре, вращающемся равномерно в однородном магнитном поле, равна произведению угловой скорости контура на индукцию В магнитного поля, на площадь контура S и на синус угла а между вектором магнитной индукции и нормалью к плоскости контура:

В случае, когда плоскость контура параллельна магнитным линиям, угол . Тогда ЭДС индукции в контуре будет максимальна.

Если контур содержит N витков, то ЭДС индукции в нем в N раз больше, чем в одном витке:

Явление возникновения ЭДС индукции и индукционного тока в контуре вследствие изменения тока, текущего в этом контуре, называется явлением самоиндукции.

Магнитный поток Ф сквозь катушку (или контур любой иной формы) прямо пропорционален силе тока в ней, т.е. между этими величинами существует прямо пропорциональная зависимость:

Здесь L — коэффициент пропорциональности между током и связанным с ним магнитным потоком. Он называется коэффициентом самоиндукции контура или его индуктивностью. Величина индуктивности зависит от формы и размеров самого контура, а также от магнитных свойств среды, и постоянна для данного контура. Индуктивность контура — скалярная положительная величина. Она не зависит от наличия или отсутствия тока в нем. Индуктивность катушек заводского изготовления указывается в их паспорте.

Единица индуктивности в СИ — генри (Гн).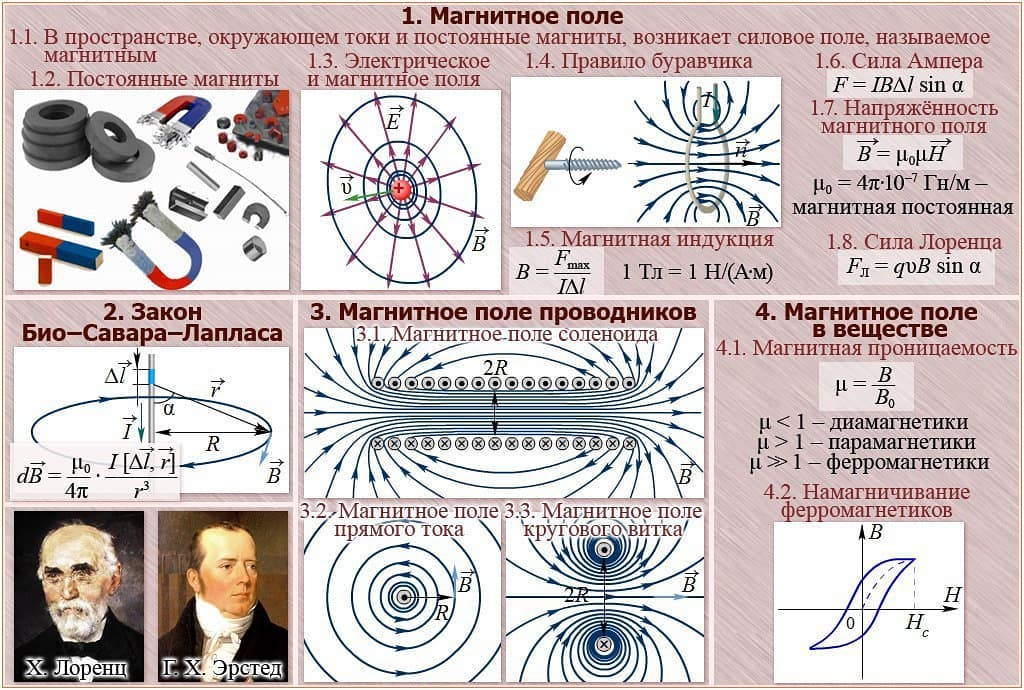

ЭДС самоиндукции , возникающая в контуре при изменении тока в нем, прямо пропорциональна скорости изменения силы тока в контуре, взятой со знаком «минус»:

Здесь —скорость изменения силы тока, т.е. изменение силы тока за единицу времени.

Если ток в контуре изменяется произвольно, то пользоваться этой формулой для определения мгновенной ЭДС самоиндукции нельзя, по ней можно определить лишь среднее значение ЭДС самоиндукции за время . Для определения мгновенного значения ЭДС самоиндукции в этом случае надо пользоваться формулой

Мгновенная ЭДС самоиндукции прямо пропорциональна первой производной силы тока по времени, взятой со знаком «минус».

Магнитное поле, как и всякое силовое поле, обладает энергией.

Энергия магнитного поля катушки с током соленоида равна половине произведения индуктивности этого соленоида на квадрат силы тока в нем:

Поскольку магнитное поле размыто по пространству, то, чтобы охарактеризовать его энергетические свойства, вводят величину, равную энергии магнитного поля в единице объема пространства, занятого этим полем. Эта величина называется объемной плотностью энергии магнитного поля .

Объемная плотность энергии магнитного поля равна отношению энергии магнитного поля к объему V пространства, занятого им:

Объемная плотность энергии магнитного поля прямо пропорциональна квадрату магнитной индукции этого поля и обратно пропорциональна относительной магнитной проницаемости окружающей среды:

Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти страницы:

3. Магнитное поле в вакууме и веществе Основные формулы:

Закон Био-Савара-Лапласа: ,

где _о=410^-7Гн/м.

Магнитная индукция в центре кругового тока: .

Магнитная индукция поля, создаваемого бесконечно длинным прямым проводником с током:

Магнитная индукция поля,

создаваемого отрезком проводника:

Связь магнитной индукции с напряженностью магнитного поля:

Магнитная индукция поля, создаваемого соленоидом в средней его части (или тороида на его оси):

Принцип суперпозиции магнитных полей:

Закон Ампера:

Сила взаимодействия двух прямых бесконечно длинных параллельных проводников с токами:

Магнитный момент контура с током: P_m=I ^. S .

Механический момент, действующий на контур с током, помещенный в однородное магнитное поле: M = p_m^.B sin 

Сила, действующая на заряд, движущийся в магнитном поле (сила Лоренца): F = q V B sin 

Закон полного тока:

Магнитный поток через плоский контур: Ф = B S cos  .

Потокосцепление, то есть полный магнитный поток, сцепленный со всеми витками соленоида или тороида: .

Магнитный поток сквозь тороид, сердечник которого составлен из двух частей, изготовленных из веществ с различными магнитными проницаемостями:

Примеры решения задач

Задача 18. Бесконечно длинный тонкий проводник с током I = 50А имеет изгиб (плоскую петлю) радиусом R = 10см. Определить в точке О магнитную индукцию В поля, создаваемого этим током.

Дано: I = 50А R = 10см	Решение.
В— ?

Магнитная индукция в точке О согласно принципа суперпозиции равна где— магнитные индукции поля в точкеО, создаваемые током, текущим соответственно на первом, втором и третьем участках проводника.

Векторы в соответствии с правилом буравчика направлены перпендикулярно плоскости чертежа в одну сторону (к нам), то есть геометрическое суммирование можно заменить алгебраическимВ = В₁ + В₂ +В₃ .

Магнитная индукция В₂ в точке О создается половиной кругового проводника с током, поэтому

Таким образом,

Ответ: B=8,05·10^-4 Тл.

Задача 19. По двум бесконечно длинным прямым параллельным проводам текут токи I₁ = 20 А и I₂ = 30 А в одном направлении. Расстояние d между проводами равно 10 см. Вычислить напряженность магнитного поля H в точке, удаленной от обоих проводов на одинаковое расстояние r = 10 см.

Дано: I1 = 20 А I 2 = 30 А d = 10см r = 10 см	Решение.
H — ?

Напряженность магнитного поля в точке А согласно принципа суперпозиции равна .Результирующая напряженность по модулю и направлению является диагональю параллелограмма, построенного на векторах

, где =60^о.

Отсюда .

Ответ: H=69,2 А/м.

Задача 20. Провод в виде тонкого полукольца радиусом R = 10 см находится в однородном магнитном поле (В = 50 мТл). По проводу течет ток I=10 А. Найти силу , действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а проводящие провода находятся вне поля.

Дано: R = 10 см В = 50 мТл = =50 . 10—3 Тл I = 10 А.	Решение.
F — ?

Выделим на проводе малый элемент dℓ с током I. На этот элемент тока действует сила Ампера. Направление этой силы определяется по правилу векторного произведения или по правилу левой руки.

Ввиду симметрии провода координатные оси удобно выбрать, как показано на рисунке.

Сила , действующая на весь провод, равна. Из соображений симметрии. Тогда. Так как вектор перпендикулярен вектору, тоdF=JBdℓ.

Из рисунка видно, что

Проинтегрировав последнее выражение в пределах от —π/2 до π/2, имеем

Сила сонаправлена с единичным вектором.

F = 2 I B R = 1 H .

Ответ: F = 1 H .

Задача 21. Электрон в атоме водорода движется вокруг ядра по круговой орбите некоторого радиуса. Найти отношение магнитного момента Р_m эквивалентного кругового тока к моменту импульса L орбитального движения электрона. Заряд электрона и его массу считать известными.

Дано: m = 9,1 . 10—31 кг e = 1,6 . 10—19 Кл	Решение.
Рm /L — ?

Эквивалентный круговой ток обусловлен движением электрона по круговой орбите с периодом T.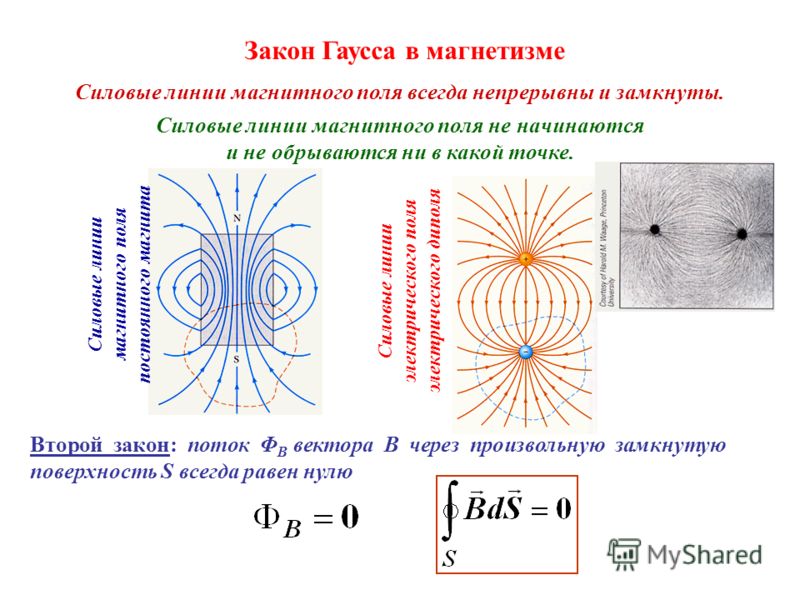

,

где V – скорость движения электрона по круговой орбите.

Магнитный момент кругового тока равен

.

Момент импульса электрона определяется по формуле L=mVr. Отсюда .

Ответ: .

Задача 22. Электрон движется в однородном магнитном поле с индукцией В=9 мТл по винтовой линии, радиус которой равен 1см и шаг h=7,8 см. Определить период Т обращения электрона и его скорость V.

Дано: В = 9 мТл R= 1 см h =7,8 см =7,8 . 10-2м m = 9,1 . 10—31 кг e = 1,6 . 10—19 Кл Т— ? V— ?

Решение.

Электрон в магнитном поле движется по винтовой линии под действием силы Лоренца. Вектор скорости V составляет угол  c направлением вектора магнитной индукции . Электрон движется по окружности радиусаR в плоскости, перпендикулярной линиям индукции со скоростью V_y=Vsinα; одновременно он движется и вдоль поля со скоростью .

Уравнение движения электрона по окружности имеет вид . Отсюда.

Шаг винтовой линии h равен пути, пройденному электроном вдоль поля за время, равное периоду обращения электрона Т по окружности h=V_xT=Vcosα·T, где . Таким образом, и угол равен .

Подставив значение sin  в формулу для скорости , получаем

V^.⁷ м/с.

Период обращения электрона Т = 3,97 ^. 10^—9 с.

Ответ: V^{. }⁷ м/с, Т = 3,97 ^. 10^—9 с.

Задача 23. Линии напряженности однородного электрического поля и линии индукции однородного магнитного поля взаимно перпендикулярны. Напряженность электрического поля 1 кВ/м, а индукция магнитного поля 1 мТл. Какими должны быть направление и модуль скорости электрона, чтобы его движение было прямолинейным?

Дано: Е = 1кВ/м =103 В/м В = 1 мТл 10—3 Тл	Решение.
V— ?

На электрон действуют две силы:

1. сила Лоренца , направленная перпендикулярно скоростии вектору магнитной индукции;

2. кулоновская сила , совпадающая по направлению с вектором напряженности электрического поля.

По первому закону Ньютона не будет испытывать отклонения при своем движении, если илиeE — eVB=0. Отсюда .

Ответ: V=10⁶ м/с.

Задача 24. Сколько витков имеет катушка, индуктивность которой L=1мГн, если при токе I = 1A магнитный поток сквозь катушку Ф=2мкВб ?

Дано: L= 1мГн I = 1A Ф = 2мкВб	Решение. Магнитный поток сквозь катушку равен Отсюда число витков
N— ?

Ответ: N = 500.

Задача 25. Железное кольцо диаметром D=11,4 см имеет обмотку из N=200 витков, по которой течет ток I₁=15 A. Какой ток I₂ должен проходить через обмотку, чтобы индукция в сердечнике осталась прежней, если в кольце сделать зазор шириной b=1 мм? Найти магнитную проницаемость  материала сердечника при этих условиях.

Дано: D = 11,4 см N = 200 I 1 = 15 A b = 1 мм B = const	Решение. Напряженность магнитного поля по средней линии кольца без воздушного зазора равна — длина средней линии кольца.
I 2 — ?	Пользуясь графиком зависимости индукции B от

напряженности H магнитного поля для железа, который находится в конце любого задачника по физике, определим индукцию магнитного поля в кольце. В = 1,8 Тл.

Пренебрегая рассеянием магнитного потока, можно принять, что индукция поля в воздушном зазоре равна индукции в железе.

По закону полного тока H₁ℓ+H_ob=I₂N, где — напряженность поля в зазоре. Отсюда токI₂ равен .

Пользуясь выражением для магнитного поля сквозь тороид, сердечник которой составлен из двух частей, запишем формулу для магнитной индукции в виде

. Отсюда магнитная проницаемость железа равна .

Ответ: I₂=21,8 А, μ≈180.

Задача 26. Проводник с активной длиной 15 см движется со скоростью 10 м/с перпендикулярно линиям индукции однородного магнитного поля с индукцией 2 Тл. Какая сила тока возникает в проводнике, если его замкнуть накоротко? Сопротивление цепи 0,5 Ом.

Дано: l = 15 см V10 м/с B = 2 Тл R = 0,5 Ом.	Решение.
I— ?

При движении проводника в магнитном поле в нем индуцируется ЭДС индукции, равная , где ∆Ф=B·∆S, ∆S – площадь, которую описывает проводник при своем движении. ∆S=ℓV∆t. Отсюда . Сила тока, возникающая в проводнике.

Ответ: I=6 А.

Задача 27. В однородном магнитном поле с индукцией 0,35 Тл равномерно с частотой 480 мин^—1 вращается рамка, содержащая 500 витков площадью 50 см² . Ось вращения лежит в плоскости рамки и перпендикулярна линиям индукции. Определить максимальную ЭДС индукции, возникшую в рамке.

Дано: B = 0,35 Тл 480 мин—1 N = 500 витков S = 50 см2 = = 5 . 10—3 м2	Решение. ЭДС индукции, возникающая в рамке, равна где Ф = N B S cos t — магнитный поток, сцепленный с рамкой.
in— ?	— циклическая частота.

Ответ: ε_max=44 В.

Задача 28. Рамка, имеющая форму квадрата, помещена в однородное магнитное поле индукции 0,1 Тл. Перпендикуляр к плоскости рамки составляет с направлением магнитного поля угол 60^о. Определить длину стороны рамки, если известно, что среднее значение ЭДС индукции, возникающей в рамке при выключении тока в течение 0,03 с, равно 10 мВ.

Дано: B1 = 0,1 Тл B2 = 0 in =10 мВ =0,032 c	Решение.
—?

ЭДС индукции, возникающая в рамке, равна

где Ф = B ^. S cos — изменение магнитного потока за время Δt,

B = B₂ — B₁ = — B₁, S=² .

. Отсюда .

Ответ: α=4·10^-2 м.

Задача 29. Имеется катушка длиной ℓ=20 см и диаметром D=2 см. Обмотка катушки состоит из N=200 витков медной проволоки, площадь поперечного сечения которой S=1 мм². Катушка включена в цепь с некоторой ЭДС. При помощи переключателя ЭДС выключается, и катушка замыкается накоротко. Через какое время t после выключения ЭДС ток в цепи уменьшится в 2 раза?

Дано: =20 см =0,2 м D=2 см = 0,02 м N=200 витков S=1 мм2 = 10—6 м2 1,7.10—8 Ом.м Io / I = 2	Решение. Вследствие явления самоиндукции при выключении ЭДС ток в цепи спадает по закону , где — сопротивление катушки,
t— ?	— индуктивность катушки,

площадь поперечного сечения катушки,

длина катушки.

, .

Отсюда .

Ответ: t=2,5·10^-4с.

Задача 30. Уравнение изменения со временем разности потенциалов на обкладках конденсатора в колебательном контуре имеет вид U= 50 cos10⁴t . Емкость конденсатора С=0,1мкФ. Найти период Т колебаний, индуктивность контура L, закон изменения со временем тока I в цепи и длину волны соответствующую этому контуру.

Дано: U= 50 cos 104t С=0,1мкФ	Решение. Из уравнения U = 50 cos104t следует, что Uo=50, 104 рад/с.
T — ? L — ? — ? I = I ( t ) — ?	. Отсюда . , , где V=3·108 м/с – скорость электромагнитных волн,

λ=6·10⁴ м.

Закон изменения тока I от времени имеет вид ,

где I_o=q_oω=U_oCω. Отсюда закон изменения тока в рассматриваемом контуре имеет вид:

Ответ: L=0,01 Гн, T= 2·10^-4 с, λ=6·10⁴ м,

I=-157·10^-3sin10⁴πt А.

Задача 31. Колебательный контур состоит из катушки с индуктивностью L=1,2мГн и конденсатора переменной емкости от С₁=12^.10^—12Ф до С₂=80^.10^—12 Ф. Определить диапазон длин электромагнитных волн, которые могут вызвать резонанс в этом контуре. Активное сопротивление контура принять равным нулю.

Дано: L= 1,2 мГн С1 = 12.10—12Ф С2 = 80.10—12 Ф v = 3 . 108 м/с	Решение. Длина электромагнитной волны, которая может вызвать резонанс в контуре, равна V.Т, где V — скорость электромагнитной волны,
1- ?, 2— ?	—период колебаний.

Следовательно, 

Ответ: λ₁=226 м, λ₂=585 м.

Задача 32. В колебательном контуре с индуктивностью 0,4 Гн и емкостью 20 мкФ максимальное значение силы тока равно 0,1мА. Каким будет напряжение на конденсаторе в момент, когда энергия электрического и магнитного полей будут равны? Колебания считать незатухающими.

Дано: L= 0,4 Гн С= 10 мФ=10—5Ф Imax= 0,1мА =10—4 А Wэ = Wм	Решение. Энергия колебательного контура в любой момент времени равна сумме энергий электрического и магнитного полей. . .
U— ?	Согласно закона сохранения энергии

. W_Э=W_М. . Отсюда.

Ответ: U=0,02 В.

Список литературы

1. Савельев И.В. Курс общей физики. Кн.2. – М.: Наука, 1999.

2. Трофимова Т.И. Курс физики. – М.: Высшая школа, 1998.

3. Детлаф А.А., Яворский Б.М. Курс физики. – М.: Высшая школа, 1998.

4. Волькенштейн В.С. Сборник задач по общему курсу физики. – СПб.: СпецЛит, 2001.

5. Чертов А.Г., Воробьев А.А. Задачник по физике. – М.: Интеграл-пресс, 1997.

Составители: СТРОКИНА Венера Рамазановна

ШАТОХИН Сергей Алексеевич

ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

к практическим занятиям

по курсу общей физики

Редактор Соколова О.А.

Подписано в печать 23.04.2003 Формат 60 х 84 1/16.

Бумага оберточная. Печать плоская. Гарнитура Times New Roman Cyr.

Усл. печ. л. 2,5. Усл.-кр.-отт. 2,4. Уч-изд.л. 2,4.

Тираж 350 экз. Заказ № .

Уфимский государственный авиационный технический университет

Редакционно-издательский комплекс УГАТУ

450000, Уфа-центр, ул. К.Маркса, 12

0

Основные формулы по физике — ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ

Физические законы, формулы, переменные	Формулы электричество и магнетизм
Закон Кулона: где q1 и q2 — величины точечных зарядов, ԑ1  — электрическая постоянная; ε — диэлектрическая проницаемость изотропной среды (для вакуума ε = 1), r — расстояние между зарядами.
Напряженность электрического поля: где Ḟ — сила, действующая на заряд q0 , находящийся в данной точке поля.
Напряженность поля на расстоянии r от источника поля: 1) точечного заряда 2) бесконечно длинной заряженной нити с линейной плотностью заряда τ: 3) равномерно заряженной бесконечной плоскости с поверхностной плотностью заряда σ: 4) между двумя разноименно заряженными плоскостями
Потенциал электрического поля: где W — потенциальная энергия заряда q0 .
Потенциал поля точечного заряда на расстоянии r от заряда:
По принципу суперпозиции полей, напряженность:
Потенциал: где Ēiи ϕi — напряженность и потенциал в данной точке поля, создаваемый i-м зарядом.
Работа сил электрического поля по перемещению заряда q из точки с потенциалом ϕ1 в точку с потенциалом ϕ2 :
Связь между напряженностью и потенциалом 1) для неоднородного поля: 2) для однородного поля:	1)    2)
Электроемкость уединенного проводника:
Электроемкость конденсатора: где U = ϕ1 — ϕ2 — напряжение.
Электроемкость плоского конденсатора: где S — площадь пластины (одной) конденсатора, d — расстояние между пластинами.
Энергия заряженного конденсатора:
Сила тока:
Плотность тока: где S — площадь поперечного сечения проводника.
Сопротивление проводника: ρ — удельное сопротивление; l — длина проводника; S — площадь поперечного сечения.
Закон Ома 1) для однородного участка цепи: 2) в дифференциальной форме: 3) для участка цепи, содержащего ЭДС:    где ε — ЭДС источника тока,    R и r — внешнее и внутреннее сопротивления цепи; 4) для замкнутой цепи:	1)   2)    3)    4)
Закон Джоуля-Ленца  1) для однородного участка цепи постоянного тока:     где Q — количество тепла, выделяющееся в проводнике с током,     t — время прохождения тока;  2) для участка цепи с изменяющимся со временем током:	1) 2)
Мощность тока:
Связь магнитной индукции и напряженности магнитного поля: где B — вектор магнитной индукции, μ √ магнитная проницаемость изотропной среды, (для вакуума μ = 1), µ0 — магнитная постоянная , H — напряженность магнитного поля.
Магнитная индукция (индукция магнитного поля):  1) в центре кругового тока      где R — радиус кругового тока,  2) поля бесконечно длинного прямого тока      где r — кратчайшее расстояние до оси проводника;  3) поля, созданного отрезком проводника с током     где ɑ1 и ɑ2 — углы между отрезком проводника и линией, соединяющей концы отрезка и точкой поля;  4) поля бесконечно длинного соленоида      где n — число витков на единицу длины соленоида.	1)   2)    3)    4)
Сила Лоренца: по модулю где F — сила, действующая на заряд, движущийся в магнитном поле, v — скорость заряда q, α — угол между векторами v и B.
Поток вектора магнитной индукции (магнитный поток через площадку S):  1) для однородного магнитного поля ,     где α — угол между вектором B и нормалью к площадке,  2) для неоднородного поля	1)   2)
Потокосцепление (полный поток): где N — число витков катушки.
Закон Фарадея-Ленца: где ԑi — ЭДС индукции.
ЭДС самоиндукции: где L — индуктивность контура.
Индуктивность соленоида: где n — число витков на единицу длины соленоида, V — объем соленоида.
Энергия магнитного поля:
Заряд, протекающий по замкнутому контуру при изменении магнитного потока через контур: где ∆Ф = Ф2 – Ф1 — изменение магнитного потока, R — сопротивление контура.
Работа по перемещению замкнутого контура с током I в магнитном поле:

Формула силы Лоренца в физике

Содержание:

Определение и формула силы Лоренца

Определение

Сила $\bar{F}$ , действующая на движущуюся заряженную частицу в магнитном поле, равная:

$$\bar{F}=q[\bar{v} \times \bar{B}](1)$$

называется силой Лоренца (магнитной силой).

Исходя из определения (1) модуль рассматриваемой силы:

$$F=q v B \sin \alpha(2)$$

где $\bar{v}$ – вектор скорости частицы, q – заряд частицы, $\bar{B}$ – вектор магнитной индукции поля в точке нахождения заряда, $\alpha$ – угол между векторами $\bar{v}$ и $\bar{B}$. Из выражения (2) следует, что если заряд движется параллельно силовым линиям магнитного поля,то сила Лоренца равна нулю. Иногда силу Лоренца стараясь выделить, обозначают, используя индекс: $\bar{F}_L$

Направление силы Лоренца

Сила Лоренца (как и всякая сила) – это вектор. Ее направление перпендикулярно вектору скорости $\bar{v}$ и вектору $\bar{B}$ (то есть перпендикулярно плоскости, в которой находятся векторы скорости и магнитной индукции) и определяется правилом правого буравчика (правого винта) рис.1 (a). Если мы имеем дело с отрицательным зарядом, тонаправление силы Лоренца противоположно результату векторного произведения (рис.1(b)).

вектор $\bar{B}$ направлен перпендикулярно плоскости рисунков на нас.

Следствия свойств силы Лоренца

Так как сила Лоренца направлена всегда перпендикулярно направлению скорости заряда, то ее работа над частицей равна нулю. Получается, что воздействуя на заряженную частицу при помощи постоянного магнитного поля нельзя изменить ее энергию.{2}}}}$ – релятивистский множитель Лоренца, c – скорость света в вакууме.

Сила Лоренца — это центростремительная сила. По направлению отклонения элементарной заряженной частицы в магнитном поле делают вывод о ее знаке (рис.2).

Формула силы Лоренца при наличии магнитного и электрического полей

Если заряженная частица перемещается в пространстве, в котором находятся одновременно два поля (магнитное и электрическое), то сила, которая действует на нее, равна:

$$\bar{F}=q \bar{E}+q[\bar{v} \times \bar{B}](4)$$

где $\bar{E}$ – вектор напряженности электрического поля в точке, в которой находится заряд. Выражение (4) было эмпирически получено Лоренцем. Сила $\bar{F}$, которая входит в формулу (4) так же называется силой Лоренца (лоренцевой силой). Деление лоренцевой силы на составляющие: электрическую $(\bar{F} = q \bar{E})$ и магнитную $(\bar{F}=q[\bar{v} \times \bar{B}])$ относительно, так как связано с выбором инерциальной системы отсчета. Так, если система отсчета будет двигаться с такой же скоростью $\bar{v}$, как и заряд, то в такой системе сила Лоренца, действующая на частицу, будет равна нулю.{2}}{R}(1.4)$$

Из выражения (1.3) получим скорость:

$$v=\frac{q B R}{m}(1.5)$$

Период обращения электрона по окружности можно найти как:

$$T=\frac{2 \pi R}{v}=\frac{2 \pi m}{q B}(1.6)$$

Зная период, можно найти угловую скорость как:

$$\omega=\frac{2 \pi}{T}=\frac{q_{e} B}{m}$$

Ответ. $\omega=\frac{q_{e} B}{m}$

Слишком сложно?

Формула силы Лоренца не по зубам? Тебе ответит эксперт через 10 минут!

Пример

Задание. Заряженная частица (заряд q, масса m) со скоростью vвлетает в область, где имеется электрическое поле напряженностью E и магнитное поле с индукцией B. Векторы $\bar{E}$ и $\bar{B}$ совпадают по направлению. Каково ускорение частицы в моментначалаперемещения в полях, если $\bar{v} \uparrow \bar{B} \uparrow \bar{E}$?

Решение. Сделаем рисунок.

На заряженную частицу действует сила Лоренца:

$$\bar{F}=q \bar{E}+q[\bar{v} \times \bar{B}](2.1)$$

Магнитная составляющая имеет направление перпендикулярное вектору скорости ($\bar{v}$) и вектору магнитной индукции ($\bar{B}$). Электрическая составляющая сонаправлена с вектором напряжённости ($\bar{E}$) электрического поля. В соответствии со вторым законом Ньютона имеем:

$$\bar{F}=q \bar{E}+q[\bar{v} \times \bar{B}]=m \bar{a}(2.2)$$

Получаем, что ускорение равно:

$$\frac{q \bar{E}+q[\bar{v} \times \bar{B}]}{m}=\bar{a}(2.3)$$

Если скорость заряда параллельна векторам $\bar{E}$ и $\bar{B}$, тогда $[\bar{v} \times \bar{B}]=0$, получим:

$$\bar{a}=\frac{q \bar{E}}{m}$$

Ответ. $\bar{a}=\frac{q \bar{E}}{m}$

Читать дальше: Формула силы натяжения нити.

определение, основные формулы, правило левой и правой руки

Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с  самого начала – дело не самое быстрое, а у нас на счету каждая минута.

Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Магнетизм: определение

Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.

Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.

Магнитная индукция

Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.

Изображение магнитного поля при помощи силовых линий

Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.

Магнитная индукция – это силовая векторная характеристика магнитного поля.

Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.

Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.

Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.

Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!

Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.

Сила Ампера

Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:

Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.

Сила Лоренца

Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.

Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:

Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.

Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:

Взаимодействие токов

Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.

В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:

Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.

Во втором случае магнитная индукция в центре кругового витка с током равна:

Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.

Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Магнитный поток и ЭДС

Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.

S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.

При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.

По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.

Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:

L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:

Формула для ЭДС самоиндукции:

Энергия магнитного поля

Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:

Объемная плотность энергии поля:

Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.

связь магнитного потока и ВМИ

Во всех областях электротехники, кроме электростатики, используется понятие о магнитном поле. Вектор магнитной индукции описывает силу и направление этого поля в определённом месте рядом с источником поля. Как и для всего в электротехнике, для расчета этого параметра используются соответствующие формулы. В этой статье рассказывается, как найти вектор магнитной индукции, как находить его направление и как найти модуль вектора магнитной индукции.

Силовые линии магнитного поля

Магнитное поле

Магниты известны людям много сотен лет. Ещё в Древней Греции использовали в качестве компаса намагниченную иголку. В 1820 году Ганс Эрстед обнаружил связь между магнетизмом и электромагнетизмом. Его опыты показали, что стрелка компаса, находящаяся возле проводника, поворачивается при прохождении по нему электрического тока так же, как и при приближении постоянного магнита. Это происходит потому, что при движении электрических зарядов всегда появляются электрический ток и магнитное поле. Параметры вектора магнитной индукции характеризуют магнитное поле в определённой точке, находящейся возле магнита.

Справка. Поле, все силовые линии которого являются замкнутыми, называется вихревым. Магнитное поле – это вихревое поле.

Наглядное отображение линий магнитной индукции

Для того чтобы наглядно увидеть линии индукции магнитного поля, есть два способа:

• Использовать компас. При этом поле стрелки взаимодействует с магнитом или проводником с током. В точке, в которой измеряется это направление, она располагается по направлению вектора индукции. Северным считается то, в которое будет направлен конец стрелки, обозначенный «N». При движении компаса вокруг прибора её направление будет меняться вместе с изменением направления силовых линий;
• Поместить провод или катушку под лист бумаги или стекло, а сверху насыпать железные опилки. Проводники можно также пропустить сквозь бумагу. При этом опилки расположатся вдоль силовых линий поля. Этот опыт демонстрирует также взаимодействие двух магнитов.

Вектор магнитной индукции

Все физические параметры делятся на две группы:

• Скалярные. Это такие величины, которые не имеют направления: вес, объём, электрическое напряжение или ток;
• Векторные. Это параметры, имеющие направление: скорость, ускорение или инерция.

Магнитная индукция – это векторная величина. Её направленность совпадает с касательной к линиям поля. Форма и направление линий индукции зависят от проводника.

Направление магнитной индукции

В прямом проводнике поле имеет форму кругов, перпендикулярно которых проходит этот проводник, а его центр совпадает с ними. Чем ближе к центру, тем больше силовых линий проходит через точку пространства и сильнее поле. Его направление определяется по правилу правой руки.

Правило правой руки

Если провод свернуть в кольцо, то поле приобретает форму тора (бублика). Если витков много, и длина превышает диаметр катушки, то внутри неё силовые линии идут равномерно и параллельно. Магнитные свойства этого прибора аналогичны постоянному магниту. Если обмотку намотать на сердечник, изготовленный из материала с высокой магнитопроницаемостью, то получится электромагнит, форма которого зависит от сердечника: плоский, квадратный или подковообразный. Направление магнитного поля, идущего через такие устройства, можно найти по правилу буравчика.

Правило буравчика

Модуль вектора

Вектор, кроме величины, имеет модуль, или размер, – это показатель, характеризующий численное значение параметра. Если сама магнитная индукция обозначается В, направленность – B→, то модуль обозначается |B|. Этот параметр зависит от тока и расстояния до проводника. Для определения модуля выражение имеет вид |В|=k*(I/r), где:

• k – коэффициент. Он зависит от конкретных условий. В катушке с магнитопроницаемым сердечником и большим количеством витков коэффициент больше, чем в прямом отрезке провода;
• I – сила тока. Чем она больше, тем сильнее создаваемое им поле и больше величина вектора;
• r – расстояние от места измерения до катушки или проводника. Чем ближе к магниту, тем плотнее расположены силовые линии, и больше модуль.

Рядом расположенные провода или катушки с электротоком влияют друг на друга. Сила этого взаимодействия находится по формуле:

F=|B|*I*l, где l – длина проводов.

Если эту формулу преобразовать по законам алгебры, чтобы определить вектор магнитной индукции, она примет следующий вид:

|B|=(F/(I*l).

С её помощью можно рассчитать величину вектора, зная силу взаимного влияния, силу тока и длину проводов.

Интересно. Это взаимодействие можно увидеть при изменении силы сварочного тока в проходящих рядом кабелях.

Магнитный поток

Параметр, количественно характеризующий уровень магнитного поля, проходящего через контур с протекающим по нему электрическим током или другую площадь, называется магнитный поток. Это скалярный параметр. Он зависит от индукции «В», площади поверхности «S» и «cos α» – косинуса угла, с которым линии магнитной индукции пересекают поверхность. Магнитный поток и вектор магнитной индукции связаны формулой:

Ф=|B|*S*cos α,

или, если преобразовать это выражение, получается:

|B|=Ф/(S*cos α), где S – площадь, через которую проходит поток в сантиметрах.

Следовательно, величина магнитного потока, проходящего перпендикулярно через 1 см2, количественно равна модулю магнитной индукции.

Интересно. Таким образом, в электродвигателе постоянного тока максимальное влияние обмотка возбуждения оказывает в положении якоря, при котором его обмотки параллельны.

Знание того, как рассчитывается направление магнитного поля, и как определяется модуль вектора магнитной индукции, а также формул, используемых при расчетах, необходимо при проектировании электродвигателей, а также во многих других областях электротехники.

Видео

Оцените статью:Магнитное поле

: определение, причины, формула, единицы и измерения (с примерами)

Обновлено 28 декабря 2020 г.

Ли Джонсон

Поля окружают нас повсюду. Будь то гравитационное поле, вызванное массой Земли, или электрические поля, создаваемые заряженными частицами, такими как электроны, везде есть невидимые поля, представляющие потенциалы и невидимые силы, способные перемещать объекты с соответствующими характеристиками.

Например, электрическое поле в области означает, что заряженный объект может отклониться от своего первоначального пути, когда он входит в область, а гравитационное поле из-за массы Земли удерживает вас на поверхности Земли, если вы этого не сделаете. некоторые работают над преодолением его влияния.

Магнитные поля являются причиной магнитных сил, а объекты, которые оказывают магнитные силы на другие объекты, делают это, создавая магнитное поле. Магнитные поля можно обнаружить по отклонению стрелок компаса, которые совпадают с силовыми линиями (магнитный север стрелки указывает на магнитный юг). Если вы изучаете электричество и магнетизм, изучение магнитных полей и магнитной силы станет важным шагом на вашем пути.

Что такое магнитное поле?

В физике в целом поля — это векторы со значениями в каждой области пространства, которые говорят вам, насколько сильным или слабым является эффект в этой точке, и о направлении эффекта.Например, объект с массой, такой как солнце, создает гравитационное поле, и в результате на другие объекты с массой, попадающие в это поле, действует сила. Вот как гравитационное притяжение Солнца удерживает Землю на орбите вокруг себя.

Дальше в солнечной системе, например, на орбите Урана, действует та же сила, но сила намного ниже. Он всегда направлен прямо на солнце; Если вы представите себе набор стрел, окружающих Солнце, все они указывают на него, но с большей длиной на близком расстоянии (более сильная сила) и меньшей длиной на больших расстояниях (более слабая сила), вы в основном вообразили гравитационное поле в Солнечной системе.

Таким же образом, объекты с зарядом создают электрические поля, а движущиеся заряды создают магнитные поля , которые могут вызвать магнитную силу в соседнем заряженном объекте или других магнитных материалах.

Эти поля немного сложнее по форме, чем гравитационные поля, поскольку они имеют петлевые линии магнитного поля, которые выходят из положительного (или северного полюса) и заканчиваются на отрицательном (или южном полюсе), но заполняют та же основная роль.Они похожи на силовые линии, которые говорят вам, как будет вести себя объект, помещенный в определенное место. Вы можете четко визуализировать это, используя железные опилки, которые будут совпадать с внешним магнитным полем.

Магнитные поля всегда дипольные поля , поэтому магнитных монополей нет. Обычно магнитные поля обозначаются буквой B , но если магнитное поле проходит через магнитный материал, он может поляризоваться и генерировать собственное магнитное поле.Это второе поле вносит вклад в первое поле, и их комбинация обозначается буквой H , где

H = \ frac {B} {\ mu_m} \ text {и} \ mu_m = K_m \ mu_0

, где μ ₀ = 4π × 10 ^{— 7} Гн / м (т.е. магнитная проницаемость свободного пространства), а K _м — относительная проницаемость рассматриваемого материала.

Величина магнитного поля, проходящего через данную область, называется магнитным потоком.Плотность магнитного потока связана с локальной напряженностью поля. Поскольку магнитные поля всегда диполярны, чистый магнитный поток через замкнутую поверхность равен 0. (Любые силовые линии, выходящие из поверхности, обязательно входят в нее снова, сокращаясь.)

Единицы измерения и измерения

Единица измерения магнитного поля в системе СИ. сила — тесла (Тл), где:

1 тесла = 1 Тл = 1 кг / А с ² = 1 В с / м ² = 1 Н / А м

Еще одна широко используемая единица измерения магнитного поля сила — это гаусс (G), где:

Тесла — довольно большая единица, поэтому во многих практических ситуациях более полезным выбором будет гаусс — например, магнит на холодильник будет иметь силу около 100 G, а Магнитное поле Земли на поверхности Земли составляет около 0.5 G.

Причины возникновения магнитных полей

Электричество и магнетизм фундаментально взаимосвязаны, потому что магнитные поля генерируются движущимся зарядом (например, электрическими токами) или изменяющимися электрическими полями, в то время как изменяющееся магнитное поле генерирует электрическое поле.

В стержневом магните или подобном магнитном объекте магнитное поле возникает в результате выравнивания нескольких магнитных «доменов», которые, в свою очередь, создаются движением заряженных электронов вокруг ядер их атомов.Эти движения создают небольшие магнитные поля внутри домена. В большинстве материалов домены будут иметь случайное выравнивание и компенсировать друг друга, но в некоторых материалах магнитные поля в соседних доменах выравниваются, и это создает более крупномасштабный магнетизм.

Магнитное поле Земли также создается движущимся зарядом, но в данном случае это движение расплавленного слоя, окружающего ядро ​​Земли, которое создает магнитное поле. Это объясняется теорией динамо , которая описывает, как вращающаяся электрически заряженная жидкость генерирует магнитное поле.Внешнее ядро ​​Земли содержит постоянно движущееся жидкое железо с электронами, движущимися через жидкость и генерирующими магнитное поле.

Солнце также обладает магнитным полем, и объяснение того, как это работает, очень похоже. Однако разные скорости вращения различных частей Солнца (то есть жидкообразного материала на разных широтах) со временем приводят к спутыванию силовых линий, а также ко многим явлениям, связанным с Солнцем, таким как солнечные вспышки и солнечные пятна. , и примерно 11-летний солнечный цикл.Солнце имеет два полюса, как стержневой магнит, но движение солнечной плазмы и постепенно возрастающая солнечная активность заставляют магнитные полюса переворачиваться каждые 11 лет.

Формулы магнитного поля

Магнитные поля, обусловленные различным расположением движущихся зарядов, должны быть получены индивидуально, но есть много стандартных формул, которые вы можете использовать, чтобы вам не приходилось каждый раз «изобретать колесо». Вы можете получить формулы практически для любого расположения движущегося заряда, используя закон Био-Савара или закон Ампера-Максвелла.Однако полученные формулы для простых схем электрического тока настолько широко используются и цитируются, что вы можете просто рассматривать их как «стандартные формулы», а не выводить их каждый раз из закона Био-Савара или Ампера-Максвелла.

Магнитное поле прямолинейного тока определяется по закону Ампера (более простая форма закона Ампера-Максвелла) как:

B = \ frac {μ_0 I} {2 π r}

Где μ ₀ соответствует определению ранее, I — ток в амперах, а r — расстояние от провода, на котором вы измеряете магнитное поле.

Магнитное поле в центре токовой петли определяется выражением:

B = \ frac {μ_0 I} {2 R}

Где R — радиус петли, а другие символы — как определено ранее.

Наконец, магнитное поле соленоида определяется выражением:

B = μ_0 \ frac {N} {L} I

Где N — количество витков, а L — длина соленоида. Магнитное поле соленоида в основном сосредоточено в центре катушки.

Примеры расчетов

Научиться использовать эти уравнения (и подобные им) — это главное, что вам нужно сделать при вычислении магнитного поля или результирующей магнитной силы, поэтому пример каждого из них поможет вам решить проблемы, с которыми вы, вероятно, столкнетесь.

Для длинного прямого провода, по которому течет ток 5 ампер (т. Е. I = 5 А), какова напряженность магнитного поля на расстоянии 0,5 м от провода?

Используя первое уравнение с I = 5 A и r = 0.{−4} \ text {T} \ end {align}

Другой пример расчета магнитного поля может работать немного по-другому — например, сообщая вам поле в центре соленоида и ток, но запрашивая N / Коэффициент L — но пока вы знакомы с уравнениями, у вас не будет проблем с ответом на них.

Магнитные термины, используемые в магнитных цепях. Определение и формулы

Магнит и магнетизм Важные термины, определения и формулы

Магнитное поле или магнитная индукция (B)

Магнит или электромагнит создает магнитное поле.Поле, в котором магнит притягивает или отталкивает магнитные материалы, такие как железо, сталь и т. Д., Может быть определено как сила, действующая на движущийся заряд,

F = qxvx B

Где

• F = Сила,
• V = скорость частиц,
• B = величина поля.

Полезно знать:

Это векторная величина, а единица магнитного поля в системе СИ — Тесла, где 1 Тесла = (Ньютон x секунда) / (кулон x метр) 10000 Гаусс.Формула для магнитного поля в СИ: B = µ _○ (H + M), а в CGS — B = H + 4π M.

Провод, по которому проходит постоянный ток или постоянный магнит, создает магнитостатическое (канцелярское) поле и его величина и направление остаются прежними. При переменном токе или пульсирующем постоянном токе проводник создает переменное магнитное поле, которое непрерывно меняет свое направление и величину.

Также прочтите

Сила магнитного поля (H)

Величина намагничивающей силы (сколько силы она имеет для намагничивания магнитных материалов, таких как железо, сталь и т. Д.) Называется силой магнитного поля, которая обозначается ( ЧАС).Он обратно пропорционален длине провода и прямо пропорционален току, проходящему по нему. В системе СИ единица измерения напряженности магнитного поля — ампер / метр (А / м), это векторная величина, а формула СИ для напряженности магнитного поля:

H = NI / 1c

, где 1c = магнитный путь в метрах.

Магнитный поток (Φ)

Проще говоря, Магнитное поле x площадь, перпендикулярная магнитному полю (B), называется Магнитным потоком, который обозначается Φ или Φ _м или Φ _B .Или это количество магнитного поля или магнитных силовых линий, проходящих через поверхность, такую ​​как проводящая область, пространство, воздух и т. Д. Единица измерения магнитного потока в системе СИ — Вб (Вебер). Формула для нахождения магнитного потока в системе СИ:

Φ = BAc

Где

Ac = площадь в м ²

А единицей измерения и формулой CGS для магнитного потока является Максвелл (м), а Φ = BAc Ac = площадь в см ² соответственно.

Намагничивание (M)

Состояние намагничиваемого материала или процесс намагничивания магнитных материалов.Это плотность дипольных моментов постоянного магнита или электромагнита в магнитных материалах. Или магнитный момент (м) на единицу объема (v) магнитным полем называется намагниченностью. Единица намагничивания в системе СИ — ампер / метр (А / м), также это векторная величина. Формула СИ для намагничивания:

M = m / V

, где

• m = общий магнитный момент
• и V = объем в м ³ .

Единица CGS и формула намагничивания: Emu / cm ³ и M = m / V соответственно, где m = общий магнитный момент, V = объем в см ³ и EMU = электромагнитные единицы.Это также может быть определено как M = (N / V) x m → M = nm ……. (N / V) = п. Где «m» — это магнитный момент, а «n» — это плотность магнитных моментов.

Магнитная проницаемость вакуума (µ _○ )

Говоря забавными словами, Perm = Разрешение и способность — это особенность или умение что-то делать. Т.е. проницаемость (µ) — это способность материала легко намагничиваться?

Магнитная проницаемость вакуума

Это величина сопротивления магнитному полю при формовании в вакууме.

Единица измерения проницаемости в системе СИ — (Г · м ⁻¹ ) или Ньютон на квадратный ампер (Н · А ⁻² ). Единица СИ и формулы для магнитной проницаемости вакуума: Ньютон / Ампер ² и µ _○ = 4πx10 ^-7 ≈ 1,2566370614 Гн · м ⁻¹ соответственно. Единица CGS магнитной проницаемости вакуума — 1.

Полезно знать: Противоположность магнитной проницаемости — это магнитная относительность.

Полезно знать: известное магнитное соотношение: B = µH, где µ — проницаемость, которая является скалярной величиной, B — магнитное поле, а H — сила намагничивания или напряженность магнитного поля.

Индуктивность (L)

Индуктивность — это свойство проводника, катушки или провода, которое препятствует изменению тока, протекающего через них. Изменение тока, протекающего по проводнику, создает напряжение, называемое обратной ЭДС или электродвижущей силой.

Равномерность Изменение тока, протекающего через проводник или катушку, вызывает в них напряжение, которое называется самоиндуцированной ЭДС, а в любых соседних катушках или проводниках — взаимная индуктивность. В системе СИ единица индуктивности (L) — это Генри «H», а формула:

L = µ _○ µ N ² Ac / 1c

Где

• N = Обороты
• Ac = Площадь в м ²
• 1c = магнитный путь в метрах

Единица CGS и формула индуктивности — Генри «H» (Джозеф Генри) и L = 0.4π мкН ² Ac / 1c x10 ^-8 соответственно

где;

• L = индуктивность
• N = витки
• Ac = площадь в см ²
• 1c = магнитный путь в см.

Полезно знать : 1 H = 1 Вт / А (Один Генри = 1 Вебер на Ампер)

Формула самоиндукции

L = µ _○ (N ² xA) / л

Где:

• L = по Генри
• μ _ο = проницаемость свободного пространства (4.π.10 ^-7 )
• N = Число витков
• A = Площадь внутреннего сердечника (π.r ² ) в м ²
• l = длина катушки в метрах

Формула взаимной индуктивности

M = μ _ο μ _r N ₁ N ₂ A / l

Где:

• µ _o = проницаемость свободного пространства (4 .π.10 ^-7 )
• µ _r = относительная проницаемость сердечника из мягкого железа
• N = в количестве витков катушки
• A = в площади поперечного сечения в м ²
• l = длина катушек в метрах

Связанные сообщения:

Voltage или E.М.Ф. (В)

Разница электрических потенциалов между двумя точками называется напряжением. Или работа, совершаемая на единицу заряда в статическом электрическом поле по перемещению заряда между двумя точками, поэтому уравнение принимает вид

V = W / q или E / q.

Где;

• В = напряжение
• E = энергия в джоулях
• q = заряд в кулонах

Или электрическая потенциальная энергия на единицу заряда называется напряжением.

По закону Ома напряжение = V = I x R, где I = ток в амперах и R = сопротивление в омах (Ом)

Единицей измерения напряжения в системе СИ является вольт (В) или джоуль на кулон.Где 1 В = 1 Джоуль / 1 Кулон

Формула СИ для напряжения:

В = -N dΦ / dt

Где;

• N = количество витков катушки
• dΦ = скорость изменения магнитного потока
• t = время

Полезно знать: Другие родственные слова, используемые для напряжений и ЭДС: Разница электрических потенциалов , Электрическое напряжение , Электрическое давление, разность потенциалов, Pd, ЭДС, электродвижущая сила и это скалярная величина, и это тип электрической энергии.

В следующей таблице показаны все вышеперечисленные основные термины, используемые в магнитных цепях, с единицами измерения СИ и СГС и формулами.

9046 / м)

Количество

Символ

Единица СИ

Уравнение СИ

Единица CGS

Уравнение CGS66

9046 904 904 904 904 904

B

Тесла (T)

B = µ ○ (H + M)

Gauss (G)

B = H + 4π M

1T = 10 4 G

Магнитное поле Прочность

H

Ампер / метр (А / м)

H = NI / 1c 1c = магнитный путь в м

Эрстед Oe

H = 0.4πNI / 1c 1c = магнитный путь в см

1A / м = 4πx10 -3 Oe

Магнитный поток

Φ

Weber (Wb)

Φ = BAc Φ = BAc м 2

Maxwell M

Φ = BAc Ac = площадь в см 2

1Wb = 10 8 M

Измеритель намагниченности

M

M = m / V m = общий магнитный момент, V = объем в м 3

Emu / cm 3 Где EMU = Электромагнитные блоки

M = m / V м = общий магнитный момент, V = объем в см 3

1 А / м = 10- 3 emu / см 3

Магнитная проницаемость вакуума

µ ○

Ньютон / Ампер 2

µ ○ 90 040 = 4πx10 -7 ≈ 1.2566370614 H · м −1

1

—

4πx10 -7

Индуктивность

L

Генри

L = µ ○ µN c Оборотов Ac = Площадь в м 2 1c = магнитный путь в м

Генри

L = 0,4π мкН 2 Ac / 1c x10 -8 N = Оборотов Ac = Площадь в см 2 1c = магнитный путь в см

1

Напряжение или ЭДС

В

Вольт

В = — NdΦ / dt N = Оборотов

В = 904 -10 -8 xNxdΦ / dt N = Обороты

1

Ниже приводится таблица в формате изображения для справки.

Похожие сообщения:

12.S: Источники магнитных полей (сводка)

Ключевые термины

Закон Ампера	физический закон, который гласит, что линейный интеграл магнитного поля вокруг электрического тока пропорционален току
Закон Био-Савара	уравнение, определяющее магнитное поле в точке, создаваемое токоведущим проводом
диамагнитные материалы	их магнитные диполи ориентированы противоположно приложенному магнитному полю; при снятии поля материал не намагничивается
ферромагнитные материалы	содержат группы диполей, называемых доменами, которые выравниваются по приложенному магнитному полю; когда это поле убирают, материал все еще намагничивается
гистерезис	свойство ферромагнетиков, которое наблюдается, когда магнитное поле материала исследуется по сравнению с приложенным магнитным полем; петля создается в результате перемещения приложенного поля вперед и назад
магнитные домены	группы магнитных диполей, которые выровнены в одном направлении и связаны друг с другом квантово-механически
магнитная восприимчивость	отношение магнитного поля в материале к приложенному в это время полю; положительные восприимчивости могут быть парамагнитными или ферромагнитными (выровненными по полю), а отрицательные восприимчивости — диамагнитными (выровненными противоположно полю)
парамагнитные материалы	их магнитные диполи частично выравниваются в том же направлении, что и приложенное магнитное поле; когда это поле убирается, материал не намагничивается
проницаемость свободного пространства	\ (\ displaystyle μ_0 \), мера способности материала, в данном случае свободного пространства, поддерживать магнитное поле
соленоид	тонкий провод, намотанный на катушку, которая создает магнитное поле при прохождении через нее электрического тока
тороид	Катушка в форме пончика, плотно намотанная на один сплошной провод

Ключевые уравнения

Проницаемость свободного пространства	\ (\ Displaystyle μ_0 = 4π × 10 ^ {- 7} T⋅m / A \)
Вклад в магнитное поле элемента тока	\ (\ Displaystyle дБ = \ гидроразрыва {μ_0} {4π} \ frac {Idlsinθ} {r ^ 2} \)
Закон Био – Савара	\ (\ displaystyle \ vec {B} = \ frac {μ_0} {4π} ∫_ {wire} \ frac {Id \ vec {l} × \ hat {r}} {r ^ 2} \)
Магнитное поле из-за длинного прямого провода	\ (\ Displaystyle B = \ гидроразрыва {μ_0I} {2πR} \)
Сила между двумя параллельными токами	\ (\ displaystyle \ frac {F} {l} = \ frac {μ_0I_1I_2} {2πr} \)
Магнитное поле токовой петли	\ (\ displaystyle B = \ frac {μ_0I} {2R} \) (в центре цикла)
Закон Ампера	\ (\ Displaystyle ∮ \ vec {B} ⋅d \ vec {l} = μ_0I \)
Напряженность магнитного поля внутри соленоида	\ (\ Displaystyle В = μ_0nI \)
Напряженность магнитного поля внутри тороида	\ (\ Displaystyle B = \ гидроразрыва {μ_oNI} {2πr} \)
Магнитная проницаемость	\ (\ Displaystyle μ = (1 + χ) μ_0 \)
Магнитное поле соленоида, заполненного парамагнитным материалом	\ (\ Displaystyle В = мкни \)

Сводка

12. {- 7} T⋅m / s \) — проницаемость свободного пространства.

Направление магнитного поля, создаваемого длинным прямым проводом, определяется правилом правой руки 2 (RHR-2): направьте большой палец правой руки в направлении тока, и пальцы согнуты в направлении магнитного поля. создаваемые им полевые петли.

12.4 Магнитная сила между двумя параллельными токами

• Сила между двумя параллельными токами \ (\ displaystyle I_1 \) и \ (\ displaystyle I_2 \), разделенными расстоянием r, имеет величину на единицу длины, определяемую выражением \ (\ displaystyle \ frac {F} {l} = \ frac {μ_0I_1I_2} {2πr} \).
• Сила притягивающая, если токи в одном направлении, и отталкивающая, если они в противоположных направлениях.

12.5 Магнитное поле токовой петли

• Напряженность магнитного поля в центре круговой петли определяется выражением \ (\ displaystyle B = \ frac {μ_0I} {2R} \) (в центре петли), , где R — радиус петли. . RHR-2 дает направление поля вокруг петли.

12.6 Закон Ампера

• Магнитное поле, создаваемое током, идущим по любому пути, является суммой (или интегралом) полей из-за сегментов вдоль пути (величина и направление, как для прямого провода), в результате чего возникает общая взаимосвязь между током и полем, известная как поле Ампера. закон.
• Закон Ампера можно использовать для определения магнитного поля по тонкой или толстой проволоке с помощью геометрически удобного пути интегрирования. Результаты соответствуют закону Био-Савара.

12.7 Соленоиды и тороиды

• Напряженность магнитного поля внутри соленоида

\ (\ Displaystyle B = μ_0nI \) (внутри соленоида)

, где n — количество петель на единицу длины соленоида. Поле внутри очень однородно по величине и направлению.

• Напряженность магнитного поля внутри тороида составляет

\ (\ displaystyle B = \ frac {μ_oNI} {2πr} \) (внутри тороида)

, где N — количество витков. Поле внутри тороида неоднородно и изменяется с расстоянием как 1 / r.

12,8 Магнетизм в веществе

• Материалы классифицируются как парамагнитные, диамагнитные или ферромагнитные в зависимости от того, как они ведут себя в приложенном магнитном поле.
• Парамагнитные материалы имеют частичное выравнивание своих магнитных диполей с приложенным магнитным полем.Это положительная магнитная восприимчивость. Остается только поверхностный ток, создающий магнитное поле, подобное соленоиду.
• Диамагнитные материалы имеют наведенные диполи, противоположные приложенному магнитному полю. Это отрицательная магнитная восприимчивость.
• Ферромагнитные материалы имеют группы диполей, называемых доменами, которые выравниваются по приложенному магнитному полю. Однако, когда поле снимается, ферромагнитный материал остается намагниченным, в отличие от парамагнитных материалов.Это намагничивание материала в зависимости от эффекта приложенного поля называется гистерезисом.

Авторы и авторство

Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Напряженность магнитного поля

— обзор

3.1 Схема компактных симметричных сверхпроводящих магнитов

Четыре компактных магнита с различной напряженностью магнитного поля (1, 3, 7 и 11.75 T) изображены для сравнения характерных черт конструкций. Все магниты имеют разное распределение поля, которое позволяет получить определенное расположение катушек, и они выделены в этом разделе. Мы также указываем на важные соображения, которые следует учитывать в отношении магнитов с низким и сильным полями, и на то, как они меняются при увеличении или уменьшении напряженности поля поля зрения.

На рисунках 4–7 соответственно представлены иллюстрации, связанные с конструкцией и функциями 1, 3, 7 и 11.Магниты 75 Т. Эти магниты были разработаны с использованием магнитной области, показанной на рисунке 2A. Домен делит магнитное поле на две несвязанные области. Источник выражения сферической гармоники (представленный на рисунке 1) или центр поля зрения помещается в центр тяжести домена. Конструкции магнитов 1, 3 и 7 Т предполагают использование сверхпроводящего провода из NbTi, подробные характеристики которого приведены в Sciver и Marken. ⁹ Следовательно, в наших конструкциях пиковое поле на любой катушке было ограничено величиной менее 9 Тл, и проводник при этой напряженности поля способен пропускать транспортный ток не более 250 А / мм. 4.2 К. В конструкции 11,75 Тл используется композит резерфордовской проволоки NbTi – Cu с критической плотностью тока 165 А / мм ² при 12 Т и 2,8 К, которая является целью для всех катушек и использовалась ранее. ⁴¹

Рис. 4. Конструкция магнита порядка 1 Т 14 градусов 4. Иллюстрации (A) распределения плотности тока MSE с местоположениями для начальных катушек затравки, (B) общее распределение магнитного поля, (C) окончательная компоновка катушки и связанное с ней внутреннее поле, (D) отсечка внешнего поля с 20 , 15, 10 и 5 G изолинии изнутри наружу и (E) напряжение относительно радиального направления внутри каждой из катушек.Знаки «+» в (C) указывают положительный транспортный ток, в противном случае транспортный ток отрицательный, и контуры соответствуют полю в (B).

Рис. 5. Конструкция магнита под углом 3 Т порядка 14 градусов и 6 градусов. Иллюстрации (A) распределения плотности тока MSE с местоположениями для начальных катушек затравки, (B) общее распределение магнитного поля, (C) окончательная компоновка катушки и связанное с ней внутреннее поле, (D) отсечка внешнего поля с 20 , 15, 10 и 5 G контуры изнутри наружу и (E) напряжение относительно радиального направления внутри каждой из катушек.Знаки «+» в (C) указывают положительный транспортный ток, в противном случае транспортный ток отрицательный, и контуры соответствуют полю в (B).

Рис. 6. Конструкция магнита 7 Т порядка 12 градусов и 4. Иллюстрации (A) распределения плотности тока MSE с местоположениями для начальных катушек затравки, (B) общее распределение магнитного поля, (C) окончательная компоновка катушки и связанное с ней внутреннее поле, (D) отсечка внешнего поля с 20 , 15, 10 и 5 G контуры изнутри наружу и (E) напряжение относительно радиального направления внутри каждой из катушек.Знаки «+» в (C) указывают положительный транспортный ток, в противном случае транспортный ток отрицательный, и контуры соответствуют полю в (B).

Рис. 7. Конструкция открытого магнита с 12 градусами и шестью магнитами порядка 11,75 Т. Иллюстрации (A) распределения плотности тока MSE с местоположениями для начальных катушек затравки, (B) общее распределение магнитного поля, (C) окончательная компоновка катушки и связанное с ней внутреннее поле, (D) отсечка внешнего поля с 20 , 15, 10 и 5 G контуры изнутри наружу и (E) напряжение относительно радиального направления внутри каждой из катушек.Знаки «+» в (C) указывают положительный транспортный ток, в противном случае транспортный ток отрицательный, и контуры соответствуют полю в (B).

На рисунках 4A, 5A, 6A и 7A изображены изолинии карты плотности тока вместе с размещением катушек затравки, используемых для оптимизации второго этапа. Затравочные катушки размещены в локальных положительных максимумах и отрицательных минимумах карты плотности тока MSE. Направление тока каждой катушки определяется полярностью этих локальных оконечностей.Также важно отметить, что локальные конечности на карте плотности тока MSE появляются по периметру магнитной области, и затравочные катушки для второго этапа оптимизации определяются соответственно.

Распределение магнитного поля окончательных конфигураций показано на рисунках 4B, 5B, 6B и 7B. Его контуры изображены как часть окончательной конфигурации катушек на рисунках 4C, 5C, 6C и 7C, где катушки с положительным транспортным током обозначены знаком «+», а другие катушки имеют отрицательный транспортный ток.Из графиков можно видеть, что для конфигурации катушки магнита 1 Т полное магнитное поле имеет тенденцию быть наибольшим между катушками среднего и внешнего слоев (то есть катушками 7 и 8 на рисунке 4B). Из напряженности поля 3 Тл магнита на рис. 5В видно, что максимальные поля теперь находятся между катушками внутреннего и среднего слоя (то есть катушками 7 и 8). В случае конфигураций 7 и 11,75 Тл, показанных на рисунках 6B и 7B, максимальные общие поля сместились к внутреннему диаметру магнита.Это важное наблюдение, поскольку проблемы пикового поля для сильнопольных магнитов, по-видимому, связаны с внутренними катушками, тогда как в конструкциях с низким полем может оказаться, что внутренние катушки испытывают меньше проблем, связанных с сильными магнитными полями. Следовательно, чтобы уменьшить пиковое поле сверхпроводящих катушек для магнитов с низким и средним полем, необходимо отрегулировать относительное расстояние между катушками в среднем слое и катушками во внутреннем или внешнем слое. Однако для сильнопольных магнитов пиковое поле можно уменьшить только за счет увеличения длины магнитной области и уменьшения плотности тока на сверхпроводящих катушках.

Рисунки 4D, 5D, 6D и 7D представляют собой контурные графики поля рассеяния, где контуры представляют собой линии 5, 10, 15 и 20 G снаружи внутрь. Во всех конструкциях линия 5 G простирается примерно на 5 м в целом. направления от центра поля зрения, что лучше, чем у клинических магнитов, предоставляемых основными производителями, с полем обзора 45–50 см.

На рисунках 4E, 5E, 6E и 7E изображены кольцевые напряжения отдельных катушек в радиальном направлении в средней плоскости каждой катушки. Особенно для высокопольного 11.75 Тл, расчет напряжения показывает, что самые внутренние катушки являются наиболее важными в конструкции, потому что они подвергаются наибольшим магнитным полям и напряжениям. Можно использовать другие сверхпроводники (то есть более дешевые) для создания внешних сверхпроводящих катушек, поскольку они находятся в пределах сверхпроводимости.

Конструкцию MSE 1 T можно сравнить с первичным магнитом на 1 Тл, описанным в Cheng et al . ²⁵ с использованием транспортного тока 110 А.Магнит Ченга имеет тот же внутренний диаметр и больший внешний диаметр (1,35 м по сравнению с нашими 1,15 м), меньшее поле обзора (30 см по сравнению с 40 см при размахе размаха в 1 ppm) и большее поле рассеяния (11,9 на 9,8 м). по сравнению с 7,8 на 7 м на линии 5 G).

В таблице 1 представлены интересующие характеристики, полученные для различных конструкций. В таблице 2 представлена ​​дополнительная информация о расположении катушек. Центральное расположение катушек с соответствующими радиальными и осевыми координатами задается как ( r _c , z _c ), а соответствующая катушка имеет размеры ( D _r , D _z ).Пиковое поле ( B _пик ) для каждой катушки сообщается вместе с расчетным кольцевым напряжением ( σ _θ ) с использованием соотношения BJr , где B — среднее осевое магнитное поле, J — плотность тока, а r — средний радиус. ⁴⁰

Таблица 1. Представляющие интерес характеристики, полученные из шести различных конструкций

90464002 2,0 9049

Спецификация	1 T	3 T	7 T	11.75 T	1 T A	1 T O
Порядок (внутренние гармоники пропали)	14	14	12	12	11	14 Градус (исчезновение внешних гармоник)	4	6	4	6	2	4
Длина (м)	1.00	1.44	1.943	1,40
Внутренний диаметр (м)	1,00	1,00	1,00	1,00	1,00	1,00
Наружный диаметр (м) 2,3	3,22	2,20	2,20
Радиальный угол обзора при 1 ppm (м)	0,40	0,46	0,43	0,58	0,34	0,56	0,56
0.40	0,46	0,41	0,56	0,35	0,66
Радиальный след при 5 G (м)	7,00	5,60	7,80 3 9046 9,20 Осевая зона охвата при 5 G (м)	7,8	6,15	9,15	10,60	10,40	7,80
Накопленная энергия (МДж)	33	58463 36	16
Пиковое кольцевое напряжение (МПа)	369	188	182	129	276	286
Пиковое магнитное поле	8.73	8,16	8,76	12,11	8,47	6,79
Плотность тока, А / мм 2

Критическая плотность тока резерфордовской проволоки NbTi / Cu, используемой в конструкции 11,75 Тл, составляет 165 А / мм ² при напряженности магнитного поля 12 Тл при 2,8 К. Критическая плотность тока используемой проволоки NbTi в других конструкциях — 250 А / мм ² при напряженности магнитного поля 9 Тл при 4.2 К. ( ^A асимметричный, ^O открытый).

Таблица 2. Конфигурации катушек для шести конструкций представлены

160

146,690

160 175 1754 9046 2 9046 2 9046 2 +

0,0970

0,003 89463 175

Магнит	Катушка	Полярность	I (А / мм 2 )	Объем (м 3 )	B пик (T)	r c (м)	z c (м)	D r (м)	D z (м)	σ θ (МПа)
1 T	1	+	160	0.0056	4,2145	0,5344	0,0122	0,0689	0,0243	155,171
	2	—	0,0123 4,446 9066 0,0128
	3	+	160	0,0088	4,0903	0,5236	0,1410	0,0472	0.0566	132,594
	4	—	160	0,0179	6,1822	0,5316	0,2217	0,0632	0,0850 19462
			5,5941	0,5433	0,3003	0,0866	0,0411	307,353
	6	—	160	0.0204	6,3448	0,5251	0,4003	0,0501	0,1233	278,592
	7	+	0,1183			8463	68,9890
	8	—	160	0,1161	8,7223	1,0832	0,4362	0,1336	0.1277	369,317
	9	+	160	0,0413	4,6549	1,1171	0,0446	0,0659	0,0893 344 9066 9066 9046 3 9046 1 9046 1 9046 3 175	0,0110	5,1712	0,5462	0,0173	0,0925	0,0347	83.0100
2	—	175 0.0082	5,0338	0,5212	0,0714	0,0424	0,0592	188,144
3	+	175	0,02134 0,0346 0,04
0,02134 904 124,006
4	—	175	0,0111	5,9871	0,5240	0,2335	0,0480	0.0703	179,269
5	+	175	0,0334	7,2336	0,5473	0,3353	0,0947	0,1025 9046 9046 9046 3 0,0947 9046 9046 0,1025 904	6,8989	0,5348	0,4538	0,0697	0,0924	88,2740
7	+	175	0.0623	7,7368	0,5495	0,6288	0,0990	0,1824	10,4410
8	—	0,0858 904		0,0856 904	175	0,0858 904 123,763
9	+	175	0,0862	7,3361	0,9800	0,4333	0,0600	0.2334	58.1230
10	—	175	0,0607	6,5604	0,9800	0,0821	0,0600 9066	0,1642	9066 9066 904 904 904 904 946 9461 9046 1 93,734	0,0477	7,0221	0,5526	0,0881	0,1052	0,1305	119,113
2	+	93.734	0,0715	7,0704	0,5504	0,3042	0,1008	0,2050	120,887
3		0,4654	54,0865
4	—	93,734	0,2175	5,8079	0,9611	0,7318	0.0777	0,4636	181,819
11,75 T	1	+	44,400	0,1912	11,757	0,6455
	44,400	0,2735	11,812	0,6455	0,3116	0,2910	0,2333	128,652
	3	44.400	1,3016	12,108	0,6455	1,0152	0,2910	1,0947	104,760
	4	73,9070
	5	—	44,400	0,3826	3,5121	1,5599	0,1953	0.1001	0,3907	93,8790
1 T A	1	—	155	0,0202	7,3588	0,5000			7,3588	0,5000
		— 0,346 2	2	+	155	0,0087	4,1991	0,5258	— 0,2235	0,0517	0,0511	175,085
		3 14	4,3260	0,5234	— 0,1425	0,0467	0,0741	94,1320
	4	+ 9066	155	0,00983 9046 0,05	83.1000
	5	—	155	0,0063	2,9329	0,5171	0,0271	0,0342	0.0567	52.2210
	6	+	155	0,0085	2,6471	0,5185	0,1149	0,0371	0,0706
	9046	2,3240	0,5153	0,2038	0,0307	0,0542	29,6750
	8	+	155	0.0086	2,6748	0,5188	0,3073	0,0377	0,0698	66,5320
	9	—	155			82.0880
	10	+	155	0,0338	4,4609	0,6525	0,5774	0,1823	0.0452	80,1380
	11	—	155	0,0697	2,2910	1,0904	— 0,0973	0,0192	0,5298 9046	0,0192	0,5298 904 9046 0,5657	8,4084	0,7269	— 0,3597	0,2338	0,5298	146,078
1 T O	1	17546 0.0068	2,8406	0,5496	0,3630	0,0760	0,0260	26,1530
	2	—	175	0,0061163 0,46 904 904 108,254
	3	+	175	0,0080	3,5979	0,5236	0,4744	0,0470	0.0520	123.876
	4	—	175	0,0142	5,7564	0,5243	0,5810	0,0490	0,0846 9046 9046 904 904 904 904 904 904 904 9046 9046 904	5,3065	0,6553	0,3754	0,0980	0,0510	182,115
	6	—	175	0.0404	6,1251	0,6731	0,6765	0,2030	0,0470	125,311
	7	+	0,0337 5404 175 285,821
	8	—	175	0,0753	6,7900	0,8922	0,3866	0,1840	0.0730	6,13800

Для каждой катушки было вычислено пиковое магнитное поле вместе со средним кольцевым напряжением. В таблице ( D _r , D _z ) указаны размеры катушки в центре ( r _c , z _c ) вдоль радиальное ( r ) и осевое ( z ) координатные направления. Кольцевое напряжение ( σ _θ ) для каждой катушки указано в последнем столбце.Предусмотрены все 12 катушек асимметричного магнита. Для симметричных магнитов предусмотрена только половина катушек. ( ^A асимметричный, ^O открытый).

Размеры магнитного поля — формулы, уравнения и производные

Физическая величина — это любая величина, которая может быть измерена устройством в единицах измерения. Весь список физических величин можно в общих чертах разделить на два типа, а именно: фундаментальные физические величины и производные физические величины.

В следующих разделах этой страницы дается краткое описание основной идеи физических величин и размерной формулы для магнитного поля. На странице также представлены различные единицы измерения.

Размерная формула магнитного поля = M1 T2 I -1

Физические величины

Все физические величины можно в целом разделить на два типа, а именно: основные или основные физические величины и производные физические величины. .В физике есть семь фундаментальных физических величин. Это масса, время, длина, электрический ток, температура, сила света и количество вещества. Эти семь величин называются измерениями физического мира. Вместо названий используются их первые буквы для обозначения базовых величин. Три механические величины: масса, длина и время представлены как M, L и T. Для обозначения размеров эти символы используются в квадратных скобках.

Важно отметить, что размеры физических величин и размеры их единиц совпадают. Это только характер единицы, представленной как [M], [L] и [T], а не ее величина. Каждая производная физическая величина представлена ​​в терминах своих основных физических величин с соответствующей степенью. Степени, до которых необходимо возвести фундаментальную физическую величину для получения производной величины, называются размерностями производной величины.

Подробнее о размерной формуле и размерном уравнении

Размерная формула — это сложное выражение, которое описывает, какие фундаментальные величины задействованы и как они участвуют в моделировании производной физической величины.Физическая величина и ее размеры уравниваются в уравнении, называемом уравнением размерностей. Другими словами, размерные уравнения — это уравнения, которые представляют размерность любой физической величины в терминах ее фундаментальных величин.

Магнитное поле

Область вокруг магнита, на которую действует сила этого магнита, называется Магнитным полем. Магнитные поля могут создаваться перемещением электрических зарядов. Магнитное поле проникает сквозь пространство и действует как движущая сила для перемещения электрических зарядов и магнитных диполей.

В случае стержневого магнита силовые линии магнитного поля сильнее на полюсах и слабее в середине стержневого магнита. Сила магнитного поля на обоих полюсах одинакова. Магнитное поле — это производная физическая величина. Размерная формула магнитного поля равна [M] 1 [T] -2 [I] -1.

Размерная формула магнитного поля

Размерная формула магнитного поля может быть определена как представление единиц магнитного поля в терминах фундаментальных физических величин с соответствующей мощностью.Размерная формула Магнитного поля задается как [M] 1 [T] -2 [I] -1. В этой формуле «M» представляет собой массу, «T» представляет время, а «I» представляет собой ток.

Вывод размерной формулы магнитного поля

Сила Лоренца задается уравнением

Сила = заряд x магнитное поле (B) x скорость

Вышеупомянутое уравнение можно переписать, чтобы найти магнитное поле как:

Магнитное поле = Сила x [Заряд x Скорость] -1 → (1)

Мы знаем, что скорость может быть записана в единицах расстояния и времени как:

Скорость = Расстояние x [Время] -1

Формула размеров скорости [L T-1] → (2)

Основная формула для электрического заряда:

Заряд = Электрический ток x время

Размерная формула для электрического заряда: [I1 T1] → (3)

Сила Лоренца определяется вторым законом движения Ньютона как:

Сила Лоренца = Масса x Ускорение → (4)

Но ускорение — это скорость изменения скорости, которая определяется как:

Ускорение = Скорость x [Время] — 1 → (5)

Подставляя (5) в (4) получаем

сила Лоренца = Масса x Скорость x [Время] -1

Формула размеров для силы Лоренца, таким образом, записывается как [ML T-2] → (6)

Подставляя измерения скорости, электрический заряд и сила Лоренца из (2), (3) и (6) в формуле для Магнитного поля, представленного как (1), получаем,

Следовательно, B = [ML T-2] {[I1 T1] [ L T-1]} — 1

B = [M1 L0 T-2 I-1]

Следовательно, магнитное поле можно представить в виде [M1 T2 I-1].

HSC Физический модуль 6 Электромагнетизм

Категория: Физика

Это Часть II серии пересмотров формул, охватывающая Модуль 6 (Электромагнетизм). Щелкните здесь, чтобы просмотреть ссылки на Модуль 5, Модуль 7 и Модуль 8.

Знание, где искать формулу, как ее применять и как ее интерпретировать, необходимо для успешной сдачи экзаменов HSC Physics или пробных экзаменов.Справочный лист — бесценный инструмент, поэтому в этом руководстве по пересмотру мы объясним данные формулы и дадим некоторое представление обо всех формулах и типах вопросов, в которых они применяются. Формулы описаны в тематическом порядке, который не всегда соответствует в том же порядке, в каком они даны в справочном листе. Однако понимание того, как они связаны и применяются, таким образом должно быть проще, поскольку многие формулы тематически «связаны». Кроме того, здесь не рассматриваются многие формулы 11-го года обучения, которые не имеют отношения к большинству вопросов по HSC Physics.

Электрические поля

Напряжение

Электрический потенциал определяется как количество энергии на единицу заряда заряженной частицы внутри электрического поля из-за ее положения. Это можно рассматривать как эквивалент гравитационной потенциальной энергии. Однако в физике нас больше интересует разность электрических потенциалов между двумя точками, а не $ ΔV $ или просто $ V $. Короче говоря, это также известно как напряжение между двумя точками. $$ V = \ frac {ΔU} {q} $$

Однородные электрические поля

Первая приведенная формула описывает напряженность однородного электрического поля между двумя металлическими пластинами.$$ E = \ frac {V} {d} $$ $ E $ представляет электрическое поле, а $ V $ — напряжение между двумя пластинами. Помните, что напряжение — это разница между двумя параллельными пластинами (в HSC Physics оно всегда должно быть положительным, поскольку мы вычисляем величину $ E $).

Электростатическая сила

Электростатическая сила — это сила, прилагаемая, когда объект или частица с зарядом $ q $ попадает в электрическое поле с напряженностью $ E $: $$ F = qE $$ E $ здесь представляет собой напряженность электрического поля. 2} $$ Эта формула иногда известна как формула силы Кулона.{-3} $
• $ q_1 $ и $ q_2 $ — это две платы соответственно
• $ r $ — расстояние между центрами двух заряженных частиц.

Направление электростатической силы в этом случае зависит от знака двух зарядов:

Работа

В справочном листе есть две формулы для расчета работы, совершаемой заряженной частицей при ее движении в электрическом поле. $$ W = qV $$ $$ W = qEd $$ В первом случае заряженная частица с зарядом $ q $ движется между двумя точками с напряжением $ V $.
Во втором случае заряженная частица с зарядом $ q $ перемещается на расстояние $ d $ внутри однородного электрического поля с напряженностью $ E $.

Здесь следует помнить, что если:
• Положительный заряд движется в том же направлении, что и силовая линия электрического поля, работа выполняется посредством частицы. Это движение спонтанное (происходит само по себе).
• Положительный заряд движется в направлении, противоположном силовой линии электрического поля, работа выполняется на частице . Это движение не является самопроизвольным (для его выполнения требуется внешняя энергия / работа).

Очевидно, что вышеупомянутые правила обратны для отрицательных зарядов.

Магнитные поля

Напряженность магнитного поля (плотность магнитного потока)

Магнитные поля возникают вокруг движущихся заряженных частиц, проводников с током, постоянных магнитов или электромагнитов. Как и другие поля, они определяются как области пространства, в которых происходят магнитные взаимодействия. Вы можете узнать больше о магнитных полях здесь.

Хотя в основном полезны в 11 классе, есть две формулы для расчета величины напряженности магнитного поля ($ B $): $$ B = \ frac {μ_0I} {2πr} $$ $$ B = \ frac {μ_0NI} {L} $$ Первая формула используется для расчета напряженности поля на расстоянии $ r $ от прямого токопровода с током $ I $.
Вторая формула используется для расчета напряженности поля внутри соленоида длиной $ L $, имеющего $ N $ витков, по которым проходит ток $ I $.

Направление силовых линий магнитного поля можно определить с помощью правила для правой руки:

Магнитный поток

Магнитный поток представляет собой количество силовых линий магнитного поля, проходящих через область. Обозначение магнитного потока $ Φ $ измеряется в Веберсах (Вб). Это зависит от площади, через которую проходят линии ($ A $), плотности магнитного потока ($ B $) и угла между силовыми линиями и нормалью к плоскости области ($ θ $).$$ Φ = BA \ cos {θ} $$ Мы можем использовать пример с количеством капель дождя (представляющих магнитный магнитный поток), проходящих через круговое кольцо под разными углами, чтобы понять концепцию магнитного потока и угла:

Отсюда следует, что:
• Максимальный магнитный поток через зону возникает, когда плоскость площадки перпендикулярна силовым линиям магнитного поля (θ = 0 °).
• Нулевой магнитный поток через зону возникает, когда плоскость площадки параллельна силовым линиям магнитного поля (θ = 90 °).

Магнитная сила на движущемся заряде

Каждый раз, когда заряженная частица с зарядом $ q $ движется в магнитном поле напряжённостью $ B $ со скоростью $ v $, на нее действует сила, равная: $$ F = qvB \ sinθ $$ Прост в использовании, вам просто нужно быть осторожным, чтобы избежать «ловушки» с углом. Угол $ θ $ здесь — угол между вектором скорости и силовыми линиями магнитного поля.

Вы также должны помнить, что направление силы определяется правилом для правой руки.2} {r} = qvB \ sinθ $$ $$ R = \ frac {mv} {qB \ sinθ} $$

Моторный эффект

Эффект двигателя и его применение в двигателях постоянного и переменного тока описано более подробно здесь.

Магнитная сила, действующая на проводник с током

Сила моторного эффекта — это магнитная сила, приложенная к проводнику с током длиной $ l $, находящемуся в магнитном поле: $$ F = liB \ sinθ $$ Несколько вещей, о которых следует соблюдать осторожность:
• Как и в случае движущихся зарядов, угол $ θ $ — это угол между силовыми линиями магнитного поля ($ B $) и током ($ I $).В большинстве случаев, когда катушка двигателя вращается в магнитном поле, это должно быть 90 градусов для двух сторон (константа) и, следовательно, $ \ sinθ = 1 $. Будьте очень осторожны с вопросами о ловушках, которые дают вам угол, но это не требуется для расчета силы моторного эффекта! Например, вопрос HSC Physics ниже:

Угол 30 ° вообще не должен использоваться в формуле силы моторного эффекта, поскольку угол между $ B $ и $ I $ фактически равен 90 ° (в 3-х измерениях). 30 ° по-прежнему полезно, чтобы найти длину проводника с помощью теоремы Пифагора.Попробуйте и посмотрите, правильно ли вы понимаете!
• Если у вас квадратная или прямоугольная катушка, вы должны применить формулу моторного эффекта для перпендикулярной и параллельной сторон поля отдельно (следовательно, углы будут 90 ° и 0 ° соответственно).
• Направление силы можно найти с помощью правила правой руки: большой палец — это направление тока, пальцы — направление силовых линий, а ладонь — направление силы моторного эффекта.

Магнитная сила на двух параллельных токоведущих проводниках

Эта формула представляет собой конкретное приложение силы воздействия двигателя, когда есть два параллельных проводника длиной $ l $, несущие токи $ I_1 $ и $ I_2 $ и разделенные расстоянием $ r $: $$ \ frac {F} {l} = \ frac {μ_0I} {2π} \ frac {I_1 I_2} {r} $$ Для этой формулы вам нужно помнить:
• Когда токи имеют одинаковое направление, проводники притягиваются.
• Когда токи имеют противоположное направление, проводники отталкиваются. (Вы можете вывести эти правила, применяя правила для ладони и захвата правой руки).
• Вы должны применять эту формулу отдельно для каждого проводника; согласно третьему закону Ньютона, существует пара сил, по одной на каждый проводник с равными величинами и противоположными направлениями.
• Длина проводника $ l $ всегда равна длине перекрытия обоих проводов — если один из них длиннее, вы должны пренебречь дополнительной длиной.

Крутящий момент на обмотке двигателя

Эта формула представляет собой конкретное приложение крутящего момента к катушкам двигателя, по которым протекает ток в магнитном поле.$$ τ = nBIA \ sin {θ} $$ Здесь $ A $ представляет площадь катушки двигателя, а $ θ $ — угол между нормалью к плоскости катушки и линиями магнитного поля. На рисунке ниже угол воздействия двигателя для расчета силы по бокам составляет 90 °, поскольку левая и правая стороны перпендикулярны силовым линиям. Нормаль к плоскости катушки под углом и силовые линии также имеют угол 90 °.

Однако имейте в виду, что углы $ θ $ в формуле крутящего момента и формуле силы воздействия двигателя не всегда одинаковы; см. примеры здесь.

Электромагнитная индукция

Более подробную информацию о явлении электромагнитной индукции можно найти здесь. Электромагнитная индукция — одно из основных понятий физики HSC. Он описывает индукцию электродвижущей силы ($ EMF $) в результате ненулевой скорости изменения потока через контур с $ N $ витками: $$ EMF = -N \ frac {ΔΦ} {Δt} $$ Эта формула иногда известна как закон Фарадея / Ленца. Перво-наперво, $ EMF $ звучит как сила (ElectroMotive Force), но на самом деле это напряжение, поэтому оно измеряется в вольтах.Каждый раз, когда изменяется количество магнитных линий, проходящих через область (из-за перемещения компонентов друг относительно друга или изменения магнитного поля), отношение $ \ frac {ΔΦ} {Δt} $ не равно нулю. а значит и будет ЭДС. На следующей диаграмме представлен возможный пошаговый подход к рассуждению, которому вы можете следовать, чтобы объяснить большинство ситуаций.

Вы всегда должны пытаться определить изменение магнитного потока на шаге 2 с точки зрения увеличения / уменьшения магнитного потока (силовых линий) через область и их направления.Например, изменение может быть «более сильным потоком, выходящим за пределы страницы». На шаге 7 закон Ленца всегда заставляет поле $ B_2 $ противодействовать этому изменению — в нашем примере это будет «меньший поток, выходящий за пределы страницы», или «более высокий поток, проходящий внутри страницы» (оба утверждения эквивалентны).

Следует отметить, что более точный способ вычисления $ EMF $ — это мгновенная скорость изменения (однако в HSC Physics расчет не используется): $$ EMF = -N \ frac {dΦ} {dt} $$

Трансформаторы

Трансформатор — это электрическое устройство, используемое для изменения переменного напряжения между двумя частями цепи.Он основан на принципе электромагнитной индукции.

Существует несколько конфигураций и типов трансформаторов в зависимости от того, для чего они нужны. В HSC Physics мы почти всегда предполагаем, что трансформатор идеален; это означает, что потери мощности при преобразовании напряжения равны нулю. Формулы трансформатора имеют следующий вид: $$ \ frac {V_p} {V_s} = \ frac {N_p} {N_s} $$ $$ V_pV_s = I_pI_s $$ Приложения в вопросах физики HSC просты: индекс «$ p $» относится к первичной катушке, «$ s $» относится к вторичной катушке, и, очевидно, $ V $, $ I $ и $ N $ представляют напряжение, ток. и количество витков соответственно.

Электрические схемы (11 класс физики)

Электрический ток

Иногда вам, возможно, придется ссылаться или рассчитывать ток, исходя из первых принципов. Ток определяется как количество электрического заряда $ q $, протекающего через поперечное сечение за время $ t $, или скорость изменения заряда. $$ I = \ frac {q} {t} $$

Закон Ома

В редких случаях вы можете получить некоторые вопросы на экзаменах по физике HSC с использованием закона Ома. Напомним, что закон Ома показывает падение напряжения $ V $, которое происходит, когда ток $ I $ проходит через резистор с сопротивлением $ R $.2R $$ Потери мощности пропорциональны квадрату тока и сопротивления, поэтому вы можете использовать эти две формулы, чтобы объяснить, почему высокое напряжение важно при передаче (высокое напряжение означает низкий ток, а низкий ток означает низкие потери мощности).

GMW Associates — Векторы и компоненты магнитного поля

Магнитное поле в любой точке пространства является векторной величиной. Это означает, что есть направление, связанное с полем, а также его напряженность.Рассмотрим стрелку ниже:

Направление стрелки можно представить как направление магнитного поля. Длину стрелки можно представить как силу поля, то есть чем длиннее стрелка, тем сильнее поле. Назовите эту длину B.

Если я помещу набор осей на стрелку, я могу разделить поле на два компонента поля, а именно компонент x и компонент y. Назовите эти длины Bx и By.

Теперь я могу описать длину стрелки или силу магнитного поля в терминах компонентов x и y.Использование теоремы Пифагора:

Теперь представьте, что существует третье направление, так что стрелка B может указывать из (или внутрь) плоскости страницы. Теперь есть третий компонент, а именно Bz, который в нашем примере представляет собой длину компонента, простирающегося от страницы к краю стрелки.

Используя ту же математику, я могу теперь описать B как:

Величина B — это сила магнитного поля. Bx, By и Bz — три составляющие, измеренные трехосевым тесламетром (гауссметром).Одноосное измерительное устройство будет изменять свои показания в зависимости от того, в какую сторону ориентирована чувствительная ось по отношению к направлению магнитного поля. Чтобы получить полное представление о магнитном поле в любой точке пространства, необходимо не только значение B, но и направление, которое может быть выражено тремя компонентами: Bx, By и Bz.

No related posts.