Максимальная энергия конденсатора: Формула энергии конденсатора, Wp

Свободные электромагниные колебания в контуре, катушка, конденсатор, сохранение энергии. Курсы по физике

Подготовка к ЕГЭ по физике Задание 18 с решением и ответами

Колебательный контур — урок. Физика, 9 класс.

§ 9 учебника К.Ю.Богданова для 11 класса

— EVE University Wiki

Определите энергию, запасенную в каждом конденсаторе при максимальном заряде.

A Энергосберегающая беспроводная система зарядки конденсаторов через индуктивную связь

Калькулятор энергии конденсатора — Calculator Academy

Тестирование онлайн

Свободные электромагнитные колебания

Период колебаний. Формула Томсона

Энергия колебательного контура

Обзор

Управление конденсатором

Скорость перезарядки конденсатора

Конденсаторное оборудование

Навыки

Ссылки

Вопрос:

Конденсатор

Ответ и объяснение: 1

Формула энергии конденсатора

Определение энергии конденсатора

Как рассчитать энергию конденсатора?

FAQ

A. Концепция зарядки конденсаторов

B. Анализ времени зарядки и эффективности

C. Реализация системы зарядки конденсаторов

Содержание

Электромагнитные колебания. Основные понятия
Электромагнитные колебания

Рассмотрим электрическую цепь, состоящую из катушки индуктивностью L и конденсатора электроемкостью C. Если предварительно зарядить конденсатор (рис. a), то получим колебательный контур (рис. б).

1) В начальный момент времени конденсатор имеет максимальный заряд, обладает максимальной энергией W_C.

2) В следующий момент времени конденсатор начинает разряжаться. В цепи появляется ток. По мере разрядки конденсатора ток в цепи и в катушке нарастает. Из-за явления самоиндукции это происходит не мгновенно. Энергия катушки W_L становится максимальной.

3) Электрические заряды вновь накапливаются на конденсаторе, но обкладка конденсатора, первоначально заряженная положительно, будет заряжена отрицательно. Энергия конденсатора максимальная.

4) Конденсатор разряжается, но ток протекает уже в обратном направлении.

Этот процесс будет повторяться снова и снова. Возникнут электромагнитные колебания. Если отсутствуют потери (R=0), то сила тока, заряд и напряжение со временем изменяются по гармоническому закону.

Наименьший промежуток времени, в течение которого происходит переход зарядов с одной обкладки конденсатора на другую и обратно, называется периодом свободных электромагнитных колебаний.

Если пренебречь потерями (R=0), то полная энергия колебательного контура остается постоянной. Выполняется закон сохранения энергии.

Мгновенное значение силы тока в катушке

Мгновенное значение ЭДС самоиндукции

1. Установите соответствие между физическими величинами, описывающими протекание постоянного тока через резистор, и формулами для их расчёта. В формулах использованы обозначения: R — сопротивление резистора; I — сила тока; U — напряжение на резисторе; ∆t — промежуток времени.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) мощность тока

Б) работа тока

ФОРМУЛЫ

Решение.

А) Мощность тока определяется как P=UI, что соответствует формуле под номером 3.

Б) Работа тока определяется как . Учитывая, что U=IR, имеем:

что соответствует формуле под номером 1.

Ответ: 31.

2. Установите соответствие между физическими величинами, описывающими протекание постоянного тока через резистор, и формулами для их расчёта. В формулах использованы обозначения: R — сопротивление резистора; I — сила тока; U — напряжение на резисторе; ∆t — промежуток времени.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) сопротивление резистора

Б) работа тока

ФОРМУЛЫ

Решение.

А) В соответствии с законом Ома, сопротивление резистора можно записать по формуле , что соответствует формуле под номером 4.

Б) Работа тока – это величина, равная , где — мощность тока. Соответственно, для работы имеем: — формула под номером 2.

Ответ: 42.

3. На рисунке показана цепь постоянного тока. Внутренним сопротивлением источника тока можно пренебречь. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (E — ЭДС источника тока; R — сопротивление резистора).

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) сила тока через источник при замкнутом ключе К

Б) мощность источника при разомкнутом ключе К

ФОРМУЛЫ

Решение.

А) При замкнутом ключе К сопротивление внешней цепи равно . Тогда по закону Ома, сила тока в цепи, равна: , что соответствует формуле под номером 1.

Б) Мощность источника при разомкнутом ключе К определяется как — формула под номером 2.

Ответ: 12.

4. На рисунке показана цепь постоянного тока. Внутренним сопротивлением источника тока можно пренебречь. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (E — ЭДС источника тока; R — сопротивление резистора).

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) сила тока через источник при разомкнутом ключе К

Б) мощность источника при замкнутом ключе К

ФОРМУЛЫ

Решение.

А) При разомкнутом ключе К сопротивление внешней цепи равно R, и согласно закону Ома, сила тока в цепи равна — формула под номером 4.

Б) Мощность источника определяется как . При замкнутом ключе К сопротивление внешней цепи равно и мощность источника: — формула под номером 3.

Ответ: 43.

5. Конденсатор колебательного контура полностью заряжён от источника постоянного напряжения (см. рисунок). В момент t = 0 переключатель К переводят из положения 1 в положение 2. Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре после этого. Т — период электромагнитных колебаний.

Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

ГРАФИКИ

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

1) сила тока в катушке

2) энергия электрического поля конденсатора

3) энергия магнитного поля катушки

4) заряд левой обкладки конденсатора

Решение.

А) Так как график уходит в отрицательную область, то это не может быть энергией конденсатора или катушки. Сила тока в катушке тоже не подходит, т.к. в начальный момент времени, при переключении ключа К, она равна 0. Следовательно, это заряд левой обкладки конденсатора. В соответствии с рисунком он изначально заряжается положительно, а затем, в процессе колебаний, постоянно меняет свое значение.

Б) Под этот график подходит изменение энергии. Энергия электрического поля конденсатора не подходит, т.к. в начальный момент времени он заряжен и его энергия максимальна. Подходит энергия магнитного поля катушки, которая возрастает по мере разрядки конденсатора, а затем, убывает.

Ответ: 43.

6. Конденсатор колебательного контура полностью заряжён от источника постоянного напряжения (см. рисунок). В момент t = 0 переключатель К переводят из положения 1 в положение 2. Графики А и Б представляют изменения физических величин, характеризующих колебания в контуре после этого. T — период электромагнитных колебаний.

ГРАФИКИ

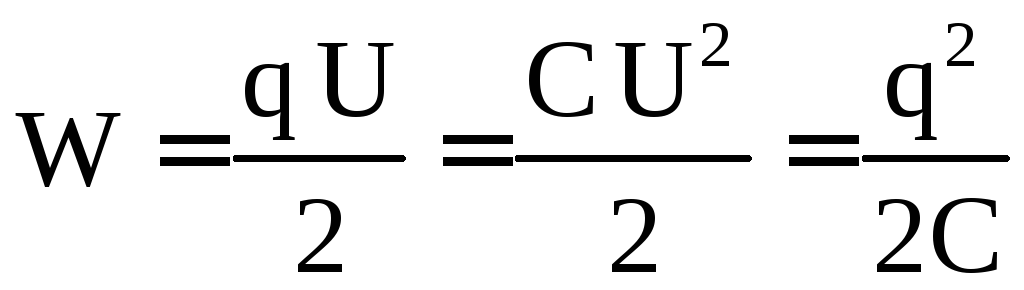
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

1) заряд правой обкладки конденсатора

2) энергия электрического поля конденсатора

3) энергия магнитного поля катушки

4) сила тока в катушке

Решение.

А) Так как график уходит в отрицательную область, то это не может быть энергией конденсатора или катушки. Сила тока в катушке тоже не подходит, т.к. в начальный момент времени, при переключении ключа К, она равна 0. Следовательно, это заряд на правой обкладке конденсатора. В соответствии с рисунком она изначально заряжается отрицательно, а затем, в процессе колебаний, постоянно меняет свое значение.

Б) Под этот график подходит изменение энергии. Энергия магнитного поля катушки не подходит, т.к. в начальный момент времени она не заряжена и ее энергия равна нулю. Подходит энергия электрического поля конденсатора, которая сначала имеет максимальное значение, а затем, убывает.

Ответ: 12.

7. Протон массой m и зарядом q движется перпендикулярно линиям индукции однородного магнитного поля B по окружности со скоростью v. Действием силы тяжести пренебречь.

Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) период обращения протона по окружности

Б) модуль ускорения протона

ФОРМУЛЫ

Решение.

Сила Лоренца, действующая на частицу со стороны магнитного поля равна

и так как в данном случае , то

Перепишем это выражение в соответствии со вторым законом Ньютона, получим:

откуда модуль ускорения протона равен:

Это центростремительное ускорение , поэтому:

откуда радиус окружности

Период обращения частицы по окружности – это время, за которое она проходит по этой окружности. Длина окружности равна

тогда время прохождения будет равно

Ответ: 14.

8. Протон массой m и зарядом q движется перпендикулярно линиям индукции однородного магнитного поля B по окружности со скоростью v. Действием силы тяжести пренебречь.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) модуль силы Лоренца, действующей на протон

Б) радиус окружности, по которой движется протон

ФОРМУЛЫ

Решение.

Сила Лоренца, действующая на частицу со стороны магнитного поля равна

и так как в данном случае , то

Перепишем это выражение в соответствии со вторым законом Ньютона, получим:

откуда модуль ускорения протона равен:

Это центростремительное ускорение , поэтому:

откуда радиус окружности

тогда время прохождения будет равно

Ответ: 23.

9. Идеальный колебательный контур состоит из конденсатора и катушки индуктивностью 4 мГн. Заряд на пластинах конденсатора изменяется во времени в соответствии с формулой (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимость от времени в условиях данной задачи. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) сила тока i(t) в колебательном контуре

Б) энергия WL(t) магнитного поля катушки

ФОРМУЛЫ

Решение.

А) Сила тока в цепи определяется как , что, в пределе означает производную от q(t) по времени t. Найдем , получим:

Б) Энергия магнитного поля катушки определяется как

Ответ: 13.

10. Идеальный колебательный контур состоит из конденсатора и катушки индуктивностью 4 мГн. Заряд на пластинах конденсатора изменяется во времени в соответствии с формулой (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимость от времени в условиях данной задачи.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) напряжение u(t) на конденсаторе

Б) энергия Wc(t) электрического поля конденсатора

ФОРМУЛЫ

Решение.

А) Сначала найдем емкость конденсатора в колебательном контуре из формулы Томпсона: , где — период колебаний.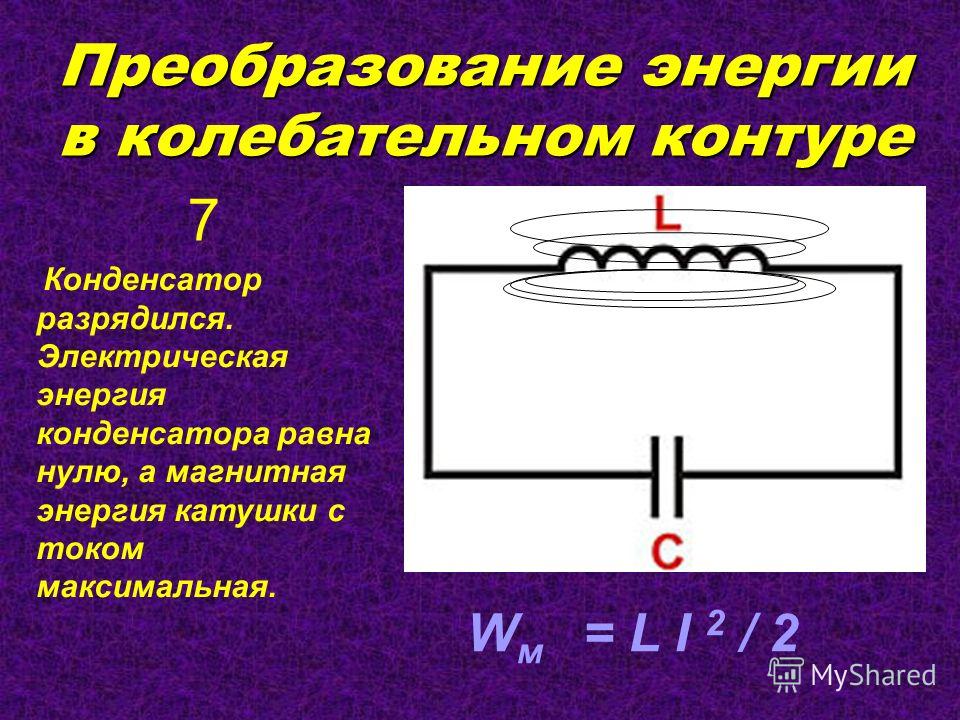 Из закона изменения заряда q(t) видно, что ω = 5000, следовательно, и емкость:

Ф.

Напряжение

Б) Энергия электрического поля конденсатора

Ответ: 24.

11. В первой экспериментальной установке отрицательно заряженная частица влетает в однородное магнитное поле так, что вектор скорости v0 перпендикулярен индукции магнитного поля (рис. 1). Во второй экспериментальной установке вектор скорости v0 такой же частицы параллелен напряжённости электрического поля (рис. 2). Установите соответствие между экспериментальными установками и траекториями движения частиц в них.

ДВИЖЕНИЕ ЧАСТИЦЫ

А) в первой установке

Б) во второй установке

ТРАЕКТОРИЯ

1) прямая линия

2) окружность

3) спираль

4) парабола

Решение.

А) На частицу со стороны магнитного поля будет действовать сила Лоренца, равная

и так как вектор скорости перпендикулярен индукции магнитного поля, то имеем и

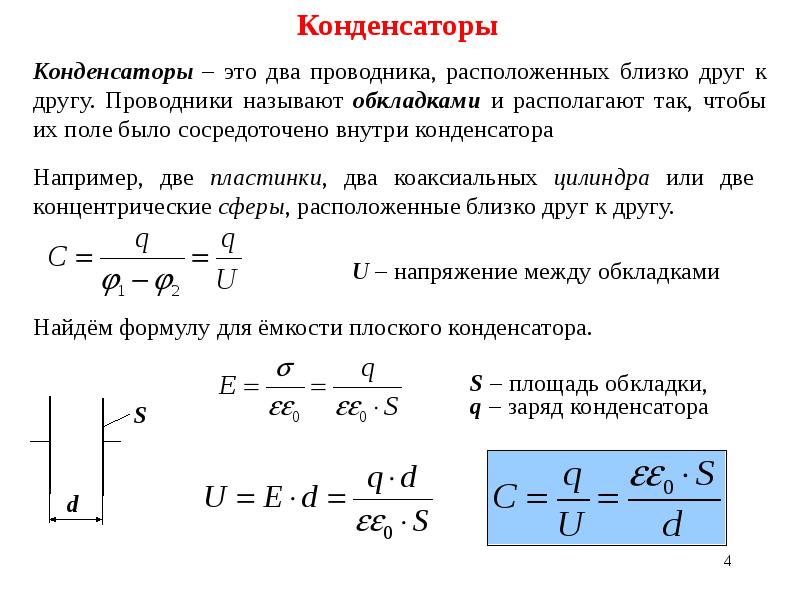
Направление силы Лоренца определяется правилом левой руки. Учитывая, что данное правило разработано для направления тока от «+» к «-», получаем направление силы Лоренца перпендикулярно направлению движения частицы (изначально она направлена вниз, так как отрицательная частица движется к положительному заряду). В результате частица будет описывать круговое движение. Ответ под номером 2.

Б) Здесь на частицу действует сила Кулона , направленная в сторону отрицательного заряда. Под действием этой силы, частица будет продолжать движение в горизонтальном направлении. Ответ под номером 1.

Ответ: 21.

12. В первой экспериментальной установке положительно заряженная частица влетает в однородное магнитное поле так, что вектор v0 перпендикулярен индукции магнитного поля (рис. 1). Во второй экспериментальной установке вектор v0 той же частицы параллелен напряжённости электрического поля (рис. 2).

Установите соответствие между экспериментальной установкой и траекторией движения частицы в ней.

ДВИЖЕНИЕ ЧАСТИЦЫ

А) в первой установке

Б) во второй установке

ТРАЕКТОРИЯ

1) спираль

2) прямая линия

3) окружность

4) парабола

Решение.

А) На частицу со стороны магнитного поля будет действовать сила Лоренца, равная

и так как вектор скорости перпендикулярен индукции магнитного поля, то имеем и

Направление силы Лоренца определяется правилом левой руки. Учитывая, что данное правило разработано для направления тока от «+» к «-», получаем направление силы Лоренца перпендикулярно направлению движения частицы (изначально она направлена вниз. В результате частица будет описывать круговое движение. Ответ под номером 3.

Б) На частицу в электрическом поле действует сила Кулона , направленная в сторону отрицательного заряда. Под действием этой силы, положительная частица будет тормозиться, а затем, полетит в обратном направлении, то есть движение будет происходить по прямой линии. Ответ под номером 2.

Ответ: 32.

13. Пучок монохроматического света переходит из воды в воздух. Частота световой волны — v, длина световой волны в воде — λ, показатель преломления воды относительно воздуха — n.

Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) скорость света в воздухе

Б) длина световой волны в воздухе

ФОРМУЛЫ

Решение.

А) Показатель преломления воды относительно воздуха n можно выразить формулой

, (1)

где — скорость света в воздухе; — скорость света в воде. Отсюда имеем:

и скорость света в воздухе

Б) Из формулы (1) имеем:

и длина волны в воздухе

Ответ: 32.

14. Пучок монохроматического света переходит из воздуха в воду. Скорость света в воздухе c, длина световой волны в воздухе — λ, показатель преломления воды относительно воздуха — n. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) длина световой волны в воде

Б) частота световой волны в воде

ФОРМУЛЫ

Решение.

А) Показатель преломления воды относительно воздуха n можно выразить формулой

, (1)

где — скорость света в воздухе; — скорость света в воде; v – частота волны (остается постоянной в разных средах). Отсюда получаем:

Б) Так как частота волны постоянна, то из формулы получаем

Ответ: 42.

15. Колебательный контур состоит из конденсатора ёмкостью C и катушки индуктивностью L. При свободных электромагнитных колебаниях, происходящих в этом контуре, максимальный заряд пластины конденсатора равен q. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. Сопротивлением контура пренебречь.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) максимальная энергия электрического поля конденсатора

Б) максимальная сила тока, протекающего через катушку

ФОРМУЛЫ

Решение.

А) Максимальная энергия электрического поля конденсатора равна

где — максимальное напряжение на конденсаторе. Отсюда получаем:

Б) Максимальное значение тока, протекающего через катушку, можно найти из формулы

где — циклическая частота колебаний колебательного контура. Объединяя эти выражения, имеем:

Ответ: 13.

16. Установите соответствие между формулами для вычисления физических величин в схемах постоянного тока и названиями этих величин. В формулах использованы обозначения: I — сила тока; U — напряжение; R — сопротивление резистора.

ФОРМУЛЫ

А)

Б)

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

1) заряд, протёкший через резистор

2) сила тока через резистор

3) мощность тока, выделяющаяся на резисторе

4) сопротивление резистора

Решение.

А) По закону Ома U=IR, следовательно — сопротивление резистора.

Б) Мощность тока, выделяемая на резисторе равна .

Ответ: 43.

17. В опыте нить накала лампочки расположена вблизи главной оптической оси тонкой линзы с фокусным расстоянием F перпендикулярно этой оси. Расстояние от линзы до спирали равно 2F. Сначала в опыте использовали рассеивающую линзу, а затем — собирающую. Установите соответствие между видом линзы, использовавшейся в опыте, и свойствами изображения. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

ВИД ЛИНЗЫ

А) линза рассеивающая

Б) линза собирающая

СВОЙСТВА ИЗОБРАЖЕНИЯ

1) действительное, перевёрнутое, равное по размерам

2) мнимое, прямое, уменьшенное

3) действительное, увеличенное, перевёрнутое

4) мнимое, увеличенное, перевёрнутое

Решение.

А) Рассеивающая линза с фокусным расстоянием F формирует мнимое прямое, уменьшенное изображение предмета (см. красная отметка на рисунке ниже), расположенного на расстоянии больше фокусного, в частности, 2F. Ответ 2.

Б) Собирающая линза формирует изображение предмета на расстоянии от линзы. Данное расстояние можно найти по формуле

где — расстояние от предмета до линзы. Получаем:

то есть предмет и его изображение находятся на одном расстоянии от линзы, следовательно, изображение является действительным, перевернутым и равное по размерам самому предмету. Ответ 1.

Ответ: 21.

18. В опыте нить накала лампочки расположена вблизи главной оптической оси тонкой линзы с фокусным расстоянием F перпендикулярно этой оси. Расстояние a от линзы до спирали равно 3F. Сначала в опыте использовали собирающую линзу, а затем — рассеивающую. Установите соответствие между видом линзы, использовавшейся в опыте, и свойствами изображения. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

ВИД ЛИНЗЫ

А) линза собирающая

Б) линза рассеивающая

СВОЙСТВА ИЗОБРАЖЕНИЯ

1) действительное, увеличенное, перевёрнутое

2) мнимое, прямое, уменьшенное

3) действительное, уменьшенное, перевёрнутое

4) мнимое, увеличенное, перевёрнутое

Решение.

А) Собирающая линза формирует изображение предмета на расстоянии от линзы. Данное расстояние можно найти по формуле

где — расстояние от предмета до линзы. Получаем:

то есть изображение предмета расположено ближе к линзе, чем сам предмет. Из этого следует, что изображение предмета получается уменьшенным. А так как используется собирающая линза, то оно также будет действительным и перевернутым. Ответ 3.

Б) Рассеивающая линза с фокусным расстоянием F формирует мнимое прямое, уменьшенное изображение предмета (см. красная отметка на рисунке ниже), расположенного на расстоянии больше фокусного, в частности, 3F. Ответ 2.

Ответ: 32.

19. На рисунке показана цепь постоянного тока. Сопротивления обоих резисторов одинаковы и равны R. Внутренним сопротивлением источника тока можно пренебречь. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (E — ЭДС источника тока). К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) тепловая мощность на резисторе R1 при замкнутом ключе К

Б) тепловая мощность на резисторе R1 при разомкнутом ключе К

ФОРМУЛЫ

Решение.

А) Тепловая мощность, выделяемая на резисторе R1, определяется выражением

При замкнутом ключе К сила тока, протекающая через сопротивление R1 равна

и выделяемая мощность

Б) При разомкнутом ключе К внешнее сопротивление цепи становится равным , а сила тока . Тогда выделяемая мощность равна

Ответ: 24.

20. Колебательный контур состоит из конденсатора ёмкостью C и катушки индуктивностью L. При свободных электромагнитных колебаниях, происходящих в этом контуре, максимальная сила тока, протекающего через катушку индуктивности, равна I. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. Сопротивлением контура пренебречь.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) максимальная энергия магнитного поля катушки индуктивности

Б) максимальный заряд конденсатора

ФОРМУЛЫ

Решение.

А) Максимальная энергия магнитного поля катушки индуктивности равна .

Б) Максимальный заряд конденсатора , где напряжение U можно найти из равенства максимальных энергий в конденсаторе и катушке:

откуда

и максимальный заряд конденсатора

Ответ: 32.

21. Установите соответствие между физическими величинами и их единицами измерения в системе СИ.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) Ёмкость конденсатора

Б) Сопротивление резистора

ЕДИНИЦЫ ИЗМЕРЕНИЯ

1) 1 Ф

2) 1 Ом

3) 1 Гн

4) 1 Тл

Решение.

А) Емкость конденсатора определяется в фарадах – ответ под номером 1.

Б) Сопротивление резистора определяется в омах – ответ под номером 2.

Ответ: 12.

22. Установите соответствие между физическими величинами и их единицами измерения в системе СИ.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) Магнитный поток

Б) Потенциал электростатического поля

ЕДИНИЦЫ ИЗМЕРЕНИЯ

1) 1 Тл

2) 1 В

3) 1 В/м

4) 1 Вб

Решение.

А) Магнитный поток измеряется в веберах – единица измерения под номером 4.

Б) Потенциал электростатического поля измеряется в вольтах – единица измерения под номером 2.

Ответ: 42.

23. Зависимость силы тока от времени в идеальном колебательном контуре описывается выражением , где Т — период колебаний. В момент энергия катушки с током равна энергии конденсатора: , — а напряжение на конденсаторе равно U. Каковы напряжение на конденсаторе в момент и амплитуда напряжения на конденсаторе?

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) напряжение на конденсаторе в момент

Б) амплитуда напряжения на конденсаторе

ФОРМУЛЫ ДЛЯ ИХ ВЫЧИСЛЕНИЯ

Решение.

Энергия катушки равна энергии конденсатора когда максимальная энергия уменьшается вдвое, то есть при

откуда напряжение на конденсаторе равно

. (1)

А) В момент сила тока равна

Используя выражение (1), напряжение на конденсаторе будет равно

Б) Максимальное напряжение на конденсаторе найдем из равенства энергий на конденсаторе и в катушке. Учитывая выражение (1), имеем:

Ответ: 32.

24. Зависимость силы тока от времени в идеальном колебательном контуре описывается выражением , где Т — период колебаний. В момент энергия катушки с током равна энергии конденсатора: , — а сила тока в контуре равна I. Каковы заряд конденсатора в момент и амплитуда заряда конденсатора?

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) заряд конденсатора в момент

Б) амплитуда заряда конденсатора

ФОРМУЛЫ ДЛЯ ИХ ВЫЧИСЛЕНИЯ

Решение.

Энергия катушки равна энергии конденсатора когда максимальная энергия уменьшается вдвое, то есть при

Так как сила тока в контуре в этот момент равна I, то из равенства

можно записать, что

, (1)

а напряжение

. (2)

Учитывая, что заряд на конденсаторе равен , а период колебаний , имеем:

. (3)

А) В момент сила тока равна

Следовательно, выполняется выражение (1) (по модулю) и заряд на конденсаторе в соответствии с (3) равен .

Б) Амплитуда заряда конденсатора достигается при максимальном токе в цепи, то есть когда ток (из выражения (1)) и заряд

Ответ: 41.

25. При подключении проводника к полюсам гальванического элемента на поверхности проводника появляются заряды: положительные вблизи положительного полюса, отрицательные вблизи отрицательного полюса — и возникает электрический ток. Заряды на поверхности проводника создают в пространстве электрическое поле, а ток — магнитное поле. Проводник, подключённый к гальваническому элементу, проходит через отверстие в доске. На рисунках 1-4 при помощи линий поля изображены электрическое и магнитное поля, создаваемые проводником в плоскости доски (вид сверху). Установите соответствие между видами поля и рисунками, изображающими линии поля.

ВИДЫ ПОЛЯ

А) электрическое поле

Б) магнитное поле

ИЗОБРАЖЕНИЯ ЛИНИЙ ПОЛЯ

Решение.

А) Вектор напряженности электрического поля исходит из положительного заряда и входит в отрицательный заряд. Так как доска расположена вблизи положительного полюса, то вокруг проводника с током будет сосредоточен положительный заряд, от которого во все стороны будут исходить линии напряженности электрического поля. Рисунок под номером 1.

Б) Направление линий магнитного поля, циркулирующих вокруг проводника с током, можно найти по правилу буравчика.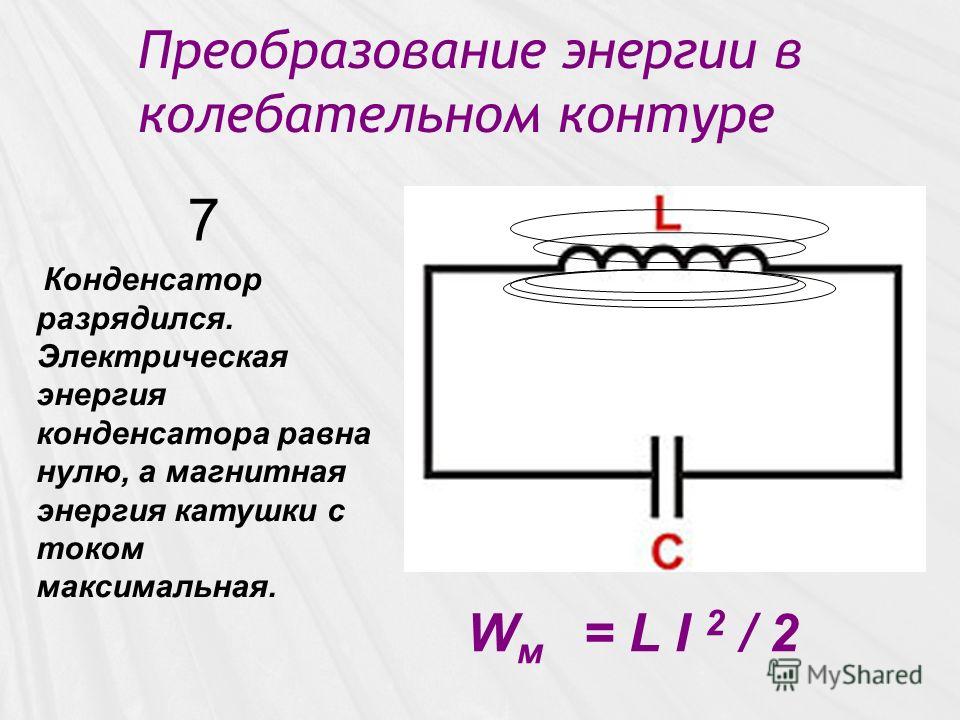 Направим буравчик от «+» к «-» и будем его ввинчивать по направлению движения тока (также от «+» к «-»). Направление вращения ручки буравчика в плоскости доски будет соответствовать рисунку 4.

Ответ: 14.

26. При подключении проводника к полюсам гальванического элемента на поверхности проводника появляются заряды: положительные вблизи положительного полюса, отрицательные вблизи отрицательного полюса — и возникает электрический ток. Заряды на поверхности проводника создают в пространстве электрическое поле, а ток — магнитное поле. Проводник, подключённый к гальваническому элементу, проходит через отверстие в доске. На рисунках 1-4 при помощи линий поля изображены электрическое и магнитное поля, создаваемые проводником в плоскости доски (вид сверху). Установите соответствие между видами поля и рисунками, изображающими линии поля.

ВИДЫ ПОЛЯ

А) электрическое поле

Б) магнитное поле

ИЗОБРАЖЕНИЯ ЛИНИЙ ПОЛЯ

Решение.

А) Вектор напряженности электрического поля исходит из положительного заряда и входит в отрицательный заряд. Так как доска расположена вблизи отрицательного полюса, то вокруг проводника с током будет сосредоточен отрицательный заряд, к которому со всех сторон будут входить линии напряженности электрического поля. Рисунок под номером 2.

Ответ: 23.

27. На рисунке показан ход луча света через стеклянную призму, находящуюся в воздухе. Точка О — центр окружности.

Установите соответствие между физическими величинами и формулами, выражающими их в рассматриваемой задаче.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) показатель преломления стекла n

Б) синус угла преломления в точке О

ФОРМУЛЫ

Решение.

А) Показатель преломления стекла n можно выразить формулой

где α – угол падения луча; γ – угол преломления луча. Так как угол падения – это угол между нормалью к призме и падающим лучом, то синус угла α равен отношению длины отрезка AB к радиусу (гипотенузе) окружности AO (см. рисунок). Аналогично для преломленного угла γ имеем, что его синус равен отношению . Таким образом, показатель преломления стекла равен (при условии, что OC=AO):

Б) Синус угла преломления в точке О – это угол COD, синус которого равен

Ответ: 23.

28. На рисунке показан ход луча света через стеклянную призму, находящуюся в воздухе. Точка О — центр окружности.

Установите соответствие между формулами и физическими величинами, которые они выражают в рассматриваемой задаче.

ФОРМУЛЫ

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

1) синус угла падения в точке О

2) синус угла преломления в точке О

3) показатель преломления воздуха

4) показатель преломления стекла

Решение.

А)-Б) Показатель преломления стекла n можно выразить формулой

Ответ: 41.

29. Колебательный контур состоит из катушки индуктивностью L и конденсатора ёмкостью С. В процессе свободных электромагнитных колебаний, происходящих в этом контуре, максимальный заряд пластины конденсатора равен q. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) максимальная энергия электрического поля конденсатора

Б) максимальная сила тока, протекающего через катушку

ФОРМУЛЫ

Решение.

А) Максимальная энергия электрического поля конденсатора равна

Заряд конденсатора q связан с емкостью C и напряжением U выражением

откуда

Подставляя это выражение в формулу энергии конденсатора, получаем:

Б) Максимальное значение тока I можно найти из равенства максимальных энергий:

откуда величина максимального тока

Ответ: 13.

30. Колебательный контур состоит из катушки индуктивностью L и конденсатора ёмкостью С. В процессе свободных электромагнитных колебаний, происходящих в этом контуре, максимальная сила тока в катушке индуктивности равна I. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А) максимальная энергия магнитного поля катушки индуктивности

Б) максимальный заряд на обкладке конденсатора

ФОРМУЛЫ

Решение.

А) Максимальная энергия магнитного поля катушки индуктивности определяется как

Б) Максимальный заряд на обкладке конденсатора найдем из равенства максимальных энергий на катушке и конденсаторе:

Учитывая, что , то

откуда максимальный заряд равен

Ответ: 34.

Колебательный контур — это устройство, в котором могут происходить свободные электромагнитные колебания.

Колебательный контур состоит из конденсатора и катушки индуктивности. Электроёмкость конденсатора — \(C\), индуктивность катушки — \(L\).

Изображение на схемах

Обрати внимание!

В колебательном контуре периодически происходит переход энергии электрического поля в энергию магнитного поля и наоборот.

На некоторое время с помощью переключателя зарядим конденсатор, замкнув его на источник тока (рис. А). Затем наш заряженный конденсатор подсоединим к катушке (рис. Б).

	t1=T4. Заряженный конденсатор, подключённый к катушке, начнёт через неё разряжаться. Нижняя обкладка заряжена положительно. Разрядный ток, проходящий по катушке, создаст вокруг неё магнитное поле. Явление самоиндукции будет препятствовать резкому возрастанию тока через катушку, поэтому ток растёт постепенно и через некоторое время приобретает максимальное значение. В этот момент конденсатор будет полностью разряжен. Произошло превращение энергии электрического поля в энергию магнитного поля.
	2t1=T2. Так как конденсатор разряжен, то в следующий момент времени ток должен мгновенно исчезнуть, но в результате самоиндукции, которая препятствует убыванию тока, он некоторое время поддерживается в цепи. Индукционный ток сонаправлен с уходящим током цепи и благодаря этому конденсатор заряжается, только заряд на обкладках поменяется на противоположный знак. Энергия магнитного поля перешла в энергию электрического поля. Если рассматривать идеальную модель колебательного контура, который не имеет сопротивления, то энергия в нём не потратится, и конденсатор вновь зарядится до максимального значения. В реальности такого не бывает, потому что часть энергия уйдёт на преодоление сопротивления проводников и превратится в тепловую энергию. В реальном колебательном контуре в этот момент времени конденсатор зарядится уже не полностью.
	3t1=3T4. В третьей четверти периода конденсатор начнёт разряжаться, только теперь ток разряда будет протекать в другом направлении, т. к. полярность напряжения на конденсаторе поменялась. Самоиндукция катушки вновь будет препятствовать быстрому росту тока, который постепенно всё же приобретёт максимальное значение, а конденсатор к тому времени полностью разрядится. Снова энергия электрического поля переходит в энергию магнитного поля.
	4t1=T. Последняя четверть периода будет похожа на вторую четверть, только ток уже будет протекать в другом направлении. Убыванию тока будет вновь препятствовать самоиндукция, поэтому ток будет убывать постепенно и вновь зарядит конденсатор. И вновь энергия магнитного поля переходит в энергию электрического поля. В идеальном контуре не было бы потерь, и амплитуда колебаний оставалась постоянной.

За промежуток времени 4t1 произошло одно полное колебание. Значит, 4t1 \(=T\), где \(T\) — период колебаний.

Период полученных свободных колебаний равен собственному периоду колебательного контура.

Обрати внимание!

Формула для определения периода свободных электромагнитных колебаний: T=2 π ·LC.

Из формулы видно, что период колебательного контура зависит от параметров составляющих его элементов: индуктивности катушки \(L\) и электроёмкости конденсатора \(C\).

Работа колебательного контура представлена на рисунке.

Колебательный контур входит в состав генератора высокочастотных электромагнитных колебаний, который применяется в радиовещании (т. е. передаче звуковой информации на большие расстояния).

§ 9. электромагнитные колебания. превращения энергии в колебательном контуре

Колебательный контур, состоящий из катушки, замкнутой на конденсатор, является источником электромагнитных колебаний, при которых электрическая энергия заряженного конденсатора периодически превращается в энергию магнитного поля катушки.

Электромагнитными колебаниями называют периодические изменения напряжённости электрического поля, магнитной индукции, силы тока, заряда и других характеристик электромагнитного поля. Электромагнитные колебания представляют основу электрической энергии используемой человеком. Они применяются в телевидении, а также в радио и телефонной связи. Работа мозга, сердца и мышц человека сопровождается появлением электромагнитных колебаний. Все световые явления тоже являются электромагнитными колебаниями.

Как и механические колебания, электромагнитные колебания бывают свободными или вынужденными. Свободные электромагнитные колебания можно наблюдать в схеме, состоящей из катушки и конденсатора, называемой колебательным контуром. Зарядим конденсатор С колебательного контура, сообщив его пластинам заряд q. При этом энергия электрического поля конденсатора составит (см. курс физики 10 класса). Замкнём конденсатор на катушку индуктивности L (рис. 9а), после чего конденсатор начнёт разряжаться через катушку, а заряд на его пластинах уменьшаться. Разряд конденсатора будет постепенным, а не мгновенным, так как ЭДС самоиндукции в катушке станет противодействовать нарастанию силы тока.

Очевидно, что, разряжаясь через катушку, конденсатор будет терять свою энергию, однако, одновременно с уменьшением электрического поля будет расти энергия магнитного поля W_M катушки, через которую течёт ток I (см. §6), . Если считать, что потерь энергии в этом контуре не происходит, то полная энергия электромагнитного поля контура будет постоянна:

Из (9.1) следует, что, когда конденсатор окажется полностью разряженным (рис. 9б), сила тока в колебательном контуре достигнет максимального значения и вся энергия электрического поля конденсатора превратится в энергию магнитного поля катушки. Однако из-за явления самоиндукции ток в катушке не может уменьшиться мгновенно, и поэтому начинается перезарядка конденсатора, которая происходит, пока сила тока в контуре не станет равной нулю (рис. 9в). В этот момент времени энергия магнитного поля катушки целиком превратится в электрическую энергию конденсатора, и при этом конденсатор будет обладать тем же зарядом, что и сначала (рис. 9а), но заряды на пластинах, просто, поменяются местами. Далее конденсатор опять начнёт разряжаться, и колебательный контур вернётся в исходное состояние (рис. 9а).

Если пренебречь потерями энергии в колебательном контуре, то колебания тока в катушке и напряжения между пластинами конденсатора являются незатухающими гармоническими колебаниями, сдвинутыми по фазе p/2 (рис. 9г). Расчёты показывают, что период Т таких колебаний зависит от индуктивности катушки L и ёмкости конденсатора С следующим образом:

Формулу (9.2) называют формулой Томсона в честь английского физика У. Томсона (Кельвина), который её впервые вывел. В действительности протекание тока в колебательном контуре всегда сопровождается потерями энергии. Одной из причин этих потерь является нагревание катушки и соединительных проводов. Поэтому со временем энергия электромагнитного поля переходит во внутреннюю энергию элементов колебательного контура, и амплитуда электромагнитных колебаний постепенно уменьшается до нуля.

Вопросы для повторения:

· Что называют электромагнитными колебаниями?

· Как происходит превращение энергии в колебательном контуре?

· От чего зависит период колебаний колебательного контура?

Рис. 9. Состояние колебательного контура в различные моменты периода колебаний (а-в) и графики зависимости напряжения между пластинами конденсатора U и силы тока в катушке I от времени t (г).

Конденсатор

Конденсатор — это дополнительный запас энергии, который ваш корабль использует для питания модулей и оборудования, требующего быстрого всплеска энергии.

Этот конденсатор имеет 1696 ГДж из максимально возможных 1725 ГДж.

Во многом конденсатор аналогичен «Мане» в других ролевых играх в жанре фэнтези. Подобно тому, как для определенных заклинаний и магии требуется мана, для определенных модулей и способностей требуется конденсатор.Однако отсутствие маны означает лишь то, что вы не можете разыгрывать заклинания какое-то время. То же самое и с Eve — исчерпание конденсатора означает, что вы не можете использовать некоторые модули какое-то время.

У каждого корабля в Еве есть внутренний генератор, и этот генератор обеспечивает энергосистему, которую вы видите в окне арматуры. Модули, которые установлены на корабле, будут подключаться к электросети и резервируют часть выходной мощности генератора для себя (следовательно, уменьшая оставшуюся электросеть при установке). Во время полета на корабле модуль будет работать от генератора.

Однако для работы некоторых модулей требуется больше энергии. Энергетическому оружию (также известному как лазерные турели), например, требуется мощность, чтобы выстрелить в вашу цель разрушительным лучом. Поскольку оружие должно выстрелить сразу после подачи команды, оно не может ждать, пока мощность генератора накопит достаточно энергии для выстрела. С другой стороны, постоянная зарядка оружия полной энергией, необходимой для выстрела, будет тратить кучу энергии энергосистемы и, вероятно, расплавить само оружие.

Решением является конденсатор . Корабельный конденсатор постоянно поглощает определенную мощность генератора, чтобы заряжаться как батарея — или, скорее, как реальный конденсатор. Когда для работы модуля требуется быстрый всплеск энергии, конденсатор разряжается, обеспечивая эту энергию. Таким образом, конденсатор позволяет вашему кораблю использовать модули и оборудование, требующие большого количества энергии.

В случае, если ваш корабль полностью разрядится от заряда конденсатора, произойдет следующее:

У вас недостаточно энергии, чтобы вызвать деформацию.(Если у вас есть только частичный заряд конденсатора, ваш корабль будет деформироваться настолько далеко, насколько сможет, и остановится на полпути. Затем вы можете снова инициировать деформацию, чтобы прибыть к месту назначения.)
Вы не сможете активировать какие-либо активные модули, требующие заряда конденсатора. Вы по-прежнему можете активировать модули, которые этого не делают.

Отсутствие заряда конденсатора НЕ останавливает ваши двигатели и не выводит ваш корабль из строя.

В окне «Моделирование фитинга» есть вкладка для моделирования уровня заряда конденсатора.

Слева вверху: емкость конденсатора, время перезарядки, дельта в ГДж / с, дельта в процентах.

Если конденсатор «Стабильный», это означает, что с каждым модулем, потребляющим конденсатор, работает без остановок, уровень энергии конденсатора в конечном итоге будет падать и бесконечно колебаться между отображаемым процентным уровнем. Если конденсатор подгонки стабилен, его называют «стабильным по конденсатору».

Если вместо этого в окне отображается «Depletes in XX: XX», это означает, что с каждым модулем, потребляющим конденсатор, работающим без остановок, уровень энергии вашего конденсатора упадет до 0% по истечении указанного времени.

Рядом с оранжевым кружком отображаются четыре элемента дополнительной информации. Верхний ряд — это просто максимальная емкость конденсатора и время перезарядки. Нижний ряд немного сложнее. «Дельта» (Δ) вашего конденсатора составляет (пиковая скорость перезарядки конденсатора) — (максимальная потребляемая мощность). Положительный треугольник означает, что конденсатор работает стабильно. Наличие большей положительной дельты означает, что вы можете позволить себе дополнительную дестабилизацию конденсаторов (чаще всего нейтрализаторов) и при этом оставаться стабильными.Отрицательный треугольник означает, что ваш конденсатор нестабилен. Наличие большего отрицательного дельта означает, что ваш конденсатор разряжается быстрее.

Хотя быть стабильным по ограничению мощности — это хорошо, это не является обязательным требованием. Во многих PvE-ситуациях редко требуется, чтобы все работало одновременно. Вместо того, чтобы ставить под угрозу способность вашего корабля обеспечивать устойчивость к ограничению емкости, вы можете просто выбрать микроуправление использованием модуля, чтобы продлить срок службы заряда конденсатора.

Вместо непрерывного запуска ремонтного модуля (усилитель щита, ремонтник брони) активируйте его только тогда, когда это необходимо.
То же самое и с силовыми модулями, особенно с микроприводами.
Всегда поддерживайте уровень конденсатора выше 25%. Падение ниже 25% резко снижает скорость пассивной перезарядки.
При столкновении с врагами, использующими нейтрализаторы энергии или носфератус, старайтесь держаться на расстоянии, чтобы снизить их эффективность.
Если вашему кораблю не хватает как устойчивости конденсаторов, так и способности танкования, постарайтесь сосредоточиться на уменьшении урона и быстром устранении вражеских целей, а не на грубом форсировании входящего DPS.Создание мощной системы защиты требует значительных вложений, как с точки зрения очков навыков, так и с точки зрения ISK.

Конденсатор пассивно заряжается от бортового генератора и не требует дополнительного «топлива» для пополнения.
Скорость перезарядки конденсатора в гигаджоулях в секунду зависит от емкости конденсатора, текущего заряда конденсатора и времени его перезарядки.
Ваш конденсатор будет заряжаться быстрее, чем ближе вы к 25% от вашего максимума.
Скорость перезарядки падает очень быстро, как только вы опускаетесь ниже этого уровня.

Экспериментальные данные по перезарядке конденсатора. Синие точки — это точки данных экспериментов Кивены. Черная линия — это уравнение, основанное на исследовании Dust Puppy, которое вы можете увидеть в верхнем левом углу изображения. На меньшем внутреннем графике (оранжевый) показан процент средней скорости перезарядки по отношению к текущему проценту конденсатора. Вы можете ясно видеть, что максимальная перезарядка в 2,5 раза превышает среднюю перезарядку и происходит при 25%.нажмите, чтобы увеличить

Скорость перезарядки конденсатора является нелинейной функцией — скорость в любой данный момент зависит от того, сколько энергии накоплено в этот момент. Близость к нулю и почти полная емкость, скорость перезарядки очень низкая и достигает пика 25 процентов.

Важно помнить, что скорость перезарядки резко снижается, когда она падает ниже 25% емкости. Поэтому, если вы участвуете в драке, оставьте себе запас прочности и подумайте о побеге, если окажется, что вы скоро упадете ниже этого уровня.

Игрок по имени «Dust Puppy» тщательно исследовал скорость перезарядки и опубликовал свои результаты ^[1]. Основываясь на своих экспериментах, он предлагает формулу для расчета скорости перезарядки:

[математика] \ displaystyle \ frac {\ text {d} C} {\ text {d} t} = \ frac {10C _ {\ rm {max}}} {T} \ left (\ sqrt {\ frac { C} {C _ {\ rm {max}}}} — \ frac {C} {C _ {\ rm {max}}} \ right) [/ math]

… где:

[math] C [/ math] — текущий уровень конденсатора в ГДж.
[math] C_ \ rm {max} [/ math] — ваш максимальный уровень конденсатора в ГДж.
[math] \ text {d} C / \ text {d} t [/ math] — текущая скорость перезарядки конденсатора в ГДж / с. (Формально: мгновенная скорость изменения заряда конденсатора [математика] C [/ математика] относительно времени.)
[math] T [/ math] — время перезарядки конденсатора.

Перезарядка конденсатора, таким образом, достигает пика на уровне 25%, и объявленное «Время перезарядки конденсатора» на самом деле является временем, за которое конденсатор полностью опустеет до 98.2 [/ math]

, где C ₀ — уровень конденсатора в момент запуска t ₀ и C ₁ — уровень конденсатора в момент времени t ₁

Навыки, связанные с прямым конденсатором:
Навыки, связанные с конкретными конденсаторами подсистемы:
- Afterburner — уменьшение длительности Afterburner на 5% и уменьшение использования конденсатора Afterburner на 10% за каждый уровень навыка.
- Capacitor Emission Systems — снижение потребности в конденсаторах передатчиков энергии и нейтрализаторов энергии на 5%.Относится только к субкапитальным модулям.
- Capital Capacitor Emission Systems — снижение на 5% потребности в конденсаторах капитальных передатчиков энергии и капитальных нейтрализаторов энергии.
- Controlled Bursts — 5% снижение потребности в конденсаторах оружейных турелей за каждый уровень навыка.
- Electronic Warfare — на 5% меньше конденсаторов для систем ECM и ECM Burst на каждый уровень квалификации.
- High Speed Maneuvering — сокращение использования конденсатора Microwarpdrive на 5% за каждый уровень навыка.
- Jump Drive Operation — 5% уменьшение потребности в конденсаторах для инициации прыжка на каждый уровень навыка.
- Propulsion Jamming — 5% уменьшение потребности Warp Scrambler, Warp Disruptor и конденсатора Stasis Web для каждого уровня навыка.
- Sensor Linking — на 5% меньше конденсатора для подключения датчика на каждый уровень навыка.
- Warp Drive Operation — 10% снижение потребности в конденсаторах для инициирования деформации на каждый уровень навыка.
- Разрушение оружия — потребность в конденсаторах для дизрапторов оружия на 5% меньше на каждый уровень навыка.

Определите энергию, запасенную в каждом конденсаторе при максимальном заряде.

Конденсатор — это электрическое устройство, которое может накапливать энергию в виде электрической энергии. 2} {2C} \ = \ \ dfrac {1} {2} QV {/ eq}

Нам дается:

Емкость первого последовательно включенного конденсатора равна {eq} \ rm C_1 \ = \ 2 \ \ rm \ mu F {/ экв}.

Емкости второго и третьего конденсаторов, которые параллельны друг другу, равны {eq} \ rm C_2 \ = \ 3 \ \ rm \ mu F {/ eq} и {eq} \ rm C_3 \ = \ 4 \ \ rm \ mu F {/ экв}.

Максимальный потенциал равен {eq} V \ = \ 60 \ \ rm V {/ eq}

Эквивалентную емкость всех конденсаторов можно рассчитать следующим образом:

{экв} \ begin {align} \ rm C_ {eq} \ & = \ \ rm \ dfrac {(C_2 + C_3) \ times C_1} {C_1 + (C_2 + C_3)} \\ [0,3 см] & = \ \ rm \ dfrac {(3 \ \ rm \ mu F + 4 \ \ rm \ mu F) \ times 2 \ \ rm \ mu F} {2 \ \ rm \ mu F + (3 \ \ rm \ mu F + 4 \ \ rm \ mu F)} \\ [0.3 см] & = \ \ dfrac {14} {9} \ \ rm \ mu F \\ [0,3 см] \ end {align} {/ eq}

Первый конденсатор включен последовательно с двумя другими конденсаторами. Следовательно. максимальный заряд на первом конденсаторе можно рассчитать следующим образом:

{экв} \ begin {align} \ rm Q_1 \ & = \ \ rm C_ {eq} \ times V \\ [0,3 см] & = \ \ rm \ dfrac {14} {9} \ \ rm \ mu F \ times 60 \ \ rm V \\ [0,3 см] & = \ \ dfrac {280} {3} \ \ rm \ mu C \ end {align} {/ eq}

Нас просят вычислить энергию, запасенную в каждом конденсаторе при максимальном заряде.{-4} \ \ rm J}} \ end {align} {/ eq}

Концепция предлагаемой системы зарядки конденсаторов начинается с использования конденсатора с последовательной инжекцией заряда в качестве источника тока, который генерирует фиксированное количество предварительно заданного зарядный ток. показана упрощенная принципиальная схема системы индуктивной зарядки конденсатора, которая заряжает пару положительных и отрицательных конденсаторов C, _P,, и C, _N,, , соответственно.Вторичная катушка L ₂ и ее параллельный резонансный конденсатор C ₂, которые генерируют напряжение катушки V _COIL, сопровождаются конденсатором последовательной инжекции заряда C _S , который обеспечивает входное напряжение В _IN до C _P и C _N через переключатели SW _P и SW _N соответственно. SW _P включается, когда V _IN> V _CP формирует положительный сигнал C _P заряжается, а SW _N включается, когда V IN V _CN для отрицательной C _N зарядки относительно земли GND.Когда V _CN < V _IN < V _CP, оба переключателя выключаются, а V _IN следует за V _COIL. Затем, когда включается SW _P или SW _N , переключатель подключает V _IN к положительному или отрицательному напряжению конденсатора V _CP или V _CN, удерживая V _IN относительно постоянным и генерируя фиксированный зарядный ток I _CH через C _S .Например, когда V _IN> V _CP, SW _P подключает V _IN к V _CP для удержания V _IN около _CP, а V _COIL продолжает увеличиваться. Таким образом, изменение напряжения на C _S , V _COIL — V _IN, генерирует положительный I _CH, пока V _COIL не достигнет своего положительного пика.Когда V _COIL начинает уменьшаться от своего пика, V _IN также уменьшается ниже V _CP, и SW _P выключается. Зарядный ток I _CH может быть выражен как

I _CH = C _S × d ( V _COIL — V ) д т .

(1)

Упрощенная принципиальная схема системы индуктивного заряда конденсатора.

Значение I _CH можно настроить, выбрав правильный C _S , который будет обсуждаться в Разделе II-B. Фиксированный I _CH минимизирует потери в переключателе, в то время как в отличие от реального источника тока падение напряжения на C _S не рассеивает мощность, повышая эффективность зарядки от L ₂ к паре конденсаторов.

Чем меньше ток зарядки, тем выше эффективность зарядки конденсатора и меньше потери мощности в переключателях, что приводит к увеличению времени зарядки.Следовательно, зарядный ток I _CH должен быть оптимизирован для эффективной зарядки конденсаторов в течение желаемого периода. Мы смоделировали время зарядки и эффективность в зависимости от I _CH с упрощенными формами напряжения и тока системы зарядки конденсатора в формате. В этом анализе f _c — это несущая частота, которая принимается через V _COIL, n — номер цикла зарядки, а t [ n ] — время перехода V _IN при V _CN < V _IN < V _CP.В этой упрощенной модели мы предполагаем следующее: 1) В _COIL синусоидален с постоянным пиковым напряжением В _Пик; 2) переключатели включаются и выключаются в идеальное время, и V _IN становится равным V _CP или V _CN с незначительным падением напряжения на замкнутых переключателях при подключении к конденсаторам; 3) во время каждого цикла зарядки V _CP и V _CN являются постоянными, и небольшие приращения напряжения ΔV _CP и ΔV _CN добавляются к V _CP и V _CN в конце каждого цикла соответственно; и 4) C _P и C _N равны и начисляются на одинаковую сумму I _CH, т.е.е., V _CP = — V _CN.

Упрощенные формы сигналов напряжения и тока системы зарядки конденсаторов для моделирования и теоретического анализа.

Когда V _IN подключен к V _CP или V _CN для зарядки, V _COIL и I _CH можно выразить как

_COIL ( t ) = V _Peak sin (2 π f _c t )

(2)

I _{4 9012 ) = 2 π f _c C _S V _{Пиковое значение} cos (2 π f _{c 9023.}}

(3)

V _CP на n -м цикле зарядки V _CP [ n ] можно получить из

VCP [n] = ∑i = 1nΔVCP [i]

(4)

, где ΔV _CP [ n ] — это приращение V _CP при n -м цикле зарядки, из начального состояния V _CP [0 ] = В _CN [0] = 0 В.

В n -м цикле зарядки t [ n ] равно времени перехода, в котором V _IN увеличивается от V _CN [ n– 1] до V _CP [ n– 1].Следовательно,

VCP [n − 1] −VCN [n − 1] = 2VCP [n − 1] = [VCOIL (t)] nfc − 14fc + t [n] nfc + 14fc = VPeak [sin (2πfct)] nfc-14fc + t [n] nfc + 14fc.

(5)

В (5) t [ n ] можно записать как

t [n] = sin − 1 (−1 + 2VCP [n − 1] VPeak) 2πfc + 14fc.

(6)

С t [ n ] в (6), ΔV _CP [ n ] может быть получено как

ΔVCP [n] = 1CP∫nfc − 14fc + t [n] nfc + 14fcICH (t) dt = CSCPVPeak [sin (2πfct)] nfc-14fc + t [n] nfc + 14fc = 2CSCPVPeak (1-VCP [n-1] VPeak).

(7)

Следовательно, период зарядки T _CH, в течение которого C _P и C _N заряжаются до заданного напряжения зарядки ± В _TG на n _CH-й цикл зарядки, можно получить из

TCH = nCHfc, где VCP [nCH] = ∑i = 1nCHΔVCP [i] = VTG.

(8)

Суммарные потери энергии в ПО _P и ПО _N в течение n _CH циклов зарядки E _SW [ n _CH] может быть рассчитывается как сумма коммутационных потерь энергии в каждом цикле ΔE _SW [ n ]

ΔESW [n] = 2∫nfc − 14fc + t [n] nfc + 14fcICh3 (t) × RSWdt

( 9)

ESW [nCH] = ∑i = 1nCHΔESW [i]

(10)

, где R _SW — сопротивление переключателя.

Эффективность заряда конденсатора η _CAP от L ₂ до пары конденсаторов C _P и C _N можно выразить как

ηCAPECP = ECP + ECN + ESW [nCH] + ESYS

(11)

, где E _CP и E _CN — сохраненные энергии в C _P и C _N , соответственно, которые равны ECP = CPVTG2 ∕ 2 и ECN = CNVTG2 ∕ 2, соответственно, и E _SYS — энергия, потребляемая остальной частью системы в течение n _CH циклов зарядки.

Меньший I _CH увеличивается T _CH в (4) — (8), а меньший I _CH и R _SW увеличивается η _CAP in (9 ) — (11). Следовательно, когда известен максимально допустимый T _CH, I _CH может быть выбран настолько малым, насколько требуется T _CH для зарядки C _P и C _N для C _S и V _{Пиковые значения} в (3) — (8). C _S должен быть меньше C _R и V _Peak> V _TG.

Общая архитектура предлагаемой системы зарядки конденсаторов показана на рис. Передатчик мощности управляет первичной катушкой L ₁ с обозначенной несущей частотой f _c , что индуцирует V _COIL через L ₂.Зарядное устройство для конденсаторов состоит из переключателей, приводимых в действие высокоскоростными активными драйверами, для зарядки батареи из четырех пар конденсаторов C _P и C _N . Блок управления устанавливает заданное пользователем целевое напряжение зарядки V, _TG и генерирует сигнал последовательности S _CH для последовательного управления четырехканальным конденсаторным зарядным устройством, которое может использоваться в программируемой многоэлектродной нейронной стимуляции [5 ]. Во время зарядки конденсаторное зарядное устройство подключает V _IN к положительным и отрицательным конденсаторам поочередно, чтобы удерживать V _IN при V _CP или V _CN, генерируя при этом фиксированный зарядный ток I _CH — C _S .Другими словами, C _S работает как источник тока, который не рассеивает мощность, одновременно уменьшая потери при переключении в конденсаторном зарядном устройстве и значительно повышая эффективность зарядки от L ₂ до конденсаторной батареи.

Общая архитектура предлагаемой энергоэффективной системы зарядки конденсаторов через индуктивную связь.

В этой системе зарядки конденсаторов вторичная резонансная емкость C _R , подключенная через L ₂, может быть выражена как

CR = C2 + CA + CSCEffCS + CEff

(12)

где C ₂ — параллельный резонансный конденсатор, C _A — конденсатор адаптивной настройки и C _Eff — эффективная емкость конденсаторной батареи, которая изменяется в зависимости от напряжения конденсаторной батареи и переключения. изменение рабочего цикла.Адаптивный тюнер конденсатора компенсирует отклонения C _Eff, автоматически регулируя C _A , чтобы поддерживать постоянным значение C _R . Следовательно, вторичный бак L ₂ C ₂ поддерживается в резонансе во время зарядки, при этом максимизируя V _COIL. После цикла зарядки сигнал окончания заряда (EOC) соединяет V _IN с GND, и адаптивный тюнер конденсатора отключается, устанавливая C _R = C ₂ + C _С .Выпрямитель с двумя выходами V _TH с компенсацией, за которым следуют регуляторы с малым падением напряжения, генерирует напряжения питания V _DD и V _SS от V _COIL, что мало влияет на операция зарядки, пока амплитуда V _COIL поддерживается постоянной адаптивным тюнером конденсатора.

Введите емкость (C) и напряжение (V) конденсатора, чтобы рассчитать энергию (E) и заряд (Q), накопленные в этом конденсаторе.Конденсатор — это электронный инструмент, используемый для хранения электрического заряда.

Следующее уравнение используется для расчета общего запаса энергии в конденсаторе.

E = 1/2 * C * V²

Где E — энергия
C — емкость
, а V — напряжение.

Этот калькулятор также определяет заряд конденсатора, который обычно рассчитывается по следующей формуле:

Q = C * V

Где Q — заряд
C — емкость
V — напряжение

Другой аспект расчета энергии, запасенной в конденсаторе, — это тип конденсатора.Это могут быть как параллельные пластины, так и сферические конденсаторы. Однако в каждом случае эти пластины несут заряженные частицы, состоящие из определенного количества энергии. Эта энергия, в свою очередь, создает электрическое поле, которое является разновидностью потенциальной энергии.

Энергия конденсатора определяется как общая энергия, которая может храниться в конденсаторе электрического компонента.

Как рассчитать энергию конденсатора?

Сначала определите емкость.
Емкость определяется конструкцией и материалом, из которого изготовлен конденсатор.
Далее определяем напряжение.
Определите напряжение, проходящее через конденсатор.
Наконец, рассчитайте энергию конденсатора.
Рассчитайте общую энергию, запасенную в конденсаторе, по приведенной выше формуле.

(постоянная Q )

( d , Q постоянная)

V ∝ E ( d постоянная)

Что такое энергия конденсатора?
Энергия конденсатора определяется как энергия, запасенная в конденсаторе из-за его емкости и проходящего через него напряжения.
Какие единицы для энергии конденсатора?
В этом калькуляторе используются следующие единицы измерения: фарады (F) для емкости, вольт (V) для напряжения, кулоны (C) для заряда и джоули (J) для энергии. Важно, чтобы единицы, введенные в приведенном выше вычислении, соответствовали им, в противном случае итоговый расчет будет неверным.
Dielectrics — The Physics Hypertextbook
Обсуждение
основная идея
Диэлектрики — изоляторы простые и простые.Эти два слова относятся к одному и тому же классу материалов, но имеют разное происхождение и используются преимущественно в разных контекстах.
Поскольку заряды в неметаллических твердых телах не могут легко перемещаться, в стекле, керамике и пластике могут быть «островки» заряда. Латинское слово «остров» — insula , от которого происходит слово изолятор . Напротив, заряды в металлических твердых телах имеют тенденцию легко перемещаться — как будто кто-то или что-то их ведет.Латинский префикс con или com означает «с». Человек, с которым у вас есть хлеб, — ваш товарищ. (По-латыни хлеб — panis .) Взять что-то с собой в дорогу — значит передать это. (Латинское слово «дорога» — это через .) Человек, с которым вы путешествуете, который указывает путь или обеспечивает безопасный проход, является кондуктором. (Латинское слово для обозначения лидера — , провод .) Материал, обеспечивающий безопасный проход электрических зарядов, — это проводник .
Вставка слоя неметаллического твердого вещества между пластинами конденсатора увеличивает его емкость.Греческий префикс di или dia означает «поперек». Линия, пересекающая углы прямоугольника, — это диагональ. (Греческое слово, обозначающее угол — gonia — γωνία.) Измерение поперек круга — это диаметр. (Греческое слово «мера» — метрон — μέτρον.) Материал, помещенный на пластины конденсатора, как небольшой непроводящий мостик, — это диэлектрик .
Пластиковое покрытие электрического шнура является изолятором. Стеклянные или керамические пластины, используемые для поддержки линий электропередач и предотвращения их замыкания на землю, являются изоляторами.Практически всегда, когда неметаллическое твердое тело используется в электрическом устройстве, оно называется изолятором. Возможно, единственный раз, когда слово диэлектрик используется в отношении непроводящего слоя конденсатора.
Диэлектрики в конденсаторах служат трем целям:
, чтобы предотвратить соприкосновение проводящих пластин, что позволяет уменьшить расстояние между пластинами и, следовательно, увеличить емкость;
для увеличения эффективной емкости за счет уменьшения напряженности электрического поля, что означает, что вы получаете такой же заряд при более низком напряжении; и
для уменьшения возможности короткого замыкания из-за искрения (более известного как пробой диэлектрика) во время работы при высоком напряжении.
что здесь происходит
Когда металл помещается в электрическое поле, свободные электроны текут против поля, пока не выйдут из проводящего материала. В кратчайшие сроки у нас будет избыток электронов с одной стороны и дефицит с другой. Одна сторона проводника заряжена отрицательно, а другая — положительно. Освободите поле, и электроны на отрицательно заряженной стороне окажутся слишком близко для комфорта. Подобные заряды отталкиваются, и электроны убегают друг от друга так быстро, как только могут, пока не распределятся равномерно по всему телу; в среднем один электрон на каждый протон в пространстве, окружающем каждый атом.Проводящий электрон в металле похож на гоночную собаку, загнанную на пастбище. Они могут свободно передвигаться сколько угодно и могут перемещаться по всей длине, ширине и глубине металла по своей прихоти.
Жизнь электрона в изоляторе гораздо более ограничена. По определению, заряды в изоляторе не могут свободно перемещаться . Это не то же самое, что сказать, что они не могут двигаться . Электрон в изоляторе похож на сторожевую собаку, привязанную к дереву: он может двигаться свободно, но в определенных пределах.Размещение электронов изолятора в присутствии электрического поля похоже на размещение привязанной собаки в присутствии почтальона. Электроны будут напрягаться против поля, насколько это возможно, почти так же, как наша гипотетическая собака будет напрягаться против своего поводка, насколько это возможно. Однако электроны в атомном масштабе больше похожи на облака, чем на собак. Электрон эффективно распространяется по всему объему атома и не концентрируется в каком-либо одном месте. Полагаю, хорошую атомную собаку не назвали бы Спотом.
Когда атомы или молекулы диэлектрика помещаются во внешнее электрическое поле, ядра толкаются полем, что приводит к увеличению положительного заряда с одной стороны, в то время как электронные облака притягиваются к нему, что приводит к увеличению отрицательного заряда с другой. боковая сторона. Этот процесс известен как поляризация , а диэлектрический материал в таком состоянии называется поляризацией . Существует два основных метода поляризации диэлектрика: растяжение и вращение.
Растяжение атома или молекулы приводит к индуцированному дипольному моменту , добавленному к каждому атому или молекуле.
Увеличить
Вращение происходит только в полярных молекулах — с постоянным дипольным моментом , как у молекулы воды, показанной на диаграмме ниже.
Увеличить
Полярные молекулы обычно поляризуются сильнее, чем неполярные. Вода (полярная молекула) имеет диэлектрическую прочность в 80 раз больше, чем у азота (неполярная молекула, которая является основным компонентом воздуха).Это происходит по двум причинам, одна из которых обычно тривиальна. Во-первых, все молекулы растягиваются в электрическом поле независимо от того, вращаются они или нет. Неполярные молекулы и атомы растягиваются, в то время как полярные молекулы растягиваются на и вращаются. Однако эта комбинация действий лишь незначительно влияет на общую степень поляризации вещества. Что еще более важно, полярные молекулы уже сильно растянуты — естественно. То, как атомы водорода сидят на рукавах электронных облаков атома кислорода, искажает молекулу в диполь.Все это происходит в межатомном или молекулярном масштабе. На таких крошечных расстояниях напряженность электрического поля относительно велика для того, что в противном случае было бы ничем не примечательным напряжением (например, 13,6 В для электрона в атоме водорода).
Когда дело доходит до поляризации, растяжение и вращение — не конец истории. Это просто методы, которые проще всего описать случайному наблюдателю. Обычно поляризация диэлектрического материала представляет собой микроскопическую электростатическую деформацию в ответ на макроскопическое электростатическое напряжение.Внешнее поле, приложенное к диэлектрику, не может заставить заряды двигаться макроскопически, но оно может растягивать и искажать их микроскопически. Он может толкнуть их в неудобное положение, а при отпускании позволить им вернуться в расслабленное состояние. То, что отличает поляризацию в изоляторе от растяжения упругого тела, такого как пружина, заключается в том, что устранение напряжения не обязательно снимает напряжение. Некоторые изоляторы будут оставаться в поляризованном состоянии в течение часов, дней, лет или даже столетий.Наиболее длинные характерные времена должны быть экстраполированы из неполных наблюдений на более разумную продолжительность. Никто не собирается сидеть сложа руки и ждать две тысячи лет, чтобы увидеть, как поляризация куска пластика уменьшится до нуля. Ждать не стоит.
Наконец, важно иметь в виду, что заряды, «хранящиеся» в диэлектрическом слое, не доступны в виде пула свободных зарядов. Для их извлечения еще понадобятся металлические пластины. Важно помнить, что единственная причина, по которой кто-то, кажется, заботится об этом явлении, заключается в том, что он помогает нам создавать лучшие конденсаторы.Я думаю, что на этом следует завершить обсуждение.
Конденсаторы с диэлектриками
Поместите диэлектрический слой между двумя параллельно заряженными металлическими пластинами, направив электрическое поле справа налево. (Почему не слева направо? Ну, я читаю справа налево, поэтому мне легче «читать» диаграммы.) Положительные ядра диэлектрика будут перемещаться на с полем вправо, а отрицательные электроны переместит против на поле слева.Силовые линии начинаются с положительных зарядов и заканчиваются отрицательными зарядами, поэтому электрическое поле внутри каждого напряженного атома или молекулы диэлектрика указывает на нашей диаграмме слева направо — напротив внешнего поля двух металлических пластин. Электрическое поле — это векторная величина, и когда два вектора указывают в противоположных направлениях, вы вычитаете их величины, чтобы получить результат. Два поля не компенсируются в диэлектрике, как в металле, поэтому общий результат — более слабое электрическое поле между двумя пластинами.
Увеличить
Позвольте мне повторить это — общий результат — более слабое электрическое поле между двумя пластинами. Давай займемся математикой.
Электрическое поле — это градиент электрического потенциала (более известного как напряжение).
.
E _x = — ∆ В
∆ x
E _y = — ∆ В ⇒ E = — ∇ V
∆ y
E _z = — ∆ В
∆ z
Емкость — это отношение заряда к напряжению.
Введение диэлектрика в конденсатор уменьшает электрическое поле, что снижает напряжение, что увеличивает емкость.
.
С ∝ 1 (постоянная Q ) ⇒ С ∝ ( d , Q постоянная)
В 1
V ∝ E ( d постоянная) E
Конденсатор с диэлектриком сохраняет тот же заряд, что и конденсатор без диэлектрика, но при более низком напряжении.Поэтому конденсатор с диэлектриком более эффективен.
ЭТА МАЛЕНЬКАЯ ЧАСТЬ НУЖДАЕТСЯ В Доработке.
О первых открытиях лейденской банки. Удаление стержня снижает емкость. (Воздух имеет более низкую диэлектрическую проницаемость, чем вода.) Напряжение и емкость обратно пропорциональны, когда заряд постоянен. Уменьшение емкости увеличивает напряжение.
восприимчивость, диэлектрическая проницаемость, диэлектрическая проницаемость
Электрический дипольный момент чего-либо — будь то атом, растянутый во внешнем электрическом поле, полярная молекула или две противоположно заряженные металлические сферы — определяется как продукт заряда и разделения.
p = q r
с единицей СИ кулонметров , у которой нет специального названия.
[см = см]
Поляризация области определяется как дипольный момент на единицу объема
с единицей СИ кулонов на квадратный метр .
⎡
⎢
⎣ см = С ⎤
⎥
⎦
м ³ м ²
Расчет поляризации из первых принципов — сложная процедура, которую лучше доверить специалистам.Не беспокойтесь о деталях того, почему поляризация имеет то значение, которое она имеет, просто примите то, что она существует и является функцией некоторых переменных. И что это за переменные? Конечно, почему они такие материалы и напряженность поля. Различные материалы поляризуются в разной степени — мы будем использовать греческую букву χ _e [chi sub e], чтобы обозначить эту величину, известную как электрическая восприимчивость, — но для большинства материалов поле сильнее ( E ) , тем больше поляризация ( P ).Добавьте коэффициент пропорциональности ε ₀, и все готово.
P = ε ₀ χ _e E
Электрическая восприимчивость — это безразмерный параметр, который зависит от материала. Его значение варьируется от 0 для пустого места до любого другого. Бьюсь об заклад, есть даже некоторые причудливые материалы, для которых этот коэффициент отрицательный (хотя я не знаю наверняка). Константа пропорциональности ε ₀ [эпсилон ноль] известна как диэлектрическая проницаемость свободного пространства и будет рассмотрена немного позже.На данный момент это просто приспособление для тренировки единиц.
⎡
⎢
⎣ С = С ² N ⎤
⎥
⎦
м ² Н м ² С
НАПИШИТЕ ОТДЫХ.
Величина κ [каппа] безразмерна.
Диэлектрическая проницаемость для выбранных материалов (~ 300 K, если не указано иное)
материал κ
воздух 1.005364
уксусная кислота 6,2
спирт этиловый (зерновой) 24,55
спирт метиловый (дерево) 32,70
янтарь 2,8
асбест 4,0
асфальт 2,6
бакелит 4,8
кальцит 8,0
карбонат кальция 8.7
целлюлоза 3,7–7,5
цемент ~ 2
кокаин 3,1
хлопок 1,3
алмаз I типа 5,87
алмаз типа IIa 5,66
эбонит 2,7
эпоксидная 3,6
мука 3-5
фреон 12, −150 ° C (жидкость) 3.5
фреон 12, +20 ° C (пар) 2,4
германий 16
стекло 4–7
стекло, пирекс 7740 5,0
гуттаперча 2,6
реактивное топливо (жиклер) 1,7
оксид свинца 25,9
ниобат свинца, магния 10 000
сульфид свинца (галенит) 200
титанат свинца 200
дейтерид лития 14.0
люцит 2,8
слюда, мусковит 5,4
слюда канадская 6,9
нейлон 3,5
масло льняное 3,4
масло минеральное 2,1
масло оливковое 3,1
масло нефтяное 2,0–2,2
масло, силикон 2.5
масло, сперма 3,2
масло трансформаторное 2,2
материал κ
бумага 3,3, 3,5
оргстекло 3,1
полиэстер 3,2–4,3
полиэтилен 2,26
полипропилен 2.2–2,3
полистирол 2,55
поливинилхлорид (пвх) 4,5
фарфор 6–8
ниобат калия 700
KTN, 0 ° C 34 000
KTN, 20 ° C 6 000
кварц кристаллический (∥) 4,60
кварц кристаллический (⊥) 4.51
кварц плавленый 3,8
каучук бутил 2,4
резина, неопрен 6,6
резина, силикон 3,2
резина вулканизированная 2,9
соль 5,9
селен 6,0
кремний 11,8
карбид кремния (αSiC) 10.2
диоксид кремния 4,5
силиконовое масло 2,7–2,8
почва 10–20
титанат стронция, +25 ° C 332
титанат стронция, −195 ° C 2080
сера 3,7
пятиокись тантала 27
тефлон 2,1
антимонид олова 147
теллурид олова 1770
диоксид титана (рутил) 114
табак 1.6–1,7
диоксид урана 24
вакуум 1 (ровно)
вода, лед, −30 ° C 99
вода, жидкость, 0 ° C 87,9
вода, жидкость, 20 ° C 80,2
вода, жидкость, 40 ° C 73,2
вода, жидкость, 60 ° C 66,7
вода, жидкость, 80 ° C 60.9
вода, жидкость, 100 ° C 55,5
воск пчелиный 2,7–3,0
воск карнубский 2,9
воск, парафин 2,1–2,5
вощеная бумага 3,7
ткани человека κ
кость губчатая 26
кость кортикальная 14.5
мозг, серое вещество 56
мозг, белое вещество 43
мозг, мозговые оболочки 58
хрящ общий 22
хрящ, ухо 47
ткани человека κ
глаз, водянистая влага 67
глаз, роговица 61
глаз, склера 67
жир 16
мышца гладкая 56
мышца поперечнополосатая 58
скин 33–44
язычок 38
пробой диэлектрика
Любой изолятор можно заставить проводить электричество.Это явление известно как пробой диэлектрика .
Пробой диэлектрика в избранных материалах
материал поле (МВ / м)
воздух 3
янтарь 90
бакелит 12, 24
алмаз типа IIa 10
стекло, пирекс 7740 13, 14
слюда, мусковит 160
нейлон 14
масло, силикон 15
масло трансформаторное 12, 27
материал поле (МВ / м)
бумага 14, 16
полиэтилен 50, 500–700, 18
полистирол 24, 25, 400–600
поливинилхлорид (ПВХ) 40
фарфор 4, 12
кварц плавленый 8
резина, неопрен 12, 12
титанат стронция 8
тефлон 60
диоксид титана (рутил) 6
пьезоэлектрический эффект
Произнесите все гласные.Пьезоэлектричество — это эффект преобразования энергии между механической и электрической формами.
Пьезо — греческое слово, обозначающее давление (πιεζω).
Обнаружен в 1880-х годах братьями Кюри.
Недорогие пьезоэлектрические микрофоны. Когда поляризованный кристалл подвергается напряжению, напряжение создает разность потенциалов. Эта разность потенциалов пропорциональна напряжению, которое пропорционально акустическому давлению.
Обратный пьезоэлектрический микрофон — это пьезоэлектрический динамик: зуммер будильника, звонок наручных часов, всевозможные электронные гудки.Когда к поляризованному кристаллу прикладывается электрический потенциал, кристалл подвергается механической деформации, которая, в свою очередь, может создавать акустическое давление.
Коллаген пьезоэлектрический. «Когда к [костному] коллагену прикладывается сила, создается небольшой электрический потенциал постоянного тока. Коллаген проводит ток в основном за счет отрицательных зарядов. Минеральные кристаллы кости (апатит), расположенные рядом с коллагеном, проводят ток с помощью положительных зарядов. из этих двух типов полупроводников ток легко течет в одном направлении, но не в другом….Считается, что силы, действующие на кости, создают потенциалы за счет пьезоэлектрического эффекта и что соединения коллаген-апатит образуют токи, которые вызывают и контролируют рост костей. Токи пропорциональны напряжению (сила на единицу площади), поэтому повышенное механическое напряжение костей приводит к усилению роста «. Physics of the Body (255).
Микрофоны и принцип их работы
тип звуков производят
изменений в… , что вызывает
изменений в… , что приводит к изменению
…
углеродистый Плотность гранул сопротивление напряжение
конденсатор разделительная пластина емкость напряжение
динамический расположение змеевика флюс напряжение
пьезоэлектрический компрессия поляризация напряжение
Путь к конденсатору со сверхвысокой плотностью энергии
Для изготовления нового материала тонкая пленка сначала осаждается с помощью процесса импульсного лазерного осаждения в этой камере.Яркий «шлейф», который вы видите, — это лазер, попадающий в цель и осаждающий материал. (Изображение любезно предоставлено Лэйном Мартином)
Конденсаторы, которые быстро накапливают и выделяют электрическую энергию, являются ключевыми компонентами современной электроники и систем питания. Однако наиболее часто используемые из них имеют низкую плотность энергии по сравнению с другими системами хранения, такими как батареи или топливные элементы, которые, в свою очередь, не могут быстро разряжаться и перезаряжаться без повреждений.
Как сообщает журнал Science, исследователи нашли лучшее из обоих миров.Вводя изолированные дефекты в коммерчески доступную тонкую пленку на этапе простой постобработки, группа ученых под руководством исследователей из Национальной лаборатории Лоуренса Беркли Министерства энергетики США (DOE) продемонстрировала, что обычный материал можно обрабатывать. в высококачественный энергоаккумулирующий материал.
Исследование проводится при поддержке Materials Project, онлайновой базы данных с открытым доступом, которая фактически предоставляет крупнейшую коллекцию свойств материалов ученым со всего мира.Сегодня проект материалов объединяет вычислительные и экспериментальные усилия, среди прочего, для ускорения разработки новых функциональных материалов. Это включает в себя понимание способов манипулирования известными материалами с целью улучшения их характеристик.
Растущие требования к снижению затрат и миниатюризации устройств подтолкнули к разработке конденсаторов с высокой плотностью энергии. Конденсаторы обычно используются в электронных устройствах для поддержания питания во время зарядки аккумулятора.Новый материал, разработанный в лаборатории Беркли, может в конечном итоге объединить эффективность, надежность и прочность конденсаторов с возможностями аккумулирования энергии крупномасштабных батарей. Приложения включают личные электронные устройства, носимые устройства и автомобильные аудиосистемы.
Материал основан на так называемом «релаксорном сегнетоэлектрике», который представляет собой керамический материал, который подвергается быстрой механической или электронной реакции на внешнее электрическое поле и обычно используется в качестве конденсатора в таких приложениях, как ультразвук, датчики давления и напряжения. генераторы.
Приложенное поле меняет ориентацию электронов в материале. В то же время поле вызывает изменение энергии, хранящейся в материалах, что делает их хорошим кандидатом для использования помимо малогабаритных конденсаторов. Проблема, которую необходимо решить, заключается в том, как оптимизировать сегнетоэлектрик, чтобы его можно было заряжать до высоких напряжений и очень быстро разряжать — в миллиарды раз и более — без повреждений, которые сделали бы его непригодным для длительного использования в таких приложениях, как компьютеры и автомобили. .
Лейн Мартин (слева) и Джиын Ким продемонстрировали, что обычный материал может быть переработан в высокопроизводительный материал для хранения энергии. (Фотографии любезно предоставлены Мартином и Ким)
Исследователи из лаборатории Лейна Мартина, научного сотрудника Отделения материаловедения (MSD) лаборатории Беркли и профессора материаловедения и инженерии Калифорнийского университета в Беркли, достигли этого путем введения локальных дефектов, которые позволили ей выдерживать большие напряжения.
«Вы, наверное, сталкивались с релаксорными сегнетоэлектриками на газовом гриле.Кнопка, которая зажигает решетку, приводит в действие подпружиненный молоток, который ударяет по пьезоэлектрическому кристаллу, который является разновидностью релаксора, и создает напряжение, которое воспламеняет газ », — объяснил Мартин. «Мы продемонстрировали, что из них также можно сделать одни из лучших материалов для хранения энергии».
Размещение сегнетоэлектрического материала между двумя электродами и увеличение электрического поля вызывает накопление заряда. Во время разряда количество доступной энергии зависит от того, насколько сильно электроны материала ориентируются или становятся поляризованными в ответ на электрическое поле.Однако большинство таких материалов обычно не могут выдерживать большое электрическое поле до того, как материал разрушится. Таким образом, основная задача состоит в том, чтобы найти способ увеличить максимально возможное электрическое поле без ущерба для поляризации.
Исследователи обратились к разработанному ими ранее подходу для «отключения» проводимости материала. Бомбардировав тонкую пленку заряженными частицами высоких энергий, известными как ионы, они смогли создать изолированные дефекты. Дефекты захватывают электроны материала, препятствуя их движению и уменьшая проводимость пленки на порядки.
«В сегнетоэлектриках, которые должны быть изоляторами, утечка заряда через них является серьезной проблемой. Бомбардируя сегнетоэлектрики пучками ионов высоких энергий, мы знали, что можем сделать их лучше изоляторов », — сказал Джиын Ким, доктор-исследователь в группе Мартина и ведущий автор статьи. «Затем мы спросили, можем ли мы использовать тот же подход, чтобы релаксорный сегнетоэлектрик выдерживал большие напряжения и электрические поля, прежде чем он катастрофически выйдет из строя?»
Ответ оказался утвердительным.Ким впервые изготовил тонкие пленки из прототипа релаксорного сегнетоэлектрика, названного свинец-магний ниобит – титанат свинца. Затем он нацелился на пленки с ионами гелия высокой энергии в Центре ионно-лучевого анализа, находящемся в ведении Отдела ускорительных технологий и прикладной физики (ATAP) в лаборатории Беркли. Ионы гелия сбивали целевые ионы со своих узлов, создавая точечные дефекты. Измерения показали, что пленка, подвергнутая ионной бомбардировке, имела более чем вдвое большую плотность накопления энергии по сравнению с ранее сообщенными значениями и на 50% более высокую эффективность.
«Первоначально мы ожидали, что эффект будет в основном от уменьшения утечки с помощью изолированных точечных дефектов. Однако мы поняли, что сдвиг в соотношении поляризация-электрическое поле из-за некоторых из этих дефектов не менее важен », — сказал Мартин. «Этот сдвиг означает, что для создания максимального изменения поляризации требуется все большее и большее приложенное напряжение». Результат предполагает, что ионная бомбардировка может помочь преодолеть компромисс между высокой поляризацией и легкостью разрушения.
Тот же подход ионного пучка может также улучшить другие диэлектрические материалы для улучшения хранения энергии и предоставляет исследователям инструмент для устранения проблем в уже синтезированных материалах. «Было бы здорово, если бы люди использовали эти ионно-лучевые методы для« исцеления »материалов в устройствах постфактум, если процесс их синтеза или производства не прошел идеально», — сказал Ким.
Это исследование было поддержано Управлением науки Министерства энергетики США и грантом Национального научного фонда.
# #
Национальная лаборатория Лоуренса Беркли и ее ученые были основаны в 1931 году с убеждением в том, что самые большие научные проблемы решаются с помощью команд. Они были отмечены 13 Нобелевскими премиями. Сегодня исследователи Berkeley Lab разрабатывают решения в области устойчивой энергетики и защиты окружающей среды, создают новые полезные материалы, расширяют границы компьютерных технологий и исследуют тайны жизни, материи и Вселенной. Ученые со всего мира полагаются на возможности лаборатории в своих научных открытиях.Berkeley Lab — это многопрограммная национальная лаборатория, управляемая Калифорнийским университетом при Управлении науки Министерства энергетики США.
Управление науки Министерства энергетики США является крупнейшим спонсором фундаментальных исследований в области физических наук в Соединенных Штатах и работает над решением некоторых из наиболее актуальных проблем современности. Для получения дополнительной информации посетите сайт energy.gov/science.
Контактное лицо для СМИ:
Лорел Келлнер: [адрес электронной почты защищен], 510-486-5375
General Atomics побила рекорд конденсаторов по энергоемкости
САН-ДИЕГО, Калифорния, 30 ИЮНЯ 2016 г. — Компания General Atomics Electromagnetic Systems (GA-EMS) объявила сегодня, что она успешно разработала и продемонстрировала импульсные силовые конденсаторы с энергоемкостью более 415 килоджоулей (кДж), что превышает предыдущий рекорд, установленный GA-EMS, более чем на 20%.
«Это представляет собой то, что мы считаем важной, установившей мировой рекорд вехой в разработке конденсаторов с более высокой плотностью энергии», — заявил Ник Буччи, вице-президент по противоракетной обороне и космическим системам в GA-EMS. «Наши постоянные исследования, разработки и совершенствование технологий конденсаторов с высокой плотностью энергии позволяют создавать системы импульсного питания, достаточно мощные и достаточно компактные, чтобы удовлетворить потребности наших клиентов как в наземных, так и в морских рельсотронах.«
Два отдельных импульсных силовых конденсатора были успешно продемонстрированы 500 выстрелов при 415 кДж в режиме повторяющегося огня. GA-EMS продолжает испытания, чтобы дополнительно продемонстрировать срок службы конденсаторов для соответствия требованиям миссии рельсотрона.
«Системы вооружения с электроприводом предъявляют огромные требования к импульсным системам питания и, в частности, к конденсаторам, из которых они состоят», — продолжил Буччи. «Раньше максимальная запасенная энергия для одного из наших конденсаторов большой платформы составляла 340 кДж. Теперь, когда в одном конденсаторе содержится более 415 кДж энергии, мы добиваемся значительного увеличения общей плотности энергии для проектирования и производства импульсных систем питания. чтобы соответствовать более компактным платформам систем вооружения рельсотрона следующего поколения.«
GA-EMS успешно провела испытания снарядов из своего 3-мегаджоульного электромагнитного рельсотрона Blitzer® с использованием импульсных систем питания предыдущего поколения с высокой плотностью энергии, приводимых в действие конденсаторами, для запуска снарядов с ускорением, превышающим ускорение силы тяжести в 30 000 раз (30 000 gees). Эта новая разработка конденсатора обеспечит значительно более высокую дульную энергию в импульсных системах питания аналогичного размера.
О компании General Atomics Electromagnetic Systems
Группа компаний General Atomics Electromagnetic Systems (GA-EMS) является мировым лидером в области исследований, проектирования и производства первых в своем роде электромагнитных систем и систем производства электроэнергии.
No related posts.

материал	κ
воздух	1.005364
уксусная кислота	6,2
спирт этиловый (зерновой)	24,55
спирт метиловый (дерево)	32,70
янтарь	2,8
асбест	4,0
асфальт	2,6
бакелит	4,8
кальцит	8,0
карбонат кальция	8.7
целлюлоза	3,7–7,5
цемент	~ 2
кокаин	3,1
хлопок	1,3
алмаз I типа	5,87
алмаз типа IIa	5,66
эбонит	2,7
эпоксидная	3,6
мука	3-5
фреон 12, −150 ° C (жидкость)	3.5
фреон 12, +20 ° C (пар)	2,4
германий	16
стекло	4–7
стекло, пирекс 7740	5,0
гуттаперча	2,6
реактивное топливо (жиклер)	1,7
оксид свинца	25,9
ниобат свинца, магния	10 000
сульфид свинца (галенит)	200
титанат свинца	200
дейтерид лития	14.0
люцит	2,8
слюда, мусковит	5,4
слюда канадская	6,9
нейлон	3,5
масло льняное	3,4
масло минеральное	2,1
масло оливковое	3,1
масло нефтяное	2,0–2,2
масло, силикон	2.5
масло, сперма	3,2
масло трансформаторное	2,2

материал	κ
бумага	3,3, 3,5
оргстекло	3,1
полиэстер	3,2–4,3
полиэтилен	2,26
полипропилен	2.2–2,3
полистирол	2,55
поливинилхлорид (пвх)	4,5
фарфор	6–8
ниобат калия	700
KTN, 0 ° C	34 000
KTN, 20 ° C	6 000
кварц кристаллический (∥)	4,60
кварц кристаллический (⊥)	4.51
кварц плавленый	3,8
каучук бутил	2,4
резина, неопрен	6,6
резина, силикон	3,2
резина вулканизированная	2,9
соль	5,9
селен	6,0
кремний	11,8
карбид кремния (αSiC)	10.2
диоксид кремния	4,5
силиконовое масло	2,7–2,8
почва	10–20
титанат стронция, +25 ° C	332
титанат стронция, −195 ° C	2080
сера	3,7
пятиокись тантала	27
тефлон	2,1
антимонид олова	147
теллурид олова	1770
диоксид титана (рутил)	114
табак	1.6–1,7
диоксид урана	24
вакуум	1 (ровно)
вода, лед, −30 ° C	99
вода, жидкость, 0 ° C	87,9
вода, жидкость, 20 ° C	80,2
вода, жидкость, 40 ° C	73,2
вода, жидкость, 60 ° C	66,7
вода, жидкость, 80 ° C	60.9
вода, жидкость, 100 ° C	55,5
воск пчелиный	2,7–3,0
воск карнубский	2,9
воск, парафин	2,1–2,5
вощеная бумага	3,7

ткани человека	κ
кость губчатая	26
кость кортикальная	14.5
мозг, серое вещество	56
мозг, белое вещество	43
мозг, мозговые оболочки	58
хрящ общий	22
хрящ, ухо	47

ткани человека	κ
глаз, водянистая влага	67
глаз, роговица	61
глаз, склера	67
жир	16
мышца гладкая	56
мышца поперечнополосатая	58
скин	33–44
язычок	38

материал	поле (МВ / м)
воздух	3
янтарь	90
бакелит	12, 24
алмаз типа IIa	10
стекло, пирекс 7740	13, 14
слюда, мусковит	160
нейлон	14
масло, силикон	15
масло трансформаторное	12, 27

материал	поле (МВ / м)
бумага	14, 16
полиэтилен	50, 500–700, 18
полистирол	24, 25, 400–600
поливинилхлорид (ПВХ)	40
фарфор	4, 12
кварц плавленый	8
резина, неопрен	12, 12
титанат стронция	8
тефлон	60
диоксид титана (рутил)	6

Микрофоны и принцип их работы
тип	звуков производят изменений в…	, что вызывает изменений в…	, что приводит к изменению …
углеродистый	Плотность гранул	сопротивление	напряжение
конденсатор	разделительная пластина	емкость	напряжение
динамический	расположение змеевика	флюс	напряжение
пьезоэлектрический	компрессия	поляризация	напряжение

Разное

E _x = —	∆ В
	∆ x
E _y = —	∆ В	⇒	E = — ∇ V
	∆ y
E _z = —	∆ В
	∆ z