Электрическая емкость (страница 1)

Решение:
При перемещении пластины емкость конденсатора в данный момент времени определяется той частью площади пластин, по которой они перекрывают друг друга. В моменты времени t₁ и t₂ площади

где l=10 см-длина стороны пластины. В эти моменты времени конденсатор имеет емкости

а заряды на его пластинах

11 Найти заряд, который нужно сообщить двум параллельно соединенным конденсаторам с емкостями C₁ = 2 мкФ и С₂=1 мкФ, чтобы зарядить их до разности потенциалов V=20кВ.

Решение:
Общий заряд параллельно соединенных конденсаторов

12 Два одинаковых плоских конденсатора соединены параллельно и заряжены до разности потенциалов V₀ = 6 В. Найти разность потенциалов V между пластинами конденсаторов, если после отключения конденсаторов от источника тока у одного конденсатора уменьшили расстояние между пластинами вдвое.

Решение:

13 Два конденсатора с емкостями С₁ = 1 мкФ и С₂ = 2мкФ зарядили до разностей потенциалов V₁=20B и V₂ = 50 В. Найти разность потенциалов V после соединения — конденсаторов одноименными полосами.

Решение:

14 Конденсатор емкости C₁ = 20 мкФ, заряженный до разности потенциалов V₁ = 100B, соединили параллельно с заряженным до разности потенциалов V₁=40 В конденсатором, емкость которого С₂ неизвестна (соединили одноименно заряженные обкладки конденсаторов). Найти емкость С₂ второго конденсатора, если разность потенциалов между обкладками конденсаторов после соединения оказалась равной V=80 В.

Решение:

15 Конденсатор емкости С₁=4мкФ, заряженный до разности потенциалов V₁ = 10B, соединен параллельно с заряженным до разности потенциалов V₂ = 20 В конденсатором емкости С₂ = 6 мкФ (соединили разноименно заряженные обкладки конденсаторов). Какой заряд окажется на пластинах первого конденсатора после соединения?

Решение:
Заряды конденсаторов до их соединения q₁ = C₁V₁ и q₂ = C₂V₂. После соединения разноименно заряженных обкладок конденсаторов общий заряд q = |q₂-q₁| = (C₁ + C₂)V и заряд первого конденсатора где V-разность потенциалов между обкладками конденсаторов после соединения; отсюда

16 Конденсатор, заряженный до разности потенциалов V₁ = 20 В, соединили параллельно с заряженным до разности потенциалов V₂ = 4 В конденсатором емкости С₂ = 33 мкФ (соединили разноименно заряженные обкладки конденсаторов). Найти емкость С1 первого конденсатора, если разность потенциалов между обкладками конденсаторов после их соединения V=2 В.

Решение:
После соединения разноименных обкладок общий заряд q = CV равен разности зарядов q₁ = C₁V₁ и q₂ = C₂V₂ отдельных конденсаторов, где С=С₁ + С₂ — общая емкость после соединения. Таким образом,


17 Конденсатор емкости С₁ = 1 мкФ, заряженный до разности потенциалов V₁ = 100B, соединили с конденсатором емкости С₂ = 2 мкФ, разность потенциалов V₂ на обкладках которого неизвестна (соединили разноименно заряженные обкладки конденсаторов). Найти разность потенциалов V₂, если разность потенциалов между обкладками конденсаторов после соединения оказалась равной V=200 В.

Решение:
До соединения заряды первого и второго конденсаторов

После соединения разноименных обкладок общий заряд

Двойной знак мы здесь поставили потому, что заранее не известно, какой из зарядов, q₂ или q₁ больше; отсюда

Решение со знаком минус соответствует случаю, когда знаки зарядов на пластинах первого конденсатора после соединения пластин не меняются, а со знаком плюс-случаю, когда эти знаки становятся обратными. Так как в нашем случае , а величина |V₂| должна быть всегда положительной, то существует лишь одно решение-со знаком плюс. В результате |V₂| = 350 В.

18 Два проводящих шара с радиусами R₁ и R₂ расположены так, что расстояние между ними во много раз больше радиуса большего шара. На шар радиуса R₁ помещен заряд q. Каковы будут заряды на шарах после соединения их проводником, если второй шар не был заряжен? Емкостью проводника, соединяющего шары, пренебречь.

Решение:


19 Два проводящих шара с радиусами R₁ = 8см и R₂ = 20 см, находящихся на большом расстоянии друг от друга, имели электрические заряды q₁=40 нКл и q₂=— 20 нКл. Как перераспределятся заряды, если шары соединить проводником? Емкостью проводника, соединяющего шары, пренебречь.

Решение:
Соединение шаров проводником эквивалентно параллельному соединению конденсаторов. После соединения


20 Два проводящих шара с радиусами R₁ = 10см и R₂ = 5см, заряженных до потенциалов φ₁=20B и φ₂=10В, соединяются проводником. Найти поверхностные плотности зарядов на шарах σ₁ и σ₂ после их соединения. Расстояние между шарами велико по сравнению с их радиусами. Емкостью проводника, соединяющего шары, пренебречь.

Решение:
Заряды на шарах до и после соединения Общий потенциал шаров после соединения определим из условия сохранения заряда
Заряды на первом и втором шарах после соединения

Поверхностные плотности зарядов на шарах


21 Плоский воздушный конденсатор, заряженный до разности потенциалов V₀ = 800 В, соединили параллельно с таким же по размерам незаряженным конденсатором, заполненным диэлектриком. Какова диэлектрическая проницаемость e диэлектрика, если после соединения разность потенциалов между пластинами конденсаторов оказалась равной V=100В?

Решение:

22 Найти емкость С трех плоских воздушных конденсаторов, соединенных параллельно. Размеры конденсаторов одинаковы: площадь пластины S=314 см², расстояние между пластинами d=1 мм. Как изменится емкость трех конденсаторов, если пространство между пластинами одного конденсатора заполнить слюдой (диэлектрическая проницаемость ε₁ = 7), а другого — парафином (диэлектрическая проницаемость ε₂ = 2)?

Решение:
Емкость трех конденсаторов без диэлектрика При заполнении двух конденсаторов диэлектриками емкость трех конденсаторов

23 В заряженном плоском конденсаторе, отсоединенном от источника тока, напряженность электрического поля равна Е₀. Половину пространства между пластинами конденсатора заполнили диэлектриком с диэлектрической проницаемостью ε (толщина диэлектрика равна расстоянию между пластинами). Найти напряженность электрического поля Е в пространстве между пластинами, свободном от диэлектрика.

Решение:
Если d-расстояние между пластинами и С₀ — емкость конденсатора без диэлектрика, то разность потенциалов между пластинами конденсатора (без диэлектрика) и заряд на пластинах Конденсатор, половина которого заполнена диэлектриком, можно рассматривать как два соединенных параллельно конденсатора (рис. 341), причем один не содержит диэлектрика и имеет емкость а в другом все пространство между пластинами заполнено диэлектриком, и поэтому его емкость Полная емкость конденсатора, половина которого заполнена диэлектриком, При отключенном источнике тока заряд на пластинах сохраняется, поэтому разность потенциалов между пластинами V=q/C, и напряженность электрического поля в пространстве между пластинами, свободном от диэлектрика,


24 Два последовательно соединенных конденсатора с емкостями C₁ = 1 мкФ и С₂ = 3 мкФ подключены к источнику тока с напряжением V =220 В. Найти напряжение на каждом конденсаторе.

Решение:
Если V₁ и V₂ — напряжения на первом и втором конденсаторах, то V= V₁ + V₂, а заряды на них одинаковы и равны
q=C₁V₁=C₂V₂; отсюда

При последовательном соединении конденсаторов на конденсаторе меньшей емкости напряжение больше, чем на конденсаторе большей емкости.

25 Два последовательно соединенных конденсатора с емкостями C₁ = 1 мкФ и С₂ = 2 мкФ подключены к источнику тока с напряжением V =900 В. Возможна ли работа такой схемы, если напряжение пробоя конденсаторов V_пр = 500 В?

Решение:
Напряжения на первом и втором конденсаторах (см. задачу 24). Работать при указанном в условии задачи напряжении пробоя конденсаторов нельзя, ибо произойдет пробой первого, а затем и второго конденсаторов.

26 Два последовательно соединенных конденсатора подключены к источнику тока с напряжением V= 200 В (рис. 79). Один конденсатор имеет постоянную емкость C₁ = 0,5 мкФ, а другой — переменную емкость С₂ (от Cmin = 0,05 мкФ до Сmах = 0,5 мкФ). В каких пределах изменяется напряжение на переменном конденсаторе при изменении его емкости от минимальной до максимальной?

Решение:
При изменении емкости переменного конденсатора С₂ от Cmin до Сmax, напряжение на нем V изменяется в пределах (см. задачу 24)

27 При последовательном соединении трех различных конденсаторов емкость цепи С₀ = 1 мкФ, а при параллельном соединении емкость цепи С=11мкФ. Найти емкости конденсаторов С₂ и С₃, если емкость конденсатора С₁ = 2 мкФ.

Решение:

28 При последовательном соединении трех различных конденсаторов емкость цепи С₀ = 0,75 мкФ, а при параллельном соединении емкость цепи С = 7 мкФ. Найти емкости конденсаторов С₂ и С₃ и напряжения на них V₂ и V₃ (при последовательном соединении), если емкость конденсатора C₁ = 3 мкФ, а напряжение на нем V₁ = 20B.

Решение:
При последовательном соединении конденсаторов имеем

при параллельном

Из этих уравнений находим

Согласно теореме Виета С2 и С3 должны быть корнями квадратного уравнения

Решая его, найдем

Заряды на всех конденсаторах при последовательном соединении равны между собой:


29 Три последовательно соединенных конденсатора с емкостями С₁ = 100пФ, С₂ = 200 пФ, С₃ = 500 пФ подключены к источнику тока, который сообщил им заряд q=10нКл. Найти напряжения на конденсаторах V₁, V₂ и V₃, напряжение источника тока V и емкость всех конденсаторов С₀.

Решение:
При последовательном соединении конденсаторов заряд каждого конденсатора равен q, поэтому

Напряжение источника тока равно полному напряжению на всех конденсаторах:

Так как при последовательном соединении
то

30 Три последовательно соединенных конденсатора с емкостями С₁=0,1мкФ, С₂ = 0,25 мкФ и С₃ = 0,5 мкФ подключены к источнику тока с напряжением V =32 В. Найти напряжения V₁, V₂ и V₃ на конденсаторах.

Решение:


31 Два одинаковых воздушных конденсатора емкости С=100пФ соединены последовательно и подключены к источнику тока с напряжением V= 10 В. Как изменится заряд на конденсаторах, если один из них погрузить в диэлектрик с диэлектрической проницаемостью ε = 2?

Решение:
При последовательном соединении конденсаторов заряды на конденсаторах равны. До погружения одного из них в диэлектрик заряд на каждом конденсаторе

после погружения одного из них в диэлектрик заряды конденсаторов будут

Учитывая, что

Изменение заряда на конденсаторах


32 Два плоских воздушных конденсатора с одинаковыми емкостями соединены последовательно и подключены к источнику тока. Пространство между пластинами одного из конденсаторов заполняют диэлектриком с диэлектрической проницаемостью ε = 9. Во сколько раз изменится напряженность электрического поля Е в этом конденсаторе?

Решение:
Первоначальная напряженность электрического поля в каждом конденсаторе

где d-расстояние между пластинами конденсатора. После заполнения одного конденсатора диэлектриком напряженность электрического поля в нем

Отношение напряженностей


33 Решить предыдущую задачу для случая, когда конденсаторы после зарядки отключаются от источника тока.

Решение:
После отключения конденсатора от источника тока и заполнения его диэлектриком заряд на нем не изменяется:

Напряженность электрического поля в конденсаторе, заполненном диэлектриком,

Отношение напряженностей

34 Два плоских воздушных конденсатора с одинаковыми емкостями С=10пФ соединены последовательно. Насколько изменится емкость конденсаторов, если пространство между пластинами одного из них заполнить диэлектриком с диэлектрической проницаемостью ε = 2?

Решение:
Изменение емкости соединенных конденсаторов


35 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d введена параллельно обкладкам проводящая пластинка, размеры которой равны размерам обкладок, а ее толщина намного меньше d. Найти емкость конденсатора с проводящей пластинкой, если пластинка расположена на расстоянии l от одной из обкладок конденсатора.

Решение:
После введения пластинки образовалось два последовательно включенных конденсатора с емкостями

(рис. 342). Их общую емкость определим из соотношения

где С-первоначальная емкость конденсатора. Таким образом, после введения пластинки при любом ее положении С₀ = С.

36 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d введена параллельно обкладкам проводящая пластинка, размеры которой равны размерам обкладок, а толщина d_п = d/3

Решение:
Введение проводящей пластинки между обкладками конденсатора приводит к образованию двух последовательно включенных конденсаторов с расстояниями между обкладками d₁ и d₂ и емкостями

(рис. 343). Их общую емкость находим из соотношения

При -первоначальная емкость конденсатора.

37 Плоский воздушный конденсатор заряжен до разности потенциалов V₀ = 50 В и отключен от источника тока. После этого в конденсатор параллельно обкладкам вносится проводящая пластинка толщины d_п= 1 мм. Расстояние между обкладками d=5 мм, площади обкладок и пластинки одинаковы. Найти разность потенциалов V между обкладками конденсатора с проводящей пластинкой.

Решение:
Емкости конденсатора до и после внесения проводящей пластинки толщины d_п (см. задачу 36)
Заряд конденсатора, отключенного от источника тока, не изменяется:

отсюда разность потенциалов между обкладками конденсатора после внесения проводящей пластинки

38 В плоский воздушный конденсатор с площадью обкладок S и расстоянием между ними d вводится параллельно обкладкам диэлектрическая пластинка толщины d₁<d/ Диэлектрическая проницаемость пластинки равна ε, площади обкладок и пластинки одинаковы и равны S. Найти емкость конденсатора с диэлектрической пластинкой.

Решение:

Задача В15. Плоский конденсатор состоит из двух обкладок площадью

Задача В15. Плоский конденсатор состоит из двух обкладок площадью 40 каждая. Между ними находится стекло с диэлектрической проницаемостью 7. Какой заряд находится на обкладках этого конденсатора, если напряженность электрического поля между ними 8 МВ/м?

Обозначим S площадь обкладок конденсатора, — диэлектрическую проницаемость стекла, Е — напряженность электрического поля между обкладками, q — заряд конденсатора, С — его емкость, — электрическую постоянную, d — расстояние между обкладками, U — напряжение на обкладках.

Решение:

Согласно определению емкости конденсатора

Кроме того, емкость плоского конденсатора

Приравняем правые части этих равенств и из полученного выражения найдем искомый заряд:

Расстояние между обкладками d определим из формулы

откуда

Подставим равенство (2) в формулу (1):

Произведем вычисления:

Ответ: q = 2 мкКл.

Эта задача взята со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:

Задачи по физике с решением

Возможно вам будут полезны эти задачи:

Задача В13. Напряжение на обкладках конденсатора 200 В, расстояние между обкладками 0,2 мм. Конденсатор отключили от источника зарядов, после чего увеличили расстояние между обкладками до 0,7 мм. Определить новое напряжение на обкладках конденсатора.

Задача В14. Между обкладками плоского конденсатора находится слюдяная пластинка с диэлектрической проницаемостью 6. Емкость конденсатора 10 мкФ, напряжение на его обкладках 1 кВ. Какую работу надо совершить, чтобы вынуть пластинку из конденсатора, не отключая его от источника напряжения?

Задача В16. Два проводника с емкостями 4 пФ и 6 пФ заряжены соответственно до потенциалов 8 В и 10 В. Найти их потенциал после соприкосновения друг с другом.

Задача В17. Плоский воздушный конденсатор зарядили до напряжения 600 В и отключили от источника зарядов, после чего расстояние между обкладками увеличили от 0,2 мм до 0,7 мм и ввели диэлектрик с проницаемостью 7. Найти новое напряжение между обкладками

Решение задач Воздушный 📝 цилиндрический конденсатор состоит из проволок

1. Сколько стоит помощь?

Цена, как известно, зависит от объёма, сложности и срочности. Особенностью «Всё сдал!» является то, что все заказчики работают со экспертами напрямую (без посредников). Поэтому цены в 2-3 раза ниже.

2. Каковы сроки?

Специалистам под силу выполнить как срочный заказ, так и сложный, требующий существенных временных затрат.

Для каждой работы определяются оптимальные сроки. Например, помощь с курсовой работой – 5-7 дней. Сообщите нам ваши сроки, и мы выполним работу не позднее указанной даты. P.S.: наши эксперты всегда стараются выполнить работу раньше срока.

3. Выполняете ли вы срочные заказы?

Да, у нас большой опыт выполнения срочных заказов.

4. Если потребуется доработка или дополнительная консультация, это бесплатно?

Да, доработки и консультации в рамках заказа бесплатны, и выполняются в максимально короткие сроки.

5. Я разместил заказ. Могу ли я не платить, если меня не устроит стоимость?

Да, конечно — оценка стоимости бесплатна и ни к чему вас не обязывает.

6. Каким способом можно произвести оплату?

Работу можно оплатить множеством способом: картой Visa / MasterCard, с баланса мобильного, в терминале, в салонах Евросеть / Связной, через Сбербанк и т.д.

7. Предоставляете ли вы гарантии на услуги?

На все виды услуг мы даем гарантию. Если эксперт не справится — мы вернём 100% суммы.

8. Какой у вас режим работы?

Мы принимаем заявки 7 дней в неделю, 24 часа в сутки.

Электроемкость, конденсатор, напряжение, потенциал.

Соединения: параллельное, последовательное конденсаторов. Тест

Вопрос 1. Модуль напряженности электрического поля в пространстве между пластинами плоского конденсатора в вакууме 60 В/м, расстояние между пластинами 4 см. Определите напряжение на пластинах конденсатора.

Вопрос 2. Определите емкость батареи (нФ) конденсаторов, если C₁=5 нФ, C₂=15 нФ.

Вопрос 3. Определите площадь (см²) каждой из обкладок плоского конденсатора с воздушным промежутком 3 мм, если его емкость 5 пФ.

Вопрос 4. Емкости конденсаторов C₁ = 12 нФ и C₂ = 24 нФ, C₃ = 36 нФ. Определите емкость батареи (нФ) конденсаторов.

Вопрос 5. Плоский конденсатор с расстоянием между пластинами 1 мм заряжен от источника тока напряжением 20 В. Определите напряжение между пластинами, если отключив конденсатор от источника тока, раздвинуть их до расстояния 5 мм.

Вопрос 6. Между пластинами плоского конденсатора емкостью 23 нФ вставляют две одинаковые по толщине пластины из диэлектрика с проницаемостями 2 и 2,5, которые плотно прилегают к обкладкам конденсатора. Определите емкость (нФ) полученного конденсатора.

Вопрос 7. Батарея конденсаторов состоит из двух плоских конденсаторов, соединенных параллельно, емкости которых 10 мкФ и 40 мкФ соответственно. Из конденсатора меньшей емкости сливают жидкий диэлектрик проницаемостью 4 и полностью заполняют им второй, бывший до этого «пустым». Во сколько раз увеличится емкость батареи?

Вопрос 8. Батарея конденсаторов состоит из двух плоских конденсаторов, соединенных последовательно, емкости которых 10 пФ и 30 пФ. Из конденсатора большей емкости сливают половину жидкого диэлектрика с диэлектрической проницаемостью 3 и наполовину заполняют им конденсатор меньшей емкости. Определите емкость (пФ) полученной батареи.

Вопрос 9. К конденсатору емкостью 60 нФ, заряженному до напряжения 80 В, параллельно присоединяют незаряженный конденсатор емкостью 90 нФ. Определите разность зарядов (мкКл, с точностью до сотых) на каждом конденсаторе после соединения.

Вопрос 10. Какой заряд необходимо сообщить земному шару, чтобы изменить его потенциал на 3 кВ? Радиус Земли 6400 км.

Вопрос 11.

Определите заряд (мкКл) плоского конденсатора, имевшего заряд 30 мкКл, если его, не отключая от источника напряжения заполнить диэлектриком проницаемостью 4.

Вопрос 12. Воздушный конденсатор емкостью 6 нФ, подключенный к батарее напряжением 12 В, заполняют парафином. Какой заряд (нКл) пройдет при этом по цепи?

Вопрос 13. К батарее конденсаторов С₁ = 1 мкФ, С₂ = 2 мкФ, С₃ = 3 мкФ подключили напряжение 100 В. Определите напряжение на конденсаторе С₁.

Вопрос 14. На батарею конденсаторов С₁ = 1 мкФ, С₂ = 2С₁, С₃ = 3 С₁ подали напряжение 100 В. Определите заряд (мКл) на конденсаторе С

3.

Вопрос 15. Имеется три различных конденсатора, причем емкость одного из них 4 мкФ. Если конденсаторы соединить последовательно, то емкость полученной батареи будет 12/11 мкФ, а если параллельно – 12 мкФ. Определите разность емкостей (мкФ) неизвестных конденсаторов.

Вопрос 16. Плоский воздушный конденсатор заряжен до разности потенциалов 50 В и отключен от источника тока. После этого в конденсатор параллельно обкладкам вносится металлический лист толщиной 1 мм. Какова разность потенциалов между обкладками конденсатора, если расстояние между ними составляет 5 мм?

Вопрос 17. Определите емкость батареи (нФ), если С = 2 нФ.

Вопрос 18. Определите емкость батареи (мкФ) конденсаторов в приведенной схеме, если С=10 мкФ.

Вопрос 19. Батарею параллельно соединенных конденсаторов с емкостями C₁ = 1 мкФ и C₂ = 2 мкФ сначала подсоединяют к источнику с ЭДС, равной 6 В (ключ К в положении 1). Затем ключ переводят в положение 2, соединяя батарею с незаряженным конденсатором C₃ = 3 мкФ. Какой заряд (мкКл) при этом получит конденсатор C₃?

Вопрос 20. Поверхностная плотность заряда на пластинах конденсатора, находящегося в вакууме, составляет . Площадь пластин 100см², емкость конденсатора 10 пФ. Определите скорость (Мм/с), которую приобретает электрон, пройдя в конденсаторе путь от одной пластины к другой.

3.6. Примеры решения задач к разделу 3

Пример 1.
Плоский конденсатор заряжен и отключен от источника. Определите силу притяжения пластин конденсатора.
Ответ: отключенный конденсатор — электрически замкнутая система (Q = const), поэтому , где .

Пример 2.
Вычислите силу взаимодействия обкладок сферического конденсатора, если он заполнен диэлектриком с проницаемостью = 6, а радиусы R₁ и R₂ равны соответственно 6 и 8 см. Конденсатор подключен к источнику с разностью потенциалов

Решение

Потенциальная энергия сферического конденсатора , подставляя выражение для емкости конденсатора получаем . Сила, действующая, например, на внешнюю обкладку составит

; F = 3 ·10^-3 Н.

Пример 3.
Цилиндрический конденсатор с радиусами обкладок соответственно R₁ = 10 и R₂ = 15 см, заполненный диэлектриком с проницаемостью = 4, подключен к источнику с разностью потенциалов = 3·10² В. Определите силу взаимодействия обкладок на единицу h = 1 м длины конденсатора.

Решение

Погонная энергия заряженного цилиндрического конденсатора есть

.

Сила взаимодействия обкладок ; F = 4,1 10^-4 Н / м.

Пример 4.
Потенциал наэлектризованного металлического шара и напряженность ЭСП на расстоянии а = 5 см от его поверхности составляют = 1,2·10⁴ В; Е = 6·10⁴ В / м. Определите энергию W шара.

Решение

Для определения энергии необходимо найти радиуса R шара и заряд Q на его поверхности. Находим их из известных соотношений: и . Тогда ; W = 4·10^-4 Дж.

Пример 5.
1) Сферическую тонкостенную оболочку радиуса R₁, равномерно заряженную по поверхности зарядом Q, расширили до радиуса R₂. Определите работу А₁₂, совершенную при расширении силами ЭСП.
Ответ: .
2) В центре сферической тонкостенной оболочки, по поверхности которой равномерно распределен заряд Q = 5 мкКл, расположен точечный заряд Q₀ = 1,5 мкКл. Определите работу сил ЭСП при расширении оболочки, т.е. при увеличении ее радиуса от R₁ = 50 мм до R₂ = 0,1 м.
Ответ: ; А₁₂ = 1,8 Дж.

Пример 6.
Система проводников состоит из двух концентрических тонкостенных металлических оболочек радиусов R₁ и R₂ и зарядами на оболочках соответственно Q₁ и Q₂. Определите полную энергию W системы.

Решение

Полная энергия системы двух сфер есть сумма их собственных энергий и потенциальной энергии взаимодействия , каждое из слагаемых есть:

; ; .
.

Пример 7.
1) У плоского конденсатора с площадью пластин S и расстоянием d между ними одна из пластин заземлена. Конденсатор заряжен и отключен от источника. Определите энергию 2-ой обкладки в ЭСП первой.

Решение

Потенциал ЭСП, создаваемого 1-ой (заземленной) обкладкой в месте расположения элементарных зарядов на 2-ой обкладке, равен . Потенциальная энергия элементарных зарядов на 2-ой обкладке в ЭСП первой составит

.

2) Плоский конденсатор с пластинами площадью S = 0,02 м2 каждая и расстоянием между ними d = 0,5 см заполнен диэлектриком с = 4. Конденсатор заряжается до разности потенциалов = 0,1 кВ после чего отключается от источника. Какую работу необходимо затратить, чтобы удалить диэлектрик из конденсатора?

Решение

Энергия конденсатора с диэлектриком , после извлечения диэлектрика . Искомая работа есть

; А = 2·10^-8 Дж.

3) Пусть имеется плоский воздушный конденсатор с площадью обкладок S. Какую работу А₁₂ против сил ЭСП надо совершить, чтобы медленно увеличить расстояние между обкладками от d₁ до d₂, если при этом поддерживать неизменными заряд Q на обкладках.

Решение

Работа внешних сил расходуется на изменение внутренней энергии конденсатора. Здесь существенно, что по условию Q = const, поэтому энергию удобно вычислять по формуле , тогда .

Пример 8.
1) Максимальная электроемкость конденсатора настройки в радиоэлектронном устройстве равна 100 пФ (1 пФ = 1·10^-12 Ф). Путем поворота подвижных пластин электроемкость конденсатора может быть уменьшена до 10 пФ. Предположим, что конденсатор подключен к источнику с разностью потенциалов = 0,3 кВ, когда его емкость максимальна. Затем ручка настройки поворачивается, и электроемкость конденсатора становится минимальной. Какая работа совершается при повороте ручки настройки?

Решение

Энергия заряженного конденсатора с электроемкостью С равна . Искомая работа (здесь внешней силы) равна разности энергий конденсатора после и до поворота ручки настройки, т. е. ; А = -4,1·10^-6 Дж.
2) Максимальная электроемкость плоского конденсатора переменной электроемкости С₁ = 400 пФ, минимальная — С₂ = 2 пФ. Изменение электроемкости в этих пределах достигается поворотом рукоятки ротора на 180⁰, при этом подвижные пластины остаются параллельными неподвижным. Момент сил трения в подшипниках ротора М = 5,00 10^-6 Н м. Какую работу надо совершить, чтобы изменить электроемкость конденсатора от максимальной до минимальной, если конденсатор подключен к источнику с разностью потенциалов = 100 В?
Ответ: ; А=13,8 10^-6 Дж.

Пример 9.
Пластины плоского многопластинчатого конденсатора площадью S = 20 см² каждая разделены слюдяным диэлектриком ( = 6) толщиной d = 5 10^-5 м. При разности потенциалов на конденсаторе = 0,33 кВ энергия ЭСП в нем W = 7,7·10^-4 Дж. Определите электроемкость конденсатора и число N пластин.
Ответ: ; С=3,21·10^-8 Ф; ; ; N = 17.

Пример 10.
Число удаленных друг от друга ртутных капелек N = 100, радиусом r = 1 мм каждая заряжены до одинакового потенциала = 9 В. Капельки соединяются в одну большую радиуса R. Определите изменение W электростатической составляющей энергии капель.

Решение

Заряд на каждой капельке , и энергия всех удаленных друг от друга капелек . После слияния капель в одну заряды и объемы складываются, поэтому и , откуда .
Энергия большой капли составит . Изменение энергии ; = 8,2·10^-9 Дж.

Пример 11.
1) Заряды на обкладках двух конденсаторов с электроемкостями С₁ и С₂ равны соответственно Q₁ и Q₂. Конденсаторы соединяют параллельно одноименными обкладками. Проанализируйте ситуацию и покажите, что при соединении конденсаторов энергия батареи уменьшается. Укажите на возможные «каналы» потери энергии. На основе полученного результата проанализируйте, возможна ли ситуация, при которой энергия не теряется.

Решение

Энергия конденсаторов до их соединения равна При параллельном соединении электроемкости конденсаторов складываются, поэтому энергия ЭСП батареи составит Изменение энергии при этом составит
Уменьшение энергии произошло за счет ее излучения во внешнее пространство и превращения во внутреннюю энергию соединительных проводов (при перераспределении зарядов). Потери энергии не происходит, если Q₁C₂ = Q₂C₁. Иначе, это отвечает условию
2) Конденсатор с электроемкостью С₁ = 1 мкФ, заряженный до разности потенциалов = 0,3 кВ, подключили параллельно к незаряженному конденсатору электроемкостью С₂ = 2 мкФ. Вычислите изменение энергии системы конденсаторов после соединения их в батарею и установления в ней равновесия.

Решение

После соединения конденсаторов в батарею ее электроемкость увеличится до значения С = (С₁ + С₂), но заряд останется неизменным. Следовательно, изменение энергии составит
3) Два конденсатора с электроемкостями С₁ = 6 и С₂ = 4 мкФ соединены последовательно и вся батарея заряжена до разности потенциалов = 1·10⁴ В. Затем конденсаторы отключаются от источника и соединяются в новую батарею параллельно одноименными обкладками. Определите изменение энергии батареи.

Решение

При последовательном соединении энергия . После параллельного соединения конденсаторов заряд на батарее , а ее электроемкость станет , поэтому энергия .
Изменение энергии:

; = — 5 Дж.

Пример 12.
Точечный заряд Q = 3,0 мкКл находится в центре сферического слоя из диэлектрика с проницаемостью = 3,0. Внутренний радиус R₁ cлоя составляет 0,25 см, внешний R₂ = 0,5 м. Вычислите энергию W ЭСП в таком слое.

Решение

В тонком сферическом слое толщиной dr и радиуса содержится энергия

Интегрируем далее это выражение по r в пределах от R₁ до R₂, получаем

; W = 27 мДж.

Пример 13.
Металлическому шару радиуса R₁ сообщен заряд Q. Шар окружен сферическим диэлектрическим слоем из материала с проницаемостью ; наружный радиус слоя R₂. Вся система находится в неограниченной однородной среде с проницаемостью . Определите энергию ЭСП заряженного шара. Определите энергетическую массу m ЭСП, заключенного в слое.

Решение

Разбиваем мысленно все пространство вокруг шара на сферические слои радиусов r, толщиной dr, объемом . Энергия ЭСП, заключенного в таком слое, составит , где есть объемная плотность энергии ЭСП.
Используя результаты исследования структуры напряженности E(r) такой системы и после интегрирования, получаем .
Для массы m ЭСП в слое согласно формуле Эйнштейна , имеем , где с₀ = 3,0·10⁸ м / с — скорость электромагнитных волн в вакууме. Поучительны цифровые оценки: если Q = 2·10^-6 Кл, R₁ = 0,1 м, R₂ = 0,2 м, = 2, то m = 1·10^-18 кг. Это намного больше, чем массы покоящихся электрона, протона, и др.

Пример 14.
Вычислите энергию W_p ЭСП между двумя эквипотенциальными поверхностями на расстояниях R₁ = 5 и R₂ = 10 см от весьма тонкого металлического провода длиной h = 1 м, линейная плотность заряда которого = 5·10^-8 Кл / м.

Решение

Предполагаем здесь проводник достаточно длинным, поэтому краевыми эффектами пренебрегаем. В тонком воображаемом цилиндрическом слое радиуса r и толщиной dr, расположенном соосно с проводником, ЭСП обладает элементарной энергией . Интегрируя эти элементарные энергии в пределах от R₁ до R₂, получаем ; W_p = 1,6·10^-5 Дж.

Конденсаторы

| на главную | доп. материалы | физика как наука и предмет | электричество и электромагнетизм |

Организационные, контрольно-распорядительные и инженерно-технические услуги
в сфере жилой, коммерческой и иной недвижимости. Московский регион. Официально.

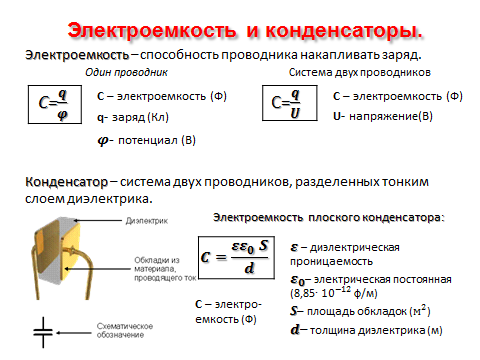
Для того чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. На практике, однако, необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать значительные по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов.

Если к заряженному проводнику приближать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, причем ближайшими к наводящему заряду Q будут заряды противоположного знака. Эти заряды, естественно, ослабляют поле, создаваемое зарядом Q, т. е. понижают потенци­ал проводника, что приводит (см. (93.1)) к повышению его электроемкости.

Конденсатор состоит из двух проводников (обкладок), разделенных диэлектриком. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми заря­дами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) два коаксиальных цилиндра; 3) две концентрические сферы. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, цилиндрические и сферические.

Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, воз­никающие на разных обкладках, являются равными по модулю разноименными зарядами. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (j₁—j₂) между его обкладками:

                                                                     (94.1)

Рассчитаем емкость плоского конденсатора, состоящего из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Если расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами можно пренебречь и поле между обкладками считать однородным. Его можно рассчитать используя формулы (86.1) и (94.1). При наличии диэлектрика между обкладками разность потенциалов между ними, согласно (86.1),

                                                       (94.2)

где e — диэлектрическая проницаемость. Тогда из формулы (94.1), заменяя Q=sS, с учетом (94.2) получим выражение для емкости плоского конденсатора:

                                                             (94.3)

Для определения емкости цилиндрического конденсатора, состоящего из двух полых коаксиаль­ных цилиндров с радиусами r₁ и r₂ (r₂ > r₁), вставленных один в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и сосредоточенным между цилиндрическими обкладками. Разность потенциалов между обкладками вычислим по формуле (86.3) для поля равномерно заряженного бесконечного цилиндра с линейной плотностью t =Q/l (l—длина обкладок). При наличии диэлектрика между обкладками разность потенциалов

                                                 (94.4)

Подставив (94.4) в (94.1), получим выражение для емкости цилиндрического конденсатора:

                                                        (94.5)

Для определения емкости сферического конденсатора, состоящего из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу (86.2) для разности потенциалов между двумя точками, лежащими на расстояниях r₁ и r₂ (r₂ > r₁) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов

                                                   (94.6)

Подставив (94.6) в (94.1), получим

Если d=r₂—r₁<<r₁, то r₂ » r₁ » r и C=4pe₀er²/d. Так как 4pr² —площадь сферической обкладки, то получаем формулу (94.3). Таким образом, при малой величине зазора по сравнению с радиусом сферы выражения для емкости сферического а плоского конденсаторов совпадают. Этот вывод справедлив и для цилиндрического конденсатора: при малом зазоре между цилиндрами по сравнению с их радиусами в формуле (94.5) ln (r₂/r₁) можно разложить в ряд, ограничиваясь только членом первого порядка. В результате опять приходим к формуле (94.3).

Из формул (94.3), (94.5) и (94.7) вытекает, что емкость конденсаторов любой формы прямо пропорциональна диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками. Поэтому применение в качестве прослойки сегнетоэлектриков значительно увеличивает емкость конденсаторов.

Конденсаторы характеризуются пробивным напряжением — разностью потенциа­лов между обкладками конденсатора, при которой происходит пробой — электричес­кий разряд через слой диэлектрика в конденсаторе. Пробивное напряжение зависит от формы обкладок, свойств диэлектрика и его толщины.

Для увеличения емкости и варьирования ее возможных значений конденсаторы соединяют в батареи, при этом используется их параллельное и последовательное соединения.

1. Параллельное соединение конденсаторов (рис. 144). У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна j_A – j_B. Если емкости отдельных конденсаторов С₁, С₂, …, С_n, то, согласно (94.1), их заряды равны

а заряд батареи конденсаторов

Полная емкость батареи

т. е. при параллельном соединении конденсаторов она равна сумме емкостей отдель­ных конденсаторов.

2. Последовательное соединение конденсаторов (рис. 145). У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи

где для любого из рассматриваемых конденсаторов Dj_i = Q/С_i. С другой стороны,

откуда

т. е. при последовательном соединении конденсаторов суммируются величины, обратные емкостям. Таким образом, при .последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, используемой в батарее.

---

Конденсатор на

А состоит из двух близко расположенных металлических проводов большая площадь, разделенная тонкой …

Конденсатор состоит из двух близко расположенных металлических проводников большая территория, разделенная тонкой …

Конденсатор состоит из двух близко расположенных металлических проводников большая площадь, разделенная тонкой изолирующей фольгой. Имеет электрическая емкость 3000,0 мкФ и заряжена до потенциала разница 60,0 В. Рассчитайте количество энергии, хранящейся в конденсатор.Попыток 0/99 Рассчитайте заряд этого конденсатора, когда электрическая запасенная в конденсаторе энергия составляет 5,40 Дж. Попыток 0/99 Если две пластины конденсатора разделены увеличился в раз …

Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонкой …

Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонкой изолирующей фольгой. Его электрическая мощность составляет 3800 В.Č Вычислить количество энергии, хранящейся в конденсаторе. Попытки ответа 0/99. Рассчитать заряд этого конденсатора, когда электрическая энергия, запасенная в конденсаторе, составляет 10,69 Дж. Отправить ответ Попытки 0/99 Если разделение двух пластин конденсатора увеличено на фактор 5, а заряд на …

Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонкой …

Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонкой изолирующей фольгой.Он имеет электрическую емкость 3400,0 мкФ и заряжается до разности потенциалов 81,0 В. Рассчитайте количество энергии, хранящейся в конденсаторе. Отправить ответ Попытки 0/99 Рассчитать заряд этого конденсатора, когда электрическая энергия, запасенная в конденсаторе, равна 12,00 Дж. Отправить ответ Попытки 0/99 Если две пластины конденсатора разделены …

Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонкой …

Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонкой изолирующей фольгой.Он имеет электрическую емкость 3200 мкФ и заряжается до разности потенциалов 0. Вычислите количество энергии, хранящейся в конденсаторе. Отправить Ansmer Tries 0/20 Рассчитать заряд этого конденсатора, когда электрическая энергия, запасенная в конденсаторе, составляет 6,35 Дж. Отправить ответ Попытки 0/20 u два элемента конденсатора имеют увеличенное разделение …

1. Конденсатор состоит из двух близко расположенных металлических проводников. большой площади, разделенные …

1.Конденсатор состоит из двух близко расположенных металлических проводников. большой площади, разделенной тонкой изолирующей фольгой. Имеет электрическая емкость 3800,0 мкФ и заряжена до потенциала разность 90,0 В. Рассчитайте количество энергии, хранящейся в конденсатор. 2. Рассчитайте заряд этого конденсатора, когда электрическая запасенная в конденсаторе энергия составляет 13,41 Дж. 3. Если две пластины конденсатора разделены увеличился в … раз

Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонким…

Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонкой изолирующей фольгой. Он имеет электрическую емкость 4000,0 мкФ и заряжается до разности потенциалов 69,0 В. Вычислите количество энергии, хранящейся в конденсаторе, 9,52 Дж. Вы правы. Предыдущие попытки Рассчитайте заряд этого конденсатора, когда электрическая энергия, запасенная в конденсаторе, составляет 12,17 Дж. 2759 ° C Емкость такая же, как и в предыдущем …

Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонким…

Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонкой изолирующей фольгой. Он имеет электрическую емкость 3600,0 мкФ и накопленную разность капацеротий в 66,0 В. Подсчитайте количество энергии 7,84 Дж. Вы правы. Предыдущие попытки Рассчитайте заряд на этом конденсаторе, когда электрическая энергия хранится в 2,48×10-1 c. Вы правы. Предыдущие попытки Если разделение двух пластин конденсатора увеличилось на …

1.) Конденсатор состоит из двух близко расположенных металлических проводников. большой площади, разделены …

1.) Конденсатор состоит из двух близко расположенных металлических проводников. большой площади, разделены тонкой изолирующей фольгой. Имеет электрическую емкость из 3800 мкФ и заряжается до разности потенциалов 75,0 V. Рассчитайте количество энергии, хранящейся в конденсаторе. 2.) Рассчитайте заряжать этот конденсатор, когда электрическая энергия, хранящаяся в конденсатор 9,85 Дж. 3.) Если два разделение пластин конденсатора увеличено в раз из 4 пока…

Конденсатор состоит из двух близко расположенных металлических проводников большая территория, разделенная тонкой …

Конденсатор состоит из двух близко расположенных металлических проводников большая площадь, разделенная тонкой изоляционной пленкой. Один из многих Практическое использование конденсатора заключается в накоплении энергии, чтобы выпускается внезапной вспышкой (как включение лампы вспышки в камера!) Приличный (не слишком дорогой) конденсатор в такой камере может составлять 100 мкФ и может вызвать полное электрическое энергия 4.8 Дж в мгновение ока. Какая разница напряжений …

Введение в физику II Главное меню Содержание Оценки Содержание курса ГЛАВНОЕ ЗАДАНИЕ »Установить 2 Таймер Примечания ОценитьОбратная связьПри …

Введение в Физику II Главное меню Содержание Оценки Содержание курса ГЛАВНОЕ ЗАДАНИЕ »Set 2 Таймер Примечания EvaluateFeedbackPri Конденсатор состоит из двух близко расположенных металлических проводников большой площади, разделенных тонкой изолирующей фольгой. Он имеет электрическую емкость 3800,0 мкФ и заряжен до разности потенциалов 87.0 В. Рассчитайте количество энергии, хранящейся в конденсаторе. Suimi Ansae Tries o / 20 Вычислить заряд этого конденсатора, когда электрическая энергия, запасенная в конденсаторе, равна …

Конденсатор

А состоит из двух круглых пластин диаметром 6,1 см, разделенных расстоянием 1,0 мм. Пластины заряжены …

Конденсатор состоит из двух круглых пластин диаметром 42 см, разделенных расстоянием 1,0 мм. Таблички …

Конденсатор состоит из двух круглых пластин диаметром 42 см, разделенных расстоянием 1.0 мм. Пластины заряжаются до 170 В, затем снимается аккумулятор (= 8 85 102 м) Сколько энергии хранится в конденсаторе? Выразите свой ответ в джоулях. ΑΣΦ. o 2 Отправить лучшее A Часть B Сколько работы необходимо сделать, чтобы раздвинуть пластинки так, чтобы расстояние между ними составляло 20 мм. Выразите свой ответ в джоулях |||| th 2 IN

Конденсатор состоит из двух круглых пластин диаметром 6,6 см. разделены на 1,0 мм. Пластины заряжены …

Конденсатор состоит из двух 6.Круглые тарелки диаметром 6 см разделены на 1,0 мм. Пластины заряжаются до 170 В, затем аккумулятор удален. Сколько энергии хранится в конденсаторе? Как необходимо проделать большую работу, чтобы раздвинуть пластины туда, где расстояние между ними 2,0 мм?

Часть A Четко покажите всю свою работу на бумаге для заметок.) ​​Электрическое поле E = …

Часть A Четко покажите всю свою работу на бумаге для заметок.) ​​Электрическое поле E = (2,0×105 Н / C, справа) заставляет шар массой 5,0 г (рис. 1) висеть под углом 20 °.(g = 9,8 м / с2) Каков заряд шара? Выразите свой ответ в нанокулонах. 10 AP? 9-89,2 нКл Отправить запрос Ответить <1 из 1 Обеспечить обратную связь 20 Ë 9 5,08 Пункт 22 Конденсатор состоит из двух круглых пластин диаметром 4,3 см ...

Две круглые металлические пластины радиусом 10,0 см разделены расстояние 0,200 …

Две круглые металлические пластины радиусом 10,0 см разделены расстояние 0,200 мм. Они подключены к клеммам автомобильный аккумулятор (трактуется как 12.0 В). (d) Теперь вы возвращаете пластины в их первоначальное положение и подождите, пока конденсатор полностью зарядится. Затем вы отсоединяете от них аккумулятор. Опять же, используя изолированные пластины, вы раздвигаете пластины, пока они не разделятся на 0,400 мм. Теперь…

А Конденсатор состоит из двух круглых пластин из круглых пластин радиус 5,0 см через …

А Конденсатор состоит из двух круглых пластин из круглых пластин радиус 5,0 см, разделенные знаком 0.Слой тефлона толщиной 01 мм (k = 2,1). Какие такое емкость?

Конденсатор состоит из квадратных проводящих пластин со стороной 27 см. и 4,9 мм друг от друга, …

Конденсатор состоит из квадратных проводящих пластин со стороной 27 см. и 4,9 мм друг от друга, несущие заряды ± 1,5 мкКл. Часть А Найдите электрическое поле между пластинами. Выразите свой ответ двумя значащими цифрами. Часть B Найдите разность потенциалов между пластинами. Выразите свой ответ двумя значащими цифрами.Часть C Найдите накопленную энергию. Выразите свой ответ двумя значащими цифрами.

5. Конденсатор с параллельными пластинами 250 нФ состоит из двух одинаковых круглые тарелки на расстоянии 1 см друг от друга, разделенные …

5. Конденсатор с параллельными пластинами 250 нФ состоит из двух одинаковых круглые пластины на расстоянии 1 см друг от друга, разделенные воздухом. а. Найдите их радиус. б. Каков был бы ответ, если бы тарелки были разделены стакан?

Конденсатор с параллельными пластинами состоит из двух металлических пластин площадью A, разделенных знаком…

Конденсатор с параллельными пластинами состоит из двух металлических пластин площадью A, разделенных расстоянием d. Этот конденсатор с параллельными пластинами подключен к батарее с напряжением AVo. Ваш ответ должен зависеть от A, d, ΔVo и любых других физических констант a. Определите заряд, накопленный на пластинах конденсатора, и энергию, накопленную в конденсаторе b. Определите напряженность электрического поля между пластинами конденсатора c. У экспериментатора пять …

Константы Часть A Конденсатор состоит из двух параллельных пластин, каждая из которых имеет площадь 15.0 …

Константы Часть A Конденсатор состоит из двух параллельных пластин, каждая площадью 15,0 см2, разделенных расстоянием 0,250 см. Материал, заполняющий пространство между пластинами, имеет диэлектрическую проницаемость 4,00. Пластины конденсатора подключены к батарее на 200 В. Какая емкость конденсатора? SubmitPrev Предыдущие ответы Запросить ответ X Неверный; Попробуйте снова; Осталось 4 попытки. Часть B Каков заряд на любой из пластин? Часть…

Первоначально заряжается конденсатор, состоящий из двух параллельных пластин, разделенных расстоянием d…

Конденсатор, состоящий из двух параллельных пластин, разделенных расстоянием d, первоначально заряжается до напряжения 1,9 В. Затем аккумулятор отключается от конденсатора. Для каждого утверждения ниже выберите True или False. на любой пластине конденсатора останется неизменным CA: True OB: False n etherteiate oi tihe napatetor Wifthemaih unichanged между пластинами увеличивается, количество накопленного заряда Увеличение расстояния d после отсоединения батареи снижает электрическую энергию…

Конденсатор

Конденсатор

Конденсаторы

Емкость

Конденсатор — это устройство для хранения разделенного заряда. Нет единого электронного компонента сегодня играет более важную роль, чем конденсатор. Это устройство используется для хранить информацию в памяти компьютера, регулировать напряжение в источниках питания, для создания электрических полей, для хранения электрической энергии, для обнаружения и производить электромагнитные волны и измерять время.Любые два проводника, разделенные изолирующей средой, образуют конденсатор.

А Параллельно-пластинчатый конденсатор состоит из двух пластин, разделенных тонкой изоляционной материал, известный как диэлектрик . В параллельной пластине Электроны конденсатора переносятся с одной параллельной пластины на другую.

Мы уже показали, что электрическое поле между пластинами постоянно с величиной E = σ / ε ₀ и указывает от положительной пластины к отрицательной.

Следовательно, разность потенциалов между отрицательной и положительной пластинами составляет предоставлено

∆U = U _pos — U _neg = -q Σ _neg ^pos E ∙ ∆ r = q E d.
При суммировании ∆ r указывает от отрицательной пластины к положительной в противоположном направлении от E .
Следовательно E ∙ ∆ r = -E∆r, а знаки минус отменяют.
Положительный пластина имеет более высокий потенциал, чем отрицательная пластина.

Силовые линии и эквипотенциальные линии для Постоянное поле между двумя заряженными пластинами показано справа. Одна пластина конденсатора удерживает положительный заряд Q, а другая — отрицательный заряд -Q. Заряд Q на пластинах пропорционален потенциалу разность V на двух пластинах. Модель емкость C — пропорциональная константа,

Q = CV, C = Q / V.

C зависит от геометрии конденсатора и типа диэлектрического материала использовал. Емкость параллельного пластинчатого конденсатора с двумя пластинами площадью А расстояние d и отсутствие диэлектрического материала между пластинами составляет

C = ε ₀ A / d.

(Электрическое поле E = σ / ε ₀ . Напряжение V = Ed = σd / ε ₀ . Заряд Q = σA. Следовательно, Q / V = σAε ₀ / σd = Aε ₀ / d.)
Единица измерения емкости в системе СИ — Кулон / Вольт = Фарад (Ф).
Типичный конденсаторы имеют емкость в диапазоне от пикофарад до микрофарад.

Емкость говорит нам, сколько заряда устройство хранит для данного Напряжение. Диэлектрик между проводниками увеличивает емкость конденсатор. Молекулы диэлектрического материала поляризованы в поле между двумя проводниками. Весь отрицательный и положительный заряд диэлектрик смещен на небольшую величину друг относительно друга.Этот приводит к эффективному положительному поверхностному заряду на одной стороне диэлектрика. и отрицательный поверхностный заряд на другой стороне диэлектрика. Эти эффективные поверхностные заряды на диэлектрике создают электрическое поле, которое противостоит полю, создаваемому поверхностными зарядами на проводниках, и, таким образом, снижает напряжение между проводниками. Чтобы поддерживать напряжение, больше заряда необходимо надеть на проводники. Таким образом, конденсатор накапливает больше заряда в течение заданное напряжение.Диэлектрическая проницаемость κ — это отношение напряжения V ₀ между проводниками без диэлектрика к напряжение V с диэлектриком, κ = V ₀ / V, для данного количества заряда Q на проводниках.

На диаграмме выше такое же количество заряда Q на проводников приводит к меньшему полю между пластинами конденсатора с диэлектрик. Чем выше диэлектрическая проницаемость κ, тем больше заряда может хранить конденсатор при заданном напряжении.Для параллельной пластины конденсатор с диэлектриком между пластинами, емкость

C = Q / V = ​​κQ / V ₀ = κε ₀ A / d = εA / d,
, где ε = κε ₀ . Статическая диэлектрическая проницаемость любого материала всегда больше 1.

Типичные диэлектрические постоянные

Материал Диэлектрическая проницаемость Воздух 1.00059 силикат алюминия от 5,3 до 5,5 Бакелит 3,7 Пчелиный воск (желтый) 2,7 Бутилкаучук 2,4 Formica XX 4,00 Германий 16 Стекло 4-10 Гуттаперча 2.6 Масло Halowax 4,8 Кел-Ф 2,6 Люцит 2,8 Слюда 4-8 Микарта 254 от 3,4 до 5,4 Майлар 3,1 Неопреновый каучук 6,7 Нейлон 3.00

Материал Диэлектрическая проницаемость Бумага 1,5 к 3 Парафин 2–3 Оргстекло 3,4 Полиэтилен 2,2 полистирол 2,56 Фарфор 5-7 Стекло Pyrex 5.6 кварцевый от 3,7 до 4,5 Силиконовое масло 2,5 Стеатит от 5,3 до 6,5 титанат стронция 233 тефлон 2,1 Tenite от 2,9 до 4,5 Вакуум 1,00000 вазелин 2.16 Вода (дистиллированная) от 76,7 до 78,2 Дерево от 1,2 до 2,1

Если диэлектрик с диэлектрической проницаемостью κ вставляется между пластинами параллельной пластины конденсатора, а напряжение поддерживается постоянным аккумулятором, заряд Q на пластинах увеличивается в κ раз. Батарея перемещает больше электронов с положительной пластины на отрицательную. Величина электрического поля между пластинами E = V / d остается неизменной. тем же.

Если диэлектрик вставлен между пластинами параллельной пластины конденсатор, и заряд на пластинах остается прежним, потому что конденсатор отключается от АКБ, то напряжение V уменьшается в раз из κ, а электрическое поле между пластиной E = V / d уменьшается в 2 раза. κ.

Модуль 2: Вопрос 2:

(a) Конденсатор с параллельными пластинами изначально имеет напряжение 12 В и остается подключенным к батарее.Если теперь расстояние между пластинами увеличено вдвое, что бывает?
(b) Конденсатор с параллельными пластинами первоначально подключается к батарее, а пластины удерживают заряд ± Q. Затем аккумулятор отключается. Если расстояние между пластинами равно теперь вдвое, что происходит?

Подсказка: аккумулятор является зарядным насосом. Может качать заряд с одной пластины к другому, чтобы поддерживать постоянную разность потенциалов.
Нет батареи <--> нет зарядного насоса. Заряд не может перемещаться с одной пластины на Другие.

Обсудите это со своими однокурсниками на дискуссионном форуме!

Ссылка: PhET Конденсаторная лаборатория (базовая)

---

Энергия, запасенная в конденсаторе

Энергия U, запасенная в конденсаторе, равна работе W сделано при разделении заряды на проводниках. Чем больше заряда уже накоплено на пластинах, тем необходимо проделать больше работы по разделению дополнительных сборов из-за сильного отталкивание между одноименными зарядами.При заданном напряжении требуется бесконечно малое объем работы ∆W = V∆Q для отделения дополнительной бесконечно малой суммы заряда ∆Q.
(Напряжение V — это количество работы на единицу заряда.)
Поскольку V = Q / C, V увеличивается линейно с Q. Общая работа, проделанная при зарядке конденсатора является

W = U = Σ V ∆Q = V _{в среднем} Q = ½VQ.
Используя Q = CV, мы также можем написать U = ½ (Q ² / C) или U = ½CV ² .

Проблема:

Каждая ячейка памяти компьютера содержит конденсатор для хранения заряда. Сохраняемый или не сохраняемый заряд соответствует двоичным цифрам 1 и 0. Для более плотной упаковки ячеек в траншейных конденсаторах часто используются пластины конденсатора установлены вертикально вдоль стенок траншеи выгравирован на кремниевом чипе. Если у нас емкость 50 фемтоФарад = 50 * 10 ^-15 F и каждая плита имеет площадь 20 * 10 ^-12 м ² (траншеи микронного размера), что такое разделение пластин?

Решение:

• Рассуждение:
  Емкость параллельного пластинчатого конденсатора с двумя пластинами площадью А разделенные расстоянием d и отсутствие диэлектрического материала между пластинами C = ε ₀ A / d.
• Детали расчета:
  C = ε ₀ A / d, d = ε ₀ A / C = (8,85 * 10 ^-12 * 20 * 10 ^-12 / (50 * 10 ^-15 )) м = 3,54 * 10 ^-9 м.
  Типичные атомные размеры порядка 0,1 нм, поэтому траншея находится на порядка 30 атомов в ширину.

---

Для любого изолятора существует максимальное поддерживаемое электрическое поле без ионизации молекул. Для конденсатора это означает наличие максимально допустимое напряжение, которое может быть приложено к проводникам.Этот максимальное напряжение зависит от диэлектрика в конденсаторе. Соответствующие максимальное поле E _b называется диэлектрической прочностью материала. Для более сильных полей конденсатор « выходит из строя » (аналогично коронный разряд) и обычно разрушается. Большинство конденсаторов, используемых в электрических схемы имеют как емкость, так и номинальное напряжение. Это напряжение пробоя V _b относится к диэлектрической прочности E _b .Для параллельной пластины конденсатор имеем V _b = E _b d.

Материал	Диэлектрическая прочность (В / м)
Воздух	3 * 10 6
Бакелит	24 * 10 6
Неопреновый каучук	12 * 10 6
Нейлон	14 * 10 6
Бумага	16 * 10 6
полистирол	24 * 10 6
Стекло Pyrex	14 * 10 6
кварцевый	8 * 10 6
Силиконовое масло	15 * 10 6
титанат стронция	8 * 10 6
тефлон	60 * 10 6

Конденсатор состоит из двух металлических пластин каждая по 10 см класса 11 по физике CBSE

Совет: Конденсатор представляет собой две параллельные пластины, разделенные небольшим расстоянием.Емкость конденсатора определяется как отношение электрического заряда на каждом проводе к разности потенциалов между ними. Емкость зависит от формы, размера и геометрического расположения проводников и среды между ними.

Полный пошаговый ответ:

Рассмотрим конденсатор с параллельными пластинами, заполненный изолятором с диэлектрической проницаемостью k с зарядом + Q и -Q, как показано ниже:

Емкость конденсатора с параллельными пластинами определяется формулой
$ C = k {{\ varepsilon} _ {0 }} \ dfrac {A} {d} \ text {farad} $ ……… (1)
Где,
k — диэлектрическая проницаемость, это связано с введением диэлектрической среды между пластинами конденсатора.{-12}} F \ simeq 360pF $
Таким образом, правильный вариант — D.

Примечание: запомните формулу емкости для решения этого типа вопросов.
Студенты обычно делают ошибки при замене k, поскольку значение электрической прочности также указывается в вопросе, но k — это диэлектрическая проницаемость, а не электрическая прочность. Чтобы легко запомнить, обратите внимание, что диэлектрическая проницаемость не имеет единицы.
Диэлектрическая прочность — это максимальная напряженность электрического поля, выше которой изолирующий материал начинает разрушаться, и ее единица измерения — В / м.{2}} $.

Конденсатор состоит из двух близких проводов. Емкость Конденсатор состоит из двух проводов

Емкость Конденсатор состоит из двух проводов, которые расположены близко друг к другу, но не соприкасаются. Конденсатор обладает способностью накапливать электрический заряд.

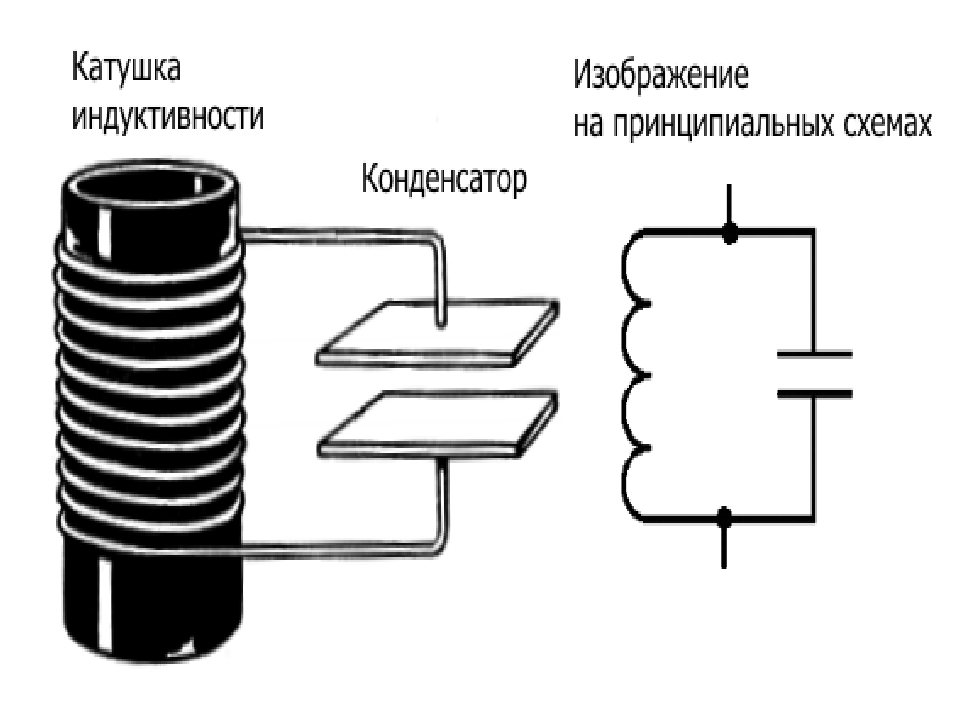
a) Конденсатор с параллельными пластинами, подключенный к батарее. (б) — принципиальная схема.

Когда конденсатор подключен к батарее, заряд на его пластинах пропорционален напряжению:

Величина C называется емкостью.

Единица емкости: фарад (F)

1 F = 1 C / V

Q = заряд (C) и V = напряжение (В)

Емкость не зависит от напряжения; это функция от геометрии и материалов конденсатора.

Для конденсатора с параллельными пластинами:

C = емкость, A = площадь, d = расстояние между пластинами и = диэлектрическая проницаемость свободного пространства

= 8,85×10-12 C2 / Нм2! 0

Диэлектрики

Диэлектрик является изолятором и характеризуется диэлектрической проницаемостью K.

Емкость конденсатора с параллельными пластинами, заполненного диэлектриком:

Диэлектрическая прочность — это максимальное поле, которое диэлектрик может испытывать без разрушения.

Молекулы в диэлектрике имеют тенденцию ориентироваться таким образом, чтобы уменьшить внешнее поле.

Это означает, что электрическое поле внутри диэлектрика меньше, чем в воздухе, что позволяет сохранять больший заряд при том же потенциале.

Накопление электрической энергии в конденсаторе

Заряженный конденсатор накапливает электрическую энергию; запасенная энергия равна работе, проделанной для зарядки конденсатора.

Плотность энергии, определяемая как энергия на единицу объема, одинакова независимо от происхождения электрического поля:

Внезапный разряд электрической энергии может быть вредным или фатальным. Конденсаторы могут сохранять свой заряд неопределенно долго, даже если они отключены от источника напряжения. Будьте осторожны!

Цепи, содержащие конденсаторы последовательно и параллельно

Параллельно подключенные конденсаторы имеют одинаковое напряжение на каждой:

В этом случае общая (эквивалентная) емкость равна сумме:

Последовательные конденсаторы имеют одинаковый заряд:

В этом случае обратные величины емкостей складываются, чтобы получить обратную величину эквивалентной емкости:

Зарядка и разрядка конденсатора Когда переключатель замкнут, конденсатор начинает заряжаться .

Как вы думаете, значение резистора и конденсатора может повлиять на скорость зарядки конденсатора?

Напряжение на конденсаторе увеличивается со временем:

Это тип экспоненты.

Эта кривая имеет характеристическую постоянную времени:

Заряд следует аналогичной кривой:

Если изолированный заряженный конденсатор подключен к резистору, он разряжается:

Сферический конденсатор состоит из двух концентрических сферических проводов, удерживаемых на месте подходящими изолирующими опорами.Покажите, что емкость сферического конденсатора равна

.

Нокаут NEET 2024

Персонализированный наставник с искусственным интеллектом и адаптивное расписание, Материал для самообучения, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.

40000 / —

купить сейчас

Выбивной NEET 2025

Персонализированный наставник с искусственным интеллектом и адаптивное расписание, Материал для самообучения, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.

₹ 45000 / —

купить сейчас

Основание NEET + нокаут NEET 2024

Персонализированный наставник с искусственным интеллектом и адаптивное расписание, Материал для самообучения, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.

54999 ₹ / — 42499 ₹ / —

купить сейчас

NEET Foundation + Knockout NEET 2024 (простая установка)

Персонализированный наставник с искусственным интеллектом и адаптивное расписание, Материал для самообучения, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.

3999 / —

купить сейчас

NEET Foundation + Knockout NEET 2025 (простая установка)

Персонализированный наставник с искусственным интеллектом и адаптивное расписание, Материал для самообучения, Неограниченные пробные тесты и персонализированные аналитические отчеты, Круглосуточная поддержка в чате сомнений.

3999 / —

купить сейчас

Конденсатор состоит из двух больших параллельных пластин площадью A, разделенных очень малым расстоянием d. Этот конденсатор подключен к

Ответ:

Объяснение:

Первый закон движения Ньютона: объект находится в движении, он остается в движении или объект находится в состоянии покоя, он остается в состоянии покоя до тех пор, пока к нему не будет приложена внешняя сила. тело.

Например, автомобиль находится в состоянии покоя, он остается в состоянии покоя, поскольку на его кузов не действует внешняя сила.

Второй закон движения Ньютона: Скорость изменения количества движения объекта прямо пропорциональна силе, приложенной к объекту.

Сила, пропорциональная скорости изменения количества движения.

Третий закон движения Ньютона: на каждое действие существует равное и противоположное противодействие.

Сила действия и противодействия, действующая на два разных тела.

Ответ:

Вопрос № 1 — Ученые соглашаются со стандартным способом представления измеренных величин, при котором количество представленных цифр отражает точность измерения — больше цифр, больше точность; меньше цифр, меньше точность. Вы только что изучили 14 семестров!

Вопрос № 2 — Единицы важны, потому что без надлежащих измерений и единиц для их выражения мы никогда не сможем точно выразить физические законы только на основе качественных рассуждений.Единицы невероятно важны для физики. Две из наиболее важных причин следующие: (1) они помогают нам. чтобы избежать ошибок в вычислениях, и (2) они служат для проверки вычислений после их завершения. В первом случае вы можете избежать добавления 3 м и 25 см и получения неправильного ответа.

Пояснение: Надеюсь, это поможет, пожалуйста, отметьте самого умного!

Ответ:

Ответ неверен

Объяснение:

Для бесконечного слоя зарядов электрическое поле перпендикулярно поверхности .Чтобы вычислить электрическое поле, мы используем гауссову поверхность (цилиндр) , получаем, что

откуда

Затем рассчитанное поле составляет половину поля проводника, заряженного , это означает, что величина заряженного проводника

Следовательно, ответ — Ложь.

No related posts.