Как определить внутреннее сопротивление. Электродвижущая сила

ЭДС и напряжение. Внутреннее сопротивление источников питания.
Ликбез так ликбез!
Закон Ома. Вот я о чем.
О законе Ома мы уже говорили. Поговорим еще раз — с несколько иной стороны. Не вдаваясь в физические подробности и выражаясь простым кошачьим языком, закон Ома гласит: чем больше э.д.с. (электродвижущая сила), тем больше ток, чем больше сопротивление, тем меньше ток.
Переведя сие заклинание на язык сухих формул получаем:

I=E/R

где:I — сила тока,E — Э.Д.С. — электродвижущая силаR — сопротивление
Ток измеряется в амперах, э.д.с. — в вольтах, а сопротивление носит гордое имя товарища Ома.Э.д.с. — это есть характеристика идеального генератора, внутренне сопротивление которого принято считать бесконечно малым. В реальной жизни такое бывает редко, поэтому в силу вступает закон Ома для последовательной цепи (более знакомый нам):

I=U/R

где:U — напряжение источника непосредственно на его клеммах.

Рассмотрим простой пример.
Представим себе обычную батарейку в виде источника э.д.с. и включенного последовательно с ним некоего резистора, который будет олицетворять собой внутреннее сопротивление батарейки. Подключим параллельно батарейке вольтметр. Его входное сопротивление значительно больше внутреннего сопротивления батарейки, но не бесконечно большое — то есть, через него потечет ток. Величина напряжения, которую покажет вольтметр будет меньше величины э.д.с. как раз на величину падения напряжения на внутреннем воображаемом резисторе при данном токе.Но, тем не менее именно эта величина и принимается за напряжение батарейки.
Формула конечного напряжения при этом будет иметь следующий вид:

U(бат)=E-U(внутр)

Так как со временем у всех элементов питания внутреннее сопротивление увеличивается, то и падение напряжения на внутреннем сопротивлении тоже увеличивается. При этом напряжение на клеммах батарейки уменьшается. Мяу!
Разобрались!
Что же происходит, если вместо вольтметра к батарейке подключить амперметр? Так как собственное сопротивление амперметра стремится к нулю, мы фактически будем измерять ток, протекающий через внутреннее сопротивление батарейки. Так как внутренне сопротивление источника очень небольшое, измеренный при этом ток может достигать н ескольких ампер.

Однако следует заметить, что внутреннее сопротивление источника является таким же элементом цепи, как и все остальные. Поэтому при увеличении тока нагрузки падение напряжения на внутреннем сопротивлении также увеличится, что приводит к уменьшению напряжения на нагрузке. Или как мы, радиокоты, любим выражаться — к просадке напруги.
Чтобы изменение нагрузки как можно меньше влияло на выходное напряжение источника его внутреннее сопротивление стараются свести к минимуму.
Можно так подобрать элементы последовательной цепи, чтобы на каком-нибудь из них получить напряжение, уменьшенное, по сравнению с исходным, во сколько угодно раз.

Двухполюсник и его эквивалентная схема

Вну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включенных генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.

Введение

Рассмотрим пример. В легковом автомобиле запитаем бортовую сеть не от штатного свинцово-кислотного аккумулятора напряжением 12 вольт и ёмкостью 55 А·ч, а от последовательно соединённых восьми батареек (например, типоразмера АА, ёмкостью около 1 А·ч). Попробуем завести двигатель. Опыт показывает, что при питании от батареек вал стартера не повернётся ни на градус. Более того, не сработает даже втягивающее реле.

Интуитивно понятно, что батарейка «недостаточно мощная» для подобного применения, однако рассмотрение её заявленных электрических характеристик — напряжения и заряда (ёмкости) — не даёт количественного описания данного явления. Напряжение в обоих случаях одинаково:

Аккумулятор: 12 вольт

Гальванические элементы: 8·1,5 вольт = 12 вольт

Ёмкости также вполне достаточно: одного ампер·часа в батарейке должно хватить, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).

Казалось бы, в соответствии с законом Ома ток в одинаковой нагрузке при электрически одинаковых источниках также должен быть одинаковым. Однако в действительности это не совсем так. Источники вели бы себя одинаково, если бы были идеальными генераторами напряжения. Для описания степени отличия реальных источников от идеальных генераторов и применяется понятие внутреннее сопротивление.

Сопротивление и внутреннее сопротивление

Основной характеристикой двухполюсника является его сопротивление (или импеданс). Однако характеризовать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=Ir не выполняется.

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:

Входное сопротивление — внутреннее сопротивление двухполюсника, которым является вход системы.

Выходное сопротивление — внутреннее сопротивление двухполюсника, которым является выход системы.

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причем активное сопротивление, то есть резистор в нем присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведет себя так, словно в нем имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление чисто активное, оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определенный предел.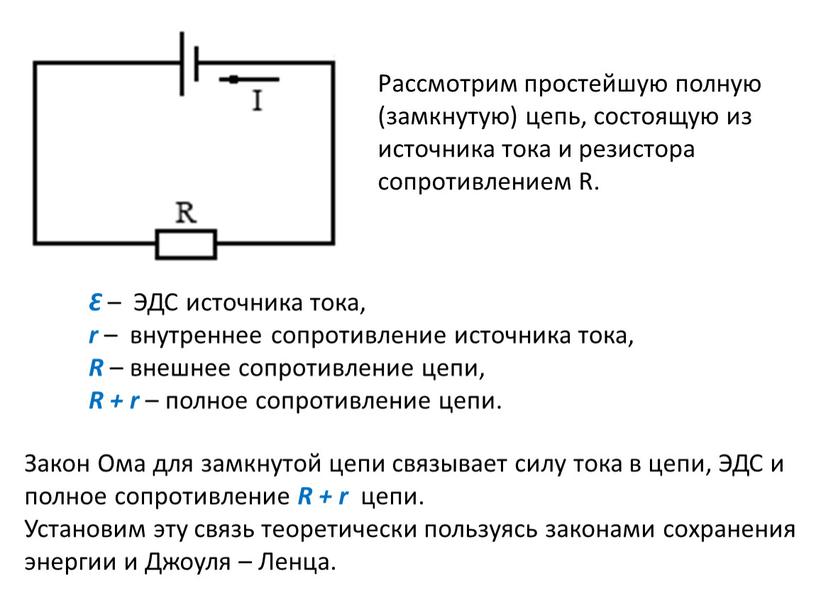 Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.

В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

Внутреннее сопротивление невозможно убрать из двухполюсника

Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних условий.

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого двухполюсника.

Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Если к источнику с ЭДС генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом.

Расчёт

Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).

Пусть, имеется двухполюсник, который может быть описан приведенной выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

ЭДС генератора напряжения U

Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов Uout = φ2 − φ1) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

где Uout1 — выходное напряжение при токе I1, Uout2 — выходное напряжение при токе I2. Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (1) записывается следующим образом:

где Uoc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; Isc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчета — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощенной формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Часто применяется следующий простой способ измерения, не требующий вычислений:

Измеряется напряжение холостого хода

В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нем составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:

Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.

В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум — десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.

На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены , его внутреннее сопротивление, а также сопротивление нагрузки. Согласно , ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен . Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает

Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:

• Автомобильный свинцово-кислотный аккумулятор напряжением 12 вольт и ёмкостью 55 А·ч
• Восемь батареек типоразмера АА, соединенных последовательно. Суммарное напряжение такой батареи также 12 вольт, ёмкость значительно меньше — примерно 1 А·ч

Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартер потребляет ток 250 ампер), а от цепочки батареек стартер вообще не вращается. Относительно небольшая емкость батареек не является причиной: одного ампер-часа в батарейках хватило бы для того, чтобы вращать стартер в течение 14 секунд (при токе 250 ампер).

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников, то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход, то часто употребляются следующие термины:

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление , то есть резистор в нём присутствует обязательно), внутреннее сопротивление не сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

• Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление практически чисто активное (если только речь не идет об очень высоких частотах), оно обусловлено физическими эффектами, которые не позволяют мощности , отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
• В случае двухполюсника, содержащего внутри электрическую схему , внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

• ЭДС генератора напряжения U
• Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U out = φ 2 − φ 1 ) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

где U out1 I 1 , U out2 — выходное напряжение при токе I 2 . Решая систему уравнений, находим искомые неизвестные:

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система () записывается следующим образом:

где U oc — выходное напряжение в режиме холостого хода (англ. open circuit ), то есть при нулевом токе нагрузки; I sc — ток нагрузки в режиме короткого замыкания (англ. short circuit ), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение , которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Иногда применяется следующий простой способ измерения, не требующий вычислений:

• Измеряется напряжение холостого хода
• В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности , то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды , то есть расчет производится методом комплексных амплитуд .

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией , а не скалярным значением:

• Можно искать различные параметры комплексного значения: модуль , аргумент , только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
• Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путем измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.

Применение

В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.

Упрощение эквивалентных схем

Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.

Согласование источника и нагрузки

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:

Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.

Понижение высоких напряжений

Иногда к источнику искусственно добавляют большое сопротивление (оно добавляется к внутреннему сопротивлению источника) для того, чтобы значительно понизить получаемое от него напряжение. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) ведёт к бесполезному выделению мощности на нём. Чтобы не расходовать энергию впустую, в системах переменного тока используют реактивные гасящие импедансы, чаще всего конденсаторы . Таким образом строятся конденсаторные блоки питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств.

Минимизация шума

При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители , однако они спроектированы таким образом, что наименьший коэффициент шума достигается лишь в определенном диапазоне выходного сопротивления источника сигнала. Например, малошумящий усилитель обеспечивает минимальный шум только в диапазоне выходных сопротивлений источника от 1 кОм до 10 кОм; если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор , который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.

Ограничения

Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения , что и для применимости эквивалентных схем.

Примеры

Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r . Тривиальные случаи двухполюсников без источников оговорены особо.

Малое внутреннее сопротивление

Большое внутреннее сопротивление

Отрицательное внутреннее сопротивление

Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:

• элементов с отрицательным дифференциальным сопротивлением , например, туннельных диодов

Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов .

См. также

Ссылки

Литература

• Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
• Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с.

Как найти общее внутреннее сопротивление

Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.

Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника. Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.

У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.

Измерение сопротивления петли фаза-нуль

Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).

Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк. з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.

Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.

На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:

• заменяются участки провода, не отвечающие требованиям по диаметру сечения;
• перекручиваются болтовые соединения с обязательной установкой врезных шайб;
• вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
• при необходимости в контур защитного заземления добавляются дополнительные элементы;
• исключается последовательное подключение корпусов устройств к общей шине заземления.

После выполнения комплекса мероприятий измерения проводятся повторно.

Нахождение внутреннего сопротивления

Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.

Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:

Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.

Выразив отсюда r, получают формулу для его вычисления:

где:

• r – внутреннее сопротивление источника;
• ε – ЭДС источника;
• I – сила тока в полной цепи;
• R – сопротивление в полной цепи.

Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.

Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.

В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.

Малое внутреннее сопротивление

Малой величины внутреннего сопротивления добиваются применением обратной связи в схемах, куда включён двухполюсник. В стабилизаторах напряжения r достигает значений менее 9*10-4 Ом. Автомобильная АКБ 6СТ-60 обладает сопротивлением около 0,01 Ом. Если произвести измерения петли фаза-ноль бытовой сети, то норма значения лежит в пределах 0,05-1 Ом.

Реактивное внутреннее сопротивление

Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.

Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.

На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.

Большое внутреннее сопротивление

Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.

Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.

Внутреннее сопротивление и импеданс

Импеданс – полное (комплексное) внутреннее сопротивление эквивалентного двухполюсника переменному току. Обозначается буквой Z и так же измеряется в Омах.

Двухполюсник и его эквивалентная схема

Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:

• цепи, содержащие источник тока или напряжения;
• двухполюсники, не являющиеся источниками.

Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.

Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.

Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.

Влияние внутреннего сопротивления на свойства двухполюсника

Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:

где:

• E – напряжение ЭДС;
• R – сопротивление нагрузки;
• r – активное внутреннее сопротивление двухполюсника.

Формула применима к двухполюсникам, не отдающим энергию.

К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.

Разрядная емкость источника

Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.

Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.

Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.

Видео

Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.

Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника. Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.

У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.

Измерение сопротивления петли фаза-нуль

Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).

Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.

Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.

На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:

• заменяются участки провода, не отвечающие требованиям по диаметру сечения;
• перекручиваются болтовые соединения с обязательной установкой врезных шайб;
• вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
• при необходимости в контур защитного заземления добавляются дополнительные элементы;
• исключается последовательное подключение корпусов устройств к общей шине заземления.

После выполнения комплекса мероприятий измерения проводятся повторно.

Нахождение внутреннего сопротивления

Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.

Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:

Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.

Выразив отсюда r, получают формулу для его вычисления:

где:

• r – внутреннее сопротивление источника;
• ε – ЭДС источника;
• I – сила тока в полной цепи;
• R – сопротивление в полной цепи.

Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.

Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.

В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.

Малое внутреннее сопротивление

Малой величины внутреннего сопротивления добиваются применением обратной связи в схемах, куда включён двухполюсник. В стабилизаторах напряжения r достигает значений менее 9*10-4 Ом. Автомобильная АКБ 6СТ-60 обладает сопротивлением около 0,01 Ом. Если произвести измерения петли фаза-ноль бытовой сети, то норма значения лежит в пределах 0,05-1 Ом.

Реактивное внутреннее сопротивление

Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.

Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.

На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.

Большое внутреннее сопротивление

Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.

Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.

Внутреннее сопротивление и импеданс

Импеданс – полное (комплексное) внутреннее сопротивление эквивалентного двухполюсника переменному току. Обозначается буквой Z и так же измеряется в Омах.

Двухполюсник и его эквивалентная схема

Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:

• цепи, содержащие источник тока или напряжения;
• двухполюсники, не являющиеся источниками.

Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.

Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.

Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.

Влияние внутреннего сопротивления на свойства двухполюсника

Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:

где:

• E – напряжение ЭДС;
• R – сопротивление нагрузки;
• r – активное внутреннее сопротивление двухполюсника.

Формула применима к двухполюсникам, не отдающим энергию.

К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.

Разрядная емкость источника

Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.

Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.

Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.

Видео

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.

В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для гальванического элемента или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум – десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.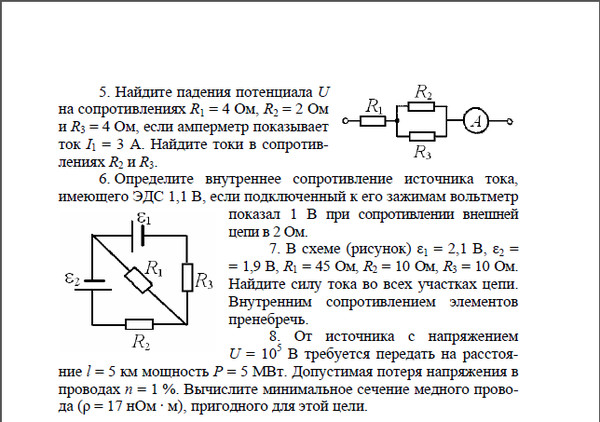

На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены ЭДС источника, его внутреннее сопротивление, а также сопротивление нагрузки. Согласно закону Ома для замкнутой цепи, ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника. Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен току короткого замыкания. Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает источник:

Ясно, что если источник развивает такую мощность, что на нагрузке получается максимум возможной мощности для данного источника, то КПД источника окажется равным 50%.

Как найти внутреннее сопротивление формула в физике. Электродвижущая сила. Внутреннее сопротивление источника тока

Цель работы: изучить метод измерения ЭДС и внутреннего сопротивления источника тока с помощью амперметра и вольтметра.

Оборудование: металлический планшет, источник тока, амперметр, вольтметр, резистор, ключ, зажимы, соединительные провода.

Для измерения ЭДС и внутреннего сопротивления источника тока собирают электрическую цепь, схема которой показана на рисунке 1.

К источнику тока подключают амперметр, сопротивление и ключ, соединенные последовательно. Кроме того, непосредствен­но к выходным гнездам источника подключают еще и вольтметр.

ЭДС измеряют по показанию вольтметра при разомкнутом ключе. Этот прием определения ЭДС основан на следствии из за­кона Ома для полной цепи, согласно которому при бесконечно большом сопротивлении внешней цепи напряжение на зажимах источника равно его ЭДС. (См. параграф «Закон Ома для полной цепи» учебника «Физика 10»).

Для определения внутреннего сопротивления источника за­мыкают ключ К. При этом в цепи можно условно выделить два участка: внешний (тот, который подключен к источнику) и внутренний (тот, который находится внутри источника тока).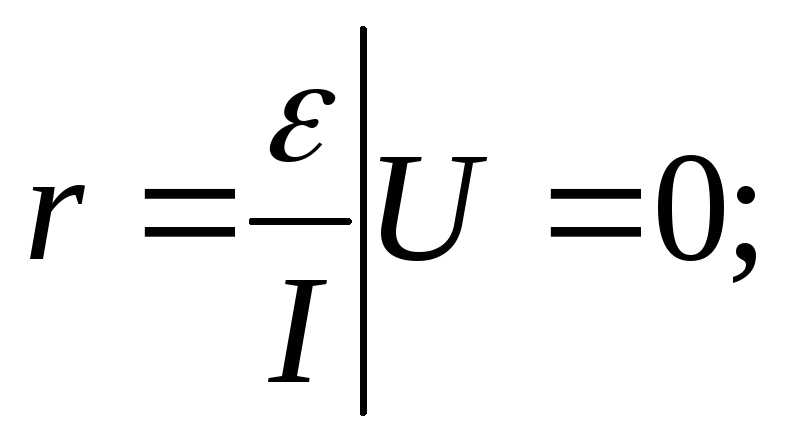 Поскольку ЭДС источника равна сумме падения напряжений на внутрен­нем и внешнем участках цепи:

ε = U r +U R , то U r = ε -U R (1)

По закону Ома для участка цепи U r = I· r (2). Подставив равенство (2) в (1) получают:

I · r = ε — U r , откуда r = (ε — U R )/ J

Следовательно, чтобы узнать внутреннее сопротивление источника тока, необходимо пред­варительно определить его ЭДС, затем замкнуть ключ и измерить падение напряжения на внеш­нем сопротивлении, а также силу тока в нем.

Ход работы

1. Подготовьте таблицу для записи результатов измерений и вычислений:

ε ,в	U r , B	i,a	r , Ом

Начертите в тетради схему для измерения ЭДС и внутреннего сопротивления источника.

После проверки схемы соберите электрическую цепь. Ключ разомкните.

Измерьте величину ЭДС источника.

Замкните ключ и определите показания амперметра и вольтметра.

Вычислите внутреннее сопротивление источника.

1. Определение эдс и внутреннего сопротивления источника тока графическим методом

Цель работы: изучить измерения ЭДС, внутреннего сопротивления и тока короткого замы­кания источника тока, основанный на анализе графика зависимости напряже­ния на выходе источника от силы тока в цепи.

Оборудование: гальванический элемент, амперметр, вольтметр, резистор R 1 , переменный резистор, ключ, зажимы, металлический планшет, соединительные провода.

Из закона Ома для полной цепи следует, что напряжение на выходе источника тока зависит прямо пропорционально от силы тока в цепи:

так как I =E/(R+r), то IR + Ir = Е, но IR = U, откуда U + Ir = Е или U = Е – Ir (1).

Если построить график зависимости U от I, то по его точкам пересечения с осями координат можно определить Е, I К.З. — силу тока короткого замыкания (ток, который потечет в цепи источни­ка, когда внешнее сопротивление R станет равным нулю).

ЭДС определяют по точке пересечения графика с осью напряжений. Эта точка графика со­ответствует состоянию цепи, при котором ток в ней отсутствует и, следовательно, U = Е.

Силу тока короткого замыкания определяют по точке пересечения графика с осью токов. В этом случае внешнее сопротивление R = 0 и, следовательно, напряжение на выходе источника U = 0.

Внутреннее сопротивление источника находят по тангенсу угла наклона графика относи­тельно оси токов. (Сравните формулу (1) с математической функцией вида У = АХ +В и вспомни­те смысл коэффициента при X).

Ход работы

Для записи результатов измерений подготовьте таблицу:

1. После проверки схемы преподавателем соберите электрическую цепь. Ползунок переменного резистора установите в положение, при котором сопротивление цепи, подключенной к источ­нику тока, будет максимальным.

Определите значение силы тока в цепи и напряжение на зажимах источника при максимальной величине сопротивления переменного резистора. Данные измерений занесите в таблицу.

Повторите несколько раз измерения силы тока и напряжения, уменьшая всякий раз величину переменного сопротивления так, чтобы напряжение на зажимах источника уменьшалось на 0,1В. Измерения прекратите, когда сила тока в цепи достигнет значения в 1А.

Нанесите полученные в эксперименте точки на график. Напряжение откладывайте по верти­кальной оси, а силу тока — по горизонтальной. Проведите по точкам прямую линию.

Продолжите график до пересечения с осями координат и определите величины Е и, I К.З.

Измерьте ЭДС источника, подключив вольтметр к его выводам при разомкнутой внешней це­пи. Сопоставьте значения ЭДС, полученные двумя способами, и укажите причину возможного расхождения результатов.

Определите внутреннее сопротивление источника тока. Для этого вычислите тангенс угла на­клона построенного графика к оси токов. Так как тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то практически это можно сделать, найдя отношение Е / I К.З

На концах проводника, а значит, и тока необходимо наличие сторонних сил неэлектрической природы, с помощью которых происходит разделение электрических зарядов .

Сторонними силами называются любые силы, действующие на электрически заряженные частицы в цепи, за исключением электростатических (т. е. кулоновских).

Сторонние силы приводят в движение заряженные частицы внут-ри всех источников тока: в генераторах, на электростанциях, в гальванических элементах, аккумуляторах и т. д.

При замыкании цепи создается электрическое поле во всех про-водниках цепи. Внутри источника тока заряды движутся под действием сторонних сил против кулоновских сил (электроны движут-ся от положительно заряженного электрода к отрицательному), а во всей остальной цепи их приводит а движение электрическое поле (см. рис. выше).

В источниках тока в процессе работы по разделению заряженных частиц происходит превращение разных видов энергии в электричес-кую. По типу преобразованной энергии различают следующие виды электродвижущей силы:

— электростатическая — в электрофорной машине, в которой происходит превращение механической энергии при трении в электрическую;

— термоэлектрическая — в термоэлементе — внутренняя энергия нагретого спая двух проволок, изготовленных из разных металлов, превращается в электрическую;

— фотоэлектрическая — в фотоэлементе. Здесь происходит превращение энергии света в элек-трическую: при освещении некоторых веществ, например, селена, оксида меди (I) , кремния наблюдается потеря отрицательного электрического заряда;

— химическая — в гальванических элементах, аккумуляторах и др. источниках, в которых происходит превращение химической энергии в электрическую.

Электродвижущая сила (ЭДС) — характеристика источников тока. Понятие ЭДС было введено Г. Омом в 1827 г. для цепей постоянного тока. В 1857 г. Кирхгофф определил ЭДС как работу сторонних сил при переносе единичного электрического заряда вдоль замкнутого контура:

ɛ = A ст /q ,

где ɛ — ЭДС источника тока, А ст — работа сторонних сил , q — количество перемещенного заряда.

Электродвижущую силу выражают в вольтах.

Можно говорить об электродвижущей силе на любом участке цепи. Это удельная работа сторонних сил (работа по перемещению единичного заряда) не во всем контуре, а только на данном участке.

Внутреннее сопротивление источника тока.

Пусть имеется простая замкнутая цепь, состоящая из источника тока (например, гальванического элемента, аккумулятора или генератора) и резистора с сопротивлением R . Ток в замкну-той цепи не прерывается нигде, следовательно, oн существует и внутри источника тока. Любой источник представляет собой некоторое сопротивление дли тока. Оно называется внутренним сопротивлением источника тока и обозначается буквой r .

В генераторе r — это сопротивление обмотки, в гальваническом элементе — сопротивление раствора электролита и электродов.

Таким образом, источник тока характеризуется величинами ЭДС и внутреннего сопротивлении, которые определяют его качество. Например, электростатические машины имеют очень большую ЭДС (до десятков тысяч вольт), но при этом их внутреннее сопротивление огромно (до со-тни Мом). Поэтому они непригодны для получения сильных токов. У гальванических элементов ЭДС всего лишь приблизительно 1 В, но зато и внутреннее сопротивление мало (приблизительно 1 Ом и меньше). Это позволяет с их помощью получать токи, измеряемые амперами.

ЭДС и напряжение. Внутреннее сопротивление источников питания.
Ликбез так ликбез!
Закон Ома. Вот я о чем.
О законе Ома мы уже говорили. Поговорим еще раз — с несколько иной стороны. Не вдаваясь в физические подробности и выражаясь простым кошачьим языком, закон Ома гласит: чем больше э.д.с. (электродвижущая сила), тем больше ток, чем больше сопротивление, тем меньше ток.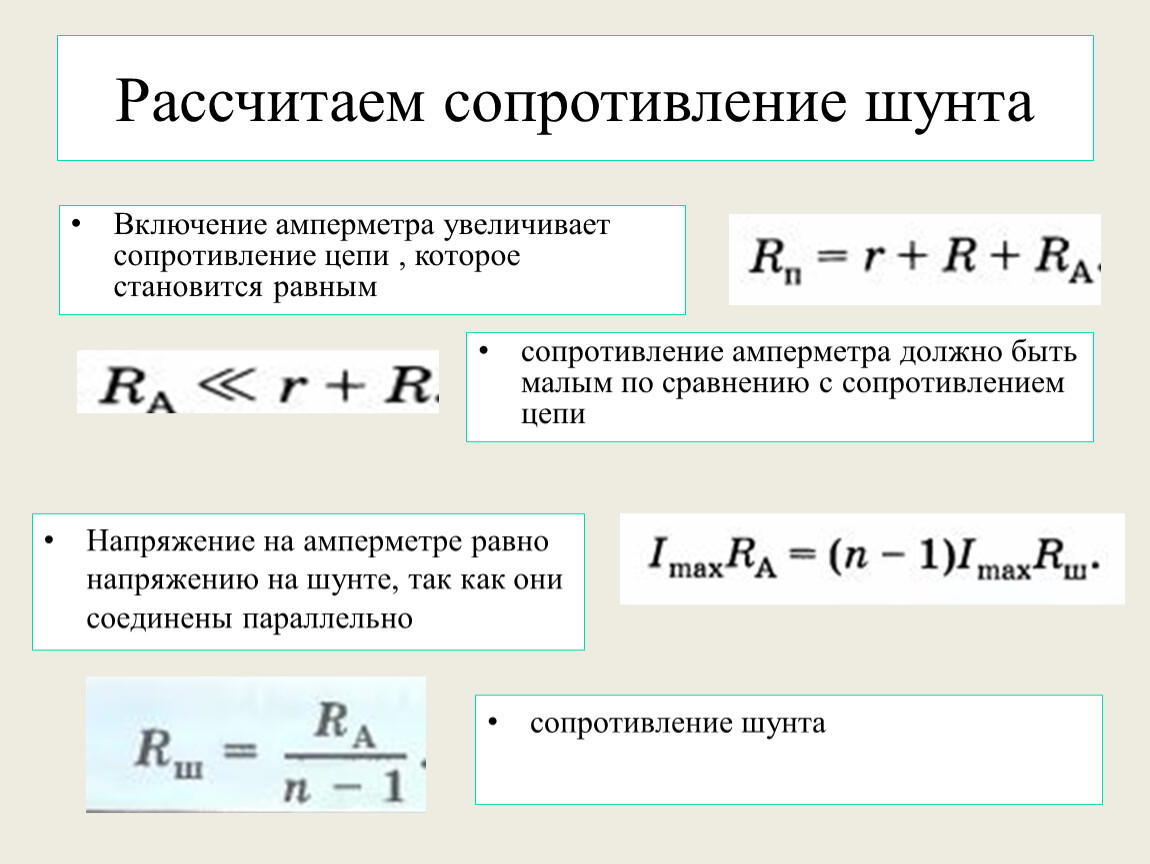
Переведя сие заклинание на язык сухих формул получаем:

I=E/R

где:I — сила тока,E — Э.Д.С. — электродвижущая силаR — сопротивление
Ток измеряется в амперах, э.д.с. — в вольтах, а сопротивление носит гордое имя товарища Ома.Э.д.с. — это есть характеристика идеального генератора, внутренне сопротивление которого принято считать бесконечно малым. В реальной жизни такое бывает редко, поэтому в силу вступает закон Ома для последовательной цепи (более знакомый нам):

I=U/R

где:U — напряжение источника непосредственно на его клеммах.
Рассмотрим простой пример.
Представим себе обычную батарейку в виде источника э.д.с. и включенного последовательно с ним некоего резистора, который будет олицетворять собой внутреннее сопротивление батарейки. Подключим параллельно батарейке вольтметр. Его входное сопротивление значительно больше внутреннего сопротивления батарейки, но не бесконечно большое — то есть, через него потечет ток. Величина напряжения, которую покажет вольтметр будет меньше величины э. д.с. как раз на величину падения напряжения на внутреннем воображаемом резисторе при данном токе.Но, тем не менее именно эта величина и принимается за напряжение батарейки.
Формула конечного напряжения при этом будет иметь следующий вид:

U(бат)=E-U(внутр)

Так как со временем у всех элементов питания внутреннее сопротивление увеличивается, то и падение напряжения на внутреннем сопротивлении тоже увеличивается. При этом напряжение на клеммах батарейки уменьшается. Мяу!
Разобрались!
Что же происходит, если вместо вольтметра к батарейке подключить амперметр? Так как собственное сопротивление амперметра стремится к нулю, мы фактически будем измерять ток, протекающий через внутреннее сопротивление батарейки. Так как внутренне сопротивление источника очень небольшое, измеренный при этом ток может достигать н ескольких ампер.
Однако следует заметить, что внутреннее сопротивление источника является таким же элементом цепи, как и все остальные. Поэтому при увеличении тока нагрузки падение напряжения на внутреннем сопротивлении также увеличится, что приводит к уменьшению напряжения на нагрузке.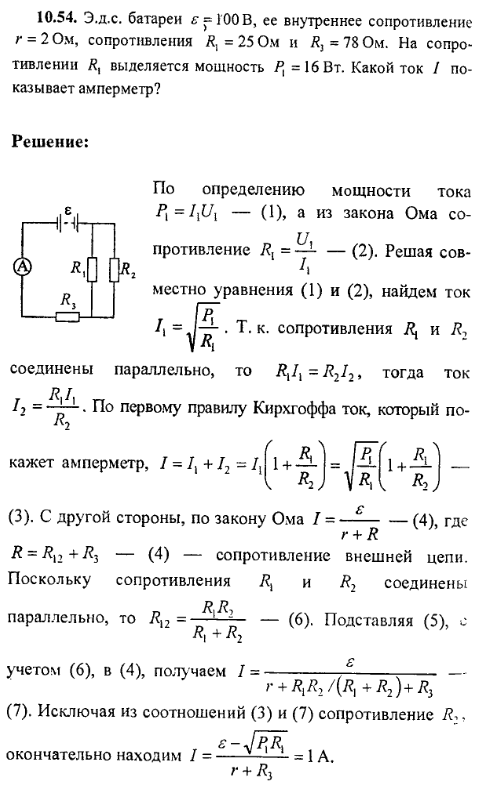 Или как мы, радиокоты, любим выражаться — к просадке напруги.
Чтобы изменение нагрузки как можно меньше влияло на выходное напряжение источника его внутреннее сопротивление стараются свести к минимуму.
Можно так подобрать элементы последовательной цепи, чтобы на каком-нибудь из них получить напряжение, уменьшенное, по сравнению с исходным, во сколько угодно раз.

Допустим, есть простейшая электрическая замкнутая цепь, включающая в себя источник тока, например генератор, гальванический элемент или аккумулятор, и резистор, обладающий сопротивлением R. Поскольку ток в цепи нигде не прерывается, то и внутри источника он течет.

В такой ситуации можно сказать, что любой источник обладает некоторым внутренним сопротивлением, препятствующим току. Это внутреннее сопротивление характеризует источник тока и обозначается буквой r. Для или аккумулятора внутреннее сопротивление — это сопротивление раствора электролита и электродов, для генератора — сопротивление обмоток статора и т. д.

Таким образом, источник тока характеризуется как величиной ЭДС, так и величиной собственного внутреннего сопротивления r – обе эти характеристики свидетельствуют о качестве источника.

Электростатические высоковольтные генераторы (как генератор Ван де Граафа или генератор Уимшурста), к примеру, отличаются огромной ЭДС измеряемой миллионами вольт, при этом их внутреннее сопротивление измеряется сотнями мегаом, потому они и непригодны для получения больших токов.

Гальванические элементы (такие как батарейка) — напротив — имеют ЭДС порядка 1 вольта, хотя внутреннее сопротивление у них порядка долей или максимум — десятка Ом, и от гальванических элементов поэтому можно получать токи в единицы и десятки ампер.

На данной схеме показан реальный источник с присоединенной нагрузкой. Здесь обозначены , его внутреннее сопротивление, а также сопротивление нагрузки. Согласно , ток в данной цепи будет равен:

Поскольку участок внешней цепи однороден, то из закона Ома можно найти напряжение на нагрузке:

Выразив из первого уравнения сопротивление нагрузки, и подставив его значение во второе уравнение, получим зависимость напряжения на нагрузке от тока в замкнутой цепи:

В замкнутом контуре ЭДС равна сумме падений напряжений на элементах внешней цепи и на внутреннем сопротивлении самого источника.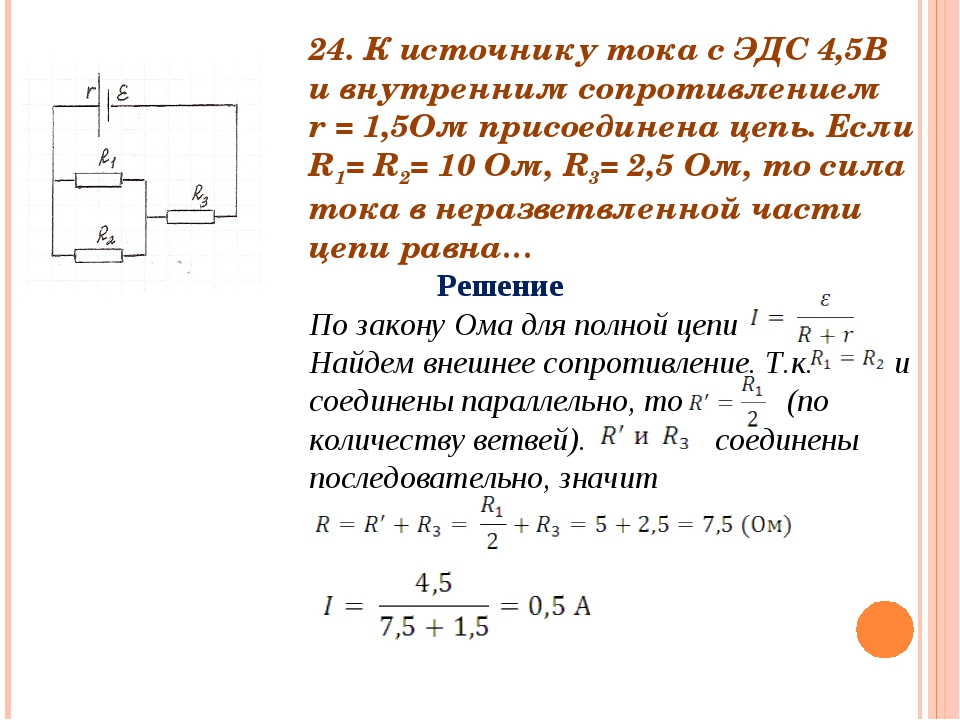 Зависимость напряжения на нагрузке от тока нагрузки в идеальном случае линейна.

График это показывает, но экспериментальные данные на реальном резисторе (крестики возле графика) всегда отличаются от идеала:

Эксперименты и логика показывают, что при нулевом токе нагрузки напряжение на внешней цепи равно ЭДС источника, а при нулевом напряжении на нагрузке ток в цепи равен . Это свойство реальных цепей помогает экспериментально находить ЭДС и внутреннее сопротивление реальных источников.

Экспериментальное нахождение внутреннего сопротивления

Чтобы экспериментально определить данные характеристики, строят график зависимости напряжения на нагрузке от величины тока, затем экстраполируют его до пересечения с осями.

В точке пересечения графика с остью напряжения находится значение ЭДС источника, а в точке пересечения с осью тока находится величина тока короткого замыкания. В итоге внутреннее сопротивление находится по формуле:

Развиваемая источником полезная мощность выделяется на нагрузке. График зависимости этой мощности от сопротивления нагрузки приведен на рисунке. Эта кривая начинается от пересечения осей координат в нулевой точке, затем возрастает до максимального значения мощности, после чего спадает до нуля при сопротивлении нагрузки равном бесконечности.

Чтобы найти максимальное сопротивление нагрузки, при котором теоретически разовьется максимальная мощность при данном источнике, берется производная от формулы мощности по R и приравнивается к нулю. Максимальная мощность разовьется при сопротивлении внешней цепи, равном внутреннему сопротивлению источника:

Это положение о максимальной мощности при R = r, позволяет экспериментально найти внутреннее сопротивление источника, построив зависимость мощности, выделяемой на нагрузке, от величины сопротивления нагрузки. Найдя реальное, а не теоретическое, сопротивление нагрузки, обеспечивающее максимальную мощность, определяют реальное внутреннее сопротивление источника питания.

КПД источника тока показывает отношение максимальной выделяемой на нагрузке мощности к полной мощности, которую в данный момент развивает

Попробуем решить эту задачу на конкретном примере.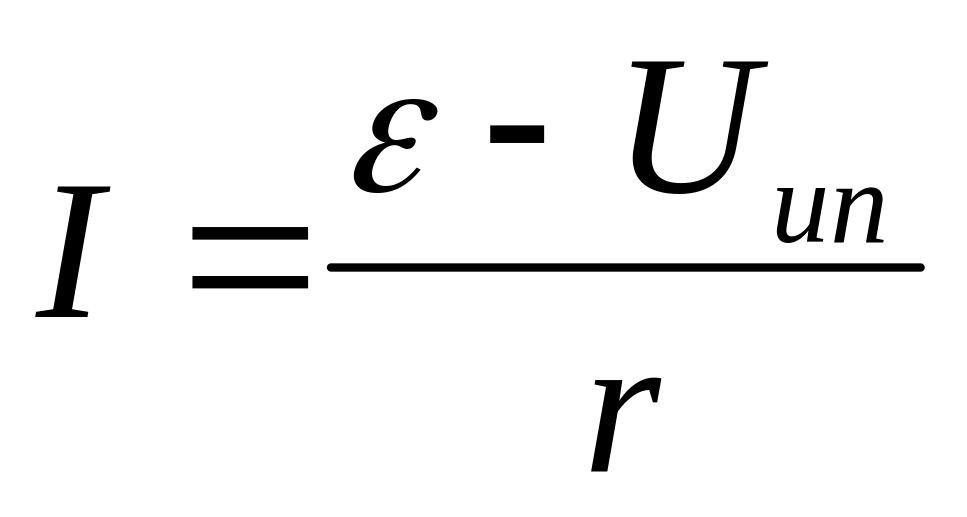 Электродвижущая сила источника питания составляет 4,5 В. К нему подключили нагрузку, и через неё потёк ток, равный 0,26 А. Напряжение при этом стало равным 3,7 В. Первым делом, представим себе, что внутри источника спрятана последовательная цепь из идеального источника напряжения в 4,5 В, внутреннее сопротивление которого равно нулю, а также резистора, номинал которого и требуется найти. Понятно, что на самом деле это не так, но для расчётов аналогия вполне сойдёт.

2 шаг

Запомните, что буквой U обозначают только напряжение под нагрузкой. Для обозначения же электродвижущей силы зарезервирована другая буква – E. Абсолютно точно её измерить невозможно, потому что потребуется вольтметр с бесконечным входным сопротивлением. Даже у электростатического вольтметра (электрометра) оно огромно, но не бесконечно. Но одно дело – абсолютно точно, а другое – с точностью, приемлемой на практике. Второе вполне осуществимо: нужно лишь, чтобы внутреннее сопротивление источника было пренебрежимо мало по сравнению с внутренним сопротивлением вольтметра. А пока суть да дело, посчитаем разницу между ЭДС источника и его напряжением под нагрузкой, потребляющей ток в 260 мА. E-U = 4,5-3,7 = 0,8. Это и будет падение напряжения на том “виртуальном резисторе”.

3 шаг

Ну а дальше всё просто, ибо в дело вступает классический закон Ома. Помним, что ток через нагрузку и “виртуальный резистор” одинаков, ведь они соединены последовательно. Падение напряжения на последнем (0,8 В) делим на силу тока (0,26 А) и получаем 3,08 Ома. Вот и готов ответ! Можно ещё посчитать, какая мощность рассеивается на нагрузке, а какая – бесполезно на источнике. На нагрузке рассеивается: 3,7*0,26=0,962 Вт. На источнике: 0,8*0,26=0,208 Вт. Процентное соотношение между ними вычислите самостоятельно. Но эта не единственный вид задач на нахождение внутреннего сопротивления источника. Есть и такие, в которых вместо силы тока указано сопротивление нагрузки, а остальные исходные данные такие же. Тогда надо вначале проделать ещё одно вычисление. Приведённое в условии напряжение под нагрузкой (не ЭДС!) поделить на сопротивление нагрузки. И получится сила тока в цепи. После чего, как говорят физики, “задача сведена к предыдущей”! Попробуйте составить такую задачу и решить её.

Как найти внутреннее сопротивление амперметра

Лабораторная работа №2

Тема. Измерение напряжения в цепях постоянного тока

Цель. Провести измерение напряжения в цепи постоянного тока прямым методом. Ознакомится со способам расширения верхних пределов измерений вольтметров постоянного тока, с методам расчета добавочных сопротивлений.

Определить внутренне сопротивление вольтметра.

Определить сопротивление добавочного резистора.

Сделать выводы по результатам работы.

Для измерения напряжения U, действующего между какими-либо двумя точками электрической цепи, вольтметр 2 (рис. 1, а) присоединяют к этим точкам, т. е. параллельно источнику 1 электрической энергии или приемнику 3.

Для того чтобы включение вольтметра не оказывало влияния на работу электрических установок и он не создавал больших потерь энергии, вольтметры выполняют с большим сопротивлением.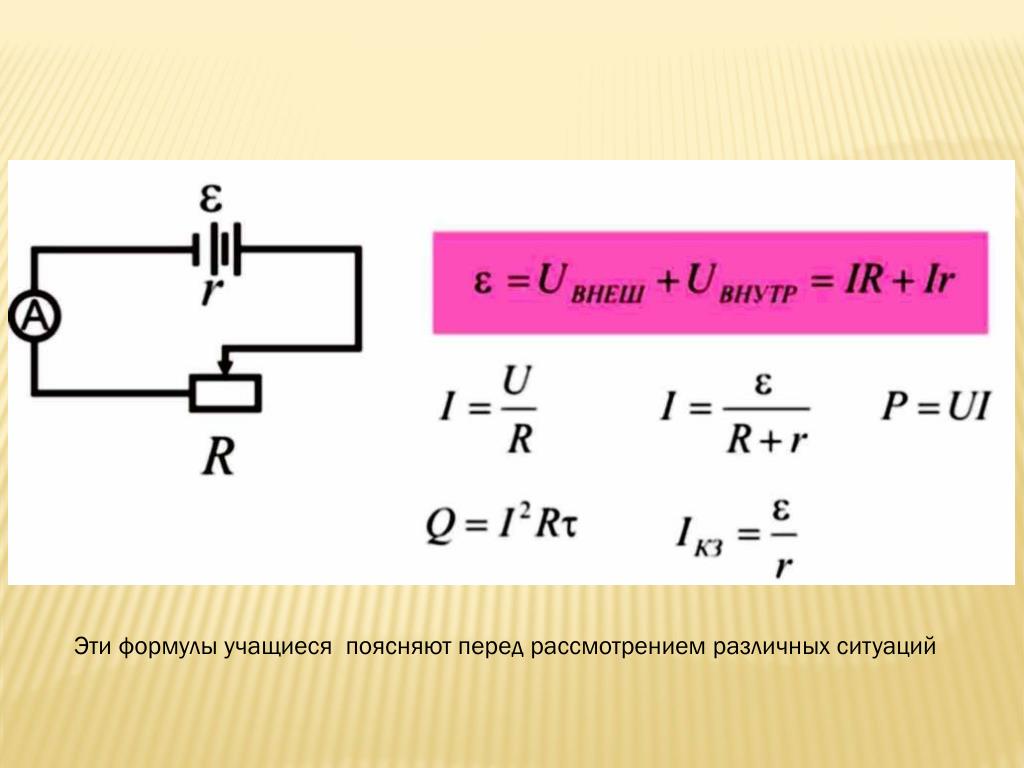 Поэтому практически можно пренебрегать проходящим по вольтметру током.

Для расширения пределов измерения вольтметров последовательно с обмоткой прибора включают добавочный резистор 4 (R_Д) (рис. 1, б). При этом на прибор приходится лишь часть U_V измеряемого напряжения U, пропорциональная сопротивлению прибора R_V.

Зная сопротивление добавочного резистора и вольтметра, можно по значению напряжения U_V, фиксируемого вольтметром, определить напряжение, действующее в цепи:

(1)

Величина показывает, во сколько раз измеряемое напряжение U больше напряжения U_V, приходящегося на прибор, т. е. во сколько раз увеличивается предел измерения напряжения вольтметром при применении добавочного резистора.

Сопротивление добавочного резистора, необходимое для измерения напряжения U, в n раз большего напряжения прибора U_V, определяется по формуле

(2)

Добавочный резистор может встраиваться в прибор и одновременно использоваться для уменьшения влияния температуры окружающей среды на показания прибора. Для этой цели резистор выполняется из материала, имеющего малый температурный коэффициент, и его сопротивление значительно превышает сопротивление катушки, вследствие чего общее сопротивление прибора становится почти независимым от изменения температуры. По точности добавочные резисторы подразделяются на те же классы точности, что и шунты.

Рис. 1. Схемы для измерения напряжения

Внутреннее сопротивление вольтметра. Для определения внутреннего сопротивления вольтметра его необходимо подключить последовательно с резистором (с ) к источнику напряжения (рис. 2) . Напряжение источника поделится между резистором и вольтметром пропорционально их сопротивлениям

(3)

(4)

Рис. 2. Схема для определения внутреннего сопротивления вольтметра

Собрать схему, как на рис. 2.

Сопротивления R выбрать с помощью магазинов сопротивлений так, чтобы напряжения U_R и U_V были приблизительно равнями ().

Собрать схему, как на рис. 3 ( ).

Рассчитать значение добавочного сопротивления R_Д (2) для каждого из значений U_ИП и коэффициент n.

Используя показание вольтметра 15 В и значение коэффициента n, определить напряжение U_ИП (1). Убедиться, что его значение совпадает с действительным.

Заполнить таблицу 1.

Рис. 3. Использование добавочного сопротивления

Для контроля величины тока применяется прибор называемый амперметром. Из практики могу сказать, что не всегда под рукой оказывается прибор с нужным диапазоном измерения. Как правило, диапазон либо мал, либо велик. Здесь мы разберем, как изменить рабочий диапазон амперметра. Амперметры на большие токи от 20 ампер и выше имеют в своём составе внешний шунтирующий резистор. Он подключается параллельно амперметру. На рисунке 1 приведена схема включения амперметра с шунтирующем резистором.

В качестве примера в экспериментах будет использован амперметр M367 со шкалой до 150 ампер, соответственно при таком токе амперметр используется с внешним шунтирующим сопротивлением.

Если убрать шунтирующий резистор, то амперметр станет миллиамперметром с максимальным током отклонения стрелки 30 мА (далее будет пояснение, откуда это значение взялось). Таким образом, используя разные шунтирующие сопротивления можно сделать амперметр практически с любым диапазоном измерения.

Рассмотрим подробнее имеющийся измерительный прибор. Из его маркировок можно узнать следующее. Маркировка в верхнем правом углу (цифра 1 на изображении). Модель измерительной головки М367. Сделан на краснодарском заводе измерительных приборов (это можно определить по ромбику с буковками ЗИП). Год выпуска 1973. Серийный номер 165266.

Маркировка в нижнем левом углу (цифра 2 на изображении). Слева на право. Прибор предназначен для измерения постоянного тока. Магнитоэлектрический прибор с подвижной рамкой. Напряжение между корпусом и мангнитоэлектрической системой не должно превышать 2 КВ. Рабочее положение шкалы прибора вертикальное. Класс точности прибора в процентах 1,5. ГОСТ8711-60. Измерительная головка рассчитана на измерения силы тока до 150 ампер с использованием внешнего шунтирующего сопротивления рассчитанного на падение на нём напряжения номиналом в 75 милливольт.

Итак, это максимум что удалось узнать из маркировки амперметра. Теперь перейдём к расчетам. Сопротивление шунта определяется по формуле:

где :
Rш – сопротивление шунтирующего резистора;
Rприб – внутреннее сопротивление амперметра;
Iприб – максимально измеримый ток амперметром без шунта;
Iраб – максимально измеримый ток с шунтом (требуемое значение)

Если все данные для расчёта имеются, то можно приступать к самому расчёту. Для упрощения можно воспользоваться онлайн калькулятором ниже:

В нашем случае из формулы видно, что данных не достаточно. Нам известен только максимальный измеряемый ток с шунтом. То есть, то, что мы хотим видеть в случае максимального отклонения стрелки амперметра.

Из маркировки прибора удалось узнать падение напряжения на шунтирующем сопротивлении. И это уже что-то. Из этого параметра ясно, что при подаче на прибор напряжения номиналом 0,075 вольт (75мВ) стрелка отклониться до крайнего значения на шкале 150 ампер. Таким образом, получается, что максимальное отклонение стрелки прибора достигается подачей напряжения 75 мВ. Вроде как данных для расчета по-прежнему не хватает. Необходимо узнать сопротивление прибора и ток, при котором стрелка откланяется до максимального значения без шунтирующего резистора. Далее предлагаю несколько способов для определения нужных параметров и решения задачи.

Способ первый. При помощи блока питания выясняем максимальное отклонение стрелки по току и напряжению без шунта. В нашем случае напряжение уже известно. Его замерять не будем. Измеряем ток и отклонение стрелки. Так как блока питания под рукой не оказалось, то пришлось воспользоваться очень разряженой батарейкой типа АА. Ток, который батарейка могла ещё отдать, составил 12 мА (по показаниям мультиметра). При этом токе стрелка прибора отклонилась до значения на циферблате 60А. Далее определяем цену деления и рассчитываем полное (максимальное) отклонение стрелки. Поскольку шкала циферблата амперметра размечена равномерно, то не составит труда узнать (рассчитать) ток максимального отклонения стрелки.

Цена деления прибора рассчитывается по формуле:

где:
х1 – меньшее значение,
х2 – большее значение,
n – количество промежутков (отрезков) между значениями

Для упрощения можно воспользоваться онлайн калькулятором ниже:

Расчёт показал, что цена деления прибора штатной шкалы составляет 5 ампер. При токе 12 мА стрелка отклонялась до показания 60А. Таким образом, цена одного деления без шунта составляет 1 мА. Всего делений 30, соответственно максимальное отклонение стрелки до значения 150А без шунта составляет 30 мА.

Далее при помощи закона Ома находим сопротивление прибора. 0,075/0,03=2,5 Ом

Расчёт:
Rш=Rприб*Iприб/(Iраб-Iприб)=2,5*0,03/(10-0,03)=0,00752 Ом для шкалы 10А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,5*0,03/(5-0,03)=0,01509 Ом для шкалы 5А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,5*0,03/(3-0,03)=0,02525 Ом для шкалы 3А мах

Для упрощения можно воспользоваться онлайн калькулятором расчёта сопротивления шунтирующего сопротивления выше.

Второй вариант. При помощи прецизионного мультиметра замеряем сопротивление амперметра и далее при помощи закона Ома (зная напряжение максимального отклонения стрелки) находим ток максимального отклонения стрелки. Измерения выполнялись прецизионными мультиметрами Mastech MS8218 и Uni-t UT71E. При измерении сопротивления амперметра значение составило 2,50-2,52 Ом прибором UT71E и 2,52-2,53 прибором MS8218.

Формула для расчёта тока отклонения стрелки до максимального значения:

Для упрощения вычислений максимального тока отклонения стрелки амперметра можно воспользоваться калькулятором ниже:

Далее, как и в первом варианте выполняем расчёт сопротивления шунтирующего резистора (калькулятор выше). Для расчёта было принято среднее показание измеренного сопротивления амперметра двумя мультиметрами Rприб = 2,52Ом

Расчёт:
Rш=Rприб*Iприб/(Iраб-Iприб)=2,52*0,02976/(10-0,02976)=0,00752 Ом для шкалы 10А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,52*0,02976/(5-0,02976)=0,01508 Ом для шкалы 5А мах
Rш=Rприб*Iприб/(Iраб-Iприб)=2,52*0,02976/(3-0,02976)=0,02524 Ом для шкалы 3А мах

Если сравнить расчёты двух методик между собой, то получились совпадение данных до четвёртого знака после запятой, а в некоторых случаях даже до пяти знаков.

О тонкостях изготовления шунтирующего сопротивления расскажу в следующей статье.

1. Необходимо измерить ток потребителя в пределах 20 – 25 А. Имеется микроамперметр с пределом измерения 200мкА, внутренним сопротивлением 300 Ом и максимальным числом делений 100. Определить сопротивление шунта для расширения предела измерения до 30 А и определить относительную погрешность измерения на отметке 85 делений, если класс точности прибора 1,0.

Решение:

2. Предел измерения I_пр амперметра с внутренним сопротивлением R_А должен быть расширен до значения 8 I_пр. Найти значение R_Ш.

Решение:

3. Предел измерения микроамперметра на 150 мкА должен быть расширен до 15 А. Определить сопротивление шунта, если внутреннее его сопротивление R_А = 400 А.

Решение:

4. Амперметр с внутренним сопротивлением R_А = 0,015 Ом и пределом измерения 20 А имеет шунт сопротивлением 0,005 Ом. Определить предел измерения амперметра с шунтом, а также ток в цепи, если его показание равно 12 А.

Решение:

5. Милливольтметр с пределом измерения 75 мВ и внутренним сопротивлением R_В = 25 Ом имеет 150 делений шкалы. Определить сопротивление шунта, чтобы прибором можно было измерять предельное значение тока 30 А. Определить цену деления прибора в обоих случаях.

Решение:

6. Микроамперметр с пределом измерения 1000 мкА и внутренним сопротивлением R_А =300 Ом необходимо использовать в качестве вольтметра на предел 30 В. Определить добавочное сопротивление.

Решение:

7. Милливольтметр с пределом измерения 750 мВ необходимо переделать в многопредельный вольтметр с пределами 7,5; 15; 75; 150В. Добавочное сопротивление на пределе 7,5 В составляет 1350 Ом. Определить добавочное сопротивление на каждом из пределов, сопротивление и ток полного отклонения прибора.

Решение:

8. У вольтметра электродинамической системы с пределом измерения U = 300 В и внутренним сопротивлением R_в = 30 кОм необходимо расширить предел до 1500 В. Определить добавочное сопротивление вольтметра и максимальную потребляемую мощность на основном и расширенном пределах.

Решение:

9. Предел измерения вольтметра электромагнитной системы составляет 7,5 В при внутреннем сопротивлении R_в = 200 Ом. Определить добавочное сопротивление, которое необходимо включить для расширения предела измерения до 600 В.

Решение:

10. Амперметром с внутренним сопротивлением R_A = 1 Ом следует измерить ток в 10, 100 и 1000 раз больше его номинального значения. Найти соотношение между сопротивлениями амперметра и шунтов, подобранных для выполнения указанных измерений.

Решение:

11. Амперметр, имеющий внутреннее сопротивление 0,2 Ом и предел измерения 10 А, необходимо использовать для измерения тока до 500 А. Определить сопротивление шунта прибора и падение напряжения на амперметре и шунте.

Решение:

12. Номинальный ток амперметра I_н = 1 А, сопротивление шунта R_ш = 0,5 Ом Определить сопротивление амперметра, если номинальное значение тока в нем было при общем токе цепи 5 А.

Решение:

13. Номинальный ток амперметра 1 А, его внутреннее сопротивление 0,08 Ом. Какой ток проходит в электрической цепи, если амперметр с шунтом сопротивлением 0,03 Ом показывает ток 0,9 А?

Решение:

14. Необходимо измерить напряжение в пределах 30-40 В. Какой из вольтметров позволяет произвести измерение с большей точностью:

1 ) с верхним пределом 50 В и классом точности 2,5;

2) с верхним пределом 100 В и классом точности 1,5;

3) с верхним пределом 300 В и классом точности 0,5; 4) с верхним пределом 150 В и классом точности 1.

Решение:

15. Вольтметром с внутренним сопротивлением R_v требуется измерить напряжение в 10, 100 и 1000 раз больше его номинального значения. Найти соотношение между внутренним сопротивлением вольтметра и сопротивлениями добавочных резисторов, подобранных для выполнения указанных условий.

Решение:

16. Номинальное напряжение вольтметра 10 В, внутреннее его сопротивление 5 кОм. Какое допустимое напряжение может быть в измеряемой цепи, если к вольтметру подключен добавочный резистор, сопротивление которого 150 кОм?

Решение:

17. Вольтметр рассчитан для измерения напряжения до 15 В. Определить сопротивление добавочного резистора, который необходимо подключить к вольтметру с R_v = 50 кОм, чтобы с его помощью измерять напряжение 220 В. Каковы при этом потери мощности в обмотке вольтметра и добавочном резисторе?

Решение:

Рис. 3.1

18. Номинальное напряжение вольтметра 30 В, его внутреннее сопротивление 10 кОм. Каково напряжение в измеряемой цепи, если показание вольтметра 10 В соответствует сопротивлению добавочного резистора 50 кОм?

Решение:

19. Для измерения ЭДС генератора к его зажимам присоединен вольтметр (рис, 3.1), сопротивление которого R_v = 10000 Ом. Сопротивление якоря генератора R_а = 0,2 Ом. Определить, на сколько процентов делаем ошибку, считая показание вольтметра, равным ЭДС генератора.

Решение:

20. Амперметр, сопротивление которого R_А = 0,3 Ом, имеет шкалу в 150 делений и постоянная прибора С_А = 0,001 А/дел. Определить сопротивление шунта R_Ш, при помощи которого можно было измерять ток до 300 А.

Решение:

21. Амперметр, сопротивление которого R_А = 0,3 Ом, имеет шкалу в 150 делений и постоянная прибора С_А = 0,001 А/дел. Определить; какое сопротивление R_Д необходимо последовательно включить с амперметром, чтобы этим прибором можно было измерять напряжение до 150В.

Решение:

22. Какой ток можно измерять амперметром (сопротивление R_А = 0,3 Ом, шкала имеет 150 делений и постоянная прибора С_А =0,001 А/дел), если имеется шунт с сопротивлением Ом?

Решение:

23. Необходимо подобрать к амперметру с сопротивлением R_А шунты, расширяющие пределы измерения в 10 и 100 раз. Каковы будут соотношения между сопротивлением амперметра и шунта?

Решение:

24. Вольтметр с ценой деления 1В/дел, шкала которого содержит 150 делений, имеет сопротивление R_В = 10 000 Ом. Какое добавочное сопротивление R_Д необходимо включить последовательно с вольтметром, чтобы им можно было измерять напряжение до 600 В?

Решение:

25. Через амперметр, включенный в цепь через трансформатор тока ТЛ-35К, рассчитанный на ток 600/5 А, проходит ток I₂ = 4,25 А, Определить ток в первичной цепи.

Решение:

26. Амперметр, рассчитанный на 5А, со шкалой 0 — 500 делений включен в цепь через трансформатор тока 400/5 А. Какой ток проходит в первичной и вторичной обмотках трансформатора, если амперметр показывает 350 делений?

Решение:

27. Ваттметр, имеющий пределы измерения U = 150 В, I = 5 А и число делений шкалы 150, включены через измерительный трансформатор, напряжения 6000/100 В и трансформатор тока 500/5 А. Определить мощность первичной цепи, если показания ваттметра — 124 деления.

Решение:

28. Через трансформатор тока 500/5А и трансформатор напряжения 6000/100В в сеть переменного тока включены амперметр, вольтметр и ваттметр. Определить ток, напряжение, активную мощность и коэффициент мощности цепи, если амперметр показал I = 4 А, вольтметр — U = 100 В, а ваттметр — 350 Вт.

Решение:

29. Обмотки ваттметра, рассчитанные на номинальную мощность Р_ном = 500 Вт, присоединены к сети переменного тока через измерительный трансформатор напряжения НОМ-6 (3000/100 В) и трансформатор тока ТПЛ-10 (400/5 А). Определять мощность первичной цепи, если мощность в цепи ваттметра Р = 380 Вт.

Решение:

30. К трансформатору напряжения НОМ-10 (номинальное напряжение первичной обмотки 10 000 В) подключили вольтметр, рассчитанный на 150 В. Определить напряжение на вольтметре, если напряжение в первичной цепи понизилось до 9950 В.

Решение:

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9825 – | 7406 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Найти внутреннее сопротивление и ЭДС батареи аккумуляторов

ВАРИАНТ 10-15-1.

1. Найти внутреннее сопротивление и ЭДС батареи аккумуляторов, если при сопротивлении внешней части цепи 2,0 Ом ток равен 0,80 А, а при сопротивлении

3 Ом — 0,60 А.

2. Три потребителя эл.энергии сопротивлением 12, 9 и 3 Ом соединены последовательно. Напря­жение на концах цепи 120 В. Найти ток в цепи и падение напряжения на каждом потребителе.

3. Каково удельное сопротивление провода, если его длина 20 м, площадь поперечного сечения 1,0 мм² и сопротивление 10 Ом?

4. Четыре проводника сопротивлением 1 Ом ; 2 Ом ; 3 Ом ; 4 Ом соединены параллельно. Определить общее сопротивление.

ВАРИАНТ 10-15-2

1. По цепи, состоящей из источника тока с ЭДС 2 В и внутренним сопротивлением

2 Ом и реостата, идет ток силой 0,5 А. Какой силы пойдет ток при уменьшении сопротивления реостата в два раза?

2. Цепь состоит из трех сопротивлений 10, 20 и 30 Ом, соединенных последовательно. Падение напряжения на первом сопротивлении 20 В. Най­ти падение напряжения на остальных сопротив­лениях и напряжение на концах цепи.

3. Восемь проводников сопротивлением по 20 0м каждый соединены по два последовательно в четыре параллельные цепи. Определить общее сопротивление.

4. Два электронагревателя сопротивлением 25 Ом и 20 Ом находятся под напряжением 100 В. Какое количество теплоты в течение 3 минут выделится нагревателями при их последовательном соединении?

ВАРИАНТ 10-15-3

1. Гальванический элемент с ЭДС 14,0 В и внутренним сопротивлением 1,0 Ом замкнут на внешнее сопротивление 20,0 Ом. Чему равно напряжение на внешнем сопротивлении?

2. Последовательно дуговой лампе сопротивлением 4 Ом включен реостат сопротивлением 8 Ом. Определить силу тока в лампе, если напряжение в сети 120 В.

3. Какого сопротивления проводник нужно соеди­нить параллельно с проводником

300 Ом, чтобы общее сопротивление их стало равным 120 Ом?

4. В каком из двух сопротивлений 2 Ом и 10 Ом, соединенных последовательно, при протекании тока выделяется большее количество теплоты?

ВАРИАНТ 10-15-4

1. ЭДС источника напряжения 6,0 В. При внеш­нем сопротивлении цепи 1,0 Ом ток равен 3,0 А. Каким будет ток короткого замыкания?

2. Определить сопротивление цепи, состоящей из эл.лампочки сопротивлением

9,5 Ом, реостата сопротивлением 12 Ом и медного проводника длиной 400 см и сечением 0,4 мм², соединенных последовательно.

3. Имеются три проводника сопротивлением по 2 Ом каждый. Как нужно соединить их между собой, чтобы общее сопротивление было равно 3 Ом.

4. Два электронагревателя 3 Ом и 4 Ом соединены параллельно. Напряжение в цепи 220 В. Какое количество теплоты выделится нагревателями за 1 минуту?

ВАРИАНТ 10-15-5

1. Определить потерю напряжения внутри источника тока и его ЭДС, если потеря напряжения на внешней части цепи 1,2 В, сопротивление внеш­ней части цепи

1,5 Ом, внутреннее сопротивле­ние источника тока 0,3 Ом.

2. Два сопротивления по 4 Ом каждый соединены параллельно. Последовательно к ним подключено сопротивление 6 Ом. Определить общее сопротив­ление.

3. Каково удельное сопротивление провода, если его длина 10,0 км, площадь поперечного сече­ния 70,0 мм² и сопротивление 4,0 0м.

4. Два электронагревателя сопротивлением 6 0м и 4 0м соединены последовательно и находятся под напряжением 110 В, Какое количество теплоты выделится ими за

2 минуты?

ВАРИАНТ 10-15-6

1. В проводнике сопротивлением 2 0м, подключен­ном к элементу с ЭДС=1,1 В, идет ток 0,5 А, Какова сила тока при коротком замыкании элемента?

2. Два сопротивления по 5 0м каждый соединены параллельно. Определить силу тока в цепи, если напряжение равно 25 В.

3. Медный и алюминиевый проводники имеют одинаковые сечения и сопротивления. Какой проводник длиннее и во сколько раз?

4. Какое количество теплоты выделится эл.плиткой сопротивлением 10 0м, если по цепи течет ток 3 А за 5 минут? 10 минут?

Нахождение внутреннего сопротивления и ЭДС источника.

В статье расчёт в маткаде переходных процессов в ёмкостном фильтре исследовался переходный процесс в фильтре поставленном на выходе однофазного однополупериодного выпрямителя, при этом в схеме замещения выпрямитель с источником переменного напряжения заменены последовательным соединением источника ЭДС и резистора, такая замена делает возможным расчёт схем но при этом для расчётов требуется найти ЭДС источника и его внутреннее сопротивление. Найти ЭДС источника и его внутреннее сопротивление эксперементально можно проделав опыт холостого хода и опыт короткого замыкания но это не всегда возможно, например когда необходимо найти ЭДС и внутреннее сопротивление источника представляющего собой вторичную обмотку трансформатора, поэтому бывает необходимо определить параметры схемы замещения источника не внося больших изменений сопротивления нагрузки в схему. Рассмотрим схему на рисунке 1:

Рисунок 1 — Схема для определения параметров схемы замещения источника.

В этой схеме значения ЭДС источника и его внутреннего сопротивления неизвестны, известны только показания амперметра и вольтметра. Учтём что тока в цепи вольтметра нет, так как у него большое сопротивление и его проводимостью можно пренебреч а сопротивление амперметра настолько мало что им тоже можно пренебреч и заменить амперметр перемычкой. Ток в этой цепи обозначим как I1 (его показывает амперметр) а напряжение на R1 и G обозначим как U1 (его показывает вольтметр) при этом будем считать что ток направлен как показано на рисунке 1, а напряжения на R1 и r направлены в туже сторону что и ток. Рассмотрим схему на рисунке 2 в которой изменено (в нашем случае увеличено) сопротивление реостата:

Рисунок 2 — Схема для определения параметров схемы замещения источника с изменённым сопротивлением реостата.

В этой схеме показание амперметра обозначим как I2 а показание вольтметра как U2.

Из схемы на рисунке 1, составим уравнение по второму закону Кирхгофа для контура который остаётся если заменить вольтметр разрывом:

Здесь E — ЭДС источника, U1 — напряжение на реостате (показывает вольтметр), I1 — ток в цепи (показывает амперметр), r — внутреннее сопротивление источника. Выразим из уравнения (1) напряжение U1:

Аналогично найдём U2, используя схему на рисунке 2:

Подставим (1) в (3):

Выразим из уравнения (4) внутреннее сопротивление источника r:

 Подставим (6) в (1) и найдём ЭДС источника:

По формулам (6) и (7) находятся параметры схемы замещения источника электрической энергии (по формуле (7) его ЭДС, по формуле (6) его внутреннее сопротивление). Последовательно с реостатом можно поставить измерительный резистор и использовать его для измерения тока вольтметром тогда измерения можно проводить одним вольтметром сначала подключая его паралельно источнику G, а потом паралельно измерительному резистору.
Для расчёта внутреннего сопротивления и ЭДС источника можно воспользоваться программой:
Первое измерение должно быть с меньшим сопротивлением реостата, а второе с большим.

эдс источника внутреннее сопротивление

эдс источника внутреннее сопротивление

---

Задача 13496

На рисунке ε₁ = 10 В, ε₂ = 20 В, ε₃ = 40 В, а сопротивления R₁ = R₂ = R₃ = 10 Ом. Определите силу токов, протекающих через сопротивления (I) и через источники ЭДС (I’). Внутреннее сопротивление источников ЭДС не учитывать.
.

---

Задача 10083

Определить ЭДС и внутреннее сопротивление источника, если при подключении к этому источнику нагрузки сопротивлением 5 Ом напряжение на ней составляет 10 В, а при подключении нагрузки сопротивлением 20 Ом напряжение на нагрузке составляет 20 В.

---

Задача 60002

Полезная мощность, выделяемая во внешней части цепи, достигает наибольшего значения 5 Вт при силе тока 5 А. Найти внутреннее сопротивление и ЭДС источника.

---

Задача 60089

При каком внешнем сопротивлении потребляемая мощность будет максимальной, если два одинаковых источника с ЭДС 6 В и внутренним сопротивлением 1 Ом каждый соединены последовательно? Чему равна эта мощность?

---

Задача 60124

Определить ЭДС и внутреннее сопротивление источника тока, если при внешнем сопротивлении 3,9 Ом сила тока в цепи равна 0,5 А, а при внешнем сопротивлении 1,9 Ом — 1 А.

---

Задача 60377

Сопротивление R₁ = 5 Ом, вольтметр и источник тока соединены параллельно. Вольтметр показывает напряжение U₁ = 10 В. Если заменить сопротивление R₁ на R₂ = 12 Ом, то вольтметр покажет напряжение U₂ = 12 В. Определить ЭДС и внутреннее сопротивление источника тока. Током через вольтметр пренебречь.

---

Задача 60435

При каком внешнем сопротивлении потребляемая мощность будет максимальна, если два одинаковых источника с ЭДС 6 В и внутренним сопротивлением 1 Ом каждый соединены параллельно? Чему равна эта мощность?

---

Задача 12316

Определить эдс и внутреннее сопротивление источника питания, если в режиме холостого хода напряжение на выводах 15 В, а в режиме короткого замыкания ток 0,5 А. Найти ток в этой цепи при подключении резистора сопротивлением 120 Ом.

---

Задача 16205

В замкнутой цепи при сопротивлении нагрузки R₁ = 3 Ом ток I₁ = 3 А, а при R₂ = 2 Ом, I₂ = 4 А. Определить эдс источника и его внутреннее сопротивление.

---

Задача 16262

Батарея из двух параллельных источников с ЭДС 2 и 1,8 В и внутренним сопротивлением 50 мОм каждый замкнута на сопротивление 2 Ом. Найти величину тока, проходящего через сопротивление и через источники.

---

Задача 17294

Мощность, выделяющаяся на нагрузке, подключенной к источнику с ЭДС 5 В и внутренним сопротивлением 2 Ом, составляет 2 Вт. Определить ток в цепи и сопротивление нагрузки.

---

Задача 21481

Ток короткого замыкания источника 48 А. При подключении к источнику резистора сопротивлением 19,5 Ом ток в цепи уменьшился до 1,2 А. Определить ЭДС источника, его внутреннее сопротивление, а также мощность источника в обоих случаях.

---

Задача 21499

Ток короткого замыкания источника 48 А. При подключении к источнику резистора сопротивлением R = 19,5 Ом ток в цепи уменьшился до 1,2 А. Определить ЭДС источника и его внутреннее сопротивление.

---

Измерение внутреннего сопротивления батарей

Добавлено в избранное Любимый 7

Внутреннее сопротивление

При проектировании схемы с аккумулятором мы часто предполагаем, что аккумулятор является идеальным источником напряжения. Это означает, что независимо от того, какую нагрузку мы прилагаем к аккумулятору, напряжение на выводах источника всегда остается неизменным.

Если мы моделируем эту батарею как идеальный источник напряжения, изменение значения R _L не влияет на напряжение между выводами батареи

На самом деле несколько факторов могут ограничить способность батареи действовать как идеальный источник напряжения.Размер батареи, химические свойства, возраст и температура — все это влияет на величину тока, которую батарея может выдавать. В результате мы можем создать лучшую модель батареи с идеальным источником напряжения и резистором, включенным в серию .

Батареи можно смоделировать как идеальный источник напряжения с последовательным резистором (обозначенным R _I )

Мы можем измерить напряжение аккумулятора на его выводах без подключенной нагрузки. Это известно как напряжение холостого хода (В _OC ).

Измерение напряжения щелочного элемента AA без нагрузки

Обратите внимание, что, поскольку через внутренний резистор не течет ток, падение напряжения на нем равно 0 В. Следовательно, мы можем предположить, что V _OC равно напряжению идеального источника напряжения в батарее.

Если мы подключим нагрузку к аккумулятору, напряжение на выводах упадет.

Здесь мы измеряем падение напряжения на резисторе 4 Ом

Это падение напряжения вызвано внутренним сопротивлением батареи.Мы можем рассчитать внутреннее сопротивление, если снимем показания напряжения холостого хода и напряжения на клеммах батареи с подключенной нагрузкой.

Для начала создадим схему, показывающую нашу схему.

Вот наша схема. Мы хотим рассчитать R _I .

Мы можем подключить измеренное нами напряжение под нагрузкой (V _L ) и значение резистора (R _L ) в закон Ома, чтобы получить ток, протекающий по цепи (I).

Нам также нужно получить напряжение на внутреннем резисторе. Мы можем сделать это, используя закон напряжения Кирхгофа. Упрощенно для этой схемы, мы можем сказать, что падение напряжения на обоих резисторах должно составлять в сумме напряжение идеального источника напряжения.

Теперь, когда мы знаем падение напряжения на внутреннем резисторе и ток через него, мы можем снова использовать закон Ома, чтобы найти его сопротивление.

Отсюда видно, что внутреннее сопротивление (на данный момент) элемента AA составляет 0.273 Ом .

ПРИМЕЧАНИЕ : С помощью этого метода мы можем только сделать снимок внутреннего сопротивления. Внутреннее сопротивление может варьироваться в зависимости от возраста батареи и температуры. Через 10 минут значение сопротивления может измениться! Обычная щелочная батарея AA может иметь внутреннее сопротивление от 0,1 Ом до 0,9 Ом.

---

← Предыдущая страница
Введение

Определение ЭДС и внутреннего сопротивления ячейки — Электрические источники и внутреннее сопротивление — Высшая физическая версия

Вольтметр и переменный резистор

Посмотрите это видео, чтобы узнать, как можно измерить ЭДС и внутреннее сопротивление ячейки.

Как показано на видео, чтобы найти ЭДС и внутреннее сопротивление ячейки, создается следующая схема.

Изменяется переменный резистор и снимаются показания разности потенциалов на выводах элемента и тока через элемент. Затем строится график этих результатов, как показано ниже.

В точке, в которой линия пересекает ось конечной разности потенциалов, нет тока , протекающего из ячейки. Это называется потенциалом разомкнутой цепи цепи.

Поскольку нет тока, не будет потерь напряжения, поэтому это значение является ЭДС ячейки. Таким образом, точка, где линия пересекает ось конечной разности потенциалов (точка пересечения оси Y), является ЭДС ячейки.

В точке, где линия пересекает текущую ось (точка пересечения оси x), из ячейки берется максимальный ток. Это происходит при сопротивлении нагрузки \ (R = 0 \ Omega. \)

. Это может быть достигнуто путем короткого замыкания ячейки (этого следует избегать, поскольку ячейка может перегреться и это потенциально опасно).Максимальный ток называется током короткого замыкания , \ (I_ {SC} \).

Для определения внутреннего сопротивления ячейки рассчитывается градиент линии. Это отрицательное значение. Внутреннее сопротивление ячейки такое же, но без знака минус. Например, если наклон линии равен \ (- 4 \), то внутреннее сопротивление равно \ (4 \ Omega \).

Внутреннее сопротивление также можно найти, разделив ЭДС \ (E \) на ток короткого замыкания \ (I_ {SC} \).

Как рассчитать ЭДС | Sciencing

Обновлено 2 ноября 2020 г.

Ли Джонсон

Электродвижущая сила (ЭДС) — понятие незнакомое для большинства людей, но оно тесно связано с более знакомым понятием напряжения. Понимание разницы между ними и того, что означает ЭДС, дает вам инструменты, необходимые для решения многих проблем в физике и электронике, а также знакомит с концепцией внутреннего сопротивления батареи. ЭДС сообщает вам напряжение батареи без уменьшения внутреннего сопротивления, как это происходит при обычных измерениях разности потенциалов.Вы можете рассчитать его несколькими способами, в зависимости от того, какая информация у вас есть.

TL; DR (слишком долго; не читал)

Рассчитайте ЭДС по формуле:

ε = V + Ir

Здесь (В) означает напряжение элемента, (I) означает ток в цепи, а (r) означает внутреннее сопротивление ячейки.

Что такое ЭДС?

Электродвижущая сила — это разность потенциалов (т. Е. Напряжение) на клеммах батареи при отсутствии тока.Может показаться, что это не имеет значения, но каждая батарея имеет «внутреннее сопротивление». Это похоже на обычное сопротивление, которое снижает ток в цепи, но оно существует внутри самой батареи. Это связано с тем, что материалы, из которых состоят элементы в батарее, имеют собственное сопротивление (так как практически все материалы имеют).

Когда ток не течет через элемент, это внутреннее сопротивление ничего не меняет, потому что нет тока для его замедления.В некотором смысле, ЭДС можно рассматривать как максимальную разность потенциалов на клеммах в идеальной ситуации, и на практике она всегда больше, чем напряжение батареи.

Уравнения для расчета ЭДС

Есть два основных уравнения для расчета ЭДС. Наиболее фундаментальное определение — это количество джоулей энергии (E), которое каждый кулон заряда (Q) забирает при прохождении через ячейку:

Где (ε) — символ электродвижущей силы, (E) — энергия в цепи, а (Q) — заряд цепи.Если вы знаете результирующую энергию и количество заряда, проходящего через ячейку, это самый простой способ рассчитать ЭДС, но в большинстве случаев у вас нет этой информации.

Вместо этого вы можете использовать определение, больше похожее на закон Ома (V = IR). Это может быть выражено как:

\ epsilon = I (R + r)

, где (I) означает ток, (R) — сопротивление рассматриваемой цепи, а (r) — внутреннее сопротивление ячейки. Расширение этого показывает тесную связь с законом Ома:

\ epsilon = IR + Ir = V + Ir

Это показывает, что вы можете рассчитать ЭДС, если вы знаете напряжение на клеммах (напряжение, используемое в реальных ситуациях) , протекающий ток и внутреннее сопротивление ячейки.

Как рассчитать ЭДС: пример

В качестве примера представьте, что у вас есть цепь с разностью потенциалов 3,2 В, протекающим током 0,6 А и внутренним сопротивлением батареи 0,5 Ом. Используя формулу выше:

\ epsilon = V + Ir = 3.2 \ text {V} + (0.6 \ text {A}) (0.5 \ text {} \ Omega) = 3.5 \ text {V}

Итак, EMF этой цепи составляет 3,5 В.

Внутреннее сопротивление, ЭДС и разность потенциалов

В любой цепи есть компоненты, которые передают энергию из в схему, и компоненты, которые отбирают энергию из .С этого момента мы будем говорить, что любое устройство, передающее энергию в цепь, обеспечивает электродвижущую силу (ЭДС) , и любое устройство, выводящее ее, имеет разность потенциалов (pd) на нем.

И ЭДС, и pd измеряются в вольтах, В, , поскольку они описывают, сколько энергии вкладывается или снимается на один кулон заряда, проходящего через этот участок цепи.

Лучше всего думать о них:

ЭДС — это количество энергии любой формы, которое превращается в электрическую энергию на кулон заряда.

pd — количество электрической энергии, которая преобразуется в другие формы энергии на один кулон заряда.

Источники ЭДС:

Элемент, аккумулятор (комбинация элементов), солнечный элемент, генератор, динамо-машина, термопара.

Элементы и батареи не идеальны (что, конечно, не считая момента окончания вашего последнего экзамена?). Используйте их некоторое время, и вы заметите, что они нагреваются.

Откуда поступает тепловая энергия?

Это от тока, проходящего через внутреннюю часть ячейки.Сопротивление внутри ячейки превращает часть производимой ею электроэнергии в тепловую при движении электронов через нее.

Это легко объяснить, если представить, что каждая ячейка идеальна, за исключением того, что по какой-то странной причине (вероятно, часть заговора по захвату мира, задуманного доктором Злом) производители включили резистор последовательно с ячейкой внутри ячейки. кожух.

Таким образом, внутри ячейки энергия передается в цепь ячейкой (ЭДС), но некоторая часть этой энергии отбирается из цепи внутренним резистором (pd).

Таким образом, pd, доступный для остальной части схемы (внешней цепи, поскольку некоторые вопросы могут относиться к ней), это ЭДС минус pd, потерянный внутри ячейки:

V = E — Ir

Где :

В = pd по внешней цепи (В)

E = ЭДС ячейки (В)

I = ток через элемент (А)

r = значение внутреннего сопротивления (& Omega;)

( Ir = p.d. на внутреннем резисторе)

Примечание: В иногда называют клеммой pd , поскольку это pd на клеммах ячейки

Пример 1:

Что такое клемма p.d. для ячейки ЭДС 2В и внутреннего сопротивления 1 Ом при подключении к резистору 9 Ом?

Ответ:

Просто представьте, что внутреннее сопротивление является одним из нормальных резисторов в цепи.Нарисуйте его на принципиальной схеме рядом с ячейкой, чтобы весь ток, проходящий через ячейку, также проходил через резистор.

Чтобы найти V, клемму pd (или напряжение, доступное для внешней цепи), вычислите ток I для всей цепи:

Примечание: V _T и R _T — это напряжение и сопротивление для всей цепи, включая внешнее и внутреннее сопротивление.

Таким образом, 9 & Omega; резистор получает V = IR = 0.2 x 9 = 1,8 В

Таким образом, эта ячейка ЭДС на 2 В фактически подает 1,8 В во внешнюю цепь.

Пример 2:

Теперь поменяйте местами 9 & Omega; резистор в последнем примере для 1 & Omega; резистор.

Ответ:

Найдите V, терминал pd, используя тот же метод снова:

Теперь ячейка ЭДС 2V подает только 1V во внешнюю цепь !!! Другой 1 В теряется, из-за чего ячейка нагревается. Не очень работоспособен.

Примечание: Вам необходимо учитывать внутреннее сопротивление при принятии решения о том, подходит ли ячейка для использования в конкретной цепи. Для максимальной эффективности внешнее сопротивление должно быть намного больше внутреннего сопротивления ячейки. Однако для максимальной мощности, передаваемой во внешнюю цепь, внутреннее сопротивление должно быть равно сопротивлению внешней цепи, хотя эффективность ячейки будет только 50%.

Источники питания с низким напряжением и более высокими токами, например автомобильный аккумулятор, должны иметь низкое внутреннее сопротивление, как показано выше.Источники питания высокого напряжения, вырабатывающие тысячи вольт, должны иметь чрезвычайно высокое внутреннее сопротивление, чтобы ограничить ток, который может протекать в случае случайного короткого замыкания.

Поскольку V = E — Ir, если вы построите график зависимости pd, V от тока, I, градиент графика будет равен внутреннему сопротивлению ячейки. (отрицательный, потому что график наклоняется вниз)

Записывая значения тока и клеммы pd по мере изменения внешнего сопротивления, вы можете построить график и найти внутреннее сопротивление и ЭДС ячейки.

Если последовательно подключено более одной ячейки, необходимо сложить внутренние сопротивления ячеек.

Внутреннее сопротивление батарейного калькулятора • Электрические, радиочастотные и электронные калькуляторы • Онлайн-преобразователи единиц

Этот калькулятор определяет внутреннее сопротивление электрической батареи по падению напряжения на нагрузочном резисторе с известным сопротивлением, а также по напряжению или току холостого хода. в нагрузочном резисторе.

Пример 1: Рассчитайте внутреннее сопротивление Li-PO батареи, если ее напряжение без нагрузки равно 3.90 В, а при нагрузке 10 Ом — 3,89 В. Ниже вы найдете еще пять примеров.

Рассчитать

R _I и I от U _NL , R _L и U _L R _I U _NL , R _L и I R _I и R _L от U _NL , U 9 и 9033 _{L L и I от U NL , R I и R L R L и I от UL 903 934 9000 R UL 903 934 9000 R I и U L R L и U L от U NL , R I и I 9333 U 903 33 I из R I , R L и U L U NL и U L из R I ,} и I U _NL и R _L от R _I , U _L и I

Напряжение на батарее, без нагрузки

_NL микровольт (мкВ) милливольт (мВ) вольт (В) киловольт (кВ) мегавольт (МВ)

Внутреннее сопротивление батареи

R _I миллиом (мОм) (Ом) кОм) мегаом (МОм)

Для расчета введите любые три из пяти значений и нажмите или коснитесь кнопки Вычислить .Исключение: при вводе только трех параметров нагрузки R _L , U _L и I невозможно рассчитать параметры батареи U _NL и R _I и никаких расчетов выполняются.

Определения и формулы

Согласно теореме Гельмгольца – Тевенина любую линейную сеть с любым количеством источников напряжения (например, шесть гальванических элементов, соединенных последовательно в автомобильном аккумуляторе), можно заменить электродвижущей силой (ЭДС ). ) или эквивалентное напряжение холостого хода U _NL источник последовательно с внутренним сопротивлением R _I или импедансом Z _I .Напряжение U _NL питает внешнюю нагрузку R _L током I .

Ток, подаваемый батареей на нагрузку, будет определяться сопротивлением внешней нагрузки, и в то же время этот ток будет ограничен внутренним сопротивлением батареи. Внутреннее сопротивление складывается из сопротивления пластин батареи, ее активного материала и электролита.

Свинцово-кислотные батареи имеют очень маленькое внутреннее сопротивление (обычно 0.01 Ом) — именно поэтому они способны обеспечить большой ток, необходимый для запуска двигателя. Внутреннее сопротивление свинцово-кислотных ячеек настолько мало, потому что в каждой ячейке есть несколько отрицательных и положительных пластин, соединенных параллельно. Кроме того, расстояние между отрицательной и положительной пластинами очень мало, и, следовательно, толщина слоя электролита между ними уменьшается, что, в свою очередь, делает их внутреннее сопротивление еще меньше. Когда батарея выдает большой ток, это внутреннее сопротивление рассеивает тепло, и батарея нагревается.

Внутреннее сопротивление батареи можно рассчитать по ее напряжению холостого хода U _NL , напряжению, измеренному на нагрузке U _L , и сопротивлению нагрузки R _L . Это напряжение холостого хода эквивалентно электродвижущей силе батареи.

Ток, протекающий через нагрузочный резистор:

Падение напряжения на внутреннем сопротивлении:

Внутреннее сопротивление:

Полная формула:

В качестве альтернативы внутреннее сопротивление батареи можно рассчитать по току I _L через сопротивление нагрузки, напряжение холостого хода аккумулятора и сопротивление нагрузки.

Напряжение на нагрузочном резисторе

Падение напряжения на внутреннем сопротивлении:

Внутреннее сопротивление:

Полная формула:

Как измерить внутреннее сопротивление батареи

As Как мы объяснили выше, для определения внутреннего сопротивления нам нужны три значения:

• напряжение холостого хода батареи U _NL , напряжение, измеренное на нагрузке U _L , и сопротивление нагрузки R _L

или

• ток I _L через сопротивление нагрузки, напряжение холостого хода батареи U _NL и сопротивление нагрузки R _L .

Чтобы правильно определить внутреннее сопротивление, нужно произвести несколько измерений с разными резисторами. Кроме того, внутреннее сопротивление может варьироваться в зависимости от температуры, возраста батареи и ряда других факторов. Таким образом, ваше измерение является лишь приблизительным, и не существует такого понятия, как «истинное» внутреннее сопротивление, которое можно было бы точно измерить.

На внутреннее сопротивление батарей влияет несколько факторов, включая их емкость, химический состав, качество элементов, возраст, температуру и скорость разряда.Дополнительную информацию о батареях вы найдете в наших калькуляторах энергии и времени работы от батарей и калькуляторе LiPo батарей для дрона.

Для измерения напряжения на нагрузке, подключенной к батарее , вольтметр подключается параллельно нагрузке или клеммам батареи. Если сопротивление нагрузки относительно низкое по сравнению с внутренним сопротивлением измерителя, вы получите достаточно точное показание напряжения нагрузки.

Для измерения тока , подаваемого на нагрузку, подключенную к батарее , между нагрузкой и батареей подключается амперметр, как показано на рисунке.Если его внутреннее сопротивление относительно мало по сравнению с сопротивлением нагрузки, вы можете предположить, что ваши измерения точны.

Конечно, теоретически и даже практически (например, для угольно-цинковой батареи) ток короткого замыкания батареи измерить путем короткого замыкания батареи амперметром вполне возможно. Однако, если батарея способна выдавать значительный ток, она может перегреться или даже загореться при коротком замыкании. Литий-ионные батареи могут даже взорваться, если их клеммы закорочены.Следовательно, ток почти всегда измеряется, когда батарея подключена к разумной нагрузке.

Для измерения напряжения холостого хода аккумулятора к его клеммам без нагрузки подключается вольтметр. Это напряжение также называется напряжением холостого хода. Если внутреннее сопротивление вольтметра намного выше внутреннего сопротивления аккумулятора, можно предположить, что напряжение холостого хода измеряется относительно точно.

Также необходимо измерить сопротивление нагрузки , если вы не используете прецизионный резистор.Помните, что если нагрузочный резистор нагревается, его сопротивление увеличивается, поэтому измерение тока необходимо проводить быстро.

Теперь вы можете поместить результаты ваших измерений в наш калькулятор и получить внутреннее сопротивление вашей батареи. Конечно, в продаже имеется множество специальных измерителей внутреннего сопротивления. Кроме того, более мощные зарядные устройства могут измерять внутреннее сопротивление батареи.

Чтобы получить полную картину, мы можем отметить, что каждая батарея имеет спектр внутренних сопротивлений или, скорее, импедансов, и для их измерения часто используется более сложная схема, которая питается от источника переменного тока с частотой изменяется от очень низкого до нескольких килогерц.Внутреннее сопротивление обычно характеризуется графиками, показывающими его зависимость от различных факторов.

Примеры расчетов

Пример 2. Батарея с ЭДС = 14,5 В выдает 25 Вт мощности на внешний нагрузочный резистор. Напряжение на выводе аккумулятора составляет 11,9 В. Определите внутреннее сопротивление аккумулятора. Намек. Воспользуйтесь нашим калькулятором закона Ома, чтобы определить ток через нагрузочный резистор. Затем используйте этот калькулятор для определения внутреннего сопротивления.

Пример 3. Лампа накаливания на 4 Ом подключена к батарее с внутренним сопротивлением 0,15 Ом. Вольтметр, подключенный к клеммам аккумулятора, показывает 11,5 В. Какая ЭДС аккумулятора?

Пример 4. Две галогенные лампы головного света мощностью 55 Вт подключены параллельно к клеммам аккумуляторной батареи грузового автомобиля, имеющей внутреннее сопротивление 0,02 Ом. Напряжение на выводах аккумулятора 23,6 В. Какая ЭДС ℰ аккумулятора? Подсказка: используйте наш калькулятор мощности постоянного тока, чтобы определить сопротивление горячей лампы.Затем используйте наш калькулятор параллельного сопротивления, чтобы определить сопротивление двух параллельно соединенных ламп. Затем используйте этот калькулятор для определения ЭДС аккумулятора.

Пример 5. Определите ток короткого замыкания автомобильного аккумулятора на 12 В с ЭДС = 13,5 В и внутренним сопротивлением 0,04 Ом. Подсказка: 12 В — это номинальное напряжение аккумулятора, и это число не используется при решении этой проблемы.

Пример 6. Батарея с ЭДС ℰ = 1.5 В замкнут накоротко с помощью неидеального амперметра с внутренним сопротивлением 0,02 Ом, которое показывает 2,7 А. Определите его внутреннее сопротивление и мощность, рассеиваемую внутри батареи. Подсказка: сначала используйте этот калькулятор для определения внутреннего сопротивления батареи, а затем воспользуйтесь нашим калькулятором мощности постоянного тока, чтобы определить мощность, рассеиваемую в батарее.

Пример 7. Контроллер запуска модели, который используется для запуска ракетного двигателя путем нагрева нихромовой проволоки воспламенителя, питается от четырех AA 1.Батареи 5 В соединены последовательно. Каждая батарея имеет внутреннее сопротивление 200 мОм. Сопротивление двух разных воспламенителей ракетных двигателей составляет 0,7 и 3 Ом. Определите ток, подаваемый на воспламенитель 0,7 Ом и воспламенитель 3 Ом. Подсказка: напряжение четырех последовательно соединенных батарей составляет 1,5 × 4 = 6 В, а их общее внутреннее сопротивление составляет 200 × 4 = 0,8 Ом.

Эту статью написал Анатолий Золотков

Внутреннее сопротивление — когда оно незначительно, а когда его нет

Батарейки потеют, если заставлять их работать слишком много

Аккумулятор преобразует химическую энергию в электрическую.Это преобразование вызвано химическими реакциями внутри батареи. Чем быстрее батарея вырабатывает энергию, тем быстрее должны происходить химические реакции.

Если вы заставляете аккумулятор работать интенсивно, то часть химической энергии преобразуется в электрическую, а часть — в тепловую. Тепловая энергия нагревает аккумулятор.

Чем тяжелее работает аккумулятор, тем больше химической энергии преобразуется в тепловую и тем сильнее нагревается аккумулятор.

Анимация, показывающая различные способы короткого замыкания всей цепи, подключив одну клемму батареи напрямую к другой.

Как заставить аккумулятор работать

Если вы заставляете батарею работать с одним компонентом, который очень быстро потребляет энергию, например очень яркой лампочкой, или с множеством компонентов, включенных параллельно, тогда батарея должна работать очень тяжело, потому что она должна очень быстро подавать энергию.

Помните, что батареи являются (или стараются быть) поставщиками постоянного напряжения. Сила тока зависит от выполняемой ими работы. Когда они много работают, они дают большой ток. Но, как мы увидим, если они выдают очень большой ток, то напряжение упадет.

Меньше электроэнергии означает меньшее напряжение

Вы можете думать о напряжении как об энергии, приходящейся на заряд.

Если доступно меньше электроэнергии (потому что часть химической энергии превращается в тепло в батарее), то напряжение на клеммах батареи упадет. Это означает, что напряжение в цепи также падает.

Практический результат состоит в том, что если вы сделаете аккумуляторную батарею большим током к

• заставляет его запускать что-то, что требует большого тока, например очень яркую (с низким сопротивлением) лампочку
• , позволяющий запускать множество операций одновременно (подключены параллельно)
• закорачивает аккумулятор (соединив один вывод с другим проводом)

напряжение упадет.

Если электрическая энергия преобразуется в тепловую, это должен быть резистор

Батареи не имеют внутри резистора, который можно вынуть и посмотреть. Но у них действительно есть источники сопротивления, например продукты химических реакций и металлические части со всеми их соединениями.

Таким образом, батареи часто моделируют как идеальный источник питания (напряжение которого никогда не падает), включенный последовательно с воображаемым резистором.

Очевидно, батарейки используются для работы чего-то вроде лампочки.Сопротивление цепи, в которой они работают, называется сопротивлением нагрузки R _L .

Внутреннее сопротивление обычно обозначается символом r. Это не значит, что он всегда маленький. Сопротивление батарейки для миниатюрных часов может составлять 100 Ом или около того. Батарея фонаря имеет внутреннее сопротивление около 0,1 Ом, а автомобильный аккумулятор — около 0,001 Ом.

Наш воображаемый внутренний резистор подчиняется закону Ома, как и любой другой резистор. Единственное отличие в том, что он спрятан внутри аккумулятора.

Почему важно внутреннее сопротивление?

Автомобильный аккумулятор на 12 В имеет такое же напряжение, как и восемь аккумуляторов 1,5 В. AA. Могли бы вы использовать эти батареи, чтобы завести машину?

Ответ — решительное нет. Есть два взгляда на это.

1. Батарейки типа AA не могут обеспечивать энергию очень быстро, в то время как вашему стартеру требуется энергия очень быстро.
2. Внутреннее сопротивление ваших батареек AA слишком велико, поэтому напряжение падает с 12 В до почти 0 В, как только вы пытаетесь запустить двигатель.

Если вы знаете, что вам нужно очень быстро подавать энергию, вам нужно очень низкое внутреннее сопротивление. Как и толстый кусок провода, большая батарея имеет меньшее сопротивление. Поэтому аккумуляторные батареи большой мощности должны быть большими, как автомобильные.

Если вам не нужна энергия очень быстро, другими словами, ваше устройство потребляет только крошечный ток, как цифровые часы, тогда внутреннее сопротивление менее важно, поэтому вы можете позволить себе уменьшить размер батареи. Это полезно, если вы хотите поместить его в часы!

Что такое «незначительное внутреннее сопротивление»?

Это выражение часто встречается в экзаменационных вопросах.

Это не означает, что сопротивление должно быть маленьким. как таковое . Это просто означает, что батарея не работает достаточно усердно, чтобы ее напряжение сильно упало.

Электродвижущая сила — это напряжение аккумулятора, когда на нем ничего не работает

Максимальное напряжение, которое вы можете получить от батареи, называется электродвижущей силой или ЭДС. Это называется так по историческим причинам, но в этом нет ничего особенного. Это просто напряжение. Обычно ему присваивается символ ε.

Если внутренним сопротивлением нельзя пренебречь и аккумулятор работает, например, от лампочки, то фактически измеренное напряжение на выводах аккумулятора (а также на лампе) будет ниже, чем ЭДС. Мы называем это нижнее напряжение напряжением нагрузки, V _L .

Определение внутреннего сопротивления и ЭДС. батареи

Вы можете измерить ЭДС. батареи, просто измерив напряжение на клеммах, когда она ни к чему не подключена.Это называется измерением напряжения в «разомкнутой цепи».

Вы не можете просто измерить внутреннее сопротивление напрямую, потому что вы не можете попасть внутрь батареи. Итак, вам нужно провести эксперимент, в котором вы изменяете ток, потребляемый от батареи (изменяя сопротивление нагрузки) и измеряя p.d. через терминалы.

Закон Кирхгофа по напряжению гласит, что если сложить напряжения на всех компонентах в последовательной цепи, они должны точно равняться напряжению батареи.

e.м.ф. = напряжение на внутреннем сопротивлении + напряжение на нагрузке (например, лампочке)

В символах это уравнение

ε = V _{внутренний} + V _L

Мы знаем, что V = IR, или используя соответствующие термины для внутреннего сопротивления V _{внутреннее} = Ir, поэтому

ε = Ir + V _L

Мы можем изменить это уравнение, чтобы получить

В _L = -rI + ε

Если вы настроили схему с переменным резистором для нагрузки, вы можете изменить ток I, потребляемый от батареи, и измерить напряжение на выводах, V _L .

График V _L относительно I дает прямую линию с величиной градиента, равной внутреннему сопротивлению r. Э.д.с. это точка пересечения на оси напряжения, другими словами, напряжение при нулевом токе.

назад к Уроку 7: Сопротивление и закон Ома

Внутреннее сопротивление | Аккумуляторы и другие источники питания

Внутреннее сопротивление | Аккумуляторы и другие источники питания

В электрических цепях, которые мы рассмотрели до сих пор, мы рассматривали источник напряжения, питающий цепь, как идеальный источник напряжения.то есть:

• Мы предположили, что напряжение, подаваемое в цепь, остается постоянным, независимо от того, какой ток подается. поставляется.
• Мы также предположили, что энергия преобразуется в тепло только за счет сопротивления во внешней цепи.

На практике это не так, поскольку:

1. Напряжение на клеммах батареи уменьшается по мере того, как ток, подаваемый в цепь, увеличивается.
   Это то же самое для всех реальных источников напряжения. (Однако разработчики блоков питания действительно производят стабилизированные блоки питания, в которых обратная связь схемы используются для поддержания относительно постоянного выходного напряжения).
2. Все блоки питания нагреваются во время использования, что свидетельствует о том, что часть выделяемой ими энергии фактически расходуется. преобразуется в тепло внутри самого блока питания!

Это показано на анимации ниже.

Это изменение напряжения питания потенциально трудно объяснить, особенно если учесть, что Причины отклонения будут зависеть от типа используемого источника питания.
Например:

• Для аккумулятора: напряжение падает из-за скорости химических реакций, передающих заряд на клеммы аккумулятора, не может соответствовать скорости, с которой заряд покидает клеммы, чтобы течь по цепи.
• Для генератора: ток создает более сильные магнитные поля внутри генератора, которые замедляют работу генератора и уменьшают напряжение питания.

К счастью, мы можем избежать этих деталей, и, независимо от фактического характера источника питания, мы можем представить его в виде модель блока питания, полностью состоящая из простых электрических компонентов. Один из способов сделать это — представить власть как идеальный источник напряжения (например,м.д.) последовательно с внутренним сопротивлением. Когда эта модель источника питания применяется к внешней цепи, ток цепи также течет через внутреннее сопротивление. Это вызывает внутреннее падение напряжения внутри источника питания, что, следовательно, снижает напряжение на клеммах источника питания. Мощность, рассеиваемая внутренним сопротивлением, представляет собой тепло, выделяемое в источнике питания. Это показано на анимации ниже.

Напряжение на клеммах (В) равно эл.м.ф. напряжение (E) за вычетом внутреннего падения напряжения (Ir).
(используя закон Ома: внутреннее падение напряжения = ток (I) x внутреннее сопротивление (r)).

Чтобы смоделировать любой реальный источник питания, нам просто нужно определить правильные значения E и r для использования.

Когда источник питания не подключен к цепи, ток не протекает, поэтому:

• V = E — 0 x r.
• В = E.
• то есть e.Напряжение m.f равно напряжению на клеммах холостого хода источника питания.

Внутреннее сопротивление можно определить, подключив цепь с известным сопротивлением и измерив протекающий ток.

• I = E / (R + r).
• , следовательно, r = (E / I) — R.

Мощность, подаваемая э.д.с., определяется как P = EI, а мощность, рассеиваемая в источнике питания, определяется как P = I ² r.
Энергия, обеспечиваемая e.m.f. определяется как W = EIt, а энергия, рассеиваемая в источнике питания, определяется как W = I ² rt.

.