Емкость конденсатора формула через напряжение и заряд
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
где – радиусы обкладок конденсатора.
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
| Задание | Каковы заряды на обкладках конденсаторов, если они имеют емкости Ф и Ф, соединены последовательно и присоединены к батарее с ЭДС равной В (рис.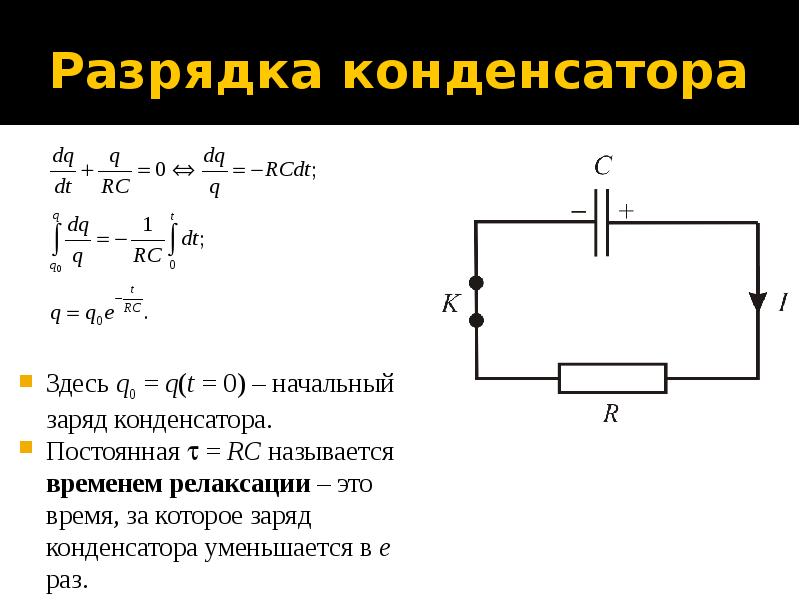 3)? Чему равен суммарный заряд соединения? 3)? Чему равен суммарный заряд соединения? |
Заряд на первом конденсаторе при этом равен:
Заряд на обкладках второго конденсатора:
Суммарный заряд системы можно найти как:
Тогда суммарный заряд равен:
| Задание | Емкость пускового устройства электрического двигателя равна C. Энергии имеющейся в конденсаторе достаточно для того чтобы поднять груз массы m на высоту h. Чему равен заряд конденсатора? |
| Решение | При поднятии груза на высоту h происходит переход энергии поля конденсатора () в потенциальную энергию тела (), поднятого над Землей, поэтому запишем: |
Энергию найдем как:
Энергию электрического поля конденсатора будет удобнее выразить:
Подставим в выражение (2.1) правые части (2.2) и (2.3), имеем:
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
где – радиусы обкладок конденсатора.
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
| Задание | Каковы заряды на обкладках конденсаторов, если они имеют емкости Ф и Ф, соединены последовательно и присоединены к батарее с ЭДС равной В (рис.3)? Чему равен суммарный заряд соединения? |
Заряд на первом конденсаторе при этом равен:
Заряд на обкладках второго конденсатора:
Суммарный заряд системы можно найти как:
Тогда суммарный заряд равен:
| Задание | Емкость пускового устройства электрического двигателя равна C. Энергии имеющейся в конденсаторе достаточно для того чтобы поднять груз массы m на высоту h. Чему равен заряд конденсатора? |
| Решение | При поднятии груза на высоту h происходит переход энергии поля конденсатора () в потенциальную энергию тела (), поднятого над Землей, поэтому запишем: |
Энергию найдем как:
Энергию электрического поля конденсатора будет удобнее выразить:
Подставим в выражение (2. 1) правые части (2.2) и (2.3), имеем:
1) правые части (2.2) и (2.3), имеем:
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.
Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU 2 /2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции.
Формула емкости конденсатора через напряжение. Зарядка конденсатора от источника постоянной эдс
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов (рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
ru.solverbook.com
Формула емкости конденсатора, С
Если q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками, то величина C, равная:
называется емкостью конденсатора.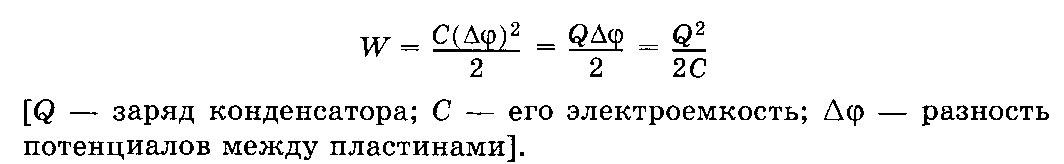 Это постоянная величина, которая зависит то размеров и устройства конденсатора.
Это постоянная величина, которая зависит то размеров и устройства конденсатора.
Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():
где – диэлектрическая проницаемость диэлектрика.
За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).
Формула электрической емкости плоского конденсатора
Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:
Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:
Формула электрической емкости цилиндрического конденсатора
Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:
Формула электрической емкости сферического конденсатора
Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:
Емкость такого конденсатора находят как:
где – радиусы обкладок конденсатора.
Примеры решения задач по теме «Емкость конденсатора»
ru.solverbook.com
Ёмкость конденсатора — Все формулы
Электрическая ёмкость — характеристика проводника (конденсатора), мера его способности накапливать электрический заряд.
Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические.
Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ1 — φ2) между его обкладками
Для получения больших ёмкостей конденсаторы соединяют параллельно. При этом напряжение между обкладками всех конденсаторов одинаково. Общая ёмкость батареи параллельно соединённых конденсаторов равна сумме ёмкостей всех конденсаторов, входящих в батарею.
Конденсаторы можно классифицировать по следующим признакам и свойствам:
1) по назначению — конденсаторы постоянной и переменной емкости;
2) по форме обкладок различают конденсаторы плоские, сферические, цилиндрические и др.;
3) по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и т.д.
Так же есть:
Энергия конденсатора:
Ёмкость цилиндрического конденсатора:
Ёмкость плоского конденсатора:
Емкость сферического конденсатора:
В формуле мы использовали:
Электрическая ёмкость (ёмкость конденсатора)
Потенциал проводника (Напряжение)
Потенциал
Относительная диэлектрическая проницаемость
Электрическая постоянная
Площадь одной обкладки
Расстояние между обкладками
xn--b1agsdjmeuf9e.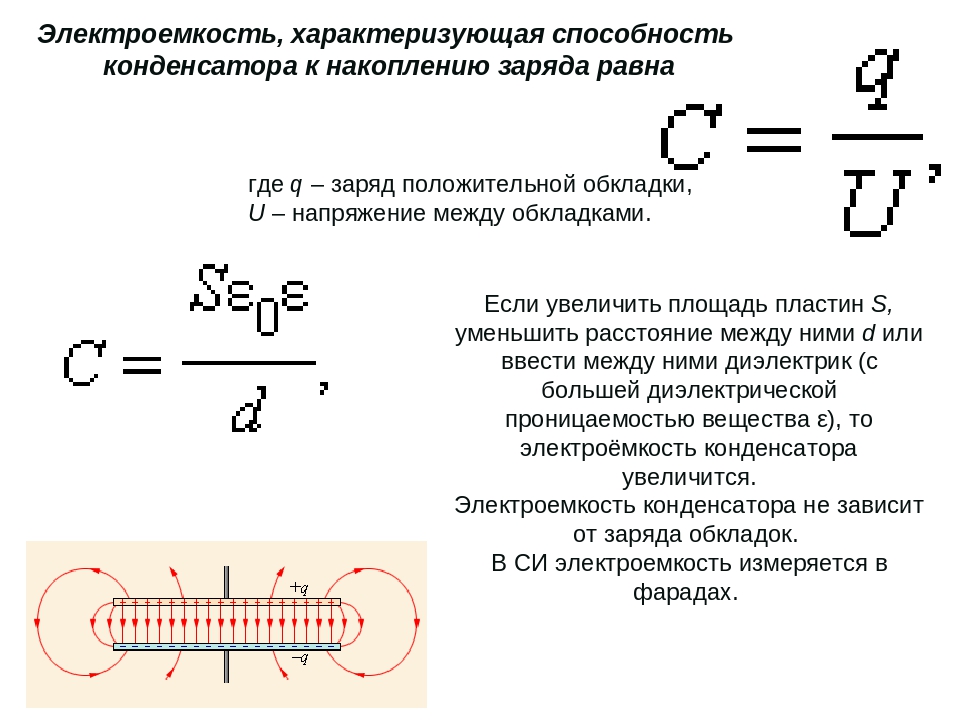 xn--p1ai
xn--p1ai
Заряд конденсатора, теория и примеры задач
Определение и заряд конденсатора
Возможность конденсатора накопить электрический заряд зависит от главной характеристики конденсатора – емкости (C).
По своему назначению конденсатор можно уподобить батарейке. Однако существует принципиальное отличие в принципах работы этих элементов. Отличаются, также максимальные емкости и скорости зарядки и разряда конденсатора и батарейки.
Если к конденсатору присоединить источник напряжения (рис.1), то на одной из пластин конденсатора станут накапливаться отрицательные заряды (электроны), на другой положительные частицы (положительные ионы). Между обкладками конденсатора находится диэлектрик, вследствие этого, заряды не могут перебраться на противоположную пластину. Однако заметим, что электроны двигаются от источника тока до пластины конденсатора.
При первоначальном соединении конденсатора и источника тока на обкладках конденсатора много свободного места. Это означает, что сопротивление току этот момент времени минимально, сам ток максимален. В ходе зарядки конденсатора сила тока в цепи постепенно падает, до того момента пока не закончится свободное место на обкладках. При полной зарядке конденсатора ток в цепи прекратится.
Время, которое затрачивается на зарядку конденсатора от нулевого заряда (максимального тока) до полностью заряженного конденсатора (минимальная или нулевая сила тока) называют переходным периодом заряда конденсатора. На практике процесс зарядки конденсатора считают законченным, если сила тока уменьшилась до 1% от начальной величины.
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
Примеры решения задач
ru.solverbook.com
Формула электроемкости конденсатора
Обкладки должны иметь такую форму и быть расположены так относительно друг друга, что поле, которое создается данной системой, было максимально сосредоточено в ограниченной области пространства, между обкладками.
Назначение конденсатора в том, чтобы накапливать и отдавать в электрической цепи заряд.
Основной характеристикой конденсатора является электрическая емкость (C). Электрическая емкость конденсатора – это взаимная емкость принадлежащих ему обкладок:
q – величина заряда на обкладке; – разность потенциалов между обкладками.
Электрическая ёмкость конденсатора зависит от диэлектрической проницаемости диэлектрика, который заполняет пространство между его обкладками. Если пространство между обкладками одного конденсатора заполнено диэлектриком с проницаемостью равной , а у второго конденсатора воздух между пластинами, то емкость конденсатора с диэлектриком (C) в раз больше, чем емкость воздушного конденсатора ():
Формула электроемкости основных типов конденсаторов
При расчете электроемкости плоского конденсатора нарушением однородности поля около краёв обкладок обычно пренебрегают. Это становится возможным, если расстояние между пластинами существенно меньше, чем линейные размеры обкладок. В таком случае электрическую емкость плоского конденсатора вычисляют при помощи формулы:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Если плоский конденсатор между обкладками имеет N слоев диэлектрика, при этом толщина каждого слоя равна , а диэлектрическая проницаемость , то его электрическую емкость рассчитывают при помощи формулы:
Цилиндрический конденсатор составляют две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполнено диэлектриком. При этом емкость цилиндрического конденсатора находят как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
У сферического конденсатора обкладками служат две концентрические сферические проводящие поверхности, пространство обкладками заполняет диэлектрик. Емкость сферического конденсатора вычисляют как:
где – радиусы обкладок конденсатора. Если , то можно считать, что , тогда, мы имеем:
Если , то можно считать, что , тогда, мы имеем:
так как – площадь поверхности сферы, и если обозначить , то получим формулу для емкости плоского конденсатора (3). Если расстояние между обкладками сферического и цилиндрического конденсаторов малы (в сравнении с их радиусами), то в приближенных расчетах используют формулу емкости для плоского конденсатора.
Электрическую емкость для линии из двух проводов находят как:
где d – расстояние между осями проводов; R – радиус проводов; l – длина линии.
Формулы для вычисления электрической емкости соединений конденсаторов
Если конденсаторы соединены параллельно, то суммарная емкость батареи (C) находится как сумма емкостей отдельных конденсаторов ():
При последовательном соединении конденсаторов емкость батареи вычисляют как:
Если последовательно соединены N конденсаторов, с емкостями то емкость батареи найдем как:
Сопротивление конденсатора
Если конденсатор включен в цепь с постоянного тока, то сопротивление конденсатора можно считать бесконечно большим.
При включении конденсатора в цепь переменного тока, его сопротивление носит название емкостного, и вычисляют его с помощью формулы:
где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.
Энергия поля конденсатора
Электрическое поле локализованное между пластинами конденсатора обладает энергией, которую можно вычислить при помощи формулы:
где –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; – разность потенциалов между обкладками конденсатора.
Энергия поля плоского конденсатора:
Примеры решения задач по теме «Электроемкость конденсатора»
ru.solverbook.com
Как найти заряд конденсатора 🚩 как определить величину заряда 🚩 Естественные науки
В обычном (без плагинов и модов) варианте Minecraft такого понятия, как конденсатор, не существует.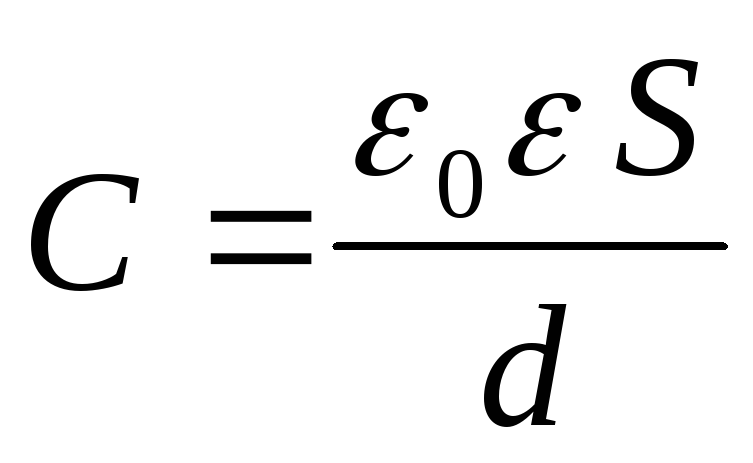 Вернее, устройство, выполняющее его функции, имеется, но название у него совершенно другое — компаратор. Некоторая путаница в этом плане произошла еще в период разработки такого прибора. Сперва — в ноябре 2012-го — представители Mojang (компании-создателя игры) объявили о скором появлении в геймплее конденсатора. Однако через месяц они высказались уже о том, что как такового этого прибора не будет, а вместо него в игре будет компаратор.
Вернее, устройство, выполняющее его функции, имеется, но название у него совершенно другое — компаратор. Некоторая путаница в этом плане произошла еще в период разработки такого прибора. Сперва — в ноябре 2012-го — представители Mojang (компании-создателя игры) объявили о скором появлении в геймплее конденсатора. Однако через месяц они высказались уже о том, что как такового этого прибора не будет, а вместо него в игре будет компаратор.
Подобное устройство существует для проверки заполненности расположенных позади него контейнеров. Таковыми могут быть сундуки (в том числе в виде ловушек), варочные стойки, раздатчики, выбрасыватели, печи, загрузочные воронки и т.п.
Помимо этого, его часто используют для сравнения двух сигналов редстоуна между собою — он выдает результат в соответствии с тем, как было запрограммировано в данной цепи, и с тем, какой режим выбран для самого механизма. В частности, компаратор может разрешить зажигание факела, если первый сигнал больше либо равен другому.
Также порой конденсатор-компаратор устанавливают рядом с проигрывателем, подключая его входом к последнему. Когда в звуковоспроизводящем устройстве проигрывается какая-либо пластинка, вышеупомянутый прибор будет выдавать сигнал, равный по силе порядковому номеру диска.
Скрафтить такой компаратор несложно, если имеется достаточно трудно добываемый ресурс — адский кварц. Его надо поставить в центральный слот верстака, над ним и по бокам от него установить три красных факела, а в нижнем ряду — такое же количество каменных блоков.
В большом количестве модов попадаются конденсаторы, имеющие самое разное предназначение. К примеру, в Galacticraft, где у геймеров есть возможность слетать на многие планеты для ознакомления с тамошними реалиями, появляется рецепт крафта кислородного конденсатора. Он служит для создания механизмов вроде коллектора и накопителя газа для дыхания, а также рамки воздушного шлюза. Для его изготовления четыре стальных пластины размещаются по углам верстака, в центре — оловянная канистра, а под нею — воздуховод. Остальные три ячейки занимают пластины из олова.
Остальные три ячейки занимают пластины из олова.
В JurassiCraft существует конденсатор потока — некий телепорт, позволяющий переместиться в удивительный игровой мир, кишащий динозаврами. Для создания такого прибора нужно поместить в два крайних вертикальных ряда шесть железных слитков, а в средний — два алмаза и между ними единицу пыли редстоуна. Дабы устройство заработало, надо поставить его на свинью либо вагонетку, а затем щелкнуть по нему правой клавишей мыши, быстро запрыгнув туда. При этом требуется поддержание высокой скорости устройства.
С модом Industrial Craft2 у игрока появляется возможность создавать как минимум два вида тепловых конденсаторов — красный и лазуритовый. Они служат исключительно для охлаждения ядерного реактора и для накопления его энергии и хороши для циклических сооружений такого типа. Остужаются они сами, соответственно, красной пылью или лазуритом.
Красный теплоконденсатор делается из семи единиц пыли редстоуна — их надо установить в виде буквы П и расставить под ними теплоотвод и теплообменник. Крафтинг же лазуритового устройства чуть посложнее. Для его создания четыре единицы пыли редстоуна расставляются по углам станка, в центр пойдет блок лазурита, по бокам от него — два красных тепловых конденсатора, сверху — теплоотвод реактора, а снизу — его же теплообменник.
В ThaumCraft, где сделан акцент на настоящем чародействе, конденсаторы тоже используются. Например, один из них — кристаллический — существует для аккумуляции и отдачи магии. Причем, что интересно, создавать его и многие другие вещи разрешено лишь после изучения особого элемента геймплея — исследования, проводимого за специальным столом и с определенными приборами.
Делается такой конденсатор из восьми тусклых осколков, в центр которых на верстаке помещается мистический деревянный блок. К сожалению, подобный прибор — равно как и его составляющие — просуществовал лишь до ThaumCraft 3, а в четвертой версии мода был упразднен.
www.kakprosto.ru
Соединение конденсаторов: формулы
Содержание:- Последовательное соединение
- Онлайн калькулятор
- Смешанное соединение
- Параллельное соединение
- Видео
В электронных и радиотехнических схемах широкое распространение получило параллельное и последовательное соединение конденсаторов. В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.
В первом случае соединение осуществляется без каких-либо общих узлов, а во втором варианте все элементы объединяются в два узла и не связаны с другими узлами, если это заранее не предусмотрено схемой.
Последовательное соединение
При последовательном соединении два и более конденсаторов соединяются в общую цепь таким образом, что каждый предыдущий конденсатор соединяется с последующим лишь в одной общей точке. Ток (i), осуществляющий зарядку последовательной цепи конденсаторов будет иметь одинаковое значение для каждого элемента, поскольку он проходит только по единственно возможному пути. Это положение подтверждается формулой: i = ic1 = ic2 = ic3 = ic4.
В связи с одинаковым значением тока, протекающего через конденсаторы с последовательным соединением, величина заряда, накопленного каждым из них, будет одинаковой, независимо от емкости. Такое становится возможным, поскольку заряд, приходящий с обкладки предыдущего конденсатора, накапливается на обкладке последующего элемента цепи. Поэтому величина заряда у последовательно соединенных конденсаторов будет выглядеть следующим образом: Qобщ= Q1 = Q2 = Q3.
Если рассмотреть три конденсатора С1, С2 и С3, соединенные в последовательную цепь, то выясняется, что средний конденсатор С2 при постоянном токе оказывается электрически изолированным от общей цепи. В конечном итоге величина эффективной площади обкладок будет уменьшена до площади обкладок конденсатора с самыми минимальными размерами. Полное заполнение обкладок электрическим зарядом, делает невозможным дальнейшее прохождение по нему тока. В результате, движение тока прекращается во всей цепи, соответственно прекращается и зарядка всех остальных конденсаторов.
Общее расстояние между обкладками при последовательном соединении представляет собой сумму расстояний между обкладками каждого элемента. В результате соединения в последовательную цепь, формируется единый большой конденсатор, площадь обкладок которого соответствует обкладкам элемента с минимальной емкостью. Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.
Расстояние между обкладками оказывается равным сумме всех расстояний, имеющихся в цепи.
Падение напряжения на каждый конденсатор будет разным, в зависимости от емкости. Данное положение определяется формулой: С = Q/V, в которой емкость обратно пропорциональна напряжению. Таким образом, с уменьшением емкости конденсатора на него падает более высокое напряжение. Суммарная емкость всех конденсаторов вычисляется по формуле: 1/Cобщ = 1/C1 + 1/C2 + 1/C3.
Главная особенность такой схемы заключается в прохождении электрической энергии только в одном направлении. Поэтому в каждом конденсаторе значение тока будет одинаковым. Каждый накопитель в последовательной цепи накапливает равное количество энергии, независимо от емкости. То есть емкость может воспроизводиться за счет энергии, присутствующей в соседнем накопителе.
Онлайн калькулятор, для расчета емкости конденсаторов соединенных последовательно в электрической цепи.
Смешанное соединение
Параллельное соединение конденсаторов
Параллельным считается такое соединение, при котором конденсаторы соединяются между собой двумя контактами. Таким образом в одной точке может соединяться сразу несколько элементов.
Данный вид соединения позволяет сформировать единый конденсатор с большими размерами, площадь обкладок которого будет равна сумме площадей обкладок каждого, отдельно взятого конденсатора. В связи с тем, что емкость конденсаторов находится в прямой пропорциональной зависимости с площадью обкладок, общая емкость составить суммарное количество всех емкостей конденсаторов, соединенных параллельно. То есть, Собщ = С1 + С2 + С3.
Поскольку разность потенциалов возникает лишь в двух точках, то на все конденсаторы, соединенные параллельно, будет падать одинаковое напряжение. Сила тока в каждом из них будет отличаться, в зависимости от емкости и значения напряжения. Таким образом, последовательное и параллельное соединение, применяемое в различных схемах, позволяет выполнять регулировку различных параметров на тех или иных участках. За счет этого получаются необходимые результаты работы всей системы в целом.
За счет этого получаются необходимые результаты работы всей системы в целом.
electric-220.ru
Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.
Расчёт конденсаторов
Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:
- C – ёмкость,
- q – заряд одной из обкладок элемента,
- U – разность потенциалов между обкладками.
В электротехнике вместо понятия «разность потенциалов между обкладками» используется «напряжение на конденсаторе».
Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:
С=Co*ε, где:
- С – реальная ёмкость,
- Со – идеальная, при условии, что между пластинами вакуум или воздух,
- ε – диэлектрическая проницаемость материала между ними.
Например, если в качестве диэлектрика используется слюда, «ε» которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.
Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).
Расчет плоской конструкции
- ε – диэлектрическая проницаемость изолирующего материала,
- d – расстояние между пластинами.
Расчет конструкции цилиндрической формы
Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.
Вычисляются параметры такого устройства по формуле:
C=(2π*l*R*ε)/d, где:
- l – длина устройства,
- R – радиус цилиндра,
- ε – диэлектрическая проницаемость изолятора,
- d – его толщина.
Расчёт сферической конструкции
Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:
C=(4π*l*R1*R2*ε)/(R2-R1), где:
- R1 – радиус внутренней сферы,
- R2 – радиус внешней сферы,
- ε – диэлектрическая проницаемость.
Ёмкость одиночного проводника
Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников. Параметры заряженного элемента рассчитывается по формуле:
- Q – заряд,
- φ – потенциал проводника.
Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.
Способы соединения элементов
Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.
Параллельное соединение
Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора. При этом вторые обкладки присоединяются к другой клемме.
При таком соединении напряжение на контактах всех элементов будет одинаковым. Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:
где C1-Cn – параметры деталей, участвующих в параллельном соединении.
Важно! Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.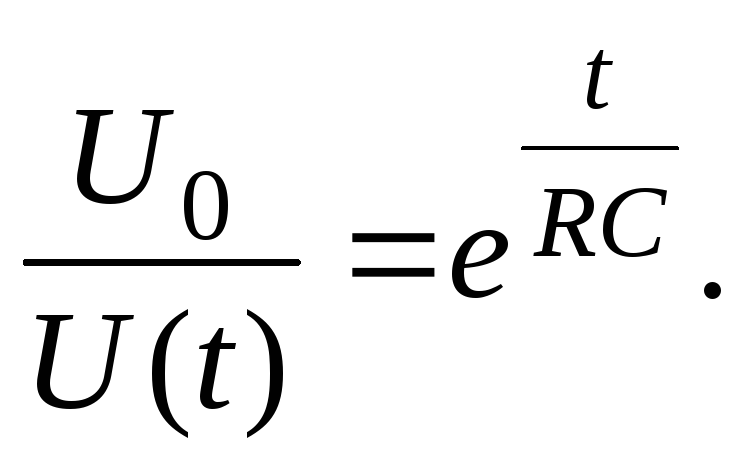
Последовательное соединение
Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.
При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов. Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.
Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.
Рассчитываются эти параметры следующим образом:
- Допустимое напряжение:
Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;
- Общая ёмкость:
1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.
Интересно. Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).
Смешанное соединение
Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:
- определяются группы элементов, соединённые параллельно;
- для каждой группы в отдельности рассчитывается эквивалентные значения;
- рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
- получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.
Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.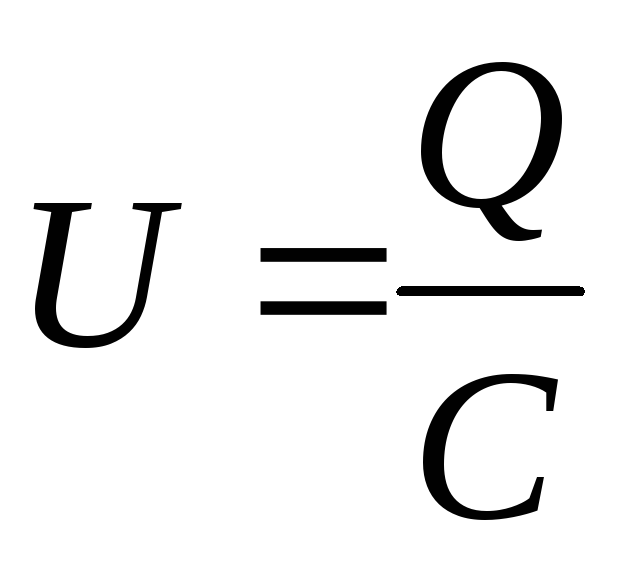
Видео
Содержание:Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица — фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q — заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов используется формула:
в которой ε 0 = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε — является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S — означает площадь обкладки, а d — зазор между обкладками.
Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как . После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде:W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: W эл = CU 2 /2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: U c = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома I зар = Е/R i , поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора — способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: I ут = U/R d , где I ут, — это ток утечки, U — напряжение, прилагаемое к конденсатору, а R d — сопротивление изоляции.
§ 6. Заряд и разряд конденсатора
Чтобы зарядить конденсатор, надо, чтобы свободные электроны перешли из одной обкладки на другую. Переход электронов с одной обкладки конденсатора на другую происходит под действием напряжения источника по проводам, соединяющим этот источник с обкладками конденсатора.
В момент включения конденсатора зарядов на его обкладках нет и напряжение на нем равно нулю μ с =0. Поэтому зарядный ток определяется внутренним сопротивлением источника r в и имеет наибольшую величину:
I З max =E/ r в.
По мере накопления зарядов на обкладках конденсатора напряжение на нем увеличивается и падение напряжения на внутреннем сопротивлении источника будет равно разности ЭДС источника и напряжения на конденсаторе (Е- μ с). следовательно, зарядный ток
i з =(Е- μ с)/ r в.
Таким образом, с увеличением напряжения на конденсаторе ток заряда снизится и при μ с =Е становится равным нулю. Процесс изменения напряжения на конденсаторе и тока заряда во времени изображен на рис. 1. В самом начале заряда напряжение на конденсаторе резко возрастает, так как зарядный ток имеет наибольшее значение и накопление зарядов на обкладках конденсатора происходит интенсивно. По мере повышения напряжения на конденсаторе зарядный ток уменьшается и накопление зарядов на обкладках замедляется. Продолжительность заряда конденсатора зависит от его емкости и сопротивления цепи, увеличение которых приводит к возрастанию продолжительности заряда. С увеличением емкости конденсатора, возрастает количество зарядов, накапливаемых на его пластинах, а если увеличить сопротивление цепи уменьшится и зарядный ток, а это замедляет процесс накопления зарядов на этих обкладках.
Если обкладки заряженного конденсатора подключить к какому-либо сопротивлению R , то за счет напряжения на конденсаторе будет протекать разрядный ток конденсатора. При разряде конденсатора электронысодной пластины (при их избытке) будут переходить на другую (при их недостатке) и будет продолжается до тех пор, пока потенциалы обкладок не выравняются, т. е. напряжение на конденсаторе станет равным нулю. Изменение напряжения в процессе разряда конденсатора изображено на рис. 2. Ток разряда конденсатора пропорционален напряжению на конденсаторе (i р =μ с /R ), и его изменение во времени подобно изменению напряжения.
В начальный момент разряда напряжение на конденсаторе наибольшее (μ с =Е) и разрядный ток максимальный (I р max =E /R ), так что разряд происходит быстро. При понижении напряжения, ток разряда снижается и процесс перехода зарядов с одной обкладки на другую затормаживается.
Время процесса разряда конденсатора зависит от сопротивления цепи и емкости конденсатора, причем возрастание как сопротивления, так и емкости увеличивает продолжительность разряда. С увеличением сопротивления разрядный ток снижается, замедляется процесс переноски зарядов с одной на другую обкладок; с увеличением емкости конденсатора повышается заряд на обкладках.
Таким образом, в цепи, содержащей конденсатор, ток проходит только в процессе его заряда и разряда, т. е. когда напряжение на обкладках претерпевает изменение во времени. При постоянстве напряжения ток через конденсатор не проходит, т. е. конденсатор не пропускает постоянный ток, так как между его обкладками помещен диэлектрик и в результате этого цепь разомкнута.
При зарядке конденсатора, последний способен накапливать электрическую энергию, потребляя ее от энергоисточника. Накопленная энергия сохраняется определенное время. При разряде конденсатора эта энергия переходит к разрядному резистору, нагревая его, т. е. энергию электрического поля превращается в тепловую. Чем выше емкость конденсатора и напряжение на его обкладках, тем будет больше энергии, запасенной на нем. Энергия электрического поля конденсатора определяется следующим выражением
W=CU 2 /2.
Если конденсатор емкостью 100 мкФ заряжен до напряжения 200 В, то энергия, запасенная в электрическом поле конденсатора, W =100· 10 -6 · 200 2 /2=2 Дж.
Вам понадобится
- — знание емкости или геометрических и физических параметров конденсатора;
- — знание энергии или заряда на конденсаторе.-12 Ф/м), ε — относительная диэлектрическая проницаемость пространства между пластинами (ее можно узнать из физических справочников). Вычислив емкость, рассчитайте напряжение одним из методов, приведенных в шагах 1-3.
Обратите внимание
Для получения корректных результатов при вычислении напряжений между обкладками конденсаторов, перед проведением расчетов приводите значения всех параметров в систему СИ.
Для того чтобы знать, можно ли использовать в том или ином месте схемы конденсатор, следует определить его . Способ нахождения этого параметра зависит от того, каким образом он обозначен на конденсаторе и обозначен ли вообще.
Вам понадобится
- Измеритель емкости
Инструкция
На крупных конденсаторах емкость обычно обозначена открытым текстом: 0,25 мкФ или 15 uF. В этом случае, способ ее определения тривиален.
На менее крупных конденсаторах (в том , SMD) емкость двумя или тремя цифрами. В первом случае, она обозначена в пикофарадах. Во втором случае, первые две цифры емкость , а третья — в каких единицах она выражена:1 — десятки пикофарад;
2 — сотни пикофарад;
3 — нанофарады;
4 — десятки нанофарад;
5 — доли микрофарады.Существует также система обозначения емкости, использующая сочетания латинских букв и цифр. Буквы обозначают следующие цифры:A — 10;
B — 11;
C — 12;
D — 13;
E — 15;
F — 16;
G — 18;
H — 20;
J — 22;
K — 24;
L — 27;
M — 30;
N — 33;
P — 36;
Q — 39;
R — 43;
S — 47;
T — 51;
U — 56;
V — 62;
W — 68;
X — 75;
Y — 82;
Z — 91.Полученное число следует умножить на число 10, предварительно возведенное в степень, равную цифре, следующей после . Результат будет выражен в пикофарадах.Встречаются конденсаторы, емкость на которых не обозначена вообще. Вы наверняка встречали их, в , в стартерах ламп дневного . В этом случае, измерить емкость можно только специальным прибором. Они цифровыми и мостовыми.В любом случае, если конденсатор впаян в то или иное устройство, его следует обесточить, разрядить в нем конденсаторы фильтра и сам конденсатор, емкость которого следует измерить, и лишь после этого выпаять его. Затем его необходимо подключить к прибору.На цифровом измерителе сначала выбирают самый грубый предел, затем переключают его до тех пор, пока он не покажет перегрузку. После этого переключатель переводят на один предел назад и читают показания, а по положению переключателя определяют, в каких единицах они выражены.На мостовом измерителе, последовательно переключая , на каждом из них прокручивают регулятор из одного конца шкалы в другой, пока звук из динамика не исчезнет. Добившись исчезновения , по шкале регулятора считывают результат, а единицы, в которых он выражен, также определяют по положению переключателя.Затем конденсатор устанавливают обратно в устройство.
Обратите внимание
Никогда не подключайте к измерителю заряженные конденсаторы.
Источники:
- Справочник по системам обозначения емкости
Найти значение электрического заряда можно двумя способами. Первый – измерить силу взаимодействия неизвестного заряда с известным и с помощью закона Кулона рассчитать его значение. Второй – внести заряд в известное электрическое поле и измерить силу, с которой оно действует на него. Для измерения заряда протекающего через поперечное сечение проводника за определенное время измерьте силу тока и умножьте ее на значение времени.
Вам понадобится
- чувствительный динамометр, секундомер, амперметр, измеритель электростатического поля, воздушный конденсатор.
Инструкция
Измерение заряда при его с известным зарядомЕсли известен одного тела, поднесите к нему неизвестный заряд и измерьте между ними в метрах. Заряды начнут взаимодействовать. С помощью динамометра измерьте силу их взаимодействия. Рассчитайте значение неизвестного заряда — для этого квадрат измеренного расстояния умножьте на значение силы и поделите на известный заряд.9)). Если заряды отталкиваются, то они одноименные, если же притягиваются – разноименные.
Измерение значения заряда , внесенного в электрическое полеИзмерьте значение постоянного электрического поля специальным прибором (измеритель электрического поля). Если такого прибора нет, возьмите воздушный конденсатор, зарядите его, измерьте напряжение на его обкладках и поделите не расстояние между пластинами – это и будет значение электрического поля внутри конденсатора в вольтах на метр. Внесите в поле неизвестный заряд. С помощью чувствительного динамометра измерьте силу, которая на него действует. Измерение проводите в . Поделите значение силы на напряженность электрического поля. Результатом будет значение заряда в Кулонах (q=F/Е).
Измерение заряда , протекающего через поперечное проводникаСоберите электрическую цепь с проводниками и последовательно подключите к ней амперметр. Замкните ее на источник тока и измерьте силу тока с помощью амперметра в амперах. Одновременно секундомером засеките , в которого в цепи был электрический ток. Умножив значение силы тока на полученное время, узнайте заряд, через поперечное сечение каждого за это время (q=I t). При измерениях следите, чтобы проводники не перегревались и не произошло короткое замыкание.
Конденсатором называется устройство, способное накапливать электрические заряды. Количество накапливаемой электрической энергии в конденсаторе характеризуется его емкостью . Она измеряется в фарадах. Считается, что емкость в один фарад соответствует конденсатору, заряженному электрическим зарядом в один кулон при разности потенциалов на его обкладках в один вольт.
Инструкция
Определите емкость плоского конденсатора по формуле С = S e e0/d, где S — площадь поверхности одной пластины, d — между пластинами, e — относительная диэлектрическая проницаемость , заполняющей пространство между пластинами (в вакууме она равна ), e0 — электрическая постоянная, равная 8,854187817 10(-12) Ф/м.Исходя из приведенной формулы, величина емкости будет зависеть от площади проводников, между ними и от материала диэлектрика. В качестве диэлектрика может применяться или слюда.
Вычислите емкость сферического конденсатора по формуле С = (4П e0 R²)/d, где П — число «пи», R — радиус сферы, d — величина зазора между его сферами.Величина емкости сферического конденсатора прямо пропорциональна концентрической сферы и обратно пропорциональна расстоянию между сферами.
Рассчитайте емкость цилиндрического конденсатора по формуле С = (2П e e0 L R1)/(R2-R1), где L — длина конденсатора , П — число «пи», R1 и R2 — радиусы его цилиндрических обкладок.
Если конденсаторы в цепи соединены параллельно, рассчитайте их общую емкость по формуле С = С1+С2+…+Сn, где С1, С2,…Сn – емкости параллельно соединенных конденсаторов.
Вычислите общую емкость последовательно соединенных конденсаторов по формуле 1/С = 1/С1+1/С2+…+1/Сn, где С1, С2,…Сn — емкости последовательно соединенных конденсаторов.
Обратите внимание
На любом конденсаторе обязательно должна быть нанесена маркировка, которая может быть буквенно-цифровая или цветовая. Маркировка отражает его параметры.
Источники:
- Цветовая маркировка резисторов, конденсаторов и индуктивностей
Емкость – величина, в системе СИ выражаемая в фарадах. Хотя используются, фактически, лишь производные от нее – микрофарады, пикофарады и так далее. Что касается электроемкости плоского конденсатора, она зависит от зазора меж обкладок и их площади, от вида диэлектрика, в данном зазоре расположенного.
Инструкция
В том случае, если обкладки конденсатора имеют одинаковую площадь и имеют расположение строго одна над другой, рассчитайте площадь одной из обкладок – любой. Если же одна из них относительно другой смещена либо они разные , нужно рассчитывать площадь области, в которой обкладки друг дружку перекрывают.
При этом используются общепринятые формулы, рассчитывать площади таких геометрических фигур, как круг (S=π(R^2)), прямоугольника (S=ab), его частного случая – квадрата (S=a^2) – и других.(-12) Ф/м и является, по сути, диэлектрической проницаемостью вакуума.
Конденсатор — урок. Физика, 9 класс.
Конденсатор — это устройство, предназначенное для накопления заряда и энергии электрического поля (от лат. kondensator — «уплотнять», «сгущать»).
Простейший плоский конденсатор состоит из двух одинаковых металлических пластин — обкладок — и слоя диэлектрика, толщина которого мала по сравнению с размерами пластин.
На схемах электрических цепей конденсатор обозначается: .Для зарядки конденсатора нужно присоединить его обкладки к полюсам источника тока. При зарядке обе обкладки получают заряды, равные по модулю, но противоположные по знаку. Под зарядом конденсаторов понимают модуль заряда одной из его обкладок. Свойство конденсатора накапливать электрический заряд характеризуется физической величиной — электроёмкостью.
Электроёмкость обозначается буквой \(C\) и определяется по формуле:
C=qU, где \(q\) — заряд конденсатора, \(U\) — напряжение между обкладками конденсатора.
Электроёмкость конденсатора зависит от площади перекрытия пластин и расстояния между ними, а также от свойств используемого диэлектрика:
C∼Sd, где \(S\) — площадь каждой обкладки, \(d\) — расстояние между обкладками.
За единицу электроёмкости в СИ принимается Фарад (Ф).
Она названа в честь Майкла Фарадея — английского физика. \(1\) Фарад равен ёмкости конденсатора, при которой заряд \(1\) Кулон создаёт между его обкладками напряжение \(1\) Вольт: 1 Фарад=1 Кулон1 Вольт.
\(1\) Ф — это очень большая ёмкость для конденсатора. Чаще всего конденсаторы имеют электроёмкость, равную дольным единицам Ф: микрофарад (мкФ) — 10−6Ф, пикофарад (пФ) — 10−12 Ф.
Для получения требуемой ёмкости конденсаторы соединяют в батареи.
Если конденсаторы соединены параллельно, то общая ёмкость равна сумме ёмкостей: Cоб=C1+C2+C3.
Если конденсаторы соединены последовательно, то общая ёмкость будет равна: 1Cоб=1C1+1C2+1C3.
При зарядке конденсатора внешними силами совершается работа по разделению положительных и отрицательных зарядов. По закону сохранения энергии работа внешних сил равна энергии поля конденсатора. При разрядке конденсатора за счёт этой энергии может быть совершена работа. Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.
Энергию электрического поля конденсатора можно рассчитать по формуле: Eэл=q22C.
Из формулы видно, что энергия конденсатора данной электроёмкости тем больше, чем больше его заряд.
Источники:
Учебник А. В. Перышкин, Е. М. Гутник «Физика. 9 класс».
https://electrosam.ru/ Виды конденсаторов.
https://elektronchic.ru/ Электронщик.
https://ru.wikipedia.org Википедия.
Заряд на обкладках конденсатора формула
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU 2 /2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции.
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
где – радиусы обкладок конденсатора.
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
Задание Каковы заряды на обкладках конденсаторов, если они имеют емкости Ф и Ф, соединены последовательно и присоединены к батарее с ЭДС равной В (рис.3)? Чему равен суммарный заряд соединения? Решение Разности потенциалов на обкладках конденсаторов будут при таком соединении равны: Заряд на первом конденсаторе при этом равен:
Заряд на обкладках второго конденсатора:
Суммарный заряд системы можно найти как:
Тогда суммарный заряд равен:
Ответ Кл; Кл; Кл Задание Емкость пускового устройства электрического двигателя равна C. Энергии имеющейся в конденсаторе достаточно для того чтобы поднять груз массы m на высоту h. Чему равен заряд конденсатора? Решение При поднятии груза на высоту h происходит переход энергии поля конденсатора () в потенциальную энергию тела (), поднятого над Землей, поэтому запишем: Энергию найдем как:
Энергию электрического поля конденсатора будет удобнее выразить:
Подставим в выражение (2.1) правые части (2.2) и (2.3), имеем:
Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.
Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:
C = q φ 1 — φ 2 = q U .
Значением φ 1 — φ 2 = U обозначают разность потенциалов, называемую напряжением, то есть U . По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.
Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.
Плоский конденсатор
Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1 .
Формула для расчета электроемкости записывается как
C = ε ε 0 S d , где S является площадью обкладки, d – расстоянием между ними, ε — диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.
При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется d i , вычисление диэлектрической проницаемости этого слоя ε i выполняется, исходя из формулы:
C = ε 0 S d 1 ε 1 + d 2 ε 2 + . . . + d N ε N .
Сферический конденсатор
Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.
Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2 . Емкость рассчитывается по формуле:
C = 4 π ε ε 0 R 1 R 2 R 2 — R 1 , где R 1 и R 2 являются радиусами обкладок.
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равняется:
C = 2 πεε 0 l ln R 2 R 1 , где l — высота цилиндров, R 1 и R 2 — радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3 .
Важной характеристикой конденсаторов считается пробивное напряжение — напряжение, при котором происходит электрический разряд через слой диэлектрика.
U m a x находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.
Электроемкость плоского конденсатора. Формулы
Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы C i , где C i — это емкость конденсатора с номером i :
При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:
Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 с м 2 с расстоянием между ними 1 м м . Пространство между обкладками находится в вакууме.Решение
Чтобы рассчитать электроемкость конденсатора, применяется формула:
ε = 1 , ε 0 = 8 , 85 · 10 — 12 Ф м ; S = 1 с м 2 = 10 — 4 м 2 ; d = 1 м м = 10 — 3 м .
Подставим числовые выражения и вычислим:
C = 8 , 85 · 10 — 12 · 10 — 4 10 — 3 = 8 , 85 · 10 — 13 ( Ф ) .
Ответ: C ≈ 0 , 9 п Ф .
Найти напряженность электростатического поля у сферического конденсатора на расстоянии x = 1 с м = 10 — 2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R 1 = 1 с м = 10 — 2 м , внешнем – R 2 = 3 с м = 3 · 10 — 2 м . Значение напряжения — 10 3 В .
Решение
Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:
E = 1 4 π ε ε 0 q r 2 , где q обозначают заряд внутренней сферы, r = R 1 + x — расстояние от центра сферы.
Нахождение заряда предполагает применение определения емкости конденсатора С:
Для сферического конденсатора предусмотрена формула вида
C = 4 π ε ε 0 R 1 R 2 R 2 — R 1 с радиусами обкладок R 1 и R 2 .
Производим подстановку выражений для получения искомой напряженности:
E = 1 4 πεε 0 U ( x + R 1 ) 2 4 πεε 0 R 1 R 2 R 2 — R 1 = U ( x + R 1 ) 2 R 1 R 2 R 2 — R 1 .
Данные представлены в системе С И , поэтому достаточно заменить буквы числовыми выражениями:
E = 10 3 ( 1 + 1 ) 2 · 10 — 4 · 10 — 2 · 3 · 10 — 2 3 · 10 — 2 — 10 — 2 = 3 · 10 — 1 8 · 10 — 6 = 3 , 45 · 10 4 В м .
Ответ: E = 3 , 45 · 10 4 В м .
Энергия поля конденсатора — Основы электроники
Вся энергия заряженного конденсатора сосредотачивается в электрическом поле между его пластинами. Энергию, накопленную в конденсаторе, можно определить следующим образом. Представим себе, что мы заряжаем конденсатор не сразу, а постепенно, перенося электрические заряды с одной его пластины на другую.
При перенесении первого заряда работа, произведенная нами, будет небольшой. На перенесение второго заряда мы затратим больше энергии, так как в результате перенесения первого заряда между пластинами конденсатора будет уже существовать разность потенциалов, которую нам придется преодолевать, третий, четвертый и вообще каждый последующий заряд будет переносить все труднее и труднее, т. е. на перенесение их придется затрачивать все больше и больше энергии. Пусть мы перенесем таким образом некоторое количество электричества, которое мы обозначим буквой Q.
Вся энергия, затраченная нами при заряде конденсатора, сосредоточится в электрическом поле между его пластинами. Напряжение между пластинами конденсатора в конце заряда мы обозначим буквой U.
Как мы уже заметили, разность потенциалов в процессе заряда не остается постоянной, а постепенно увеличивается от нуля — в начале заряда — до своего конечного значения U.
Для упрощения вычисления энергии допустим, что мы перенесли весь электрический заряд Q с одной пластины конденсатора на другую не маленькими порциями, а сразу. Но при этом мы должны считать, что напряжение между пластинами конденсатора было не ноль, как в начале заряда, и не U, как в конце заряда, а равнялось среднему значению между нулем и U, т. е. половине U. Таким образом, энергия, запасенная в электрическом поле конденсатора, будет равна половине напряжения U, умноженной на общее количество перенесенного электричества Q.
Полученный результат мы можем записать в виде следующей математической формулы:
W = UQ/2 (1)
Если напряжение в этой формуле будет выражено в вольтах, а количество электричества — в кулонах, то энергия W получится в джоулях. Если мы вспомним, что заряд, накопленный на конденсаторе, равен Q = CU, то формулу (1) можно будет записать окончательно в следующем виде:
W = CU2/2 (2)
Выражение (2) говорит нам о том, что энергия, сосредоточенная в поле конденсатора, равна половине произведения емкости конденсатора на квадрат напряжения между его пластинами.
Этот вывод имеет очень важное значение при изучении раздела радиотехники о колебательных контурах.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Как найти напряжение на конденсаторе формула
Одним из важных элементов электрической цепи является конденсатор, формулы для которого позволяют рассчитать и подобрать наиболее подходящий вариант. Основная функция данного устройства заключается в накоплении определенного количества электроэнергии. Простейшая система включает в себя два электрода или обкладки, разделенные между собой диэлектриком.
В чем измеряется емкость конденсатора
Одной из важнейших характеристик конденсатора является его емкость. Данный параметр определяется количеством электроэнергии, накапливаемой этим прибором. Накопление происходит в виде электронов. Их количество, помещающееся в конденсаторе, определяет величину емкости конкретного устройства.
Для измерения емкости применяется единица – фарада. Емкость конденсатора в 1 фараду соответствует электрическому заряду в 1 кулон, а на обкладках разность потенциалов равна 1 вольту. Эта классическая формулировка не подходит для практических расчетов, поскольку в конденсаторе собираются не заряды, а электроны. Емкость любого конденсатора находится в прямой зависимости от объема электронов, способных накапливаться при нормальном рабочем режиме. Для обозначения емкости все равно используется фарада, а количественные параметры определяются по формуле: С = Q / U, где С означает емкость, Q – заряд в кулонах, а U является напряжением. Таким образом, просматривается взаимная связь заряда и напряжения, оказывающих влияние на способность конденсатора к накоплению и удержанию определенного количества электричества.
Для расчетов емкости плоского конденсатора используется формула:
в которой ε = 8,854187817 х 10 -12 ф/м представляет собой постоянную величину. Прочие величины: ε – является диэлектрической проницаемостью диэлектрика, находящегося между обкладками, S – означает площадь обкладки, а d – зазор между обкладками.Формула энергии конденсатора
С емкостью самым тесным образом связана другая величина, известная как энергия заряженного конденсатора. После зарядки любого конденсатора, в нем образуется определенное количество энергии, которое в дальнейшем выделяется в процессе разрядки. С этой потенциальной энергией вступают во взаимодействие обкладки конденсатора. В них образуются разноименные заряды, притягивающиеся друг к другу.
В процессе зарядки происходит расходование энергии внешнего источника для разделения зарядов с положительным и отрицательным значением, которые, затем располагаются на обкладках конденсатора. Поэтому в соответствии с законом сохранения энергии, она не исчезает бесследно, а остается внутри конденсатора в виде электрического поля, сосредоточенного между пластинами. Разноименные заряды образуют взаимодействие и последующее притяжение обкладок между собой.
Каждая пластина конденсатора под действием заряда создает напряженность электрического поля, равную Е/2. Общее поле будет складываться из обоих полей, возникающих в каждой обкладке с одинаковыми зарядами, имеющими противоположные значения.
Таким образом, энергия конденсатора выражается формулой: W=q(E/2)d. В свою очередь, напряжение выражается с помощью понятий напряженности и расстояния и представляется в виде формулы U=Ed. Это значение, подставленное в первую формулу, отображает энергию конденсатора в таком виде: W=qU/2. Для получения окончательного результата необходимо использовать определение емкости: C=q/U, и в конце концов энергия заряженного конденсатора будет выглядеть следующим образом: Wэл = CU 2 /2.
Формула заряда конденсатора
Для выполнения зарядки, конденсатор должен быть подключен к цепи постоянного тока. С этой целью может использоваться генератор. У каждого генератора имеется внутреннее сопротивление. При замыкании цепи происходит зарядка конденсатора. Между его обкладками появляется напряжение, равное электродвижущей силе генератора: Uc = E.
Обкладка, подключенная к положительному полюсу генератора, заряжается положительно (+q), а другая обкладка получает равнозначный заряд с отрицательной величиной (- q). Величина заряда q находится в прямой пропорциональной зависимости с емкостью конденсатора С и напряжением на обкладках Uc. Эта зависимость выражается формулой: q = C x Uc.
В процессе зарядки одна из обкладок конденсатора приобретает, а другая теряет определенное количество электронов. Они переносятся по внешней цепи под влиянием электродвижущей силы генератора. Такое перемещение является электрическим током, известным еще как зарядный емкостной ток (Iзар).
Течение зарядного тока в цепи происходит практически за тысячные доли секунды, до того момента, пока напряжение конденсатора не станет равным электродвижущей силе генератора. Напряжение увеличивается плавно, а потом постепенно замедляется. Далее значение напряжения конденсатора будет постоянным. Во время зарядки по цепи течет зарядный ток. В самом начале он достигает максимальной величины, так как напряжение конденсатора имеет нулевое значение. Согласно закона Ома Iзар = Е/Ri, поскольку к сопротивлению Ri приложена вся ЭДС генератора.
Формула тока утечки конденсатора
Ток утечки конденсатора вполне можно сравнить с воздействием подключенного к нему резистора с каким-либо сопротивлением R. Ток утечки тесно связан с типом конденсатора и качеством используемого диэлектрика. Кроме того, важным фактором становится конструкция корпуса и степень его загрязненности.
Некоторые конденсаторы имеют негерметичный корпус, что приводит к проникновению влаги из воздуха и возрастанию тока утечки. В первую очередь это касается устройств, где в качестве диэлектрика использована промасленная бумага. Значительные токи утечки возникают из-за снижения электрического сопротивления изоляции. В результате нарушается основная функция конденсатора – способность получать и сохранять заряд электрического тока.
Основная формула для расчета выглядит следующим образом: Iут = U/Rd, где Iут, – это ток утечки, U – напряжение, прилагаемое к конденсатору, а Rd – сопротивление изоляции.
По назначению конденсатор можно сравнить с батарейкой. Но имеется принципиальное отличие в работе данных элементов. Существуют отличия в предельной емкости и скорости зарядки конденсатора и батарейки.
Формула заряда конденсатора
Величина заряда конденсатора (q) связана с его емкостью (C) и разностью потенциалов (U) между его обкладками как:
где q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками.
Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Заряд на пластинах плоского конденсатора равен:
где – электрическая постоянная; – площадь каждой (или наименьшей) пластины; – расстояние между пластинами; – диэлектрическая проницаемость диэлектрика, который находится между пластинами конденсатора.
Заряд на обкладках цилиндрического конденсатора вычисляется при помощи формулы:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Заряд на обкладках сферического конденсатора найдем как:
где – радиусы обкладок конденсатора.
Заряд конденсатора связан с энергией поля (W) внутри него:
Из формулы (6) следует, что заряд можно выразить как:
Рассмотрим последовательное соединение из N конденсаторов ( рис. 1).
Здесь (рис.1) положительная обкладка одного конденсатора соединяется с отрицательной обкладкой следующего конденсатора. При таком соединении, обкладки соседних конденсаторов создают единый проводник. У всех конденсаторов, соединенных последовательно на обкладках имеются равные по величине заряды.
При параллельном соединении конденсаторов (рис.2), соединяют обкладки, имеющие заряды одного знака. Суммарный заряд соединения (q) равен сумме зарядов конденсаторов.
Примеры решения задач по теме «Заряд конденсатора»
Задание Каковы заряды на обкладках конденсаторов, если они имеют емкости Ф и Ф, соединены последовательно и присоединены к батарее с ЭДС равной В (рис.3)? Чему равен суммарный заряд соединения? Решение Разности потенциалов на обкладках конденсаторов будут при таком соединении равны: Заряд на первом конденсаторе при этом равен:
Заряд на обкладках второго конденсатора:
Суммарный заряд системы можно найти как:
Тогда суммарный заряд равен:
Ответ Кл; Кл; Кл Задание Емкость пускового устройства электрического двигателя равна C. Энергии имеющейся в конденсаторе достаточно для того чтобы поднять груз массы m на высоту h. Чему равен заряд конденсатора? Решение При поднятии груза на высоту h происходит переход энергии поля конденсатора () в потенциальную энергию тела (), поднятого над Землей, поэтому запишем: Энергию найдем как:
Энергию электрического поля конденсатора будет удобнее выразить:
Подставим в выражение (2.1) правые части (2.2) и (2.3), имеем:
Один из наиболее важных эффектов, используемых в электронике, — ёмкость конденсаторов. Способность накапливать и хранить электрический заряд нашла применение практически во всех аналоговых цепях и логических схемах. Пассивные устройства, запасающие энергию в виде электрического поля, называли конденсаторами уже в те времена, когда учёные ещё очень мало знали о природе электричества.
История накопителей заряда
Самое раннее письменное свидетельство получения зарядов с помощью трения принадлежит учёному Фалесу из Милета (635—543 гг. до н. э.), который описал трибоэлектрический эффект от взаимодействия янтаря и сухой шерсти. Для приблизительно 2300 последующих лет любое получение электричества заключалось в трении двух различных материалов друг о друга.
Качественный рывок в знаниях о зарядах произошёл в эпоху Просвещения — период революционного развития научной мысли в образованных кругах. В это время электричество становится популярной темой, а энтузиастами было произведено немало опытов и экспериментов с генераторами на основе трения.
Первое устройство для хранения полученных зарядов было создано в 1745 г. двумя электриками (так тогда называли людей, изучающих природу статического электричества), работающими независимо друг от друга: Эвальдом фон Клейстом, деканом собора в Пруссии, и Питером ван Мюссенбруком, профессором математики и физики в университете Лейдена.
Открытие явления произошло во время опытов у обоих экспериментаторов, но с той разницей, что Мюссенбрук, во-первых, сделал немало усовершенствований первоначально созданного оборудования, а во-вторых, письменно сообщил коллегам о своих достижениях. Прошло совсем немного времени и учёные мира стали создавать накопители зарядов собственных конструкций. Это были первые шаги в эволюции конденсаторов, продолжающейся и в наши дни. Основные даты хронологии появления устройств для хранения зарядов:
- 1746 г. — изобретение лейденской банки в результате экспериментов по доработке устройства Клейста;
- 1750 г. — опыты Бенджамина Франклина с батареями конденсаторов;
- 1837 г. — публикация Майклом Фарадеем теории диэлектрической поляризации — научной основы работы накопителей;
- конец XIX в. — начало практического применения лейденских банок вместе с первыми устройствами постоянного тока;
- начало XX в. — изобретение слюдяных и керамических конденсаторов.
Физика ёмкостных характеристик
Устройства, обладающие способностью хранения энергии в форме электрического заряда и производящие при этом разность потенциалов, называют конденсаторами. В простейшем виде они состоят из двух или более параллельных проводящих пластин, находящихся на небольшом расстоянии друг от друга, но электрически разделённых либо воздухом, либо каким-либо другим изоляционным материалом, например, вощёной бумагой, слюдой, керамикой, пластмассой или специальным гелем.
Если подключить к пластинам источник напряжения, то одна из них получит избыток электронов, а на другой сформируется их дефицит. Ионы и электроны на каждой из этих пластин притягиваются друг к другу, но благодаря диэлектрическому барьеру они не соединяются, а накапливаются на плоскостях проводников. В результате первая пластина (электрод) окажется заряженной отрицательно, а вторая — положительно. Неподвижные заряды создают постоянное электрическое поле, теоретически сохраняемое неограниченное количество времени в незамкнутой электрической цепи.
Поток электронов на пластины называется зарядным током, продолжающим присутствовать до тех пор, пока напряжение на пластинах не сравняется с приложенным. В этот момент конденсатор считается полностью заряженным, то есть зарядов на пластинах становится так много, что они отталкивают вновь поступающие. При подключении к заряженному устройству нагрузки электроны и ионы находят новый путь друг к другу. В этом случае конденсатор работает как источник тока до момента потери разности потенциалов на электродах.
Способность конденсатора хранить заряд Q (измеряется в кулонах) называют ёмкостью. Чем больше площадь пластин и меньше расстояние между ними (благодаря усилению эффекта притяжения зарядов между обкладками), тем большая ёмкость устройства. Степень приближения пластин ограничивается способностью диэлектрика сопротивляться разрядке пробоем между ними. Таким образом, три характеристики определяют производительность конденсатора:
- геометрия пластин;
- расстояние между ними;
- диэлектрический материал между пластинами.
Единица и формулы расчёта
Ёмкость в виде электрического свойства, способного хранить заряды, измеряется в фарадах (Ф) и обозначается С. Величина названа в честь английского физика Майкла Фарадея. Конденсатор ёмкостью 1 фарад способен хранить заряд в 1 кулон на пластинах с напряжением 1 вольт. Значение С всегда положительно.
Математическое выражение фарада
Ёмкость конденсатора — постоянная величина, означающая потенциальную способность хранить энергию. Количество заряда, хранимое в отдельно взятый момент, определяется уравнением Q=CV, где V — приложенное напряжение. Таким образом, регулируя напряжение на пластинах, можно увеличивать или уменьшать заряд. Эта формула ёмкости в виде C=Q/V в единичных значениях определяет, в чём измеряется ёмкость конденсатора в СИ, и является математическим выражением фарада.
Специалисты по электронике единицу в один фарад считают не совсем практичной, поскольку она представляет собой огромное значение. Даже 1/1000 F — это очень большая ёмкость. Как правило, для реальных электрических компонентов применяют следующие величины:
- пикофарад — 10—12 Ф;
- нанофарад — 10—9 Ф;
- микрофарад — 10—6 Ф.
Диэлектрическая проницаемость
Фактор, благодаря которому изолятор определяет ёмкость конденсатора, называется диэлектрической проницаемостью. Обобщённая формула расчёта ёмкости конденсатора с параллельными пластинами представлена выражением C= ε (A / d), где:
- А — площадь меньшей пластины;
- d — расстояние между ними;
- ε — абсолютная проницаемость используемого диэлектрического материала.
Диэлектрическая проницаемость вакуума ε0 является константой и имеет значение 8,84х10—12 фарад на метр. Как правило, проводящие пластины разделены слоем изоляционного материала, а не вакуума. Чтобы найти ёмкость конденсатора, пластины которого находятся в воздухе, можно воспользоваться значением ε0. Разницей диэлектрической проницаемости атмосферы и вакуума можно пренебречь, поскольку их значения очень близки.
На практике в формулах нахождения ёмкости конденсатора используется относительная диэлектрическая проницаемость в качестве коэффициента, означающая, насколько электрическое поле между зарядами уменьшается в диэлектрике по сравнению с вакуумом. Некоторые значения этой величины для различных материалов:
Поскольку эффективность конденсатора зависит от применяемого в нём изолятора, его качество как накопителя можно определить через удельную ёмкость — величину, равную отношению ёмкости к объёму диэлектрика.
Практические измерения
Значение ёмкости конденсатора обозначается на корпусе в дробных фарадах или с помощью цветового кода. Но со временем компоненты способны потерять свои качества, поэтому для некоторых критических случаев последствия могут быть неприемлемыми. Существуют и другие обстоятельства, требующие измерений. Например, необходимость знать общую ёмкость цепи или части электрооборудования. Приборов, осуществляющих непосредственное считывание ёмкости, не существует, но значение может быть вычислено вручную или интегрированными в измерительные устройства процессорами.
Для обнаружения фактической ёмкости нередко используют осциллограф как средство измерения постоянной времени (т). Эта величина обозначает время в секундах, за которое конденсатор заряжается на 63%, и равна произведению сопротивления цепи в омах на ёмкость цепи в фарадах: т=RC. Осциллограф позволяет легко определить постоянную времени и даёт возможность с помощью расчётов найти искомую ёмкость.
Существует также немало моделей любительского и профессионального электронного измерительного оборудования, оснащённого функциями для тестирования конденсаторов. Многие цифровые мультиметры обладают возможностью определять ёмкость. Эти устройства способны контролируемо заряжать и разряжать конденсатор известным током и, анализируя нарастание результирующего напряжения, выдавать довольно точный результат. Единственный недостаток большинства таких приборов — сравнительно узкий диапазон измеряемых величин.
Более сложные и специализированные инструменты — мостовые измерители, испытывающие конденсаторы в мостовой схеме. Этот метод косвенного измерения обеспечивает высокую точность. Современные устройства такого типа оснащены цифровыми дисплеями и возможностью автоматизированного использования в производственной среде, они могут быть сопряжены с компьютерами и экспортировать показания для внешнего контроля.
Идея суперконденсатора
Электричество — чрезвычайно универсальный вид энергии, обладающий одним недостатком — его трудно саккумулировать быстро. Химические батареи способны сохранять большое количество энергии, но требуют нескольких часов для полной зарядки. Этого недостатка лишены конденсаторы — они могут заряжаться практически мгновенно. Но их ёмкость не позволяет хранить большое количество энергии, поэтому весьма заманчивой выглядит идея суперконденсатора, сочетающего лучшие качества химических и электростатических накопителей электричества.
Несмотря на функциональную схожесть, аккумуляторные батареи и конденсаторы устроены совершенно по-разному. Гальванические элементы работают на принципе высвобождения электрической энергии во время химической реакции веществ внутри них. При истощении запаса активных реагентов они прекращают генерировать разность потенциалов и для нового цикла требуют инициирования током обратных химических реакций для восстановления активных веществ. Основные недостатки аккумуляторов по сравнении и конденсаторами:
- непродолжительный жизненный цикл;
- невысокая удельная мощность;
- узкий диапазон температур зарядки и разрядки;
- неспособность быстро отдать весь запас энергии.
Тем не менее обычные конденсаторы не используются в качестве активных источников напряжения из-за низкой ёмкости. Теоретические и практические суперконденсаторы (ультраконденсаторы) отличаются от обычных крайне высокой ёмкостью при большой плотности хранимой энергии, что позволяет их рассматривать как альтернативу химическим элементам.
Крупнейшие коммерческие устройства обладают ёмкостью до нескольких тысяч фарад, но их возможности всё равно несопоставимы с аккумуляторами, поэтому подобные устройства используются для хранения зарядов в течение относительно короткого периода времени. Они нашли широкое применение в качестве электрических эквивалентов механических маховиков, чтобы сглаживать напряжение источников питания, например, в ветровых турбинах или рекуперативных тормозных системах электрических транспортных средств.
Первые ультраконденсаторы появились в середине прошлого века и обладали не очень впечатляющими ёмкостями. С тех пор прогресс в совершенствовании материалов привёл к утоньшению диэлектрического слоя до одной молекулы, что позволило создавать устройства с выдающимися характеристиками. Дальнейшее развитие наноиндустрии стало основой для фундаментальных перемен в накоплении электричества. Возможно, в скором времени экологически опасные и капризные химические аккумуляторы заменят суперконденсаторы на основе молекулярно структурированных пластин и диэлектрического слоя.
Накопление электрической энергии
Публикации по материалам Д. Джанколи. «Физика в двух томах» 1984 г. Том 2.
В заряженном конденсаторе накоплена (аккумулирована) электрическая энергия. Эта энергия конденсатора равна работе, необходимой для зарядки конденсатора.
Процесс зарядки конденсатора состоит, по сути, в том, что заряд с одной пластины переносится на другую. Именно это совершает источник напряжения, когда его подключают к конденсатору. Сначала, когда конденсатор не заряжен, для переноса первой порции заряда не требуется работы.
Но когда на каждой из пластин уже имеется заряд, для пополнения его приходится совершать работу против сил электрического отталкивания. Чем больше накопленный пластинами заряд, тем большую работу, необходимо совершить для его увеличения. Если на пластинах существует разность потенциалов V, работа по переносу элемента заряда dq равна dW = Vdq. Поскольку V= q/C , где С — емкость конденсатора, тогда работа по его заряду составит:Итак, мы можем сказать, что энергия, запасенная, или аккумулированная, конденсатором, равна
если заряды обкладок конденсатора емкостью С равны соответственно +Q и -Q. А так как Q = СV, где V — разность потенциалов между обкладками, мы можем написать
Пример 25.5. Конденсатор емкостью 20 мкФ подключен к батарее напряжением 12 В. Какую энергию может запасти конденсатор?
Решение. Согласно (25.5),
Энергия не является «вещественной субстанцией», поэтому она вовсе не должна быть где-то сосредоточена. Тем не менее принято считать, что она запасена электрическим полем между пластинами.
Для примера выразим энергию плоского конденсатора через напряженность электрического поля. Мы показали [см. (24.3)], что между параллельными пластинами существует приблизительно однородное электрическое поле Е и его напряженность связана с разностью потенциалов соотношением V = Ed, где d — расстояние между пластинами.
Кроме того, согласно (25.2), емкость плоского конденсатора равна С = s0 A/d. ТогдаПроизведение Ad характеризует объем, занимаемый электрическим полем Е. Разделив обе части формулы на объем, получим выражение для энергии, запасенной в единице объема, или плотности энергии u:
Плотность электростатической энергии, запасенной в любой части пространства, пропорциональна квадрату напряженности электрического поля в этой области.
Выражение (25.6) получено для частного случая плоского конденсатора. Можно показать, однако, что оно справедливо для любой области пространства, в которой существует электрическое поле.
Продолжение следует. Коротко о следующей публикации:
Диэлектрики.
В конденсаторах между пластинами проложен изолирующий материал (диэлектрик), например слюда или пластмассовая пленка. Этим достигается сразу несколько целей. Во-первых, диэлектрики лучше противостоят электрическому пробою, чем воздух, и к конденсатору можно приложить более высокое напряжение. Во-вторых, при наличии диэлектрика пластины можно расположить ближе друг к другу без опасения, что они могут соприкасаться. В третьих, ёмкость конденсатора увеличится в несколько раз благодаря электрической поляризации диэлектрика.Альтернативные статьи: Переменный ток, Закон Ома.
Замечания и предложения принимаются и приветствуются!
Как рассчитать заряд конденсатора — Onlinecomponents.com
Конденсатор — это устройство, которое используется для хранения электрического заряда и электрической энергии. Основной конденсатор состоит из двух металлических пластин, разделенных некоторым изолятором, называемым диэлектриком. Способность конденсатора удерживать заряд называется емкостью.
Когда клеммы батареи соединены через конденсатор, потенциал батареи перемещает заряд, и он начинает накапливаться на пластинах конденсатора.Клемма конденсатора, подключенная к катоду батареи, будет заряжена положительно (+ Q), а клемма, подключенная к аноду батареи, будет заряжена отрицательно (-Q). Конденсатор в целом остается нейтральным, но заряды разделены на противоположных пластинах, которые находятся на заданном расстоянии друг от друга с расстоянием (d). Базовый конденсатор показан на рис. 1
.Рис.1
Заряд, накопленный на пластинах конденсатора, прямо пропорционален приложенному напряжению, поэтому [1]
В α Q
Где
В = Напряжение
Q = Заряд
Конденсаторы с разными физическими параметрами могут удерживать разное количество заряда, когда на конденсаторы подается одинаковое напряжение.Эта способность конденсатора называется емкостью. Емкость конденсатора можно определить как отношение количества максимального заряда (Q), который конденсатор может хранить, к приложенному напряжению (V).
V = C Q
Q = C / V
Таким образом, количество заряда конденсатора можно определить по вышеупомянутой формуле.
Конденсаторы заряжаются предсказуемым образом, и для зарядки конденсатора требуется время. Рассматривая зарядку как функцию времени, мы также можем определить количество заряда конденсатора через определенный период времени, когда он подключен к батарее, как показано на рис.2
Рис.2 Конденсатор, включенный в RC-цепочку
Предположим, что конденсатор (C) полностью разряжен, а переключатель разомкнут, конденсатор не заряжается. Эта ситуация представляет собой сценарий, когда при t = 0, I = 0, и заряд, накопленный на конденсаторе C, также будет равен нулю.
Теперь, как только переключатель замкнут, ток начнет течь по цепи, максимальное количество тока, которое будет протекать по цепи, ограничено резистором (R), который подключен последовательно с конденсатором.Ток, который будет протекать по цепи, можно найти с помощью закона напряжения Кирхгофа [2]
V = I (t) R + V C Q = C / V C и V C = Q / C
где
В = Напряжение
I (t) = Ток в цепи в любой момент времени
Vc = напряжение на конденсаторе
Q = Заряд
C = Емкость, включенная в цепь
R = Сопротивление, подключенное в цепи
В = I (t) R + Q / C
Q = CV [1-e -t / RC ]
Количество заряда в любой момент можно найти с помощью вышеупомянутого уравнения.График зарядки конденсатора показан на рис. 3
.Рис. 3 Заряд конденсатора по времени
Из графика можно сказать, что первоначально зарядный ток будет максимальным и конденсатор начнет быстро изменяться, а после одноразовой постоянной, равной T = RC, конденсатор будет заряжаться примерно на 63% от своего общего значения. Конденсатор продолжит заряжаться, зарядный ток будет уменьшаться, и скорость, с которой заряжался конденсатор, также уменьшится.
После пятикратной постоянной времени конденсатор будет полностью заряжен и зарядный ток будет равен нулю. Рассматривая заряд конденсатора как функцию времени, когда он включен в цепь, можно определить количество заряда в любой момент времени.
Артикул
[1] Основы электротехники В.К. Мехта, Рохит Мехта, стр. 296
[2] Конденсаторы от Р.П. Дешпанде, стр. 29
5.19: Зарядка конденсатора через резистор
На этот раз заряд конденсатора увеличивается, поэтому потребляемый ток равен \ (+ \ точка Q \) .{-t / (RC)} \ right). \ label {5.19.3} \]
Таким образом, заряд конденсатора асимптотически приближается к своему окончательному значению \ (CV \), достигая 63% (1 — e -1 ) окончательного значения во времени \ (RC \) и половины окончательного значения во времени \ (RC \ ln 2 = 0,6931 \, RC \).
Разность потенциалов на пластинах увеличивается с той же скоростью. Разница потенциалов не может измениться мгновенно в любой цепи, содержащей емкость.
Как ток меняется со временем? Это находится путем дифференцирования уравнения \ ref {5.{-t / (RC)}. \]
Это говорит о том, что ток мгновенно возрастает от нуля до \ (V / R \), как только переключатель замкнут, а затем он спадает экспоненциально с постоянной времени \ (RC \) до нуля. Это реально возможно? В принципе это возможно, если индуктивность (см. Главу 12) цепи равна нулю. Но индуктивность любой замкнутой цепи не может быть точно равна нулю, а схема, изображенная без какой-либо индуктивности, недостижима ни в одной реальной цепи, и поэтому в реальной цепи не будет мгновенного изменения тока.2, \]
так что все хорошо. Энергия, теряемая аккумулятором, распределяется поровну между \ (R \) и \ (C \) .
Неоновая лампа
Вот способ заставить неоновую лампу периодически мигать.
На Рисунке \ (V. \) 25 \ (\ frac {1} {2} \) (извините за дробь — я подсунул фигуру в последнюю очередь!), Вещь, которая выглядит как счастливое лицо на справа — газоразрядная трубка; точка внутри указывает на то, что внутри не полный вакуум, но внутри есть немного газа.
\ (\ text {РИСУНОК V.25} \ frac {1} {2} \)
Он разряжается, когда разность потенциалов на электродах превышает определенный порог. Когда к трубке прикладывается электрическое поле, электроны и положительные ионы ускоряются, но вскоре замедляются из-за столкновений. Но если поле достаточно велико, электроны и ионы будут иметь достаточно энергии при столкновении, чтобы ионизировать атомы, с которыми они сталкиваются, поэтому произойдет каскадный разряд. Разность потенциалов экспоненциально возрастает во временной шкале \ (RC \), пока не достигнет порогового значения, и неоновая трубка внезапно разряжается.Затем все начинается сначала.
Аналогичная проблема с индуктором описана в главе 10, раздел 10.12.
Интегрирующие и дифференцирующие схемы
Теперь мы посмотрим, что произойдет, если мы подключим последовательно резистор и конденсатор к источнику напряжения, изменяющемуся во времени, и покажем, что, при условии выполнения некоторых условий разность потенциалов на конденсаторе — это интеграл по времени от входного напряжения, а разность потенциалов на резисторе — это производная по времени входного напряжения.{-1} = 0,632 \) этого значения во времени \ (RC \). Обратите внимание, что когда \ (t << RC \), ток будет большим, а заряд в конденсаторе будет небольшим. Большая часть падения потенциала в цепи будет на резисторе и относительно небольшая - на конденсаторе. Однако по прошествии длительного времени ток станет низким, а заряд будет высоким, так что большая часть падения потенциала будет приходиться на конденсатор и сравнительно небольшое - на резистор. Потенциал перепадов на R и C будет равен одновременно
\ [t = RC \ ln 2 = 0.693RC. \]
Предположим, что вместо подключения \ (R \) и \ (C \) к батарее постоянной ЭДС, мы подключаем ее к источнику, напряжение которого изменяется со временем, \ (V (t) \) . Как заряд в \ (C \) будет меняться со временем?
Соответствующим уравнением является \ (V = IR + Q / C \), в котором \ (I, \, Q \ text {и} V \) — все функции времени.
Поскольку \ (I = \ dot Q \), дифференциальное уравнение, показывающее, как \ (Q \) изменяется со временем, составляет
\ [\ dfrac {dQ} {dt} + \ dfrac {1} {RC} Q = \ dfrac {V} {R} \ label {5.{\ dfrac {t} {RC}} \, dt \ right) \\ & = \ dfrac {dV} {dt} — \ dfrac {1} {RC} (V-V_C) = \ dfrac {dV} {dt } — \ dfrac {V_R} {RC} \\ \ end {align} \ label {5.19.22} \]
Если постоянная времени мала, так что \ (\ dfrac {dV_R} {dt} \ ll <\ dfrac {V_R} {RC} \), это становится
\ [V_R = RC \ dfrac {dV} {dR}, \ label {5.20.23} \]
, так что напряжение на \ (R \) \ (RC \) умножить на производную входного напряжения по времени \ (V. \). Таким образом, мы имеем дифференцирующую цепь .
Обратите внимание, что в интегрирующей схеме схема должна иметь большую постоянную времени (большие \ (R \) и \ (C \)), а временные изменения \ (V \) составляют быстрые по сравнению с \ (RC \).Выходное напряжение на \ (C \) тогда равно \ (\ dfrac {1} {RC} \ int V \, dt \). В дифференцирующей схеме схема должна иметь малое время постоянную , а временные изменения в \ (V \) должны быть медленными по сравнению с \ (RC \). Выходное напряжение на \ (R \) тогда равно \ (\ dfrac {dV} {dR} \).
домашних заданий и упражнений — Как правильно рассчитать заряд конденсатора?
домашнее задание и упражнения — Как правильно рассчитать заряд конденсатора? — Обмен физическими стекамиСеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange- 0
- +0
- Авторизоваться Зарегистрироваться
Physics Stack Exchange — это сайт вопросов и ответов для активных исследователей, ученых и студентов-физиков.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществуКто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 53k раз
$ \ begingroup $ Закрыто. Это вопрос не по теме. В настоящее время он не принимает ответы.Хотите улучшить этот вопрос? Обновите вопрос, чтобы он соответствовал теме Physics Stack Exchange.
Закрыт 4 года назад.
Сколько заряда на каждой пластине 4.-5 С
Почему?
Дэвид З71.8k2424 золотых знака163163 серебряных знака274274 бронзовых знака
задан 3 мая ’12 в 19: 182012-05-03 19:18
Ястреб89722 золотых знака1818 серебряных знаков3232 бронзовых знака
$ \ endgroup $ 0 $ \ begingroup $Заряд на двух пластинах противоположен и равен ключевому ответу.Параметр Q — это заряд одной пластин, а не сумма абсолютных значений двух зарядов. Емкость определяется как заряд на единицу напряжения, так что $ Q = CV $, поэтому 4F умножить на 12 В — это 48 единиц заряда, что для единицы «F» составляет миллионные доли кулоновского C. Это дает ответ в книге.
Создан 03 мая 2012, 19:27.
$ \ endgroup $ 0 $ \ begingroup $Чистый заряд конденсатора всегда равен нулю, потому что на пластинах одинаковые и различающиеся заряды.-6 * 12 кулонов т.е. q = 48 микрокулонов
Создан 03 мая ’13 в 9: 132013-05-03 09:13
$ \ endgroup $ $ \ begingroup $Формула $ V = \ frac {Q} {C} $ дает количество заряда, которое находится на одной из пластин. Общая сумма заряда на обеих пластинах, вместе взятых, равна нулю! Оба они заряжены противоположно.
Создан 05 мая 2013, 11:40:56
$ \ endgroup $ Очень активный вопрос . Заработайте 10 репутации, чтобы ответить на этот вопрос.Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов. Physics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Электрические свойства цепей RC:
В простейшем виде цепь R-C содержит сопротивление R, конденсатор C и электродвижущую силу ЭДС (обычно аккумулятор).Принципиальная схема цепи R-C выглядит так:Когда тумблер находится в разомкнутом положении, показанном на схеме, к конденсатору не подключена электродвижущая сила, ЭДС, и, если конденсатор не был ранее заряжен, в конденсаторе не будет храниться зарядов (т. Е. Q = 0). и разность потенциалов между пластинами конденсатора, соответственно, также будет равна нулю.
V c = e,
Если переключатель переключен так, что он соединяет конденсатор с электродвижущей силой, заряды будут накапливаться на пластинах конденсатора, + на одной пластине, _ на другой.Это будет продолжаться до тех пор, пока накопленный заряд не создаст разность потенциалов (V c ) между двумя пластинами, численно равную электродвижущей силе. То есть, когда:ток через соединительные провода прекратится (т. Е. I = 0).
Когда переключатель переведен в свое альтернативное положение, (i) ЭДС обходится, (ii) две пластины конденсатора соединены, и (iii) заряды, накопленные на конденсаторе, будут стремиться пройти через соединительный провод к конденсатору. противоположная пластина.Другими словами, заряженный конденсатор разрядится.
Об электрических свойствах цепей R-C следует помнить две важные вещи:1. Когда конденсатор (C) полностью заряжен, выполняется следующее соотношение:
q = Ce Уравнение 1a где q — общее количество заряда, накопленного конденсатором, C — емкость конденсатора, а e — электродвижущая сила, которая фактически заряжает конденсатор.Обратите внимание, что q = 0, когда конденсатор разряжен. Также обратите внимание, что уравнение можно переставить так:
q / C = e = V c Уравнение 1b Это означает, что размещение избытка + на одной пластине конденсатора и избытка на другой пластине создаст разность потенциалов между пластинами.
2. Из-за наличия сопротивления (R) в цепи ток через цепь замедляется. В результате для изменения количества заряда, хранящегося на пластинах конденсатора, требуется время. Например, если вы начнете с полностью разряженного конденсатора (т.е. q = 0 и V c = 0) и подключите его к батарее, зарядка конденсатора будет описана экспоненциальным уравнением ,
q t = Ce (1 e -t / RC ) Уравнение 2a и если C = 1, e = 10 и R = 1 график зависимости q t отвремя будет выглядеть так:
Аналогично, если бы вы начали с того же конденсатора в полностью заряженном состоянии (т.е. q = Ce и V c = e ) и соедините две его пластины друг с другом, разряд конденсатора будет описан экспоненциальным уравнением:
q т = Ce e -t / RC Уравнение 2b и график q т vs.время будет выглядеть так:
Упражнения:
1. Имея в виду уравнения 1b, 2a и 2b и определение тока, можете ли вы предсказать внешний вид графиков V c и тока (I) в зависимости от времени для той же цепи R-C?
2. Запустите моделирование электрических свойств RC-цепи и получите качественное представление о влиянии изменения e на электрическое поведение RC-цепи.
3. Величина RC называется постоянной времени цепи R-C и иногда обозначается как t (= RC).Исследуйте влияние изменения t на электрическое «поведение» RC-цепи, повторяя упражнение 2, на этот раз изменяя R и / или C. плазматическая мембрана возбудимых клеток (подсказка: вспомните модель эквивалентного контура)?
Страница не найдена | MIT
Перейти к содержанию ↓- Образование
- Исследовать
- Инновации
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
- Подробнее ↓
- Прием + помощь
- Студенческая жизнь
- Новости
- Выпускников
- О MIT
Попробуйте поискать что-нибудь еще! Что вы ищете? Увидеть больше результатовПредложения или отзывы?
Кафедра физики и астрономии
Основные исследования
Миссии астронома из ЛГУ и НАСА разоблачили космические извержения в соседних галактиках
Короткая вспышка высокоэнергетического света пронеслась по Солнечной системе 15 апреля 2020 г. запускать космические инструменты, в том числе на борту НАСА и европейских миссий.Теперь несколько intl. научные группы пришли к выводу, что взрыв произошел от сверхмагниченной звездной Остаток, известный как магнетар, находится в соседней галактике.
Отслеживание тенденций COVID-19 в наиболее пострадавших государствах
Исследователи LSU применили вычислительные модели для исследования инфекции COVID-19 ставки в отношении мер социального дистанцирования.Их статья, Эффект смягчения меры по распространению COVID-19 в наиболее пострадавших штатах США, опубликованные в PLOS ONE., Исследует изменение уровня заражения из-за усилий по смягчению и прогнозируют количество смертей и инфекций до сентября 2020 г. для некоторых из наиболее сильно затронутые состояния.
LIGO и Дева объявляют о новых открытиях в обновленном каталоге гравитационных волн
После нескольких месяцев тщательного анализа LIGO Scientific Collaboration и Компания Virgo Collaboration выпустила обновленный каталог обнаружений гравитационных волн.Каталог содержит 39 новых обнаруженных сигналов от столкновений черных дыр или нейтронных звезд. с 1 апреля по окт. 1 января 2019 г., что более чем втрое увеличивает количество подтвержденных обнаружений.
Физики LSU разрабатывают и демонстрируют метод устранения давления квантового излучения Шум в детекторах гравитационных волн
Детекторы гравитационных волн открыли новое окно во Вселенную, измеряя рябь в пространстве-времени, вызванная столкновением черных дыр и нейтронных звезд, но в конечном итоге они ограничены квантовыми флуктуациями, вызванными отражением света от зеркал.LSU Ph.D. выпускник физики Джонатан Крайп, научный сотрудник, NIST, и его команда исследователей LSU провела новый эксперимент с учеными из Калифорнийского технологического института. и Thorlabs, чтобы изучить способ отменить это квантовое обратное действие и улучшить детектор. чувствительность.
Цепи конденсаторов
Конденсаторы используются в цепях постоянного тока, чтобы обеспечить «всплески» энергия.»Типичными примерами могут служить конденсатор для запуска двигателя от внешнего источника или конденсатор, используемый для работы вспышки фотоаппарата.Зарядка
В схеме, показанной ниже, когда переключатель замкнут, заряды сразу начинают течь с аккумулятора на пластины конденсатора. По мере увеличения заряда обкладок конденсатора это переходный ток уменьшается; пока, наконец, ток не перестанет течь и конденсатор полностью заряжен.На схеме, показанной ниже, правая пластина конденсатора будет быть положительно заряженным, а его левая пластина — отрицательно, поскольку пластины произвольно обозначены как + и — в зависимости от их близости к ближайшей батарее Терминал.
Графики зависимости заряда от времени и тока от времени для зарядки конденсаторов показаны ниже. Математически оба этих графика являются экспоненциальными функциями — ток — экспоненциальным распадаются, а заряд — экспоненциальный рост.
Графики зарядного конденсатора
заряд в зависимости от времени
текущая и времяКогда переключатель изначально замкнут, конденсатор не имеют никакого заряда, и правило петли Кирхгофа приведет к уравнение:
— Р- В с = 0
знак равно R
знак равно / RГде представляет собой начальный максимальный ток, протекающий от батареи к пластины конденсатора.Однако этот ток непостоянен. Как раз проходит, на конденсаторе накапливается все больше и больше зарядов. Это в свою очередь увеличивает напряжение на конденсаторе Q = CV. Когда напряжение конденсатор равняется напряжению батареи, заряды перестанут течь. В ток уменьшается со временем.
Теперь мы выведем уравнение для переходного заряда конденсатора. В этом выводе i представляет переходный ток в цепи, когда конденсатор заряжается, q представляет собой переходный процесс заряд, присутствующий на конденсаторе, q (t) представляет собой заряд в любом В данное время t и C — это емкость конденсатора.
Мы будем использовать в качестве начального условия: t = 0, I = / R, и V c = 0. Применяя правило цикла Кирхгофа, получаем
где
Подставляем эти значения и решаем выражение dq / dt получаем
Разделение переменных и интегрирование дает
Чтобы решить для q (t) , мы должны извлечь его из в естественном логарифмическом выражении .
Sincewe теперь возведет обе части нашего уравнения в степень e .
В приведенном выше уравнении Ce представляет собой окончательный общий заряд, присутствующий на пластинах, исходя из Q = CV.
Чтобы вычислить уравнение переходного тока, мы будем используйте тот факт, что и продифференцируем только что выведенное нами уравнение для q (t).
В этих уравнениях произведение RC должно иметь единицы времени, поскольку функция f (x) = e x должна быть безразмерной.Давайте исследуйте эти отношения.
т RC
сек Ом (фарады)
(вольт / ампер) (кулоны / вольт)
кулоны / амперы
кулонов / (кулонов / сек)
секЭтот продукт называется постоянной времени RC .Это сказать нам, когда произошли определенные процентные изменения. Например, при t = 1 RC,
Выгрузка
Когда переключатель замкнут в цепи как показано ниже, зарядка начинается немедленно стекание обкладок конденсатора. Как заряд на обкладках конденсатора уменьшается, ток уменьшается; пока, наконец, ток не перестанет течь и конденсатор полностью разряжен.
Графики зависимости тока от времени и заряда от времени обе будут функциями распада поскольку ток, протекающий через резистор, будет падать в соответствии с потоком зарядить пластины конденсатора.
Разрядный конденсатор графики
текущая и время
заряд в зависимости от времениТеперь мы выведем уравнение для переходного заряда конденсатора.В этом выводе i представляет переходный ток в цепи, когда конденсатор заряжается, q представляет собой переходный процесс заряд, оставшийся на конденсаторе, q (t) представляет собой заряд в любом В данное время t и C — это емкость конденсатора.
Начальный условия таковы, что когда t = 0 и I = V c / Р. Применяя правило петли Кирхгофа, получаем
Чтобы вычислить уравнение переходного тока, мы будем используйте тот факт, что и продифференцируем только что выведенное нами уравнение для q (t).
