где $\bar{p}=m \bar{v}$ — импульс тела, m–масса рассматриваемого тела, $\bar{v}$ — скорость. Надо отметить, что уравнение (1) строго применимо только относительно материальной точки. Если рассматривается протяженное тело, то под скоростью понимают скорость движения центра масс тела.
Если масса материальной точки (m)не изменяется во времени, то формула, определяющая результирующую силу, приложенную к ней (второй закон Ньютона) можно представить в виде:
$$\bar{F}=m \frac{d \bar{v}}{d t}=m \bar{a}(2)$$где $\bar{a}$ – ускорение, которое материальная точка приобретает в результате воздействия на нее силы. Выражение (2) показывает то, что если $\bar{F}$=0, то тело (материальная точка) движется равномерно и прямолинейно или покоится.
Если сила, приложенная к телу, является постоянной (по модулю и направлению), то формулу для нее можно представить в виде:
$$F=\frac{\Delta p}{\Delta t}=\frac{m\left(v_{2}-v_{1}\right)}{t_{2}-t_{1}}$$Единицы измерения силы
В СГС: [F]=дин
1Н=105 дин
Примеры решения задач
Пример
Задание. то, учитывая выражения (1.2) и (1.3), получаем: Так как ay=0, то получаем, что сила, которая действует на нашу точку, направлена по оси X, так как направление ускорение
и силы совпадают, а мы получили: где $\bar{i}$ – единичный вектор, направленный по оси X. Исходя из второго закона Ньютона, имеем: Ответ. Так как $F=m \cdot 6 \alpha t$, то с течением времени сила увеличивается по модулю. Слишком сложно? Формула силы не по зубам? Тебе ответит эксперт через 10 минут! Пример Задание. Два параллелепипеда лежат на горизонтальной поверхности. Они соприкасаются. Данные тела могут
скользить по поверхности опоры без трения. Масса одного тела равна m1, второго — m2. Первое тело толкнули с силой F0. {2}}(1.4)$$
{2}}(1.4)$$ {\prime}}=\left(m_{1}+m_{2}\right) \bar{a}(2.3)$$
{\prime}}=\left(m_{1}+m_{2}\right) \bar{a}(2.3)$$
Из уравнения (2.4) выразим ускорение:
$$a=\frac{F_{0}}{m_{1}+m_{2}}$$Подставим правую часть выражения (2.5) в (2.2) вместо ускорения:
$$F=F_{0}-m_{1} \cdot \frac{F_{0}}{m_{1}+m_{2}}$$Ответ. $F=F_{0}-m_{1} \cdot \frac{F_{0}}{m_{1}+m_{2}}$
Читать дальше: Формула сопротивления.
Все главные формулы по физике — Физика — Теория, тесты, формулы и задачи
Оглавление:
Кинематика
К оглавлению…
Путь при равномерном движении:
Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):
Средняя скорость пути:
Средняя скорость перемещения:
Определение ускорения при равноускоренном движении:
Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:
Средняя скорость при равноускоренном движении:
Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Формула для тормозного пути тела:
Время падения тела при горизонтальном броске с высоты
Дальность полета тела при горизонтальном броске с высоты H:
Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.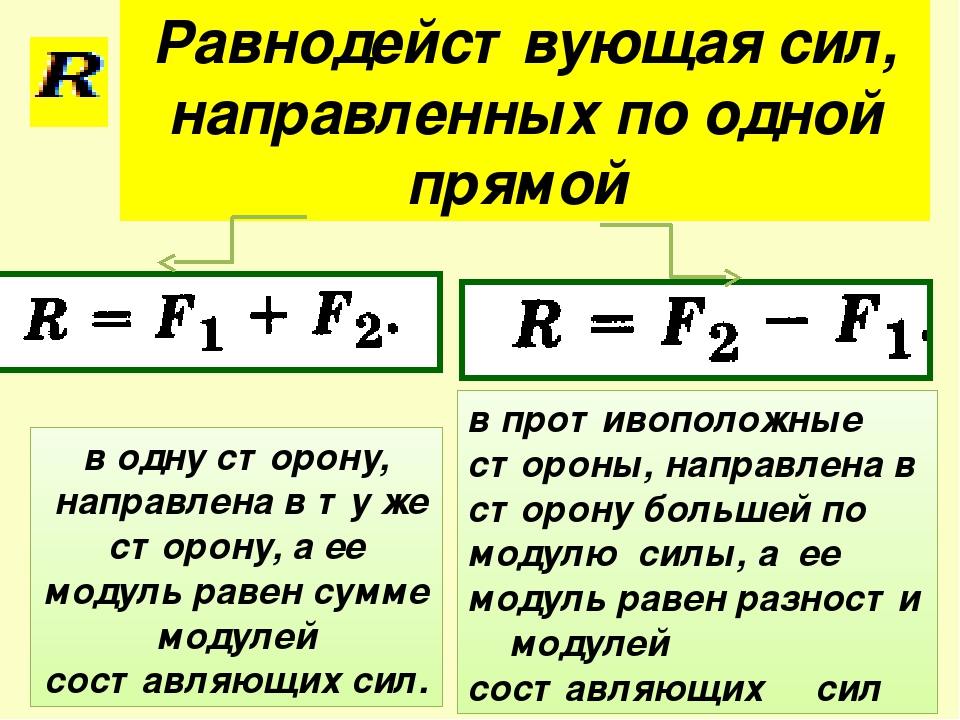 е. тело бросали, например, с земли на землю):
е. тело бросали, например, с земли на землю):
Определение периода вращения при равномерном движении по окружности:
Определение частоты вращения при равномерном движении по окружности:
Связь периода и частоты:
Линейная скорость при равномерном движении по окружности может быть найдена по формулам:
Угловая скорость вращения при равномерном движении по окружности:
Связь линейной и скорости и угловой скорости выражается формулой:
Связь угла поворота и пути при равномерном движении по окружности радиусом R (фактически, это просто формула для длины дуги из геометрии):
Динамика
К оглавлению…
Второй закон Ньютона:
Здесь: F — равнодействующая сила, которая равна сумме всех сил действующих на тело:
Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):
Третий закон Ньютона (сила действия равна силе противодействия):
Сила упругости:
Общий коэффициент жесткости параллельно соединённых пружин:
Общий коэффициент жесткости последовательно соединённых пружин:
Закон всемирного тяготения:
Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:
Где: g — ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:
Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:
Скорость спутника на круговой орбите:
Первая космическая скорость:
Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:
Статика
 ..
..Момент силы определяется с помощью следующей формулы:
Условие при котором тело не будет вращаться:
Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):
Гидростатика
К оглавлению…
Определение давления задаётся следующей формулой:
Давление, которое создает столб жидкости находится по формуле:
Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:
Идеальный гидравлический пресс:
Любой гидравлический пресс:
КПД для неидеального гидравлического пресса:
Сила Архимеда (выталкивающая сила, V — объем погруженной части тела):
Импульс
К оглавлению…
Импульс тела находится по следующей формуле:
Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):
Общий импульс системы тел (важно то, что сумма векторная):
Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:
Закон сохранения импульса.
Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:
Работа, мощность, энергия
К оглавлению…
Механическая работа рассчитывается по следующей формуле:
Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):
Мгновенная механическая мощность:
Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:
Формула для кинетической энергии:
Потенциальная энергия тела поднятого на высоту:
Потенциальная энергия растянутой (или сжатой) пружины:
Полная механическая энергия:
Связь полной механической энергии тела или системы тел и работы внешних сил:
Закон сохранения механической энергии (далее – ЗСЭ). Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):
Молекулярная физика
К оглавлению…
Химическое количество вещества находится по одной из формул:
Масса одной молекулы вещества может быть найдена по следующей формуле:
Связь массы, плотности и объёма:
Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:
Определение концентрации задаётся следующей формулой:
Для средней квадратичной скорости молекул имеется две формулы:
Средняя кинетическая энергия поступательного движения одной молекулы:
Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:
Следствия из основного уравнения МКТ:
Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):
Газовые законы. Закон Бойля-Мариотта:
Закон Бойля-Мариотта:
Закон Гей-Люссака:
Закон Шарля:
Универсальный газовый закон (Клапейрона):
Давление смеси газов (закон Дальтона):
Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:
Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:
Термодинамика
К оглавлению…
Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:
Теплоемкость (С — большое) тела может быть рассчитана через удельную теплоёмкость (c — маленькое) вещества и массу тела по следующей формуле:
Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:
Фазовые превращения.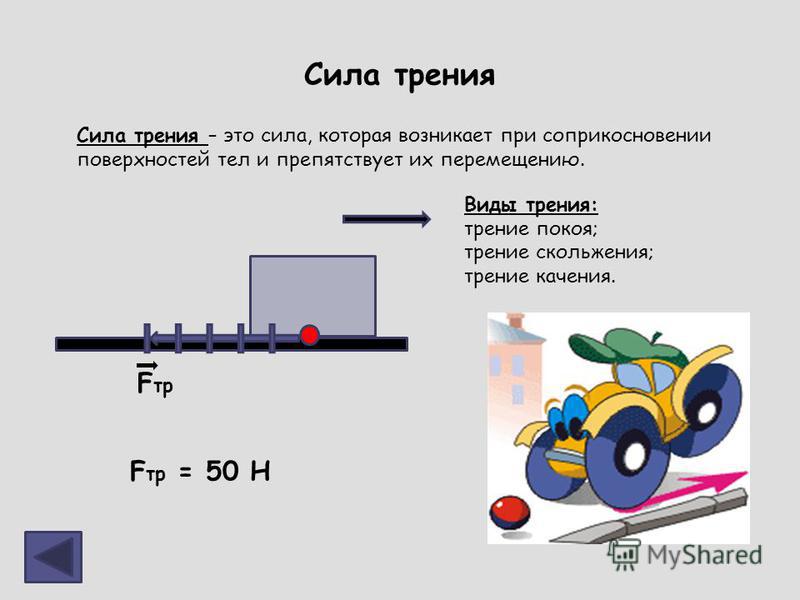 При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:
При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:
При сгорании топлива выделяется количество теплоты равное:
Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):
Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:
Работа идеального газа:
Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа:
Изменение внутренней энергии рассчитывается по формуле:
Первый закон (первое начало) термодинамики (ЗСЭ):
Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):
Изохорный процесс (V = const):
Изобарный процесс (p = const):
Изотермический процесс (T = const):
Адиабатный процесс (Q = 0):
КПД тепловой машины может быть рассчитан по формуле:
Где: Q1 – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q2 – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:
Наибольший КПД при заданных температурах нагревателя T1 и холодильника T2, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:
Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):
Относительная влажность воздуха может быть рассчитана по следующим формулам:
Потенциальная энергия поверхности жидкости площадью S:
Сила поверхностного натяжения, действующая на участок границы жидкости длиной L:
Высота столба жидкости в капилляре:
При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:
В этом случае высота столба жидкости в капилляре станет равной:
При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Электростатика
К оглавлению…
Электрический заряд может быть найден по формуле:
Линейная плотность заряда:
Поверхностная плотность заряда:
Объёмная плотность заряда:
Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):
Где: k — некоторый постоянный электростатический коэффициент, который определяется следующим образом:
Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):
Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):
Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:
Напряженность электрического поля, которую создает заряженная плоскость:
Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:
Электрическое напряжение это просто разность потенциалов, т. е. определение электрического напряжения может быть задано формулой:
е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
Определение потенциала задаётся выражением:
Потенциал, который создает точечный заряд или заряженная сфера:
Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):
Для диэлектрической проницаемости вещества верно следующее:
Определение электрической ёмкости задаётся формулой:
Ёмкость плоского конденсатора:
Заряд конденсатора:
Напряжённость электрического поля внутри плоского конденсатора:
Сила притяжения пластин плоского конденсатора:
Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):
Объёмная плотность энергии электрического поля:
Электрический ток
К оглавлению. ..
..
Сила тока может быть найдена с помощью формулы:
Плотность тока:
Сопротивление проводника:
Зависимость сопротивления проводника от температуры задаётся следующей формулой:
Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):
Закономерности последовательного соединения:
Закономерности параллельного соединения:
Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:
Закон Ома для полной цепи:
Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):
Сила тока короткого замыкания:
Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:
Мощность электрического тока:
Энергобаланс замкнутой цепи
Полезная мощность или мощность, выделяемая во внешней цепи:
Максимально возможная полезная мощность источника достигается, если R = r и равна:
Если при подключении к одному и тому же источнику тока разных сопротивлений R1 и R2 на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:
Мощность потерь или мощность внутри источника тока:
Полная мощность, развиваемая источником тока:
КПД источника тока:
Электролиз
Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:
Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:
Он может быть рассчитан по формуле:
Где: n – валентность вещества, NA – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:
Магнетизм
К оглавлению…
Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:
Момент сил действующих на рамку с током:
Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:
Радиус траектории полета заряженной частицы в магнитном поле:
Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:
Индукция поля в центре витка с током радиусом R:
Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:
Магнитная проницаемость вещества выражается следующим образом:
Магнитным потоком Φ через площадь S контура называют величину заданную формулой:
ЭДС индукции рассчитывается по формуле:
При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):
Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:
Индуктивность катушки:
Где: n — концентрация витков на единицу длины катушки:
Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:
ЭДС самоиндукции возникающая в катушке:
Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):
Объемная плотность энергии магнитного поля:
Колебания
К оглавлению. ..
..
Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω0:
Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:
Период колебаний вычисляется по формуле:
Частота колебаний:
Циклическая частота колебаний:
Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:
Максимальное значение скорости при гармонических механических колебаниях:
Зависимость ускорения от времени при гармонических механических колебаниях:
Максимальное значение ускорения при механических гармонических колебаниях:
Циклическая частота колебаний математического маятника рассчитывается по формуле:
Период колебаний математического маятника:
Циклическая частота колебаний пружинного маятника:
Период колебаний пружинного маятника:
Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:
Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:
Взаимосвязь энергетических характеристик механического колебательного процесса:
Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:
Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:
Циклическая частота колебаний в электрическом колебательном контуре:
Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:
Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:
Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:
Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:
Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:
Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом.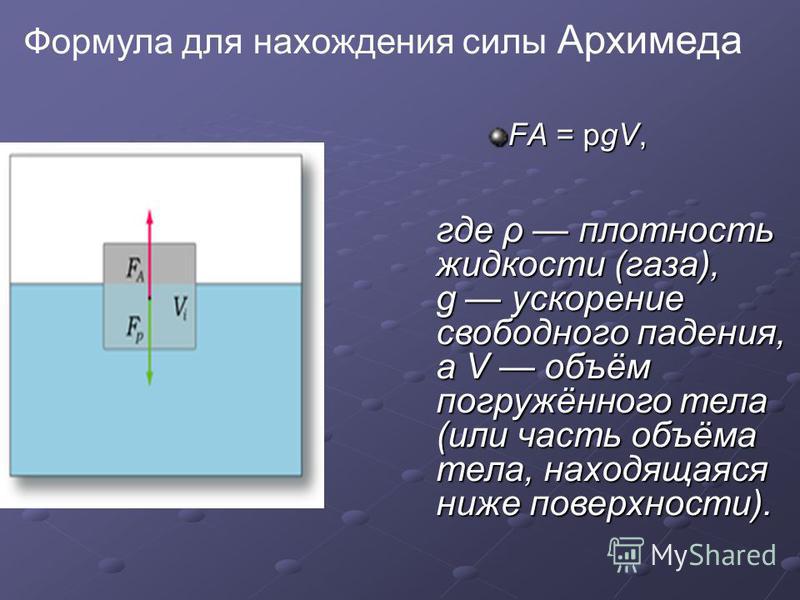 Действующее значение силы тока:
Действующее значение силы тока:
Действующее значение напряжения:
Мощность в цепи переменного тока:
Трансформатор
Если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2, то выполняется следующее соотношение:
Коэффициент трансформации вычисляется по формуле:
Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):
В неидеальном трансформаторе вводится понятие КПД:
Волны
Длина волны может быть рассчитана по формуле:
Разность фаз колебаний двух точек волны, расстояние между которыми l:
Скорость электромагнитной волны (в т.ч. света) в некоторой среде:
Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙108 м/с, она также может быть вычислена по формуле:
Скорости электромагнитной волны (в т. ч. света) в среде и в вакууме также связаны между собой формулой:
ч. света) в среде и в вакууме также связаны между собой формулой:
При этом показатель преломления некоторого вещества можно рассчитать используя формулу:
Оптика
К оглавлению…
Оптическая длина пути определяется формулой:
Оптическая разность хода двух лучей:
Условие интерференционного максимума:
Условие интерференционного минимума:
Формула дифракционной решетки:
Закон преломления света на границе двух прозрачных сред:
Постоянную величину n21 называют относительным показателем преломления второй среды относительно первой. Если n1 > n2, то возможно явление полного внутреннего отражения, при этом:
Формула тонкой линзы:
Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета:
Атомная и ядерная физика
К оглавлению. ..
..
Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:
Импульс фотона:
Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):
Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение Uз и элементарный заряд е:
Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:
Второй постулат Бора или правило частот (ЗСЭ):
В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:
На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:
Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:
Дефект массы:
Энергия связи ядра выраженная в единицах СИ:
Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):
Формула альфа-распада:
Формула бета-распада:
Закон радиоактивного распада:
Ядерные реакции
Для произвольной ядерной реакции описывающейся формулой вида:
Выполняются следующие условия:
Энергетический выход такой ядерной реакции при этом равен:
Основы специальной теории относительности (СТО)
К оглавлению. ..
..
Релятивистское сокращение длины:
Релятивистское удлинение времени события:
Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:
Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:
Энергия покоя тела:
Любое изменение энергии тела означает изменение массы тела и наоборот:
Полная энергия тела:
Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:
Релятивистское увеличение массы:
Кинетическая энергия тела, движущегося с релятивистской скоростью:
Между полной энергией тела, энергией покоя и импульсом существует зависимость:
Равномерное движение по окружности
К оглавлению…
В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, an – центростремительное ускорение, L – длина дуги окружности, t – время):
Расширенная PDF версия документа «Все главные формулы по школьной физике»:
К оглавлению. ..
..
Сила тяжести, трения, реакции опоры, упругости, Архимеда, сопротивления, вес. Направление, точка приложения, природа возникновения
Тестирование онлайн
Что надо знать о силе
Сила — векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле
Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
Сила тяжести всегда направлена вертикально вниз.
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:
Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы «говорит» реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, «сопротивляются».
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину — уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Во всех этих примерах возникает сила, которая препятствует деформации — сила упругости.
Закон Гука
Сила упругости направлена противоположно деформации.
Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле
При параллельном соединении жесткость
Жесткость образца. Модуль Юнга.
Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
Вес тела
Вес тела — это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
Сила тяжести — сила, которая возникает в результате взаимодействия с Землей. Вес — результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же — сила, которая приложена на опору (не на предмет)!
Формулы определения веса нет. Обозначается эта силы буквой .
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.
Сила реакции опоры и вес — силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес — это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость — состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!
Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес — сила, измеряется в Ньютонах. Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Как верно ответить на вопрос: «Сколько ты весишь»? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка — отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше — тонет.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Поэтому на схемах различные точки приложения переносят в одну точку — в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Рассмотрим взаимное притяжение предмета и Земли. Между ними, согласно закону гравитации возникает сила
А сейчас сравним закон гравитации и силу тяжести
Величина ускорения свободного падения зависит от массы Земли и ее радиуса! Таким образом, можно высчитать, с каким ускорением будут падать предметы на Луне или на любой другой планете, используя массу и радиус той планеты.
Расстояние от центра Земли до полюсов меньше, чем до экватора. Поэтому и ускорение свободного падения на экваторе немного меньше, чем на полюсах. Вместе с тем, следует отметить, что основной причиной зависимости ускорения свободного падения от широты местности, является факт вращения Земли вокруг своей оси.
При удалении от поверхности Земли сила земного тяготения и ускорения свободного падения изменяются обратно пропорционально квадрату расстояния до центра Земли.
Сила тяжести: формула, единицы измерения, особенности
Сила тяжести и ее источник: FreepickРазбираетесь с такой физической категорией, как сила тяжести? Формула, ее составляющие и единицы измерения укажут, что сильнее притянет Земля — яблоко или поезд. Отличается ли сила тяжести от силы тяготения? Объясним, как не перепутать эти две величины.
Что такое сила тяжести
Каждый день наблюдаем, как тела вокруг деформируются (меняют форму или размеры), ускоряются или тормозят, падают. В реальной жизни с различными телами происходят самые разнообразные вещи. Причина всех действий и взаимодействий кроется в некой силе. О чем идет речь?
В реальной жизни с различными телами происходят самые разнообразные вещи. Причина всех действий и взаимодействий кроется в некой силе. О чем идет речь?
Понятие силы
Силой называют физическую векторную величину, которая оказывает воздействие на тело, а ее источниками становятся другие тела. Что означает понятие векторной величины? Это говорит о том, что сила наделена направлением. В зависимости от того, куда она направлена, можно получить разные результаты.
Это как если стоять на вершине горы на сноуборде, то от направления толчка будет зависеть дальнейшее движение. Таков результат приложения силы в этом случае. Силы, которые изучают ученые-физики, разнообразны и очень важны для нашей повседневной жизни.
Определение и значение силы тяжести
Одна из них носит название сила тяжести. Физика предлагает следующее определение: сила тяжести — это величина, которая показывает, насколько сильно Земля притягивает тело, которое расположено на ее поверхности или рядом с ней.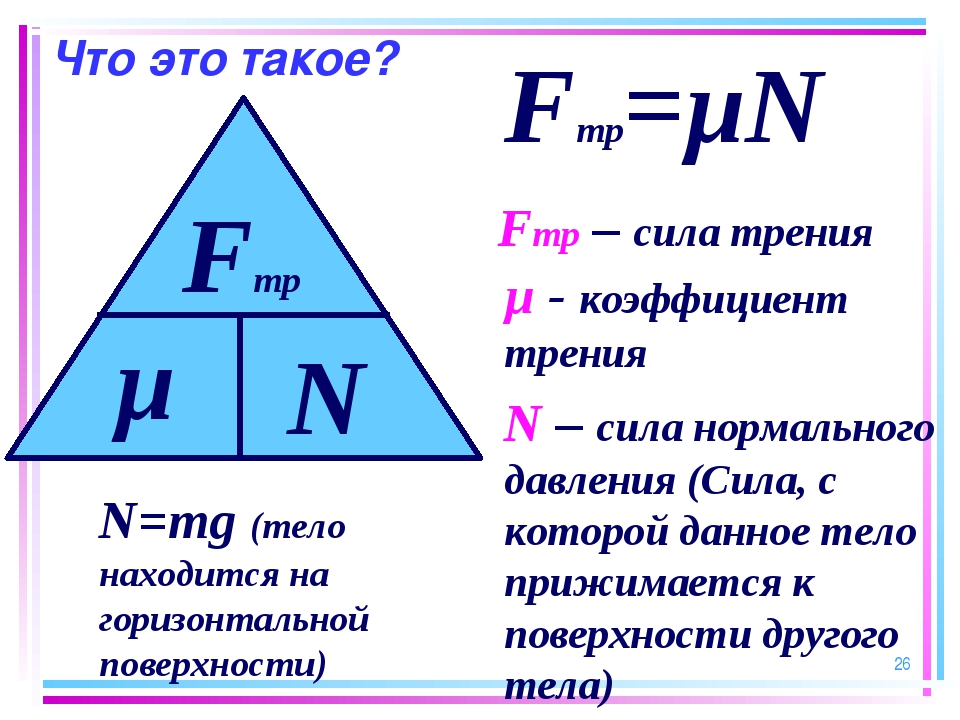 Таким образом, направление этой силы — центр нашей планеты.
Таким образом, направление этой силы — центр нашей планеты.
Сила тяжести на Земле крайне важна по следующим причинам:
- Наша планета притягивает все, что попадает в сферу действия этой силы, будь то твердое тело, жидкость или газ.
- Благодаря ее существованию стало возможным создание атмосферы (молекулы газов, которые ее составляют, не улетают в космические просторы), появились и остаются на своих местах моря и океаны.
- Любой предмет, который приподнимаем и роняем, обязательно упадет вниз по направлению к Земле.
Кстати, именно из-за воздействия этой силы люди не могут летать. Самостоятельно развить скорость, на которой полет становится возможным (так называемую первую космическую) человек не способен, а потому в обычной жизни всегда твердо стоит ногами на Земле.
Сила тяжести и сила тяготения: отличия
Падение перьев как пример силы тяжести: FreepickСила тяжести, определение которой дали выше, схожа с силой тяготения. Оба варианта связывает сила притяжения.
Однако эти две силы не одно и то же, хоть их и часто путают. Давайте разберемся, в чем тут дело.
Еще в 1682 году Исаак Ньютон открыл закон о всемирном тяготении. Сформулирован он был так: тела притягивают друг друга, а сила этого тяготения — величина, прямо пропорциональная произведению их масс и обратно пропорциональна расстоянию, возведенному в квадрат.
Математически силу тяготения записывают так: F = G×M×m/R², где:
- F — сила тяготения, Н;
- M — масса первого тела (часто планеты), кг;
- m — масса второго тела, кг;
- R — дистанция между ними, м;
- G — постоянная величина (G = 6,67×10⁻¹¹ м³×кг⁻¹×с⁻²).
Продемонстрировать эту силу легко — достаточно встать на весы. Стрелка сразу же отклонится, показывая вес тела. Так происходит из-за очень большой массы Земли, благодаря которой мы придавлены к ней. На Луне, масса которой меньше, вес человека меньше в несколько раз.
Итак, закон о всемирном тяготении и соответствующая сила необходимы для вычисления силы взаимодействий между разнообразными телами. При этом их размеры должны быть меньше, чем расстояние между ними.
При этом их размеры должны быть меньше, чем расстояние между ними.
Теперь вернемся к нашей теме и рассмотрим подробно, что же такое сила тяжести, обозначение которой дали выше, и как она связана с силой тяготения.
Сила тяжести: формула, единицы измерения
Напомним, что когда говорим о силе тяжести, то имеем в виду силу, с которой осуществляет притяжение наша планета.
Формула силы тяжести такова: F = m×g, где:
- F — сила тяжести, Н;
- m — масса тела, кг;
- g — ускорение свободного падения, м/с².
В этой формуле видим новую величину — ускорение свободного падения. Так называют ускорение, которое приобретает тело рядом с Землей во время свободного и беспрепятственного падения. Рядом с поверхностью Земли значение этой величины примерно равняется 9,81 м/с², а в приблизительных расчетах используют округленное значение 10 м/с².
По этой формуле рассчитывается сила тяжести, единица измерения которой — Ньютоны (в честь Исаака Ньютона).
Чему равна сила тяжести? Глядя на эту формулу, можно сказать, что сила тяжести схожа с весом тела. В покое на Земле эта величина и вес будут идентичны. Но это не одно и то же. Почему? Объяснение не сложное:
- Силой, с которой на тела действует Земля, называют силу тяжести.
- Вес тоже сила, с которой тела действуют на опору.
- То есть у них отличаются точки действия: первая направлена на центр массы тел, а вес направлен на опору.
Кроме того, на величину силы тяжести влияет масса и планета, на которой проводятся измерения. Вес определяется также ускорением, с которым происходит движение тела и опоры.
К примеру, вес тела в лифте определяется тем, в каком направлении и как быстро происходит движение тела. Сила тяжести не учитывает, куда и что движется: эти внешние факторы на нее не влияют.
Итак, с весом разобрались. А что же с силой тяготения, которую упоминали выше? Можем ли две эти силы приравнять? На этот раз ответ будет утвердительным. Но только, когда мы говорим о Земле и теле, которое к ней притягивается. В этом случае обе силы будут равны.
Но только, когда мы говорим о Земле и теле, которое к ней притягивается. В этом случае обе силы будут равны.
Выразим это математически:
- F = m×g.
- F = G×M×m/R².
- m×g = G×M×m/R².
Если обе части полученного уравнения разделить на массу, то получим такую формулу: g = G×M/R².
Величина g (ускорение свободного падения) уникальна для каждой планеты:
- На нашей Земле свободно падающее тело с каждой секундой ускоряется примерно на 9,81 метр (м/с²).
- Ускорение свободного падения рядом с Луной имеет величину всего 1,62 м/с².
- На Юпитере это значение достигает 26,2 м/с². Человек, который весит 60 кг, на этой планете почувствует себя так, будто бы поправился на 100 кг.
Как изменится величина, если тело будет падать 4 секунды? Попробуем подсчитать:
- Скорость падения в начальной точке составит 0 м/с².
- В течение первой секунды она увеличится до 9,81 м/с².
- За вторую секунду величина вырастет вдвое и составит 19,62 м/с².

- Третья секунда добавить еще одну величину ускорения и получится 29,43 м/с².
- В четвертую секунду скорость движения тела достигнет 39,24 м/с², что равняется приблизительно 141 км/ч.
Отметим, что яблоко и кирпич будут падать с равной скоростью. Только очень легкие предметы во время падения замедляет воздух, оказывая им ощутимое сопротивление. Так, птичье перышко будет совершать падение очень медленно и плавно.
Задумываемся об этом или нет, на каждого из нас оказывает воздействие сила тяжести. Формула ее расчета состоит из массы, умноженной на величину ускорения свободного падения. Эта сила показывает воздействие планет на тела, которые находятся рядом с их поверхностями. Поэтому ее величина отличается на Земле и на Луне.
Оригинал статьи: https://www.nur.kz/family/school/1909020-sila-tyazhesti-formula-edinitsy-izmereniya-osobennosti/
Формулы по физике 7 класс
Формула Обозначение Ед. измерения
измерения
S=ab a-длина м
b-ширина м
с- высота м
S- площадь м2
V=abc V- объем м3
ѵ=s / t ѵ-скорость м/с
s-путь м
t-время с
m=𝛒 V m-масса кг
V-объем м3
𝛒- плотность кг/м3 стр 50-51
Fтяж=mg Fтяж-сила тяжести Н
g=10Н\кг ускорение свободного
падения
Р=mg P-вес тела Н
Fупр=к 𝛥х Fупр— сила упругости Н
к- жесткость пружины Н/м
𝛥х- удлинение пружины м
Fтр=𝜇 N Fтр-сила трения Н
𝜇-коэффициент трения
N- сила реакции опоры ( N=mg)
R=F1+F2R-равнодействующая сила
R=F2-F1
p=F / S p-давление Па
( твердые тела)
p= g𝛒h 𝛒-плотность жидкости
(в жидкости) h-глубина
1мм рт.ст. =133,3 Па
F2/F1=S2/S1F1,F2-силы действующие на пресс
S1,S2-площади поршней пресса
А= Fs A-работа Дж
N= A/t N-мощность Вт
N= F ѵ ѵ скорость
F1*L1= F2*L2 равновесие рычага
М=F*L M-момент силы Нм
КПД= Ап / Аз
Формула Обозначение Ед.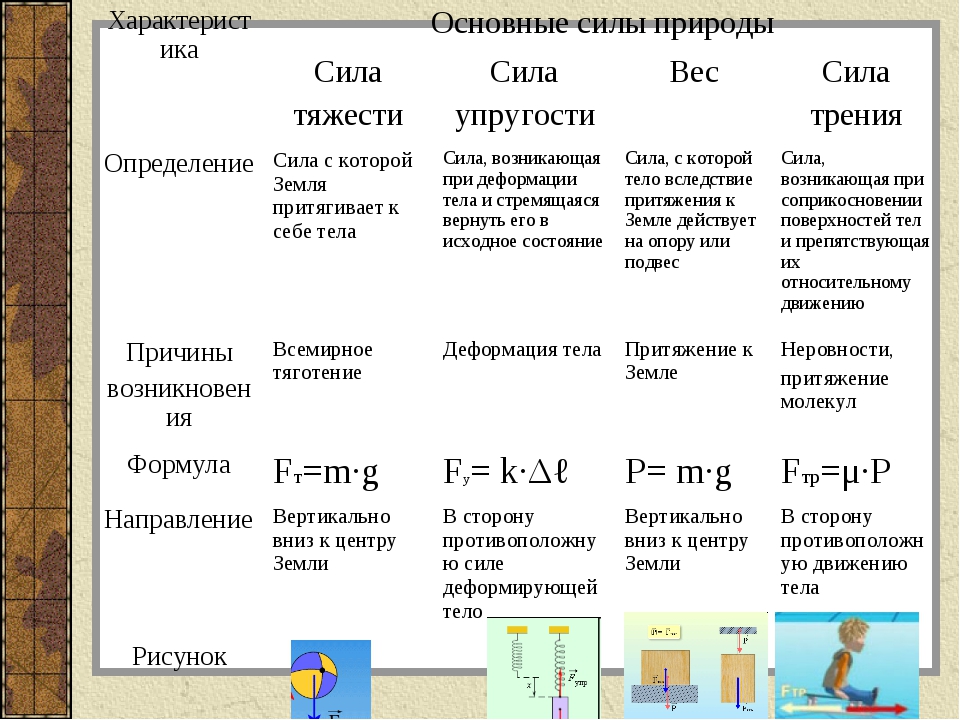 измерения
измерения
S=ab a-длина м
b-ширина м
с- высота м
S- площадь м2
V=abc V- объем м3
ѵ=s / t ѵ-скорость м/с
s-путь м
t-время с
m=𝛒 V m-масса кг
V-объем м3
𝛒- плотность кг/м3 стр 50-51
Fтяж=mg Fтяж-сила тяжести Н
g=10Н\кг ускорение свободного
падения
Р=mg P-вес тела Н
Fупр=к 𝛥х Fупр— сила упругости Н
к- жесткость пружины Н/м
𝛥х- удлинение пружины м
Fтр=𝜇 N Fтр-сила трения Н
𝜇-коэффициент трения
N- сила реакции опоры ( N=mg)
R=F1+F2R-равнодействующая сила
R=F2-F1
p=F / S p-давление Па
( твердые тела)
p= g𝛒h 𝛒-плотность жидкости
(в жидкости) h-глубина
1мм рт.ст. =133,3 Па
F2/F1=S2/S1F1,F2-силы действующие на пресс
S1,S2-площади поршней пресса
А= Fs A-работа Дж
N= A/t N-мощность Вт
N= F ѵ ѵ скорость
F1*L1= F2*L2 равновесие рычага
М=F*L M-момент силы Нм
КПД= Ап / Аз
Формула Обозначение Ед. измерения
измерения
S=ab a-длина м
b-ширина м
с- высота м
S- площадь м2
V=abc V- объем м3
ѵ=s / t ѵ-скорость м/с
s-путь м
t-время с
m=𝛒 V m-масса кг
V-объем м3
𝛒- плотность кг/м3 стр 50-51
Fтяж=mg Fтяж-сила тяжести Н
g=10Н\кг ускорение свободного
падения
Р=mg P-вес тела Н
Fупр=к 𝛥х Fупр— сила упругости Н
к- жесткость пружины Н/м
𝛥х- удлинение пружины м
Fтр=𝜇 N Fтр-сила трения Н
𝜇-коэффициент трения
N- сила реакции опоры ( N=mg)
R=F1+F2R-равнодействующая сила
R=F2-F1
p=F / S p-давление Па
( твердые тела)
p= g𝛒h 𝛒-плотность жидкости
(в жидкости) h-глубина
1мм рт.ст. =133,3 Па
F2/F1=S2/S1F1,F2-силы действующие на пресс
S1,S2-площади поршней пресса
А= Fs A-работа Дж
N= A/t N-мощность Вт
N= F ѵ ѵ скорость
F1*L1= F2*L2 равновесие рычага
М=F*L M-момент силы Нм
КПД= Ап / Аз
Определение работы силы с помощью интеграла
Известную формулу из физики A = Fs
для определения работы силы можно использовать лишь тогда, когда на тело воздействует постоянная сила,
направленная по направлению движения.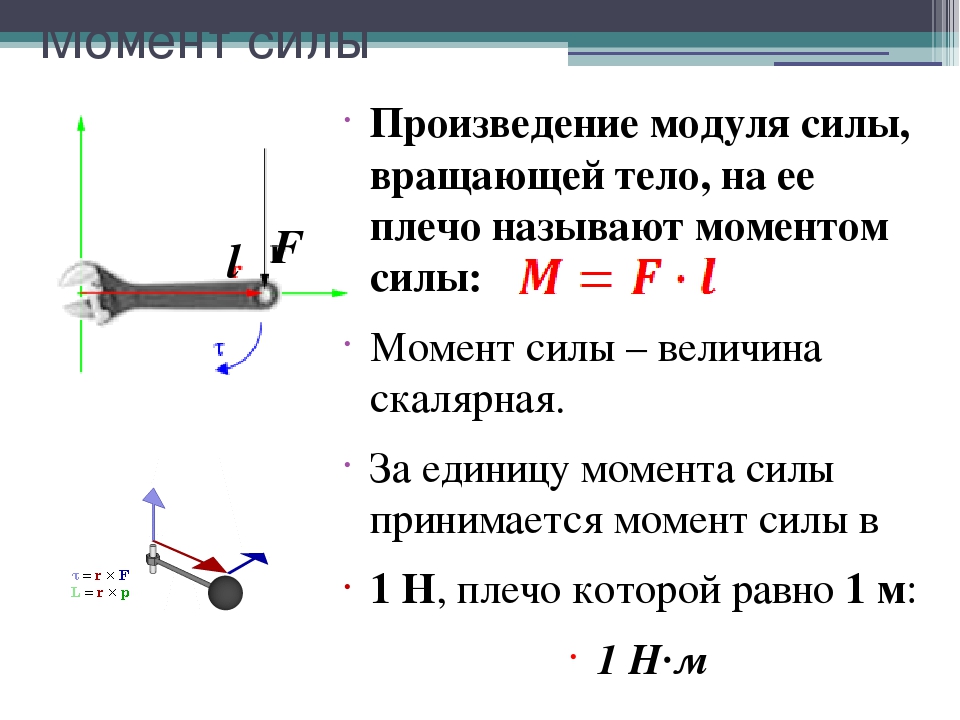 Однако часто требуется определить работу тогда, когда сила изменяется
с пройденным путём. Например, чтобы растянуть пружину, нужно приложить силу, которая пропорциональна
пройденному пути — удлиннению пружины.
Однако часто требуется определить работу тогда, когда сила изменяется
с пройденным путём. Например, чтобы растянуть пружину, нужно приложить силу, которая пропорциональна
пройденному пути — удлиннению пружины.
Пусть тело перемещается по отрезку [a, b] оси Ox, при этом проекция вектора силы на ось Ox является функцией F(x) аргумента x. Чтобы определить работу, совершённую силой, разделим отрезок [a, b] на n частей точками a = x0 < x1 < x2 < …xn = b. Таким образом, всё перемещение тела из a в b состоит из n участков пути.
Приложенная сила A будет равна сумме элементарных работ, совершённых при перемещении тела по каждому из участков пути.
Поэтому вся приложенная сила для перемещения тела по прямой будет равна пределу интегральной суммы или определённому интегралу
. (1)
(1)
Это и есть формула для определения работы силы.
Пример 1. Сжатие S винтовой пружины пропорционально приложенной силе F. Вычислить работу силы F при сжатии пружины на 5 см, если для сжатия её на 1 см нужна сила в 1 кг.
Решение. Сила F и перемещение S связаны по условию зависимостью F=kS, где k — постоянная. Будем выражать S в метрах, F — в килограммах. При S=0,01 F=1, то есть 1=k*0,01, откуда k=100, F=100S.
По формуле (1) определяем работу силы:
.
Пример 2. Сила F, с которой электрический заряд e1 отталкивает заряд e2 (того же знака), находящийся от него на расстоянии r, выражается формулой
,
где k — постоянная.
Вычислить работу силы F при перемещении заряда e2 из точки A1, отстоящей от e1 на расстоянии r1, в точку A2, отстоящую от e1 на расстоянии r2, полагая, что заряд e1 помещён в точке A0, принятой за начала отсчёта.
Решение. По формуле (1) вычисляем работу силы:
.
При получим
.
При получим . Последняя величина называется потенциалом поля, создаваемого зарядом e1.
Пример 3. Вычислить работу, которую нужно совершить, чтобы вытащить шарик массой 9 г из бочки, высота которой 3 м.
Решение. Из физики известно, что F=Ph, то есть
. Вес шарика будет
равен произведению массы на ускорение свободного падения, то есть P=gm, где
g=9,8. Теперь можем вычислить работу силы:
Теперь можем вычислить работу силы:
Начало темы «Интеграл»
Теория для 2 задания ЕГЭ по физике
2 задание в ЕГЭ по физике связано с основными силами в природе: трением, тяжестью и упругостью, законами Ньютона и законом всемирного тяготения. Теории по этим темам несложные, а вот решение задач часто вызывает у школьников затруднения. Дело в том, что нужно не просто знать формулы, но и уметь правильно их применять, понимать особенности разных физических процессов. Всему этому учат на курсах подготовки к ЕГЭ. Там вам расскажут, как решать 2 задание из ЕГЭ по физике. А если вы хотите понять основы этой темы, читайте нашу статью.
Первый закон Ньютона
Первый закон Ньютона существует только в инерциальных системах отсчета. Это такие системы, в которых материальная точка без воздействия внешних сил не двигается, либо двигается равномерно и прямолинейно. На самом деле, настоящие инерциальные системы невозможны. Для существования системы нужна связь с каким-то объектом, например, полом. Но любые объекты во Вселенной движутся с определенным ускорением, поэтому деление систем на инерциальные и неинерциальные носит условный характер. Эта информация не нужна для 2 задания по физике, но ее нужно понимать.
На самом деле, настоящие инерциальные системы невозможны. Для существования системы нужна связь с каким-то объектом, например, полом. Но любые объекты во Вселенной движутся с определенным ускорением, поэтому деление систем на инерциальные и неинерциальные носит условный характер. Эта информация не нужна для 2 задания по физике, но ее нужно понимать.
Сам первый закон Ньютона (закон инерции) звучит так: «До тех пор, пока к телу не приложится сила извне, оно находится в покое или движется равномерно и прямолинейно». Это один из трех основных законов механики. Он не определяется формулами, поэтому не используется в задачах 2 задания физики. Но, он дает понимание того, что в механике изучаются только инерциальные системы отсчета.
Принцип относительности Галилея
Галилей занимался изучением разных инерциальных систем. В частности, он создал так называемые преобразования Галилея, которые показывают, как меняются координаты при переходе из одной системы отсчета в другую. При этом основные уравнения, объясняющие законы механики, не изменяются. Принцип относительности выглядит так: «Законы механики одинаковы для всех инерциальных систем отсчета». Сами преобразования довольно сложны, они не нужны для решения 2 задания из ЕГЭ по физике, поэтому здесь мы их приводить не будем. Галилей доказал, что невозможно изучать движение одной системы координат относительно другой. Мы не можем понять, как двигается поезд, находясь внутри него. Для нас он неподвижен, а для людей, стоящих на перроне, быстро проезжает мимо. Нужно понимать и то, что тождественно не само движение, а лишь его законы. Если мы встанем у окна движущегося поезда и подкинем камень, относительно поезда его траектория будет вертикальной. Люди, заглянувшие к нам в окно, увидят параболу.
При этом основные уравнения, объясняющие законы механики, не изменяются. Принцип относительности выглядит так: «Законы механики одинаковы для всех инерциальных систем отсчета». Сами преобразования довольно сложны, они не нужны для решения 2 задания из ЕГЭ по физике, поэтому здесь мы их приводить не будем. Галилей доказал, что невозможно изучать движение одной системы координат относительно другой. Мы не можем понять, как двигается поезд, находясь внутри него. Для нас он неподвижен, а для людей, стоящих на перроне, быстро проезжает мимо. Нужно понимать и то, что тождественно не само движение, а лишь его законы. Если мы встанем у окна движущегося поезда и подкинем камень, относительно поезда его траектория будет вертикальной. Люди, заглянувшие к нам в окно, увидят параболу.
Взаимодействие
Тела и частицы постоянно сталкиваются и действуют друг на друга. Это приводит к изменению траектории движения. Это явление физики называют взаимодействием. Оно осуществляется через поля (электромагнитное, гравитационное), действующие на все объекты во Вселенной. Существуют фундаментальные взаимодействия. Они являются основой всех процессов, их нельзя свести к еще более простым явлениям. Некоторые ученые предполагают, что фундаментальные взаимодействия — лишь частный случай одного объединенного. Для решения 2 задания по физике нужно знать, что из себя представляют эти взаимодействия:
Существуют фундаментальные взаимодействия. Они являются основой всех процессов, их нельзя свести к еще более простым явлениям. Некоторые ученые предполагают, что фундаментальные взаимодействия — лишь частный случай одного объединенного. Для решения 2 задания по физике нужно знать, что из себя представляют эти взаимодействия:
- гравитационное. Распространяется на все объекты во Вселенной, от мельчайших частиц до огромных планет. Радиус действия бесконечен, а относительную интенсивность принимают за единицу. Но, для небольших объектов эти взаимодействия столь незначительны, что ими принято пренебрегать. Они приобретает значение при изучении небесных объектов;
- слабое. Присуще всем частицам кроме фотона. Благодаря этому взаимодействию проходят почти все ядерные реакции. Радиус равен 10-17 (поэтому не ощущается человеком и влияет лишь на мельчайшие частицы), а относительная интенсивность — 1032;
- электромагнитное.
 Связывает электроны с ядром, объединяет атомы в молекулы, а молекулы в вещества. Это взаимодействие объясняет многие механические процессы. У него бесконечный радиус действия, но оно почти не оказывает влияния на макрообъекты, так как они нейтральны. Относительная интенсивность — 1036;
Связывает электроны с ядром, объединяет атомы в молекулы, а молекулы в вещества. Это взаимодействие объясняет многие механические процессы. У него бесконечный радиус действия, но оно почти не оказывает влияния на макрообъекты, так как они нейтральны. Относительная интенсивность — 1036; - сильное. Действует только на адроны, обеспечивает нахождение нуклонов в ядре. Радиус действия — 10-15, а относительная интенсивность равна 1038.
Сила
Следующая часть теории ко 2 заданию по физике связана с понятием силы. Это величина, которая показывает, как тела влияют друг на друга. Силы в механике обусловлены только теми взаимодействиями, у которых есть неограниченный радиус действия. Сильные и слабые существуют при таких малых масштабах, что законы Ньютона к ним неприменимы. В рамках механики считается, что возникновение силы приводит к изменению скорости. Она может действовать напрямую или посредством образования полей. Кроме того, она придает объекту ускорение. Величина обозначается как F и измеряется в Ньютонах (Н). При решении задач нужно указывать точку приложения.
Величина обозначается как F и измеряется в Ньютонах (Н). При решении задач нужно указывать точку приложения.
Принцип суперпозиции
В реальном мире тела подвержены воздействию нескольких сил одновременно. В таком случае гораздо удобнее пользоваться суммарной силой. Она равна векторной сумме всех сил, действующих на предмет или частицу. В этом и заключается принцип суперпозиции тел. Не забывайте, что при расчете нужно пользоваться правилами векторного сложения. Запомните это правило, оно пригодится при решении 2 задания по физике.
Второй закон Ньютона
Второй закон Ньютона называют также законом ускорения. Он позволяет связать силу, ускорение и массу тела. Закон также представляет собой важнейшую формулу для 2 задания ЕГЭ по физике: a = F / m. Получается, что ускорение растет с увеличением приложенной к телу силы. Увеличение массы, наоборот, уменьшает ускорение.
Третий закон Ньютона
Объектом исследования первых двух законов Ньютона является одно тело, на которое действует бесконечное количество других. В третьем анализируется система, состоящая из двух тел, действующих друг на друга. Ньютон доказал, что сила этих взаимодействий равна, потому что иначе система потеряла бы устойчивость. Закон сформулирован так: «У каждой силы есть противодействующая, они равны и противоположны по направлению». Но нужно понимать, что силы при этом не могут уравновесить друг друга, так как относятся к разным телам. В математическом виде это записывается так: F1 = -F2. Для решения 2 задания по физике может пригодиться и другая форма записи: a1 / a2 = m1 / m2.
В третьем анализируется система, состоящая из двух тел, действующих друг на друга. Ньютон доказал, что сила этих взаимодействий равна, потому что иначе система потеряла бы устойчивость. Закон сформулирован так: «У каждой силы есть противодействующая, они равны и противоположны по направлению». Но нужно понимать, что силы при этом не могут уравновесить друг друга, так как относятся к разным телам. В математическом виде это записывается так: F1 = -F2. Для решения 2 задания по физике может пригодиться и другая форма записи: a1 / a2 = m1 / m2.
Упругость
Упругость — свойство, которое позволяет телам деформироваться (менять форму и размер), а потом возвращаться в первоначальное состояние. Деформации при этом могут быть любыми, упругость есть и у твердых тел, и у жидкостей, и у газов. Деформированное тело стремится вернуть свою привычную форму и размер, при этом возникает сила упругости. Она часто встречается во 2 задании.
Она часто встречается во 2 задании.
Закон Гука
Закон Гука тоже связан с упругостью. Для решения задач нужно знать его математическое отражение, оно является еще одной формулой для 2 задания ЕГЭ по физике: Fупр = -kx. x означает удлинение тела (в случае с пружиной), а минус показывает, что удлинение направлено против силы упругости. k — это коэффициент пропорциональности или жесткость. Она своя для каждого тела. Чем выше ее значение, тем сложнее деформировать объект. Еще один важный момент: закон Гука можно использовать, только если деформации незначительные. Если они большие, зависимость перестает быть линейной, а при дальнейшем воздействии тело разрушается.
Трение
Еще одна часть теории для 2 задания ЕГЭ по физике — сила трения. Трение возникает при соприкосновении тел, оно препятствует их движению. При этом возникает сила трения. Она имеет электромагнитную природу и бывает трех типов:
- трение покоя возникает, если тела не двигаются.
 Оно не дает шнуркам развязываться, а гвоздям — выпадать из стены. Иными словами, оно мешает одному телу двигаться относительно другого. Она направлена против силы предполагаемого движения, но имеет максимальное значение. В какой-то момент трение покоя не сможет уравновешивать внешнюю силу, и тела начнут перемещаться. Максимальное значение зависит от свойств предметов и определяется формулой Fтр. пок. макс. = μпN, где N — сила реакции опоры, а μп — коэффициент трения покоя;
Оно не дает шнуркам развязываться, а гвоздям — выпадать из стены. Иными словами, оно мешает одному телу двигаться относительно другого. Она направлена против силы предполагаемого движения, но имеет максимальное значение. В какой-то момент трение покоя не сможет уравновешивать внешнюю силу, и тела начнут перемещаться. Максимальное значение зависит от свойств предметов и определяется формулой Fтр. пок. макс. = μпN, где N — сила реакции опоры, а μп — коэффициент трения покоя; - трение скольжения возникает при переходе через Fтр. пок. макс.. При этом объект начинает перемещаться, а трение направлено против этого движения. Сама сила определяется формулой F тр. скольж. = μN, где μ — коэффициент трения скольжения. Величина силы трения скольжения определяется также скоростями тел, но если их значения невелики, то этим фактором можно пренебречь;
- трение качения возникает, когда предмет катится по поверхности, как колесо или цилиндр.
 При этом оно как бы вдавливается в землю, поэтому при каждом обороте телу нужно пересечь небольшое возвышение. Получается, сила трения растет с уменьшением твердости опоры. Она определяется формулой F тр.кач. = μкач.N, где μкач — коэффициент трения качения. μкач << μ — сила трения качения значительно меньше силы трения скольжения, поэтому катить что-то всегда проще, чем просто тащить по земле.
При этом оно как бы вдавливается в землю, поэтому при каждом обороте телу нужно пересечь небольшое возвышение. Получается, сила трения растет с уменьшением твердости опоры. Она определяется формулой F тр.кач. = μкач.N, где μкач — коэффициент трения качения. μкач << μ — сила трения качения значительно меньше силы трения скольжения, поэтому катить что-то всегда проще, чем просто тащить по земле.
Сопротивление твердого тела, движущегося в жидкости и газе
Разбираем последнюю тему для 2 задания по физике. Когда тело перемещается внутри жидкости или газа, оно сталкивается с сопротивлением среды. Оно похоже на силу трения, но появляется только когда объект начинает движение. Аналога силы трения покоя нет, поэтому перемещать предметы в воде проще, чем на суше. При малых скоростях Fc = k1v, а при больших Fc = k2v2. k1 и k2 — коэффициенты, отличные друг от друга. k1 — коэффициент, зависящий от размеров, формы, состояния поверхности тела и вязкости среды; k2 — коэффициент сопротивления.
k1 — коэффициент, зависящий от размеров, формы, состояния поверхности тела и вязкости среды; k2 — коэффициент сопротивления.
Примеры задач
А теперь проведем разбор 2 задания ЕГЭ по физике.
Задание 1. Брусок массой 5 кг перемещается по горизонтальной поверхности. На него действует сила трения скольжения, равная 10 Н. Рассчитайте силу трения скольжения при уменьшении массы бруска в 2 раза, если учитывать, что коэффициент трения не изменился.
Решение. Сила трения скольжения определяется формулой F = μN. Брусок находится на горизонтальной поверхности, поэтому силу реакции опоры можно определить через второй закон Ньютона: N = mg. Таким образом, F = mgμ. Первые две величины не меняются, значит, на силу будет влиять только уменьшение массы. Необходимо 10 Н разделить на 2.
Ответ: 5 Н.
Задание 2. Мальчик взял камень массой 200 г и бросил его вверх под углом 60° к горизонту. Рассчитайте, чему равна сила тяжести в момент броска. Ускорение свободного падения равно 10 м/с2.
Ускорение свободного падения равно 10 м/с2.
Решение. Сила тяжести постоянна. Она не зависит от угла наклона и скорости. Сила тяжести в момент броска равна силе в любой другой момент времени и определяется формулой F = mg. Следовательно, F = 0,2 кг • 10 м/с2 = 2 Н.
Ответ: 2 Н.
Мы провели разбор 2 задания по физике, причем как по теории, так и по практике. Этот материал представляет собой лишь основы предмета, но он обязательно поможет подготовиться к ЕГЭ. А если вы хотите знать больше, записывайтесь на курсы. Лучше всего выбрать комплексный вариант, например, русский + математика + физика. Так у вас будет больше шансов получить хорошие баллы. А мы желаем вам удачи на экзамене.
Расчет гравитационных сил | IOPSpark
Закон всемирного тяготения Ньютона
Земля и космос
Расчет гравитационных сил
Повествование о физике для 11-14
Узнайте, как рассчитать гравитационные силы
Предположим, вы хотите рассчитать величину гравитационной силы, действующей между вами и вашим коллегой, когда вы приближаетесь друг к другу (на расстоянии одного метра) в коридоре. Мы можем сделать это довольно просто, используя уравнение Ньютона: сила сила тяжести = G × M × м расстояние 2 .
Мы можем сделать это довольно просто, используя уравнение Ньютона: сила сила тяжести = G × M × м расстояние 2 .
Предположим: ваша масса м 60 кг; масса вашего коллеги M 70 кг; расстояние между центрами, r , составляет 1 м; и G составляет 6,67 × 10 -11 ньютон квадратный метр килограмм -2 .
Подставляя эти значения в уравнение, получаем 6.67 × 10 -11 ньютон квадратный метр килограмм -2 × 60 килограмм × 70 килограмм1 метр 2 . Вы можете выработать эту силу, и вы получите 2,8 × 10 -7 ньютона.
Другими словами, вы прикладываете к своему коллеге силу притяжения в 0,28 миллионных долей ньютона! Сила существует, но она слишком мала, чтобы ее можно было заметить на практике.
Из чисел ясно, что из-за того, что величина G настолько мала, величина гравитационной силы будет очень мала, если только тот или иной объект не имеет очень большую массу.
Вы можете использовать уравнение Ньютона, чтобы проверить эмпирическое наблюдение, что масса в 1 килограмм испытывает гравитационное притяжение около 10 Н на поверхности Земли. Это расчет гравитационного притяжения на поверхности Земли
сила сила тяжести = G × M × м отрыв 2
Где: масса, м, , 1 килограмм; масса Земли, M , составляет 6,0 × 10 24 килограмм; радиус Земли (разделение масс), r , равен 6.4 × 10 6 м; и G составляет 6,67 × 10 -11 ньютон на квадратный метр килограмм-2 }.
Подставляем эти значения в уравнение и вычисляем его, чтобы получить силу в 9,8 ньютона.
Как и ожидалось, сила притяжения Земли на массу в 1 килограмм на ее поверхности составляет около 10 Н.
8.1 Линейный импульс, сила и импульс — Физика
Задачи обучения разделу
К концу этого раздела вы сможете делать следующее:
- Опишите импульс, то, что может изменить импульс, импульс и теорему об импульсе-импульсе
- Опишите второй закон Ньютона с точки зрения количества движения
- Решение задач с помощью теоремы об импульсе-импульсе
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (6) Научные концепции.Учащийся знает, что в физической системе происходят изменения, и применяет законы сохранения энергии и количества движения. Ожидается, что студент:
- (C) вычислить механическую энергию, мощность, генерируемую внутри, импульс, приложенный к, и импульс физической системы.
Раздел Основные термины
| изменение импульса | импульс | теорема об импульсе-импульсе | момент импульса |
Поддержка учителя
Поддержка учителя
[BL] [OL] Изучите инерцию и законы движения Ньютона.
[AL] Начать обсуждение движения и столкновения. На примере футболистов укажите, что и масса, и скорость объекта являются важными факторами при определении воздействия столкновений. Направление, а также величина скорости очень важны.
Импульс, импульс и теорема импульс-импульс
Линейный импульс — это произведение массы системы на ее скорость. В форме уравнения импульс движения p равен
.Из уравнения видно, что импульс прямо пропорционален массе объекта ( м ) и скорости ( v ).Следовательно, чем больше масса объекта или чем больше его скорость, тем больше его импульс. Большой, быстро движущийся объект имеет больший импульс, чем более мелкий и медленный объект.
Импульс является вектором и имеет то же направление, что и скорость v . Поскольку масса является скаляром, когда скорость имеет отрицательное направление (т. Е. Противоположно направлению движения), импульс также будет иметь отрицательное направление; и когда скорость в положительном направлении, импульс также будет в положительном направлении.В системе СИ для количества движения используется кг м / с.
Импульс настолько важен для понимания движения, что физики, такие как Ньютон, назвали его величиной движения . Сила влияет на импульс, и мы можем изменить второй закон движения Ньютона, чтобы показать взаимосвязь между силой и импульсом.
Вспомните наше исследование второго закона движения Ньютона ( F net = м a ). Ньютон фактически сформулировал свой второй закон движения в терминах количества движения: чистая внешняя сила равна изменению количества движения системы, деленному на время, в течение которого он изменяется.Изменение импульса — это разница между конечным и начальным значениями импульса.
В форме уравнения этот закон имеет вид
, где F net — чистая внешняя сила, ΔpΔp — изменение количества движения, а ΔtΔt — изменение во времени.
Мы можем найти ΔpΔp, переписав уравнение
будет
FnetΔtFnetΔt называется импульсом, и это уравнение известно как теорема импульса-импульса. Из уравнения мы видим, что импульс равен средней чистой внешней силе, умноженной на время ее действия.Это равно изменению импульса. Действие силы на объект зависит от того, как долго он действует, а также от силы силы. Импульс — полезное понятие, поскольку оно позволяет количественно оценить влияние силы. Очень большая сила, действующая в течение короткого времени, может иметь большое влияние на импульс объекта, например, сила удара ракетки по теннисному мячу. Небольшая сила может вызвать такое же изменение импульса, но действовать ей придется гораздо дольше.
Поддержка учителя
Поддержка учителя
[OL] [AL] Объясните: большой, быстро движущийся объект имеет больший импульс, чем меньший и более медленный объект.Это качество называется импульсом.
[BL] [OL] Просмотрите уравнение второго закона движения Ньютона. Укажите на два разных уравнения закона.
Второй закон Ньютона в терминах количества движения
Когда второй закон Ньютона выражается в единицах количества движения, его можно использовать для решения задач, в которых масса изменяется, поскольку Δp = Δ (mv) Δp = Δ (mv). В более традиционной форме закона, с которым вы привыкли работать, масса считается постоянной. Фактически, эта традиционная форма является частным случаем закона, в котором масса постоянна.Fnet = maFnet = ma фактически выводится из уравнения:
Чтобы понять взаимосвязь между вторым законом Ньютона в его двух формах, давайте воссоздадим вывод Fnet = maFnet = ma из
., заменив определения ускорения и импульса.
Изменение количества движения ΔpΔp определяется как
Если масса системы постоянна, то
При замене ΔpΔp mΔvmΔv второй закон движения Ньютона становится
Fnet = ΔpΔt = mΔvΔtFnet = ΔpΔt = mΔvΔtдля постоянной массы.
Потому что
мы можем заменить, чтобы получить знакомое уравнение
, когда масса системы постоянна.
Поддержка учителей
Поддержка учителей
[BL] [OL] [AL] Покажите две разные формы второго закона Ньютона и то, как одна может быть получена из другой.
Советы для успеха
Мы только что показали, как Fnet = maFnet = ma применяется только тогда, когда масса системы постоянна. Примером, когда эта формула неприменима, может быть движущаяся ракета, которая сжигает достаточно топлива, чтобы значительно изменить массу ракеты.В этом случае вам нужно будет использовать второй закон Ньютона, выраженный в единицах количества движения, чтобы учесть изменение массы.
Snap Lab
Движение рук и импульс
В этом упражнении вы будете экспериментировать с различными типами движений рук, чтобы получить интуитивное понимание взаимосвязи между силой, временем и импульсом.
- один мяч
- одна ванна с водой
Процедура:
- Попробуйте поймать мяч, пока дает мячом, подтягивая руки к телу.
- Затем попробуйте поймать мяч, не двигая руками.
- Попадать в ванну полной ладонью. Ваша полная ладонь изображает пловца, который делает шлепок животом.
- После того, как вода осядет, снова ударьте по воде, погрузив руку сначала в воду пальцами. Ваша рука для ныряния изображает ныряющего пловца.
- Объясните, что происходит в каждом случае и почему.
Проверка захвата
Какие еще примеры движений, на которые влияет импульс?
- столкновение футболиста с другим игроком или автомобиль, движущийся с постоянной скоростью
- Автомобиль, движущийся с постоянной скоростью, или объект, движущийся снарядом
- Автомобиль, движущийся с постоянной скоростью, или ракетка, ударяющая по мячу
- Столкновение футболиста с другим игроком или удар ракеткой по мячу
Поддержка учителя
Поддержка учителя
[OL] [AL] Обсудите удар, который ощущается при падении или прыжке.Перечислите факторы, влияющие на это влияние.
Ссылки на физику
Инженерное дело: спасение жизней с помощью концепции импульса
Автомобили за последние несколько десятилетий стали намного безопаснее. Ремни безопасности играют важную роль в обеспечении безопасности автомобиля, предотвращая попадание людей в лобовое стекло в случае аварии. Другие функции безопасности, такие как подушки безопасности, менее заметны или очевидны, но они также эффективны для снижения смертельных исходов при автокатастрофах (см. Рис. 8.2). Многие из этих функций безопасности используют концепцию импульса из физики.Напомним, что импульс — это чистая сила, умноженная на продолжительность удара. Математически это выражалось как Δp = FnetΔtΔp = FnetΔt.
Рис. 8.2 На автомобилях установлены такие устройства безопасности, как подушки безопасности и ремни безопасности.
Подушки безопасностипозволяют пассажирам в автомобиле действовать в течение более длительного времени при внезапной остановке. Изменение импульса для пассажира одинаково независимо от того, сработала подушка безопасности или нет. Но сила, заставляющая человека остановиться, будет намного меньше, если она будет действовать в течение большего времени.Изменив уравнение для импульса, чтобы найти силу Fnet = ΔpΔt, Fnet = ΔpΔt, вы можете увидеть, как увеличение ΔtΔt при неизменном ΔpΔp приведет к уменьшению F net . Это еще один пример обратной зависимости. Точно так же мягкая приборная панель увеличивает время действия силы удара, тем самым уменьшая силу удара.
Сегодня автомобили состоят из множества пластиковых компонентов. Одним из преимуществ пластмасс является их меньший вес, что приводит к лучшему расходу топлива.Еще одно преимущество заключается в том, что автомобиль может смяться при столкновении, особенно в случае лобового столкновения. Более длительное время столкновения означает, что сила, действующая на пассажиров в автомобиле, будет меньше. Смертность во время автомобильных гонок резко снизилась, когда жесткие рамы гоночных автомобилей были заменены деталями, которые могли смяться или разрушиться в случае аварии.
Проверка захвата
Возможно, вы слышали совет сгибать колени при прыжках. В этом примере друг предлагает вам спрыгнуть со скамейки в парке на землю, не сгибая колен.Вы, конечно, отказываетесь. Объясните другу, почему это было бы глупо. Покажите это с помощью теоремы об импульсе-импульсе.
- Сгибание колен увеличивает время удара, тем самым уменьшая силу.
- Сгибание коленей сокращает время удара, тем самым уменьшая силу.
- Сгибание колен увеличивает время удара, увеличивая, таким образом, силу.
- Сгибание коленей сокращает время удара, увеличивая, таким образом, силу.
Решение задач с использованием теоремы об импульсе-импульсе
Поддержка учителей
Поддержка учителей
Расскажите о различных стратегиях, которые следует использовать при решении задач. Убедитесь, что учащиеся знают допущения, сделанные в каждом уравнении относительно того, что определенные величины являются постоянными или некоторые величины пренебрежимо малы.
Рабочий пример
Расчет импульса: футболист и футбол
(a) Рассчитайте импульс футболиста массой 110 кг, бегущего со скоростью 8 м / с.(b) Сравните импульс игрока с импульсом футбольного мяча весом 0,410 кг, брошенного со скоростью 25 м / с.
Стратегия
Нет информации о направлении футболиста или футбольного мяча, поэтому мы можем вычислить только величину импульса, p . (Курсивом обозначена величина.) В обеих частях этого примера величина импульса может быть вычислена непосредственно из определения импульса:
Решение для (а)
Чтобы найти импульс игрока, подставьте известные значения массы и скорости игрока в уравнение.
pplayer = (110 кг) (8 м / с) = 880 кг⋅м / сpplayer = (110 кг) (8 м / с) = 880 кг⋅м / сРешение для (b)
Чтобы найти импульс мяча, подставьте известные значения массы и скорости мяча в уравнение.
мяч = (0,410 кг) (25 м / с) = 10,25 кг⋅м / мяч = (0,410 кг) (25 м / с) = 10,25 кг⋅м / сОтношение количества движения игрока к импульсу мяча составляет
pplayerpball = 88010.3 = 85.9. pplayerpball = 88010.3 = 85.9.Обсуждение
Хотя мяч имеет большую скорость, игрок имеет гораздо большую массу.Следовательно, импульс игрока примерно в 86 раз больше, чем импульс футбола.
Рабочий пример
Расчетное усилие: ракетка Винус Уильямс
Во время Открытого чемпионата Франции 2007 года Винус Уильямс (рис. 8.3) показала самую быструю подачу в матче лучших женщин, достигнув скорости 58 м / с (209 км / ч). Какая средняя сила была приложена к теннисному мячу весом 0,057 кг ракеткой Williams? Предположим, что скорость мяча сразу после удара составляла 58 м / с, горизонтальная скорость до удара незначительна и что мяч оставался в контакте с ракеткой в течение 5 мс (миллисекунд).
Рис. 8.3. Винус Уильямс играет на US Open 2013 (Эдвин Мартинес, Flickr)
Стратегия
Напомним, что второй закон Ньютона, выраженный в единицах количества движения, равен
.Как отмечалось выше, когда масса постоянна, изменение количества движения определяется как
Δp = mΔv = m (vf − vi), Δp = mΔv = m (vf − vi),, где v f — конечная скорость, а v i — начальная скорость. В этом примере даны скорость сразу после удара и изменение во времени, поэтому после решения для ΔpΔp мы можем использовать Fnet = ΔpΔtFnet = ΔpΔt, чтобы найти силу.
Решение
Чтобы определить изменение количества движения, подставьте значения массы, начальной и конечной скоростей в приведенное выше уравнение.
Δp = m (vf − vi) = (0,057 кг) (58 м / с — 0 м / с) = 3,306 кг · м / с ≈ 3,3 кг · м / с Δp = m (vf − vi) = (0,057 кг) (58 м / с — 0 м / с) = 3,306 кг · м / с ≈ 3,3 кг · м / с8,1
Теперь мы можем найти величину чистой внешней силы, используя Fnet = ΔpΔtFnet = ΔpΔt
Fnet = ΔpΔt = 3,3065 × 10−3 = 661 N≈660 Н.Fnet = ΔpΔt = 3,3065 × 10−3 = 661 N≈660 Н.8,2
Обсуждение
Эта величина была средней силой, прилагаемой ракеткой Винус Уильямс к теннисному мячу во время его кратковременного удара. Эту проблему также можно решить, сначала найдя ускорение, а затем используя F net = м a , но нам пришлось бы сделать еще один шаг. В этом случае использование импульса было сокращением.
Практические задачи
1.Каков импульс шара для боулинга с массой 5 \, \ text {кг} и скоростью 10 \, \ text {м / с}?
- 0.5 \, \ text {кг} \ cdot \ text {м / с}
- 2 \, \ text {кг} \ cdot \ text {м / с}
- 15 \, \ text {кг} \ cdot \ text {m / s}
- 50 \, \ text {кг} \ cdot \ text {м / с}
Каким будет изменение количества движения, вызванное чистой силой 120 \, \ text {N}, действующей на объект в течение 2 секунд?
- 60 \, \ text {кг} \ cdot \ text {m / s}
- 118 \, \ text {kg} \ cdot \ text {m / s}
- 122 \, \ text {кг} \ cdot \ text {m / s}
- 240 \, \ текст {кг} \ cdot \ text {м / с}
Проверьте свое понимание
3.Что такое импульс?
- сумма массы системы и ее скорости
- отношение массы системы к ее скорости
- произведение массы системы на ее скорость
- произведение момента инерции системы на ее скорость
Если масса объекта постоянна, каков его импульс?
- Его скорость
- Его вес
- Рабочий объем
- Его момент инерции
Каково уравнение второго закона движения Ньютона в терминах массы, скорости и времени, когда масса системы постоянна?
- Fnet = ΔvΔmΔtFnet = ΔvΔmΔt
- Fnet = mΔtΔvFnet = mΔtΔv
- Fnet = mΔvΔtFnet = mΔvΔt
- Fnet = ΔmΔvΔtFnet = ΔmΔvΔt
Приведите пример системы, масса которой непостоянна.
- Волчок
- Бейсбольный мяч, летящий по воздуху
- Ракета, запущенная с Земли
- Блок, скользящий по наклонной плоскости без трения
Поддержка учителей
Поддержка учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, усвоили ли учащиеся учебные цели этого раздела.Если учащимся не удается решить конкретную задачу, оценка поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
Обзор силы гравитации Рона Куртуса
SfC Home> Физика> Гравитация>
от Рона Куртуса
Гравитация — это сила , которая притягивает объекты к Земле. Это приближение гравитационной силы , которая притягивает объекты массы друг к другу на больших расстояниях.
( Примечание : Гравитация на Луне — это сила, которая притягивает объекты к поверхности Луны.)
Уравнение силы тяжести: F = mg , где g — ускорение свободного падения. Единицы могут быть обозначены в метрической (СИ) или английской системе. Уравнение также указывает вес объекта ( Вт = мг).
Основной особенностью этой силы является то, что все объекты падают с одинаковой скоростью, независимо от их массы.Гравитация на Луне и на других планетах имеет разные значения ускорения свободного падения. Однако эффекты силы похожи.
Вопросы, которые могут у вас возникнуть:
- Что такое уравнение гравитации?
- Какая самая выдающаяся характеристика гравитации?
- Что такое гравитация в другом месте?
Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц
Уравнение гравитации
Согласно Закону всемирного тяготения Ньютона , гравитация — это сила, притягивающая объекты друг к другу.Для объектов, относительно близких к Земле, эта сила называется гравитацией, и ее уравнение:
F = мг
где
- F — сила, притягивающая объекты к Земле
- м — масса объекта
- g — ускорение свободного падения; это число является постоянным для всех масс вещества
- мг — произведение м умноженное на г
Примечание : Для проверки того, что сила тяжести равна силе тяжести для объектов, близких к Земле, см. Постоянные факторы гравитации.
Ускорение свободного падения
Ускорение силы тяжести на Земле обозначено g . Его значение:
г = 9,807 метров на секунду в квадрате (м / с 2 ) в метрической системе измерения или системе СИ
г = 32,2 фута на секунду в квадрате (фут / с 2 ) в английской системе измерения
Примечание : Поскольку в большинстве учебников используется г = 9.8 м / с 2 и 32 фут / с 2 , в этих уроках мы также будем использовать округленную версию.
В уравнении F = mg вы должны использовать ту же систему измерения для массы, m , что и для g .
Примечание: Некоторые учебники небрежно определяют g как ускорение силы тяжести . Это неверно и вводит в заблуждение, поскольку сила тяжести не ускоряется.Выражение должно быть ускорение из-за силы тяжести , что является правильным описанием g .
Следует проявлять осторожность при определении научных терминов.
Масса и масса
Вес объекта данной массы — это сила тяжести, действующая на этот объект:
w = мг
где
- w вес в ньютонах (Н) или фунт-сила (фунт)
- м — масса в килограммах или фунт-масса (фунт-масса)
Примечание : Часто возникает путаница относительно обозначения веса и массы.
Хотя килограмм считается единицей массы, он часто используется для обозначения веса. Вы должны знать, что вес 1 кг массы равен w = 9,8 ньютона.
Кроме того, фунт считается силой, но его часто называют массой. Масса 1 фунт-сила равна 1/32 массы фунта.
Опять же, вы должны быть точными в формулировке научных терминов.
Взвешивание объекта
Вы можете определить вес объекта на откалиброванных весах — обычно с пружиной, сопротивляющейся силе груза.
Массу объекта можно измерить с помощью весов, сравнивая с объектом данной массы.
Объекты падают с одинаковой скоростью
Наиболее выдающейся характеристикой силы тяжести является тот факт, что все объекты падают с одинаковой скоростью — если предположить, что влияние сопротивления воздуха незначительно. Это связано с тем, что ускорение свободного падения g является константой для всех объектов, независимо от их массы.
Это кажется нелогичным, поскольку можно ожидать, что тяжелый предмет упадет быстрее, чем предмет, который весит меньше.Но это факт. Попробуйте уронить два объекта одновременно с одинаковой высоты, убедившись, что они достаточно тяжелые, чтобы на них не влияло сопротивление воздуха. Вы увидите, что они одновременно упали на землю.
( Для получения дополнительной информации см. Принцип эквивалентности силы тяжести. )
Гравитация в другом месте
Когда вы говорите о гравитации, вы имеете в виду гравитацию около Земли. Однако то же самое уравнение гравитации справедливо для объектов вблизи Луны или других планет, за исключением того, что значение g другое.В таких случаях вы обычно указываете, где находится гравитация, например «гравитация на Луне» или «гравитация на Марсе».
Гравитация на Луне
Сила тяжести на Луне составляет примерно 1/6 от силы тяжести на Земле для данной массы. Таким образом:
F м = мг м
где
- F м — сила или вес на Луне
- м — масса объекта
- g m — ускорение свободного падения на Луне
Значение для г м равно 1.6 м / с 2 или 5,3 фут / с 2 .
Вес и масса на Луне
Значение для г м составляет примерно 1/6 значения для г на Земле. Таким образом, объект на Луне будет весить около 1/6 своего веса на Земле.
Используя пружинные весы, если вы весите на Земле 60 кг (132 фунта), то на Луне вы будете весить всего 10 кг (22 фунта). Однако, используя шкалу баланса и на Земле, и на Луне, ваша масса будет одинаковой.
Упавшие предметы
Если вы уроните на Луну два объекта разного веса, они упадут на землю с одинаковой скоростью. Вам не придется беспокоиться о влиянии сопротивления воздуха, поскольку на Луне нет воздуха.
Поскольку g m = g /6, объекты будут падать с меньшей скоростью.
( См. Уравнения силы тяжести для падающих предметов, а затем примените g m , чтобы получить другие значения.)
Сводка
Гравитация — это сила, притягивающая объекты к Земле. Это частный случай гравитации. Уравнение силы тяжести: F = мг, в результате чего все объекты падают с одинаковой скоростью, независимо от их массы. Гравитация на Луне и гравитация на других планетах имеют разные значения ускорения свободного падения, но эффекты силы схожи.
Будьте как можно лучше
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайты
Гравитационные ресурсы
Сила гравитации — Журнал «Вселенная сегодня»
Притяжение Земли — Википедия
Как работает гравитация? — Как работает материал
Стандартная сила тяжести — Среднее значение по сравнению с вариацией из-за положения на Земле — Википедия
Международная формула силы тяжести — Изменение силы тяжести в зависимости от расстояния от экватора — Отдел геофизики.Университет Оклахомы
Я чувствую себя легче, когда поднимаюсь в гору, но разве я? — Национальная физическая лаборатория FAQ
Книги
(Примечание: Школа чемпионов может получать комиссионные от покупки книг)
Книги с самым высоким рейтингом по простой науке о гравитации
Книги с самым высоким рейтингом по продвинутой физике гравитации
Вопросы и комментарии
Есть ли у вас какие-либо вопросы, комментарии или мнения по этой теме? Если да, отправьте свой отзыв по электронной почте.Я постараюсь вернуться к вам как можно скорее.
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/
gravity_overview.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или тезисе.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
Гравитационные темы
Обзор силы тяжести
4.3: Второй закон движения Ньютона — концепция системы
Цели обучения
К концу этого раздела вы сможете:
- Определите чистую силу, внешнюю силу и систему.
- Поймите второй закон движения Ньютона.
- Примените второй закон Ньютона для определения веса объекта.
Второй закон движения Ньютона тесно связан с первым законом движения Ньютона. Он математически устанавливает причинно-следственную связь между силой и изменениями в движении. Второй закон движения Ньютона является более количественным и широко используется для расчета того, что происходит в ситуациях, связанных с действием силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, дающего точное соотношение силы, массы и ускорения, нам необходимо отточить некоторые идеи, которые уже упоминались.
Во-первых, что мы подразумеваем под изменением движения? Ответ в том, что изменение движения эквивалентно изменению скорости. Изменение скорости по определению означает наличие ускорения . Первый закон Ньютона гласит, что чистая внешняя сила вызывает изменение движения; таким образом, мы видим, что чистая внешняя сила вызывает ускорение .
Сразу возникает еще один вопрос. Что мы подразумеваем под внешней силой? Интуитивное представление о внешнем является правильным — внешняя сила действует извне из интересующей системы .Например, на рисунке \ (\ PageIndex {1a} \) интересующей системой является вагон плюс его дочерний элемент. Две силы, действующие со стороны других детей, — это внешние силы. Между элементами системы действует внутренняя сила. Снова посмотрев на рисунок \ (\ PageIndex {1a} \), можно увидеть, что сила, которую ребенок в тележке прикладывает, чтобы повиснуть на тележке, является внутренней силой между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы. (Внутренние силы фактически отменяются, как мы увидим в следующем разделе.) Вы должны определить границы системы, прежде чем сможете определить, какие силы являются внешними . Иногда система очевидна, тогда как в других случаях определение границ системы более тонкое. Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция будет неоднократно пересматриваться в нашем путешествии по физике.
Рисунок \ (\ PageIndex {1} \): Различные силы, действующие на одну и ту же массу, вызывают разное ускорение.а) Двое детей толкают тележку с ребенком в ней. Показаны стрелки, представляющие все внешние силы. Интересующая система — это повозка и ее водитель. Вес \ (w \) системы и опора основания \ (N \) также показаны для полноты и, как предполагается, сокращаются. Вектор \ (f \) представляет трение, действующее на вагон, и действует влево, противодействуя движению вагона. (b) Все внешние силы, действующие на систему, складываются вместе, образуя результирующую силу \ (F_ {net} \).На диаграмме свободного тела показаны все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки. Поскольку справа действуют две силы, мы рисуем векторы коллинеарно. (c) Большая чистая внешняя сила вызывает большее ускорение \ ((al> a) \), когда взрослый толкает ребенка.Теперь кажется разумным, что ускорение должно быть прямо пропорционально и в том же направлении, что и чистая (полная) внешняя сила, действующая на систему.Это предположение было проверено экспериментально и показано на рисунке. В части (а) меньшая сила вызывает меньшее ускорение, чем большая сила, показанная в части (с). Для полноты картины также показаны вертикальные силы; предполагается, что они отменяются, поскольку нет ускорения в вертикальном направлении. Вертикальные силы — это вес \ (w \) и опора на землю \ (N \), а горизонтальная сила \ (f \) представляет собой силу трения. Они будут обсуждаться более подробно в следующих разделах.А пока мы определим трение как силу, противодействующую движению соприкасающихся объектов друг за другом. На рисунке \ (\ PageIndex {1b} \) показано, как векторы, представляющие внешние силы, складываются вместе, образуя чистую силу, \ (F_ {net} \).
Чтобы получить уравнение для второго закона Ньютона, сначала запишем соотношение ускорения и чистой внешней силы как пропорциональность
\ [a \ propto F_ {net} \]
, где символ \ (\ propto \) означает «пропорционально», а \ (F_ {net} \) — чистая внешняя сила .(Чистая внешняя сила представляет собой векторную сумму всех внешних сил и может быть определена графически, используя метод «голова к хвосту», или аналитически, используя компоненты. Методы такие же, как и для сложения других векторов, и рассматриваются в главе, посвященной двумерной кинематике.) Эта пропорциональность выражает то, что мы сказали словами: ускорение прямо пропорционально чистой внешней силе . После выбора интересующей системы важно определить внешние силы и игнорировать внутренние.Это огромное упрощение — не учитывать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в теле ребенка, не говоря уже о мириадах сил между атомами в объектах, но, делая это, мы можем легко решить некоторые очень сложные задачи с минимальной ошибкой благодаря нашему упрощению
Теперь также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой.И действительно, как показано на рисунке, та же самая чистая внешняя сила, приложенная к автомобилю, вызывает гораздо меньшее ускорение, чем при приложении к баскетбольному мячу. Пропорциональность записывается как
.\ [a \ propto \ dfrac {1} {m}, \]
где \ (m \) — масса системы. Эксперименты показали, что ускорение прямо обратно пропорционально массе, точно так же, как оно прямо линейно пропорционально чистой внешней силе.
Рисунок \ (\ PageIndex {2} \): Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение.(a) Баскетболист толкает баскетбольный мяч, чтобы сделать передачу. (Влияние силы тяжести на мяч игнорируется.) (B) Тот же игрок оказывает идентичное усилие на остановившийся внедорожник и производит гораздо меньшее ускорение (даже если трение незначительно). (c) Диаграммы свободного тела идентичны, что позволяет напрямую сравнить две ситуации. По мере того, как вы будете решать больше задач, появится серия паттернов для диаграммы свободного тела.Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта.Комбинирование двух только что приведенных пропорциональностей дает второй закон движения Ньютона.
Второй закон движения Ньютона
Ускорение системы прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении, и обратно пропорционально ее массе. В форме уравнения второй закон движения Ньютона равен
.\ [a = \ dfrac {F_ {net}} {m} \]
Это часто записывается в более знакомой форме
\ [F_ {net} = ma.\]
Если рассматривать только величину силы и ускорения, это уравнение просто
\ [F_ {net} = ma. \]
Хотя эти последние два уравнения на самом деле одинаковы, первое дает больше понимания того, что означает второй закон Ньютона. Закон представляет собой причинно-следственную связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона полностью основана на экспериментальной проверке.
Единицы силы
\ (F_ {net} = ma \) используется для определения единиц силы в терминах трех основных единиц массы, длины и времени.2 \]
В то время как почти весь мир использует ньютон в качестве единицы силы, в Соединенных Штатах наиболее известной единицей силы является фунт (фунт), где 1 Н = 0,225 фунта.
Вес и гравитационная сила
Когда объект падает, он ускоряется к центру Земли. Второй закон Ньютона гласит, что общая сила, действующая на объект, отвечает за его ускорение. Если сопротивление воздуха незначительно, результирующая сила, действующая на падающий объект, — это сила тяжести, обычно называемая его весом \ (w \).Вес можно обозначить как вектор \ (w \), потому что он имеет направление; Вниз по определению является направлением силы тяжести, и, следовательно, вес — это сила, направленная вниз. Величина веса обозначается как \ (w \). Галилей сыграл важную роль в демонстрации того, что при отсутствии сопротивления воздуха все объекты падают с одинаковым ускорением \ (w \). Используя результат Галилея и второй закон Ньютона, мы можем вывести уравнение для веса.
Рассмотрим объект с массой \ (m \), падающий вниз к Земле. Он испытывает только нисходящую силу тяжести, величина которой равна \ (w \).Второй закон Ньютона гласит, что величина чистой внешней силы, действующей на объект, равна \ (F_ {net} = ma \).
Поскольку на объект действует только сила тяжести, направленная вниз, \ (F_ {net} = w \). Мы знаем, что ускорение объекта под действием силы тяжести равно \ (g \) или \ (a = g \). Подставляя их во второй закон Ньютона, получаем
ВЕС
Это уравнение веса — силы тяжести, действующей на массу \ (m \):
\ [w = мг \]
Так как вес \ (g = 9.2) = 9,8 Н. \]
Напомним, что \ (g \) может принимать положительное или отрицательное значение, в зависимости от положительного направления в системе координат. Обязательно учтите это при решении задач с весом.
Когда чистая внешняя сила, действующая на объект, равна его весу, мы говорим, что он находится в свободном падении . То есть единственная сила, действующая на объект, — это сила тяжести. В реальном мире, когда объекты падают вниз к Земле, они никогда не находятся в состоянии свободного падения, потому что на объект всегда действует некоторая восходящая сила воздуха.2 \). Таким образом, масса в 1,0 кг имеет вес 9,8 Н на Земле и всего около 1,7 Н на Луне.
Самое широкое определение веса в этом смысле состоит в том, что вес объекта — это сила тяжести, действующая на него со стороны ближайшего крупного тела , такого как Земля, Луна, Солнце и так далее. Это наиболее распространенное и полезное определение веса в физике. Однако оно кардинально отличается от определения веса, используемого НАСА и популярными СМИ в отношении космических путешествий и исследований.Когда они говорят о «невесомости» и «микрогравитации», они на самом деле имеют в виду явление, которое мы называем «свободным падением» в физике. Мы будем использовать приведенное выше определение веса и проведем тщательное различие между свободным падением и фактической невесомостью.
Важно знать, что вес и масса — очень разные физические величины, хотя они тесно связаны. Масса — это количество материи (сколько «вещества») и не изменяется в классической физике, тогда как вес — это сила тяжести, которая зависит от силы тяжести.Заманчиво приравнять эти два понятия, поскольку большинство наших примеров имеет место на Земле, где вес объекта лишь немного зависит от его местоположения. Кроме того, в повседневном языке термины масса и вес используются взаимозаменяемо; например, в наших медицинских записях наш «вес» часто указывается в килограммах, но никогда в правильных единицах — ньютонах.
РАСПРОСТРАНЕННЫЕ Заблуждения: МАССА VS. ВЕС
В обиходе масса и вес часто используются как синонимы.Однако в науке эти термины существенно отличаются друг от друга. Масса — это мера количества вещества в объекте. Типичной мерой массы является килограмм (или «слизняк» в английских единицах измерения). С другой стороны, вес — это мера силы тяжести, действующей на объект. Вес равен массе объекта \ ((m) \), умноженной на ускорение свободного падения \ ((g) \). Как и любая другая сила, вес измеряется в ньютонах (или фунтах в английских единицах).
Предполагая, что масса объекта остается неизменной, она останется неизменной независимо от его местоположения.2 \)). Если вы измерили свой вес на Земле, а затем измерили свой вес на Луне, вы бы обнаружили, что «весите» намного меньше, хотя и не выглядите худее. Это потому, что сила тяжести на Луне слабее. Фактически, когда люди говорят, что они «худеют», они на самом деле имеют в виду, что они теряют «массу» (что, в свою очередь, заставляет их весить меньше)
ЭКСПЕРИМЕНТ НА ДОМУ: МАССА И ВЕС
Что измеряют весы для ванной? Когда вы стоите на весах в ванной, что происходит с весами? Слегка угнетает.Весы содержат пружины, которые сжимаются пропорционально вашему весу — подобно резиновым лентам, расширяющимся при натяжении. Пружины позволяют измерить ваш вес (для объекта, который не ускоряется). Это сила в ньютонах (или фунтах). В большинстве стран результат делится на 9,80, чтобы получить значение в килограммах. Весы измеряют вес, но откалиброваны для предоставления информации о массе. Стоя на весах в ванной, нажмите на соседний стол. Что происходит с чтением? Почему? Будет ли ваша шкала измерять ту же «массу» на Земле, что и на Луне?
Пример \ (\ PageIndex {1} \): какое ускорение может дать человек, толкая газонокосилку?
Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н (около 11 фунтов) параллельно земле.Масса косилки 24 кг. Какое у него ускорение?
Рисунок \ (\ PageIndex {3} \): Чистое усилие на газонокосилке составляет 51 Н. вправо. С какой скоростью газонокосилка ускоряется вправо?Стратегия
Поскольку даны \ (F_ {net} \) и \ (m \), ускорение можно вычислить непосредственно из второго закона Ньютона, как указано в \ (F_ {net} = ma \).
Решение
Величина ускорения \ (a \) равна \ (a = \ frac {F_ {net}} {m} \).2 \]
Обсуждение
Направление ускорения совпадает с направлением результирующей силы, параллельной земле. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах. Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны нейтрализоваться, если не должно быть ускорения в вертикальном направлении ( косилка движется только горизонтально).Обнаруженное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не будет длиться слишком долго, потому что человек скоро достигнет максимальной скорости.
Пример \ (\ PageIndex {2} \): Какая ракетная тяга ускоряет этот снегоход?
До пилотируемых космических полетов ракетные сани использовались для испытаний самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.2 \) масса системы 2100 кг, а сила трения, препятствующая движению, известна как 650 Н.
Рисунок 4.4.4. Салазки испытывают ракетную тягу, разгоняющую их вправо. Каждая ракета создает одинаковую тягу \ (T \). Как и в других ситуациях, когда есть только горизонтальное ускорение, вертикальные силы нейтрализуются. Земля оказывает на систему направленную вверх силу \ (N \), равную по величине и противоположную по направлению ее весу, \ (w \). Система здесь — сани, его ракеты и всадник, поэтому никакие силы между этими объектами не рассматриваются.Стрелка, обозначающая трение \ ((f) \), нарисована больше масштаба.Стратегия
Несмотря на то, что существуют силы, действующие вертикально и горизонтально, мы предполагаем, что вертикальные силы компенсируются, поскольку нет вертикального ускорения. Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на рисунке.
Решение
Поскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей.Поскольку мы определили направление силы и ускорения как действующие «вправо», нам нужно учитывать в расчетах только величины этих величин. Следовательно, мы начинаем с \ [F_ {net} = ma. \], где \ (F_ {net} \) — чистая сила в горизонтальном направлении. Из рисунка видно, что тяга двигателя увеличивается, а трение противодействует тяге. В форме уравнения чистая внешняя сила равна \ [F_ {net} = 4T — f. \]
Подставляя это во второй закон Ньютона, получаем \ [F_ {net} = ma = 4T — f.2 \)). Пока живые предметы больше не используются, с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч. В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.
Второй закон движения Ньютона — это больше, чем определение; это соотношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе.В следующем разделе представлен третий и последний закон движения.
Сводка
- Ускорение, \ (a \), определяется как изменение скорости, означающее изменение ее величины или направления, или и того, и другого.
- Внешняя сила — это сила, действующая на систему извне, в отличие от внутренних сил, которые действуют между компонентами внутри системы.
- Второй закон движения Ньютона гласит, что ускорение системы прямо пропорционально и в том же направлении, что и чистая внешняя сила, действующая на систему, и обратно пропорционально ее массе.
- В форме уравнения второй закон движения Ньютона: \ (a = \ frac {F_ {net}} {m} \)
- Это часто записывается в более знакомой форме: \ (F_ {net} = ma. \)
- Вес \ (w \) объекта определяется как сила тяжести, действующая на объект массы \ (m. \). Объект испытывает ускорение, вызванное гравитацией \ (g \): \ [w = mg. \]
- Если единственная сила, действующая на объект, вызвана гравитацией, объект находится в свободном падении.
- Трение — это сила, которая препятствует движению соприкасающихся объектов друг за другом.
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Оклендский университет) и Манджула Шарма (Сиднейский университет). Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Часто используемых уравнений — Гипертекст по физике
Часто используемые уравнения — Гипертекст по физике- обсуждение
- сводка
- практика
- проблемы
- ресурсов
Номер ссылки
механика теплофизика, волны и оптика, электричество и маджентизм, современная физикаМеханика
| уравнения движения |
|---|
| v = v 0 + при s = s 0 + v 0 t + ½ при 2 v 2 = v 0 2 + 2 a ( с — с 0 ) v = ½ ( v + v 0 ) |
| уравнения вращения |
|---|
| ω = ω 0 + α t θ = θ 0 + ω 0 t + ½α t 2 ω 2 = ω 0 2 + 2α (θ — θ 0 ) ω = ½ (ω + ω 0 ) |
| крутящий момент |
|---|
| τ = rF sin θ |
| τ = r × F |
Теплофизика
| c.o.p. | |||
|---|---|---|---|
| T C | ||
| T H — T C |
Waves & Optics
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ∆ f | ≈ | ∆λ | ≈ | ∆ v | ||||||
| f | λ | c | ||||||||
| Закон Фарадея | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||
|
Современная физика
| релятивистская k.е. | |||||||
|---|---|---|---|---|---|---|---|
| |||||||
| K = (γ — 1) mc 2 |
| 9909090 уравнение Шредингера90 | i ℏ | ∂ | Ψ ( r , t ) = — | ℏ 2 | ∇ 2 Ψ ( r ) + t t U ( r ) Ψ ( r , t ) |
|---|---|---|---|---|---|
| ∂t | 2 м |
| E E = — 9012 2 | ℏ 2 | ∇ 2 ψ ( r ) + U ( r ) ψ ( r ) |
| 2 m |
- обсуждение
- сводка
- практика
- проблемы
- ресурсов
Нет постоянных условий.
- Механика
- Кинематика
- Движение
- Расстояние и перемещение
- Скорость и скорость
- Разгон
- Уравнения движения
- Свободное падение
- Графики движения
- Кинематика и расчет
- Кинематика в двух измерениях
- Снаряды
- Параметрические уравнения
- Dynamics I: Force
- Сил
- Сила и масса
- Действие-реакция
- Вес
- Динамика
- Статика
- Трение
- Силы в двух измерениях
- Центростремительная сила
- Кодовые рамки
- Энергия
- Работа
- Энергия
- Кинетическая энергия
- Потенциальная энергия
- Сохранение энергии
- Мощность
- Простые станки
- Dynamics II: Импульс
- Импульс и импульс
- Сохранение импульса
- Импульс и энергия
- Импульс в двух измерениях
- Вращательное движение
- Кинематика вращения
- Инерция вращения
- Динамика вращения
- Вращательная статика
- Угловой момент
- Энергия вращения
- Прокатный
- Вращение в двух измерениях
- Сила Кориолиса
- Планетарное движение
- Геоцентризм
- Гелиоцентризм
- Вселенская гравитация
- Орбитальная механика I
- Гравитационная потенциальная энергия
- Орбитальная механика II
- Плотность вытянутых тел
- Периодическое движение
- Пружины
- Простой генератор гармоник
- Маятники
- Резонанс
- Эластичность
- Жидкости
- Плотность
- Давление
- Плавучесть
- Расход жидкости
- Вязкость
- Аэродинамическое сопротивление
- Режимы потока
- Кинематика
- Теплофизика
- Тепло и температура
- Температура
- Тепловое расширение
- Атомная природа материи
- Закон о газе
- Кинетико-молекулярная теория
- Фазы
- Калориметрия
- Явное тепло
- Скрытое тепло
- Химическая потенциальная энергия
- Теплопередача
- Проводимость
- Конвекция
- Радиация
- Термодинамика
- Тепло и работа
- Диаграммы давление-объем
- Двигатели
- Холодильники
- Энергия и энтропия
- Абсолютный ноль
- Тепло и температура
- Волны и оптика
- Волновые явления
- Природа волн
- Периодические волны
- Интерференция и суперпозиция
- Интерфейсы и барьеры
- Звук
- Природа звука
- Интенсивность
- Эффект Доплера (звук)
- Ударные волны
- Дифракция и интерференция (звук)
- Стоячие волны
- ударов
- Музыка и шум
- Физическая оптика
- Природа света
- Поляризация
- Эффект Доплера (свет)
- Черенковское излучение
- Дифракция и интерференция (свет)
- Тонкопленочная интерференция
- Цвет
- Геометрическая оптика
- Отражение
- Преломление
- Зеркала сферические
- Сферические линзы
- Аберрация
- Волновые явления
- Электричество и магнетизм
- Электростатика
- Электрический заряд
- Закон Кулона
- Электрическое поле
- Электрический потенциал
- Закон Гаусса
- Проводников
- Электростатические приложения
- Конденсаторы
- Диэлектрики
- Батареи
- Электрический ток
- Электрический ток
- Электрическое сопротивление
- Электроэнергия
- цепей постоянного тока
- Резисторы в цепях
- Батареи в цепях
- Конденсаторы в цепях
- Правила Кирхгофа
- Магнитостатика
- Магнетизм
- Электромагнетизм
- Закон Ампера
- Электромагнитная сила
- Магнитодинамика
- Электромагнитная индукция
- Закон Фарадея
- Закон Ленца
- Индуктивность
- Цепи переменного тока
- Переменный ток
- RC-цепи
- Цепи RL
- LC цепи
- Электромагнитные волны
- Уравнения Максвелла
- Электромагнитные волны
- Электромагнитный спектр
- Электростатика
- Современная физика
- Теория относительности
- Пространство-время
- Масса-энергия
- Общая теория относительности
- Quanta
- Излучение черного тела
- Фотоэффект
- Рентгеновские снимки
- Антиматерия
- Волновая механика
- Волны материи
- Атомарные модели
- Полупроводники
- Конденсированное вещество
- Ядерная физика
- Изотопы
- Радиоактивный распад
- Период полураспада
- Энергия связи
- Деление
- Fusion
- Нуклеосинтез
- Ядерное оружие
- Радиобиология
- Физика элементарных частиц
- Квантовая электродинамика
- Квантовая хромодинамика
- Квантовая динамика ароматов
- Стандартная модель
- Помимо стандартной модели
- Теория относительности
- Фундаменты
- шт.
- Международная система единиц
- Гауссова система единиц
- Британо-американская система единиц
- Разные единицы
- Время
- Преобразование единиц
- Измерение
- Значащие цифры
- По порядку величины
- Графики
- Графическое представление данных
- Линейная регрессия
- Подгонка кривой
- Исчисление
- Векторы
- Тригонометрия
- Сложение и вычитание векторов
- Векторное разрешение и компоненты
- Умножение вектора
- ссылку
- Специальные символы
- Часто используемые уравнения
- Физические константы
- Астрономические данные
- Периодическая система элементов
- Люди в физике
- шт.
- Назад дело
- Предисловие
- Об этой книге
- Связаться с автором
- гленнелерт.сша
- Behance
- Твиттер
- YouTube
- аффилированных веб-сайтов
- hypertextbook.com
- midwoodscience.org
- Предисловие
Рычаги и момент
Рычаги и моментРычаги и крутящий момент
Цели
| Настройка
|
Теория
Рычаги используют крутящий момент, чтобы помочь нам поднимать или перемещать объекты. Крутящий момент крест произведение силы на расстояние от точки опоры (центральной точки о котором крутится система). Перекрестное произведение берет только компонент сила, действующая перпендикулярно расстоянию. С помощью тригонометрии определяется крутящий момент. как:
Крутящий момент = Сила × Расстояние до точки опоры × sin (θ)
Помните, что работа также была силой, умноженной на расстояние, но это была точка произведение и использовал косинус угла между силой и расстоянием: сила × расстояние × cos (θ).
В этой лаборатории сила будет перпендикулярна (90 °) расстоянию. В синус 90 ° равен единице, поэтому крутящий момент будет:
Крутящий момент = Сила × Расстояние до точки опоры × sin (θ)
Крутящий момент = Сила × Расстояние до точки опоры × sin (90 °)
Крутящий момент = Сила × Расстояние до точки опоры × 1
Крутящий момент = Сила × Расстояние до точки опоры
Процедура, сбор данных и расчеты
Пробный рычаг I класса: d
e = d rВ рычаге класса 1 точка опоры находится между силой сопротивления (F r ) и сила усилия (F e ).В классе один рычаг сила усилие (F e ), умноженное на расстояние усилия от точки опоры (d e ) равна силе сопротивления (F r ), умноженной на расстояние сопротивление от точки опоры (d r ). Усилие и сопротивление продолжаются. противоположные стороны точки опоры. Плоскогубцы являются примером рычага первого класса.
На диаграмме масса обеспечивает сопротивление, пружинная шкала измеряет наше сопротивление. усилия. Пружинная шкала откалибрована в граммах.Граммы — это не единица измерения силы как таковой, но в этой лаборатории мы будем использовать термин «грамм-сила» как сила, действующая на один грамм у поверхности Земли за счет ускорения свободного падения. Один «грамм-сила» будет эквивалентна 980 см / сек 2 (дин).
Для диаграммы: F e × d e = F r × d r
Механическое преимущество = F r / F e
- Повесьте гирю 200 граммов на 10 см, подвесьте пружинную шкалу на отметке 90 см, подвесьте измеритель на отметке 50 см.
- Найдите F e , d e , F r , d r в граммах-силе. К Определите грамм-силу массы (F r ) с помощью весов балансира. d e и d r при правильной настройке должно быть 40 см. F e можно прочитать из Весенняя граммовая шкала напрямую.
- Вычислить F e × d e и F r × d r .
- Укажите, является ли F e × d e = F r × d r .
- Рассчитайте механическое преимущество F r / F e .
| F e | d e | F e × d e | F r | d r | F r × d r | F e d e = F r d r ? | M.A. |
|---|---|---|---|---|---|---|---|
| ________ | ________ | ________ | ________ | ________ | ________ | Да | Нет | ________ |
Класс I Рычаги испытательные два: d
e > d r Для диаграммы: F e × d e = F r × d r
Механическое преимущество = F r / F e
- Переключите массы на массу 500 грамм или две 200-граммовые гирьки вместе.
- Поместите груз массой 500 грамм на отметку 10 см, а шкалу пружины на отметку 90 см, подвесьте метр от отметки 30 см.
- Найдите F e , d e , F r , d r в граммах-силе.
- Вычислить F e × d e и F r × d r .
- Укажите, является ли F e × d e = F r × d r .
- Рассчитайте механическое преимущество F r / F e .
| F e | d e | F e × d e | F r | d r | F r × d r | F e d e = F r d r ? | M.A. |
|---|---|---|---|---|---|---|---|
| ________ | ________ | ________ | ________ | ________ | ________ | Да | Нет | ________ |
Рычаги класса II
В рычаге второго класса сопротивление находится между силой усилия и силой точка опоры.В рычаге класса два сила усилия, умноженная на расстояние усилие от точки опоры противоположно и равно силе сопротивления умноженное на расстояние сопротивления от точки опоры. Усилия и Сопротивления находятся с одной стороны от точки опоры, но направлены в противоположные стороны.
Расстояние усилия (также иногда называемое «рычагом усилия») на длиннее чем расстояние сопротивления.
Тачки и гигантские столбы для раскопок таро (когда мы отжимаемся на шесте) являются примерами рычаги второго класса.
Обратите внимание, что наш выбор пуха как положительного в первой части лабораторной работы означает, что вверх теперь отрицательный в этом разделе. Итак, F e — отрицательная сила. Запишите F e как отрицательное в таблице, а затем -F e × d e будет быть положительным.
Для диаграммы: -F e × d e = F r × d r
Механическое преимущество = | F r / F e | где | означает «абсолютный
значение. «Механическое преимущество всегда положительно.
- Переместите гирю 500 грамм (или две гири по 200 грамм) примерно на 30 см. Отметьте метку и пружинную шкалу на отметке 90 см, подвесьте измерительную штангу на отметке 10 см. Возможно, вам придется отрегулировать положение вашей массы в соответствии с возможностями вашего пружинная шкала для обеспечения точных показаний. Вы не хотите читать очень маленькие граммовые силы или граммовые силы слишком большие для вашей пружинной шкалы. Если вы отрегулируете положения, не забудьте измерить фактические d e и d r , которые вы используете!
- Найдите F e , d e , F r , d r в граммах-силе.
- Вычислить F e × d e и F r × d r .
- Укажите, является ли -F e × d e = F r × d r .
- Рассчитайте механическое преимущество F r / F e .
| F e | d e | -F e × d e | F r | d r | F r × d r | -F e d e = F r d r ? | М.А. |
|---|---|---|---|---|---|---|---|
| ________ | ________ | ________ | ________ | ________ | ________ | Да | Нет | ________ |
Рычаги класса III
В рычаге третьего класса сопротивление находится между силой усилия и силой точка опоры. В рычаге третьего класса сила усилия, умноженная на расстояние усилия от точки опоры противоположны и равны силе сопротивления умноженное на расстояние сопротивления от точки опоры.Усилия и Сопротивления находятся с одной стороны от точки опоры, но направлены в противоположные стороны.
Расстояние усилия (также иногда называемое «рычагом усилия») на короче чем расстояние сопротивления.
Для диаграммы: -F e × d e = F r × d r
Механическое преимущество = | F r / F e | где | означает «абсолютный
значение. «Механическое преимущество всегда положительно.
- Перейти на массу 100 граммов.
- Переместите гирю 100 грамм на отметку 90 см, а шкалу пружины примерно на отметку 65 см. см до отметки 70 см, удерживая измерительную линейку подвешенной на отметке 10 см. Снова при необходимости отрегулируйте шкалу пружины и положение масс, чтобы получить точные показания Весенняя шкала.
- Найдите F e , d e , F r , d r в граммах-силе.
- Вычислить F e × d e и F r × d r .
- Укажите, является ли -F e × d e = F r × d r .
- Рассчитайте механическое преимущество F r / F e .
| F e | d e | -F e × d e | F r | d r | F r × d r | -F e d e = F r d r ? | М.А. |
|---|---|---|---|---|---|---|---|
| ________ | ________ | ________ | ________ | ________ | ________ | Да | Нет | ________ |
В рычаге класса III механическое преимущество можно назвать механическим недостаток. Почему? (Предложение: подумайте о силе усилия, меньше силы сопротивления или больше силы сопротивления?)
Обратите внимание, что нижняя часть руки человека — это рычаг третьего класса: бицепс, прикрепленный чуть ниже локоть, можно использовать для поднятия груза, удерживаемого в руке в конце нижнего рука.
Рычаги непрерывного действия: Отвертки
Отвертка на самом деле представляет собой форму рычага, в которой ручка с большим радиусом обеспечивает механическое преимущество при повороте лезвия с меньшим радиусом. Всевозможные циркулярные устройства используют эту форму механического преимущества. Круглые ручки водяного клапана, шина утюги, торцевые ключи, гаечные ключи и многие другие предметы используют это время круговой рычаг.
Измерьте радиус ручки отвертки, а затем измерьте радиус лезвие.Рассчитайте механическое преимущество: d e / d r .
Обратите внимание, что механическое преимущество круглого устройства снижается, в то время как мех. нареч. для рычага было Fr / Fe. Обратите внимание, что кажущийся «триггер» дроби не ошибка.
Считаем, что F e × d e = F r × d r . Крест деление на F e и d r дает:
d e = F r - - = механическое преимущество d r F e
SC 130 Домашняя страница
Домашняя страница курсов Ли Линга
На главную страницу COM-FSM
Формула работы: физическое уравнение с примерами
В физике мы говорим, что сила выполняет работу , если приложение силы перемещает объект в направлении силы.Другими словами, работа эквивалентна приложению силы на расстоянии. Количество работы, выполняемой силой, прямо пропорционально тому, насколько далеко эта сила перемещает объект. Общая формула для работы и определения объема работы, выполняемой над объектом:
, где W — объем работы, F — вектор силы, D — величина смещения, — угол между вектором силы и вектором смещения.Единица СИ для работы — джоуль ( Дж ), а ее размеры составляют кг • м 2 / с 2 . Другой способ понять это состоит в том, что один джоуль эквивалентен количеству энергии, передаваемой, когда сила в один ньютон перемещает объект на расстояние в один метр.
Формула для работы
Каждый раз, когда сила перемещает объект, мы говорим, что работа выполнена. Когда мяч катится с холма под действием силы тяжести, когда вы поднимаете рюкзак с земли, когда внутренний двигатель вашего автомобиля прикладывает силу, заставляющую ваши колеса двигаться; все эти события связаны с силой, перемещающей объект на расстояние, и поэтому требуют некоторой работы.В случаях, когда к объекту прикладывается сила, но он не перемещается, работа не выполняется. Таким образом, сила человека, толкающего край небоскреба, не работает, поскольку небоскреб не двигается. Давайте рассмотрим несколько простых примеров, чтобы проиллюстрировать концепцию работы.
Примеры задач
(1)
Сила в 100 Ньютонов прикладывается к ящику весом 15 кг в горизонтальном направлении и перемещает его на 5 метров по горизонтали. Сколько работы было сделано?
В этом случае мы знаем, что сила равна 100 Н, а расстояние составляет 5 метров.Мы также знаем, что, поскольку сила приложена в том же направлении, что и смещение, Θ равно 0. Таким образом, мы подставляем эти значения в наше уравнение
и получаем:
- W = 100 (5) cos (0 ) = 500 Дж
Итак, сила 100 Н выполнила 500 джоулей работы, переместив блок на 5 метров.
(2)
На столе лежит книга весом 2 кг. К книге прилагается сила 64 Н под углом 120 ° от горизонтали и перемещает книгу на 3 метра в горизонтальном направлении.Сколько работы было сделано?
В данном случае нам известна сила 64 Н и расстояние 3 м. Мы также знаем, что существует угол 120 ° между углом направления приложенной силы и направлением движения. Таким образом, включение этих значений в наше удобное уравнение дает:
- W = 64 (3) cos (120) = 156,32 Джоулей
Таким образом, сила 64 Н под углом 120 ° составила 156,32 Дж работы. перемещение книги 3 метра .
(3)
Линда поднимает чемодан 300 Н на 3 лестничных пролета на общее расстояние по вертикали 16 метров.Затем она толкает чемодан с силой 100 Н на оставшиеся 8 метров к своему гостиничному номеру. Сколько работы было проделано за всю поездку?
Этот вопрос требует 2 отдельных шагов. Ее поездка состоит из двух основных частей, поэтому мы можем рассчитать работу, проделанную для каждой части индивидуально, а затем объединить эти два значения, чтобы получить общий объем проделанной работы. В первой части поездки она прилагает усилие 300 Н, чтобы переместить чемодан на 16 метров по вертикали, поэтому объем проделанной работы составит:
- W 1 = 300 (16) cos (0) = 4800 Джоули
Итак, первая часть пути составила 4800 джоулей.Что касается второй части, мы знаем, что сила 100 Н перемещает чемодан по горизонтали на 8 метров, поэтому общий объем работы, проделанной во второй части поездки, составляет:
- W 2 = 100 (8) cos (0) = 800 Дж
Объединение двух значений из каждой части маршрута дает:
- W всего = W 1 + W 2 = 4800 + 800 = 5600 Джоули
Итак, за все время путешествия Линды было выполнено 5600 Джоулей работы.
Отношение работа / энергия
Три основных уравнения, представляющих отношения между энергией, работой и силой.Работа и энергия в физике тесно связаны. Согласно принципу работы-энергии, увеличение кинетической энергии твердого тела вызывается равным объемом работы, совершаемой над этим телом силой, приложенной к этому телу. В более математических терминах это соотношение может быть выражено как:
, где KE означает кинетическую энергию. Другими словами, изменение кинетической энергии тела равно количеству работы, выполняемой этим телом.В общем, формула кинетической энергии объекта:
, где v обозначает скорость объекта. Единица кинетической энергии такая же, как и работа, джоуль. Давайте рассмотрим некоторые задачи, чтобы исследовать эти математические отношения.
(4)
Осел и Дидди Конг сидят в 90-килограммовой вагонетке, которая первоначально движется горизонтально со скоростью 5 м / с. Носорог Рамби толкает вагонетку сзади и ускоряет ее, так что теперь она движется со скоростью 11 м / с.Сколько работы Рамби проделал с вагонеткой?
Чтобы решить эту проблему, нам сначала нужно вычислить начальную кинетическую энергию вагонетки и ее конечную кинетическую энергию. Зная эти значения, мы можем определить общий объем работы. Нам известны скорость и масса вагонетки, поэтому мы можем определить общую кинетическую энергию в начале и в конце. Начальная кинетическая энергия вагонетки:
- KE начальная = (1/2) (90) (5) 2 = 1125 Дж
Конечная кинетическая энергия вагонетки
- KE final = (1/2) (90) (11) 2 = 5445 Дж
Таким образом, общий объем выполненных работ на тележке составляет 5545-1125 = 4420 Дж .
«Наука — это знание последствий и зависимости одного факта от другого». — Томас Гоббс
(5)
Автомобиль весом 1300 кг движется со скоростью 18 м / с. Если с автомобилем будет проделано 60000 джоулей работы, какова будет его конечная скорость?
Вопрос потребует немного алгебры. Во-первых, мы должны определить начальную кинетическую энергию автомобиля. Начальная кинетическая энергия автомобиля:
- (1/2) (1300) (18) 2 = 210600 Дж
Поскольку нам известен общий объем работы, проделанной в системе (60000 J) мы можем вычислить конечную кинетическую энергию автомобиля:
- 60000 = KE final −210600
- 270600 = KE final
Теперь, поскольку мы знаем конечную кинетическую энергию и массу автомобиля, мы можем определить его конечную скорость следующим образом:
- KE final = (1/2) кг * v 2
- 270600 = (1/2) (1300) v 2
- 270600 = 650 v 2
- 416.3 = v 2
- v = 20,4 м / с
Конечная скорость автомобиля составит 20,4 м / с .
Итак, суммируя, мы говорим, что работа выполняется всякий раз, когда сила перемещает объект на расстояние.
Разное
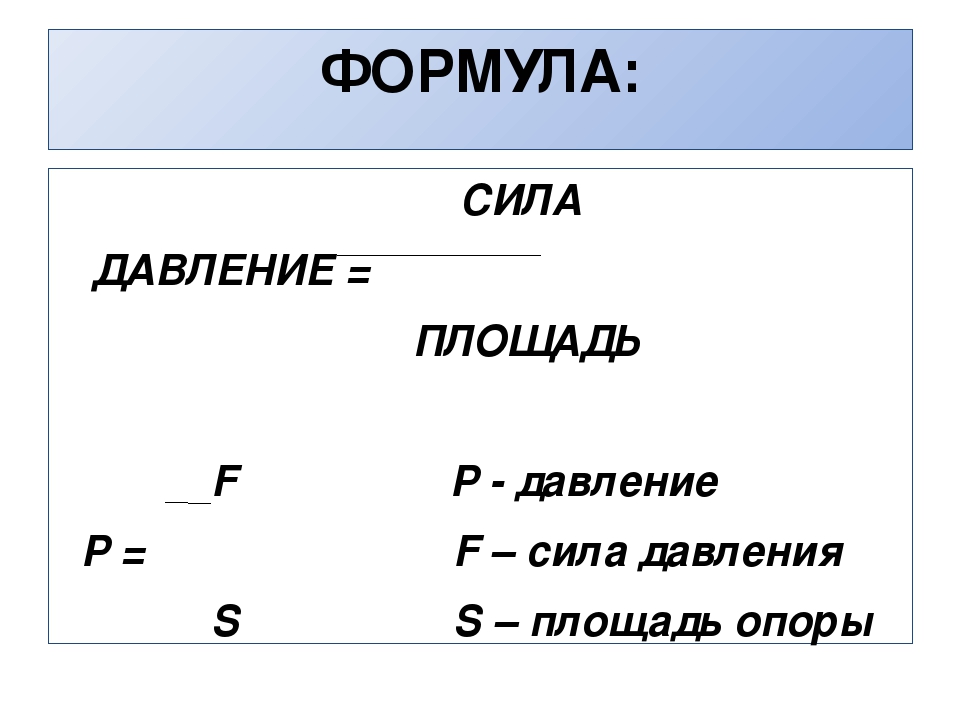
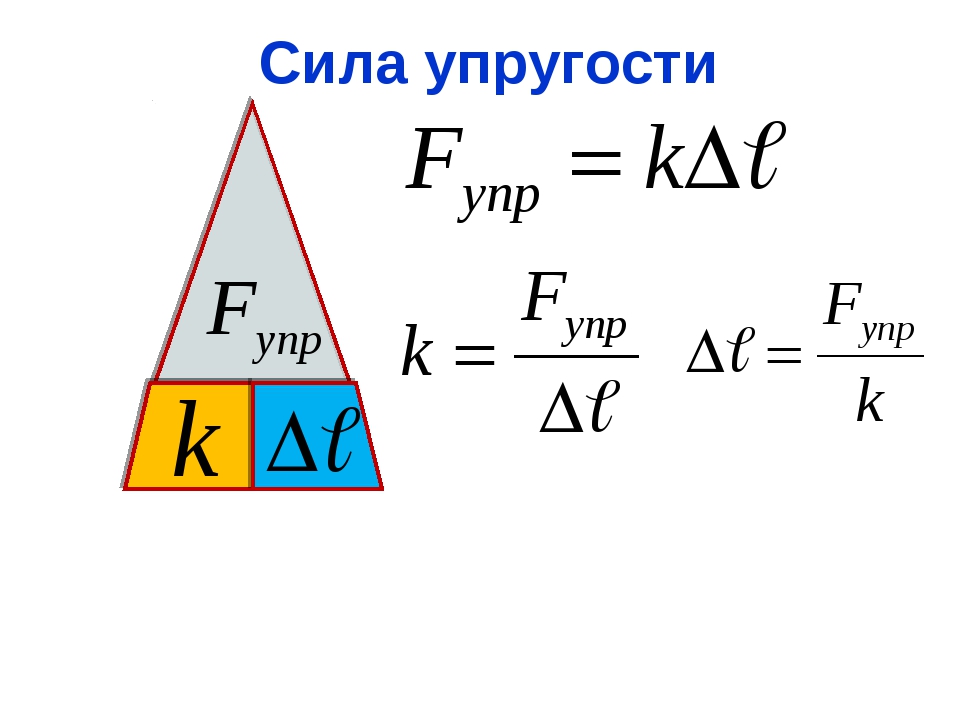 Связывает электроны с ядром, объединяет атомы в молекулы, а молекулы в вещества. Это взаимодействие объясняет многие механические процессы. У него бесконечный радиус действия, но оно почти не оказывает влияния на макрообъекты, так как они нейтральны. Относительная интенсивность — 1036;
Связывает электроны с ядром, объединяет атомы в молекулы, а молекулы в вещества. Это взаимодействие объясняет многие механические процессы. У него бесконечный радиус действия, но оно почти не оказывает влияния на макрообъекты, так как они нейтральны. Относительная интенсивность — 1036;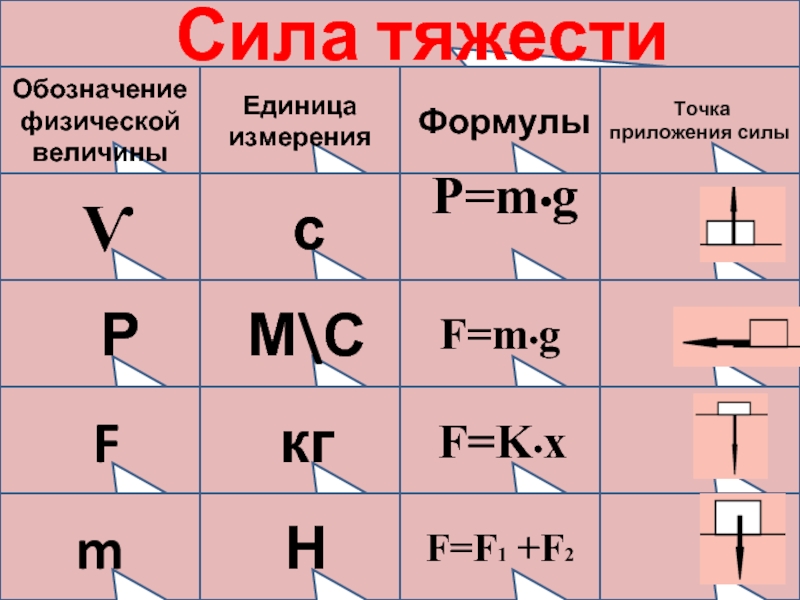 Оно не дает шнуркам развязываться, а гвоздям — выпадать из стены. Иными словами, оно мешает одному телу двигаться относительно другого. Она направлена против силы предполагаемого движения, но имеет максимальное значение. В какой-то момент трение покоя не сможет уравновешивать внешнюю силу, и тела начнут перемещаться. Максимальное значение зависит от свойств предметов и определяется формулой Fтр. пок. макс. = μпN, где N — сила реакции опоры, а μп — коэффициент трения покоя;
Оно не дает шнуркам развязываться, а гвоздям — выпадать из стены. Иными словами, оно мешает одному телу двигаться относительно другого. Она направлена против силы предполагаемого движения, но имеет максимальное значение. В какой-то момент трение покоя не сможет уравновешивать внешнюю силу, и тела начнут перемещаться. Максимальное значение зависит от свойств предметов и определяется формулой Fтр. пок. макс. = μпN, где N — сила реакции опоры, а μп — коэффициент трения покоя; При этом оно как бы вдавливается в землю, поэтому при каждом обороте телу нужно пересечь небольшое возвышение. Получается, сила трения растет с уменьшением твердости опоры. Она определяется формулой F тр.кач. = μкач.N, где μкач — коэффициент трения качения. μкач << μ — сила трения качения значительно меньше силы трения скольжения, поэтому катить что-то всегда проще, чем просто тащить по земле.
При этом оно как бы вдавливается в землю, поэтому при каждом обороте телу нужно пересечь небольшое возвышение. Получается, сила трения растет с уменьшением твердости опоры. Она определяется формулой F тр.кач. = μкач.N, где μкач — коэффициент трения качения. μкач << μ — сила трения качения значительно меньше силы трения скольжения, поэтому катить что-то всегда проще, чем просто тащить по земле.