Формула эдс индукции: расчет электродвижущей силы по формуле

Содержание

расчет электродвижущей силы по формуле

Электромагнитная индукция – генерирование электротоков магнитными полями, изменяющимися во времени. Открытие Фарадеем и Генри этого феномена ввело определенную симметрию в мир электромагнетизма. Максвеллу в одной теории удалось собрать знания об электричестве и магнетизме. Его исследования предсказывали существование электромагнитных волн перед экспериментальными наблюдениями. Герц доказал их существование и открыл человечеству эпоху телекоммуникаций.

Эксперименты Фарадея

Законы Фарадея и Ленца

Электрические токи создают магнитные эффекты. А возможно ли, чтобы магнитное поле порождало электрическое? Фарадей обнаружил, что искомые эффекты возникают вследствие изменения МП во времени.

Когда проводник пересекается переменным магнитным потоком, в нем индуцируется электродвижущая сила, вызывающая электроток. Системой, которая генерирует ток, может быть постоянный магнит или электромагнит.

Явление электромагнитной индукции регулируется двумя законами: Фарадея и Ленца.

Закон Ленца позволяет охарактеризовать электродвижущую силу относительно ее направленности.

Важно! Направление индуцированной ЭДС такое, что вызванный ею ток стремится противостоять создающей его причине.

Фарадей заметил, что интенсивность индуцированного тока растет, когда быстрее изменяется число силовых линий, пересекающих контур. Другими словами, ЭДС электромагнитной индукции находится в прямой зависимости от скорости движущегося магнитного потока.

ЭДС индукции

Формула ЭДС индукции определена как:

Е = — dФ/dt.

Знак «-» показывает, как полярность индуцированной ЭДС связана со знаком потока и меняющейся скоростью.

Получена общая формулировка закона электромагнитной индукции, из которой можно вывести выражения для частных случаев.

Движение провода в магнитном поле

Когда провод длиной l движется в МП, имеющем индукцию В, внутри него будет наводиться ЭДС, пропорциональная его линейной скорости v. Для расчета ЭДС применяется формула:

в случае движения проводника перпендикулярно направлению магнитного поля:

Е = — В x l x v;

в случае движения под другим углом α:

Е = — В x l x v х sin α.

Индуцированная ЭДС и ток будут направлены в сторону, которую находим, пользуясь правилом правой руки: расположив руку перпендикулярно силовым линиям магнитного поля и указывая большим пальцем в сторону перемещения проводника, можно узнать направление ЭДС по оставшимся четырем распрямленным пальцам.

Перемещение провода в МП

Вращающаяся катушка

Работа генератора электроэнергии основана на вращении контура в МП, имеющего N витков.

ЭДС индуцируется в электроцепи всегда, когда магнитный поток ее пересекает, в соответствии с определением магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на поверхностную площадь, через которую проходит МП, и косинус угла, образованного вектором В и перпендикулярной линией к плоскости S).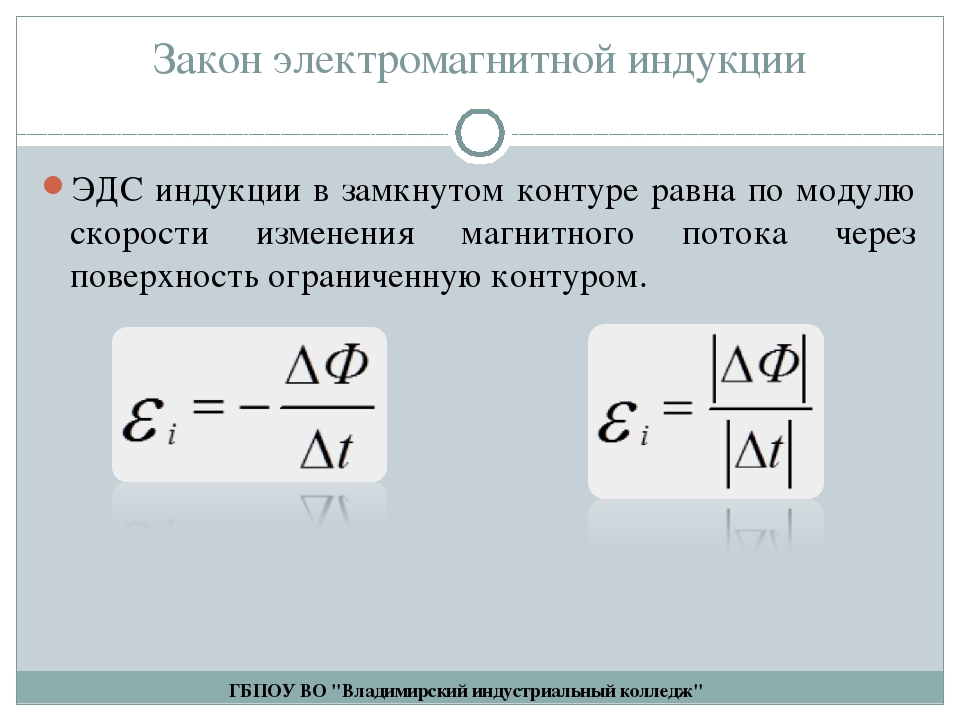

Из формулы следует, что Ф подвержен изменениям в следующих случаях:

меняется интенсивность МП – вектор В;
варьируется площадь, ограниченная контуром;
изменяется ориентация между ними, заданная углом.

В первых опытах Фарадея индуцированные токи были получены путем изменения магнитного поля В. Однако можно индуцировать ЭДС, не двигая магнит или не меняя ток, а просто вращая катушку вокруг своей оси в МП. В данном случае магнитный поток меняется из-за изменения угла α. Катушка при вращении пересекает линии МП, возникает ЭДС.

Если катушка вращается равномерно, это периодическое изменение приводит к периодическому изменению магнитного потока. Или количество силовых линий МП, пересекаемых каждую секунду, принимает равные значения с равными интервалами времени.

Вращение контура в МП

Важно! Наведенная ЭДС меняется вместе с ориентацией с течением времени от положительной до отрицательной и наоборот. Графическое представление ЭДС представляет собой синусоидальную линию.

Для формулы ЭДС электромагнитной индукции применяется выражение:

Е = В х ω х S x N x sin ωt, где:

S – площадь, ограниченная одним витком или рамкой;
N – количество витков;
ω – угловая скорость, с которой вращается катушка;
В – индукция МП;
угол α = ωt.

На практике в генераторах переменного тока часто катушка остается неподвижной (статор), а электромагнит вращается вокруг нее (ротор).

ЭДС самоиндукции

Когда через катушку проходит переменный ток, он генерирует переменное МП, обладающее изменяющимся магнитным потоком, индуцирующим ЭДС. Этот эффект называется самоиндукцией.

Поскольку МП пропорционально интенсивности тока, то:

Ф = L x I,

где L – индуктивность (Гн), определяемая геометрическими величинами: количеством витков на единицу длины и размерами их поперечного сечения.

Для ЭДС индукции формула принимает вид:

Е = — L x dI/dt.

Взаимоиндукция

Если две катушки расположены рядом, то в них наводится ЭДС взаимоиндукции, зависящая от геометрии обеих схем и их ориентации относительно друг друга. Когда разделение цепей возрастает, взаимоиндуктивность снижается, так как уменьшается соединяющий их магнитный поток.

Взаимоиндукция

Пусть имеется две катушки. По проводу одной катушки, обладающей N1 витками, протекает ток I1, создающий МП, проходящее через катушку с N2 витками. Тогда:

Взаимоиндуктивность второй катушки относительно первой:

М21 = (N2 x F21)/I1;

Магнитный поток:

Ф21 = (М21/N2) x I1;

Найдем индуцированную ЭДС:

Е2 = — N2 x dФ21/dt = — M21x dI1/dt;

Идентично в первой катушке индуцируется ЭДС:

Е1 = — M12 x dI2/dt;

Важно! Электродвижущая сила, вызванная взаимоиндукцией в одной катушке, всегда пропорциональна изменению электротока в другой.

Взаимную индуктивность можно признать равной:

М12 = М21 = М.

Соответственно, E1 = — M x dI2/dt и E2 = M x dI1/dt.

М = К √ (L1 x L2),

где К – коэффициент связи между двумя индуктивностями.

Явление взаимоиндукции используется в трансформаторах – электроаппаратах, позволяющих изменить значение напряжения переменного электротока. Аппарат представляет собой две катушки, намотанные вокруг одного сердечника. Ток, присутствующий в первой, создает меняющееся МП в магнитопроводе и электроток в другой катушке. Если количество витковых оборотов первой обмотки меньше, чем другой, напряжение увеличивается, и наоборот.

Кроме генерирования, трансформации электроэнергии магнитная индукция применяется в иных устройствах. Например, в магнитных левитационных поездах, которые двигаются не в непосредственном контакте с рельсами, а на несколько сантиметров выше из-за электромагнитной силы отталкивания.

Видео

Оцените статью:

что это такое, основные формулы, в чем измеряется, от чего зависит.

В материале разберемся в понятии ЭДС индукции в ситуациях ее возникновения. Также рассмотрим индуктивность в качестве ключевого параметра возникновения магнитного потока при появлении электрического поля в проводнике.

Электромагнитная индукция представляет собой генерирование электрического тока магнитными полями, которые изменяются во времени. Благодаря открытиям Фарадея и Ленца закономерности были сформулированы в законы, что ввело симметрию в понимание электромагнитных потоков. Теория Максвелла собрала воедино знания об электрическом токе и магнитных потоках. Благодаря открытия Герца человечество узнало о телекоммуникациях.

Магнитный поток

Вокруг проводника с электротоком появляется электромагнитное поле, однако параллельно возникает также обратное явление – электромагнитная индукция. Рассмотрим магнитный поток на примере: если рамку из проводника поместить в электрическое поле с индукцией и перемещать ее сверху вниз по магнитным силовым линиям или вправо-влево перпендикулярно им, тогда магнитный поток, проходящий через рамку, будет постоянной величиной.

При вращении рамки вокруг своей оси, тогда через некоторое время магнитный поток изменится на определенную величину. В результате в рамке возникает ЭДС индукции и появится электрический ток, который называется индукционным.

ЭДС индукции

Разберемся детально, что такое понятие ЭДС индукции. При помещении в магнитное поле проводника и его движении с пересечением силовых линий поля, в проводнике появляется электродвижущая сила под названием ЭДС индукции. Также она возникает, если проводник остается в неподвижном состоянии, а магнитное поле перемещается и пересекается с проводником силовыми линиями.

Когда проводник, где происходит возникновение ЭДС, замыкается на вешнюю цепь, благодаря наличию данной ЭДС по цепи начинает протекать индукционный ток. Электромагнитная индукция предполагает явление индуктирования ЭДС в проводнике в момент его пересечения силовыми линиями магнитного поля.

Электромагнитная индукция являет собой обратный процесс трансформации механической энергии в электроток. Данное понятие и его закономерности широко используются в электротехнике, большинство электромашин основывается на данном явлении.

Законы Фарадея и Ленца

Законы Фарадея и Ленца отображают закономерности возникновения электромагнитной индукции.

Фарадей выявил, что магнитные эффекты появляются в результате изменения магнитного потока во времени. В момент пересечения проводника переменным магнитным током, в нем возникает электродвижущая сила, которая приводит к возникновению электрического тока. Генерировать ток может как постоянный магнит, так и электромагнит.

Ученый определил, что интенсивность тока возрастает при быстром изменении количества силовых линий, которые пересекают контур. То есть ЭДС электромагнитной индукции пребывает в прямой зависимости от скорости магнитного потока.

Согласно закону Фарадея, формулы ЭДС индукции определяются следующим образом:

Е = — dФ/dt.

Знак «минус» указывает на взаимосвязь между полярностью индуцированной ЭДС, направлением потока и изменяющейся скоростью.

Согласно закону Ленца, можно охарактеризовать электродвижущую силу в зависимости от ее направленности. Любое изменение магнитного потока в катушке приводит к появлению ЭДС индукции, причем при быстром изменении наблюдается возрастающая ЭДС.

Если катушка, где есть ЭДС индукции, имеет замыкание на внешнюю цепь, тогда по ней течет индукционный ток, вследствие чего вокруг проводника появляется магнитное поле и катушка приобретает свойства соленоида. В результате вокруг катушки формируется свое магнитное поле.

Э.Х. Ленц установил закономерность, согласно которой определяется направление индукционного тока в катушке и ЭДС индукции. Закон гласит, что ЭДС индукции в катушке при изменении магнитного потока формирует в катушке ток направления, при котором данный магнитный поток катушки дает возможность избежать изменения постороннего магнитного потока.

Закон Ленца применяется для всех ситуаций индуктирования электротока в проводниках, вне зависимости от их конфигурации и метода изменения внешнего магнитного поля.

Движение провода в магнитном поле

Значение индуктированной ЭДС определяется в зависимости от длины проводника, пересекаемого силовыми линиями поля. При большем количестве силовых линий возрастает величина индуктируемой ЭДС. При увеличении магнитного поля и индукции, большее значение ЭДС возникает в проводнике. Таким образом, значение ЭДС индукции в движущемся в магнитном поле проводнике находится в прямой зависимости от индукции магнитного поля, длины проводника и скорости его движения.

Данная зависимость отражена в формуле Е = Blv, где Е — ЭДС индукции; В — значение магнитной индукции; I — длина проводника; v —скорость его перемещения.

Отметим, что в проводнике, который движется в магнитном поле, ЭДС индукции появляется, только когда он пересекает силовые линии магнитного поля. Если проводник движется по силовым линиям, тогда ЭДС не индуктируется. По этой причине формула применяется только в случаях, когда движением проводника направлено перпендикулярно силовым линиям.

Направление индуктированной ЭДС и электротока в проводнике определяется направлением движения самого проводника. Для выявления направления разработано правило правой руки. Если держать ладонь правой руки таким образом, чтобы в ее направлении входили силовые линии поля, а большой палец указывает направление движения проводника, тогда остальные четыре пальца показывают направление индуктированной ЭДС и направление электротока в проводнике.

Вращающаяся катушка

Функционирование генератора электротока основывается на вращении катушки в магнитном потоке, где имеется определенное количество витков. ЭДС индуцируется в электрической цепи всегда при пересечении ее магнитным потоком, на основании формулы магнитного потока Ф = B x S х cos α (магнитная индукция, умноженная на площадь поверхности, через которую проходит магнитный поток, и косинус угла, сформированный вектором направления и перпендикулярной плоскости линии).

Согласно формуле, на Ф воздействуют изменения в ситуациях:

при изменении магнитного потока меняется вектор направления;
изменяется площадь, заключенная в контур;
меняется угол.

Допускается индуцирование ЭДС при неподвижном магните или неизменном токе, а просто при вращении катушки вокруг своей оси в пределах магнитного поля. В данном случае магнитный поток изменяется при смене значения угла. Катушка в процессе вращения пересекает силовые линии магнитного потока, в итоге появляется ЭДС. При равномерном вращении возникает периодическое изменение магнитного потока. Также число силовых линий, которые пересекаются ежесекундно, становится равным значениям через равные временные промежутки.

На практике в генераторах переменного электротока катушка остается в неподвижном состоянии, а электромагнит выполняет вращения вокруг нее.

ЭДС самоиндукции

При прохождении через катушку переменного электротока генерируется переменное магнитное поле, которое характеризуется меняющимся магнитным потоком, индуцирующим ЭДС. Данное явление называется самоиндукцией.

В силу того, что магнитный поток пропорционален интенсивности электротока, тогда формула ЭДС самоиндукции выглядит таким образом:

Ф = L x I, где L – индуктивность, которая измеряется в Гн. Ее величина определяется числом витков на единицу длины и величиной их поперечного сечения.

Взаимоиндукция

При расположении двух катушек рядом в них наблюдается ЭДС взаимоиндукции, которая определяется конфигурацией двух схем и их взаимной ориентацией. При возрастании разделения цепей значение взаимоиндуктивности уменьшается, поскольку наблюдается уменьшение общего для двух катушек магнитного потока.

Рассмотрим детально процесс возникновения взаимоиндукции. Есть две катушки, по проводу одной с N1 витков течет ток I1, которым создается магнитный поток и идет через вторую катушку с N2 числом витков.

Значение взаимоиндуктивности второй катушки в отношении первой:

М21 = (N2 x F21)/I1.

Значение магнитного потока:

Ф21 = (М21/N2) x I1.

Индуцированная ЭДС вычисляется по формуле:

Е2 = — N2 x dФ21/dt = — M21x dI1/dt.

В первой катушке значение индуцируемой ЭДС:

Е1 = — M12 x dI2/dt.

Важно отметить, что электродвижущая сила, спровоцированная взаимоиндукцией в одной из катушек, в любом случае прямо пропорциональна изменению электрического тока в другой катушке.

Тогда взаимоиндуктивность считается равной:

М12 = М21 = М.

Вследствие этого , E1 = — M x dI2/dt и E2 = M x dI1/dt. М = К √ (L1 x L2), где К является коэффициентом связи между двумя значениями инжуктивности.

Взаимоиндукция широко используется в трансформаторах, которые дают возможность менять значения переменного электротока. Прибор представляет собой пару катушек, которые намотаны на общий сердечник. Ток в первой катушке формирует изменяющийся магнитный поток в магнитопроводе и ток во второй катушке. При меньшем числе витков в первой катушке, чем во второй, возрастает напряжение, и соответственно при большем количестве витков в первой обмотке напряжение снижается.

Помимо генерирования и трансформации электрической энергии, явление магнитной индукции используется в прочих приборах. К примеру, в магнитных левитационных поездах, движущихся без непосредственного контакта с током в рельсах, а на пару сантиметров выше по причине электромагнитного отталкивания.

формула через силу тока, индуктивность или площадь, единица измерения в физике

Что такое ЭДС индукции — когда возникает, при каких условиях

Определение

Электродвижущая сила, ЭДС — физическая величина, описывающая работу любых сил, которые действуют в квазистационарных цепях постоянного или переменного тока, за исключением диссипативных и электростатических сил.

При замкнутой цепи можно найти ЭДС, воспользовавшись законом Ома:

$\varepsilon\;=\;I\;\times\;(R\;+\;r).$

R здесь — сопротивление цепи, r — внутреннее сопротивление источника.
Создание Алессандро Вольтой надежного источника электричества, гальванического элемента, и открытие Хансом Кристианом Эрстедом магнитного действия электрического тока послужили толчком к интенсивному развитию техники электрических измерений в XIX веке.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Выдающаяся роль здесь принадлежит немецкому физику Георгу Симону Ому. Для определения силы тока он использовал принцип крутильных весов Кулона. На длинной тонкой нити подвешено горизонтальное коромысло с заряженным шариком на конце. Второй заряд закреплен на спице, пропущенной сквозь крышку весов.

При их взаимодействии коромысло поворачивается. Вращение головки в верхней части весов закручивало нить, возвращая коромысло в исходное состояние. По углу закручивания можно рассчитать силу взаимодействия зарядов в зависимости от расстояния между ними.

Ом по величине угла закрутки судил о силе тока I в проводнике, т. е. количестве электричества, перенесенном через поперечное сечение проводника за единицу времени.

В качестве основной характеристики источника тока Ом брал величину напряжения \varepsilon на электродах гальванического элемента при разомкнутой цепи. Эту величину \varepsilon он назвал электродвижущей силой, сокращенно ЭДС.

Движущиеся заряды создают вокруг себя магнитное поле. Однако действующая в нем на магнит или другой ток сила отличается от электрической своим направлением — магнитная стрелка старается развернуться перпендикулярно проводу.

Изучение действующей на другой ток силы переросло в отдельное исследование с неожиданным результатом: сила оказалась направленной всегда перпендикулярно внесенному в магнитное поле проводнику, который для простоты исследования был прямолинейным.

Математическое выражение для этой силы, названной силой Ампера, проще всего записать в виде векторного произведения:

$d\overrightarrow F\;=\;Id\overrightarrow l\;\times\;\overrightarrow B$.

I здесь — сила тока, протекающего через проводник; l — вектор длины проводника, направленный в ту же сторону, куда течет ток; В — характеристика поля. Величина В называется магнитной индукцией и является аналогом электрической напряженности.

Максвелл поставил целью создать теорию эфира, связав его механические характеристики с электрическими и магнитными силами. Тщательно изучив труды Фарадея, он пришел к выводу, что напряженность $\overrightarrow Е$ электрического поля объясняется упругими напряжениями в эфире, а магнитная индукция $\overrightarrow B$ — его вихревыми движениями.

Рассматривая замкнутый проводящий контур С, где действует ЭДС индукции $\varepsilon_i$, Максвелл для получения числа силовых линий магнитного потока $\triangle Ф$, пересекаемых контуром за время \triangle t, «натягивал» на него некую поверхность S, разбитую на элементарные площадки $\triangle S$, и отождествлял Ф с магнитным потоком сквозь всю поверхность. Математически это можно выразить так:

$Ф\;=\;\sum_{\triangle S}\;\;B\triangle S. $

Объединив это соотношение с идеей Фарадея, Максвелл пришел к собственной формуле:

$\varepsilon_i\;=\;-\;\frac1с\;\times\;\frac{dФ}{dt}. $

Выбор коэффициента пропорциональности $\alpha$ здесь обусловлен необходимостью согласования формулы с законом Био — Савара — Лапласа, в котором появляется та же электродинамическая постоянная с.

Определение

Электродинамическая постоянная с — универсальная постоянная, равная скорости распространения электромагнитных волн в вакууме.

Но в опытах Фарадея ЭДС индукции регистрировалась как в движущемся, так и в покоящемся проводящем контуре С, если последний находился в переменном магнитном поле. И здесь встал вопрос, что конкретно перемещает заряды в неподвижном проводнике.

Само по себе магнитное поле не воздействует на заряды, находящиеся в покое, из чего следует: условие возникновения индукционного тока — возникающее в контуре электрическое поле \overrightarrow Е. Так как электростатическое поле в замкнутом контуре не совершает работы, значит, происходит работа вихревого поля, и она равна ЭДС индукции:

$\varepsilon_i\;=\;\underset С{\oint\;}\;(\overrightarrow{Е\;}\times\;d\overrightarrow l)$

Определение

Самоиндукция — частный случай магнитной индукции, возникновение ЭДС индукции в проводящем контуре, когда в нем меняется ток.

Источником энергии, возникающей в цепи, является в этом случае запас энергии магнитного поля. Полное количество выделившейся джоулевой теплоты можно вычислить, изобразив на графике зависимость магнитного потока Ф(I) от силы тока I:

Источник: physics.ru

ЭДС в быту, как обозначается, единицы измерения

В быту явление электромагнитной индукции используют для изменения величины напряжения тока в трансформаторах и дросселях. На принципе магнитной индукции работают электрические счетчики, реле мощности, успокоительные системы стрелочных измерительных приборов.

Существуют также магнитные газовые генераторы, в которых благодаря магнитному полю возникает электродвижущая сила, создающая ток.

Электродвижущая сила индукции в системе СИ измеряется в вольтах. Просто электродвижущая сила обозначается греческой буквой $\varepsilon $, электродвижущая сила индукции —$ \varepsilon_i.$

Законы Фарадея и Ленца

Фарадей опытным путем выяснил, что при пересечении проводником магнитных силовых линий по нему проходит заряд $\triangle Q$.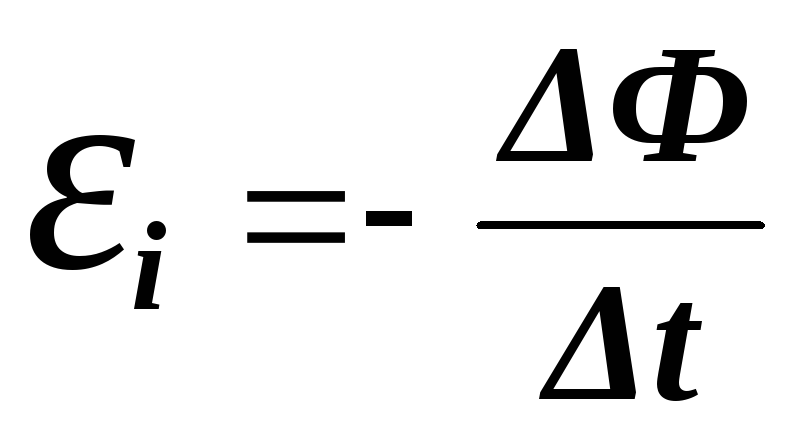

Он связан с числом пересеченных силовых линий $ \triangle Ф$ и электрическим сопротивлением контура R, что выражается законом Фарадея:

$\triangle Q\;=\;\alpha\frac{\triangle Ф}R. $

Соприкосновение поля и проводника вызвано либо движением проводника, либо изменениями самого магнитного поля.

Саму электродвижущую силу индукции, связанную с сопротивлением контура и силой тока согласно закону Ома, можно найти по формуле

$\varepsilon_i\;=\;\alpha\frac{\triangle Ф}{\triangle t}. $

$\triangle t$ здесь — время, за которое проходит через поперечное сечение проводника количество электричества $\triangle Q.$

Ленц доказал, что индукционный ток всегда направлен так, чтобы противодействовать вызвавшей его причине. Согласно правилу Ленца, в вышеприведенном соотношении следует выбрать отрицательный знак, считая коэффициент$ \alpha $ положительным:

$\varepsilon_i\;=\;-\;\alpha\frac{\triangle Ф}{\triangle t}. $

Как рассчитать электродвижущую силу индукции, формулы

Через магнитный поток

$\varepsilon_i\;=\;-\;\alpha\frac{\triangle Ф}{\triangle t}. $

Через силу тока

ЭДС самоиндукции зависит от изменения силы тока, при этом магнитный поток собственного поля через цепь пропорционален току в ней:

$\varepsilon_{is\;}\;=\;-\;L\frac{\triangle I}{\triangle t}. $

L здесь — индуктивность проводника.

Через сопротивление

Для ЭДС индукции уравнение закона Ома можно переписать в виде:
$\varepsilon_{i\;}\;=\;IR\;-\;\varepsilon.$

Через угловую скорость

$\varepsilon_i\;=\;В\omega SN\sin\left(\alpha\right). $

B здесь — индукция магнитного поля, $\omega$ — угловая скорость вращения рамки, S — площадь рамки, N — число витков, $\alpha$ — угол между векторами индукции магнитного поля и скорости движения проводника.

Через площадь

Если магнитный поток изменяется без деформации витков, т. е. их количество и площадь не меняются, то можно найти электродвижущую силу индукции через площадь.
Угол \alpha между вектором магнитного поля и нормалью к плоскости витков будет равен:

$2\mathrm\pi\;\times\;\mathrm v\;\times\;\mathrm t. $Полный магнитный поток в момент времени t будет равен:

$\psi_B\;=\;N\;\times\;B\;\times\;S\;\times\;\cos\left(\alpha\right)=\;N\;\times\;B\;\times\;S\;\times\;\cos\left(2\mathrm\pi\;\times\;\mathrm v\;\times\;\mathrm t\right).$

Тогда $\varepsilon_i\;=\;-\;\frac{d\psi_B}{dt}=\;2\mathrm{pivNBSsin}\left(2\mathrm{pivt}\right).$

Способы определения ЭДС индукции в движущихся проводниках

Нахождение ЭДС индукции через силу Лоренца

Магнитный поток через контур может изменяться по следующим причинам:

В обоих этих случаях будет выполняться закон электромагнитной индукции. При этом происхождение электродвижущей силы в этих случаях различное. Рассмотрим подробнее второй из этих случаев

В данном случае проводник движется в магнитном поле. Вместе с проводником совершают движение и все заряды, которые находятся внутри проводника. На каждый из таких зарядов со стороны магнитного поля будет действовать сила Лоренца. Она и будет способствовать перемещению зарядов внутри проводника.

ЭДС индукции в данном случае будет иметь магнитное происхождение.

Рассмотрим следующий опыт: магнитный контур, у которого одна сторона подвижная, помещают в однородное магнитное поле. Подвижная сторона длиной l начинает скользить вдоль сторон MD и NC с постоянной скоростью V. При этом она постоянно остаётся параллельной стороне СD. Вектор магнитной индукции поля будет перпендикулярен проводнику и составлять угол а с направлением его скорости. На следующем рисунке представлена лабораторная установка для этого опыта:

Сила Лоренца, действующая на движущуюся частицу, вычисляется по следующей формуле:

Fл = |q|*V*B*sin(a).

Сила Лоренца будет направлена вдоль отрезка MN. Рассчитаем работу силы Лоренца:

A = Fл*l = |q|*V*B*l*sin(a).

ЭДС индукции — это отношение работы, совершаемой силой при перемещении единичного положительного заряда, к величине этого заряда. Следовательно, имеем:

Ei = A/|q| = V*B*l*sin(a).

Эта формула будет справедлива для любого проводника, движущегося в с постоянной скоростью в магнитном поле. ЭДС индукции будет только в этом проводнике, так как остальные проводники контура остаются неподвижными. Очевидно, что ЭДС индукции во всем контуре будет равняться ЭДС индукции в подвижном проводнике.

ЭДС из закона электромагнитной индукции

Магнитный поток через тот же контур, что и в примере выше, будет равняться:

Ф = B*S*cos(90-a) = B*S*sin(a).

Здесь угол (90-а) = угол между вектором магнитной индукции и нормалью к поверхности контура. За некоторое время ∆t площадь контура будет изменяться на ∆S = -l*V*∆t. Знак «минус» показывает, что площадь уменьшается. При этом за это время магнитный поток изменится:

∆Ф = -B*l*V*sin(a).

Тогда ЭДС индукции равна:

Ei = -∆Ф/∆t = B*l*V*sin(a).

Если весь контур будет двигаться внутри однородного магнитного поля с постоянной скоростью, то ЭДС индукции будет равняться нулю, так как будет отсутствовать изменение магнитного потока.

ЭДС индукции будет возникать и при повороте рамки внутри магнитного поля.

Нужна помощь в учебе?

Предыдущая тема: Закон электромагнитной индукции:магнитный поток и электродвижущая сила
Следующая тема:&nbsp&nbsp&nbspЭлектродинамический микрофон: самоиндукция

Эдс самоиндукции расчет. Формула ЭДС индукции определена как

Э. д. с. самоиндукции. Э. д. с. e L , индуцирования в проводнике или катушке в результате изменения магнитного потока, созданного током, проходящим по этому же проводнику или катушке, носит название э. д. с. самоиндукции (рис. 60). Эта э. д. с. возникает при всяком изменении тока, например при замыкании и размыкании электрических цепей, при изменении нагрузки электродвигателей и пр. Чем быстрее изменяется ток в проводнике или катушке, тем больше скорость изменения пронизывающего их магнитного потока и тем большая э. д. с. самоиндукции в них индуцируется. Например, э. д. с. самоиндукции e L возникает в проводнике АБ (см. рис. 54) при изменении протекающего по нему тока i 1 . Следовательно, изменяющееся магнитное поле индуцирует э. д. с. в том же самом проводнике, в котором изменяется ток, создающий это поле.

Направление э. д. с. самоиндукции определяется по правилу Ленца. Э. д. с. самоиндукции имеет всегда такое направление, при котором она препятствует изменению вызвавшего ее тока. Следовательно, при возрастании тока в проводнике (катушке) индуцированная в них э. д. с. самоиндукции будет направлена против тока, т. е. будет препятствовать его возрастанию (рис. 61, а), и наоборот, при уменьшении тока в проводнике (катушке) возникает э. д. с. самоиндукции, совпадающая по направлению с током, т. е. препятствующая его убыванию (рис. 61, б). Если же ток в катушке не изменяется, то э. д. с. самоиндукции не возникает.

Из рассмотренного выше правила для определения направления э. д. с. самоиндукции вытекает, что эта э. д. с. оказывает тормозящее действие на изменение тока в электрических цепях. В этом отношении ее действие аналогично действию силы инерции, которая препятствует изменению положения тела. В электрической цепи (рис. 62, а), состоящей из резистора с сопротивлением R и катушки К, ток i создается совместным действием напряжения U источника и э. д. с. самоиндукции e L индуцируемой в катушке. При подключении рассматриваемой цепи к источнику э. д. с. самоиндукции e L (см. сплошную стрелку) сдерживает нарастание силы тока. Поэтому ток i достигает установившегося значения I=U/R (согласно закону Ома) не мгновенно, а в течение определенного промежутка времени (рис. 62, б). За это время в электрической цепи происходит переходный процесс, при котором изменяются e L и i. Точно

так же при выключении электрической цепи ток i не уменьшается мгновенно до нуля, а из-за действия э. д. с. e L (см. штриховую стрелку) постепенно уменьшается.

Индуктивность. Способность различных проводников (катушек) индуцировать э. д. с. самоиндукции оценивается индуктивностью L. Она показывает, какая э. д. с. самоиндукции возникает в данном проводнике (катушке) при изменении тока на 1 А в течение 1 с. Индуктивность измеряется в генри (Гн), 1 Гн = 1 Ом*с. На практике индуктивность часто измеряют в тысячных долях генри — миллигенри (мГн) и в миллионных долях генри — микрогенри (мкГн).

Индуктивность катушки зависит от числа витков катушки? и магнитного сопротивления R м ее магнитопровода, т. е. от его магнитной проницаемости? а и геометрических размеров l и s. Если в катушку вставить стальной сердечник, ее индуктивность резко возрастает из-за усиления магнитного поля катушки. В этом случае ток 1 А создает значительно больший магнитный поток, чем в катушке без сердечника.

Используя понятие индуктивности L, можно получить для э. д. с. самоиндукции следующую формулу:

e L = – L ?i / ?t (53)

Где?i – изменение тока в проводнике (катушке) за промежуток времени?t.

Следовательно, э. д. с. самоиндукции пропорциональна скорости изменения тока.

Включение и отключение цепей постоянного тока с катушкой индуктивности. При подключении к источнику постоянного тока с напряжением U электрической цепи, содержащей R и L, выключателем B1 (рис. 63, а) ток i возрастает до установившегося значения I уст =U/R не мгновенно, так как э. д. с. самоиндукции e L , возникающая в индуктивности, действует против приложенного напряжения V и препятствует нарастанию тока. Для рассматриваемого процесса характерным является постепенное изменение тока i (рис. 63, б) и напряжений u а и u L по кривым — экспонентам. Изменение i, u а и u L по указанным кривым называется апериодическим.

Скорость нарастания силы тока в цепи и изменения напряжений u а и u L характеризуется постоянной времени цепи

T = L/R (54)

Она измеряется в секундах, зависит только от параметров R и L данной цепи и позволяет без построения графиков оценить длительность процесса изменения тока. Эта длительность теоретически бесконечно велика. Практически же обычно считают, что она составляет (3-4) Т. За это время ток в цепи достигает 95-98 % установившегося значения. Следовательно, чем больше сопротивление и чем меньше индуктивность L, тем быстрее протекает процесс изменения тока в электрических цепях с индуктивностью. Постоянную времени Т при апериодическом процессе можно определить как отрезок АВ, отсекаемый касательной, проведенной из начала координат к рассматриваемой кривой (например, тока i) на линии, соответствующей установившемуся значению данной величины.
Свойством индуктивности замедлять процесс изменения тока пользуются для создания выдержек времени при срабатывании различных аппаратов (например, при управлении работой песочниц для периодической подачи порций песка под колеса локомотива). На использовании этого явления основана также работа электромагнитного реле времени (см. § 94).

Коммутационные перенапряжения. Особенно сильно проявляет себя э. д. с. самоиндукции при размыкании цепей, содержащих катушки с большим числом витков и со стальными сердечниками (например, обмотки генераторов, электродвигателей, трансформаторов и пр.), т. е. цепей, обладающих большой индуктивностью. В этом случае возникающая э. д. с. самоиндукции e L может во много раз превысить напряжение U источника и, суммируясь с ним, послужить причиной возникновения перенапряжений в электрических цепях (рис. 64, а), называемых коммутационными (возникающими при коммутации — переключениях электрических цепей). Они являются опасными для обмоток электродвигателей, генераторов и трансформаторов, так как могут вызвать пробой их изоляции.

Большая э. д. с. самоиндукции способствует также возникновению электрической искры или дуги в электрических аппаратах, осуществляющих коммутацию электрических цепей. Например, в момент размыкания контактов рубильника (рис. 64, б) образующаяся э. д. с. самоиндукции сильно увеличивает разность потенциалов между разомкнутыми контактами рубильника и пробивает воздушный промежуток. Возникающая при этом электрическая дуга поддерживается в, течение некоторого времени э. д. с. самоиндукции, которая, таким образом, затягивает процесс отключения тока в цепи. Это явление весьма нежелательно, так как дуга оплавляет контакты отключающих аппаратов, что приводит к быстрому выходу их из строя. Поэтому во всех аппаратах, служащих для размыкания электрических цепей, предусматриваются специальные дугогасительные устройства, обеспечивающие ускорение гашения дуги.

Кроме того, в силовых цепях, обладающих значительной индуктивностью (например, обмотки возбуждения генераторов), параллельно цепи R-L (т. е. соответствующей обмотке) включают разрядный резистор R р (рис. 65, а). В этом случае после отключения выключателя В1 цепь R-L не прерывается, а оказывается замкнутой на резистор R р. Ток в цепи i при этом уменьшается не мгновенно, а постепенно — по экспоненте (рис. 65,6), так как э. д. с. самоиндукции e L , возникающая в индуктивности L, препятствует уменьшению тока. Напряжение u p на разрядном резисторе в течение процесса изменения тока также изменяется по экспоненте. Оно равно напряжению, приложенному к цепи R-L, т. е. к зажимам соответ-

ствующей обмотки. В начальный момент U p нач = UR p /R, т. е. зависит от сопротивления разрядного резистора; при больших значениях Rp это напряжение может оказаться чрезмерно большим и опасным для изоляции электрической установки. Практически для ограничения возникающих перенапряжений сопротивление R p разрядного резистора берут не более чем в 4-8 раз больше сопротивления R соответствующей обмотки.

Условия возникновения переходных процессов. Рассмотренные выше процессы при включении и выключении цепи R-L называют переходными процессами . Они возникают при включении и выключении источника или отдельных участков цепи, а также при изменении режима работы , например при скачкообразном изменении нагрузки, обрывах и коротких замыканиях. Такие же переходные процессы имеют место при указанных условиях и в цепях, содержащих конденсаторы, обладающие емкостью С. В ряде случаев переходные процессы являются опасными для источников и приемников, так как возникающие токи и напряжения могут во много раз превышать номинальные значения, на которые рассчитаны эти устройства. Однако в некоторых элементах электрооборудования, в частности в устройствах промышленной электроники, переходные процессы являются рабочими режимами.

Физически возникновение переходных процессов объясняется тем, что катушки индуктивности и конденсаторы являются накопителями энергии, а процесс накопления и отдачи энергии в этих элементах не может происходить мгновенно, следовательно, не может мгновенно измениться ток в катушке индуктивности и напряжение на конденсаторе. Время переходного процесса, в течение которого при включениях, выключениях и изменениях режима работы цепи происходит постепенное изменение тока и напряжения, определяется значениями R, L и С цепи и может составить доли и единицы секунд. После окончания переходного процесса ток и напряжение приобретают новые значения, которые называют установившимися .

Магнитное поле контура, в котором сила тока изменяется, индуцирует ток не только в других контурах, но и в себе самом. Это явление получило название самоиндукции.

Опытным путём установлено, что магнитный поток вектора магнитной индукции поля, создаваемого текущим в контуре током, пропорционален силе этого тока:

где L– индуктивность контура. Постоянная характеристика контура, которая зависит от его формы и размеров, а так же от магнитной проницаемости среды, в которой находится контур. [L] = Гн (Генри,

1Гн = Вб/А).

Если за время dtток в контуре изменится наdI, то магнитный поток, связанный с этим током, изменится наdФ =LdIв результате чего в этом контуре появится ЭДС самоиндукции:

Знак минус показывает, что ЭДС самоиндукции (а, следовательно, и ток самоиндукции) всегда препятствует изменению силы тока, который вызвал самоиндукцию.

Наглядным примером явления самоиндукции служат экстратоки замыкания и размыкания, возникающие при включении и выключении электрических цепей, обладающей значительной индуктивностью.

Энергия магнитного поля

Магнитное поле обладает потенциальной энергией, которая в момент его образования (или изменения) пополняется за счёт энергии тока в цепи, совершающего при этом работу против ЭДС самоиндукции, возникающей вследствие изменения поля.

Работа dAза бесконечно малый промежуток времениdt, в течении которого ЭДС самоиндукциии токIможно считать постоянными, равняется:

. (5)

Знак минус указывает, что элементарная работа совершается током против ЭДС самоиндукции. Чтобы определить работу при изменении тока от 0 до I, проинтегрируем правую часть, получим:

. (6)

Эта работа численно равна приросту потенциальной энергии ΔW п магнитного поля, связанного с этой цепью, т.е.A= -ΔW п.

Выразим энергию магнитного поля через его характеристики на примере соленоида. Будем считать, что магнитное поле соленоида однородно и в основном расположено внутри его. Подставим в (5) значение индуктивности соленоида, выраженное через его параметры и значение силы тока I, выраженное из формулы индукции магнитного поля соленоида:

, (7)

где N – общее число витков соленоида; ℓ – его длина; S – площадь сечения внутреннего канала соленоида.

, (8)

После подстановки имеем:

Разделив обе части на V, получим объёмную плотность энергии поля:

(10)

или, с учётом, что
получим,
. (11)

Переменный ток

2.1 Переменный ток и его основные характеристики

Переменным называется ток, изменяющийся с течением времени и по величине и по направлению. Примером переменного тока может служить потребляемый промышленный ток. Этот ток является синусоидальным, т.е. мгновенное значение его параметров меняются со временем по закону синуса (или косинуса):

i = I 0 sinωt, u = U 0 sin(ωt + φ 0). (12)

Переменный синусоидальный ток можно получить, если вращать рамку (контур) с постоянной скоростью

в однородном магнитном поле с индукцией B (рис.5). При этом магнитный поток, пронизывающий контур, изменяется по закону

где S– площадь контура, α = ωt– угол поворота рамки за время t. Изменение потока приводит к возникновению ЭДС индукции

, (17)

направление которой определяется по правилу Ленца.

Если контур замкнут (рис.5), то по нему идёт ток:

. (18)

График изменения электродвижущей силыи индукционного токаi представлен на рис. 6.

Переменный ток характеризуется периодом Т, частотой ν = 1/Т, циклической частотой
и фазой φ = (ωt + φ 0) Графически значения напряжения и силы переменного тока на участке цепи будут представляться двумя синусоидами, в общем случае сдвинутыми по фазе на φ.

Для характеристики переменного тока вводятся понятия действующего (эффективного) значения тока и напряжения. Эффективным значением силы переменного тока называется сила такого постоянного тока, который выделяет в данном проводнике столько же тепла за время одного периода, сколько выделяет тепла и данный переменный ток.

,
. (13)

Приборы, включенные в цепь переменного тока (амперметр, вольтметр), показывают эффективные значения тока и напряжения.

Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/1-14-210×140..jpg 614w»>

Эксперименты Фарадея

Законы Фарадея и Ленца

Явление электромагнитной индукции регулируется двумя законами: Фарадея и Ленца.

Закон Ленца позволяет охарактеризовать электродвижущую силу относительно ее направленности.

Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/2-10-768×454..jpg 960w»>

ЭДС индукции

Формула ЭДС индукции определена как:

Е = — dФ/dt.

Знак «-» показывает, как полярность индуцированной ЭДС связана со знаком потока и меняющейся скоростью.

Движение провода в магнитном поле

в случае движения проводника перпендикулярно направлению магнитного поля:

Е = — В x l x v;

в случае движения под другим углом α:

Е = — В x l x v х sin α.

Jpg?x15027″ alt=»Перемещение провода в МП»>

Перемещение провода в МП

Вращающаяся катушка

Работа генератора электроэнергии основана на вращении контура в МП, имеющего N витков.

Из формулы следует, что Ф подвержен изменениям в следующих случаях:

меняется интенсивность МП – вектор В;
варьируется площадь, ограниченная контуром;
изменяется ориентация между ними, заданная углом.

Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/4-10-768×536..jpg 900w»>

Вращение контура в МП

Для формулы ЭДС электромагнитной индукции применяется выражение:

Е = В х ω х S x N x sin ωt, где:

S – площадь, ограниченная одним витком или рамкой;
N – количество витков;
ω – угловая скорость, с которой вращается катушка;
В – индукция МП;
угол α = ωt.

ЭДС самоиндукции

Поскольку МП пропорционально интенсивности тока, то:

Для ЭДС индукции формула принимает вид:

Е = — L x dI/dt.

Взаимоиндукция

Jpg?.jpg 600w, https://elquanta.ru/wp-content/uploads/2018/03/5-5. jpg 680w»>

Взаимоиндукция

Взаимоиндуктивность второй катушки относительно первой:

М21 = (N2 x F21)/I1;

Магнитный поток:

Ф21 = (М21/N2) x I1;

Найдем индуцированную ЭДС:

Е2 = — N2 x dФ21/dt = — M21x dI1/dt;

Идентично в первой катушке индуцируется ЭДС:

Е1 = — M12 x dI2/dt;

Взаимную индуктивность можно признать равной:

М12 = М21 = М.

Соответственно, E1 = — M x dI2/dt и E2 = M x dI1/dt.

М = К √ (L1 x L2),

где К – коэффициент связи между двумя индуктивностями.

При изменении тока в контуре меняется поток магнитной индукции через поверхность , ограниченную этим контуром, изменение потока магнитной индукции приводит к возбуждению ЭДС самоиндукции. Направление ЭДС оказывается таким, что при увеличении тока в цепи эдс препятствует возрастанию тока, а при уменьшении тока — убыванию.

Величина ЭДС пропорциональна скорости изменения силы тока I и индуктивности контура L :

За счёт явления самоиндукции в электрической цепи с источником ЭДС при замыкании цепи ток устанавливается не мгновенно, а через какое-то время. Аналогичные процессы происходят и при размыкании цепи , при этом величина ЭДС самоиндукции может значительно превышать ЭДС источника. Чаще всего в обычной жизни это используется в катушках зажигания автомобилей. Типичное напряжение самоиндукции при напряжении питающей батареи 12В составляет 7-25кВ.

Wikimedia Foundation . 2010 .

Смотреть что такое «ЭДС самоиндукции» в других словарях:

эдс самоиндукции — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN self induced emfFaraday voltageinductance voltageself induction… …

Это явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока. При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение… … Википедия

— (от лат. inductio наведение, побуждение), величина, характеризующая магн. св ва электрич. цепи. Ток, текущий в проводящем контуре, создаёт в окружающем пр ве магн. поле, причём магнитный поток Ф, пронизывающий контур (сцепленный с ним), прямо… … Физическая энциклопедия

реактивная мощность — Величина, равная при синусоидальных электрическом токе и электрическом напряжении произведению действующего значения напряжения на действующее значение тока и на синус сдвига фаз между напряжением и током двухполюсника. [ГОСТ Р 52002 2003]… … Справочник технического переводчика

Раздел физики, охватывающий знания о статическом электричестве, электрических токах и магнитных явлениях. ЭЛЕКТРОСТАТИКА В электростатике рассматриваются явления, связанные с покоящимися электрическими зарядами. Наличие сил, действующих между… … Энциклопедия Кольера

Электрический машина, не имеющая подвижных частей и преобразующая переменный ток одного напряжения в переменный ток другого напряжения. В простейшем случае состоит из магнитопровода (сердечника) и расположенных на нём двух обмоток первичной и… … Энциклопедический словарь

САМОИНДУКЦИЯ

Каждый проводник, по которому протекает эл. ток, находится в собственном магнитном поле.

При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл. поля и в цепи появляется ЭДС индукции.

Это явление называется самоиндукцией.
Самоиндукция — явление возникновения ЭДС индукции в эл. цепи в результате изменения силы тока.
Возникающая при этом ЭДС называетсяЭДС самоиндукции

Замыкание цепи

При замыкании в эл. цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл. поле, направленное против тока, т. е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
В результатеЛ1 загорается позже, чем Л2.

Размыкание цепи

При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
В результате Л при выключенииярко вспыхивает.

Вывод

в электротехнике явление самоиндукции проявляется при замыкании цепи (эл.ток нарастает постепенно) и при размыкании цепи (эл.ток пропадает не сразу).

От чего зависит ЭДС самоиндукции?

Эл. ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике
(B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I).
ЭДС самоиндукции зависит от скорости изменения силы тока в эл. цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.

Индуктивность — физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:

где Ф — магнитный поток через контур, I — сила тока в контуре.

Единицы измерения индуктивности в системе СИ:

Индуктивность катушки зависит от:
числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды
(возможен сердечник).

ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.

Вокруг проводника с током существует магнитное поле, которое обладает энергией.
Откуда она берется? Источник тока, включенный в эл. цепь, обладает запасом энергии.
В момент замыкания эл. цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.

Энергия магнитного поля равнасобственной энергии тока.
Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.

Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока.
Куда пропадает энергия магнитного поля после прекращения тока? — выделяется (при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)

ВОПРОСЫ К ПРОВЕРОЧНОЙ РАБОТЕ
по теме «Электромагнитная индукция»

1. Перечислить 6 способов получения индукционного тока.
2. Явление электромагнитной индукции (определение).
3. Правило Ленца.
4. Магнитный поток (определение, чертеж, формула, входящие величины, их ед. измерения).
5. Закон электромагнитной индукции (определение, формула).
6. Свойства вихревого электрического поля.
7. ЭДС индукции проводника, движущегося в однородном магнитном поле (причина появления, чертеж, формула, входящие величины, их ед. измерения).
7. Самоиндукция (кратко проявление в электротехнике, определение).
8. ЭДС самоиндукции (ее действие и формула).
9. Индуктивность (определение, формулы, ед. измерения).
10. Энергия магнитного поля тока (формула, откуда появляется энергия м. поля тока, куда пропадает при прекращении тока).

Самоиндукция. Энергия магнитного поля.

Определение 1

Самоиндукция – это значимый частный случай электромагнитной индукции, когда магнитный поток, изменяясь и вызывая ЭДС индукции, создается током в самом контуре.

В случае, когда ток рассматриваемого контура по каким-либо причинам изменен, то имеет место изменение и магнитного поля этого тока, а значит и собственного магнитного потока, проходящего через контур. В контуре создается ЭДС самоиндукции, создавая препятствие для изменений тока в контуре (по правилу Ленца).

Собственный магнитный поток Φ, который проходит через контур или катушку с током, является пропорциональным силе тока I: Φ=LI.

Определение 2

Коэффициент пропорциональности L в формуле Φ=LI есть коэффициент самоиндукции или индуктивность катушки. Единица индуктивности в СИ носит название генри (Гн). Индуктивность контура или катушки равна 1 Гн, когда при силе постоянного тока 1 А собственный поток составляет 1 Вб: 1 Гн=1 Вб1 А.

Расчет индуктивности

Пример 1

Для наглядности произведем расчет индуктивности длинного соленоида, который имеет N витков, площадь сечения S и длину l. Соленоид – это цилиндрическая катушка индуктивности, у которой длина много больше диаметра. Магнитное поле соленоида задается формулой:

B=μ0nI,

где I является обозначением тока в соленоиде, n = Ne указывает число витков на единицу длины соленоида.

Магнитный поток внутри катушки соленоида, проходящий через все N витков, составляет:

Φ=B·S·N=μ0n2Sl

Таким образом, индуктивность соленоида будет выражена формулой:

L=μ0n2S·l=μ0n2V,

где V=Sl – объем соленоида, содержащий магнитное поле.

Результат, который мы получили, не берет в расчет краевых эффектов, а значит он является приближенно верным лишь для катушек достаточной длины. Когда соленоид заполнен веществом, имеющим магнитную проницаемость μ, при заданном токе I индукция магнитного поля будет возрастать по модулю в μ раз, а значит и индуктивность катушки с сердечником тоже получит увеличение в μ раз:

Lμ=μ·L=μ0·μ·n2·V.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Определение 3

ЭДС самоиндукции, которая возникает в катушке при постоянном значении индуктивности, в соответствии с законом Фарадея записывается в виде формулы:

δинд=δL=-∆Φ∆t=-L∆I∆t.

ЭДС самоиндукции является прямо пропорциональной индуктивности катушки и скорости изменения силы тока в ней.

Магнитное поле выступает носителем энергии. Так же, как заряженный конденсатор обладает запасом электрической энергии, катушка, по виткам которой проходит ток, обладает запасом магнитной энергии. Включив электрическую лампу параллельно катушке с большой индуктивностью в электрическую цепь постоянного тока, при размыкании ключа будем наблюдать короткую вспышку лампы (рис. 1.21.1). Ток в цепи появится под влиянием ЭДС самоиндукции. Источником энергии, которая будет выделяться в этом процессе электрической цепью, будет служить магнитное поле катушки.

Рисунок 1.21.1. Магнитная энергия катушки. В момент размыкания ключа K лампа ярко вспыхнет.

Закон сохранения энергии позволяет говорить, что вся энергия, составляющая запас катушки, будет выделена в виде джоулева тепла. Обозначим как Rполное сопротивление цепи, тогда за время Δt будет выделено количество теплоты ΔQ=I2·R·Δt.

Ток в цепи составляет:

I=δLR=-LR∆I∆t

Выражение для ΔQ можем записать так:

∆Q=-L·I·∆I=-Φ(I)∆I

В данной записи ΔI < 0; значение тока в цепи постепенно снижается от изначального I0 до нуля. Полное количество теплоты, которое выделится в цепи, возможно получить, осуществив действие интегрирования в пределах от I0 до 0. Тогда получим:

Q=LI022

Графический вывод формулы

Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:

Рисунок 1.21.2. Вычисление энергии магнитного поля.

В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:

Wм=ΦI2=LI22=Φ22L

Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:

Wм=μ0·μ·n2·I22V=B22μ0·μV

В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.

Определение 4

Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.

В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.

Репетитор-онлайн — подготовка к ЦТ

Пример 13. Проводящий контур, имеющий форму квадрата со стороной 20 см, помещен в однородное магнитное поле с индукцией 45 мТл. Плоскость контура составляет угол 30° с направлением силовых линий поля. За 0,15 с контур поворачивают таким образом, что его плоскость устанавливается перпендикулярно силовым линиям поля. Найти среднее значение ЭДС индукции, возникающей в контуре при его повороте в магнитном поле.

Решение. Появление ЭДС индукции в контуре вызвано изменением потока вектора индукции, пронизывающего плоскость квадрата, при повороте контура в магнитном поле.

Поток индукции магнитного поля через площадь квадрата определяется формулами:

в первом положении контура (до поворота)

Ф₁ = BS cos α₁,

где B — модуль индукции магнитного поля, B = 45 мТл; S — площадь квадрата, S = a ²; a — сторона квадрата, a = 20 см; α₁ — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата в первом положении контура, α₁ = = 90° − 30° = 60°;

во втором положении контура (после поворота)

Ф₂ = BS cos α₂,

где α₂ — угол между направлениями вектора магнитной индукции и вектора нормали (перпендикуляра) к плоскости квадрата во втором положении контура, α₂ = 0°.

Изменение потока вектора индукции магнитного поля определяется разностью

ΔФ=Ф2−Ф1=BScos0°−BScos60°=BS2.

Среднее значение ЭДС индукции, возникающей в контуре при его повороте в магнитном поле:

〈ℰi〉=|ΔФΔt|=−BS2Δt=Ba22Δt,

где ∆t — интервал времени, за который происходит поворот контура, ∆t = 0,15 с.

Расчет дает значение:

〈ℰi〉=45⋅10−3⋅(20⋅10−2)22⋅0,15=6,0⋅10−3 В=6,0 мВ.

При повороте контура в нем возникает ЭДС индукции, среднее значение которой равно 6,0 мВ.

Закон Фарадея

Концепция закона Фарадея состоит в том, что любое изменение магнитной среды катушки с проволокой вызывает «индуцирование» в катушке напряжения (ЭДС). Независимо от того, как производится изменение, напряжение будет генерироваться. Изменение может быть произведено изменением напряженности магнитного поля, перемещением магнита к катушке или от нее, перемещением катушки в магнитное поле или из него, вращением катушки относительно магнита и т. Д.

Слева вверху на иллюстрации две катушки пронизаны изменяющимся магнитным полем.Магнитный поток F определяется как F = BA, где B — магнитное поле или среднее магнитное поле, а A — площадь, перпендикулярная магнитному полю. Обратите внимание, что для данной скорости изменения потока через катушку генерируемое напряжение пропорционально количеству витков N, через которые проходит поток. Этот пример относится к работе трансформаторов, где магнитный поток обычно следует за железным сердечником от первичной катушки ко вторичной катушке и генерирует вторичное напряжение, пропорциональное количеству витков во вторичной катушке.

По часовой стрелке второй пример показывает напряжение, генерируемое при перемещении катушки в магнитное поле. Иногда это называют «ЭДС движения», и она пропорциональна скорости, с которой катушка перемещается в магнитное поле. Эта скорость может быть выражена через скорость изменения области, находящейся в магнитном поле.

Следующий пример — это стандартная геометрия генератора переменного тока, в которой катушка с проволокой вращается в магнитном поле. Вращение изменяет перпендикулярную площадь катушки по отношению к магнитному полю и генерирует напряжение, пропорциональное мгновенной скорости изменения магнитного потока.При постоянной скорости вращения генерируемое напряжение является синусоидальным.

Последний пример показывает, что напряжение можно генерировать, перемещая магнит к катушке с проволокой или от нее. При постоянной площади изменяющееся магнитное поле вызывает генерируемое напряжение. Направление или «чувство» генерируемого напряжения таково, что любой результирующий ток создает магнитное поле, противодействующее изменению магнитного поля, которое его создало. Это значение знака минус в законе Фарадея, и это называется законом Ленца.

Формула для наведенной ЭДС в катушке из-за изменения класса 12 физики JEE_Main

Подсказка: Понятие индуцированной ЭДС дается законом Фарадея, который гласит:
Любое изменение магнитного поля или магнитного потока катушки вызовет наведенную ЭДС.
$ e = — N \ dfrac {{d \ phi}} {{dt}} $ (e — наведенная ЭДС, N — количество витков катушки, а $ \ phi $ — магнитный поток)
Знак минус вышеприведенное уравнение связано с законом Ленца.
Обсудим вышеупомянутые два закона более подробно и решим поставленную задачу.

Полное пошаговое решение:
Давайте сначала объясним закон Ленца и закон Фарадея более подробно. Закон
Фарадея гласит, что: Индуцированная ЭДС прямо пропорциональна скорости изменения магнитного потока, создаваемого в катушке из-за протекающего тока в проводнике с конечным числом витков.
В математических терминах закон Фарадея имеет вид:
$ e = — N \ dfrac {{d \ phi}} {{dt}} $
Знак минус уравнения дается законом Ленца, который гласит:
Направление электрического тока, который индуцируется в проводнике изменяющимся магнитным полем, таково, что магнитное поле таково, что магнитное поле, создаваемое индуцированным током, противодействует начальному изменяющемуся магнитному полю.
На языке непрофессионалов мы можем сформулировать закон Ленца как; Ток или напряжение, которые индуцируются в цепи, противодействуют изменению, которое их вызывает.
Теперь вычислим формулу наведенной ЭДС.
Магнитное поле задается как:
$ B = \ dfrac {\ phi} {A} $ (B — магнитное поле, A — площадь, а $ \ phi $ — поток)
Следовательно, поток задается как, $ \ phi $ = BA
Согласно определению наведенной ЭДС, скорость изменения потока равна наведенной ЭДС, поэтому формула принимает следующий вид:
$ e = — \ dfrac {{дБ.A}} {{dt}} $

Следовательно, вариант C верен.

Примечание: Закон Фарадея применим во многих электрических устройствах, таких как трансформаторы, где повышение или понижение тока или напряжения происходит из-за электромагнитной индукции, генераторы переменного тока, которые создают вращающиеся магнитные поля, двигатели постоянного тока, измерительные приборы, такие как счетчики энергии и др.

Закон электромагнитной индукции Фарадея | Электромагнетизм

10.3 Закон электромагнитной индукции Фарадея (ESBPY)

Ток, индуцированный изменяющимся магнитным полем (ESBPZ)

Хотя удивительное открытие электромагнетизма Эрстедом проложило путь для более практического применения электричества, именно Майкл Фарадей дал нам ключ к практическому производству электричества: электромагнитная индукция .

Фарадей обнаружил, что когда он перемещал магнит рядом с проводом, на нем генерировалось напряжение. Если магнит удерживался в неподвижном состоянии, напряжение не генерировалось, оно существовало только во время движения магнита. Мы называем это напряжение индуцированной ЭДС (\ (\ mathcal {E} \)).

Контурная петля, подключенная к чувствительному амперметру, будет регистрировать ток, если он настроен, как показано на этом рисунке, и магнит перемещается вверх и вниз:

Магнитный поток

Прежде чем мы перейдем к определению закона электромагнитной индукции Фарадея и примерам, нам сначала нужно потратить некоторое время на изучение магнитного потока.Для петли площадью \ (A \) в присутствии однородного магнитного поля \ (\ vec {B} \) магнитный поток (\ (φ \)) определяется как: \ [\ phi = BA \ cos \ theta \] Где: \ begin {align *} \ theta & = \ text {угол между магнитным полем B и нормалью к петле в области A} \\ A & = \ text {область петли} \\ B & = \ text {магнитное поле} \ end {align *}

Единицей измерения магнитного потока является Вебер (Вб).

Вы можете спросить себя, почему включен угол \ (\ theta \). Поток зависит от магнитного поля, проходящего через поверхность. Мы знаем, что поле, параллельное поверхности, не может вызвать ток, потому что оно не проходит через поверхность. Если магнитное поле не перпендикулярно поверхности, то есть компонент, который перпендикулярен, и компонент, который параллелен поверхности. Параллельная составляющая не может вносить вклад в поток, только вертикальная составляющая может.

На этой диаграмме мы показываем, что магнитное поле под углом, отличным от перпендикулярного, может быть разбито на составляющие.Компонент, перпендикулярный поверхности, имеет величину \ (B \ cos (\ theta) \), где \ (\ theta \) — угол между нормалью и магнитным полем.

Закон электромагнитной индукции Фарадея

ЭДС \ (\ mathcal {E} \), создаваемая вокруг контура проводника, пропорциональна скорости изменения магнитного потока φ через площадь A контура. Математически это можно выразить как:

\ [\ mathcal {E} = -N \ frac {\ Delta \ phi} {\ Delta t} \]

где \ (\ phi = B · A \), а B — напряженность магнитного поля.\ (N \) — количество контуров схемы. Магнитное поле измеряется в теслах (Тл). Знак минус указывает направление и то, что наведенная ЭДС имеет тенденцию противодействовать изменению магнитного потока. Знак минус можно не учитывать при вычислении звездных величин.

Закон Фарадея связывает наведенную ЭДС со скоростью изменения магнитного потока, который является произведением магнитного поля и площади поперечного сечения, через которое проходят силовые линии.

Это не площадь самого провода, а площадь, которую он ограничивает.Это означает, что если вы согнете проволоку в круг, площадь, которую мы будем использовать при вычислении потока, будет площадью поверхности круга, а не проволоки.

На этой иллюстрации, где магнит находится в той же плоскости, что и контур цепи, не будет тока, даже если магнит перемещается все ближе и дальше. Это связано с тем, что силовые линии магнитного поля не проходят через замкнутое пространство, а параллельны ему. Силовые линии магнитного поля должны проходить через область, ограниченную контуром цепи, чтобы возникла ЭДС.

Направление индуцированного тока (ESBQ2)

Самое важное, что нужно помнить, это то, что индуцированный ток противодействует происходящему изменению.

На первом рисунке (слева) контурная петля имеет южный полюс приближающегося магнита. Величина поля от магнита становится больше. Реакция наведенной ЭДС будет заключаться в том, чтобы попытаться противодействовать усилению поля по направлению к полюсу. Поле является вектором, поэтому ток будет течь в таком направлении, чтобы поля, возникающие из-за тока, имели тенденцию нейтрализовать поля от магнита, сохраняя результирующее поле неизменным.

Чтобы противостоять переходу от приближающегося южного полюса сверху, ток должен приводить к силовым линиям, удаляющимся от приближающегося полюса. Следовательно, индуцированное магнитное поле должно иметь силовые линии, идущие вниз внутри петли. Направление тока, указанное стрелками на контуре цепи, будет достигнуто. Проверьте это, используя Правило правой руки. Поместите большой палец правой руки в направлении одной из стрелок и обратите внимание на то, что поле закручивается вниз в область, ограниченную петлей.

На второй диаграмме южный полюс удаляется. Это означает, что поле от магнита станет слабее. Отклик от индуцированного тока будет заключаться в создании магнитного поля, которое добавляется к существующему от магнитного поля, чтобы противостоять его уменьшению в силе.

Другой способ представить ту же функцию — использовать полюса. Чтобы противостоять приближающемуся южному полюсу, индуцируемый ток создает поле, которое выглядит как другой южный полюс со стороны приближающегося южного полюса.Подобно отталкиванию полюсов, вы можете представить себе, как течение создает южный полюс, чтобы отразить приближающийся южный полюс. На второй панели ток устанавливает северный полюс, чтобы привлечь южный полюс и остановить его движение.

Мы также можем использовать вариант правила правой руки, помещая пальцы в направлении течения, чтобы большой палец указывал в направлении силовых линий (или северного полюса).

Мы можем проверить все это на случаях, когда северный полюс перемещается ближе или дальше от цепи.В первом случае приближения северного полюса ток будет сопротивляться изменению, создавая поле в направлении, противоположном полю, исходящему от магнита, который становится сильнее. Используйте Правило правой руки, чтобы убедиться, что стрелки создают поле с линиями поля, которые изгибаются вверх в замкнутой области, нейтрализуя те, которые изгибаются вниз от северного полюса магнита.

Подобно отталкиванию полюсов, в качестве альтернативы проверьте, что если поместить пальцы правой руки в направлении течения, большой палец будет указывать вверх, указывая на северный полюс.

Для второго рисунка, где северный полюс удаляется, ситуация обратная.

Направление индуцированного тока в соленоиде (ESBQ3)

Подход к изучению направления тока в соленоиде аналогичен подходу, описанному выше. Единственная разница в том, что в соленоиде есть несколько витков проволоки, поэтому величина наведенной ЭДС будет другой. Поток будет рассчитан с использованием площади поверхности соленоида, умноженной на количество петель.

Помните: направления токов и связанных с ними магнитных полей можно найти, используя только Правило правой руки. Когда пальцы правой руки направлены в направлении магнитного поля, большой палец указывает в направлении тока. Когда большой палец направлен в направлении магнитного поля, пальцы указывают в направлении тока.

Направление тока будет таким, чтобы препятствовать изменению. Мы бы использовали установку, как в этом скетче, для проведения теста:

В случае, когда северный полюс направлен к соленоиду, ток будет течь так, чтобы северный полюс установился на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его (проверьте, используя Правило правой руки):

В случае, когда северный полюс движется от соленоида, ток будет течь так, что южный полюс устанавливается на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:

В случае, когда южный полюс движется от соленоида, ток будет течь так, что северный полюс будет установлен на конце соленоида, ближайшем к удаляющемуся магниту, чтобы притягивать его:

В случае, когда южный полюс направлен к соленоиду, ток будет течь так, что южный полюс будет установлен на конце соленоида, ближайшем к приближающемуся магниту, чтобы оттолкнуть его:

Простой способ создать магнитное поле изменяющейся интенсивности — переместить постоянный магнит рядом с проволокой или катушкой с проволокой.Магнитное поле должно увеличиваться или уменьшаться по напряженности перпендикулярно к проводу (так, чтобы силовые линии магнитного поля «пересекали» проводник), иначе не будет индуцироваться напряжение.

Индуцированный ток создает магнитное поле. Индуцированное магнитное поле имеет направление, которое стремится нейтрализовать изменение магнитного поля в петле из проволоки. Итак, вы можете использовать Правило правой руки, чтобы найти направление индуцированного тока, помня, что индуцированное магнитное поле противоположно направлению изменения магнитного поля.

Индукция

Электромагнитная индукция находит практическое применение в конструкции электрических генераторов, которые используют механическую энергию для перемещения магнитного поля мимо катушек с проволокой для генерации напряжения. Однако это далеко не единственное практическое применение этого принципа.

Если мы вспомним, магнитное поле, создаваемое проводом с током, всегда перпендикулярно проводу, и что сила потока этого магнитного поля зависит от величины тока, который проходит через него.Таким образом, мы можем видеть, что провод может создавать напряжение на своей собственной длине , если ток изменяется. Этот эффект называется самоиндукцией . Самоиндукция — это когда изменяющееся магнитное поле создается изменением тока через провод, вызывая напряжение по длине того же провода.

Если магнитный поток усиливается путем сгибания проволоки в форме катушки и / или наматывания этой катушки на материал с высокой проницаемостью, этот эффект самоиндуцированного напряжения будет более интенсивным.Устройство, сконструированное для использования этого эффекта, называется индуктором .

Помните, что индуцированный ток создает магнитное поле, которое противодействует изменению магнитного потока. Это известно как закон Ленца.

Рабочий пример 1: Закон Фарадея

Рассмотрим плоскую квадратную катушку с 5 витками. Катушка находится \ (\ text {0,50} \) \ (\ text {m} \) с каждой стороны и имеет магнитное поле \ (\ text {0,5} \) \ (\ text {T} \) проходящий через него. Плоскость катушки перпендикулярна магнитному полю: поле направлено за пределы страницы.Используйте закон Фарадея для вычисления наведенной ЭДС, если магнитное поле увеличивается равномерно от \ (\ text {0,5} \) \ (\ text {T} \) до \ (\ text {1} \) \ (\ текст {T} \) в \ (\ text {10} \) \ (\ text {s} \). Определите направление индуцированного тока.

Определите, что требуется

Мы обязаны использовать Закон Фарадея для расчета наведенной ЭДС.

Запишите закон Фарадея

\ [\ mathcal {E} = — N \ frac {\ Delta \ phi} {\ Delta t} \] Мы знаем, что магнитное поле расположено под прямым углом к поверхности и поэтому выровнено с нормалью.Это означает, что нам не нужно беспокоиться об угле, который поле образует с нормалью и \ (\ phi = BA \). Начальное или начальное магнитное поле, \ (B_i \), задается как конечная величина поля, \ (B_f \). Мы хотим определить величину ЭДС, чтобы можно было игнорировать знак минус.

Площадь \ (A \) — это площадь квадратной катушки. 2 (\ text {1} — \ text {0,50})} {\ text {10}} \\ & = \ текст {0,0625} \ текст {V} \ end {выровнять *}

Наведенный ток направлен против часовой стрелки, если смотреть со стороны нарастающего магнитного поля.

Рабочий пример 2: закон Фарадея

Рассмотрим соленоид из 9 витков с неизвестным радиусом \ (r \). На соленоид действует магнитное поле \ (\ text {0,12} \) \ (\ text {T} \). Ось соленоида параллельна магнитному полю. Когда поле равномерно переключается на \ (\ text {12} \) \ (\ text {T} \) в течение 2 минут, ЭДС величиной \ (- \ text {0,3} \) \ (\ text {V} \) индуцируется. Определите радиус соленоида.

Определите, что требуется

Требуется определить радиус соленоида.Мы знаем, что связь между наведенной ЭДС и полем регулируется законом Фарадея, который включает геометрию соленоида. Мы можем использовать это соотношение, чтобы найти радиус.

Запишите закон Фарадея

\ [\ mathcal {E} = — N \ frac {\ Delta \ phi} {\ Delta t} \] Мы знаем, что магнитное поле расположено под прямым углом к поверхности и поэтому выровнено с нормалью. Это означает, что нам не нужно беспокоиться об угле, который поле образует с нормалью и \ (\ phi = BA \).{- \ text {2}} \) \ (\ text {m} \). На соленоид действует переменное магнитное поле, которое равномерно изменяется от \ (\ text {0,4} \) \ (\ text {T} \) до \ (\ text {3,4} \) \ (\ text { T} \) в интервале \ (\ text {27} \) \ (\ text {s} \). Ось соленоида составляет угол \ (\ text {35} \) \ (\ text {°} \) к магнитному полю. Найдите наведенную ЭДС.

Определите, что требуется

Мы обязаны использовать Закон Фарадея для расчета наведенной ЭДС.

Запишите закон Фарадея

\ [\ mathcal {E} = — N \ frac {\ Delta \ phi} {\ Delta t} \] Мы знаем, что магнитное поле расположено под углом к нормали к поверхности.{- \ text {3}} \ text {V} \ end {выровнять *}

Наведенный ток направлен против часовой стрелки, если смотреть со стороны нарастающего магнитного поля.

Реальные приложения

Следующие устройства используют в своей работе закон Фарадея.

индукционные плиты
магнитофонов
металлоискатели
трансформаторы

Реальные применения закона Фарадея

Выберите одно из следующих устройств и поищите в Интернете или библиотеке, как работает ваше устройство.В объяснении вам нужно будет сослаться на закон Фарадея.

индукционные плиты
магнитофонов
металлоискатели
трансформаторы

Присоединяйтесь к тысячам учащихся, улучшающих свои научные оценки онлайн с помощью Siyavula Practice.

Зарегистрируйтесь здесь

Закон Фарадея

Упражнение 10.2

Изложите закон электромагнитной индукции Фарадея словами и запишите математическое соотношение.

\ [\ mathcal {E} = -N \ frac {\ Delta \ phi} {\ Delta t} \]

Опишите, что происходит, когда стержневой магнит вдавливается в соленоид, подключенный к амперметру, или вытягивается из него. Нарисуйте картинки, подтверждающие ваше описание.

Объясните, как магнитный поток может быть равен нулю, когда магнитное поле не равно нулю.

Поток связан с магнитным полем:

\ (\ phi = BA \ cos \ theta \)

Если \ (\ cos \ theta \) равно 0, то магнитный поток будет равен 0, даже если есть магнитное поле. В этом случае магнитное поле параллельно поверхности и не проходит через нее.

Используйте правило правой руки, чтобы определить направление индуцированного тока в соленоиде ниже.

Южный полюс магнита приближается к соленоиду.Закон Ленца говорит нам, что ток будет течь, чтобы противодействовать изменению. Южный полюс на конце соленоида будет противодействовать приближающемуся южному полюсу. Ток будет циркулировать по странице в верхней части катушки, так что большой палец правой руки будет указывать влево.

Рассмотрим круговую катушку из 5 витков с радиусом \ (\ text {1,73} \) \ (\ text {m} \). Катушка подвергается воздействию переменного магнитного поля, которое равномерно изменяется от \ (\ text {2,18} \) \ (\ text {T} \) до \ (\ text {12,7} \) \ (\ text { T} \) в интервале \ (\ text {3} \) \ (\ text {minutes} \). {2} & = \ текст {0,0479} \\ г & = \ текст {0,22} \ текст {м} \ end {выровнять *}

Найдите изменение потока, если ЭДС равна \ (\ text {12} \) \ (\ text {V} \) за период \ (\ text {12} \) \ (\ text {s} \) .

\ begin {align *} \ mathcal {E} & = N \ frac {\ Delta \ phi} {\ Delta t} \\ 12 & = 5 \ left (\ frac {\ Delta \ phi} {12} \ right) \\ \ Delta \ phi & = \ text {28,8} \ text {Wb} \ end {выровнять *}

Если угол изменить на \ (\ text {45} \) \ (\ text {°} \), на какой временной интервал нужно изменить, чтобы наведенная ЭДС оставалась прежней?

\ begin {align *} \ mathcal {E} & = N \ frac {\ Delta \ phi} {\ Delta t} \\ & = N \ frac {\ phi_ {f} — \ phi_ {i}} {\ Delta t} \\ & = N \ frac {B_ {f} A \ cos \ theta — B_ {i} A \ cos \ theta} {\ Delta t} \\ & = \ cos \ theta \ times N \ frac {B_ {f} A — B_ {i} A} {\ Delta t} \ end {выровнять *}

Все значения остаются неизменными между двумя описанными ситуациями, за исключением угла и времени.Мы можем приравнять уравнения для двух сценариев:

\ begin {align *} \ mathcal {E} _1 & = \ mathcal {E} _2 \\ \ cos \ theta_1 \ times N \ frac {B_ {f} A — B_ {i} A} {\ Delta t_1} & = \ cos \ theta_2 \ times N \ frac {B_ {f} A — B_ {i} A } {\ Delta t_2} \\ \ cos \ theta_1 \ frac {1} {\ Delta t_1} & = \ cos \ theta_2 \ frac {1} {\ Delta t_2} \\ \ Delta t_2 & = \ frac {\ Delta t_1 \ cos \ theta_2} {\ cos \ theta_1} \\ \ Delta t_2 & = \ frac {(\ text {12} \ cos (\ text {45}} {\ cos (\ text {23})} \\ \ Delta t_2 & = \ text {9,22} \ text {s} \ end {выровнять *}

Закон Ленца и обратная ЭМП

Закон Ленца и обратная ЭДС работают рука об руку.При работе электродвигателя, когда якорь вращается внутри магнитного поля, создается напряжение. Это напряжение обычно называют обратной ЭДС (электродвижущей силой), поскольку оно действует против напряжения, приводящего в действие двигатель.

Законы электромагнетизма

Одним из фундаментальных законов, регулирующих работу электродвигателя, является закон Фарадея, который гласит, что любое изменение магнитной среды катушки с проволокой вызывает «индуцирование» напряжения (ЭДС) в катушке. Независимо от того, как происходит изменение — перемещая магнит и катушку относительно друг друга или изменяя магнитное поле, — будет генерироваться напряжение.Уравнение для этой наведенной ЭДС:

Рука об руку с законом Фарадея работает закон Ленца, который гласит, что полярность наведенной ЭДС такова, что она производит ток, магнитное поле которого противодействует изменению, которое его вызывает. Индуцированное магнитное поле внутри любой проволочной петли всегда поддерживает постоянный магнитный поток в петле. Проще говоря, согласно закону Ленца, индуцированное напряжение (ЭДС) будет противодействовать управляющему напряжению. Следовательно, отрицательный знак в уравнении.

Закон Ленца применяется к цепям двигателей

Рассматривая простую схему двигателя и принимая во внимание сохранение энергии, мы видим, что сетевое напряжение на двигателе всегда будет равно напряжению питания плюс обратная ЭДС:

Напряжение сети = напряжение питания + обратная ЭДС

Показано графически:

Напряжение питания = 195 В
Противо-ЭДС = -45 В
Напряжение сети на двигателе = 150 В

Напряжение питания = 195 В.

Задняя ЭДС = -45 В.

Напряжение сети на двигателе, рассчитанное по закону Ома (V = I x R = 10 A x 15 Ом), = 150 В.

Это согласуется с уравнением для сетевого напряжения:

150 В = 195 В + -45 В

Обратная ЭДС на практике

Теперь давайте посмотрим, что происходит, когда на двигатель прикладывается нагрузка.

Во-первых, повышенная нагрузка вызывает снижение скорости двигателя. Обратная ЭДС напрямую связана со скоростью, поэтому, когда скорость уменьшается, уменьшается и наведенная обратная ЭДС.Из приведенного выше уравнения мы видим, что при меньшей обратной ЭДС напряжение (и, следовательно, ток) на двигателе увеличится. Этот дополнительный ток создает дополнительный крутящий момент, необходимый двигателю для восстановления скорости при увеличении нагрузки.

В конструкции двигателя на обратную ЭДС влияет количество витков в обмотках статора и магнитное поле. Двигатели спроектированы с постоянной обратной ЭДС, которая позволяет двигателю потреблять номинальный ток и обеспечивать номинальный крутящий момент при работе на номинальной скорости.

Обратная ЭДС может иметь синусоидальную (переменный ток) или трапециевидную (постоянный ток) форму волны. Форма обратной ЭДС важна, поскольку она определяет тип управляющего тока и метод коммутации, который следует использовать для двигателя.

Принципиальная схема и пример взяты из Департамента образования и профессиональной подготовки Нового Южного Уэльса, 2007 г.

Закон Фарадея Электромагнитная индукция | Electrical4u

Закон Фарадея Электромагнитная индукция:

Электромагнитная индукция была независимо открыта Майклом Фарадеем в 1831 году и Джозефом Генри в 1832 году.Фарадей был первым, кто опубликовал результаты своих экспериментов 29 августа 1831 года. Майкл Фарадей, английский физик, дал один из самых основных законов электромагнетизма, называемый законом электромагнитной индукции Фарадея. Сначала закон был отклонен из-за отсутствия математических и теоретических расчетов. Этот закон говорит об электрической цепи и магнитном поле. Этот принцип используется в большинстве электросетей. Как мы знаем, названиями некоторых приложений являются электродвигатели, генераторы, электрические трансформаторы и цепи магнитного управления, такие как контакторы, реле и т. Д.

[wp_ad_camp_1]

Закон электромагнитной индукции Фарадея:

Закон Фарадея об электромагнитной индукции гласит, что ЭДС, индуцированная в замкнутой электрической цепи, равна скорости изменения потоковых связей.

Здесь N — количество витков в катушке, а Φ — магнитная связь со всеми из них.

Закон электромагнитной индукции Фарадея

В большинстве случаев поток Φ не связан со всеми витками, в этих случаях суммирование всех произведений магнитного потока на полные витки магнитной цепи дает общее значение потоковых связей. …

Следовательно, общая стоимость потокосцеплений составляет..

Здесь N _k — количество витков, которые связаны с магнитным потоком Φ _k.

В случае изменения значения потокосцеплений катушки в ней создается наведенная ЭДС, значение которой равно…

Здесь отрицательный знак указывает на то, что направление наведенной ЭДС таково, что создаваемый им ток противодействует изменению магнитных связей.

Изменение магнитных связей может быть вызвано тремя способами.

Катушка неподвижна относительно магнитного потока, а величина магнитного потока изменяется во времени.

В этом методе, когда катушка или витки неподвижны (катушка не движется) и поток изменяется во времени, здесь ЭДС называется трансформаторной или (пульсационной) ЭДС. Поскольку движение не задействовано, преобразование энергии не происходит, и действительно происходит процесс передачи энергии. Этот принцип используется в трансформаторах, в которых используются неподвижные катушки и изменяющиеся во времени потоки для передачи энергии с одного уровня на другой.

Пример: трансформатор.

Поток постоянен во времени и неподвижен, и катушка движется через него

В этом случае правило отсечения магнитного потока может использоваться для иллюстрации ЭДС, генерируемой в проводнике, движущемся в постоянном стационарном поле. ЭДС, генерируемая в проводнике длины, движущемся под прямым углом к однородному, стационарному, не зависящему от времени магнитному полю, равна

[wp_ad_camp_1]
Сгенерированная ЭДС в этом случае называется «ЭДС движения», потому что она вызвана движением проводника.Поскольку движение участвует в создании этой ЭДС, процесс включает электромеханическое преобразование энергии. Этот принцип используется во вращающихся машинах, таких как машины постоянного тока, машины переменного тока, такие как индукционные и синхронные машины.

Пример: двигатели переменного тока, генератор и т. Д.

Оба упомянутых выше изменения происходят вместе, т. Е. Катушка движется через изменяющееся во времени поле.

В этом случае проводник или катушка движется через стационарное изменяющееся во времени магнитное поле (поток), и, следовательно, как трансформатор, так и ЭДС движения создаются в проводнике или катушке.Таким образом, этот процесс включает в себя как передачу, так и преобразование энергии.

Пример: Коммутаторная машина.

Ключевые точки:

Чтобы вызвать ЭДС в катушке или проводнике, проводник должен находиться в мгновенном положении, иначе поток должен изменяться во времени.

Пример машины для перемещения проводов: генератор и генератор переменного тока

Пример для машины с изменяющимся потоком: Трансформатор

Скорость изменения магнитного потока прямо пропорциональна наведенной ЭДС.

Как увеличить наведенную ЭДС в катушке

Увеличить наведенную ЭДС в катушке можно четырьмя способами

Увеличение числа витков увеличивает потокосцепление в цепи, когда потокосцепление увеличивается, автоматически увеличивается наведенная ЭДС.

Увеличьте скорость кондуктора. Частота f говорит о скорости проводника. Обычно в синхронной машине это называется синхронной скоростью.
Увеличение плотности потока в цепи увеличивает наведенную ЭДС в проводнике. См. Формулу 2
Увеличение длины проводника увеличивает наведенную ЭДС в катушке. См. Формулу 2.

Видеообъяснение закона Фарадея Электромагнитная индукция:

1) В формуле наведенной ЭДС в законе Фарадея, которая

Транскрибируемый текст изображения: 1) В формуле наведенной ЭДС в законе Фарадея, которая дается как Sm = -N, магнитный поток o, на самом деле является суммой внешний магнитный поток s.c. из-за внешней плотности магнитного потока B и внутреннего магнитного потока из-за индуцированной плотности магнитного потока Bd. В большинстве вопросов (даже тех, которые решаются в теоретических часах и часах решения проблем этого курса) учитывается вклад только внешнего магнитного потока, так что вклад внутреннего магнитного потока не учитывается. Однако эти вопросы не должны вводить в заблуждение, что наведенная ЭДС зависит от производной по времени только внешнего магнитного потока Z. Рассмотрим очень длинный соленоид с радиусом a = 1 см, h = 0.2 м и N = 200 витков. Проводящие провода соленоида не имеют сопротивлений, что может быть физически возможно со сверхпроводящими проводами. Плотность внешнего магнитного потока, который существует только внутри соленоида, определяется как B (t) = 5 cos (2000×1) â, мВт / м². Среда — свободное пространство. O a) Если конечные точки соленоида (точки C и D) оставлены открытыми и не подключены к какой-либо другой цепи, то каковы наведенная ЭДС и наведенный ток (величина и направление) на соленоиде? Op b) Если концы соленоида (точки C и D) замкнуты накоротко (подключены к резистору с нулевым сопротивлением), то каковы наведенная ЭДС и наведенный ток (величина и направление) на соленоиде? Если бы закон Фарадея включал только внешний магнитный поток, какими должны быть значения наведенной ЭДС и наведенного тока (величина и направление)? Прокомментируйте свои результаты.c) Предположим, что теперь конечные точки соленоида (точки C и D) подключены к сопротивлению R, значение которого не равно нулю. Найдите и выразите условие для значения R, при котором вкладом внутреннего магнитного потока можно пренебречь. Соответственно, найдите и выразите общее условие для значения R для любой геометрии замкнутого контура (не обязательно только для этого примера соленоида)

Предыдущий вопрос Следующий вопрос

Электромагнитная индукция

Магнитное поле в контуре можно изменить либо путем изменения величины поля или изменением площади петли.Чтобы иметь возможность количественно описать эти изменения, магнитный поток определяется как Φ = BA cosθ, где θ — угол между B и направлением, перпендикулярным плоскости петли (вдоль оси петли). .

Закон Фарадея

При изменении магнитного потока через проволочную петлю индуцируется ток. Закон Фарадея гласит, что ЭДС, индуцированная в проводе, пропорциональна скорости потока, проходящего через петлю.Математически

, где N — количество витков, ΔΦ — изменение потока во времени, Δ t . Знак минус указывает полярность наведенной ЭДС.

Предыдущее уравнение легко использовать, когда магнитный поток задается электромагнитом. Если электромагнит включен или выключен, наведенная ЭДС равна количеству витков в контуре, умноженному на скорость изменения магнитного потока. Поток также можно изменить с помощью петли, изменяя размер петли.Представьте скользящую проволоку, как показано на рисунке 1, где l — длина проволоки, которая движется в контакте с U-образной проволокой. В этом случае ε = Blv , где v — скорость длины скольжения.

Обратите внимание, что эта наведенная ЭДС неотличима от ЭДС батареи и что ток по-прежнему является просто скоростью движения зарядов; поэтому закон Ома и другие соотношения для токов в проводах остаются в силе.

Закон Ленца

Направление индуцированного тока можно найти из закона Ленца, который гласит, что магнитное поле, создаваемое индуцированной ЭДС, создает ток, магнитное поле которого противодействует первоначальному изменению потока через проволочную петлю.Снова рассмотрим рисунок и предположим, что слайд движется вправо. Фигуры x указывают на то, что B находится на странице; таким образом, когда слайд перемещается вправо, поле, проходящее через слайд, увеличивается на странице. (Изменение магнитного потока является решающей величиной.) Магнитное поле индуцированного тока будет направлено за пределы страницы, потому что оно будет противодействовать изменению магнитного потока. Воспользуйтесь правилом из вторых рук и поместите изгиб пальцев из страницы в центр петли.Направление большого пальца указывает на то, что ток будет течь против часовой стрелки. (Неправильно утверждать, что ток направлен вправо, потому что он находится слева в верхней части петли.) И наоборот, если ползун перемещается влево, B будет уменьшаться по петле. Изменение потока будет вне страницы, а индуцированный ток будет по часовой стрелке. Тот же анализ используется, если электромагнит включен или выключен.

Рисунок 1

Цепь скользящей проволоки генерирует ЭДС.

Закон Ленца также является законом сохранения. Если бы магнитное поле, создаваемое индуцированным током, могло быть в том же направлении, что и исходное изменение магнитного потока, изменение стало бы больше, а индуцированный ток больше. Это невозможное условие было бы лучшим обменом энергии, чем вечный двигатель.

Генераторы и двигатели

Генераторы и двигатели — это применение электромагнитной индукции.На рисунке показан простой электрический генератор.

Рисунок 2

Простой электрогенератор.

Кривошип представляет собой механический метод поворота проволочной петли в магнитном поле. Изменение магнитного потока через петлю генерирует индуцированный ток; таким образом, генератор преобразует механическую энергию в электрическую. Работа двигателя аналогична работе генератора, но в обратном порядке.Двигатель имеет аналогичные физические компоненты, за исключением того, что электрический ток, подаваемый в контур, создает крутящий момент, который поворачивает контур. Таким образом, двигатель преобразует электрическую энергию в механическую.

Взаимная индуктивность и самоиндукция

Взаимная индуктивность возникает, когда две цепи расположены так, что изменение тока в одной вызывает наведение ЭДС в другой.

Представьте себе простую схему переключателя, катушки и батареи.Когда переключатель замкнут, ток через катушку создает магнитное поле. По мере увеличения тока магнитный поток через катушку также изменяется. Этот изменяющийся магнитный поток генерирует ЭДС, противоположную ЭДС батареи. Этот эффект возникает только тогда, когда ток либо увеличивается до своего установившегося значения сразу после замыкания переключателя, либо уменьшается до нуля при размыкании переключателя. Этот эффект называется самоиндуктивностью . Пропорциональная константа между самоиндуцированной ЭДС и скоростью изменения тока во времени называется индуктивностью , (L) и выражается выражением

Единицей измерения индуктивности в системе СИ является генри, а 1 генри = 1 (Вс / А).

Используя закон Фарадея, индуктивность можно выразить через изменение магнитного потока и тока:

, где N — количество витков катушки.

Уравнения Максвелла и электромагнитные волны

Уравнения Максвелла суммируют электромагнитные эффекты в четырех уравнениях. Уравнения слишком сложны для этого текста, но концепции, заложенные в них, важно учитывать. Максвелл объяснил, что электрические и магнитные волны могут генерироваться колебаниями электрических зарядов.Эти электромагнитные волны могут быть изображены как скрещенные электрические и магнитные поля, распространяющиеся в пространстве перпендикулярно направлению движения и друг к другу, как показано на рисунке 3.

Рисунок 3

Электромагнитная волна состоит из перпендикулярных колеблющихся магнитного и электрического полей.

Разное