Определение активных и индуктивных сопротивлений проводов
Доброго времени суток. В данной статье речь пойдет о расчете активных и индуктивных сопротивлений для воздушных и кабельных линий из цветных металлов, таких как медь и алюминий. Данные расчеты обычно приходится выполнять, когда нужно выполнить расчет токов короткого замыкания в распределительных сетях.
Определение активного сопротивления проводов
Активное сопротивлении проводов проще всего определять по справочным данным, составленным на основании ГОСТ 839-80 – «Провода неизолированные для воздушных линий электропередач» таблицы 1 – 4. Данные таблицы вы сможете найти непосредственно в самом ГОСТ, приведу лишь не которые.
Пользоваться всеми известными формулами по определению активного сопротивления — не рекомендуется [Л1. с.18],связано это с тем, что действительное сечение отличается от номинального сечения, провода выпускались в разное время, по разным ГОСТ и ТУ и величины удельной проводимости (ρ) и удельного сопротивления (γ) у них разные:
где:
- γ – значение удельной проводимости для медных и алюминиевых проводов при температуре 20 °С принимается: для медных проводов – 53 м/Ом*мм2; для алюминиевых проводов – 31,7 м/Ом*мм2;
- s – номинальное сечение провода(кабеля),мм2;
- l – длина линии, м;
- ρ – значение удельного сопротивления принимается: для медных проводов — 0,017-0,018 Ом*мм2/м; для алюминиевых проводов – 0,026 — 0,028 Ом*мм2/м, см.
 таблицу 1.14 [Л2. с.30].
таблицу 1.14 [Л2. с.30].
Активные сопротивления стальных проводов математическому расчету не поддаются. Поэтому рекомендую для определения активного сопротивления использовать приложения П23 – П25 [Л1. с.80,81].
Определение индуктивного сопротивления проводов
Индуктивное сопротивление воздушных линий для стандартной частоты f = 50 Гц и относительной магнитной проницаемости для цветных металлов µ = 1, определяется по известной всем формуле [Л1.с.19]:
где:
- Dср. – среднее геометрическое расстояние между проводами, мм;
- dр – расчетный диаметр провода (мм2), определяется по ГОСТ 839-80, таблицы 1 -4;
Среднее геометрическое расстояние между проводами определяется по формуле [Л1.с.19]:
где:
- D1-2 — расстояние между проводами первой и второй фазы;
- D2-3 — расстояние между проводами второй и третей фазой;
- D1-3 — расстояние между первой и третей фазой.

Данные значения определяются по чертежам опор линий электропередачи.
Для упрощения расчетов индуктивного сопротивления проводов рекомендуется использовать приложения П28-П31 [Л1.с.83-85], предварительно определив значение Dср.
Если же нужно выполнить приближенный расчет, то можно использовать в расчетах средние значения сопротивлений:
- для линий 0,4 – 10 кВ х = 0,3 Ом/км;
- для линий 35 кВ х = 0,4 Ом/км;
Индуктивное сопротивление кабелей рассчитать довольно сложно, из-за различной их конструкции. Поэтому активные и индуктивные сопротивления кабелей рекомендуется принимать по справочникам, приложение П7 [Л1.с.70].
Если же нужно выполнить приближенный расчет, можно принять индуктивные сопротивления:
- для кабелей сечением 16 – 240 мм2 х = 0,06 Ом/км для напряжения до 1000 В;
- для кабелей сечением 16 – 240 мм2 х = 0,08 Ом/км для напряжения 6 – 10 кВ;
- для проводов проложенных на роликах х = 0,20 Ом/км;
- для проводов проложенных на изоляторах х = 0,25 Ом/км;
Литература:
1. Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
Расчет токов короткого замыкания в электросетях 0,4-35 кВ, Голубев М.Л. 1980 г.
2. Справочная книга электрика. Григорьева В.И. 2004 г.
Всего наилучшего! До новых встреч на сайте Raschet.info.
Поделиться в социальных сетях
Учет температуры при расчете активного сопротивления
Согласно ГОСТ 28249-93 «Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением до 1 кВ.» [1], п.1.5.:
1.5. При расчетах токов КЗ рекомендуется учитывать:
…
2) изменение активного сопротивления проводников короткозамкнутой цепи вследствие их нагрева при КЗ;
…
КЗ – короткое замыкание.
При этом в приложении 2 приводится следующая формула для расчета изменения удельного сопротивления при повышении температуры:
где
ρΘ и ρΘнорм — удельные сопротивления, Ом×м, материала кабеля при температуре Θ и начальной нормированной температуре Θнорм (Θ0).
К сожалению, в ГОСТ отсутствует расшифровка для символа Т, используемого в формуле (2).
Аналогичная методика расчета сопротивления с учетом температуры приводится в РД 153-34.0-20.527-98 «Руководящие указания по расчету токов короткого замыкания и выбору электрооборудования»
где Rн – начальное сопротивление проводника;
KΘ — коэффициент увеличения активного сопротивления проводника, который зависит от материала, а также начальной и конечной температур проводника и определяется по формуле
где Θн и Θкн – соответственно начальная и конечная температуры проводника;
τp — условная температура, равная: для меди τ
Чтобы привести формулы к одному виду, договоримся, что начальная температура и нормированная температура совпадают Θнорм = Θн = Θ0. Также, обозначим Θкн как Θ.
Также, обозначим Θкн как Θ.
Очевидно, если в выражение (3) подставить формулы нахождения активного сопротивления проводника (5) и (6):
где L – длина проводника;
S – сечение проводника,
получим выражение, соответствующее формуле (1), в котором величина K
Итак, подставим (4) в (3) и перепишем новую формулу, используя введенные обозначения:
где RΘ – активное сопротивление проводника с учетом изменения температуры, Ом;
Rн – начальное (нормированное) активное сопротивление проводника, Ом;
Θ0 и Θ – соответственно начальная и конечная температуры проводника, °С;
τp — условная температура, равная: для меди τp = 234 °С, для алюминия τp = 236 °С.
И вот теперь, после согласования методик учета температуры при расчете активного сопротивления проводника по двум нормативным документам
«А что за величина такая — условная температура – используемая в формуле (7)? Какой у нее физический смысл? Где найти подтверждение значениям: для меди tp = 234 °С, для алюминия tp = 236 °С, приведенным в [2]?».
Действительно, ни один из рассматриваемых документов на это ответ не дает. Более того, в [1] эта величина даже не имеет расшифровки.
К счастью, (7) не является единственной формулой расчета активного сопротивления проводника с учетом температуры. Например, ГОСТ Р МЭК 60287-1-1-2009 «Кабели электрические. Расчет номинальной токовой нагрузки. Часть 1-1.»
где R0 – погонное сопротивление жилы постоянному току при 20 °С, Ом/м;
R’ – погонное сопротивление жилы постоянному току при температуре Θ, Ом/м;
α20 – температурный коэффициент при 20 °С, 1/К.
Температурный коэффициент электрического сопротивления — величина, равная относительному изменению электрического сопротивления участка электрической цепи или удельного сопротивления вещества при изменении температуры на единицу.

Заменив обозначения в (8) на обозначения, принятые в данной статье, а также умножив левую и правую часть (8) на длину проводника L, получим:
где αнорм – температурный коэффициент материала проводника при нормированной температуре Θ0, 1/К.
Следует заметить, что в (8) Θ0 =20 °С.
Теперь, приравняв правые части выражений для расчета активных сопротивлений с учетом температуры (7) и (9), и сократив Rн, получим следующее выражение:
Выразим величину τp в выражении (10). Для этого, перенесем 1 в левую часть и умножим левую и правую части уравнения на знаменатель левой части. Получим промежуточное выражение:
Разделим левую и правую части выражения (11) на его левую часть:
и выразим величину τp:
Итак, условная температура τp численно равна обратному значению температурного коэффициента электрического сопротивления αнорм при нормированной температуре Θ0 = 0 °С.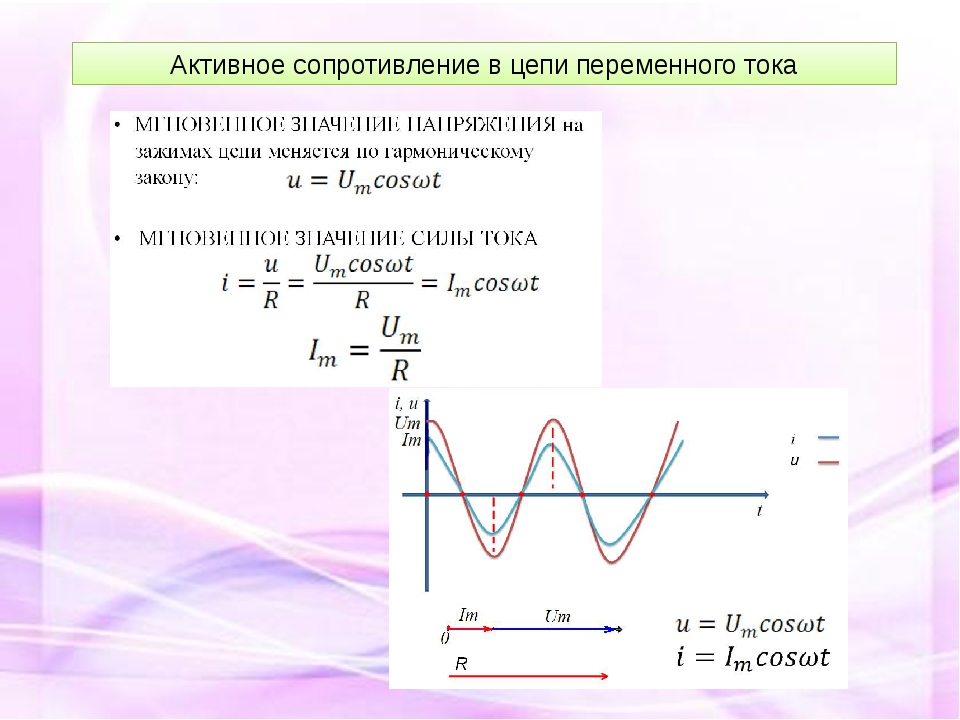 При другом значении нормированной температуры величина условной температуры определяется согласно выражению (13).
При другом значении нормированной температуры величина условной температуры определяется согласно выражению (13).
Теперь можно проверить, соответствуют ли значения условной температуры и температурного коэффициента, приводимые в [2] и [3] соответственно, друг другу.
Для меди: αнорм = 3,93*10-3 1/К, см. [3], табл.1
Для алюминия: αнорм = 4,03*10-3 1/К, см. [3], табл.1
Исходные и полученные данные об условной температуре сведены в таблицу.
Наименование источника | Θ0 , °С | Медь | Алюминий | ||
αнорм, 1/К | τp, °С | αнорм, 1/К | τp, °С | ||
ГОСТ Р МЭК 60287-1-1-2009, табл. | 20 | 3,93*10-3 | 234 | 4,03*10-3 | 228 |
РД 153-34.0-20.527-98, п.5.10.4 | — | — | 234 | — | 236 |
К сожалению, в [2] не указано, для какой нормированной температуры приведена условная температура материалов. Будем считать, что Θ0 =20 °С.
Из таблицы видно, что справочные данные значений условной температуры отличаются для алюминия, а значит, и результаты расчетов активных сопротивлений с учетом температуры будут отличаться.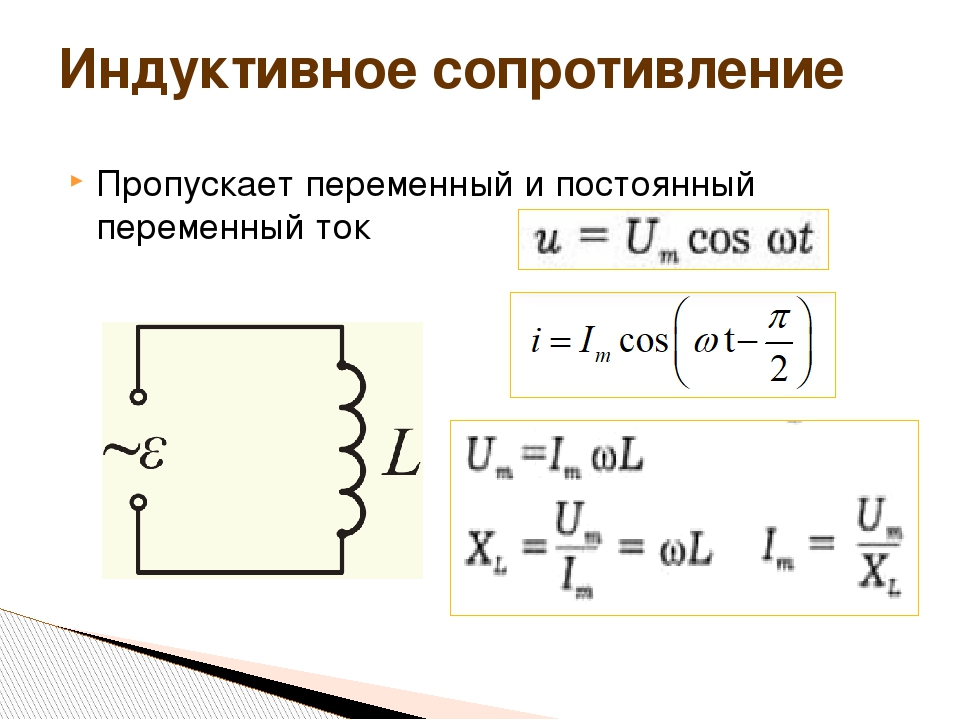 Следует заметить, что в интернет содержится много сайтов со справочными значениями температурных коэффициентов, отличающихся от приведенных в таблице. Возникает законный вопрос: «Какие значения использовать в расчетах?». На это можно ответить только одно – все значения, используемые в расчетах, подлежат проверке. В данном случае, точно такие же значения температурного коэффициента есть в справочнике «Электрические кабели, провода и шнуры», 1971 г., под авторством Бачелис Д.С и др. [4], п.2.1, стр. 81.
Следует заметить, что в интернет содержится много сайтов со справочными значениями температурных коэффициентов, отличающихся от приведенных в таблице. Возникает законный вопрос: «Какие значения использовать в расчетах?». На это можно ответить только одно – все значения, используемые в расчетах, подлежат проверке. В данном случае, точно такие же значения температурного коэффициента есть в справочнике «Электрические кабели, провода и шнуры», 1971 г., под авторством Бачелис Д.С и др. [4], п.2.1, стр. 81.
- В нормативной литературе при расчетах активного сопротивления с учетом температуры используется понятие «условная температура», но при этом не дается определение этому понятию; также, нельзя проверить корректность табличных значений этой величины.
- Для расчетов активного сопротивления с учетом температуры рекомендуется использовать формулу (11) из [3] (также, см. формулу (9) данной статьи).
- Для перехода от величины температурного коэффициента электрического сопротивления к величине условной температуры можно использовать формулу (13) данной статьи.

- Значения температурного коэффициента рекомендуется брать из [3], табл.1.
- ГОСТ 28249-93 «Короткие замыкания в электроустановках. Методы расчета в электроустановках переменного тока напряжением до 1 кВ.»
- РД 153-34.0-20.527-98 «Руководящие указания по расчету токов короткого замыкания и выбору электрооборудования».
- ГОСТ Р МЭК 60287-1-1-2009 «Кабели электрические. Расчет номинальной токовой нагрузки. Часть 1-1.»
- Бачелис Д.С. и др. Электрические кабели, провода и шнуры (справочник). Под общ. ред. Н. И. Белоруссова. Изд. 3-е, перераб. М.: «Энергия», 1971.
Эту статью можно обсудить ниже в комментариях или на форуме.
Реактивное сопротивление ёмкости |
Мы знаем, что на встречу нарастающему току генератора идет ток самоиндукции катушки. Вот это противодействие тока самоиндукции катушки нарастающему току генератора и называется индуктивным сопротивлением.
На преодоление этого противодействия затрачивается часть энергии переменного тока генератора. Вся эта часть энергии полностью превращается в энергию магнитного поля катушки. Когда ток генератора будет убывать, магнитное поле катушки также будет убывать, пресекая катушку и индуктируя в цепи ток самоиндукции. Теперь ток самоиндукции будет идти в одном направлении с убывающим током генератора.
Таким образом вся энергия затраченная током генератора на преодоление противодействия тока самоиндукции катушки полностью вернулась в цепь в виде энергии электрического тока. Поэтому индуктивное сопротивление является реактивным, т. е. не вызывающим безвозвратных потерь энергии.
Единицей измерения индуктивного сопротивления является Ом
Индуктивное сопротивление обозначается X L .
Буква X- означает реактивное сопротивление, а L означает что это реактивное сопротивление является индуктивным.
f- частота Гц, L- индуктивность катушки Гн, X L- индуктивное сопротивление Ом
Соотношение между фазами U и I на X L
Так как активное сопротивление катушки по условию равно нулю (чисто индуктивное сопротивление), то все напряжение приложенное генератором к катушке идет на преодоление э. д. с. самоиндукции катушки. Это значит что график напряжения приложенного генератором к катушке равен по амплитуде графику э. д. с. самоиндукции катушки и находится с ним в противофазе.
Напряжение приложенное генератором к чисто индуктивному сопротивлению и ток идущий от генератора по чисто индуктивному сопротивлению сдвинуты по фазе на 90 0 ,т. е. напряжение опережает ток на 90 0.
Реальная катушка кроме индуктивного сопротивления имеет еще и активное сопротивление. Эти сопротивления следует считать соединенными последовательно.
На активном сопротивлении катушки напряжение приложенное генератором и ток идущий от генератора совпадают по фазе.
На чисто индуктивном сопротивлении напряжение приложенное генератором и ток идущий от генератора сдвинуты по фазе на 90 0 . Напряжение опережает ток на 90 0 . Результирующее напряжение приложенное генератором к катушке определяется по правилу параллелограмма.
кликните по картинке чтобы увеличить
Результирующее напряжение приложенное генератором к катушке всегда опережает ток на на угол меньший 90 0 .
Величина угла φ зависит от величин активного и индуктивного сопротивлений катушки.
О результирующем сопротивлении катушки
Результирующее сопротивление катушки нельзя находить суммированием величин её активного и реактивного сопротивлений .
Результирующее сопротивление катушки Z равно
Ac — обзор
Для трехфазного экранированного кабеля, проложенного под землей и имеющего броневую защиту, сердечник, оболочка и броня будут иметь собственное сопротивление с заземлением. Электромагнитная связь и, следовательно, взаимные импедансы существуют между сердечником, оболочкой и броней в каждой фазе. Хотя три фазы обычно располагаются параллельно друг другу и поверхности земли, земля не действует как электромагнитный экран между ними. Следовательно, между всеми проводниками всех фаз существуют взаимные сопротивления.Рисунки 3.22 и 3.24 используются при расчете собственного и взаимного импеданса подземных кабелей для использования в анализе частоты установившейся мощности.
Рисунок 3.24. Иллюстрация пространственных размеров двух подземных фаз кабеля
Собственное сопротивление жилы жилы с заземлением определяется как
(3.100a) ZCC = Rc (ac) + π210-4f + j4π10-4f [μc4 × f ( roc, ric) + loge (Dercroc)] Ω / km
, где
(3.100b) f (roc, ric) = 1-2ric2 (roc2-ric2) + 4ric4 (roc2-ric2) 2loge (rocric)
и D erc — глубина эквивалентного заземляющего заземляющего проводника, заданная в уравнении (3.15), а μ c — относительная магнитная проницаемость жилы проводника.
Собственное сопротивление брони с заземлением составляет
(3.102a) Zaa = Ra (ac) + π210-4f + j4π10-4f [μa4 × f (roa, ria) + loge (Dercroa)] Ω / km
, где
(3.102b) f (ros, ris) = 1-2ris2 (ros2-ris2) + 4ris4 (ros2-ris2) 2loge (rosris)
и μ a — относительная проницаемость брони. дирижер.
Взаимное сопротивление между сердечником, оболочкой или броней i и сердечником, или оболочкой, или броней j, с заземлением, равно
(3.103) Zij = π210-4f + j4π10-4f × loge (DercSij) Ом / км
, где S ij — расстояние между центрами кабелей i и j, если жилы принадлежат разным кабелям. Если проводники принадлежат одному кабелю, S ij — это среднее геометрическое расстояние между двумя проводниками, например GMD между сердечником и оболочкой кабеля j определяется выражением S jj = ( r os + r = ) / 2, что достаточно точно для практических размеров кабеля.
Сопротивление переменному току
Сопротивление переменному току сердечника, оболочки или брони можно рассчитать из сопротивления постоянному току по следующей формуле:
(3.104a) R (ac) = R (dc) [1 + y (kS + кП)] Ом / км
, где y = 1 для одножильных, двухжильных и трехжильных кабелей, но y = 1,5 для трубчатых кабелей. k S и k P — факторы скин-эффекта и эффекта близости, соответственно. Кроме того,
(3,104b) R (dc) = 1000ρA [1 + α20 × (T-20)] Ом / км
ρ — удельное сопротивление проводника в Ом · м, A — номинальная площадь поперечного сечения проводника в м 2 , T — температура проводника в ° C, а α 20 в ° C -1 — постоянный массовый температурный коэффициент при 20 ° C.В таблице 3.1 приведены типичные значения для α 20 и удельного сопротивления при 20 ° C.
Таблица 3.1. Типичные значения α 20 и удельного сопротивления проводника при 20 ° C
| Материал | Температурный коэффициент α 20 (° C -1 ) при 20 ° C | Удельное сопротивление ρ 20 (Ом · м) при 20 ° C |
|---|---|---|
| Сердечники | ||
| Медь | 3,93 × 10 −3 | 1.7241 × 10 −8 |
| Алюминий | 4,03 × 10 −3 | 2,8264 × 10 −8 |
| Оболочки или броня | ||
| Свинец 10 −3 | 21,4 × 10 −8 | |
| Бронза | 3 × 10 −3 | 3,5 × 10 −8 |
| Сталь | 4,5 × 10 −3 | 13.8 × 10 −8 |
| Нержавеющая сталь | 0 | 70 × 10 −8 |
Фактор скин-эффекта — это фактор дополнительного сопротивления, создаваемый переменным током в изолированном проводнике за счет кожи эффект и определяется выражением
(3,105) kS = {z40,8 × z4 + 1920
, где z = 8πfaz / (104Rdc). Для медных проводников a z = 1 для нормально скрученных круглых и секторных проводников, но a z = 0.43 для сегментных проводников или проводников Милликена. Для многожильных кольцевых проводников a z = [( r o — r i ) / ( r o + r i )] [( r o + 2 r i ) / ( r o + r i )] 2 , где r i и r o — кондукторные внутренний и внешний радиусы соответственно.Как правило, z меньше 2,8 для большинства практических приложений. Хотя уравнение (3.105) для скин-фактора основано на упрощенном подходе, оно содержит ошибку менее 0,5% на промышленной частоте.
Фактор эффекта близости — это коэффициент дополнительного сопротивления из-за близости других проводников с переменным током, он равен
(3,106a) кП {2,9 × F (p) (dcS) 2 для двухжильных и двухжильных проводов. кабели F (p) (dcS) 2 [0,312 (dcS) 2 + 1,18F (p) +0,27] для трехжильных и трехжильных кабелей
, где
(3.106b) F (p) = p40,8 × p4 + 192andp = 8πfap104Rdc
d c — диаметр проводника, а S — осевое расстояние между проводниками. Как для меди, так и для алюминия значение a p равно 0,8 для круглых, секторных и кольцевых многожильных проводников. a p равно 0,37 для круглых сегментных жил.
Значения различных коэффициентов, используемых в уравнениях (3.104), (3.105) и (3.106), обычно предоставляются производителем кабеля.
Для трехфазного подводного кабеля можно использовать уравнения промышленной частоты, приведенные для подземных кабелей. Тем не менее, море теперь будет преимущественно заменять землю в качестве обратного пути и представлено следующим образом:
(3,107) RSea = 399,63 × ρSeafm
, где R море — внешний радиус возврата в море, представленный как эквивалентный проводник. и ρ Sea — удельное сопротивление морской воды. Эта концепция основана на расчете обратного импеданса в море, когда предполагается, что кабель полностью окружен бесконечным морем, которое действует как эквивалентный обратный проводник с внешним радиусом R Sea .Например, для типичного значения удельного сопротивления морской воды ρ Sea = 0,5 Ом, R Sea ≅ 40 м при 50 Гц. Интересно отметить, что в глубокой морской воде, где фазы кабеля проложены на расстоянии 100-500 м друг от друга, электромагнитная связь между фазами будет очень слабой, и ее обычно можно игнорировать. Внутренний импеданс морского возврата, представленный как эквивалентный проводник с радиусом R Sea , определяется как
(3,108) ZSea = π210-4f [1 + 4πkei (α)] + j4π10-4f [loge (RSear) -ker (α)] Ом / км
, где α = 1.123 × D / R Sea , D — среднее расстояние между фазами кабеля в м, r — радиус проводника в м, а ker (α) и kei (α) — функции Кельвина с вещественный аргумент α.
Для трубчатых кабелей расчет собственного и взаимного импедансов более сложен, чем для подземных кабелей. Расчет потокосцеплений внутри стенки стальной трубы и снаружи трубы дополнительно осложняется нелинейной проницаемостью стальной трубы, которая сама по себе изменяется в зависимости от величины тока ZPS, протекающего по трубе в условиях замыкания на землю из-за трубы. насыщенность.Эффект насыщения должен вызвать снижение эффективного сопротивления ZPS кабеля; чем больше ток ZPS, тем больше снижение импеданса ZPS. Производители кабелей обычно обязаны предоставлять такие данные сетевым компаниям. Для анализа промышленной частоты обычно предполагается, что толщина трубы больше, чем глубина проникновения в стенку трубы, и что это предположение остается приблизительно верным при увеличении тока ZPS трубы. Это означает, что, помимо оболочек трех кабелей, труба является единственным каналом возврата тока и что ток не возвращается через землю.Тогда кабели внутри трубы можно рассматривать как три автономных одножильных кабеля, но с трубой, заменяющей землю, в качестве пути возврата тока. Глубина проникновения в трубу может быть рассчитана с использованием формулы глубины скин-слоя из уравнения (3.7b) δ = 503,292 × ρp / fμp, где ρ p и μ p — удельное сопротивление и относительная проницаемость трубы соответственно. Чтобы проиллюстрировать предположение о бесконечной толщине трубы, рассмотрим стальную трубу трубчатого кабеля на 132 кВ, имеющую толщину 6.3 мм, удельное сопротивление ρ p = 3,8 × 10 −8 Ом м и относительная магнитная проницаемость μ p = 400. Глубина проникновения в трубу при 50 Гц равна δ = 1,32 мм. Это меньше, чем толщина трубы, и показывает, что обратный ток будет течь к внутренней стенке трубы и что обратным током через землю можно пренебречь. На рисунке 3.23 мы предполагаем, что каждая фаза кабеля состоит из сплошного проводника с радиусом r c , изоляции жилы и проводника оболочки с внутренним и внешним радиусами r и r os , соответственно.Из рисунка 3.23 матрица собственного сопротивления фазы k кабеля внутри трубы равна
(3.109) Zk = [Zcc-kZcs-kZcs-kZss-k] = [Z1 + Z2 + Z3 + Z4 + Z5-2Z6Z4 + Z5-Z6Z4 + Z5-Z6Z4 + Z5]
, где Z 1 соответствует уравнению (3.7), а
(3.110a) Z2 = j4πf10-4loge (ris / rc) Z3 = 1000ρm2πrisD [ Io (mris) K1 (mros) + Ko (mris) I1 (mros)]
(3.110b) Z4 = 1000ρm2πrosD [Ио (mros) K1 (mris) + Ko (mros) I1 (mris)] Z5 = j4πf10- 4loge (q2-qk2qros)
(3,110c) Z6 = 1000ρ2πrisrosDm = 2δ-1ejπ / 4D = I1 (mros) K1 (mris) -K1 (mros) I1 (mris)
где Z от 1 до Z 6 в ю / км. I i и K i — это модифицированные функции Бесселя первого и второго типа порядка i соответственно. Внутреннее сопротивление трубы с обратным каналом, являющимся внутренней стенкой трубы, определяется выражением
(3.111) ZP-int = j4πμp10-4 {Ko (mq) mqK1 (mq) + 2∑n = 1∞ [(diq) 2nKn (mq) nμpKn (mq) -K′n (mq)]} Ом / км
Дано взаимное сопротивление в ω / км между проводниками i и k по отношению к внутренней стенке трубы. по
(3.112) Zi-k = j4πf10-4 {μpKo (mq) mqK1 (mq) + loge [qdi2 + dk2-2didkcosθik] + ∑n = 1∞ (didkq2) ncos (nθik) [2μpKn (mq) nμpKn (mq) — mqK′n (mq) -1n]}
, где K ′ n является производной от K n .
Значения действующего напряжения и тока.Определение. Соотношение амплитуд для разных форм. (10+) Понятие эффективных (действующих) значений напряжения и тока Когда мы говорим о переменных напряжениях или токах, особенно сложной формы, возникает вопрос, как их измерить. Ведь напряжение постоянно меняется. Вы можете измерить амплитуду сигнала, то есть максимальный модуль значения напряжения. Этот метод измерения подходит для относительно гладких сигналов, но наличие коротких всплесков портит картинку.Еще один критерий выбора метода измерения — с какой целью производится измерение. Поскольку в большинстве случаев представляет интерес мощность, которую может дать конкретный сигнал, используется эффективное (действующее) значение.
|
% PDF-1.4 % 1 0 объект > поток iText 4.2.0 от 1T3XTMicrosoft® Word 20102019-03-29T07: 04: 41 + 02: 002021-11-25T21: 57: 07-08: 002021-11-25T21: 57: 07-08: 00uuid: 93FCF189-8FA6- 40FE-8B82-175FD867A34Buuid: ac30ac3a-04cd-4c63-b664-64d942ba3fb1uid: 93FCF189-8FA6-40FE-8B82-175FD867A34B
Разница между сопротивлением и импедансом (со сравнительной таблицей)
Разница между сопротивлением и Импеданс объясняется ниже с учетом различных факторов, таких как основное определение сопротивления и импеданса, тип схемы, в которой они работают, элементы, от которых они зависят, их символическое представление, реальное и мнимое. чисел, влияние частоты на них, фазовый угол, рассеиваемая мощность и запасенная энергия.
Разница между сопротивлением и импедансом приведена ниже в виде таблицы .
| ОСНОВАНИЕ | СОПРОТИВЛЕНИЕ | ИМПЕДАНС |
|---|---|---|
| Определение | Противодействие протеканию тока в электрической цепи известно как сопротивление. | Сопротивление протеканию тока в цепи переменного тока из-за сопротивления, емкости и индуктивности известно как импеданс. |
| Цепь | Сопротивление возникает как в цепи переменного, так и постоянного тока. | Импеданс возникает только в цепи переменного тока. |
| Элементы | Вклад резистивного элемента в схему. | Это вклад как сопротивления, так и реактивного сопротивления. |
| Символ | Обозначается R | Обозначается Z |
| Действительное и мнимое значение | Сопротивление — это простое значение, состоящее только из действительных чисел.Например: 3,4 Ом, 6,2 Ом и т. Д. | Импеданс — это комплексное значение, состоящее из действительных и мнимых значений. Например: R + ij |
| Частота | Сопротивление в цепи постоянно и не меняется в зависимости от частоты переменного или постоянного тока. | Импеданс зависит от частоты переменного тока. |
| Фазовый угол | У сопротивления нет фазового угла. | Импеданс имеет величину и фазовый угол. |
| Рассеиваемая мощность и запасенная энергия | Представляет собой рассеиваемую мощность в любом материале, только если он находится в электромагнитном поле. | Если держать в электромагнитном поле, он представляет собой как рассеиваемую мощность, так и запасенную энергию. |
Сопротивление просто определяется как сопротивление потоку электрического тока в цепи.
Импеданс — это противодействие прохождению переменного тока из-за любых трех компонентов: резистивных, индуктивных или емкостных. Это комбинация сопротивления и реактивного сопротивления в цепи.
Ключевые различия между сопротивлением и импедансом
- Противодействие протеканию тока в электрической цепи, будь то переменный или постоянный ток, известно как сопротивление.Противодействие протеканию тока в цепи переменного тока из-за сопротивления, емкости и индуктивности известно как импеданс.
- Сопротивление возникает как в цепи переменного тока, так и в цепи постоянного тока, тогда как полное сопротивление имеет место только в цепи переменного тока.
- Сопротивление — это вклад резистивного элемента в цепи, тогда как вклад как сопротивления, так и реактивного сопротивления формирует импеданс.
- Сопротивление обозначается (R), а полное сопротивление — (Z).
- Сопротивление — это простое значение, состоящее только из действительных чисел.Пример: 3,4 Ом, 6,2 Ом и т. Д. Импеданс состоит из действительных и мнимых чисел. Пример: R + ij, где R — действительное число, а ij — мнимая часть.
- Сопротивление цепи не меняется в зависимости от частоты переменного или постоянного тока, тогда как полное сопротивление изменяется с изменением частоты.
- Импеданс имеет как величину, так и фазовый угол, тогда как сопротивление не имеет фазового угла.
- Сопротивление в электромагнитном поле представляет собой рассеивание мощности в любом материале.Точно так же, если импеданс подвергается воздействию магнитного поля, он представляет собой как рассеивание мощности, так и накопление энергии.
Таким образом, сопротивление и импеданс — это две совершенно разные терминологии.
Измерение деформации тензодатчиками
Деформацию можно измерить несколькими методами, но наиболее распространенным является тензодатчик. Электрическое сопротивление тензодатчика изменяется пропорционально величине напряжения в устройстве. Самым распространенным тензодатчиком является металлический тензодатчик.Металлический тензодатчик состоит из очень тонкой проволоки или, чаще, металлической фольги, расположенной в виде сетки. Сетчатый рисунок максимизирует количество металлической проволоки или фольги, подверженной деформации в параллельном направлении. Сетка приклеивается к тонкой подложке, называемой держателем, которая прикрепляется непосредственно к образцу для испытаний. Таким образом, напряжение, испытываемое испытуемым образцом, передается непосредственно на тензодатчик, который реагирует линейным изменением электрического сопротивления.
Рисунок 3. Электрическое сопротивление металлической сетки изменяется пропорционально степени деформации испытательного образца.
Основным параметром тензорезистора является его чувствительность к деформации, количественно выражаемая как коэффициент измерения (GF). GF — это отношение частичного изменения электрического сопротивления к частичному изменению длины или деформации:
GF для металлических тензодатчиков обычно составляет около 2. Фактический GF конкретного тензодатчика можно получить у поставщика датчика или в документации по датчику.
На практике измерения деформации редко включают величины, превышающие несколько миллиштренов (например, 10 -3 ). Следовательно, чтобы измерить деформацию, вы должны точно измерить очень небольшие изменения сопротивления. Например, предположим, что испытуемый образец подвергается деформации в 500 мэ. Тензорезистор с GF 2 показывает изменение электрического сопротивления всего на 2 (500 x 10 -6 ) = 0,1%. Для манометра на 120 Ом это изменение составляет всего 0,12 Ом.
Для измерения таких небольших изменений сопротивления конфигурации тензодатчиков основаны на концепции моста Уитстона.Общий мост Уитстона, показанный на рисунке 4, представляет собой сеть из четырех резистивных плеч с напряжением возбуждения V EX , приложенным к мосту.
Рис. 4. Тензорезисторы сконфигурированы в схемах моста Уитстона для обнаружения небольших изменений сопротивления.
Мост Уитстона является электрическим эквивалентом двух параллельных цепей делителя напряжения. R 1 и R 2 составляют одну схему делителя напряжения, а R 4 и R 3 составляют вторую схему делителя напряжения.Выходной сигнал моста Уитстона, Vo , измеряется между средними узлами двух делителей напряжения.
Из этого уравнения видно, что когда R 1 / R 2 = R 4 / R 3 , выходное напряжение В O равно нулю. В этих условиях считается, что мост уравновешен. Любое изменение сопротивления в любом плече моста приводит к ненулевому выходному напряжению.Следовательно, если вы замените R 4 на рис. 4 активным тензодатчиком, любые изменения сопротивления тензодатчика приведут к дисбалансу моста и получению ненулевого выходного напряжения, которое является функцией деформации.
F.I.T.T. для тренировок с отягощениями | Кардиологический колледж
Принцип FITT, использованный при разработке вашей программы аэробных тренировок, также используется при разработке вашей программы тренировок с отягощениями.
FITT означает:
Запомните эти термины тренировки с отягощениями:
Повторение:
- 1 выполнение упражнения
- Пример: выполнение 1 подъема на бицепс
Набор:
- Пример конкретного количества повторений
- выполнение 1 подхода из 10 сгибаний на бицепс
Схема:
- Серия упражнений
- Пример: выполнение 1 подхода из 10 повторений на 10 упражнений
Важные советы для вашей программы тренировки с отягощениями
- Разминка перед выполнением упражнений упражнения.Перед тренировкой с отягощениями ходите медленно в течение 5 минут.
- Выполняйте упражнения правильной техникой.
- Не задерживайте дыхание.
- Не позволяйте вашему RPE превышать 16.
- Делайте не менее 30 секунд отдыха между подходами.
- После тренировки остынет и потянется.
- Между днями тренировок с отягощениями требуется не менее 1 дня на восстановление.
Болезненность и скованность в мышцах
Болезненность и скованность в мышцах являются нормальным явлением, когда вы начинаете тренировку с отягощениями.Это может произойти через несколько часов после выполнения упражнений. Это может длиться до 3-4 дней.
Прекратите все тренировки с отягощениями, если болезненность или скованность сохраняется более 3-4 дней. Это может быть признаком того, что вы подняли слишком большой вес или использовали неправильную технику. Поговорите со своим врачом или командой по профилактике сердечно-сосудистых заболеваний и реабилитации, прежде чем делать что-то еще.
Частота
Тренируйтесь с отягощениями 2–3 раза в неделю.
Не тренируйтесь с отягощениями 2 или более дней подряд.Убедитесь, что у вас есть день отдыха, чтобы восстановиться.
Back to TopИнтенсивность
При тренировке с отягощениями:
- Вы должны дышать комфортно. Не задерживай дыхание! Задержка дыхания может повысить кровяное давление во время упражнения.
- Не поднимайте настолько тяжелый вес, что вам нужно напрячься и задержать дыхание, чтобы поднять его. Используйте более легкий вес, если вы не можете поднять вес, не задерживая дыхание.
- Следуйте программе тренировок с отягощениями, разработанной вашей командой по профилактике сердечно-сосудистых заболеваний и реабилитации.
Для достижения наилучших результатов важно поднимать правильный вес. Используйте приведенную ниже шкалу воспринимаемой нагрузки (RPE), чтобы помочь вам. Ваше последнее повторение в вашем наборе упражнений должно оцениваться как оценка от 11 до 16 по шкале RPE.
Не выполняйте упражнения с такими симптомами, как:
- боль в груди
- стенокардия
- одышка
- учащенное сердцебиение
- головокружение
- боли в теле
Если вы чувствуете какой-либо из этих симптомов, сообщите сердечно-сосудистые меры и команду реабилитации, чтобы они могли помочь вам отрегулировать интенсивность ваших упражнений.
Шкала оценки воспринимаемой нагрузки (RPE)
| Число Рейтинг | Устная оценка | Пример |
|---|---|---|
| 6 | Никаких усилий. Сидеть и ничего не делать | |
| 7 | Очень-очень легкий | Ваши усилия просто заметны |
| 8 | ||
| 9 | Очень легкий | |
| 10 | Легкое усилие | |
| 11 | Достаточно легкий | По-прежнему кажется, что у вас достаточно энергии для продолжения упражнений |
| 12 | ||
| 13 | Сильно | |
| 14 | Требуются большие усилия | |
| 15 | Жесткий | |
| 16 | Требуется очень большое усилие | |
| 17 | Очень сложно | Вы все еще можете продолжать, но вам действительно нужно подтолкнуть себя.Он кажется очень тяжелым, и вы очень устали |
| 18 | ||
| 19 | Очень, очень сложно | Для большинства людей это самое тяжелое упражнение, которое они когда-либо выполняли. Практически максимальное усилие |
| 20 | Абсолютное максимальное усилие (максимально возможное). Истощение. |
Для тренировок с отягощениями ваше RPE должно быть между 11 и 16.Вот как вы должны себя чувствовать, когда закончите последнее повторение вашего подхода.
Back to TopВремя
После того, как вы проработаете до двух подходов по 10-15 повторений каждого упражнения, вам, вероятно, потребуется около 20-30 минут, чтобы завершить вашу программу.
Back to TopТип
Существует множество различных упражнений для улучшения силы и выносливости ваших мышц. Ваша команда по профилактике сердечно-сосудистых заболеваний и реабилитации может порекомендовать от 7 до 10 различных упражнений, которые безопасны и проработают все ваши основные группы мышц.При необходимости эти упражнения можно изменить, чтобы вам было удобно и безопасно.
Эти упражнения можно выполнять с различными типами оборудования, такими как:
- ручные гири
- ленты или трубки
- тренажеры
- собственный вес
В этом примере для простоты каждое значение следует читать как среднеквадратичное значение, даже если это пиковое значение.Обычно применяется правило [1.41] [0.707] !!! Во-первых, хочу отметить, что очень часто я нахожу трансформатор вообще без указания его параметров. Вот шаги, которые я использую для определения параметров трансформатора. 1. Непосредственно подавать 220 В на неизвестный трансформатор нецелесообразно, потому что вы можете не знать, какая первичная, а какая вторичная. Более того, это может быть аудиопреобразователь, который может его сжечь. Итак, сначала вы берете известный трансформатор и понижаете напряжение сети до более контролируемого уровня.Допустим, 16Vrms. 2. Вы измеряете активное сопротивление постоянному току катушек неизвестного трансформатора с помощью омметра. То, что имеет более высокое сопротивление, является первичным (это не всегда применимо, но в случае понижающих трансформаторов) 3. Вы подключаете первичную обмотку неизвестного трансформатора к стороне 16 В среднеквадратического значения известного трансформатора и измеряете напряжение на вторичной обмотке неизвестного трансформатора. В нашем случае это 297мВ. ⚠ Будьте осторожны, потому что если вы поменяете местами первичную обмотку с вторичной, вы можете в конечном итоге повысить напряжение до уровня даже выше сетевого, что является летальным исходом.Будьте осторожны на этом этапе. 4. Теперь, когда мы знаем напряжения на обеих сторонах неизвестного трансформатора, мы можем рассчитать коэффициент его намотки. Вы просто делите первичное напряжение на вторичное. 16 В / 0,297 В = 54. Следовательно, передаточное число намотки составляет 54: 1. Несмотря на то, что трансформатор здесь говорит 50:10, когда активное сопротивление снижает напряжение, соотношение становится 54: 1. Разное |

 таблицу 1.14 [Л2. с.30].
таблицу 1.14 [Л2. с.30].
 1
1
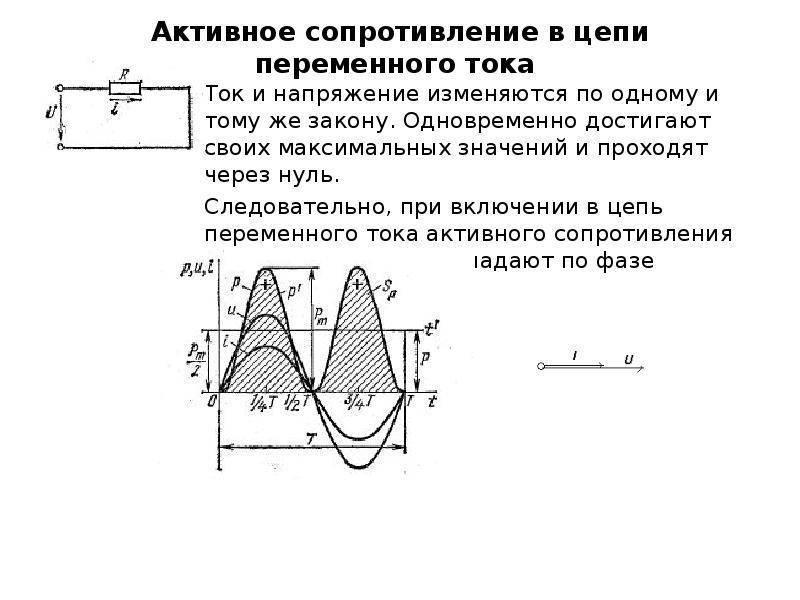
 Типичными представителями активных сопротивлений являются резисторы, лампы накаливания, электрические печи и т.д.
Типичными представителями активных сопротивлений являются резисторы, лампы накаливания, электрические печи и т.д. Индуктивность в цепи переменного тока
Индуктивность в цепи переменного тока 
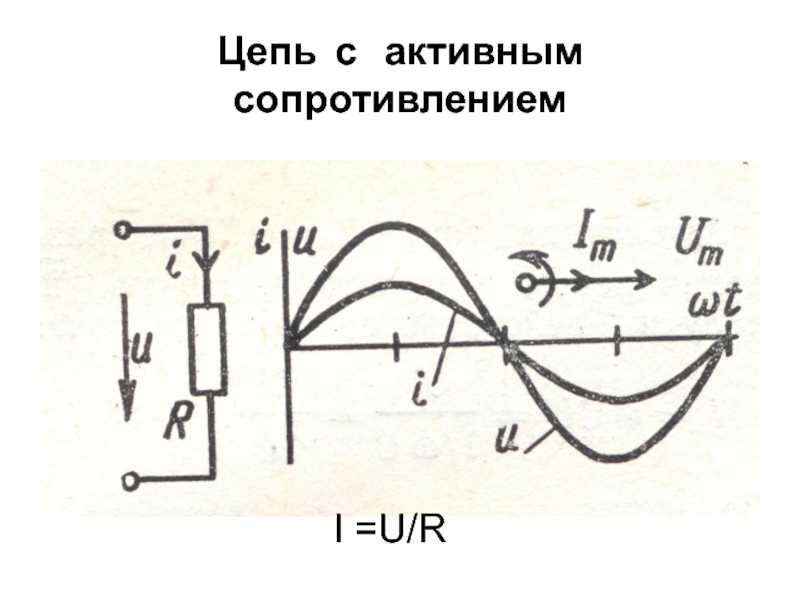

 Необходимо также иметь в виду, что в цепи с индуктивностью, не содержащей г, в каждый момент времени электродвижущая сила самоиндукции направлена навстречу напряжению генератора U . В связи с этим напряжение и э. д. с. самоиндукции е с также сдвинуты по фазе друг относительно друга на 180°.
Необходимо также иметь в виду, что в цепи с индуктивностью, не содержащей г, в каждый момент времени электродвижущая сила самоиндукции направлена навстречу напряжению генератора U . В связи с этим напряжение и э. д. с. самоиндукции е с также сдвинуты по фазе друг относительно друга на 180°.