Формулы конденсатора

Формулы емкости конденсаторов

Для любого конденсатора справедлива формула:

   

где C – емкость конденсатора; q – величина заряда одной из обкладок конденсатора; – разность потенциалов между его обкладками.

Емкость конденсатора, между пластинами которого находится диэлектрик (C) (диэлектрическая проницаемость которого равна в раз больше, чем емкость такого же воздушного конденсатора ():

   

Для расчета емкости плоского конденсатора применяют формулу:

   

где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.

Емкость плоского конденсатора, содержащего N слоев диэлектрика (толщина i-го слоя равна , диэлектрическая проницаемость i-го слоя , определяется как:

   

Электрическая емкость цилиндрического конденсатора вычисляют как:

   

где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.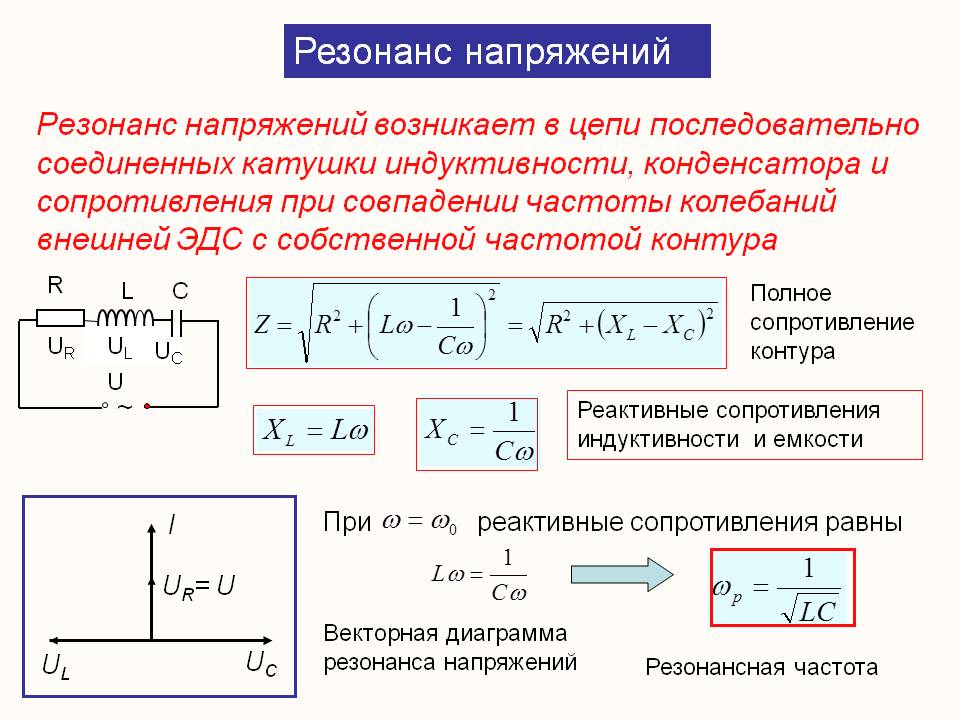

Емкость сферического (шарового) конденсатора находят по формуле:

   

где – радиусы обкладок конденсатора.

Формулы для расчета емкости соединения конденсаторов

При параллельном соединении конденсаторов суммарная емкость батареи (C) равна сумме емкостей отдельных конденсаторов (), ее составляющих:

   

Электрическая емкость последовательного соединения конденсаторов может быть вычислена по формуле:

   

Если последовательно соединены N конденсаторов, с емкостями то емкость батареи вычислим как:

   

Сопротивление конденсатора

При включении конденсатора в цепь с постоянным током сопротивление конденсатора считают бесконечно большим.

Если конденсатор включен в цепь переменного тока, то его сопротивление называют емкостным и вычисляют при помощи формулы:

   

где – частота переменного тока; – угловая частота тока; C – емкость конденсатора.

Формула энергии поля конденсатора

   

где –энергия поля конденсатора; q – заряд конденсатора; C – емкость конденсатора; – разность потенциалов между обкладками конденсатора.

Энергия поля плоского конденсатора:

   

Примеры решения задач по теме «Конденсатор»

Емкость частота конденсатора и их искажения

электролитические конденсаторы для hi-end     …Одна из причин, которые препятствуют усилению звуковых программ с высокой достоверностью, кроется в нелинейных искажениях, возникающих в активных элементах усилителя. При этом возникают такие виды искажений, как гармонические и кроссмодуляционные. Современное же развитие полупроводниковой техники и схемотехники позволяет значительно снизить влияние нелинейных искажений активных элементов на качество воспроизведения.     Как известно, звуковые сигналы имеют сложную форму, их спектр состоит из основных частот и гармонических составляющих. Именно гармонические составляющие маскируются шумовым сигналом, при этом снижается четкость воспроизведения. Были проведены тщательные исследования, в результате которых выяснилось, что источником искажений являются пассивные элементы, особенно электролитические конденсаторы большой емкости, которые широко используются в транзисторных усилителях благодаря их большой удельной емкости.     Вольтамперная характеристика электролитического конденсатора похожа на характеристику полупроводникового диода. При нормальной полярности приложенного напряжения через конденсатор протекает небольшой ток утечки, а при противоположной полярности приложенного напряжения через конденсатор будет протекать большой ток, т. е. характеристика конденсатора существенно нелинейна. Поэтому если к электролитическому конденсатору приложить переменное синусоидальное напряжение, то будут возникать гармоники основной частоты, которые уменьшаются при увеличении постоянного запирающего напряжения.     Кроме того, внутренние потери конденсатора зависят от частоты приложенного сигнала. На рис. 1 показан график зависимости потерь tg б электролитического конденсатора от частоты сигнала. На нем видно, что, начиная с некоторой частоты, потери резко возрастают. При этом их уровень зависит от приложенного постоянного напряжения и возрастает при его увеличении. Для конденсаторов К50-6 на частоте 10 кГц tg б становится значительно больше 1, т. е. конденсатор ведет себя как нелинейный резистор. Все это свидетельствует о том, что электролитические конденсаторы большой емкости являются источниками высокочастотных искажений звукового сигнала. Чтобы уменьшить нелинейные искажения в электролитических конденсаторах,параллельно им включают бумажный, металлобумажный или пленочный конденсатор. Потери в этих конденсаторах гораздо меньше (tg 6     Существенное влияние на звуковые свойства конденсатора оказывает коэффициент абсорбции. Если зарядить конденсатор, а потом произвести его разряд (1-2сек), то через некоторое время мы обнаружим на его обкладках напряжение отличное от нуля. Таким образом конденсатор накапливает энергию в диэлектрике, а потом постепенно ее отдает. Вы можете представить, что происходит со звуком, когда напряжение на конденсаторе изменяется не с изменением сигнала, а по «ЗАКОНАМ КОНДЕНСАТОРА».     Сейчас разработано множество АУДИОФИЛЬСКИХ конденсаторов. Я думаю нет смысла приводить их список. Он всем известен. Выбор в данном случае ограничивается лишь размером кошелька. Из недорогих пленочных мне нравится SOLEN.     Среди отечественных я отмечу К73-полиэтилентерефталатные К78-полипропиленовые, К70, К71-полистирольные Фт-фторопластовые. Наименьший tg б у серий Фт, К71, К78 (tg б = 0,008— 0,015). Звучат они все по-разному. Здесь выбор—дело вкуса.     Мы незаслужено забыли о бумажных конденсаторах. Они дают более высокое разрешение и мягкое звучание. Но к сожалению имеют слишком большие габариты и поэтому применяются как правило только в ламповой звукотехнике.

Электроника НТБ — научно-технический журнал — Электроника НТБ

ПОМЕХОПОДАВЛЯЮЩИЕ КОНДЕНСАТОРЫ: ТРЕБОВАНИЯ И КОНСТРУКЦИИ[1]
Обеспечение помехоустойчивости – одна из основных проблем при проектировании радиоэлектронных устройств. Ее особая актуальность обусловлена широким применением источников вторичного электропитания, которые могут служить генераторами высокочастотных помех. Применение высокоскоростных цифровых устройств также приводит к возрастанию частоты помех. Если раньше требования к максимальной частоте помехоподавления составляли не более 50 МГц, то теперь увеличены до 100 МГц и выше. Наиболее опасными являются кондуктивные помехи, распространяющиеся в проводящих цепях питания, управления, коммутации.

Для устранения таких помех применяются блокировочные конденсаторы, предназначенные для замыкания их на корпус аппаратуры, «землю». Опорными называются помехоподавляющие конденсаторы, в конструкции которых есть опорный вывод, обеспечивающий малую индуктивность соединения одного из электродов конденсатора с корпусом аппаратуры. Опорные конденсаторы отличаются от аналогичных устройств лишь конструкцией и некоторыми дополнительными требованиями к электрическим параметрам (эквивалентному последовательному сопротивлению и частоте помехоподавления).

Амплитудно-частотная характеристика (АЧХ) полного сопротивления (Z) конденсаторов (рис.1) имеет U-образную форму, в левой ветви которой Z уменьшается пропорционально частоте и достигает минимального значения на частоте собственного последовательного резонанса fрез. На этой частоте величины емкостного и индуктивного реактивных сопротивлений одинаковы и противоположны по знаку, а результирующее реактивное сопротивление равно нулю. На частоте собственного последовательного резонанса общий импеданс будет равен эквивалентному последовательному сопротивлению (Rэпс). На частотах ниже частоты последовательного резонанса Z определяется емкостью, а выше – индуктивностью, увеличиваясь пропорционально частоте. Для устранения кондуктивных помех их (помехи) по цепям распространения нужно накоротко замкнуть по переменному току на заземленный корпус. Но наличие в цепи конденсаторов активного сопротивления Rэпс не позволяет этого сделать. По этой причине минимально достижимые значения эквивалентного последовательного сопротивления – одно из главных требований к опорным помехоподавляющим конденсаторам.

Достижение максимальной частоты помехоподавления зависит от значений частоты собственного последовательного резонанса fрез и собственной индуктивности L, определяемых конструкцией электродов и выводов конденсатора. Для повышения частоты fрез необходимо обеспечить минимально возможные значения индуктивности. Для оценки параметра помехоподавления обычно используются термины «ослабление» или «вносимое затухание». В настоящей статье предпочтение отдано второму варианту. Вносимое затухание соответствует ослаблению электрического сигнала переменного тока, вызванному включением конденсатора в электрическую схему.
Значение вносимого затухания (А, дБ) вычисляют по формуле:
А = 20 lg U1 / U2, (1)
где
U1 – напряжение в цепи без конденсатора,
U2 – напряжение с установленным конденсатором.

Разработка помехоподавляющих конденсаторов в НИИ «Гириконд» началась с 1950-х годов. Были созданы дисковые керамические опорные конденсаторы КДО, трубчатые опорные конденсаторы КО, другие опорные конденсаторы с органическим диэлектриком. Конденсаторы КО, КДО до последнего времени выпускались заводом «Номинал» на Украине и использовались на ряде предприятий России. В связи с прекращением поставок встал вопрос об их замещении. Конденсаторы КДО имеют металлический фланец с резьбовой шпилькой (опорный вывод), на котором размещен емкостной элемент в виде однослойного керамического дискового диэлектрика. Максимальная номинальная емкость КДО равняется 2 200 пФ. В случае такой емкости нижняя граница диапазона частот помехоподавления, при которой вносимое затухание равняется 3 дБ (частота среза), составляет 2,9 МГц. Максимальная номинальная емкость конденсаторов КО также небольшая – 4 700 пФ, поэтому они не могут обеспечить эффективное помехоподавление в области низких частот. В этом диапазоне частот с такой задачей справляются опорные конденсаторы с органическим диэлектриком К73-57, однако у них большая собственная индуктивность, ограничивающая помехоподавление в высокочастотной области. На частоте 100 МГц вносимое затухание составляет всего 10 дБ (рис. 2).
В конце 1950-х – начале 1960-х годов в конструкциях и технологии изготовления керамических конденсаторов произошли принципиальные изменения. Были разработаны методы литья тонких керамических пленок, с применением которых создан новый тип керамических конденсаторов – многослойные. Максимальная и удельная емкость таких конденсаторов по сравнению с однослойными увеличилась в тысячи раз. Наибольшее распространение получили конденсаторы для поверхностного монтажа, имеющие форму параллелепипеда (чип-конденсаторы). Такие устройства могут применяться и как блокировочные, например конденсаторы К10-67в‑500 В‑0,022 мкФ размером 5,7 Ч 5,0 Ч 3,0 мм в цепях с источниками вторичного электропитания. Спустя время появились помехоподавляющие шайбовые конденсаторы (рис.3).
Чередующиеся слои керамического диэлектрика и электродов конденсаторов, отдельные слои которых соединены параллельно, образуют емкость между внутренней и внешней контактными поверхностями. Благодаря данной конструкции можно получать значения емкости от единиц пикофарад до нескольких десятков микрофарад [1]. В иностранных каталогах [2, 3] такие конденсаторы называют в основном Multilayer Discoidal Capacitors, а в отдельных источниках отечественной технической литературы – «дискоидальными». В соответствии с конструкцией мы называем такие конденсаторы шайбовыми. Устройства применяются как самостоятельные помехоподавляющие элементы, так и в составе фильтров низкой частоты [4]. Коаксиальная конструкция и параллельное соединение внутренних электродов обеспечивают минимальные значения собственной индуктивности и максимальную частоту собственного резонанса.
МАЛОИНДУКТИВНЫЕ ОПОРНЫЕ
КОНДЕНСАТОРЫ К10-85
Конструкция конденсаторов. Малоиндуктивные опорные конденсаторы К10-85 (рис.4) были разработаны с использованием преимуществ шайбовых конденсаторов. Устройства номинальным напряжением 250, 500, 750 и 1 000 В, их корпуса выполнены из латуни с покрытием серебром. Корпус с резьбой служит опорным выводом. Конструкции и основные размеры конденсаторов приведены в табл.1 и на рис.5, 6. Типоразмеры, группы температурной стабильности (ТСЕ) и номинальные емкости представлены в табл. 2. Материалы группы ТСЕ Н90 для конденсаторов не использовались из-за высокой их нестабильности при воздействии температуры и рабочего напряжения.

Параметры помехоподавления. Вносимое затухание конденсаторов А в диапазоне частот от 0,3 до 1 300 МГц определялось с помощью измерителей комплексных коэффициентов передач «Обзор‑103» и в диапазоне частот от 0,3 до 3 200 МГц – «Обзор‑304». Эти приборы предназначены для измерения комплексных S-параметров, из которых вносимому затуханию соответствует коэффициент передачи S21. АЧХ вносимого затухания конденсаторов с минимальным и максимальным значениями номинальной емкости приведены на рис.7 и 8.
Частота среза АЧХ, при которой вносимое затухание А равняется 3 дБ, точно соответствует соотношению:
Fc = 1 / π R C, (2)
где
Fc – частота среза, Гц;
R – сопротивление измерительной системы, 50 Ом;
С – емкость конденсатора, Ф.

Значения Fc составляют от 20 кГц для емкости 0,33 мкФ и до 900 МГц для емкости 4,7 пФ. На частотах до резонансной частоты вносимое затухание увеличивается (крутизна около 20 дБ/декаду). Значения fрез находятся в пределах от 4,4 до 1 150 МГц. После резонансной частоты вносимое затухание начинает уменьшаться с такой же крутизной – около 20 дБ/декаду. При этом минимальные значения вносимого затухания составляют 8–12 дБ на частоте 1,4 ГГц. На более высокой частоте вносимое затухание увеличивается до 20 дБ. Таким образом, полоса помехоподавления по сравнению с конденсаторами К73-57 (до 20 МГц) была существенно расширена.
На основании измеренных АЧХ были рассчитаны значения эквивалентного последовательного сопротивления Rэпс и собственной индуктивности (L = 3,5–4,5 нГн). Значения L изменяются на 0,2–0,3 нГн/мм в зависимости от расстояния до подключения вывода конденсаторов. Значения резонансной частоты и вносимого затухания в технических условиях представлены в табл.3. Так как фактические значения емкости конденсаторов отличаются от их номинального значения в пределах допустимого отклонения, изменяются и значения резонансных частот. Поэтому значения резонансной частоты fрез были пересчитаны для номинального значения емкости по формуле:
fрез = fрез.изм., (3)
где
fрез.изм. – измеренное значение резонансной частоты,
Сф – фактическое значение емкости,
Сном – номинальное значение емкости.

Формула справедлива, так как собственная индуктивность конкретного измеренного конденсатора оставалась постоянной. Вместе с указанием резонансной частоты fрез в табл.3 приводятся значения вносимого затухания на этой частоте.
Для проверки возможного расширения полосы помехоподавления было опробовано параллельное соединение двух опорных конденсаторов – разной емкости, с разнесенными частотами собственного резонанса. АЧХ параллельно соединенных конденсаторов К10-85 номинальной емкостью 0,33 мкФ и 150 пФ приведена на рис.9.
Предполагалось, что конденсатор большей емкости и с меньшей частотой собственного резонанса обеспечит низкое значение полного сопротивления Z в низкочастотной области.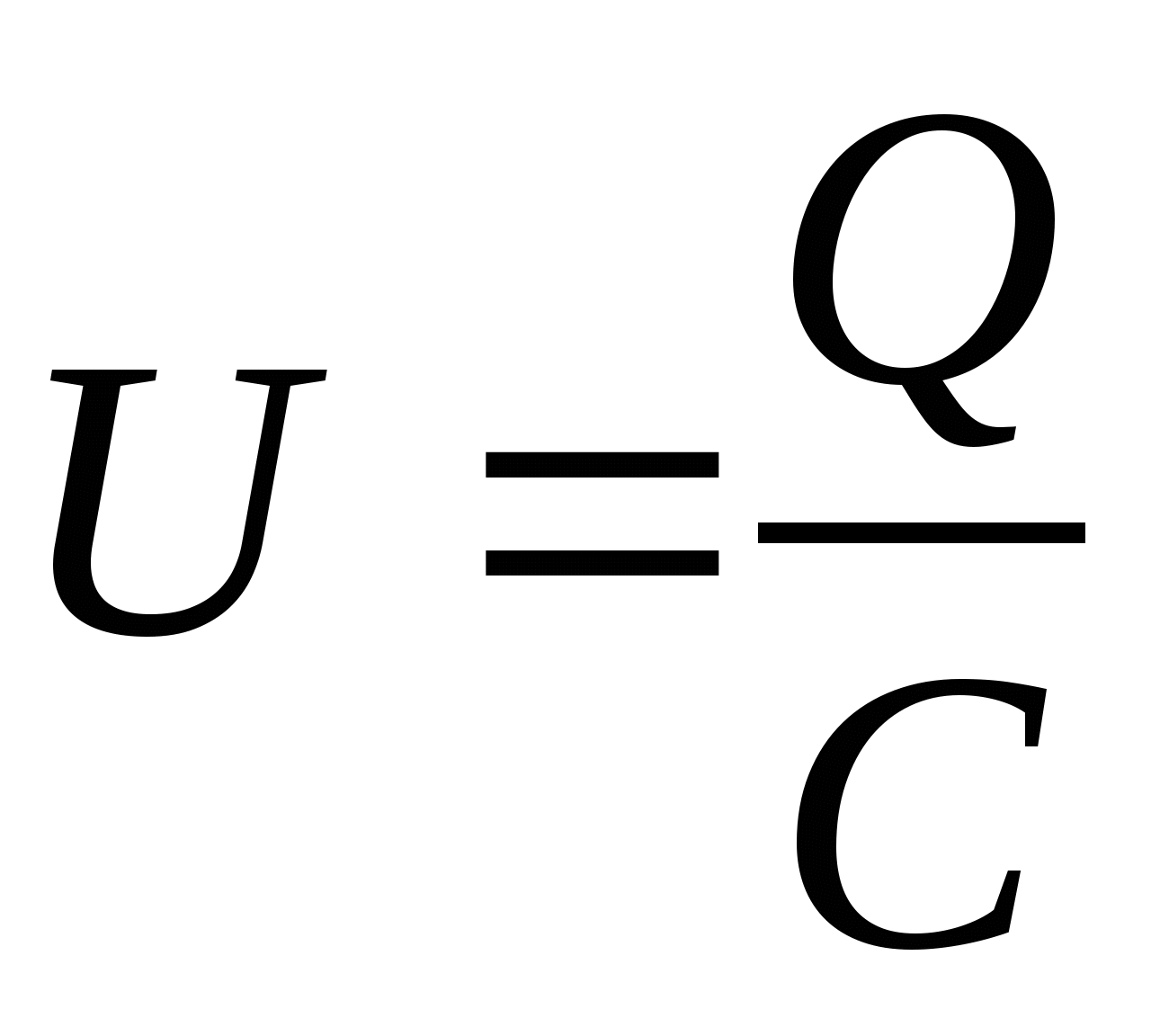 И наоборот, конденсатор меньшей емкости и с большей частотой собственного резонанса – низкое значение Z в высокочастотной области требуемого помехоподавления.
Однако предположение подтвердилось не полностью. Конденсатор емкостью 0,33 мкФ находится в индуктивной области, параллельно подключенный конденсатор емкостью 150 пФ – в емкостной. У образовавшегося таким образом колебательного контура на параллельном резонансе с частотой 104,9 МГц резко увеличилось полное сопротивление Z, что отразилось на АЧХ вносимого затухания (см. рис.9). Такое соединение опорных конденсаторов разной емкости может применяться при формировании полосы помехоподавления с заданной АЧХ.
Результат эксперимента был проверен расчетным путем: определена частота резонанса параллельного соединения конденсаторов с помощью формул (4) и (5). Результаты АЧХ (см. рис.9) и рассчитанные по формуле (5) практически совпали.
, (4)
где
– комплексное сопротивление параллельного соединения конденсаторов;
и – комплексные сопротивления первого и второго конденсаторов соответственно.

(5)
где
L1 и L2 – фактические индуктивности первого и второго конденсаторов соответственно, С1 и С2 – фактические емкости первого и второго конденсаторов соответственно.

Допустимые реактивные параметры. Предельно допустимые значения реактивных параметров в режимах переменного напряжения необходимы для определения допустимого рабочего переменного напряжения Uраб. При этих значениях Uраб температура поверхности конденсаторов не должна превышать температуру окружающей среды более чем на 5 °С, а параметры конденсатора должны оставаться в пределах нормы. Для определения этих параметров температура корпуса конденсаторов измерялась в различных режимах нагрузки переменным током на частотах от 300 Гц до 200 кГц. Керамический диэлектрик группы МПО имеет низкие диэлектрические потери (tgδ = 0,0001–0,001), и конденсаторы этой группы ТСЕ нагревались только за счет нагрева реактивным током Ip металлических частей конденсатора. Нагрев конденсаторов групп Н20, Н50 происходит за счет диэлектрических потерь (tgδ = 0,005–0,02) при реактивной мощности Рр.  Однако на определенной частоте f0 потери в металле сравниваются с потерями в диэлектрике, а при более высоких частотах – превосходят их. Поэтому на частотах > f0 допустимые значения Рр и Ip необходимо снижать пропорционально отношению f / f0. На основании анализа полученных данных определены предельно допустимые значения реактивных мощности и тока, а также формула для расчета f0 при разных значениях емкости С (табл.4).
* * *
Новые керамические опорные помехоподавляющие конденсаторы, разработанные в АО «НИИ «Гириконд», удовлетворяют основным требованиям обеспечения помехоустойчивости радиоэлектронных устройств, отличаются низкими значениями собственной индуктивности, для них характерна широкая линейка напряжений и емкостей.

ЛИТЕРАТУРА
1. Красильщиков М., Смирнов В., Шалаева А. Новые керамические помехоподавляющие конденсаторы // Компоненты и технологии. 2010. № 7. С. 60–63.
2. Ceramic capacitors. Каталог фирмы Eurofarad. Франция.
3. Discoidal capacitors. Каталог фирмы Syfer. Англия.
4. Красильщиков М., Смирнов В., Шалаева А. Керамические проходные фильтры нижних частот с малыми потерями // ЭЛЕКТРОНИКА: Наука, Технология, Бизнес. 2009. № 7. С. 28–32, № 8. С. 22–26.
5. Патент на полезную модель № 158534. Керамический опорный помехоподавляющий конденсатор. Авторы: Смирнов В. Ф., Шалаева А. А., Кузьмичев З. В. Приоритет полезной модели от 23 июня 2015 года.
6. Конденсаторы керамические помехоподавляющие К10-85, технические условия АДПК.673511.019 ТУ.

Таблица. Реактивное сопротивление емкости (конденсатора) в зависимости от частоты.(от 1 пф до 1000 мкФ ; от 50 Гц до 100 МГц)

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Физический справочник / / Электрические и магнитные величины / / Электрическое сопротивление и проводимость проводников, растворов, почв.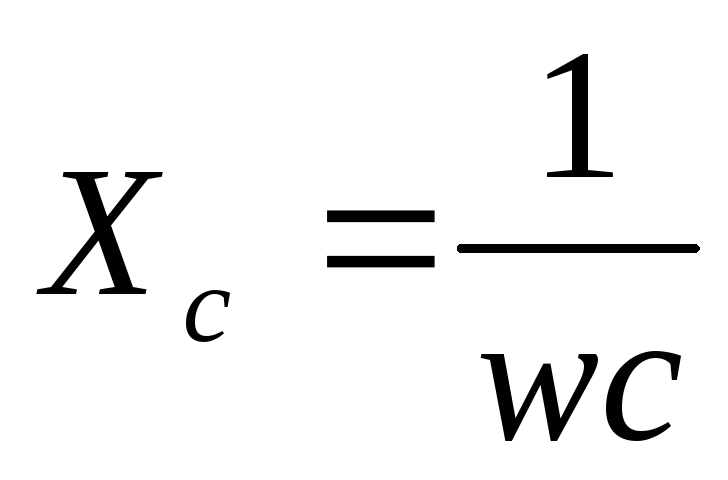 …  / / Таблица. Реактивное сопротивление емкости (конденсатора) в зависимости от частоты.(от 1 пф до 1000 мкФ ; от 50 Гц до 100 МГц) Поделиться:    Таблица. Реактивное сопротивление емкости (конденсатора) в зависимости от частоты. (от 1 пф до 1000 мкФ ; от 50 Гц до 100 МГц) Таблица. Реактивное сопротивление емкости. 50 Гц 100 Гц 1 кГц 10 кГц 100 кГц 1 МГц 10 МГц 100 МГц 1 пФ — — — — 1. 6 МОм 160 кОм 16 кОм 1.6 кОм 10 пФ — — — 1.6 МОм 160 кОм 16 кОм 1.6 кОм 160 Ом 50 пФ — — 3.2 МОм 320 кОм 32 кОм 3.2 кОм 320 Ом 32 Ом 250 пФ — 6.4 МОм 640 кОм 64 кОм 6.4 кОм 640 Ом 64 Ом 6.4 Ом 1000пф 3.2 МОм 1.6 МОм 160 кОм 16 кОм 1. 6 кОм 160 Ом 16 Ом 1.6 Ом 2000 пф 1.6 МОм 800 кОм 80 кОм 8 кОм 800 Ом 80 Ом 8 Ом 0.8 Ом 0.01 мкФ 320 кОм 160 кОм 16 кОм 1.6 кОм 160 Ом 16 Ом 1.6 Ом 0.16 Ом 0.05 мкФ 64 кОм 32 кОм 3.2 кОм 320 Ом 32 Ом 3.2 Ом 0.32 Ом — 0.1 мкФ 32 кОм 16 кОм 1. 6 кОм 160 Ом 16 Ом 1.6 Ом 0.16 Ом — 1 мкФ 3.2 кОм 1.6 Ом 160 Ом 16 Ом 1.6 Ом 0.16 Ом — — 2.5 мкФ 1.3 кОм 640 Ом 64 Ом 6.4 Ом 0.64 Ом — — — 5 мкФ 640 Ом 320 Ом 32 Ом 3.2 Ом 0.32 Ом — — — 10 мкФ 320 Ом 160 Ом 16 Ом 1. 6 Ом 0.16 Ом — — — 30 мкФ 107 Ом 53 Ом 5.3 Ом 0.53 Ом — — — — 100 мкФ 32 Ом 16 Ом 1.6 Ом 0.16 Ом — — — — 1000 мкФ 3.2 Ом 1.6 Ом 0.16 Ом — — — — — Поиск в инженерном справочнике DPVA. Введите свой запрос: Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая поддержка сайта: Zavarka Team	Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator

Измеряем конденсаторы «большой» емкости используя VNA

Зашла тут речь о полезности частот выше 100 КГц применительно к измерениям конденсаторов достаточно большой емкости 10-100 мкФ

Колхозить нормальную схему мне было лень и калибровать её.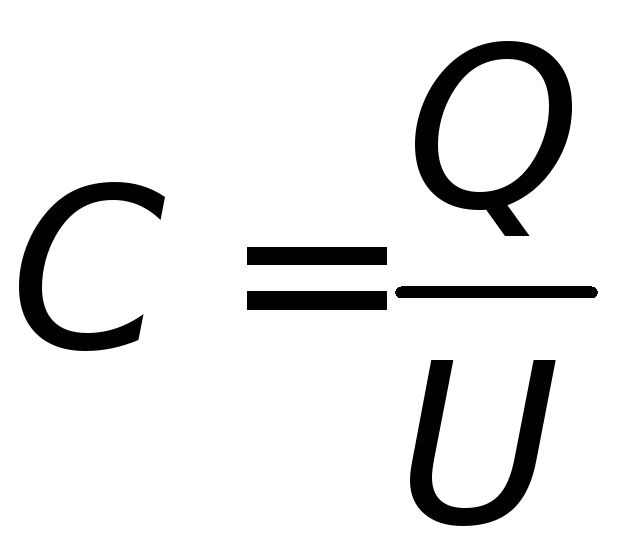 Поэтому будет с некоторым смещением все. Но для частот до 10 МГц сойдет.
О графиках. По оси X — частота, экспоненциально нарастающая от 10 КГц до 10 МГц. По оси Y — сопротивление в омах. Красный график — реальная часть сопротивления, синий график — комплексная часть сопротивления.

Дополнительное сопротивление относительно откалиброванного SMA провода оказалось порядка 50-70 мОм, дополнительная индукктивность 11 nH.

Электролит выдал на удивление хорошую частоту последовательного резонанса — 1 МГц! ESR равный почти 1 ому вполне типичен для электролитов такой емкости. Частота последовательного резонанса в том месте, где комплексное сопротивление пересекает нулевую линию. Резонансная частота такая высокая из-за того, что емкость электролита стремительно деградирует с ростом частоты. На частоте 100 КГц она равна примерно 9 uF. По резонансной частоте можно прикинуть, какая емкость примерно остается у этого конденсатора на частоте 1 МГц. Получается, что всего 2 uF для 1 МГц частоты.

SMD конденсатор типоразмера 1206 имеет оочень низкий ESR = 57 мОм на частоте 10 KHz. Почти как у короткозамкнутой перемычки, которую видимо надо было залудить для лучшего контакта. Частота последовательного резонанса оказалась 248 KHz. Причина этого тоже прозаична. Я припаял к нему проводки немного большей длинны, чем выводы электролитического конденсатора. Вот эти дополнительные 5 мм длинны и дали нам дополнительные 7-8 nH индуктивности. Вместе с большей ёмкостью они понизили резонансную частоту. На резонансной частоте у этого конденсатора остаются еще вполне приличные 22 uF емкости.

Выводов могу сделать парочку (хотя эта полная банальщина всем известная).
1. Электролиты бесполезно применять в современных импульсных цепях, слишком большой ESR.
2. Следуйте рекомендациям производителей Step-Down/Step-Up микросхем и ставьте конденсаторы максимально близко к ним. Важен буквально каждый миллиметр. Ну и естественно не экономьте на количестве переходных отверстий.

Разделительный конденсатор

Создание связи по переменному току необходимо, чтобы запретить протекание постоянного тока между определенными точками схемы и обес­печить при этом свободное прохождение переменного тока. Электрон­ные компоненты, обеспечивающие связь по переменному току, например конденсаторы или трансформаторы, обычно устанавливаются на входе и выходе усилителя. Таким образом, заданный режим покоя (статический режим) транзистора не влияет на статические режимы предыдущего и последующего каскадов.

В схеме, приведенной на рис. 23.1. конденсатор связывает точки А и В по переменному току, aR – нагрузочный резистор. Для постоянного тока конденсатор действует как разрыв цепи, полностью блокируя протекание постоянного тока между точками А и В. По этой причине конденсатор связи называют блокировочным или разделительным конденсатором.

Удовлетворительное качество связи по переменному току достигается только в том случае, когда реактивное сопротивление Х_с конденсатора на рабочей частоте много меньше сопротивления нагрузочного резистора R.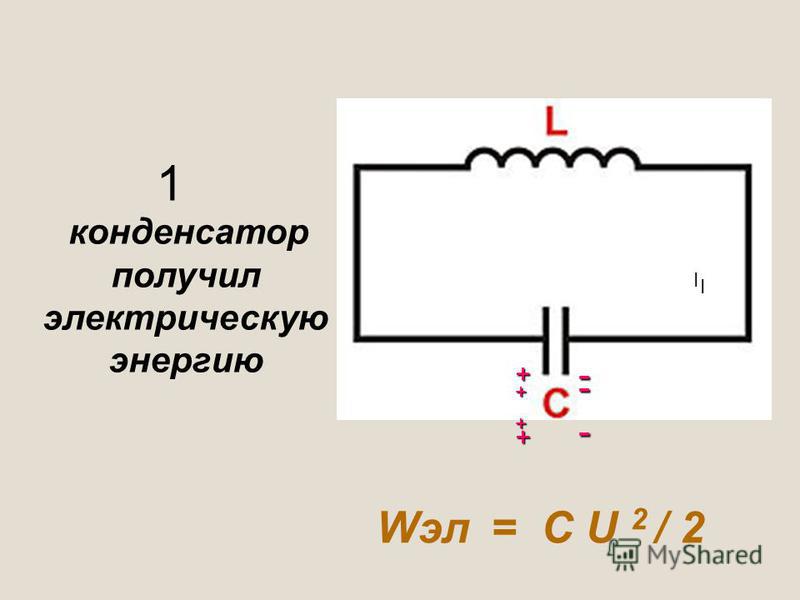 Тогда на этом конденсаторе падает (и теряется) очень малая часть напряжения входного сигнала. Например, если V_вх = 100 мВ, то связь по переменному току можно считать удовлетворительной, когда выходное напряжение          V_вых = 95 мВ и на разделительном конденсаторе падает 5 мВ (5%). Требуемую емкость разделительного конденсатора определяют два фактора.

1.                   Сопротивление загрузочного резистора R. Считая, что удовлетвори­тельная связь но переменному току достигается, когда Х_с = R/20, для R = 1 кОм получаем Х_с = 50 Ом.

 

 

Рис. 23.1. Установка разделительного                                      Рис. 23.2.  Влияние развязывающего конденсатора.                                                                          конденсатора.

                                                           

Указаны потен­циалы точки А без развязывающего конденсатора (а) и с развязывающим конденсатором (б).

Предположим, что рабочая частота f = 300 Гц. Поскольку Х_c = 1/2πfC₁, то

Если сопротивление нагрузочного резистора увеличить до 100 кОм, то Х_c= R/20 = 1/20·100 = 5 кОм

Таким образом, если сопротивление нагрузочного резистора увеличить в 100 раз (с 1 кОм до 100 кОм), то емкость разделительного конденсатора можно уменьшить в той же пропорции (с 10 мкФ до 0,1 мкФ).

Вообще, чем больше сопротивление нагрузочного резистора, тем мень­ше требуемая емкость разделительного конденсатора.

2. Рабочая частота. Возьмем в качестве исходного вышеприведенный пример, где удовлетворительная связь по переменному току достига­лась при С = 10 мкФ и R = 1 кОм для f = 300 Гц.

Если теперь рабочую частоту увеличить до 300 кГц, то с учетом усло­вия Хс = R/20 = 50Ом получаем

Таким образом, если рабочую частоту увеличить в 1000 раз (с 300 Гц до 300 кГц), то емкость разделительного конденсатора можно уменьшить в 1000 раз (с 10 мкФ до 0,01 мкФ). .1) в точке А постоянный потенциал равен 10 В, а переменный потенциал сигнала — 10 мВ. Кон­денсатор, представляющий собой разрыв цени для постоянного тока, не оказывает никакого влияния на постоянный потенциал точки А, Одна­ко если емкость этого конденсатора такова, что па рабочей частоте его реактивное сопротивление существенно меньше сопротивления резистора R, то конденсатор будет эффективно осуществлять короткое замыкание сигнала переменного тока на землю. Таким образом, потенциал точки А по переменному току будет равен нулю. ёмкость конденсатора С, обес­печивающая удовлетворительную развязку, определяется сопротивлени­ем резистора R и рабочей частотой — но тем же самым формулам, ко­торые использовались для расчета емкости разделительного конденса­тора.

Усилитель с ДС-связью

На рис. 23.3 приведена схема усилителя с ДС-связыо, где С} — входной разделительный конденсатор. Емкость этого конденсатора должна быть сравнительно велика в силу низкого входного сопротивления транзистора в схеме с ОЭ (это сопротивление становится еще меньше за счет шунтиро-вания входа, усилителя резистором R^}. связывает выход усилителя с нагрузкой или следующим каскадом, его емкость сравнима с емкостью конденсатора Ci. Типичные значения емкостей разделитель-ьшх конденсаторов следующие:

10-50 мкФ. 0.01-0,1 мкФ.

для звуковых частот:

для радиочастот:

 

Рис. 23.3. Усилитель с RC-связью с

развязывающим конденсатором С₃ в цепи эмиттера.            Рис. 23.4. Инвертирование (измене­ние на 180°) фазы сигнала в усили­теле с ОЭ.

Развязывающий конденсатор

Отрицательная обратная связь через резистор R₄ в усилителе на рис. 23.3, с одной стороны, обеспечивает необходимую стабильность усилителя по постоянному току, а с другой стороны, снижает его коэффициент усиле­ния до очень малой величины (2-3). Снижение коэффициента усиления связано с действием отрицательной обратной связи по переменному току, обусловленной падением напряжения сигнала на резисторе R₄. Для устранения этой отрицательной обратной связи по переменному току и одновременного сохранения стабильности по постоянному току применя­ется эмиттерный развязывающий конденсатор С₃.

Типичные значения емкости эмиттерного развязывающего конденса­тора того же порядка, что и для разделительного конденсатора.

Усиление

Схема, приведенная на рис. 23.3, является законченной схемой однокас­кадного усилителя с ОЭ. При подаче сигнала (например, синусоидальной формы) на вход усилителя этот сигнал передается через конденсатор С₁ на базу транзистора. В начале положительного полупериода входного сигнала потенциал базы возрастает относительно потенциала эмиттера, напряжение V_BEувеличивается, ток эмиттера I_e, а с ним и ток коллек­тора I_c, возрастают, в результате уменьшается напряжение на коллекторе V_c. Это означает, что положительному полу периоду входного сигнала со­ответствует отрицательный полупериод выходного сигнала. С другой сто­роны, отрицательному полупериоду входного сигнала соответствует поло­жительный полупериод изменения коллекторного напряжения. Таким образом, сигналы на входе и выходе усилителя противофазны, как по­казано на рис. 23.4. Усиление сигнала происходит в силу того, что очень малый размах напряжения V_BEприводит к большому размаху тока транзистора, который, проходя через резисторR₃, вызывает большой размах коллекторного напряжения.

Линия нагрузки

Выходные характеристики транзистора дают общее представление о рабо­те транзистора. Для того чтобы получить представление о работе транзи­стора в конкретной схеме, нужно начертить линию нагрузки. На рис. 23.5 изображены семейство выходных характеристик транзистора, работаю­щего в схеме усилителя на рис. 23.3, и линия нагрузки XY.

Прежде чем проводить линию нагрузки, нужно сначала зафиксиро­вать две точки, попадающие на эту линию. Лучше всего использовать точку Х на оси х, где ток I_c = 0, и точку Y на оси у, где V_c = 0. Через эти две точки проводится прямая линия — линия нагрузки. Предполагается, что V_c = V_CE.

Точка X. В этой точке ток транзистора I_c = 0. Транзистор находится в состоянии отсечки. Следовательно, напряжение на коллекторе V_c = V_CC.

Точка Y. Здесь коллекторное напряжение V_c = 0. Подставляя V_c = 0 в уравнение               V_CC = V_c + V_R3, получаем V_CC = V_R3. Но V_R3 = I_c R₃, поэтому V_CC = I_c R₃. Следовательно,

I_c = V_CC / R₃.

Рис. 23.5. Линия нагрузки.

Для величин, указанных на рис. 23.3, положение точек Х и Y будет определяться следующими параметрами:

Точка Х          I_c = 0, V_c = V_CC = 10 В.

Точка Y         V_c = 0, I_c = V_CC/ R₃ = 10/3,3 = 3 мА.

Таким образом, XY — это линия нагрузки для нагрузочного резистора сопротивлением        R₃ = 3,3 кОм.

При использовании нагрузочного резистора меньшего номинала (2,2 кОм) получаем линию нагрузки ХY_a. Положение точки Х не изменяется по сравнению с предыдущим случаем, поскольку напряжение V_СС остается тем же самым — 10 В. Для точки Y_b получаем I_c = V_CC / R₃ = 10 В/2,2кОм = 4,55мА.

Нагрузочному резистору более высокого номинала, например 4,9 кОм, соответствует линия нагрузки ХY_b с точкой Y_b при I_c = 10 В/4, 9 кОм ≈ 2 мА.

Графический анализ

Процесс усиления сигнала осуществляется вдоль линии нагрузки и может быть представлен графически, как показано на рис. 23.6. Точка Q есть статическая рабочая точка, представляющая режим работы усилителя по постоянному току, т. е. в отсутствие сигнала. Рабочая точка задает смещение транзистора в статическом режиме. В рассматриваемом случае смещение определяется следующими величинами:

I_b = 20 мкА, I_c = 1,5 мА, V_c = 5 В.

Рис. 23.6. Графическое представление работы усилителя.

 

Рис. 23.7. Перегрузка усилителя, приводящая к ограничению выходного сиг­нала.

При подаче сигнала базовый ток изменяется по синусоиде с амплитудой 20 мкА (от 0 до 40 мкА). Это приводит к изменению коллекторного тока I_c с размахом 2,8 мА и изменению коллекторного напряжения с размахом около 9 В.

С одной стороны размах входного сигнала ограничен линией I_b = 0, соответствующей отсечке транзистора (точка М на линии нагрузки), а с другой стороны – линией I_b = 40 мкА, соответствующей насыщению транзистора (точка N на линии нагрузки). Для рассматриваемого уси­лителя рабочая точка Q выбирается в середине линии нагрузки. В этом случае при подаче сигнала с амплитудой 20 мкА на базу транзистора базовый ток изменяется в пределах от 0 до 40 мкА, обеспечивая максимальную величину неискаженного выходного сигнала.

 

Рис. 23.8. Графическое представление работы усилителя с использованием пе­редаточной характеристики.

Любая попыт­ка превышения этой величины входного сигнала приводит к искажению формы выходного сигнала. Это хорошо видно на рис. 23.7, где иллюстри­руется случай перегрузки усилителя с результирующим ограничением синусоидального сигнала. Входной и выходной сигналы могут быть так­же представлены графически с помощью передаточной характеристики транзистора (рис. 23.8). Рабочий диапазон усилителя ограничен линей­ным участком характеристики передачи, выход за границы этого участка приводит к искажениям.

Добавить комментарий

Увеличивается ли емкость с частотой? — MVOrganizing

Увеличивается ли емкость с частотой?

Емкость не меняется с частотой. Скорее, это емкостное реактивное сопротивление, которое фактически изменяется с частотой. Емкость — это просто заряд конденсатора на напряжение на его пластинах.

Что происходит с емкостным реактивным сопротивлением при увеличении рабочей частоты?

Емкостное реактивное сопротивление конденсатора уменьшается с увеличением частоты на нем, поэтому емкостное реактивное сопротивление обратно пропорционально частоте.Также, когда частота увеличивается, ток, протекающий через конденсатор, увеличивается в значении, потому что скорость изменения напряжения на его пластинах увеличивается.

Что произойдет, если увеличить емкость?

В емкостной цепи, когда емкость увеличивается, емкостное реактивное сопротивление XC уменьшается, что приводит к увеличению тока цепи и наоборот. Когда сопротивление увеличивается, ток в цепи уменьшается, и наоборот. Емкость обратно пропорциональна емкостному сопротивлению.

Какова связь между постоянной времени τ сопротивлением R и емкостью C?

Постоянная времени RC, также называемая тау, постоянная времени (в секундах) RC-цепи, равна произведению сопротивления цепи (в омах) на емкость цепи (в фарадах), то есть

Какая связь между емкостью и сопротивлением?

Если у конденсатора есть какое-то «внутреннее» сопротивление, то нам нужно представить полное сопротивление конденсатора как сопротивление, соединенное последовательно с емкостью и в цепи переменного тока, которая содержит как емкость, C, так и сопротивление, R вектор напряжения, V на комбинация будет равна векторной сумме двух…

Какое сопротивление идеального конденсатора?

Сопротивление идеального конденсатора равно нулю.Реактивное сопротивление идеального конденсатора и, следовательно, его полное сопротивление отрицательны для всех значений частоты и емкости. Эффективный импеданс (абсолютное значение) конденсатора зависит от частоты, и для идеальных конденсаторов всегда уменьшается с частотой.

Есть ли у конденсатора внутреннее сопротивление?

Конденсаторы, как и батареи, имеют внутреннее сопротивление, поэтому их выходное напряжение не является ЭДС, если ток не равен нулю. На практике это сложно измерить, поэтому мы ссылаемся на напряжение конденсатора, а не на его ЭДС.Но источник разности потенциалов в конденсаторе является фундаментальным, и это ЭДС.

Как определить внутреннее сопротивление конденсатора?

Внутреннее сопротивление или импеданс постоянного тока равен напряжению ступени, деленному на 1 ампер. Для устройств с более низким внутренним сопротивлением, чем в этом примере, требуется более высокий постоянный ток.

Что происходит с индуктивным сопротивлением при увеличении рабочей частоты?

Что происходит с индуктивным сопротивлением при увеличении рабочей частоты? Пояснение: Индуктивное реактивное сопротивление прямо пропорционально рабочей частоте и определяется формулой Xf = 2πfL, где L — значение индуктивности в Генри.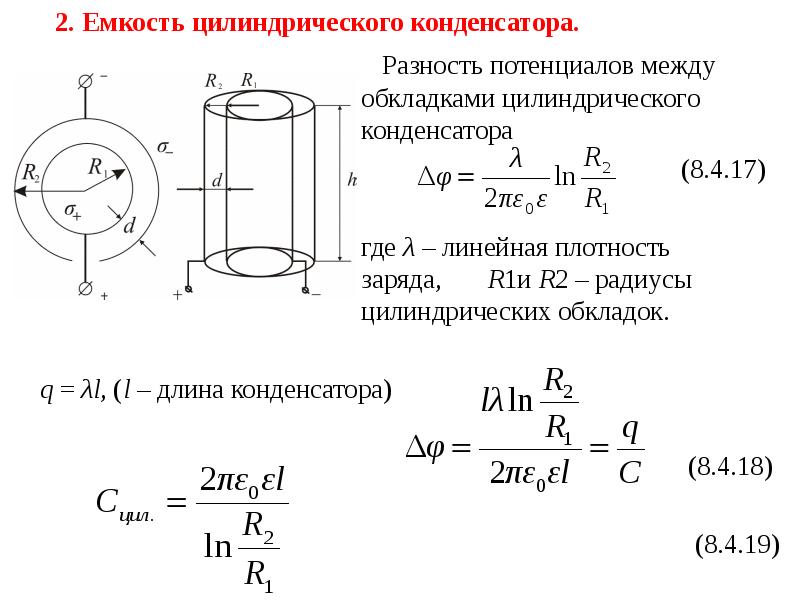 9. Каково индуктивное сопротивление катушки 40 мкГн на частоте 18 МГц?

Имеет ли конденсатор бесконечное сопротивление?

Конденсатор имеет бесконечное сопротивление (ну, если напряжение не станет настолько высоким, что оно сломается). В цепи постоянного тока конденсатор действует как разомкнутая цепь и не пропускает ток. В цепи переменного тока конденсатор имеет значение, потому что он действует как резервуар тока при изменении тока.

Какой конденсатор имеет бесконечную емкость?

Ответ.Бесконечная емкость означает бесконечную емкость для удержания заряда при приложении напряжения. Это означает короткое замыкание, поскольку I = C dv / dt. Поскольку C бесконечно, ток также будет бесконечным.

Что влияет на емкость конденсатора?

На емкость влияют три фактора: размер проводников, размер зазора между ними и материал между ними (диэлектрик). Чем больше проводники, тем больше емкость. Чем меньше зазор, тем больше емкость.

Как можно увеличить емкость конденсатора?

Следовательно, с увеличением площади пластин увеличивается емкость. Емкость прямо пропорциональна электростатическому силовому полю между пластинами. Это поле тем сильнее, когда пластины расположены ближе друг к другу. Следовательно, с уменьшением расстояния между пластинами емкость увеличивается.

Что не влияет на емкость конденсатора?

Кривизна пластин означает, что пластина представляет собой сферическую пластину или цилиндрическую пластину.Таким образом, тип материала пластин является единственным фактором, не влияющим на емкость конденсатора.

Как увеличить емкость цепи?

Если два или более конденсатора соединены параллельно, общий эффект будет таким, как у одного эквивалентного конденсатора, имеющего общую площадь пластин отдельных конденсаторов. Как мы только что видели, увеличение площади пластины без изменения всех других факторов приводит к увеличению емкости.

Какое количество одинаково для всех конденсаторов, подключенных параллельно?

Общий заряд Q — это сумма отдельных зарядов: Q = Q1 + Q2 + Q3. Рисунок 2. (а) Конденсаторы, включенные параллельно. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, поэтому общая параллельная емкость — это просто сумма отдельных емкостей.

Имеют ли параллельно подключенные конденсаторы одинаковую разность потенциалов?

Когда конденсаторы подключены параллельно, они имеют одинаковую разность потенциалов на каждом, и параллельный подход заключается в суммировании накопленных зарядов.

Почему конденсатор подключается параллельно для повышения коэффициента мощности?

Для повышения коэффициента мощности статические конденсаторы подключаются параллельно к тем устройствам, которые работают с низким коэффициентом мощности.Статические конденсаторы обеспечивают опережающий ток, который нейтрализует запаздывающую индуктивную составляющую тока нагрузки. Реактивная мощность конденсатора будет напрямую вычитаться из реактивной мощности нагрузки.

Каковы частотные характеристики импеданса / ESR конденсаторов?

Направляющая конденсатора

14. 02.2013

Основные сведения о конденсаторах описаны в этой технической колонке.
Сегодняшний столбец описывает частотные характеристики величины импеданса | Z | и эквивалентное последовательное сопротивление (ESR) в конденсаторах.

Понимание частотных характеристик конденсаторов позволяет определить, например, возможности подавления шума или возможности управления колебаниями напряжения линии питания. Поэтому частотные характеристики являются важными параметрами, необходимыми для проектирования схем. В этом столбце описаны два типа частотных характеристик: импеданс | Z | и СОЭ.

1. Частотные характеристики конденсаторов

Полное сопротивление Z идеального конденсатора (рис. 1) показано формулой (1), где ω — угловая частота, а C — электростатическая емкость конденсатора.

Из формулы (1) величина импеданса | Z | уменьшается обратно пропорционально частоте, как показано на рисунке 2. В идеальном конденсаторе потери отсутствуют, а эквивалентное последовательное сопротивление (ESR) равно нулю.

В реальных конденсаторах (рис.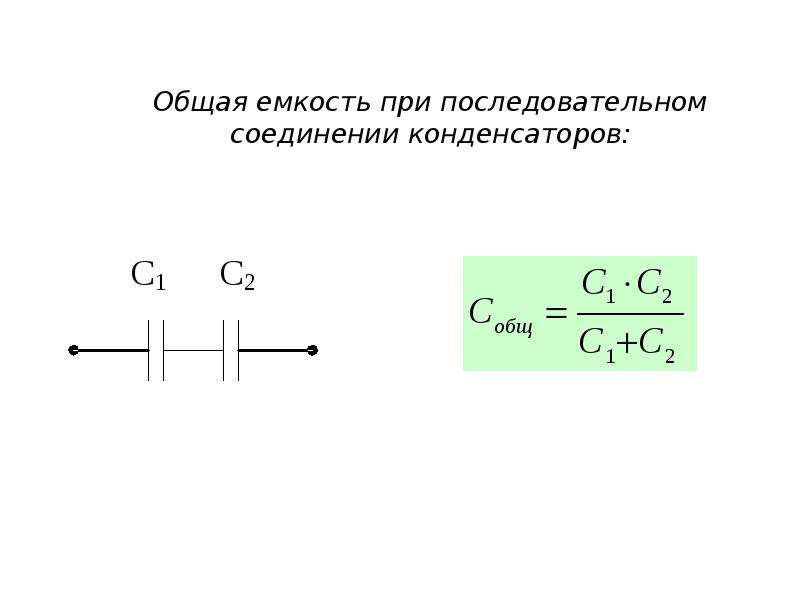 3), однако существует некоторое сопротивление (ESR) из-за потерь из-за диэлектрических веществ, электродов или других компонентов в дополнение к компоненту емкости C и некоторой паразитной индуктивности (ESL) из-за электродов, выводов и других компонентов. В результате частотные характеристики | Z | образуют V-образную кривую (или U-образную кривую в зависимости от типа конденсатора), как показано на рисунке 4, а ESR также показывает частотные характеристики для значений, эквивалентных потерям.

Причина, по которой | Z | и кривые формы СОЭ, подобные показанным на рисунке 4, можно объяснить следующим образом.

Область низких частот:

| Z | в регионах с низкой частотой частота уменьшается обратно пропорционально частоте, как в идеальном конденсаторе. ESR показывает величину, эквивалентную диэлектрическим потерям из-за задержки поляризации в диэлектрическом веществе.

Рядом с точкой резонанса:

При повышении частоты ESR в результате паразитной индуктивности, удельного сопротивления электродов и других факторов вызывает | Z | поведение отклоняется от идеального конденсатора (красная пунктирная линия) и достигает минимального значения. Частота, на которой | Z | это минимальное значение, называемое собственной резонансной частотой, и в это время | Z | = ESR. При превышении собственной резонансной частоты характеристика элемента меняется от конденсатора к катушке индуктивности, и | Z | начинает увеличиваться. Область ниже собственной резонансной частоты называется емкостной, а область выше — индуктивной.

На

ESR помимо диэлектрических потерь влияют потери, вызванные электродом.

Область высоких частот:

В частотных зонах даже выше точки резонанса | Z | характеристики определяются паразитной индуктивностью (L).| Z | в высокочастотной области приближается к формуле (2) и увеличивается пропорционально частоте.

Что касается СОЭ, начинают проявляться скин-эффекты электродов, эффекты близости и другие эффекты.

Выше было объяснение частотных характеристик реального конденсатора. Главное помнить, что при повышении частоты нельзя игнорировать ESR и ESL.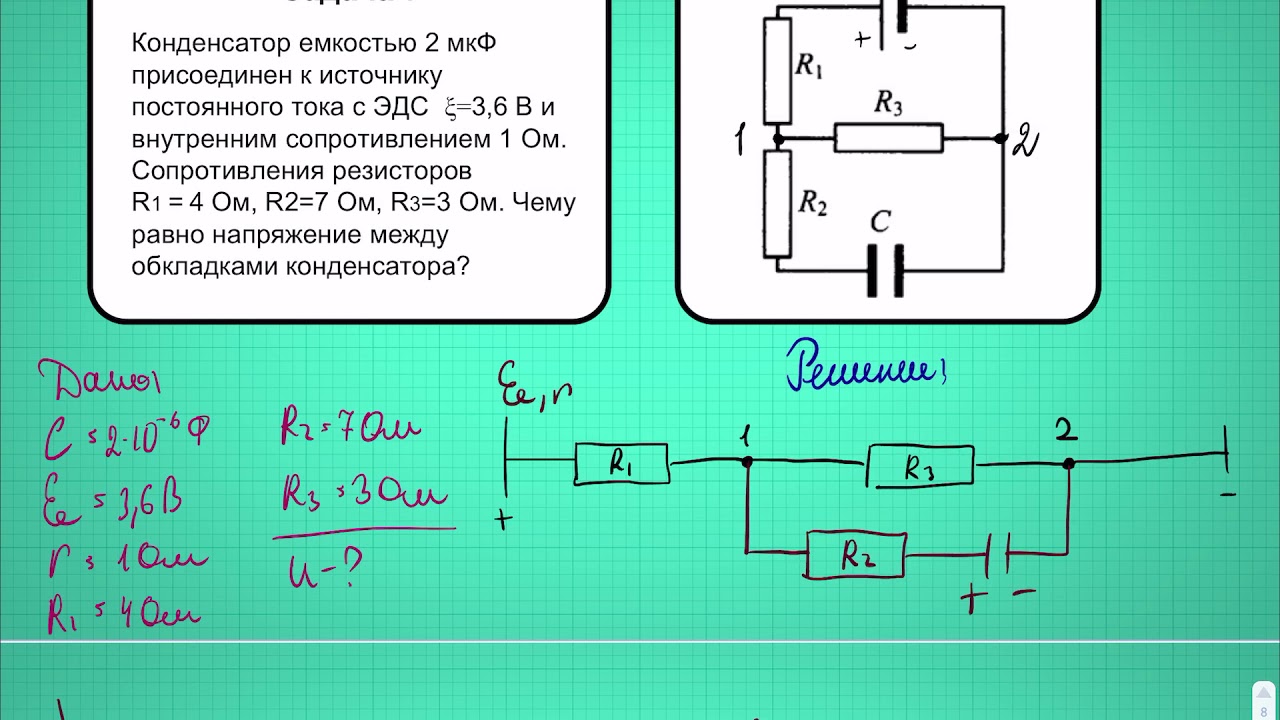 Поскольку растет число приложений, в которых конденсаторы используются на высоких частотах, ESR и ESL становятся важными параметрами, которые показывают характеристики конденсатора в дополнение к значениям электростатической емкости.

2. Частотные характеристики различных типов конденсаторов

В предыдущем разделе объяснялось, что паразитные компоненты конденсаторов, такие как ESR и ESL, сильно влияют на их частотные характеристики. Поскольку типы паразитных компонентов различаются в зависимости от типа конденсатора, давайте посмотрим на различные частотные характеристики разных типов конденсаторов.

На рисунке 5 показан | Z | и частотные характеристики ESR различных конденсаторов электростатической емкостью 10 мкФ.За исключением пленочного конденсатора, все конденсаторы относятся к типу SMD.

Поскольку электростатическая емкость всех конденсаторов, показанных на Рисунке 5, составляет 10 мкФ, | Z | значение одинаково для всех типов в емкостной области на частотах ниже 1 кГц. Повышаясь выше 1 кГц, | Z | значения увеличиваются намного выше в алюминиевом электролитическом конденсаторе и танталовом электролитическом конденсаторе, чем в многослойном керамическом конденсаторе и пленочном конденсаторе. Это связано с высоким удельным сопротивлением материала электролита и большим ESR алюминиевого электролитического конденсатора и танталового электролитического конденсатора.Пленочный конденсатор и многослойный керамический конденсатор используют металлические материалы для своих электродов и поэтому демонстрируют очень минимальное ESR.

Многослойный керамический конденсатор и этилированный пленочный конденсатор показывают примерно одинаковые характеристики до точки резонанса, но собственная резонансная частота выше и | Z | в индуктивной области ниже в многослойном керамическом конденсаторе. Это связано с тем, что в этилированных пленочных конденсаторах индуктивность не больше индуктивности выводного провода.

Эти результаты показывают, что в многослойных керамических конденсаторах SMD-типа в широком диапазоне частот полное сопротивление невелико, что делает их наиболее подходящими конденсаторами для высокочастотных приложений.

3. Частотные характеристики многослойных керамических конденсаторов

Существуют также разные типы многослойных керамических конденсаторов из разных материалов и различной формы. Давайте посмотрим, как эти факторы влияют на частотные характеристики.

(1) СОЭ
ESR в емкостной области зависит от диэлектрических потерь, вызванных диэлектрическим материалом. Материалы с высокой диэлектрической проницаемостью класса 2 обычно имеют более высокие уровни ESR, поскольку в них используются сегнетоэлектрики. В материалах с температурной компенсацией класса 1 используются параэлектрики, поэтому они обладают очень небольшими диэлектрическими потерями и низким уровнем ESR.
В дополнение к удельному сопротивлению материала электрода, форма электрода (толщина, длина, ширина) и количество слоев, уровни ESR на высоких частотах от точки резонанса до индуктивной области также зависят от скин-эффекта и эффектом близости.В качестве электродного материала часто используется никель, но для конденсаторов с низкими потерями иногда выбирают медь с низким удельным сопротивлением.

(2) ESL
На ESL многослойных керамических конденсаторов сильно влияет структура внутреннего электрода. Если размер внутреннего электрода обозначен как длина l, ширина w и толщина d, индуктивность ESL электрода может быть выражена формулой (3) согласно Ф. В. Гроверу.

Из этой формулы очевидно, что ESL уменьшается по мере того, как электроды конденсатора становятся короче, шире и толще.

На рисунке 6 показано соотношение между номинальной емкостью и собственной резонансной частотой для многослойных керамических конденсаторов различных размеров. Вы можете видеть, что при уменьшении размера частота собственного резонанса увеличивается, а ESL уменьшается при той же емкости. Это означает, что малые конденсаторы с короткой длиной l лучше всего подходят для высокочастотных приложений.

На рисунке 7 показан обратный конденсатор LW с короткой длиной l и большой шириной w. Из частотных характеристик, показанных на рисунке 8, вы можете видеть, что обратные конденсаторы LW имеют более низкий импеданс и лучшие характеристики, чем обычные конденсаторы той же емкости.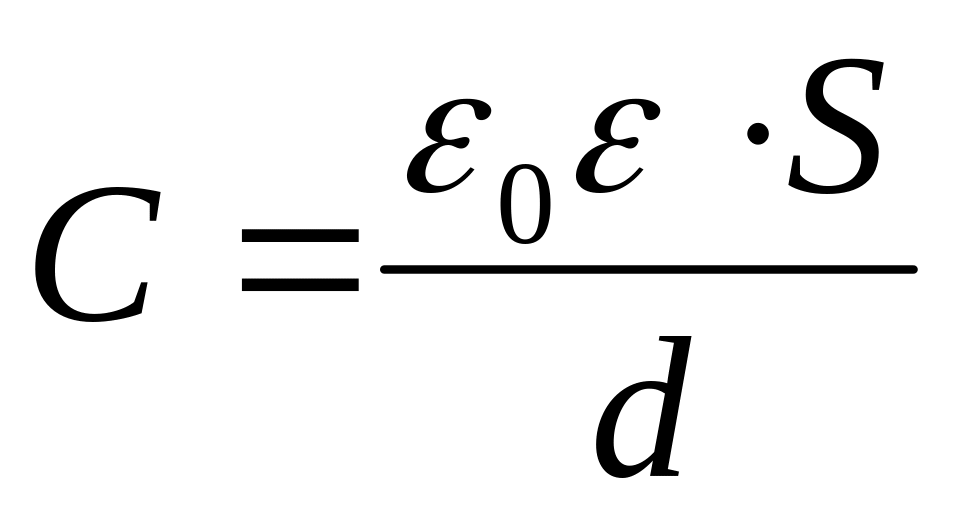 Используя обратные конденсаторы LW, можно достичь тех же характеристик, что и у обычных конденсаторов с меньшим количеством единиц. Уменьшение количества единиц позволяет снизить затраты и уменьшить монтажное пространство.

4. Как получить данные частотных характеристик

Хотя данные о частотных характеристиках можно получить с помощью анализатора импеданса или векторного анализатора цепей, теперь такие данные также доступны на веб-сайтах производителей запчастей.

На рис. 9 показан вид экрана инструмента дизайна Murata «SimSurfing». Характеристики можно отобразить, просто введя номер модели и элементы, которые вы хотите проверить. Кроме того, вы можете загрузить сетевые списки SPICE и данные S2P в качестве данных для моделирования. Не стесняйтесь использовать их для проектирования всех типов электронных схем.

zoom_in Рис. 9. Пример экрана средства проектирования «SimSurfing» （Щелкните изображение, чтобы увидеть увеличенное изображение）

См. Здесь для SimSurfing

Ответственное лицо: А.S., Подразделение компонентов, Murata Manufacturing Co., Ltd.

Сопутствующие товары

Конденсатор

Статьи по теме

14.02.2013

Будьте в курсе!

Получайте электронные письма от Мураты с последними обновлениями на этом сайте.
Информационный бюллетень Murata (электронный информационный бюллетень) запуск

mail_outline

Колебаний в LC-цепи — Университетская физика, том 2

Цели обучения

К концу этого раздела вы сможете:

• Объясните, почему заряд или ток колеблются между конденсатором и катушкой индуктивности, соответственно, при последовательном соединении
• Опишите взаимосвязь между зарядом и током, колеблющимся между конденсатором и катушкой индуктивности, соединенными последовательно

Следует отметить, что и конденсаторы, и катушки индуктивности накапливают энергию в своих электрических и магнитных полях соответственно.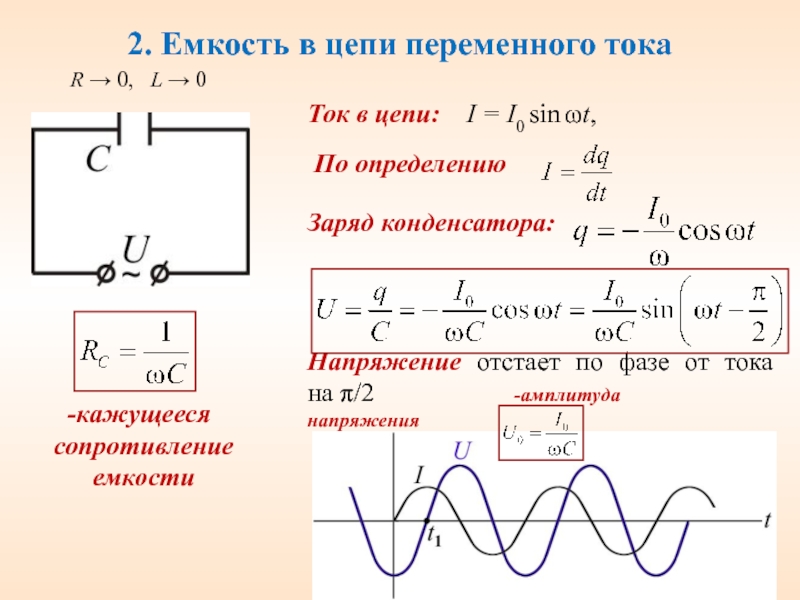 Цепь, содержащая как катушку индуктивности ( L, ), так и конденсатор ( C ), может колебаться без источника ЭДС путем сдвига энергии, накопленной в цепи, между электрическим и магнитным полями. Таким образом, концепции, которые мы развиваем в этом разделе, непосредственно применимы к обмену энергией между электрическим и магнитным полями в электромагнитных волнах или свете. Начнем с идеализированной схемы с нулевым сопротивлением, содержащей индуктивность и конденсатор, — это схема LC .

Схема LC показана на (Рисунок). Если конденсатор содержит заряд до того, как переключатель замкнут, тогда вся энергия цепи первоначально хранится в электрическом поле конденсатора ((Рисунок) (a)). Эта энергия

Когда переключатель замкнут, конденсатор начинает разряжаться, создавая ток в цепи. Ток, в свою очередь, создает в индукторе магнитное поле. Конечным результатом этого процесса является передача энергии от конденсатора с его уменьшающимся электрическим полем к индуктору с его увеличивающимся магнитным полем.

(a – d) Колебание накопителя заряда при изменении направления тока в цепи LC . (e) Графики показывают распределение заряда и тока между конденсатором и катушкой индуктивности.

В (Рисунок) (b) конденсатор полностью разряжен, и вся энергия хранится в магнитном поле индуктора. В этот момент ток достигает максимального значения, а энергия в катушке индуктивности равна

.

Поскольку в цепи нет сопротивления, энергия не теряется из-за джоулева нагрева; таким образом, максимальная энергия, запасенная в конденсаторе, равна максимальной энергии, сохраненной позже в катушке индуктивности:

В произвольный момент, когда заряд конденсатора равен q (t) , а ток равен i (t) , полная энергия U в цепи равна

Поскольку нет рассеивания энергии,

После достижения максимума ток i (t) продолжает переносить заряд между пластинами конденсатора, тем самым перезаряжая конденсатор. Поскольку катушка индуктивности сопротивляется изменению тока, ток продолжает течь, даже если конденсатор разряжен. Этот непрерывный ток заставляет конденсатор заряжаться с противоположной полярностью. Электрическое поле конденсатора увеличивается, в то время как магнитное поле индуктора уменьшается, и общий эффект заключается в передаче энергии от индуктора обратно к конденсатору. Согласно закону сохранения энергии, максимальный заряд, который повторно приобретает конденсатор, составляет. Однако, как показано (Рисунок) (c), пластины конденсатора заряжены на напротив по сравнению с тем, что было изначально.

После полной зарядки конденсатор снова передает свою энергию катушке индуктивности до тех пор, пока он снова полностью не разрядится, как показано на (Рисунок) (d). Затем, в последней части этого циклического процесса, энергия возвращается к конденсатору, и исходное состояние схемы восстанавливается.

Мы проследили цепь через один полный цикл. Его электромагнитные колебания аналогичны механическим колебаниям массы на конце пружины. В последнем случае энергия передается назад и вперед между массой, имеющей кинетическую энергию, и пружиной, имеющей потенциальную энергию.При отсутствии трения в системе масса-пружина колебания будут продолжаться бесконечно. Точно так же колебания цепи LC без сопротивления будут продолжаться вечно, если не будут нарушены; однако эта идеальная схема LC с нулевым сопротивлением неприменима, и любая схема LC будет иметь, по крайней мере, небольшое сопротивление, которое со временем будет излучать и терять энергию.

Частоту колебаний в цепи без сопротивления LC можно найти по аналогии с системой масса-пружина.Для схемы, полная электромагнитная энергия U составляет

Для системы масса-пружина, полная механическая энергия E составляет

Эквивалентность двух систем очевидна. Чтобы перейти от механической системы к электромагнитной, мы просто заменяем m на L , v на i , k на 1/ C и x на q . Теперь x (t) даёт

, где Следовательно, заряд конденсатора в цепи LC равен

, где угловая частота колебаний в контуре

Наконец, ток в цепи LC находится путем взятия производной по времени от q (t) :

Временные изменения q и I показаны на (Рисунок) (e) для.

Цепь LC В цепи LC собственная индуктивность равна H, а емкость равна F. Вся энергия хранится в конденсаторе, который имеет заряд C. (a) Какова угловая частота колебания в цепи? б) Каков максимальный ток, протекающий через цепь? (c) Сколько времени нужно, чтобы конденсатор полностью разрядился? (d) Найдите уравнение, которое представляет q (t) .

Стратегия

Угловая частота цепи LC указана на (Рисунок).Чтобы найти максимальный ток, максимальная энергия в конденсаторе устанавливается равной максимальной энергии в катушке индуктивности. Время разряда конденсатора, если он изначально заряжен, составляет четверть периода цикла, поэтому, если мы вычислим период колебаний, мы сможем выяснить, какая четверть от этого времени составляет это время. Наконец, зная начальный заряд и угловую частоту, мы можем составить уравнение косинуса, чтобы найти q ( t ).

Решение

1. Из (рисунок) угловая частота колебаний составляет
   
2. Ток максимален, когда вся энергия хранится в катушке индуктивности.Из закона сохранения энергии,
   

   
   т.о.
   

   
   Этот результат также можно найти по аналогии с простым гармоническим движением, где ток и заряд — это скорость и положение осциллятора.

3. Конденсатор полностью разряжается за одну четверть цикла или за время T /4, где T — период колебаний. С
   г.

   
   время, необходимое для полной разрядки конденсатора, составляет

4. Конденсатор полностью заряжен, поэтому Используя (рисунок), получаем
   

   
   Таким образом, и
   

Значение Энергетическая зависимость, установленная в части (b), — не единственный способ приравнять энергии.В большинстве случаев часть энергии накапливается в конденсаторе, а часть энергии — в катушке индуктивности. Мы можем поместить оба члена в каждую сторону уравнения. Исследуя схему только при отсутствии заряда конденсатора или тока в катушке индуктивности, мы упрощаем уравнение энергии.

Проверьте свое понимание Угловая частота колебаний в цепи LC составляет рад / с. (а) Если, что такое C ? (б) Предположим, что вся энергия хранится в катушке индуктивности.Каково значение (c) Второй идентичный конденсатор подключен параллельно исходному конденсатору. Какая угловая частота этой схемы?

Сводка

• Энергия, передаваемая колебательным образом между конденсатором и катушкой индуктивности в цепи LC , происходит с угловой частотой.
• Заряд и ток в цепи соответствуют
  

Концептуальные вопросы

Применяются ли правила Кирхгофа к цепям, содержащим катушки индуктивности и конденсаторы?

Может ли элемент схемы иметь как емкость, так и индуктивность?

Что в цепи LC определяет частоту и амплитуду колебаний энергии в катушке индуктивности или конденсаторе?

Амплитуда колебаний энергии зависит от начальной энергии системы.Частота в цепи LC зависит от значений индуктивности и емкости.

Проблемы

Конденсатор емкостью 5000 пФ заряжается до 100 В и затем быстро подключается к катушке индуктивности 80 мГн. Определите (а) максимальную энергию, запасенную в магнитном поле индуктора, (б) пиковое значение тока и (в) частоту колебаний цепи.

Собственная индуктивность и емкость цепи LC составляют 0,20 мГн и 5,0 пФ.Какая угловая частота колеблется в цепи?

Какова собственная индуктивность цепи LC , которая колеблется с частотой 60 Гц при емкости?

В колеблющейся цепи LC максимальный заряд конденсатора составляет, а максимальный ток через катушку индуктивности составляет 8,0 мА. а) Каков период колебаний? (б) Сколько времени проходит между моментом, когда конденсатор не заряжен, и следующим моментом, когда он полностью заряжен?

а.; б.

Собственная индуктивность и емкость колеблющегося контура LC равны соответственно. а) Какова частота колебаний? (b) Если максимальная разность потенциалов между пластинами конденсатора составляет 50 В, каков максимальный ток в цепи?

В колеблющейся цепи LC максимальный заряд конденсатора составляет. Определите заряд конденсатора и ток через катушку индуктивности, когда энергия распределяется поровну между электрическим и магнитным полями.Выразите свой ответ в виде L и C .

В схеме, показанной ниже, одновременно размыкается и замыкается. Определите (а) частоту возникающих колебаний, (б) максимальный заряд конденсатора, (в) максимальный ток через катушку индуктивности и (г) электромагнитную энергию колебательного контура.

Схема LC в тюнере AM (в автомобильной стереосистеме) использует катушку с индуктивностью 2.5 мГн и конденсатор переменной емкости. Если собственная частота схемы должна регулироваться в диапазоне от 540 до 1600 кГц (диапазон AM), какой диапазон емкости требуется?

Глоссарий

LC контур

Цепь

, состоящая из источника переменного тока, катушки индуктивности и конденсатора

Высокочастотные многослойные конденсаторы с высокой добротностью

Одним из наиболее важных параметров при оценке конденсатора высокочастотной микросхемы является добротность или соответствующее эквивалентное последовательное сопротивление (ESR).Помимо предоставления высокопроизводительных радиочастотных компонентов, JTI стремится предоставлять нашим клиентам точные и полные данные. С этой целью следует более подробное обсуждение вопросов измерения Q & ESR.

Теоретически, «идеальный» конденсатор имел бы ESR 0 (ноль) Ом и был бы чисто реактивным без реальной (резистивной) составляющей. Ток, проходящий через конденсатор, приведет к увеличению напряжения на конденсаторе ровно на 90 градусов на всех частотах.

В реальных условиях нет идеального конденсатора, который всегда будет показывать некоторое конечное значение ESR.ESR изменяется в зависимости от частоты для данного конденсатора и является «эквивалентным», поскольку его источник зависит от характеристик структур проводящих электродов и изолирующей диэлектрической структуры. Для целей моделирования ESR представлен как единый паразитный элемент серии. В прошлые десятилетия все параметры конденсаторов измерялись при стандартной частоте 1 МГц, но в сегодняшнем мире высоких частот этого далеко не достаточно. Типичные значения для хорошего высокочастотного конденсатора данного номинала могут быть порядка 0.05 Ом на 200 МГц, 0,11 Ом на 900 МГц и 0,14 Ом на 2000 МГц.

Добротность Q — это безразмерное число, равное реактивному сопротивлению конденсатора, деленному на паразитное сопротивление конденсатора (ESR). Значение Q сильно меняется с частотой, так как реактивное сопротивление и сопротивление изменяются с частотой. Реактивное сопротивление конденсатора сильно меняется в зависимости от частоты или значения емкости, и поэтому значение Q может сильно варьироваться. См. Уравнения 1 и 2.

Johanson Technology измеряет ESR и Q на резонансной линии Boonton 34A. Тестируемый конденсатор резонирует с индуктивной линией с точно определенным импедансом и Q. Из полученных данных (центральная частота и ширина полосы результирующего пика) выводятся значения Q, ESR и емкости устройства. Этот метод является давним промышленным стандартом для измерения Q и ESR на радиочастотах. Поскольку этот метод зависит от точности частоты генератора сигналов (которая может быть измерена с чрезвычайной точностью), данные, полученные таким образом, являются довольно точными.Поскольку ESR современных конденсаторов становится все ниже, точность даже этого метода будет приближаться к +/- 10% (см. Руководство по эксплуатации Boonton 34A, стр. 2.2). Это все еще самый точный метод измерения Q и ESR на радиочастотах, доступный в настоящее время. См. Рисунок 1 для блок-схемы испытательной установки. См. Рисунки 2 и 3 с изображениями установки.

Использование данных S-параметров, собранных с помощью векторного анализатора цепей, для получения ESR неприемлемо. Основная причина заключается в том, что точность этих данных ограничена точностью анализатора цепей в системе с сопротивлением 50 Ом (типичная калибровка амплитуды ±.Значение 05 дБ недостаточно точно в конденсаторе с малыми потерями, которое может составлять 0,01 дБ). Использование данных Q / ESR, полученных с помощью измерителя LCR, также неприемлемо для этих высокодобротных устройств. Когда Q устройства очень велико, измеритель LCR просто не может сопоставить чрезвычайно малое сопротивление (R) с чрезвычайно большим реактивным сопротивлением (X). По этой причине параметры ESR и Q, представленные в опубликованном каталоге Johanson Technology и в программе MLCSoft®, основаны на стандартном промышленном методе тестирования резонансных линий.

Для получения дополнительной информации свяжитесь с нашими инженерами по приложениям.

Конденсатор

с частотно-зависимой емкостью, паразитными параметрами и потерями: CAPQP

Конденсатор с частотно-зависимой емкостью, паразитный и без потерь: CAPQP

CAPQP моделирует конденсатор с заданной пользователем частотной зависимостью емкости и потеря.Частотные зависимости указываются в качестве справочных таблиц (векторов) в модели. параметры. Эта модель использует интерполяцию для получения значений параметров в каждом проекте. частота оценки.

Имя	Описание	Агрегат Тип	По умолчанию
ID	Имя	Текст	КЕПКА #
Ф	Вектор частот, на которых заданы C, Q и R.	Частота	{1}
С	Емкость (вектор)	Емкость	Li
Q	Добротность (вектор)	Скаляр	{1000}
л	Индуктивность	Паразитная индуктивность	С
R	Последовательное сопротивление (вектор)	Сопротивление	{0}

Ф. Вектор частот, на которых L, Q и R параметры указаны. Частоты должны быть последовательными и указываться по возрастанию. порядок.

C. Вектор последовательной емкости C (f) (см. Раздел «Эквивалентная схема»), указанные в единицах измерения емкости. Вы должны указать каждый элемент вектора в соответствующем элементе частоты из вектора частоты F.

Q. Вектор добротности; указывает серию сопротивление Rq (f) (см. раздел «Эквивалентная схема»). Вы должны указать каждый вектор запись в соответствующем частотном входе из частотного вектора F.

L. Паразитная индуктивность (см. «Эквивалентную схему» раздел).

р. Вектор шунтирующего сопротивления R (f) (см. Раздел «Эквивалентная схема»), указанные в единицах проектного сопротивления. Вы должны указать каждый элемент вектора в соответствующем элементе частоты из вектора частоты F.

Ограничения и рекомендации по параметрам

1. Размер векторных параметров C, Q и R должен быть равен размеру частотный вектор F.

2. Если частота оценки проекта выходит за пределы диапазона частот в F, то Параметры C, Q и R экстраполируются как постоянные значения, равные первые / последние записи соответствующих векторов. Предупреждение не выдается.

3. Вы можете указать вектор тремя способами: во-первых, введя его как правый побочное значение параметра модели, например R = {100,102,110,113,120}; во-вторых, указание вектора в другом месте уравнения; и в-третьих, указав вектор в столбце или строке текстового файла.Третий способ обеспечивает удобный и гибкий метод указания параметров C, Q и R на одном место нахождения. Например, вы можете создать файл capqp.txt содержащие столбцы C, Q и R, разделенные пробелами. Первый столбец должен представляют частоту в единицах проекта (обратите внимание, что изменение проекта по умолчанию частотные единицы требует ручного масштабирования частот в этом файле).Импорт или свяжите этот файл со своим проектом и назовите его, например, CAPQP_1. Теперь вы можете укажите, например, параметр R как R = Col (файл данных («CAPQP_1»), 4), чтобы значения вектора R копируются в модель из столбца 4 таблицы capqp.txt импортирован под именем capqp_1. если ты предпочитают развертывать данные построчно, используя R = Row (файл данных («CAPQP_1»), 2).

4. Если ваш проект использует ввод текстового файла для передачи данных в эту модель, имейте в виду, что единицы измерения частоты, сопротивления, индуктивности или проводимости, которые подразумеваются в этом файле. Ваш единицы проекта по умолчанию могут отличаться от единиц в вашем файле данных. Если это произойдет, вы должны масштабировать входные значения, умножая вызов функции Col или Row на коэффициент масштабирования.Например, если в вашем проекте используется емкость в пикофарадах а файл данных содержит данные в фарадах, которые вы можете получить из столбец 2 файла данных CAPQP_1, например: C = 1e + 12 * Col (файл данных («CAPQP_1»), 2).

Данная модель реализована как последовательное соединение конденсатора с потерями и частотно-зависимый резистор.Паразитная индуктивность последовательно с потерями конденсатор.

Реализация модели основана на линейной интерполяции параметров C, Q и R при частота оценки каждого проекта. Интерполяция использует предоставленные пользователем таблицы поиска через параметры. Если частота оценки проекта выходит за пределы диапазона частот в F, затем параметры C, Q и R экстраполируются как постоянные значения, равные первому / последнему элементы соответствующих векторов.

Анализ переходных процессов во времени чувствителен к количеству частотных точек. Также время измерения области могут быть неточными из-за непричинного поведения модели на заданные значения параметров.

Простые схемы с резисторами и конденсаторами · Мэтт Лейси

Вы здесь: Дом » Наука »Eis »Простые схемы

<< Вернуться к Принципы спектроскопии электрохимического импеданса

Итак, теперь, когда я представил математику, лежащую в основе импеданса, и графики, которые мы используем для его представления, мы можем начать рассматривать математические определения и характеристики импеданса двух основных компонентов электрической схемы и их комбинации. из них.

---

Резисторы

Это простейшая электрическая схема, которую легче всего понять. Резисторы, как вы наверняка знаете, подчиняются закону Ома, поэтому ток всегда пропорционален напряжению, отсутствует реактивная часть (то есть фазовый сдвиг) и, следовательно, нет никакой зависимости от частоты. Мы можем просто записать это так:

$$ \ displaystyle \ pmb {Z} _R = R $$

где R — сопротивление. Тогда график Найквиста для резистора очень прост — это всего лишь одна точка на оси x на любой частоте:

---

Конденсаторы

Конденсаторы

имеют чисто реактивное сопротивление .Идеальный конденсатор имеет нулевое сопротивление. Когда на конденсатор подается переменное напряжение, ток опережает напряжение (фаза -90 °), а полное сопротивление обратно пропорционально частоте. То есть сопротивление увеличивается с уменьшением частоты. Рассмотрите возможность подачи постоянного напряжения на конденсатор — через достаточно долгое время конденсатор полностью заряжен и ток больше не течет. Импеданс фактически бесконечен. Уравнение, описывающее конденсатор:

$$ \ displaystyle \ pmb {Z} _C = \ frac {1} {j \ omega C} $$

, где \ (j \) — мнимая единица, \ (\ omega = 2 \ pi f \), а C — емкость.

Таким образом, график Найквиста для конденсатора выглядит как вертикальная линия, где Z ’= 0 для всех частот. Емкости возникают повсюду в электрохимических системах, практически везде, где у вас есть интерфейс — чаще всего из-за емкости двойного слоя, но также и из-за диэлектрической емкости или на границах зерен в твердых телах и так далее.

Пока это все довольно просто, поэтому теперь мы собираемся рассмотреть возможность объединения некоторых из этих различных схем вместе.

---

RC-цепи

В серии полные сопротивления складываются :

$$ \ Displaystyle \ pmb {Z} = \ sum_n \ pmb {Z} _n $$

Таким образом, полное сопротивление последовательной RC-цепи — это просто сложение отдельных сопротивлений резистора и конденсатора вместе:

$$ \ displaystyle \ pmb {Z} = \ pmb {Z} _R + \ pmb {Z} _C = R + \ frac {1} {j \ omega C} $$

График Найквиста для этой схемы показан слева.Как и следовало ожидать, реальный импеданс Z ’равен сопротивлению резистора для всех частот, а мнимая часть импеданса соответствует тому же поведению, что и для идеального конденсатора.

Вы можете рассматривать последовательную RC-цепь как простую модель для таких вещей, как блокирующий интерфейс — например, инертный электрод, погруженный в проводящий электролит, — где R представляет ионное сопротивление электролита, а C представляет емкость двойного слоя на поверхность электрода.

Это также представляет собой два электрода в электролите (т. Е. Целую ячейку), потому что последовательная цепь с двумя конденсаторами (т. Е. C-R-C) в любом случае упрощается до одного RC-блока, если следовать приведенным выше уравнениям.

Хорошо, давайте рассмотрим параллельный случай.

Параллельно, проводников (т. Е. Обратные импедансам) складываются :

$$ \ displaystyle \ pmb {Y} = \ frac {1} {\ pmb {Z}} = \ sum_n \ frac {1} {\ pmb {Z} _n} $$

Итак, мы можем записать выражение для параллельной RC-цепи следующим образом:

$$ \ displaystyle \ frac {1} {\ pmb {Z}} = \ frac {1} {R} + j \ omega C $$

Если мы изменим это уравнение для Z (сначала умножив все члены на R), то получим:

$$ \ displaystyle \ pmb {Z} = \ frac {R} {1 + j \ omega RC} $$

Из этого уравнения вы можете видеть, что на высокой частоте, т.е.е., \ (\ omega \ rightarrow \ infty \), нижний член дроби стремится к бесконечности, поэтому импеданс стремится к нулю; идеальная схема ведет себя как конденсатор на бесконечной частоте — она ​​имеет нулевое сопротивление. Однако на низкой частоте, то есть \ (\ omega \ rightarrow 0 \), вы можете видеть, что нижний член становится равным 1, поэтому общий импеданс цепи равен R, то есть при постоянном токе цепь ведет себя как резистор (это имеет смысл, не так ли? В конце концов, при постоянном токе конденсатор становится полностью заряженным, и ток проходит только через резистор).Таким образом, график Найквиста для этой схемы представляет собой полукруг, пересекающий реальную ось (Z ’) в точках 0 и R:

.

Полукруги на графике Найквиста очень распространены в электрохимическом импедансе и обычно связаны с такими процессами, как перенос заряда , потому что на поверхности электрода перенос заряда происходит параллельно с зарядкой емкости двойного слоя — отсюда и полукруг .

Также обратите внимание, что я обозначил самую верхнюю часть полукруга цветом f * .Это известно как частота релаксации и относится к постоянной времени RC цепи. Из предыдущего уравнения вы увидите, что пик полукруга возникает, когда \ (\ omega RC = 1 \). Тогда постоянная времени определяется следующим образом:

$$ \ tau = \ frac {1} {\ omega} = \ frac {1} {2 \ pi f} = RC $$

Это важное понятие в EIS, потому что оно говорит нам кое-что о временных рамках, в которых происходят различные процессы. Это уравнение также позволяет рассчитать емкости этих элементов, зная только сопротивление (от диаметра) и частоту релаксации.

Вот здесь и пригодится сюжет Боде. Вершина полукруга просто появляется как пик на графике зависимости мнимой части от частоты с логарифмическим масштабированием:

Фактические значения, которые я использовал для моделирования полукруга на предыдущем графике, раньше не имели значения, но на этот раз я оставил их для демонстрации. {- 6} \ текст {F}} = 15.9 \ text {Hz} $$

и на графике Боде выше видно, что пик находится примерно на 16 Гц.

Другая причина, по которой это важно, заключается в том, что постоянная времени (то есть частотная зависимость) этих элементов, конечно, влияет на порядок, в котором они появляются на графике Найквиста. Элементы с меньшей постоянной времени (т. Е. Более высокой частотой релаксации), естественно, будут появляться на более высоких частотах в спектре импеданса. Однако большее беспокойство вызывает то, что элементы с очень похожими или одинаковыми постоянными времени будут иметь тенденцию перекрываться.Я включил приложение Shiny для моделирования схемы, состоящей из двух последовательно соединенных параллельных RC-модулей, чтобы показать это. Попробуйте изменить параметры и посмотрите, как они влияют на то, как выглядит график Найквиста.

Далее: Моделирование RC-RC цепи >>

---

Спасибо за внимание!

Эти страницы останутся открытыми для всех и на 100% свободными от рекламы, сейчас и всегда. Если вам понравилась эта страница и вы хотите увидеть больше, подумайте о том, чтобы купить мне чашку кофе, чтобы поддержать мою мотивацию и помочь с текущими расходами на этот сайт!

Микроволны101 | Математика конденсаторов

Щелкните здесь, чтобы перейти на нашу главную страницу о конденсаторах

Щелкните здесь, чтобы перейти к нашему калькулятору реактивного сопротивления

Ниже приведен индекс нашего математического обсуждения конденсаторов:

Емкостное реактивное сопротивление

Емкость ЛЭП (отдельная страница)

Фактор качества

Параллельно-пластинчатая емкость

Емкость листа

Резонанс конденсатора

Расчет емкости накопителя заряда (отдельная страница, новинка марта 2007 г.!

Эффект ESR конденсатора (отдельная страница, новинка февраля 2009 года!)

Емкостное реактивное сопротивление

Воспользуйтесь нашим калькулятором реактивного сопротивления, если вам интересна эта тема!

Емкостное реактивное сопротивление — это «воображаемое» полное сопротивление конденсатора, выраженное в омах.Обратите внимание на отрицательный знак, который означает, что на диаграмме Смита добавление последовательной емкости приводит к повороту коэффициента отражения против часовой стрелки. Это функция частоты.

Привет, Билл Гейтс, прежде чем мы продолжим работу с этой страницей, мы хотим сказать вам, что Microsoft Equation Editor 3.0 — отстой! Теперь давайте исправим эту формулу для более практичных единиц пикофарад и ГГц:

Фактор качества

Коэффициент качества — это мера того, насколько без потерь конденсатор:

Обратите внимание, что по мере увеличения частоты коэффициент качества всегда ухудшается (уменьшается).Положим уравнение в ГГц и пикофарады:

Таким образом, конденсатор на 1 пФ с сопротивлением в одну десятую Ом будет иметь добротность 159 на частоте 10 ГГц. Коэффициент рассеяния — это просто величина, обратная фактору качества:

.

Рассеивание того же конденсатора 1 пФ на частоте 10 ГГц составит 0,6%.

Емкость параллельных пластин

Известная формула для конденсаторов с параллельными обкладками «бесконечного размера» приведена ниже. Большинство конденсаторов с параллельными пластинами ведут себя почти идеально, потому что их размеры (длина и ширина) намного больше, чем расстояние между пластинами.Обычно нет необходимости учитывать окаймляющие поля, если вы не работаете с очень маленькими конденсаторами (возможно, менее 1 пикофарада).

Это тот случай, когда микроволновая техника предпочитает метрическую систему, потому что диэлектрическая проницаемость свободного пространства всегда выражается в фарадах на метр, а не в фарадах на дюйм. Поскольку практические микроволновые схемы намного меньше метров и фарадов, мы перепишем формулу емкости, используя миллиметры и пикофарады:

Емкость листа

Листовая емкость — полезное упрощение формулы конденсатора, если вы всегда используете заданный диэлектрик и толщину для создания конденсаторов (например, на MMIC):

Таким образом, если вы работаете с литейным предприятием MMIC, предлагающим 2000 ангстрем (0.2 мкм) нитрид кремния (er = 7,5) для тонкопленочных конденсаторов, емкость листа:

7,5 x 0,00885 / 0,0002 = 332 пФ / мм ²

Если вы сконструируете конденсатор 100 x 100 микрон (0,1 x 0,1 мм), он будет иметь значение 3,3 пФ.

Резонанс конденсатора

Первый резонанс конденсатора — это последовательная резонансная частота. Что касается модели ниже, это частота, при которой емкостное реактивное сопротивление и индуктивное реактивное сопротивление из-за L _S отменяются.

Последовательная резонансная частота (SRF)
Частота, при которой последовательная индуктивность конденсатора равна, но противоположна его емкости. Щелкните здесь для объяснения последовательного резонанса на нашей странице фильтров. Здесь конденсатор ведет себя как резистор низкого номинала (равный значению ESR).

Большинство производителей конденсаторов указывают последовательную резонансную частоту, а не индуктивность L _S . Чтобы определить L _S в нано-Генри, используйте следующее уравнение (исправлено 3 февраля 2006 г.!):

Параллельная резонансная частота (PRF)
Обычно это происходит на двойной частоте SRF.Щелкните здесь для объяснения параллельного резонанса на нашей странице фильтров. Обычно у вас нет никакого дела до эксплуатации конденсатора на или рядом с PRF, потому что в этом случае он действует как разомкнутая цепь!

На этом пока все!

.

No related posts.