Урок 28. электрическая ёмкость. конденсатор — Физика — 10 класс
Физика, 10 класс
Урок 28. Электрическая ёмкость. Конденсатор
Перечень вопросов, рассматриваемых на уроке:
- Электрическая ёмкость
- Плоский конденсатор
- Энергия конденсатора
Глоссарий по теме:
Конденсатор – устройство для накопления электрического заряда.
Электроёмкостью конденсатора называют физическую величину, численно равную отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Под зарядом конденсатора понимают модуль заряда одной из его обкладок.
Последовательное соединение – электрическая цепь не имеет разветвлений. Все элементы цепи включают поочередно друг за другом. При параллельном соединении концы каждого элемента присоединены к одной и той же паре точек.
Смешанное соединение — это такое соединение, когда в цепи присутствует и последовательное, и параллельное соединение.
Энергия конденсатора прямо пропорциональна квадрату напряжённости электрического поля внутри его:
Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения.
Основная и дополнительная литература по теме:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. С. 321-330.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. С. 97-100.
Теоретический материал для самостоятельного изучения
Конденсатор при переводе с латиницы означает, то что уплотняет, сгущает – устройство, предназначенное для накопления зарядов энергии электрического поля. Конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга. Главной характеристикой этого прибора, является его электроёмкость, которая зависит от площади его пластин, расстояния между ними и свойств диэлектрика.
Заряд конденсатора определяется – модулем заряда на любой одной из её обкладок. Заряд конденсатора прямо пропорционален напряжению между обкладками конденсатора. Коэффициент пропорциональности С называется электрической ёмкостью, электроёмкостью или просто ёмкостью конденсатора.
Электрической ёмкостью конденсатора называется физическая величина, которая численно равна отношению заряда, одного из проводников конденсатора к разности потенциалов между его обкладками.
Чем больше площадь проводников и чем меньше пространство заполняющего диэлектриком, тем больше увеличивается ёмкость обкладок конденсатора.
Измеряется электрическая ёмкость в Международной системе СИ в Фарадах. Эта единица имеет своё название в честь английского физика экспериментатора Майкла Фарадея который внёс большой вклад в развитие теории электромагнетизма. Один Фарад равен ёмкости такого конденсатора, между пластинами которого возникает напряжение, равное одному Вольту, при сообщении заряда в один Кулон.
Электрическая ёмкость конденсаторов определяется их конструкцией, самыми простыми из них являются плоские конденсаторы.
Чем больше площадь взаимного перекрытия обкладок и чем меньше расстояние между ними, тем значительнее будет увеличение ёмкости обкладок конденсатора. При заполнении в пространство между обкладками стеклянной пластины, электрическая ёмкость конденсатора значительно увеличивается, получается, что она зависит от свойств используемого диэлектрика.
Электрическая ёмкость плоского конденсатора зависит от площади его обкладок, расстояния между ними, диэлектрической проницаемости диэлектрика, заполняющего пространство между обкладками и определяется по формуле:
где – электрическая постоянная.
Для того чтобы получить необходимую определённую ёмкость, берут несколько конденсаторов и собирают их в батарею применяя при этом параллельное, последовательное или смешанное соединения.
Параллельное соединение:
q = q1 + q2 + q3
u = u1 = u2 = u3
с = с1+с2+с3
с = n∙с
Последовательное соединение:
q = q1 = q2 = q3
u = u
Энергия конденсатора равна половине произведения заряда конденсатора напряжённости поля и расстояния между пластинами конденсатора: u = Еd
Эта энергия равна работе, которую совершит электрическое поле при сближении пластин, это поле совершает положительную работу. При этом энергия электрического поля уменьшается:
При этом энергия электрического поля уменьшается:
Для любых конденсаторов энергия равна половине произведения электроёмкости и квадрата напряжения:
Примеры и разбор решения заданий:
1. Плоский конденсатор, расстояние между пластинами которого равно 3 мм, заряжен до напряжения 150 В и отключен от источника питания. Разность потенциалов между пластинами возросла до 300 В.
- Во сколько раз увеличилась разность потенциалов между пластинами?
- Какое расстояние между пластинами конденсатора стало после того, как пластины были раздвинуты?
- Во сколько раз изменилось расстояние между пластинами.
Решение:
Электрическая ёмкость конденсатора определяется по формуле:
1.По условию разность потенциалов увеличилось в два раза. U1 = 150В→ U2 = 300В.
2.По условию d = 3 мм, если разность потенциалов увеличилось в два раза, по формуле соответственно и расстояние между пластинами увеличилось в два раза, и d =2·3 мм = 6 мм.
3.Расстояние между пластинами увеличилось в два раза.
Ответ:
1. 2
2. 6мм
3. 2
2. Конденсатор электроёмкостью 20 мкФ имеет заряд 4 мкКл. Чему равна энергия заряженного конденсатора?
Дано: С = 20 мкФ = 20 · 10-6 Ф, q = 4 мкКл = 4·10-6 Кл.
Найти: W.
Решение:
Энергия заряженного конденсатора W через заряд q и электрическую ёмкость С определяется по формуле:
Ответ: W = 0,4 мкДж.
Глава 20. Конденсаторы
Для накопления разноименных электрических зарядов служит устройство, которое называется конденсатором. Конденсатор — система двух изолированных друг от друга проводников (которые часто называют обкладками конденсатора), один из которых заряжен положительным, второй — таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластинки, расположенные на небольшом рас-стоянии друг от друга, то конденсатор называется плоским.
Для характеристики способности конденсатора накапливать заряд вводится понятие электроемкости (часто говорят просто емкости). Емкостью конденсатора называется отношение заряда конденсатора к той разности потенциалов , которая возникает между обкладками при их заряжении зарядами и (эту разность потенциалов проводников часто называют электрическим напряжением между обкладками и обозначают буквой ):
(20.1) |
Поскольку величины и (или ) в формуле (20.1) зависимы, то емкость (20.1) не зависит от и , а является характеристикой геометрии системы проводников. Действительно, при сообщении проводникам зарядов и проводники приобретут потенциалы, разность которых будет пропорциональна заряду . Поэтому в отношении (20.1) заряд сокращается.
Выведем формулу для емкости плоского конденсатора (эта формула входит в программу школьного курса физики). При заряжении параллельных пластин, расположенных на небольшом расстоянии друг от друга, зарядами и , в пространстве между ними возникает однородное электрическое поле с напряженностью (см. гл. 18):
гл. 18):
(20.2) |
Разность потенциалов между пластинами равна
(20.3) |
где — площадь пластин, — расстояние между ними. Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора
(20.4) |
Если все пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью , то поле (20.2) и разность потенциалов (20.3) убывает в раз, а емкость конденсатора в раз взрастает
(20.5) |
Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости, как емкости одного конденсатора, который при заряжении его тем же зарядом, что и батарея дает ту же разность потенциалов, что и батарея конденсаторов.
Последовательное соединение (см. рисунок). При сообщении левой пластине левого конденсатора заряда , а правой пластине правого заряда , на внутренних пластинах благодаря поляризации будут индуцироваться заряды (см. рисунок; значения индуцированных зарядов приведены под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен такими же зарядами и , как и заряды крайних пластин, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом, а обратная эквивалентная емкость батареи — сумме обратных емкостей всех конденсаторов
(20.6) |
Параллельное соединение (см. рисунок). В этом случае если сообщить левому проводнику заряд , правому сообщить заряд , заряд распределится между конденсаторами, вообще говоря, не одинаково, но по закону сохранения заряда .
Поскольку правые пластины всех конденсаторов соединены между собой, левые — тоже, то они представляют собой единые проводники, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинакова: . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов
(20.7) |
Заряженный конденсатор обладает определенной энергией. Если конденсатор емкости заряжен зарядом , то энергия этого конденсатора (можно говорить энергия электрического поля конденсатора) равна
(20.8) |
С помощью определения электрической емкости (20.1) можно переписать формулу (20.8) еще в двух формах:
(20.9) |
Рассмотрим в рамках этого минимума сведений о конденсаторах типичные задачи ЕГЭ по физике, которые были предложены в первой части книги.
Электроемкость конденсатора — его геометрическая характеристика, которая при неизменной геометрии не зависит от заряда конденсатора (задача 20.1.1 — ответ 3). Аналогично не меняется емкость конденсатора при увеличении напряжения на конденсаторе (задача 20.1.2 — ответ 3).
Связь между единицами измерений (задача 20.1.3) следует из определения емкости (20.1). Единица электрической емкости в международной системе единиц измерений СИ называется Фарада. 1 Фарада — это емкость такого конденсатора, между пластинами которого возникает напряжение 1 В при зарядах пластин 1 Кл и -1 Кл (ответ 4).
Поскольку электрическое поле в плоском конденсаторе однородно, то напряженность поля в конденсаторе и напряжение между пластинами связаны соотношением (см. формулу (18.9)) , где — расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в задаче 20.1.4
(ответ 4).
Согласно определению электрической емкости имеем в задаче 20.1.5
(ответ 2).
Из формулы (20.4) для емкости плоского конденсатора заключаем, что при увеличении площади его пластин в 3 раза (задача 20.1.6) его емкость увеличивается в 3 раза (ответ 1).
При уменьшении в раз расстояния между пластинами емкость плоского конденсатора возрастет в раз. Поэтому новое напряжение на конденсаторе (задача 20.1.7) можно найти из следующей цепочки формул
где и — новый заряд конденсатора (ответ 3).
Так как конденсатор в задаче 20.1.8 подключен к источнику, то между его пластинами поддерживается постоянное напряжение независимо от расстояния между ними. Поэтому заряд конденсатора изменяется при раздвигании пластин так же, как изменяется его емкость. А поскольку при увеличении расстояния между пластинами вдвое емкость конденсатора уменьшается вдвое (см. формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).
формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).
В задаче 20.1.9 конденсатор отключен от источника в процессе сближения пластин. Поэтому не меняется их заряд. А поскольку напряженность электрического поля между пластинами определяется соотношением (20.2)
то напряженность электрического поля между пластинами также не изменяется (ответ 3). Этот же результат можно получить и через определение емкости с учетом того, что
произведение от расстояния между пластинами не зависит (см. формулу (20.4)).
Из формул (20.8), (20.9) видим, что только одно из приведенных в качестве ответов к задаче 20.1.10 соотношений (а именно — 2) определяет энергию конденсатора.
При последовательном соединении конденсаторов (задача 20.2.1) одинаковыми будут их заряды независимо от значений их электрических емкостей (ответ 2). При параллельном соединении конденсаторов (задача 20. 2.2) одинаковыми будут напряжения на каждом из них (ответ 3).
2.2) одинаковыми будут напряжения на каждом из них (ответ 3).
Поскольку конденсатор в задаче 20.2.3 отключен от источ-ника напряжения, его заряд не меняется в процессе раздвигания пластин. Поэтому для исследования изменения энергии конденсатора удобно воспользоваться формулой (20.8)
(1) |
Так как при увеличении расстояния между пластинами в раз электрическая емкость конденсатора уменьшается в раз, то согласно формуле (1) энергия конденсатора увеличится в раз (ответ 1).
В задаче 20.2.4 не изменяется напряжение на конденсаторе. Поэтому воспользуемся первой из формул (20.9)
Из этой формулы заключаем, что при увеличении в раз расстояния между пластинами энергия конденсатора уменьшится в раз — ответ 2. (Разница с предыдущей задачей связана с тем, что здесь кроме внешних сил, совершающих работу при раздвигании пластин, совершает работу источник напряжения. )
)
В задаче 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора. Поэтому удобно воспользоваться формулой (20.8)
Из этой формулы заключаем, что при увеличении расстояния между пластинами в 2 раза и увеличении заряда конденсатора в 2 раза его энергия возрастет в 8 раз (ответ 4).
Поскольку в задаче 20.2.6 конденсаторы соединены последовательно, емкость батареи конденсаторов можно найти по формуле (20.6), откуда находим емкость батареи конденсаторов (ответ 2).
В задаче 20.2.7 конденсаторы соединены параллельно, поэтому емкость батареи конденсаторов можно найти по формуле (20.7): (ответ 2).
Основной вопрос, на который нужно ответить в задаче 20.2.8, это как соединены конденсаторы? Последовательно, параллельно, по-другому? Попробуем по-другому расположить в пространстве и изменить длину соединительных проводов, чтобы схема стала более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно. Поэтому (ответ 1).
Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно. Поэтому (ответ 1).
Когда в заряженный плоский конденсатор вставляют металлическую пластинку (задача 20.2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — заряд конденсатора, — площадь его пластин. Поэтому напряжение между обкладками конденсатора определяется соотношением:
где — расстояние между обкладками конденсатора, — толщина пластинки. Отсюда находим емкость рассматриваемого конденсатора
(ответ 4).
Чтобы найти емкость сферического конденсатора (задача 20. 2.10) сообщим его обкладкам заряды и , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами и (напряжение между обкладками сферического конденсатора), определена в задаче 19.2.5., откуда находим электрическую емкость сферического конденсатора (ответ 3):
2.10) сообщим его обкладкам заряды и , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами и (напряжение между обкладками сферического конденсатора), определена в задаче 19.2.5., откуда находим электрическую емкость сферического конденсатора (ответ 3):
Электрическая емкость • Электротехника • Компактный калькулятор • Онлайн-конвертеры единиц измерения
Конвертер длины и расстоянияКонвертер массыКонвертер мер объема сыпучих продуктов и продуктов питанияКонвертер площадиКонвертер объема и единиц измерения в кулинарных рецептахКонвертер температурыКонвертер давления, механического напряжения, модуля ЮнгаКонвертер энергии и работыКонвертер мощностиКонвертер силыКонвертер времениКонвертер линейной скоростиПлоский уголКонвертер тепловой эффективности и топливной экономичностиКонвертер чисел в различных системах счисления.Конвертер единиц измерения количества информацииКурсы валютРазмеры женской одежды и обувиРазмеры мужской одежды и обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаКонвертер момента инерцииКонвертер момента силыКонвертер вращающего моментаКонвертер удельной теплоты сгорания (по массе)Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему)Конвертер разности температурКонвертер коэффициента теплового расширенияКонвертер термического сопротивленияКонвертер удельной теплопроводностиКонвертер удельной теплоёмкостиКонвертер энергетической экспозиции и мощности теплового излученияКонвертер плотности теплового потокаКонвертер коэффициента теплоотдачиКонвертер объёмного расходаКонвертер массового расходаКонвертер молярного расходаКонвертер плотности потока массыКонвертер молярной концентрацииКонвертер массовой концентрации в раствореКонвертер динамической (абсолютной) вязкостиКонвертер кинематической вязкостиКонвертер поверхностного натяженияКонвертер паропроницаемостиКонвертер плотности потока водяного параКонвертер уровня звукаКонвертер чувствительности микрофоновКонвертер уровня звукового давления (SPL)Конвертер уровня звукового давления с возможностью выбора опорного давленияКонвертер яркостиКонвертер силы светаКонвертер освещённостиКонвертер разрешения в компьютерной графикеКонвертер частоты и длины волныОптическая сила в диоптриях и фокусное расстояниеОптическая сила в диоптриях и увеличение линзы (×)Конвертер электрического зарядаКонвертер линейной плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объемной плотности зарядаКонвертер электрического токаКонвертер линейной плотности токаКонвертер поверхностной плотности токаКонвертер напряжённости электрического поляКонвертер электростатического потенциала и напряженияКонвертер электрического сопротивленияКонвертер удельного электрического сопротивленияКонвертер электрической проводимостиКонвертер удельной электрической проводимостиЭлектрическая емкостьКонвертер индуктивностиКонвертер реактивной мощностиКонвертер Американского калибра проводовУровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
единицахКонвертер магнитодвижущей силыКонвертер напряженности магнитного поляКонвертер магнитного потокаКонвертер магнитной индукцииРадиация. Конвертер мощности поглощенной дозы ионизирующего излученияРадиоактивность. Конвертер радиоактивного распадаРадиация. Конвертер экспозиционной дозыРадиация. Конвертер поглощённой дозыКонвертер десятичных приставокПередача данныхКонвертер единиц типографики и обработки изображенийКонвертер единиц измерения объема лесоматериаловВычисление молярной массыПериодическая система химических элементов Д. И. Менделеева
Сенсорный экран этого планшета выполнен с использованием проекционно-емкостной технологии.
Общие сведения
Измерение емкости конденсатора номинальной емкостью 10 мкФ с помощью осциллографа-мультиметра
Электрическая емкость — это величина, характеризующая способность проводника накапливать заряд, равная отношению электрического заряда к разности потенциалов между проводниками:
C = Q/∆φ
Здесь Q — электрический заряд, измеряется в кулонах (Кл), — разность потенциалов, измеряется в вольтах (В).
В системе СИ электроемкость измеряется в фарадах (Ф). Данная единица измерения названа в честь английского физика Майкла Фарадея.
Фарад является очень большой емкостью для изолированного проводника. Так, металлический уединенный шар радиусом в 13 радиусов Солнца имел бы емкость равную 1 фарад. А емкость металлического шара размером с Землю была бы примерно 710 микрофарад (мкФ).
Так как 1 фарад — очень большая емкость, поэтому используются меньшие значения, такие как: микрофарад (мкФ), равный одной миллионной фарада; нанофарад (нФ), равный одной миллиардной; пикофарад (пФ), равный одной триллионной фарада.
В системе СГСЭ основной единицей емкости является сантиметр (см). 1 сантиметр емкости — это электрическая емкость шара с радиусом 1 сантиметр, помещенного в вакуум. СГСЭ — это расширенная система СГС для электродинамики, то есть, система единиц в которой сантиметр, грам, и секунда приняты за базовые единицы для вычисления длины, массы и времени соответственно. В расширенных СГС, включая СГСЭ, некоторые физические константы приняты за единицу, чтобы упростить формулы и облегчить вычисления.
Использование емкости
Конденсаторы — устройства для накопления заряда в электронном оборудовании
Условные обозначения конденсаторов на принципиальных схемах
Понятие электрической емкости относится не только к проводнику, но и к конденсатору.
Конденсатор — система двух проводников, разделенных диэлектриком или вакуумом. В простейшем варианте конструкция конденсатора состоит из двух электродов в виде пластин (обкладок). Конденсатор (от лат. condensare — «уплотнять», «сгущать») — двухэлектродный прибор для накопления заряда и энергии электромагнитного поля, в простейшем случае представляет собой два проводника, разделённые каким-либо изолятором. Например, иногда радиолюбители при отсутствии готовых деталей изготавливают подстроечные конденсаторы для своих схем из отрезков проводов разного диаметра, изолированных лаковым покрытием, при этом более тонкий провод наматывается на более толстый. Регулируя число витков, радиолюбители точно настраивают контура аппаратуры на нужную частоту. Примеры изображения конденсаторов на электрических схемах приведены на рисунке.
Примеры изображения конденсаторов на электрических схемах приведены на рисунке.
Параллельная RLC-цепь, состоящая из резистора, конденсатора и катушки индуктивности
Историческая справка
Еще 275 лет назад были известны принципы создания конденсаторов. Так, в 1745 г. в Лейдене немецкий физик Эвальд Юрген фон Клейст и нидерландский физик Питер ван Мушенбрук создали первый конденсатор — «лейденскую банку» — в ней диэлектриком были стенки стеклянной банки, а обкладками служили вода в сосуде и ладонь экспериментатора, державшая сосуд. Такая «банка» позволяла накапливать заряд порядка микрокулона (мкКл). После того, как ее изобрели, с ней часто проводили эксперименты и публичные представления. Для этого банку сначала заряжали статическим электричеством, натирая ее. После этого один из участников прикасался к банке рукой, и получал небольшой удар током. Известно, что 700 парижских монахов, взявшись за руки, провели лейденский эксперимент. В тот момент, когда первый монах прикоснулся к головке банки, все 700 монахов, сведенные одной судорогой, с ужасом вскрикнули.
В Россию «лейденская банка» пришла благодаря русскому царю Петру I, который познакомился с Мушенбруком во время путешествий по Европе, и подробнее узнал об экспериментах с «лейденской банкой». Петр I учредил в России Академию наук, и заказал Мушенбруку разнообразные приборы для Академии наук.
В дальнейшем конденсаторы усовершенствовались и становились меньше, а их емкость — больше. Конденсаторы широко применяются в электронике. Например, конденсатор и катушка индуктивности образуют колебательный контур, который может быть использован для настройки приемника на нужную частоту.
Существует несколько типов конденсаторов, отличающихся постоянной или переменной емкостью и материалом диэлектрика.
Примеры конденсаторов
Оксидные конденсаторы в блоке питания сервера.
Промышленность выпускает большое количество типов конденсаторов различного назначения, но главными их характеристиками являются ёмкость и рабочее напряжение.
Типичные значение ёмкости конденсаторов изменяются от единиц пикофарад до сотен микрофарад, исключение составляют ионисторы, которые имеют несколько иной характер формирования ёмкости – за счёт двойного слоя у электродов – в этом они подобны электрохимическим аккумуляторам. Суперконденсаторы на основе нанотрубок имеют чрезвычайно развитую поверхность электродов. У этих типов конденсаторов типичные значения ёмкости составляют десятки фарад, и в некоторых случаях они способны заменить в качестве источников тока традиционные электрохимические аккумуляторы.
Суперконденсаторы на основе нанотрубок имеют чрезвычайно развитую поверхность электродов. У этих типов конденсаторов типичные значения ёмкости составляют десятки фарад, и в некоторых случаях они способны заменить в качестве источников тока традиционные электрохимические аккумуляторы.
Вторым по важности параметром конденсаторов является его рабочее напряжение. Превышение этого параметра может привести к выходу конденсатора из строя, поэтому при построении реальных схем принято применять конденсаторы с удвоенным значением рабочего напряжения.
Для увеличения значений ёмкости или рабочего напряжения используют приём объединения конденсаторов в батареи. При последовательном соединении двух однотипных конденсаторов рабочее напряжение удваивается, а суммарная ёмкость уменьшается в два раза. При параллельном соединении двух однотипных конденсаторов рабочее напряжение остаётся прежним, а суммарная ёмкость увеличивается в два раза.
Третьим по важности параметром конденсаторов является температурный коэффициент изменения ёмкости (ТКЕ). Он даёт представление об изменении ёмкости в условиях изменения температур.
Он даёт представление об изменении ёмкости в условиях изменения температур.
В зависимости от назначения использования, конденсаторы подразделяются на конденсаторы общего назначения, требования к параметрам которых некритичны, и на конденсаторы специального назначения (высоковольтные, прецизионные и с различными ТКЕ).
Маркировка конденсаторов
Подобно резисторам, в зависимости от габаритов изделия, может применяться полная маркировка с указанием номинальной ёмкости, класса отклонения от номинала и рабочего напряжения. Для малогабаритных исполнений конденсаторов применяют кодовую маркировку из трёх или четырёх цифр, смешанную цифро-буквенную маркировку и цветовую маркировку.
Соответствующие таблицы пересчёта маркировок по номиналу, рабочему напряжению и ТКЕ можно найти в Интернете, но самым действенным и практичным методом проверки номинала и исправности элемента реальной схемы остаётся непосредственное измерение параметров выпаянного конденсатора с помощью мультиметра.
Оксидный конденсатор собран из двух алюминиевых лент и бумажной прокладки с электролитом. Одна из алюминиевых лент покрыта слоем оксида алюминия и служит анодом. Катодом служит вторая алюминиевая лента и бумажная лента с электролитом. На алюминиевых лентах видны следы электрохимического травления, позволяющего увеличить их площадь поверхности, а значит и емкость конденсатора.
Предупреждение: поскольку конденсаторы могут накапливать большой заряд при весьма высоком напряжении, во избежание поражения электрическим током необходимо перед измерением параметров конденсатора разряжать его, закоротив его выводы проводом с высоким сопротивлением внешней изоляции. Лучше всего для этого подходят штатные провода измерительного прибора.
Оксидные конденсаторы: данный тип конденсатора обладает большой удельной емкостью, то есть, емкостью на единицу веса конденсатора. Одна обкладка таких конденсаторов представляет собой обычно алюминиевую ленту, покрытую слоем оксида алюминия. Второй обкладкой служит электролит. Так как оксидные конденсаторы имеют полярность, то принципиально важно включать такой конденсатор в схему строго в соответствии с полярностью напряжения.
Второй обкладкой служит электролит. Так как оксидные конденсаторы имеют полярность, то принципиально важно включать такой конденсатор в схему строго в соответствии с полярностью напряжения.
Твердотельные конденсаторы: в них вместо традиционного электролита в качестве обкладки используется органический полимер, проводящий ток, или полупроводник.
Трехсекционный воздушный конденсатор переменной емкости
Переменные конденсаторы: емкость может меняться механическим способом, электрическим напряжением или с помощью температуры.
Пленочные конденсаторы: диапазон емкости данного типа конденсаторов составляет примерно от 5 пФ до 100 мкФ.
Имеются и другие типы конденсаторов.
Ионисторы
В наши дни популярность набирают ионисторы.
Ионистор (суперконденсатор) — это гибрид конденсатора и химического источника тока, заряд которого накапливается на границе раздела двух сред — электрода и электролита. Начало созданию ионисторов было положено в 1957 году, когда был запатентован конденсатор с двойным электрическим слоем на пористых угольных электродах. Двойной слой, а также пористый материал помогли увеличить емкость такого конденсатора за счет увеличения площади поверхности. В дальнейшем эта технология дополнялась и улучшалась. На рынок ионисторы вышли в начале восьмидесятых годов прошлого века.
Двойной слой, а также пористый материал помогли увеличить емкость такого конденсатора за счет увеличения площади поверхности. В дальнейшем эта технология дополнялась и улучшалась. На рынок ионисторы вышли в начале восьмидесятых годов прошлого века.
С появлением ионисторов появилась возможность использовать их в электрических цепях в качестве источников напряжения. Такие суперконденсаторы имеют долгий срок службы, малый вес, высокие скорости зарядки-разрядки. В перспективе данный вид конденсаторов может заменить обычные аккумуляторы. Основными недостатками ионисторов является меньшая, чем у электрохимических аккумуляторов удельная энергия (энергия на единицу веса), низкое рабочее напряжение и значительный саморазряд.
Ионисторы применяются в автомобилях Формулы-1. В системах рекуперации энергии, при торможении вырабатывается электроэнергия, которая накапливается в маховике, аккумуляторах или ионисторах для дальнейшего использования.
Электромобиль А2В Университета Торонто. Общий вид
Общий вид
В бытовой электронике ионисторы применяются для стабилизации основного питания и в качестве резервного источника питания таких приборов как плееры, фонари, в автоматических коммунальных счетчиках и в других устройствах с батарейным питанием и изменяющейся нагрузкой, обеспечивая питание при повышенной нагрузке.
В общественном транспорте применение ионисторов особенно перспективно для троллейбусов, так как становится возможна реализация автономного хода и увеличения маневренности; также ионисторы используются в некоторых автобусах и электромобилях.
Электромобиль А2В Университета Торонто. Под капотом
Электрические автомобили в настоящем времени выпускают многие компании, например: General Motors, Nissan, Tesla Motors, Toronto Electric. Университет Торонто совместно с компанией Toronto Electric разработали полностью канадский электромобиль A2B. В нем используются ионисторы вместе с химическими источниками питания, так называемое гибридное электрическое хранение энергии. Двигатели данного автомобиля питаются от аккумуляторов весом 380 килограмм. Также для подзарядки используются солнечные батареи, установленные на крыше электромобиля.
Двигатели данного автомобиля питаются от аккумуляторов весом 380 килограмм. Также для подзарядки используются солнечные батареи, установленные на крыше электромобиля.
Емкостные сенсорные экраны
В современных устройствах все чаще применяются сенсорные экраны, которые позволяют управлять устройствами путем прикосновения к панелям с индикаторами или экранам. Сенсорные экраны бывают разных типов: резистивные, емкостные и другие. Они могут реагировать на одно или несколько одновременных касаний. Принцип работы емкостных экранов основывается на том, что предмет большой емкости проводит переменный ток. В данном случае этим предметом является тело человека.
Поверхностно-емкостные экраны
Cенсорный экран iPhone выполнен по проекционно-емкостной технологии.
Таким образом, поверхностно-емкостный сенсорный экран представляет собой стеклянную панель, покрытую прозрачным резистивным материалом. В качестве резистивного материала обычно применяется имеющий высокую прозрачность и малое поверхностное сопротивление сплав оксида индия и оксида олова. Электроды, подающие на проводящий слой небольшое переменное напряжение, располагаются по углам экрана. При касании к такому экрану пальцем появляется утечка тока, которая регистрируется в четырех углах датчиками и передается в контроллер, который определяет координаты точки касания.
Электроды, подающие на проводящий слой небольшое переменное напряжение, располагаются по углам экрана. При касании к такому экрану пальцем появляется утечка тока, которая регистрируется в четырех углах датчиками и передается в контроллер, который определяет координаты точки касания.
Преимущество таких экранов заключается в долговечности (около 6,5 лет нажатий с промежутком в одну секунду или порядка 200 млн. нажатий). Они обладают высокой прозрачностью (примерно 90%). Благодаря этим преимуществам, емкостные экраны уже с 2009 года активно начали вытеснять резистивные экраны.
Недостаток емкостных экранов заключается в том, что они плохо работают при отрицательных температурах, есть трудности с использованием таких экранов в перчатках. Если проводящее покрытие расположено на внешней поверхности, то экран является достаточно уязвимым, поэтому емкостные экраны применяются лишь в тех устройствах, которые защищены от непогоды.
Проекционно-емкостные экраны
Помимо поверхностно-емкостных экранов, существуют проекционно-емкостные экраны. Их отличие заключается в том, что на внутренней стороне экрана нанесена сетка электродов. Электрод, к которому прикасаются, вместе с телом человека образует конденсатор. Благодаря сетке, можно получить точные координаты касания. Проекционно-емкостный экран реагирует на касания в тонких перчатках.
Их отличие заключается в том, что на внутренней стороне экрана нанесена сетка электродов. Электрод, к которому прикасаются, вместе с телом человека образует конденсатор. Благодаря сетке, можно получить точные координаты касания. Проекционно-емкостный экран реагирует на касания в тонких перчатках.
Проекционно-емкостные экраны также обладают высокой прозрачностью (около 90%). Они долговечны и достаточно прочные, поэтому их широко применяют не только в персональной электронике, но и в автоматах, в том числе установленных на улице.
Автор статьи: Sergey Akishkin, Tatiana Kondratieva
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
емкость, напряжение, напряженность и прочее
В этой статье мы начнем разбирать конденсаторы “по косточкам”. Мы узнаем, как зависит напряжение на конденсаторе от расстояния между пластин, в чем отличие поведения конденсатора в случаях, когда он подключен к источнику и когда нет. В последующих статьях – продолжение.
В последующих статьях – продолжение.
Задача 1. Найти емкость сферического конденсатора, состоящего из двух концентрических сфер радиусами м и м. Пространство между сферами заполнено маслом. Какого радиуса должен быть изолированный шар, чтобы он имел емкость, равную емкости такого конденсатора?
Как известно,
Запишем потенциалы сфер:
Разность потенциалов:
Тогда емкость конденсатора равна (диэлектрическая проницаемость масла равна ):
А радиус шара был бы равен
Ответ: пФ, м.
Задача 2. Найти емкость плоского конденсатора, состоящего из двух круглых пластин диаметром см, разделенных парафиновой прослойкой толщиной мм.
Диэлектрическая проницаемость парафина .
По формуле
Ответ: 556 мкФ
Задача 3. Площадь каждой пластины плоского конденсатора см. На каком расстоянии друг от друга надо расположить в воздухе пластины, чтобы емкость конденсатора была пФ?
Диэлектрическая проницаемость воздуха .
Из формулы
«вытащим» :
Ответ: 1 см
Задача 4. Расстояние между обкладками плоского конденсатора увеличивают. Как изменится: а) электроемкость конденсатора; б) напряженность электрического поля; в) напряжение? Рассмотреть два случая: 1) конденсатор заряжен и отключен от источника тока; 2) конденсатор подключен к источнику тока.
Здесь необходимо запомнить: если конденсатор заряжен и после этого отключен, то заряд на нем сохраняется. Действительно, куда ему деваться? А если начать что-либо менять, то будут меняться емкость и напряжение.
Если же конденсатор подключен к источнику, то напряжение на нем постоянно, и при любых вмешательствах (раздвинули пластины, вложили диэлектрик) будет меняться емкость и заряд.
Тогда в первом случае (заряд постоянен!): так как зависимость емкости от обратная, то емкость будет падать при увеличении расстояния между пластинами. Напряженность – никак не зависит от расстояния между обкладками, она не изменится; напряжение – увеличится, оно от величины зависит прямо.
Во втором случае (напряжение постоянно): напряженность поля уменьшится; емкость уменьшится.
Задача 5. Плоский конденсатор состоит из двух пластин, площадью см каждая, расположенных на расстоянии мм друг от друга, между которыми находится слой слюды. Какой наибольший заряд можно сообщить конденсатору, если допустимое напряжение кВ?
Диэлектрическая проницаемость слюды .
Ответ: 1,59 мкКл
Задача 6. Плоский воздушный конденсатор, расстояние между пластинами которого мм, заряжен до напряжения В и отключен от источника. Каким будет напряжение , если пластины раздвинуть до расстояния мм?
Если конденсатор заряжен и после этого отключен, то заряд на нем сохраняется. Тогда
Ответ: В
Задача 7. С какой силой взаимодействуют пластины плоского воздушного конденсатора площадью м, если напряжение на пластинах В и расстояние между ними м?
Сила взаимодействия пластин может быть вычислена как произведение заряда пластины на напряженность поля пластины: – делим пополам, потому что напряженность поля одной пластины вдвое меньше напряженности поля конденсатора – там пластин две штуки.
Ответ: мН.
Конденсатор — Физикон
КОНДЕНСАТОРЫ Презентация…загрузить
! Конденсатор — это устройство, предназначенное для накопления заряда и энергии электрического поля (от лат. kondensator — «уплотнять», «сгущать»).
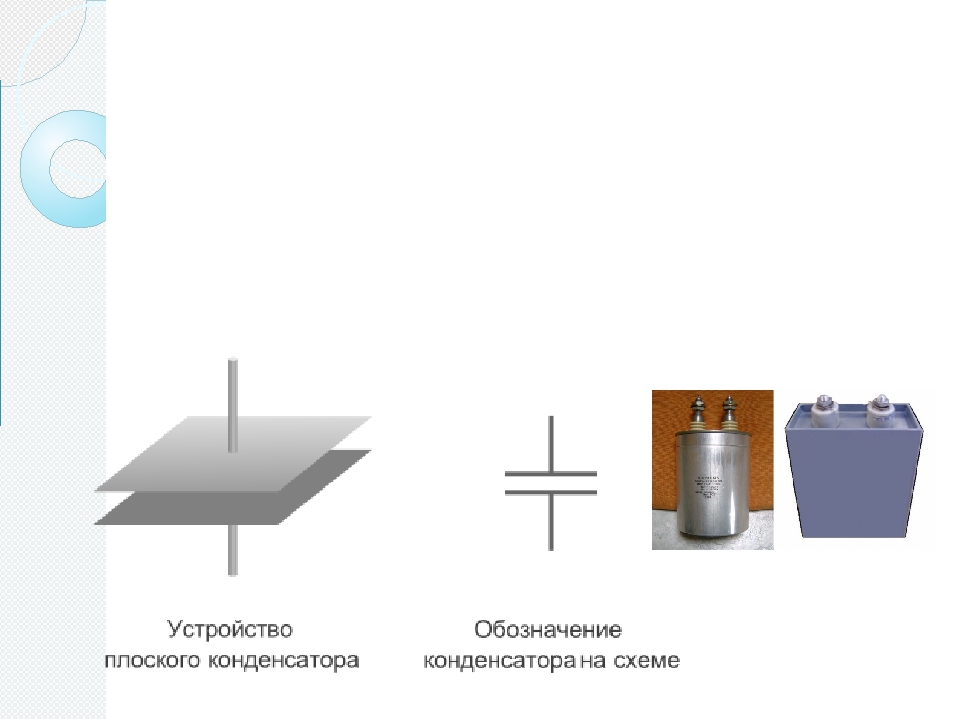
Простейший плоский конденсатор состоит из двух одинаковых металлических пластин — обкладок — и слоя диэлектрика, толщина которого мала по сравнению с размерами пластин.
На схемах электрических цепей конденсатор обозначается: .
Конденсатор — два проводника, разделенные диэлектриком, служащие для накопления электрического заряда. Под зарядом конденсатора понимают модуль заряда одной из его пластин или обкладок.
YouTube Video
Типы конденсаторов
Для зарядки конденсатора нужно присоединить его обкладки к полюсам источника тока.
 При зарядке обе обкладки получают заряды, равные по модулю, но противоположные по знаку. Под зарядом конденсаторов понимают модуль заряда одной из его обкладок. Свойство конденсатора накапливать электрический заряд характеризуется физической величиной — электроёмкостью.
При зарядке обе обкладки получают заряды, равные по модулю, но противоположные по знаку. Под зарядом конденсаторов понимают модуль заряда одной из его обкладок. Свойство конденсатора накапливать электрический заряд характеризуется физической величиной — электроёмкостью.Электроёмкость обозначается буквой C и определяется по формуле:
C=qU, где q — заряд конденсатора, Кл U — напряжение между обкладками конденсатора, В.
Электроёмкость конденсатора зависит от площади перекрытия пластин и расстояния между ними, а также от свойств используемого диэлектрика:
C∼Sd, где S — площадь каждой обкладки , d — расстояние между обкладками.
За единицу электроёмкости в СИ принимается Фарад (Ф).
Она названа в честь Майкла Фарадея — английского физика. 1 Фарад равен ёмкости конденсатора, при которой заряд 1 Кулон создаёт между его обкладками напряжение 1 Вольт: 1 Фарад=1 Кулон1 Вольт.
1 Ф — это очень большая ёмкость для конденсатора. Чаще всего конденсаторы имеют электроёмкость, равную дольным единицам Ф: микрофарад (мкФ) — 10−6Ф, пикофарад (пФ) — 10−12 Ф.
Чаще всего конденсаторы имеют электроёмкость, равную дольным единицам Ф: микрофарад (мкФ) — 10−6Ф, пикофарад (пФ) — 10−12 Ф.
Для получения требуемой ёмкости конденсаторы соединяют в батареи.
Если конденсаторы соединены параллельно, то общая ёмкость равна сумме ёмкостей: Cоб=C1+C2+C3.
Если конденсаторы соединены последовательно, то общая ёмкость будет равна: 1Cоб=1C1+1C2+1C3.
При зарядке конденсатора внешними силами совершается работа по разделению положительных и отрицательных зарядов. По закону сохранения энергии работа внешних сил равна энергии поля конденсатора. При разрядке конденсатора за счёт этой энергии может быть совершена работа. Энергия конденсатора есть не что иное, как энергия заключённого внутри него электрического поля.
C — ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ
YouTube Video
Величина С характеризует способность проводника накапливать электрический заряд и называется электрической емкостью.
!Электроёмкость проводника зависит от его размеров, формы, а также электрических свойств среды.
Емкость плоского конденсатора прямо пропорциональна площади пластин S , диэлектрической проницаемости среды , и обратно пропорциональна расстоянию между пластинами d:
! Величина, измеряемая отношением заряда одной из пластин конденсатора к напряжению между пластинами, называется электроёмкостью конденсатора.
Способность конденсатора накапливать заряд характеризуется электроемкостью, которая равна отношению заряда конденсатора к напряжению:
C=q/U
Емкость конденсатора равна 1 Ф, если при напряжении 1 В его заряд равен 1 Кл.
Опыт для наблюдения зависимости электроемкости плоского конденсатора от расстояния между пластинамиYouTube Video
ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА.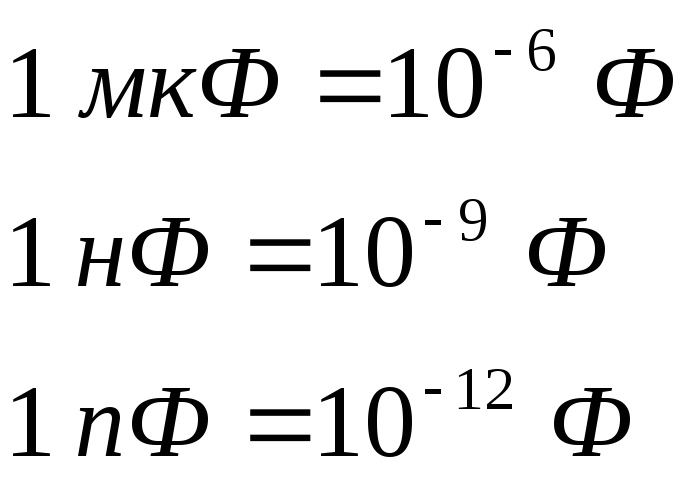
Энергию электрического поля конденсатора можно рассчитать по формуле:
Из формулы видно, что энергия конденсатора данной электроёмкости тем больше, чем больше его заряд.
YouTube Video
Конденсаторы в клавиатуре
Пластины конденсатора располагаются на тыльной стороне клавиши и на плате.
При нажатии на клавишу, меняется расстояние между пластинами. Это приводит к изменению электроемкости конденсатора, на которое реагирует микросхема клавиатуры. Далее, микросхема преобразует сигнал в соответствующий код, который передается компьютеру.
Для закрепления и проверки знаний пройдите тест по теме «КОНДЕНСАТОР»
Тестирование
Тестирование
Источники:
Учебник А. В. Перышкин, Е. М. Гутник «Физика. 9 класс».
https://electrosam. ru/ Виды конденсаторов.
ru/ Виды конденсаторов.
https://elektronchic.ru/ Электронщик.
https://ru.wikipedia.org Википедия.
Емкость плоского и других конденсаторов
Конфигурация конденсатора такова, что поле, которое создается зарядами, локализовано между обкладками. В общем случае электроемкость конденсатора равна:
\[C=\frac{q}{{\varphi }_1-{\varphi }_2}=\frac{q}{U}\left(1\right),\]где ${\varphi }_1-{\varphi }_2=U$ — разность потенциалов обкладок, которую называют напряжением и обозначают $U$. Емкость по определению считается положительной величиной. Она зависит только от геометрии обкладок конденсатора их взаиморасположения и диэлектрика. Форму обкладок и их расположение подбирают так, чтобы внешние поля минимально влияли на внутреннее поле конденсатора. Силовые линии поля конденсатора начинались на проводнике с положительным зарядом и заканчивались на проводнике с отрицательным зарядом. Конденсатор может быть проводником, который помещен в полость, окруженную замкнутой оболочкой.
В соответствии с конфигураций конденсаторов можно выделить три большие группы: плоские, сферические и цилиндрические (по форме обкладок). Вычисление емкости конденсатора сводится к определению $напряжения$ конденсатора при известном заряде на его обкладках.
Плоский конденсатор
Плоский конденсатор (рис.1) — это две разноименно заряженные пластины, разделенные тонким слоем диэлектрика. Формула для расчета емкости такого конденсатора представляет собой выражение:
\[С=\frac{\varepsilon {\varepsilon }_0S}{d}\left(2\right),\]где $S$ — площадь обкладки, $d$ — расстояние между обкладками, $\varepsilon $ — диэлектрическая проницаемость вещества. Чем меньше $d$, тем больше совпадает расчётная емкость конденсатора (2), с реальной емкостью.
Рис. 1
Электроемкость плоского конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равна $d_i$, диэлектрическая проницаемость этого слоя ${\varepsilon }_i$ вычисляется по формуле:
\[C=\frac{{\varepsilon }_0S}{\frac{d_1}{{\varepsilon }_1}+\frac{d_2}{{\varepsilon }_2}+\dots +\frac{d_N}{{\varepsilon }_N}}\ \left(3\right). \]
\]Сферический конденсатор
В том случае, если внутренний проводник шар или сфера, внешняя замкнутая оболочка — концентрическая ему сфера, то конденсатор является сферическим. Сферический конденсатор (рис.2) состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком. Емкость его можно рассчитать по формуле:
\[C=4\pi \varepsilon {\varepsilon }_0\frac{R_1R_2}{R_2-R_1}\ \left(4\right),\]где $R_1{\ и\ R}_2$ — радиусы обкладок.
Рис. 2
Цилиндрический конденсатор
Емкость цилиндрического конденсатора равна:
\[C=\frac{2\pi \varepsilon {\varepsilon }_0l}{{ln \left({R_2}/{R_1}\right)\ }}\left(5\right),\]где $l$ — высота цилиндров, $R_1$ и $R_2$ — радиусы обкладок. Этот вид конденсаторов представляет собой две коаксиальных (соосных) проводящих цилиндрических поверхности (рис.3).
Рис. 4\frac{В}{м}.$
4\frac{В}{м}.$
Физики научились измерять давление через емкость
PTB
Ученым впервые удалось определить давление газа на основе измерения электрической емкости наполненного им конденсатора. Этот способ относится к первичным методам и позволит независимо проверять показания стандартных грузопоршневых манометров с высокой точностью, пишут авторы в журнале Nature Physics.
Физические величины можно измерить различными
способами. Некоторые позволяют сразу получить оценку искомой величины — такие
методы называются прямыми, но они существуют не для всех величин и, как
правило, обладают значительными ограничениями. Поэтому обычно проводят косвенные
измерения, при которых непосредственно определяется вспомогательная величина,
которая затем позволяет вычислить искомую.
Некоторые позволяют сразу получить оценку искомой величины — такие
методы называются прямыми, но они существуют не для всех величин и, как
правило, обладают значительными ограничениями. Поэтому обычно проводят косвенные
измерения, при которых непосредственно определяется вспомогательная величина,
которая затем позволяет вычислить искомую.
Процесс пересчета в рамках косвенного измерения также может проходить по-разному. В некоторых ситуациях измерительные приборы необходимо подвергать калибровке, то есть соотносить их показания с измерениями других инструментов. В таком случае точность измерения таким устройством не может быть лучше, чем у эталонного, с которым проходило сравнение.
Однако бывают случаи, когда можно обойтись и без калибровки — тогда говорят о первичном методе измерения. Его точность опирается на
неопределенности в других используемых величинах и значениях физических констант.
Использование нескольких высокоточных первичных методов разного рода для измерения
одной величины позволяет добиться надежной оценки.
На данный момент стандартным методом измерения давления в области точной метрологии является механический — на основе грузопоршневых
манометров. Он заключается в уравновешивании давления газа снизу от поршня тяжестью груза известной массы. Таким образом удается получать данные с относительной точностью на уровне одной миллионной
вплоть до давления в семь мегапаскалей. Однако выше 0,1 мегапаскаля не существует другого
первичного метода, который помогал бы сверять показания и искать источники
систематических ошибок, что необходимо для расширения охватываемого диапазона.
Метод, предложенный физиками из Федерального физико-технического центра в Германии при участии Кристофа Гайзера (Christof Gaiser), как раз занимает эту нишу: им впервые удалось воплотить первичный метод измерения давления в газах на основе электрической емкости — впервые измерять давление таким способом предложили еще 20 лет назад.
Сам метод основан на предсказуемом изменении параметров конденсатора при его заполнении гелием, так как давление газа деформирует устройство, а сам он обладает диэлектрическими свойствами. Практическая реализация этой идеи была невозможна, так как не существовало достаточно стабильных
конденсаторов, а параметры гелия, вычисляемые теоретически из первых принципов,
не были известны с достаточной точностью. Также диэлектрическая проницаемость
гелия весьма мала, что
дополнительно осложняет ситуацию.
Практическая реализация этой идеи была невозможна, так как не существовало достаточно стабильных
конденсаторов, а параметры гелия, вычисляемые теоретически из первых принципов,
не были известны с достаточной точностью. Также диэлектрическая проницаемость
гелия весьма мала, что
дополнительно осложняет ситуацию.
Эти проблемы были решены в рамках разработки новых эталонов величин системы СИ (в частности, кельвина) на протяжении последних лет. Это позволило провести сравнение показаний двух методов, которые показали одинаковые величины при давлениях до 7 мегапаскалей с точностью в 5 миллионных долей.
С точки зрения метрологии этот способ очень важен: это единственный первичный метод, который можно использовать для
проверки показаний стандартного грузопоршневого манометра в диапазоне от 0,1 до
7 мегапаскалей с точностью на уровне нескольких миллионных долей. Авторы
отмечают, что созданная ими установка слишком сложна для проведения массовых
измерений. Ее можно было бы значительно упростить в случае использования газа с
более высоким значением диэлектрической проницаемости. Подходящими значениями обладают
неон и аргон, но теоретические значения их свойств пока недостаточно точно
известны для проведения измерений с ошибками на уровне единиц миллионных долей.
Подходящими значениями обладают
неон и аргон, но теоретические значения их свойств пока недостаточно точно
известны для проведения измерений с ошибками на уровне единиц миллионных долей.
В последние годы произошло масштабное переопределение единиц СИ: о начале процесса мы рассказывали в материале «Последний эталон», а завершился он 20 мая этого года. Отдельно мы писали о том, что килограмм стал нематериальным. О том как выглядят и как «живут» идеальные единицы измерения можно прочитать в тексте «Эталонный быт».
Тимур Кешелава
Удельная теплоемкость | Безграничная физика
Тепловая мощность
Теплоемкость измеряет количество тепла, необходимое для повышения температуры объекта или системы на один градус Цельсия.
Цели обучения
Объясните энтальпию в системе с постоянным объемом и давлением
Основные выводы
Ключевые моменты
- Теплоемкость — это измеримая физическая величина, которая характеризует количество тепла, необходимое для изменения температуры вещества на заданную величину.
 Он измеряется в джоулях на Кельвин и выражается в.
Он измеряется в джоулях на Кельвин и выражается в. - Теплоемкость — это обширное свойство, которое зависит от размера системы.
- Теплоемкость большинства систем непостоянна (хотя ее часто можно рассматривать как таковую). Это зависит от температуры, давления и объема рассматриваемой системы.
Ключевые термины
- теплоемкость : количество тепловой энергии, необходимое для повышения температуры объекта или единицы вещества на один градус Цельсия; в джоулях на кельвин (Дж / К).
- энтальпия : общее количество энергии в системе, включая как внутреннюю энергию, так и энергию, необходимую для вытеснения окружающей среды
Тепловая мощность
Теплоемкость (обычно обозначается заглавной буквой C, часто с индексами) или теплоемкость — это измеряемая физическая величина, которая характеризует количество тепла, необходимое для изменения температуры вещества на заданную величину. В единицах СИ теплоемкость выражается в джоулях на кельвин (Дж / К).
В единицах СИ теплоемкость выражается в джоулях на кельвин (Дж / К).
Теплоемкость объекта (обозначение C ) определяется как отношение количества тепловой энергии, переданной объекту, к результирующему увеличению температуры объекта.
[латекс] \ displaystyle {\ text {C} = \ frac {\ text {Q}} {\ Delta \ text {T}}.} [/ Latex]
Теплоемкость — это обширное свойство, поэтому она масштабируется в зависимости от размера системы. Образец, содержащий в два раза больше вещества, чем другой образец, требует передачи вдвое большего количества тепла (Q) для достижения такого же изменения температуры (ΔT).Например, если для нагрева блока железа требуется 1000 Дж, то потребуется 2000 Дж для нагрева второго блока железа, масса которого в два раза больше, чем у первого.
Измерение теплоемкости
Тепловая мощность большинства систем непостоянна. Скорее, он зависит от переменных состояния исследуемой термодинамической системы. В частности, это зависит от самой температуры, а также от давления и объема системы, а также от способов изменения давлений и объемов при переходе системы от одной температуры к другой. Причина этого заключается в том, что работа давления и объема, выполняемая в системе, повышает ее температуру за счет механизма, отличного от нагрева, в то время как работа объема давления, выполняемая системой, поглощает тепло, не повышая температуру системы. (Температурная зависимость объясняет, почему определение калории — это формально энергия, необходимая для нагрева 1 г воды с 14,5 до 15,5 ° C, а не на 1 ° C, как правило.)
Причина этого заключается в том, что работа давления и объема, выполняемая в системе, повышает ее температуру за счет механизма, отличного от нагрева, в то время как работа объема давления, выполняемая системой, поглощает тепло, не повышая температуру системы. (Температурная зависимость объясняет, почему определение калории — это формально энергия, необходимая для нагрева 1 г воды с 14,5 до 15,5 ° C, а не на 1 ° C, как правило.)
Таким образом, можно выполнять различные измерения теплоемкости, чаще всего при постоянном давлении и постоянном объеме.Измеренные таким образом значения обычно имеют нижний индекс (соответственно p и V) для обозначения определения. Газы и жидкости обычно также измеряются при постоянном объеме. Измерения при постоянном давлении дают более высокие значения, чем измерения при постоянном объеме, потому что значения постоянного давления также включают тепловую энергию, которая используется для выполнения работы по расширению вещества против постоянного давления при повышении его температуры. Эта разница особенно заметна для газов, где значения при постоянном давлении обычно составляют от 30% до 66.На 7% больше, чем при постоянной громкости.
Эта разница особенно заметна для газов, где значения при постоянном давлении обычно составляют от 30% до 66.На 7% больше, чем при постоянной громкости.
Термодинамические соотношения и определение теплоемкости
Внутренняя энергия замкнутой системы изменяется либо за счет добавления тепла в систему, либо за счет выполнения системой работы. Вспоминая первый закон термодинамики,
[латекс] \ text {dU} = \ delta \ text {Q} — \ delta \ text {W} [/ latex].
За работу в результате увеличения объема системы можем написать:
[латекс] \ text {dU} = \ delta \ text {Q} — \ text {PdV} [/ latex].
Если тепло добавляется при постоянном объеме, то второй член этого соотношения обращается в нуль и легко получается
[латекс] \ displaystyle {\ left (\ frac {\ partial \ text {U}} {\ partial \ text {T}} \ right) _ {\ text {V}} = \ left (\ frac {\ partial \ text {Q}} {\ partial \ text {T}} \ right) _ {\ text {V}} = \ text {C} _ {\ text {V}}} [/ latex].
Это определяет теплоемкость при постоянном объеме , C V . Еще одна полезная величина — теплоемкость при постоянном давлении , C P .При энтальпии системы из
[латекс] \ text {H} = \ text {U} + \ text {PV} [/ latex],
наше уравнение для d U меняется на
[латекс] \ text {dH} = \ delta \ text {Q} + \ text {VdP} [/ latex],
и, следовательно, при постоянном давлении имеем
[латекс] (\ frac {\ partial \ text {H}} {\ partial \ text {T}}) _ {\ text {P}} = (\ frac {\ partial \ text {Q}} {\ partial \ text {T}}) _ {\ text {P}} = \ text {C} _ {\ text {P}} [/ latex].
Удельная теплоемкость
Удельная теплоемкость — это интенсивное свойство, которое описывает, сколько тепла необходимо добавить к определенному веществу, чтобы повысить его температуру.
Цели обучения
Обобщите количественную взаимосвязь между теплопередачей и изменением температуры
Основные выводы
Ключевые моменты
- В отличие от общей теплоемкости, удельная теплоемкость не зависит от массы или объема.
 Он описывает, сколько тепла необходимо добавить к единице массы данного вещества, чтобы повысить его температуру на один градус Цельсия. Единицы измерения удельной теплоемкости — Дж / (кг ° C) или эквивалентно Дж / (кг · K).
Он описывает, сколько тепла необходимо добавить к единице массы данного вещества, чтобы повысить его температуру на один градус Цельсия. Единицы измерения удельной теплоемкости — Дж / (кг ° C) или эквивалентно Дж / (кг · K). - Теплоемкость и удельная теплоемкость связаны соотношением C = см или c = C / м.
- Масса m, удельная теплоемкость c, изменение температуры ΔT и добавленное (или вычитаемое) тепло Q связаны уравнением: Q = mcΔT.
- Значения удельной теплоемкости зависят от свойств и фазы данного вещества. Поскольку их нелегко рассчитать, они измеряются эмпирическим путем и доступны для справки в таблицах.
Ключевые термины
- удельная теплоемкость : Количество тепла, которое должно быть добавлено (или удалено) из единицы массы вещества, чтобы изменить его температуру на один градус Цельсия.Это интенсивное свойство.
Удельная теплоемкость
Теплоемкость — это обширное свойство, которое описывает, сколько тепловой энергии требуется для повышения температуры данной системы. Однако было бы довольно неудобно измерять теплоемкость каждой единицы вещества. Нам нужно интенсивное свойство, которое зависит только от типа и фазы вещества и может применяться к системам произвольного размера. Эта величина известна как удельная теплоемкость (или просто удельная теплоемкость), которая представляет собой теплоемкость на единицу массы материала.Эксперименты показывают, что передаваемое тепло зависит от трех факторов: (1) изменения температуры, (2) массы системы и (3) вещества и фазы вещества. Последние два фактора заключены в значении удельной теплоемкости.
Однако было бы довольно неудобно измерять теплоемкость каждой единицы вещества. Нам нужно интенсивное свойство, которое зависит только от типа и фазы вещества и может применяться к системам произвольного размера. Эта величина известна как удельная теплоемкость (или просто удельная теплоемкость), которая представляет собой теплоемкость на единицу массы материала.Эксперименты показывают, что передаваемое тепло зависит от трех факторов: (1) изменения температуры, (2) массы системы и (3) вещества и фазы вещества. Последние два фактора заключены в значении удельной теплоемкости.
Теплопередача и удельная теплоемкость : Тепло Q, передаваемое для изменения температуры, зависит от величины изменения температуры, массы системы, а также от вещества и фазы. (а) Количество переданного тепла прямо пропорционально изменению температуры.Чтобы удвоить изменение температуры массы m, вам нужно добавить в два раза больше тепла. (б) Количество переданного тепла также прямо пропорционально массе. Чтобы вызвать эквивалентное изменение температуры в удвоенной массе, вам нужно добавить в два раза больше тепла. (c) Количество передаваемого тепла зависит от вещества и его фазы. Если требуется количество тепла Q, чтобы вызвать изменение температуры ΔT в данной массе меди, потребуется в 10,8 раз больше тепла, чтобы вызвать эквивалентное изменение температуры в той же массе воды, при условии отсутствия фазовых изменений ни в одном из веществ.
Чтобы вызвать эквивалентное изменение температуры в удвоенной массе, вам нужно добавить в два раза больше тепла. (c) Количество передаваемого тепла зависит от вещества и его фазы. Если требуется количество тепла Q, чтобы вызвать изменение температуры ΔT в данной массе меди, потребуется в 10,8 раз больше тепла, чтобы вызвать эквивалентное изменение температуры в той же массе воды, при условии отсутствия фазовых изменений ни в одном из веществ.
Удельная теплоемкость : В этом уроке тепло связано с изменением температуры. Мы обсуждаем, как количество тепла, необходимое для изменения температуры, зависит от массы и вещества, и это соотношение представлено удельной теплоемкостью вещества C.
Зависимость от изменения температуры и массы легко понять. Поскольку (средняя) кинетическая энергия атома или молекулы пропорциональна абсолютной температуре, внутренняя энергия системы пропорциональна абсолютной температуре и количеству атомов или молекул.Поскольку переданное тепло равно изменению внутренней энергии, тепло пропорционально массе вещества и изменению температуры. Передаваемое тепло также зависит от вещества, так что, например, для повышения температуры требуется меньше тепла, чем для воды. Для одного и того же вещества передаваемое тепло также зависит от фазы (газ, жидкость или твердое тело).
Поскольку (средняя) кинетическая энергия атома или молекулы пропорциональна абсолютной температуре, внутренняя энергия системы пропорциональна абсолютной температуре и количеству атомов или молекул.Поскольку переданное тепло равно изменению внутренней энергии, тепло пропорционально массе вещества и изменению температуры. Передаваемое тепло также зависит от вещества, так что, например, для повышения температуры требуется меньше тепла, чем для воды. Для одного и того же вещества передаваемое тепло также зависит от фазы (газ, жидкость или твердое тело).
Количественная связь между теплопередачей и изменением температуры включает все три фактора:
[латекс] \ text {Q} = \ text {mc} \ Delta \ text {T} [/ latex],
где Q — обозначение теплопередачи, m — масса вещества, а ΔT — изменение температуры.Символ c обозначает удельную теплоемкость и зависит от материала и фазы.
Удельная теплоемкость — это количество тепла, необходимое для изменения температуры 1,00 кг массы на 1,00 ° C. Удельная теплоемкость c — это свойство вещества; его единица СИ — Дж / (кг⋅К) или Дж / (кг⋅К). Напомним, что изменение температуры (ΔT) одинаково в единицах кельвина и градусов Цельсия. Обратите внимание, что общая теплоемкость C — это просто произведение удельной теплоемкости c и массы вещества m, i.е.,
Удельная теплоемкость c — это свойство вещества; его единица СИ — Дж / (кг⋅К) или Дж / (кг⋅К). Напомним, что изменение температуры (ΔT) одинаково в единицах кельвина и градусов Цельсия. Обратите внимание, что общая теплоемкость C — это просто произведение удельной теплоемкости c и массы вещества m, i.е.,
[латекс] \ text {C} = \ text {mc} [/ latex] или [латекс] \ text {c} = \ frac {\ text {C}} {\ text {m}} = \ frac {\ текст {C}} {\ rho \ text {V}} [/ latex],
где ϱ — плотность вещества, V — его объем.
Значения удельной теплоемкости обычно нужно искать в таблицах, потому что нет простого способа их вычислить. Вместо этого они измеряются эмпирически. Как правило, удельная теплоемкость также зависит от температуры. В таблице ниже приведены типичные значения удельной теплоемкости для различных веществ.За исключением газов, температурная и объемная зависимость удельной теплоемкости большинства веществ слабая. Удельная теплоемкость воды в пять раз больше, чем у стекла, и в десять раз больше, чем у железа, что означает, что требуется в пять раз больше тепла, чтобы поднять температуру воды на такое же количество, что и у стекла, и в десять раз больше тепла, чтобы повысить температуру. воды как для железа. Фактически, вода имеет одну из самых высоких удельной теплоемкости из всех материалов, что важно для поддержания жизни на Земле.
воды как для железа. Фактически, вода имеет одну из самых высоких удельной теплоемкости из всех материалов, что важно для поддержания жизни на Земле.
Удельная теплоемкость : Указана удельная теплоемкость различных веществ.Эти значения идентичны в единицах кал / (г⋅C) .3. cv при постоянном объеме и 20,0 ° C, если не указано иное, и среднем давлении 1,00 атм. В скобках указаны значения cp при постоянном давлении 1,00 атм.
Калориметрия
Калориметрия — это измерение теплоты химических реакций или физических изменений.
Цели обучения
Проанализировать взаимосвязь между газовой постоянной для получения идеального выхода газа и объемом
Основные выводы
Ключевые моменты
- Калориметр используется для измерения тепла, выделяемого (или поглощаемого) в результате физических изменений или химической реакции.Наука об измерении этих изменений известна как калориметрия.
- Для проведения калориметрии очень важно знать удельную теплоемкость измеряемых веществ.

- Калориметрия может выполняться при постоянном объеме или постоянном давлении. Тип выполняемого расчета зависит от условий эксперимента.
Ключевые термины
- Калориметр постоянного давления : прибор, используемый для измерения тепла, выделяемого во время изменений, не связанных с изменениями давления.
- калориметр : Устройство для измерения тепла, выделяемого или поглощаемого в результате химической реакции, изменения фазы или какого-либо другого физического изменения.
- Калориметр постоянного объема : прибор, используемый для измерения тепла, выделяемого во время изменений, не связанных с изменением объема.
Калориметрия
Обзор
Калориметрия — это наука об измерении теплоты химических реакций или физических изменений. Калориметрия выполняется калориметром.Простой калориметр состоит из термометра, прикрепленного к металлическому контейнеру с водой, подвешенному над камерой сгорания. Слово калориметрия происходит от латинского слова calor , что означает тепло. Шотландский врач и ученый Джозеф Блэк, который первым осознал различие между теплом и температурой, считается основоположником калориметрии.
Слово калориметрия происходит от латинского слова calor , что означает тепло. Шотландский врач и ученый Джозеф Блэк, который первым осознал различие между теплом и температурой, считается основоположником калориметрии.
Калориметрия требует, чтобы нагреваемый материал имел известные тепловые свойства, то есть удельную теплоемкость.Классическое правило, признанное Клаузиусом и Кельвином, состоит в том, что давление, оказываемое калориметрическим материалом, полностью и быстро определяется исключительно его температурой и объемом; это правило применяется для изменений, не связанных с фазовым переходом, таких как таяние льда. Есть много материалов, которые не соответствуют этому правилу, и для них требуются более сложные уравнения, чем приведенные ниже.
Ледяной калориметр : первый в мире ледяной калориметр, использованный зимой 1782-83 гг. Антуаном Лавуазье и Пьером-Симоном Лапласом для определения тепла, выделяемого при различных химических изменениях; расчеты, основанные на предыдущем открытии скрытой теплоты Джозефом Блэком. Эти эксперименты составляют основу термохимии.
Эти эксперименты составляют основу термохимии.
Базовая калориметрия при постоянном значении
Калориметрия постоянного объема — это калориметрия, выполняемая при постоянном объеме. Это предполагает использование калориметра постоянного объема (один из типов называется калориметром бомбы). Для калориметрии постоянного объема:
[латекс] \ delta \ text {Q} = \ text {C} _ {\ text {V}} \ Delta \ text {T} = \ text {mc} _ {\ text {V}} \ Delta \ text {T} [/ латекс]
, где δQ — приращение тепла, полученного образцом, C V — теплоемкость при постоянном объеме, c v — удельная теплоемкость при постоянном объеме, а ΔT — изменение температуры.
Измерение изменения энтальпии
Чтобы найти изменение энтальпии на массу (или на моль) вещества A в реакции между двумя веществами A и B, вещества добавляются в калориметр, а начальная и конечная температуры (до начала реакции и после ее завершения) ) отмечены. Умножение изменения температуры на массу и удельную теплоемкость веществ дает значение энергии, выделяемой или поглощаемой во время реакции:
[латекс] \ delta \ text {Q} = \ Delta \ text {T} (\ text {m} _ {\ text {A}} \ text {c} _ {\ text {A}} + \ text { m} _ {\ text {B}} \ text {c} _ {\ text {B}}) [/ latex]
Разделение изменения энергии на количество присутствующих граммов (или молей) A дает изменение энтальпии реакции. Этот метод используется в основном в академическом обучении, поскольку он описывает теорию калориметрии. Он не учитывает потери тепла через контейнер или теплоемкость термометра и самого контейнера. Кроме того, объект, помещенный внутри калориметра, показывает, что объекты передают свое тепло калориметру и жидкости, а тепло, поглощаемое калориметром и жидкостью, равно теплу, выделяемому металлами.
Этот метод используется в основном в академическом обучении, поскольку он описывает теорию калориметрии. Он не учитывает потери тепла через контейнер или теплоемкость термометра и самого контейнера. Кроме того, объект, помещенный внутри калориметра, показывает, что объекты передают свое тепло калориметру и жидкости, а тепло, поглощаемое калориметром и жидкостью, равно теплу, выделяемому металлами.
Калориметрия постоянного давления
Калориметр постоянного давления измеряет изменение энтальпии реакции, протекающей в растворе, в течение которой атмосферное давление остается постоянным.Примером может служить калориметр кофейной чашки, который состоит из двух вложенных друг в друга чашек из пенополистирола и крышки с двумя отверстиями, в которую можно вставить термометр и стержень для перемешивания. Внутренняя чашка содержит известное количество растворенного вещества, обычно воды, которое поглощает тепло от реакции. Когда происходит реакция, внешняя чашка обеспечивает изоляцию. Тогда
Тогда
[латекс] \ text {C} _ {\ text {P}} = \ frac {\ text {W} \ Delta \ text {H}} {\ text {M} \ Delta \ text {T}} [/ латекс]
где C p — удельная теплоемкость при постоянном давлении, ΔH — энтальпия раствора, ΔT — изменение температуры, W — масса растворенного вещества, а M — молекулярная масса растворенного вещества.Измерение тепла с помощью простого калориметра, такого как калориметр для кофейной чашки, является примером калориметрии постоянного давления, поскольку давление (атмосферное давление) остается постоянным во время процесса. Калориметрия постоянного давления используется для определения изменений энтальпии, происходящих в растворе. В этих условиях изменение энтальпии равно теплоте (Q = ΔH).
Удельная теплоемкость идеального газа при постоянном давлении и объеме
Идеальный газ имеет различную удельную теплоемкость при постоянном объеме или постоянном давлении.
Цели обучения
Объясните, как рассчитать индекс адиабаты
Основные выводы
Ключевые моменты
- Удельная теплоемкость газа при постоянном объеме задается как [латекс] (\ frac {\ partial \ text {U}} {\ partial \ text {T}}) _ {\ text {V}} = \ text {c} _ {\ text {v}} [/ latex].

- Удельная теплоемкость идеального газа при постоянном давлении определяется как [latex] (\ frac {\ partial \ text {H}} {\ partial \ text {T}}) _ {\ text {V}} = \ text {c} _ {\ text {p}} = \ text {c} _ {\ text {v}} + \ text {R} [/ latex].
- Коэффициент теплоемкости (или индекс адиабаты) — это отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.
Ключевые термины
- Фундаментальная термодинамическая связь : В термодинамике фундаментальное термодинамическое соотношение выражает бесконечно малое изменение внутренней энергии в терминах бесконечно малых изменений энтропии и объема для замкнутой системы, находящейся в тепловом равновесии, следующим образом: dU = TdS-PdV. Здесь U — внутренняя энергия, T — абсолютная температура, S — энтропия, P — давление, V — объем.
- Индекс адиабаты : Отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме.

- удельная теплоемкость : отношение количества тепла, необходимого для повышения температуры единицы массы вещества на единицу градуса, к количеству тепла, необходимому для повышения температуры той же массы воды на такое же количество.
Удельная теплоемкость идеального газа при постоянном давлении и объеме
Теплоемкость при постоянном объеме nR = 1 Дж · К −1 любого газа, включая идеальный, составляет:
[латекс] (\ frac {\ partial \ text {U}} {\ partial \ text {T}}) _ {\ text {V}} = \ text {c} _ {\ text {v}} [/ латекс]
Это безразмерная теплоемкость при постоянном объеме; обычно это функция температуры из-за межмолекулярных сил.При умеренных температурах константа для одноатомного газа c v = 3/2, а для двухатомного газа c v = 5/2 (см.). Макроскопические измерения теплоемкости дают информацию о микроскопической структуре молекул.
Молекулярные внутренние колебания : Когда газ нагревается, поступательная kientic энергия молекул в газе увеличивается. Кроме того, молекулы газа могут улавливать множество характерных внутренних колебаний. Потенциальная энергия, накопленная в этих внутренних степенях свободы, вносит вклад в удельную теплоемкость газа.
Кроме того, молекулы газа могут улавливать множество характерных внутренних колебаний. Потенциальная энергия, накопленная в этих внутренних степенях свободы, вносит вклад в удельную теплоемкость газа.
Теплоемкость при постоянном давлении 1 Дж · К −1 идеального газа составляет:
[латекс] (\ frac {\ partial \ text {H}} {\ partial \ text {T}}) _ {\ text {V}} = \ text {c} _ {\ text {p}} = \ текст {c} _ {\ text {v}} + \ text {R} [/ latex]
где H = U + pV — энтальпия газа.
Измерение теплоемкости при постоянном объеме может быть чрезвычайно трудным для жидкостей и твердых тел. То есть небольшие изменения температуры обычно требуют большого давления для поддержания постоянного объема жидкости или твердого вещества (это означает, что содержащий сосуд должен быть почти жестким или, по крайней мере, очень прочным).Легче измерить теплоемкость при постоянном давлении (позволяющем материалу свободно расширяться или сжиматься) и определить теплоемкость при постоянном объеме, используя математические соотношения, выведенные из основных термодинамических законов.
Используя фундаментальную термодинамическую связь, мы можем показать:
[латекс] \ text {C} _ {\ text {p}} — \ text {C} _ {\ text {V}} = \ text {T} (\ frac {\ partial \ text {P}} { \ partial \ text {T}}) _ {\ text {V}, \ text {N}} (\ frac {\ partial \ text {V}} {\ partial \ text {T}}) _ {\ text { p}, \ text {N}} [/ latex]
, где частные производные взяты при постоянном объеме и постоянном числе частиц, а также при постоянном давлении и постоянном количестве частиц, соответственно.
Коэффициент теплоемкости или показатель адиабаты — это отношение теплоемкости при постоянном давлении к теплоемкости при постоянном объеме. Иногда его также называют коэффициентом изоэнтропического расширения:
.[латекс] \ gamma = \ frac {\ text {C} _ {\ text {P}}} {\ text {C} _ {\ text {V}}} = \ frac {\ text {c} _ { \ text {p}}} {\ text {c} _ {\ text {v}}} [/ latex]
Для идеального газа оценка приведенных выше частных производных в соответствии с уравнением состояния, где R — газовая постоянная для идеального газа, дает:
[латекс] \ text {pV} = \ text {RT} [/ латекс]
[латекс] \ text {C} _ {\ text {p}} — \ text {C} _ {\ text {V}} = \ text {T} (\ frac {\ partial \ text {P}} { \ partial \ text {T}}) _ {\ text {V}} (\ frac {\ partial \ text {V}} {\ partial \ text {T}}) _ {\ text {p}} [/ latex ]
[латекс] \ text {C} _ {\ text {p}} — \ text {C} _ {\ text {V}} = — \ text {T} (\ frac {\ partial \ text {P}} {\ partial \ text {V}}) _ {\ text {V}} (\ frac {\ partial \ text {V}} {\ partial \ text {T}}) _ {\ text {p}} ^ { 2} [/ латекс]
[латекс] \ text {P} = \ frac {\ text {RT}} {\ text {V}} \ text {n} \ to (\ frac {\ partial \ text {P}} {\ partial \ text {V}}) _ {\ text {T}} = \ frac {- \ text {RT}} {\ text {V} ^ {2}} = \ frac {- \ text {P}} {\ text { V}} [/ латекс]
[латекс] \ text {V} = \ frac {\ text {RT}} {\ text {P}} \ text {n} \ to (\ frac {\ partial \ text {V}} {\ partial \ text {T}}) ^ {2} _ {\ text {p}} = \ frac {\ text {R} ^ {2}} {\ text {P} ^ {2}} [/ latex]
заменяющий:
[латекс] — \ text {T} (\ frac {\ partial \ text {P}} {\ partial \ text {V}}) _ {\ text {V}} (\ frac {\ partial \ text {V }} {\ partial \ text {T}}) _ {\ text {p}} ^ {2} = — \ text {T} \ frac {- \ text {P}} {\ text {V}} \ frac {\ text {R} ^ {2}} {\ text {P} ^ {2}} = \ text {R} [/ latex]
Это уравнение сводится просто к тому, что известно как соотношение Майера:
Юлиус Роберт Майер : Юлиус Роберт фон Майер (25 ноября 1814 — 20 марта 1878), немецкий врач и физик, был одним из основоположников термодинамики.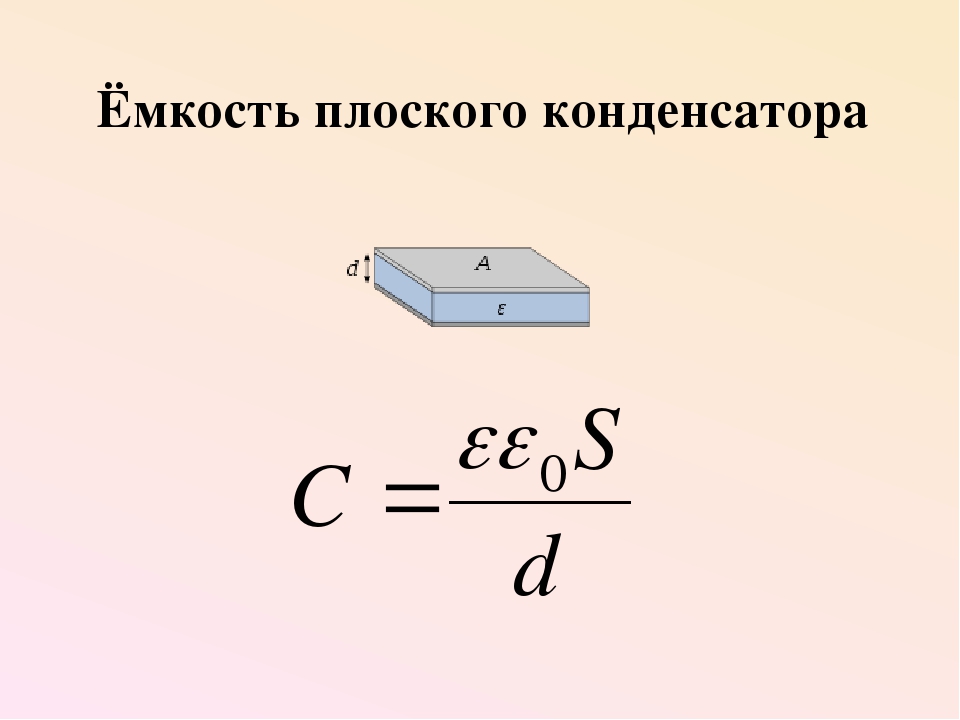 Он известен прежде всего тем, что в 1841 году сформулировал одно из первоначальных утверждений о сохранении энергии (или то, что сейчас известно как одна из первых версий первого закона термодинамики): «Энергия не может быть ни создана, ни уничтожена. В 1842 году Майер описал жизненно важный химический процесс, который теперь называют окислением, как основной источник энергии для любого живого существа. Его достижения не были замечены, и заслуга в открытии механического эквивалента тепла была приписана Джеймсу Джоулю в следующем году.фон Майер также предположил, что растения превращают свет в химическую энергию.
Он известен прежде всего тем, что в 1841 году сформулировал одно из первоначальных утверждений о сохранении энергии (или то, что сейчас известно как одна из первых версий первого закона термодинамики): «Энергия не может быть ни создана, ни уничтожена. В 1842 году Майер описал жизненно важный химический процесс, который теперь называют окислением, как основной источник энергии для любого живого существа. Его достижения не были замечены, и заслуга в открытии механического эквивалента тепла была приписана Джеймсу Джоулю в следующем году.фон Майер также предположил, что растения превращают свет в химическую энергию.
[латекс] \ text {C} _ {\ text {P}} — \ text {C} _ {\ text {V}} = \ text {R} [/ latex].
Это простое уравнение, связывающее теплоемкость при постоянной температуре и постоянном давлении.
Решение задач калориметрии
Калориметрия используется для измерения количества тепла, выделяемого или потребляемого в химической реакции.
Цели обучения
Объясните, что калориметр бомбы используется для измерения тепла, выделяемого в реакции горения
Основные выводы
Ключевые моменты
- Калориметрия используется для измерения количества тепла, передаваемого веществу или от него.

- Калориметр — это устройство, используемое для измерения количества тепла, участвующего в химическом или физическом процессе.
- Это означает, что количество тепла, производимого или потребляемого в реакции, равно количеству тепла, поглощаемого или теряемого раствором.
Ключевые термины
- теплота реакции : изменение энтальпии в химической реакции; количество тепла, которое система отдает своему окружению, чтобы она могла вернуться к исходной температуре.
- горение : Процесс, в котором два химических вещества объединяются для получения тепла.
предназначены для минимизации обмена энергией между исследуемой системой и ее окружением. Они варьируются от простых калориметров для кофейных чашек, используемых студентами начального курса химии, до сложных калориметров-бомб, используемых для определения энергетической ценности пищи.
Калориметрия используется для измерения количества тепла, передаваемого веществу или от него. Для этого происходит обмен тепла с калиброванным объектом (калориметром).Изменение температуры измерительной части калориметра преобразуется в количество тепла (поскольку предыдущая калибровка использовалась для определения его теплоемкости). Измерение теплопередачи с использованием этого подхода требует определения системы (вещества или веществ, подвергающихся химическому или физическому изменению) и ее окружения (других компонентов измерительного устройства, которые служат для обеспечения теплом системы или поглощения тепла от система). Знание теплоемкости окружающей среды и тщательные измерения масс системы и окружающей среды, а также их температуры до и после процесса позволяют рассчитать передаваемое тепло, как описано в этом разделе.
Для этого происходит обмен тепла с калиброванным объектом (калориметром).Изменение температуры измерительной части калориметра преобразуется в количество тепла (поскольку предыдущая калибровка использовалась для определения его теплоемкости). Измерение теплопередачи с использованием этого подхода требует определения системы (вещества или веществ, подвергающихся химическому или физическому изменению) и ее окружения (других компонентов измерительного устройства, которые служат для обеспечения теплом системы или поглощения тепла от система). Знание теплоемкости окружающей среды и тщательные измерения масс системы и окружающей среды, а также их температуры до и после процесса позволяют рассчитать передаваемое тепло, как описано в этом разделе.
Калориметр — это устройство, используемое для измерения количества тепла, участвующего в химическом или физическом процессе. Например, когда в растворе в калориметре происходит экзотермическая реакция, тепло, выделяемое в результате реакции, поглощается раствором, что увеличивает его температуру. Когда происходит эндотермическая реакция, необходимое тепло поглощается тепловой энергией раствора, что снижает его температуру. Изменение температуры, а также удельная теплоемкость и масса раствора затем можно использовать для расчета количества тепла, задействованного в любом случае.
Когда происходит эндотермическая реакция, необходимое тепло поглощается тепловой энергией раствора, что снижает его температуру. Изменение температуры, а также удельная теплоемкость и масса раствора затем можно использовать для расчета количества тепла, задействованного в любом случае.
Калориметры кофейных чашек
Студенты-общехимики часто используют простые калориметры, изготовленные из полистирольных стаканчиков. Эти простые в использовании калориметры типа «кофейная чашка» обеспечивают больший теплообмен с окружающей средой и, следовательно, дают менее точные значения энергии.
Устройство калориметра постоянного объема (или «бомбы»)
Калориметр бомбы : Это изображение типичной установки калориметра бомбы.
Калориметр другого типа, который работает с постоянным объемом, в просторечии известный как калориметр бомбы, используется для измерения энергии, производимой в реакциях, которые дают большое количество тепла и газообразных продуктов, таких как реакции горения. (Термин «бомба» исходит из наблюдения, что эти реакции могут быть достаточно интенсивными, чтобы напоминать взрывы, которые могут повредить другие калориметры.) Калориметр этого типа состоит из прочного стального контейнера («бомба»), который содержит реагенты и сам является погружен в воду. Образец помещается в бомбу, которая затем заполняется кислородом под высоким давлением. Для воспламенения образца используется небольшая электрическая искра. Энергия, производимая в результате реакции, улавливается стальной бомбой и окружающей водой.Повышение температуры измеряется и вместе с известной теплоемкостью калориметра используется для расчета энергии, произведенной в результате реакции. Калориметры бомбы требуют калибровки, чтобы определить теплоемкость калориметра и гарантировать точные результаты. Калибровка выполняется с использованием реакции с известным q, например измеренного количества бензойной кислоты, воспламененного искрой от никелевой плавкой проволоки, которая взвешивается до и после реакции.
(Термин «бомба» исходит из наблюдения, что эти реакции могут быть достаточно интенсивными, чтобы напоминать взрывы, которые могут повредить другие калориметры.) Калориметр этого типа состоит из прочного стального контейнера («бомба»), который содержит реагенты и сам является погружен в воду. Образец помещается в бомбу, которая затем заполняется кислородом под высоким давлением. Для воспламенения образца используется небольшая электрическая искра. Энергия, производимая в результате реакции, улавливается стальной бомбой и окружающей водой.Повышение температуры измеряется и вместе с известной теплоемкостью калориметра используется для расчета энергии, произведенной в результате реакции. Калориметры бомбы требуют калибровки, чтобы определить теплоемкость калориметра и гарантировать точные результаты. Калибровка выполняется с использованием реакции с известным q, например измеренного количества бензойной кислоты, воспламененного искрой от никелевой плавкой проволоки, которая взвешивается до и после реакции. Изменение температуры, вызванное известной реакцией, используется для определения теплоемкости калориметра.Калибровка обычно выполняется каждый раз перед использованием калориметра для сбора данных исследования.
Изменение температуры, вызванное известной реакцией, используется для определения теплоемкости калориметра.Калибровка обычно выполняется каждый раз перед использованием калориметра для сбора данных исследования.
Пример: идентификация металла путем измерения удельной теплоемкости
Кусок металла весом 59,7 г, который был погружен в кипящую воду, был быстро перенесен в 60,0 мл воды при начальной температуре 22,0 ° C. Конечная температура составляет 28,5 ° C. Используйте эти данные, чтобы определить удельную теплоемкость металла. Используйте этот результат, чтобы идентифицировать металл.
Решение
Предполагая идеальную теплопередачу, тепло, выделяемое металлом, является отрицательной величиной тепла, поглощаемого водой, или:
[латекс] \ text {q} _ {\ text {metal}} = — \ text {q} _ {\ text {water}} [/ latex]
В развернутом виде это:
[латекс] \ text {c} _ {\ text {metal}} \ times \ text {m} _ {\ text {metal}} \ times \ left (\ text {T} _ {\ text {f, металл }} — \ text {T} _ {\ text {i, metal}} \ right) = \ text {c} _ {\ text {water}} \ times \ text {m} _ {\ text {water}} \ times \ left (\ text {T} _ {\ text {f, water}} — \ text {T} _ {\ text {i, water}} \ right) [/ latex]
Отметив, что, поскольку металл был погружен в кипящую воду, его начальная температура была 100. {\ text {o}} \ text {C} [/ latex]
{\ text {o}} \ text {C} [/ latex]
Наша экспериментальная удельная теплоемкость наиболее близка к значению для меди (0,39 Дж / г ° C), поэтому мы идентифицируем металл как медь.
Что такое теплоемкость? | Sciencing
Обновлено 14 ноября 2018 г.
Автор: Кевин Бек
Теплоемкость — это термин в физике, который описывает, сколько тепла необходимо добавить к веществу, чтобы повысить его температуру на 1 градус Цельсия. Это связано с удельной теплоемкостью , но отличается от нее, — это количество тепла, необходимое для подъема ровно 1 грамма (или другой фиксированной единицы массы) вещества на 1 градус Цельсия.Чтобы получить теплоемкость C вещества из его удельной теплоемкости S, нужно умножить его на количество вещества, которое присутствует, и убедиться, что вы используете одни и те же единицы массы во всей задаче. Проще говоря, теплоемкость — это показатель способности объекта сопротивляться нагреванию за счет добавления тепловой энергии.
Материя может существовать в твердом, жидком или газообразном состоянии. В случае газов теплоемкость может зависеть как от давления окружающей среды, так и от температуры окружающей среды.Ученые часто хотят знать теплоемкость газа при постоянном давлении, в то время как другие переменные, такие как температура, могут изменяться; он известен как C p . Точно так же может быть полезно определить теплоемкость газа при постоянном объеме, или C v . Отношение C p к C v дает важную информацию о термодинамических свойствах газа.
Наука термодинамики
Прежде чем приступить к обсуждению теплоемкости и удельной теплоемкости, полезно сначала понять основы теплообмена в физике и концепцию тепла в целом, а также ознакомиться с некоторыми фундаментальными уравнения дисциплины.
Термодинамика — раздел физики, изучающий работу и энергию системы. Работа, энергия и тепло имеют одни и те же единицы в физике, несмотря на различное значение и применение.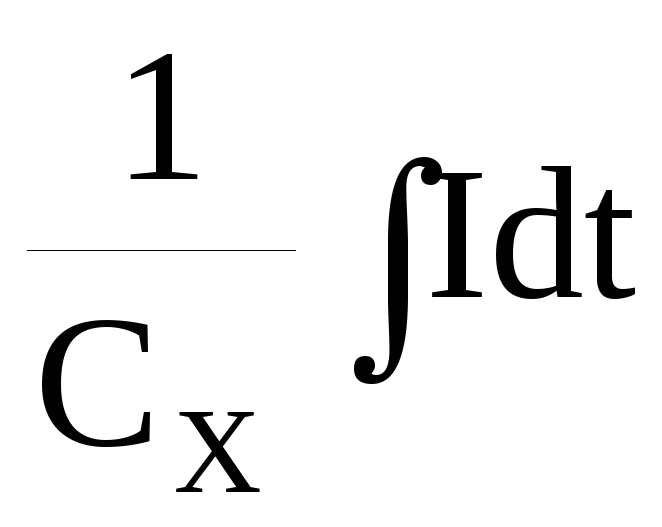 Единицей измерения тепла в системе СИ (международной стандартной) является джоуль. Работа определяется как сила, умноженная на расстояние, поэтому, учитывая единицы СИ для каждой из этих величин, джоуль — это то же самое, что и ньютон-метр. Другие единицы измерения тепла, с которыми вы, вероятно, столкнетесь, включают калории (cal), британские тепловые единицы (btu) и эрг.(Обратите внимание, что «калории», которые вы видите на этикетках пищевых продуктов, на самом деле являются килокалориями, «кило-» — это греческий префикс, обозначающий «тысяча»; таким образом, если вы заметите, что, скажем, банка газировки на 12 унций включает 120 » калорий », это фактически равно 120 000 калорий в формальном физическом выражении.)
Единицей измерения тепла в системе СИ (международной стандартной) является джоуль. Работа определяется как сила, умноженная на расстояние, поэтому, учитывая единицы СИ для каждой из этих величин, джоуль — это то же самое, что и ньютон-метр. Другие единицы измерения тепла, с которыми вы, вероятно, столкнетесь, включают калории (cal), британские тепловые единицы (btu) и эрг.(Обратите внимание, что «калории», которые вы видите на этикетках пищевых продуктов, на самом деле являются килокалориями, «кило-» — это греческий префикс, обозначающий «тысяча»; таким образом, если вы заметите, что, скажем, банка газировки на 12 унций включает 120 » калорий », это фактически равно 120 000 калорий в формальном физическом выражении.)
Газы ведут себя иначе, чем жидкости и твердые вещества. Поэтому физики, занимающиеся аэродинамикой и смежными дисциплинами, которые, естественно, очень озабочены поведением воздуха и других газов в их работе с высокоскоростными двигателями и летательными аппаратами, особенно озабочены теплоемкостью и другими измеряемыми физическими параметрами, связанными с иметь значение в этом состоянии. Одним из примеров является энтальпия , которая является мерой внутреннего тепла замкнутой системы. Это сумма энергии системы плюс произведение ее давления на объем:
Одним из примеров является энтальпия , которая является мерой внутреннего тепла замкнутой системы. Это сумма энергии системы плюс произведение ее давления на объем:
Более конкретно, изменение энтальпии связано с изменением объема газа соотношением:
Греческий символ ∆, или дельта, означает «изменение» или «различие» по соглашению в физике и математике. Кроме того, вы можете убедиться, что умножение давления на объем дает единицы работы; давление измеряется в ньютонах / м 2 , а объем может быть выражен в м 3 .
Кроме того, давление и объем газа связаны уравнением:
, где T — температура, а R — константа, имеющая разные значения для каждого газа.
Вам не нужно сохранять эти уравнения в памяти, но они будут повторно рассмотрены позже при обсуждении C p и C v .
Что такое теплоемкость?
Как уже отмечалось, теплоемкость и удельная теплоемкость взаимосвязаны.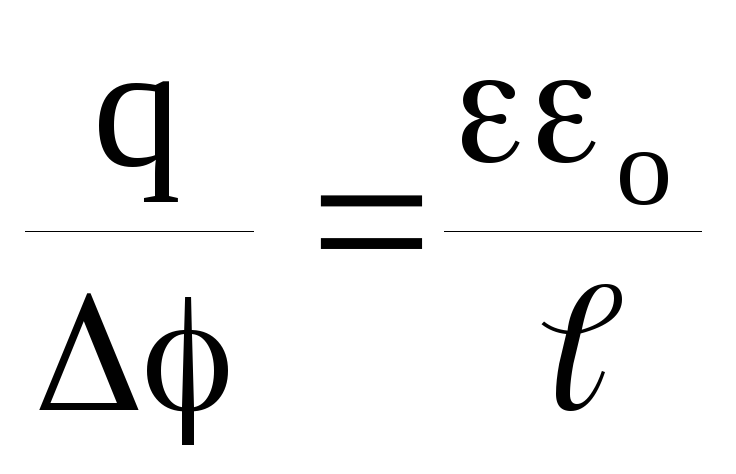 Первое на самом деле возникает из второго.Удельная теплоемкость — это переменная состояния, означающая, что она относится только к внутренним свойствам вещества, а не к тому, сколько из них присутствует. Поэтому он выражается как количество тепла на единицу массы. Теплоемкость, с другой стороны, зависит от того, какая часть рассматриваемого вещества подвергается теплопередаче, и не является переменной состояния.
Первое на самом деле возникает из второго.Удельная теплоемкость — это переменная состояния, означающая, что она относится только к внутренним свойствам вещества, а не к тому, сколько из них присутствует. Поэтому он выражается как количество тепла на единицу массы. Теплоемкость, с другой стороны, зависит от того, какая часть рассматриваемого вещества подвергается теплопередаче, и не является переменной состояния.
С любой материей связана температура. Возможно, это не первое, что приходит в голову, когда вы замечаете объект («Интересно, насколько теплая эта книга?»), Но по пути вы, возможно, узнали, что ученым никогда не удавалось достичь температуры абсолютного нуля. при любых условиях, хотя они подошли мучительно близко.(Причина, по которой люди стремятся сделать это, связана с чрезвычайно высокими свойствами проводимости чрезвычайно холодных материалов; просто подумайте о стоимости физического электрического проводника, практически не имеющего сопротивления.) Температура — это мера движения молекул. . В твердых материалах вещество организовано в виде решетки или сетки, и молекулы не могут свободно перемещаться. В жидкости молекулы более свободны в движении, но все еще в значительной степени ограничены. В газе молекулы могут очень свободно перемещаться.В любом случае просто помните, что низкая температура подразумевает небольшое движение молекул.
. В твердых материалах вещество организовано в виде решетки или сетки, и молекулы не могут свободно перемещаться. В жидкости молекулы более свободны в движении, но все еще в значительной степени ограничены. В газе молекулы могут очень свободно перемещаться.В любом случае просто помните, что низкая температура подразумевает небольшое движение молекул.
Когда вы хотите переместить объект, в том числе себя, из одного физического места в другое, вы должны затратить энергию — или, наоборот, выполнить работу — для этого. Вы должны встать и пройти через комнату, или вы должны нажать педаль акселератора автомобиля, чтобы прогнать топливо через двигатель и заставить автомобиль двигаться. Точно так же на микроуровне требуется ввод энергии в систему, чтобы заставить ее молекулы двигаться.Если этого ввода энергии достаточно, чтобы вызвать увеличение молекулярного движения, то, исходя из приведенного выше обсуждения, это обязательно означает, что температура вещества также увеличивается.
Различные обычные вещества имеют сильно различающиеся значения удельной теплоемкости. Среди металлов, например, золото проверяется при 0,129 Дж / г ° C, что означает, что 0,129 джоулей тепла достаточно, чтобы поднять температуру 1 грамма золота на 1 градус Цельсия. Помните, что это значение не меняется в зависимости от количества присутствующего золота, потому что масса уже учтена в знаменателе единиц удельной теплоемкости.Как вы скоро обнаружите, это не относится к теплоемкости.
Среди металлов, например, золото проверяется при 0,129 Дж / г ° C, что означает, что 0,129 джоулей тепла достаточно, чтобы поднять температуру 1 грамма золота на 1 градус Цельсия. Помните, что это значение не меняется в зависимости от количества присутствующего золота, потому что масса уже учтена в знаменателе единиц удельной теплоемкости.Как вы скоро обнаружите, это не относится к теплоемкости.
Теплоемкость: простые вычисления
Многих студентов, изучающих вводную физику, удивляет, что удельная теплоемкость воды 4,179 значительно выше, чем у обычных металлов. (В этой статье все значения удельной теплоемкости приведены в Дж / г ° C.) Кроме того, теплоемкость льда 2,03 меньше половины теплоемкости воды, хотя оба они состоят из H 2 O Это показывает, что состояние соединения, а не только его молекулярный состав, влияет на значение его удельной теплоемкости.
В любом случае, скажем, вас просят определить, сколько тепла требуется для повышения температуры 150 г железа (с удельной теплоемкостью, или S, равной 0,450) на 5 C. Как бы вы это сделали?
Как бы вы это сделали?
Расчет очень прост; умножьте удельную теплоемкость S на количество материала и изменение температуры. Поскольку S = 0,450 Дж / г ° C, количество тепла, которое необходимо добавить в Дж, равно (0,450) (г) (∆T) = (0,450) (150) (5) = 337,5 Дж. Другой способ выразить это означает, что теплоемкость 150 г железа равна 67.5 Дж, что представляет собой не что иное, как удельную теплоемкость S, умноженную на массу присутствующего вещества. Очевидно, что даже несмотря на то, что теплоемкость жидкой воды постоянна при данной температуре, для нагрева одного из Великих озер даже на десятую долю градуса потребуется гораздо больше тепла, чем для нагрева пинты воды на 1 градус. , или 10, или даже 50.
Что такое отношение Cp к Cv γ?
В предыдущем разделе вы познакомились с идеей условной теплоемкости для газов, то есть значений теплоемкости, которые применяются к данному веществу в условиях, в которых либо температура (T), либо давление (P) являются оставался неизменным на протяжении всей проблемы. Вам также были даны основные уравнения ∆H = E + P∆V и P∆V = R∆T.
Вам также были даны основные уравнения ∆H = E + P∆V и P∆V = R∆T.
Из последних двух уравнений видно, что другой способ выразить изменение энтальпии, ∆H, это:
Хотя здесь не приводится никакого вывода, один способ выразить первый закон термодинамики, который применяется к замкнутым системам и который Вы, возможно, слышали, что в просторечии говорится, что «Энергия не создается и не уничтожается»:
Простым языком это означает, что когда определенное количество энергии добавляется в систему, включая газ, а объем этого газа не может измениться (обозначено индексом V в C v ), его температура должна повыситься прямо пропорционально значению теплоемкости этого газа.
Между этими переменными существует еще одна взаимосвязь, которая позволяет определить теплоемкость при постоянном давлении, C p, , а не при постоянном объеме. Это соотношение является еще одним способом описания энтальпии:
Если вы разбираетесь в алгебре, вы можете прийти к критическому соотношению между C v и C p :
То есть, теплоемкость газа при постоянной давление превышает его теплоемкость при постоянном объеме на некоторую постоянную величину R, которая связана со специфическими свойствами исследуемого газа. Это имеет интуитивный смысл; если вы вообразите, что газу позволено расширяться в ответ на увеличение внутреннего давления, вы, вероятно, можете понять, что он должен будет меньше нагреваться в ответ на данное добавление энергии, чем если бы он был ограничен тем же пространством.
Это имеет интуитивный смысл; если вы вообразите, что газу позволено расширяться в ответ на увеличение внутреннего давления, вы, вероятно, можете понять, что он должен будет меньше нагреваться в ответ на данное добавление энергии, чем если бы он был ограничен тем же пространством.
Наконец, вы можете использовать всю эту информацию для определения другой переменной, зависящей от вещества, γ, которая представляет собой отношение C p к C v или C p / C v . Из предыдущего уравнения видно, что это соотношение увеличивается для газов с более высокими значениями R.
Cp и Cv воздуха
C p и C v воздуха важны для изучения гидродинамики, поскольку воздух (состоящий в основном из смеси азота и кислорода) является наиболее распространенным газом, который человеческий опыт. И C p , и C v зависят от температуры, но не в одинаковой степени; как это бывает, C v растет немного быстрее с повышением температуры. Это означает, что «постоянная» γ на самом деле не является постоянной, но она удивительно близка в диапазоне вероятных температур.Например, при 300 градусах Кельвина или K (равных 27 C) значение γ составляет 1,400; при температуре 400 К, что составляет 127 ° С и значительно выше точки кипения воды, значение γ составляет 1,395.
Это означает, что «постоянная» γ на самом деле не является постоянной, но она удивительно близка в диапазоне вероятных температур.Например, при 300 градусах Кельвина или K (равных 27 C) значение γ составляет 1,400; при температуре 400 К, что составляет 127 ° С и значительно выше точки кипения воды, значение γ составляет 1,395.
Тепловая мощность | Мини-физика
Тепловая мощность
- Теплоемкость тела C определяется как количество тепла (Q), необходимое для повышения его температуры (θ) на один градус без изменения состояния.
- Количество тепла, необходимое для повышения температуры объекта, зависит от массы объекта.
- Теплоемкость также зависит от материала объекта. Некоторые материалы нагреть труднее, чем другие. Молекулам в жидкости, такой как вода, требуется больше энергии, чтобы двигаться быстрее, чем атомам меди в твердом теле. Таким образом, чтобы зафиксировать повышение температуры на 1 ° C, жидкостям потребуется больше тепловой энергии, чем твердым телам.

- SI. единицей теплоемкости является джоуль на кельвин (Дж К -1 ) или джоуль на градус Цельсия (Дж ° C -1 ).
$ C = \ frac {Q} {\ Delta \ theta} $, где
C = теплоемкость (JK -1 , Дж ° C -1 )
Q = поглощенная или выделенная тепловая энергия (Дж)
Δθ = изменение температуры (K или ° C)
| Теплоемкость | Время остывать / нагреваться | Причина |
|---|---|---|
| Высокая | длиннее | Необходимость терять больше энергии (охлаждение) или поглощать больше энергии (нагрев) |
| Низкий | Короче | Потребность в меньших потерях энергии (охлаждение) или меньшем потреблении энергии (нагрев) |
Рабочий пример:
В простом эксперименте 100 г воды требует 12 600 Дж тепла, чтобы поднять ее с 30 ° C до 60 ° C.
i) Найдите теплоемкость 100 г воды.
ii) Найдите теплоемкость 1000 г воды.
iii) Найдите температуру, необходимую для повышения температуры 1000 г воды с 30 ° C до 40 ° C.
Показать / скрыть ответi) $ C = \ frac {Q} {\ Delta \ theta} = \ frac {12600} {30}
долларов СШАС = 420 Дж -1
ii) Так как масса 1000 г воды в 10 раз превышает массу 100 г воды, теплоемкость 1000 г воды = 10-кратная теплоемкость 100 г воды.
Следовательно, C на 1000 г воды = 4200 Дж -1
iii) Требуется тепло, $ Q = C \ Delta \ theta = 4200 (40-30) = 42000 Дж $
Определение удельной теплоемкости
Определение удельной теплоемкости
Удельная теплоемкость — это количество тепловой энергии, необходимое для повышения температуры вещества на единицу массы. Удельная теплоемкость материала — это физическое свойство. Это также пример обширного свойства, поскольку его значение пропорционально размеру исследуемой системы.
Ключевые выводы: удельная теплоемкость
- Удельная теплоемкость — это количество тепла, необходимое для повышения температуры на единицу массы.
- Обычно это количество тепла в Джоулях, необходимое для повышения температуры 1 грамма образца на 1 Кельвин или 1 градус Цельсия.
- Вода имеет чрезвычайно высокую удельную теплоемкость, что делает ее удобной для регулирования температуры.
В единицах СИ удельная теплоемкость (обозначение: c) — это количество тепла в джоулях, необходимое для подъема 1 грамма вещества на 1 градус Кельвина.Его также можно выразить как Дж / кг · К. Удельная теплоемкость также может быть выражена в калориях на грамм-градус Цельсия. Связанные значения — молярная теплоемкость, выраженная в Дж / моль · К, и объемная теплоемкость, выраженная в Дж / м 3 · К.
Теплоемкость определяется как отношение количества энергии, переданной материалу, к произведенному изменению температуры:
C = Q / ΔT
где C — теплоемкость, Q — энергия (обычно выражается в джоулях), а ΔT — изменение температуры (обычно в градусах Цельсия или Кельвинах).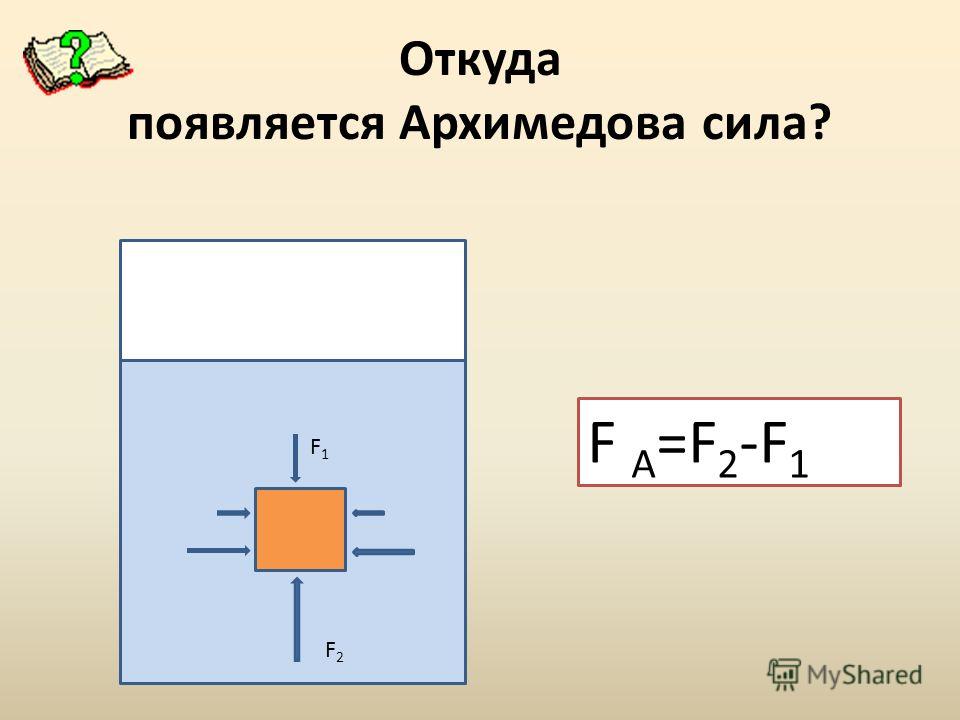 В качестве альтернативы уравнение можно записать:
В качестве альтернативы уравнение можно записать:
Q = CmΔT
Удельная теплоемкость и теплоемкость связаны по массе:
С = м * S
Где C — теплоемкость, m — масса материала, а S — удельная теплоемкость. Обратите внимание, что, поскольку удельная теплоемкость рассчитана на единицу массы, ее значение не меняется независимо от размера образца. Итак, удельная теплоемкость галлона воды такая же, как удельная теплоемкость капли воды.
Важно отметить, что связь между добавленным теплом, удельной теплотой, массой и изменением температуры не применяется во время фазового перехода .Причина этого в том, что тепло, которое добавляется или удаляется при фазовом переходе, не изменяет температуру.
Также известен как: удельная теплоемкость, удельная теплоемкость по массе, теплоемкость
Вода имеет удельную теплоемкость 4,18 Дж (или 1 калорию на грамм ° C). Это намного более высокое значение, чем у большинства других веществ, что делает воду исключительно хорошей при регулировании температуры. В отличие от меди, удельная теплоемкость составляет 0,39 Дж.
В отличие от меди, удельная теплоемкость составляет 0,39 Дж.
Таблица общих значений удельной теплоемкости и теплоемкости
Эта таблица значений удельной теплоемкости и теплоемкости должна помочь вам лучше понять типы материалов, которые хорошо проводят тепло, а не те, которые этого не делают.Как и следовало ожидать, металлы имеют относительно низкую удельную теплоемкость.
| Материал | Удельная теплоемкость (Дж / г ° C) | Теплоемкость (Дж / ° C на 100 г) |
| золото | 0,129 | 12,9 |
| ртуть | 0,140 | 14,0 |
| медь | 0,385 | 38,5 |
| утюг | 0.450 | 45,0 |
| соль (Nacl) | 0,864 | 86,4 |
| алюминий | 0,902 | 90,2 |
| воздух | 1. 01 01 | 101 |
| лед | 2,03 | 203 |
| вода | 4,179 | 417,9 |
Источники
- Холлидей, Дэвид; Резник, Роберт (2013). Основы физики . Вайли. п. 524. , ,
- , , Киттель, Чарльз (2005). Введение в физику твердого тела (8-е изд.). Хобокен, Нью-Джерси, США: John Wiley & Sons. п. 141. ISBN 0-471-41526-X.
- Лейдер, Кейт Дж. (1993). Мир физической химии . Издательство Оксфордского университета. ISBN 0-19-855919-4.
- у А. Ценгеля и Майкла А. Болеса (2010). Термодинамика: инженерный подход (7-е издание).Макгроу-Хилл. ISBN 007-352932-X.
| Рассмотрим две сковороды, показанные ниже. | |||||
| Сковороды подобный тип, но другой размер. | |||||
Каждая кастрюля наполнена водой. | |||||
| Устанавливаются на нагреватели с одинаковым мощность. | |||||
| В какой кастрюле сначала закипит вода? (Не волнуйтесь, это не вопрос с подвохом…) | |||||
| Очевидно, меньшего размера. Это легко объяснить: | |||||
| Температура тела является мерой средняя кинетическая энергия частиц тела. | |||||
| Если оба тела получают энергию на та же ставка, то та, содержащая большее количество частицам потребуется больше времени, чтобы изменить температуру на заданный количество. | |||||
| Чтобы описать эту ситуацию, мы говорим, что большая кастрюля с водой имеет большую теплоемкость , чем поменьше. | |||||
| Определение: | |||||
| Теплоемкость тела количество энергии , необходимое для того, чтобы его температура сменить на 1С . | |||||
Следовательно, единицы тепловой мощности — JC -1 или JK -1 (помните, что
размер градуса одинаков по Цельсию и Кельвину
напольные весы). | |||||
| Теплоемкость кузов зависит от: | |||||
| 1. вещества это из | |||||
| 2. массы разные вещества в организме. | |||||
| Теплоемкость тела явно полезно знать цифру, однако представьте, что вы должны были сесть и напишите список теплоемкости всех тел, которые вы могли бы думать о… Думаю, это будет довольно длинный список! | |||||
| Еще полезнее будет список из которого можно было бы вычислить теплоемкости различных тел . | |||||
| Удельная теплоемкость Вещество (с) | |||||
| Рассматривая снова две кастрюли с водой. | |||||
| Предположим, что маленькая сковорода удерживает 1 кг воды, а больший вмещает 3 кг воды. | |||||
Разумно ожидать, что изменится
температура 3 кг воды на определенное количество потребует
в три раза больше энергии, чем изменение температуры
1 кг
воды. | |||||
| Мы предполагаем, что 1 кг воды всегда требуется такое же количество энергии, чтобы изменить свою температуру на заданная сумма. | |||||
| Теперь определим удельная теплоемкость вещества составляет: | |||||
| Удельная теплоемкость вещество — это количество энергии, необходимое для изменения температура 1кг вещество по 1С . | |||||
| Итак, агрегаты удельной теплоемкости грузоподъемность Джкг -1 C -1 или Jkg -1 K -1 | |||||
| Вполне разумно представить себе довольно исчерпывающий перечень из удельных теплоемкостей различных вещества , из которого мы можем затем рассчитать тепло вместимость любого тела мы можем найти (при условии, что мы также знаем массы разных веществ, конечно). | |||||
| Из этого определения имеем следующее полезное уравнение для расчета количества энергии Q, необходимой для изменить температуру ΔT данной массы m известного вещества: | |||||
| Сравнение Удельная теплоемкость различных веществ | |||||
Изменить температуру тела — значит
изменить среднюю кинетическую энергию его частиц. | |||||
| Частицы различных веществ имеют разной массы . | |||||
| Номер частиц в 1 кг вещество, очевидно, зависит от массы этих частиц . | |||||
| Это объясняет, почему разные вещества имеют разные удельные теплоемкости. | |||||
| Например, масса атома железа равна примерно в два раза больше массы атома алюминия. | |||||
| Итак, 1кг алюминий должен содержать примерно в два раза больше атомов , чем 1 кг утюг. | |||||
| Следовательно, можно ожидать, что удельная теплоемкость емкость алюминия примерно вдвое больше, чем у железа. | |||||
| |||||
. .. Я отдыхаю … .. Я отдыхаю … | |||||
| NB | |||||
| Удельная теплоемкость воды высокая по сравнению с большинством других веществ, c вода = (приблизительно) 4200Jkg -1 C -1 , это означает, что воде требуется единиц энергии для изменения его температура. | |||||
| Помните, что в следующий раз примете душ … |
14.2: Изменение температуры и теплоемкость
Одним из основных эффектов теплопередачи является изменение температуры: нагревание увеличивает температуру, а охлаждение снижает ее. Мы предполагаем, что фазового перехода нет и что система не выполняет никаких работ. Эксперименты показывают, что передаваемое тепло зависит от трех факторов: изменения температуры, массы системы, а также вещества и фазы вещества.
Рисунок \ (\ PageIndex {1} \): Тепло \ (Q \), передаваемое для изменения температуры, зависит от величины изменения температуры, массы системы, а также вещества и фазы. (а) Количество переданного тепла прямо пропорционально изменению температуры. Чтобы удвоить изменение температуры массы \ (m \), вам нужно добавить вдвое больше тепла. (б) Количество переданного тепла также прямо пропорционально массе. Чтобы вызвать эквивалентное изменение температуры в удвоенной массе, вам нужно добавить в два раза больше тепла. (c) Количество передаваемого тепла зависит от вещества и его фазы. Если требуется количество \ (Q \) тепла, чтобы вызвать изменение температуры \ (\ Delta T \) в данной массе меди, потребуется 10.В 8 раз больше тепла, чтобы вызвать эквивалентное изменение температуры в той же массе воды, при условии отсутствия фазовых изменений ни в одном из веществ.
(а) Количество переданного тепла прямо пропорционально изменению температуры. Чтобы удвоить изменение температуры массы \ (m \), вам нужно добавить вдвое больше тепла. (б) Количество переданного тепла также прямо пропорционально массе. Чтобы вызвать эквивалентное изменение температуры в удвоенной массе, вам нужно добавить в два раза больше тепла. (c) Количество передаваемого тепла зависит от вещества и его фазы. Если требуется количество \ (Q \) тепла, чтобы вызвать изменение температуры \ (\ Delta T \) в данной массе меди, потребуется 10.В 8 раз больше тепла, чтобы вызвать эквивалентное изменение температуры в той же массе воды, при условии отсутствия фазовых изменений ни в одном из веществ. Зависимость от изменения температуры и массы легко понять. В связи с тем, что (средняя) кинетическая энергия атома или молекулы пропорциональна абсолютной температуре, внутренняя энергия системы пропорциональна абсолютной температуре и количеству атомов или молекул. Благодаря тому, что переданное тепло равно изменению внутренней энергии, тепло пропорционально массе вещества и изменению температуры. Передаваемое тепло также зависит от вещества, так что, например, для повышения температуры требуется меньше тепла, чем для воды. Для одного и того же вещества передаваемое тепло также зависит от фазы (газ, жидкость или твердое тело).
Передаваемое тепло также зависит от вещества, так что, например, для повышения температуры требуется меньше тепла, чем для воды. Для одного и того же вещества передаваемое тепло также зависит от фазы (газ, жидкость или твердое тело).
Теплопередача и изменение температуры
Количественная связь между теплопередачей и изменением температуры включает все три фактора: \ [Q = mc \ Delta T, \], где \ (Q \) — символ теплопередачи, \ (m \) — масса вещества. , а \ (\ Delta T \) — изменение температуры.oC) \).
Значения удельной теплоемкости обычно нужно искать в таблицах, потому что нет простого способа их вычислить. Как правило, удельная теплоемкость также зависит от температуры. В таблице \ (\ PageIndex {1} \) перечислены типичные значения теплоемкости для различных веществ. За исключением газов, температурная и объемная зависимость удельной теплоемкости большинства веществ слабая. Из этой таблицы видно, что удельная теплоемкость воды в пять раз больше, чем у стекла и в десять раз больше, чем у железа, что означает, что требуется в пять раз больше тепла, чтобы поднять температуру воды на такую же величину, что и у стекла, и в десять раз больше. много тепла для повышения температуры воды, как для утюга.oC \).
много тепла для повышения температуры воды, как для утюга.oC \).
(а) Сколько тепла требуется? Какой процент тепла используется для повышения температуры (б) сковороды и (в) воды?
Стратегия
Кастрюля и вода всегда имеют одинаковую температуру. Когда вы ставите кастрюлю на плиту, температура воды и кастрюли
увеличился на такую же сумму. Мы используем уравнение теплопередачи для данного изменения температуры и массы воды и алюминия. Значения удельной теплоемкости воды и алюминия приведены в таблице \ (\ PageIndex {1} \).oC) = 27,0 кДж. \]
Обсуждение
В этом примере тепло, передаваемое контейнеру, составляет значительную долю от общего переданного тепла. Хотя вес кастрюли в два раза больше, чем у воды, удельная теплоемкость воды более чем в четыре раза больше, чем у алюминия. Следовательно, для достижения заданного изменения температуры воды требуется чуть более чем в два раза больше тепла по сравнению с алюминиевым поддоном.
Хотя вес кастрюли в два раза больше, чем у воды, удельная теплоемкость воды более чем в четыре раза больше, чем у алюминия. Следовательно, для достижения заданного изменения температуры воды требуется чуть более чем в два раза больше тепла по сравнению с алюминиевым поддоном.
Пример \ (\ PageIndex {2} \): Расчет повышения температуры в результате работы, проделанной с веществом: перегрев тормозов грузовика на спуске
Тормоза грузовика, используемые для управления скоростью на спуске, работают, преобразуя гравитационную потенциальную энергию в повышенную внутреннюю энергию (более высокую температуру) тормозного материала.oC \), если материал удерживает 10% энергии от грузовика массой 10 000 кг, спускающегося на 75,0 м (в вертикальном перемещении) с постоянной скоростью.
Стратегия
Если тормоза не применяются, потенциальная гравитационная энергия преобразуется в кинетическую энергию.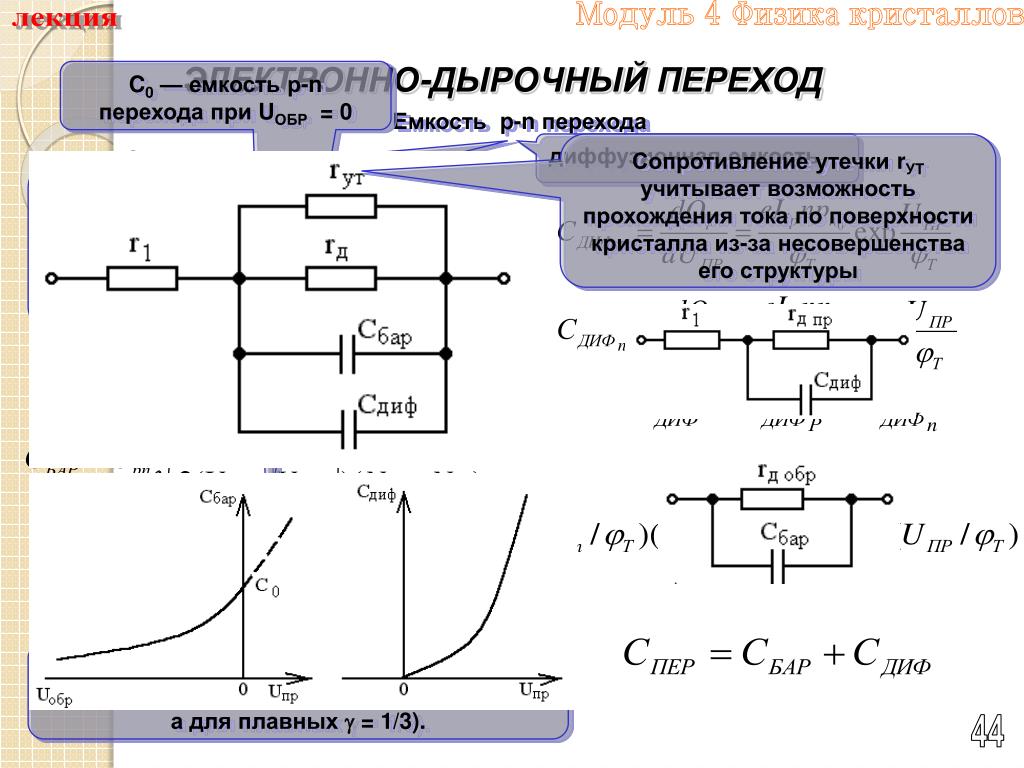 При срабатывании тормозов потенциальная гравитационная энергия преобразуется во внутреннюю энергию тормозного материала. Сначала мы вычисляем гравитационную потенциальную энергию \ ((Mgh) \), которую весь грузовик теряет при спуске, а затем находим повышение температуры, возникающее только в тормозном материале.oC. \]
При срабатывании тормозов потенциальная гравитационная энергия преобразуется во внутреннюю энергию тормозного материала. Сначала мы вычисляем гравитационную потенциальную энергию \ ((Mgh) \), которую весь грузовик теряет при спуске, а затем находим повышение температуры, возникающее только в тормозном материале.oC. \]
Обсуждение
Эта температура близка к температуре кипения воды. Если бы грузовик ехал какое-то время, то непосредственно перед спуском температура тормозов, вероятно, была бы выше температуры окружающей среды. Повышение температуры при спуске, скорее всего, приведет к повышению температуры тормозного материала выше точки кипения воды, поэтому этот метод нецелесообразен. Однако та же самая идея лежит в основе недавней гибридной технологии автомобилей, где механическая энергия (гравитационная потенциальная энергия) преобразуется тормозами в электрическую энергию (аккумулятор).° C \)
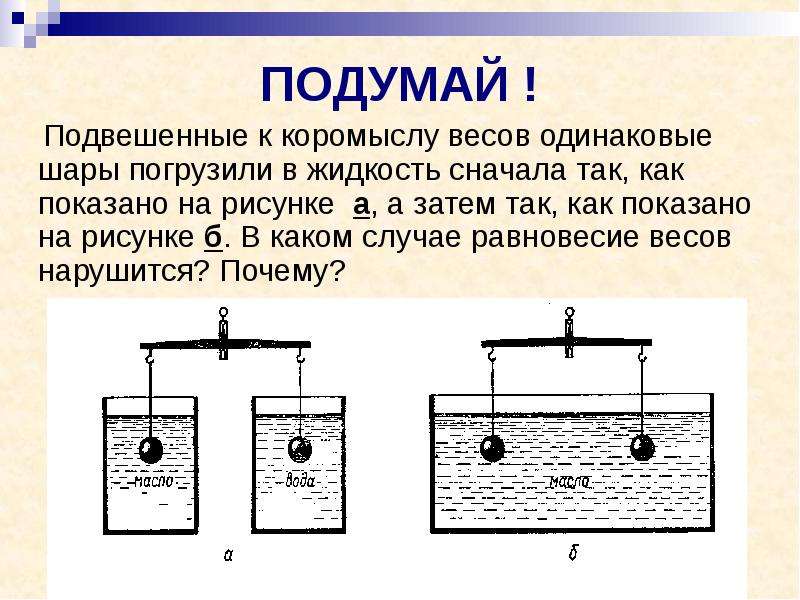 20
20 586
586 oC \). Предположим, что поддон стоит на изолированной подушке и выкипает незначительное количество воды. Какова температура, когда вода и поддон через короткое время достигают теплового равновесия?
oC \). Предположим, что поддон стоит на изолированной подушке и выкипает незначительное количество воды. Какова температура, когда вода и поддон через короткое время достигают теплового равновесия?Стратегия
Кастрюлю кладут на изолирующую подкладку, чтобы тепло не передавалось с окружающей средой. Изначально кастрюля и вода не находятся в тепловом равновесии: кастрюля имеет более высокую температуру, чем вода. Затем теплообмен восстанавливает тепловое равновесие, когда вода и поддон соприкасаются.Поскольку теплообмен между поддоном и водой происходит быстро, масса испарившейся воды ничтожна, а величина тепла, теряемого поддоном, равна теплу, полученному водой. Обмен тепла прекращается, когда достигается тепловое равновесие между кастрюлей и водой. Теплообмен можно записать как \ (| Q_ {hot} | = Q_ {cold}. \)
Решение
- Используйте уравнение теплопередачи \ (Q = mc \ Delta T \), чтобы выразить тепло, потерянное алюминиевой сковородой, через массу сковороды, удельную теплоемкость алюминия, начальную температуру сковороды и конечная температура: \ [Q_ {hot} = m_ {Al} c_ {Al} (T_f — 150 ° C).
 oC). \]
oC). \] - Переместите все термины, содержащие \ (T_f \), в левую часть, а все остальные термины — в правую. Решить относительно \ (T_f \),
\ (T_f = \ dfrac {m_ {Al} c_ {Al} (150ºC) + m_Wc_W (20,0ºC)} {m_ {Al} c_ {Al} + m_Wc_W} \),
и введите числовые значения:
\ (T_f = \ dfrac {(0,500 кг) (900 Дж / кгºC) (150ºC) + (0,250 кг) (4186 Дж / кгºC) (20,0ºC)} {(0,500 кг) (900 Дж / кгºC) + ( 0,250 кг) (4186 Дж / кгºC)} = \ dfrac {88430 Дж} {1496,5 Дж / ºC} = 59,1ºC. \)
Обсуждение
Это типичная проблема калориметрии — два тела при разных температурах приводят в контакт друг с другом и обмениваются теплом, пока не будет достигнута общая температура.Почему конечная температура намного ближе к 20,0ºC , чем к 150ºC ? Причина в том, что вода имеет большую удельную теплоемкость, чем большинство обычных веществ, и, следовательно, претерпевает небольшое изменение температуры при данной теплопередаче. Большой водоем, например озеро, требует большого количества тепла для значительного повышения температуры. Это объясняет, почему температура в озере остается относительно постоянной в течение дня, даже когда изменение температуры воздуха велико. Однако температура воды действительно меняется в течение длительного времени (например,г., с лета на зиму).
Большой водоем, например озеро, требует большого количества тепла для значительного повышения температуры. Это объясняет, почему температура в озере остается относительно постоянной в течение дня, даже когда изменение температуры воздуха велико. Однако температура воды действительно меняется в течение длительного времени (например,г., с лета на зиму).
ЭКСПЕРИМЕНТ НА ДОМУ: ИЗМЕНЕНИЕ ТЕМПЕРАТУРЫ ЗЕМЛИ И ВОДЫ
Что нагревается быстрее, земля или вода?
Для изучения разницы в теплоемкости:
- Поместите равные массы сухого песка (или почвы) и воды одинаковой температуры в две небольшие банки. (Средняя плотность почвы или песка примерно в 1,6 раза больше плотности воды, поэтому вы можете получить примерно равную массу, используя на \ (50% \) больше воды по объему.)
- Нагрейте и то, и другое (с помощью духовки или нагревательной лампы) одинаковое время.
- Запишите конечную температуру двух масс.
- Теперь доведите обе банки до одинаковой температуры, нагревая в течение более длительного периода времени.

- Снимите банки с источника тепла и измеряйте их температуру каждые 5 минут в течение примерно 30 минут.
Какой образец остывает быстрее всего? Эта деятельность воспроизводит явления, ответственные за дующий с суши и морской бриз.
Упражнение \ (\ PageIndex {1} \)
Если 25 кДж необходимо для повышения температуры блока с 25ºC до 30ºC , сколько тепла необходимо для нагрева блока с 45ºC до 50ºC ?
- Ответ
Теплопередача зависит только от разницы температур.Поскольку разница температур в обоих случаях одинакова, во втором случае необходимы те же 25 кДж.
Сводка
- Передача тепла \ (Q \), которая приводит к изменению \ (ΔT \) температуры тела с массой \ (m \), равна \ (Q = mcΔT \), где \ (c \) — удельная теплоемкость материала. Это соотношение также можно рассматривать как определение удельной теплоемкости.

Сноски
1 Значения для твердых веществ и жидкостей даны при постоянном объеме и при 25ºC , за исключением случаев, указанных выше.
2 Эти значения идентичны в единицах кал / г⋅ºC .
3 cv при постоянном объеме и 20,0 ° C , если не указано иное, при среднем давлении 1,00 атм. В скобках указаны значения \ (c_p \) при постоянном давлении 1,00 атм.
Глоссарий
удельная теплоемкостьколичество тепла, необходимое для изменения температуры 1,00 кг вещества на 1,00 ºC
Авторы и авторство
Пол Питер Урон (почетный профессор Калифорнийского государственного университета, Сакраменто) и Роджер Хинрикс (Государственный университет Нью-Йорка, колледж в Освего) с участвующими авторами: Ким Диркс (Университет Окленда) и Манджула Шарма (Университет Сиднея).Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.
 0).
0).
Изменение температуры и теплоемкость — College Physics
Цели обучения
- Наблюдать за теплопередачей, а также за изменением температуры и массы.
- Рассчитать конечную температуру после теплопередачи между двумя объектами.
Одним из основных эффектов теплопередачи является изменение температуры: нагрев увеличивает температуру, а охлаждение снижает ее.Мы предполагаем, что фазового перехода нет и что система не выполняет никаких работ. Эксперименты показывают, что передаваемое тепло зависит от трех факторов: изменения температуры, массы системы, а также вещества и фазы вещества.
Зависимость от изменения температуры и массы легко понять. В связи с тем, что (средняя) кинетическая энергия атома или молекулы пропорциональна абсолютной температуре, внутренняя энергия системы пропорциональна абсолютной температуре и количеству атомов или молекул.Благодаря тому, что переданное тепло равно изменению внутренней энергии, тепло пропорционально массе вещества и изменению температуры. Передаваемое тепло также зависит от вещества, так что, например, для повышения температуры требуется меньше тепла, чем для воды. Для одного и того же вещества передаваемое тепло также зависит от фазы (газ, жидкость или твердое тело).
Передаваемое тепло также зависит от вещества, так что, например, для повышения температуры требуется меньше тепла, чем для воды. Для одного и того же вещества передаваемое тепло также зависит от фазы (газ, жидкость или твердое тело).
Значения удельной теплоемкости обычно нужно искать в таблицах, потому что нет простого способа их вычислить.Как правило, удельная теплоемкость также зависит от температуры. (Рисунок) показывает типичные значения теплоемкости для различных веществ. За исключением газов, температурная и объемная зависимость удельной теплоемкости большинства веществ слабая. Из этой таблицы видно, что удельная теплоемкость воды в пять раз больше, чем у стекла и в десять раз больше, чем у железа, что означает, что требуется в пять раз больше тепла, чтобы поднять температуру воды на такую же величину, что и у стекла, и в десять раз больше. много тепла для повышения температуры воды, как для утюга.Фактически, вода имеет одну из самых высоких удельной теплоемкости из всех материалов, что важно для поддержания жизни на Земле.
Расчет необходимого тепла: нагрев воды в алюминиевой кастрюле
Алюминиевый поддон массой 0,500 кг на плите используется для нагрева 0,250 литров воды от до. а) Сколько тепла требуется? Какой процент тепла используется для повышения температуры (б) сковороды и (в) воды?
Стратегия
Кастрюля и вода всегда имеют одинаковую температуру.Когда вы ставите кастрюлю на плиту, температура воды и кастрюли повышается на одинаковую величину. Мы используем уравнение теплопередачи для данного изменения температуры и массы воды и алюминия. Значения удельной теплоемкости воды и алюминия приведены на (Рисунок).
Решение
Поскольку вода находится в тепловом контакте с алюминием, кастрюля и вода имеют одинаковую температуру.
- Рассчитайте разницу температур:
- Рассчитайте массу воды.Поскольку плотность воды равна, один литр воды имеет массу 1 кг, а масса 0,250 литра воды.
- Рассчитайте тепло, передаваемое воде.
 Используйте удельную теплоемкость воды в (рисунок):
Используйте удельную теплоемкость воды в (рисунок): - Рассчитайте тепло, передаваемое алюминию. Используйте удельную теплоемкость алюминия в (рисунок):
- Сравните процент тепла, поступающего в сковороду, и в воду. Сначала найдите общее переданное тепло:
Таким образом, количество тепла, идущего на нагревание сковороды, равно
., а на нагрев воды —
.Обсуждение
В этом примере тепло, передаваемое контейнеру, составляет значительную долю от общего переданного тепла.Хотя вес кастрюли в два раза больше, чем у воды, удельная теплоемкость воды более чем в четыре раза больше, чем у алюминия. Следовательно, для достижения заданного изменения температуры воды требуется чуть более чем в два раза больше тепла по сравнению с алюминиевым поддоном.
Дымящиеся тормоза этого грузовика — видимое свидетельство механического эквивалента тепла.
Расчет повышения температуры в результате работы, проделанной с веществом: перегрев тормозов грузовика на спуске
Тормоза грузовика, используемые для управления скоростью на спуске, работают, преобразуя гравитационную потенциальную энергию в повышенную внутреннюю энергию (более высокую температуру) тормозного материала. Это преобразование предотвращает преобразование потенциальной гравитационной энергии в кинетическую энергию грузовика. Проблема в том, что масса грузовика велика по сравнению с массой тормозного материала, поглощающего энергию, и повышение температуры может происходить слишком быстро, чтобы тепло передавалось от тормозов в окружающую среду.
Это преобразование предотвращает преобразование потенциальной гравитационной энергии в кинетическую энергию грузовика. Проблема в том, что масса грузовика велика по сравнению с массой тормозного материала, поглощающего энергию, и повышение температуры может происходить слишком быстро, чтобы тепло передавалось от тормозов в окружающую среду.
Рассчитайте повышение температуры 100 кг тормозного материала со средней удельной теплоемкостью, если материал удерживает 10% энергии от спускающегося грузовика массой 10 000 кг 75.0 м (при вертикальном перемещении) с постоянной скоростью.
Стратегия
Если тормоза не применяются, потенциальная гравитационная энергия преобразуется в кинетическую энергию. При срабатывании тормозов потенциальная гравитационная энергия преобразуется во внутреннюю энергию тормозного материала. Сначала мы вычисляем гравитационную потенциальную энергию, которую весь грузовик теряет при спуске, а затем находим повышение температуры, возникающее только в тормозном материале.
Решение
- Рассчитать изменение гравитационной потенциальной энергии при спуске грузовика
- Рассчитайте температуру по передаваемому теплу, используя и
где — масса тормозного материала.Вставьте значения и найдите
Обсуждение
Эта же идея лежит в основе новейшей гибридной технологии автомобилей, в которой механическая энергия (гравитационная потенциальная энергия) преобразуется тормозами в электрическую энергию (аккумулятор).
| Вещества | Удельная теплоемкость ( c ) | |
|---|---|---|
| Твердые тела | Дж / кг⋅ºC | ккал / кг⋅ºC 2 |
| Алюминий | 900 | 0. 215 215 |
| Асбест | 800 | 0,19 |
| Бетон, гранит (средний) | 840 | 0,20 |
| Медь | 387 | 0,0924 |
| Стекло | 840 | 0,20 |
| Золото | 129 | 0,0308 |
| Человеческое тело (в среднем при 37 ° C) | 3500 | 0,83 |
| Лед (в среднем, от -50 ° C до 0 ° C) | 2090 | 0.50 |
| Чугун, сталь | 452 | 0,108 |
| Свинец | 128 | 0,0305 |
| Серебро | 235 | 0,0562 |
| Дерево | 1700 | 0,4 |
| Жидкости | ||
| Бензол | 1740 | 0,415 |
| Этанол | 2450 | 0.586 |
| Глицерин | 2410 | 0,576 |
| Меркурий | 139 | 0,0333 |
| Вода (15,0 ° C) | 4186 | 1. 000 000 |
| Газы | ||
| Воздух (сухой) | 721 (1015) | 0,172 (0,242) |
| Аммиак | 1670 (2190) | 0,399 (0,523) |
| Двуокись углерода | 638 (833) | 0.152 (0,199) |
| Азот | 739 (1040) | 0,177 (0,248) |
| Кислород | 651 (913) | 0,156 (0,218) |
| Пар (100 ° C) | 1520 (2020) | 0,363 (0,482) |
Обратите внимание, что (Рисунок) иллюстрирует механический эквивалент тепла. В качестве альтернативы повышение температуры может быть произведено с помощью паяльной лампы, а не механически.
Расчет конечной температуры при передаче тепла между двумя телами: налив холодной воды в горячую кастрюлю
Допустим, вы налили 0.250 кг воды (около чашки) в алюминиевую кастрюлю массой 0,500 кг, снятую с плиты, и температуру Предположим, что поддон стоит на изолированной подушке и выкипает незначительное количество воды. Какова температура, когда вода и поддон через короткое время достигают теплового равновесия?
Какова температура, когда вода и поддон через короткое время достигают теплового равновесия?
Стратегия
Кастрюлю кладут на изолирующую подкладку, чтобы тепло не передавалось с окружающей средой. Изначально кастрюля и вода не находятся в тепловом равновесии: кастрюля имеет более высокую температуру, чем вода.Затем теплообмен восстанавливает тепловое равновесие, когда вода и поддон соприкасаются. Поскольку теплообмен между поддоном и водой происходит быстро, масса испарившейся воды ничтожна, а величина тепла, теряемого поддоном, равна теплу, полученному водой. Обмен тепла прекращается, когда достигается тепловое равновесие между кастрюлей и водой. Теплообмен можно записать как.
Решение
- Используйте уравнение теплопередачи, чтобы выразить тепло, теряемое алюминиевой сковородой, через массу сковороды, удельную теплоемкость алюминия, начальную температуру сковороды и конечную температуру:
- Выразите количество тепла, приобретаемое водой, через массу воды, удельную теплоемкость воды, начальную температуру воды и конечную температуру:
- Обратите внимание, что и и что они должны быть суммированы до нуля, потому что тепло, теряемое горячей сковородой, должно быть таким же, как тепло, полученное холодной водой:
- Поместите все термины с левой стороны, а все остальные термины с правой стороны.
 Решить,
Решить,и введите числовые значения:
Обсуждение
Это типичная проблема калориметрии — два тела при разных температурах приводят в контакт друг с другом и обмениваются теплом, пока не будет достигнута общая температура. Почему конечная температура намного ближе к? Причина в том, что вода имеет большую удельную теплоемкость, чем большинство обычных веществ, и, следовательно, претерпевает небольшое изменение температуры при данной теплопередаче.Большой водоем, например озеро, требует большого количества тепла для значительного повышения температуры. Это объясняет, почему температура в озере остается относительно постоянной в течение дня, даже когда изменение температуры воздуха велико. Однако температура воды действительно меняется в течение длительного времени (например, с лета на зиму).
Эксперимент на вынос: изменение температуры земли и воды
Что нагревается быстрее, земля или вода?
Для изучения разницы в теплоемкости:
Какой образец остывает быстрее всего? Эта деятельность воспроизводит явления, ответственные за дующий с суши и морской бриз.
Проверьте свое понимание
Если 25 кДж необходимо для повышения температуры блока от до, сколько тепла необходимо для нагрева блока от до?
Теплопередача зависит только от разницы температур. Поскольку разница температур в обоих случаях одинакова, во втором случае необходимы те же 25 кДж.
Концептуальные вопросы
Какие три фактора влияют на теплопередачу, необходимую для изменения температуры объекта?
Тормоза в автомобиле нагреваются при остановке со скорости.Насколько больше было бы, если бы машина изначально имела вдвое большую скорость? Вы можете предположить, что автомобиль останавливается достаточно быстро, чтобы не отводить тепло от тормозов.
Задачи и упражнения
В жаркий день температура в бассейне на 80 000 л повышается на. Какова чистая теплопередача при этом нагреве? Игнорируйте любые осложнения, такие как потеря воды из-за испарения.
Покажи это.
Для стерилизации стеклянной детской бутылочки на 50,0 г необходимо повысить ее температуру с до.Какая требуется теплопередача?
Одинаковая передача тепла идентичным массам разных веществ вызывает разные изменения температуры. Рассчитайте конечную температуру, когда 1,00 ккал тепла передается 1,00 кг следующих веществ, первоначально при: (а) воде; (б) бетон; (в) сталь; и (d) ртуть.
Потирание рук согревает их, превращая работу в тепловую энергию. Если женщина потирает руки взад и вперед в общей сложности 20 движений, на расстоянии 7.50 см на руб, а при средней силе трения 40,0 Н, что такое повышение температуры? Масса согреваемых тканей всего 0,100 кг, преимущественно в ладонях и пальцах.
Блок чистого материала массой 0,250 кг нагревается от до 4,35 кДж энергии. Вычислите его удельную теплоемкость и определите вещество, из которого он, скорее всего, состоит.
Предположим, что одинаковые количества тепла передаются различным массам меди и воды, вызывая одинаковые изменения температуры. Какое отношение массы меди к воде?
Какое отношение массы меди к воде?
(a) Количество килокалорий в пище определяется калориметрическими методами, при которых пища сжигается и измеряется теплопередача. Сколько килокалорий на грамм содержится в арахисе весом 5,00 г, если энергия его горения передается 0,500 кг воды, содержащейся в алюминиевой чашке весом 0,100 кг, вызывая повышение температуры? (b) Сравните свой ответ с информацией на этикетке, указанной на упаковке арахиса, и прокомментируйте, согласуются ли значения.
После интенсивных тренировок температура тела человека весом 80,0 кг составляет. С какой скоростью в ваттах человек должен передавать тепловую энергию, чтобы снизить температуру тела за 30,0 мин, если организм продолжает вырабатывать энергию со скоростью 150 Вт? .
Бассейн с радиоактивным отработавшим топливом на атомной электростанции. Отработанное топливо долгое время остается горячим. (кредит: Министерство энергетики США)
Сноски
- 1 Значения для твердых и жидких тел даны при постоянном объеме и при, если не указано иное.
 Разное
Разное

 Он измеряется в джоулях на Кельвин и выражается в.
Он измеряется в джоулях на Кельвин и выражается в. Он описывает, сколько тепла необходимо добавить к единице массы данного вещества, чтобы повысить его температуру на один градус Цельсия. Единицы измерения удельной теплоемкости — Дж / (кг ° C) или эквивалентно Дж / (кг · K).
Он описывает, сколько тепла необходимо добавить к единице массы данного вещества, чтобы повысить его температуру на один градус Цельсия. Единицы измерения удельной теплоемкости — Дж / (кг ° C) или эквивалентно Дж / (кг · K).




 oC). \]
oC). \]

 0).
0). Используйте удельную теплоемкость воды в (рисунок):
Используйте удельную теплоемкость воды в (рисунок): Решить,
Решить,