Закон Джоуля — Ленца — Википедия

Закон Джо́уля — Ле́нца — физический закон, дающий количественную оценку теплового действия электрического тока. Установлен в 1841 году Джеймсом Джоулем и независимо от него в 1842 году Эмилием Ленцем^[1].

В словесной формулировке звучит следующим образом^[2]:

Мощность тепла, выделяемого в единице объёма среды при протекании постоянного электрического тока, равна произведению плотности электрического тока на величину напряженности электрического поля.

Математически может быть выражен в следующей форме:

w=j→⋅E→=σE2,{\displaystyle w={\vec {j}}\cdot {\vec {E}}=\sigma E^{2},}

где w{\displaystyle w} — мощность выделения тепла в единице объёма, j→{\displaystyle {\vec {j}}} — плотность электрического тока, E→{\displaystyle {\vec {E}}} — напряжённость электрического поля, σ — проводимость среды, а точкой обозначено скалярное произведение.

Закон также может быть сформулирован в интегральной форме для случая протекания токов в тонких проводах^[3]:

Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивления участка.

В интегральной форме этот закон имеет вид

dQ=I2Rdt,{\displaystyle dQ=I^{2}Rdt,}

Q=∫t1t2I2Rdt,{\displaystyle Q=\int \limits _{t_{1}}^{t_{2}}I^{2}Rdt,}

где dQ{\displaystyle dQ} — количество теплоты, выделяемое за промежуток времени dt{\displaystyle dt}, I{\displaystyle I} — сила тока, R{\displaystyle R} — сопротивление, Q{\displaystyle Q} — полное количество теплоты, выделенное за промежуток времени от t1{\displaystyle t_{1}} до t2{\displaystyle t_{2}}. В случае постоянных силы тока и сопротивления:

Q=I2Rt.{\displaystyle Q=I^{2}Rt.}

Применяя закон Ома, можно получить следующие эквивалентные формулы:

Q=U2t/R =IUt.{\displaystyle Q=U^{2}t/R\ =IUt.}

Снижение потерь энергии[править | править код]

При передаче электроэнергии тепловое действие тока в проводах является нежелательным, поскольку ведёт к потерям энергии. Подводящие провода и нагрузка соединены последовательно, значит ток в сети I{\displaystyle I} на проводах и нагрузке одинаков. Мощность нагрузки и сопротивление проводов не должны зависеть от выбора напряжения источника. Выделяемая на проводах и на нагрузке мощность определяется следующими формулами

Qw=Rw⋅I2,{\displaystyle Q_{w}=R_{w}\cdot I^{2},}

Qc=Uc⋅I.{\displaystyle Q_{c}=U_{c}\cdot I.}

Откуда следует, что Qw=Rw⋅Qc2/Uc2{\displaystyle Q_{w}=R_{w}\cdot Q_{c}^{2}/U_{c}^{2}}. Так как в каждом конкретном случае мощность нагрузки и сопротивление проводов остаются неизменными и выражение Rw⋅Qc2{\displaystyle R_{w}\cdot Q_{c}^{2}} является константой, то тепло выделяемое на проводе обратно пропорционально квадрату напряжения на потребителе. Повышая напряжение мы снижаем тепловые потери в проводах. Это, однако, снижает электробезопасность линий электропередачи.

Выбор проводов для цепей[править | править код]

Тепло, выделяемое проводником с током, в той или иной степени выделяется в окружающую среду. В случае, если сила тока в выбранном проводнике превысит некоторое предельно допустимое значение, возможен столь сильный нагрев, что проводник может спровоцировать возгорание находящихся рядом с ним объектов или расплавиться сам. Как правило, при выборе проводов, предназначенных для сборки электрических цепей, достаточно следовать принятым нормативным документам, которые регламентируют выбор сечения проводников.

Электронагревательные приборы[править | править код]

Если сила тока одна и та же на всём протяжении электрической цепи, то в любом выбранном участке будет выделять тепла тем больше, чем выше сопротивление данного участка.

За счёт сознательного увеличения сопротивления участка цепи можно добиться локализованного выделения тепла в этом участке. По этому принципу работают

электронагревательные приборы. В них используется нагревательный элемент — проводник с высоким сопротивлением. Повышение сопротивления достигается (совместно или по отдельности) выбором сплава с высоким удельным сопротивлением (например, нихром, константан), увеличением длины проводника и уменьшением его поперечного сечения. Подводящие провода имеют обычное низкое сопротивление и поэтому их нагрев, как правило, незаметен.

Плавкие предохранители[править | править код]

Для защиты электрических цепей от протекания чрезмерно больших токов используется отрезок проводника со специальными характеристиками. Это проводник относительно малого сечения и из такого сплава, что при допустимых токах нагрев проводника не перегревает его, а при чрезмерно больших перегрев проводника столь значителен, что проводник расплавляется и размыкает цепь.

ru.wikipedia.org

Закон Джоуля-Ленца: определение, формула, применение

Мы ежедневно пользуемся электронагревательными приборами, не задумываясь, откуда берётся тепло. Разумеется, вы знаете, что тепловую энергию вырабатывает электричество. Но как это происходит, а тем более, как оценить количество выделяемого тепла, знают не все. На данный вопрос отвечает закон Джоуля-Ленца, обнародованный в позапрошлом столетии.

В 1841 году усилия английского физика Джоуля, а в 1842 г. исследования русского учёного Ленца увенчались открытием закона, применение которого позволяет количественно оценить результаты теплового действия электрического тока [ 1 ]. С тех пор изобретено множество приборов, в основе которых лежит тепловое действие тока. Некоторые из них, изображены на рис. 1.

Рис. 1. Тепловые приборы

Определение и формула

Тепловой закон можно сформулировать и записать в следующей редакции: «Количество тепла, выработанного током, прямо пропорционально квадрату приложенного к данному участку цепи тока, сопротивления проводника и промежутка времени, в течение которого электричество действовало на проводник».

Обозначим символом Q количество выделяемого тепла, а символами I, R и Δt – силу тока, сопротивление и промежуток времени, соответственно. Тогда формула закона Джоуля-Ленца будет иметь вид: Q = I²*R*Δt

Согласно законам Ома I=U/R, откуда R = U/I. Подставляя выражения в формулу Джоуля-Ленца получим: Q = U²/R * Δt ⇒ Q = U*I*Δt.

Выведенные нами формулы – различные формы записи закона Джоуля-Ленца. Зная такие параметры как напряжение или силу тока, можно легко рассчитать количество тепла, выделяемого на участке цепи, обладающем сопротивлением R.

Дифференциальная форма

Чтобы перейти к дифференциальной форме закона, проанализируем утверждение Джоуля-Ленца применительно к электронной теории. Приращение энергии электрона ΔW за счёт работы электрических сил поля равно разности энергий электрона в конце пробега (m/2)*(u=υ_max)² и в начале пробега (mu²)/2 , то есть

Здесь u – скорость хаотического движение (векторная величина), а

υ_max – максимальная скорость электрического заряда в данный момент времени.

Поскольку установлено, что скорость хаотического движения с одинаковой вероятностью совпадает с максимальной (по направлению и в противоположном направлении), то выражение 2*u*υ_max в среднем равно нулю. Тогда полная энергия, выделяющаяся при столкновениях электронов с атомами, образующими узлы кристаллической решётки, составляет:

Это и есть закон Джоуля-Ленца, записанный в дифференциальной форме. Здесь γ – согласующий коэффициент, 

E – напряжённость поля.

Интегральная форма

Предположим, что проводник имеет цилиндрическую форму с сечением S. Пусть длина этого проводника составляет l. Тогда мощность P, выделяемая в объёме V= lS составляет:

гдеR – полное сопротивление проводника.

Учитывая, чтоU = I×R, из последней формулы имеем:

• P = U×I;
• P = I²R;
• P = U²/R.

Если величина тока со временем меняется, то количество теплоты вычисляется по формуле:

Данное выражение, а также вышеперечисленные формулы, которые можно переписать в таком же виде, принято называть интегральной формой закона Джоуля-Ленца.

Формулы очень удобны при вычислении мощности тока в нагревательных элементах. Если известно сопротивление такого элемента, то зная напряжение бытовой сети легко определить мощность прибора, например, электрочайника или паяльника.

Физический смысл

Вспомним, как электрический ток протекает по металлическому проводнику. Как только электрическая цепь замкнётся, то под действием ЭДС движение свободных электронов упорядочивается, и они устремляются к положительному полюсу источника питания. Однако на их пути встречаются стройные ряды кристаллических решёток, атомы которых создают препятствия упорядоченному движению, то есть оказывают сопротивление.

На преодоление сопротивления уходит часть энергии движущихся электронов. В соответствии с фундаментальным законом сохранения энергии, она не может бесследно исчезнуть. Она-то и превращается в тепло, вызывающее нагревание проводника. Накапливаемая тепловая энергия излучается в окружающее пространство или нагревает другие предметы, соприкасающиеся с проводником.

На рисунке 2 изображёна схема опыта, демонстрирующего закон теплового действия тока, разогревающего участок провода в электрической цепи.

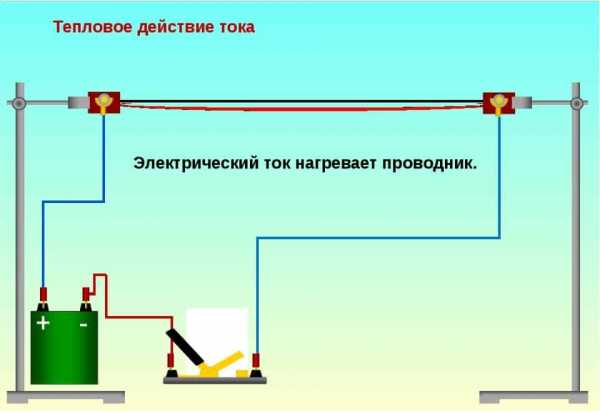Рис. 2. Тепловое действие тока

Явление нагревания проводников было известно практически с момента получения электротока, но исследователи не могли тогда объяснить его природу, и тем более, предложить способ оценки количества выделяемого тепла. Эту проблему решает закон  Джоуля-Ленца, которым мы пользуемся по сегодняшний день.

Практическая польза закона Джоуля-Ленца

При сильном нагревании можно наблюдать излучение видимого спектра света, что происходит, например, в лампочке накаливания. Слабо нагретые тела тоже излучают тепловую энергию, но в диапазоне инфракрасного излучения, которого мы не видим, но можем ощутить своими тепловыми рецепторами.

Допускать сильное нагревание проводников нельзя, так как чрезмерная температура разрушает структуру металла, проще говоря – плавит его. Это может привести к выводу из строя электрооборудования, а также стать причиной пожара. Для того, чтобы не допустить критических параметров нагревания необходимо делать расчёты тепловых элементов, пользуясь формулами, описывающими закон Джоуля-Ленца.

Проанализировав выражение U²/R убеждаемся, что когда сопротивление стремится к нулю, то количество выделенного тепла стремится к бесконечности. Такая ситуация возникает при коротких замыканиях. В это основная опасность КЗ.

В борьбе с короткими замыканиями используют:

• автоматические выключатели:
• электронные защитные блоки;
• плавкие предохранители;
• другие защитные устройства.

Применение и практический смысл

Непосредственное превращение электричества в тепловую энергию нельзя назвать экономически выгодным. Однако, с точки зрения удобства и доступности современного человечества к источникам электроэнергии различные нагревательные приборы продолжают массово применяться как в быту, так и на производстве.

Перечислим некоторые из них:

• электрочайники;
• утюги;
• фены;
• варочные плиты;
• паяльники;
• сварочные аппараты и многое другое.

На рисунке 3 изображены бытовые нагревательные приборы, которыми мы часто пользуемся.

Рис. 3. Бытовые нагревательные приборы

Использование тепловых мощностей в химической, металлургической и в других промышленных отраслях тесно связно с использованием электрической энергии.

Без знания физического закона Джоуля-Ленца было бы невозможно сконструировать безопасный нагревательный прибор. Для этого нужны расчёты, которые невозможно сделать без применения рассмотренных нами формул. На основе расчётов происходит выбор материалов с нужным удельным сопротивлением, влияющим на нагревательную способность устройств.

Закон Джоуля-Ленца без преувеличения можно назвать гениальным. Это один из тех законов, которые повлияли на развитие электротехники.

www.asutpp.ru

Закон Джоуля-Ленца и его применение

Закон Джоуля-Ленца и его применение

Раздел ОГЭ по физике: 3.9.Закон Джоуля-Ленца
Раздел ЕГЭ по физике: 3.2.8. Работа электрического тока. Закон Джоуля–Ленца

---

---

Рассмотрим Закон Джоуля-Ленца и его применение.

При прохождении электрического тока по проводнику он нагревается. Это происходит потому, что перемещающиеся под действием электрического поля свободные электроны в металлах и ионы в растворах электролитов сталкиваются с молекулами или атомами проводников и передают им свою энергию. Таким образом, при совершении током работы увеличивается внутренняя энергия проводника, в нём выделяется некоторое количество теплоты, равное работе тока, и проводник нагревается: Q = А или Q = IUt. Учитывая, что U = IR, в результате получаем формулу:

Q = I²Rt , где

Q — количество выделяемой теплоты (в Джоулях)
I — сила тока (в Амперах)
R — сопротивление проводника (в Омах)
t — время прохождения (в секундах)

♦ Закон Джоуля–Ленца: количество теплоты, выделяемое проводником с током, равно произведению квадрата силы тока, сопротивления проводника и времени прохождения тока.

В XIX в. независимо друг от друга англичанин Д. Джоуль и россиянин Э. Ленц изучали нагревание проводников при прохождении электрического тока и опытным путём обнаружили закономерность: количество теплоты, выделяющееся при прохождении тока по проводнику, равно произведению квадрата силы тока, сопротивления проводника и времени: Q = I²Rt  (в случае постоянных силы тока и сопротивления). Эту закономерность называют законом Джоуля-Ленца. Данный закон дает количественную оценку теплового действия электрического тока.

Применяя закон Ома, можно получить эквивалентные формулы: Q = IUt,  Q= U²t/R

 

---

 

Где применяется закон Джоуля-Ленца ?

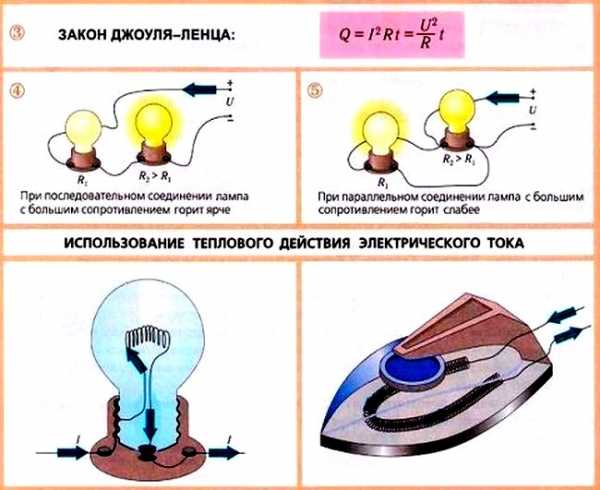
1. Например, в лампах накаливания и в электронагревательных приборах применяется закон Джоуля-Ленца. В них используют нагревательный элемент, который является проводником с высоким сопротивлением. За счет этого элемента можно добиться локализованного выделения тепла на определенном участке. Выделение тепла будет появляться при повышении сопротивления, увеличении длины проводника, выбором определенного сплава.

2. Одной из областей применения закона Джоуля-Ленца является снижение потерь энергии. Тепловое действие силы тока ведет к потерям энергии. При передаче электроэнергии, передаваемая мощность линейно зависит от напряжения и силы тока, а сила нагрева зависит от силы тока квадратично, поэтому если повышать напряжение, при этом понижая силу тока перед подачей электроэнергии, то это будет более выгодно. Но повышение напряжения ведет к снижению электробезопасности. Для повышения уровня электробезопасности повышают сопротивление нагрузки соответственно повышению напряжения в сети.

3. Также закон Джоуля-Ленца влияет на выбор проводов для цепей. Потому что при неправильном подборе проводов возможен сильный нагрев проводника, а также его возгорание. Это происходит когда сила тока превышает предельно допустимые значения и выделяется слишком много энергии.

Нагревание проводов является вредным, поскольку приводит к потерям электроэнергии при передаче ее от источника к потребителю. Для уменьшения этих потерь силу тока уменьшают, повышая напряжение источника с тем, чтобы передаваемая мощность осталась прежней. Чтобы избежать электрического пробоя изоляции проводов, их поднимают на большую высоту на мачтах высоковольтных линий электропередач, связывающих крупные электростанции с городами и поселками, отстоящими от них на десятки и сотни километров.

---

Вы смотрели конспект урока физики в 8 классе «Закон Джоуля-Ленца и его применение».
Выберите дальнейшие действия:

 

uchitel.pro

Закон Джоуля – Ленца: определение, формула, физический смысл

Закон Джоуля – Ленца – закон физики, определяющий количественную меру теплового действия электрического тока. Сформулирован этот закон был в 1841 году английским учёным Д. Джоулем и совершенно отдельно от него в 1842 году известным русским физиком Э. Ленцем. Поэтому он получил своё двойное название — закон Джоуля – Ленца.

Определение закона и формула

Словесная формулировка имеет следующий вид: мощность тепла, выделяемого в проводнике при протекании сквозь него электрического тока, пропорционально произведению значения плотности электрического поля на значение напряженности.

Математически закон Джоуля — Ленца выражается следующим образом:

ω = j • E = ϭ E²,

где ω — количество тепла, выделяемого в ед. объема;

E и j – напряжённость и плотность, соответственно, электрического полей;

σ — проводимость среды.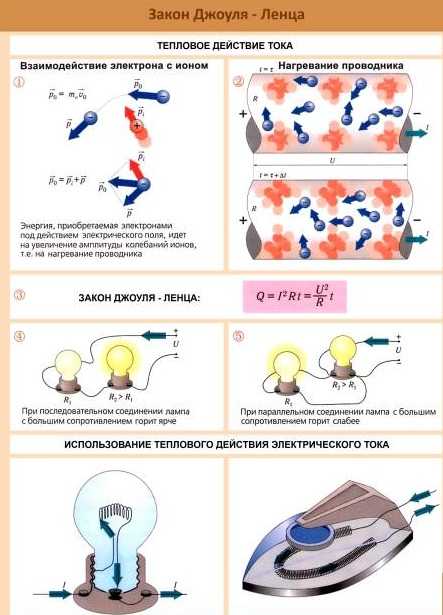

Физический смысл закона Джоуля – Ленца

Закон можно объяснить следующим образом: ток, протекая по проводнику, представляет собой перемещение электрического заряда под воздействием электрического поля. Таким образом, электрическое поле совершает некоторую работу. Эта работа расходуется на нагрев проводника.

Другими словами, энергия переходит в другое свое качество – тепло.

Но чрезмерный нагрев проводников с током и электрооборудования допускать нельзя, поскольку это может привести к их повреждению. Опасен сильный перегрев при коротких замыканиях проводов, когда по проводниках могут протекать достаточно большие токи.

В интегральной форме для тонких проводников закон Джоуля – Ленца звучит следующим образом: количество теплоты, которое выделяется в единицу времени в рассматриваемом участке цепи, определяется как произведение квадрата силы тока на сопротивление участка.

Математически эта формулировка выражается следующим образом:

Q = ∫ k • I² • R • t,

при этом Q – количество выделившейся теплоты;

I – величина тока;

R — активное сопротивление проводников;

t – время воздействия.

Значение параметра k принято называть тепловым эквивалентом работы. Величина этого параметра определяется в зависимости от разрядности единиц, в которых выполняются измерения значений, используемых в формуле.

Закон Джоуля-Ленца имеет достаточно общий характер, поскольку не имеет зависимости от природы сил, генерирующих ток.

Из практики можно утверждать, что он справедлив, как для электролитов, так проводников и полупроводников.

Область применения

Областей применения в быту закона Джоуля Ленца – огромное количество. К примеру, вольфрамовая нить в лампе накаливания, дуга в электросварке, нагревательная нить в электрообогревателе и мн. др. Это наиболее широко распространенный физический закон в повседневной жизни.

pue8.ru

Нагревание проводников электрическим током. Закон Джоуля-Ленца (Гребенюк Ю.В.)

Этот урок посвящён изучению теплового действия электрического тока. Мы проведём ряд опытов, демонстрирующих зависимость количества теплоты от силы тока и сопротивления, а также  рассмотрим закон Джоуля – Ленца

Мы уже знаем, что при прохождении тока через электрическую лампочку её спираль нагревается и излучает видимый свет. Таким образом, мы наблюдаем тепловое действие электрического тока. Благодаря этому действию, нагреваются, например, утюг или чайник. Но при работе вентилятора или пылесоса практически не наблюдается тепловое действие, также в нормальном состоянии слабо греются провода. На этом уроке, тема которого: «Нагревание проводников электрическим током. Закон Джоуля – Ленца», мы определим, от чего зависит тепловое действие электрического тока.

Факт нагрева проводника при протекании по нему тока объясняется тем, что во время движения заряженных частиц под действием электрического поля они сталкиваются с частицами проводника, в результате часть энергии передаётся этим частицам проводника, то есть средняя скорость хаотического (теплового) движения частиц проводника увеличивается, и проводник нагревается. По закону сохранения энергии кинетическая энергия свободных заряженных частиц, приобретённая под действием электрического поля, превратится во внутреннюю энергию проводника. Следовательно, можно предположить:

1. чем больше сопротивление проводника, тем больше тепла выделяется при прохождении электрического тока по проводнику, то есть количество теплоты, которое выделяется в проводнике при прохождении по нему электрического тока, прямо пропорционально сопротивлению проводника;

2. количество теплоты, выделяемое в проводнике при прохождении по нему электрического тока, зависит от силы тока (чем больше сила тока, тем большее количество свободных частиц проходит через сечение проводника в единицу времени, происходит больше столкновений, следовательно, больше энергии передаётся частицам проводника).
Можно подтвердить данные предположения с помощью опытов.

Соберём электрическую цепь, в которой последовательно с источником тока подключены два нагревателя с разными сопротивлениями, которые опущены в калориметры (прибор для измерения количества теплоты) с одинаковым количеством воды при одинаковой температуре. При прохождении электрического тока через нагреватели будет наблюдаться повышение температуры воды, причём вода будет нагреваться быстрее в том калориметре, в который помещён нагреватель с бльшим сопротивлением (см. Рис. 1). То есть подтверждается предположение 1.

Для подтверждения предположения 2 соберём электрическую цепь, в которой последовательно к источнику тока подключен амперметр, лампочка накаливания и реостат. Регулируя сопротивление реостата, меняем силу тока в цепи при постоянном напряжении. При увеличении силы тока увеличивается яркость лампочки (см. Рис. 2), то есть увеличивается количество теплоты, которое выделяет нить накаливания.

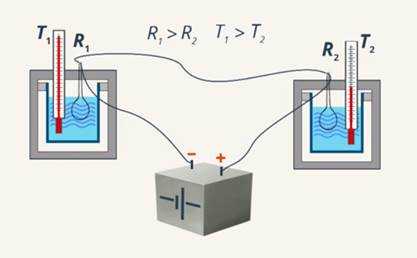
Рис. 1. Нагреватель с бльшим сопротивлением нагревает воду быстрее

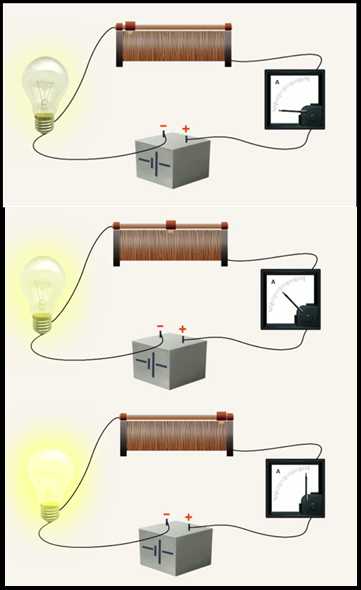
Рис. 2. Увеличение яркости лампочки при увеличении силы тока    

Тепловое действие тока опытным путём независимо друг от друга изучали английский учёный Джоуль и русский учёный Ленц. Они пришли к выводу, который впоследствии назвали закон Джоуля – Ленца: количество теплоты, выделяющееся при прохождении тока в проводнике, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока:

,

где  – количество теплоты, I – сила тока, R – сопротивление проводника, t – время прохождения тока.

Закон Джоуля – Ленца был получен экспериментально, но так как мы знаем формулу для работы электрического тока (), то сможем вывести его с помощью несложных математических вычислений. Если на участке цепи, в котором течёт электрический ток, не выполняется механическая работа и не происходят химические реакции, то результатом работы электрического тока будет нагревание проводника. В результате этого нагревания проводник будет отдавать тепло окружающим телам. Следовательно, в данном случае, согласно закону сохранения энергии, количество выделенной теплоты () будет равно работе тока (A). Зная формулу для работы тока и напряжения, получим следующие преобразования:

 

Если сила тока неизвестна, а известно напряжение на концах участка цепи, то, воспользовавшись законом Ома, получаем:

 

Формулы  и   можно использовать только тогда, когда вся работа электрического тока расходуется только на нагревание. Если на участке цепи есть потребители энергии, в которых выполняется механическая работа или происходят химические реакции, эти формулы использовать нельзя (в таких случаях применяются сложные математические расчёты).

На этом уроке мы узнали о том, что прохождение тока в проводнике сопровождается выделением тепла, при этом количество теплоты, выделяющееся при прохождении тока в проводнике, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока. Таким образом, мы сформулировали закон Джоуля – Ленца.

По проводнику сопротивлением R течёт ток I. Как изменится количество теплоты, выделяющееся в проводнике в единицу времени, если его сопротивление увеличить в два раза, а силу тока уменьшить в два раза? Варианты ответа: а) увеличится в два раза; б) уменьшится в два раза; в) не изменится; г) уменьшится в восемь раз.

Решение

Воспользуемся законом Джоуля – Ленца:

 

Количество теплоты, выделяющееся в проводнике в единицу времени, равно:

 

Так как сопротивление увеличивается в два раза, а сила тока уменьшается в два раза:

 

 

Следовательно, новое значение количества теплоты будет равно:

 

  

Ответ: б) уменьшится в два раза

Ещё в 1832-1833-х годах Эмилий Христианович Ленц обратил внимание на то, что проводимость проводника сильно зависит от его нагревания, это осложняло расчёты электрических цепей, так как не представлялось возможным вычислить зависимость тока от теплоты, которую он выделяет.

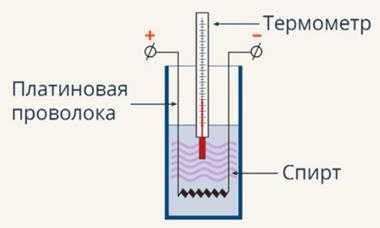
Рис. 3. Опыт Ленца

Ленц сконструировал специальный прибор-сосуд, служивший для измерения количества тепла, выделявшегося в проволоке. В сосуд учёный заливал разбавленный спирт (спирт обладает меньшей электропроводностью, чем вода, которую использовал в своих опытах Джеймс Джоуль). В раствор спирта помещалась платиновая проволока, через которую пропускался электрический ток (см. Рис. 3). Была произведена большая серия опытов, в которых Ленц замерял время, затраченное на нагревание раствора на . Получив достаточное количество убедительных данных, в 1843 году учёный опубликовал закон: «нагревание проволоки гальваническим током пропорционально квадрату служащего для нагревания тока». Однако аналогичный закон уже был опубликован Джоулем в 1841 году, но Ленц вполне обоснованно обратил внимание на то, что англичанин провёл свои эксперименты с большим количеством погрешностей. Именно поэтому закон о тепловом действии тока был назван в честь двух выдающихся учёных.

Задача 1

Определите длину нихромового провода, с площадью сечения 0,25 , из которого изготовлен нагреватель электрического чайника. Чайник питается от сети напряжением 220 В и нагревает 1,5 литра воды от  до  за 10 минут. КПД чайника составляет .

Дано: ; ; ; ; ; ;  – теплоёмкость воды;  – плотность воды;  – удельное сопротивление нихрома;  

Найти:l

Решение

Так как вся электрическая энергия идёт на нагревание воды, то воспользуемся законом Джоуля – Ленца:

 

Отсюда сопротивление проводника (н

interneturok.ru

формулировка закона, расчет теплоты по формуле i2rt

Одной из основополагающих, теоретически и практически значимых закономерностей физики можно смело назвать закон Джоуля Ленца, который англичанин Дж. Джоуль и россиянин Э.Х. Ленц вывели примерно в одно время (в 1840-1841 годах), однако при этом, не работая совместно.

Авторы закона: Джеймс Джоуль и Эмилий Ленц

Как был открыт закон

Оба физика проводили множество экспериментов, в которых главным действующим прибором был калориметр. Агрегат представлял собой устройство, изолированное от теплопотерь, у которого была измерена и зафиксирована теплоемкость. Калориметр был оснащен термометром, в него также вставлялся проводник с определенным электросопротивлением.

В результате опытов физики заметили, что при подключении проводника к электропитанию начинает выделяться тепло.

Воспроизведение опытов, с помощью которых была сформулирована закономерность Джоуля-Ленца

Джоуль проводил эти исследования в рамках изучения закона сохранения энергии. Он хотел оценить, какова величина механической энергии, давшей полученное количество теплоты. Для этого к динамо-машине, вращавшей ротор для выработки электричества, он привязывал некий груз и делал вывод, что разница между механической энергией груза в поле и вне поля тяготения и есть искомая величина. Англичанин доказал, что сделанные им выводы о преобразовании энергии применимы и для электролитических растворов.

Опыты Ленца более точные. Он определил, что открытая им закономерность не действует, если проводники двигаются, когда через них течет электроток (они называются проводники второго типа), такие как индуктивная катушка, находящаяся внутри электромотора.

Суть теплового закона

В проводнике, являющимся активным сопротивлением, по которому пропускается постоянное электричество, имеется электрическое поле, в котором упорядоченно протекают заряженные частицы. Электрофизические силы, присущие ему, оказывают воздействие на электроны, что имеет определение «работа тока» (Aэл.). Та работа, которая замеряется в единицу времени (как правило, час), считается мощностью тока (Nэл.). Обозначенные электромеханические показатели измеряются при помощи приборов: амперметра, вольтметра и ваттметра. Эти 2 понятия: работа и мощность тока, формируют закон Джоуля Ленца.

Работа тока на подключенном участке преобразовывает электроэнергию во внутреннюю. Это происходит за счет того, что свободные электроны натыкаются на нейтральные молекулы (лишенные электронов) проводника, и присущая им механическая энергия превращается в тепловую. Она способствует увеличению температуры проводника. Согласуясь со всемирным законом сохранения энергии, тот объем тепла (q) приравнивается к работе тока.

Всякое преодоление сопротивления неизбежно сопровождается затратами энергии. Если, к слову, что-то тяжелое приходится тянуть, преодолевая силу трения, то работа по ее преодолению становится теплом. В случае с током и полупроводником электросопротивление выступает в роли трения.

Российский и английский ученые пришли к выводу, что количество теплоты q, получаемое в полупроводнике при прохождении постоянного тока, прямо пропорционально величине тока (I), возведенной во вторую степень, и тому времени (t), что ток пропускался по проводнику, испытывая сопротивление (R).

Знаменитый закон Лжоуля Ленца можно описать формулой:

Q =I2Rt.

Это закономерность – закон Джоуля-Ленца, применимый на однородном участке электроцепи. При этом количество тепла q может вычисляться в Джоулях (если сила тока равна 1) и в малых калориях (если сила тока 0,24). Малая калория – это количество тепла, расходуемое на нагрев 1 грамма воды на один градус.

Интегральная и дифференциальная формулы закона

Если обратить внимание на величину, представляющую разность внутренней энергии проводника за время прохождения по нему тока, можно заметить, что постепенно при нагревании эта энергия будет увеличиваться. Следуя закону Ньютона, можно предположить, что увеличится и мощность отдачи тепла q проводником. Через определенный промежуток времени температура полупроводника зафиксируется и перестанет расти. В это время внутренняя энергия перестанет меняться, и значение «дельта U» станет равно нулю. В таком равновесии формулировка 1-го термодинамического закона будет следующей:

A = – Q, т.е. работа тока полностью переходит в тепло.

Основываясь на этом выводе, можно представить тепловую закономерность Джоуля Ленца в несколько другом виде, а именно в ее интегральном и дифференциальном видах.

Закон Джоуля Ленца в интегральной и дифференциальной формах

Формула интегрального закона Джоуля-Ленца справедлива при любых данных, поэтому она считается законом. Другие же формулировки типа:

q=I*Ut и q=u2/R*t

работают лишь при определенных условиях, и их нельзя считать законом.

Дополнительная информация. Если углубляться в теорию и проводить дальнейшие расчеты, то можно вывести и другие формы данного теплового закона.

Теоретическая значимость

Открытие двух знаменитых физиков стало заметной вехой на пути к исследованию и всемирному принятию закона сохранения энергии. Благодаря ему, сегодня общеизвестно, что и тепло, и электроток, и движение механических частиц – есть формы материи, обладающие своей энергией, которую можно измерить. Закон Джоуля-Ленца (и последующие работы Джоуля) помогли установить соответствия для электрического, механического и теплового вида энергии и определить переводные соотношения между единицами различных видов (калории и джоули). Тепловая закономерность применяется и в разработке теории тока в металлах.

Обратите внимание! Поскольку тепло всегда вырабатывается в проводнике, находящемся под электрическим током, может случиться его перегрев и, как следствие, выход из строя электрических устройств. Особенно опасным явлением является короткое замыкание, когда сопротивление проводников стремится к нулю, ток становится очень сильным, соответственно, выделяется огромное количество тепла, приводящее к аварийным состояниям.

Чрезмерное выделение тепловой энергии при коротком замыкании

С помощью закона Джоуля-Ленца можно рассчитать оптимальную силу электротока, чтобы предотвратить перегрев проводников.

Попробуйте сформулируйте положение о том, как электричество переходит в тепло? Англичанину Джоулю и россиянину Ленцу это блестяще удалось: в открытом ими тепловом законе, гласящем, что электрический ток, проходящий по проводнику, выделяет тепло, равное работе электрических сил. Это наблюдение оказало большое влияние на дальнейшее развитие физики как науки.

Видео

Оцените статью:

jelectro.ru

Закон Джоуля — Ленца — Вікіпедія

Матеріал з Вікіпедії — вільної енциклопедії.

Закон Джо́уля — Ле́нца — фізичний закон, що дає кількісну оцінку теплової дії електричного струму. Закон був експериментально встановлений у 1840 році англійським фізиком Джеймсом Прескоттом Джоулем і незалежно від нього російським вченим Еміліем Ленцом в 1842 році^[1].

Фізичною природою виділення тепла при проходженні струму через провідник є те, що потенціальна енергія носіїв заряду, які подолали ділянку кола зменшується, а кінетична енергія залишається в середньому однаковою на початку й у кінці шляху. Втрачена носіями заряду енергія дисипує, тобто передається коливанням атомів провідника і переходить у тепло.

Формулювання закону звучить наступним чином:

Кількість теплоти, що виділяється в провіднику зі струмом, пропорційна силі струму, напрузі і часу проходження струму через провідник.

Математичний запис закону:

Q=IUt{\displaystyle Q=IUt},

де I{\displaystyle I} — сила струму, U{\displaystyle U} — cпад напруги на ділянці кола, t{\displaystyle t} — час проходження струму.

Застосувавши закон Ома для ділянки кола, закон Джоуля-Ленца можна записати як

Q=I2Rt{\displaystyle Q=I^{2}Rt},

де R{\displaystyle R} — опір провідника.

Закон Джоуля-Ленца в диференційній формі[ред. | ред. код]

Закон Джоуля-Ленца можна записати також для елементарного об’єму провідника dV=ds⋅dl{\displaystyle \!dV=ds\cdot dl}, в якому за час dt{\displaystyle dt} виділятиметься теплота:

dQ=(dI)2RdVdt{\displaystyle \!dQ=(dI)^{2}R_{dV}{dt}}

де RdV{\displaystyle \!R_{dV}} — опір елементарного об’єму, а dI{\displaystyle dI} — елементарна сила струму, що протікає через елемент поверхні площею ds{\displaystyle ds}

RdV=ρdlds{\displaystyle \!R_{dV}=\rho {\frac {dl}{ds}}},

де ρ{\displaystyle \rho } — питомий опір.

З закону Ома j=σE{\displaystyle \!j=\sigma E}. З другого боку,

dI=jds=σEds{\displaystyle \!dI=jds=\sigma Eds},

де σ{\displaystyle \sigma } — електропровідність, а E{\displaystyle \!E} — напруженість електричного поля.

ρ=1σ{\displaystyle \!\rho ={\frac {1}{\sigma }}}

dQ=σ2E2ds2ρdldsdt{\displaystyle \!dQ=\sigma ^{2}E^{2}{ds}^{2}\rho {\frac {dl}{ds}}dt}

dQ=σE2dVdt{\displaystyle \!dQ=\sigma E^{2}dVdt}

Ввівши поняття елементарної питомої потужності струму — кількості теплоти, що виділяється в одиниці об’єму за одиницю часу, можна записати:

ω=dQdVdt{\displaystyle \!\omega ={\frac {dQ}{dVdt}}}.

Тоді

ω=σE2{\displaystyle \!\omega =\sigma E^{2}}.

Питома теплова потужність струму дорівнює добутку провідності на квадрат напруженості.

Зниження втрат енергії[ред. | ред. код]

При передаванні електроенергії теплова дія струму є небажаною, оскільки це призводить до втрат енергії. Оскільки потужність, що передається, лінійно залежить як від напруги, так і від сили струму, а потужність нагріву залежить від сили струму квадратично, то вигідно підвищувати напругу перед передачею електроенергії, знижуючи при цьому силу струму. Однак, підвищення напруги знижує електробезпеку ліній електропередачі.

Електронагрівальні прилади[ред. | ред. код]

В основі роботи багатьох електронагрівальних приладів лежить закон Джоуля — Ленца. Такі прилади використовують нагрівальний елемент, що є провідником з високим опором. Підвищення опору досягається вибором сплаву з високим питомим опором (наприклад, ніхрому, константану), збільшенням довжини провідника і зменшенням його поперечного перерізу.

Плавкі запобіжники[ред. | ред. код]

Для захисту електричних кіл від протікання надмірно великих струмів використовується відрізок провідника зі спеціальними характеристиками. Це провідник малого перерізу і виготовлений з такого сплаву, що при допустимому струмі нагрів провідника не перегріває його, а при надмірно великих струмах перегрів провідника стає настільки значним, що провідник розплавлюється і розмикає коло.

1. ↑ Закон Джоуля — Ленца // Большая советская энциклопедия : в 30 т. / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1972. — Т. 8 : Дебитор — Евкалипт. — 592 с. (рос.)

uk.wikipedia.org