Диэлектрик в конденсаторе
Физика > Конденсаторы с диэлектриками
Как выглядит конденсатор, заполненный диэлектриком: применение диэлектрика между пластинами, емкость конденсатора и формула, сопротивление ионизации.
Диэлектрик вступает в частичное сопротивление к электрическому полю конденсатора. Он может увеличить емкость и избавить пластины от касания.
Задача обучения
- Охарактеризовать поведение диэлектрического материала в электрическом поле конденсатора.
Основные пункты
- Если применяется диэлектрик в конденсаторе, то помещенный между пластинами материал будет поляризоваться, чтобы сопротивляться полю.
- Емкость конденсатора с параллельной пластиной вычисляется по формуле: c = εA/d (ε – диэлектрическая проницаемость, A – площадь пластин конденсатора, а d – толщина диэлектрика).
- В качестве диэлектрика выбирают материал со способностью противостоять ионизации.
Термины
- Емкость – умение электрической цепи сберегать заряд.
- Диэлектрик – изолирующий или непроводящий материал.
- Конденсатор – электронная составляющая, способная сберечь электрический заряд.
Чтобы конденсатор сохранил заряд, цепь между двумя сторонами должна прерваться. Это может произойти из-за вакуума или диэлектрика.
Когда мы используем конденсатор, заполненный диэлектриком, то материал между параллельными пластинами конденсатора начинает поляризоваться. Часть возле положительного конца обретет избыток отрицательного заряда, а часть возле отрицательного – избыток положительного. В итоге, подобное перераспределение формирует электрическое поле, вступающее в противостояние созданному конденсатором полю. Ниже представлена схема диэлектрика между пластинами конденсатора.
Заряды в линии диэлектрического материала противостоят зарядам пластин. Между ними формируется электрическое поле
Именно поэтому, созданное конденсатором чистое поле будет частично сокращаться вместе с разностью потенциалов.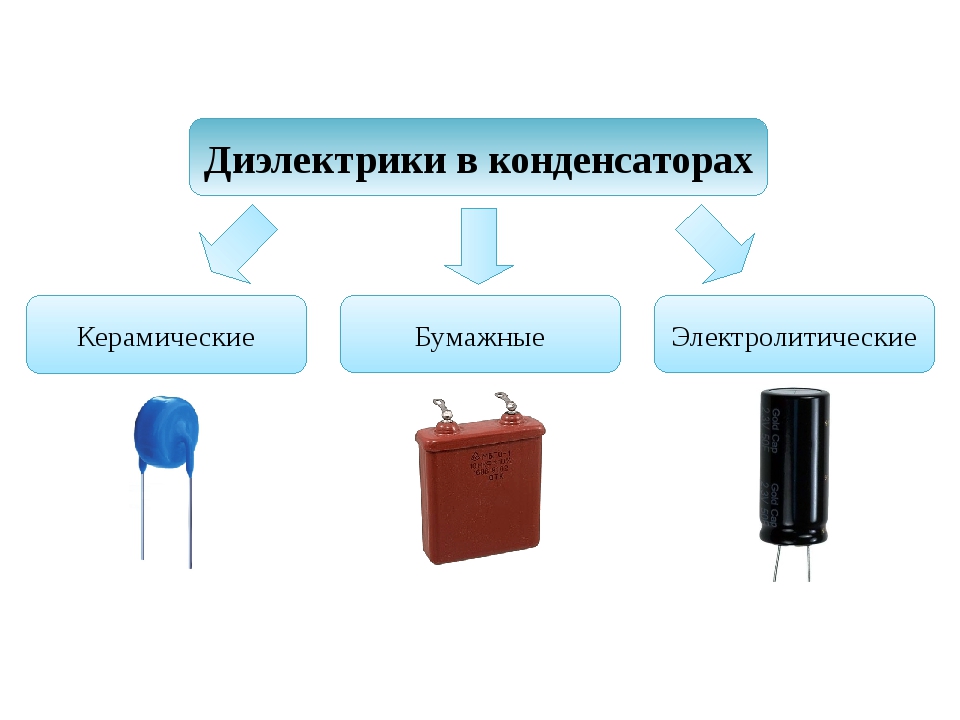 Но диэлектрик не позволяет пластинам вступать в прямой контакт. Если присутствует высокая проницаемость, то увеличивается емкость для любого конкретного напряжения. Емкость вычисляется по формуле:
Но диэлектрик не позволяет пластинам вступать в прямой контакт. Если присутствует высокая проницаемость, то увеличивается емкость для любого конкретного напряжения. Емкость вычисляется по формуле:
c = εA/d (ε – диэлектрическая проницаемость, A – площадь пластин конденсатора, а d – толщина диэлектрика).
В качестве диэлектриков выбирают материалы со способностью сопротивляться ионизации. Чем выше устойчивость, тем лучше всего он подходит для работы с высоким напряжением. У каждого материала есть точка пробоя диэлектрика, где разность потенциалов становится крайне высокой для изоляции. Тогда она ионизирует и пропускает ток.
Электричество и магнетизм
Если, к примеру, в однородное электрическое поле (как в идеальном плоском конденсаторе) поместить плоскопараллельную диэлектрическую пластину так, что её поверхности составят некоторый угол с направлением поля и, тем самым, они не будут совпадать с его эквипотенциальными поверхностями, то величина поля внутри этой пластины будет довольно сложным образом зависеть от угла
Рис. 3.4. Напряженность поля на оси тонкого диэлектрического стержня
Уменьшение разности потенциалов между обкладками и увеличение емкости конденсатора мы наблюдали в решенной выше задаче о сферическом конденсаторе с металлической оболочкой между обкладками. Там причина уменьшения разности потенциалов была ясна: на оболочке наводились индуцированные заряды, которые компенсировали внешнее поле от обкладок.
В диэлектрике нет зарядов, способных перемещаться по всему его объёму, но идея возникновения на его поверхности каких-то дополнительных зарядов (их называют в этом случае
Рис. 3.5. Сферическая частица в однородном электрическом поле напряжённостью Е.
Знаками «+» и «–» показаны связанные заряды, возникшие на поверхности частицы при её поляризации.
Поляризационные заряды создают дополнительное электрическое поле , направленное противоположно полю от зарядов на обкладках (см. рис. 3.3). Это и объясняет меньшую величину результирующего поля Е по сравнению с полем E0. Действительно, для простейшей геометрии плоского конденсатора (см. выше замечание о форме поверхности диэлектрика) изменение поля в диэлектрике сводится только к изменению величины его напряженности в
|
(3.2) |
Отсюда мы находим, какая часть результирующего поля создается поляризационными зарядами, а какая — зарядами на обкладках
|
(3. |
Отрицательный знак указывает на противоположное направление поля поляризационных зарядов. Зная связь поверхностной плотности зарядов с напряженностью создаваемого ими поля
Находим плотность поляризационных зарядов
|
|
(3.4) |
Заметим, что случаю проводника соответствует предел
Действительно, тогда , а поле внутри материала полностью компенсируется, получаем
откуда
Значения e для некоторых диэлектриков приведены в таблице (для газов — при нормальных условиях).
Таблица
Значения диэлектрической проницаемости для некоторых веществ
|
Диэлектрик |
|
Диэлектрик |
|
Гелий |
1,00007 |
Жидкий гелий |
1,047 |
|
Водород |
1,00027 |
Жидкий водород |
1,23 |
|
Азот |
1,00058 |
Жидкий азот |
1,43 |
|
Бумага |
3,5 |
Трансформаторное масло |
4,5 |
|
Фарфор |
6,5 |
Лёд |
16 |
|
Этиловый спирт |
25,1 |
Глицерин |
56,2 |
|
Вода |
81,1 |
Титанат стронция |
310 |
|
|
|
|
|
Обратите внимание: одни и те же вещества при разных условиях имеют различные диэлектрические свойства. Значит, для их объяснения необходимо построить теорию на микроскопическом уровне, исходящую из свойств атомов и молекул и учитывающую состояние вещества.
Значит, для их объяснения необходимо построить теорию на микроскопическом уровне, исходящую из свойств атомов и молекул и учитывающую состояние вещества.
Дополнительная информация
http://chemister.da.ru/Chemie/Tables/dielectric.htm — диэлектрические проницаемости некоторых веществ;
http://www.radioland.net.ua/contentid-381-page1.html — основные типы диэлектриков, применяемые в конденсаторах;
http://ufn.ru/ufn67/ufn67_11/Russian/r6711n.pdf — статья «Вещества с высокой и сверхвысокой диэлектрической проницаемостью»;
http://www.chipdip.ru/video.aspx?vid=ID000292886&tag=dielectric — видео «Пироэлектрики»;
http://gos-rz.narod.ru/2/20.htm — сегнетоэлектрики, их применение;
http://www.rci.rutgers.edu/~ecerg/projects/ferroelectric.html — керамические сегнетоэлектрики;
http://www.chipdip.ru/video.aspx?vid=ID000292814&tag=dielectric — видео «Сегнетокерамика».
НАЧАЛА ФИЗИКИ
Поэтому, когда мы вставляем между обкладками отключенного от источника конденсатора диэлектрик (случай (а)), то его емкость увеличивается в ε раз, заряд не изменяется, напряжение на конденсаторе уменьшается в ε раз. Чтобы понять, как изменяется напряженность поля в конденсаторе, можно рассуждать так. Поскольку заряд обкладок не изменяется, а в конденсаторе оказывается диэлектрик, на основании формулы (26.2) для напряженности поля заряженной пластины заключаем, что напряженность поля между пластинами убывает в ε раз. Для оценки изменения энергии конденсатора удобно воспользоваться формулой (26.8), выражающей энергию конденсатора через заряд и емкость. В результате заключаем, что энергия убывает в ε раз.
Если вставить диэлектрик в конденсатор без отключения его от источника (случай (б)), то процесс пойдет по-другому. Поскольку обкладки конденсатора соединены с источником, между ними поддерживается фиксированное напряжение источника. Поэтому из определения емкости (26.10) заключаем, что при увеличении емкости конденсатора в ε раз при фиксированном напряжении между обкладками, их заряд увеличится в ε раз. Из формулы (26.8) для напряженности поля заряженной пластины следует, что при увеличении заряда в ε раз и одновременном появлении диэлектрика с диэлектрической проницаемостью ε, напряженность поля между обкладками не изменится. Чтобы понять, как изменяется энергия конденсатора, проще всего воспользоваться первой из формул (26.9). Поскольку напряжение на конденсаторе не изменяется, а емкость увеличивается в ε раз, то в ε раз увеличивается и энергия конденсатора.
Поэтому из определения емкости (26.10) заключаем, что при увеличении емкости конденсатора в ε раз при фиксированном напряжении между обкладками, их заряд увеличится в ε раз. Из формулы (26.8) для напряженности поля заряженной пластины следует, что при увеличении заряда в ε раз и одновременном появлении диэлектрика с диэлектрической проницаемостью ε, напряженность поля между обкладками не изменится. Чтобы понять, как изменяется энергия конденсатора, проще всего воспользоваться первой из формул (26.9). Поскольку напряжение на конденсаторе не изменяется, а емкость увеличивается в ε раз, то в ε раз увеличивается и энергия конденсатора.
В задачах школьного курса физики часто рассматривают ситуации, когда в плоский конденсатор вставляют металлическую пластинку, параллельную пластинам конденсатора. Это приводит к значительному изменению геометрии конденсатора и, следовательно, его емкости. Благодаря сохранению плоской геометрии такого типа задачи легко решаются. Давайте рассмотрим следующий пример.
Пример 26.3. Заряд плоского воздушного конденсатора, соединенного с источником напряжения, равен Q. Каким будет заряд конденсатора, если, не отключая его от источника, вставить между обкладками плоскую металлическую пластину толщиной ?
Диэлектрик — конденсатор — Большая Энциклопедия Нефти и Газа, статья, страница 1
Диэлектрик — конденсатор
Cтраница 1
Диэлектрик конденсатора должен обладать высокой электрической прочностью и диэлектрической проницаемостью, малыми потерями и должен образовывать тонкие пленки без дефектов ( сквозной пористости и участков с повышенной проводимостью), обладать хорошей адгезией к металлам обкладок, быть устойчивым к температурным воздействиям на всех этапах изготовления микросборки, обладать минимальной гигроскопичностью. От всех этих свойств диэлектрика зависит надежность конденсатора. [2]
[2]
Диэлектрик конденсатора никогда не может быть идеальным. Электроны с отрицательно заряженной обкладки постепенно переходят через диэлектрик на другую обкладку, образуя небольшой ток, называемый током утечки. Поэтому заряженный конденсатор постепенно уменьшает свой заряд. [3]
Диэлектрик конденсатора состоит из слоя слюды 3 и слоя воздуха. При изменении давления, оказываемого на диафрагму /, являющуюся вторым электродом, изменяется расстояние между диафрагмой / и неподвижным электродом 2, что вызывает изменение емкости конденсатора. [4]
Диэлектрики конденсаторов изготовляют из одноокиси кремния, которую, используя соответствующие маски, наносят также поверх пленочных резисторов как дополнительный защитный слой перед покрытием смолой или лаком. [5]
Диэлектрик конденсаторов следует обозначать штрих-пунктирной линией без штриховки площади диэлектрика, а защитный слой — пунктирной линией без штриховки площади защищенных участков. [6]
Диэлектрик конденсатора представляет собой тесную смесь двух керамических материалов типа термоконда Т-20 на основе ти-таната циркония и типа ультрафарфора. Каково должно быть соотношение составных частей, чтобы температурный коэффициент диэлектрической проницаемости смеси был равен нулю. Чему равна диэлектрическая проницаемость такой смеси. [7]
Диэлектрик конденсатора формируется методами термического напыления, ионно-плазменного и реактивного распыления. [8]
Диэлектрик конденсаторов МБГП на рабочие напряжения 160 и 200 в однослойный из конденсаторной бумаги толщиной 8 а. [10]
[10]
Диэлектриком конденсатора служит слой окиси. Положительной обкладкой ( анодом) является та лента, которая имеет слой окиси. Она соединяется с изолированным от корпуса лепестком. Вторая, отрицательная обкладка ( катод) — бумага, пропитанная электролитом через ленту, на которой нет слоя окиси, соединяется с металлическим корпусом. Таким образом, корпус является выводом отрицательной, а изолированный от него лепесток-выводом положительной обкладки электролитического конденсатора. Конденсаторы КЭ-2 отличаются от конденсаторов типов КЭ только пластмассовой втулкой с резьбой и гайкой для крепления на панели. [12]
Диэлектриком конденсатора служит воздух. [13]
Диэлектриком конденсатора служат изоляцишные1 шайбы или втулки, фиксирующие, кроме того, положение телескопической штыревой антенны в рабочем положении и предотвращаю-щие возможность ее замыкания на корпус. [15]
Страницы: 1 2 3 4 5
Как изменяется электроемкость плоского конденсатора. Что такое электроемкость конденсатора? Электрическая емкость цилиндрического конденсатора
Одним их важнейших параметров, при помощи которого характеризуют конденсатор, является его электроёмкость (C). Физическая величина C, равная:
называется емкостью конденсатора. Где q — величина заряда одной из обкладок конденсатора, а — разность потенциалов между его обкладками. Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.
Для конденсаторов с одинаковым устройством и при равных зарядах на его обкладках разность потенциалов воздушного конденсатора будет в раз меньше, чем разность потенциалов между обкладками конденсатора, пространство которого между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Значит емкость конденсатора с диэлектриком (C) в раз больше, чем электроемкость воздушного конденсатора ():
Значит емкость конденсатора с диэлектриком (C) в раз больше, чем электроемкость воздушного конденсатора ():
где — диэлектрическая проницаемость диэлектрика.
Единицей емкости конденсатора считают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) является фарад (Ф).
Электроемкость плоского конденсатора
Поле между обкладками плоского конденсатора в большинстве случаев считают однородным. Однородность нарушается только около краев. При расчете емкости плоского конденсатора данными краевыми эффектами обычно пренебрегают. Это возможно, если расстояние между пластинами мало в сравнении с их линейными размерами. В таком случае емкость плоского конденсатора вычисляют как:
где — электрическая постоянная; S — площадь каждой (или наименьшей) пластины; d — расстояние между пластинами.
Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:
Электрическая емкость цилиндрического конденсатора
Конструкция цилиндрического конденсатора включает две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость такого конденсатора находят как:
где l — высота цилиндров; — радиус внешней обкладки; — радиус внутренней обкладки.
Емкости сферического конденсатора
Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:
где — радиусы обкладок конденсатора.
Примеры решения задач
ПРИМЕР 1
| Задание | Пластины плоского воздушного конденсатора несут заряд, который равномерно распределен с поверхностной плотностью . При этом расстояние между его обкладками, равно . На какую величину изменится разность потенциалов на обкладках этого конденсатора, если его пластины раздвинуть до расстояния ? При этом расстояние между его обкладками, равно . На какую величину изменится разность потенциалов на обкладках этого конденсатора, если его пластины раздвинуть до расстояния ? |
| Решение | Сделаем рисунок. В задаче при изменении расстояния между пластинами конденсатора заряд на его обкладках не изменяется, изменяются емкость и разность потенциалов на обкладках. Емкость плоского воздушного конденсатора равна: где . Емкость этого же конденсатора можно определить как: где U — разность потенциалов на обкладках конденсатора. Для конденсатора в первом случае имеем: Для того же конденсатора, но после того как пластины раздвинули, имеем: Используя формулу (1.3) и применяя соотношение: выразим разность потенциалов Следовательно, для конденсатора во втором состоянии получим: Найдем изменение разности потенциалов: |
| Ответ |
Рассмотрим два заряженных проводника. Предположим, что все силовые линии, начинающиеся на одном из них, заканчиваются на другом. Для этого, разумеется, они должны иметь равные и противоположные по знаку заряды. Такая система двух проводящих тел называется конденсатором.
Примеры конденсаторов. Примерами конденсаторов могут служить две концентрические проводящие сферы (сферический, или шаровой, конденсатор), две параллельные плоские проводящие пластины при условии, что расстояние между ними мало по сравнению с размерами пластин (плоский конденсатор), два коаксиальных проводящих цилиндра при условии, что их длина велика по сравнению с зазором между цилиндрами (цилиндрический конденсатор).
Два проводника, образующие конденсатор, называются его обкладками.
Рис. 41. Электрическое поле в сферическом, плоском и цилиндрическом конденсаторах
Во всех таких системах при сообщении обкладкам равных по модулю и противоположных по знаку зарядов электрическое поле практически целиком заключено в пространстве между обкладками (рис. 41). Внешний вид некоторых используемых в технике конденсаторов показан на рис. 42.
41). Внешний вид некоторых используемых в технике конденсаторов показан на рис. 42.
Основная характеристика конденсатора — электроемкость или просто емкость С, определяемая как отношение заряда одной из
обкладок к разности потенциалов т. е. к напряжению, между ними:
Распределение зарядов на обкладках будет одинаковым независимо от того, большой или малый заряд им сообщен. Это значит, что напряженность поля, а следовательно, и разность потенциалов между обкладками, пропорциональны сообщенному конденсатору заряду. Поэтому емкость конденсатора не зависит от его заряда.
Рис. 42. Устройство, внешний вид и условные обозначения на электрических схемах некоторых конденсаторов
В вакууме емкость определяется исключительно геометрическими характеристиками конденсатора, т. е. формой, размерами и взаимным расположением обкладок.
Единицы емкости. В СИ за единицу электроемкости принят фарад Емкостью 1 Ф обладает конденсатор, между обкладками которого устанавливается напряжение 1 В при сообщении заряда 1 Кл:
В абсолютной электростатической системе единиц СГСЭ электроемкость имеет размерность длины и измеряется в сантиметрах:
На практике обычно приходится иметь дело с конденсаторами, емкость которых значительно меньше 1 Ф. Поэтому используются доли этой единицы — микрофарад (мкФ) и пикофарад . Соотношение между фарадом и сантиметром легко установить, учитывая, что
Электроемкость и геометрия конденсатора. Зависимость емкости конденсатора от его геометрических характеристик легко проиллюстрировать простыми опытами. Воспользуемся для этого электрометром, подключенным к двум плоским пластинам, расстояние между которыми можно изменять (рис. 43). Чтобы заряды пластин были одинаковы и все поле было сосредоточено только между ними, следует заземлить вторую пластину и корпус электрометра. Отклонение стрелки электрометра пропорционально напряжению между обкладками. Если сдвигать или раздвигать пластины конденсатора, то при неизменном заряде напряжение будет соответственно уменьшаться или увеличиваться: емкость тем больше, чем меньше расстояние между пластинами.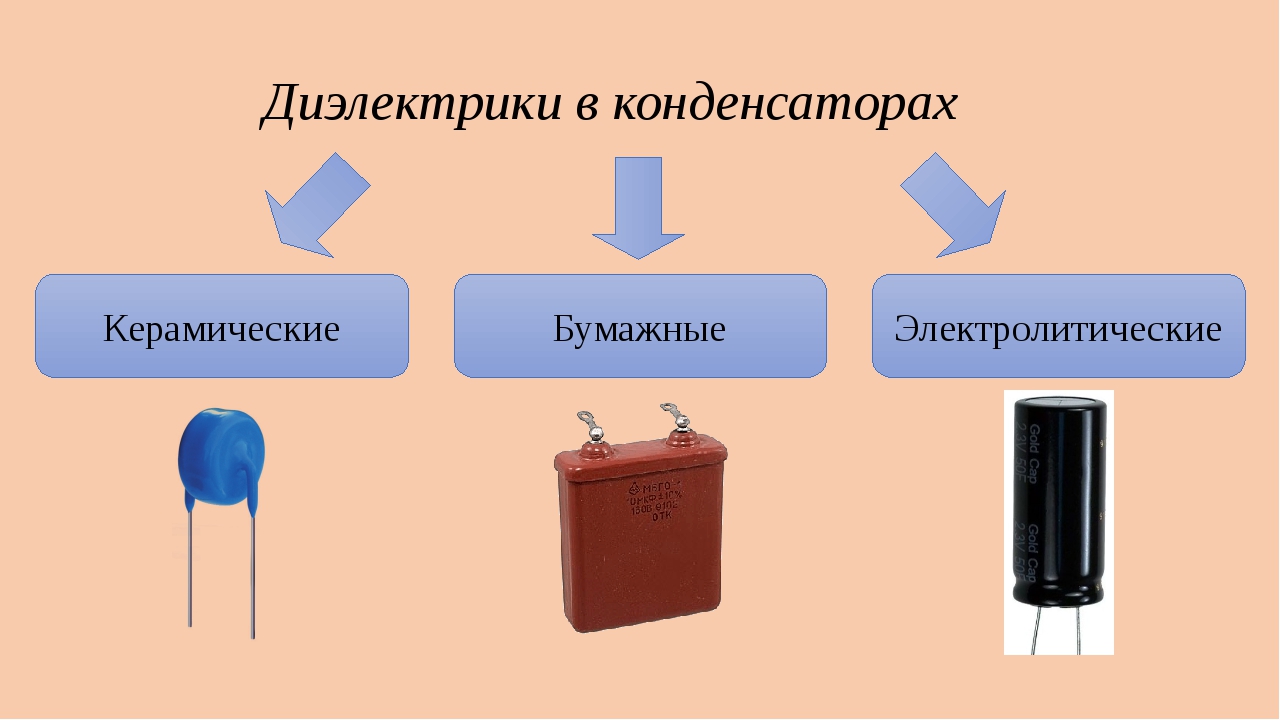 Аналогично можно убедиться в том, что емкость конденсатора тем больше, чем больше площадь его пластин. Для этого можно просто сдвигать пластины при неизменном зазоре между ними.
Аналогично можно убедиться в том, что емкость конденсатора тем больше, чем больше площадь его пластин. Для этого можно просто сдвигать пластины при неизменном зазоре между ними.
Рис. 43. Емкость конденсатора зависит от расстояния между пластинами
Емкость плоского конденсатора. Получим формулу для емкости плоского конденсатора. Поле между его обкладками однородно за исключением небольшой области вблизи краев пластин. Поэтому напряжение между обкладками равно произведению напряженности поля Е на расстоянии между ними: Для нахождения напряженности поля Е можно воспользоваться формулой (1) § 6, которая связывает Е вблизи поверхности проводника с поверхностной плотностью зарядов с: Выразим а через заряд конденсатора и площадь пластины, считая распределение заряда равномерным, что согласуется с используемым предположением об однородности поля: Подставляя приведенные соотношения в общее определение емкости (1), находим
В СИ, где емкость плоского конденсатора имеет вид
В системе единиц СГСЭ k = 1 и
Емкость сферического конденсатора. Совершенно аналогично можно вывести формулу для емкости сферического конденсатора, рассматривая электрическое поле в промежутке между двумя заряженными концентрическими сферами радиусов Напряженность поля там такая же, как в случае уединенного заряженного шара радиуса Поэтому для напряжения между обкладками радиусов справедливо
Выражение для емкости получаем, подставляя в формулу (1):
Емкость уединенного проводника. Иногда вводят понятие емкости уединенного проводника, рассматривая предельный случай конденсатора, одна из обкладок которого удалена на бесконечность. В частности, емкость уединенного проводящего шара получается из (5) в результате предельного перехода что соответствует неограниченному увеличению радиуса внешней обкладки при неизменном радиусе внутренней
В системе единиц СГСЭ, где емкость уединенного шара равна его радиусу. Если проводник имеет несферическую форму, его емкость по порядку величины равна характерному линейному размеру, хотя, конечно же, зависит и от его формы. В отличие от уединенного проводника, емкость конденсатора гораздо больше его линейных размеров. Например, у плоского конденсатора характерный линейный размер равен причем Как видно из формулы (4), при этом
В отличие от уединенного проводника, емкость конденсатора гораздо больше его линейных размеров. Например, у плоского конденсатора характерный линейный размер равен причем Как видно из формулы (4), при этом
Конденсатор с диэлектриком. В рассмотренных выше примерах конденсаторов пространство между обкладками считалось пустым. Тем не менее полученные выражения для емкости справедливы и тогда, когда это пространство заполнено воздухом, как это было в описанных простых опытах. Если пространство между обкладками заполнить каким-либо диэлектриком, емкость конденсатора увеличивается. В этом легко убедиться на опыте, вдвигая диэлектрическую пластину в промежуток между обкладками заряженного конденсатора, подключенного к электрометру (рис. 43). При неизменном заряде конденсатора напряжение между обкладками уменьшается, что свидетельствует о возрастании емкости.
Уменьшение разности потенциалов между обкладками при внесении туда диэлектрической пластины свидетельствует о том, что напряженность электрического поля в зазоре становится меньше. Это уменьшение зависит от того, какой именно диэлектрик используется в опыте.
Диэлектрическая проницаемость. Для характеристики электрических свойств диэлектрика вводят физическую величину, называемую диэлектрической проницаемостью. Диэлектрическая проницаемость — это безразмерная величина, показывающая, во сколько раз напряженность электрического поля в заполненном диэлектриком конденсаторе (или напряжение между его обкладками) меньше, чем в отсутствие диэлектрика при том же заряде конденсатора. Другими словами, диэлектрическая проницаемость показывает, во сколько раз увеличивается емкость конденсатора при заполнении его диэлектриком. Например, емкость плоского конденсатора, заполненного диэлектриком с проницаемостью равна
Приведенное здесь определение диэлектрической проницаемости соответствует феноменологическому подходу, при котором рассматриваются только макроскопические свойства вещества в электрическом поле. Микроскопический подход, основанный на рассмотрении поляризации атомов или молекул, из которых состоит вещество, предполагает исследование какой-либо конкретной модели и позволяет не только подробно описывать электрические и магнитные поля внутри вещества, но и понять, как протекают макроскопические электрические и магнитные явления в веществе. На этом этапе мы ограничиваемся только феноменологическим подходом.
Микроскопический подход, основанный на рассмотрении поляризации атомов или молекул, из которых состоит вещество, предполагает исследование какой-либо конкретной модели и позволяет не только подробно описывать электрические и магнитные поля внутри вещества, но и понять, как протекают макроскопические электрические и магнитные явления в веществе. На этом этапе мы ограничиваемся только феноменологическим подходом.
Рис. 44. Параллельное соединение конденсаторов
У твердых диэлектриков значение лежит в пределах от 4 до 7, а у жидких — от 2 до 81. Такой аномально большой диэлектрической проницаемостью обладает обыкновенная чистая вода. Кроме воздушного конденсатора переменной емкости (см. рис. 42), используемого для настройки радиоприемников, все другие применяемые в технике конденсаторы заполнены диэлектриком.
Батареи конденсаторов. При использовании конденсаторов их иногда соединяют в батареи. При параллельном соединении (рис. 44) напряжения на конденсаторах одинаковы, а полный заряд батареи равен сумме зарядов конденсаторов для каждого из которых, очевидно, справедливо Рассматривая батарею как один
конденсатор, имеем
С другой стороны,
Сравнивая (8) и (9), получаем, что емкость батареи параллельно соединенных конденсаторов равна сумме их емкостей:
Рис. 45. Последовательное соединение конденсаторов
При последовательном соединении предварительно незаряженных конденсаторов (рис. 45) заряды на всех конденсаторах одинаковы, а полное напряжение равно сумме напряжений на отдельных конденсаторах:
С другой стороны, рассматривая батарею как один конденсатор, имеем
Сравнивая (11) и (12), видим, что при последовательном соединении конденсаторов складываются обратные емкостям величины:
При последовательном соединении емкость батареи меньше самой малой из емкостей соединенных конденсаторов.
В каком случае два проводящих тела образуют конденсатор?
Что называется зарядом конденсатора?
Как установить связь между единицами емкости СИ и СГСЭ?
Объясните качественно, почему емкость конденсатора увеличивается при уменьшении зазора между обкладками.
Получите формулу для емкости плоского конденсатора, рассматривая электрическое поле в нем как суперпозицию полей, создаваемых двумя плоскостями, заряженными разноименно.
Получите формулу для емкости плоского конденсатора, рассматривая его как предельный случай сферического конденсатора, у которого стремятся к бесконечности так, что разность остается постоянной.
Почему нельзя говорить о емкости уединенной бесконечной плоской пластины или отдельного бесконечно длинного цилиндра?
Охарактеризуйте кратко различие между феноменологическим и микроскопическим подходами при исследовании свойств вещества в электрическом поле.
Каков смысл диэлектрической проницаемости вещества?
Почему при расчете емкости батареи последовательно соединенных конденсаторов оговаривалось условие, чтобы они предварительно не были заряжены?
В чем смысл последовательного соединения конденсаторов, если оно приводит лишь к уменьшению емкости?
Поле внутри и вне конденсатора. Чтобы подчеркнуть различие между тем, что называют зарядом конденсатора, и полным зарядом обкладок, рассмотрим следующий пример. Пусть наружная обкладка сферического конденсатора заземлена, а внутренней сообщен заряд д. Весь этот заряд равномерно распределится по внешней поверхности внутренней обкладки. Тогда на внутренней поверхности наружной сферы индуцируется заряд , следовательно, заряд конденсатора равен . А что будет на внешней поверхности наружной сферы? Это зависит от того, что окружает конденсатор. Пусть, например, на расстоянии от поверхности внешней сферы находится точечный заряд (рис. 46). Этот заряд никак не повлияет на электрическое состояние внутреннего пространства конденсатора, т. е. на поле между его обкладками. В самом деле, внутреннее и внешнее пространства разделены толщей металла наружной обкладки, в которой электрическое поле равно нулю.
Рис. 46. Сферический конденсатор во внешнем электрическом поле
Заряд на внешней поверхности обкладки. Но характер поля во внешнем пространстве и заряд, индуцированный на наружной поверхности внешней сферы, зависят от величины и положения заряда Это поле будет точно таким же, как и в случае, коща заряд находится на расстоянии от поверхности сплошного заземленного металлического шара, радиус которого равен радиусу внешней сферы конденсатора (рис. 47). Таким же будет и индуцированный заряд.
Но характер поля во внешнем пространстве и заряд, индуцированный на наружной поверхности внешней сферы, зависят от величины и положения заряда Это поле будет точно таким же, как и в случае, коща заряд находится на расстоянии от поверхности сплошного заземленного металлического шара, радиус которого равен радиусу внешней сферы конденсатора (рис. 47). Таким же будет и индуцированный заряд.
Для нахождения величины индуцированного заряда будем рассуждать следующим образом. Электрическое поле в любой точке пространства создается зарядом и зарядом, индуцированным
на поверхности шара, который распределен там, разумеется, неравномерно — как раз так, чтобы обратилась в нуль результирующая напряженность поля внутри шара. Согласно принципу суперпозиции потенциал в любой точке можно искать в виде суммы потенциалов полей, создаваемых точечным зарядом и точечными зарядами, на которые можно разбить распределенный по поверхности шара индуцированный заряд. Поскольку все элементарные заряды на которые разбит индуцированный на поверхности шара заряд находятся на одинаковом расстоянии от центра шара, то потенциал создаваемого им поля в центре шара будет равен
Рис. 47. Поле точечного заряда вблизи заземленного проводящего шара
Тогда полный потенциал в центре заземленного шара равен
Знак минус отражает тот факт, что индуцированный заряд всегда противоположного знака.
Итак, мы видим, что заряд на наружной поверхности внешней сферы конденсатора определяется тем окружением, в котором находится конденсатор, и не имеет никакого отношения к заряду конденсатора д. Полный заряд внешней обкладки конденсатора, разумеется, равен сумме зарядов ее внешней и внутренней поверхностей, однако заряд конденсатора определяется только зарядом внутренней поверхности этой обкладки, который связан силовыми линиями поля с зарядом внутренней обкладки.
В разобранном примере независимость электрического поля в пространстве между обкладками конденсатора и, следовательно, его емкости от внешних тел (как заряженных, так и незаряженных) обусловлена электростатической защитой, т. е. толщей металла внешней обкладки. К чему может привести отсутствие такой защиты, можно увидеть на следующем примере.
е. толщей металла внешней обкладки. К чему может привести отсутствие такой защиты, можно увидеть на следующем примере.
Плоский конденсатор с экраном. Рассмотрим плоский конденсатор в виде двух параллельных металлических пластин, электрическое поле которого практически целиком сосредоточено в пространстве между пластинами. Заключим конденсатор в незаряженную плоскую металлическую коробку, как показано на рис. 48. На первый взгляд может показаться, что картина поля между обкладками конденсатора не изменится, так как все поле сосредоточено между пластинами, а краевым эффектом мы пренебрегаем. Однако легко видеть, что это не так. Снаружи конденсатора напряженность поля равна нулю, поэтому во всех точках слева от конденсатора потенциал одинаков и совпадает с потенциалом левой пластины. Точно так же потенциал любой точки справа от конденсатора совпадает с потенциалом правой пластины (рис. 49). Поэтому, заключая конденсатор в металлическую коробку, мы соединяем проводником точки, имеющие разный потенциал.
В результате в металлической коробке будет происходить перераспределение зарядов до тех пор, пока не выравняются потенциалы всех ее точек. На внутренней поверхности коробки индуцируются заряды, и появится электрическое поле внутри коробки, т. е. снаружи конденсатора (рис. 50).
Рис. 48. Конденсатор в металлической коробке
Рис. 49. Электрическое поле заряженного плоского конденсатора
Рис. 50. Электрическое поле заряженного конденсатора, помещенного в металлическую коробку
Но это означает, что на внешних поверхностях пластин конденсатора тоже появятся заряды. Так как при этом полный заряд изолированной пластины не меняется, то заряд на ее внешней поверхности может возникнуть только за счет перетекания заряда с внутренней поверхности. Но при изменении заряда на внутренних поверхностях обкладок изменится напряженность поля между пластинами конденсатора.
Таким образом, заключение рассмотренного конденсатора в металлическую коробку приводит к изменению электрического состояния внутреннего пространства.
Изменение зарядов пластин и электрического поля в этом примере может быть легко рассчитано. Обозначим заряд изолированного конденсатора через Заряд, перетекающий на наружные поверхности пластин при надевании коробки, обозначим через Такой же заряд противоположного знака будет индуцирован на внутренних поверхностях коробки. На внутренних поверхностях пластин конденсатора останется заряд Тогда в пространстве между пластинами напряженность однородного поля будет равна в единицах СИ, а вне конденсатора поле направлено в противоположную сторону и его напряженность равна где — площадь пластины. Требуя, чтобы разность потенциалов между противоположными стенками металлической коробки была равна нулю, и считая для простоты расстояния между всеми пластинами одинаковыми и равными то
Этот результат легко понять, если учесть, что после надевания коробки поле существует во всех трех промежутках между пластинами, т. е. фактически имеются три одинаковых конденсатора, эквивалентная схема включения которых показана на рис. 51. Вычисляя емкость получившейся системы конденсаторов, получаем .
Надетая на конденсатор металлическая коробка осуществляет электростатическую защиту системы. Теперь мы можем подносить снаружи к коробке любые заряженные или незаряженные тела и при этом электрическое поле внутри коробки не изменится. Значит, не изменится и емкость системы.
Обратим внимание на то, что в разобранном примере, выяснив все, что нас интересовало, мы тем не менее обошли стороной вопрос о том, какие же силы осуществили перераспределение зарядов. Какое электрическое поле вызвало движение электронов в материале проводящей коробки?
Очевидно, что это может быть только то неоднородное поле, которое выходит за пределы конденсатора вблизи краев пластины (см. рис. 39). Хотя напряженность этого поля мала и не принимается во внимание при расчете изменения емкости, именно она определяет суть рассматриваемого явления — перемещает заряды и этим вызывает изменение напряженности электрического поля внутри коробки.
Почему под зарядом конденсатора следует понимать не полный заряд обкладки, а только ту его часть, что находится на ее внутренней стороне. обращенной к другой обкладке?
В чем проявляется роль краевых эффектов при рассмотрении электростатических явлений в конденсаторе?
Как изменится емкость батареи конденсаторов, если замкнуть между собой обкладки одного из них?
Формула электроемкости следующая.
Измеряется эта величина в фарадах. Как правило, емкость элемента очень мала и измеряется в пикофарадах.
В задачах часто спрашивается, как изменится электроемкость конденсатора, если увеличить заряд или напряжение. Это вопрос с подвохом. Проведем другую аналогию.
Представьте, что речь идет про обычную банку, а не конденсатор. Например, у вас она трехлитровая. Аналогичный вопрос: что произойдет со вместимостью банки, если туда налить 4 литра воды? Разумеется, вода просто выльется, но при этом размеры банки никак не изменятся.
То же самое с конденсаторами. Заряд и напряжение никак не влияют на емкость. Этот параметр зависит только от реальных физических размеров.
Формула будет следующей
Только эти параметры влияют на реальную электроемкость конденсатора.
На любом конденсаторе есть маркировка с техническими параметрами.
Разобраться несложно. Достаточно минимальных знаний по электричеству.
Соединение конденсаторов
Конденсаторы, так же как и сопротивления, можно подключать последовательно и параллельно. Кроме этого, в схемах бывают и смешанные соединения.
Как видите, электроемкость конденсатора в обоих случаях считается по-разному. Это также относится к напряжению и заряду. По формулам видно, что электроемкость конденсатора, вернее, их совокупности в схеме, будет наибольшей при параллельном соединении. При последовательном общая емкость значительно уменьшается.
При подключении последовательно заряд размещается равномерно. Он будет везде одинаков — как суммарный, так и на каждом конденсаторе. А когда соединение параллельное, суммарный заряд складывается. Это важно помнить при решении задач.
А когда соединение параллельное, суммарный заряд складывается. Это важно помнить при решении задач.
Напряжение считается наоборот. При последовательном соединении складываем, а при параллельном оно равно везде.
Здесь приходится выбирать: если вам нужно больше напряжения, тогда жертвуем емкостью. Если емкость, то огромного напряжения не будет.
Виды конденсаторов
Существует огромное количество конденсаторов. Они отличаются как по размеру, так и по форме.
Разумеется, емкость вычисляется у всех по-разному.
Электроемкость плоского конденсатора
Электроемкость плоского конденсатора определяется проще всего. Эту формулу в основном все и помнят, в отличии от других.
Здесь всё зависит от физических параметров и среды между пластинами.
Здесь также большое значение имеет, какой диэлектрик или материал помещен внутрь. Так как деталь имеет размер сферы, ее емкость зависит от радиуса.
В случае с цилиндрической формой, кроме среды внутри, значение имеют радиусы и длина цилиндра.
Подумайте, как изменится электроемкость плоского конденсатора, если на нем будут повреждения? Существуют различные сбои, которые могут повлиять на работоспособность конденсаторов.
Например, они рассыхаются или вздуваются. После этого они становятся непригодными для нормальной работы устройства, куда установлены.
Рассмотрим примеры повреждений и выхода из строя конденсаторов. Вздуться могут все сразу.
Иногда из строя выходят только несколько. Такое бывает, когда конденсаторы разных параметров или качества.
Наглядный пример порчи (вздутие, разрыв и выход наружу содержимого).
Если вы увидите вот такие ленты, это крайняя степень повреждения. Хуже и быть не может.
Если вы заметите на устройстве (например на видеокарте в компьютере) такие вздутые конденсаторы, это повод задуматься о замене детали.
Подобные проблемы можно устранить только заменой на аналогичную деталь. У вас должны совпадать все параметры один в один. Иначе работа может быть некорректной или очень кратковременной.
У вас должны совпадать все параметры один в один. Иначе работа может быть некорректной или очень кратковременной.
Менять конденсаторы нужно аккуратно, не повредив платы. Выпаивать нужно быстро, не допуская перегрева. Если вы не умеете этого делать, лучше отнесите деталь в ремонт.
Основной причиной разрушения является перегрев, который возникает в случае старения или большого сопротивления в цепи.
Рекомендуется не затягивать с ремонтом. Поскольку у поврежденных конденсаторов изменяется емкость, устройство, где они расположены, будет работать с отклонением от нормы. И со временем это может стать причиной выхода из строя.
Если у вас на видеокарте вздулись конденсаторы, то их своевременная замена может исправить ситуацию. В противном случае может сгореть микросхема или что-то еще. В таком случае ремонт будет стоить очень дорого или вовсе окажется невозможным.
Меры предосторожности
Выше был приведен пример с банкой воды. Там говорилось, что если воды налить больше, то воды выльется. А теперь подумайте, куда могут «вылиться» электроны в конденсаторе? Ведь он запечатан полностью!
Если вы подадите в цепи больше тока, чем тот, на который рассчитан конденсатор, то как только он зарядится, его излишек попытается выйти куда-то. А пространства свободного нет. Результатом будет взрыв. В случае незначительного превышения заряда хлопок будет небольшой. Но если подать колоссальное количество электронов на конденсатор, его просто разорвет, и диэлектрик вытечет.
Будьте аккуратны!
Плоским конденсатором обычно называ-ют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Про-стота конструкции такого конденсатора по-зволяет сравнительно просто рассчитывать его электроемкость и получать значения, совпадающие с результатами эксперимента.
Укрепим две металлические пластины на изоляционных подставках и соединим с электрометром так, что одна из пластин будет присоединена к стержню электромет-ра, а вторая — к его металлическому кор-пусу (рис. 4.71). При таком соединении электрометр будет измерять разность по-тенциалов между пластинами, которые об-разуют плоский конденсатор из двух пла-стин. Проводя исследования, необходимо пом-нить, что
4.71). При таком соединении электрометр будет измерять разность по-тенциалов между пластинами, которые об-разуют плоский конденсатор из двух пла-стин. Проводя исследования, необходимо пом-нить, что
при постоянном значении заряда пластин уменьшение разности потенциалов свидетельствует об увеличении электроем-кости конденсатора, и наоборот.
Сообщим пластинам разноименные заря-ды и отметим отклонение стрелки электро-метра. Приближая пластины друг к другу (уменьшая расстояние между ними), заме-тим уменьшение разности потенциалов. Та-ким образом, при уменьшении расстояния между пластинами конденсатора его элект-роемкость увеличивается. При увеличении расстояния показания стрелки электрометра увеличиваются, что является свидетельст-вом уменьшения электроемкости.
об-ратно пропорциональна расстоянию между его обкладками.
C ~ 1 / d ,
где d — расстояние между обкладками.
Эту зависимость можно изобразить гра-фиком обратной пропорциональной зависи-мости (рис. 4.72).
Будем смещать пластины одну относи-тельно другой в параллельных плоскостях, не изменяя расстояния между ними.
При этом площадь перекрытия пластин будет уменьшаться (рис. 4.73). Увеличение разности потенциалов, отмеченное электрометром, будет свидетельствовать об умень-шении электроемкости.
Увеличение площади перекрытия пластан приведет к увеличению емкости.
Электроемкость плоского конденсатора про-порциональна площади пластин, которые пере-крываются.
C ~ S,
где S — площадь пластин.
Эту зависимость можно представить гра-фиком прямой пропорциональной зависи-мости (рис. 4.74).
Возвратив пластины в начальное поло-жение, внесем в пространство между ними плоский диэлектрик. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увели-чении электроемкости конденсатора. Если между пластинами поместить другой диэлек-трик, то изменение электроемкости будет иным.
Электроемкость плоского конденсатора за-висит от диэлектрической проницаемости ди-электрика.
C ~ ε ,
где ε — диэлектрическая проницаемость ди-электрика. Материал с сайта
Такая зависимость показана на графике рис. 4.75.
Результаты опытов можно обобщить в ви-де формулы ёмкости плоского конденсатора :
C = εε 0 S / d,
где S — площадь пластины; d — расстояние между ними; ε — диэлектрическая прони-цаемость диэлектрика; ε 0 — электрическая постоянная.
Конденсаторы, которые состоят из двух пластин, в практике применяются очень редко. Как правило, конденсаторы имеют много пластин, соединенных между собой по определенной схеме.
На этой странице материал по темам:
Решение задач по теме электроемкость плоского конденсатора
Как влияет диэлектрик на электроёмкость?
Теория плоских конденсаторов
График электроемкости плоского конденсатора от площади его пластин
Заключение по электроемкости
Вопросы по этому материалу:
Какое строение плоского конденсатора?
По изменению какой величины в опыте можно делать заключение об изменении электроемкости?
Конденсаторы: меняем толщину диэлектрика
В этой статье предложены задачи, которые помогут отработать формулы пересчета последовательного и параллельного соединения конденсаторов в эквивалентную емкость, причем одновременно будем менять либо диэлектрическую проницаемость, либо толщину слоя диэлектрика.
Задача 1. Плоский воздушный конденсатор, расстояние между пластинами которого м, до половины погрузили в масло. На какое расстояние следует раздвинуть пластины, чтобы емкость конденсатора не изменилась?
Сначала емкость конденсатора была равна
Затем, когда половину площади пластин погрузили в масло, мы получили словно два конденсатора, соединенных параллельно: один с масляным диэлектриком, второй – без. Площади их пластин одинаковы и равны . Тогда емкость такой системы будет равна
Площади их пластин одинаковы и равны . Тогда емкость такой системы будет равна
– это то новое расстояние, на которое мы раздвинем пластины, чтобы емкость не изменилась. Приравняем обе емкости:
Расстояние изменили на
Ответ: нужно раздвинуть пластины на 6 мм.
Задача 2. Конденсатор какой емкости следует подключить последовательно к конденсатору емкостью пФ, чтобы емкость батареи была С = 160 пФ?
При последовательном соединении двух конденсаторов их эквивалентная емкость будет равна
(Она получается из формулы приведением к общему знаменателю.)
Тогда:
Ответ: 200 пФ
Задача 3. Два последовательно соединенных конденсатора емкостями мкФ и мкФ присоединены к источнику постоянного напряжения В. Определить напряжение на каждом конденсаторе.
Так как конденсаторы соединены последовательно, их заряды одинаковы. Тогда
Сумма напряжений на последовательно соединенных элементах равна напряжению на источнике:
Тогда можно записать:
Тогда В.
Ответ: В, В.
Задача 4. Два одинаковых воздушных конденсатора соединены последовательно и подключены к батарее с постоянной ЭДС. Один из них заполняют диэлектриком с диэлектрической проницаемостью . Во сколько раз изменится напряженность электрического поля в этом конденсаторе?
Так как напряженность непосредственно связана с напряжением на конденсаторе, то определим, как изменится напряжение на каждом из конденсаторов.
Сначала на конденсаторах одинаковое напряжение, так как они соединены последовательно, и емкости у них одинаковые – . Затем емкость второго конденсатора меняется в раз, и заряды по-прежнему остаются одинаковыми на обоих конденсаторах, а напряжения – нет:
Решаем систему:
Найдем отношение напряженностей:
Ответ: напряженность изменится в 0,4 раза.
Задача 5. Пространство между обкладками плоского конденсатора заполнено двумя слоями диэлектриков толщиной и , которые параллельны обкладкам конденсатора. Диэлектрические проницаемости диэлектриков и соответственно. Площадь пластин . Найти емкость конденсатора С.
Такое расположение слоев диэлектриков приводит к тому, что емкость такого конденсатора равна (эквивалентна) двум последовательно соединенным конденсаторам с емкостями и .
Эквивалентная емкость двух последовательно соединенных конденсаторов:
Задача 6. У плоского конденсатора, заполненного твердым диэлектриком с диэлектрической проницаемостью одну пластину отодвигают от диэлектрика на расстояние, равное половине толщины диэлектрического слоя. При каком значении емкость конденсатора изменится в 2 раза?
Полученный конденсатор эквивалентен двум последовательно включенным: один с диэлектриком, второй воздушный.
Первоначальная емкость:
После изменения:
Где :
Так как по условию
(емкость уменьшается, ведь мы увеличиваем расстояние между пластинами),то
Ответ:
Задача 7. У плоского воздушного конденсатора, заполненного слюдой, удаляют треть толщины диэлектрического слоя. Как и во сколько раз меняется при этом емкость конденсатора?
Первоначальная емкость:
После изменения:
Где – емкость конденсатора с утонченным слоем диэлектрика, а – емкость воздушного конденсатора:
Найдем отношение:
Ответ: емкость уменьшится, в 2,66 раза.
Пассивность (инженерия) — Passivity (engineering)
Системы, которые не производят и не потребляют энергию
Пассивность — это свойство инженерных систем, которое используется в различных инженерных дисциплинах, но чаще всего встречается в аналоговой электронике и системах управления . Пассивный компонент , в зависимости от области, может представлять собой либо компонент , который потребляет , но не производит энергию (термодинамическое пассивность) или компонент , который не способен усиление мощности (инкрементные пассивности).
Пассивный компонент , в зависимости от области, может представлять собой либо компонент , который потребляет , но не производит энергию (термодинамическое пассивность) или компонент , который не способен усиление мощности (инкрементные пассивности).
Компонент, который не является пассивным, называется активным компонентом . Электронная схема , состоящая целиком из пассивных компонентов называется пассивной цепью и имеет то же свойство, что и пассивный компонент. Термин пассивный, используемый вне контекста и без квалификатора, неоднозначен. Обычно разработчики аналоговых устройств используют этот термин для обозначения постепенно пассивных компонентов и систем, в то время как инженеры систем управления используют его для обозначения термодинамически пассивных компонентов .
Термодинамическая пассивность
В теории систем управления и схемных сетей пассивный компонент или схема — это тот, который потребляет энергию, но не производит ее. Согласно этой методологии источники напряжения и тока считаются активными, а резисторы , конденсаторы , катушки индуктивности , транзисторы , туннельные диоды , метаматериалы и другие диссипативные и энергонезависимые компоненты считаются пассивными. Разработчики схем иногда называют этот класс компонентов диссипативными или термодинамически пассивными.
Хотя во многих книгах даются определения пассивности, многие из них содержат тонкие ошибки в том, как обрабатываются начальные условия, а иногда определения не обобщаются на все типы нелинейных нестационарных систем с памятью. Ниже приводится правильное формальное определение, взятое из Wyatt et al. что также объясняет проблемы со многими другими определениями. Дано п — порт R с государственным представлением S , и начальное состояние х , определить доступную энергию E A , как:
- E А ( Икс ) знак равно Как дела Икс → Т ≥ 0 ∫ 0 Т — ⟨ v ( т ) , я ( т ) ⟩ d т {\ displaystyle E_ {A} (x) = \ sup _ {x \ to T \ geq 0} \ int _ {0} ^ {T} — \ langle v (t), i (t) \ rangle \, { \ mathord {\ operatorname {d}}} t}
где обозначение sup x → T ≥0 означает, что супремум берется по всем T ≥ 0 и всем допустимым парам { v (·), i (·)} с фиксированным начальным состоянием x (например, по всем вольт-амперным траекториям для заданное начальное состояние системы). Система считается пассивной, если E A конечно для всех начальных состояний x . В противном случае система считается активной. Грубо говоря, внутренний продукт — это мгновенная мощность (например, произведение напряжения и тока), а E A — это верхняя граница интеграла мгновенной мощности (например, энергии). Эта верхняя граница (взятая по всем T ≥ 0) представляет собой доступную энергию в системе для конкретного начального условия x . Если для всех возможных начальных состояний системы доступная энергия конечна, то система называется пассивной. ⟨ v ( т ) , я ( т ) ⟩ {\ Displaystyle \ langle v (т), я (т) \ rangle}
Система считается пассивной, если E A конечно для всех начальных состояний x . В противном случае система считается активной. Грубо говоря, внутренний продукт — это мгновенная мощность (например, произведение напряжения и тока), а E A — это верхняя граница интеграла мгновенной мощности (например, энергии). Эта верхняя граница (взятая по всем T ≥ 0) представляет собой доступную энергию в системе для конкретного начального условия x . Если для всех возможных начальных состояний системы доступная энергия конечна, то система называется пассивной. ⟨ v ( т ) , я ( т ) ⟩ {\ Displaystyle \ langle v (т), я (т) \ rangle}
Инкрементная пассивность
В схемотехнике , неформально, пассивные компоненты относятся к компонентам, которые не способны увеличивать мощность ; это означает, что они не могут усиливать сигналы. Согласно этому определению, пассивные компоненты включают конденсаторы , катушки индуктивности , резисторы , диоды , трансформаторы , источники напряжения и источники тока. Они исключают такие устройства, как транзисторы , электронные лампы , реле , туннельные диоды и светящиеся лампы . Формально, в течение двух-концевого элемента без памяти, это означает , что вольтамперная характеристика является монотонно возрастающей . По этой причине теоретики систем управления и схемотехнических сетей называют эти устройства локально пассивными, постепенно пассивными, увеличивающимися, монотонно увеличивающимися или монотонными. Неясно, как это определение будет формализовано для многопортовых устройств с памятью — на практике разработчики схем используют этот термин неформально, поэтому, возможно, нет необходимости его формализовать.
Этот термин используется в разговорной речи в ряде других контекстов:
- Пассивный адаптер USB-PS / 2 состоит из проводов, потенциально резисторов и аналогичных пассивных (как в инкрементальном, так и в термодинамическом смысле) компонентов.
 Активный адаптер USB-PS / 2 состоит из логики для преобразования сигналов (активен в инкрементальном смысле)
Активный адаптер USB-PS / 2 состоит из логики для преобразования сигналов (активен в инкрементальном смысле) - Пассивный смеситель состоит только из резисторов (постепенно пассивных), тогда как активный смеситель включает компоненты, способные к усилению (активные).
- В работе со звуком также можно найти как (постепенно) пассивные и активные преобразователи между симметричными и несимметричными линиями. Пассивный балансный / небалансный преобразователь, как правило, представляет собой просто трансформатор вместе, конечно, с необходимыми разъемами, в то время как активный преобразователь обычно состоит из дифференциального привода или инструментального усилителя.
Другие определения пассивности
В электронной технике устройства с функцией усиления или выпрямления (например, диоды ) считаются активными. Пассивными считаются только конденсаторы, катушки индуктивности и резисторы. С точки зрения абстрактной теории диоды можно рассматривать как нелинейные резисторы, но нелинейность резистора обычно не является направленной, что является свойством, которое приводит к тому, что диоды классифицируются как активные. Бюро патентов и товарных знаков США входит в число организаций, классифицирующих диоды как активные устройства.
Системы, для которых модель малого сигнала не является пассивной, иногда называют локально активными (например, транзисторы и туннельные диоды). Системы, которые могут генерировать энергию в изменяющемся во времени невозмущенном состоянии, часто называют параметрически активными (например, некоторые типы нелинейных конденсаторов).
Стабильность
Пассивность в большинстве случаев может использоваться для демонстрации того, что пассивные цепи будут стабильными при определенных критериях. Обратите внимание, что это работает, только если используется только одно из приведенных выше определений пассивности — если компоненты из двух смешаны, системы могут быть нестабильными по любым критериям. Кроме того, пассивные схемы не обязательно будут стабильными по всем критериям стабильности. Например, резонансная последовательная LC-цепь будет иметь неограниченное выходное напряжение для ограниченного входного напряжения, но будет стабильной в смысле Ляпунова , и при ограниченном вводе энергии будет ограниченная выходная энергия.
Кроме того, пассивные схемы не обязательно будут стабильными по всем критериям стабильности. Например, резонансная последовательная LC-цепь будет иметь неограниченное выходное напряжение для ограниченного входного напряжения, но будет стабильной в смысле Ляпунова , и при ограниченном вводе энергии будет ограниченная выходная энергия.
Пассивность часто используется в системах управления для разработки стабильных систем управления или для демонстрации стабильности в системах управления. Это особенно важно при проектировании больших сложных систем управления (например, устойчивости самолетов). Пассивность также используется в некоторых областях схемотехники, особенно в конструкции фильтров.
Пассивный фильтр
Пассивный фильтр — это разновидность электронного фильтра, который состоит только из пассивных компонентов — в отличие от активного фильтра, он не требует внешнего источника питания (помимо сигнала). Поскольку большинство фильтров являются линейными, в большинстве случаев пассивные фильтры состоят всего из четырех основных линейных элементов — резисторов, конденсаторов, катушек индуктивности и трансформаторов. Более сложные пассивные фильтры могут включать нелинейные элементы или более сложные линейные элементы, такие как линии передачи.
Разделитель телевизионного сигнала, состоящий из пассивного фильтра верхних частот (слева) и пассивного фильтра нижних частот (справа). Антенна подключается к винтовым клеммам слева от центра.Пассивный фильтр имеет несколько преимуществ перед активным фильтром :
- Гарантированная стабильность
- Лучшее масштабирование для больших сигналов (десятки ампер, сотни вольт), где активные устройства часто непрактичны
- Блок питания не требуется
- Часто дешевле в дискретных конструкциях (если не требуются большие катушки)
- Для линейных фильтров потенциально большая линейность в зависимости от требуемых компонентов
Они обычно используются в конструкции кроссовера динамиков (из-за умеренно больших напряжений и токов и отсутствия легкого доступа к источнику питания), фильтров в распределительных сетях (из-за больших напряжений и токов), обхода источника питания (из-за низкой стоимости, а в некоторых случаях и требований к питанию), а также множеству дискретных схем и схем домашнего приготовления (для низкой стоимости и простоты). Пассивные фильтры необычны в конструкции монолитных интегральных схем , где активные устройства недороги по сравнению с резисторами и конденсаторами, а катушки индуктивности чрезмерно дороги. Однако пассивные фильтры все еще встречаются в гибридных интегральных схемах . В самом деле, может возникнуть желание включить пассивный фильтр, который заставит проектировщика использовать гибридный формат.
Пассивные фильтры необычны в конструкции монолитных интегральных схем , где активные устройства недороги по сравнению с резисторами и конденсаторами, а катушки индуктивности чрезмерно дороги. Однако пассивные фильтры все еще встречаются в гибридных интегральных схемах . В самом деле, может возникнуть желание включить пассивный фильтр, который заставит проектировщика использовать гибридный формат.
Примечания
Рекомендации
дальнейшее чтение
- Халил, Хасан (2001). Нелинейные системы (3-е издание) . Прентис Холл. ISBN 0-13-067389-7 . —Очень удобочитаемое вводное обсуждение пассивности в системах управления.
- Чуа, Леон ; Десоэр, Чарльз; Кух, Эрнест (1987). Линейные и нелинейные схемы . McGraw – Hill Companies. ISBN 0-07-010898-6 . — Хороший набор теорем о пассивной стабильности, но только для однопортов без памяти. Разборчиво и формально.
- Десоэр, Чарльз; Кух, Эрнест (1969). Основная теория схем . McGraw – Hill Education. ISBN 0-07-085183-2 . — Несколько менее читабельно, чем Чуа, и более ограничены по объему и формальности теорем.
- Круз, Хосе; Ван Валкенберг, ME (1974). Сигналы в линейных цепях . Хоутон Миффлин. ISBN 0-395-16971-2 . — Дает определение пассивности для мультипортов (в отличие от приведенного выше), но общее обсуждение пассивности весьма ограничено.
- Wyatt, JL; Чуа, Ло; Gannett, J .; Göknar, IC; Грин, Д. (1978). Основы теории нелинейных сетей, часть I: пассивность . Меморандум UCB / ERL M78 / 76, Лаборатория исследований электроники, Калифорнийский университет, Беркли.
Wyatt, JL; Чуа, Ло; Gannett, J .; Göknar, IC; Грин, Д. (1980). Основы теории нелинейных сетей, часть II: Без потерь . Меморандум UCB / ERL M80 / 3, Лаборатория исследований электроники, Калифорнийский университет, Беркли.
— Пара заметок, в которых хорошо обсуждается пассивность. - Брольято, Бернар; Лозано, Рохелио; Машке, Бернхард; Эгеланн, Олав (2007). Диссипативные системы: анализ и управление, 2-е издание . Springer Verlag London. ISBN 1-84628-516-X . — Полное изложение диссипативных систем с акцентом на знаменитую лемму KYP, а также на диссипативность Виллемса и ее использование в управлении.
Конденсаторы и диэлектрики | Физика
Цели обучения
К концу этого раздела вы сможете:
- Опишите действие конденсатора и определите емкость.
- Объясните, что такое конденсаторы с параллельными пластинами и их емкости.
- Обсудите процесс увеличения емкости диэлектрика.
- Определите емкость при заданном заряде и напряжении.
Конденсатор — это устройство, используемое для хранения электрического заряда.Конденсаторы имеют разные применения: от фильтрации статического электричества при радиоприеме до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как показано на рисунке 1. (В большинстве случаев между двумя пластинами используется изолятор для обеспечения разделения — см. Обсуждение диэлектриков ниже). Клеммы батареи подключены к первоначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, + Q и — Q , разделены на его две пластины.Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд Q .
Рис. 1. Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них разделены заряды + Q и — Q на своих двух половинах. (а) Конденсатор с параллельными пластинами. (b) Скрученный конденсатор с изоляционным материалом между двумя проводящими листами.
Конденсатор
Конденсатор — это устройство, используемое для хранения электрического заряда.
Количество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.
Количество заряда
Q конденсатор может хранитьКоличество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.
Рис. 2. Линии электрического поля в этом конденсаторе с параллельными пластинами, как всегда, начинаются с положительных зарядов и заканчиваются отрицательными.Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.
Система, состоящая из двух идентичных параллельных проводящих пластин, разделенных расстоянием, как на рисунке 2, называется конденсатором с параллельными пластинами . Легко увидеть взаимосвязь между напряжением и накопленным зарядом для конденсатора с параллельными пластинами, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поля будет больше. линии, если есть больше заряда.(Рисование одной силовой линии для каждого заряда — это только удобство. Мы можем нарисовать много силовых линий для каждого заряда, но их общее количество пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна Ом. .
Поле пропорционально начислению:
E ∝ Q ,
, где символ ∝ означает «пропорционально». Из обсуждения в разделе «Электрический потенциал в однородном электрическом поле» мы знаем, что напряжение на параллельных пластинах равно
. V = Ed .
Таким образом, V ∝ E . Отсюда следует, что V ∝ Q , и, наоборот,
Q ∝ V .
В целом это верно: чем больше напряжение, приложенное к любому конденсатору, тем больше в нем хранится заряд.
Различные конденсаторы будут накапливать разное количество заряда для одного и того же приложенного напряжения, в зависимости от их физических характеристик. Мы определяем их емкость C так, чтобы заряд Q , хранящийся в конденсаторе, был пропорционален C .Заряд, накопленный в конденсаторе, равен
.Q = CV .
Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора C и напряжение В . Изменив уравнение, мы видим, что емкость C — это количество заряда, накопленного на вольт, или
.[латекс] C = \ frac {Q} {V} \\ [/ latex].
Емкость
Емкость C — это величина накопленного заряда на вольт, или
[латекс] C = \ frac {Q} {V} \\ [/ latex]
Единица измерения емкости — фарад (Ф), названная в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость — это заряд на единицу напряжения, мы видим, что фарад — это кулон на вольт, или
.[латекс] 1 \ text {F} = \ frac {1 \ text {C}} {1 \ text {V}} \\ [/ latex].
Конденсатор емкостью 1 фарад может хранить 1 кулон (очень большое количество заряда) при подаче всего 1 вольт. Таким образом, одна фарада — это очень большая емкость. Типичный диапазон конденсаторов составляет от долей пикофарада (1 пФ = 10 −12 Ф) до миллифарадов (1 мФ = 10 −3 Ф).
На рисунке 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.
Как обсуждается ниже, в их конструкции обычно используются изоляционные материалы, называемые диэлектриками.
Рисунок 3. Некоторые типичные конденсаторы. Размер и значение емкости не обязательно связаны. (Источник: Windell Oskay)
Конденсатор с параллельными пластинами
Рис. 4. Конденсатор с параллельными пластинами, разделенные пластинами на расстояние d. Каждая пластина имеет площадь A.
Конденсатор с параллельными пластинами, показанный на рисунке 4, имеет две идентичные проводящие пластины, каждая из которых имеет площадь поверхности A, , разделенных расстоянием d (без материала между пластинами).Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость зависит от A и d , рассмотрев характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, в отличие от зарядов притягиваются, и сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут расходиться больше. Таким образом, C должен быть больше для большего A .Точно так же, чем ближе пластины расположены друг к другу, тем сильнее на них притяжение противоположных зарядов. Значит, C должно быть больше для меньшего d .
Можно показать, что для конденсатора с параллельными пластинами есть только два фактора ( A, и d ), которые влияют на его емкость C . Емкость конденсатора с параллельными пластинами в форме уравнения равна
.[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].
Емкость параллельного пластинчатого конденсатора
[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex]
A — это площадь одной пластины в квадратных метрах, а d — это расстояние между пластинами в метрах.Константа ε 0 — диэлектрическая проницаемость свободного пространства; его числовое значение в единицах СИ составляет ε 0 = 8,85 × 10 −12 Ф / м. Единицы измерения Ф / м эквивалентны C 2 / Н · м 2 . Небольшое числовое значение ε 0 связано с большим размером фарада. Конденсатор с параллельными пластинами должен иметь большую площадь, чтобы его емкость приближалась к фараду. (Обратите внимание, что приведенное выше уравнение действительно, когда параллельные пластины разделены воздухом или свободным пространством.Когда между пластинами помещается другой материал, уравнение изменяется, как обсуждается ниже.)
Единицы измерения Ф / м эквивалентны C 2 / Н · м 2 . Небольшое числовое значение ε 0 связано с большим размером фарада. Конденсатор с параллельными пластинами должен иметь большую площадь, чтобы его емкость приближалась к фараду. (Обратите внимание, что приведенное выше уравнение действительно, когда параллельные пластины разделены воздухом или свободным пространством.Когда между пластинами помещается другой материал, уравнение изменяется, как обсуждается ниже.)
Пример 1. Емкость и заряд в параллельном пластинчатом конденсаторе
- Какова емкость конденсатора с параллельными пластинами, каждая из которых имеет площадь 1,00 м 2 , разделенных расстоянием 1,00 мм?
- Какой заряд хранится в этом конденсаторе, если к нему приложено напряжение 3,00 × 10 3 В?
Стратегия
Определение емкости C представляет собой прямое приложение уравнения [латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].{-9} \ text {F} = 8.85 \ text {nF} \ end {array} \\ [/ latex]
Обсуждение части 1
Это небольшое значение емкости указывает на то, насколько сложно изготовить устройство с большой емкостью. Помогают специальные методы, например, использование тонких пленок очень большой площади, расположенных близко друг к другу.
Решение для Части 2
Заряд любого конденсатора определяется уравнением Q = CV . Ввод известных значений в это уравнение дает
[латекс] \ begin {array} {lll} Q & = & CV = \ left (8.{3} \ text {V} \ right) \\\ text {} & = & 26.6 \ mu \ text {C} \ end {array} \\ [/ latex]
Обсуждение части 2
Этот заряд лишь немного больше, чем у обычного статического электричества. Поскольку воздух разрывается при примерно 3,00 × 10 6 В / м, на этом конденсаторе не может быть накоплено больше заряда за счет увеличения напряжения.
Другой интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. {6} \ text {V / m} \\ [/ latex]
{6} \ text {V / m} \\ [/ latex]
Этого электрического поля достаточно, чтобы вызвать пробой в воздухе.
Диэлектрик
Предыдущий пример подчеркивает сложность сохранения большого количества заряда в конденсаторах. Если d сделать меньше, чтобы обеспечить большую емкость, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс] E = \ frac {V} {d} \\ [/ latex]). Важным решением этой проблемы является размещение изоляционного материала, называемого диэлектриком , между пластинами конденсатора и обеспечение минимально возможного размера d .Мало того, что меньший d увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, прежде чем сломаться.
Есть еще одно преимущество использования диэлектрика в конденсаторе. В зависимости от используемого материала емкость больше, чем заданная уравнением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], на коэффициент κ , называемый диэлектрическая проницаемость . Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex] (конденсатор с параллельными пластинами с диэлектриком).
Значения диэлектрической проницаемости κ для различных материалов приведены в таблице 1. Обратите внимание, что κ для вакуума равно 1, поэтому приведенное выше уравнение справедливо и в этом случае. Если использовать диэлектрик, например, поместив тефлон между пластинами конденсатора в примере 1, то емкость будет больше в κ раз, что для тефлона составляет 2,1.
Эксперимент на вынос: создание конденсатора
Насколько большой конденсатор можно сделать из обертки от жевательной резинки? Пластины будут из алюминиевой фольги, а разделитель (диэлектрик) между ними — из бумаги.
Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC | ||
|---|---|---|
| Материал | Диэлектрическая проницаемость κ | Электрическая прочность (В / м) |
| Вакуум | 1,00000 | – |
| Воздух | 1.00059 | 3 × 10 6 |
| Бакелит | 4,9 | 24 × 10 6 |
| Плавленый кварц | 3.78 | 8 × 10 6 |
| Неопреновый каучук | 6,7 | 12 × 10 6 |
| Нейлон | 3,4 | 14 × 10 6 |
| Бумага | 3,7 | 16 × 10 6 |
| Полистирол | 2,56 | 24 × 10 6 |
| Стекло Pyrex | 5,6 | 14 × 10 6 |
| Кремниевое масло | 2.5 | 15 × 10 6 |
| титанат стронция | 233 | 8 × 10 6 |
| Тефлон | 2,1 | 60 × 10 6 |
| Вода | 80 | – |
Обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что заполненные воздухом конденсаторы действуют так же, как конденсаторы с вакуумом между пластинами за исключением , что воздух может стать проводящим, если напряженность электрического поля становится равной. слишком большой.(Напомним, что [латекс] E = \ frac {V} {d} \\ [/ latex] для конденсатора с параллельными пластинами.) В таблице 1 также показаны максимальные напряженности электрического поля в В / м, которые называются диэлектрической прочностью , для нескольких материалов. Это поля, над которыми материал начинает разрушаться и проводить. 6 \ text {V / m} \ right) \ left ( 1.{-3} \ text {m} \ right) \\\ text {} & = & 3000 \ text {V} \ end {array} \\ [/ latex]
6 \ text {V / m} \ right) \ left ( 1.{-3} \ text {m} \ right) \\\ text {} & = & 3000 \ text {V} \ end {array} \\ [/ latex]
Однако предел для расстояния в 1,00 мм, заполненного тефлоном, составляет 60 000 В, поскольку диэлектрическая прочность тефлона составляет 60 × 10 6 В / м. Таким образом, тот же конденсатор, заполненный тефлоном, имеет большую емкость и может подвергаться гораздо большему напряжению. Используя емкость, которую мы рассчитали в приведенном выше примере для конденсатора с параллельными пластинами, заполненного воздухом, мы обнаружили, что конденсатор с тефлоновым заполнением может хранить максимальный заряд
[латекс] \ begin {array} {lll} Q & = & CV \\\ text {} & = & \ kappa {C} _ {\ text {air}} V \\\ text {} & = & (2.4 \ text {V}) \\\ text {} & = & 1.1 \ text {mC} \ end {array} \\ [/ latex]
Это в 42 раза больше заряда того же конденсатора, заполненного воздухом.
Диэлектрическая прочность
Максимальная напряженность электрического поля, при превышении которой изолирующий материал начинает разрушаться и становится проводником, называется его диэлектрической прочностью.
Микроскопически, как диэлектрик увеличивает емкость? За это отвечает поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость κ .Вода, например, представляет собой полярную молекулу , потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды обуславливает ее относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации лучше всего объясняется характеристиками кулоновской силы. На рис. 5 схематично показано разделение зарядов в молекулах диэлектрического материала, помещенных между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень сильна, поскольку они расположены очень близко друг к другу. Это притягивает больше заряда к пластинам, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии d друг от друга.
Это притягивает больше заряда к пластинам, чем если бы пространство было пустым, а противоположные заряды находились на расстоянии d друг от друга.
Рис. 5. (a) Молекулы изоляционного материала между пластинами конденсатора поляризованы заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда на пластину, увеличивая ее емкость. (б) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к уменьшению напряжения между пластинами при одинаковом заряде.Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.
Другой способ понять, как диэлектрик увеличивает емкость, — это рассмотреть его влияние на электрическое поле внутри конденсатора. На рисунке 5 (b) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются зарядами в диэлектрике, их меньше, идущих от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, даже если бы на пластинах был одинаковый заряд.Напряжение между пластинами составляет В, = Ед, , поэтому оно тоже снижается за счет диэлектрика. Таким образом есть меньшее напряжение В, для того же заряда Q ; поскольку [латекс] C = \ frac {Q} {V} \\ [/ latex], емкость C больше.
Диэлектрическая проницаемость обычно определяется как [латекс] \ kappa = \ frac {E_0} {E} \\ [/ latex], или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале, и в конечном итоге связанных с поляризуемостью материала.
Великие и малые вещи: субмикроскопическое происхождение поляризации
Поляризация — это разделение зарядов внутри атома или молекулы. Как уже отмечалось, планетарная модель атома описывает его как имеющее положительное ядро, вращающееся вокруг отрицательных электронов, аналогично планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в других местах, например, в атомной физике. Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рисунке 6.
Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в других местах, например, в атомной физике. Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рисунке 6.
Рис. 6. Художественное представление о поляризованном атоме. Орбиты электронов вокруг ядра слегка смещены внешними зарядами (показаны в преувеличении). Получающееся разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что непохожий заряд теперь ближе к внешним зарядам, вызывая поляризацию.
В атомной физике мы обнаружим, что орбиты электронов более правильно рассматривать как электронные облака с плотностью облака, связанной с вероятностью нахождения электрона в этом месте (в отличие от определенных положений и путей движения планет на их орбитах). вокруг Солнца).Это облако сдвигается кулоновской силой, так что в среднем атом имеет разделенный заряд. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.
Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому они называются полярными молекулами. На рисунке 7 показано разделение зарядов в молекуле воды, которая имеет два атома водорода и один атом кислорода (H 2 O).Молекула воды несимметрична — атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды более сконцентрированы вокруг более заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец — слегка положительным. Внутреннее разделение зарядов в полярных молекулах облегчает их выравнивание с внешними полями и зарядами. Следовательно, полярные молекулы проявляют более сильные поляризационные эффекты и имеют более высокие диэлектрические проницаемости.Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды собирают ионы гораздо эффективнее, потому что у них есть электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как было показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.
Например, молекулы воды собирают ионы гораздо эффективнее, потому что у них есть электрическое поле и разделение зарядов для притяжения зарядов обоих знаков. Кроме того, как было показано в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.
Рис. 7. Художественная концепция молекулы воды. Существует внутреннее разделение зарядов, поэтому вода — полярная молекула.Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда около двух ядер водорода. (Обратите внимание, что схема справа является приблизительной иллюстрацией распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.)
Исследования PhET: лаборатория конденсаторов
Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость.Измените напряжение и посмотрите, как на пластинах образовались заряды. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
- Конденсатор — это устройство для накопления заряда.
- Количество заряда Q , которое может хранить конденсатор, зависит от двух основных факторов — приложенного напряжения и физических характеристик конденсатора, таких как его размер.
- Емкость C — это количество заряда, накопленного на вольт, или [латекс] C = \ frac {Q} {V} \\ [/ latex].
- Емкость конденсатора с параллельными пластинами составляет [латекс] C = {\ epsilon} _ {0} \ frac {A} {d} \\ [/ latex], когда пластины разделены воздухом или свободным пространством. [latex] {\ epsilon} _ {\ text {0}} [/ latex] называется диэлектрической проницаемостью свободного пространства.
- Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], где κ — диэлектрик.
 константа материала.
константа материала. - Максимальная напряженность электрического поля, при превышении которой изолирующий материал начинает разрушаться и становится проводником, называется электрической прочностью.
Концептуальные вопросы
- Зависит ли емкость устройства от приложенного напряжения? А как насчет хранимого в нем заряда?
- Используйте характеристики кулоновской силы, чтобы объяснить, почему емкость должна быть пропорциональна площади пластины конденсатора. Аналогичным образом объясните, почему емкость должна быть обратно пропорциональна расстоянию между пластинами.
- Объясните причину, по которой диэлектрический материал увеличивает емкость по сравнению с тем, что было бы с воздухом между пластинами конденсатора.Какова независимая причина того, что диэлектрический материал также позволяет приложить большее напряжение к конденсатору? (Таким образом, диэлектрик увеличивает C и допускает более В .)
- Как полярный характер молекул воды помогает объяснить относительно большую диэлектрическую проницаемость воды? (См. Рисунок 7.)
- Искры возникают между пластинами заполненного воздухом конденсатора при более низком напряжении, когда воздух влажный, чем когда сухой. Объясните почему, учитывая полярный характер молекул воды.
- Вода имеет большую диэлектрическую проницаемость, но редко используется в конденсаторах. Объяснить, почему.
- Мембраны в живых клетках, в том числе в человеческих, характеризуются разделением заряда через мембрану. Таким образом, мембраны представляют собой заряженные конденсаторы, важные функции которых связаны с разностью потенциалов на мембране. Требуется ли энергия для разделения этих зарядов в живых мембранах, и если да, то является ли ее источником метаболизм пищевой энергии или каким-либо другим источником?
Рисунок 8.Полупроницаемая мембрана клетки имеет разную концентрацию ионов внутри и снаружи. Диффузия перемещает ионы K + (калий) и Cl — (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Это приводит к слою положительного заряда снаружи, слою отрицательного заряда внутри и, следовательно, к напряжению на клеточной мембране. Мембрана обычно непроницаема для Na + (ионы натрия).
Это приводит к слою положительного заряда снаружи, слою отрицательного заряда внутри и, следовательно, к напряжению на клеточной мембране. Мембрана обычно непроницаема для Na + (ионы натрия).
Задачи и упражнения
- Какой заряд сохраняется в конденсаторе 180 мкФ, когда к нему приложено 120 В?
- Найдите накопленный заряд, когда 5.50 В подается на конденсатор емкостью 8,00 пФ.
- Какой заряд хранится в конденсаторе в Примере 1?
- Рассчитайте напряжение, приложенное к конденсатору 2,00 мкФ, когда он имеет заряд 3,10 мкКл.
- Какое напряжение необходимо подать на конденсатор емкостью 8,00 нФ для накопления заряда 0,160 мкКл?
- Какая емкость необходима для хранения заряда 3,00 мкКл при напряжении 120 В?
- Какая емкость терминала большого генератора Ван-де-Граафа, учитывая, что он хранит 8?00 мкКл заряда при напряжении 12,0 МВ?
- Найдите емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 5,00 м 2 , разделенных слоем тефлона 0,100 мм.
- (a) Какова емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 1,50 м 2 , разделенных 0,0200 мм неопреновой резины? (b) Какой заряд он держит, когда к нему приложено 9,00 В?
- Интегрированные концепции. Шутник подает 450 В на 80.Конденсатор 0 мкФ, а затем бросает его ничего не подозревающей жертве. Палец пострадавшего обгорел от разряда конденсатора через 0,200 г мяса. Какое повышение температуры мяса? Разумно ли предполагать отсутствие изменения фазы?
- Необоснованные результаты. (a) Конденсатор с параллельными пластинами имеет площадь пластин 4,00 м 2 , разделенных нейлоном толщиной 0,0100 мм, и накапливает 0,170 Кл заряда. Какое приложенное напряжение? б) Что неразумного в этом результате? (c) Какие допущения являются ответственными или противоречивыми?
Глоссарий
конденсатор: устройство, накапливающее электрический заряд
емкость: количество заряда на единицу вольт
диэлектрик: изоляционный материал
диэлектрическая прочность: максимальное электрическое поле, выше которого изоляционный материал начинает разрушаться и проводить
Конденсатор с параллельными пластинами: две идентичные проводящие пластины, разделенные расстоянием
полярная молекула: молекула с внутренним разделением заряда
Избранные решения проблем и упражнения
1. 21,6 мК
21,6 мК
3. 80.0 мС
5. 20,0 кВ
7. 667 пФ
9. (а) 4,4 мкФ; (б) 4.0 × 10 −5 C
11. (а) 14,2 кВ; (b) Напряжение неоправданно велико, более чем в 100 раз превышает напряжение пробоя нейлона; (c) Предполагаемый заряд неоправданно велик и не может храниться в конденсаторе таких размеров.
5.16: Вставка диэлектрика в конденсатор
Предположим, вы начали с двух пластин, разделенных вакуумом или воздухом, с разностью потенциалов на пластинах, а затем вставляете диэлектрический материал с диэлектрической проницаемостью \ (\ epsilon_0 \) между пластинами. тарелки.Меняется ли интенсивность поля или остается прежней? Если первое, оно увеличивается или уменьшается?
Ответ на эти вопросы
- зависит от того, ссылаетесь ли вы под полем на поле \ (E \) или на поле \ (D \);
- от того, являются ли пластины изолированными или они соединены с полюсами батареи .
Начнем с предположения, что пластины изолированные . Смотрите рисунок \ (V.\) 20.
\ (\ text {РИСУНОК V.20} \)
Пусть \ (Q \) будет зарядом на пластинах, а \ (\ sigma \) — поверхностной плотностью заряда. Они не изменяются введением диэлектрика. Закон Гаусса предусматривает, что \ (D = \ sigma \), так что это тоже не изменяется при введении диэлектрика. Первоначально электрическое поле было \ (E_1 = D / \ epsilon_0 \). После введения диэлектрика оно немного меньше, а именно \ (E_1 = D / \ epsilon \).
Примем потенциал нижней пластины равным нулю.До введения диэлектрика потенциал верхней пластины был \ (V_1 = \ sigma d / \ epsilon_0 \). После введения диэлектрика его немного меньше, а именно \ (V_1 = \ sigma d / \ epsilon \).
Почему электрическое поле \ (E \) меньше после введения диэлектрического материала? Это потому, что диэлектрический материал становится поляризованным на . В разделе 3.6 мы видели, как материя может поляризоваться.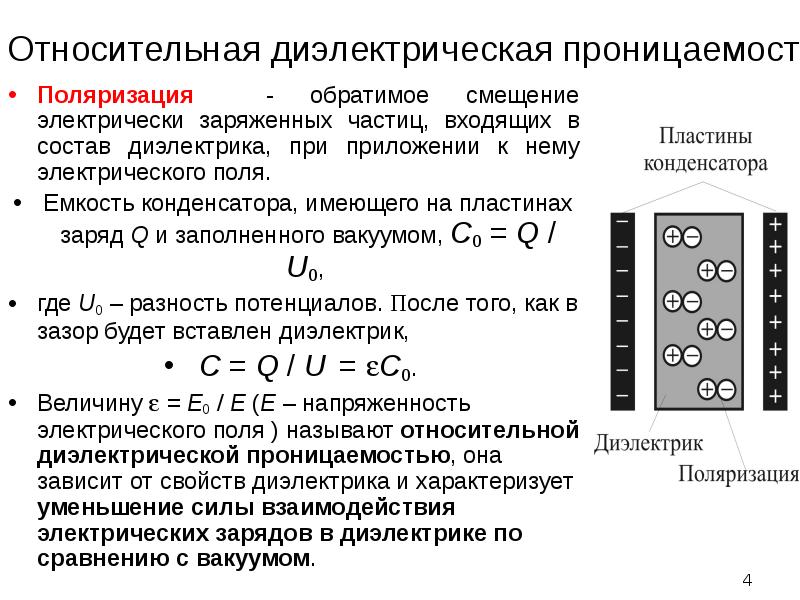 Либо молекулы с уже существующими дипольными моментами выравниваются с наложенным электрическим полем, либо, если у них нет постоянного дипольного момента или они не могут вращаться, дипольный момент может быть индуцирован в отдельных молекулах.В любом случае эффект выравнивания всех этих молекулярных диполей состоит в том, что на поверхности диэлектрического материала рядом с отрицательной пластиной имеется небольшой избыток положительного заряда, а на поверхности диэлектрика — небольшой избыток отрицательного заряда. материал рядом с положительной пластиной. Это создает электрическое поле, противоположное направлению приложенного поля, и, таким образом, общее электрическое поле несколько уменьшается.
Либо молекулы с уже существующими дипольными моментами выравниваются с наложенным электрическим полем, либо, если у них нет постоянного дипольного момента или они не могут вращаться, дипольный момент может быть индуцирован в отдельных молекулах.В любом случае эффект выравнивания всех этих молекулярных диполей состоит в том, что на поверхности диэлектрического материала рядом с отрицательной пластиной имеется небольшой избыток положительного заряда, а на поверхности диэлектрика — небольшой избыток отрицательного заряда. материал рядом с положительной пластиной. Это создает электрическое поле, противоположное направлению приложенного поля, и, таким образом, общее электрическое поле несколько уменьшается.
До введения диэлектрического материала энергия, запасенная в конденсаторе, составляла \ (\ dfrac {1} {2} QV_1 \).После введения материала это будет \ (\ dfrac {1} {2} QV_2 \), что немного меньше. Таким образом, потребуется работа по удалению материала между пластинами. Пустой конденсатор будет иметь тенденцию всасывать материал, так же как заряженный стержень в главе 1 притягивает незаряженный пробковый шар.
Теперь предположим, что пластины подключены к батарее . (Рисунок \ (V. \) 21)
\ (\ text {РИСУНОК V.21} \)
На этот раз разность потенциалов остается постоянной, и, следовательно, поле \ (E \), которое это просто \ (V / d \).Но поле \ (D \) увеличивается с \ (\ epsilon_0 E \) до \ (\ epsilon E \), и, следовательно, плотность поверхностного заряда на пластинах увеличивается. Эта дополнительная зарядка происходит от аккумулятора.
Емкость увеличивается с \ (\ dfrac {\ epsilon_0A} {d} \ text {до} \ dfrac {\ epsilon A} {d} \), а заряд, накопленный на пластинах, увеличивается с \ (Q_1 = \ dfrac { \ epsilon_0AV} {d} \ text {to} Q_2 \ dfrac {\ epsilon AV} {d} \). Энергия, запасенная в конденсаторе, увеличивается с \ (\ dfrac {1} {2} Q_1V \ text {до} \ dfrac {1} {2} Q_2V \).
Энергия, поставляемая батареей = энергия, сбрасываемая в конденсатор + энергия, необходимая для всасывания диэлектрического материала в конденсатор:
\ [(Q_2-Q_1) V = \ dfrac {1} {2} (Q_2- Q_1) V + \ dfrac {1} {2} (Q_2-Q_1) V. \ nonumber \]
\ nonumber \]
Вам нужно будет выполнить работу по удалению материала с конденсатора; половина работы, которую вы выполняете, — это механическая работа, выполняемая при вытягивании материала; другая половина будет использоваться для зарядки аккумулятора.
В п. 5.15 Я изобрел один тип зарядного устройства. Теперь я собираюсь заработать состояние на изобретении зарядного устройства другого типа.
Пример 1 .
\ (\ text {РИСУНОК V.22} \)
Конденсатор состоит из двух квадратных пластин, каждая размером \ (a \ times a \), разделенных \ (d \), подключенных к батарее. Между пластинами находится диэлектрическая среда с проницаемостью \ (\ epsilon \). Вытягиваю диэлектрическую среду со скоростью \ (\ dot x \). Рассчитайте ток в цепи при подзарядке аккумулятора.2 — (\ epsilon — \ epsilon_0) ax} {d} \ right] V. \ nonumber \]
Если диэлектрик перемещается со скоростью \ (\ dot x \), заряд, удерживаемый конденсатором, будет увеличиваться на коэффициент
\ [\ dot Q = \ dfrac {- (\ epsilon- \ epsilon_0) a \ dot xV} {d}. \ nonumber \]
(Это отрицательно, поэтому \ (Q \) уменьшается.) A Таким образом, ток такой величины течет по цепи по часовой стрелке в батарею. Вы должны убедиться, что выражение имеет правильные размеры для тока.
Пример 2.
\ (\ text {РИСУНОК V.23} \)
Конденсатор состоит из двух пластин, каждая площадью \ (A \), разделенных расстоянием \ (x \), подключенных к батарее EMF \ (V. \) Чашка опирается на нижнюю пластину. Чашка постепенно заполняется непроводящей жидкостью с диэлектрической проницаемостью \ (\ epsilon \), поверхность поднимается со скоростью \ (\ dot x \). Рассчитайте величину и направление тока в цепи.
Легко подсчитать, что, когда жидкость имеет глубину x , емкость конденсатора составляет
\ [C = \ dfrac {\ epsilon \ epsilon_0A} {\ epsilon d — (\ epsilon — \ epsilon_0 ) x} \ nonumber \]
, и тогда заряд, удерживаемый конденсатором, равен
\ [\ nonumber Q = \ dfrac {\ epsilon \ epsilon_0AV} {\ epsilon d — (\ epsilon- \ epsilon_0) x}. 2} \).
2} \).
Влияние диэлектрика на емкость — учебный материал для IIT JEE
Что такое диэлектрик?
Диэлектрики — это непроводящие вещества, которые являются изоляционными материалами и плохо проводят электрический ток. Диэлектрические материалы могут удерживать электростатический заряд, рассеивая при этом минимальную энергию в виде тепла. Примеры диэлектрика: Слюда , Пластмасса , Стекло , Фарфор и различные оксиды металлов , и даже сухой воздух также является примером диэлектрика.
Рисунок 1.1 Диэлектрический конденсатор
Что такое диэлектрическая постоянная?В конденсаторе с параллельными пластинами, когда диэлектрическая пластина помещается между двумя пластинами, отношение напряженности приложенного электрического поля к напряженности уменьшенного значения конденсатора электрического поля называется диэлектрической постоянной, то есть:
K = E или / E
K — диэлектрическая проницаемость
E 0 больше или равно E
Где E o диэлектрик
А поле нетто
Чем больше диэлектрическая проницаемость, тем больше заряда может сохраняться.Полное заполнение пространства между пластинами конденсатора диэлектриком увеличивает емкость на коэффициент диэлектрической проницаемости:
C = KC o , где C o — емкость без диэлектрика между пластинами.
Диэлектрики обычно помещают между двумя пластинами конденсаторов с параллельными пластинами. Они могут полностью или частично занимать область между пластинами.
Когда диэлектрик помещается между двумя пластинами конденсатора с параллельными пластинами, он поляризуется присутствующим электрическим полем. Плотности поверхностных зарядов рассматриваются как σ p и — σ p .
Плотности поверхностных зарядов рассматриваются как σ p и — σ p .
Когда диэлектрик полностью помещен между двумя пластинами конденсатора, его диэлектрическая постоянная увеличивается по сравнению с вакуумным значением.
Рисунок 1.2 Диэлектрик, расположенный между двумя пластинами
Электрическое поле внутри конденсатора определяется значением
.Итак,
А,
Ɛ — диэлектрическая проницаемость вещества.
Разница потенциалов между пластинами равна
Для линейных диэлектриков
Где k — диэлектрическая проницаемость вещества
K = 1 иначе,
Как диэлектрик увеличивает емкость конденсатора?Электрическое поле между пластинами конденсатора с параллельными пластинами прямо пропорционально емкости C конденсатора. Напряженность электрического поля уменьшается из-за наличия диэлектрика, и если общий заряд на пластинах поддерживается постоянным, то уменьшается разность потенциалов на пластинах конденсатора.
Таким образом, диэлектрик увеличивает емкость конденсатора.
Рисунок 1.3 Параллельно-пластинчатый конденсатор с диэлектриком
Доказательство
Рассмотрим следующую схему
Рис. 1.4 диэлектрик между двумя конденсаторами
Диэлектрическая поляризацияКогда к диэлектрическому материалу прикладывают внешнее электрическое поле, его поведение может быть определено и известно как Диэлектрическая поляризация , что можно понять по смещению зарядов (положительных и отрицательных) при приложении электрического поля
Основная задача диэлектрической поляризации — связать макроскопические свойства с микроскопическими свойствами.Где макроскопические свойства могут быть от диэлектрической проницаемости до поляризуемости
Поляризация возникает под действием электрического поля или других внешних факторов, таких как механическое напряжение в случае пьезоэлектрических кристаллов (пьезоэлектрические кристаллы — это те твердые материалы, которые накапливают в них электрический заряд). Диэлектрическая поляризация может также возникать спонтанно в пироэлектрических кристаллах, особенно в сегнетоэлектриках (сегнетоэлектричество — это свойство некоторых материалов, которые имеют спонтанную электрическую поляризацию, которую можно обратить на противоположную путем приложения внешнего электрического поля).
Диэлектрическая поляризация может также возникать спонтанно в пироэлектрических кристаллах, особенно в сегнетоэлектриках (сегнетоэлектричество — это свойство некоторых материалов, которые имеют спонтанную электрическую поляризацию, которую можно обратить на противоположную путем приложения внешнего электрического поля).
1,5 Диэлектрическая поляризация
Вставка диэлектрика в конденсаторКогда диэлектрический материал вводится между пластинами А, когда диэлектрический материал помещается между пластинами конденсатора с параллельными пластинами, тогда из-за поляризации зарядов по обе стороны от диэлектрика он создает собственное электрическое поле, которое действует в направлении противоположно полю из-за источника.
Это делает чистый электрический поток равным нулю.Этот эффект приводит к появлению емкости.
Вставка диэлектрика между пластинами конденсатора при постоянном напряжении или заряде имеет тот же эффект, что и отношение заряда к напряжению.
| Рисунок 1.6 Влияние диэлектрика на пластины при постоянном напряжении или заряде | |
Что диэлектрик делает с конденсатором?
Диэлектрики часто называют изоляторами , когда изолятор помещен между двумя пластинами конденсатора.
Сторона изолятора, ближайшая к положительной пластине, будет отрицательной, а сторона, ближайшая к отрицательной пластине, будет положительной.
Чистое поле внутри конденсатора и разность потенциалов на конденсаторе уменьшаются, когда электрическое поле от заряда пластин конденсатора компенсируется электрическим полем поляризованного диэлектрика. Конденсатору требуется больший заряд, чтобы вернуться к своему первоначальному потенциалу разница.
Конденсатору требуется больший заряд, чтобы вернуться к своему первоначальному потенциалу разница.
Чистый эффект диэлектрика заключается в увеличении количества заряда, который конденсатор может хранить при заданной разности потенциалов.Весь смысл использования конденсатора заключается в накоплении заряда, поэтому придумать способ накопить больше заряда при том же количестве усилий — это хорошо.
Добавление диэлектрика к конденсатору увеличивает емкость в K и
раз.Заряд конденсатора увеличивается, когда напряжение остается постоянным, и
Если конденсатор отключен, то есть заряд остается постоянным, потенциал на конденсаторе будет уменьшаться.
Емкость конденсатора с параллельными пластинами зависит от:
Расстояние d между двумя пластинами
Область среды А между пластинами
Согласно закону Гаусса электрическое поле можно записать как
Поскольку мы знаем, что емкость определяется как V = Q / C, поэтому емкость можно переписать как
Когда пластины расположены очень близко и , площадь пластин большая , мы получаем максимальную емкость .
Рис. 1.7 диэлектрик, расположенный между двумя электродами
На двух пластинах микроскопический дипольный момент материала будет экранировать заряды. Таким образом, изменится влияние диэлектрического материала, который вставлен между двумя пластинами. Материалы имеют проницаемость , которая задается относительной проницаемостью K
Таким образом, емкость определяется как:
Емкость конденсатора с параллельными пластинами может быть увеличена путем введения диэлектрика между пластинами, так как диэлектрик имеет проницаемость k, которая больше 1. K также иногда называют диэлектрической постоянной .
K также иногда называют диэлектрической постоянной .
1. Когда диэлектрик полностью заполнен между пластинами
Когда пространство между двумя пластинами полностью заполнено диэлектриком, то относительная проницаемость er,
C 0 = C x e r
2. Когда диэлектрик частично заполнен между пластинами
Когда в конденсаторе с параллельными пластинами, пространство между пластинами частично заполнено воздухом и частично другим веществом, его емкость можно рассчитать.
Пусть существует конденсатор с параллельными пластинами, в котором среда между параллельными пластинами состоит в основном из воздуха и частично из другого вещества.
Дополнительная информация
Влияние диэлектриков на емкость
Конденсатор с диэлектриком | Репетитор 4 по физике
Что такое диэлектрик
Диэлектрический материал — это изолятор, в котором нет свободных электронов.
Это означает, что диэлектрик не может проводить ток.
Диэлектрическая проницаемость
Диэлектрическую проницаемость K можно записать как отношение диэлектрической проницаемости среды. разрешению свободного пространства.
Его также можно определить как отношение емкость с диэлектриком в качестве среды и — емкость с воздухом или вакуумом между пластинами.
Далее его также можно определить как отношение электрическое поле между пластинами с воздухом или вакуумом в качестве среды и — электрическое поле между пластинами с диэлектриком в качестве среды.
Полярные и неполярные материалы
Материалы можно разделить на полярные и неполярные.
Полярные материалы
Материалы и называются полярными материалами, когда молекулы обладают суммарным дипольным моментом. Это означает, что центр масс положительного заряда и центр масс отрицательный заряд в молекуле незначительно отделен
Неполярные материалы
Материалы и называются неполярными материалами, когда молекулы не имеют чистого диапольного момента.Это означает, что центр масс положительного заряда и центр масс отрицательные заряды в молекуле совпадают и не способны создать дипольный момент
Атомы из-за своей сферической симметрии всегда неполярны
Конденсатор с диэлектриком
Если поместить диэлектрик между пластинами парелеля конденсатора и дать заряд к конденсатору, то при отсутствии диэлектрика возникает электрическое поле . Скажем, расстояние между пластинами d а толщина диэлектрика t.Теперь, поскольку положительный заряд находится на одной пластине а отрицательный заряд находится на другой пластине, он будет вызывать диапольный момент в молекулах диэлектрика. Если бы молекулы были изначально неполярными, у них это индуцировалось бы, однако, если у них уже был диапольный момент, они будут перестроены в соответствии с положительным и отрицательным зарядом на пластинах, ориентируясь таким образом в направлении электрического поля. Теперь слева сторона диэлектрика будет иметь чистый отрицательный заряд, а правая сторона — чистый положительный заряд.И, в результате направление индуцированного электрического поля внутри диэлектрика будет справа налево.
Итак, поскольку слева есть электрическое поле из-за индукции, чистое электрическое поле внутри диэлектрик уменьшится и будет:
Однако направление будет таким же, как и направление
Влияние диэлектрика на емкость конденсатора
Позвольте быть площадь каждой пластины
При отсутствии диэлектрика емкость можно записать как:
Однажды диэлектрик, имеющий толщину помещается между пластинами, емкость изменится.
потенциал между пластинами будет:
Вот продукт электрического поля и расстояния пространства, свободного от диэлектрика, что определяется выражением . это продукт электрического поля внутри диалектика и толщины диэлектрика.
Сейчас
следовательно
мы знаем, что
следовательно
или
Из закона Гаусса мы знаем, что где — поверхностная плотность заряда, т. е. плата за единицу площади
, поэтому мы можем сказать, что если это заряд на каждой пластине, которая отрицательна на одной и положительна на другой, затем
или
мы знаем, что
следовательно
, следовательно,
мы знаем, что емкость
, следовательно,
Это формула емкости при неполном заполнении диэлектриком. тарелки
Отсюда видно, что если диэлектрик полностью заполняет пластины, то t будет равно d.Когда мы подставляем это, получаем
мы видели, что
следовательно
Теперь, поскольку K всегда больше 1, означает, что
Или, если мы поместим диэлектрик между пластинами конденсатора, его емкость будет равна увеличить
Диэлектрическая прочность
Это максимальное значение электрического поля, которое диэлектрик может выдержать без электрический пробой.
Часть 4 — Диэлектрическая поляризация
Добро пожаловать в серию «Основы работы с конденсаторами», в которой мы расскажем вам обо всех особенностях микросхем конденсаторов — их свойствах, классификации продукции, стандартах испытаний и сценариях использования — чтобы помочь вам принимать обоснованные решения о подходящие конденсаторы для ваших конкретных приложений.После описания факторов, влияющих на емкость, в нашей предыдущей статье, давайте обсудим диэлектрическую поляризацию и ее связь с частотой
.Что такое диэлектрическая поляризация?
Когда к конденсатору прикладывается электрическое поле, диэлектрический материал (или электрический изолятор) становится поляризованным, так что отрицательные заряды в материале ориентируются в направлении положительного электрода, а положительные заряды смещаются в сторону отрицательного электрода. Поскольку заряды не могут свободно перемещаться в изоляторе, эффект поляризации, который противодействует приложенному полю, притягивает заряды к электродам, таким образом сохраняя энергию в конденсаторе.
Чем легче поляризовать материал, тем большее количество заряда может храниться в конденсаторе. Эта способность накапливать энергию в электрическом поле называется диэлектрической проницаемостью K или относительной диэлектрической проницаемостью ε r . Степень поляризации P связана с диэлектрической проницаемостью K и напряженностью электрического поля E следующим образом:
P = ε 0 (К-1) E
, где ε 0 — физическая постоянная, известная как диэлектрическая проницаемость вакуума
Полная поляризация диэлектрика складывается из четырех источников смещения заряда: электронного смещения P e , ионного смещения P i , ориентации постоянных диполей P d и смещения пространственного заряда P s .
P t = P e + P i + P d + P s
Рисунок 1. Четыре типа механизмов поляризации (источник: ACRHEM )
Электронная поляризация: Этот эффект возникает во всех атомах под действием электрического поля. Ядро атома и центр его электронного облака удаляются друг от друга, создавая крошечный диполь с очень небольшим эффектом поляризации.
Ионная поляризация: В ионных твердых телах, таких как керамические материалы, ионы симметрично расположены в кристаллической решетке с чистой нулевой поляризацией. При приложении электрического поля катионы и анионы притягиваются в противоположных направлениях. Это создает относительно большое ионное смещение (по сравнению с электронным смещением), которое может привести к высоким диэлектрическим постоянным в керамике, широко используемой в конденсаторах.
Поляризация диполя (или ориентации) : Некоторые твердые тела имеют постоянные молекулярные диполи, которые под действием электрического поля вращаются в направлении приложенного поля, создавая суммарный средний дипольный момент на молекулу.Дипольная ориентация более распространена в полимерах, поскольку их атомная структура допускает переориентацию.
Поляризация пространственного заряда (или межфазной): В керамике это явление возникает из-за посторонних зарядов, которые возникают из-за загрязнений или неправильной геометрии на границах раздела поликристаллических твердых тел. Эти заряды частично подвижны и мигрируют под действием приложенного поля, вызывая этот внешний тип поляризации.
Как частота влияет на поляризацию и диэлектрические потери?
Интересно, что каждый тип поляризации имеет разную временную реакцию на частоту приложенного поля, что означает, что суммарный эффект поляризации для диэлектрической проницаемости зависит от частоты.
- Электронное смещение очень быстрое, поэтому эта поляризация происходит на частотах до 10 17
- Ионная поляризация немного медленнее и происходит на частотах до 10 13
- Дипольная поляризация происходит на частотах меньше 10 10
- Поляризация пространственного заряда является самой медленной и происходит при значениях менее 10 4
Следовательно, диэлектрическая проницаемость (и, следовательно, значение емкости) всегда уменьшается с увеличением частоты, поскольку механизмы поляризации становятся менее эффективными.
Рисунок 2. Влияние частоты на механизмы поляризации
В цепи переменного тока напряжение и ток на идеальном конденсаторе сдвинуты по фазе на 90 градусов. Однако реальные диэлектрики не идеальны, и поэтому запаздывание или «время релаксации» механизмов поляризации с частотой порождает диэлектрические потери. Можно определить угол, на который ток конденсатора не совпадает по фазе с идеальным, и тангенс этого угла является свойством материала, называемым тангенсом потерь (Tan δ) или коэффициентом рассеяния.На практике материалы с более высокими диэлектрическими постоянными (и, следовательно, с высокими механизмами поляризации) демонстрируют более высокие коэффициенты рассеяния.
Рис. 3. Касательные потери или коэффициент рассеяния реального конденсатора
Частота, на которой используется диэлектрик, имеет важное влияние на механизмы поляризации, особенно на время релаксации, отображаемое материалом при следовании инверсии поля в переменной цепи.
- Случай 1: Если время релаксации поляризации намного больше и медленнее, чем инверсия поля, ионы вообще не могут следовать за полем и потери малы.
- Случай 2: Если время релаксации намного быстрее, чем инверсия поля, поляризационные процессы могут легко следовать за частотой поля, а потери невелики.
- Случай 3: Если время релаксации и частота поля одинаковы, значки могут следовать за полем, но ограничены своим запаздыванием, таким образом, генерируя самые высокие потери с частотой.
Следовательно, диэлектрические потери максимальны на частоте, на которой приложенное поле имеет такой же период релаксации.Керамические диэлектрические составы всегда показывают диапазон времен релаксации по частотному спектру, поскольку эти материалы состоят из поликристаллического вещества. В высокочастотных приложениях этот параметр часто называют Q-фактором, который является обратной величиной тангенса угла потерь: Q = 1 / (tan δ)
Рисунок 4. Изменения диэлектрической проницаемости и диэлектрических потерь, вызванные частотой
Надеюсь, часть 4 дала вам лучшее понимание диэлектрической поляризации и того, как она влияет на ваше конкретное приложение.В Части 5 мы рассмотрим диэлектрические свойства, такие как сопротивление изоляции и электрическую прочность. Также ознакомьтесь с нашими конденсаторами Knowles Precision Devices, чтобы ознакомиться с полным ассортиментом нашей продукции.
Чтобы узнать больше о конденсаторах, загрузите нашу электронную книгу «Руководство по выбору правильного конденсатора для вашего конкретного применения».
диэлектрическая проницаемость | Определение, формула, единицы и факты
Диэлектрическая постоянная , также называемая относительной диэлектрической проницаемостью или удельная индуктивная емкость , свойство электроизоляционного материала (диэлектрика), равное отношению емкости конденсатора, заполненного данный материал соответствует емкости идентичного конденсатора в вакууме без диэлектрического материала.Введение диэлектрика между пластинами, скажем, конденсатора с параллельными пластинами всегда увеличивает его емкость или способность накапливать противоположные заряды на каждой пластине по сравнению с этой способностью, когда пластины разделены вакуумом. Если C — это значение емкости конденсатора, заполненного данным диэлектриком, а C 0 — емкость идентичного конденсатора в вакууме, диэлектрическая постоянная, обозначенная греческой буквой каппа, κ, равна просто выражается как κ = C / C 0 .Диэлектрическая проницаемость — это число без размеров. В системе сантиметр-грамм-секунда диэлектрическая проницаемость идентична диэлектрической проницаемости. Он обозначает крупномасштабное свойство диэлектриков без определения электрического поведения в атомном масштабе.
многослойный конденсаторМногослойный конденсатор с чередующимися слоями металлических электродов и керамического диэлектрика.
Британская энциклопедия, Inc.Британская викторина
Викторина «Все о физике»
Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.
Значение статической диэлектрической проницаемости любого материала всегда больше единицы, ее значение для вакуума. Значение диэлектрической проницаемости при комнатной температуре (25 ° C или 77 ° F) составляет 1.00059 для воздуха, 2.25 для парафина, 78.2 для воды и около 2000 для титаната бария (BaTiO 3 ) при приложении электрического поля. перпендикулярно главной оси кристалла. Поскольку значение диэлектрической проницаемости для воздуха почти такое же, как и для вакуума, для всех практических целей воздух не увеличивает емкость конденсатора.Диэлектрическая проницаемость жидкостей и твердых тел может быть определена путем сравнения значения емкости, когда диэлектрик находится на месте, с ее значением, когда конденсатор заполнен воздухом.
Конденсатор с диэлектриком — Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Опишите влияние диэлектрика в конденсаторе на емкость и другие свойства
- Вычислить емкость конденсатора, содержащего диэлектрик
Как мы обсуждали ранее, изоляционный материал, помещенный между пластинами конденсатора, называется диэлектриком.Вставка диэлектрика между пластинами конденсатора влияет на его емкость. Чтобы понять, почему, давайте рассмотрим эксперимент, описанный на (рис.). Первоначально конденсатор с емкостью, когда между его пластинами находится воздух, заряжается аккумулятором до напряжения. Когда конденсатор полностью заряжен, аккумулятор отключается. Затем на пластинах остается заряд, и измеряется разность потенциалов между пластинами. Теперь предположим, что мы вставляем диэлектрик, который полностью заполняет промежуток между пластинами.Если мы будем следить за напряжением, мы обнаружим, что показание вольтметра упало до меньшего значения В . Мы запишем это новое значение напряжения как часть исходного напряжения с положительным числом:
.Постоянная в этом уравнении называется диэлектрической проницаемостью материала между пластинами, и ее значение является характерным для материала. Подробное объяснение того, почему диэлектрик снижает напряжение, дается в следующем разделе. У разных материалов разная диэлектрическая проницаемость (таблица значений для типичных материалов приведена в следующем разделе).Как только батарея отсоединяется, заряд от пластин конденсатора не может течь к батарее. Следовательно, введение диэлектрика не влияет на заряд на пластине, который остается на уровне. Следовательно, находим, что емкость конденсатора с диэлектриком составляет
Это уравнение говорит нам, что емкость пустого (вакуумного) конденсатора может быть увеличена в раз, когда мы вставляем диэлектрический материал, чтобы полностью заполнить пространство между его пластинами .Обратите внимание, что (рисунок) также можно использовать для пустого конденсатора, установив. Другими словами, мы можем сказать, что диэлектрическая проницаемость вакуума равна 1, что является справочным значением.
(а) Полностью заряженный вакуумный конденсатор имеет напряжение и заряд (заряды остаются на внутренних поверхностях пластины; на схеме указан знак заряда на каждой пластине). (b) На шаге 1 аккумулятор отключается. Затем, на этапе 2, в заряженный конденсатор вставляется диэлектрик (то есть электрически нейтральный).Когда теперь измеряется напряжение на конденсаторе, обнаруживается, что значение напряжения уменьшилось до. Схема показывает знак индуцированного заряда, который теперь присутствует на поверхностях диэлектрического материала между пластинами.Принцип, выраженный (Рисунок), широко используется в строительной отрасли ((Рисунок)). Металлические пластины в электронном устройстве поиска контактов эффективно действуют как конденсатор. Вы кладете прибор для поиска гвоздей плоской стороной на стену и постоянно перемещаете его в горизонтальном направлении.Когда искатель перемещается по деревянной стойке, емкость его пластин изменяется, потому что древесина имеет диэлектрическую проницаемость, отличную от диэлектрической проницаемости гипсовой стены. Это изменение запускает сигнал в цепи, и, таким образом, шпилька обнаруживается.
Электронный поиск стоек используется для обнаружения деревянных стоек за гипсокартоном. (кредит вверху: модификация работы Джейн Уитни)
На электрическую энергию, запасаемую конденсатором, также влияет присутствие диэлектрика. Когда энергия, запасенная в пустом конденсаторе, равна, энергия U , запасенная в конденсаторе с диэлектриком, меньше в
раз.Когда образец диэлектрического материала приближается к пустому заряженному конденсатору, образец реагирует на электрическое поле зарядов на пластинах конденсатора.Точно так же, как мы узнали из «Электрических зарядов и полей» по электростатике, на поверхности образца будут индуцированные заряды; однако они не являются свободными зарядами, как в проводнике, потому что идеальный изолятор не имеет свободно движущихся зарядов. Эти наведенные заряды на диэлектрической поверхности имеют противоположный знак свободным зарядам на пластинах конденсатора, и поэтому они притягиваются свободными зарядами на пластинах. Следовательно, диэлектрик «втягивается» в зазор, и работа по поляризации диэлектрического материала между пластинами выполняется за счет накопленной электрической энергии, которая уменьшается в соответствии с (Рисунок).
Проверьте свое понимание Когда диэлектрик вставлен в изолированный и заряженный конденсатор, запасенная энергия уменьшается до 33% от своего первоначального значения. а) Что такое диэлектрическая проницаемость? б) Как изменяется емкость?
а. 3.0; б.
Сводка
- Емкость пустого конденсатора увеличивается в раз, когда пространство между его пластинами полностью заполняется диэлектриком с диэлектрической проницаемостью.
- Каждый диэлектрический материал имеет определенную диэлектрическую проницаемость.
- Энергия, запасенная в пустом изолированном конденсаторе, уменьшается в раз, когда пространство между его пластинами полностью заполнено диэлектриком с диэлектрической проницаемостью.
Концептуальные вопросы
Обсудите, что произойдет, если вставить проводящую пластину, а не диэлектрик, в зазор между пластинами конденсатора.
Обсудите, как энергия, запасенная в пустом, но заряженном конденсаторе, изменяется, когда вставляется диэлектрик, если (а) конденсатор изолирован, так что его заряд не меняется; (б) конденсатор остается подключенным к батарее, так что разность потенциалов между его пластинами не меняется.
Проблемы
Покажите, что для данного диэлектрического материала максимальная энергия, которую может хранить конденсатор с параллельными пластинами, прямо пропорциональна объему диэлектрика.
Конденсатор, заполненный воздухом, состоит из двух плоских параллельных пластин, расположенных на расстоянии 1,0 мм друг от друга. Внутренняя площадь каждой пластины составляет. а) Какова емкость этого набора пластин? (б) Если область между пластинами заполнена материалом с диэлектрической проницаемостью 6,0, какова новая емкость?
Конденсатор состоит из двух концентрических сфер, одна из которых имеет радиус 5.00 см, другой радиусом 8,00 см. а) Какова емкость этого набора проводников? (б) Если область между проводниками заполнена материалом с диэлектрической проницаемостью 6,00, какова емкость системы?
Конденсатор с параллельными пластинами имеет заряд величины на каждой пластине и емкость, когда между пластинами есть воздух. Пластины разделены на 2,00 мм. При постоянном заряде пластин между пластинами вставляется диэлектрик, полностью заполняющий пространство между пластинами.а) Какова разность потенциалов между пластинами конденсатора до и после установки диэлектрика? б) Каково электрическое поле в точке посередине между пластинами до и после введения диэлектрика?
а. до 3,00 В; после 0,600 В; б. до 1500 В / м; после 300 В / м
Некоторые клеточные стенки человеческого тела имеют на внутренней поверхности слой отрицательного заряда. Предположим, что поверхностные плотности заряда равны, стенка ячейки толстая, а материал стенки ячейки имеет диэлектрическую проницаемость.(а) Найдите величину электрического поля в стенке между двумя заряженными слоями.

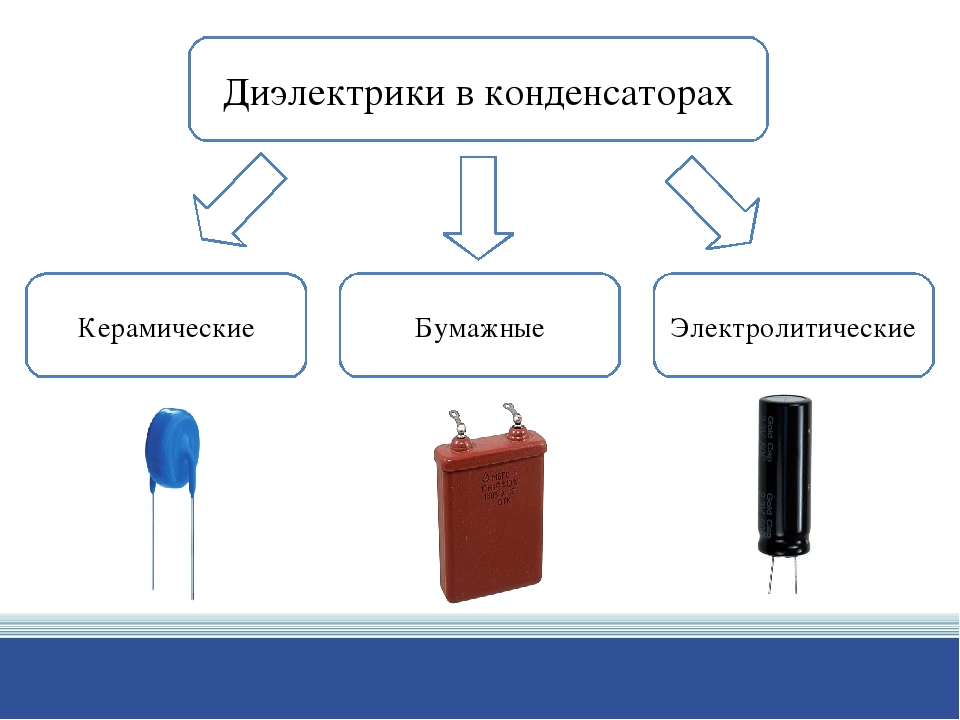 3)
3) Активный адаптер USB-PS / 2 состоит из логики для преобразования сигналов (активен в инкрементальном смысле)
Активный адаптер USB-PS / 2 состоит из логики для преобразования сигналов (активен в инкрементальном смысле)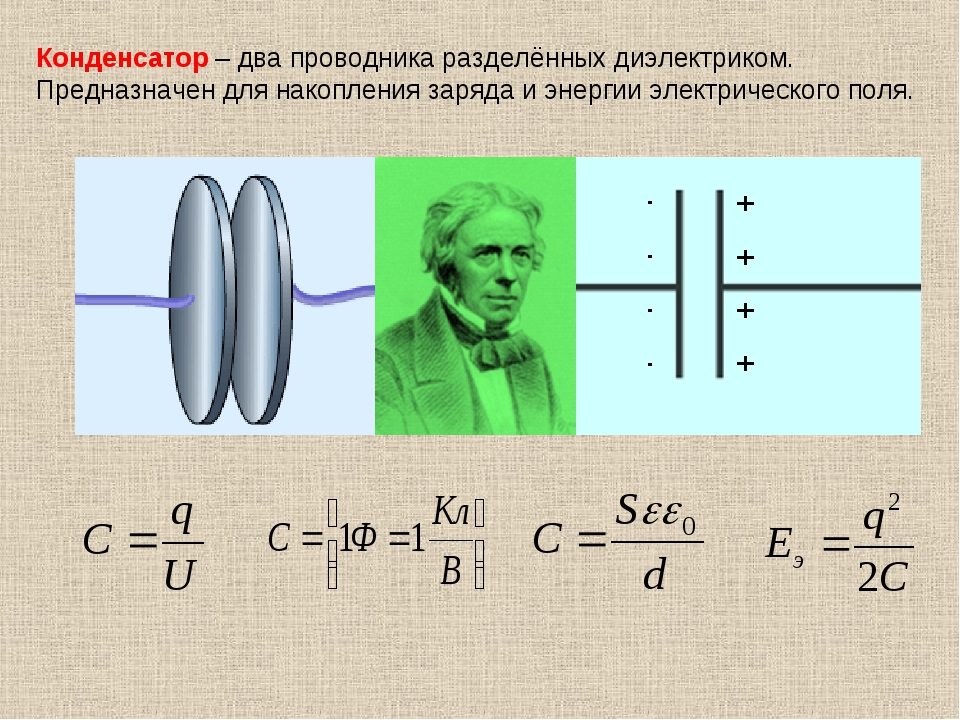
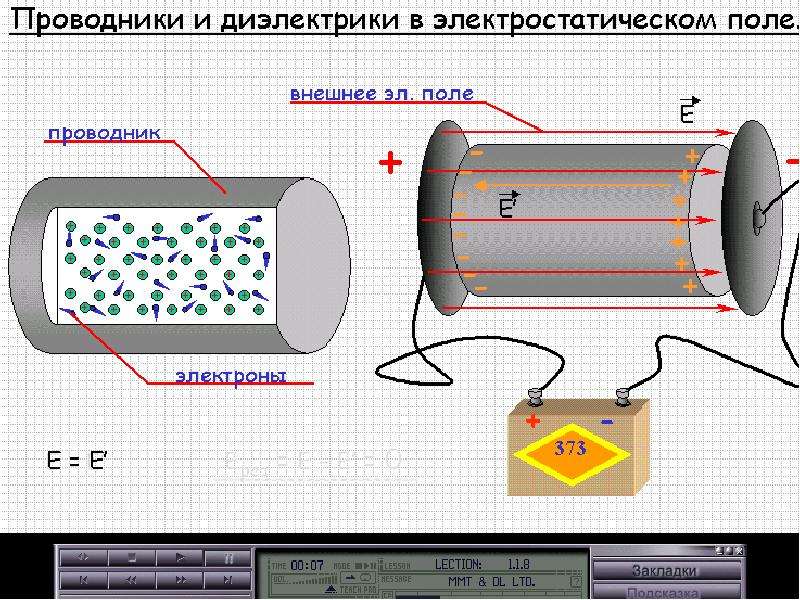 константа материала.
константа материала.