Колебания — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Гармонические колебания

К оглавлению…

В технике и окружающем нас мире часто приходится сталкиваться с периодическими процессами, которые повторяются через одинаковые промежутки времени. Такие процессы называют колебательными. Колебаниями называют изменения физической величины, происходящие по определенному закону во времени. Колебательные явления различной физической природы подчиняются общим закономерностям. Например, колебания тока в электрической цепи и колебания математического маятника могут описываться одинаковыми уравнениями. Общность колебательных закономерностей позволяет рассматривать колебательные процессы различной природы с единой точки зрения.

Механическими колебаниями называют движения тел, повторяющиеся точно через одинаковые промежутки времени.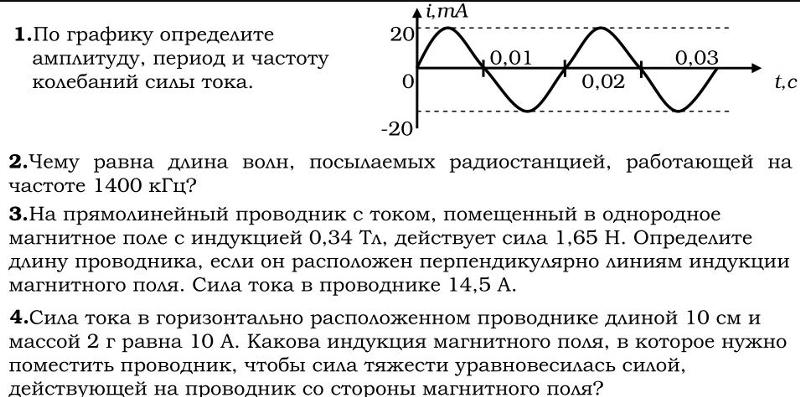 Примерами простых колебательных систем могут служить груз на пружине или математический маятник. Для существования в системе

гармонических колебаний необходимо, чтобы у нее было положение устойчивого равновесия, то есть такое положение, при выведении из которого на систему начала бы действовать возвращающая сила.

Механические колебания, как и колебательные процессы любой другой физической природы, могут быть свободными и вынужденными. Свободные колебания совершаются под действием внутренних сил системы, после того, как система была выведена из состояния равновесия. Колебания груза на пружине или колебания маятника являются свободными колебаниями. Колебания, происходящие под действием внешних периодически изменяющихся сил, называются

вынужденными.

Простейшим видом колебательного процесса являются колебания, происходящие по закону синуса или косинуса, называемые гармоническими колебаниями.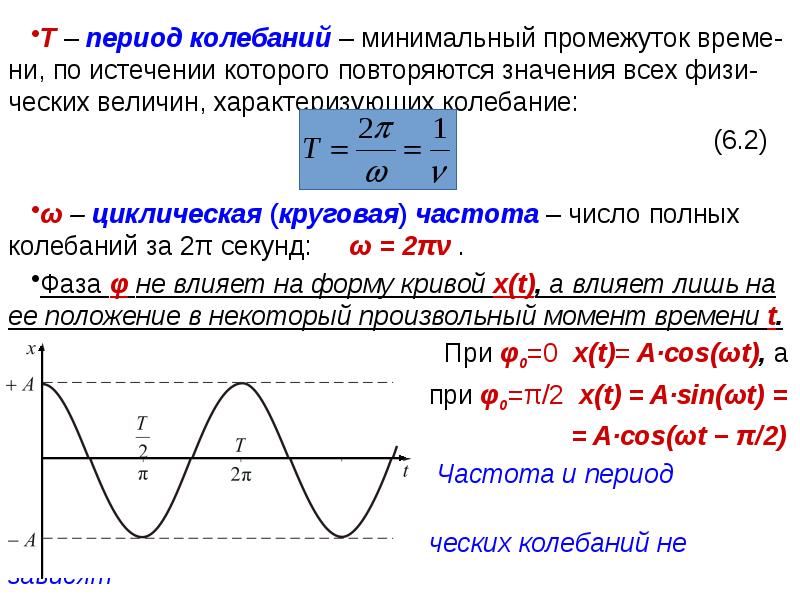  Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω₀ задаётся следующим образом:

Решение предыдущего уравнения является уравнением движения для гармонических колебаний, которое имеет вид:

где: x – смещение тела от положение равновесия,

A – амплитуда колебаний, то есть максимальное смещение от положения равновесия, ω – циклическая или круговая частота колебаний (ω = 2Π/T), t – время. Величина, стоящая под знаком косинуса: φ = ωt + φ₀, называется фазой гармонического процесса. Смысл фазы колебаний: стадия, в которой колебание находится в данный момент времени. При t = 0 получаем, что φ = φ₀, поэтому φ₀ называют начальной фазой (то есть той стадией, из которой начиналось колебание).

Минимальный интервал времени, через который происходит повторение движения тела, называется периодом колебаний T. Если же количество колебаний N, а их время t, то период находится как:

Физическая величина, обратная периоду колебаний, называется частотой колебаний:

Частота колебаний ν показывает, сколько колебаний совершается за 1 с. Единица частоты – Герц (Гц). Частота колебаний связана с циклической частотой ω и периодом колебаний T соотношениями:

Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:

Максимальное значение скорости при гармонических механических колебаниях:

Максимальные по модулю значения скорости υ_m = ωA достигаются в те моменты времени, когда тело проходит через положения равновесия (x = 0). Аналогичным образом определяется ускорение a = a_x тела при гармонических колебаниях.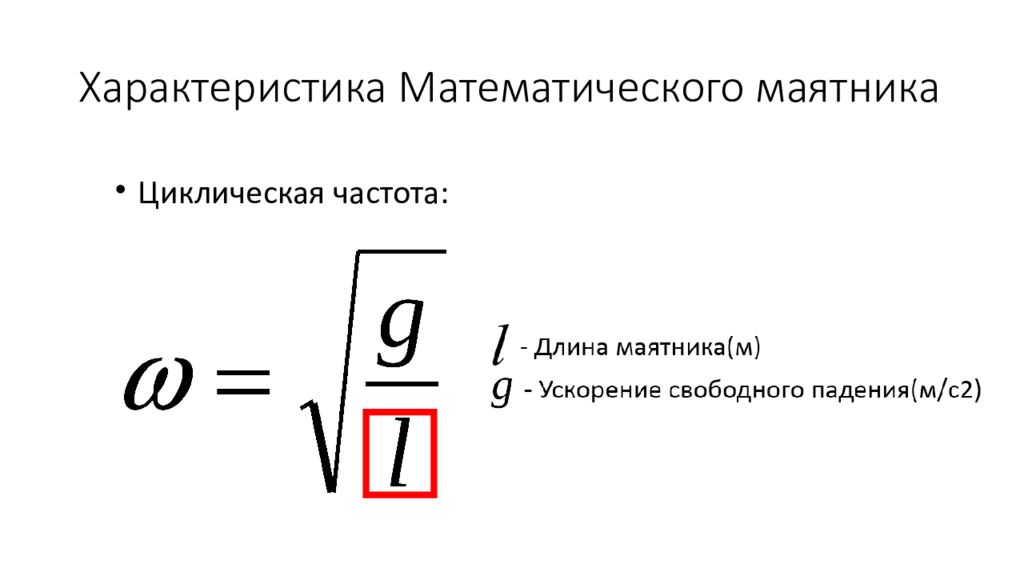  Зависимость ускорения от времени при гармонических механических колебаниях:

Максимальное значение ускорения при механических гармонических колебаниях:

Знак минус в предыдущем выражении означает, что ускорение a(t) всегда имеет знак, противоположный знаку смещения x(t), и, следовательно, возвращает тело в начальное положение (x = 0), т.е. заставляет тело совершать гармонические колебания.

Следует обратить внимание на то, что:

• физические свойства колебательной системы определяют только собственную частоту колебаний ω₀ или период T.
• Такие параметры процесса колебаний, как амплитуда A = x_m и начальная фаза φ₀, определяются способом, с помощью которого система была выведена из состояния равновесия в начальный момент времени, т.е. начальными условиями.
• При колебательном движении тело за время, равное периоду, проходит путь, равный 4 амплитудам. При этом тело возвращается в исходную точку, то есть перемещение тела будет равно нулю. Следовательно, путь равный амплитуде тело пройдет за время равное четверти периода.

Чтобы определить, когда в уравнение колебаний подставлять синус, а когда косинус, нужно обратить внимание на следующие факторы:

• Проще всего, если в условии задачи колебания названы синусоидальными или косинусоидальными.
• Если сказано, что тело толкнули из положения равновесия – берем синус с начальной фазой, равной нулю.
• Если сказано, что тело отклонили и отпустили – косинус с начальной фазой, равной нулю.
• Если тело толкнули из отклоненного от положения равновесия состояния, то начальная фаза не равна нолю, а брать можно и синус и косинус.

 

Математический маятник

К оглавлению…

Математическим маятником называют тело небольших размеров, подвешенное на тонкой, длинной и нерастяжимой нити, масса которой пренебрежимо мала по сравнению с массой тела.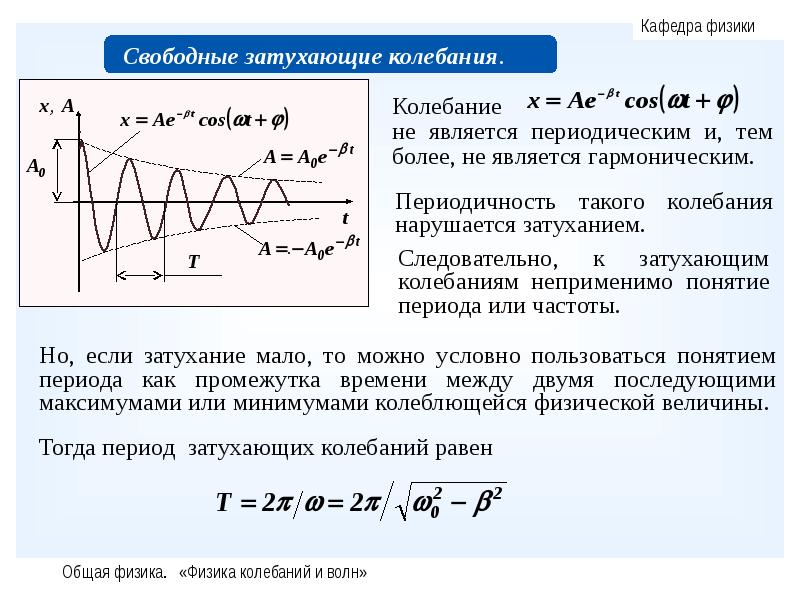  Только в случае малых колебаний математический маятник является гармоническим

осциллятором, то есть системой, способной совершать гармонические (по закону sin или cos) колебания. Практически такое приближение справедливо для углов порядка 5–10°. Колебания маятника при больших амплитудах не являются гармоническими.

Циклическая частота колебаний математического маятника рассчитывается по формуле:

Период колебаний математического маятника:

Полученная формула называется формулой Гюйгенса и выполняется, когда точка подвеса маятника неподвижна. Важно запомнить, что период малых колебаний математического маятника не зависит от амплитуды колебаний. Такое свойство маятника называется

изохронностью. Как и для любой другой системы, совершающей механические гармонические колебания, для математического маятника выполняются следующие соотношения:

1. Путь от положения равновесия до крайней точки (или обратно) проходится за четверть периода.
2. Путь от крайней точки до половины амплитуды (или обратно) проходится за одну шестую периода.
3. Путь от положения равновесия до половины амплитуды (или обратно) проходится за одну двенадцатую долю периода.

 

Пружинный маятник

К оглавлению…

Свободные колебания совершаются под действием внутренних сил системы после того, как система была выведена из положения равновесия. Для того, чтобы свободные колебания совершались по гармоническому закону, необходимо, чтобы сила, стремящаяся возвратить тело в положение равновесия, была пропорциональна смещению тела из положения равновесия и направлена в сторону, противоположную смещению. Таким свойством обладает сила упругости.

Таким образом, груз некоторой массы m, прикрепленный к пружине жесткости k, второй конец которой закреплен неподвижно, составляют систему, способную совершать в отсутствие трения свободные гармонические колебания. Груз на пружине называют пружинным маятником.

Циклическая частота колебаний пружинного маятника рассчитывается по формуле:

Период колебаний пружинного маятника:

При малых амплитудах период колебаний пружинного маятника не зависит от амплитуды (как и у математического маятника). При горизонтальном расположении системы пружина–груз сила тяжести, приложенная к грузу, компенсируется силой реакции опоры. Если же груз подвешен на пружине, то сила тяжести направлена по линии движения груза. В положении равновесия пружина растянута на величину x₀, равную:

А колебания совершаются около этого нового положения равновесия. Приведенные выше выражения для собственной частоты

ω₀ и периода колебаний T справедливы и в этом случае. Таким образом, полученная формула для периода колебаний груза на пружине остается справедливой во всех случаях, независимо от направления колебаний, движения опоры, действия внешних постоянных сил.

При свободных механических колебаниях кинетическая и потенциальная энергии периодически изменяются. При максимальном отклонении тела от положения равновесия его скорость, а, следовательно, и кинетическая энергия обращаются в нуль. В этом положении потенциальная энергия колеблющегося тела достигает максимального значения. Для груза на пружине потенциальная энергия – это энергия упругой деформации пружины. Для математического маятника – это энергия в поле тяготения Земли.

Когда тело при своем движении проходит через положение равновесия, его скорость максимальна. Тело проскакивает положение равновесия по инерции. В этот момент оно обладает максимальной кинетической и минимальной потенциальной энергией (как правило, потенциальную энергию в положении равновесия полагают равной нулю). Увеличение кинетической энергии происходит за счет уменьшения потенциальной энергии. При дальнейшем движении начинает увеличиваться потенциальная энергия за счет убыли кинетической энергии и так далее.

Таким образом, при гармонических колебаниях происходит периодическое превращение кинетической энергии в потенциальную и наоборот.  Если в колебательной системе отсутствует трение, то полная механическая энергия при свободных колебаниях остается неизменной. При этом, максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:

Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:

Взаимосвязь энергетических характеристик механического колебательного процесса (полная механическая энергия равна максимальным значениям кинетической и потенциальной энергий, а также сумме кинетической и потенциальной энергий в произвольный момент времени):

 

Механические волны

К оглавлению…

Если в каком-нибудь месте твердой, жидкой или газообразной среды возбуждены колебания частиц, то вследствие взаимодействия атомов и молекул среды колебания начинают передаваться от одной точки к другой с конечной скоростью. Процесс распространения колебаний в среде называется волной.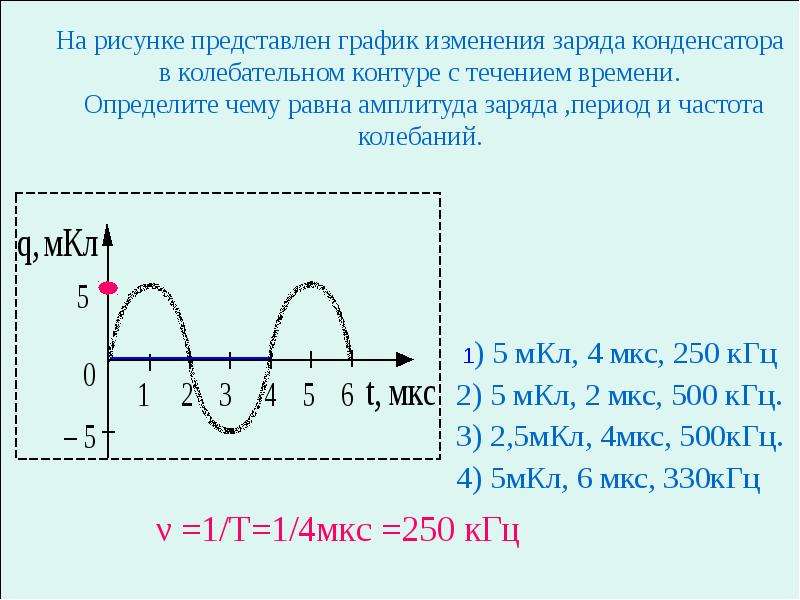

Механические волны бывают разных видов. Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной. Если смещение частиц среды происходит в направлении распространения волны, такая волна называется продольной.

Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

Характерной особенностью механических волн является то, что они распространяются в материальных средах (твердых, жидких или газообразных). Существуют немеханические волны, которые способны распространяться и в пустоте (например, световые, т.е. электромагнитные волны могут распространяться в вакууме).

• Продольные механические волны могут распространяться в любых средах – твердых, жидких и газообразных.
• Поперечные волны не могут существовать в жидкой или газообразной средах.

Значительный интерес для практики представляют простые гармонические или синусоидальные волны. Они характеризуются амплитудой A колебания частиц, частотой ν и длиной волны λ. Синусоидальные волны распространяются в однородных средах с некоторой постоянной скоростью υ.

Длиной волны λ называют расстояние между двумя соседними точками, колеблющимися в одинаковых фазах. Расстояние, равное длине волны λ, волна пробегает за время равное периоду T, следовательно, длина волны может быть рассчитана по формуле:

где: υ – скорость распространения волны. При переходе волны из одной среды в другую длина волны и скорость ее распространения меняются. Неизменными остаются только частота и период волны.

Разность фаз колебаний двух точек волны, расстояние между которыми l рассчитывается по формуле:

 

Электрический контур

К оглавлению. ..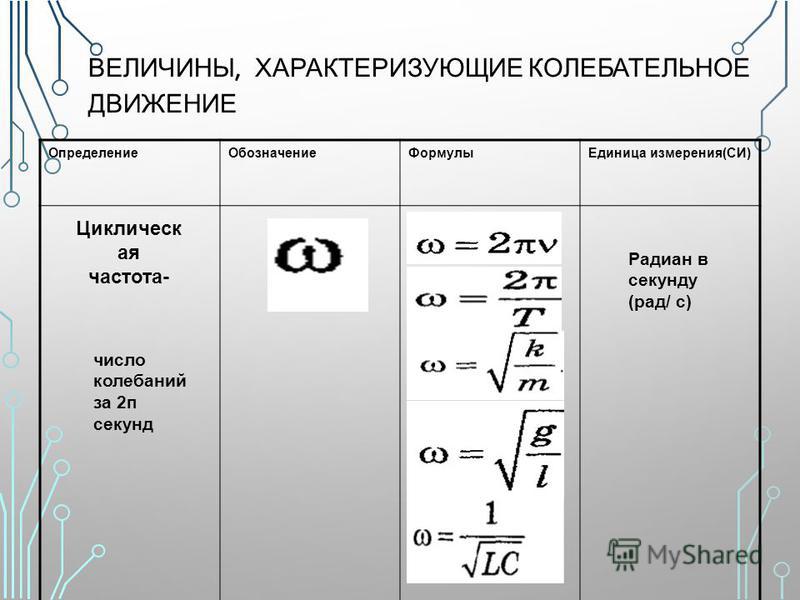

В электрических цепях, так же, как и в механических системах, таких как груз на пружине или маятник, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный LC-контур. В отсутствие затухания свободные колебания в электрическом контуре являются гармоническими. Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:

Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:

Циклическая частота колебаний в электрическом колебательном контуре:

Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:

Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:

Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:

Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:

Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:

Все реальные контура содержат электрическое сопротивление R. Процесс свободных колебаний в таком контуре уже не подчиняется гармоническому закону. За каждый период колебаний часть электромагнитной энергии, запасенной в контуре, превращается в теплоту, выделяющуюся на резисторе, и колебания становятся затухающими.

 

Переменный ток. Трансформатор

К оглавлению…

Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими синусоидальное напряжение. Они позволяют наиболее просто и экономно осуществлять передачу, распределение и использование электрической энергии.

Устройство, предназначенное для превращения механической энергии в энергию переменного тока, называется генератором переменного тока. Он характеризуется переменным напряжением U(t) (индуцированной ЭДС) на его клеммах. В основу работы генератора переменного тока положено явление электромагнитной индукции.

Переменным током называется электрический ток, который изменяется с течением времени по гармоническому закону. Величины U₀, I₀ = U₀/R называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.

Переменный ток характеризуется действующими значениями силы тока и напряжения. Действующим (эффективным) значением переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделил бы в единицу времени такое же количество теплоты, что и данный переменный ток. Для переменного тока действующее значение силы тока может быть рассчитано по формуле:

Аналогично можно ввести действующее (эффективное) значение и для напряжения, рассчитываемое по формуле:

Таким образом, выражения для мощности постоянного тока остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

Обратите внимание, что если идет речь о напряжении или силе переменного тока, то (если не сказано иного) имеется в виду именно действующее значение. Так, 220В – это действующее напряжение в домашней электросети.

Конденсатор в цепи переменного тока

Строго говоря, конденсатор ток не проводит (в том смысле, что носители заряда через него не протекают). Поэтому, если конденсатор подключен в цепь постоянного тока, то сила тока в любой момент времени в любой точке цепи равна нулю. При подключении в цепь переменного тока из-за постоянного изменения ЭДС конденсатор перезаряжается. Ток через него по-прежнему не течет, но ток в цепи существует. Поэтому условно говорят, что конденсатор проводит переменный ток. В этом случае вводится понятие сопротивления конденсатора в цепи переменного тока (или емкостного сопротивления). Это сопротивление определяется выражением:

Обратите внимание, что емкостное сопротивление зависит от частоты переменного тока. Оно в корне отличается от привычного нам сопротивления R. Так, на сопротивлении R выделяется теплота (поэтому его часто называют активным), а на емкостном сопротивлении теплота не выделяется.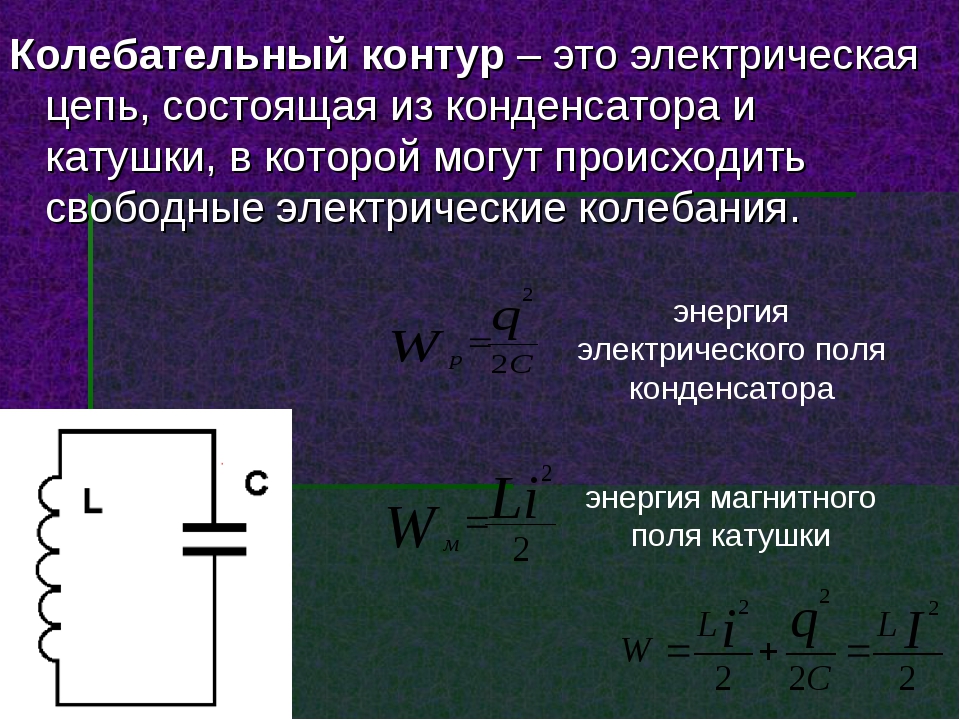 Активное сопротивление связано со взаимодействием носителей заряда при протекании тока, а емкостное – с процессами перезарядки конденсатора.

Катушка индуктивности в цепи переменного тока

При протекании переменного тока в катушке возникает явление самоиндукции, и, следовательно, ЭДС. Из-за этого напряжение и сила тока в катушке не совпадают по фазе (когда сила тока равна нулю, напряжение имеет максимальное значение и наоборот). Из-за такого несовпадения средняя тепловая мощность, выделяющаяся в катушке, равна нулю. В этом случае вводится понятие сопротивления катушки в цепи переменного тока (или индуктивного сопротивления). Это сопротивление определяется выражением:

Обратите внимание, что индуктивное сопротивление зависит от частоты переменного тока. Как и емкостное сопротивление, оно отличается от сопротивления R. Как и на емкостном сопротивлении, на индуктивном сопротивлении теплота не выделяется. Индуктивное сопротивление связано с явлением самоиндукции в катушке.

Трансформаторы

Среди приборов переменного тока, нашедших широкое применение в технике, значительное место занимают трансформаторы. Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении электромагнитной индукции. Простейший трансформатор состоит из сердечника замкнутой формы, на который намотаны две обмотки: первичная и вторичная. Первичная обмотка подсоединяется к источнику переменного тока с некоторым напряжением U₁, а вторичная обмотка подключается к нагрузке, на которой появляется напряжение U₂. При этом, если число витков в первичной обмотке равно n₁, а во вторичной n₂, то выполняется следующее соотношение:

Коэффициент трансформации вычисляется по формуле:

Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):

В неидеальном трансформаторе вводится понятие КПД:

 

Электромагнитные волны

К оглавлению. ..

Электромагнитные волны – это распространяющееся в пространстве и во времени электромагнитное поле. Электромагнитные волны поперечны – векторы электрической напряженности и магнитной индукции перпендикулярны друг другу и лежат в плоскости, перпендикулярной направлению распространения волны. Электромагнитные волны распространяются в веществе с конечной скоростью, которая может быть рассчитана по формуле:

где: ε и μ – диэлектрическая и магнитная проницаемости вещества, ε₀ и μ₀ – электрическая и магнитная постоянные: ε₀ = 8,85419·10^–12 Ф/м, μ₀ = 1,25664·10^–6 Гн/м. Скорость электромагнитных волн в вакууме (где ε = μ = 1) постоянна и равна с = 3∙10⁸ м/с, она также может быть вычислена по формуле:

Скорость распространения электромагнитных волн в вакууме является одной из фундаментальных физических постоянных.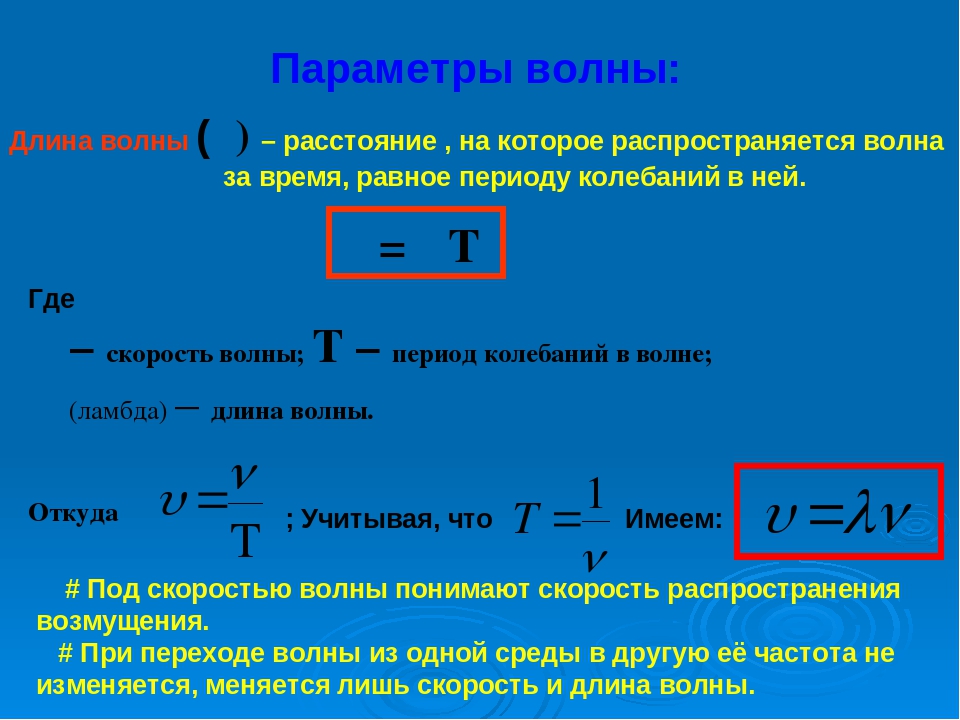 Если электромагнитная волна распространяется в какой-либо среде, то скорость ее распространения также выражается следующим соотношением:

где: n – показатель преломления вещества – физическая величина, показывающая во сколько раз скорость света в среде меньше чем в вакууме. Показатель преломления, как видно из предыдущих формул, может быть рассчитан следующим образом:

• Электромагнитные волны переносят энергию. При распространении волн возникает поток электромагнитной энергии.
• Электромагнитные волны могут возбуждаться только ускоренно движущимися зарядами. Цепи постоянного тока, в которых носители заряда движутся с неизменной скоростью, не являются источником электромагнитных волн. А вот цепи, в которых протекает переменный ток, т.е. такие цепи в которых носители заряда постоянно меняют направление своего движения, т.е. двигаются с ускорением – являются источником электромагнитных волн. В современной радиотехнике излучение электромагнитных волн производится с помощью антенн различных конструкций, в которых возбуждаются быстропеременные токи.

Связь между периодом колебаний и циклической частотой. Циклическая частота колебаний

Время, в течение которого совершается одно полное изме­нение ЭДС, то есть один цикл колебания или один полный оборот радиуса-вектора, называется периодом колебания пере­менного тока (рисунок 1).

Рисунок 1. Период и амплитуда синусоидального колебания. Период — время одного колебания; Аплитуда — его наибольшее мгновенное значение.

Период выражают в секундах и обозначают буквой Т .

Так же используются более мелкие единицы измерения периода это миллисекунда (мс)- одна тысячная секунды и микросекунда (мкс)- одна миллионная секунды.

1 мс =0,001сек =10 -3 сек.

1 мкс=0,001 мс = 0,000001сек =10 -6 сек.

1000 мкс = 1 мс.

Число полных изменений ЭДС или число оборотов ради­уса-вектора, то есть иначе говоря, число полных циклов колеба­ний, совершаемых переменным током в течение одной секунды, называется частотой колебаний переменного тока .

Частота обо­значается буквой f и выражается в периодах в секунду или в герцах.

Одна тысяча герц называется килогерцом (кГц), а миллион герц — мегагерцом (МГц). Существует так же единица гигагерц (ГГц) равная одной тысячи мегагерц.

1000 Гц = 10 3 Гц = 1 кГц;

1000 000 Гц = 10 6 Гц = 1000 кГц = 1 МГц;

1000 000 000 Гц = 10 9 Гц = 1000 000 кГц = 1000 МГц = 1 ГГц;

Чем быстрее происходит изменение ЭДС, то есть чем бы­стрее вращается радиус-вектор, тем меньше период колебания Чем быстрее вращается радиус-вектор, тем выше частота. Таким образом, частота и период переменного тока являются величинами, обратно пропорциональными друг другу. Чем больше одна из них, тем меньше другая.

Математическая связь между периодом и частотой переменного тока и напряжения выра­жается формулами

Например, если частота тока равна 50 Гц, то период будет равен:

Т = 1/f = 1/50 = 0,02 сек.

И наоборот, если известно, что период тока равен 0,02 сек, (T=0,02 сек. ), то частота будет равна:

f = 1/T=1/0,02 = 100/2 = 50 Гц

Частота переменного тока, используемого для освещения и промышленных целей, как раз и равна 50 Гц.

Частоты от 20 до 20 000 Гц называются звуковыми часто­тами. Токи в антеннах радиостанций колеблются с частотами до 1 500 000 000 Гц или, иначе говоря, до 1 500 МГц или 1,5 ГГц. Такие вы­сокие частоты называются радиочастотами или колебаниями высокой частоты.

Наконец, токи в антеннах радиолокационных станций, станций спутниковой связи, других спецсистем (например ГЛАНАСС, GPS) колеблются с частотами до 40 000 МГц (40 ГГц) и выше.

Амплитуда переменного тока

Наибольшее значение, которого достигает ЭДС или сила тока за один период, называется амплитудой ЭДС или силы переменного тока . Легко заметить, что амплитуда в масштабе равна длине радиуса-вектора. Амплитуды тока, ЭДС и напряжения обозначаются соответственно бук­вами Im, Em и Um (рисунок 1).

Угловая (циклическая) частота переменного тока.

Скорость вращения радиуса-вектора, т. е. изменение ве­личины угла поворота в течение одной секунды, называется угловой (циклической) частотой переменного тока и обозначается греческой буквой ? (оме­га). Угол поворота радиуса-вектора в любой данный момент относительно его начального положения измеряется обычно не в градусах, а в особых единицах — радианах.

Радианом называется угловая величина дуги окружности, длина которой равна радиусу этой окружности (рисунок 2). Вся окружность, составляющая 360°, равна 6,28 радиан, то есть 2.

Рисунок 2.

1рад = 360°/2

Следовательно, конец радиуса-вектора в течение одного периода пробегают путь, равный 6,28 радиан (2). Так как в тече­ние одной секунды радиус-вектор совершает число оборотов, равное частоте переменного тока f , то за одну секунду его ко­нец пробегает путь, равный 6,28 * f радиан. Это выражение, характеризующее скорость вращения радиуса-вектора, и будет угловой частотой переменного тока — ? .

? = 6,28*f = 2f

Угол поворота радиуса-вектора в любое данное мгновение относительно его начального положения называется фазой переменного тока . Фаза характеризует величину ЭДС (или тока) в данное мгновение или, как говорят, мгновенное значение ЭДС, ее направление в цепи и направление ее изменения; фаза пока­зывает, убывает ли ЭДС или возрастает.

Рисунок 3.

Полный оборот радиуса-вектора равен 360°. С началом но­вого оборота радиуса-вектора изменение ЭДС происходит в том же порядке, что и в течение первого оборота. Следова­тельно, все фазы ЭДС будут повторяться в прежнем поряд­ке. Например, фаза ЭДС при повороте радиуса-вектора на угол в 370° будет такой же, как и при повороте на 10°. В обо­их этих случаях радиус-вектор занимает одинаковое положе­ние, и, следовательно, мгновенные значения ЭДС будут в обоих этих случаях одинаковыми по фазе.

В мире, окружающем нас, есть много явлений и процессов, которые, по большому счету, незаметны не потому, что их нет, а потому, что мы их попросту не замечаем. Они присутствуют всегда и являются такой же незаметной и обязательной сущностью вещей, без которой нашу жизнь и представить трудно. Каждому, например, известно, что такое колебание: в самом общем виде — это отклонение от состояния равновесия. Ну, хорошо, отклонилась верхушка Останкинской башни на свои 5 м, а что дальше? Так и застынет? Ничего подобного, начнет возвращаться назад, проскочит состояние равновесия и будет отклоняться в другую сторону, и так вечно, пока она будет существовать. А скажите, много людей реально видели эти вполне серьезные колебания такого огромного сооружения? Все знают, колеблется, сюда-туда, сюда-туда, и днем и ночью, зимой и летом, но как-то… не заметно. Причины колебательного процесса — это другой вопрос, но его наличие — неотделимый признак всего сущего.

Колеблется все вокруг: здания, сооружения, маятники часов, листья на деревьях, струны скрипки, поверхность океана, ножки камертона… Среди колебаний различают хаотичные, которые не имеют строгой повторяемости, и циклические, у которых за временной период Т колеблющееся тело проходит полный набор своих изменений, а затем этот цикл в точности повторяется, вообще говоря, бесконечно долго. Обычно эти изменения подразумевают последовательный перебор пространственных координат, как это можно наблюдать на примере колебаний маятника или той же башни.

Количество колебаний в единицу времени называется частотой F = 1/T. Единица измерения частоты — Гц = 1/сек. Понятное дело, что циклическая частота является параметром одноименных колебаний любого вида. Тем не менее, на практике принято это понятие, с некоторыми дополнениями, относить преимущественно к колебаниям вращательного характера. Так уж сложилось в технике, что является основой большинства станков, механизмов, устройств. Для таких колебаний один цикл составляет один оборот, и тогда удобнее использовать угловые параметры перемещения. Исходя из этого, вращательное перемещение измеряют угловыми единицами, т.е. один оборот равен 2π радиан, а циклическая частота ῳ = 2π / T. Из этого выражения легко просматривается связь c частотой F: ῳ = 2πF. Это позволяет сказать, что циклическая частота — это количество колебаний (полных оборотов) за 2π секунд.

Казалось бы, не в лоб, так… Не совсем так. Множители 2π и 2πF применяются во многих уравнениях электроники, математической и теоретической физики в разделах, где колебательные процессы изучаются с использованием понятия циклическая частота. Формула резонансной частоты, например, сокращается на два сомножителя. В случае использования в расчетах единицы «об./сек» угловая, циклическая, частота ῳ численно совпадает со значением частоты F.

Колебания, как суть и форма существования материи, и ее вещественного воплощения — предметов нашего бытия, имеют большое значение в жизни человека. Знание законов колебаний позволило создать современную электронику, электротехнику, многие современные машины. К сожалению, колебания не всегда приносят положительный эффект, иногда они приносят горе и разрушения. Неучтённые колебания, причина многих аварий, вызывают материалов, а циклическая частота резонансных колебаний мостов, плотин, деталей машин приводит к их преждевременному выходу из строя. Изучение колебательных процессов, умение предсказать поведение природных и технических объектов с целью предотвратить их разрушение или выход из рабочего состояния — основная задача многих инженерных приложений, а обследование промышленных объектов и механизмов на виброустойчивость — обязательный элемент эксплуатационного обслуживания.

При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период колебани.

Надо иметь в виду, что во всякой реальной колебательной системе есть сопротивления среды, т.е. колебания будут затухающими. Для характеристики затухания колебаний вводится коэффициент затухания и логарифмический декремент затухани.

Если колебания совершаются под действием внешней, периодически изменяющейся силы, то такие колебания называют вынужденными. Они будут незатухающими. Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении частоты вынужденных колебаний к частоте собственных колебаний амплитуда вынужденных колебаний резко возрастает. Это явление называется резонансом.

Переходя к изучению электромагнитных волн нужно четко представлять, что электромагнитная волна — это распространяющееся в пространстве электромагнитное поле. Простейшей системой, излучающей электромагнитные волны, является электрический диполь. Если диполь совершает гармонические колебания, то он излучает монохроматическую волну.

Таблица формул: колебания и волны

Физические законы, формулы, переменные	Формулы колебания и волны
Уравнение гармонических колебаний: где х — смещение (отклонение) колеблющейся величины от положения равновесия; А — амплитуда; ω — круговая (циклическая) частота; α — начальная фаза; (ωt+α) — фаза.
Связь между периодом и круговой частотой:
Частота:
Связь круговой частоты с частотой:
Периоды собственных колебаний 1) пружинного маятника: где k — жесткость пружины; 2) математического маятника: где l — длина маятника, g — ускорение свободного падения; 3) колебательного контура: где L — индуктивность контура, С — емкость конденсатора.
Частота собственных колебаний:
Сложение колебаний одинаковой частоты и направления: 1) амплитуда результирующего колебания где А 1 и А 2 — амплитуды составляющих колебаний, α 1 и α 2 — начальные фазы составляющих колебаний; 2) начальная фаза результирующего колебания
Уравнение затухающих колебаний: е = 2,71… — основание натуральных логарифмов.
Амплитуда затухающих колебаний: где А 0 — амплитуда в начальный момент времени; β — коэффициент затухания;
Коэффициент затухания: колеблющегося тела где r — коэффициент сопротивления среды, m — масса тела; колебательного контура где R — активное сопротивление, L — индуктивность контура.
Частота затухающих колебаний ω:
Период затухающих колебаний Т:
Логарифмический декремент затухания:

(лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.

Для маятника это максимальное расстояние, на которое удаляется ша-рик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.

Амплитуда колебаний измеряется в единицах длины — метрах , санти-метрах и т. д. На графике колебаний амплитуда определяется как макси-мальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).

Период колебаний.

Период колебаний — это наименьший промежуток времени, через который система, соверша-ющая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.

Другими словами, период колебаний (Т ) — это время, за которое совершается одно полное ко-лебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.

За полный период колебаний, таким образом, тело проходит путь, равный четы-рем амплитудам. Период колебаний измеряется в единицах времени — секундах , минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).

Понятие «период колебаний», строго говоря, справедливо, лишь когда значения колеблющей-ся величины точно повторяются через определенный промежуток времени, т. е. для гармоничес-ких колебаний. Однако это понятие применяется также и для случаев приблизительно повторяю-щихся величин, например, для затухающих колебаний .

Частота колебаний.

Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с .

Единица частоты в СИ названа герцем (Гц ) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v ) равна 1 Гц , то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:

В теории колебаний пользуются также понятием циклической , или круговой частоты ω . Она связана с обычной частотой v и периодом колебаний Т соотношениями:

.

Циклическая частота — это число колебаний, совершаемых за 2π секунд.

Таким образом, полная энергия гармонического колебания постоянна и пропорциональна квадрату амплитуды смещения. Это – одно из характерных свойств гармонических колебаний. Здесь постоянный коэффициент k в случае пружинного маятника означает жёсткость пружины, а для математического маятника k=mgH. В обоих случаях коэффициент k передаётся параметрами колебательной системы.

Полная энергия механической колебательной системы состоит из кинетической и потенциальной энергий и равна максимальному значению любой из этих двух составляющих:

Следовательно, полная энергия колебаний прямо пропорциональна квадрату амплитуды смещения или квадрату амплитуды скорости.

Из формулы:

можно определить амплитуду x m колебаний смещения:

Амплитуда смещения при свободных колебаниях прямо пропорциональна корню квадратному из энергии, сообщённой колебательной системе в начальный момент, когда систему выводили из состояния равновесия.

Кинематика механических свободных колебаний

1 Смещение, скорость, ускорение. Для нахождения кинематических характеристик (смещения, скорости и ускорения) свободных колебаний воспользуемся законом сохранения и превращения энергии, которой для идеальной механической колебательной системы записывается так:

Так как производная по времени φ » постоянна, то угол φ зависит от времени линейно:

Учитывая это можно записать:

x = x m sin ω 0 t, υ = x m ω 0 cos ω 0 t

Здесь величина

есть амплитуда изменения скорости:

υ = υ m cos ω 0 t

Зависимость мгновенного значения ускорения a от времени t мы найдём как производную скорости υ по времени:

a = υ » = — ω 0 υ m sin ω 0 t,

a = -a m sin ω 0 t

знак «-» в полученной формуле указывает на то, что знак проекции вектора ускорения на ось, вдоль которой происходят колебания, противоположен знаку смещения x.

Итак, мы видим, что при гармонических колебаниях не только смещение, но и скорость и ускорение изменяются синусоидально.

2 Циклическая частота колебаний. Величина ω 0 называется циклической частотой колебаний. Так как функция sin α имеет по аргументу α период 2π, а гармонические колебания имеют по времени период T, то

Тест по физике на тему «КОЛЕБАНИЯ И ВОЛНЫ. 2 ВАРИАНТ.» (11 класс)

КОЛЕБАНИЯ И ВОЛНЫ. 2 ВАРИАНТ.

Предмет	Физика
Класс	11
Учебник	Физика (базовый уровень)
Тема	Колебания и волны

На рисунке 1 представлен график зависимости от времени

координаты х тела, совершающего гармонические колебания вдоль оси Ох. Чему равна амплитуда колебаний. A) 0,4 м.

B)     0,1 м.

C)     0,2 м.

D)    0,3 м.

   Электрические колебания в колебательном контуре заданы уравнением I = 2 sin 10t (А). Чему равна циклическая частота колебаний силы тока?

A)     4 с-¹

B)     10 с-¹

C)     2 с-¹

D)    8 с-¹

Колебания силы тока в колебательном контуре происходят происходят с циклической частотой

4 c-1 .

Чему равен период колебаний силы тока? A) 2 с.

B)     4л с.

C)     0.5 с.

D)    2л с.

При гармонических колебаниях тела вдоль оси О_Х  ускорение изменяется по закону а_х =4 соs 2t (м/с²). Чему равна амплитуда колебаний координаты х тела. A) 3 м.

B)     2 м.

C)     1 м.

D)    4 м.

     Груз, подвешенный на пружине жесткостью k совершает гармонические колебания с циклической частотой w₁ Чему равна циклическая частота w₂ колебаний того же груза на пружине жесткостью k = 4k₁?  w₂ =w₁. A) w2 =w1​.

B)     w2 =2w1​.

C)     w2 =4w1​.

D)    w2 =w1/2​.

     Как изменится период колебаний математического маятника, если его длину уменьшить в 4 раза?

A) Уменьшится в 4 раза. B) Увеличится в 2 раза

C)     Уменьшится в 2 раза.

D)    Увеличится в 4 раза

    Ротор генератора переменного тока вращается в однородном магнитном поле. Как изменится амплитуда ЭДС индукции при увеличении частоты его вращения в 2 раза? A) Увеличится в 2 раза.

B)     Уменьшится в 2 раза.

C)     Увеличится в 4 раза.

D)    Уменьшится в 4 раза.

   Как изменится амплитуда колебаний силы тока, протекающего через активное сопротивление, если при неизменной амплитуде колебаний напряжения частоту колебаний приложенного напряжения увеличить в 2 раза? A) Уменьшится в 4 раза.

B)     Не изменится.

C)     Уменьшится в 2 раза.

D)    Увеличится в 2 раза.

    При гармонических электрических колебаниях в колебательном контуре максимальное значение энергии электрического поля конденсатора . равно 50 Дж, максимальное значение энергии магнитного поля катушки 50 Дж. Как изменяется во времени полная энергия электромагнитного поля контура?

A)     Изменяется от 0 до 100 Дж.

B)     Не изменяется и равна 50 Дж.

C)     Изменяется от 0 до 50 Дж.

D)    Не изменяется и равна 100 Дж.

    Какие из перечисленных ниже колебаний являются вынужденными: 1 — колебания математического маятника; 2 — колебания поршня в цилиндре автомобильного двигателя; 3 — колебания силы тока в индукционном генераторе; 4 — колебания силы тока в ламповом генераторе; 5 — колебания силы тока в колебательном контуре.

A)     2, 2.

B)     1, 3.

C)     2, 3.

D)    1, 5.

Правильные ответы, решения к тесту:

Правильный ответ — C

Решение: 0,2 м.

Правильный ответ — B

Решение: 10 с-¹

Правильный ответ — C

Решение: 0,5 с.

Правильный ответ — C

Решение: 1 м.

Вопрос №5 Правильный ответ — B

Решение: w₂ =2w₁​.

Правильный ответ — C

Решение: Уменьшится в 2 раза.

Правильный ответ — A

Решение: Увеличится в 2 раза.

Вопрос №8 Правильный ответ — B

Решение: Не изменится.

Правильный ответ — B

Решение: Не изменяется и равна 50 Дж.

Правильный ответ — C Решение: 2, 3.

Контрольная работа по теме «Электрические колебания»

Цель работы:

• При оценивании знаний необходим в подборе знаний учет индивидуальности. Работа по 30 вариантам дает возможность осуществить личностный ориентированный подход.
• Проверка знаний по теме «Электрические колебания включает».
  • cвободные электрические колебания в контуре
  • период, частота, напряжение и сила электрического тока.
  • индуктивность и емкость сопротивления;
  • мощность переменного тока;
  • производство, передача и использование электрической энергии.

В контурной работе предлагается 30 задач с разноуровневым подходом.

• 1-10 задачу-первый уровень сложности
• 11-19 задачу- второй уровень сложности
• 20-30 задачу- третий уровень сложности

Первый и второй уровень сложности имеет по 3 задачи, третий уровень 5 задач.

В каждом варианте

• На первом и втором уровне решение любой одной задачи оценивается в «3» балла.
• На третьем уровне на два балла оценивается решение только первой задачи, без анализа последующих. При решении одной из последующих задач оценивание увеличивается на один балл

Система оценивания работы.

• 1-2 уровень
• 3 задачи- «5»
• 2 задачи — «4»
• 1 задача- «3»
• 3 уровень
• 5 задач- «5»
• 4 задачи- «4»
• 3 задачи- «3»
• 2 задачи- «3»
• 1 задача- «2»

Вариант 1

1. В колебательном контуре емкости конденсатор 3 мкФ, а максимальное напряжение на нем 4 В. Найдите максимальную энергию магнитного поля катушки. Активное сопротивление примите равным нулю.
2. Почему в колебательном контуре, изображенном на рисунке, существуют только затухающие электромагнитные колебания?
3. По графику изображенному на рисунке, определите амплитуду ЭДС, период .ока и частоту. Напишите уравнение ЭДС.

Вариант 2

1. Индуктивность и емкость колебательного контура соответственно равны 70 Гн и 70 мкФ. Определите период колебаний в контуре. Можно ли эти колебания назвать высококачественными?
2. Что можно сказать о значении энергии магнитного поля катушки колебательного контура, когда энергия электрического поля конденсатора достигнет максимума?
3. По графику, изображенному на рисунке, определите амплитуду напряжения, период и значение напряжения для фазы рад.

Вариант 3

1. Определите циклическую частоту колебаний в контуре, если емкость конденсатора контура 10 мкФ, а индуктивность его катушки 100мГн.
2. Где будет в колебательном контуре, изображенном на рисунке, сосредоточена энергия через четверть периода?
3. По графику, изображенном на рисунке, определите амплитуду силы тока, период и частоту. Напишите уравнение мгновенного значения силы переменного тока.

Вариант 4

1. В колебательном контуре при напряжении на обкладках конденсатора 3 В энергия магнитного поля равна 0,9?10 Дж. Определите емкость конденсатора, считая активное сопротивление контура равным нулю.
2. Начертите схему колебательного контура, конденсатора которого можно было периодически подзаряжать от источника постоянного тока.
3. По графику, изображенному на рисунке, определите амплитуду силы тока, частоту и значение силы тока для фазы рад.

Вариант 5

1. Индуктивность катушки колебательного контура 5*10? Гн.
2. Требуется настроить этот контур на частоту 1МГц. Какова должна быть емкость конденсатора в этом контуре?
3. Что можно сказать о значении энергии электрического поля конденсатора в контуре, когда энергия магнитного поля достигнет минимума?
4. По графику, изображенному на рисунке, определите амплитуду ЭДС, период и частоту ЭДС. Напишите уравнение ЭДС.

Вариант 6

1)Определите индуктивность катушки колебательного контура, если емкость конденсатора равна 5мкФ, а период колебаний 0,001 с.

2) Где в колебательном контуре, изображенном на рисунке, будет сосредоточена энергия через четверть периода?

3)По графику, изображенному на рисунке, определите амплитуду напряжения и период колебания. Запишите уравнение мгновенного значения напряжения.

Вариант 7

1. Значение силы тока, измеренное в амперах, задано уравнением i= 0,28 sin 50Пt, где t выражено в секундах. Определите амплитуду силы тока, частоту и период.
2. Каково индуктивное сопротивление проводника с индуктивностью 0,05 Гн в цепи переменного тока частотой 50 ГЦ.?
3. Ваттметр, включенный в сеть переменного тока, отмечает мощность 650 Вт. Правильно ли показание ваттметра, если напряжение в сети 120 В, сила тока 6 А и cos ? 0,85?

Вариант 8

1. Значение ЭДС, измерено в вольтах, задано уравнением e = 50 sin 50 Пt., где t выражено в секундах. Определите амплитуду силы тока, частоту и период.
2. Определите емкость конденсатора, сопротивление которого в цепи переменного тока частотой 50 Гц равно 10 Ом.
3. Определите коэффициент мощности, если при включении электродвигателя в сеть переменного тока вольтмера показал 220 В, амперметра 4 А, а ваттметр 600 Вт.

Вариант 9

1. Амплитуда ЭДС, переменного тока с частотой 50 Гц равна 100 В. Каковы значения ЭДС через 0,0025 и 0,005с, считая от начала периода?
2. В цепь переменного тока с действующим значением напряжения 220 В включено активное сопротивление 50 Ом. Найдите действующее и амплитудное значение силы тока.
3. Какова активная мощность, развиваемая генератором во внешней цепи, если напряжение на зажимах генератора переменного тока равно 220 в, сила тока во внешней цепи равна 10 А и cos =0,8?

Вариант 10

1. Значение напряжения, измеренное в вольтах, задано уравнением U=120 cos 40Пt, где t выражено в секундах. Чему равна амплитуда напряжения, периода и частоты?
2. Индуктивное сопротивление катушки 80 Ом. Определите индуктивность катушки, если циклическая частота переменного тока 1000 Гц.
3. С каким коэффициентом мощности работает двигатель , включенный в сеть переменного тока с напряжением 120 В и силой тока 8 А, если показание ваттметра равно 600 Вт.?

Вариант 11

1. Мгновенное значение силы переменного тока частотой 50Гц равно 2А для фазы П./4рад. Какова амплитуда силы тока? Найдите мгновенное значение силы тока через 0,015 с, считая от начала периода.
2. Индуктивность и емкость в цепи переменного тока соответственно равны 0,1 Гн и 1 мкФ. Найдите отношение индуктивного сопротивления к емкостному при частоте 5кГц.
3. Коэффициент мощности работающего электродвигателя 0,8. Найдите значение силы тока, если электродвигатель, включенный в данную сеть, потребляет мощность 8 кВт, а напряжение в сети 380 В.

Вариант 12

1. Мгновенное значение силы переменного тока для фазы 60^о равно 120 В. Какова амплитуда ЭДС? Чему равно мгновенное значение ЭДС через 0,25 с, считая от начала периода? Частота тока 50 Гц.
2. Определите период переменного тока, для которого конденсатор емкостью 2 мкФ представляет сопротивление 8 Ом.
3. Активная мощность в цепи переменного тока равна 40 Вт, cos = 0,2 сила тока 1 А. Определите напряжение в данной цепи.

Вариант 13

1. В сеть переменного тока напряжением 127 В включена цепь, состоящая из последовательных соединенных резисторов сопротивлением 100 Ом и конденсатора емкостью 40 мкФ Определите амплитуду силы тока в цепи, если частота тока равна 50 Гц.
2. написать уравнение ЭДС, если амплитудное значение равно 10 В, а период колебания 10с. Начальная фаза равна нулю..
3. Трансформатор повышает напряжение с 220 В до 660 В и содержит в первичной обмотке 850 витков. Определите коэффициент трансформации и число витков во вторичной обмотке. В какой обмотке сила тока больше?

Вариант 14

1. Емкость конденсатора колебательного контура 0,05 мкФ. Какой должна быть индуктивность катушки контура, чтоб при циклической частоте 1000 с в цепи наступил электрический резонанс?
2. Значение силы тока задано x = 10 cos 1/3 Пt. Найдите амплитуду силы тока, частоту и период колебания.
3. Сила тока в первичной обмотке трансформатора 0,5 А, напряжение на ее концах- 10 В. Определите КПД трансформатора

Вариант 15

1. Период колебания в электрическом контуре с катушкой, индуктивностью 0,1 Гц 1 Определите период колебания в колебательном контуре с индуктивностью при одном и том же конденсаторе.
2. Значение ЭДС переменного тока, измеренное в вольтах, задано уравнением e=100 sin 120 Пt, где t выражено в секундах. Найдите амплитуду ЭДС, частоту и период тока.
3. Первичная обмотка понижающего трансформатора с коэффициентом трансформации 5 включена в сеть с напряжение 220 в. Определите напряжение на зажимах вторичной обмотки.

Вариант 16

1. В сеть переменного тока напряжением120 В последовательно включены проводник сопротивлением 15 Ом и катушка индуктивностью 50 мГн. Найдите частоту тока в цепи, если I=7 А.
2. Определить период колебания в колебательном контуре с катушкой индуктивностью 0,25 Гц и конденсатором емкостью 2 МФ
3. Напряжение на зажимах вторичной обмотки понижающегося трансформатора 60 В, сила тока во вторичной цепи 40 А. Первичная обмотка включена в цепь с напряжением 240 В. Найдите силу тока в первичной обмотке трансформатора.

Вариант 17

1. Цепь состоит из последовательных соединений катушки индуктивностью 16 мГн и конденсатора емкостью 2,5 мкФ. Какой должна быть циклическая частота тока в цепи, чтоб возникло явление резонанса?
2. Значение напряжения в колебательном контуре задано уравнением x= 5 cos П/6 t. Каково амплитудное значение и период колебаний? Определите смещение точки для момента времени I/6.
3. Трансформатор имеет коэффициент трансформации 20. напряжение на первичной обмотке 120 В. Определите напряжение на вторичной обмотке и число витков в ней, если первичная обмотка имеет 200 витков.

Вариант 18

1. В колебательном контуре с конденсатором емкостью 2 мкФ за 36 с совершается 1200 колебаний. Какова индуктивность контура?
2. Мгновенное значение ЭДС переменного тока для фазы 60 равно 120 В. Каково амплитудное значение и действующее значение ЭДС?
3. Первичная обмотка силового трансформатора для питания цепей радиоприемника имеет 1200 витков. Какое количество витков должна иметь вторичная обмотка трансформатора для питания кенотрона ( необходимое напряжение 3,5 В)? Напряжение в сети 129 В.

Вариант 19

1. Двухпроводная линия длиной 800 м от понижающего трансформатора выполнена медным проводом сечением 20 мм. Приемники энергии потребляют 2,58 кВт при напряжении 215В. Определите напряжение на зажимах трансформатора и потерю мощности в проводах линии.
2. Начальный заряд, сообщенный конденсатору колебательного контура, уменьшили в 2 раза . Во сколько раз изменилась: амплитуда, напряжение, амплитуда силы тока?
3. Конденсатор емкостью с и две катушки индуктивностями L и L образуют колебательный контур. Определить максимальную силу тока в этом контуре, если максимальная разность потенциалов на обкладках конденсатора достигает Um.

Вариант 20

1. В чем сходство и различие между свободными колебаниями в механических и в электромагнитных колебательных системах?
2. Вторичная обмотка трансформатора, имеющая 200 витков, пронизывается магнитным потоком, изменяющимся со временем закону Ф = 0,2 cos 314 t. Напишите формулу, выражающую зависимость ЭДС вторичной обмотки от времени, найдите действующее значение ЭДС.
3. Колебательный контур составлен из дросселя с индуктивностью 0,2 Гн и конденсатора с емкостью Ф. В момент, когда напряжение на конденсаторе 1 В, ток к контуре 0,01 А. Каков заряд конденсатора в момент, когда ток равен 0,005 А?
4. Определите мгновенные значения силы тока, изменяющегося по закону i = 12 sin t для начальной фазы /6, и моментов времени Т/2.
5. Последовательно с проводником с активным сопротивлением 1 кОм включены катушка индуктивностью 0,5 Гн и конденсатор емкостью 1 мкФ. Определите индуктивное сопротивление, емкостное сопротивление и полное сопротивление цепи переменного тока при частотах 50 Гц.

Вариант 21

1. Почему необходимо повышать напряжение при передаче электроэнергии на большие расстояния? Ответ обоснуйте.
2. Повышающий трансформатор создает во вторичной цепи ток 2А при напряжении 2200 В, напряжение в первичной обмотке равно 110 В. Чему равен ток в первичной обработке, а также входная и выходная мощности трансформатора, если потерь в энергии в нем нет?
3. ЭДС переменного тока выражается уравнением Е = 125sm628t. Определить действующее значение ЭДС и период ее изменения.
4. Колебательный контур имеет собственную частоту 30 к Гц. Какой будет его собственная частота, если расстояние между пластинами плоского конденсатора увеличить в 1,44 раза?
5. Катушка с активным сопротивлением 15 Ом и индуктивностью 52 мГн включена в сеть стандартной частоты последовательно с конденсатором емкостью 120 мк Ф. Напряжение в сети 220 В. Определите силу тока в цепи, активную мощность и коэффициент мощности.

Вариант 22

1. Потери в производстве, передаче и использовании электроэнергии и пути их устранения.
2. Если на первичную обмотку ненагруженного трансформатора с коэффициентом трансформации 8 включена в сеть напряжением 200 В. Сопротивление вторичной обмотки 2 Ом, ток во вторичной обмотке трансформатора 3 А. Определите напряжение на зажимах вторичной обмотки. Потерями в первичной обмотке пренебречь.
3. Передающий контур имеет параметры:
4. С1=10^-5Ф,L(1)=4 * 10^-3Гн. Какой емкости надо подобрать конденсатор, чтобы настроить этот контур в резонанс с другим контуром, имеющим индуктивность 1,6 * 10^-3Гн?
5. Сила тока изменяется по закону i = 90sin (314 + (П)/4). Определить действующее значение силы тока и частоту.
6. Катушка с активным сопротивлением 10 Ом и индуктивностью включена в цепь переменного тока и частотой 50 Гц. Найдите индуктивность катушки, если известен сдвиг фаз между напряжением и силой тока 60°.

Вариант 23

1. Передача электроэнергии: достоинства и недостатки переменного тока.
2. На первичную обмотку понижающего трансформатора с коэффициентом трансформации 10 подается напряжение 220 В. При этом во вторичной обмотке, сопротивление которой 2 Ом, течет ток 4 А. Пренебрегая потерями в первичной обмотке, определите напряжение на выходе трансформатора.
3. Когда в колебательный контур был включен 1-ый конденсатор, собственная частота контура равна 30 кГц, а когда 2-й-40 кГц. Какой будет частота контура при параллельном соединении конденсаторов?
4. Мгновенное значение переменного тока в проводнике определяется по закону I = 0,564sin12,56 t. Какое количество теплоты выделится в проводнике с активным сопротивлением 15 Ом за время, равное 10 периодам?
5. В цепь переменного тока напряжением 220 В и частотой 50 Гц включены последовательно конденсатор емкостью 35,4 мкФ, проводник сопротивлением 100 Ом и катушка индуктивностью 0,7 Гн. Найдите ток в цепи и падение напряжения на конденсаторе, проводнике и катушке.

Вариант 24

1. Укажите характерные черты свободных, вынужденных колебаний и автоколебаний.
2. Понижающий трансформатор с коэффициентом трансформации К= 10 включен в сеть с напряжением U= 127B. Сопротивление вторичной обмотки R= 2 Ом, сила тока J= 3A. Определите напряжение на зажимах вторичной обмотки. Потерями энергии первичной обмотки пренебречь.
3. Найдите индуктивность катушки, в которой равномерное изменение силы тока на 0,8А в течение 10^-5с возбуждает ЭДС самоиндукции 0,2В.
4. Изменение силы тока в зависимости от времени задано (в ед. СИ) уравнением i=cos(100/7t). Определите амплитуду силы тока, циклическую частоту, период и частоту колебаний.
5. Когда в колебательный контур был включен 1-й конденсатор, то собственная частота контура стала равной 30 кГц, а когда 2-й — 40 кГц. Какой будет частота контура при параллельном соединении конденсаторов?

Вариант 25

1. Назовите условия возникновения резонанса в механических и электромагнитных системах. По каким признакам можно обнаружить эти явления?
2. Линия электропередачи длинной 10 метров работает при напряжении 200 000 В. Определить КПД линии / отношение напряжения на нагрузке к напряжению, подводимому к линии/. Линия выполнена алюминиевым кабелем площадью поперечного сечения 150 кв. мм. Передаваемая мощность 30000 КВТ.
3. Сила тока изменяется по закону I=90 sin /314t + Определить действующее значение силы тока.
4. Когда в колебательный контур был включен 1-й конденсатор то собственная частота контура равна 30 кГц, а когда второй — 40 кГц. Какой будет частота контура при параллельном соединении конденсаторов?
5. Катушка с индуктивностью 45 мГн и активным сопротивлением 10 Ом включена в сеть переменного тока с частотой 20 Гц. Напряжение в 220 В. Определите силу тока в катушке и сдвиг фаз между силой тока и напряжением.

Вариант 26

1.  Нарисуйте схему преобразования энергии от внутренней энергии топлива на электростанции до механической энергии на каждом этапе ее передачи и преобразования.
2. Определить емкость конденсатора, сопротивление которого в цепи переменного тока частотой 50 Гц равно 800 ОМ.
3. Понижающий трансформатор дает ток 20 А при напряжении 120 В. Первичное напряжение равно 22 000 В. Чему равны ток в первичной обмотке, а также входная и выходная мощности трансформатора, если его КПД равен 90%.
4. Передающий контур имеет параметры: С 1 = 10 Ф, L 1 = 4 10 Гн. Какой емкости надо подобрать конденсатор, чтобы настроить этот контур в резонанс с другим контуром, имеющим индуктивность 1,6 * 10 Гн?
5. Катушка индуктивностью 0,2 Гн включена в цепь напряжением 220 В стандартной частоты. Напишите уравнение зависимости силы тока, текущего по катушке, от времени. Изобразите график этой зависимости.

Вариант 27

1.  Почему наличие очень высокого напряжения во вторичной обмотке повышающего трансформатора не приводит к большим потерям энергии на выделение теплоты в самой обмотке?
2. В колебательный контур включен конденсатор емкостью 0,2 мкФ. Какую индуктивность нужно включить в контур, чтобы получить в нем электромагнитные колебания частотой 400Гц.
3. Зависимость силы тока, текущего по катушке, от времени записано уравнением i=3,5sin314t. Изобразите график этой зависимости.
4. Когда в колебательный контур был включен 1-й конденсатор то собственная частота контура стала равной 30 кГц, а когда 2-й — 40 кГц. Какой будет частота контура при последовательном соединении конденсаторов?
5. Катушка с активным сопротивлением 10 ом и индуктивностью включена в цепь переменного тока напряжением 127 В и частотой 50 Гц. Найдите индуктивность катушки, если известно, что катушка поглощает мощность 400 ВТ.

Вариант 28

1. Что произойдет с собственными колебаниями в контуре, если его емкость увеличить в 3 раза, а индуктивность уменьшить в 3 раза. Активным сопротивлением можно пренебречь.
2. Ротор генератора имеет 50 пар полюсов и вращается с частотой 2,400. Найти частоту ЭДС в цепи генератора.
3. Колебательный контур состоит из катушки индуктивностью 6 Гн и конденсатора емкостью 2 мкФ. Амплитуда колебаний заряда на обкладках конденсатора равна 100 мк. Напишите уравнение зависимости g(t),i(t).
4. К зажимам генератора присоединен конденсатор емкостью 0,1 мкФ. Определите амплитуду напряжения на зажимах конденсатора, если сила тока 1,6А, а период изменения тока равен 0,2 мс.
5. Катушка с активным сопротивлением 15 ом и индуктивностью 52 мГн, включена в сеть стандартной частоты последовательно с конденсатором емкостью 120 мкФ. Напряжение в сети 220 В. Определите силу тока в цепи, активную мощность и коэффициент мощности.

Вариант 29

1. Пластины плоского конденсатора, включенного в колебательный контур, сближают. Как будет меняться при этом частота колебаний контура?
2. Вторичная обмотка трансформатора, имеющая 100 витков, пронизывается переменным магнитным потоком, изменяющимся со временем по закону Ф=0,01cos314t Вб. Написать уравнение,выражающее зависимость ЭДС индукции от времени в этой обмотке и найти действующее значение.
3. Заряд на обладках конденсатора колебательного контура меняется по закону g=4cosКл. Найдите действующее значение силы тока, период и частоту колебаний.
4. Два конденсатора емкостью 0,2мкФ и 0,1мкФ включены последовательно в цепь переменного тока напряжением 220В. Найдите силу тока в цепи и падение напряжение на каждом конденсаторе.
5. Катушка с активным сопротивлением 2ом и индуктивностью 75мГн включена последовательно с конденсатором в сеть переменного тока, с напряжением 50В и частотой 50Гц. Чему равна емкость конденсатора при резонансе напряжений в цепи? Определите напряжение на катушке и конденсаторе в режиме резонанса.

Вариант 30

1. Какое влияние на свободные электромагнитные колебания в контуре окажет увеличение активного сопротивления катушки при прочих равных условиях?
2. Ротор электрического генератора 7 м и диаметром 1,25 м вращается с частотой 3000. Индукция магнитного поля 2 Тл. Определите амплитуду колебаний ЭДС индукции в одном витке обмотки статора.
3. Определите мгновенное значение силы тока, изменяющегося по закону i=12sint для фазы 320° и момента времени .
4. Последовательно с проводником, с активным сопротивлением 1 кОн включены катушка, индуктивностью 0,5 Гн и конденсатора емкость 1 мкФ. Определите индуктивное сопротивление, емкостное сопротивление и полное сопротивление цепи переменного тока при частоте 10 кГц.
5. В какой момент времени, считая от начала колебаний, мгновенное значение силы переменного тока i будет ровно его действующему значению? Период колебания считать известным, и равным 2 с.

Ответы.

Список используемой литературы.

1. А.Т.Глазунов, О.Ф. Кабардин, А.Н. Малинин, В.А. Орлов, А.А. Пинский. Физика-11. Издательство «Просвещение» 1998 г.

2. И.М. Мартынов, Э.Н. Хозяинова, В.А. Буров. Дидактический материал по физике. Издательство «Просвещение» 1990 г.

3. Г.Н. Степанова. Сборник задач по физике для 9-11 классов общеобразовательных учреждений. Издательство «Просвещение» 1996 г.

Переменный ток — MagLab

Переменный ток ведет себя по-разному, в зависимости от того, какие компоненты находятся в цепи.

Переменный ток (AC) — это электрический ток, который циклически меняет направление, в отличие от постоянного тока (DC), который всегда движется одинаково, как, например, в случае с чем-либо, питаемым от батареи. Переменный ток — это ток, протекающий по электрическим проводам и приборам в вашем доме. Величина переменного тока меняется, возрастая от нуля до положительного максимума, а затем снова снижаясь до нуля до того, как реверсирование тока заставит ток постепенно достичь отрицательного максимума, а затем снова вернуться к нулю.Число раз, когда переменный ток повторяет полный цикл в секунду, составляет , частота , а максимум, которого достигает ток в любом направлении, — это его амплитуда . Форма волны силовой цепи переменного тока представляет собой синусоидальную волну.

Размещение различных компонентов в цепи, питаемой от источника переменного тока, может повлиять на синусоидальные волны для тока и напряжение в цепи, которая запускает ток, как показано в этом руководстве. Ниже показана простая схема с источником питания переменного тока.Идеальный резистор , , конденсатор или индуктор можно включить в схему, выбрав соответствующий пункт в раскрывающемся меню . Выберите компонент . Напряжение (измеренное в вольтах) и ток (измеренное в амперах) в цепи колеблются из-за переменного тока, что видно по показаниям счетчиков в цепи.

Связь между напряжением и током дополнительно подчеркивается векторной диаграммой в нижнем левом углу, которая показывает их колебания как вращающиеся векторы.Когда вектор направлен вверх по оси Y, напряжение или ток достигли своего положительного максимального значения, а когда он направлен вниз по той же оси, был достигнут отрицательный максимум. Горизонтальная ось абсцисс показывает нулевое значение. В правом нижнем углу учебного окна график показывает амплитуду (ось y) как напряжения, так и тока во времени (ось x). Обратите внимание на изменения на диаграмме и графике, когда в схему вставляются разные компоненты.

Когда схема содержит только чистый резистор, ток и напряжение постоянно находятся в фазе друг с другом.Однако, когда в цепи присутствует чистый конденсатор, ток достигает максимального пика, когда напряжение равно нулю; в этом случае говорят, что ток опережает напряжение на 90 градусов. Если выбран чистый индуктор, происходит обратное: напряжение опережает ток на 90 градусов. Конечно, чистое сопротивление, емкость и индуктивность обычно не встречаются в реальных приложениях. В результате различия в фазовом соотношении между током и напряжением могут значительно отличаться от идеализированной корреляции, представленной в учебном пособии.

Вы можете настроить скорость воспроизведения этой интерактивной анимации с помощью ползунка Applet Speed ​​. Притормози, чтобы хорошо рассмотреть взаимосвязи между различными компонентами учебника. Ускорьте его, чтобы получить более реалистичное представление о том, насколько быстро эти изменения на самом деле происходят. Учебное пособие не может проиллюстрировать истинную скорость колебаний напряжения переменного тока, которая проходит полный цикл — изменение от положительного до отрицательного и обратно — 60 раз в секунду в США., 50 раз в секунду в Европе.

(PDF) Колебания частоты в морских микросетях: источники и инструменты идентификации

Для дальнейшего чтения

• OB Fosso и M. Molinas, «EMD Mode Mixing Selection of Signals with Close Spectral

Proximity in Smart Grids», 2018 IEEE Конференция PES Innovative Smart Grid Technologies Conference

Europe (ISGT-Europe), Сараево, 2018, стр. 1-6. DOI: 10.1109 / ISGTEurope.2018.8571816

• Норден Э. Хуанг, Чжэн Шен, Стивен Р.Лонг, Манли К. Ву, Син Х. Ши, Куанан Чжэн,

Най-Чьюань Йен, Чи Чао Тунг и Генри Х. Лю., Эмпирическое разложение по модам

и гильбертовый спектр для нелинейного и нестационарного времени анализ серий. Слушания

Лондонского королевского общества, 1998. doi: 10.1098 / rspa.1998.0193

• Ван Т., Z-преобразование сегментированного щебета и его применение в спектральном анализе, IEEE

Transactions on Instrumentation and Measurement, vol.39, выпуск 2, апрель 1990 г., стр. 318-323.

Об авторах

Томаш Тарасюк — профессор кафедры морской электротехники в Гдыне

Морской университет в Гдыне, Польша, электронная почта: [email protected]

Юрий Зунино имеет степень магистра в области электротехники в Университете Генуи, Генуя,

Италия; электронная почта: [email protected]

Максимилиано Буэно-Лопес — профессор кафедры электроники, контрольно-измерительной аппаратуры и управления

Университета дель Каука в Попаяне, Колумбия; электронная почта: mbuenol @ unicauca.edu.co

Федерико Сильвестро — доцент кафедры электротехники, электроники,

Телекоммуникационная инженерия и военно-морская архитектура Университета Генуи, Генуя, Италия;

электронная почта: [email protected]

Анджей Пилатис ассистент кафедры морской электротехники в Гдыне Морской

университет в Гдыне, Польша, электронная почта: [email protected]

Марта Молинас является профессором кафедры инженерной кибернетики Норвежского научно-технического университета

Тронхейм, Норвегия; электронная почта: Марта[email protected]

гелиогнозис

Экспериментальный Отчет 2: Наблюдения за колебаниями вакуума позволяют предположить существование энергии нулевой точки (ZPE) от Heliognosis Абстрактные Недавний экспериментальные данные предполагают, что неуловимая энергия нулевой точки (ZPE) флуктуации вакуума можно обнаружить с помощью электрического поля. Исходные данные показывают, что увеличение напряженности электрического поля приводит к в повышенной связи с колебаниями вакуума.Это было определяется изменением как напряжения электрического поля, так и за счет увеличения площади радиаторной пластины. С AC электрическое поле 246 В от пика до пика, присутствуют колебания вакуума сами по себе как динамические квазициклические колебания тока в самом низкочастотный (vlf) и сверхнизкочастотный (ulf) диапазон с величина 0,02%. Хотя в вакууме энергии нулевой точки Колебания стали хорошо изученной концепцией квантовой механики, мало выдвинуто экспериментальное свидетельство в отношении электрического поле.Недавнее исследование Р. Бланко, Х. М. Франка, Э. Сантоса и Р. К. Sponchiado (1) в Physics Letters A предполагает, что флуктуации вакуума для магнитного поле может быть обнаружено. Эти колебания магнитного напряжения показаны быть экспериментально отличимым от колебаний напряжения связанный с хорошо известным шумом Найквиста (1). Пока изучение поглощения электрического поля у живых субъектов на расстояния наблюдалась флуктуация на очень низкой частоте (vlf) диапазон. Наблюдения проводились с помощью металлической пластины, заряженной переменным током. высокое напряжение.Текущий поток к пластине и от пластины контролировался с помощью усилитель электрического тока с высоким сопротивлением и высоким коэффициентом усиления. Улучшения в конструкция усилителя снизила «тепловой шум Джонсона» до второго уровня. на порядки меньше, чем размах интенсивности колебания наблюдаются изначально. Собрана аппаратура для изучения эти колебания показаны на рисунке 1. Рисунок 1 Рисунок 2

Настройка

An сверхстабильный регулируемый источник питания постоянного тока был модулирован прерывателем и импульсное колебание постоянного тока было подключено к пластине в вакууме трубка.Переменный ток, протекающий к пластине и от нее, наблюдался с помощью датчик тока. Токовый сигнал подвергался полуволновому выпрямлению и фильтрации. чтобы убрать несущую частоту и затем усилить. Среднее значение положительной части тока затем наблюдали на приборе Tektronix Цифровой стробоскопический осциллограф TDS320. Второй идентичный усилитель отслеживали изменения размаха напряжения генератора. Целый прибор, за исключением прицела, был помещен в заземленный Клетка Фарадея для предотвращения помех от внешних электрических полей, таких как как 60 Гц.Вся мощность в клетке обеспечивалась стеками 12В. гелевые батареи.

Импульсное поле возбуждения постоянного тока представляло собой форму волны с медленным нарастанием и крутым спадом с частотой 66 кГц. Импеданс датчика тока был выбран равным 100 кОм. Электрод В качестве платформы для излучения электрического поля использовалась одна из пластин. от двухполупериодной высоковольтной выпрямительной лампы Raytheon JAN5R4WGB. В площадь одной стороны этой пластины составляла примерно 2,25 кв. дюймы.

Наблюдения

An начальный тест калибровки шума проводился с малым возбуждением. напряжения и только с датчиком тока на месте (без нагрузки).Вход Напряжение P-P составляло 16,8 В в контрольной точке (2a). Импеданс датчика тока составлял 100 кОм, а общее усиление составляло 50X. На рисунке 3 a 25 мс на кривую деления показывает колебания датчика тока напряжение на дорожке 1, контрольной точке (1b) и в напряжении генератора на кривая 2, контрольная точка (2b). Ток пластины тогда имеет размах переменного тока. изменение 2,88 мВ / 50 = 58 мкВ, 58 мкВ / 100 кОм = 580 пА. Осциллятор размах напряжения составляет 58 мкВ. Это очевидно из отслеживает, что форма волны тока не зависит от напряжения вариации.

Рисунок 3

Затем напряжение аккумуляторной батареи увеличивалось поэтапно, обеспечивая достаточное время стабилизации напряжения на входном фильтре R-C. На каждый шаг, ток пластины переменного тока, входное напряжение, размах тока колебания и колебания напряжения от пика до пика были измерены. В На рисунке 4 представлены графики размах колебаний тока в зависимости от увеличение входного напряжения генератора. На рисунке 4 представлен график, показывающий эти полученные результаты.

Рисунок 4

В фиг.5 осциллограмма тока трубчатого электрода на максимуме показано испытательное напряжение.Это измерение производится в точке (1a) из цифра 2 без какого-либо усиления. Положительная часть форма волны показывает часть цикла, когда электроны вытянутый из пластины, чтобы создать положительно заряженное электрическое поле в вакуум. Отрицательный всплеск возникает, когда прерыватель подключает пластина к земле, и электроны устремляются обратно к пластине и нейтрализуют поле. Поскольку детектор тока имеет аттенюатор 20x на входной, соответствующая шкала тока составляет 200 мкА на деление.

Рисунок 5

Аналогично На рисунке 6 показано входное напряжение генератора. Напряжение было измерено в точке (2а) из рисунка 2 без усиления.

Рисунок 6

Рисунок 7 — осциллограф 50-секундного графика вакуумного тока. колебания. Это измерение производится в точках (1b) для текущего (верхняя кривая) и (2b) для напряжения (нижняя кривая). Как это может быть хорошо видно, колебания тока не следуют за напряжением колебания.Ток и напряжение уменьшаются в 20 раз за счет цепь детектора, а затем усилена в 1000 раз. Общее усиление тогда 50x. Наблюдаемое колебание тока составляет 296 мВ / 50 = 5,92 мВ. 5,92 мВ / 100 кОм = 59,2 нА. Пиковая положительная часть тока форма волны на рисунке 5 составляет 290 мкА. Это колебание 0,0204%. Для Для сравнения, колебание напряжения составляет 0,0256%.

Рисунок 7

тарелки с большой площадью поверхности позволяют формировать гораздо более прочные электрические поля при том же напряжении по сравнению с относительно небольшими вакуумная плита.Для сравнения на рисунке 8 показана форма кривой тока для Изолированная плита площадью 300 кв. Дюймов в воздухе. Этот ток измеряется в точке (1а) перед выпрямлением, фильтрацией и усилением. Вертикаль шкала составляет 400 мкА на деление, а пиковая положительная часть составляет 1,03 мА.

Рисунок 8

Аналогично форма волны напряжения и колебания сверхнизкой частоты (ulf) показаны на рисунках 9 и 10 соответственно. На рисунке 10 текущий колебания (верхняя кривая) имеют шкалу 40 нА на деление.В размах колебаний тока составил 81,6 нА или 0,0079%. Напряжение колебание составило 0,0081%.

Рисунок 9

Рисунок 10

Демонстрация флуктуации вакуума с использованием модели Heliognosis LM2

А коммерческая версия вышеупомянутой схемы, Heliognosis Experimental Измеритель жизненной энергии LM2 был подключен к клетке Фарадея и работал от гелевой батареи 12 В. Счетчику давали прогреться в течение 30 минут до проведения измерений для обеспечения стабильности.Исключить влияние температуры, все показания были сняты за период 30 минут и температуру контролировали ртутным термометр. Температура в начале эксперимента составляла 17,4 ° С. В конце опыта температура составила 17,1 ° С. LM2 имеет гораздо более сильный демпфирующий фильтр, чем использованная лабораторная версия. выше, чтобы можно было наблюдать флуктуации вне фарадеевского клетка. Более сильная фильтрация снижает наблюдаемые колебания несколько, но также более эффективно фильтрует 60 Гц.Плоская тарелка меньшего размера был впервые протестирован (40 кв. дюймов) с усилением, установленным на x1000, и задний переключатель в положении большой пластины (сопротивление датчика 200 кОм). А большая тарелка, модель LM03-AC, площадью 300 кв. дюймов был соединен с тем же условия эксплуатации. Нулевые контроли были отрегулированы для каждого планшета, чтобы держите среднее значение на аналоговом измерителе около 10%. График выход регистратора был подключен к TDS320 DSO и обеспечен осциллографы колебаний vlf и ulf.

Наблюдения

Чтения были сняты с помощью осциллографа в режиме переменного тока для наблюдения vlf колебания в нижнем диапазоне Герц. Эти показания были приняты периоды 250 мс и 1 секунда. Осциллограф был переведен в режим постоянного тока. чтобы увидеть колебания vlf и ulf вместе за период 100 секунд. Было снято несколько показаний в обоих режимах с малым и большие пластины и усредненные данные показаны ниже.

от пика до пика колебания:

	AC (только vlf)	DC (vlf + ulf)
маленькая пластина	7.9nA	11,2 нА
пластина большая	12,3 нА	21,4 нА

Фигура 11 показан пример больших колебаний переменного тока пластины за период 0,25 секунды. Как видно, флуктуация тока vlf равна квазициклический с несколькими частотами, такими как 11,5 Гц, 25 Гц и 40 Гц. Электромагнитные помехи, такие как 60 Гц, эффективно блокируются Клетка Фарадея и не видна на осциллограмме.

Рисунок 11

Рисунок 12 показан пример колебаний постоянного тока для большой пластины над 100 секундный интервал.Комбинированное колебание vlf и ulf соответствует до максимального значения 21,4 нА.

Рисунок 12

Выводы

Из Из приведенных выше результатов видно, что электрическое поле вокруг вакуумная пластина динамически колеблется с квазициклическими колебаниями в диапазон vlf и ulf. Переменный ток на вакуумной пластине изменяется как примерно 0,0204% в исследованном диапазоне входного напряжения и тока. В было обнаружено, что колебания вакуума увеличиваются пропорционально входному пластина напряжения.Также было обнаружено, что увеличение площади пластины также увеличивает колебания. Эффективный вывод состоит в том, что электрическая диэлектрическая проницаемость не является постоянной, а скорее функцией локального нулевая энергия вакуумных колебаний.

Список литературы

(1) Радиационная шум в цепях с индуктивностью
Физика Письма A, том 282, выпуск 6, 30 апреля 2001 г., страницы 349-356
R. Бланко, Х. М. Франка, Э. Сантос и Р. К. Спонкиадо

% PDF-1.5 % 11 0 объект >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 4 0 obj >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 7 0 объект >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 1 0 объект >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A».N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 13 0 объект >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 15 0 объект >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 6 0 obj >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 14 0 объект >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 5 0 obj >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 12 0 объект >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 3 0 obj >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A».N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 8 0 объект >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 16 0 объект >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 9 0 объект >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 10 0 obj >>> / BBox [0 0 595.44 841.68] / Длина 116 >> поток x% ̱0% Q ګ G «N% = SP ۋ qƯ2WF `X8Oe] A» .N> F8G? 3 ‘? /; 4 ᦯ q \ D6B_9 D конечный поток эндобдж 18 0 объект > поток ; изменено с помощью iText 4.2.0 пользователем 1T3XT2021-11-23T14: 09: 10-08: 00

конечный поток эндобдж 19 0 объект > поток x +

Что такое частота? | Fluke

Частота переменного тока (ac) — это количество циклов в секунду в синусоидальной волне переменного тока.Частота — это скорость изменения направления тока в секунду. Он измеряется в герцах (Гц), международной единице измерения, где 1 герц равен 1 циклу в секунду.

• Герц (Гц) = Один герц равен одному циклу в секунду.
• Цикл = Одна полная волна переменного тока или напряжения.
• Чередование = половина цикла.
• Период = время, необходимое для создания одного полного цикла сигнала.

В самом основном, частота — это то, как часто что-то повторяется.В случае электрического тока частота — это количество раз, когда синусоидальная волна повторяет или завершает цикл от положительного к отрицательному.

Чем больше циклов происходит в секунду, тем выше частота.

Пример: Если переменный ток имеет частоту 3 Гц (см. Диаграмму ниже), это означает, что его форма волны повторяется 3 раза за 1 секунду.

Частота обычно используется для описания работы электрического оборудования. Ниже приведены некоторые распространенные диапазоны частот:

• Частота сети питания (обычно 50 Гц или 60 Гц).
• Преобразователи частоты, которые обычно используют несущую частоту 1–20 килогерц (кГц).
• Диапазон звуковых частот: от 15 Гц до 20 кГц (диапазон человеческого слуха).
• Радиочастота: 30-300 кГц.
• Низкая частота: от 300 кГц до 3 мегагерц (МГц).
• Средняя частота: 3-30 МГц.
• Высокая частота: 30-300 МГц.

Цепи и оборудование часто предназначены для работы с фиксированной или переменной частотой. Оборудование, предназначенное для работы на фиксированной частоте, работает ненормально, если оно работает на частоте, отличной от указанной.Например, двигатель переменного тока, предназначенный для работы на частоте 60 Гц, работает медленнее, если частота падает ниже 60 Гц, и быстрее, если она превышает 60 Гц. Для двигателей переменного тока любое изменение частоты вызывает пропорциональное изменение скорости двигателя. Другой пример: уменьшение частоты на 5% приводит к снижению скорости двигателя на 5%.

Как измерить частоту

Цифровой мультиметр, который включает режим частотомера, может измерять частоту сигналов переменного тока, а также может предлагать следующее:

• Запись MIN / MAX, что позволяет записывать измерения частоты в течение определенного периода или таким же образом записываются измерения напряжения, тока или сопротивления.
• Автоматический диапазон, который автоматически выбирает частотный диапазон, за исключением случаев, когда измеренное напряжение выходит за пределы диапазона измерения частоты.

Электросети различаются в зависимости от страны. В США сетка основана на высокостабильном сигнале с частотой 60 Гц, что означает, что она циклически повторяется 60 раз в секунду.

В США для электроснабжения домашних хозяйств используется однофазный источник питания переменного тока на 120 вольт. Мощность, измеренная в настенной розетке дома в США, будет давать синусоидальные волны, колеблющиеся в пределах ± 170 вольт, при измерении истинного среднеквадратичного напряжения 120 вольт.Частота колебаний составит 60 циклов в секунду.

Hertz назван в честь немецкого физика Генриха Герца (1857–1894), который первым начал передавать и принимать радиоволны. Радиоволны распространяются с частотой один цикл в секунду (1 Гц). (Точно так же часы отсчитывают 1 Гц.)

Ссылка: Принципы цифрового мультиметра, автор — Глен А. Мазур, American Technical Publishers.

Урезанная оценка Уиттла SVAR по сравнению с фильтрацией низкочастотных колебаний: приложения к технологическим шокам , низкочастотные колебания, которые могут возникнуть в макроэкономических данных.Предварительная фильтрация разрушает низкочастотный диапазон спектра, тем самым искажая оценочные параметры и реакцию переменных на шоки. Предлагаемый метод, напротив, учитывает нежелательные колебания при преодолении этих недостатков. Более того, этот метод остается надежным даже тогда, когда наблюдаемая низкочастотная изменчивость ошибочно считалась внешней по отношению к SVAR. Для иллюстрации результатов предлагается эмпирическое приложение, которое исследует влияние технологических шоков на отработанное время.Мы находим положительный и аналогичный отклик часов при использовании как долгосрочных, так и краткосрочных идентификационных ограничений, что позволяет решить широкую дискуссию в литературе о бизнес-циклах.

Список литературы

Бакстер М. и Р. Дж. Кинг. 1999. «Измерение бизнес-циклов: приблизительные полосовые фильтры для экономических временных рядов». Обзор экономики и статистики 81: 575–593. Искать в Google Scholar

Канова, Ф., Д. Лопес-Салидо и К. Мичелаччи. 2010 г.«Влияние технологического шока на часы работы и производительность: анализ надежности». Журнал прикладной эконометрики 25: 755–773. Искать в Google Scholar

Кристиано, Л. Дж., М. Эйхенбаум и Р. Вигфуссон. 2003. «Что происходит после технологического шока?» Рабочие документы NBER 9819, Национальное бюро экономических исследований, Inc. Поиск в Google Scholar

Когли Т. и Дж. М. Нейсон. 1995. «Влияние фильтра Ходрика-Прескотта на тренд и разность стационарных временных рядов: значение для исследования бизнес-цикла. Журнал экономической динамики и управления 19: 253–278. Искать в Google Scholar

Дальхаус, Р. 1988. «Эффекты малых выборок в анализе временных рядов: новая асимптотическая теория и новая оценка». Анналы статистики 16: 808–841. Искать в Google Scholar

Энгл, Р. Ф. 1974. «Регрессия полосового спектра». Международный экономический обзор 1–11. Искать в Google Scholar

Фернальд, Дж. Г. 2007. «Сломанные тенденции, долгосрочные ограничения и сдерживающие усовершенствования технологий.” Журнал денежно-кредитной экономики 54: 2467–2485. Искать в Google Scholar

Фрэнсис Н. и В. А. Рэми. 2009. «Измерение количества часов на душу населения и их значение для дебатов о количестве часов на душу населения». Журнал денег, кредита и банковского дела 41: 1071–1097. Искать в Google Scholar

Господинов, Н. 2010. «Вывод в почти нестационарных моделях SVAR с долгосрочными ограничениями идентификации». Журнал деловой и экономической статистики 28: 1–12.Искать в Google Scholar

Господинов, Н., А. Мейнард, Э. Песавенто. 2011. «Чувствительность импульсных откликов к небольшим низкочастотным колебаниям: согласование данных о влиянии технологических шоков». Журнал деловой и экономической статистики 29: 455–467. Искать в Google Scholar

Гамильтон, Дж. Д. 2018. «Почему никогда не следует использовать фильтр Ходрика-Прескотта». Обзор экономики и статистики 100: 831–834. Искать в Google Scholar

Хансен, Л.П. и Т. Дж. Сарджент. 1993. «Сезонность и ошибки аппроксимации в моделях рациональных ожиданий». Journal of Econometrics 55: 21–55. Искать в Google Scholar

Харви, А. С. 1989. Прогнозирование, модели структурных временных рядов и фильтр Калмана . Кембридж, Великобритания: Издательство Кембриджского университета. Искать в Google Scholar

Харви А. и А. Джегер. 1993. «Разоблачение тенденций, стилизованные факты и деловой цикл». Журнал прикладной эконометрики 8: 231–247.Искать в Google Scholar

Hodrick, R.J. и E.C. Prescott. 1997. «Послевоенные деловые циклы в США: эмпирическое исследование». Журнал денег, кредита и банковского дела 2: 1–16. Искать в Google Scholar

Hou, J., and P. Perron. 2014. «Модифицированная локальная оценка Уиттла для процессов с длительной памятью в присутствии низкочастотных (и других) загрязнений». Эконометрический журнал 182: 309–328. Искать в Google Scholar

Кинг, Р. Г. и С.Т. Ребело. 1993. «Низкочастотная фильтрация и реальные деловые циклы». Журнал экономической динамики и управления 17: 207–231. Искать в Google Scholar

Ловча Ю. и А. Перес-Лаборда. 2015. «Часы работы — Загадка производительности: идентификация в настройках дробной интеграции». Макроэкономическая динамика 19: 1593–1621. Искать в Google Scholar

Макклоски, А. 2013. «Оценка параметров модели стохастической волатильности с длительной памятью, устойчивой к сдвигам уровней и детерминированным тенденциям.» Журнал анализа временных рядов 4: 285–301. Искать в Google Scholar

Макклоски А. и Дж. Б. Хилл. 2014. «Надежная оценка в частотной области с тяжелым хвостом». Машинопись, сентябрь 2014 г. Поиск в Google Scholar

Макклоски А. и Дж. Б. Хилл. 2017. «Устойчивость оценки параметров к низкочастотному загрязнению», журнал , Журнал деловой и экономической статистики, , 35: 598–610. Искать в Google Scholar

Цюй З., Ткаченко Д. 2012. «Идентификация и оценка квазимаксимального правдоподобия в частотной области линеаризованных динамических стохастических моделей общего равновесия.” Количественная экономика 3: 95–132. Искать в Google Scholar

Рэми, В. А. 2016. «Макроэкономические шоки и их распространение». В Справочнике по макроэкономике под редакцией Дж. Б. Тейлора и Х. Улига, Vol. 2, стр. 271–162, Северная Голландия, Амстердам: Elsevier. Искать в Google Scholar

Сала, Л. 2015. «Модели DSGE в частотной области». Журнал прикладной эконометрики 30: 219–240. Искать в Google Scholar

Тьюки, Дж. У. 1967.«Введение в вычисления численного анализа спектра». В Расширенный семинар по спектральному анализу временных рядов , под редакцией Б. Харриса, Нью-Йорк: Wiley. Искать в Google Scholar

Веласко, C. 1999. «Гауссовская полупараметрическая оценка нестационарных временных рядов». Журнал анализа временных рядов 20: 87–127. Искать в Google Scholar

Whittle, P. 1963. «О согласовании многомерных авторегрессий и приближенной канонической факторизации матрицы спектральной плотности.” Биометрика 50: 129–134. Искать в Google Scholar

Чжан, Х. С. 1991. «Снижение асимптотического смещения авторегрессионных и спектральных оценок за счет сужения». Журнал анализа временных рядов 13: 451–469. Искать в Google Scholar

Чувствительность роста трещин к величине и частоте колебаний нагрузки на стадии 1b коррозионного растрескивания под напряжением при высоком pH

Трубопроводы проходят последовательные стадии до выхода из строя, вызванного коррозионным растрескиванием под высоким pH.Этими последовательными стадиями являются стадия инкубации, зарождение межкристаллитной трещины (стадия 1a), эволюция трещины для обеспечения условий для роста трещин, вызванных механическим воздействием (стадия 1b), устойчивого механического распространения трещин (стадия 2) и быстрого распространения трещины до разрушения (стадия 3). Механизмы распространения трещин на этапе 1b состоят из зарождения и роста вторичных трещин на свободной поверхности и слияния вторичных трещин друг с другом и с первичной трещиной.Эти механизмы продолжаются до тех пор, пока коэффициент интенсивности напряжения (K) в вершине трещины не достигнет критического значения, известного как K _ISCC . В этом исследовании использовался новый подход к изучению этапа 1b при использовании предварительно растрескавшихся компактных образцов на растяжение (CT). Использование предварительно растрескавшихся образцов и поддержание K на уровне ниже K _ISCC дало возможность изучить зарождение трещин на поверхности образца в условиях плоского напряжения при наличии ранее существовавшей трещины. В настоящей работе изучалось влияние характеристик циклического нагружения на характер роста трещин на этапе 1b.Было замечено, что существовавшие ранее трещины на этапе 1b привели к возникновению вторичных трещин. Возникновение вторичных трещин в вершине трещины зависело от характеристик нагружения, т. Е. От амплитуды и частоты колебаний нагрузки. Вторичные трещины на вершине трещины можно разделить на четыре категории в зависимости от их положения относительно первичной трещины. Циклы с низким R-соотношением генерировали явную циклическую пластическую зону, в которой образовывались межкристаллитные трещины высокой плотности.Чем выше частота циклов с низким отношением R, тем выше плотность межзеренных трещин, образующихся в зоне циклической пластичности. Скорость роста трещины увеличивалась с увеличением либо амплитуды, либо частоты колебаний нагрузки. Минимальная и максимальная скорость роста трещины составляла 8 × 10 ⁻⁹ мм / с и 4,2 × 10 ⁻⁷ мм / с, соответственно, с коэффициентом R от 0,2 до 0,9, с частотой от 10 ^−4. Гц и 5 × 10 ⁻² Гц, и при фиксированном коэффициенте интенсивности напряжений 15 МПа · м.Было обнаружено, что предотвращение быстрых и больших колебаний нагрузки замедлило эволюцию геометрии трещины и задержало начало Этапа 2.

No related posts.