Комплексные числа в электротехнике
Господа, в сегодняшней статье я хотел бы вам немного рассказать про комплексные числа и сигналы. Данная статья будет в основном теоретической. Ее задача – подготовить некоторый фундамент для возможности понимания дальнейших статей. Просто когда речь заходит про фазу или, допустим, про поведение конденсатора в цепи переменного тока, так сразу и начинаю лезть все эти комплексности. А про фазу все-таки хочется поговорить, штука важная. Нет, эта статья ни в коем случае не будет кратким курсом ТФКП, мы рассмотрим только лишь очень узкую область из этой вне всякого сомнения интересной и обширной темы. Итак, поехали!
Но прежде чем начать говорить непосредственно про комплексные числа, я бы хотел еще рассказать про такую любопытную штуку, как тригонометрический круг. Господа, вот мы с вами уже на протяжении аж трех (раз, два, три) статей говорим про синусоидальный ток. Но как вообще формируется функция синуса? Да и косинуса тоже? Можно по-разному ответить на этот вопрос, но в контексте данной статьи я выбрал следующее объяснение. Взгляните, пожалуйста, на рисунок 1. На нем изображен так называемый тригонометрический круг.
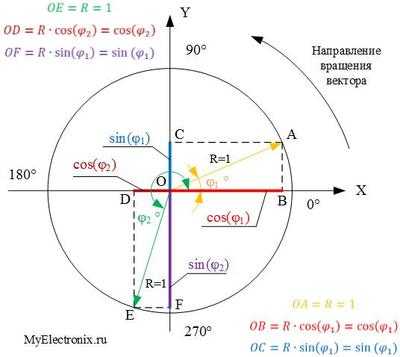
Рисунок 1 – Тригонометрический круг
Там много всего намалевано, поэтому давайте разбираться постепенно что там есть что. Во-первых, там есть, собственно, некоторая окружность, центр которой совпадает с центром системы координат с осями Х и Y. Радиус этой окружности равен единице. Просто единице, без всяких вольт, ампер и прочего. Далее из центра этой окружности проведены два радиус-вектора ОА и ОЕ. Очевидно, длина этих векторов равна единице, потому что у нас окружность единичного радиуса. Угол между вектором
А теперь самое интересное, господа. Давайте рассмотрим, чему равны проекции этих векторов на оси Х и Y. Проекция вектора ОА на ось Х – это отрезок ОВ, а на ось Y – это отрезок ОС. И все вместе (сам вектор ОА и его проекции ОВ и ОС) образует прямоугольный треугольник ОАВ. По правилам работы с прямоугольным треугольником мы можем найти его стороны ОВ и ОС, то есть проекции радиус вектора ОА
Абсолютно аналогично можно найти соотношения для вектора OE:
Если не понятно почему так, советую погуглить про соотношения сторон в прямоугольном треугольнике. Ну а мы для себя сейчас выносим один немаловажный вывод – проекция единичного вектора на ось Х равна косинусу угла между вектором и осью Х, а проекция на ось Y – синусу этого угла.
А теперь давайте начнем вращать радиус-вектор против часовой стрелки с некоторой частотой. Ну, так, чтобы он своим концом вычерчивал окружность. И, как вы уже, вероятно, догадались, при таком вращении проекция вектора на ось Х будет вырисовывать функцию косинуса, а проекция на ось Y – функцию синуса. То есть, если этот наш радиус-вектор делает за секунду, например, 50 оборотов (то есть вращается с частотой 50 Гц), то это значит, что его проекция на ось Х формирует функцию
а его проекция на ось Y – вырисовывает функцию
Довольно интересный факт на мой взгляд. И вообще тригонометрический круг – любопытная штука. Рекомендую познакомиться с ним поближе, погуглив на эту тему. Он позволяет многое лучше понять. Мы же сейчас рассмотрели только немногие из фич, которые нам будут нужны. Сейчас давайте пока временно оставим этот факт и поговорим непосредственно про комплексные числа.
a – это действительная часть комплексного числа z.
b – это мнимая часть комплексного числа z.
На самом деле в серьезных книжках по математике комплексное число определяют несколько по-другому, однако нас вполне устроит и такой вариант.
По-научному – это алгебраическая форма записи комплексного числа. Есть еще и другие, с ними познакомимся чуть позже.
а и b – это обычные числа, к которым мы с вами все привыкли. Например, 42, 18, -94, 100500, 1.87 ну и так далее. То есть абсолютно любые. Например, могут иметь место вот такие записи
А число j – это так называемая мнимая единица. Часто ее обозначают не j, а i, но i – это обычно ток в электротехнике, поэтому мы будем использовать буковку j. Что это такое? Формально, это можно записать так
Немного не понятно, как это может быть корень из отрицательного числа . Все мы с детства привыкли, что под корнем у нас только лишь положительные числа. Но математики ввели вот такую вот абстракцию, которая позволяет извлечь корень и из отрицательных чисел. И, как ни странно, подобная абстракция неплохо помогает описывать вполне себе реальные, а вовсе никакие не абстрактные процессы в электротехнике.
То есть мы видим, что комплексное число само по себе как бы просто состоит из двух самых обычных чисел. Да, перед втором стоит некоторое мифическое j, но сути дела это не меняет.
Давайте теперь познакомимся с графическим представление комплексных чисел.
Господа, взгляните на рисунок 2. Там как раз-таки это представление и изображено.
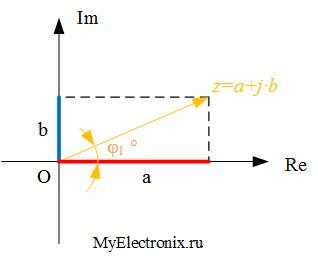
Рисунок 2 – Комплексная плоскость
Итак, в чем здесь, собственно, фишка? А фишка в том, что мы берем и рисуем систему координат. В ней мы ось Х обзываем Re, а ось Y – Im. Re – это ось действительных чисел, а
Интересный факт: давайте представим, что b равно 0. Тогда получается, что комплексное число вырождается в самое обыкновенно, «одномерное»: мнимая часть просто обнуляется. И, естественно, вектор в этом случае будет лежать на оси Re. То есть, можно сказать, что все числа, которые нас окружают в обычной жизни, находятся на оси
Давайте лучше углубимся в другое. А именно в то, как еще можно представить комплексные числа. Только что мы пришли к выводу, что комплексное число – по сути это вектор. А вектор можно характеризовать длинной и углом наклона, например, к оси Х. Действительно, эти два параметра полностью определяют любой вектор при условии, что у нас двумерное пространство, само собой. Для объема или какого-нибудь многомерного пространства (ужас какой) это не верно, а для двумерного – это так. Давайте теперь выразим сказанное математически. Итак, давайте теперь исходить из того, что нам известна длина вектора (обзовем ее
Что мы можем найти, исходя из этих знаний? Да вообще говоря, довольно много. По сути нам известна гипотенуза прямоугольного треугольника и один из его углов, то есть, согласно каким-то там теоремам геометрии, прямоугольный треугольник полностью определен. Поэтому давайте найдем его катеты а и b:
А теперь, господа, можно сделать небольшой финт ушами? Помните алгебраическую запись комплексного числа? Ну, вот эту
Давайте-ка подставим сюда a и b, представленные через синусы с косинусами. Получим
Мы получили интересное выражение. Выражение вида
называется тригонометрической формой записи комплексного числа. Она хороша, если нам известна длина нашего вектора |z| и угол его наклона φ1. Когда речь пойдет об электротехнике, длина вектора внезапно превратится в амлитуду сиганала, а угол наклона – в фазу сигнала. Кстати, обратите внимание, что тригонометрическая форма записи комплексного числа чем-то близка к тригонометрическому кругу, который мы нарисовали в начале статьи. Но к этому сходству мы вернемся чуть позже.
Господа, теперь нам осталось познакомиться с последней формой записи комплексного числа –
где е – это экспонента или, как ее еще называют, показательная функция. Для математиков это некоторый предел при стремлении чего-то там к бесконечности, а если по-простому – обычное число
А теперь сравните формулу Эйлера и тригонометрической записью комплексного числа. Не замечаете интереснейшего сходства? Скрестив эти два выражения, можно получить как раз-таки показательную форму записи комплексного числа:
Как ни странно, эта мудреная запись используется в электротехнике не так уж и редко.
Итак, мы познакомились с основными вариантами записи комплексных числе. Теперь давайте постепенно продвигаться к нашей любимой электротехнике. Запишем закон изменения косинусоидального напряжения.
Мы уже записывали этот закон неоднократно, например, в самой первой статье, посвященной переменному току. Правда, там был синус, а здесь косинус, но это абсолютно ничего не меняет по сути, просто тут косинус немного удобнее для объяснения.
А сейчас внимание, господа. Очень хитрая последовательность действий.
Во-первых, никто нам не мешает рассмотреть косинус, который стоит в этом выражении, на тригонометрическом круге, который мы чертили на рисунке 1 в самом начале статьи. А что? Почему нет? Будем представлять себе, что некоторый вектор Ám, равный амплитуде нашего косинусоидального напряжения, вращается в прямоугольной системе координат с круговой частотой ω. И тогда в силу выше изложенных обстоятельств его проекция на оси Х будет вырисовывать как раз наш закон v(t). Вроде бы никакого подвоха пока нет.
Смотрим дальше. На оси Х проекция рисует нашу функцию времени, а ось Y пока что вообще не при делах. А что б она просто так не простаивала – давайте-ка считать, что это не просто абы какая ось Y, а ось мнимых чисел. То есть мы сейчас вводим то самое комплексное пространство. В этом пространстве при вращении вектора Ám (вектора обычно обозначаются буквой с точкой или стрелочкой сверху) в то время как его проекция на оси Х рисует косинус, на оси Y у нас будет рисоваться функция синуса. Вся фишка в том, что мы сейчас как бы скрещиваем тригонометрический круг с комплексной плоскостью. И в результате получаем что-то типа того, что показано на рисунке 3 (картинка кликабельна).
Рисунок 3 – Представление напряжения на комплексной плоскости
Что мы на нем видим? Собственно, то, о чем только что говорили. Вектор, равный по длине амплитуде нашего напряжения, вращается в системе координат, на оси Х (которая Re) вырисовывается закон косинуса (он полностью совпадает нашим сигналом v(t)). А на оси Y (которая Im) вырисовывается закон синуса. Итого на основе вышесказанного наш исходный сигнал
мы можем представить в тригонометрической форме вот так
или в показательной форме вот так
Давайте представим теперь, что у нас не косинусоидальный сигнал, а синусоидальный. К нему мы как-то больше привыкли. То есть, пусть напряжение изменяется вот по такому закону
Проведем все рассуждения аналогичным образом. Единственное отличие будет в том, что теперь наш сигнал «рисуется» на мнимой оси Im, а ось Re как бы не при делах. Но вводя комплексное пространство, мы внезапно получаем, что комплексная запись сигнала для данного случая точно такая же, как и для случая косинуса. То есть и для сигнала
мы можем записать комплексное представление в тригонометрической форме вот так
или в показательной форме вот так
Выходит, что комплексное представление для случая синусоидального и косинусоидального сигнала имеет один и тот же вид. Кстати, это довольно очевидно, если вспомнить, что при вращении вектора по окружности и синус и косинус вырисовываются одновременно на разных осях. А само комплексное число описывает именно этот вращающийся вектор и, таким образом, содержит в себе инфу как про ось Х, так и про ось Y.
Давайте теперь пойдем от обратного и представим, что у нас есть запись некоторого комплексного сигнала в виде
Или, например, в таком виде
Как понять – что он описывает: синус или косинус? Ответ – да никак. Он описывает и то, и то одновременно. И если мы имеем косинусоидальный сигнал, то мы должны взять действительную часть этого комплексного сигнала, а если синусоидальный – мнимую. То есть для случая косинуса это выглядит как-то так:
или так
А для случая синуса это выглядит вот так
или так
Здесь Re() и Im() – функции взятия действительной или мнимой части комплексного числа. Кстати, они определены во многих математических САПРах и их можно прям вот в таком виде использовать. То есть передавать им комплексное число, а на выходе получать дейтсвительную или мнимую часть.
Возможно, вы спросите: а зачем так все усложнять? Какая с этого выгода? В чем профит? Профит, безусловно, есть, но о нем мы поговорим чуть позже, в следующих статьях. На сегодня пока все, господа. Спсибо что прочитали и пока!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
myelectronix.ru
КОМПЛЕКСНЫЕ ЧИСЛА В ЭЛЕКТРОТЕХНИКЕ | sibac.info
КОМПЛЕКСНЫЕ ЧИСЛА В ЭЛЕКТРОТЕХНИКЕ
Мангушев Виталий Иванович
студент 2 курса, факультет электроэнергетики и электротехники ДВФУ, г. Владивосток
E-mail: vitalya-53@mail.ru
Дмух Галина Юрьевна
научный руководитель, канд. пед. наук, доцент кафедры алгебры, геометрии и анализа ДВФУ, г. Владивосток
В математике очень широко применяется решение задач с помощью комплексных чисел, но что такое комплексные числа и как они нашли себя в электротехнике?
Первоначально математики столкнулись с мнимой единицей i=, когда стало не хватать действительного числа, а именно при решении простейшего квадратного уравнения , где «p» и «q» — действительные числа. При вычислении его корней по всем известным формулам, математики еще до XVI века сталкивались с проблемой отрицательного корня. В действительности, никто не мог объяснить какой смысл следует придавать этому выражению и, в следствие, решили, что корень из отрицательного числа не имеет смысла. И это работало, было легко показать, что при отрицательном корне, решением было ни положительное число, ни отрицательное, ни нуль.
Однако в дальнейшем, при решении кубических уравнений отказываться от отрицательного корня уже было невозможно. В 1543 году несколько итальянских ученых выдвинули формулу «Кардано» позволяющую решать уравнения третьей степени вида:
, а именно: , где , она вполне рабочая, но при решении уравнений имеющих три различных действительных корня она не дает ожидаемого результата. Например, корнями уравнения легко доказать, являются числа 0,1,–1, но при решении уравнения методом, изложенным выше, результат удивляет: и как же получить из этого три нужных нам корня?
После этого математики пошли на изучение мнимых чисел, дали возможность им существовать. Затем было обнаружено, что многие громоздкие задачи в математике решаются гораздо проще, если пользоваться мнимыми числами. К.Ф. Гаусс предложил называть мнимые числа комплексными, что впоследствии прижилось.
С похожей проблемой ученые столкнулись при решении задач электротехники.
Описание электромагнитных процессов в цепях переменного тока сводится к решению множества интегралов, а решение их становится столь сложным, что взять их не пол силу даже опытным математикам. Определение крайне упростилось и стало более элегантно при применении комплексных чисел.
Из физики мы знаем, что переменным током называется ток, изменяющийся во времени. Из всех возможных форм периодических токов наибольшее распространение имеет синусоидальный ток, так как у него есть преимущество в плане экономии энергоресурсов.
Любая синусоидальная функция времени «a(t)» может быть однозначно задана тремя параметрами: амплитудой, частотой и начальной фазой. Ее формула для любого момента времени «t»: , где — максимальное значение функции или её амплитуда; – угловая частота, начальная фаза (угол функции в момент времени принятый за начало отсчета, т. е. при ), аргумент называется фаза или фазовый угол, он определяет значение функции в любой момент времени. В электрических цепях переменного тока синусоидальными функциями времени являются ток, падение напряжения и ЭДС:
В электротехнике принято обозначать мгновенные значения токов строчными буквами в виде: ; А амплитуду заглавной с нижним индексом «» : .
Так же существует действующий(эффективный) ток. По закону Джоуля-Ленца на участке тока сопротивлением «r», за время «T», соответствующее периоду тока «i», будет выделено количество тепла равное: , с другой стороны при постоянном токе на этом же участке выделится равное количество энергии: , если приравнять данные формулы, можно вывести действующее значение тока .
Отсюда — действующий ток это среднеквадратичное значение переменного тока. По аналогии можно рассчитать действующее значение напряжения и ЭДС, которые так же равняются среднеквадратичной своей соответствующей.

Рисунок 1. Представление синусоиды тока в виде вращающегося вектора
Из курса математики известно, что синусоидальная функция времени может быть представлена в виде вращающегося вектора длиной с угловой частотой . Положение этого вектора в начальный момент времени t = 0 должно составлять угол с осью абсцисс.
Наиболее удобная для проведения расчетов координатная система стала комплексная, так как вектор можно определить четырьмя различными формами записи:
· Алгебраическая форма: , надо заметить, что в математике знак мнимой части используется как «», но в электротехнике этим знаком обозначается ток, по этому было решено заменить его на «». Знак «» не говорит ни о каком-либо сложении, он только указывает на то, что мы объединяем два действительных числа в нечто единое. На комплексной плоскости «» и «» координаты конца вектора тока, по мнимой и действительной оси.
· Тригонометрическая форма: запись результата вещественной и мнимой части через модуль «» и аргумент «»
· Показательная форма: — получается путем применения формулы Эйлера к тригонометрической.
· Полярная форма: — запись, не использующаяся для расчетов.
Рассмотрим типичную задачу в электротехнике: сложение токов.
Включим в цепь переменного тока две параллельные ветви, содержащие некое сопротивление. Нам известны: амплитуда, частота и начальная фаза токов, равная нулю. ,
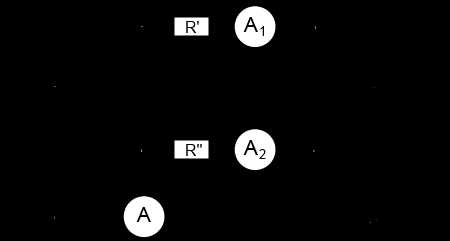
Рисунок 2. Токи в параллельных ветвях цепи переменного тока
По одному из главных постулатов электротехники, а именно по I-му закону Кирхгофа (Алгебраическая сумма токов в узле равна нулю ) , отсюда , графически это можно определить так:
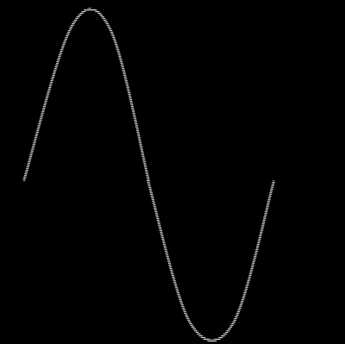
Рисунок 3. Сложение синусоид тока
Как видно, это было легко, при фазе равной нулю решение такой задачи обуславливается сложением значения амплитуд в каждый момент времени. . Всё просто.
А теперь представим, что фаза у токов отличается. Например, равняется не нулю, а скажем, 30, попробуем проделать задачу тем же способом:

Рисунок 4. Синусоиды тока с разной фазой
Решение:
;
по формуле суммы углов:
Воспользуемся методом введения дополнительного угла, чтобы привести уравнение к виду: ;
Так как у нас есть составляющие: и, найдем и .
По основному тождеству тригонометрии: , значит:
Находим и через и :
Подставляем в :
.
Как видим, такая, простая на первый взгляд, задача переливается в уравнение, которое заставит посидеть и подумать «как же оно решается?», а ведь это самое наипростейшее усложнение.
Теперь рассмотрим эту задачу с применением комплексных чисел, мы уже знаем, что такое комплексное число и в состоянии перевести в него уравнение синусоиды тока.
Итак:
; ,
сложим:
.
Решение в 2 строки, а результаты те же.
Проверим это на векторной диаграмме:
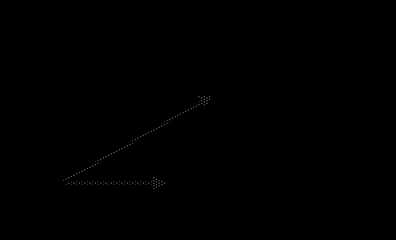
Рисунок 5. Векторная диаграмма
Выводы: На этом простейшем примере хорошо видно как комплексные числа упростили решение. Сейчас же ни одна задача в электротехнике не решается без них. Мнимые числа необходимая составляющая электротехники.
Список литературы:
1.Балк М.Б., Балк Г.Д., Полухин А.А. «Реальные применения мнимых чисел» // изд. «Радянська школа», 1988 г — 5—16 с.
2.Голубев А.Н. Доктор техн. наук, профессор, «Лекция по ТОЭ № 3 — Представление синусоидальных величин с помощью векторов и комплексных чисел».
3.Ландсберг Г.С. Элементарный учебник физики, том 2. «Электричество и магнетизм», § 160 «Сложение токов при параллельном включении сопротивлений в цепь переменного тока» — 384—389 с.
4.Мацкевич И.Ю. «Высшая математика приложения в физике и электронике» учебно-методическое пособие// МГВРК Минск 2008 — 5—7 с.
sibac.info
J в электротехнике
Господа, в сегодняшней статье я хотел бы вам немного рассказать про комплексные числа и сигналы. Данная статья будет в основном теоретической. Ее задача — подготовить некоторый фундамент для возможности понимания дальнейших статей. Просто когда речь заходит про фазу или, допустим, про поведение конденсатора в цепи переменного тока, так сразу и начинаю лезть все эти комплексности. А про фазу все-таки хочется поговорить, штука важная. Нет, эта статья ни в коем случае не будет кратким курсом ТФКП, мы рассмотрим только лишь очень узкую область из этой вне всякого сомнения интересной и обширной темы.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.
По завершению появится ссылка для доступа к найденным материалам.
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Основы электротехники Курс Электрика своими руками ч1Приложение комплексных чисел в электротехнике
В международном фонетическом алфавите символ [ j ] обозначает палатальный аппроксимант. На компьютерной клавиатуре с QWERTY-раскладкой на клавишах F и J обычно находится небольшой выступ в виде точки или полосы для удобства слепого позиционирования пальцев на этих клавишах.
Изначально символ j использовался как вариант символа i например, сочетание ii писалось как ij. Однако в романских языках появлялись звуки, отличные от прежнего звучания кроме итальянского языка. Так произношение буквы J во французском и в испанском языках сильно отличается от произношения I. В латинском языке буква произносится как [ j ]. Такое же произношение имеется в большинстве германских языков кроме английского , в балтийских языках , всех славянских , использующих латинский алфавит, албанском , венгерском , финском , эстонском языках и в эсперанто.
В современном итальянском языке буква J используется в основном в заимствованных словах. До XIX века J использовалась в дифтонгах вместо I , вместо заключительного -ii и при разбиении группы гласных как в слове Savoja.
Материал из Википедии — свободной энциклопедии. У этого термина существуют и другие значения, см. J значения. Производные латинской буквы J, j. Категории : Буквы латинского алфавита Производные буквы J. Скрытая категория: Статьи со ссылками на Викисловарь. Пространства имён Статья Обсуждение. Просмотры Читать Править Править код История. В других проектах Викисклад. Эта страница в последний раз была отредактирована 4 июня в Текст доступен по лицензии Creative Commons Attribution-ShareAlike ; в отдельных случаях могут действовать дополнительные условия.
Подробнее см. Условия использования. Политика конфиденциальности Описание Википедии Отказ от ответственности Свяжитесь с нами Разработчики Заявление о куки Мобильная версия. Название по-русски : й. Семафорная азбука. Флаги международного свода сигналов.
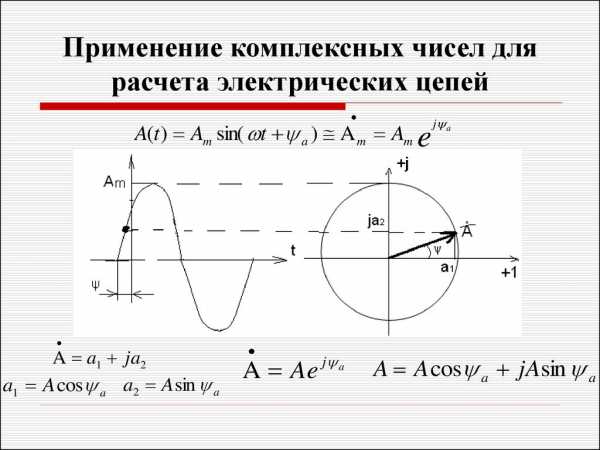
№15 Основные сведения о комплексных числах.
Формула электрического тока: Электрический ток измеряется в амперах. СИ: А. Электрический ток обозначается латинскими буквами i или I. В частном случае он может быть постоянным или переменным. Прописной латинской буквой I обозначается, как правило, постоянное значение тока. В любом участке неразветвленной электрической цепи протекает одинаковый по величине ток, который прямо пропорционален напряжению на концах участка и обратно пропорционален его сопротивлению. Величина тока определяется по закону Ома: 1 для цепи постоянного тока 2 для цепи переменного тока , где U — напряжение, В ; R — омическое сопротивление, Ом ; Z — полное сопротивление, Ом.
КОМПЛЕКСНЫЕ ЧИСЛА Комплексное число – упорядоченная пара чисел. I = a + j·b, где a, b – вещественные числа; j – мнимая единица (в математике.
Переменный ток. Метод комплексных амплитуд
В английском языке словом Real принято характеризовать действительность, а термином Imaginary — мнимые свойства. От этих слов были созданы обозначения Re и Im , которые используются для выражения величин «а» и «b» следующим способом:. Для геометрического отображения КЧ в векторной форме применяется комплексная плоскость. Термин действительной реже вещественной части используется для наименования горизонтальной оси, а для вертикальной — мнимой. Обе составляющие действительная и мнимая КЧ являются прямоугольными проекциями вектора на соответствующие оси. К КЧ применимо понятие сопряжения. Им называют те числа, которые равны по величине модулей и аргументов, но имеют разные знаки у аргументов. КЧ и математические действия. Для их сложения или вычитания делается запись в алгебраическом выражении:.
Калькулятор комплексных чисел
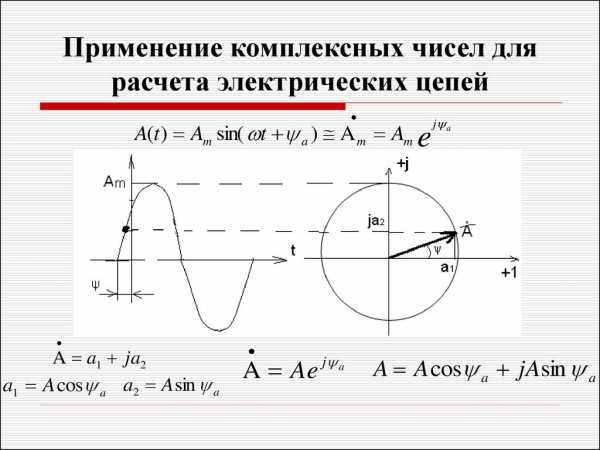
В общем случае алгебраическая форма записи комплексной величины выглядит следующим образом:. Но это математическая запись. В электротехнике принято мнимую единицу обозначать не «i», а буквой «j» это сделано для того, чтобы не было путаницы с токами, которые чаще всего и обозначаются латинской буквой «i». Тогда в электротехнике вы скорее всего увидите запись:.
Формула двух узлов :.
Теоретические основы электротехники — ТОЭ. В помощь студенту
Отправьте статью сегодня! Журнал выйдет 19 октября , печатный экземпляр отправим 23 октября. Автор : Шмидт Надежда Михайловна. Статья просмотрена: раза. Шмидт Н. Итальянский ученый Джироламо Кардано в году опубликовал работу, в которой, пытаясь решить уравнение , он пришел к выражению.
Мнимая единица
Переход от алгебраической формы записи комплексного числа к показательной или к форме записи в полярных координатах. Пусть комплекс сопротивления дан в алгебраической форме записи:. Необходимо преобразовать алгебраическую форму записи в показательную в форму записи в полярных координатах. Воспользуемся вышеприведенными формулами перехода. Тогда комплекс сопротивления Z в показательной форме в форме записи в полярных координатах будет:. Переход от показательной формы записи комплексного числа в форме записи в полярных координатах к алгебраической. Пусть комплекс сопротивления дан в показательной форме записи в форме записи в полярных координатах :.
Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице). Термин может употребляться также в обобщённом смысле не.
Комплексное число
Она позволяет расширить поле вещественных чисел до поля комплексных чисел. Точное определение зависит от способа расширения. Исторически мнимая единица сначала была введена для решения вещественного кубического уравнения : нередко, при наличии трёх вещественных корней, для получения двух из них формула Кардано требовала брать кубический корень в комплексных числах.
Приложение комплексных чисел в электротехнике
Символы Re и Im — есть начальные буквы английских слов Real — действительный и Imaginary — мнимый. Геометрически комплексное число изображается вектором на комплексной плоскости рис. Действительная и мнимая составляющие комплексного числа представляют собой проекции вектора на эти оси. Сложение и вычитание производится над числами, записанными в алгебраической форме:. Операции сложения комплексных чисел соответствует сложение изображающих их векторов.
Из курса математики известно, что комплексное число Z может быть представлено в следующих трех формах : показательной, тригонометрической и алгебраической :.
Комплексные числа в электротехнике для синусоидальных функций
Как известно, для решения некоторых типичных задач электротехники применяют комплексные числа. Но для чего их используют и почему это делают именно так? В этом мы и постараемся разобраться по ходу данной статьи. Дело в том, что комплексный метод, или метод комплексных амплитуд, удобен при расчетах сложных цепей переменного тока. И для начала вспомним немного математических основ:.
Состояние отпатрулирована. Первоначально идея о необходимости использования комплексных чисел возникла в результате формального решения кубических уравнений , при котором в формуле Кардано под знаком квадратного корня получалось отрицательное число [3]. Преобразования комплексной плоскости оказались полезны в картографии и гидродинамике.
all-audio.pro
Решение задач и курсовых по электротехнике Сайт Электротехника и электроника на «пять»
В общем случае алгебраическая форма записи комплексной величины выглядит следующим образом:
x = a + i*bНо это математическая запись. В электротехнике принято мнимую единицу обозначать не «i», а буквой «j» (это сделано для того, чтобы не было путаницы с токами, которые чаще всего и обозначаются латинской буквой «i»). Тогда в электротехнике вы скорее всего увидите запись:
x = a+j*bПри этом мнимая единица может стоять как первым множителем, так и вторым. То есть это же число можно записать:
x = a+b*jЧасть комплексного числа без мнимой единицы называется «Действительной» и чаще всего обозначается Re (от английского Real — действительный, настоящий)
Часть комплексного числа с мнимой единицой называется также «Мнимой» и обозначается Im (от английского Imaginary — воображаемый)
Что касается показательной формы записи, то в она обычно выглядит так:
x=A*ejφЗдесь буква «А» — модуль величины, буква «е» ничего не значит и просто указывает, что это показательная форма записи (так как остальные данные записаны в показатель степени). Буква «j» в степени тоже просто обозначает комплексное число, а вот «φ» — это угол в градусах или радианах.
Чтобы легко понять как эти формы записи связаны друг с другом, достаточно рассмотреть изображение вектора на комплексной плоскости:
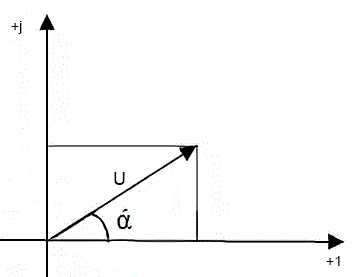
Очевидно, что такой вектор можно задать, указав его длину и угол поворота — это и есть показательная форма записи комплексных числел. То, что в нашем примере обозначено буквой «А» — длина вектора, а число в показателе степени — угол поворота
Еще один споосб точного описания вектора — указать его проекции на координатные оси. Например «отложим пять единиц по горизонтальной оси и три по вертикальной». Именно так и работает алгебраическая форма записи:
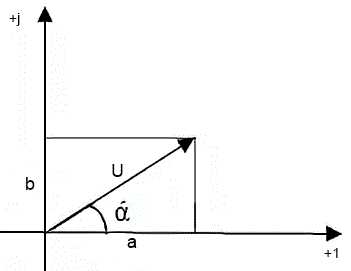
Очевидно — чтобы перевести из показательной формы записи в алгебраическую, нужно определить проекции вектора на оси координат. Известно, что косинус угла есть отношение прилежащего катета к гипотенузе:
Отсюда действительная часть комплексного числа:
Синус угла — отношение противолежащего катета к гипотенузе:
Значит, мнимая часть комплексного числа:
Разберем пример. Пусть задано напряжение в показательной форме:
Определим действительную часть алгебраической формы записи:
Теперь мнимую часть:
В принципе, все. Можно записать результат (не забывайте к мнимой части дописывать указатель мнимой единицы — j или i):
В качестве итога, запишем алгоритм перевода показательной формы записи комплексного числа в алгебраическую:
Как видите — ничего сложного.
toe5.ru
Наименование величины | Обозначение | ||||
главное | запасное | ||||
1 | 2 | 3 | |||
Емкость электрическая | С | — | |||
Заряд электрический | Q | — | |||
Индуктивность взаимная | м | Lmn | |||
Индуктивность собственная | L | — | |||
Индукция магнитная | В | — | |||
Коэффициент затухания | 6 |
| |||
Коэффициент магнитного рассеивания | ст |
| |||
Коэффициент мощности при синусоидальных напряжении и токе | cosφ |
| |||
Коэффициент трансформации | п |
| |||
Коэффициент трансформации трансформатора напряжения (TH) | К | Ки | |||
Коэффициент трансформации трансформатора тока (ТТ) | К | Кт | |||
Мощность, мощность активная | Р | — | |||
Мощность полная | S | Ps | |||
Мощность реактивная | Q | PQ | |||
Напряжение электрическое | и | — | |||
Напряженность магнитного поля | н |
| |||
Напряженность электрического поля | Е | — | |||
Период колебаний электрической или магнитной величины | Т |
| |||
1 | 2 | 3 |
| ||
Плотность тока | J | — |
| ||
Постоянная времени электрической цепи | т | т |
| ||
Постоянная магнитная | Цо | — |
| ||
Постоянная электрическая | So | — |
| ||
Поток магнитный | Ф | — |
| ||
Потокосцепление | V | — |
| ||
Проводимость магнитная | Л | — |
| ||
Проводимость электрическая активная | G | g |
| ||
Проводимость электрическая полная | Y | — |
| ||
Проводимость реактивная | В | ь |
| ||
Сдвиг фаз между напряжением и током | Ф | — |
| ||
Сила коэрцитивная | Не | — |
| ||
Сила магнитодвижущая (МДС) вдоль замкнутого контура | F | Fm |
| ||
Сила электродвижущая (ЭДС) | Е | — |
| ||
Скольжение | s | — |
| ||
Сопротивление магнитное | Rm | rm |
| ||
Сопротивление электрическое, то же постоянному току, то же актив |
|
|
| ||
ное | R | г |
| ||
Сопротивление электрическое полное | Z | — |
| ||
Сопротивление электрическое реактивное | X | X |
| ||
Сопротивление электрическое удельное | Р |
|
| ||
Ток | I |
|
| ||
Частота колебаний электрической или магнитной величины | f | У |
| ||
Частота колебаний угловая электрической или магнитной величины | со | Q |
| ||
Число витков | N | W |
| ||
Число пар полюсов | Р | — |
| ||
Число фаз многофазной системы | m |
|
| ||
Энергия электромагнитная | W |
|
| ||
leg.co.ua
Величина | Обозначение |
Добротность | Q |
Емкость электрическая | C |
Заряд электрона | e |
Индуктивность: собственная взаимная |
L M |
Индукция магнитная | B |
Количество электричества | Q |
Коэффициент: затухания цепи контура мощности при синусоидальных токах и напряжениях мощности при несинусоидальных токах и напряжениях распространения трансформации, отношения числа витков трансформации по току, напряжению связи фазы |
α δ cosφ
λ γ n Kт, Кυ k β |
Мощность: электрическая полная реактивная |
P S Q |
Напряжение электрическое | U |
Напряженность: магнитного поля электрического поля |
H E |
Период колебаний электрической или магнитной величины | Т |
Плотность электрического заряда: линейная объемная поверхностная |
τ ρ σ |
Плотность тока | J |
Постоянная времени цепи | τ |
Потенциал электрический | V |
Поток магнитный | Ф |
Проводимость: магнитная удельная электрическая активная электрическая комплексная, электрическая полная реактивная электрическая |
Λ γ G Y B |
Проницаемость: диэлектрическая магнитная |
ε μ |
Разность: электрических потенциалов фаз (сдвиг фаз между Iи U) |
U φ |
Сила электродвижущая | Е |
Сопротивления: волновое магнитное удельное электрическое характеристическое |
ZB RM ρ Zc |
Электрическое сопротивление: постоянному току и активное полное реактивное |
R Z X |
Сила тока | I |
Угол диэлектрических потерь | δ |
Частота: угловая колебания электрической или магнитной величины |
ω f |
Число витков | N |
Энергия электромагнитная | W |
ldsound.ru
Что такое j в электротехнике. Онлайн журнал электрика
Электротехника — это… Что такое Электротехника?
Электротехника — область технических наук, изучающая получение, распределение, преобразование и использование электрической энергии.
Электротехника выделилась в самостоятельную науку из физики в конце XIX века.
В настоящее время электротехника включает в себя несколько наук: электроэнергетику, электронику, системы управления, обработку сигналов и телекоммуникации. Основное отличие от электроники заключается в том, что электротехника изучает проблемы, связанные с силовыми крупногабаритными электронными компонентами: линии электропередачи, электрические приводы, в то время как в электронике основными компонентами являются компьютеры и интегральные схемы[1]. В другом смысле, в электротехнике основной задачей является передача электрической энергии, а в электронике — информации.
История
Разделы
Электротехника имеет множество разделов, самые важные из которых описаны ниже. Хотя инженеры работают каждый в своей области, но многие из них имеют дело с комбинацией из нескольких наук.
Электроэнергетика
Электроэнергетика — наука о выработке, передаче и потреблении электроэнергии, а также о разработке устройств для этих целей. К таким устройствам относят: трансформаторы, электрические генераторы, ТЭНы, электродвигатели, низковольтную аппаратуру и электронику для управления силовыми приводами. Многие государства мира имеют электрическую сеть, называемую электроэнергетической системой, которая соединяет множество генераторов с потребителями энергии. Потребители получают энергию из сети, не тратя ресурсы на выработку своей собственной энергии. Энергетики работают как над проектированием и обслуживанием сети, так и над энергетическими системами, присоединёнными к сети. Такие системы называются внутрисетевыми и могут как поставлять энергию в сеть, так и потреблять её. Энергетики работают также и над системами не присоединёнными к сети, называемыми внесетевыми, которые в некоторых случаях являются более предпочтительными, чем внутрисетевые системы. Имеется перспектива создания энергетических систем, контролируемых со спутника, имеющих обратную связь в реальном времени, что позволит избежать скачков напряжения и предотвратить нарушения энергоснабжения.
Системы автоматического управления
Задачами автоматических систем управления (и автоматизации в целом) является моделирование различных динамических систем и разработка систем управления, которые заставляют работать динамические системы нужным образом. Для создания таких устройств могут использоваться электрические схемы, процессоры цифровой обработки сигналов, микроконтроллеры и программируемые логические контроллеры. Системы управления имеют широкую область применения от систем, встраиваемых в энергетические установки (например, на коммерческих авиалайнерах), автоматов постоянной скорости (имеющихся во множестве современных автомобилей) и ЧПУ в станках до систем управления на базе промышленных ПК в автоматизации промышленного производства.
Инженеры часто используют обратную связь при проектировании систем управления. Например в автомобиле с автоматом постоянной скорости скорость транспортного средства постоянно отслеживается и данные передаются системе, которая соответственно регулирует выходную мощность двигателя. Если имеется стандартная система обратной связи, можно использовать теорию управления для определения того, как система должна реагировать на поступающую информацию.
Микроэлектроника
Микроэлектроника занимается разработкой и изготовлением очень малых компонентов электронных цепей для использования в интегральных схемах или, в некоторых случаях, для использования в качестве основных электронных компонентов. Самыми распространенными микроэлектронными компонентами являются полупроводниковые транзисторы, хотя все основные электронные компоненты (резисторы, конденсаторы, индукторы) могут быть созданы на микроскопическом уровне.
Микроэлектронные компоненты создаются химическим изготовлением пластин из полупроводников, например, кремния (при более высоких частотах — полупроводниковых соединений, таких как арсенид галлия, фосфид индия,
10i5.ru
