Что такое активная и реактивная электроэнергия?

Расчет электрической энергии, используемой бытовым или промышленным электротехническим прибором, производится обычно с учетом полной мощности электрического тока, проходящего через измеряемую электрическую цепь.

При этом выделяются два показателя, отражающие затраты полной мощности при обслуживании потребителя. Эти показатели называются активная и реактивная энергия. Полная мощность представляет собой сумму этих двух показателей.

Полная мощность.
По сложившейся практике потребители оплачивают не полезную мощность, которая непосредственно используется в хозяйстве, а полную, которую отпускает предприятие-поставщик. Различают эти показатели по единицам измерения – полная мощность измеряется в вольт-амперах (ВА), а полезная – в киловаттах. Активная и реактивная электроэнергия используется всеми запитанными от сети электроприборами.

Активная электроэнергия.
Активная составляющая полной мощности совершает полезную работу и преобразовывается в те виды энергии, которые нужны потребителю. У части бытовых и промышленных электроприборов в расчетах активная и полная мощность совпадают. Среди таких устройств – электроплиты, лампы накаливания, электропечи, обогреватели, утюги и гладильные прессы и прочее. Если в паспорте указана активная мощность 1 кВт, то полная мощность такого прибора будет составлять 1 кВА.

Понятие реактивной электроэнергии.
Этот вид электроэнергии присущ цепям, в составе которых имеются реактивные элементы. Реактивная электроэнергия — это часть полной поступаемой мощности, которая не расходуется на полезную работу. В электроцепях постоянного тока понятие реактивной мощности отсутствует. В цепях переменного тока реактивная составляющая возникает только в том случае, когда присутствует индуктивная или емкостная нагрузка. В таком случае наблюдается несоответствие фазы тока с фазой напряжения. Данный сдвиг фаз между напряжением и током обозначается символом «φ». При индуктивной нагрузке в цепи наблюдается отставание фазы, при емкостной – ее опережение. Поэтому потребителю приходит только часть полной мощности, а основные потери происходят из-за бесполезного нагревания устройств и приборов в процессе эксплуатации. Потери мощности происходят из-за наличия в электрических устройствах индуктивных катушек и конденсаторов. Из-за них в цепи в течение некоторого времени происходит накопление электроэнергии. После этого запасенная энергия поступает обратно в цепь. К приборам, в составе потребляемой мощности которых имеется реактивная составляющая электроэнергии, относятся переносные электроинструменты, электродвигатели и различная бытовая техника. Эта величина рассчитывается с учетом особого коэффициента мощности, который обозначается как cos φ.

Расчет реактивной электроэнергии.
Коэффициент мощности лежит в пределах от 0,5 до 0,9; точное значение этого параметра можно узнать из паспорта электроприбора. Полная мощность должна быть определена как частное от деления активной мощности на коэффициент. Например, если в паспорте электрической дрели указана мощность в 600 Вт и значение 0,6, тогда потребляемая устройством полная мощность будет равна 600/06, то есть 1000 ВА. При отсутствии паспортов для вычисления полной мощности прибора коэффициент можно брать равным 0,7. Поскольку одной из основных задач действующих систем электроснабжения является доставка полезной мощности конечному потребителю, реактивные потери электроэнергии считаются негативным фактором, и возрастание этого показателя ставит под сомнение эффективность электроцепи в целом.

Значение коэффициента при учете потерь.
Чем выше значение коэффициента мощности, тем меньше будут потери активной электроэнергии – а значит конечному потребителю потребляемая электрическая энергия обойдется немного дешевле. Для того чтобы повысить значение этого коэффициента, в электротехнике используются различные приемы компенсации нецелевых потерь электроэнергии. Компенсирующие устройства представляют собой генераторы опережающего тока, сглаживающие угол сдвига фаз между током и напряжением. Для этой же цели иногда используются батареи конденсаторов. Они подключаются параллельно к рабочей цепи и используются как синхронные компенсаторы.

Расчет стоимости электроэнергии для частных клиентов.
Для индивидуального пользования активная и реактивная электроэнергия в счетах не разделяется – в масштабах потребления доля реактивной энергии невелика. Поэтому частные клиенты при потреблении мощности до 63 А оплачивают один счет, в котором вся потребляемая электроэнергия считается активной. Дополнительные потери в цепи на реактивную электроэнергию отдельно не выделяются и не оплачиваются. Учет реактивной электроэнергии для предприятий Другое дело – предприятия и организации. В производственных помещениях и промышленных цехах установлено огромное число электрооборудования, и в общей поступаемой электроэнергии имеется значительная часть энергии реактивной, которая необходима для работы блоков питания и электродвигателей. Активная и реактивная электроэнергия, поставляемая предприятиям и организациям, нуждается в четком разделении и ином способе оплаты за нее. Основанием для регуляции отношений предприятия-поставщика электроэнергии и конечных потребителей в этом случае выступает типовой договор. Согласно правилам, установленным в этом документе, организации, потребляющие электроэнергию свыше 63 А, нуждаются в особом устройстве, предоставляющем показания реактивной энергии для учета и оплаты. Сетевое предприятие устанавливает счетчик реактивной электроэнергии и начисляет оплату согласно его показаниям.

Коэффициент реактивной энергии.
Как говорилось ранее, активная и реактивная электроэнергия в счетах на оплату выделяются отдельными строками. Если соотношение объемов реактивной и потребленной электроэнергии не превышает установленной нормы, то плата за реактивную энергию не начисляется. Коэффициент соотношения бывает прописан по-разному, его среднее значение составляет 0,15. При превышении данного порогового значения предприятию-потребителю рекомендуют установить компенсаторные устройства.

Реактивная энергия в многоквартирных домах.
Типичным потребителем электроэнергии является многоквартирный дом с главным предохранителем, потребляющий электроэнергию свыше 63 А. Если в таком доме имеются исключительно жилые помещения, плата за реактивную электроэнергию не взимается. Таким образом, жильцы многоквартирного дома видят в начислениях оплату только за полную электроэнергию, поставленную в дом предприятием-поставщиком. Та же норма касается жилищных кооперативов.

Частные случаи учета реактивной мощности.

Бывают случаи, когда в многоэтажном здании имеются и коммерческие организации, и квартиры. Поставка электроэнергии в такие дома регулируется отдельными Актами. Например, разделением могут служить размеры полезной площади. Если в многоквартирном доме коммерческие организации занимают менее половины полезной площади, то оплата за реактивную энергию не начисляется. Если пороговый процент был превышен, то возникают обязательства оплаты за реактивную электроэнергию. В ряде случаев жилые дома не освобождаются от оплаты за реактивную энергию. Например, если в доме установлены пункты подключения лифтов для квартир, начисление за использование реактивной электроэнергии происходит отдельно, лишь для этого оборудования. Владельцы квартир по-прежнему оплачивают лишь активную электроэнергию.

circutor-rus.ru

Что такое полная, активная и реактивная мощность?

ЧТО ТАКОЕ ПОЛНАЯ, АКТИВНАЯ И РЕАКТИВНАЯ МОЩНОСТЬ? ОТ СЛОЖНОГО К ПРОСТОМУ.

 

В повседневной жизни практически каждый сталкивается с понятием «электрическая мощность», «потребляемая мощность» или «сколько эта штука «кушает» электричества». В данной подборке мы раскроем понятие электрической мощности переменного тока для технически подкованных специалистов и покажем на картинке электрическую мощность в виде «сколько эта штука кушает электричества» для людей с гуманитарным складом ума :-). Мы раскрываем наиболее практичное и применимое понятие электрической мощности и намеренно уходим от описания дифференциальных выражений электрической мощности.

 

ЧТО ТАКОЕ МОЩНОСТЬ ПЕРЕМЕННОГО ТОКА?

В цепях переменного тока формула для мощности постоянного тока может быть применена лишь для расчёта мгновенной мощности, которая сильно изменяется во времени и для практических расчётов бесполезна. Прямой расчёт среднего значения мощности требует интегрирования по времени. Для вычисления мощности в цепях, где напряжение и ток изменяются периодически, среднюю мощность можно вычислить, интегрируя мгновенную мощность в течение периода. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.

Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Активная мощность (Real Power)

Единица измерения — ватт (русское обозначение: Вт, киловатт — кВт; международное: ватт -W, киловатт — kW).

Среднее за период Τ  значение мгновенной мощности называется активной  мощностью, и

 

выражается формулой:  

В цепях однофазного синусоидального тока , где υ и Ι это  среднеквадратичные значения напряжения и тока,  а φ — угол сдвига фаз между ними.Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле . В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S, активная связана соотношением . 

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.

Реактивная мощность (Reactive Power)

Единица измерения — вольт-ампер реактивный (русское обозначение: вар, кВАР; международное: var).

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними:

 (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью P  соотношением:  .

Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.

Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до минус 90° является отрицательной величиной. В соответствии с формулой    

реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например,асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

 Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.

 Мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например,асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

 Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

 Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения

Полная мощность (Apparent Power)

Единица полной электрической мощности — вольт-ампер (русское обозначение: В·А, ВА, кВА-кило-вольт-ампер; международное: V·A, kVA).

Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: ; соотношение полной мощности с активной и реактивной мощностями выражается в следующем виде:     где P — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q›0, а при ёмкостной Q‹0).Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому полная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.

 

Визуально и интуитивно-понятно все вышеперечисленные формульные и текстовые описания полной, реактивной и активной мощностей передает следующий рисунок 🙂 

Специалисты компании НТС-групп (ТМ Электрокапризам-НЕТ) имеют огромный опыт подбора специализированного оборудования для построения систем обеспечения жизненно важных объектов бесперебойным электропитанием. Мы умеем максимально качественно учитывать множество электрических и эксплуатационных параметров, которые позволяют выбрать экономически обоснованный вариант построения системы бесперебойного электропитанияс применением стабилизаторов напряжения, топливных электростанций, источников бесперебойного питания и др. сопутствующего оборудования.

 

© Материал подготовлен специалистами компании НТС-групп (ТМ Электрокапризам-НЕТ) с использованием информации из открытых источников, в т.ч. из свободной энциклопедии ВикипедиЯ https://ru.wikipedia.org  

 

electrokaprizam.net

Преобразование энергии в электрической цепи. Мгновенная, активная, реактивная и полная мощности синусоидального тока. (Лекция №7)

Передача энергии w по электрической цепи (например, по линии электропередачи), рассеяние энергии, то есть переход электромагнитной энергии в тепловую, а также и другие виды преобразования энергии характеризуются интенсивностью, с которой протекает процесс, то есть тем, сколько энергии передается по линии в единицу времени, сколько энергии рассеивается в единицу времени. Интенсивность передачи или преобразования энергии называется мощностью р. Сказанному соответствует математическое определение:

.

(1)

Выражение для мгновенного значения мощности в электрических цепях имеет вид:

.

(2)

Приняв начальную фазу напряжения за нуль, а сдвиг фаз между напряжением и током за , получим:

.

(3)

Итак, мгновенная мощность имеет постоянную составляющую и гармоническую составляющую, угловая частота которой в 2 раза больше угловой частоты напряжения и тока.

Когда мгновенная мощность отрицательна, а это имеет место (см. рис. 1), когда u и i разных знаков, т.е. когда направления напряжения и тока в двухполюснике противоположны, энергия возвращается из двухполюсника источнику питания.

Такой возврат энергии источнику происходит за счет того, что энергия периодически запасается в магнитных и электрических полях соответственно индуктивных и емкостных элементов, входящих в состав двухполюсника. Энергия, отдаваемая источником двухполюснику в течение времени t равна .

Среднее за период значение мгновенной мощности называется

активной мощностью .

Принимая во внимание, что , из (3) получим:

.

(4)

Активная мощность, потребляемая пассивным двухполюсником, не может быть отрицательной (иначе двухполюсник будет генерировать энергию), поэтому , т.е. на входе пассивного двухполюсника . Случай Р=0, теоретически возможен для двухполюсника, не имеющего активных сопротивлений, а содержащего только идеальные индуктивные и емкостные элементы.

1. Резистор (идеальное активное сопротивление).

Здесь напряжение и ток (см. рис. 2) совпадают по фазе , поэтому мощность всегда положительна, т.е. резистор потребляет активную мощность

2. Катушка индуктивности (идеальная индуктивность)

При идеальной индуктивности ток отстает от напряжения по фазе на . Поэтому в соответствии с (3) можно записать
.

Участок 1-2: энергия , запасаемая в магнитном поле катушки, нарастает.

Участок 2-3: энергия магнитного поля убывает, возвращаясь в источник.

3. Конденсатор (идеальная емкость)

Аналогичный характер имеют процессы и для идеальной емкости. Здесь . Поэтому из (3) вытекает, что . Таким образом, в катушке индуктивности и конденсаторе активная мощность не потребляется (Р=0), так как в них не происходит необратимого преобразования энергии в другие виды энергии. Здесь происходит только циркуляция энергии: электрическая энергия запасается в магнитном поле катушки или электрическом поле конденсатора на протяжении четверти периода, а на протяжении следующей четверти периода энергия вновь возвращается в сеть. В силу этого катушку индуктивности и конденсатор называют реактивными элементами, а их сопротивления Х_L и Х_С , в отличие от активного сопротивления R резистора, – реактивными.

Интенсивность обмена энергии принято характеризовать наибольшим значением скорости поступления энергии в магнитное поле катушки или электрическое поле конденсатора, которое называется реактивной мощностью.

В общем случае выражение для реактивной мощности имеет вид:

(5)

Она положительна при отстающем токе (индуктивная нагрузка- ) и отрицательна при опережающем токе (емкостная нагрузка- ). Единицу мощности в применении к измерению реактивной мощности называют вольт-ампер реактивный (ВАр).

В частности для катушки индуктивности имеем:

, так как .

.

Из последнего видно, что реактивная мощность для идеальной катушки индуктивности пропорциональна частоте и максимальному запасу энергии в катушке. Аналогично можно получить для идеального конденсатора:

.

Полная мощность

Помимо понятий активной и реактивной мощностей в электротехнике широко используется понятие полной мощности:

.

(6)

Активная, реактивная и полная мощности связаны следующим соотношением:

.

(7)

Отношение активной мощности к полной называют коэффициентом мощности. Из приведенных выше соотношений видно, что коэффициент мощности равен косинусу угла сдвига между током и напряжением. Итак,

.

(8)

Комплексная мощность

Активную, реактивную и полную мощности можно определить, пользуясь комплексными изображениями напряжения и тока. Пусть , а . Тогда комплекс полной мощности:

,

(9)

где — комплекс, сопряженный с комплексом .

.

Комплексной мощности можно поставить в соответствие треугольник мощностей (см. рис. 4). Рис. 4 соответствует (активно-индуктивная нагрузка), для которого имеем:

Применение статических конденсаторов для повышения cos

Как уже указывалось, реактивная мощность циркулирует между источником и потребителем. Реактивный ток, не совершая полезной работы, приводит к дополнительным потерям в силовом оборудовании и, следовательно, к завышению его установленной мощности. В этой связи понятно стремление к увеличению в силовых электрических цепях.

Следует указать, что подавляющее большинство потребителей (электродвигатели, электрические печи, другие различные устройства и приборы) как нагрузка носит активно-индуктивный характер.

Если параллельно такой нагрузке (см. рис. 5), включить конденсатор С, то общий ток , как видно из векторной диаграммы (рис. 6), приближается по фазе к напряжению, т.е. увеличивается, а общая величина тока (а следовательно, потери) уменьшается при постоянстве активной мощности . На этом основано применение конденсаторов для повышения .

Какую емкость С нужно взять, чтобы повысить коэффициент мощности от значения до значения ?

Разложим на активную и реактивную составляющие. Ток через конденсатор компенсирует часть реактивной составляющей тока нагрузки :

;

(10)

;

(11)

.

(12)

Из (11) и (12) с учетом (10) имеем

,

но , откуда необходимая для повышения емкость:

.

(13)

Баланс мощностей

Баланс мощностей является следствием закона сохранения энергии и может служить критерием правильности расчета электрической цепи.

а) Постоянный ток

Для любой цепи постоянного тока выполняется соотношение:

(14)

Это уравнение представляет собой математическую форму записи баланса мощностей: суммарная мощность, генерируемая источниками электрической энергии, равна суммарной мощности, потребляемой в цепи.

Следует указать, что в левой части (14) слагаемые имеют знак “+”, поскольку активная мощность рассеивается на резисторах. В правой части (14) сумма слагаемых больше нуля, но отдельные члены здесь могут иметь знак “-”, что говорит о том, что соответствующие источники работают в режиме потребителей энергии (например, заряд аккумулятора).

б) Переменный ток.

Из закона сохранения энергии следует, что сумма всех отдаваемых активных мощностей равна сумме всех потребляемых активных мощностей, т.е.

(15)

В ТОЭ доказывается (вследствие достаточной громоздкости вывода это доказательство опустим), что баланс соблюдается и для реактивных мощностей:

,

(16)

где знак “+” относится к индуктивным элементам , “-” – к емкостным .

Умножив (16) на “j” и сложив полученный результат с (15), придем к аналитическому выражению баланса мощностей в цепях синусоидального тока (без учета взаимной индуктивности):

или

.

Литература

1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Что такое активная мощность?
2. Что такое реактивная мощность, с какими элементами она связана?
3. Что такое полная мощность?
4. Почему необходимо стремиться к повышению коэффициента мощности ?
5. Критерием чего служит баланс мощностей?
6. К источнику с напряжением подключена активно-индуктивная нагрузка, ток в которой . Определить активную, реактивную и полную мощности.

Ответ: Р=250 Вт; Q=433 ВАр; S=500 ВА.

7. В ветви, содержащей последовательно соединенные резистор R и катушку индуктивности L, ток I=2 A. Напряжение на зажимах ветви U=100 B, а потребляемая мощность Р=120 Вт. Определить сопротивления R и XL элементов ветви.

Ответ: R=30 Ом; XL=40 Ом.

8. Мощность, потребляемая цепью, состоящей из параллельно соединенных конденсатора и резистора, Р=90 Вт. Ток в неразветвленной части цепи I1=5 A, а в ветви с резистором I2=4 A. Определить сопротивления R и XC элементов цепи.

Ответ: R=10 Ом; XС=7,5 Ом.

toehelp.ru

Электрическая мощность — это… Что такое Электрическая мощность?

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

Мгновенная электрическая мощность

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки А в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем:

Для единичного заряда на участке A-B:

Для всех зарядов:

Поскольку ток есть не что иное, как количество зарядов в единицу времени, то есть по определению, в результате получаем:

Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:

мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке:

Если участок цепи содержит резистор c электрическим сопротивлением R, то

Дифференциальные выражения для электрической мощности

Мощность, выделяемая в единице объёма, равна:

В линейном изотропном приближении:

В линейном анизотропном приближении (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла):

Мощность постоянного тока

Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:

Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:

Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:

где — ЭДС.

Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность прибавляется к поглощаемой или вычитается из отдаваемой.

Мощность переменного тока

В переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.

Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Активная мощность

Единица измерения — ватт (W, Вт).

Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U и I — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.

Реактивная мощность

Единица измерения — вольт-ампер реактивный (var, вар)

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: .

Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.

Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до −90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ, реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.

Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sin φ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.^{[источник не указан 124 дня]}

Полная мощность

Единица полной электрической мощности — вольт-ампер (V·A, В·А)

Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U·I; связана с активной и реактивной мощностями соотношением: где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0).

Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому номинальная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.

Комплексная мощность

Мощность, аналогично импедансу, можно записать в комплексном виде:

где  — комплексное напряжение,  — комплексный ток, — импеданс, * — оператор комплексного сопряжения.

Модуль комплексной мощности равен полной мощности S. Действительная часть равна активной мощности Р, а мнимая  — реактивной мощности Q с корректным знаком в зависимости от характера нагрузки.

Неактивная мощность

Неактивная мощность (пассивная мощность)^{[источник не указан 172 дня]} — это мощность нелинейных искажений тока, равная корню квадратному из разности квадратов полной и активной мощностей в цепи переменного тока. В цепи с синусоидальным напряжением неактивная мощность равна корню квадратному из суммы квадратов реактивной мощности и мощностей высших гармоник тока^{[источник не указан 172 дня]}. При отсутствии высших гармоник неактивная мощность равна модулю реактивной мощности.

Под мощностью гармоники тока понимается произведение действующего значения силы тока данной гармоники на действующее значение напряжения^{[источник не указан 172 дня]}.

Наличие нелинейных искажений тока в цепи означает нарушение пропорциональности между мгновенными значениями напряжения и силы тока, вызванное нелинейностью нагрузки, например когда нагрузка имеет реактивный или импульсный характер. При линейной нагрузке сила тока в цепи пропорциональна мгновенному напряжению, вся потребляемая мощность является активной. При нелинейной нагрузке увеличивается кажущаяся (полная) мощность в цепи за счёт мощности нелинейных искажений тока, которая не принимает участия в совершении работы^{[источник не указан 172 дня]}. Мощность нелинейных искажений не является активной и включает в себя как реактивную мощность, так и мощность прочих искажений тока. Данная физическая величина имеет размерность мощности, поэтому в качестве единицы измерения неактивной мощности можно использовать В∙А (вольт-ампер) или вар (вольт-ампер реактивный). Вт (ватт) использовать нежелательно, чтобы неактивную мощность не спутали с активной.

Связь неактивной, активной и полной мощностей

Величину неактивной мощности обозначим N. Через i обозначим вектор тока, через u — вектор напряжения. Буквами I и U будем обозначать соответствующие действующие значения:

Представим вектор тока i в виде суммы двух ортогональных составляющих i_a и i_p, которые назовём соответственно активной и пассивной. Поскольку в совершении работы участвует только составляющая тока, коллинеарная напряжению, потребуем, чтобы активная составляющая была коллинеарна напряжению, то есть i_a = λu, где λ — некоторая константа, а пассивная — ортогональна, то есть Имеем

Запишем выражение для активной мощности P, скалярно умножив последнее равенство на u:

Отсюда находим

Выражение для величины неактивной мощности имеет вид где S = U I — полная мощность.

Для полной мощности цепи справедливо представление, аналогичное выражению для цепи с гармоническими током и напряжением, только вместо реактивной мощности используется неактивная мощность:

Таким образом, понятие неактивной мощности представляет собой один из способов обобщения понятия реактивной мощности для случая несинусоидальных тока и напряжения. Неактивная мощность иногда называется реактивной мощностью по Фризе.

Измерения

• Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра и амперметра.
• Для измерения коэффициента реактивной мощности применяют фазометры
• Государственный эталон — ГЭТ 153-86 Государственный специальный эталон единицы электрической мощности в диапазоне частот 40-2500 Гц. Институт-хранитель: ВНИИМ

Мощность некоторых электрических приборов

В таблице указаны значения мощности некоторых потребителей электрического тока:

Электрический прибор	Мощность,Вт
Лампочка фонарика	1
Лампа люминесцентная бытовая	5…30
Лампа накаливания бытовая	25…150
Холодильник бытовой	15…200
Электропылесос	100…2 000
Электрический утюг	300…2 000
Стиральная машина	350…2 000
Электрическая плитка	1 000…2 000
Сварочный аппарат бытовой	1 000…5 500
Двигатель трамвая	45 000…50 000
Двигатель электровоза	650 000
Электродвигатели прокатного стана	6 000 000…9 000 000

Большинство бытовых приборов рассчитаны на напряжение 220 В, но на разную силу тока. Поэтому мощность потребителей электроэнергии разная.

Литература

• ГОСТ 8.417-2002 Единицы величин
• ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации
• Бессонов Л. А. Теоретические основы электротехники. — М: Высшая школа, 1984.
• Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193—2009. — 146 с.

Дополнительная литература

• Агунов М. В., Агунов А. В. Об энергетических соотношениях в электрических цепях с несинусоидальными режимами // Электричество, 2005, № 4, С. 53-56.
• Агунов М. В., Агунов А. В., Вербова Н. М. Новый подход к измерению электрической мощности // Промышленная энергетика, 2004, № 2, С. 30-33.
• Агунов М. В., Агунов А. В., Вербова Н. М. Определение составляющих полной мощности в электрических цепях с несинусоидальными напряжениями и токами методами цифровой обработки сигналов // Электротехника, 2005, № 7, С. 45-48.
• Агунов А. В. Неактивные составляющие полной мощности в автономных электротехнических системах судостроения. Автореферат диссертации на соискание ученой степени кандидата технических наук. СПб., СПбГМТУ, 1997, 20 с.
• Агунов М. В. Энергетические процессы в электрических цепях с несинусоидальными режимами и их эффективность. Кишинев-Тольятти: МолдНИИТЭИ, 1997, 84 с.
• Агунов М. В., Агунов А. В. Об энергетических соотношениях в электрических цепях с несинусоидальными режимами // Электричество, 2005, № 4, С. 53-56.
• Агунов А. В. Управление качеством электроэнергии при несинусоидальных режимах. СПб., СПбГМТУ, 2009, 134 с.
• Агунов М. В., Агунов А. В., Вербова Н. М. Новый подход к измерению электрической мощности // Промышленная энергетика, 2004, № 2, С. 30-33.
• Агунов А. В. Статический компенсатор неактивных составляющих мощности с полной компенсацией гармонических составляющих тока нагрузки // Электротехника, 2003, № 2, С. 47-50.

Ссылки

См. также

dic.academic.ru

Электрическая мощность — это… Что такое Электрическая мощность?

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

Мгновенная электрическая мощность

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки А в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем:

Для единичного заряда на участке A-B:

Для всех зарядов:

Поскольку ток есть не что иное, как количество зарядов в единицу времени, то есть по определению, в результате получаем:

Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:

мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке:

Если участок цепи содержит резистор c электрическим сопротивлением R, то

Дифференциальные выражения для электрической мощности

Мощность, выделяемая в единице объёма, равна:

В линейном изотропном приближении:

В линейном анизотропном приближении (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла):

Мощность постоянного тока

Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:

Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:

Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:

где — ЭДС.

Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность прибавляется к поглощаемой или вычитается из отдаваемой.

Мощность переменного тока

В переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.

Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Активная мощность

Единица измерения — ватт (W, Вт).

Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U и I — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.

Реактивная мощность

Единица измерения — вольт-ампер реактивный (var, вар)

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: .

Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.

Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до −90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ, реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.

Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sin φ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.^{[источник не указан 124 дня]}

Полная мощность

Единица полной электрической мощности — вольт-ампер (V·A, В·А)

Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U·I; связана с активной и реактивной мощностями соотношением: где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0).

Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому номинальная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.

Комплексная мощность

Мощность, аналогично импедансу, можно записать в комплексном виде:

где  — комплексное напряжение,  — комплексный ток, — импеданс, * — оператор комплексного сопряжения.

Модуль комплексной мощности равен полной мощности S. Действительная часть равна активной мощности Р, а мнимая  — реактивной мощности Q с корректным знаком в зависимости от характера нагрузки.

Неактивная мощность

Неактивная мощность (пассивная мощность)^{[источник не указан 172 дня]} — это мощность нелинейных искажений тока, равная корню квадратному из разности квадратов полной и активной мощностей в цепи переменного тока. В цепи с синусоидальным напряжением неактивная мощность равна корню квадратному из суммы квадратов реактивной мощности и мощностей высших гармоник тока^{[источник не указан 172 дня]}. При отсутствии высших гармоник неактивная мощность равна модулю реактивной мощности.

Под мощностью гармоники тока понимается произведение действующего значения силы тока данной гармоники на действующее значение напряжения^{[источник не указан 172 дня]}.

Наличие нелинейных искажений тока в цепи означает нарушение пропорциональности между мгновенными значениями напряжения и силы тока, вызванное нелинейностью нагрузки, например когда нагрузка имеет реактивный или импульсный характер. При линейной нагрузке сила тока в цепи пропорциональна мгновенному напряжению, вся потребляемая мощность является активной. При нелинейной нагрузке увеличивается кажущаяся (полная) мощность в цепи за счёт мощности нелинейных искажений тока, которая не принимает участия в совершении работы^{[источник не указан 172 дня]}. Мощность нелинейных искажений не является активной и включает в себя как реактивную мощность, так и мощность прочих искажений тока. Данная физическая величина имеет размерность мощности, поэтому в качестве единицы измерения неактивной мощности можно использовать В∙А (вольт-ампер) или вар (вольт-ампер реактивный). Вт (ватт) использовать нежелательно, чтобы неактивную мощность не спутали с активной.

Связь неактивной, активной и полной мощностей

Величину неактивной мощности обозначим N. Через i обозначим вектор тока, через u — вектор напряжения. Буквами I и U будем обозначать соответствующие действующие значения:

Представим вектор тока i в виде суммы двух ортогональных составляющих i_a и i_p, которые назовём соответственно активной и пассивной. Поскольку в совершении работы участвует только составляющая тока, коллинеарная напряжению, потребуем, чтобы активная составляющая была коллинеарна напряжению, то есть i_a = λu, где λ — некоторая константа, а пассивная — ортогональна, то есть Имеем

Запишем выражение для активной мощности P, скалярно умножив последнее равенство на u:

Отсюда находим

Выражение для величины неактивной мощности имеет вид где S = U I — полная мощность.

Для полной мощности цепи справедливо представление, аналогичное выражению для цепи с гармоническими током и напряжением, только вместо реактивной мощности используется неактивная мощность:

Таким образом, понятие неактивной мощности представляет собой один из способов обобщения понятия реактивной мощности для случая несинусоидальных тока и напряжения. Неактивная мощность иногда называется реактивной мощностью по Фризе.

Измерения

• Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра и амперметра.
• Для измерения коэффициента реактивной мощности применяют фазометры
• Государственный эталон — ГЭТ 153-86 Государственный специальный эталон единицы электрической мощности в диапазоне частот 40-2500 Гц. Институт-хранитель: ВНИИМ

Мощность некоторых электрических приборов

В таблице указаны значения мощности некоторых потребителей электрического тока:

Электрический прибор	Мощность,Вт
Лампочка фонарика	1
Лампа люминесцентная бытовая	5…30
Лампа накаливания бытовая	25…150
Холодильник бытовой	15…200
Электропылесос	100…2 000
Электрический утюг	300…2 000
Стиральная машина	350…2 000
Электрическая плитка	1 000…2 000
Сварочный аппарат бытовой	1 000…5 500
Двигатель трамвая	45 000…50 000
Двигатель электровоза	650 000
Электродвигатели прокатного стана	6 000 000…9 000 000

Большинство бытовых приборов рассчитаны на напряжение 220 В, но на разную силу тока. Поэтому мощность потребителей электроэнергии разная.

Литература

• ГОСТ 8.417-2002 Единицы величин
• ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации
• Бессонов Л. А. Теоретические основы электротехники. — М: Высшая школа, 1984.
• Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193—2009. — 146 с.

Дополнительная литература

• Агунов М. В., Агунов А. В. Об энергетических соотношениях в электрических цепях с несинусоидальными режимами // Электричество, 2005, № 4, С. 53-56.
• Агунов М. В., Агунов А. В., Вербова Н. М. Новый подход к измерению электрической мощности // Промышленная энергетика, 2004, № 2, С. 30-33.
• Агунов М. В., Агунов А. В., Вербова Н. М. Определение составляющих полной мощности в электрических цепях с несинусоидальными напряжениями и токами методами цифровой обработки сигналов // Электротехника, 2005, № 7, С. 45-48.
• Агунов А. В. Неактивные составляющие полной мощности в автономных электротехнических системах судостроения. Автореферат диссертации на соискание ученой степени кандидата технических наук. СПб., СПбГМТУ, 1997, 20 с.
• Агунов М. В. Энергетические процессы в электрических цепях с несинусоидальными режимами и их эффективность. Кишинев-Тольятти: МолдНИИТЭИ, 1997, 84 с.
• Агунов М. В., Агунов А. В. Об энергетических соотношениях в электрических цепях с несинусоидальными режимами // Электричество, 2005, № 4, С. 53-56.
• Агунов А. В. Управление качеством электроэнергии при несинусоидальных режимах. СПб., СПбГМТУ, 2009, 134 с.
• Агунов М. В., Агунов А. В., Вербова Н. М. Новый подход к измерению электрической мощности // Промышленная энергетика, 2004, № 2, С. 30-33.
• Агунов А. В. Статический компенсатор неактивных составляющих мощности с полной компенсацией гармонических составляющих тока нагрузки // Электротехника, 2003, № 2, С. 47-50.

Ссылки

См. также

biograf.academic.ru

Электрическая мощность — это… Что такое Электрическая мощность?

Электри́ческая мо́щность — физическая величина, характеризующая скорость передачи или преобразования электрической энергии.

Мгновенная электрическая мощность

Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки А в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале Δt), Q — количество зарядов, прошедших от А к B за время Δt. А — работа, совершённая зарядом Q при движении по участку A-B, P — мощность. Записывая вышеприведённые рассуждения, получаем:

Для единичного заряда на участке A-B:

Для всех зарядов:

Поскольку ток есть не что иное, как количество зарядов в единицу времени, то есть по определению, в результате получаем:

Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности:

мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке:

Если участок цепи содержит резистор c электрическим сопротивлением R, то

Дифференциальные выражения для электрической мощности

Мощность, выделяемая в единице объёма, равна:

В линейном изотропном приближении:

В линейном анизотропном приближении (например, в монокристалле или жидком кристалле, а также при наличии эффекта Холла):

Мощность постоянного тока

Так как значения силы тока и напряжения постоянны и равны мгновенным значениям в любой момент времени, то мощность можно вычислить по формуле:

Для пассивной линейной цепи, в которой соблюдается закон Ома, можно записать:

Если цепь содержит источник ЭДС, то отдаваемая им или поглощаемая на нём электрическая мощность равна:

где — ЭДС.

Если ток внутри ЭДС противонаправлен градиенту потенциала (течёт внутри ЭДС от плюса к минусу), то мощность поглощается источником ЭДС из сети (например, при работе электродвигателя или заряде аккумулятора), если сонаправлен (течёт внутри ЭДС от минуса к плюсу), то отдаётся источником в сеть (скажем, при работе гальванической батареи или генератора). При учёте внутреннего сопротивления источника ЭДС выделяемая на нём мощность прибавляется к поглощаемой или вычитается из отдаваемой.

Мощность переменного тока

В переменном электрическом поле формула для мощности постоянного тока оказывается неприменимой. На практике наибольшее значение имеет расчёт мощности в цепях переменного синусоидального напряжения и тока.

Для того, чтобы связать понятия полной, активной, реактивной мощностей и коэффициента мощности, удобно обратиться к теории комплексных чисел. Можно считать, что мощность в цепи переменного тока выражается комплексным числом таким, что активная мощность является его действительной частью, реактивная мощность — мнимой частью, полная мощность — модулем, а угол φ (сдвиг фаз) — аргументом. Для такой модели оказываются справедливыми все выписанные ниже соотношения.

Активная мощность

Единица измерения — ватт (W, Вт).

Среднее за период T значение мгновенной мощности называется активной мощностью: В цепях однофазного синусоидального тока где U и I — среднеквадратичные значения напряжения и тока, φ — угол сдвига фаз между ними. Для цепей несинусоидального тока электрическая мощность равна сумме соответствующих средних мощностей отдельных гармоник. Активная мощность характеризует скорость необратимого превращения электрической энергии в другие виды энергии (тепловую и электромагнитную). Активная мощность может быть также выражена через силу тока, напряжение и активную составляющую сопротивления цепи r или её проводимость g по формуле В любой электрической цепи как синусоидального, так и несинусоидального тока активная мощность всей цепи равна сумме активных мощностей отдельных частей цепи, для трёхфазных цепей электрическая мощность определяется как сумма мощностей отдельных фаз. С полной мощностью S активная связана соотношением

В теории длинных линий (анализ электромагнитных процессов в линии передачи, длина которой сравнима с длиной электромагнитной волны) полным аналогом активной мощности является проходящая мощность, которая определяется как разность между падающей мощностью и отраженной мощностью.

Реактивная мощность

Единица измерения — вольт-ампер реактивный (var, вар)

Реактивная мощность — величина, характеризующая нагрузки, создаваемые в электротехнических устройствах колебаниями энергии электромагнитного поля в цепи синусоидального переменного тока, равна произведению среднеквадратичных значений напряжения U и тока I, умноженному на синус угла сдвига фаз φ между ними: (если ток отстаёт от напряжения, сдвиг фаз считается положительным, если опережает — отрицательным). Реактивная мощность связана с полной мощностью S и активной мощностью Р соотношением: .

Физический смысл реактивной мощности — это энергия, перекачиваемая от источника на реактивные элементы приёмника (индуктивности, конденсаторы, обмотки двигателей), а затем возвращаемая этими элементами обратно в источник в течение одного периода колебаний, отнесённая к этому периоду.

Необходимо отметить, что величина sin φ для значений φ от 0 до плюс 90° является положительной величиной. Величина sin φ для значений φ от 0 до −90° является отрицательной величиной. В соответствии с формулой Q = UI sin φ, реактивная мощность может быть как положительной величиной (если нагрузка имеет активно-индуктивный характер), так и отрицательной (если нагрузка имеет активно-ёмкостный характер). Данное обстоятельство подчёркивает тот факт, что реактивная мощность не участвует в работе электрического тока. Когда устройство имеет положительную реактивную мощность, то принято говорить, что оно её потребляет, а когда отрицательную — то производит, но это чистая условность, связанная с тем, что большинство электропотребляющих устройств (например, асинхронные двигатели), а также чисто активная нагрузка, подключаемая через трансформатор, являются активно-индуктивными.

Синхронные генераторы, установленные на электрических станциях, могут как производить, так и потреблять реактивную мощность в зависимости от величины тока возбуждения, протекающего в обмотке ротора генератора. За счёт этой особенности синхронных электрических машин осуществляется регулирование заданного уровня напряжения сети. Для устранения перегрузок и повышения коэффициента мощности электрических установок осуществляется компенсация реактивной мощности.

Применение современных электрических измерительных преобразователей на микропроцессорной технике позволяет производить более точную оценку величины энергии возвращаемой от индуктивной и емкостной нагрузки в источник переменного напряжения.

Измерительные преобразователи реактивной мощности, использующие формулу Q = UI sin φ, более просты и значительно дешевле измерительных преобразователей на микропроцессорной технике.^{[источник не указан 124 дня]}

Полная мощность

Единица полной электрической мощности — вольт-ампер (V·A, В·А)

Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах: S = U·I; связана с активной и реактивной мощностями соотношением: где Р — активная мощность, Q — реактивная мощность (при индуктивной нагрузке Q > 0, а при ёмкостной Q < 0).

Векторная зависимость между полной, активной и реактивной мощностью выражается формулой:

Полная мощность имеет практическое значение, как величина, описывающая нагрузки, фактически налагаемые потребителем на элементы подводящей электросети (провода, кабели, распределительные щиты, трансформаторы, линии электропередачи), так как эти нагрузки зависят от потребляемого тока, а не от фактически использованной потребителем энергии. Именно поэтому номинальная мощность трансформаторов и распределительных щитов измеряется в вольт-амперах, а не в ваттах.

Комплексная мощность

Мощность, аналогично импедансу, можно записать в комплексном виде:

где  — комплексное напряжение,  — комплексный ток, — импеданс, * — оператор комплексного сопряжения.

Модуль комплексной мощности равен полной мощности S. Действительная часть равна активной мощности Р, а мнимая  — реактивной мощности Q с корректным знаком в зависимости от характера нагрузки.

Неактивная мощность

Неактивная мощность (пассивная мощность)^{[источник не указан 172 дня]} — это мощность нелинейных искажений тока, равная корню квадратному из разности квадратов полной и активной мощностей в цепи переменного тока. В цепи с синусоидальным напряжением неактивная мощность равна корню квадратному из суммы квадратов реактивной мощности и мощностей высших гармоник тока^{[источник не указан 172 дня]}. При отсутствии высших гармоник неактивная мощность равна модулю реактивной мощности.

Под мощностью гармоники тока понимается произведение действующего значения силы тока данной гармоники на действующее значение напряжения^{[источник не указан 172 дня]}.

Наличие нелинейных искажений тока в цепи означает нарушение пропорциональности между мгновенными значениями напряжения и силы тока, вызванное нелинейностью нагрузки, например когда нагрузка имеет реактивный или импульсный характер. При линейной нагрузке сила тока в цепи пропорциональна мгновенному напряжению, вся потребляемая мощность является активной. При нелинейной нагрузке увеличивается кажущаяся (полная) мощность в цепи за счёт мощности нелинейных искажений тока, которая не принимает участия в совершении работы^{[источник не указан 172 дня]}. Мощность нелинейных искажений не является активной и включает в себя как реактивную мощность, так и мощность прочих искажений тока. Данная физическая величина имеет размерность мощности, поэтому в качестве единицы измерения неактивной мощности можно использовать В∙А (вольт-ампер) или вар (вольт-ампер реактивный). Вт (ватт) использовать нежелательно, чтобы неактивную мощность не спутали с активной.

Связь неактивной, активной и полной мощностей

Величину неактивной мощности обозначим N. Через i обозначим вектор тока, через u — вектор напряжения. Буквами I и U будем обозначать соответствующие действующие значения:

Представим вектор тока i в виде суммы двух ортогональных составляющих i_a и i_p, которые назовём соответственно активной и пассивной. Поскольку в совершении работы участвует только составляющая тока, коллинеарная напряжению, потребуем, чтобы активная составляющая была коллинеарна напряжению, то есть i_a = λu, где λ — некоторая константа, а пассивная — ортогональна, то есть Имеем

Запишем выражение для активной мощности P, скалярно умножив последнее равенство на u:

Отсюда находим

Выражение для величины неактивной мощности имеет вид где S = U I — полная мощность.

Для полной мощности цепи справедливо представление, аналогичное выражению для цепи с гармоническими током и напряжением, только вместо реактивной мощности используется неактивная мощность:

Таким образом, понятие неактивной мощности представляет собой один из способов обобщения понятия реактивной мощности для случая несинусоидальных тока и напряжения. Неактивная мощность иногда называется реактивной мощностью по Фризе.

Измерения

• Для измерения электрической мощности применяются ваттметры и варметры, можно также использовать косвенный метод, с помощью вольтметра и амперметра.
• Для измерения коэффициента реактивной мощности применяют фазометры
• Государственный эталон — ГЭТ 153-86 Государственный специальный эталон единицы электрической мощности в диапазоне частот 40-2500 Гц. Институт-хранитель: ВНИИМ

Мощность некоторых электрических приборов

В таблице указаны значения мощности некоторых потребителей электрического тока:

Электрический прибор	Мощность,Вт
Лампочка фонарика	1
Лампа люминесцентная бытовая	5…30
Лампа накаливания бытовая	25…150
Холодильник бытовой	15…200
Электропылесос	100…2 000
Электрический утюг	300…2 000
Стиральная машина	350…2 000
Электрическая плитка	1 000…2 000
Сварочный аппарат бытовой	1 000…5 500
Двигатель трамвая	45 000…50 000
Двигатель электровоза	650 000
Электродвигатели прокатного стана	6 000 000…9 000 000

Большинство бытовых приборов рассчитаны на напряжение 220 В, но на разную силу тока. Поэтому мощность потребителей электроэнергии разная.

Литература

• ГОСТ 8.417-2002 Единицы величин
• ПР 50.2.102-2009 Положение о единицах величин, допускаемых к применению в Российской Федерации
• Бессонов Л. А. Теоретические основы электротехники. — М: Высшая школа, 1984.
• Гольдштейн Е. И., Сулайманов А. О., Гурин Т. С. Мощностные характеристики электрических цепей при несинусоидальных токах и напряжениях. ТПУ, — Томск, 2009, Деп. в ВИНИТИ, 06.04.09, № 193—2009. — 146 с.

Дополнительная литература

• Агунов М. В., Агунов А. В. Об энергетических соотношениях в электрических цепях с несинусоидальными режимами // Электричество, 2005, № 4, С. 53-56.
• Агунов М. В., Агунов А. В., Вербова Н. М. Новый подход к измерению электрической мощности // Промышленная энергетика, 2004, № 2, С. 30-33.
• Агунов М. В., Агунов А. В., Вербова Н. М. Определение составляющих полной мощности в электрических цепях с несинусоидальными напряжениями и токами методами цифровой обработки сигналов // Электротехника, 2005, № 7, С. 45-48.
• Агунов А. В. Неактивные составляющие полной мощности в автономных электротехнических системах судостроения. Автореферат диссертации на соискание ученой степени кандидата технических наук. СПб., СПбГМТУ, 1997, 20 с.
• Агунов М. В. Энергетические процессы в электрических цепях с несинусоидальными режимами и их эффективность. Кишинев-Тольятти: МолдНИИТЭИ, 1997, 84 с.
• Агунов М. В., Агунов А. В. Об энергетических соотношениях в электрических цепях с несинусоидальными режимами // Электричество, 2005, № 4, С. 53-56.
• Агунов А. В. Управление качеством электроэнергии при несинусоидальных режимах. СПб., СПбГМТУ, 2009, 134 с.
• Агунов М. В., Агунов А. В., Вербова Н. М. Новый подход к измерению электрической мощности // Промышленная энергетика, 2004, № 2, С. 30-33.
• Агунов А. В. Статический компенсатор неактивных составляющих мощности с полной компенсацией гармонических составляющих тока нагрузки // Электротехника, 2003, № 2, С. 47-50.

Ссылки

См. также

dikc.academic.ru

Активная мощность

Мгновенная мощность pпроизвольного участка цепи, напряжение и ток которого изменяются по законуu=U_msin(t), i = I_msin(t–), имеет вид

p = ui= U_msin(t)I_msin(t–) = U_mI_m[cos — cos(2t — )]/2 =

= Uicos — UIcos(2t — ) = (UIcos – UIcos cos2t) – UIsin sin2t. (1)

Активная мощность цепи переменного тока Pопределяется как среднее значение мгновенной мощностиp(t) за период:

P = ,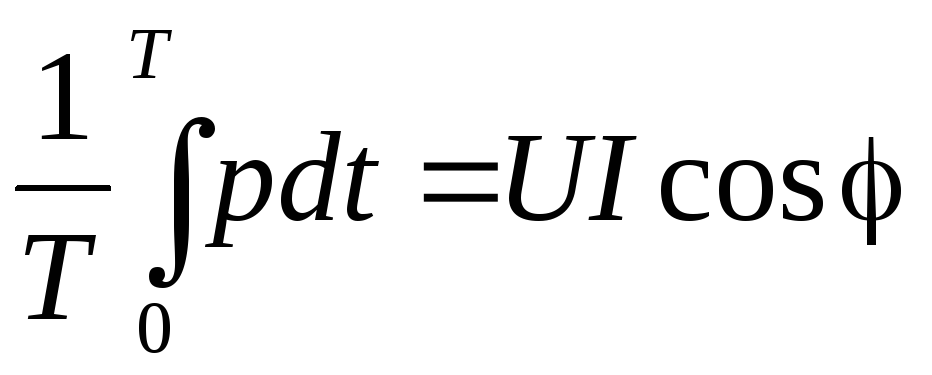

так как среднее за период значение гармонической функции равно 0.

Из этого следует, что средняя за период мощность зависит от угла сдвига фаз между напряжением и током и не равна нулю, если участок цепи имеет активное сопротивление. Последнее объясняет ее название активная мощность. Подчеркнем еще раз, что в активном сопротивлении происходит необратимое преобразование электрической энергии в другие виды энергии, например в тепловую. Активная мощность может быть определена как средняя за период скорость поступления энергии в участок цепи. Активная мощность измеряется в ваттах (Вт).

Реактивная мощность

При расчетах электрических цепей находит широкое применение так называемая реактивнаямощность. Она характеризует процессы обмена энергией между реактивными элементами цепи и источниками энергии и численно равна амплитуде переменной составляющей мгновенной мощности цепи. В соответствии с этим реактивная мощность может быть определена из (1) как

Q = UIsin.

В зависимости от знака угла реактивная мощность может быть положительной или отрицательной. Единицу реактивной мощности, чтобы отличить ее от единицы активной, называют не ватт, а вольт-ампер реактивныйвар. Реактивные мощности индуктивного и емкостного элементов равны амплитудам их мгновенных мощностейp_L иp_C. С учетом сопротивленийэтих элементов реактивные мощности катушки индуктивности и конденсатора равныQ_L=UI=x_LI ²иQ_C=UI= x_CI ², соответственно.

Результирующая реактивная мощность разветвленной электрической цепи находится как алгебраическая сумма реактивных мощностей элементов цепи с учетом их характера (индуктивный или емкостный): Q=Q_L–Q_С. ЗдесьQ_Lесть суммарная реактивная мощность всех индуктивных элементов цепи, аQ_С представляет собой суммарную реактивную мощность всех емкостных элементов цепи.

Полная мощность

Кроме активной и реактивной мощностей цепь синусоидального тока характеризуется полной мощностью, обозначаемой буквой S. Под полной мощностью участка понимают максимально возможную активную мощность при заданных напряженииUи токеI. Очевидно, что максимальная активная мощность получается при cos= 1, т. е. при отсутствии сдвига фаз между напряжением и током:

S = UI.

Необходимость во введении этой мощности объясняется тем, что при конструировании электрических устройств, аппаратов, сетей и т. п. их рассчитывают на определенное номинальное напряжение U_номи определенный номинальный токI_номи их произведениеU_ном I_ном= S_номдает максимально возможную мощность данного устройства (полная мощность S_номуказывается в паспорте большинства электрических устройств переменного тока.). Для отличия полной мощности от других мощностей ее единицу измерения называют вольт-ампер и сокращенно обозначают ВА. Полная мощность численно равна амплитуде переменной составляющей мгновенной мощности.

Из приведенных соотношений можно найти связь между различными мощностями:

P = S cos,  Q = S sin,  S = UI =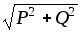 

и выразить угол сдвига фаз через активную и реактивную мощности:

.

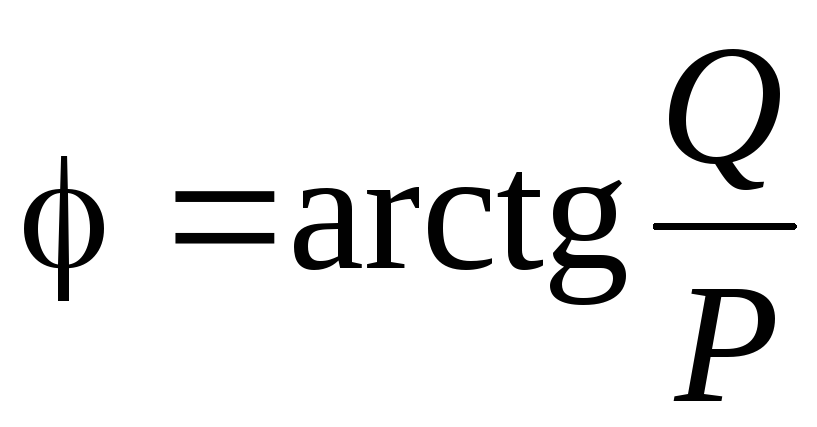Рассмотрим простой прием, который позволяет найти активную и реактивную мощности участка цепи по комплексным напряжению и току. Он заключается в том, что нужно взять произведение комплексного напряжения 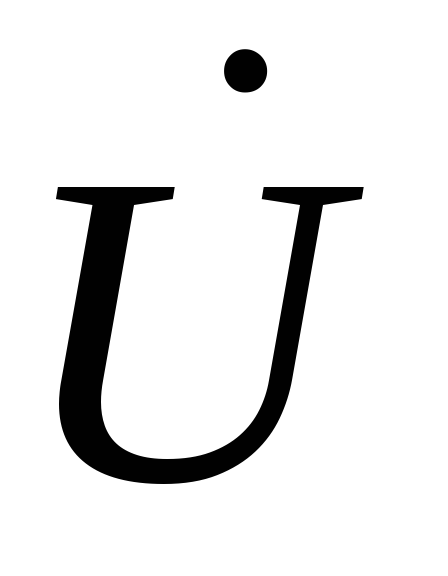и тока, комплексно сопряженного току рассматриваемого участка цепи. Операция комплексного сопряжения состоит в смене знака на противоположный перед мнимой частью комплексного числа либо в смене знака фазы комплексного числа, если число представлено в экспоненциальной форме записи. В результате получим величину, которая называетсяполной комплексной мощностьюи обозначается. 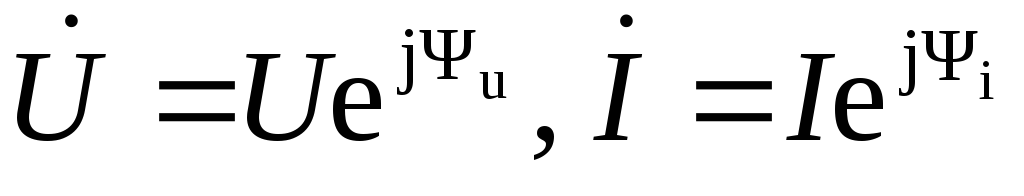Если, то для полной комплексной мощности получаем:

.

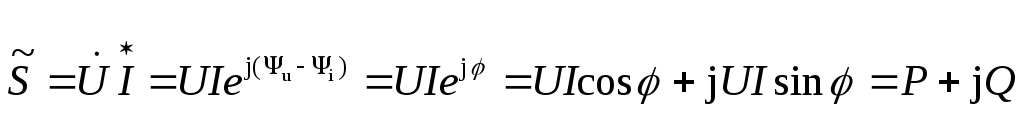Отсюда видно, что активная и реактивная мощности представляют собой вещественную и мнимую части полной комплексной мощности, соответственно. Для облегчения запоминания всех формул, связанных с мощностями, на рис. 7, б(с. 38) построен треугольник мощностей.

studfile.net