17 часто задаваемых вопросов о преобразователе частоты и электродвигателе — Статьи
Дата публикации: 21.08.2019
В данной статье мы подобрали для вас ответы на наиболее часто задаваемые вопросы по работе электродвигателей и частотных преобразователей.
1. Что такое электромеханический привод?
Ответ: Электромеханический привод – это система, состоящая из электродвигателя, механического передаточного устройства, электрического силового преобразователя и электронного устройства управления, осуществляющая управляемое преобразование электрической энергии в энергию движения механического объекта.
2. Что такое преобразователь частоты?
Ответ: Преобразователь частоты – это устройство для управляемого питания электродвигателя.
3. В чем заключается назначение преобразователя частоты?
Ответ: Назначение преобразователя частоты – это управление моментом/скоростью вращения электродвигателя за счет изменения частоты и напряжения питания.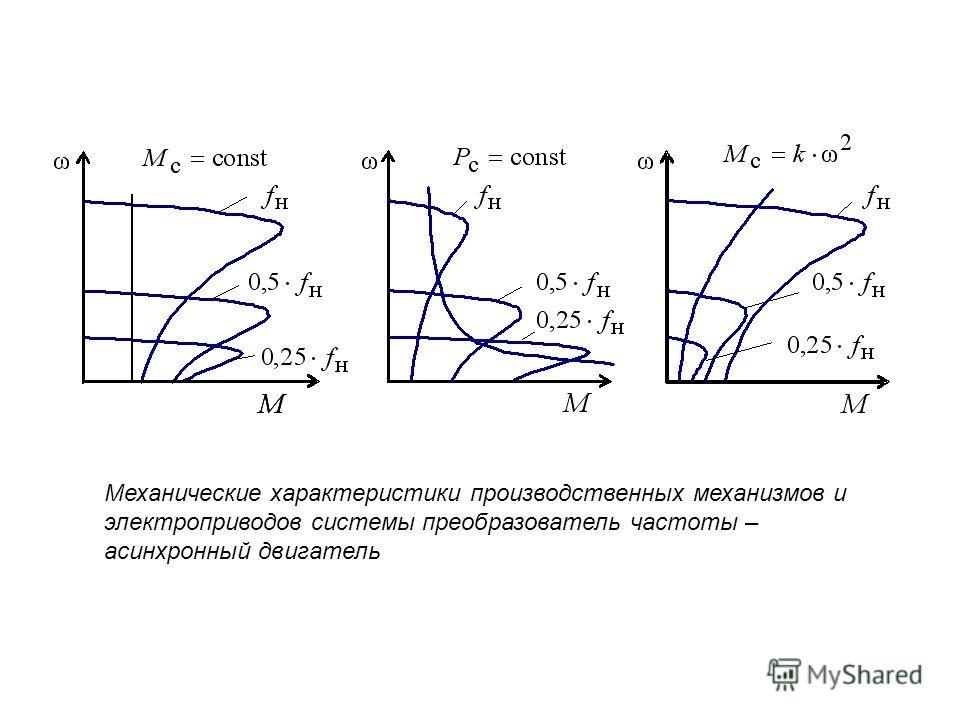
4. Что такое ШИМ?
Ответ: ШИМ (Широтно импульсная модуляция) – это метод получения регулируемого выходного напряжения путем изменения длительности коммутации.
5. Как согласуется выходное напряжение ПЧ с входным?
Ответ: Выходное напряжение может меняться от 0 до уровня входного напряжения ПЧ (возможна перегрузка в несколько процентов). Соответственно при питании ПЧ от сети 220В не возможно развить номинальный момент на двигателе подключенным по схеме питания 380В.
6. Как согласуется выходная частота ПЧ с номинальной входной?
Ответ: Выходная частота формируется посредством ШИМ и может меняться в диапазоне от 0 до 400 -590 Гц (в зависимости от модели ПЧ). В зависимости от выходной частоты ПЧ меняется скорость вращения вала двигателя.
7. Возможно ли управлять ПЧ однофазными двигателями?
Ответ: Нет.
8. Возможно ли управлять ПЧ с однофазным питанием, трехфазными двигателями?
Ответ: Да, до 2,2 кВт.
9. Основные плюсы использования преобразователей частоты?
Ответ: Их 2. Во-первых, экономия электроэнергии при работе электродвигателя. Во-вторых, реализация сложных технологических процессов за счет изменения частоты вращения приводов.
10. Какой принцип работы асинхронного двигателя с короткозамкнутым ротором?
Ответ: ПЧ создает вращающееся магнитное поле в статоре, а оно создает электрическое поле в короткозамкнутом роторе (принцип магнитной индукции). Происходит взаимодействие между полями ротора и статора. Поле ротора стремится вращаться также как поле статора, тем самым ротор приходит во вращение.
11. От чего зависит номинальная скорость вращения ротора асинхронного двигателя с короткозамкнутым ротором?
Ответ: Она зависит от частоты питающего напряжения и количества пар полюсов и скольжения. Преобразователь частоты позволяет регулировать частоту питающего напряжения и тем самым скорость вращения вала ЭД.
Преобразователь частоты позволяет регулировать частоту питающего напряжения и тем самым скорость вращения вала ЭД.
12. Какое значение имеет скорость вращения вала электродвигателя при его работе от сети?
Ответ: Скорость равна номинальной частоте двигателя.
13. Какова скорость вращения вала электродвигателя при его работе от ПЧ?
Ответ: Скорость регулируется от ПЧ .
14. Как связан момент с током электродвигателя?
Ответ: Для двигателя с постоянными магнитами момент пропорционален току статора. Для асинхронных двигателей зависимость между током и моментом нелинейная, но в рабочей зоне рост тока приводит к росту момента.
15: Какие существуют способы подключения обмоток двигателя?
Ответ: Треугольник, Звезда (изменяется номинальное напряжение и ток двигателя).
16: При подключении в звезду или треугольник будет больше номинальное линейное напряжение двигателя?
Ответ: Линейное напряжение будет больше для звезды (соответственно ток наоборот меньше).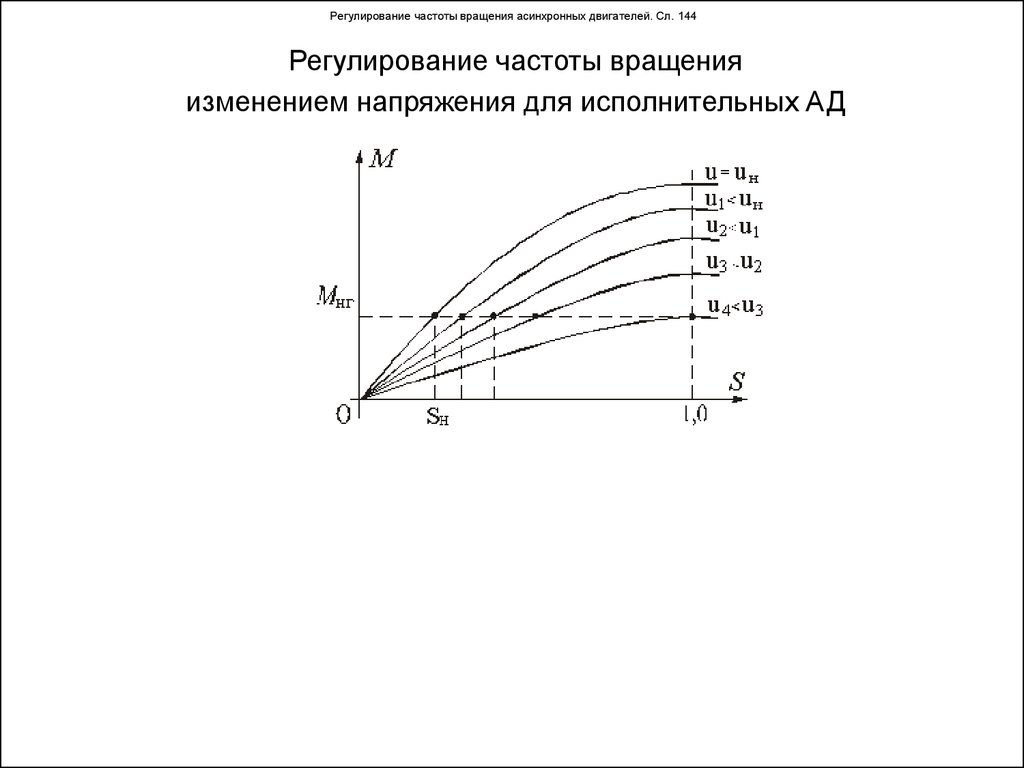
17: Что такое скольжение?
Ответ: Скольжение – это разница между скоростью поля статора и частотой вращения ротора в процентах.
Смотрите так же:
Функция «Спящий режим» преобразователя частоты Danfoss FC-051 (Реализация на встроенном контроллере)
Управление частотным преобразователем Danfoss серии FC51 с панели оператора Weintek MT8121XE1WK
Для заказа преобразователя частоты перейдите в каталог по ссылке — VLT Micro Drive
Асинхронный двигатель
Если поместить во вращающееся магнитное поле короткозамкнутую медную или алюминиевую рамку на валу электродвигателя, то она вместе с валом придет во вращение по направлению вращения поля. Явление это объясняется следующим образом. Пусть угловая скорость вращения рамки n несколько меньше угловой скорости вращения поля no (асинхронное вращение). В этом случае рамка «проскальзывает» относительно поля. Величину s = (n0—n)/n0 называют скольжением. Относительно магнитного поля рамка вращается с угловой скоростью, пропорциональной скольжению. Поэтому в ней возникает индукционный ток, пропорциональный относительной скорости вращения рамки, т. е. скольжению. По закону Ленца, индуцированный ток взаимодействует с полем так, что рамка увлекается полем.
Относительно магнитного поля рамка вращается с угловой скоростью, пропорциональной скольжению. Поэтому в ней возникает индукционный ток, пропорциональный относительной скорости вращения рамки, т. е. скольжению. По закону Ленца, индуцированный ток взаимодействует с полем так, что рамка увлекается полем.
А так как магнитное поле вращается, то это приводит к вращению рамки. Вращающий момент, действующий на рамку, пропорционален индуцированному току и тем самым скольжению. Этот вращающий момент уравновешивается внешней нагрузкой. Таким образом, в установке данного типа рамка всегда вращается несколько медленнее вращения поля. Такое вращение называют асинхронным (т. е. неодновременным, несогласованным). Сам двигатель получил название асинхронного.
Асинхронный двигатель наиболее распространен в качестве электропривода различных механизмов благодаря своей простоте и надежности. Их применяют для привода машин и механизмов, не требующих строго постоянной частоты вращения и ее регулировки. Важнейшими достоинствами данного двигателя являются простота его устройства и большая надежность, вызванная отсутствием скользящих контактов. Двигатель имеет достаточный пусковой момент, легко реверсируется (т. е. в нем легко меняется направление вращения ротора). В результате этого асинхронные двигатели являются самыми распространенными в технике электрическими машинами. Более 60 % всей вырабатываемой в мире энергии преобразуется в механическую, в основном, с помощью асинхронных двигателей. Мощность двигателей колеблется от десятков ватт до сотен киловатт.
Важнейшими достоинствами данного двигателя являются простота его устройства и большая надежность, вызванная отсутствием скользящих контактов. Двигатель имеет достаточный пусковой момент, легко реверсируется (т. е. в нем легко меняется направление вращения ротора). В результате этого асинхронные двигатели являются самыми распространенными в технике электрическими машинами. Более 60 % всей вырабатываемой в мире энергии преобразуется в механическую, в основном, с помощью асинхронных двигателей. Мощность двигателей колеблется от десятков ватт до сотен киловатт.
Асинхронный двигатель изготавливается в однофазном, двухфазном и трехфазном исполнении.
Принцип работы
Рассмотрим вращающееся поле переменного тока трехфазной цепи короткозамкнутого асинхронного двигателя с тремя обмотками, сдвинутыми по окружности на 120° и соединенными звездой .
Обмотки статора питаются симметричным трехфазным напряжением. Начальную фазу тока в обмотке А-х принимаем равной нулю. Тогда:
Конструкция
Асинхронный двигатель состоит из статора и ротора. Статор представляет собой литой корпус (стальной или чугунный) цилиндрической формы. Внутри статора располагается магнитопровод с вырубленными пазами, в которые укладывается статорная обмотка. Концы обмоток выводятся в клеммную коробку и могут быть соединены как треугольником, так и звездой. Корпус статора с торцов закрыт подшипниковыми щитами, в которые запрессовываются подшипники вала ротора. Ротор состоит из стального вала с напрессованным на него магнитопроводом.
Статор представляет собой литой корпус (стальной или чугунный) цилиндрической формы. Внутри статора располагается магнитопровод с вырубленными пазами, в которые укладывается статорная обмотка. Концы обмоток выводятся в клеммную коробку и могут быть соединены как треугольником, так и звездой. Корпус статора с торцов закрыт подшипниковыми щитами, в которые запрессовываются подшипники вала ротора. Ротор состоит из стального вала с напрессованным на него магнитопроводом.
По конструкции роторов двигатели делятся на две группы. Первая — с короткозамкнутым ротором и вторая — с фазным. У двигателя с короткозамкнутым ротором в пазы заливаются алюминиевые стержни и накоротко замыкаются по торцам. У фазового ротора имеются три обмотки, соединенные в звезду. Выводы обмоток присоединены к кольцам, закрепленным на валу. К кольцам при пуске прижимаются неподвижные щетки, к которым подключаются сопротивления. В начальный момент пуска ротор находится в заторможенном состоянии, затем сопротивление уменьшается и двигатель плавно запускается, что позволяет снизить пусковой ток.
К обмоткам статора подводится трехфазное напряжение, а ротор вращается посредством вращающегося магнитного поля, создаваемого системой трехфазного тока.
В момент времени t1: . Если ток фазы А положителен, т.е. течет от начала к концу, то, пользуясь правилом правоходового винта, можно найти картину распределения магнитного поля для времени t1.
В момент времени t2 вектор результирующей магнитной индукции Вm развернется на угол α1 и далее по часовой стрелке с периодом обращения 360°. Для данного примера угол α1 = 60°.
Таким образом, магнитная индукция представляет собой вращающееся поле с амплитудой
За период поле делает один оборот, , (где f = 50 Гц), и является промышленной частотой питающего переменного напряжения и тока.
При синусоидальном характере вращающегося поля его скорость no равна отношению αf/p (где р — число пар полюсов).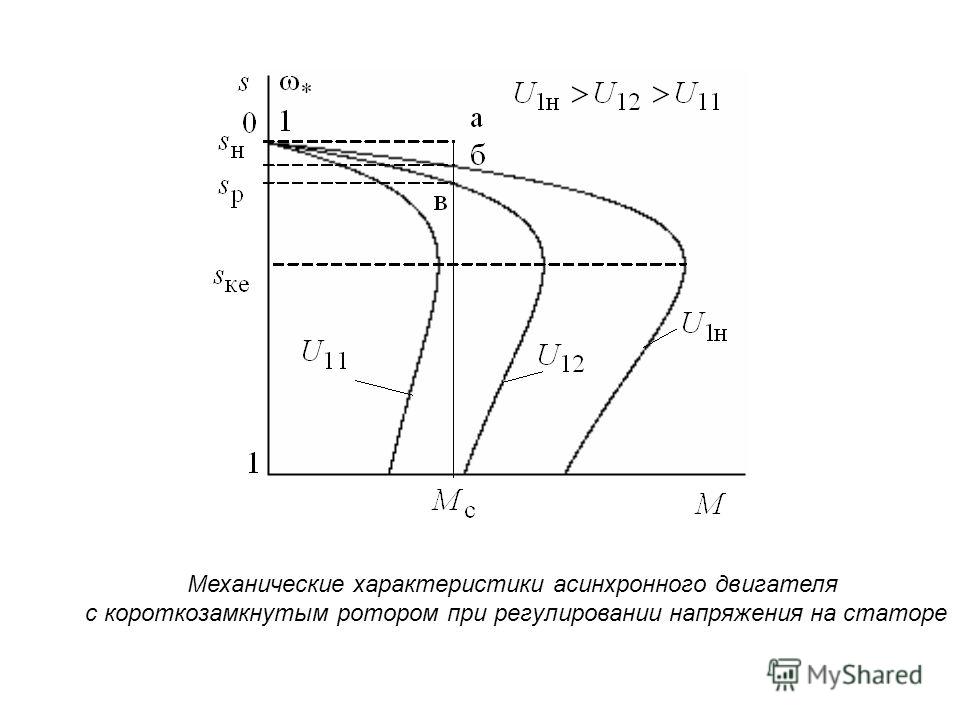 В рассматриваемом примере р = 1 и частота вращения равна соответственно 3000 оборотам в минуту. Если число катушек в каждой фазе увеличить в два раза, а сдвиг фаз между токами сохранить 120°, то частота вращения уменьшится в два раза за счет увеличения числа пар полюсов. Особенностью короткозамкнутого асинхронного двигателя является наличие постоянной частоты вращения поля статора, определяемой числом пар полюсов.
В рассматриваемом примере р = 1 и частота вращения равна соответственно 3000 оборотам в минуту. Если число катушек в каждой фазе увеличить в два раза, а сдвиг фаз между токами сохранить 120°, то частота вращения уменьшится в два раза за счет увеличения числа пар полюсов. Особенностью короткозамкнутого асинхронного двигателя является наличие постоянной частоты вращения поля статора, определяемой числом пар полюсов.
Если поменять местами любые две фазы, то возникнет поле обратной последовательности и ротор начнет вращаться в другую сторону. Еще одной особенностью асинхронных двигателей является разность частоты вращения полей статора no и ротора n, что делает возможным их электромагнитное взаимодействие. При этом поле ротора будет как бы скользить относительно поля статора
где s — скольжение, при номинальной мощности двигателя скольжение составляет 0,01-0,03.
Основное вращающееся магнитное поле индуцирует в обмотках статора и ротора ЭДС, аналогично трансформатору, так как при разомкнутом роторе асинхронный двигатель представляет собой трансформатор в режиме холостого хода:
где индекс 1 относится к параметрам статора, а 2 — к параметрам ротора; Kобм — обмоточные коэффициенты, определяемые способом укладки обмоток (петлевая или волновая). Kобм=0,92-0,98; E2s=E2s; E2 — действующее значение ЭДС неподвижного ротора при s = 1; f2=f1s.
Kобм=0,92-0,98; E2s=E2s; E2 — действующее значение ЭДС неподвижного ротора при s = 1; f2=f1s.
В асинхронном двигателе кроме основного магнитного потока создаются потоки рассеяния. Один охватывает проводники статора, другой — ротора. Потоки рассеяния характеризуются соответствующими индуктивными сопротивлениями X1 и X2s.
Уравнения электрического состояния фаз обмоток статора и ротора:
Момент асинхронного двигателя
Вращающий электромагнитный момент двигателя в соответствии с законом электромагнитных сил
где
Cм — конструктивная постоянная;
φ2s — фазовый сдвиг между током и магнитным потоком.
Отношение максимального момента Mmax к номинальному Mн определяет перегрузочную способность двигателя и составляет 2,0-2,2 (дается в каталожных данных). Максимальный момент соответствует критическому скольжению sк, определяемому активными и индуктивными сопротивлениями двигателя, и пропорционален активному сопротивлению цепи ротора.
Максимальный момент соответствует критическому скольжению sк, определяемому активными и индуктивными сопротивлениями двигателя, и пропорционален активному сопротивлению цепи ротора.
Потери в асинхронном двигателе
Потери делятся на потери в статоре и в роторе. Потери в статоре состоят из электрических потерь в обмотке Рэ1 и потерь в стали Рст, а потери в роторе — из электрических Рэ2 и механических Рмех плюс добавочные потери на трение и вентиляцию Рдоб.
где К = 2,9-3,6 определяется диаметром статора D1.
Потери в стали в рабочем режиме во много раз меньше электрических потерь в роторе и ими обычно пренебрегают.
КПД асинхронного двигателя составляет от 0,75 до 0,95.
Рабочий момент двигателя пропорционален квадрату напряжения, что необходимо учитывать при включении двигателя в протяженных распределительных сетях. Номинальному моменту соответствует номинальное скольжение, а пусковому — sп.
Номинальному моменту соответствует номинальное скольжение, а пусковому — sп.
Зависимость момента двигателя от скольжения М=f(s) приведена на рисунке.
На участке от 0 до Mmax двигатель работает в устойчивом режиме, а участок от Sk называется режимом опрокидывания двигателя, при котором двигатель в результате перегрузки останавливается и не может вернуться в рабочий режим без очередного запуска. Пусковые свойства двигателя определяются соотношением пускового момента Mп и номинального. В соответствии с каталожными данными оно составляет 1,6-1,7. При пуске асинхронного двигателя cosj очень мал и пусковой ток в обмотке статора может возрастать в 5-7 раз по сравнению с номинальным. Ограничение его осуществляется изменением частоты питающего напряжения для двигателя с короткозамкнутым ротором и увеличением активного сопротивления в цепи ротора для двигателя с фазовым ротором. Для механизмов, имеющих тяжелые условия пуска, где желательно использовать асинхронный двигатель с короткозамкнутым ротором, применяются двигатели с улучшенными пусковыми свойствами: с большим пусковым моментом и меньшим пусковым током, чем у двигателей общего назначения.
Механическая характеристика асинхронного двигателя
Зависимость скорости вращения от нагрузки на валу двигателя называется механической характеристикой асинхронного двигателя.
Участок АВ механической характеристики соответствует устойчивому режиму работы асинхронного двигателя. Увеличение нагрузки (тормозного момента) ведет к некоторому снижению частоты вращения ротора, что вызывает увеличение вращающего момента. При превышении тормозным моментом критического, двигатель останавливается. Точка В на графике соответствует точке критического или опрокидывающего момента.
Регулирование частоты вращения
Регулирование частоты вращения может быть осуществлено тремя способами: изменением частоты питающего напряжения, переключением числа пар полюсов и изменением скольжения.
Для регулирования частоты вращения двигателей с короткозамкнутым ротором в настоящее время широко используются частотные преобразователи с микропроцессорным управлением.
Тормозные режимы
Тормозные режимы возникают в машине при определенных условиях или создаются искусственно с целью ускорения процесса остановки двигателя.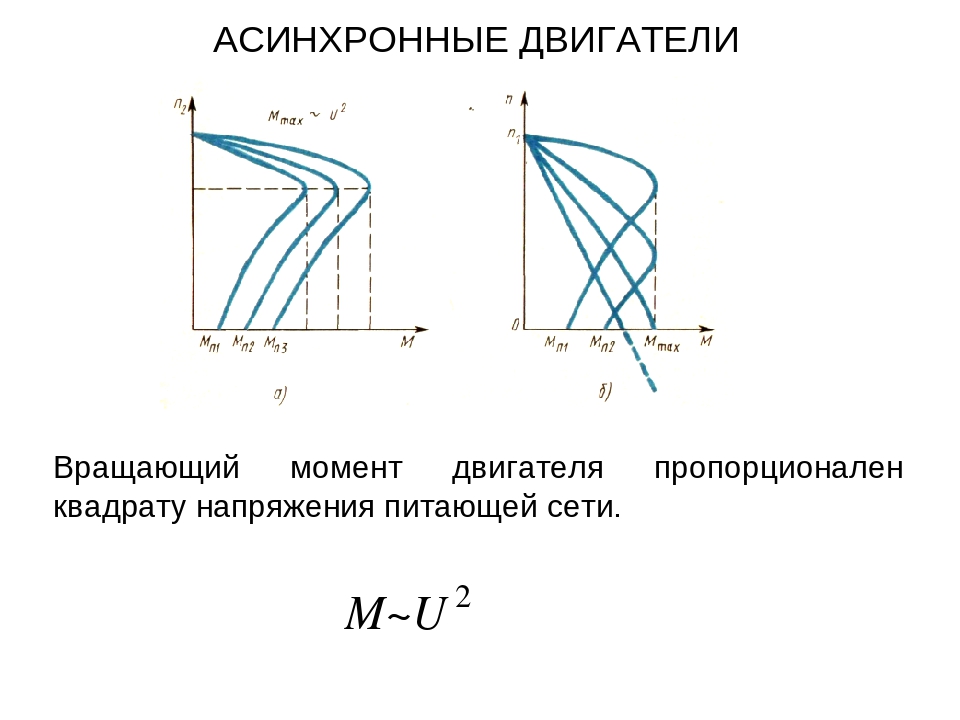 Торможение может быть:
Торможение может быть:
- генераторное с отдачей энергии в сеть;
- противовключением;
- динамическое.
Генераторным тормозным режимом называется режим работы двигателя, когда под действием внешнего момента ротор двигателя вращается в том же направлении, что и магнитное поле, но с большей скоростью.
Тормозной режим противовключения возникает в том случае, когда под действием внешнего момента, приложенного к валу двигателя, ротор вращается в противоположную сторону относительно вращающегося магнитного поля.
Динамический тормозной режим получается при отключении обмотки статора от сети трехфазного тока и подключении ее на время торможения к источнику энергии постоянного тока.
Выбор двигателя
Расчетные формулы для выбора двигателя имеют вид:
Выбор двигателя по каталогу осуществляется следующим образом. По заданному моменту рабочего механизма и частоте вращения определяется необходимая мощность. После этого определяются условия окружающей среды, выбирается исполнение по типу монтажа и высоте оси рабочего вала двигателя. Зная эти параметры, по каталогу проверяют необходимую перегрузочную способность, КПД, массу и момент инерции.
Зная эти параметры, по каталогу проверяют необходимую перегрузочную способность, КПД, массу и момент инерции.
Для шахтных условий используются двигатели взрывозащищенного исполнения; для крановых механизмов — двигатели с повышенным скольжением и т.д.
В бытовых приборах используются однофазные двигатели. Однофазный двигатель отличается от трехфазного тем, что его статорная обмотка подключается к однофазному источнику питания. Ротор выполняется короткозамкнутым. На статоре размещаются две обмотки, оси которых смещены друг относительно друга на 90 электрических градусов. Одна называется рабочей, а другая -пусковой.
Рабочие характеристики асинхронного двигателя
Рабочими характеристиками асинхронного двигателя являются зависимости от мощности на валу Р2 таких параметров, как момент, частота вращения, ток статора, КПД и cosφ. Анализ характеристик показывает, что частота вращения ротора падает с увеличением нагрузки, а момент пропорционален ей. Ток статора изменяется по нелинейному закону, что связано с магнитной системой двигателя и при Р2=0 определяется током холостого хода, составляющего до 40% его номинального значения.
Ток статора изменяется по нелинейному закону, что связано с магнитной системой двигателя и при Р2=0 определяется током холостого хода, составляющего до 40% его номинального значения.
В системах управления используются двигатели, в которых одна из обмоток статора постоянно подключена к сети переменного тока (обмотка возбуждения), а ко второй (обмотка управления) подводится напряжение управления. Такие двигатели относятся к классу микромашин.
Микромашины используются в информационных системах, где они выполняют функции первичных преобразователей для вычислительных операций в системах автоматики и телемеханики.
Одним из примеров является сельсин, предназначенный для передачи на расстояние угловых перемещений валов, механически не связанных друг с другом. По конструкции сельсины делятся на контактные и бесконтактные. Контактные сельсины выполняются в двух вариантах. В одном обмотка возбуждения располагается на роторе, а трехфазная обмотка, называемая обмоткой синхронизации, в пазах статора. В другом варианте наоборот. При включении обмотки возбуждения сельсина на однофазное напряжение ток создает пульсирующее магнитное поле, которое индуцирует в каждой фазе обмотки синхронизации переменную ЭДС. Действующее значение ЭДС каждой фазы зависит от расположения осей этих фаз относительно оси потока возбуждения.
В другом варианте наоборот. При включении обмотки возбуждения сельсина на однофазное напряжение ток создает пульсирующее магнитное поле, которое индуцирует в каждой фазе обмотки синхронизации переменную ЭДС. Действующее значение ЭДС каждой фазы зависит от расположения осей этих фаз относительно оси потока возбуждения.
В простейшем случае схема дистанционной передачи угловых перемещений состоит из двух одинаковых сельсинов, у которых одноименные зажимы обмоток синхронизации соединены проводами линии связи, а на обмотки возбуждения подается напряжение сети. Один из сельсинов называют сельсин-датчиком, другой — сельсин-приемником.
Электромагнитные дефекты | Спектральная вибродиагностика
«Диагностика дефектов вращающегося оборудования по вибрационным сигналам» 2012 г.
Анализируя сигналы с датчиков вибрации, установленных
на опорных подшипниках электрических машин, можно выявить достаточно много
специфических дефектов состояния, возникающих только в электродвигателях и
генераторах различного типа. Причиной повышенной вибрации электрических машин могут
являться как различные внутренние электромагнитные дефекты электрических машин,
так некоторые специфические особенности проявления электромагнитных процессов в
обмотках и сердечниках, т. е. это просто может отражать особенности нормальной
работы электродвигателей и генераторов во вращающихся агрегатах.
Причиной повышенной вибрации электрических машин могут
являться как различные внутренние электромагнитные дефекты электрических машин,
так некоторые специфические особенности проявления электромагнитных процессов в
обмотках и сердечниках, т. е. это просто может отражать особенности нормальной
работы электродвигателей и генераторов во вращающихся агрегатах.
Применение вибрационных методов диагностики дефектов состояния электродвигателей и генераторов обычно является первым этапом в оценке их состояния. Так происходит потому, что они позволяют оперативно анализировать состояние оборудования непосредственно во время его работы, или как это принято называть в литературе, реализуют диагностику и мониторинг технического состояния в режиме «on-line».
После применения вибрационного анализа для диагностики дефектов в электрических машинах, и выявления основных характерных признаков существования того или иного дефекта, можно, а иногда даже необходимо, применять другие, специализированные и, естественно, более точные методы диагностики состояния электрических машин.
Очевидно, что описание этих методов выходит за рамки данной работы, и ознакомиться с ними можно, если обратиться к другой, более специализированной литературе. Частично, но все равно более широко, чем это обычно делается в «обычной» литературе по вибрационной диагностике, эти методы рассмотрены в данном разделе. Некоторые аспекты диагностики электротехнического оборудования приведены ниже, в соответствующем разделе.
При выборе дефектов, которые мы описываем в данном разделе, мы исходили из простого определения. Если дефект можно диагностировать при помощи установки датчиков вибрации на опорных подшипниках, то его описание включено в данный раздел. Если же для диагностики необходимо устанавливать датчики вибрации в других точках контролируемой электрической машины, то описание диагностики таких дефектов вынесено в особый раздел данного методического руководства.
Обычные, достаточно широко распространенные причины повышенной вибрации электрических машин «не электромагнитного характера», такие как небаланс, проблемы подшипников, наличие изогнутого вала, и т. д. в данном разделе методического руководства никак не рассматриваются. По вопросам диагностики этих дефектов в двигателях и генераторах вибрационными методами следует обращаться к соответствующим разделам данного руководства.
Для проведения диагностики различных электромагнитных дефектов в электрических машинах необходимо использовать измерительное оборудование, имеющее достаточно высокие эксплуатационные параметры. Не все приборы, хорошо подходящие для диагностики дефектов механической природы возникновения, такие как небаланс, расцентровка, и т. д., могут быть использованы для анализа технического состояния электрических машин переменного тока.
Для успешной диагностики различных электромагнитных проблем в электрических двигателях и генераторах необходим анализатор спектров вибросигналов с очень высокой разрешающей способностью, с числом спектральных линий, не меньшем, чем 3200, а желательно и лучше. Кроме того, такой прибор должен иметь возможность проводить регистрацию вибрационных сигналов в течение достаточно длительного интервала времени, не менее 10 — 20 секунд. Это необходимо делать для эффективного разделения проблем механической и электромагнитной природы возникновения, что возможно сделать только в момент отключения контролируемого агрегата от питающей сети.
Измерение вибрации на подшипниках электродвигателей и генераторов нужно всегда проводить в трех направлениях — вертикальном, поперечном и осевом, иначе потом будет невозможно провести полную диагностику состояния. Идеальным является синхронная регистрация (не путать с синхронизированной регистрацией, которая гораздо менее эффективна) сразу шести вибросигналов с двух подшипников электрической машины. Обычно это повышает достоверность диагнозов дополнительно не менее чем на 10 %.
3.2.6.1. Описание физических процессов в электрических машинах
Вопросами диагностики текущего технического состояния и поиска дефектов в электрических машинах обычно занимаются специальные электротехнические службы, знакомые с особенностями физических процессов в двигателях и генераторах. Для тех, кто раньше не был практически связан с процедурой оценки состояния электротехнического оборудования, необходимо обязательно ознакомиться со специальной литературой, описывающей основные особенности его работы.
Дело в том, что существует несколько типов электрических машин, процессы в которых значительно отличаются друг от друга. Кроме того, в каждом типе электрических машин существует несколько специфических особенностей, не зная которые очень сложно проводить корректную оценку их технического состояния.
В самом начале данного раздела, на первом этапе описаний, кратко вспомним некоторые основные определения и понятия из минимального, по объему, курса электрических машин. Сделаем это для простоты объяснения причин возникновения вибрации в электрических машинах, а так же для того, чтобы не загромождать эти объяснения в дальнейшем, Знание этих основополагающих понятий совершенно необходимо для проведения корректного диагностирования дефектов электрических машин, для правильного толкования спектрального состава регистрируемых вибрационных сигналов.
По принципу действия различают три основных типа широко применяемых электрических машин:
- Синхронные машины переменного тока, в которых частота вращения ротора совпадает с частотой вращения электромагнитного поля в зазоре. Эти машины могут работать в режимах двигателя и генератора, в практике встречаются и те, и другие.
- Асинхронные машины переменного тока, в которых ротор вращается несколько медленнее. Величина отставания ротора от статора составляет несколько процентов, и характеризуется термином «скольжение». Теоретически также могут работать в режимах двигателя и генератора, но на практике встречаются практически одни двигатели.
- Машины постоянного тока. Это также обратимые электрические машины, допускающие двигательный и генераторный режимы работы. На практике встречаются и те, и другие исполнения машин постоянного тока.
В данном разделе методического руководства будут рассмотрены основные способы диагностики состояния и поиска дефектов состояния электрических машин переменного тока, синхронных и асинхронных, как наиболее распространенных в промышленности и в быту. Электромагнитные проблемы машин постоянного тока очень сложно поддаются диагностике, в основе которой лежит анализ вибрационных сигналов с опорных подшипников, поэтому рассматриваться здесь не будут.
Синхронные и асинхронные машины являются по своему принципу действия обратимыми, т. е. могут работать в как режиме двигателя, так и в режиме генератора. В дальнейшем диагностика дефектов статоров синхронных и асинхронных машин, двигателей и генераторов, не будет подразделяться, т. к. они имеют одинаковые по конструкции статоры. Синхронные машины отличаются от асинхронных только конструкцией ротора, что найдет отражение в специальном подразделе, где будут описаны наиболее часто встречающиеся дефекты короткозамкнутых роторов.
Очень важно уже на самом первом этапе диагностики, заранее, определиться с диапазоном численных значений частоты вращения ротора и электромагнитного поля в зазоре. Для этого необходимо знать оборотную частоту вращения электромагнитного поля статора и оборотную частоту вращения ротора электрической машины переменного тока. Именно они определяют требования к приборам вибрационного контроля.
Максимальная частота вращения ротора электрической машины переменного тока определяется в размерности «обороты в минуту». В иностранной литературе широко используется термин RPM, что является сокращением стандартного параметра «Rotation Per Minute», т. е. те же «обороты в минуту». Эта максимальная частота вращения также является и номинальной, так как в нормальных условиях частота вращения машины переменного тока редко регулируется, а если и регулируется, то практически всегда с использованием преобразователей частоты.
Частота вращения ротора численно равна произведению частоты питающей сети, измеряемой в [Гц], умноженной на переводной коэффициент, равный 60 (количество секунд в одной минуте). В России принят стандарт частоты питающей сети в 50 Гц. Поэтому максимально возможная частота вращения роторов двигателей и генераторов переменного тока составляет 3000 об/мин. При частоте питающей сети в 60 Гц, что являющейся стандартной в Америке и в Японии, максимальная частота вращения ротора машины переменного тока составит 3600 об/мин.
В зависимости от особенностей конструкции статоров машин переменного тока частота вращения электромагнитного поля в зазоре может изменяться. Для определения этой частоты формула определения частоты вращения поля должна быть дополнена еще одним сомножителем «Р», находящимся в знаменателе:
N0 = 60 * F1 / P
Таким образом, частота вращения электромагнитного поля в зазоре электрической машины N0 равняется частному от деления максимальной частоты вращения электромагнитного поля в зазоре на число «пар полюсов статора – Р». Это конструктивный параметр обмотки статора, и он может принимать только целые значения, равные 1, 2, 3, 4, 5 и т. д. При этом частота вращения поля в зазоре электрической машины будет равна соответственно 3000 об/мин, 1500, 1000, 750, 600 и т. д.
При числе пар полюсов, отличном от единицы, частота вращения поля в зазоре электрической машины отлична от частоты питающей сети, причем в меньшую сторону от стандартных 3000 об/мин. Это очень важно учитывать при первой диагностике состояния «мало знакомых» электрических машин по спектрам вибросигналов.
В синхронных электрических машинах переменного тока частота вращения ротора всегда совпадает с частотой вращения электромагнитного поля в зазоре. Именно поэтому такие машины называются синхронными. Такие электрические машины имеют достаточно большую мощность, что связано с особенностями их конструкции. Можно смело утверждать, что «встретить» синхронную машину с мощностью менее 1000 кВт на практике очень сложно. Их мало, но они имеют большую единичную мощность, генераторы достигают мощностей до 800 МВт и более.
В асинхронных машинах переменного тока частота вращения ротора всегда меньше частоты вращения электромагнитного поля в зазоре на небольшую величину, ротор отстает от электромагнитного поля. Это отставание обычно называется скольжением «s» и измеряется в долях от единицы или в процентах. Имеющаяся небольшая разница в частотах вращения поля и ротора называется частотой скольжения ротора, которая измеряется в герцах или в процентах. В диагностике дефектов ротора асинхронного двигателя эта частота имеет большое значение.
Стандартный ряд рабочих частот вращения роторов асинхронных двигателей, в зависимости от числа пар полюсов обмотки статора, можно примерно представить в виде последовательности чисел — 2900 об/мин, 1450 об/мин, 970 об/мин.
Из этого ряда» хорошо видно, что частота вращения ротора асинхронной электрической машины всегда отстает от частоты вращения электромагнитного поля в зазоре электрической машины. Для сравнения напомним, что в синхронных машинах переменного тока, где частота вращения ротора совпадает с частотой вращения поля в зазоре, этот ряд рабочих частот вращения электрических машин составляет 3000, 1500, 1000 об/мин.
Отдельно необходимо остановиться на термине, который практические диагносты достаточно широко используют на практике, но, может быть, не совсем корректно понимают его смысл. В самом общем случае этот термин звучит примерно как «электромагнитные вибрации и электромагнитные гармоники в спектре вибрационного сигнала».
В электрических машинах переменного тока возможно возникновение специфических вибраций двух типов. Конечно, реальных причин повышения вибрации в электродвигателях и генераторах может быть гораздо больше, но при измерении вибрационных сигналов на опорных подшипниках реально зарегистрировать можно только «отклики» от этих двух причин. В другом разделе нашего руководства мы частично затронем некоторые другие аспекты вибрационной диагностики состояния электротехнической составляющей электрических машин, здесь же мы рассмотрим только способы диагностики возможных «механических дефектов» электрических машин.
Для начала дадим определение основным электромагнитным вибрациям, которые можно зарегистрировать на опорных подшипниках синхронных и асинхронных электрических машин. Как мы уже говорили, они могут возникать по нескольким причинам.
Во-первых, это электромагнитные вибрации ферромагнитных сердечников и стальных конструктивных элементов электротехнического оборудования, по которым во время работы оборудования протекает переменный магнитный поток.
Эти вибрации возникают за счет специфического процесса, который в литературе называется магнитострикцией. Этот эффект обусловлен тем, что при перемагничивании ферромагнитных материалов сердечника происходит изменение внутренней ориентации элементарных намагниченных частиц, доменов. При каждом перемагничивании сердечника происходит поворот доменов на 180 градусов, что в итоге и приводит к небольшому «линейному расширению» ферромагнитного материала. Чем больше величина магнитного потока в сердечнике, тем больше размеры элементарных доменов в ферромагнитном сердечнике, и тем больше будут вибрации сердечника электрической машины.
Поскольку перемагничивание сердечника магнитным потоком происходит дважды за один период питающей сети, то и частота вибрации, обусловленная эффектом магнитострикции, равняется удвоенной частоте питающей сети, т. е. она равняется 100 Гц. Мы обращаем дополнительное внимание читателя на то, что вне зависимости от оборотной частоты вращения ротора электрической машины, частота вибрации сердечника (пакета стали статора) всегда равняется 100 Гц.
Если оборотная частота ротора равняется 50 Гц, то гармоника электромагнитной вибрации располагается на спектре «в том месте», где может находиться вторая гармоника оборотной частоты. Если же оборотная частота ротора равняется, например, 25 Гц, то гармоника электромагнитной вибрации на спектре будет располагаться на месте четвертой гармоники оборотной частоты. Этими двумя простыми примерами мы еще раз подчеркнули, что электромагнитная гармоника не связана с частотой вращения ротора электрической машины, а зависит только от частоты питающей сети.
Во-вторых, вибрации в электрической машине вызываются специфическими электродинамическими силами, которые в литературе принято называть «амперовыми силами», т. к. их величина определяется по закону Ампера. Смысл закона Ампера звучит следующим образом – на два проводника с током действует сила взаимного притяжения, пропорциональная квадрату протекающего по проводникам тока, и обратно пропорциональная расстоянию между проводниками. Если направление тока в обоих проводниках одинаковое, то проводники притягиваются друг к другу. Если токи в параллельных проводниках текут в разные стороны, то проводники отталкиваются друг от друга.
Самое важное для нас в этом законе заключается в том, что в числителе стоит произведение токов в проводниках, т. е. квадрат тока промышленной частоты. Из тригонометрии следует известное соотношение, гласящее, что квадрат синусоидального сигнала есть другой гармонический сигнал, но имеющий удвоенную частоту. Таким образом, мы аналогично получаем, что сила электродинамического воздействия между двумя проводниками с синусоидальными токами промышленной частоты имеет удвоенную частоту, относительно частоты питающей сети.
Таким образом, мы определили, что вибрации электрической машины, не вызванные механическими проблемами, имеют удвоенную частоту относительно частоты питающей сети, т. е. равную 100 Гц. Это определение относится как к электромагнитным причинам повышенной вибрации, возникающим в сердечниках электрических машин силами магнитострикции, так и к электродинамическим силам взаимодействия проводников друг с другом, возникающим при протекании токов по обмоткам электрической машины.
Все это можно сказать несколько иначе. Основная, или, говоря терминами, принятыми в вибрационной диагностике, оборотная частота электромагнитных сил и вибраций в электрической машине равна удвоенной частоте питающей сети. Это совершенно отдельная сила, не связанная с частотой вращения ротора, что может быть легко выяснено при помощи средств кепстрального анализа. Она просто имеет частоту, равную удвоенной частоте питающей сети. Гармоники основной частоты этой силы имеют значения 200 Гц, 300, 400 и т. д. В чистом виде эта сила очень явно проявляется в статическом электрооборудовании. Примером этого является трансформатор, в котором гармоника вибрации с частотой питающей сети в 50 Гц практически отсутствует, а максимальное значение имеет гармоника вибрации с частотой 100 Гц.
Есть еще и третья (по порядку нашего повествования, а не по порядковому номеру в спектре) гармоника вибрации, имеющая электромагнитную природу возникновения. Она называется зубцово – пазовой гармоникой. Она не всегда столь значительна, как первые две, но сказать о ней все равно нужно.
Зубцово – пазовая гармоника вызывается особенностями конструктивного исполнения электрической машины переменного тока. У нее на статоре и на роторе обмотка всегда укладывается в пазах. При вращении ротора в зазоре статора возникает периодическое чередование ферромагнитных зубцов и пазов на статоре и роторе. Это приводит к модуляции магнитного потока в зазоре частотой, связанной с количеством пазов на роторе и статоре электрической машины.
При разработке электрических машин принимаются все меры, чтобы исключить влияние зубцово — пазовой структуры на работу машины. На статоре и роторе всегда различное число пазов, на роторе применяется «скос» пазов, когда ось паза идет не вдоль оси ротора, а как бы немного закручена вокруг оси и т. д. Тем не менее, существуют типы электрических машин, в которых «пазовая» гармоника оборотной частоты ротора является явно выраженной на спектре.
Необходимо хорошо понимать, что все эти три гармоники в спектре вибросигнала, имеющие электромагнитную природу возникновения, не всегда являются признаками наличия дефектов в контролируемой электрической машине, они практически всегда сопровождают ее работу. Признаком наличия дефекта обычно является увеличение амплитуд электромагнитных гармоник выше некоторого уровня, являющегося порогом нормального состояния оборудования.
Основной признак того, что анализируемая гармоника в спектре сигнала вибрации имеет электромагнитную причину возникновения — мгновенное исчезновение этой гармоники сразу после отключения электрической машины от сети.
Очень важным является то, что диагностика причин повышенной вибрации электрических машин должна проводиться при возможно большей нагрузке двигателя. Если исследования будут проводиться на холостом ходу, или же при небольшой нагрузке, то диагностика дефектов будет затруднена.
3.2.6.2. Сводка электромагнитных проблем ротора и статора
Приведем краткую сводку по электромагнитным проблемам электрических машин, которые можно эффективно диагностировать по спектрам вибросигналов. Здесь же приведем все характерные признаки каждого вида дефекта.
Для описания дефектов здесь и далее будем использовать термины:
F1 — частота питающей сети, в России равна 50 Гц.
FЭМ — частота электромагнитных сил в электрических машинах, равна удвоенной частоте сети, в России 100 Гц.
N0 — частота вращения поля в зазоре электрической машины, численно равна частному от деления 3000 на число пар полюсов Р, которое может принимать целые значения от единицы и более (об/мин).
F0 — частота электромагнитного поля в зазоре, Гц.
FP — собственная частота вращения ротора электрической машины. Для синхронных машин она равна частоте вращения поля. Для асинхронных машин она меньше на величину скольжения ротора.
FP = F0 (1 — s)
s - скольжение ротора относительно электромагнитного поля в асинхронных машинах, безразмерная величина, численно равняется разнице между частотой вращения поля в зазоре и частотой вращения ротора, отнесенной к частоте вращения поля в зазоре
s = (N0 — FP) / N0
FП — зубцово — пазовая частота вибрации, численно равная произведению числа пазов (на роторе или статоре) на частоту электромагнитного поля в зазоре. Может быть повышенной относительно статора, относительно ротора, может быть разностная или суммарная частота биений пазовых частот ротора и статора.
Наиболее важные проблемы статора, которые можно диагностировать на основе анализа вибрационных сигналов:
- Ослабление прессовки пакета стали, обрыв или замыкание стержней, витков, или даже секций в обмотке статора. Соответствующие вибрации проявляются на частоте действия электромагнитных сил FЭМ, равной удвоенной частоте питающей сети. Особое внимание при диагностике такого дефекта следует уделять наличию дробных гармоник электромагнитной частоты — 1/2, 3/2, 5/2 и т. д. от основной частоты. По значению частоты эти гармоники соответствуют основной и нечетным гармоникам питающей сети. Появление этих гармоник в спектре вибрационного сигнала говорит об опасной степени развития дефекта, о необходимости оперативного принятия соответствующих мер.
- Эксцентриситет, эллипсность внутренней расточки статора относительно оси вращения ротора. Возникает обычно как дефект монтажа подшипниковых стоек, дефект состояния подшипниковых щитов или при общей деформации корпусных элементов самого статора. В вибрации проявляется на частоте вращения поля в зазоре, а также и на частоте действия электромагнитных сил в электрической машине, равной 100 Гц. Иногда сопровождается появлением боковых гармоник вблизи частоты 100 Гц. Дефект обычно сопровождается неравенством вертикальной и поперечной составляющих соответствующих гармоник. Пространственный максимум гармоник соответствует направлению эксцентриситета смещения оси статора. Наиболее просто направление смещения оси статора относительно оси ротора диагностируется при снятии «розы вибраций», когда датчик последовательно перемещается по огибающей вокруг подшипника со смещением при каждом измерении на угол 30 — 45 градусов.
- Неправильный взаимный осевой монтаж активных пакетов ротора и статора. Иногда для данного дефекта используется термин: «неправильная установка электромагнитных осевых разбегов». При работе электрической машины, в результате сил магнитного притяжения, пакет ротора всегда стремится к положению точно под пакетом статора.
Если этому стремлению будут препятствовать неправильно смонтированные в осевом направлении подшипники, то в них будут возникать компенсирующие осевые усилия, которые и вызовут осевые вибрации подшипников. Подшипники достаточно быстро нагреются и выйдут из строя. Иногда ротор двигателя «утягивается» в осевом направлении валом механизма, что возможно при неправильном осевом монтаже приводного механизма, сопровождающемся малой осевой подвижностью в соединительной муфте.
Основные проблемы ротора, диагностируемые по вибрации:
- Эксцентриситет внешней поверхности ротора относительно оси его вращения. На спектре вибросигнала этот дефект проявляется в усилении первой гармоники частоты вращения ротора. Усиливается частота действия электромагнитной силы, вокруг которой иногда появляются боковые гармоники, сдвинутые друг от друга на частоту скольжения ротора, умноженную на число полюсов.
- Обрыв или нарушение контакта в стержнях или кольцах «беличьей клетки» в асинхронном двигателе. Обычно проявляется на спектре вибрационного сигнала вблизи частоты вращения вала ротора. Кроме того, этот дефект всегда сопровождается появлением вблизи основной гармоники частоты вращения ротора боковых гармоник, сдвинутых относительно гармоники частоты вращения ротора на интервал, равный произведению частоты скольжения на число полюсов двигателя. Очевидно, что этот дефект присущ только асинхронным двигателям, а в синхронных машинах он никак не проявляется.
- Ослабление прессовки всего пакета стали ротора или только в области зубцов. Сопровождается усилением второй гармоники питающей сети или, при ослаблении стали в области зубцов, появлением пазовой частоты ротора с боковыми полосами, сдвинутыми друг от друга на частоту, равную двойной питающей частоте. Такой дефект на практике диагностируется достаточно сложно, так как его спектральные признаки напоминают признаки других дефектов, и проявляются не очень сильно, чаще всего неявно.
3.2.6.3. Диагностика электромагнитных проблем статора
При всех проблемах статора синхронной или асинхронной электрической машины, имеющих в своей основе первопричину электромагнитной природы, в спектре вибросигнала возникает весьма специфическая картина. В основном она сопровождается возникновением высокой амплитуды основной гармоники на частоте электромагнитных процессов FЭМ. Как уже неоднократно говорилось выше, ее частота равна удвоенной частоте питающей сети, т. е. всегда равняется 100 Гц. Еще раз напоминаем, что эта частота никак не связана с оборотной частотой вращения ротора.
Этот эффект достаточно хорошо объясняется с точки зрения физики происходящих в стали статора процессов. Силы взаимного притяжения, действующие между «распрессоваными» листами электротехнического железа или элементами крепления пакета стали, имеют максимум амплитуды дважды за один период изменения питающей сети — во время абсолютного минимума и максимума магнитного потока. Чем сильнее будет распрессован пакет статора электрической машины, тем большую амплитуду в спектре будет иметь основная электромагнитная гармоника.
Аналогично выглядит картина взаимодействия между элементами обмотки статора. Математически это объясняется тем, что электромагнитные силы пропорциональны квадрату тока или магнитного потока. Поскольку и тот и другой синусоидальны, то их произведение также пропорционально синусоиде, но изменяющейся уже с удвоенной частотой, относительно исходной частоты питающей сети.
На спектре вибрационного сигнала, приведенном на рисунке 3.2.6.1., картина появления электромагнитных проблем в статоре выражается в усилении пика на электромагнитной частоте. При значительных дефектах в стали могут появиться и вторая (200 Гц) гармоника электромагнитной частоты FЭМ, и даже третья (300 Гц).
Кроме того, в спектре может появиться также целый ряд дробных гармоник, имеющих кратность 1/2 от электромагнитной гармоники. В данной ситуации, по своей частоте, эти гармоники будут численно соответствовать нечетным целым гармоникам частоты питающей сети. Такое совпадение двух семейств гармоник усложняет их разделение частоте, требуя большей внимательности и применения дополнительных диагностических средств.
Очень важно хорошо понимать и помнить основное различие синхронных и асинхронных электрических машин, значительно влияющих на диагностику дефектов по спектрам вибрационных сигналов.
Гармоники вибрации от электромагнитных процессов в статоре синхронной машины, по своей физической природе, являются синхронными относительно частоты вращения ротора. В асинхронном двигателе эти же семейства гармоник являются несинхронными, т. к. частота вращения ротора и частота питающей сети не кратны между собой, а различаются между собой пропорционально частоте скольжения. В данном определении под коэффициентом кратности соотношений частот мы понимаем влияние числа пар полюсов обмотки, уложенной в пазах статора.
Ослабление прессовки активного железа статора в электрической машине обуславливается, в основном, двумя часто встречающимися причинами — или общим ослаблением элементов крепления железа статора, или же явлением «отслоения» крайних листов и пакетов стали.
При этих локализациях дефекта железа статора важную роль начинает играть место установки вибродатчика. Чем ближе он устанавливается к дефектному месту пакета статора, чем короче будет путь прохождения «полезного» вибрационного сигнала, тем более корректно можно будет проводить диагностирование и, достаточно часто, удается даже локализовать место проявления дефекта. Наиболее эффективно датчик вибрации устанавливать не на опорных подшипниках ротора, а непосредственно на корпусе сердечника статора, а еще лучше и на самом пакете активной стали.
Аналогично обстоит дело и с особенностями проявления в спектрах вибросигналов различных дефектов обмоток статора, но поиск их и локализация происходят гораздо сложнее. Более подробно мы рассмотрим этот вопрос в другом разделе данного руководства, однако основные требования к месту установки датчика вибрации останутся прежними – как можно ближе к возможному месту возникновения предполагаемого дефекта пакета или обмотки статора.
Самое главное, что нужно помнить при диагностике дефектов, что различить тип диагностируемого в статоре электрической машины дефекта, имеет — ли он «чисто электрическую природу возникновения», или же он обусловлен одними «магнитными проблемами», методами спектральной вибрационной диагностики практически невозможно. Единственный, достаточно корректный признак наличия короткозамкнутого витка в обмотке статора (электрическая причина возникновения повышенных вибраций) — наличие боковой гармоники вблизи частоты 100 Гц, и ее чаще всего обнаружить не удается. В большинстве практических случаев необходимо применение более специализированных методов диагностики состояния электрических машин.
3.2.6.4. Проблемы эксцентричности пакета статора
Эксцентриситет статора возникает чаще всего как дефект изготовления «шихтованного» пакета стали статора, или как дефект монтажа статора. Очень высока вероятность возникновения эксцентриситета статора в процессе монтажа электрической машины, особенно, если статор и подшипниковые опоры монтируются раздельно. Данный дефект статора может возникнуть в результате ослабления фундамента или как итог тепловых и иных деформаций в агрегате и фундаменте.
Для примера на рисунке 3.2.6.2. приведен спектр вибросигнала, зарегистрированного на подшипнике асинхронного двигателя, имеющего номинальную частоту вращения ротора, равную n0 = 1480 об/мин. Этот спектр соответствует наличию в электрической машине достаточно развитого дефекта типа «эксцентриситет статора».
Эксцентриситет статора приводит, с точки зрения физики протекания электромагнитных процессов, к периодическому изменению магнитной проводимости воздушного зазора, к ее пульсации, или, говоря иными словами, к ее модуляции. Эта пульсация происходит с удвоенной частотой сети, т. е. с частотой воздействия электромагнитных сил.
Удвоение частоты пульсации относительно питающей сети возникает из — за того, что мимо зоны окружности статора, где произошло изменение величины зазора, поочередно проходят и северный, и южный полюса электромагнитного поля, вращающегося в зазоре электрической машины. Удвоенные пульсации магнитной проводимости приводят к такой же пульсации магнитного потока и, как результат, к пульсации электромагнитной силы и вибрации с частотой 100 Гц.
Дополнительно несколько возрастает амплитуда гармоники на частоте вращения электромагнитного поля в зазоре. Это позволяет в асинхронных двигателях хорошо дифференцировать эксцентричность статора от эксцентричности ротора, где вибрация идет с частотой вращения ротора. Для выявления этого различия необходимо наличие спектроанализатора с хорошим разрешением.
Для разделения эксцентриситетов статора и ротора в синхронной машине между собой, при диагностике следует помнить, что эксцентриситет статора неподвижен в пространстве и различен по амплитуде вибрации в направлениях измерения вибрации. Благодаря такой локализации эксцентриситет статора приводит к возникновению направленной в пространстве вибрации. Это можно выявить при помощи последовательного перемещения вибродатчика по контролируемому подшипнику «вокруг вала». Эксцентриситет же ротора всегда «вращается» вместе с ротором, поэтому он не имеет стационарного максимума при определенном значении угла установки датчика. При эксцентриситете статора такой максимум явно выражен.
Для исключения проявления эксцентриситета в вибрации электрических машин необходимо, чтобы воздушный зазор между статором и ротором должен быть неизменным по окружности. Обязательно должно соблюдаться требование к качеству взаимного монтажа статора и ротора, что различие в величине воздушного зазора вдоль окружности не должно превышать значение в 5% для асинхронных двигателей и генераторов, и не превышать 10 % для синхронных двигателей. Значение этого параметра жестко контролируется при помощи специальных щупов при монтаже электрической машины. Такая процедура измерения должна производиться при нескольких взаимных положениях ротора и статора.
3.2.6.5. Эксцентричный ротор
Это достаточно часто встречающаяся в практике причина повышенной вибрации асинхронных электрических машин. У синхронных электрических машин переменного тока этот дефект менее заметен из-за больших рабочих зазоров.
При наличии эксцентриситета ротора в характере распределения электромагнитного поля в зазоре двигателя возникает ряд особенностей. Плотность электромагнитного поля вдоль окружности зазора изменяется вместе с поворотом ротора. Это приводит, из-за переменного зазора, к неравномерности тягового усилия двигателя. При совпадении оси поля статора с зоной увеличенного зазора тяговое усилие несколько уменьшается, при этом возрастает величина частоты скольжения. При смещении оси поля в зону меньшего зазора тяговое усилие растет, частота скольжения падает. При числе пар полюсов статора, большем единицы, такой процесс повторяется «Р» раз.
Если бы мы имели очень чувствительные приборы для измерения частоты вращения ротора, то мы бы обнаружили следующее. В интервале перемещения ротора от зоны, с увеличенным зазором в сторону зоны, с уменьшенным зазором, ротор бы ускорился в своей частоте вращения на небольшое значение. На интервале перехода ротора обратно, к зоне с увеличенным зазором, ротор бы замедлился на то же значение. Конечно, таких приборов у нас нет, но это видно на спектре с большой разрешающей способностью, где появляются признаки таких изменений скорости.
На спектре вибросигнала, показанном на рисунке 3.2.6.3., вокруг основной частоты вращения ротора, должны появиться симметрично расположенные боковые пики, гармоники, напоминающие зубцы короны. Симметрия пиков относительно основной частоты достаточно хорошо понятна — это следствие «мини ускорений и мини замедлений» частоты вращения ротора вокруг своего среднего значения. Аналогичные зубцы, даже еще большей интенсивности, появляются и вокруг пика электромагнитной силы, на частоте, равной второй гармонике питающей сети.
Необходимо пояснить причины проявления эксцентричности ротора на этой частоте.
Вращение эксцентричного ротора модулирует проводимость зазора с удвоенной частотой. При числе пар полюсов, равном единице частота вращения поля равна 50 Гц, удвоенная частота сети, частота электромагнитной вибрации равна 100 Гц. Эксцентричность ротора приводит к модуляции электромагнитной силы. При уменьшении числа пар полюсов частота вращения поля в зазоре уменьшится в Р раз. Переменный зазор ротора за один свой оборот будет модулировать электромагнитную силу 2 х Р раз больше частоты своего вращения, что как раз и соответствует частоте электромагнитной силы.
Эксцентричный ротор генерирует вокруг FP и вокруг FЭМ семейства гармоник, представляющих из себя пики, сдвинутые на одинаковый шаг по частоте. Сдвиг между этими гармониками равен произведению частоты скольжения на число полюсов обмотки статора
DF = FS * 2 * P
Причина такого шага между зубцами на спектре по частоте достаточно корректно объясняется. Частота скольжения есть разностная частота биений между частотой вращения поля и частотой вращения ротора. В течении одного оборота эксцентриситет ротора влияет «2 х Р» раз на тяговое усилие двигателя, которое связано с частотой скольжения ротора. Сама частота скольжения FS иногда видна на спектре, на начальном участке, на самой низкой частоте. Она проявляется обычно в диапазоне от 0,3 до 2,0 Гц. Для ее регистрации нужен низкочастотный датчик.
Необходимо помнить, что во временном сигнале эксцентриситет ротора проявляется в виде пульсирующей вибрации, средняя частота которой располагается в диапазоне частот (или вблизи него) между FЭМ и гармоникой оборотной частоты ротора, по частоте чуть меньшей, чем у электромагнитной силы (порядковый номер этой гармоники ротора равен удвоенному числу пар полюсов статора). Разделить эти гармоники на спектре можно только при высоком частотном разрешении используемого анализатора вибрационных сигналов.
Эксцентричность ротора обычно проявляется и в вертикальной, и в поперечной проекции вибрации. Иногда ее удается обнаружить даже и в осевой проекции. Так бывает при наличии эксцентричности ротора не по всей его длине, а только в районе одного, если смотреть вдоль оси ротора, края пакета электротехнической стали.
Эксцентричность ротора часто носит нестационарный характер, когда в спектре работающего двигателя имеется характерная картина, а практические измерения зазора не подтверждают диагноз. Причина здесь обычно в термических процессах, когда по тем или иным причинам ротор несимметрично нагревается, изгибается и дает картину эксцентриситета.
После останова двигателя, в процессе его разборки для измерения зазора, температуры быстро выравниваются и диагноз не подтверждается. Часто так бывает при обрывах стержней или «частичных задеваниях» ротора об неподвижные элементы, когда ротор так же начинает односторонне нагреваться.
3.2.6.6. Неправильный осевой монтаж двигателя
Принцип действия всех электрических машин переменного тока примерно одинаков - вращающий момент создается за счет взаимодействия магнитного поля статора с магнитным полем ротора (синхронные машины) или с роторными проводниками с током (асинхронные машины).
Простейший аналог, характеризующий работу синхронной электрической машины переменного тока – притяжение двух постоянных магнитов, из которых один есть вращающееся магнитное поле статора, а второй жестко зафиксирован на роторе. В асинхронной машине переменного тока все выглядит немного иначе – вращающееся магнитное поле статора увлекает за собой проводники с током, которыми являются стержни короткозамкнутой клетки ротора.
В синхронном электродвигателе машине энергия подается одновременно в ротор от источника постоянного тока, и в статор из питающей промышленной сети. В асинхронном электродвигателе внешняя энергия подается только из питающей сети в статор, поэтому для работы двигателя часть энергии должна быть передана (трансформирована) через зазор во вращающийся ротор. Только в этом случае возникает электромагнитное взаимодействие между полями ротора и статора. Наличие передачи энергии через зазор объясняет необходимость максимального уменьшения воздушного зазора в асинхронных машинах, а так же их большую чувствительность этого типа электрических машин к нелинейности величины зазора между ротором и статором.
Сила взаимного притяжения между ротором и статором является векторной величиной и состоит из трех составляющих — радиальной составляющей, касательной, полезной, и осевой. Касательная составляющая электромагнитной силы в зазоре является полезной, т. к. именно она создает вращающий момент. Радиальная составляющая есть сила притяжения ротора к статору и при постоянстве величины воздушного зазора эти силы, диаметрально противоположно, взаимно компенсируются.
Рассмотрим чуть подробнее осевую составляющую сил взаимного притяжения в зазоре электрической машины. Если магнитные сердечники ротора и статора в осевом направлении расположены непосредственно друг против друга, то и суммарная осевая составляющая силы электромагнитного притяжения ротора и статора равна нулю. Иначе будет происходить в том случае, когда произойдет взаимное осевое смещении сердечников ротора и статора. При этом итоговая осевая сила не будет равна нулю, она будет стремиться вернуть ротор в исходное нейтральное положение. Чем больше будет величина осевого смещения, тем больше будет величина осевого усилия, втягивающего ротор внутрь статора.
Величина допустимого свободного осевого перемещения ротора относительно статора определяется особенностями монтажа опорных подшипников ротора. Она максимальна при использовании подшипников скольжения, и минимальна при использовании подшипников качения, особенно радиально – упорного типа.
Если осевая подвижность ротора достаточна для перемещения его в нейтральное положение, то проблем с увеличением вибраций не будет. Если же возникнет препятствие к такому осевому перемещению, то на нем возникнет значительная осевая вибрация. Частота этой вибрации, как это показано на рисунке 3.2.8.4., обычно равняется частоте электромагнитных сил. Иногда гармоники вибрации возникают и частоте вращения ротора, это зависит от состояния поверхностей в месте препятствии к осевому смещению. Наиболее часто такая проблема возникает у асинхронных электродвигателей с подшипниками качения, осевая подвижность которых почти нулевая.
Осевая вибрация в электродвигателях, оборудованных подшипниками качения, обычно возникает при следующих основных причинах:
- При осевом смещении магнитных пакетов статора и ротора, обусловленном особенностями их взаимного первичного монтажа.
- При неполной посадке подшипников на вал, или в подшипниковых щитах, после проведения ремонтных работ.
- При смещении подшипниковых щитов, или посадочных мест подшипников после выполнения ремонтных и восстановительных работ.
Вне зависимости от причины возникновения повышенных осевых усилий на опорные подшипники качения, это довольно опасный дефект. Большинство подшипников качения не предназначены для компенсации осевых усилий, и поэтому в такой ситуации достаточно быстро выходят из строя.
У подшипников скольжения обычно существует больший конструктивный «осевой разбег», поэтому осевые вибрации в них возникают гораздо реже. Кроме того, подшипники скольжения обычно используются в крупных синхронных электрических машинах, в которых вопрос компенсации осевых усилий, по причине наличия больших воздушных зазоров, стоит менее остро.
Тем не менее, и в таких условиях осевая подвижность подшипников скольжения может оказаться недостаточной для компенсации дефектов монтажа. В таком случае возникает осевая вибрация, обычно выражающаяся в возникновении трения галтели вала о торцевую поверхность подшипникового вкладыша.
Для устранения осевой вибрации в насосных агрегатах необходимо корректно и комплексно выставлять при монтаже все три так называемых в практике «осевых разбега», расположенных в насосе, в муфте и в электродвигателе.
Достаточно часто вал электродвигателя «утягивается в осевые вибрации» валом насоса при дефектах системы осевой разгрузки рабочего колеса насоса. Парадокс диагностики — дефект в насосе, а вибрация в двигателе.
На практике бывают случаи, когда для борьбы с осевыми вибрациями ротор в подшипниках скольжения, перед пуском, принудительно смещают в осевом направлении, например, при помощи лома, и после этого двигатель некоторое время хорошо работает. С течением времени, в процессе работы, ротор смещается обратно, и осевые вибрации агрегата снова возрастают до прежнего значения.
3.2.6.7. Обрыв стержней ротора
Наиболее распространенным конструктивным исполнением обмотки ротора асинхронного двигателя является короткозамкнутый ротор с «беличьей клеткой». У такого ротора в пазах, без изоляции, забиваются медные или латунные стержни, или же пазы полностью залиты сплавом алюминия. Концы стержней, по торцам ротора, объединяются замыкающими кольцами из такого же материала.
В процессе работы, а особенно при пуске асинхронного электродвигателя, по стержням беличьей клетки протекает большой ток, и они сильно нагреваются. Частой причиной выхода из строя двигателя является нарушение контакта стержней с замыкающими кольцами, называемые в практике «отгоранием стрежней». Появление такого дефекта в отдельных стержнях приводит к увеличению нагрузки на оставшиеся стержни, дополнительному перегреву их, и также к последующему «отгоранию», и т. д. Весь этот лавинообразный процесс разрушения обмотки ротора сопровождается потерей мощности электродвигателя, к его постепенному перегреву и выходу из строя.
Выявление начальных признаков повреждений стержней клетки ротора является очень актуальной задачей и позволяет повысить надежность работы асинхронных двигателей с короткозамкнутой клеткой на роторе.
Рассмотрим особенности физических процессов и вибрационных признаков этого в роторе, имеющем характерные признаки начальной стадии данного дефекта. Будем считать, что повредился один стержень короткозамкнутой клетки.
Необходимо сразу же сказать, что спектр вибрации асинхронного электродвигателя с отгоревшим стержнем во многом похож на спектр вибрации двигателя, имеющего эксцентричный ротор. На первый взгляд между этими дефектами мало общего, но при ближайшем рассмотрении можно выявить причины возникновения сходства вибрационных сигналов, зарегистрированных на опорных подшипниках.
Как и при эксцентричном роторе, отгоревший стержень приводит к модулированию величины тягового усилия двигателя. В момент прохождения зоны отгоревшего стержня мимо электромагнитного полюса (скорее наоборот, т. к. поле асинхронного электродвигателя обгоняет ротор) тяговое усилие импульсно уменьшиться, ротор чуть-чуть замедлится. В это время под полюс поля подойдет зона бездефектного стержня, в нем за счет возросшего скольжения будет несколько больший ток, тяговое усилие также импульсно возрастет, и ротор чуть-чуть ускорится.
Эти импульсные мини ускорения и мини замедления ротора на спектре будут характеризоваться возникновением боковых зубцов вокруг основной гармоники частоты вращения ротора. Такой спектр для двигателя с частотой вращения ротора 2920 об/мин показан на рис 3.2.6.5. Понятно, что зубец (гармоника) с чуть меньшей частотой будет соответствовать моменту времени с замедлением, а зубец (гармоника) с чуть большей частотой будет принадлежать участку времени с ускорением ротора.
Сразу же напрашивается аналогия, что если поврежденных стержней в роторе будет не один, а два, то боковых гармоник будет по две с каждой стороны оборотной частоты, если будет три дефектных стержня – три пары боковых гармоник, и так далее. Это так, и не так. Примерно в половине практических случаев такой эффект соответствия количества дефектных стержней и боковых гармоник будет соблюдаться, а в половине случаев такого количественного соответствия не будет.
Корректное описание такой особенности картины спектрального отображения «дефектных» стержней на спектре вибрационных сигналов является очень сложным, и мы его здесь опустим. Мы ограничимся простой констатацией факта, что если боковых гармоник на спектре более двух (пар), то на роторе находится больше двух отгоревших стержней, или, говоря точнее, стержней с дефектами контакта. Если боковых гармоник всего две, то количество стержней с дефектами точно не определено.
Разделить две причины повышенной вибрации, о которых мы начали рассуждение, это эксцентриситет ротора и отгоревшие стержни беличьей клетки, возможно, но только при наличии у диагноста «хорошего анализатора спектров вибрационных сигналов». В данном случае речь идет о хорошем спектральном разрешении прибора, он должен рассчитывать спектры с разрешением не хуже 3200 частотных линий. В этом случае дефекты можно разделить, учитывая особенности различия их спектрах вибрационных сигналов.
Это следующие различия:
- Характерная «корона» из зубцовых гармоник вокруг пика электромагнитной частоты FЭМ проявляется на спектре различно — при эксцентриситете ротора она имеется во всех режимах работы диагностируемой электрической машины. При наличии в роторе дефекта типа «дефектный стержень», корона на спектре появляется только при значительной нагрузке электрической машины, на холостом ходу она отсутствует.
- При эксцентриситете ротора «корона» практически симметрична по величинам зубцовых гармоник относительно центрального пика, а при дефектах стержней пик на меньшей частоте всегда меньше «зеркального» пика на большей частоте. Этот факт достаточно хорошо сообразуется с картиной физических процессов. Уменьшение скорости происходит при нормальном скольжении и нормальном токе в последнем (перед дефектным) «хорошем» стержне клетки. Ускорение же ротора происходит при увеличенном скольжении, большем токе в первом «хорошем» стержне и, как результат, с большим ускорением.
- За счет колебательного «успокоения» пульсации частоты вращения ротора, после прохождения стержня с дефектом, что может возникать при определенных параметрах нагрузки на валу электродвигателя, на спектре вибрационного сигнала может возникнуть несколько гармоник частоты вращения ротора, и обычно все они окружены «коронами». Такая же картина может возникать при наличии механических или электромагнитных ослаблений в электрической машине. Параметр «электромагнитное ослабление» раскрывать мы не будем из-за его специфичности, оставив его для исследования специалистам по электрическим машинам.
В качестве численного ограничения степени проявления этого дефекта можно считать, что «короны» у исправного двигателя быть не должно. Если она появилась, и наибольший пик «короны» превысил 10 % от центрального пика — вероятность существования отгоревших стержней в обмотке ротора очень большая. Для контроля количественного значения признаков этого дефекта лучше использовать спектры с логарифмической шкалой по амплитуде. Если на нем пики «короны» будут меньше основного пика менее, чем на 20 dВ, то предполагаемый дефект имеет место.
В заключение, подчеркивая особенности диагностики данной причине повышенной вибрации, необходимо еще раз указать, что такая диагностика возможно только с применением анализаторов спектров с высокой разрешающей способностью. Это нужно для разделения на спектре частот вращения поля, ротора и боковых гармоник. Центральный пик «короны» должен соответствовать частоте вращения ротора, а не быть равным частоте вращения поля в зазоре.
3.2.6.8. Дефекты зубцово — пазовой структуры
Такая неисправность не очень часто встречается в практике, но, тем не менее, ее можно достаточно просто описать и успешно диагностировать.
Условно эту неисправность можно представить в виде ротора, у которого отсутствует один ферромагнитный зуб. Это приводит к тому, что мимо пазов статора перемещается «магнитный непериодический» элемент, наводящий в обмотке статора импульсы, число которых за один оборот будет численно равно числу пазов на статоре. На спектре вибрационного сигнала это будет представлено пиком на частоте, равной произведению частоты вращения ротора на число пазов статора.
Не вдаваясь в тонкости физического описания, следует также сказать, что дефектный зуб будет модулировать и электромагнитную силу статора. Это будет происходить потому, что дважды за свой один оборот вращающееся поле «будет натыкаться» на дефект магнитной проводимости воздушного зазора двигателя, на «отсутствующий» зуб ротора. На спектре вблизи пика зубцовой частоты появятся два зеркально расположенных пика, сдвинутых относительно своего «главного пика» на частоту электромагнитной силы FЭМ, как уже неоднократно говорилось равную удвоенной частоте питающей сети.
Наиболее сложным для диагностики будет спектр вибрации при наличии магнитных дефектов на роторе и статоре одновременно, причем дефектов множественных. На спектре будут присутствовать зубцовые частоты ротора и статора, а также будут частоты их биения, зашумленные множественными «зеркальными» пиками.
«Положительным» при этом будет то, что при таком дефекте обычно сильно падает тяговое усилие, возрастает потребляемый ток и двигатель очень быстро выходит из строя, обычно раньше, чем персоналу удается записать спектры и выявить множественный магнитный дефект методами вибрационной диагностики.
Приборы нашего производства для диагностики электромагнитных дефектов
- ViAna-4 – универсальный 4-хканальный регистратор и анализатор вибросигналов, диагностика электромагнитных дефектов по току
Рабочие характеристики асинхронного двигателя — Инструкции по эксплуатации (разное).
Рабочие характеристики асинхронного двигателя представляют собой графически выраженные зависимости частоты вращения n2, КПД η, полезного момента (момента на валу) М2, коэффициента мощности cos φ, и тока статора I1 от полезной мощности Р2 при U1 = const f1 = const.
Скоростная характеристика n2 = f(P2). Частота вращения ротора асинхронного двигателя n2 = n1(1 — s).
Скольжение s = Pэ2/Pэм, т. е. скольжение асинхронного двигателя, а следовательно, и его частота вращения определяются отношением электрических потерь в роторе к электромагнитной мощности. Пренебрегая электрическими потерями в роторе в режиме холостого хода, можно принять Рэ2 = 0, а поэтому s ≈ 0 и n20 ≈ n1.
По мере увеличения нагрузки на валу асинхронного двигателя отношение s = Pэ2/Pэм растет, достигая значений 0,01 — 0,08 при номинальной нагрузке. В соответствии с этим зависимость n2 = f(P2) представляет собой кривую, слабо наклоненную к оси абсцисс. Однако при увеличении активного сопротивления ротора двигателя r2′ угол наклона этой кривой увеличивается. В этом случае изменения частоты асинхронного двигателя n2 при колебаниях нагрузки Р2 возрастают. Объясняется это тем, что с увеличением r2′ возрастают электрические потери в роторе.
Рис. 1. Рабочие характеристики асинхронного двигателя двигателя
Зависимость М2 =f(P2). Зависимость полезного момента на валу асинхронного двигателя М2 от полезной мощности Р2 определяется выражением M2 = Р2/ ω2 = 60 P2/ (2πn2) = 9,55Р2/ n2,
где Р2 — полезная мощность, Вт; ω2 = 2πf 2/ 60 — угловая частота вращения ротора.
Из этого выражения следует, что если n2 = const, то график М2 =f2(Р2) представляет собой прямую линию. Но в асинхронном двигателе с увеличением нагрузки Р2 частота вращения ротора уменьшается, а поэтому полезный момент на валу М2 с увеличением нагрузки возрастает не сколько быстрее нагрузки, а следовательно, график М2 =f (P2) имеет криволинейный вид.
Рис. 2. Векторная диаграмма асинхронного двигателя при небольшой нагрузке
Зависимость cos φ1 = f (P2). В связи с тем что ток статора асинхронного двигателя I1 имеет реактивную (индуктивную) составляющую, необходимую для создания магнитного поля в статоре, коэффициент мощности асинхронных двигателей меньше единицы. Наименьшее значение коэффициента мощности соответствует режиму холостого хода. Объясняется это тем, что ток холостого хода электродвигателя I0 при любой нагрузке остается практически неизменным. Поэтому при малых нагрузках двигателя ток статора невелик и в значительной части является реактивным (I1 ≈ I0). В результате сдвиг по фазе тока статора относительно напряжения получается значительным (φ1 ≈ φ0), лишь немногим меньше 90° (рис. 2).
Коэффициент мощности асинхронных двигателей в режиме холостого хода обычно не превышает 0,2. При увеличении нагрузки на валу двигателя растет активная составляющая тока I1 и коэффициент мощности возрастает, достигая наибольшего значения (0,80 — 0,90) при нагрузке, близкой к номинальной. Дальнейшее увеличение нагрузки на валу двигателя сопровождается уменьшением cos φ1 что объясняется возрастанием индуктивного сопротивления ротора (x2s) за счет увеличения скольжения, а следовательно, и частоты тока в роторе.
В целях повышения коэффициента мощности асинхронных двигателей чрезвычайно важно, чтобы двигатель работал всегда или по крайней мере значительную часть времени с нагрузкой, близкой к номинальной. Это можно обеспечить лишь при правильном выборе мощности двигателя. Если же двигатель работает значительную часть времени недогруженным, то для повышения cos φ1, целесообразно подводимое к двигателю напряжение U1 уменьшить. Например, в двигателях, работающих при соединении обмотки статора треугольником, это можно сделать пересоединив обмотки статора в звезду, что вызовет уменьшение фазного напряжения в раз. При этом магнитный поток статора, а следовательно, и намагничивающий ток уменьшаются примерно в раз. Кроме того, активная составляющая тока статора несколько увеличивается. Все это способствует повышению коэффициента мощности двигателя.
На рис. 3 представлены графики зависимости cos φ1, асинхронного двигателя от нагрузки при соединении обмоток статора звездой (кривая 1) и треугольником (кривая 2).
Рис. 3. Зависимость cos φ1,от нагрузки при соединении обмотки статора двигателя звездой (1) и треугольником (2)
асинхронный двигатель
Всего комментариев: 0
Мощность и вращающий момент электродвигателя. Что это такое?
Мощность и вращающий момент электродвигателя
Данная глава посвящена вращающему моменту: что это такое, для чего он нужен и др. Мы также разберём типы нагрузок в зависимости от моделей насосов и соответствие между электродвигателем и нагрузкой насоса.
Вы когда-нибудь пробовали провернуть вал пустого насоса руками? Теперь представьте, что вы поворачиваете его, когда насос заполнен водой. Вы почувствуете, что в этом случае, чтобы создать вращающий момент, требуется гораздо большее усилие.
А теперь представьте, что вам надо крутить вал насоса несколько часов подряд. Вы бы устали быстрее, если бы насос был заполнен водой, и почувствовали бы, что потратили намного больше сил за тот же период времени, чем при выполнении тех же манипуляций с пустым насосом. Ваши наблюдения абсолютно верны: требуется большая мощность, которая является мерой работы (потраченной энергии) в единицу времени. Как правило, мощность стандартного электродвигателя выражается в кВт.
Вращающий момент (T) — это произведение силы на плечо силы. В Европе он измеряется в Ньютонах на метр (Нм).
Как видно из формулы, вращающий момент увеличивается, если возрастает сила или плечо силы — или и то и другое. Например, если мы приложим к валу силу в 10 Н, эквивалентную 1 кг, при длине рычага (плече силы) 1 м, в результате, вращающий момент будет 10 Нм. При увеличении силы до 20 Н или 2 кг, вращающий момент будет 20 Нм. Таким же образом, вращающий момент был бы 20 Нм, если бы рычаг увеличился до 2 м, а сила составляла 10 Н. Или при вращающем моменте в 10 Нм с плечом силы 0,5 м сила должна быть 20 Н.
Работа и мощность
Теперь остановимся на таком понятии как «работа», которое в данном контексте имеет особое значение. Работа совершается всякий раз, когда сила — любая сила — вызывает движение. Работа равна силе, умноженной на расстояние. Для линейного движения мощность выражается как работа в определённый момент времени.
Если мы говорим о вращении, мощность выражается как вращающий момент (T), умноженный на частоту вращения (w).
Частота вращения объекта определяется измерением времени, за которое определённая точка вращающегося объекта совершит полный оборот. Обычно эта величина выражается в оборотах в минуту, т.е. мин-1 или об/мин. Например, если объект совершает 10 полных оборотов в минуту, это означает, что его частота вращения: 10 мин-1 или 10 об/мин.
Итак, частота вращения измеряется в оборотах в минуту, т.е. мин-1.
Приведем единицы измерения к общему виду.
Для наглядности возьмём разные электродвигатели, чтобы более подробно проанализировать соотношение между мощностью, вращающим моментом и частотой вращения. Несмотря на то, что вращающий момент и частота вращения электродвигателей сильно различаются, они могут иметь одинаковую мощность.
Например, предположим, что у нас 2-полюсный электродвигатель (с частотой вращения 3000 мин-1) и 4-полюсной электродвигатель (с частотой вращения 1500 мин-1). Мощность обоих электродвигателей 3,0 кВт, но их вращающие моменты отличаются.
Таким образом, вращающий момент 4-полюсного электродвигателя в два раза больше вращающего момента двухполюсного электродвигателя с той же мощностью.
Как образуется вращающий момент и частота вращения?
Теперь, после того, как мы изучили основы вращающего момента и скорости вращения, следует остановиться на том, как они создаются.
В электродвигателях переменного тока вращающий момент и частота вращения создаются в результате взаимодействия между ротором и вращающимся магнитным полем. Магнитное поле вокруг обмоток ротора будет стремиться к магнитному полю статора. В реальных рабочих условиях частота вращения ротора всегда отстаёт от магнитного поля. Таким образом, магнитное поле ротора пересекает магнитное поле статора и отстает от него и создаёт вращающий момент. Разницу в частоте вращения ротора и статора, которая измеряется в %, называют скоростью скольжения.
Скольжение является основным параметром электродвигателя, характеризующий его режим работы и нагрузку. Чем больше нагрузка, с которой должен работать электродвигатель, тем больше скольжение.
Помня о том, что было сказано выше, разберём ещё несколько формул. Вращающий момент индукционного электродвигателя зависит от силы магнитных полей ротора и статора, а также от фазового соотношения между этими полями. Это соотношение показано в следующей формуле:
Сила магнитного поля, в первую очередь, зависит от конструкции статора и материалов, из которых статор изготовлен. Однако напряжение и частота тока также играют важную роль. Отношение вращающих моментов пропорционально квадрату отношения напряжений, т.е. если подаваемое напряжение падает на 2%, вращающий момент, следовательно, уменьшается на 4%.
Потребляемая мощность электродвигателя
Ток ротора индуцируется через источник питания, к которому подсоединён электродвигатель, а магнитное поле частично создаётся напряжением. Входную мощность можно вычислить, если нам известны данные источника питания электродвигателя, т.е. напряжение, коэффициент мощности, потребляемый ток и КПД.
В Европе мощность на валу обычно измеряется в киловаттах. В США мощность на валу измеряется в лошадиных силах (л.с.).
Если вам необходимо перевести лошадиные силы в киловатты, просто умножьте соответствующую величину (в лошадиных силах) на 0,746. Например, 20 л.с. равняется (20 • 0,746) = 14,92 кВт.
И наоборот, киловатты можно перевести в лошадиные силы умножением величины в киловаттах на 1,341. Это значит, что 15 кВт равняется 20,11 л.с.
Момент электродвигателя
Мощность [кВт или л.с.] связывает вращающий момент с частотой вращения, чтобы определить общий объём работы, который должен быть выполнен за определённый промежуток времени.
Рассмотрим взаимодействие между вращающим моментом, мощностью и частотой вращения, а также их связь с электрическим напряжением на примере электродвигателей Grundfos. Электродвигатели имеют одну и ту же номинальную мощность как при 50 Гц, так и при 60 Гц.
Это влечёт за собой резкое снижение вращающего момента при 60 Гц: частота 60 Гц вызывает 20%-ное увеличение числа оборотов, что приводит к 20%-ному уменьшению вращающего момента. Большинство производителей предпочитают указывать мощность электродвигателя при 60 Гц, таким образом, при снижении частоты тока в сети до 50 Гц электродвигатели будут обеспечивать меньшую мощность на валу и вращающий момент. Электродвигатели обеспечивают одинаковую мощность при 50 и 60 Гц.
Графическое представление вращающего момента электродвигателя изображено на рисунке.
Иллюстрация представляет типичную характеристику вращающий момент/частота вращения. Ниже приведены термины, используемые для характеристики вращающего момента электродвигателя переменного тока.
Пусковой момент (Мп): Механический вращающий момент, развиваемый электродвигателем на валу при пуске, т.е. когда через электродвигатель пропускается ток при полном напряжении, при этом вал застопорен.
Минимальный пусковой момент (Ммин): Этот термин используется для обозначения самой низкой точки на кривой вращающий момент/частота вращения электродвигателя, нагрузка которого увеличивается до полной скорости вращения. Для большинства электродвигателей Grundfos величина минимального пускового момента отдельно не указывается, так как самая низкая точка находится в точке заторможенного ротора. В результате для большинства электродвигателей Grundfos минимальный пусковой момент такой же, как пусковой момент.
Блокировочный момент (Мблок): Максимальный вращающий момент — момент, который создаёт электродвигатель переменного тока с номинальным напряжением, подаваемым при номинальной частоте, без резких скачков скорости вращения. Его называют предельным перегрузочным моментом или максимальным вращающим моментом.
Вращающий момент при полной нагрузке (Мп.н.): Вращающий момент, необходимый для создания номинальной мощности при полной нагрузке.
Нагрузка насосов и типы нагрузки электродвигателя
Выделяют следующие типы нагрузок:
Постоянная мощность
Термин «постоянная мощность» используется для определённых типов нагрузки, в которых требуется меньший вращающий момент при увеличении скорости вращения, и наоборот. Нагрузки при постоянной мощности обычно применяются в металлообработке, например, сверлении, прокатке и т.п.
Постоянный вращающий момент
Как видно из названия — «постоянный вращающий момент» — подразумевается, что величина вращающего момента, необходимого для приведения в действие какого- либо механизма, постоянна, независимо от скорости вращения. Примером такого режима работы могут служить конвейеры.
Переменный вращающий момент и мощность
«Переменный вращающий момент» — эта категория представляет для нас наибольший интерес. Этот момент имеет отношение к нагрузкам, для которых требуется низкий вращающий момент при низкой частоте вращения, а при увеличении скорости вращения требуется более высокий вращающий момент. Типичным примером являются центробежные насосы.
Вся остальная часть данного раздела будет посвящена исключительно переменному вращающему моменту и мощности.
Определив, что для центробежных насосов типичным является переменный вращающий момент, мы должны проанализировать и оценить некоторые характеристики центробежного насоса. Использование приводов с переменной частотой вращения обусловлено особыми законами физики. В данном случае это законы подобия, которые описывают соотношение между разностями давления и расходами.
Во-первых, подача насоса прямо пропорциональна частоте вращения. Это означает, что если насос будет работать с частотой вращения на 25% больше, подача увеличится на 25%.
Во-вторых, напор насоса будет меняться пропорционально квадрату изменения скорости вращения. Если частота вращения увеличивается на 25%, напор возрастает на 56%.
В-третьих, что особенно интересно, мощность пропорциональна кубу изменения скорости вращения. Это означает, что если требуемая частота вращения уменьшается на 50%, это равняется 87,5%-ному уменьшению потребляемой мощности.
Итак, законы подобия объясняют, почему использование приводов с переменной частотой вращения более целесообразно в тех областях применения, где требуются переменные значения расхода и давления. Grundfos предлагает ряд электродвигателей со встроенным частотным преобразователем, который регулирует частоту вращения для достижения именно этой цели.
Так же как подача, давление и мощность, потребная величина вращающего момента зависит от скорости вращения.
На рисунке показан центробежный насос в разрезе. Требования к вращающему моменту для такого типа нагрузки почти противоположны требованиям при «постоянной мощности». Для нагрузок при переменном вращающем моменте потребный вращающий момент при низкой частоте вращения — мал, а потребный вращающий момент при высокой частоте вращения — велик. В математическом выражении вращающий момент пропорционален квадрату скорости вращения, а мощность — кубу скорости вращения.
Это можно проиллюстрировать на примере характеристики вращающий момент/частота вращения, которую мы использовали ранее, когда рассказывали о вращающем моменте электродвигателя:
Когда электродвигатель набирает скорость от нуля до номинальной скорости, вращающий момент может значительно меняться. Величина вращающего момента, необходимая при определённой нагрузке, также изменяется с частотой вращения. Чтобы электродвигатель подходил для определённой нагрузки, необходимо чтобы величина вращающего момента электродвигателя всегда превышала вращающий момент, необходимый для данной нагрузки.
В примере, центробежный насос при номинальной нагрузке имеет вращающий момент, равный 70 Нм, что соответствует 22 кВт при номинальной частоте вращения 3000 мин-1. В данном случае насосу при пуске требуется 20% вращающего момента при номинальной нагрузке, т.е. приблизительно 14 Нм. После пуска вращающий момент немного падает, а затем, по мере того, как насос набирает скорость, увеличивается до величины полной нагрузки.
Очевидно, что нам необходим насос, который будет обеспечивать требуемые значения расход/напор (Q/H). Это значит, что нельзя допускать остановок электродвигателя, кроме того, электродвигатель должен постоянно ускоряться до тех пор, пока не достигнет номинальной скорости. Следовательно, необходимо, чтобы характеристика вращающего момента совпадала или превышала характеристику нагрузки на всём диапазоне от 0% до 100% скорости вращения. Любой «избыточный» момент, т.е. разница между кривой нагрузки и кривой электродвигателя, используется как ускорение вращения.
Соответствие электродвигателя нагрузке
Если нужно определить, отвечает ли вращающий момент определённого электродвигателя требованиям нагрузки, Вы можете сравнить характеристики скорости вращения/вращающего момента электродвигателя с характеристикой скорости вращения/ вращающего момента нагрузки. Вращающий момент, создаваемый электродвигателем, должен превышать потребный для нагрузки вращающий момент, включая периоды ускорения и полной скорости вращения.
Характеристика зависимости вращающего момента от скорости вращения стандартного электродвигателя и центробежного насоса.
Если мы посмотрим на характеристику , то увидим, что при ускорении электродвигателя его пуск производится при токе, соответствующем 550% тока полной нагрузки.
Когда двигатель приближается к своему номинальному значению скорости вращения, ток снижается. Как и следовало ожидать, во время начального периода пуска потери на электродвигателе высоки, поэтому этот период не должен быть продолжительным, чтобы не допустить перегрева.
Очень важно, чтобы максимальная скорость вращения достигалась как можно точнее. Это связано с потребляемой мощностью: например, увеличение скорости вращения на 1% по сравнению со стандартным максимумом приводит к 3%-ному увеличению потребляемой мощности.
Потребляемая мощность пропорциональна диаметру рабочего колеса насоса в четвертой степени.
Уменьшение диаметра рабочего колеса насоса на 10% приводит к уменьшению потребляемой мощности на (1- (0.9 * 0.9 * 0.9 * 0.9)) * 100 = 34%, что равно 66% номинальной мощности. Эта зависимость определяется исключительно на практике, так как зависит от типа насоса, конструкции рабочего колеса и от того, насколько вы уменьшаете диаметр рабочего колеса.
Время пуска электрдвигателя
Если нам необходимо подобрать типоразмер электродвигателя для определённой нагрузки, например для центробежных насосов, основная наша задача состоит в том, чтобы обеспечить соответствующий вращающий момент и мощность в номинальной рабочей точке, потому что пусковой момент для центробежных насосов довольно низкий. Время пуска достаточно ограниченно, так как вращающий момент довольно высокий.
Нередко для сложных систем защиты и контроля электродвигателей требуется некоторое время для их пуска, чтобы они могли замерить пусковой ток электродвигателя. Время пуска электродвигателя и насоса рассчитывается с помощью следующей формулы:
tпуск = время, необходимое электродвигателю насоса, чтобы достичь частоты вращения при полной нагрузке
n = частота вращения электродвигателя при полной нагрузке
Iобщ = инерция, которая требует ускорения, т.е. инерция вала электродвигателя, ротора, вала насоса и рабочих колёс.
Момент инерции для насосов и электродвигателей можно найти в соответствующих технических данных.
Мизб = избыточный момент, ускоряющий вращение. Избыточный момент равен вращающему моменту электродвигателя минус вращающий момент насоса при различных частотах вращения.
Мизб можно рассчитать по следующим формулам:
Как видно из приведённых вычислений, выполненных для данного примера с электродвигателем мощностью 4 кВт насоса CR, время пуска составляет 0,11 секунды.
Число пусков электродвигателя в час
Современные сложные системы управления электродвигателями могут контролировать число пусков в час каждого конкретного насоса и электродвигателя. Необходимость контроля этого параметра состоит в том, что каждый раз, когда осуществляется пуск электродвигателя с последующим ускорением, отмечается высокое потребление пускового тока. Пусковой ток нагревает электродвигатель. Если электродвигатель не остывает, продолжительная нагрузка от пускового тока значительно нагревает обмотки статора электродвигателя, что приводит к выходу из строя электродвигателя или сокращению срока службы изоляции.
Обычно за количество пусков, которое может выполнить электродвигатель в час, отвечает поставщик электродвигателя. Например, Grundfos указывает максимальное число пусков в час в технических данных на насос, так как максимальное количество пусков зависит от момента инерции насоса.
Мощность и КПД (eta) электродвигателя
Существует прямая связь между мощностью, потребляемой электродвигателем от сети, мощностью на валу электродвигателя и гидравлической мощностью, развиваемой насосом.
При производстве насосов используются следующие обозначения этих трёх различных типов мощности.
P1 (кВт) Входная электрическая мощность насосов — это мощность, которую электродвигатель насоса получает от источника электрического питания. Мощность P! равна мощности P2, разделённой на КПД электродвигателя.
P2 (кВт) Мощность на валу электродвигателя — это мощность, которую электродвигатель передает на вал насоса.
Р3 (кВт) Входная мощность насоса = P2, при условии, что соединительная муфта между валами насоса и электродвигателя не рассеивает энергию.
Р4 (кВт) Гидравлическая мощность насоса.
§79. Характеристики асинхронных двигателей | Электротехника
Характеристики асинхронных двигателей.
Для правильной эксплуатации асинхронного двигателя необходимо знать его характеристики: механическую и рабочие.
Механическая характеристика.
Зависимость частоты вращения ротора от нагрузки (вращающегося момента на валу) называется механической характеристикой асинхронного двигателя (рис. 262, а). При номинальной нагрузке частота вращения для различных двигателей обычно составляет 98—92,5 % частоты вращения n1 (скольжение sном = 2 – 7,5 %). Чем больше нагрузка, т. е. вращающий момент, который должен развивать двигатель, тем меньше частота вращения ротора.
Как показывает кривая на рис. 262, а, частота вращения асинхронного двигателя лишь незначительно снижается при увеличении нагрузки в диапазоне от нуля до наибольшего ее значения. Поэтому говорят, что такой двигатель обладает жесткой механической характеристикой.
Наибольший вращающий момент Mmax двигатель развивает при некотором скольжении skp, составляющем 10—20%. Отношение Mmax/Mном определяет перегрузочную способность двигателя, а отношение Мп/Мном — его пусковые свойства.
Рис. 262. Механические характеристики асинхронного двигателя: а — естественная; б — при включении пускового реостата
Двигатель может устойчиво работать только при обеспечении саморегулирования, т. е. автоматическом установлении равновесия между приложенным к валу моментом нагрузки Мвн и моментом М, развиваемым двигателем. Этому условию соответствует верхняя часть характеристики до достижения Mmax (до точки В).
Если нагрузочный момент Мвн превысит момент Mmax, то двигатель теряет устойчивость и останавливается, при этом по обмоткам машины будет длительно проходить ток в 5—7 раз больше номинального, и они могут сгореть.
При включении в цепь обмоток ротора пускового реостата получаем семейство механических характеристик (рис. 262,б). Характеристика 1 при работе двигателя без пускового реостата называется естественной. Характеристики 2, 3 и 4, получаемые при подключении к обмотке ротора двигателя реостата с сопротивлениями R1п (кривая 2), R2п (кривая 3) и R3п (кривая 4), называют реостатными механическими характеристиками.
При включении пускового реостата механическая характеристика становится более мягкой (более крутопадающей), так как увеличивается активное сопротивление цепи ротора R2 и возрастает sкp. При этом уменьшается пусковой ток. Пусковой момент Мп также зависит от R2. Можно так подобрать сопротивление реостата, чтобы пусковой момент Мп был равен наибольшему Мmax.
В двигателе с повышенным пусковым моментом естественная механическая характеристика приближается по своей форме к характеристике двигателя с включенным пусковым реостатом. Вращающий момент двигателя с двойной беличьей клеткой равен сумме двух моментов, создаваемых рабочей и пусковой клетками.
Поэтому характеристику 1 (рис. 263) можно получить путем суммирования характеристик 2 и 3, создаваемых этими клетками. Пусковой момент Мп такого двигателя значительно больше, чем момент М’п обычного короткозамкнутого двигателя. Механическая характеристика двигателя с глубокими пазами такая же, как и у двигателя с двойной беличьей клеткой.
Рис. 263. Механическая характеристика асинхронного двигателя с повышенным пусковым моментом (с двойной беличьей клеткой)
Рабочие характеристики.
Рабочими характеристиками асинхронного двигателя называются зависимости частоты вращения n (или скольжения s), момента на валу М2, тока статора I1 коэффициента полезного действия η и cosφ1, от полезной мощности Р2 = Рmx при номинальных значениях напряжения U1 и частоты f1 (рис. 264).
Рис. 264. Рабочие характеристики асинхронного двигателя
Они строятся только для зоны практической устойчивой работы двигателя, т. е. от скольжения, равного нулю, до скольжения, превышающего номинальное на 10—20%. Частота вращения n с ростом отдаваемой мощности Р2 изменяется мало, так же как и в механической характеристике; вращающий момент на валу М2 пропорционален мощности Р2, он меньше электромагнитного момента М на значение тормозящего момента Мтр, создаваемого силами трения.
Ток статора I1, возрастает с увеличением отдаваемой мощности, но при Р2 = 0 имеется некоторый ток холостого хода I0. К. п. д. изменяется примерно так же, как и в трансформаторе, сохраняя достаточно большое значение в сравнительно широком диапазоне нагрузки.
Наибольшее значение к. п. д. для асинхронных двигателей средней и большой мощности составляет 0,75—0,95 (машины большой мощности имеют соответственно больший к. п. д.). Коэффициент мощности cosφ1 асинхронных двигателей средней и большой мощности при полной нагрузке равен 0,7—0,9.
Следовательно, они загружают электрические станции и сети значительными реактивными токами (от 70 до 40% номинального тока), что является существенным недостатком этих двигателей.
При нагрузках 25—50 % номинальной, которые часто встречаются при эксплуатации различных механизмов, коэффициент мощности уменьшается до неудовлетворительных с энергетической точки зрения значений (0,5—0,75).
При снятии нагрузки с двигателя коэффициент мощности уменьшается до значений 0,25—0,3, поэтому нельзя допускать работу асинхронных двигателей при холостом ходе и значительных недогрузках.
Работа при пониженном напряжении и обрыве одной из фаз.
Понижение напряжения сети не оказывает существенного влияния на частоту вращения ротора асинхронного двигателя. Однако в этом случае сильно уменьшается наибольший вращающий момент, который может развить асинхронный двигатель (при понижении напряжения на 30% он уменьшается примерно в 2 раза). Поэтому при значительном падении напряжения двигатель может остановиться, а при низком напряжении — не включиться в работу.
На э. п. с. переменного тока при уменьшении напряжения в контактной сети соответственно уменьшается и напряжение в трехфазной сети, от которой питаются асинхронные двигатели, приводящие во вращение вспомогательные машины (вентиляторы, компрессоры, насосы).
Для того чтобы обеспечить нормальную работу асинхронных двигателей при пониженном напряжении (они должны нормально работать при уменьшении напряжения до 0,75Uном), мощность всех двигателей вспомогательных машин на э. п. с. берется примерно в 1,5—1,6 раза большей, чем это необходимо для привода их при номинальном напряжении.
Такой запас по мощности необходим также из-за некоторой несимметрии фазных напряжений, так как на э. п. с. асинхронные двигатели питаются не от трехфазного генератора, а от расщепителя фаз.
При несимметрии напряжений фазные токи двигателя будут неодинаковы и сдвиг между ними по фазе не будет равен 120°. В результате по одной из фаз будет протекать больший ток, вызывающий увеличенный нагрев обмоток данной фазы. Это заставляет ограничивать нагрузку двигателя по сравнению с работой его при симметричном напряжении.
Кроме того, при несимметрии напряжений возникает не круговое, а эллиптическое вращающееся магнитное поле и несколько изменяется форма механической характеристики двигателя. При этом уменьшаются его наибольший и пусковой моменты.
Несимметрию напряжений характеризуют коэффициентом несимметрии, который равен среднему относительному (в процентах) отклонению напряжений в отдельных фазах от среднего (симметричного) напряжения. Систему трехфазных напряжений принято считать практически симметричной, если этот коэффициент меньше 5 %.
При обрыве одной из фаз двигатель продолжает работать, но по неповрежденным фазам будут протекать повышенные токи, вызывающие увеличенный нагрев обмоток; такой режим не должен допускаться. Пуск двигателя с оборванной фазой невозможен, так как при этом не создается вращающееся магнитное поле, вследствие чего ротор двигателя не будет вращаться.
Использование асинхронных двигателей для привода вспомогательных машин э. п. с. обеспечивает значительные преимущества по сравнению с двигателями постоянного тока. При уменьшении напряжения в контактной сети частота вращения асинхронных двигателей, а следовательно, и подача компрессоров, вентиляторов, насосов практически не изменяются. В двигателях же постоянного тока частота вращения пропорциональна питающему напряжению, поэтому подача этих машин существенно уменьшается.
Зависимость скольжения, мощности и вращающего момента асинхронных машин от частоты сети при переходном режиме работы Текст научной статьи по специальности «Электротехника, электронная техника, информационные технологии»
УДК 621.313.333: 621.317.3
ЗАВИСИМОСТЬ СКОЛЬЖЕНИЯ, МОЩНОСТИ И ВРАЩАЮЩЕГО МОМЕНТА АСИНХРОННЫХ МАШИН ОТ ЧАСТОТЫ СЕТИ ПРИ ПЕРЕХОДНОМ РЕЖИМЕ РАБОТЫ
Бекиров Э.А., Воскресенская С.Н., Абибуллаев А.Н.
Физико-технический институт ФГАОУ ВО «КФУ им. В. И. Вернадского»
Симферополь, ул. Киевская, 181, е-mail: [email protected]
Аннотация. Проведен анализ изменения скольжения и вращающего момента асинхронных двигателей при изменении частоты питающей сети. Для асинхронных машин приведены выражения для расчета активной и реактивной мощностей. Уменьшение частоты ведет к уменьшению рабочего скольжения и к росту суммарной реактивной мощности и вращающего электромагнитного момента. Показаны расчетные и экспериментальные данные колебания и биения напряжения в сети при изменении частоты. Также рассмотрено влияние величины скольжения на электромагнитный вращающий момент.
Ключевые слова: асинхронная машина, скольжение, вращающий момент, частота, мощность.
ВВЕДЕНИЕ
Одним из главных условий обеспечения нормальной работы электродвигателей является питание их электроэнергией, параметры которой соответствуют определенным требованиям к ее качеству.
Основные показатели качества электроэнергии (ПКЭ) связаны с такими параметрами, как отклонения частоты и напряжения, колебания напряжения, несинусоидальность и несимметрия напряжения [1]. Напряжение сети, в свою очередь, зависит от реактивной мощности [2, 3] и при ее нехватке возникает необходимость в дополнительном регулировании. Изменение ПКЭ сети приводит к протеканию переходных процессов в асинхронных машинах, которые используются как для генерации электроэнергии, так и в качестве потребителей [4 — 6].
Во избежание длительного нарушения нормальной работы электродвигателей основные ПКЭ не должны выходить за пределы своих нормальных значений, а в послеаварийных режимах — за пределы определенных максимальных значений.
АНАЛИЗ ПУБЛИКАЦИЙ
При протекании переходных процессов в энергосети существенно могут меняться ПКЭ.
Жесткие требования стандарта к отклонениям частоты питающего напряжения обусловлены ее значительным влиянием на режимы работы электрооборудования, ход технологических процессов производства и, как следствие, технико-экономические показатели работы промышленных предприятий. То есть, предприятия терпят убытки, которые могут быть выражены в виде двух составляющих:
— Электромагнитная составляющая ущерба (уменьшение электромагнитной индукции и выработки двигателей) обусловлена увеличением потерь активной мощности в электрических сетях и ростом потребления активной и реактивной мощностей. Известно, что снижение частоты на 1% увеличивает потери в электрических сетях на 2% [7].
— Технологическая составляющая ущерба вызвана в основном недовыпуском промышленными предприятиями своей продукции и стоимостью дополнительного времени работы предприятия для выполнения задания.
Согласно экспертным оценкам значение технологического ущерба на порядок выше электромагнитного. Оборудование любого предприятия должно работать в режиме, способствующем энергосбережению [8 — 10].
Отклонения частоты отрицательно влияют на работу электронной техники: изменение на величину более +0,1 Гц приводит к яркостным геометрическим фоновым искажениям
телевизионного изображения; если ее значение лежит в диапазоне от 49,9 до 49,5 Гц, это влечет за собой почти четырехкратное увеличение допустимого размаха телевизионного сигнала по сравнению со значением новой помехи [11].
Пониженная частота электрической сети влияет на срок службы оборудования, содержащего элементы со сталью (электродвигатели, трансформаторы, реакторы со стальным магнитопроводом), за счет увеличения тока намагничивания в таких аппаратах и дополнительного нагрева стальных сердечников. Например, отклонение частоты влияет на надежность и долговечность работы электродвигателей, а также на их тепловой режим. Кроме того, для асинхронных и синхронных двигателей тепловой режим зависит не только от величины напряжения, но и от степени загрузки.
Анализ работы предприятий с непрерывным циклом производства показал, что большинство основных технологических линий оборудовано механизмами с постоянными и вентиляторными моментами сопротивлений, а их приводами служат асинхронные двигатели. Частота вращения роторов двигателей пропорциональна изменению частоты сети, а производительность технологических линий зависит от частоты вращения двигателя. В связи с этим целесообразно выявить ее влияние на момент и мощность.
Наиболее чувствительны к понижению частоты двигатели собственных нужд электростанций. Результатом такого изменения параметров сети является уменьшение их производительности, что сопровождается снижением располагаемой мощности генераторов и частоты (имеет место лавина частоты) из-за дальнейшего дефицита активной мощности.
Такие электропотребители, как лампы
накаливания, печи сопротивления, дуговые
электрические печи на колебание частоты практически не реагируют.
МАТЕРИАЛЫ И МЕТОДЫ ИССЛЕДОВАНИЙ
Целью исследования является анализ параметров асинхронных машин при отклонении частоты сети от номинального значения. Задачи
включают: получение зависимостей скорости изменения скольжения и вращающего момента двигателя от частоты; анализ изменения мощности; рассмотрение случаев возникновения колебаний и биений напряжения в энергосистемах при отклонении частоты.
Используемые методы исследований: математический анализ, составление
дифференциальных уравнений, экспериментальные измерения параметров и графические построения. cos W2
(4)
При уменьшении частоты магнитный поток и ток холостого хода 10 увеличиваются, причем ток 10 из-за насыщения стали магнитопровода возрастает быстрее, чем магнитный поток. Уменьшение частоты / на 10% вызывает увеличение тока 10 на 20-30%. Ток 10 является практически реактивным, это приводит к снижению коэффициента мощности двигателя. С увеличением частоты / пропорционально возрастает частота вращения. Магнитный поток Фм уменьшается обратно пропорционально частоте. Согласно формуле (4) это приводит к резкому увеличению тока 12. При неизменном нагрузочном моменте увеличение частоты повышает опасность нарушения устойчивости двигателя, так как снижается максимальный момент двигателя пропорционально квадрату частоты /2.
Характеристики асинхронного двигателя при частотах питающего напряжения, отличающихся от номинального значения, зависят от соотношения между напряжением сети и частотой /1.г, + (х, + С, • х2)2]}
(5)
где ш1 — число фаз в обмотке статора;
= 2 • п • /1/р —
угловая частота вращения магнитного поля
статора;
С1 — коэффициент, равный У1/Е1;
71 — активное сопротивление обмотки статора;
х-
— реактивное сопротивление обмотки
статора;
х2 — реактивное сопротивление обмотки ротора в схеме замещения асинхронного двигателя.
При Сх=1 (для упрощенной схемы замещения с вынесенным получаем
намагничивающим контуром),
М = +
‘ %ах —
тл • U2
{4^/1^+г1 + Уг12 + (х1+х2)2]} ‘
(6)
а пренебрегая величиной 71 ввиду его малого значения, имеем
М
тах —
+
т1 • Ul • р
=+
т
U12 •р
4 • л • • (х1 + х2) 8 • л • /i2 • (L1 + i’2)
=+
C^Uj2
/12
(7)
где С — постоянная величина.
При изменении частоты /1 изменяется максимальный момент, то есть отношение максимального момента Мтиж к нагрузочному моменту Мном. Для устойчивой работы двигателя необходимо обеспечить перегрузочную способность Мтах/Мном > (1,7 — 2).
Характеристики зависимости величины электромагнитного момента в относительных единицах М;/Мном от частоты ротора /2 при различных значениях частоты питающего напряжения /1 и законе регулирования и,//, = const приводятся в литературе [12].
Схемы замещения асинхронного двигателя представлены на рисунке 1.
р
ri jXi
Ui
jXt
а)
jX2
г/ S
P
U,
t-
jXs
/YYV
jX,
б)
г/ s
H
Рис.,
(12)
то при подстановке (11) в (12) получаем после преобразований
и, = —
Б +]’х—)
(Г1+]х1) +
2/Б+](Х2 +
,(13)
(Ш0-Ш2)
где 5 =- — скольжение ротора
ш0
асинхронного двигателя относительно поля статора, вращающегося с угловой скоростью ш0.
Выражение (10) можно получить их схемы замещения (рис. 1, а), пользуясь соотношением
шо • Мэл = 1р-—. (14)
Пренебрегая активным сопротивлением обмотки статора (г-1) вследствие его малого значения, выражение электромагнитного момента приобретает вид
М =— •
ГпБ
ш0 (Х1 + х—С1)2б2 + с—г— ‘ (15)
Максимум характеристики Мэл = [(б) наступает при скольжении, равном критическому
(16)
Р Х-1 + Х2С1
и определяется выражением
и— 1
М = ——
элтах щ 2С1(Х1 + Х2С1) ‘
Для рисунка 1, б
х5 =Х1+ х2, (18) Ъ
, (19)
(17)
М.
_ щ 1
эл.тах _ „ • ‘
ш0 2Х8
(20)
При ш0 = 2п[1; хБ = 2п[Ь
Мч
8п2[2Ь
(21)
Уменьшение частоты ведет к увеличению Мэлтах, к уменьшению рабочего скольжения и к росту суммарной реактивной мощности.
2
2
с
и?
Частота вращающегося магнитного поля в статоре зависит от частоты питающего напряжения
сети. На рисунке 2 показана зависимость частоты вращения поля статора от частоты напряжения сети.
n1 1600 1500 1400 1300 1200 1100 1000
38
40
42
44
46
48
50
f1, Гц
Рис. 2. Зависимость частоты вращающегося магнитного поля статора ni от частоты /, напряжения сети Fig. 2. Dependence of the frequency of rotating magnetic field of the stator ni on the frequency /, of the network voltage
Скольжение асинхронной машины, работающей в режиме двигателя, изменяется от нуля до единицы. A/ /i /1 /1
(23)
Найдем производную скольжения s по частоте /,
ds d/
‘(i-Af) 1
d/
/12
(24)
Из уравнения (24) видно, что скорость изменения скольжения при изменении частоты имеет обратно пропорциональную квадратичную зависимость. Построим график данной зависимости (рисунок 3).
ds/df 0,00073 0,00068 0,00063 0,00058 0,00053 0,00048 0,00043 0,00038
38
40
42
44
46
48
50
f1
Рис. — индуктивное сопротивление заторможенного ротора.
Реактивное сопротивление обмотки ротора
х2 = • L2 = 2ro?/1L2 = s • x2fc
(27)
и при 5 = 0, Мэл = 0; при 5 = 1, Мэл = Мпуск; при 5 = 5кр, Мэл = Мтах.
Чтобы определить максимальный момент, продифференцируем вращающий момент Мэм, описываемый выражением (26), по скольжению 5 и приравняем результат к нулю
dM
d5
3 2
■у • ‘ -у . ‘V
12__’ 2 Х2У
ЭЛ — г ц2 54
= °Ми1
2
(G2)2+xb)
(28)
Так как скольжение sk = то
* I2K
Mmai = «
1
2 x
(29)
Величина максимального вращающего момента не зависит от активного сопротивления цепи ротора, при этом при увеличении активного
сопротивления максимальный вращающий момент будет смещаться в область больших скольжений. С уменьшением частоты сети /1 будет увеличиваться критическое скольжение, максимальный вращающий момент также будет смещаться в область больших скольжений.
Из формулы (25) видно, что для регулирования частоты вращения асинхронного двигателя можно изменять частоту питающего напряжения (использование частотных преобразователей).
Мощность асинхронного двигателя напрямую зависит от вращающего момента, следовательно, с увеличением вращающего момента будет расти и мощность. В двигательном режиме максимальный момент существенно снижается при уменьшении частоты ввиду возрастающего влияния падения напряжения на активное сопротивление статора, что приводит к уменьшению э.д.с. Е1 и магнитного потока двигателя. В генераторном режиме максимальный момент с понижением частоты возрастает, при этом магнитный поток машины увеличивается. Такие явления в генераторном режиме нежелательны, так как при малых частотах резко возрастает электромагнитный момент, что может привести к поломке вала машины.
Рассмотрим активные и реактивные мощности асинхронной машины. На рисунке 4 приведена эквивалентная схема замещения.
Рис. 4. Эквивалентная схема замещения при расчете мощностей Fig 4. Equivalent chart of substitution at the calculation of powers
Реактивная мощность
выражениями:
Г Çad = ÇM + çs ;
y2
определяется
(30)
Çs = 3 • /s • xs ,
где Çad — суммарная реактивная мощность;
— мощность, связанная с намагничивающим
током;
— мощность от полей рассеяния в статоре и
роторе;
— ток холостого хода.•s2
п = 3 • I2 • х = —1—
VS j ‘S AS г)2 i 7 7 ‘
R2 + x2 • s2
следовательно, s
Qs = Pad~ .
S,
(32)
(33)
кр
Активная и реактивная мощности асинхронной машины зависят от изменения частоты питающего напряжения. Снижение частоты уменьшает рабочее
скольжение, увеличивается суммарная реактивная мощность.
При генерации электрической энергии в общую энергосистему необходимо обеспечивать требования качества электрической энергии по
напряжению UreH — ^энергосети; freH fceju> фген
фсети. При несоблюдении этих условий в электроэнергетической системе могут возникать модулированные колебания (рис. 5) и даже биения (рис. 6). Графики приведены для функции f = U1 sinш1Ь + U1 sinш21. Причем на рис. 5 синусоида с напряжением U1 = 380 В и частотами 50 Гц и 49 Гц, а на рис. 6 синусоида с аналогичным напряжением, но частотами 50 Гц и 45 Гц.
Рис. 5. Возникновение модулированных колебаний при изменении частоты Fig. 5. Origin of the modulated vibrations at the change of frequency
Рис. 6. Возникновение биений при изменении частоты Fig. 6. Origin of beatings at the change of frequency
Электроэнергетические службы,
обеспечивающие работу энергосистем с соблюдением требуемых нормативных данных по качеству электрической энергии, внимательно следят за изменением характеристик при подключении электрогенерирующих устройств и станций к общей системе, так как они могут генерировать напряжение с отличающимися частотами и фазами. При отключениях в общей энергосистеме частота напряжений малых генерирующих станций уменьшается и может падать до 38 Гц и ниже, при этом энергоагрегаты либо переводятся на электропитание собственных нужд, либо в худшем случае выходят из строя.
На рисунке 7 показаны биения напряжений и токов на энергоагрегатах генерирующей станции в Крыму. При аварийных режимах необходимо их
отключение либо автоматическое частотное регулирование
Частота в первый момент времени составила 46,97 Гц, а затем продолжила снижаться и в течение 1,6 секунды достигла критического значения 38,07 Гц. При этом напряжение так же снизилось. Так как при подобных условиях невозможно было провести регулировку, то это привело к отключению энергоблока.
Для обеспечения лучшего качества электрической энергии необходима
энергонезависимость Крыма, так как любые аварии на достаточно протяженном маршруте передачи электроэнергии приведут к возникновению модуляций. Крым почти на 80% обеспечивается за счет внешних мощностей. Это приводит к тому, что на настоящий момент нет собственных
электростанций, способных обеспечить потребителей от энергосистемы для стабилизации
балансирование по частоте. Таким образом, в работы. аварийных ситуациях потребуется отключение
Файл:RECON492.206 Объект:SIM_TEC рекон 492 дата процесса: 03/12/2014 время процесса:08:31:54.597 с
Рис. 7. Биения напряжений и токов на энергоагрегатах генерирующей станции
Fig. 7. Beatings of voltages and currents on the power unit of the generating station
ВЫВОДЫ
Таким образом, в работе получены зависимости скорости изменения скольжения и вращающего момента асинхронного двигателя при изменении частоты питающей сети, приведены выражения для расчета мощности асинхронных машин. Активная и реактивная мощности зависят от частоты питающего напряжения по следующему алгоритму: снижение приводит к уменьшению рабочего скольжения, увеличению суммарной реактивной мощности и момента вращения. При переходных процессах колебания и биения напряжения могут привести к необходимости отключения энергоагрегатов от сети.
СПИСОК ЛИТЕРАТУРЫ
1. Семёнов А.С., Матул Г.А., Хазиев Р.Р., Шевчук В.А., Черенков Н.С. Анализ показателей качества электрической энергии при работе асинхронного двигателя от трёхфазного источника
питания // Фундаментальные исследования. 2014. № 9-6. С. 1210 — 1215.
2. Филюшов Ю.П., Филюшов В.Ю. Управление асинхронной машиной в условиях минимума реактивной мощности // Электротехника. 2014. № 2. С. 15 — 20.
3. Симаков Г.М., Филюшов Ю.П. Управление асинхронной машиной тягового электропривода в условиях минимизации реактивной мощности // Вестник транспорта Поволжья. 2015. № 2 (50). С. 39 — 46.
4. Лустенберг Г.Е. Расчет электромеханических переходных процессов в трехфазной асинхронной машине с применением свободного программного обеспечения // Транспортная инфраструктура Сибирского региона. 2013. Т. 1. С. 259 — 263.
5. Ким К.И., Ким К.К. Переходные процессы в асинхронной машине. Санкт-Петербург: Издательство ОМ-Пресс, 2013. 90 с.
6. Христосенков С.А., Чуйко А.Д. Исследование переходных процессов протекающих в асинхронной машине // Транспортная инфраструктура Сибирского региона. 2015. Т. 2. С. 421 — 425.
7. Астахов Ю.Н., Веников В.А., Ежков В.В. Электроэнергетические системы в примерах и
иллюстрациях. Учебное пособие для вузов / под ред. В.А. Веникова. М.: Энергоатомиздат, 1983. 504 с.
8. Дейнего В., Дуюнов Д., Иванов В. Повышение энергоэффективности асинхронных двигателей вторичного рынка как способ энергосбережения // Электрик. 2015. № 5. С. 30 — 35.
9. Цопа Н.В., Малахова В.В., Ковальская Л.С. О необходимости нормативного регулирования современной энергосберегающей политики в строительном комплексе // Строительство и техногенная безопасность. 2017. № 6 (58). С. 91 — 98.
10. Цопа Н. Особенности управления энергосбережением в инвестицонно-строительном комплексе // Строительство и техногенная безопасность. 2016. № 2 (54). С. 54 — 59.
11. Вольдек А.И. Электрические машины. Учебник для студентов ВТУЗ. Изд. 2-е, перераб. и доп. — Л.: Энергия, 1974. — 840 с.
12. Брускин Д.Э., Зорохович А.Е., Хвостов В.С. Электрические машины и микромашины. Учебник для вузов. 2-е изд., перераб. и доп. М.: Высшая школа, 1981. 432 с.
REFERENCES
1. Semyonov A.S., Matul G.A., Haziev R.R., Shevchuk V.A., Cherenkov N.S. Analysis of the quality of electrical energy during the operation of an induction motor from a three-phase power source. Fundamental’nye issledovaniya. 2014. No. 9-6, рр. 1210 — 1215. (In Russian).
2. Filyushov Yu.P., Filyushov V.Yu. Control of an asynchronous machine in conditions of minimum reactive power. Ehlektrotekhnika. 2014. No. 2, pp. 15 -20. (In Russian).
3. Simakov G.M., Filyushov Yu.P. Control of an asynchronous machine of traction electric drive in conditions of minimizing reactive power. Vestnik transporta Povolzh’ya. 2015. No. 2 (50), pp. 39 — 46. (In Russian).
4. Lustenberg G.E. Calculation of electromechanical transients in a three-phase asynchronous machine using free software. Transportnaya infrastruktura Sibirskogo regiona. 2013. No. 1, pp. 259 — 263. (In Russian).
5. Kim K.I., Kim K.K. Perekhodnye processy v asinhronnoj mashine [Transients in an asynchronous machine]. St. Petersburg: Izdatel’stvo OM-Press. 2013. 90 p.
6. Hristosenkov S.A., CHujko A.D. Investigation of transients in an asynchronous machine. Transportnaya infrastruktura Sibirskogo regiona. 2015. No. 2, pp. 421
— 425. (In Russian).
7. Astahov YU.N., Venikov V.A., Ezhkov V.V. EHlektroehnergeticheskie sistemy v primerah i illyustraciyah. Uchebnoe posobie dlya vuzov [Electric power systems in examples and illustrations. Textbook for high schools] / red. V.A. Venikov. Moscow: EHnergoatomizdat. 1983. 504 p.
8. Dejnego V., Dujunov D., Ivanov V. Increase of the energoefficiency of asynchronous engines of the second market as method of energy-savings. Jelektrik. 2015, No. 5, pp. 30 — 35. (in Russian).
9. Copa N.V., Malahova V.V., Koval’skaya L.S. On the need for regulatory regulation of modern energy-saving policies in the construction sector. Stroitel’stvo i tekhnogennaya bezopasnost’. 2017. No. 6 (58), pp. 91 -98. (in Russian).
10. Copa N. Features of energy saving management in the investment and construction complex. Stroitel’stvo i tekhnogennaya bezopasnost’. 2016. No. 2 (54), pp. 54
— 59. (in Russian).
11. Vol’dek A.I. EHlektricheskie mashiny. Uchebnik dlya studentov VTUZ [Electric machine. A textbook for students of technical colleges]. — EHnergiya. 1974. 840 p.
12. Bruskin D.Eh., Zorohovich A.E., Hvostov V.S. EHlektricheskie mashiny i mikromashiny. Uchebnik dlya vuzov { Electric machines and micromachines. Textbook for universities]. Moscow: Vysshaya shkola, 1981. 432 p.
DEPENDENCE OF SLIDING, POWER, AND ROTATING MOMENT OF ASYNCHRONOUS MACHINES FROM THE NETWORK FREQUENCY IN TRANSITION MODE OF OPERATION
Bekirov E.A., Voskresenskaya S.N.,. Abibullaev A.N
Summary The analysis of the sliding and rotating moment changes of asynchronous motors at the change of the supply network frequency is carried out. For asynchronous machines, expressions for the calculation of active and reactive power are given. The decrease in frequency leads to a decrease in the working sliding and to an increase in the total reactive power and rotating moment. The calculated and experimental data of the voltage fluctuation and beating in the network at the frequency change are shown. The effect of the sliding magnitude on the electromagnetic rotating moment is also considered.
Key words: asynchronous machine, sliding, rotating moment, frequency, power.
(PDF) Обратимая зависимость скорости и времени асинхронной машины при прямом пуске без нагрузки
142 MP ĆALASAN
processdurationisveryimportant forpropermachine
уставки реле защиты (например, уставка реле максимального тока
защитные устройства) [3–5,22,23]. Кроме того, высокий фазный ток IM
может вызвать провалы напряжения
(например, в распределительных энергосистемах, на небольших участках энергосистемы
и т. Д.), что может иметь очень негативные последствия для других нагрузок (особенно для чувствительных нагрузок
, таких как освещение) [25–27]. Кроме того, высокое значение
фазного тока и длительность запуска машины могут вызвать перегрев машины. По этой причине
многие производители электрических машин и нагрузок
предоставляют уравнения для определения крутящего момента и мощности
и их взаимосвязь со временем пуска [28,29]. Техническое описание низковольтных ИД
приведено в [28], а уравнения
, описывающие трехфазные ИД, и положения
для согласования защитных устройств представлены в [29]. ].В этой статье представлена математическая модель
обратимой зависимости скорости и
времени АД при прямом пуске без нагрузки
.
Исследования по расчету времени старта IM
представлены в нескольких статьях [3,4,28–32]. А именно, простое математическое уравнение
для расчета времени пуска
, основанное на скорости машины, крутящем моменте и механических параметрах
, представлено в [30].Однако методы
, представленные в технической документации производителя станков
[28,29], а также методы, представленные
в [30], не могут применяться для всех станков (например,
для старых станков). , машины без паспортных данных,
и т. д.), поскольку они основаны на машинных данных производителя.
С другой стороны, время начала IM и
кривые скорость – время также могут быть определены с помощью методов
числовых вычислений во временной области (NTDC)
[3,4,30].Методы NTDC предполагают описание
машины с помощью набора дифференциальных уравнений (дифференциальных уравнений
для описания электрических цепей машины
, а также дифференциальных уравнений для описания
механического движения) и их реализации или реализации.
в определенных программных пакетах (например,
PSpice, Matlab, Mathematica и т. Д.). Однако все пакеты pro
граммов решают дифференциальные уравнения, используя численные методы
(например, метод Backward Euler
, метод Дорманда – Принса, метод Bogacki-Shampine
и т. Д.) [3,4,30], и поэтому требуют использования
специальных программных пакетов.
Конкретное исследование по определению пусковых характеристик
ИД, приводящих в движение ленточные транспортеры
портовых конвейеров, показано в [32]. Однако в упомянутой статье
не исследуются скоростно-временные характеристики IM start-
в режиме холостого хода.
В работах [3,4] также представлены исследования по расчету времени пуска IM
и определению пусковых характеристик
.Точнее, метод расчета времени
больших ИД при традиционных методах запуска —
(метод прямого запуска, метод
звезда – треугольник, метод автотрансформатора и метод пускателя резистора
): представлены в [3]. Вышеупомянутая статья
представляет формулу для описания времени-скорости IM
, которая основана на общем типе механической нагрузки
. Тем не менее, для того, чтобы предотвратить неповторимость
времени пуска и сингулярность момента разгона
, при выводе формулы автор
предлагает определенный поправочный коэффициент.Кроме того, в [3]
не рассматривается обратная зависимость скорости от времени.
Наконец, математическое моделирование зависимостей скорости IM
и времени от скорости во время прямого пуска без нагрузки
также представлено в [4]. Для получения упомянутых соотношений
крутящий момент машины представлен
с использованием уравнения Клосса. По этой причине определенное несоответствие
между результатами, полученными с использованием предложенного выражения
и экспериментально определенными результатами
, отмечено в [4].
Целью данной статьи является определение зависимостей скорость-время
и время-скорость во время запуска IM без нагрузки
вверх, без использования какой-либо приблизительной формулы
(такой как уравнение Клосса) или каких-либо поправок. факс
торс. Также цель состоит в том, чтобы сравнить кривую скорость-время
, полученную с использованием предложенного выражения, с результатами
, полученными с использованием выражений, известных из литературы
(например, представленных в [3,4]), а также
как с соответствующими экспериментальными результатами.Обратите внимание на
, что обратимая зависимость очень важна, поскольку,
в любой момент времени, мы можем вычислить значение скорости
и наоборот, для любого значения скорости мы можем вычислить соответствующее значение времени
.
Работа разделена на несколько разделов. Математическое выражение math-
для зависимости скорости от времени,
во время прямого пуска без нагрузки, получено и представлено
в Разделе II. Аналогично, обратная зависимость скорости от времени в этом рабочем режиме предлагается в разделе
III.Результаты моделирования прямого запуска IM без нагрузки —
up, fortwoIMs, на основе выражений привода, а также
, результаты, основанные на выражениях, известных в литературе
, и результаты, полученные с использованием метода NTDC
, сравниваются в Раздел IV. В этом разделе также представлены
определенных численных результатов, которые дополнительно описывают
предложенное выражение «скорость – время». Сравнение
экспериментально определенной кривой скорость – время в течение
прямого пуска IM и соответствующих кривых
, определенных с использованием предложенного выражения , а также
, как и в выражениях, известных из литературы, — это
, представленные в разделе V.Выводы приведены в
Разделе VI — заключении.
Новое выражение для кривой время-скорость IM
при прямом пуске без нагрузки
Механическое уравнение для любой вращающейся электрической машины
выглядит следующим образом:
Jdω
dt = M (1)
, где ω, J и M представляют скорость машины,
момента инерции и крутящие моменты машины,
Синхронный двигатель— обзор
Шаговые двигателиВ и двигатели с регулируемым сопротивлением
Реактивные двигателибыли упомянуты в разделе III.C применительно к синхронным двигателям без возбуждения поля. Эти машины имеют гладкий якорь, обычно расположенный на статоре, и ротор, имеющий количество выступающих полюсов, равное количеству полюсов в обмотке якоря. В последнее время, с появлением цифровых компьютеров, популярность приобрела новая машина. Его главное преимущество состоит в том, что он может обеспечивать очень точное позиционирование, когда он запитывается соответствующей последовательностью цифровых сигналов, генерируемых микропроцессором и усиливаемых твердотельным стабилизатором мощности.Поэтому он нашел множество применений, особенно в компьютерных приводах, роботах и станках. Еще одно преимущество — простая и прочная конструкция. Его простейшая форма показана на рис. 34.
РИСУНОК 34. Эскиз реактивной машины, имеющей разное количество полюсов на статоре и роторе.
Двигатель состоит из пакетов пластин статора и ротора. В отличие от обычных машин, двигатель имеет двойное преимущество; то есть он имеет выступающие полюса по обе стороны от воздушного зазора.Кроме того, количество полюсов статора и ротора не равнозначно. На диаметрально противоположных полюсах статора расположены последовательно соединенные катушки, которые составляют одну фазу обмотки. На каждую фазу последовательно подается импульс напряжения от источника постоянного тока. Твердотельное устройство переключения называется прерывателем. Чтобы избежать насыщения железа, поток должен быть «сброшен» в конце каждого импульса, подавая на обмотку напряжение противоположной полярности. Это достигается схемами, показанными на рис. 35.В схеме (а) необходим отдельный источник постоянного тока; в схеме (б) фазная обмотка состоит из двух тесно связанных катушек. Диод позволяет току течь во вспомогательном контуре только после размыкания переключателя и позволяет восстанавливать энергию, накопленную в магнитном поле, и передавать ее обратно в источник постоянного тока.
РИСУНОК 35. Схемы питания реактивных двигателей. (а) Схема с двумя источниками постоянного тока; (б) схема с бифилярной обмоткой.
Работу двигателя можно понять по рис.34. Крутящий момент возникает из-за тенденции магнитной цепи принимать конфигурацию с минимальным сопротивлением, то есть для того, чтобы полюса ротора совпадали с полюсами статора, так что индуктивность катушек, находящихся под напряжением, максимальна. Следовательно, если фазная обмотка 1 будет запитана первой, полюса 1 ‘ротора будут совмещены с полюсами 1 статора. Поскольку на этом рисунке количество полюсов ротора меньше, чем количество полюсов статора, шаг полюсов ротора больше. Отсюда следует, что, когда полюса 1 ‘и 1 выровнены, полюса 2’ перекрывают поверхности полюсов статора только частично и в той части, которая наиболее удалена от оси фазы 1.Если затем будет запитана фаза 2, полюса 2 ‘ротора будут совмещены с полюсами 2 статора. Таким образом, двигатель переместится на один шаг по часовой стрелке. Если вместо фазы 2 подается питание на фазу 3 после фазы 1, ротор будет двигаться против часовой стрелки. Следовательно, когда шаг полюсов ротора больше, чем у статора, ротор движется в направлении, противоположном направлению включения фазы. Когда шаг полюсов ротора меньше, ротор следует последовательности включения фазы.
Видно, что в случае рис.34 угловое смещение ротора за один шаг составляет
(83) α = 90 ° −60 ° = 30 °,
или, если N s и N r обозначают количество полюсов в статора и ротора соответственно
(84) α = 2π / Nr − 2π / Ns.
Связь между f ph , частотой импульсов в одной фазной обмотке и оборотами в минуту можно найти, наблюдая, что в двигателе, имеющем q фаз, ротор движется вперед на q шагов или на угол, равный q α за один период.Следовательно, количество импульсов (в одной фазной обмотке) на оборот ротора составляет 2π / q α, а частота равна
(85) fph = 2πqαrpm60 = NrNsq (Ns − Nr) rpm60.
Частота импульсного источника, который последовательно подает импульсы на фазы статора q , тогда равна
(86) fs = NrNsNs − Nrrpm60.
Приблизительное соотношение между крутящим моментом, развиваемым двигателем, и током i , протекающим в фазной обмотке, можно получить, если предположить, что i остается постоянным во время импульса, и пренебрегая эффектами насыщения в утюге.В этом случае запасенная в магнитном поле энергия и коэнергия равны
(87) Wmag = 12Li2,
, где L — индуктивность фазной обмотки. Принцип сохранения энергии приводит к следующей функциональной зависимости крутящего момента T от углового смещения ротора θ и тока возбуждения i :
(88) T (θ, i) = ∂Wmag (θ, i) ∂θ = 12i2dLdθ.
Если учесть два предельных положения — (1) когда полюса статора и ротора выровнены и (2) когда полюс статора обращен к межполюсному пространству ротора, угловое смещение составляет π / Н r и среднее крутящий момент
(89) T― = 12Nrπi2 (L1 − L2).
Крутящий момент фактически исчезает в этих двух предельных положениях и достигает пиков где-то посередине. В первом приближении крутящий момент при включении только одной фазы показывает синусоидальное изменение с угловым смещением. Аналогичная кривая, смещенная на угол шага α, с соответствующим знаком согласно формуле. (84) отображается, когда одна фаза обесточена, а соседняя — под напряжением. Шаговые операции в предположении, что электрические и механические переходные процессы не учитываются, показаны на рис.36. Шаги по часовой стрелке (путь a – d – e) и против часовой стрелки (путь a – b – c) показаны с нулевым моментом нагрузки T L на (a) и с конечным моментом нагрузки на (b). Поскольку разница между крутящим моментом, развиваемым двигателем, и крутящим моментом, приложенным к валу, является ускоряющим моментом, ротор быстрее достигнет своего нового положения покоя в направлении, благоприятствующем приложенному крутящему моменту.
РИСУНОК 36. Тактовый режим трехфазного шагового двигателя с N s = 6 и N r = 2.(а) T L = 0; (b) T L ≠ 0.
Машина принимает разные формы в зависимости от области применения. Когда он используется в качестве устройства позиционирования, желательно, чтобы шаг α был небольшим. Согласно формуле. (84) это означает большое количество полюсов. Поскольку было бы непрактично запитывать каждый полюс статора отдельно, используется нониусное устройство, при котором каждая фаза питает большой сердечник, содержащий несколько полюсов на своей поверхности. Типичный разрез такой машины показан на рис.37. Шаг может быть уменьшен до половины исходного шага в «полушаговом» режиме работы путем последовательного возбуждения одной или двух соседних фазных обмоток в любой момент времени. Работа, приводящая к полушагу по часовой стрелке, показана на рис. 38. Крутящий момент, развиваемый двигателем заданного размера, может быть увеличен за счет возбуждения ротора постоянными магнитами. В обычной конструкции ротор разделен на две группы с разнесением полюсов на половину шага. Постоянный магнит ориентирован в осевом направлении и помещен между двумя пакетами ротора под их выступающими полюсами.
РИСУНОК 37. Поперечный разрез шагового двигателя с нониусом.
РИСУНОК 38. Полушаговый режим трехфазного шагового двигателя с переменным сопротивлением (VR).
График зависимости крутящего момента от угла смещения показан на рис. 39. Небольшой (менее 10%) detente крутящий момент T d развивается даже в отсутствие возбуждения статора из-за зависимости сопротивления от положения ротора. Машины с постоянными магнитами (PM) обеспечивают вращение в обоих направлениях с двумя фазами вместо минимум трех, необходимых для машин с переменным магнитным сопротивлением (VR).Однако последующее упрощение стабилизатора мощности необходимо сопоставить с необходимостью в машинах с постоянным магнитом либо в двунаправленном источнике тока, либо в полноразмерной бифилярной обмотке.
РИСУНОК 39. Крутящий момент как функция угла смещения для шагового двигателя с постоянным магнитом (PM).
Машины, используемые для точного позиционирования, называются шаговыми двигателями или шаговыми двигателями . Когда желательно управление скоростью, а не позиционирование, большое количество полюсов не требуется, и, согласно формуле.(86), это привело бы к большой частоте источника. Эти машины, имеющие небольшое количество полюсов, называются реактивными двигателями с переключаемым сопротивлением и имеют мощность до нескольких десятков киловатт.
Момент нагрузки — обзор
11.4.1 Нагрузка с постоянным крутящим моментом
Нагрузка с постоянным крутящим моментом подразумевает, что крутящий момент, необходимый для поддержания нагрузки в рабочем состоянии, одинаков на всех скоростях. Хорошим примером является подъемник барабанного типа, в котором требуемый крутящий момент зависит от нагрузки на крюк, но не от скорости подъема.Пример показан на рис. 11.7.
Рис. 11.7. Таль с приводом от двигателя — нагрузка с постоянным крутящим моментом.
Диаметр барабана составляет 0,5 м, поэтому, если максимальная нагрузка (включая трос) составляет, скажем, 1000 кг, натяжение троса (мг) будет 9810 Н, а крутящий момент, приложенный нагрузкой на барабан, будет задан. на Усилие × радиус = 9810 × 0,25 ≈ 2500 Нм. Когда скорость постоянна (т. Е. Нагрузка не ускоряется), крутящий момент, создаваемый двигателем на барабане, должен быть равен и противоположен крутящему моменту, создаваемому на барабане нагрузкой.(Слово «противоположный» в последнем предложении часто опускается, при этом подразумевается, что установившийся двигатель и момент нагрузки обязательно должны действовать противоположно.)
Предположим, что скорость подъема должна контролироваться при любом значении вплоть до максимального. 0,5 м / с, и мы хотим, чтобы это соответствовало максимальной скорости двигателя около 1500 об / мин, что является разумной скоростью для широкого диапазона двигателей. Скорость подъема 0,5 м / с соответствует скорости барабана 19 об / мин, поэтому подходящее передаточное число будет, скажем, 80: 1, что дает максимальную скорость двигателя 1520 об / мин.
Нагрузочный момент со стороны двигателя редуктора будет снижен в 80 раз, с 2500 Нм до 31 Нм на двигателе. Мы также должны учитывать трение в коробке передач, эквивалентное, возможно, 20% крутящего момента полной нагрузки, поэтому максимальный крутящий момент двигателя, необходимый для подъема, будет составлять 37 Нм, и этот крутящий момент должен быть доступен на всех скоростях вплоть до 1520 об / мин. / мин.
Теперь мы можем нарисовать установившуюся кривую крутящего момента-скорости нагрузки, видимой двигателем, как показано на рис.11.8.
Рис. 11.8. Требования к крутящему моменту для двигателя в подъемном устройстве (рис. 11.7).
Мощность двигателя в установившемся режиме получается как произведение крутящего момента (Нм) и угловой скорости (рад / с). Таким образом, максимальная продолжительная мощность двигателя для подъема равна
(11,1) Pmax = 37 × 1520 × 2π60 = 5,9 кВт
На этом этапе всегда полезно проверить, что мы получим примерно такой же ответ для мощности. с учетом работы, проделанной за секунду при нагрузке. Сила ( F, ) на груз составляет 9810 Н, скорость ( v ) равна 0.5 м / с, поэтому мощность (Fv) составляет 4,9 кВт. Это на 20% меньше, чем мы получили выше, потому что здесь мы проигнорировали потерю мощности в коробке передач.
На данный момент мы установили, что нам нужен двигатель, способный непрерывно выдавать 5,9 кВт при 1520 об / мин, чтобы поднимать самый тяжелый груз с максимальной необходимой скоростью. Однако мы еще не рассмотрели вопрос о том, как груз ускоряется из состояния покоя и доводится до максимальной скорости. Во время фазы ускорения двигатель должен создавать крутящий момент, превышающий крутящий момент нагрузки, иначе нагрузка снизится, как только будет снят тормоз.Чем больше разница между крутящим моментом двигателя и крутящим моментом нагрузки, тем выше ускорение. Предположим, мы хотим, чтобы самый тяжелый груз достиг полной скорости из состояния покоя, скажем, за 1 секунду, и предположим, что мы решили, что ускорение должно быть постоянным. Мы можем рассчитать необходимый ускоряющий момент из уравнения движения, т.е.
(11.2) TorqueNm = Inertiakgm2 × Angularaccelerationradsec2.
Обычно мы считаем, что лучше всего работать с переменными, видимыми двигателем, и поэтому нам сначала нужно найти эффективную полную инерцию, видимую на валу двигателя, затем рассчитать ускорение двигателя и, наконец, использовать уравнение.(11.2) для получения ускоряющего момента.
Эффективная инерция складывается из инерции самого двигателя, указанной инерции барабана и редуктора и указанной инерции груза на крюке. Термин «приведенная инерция» означает кажущуюся инерцию, если смотреть на редуктор со стороны двигателя. Если коробка передач имеет передаточное число n : 1 (где n больше 1), инерция J на низкой скорости оказывается инерцией J / n 2 на высокой скорости. боковая сторона.В этом примере нагрузка на самом деле движется по прямой линии, поэтому нам нужно спросить, какова эффективная инерция груза, «видимая» на барабане. Геометрия здесь проста, и нетрудно увидеть, что с точки зрения инерции, наблюдаемой барабаном, груз кажется прикрепленным к поверхности барабана. Затем инерция нагрузки на барабане получается с использованием формулы для инерции массы m, расположенной на радиусе r , то есть Дж = mr 2 , что дает эффективную инерцию нагрузки на барабане как 1000 кг × ( 0.25 м) 2 = 62,5 кгм 2 .
Эффективная инерция нагрузки со стороны двигателя составляет 1 / (80) 2 × 62,5 ≈ 0,01 кгм 2 . К этому следует добавить в первую очередь инерцию двигателя, которую мы можем получить, проконсультировавшись с каталогом производителя для двигателя 5,9 кВт, 1520 об / мин. Это будет просто для постоянного тока. мотор, но переменный ток каталоги двигателей, как правило, дают номинальные значения только для рабочих частот, и здесь необходимо выбрать двигатель с правильным крутящим моментом и возможную кривую крутящего момента и скорости для рассматриваемого типа привода.Для простоты предположим, что мы нашли двигатель точно требуемой мощности с инерцией ротора 0,02 кгм 2 . Приведенная инерция барабана и коробки передач должна быть добавлена, и мы снова должны вычислить или найти. Предположим, это дает дополнительные 0,02 кгм 2 . Таким образом, общая эффективная инерция составляет 0,05 кгм 2 , из которых 40% приходится на сам двигатель.
Ускорение получить просто, поскольку мы знаем, что скорость двигателя должна повыситься с нуля до 1520 об / мин за 1 с.Угловое ускорение определяется увеличением скорости, деленным на затраченное время, то есть
1520 × 2π60 ÷ 1 = 160рад / сек2
Теперь мы можем рассчитать ускоряющий момент по формуле. (11.2) как
T = 0,05 × 160 = 8 Нм
Следовательно, чтобы удовлетворить требованиям как установившегося, так и динамического крутящего момента, привод, способный обеспечить крутящий момент 45 Нм (= 37 + 8) на всех скоростях до 1520 об / мин не требуется, как указано на рис. 11.8.
В случае подъемника ожидаемый режим работы может быть неизвестен, но вполне вероятно, что двигатель будет проводить большую часть своего времени подъема, а не ускорения.Следовательно, хотя пиковый крутящий момент 45 Нм должен быть доступен на всех скоростях, это не будет постоянным требованием и, вероятно, будет в пределах кратковременной перегрузочной способности привода, который постоянно рассчитан на 5,9 кВт.
Мы также должны учитывать, что произойдет, если необходимо опустить полностью загруженный крюк. Мы учли трение в 20% от момента нагрузки (31 Нм), поэтому во время спуска можно ожидать, что трение создаст тормозной момент, эквивалентный 6,2 Нм. Но чтобы крюк не соскочил с места, нам понадобится общий крутящий момент 31 Нм, поэтому для сдерживания нагрузки двигатель должен будет развивать крутящий момент 24.8 Нм. Мы, естественно, будем называть это тормозным моментом, потому что это необходимо для предотвращения разрыва груза на крюке, но на самом деле крутящий момент остается в том же направлении, что и при подъеме. Однако скорость отрицательна, и с точки зрения «четырехквадрантной» диаграммы (например, рис. 3.12) мы переместились из квадранта 1 в квадрант 4, и, таким образом, поток мощности меняется на противоположный, и двигатель регенерирует, потеря потенциала энергия нисходящей нагрузки преобразуется обратно в электрическую форму (и потери).Следовательно, если мы хотим удовлетворить эту ситуацию, мы должны выбрать привод, способный к непрерывной регенерации: такой привод также будет иметь возможность работать в квадранте 3, чтобы создавать отрицательный крутящий момент для опускания пустого крюка, если его вес был недостаточным. спуститься.
В этом примере в крутящем моменте преобладает требование установившегося режима, а зависящий от инерции ускоряющий крутящий момент сравнительно невелик. Конечно, если бы мы указали, что нагрузка должна быть ускорена за одну пятую секунды, а не за 1 секунду, нам потребуется ускоряющий крутящий момент 40 Нм, а не 8 Нм, и что касается требований к крутящему моменту, то ускоряющий крутящий момент будет быть более или менее таким же, как установившийся рабочий момент.В этом случае необходимо проконсультироваться с производителем привода, чтобы определить номинальные параметры привода, которые будут зависеть от частоты последовательности пуска / останова.
Вопрос о том, как оценить двигатель при прерывистой нагрузке, будет рассмотрен более подробно позже, но стоит отметить, что, если инерция заметна, накопленная кинетическая энергия вращения (12 Джω2) может стать очень значительной, особенно когда привод требуется для остановки груза. Любая накопленная энергия должна либо рассеиваться в двигателе и самом приводе, либо возвращаться в источник питания.Все двигатели по своей природе способны к регенерации, поэтому устройство, при котором кинетическая энергия рекуперируется и сбрасывается в виде тепла в резисторе внутри корпуса привода, является более дешевым вариантом, но практически осуществимо только в том случае, если энергия, которая должна поглощаться, невелика. Если накопленная кинетическая энергия велика, привод должен иметь возможность возвращать энергию источнику питания, а это неизбежно увеличивает стоимость преобразователя.
В случае нашего подъемника накопленная кинетическая энергия составляет всего
12 × 0.051520 × 2π602 = 633Дж
или около 1% энергии, необходимой для нагрева кружки воды для чашки кофе. Такая скромная энергия может быть легко поглощена резистором, но, учитывая, что в этом случае мы обеспечиваем рекуперативный привод, эта энергия также будет возвращена источнику питания.
Связь между скоростью, частотой и напряжением в асинхронном двигателе?
Наша компания планирует запрограммировать частотно-регулируемый привод для управления скоростью трехфазного асинхронного двигателя.Если мы изменим амплитуду (напряжение), что произойдет с частотой? Какая частота для какой амплитуды подходит?Асинхронный двигатель работает с частотой питающего его источника. Можно изменять скорость, изменяя применяемую частоту.
Для работы двигателю необходим магнитный поток в железе — или, точнее, в зазоре между ротором и статором. Ротор обычно вращается со скоростью, немного меньшей, чем скорость вращения поля статора (которая зависит от частоты).Эта разница в скорости называется скольжением и зависит от нагрузки (примечание: двигатели переменного тока с постоянными магнитами ротора работают без проскальзывания (синхронно)). Скольжение заставляет магнитный поток прорезать обмотки ротора, заставляя ток течь в роторе. Частота протекания тока равна частоте скольжения и никогда не может быть нулевой.
Асинхронный двигатель разработан как компромисс между потерями в стали и в меди. Если вы уменьшите количество витков статора, потери в меди уменьшатся из-за более низкого сопротивления, но поток в железе увеличится, что приведет к увеличению потерь в стали.Если поток в железе слишком велик, потери резко возрастают, и железо считается насыщенным. Цель состоит в том, чтобы работать близко к насыщению, чтобы минимизировать потери меди, но не в режиме насыщения, чтобы минимизировать потери в железе. Номинальное напряжение отражает оптимальный магнитный поток при номинальной частоте. По мере того, как вы уменьшаете частоту, подаваемую на двигатель, вам необходимо уменьшать напряжение, чтобы сохранить ту же плотность магнитного потока. Если вы этого не сделаете, плотность магнитного потока увеличится, и железо станет насыщенным.
Преобразователь частоты обычно демонстрирует постоянное соотношение напряжение / частота от номинальной частоты до низкой частоты.Проще говоря, вы можете провести прямую линию от нуля вольт при нулевой Гц до номинального напряжения при номинальной частоте.
На низких частотах с постоянным соотношением напряжение / частота магнитный поток будет уменьшаться из-за соотношения между реактивной составляющей и резистивной составляющей статора; поэтому для увеличения низкочастотного крутящего момента нормальным является обеспечение некоторого повышения напряжения (амплитуды) на очень низких частотах. Это необходимо только при тяжелых нагрузках.
По сути, если вы посмотрите на эквивалентную схему асинхронного двигателя, вы хотите, чтобы ток, протекающий через намагничивающую катушку, оставался постоянным на всех частотах.Это обеспечит постоянный поток.
Электрические асинхронные двигатели — синхронная скорость
Синхронная скорость для электрического асинхронного двигателя определяется
- частотой источника питания и
- числом полюсов в обмотке двигателя.
Синхронная скорость может быть рассчитана как:
n = f (2 / p) 60 (1)
где
n = скорость вращения вала (об / мин, об / мин)
f = частота электропитания (Гц, циклов / с, 1 / с)
p = количество полюсов
Примечание — an асинхронный двигатель никогда не достигнет своей синхронной скорости.Если бы это было так — ротор казался бы неподвижным по отношению к вращающемуся полю статора, поскольку он вращался бы с той же скоростью. При отсутствии относительного движения между статором и полем ротора в двигателе не будет индуцироваться напряжение. Поэтому скорость асинхронного двигателя ограничена скоростью ниже синхронной, а разница между синхронной скоростью и фактической скоростью называется скольжением.
Пример — синхронная скорость двухполюсного электродвигателя
На двухполюсный двигатель подается мощность с частотой 50 Гц (1 / с) .Скорость вращения можно рассчитать как
n = (50 1 / с) (2/2) (60 с / мин)
= 3000 об / мин (1 / мин)
Синхронный скорость вращения при разных частотах и количестве полюсов
| Скорость вращения вала — n — (об / мин, об / мин) | ||||||
|---|---|---|---|---|---|---|
| Частота — f — (Гц) | Количество полюса — p — | |||||
| 2 | 4 | 6 | 8 | 10 | 12 | |
| 10 | 600 | 300 200 9057 9057 9057 9057 100 | ||||
| 20 | 1200 | 600 | 400 | 300 | 240 | 200 |
| 30 | 1800 | 900 | 600 | 90 570450360 | 300 | |
| 40 | 2400 | 1200 | 800 | 600 | 480 | 400 |
| 50 1) 9057 9057 9057 9057 9057 | 750 | 600 | 500 | |||
| 60 2) | 3600 | 1800 | 1200 | 900 | 720 | 600 |
| 9057 9057 905 | 1050 | 840 | 700 | |||
| 80 | 4800 | 2400 | 1600 | 1200 | 960 | 800 |
| 54705 | 9057 9057 905 1080900 | |||||
| 100 | 6000 | 3000 | 2000 | 1500 | 1200 | 1000 |
- Двигатели, рассчитанные на 50 Гц, чаще всего встречаются за пределами U.S
- Двигатели, рассчитанные на 60 Гц, наиболее распространены в США.
Частотно-регулируемый привод
Частотно-регулируемый привод модулирует скорость электродвигателя путем изменения частоты источника питания.
Бездатчиковое прямое управление крутящим моментом шестифазного асинхронного двигателя с помощью быстрого уменьшенного порядка Расширенный фильтр Калмана
В этой статье простой расширенный контроллер с фильтром Калмана (EKF) для прямого управления крутящим моментом (DTC) шестифазной асинхронной машины в предлагаются все диапазоны скоростей.Целью данной статьи является сокращение времени выполнения EKF-моделирования шестифазного асинхронного двигателя. Предлагаемый метод быстр и может работать онлайн. Если параметры машины изменяются во время работы, активируется алгоритм EKF для поиска параметров, используемых для управления двигателем. На низкой скорости затруднено не только измерение скорости двигателя, но и диагностический код неисправности машины. Модель EKF может оценивать скорость, магнитный поток, момент нагрузки и сопротивление статора на низкой скорости; таким образом, оптимизация может выполняться во всех диапазонах нагрузок и скоростей.Предлагаемый метод позволяет повысить точность определения ДКН шестифазной асинхронной машины и снизить вычислительную стоимость системы с использованием упрощенного алгоритма. Результаты моделирования и экспериментов подтверждают эффективность и устойчивость предложенного метода к изменениям параметров.
1. Введение
Шестифазные и пятифазные машины — это два обычных типа многофазных машин, которые используются в нескольких приложениях [1–4]. Увеличение фаз машины дает некоторые преимущества, такие как более высокое резервирование и уменьшение пульсации крутящего момента [5–7].Методики полевого управления (FOC) и прямого управления крутящим моментом (DTC) применяются для управления скоростью шестифазных и пятифазных машин [8–11]. Эти методы не дают удовлетворительного отклика в низкоскоростных приложениях. В низкоскоростных приложениях требуется подходящий метод для оценки параметров и скорости. Метод DTC — это простой и надежный метод защиты от изменений параметров. Этот метод имеет очень быструю динамическую реакцию на изменение нагрузки. Таким образом, этот метод используется во многих промышленных приложениях.DTC — это мощный метод управления несколькими типами машин переменного тока. Этот метод хорошо реагирует на управление шестифазными и пятифазными асинхронными машинами [12]. Одна из основных ошибок метода DTC вызвана изменением сопротивления статора, что более серьезно в условиях низкой скорости. Сопротивление статора изменяется при изменении температуры двигателя. Если изменение сопротивления статора не учитывается в методе DTC, это вызывает ошибку на выходах контроллера [13–16]. Таким образом, для повышения точности метода DTC необходим подходящий метод оценки сопротивления статора [14].Для оценки сопротивления статора в литературе используется несколько методов. Антонелло и др. [17] предложили новый метод онлайн-оценки сопротивления статора, который подходит для анизотропных двигателей. Показано, что этот метод измеряет сопротивление статора без информации о параметрах двигателя, а отношение сигнал / шум (SNR) улучшается. Подходящий метод оценки сопротивления статора на основе механических потерь и крутящего момента предложен в исследовании Salomon et al.[18]. Этот метод подходит для автономной оценки сопротивления и в сервисных приложениях асинхронного двигателя. В этой статье используется алгоритм оптимизации роя частиц (PSO) на основе уравнений потока с минимизацией ошибки крутящего момента. Аналитический метод оценки сопротивления статора синхронного двигателя и DTC, основанный на этом методе, предложен в исследовании Sangsefidi et al. [19]. В этом методе используется влияние ошибки сопротивления статора на расчетный угол между потоком статора и векторами тока.Температура обмотки в двухфазной трехфазной машине оценивается с помощью подачи сигнала постоянного тока в исследовании Baneira et al. [20]. Этот сигнал вводится в подпространство, чтобы нейтрализовать пульсацию крутящего момента и воздушный зазор. Этот метод можно использовать только в многофазной машине с такой свободой моделирования. Проблема идентификации в бессенсорной ИМ предложена в исследовании Yin et al. [21]. В этой статье используется аппроксимация первого порядка динамики ошибок адаптивного наблюдателя. Асинхронный двигатель включал только известные сигналы; таким образом, этот метод осуществим.Оценка сопротивления статора на основе компенсатора фазового сдвига представлена в исследовании Barut et al. [22]. Этот метод отделен от устройства оценки скорости коэффициентом компенсации слежения за рабочей точкой.
Расширенный фильтр Калмана (EKF) является мощным средством оценки не только сопротивления статора, но также момента нагрузки и магнитного потока машины [23–29]. Этот метод используется в нескольких работах для оценки параметров машины. Этот метод подходит для оценки параметров машины с вариациями нагрузки и параметров [25–28].В настоящее время, с увеличением скорости обработки в DSP, возможен онлайн-эксперимент с EKF. Асинхронный двигатель обладает стохастическими свойствами; таким образом, EKF можно легко использовать для его моделирования. Кроме того, его можно использовать для управления машиной, когда машина используется на низкой скорости или параметры машины меняются. Другие оценщики используются для оценки параметров асинхронных машин [30–33]. EKF используется для моделирования шестифазной индукционной машины с хорошими результатами [34, 35].
Предлагается простой контроллер модели потерь (LMC) с простым расширенным фильтром Калмана (EKF) для повышения эффективности шестифазной асинхронной машины во всех диапазонах скоростей [36].Предлагаемый метод быстр и может работать онлайн. Если параметры машины изменяются во время работы, активируется алгоритм EKF для поиска параметров, обеспечивающих оптимальную эффективность работы. Модель EKF может оценивать скорость, нагрузку и КПД двигателя в диапазонах низких скоростей, так что оптимизация может выполняться во всех диапазонах нагрузок и скоростей. В отличие от обычного метода LMC, предлагаемый метод не зависит от изменения параметров [36].
Для оценки момента нагрузки в асинхронном двигателе предложены методы оценки многоскоростных параметров и состояния асинхронного двигателя, основанные на теории EKF.Методы реализуются в режиме реального времени на узле кластера ПК, который действует как контроллер для экспериментальной установки асинхронного двигателя. Многоскоростная эталонная адаптивная система (MRAS) предлагается для оценки постоянной времени ротора, чтобы гарантировать высокопроизводительное управление асинхронным двигателем [37].
Зависимое от температуры изменение сопротивлений статора и ротора, которое вызывает большую ошибку оценки скорости и потока, было критической проблемой для управления без датчика скорости.Для оценки одновременных изменений сопротивлений статора и ротора при бессенсорном управлении IM при различных рабочих условиях разработан блок оценки, основанный на методе расширенного фильтра Калмана (EKF). Чтобы решить проблему нестабильности одновременной оценки сопротивлений статора и ротора, сопротивление статора оценивается с учетом его температурной зависимости и тепловой динамики обмоток статора, а сопротивление ротора оценивается как постоянное состояние [38].DTC привода IM с EKF для оценки составляющих неподвижной оси статора токов статора, потоков статора, сопротивления статора и ротора с допущением имеющихся напряжений / токов статора и скорости ротора представлен в исследовании Демира и др. [39] . Онлайн-оценки сопротивлений ротора и статора дают хорошие результаты благодаря использованию единого алгоритма EKF и датчика скорости [39].
Предлагается подходящий блок оценки EKF для точной оценки потока и скорости при очень низкой и нулевой скорости.Этот метод применяется с прямым векторным управлением без датчика скорости и двумя алгоритмами EKF путем переключения с одного алгоритма на другой в каждый момент выборки. Метод переключения требует точной и увеличенной оценки параметров. Оценка переходного и установившегося состояний сопротивлений ротора и статора является важной проблемой при управлении IM без датчиков скорости, о чем сообщается в исследовании Barut et al. [40].
Целью данной статьи является сокращение времени выполнения EKF-моделирования шестифазного асинхронного двигателя.Предлагаемый метод увеличивает точность и снижает вычислительные затраты системы. Кроме того, точность DTC шестифазной асинхронной машины повышается за счет оценки сопротивления статора. Предлагаемый метод использует подходящий алгоритм EKF для оценки магнитного потока и момента нагрузки. Точность метода DTC повышается благодаря онлайн-оценке сопротивления статора. EKF-моделирование 6PIM является точным и устойчивым к изменениям параметров. В этой статье представлены подходящие коды неисправности 6PIM для всех диапазонов скоростей.При изменении нагрузки алгоритм EKF быстро и точно оценивает нагрузку и скорость. Также представленный алгоритм устойчив к изменению сопротивления. Оценка скорости — мощный инструмент при расчете скорости во всех диапазонах скоростей, потому что расчет скорости двигателя на низкой и нулевой скорости чрезвычайно сложен и содержит ошибки.
В этой статье сначала выводятся моделирование шестифазного асинхронного двигателя и DTC 6PIM. EKF-моделирование 6PIM описано в следующем разделе.Описывается подходящий DTC 6PIM, который использовал оценку параметров EKF. Наконец, показаны результаты моделирования предложенных методов, а затем экспериментальные результаты подтверждают правильность предложенных методов во всех диапазонах скоростей.
2. Шестифазный асинхронный двигатель модели
2.1. Моделирование и DTC шестифазного асинхронного двигателя
Метод разложения в векторном пространстве (VSD) используется при моделировании 6PIM. С помощью этого метода и применения 66 матриц шестифазные уравнения напряжения, тока и магнитного потока преобразуются в три подпространства.Эти подпространства называются. Поток двигателя создается с помощью основных гармоник тока и напряжения, которые отображаются в подпространстве. DTC 6PIM реализован в подпространстве, а ссылки на другие текущие подпространства установлены равными нулю. Потому что гармоники, отображаемые в единственном, приводят к потерям и считаются нулевыми в различных методах управления. Моделирование 6PIM методом VSD показано в следующих уравнениях. Все символы двигателей указаны в таблице 1.
| ||||||||||||||
Динамическая модель шестифазного асинхронного двигателя в подпространстве может быть представлена как
X , вектор состояния системы Y — измеряемый параметр двигателя, а U — входной вектор в подпространстве.Весь шум системы есть, и измерительное оборудование в этом подпространстве есть.
В то время как
Все шумы приводной системы и измерительного оборудования в этом подпространстве моделируются с помощью. Подходящая дискретная модель двигателя необходима для управления двигателем на основе DSP. Дискретная модель 6PIM выводится путем дискретизации векторов состояния. Если время выборки равно, дискретный вектор состояния в подпространстве находится где-то.
2.2. Моделирование 6PIM
EKF в уменьшенном порядке При низкой скорости качество датчиков скорости значительно ухудшается.EKF — это мощный инструмент оценки, который можно использовать для повышения точности оценки. Выходные данные EKF используются обеими секциями с ответом в реальном времени. Модель EKF шестифазного асинхронного двигателя может быть обозначена рекурсивными уравнениями, как показано ниже: где
Три ковариационные матрицы ( Q , R и) используются для моделирования системы, измерения и входного шума двигателя. система. Вышеупомянутые уравнения запускаются рекурсивно, чтобы уменьшить ошибку оценки. Поскольку для выполнения вышеуказанного алгоритма EKF требуется много времени, модель EKF можно упростить следующим образом:
Предлагаемое EKF-моделирование шестифазной асинхронной машины в сокращенном порядке можно использовать для сокращения времени выполнения EKF-моделирования двигателя.В предлагаемом способе сокращается время выполнения, а также снижается сложность системы. Схема предлагаемого EKF (ROEKF) моделирования DTC шестифазного асинхронного двигателя показана на рисунке 1.
Динамические характеристики EKF и ROEKF связаны с начальными значениями Q и R . При изменении этих параметров отклик фильтра Калмана будет несколько улучшен. Оценщик EKF имеет большую первичную ошибку во времени начала, которая связана с матрицей Q и R и настраивается с помощью начальных значений.Кроме того, если начальные значения матрицы состояний будут близки к реальным значениям, улучшается динамический отклик оценщика. В данной работе начальные значения параметров считаются неопределенными и оцениваются независимо от начальных значений.
В различных приложениях оценщик EKF часто настраивается так, чтобы иметь постоянные матрицы параметров. В оценщике EKF Q количественно определяет неточности моделирования системы, а R количественно определяет шумы измерения, преобладающие в системе.Низкое значение Q приводит к медленной переходной характеристике, а высокое значение Q приводит к высокому шуму при оценке сопротивления в установившемся режиме. Согласно предложению рецензента, мы используем адаптивную настройку, которая изменяет матрицу Q в зависимости от ошибки оценки, при этом высокое значение Q выбирается в переходных процессах, низкое значение в установившемся состоянии и линейное изменение обеспечивается в пределах. В литературе сообщается, что адаптивная настройка EKF может быть реализована с использованием различных механизмов адаптации для матриц Q и R на основе снижения расчетных уровней шума.В этой статье мы используем простой механизм адаптации, подходящий для DTC машины. Альтернативно, время установления наблюдателя должно быть меньше, чем время установления регулятора. В используемом адаптивном методе матрица Q изменяется до определенных предельных значений, что не ухудшает сходимость фильтра и, следовательно, не оказывает неблагоприятного воздействия на полосу пропускания контроллера.
Эти параметры были выбраны на основе производительности замкнутого цикла и вычислительной стоимости алгоритма.Значения параметров системы и элементы ковариационной матрицы очень эффективны для выполнения оценки EKF. В этой статье, чтобы избежать вычислительной сложности, ковариационная матрица шума системы Q выбрана в диагональной форме, также удовлетворяющей условию положительной определенности. Согласно теории КФ, матрицы Q и R должны быть получены с учетом стохастических свойств соответствующих шумов. Однако, поскольку Q и R обычно неизвестны, в большинстве случаев элементы ковариационной матрицы используются в качестве весовых коэффициентов или параметров настройки.В общем, в то время как настройка начальных значений (ковариационной матрицы ошибок оценки) и Q выполняется экспериментальным методом проб и ошибок для достижения быстрой начальной сходимости и желаемых переходных и устойчивых режимов, Q и R определяются с учетом ошибок измерения датчиков тока и напряжения и ошибок квантования АЦП.
При реализации метода фильтра Калмана некоторые вычисления только увеличивают время вычислений, хотя они не приводят к оценке параметров, в основном учитывающей объем вычислений ЦП.Требуемая память кода немного увеличена, но требуемая память данных уменьшена в предложенном способе. Также сокращение времени вычислений повысит точность предложенного алгоритма и снизит стоимость реализации. С вектором состояния как (4) в предыдущих методах EKF все размеры матрицы были бы выбраны равными шести. Например, матрица имеет 66 измерений, но в предлагаемом методе размерность матрицы выбрана как (16). Если вектор состояния имеет восемь переменных, предлагаемый метод сокращает время выполнения почти на четверть.Это означает уменьшение расчета на 75%. При сокращении расчета EKF выбранное время выборки уменьшается.
3. Моделирование и экспериментальные результаты
В этом разделе, во-первых, производительность ROEKF для оценки параметров в 6PIM показана на рисунках 2 и 3. В этом моделировании эталонная скорость двигателя составляет 50 рад / с и 2 рад / с, соответственно. . Алгоритм EKF активен и оценивает все состояния. Согласно этому рисунку сопротивление статора изменяется через 6 секунд, а нагрузка изменяется через 2 секунды, а затем 5 секунд, но алгоритм EKF может очень хорошо оценить эти изменения.На рисунке 2 показаны ток статора, магнитный поток, сопротивление статора, момент нагрузки и оценка скорости шестифазного асинхронного двигателя при 50 рад / с. Согласно рисунку 2, крутящий момент нагрузки составляет 0,1 Нм во время пуска и изменяется до 4,5 Нм за 2 секунды. По результатам предлагаемый метод имеет хороший отклик, погрешность оценки невысока.
На рисунке 3 показаны результаты оценки параметров ROEKF в условиях низкой скорости. На этом рисунке скорость двигателя составляет 1 рад / сек, и предлагаемый метод позволяет полностью оценить все параметры на низкой скорости.На рисунке 3 крутящий момент нагрузки составляет 0,1 Нм во время пуска и изменяется до 4,5 Нм за 2 секунды. На рисунке 3 показаны ток и магнитный поток по осям (d-q), момент нагрузки, сопротивление статора, скорость двигателя и оценка фазного тока. Согласно результатам, предложенная методика ROEKF активна при изменении нагрузки и сопротивления статора и может быстро и точно оценивать реальные значения. Точность метода DTC тесно связана с точной оценкой сопротивления статора. Метод DTC сильно зависит от фактического значения сопротивления статора, и любая ошибка в вычислении сопротивления приведет к сбою этого метода.Зависимость метода DTC от фактического значения сопротивления очень высока, особенно на низких скоростях. Любая ошибка в фактическом значении резистора статора вызовет ошибку в управлении и нестабильность системы.
Эта машина питается от шестифазного постоянного и переменного тока VSI. Чтобы выполнить диагностический код неисправности с обратной связью 6PIM, шесть фазных токов статора измеряются с помощью датчиков тока LEM. Четыре датчика тока используются для измерения фазных токов VSI. Выходы датчиков, используемых в качестве параметров, оцифровываются с использованием шести 12-битных аналогово-цифровых преобразователей на плате TMS.Шестифазный асинхронный двигатель изготовлен из трехфазного асинхронного двигателя путем перемотки статора.
Экспериментальный результат предложенного метода в 50 рад / сек показан на рисунке 4. Параметры шестифазного асинхронного двигателя показаны в таблице 1. Скорость двигателя составляет 50 рад / сек, а нагрузка двигателя — без нагрузки и изменена на 1,5. Нм при т = 2,7 сек. Предлагаемый алгоритм EKF может оценивать все параметры совершенно аналогично части моделирования. По результатам, предложенный алгоритм действует после изменения сопротивления статора и изменения нагрузки.Коммутируемая решетка с шестью сопротивлениями 7,8 Ом подключена к статору. Одно реле переводит резисторы в состояние короткого замыкания. В этом состоянии сопротивление статора равно Rs. Управляя сопротивлением коммутируемой матрицы, можно добавить или убрать дополнительное сопротивление к сопротивлению статора в заданное время.
Сравнение номеров математических операций в EKF и ROEKF показано в таблице 2. В этой таблице сравниваются различные функции, используемые в этих алгоритмах. В ROEKF сокращено количество математических функций; таким образом, время выполнения алгоритма сокращается.Несмотря на сокращение времени выполнения, точность оценки алгоритма не изменилась. В предлагаемом методе исключается ненужный расчет, что сокращает время расчета.
| ||||||||||||||||||
Кроме того, в предлагаемом методе было уменьшено место в памяти в байтах.В таблице 3 показано сравнение объема памяти, используемого в методах EKF и ROEKF. Согласно таблицам 2 и 3, время выполнения алгоритма уменьшено почти на 50%, а объем используемой памяти уменьшен на 35%. Обозначения двигателей, которые используются в этой статье, показаны в Таблице 4.
| ||||||||||||
| |||||||||||||||||||||||||
EKF DTC шестифазного асинхронного двигателя, представленного в этой статье, может управлять двигателем во всех диапазонах скоростей. По результатам предлагаемый способ активен при изменении нагрузки и изменении параметров. Если скорость двигателя низкая, предлагаемый метод позволяет точно оценить скорость и сопротивление статора. Если сопротивление статора оценено неправильно, код неисправности содержит ошибку и, возможно, нестабилен. Предлагаемый метод РОЭКФ имеет высокую скорость оценки. Предлагаемый алгоритм может быть реализован в недорогом микропроцессоре.В предлагаемом способе сокращается время выполнения, а также снижается сложность системы. Предлагаемый метод сокращает время выполнения и предотвращает неиспользуемые вычисления в реализации DSP и FPGA. Работоспособность предложенного метода подтверждена результатами моделирования и эксперимента.
Доступность данных
Данные файлов MATLAB, используемые для подтверждения результатов этого исследования, доступны у соответствующего автора по запросу.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.Благодарности и интеллектуальная обработка информации (2020CP01).
Обратимая зависимость скорости и времени асинхронной машины при прямом пуске без нагрузки
% PDF-1.4 % 1 0 объект > поток Индукционная машина; математическое моделирование; запуск; обратимое уравнение Текст 4.2.0 от 1T3XTapplication / pdf10.1080 / 00051144.2019.1689725en
