Электростатика — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Электрический заряд и его свойства

К оглавлению…

Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами q или Q. В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10^–6 Кл), нанокулонами (1 нКл = 10^–9 Кл) и пикокулонами (1 пКл = 10^–12 Кл). Электрический заряд обладает следующими свойствами:

1. Электрический заряд является видом материи.

2. Электрический заряд не зависит от движения частицы и от ее скорости.

3. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела. Одно и то же тело в разных условиях может иметь разный заряд.

4. Существует два рода электрических зарядов, условно названных положительными и отрицательными.

5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.

6. Существует минимально возможный (по модулю) электрический заряд, называемый

элементарным зарядом. Его значение:

e = 1,602177·10^–19 Кл ≈ 1,6·10^–19 Кл.

Электрический заряд любого тела всегда кратен элементарному заряду:

где: N – целое число. Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.

7. Закон сохранения электрического заряда.

В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q₁ и q₂ (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:

С современной точки зрения, носителями зарядов являются элементарные частицы.

Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.

В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов, или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. Обратите внимание, что положительные протоны входят в состав ядра атома, поэтому их число может изменяться только при ядерных реакциях. Очевидно, что при электризации тел ядерных реакций не происходит. Поэтому в любых электрических явлениях число протонов не меняется, изменяется только число электронов.

Так, сообщение телу отрицательного заряда означает передачу ему лишних электронов. А сообщение положительного заряда, вопреки частой ошибке, означает не добавление протонов, а отнимание электронов. Заряд может передаваться от одного тела к другому только порциями, содержащими целое число электронов.

Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:

1. Линейная плотность заряда. Используется для описания распределения заряда по нити:

где: L – длина нити. Измеряется в Кл/м.

2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:

где: S – площадь поверхности тела. Измеряется в Кл/м².

3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:

где: V – объем тела. Измеряется в Кл/м³.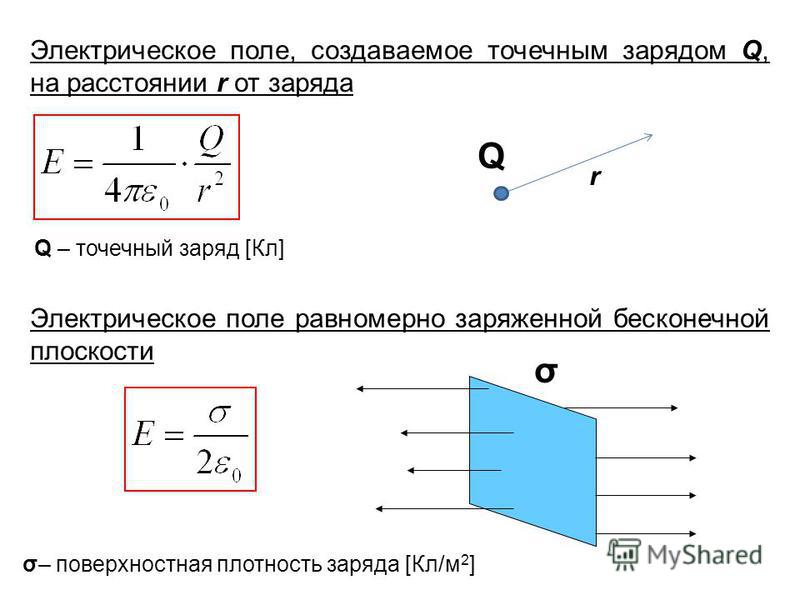

Обратите внимание на то, что масса электрона равна:

m_e = 9,11∙10^–31 кг.

 

Закон Кулона

К оглавлению…

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:

k = 9∙10⁹ м/Ф.

Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют

электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:

где: ε₀ = 8,85∙10^–12 Ф/м – электрическая постоянная.

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.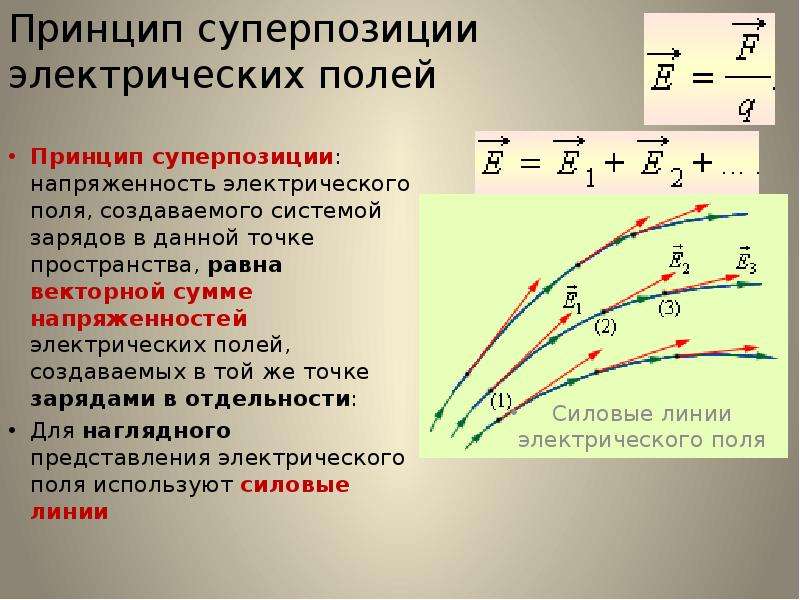

Запомните также два важных определения:

Проводники – вещества, содержащие свободные носители электрического заряда. Внутри проводника возможно свободное движение электронов – носителей заряда (по проводникам может протекать электрический ток). К проводникам относятся металлы, растворы и расплавы электролитов, ионизированные газы, плазма.

Диэлектрики (изоляторы) – вещества, в которых нет свободных носителей заряда. Свободное движение электронов внутри диэлектриков невозможно (по ним не может протекать электрический ток). Именно диэлектрики обладают некоторой не равной единице диэлектрической проницаемостью ε.

Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):

 

Электрическое поле и его напряженность

К оглавлению…

По современным представлениям, электрические заряды не действуют друг на друга непосредственно.

Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика —

напряженность электрического поля E.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:

Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.

Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.

• Силовые линии электростатического поля никогда не пересекаются.
• Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным.
• При изображении электрического поля с помощью силовых линий их густота должна быть пропорциональна модулю вектора напряженности поля.
• Силовые линии начинаются на положительном заряде или бесконечности, а заканчиваются на отрицательном или бесконечности. Густота линий тем больше, чем больше напряжённость.
• В данной точке пространства может проходить только одна силовая линия, т.к. напряжённость электрического поля в данной точке пространства задаётся однозначно.

Электрическое поле называют однородным, если вектор напряжённости одинаков во всех точках поля. Например, однородное поле создаёт плоский конденсатор – две пластины, заряженные равным по величине и противоположным по знаку зарядом, разделённые слоем диэлектрика, причём расстояние между пластинами много меньше размеров пластин.

Во всех точках однородного поля на заряд q, внесённый в однородное поле с напряжённостью E, действует одинаковая по величине и направлению сила, равная F = Eq. Причём, если заряд q положительный, то направление силы совпадает с направлением вектора напряжённости, а если заряд отрицательный, то вектора силы и напряжённости противоположно направлены.

Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:

 

Принцип суперпозиции

К оглавлению. ..

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q < 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.

Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:

Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:

1. Нарисовать рисунок.
2. Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
3. Вычислить каждую из напряжённостей по соответствующей формуле.
4. Сложить вектора напряжённостей геометрически (т.е. векторно).

 

Потенциальная энергия взаимодействия зарядов

К оглавлению…

Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывается потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:

Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.

Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.

Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью. Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.

 

Потенциал. Разность потенциалов. Напряжение

К оглавлению…

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля.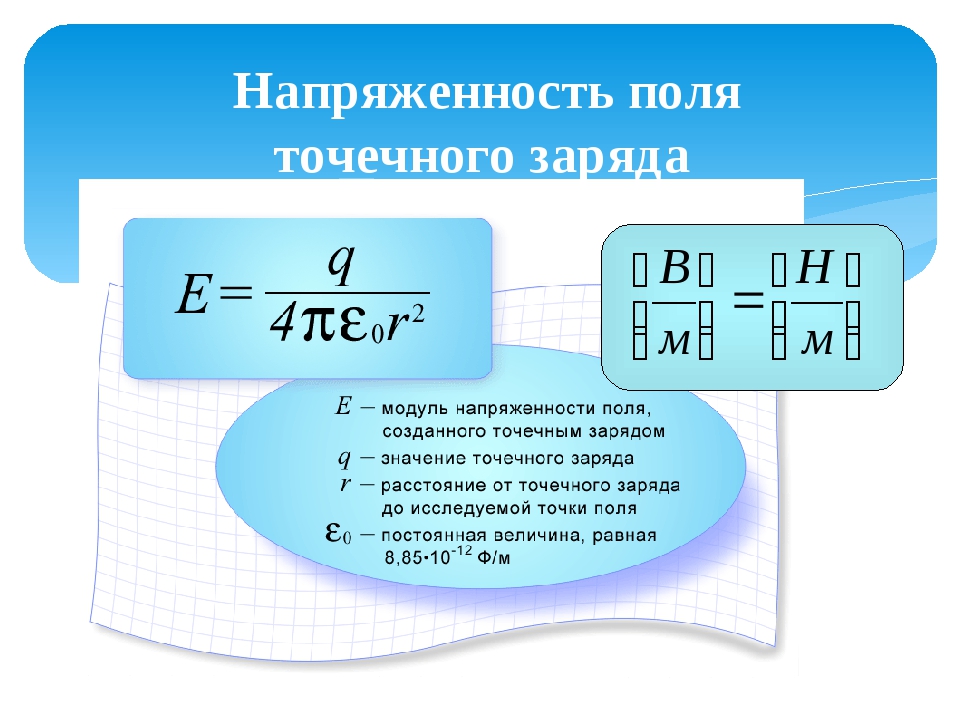 В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.

Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

В этих формулах:

• φ – потенциал электрического поля.
• ∆φ – разность потенциалов.
• W – потенциальная энергия заряда во внешнем электрическом поле.
• A – работа электрического поля по перемещению заряда (зарядов).
• q – заряд, который перемещают во внешнем электрическом поле.
• U – напряжение.
• E – напряженность электрического поля.
• d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.

Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.

Принцип суперпозиции потенциала

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):

Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.

 

Электрическая емкость. Плоский конденсатор

К оглавлению…

При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:

В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.

Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:

За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0.  Электроёмкость плоского конденсатора может быть рассчитана по формуле:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.

Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:

Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:

Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):

Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.

Энергия электрического поля

Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):

 

Соединения конденсаторов

К оглавлению…

Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:

При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:

Из закона сохранения заряда следует, что заряды на соседних обкладках равны:

Напряжение равно сумме напряжений на отдельных конденсаторах.

Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:

Для N одинаковых последовательно соединённых конденсаторов:

 

Проводящая сфера

К оглавлению…

Напряженность поля внутри заряженного проводника равна нулю. В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.

Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.

На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.

Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю). Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.

Электрическая емкость шара радиуса R:

Если шар окружен диэлектриком, то:

 

Свойства проводника в электрическом поле

К оглавлению…

1. Внутри проводника напряженность поля всегда равна нулю.
2. Потенциал внутри проводника во всех точках одинаков и равен потенциалу поверхности проводника. Когда в задаче говорят, что «проводник заряжен до потенциала … В», то имеют в виду именно потенциал поверхности.
3. Снаружи от проводника вблизи от его поверхности напряженность поля всегда перпендикулярна поверхности.
4. Если проводнику сообщить заряд, то он весь распределится по очень тонкому слою вблизи поверхности проводника (обычно говорят, что весь заряд проводника распределяется на его поверхности). Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся.
5. Снаружи проводника напряженность поля тем больше, чем кривее поверхность проводника. Максимальное значение напряженности достигается вблизи остриев и резких изломов поверхности проводника.

 

Замечания к решению сложных задач

К оглавлению…

1. Заземление чего-либо означает соединение проводником данного объекта с Землей. При этом потенциалы Земли и имеющегося объекта выравниваются, а необходимые для этого заряды перебегают по проводнику с Земли на объект либо наоборот. При этом нужно учитывать несколько факторов, которые следуют из того, что Земля несоизмеримо больше любого объекта находящегося не ней:

• Общий заряд Земли условно равен нолю, поэтому ее потенциал также равен нолю, и он останется равным нолю после соединения объекта с Землей. Одним словом, заземлить – означает обнулить потенциал объекта.
• Для обнуления потенциала (а значит и собственного заряда объекта, который мог быть до этого как положительным так и отрицательным), объекту придется либо принять либо отдать Земле некоторый (возможно даже очень большой) заряд, и Земля всегда сможет обеспечить такую возможность.

2. Еще раз повторимся: расстояние между отталкивающимися телами минимально в тот момент, когда их скорости становятся равны по величине и направлены в одну сторону (относительная скорость зарядов равна нулю). В этот момент потенциальная энергия взаимодействия зарядов максимальна. Расстояние между притягивающимися телами максимально, также в момент равенства скоростей, направленных в одну сторону.

3. Если в задаче имеется система, состоящая из большого количества зарядов, то необходимо рассматривать и расписывать силы, действующие на заряд, который не находится в центре симметрии.

Электрическое поле: определение, классификация, характеристики

Нас окружает материальный мир. Материю мы воспринимаем с помощью зрения и других органов чувств. Отдельным видом материи является электрическое поле, которое можно выявить только через его влияние на заряженные тела или с помощью приборов. Оно порождает магнитные поля и взаимодействует с ними. Эти взаимодействия нашли широкое практическое применение.

Определение

Электрическое поле неразрывно связано с магнитным полем, и возникает в результате его изменения. Эти два вида материи являются компонентами электромагнитных полей, заполняющих пространство вокруг заряженных частиц или заряженных тел.

Таким образом, данный термин означает особый вид материи, обладающий собственной энергией, являющийся составным компонентом векторного электромагнитного поля. У электрического поля нет границ, однако его силовое воздействие стремится к нулю, при удалении от источника – заряженного тела или точечных зарядов [1].

Важным свойством полевой формы материи является способность электрического поля поддерживать упорядоченное перемещение носителей зарядов.

Рис. 1. Определение понятия «электрическое поле»

Энергия электрического поля подчиняется действию закона сохранения. Её можно преобразовать в другие виды или направить на выполнение работы.

Силовой характеристикой полей выступает их напряжённость – векторная величина, численное значение которой определяется как отношение силы, действующей на пробный положительный заряд, к величине этого заряда.

Характерные физические свойства:

• реагирует на присутствие заряженных частиц;
• взаимодействует с магнитными полями;
• является движущей силой по перемещению зарядов – как положительных ионов, таки отрицательных зарядов в металлических проводниках;
• поддаётся определению только по результатам наблюдения за проявлением действия.

Оно всегда окружает неподвижные статичные (не меняющиеся со временем) заряды, поэтому получило название – электростатическое. Опыты подтверждают, что в  электростатическом поле действуют такие же силы, как и в электрическом.

Электростатическое взаимодействие поля на заряженные тела можно наблюдать при поднесении наэлектризованной эбонитовой палочки к мелким предметам. В зависимости от полярности наэлектризованных частиц, они будут либо притягиваться, либо отталкиваться от палочки.

Сильные электростатические поля образуются вблизи мощных электрических разрядов. На поверхности проводника, оказавшегося в зоне действия разряда, происходит перераспределение зарядов.

Вследствие распределения зарядов проводник становится заряженным, что является признаком влияния электрического поля.

Классификация

Электрические поля бывают двух видов: однородные и неоднородные.

Однородное электрическое поле

Состояние поля определяется пространственным расположением линий напряжённости. Если векторы напряжённости идентичны по модулю и они при этом сонаправлены во всех точках пространства, то электрическое поле – однородно. В нём линии напряжённости расположены параллельно.

В качестве примера является электрическое поле, образованное разноимёнными зарядами на участке плоских металлических пластин (см. рис. 2).

Рис. 2. Пример однородности

Неоднородное электрическое поле

Чаще встречаются поля, напряжённости которых в разных точках отличаются. Линии напряжённости у них имеют сложную конфигурацию. Простейшим примером неоднородности является электрический диполь, то есть система из двух разноимённых зарядов, влияющих друг на друга (см. рис. 3). Несмотря на то, что векторы напряжённости электрического диполя образуют красивые линии, но поскольку они не равны, то такое поле неоднородно. Более сложную конфигурацию имеют вихревые поля (рис 4).  Их неоднородность очевидна.

Рис. 3. Электрический диполь Рис. 4. Вихревые поля

Характеристики

Основными характеристиками являются:

• потенциал;
• напряжённость;
• напряжение.

Потенциал

Термин означает отношение потенциальной энергии W, которой обладает пробный заряд q′ в данной точке к его величине. Выражение φ =W/q′. называется потенциалом электрического поля в этой точке.

Другими словами: количество накопленной энергии, которая потенциально может быть потрачена на выполнение работы, направленной на перемещение единичного заряда в бесконечность, или в другую точку с условно нулевой энергией,  называется потенциалом рассматриваемого электрического поля в данной точке.

Энергия поля учитывается по отношению к данной точке. Её ещё называют потенциалом в данной точке. Общий потенциал системы равен сумме потенциалов отдельных зарядов. Это одна из важнейших характеристик поля. Потенциал можно сравнить с энергией сжатой пружины, которая при высвобождении способна выполнить определённую работу.

Единица измерения потенциала – 1 вольт. При бесконечном удалении точки от наэлектризованного тела, потенциал в этой точке уменьшается до 0: φ_∞=0.

Напряжённость поля

Достоверно известно, что электрическое поле отдельно взятого заряда q действует с определённой силой F на точечный пробный заряд, независимо от того, на каком расстоянии он находится. Сила, действующая на изолированный положительный пробный заряд, называется напряжённостью и обозначается символом E.

Напряжённость – векторная величина. Значение модуля вектора напряжённости: E=F/q′.

Линиями напряжённости электрического поля (известные как силовые линии), называются касательные, которые в точках касания совпадают с ориентацией векторов напряжённости. Плотность силовых линий определяет величину напряжённости.

Рис. 5. Электрическое поле положительного и отрицательного вектора напряжённости

Напряженность вокруг точечного заряда Q на расстоянии r от него, определяется по закону Кулона: E = 14πε₀⋅Qr2. Такие поля называют кулоновскими.

Векторы напряженности положительного точечного заряда направлены от него, а отрицательного – до центра (к заряду). Направления векторов кулоновского поля видно на рис. 6.

Рис. 6. Направление линий напряжённости положительных и отрицательных зарядов

Для кулоновских полей справедлив принцип суперпозиции. Суть принципа в следующем:вектор напряжённости нескольких зарядов может быть представлен в виде геометрической суммы напряжённостей, создаваемых каждым отдельно взятым зарядом, входящих в эту систему.

Для общего случая распределения зарядов имеем:

Линии напряжённости схематически изображены на рисунке 7. На картинке видно линии, характерные для полей:

• электростатического;
• дипольного;
• системы и одноимённых зарядов;
• однородного поля.

Рис. 7. Линии напряжённости различных полей

Напряжение

Поскольку силы электрического поля способны выполнять работу по перемещению носителей элементарных зарядов, то наличие поля является условием для существования электрического тока. Электроны и другие элементарные заряды всегда двигаются от точки, обладающей более высоким потенциалом, к точке с низшим потенциалом. При этом часть энергии расходуется на выполнение работы по перемещению.

Для поддержания постоянного тока (упорядоченного движения носителей элементарных зарядов) необходимо на концах проводника поддерживать разницу потенциалов, которую ещё называют напряжением. Чем больше эта разница, тем активнее выполняется работа, тем мощнее ток на этом участке. Функции по поддержанию разницы потенциалов возложены на источники тока.

Методы обнаружения

Органы чувств человека не воспринимают электрических полей. Поэтому мы не можем их увидеть, попробовать на вкус или определить по запаху. Единственное, что может ощутить человек – это выпрямление волос вдоль линий напряжённости. Наличие слабых воздействий мы просто не замечаем.

Обнаружить их можно через воздействие на мелкие кусочки бумаги, бузиновые шарики и т.п. Электрическое поле воздействует на электроскоп – его лепестки реагируют на такие воздействия.

Очень простой и эффективный метод обнаружения с помощью стрелки компаса. Она всегда располагается вдоль линий напряжённости.

Существуют очень чувствительные электронные приборы, с лёгкостью определяющие наличие электростатических полей.

Методы расчета электрического поля

Для расчётов параметров используются различные аналитические или численные методы:

• метод сеток или конечных разностей;
• метод эквивалентных зарядов;
• вариационные методы;
• расчёты с использованием интегральных уравнений и другие.

Выбор конкретного метода зависит от сложности задачи, но в основном используются численные методы, приведённые в списке.

Использование

Изучение свойств электрического поля открыло перед человечеством огромные возможности. Способность поля перемещать электроны в проводнике позволила создавать источники тока.

На свойствах электрических полей создано различное оборудование, применяемое в медицине, химической промышленности, в электротехнике. Разрабатываются приборы, применяемые в сфере беспроводной передачи энергии к потребителю. Примером могут послужить устройства беспроводной зарядки гаджетов. Это пока только первые шаги на пути к передачи электричества на большие расстояния.

Сегодня, благодаря знаниям о свойствах полевой формы материи, разработаны уникальные фильтры для очистки воды. Этот способ оказался дешевле, чем использование традиционных сменных картриджей.

К сожалению, иногда приходится нейтрализовать силы полей. Обладая способностью электризации предметов, оказавшихся в зоне действия, электрические поля создают серьёзные препятствия для нормальной работы радиоэлектронной аппаратуры. Накопленное статическое электричество часто является причиной выхода из строя интегральных микросхем и полевых транзисторов.

Формула напряженности электрического поля в физике

Содержание:

Определение и формула напряженности электрического поля

Определение

Вектор напряженности $\bar{E}$ – это силовая характеристика электрического поля. В некоторой точке поля, напряженность равна силе, с которой поле действует на единичный положительный заряд, размещенный в указанной точке, при этом направление силы и напряженности совпадают. Математическое определение напряженности записывается так:

$$\bar{E}=\frac{\bar{F}}{q}$$

где $\bar{F}$ – сила, с которой электрическое поле действует на неподвижный, «пробный», точечный заряд q, который размещают в рассматриваемой точке поля. При этом считают, что «пробный» заряд мал на столько, что не искажает исследуемого поля.

Если поле является электростатическим, то его напряженность от времени не зависит.{n} \bar{E}_{i}(2)$$

Допустим, что поле создается системой точечных зарядов и их распределение непрерывно, тогда результирующая напряженность находится как:

$$\bar{E}=\int d \bar{E}(3)$$

интегрирование в выражении (3) проводят по всей области распределения заряда.

Напряженность поля в диэлектрике

Напряженность поля $\bar{E}$ в диэлектрике равна векторной сумме напряженностей полей, создаваемых свободными зарядами $\bar{E}_0$ и связанными (поляризационными зарядами) $\bar{E}_p$:

$$\bar{E}=\bar{E}_{0}+\bar{E}_{p}(4)$$

В том случае, если вещество, которое окружает свободные заряды однородный и изотропный диэлектрик, то напряженность $\bar{E}$ равна:

$$\bar{E}=\frac{\bar{E}_{0}}{\varepsilon}(5)$$

где $\varepsilon$ – относительная диэлектрическая проницаемость вещества в исследуемой точке поля. Выражение (5) обозначает то, что при заданном распределении зарядов напряженность электростатического поля в однородном изотропном диэлектрике меньше, чем в вакууме в $\varepsilon$ раз.{-12}$ Ф/м (система СИ) — электрическая постоянная.

Связь напряженности и потенциала

В общем случае напряженность электрического поля связана с потенциалом как:

$$\bar{E}=-\operatorname{grad} \varphi-\frac{\partial \bar{A}}{\partial t}(7)$$

где $\varphi$ – скалярный потенциал, $\bar{a}$ – векторный потенциал.

Для стационарных полей выражение (7) трансформируется в формулу:

$$\bar{E}=-\operatorname{grad} \varphi(8)$$

Единицы измерения напряженности электрического поля

Основной единицей измерения напряженности электрического поля в системе СИ является: [E]=В/м(Н/Кл)

Примеры решения задач

Пример

Задание. Каков модуль вектора напряженности электрического поля $\bar{E}$ в точке, которая определена радиус- вектором $\bar{r}_{2}=7 \bar{i}+3 \bar{j}$ (в метрах), если электрическое поле создает положительный точечный заряд (q=1Кл), который лежит в плоскости XOY и его положение задает радиус вектор $\bar{r}_{1}=\bar{i}-5 \bar{j}$, (в метрах)?

Решение.{\prime}-\bar{r}\right) d V$

Читать дальше: Формула пути.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. НАПРЯЖЁННОСТЬ. ПРИНЦИП СУПЕРПОЗИЦИИ ПОЛЕЙ.

Закон Кулона, позволяет вычислить силу взаимодействия между двумя зарядами, но не объясняет, как один заряд действует на другой. Через какое время, например, один из зарядов «почувствует», что другой заряд стал приближаться или отдаляться от него? Связаны ли чем-нибудь между собой заряды? Чтобы ответить на эти вопросы, великие английские физики М. Фарадей и Дж. Максвелл ввели понятие электрического поля – материального объекта, существующего вокруг электрических зарядов. Таким образом, заряд q₁ порождает вокруг себя электрическое поле, а другой заряд q₂, оказавшись в этом поле, испытывает на себе действие заряда q₁ согласно закону Кулона . При этом, если положение заряда q₁ изменились, то изменение его электрического поля будет происходить постепенно, а не мгновенно, так, что на расстоянии L от q₁ изменения поля произойдут через промежуток времени L/c, где с – скорость света, 3^.10⁸ м/с. Запаздывание изменений электрического поля доказывает то, что взаимодействие между зарядами согласуется с теорией близкодействия. Эта теория объясняет любое взаимодействие между телами, даже отдалёнными друг от друга, существованием каких-либо материальных объектов или процессов между ними. Материальным объектом, осуществляющим взаимодействие между заряженными телами, является их электрическое поле.

Чтобы охарактеризовать данное электрическое поле, достаточно измерить силу, действующую на точечный заряд в различных областях этого поля. Опыты и закон Кулона  показывают, что сила, действующая на заряд со стороны поля, пропорциональна величине этого заряда. Поэтому отношение силы F, действующей на заряд в данной точке поля, к величине этого заряда q, уже не зависит от q и является характеристикой электрического поля, называемой его напряжённостью, E:

Напряжённость электрического поля, как следует из (35.1), является вектором, направление которого совпадает с направлением силы, действующей в данной точке поля на положительный заряд. Из закона Кулона (34.1) следует, что модуль напряжённости E поля точечного заряда q зависит от расстояния r до него следующим образом:

Векторы напряжённости в различных точках электрического поля положительного и отрицательного зарядов показаны на рис. 35а.

Если электрическое поле образовано несколькими зарядами (q₁, q₂, q₃ и т.д.), то, как показывает опыт, напряжённость E в любой точке этого поля равна сумме напряжённостей E₁, E₂, E₃ и т.д. электрических полей, создаваемых зарядами q₁, q₂, q₃ и т.д., соответственно:

В этом и состоит принцип суперпозиции (или наложения) полей, который позволяет определить напряжённость поля, созданного несколькими зарядами .

Чтобы показать, как изменяется напряжённость поля в различных его областях, рисуют силовые линии — непрерывные линии, касательные к которым в каждой точке совпадают с векторами напряжённости . Силовые линии не могут пересекаться между собой, т.к. в каждой точке вектор напряжённости поля имеет вполне определённое направление. Они начинаются и заканчиваются на заряженных телах, вблизи которых модуль напряжённости и густота силовых линий возрастает. Густота силовых линий пропорциональна модулю напряжённости электрического поля.

Различные тела можно наэлектризовать по-разному: передать им положительный или отрицательный заряд, сделать его большим или малым. После этого тела будут по-разному действовать на другие тела: отталкивать или притягивать их, делать это сильнее или слабее. Но как одно тело «узнаёт» заряд другого (например, чтобы «знать»: притягивать его или отталкивать)? Для ответа на этот вопрос рассмотрим понятие «электрическое поле».

Наэлектризуем одноимённо металлический шар на пластмассовой подставке и лёгкий пробковый или пенопластовый шарик на нити (назовём его пробным шариком). Будем переносить его в различные точки пространства вокруг большого шара (см. рисунок). Мы заметим, что в каждой точке пространства вокруг наэлектризованного тела обнаруживается сила, действующая на пробный шарик.

О том, что существует сила, мы судим по отклонению нити шарика от вертикали. По мере удаления от заряженного шара пробный шарик отклоняется всё слабее, следовательно, действующая на него сила становится всё меньше (сравните положения а, б, в).

Для следующего опыта используем магнит и стальной шарик, который положим на горизонтальную поверхность стола. Приблизим магнит к шарику сверху, и он незамедлительно покатится по столу вслед за магнитом. Следовательно, в каждой точке пространства вокруг намагниченного тела есть сила, действующая на стальной шарик.

Итак, в каждой точке пространства вокруг наэлектризованных или намагниченных тел существует так называемое силовое поле, способное воздействовать на другие тела. Заметим, что действие силы тяжести также обнаруживается во всех точках пространства вокруг Земли. Поэтому по аналогии говорят, что в пространстве вокруг планет также существует силовое поле; его называют гравитационным полем.

Обобщаем: гравитационное, магнитное и электрическое поле являются разновидностями силовых полей. На примере электрического поля рассмотрим один из методов изучения полей – метод силовых линий.

Проведём опыт. Возьмём два металлических шара на пластмассовых подставках, а также иглу, тоже укреплённую на подставке. Расположим шары на расстоянии 40–50 см друг от друга, а между ними – подставку с иглой. Уравновесим на ней сухую деревянную щепку.

Если зарядить шары разноимённо, мы увидим, что щепка развернётся так, чтобы находиться на прямой, соединяющей шары (см. верхнюю часть рисунка).

Будем помещать щепку в различные места вокруг шаров (см. нижнюю часть рисунка, слева). Заметим, что щепка занимает такие положения, которые «ложатся» на мысленно проведённые дугообразные линии, соединяющие шары; их называют силовыми линиями электрического поля.

Если тела наэлектризованы одноимённо или если мы имеем только одно тело, силовые линии также можно изучать с помощью щепки на игле. Однако проще – при помощи мелко стриженных волос. Опишем этот способ. Над заряженными телами необходимо поместить стекло и посыпать его стриженным волосом. Под действием поля каждый волосок поворачивается определённым образом, и образуется «картина» (см. рисунки). Слева и справа показано расположение волос вокруг одноимённо заряженных шаров, а в центре – разноимённо заряженных шаров, как в опыте со щепкой.

Изображение силовых линий поля – метод для описания электрических полей. Силовые линии изображают более «густыми» там, где обнаруживается большая сила воздействия поля на тело или тела. Но не следует думать, что силовые линии действительно существуют внутри поля; это физическая модель. Она описывает силу и направление действия поля на помещаемые в него тела (в последнем примере – электрического поля).

В заключение осталось лишь добавить очевидное: электрическое поле всегда «привязано» к заряду, его создавшему, и при перемещении заряда в другую точку пространства электрическое поле практически мгновенно перемещается вслед за зарядом, действуя на другие тела.

Электрическое поле. Напряженность электрического поля.

Электростатическое поле

Электростатическое поле — это особая форма материи, которая возникает вокруг неподвижного электрического заряда. Это поле нет возможности увидеть, понюхать. Поле можно представить при помощи линий напряженности (силовых линий).

На рисунке видно, какое условное направление имеют силовые линии: начинаются на положительных зарядах и заканчиваются на отрицательных. Изображено и то, как линии напряженности распределяются при взаимодействии одноименных и разноименных зарядов.В реальности силовые линии можно увидеть при помощи железных опилок.

Чем дальше удаляться от заряда, тем меньше сила поля (силовые линии редеют), тем слабее взаимодействуют заряженные тела, посредством создаваемого ими поля.
Поле бывает однородным. В этом случае линии напряженности параллельные.

Поле однородное между пластинами в центре

Напряженность поля

Как оценить силу поля вокруг некоторого заряда? Для этого используют пробный заряд q₀. Пробный заряд — это всегда положительный заряд, его собственное электростатическое поле ничтожно мало, относительно исследуемого поля.
Сила, с которой поле действует на пробный заряд в данной точке поля, называется напряженностью электростатического поля в этой точке
Напряженность поля — векторная величина. Вектора — это касательная к линиям напряженности в данной точке поля. Направлен вектор туда же, куда силовая линия (линия напряженности).

Вектор напряженности в различных точках поля: А, B, C и D

Вектор напряженности в точках 1, 2 и 3

Можно вывести формулу
— напряженность поля точечного заряда q на расстоянии r от него.

Принцип суперпозиции

Если поле создается несколькими зарядами, то напряженность в некоторой точке равна векторной сумме напряженностей каждого из полей в отдельности

 

??? Вопросы

1. Какими зарядами создается электрическое поле?

2. Что называют электрическим полем?

3. Какими величинами характеризуется электрическое поле?

4. Запишите формулу напряженности электрического поля?

5. Запишите формулу напряженности электрического поля точечного заряда?

6. Назовите единицу измерения напряженности электрического поля?

7. Как изображается электрическое поле? 

8. Какое направлений силовых линий электрического поля?

9. Как называется электрическое поле, если его напряженность одинакова во всех точках?

10. В чем заключается принцип суперпозиции?

Электрическое поле: основные понятия

Электрические заряды не воздействуют непосредственно друг на друга. Согласно современным представлениям, заряженные тела взаимодействуют посредством силового поля, которое создают вокруг себя.

Это силовое поле воздействует на заряженные тела с некоторой силой. Исследовать электрическое поле, которое окружает тело, несущее заряд, можно с помощью пробного заряда, величина которого незначительна. Особенностью электрического поля точечного заряда является тот факт, что оно не производит заметного перераспределения исследуемых зарядов.

Понятие напряженности электрического поля

Определение 1

Напряженность электрического поля – это силовая характеристика, которая используется для количественного определения электрического поля.

Второе значение термина – физическая величина, равная отношению силы, с которой поле действует на положительный пробный заряд, помещенный в данную точку пространства, к величине этого заряда.

Напряженность электрического поля можно задать формулой:

E→=F→q.

Напряжение электрического поля является векторной величиной. Направление вектора E→ совпадает с направлением силы, которая воздействует на положительный пробный заряд в пространстве.

Напряженность электрического поля

Какое поле называют электростатическим?

Определение 2

Электростатическое поле – это электрическое поле, которое окружает неподвижные и не меняющиеся со временем заряды.

Очень часто в контексте темы электростатическое поле будет именоваться электрическим для краткости.

Электрическое поле может быть создано сразу несколькими заряженными телами. Такое поле также можно исследовать с помощью пробного заряда. В этом случае мы будем оценивать результирующую силу, которая будет равна геометрической сумме сил каждого из заряженных тем в отдельности.

Определение 3

Напряженность электрического поля, которая создается в определенной точке пространства системой зарядов, будет равна векторной сумме напряженностей электрических полей:

E→=E1→+E2→+…

Электрическое поле подчиняется принципу суперпозиции.

Определение 4

Согласно формуле, напряженность электростатического поля, которое создается точечным зарядом Q на расстоянии r от него, в соответствии с законом Кулона, будет равна по модулю:

E=14πε0·Qr2.

Это поле называется кулоновским.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание

В кулоновском поле направление вектора E⇀ зависит от знака заряда Q: если Q>0, то вектор E⇀ направлен по радиусу от заряда, если Q<0, то вектор E⇀ направлен к заряду.

Обратимся к иллюстрации. На рисунке для большей наглядности мы используем силовые линии электрического поля. Они проходят таким образом, чтобы направление вектора E⇀ в каждой из точек пространства совпадало с направлением касательной к силовой линии. Густота силовых линий соответствует модулю вектора напряженности поля.

Рисунок 1.2.1. Силовые линии электрического поля.

Мы можем использовать как положительные, так и отрицательные точечные заряды. Оба эти случая мы изобразили на рисунке. Электростатическое поле, которое создается системой зарядов, мы можем представить как суперпозицию кулоновских полей точечных зарядов. В связи с этим мы можем рассматривать поля точечных зарядов как элементарные структурные единицы любого электрического поля.

Рисунок 1.2.2. Силовые линии кулоновских полей.

Кулоновское поле точечного заряда Q удобно записать в векторной форме. Для этого нужно провести радиус-вектор r→от заряда Q к точке наблюдения. Тогда при Q>0 вектор E→ параллелен r→, а при Q<0 вектор E→ антипараллелен r→.

Следовательно можно записать:

E→=14πε0·Qr3r→,

где r – модуль радиус-вектора r→.

По заданному распределению зарядов можно определить электрическое поле E→. Такие задачи часто встречаются в таком разделе физики как электростатика. Рассмотрим пример такой задачи.

Пример 1

Предположим, что нам нужно найти электрическое поле длинной однородно заряженной нити на расстоянии R от нее. Для большей наглядности мы привели схему на рисунке ниже.

Рисунок 1.2.3. Электрическое поле заряженной нити.

Поле в точке наблюдения P может быть представлено в виде суперпозиции кулоновских полей, создаваемых малыми элементами Δx нити, с зарядом τΔx, где τ – заряд нити на единицу длины. Задача сводится к суммированию (интегрированию) элементарных полей ∆E→. Результирующее поле оказывается равным

E=τ2πε0R.

Вектор E→ везде направлен по радиусу R→. Это следует из симметрии задачи.

Даже в таком простом примере вычисления могут быть достаточно громоздкими. Упростить математические расчеты позволяет теорема Гаусса, которая выражает фундаментальное свойство электрического поля.

Рисунок 1.2.4. Модель электрического поля точечных зарядов.

Рисунок 1.2.5. Модель движения заряда в электрическом поле.

Понятие о диполях

Определение 5

Электрический диполь – это система из двух одинаковых по модулю зарядов, которые отличаются знаками и расположены на некотором расстоянии друг от друга.

Эта система может послужить нам хорошим примером применения принципа суперпозиции полей, а также электрической моделью многих молекул.

Рисунок 1.2.6. Силовые линии поля электрического диполя E→=E1→+E2→.

Дипольный момент p→ является одной из наиболее важных характеристик электрического диполя:

p→=l→q,

где l→ – вектор, направленный от отрицательного заряда к положительному, модуль l→=l.

Электрическим дипольным моментом обладает, например, нейтральная молекула воды (h3O), так как центры двух атомов водорода располагаются не на одной прямой с центром атома кислорода, а под углом 105°. Дипольный момент молекулы воды p=6,2·10–30 Кл · м.

Рисунок 1.2.7. Дипольный момент молекулы воды.

1.3 Напряженность электрического поля

Электрическое поле. Для объяснения природы электрических взаимодействий заряженных тел необходимо допустить наличие в окружающем заряды пространстве физического агента, осуществляющего это взаимодействие. В соответствии с теорией близкодействия, утверждающей, что силовые взаимодействия между телами осуществляются через посредство особой материальной среды, окружающей взаимодействующие тела и передающей любые изменения таких взаимодействий в пространстве с конечной скоростью, таким агентом является электрическое поле.

Электрическое поле создается как неподвижными, так и движущимися зарядами. О наличии электрического поля можно судить, прежде всего, по его способности оказывать силовое действие на электрические заряды, движущиеся и неподвижные, а также по способности индуцировать электрические заряды на поверхности проводящих нейтральных тел.

Поле, создаваемое неподвижными электрическими зарядами, называют стационарным электрическим, или электростатическим полем. Оно представляет собой частный случай электромагнитного поля, посредством которого осуществляются силовые взаимодействия между электрически заряженными телами, движущимся в общем случае произвольным образом относительно системы отсчета.

Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.

E = F / q _пр.

Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд q_пр, помещенный в рассматриваемую точку поля, к величине этого заряда.

Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл.

Напряженность поля точечного заряда. Используя закон Кулона (1.1) найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:

  (1.2)

В этой формуле r – радиус-вектор, соединяющий заряды q и q_пр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.

Принцип суперпозиции. Напряжённость поля, создаваемого системой неподвижных точечных зарядов q₁, q₂, q₃, ¼, q_n, равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности:
                                          

где r_i – расстояние между зарядом q_i и рассматриваемой точкой поля.

Принцип суперпозиции, позволяет рассчитывать не только напряжённость поля системы точечных зарядов, но и напряженность поля в системах, где имеет место непрерывное распределение заряда. Заряд тела можно представить как сумму элементарных точечных зарядов dq.

При этом, если заряд распределен с линейной плотностью t, то dq = t dl; если заряд распределен с поверхностной плотностью s, то dq = dl и dq = r dl, если заряд распределен с объёмной плотностью r.

Графическое изображение электрического поля. Метод графического изображения электрического поля был предложен английским физиком Майклом Фарадеем. Суть метода заключается в том, что на чертеже изображаются непрерывные линии, которые называют линиями напряженности, или силовыми линиями.

Правило построения линий напряженности заключается в том, что касательные к ним в каждой точке чертежа совпадают с направлением вектора напряженности поля в изображаемой точке.

Таким образом, силовые линии имеют то же направление, что и напряжённость поля и не пересекаются, так как в каждой точке электрического поля вектор E имеет лишь одно направление.

С помощью силовых линий можно дать количественную характеристику напряжённости электрического поля. Для этого густота, или плотность, силовых линий выбирается пропорционально модулю вектора напряженности. Плотность силовых линий определяется как число линий, пронизывающих единичную поверхность в направлении, перпендикулярном к этой поверхности.

Изображение силовых линий позволяет получать картину поля, которая наглядно показывает, чему равна напряженность в разных частях поля и как она изменяется в пространстве.

Индукция электрического поля. Напряженность электрического поля является силовой характеристикой поля и определяется не только зарядами, создающими поле, но зависит и от свойств среды, в которой находятся эти заряды.

Часто бывает удобно исследовать электрическое поле, рассматривая только заряды и их расположение в пространстве, не принимая во внимание свойств окружающей среды. Для этой цели используется векторная величина, которая называется электрической индукцией или электрическим смещением. Вектор электрической индукции D в однородной изотропной среде связан с вектором напряженности Е соотношением

.

Единицей измерения индукции электрического поля служит 1 Кл/ м². Направление вектора электрического смещения совпадает с вектором Е. Графическое изображение электрического поля можно построить с помощью линий электрической индукции по тем же правилам, что и для линий напряженности.

Вычисление характеристик электрического поля во многих случаях сильно упрощается применением важной теоремы, излагаемой ниже.

---

Вопросы

1)      Какие поля называются электростатическими

2)      Что такое напряженность электростатического поля. Каково направление вектора напряженности. Какова размерность

3)      Изобразите качественно линии поля Е для следующих систем зарядов: а) точечного заряда; б) однородного электрического поля; в) диполя. Изобразите также эквипотенциальные поверхности

4)      Какие системы зарядов создают однородное поле

5)      Точечный заряд q находится в начале координат. Написать выражение для напряженности поля заряда. Ответ выразить через а) радиус вектор точки r; б) декартовы координаты x, y, z

6)      Как определяется вектор электрического смещения. Каково его направление и что он характеризует

наверх

Возвращение к электрическому полю | Безграничная физика

Электрическое поле точечного заряда

Точечный заряд создает электрическое поле, которое можно рассчитать по закону Кулона.

Цели обучения

Определить закон, который можно использовать для расчета электрического поля, создаваемого точечным зарядом

Основные выводы

Ключевые моменты

• Электрическое поле — это векторное поле вокруг заряженной частицы. Он представляет силу, которую почувствовали бы другие заряженные частицы, если бы их поместили рядом с частицей, создающей электрическое поле.
• Учитывая точечный заряд или частицу бесконечно малого размера, которая содержит определенный заряд, силовые линии электрического поля исходят одинаково во всех радиальных направлениях.
• Если точечный заряд положительный, силовые линии направлены в сторону от него; если заряд отрицательный, на него указывают силовые линии.

Ключевые термины

• закон Кулона : математическое уравнение, вычисляющее вектор электростатической силы между двумя заряженными частицами
• векторное поле : конструкция, в которой каждая точка в евклидовом пространстве связана с вектором; функция, диапазон которой является векторным пространством

Электрическое поле точечного заряда, как и любое другое электрическое поле, представляет собой векторное поле, которое представляет эффект, который точечный заряд оказывает на другие заряды вокруг него.Эффект ощущается как сила, и когда заряженные частицы не движутся, эта сила известна как электростатическая сила. Электростатическая сила, как и сила тяжести, действует на расстоянии. Поэтому мы рационализируем это действие на расстоянии, говоря, что заряды создают вокруг себя поля, которые влияют на другие заряды.

Учитывая точечный заряд или частицу бесконечно малого размера, которая содержит определенный заряд, силовые линии электрического поля излучаются радиально во всех направлениях.Если заряд положительный, силовые линии направлены радиально от него; если заряд отрицательный, силовые линии направлены радиально к нему.

Электрическое поле положительного точечного заряда : электрическое поле положительно заряженной частицы направлено радиально от заряда.

Электрическое поле точечного отрицательного заряда : электрическое поле отрицательно заряженной частицы направлено радиально к частице.

Причину этих направлений можно увидеть в выводе электрического поля точечного заряда. 2} \ hat {\ text {r}}} [/ latex]

Радиальная система координат : электрическое поле точечного заряда определяется в радиальных координатах.Положительное направление r указывает от начала координат, а отрицательное направление r указывает на начало координат. Электрическое поле точечного заряда симметрично относительно направления θ.

Следует иметь в виду, что указанная выше сила действует на испытательный заряд Q в положительном радиальном направлении, определяемом исходным зарядом q . Это означает, что поскольку оба заряда являются положительными и будут отталкиваться друг от друга, сила, действующая на тестовый заряд, направлена ​​в сторону от исходного заряда.2} \ hat {\ text {r}} [/ latex]

Обратите внимание, что это указывает в отрицательном направлении [latex] \ hat {\ text {r}} [/ latex], то есть к исходному заряду. Это имеет смысл, потому что противоположные заряды притягиваются, и сила, действующая на тестовый заряд, будет стремиться подтолкнуть его к исходному положительному заряду, создающему поле. Приведенное выше математическое описание электрического поля точечного заряда известно как закон Кулона.

Наложение полей

Результат нескольких электрических полей, действующих на одну и ту же точку, является суммой напряженности сил, приложенных каждым полем в этой точке.

Цели обучения

Сформулируйте принцип суперпозиции для линейной системы

Основные выводы

Ключевые моменты

• Принцип суперпозиции гласит, что для всех линейных систем чистый ответ на множественные стимулы в данном месте и в определенное время равен сумме ответов, которые были бы вызваны каждым стимулом индивидуально.
• Возможные стимулы включают, помимо прочего, числа, функции, векторы, векторные поля и изменяющиеся во времени сигналы.
• Принцип суперпозиции применим к любой линейной системе, включая алгебраические уравнения, линейные дифференциальные уравнения и системы уравнений вышеупомянутых форм.
• Электрические поля — это непрерывные поля векторов, поэтому в данной точке можно найти силы, которые несколько полей будут применять к испытательному заряду, и сложить их, чтобы найти результат.

Ключевые термины

• ортогонально : из двух объектов под прямым углом; перпендикулярны друг другу.
• принцип суперпозиции : принцип, согласно которому линейная комбинация двух или более решений уравнения сама по себе является решением; это особенность многих физических законов.
• вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.

Как векторные поля, электрические поля подчиняются принципу суперпозиции. Этот принцип гласит, что для всех линейных систем чистый ответ на множественные стимулы в определенном месте и в определенное время равен сумме ответов, которые были бы вызваны каждым стимулом индивидуально.

Возможные стимулы включают, помимо прочего: числа, функции, векторы, векторные поля и изменяющиеся во времени сигналы. Следует отметить, что принцип суперпозиции применим к любой линейной системе, включая алгебраические уравнения, линейные дифференциальные уравнения и системы уравнений вышеупомянутых форм.

Например, если силы A и B постоянны и одновременно действуют на объект, обозначенный буквой O in, результирующая сила будет суммой сил A и B.Сложение векторов является коммутативным, поэтому добавление A к B или B к A не влияет на результирующий вектор; это также относится к вычитанию векторов.

Сложение векторов : Силы a и b действуют на объект в точке O. Их сумма коммутативна и дает результирующий вектор c.

Электрические поля — это непрерывные поля векторов, поэтому в данной точке можно найти силы, которые несколько полей будут применять к испытательному заряду, и сложить их, чтобы найти результат.Для этого сначала найдите составляющие вектора силы, прикладываемой каждым полем в каждой из ортогональных осей. Это можно сделать с помощью тригонометрических функций. Затем, как только векторы-компоненты найдены, добавьте компоненты по каждой оси, которые применяются объединенными электрическими полями.

Это единственная форма решения. Общий результирующий вектор можно найти, используя теорему Пифагора, чтобы найти результирующую (гипотенузу треугольника, созданного с помощью приложенных сил как катетов) и угол по отношению к данной оси, приравняв арктангенс угла к отношению силы соседних и противоположных ног.

Линии электрического поля: многократные заряды

Электрические поля, создаваемые множеством зарядов, взаимодействуют, как и любые другие векторные поля; их силы можно подвести.

Цели обучения

Вычислить результирующую силу нескольких электрических зарядов на испытательном заряде

Основные выводы

Ключевые моменты

• Когда взаимодействуют несколько электрических зарядов, их результирующая сила на испытательном заряде может быть вычислена с помощью векторного сложения.
• Если рассматриваются противоположные заряды, соедините один с другим с помощью силовых линий. Если заряды одинаковые, ни в коем случае не подключайте их.
• При моделировании электрических полей нескольких зарядов учитывайте знак и величину каждого заряда. Количество силовых линий должно быть пропорционально величине заряда, который их вызывает.

Ключевые термины

• вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.

До сих пор мы рассматривали силовые линии электрического поля, относящиеся к изолированным точечным зарядам. Но что, если будет введено другое обвинение? У каждого будет свое собственное электрическое поле, и эти два поля будут взаимодействовать.

При моделировании электрических полей нескольких зарядов важно учитывать знак и величину каждого заряда. Такие модели не должны быть абсолютными, но должны быть непротиворечивыми. Например, числовое поле линий должно быть пропорционально величине заряда, который их порождает.Это означает, что если заряды q ₁ (со значением +1) q ₂ (заряд +2) и q ₃ (заряд +3) находятся в одном поле, можно соединить 4, 8 и 12 силовые линии соответственно зарядам. Можно также выбрать подключение 3, 6 и 9 силовых линий соответственно к q ₁ , q ₂ и q ₃ ; важно то, что количество линий связано со значениями заряда одной и той же константой пропорциональности. Линии поля всегда должны быть направлены от положительных зарядов в сторону отрицательного заряда.

Силовые линии между подобными и непохожими зарядами : Пример a показывает, насколько слабое электрическое поле между подобными зарядами (концентрация силовых линий между ними мала). Пример b, напротив, имеет сильное поле между зарядами, о чем свидетельствует высокая концентрация соединяющих их силовых линий.

Если рассматриваются противоположные заряды, соедините один с другим с помощью силовых линий. Если заряды одинаковые, ни в коем случае не подключайте их.

Напряженность электрического поля пропорционально зависит от расстояния между силовыми линиями.Больше силовых линий на единицу площади, перпендикулярных линиям, означает более сильное поле. Также следует отметить, что в любой точке направление электрического поля будет касательным к силовой линии.

Определение чистой силы при испытательном заряде

Как векторные поля, электрические поля проявляют свойства, типичные для векторов, и поэтому могут складываться друг с другом в любой интересующей точке. Таким образом, для заданных зарядов q ₁ , q ₂ ,… q _n , можно найти их равнодействующую силу на испытательном заряде в определенной точке с помощью векторного сложения: сложения составляющих векторов в каждом направлении и использования обратной тангенса функция, чтобы найти угол результирующей по отношению к данной оси.

Конденсатор с параллельными пластинами

Конденсатор с параллельными пластинами — это электрический компонент, используемый для хранения энергии в электрическом поле между двумя заряженными плоскими поверхностями.

Цели обучения

Опишите общую конструкцию конденсатора

Основные выводы

Ключевые моменты

• Конденсаторы могут быть разных форм, но все они состоят из двух проводников, разделенных диэлектрическим материалом.
• Все конденсаторы собирают заряд на двух отдельных проводящих поверхностях; одна сторона положительная, а другая отрицательная.Электрическое поле создается, когда заряд накапливается на противоположных поверхностях, накапливая энергию. Диэлектрик действует как изолятор, изолируя заряженные поверхности.
• Способность конденсаторов удерживать заряд измеряется в Фарадах (Ф). Конденсаторы обычно допускают небольшую утечку тока через диэлектрик, но после определенного напряжения весь конденсатор выходит из строя, поскольку диэлектрик становится проводником.

Ключевые термины

• конденсатор : Электронный компонент, способный накапливать электрический заряд, особенно тот, который состоит из двух проводников, разделенных диэлектриком.
• диэлектрик : Электроизоляционный или непроводящий материал, рассматриваемый на предмет его электрической восприимчивости (т. Е. Его свойства поляризации при воздействии внешнего электрического поля).
• проводник : Материал, содержащий подвижные электрические заряды.

Обзор

Конденсатор — это электрический компонент, используемый для хранения энергии в электрическом поле. Конденсаторы могут быть разных форм, но все они состоят из двух проводников, разделенных диэлектрическим материалом.Для этого атома мы сосредоточимся на конденсаторах с параллельными пластинами.

Схема конденсатора с параллельными пластинами : Заряды в диэлектрическом материале выравниваются, чтобы противостоять зарядам каждой пластины конденсатора. Электрическое поле создается между пластинами конденсатора по мере накопления заряда на каждой пластине.

Емкость

Все конденсаторы собирают заряд на двух отдельных проводящих поверхностях; одна сторона положительная, а другая отрицательная. Электрическое поле создается, когда заряд накапливается на противоположных поверхностях, накапливая энергию.Диэлектрик между проводниками должен действовать как изолятор, не позволяя заряду перекрывать зазор между двумя пластинами. Такие диэлектрики обычно состоят из стекла, воздуха, бумаги или пустого пространства (вакуума). На практике диэлектрики не действуют как идеальные изоляторы и пропускают через них небольшой ток утечки.

Конденсаторы ограничены в своей способности предотвращать перетекание заряда с одной проводящей поверхности на другую; их способность удерживать заряд измеряется в фарадах (Ф), которые, среди прочего, определяются как 1 ампер-секунда на вольт, один джоуль на квадратный вольт и один кулон на вольт.

Для конденсатора с параллельными пластинами емкость (C) связана с диэлектрической проницаемостью (ε), площадью поверхности (A) и расстоянием между пластинами (d):

[латекс] \ text {C} = \ frac {\ epsilon \ text {A}} {\ text {d}} [/ latex]

Напряжение (В) конденсатора зависит от расстояния между пластинами, диэлектрической проницаемости, площади поверхности проводника и заряда (Q) на пластинах:

[латекс] \ text {V} = \ frac {\ text {Qd}} {\ epsilon \ text {A}} [/ latex]

В зависимости от диэлектрической прочности (E _ds ) и расстояния (d) между пластинами, конденсатор «сломается» при определенном напряжении (V _bd ).Рассчитывается по:

[латекс] \ text {V} _ {\ text {bd}} = \ text {E} _ {\ text {ds}} \ text {d} [/ latex]

Параллельные пластины и эквипотенциальные линии : Краткий обзор параллельных пластин и эквипотенциальных линий с точки зрения электростатики.

Электрические поля и проводники

Электрические поля в присутствии проводников обладают несколькими уникальными и не обязательно интуитивно понятными свойствами.

Цели обучения

Описывать уникальные свойства, выражаемые электрическими полями в присутствии проводников

Основные выводы

Ключевые моменты

• Внутри заряженного проводника отсутствует электрическое поле.Это связано с тем, что заряды, которые расположены на поверхности проводника, симметрично противоположны друг другу и в сумме равны 0 во всех местах.
• Заряженные поверхности выравниваются перпендикулярно электрическим полям для достижения электростатического равновесия. Если заряды не распределяются как таковые, они будут оказывать друг на друга общую силу, которая перемещает их. В таком случае заряды не будут находиться в статическом равновесии.
• Искривление поверхности поля позволяет увеличить концентрацию заряда.Большая часть зарядов отталкивания происходит в направлении от поверхности проводника, а не вдоль его поверхности. Таким образом, заряды слабее толкают друг друга по поверхности изогнутого проводника.

Ключевые термины

• векторное поле : конструкция, в которой каждая точка в евклидовом пространстве связана с вектором; функция, диапазон которой является векторным пространством
• равновесие : Состояние тела в состоянии покоя или равномерного движения, равнодействующая всех сил, действующая на него, равна нулю.

Электрическое поле, как и другие поля (например, гравитационные или магнитные), представляет собой векторное поле, окружающее объект. Электрические поля находятся вокруг электрических зарядов и помогают определить направление и величину силы, которую заряд оказывает на соседнюю заряженную частицу. Он измеряет единицы силы, прилагаемой к единице заряда, и его единицы СИ — N / C.

Линии поля, созданные точечным зарядом : Линии вокруг положительного заряда представляют электрическое поле, которое он создает.

Электрические проводники — это материалы, в которых внутренние заряды могут свободно перемещаться. Следовательно, они могут способствовать прохождению заряда или тока. Когда проводник помещается в электрическое поле, он проявляет некоторые интересные свойства:

1. Внутри заряженного проводника отсутствует электрическое поле. Заряженный проводник в электростатическом равновесии будет содержать заряды только на своей внешней поверхности и не будет иметь внутри себя электрического поля. Это связано с тем, что все заряды в таком проводнике будут симметрично противостоять другим зарядам внутри проводника, в результате чего итоговый результат будет равен 0.
2. Заряженные поверхности выравниваются перпендикулярно электрическим полям. Если проводник находится в электростатическом равновесии, электрическое поле на поверхности будет выровнено перпендикулярно этой поверхности. Если бы существовала ненулевая параллельная составляющая электрического поля по отношению к любому заряду на поверхности проводника, этот заряд проявил бы силу и переместился бы. Если проводник находится в равновесии, такая сила не может существовать, и поэтому направление электрического поля должно быть полностью перпендикулярно поверхности.
3. Кривизна поверхности проводника позволяет увеличить концентрацию заряда. Заряд не обязательно будет равномерно распределяться по поверхности проводника. Если поверхность проводника плоская, заряд будет распределяться очень равномерно. Но по мере того, как поверхность становится более изогнутой, заряд может обнаруживаться более плотно упакованным в областях, даже если проводник находится в электростатическом равновесии. Заряды на изогнутой поверхности отталкиваются друг от друга менее сильно, чем на гладкой поверхности.Это связано с тем, что в зависимости от того, как расположены заряды, большая часть отталкивания, которую они оказывают, происходит в направлении от поверхности проводника, а не вдоль его поверхности. И заряды оттолкнуть от поверхности сложнее, чем по ней. Следовательно, отталкивание между зарядами на искривленной поверхности слабее.

Электрический заряд на острой части проводника : Силы отталкивания в направлении более резко изогнутой поверхности справа направлены больше наружу, чем вдоль поверхности проводника.

Проводники и поля в статическом равновесии

В присутствии заряда или электрического поля заряды в проводнике будут перераспределяться, пока не достигнут статического равновесия.

Цели обучения

Описать поведение зарядов в проводнике в присутствии заряда или электрического поля и при статическом равновесии

Основные выводы

Ключевые моменты

• Присутствие заряда или электрического поля заставляет заряды в проводнике перераспределяться по поверхности проводника до тех пор, пока не будет достигнуто статическое равновесие.
• В статическом равновесии заряд будет больше концентрироваться в острых, заостренных участках проводников, чем где-либо еще.
• В статическом равновесии внутренняя часть проводника будет полностью защищена от внешнего электрического поля.

Ключевые термины

• статическое равновесие : физическое состояние, в котором все компоненты системы находятся в состоянии покоя, а результирующая сила равна нулю во всей системе

Проводники — это материалы, в которых заряды могут свободно перемещаться.Если проводники подвергаются воздействию заряда или электрического поля, их внутренние заряды быстро перестраиваются. Например, если нейтральный проводник соприкасается со стержнем, содержащим отрицательный заряд, часть этого отрицательного заряда передается проводнику в точке контакта. Но заряд не будет оставаться локальным в точке контакта — он будет равномерно распределяться по поверхности проводника. После перераспределения зарядов проводник находится в состоянии электростатического равновесия.Следует отметить, что распределение зарядов зависит от формы проводника и что статическое равновесие может не обязательно включать равномерное распределение зарядов, которые имеют тенденцию собираться в более высоких концентрациях вокруг острых точек. Это объясняется в.

.

Электрический заряд в острой точке проводника : Силы между одинаковыми зарядами на обоих концах проводника идентичны, но компоненты сил, параллельных поверхностям, различны. Компонент, параллельный поверхности, имеет наибольшее значение на самой плоской поверхности и поэтому более свободно перемещает заряды друг от друга.Это объясняет разницу в концентрации заряда на плоских и заостренных участках проводника.

Точно так же, если проводник помещен в электрическое поле, заряды внутри проводника будут перемещаться до тех пор, пока поле не станет перпендикулярным поверхности проводника. Отрицательные заряды в проводнике будут выравниваться по направлению к положительному концу электрического поля, оставляя положительные заряды на отрицательном конце поля. Таким образом, проводник становится поляризованным, электрическое поле становится сильнее вблизи проводника, но распадается внутри него.Это явление похоже на то, что наблюдается в клетке Фарадея, которая представляет собой корпус, сделанный из проводящего материала, который экранирует внутреннюю часть от внешнего электрического заряда или поля или экранирует внешнюю часть от внутреннего электрического заряда или поля.

зарядов и полей — электрическое поле | Электростатика | Эквипотенциальный

UG-Intro

Физика на основе алгебры 1 уроки, вопросы для кликеров и расписание в pdf (на основе запросов)			Триш Лёблейн	HS UG-Intro	Демо HW Лаборатория	Физика
Концептуальные вопросы по физике с использованием PhET (на основе запросов)			Триш Лёблейн	UG-Intro HS	MC	Физика
Заряды и поля Удаленная лаборатория Введение в статическое электричество			Триш Лёблейн	HS UG-Intro	Удаленный Лаборатория	Физика
Использование PhET в электроэнергетике			Триш Лёблейн	HS UG-Intro	Демо Лаборатория	Физика
Введение в статическое электричество с использованием электрического хоккея на траве, сборов и полей (на основе запроса)			Триш Лёблейн	HS	Лаборатория	Физика
Демонстрация электрической энергии и емкости (по запросу)			Триш Лёблейн	HS UG-Intro	Демо	Физика
Статический магнитный и электрический блок (по запросу)			Триш Лёблейн	HS	Lab HW Demo	Физика
Картирование электрических полей			Элиз Циммер	HS	Лаборатория	Физика
Согласование PhET sim с NGSS			Trish Loeblein (обновлено Дианой Лопес)	MS	Другое	Химия Науки о Земле Физика Биология
Симы PhET присоединились к учебной программе по химии			Джулия Чемберлен	UG-Intro HS	Другое	Химия
Каким образом симуляции PhET подходят для моей программы средней школы?			Сара Боренштейн	MS	Другое	Науки о Земле Физика Биология Химия
Заряды и поля PhET Lab			Стив Стерн	HS	Лаборатория	Физика
Видео: Самостоятельное обучение работе с электрическими эквипотенциальными линиями			Луи Вонг	МС HS	HW Guided Remote Lab	Физика
Выравнивание MS и HS TEK с Sim			Элиз Циммер	МС HS	Другое	Химия Физика Биология
Электрические и магнитные поля			ДжанаЛи Мозес	MS	Remote Guided HW Lab	Физика
Лаборатория электрического поля			Дэвид Вирт	HS UG-Intro	HW Обсудить Guided Lab Remote	Физика
Лабораторная работа: электрическое поле и потенциал.			Инна Шпиро	UG-Intro	Лаборатория	Физика
Конденсатор и диэлектрик 2			Бассам Рашед	UG-Intro UG-Adv Другое HS	HW Guided Lab Remote Demo	Физика
Конденсаторы — Введение-			Бассам Рашед	HS UG-Intro UG-Adv	Lab Guided HW Remote Demo	Физика
Электрическое поле и потенциальная лаборатория			Дэвид Уотерс	HS UG-Intro	Лаборатория HW	Физика
Сборы и поля			Джон Бергманн	HS	Лаборатория	Физика
MYP Physics: Electric Force vs.Расстояние			Мехмет Салих Генчер	МС HS	Другое Лаборатория	Физика
Отображение физики PhET и IBDP			Джая Рамчандани	HS	Другое	Физика
Исследование электрических полей			Крис Страуган	HS	Lab HW Guided	Физика
Моделирование PhET адаптировано для AP Physics C			Роберта Таннер	HS	Другое	Физика
Сборы и поля			SK Gupta, Chaithra Navada	HS	Лаборатория	Физика
Рабочий лист учащегося «Введение в электрические поля»			Рэйчел Кифт	HS	Lab HW Guided	Физика
Исследование связи между полем и потенциалом вокруг точечных зарядов			Лори Фриц	HS	С направляющей	Физика
Электрическое поле против электрического потенциала			Обри Фаренгольц	HS UG-Intro	Обсудить Demo Guided	Физика
Управляемый запрос — электрические поля			Райан Томпсон	HS	Управляемая Лаборатория	Физика
Serie de actividades para Electrostática: de Electrización, Campos y Fuerzas			Триш Лёблейн (перевод Диана Лопес)	HS MS UG-Intro	Lab Discuss Remote MC Guided HW	Физика
ПРЕПАРАТОРИЯ: Alineación de PhET con programas de la DGB México (2017)			Диана Лопес	HS UG-Intro	Другое	Физика Математика Химия
Предварительные требования к разным моделям HTML5			Диана Лопес	HS UG-Intro Grad K-5 UG-Adv MS	HW Обсудить	Астрономия Химия Физика Математика
Лагерь elèctric			Хорди Плана	MS	Лаборатория	Физика
Inleiding elektrisch veld			Лоран де Фрис	MS	Удаленный Лаборатория HW	Физика
Сборы и поля			SK Gupta, Chaithra Navada, Vaibhav Gupta	HS	Лаборатория	Физика
Prática 02- Potencial elétrico			Ялвес С.Фигейра и Висенте В. Фигейра,	UG-Intro	Пульт	Физика
Prática 01- Cargas e Campos			Jalves S. Figueira e Vicente V. Figueira	HS UG-Intro	Lab Remote	Физика
Simulação virtual para os tipos de eletrização e a relação entre as cargas.			Денис Алвес	HS	Лаборатория Демо	Физика
Eletrodinâmica (Atividades) nos OA’s do PhET			Artur Araújo Cavalcante e Gilvandenys Leite Продажи	Другое HS MS	Guided Other HW Обсудить	Физика Другое Математика
Atividades sobre Eletricidade nos OA’s do PhET			Artur Araújo Cavalcante e Gilvandenys Leite Продажи	Другое HS UG-Intro MS	Lab HW Demo Обсудить Guided	Науки о Земле Физика Другое
Potencial Elétrico no «Charges And Fields (HTML5)»			Artur Araújo Cavalcante e Gilvandenys Leite Продажи	MS Другое HS	Направляемые HW Другое	Другое Математика Физика Науки о Земле
Lei de Coulomb no «Charges And Fields (HTML5)»			Artur Araújo Cavalcante e Gilvandenys Leite Продажи	HS Другое MS	Направляющая Прочее HW	Другое Физика Науки о Земле Математика
Vetor Campo Elétrico no «Charges and Fields (HTML5)»			Artur Araújo Cavalcante e Gilvandenys Leite Продажи	HS Другое MS	Другое HW С направляющей	Другое Физика Науки о Земле
Campo Eléctrico			Laboratorio de Fisica EPN	UG-Intro UG-Adv	Лаборатория	Физика
Виртуальная лаборатория: Cargas y Campos Eléctricos			Доцент Виллианс Фабрегас	МС HS	Remote Demo HW Lab	Математика Физика
Trazado de líneas equipotenciales y de campo eléctrico correientes a una configuración de electrodos			Луис Наваррете Наваррете, Альма Патрисия Пуэрто Коваррубиас, Фелипе Наваррете Наваррете.	HS UG-Intro	Удаленный Лаборатория Управляемый	Физика
Campo eléctrico y Potencial eléctrico de cargas y distribuciones de carga, analysisados ​​a partir de simulaciones.			Луис Наваррете Наваррете, Альма Патрисия Пуэрто Коваррубиас, Хайме Ф.Альмагер Медина	UG-Intro HS	С направляющей	Физика
Laboratorio campo eléctrico — введение			Юбер Монсальве	MS	Remote HW Guided Lab	Физика
CARGAS Y CAMPOS ELÉCTRICOS			JORGE ENRIQUE CASALLAS LOPEZ	HS MS	Обсудить Lab HW Demo	Физика
Лаборатория	Физика
Taller Virtual Campo eléctrico para cargas puntuales			Александр Перес Гарсия	UG-Intro	Обсудить Ведомый	Физика
Laboratorio Virtual Potencial Eléctrico			Диего Фернандо Бесерра Родригес	UG-Intro	Lab Guided Обсудить HW	Физика

Что такое электрическое поле? Определение, формула, пример

Когда воздушный шар трется о свитер, он заряжается.Из-за этого заряда воздушный шар может прилипать к стенкам, но когда его помещают рядом с другим воздушным шариком, который также был натерт, первый воздушный шар летит в противоположном направлении.

Ключевые выводы: электрическое поле

• Электрический заряд — это свойство вещества, которое заставляет два объекта притягиваться или отталкиваться в зависимости от их заряда (положительного или отрицательного).
• Электрическое поле — это область пространства вокруг электрически заряженной частицы или объекта, в которой электрический заряд может ощущать силу.
• Электрическое поле — это векторная величина, которую можно представить в виде стрелок, идущих к зарядам или от них. Линии определены как направленные радиально наружу, , от положительного заряда, или радиально внутрь, , к отрицательному заряду.

Это явление является результатом свойства вещества, называемого электрическим зарядом. Электрические заряды создают электрические поля: области пространства вокруг электрически заряженных частиц или объектов, в которых другие электрически заряженные частицы или объекты будут ощущать силу.

Определение электрического заряда

Электрический заряд, который может быть как положительным, так и отрицательным, — это свойство материи, которое заставляет два объекта притягиваться или отталкиваться. Если предметы заряжены противоположно (положительно-отрицательно), они будут притягиваться; если они заряжены одинаково (положительно-положительно или отрицательно-отрицательно), они будут отталкиваться.

Единицей электрического заряда является кулон, который определяется как количество электричества, которое переносится электрическим током силой 1 ампер за 1 секунду.

Атомы, которые являются основными единицами материи, состоят из трех типов частиц: электронов, нейтронов и протонов. Сами электроны и протоны электрически заряжены и имеют соответственно отрицательный и положительный заряд. Нейтрон электрически не заряжен.

Многие объекты электрически нейтральны и имеют нулевой общий заряд. Если имеется избыток электронов или протонов, в результате чего суммарный заряд не равен нулю, объекты считаются заряженными.

Один из способов количественно определить электрический заряд — использовать константу e = 1,602 * 10 ^-19 кулон. Электрон, который представляет собой наименьшее количество отрицательного электрического заряда ( ), имеет заряд -1,602 * 10 ^-19 кулон. Протон, который представляет собой наименьшее количество положительного электрического заряда, имеет заряд +1,602 * 10 ^-19 кулон. Таким образом, 10 электронов имели бы заряд -10 э, а 10 протонов имели бы заряд +10 э.

Закон Кулона

Электрические заряды притягивают или отталкивают друг друга, потому что они действуют друг на друга.Сила между двумя точечными электрическими зарядами — идеализированными зарядами, которые сосредоточены в одной точке пространства — описывается законом Кулона. Закон Кулона гласит, что сила или величина силы между двумя точечными зарядами составляет пропорционально величине зарядов и обратно пропорционально расстоянию между двумя зарядами.

Математически это выглядит как:

F = (k | q ₁ q ₂ |) / r ²

где q ₁ — заряд первого точечного заряда, q ₂ — заряд второго точечного заряда, k = 8.988 * 10 ⁹ Нм ² / C ² — постоянная Кулона, а r — расстояние между двумя точечными зарядами.

Хотя технически нет реальных точечных зарядов, электроны, протоны и другие частицы настолько малы, что могут быть приблизительно или точечным зарядом.

Формула электрического поля

Электрический заряд создает электрическое поле, которое представляет собой область пространства вокруг электрически заряженной частицы или объекта, в которой электрический заряд будет ощущать силу.Электрическое поле существует во всех точках пространства, и его можно наблюдать, добавляя другой заряд в электрическое поле. Однако для практических целей электрическое поле можно приблизить к нулю, если заряды расположены достаточно далеко друг от друга.

Электрические поля — это векторная величина, которую можно представить в виде стрелок, направленных к зарядам или от них. Линии определены как направленные радиально наружу, , от положительного заряда, или радиально внутрь, , к отрицательному заряду.

Величина электрического поля определяется формулой E = F / q, где E — напряженность электрического поля, F — электрическая сила, а q — пробный заряд, который используется для «ощущения» электрического поля. .

Пример: электрическое поле двухточечных зарядов

Для двухточечных зарядов F определяется законом Кулона выше.

• Таким образом, F = (k | q ₁ q ₂ |) / r ² , где q ₂ определяется как испытательный заряд , который используется для «ощущения» электрического поле.
• Затем мы используем формулу электрического поля, чтобы получить E = F / q ₂ , поскольку q ₂ был определен как пробный заряд.
• После замены F, E = (k | q ₁ |) / r ² .

Источники

• Фитцпатрик, Ричард. «Электрические поля». Техасский университет в Остине , 2007 г.
• Левандовски, Хизер и Чак Роджерс. «Электрические поля». Университет Колорадо в Боулдере , 2008 г.
• Ричмонд, Майкл. «Электрический заряд и закон Кулона». Рочестерский технологический институт.

Электрический заряд и электрическое поле

Откуда берется заряд?

Мы знаем, что все объекты состоят из атомов, а атомы состоят из более мелких частиц, называемых протонами, электронами и нейтронами. Протоны и нейтроны находятся в ядре атома, а электроны находятся в области за пределами, часто описываемой как электронное облако (см. Что такое атомные орбитали для более подробного описания).Помните, что атом водорода состоит только из одного протона и электрона. Он не содержит нейтрона.

И протоны, и электроны обладают основным свойством, называемым зарядом. Это свойство не похоже на другие физические свойства материи. Однако заряд можно измерить, и он влияет на поведение частиц.

Количество или величина заряда у протонов такая же, как у электронов. Протоны заряжены положительно, электроны заряжены отрицательно, а нейтроны нейтральны.Термины «положительный заряд» и «отрицательный заряд» были первоначально описаны Бенджамином Франклином.

Заряды проявляют силу

Сила определяется как толкающая или тянущая. Заряженные частицы демонстрируют аналогичное поведение при толчке и заполнении. Сила, которая сближает частицы, называется силой притяжения. Итак, электроны притягиваются к протонам, и это то, что удерживает атомы вместе. Сила, которая отталкивает частицы, является силой отталкивания. Между противоположно заряженными частицами существует сила притяжения — поэтому электроны и протоны притягиваются друг к другу.Подобные заряды будут отталкиваться, поэтому отрицательные электроны отталкиваются друг от друга. Простое правило для электрических зарядов: Подобные заряды отталкиваются друг от друга, а разные заряды притягиваются друг к другу.

Что такое электрическое поле?

Понятие электрического поля используется для объяснения того, почему заряженные частицы действуют друг на друга. Когда электрон попадает в электрическое поле протона, он притягивается к протону. Электрическое поле становится сильнее по мере приближения к частице.

Электрические поля визуализируются вытянутыми линиями, как показано на изображении ниже. Обратите внимание, что при положительном заряде силовые линии направлены наружу, а при отрицательном — внутрь.

Линии электрического поля между положительным и отрицательным зарядом показаны ниже. Как и выше, линии направлены к отрицательному заряду.

Что такое электроскоп и для чего он используется?

Электроскоп — это научный инструмент, который используется для определения наличия и величины электрического заряда на теле.Это был первый электроизмерительный прибор серии . Типичный классный электроскоп состоит из металлической ручки вверху и металлического стержня с тонкими металлическими пластинами внизу. Стержень вставляется в колбу с резиновой пробкой (см. Изображение ниже). В незаряженном электроскопе листья свешиваются вниз. Когда отрицательно заряженный объект, такой как отрицательно заряженный стеклянный стержень , касается ручки, электрический заряд проходит вниз по трубке к металлическим листам. поскольку оба листа теперь содержат отрицательные заряды, они будут отталкиваться.Точно так же, если ручка касается положительно заряженного стержня, электроны будут вытягиваться вверх по металлическому стержню, оставляя положительно заряженные листья. Листья снова оттолкнутся.

---

Проверьте свой Понимание:

18,3 Электрическое поле | Texas Gateway

Задачи обучения

К концу этого раздела вы сможете делать следующее:

• Рассчитывать напряженность электрического поля
• Создание и интерпретация чертежей электрических полей

Раздел Ключевые термины

электрическое поле

пробный заряд

Возможно, вы слышали о силовом поле в научно-фантастических фильмах, где такие поля применяют силы в определенных позициях в космосе, чтобы удержать злодея в ловушке или защитить космический корабль от вражеского огня.Концепция поля очень полезна в физике, хотя несколько отличается от того, что вы видите в фильмах.

Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю и все другие массы, представляет собой гравитационную силу, которая возникла бы, если бы другая масса была помещена в заданную точку внутри поля.Майкл Фарадей, английский физик XIX века, предложил концепцию электрического поля. Если вы знаете электрическое поле, вы можете легко вычислить силу (величину и направление), приложенную к любому электрическому заряду, который вы помещаете в это поле.

Электрическое поле создается электрическим зарядом и сообщает нам силу на единицу заряда во всех точках пространства вокруг распределения заряда. Распределение зарядов может быть единственной точечной зарядкой; распределение заряда, скажем, по плоской пластине; или более сложное распределение заряда.Электрическое поле распространяется в пространство вокруг распределения заряда. Теперь рассмотрите возможность размещения пробного заряда в полевых условиях. Пробный заряд — это положительный электрический заряд, заряд которого настолько мал, что он не вызывает значительного возмущения зарядов, создающих электрическое поле. Электрическое поле действует на пробный заряд в заданном направлении. Приложенная сила пропорциональна заряду испытательного заряда. Например, если мы удвоим заряд испытательного заряда, сила, приложенная к нему, удвоится.Математически, говоря, что электрическое поле — это сила на единицу заряда, записывается как

18,15. E → = F → qtestE → = F → qtest

, где мы рассматриваем только электрические силы. Обратите внимание, что электрическое поле — это векторное поле, которое направлено в том же направлении, что и сила, действующая на положительный тестовый заряд. Единицы электрического поля — N / C.

Если электрическое поле создается точечным зарядом или сферой с однородным зарядом, то величина силы между этим точечным зарядом Q и пробным зарядом определяется законом Кулона

F = k | Qqtest | r2F = k | Qqtest | r2

, где используется абсолютное значение, потому что мы учитываем только величину силы.Величина электрического поля тогда равна

18,16. E = Fqtest = k | Q | r2.E = Fqtest = k | Q | r2.

Это уравнение дает величину электрического поля, создаваемого точечным зарядом Q . Расстояние r в знаменателе — это расстояние от точечного заряда Q или от центра сферического заряда до интересующей точки.

Если тестовый заряд удалить из электрического поля, электрическое поле все еще существует. Чтобы создать трехмерную карту электрического поля, представьте, что тестовый заряд размещается в разных местах поля.В каждом месте измерьте силу, действующую на заряд, и используйте векторное уравнение E → = F → / qtestE → = F → / qtest для расчета электрического поля. Нарисуйте стрелку в каждой точке, куда вы помещаете тестовый заряд, чтобы обозначить силу и направление электрического поля. Длина стрелок должна быть пропорциональна напряженности электрического поля. Если соединить эти стрелки вместе, получатся линии. На рисунке 18.18 показано изображение трехмерного электрического поля, созданного положительным зарядом.

Рисунок 18.18 Трехмерное представление электрического поля, создаваемого положительным зарядом.

Простое рисование силовых линий электрического поля в плоскости, пересекающей заряд, дает двумерные карты электрического поля, показанные на рис. 18.19. Слева — электрическое поле, созданное положительным зарядом, а справа — электрическое поле, созданное отрицательным зарядом.

Обратите внимание, что линии электрического поля направлены от положительного заряда в сторону отрицательного заряда.Таким образом, положительный тестовый заряд, помещенный в электрическое поле положительного заряда, будет отталкиваться. Это согласуется с законом Кулона, который гласит, что одинаковые заряды отталкивают друг друга. Если мы поместим положительный заряд в электрическое поле отрицательного заряда, положительный заряд будет притягиваться к отрицательному заряду. Обратное верно для отрицательных тестовых зарядов. Таким образом, направление силовых линий электрического поля согласуется с тем, что мы находим с помощью закона Кулона.

Уравнение E = k | Q | / r2E = k | Q | / r2 говорит, что электрическое поле становится сильнее по мере приближения к заряду, который его генерирует.Например, на расстоянии 2 см от заряда Q ( r = 2 см) электрическое поле в четыре раза сильнее, чем на расстоянии 4 см от заряда ( r = 4 см). Снова посмотрев на рисунок 18.18 и рисунок 18.19, мы видим, что силовые линии электрического поля становятся более плотными по мере приближения к заряду, который его генерирует. Фактически, плотность силовых линий электрического поля пропорциональна напряженности электрического поля!

Рисунок 18.19 Силовые линии электрического поля от двух точечных зарядов. Красная точка слева несет заряд +1 нКл, а синяя точка справа несет заряд –1 нКл.Стрелки указывают направление движения положительного тестового заряда. Линии поля становятся более плотными по мере приближения к точечному заряду.

Карты электрического поля могут быть составлены для нескольких зарядов или для более сложных распределений зарядов. Электрическое поле из-за нескольких зарядов можно найти, сложив электрическое поле от каждого отдельного заряда. Поскольку эта сумма может быть только одним числом, мы знаем, что только одна линия электрического поля может проходить через любую заданную точку. Другими словами, линии электрического поля не могут пересекать друг друга.

На рисунке 18.20 (а) показана двумерная карта электрического поля, создаваемого зарядом + q и ближайшим зарядом — q . Трехмерная версия этой карты получается вращением этой карты вокруг оси, проходящей через оба заряда. Положительный испытательный заряд, помещенный в это поле, будет испытывать силу в направлении силовых линий в его местоположении. Таким образом, он будет отталкиваться от положительного заряда и притягиваться к отрицательному. Рисунок 18.20 (b) показано электрическое поле, создаваемое двумя зарядами — q . Обратите внимание на то, как линии поля имеют тенденцию отталкиваться друг от друга и не перекрываются. Положительный тестовый заряд, помещенный в это поле, будет притягиваться к обоим зарядам. Если вы находитесь далеко от этих двух зарядов, где «далеко» означает намного больше, чем расстояние между зарядами, электрическое поле выглядит как электрическое поле от одного заряда −2 q .

Рис. 18.20 (a) Электрическое поле, создаваемое положительным точечным зарядом (слева) и отрицательным точечным зарядом той же величины (справа).(б) Электрическое поле, создаваемое двумя равными отрицательными зарядами.

Виртуальная физика

Исследование электрического поля

Это моделирование показывает электрическое поле, создаваемое зарядами, которые вы размещаете на экране. Начните с установки верхнего флажка на панели параметров справа, чтобы отобразить электрическое поле. Перетаскивайте заряды из ведер на экран, перемещайте их и наблюдайте за электрическим полем, которое они образуют. Чтобы более точно увидеть величину и направление электрического поля, перетащите датчик электрического поля или датчик E-field из нижнего ведра и перемещайте его по экрану.

Проверка захвата

Если поместить на экран положительный и отрицательный заряды, где будет нулевое электрическое поле?

1. Электрическое поле равно нулю вблизи положительного заряда.
2. Электрическое поле равно нулю около отрицательного заряда.
3. Электрическое поле равно нулю на полпути между двумя зарядами.
4. Электрическое поле равно нулю на расстоянии одной четвертой от положительного заряда.

Watch Physics

Электростатика (часть 2): интерпретация электрического поля

В этом видео объясняется, как рассчитать электрическое поле точечного заряда и как интерпретировать карты электрического поля в целом. Обратите внимание, что лектор использует d для расстояния между частицами вместо r . Обратите внимание, что точечные заряды бесконечно малы, поэтому все их заряды сосредоточены в одной точке. Когда рассматриваются более крупные заряженные объекты, расстояние между ними необходимо измерять между центрами объектов.

Проверка захвата

Верно или неверно — если точечный заряд имеет линии электрического поля, направленные внутрь, заряд должен быть положительным.

1. правда
2. ложь

Рабочий пример

Какая плата?

Посмотрите на рисунок электрического поля на рис. 18.22. Какова относительная сила и знак трех зарядов?

Рисунок 18.22 Карта электрического поля от трех заряженных частиц.

СТРАТЕГИЯ

Мы знаем, что электрическое поле исходит от положительного заряда и заканчивается отрицательным зарядом.Мы также знаем, что количество силовых линий электрического поля, которые касаются заряда, пропорционально заряду. Заряд 1 имеет 12 выходящих полей. Заряд 2 имеет шесть линий поля, входящих в него. Заряд 3 имеет 12 линий поля, входящих в него.

Решение

Силовые линии электрического поля исходят из заряда 1, поэтому это положительный заряд. Линии электрического поля переходят в заряды 2 и 3, поэтому они являются отрицательными зарядами. Отношение зарядов q1: q2: q3 = + 12: −6: −12q1: q2: q3 = + 12: −6: −12. Таким образом, величина зарядов 1 и 3 вдвое больше, чем у заряда 2.

Обсуждение

Хотя мы не можем определить точный заряд каждой частицы, мы можем получить много информации из электрического поля о величине и знаке зарядов, а также о том, где сила на пробном заряде будет наибольшей (или наименьшей).

Рабочий пример

Электрическое поле от дверной ручки

Дверная ручка, которую можно принять за сферический металлический проводник, приобретает заряд статического электричества q = -1,5 нКл. Q = -1,5 нКл. Что такое электрическое поле 1.0 см перед дверной ручкой? Диаметр дверной ручки 5,0 см.

СТРАТЕГИЯ

Поскольку дверная ручка является проводником, весь заряд распределяется по внешней поверхности металла. Кроме того, поскольку предполагается, что дверная ручка имеет идеально сферическую форму, заряд на поверхности распределен равномерно, поэтому мы можем рассматривать дверную ручку так, как если бы весь заряд находился в центре дверной ручки. Справедливость этого упрощения будет доказана в более позднем курсе физики.Теперь нарисуйте дверную ручку и определите свою систему координат. Используйте + x + x, чтобы указать направление наружу, перпендикулярное двери, с x = 0x = 0 в центре дверной ручки (как показано на рисунке ниже).

Если диаметр дверной ручки 5,0 см, ее радиус равен 2,5 см. Нам нужно знать электрическое поле на расстоянии 1,0 см от поверхности дверной ручки, что составляет расстояние r = 2,5 см + 1,0 см = 3,5 см = 2,5 см + 1,0 см = 3,5 см от центра дверной ручки. Мы можем использовать уравнение E = k | Q | r2E = k | Q | r2, чтобы найти величину электрического поля.Направление электрического поля определяется знаком заряда, который в данном случае отрицательный.

Решение

Вставив заряд Q = -1,5 нКл = -1,5 · 10-9 CQ = -1,5 нКл = -1,5 · 10-9 Кл и расстояние r = 3,5 см = 0,035 mr = 3,5 см = 0,035 м в уравнение E = k | Q | r2E = k | Q | r2 дает

18,17E = k | Q | r2 = (8,99 × 109 Н · м2 / C2) | −1,5 × 10−9 C | (0,035 м) 2 = 1,1 × 104 N / CE = k | Q | r2 = (8,99 × 109 Н · м2 / C2) | −1,5 · 10−9 C | (0,035 м) 2 = 1,1 · 104 N / C.

Поскольку заряд отрицательный, силовые линии электрического поля направлены к центру дверной ручки..

Обсуждение

Это похоже на огромное электрическое поле. К счастью, электрическое поле примерно в 100 раз сильнее (3 × 106 Н / К3 × 106 Н / К), чтобы вызвать разрушение воздуха и провести электричество. Кроме того, вес взрослого человека составляет около 70 кг × 9,8 м / с2≈700 Н70 кг × 9,8 м / с2≈700 Н, так почему бы вам не почувствовать силу протонов в руке, когда вы тянетесь к дверной ручке? ? Причина в том, что ваша рука содержит равное количество отрицательного заряда, который отталкивает отрицательный заряд дверной ручки.Из-за поляризации в вашей руке может развиться очень небольшая сила, но вы никогда этого не заметите.

линий электрического поля — Университетская физика, том 2

Цели обучения

К концу этого раздела вы сможете:

• Объясните назначение схемы электрического поля
• Опишите взаимосвязь между векторной диаграммой и диаграммой линий поля
• Объясните правила создания диаграммы поля и почему эти правила имеют физический смысл
• Набросок поля произвольного заряда источника

Теперь, когда у нас есть некоторый опыт вычисления электрических полей, давайте попробуем разобраться в геометрии электрических полей.Как упоминалось ранее, наша модель состоит в том, что заряд объекта (исходный заряд) изменяет пространство в области вокруг него таким образом, что когда другой заряженный объект (тестовый заряд) помещается в эту область пространства, этот тестовый заряд испытывает электрическую силу. Концепция силовых линий электрического поля s и диаграмм силовых линий электрического поля позволяет нам визуализировать способ изменения пространства, позволяя визуализировать поле. Цель этого раздела — дать вам возможность создавать эскизы этой геометрии, поэтому мы перечислим конкретные шаги и правила, необходимые для создания точного и полезного эскиза электрического поля.

Важно помнить, что электрические поля трехмерны. Хотя в эту книгу мы включаем некоторые псевдотрехмерные изображения, некоторые из диаграмм, которые вы увидите (здесь и в последующих главах), будут двумерными проекциями или поперечными сечениями. Всегда помните, что на самом деле вы смотрите на трехмерное явление.

Наша отправная точка — это физический факт, что электрическое поле исходного заряда заставляет испытательный заряд в этом поле испытывать силу.По определению, векторы электрического поля указывают в том же направлении, что и электрическая сила, которую испытывает (гипотетический) положительный испытательный заряд, если поместить его в поле ((Рисунок))

Электрическое поле точечного положительного заряда. Показано большое количество векторов поля. Как и все векторные стрелки, длина каждого вектора пропорциональна величине поля в каждой точке. а) поле в двух измерениях; (б) поле в трех измерениях.

Мы изобразили множество векторов поля на рисунке, которые равномерно распределены вокруг заряда источника.Поскольку электрическое поле является вектором, стрелки, которые мы рисуем, соответствуют в каждой точке пространства величине и направлению поля в этой точке. Как всегда, длина стрелки, которую мы рисуем, соответствует величине вектора поля в этой точке. Для заряда точечного источника длина уменьшается на квадрат расстояния от источника заряда. Вдобавок направление вектора поля радиально от источника заряда, потому что направление электрического поля определяется направлением силы, которую испытательный положительный заряд будет испытывать в этом поле.(Опять же, имейте в виду, что фактическое поле является трехмерным; есть также линии поля, указывающие наружу и внутрь страницы.)

Эта диаграмма верна, но она становится менее полезной по мере усложнения распределения заряда источника. Например, рассмотрим диаграмму векторного поля диполя ((Рисунок)).

Векторное поле диполя. Даже с двумя одинаковыми зарядами становится трудно понять диаграмму векторного поля.

Есть более удобный способ представить ту же информацию.Вместо того, чтобы рисовать большое количество векторных стрелок все меньшего размера, мы соединяем их все вместе, образуя непрерывные линии и кривые, как показано на (Рисунок).

(а) Схема силовых линий электрического поля точечного положительного заряда. (б) Схема силовых линий диполя. На обеих диаграммах величина поля обозначена плотностью силовых линий. Векторы поля (здесь не показаны) касаются всех линий поля.

Хотя на первый взгляд это может быть неочевидно, эти диаграммы поля несут ту же информацию об электрическом поле, что и векторные диаграммы.Во-первых, направление поля в каждой точке — это просто направление вектора поля в той же точке. Другими словами, в любой точке пространства вектор поля в каждой точке касается линии поля в этой же точке. Стрелка, размещенная на линии поля, указывает ее направление.

Что касается величины поля, она обозначается плотностью силовых линий, то есть количеством силовых линий на единицу площади, проходящих через небольшую площадь поперечного сечения, перпендикулярную электрическому полю.Эта плотность силовых линий изображена пропорциональной величине поля в этом поперечном сечении. В результате, если силовые линии расположены близко друг к другу (то есть плотность силовых линий больше), это указывает на то, что величина поля в этой точке велика. Если силовые линии далеко друг от друга в поперечном сечении, это означает, что величина поля мала. (Рисунок) показывает идею.

Силовые линии электрического поля, проходящие через воображаемые области. Поскольку количество линий, проходящих через каждую область, одинаково, но сами области разные, плотность силовых линий разная.Это указывает на разные величины электрического поля в этих точках.

На (Рисунок) одинаковое количество силовых линий проходит через обе поверхности ( S , но поверхность S больше, чем поверхность. Следовательно, плотность силовых линий (количество линий на единицу площади) больше при расположение, указывающее, что электрическое поле сильнее в месте, чем в S . Правила создания диаграммы электрического поля следующие.

Стратегия решения проблем: построение линий электрического поля

1. Линии электрического поля либо берут начало на положительных зарядах, либо исходят из бесконечности, либо заканчиваются на отрицательных зарядах, либо простираются до бесконечности.
2. Количество силовых линий, начинающихся или заканчивающихся зарядом, пропорционально величине этого заряда. Плата 2 q будет иметь в два раза больше линий, чем плата q .
3. В каждой точке пространства вектор поля в этой точке касается линии поля в этой же точке.
4. Плотность силовых линий в любой точке пространства пропорциональна величине поля в этой точке пространства (и поэтому является репрезентативной).
5. Линии поля никогда не пересекаются. Поскольку силовая линия представляет направление поля в данной точке, если две силовые линии пересекаются в некоторой точке, это будет означать, что электрическое поле было направлено в двух разных направлениях в одной точке. Это, в свою очередь, предполагает, что (чистая) сила на испытательном заряде, помещенном в эту точку, будет указывать в двух разных направлениях.Поскольку это, очевидно, невозможно, из этого следует, что силовые линии никогда не должны пересекаться.

Всегда помните, что силовые линии служат только удобным способом визуализации электрического поля; они не физические лица. Хотя направление и относительную напряженность электрического поля можно определить по набору силовых линий, эти линии также могут вводить в заблуждение. Например, силовые линии, изображающие электрическое поле в определенной области, по необходимости должны быть дискретными. Однако реальное электрическое поле в этой области существует в каждой точке пространства.

Полевые линии для трех групп дискретных зарядов показаны на (Рисунок). Поскольку заряды в частях (а) и (b) имеют одинаковую величину, показано одинаковое количество силовых линий, начинающихся или заканчивающихся на каждом заряде. Однако в (c) мы рисуем в три раза больше линий поля на выходе из заряда, чем на входе. Силовые линии, которые не заканчиваются на, исходят из зарядовой конфигурации наружу в бесконечность.

Три типичных диаграммы электрического поля. (а) Диполь.(b) Два идентичных обвинения. (c) Два заряда противоположных знаков и разной величины. Можете ли вы сказать по диаграмме, какой заряд имеет большую величину?

Умение построить точную диаграмму электрического поля — важный и полезный навык; это значительно упрощает оценку, прогнозирование и, следовательно, вычисление электрического поля заряда источника. Лучший способ развить этот навык — использовать программное обеспечение, которое позволяет вам выставлять исходные платежи, а затем рисовать сетевое поле по запросу.Мы настоятельно рекомендуем вам поискать программу в Интернете. Как только вы найдете тот, который вам нравится, запустите несколько симуляций, чтобы получить основные идеи построения полевой диаграммы. Затем потренируйтесь рисовать диаграммы полей и проверять свои прогнозы с помощью компьютерных диаграмм.

Сводка

• Диаграммы электрического поля помогают визуализировать поле заряда источника.
• Величина поля пропорциональна плотности силовых линий.
• Векторы поля везде касаются линий поля.

Концептуальные вопросы

Если точечный заряд высвобождается из состояния покоя в однородном электрическом поле, будет ли он следовать за силовой линией? Будет ли так, если электрическое поле неоднородно?

При каких условиях, если таковые имеются, траектория заряженной частицы не будет следовать силовой линии?

Как бы вы экспериментально отличили электрическое поле от гравитационного?

На поверхности Земли гравитационное поле всегда направлено к центру Земли.Электрическое поле могло двигать заряженную частицу в другом направлении, чем к центру Земли. Это указывало бы на наличие электрического поля.

Представление электрического поля показывает 10 силовых линий, перпендикулярных квадратной пластине. Сколько силовых линий должно пройти через пластину перпендикулярно, чтобы изобразить поле с удвоенной величиной?

Каково отношение количества силовых линий электрического поля, оставляющих заряд 10 q и заряд q ?

Проблемы

Какие из следующих силовых линий электрического поля неверны для точечных зарядов? Объяснить, почему.

Изобразите электрическое поле для системы из трех частиц зарядов, закрепленных в углах равностороннего треугольника со стороной 2 см.

Два заряда одинаковой величины, но противоположного знака составляют электрический диполь. Квадруполь состоит из двух электрических диполей, расположенных антипараллельно по двум краям квадрата, как показано.

Изобразите электрическое поле распределения заряда.

Предположим, что электрическое поле изолированного точечного заряда уменьшается с расстоянием как, а не как.Покажите, что тогда невозможно провести непрерывные линии поля так, чтобы их количество на единицу площади было пропорционально E .

Глоссарий

полевая линия

гладкая, обычно изогнутая линия, указывающая направление электрического поля

Плотность силовых линий

количество силовых линий на квадратный метр, проходящих через воображаемую область; его цель — указать напряженность поля в разных точках пространства

Электрическое поле и движение заряда — Видео и стенограмма урока

Электрическое поле и движение

Одна важная вещь, о которой нужно помнить, — это не путать электрические поля с движением зарядов.Если я выпущу положительный тестовый заряд из состояния покоя в каком-либо положении, заряд действительно будет следовать за линиями электрического поля. Но на самом деле силовые линии говорят вам о силе, которую ощущает заряд. При начальной скорости, равной нулю, любой объект будет двигаться в направлении силы. Но так бывает не всегда.

Например, если ваш положительный тестовый заряд движется на север, а вы входите в поле, указывающее на запад, заряд будет изгибаться по кругу, неопределенно северо-восточному. В конце концов, он будет следовать за линиями поля и двигаться на запад, но сначала он может двигаться в любом направлении в зависимости от своей начальной скорости.

Чистая сила, приложенная к объекту, создает ускорение. Таким образом, силовые линии действительно только говорят вам, в каком направлении направлена ​​сила (и, следовательно, вектор ускорения).

Уравнение

Есть два основных уравнения для электрического поля. Одно из них — общее определение, которое гласит, что это сила на единицу заряда. Здесь E — напряженность электрического поля в ньютонах на кулон, F — сила, действующая на заряд q , измеренная в ньютонах, и q — это заряд, который вы вкладываете в поле, измеренный в кулонах.Так что, если вы поместите в поле заряд кулонов +2 вместо заряда +1 кулонов, оно почувствует вдвое большую силу.

Общее уравнение для электрического поля

Второе уравнение говорит вам об электрическом поле, которое создает точечный заряд. Заряд q создаст собственное электрическое поле. И чем ближе вы к нему, тем сильнее будет напряженность электрического поля. В этом уравнении E — это снова напряженность электрического поля, q — размер заряда, создающего поле на этот раз, эпсилон-ноль — постоянная, которая всегда равна 8.-12, а r — это расстояние, на котором вы находитесь от этого заряда q .

Уравнение для расчета электрического поля, создаваемого точечным зарядом

Итак, используя второе уравнение, мы можем выяснить, что создают заряды электрического поля. И мы можем использовать первое уравнение, чтобы вычислить силу, которую будет ощущать второй заряд при помещении в это электрическое поле или любое другое электрическое поле, если на то пошло.-17 ньютонов.

Вот и все — ответы есть.

Краткое содержание урока

Электрическое поле — это электрическая сила на единицу заряда. Или, другими словами, это сила, которую может почувствовать положительный испытательный заряд в 1 кулон. Чтобы вычислить напряженность электрического поля в определенном месте, все, что вам нужно сделать, это взять заряд +1 кулон, поместить его в это место и измерить силу, которую он ощущает. Электрическое поле измеряется в ньютонах на кулон (Н / Кл).

Электрические поля могут быть представлены схематически с использованием линий электрического поля или векторов электрического поля.Например, электрическое поле вокруг точечного положительного заряда выглядит так. А электрическое поле вокруг точечного отрицательного заряда выглядит так. Это показывает направление силы, которую будет ощущать положительный тестовый заряд. В случае силовых линий ближе друг к другу — значит сильнее. Для векторов поля чем больше, тем сильнее.

Одна важная вещь, о которой следует соблюдать осторожность, — это не путать электрические поля с движением зарядов. На самом деле силовые линии говорят вам о силе, которую ощущает один заряд, и, следовательно, об ускорении, которому он будет подвергаться.Однако точное движение будет зависеть от первоначального движения — было ли оно уже в движении, или в состоянии покоя и т. Д.

Есть два основных уравнения для электрического поля. Одно из них — общее определение, которое гласит, что это сила на единицу заряда. Здесь E — напряженность электрического поля в ньютонах на кулон, F — сила, действующая на заряд q , измеренная в ньютонах, и q — это заряд, который вы вкладываете в поле, измеренный в кулонах.

Второе уравнение говорит вам об электрическом поле, которое создает точечный заряд.

No related posts.