формулы и определения / Блог :: Бингоскул
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
- I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=\frac{U}{R}
- U — напряжение (в системе СИ измеряется — Вольт)
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
- Формула: U=IR
- R — электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=\frac{U}{I}
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=\frac{\varepsilon}{R+r}
- \varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Закон Ома кратко и понятно для чайников
Закон Ома является одним из фундаментальных законов электродинамики, который определяет взаимосвязь между напряжением, сопротивлением и силой тока. Его важно знать и понимать. Понятное объяснение вы найдёте в статье.
Закон Ома официально и абсолютно оправдано можно отнести к ряду основополагающих в физике по нескольким признакам. Данный закон объясняют в школе на базовом уровне, а после, более углубленно, в учреждениях, специализирующихся на изучении технических аспектов технологий.
Закон Ома – определение
Впервые данный закон был официально зафиксирован и сформулирован в восемнадцатом веке, благодаря сделанному сейчас уже широко известным всем Георгом Симоном Омом открытию. Благодаря данному закону получило грамотное и исчерпывающее объяснение наличие количественной связи между тремя фигурирующими в определении параметрами. Зависимость рассматривается как пропорциональная. Когда данное явление только было выявлено, закон несколько раз формулировали. В итоге сейчас всем известно данное определение: «величина тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению».
Для лучшего понимания разделим определение на две части и разберём отдельно более понятным языком смысл каждой.
- Первая часть определения указывает на то, что если на определенной отрезке цепи происходит количественный скачок напряжения, то величина тока также увеличивается на данном участке. Важно упомянуть, что становится больше и величина тока на заданном участке цепи.
- Концовка определения расшифровывается также просто. Выше напряжение – меньше сила тока.
Закон Ома – формула

 Иллюстрация связи сопротивления
Иллюстрация связи сопротивленияРисунок наглядно демонстрирует связь фигурирующих в понятии «участников». Таким образом, вытекают простые выводы:
1. При данных условиях: на конкретном отрезке увеличивается напряжение, но при том сопротивление остаётся прежним, ток резко возрастает;
2. Иная ситуация: наоборот, изменяется сопротивление, а точнее возрастает, при том что уровень напряжения не меняется вовсе, тока становится меньше.
В итоге в законе Ома участвуют всего три величины.
Готовая формула выглядит так:
I = U/R
Фигурируют и другие две переменные, их также можно вычислить, при условии, что другие два значения известны. Видоизменив формулу, получим:
| Формула сопротивления | R = U/I |
| Формула напряжения | U = I × R |
| Формула силы тока | I = U/R |
Важно!

 Шпаргалка для закона Ома
Шпаргалка для закона ОмаНа начальном этапе, когда составлять формулы ещё сложно, можно воспользоваться небольшой шпаргалкой.
На треугольнике просто нужно закрыть то значение, которое необходимо найти.
Закон Ома для участка цепи
Итоговая формула не видоизменяется вовсе. Обычно сопротивление в данном законе является явной характеристикой проводника, потому что это значение не постоянная величина: в зависимости от материала и других параметров число может увеличиваться или уменьшаться. Закон применим как при расчёте с использованием металлов, так и растворов электролитов, однако существует важный нюанс: в цепи не должно быть реального источника тока, или же источник должен быть идеальным, то есть он не должен создавать дополнительное сопротивление.

 Шпаргалка для использования закона Ома
Шпаргалка для использования закона ОмаС ЭДС
Обобщённый закон Ома формулируется так:
I = (Uab+E)/R
Также формулу можно выразить через проводимость:
I = (Uab + E) × G, как понятно, G – проводимость участка электрической цепи. Эти формулы можно использовать, если сохраняются условия, зафиксированные на рисунке.

 Участок цепи с ЭДС
Участок цепи с ЭДСБез ЭДС
Для начала определим, что положительное направление – это то, что слева направо. Только в этом случае напряжение на участке будет равняться разности потенциалов.

 Разность потенциалов
Разность потенциаловЕсли сохраняется условие и потенциал конечный меньше потенциала начального, то напряжение будет больше нуля. Значит, как и полагается, направление линий напряженности в проводнике будет от начала к концу, следовательно, направление тока будет идентичным. Именно такое направление тока принято считать положительным, I > O. Данный вариант самый простой для расчётов. Формула действительна с любыми числами.
Закон Ома для полной (замкнутой) цепи
При данной вариации закона выявляется значение тока при реальных условиях, то есть в настоящей полной цепи. Важно учитывать то, что получившееся в результате расчетов число зависит от нескольких параметров, а не только от сопротивления нагрузки.
Сопротивление нагрузки – внешнее сопротивление, а сопротивление самого источника тока – внутреннее сопротивление (обозначается маленькой r).
Вывод формулы закона Ома для замкнутой цепи
Если к цепи подключено напряжение и в цепи замечено напряжение (ток), то, чтобы поддержать его во внешней цепи, необходимо создать условия, при которых между её концами возникнет разность потенциалов. Это число будет равняться I × R. Однако важно помнить о том, что вышеупомянутый ток будет и во внутренней цепи и его также необходимо поддерживать, поэтому нужно создать разность потенциалов между концами сопротивления r. Эта разность равняется I × r.
Чтобы поддержать ток в цепи, электродвижущая сила (ЭДС) аккумулятора должна иметь величину:
E = I × r + I × R
Эта формула показывает, что электродвижущая сила в цепи равна сумме внешнего и внутреннего падений напряжения. Вынося I за скобки, получим:
E = I(r + R)
или
I = E / (r + R)
Две последние формулы выражают закона Ома для полной цепи.
Закон Ома в дифференциальной форме

 Дифференциальная форма закона Ома
Дифференциальная форма закона ОмаЗакон можно представить таким образом, чтобы он не был привязан к размерам проводника. Для этого выделим участок проводника Δl, на концах которой расположены ф1 и ф2. Среднюю площадь проводника обозначают ΔS , а плотность тока j, при таких условиях сила тока будет равняться:
I = jΔS = (ф1- ф2) / R = -(((ф1 — ф2)ΔS) / pΔl , отсюда следует, что j = -y × (Δф/Δl)
При условии, что Δl будет равен 0, то, взяв предел отношения:
lim (-(Δф/Δl)) = -(dф/dl) = Е,
окончательное выражение будет выглядеть так:
j = yE
Данное выражение закона находит силу тока в произвольной точке проводника в зависимости от его свойств и электрического состояния.
Закон Ома в интегральной форме
В данной интерпретации закона не содержится в условиях ЭДС, то есть формула выглядит так:
I = U/R
Чтобы найти значение для однородного линейного проводника, выразим R через p и получим:
R = p (l/S), где за р принимаем удельное объёмное сопротивление.
Линией тока принято называть кривую, в каждой точке которой вектор плотности тока направлен по касательной к этой кривой. При таких условиях вектор плотности находится из отношения J = jt, где t – это единичный вектор касательной к линии тока.
Для лучшего понимания предположим, что удельное сопротивление, а также напряженность поля движущих сил на поперечном сечении проводника однородны. При таком условии Е однородна, а значит, и j также однородная величина. Примем произвольное значение поперечного сечения цепи S, тогда pl/s = E. Получившееся равенство умножим на dl. Тогда Edl = (Е эл.ст.+Е стор.) dl = Е эл.ст. dl + Е стор. dl = -dф + dE. Отсюда получим (pI/S) dl = -dф + dE. Возьмём в учёт, что p/s dl = dR и запишем закон Ома в интегральной форме:
IdR = -dф + dE.
Закон Ома в комплексной форме
Чтобы провести анализ электрических цепей синусоидального тока, комфортнее использовать закон Ома в комплексной форме. Для лучшего понимания введем основное понятие, фигурирующее в данной интерпретации закона: синусоидальный ток – это линейные цепи с установившимся режимом работы, после того, как переходные процессы в них завершены, уровень напряжения резко уменьшается на конкретной дистанции, токи в ветвях и ЭДС источников являются синусоидальными функциями времени. В противном случае, когда данные параметры не соблюдаются, закон не может быть применим. Чем отличается эта форма от обычной? Ответ прост: токи, сопротивление и ЭДС фиксируются как комплексные числа. Это обусловлено тем, что существуют как активные так и реактивные значения напряжений, токов и сопротивлений, а в результате этого требуется внесение определенных коррективов.
Вместо активного сопротивления используется полное, то есть комплексное сопротивление цепи Z. Падение напряжения, ток и ЭДС тоже превращаются в комплексные величины. При реальных расчетах лучше и удобнее применять действующие значения. Итак, закон в комплексной форме выглядит так:
i = U/Z, i = UY
В данной формуле Z – комплексное сопротивление, Y – комплексная проводимость.
Чтобы выявить эти величины, выведены формулы. Пропустим шаги их создания и приведем готовые формулы:
Z = ze = z cosф + jz sinф = r + jx
Y = 1/ ze = ye = y cos ф — jy sin ф = g + jb
Закон Ома для переменного тока
После того как Фарадей открыл электромагнитную индукцию, стали активно использовать генераторы сперва постоянного, а после и переменного тока.
Используется уже известная формула:
I = U/Z
Полное сопротивление тока – это совокупность активного, а также индуктивного и емкостного сопротивлений. Проще говоря, ток в цепи переменного тока зависит от многих параметров, в том числе от величины ёмкости и индуктивности. Полное сопротивление вычисляется по формуле.

 Формула полного сопротивления
Формула полного сопротивленияПолное сопротивление можно изобразить как гипотенузу прямоугольного треугольника, катетами которого является активное и индуктивное сопротивление.

 Треугольник полного сопротивления
Треугольник полного сопротивленияИтак, формула амплитудного значения силы тока будет выглядеть так:
Im = Um/ ((R^2 + (ωL — (1/ωC)^2

 Цепь
ЦепьВ такой цепи колебания тока и напряжения разные по фазе, а разность фаз зависит от индуктивности катушки и ёмкости конденсатора:
U = Um sin (ωt)
I = Im sin (ωt + ф)
Закон Ома для постоянного тока
В данном случае частота будет равняться нулевому значению, поэтому остальные показатели также будут нулевыми соответственно, в то время как значение ёмкости достигнет бесконечности. Цепь разорвётся. Поэтому отсюда вытекает логичный вывод: реактивное сопротивление элементов в цепях постоянного напряжения отсутствует.
Закон Ома для однородного участка цепи
Формула выглядит уже известным образом:
I = U/R
В данном случае главной характеристикой проводника остаётся сопротивление. От того, как выглядит проводник, зависит количество узлов кристаллической решётки и атомов примесей. Поэтому электроны могут замедляться или ускоряться.
Сопротивление будет зависеть от вида проводника, а именно от его сечения, материала и длины:
R = p (L/S)
Закон Ома для неоднородного участка цепи
При решении задачи становится понятным, что для того, чтобы поддерживался стабильный ток в замкнутой цепи, нужны силы совершенной другой природы, а не кулоновские. В этом случае можно заметить такую закономерность: заряды, которые никак не соприкасаются друг с другом, выступают в двух ролях одновременно, то есть они являются силами электрического поля и силами иного вида – сторонними в это же время. Участок, на котором замечена данная закономерность, называется неоднородным.

 Неоднородный участок цепи
Неоднородный участок цепиФормула принимает вид:
E = Eq + Est
Закон Ома в данном подразделе был сформулирован таким образом: сила тока прямо пропорциональна напряжению на данном участке и обратно пропорциональна его полному сопротивлению.
Итак, готовая формула:
I = U12/R, где U12
Закон Ома для магнитной цепи
В каждом электромагните совмещены несколько важных элементов: стальной сердечник и катушка. По последней протекает ток. При совмещении нескольких участков образуется магнитная цепь.
При кольцевом магнитопроводе все поле находится внутри кольца. Тогда поток в магнитопроводе равен:
Ф = Вср S = μHср S
Формула закона для магнитной цепи:

 Формула закона ома для магнитной цепи
Формула закона ома для магнитной цепиЗадачи с решениями на закон Ома
Задача №1
Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 127 В. Определить силу тока в проволоке.
Дано:
- l = 120 м,
- S = 0,5 мм,
- U = 127 В,
- p = 1,1 Ом*мм2 /м.
Найти: I — ?
Решение:
- R = p * l / S,
- R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
- I = 127 В : 264 Ом = 0,48 А.
Ответ: I = 0,48 Ом
Задача №2
Нихромовая проволока длиной 120 м и площадью сечения 0,5 мм включена в цепь с напряжением 220 В. Определить силу тока в проволоке.
Дано:
- l = 120 м,
- S = 0,5 мм,
- U = 220 В,
- p = 1,1 Ом*мм2 /м.
Найти: I — ?
Решение:
- R = p * l / S,
- R = 1,1 Ом*мм2 /м * 120 м : 0,5 мм = 264 Ом,
- I = 220 В : 264 Ом = 0,83 А.
Ответ: I = 0,83 Ом
Задача №3
Дано:
- U = 15 В,
- R1 = 3 Ом,
- R2 = R3 = 4 Ом.
Найти: I — ?
Решение:
- R2 и R3 соединены параллельно R2 = R3, R2.3 = R2 / 2 = 2 Ом, составим эквивалентную схему:


- R = R1 + R2,3
- R = 3 Ом + 2 Ом = 5 Ом
- Найдем силу тока на участке цепи по закону Ома I = U / R
- I = 15 В / 5 Ом = 3 А
Ответ: I = 3 A.
Закон Ома

В 1826 величайший немецкий физик Георг Симон Ом публикует свою работу «Определение закона, по которому металлы проводят контактное электричество», где дает формулировку знаменитому закону. Ученые того времени встретили враждебно публикации великого физика. И лишь после того, как другой ученый – Клод Пулье, пришел к тем же выводам опытным путем, закон Ома признали во всем мире.
Закон Ома – физическая закономерность, которая определяет взаимосвязь между током, напряжением и сопротивлением проводника. Он имеет две основные формы.
Закон Ома для участка цепи
Формулировка закона Ома для участка цепи – сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению.


Это простое выражение помогает на практике решать широчайший круг вопросов. Для лучшего запоминания решим задачу.
Задача 1.1
Рассчитать силу тока, проходящую по медному проводу длиной 100 м, площадью поперечного сечения 0,5 мм2, если к концам провода приложено напряжение 12 B.
Задача простая, заключается в нахождении сопротивления медной проволоки с последующим расчетом силы тока по формуле закона Ома для участка цепи. Приступим.

Закон Ома для полной цепи
Формулировка


Здесь могут возникнуть вопросы. Например, что такое ЭДС? Электродвижущая сила — это физическая величина, которая характеризует работу внешних сил в источнике ЭДС. К примеру, в обычной пальчиковой батарейке, ЭДС является химическая реакция, которая заставляет перемещаться заряды от одного полюса к другому. Само слово электро
В каждом источнике присутствует внутреннее сопротивление r, оно зависит от параметров самого источника. В цепи также существует сопротивление R, оно зависит от параметров самой цепи.
Формулу закона Ома для полной цепи можно представить в другом виде. А именно: ЭДС источника цепи равна сумме падений напряжения на источнике и на внешней цепи.

Задача 2.1
Найти силу тока в цепи, если известно что сопротивление цепи 11 Ом, а источник подключенный к ней имеет ЭДС 12 В и внутреннее сопротивление 1 Ом.

Теперь решим задачу посложнее.
Задача 2.2
Источник ЭДС подключен к резистору сопротивлением 10 Ом с помощью медного провода длиной 1 м и площадью поперечного сечения 1 мм2. Найти силу тока, зная что ЭДС источника равно 12 В, а внутреннее сопротивление 1,9825 Ом.
Приступим.
Мнемоническая диаграмма
Для лучшего запоминания закона Ома существует мнемоническая диаграмма, благодаря которой можно всегда напомнить себе формулу. Пользоваться этой диаграммой очень просто. Достаточно закрыть искомую величину и две другие укажут, как её найти. Потренируйтесь, это может вам пригодится.
Успехов в изучении электричества! Рекомендуем прочесть статью — законы Кирхгофа.
Закон Ома для полной цепи
Закон Ома для полной цепи – эмпирический (полученный из эксперимента) закон, который устанавливает связь между силой тока, электродвижущей силой (ЭДС) и внешним и внутренним сопротивлением в цепи.
При проведении реальных исследований электрических характеристик цепей с постоянным током необходимо учитывать сопротивление самого источника тока. Таким образом в физике осуществляется переход от идеального источника тока к реальному источнику тока, у которого есть свое сопротивление (см. рис. 1).

Рис. 1. Изображение идеального и реального источников тока
Рассмотрение источника тока с собственным сопротивлением обязывает использовать закон Ома для полной цепи.

Рис. 2. Схема закона Ома для полной цепи.
Формула закона Ома для полной цепи

- R – внешнее сопротивление [Ом];
- r – сопротивление источника ЭДС (внутреннее) [Ом];
- I – сила тока [А];
- ε– ЭДС источника тока [В].
Рассмотрим некоторые задачи на данную тему. Задачи на закон Ома для полной цепи, как правило, дают ученикам 10 класса, чтобы они могли лучше усвоить указанную тему.
I. Определите силу тока в цепи с лампочкой, сопротивлением 2,4 Ом и источником тока, ЭДС которого равно 10 В, а внутреннее сопротивление 0,1 Ом.
По определению закона Ома для полной цепи, сила тока равна:

II. Определить внутреннее сопротивление источника тока с ЭДС 52 В. Если известно, что при подключении этого источника тока к цепи с сопротивлением 10 Ом амперметр показывает значение 5 А.
Запишем закон Ома для полной цепи и выразим из него внутреннее сопротивление:

III. Однажды школьник спросил у учителя по физике: «Почему батарейка садится?» Как грамотно ответить на данный вопрос?
Мы уже знаем, что реальный источник обладает собственным сопротивлением, которое обусловлено либо сопротивлением растворов электролитов для гальванических элементов и аккумуляторов, либо сопротивлением проводников для генераторов. Согласно закону Ома для полной цепи:

следовательно, ток в цепи может уменьшаться либо из-за уменьшения ЭДС, либо из-за повышения внутреннего сопротивления. Значение ЭДС у аккумулятора почти постоянный. Следовательно, ток в цепи понижается за счет повышения внутреннего сопротивления. Итак, «батарейка» садится, так как её внутреннее сопротивление увеличивается.
для участка цепи, для полной цепи +ВИДЕО
Чтобы хоть немного разбираться в электрике, необходимо знать основополагающие законы. Один из них — закон Ома. С него начинают изучение электрики и не зря. Он иллюстрирует зависимость параметров электрической цепи друг от друга.
Содержание статьи
Как звучит закон Ома для участка цепи
Есть говорить об официальной формулировке, то закон Ома можно озвучить так:
Сила тока имеет прямую зависимость от напряжения и обратную от сопротивления. Это высказывание справедливо для участка цепи с каким-то определенным и стабильным сопротивлением.
Формула этой зависимости на рисунке. Тут I — это сила тока, U — напряжение, R — сопротивление.

Формула закона Ома
- Чем больше напряжение, тем больше ток.
- Чем больше сопротивление, тем ток меньше.
Не так легко представить себе смысл этого выражения. Ведь электричество нельзя увидеть. Мы только приблизительно знаем что это такое. Попытаемся уяснить себе смысл этого закона при помощи аналогий.
Разбираемся что такое ток и сопротивление
Начнем с понятия электрического тока. Если говорить коротко, электрический ток применительно к металлам — это направленное движение электронов — отрицательно заряженных частиц. Их обычно представляют в виде небольших кружочков. В спокойном состоянии они передвигаются хаотически, постоянно меняя свое направление. При определенных условиях — возникновении разницы потенциалов — эти частицы начинают определенное движение в какую-то сторону. Вот это движение и есть электрический ток.
Чтобы было понятнее, можно сравнить электроны с водой, разлитой на какой-то плоскости. Пока плоскость неподвижна, вода не движется. Но, как только появился наклон (возникла разница потенциалов), вода пришла в движение. С электронами примерно так же.

Примерно так можно себе представить электрический ток
Теперь надо понять, что такое сопротивление и почему с силой тока у них обратная связь: чем выше сопротивление, тем меньше ток. Как известно, электроны движутся по проводнику. Обычно это металлические провода, так как металлы обладают хорошей способностью проводить электрический ток. Мы знаем, что металл имеет плотную кристаллическую решетку: много частиц, которые расположены близко и связаны между собой. Электроны, пробираясь между атомами металла, на них наталкиваются, что затрудняет их движение. Это помогает проиллюстрировать сопротивление, которое оказывает проводник. Вот теперь становится понятным, почему, чем выше сопротивление, тем меньше сила тока — чем больше частиц, тем электронам сложнее преодолевать путь, делают они это медленнее. С этим, вроде, разобрались.
Если у вас есть желание проверить эту зависимость опытным путем, найдите переменный резистор, соедините последовательно резистор — амперметр — источник тока (батарейка). Еще желательно в цепь вставить выключатель — обычный тумблер.

Цепь для проверки зависимости силы тока от сопротивления
Крутя ручку резистора вы изменяете сопротивление. При этом показания на амперметре, который измеряет силу тока, тоже меняются. Причем чем больше сопротивление, тем меньше отклоняется стрелка — меньше ток. Чем сопротивление меньше — тем сильнее отклоняется стрелка — ток больше.
Вместо стрелочного прибора можно использовать цифровой мультиметр в режиме измерения постоянного тока. В этом случае отслеживаются показания на жидкокристаллическом цифровом табло.
Зависимость тока от сопротивления почти линейная, то есть на графике отражается почти прямой линией. Почему почти — об этом надо говорить отдельно, но это другая история.
Говорим о напряжении
Не менее важно понять что такое напряжение. Давайте сразу начнем с аналогии и снова используем воду. Пусть в воронке находится вода. Она просачивается через узкое горлышко, которое создает сопротивление. Если представить, что на воду уложили груз, движение воды ускорится. Этот груз — и есть напряжение. И теперь тоже понятно, почему чем выше напряжение, тем сильнее ток — чем сильнее давление, тем быстрее будет двигаться вода. То есть, зависимость прямая: больше напряжение — больше ток. И именно это положение отражает закон Ома — «давление» стоит в числителе (в верхней части дроби).
Можно попробовать представить напряжение по-другому. Есть все те же электроны, которые скопились на одном краю источника питания. На втором краю их мало. Так как каждый из электронов имеет какой-то заряд, там, где их много, суммарный заряд больше, где мало — меньше. Разница между зарядами и есть напряжение. Это тоже несложно представить. С точки зрения электричества — это более корректное представление, хоть и не точное.
На тему закона Ома есть немало забавных картинок, позволяющих чуть лучше понять все эти явления. Одна из них перед вами и иллюстрирует, как ток зависит от напряжения и сопротивления. Смотрите что получается: сопротивление старается уменьшить ток (обратная зависимость), а с ростом напряжения он увеличивается (прямая зависимость). Это и есть закон Ома, но переданный простыми словами.

Благодаря картинке просто понять зависимость тока от напряжения и сопротивления
Если вы хотите убедиться и в этой зависимости, тоже надо создать простенькую цепь. Но нужен будет либо регулируемый источник питания, либо несколько батареек, которые выдают разное напряжение. Или можно последовательно включать несколько батареек — тоже вариант. Но менять/подпаивать батарейки надо при разорванной цепи (выключенном тумблере).
В этой схеме используются два измерительных прибора: амперметр включается последовательно с нагрузкой (резистор на схеме ниже), вольтметр параллельно нагрузке.

Схема для иллюстрации закона Ома
Так как другие параметры цепи остаются в норме, при увеличении напряжения мы увидим увеличение силы тока. Чем больше напряжение подаем, тем больше отклоняются стрелки вольтметра и амперметра. Если задаться целью построить график, он будет в виде прямой. Если поставить другое сопротивление, график также будет в виде прямой, но угол наклона ее изменится.
Что изменится для полной цепи
В ситуации выше рассмотрен только некоторый участок цепи, обладающий каким-то фиксированным сопротивлением. Мы предполагаем, что при определенных условиях электроны начнут движение. Причина этого движения — тот самый груз на картинке. В реальных условиях это — источник тока. Это может быть батарейка, генератор постоянного тока, подключенный шнур блока питания и т.д. При подключении источника питания к проводнику в нем начинает протекать ток. Это мы тоже знаем и наблюдаем, когда включаем лампу в сеть, ставим заряжаться мобильный телефон и т.д.

Полная цепь включает в себя источник питания
Участок цепи имеет какое-то сопротивление. Это понятно. Но источник питания тоже имеет сопротивление. Его обычно обозначают маленько буквой r. Так как ток бежит по кругу, ему приходится преодолевать сопротивление провода и сопротивление источника тока. Вот это суммарное сопротивление цепи и источника питания — называют импеданс. Говорят еще что это комплексное сопротивление. В формуле Ома для полной цепи его отображают при помощи суммы. В знаменателе стоит сумма сопротивлений цепи и внутреннего сопротивления источника тока (R + r).
Всем, наверное, понятно, что именно источник тока создает нужные условия для движения электронов. Все благодаря тому, что он обладает ЭДС — электродвижущей силой. Эта величина обозначается обычно E. Чем больше эта сила, тем больше ток. Это тоже, вроде, понятно. Поэтому обозначение ЭДС — латинскую букву E — ставят в числитель. Таким образом, формулировка закона Ома для полной цепи звучит так:
Сила тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника тока.
Вроде не слишком сложно, но можно попробовать еще проще:
- Чем выше ЭДС источника тока, тем больше ток.
- Чем больше суммарное сопротивление, тем ток меньше.
Как найти сопротивление, напряжение
Зная формулу закона Ома для участка цепи, мы можем рассчитать напряжение и сопротивление. Напряжение находится как произведение силы тока и сопротивления.

Формула напряжения и сопротивления по закону Ома
Сопротивление можно найти, разделив напряжение на ток. Все действительно несложно. Если мы знаем, что к участку цепи было проложено определенное напряжение и знаем какой при этом был ток, мы можем рассчитать сопротивление. Для этого напряжение делим на ток. Получаем как раз величину сопротивления этого куска цепи.
С другой стороны, если мы знаем сопротивление и силу тока, которая должна быть, мы сможем рассчитать напряжение. Надо всего лишь перемножить силу тока и сопротивление. Это даст напряжение, которое необходимо подать на этот участок цепи чтобы получить требуемый ток.
Параллельное и последовательное соединение
В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения
Последовательное соединение
Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

Последовательное соединение и параметры этого участка цепи
При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.
Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.
Параллельное соединение
Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.
Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Законы для параллельного соединения
Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.
Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.
Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.
Что нам дает параллельное и последовательное соединение?
Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:
- Если в наличии нет резистора большого номинала, но есть несколько более «мелких», нужное сопротивление можно получить соединив последовательно несколько резисторов. Как видите, это полезный прием.
- Для продления срока жизни батареек, их можно соединять параллельно. Напряжение при этом, согласно закону Ома, останется прежним (можно убедиться, измерив напряжение мультиметром). А «срок жизни» сдвоенного элемента питания будет значительно больше, нежели у двух элементов, которые сменят друг друга. Только обратите внимание: параллельно соединять можно только источники питания с одинаковым потенциалом. То есть, севшую и новую батарейки соединять нельзя. Если все-таки соединить, та батарейка которая имеет больший заряд, будет стремиться зарядить менее заряженную. В результате общий их заряд упадет до низкого значения.

Практическое применение закона Ома: можно создавать источники питания с нужным напряжением и силой тока
В общем, это наиболее распространенные варианты использования этих соединений.
ЭДС. Закон Ома для полной цепи
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электродвижущая сила, внутреннее сопротивление источника тока, закон Ома для полной электрической цепи.
До сих пор при изучении электрического тока мы рассматривали направленное движение свободных зарядов во внешней цепи, то есть в проводниках, подсоединённых к клеммам источника тока.
Как мы знаем, положительный заряд :
• уходит во внешнюю цепь с положительной клеммы источника;
• перемещается во внешней цепи под действием стационарного электрического поля, создаваемого другими движущимися зарядами;
• приходит на отрицательную клемму источника, завершая свой путь во внешней цепи.
Теперь нашему положительному заряду нужно замкнуть свою траекторию и вернуться на положительную клемму. Для этого ему требуется преодолеть заключительный отрезок пути — внутри источника тока от отрицательной клеммы к положительной. Но вдумайтесь: идти туда ему совсем не хочется! Отрицательная клемма притягивает его к себе, положительная клемма его от себя отталкивает, и в результате на наш заряд внутри источника действует электрическая сила , направленная против движения заряда (т.е. против направления тока).
Сторонняя сила
Тем не менее, ток по цепи идёт; стало быть, имеется сила, «протаскивающая» заряд сквозь источник вопреки противодействию электрического поля клемм (рис. 1).

Рис. 1. Сторонняя сила
Эта сила называется сторонней силой; именно благодаря ей и функционирует источник тока. Сторонняя сила не имеет отношения к стационарному электрическому полю — у неё, как говорят, неэлектрическое происхождение; в батарейках, например, она возникает благодаря протеканию соответствующих химических реакций.
Обозначим через работу сторонней силы по перемещению положительного заряда q внутри источника тока от отрицательной клеммы к положительной. Эта работа положительна, так как направление сторонней силы совпадает с направлением перемещения заряда. Работа сторонней силы называется также работой источника тока.
Во внешней цепи сторонняя сила отсутствует, так что работа сторонней силы по перемещению заряда во внешней цепи равна нулю. Поэтому работа сторонней силы по перемещению заряда вокруг всей цепи сводится к работе по перемещению этого заряда только лишь внутри источника тока. Таким образом, — это также работа сторонней силы по перемещению заряда по всей цепи.
Мы видим, что сторонняя сила является непотенциальной — её работа при перемещении заряда по замкнутому пути не равна нулю. Именно эта непотенциальность и обеспечивает циркулирование электрического тока; потенциальное электрическое поле, как мы уже говорили ранее, не может поддерживать постоянный ток.
Опыт показывает, что работа прямо пропорциональна перемещаемому заряду . Поэтому отношение уже не зависит от заряда и является количественной характеристикой источника тока. Это отношение обозначается :
(1)
Данная величина называется электродвижущей силой (ЭДС) источника тока. Как видим, ЭДС измеряется в вольтах (В), поэтому название «электродвижущая сила» является крайне неудачным. Но оно давно укоренилось, так что приходится смириться.
Когда вы видите надпись на батарейке: «1,5 В», то знайте, что это именно ЭДС. Равна ли эта величина напряжению, которое создаёт батарейка во внешней цепи? Оказывается, нет! Сейчас мы поймём, почему.
Закон Ома для полной цепи
Любой источник тока обладает своим сопротивлением , которое называется внутренним сопротивлением этого источника. Таким образом, источник тока имеет две важных характеристики: ЭДС и внутреннее сопротивление.
Пусть источник тока с ЭДС, равной , и внутренним сопротивлением подключён к резистору (который в данном случае называется внешним резистором, или внешней нагрузкой, или полезной нагрузкой). Всё это вместе называется полной цепью (рис. 2).

Рис. 2. Полная цепь
Наша задача — найти силу тока в цепи и напряжение на резисторе .
За время по цепи проходит заряд . Согласно формуле (1) источник тока совершает при этом работу:
(2)
Так как сила тока постоянна, работа источника целиком превращается в теплоту, которая выделяется на сопротивлениях и . Данное количество теплоты определяется законом Джоуля–Ленца:
(3)
Итак, , и мы приравниваем правые части формул (2) и (3):
После сокращения на получаем:
Вот мы и нашли ток в цепи:
(4)
Формула (4) называется законом Ома для полной цепи.
Если соединить клеммы источника проводом пренебрежимо малого сопротивления , то получится короткое замыкание. Через источник при этом потечёт максимальный ток — ток короткого замыкания:
Из-за малости внутреннего сопротивления ток короткого замыкания может быть весьма большим. Например, пальчиковая батарейка разогревается при этом так, что обжигает руки.
Зная силу тока (формула (4)), мы можем найти напряжение на резисторе с помощью закона Ома для участка цепи:
(5)
Это напряжение является разностью потенциалов между точками и (рис. 2). Потенциал точки равен потенциалу положительной клеммы источника; потенциал точки равен потенциалу отрицательной клеммы. Поэтому напряжение (5) называется также напряжением на клеммах источника.
Мы видим из формулы (5), что в реальной цепи будет — ведь умножается на дробь, меньшую единицы. Но есть два случая, когда .
1. Идеальный источник тока. Так называется источник с нулевым внутренним сопротивлением. При формула (5) даёт .
2. Разомкнутая цепь. Рассмотрим источник тока сам по себе, вне электрической цепи. В этом случае можно считать, что внешнее сопротивление бесконечно велико: . Тогда величина неотличима от , и формула (5) снова даёт нам .
Смысл этого результата прост: если источник не подключён к цепи, то вольтметр, подсоединённый к полюсам источника, покажет его ЭДС.
КПД электрической цепи
Нетрудно понять, почему резистор называется полезной нагрузкой. Представьте себе, что это лампочка. Теплота, выделяющаяся на лампочке, является полезной, так как благодаря этой теплоте лампочка выполняет своё предназначение — даёт свет.
Количество теплоты, выделяющееся на полезной нагрузке за время , обозначим .
Если сила тока в цепи равна , то
Некоторое количество теплоты выделяется также на источнике тока:
Полное количество теплоты, которое выделяется в цепи, равно:
КПД электрической цепи — это отношение полезного тепла к полному:
КПД цепи равен единице лишь в том случае, если источник тока идеальный .
Закон Ома для неоднородного участка
Простой закон Ома справедлив для так называемого однородного участка цепи — то есть участка, на котором нет источников тока. Сейчас мы получим более общие соотношения, из которых следует как закон Ома для однородного участка, так и полученный выше закон Ома для полной цепи.
Участок цепи называется неоднородным, если на нём имеется источник тока. Иными словами, неоднородный участок — это участок с ЭДС.
На рис. 3показан неоднородный участок, содержащий резистор и источник тока. ЭДС источника равна , его внутреннее сопротивление считаем равным нулю (усли внутреннее сопротивление источника равно , можно просто заменить резистор на резистор ).

Рис. 3. ЭДС «помогает» току:
Сила тока на участке равна , ток течёт от точки к точке . Этот ток не обязательно вызван одним лишь источником . Рассматриваемый участок, как правило, входит в состав некоторой цепи (не изображённой на рисунке), а в этой цепи могут присутствовать и другие источники тока. Поэтому ток является результатом совокупного действия всех источников, имеющихся в цепи.
Пусть потенциалы точек и равны соответственно и . Подчеркнём ещё раз, что речь идёт о потенциале стационарного электрического поля, порождённого действием всех источников цепи — не только источника, принадлежащего данному участку, но и, возможно, имеющихся вне этого участка.
Напряжение на нашем участке равно: . За время через участок проходит заряд , при этом стационарное электрическое поле совершает работу:
Кроме того, положительную работу совершает источник тока (ведь заряд прошёл сквозь него!):
Сила тока постоянна, поэтому суммарная работа по продвижению заряда , совершаемая на участке стационарным элетрическим полем и сторонними силами источника, целиком превращается в тепло: .
Подставляем сюда выражения для , и закон Джоуля–Ленца:
Сокращая на , получаем закон Ома для неоднородного участка цепи:
(6)
или, что то же самое:
(7)
Обратите внимание: перед стоит знак «плюс». Причину этого мы уже указывали — источник тока в данном случае совершает положительную работу, «протаскивая» внутри себя заряд от отрицательной клеммы к положительной. Попросту говоря, источник «помогает» току протекать от точки к точке .
Отметим два следствия выведенных формул (6) и (7).
1. Если участок однородный, то . Тогда из формулы (6) получаем — закон Ома для однородного участка цепи.
2. Предположим, что источник тока обладает внутренним сопротивлением . Это, как мы уже упоминали, равносильно замене на :
Теперь замкнём наш участок, соединив точки и . Получим рассмотренную выше полную цепь. При этом окажется, что и предыдущая формула превратится в закон Ома для полной цепи:
Таким образом, закон Ома для однородного участка и закон Ома для полной цепи оба вытекают из закона Ома для неоднородного участка.
Может быть и другой случай подключения, когда источник «мешает» току идти по участку. Такая ситуация изображена на рис. 4. Здесь ток, идущий от к , направлен против действия сторонних сил источника.

Рис. 4. ЭДС «мешает» току:
Как такое возможно? Очень просто: другие источники, имеющиеся в цепи вне рассматриваемого участка, «пересиливают» источник на участке и вынуждают ток течь против . Именно так происходит, когда вы ставите телефон на зарядку: подключённый к розетке адаптер вызывает движение зарядов против действия сторонних сил аккумулятора телефона, и аккумулятор тем самым заряжается!
Что изменится теперь в выводе наших формул? Только одно — работа сторонних сил станет отрицательной:
Тогда закон Ома для неоднородного участка примет вид:
(8)
или:
где по-прежнему — напряжение на участке.
Давайте соберём вместе формулы (7) и (8) и запишем закон Ома для участка с ЭДС следующим образом:
Ток при этом течёт от точки к точке . Если направление тока совпадает с направлением сторонних сил, то перед ставится «плюс»; если же эти направления противоположны, то ставится «минус».
 Одним из принципов электротехники является закон Ома для полной цепи. Используя установленную учёным закономерность, можно вычислить сопротивление электрической цепи или источника тока, рассчитать электродвижущую силу (ЭДС). Практическое же применение полученным при расчёте данным велико. Это подбор шунтирующих и предохранительных элементов, вычисление необходимой мощности используемых деталей, согласование электронных узлов.
Одним из принципов электротехники является закон Ома для полной цепи. Используя установленную учёным закономерность, можно вычислить сопротивление электрической цепи или источника тока, рассчитать электродвижущую силу (ЭДС). Практическое же применение полученным при расчёте данным велико. Это подбор шунтирующих и предохранительных элементов, вычисление необходимой мощности используемых деталей, согласование электронных узлов.
История открытия
Зависимость между током, напряжением и сопротивлением в электрической цепи была установлена опытным путём в 1827 году. Занимаясь исследованиями электричества, Георг Симон Ом проводил ряд экспериментов над проводниками, изучая их проводимость, и в частности, подключая последовательно к источнику энергии тонкие проводники, выполненные из различных материалов. Изменяя их длину, он получал определённую силу тока. Им было установлено, что на результаты экспериментов влияет источник электрической энергии, сопротивление которого оказывалось выше, чем у используемых в опытах проводников.
 По совету своего наставника Поггендорфа Ом собрал термоэлектрическую батарею, отказавшись от использования химических элементов, применив вместо них открытую Зеебеком термопару медь-висмут. Для измерения параметров цепи им использовались крутильные весы, с магнитной стрелкой сконструированные Кулоном.
По совету своего наставника Поггендорфа Ом собрал термоэлектрическую батарею, отказавшись от использования химических элементов, применив вместо них открытую Зеебеком термопару медь-висмут. Для измерения параметров цепи им использовались крутильные весы, с магнитной стрелкой сконструированные Кулоном.
На основании своих исследований физик-экспериментатор пришёл к выводу, что отклонение стрелки зависит от определённой силы, названной силой тока. Когда стрелка отклонялась, Ом закручивал весы таким образом, чтобы она возвращалась в своё начальное положение. Угол, на который закручивалась нить, он считал пропорциональной силе тока. Изменяя условия, Ом вывел математическую зависимость, составив уравнение. Выглядело оно следующим образом: Х = а/b + x, где за Х принималась сила, отклоняющая магнитную стрелку, за а — длина исследуемого образца, а b+x обозначали интенсивность и считались постоянной величиной.
В 1862 году в журнале «Физика и химия» публикуется статья Ома под названием «Определение закона, по которому металлы проводят контактное электричество». Результаты его исследований не производят впечатления на других ученых, и его выводы остаются незамеченными. Ом продолжает эксперименты, выясняя, что электричество можно рассмотреть наподобие теплового потока. Подобно разнице температур, благодаря которой совершается тепловое движение, некой величиной можно описать движение электрического заряда. Так он вводит понятие ЭДС.
Открытие Ома было принято учёным миром уже после его смерти. Существенный вклад в это внесли русские учёные Ленц и Якоби. В 1842 году Лондонское Королевское общество наградило физика золотой медалью, а закон, открытый им, был назван его именем.
Понятие тока и напряжения
Закономерность учёного устанавливает зависимость между собой трёх электрических величин: тока, напряжения и сопротивления. Поэтому для того чтобы разобраться в сути закона Ома для полной электрической цепи, необходимо понимать, что же из себя они представляют.
 В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.
В любом теле существуют свободные элементарные частички, обладающие определённым количеством энергии — зарядом. Если тело находится в спокойном состоянии, то есть на него не оказывается никакого воздействия, то происходит их хаотичное перемещение. Если же к телу приложено электрическое поле, то их перемещение становится упорядоченным, и они начинают передвигаться в одну сторону.
Такое направленное движение называют электрическим током. Мерой его служит сила тока, скалярная величина, определяемая отношением количества зарядов прошедших через поперечное сечение проводника за единицу времени: I = dq/dt. За единицу измерения силы тока принят ампер.
Если направление перемещения зарядов остаётся неизменным, то движение тока считается постоянным, а если изменяется — переменным. Возникновение тока возможно только в замкнутой цепи. Для того чтобы заряд переместился, приложенное поле должно выполнить работу. То есть затратить какую-то энергию для перемещения заряда с одной точки в другую. Если принять, что в начальном положении частичка обладает нулевым зарядом, то тогда переместившись, она уже будет иметь другое его значение. Разность между этими величинами называется разностью потенциалов или напряжением.
Для поддержания силы тока в полной цепи необходим источник, постоянно воздействующий на свободные заряды и поддерживающий разности потенциалов на различных участках цепи. Величина силы, которая действует на цепь, называется ЭДС. Физически она представляет собой отношение работы, затрачиваемой на передвижение заряда от одного своего полюса к другому, к значению заряда: E = A/q. Измеряется ЭДС, так же как и напряжение, в вольтах.
При перемещении заряд из-за особенностей строения кристаллической решётки вещества, он сталкивается с различными дефектами и примесями. В результате этого происходит частичное рассеивание его потенциала, а скорость движения замедляется. Потеря энергии характеризуется электрической величиной-сопротивлением. Другими словами, сопротивление — это величина, препятствующая прохождению тока.
Импеданс цепи
Немецкий физик, проводя эксперименты, смог обнаружить зависимость между током и напряжением. Их связь определялась через постоянную величину, которая после была названа сопротивлением. Так, формула закона Ома для полной цепи может быть записана в виде выражения:
I = E/Z, где:
- I — сила тока цепи;
- E — электродвижущая сила, приложенная к цепи;
- Z — постоянная величина (полное сопротивление).
Полное сопротивление (импеданс) электрической цепи важный параметр, определяющий силу тока и полезную мощность. Состоит она из нескольких составляющих: внутреннего сопротивления источника тока и сопротивления элементов, из которых состоит схема.

Поэтому в отличие от участка цепи, где берётся во внимание только сопротивление проводников, закон для всей цепи учитывает и электрическое сопротивление источника тока. В то же время характер происхождения сопротивления может носить как активную составляющую, так и реактивную, учитывающуюся для переменного тока.
Активная составляющая
Такое сопротивление называется активным, так как оно забирает на себя часть мощности, поступающей от источника питания. Эта забираемая энергия, проходя через проводник, превращается в тепло. При этом можно обнаружить, что если проводник подключить к переменному источнику сигнала, то его сопротивление будет немного больше. Связано это с тем, что индуцируемая ЭДС в материале в любой его точке неодинаковая. Ближе к центру она будет больше, чем у поверхности. То есть при переменном сигнале как бы происходит уменьшение полезного сечения проводника.

Сопротивление зависит от физических параметров материала. Математически это может быть описано выражением: R = p*L/S, где L — длина проводника, S — поперечное сечение, p — удельное сопротивление (табличное значение). Активное сопротивление слабо зависит от частоты сигнала, но при его увеличении возрастает.
Отличительной чертой элемента, обладающего активным сопротивлением, будет совпадение по фазе, протекающего через него тока и напряжения. Поэтому вычисляться оно по формуле: R = U/I.
Реактивное сопротивление
Индуктивное сопротивление связано с ЭДС самоиндукции. При протекании через элемент, обладающий индуктивностью, переменного тока, возникает магнитное поле, создающее ЭДС. Эта сила противодействует внешнему полю и препятствует его распространению. Затрачиваемая энергия увеличивает мощность магнитного поля. Как только ток уменьшается, значение магнитного поля начинает тоже снижаться, индуцируя ток самоиндукции. Его направление совпадает с убывающим током. В результате энергия, отобранная магнитным полем, начинает отдаваться обратно в цепь. То есть фактически, в отличие от активного сопротивления, потерь энергии не возникает.
Величина индуктивного сопротивления находится по формуле X L = 2 p * f * L, где: f — частота сигнала, L — значение индуктивности. Напряжение, приложенное к индуктивности и ток, поступающий от источника энергии, сдвинуты относительно друг друга по фазе на 90, при этом ток отстаёт от напряжения.

Ёмкостное же сопротивление обусловлено возникновением электродвижущей силы. При прохождении через ёмкость энергия, поступающая от источника питания должна преодолеть ёмкостное сопротивление, затрачивая часть мощности для её заряда. Но как только подаваемый сигнал изменит знак, весь накопленный заряд ёмкостью начнёт возвращаться в цепь, увеличивая энергию электрического поля.
Другими словами, ёмкость становится источником ЭДС. Ёмкостное сопротивление описывается выражением: X c = 1/ (2 p * f * C), где: C — величина ёмкости. При таком роде сопротивления ток будет опережать напряжение по фазе на 90.
Таким образом, реактивное сопротивление зависит от частоты сигнала. Общий же импеданс определяется не как сумма всех сопротивлений, а по формуле Z = (R2+ X l2+ X c2)½.
Суть закона
Общепринятая формулировка закона Ома гласит, что сила тока в полной цепи прямо пропорциональна электродвижущей силе источника, делённой на общее сопротивление всех элементов замкнутой цепи. Классическая формула закона Ома для цепи постоянного тока выглядит следующим образом:
I = E /(r+R), где:
- R — сопротивление внешней части цепи, Ом;
- r — внутренний импеданс источника энергии.
В замкнутой схеме ток течёт от источника энергии, протекает через различные элементы, последовательно или параллельно подключённые к нему, и возвращается обратно. Изучая открытие Ома можно сформулировать основной физический принцип, на котором строится электротехника. Заключается он в том, что чем больше ЭДС, тем большей энергией будут обладать носители заряда, а значит и их скорость перемещения будет больше. При увеличении сопротивления в цепи скорость движения, а значит, и энергия носителей заряда уменьшается, соответственно снижается и ток.

Величина ЭДС зависит от характеристик источника энергии, а сопротивление от физических параметров материала и температуры. Значение активного сопротивления не может быть изменено увеличением направленного движения частиц или напряжения, но при этом реактивная составляющая зависит от частоты сигнала.
Поэтому закон Ома для полного участка цепи переменного тока и учитывает индуктивную и ёмкостную составляющую, причём как источника питания, так и самой цепи. Описывается математически он формулой: I = Um /Z, где:
- Um — ЭДС источника питания;
- Z — импеданс всей замкнутой цепи: Z = (R2+(wL — 1/wC)2)½.
То есть для переменного тока закон будет описываться выражением вида:
I = Um/ (R2+(wL -1/wC)2)½.
Однако следует понимать, что в формуле используются амплитудные значения величин, а не мгновенные.
Дифференциальное уравнение
Так как сопротивление зависит не только от физических свойств материала, но и от его геометрических параметров, часто последнее при использовании закона Ома исключается из формулы. Открытие учёного, учитывающее только электропроводящие свойства, записывают в так называемой дифференциальной форме.
Такая формула имеет вид: J = σ*E, где:
- J — плотность, характеризующая силу электричества протекающего через единицу площади;
- σ — удельная проводимость, величина обратная удельному сопротивлению;
- E — напряжённость поля, определяется в определённой точке как отношение силы действующей на неподвижный заряд к его величине.
Составляющие уравнения представляются в виде функции координат и времени. Удельная проводимость выражается в виде единичной матрицы. Поэтому закон можно представить формулой:

Таким образом, закон Ома для замкнутой цепи практически ничем не отличается от его формулировки для неполной схемы, лишь только дополнительно учитывает внутреннее сопротивление источника ЭДС. При этом его формулировка не изменяется.
ЗаконОм
ЗаконОма показывает линейную зависимость между напряжением и током в электрической цепи.
Падение напряжения и сопротивление резистора задают постоянный ток, протекающий через резистор.
По аналогии с потоком воды мы можем представить электрический ток как ток воды через трубу, резистор как тонкую трубу, которая ограничивает поток воды, напряжение как перепад высот воды, который обеспечивает поток воды.
формула закона Ома
Ток I резистора в амперах (A) равен сопротивлению резистора напряжение V в вольтах (В), деленное на сопротивление R в омах (Ом):
В — падение напряжения на резисторе, измеренное в вольтах (В).В некоторых случаях закон Ома использует букву E для обозначения напряжения. E обозначает электродвижущую силу.
I — электрический ток, протекающий через резистор, измеренный в амперах (A)
R — сопротивление резистора, измеряется в Ом (Ω)
Расчет напряжения
Когда мы знаем ток и сопротивление, мы можем рассчитать напряжение.
Напряжение V в вольтах (В) равно току I в амперах (A), умноженному на сопротивление R в омах (Ом):
Расчет сопротивления
Когда мы знаем напряжение и ток, мы можем рассчитать сопротивление.
Сопротивление R в омах (Ом) равно напряжению V в вольтах (В), деленному на ток I в амперах (A):
Поскольку ток определяется значениями напряжения и сопротивления, формула закона Ома может показать, что:
- Если мы увеличим напряжение, ток увеличится.
- Если мы увеличим сопротивление, ток уменьшится.
Пример №1
Найти ток электрической цепи с сопротивлением 50 Ом и напряжением питания 5 Вольт.
Решение:
В = 5 В
R = 50Ω
I = В / R = 5 В / 50 Ом = 0,1 А = 100 мА
Пример №2
Найти сопротивление электрической цепи, которая имеет напряжение питания 10 Вольт и ток 5 мА.
Решение:
В = 10 В
I = 5 мА = 0,005A
R = В / I = 10 В / 0,005 А = 2000 Ом = 2 кОм
ЗаконОм для цепи переменного тока
Ток нагрузки I в амперах (A) равен напряжению нагрузки V Z = V в вольтах (В), деленному на полное сопротивление Z в омах (Ом):
В — падение напряжения на нагрузке, измеряется в Вольтах (В)
I — электрический ток, измеренный в амперах (A)
Z — полное сопротивление нагрузки, измеряется в Ом (Ω)
Пример № 3
Найти ток в цепи переменного тока с напряжением питания 110 В ± 70 ° и нагрузкой 0.5kΩ∟20 °.
Решение:
В = 110 В∟70 °
Z = 0,5 кОм20 ° = 500 кОм20 °
I = В / Z = 110 В ~ 70 ° / 500 Ом ~ 20 ° = (110 В / 500 Ом) ∟ (70 ° -20 °) = 0,22 А ~ 50 °
Калькулятор закона Ома (краткая форма)
Ом закон калькулятора: рассчитывает соотношение между напряжением, током и сопротивлением.
Введите 2 значений, чтобы получить третье значение, и нажмите кнопку Рассчитать :
закон закона Ома II ►
См. Также
,Принципиальная схема законаОм [Как читать символы] • Закон Ома
Простая принципиальная схема Ома содержит сопротивление, соединенное последовательно с источником постоянного напряжения.
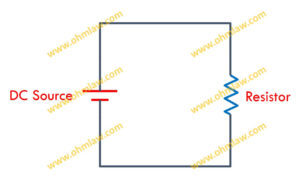
Две параллельные линии, одна из которых имеет сравнительно большую длину, представляют источник постоянного тока, а зигзагообразный символ представляет резистор. В то время как простые линии используются для представления проводов.
Приведенная выше диаграмма верна для общего случая, практически нам нужно добавить амперметр и вольтметр для целей измерения.Теперь наша диаграмма с инструментами будет выглядеть так:
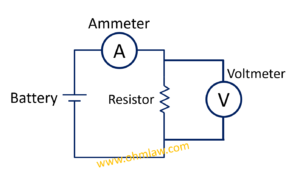
Давайте разберемся в компонентах нашей принципиальной схемы.
Батарея: это источник постоянного напряжения, обеспечивающий питание внутренней цепи. Когда мы изучали утверждение Ома: V = IR. На самом деле, V — это аккумулятор или источник напряжения, который питает всю цепь.
Амперметр: считывает ток, который течет по всей цепи. Помните, что амперметр всегда подключается последовательно к цепи.
Вольтметр: считывает напряжение на резисторе. Помните, что вольтметр всегда включается параллельно компоненту.
Теперь давайте начнем изучать базовую математику права, используя 5 различных примеров.
Пример 1: батарея 10 В подключается последовательно с сопротивлением 20 кОм. Найти ток, протекающий по цепи.
Решение: Использование V 1 = I 1 R 1 .
I 1 = V 1 / R 1 = 0.5 мА
Пример 2: источник 15 В соединяется с неизвестным резистором. Значение тока измеряется как 5 мА. Найдите значение R.
Решение: R 2 = V 2 / I 2 = 15 В / 5 мА = 3 кОм
Пример 3: резистор 50 кОм включается с переменным напряжением 25 В постоянного тока. Найти значение неизвестного тока, который течет через эту цепь.
Решение: I 3 = V 3 / R 3 = 25 В / 50 к = 0,5 мА
Пример 4. Рассеиваемая мощность при сопротивлении 29 кОм составляет 15 Вт.Найти значение тока и входного напряжения, подаваемого источником.
Решение: Здесь будут использоваться формулы: I = SQRT (P / R) и V = SQRT (P * R). Вы можете узнать обо всех этих формулах из Ohmic Wheel.
Пример 5: R5 = 10 Ом и P5 = 20 Вт
Решение: V5 = 14,14 и I5 = 1,414
,Закон- Классы
- Класс 1 — 3
- Класс 4 — 5
- Класс 6 — 10
- Класс 11 — 12
- КОНКУРСЫ
- BBS
- 000000000 Книги
- NCERT Книги для 5 класса
- NCERT Книги Класс 6
- NCERT Книги для 7 класса
- NCERT Книги для 8 класса
- NCERT Книги для 9 класса
- NCERT Книги для 10 класса
- NCERT Книги для 11 класса
- NCERT Книги для 12-го класса
- NCERT Exemplar
- NCERT Exemplar Class 8
- NCERT Exemplar Class 9
- NCERT Exemplar Class 10
- NCERT Exemplar Class 11
- NCERT Exemplar Class 12 9000al Aggar
Agard Agard Agard Agard Agulis Class 12- Классы
- RS Решения Aggarwal класса 10
- RS Решения Aggarwal класса 11
- RS Решения Aggarwal класса 10 90 003 Решения RS Aggarwal класса 9
- Решения RS Aggarwal класса 8
- Решения RS Aggarwal класса 7
- Решения RS Aggarwal класса 6
- Решения RD Sharma
- Решения класса RD Sharma
- Решения класса 9 Шарма 7 Решения RD Sharma Class 8
- Решения RD Sharma Class 9
- Решения RD Sharma Class 10
- Решения RD Sharma Class 11
- Решения RD Sharma Class 12
- ФИЗИКА
- Механика
- 000000 Электромагнетизм
- ХИМИЯ
- Органическая химия
- Неорганическая химия
- Периодическая таблица
- МАТС
- Теорема Пифагора
- Отношения и функции
- Последовательности и серии
- Таблицы умножения
- Детерминанты и матрицы
- Прибыль и убыток
- Полиномиальные уравнения
- Делительные дроби
- 000 ФОРМУЛЫ
- Математические формулы
- Алгебровые формулы
- Тригонометрические формулы
- Геометрические формулы
- КАЛЬКУЛЯТОРЫ
- Математические калькуляторы
- S000
- S0003
- Pегипс Класс 6
- Образцы документов CBSE для класса 7
- Образцы документов CBSE для класса 8
- Образцы документов CBSE для класса 9
- Образцы документов CBSE для класса 10
- Образцы документов CBSE для класса 11
- Образец образца CBSE pers for Class 12
- CBSE Документ с вопросами о предыдущем году
- CBSE Документы за предыдущий год Class 10
- CBSE Вопросы за предыдущий год Class 12
- HC Verma Solutions
- HC Verma Solutions Класс 11 Физика
- Решения HC Verma Class 12 Physics
- Решения Lakhmir Singh
- Решения Lakhmir Singh Class 9
- Решения Lakhmir Singh Class 10
- Решения Lakhmir Singh Class 8
- Примечания
- CBSE
- Notes
- CBSE Класс 7 Примечания CBSE
- Класс 8 Примечания CBSE
- Класс 9 Примечания CBSE
- Класс 10 Примечания CBSE
- Класс 11 Примечания CBSE
- Класс 12 Примечания CBSE
- Дополнительные вопросы CBSE 8 класса
- Дополнительные вопросы CBSE 8 по естественным наукам
- CBSE 9 класса Дополнительные вопросы
- CBSE 9 дополнительных вопросов по науке CBSE 9000 Класс 10 Дополнительные вопросы по математике
- Класс 3
- Класс 4
- Класс 5
- Класс 6
- Класс 7
- Класс 8
- Класс 9
- Класс 10
- Класс 11
- Класс 12
- Решения NCERT для класса 11
- Решения NCERT для физики класса 11
- Решения NCERT для класса 11 Химия Решения для класса 11 Биология
- NCERT Solutions для Класс 12 Физика
- Решения NCERT для 12 класса Химия
- Решения NCERT для 12 класса Биология
- Решения NCERT для 12 класса Математика
- Решения NCERT Класс 12 Бухгалтерский учет
- Решения NCERT Класс 12 Бизнес исследования
- Решения NCERT Класс 12 Экономика
- NCERT Solutions Class 12 Бухгалтерский учет Часть 1
- NCERT Solutions Class 12 Бухгалтерский учет Часть 2
- NCERT Solutions Class 12 Микроэкономика
- NCERT Solutions Class 12 Коммерция
- NCERT Solutions Class 12 Макроэкономика
- Решения NCERT для математики класса 4
- Решения NCERT для класса 4 EVS
- Решения NCERT для математики класса 5
- Решения NCERT для класса 5 EVS
- Решения NCERT для класса 6 Maths
- Решения NCERT для класса 6 Science
- Решения NCERT для класса 6 Общественные науки
- Решения NCERT для класса 6 Английский
- Решения NCERT для класса 7 Математика
- Решения NCERT для 7 класса Science
- Решения NCERT для 7 класса Общественные науки
- Решения NCERT для 7 класса Английский
- для 8 класса Математика
- Решения NCERT для класса 8 Science
- Решения NCERT для класса 8 Общественные науки
- NCERT Solutio ns для класса 8 Английский
- Решения NCERT для класса 9 Общественные науки
- Решения NCERT для класса 9 Математика Глава 1
- Решения NCERT Для класса 9 Математика 9 класса Глава 2
- Решения NCERT для математики 9 класса Глава 3
- Решения NCERT для математики 9 класса Глава 4
- Решения NCERT для математики 9 класса Глава 5
- Решения NCERT для математики 9 класса Глава 6
- Решения NCERT для Математика 9 класса Глава 7
- Решения NCERT для математики 9 класса Глава 8
- Решения NCERT для математики 9 класса Глава 9
- Решения NCERT для математики 9 класса Глава 10
- Решения NCERT для математики 9 класса Глава 11
- Решения NCERT для Математика 9 класса Глава 12
- Решения NCERT для математики 9 класса Глава 13
- Решения NCERT для математики 9 класса Глава 14
- Решения NCERT для математики класса 9 Глава 15
- Решения NCERT 9000 для науки 9 класса Глава 1
- Решения NCERT для класса 10 Общественные науки
- Решения NCERT для математики класса 10 Глава 1
- Решения NCERT для математики класса 10 Глава 2
- решения NCERT для математики класса 10 глава 3
- решения NCERT для математики класса 10 глава 4
- решения NCERT для математики класса 10 глава 5
- решения NCERT для математики класса 10 глава 6
- решения NCERT для математики класса 10 Глава 7
- решения NCERT для математики класса 10 глава 8
- решения NCERT для математики класса 10 глава 9
- решения NCERT для математики класса 10 глава 10
- решения NCERT для математики класса 10 глава 11
- решения NCERT для математики класса 10 Глава 12
- Решения NCERT для математики класса 10 глава 13
- Sol NCERT Решения для математики класса 10 Глава 14
- Решения NCERT для математики класса 10 Глава 15
- Решения NCERT для науки 10 класса Глава 1 Решения NCERT для науки 10 класса Глава 2
- Класс 11 Коммерческая программа Syllabus
- Учебный курс по бизнес-классу 11000
- Учебная программа по экономическому классу
- Учебная программа по 12 классу
- Учебная программа по 12 классу
- Учебная записка по 12-му классу 000000
- Решения TS Grewal Класс 12 Бухгалтерский учет
- Решения TS Grewal Класс 11 Бухгалтерский учет
- ML Решения Aggarwal Class 10 Maths
- ML Решения Aggarwal Class 9 Математика
- ML Решения Aggarwal Class 8 Maths
- ML Решения Aggarwal Class 7 Математические решения
- ML 6 0004
- ML 6
- Selina Solution для 8 класса
- Selina Solutions для 10 класса
- Selina Solution для 9 класса 9
- Frank Solutions для класса 10 Maths
- Frank Solutions для класса 9 Maths
- IAS 2019 Mock Test 1
- IAS 2019 Mock Test 2
- KPSC KAS экзамен
- UPPSC PCS экзамен
- MPSC экзамен
- RPSC RAS экзамен
- TNPSC группа 1
- APPSC группа 1
- BPSC экзамен
- экзамен
- экзамен
- WPSS
- экзамен
- WPSS
- экзамен
- JPS
- экзамен
- экзамен
- PMS
- экзамен
- PMS
- экзамен
- экзамен
- экзамен
- 9000
- Ключ ответа UPSC 2019
- IA S Коучинг Бангалор
- IAS Коучинг Дели
- IAS Коучинг Ченнаи
- IAS Коучинг Хайдарабад
- IAS Коучинг Мумбаи
- Бумага
- JEE JEE 9000
- JEE
- JEE-код
- JEE-код
- JEE J000
- J0004 JEE
- JEE Вопрос
- Биномиальная теорема
- JEE Статьи
- Квадратичное уравнение
- Программа Бьюя NEET
- NEET 2020
- NEET Приемлемость Критерии NEET 2020 S000 S000
- Жалоба Разрешение
- Customer Care
- Поддержка центр
- GSEB
- GSEB Силабус
- GSEB Вопрос бумаги
- GSEB образец бумаги
- GSEB Книги
- MSBSHSE
- MSBSHSE Syllabus
- MSBSHSE Учебники
- MSBSHSE Образцы документов
- MSBSHSE Вопросные записки
- AP Board
- -й год APSERT
- -й год SBSUS
- -й год
- SUBSUS
- SUBSUS
- SUBSUS
- SUBSUS
- SUBSUS
- SUBSUS
- SUBSUS SUBSUS
- SUBSUS SUBSUS
- SUBSUS SUBSUS
SUBSUS
- MP Board Syllabus
- MP Board Образцы документов
- MP Board Учебники
- Assam Board Syllabus
- Assam Board Учебники Sample Board Paperss
- Бихарская доска Syllabus
- Бихарская доска Учебники
- Бихарская доска Вопросные бумаги
- Бихарская модель Бумажные макеты
- доска
- Sislabus
- Совет 9408 S0008
- Sisplus
- S0008
- Sample P000S
- Sample
- S000S PSEB Syllabus
- Учебники PSEB
- Документы PSEB
- Учебное пособие Раджастхана Syllabus
- Учебники RBSE
- Документы RBSE
- JKBOSE Syllabus
- JKBOSE Образцы документов
- JKBOSE Образец экзаменационной таблицы
- TN Board Syllabus
- TN Board Книги для печати
- TNP Бумага для вопросов
Закон Ома является одним из самых фундаментальных законов в теории электричества. Формула или уравнение закона Ома связывает напряжение и ток со свойствами проводника, то есть его сопротивления в цепи.
Сопротивление Учебник включает в себя:
Что такое сопротивление
Закон Ома
удельное сопротивление
Таблица удельного сопротивления для обычных материалов
Коэффициент температуры сопротивления
Электрическая проводимость
Последовательные и параллельные резисторы
Таблица параллельных резисторов
Параллельный калькулятор резисторов
Закон Ома
является одним из наиболее фундаментальных и важных законов, регулирующих электрические и электронные схемы.Он связывает ток, напряжение и сопротивление для линейного устройства, так что если два известны, третий может быть вычислен.
Учитывая то, что ток, напряжение и сопротивление являются тремя основными величинами цепи, это означает, что закон Ома также очень важен.
Закон Омаиспользуется во всех отраслях электротехники и электроники. Он используется для расчета значения резисторов, требуемых в цепях, и также может использоваться для определения тока, протекающего в цепи, где напряжение можно легко измерить через известный резистор, но более того, закон Ома используется в огромное количество вычислений во всех формах электрических и электронных схем — фактически везде, где течет ток.
Открытие закона Ома
Существует математическая зависимость, которая связывает ток, напряжение и сопротивление. Немецкий ученый по имени Георг Ом провел много экспериментов, чтобы показать связь между ними. В те дни, когда он проводил свои эксперименты, метров не было, как мы их знаем сегодня.
Только после значительных усилий и со второй попытки ему удалось придумать то, что мы знаем сегодня как Закон Ома.
Примечание по Георгу Ом:
Георг Ом, родившийся в Эрлангене, примерно в 50 милях к северу от Мюнхена в 1879 году, стал одним из тех, кто много исследовал новую науку, связанную с электричеством, обнаруживая связь между напряжением и током в проводнике — этот закон сейчас назвал закон Ома, чтя работу, которую он сделал.
Подробнее о Георг Ом.
Что такое закон Ома?
ЗаконОма описывает, как ток протекает через материал, когда применяются различные уровни напряжения. Некоторые материалы, такие как электрические провода, имеют небольшое сопротивление току, и этот тип материала называется проводником. Следовательно, если этот проводник расположен, например, непосредственно через батарею, большой ток будет течь.
В других случаях другой материал может препятствовать протеканию тока, но, тем не менее, допускает его использование. В электрических цепях эти компоненты часто называют резисторами. Однако другие материалы практически не пропускают ток, и эти материалы называются изоляторами.
Ом посмотрел, как течет ток в различных материалах, и он смог разработать свой закон, который мы теперь называем Законом Ома.
Чтобы получить первое представление о происходящем, можно сравнить электрическую ситуацию с течением воды в трубе.Напряжение представлено давлением воды в трубе, ток — количеством воды, протекающей по трубе, и, наконец, сопротивление эквивалентно размеру трубы.
Можно представить, что чем шире труба, тем больше воды будет течь. Причина этого в том, что больше воды протекает через более широкую трубу, чем более узкую — более узкая из них обеспечивает большее сопротивление потоку воды. Кроме того, если в трубе больше давления, то для той же трубы будет течь больше воды.
Ом определили, что для обычных материалов удвоение напряжения удваивает поток тока для данного компонента. Различные материалы или одинаковые материалы с различными формами будут иметь разные уровни сопротивления течению тока.
Закон определения Ома
Закон Ом гласит, что ток, протекающий в цепи, прямо пропорционален приложенной разности потенциалов и обратно пропорционален сопротивлению в цепи.
Другими словами, удваивая напряжение на цепи, ток также удваивается. Однако, если сопротивление удвоится, ток упадет вдвое.
В этом математическом соотношении единица сопротивления измеряется в Омах.

Формула закона Ома
Формула или уравнение закона Ома очень просты.
Закон Омаможно выразить в математической форме:
Где:В = напряжение, выраженное в вольтах.
I = ток, выраженный в амперах.
R = сопротивление, выраженное в омах.
Формула может быть изменена так, что, если известны какие-либо две величины, можно рассчитать третью.
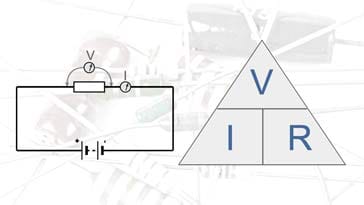
закон закона треугольника
Чтобы помочь запомнить формулу, можно использовать треугольник с одной горизонтальной стороной и вершиной сверху, как пирамиду. Это иногда называют законом треугольника Ома.
В верхнем углу треугольника закона Ом находится буква V, в левом углу — буква I, а в правом нижнем углу — R.

Чтобы использовать треугольник, прикрыть неизвестное количество, а затем, а затем вычислить его из двух других.Если они находятся на одной линии, они умножаются, но если одна находится над другой, их следует разделить. Другими словами, если нужно рассчитать ток, напряжение делится на сопротивление, то есть V / R и так далее.

Если необходимо рассчитать напряжение, то оно определяется путем умножения тока на сопротивление, т. Е. I x R.
Пример расчета закона вОм
Если на резистор 500 Ом подается напряжение 10 В, определите величину тока, который будет течь.

Глядя на треугольник закона Ома, ток является неизвестным, оставляя напряжение и сопротивление в качестве известных значений.

Таким образом, ток определяется путем деления напряжения на сопротивление.
я знак равно В р знак равно 10 500 знак равно 0.02 знак равно 20 м
Пример 2
Аналогичным образом можно использовать закон Ома, чтобы найти сопротивление, если известны ток и напряжение.Взять, к примеру, напряжение 10 вольт и ток 0,1А. Используя треугольник закона Ома, можно увидеть, что:
р знак равно В я знак равно 10 0,1 знак равно 100 Ω
Пример 3
Наконец, другая комбинация состоит в том, что сопротивление и ток известны, тогда можно рассчитать ожидаемое напряжение на сопротивлении. Возьмите пример расстояния 250 Ом, которое имеет ток 0.1 А через него течет, тогда напряжение можно рассчитать, как показано ниже:
В знак равно я р знак равно 0,1 × 250 знак равно 25 вольт
Линейный график
Можно видеть, что если бы напряжение и ток были построены для фиксированного резистора или длины провода и т. Д., Была бы линейная кривая.
 График напряжения и тока для линейного сопротивления
График напряжения и тока для линейного сопротивленияВидно, что удвоение напряжения удваивает ток, который проходит через конкретный элемент схемы.
На графике есть две линии, одна для более высокого сопротивления — эта требует, чтобы большее напряжение было приложено для данного тока. Соответственно это должно иметь более высокое сопротивление. И наоборот, кривая для более низкого сопротивления показывает компонент, который требует применения более низкого напряжения для данного тока.
Нелинейные компоненты
ЗаконОм в его основной форме, где удвоение напряжения приводит к удвоению тока, применяется к линейным компонентам, таким как обычные резисторы.Некоторые компоненты, такие как диоды, имеют нелинейные кривые, на которые сопротивление влияет приложенным напряжением.
Закон Омаявляется одним из самых основных понятий в области электротехники и электроники. Концепция элемента, имеющего определенное сопротивление, которое определяет величину тока, протекающего через него при определенном напряжении, является ключом к работе практически всех цепей.
Более основные понятия:
Напряжение
Текущий
сопротивление
емкость
Мощность
трансформеры
РЧ шум
Децибел, дБ
Q, добротность
Возврат в меню основных концепций., ,

