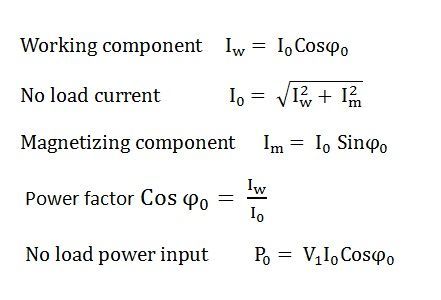Векторная диаграмма токов и напряжений: график, обозначения, виды
 Использование векторных диаграмм при анализе, расчете цепей переменного тока делает возможным рассмотреть более доступно и наглядно происходящие процессы, а также в некоторых случаях значительно упростить выполняемые расчеты.
Использование векторных диаграмм при анализе, расчете цепей переменного тока делает возможным рассмотреть более доступно и наглядно происходящие процессы, а также в некоторых случаях значительно упростить выполняемые расчеты.
Векторной диаграммой принято называть геометрическое представление изменяющихся по синусоидальному (либо косинусоидальному) закону направленных отрезков — векторов, отображающих параметры и величины действующих синусоидальных токов, напряжений либо их амплитудных величин.
Широкое применение векторные диаграммы нашли в электротехнике, теории колебаний, акустике, оптике и т.д.
Различают 2-х вида векторных диаграмм:
- точные;
- качественные.
Интересное видео о векторных диаграммах смотрите ниже:
Точные изображаются по результатам численных расчетов при условии соответствия масштабов действующих значений. При их построении можно геометрически определить фазы и амплитудные значения искомых величин.
Качественные диаграммы изображаются с учетом взаимных соотношений между электрическими величинами, без указания численных характеристик.
Они являются одним из основных средств анализа электрических цепей, позволяя наглядно иллюстрировать и качественно контролировать ход решения задачи и легко установить квадрант, в котором располагается искомый вектор.
 Для удобства при построении диаграмм анализируют неподвижные векторы для определенного момента времени, который выбирается таким образом, чтобы диаграмма имела удобный для понимания вид. Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
Для удобства при построении диаграмм анализируют неподвижные векторы для определенного момента времени, который выбирается таким образом, чтобы диаграмма имела удобный для понимания вид. Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
Векторы, изображаемые на такой диаграмме, характеризуются равновеликой угловой частотой ω. В виду чего при вращении их взаимное расположение не изменяется.
Ещё одно полезное видео о векторных диаграммах:
Поэтому при изображении векторных диаграмм один вектор можно направить произвольным образом (например, по оси ОХ).
А остальные — изображать по отношению к исходному под различными углами, соответственно равными углам сдвига фаз.
Таким образом, векторная диаграмма дает отчетливое представление об опережении либо отставании различных электрических величин.
Допустим у нас есть ток, величина которого изменяется по некоторому закону:
i = Im sin (ω t + φ).
С начала координат 0 под углом φ проведем вектор Im, величина которого соответствует Im. Его направление выбирается так, чтобы с положительным направлением оси OX вектор составлял угол — соответствующий фазе φ.
Проекция вектора на вертикальную ось и определяет значение мгновенного тока в начальный момент времени.
В основном векторные диаграммы изображают для действующих значений, а не амплитудных. Векторы действующих значений количественно отличаются от амплитудных значений — масштабом, поскольку:
I = Im /√2.

Основным преимуществом векторных диаграмм называют возможность простого и быстрого сложения и вычитания 2-х параметров при расчете электроцепей.
Векторные диаграммы электрических цепей | FaultAn.ru
При исследовании электрических цепей и моделировании часто пользуются векторными диаграммами токов и напряжений. Под векторной диаграммой понимается совокупность векторов, изображающих синусоидальные функции времени [1].
Воспользуйтесь программой расчёта электрических цепей для построения векторных диаграмм онлайн.
Представление синусоидальных функций в виде комплексных чисел
Векторная диаграмма – это удобный инструмент представления синусоидальных функций времени, коими являются, к примеру, напряжения и токи электрической цепи переменного тока.
Рассмотрим, например, произвольный ток, представленный в виде синусоидальной функции
i(t) = 10 sin(ωt + 30°).
Данный синусоидальный сигнал можно представить в виде комплексной величины
I = 10∠30°.
Для формирования комплексного числа используются модуль и фаза синусоидального сигнала.
Закон Ома в комплексной форме
Известно [1], что напряжение U на сопротивлении Z связано с током
U = Z ∙ I.
Кроме того, известны соотношения, определяющие активное сопротивление резистора, индуктивное сопротивление катушки и ёмкостное сопротивление конденсатора:
ZR = R, ZL = jXL, ZC = −jXC,
где XL = ωL, XC = 1/(ωC), R – сопротивление резистора, L – индуктивность катушки, C – ёмкость конденсатора,
Векторная диаграмма при последовательном соединении элементов
Для построения векторных диаграмм сперва составляют уравнения по законам Кирхгофа для рассматриваемой электрической цепи.
Рассмотрим электрическую цепь, представленную на рис. 1, и нарисуем для неё векторную диаграмму напряжений. Обозначим падение напряжение на элементах.
 Рис. 1. Последовательное соединение элементов цепи
Рис. 1. Последовательное соединение элементов цепи
Составим уравнение для данной цепи по второму закону Кирхгофа:
UR + UL + UC = E.
По закону Ома падение напряжений на элементах определяется по следующим выражениям:
UR = I ∙ R,
UL = I ∙ jXL,
UC = −I ∙ jXC.
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости. Обычно вектора токов и напряжений отображаются в своих масштабах: отдельно для напряжений и отдельно для токов.
Из курса математики известно, что j = 1∠90°, −j = 1∠−90°. Отсюда при построении векторной диаграммы умножение какого-либо вектора на мнимую единицу j приводит к повороту этого вектора на 90 градусов против часовой стрелки, а умножение на −j приводит к повороту этого вектора на 90 градусов по часовой стрелке.
При построении векторной диаграммы напряжений на комплексной плоскости сперва отобразим вектор тока I, после чего относительного него будем отображать вектора падений напряжений (рис. 2) с учётом приведённых выше соотношений для мнимой единицы.
Падение напряжения на резисторе

Рис. 2. Векторная диаграмма напряжений при последовательном соединении элементов цепи
Следует обратить внимание, что на одной векторной диаграмме изображают только векторы тех величин, у которых частота совпадает!
Векторная диаграмма при параллельном соединении элементов
Рассмотрим электрическую цепь, представленную на рис. 3, и нарисуем для неё векторную диаграмму токов. Обозначим направление токов в ветвях.

Рис. 3. Параллельное соединение элементов цепи
Составим уравнение для данной цепи по первому закону Кирхгофа:
I – IR – IL – IC = 0,
откуда
I = IR + IL + IC.
Определим по закону Ома токи в ветвях по следующим выражениям, учитывая, что 1 / j = −j:
IR = E / R,
IL = E
IC = E / (−jXC) = j ∙ E / XC,
Для построения векторной диаграммы необходимо отобразить приведённые в уравнении слагаемые на комплексной плоскости.
При построении векторной диаграммы токов на комплексной плоскости сперва отобразим вектор ЭДС E, после чего относительного него будем отображать вектора токов токов (рис. 4) с учётом приведённых выше соотношений для мнимой единицы.
Ток в резисторе IR совпадает по направлению с ЭДС

Рис. 4. Векторная диаграмма токов при параллельном соединении элементов цепи
Для произвольной цепи алгоритм построения векторных диаграмм аналогичен вышеизложенному с учётом протекаемых в ветвях токов и прикладываемых напряжений.
Обращаем ваше внимание, что на сайте представлен инструмент для построения векторных диаграмм онлайн для трёхфазных цепей.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Если вам нравится наш контент, помогите в развитии сайта.
Рекомендуемые записи
Построение векторной диаграммы напряжений. Катушка. Конденсатор. Сопротивление. Сдвиг фаз.
Достаточно сложным и чаще всего не изучаемым аспектом темы переменный ток является метод построения векторных диаграмм. Анализируя вынужденные электромагнитные колебания, мы уже обсудили сдвиг тока и напряжения на реактивных сопротивлениях (катушка индуктивности и конденсатор) по сравнению с активным сопротивлением (резистор). Тогда одним из задаваемых вопросов задачи является вопрос о направлении суммарного тока или напряжения в данный конкретный момент времени. Для ответа на этот вопрос и используется метод построения векторных диаграмм.
Векторная диаграмма — это изображение гармонически изменяющихся величин (текущего тока и напряжения) в виде векторов на плоскости.
Рис. 1. Векторная диаграмма
Построение векторных диаграмм происходит в прямоугольной декартовой системе координат. Построение начинается с проведения вектора, численно равного амплитудному значению тока в цепи. Данный вектор сонаправим в осью ОХ (рис. 1.1).
Т.к. напряжение на активном сопротивлении находится в одной фазе с током, то вектор амплитуды напряжения сонаправлен с вектором тока (рис. 1.2. красный).
На катушке напряжение опережает ток, поэтому отложим вектор амплитуды напряжения на катушке () вверх под углом относительно вектора тока (рис. 1.2. синий).
На конденсаторе напряжение отстаёт от тока, поэтому отложим вектор амплитуды напряжения на конденсаторе () вниз под углом относительно вектора тока (рис. 1.2. зелёный).
Угол , используемый в логике построений, используется в случае идеальности контура и катушки.
Для построения общего вектора напряжения достаточно векторно сложить напряжения:
(1)
Проще всего сначала найти вектор-сумму (т.к. они расположены вдоль одной прямой). В нашем случае, эти вектора разнонаправлены, найдём (рис. 1.3. жёлтый).
И последнее, осталось сложить получившийся вектор с вектором для получения значения полного напряжения в цепи (рис. 1.4. оранжевый). Для получения модуля вектора воспользуемся теоремой Пифагора, т.к. вектора находятся под прямым углом. Тогда:
(2)
Угол — угол между вектором силы тока и полного напряжения называется сдвигом фаз между колебаниями силы тока и напряжения. Данный параметр можно найти и исходя из параметров системы:
(3)
Вывод: задачи на данную тематику касаются поиска сдвига фаз между колебаниями силы тока и напряжения через график (рис. 1.4) или через соотношение (3), а также поиска полного напряжения в цепи также через график (рис. 1.4) или через соотношение (2).
Поделиться ссылкой:
РЕЛЕЙКА: Векторные диаграммы
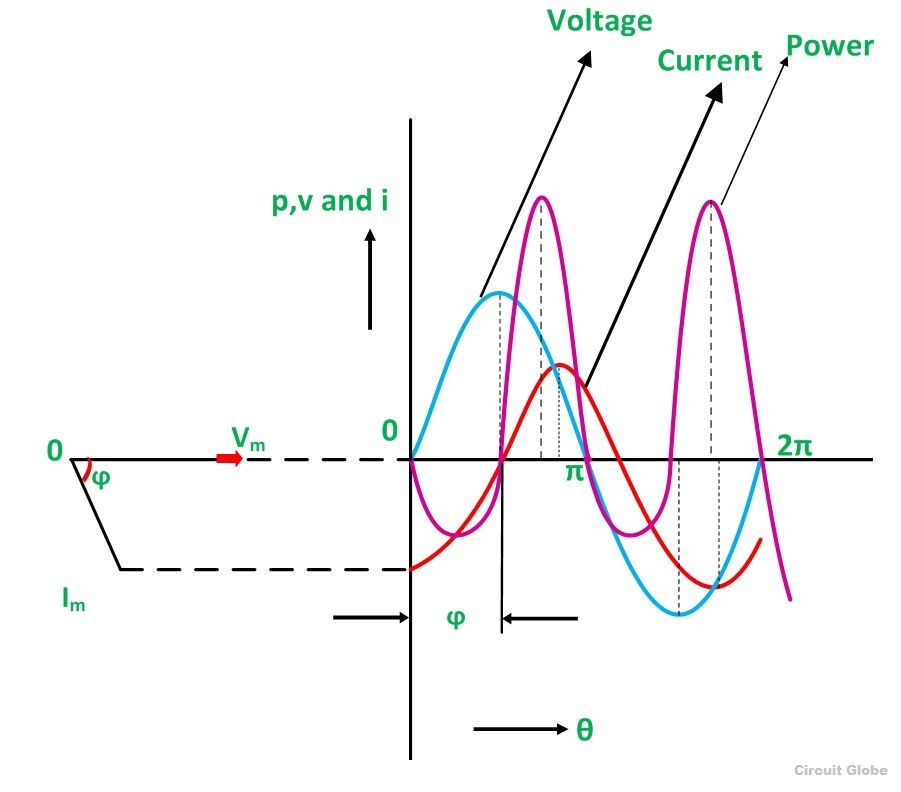
Понятие о векторах. На рис.1.4 приведена кривая изменения переменного тока во времени. Ток сначала растет от нуля (при φ=0º) до максимального положительного значения + Imax (при φ=90о), затем убывает, переходит через нуль (при φ=180о), достигает максимального отрицательного значения – Imax (при φ=270о) и, наконец, возвращается к нулю (при φ=360о). после этого цикл изменения тока повторяется.
Кривая изменения переменного тока во времени, приведенная на рис.1.4, называется синусоидой. Время
Где i – мгновенное значение тока, т.е. значение тока в каждый момент времени; Imax – максимальное значение тока; ω=2πf – угловая частота переменного тока, f=50 Гц, ω=2π·50=314; α – начальный угол, соответствующий моменту времени, с которого начинается отсчет времени (при t=0). Для частного случая, показанного на рис.1.4, α=0
Анализируя действие устройств релейной защиты и автоматики, необходимо сопоставлять токи и напряжения, складывать или вычитать их, определять углы между ними и производить другие операции. Пользоваться при этом кривыми, подобными приведенной на рис.1.4, неудобно, поскольку построение синусоид тока и напряжения занимает много времени и не дает простого и наглядного результата. Поэтому для упрощения принято изображать токи и напряжения в виде отрезков прямых линий, имеющих определенную длину и направление, — так называемых векторов (А0 на рис.1.4). один конец вектора закреплен на точке 0 – начало координат, а второй вращается против часовой стрелки.
Мгновенное значение тока или напряжения в каждый момент времени определяется проекцией на вертикальную ось вектора, длина которого равна максимальному значению тока или напряжения. Эта проекция будет становится то положительной, то отрицательной, принимая максимальные значения при вертикальном расположении вектора. За время Т, равное периоду переменного тока, вектор совершит полный оборот по окружности (360о), занимая последовательно положения 0А’,0A”, 0A’’’ и т.д. При частоте переменного тока 50 Гц вектор будет совершать 50 об/с.
Таким образом, вектор тока или напряжения – это отрезок прямой, равный по величине максимальному значению тока или напряжения, вращающийся относительно точки 0 против движения часовой стрелки со скоростью, определяемой частотой переменного тока. Зная положение вектора в каждый момент времени, можно определить мгновенное значение тока или напряжения в данный момент. Так, для положения вектора тока 0А, показанного на рис.1.5, его мгновенное значение определяется проекцией на вертикальную ось, т.е. 0А”=0А sin φ.
На основании рис.1.5 можно также сказать, что ток в данный момент времени имеет положительное значение. Однако это ещё не дает полного представления о протекании процесса в цепи переменного тока, так как неизвестно, что значит положительный или отрицательный ток, положительное или отрицательное напряжение.
Для того чтобы векторные диаграммы токов и напряжений давали полную картину, их нужно увязать с фактическим протеканием процесса в цепи переменного тока, т.е. необходимо предварительно принять условные положительные направления токов и напряжений в рассматриваемой схеме. Без выполнения этого условия, если не заданы положительные направления токов и напряжений, любая векторная диаграмма не имеет никакого смысла.
Рассмотрим простую однофазную цепь переменного тока, приведенную на рис.1.6, а. От однофазного генератора энергия предается в активное сопротивление нагрузкиR. Зададимся положительными направлениями токов и напряжений в рассматриваемой цепи. За условное положительное направление напряжения и ЭДС примем направление, когда потенциал вывода генератора или нагрузки, связанного с линией, выше потенциала вывода, соединенного с землей. В соответствии с правилами, принятыми в электротехнике, положительное направление для ЭДС обозначено стрелкой, направленной в сторону более высокого потенциала (от земли к линейному выводу), а для напряжения – стрелкой, направленной в сторону более низкого потенциала (от линейного вывода к земле).
Переменный ток будет считать положительным, когда во внешней цепи он проходит от шин генератора к нагрузке (обозначено стрелкой). Построим векторы ЭДС и тока, характеризующие работу рассматриваемой цепи (рис.1.6, б). Вектор ЭДС произвольно обозначим вертикальной линией со стрелкой, направленной вверх. Для построения вектора тока запишем для цепи уравнение согласно второму закону Кирхгофа:
отсюда
Поскольку знаки векторов тока и ЭДС в выражении совпадают, вектор тока будет совпадать с вектором ЭДС и на рис.1.6, б.
Здесь и в дальнейшем при построении векторов будем откладывать их по величине равным эффективному значению тока и напряжения, что удобно для выполнения различных математических операций с векторами. Как известно, эффективные значения тока и напряжений в √2 раз меньше соответствующих максимальных (амплитудных).
При заданных положительных направлениях тока и напряжения однозначно определяется и знак мощности. Положительной в рассматриваемом случае будем считать мощность, направленная от шин генератора в линию:
так как векторы тока и ЭДС на рис.1.6, б совпадают.
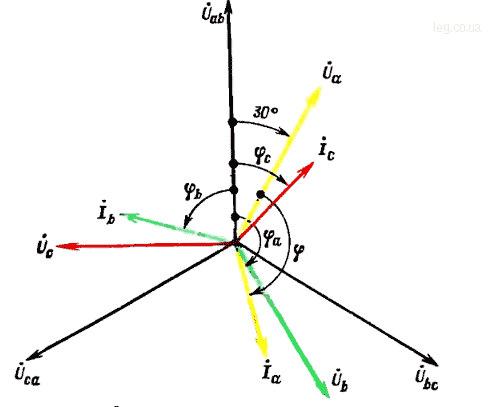
Аналогичные соображения могут быть высказаны и для трехфазной цепи переменного тока, показанной на рис.1.7, а. В этом случае во всех фазах приняты одинаковые положительные направления, чему соответствует симметричная диаграмма токов и напряжений, приведенная на рис.1.7, б. Отметим, что симметричной называется такая трехфазная система векторов, когда все три вектора равны по величине и сдвинуты относительно друг друга на угол 120о.
Операции с векторами. Когда мы рассматриваем только одну кривую тока или напряжения, начальное значение угла, с которого начинается отсчет, или, иначе говоря, положение вектора на диаграмме, соответствующее начальному моменту времени, может быть принято произвольным. Если же одновременно рассматриваются два или несколько токов и напряжений, то, задавшись начальным положением на диаграмме одного из векторов, мы тем самым уже определяем положение всех других векторов.
Все три вектора фазных напряжений: , показанные на рис.1.7, б, вращаются против часовой стрелки с одинаковой скоростью, определяемой частотой переменного тока. При этом они пересекают вертикальную ось, совпадающую с направлением вектора на рис.1.7, б, поочередно с определенной последовательностью, а именно ,,, которая называется чередованием фаз напряжения (или тока). Для того чтобы определить взаимное расположение двух векторов, обычно говорят, что один из них опережает или отстает от другого. При этом опережающим считается вектор, который при вращении против часовой стрелки раньше пересечет вертикальную ось. Так, например, можно сказать, что вектор напряжения на рис.1.7, б опережает на угол 120о или, с другой стороны, вектор отстает от вектора на угол 120о. Как видно из рис.1.7, выражение «вектор отстает на угол 120о», равноценно выражению «вектор опережает на угол 240о». Сложение векторов производится геометрическим суммированием по правилу параллелограмма, как показано на рис.1.8, а, на котором построена сумма токов (). Так как вычитание – действие, обратное сложению, для определения разности токов (например, ) достаточно к току прибавить вектор, обратный . Вместе с тем на рис.1.8, а показано, что вектор разности токов () можно построить проще, соединив линией концы векторов и . При этом стрелка вектора разности токов направляется в сторону первого вектора, т.е. . Аналогично строится векторная диаграмма межфазных напряжений, например, (рис.1.8, б).Очевидно, что положение вектора на плоскости определяется его проекциями на две любые оси. Так, например, для того чтобы определить положение вектора 0А(рис.1.9), достаточно знать его проекции на взаимно перпендикулярные оси:
0A’= 0A cos φ;
0A’’= 0A sin φ = 0A cos (90o – φ).
Отложим на осях координат проекции векторов 0А’ и 0А’’ и восстановим из точек А’ и A’’ перпендикуляры к осям. Точка пересечения этих перпендикуляров и есть точка А – один конец вектора, вторым концов которого является точка 0 – начало координат.
Назначение векторных диаграмм. Работникам, занимающимся проектированием и эксплуатацией релейной защиты, часто приходится использовать в своей работе так называемые векторные диаграммы – векторы токов и напряжений, построенные на плоскости в определенном сочетании, соответствующем электрическим процессам, происходящим в рассматриваемой схеме.
Анализ векторных диаграмм токов и напряжений является одним из важных, а в ряде случаев единственным способом проверки правильности соединения цепей тока и напряжения и включения реле в схемах дифференциальных и направленных защит.
По сути построение векторной диаграммы целесообразно во всех случаях, когда к рассматриваемому реле подаются две или более электрические величины: разность токов в максимальной токовой или дифференциальной защите, ток и напряжение в реле направления мощности или в направленном реле сопротивления. Векторная диаграмма позволяет сделать заключение о том, как рассматриваемая защита будет работать при КЗ, т.е. оценить правильность ее включения. Взаимное расположение векторов токов и напряжений на диаграмме определяется характеристикой рассматриваемой цепи, а также условно принятыми положительными направлениями токов и напряжений. Для примера рассмотрим две векторные диаграммы.
На рис.1.10 показана однофазная цепь переменного тока, состоящая из генератора и последовательно соединенных емкостного, активного и индуктивного сопротивлений (примем при этом, что индуктивное сопротивление больше емкостного ХL > XC). Положительные направления токов и напряжений, так же как и в случаях, рассмотренных выше, обозначены на рис.1.10, а стрелками.
Построение векторной диаграммы начнем с вектора ЭДС Е, который расположим на рис.1.10, б вертикально. Ток, проходящий в рассматриваемой цепи, определится из следующего выражения:
Поскольку в рассматриваемой цепи имеются активные и реактивные сопротивления, причем ХL > XC, вектор тока отстает от вектора напряжения на угол φ:
Напряжение в точке n на рис.1.10, а определится согласно следующему выражению:
Как видно из рис.1.10, б, этот последний вектор будет равен падению напряжения в индуктивном сопротивлении .Рассмотрим другую цепь переменного тока, приведенную на рис.1.11, а, и построим векторную диаграмму, характеризирующую распределение токов в параллельных ветвях. Для построения диаграммы примем, что активное и емкостное сопротивление равны R=XC.
Построение векторной диаграммы начнем с вектора , который расположим горизонтально. Затем построим вектор падения напряжения на сопротивлениях , отстающий от вектора на угол φ, так как результирующее сопротивление имеет активно-емкостной характер. Угол φ определяется следующим выражением: В рассматриваемом случае φ=45о. Вектор тока , проходящего по активному сопротивлению, совпадает с , а опережает на 90о, как показано на рис.1.11, б.Вопросы для самопроверки:
Что такое вектор? Зачем нужны векторные диаграммы?
Что такое частота переменного тока?
Что означает, когда говорят, что один вектор «опережает» или «отстает» от другого вектора?
Как производится сложение и вычитание векторов?
правила построения диаграмм, онлайн построение
В целом, для лучшего понимания процедур, происходящих в радиотехнических цепях, их взаимосвязи между собой, бывает недостаточно оперировать характеристиками и параметрами данной цепи, имеющими цифровое отображение. В связи с тем, что основная масса цепей характеризуется переменными значениями приложенного напряжения и протекающего тока, являющимися синусоидальными функциями времени, то исчерпывающий ответ по состоянию цепи может дать ее графическая презентация посредством векторной гистограммы.
Векторная диаграмма напряжений и токов
Разновидности векторных диаграмм
Любую характеристику электротехнической цепи, изменяющуюся по синусоидальному или косинусоидальному принципу, можно отобразить посредством точки на поверхности, в соответствующей системе величин. В качестве размерности по оси Х выступает действительный компонент параметра, по оси Y размещается воображаемая составляющая. Именно такие составляющие входят в алгебраическую модель записи комплексной величины. Последующее соединение точки на поверхности и нулевой точки системы координат позволит рассматривать эту прямую и ее угол с действительной осью как изображение комплексного числа. На практике положительно направленный отрезок принято называть вектором.
Векторной диаграммой принято называть множество положительно направленных отрезков на комплексной поверхности, которая соответствует комплексным значениям и параметрам гальванической цепи и их взаимосвязям. По своему характеру векторные диаграммы подразделяются на:
- Точные гистограммы;
- Качественные гистограммы.
Особенностями достоверных гистограмм является соблюдение пропорций всех характеристик и параметров, полученных путем вычислений. Данные диаграммы находят свое применение в проверке ранее проведенных расчетов. В основе использования качественных гистограмм лежит учет взаимного влияния характеристик друг на друга, и в основном они предшествуют расчетам либо заменяют их.
Векторные диаграммы токов и напряжений визуально отображают процесс достижения цели по расчету электротехнической цепи. При соблюдении всех правил по построению векторных отрезков можно просто из гистограммы установить фазы и амплитуды вещественных характеристик. Построение качественных гистограмм поможет контролировать правильный процесс решения задачи и с легкостью определить сектор с определяемыми векторами. В зависимости от особенностей построения, графические диаграммы делятся на такие типы:
- Круговая диаграмма, представляющая собой графическую гистограмму, образованную вектором, описывающим своим концом круг или полукруг, при любых изменениях характеристик цепи;
- Линейная диаграмма, представляющая собой графический рисунок в виде прямой линии, образованной вектором, посредством изменения характеристик цепи.
Построение векторной диаграммы напряжений и токов
Для лучшего понимания того, как построить векторную диаграмму токов и напряжений, следует рассматривать RLC цепь, состоящую из пассивного элемента в виде резистора и реактивных элементов в виде катушки индуктивности и конденсатора.
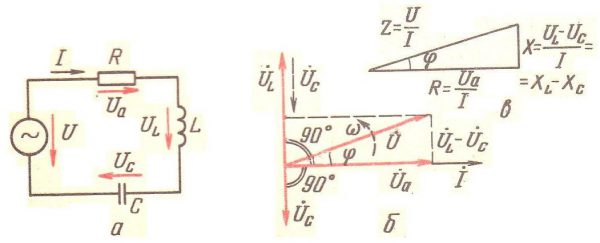
Схема цепи с последовательным соединением элементов
Перед тем, как построить векторную диаграмму токов и напряжений, необходимо охарактеризовать все известные параметры цепи. Согласно схемы цепи, изображенной на картинке а:
- U – величина переменного напряжения в текущий момент времени;
- I – мощность тока в заданный момент времени;
- UА – напряжение, падающее на активном сопротивлении;
- UC – напряжение, падающее на емкостной нагрузке;
- UL – напряжение, падающее на индуктивной нагрузке.
Поскольку входное напряжение U изменяется по колебательному закону, то сила тока характеризуется уравнением:
I=Im*cosωt, где:
- Im – максимальная амплитуда тока;
- ω – частота тока;
- t – время.
Суммарное входное напряжение, в соответствии со вторым законом Кирхгофа, равно общей величине напряжений на всех элементах цепи:
U=UC+UL+UA.
В соответствии с законом Ома, падение напряжения на резистивном компоненте равняется:
UA= Im*R*cosωt.
Противодействие току активного элемента зависит сугубо от свойства проводника и не обуславливается ни характеристиками тока, ни аспектом времени и, соответственно, имеет идентичный с напряжением фазовый сдвиг.
Поскольку конденсатору в цепи с электротоком, изменяющимся по синусоиде, свойственно наличие реактивного емкостного сопротивления, и ввиду того, что напряжение на нем постоянно имеет фазовое отставание от протекающего тока на π/2, то уместно выражение:
- RC=XC=1/ωC;
- UC=Im*RС*cos(ωt-π/2), где:
- RC – сопротивление конденсатора;
- XC – реактивный импеданс конденсатора;
- C – емкость конденсатора.
Реактивное индуктивное сопротивление катушки индуктивности обуславливается наличием изменяющегося по синусоидальному закону электротока, и поскольку напряжение на любом отрезке времени имеет фазовое опережение по отношению к электротоку на π/2, то формула, описывающая колебательный процесс на элементе, выглядит как:
- RL=XL=ωL;
- UL=Im*RL*cos(ωt+π/2), где:
- RL – сопротивление катушки индуктивности;
- XL – реактивный импеданс катушки индуктивности;
- L – индуктивность катушки.
Следовательно, общее напряжение, подведенное к цепи, выглядит:
U=Um*cos(ωt±φ), где:
- Um – максимальная величина напряжения;
- φ – фазовый сдвиг.
Ввиду того, что напряжение и электроток изменяются по синусоидальному закону, и их фиксированные показатели отличаются лишь фазовым сдвигом, то данные величины строятся как вектора.
В соответствии с законом сохранения электрического заряда, в любой момент времени сила протекающего тока одинакова, то целесообразно сформировать векторную гистограмму токов.
Векторная диаграмма токов и напряжений RLC цепочке
Пусть по оси Х отображается амплитудное значение электротока в цепочке. Поскольку напряжение и электроток на резисторе имеют одинаковый фазовый сдвиг, то вектора данных характеристик будут ориентированы в одну сторону, согласно картинке а.
Напряжение на емкостной нагрузке отстает от электрического тока на π/2, и его вектор будет направлен под прямым углом вниз, перпендикулярно напряжению активного сопротивления, согласно картинке в.
Напряжение на индуктивной нагрузке опережает электрический ток на π/2, и ее вектор будет ориентирован под прямым углом вверх, перпендикулярно напряжению на активном сопротивлении, согласно картинке б.
Для наглядности векторных преобразований пусть UL>UС. Сложив вектора напряжений на реактивных компонентах, получаем, что вектор UL-UС будет направлен перпендикулярно вверх. Суммировав вектора разности напряжений на реактивных компонентах и напряжения на сопротивлении получаем вектор, характеризующий дисперсное значение общего напряжения, согласно картинке 2(б).
Аналогично электрическому току, изменяющемуся по синусоидальному закону, напряжение меняется по такому же закону, однако с некоторым фазовым сдвигом. Наблюдается постоянный фазовый сдвиг между напряжением и током.
После простых преобразований по постулату Ома, уравнение полного импеданса заданной электрической цепи выглядит как:
Z=√R2+(1/ωC- ωL)2.
Векторная гистограмма общего и реактивных сопротивлений изображена на картинке 2в.
Построение векторных диаграмм токов и напряжений может значительно упростить процесс расчета характеристик контура. Вместе с тем сама процедура позволит наглядно видеть поведение исследуемых характеристик, в зависимости от входных величин. При большом объеме вычислительных операций целесообразно воспользоваться одной из онлайн программ по построению векторных графиков.
Видео
Оцените статью:Элементы цепи синусоидального тока. Векторные диаграммы и комплексные соотношения для них. (Лекция N 4)
1. Резистор
Идеальный резистивный элемент не обладает ни индуктивностью, ни емкостью. Если к нему приложить синусоидальное напряжение (см. рис. 1), то ток i через него будет равен
| . | (1) |
Соотношение (1) показывает, что ток имеет ту же начальную фазу, что и напряжение. Таким образом, если на входе двухлучевого осциллографа подать сигналы u и i, то соответствующие им синусоиды на его экране будут проходить (см. рис. 2) через нуль одновременно, т.е. на резисторе напряжение и ток совпадают по фазе.
Из (1) вытекает:
;
.
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
;
,
— разделим первый из них на второй:
или
| . | (2) |
Полученный результат показывает, что отношение двух комплексов есть вещественная константа. Следовательно, соответствующие им векторы напряжения и тока (см. рис. 3) совпадают по направлению.
2. Конденсатор
Идеальный емкостный элемент не обладает ни активным сопротивлением (проводимостью), ни индуктивностью. Если к нему приложить синусоидальное напряжение (см. рис. 4), то ток i через него будет равен
| . | (3) |
Полученный результат показывает, что напряжение на конденсаторе отстает по фазе от тока на /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране будет иметь место картинка, соответствующая рис. 5.
Из (3) вытекает:
;
.
Введенный параметр называют реактивным емкостным сопротивлением конденсатора. Как и резистивное сопротивление, имеет размерность Ом. Однако в отличие от R данный параметр является функцией частоты, что иллюстрирует рис. 6. Из рис. 6 вытекает, что при конденсатор представляет разрыв для тока, а при .
Переходя от синусоидальных функций напряжения и тока к соответствующим им комплексам:
;
,
— разделим первый из них на второй:
или
| . | (4) |
В последнем соотношении — комплексное сопротивление конденсатора. Умножение на соответствует повороту вектора на угол по часовой стрелке. Следовательно, уравнению (4) соответствует векторная диаграмма, представленная на рис. 7.
3. Катушка индуктивности
Идеальный индуктивный элемент не обладает ни активным сопротивлением, ни емкостью. Пусть протекающий через него ток (см. рис. 8) определяется выражением . Тогда для напряжения на зажимах катушки индуктивности можно записать
| . | (5) |
Полученный результат показывает, что напряжение на катушке индуктивности опережает по фазе ток на /2. Таким образом, если на входы двухлучевого осциллографа подать сигналы u и i, то на его экране (идеальный индуктивный элемент) будет иметь место картинка, соответствующая рис. 9.
Из (5) вытекает:
.
Введенный параметр называют реактивным индуктивным сопротивлением катушки; его размерность – Ом. Как и у емкостного элемента этот параметр является функцией частоты. Однако в данном случае эта зависимость имеет линейный характер, что иллюстрирует рис. 10. Из рис. 10 вытекает, что при катушка индуктивности не оказывает сопротивления протекающему через него току, и при .
Переходя от синусоидальных функций напряжения и тока к соответствующим комплексам:
;
,
разделим первый из них на второй:
или
| . | (6) |
В полученном соотношении — комплексное
сопротивление катушки индуктивности. Умножение на соответствует повороту вектора на угол против часовой стрелки. Следовательно, уравнению (6) соответствует векторная диаграмма, представленная на рис. 11
4. Последовательное соединение резистивного и индуктивного элементов
Пусть в ветви на рис. 12 . Тогда
где
, причем пределы изменения .
Уравнению (7) можно поставить в соответствие соотношение
,
которому, в свою очередь, соответствует векторная диаграмма на рис. 13. Векторы
на рис. 13 образуют фигуру, называемую треугольником напряжений. Аналогично
выражение
графически может быть представлено треугольником сопротивлений (см. рис. 14), который подобен треугольнику напряжений.
5. Последовательное соединение резистивного и емкостного элементов
Опуская промежуточные выкладки, с использованием соотношений (2) и (4) для ветви на рис. 15 можно записать
| ., | (8) |
где
, причем пределы изменения .
На основании уравнения (7) могут быть построены треугольники напряжений (см.
рис. 16) и сопротивлений (см. рис. 17), которые являются подобными.
6. Параллельное соединение резистивного и емкостного элементов
Для цепи на рис. 18 имеют место соотношения:
;
, где [См] – активная проводимость;
, где [См] – реактивная проводимость конденсатора.
Векторная диаграмма токов для данной цепи, называемая треугольником токов, приведена на рис. 19. Ей соответствует уравнение в комплексной форме
,
где ;
— комплексная проводимость;
.
Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 20.
Для комплексного сопротивления цепи на рис. 18 можно записать
.
Необходимо отметить, что полученный результат аналогичен известному из курса физики выражению для эквивалентного сопротивления двух параллельно соединенных резисторов.
7. Параллельное соединение резистивного и индуктивного элементов
Для цепи на рис. 21 можно записать
;
, где [См] – активная проводимость;
, где [См] – реактивная проводимость катушки индуктивности.
Векторной диаграмме токов (рис. 22) для данной цепи соответствует уравнение в комплексной форме
,
где ;
— комплексная проводимость;
.
Треугольник проводимостей, подобный треугольнику токов, приведен на рис. 23.
Выражение комплексного сопротивления цепи на рис. 21 имеет вид:
.
Литература
1. Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
Контрольные вопросы и задачи
1. В чем сущность реактивных сопротивлений?
2. Какой из элементов: резистор, катушку индуктивности или конденсатор – можно использовать в качестве шунта для наблюдения за формой тока?
3. Почему катушки индуктивности и конденсаторы не используются в цепях постоянного тока?
4.
В ветви на рис. 12 . Определить комплексное сопротивление
ветви, если частота тока .
Ответ: .
5.
В ветви на рис. 15 . Определить комплексное сопротивление
ветви, если частота тока .
Ответ: .
6.
В цепи на рис. 18 . Определить комплексные проводимость
и сопротивление цепи для .
Ответ: ; .
7. Протекающий
через катушку индуктивности ток изменяется по закону А. Определить комплекс
действующего значения напряжения на катушке.
Ответ: .
Векторные диаграммы. Построение векторных диаграмм

При расчете электрических цепей переменного тока пользуются весьма простым и наглядным способом графического изображения синусоидальных величин при помощи вращающихся векторов.
Обоснование векторной диаграммы
Предположим, что ток задан уравнением
i = Imsin(ωt +Ψ)
Проведем две взаимно перпендикулярные оси и из точки пересечения осей проведем вектор Im, длина которого в определённом масштабе Mi выражает амплитуду тока Im:
Im = Im/Mi

Направление вектора выберем так, чтобы с положительным направлением горизонтальной оси вектор составлял угол, равный начальной фазе Ψ (рис. 12.10).
Проекция этого вектора на вертикальную ось определяет мгновенный ток в начальный момент времени: i0 = ImsinΨ.
Представим себе, что вектор Im вращается против движения часовой стрелки с угловой скоростью, равной угловой частоте ω. Его положение в любой момент времени определяется углом ωt +Ψ ,
Тогда мгновенный ток для произвольного момента времени t можно определить проекцией вектора Im на вертикальную ось в этот момент времени.
Следующая статья сложение и вычитания векторов векторной диаграммы.
Например, для t = t1
i1 = Imsin(ωt1 +Ψ)
в общем случае
i = Imsin(ωt +Ψ)
Получили такое же уравнение, каким был задан переменный ток, что свидетельствует о возможности изображения тока вращающимся вектором при нанесении его на чертеж в начальном положении.
Построение векторной диаграммы
Вращая вектор Im‘ против движения часовой стрелки, в прямоугольной системе координат построим график изменения проекции его на вертикальную ось в пределах одного оборота (одного периода). Получим известный уже график синусоидальной функции, соответствующий заданному уравнению.
При построении векторов положительные углы отсчитывают от положительного направления горизонтальной оси против вращения часовой стрелки, а отрицательные — по ее движению.
В процессе расчета электрической цепи определяется ряд синусоидальных величин. Все их можно изобразить на одном чертеже при помощи вращающихся векторов, привязав к одной паре взаимно перпендикулярных осей.
Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты в начальный момент времени, называется векторной диаграммой.
Например, напряжение и ток в электрической цепи выражаются уравнениями:
u = 125 sin(ωt + 30°)
i = 12 sin(ωt — 20°).
Векторная диаграмма такой цепи изображена на рис. 12.11. Если выбрать масштабы напряжения и тока
Mu = 50 В/см; Mi = 4 А/см;
то
Um = Um/Mu = 125/50 = 2,5 см; Im = Im = im/Mi = 12/4 = 3 см.

Векторная диаграмма содержит векторы синусоидальных величин одинаковой частоты, поэтому они вращаются с одинаковой частотой и их взаимное расположение не меняется.
Начало отсчета времени выбирают произвольно, поэтому один из векторов диаграммы можно направить произвольно; остальные же нужно располагать с учетом сдвига фаз по отношению к первому или предыдущему вектору.
Сложение и вычитание векторов
Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями

Сложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:
Im = Im1 + Im2
Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель
но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.
Вектор Im, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).
Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):

При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.
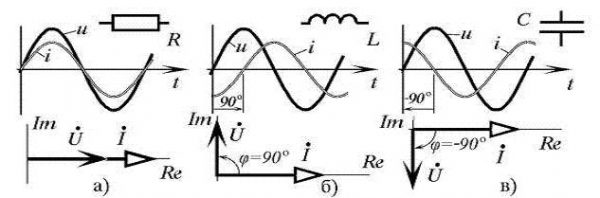
Что такое цепь серии RC? Диаграмма фазора и кривая мощности
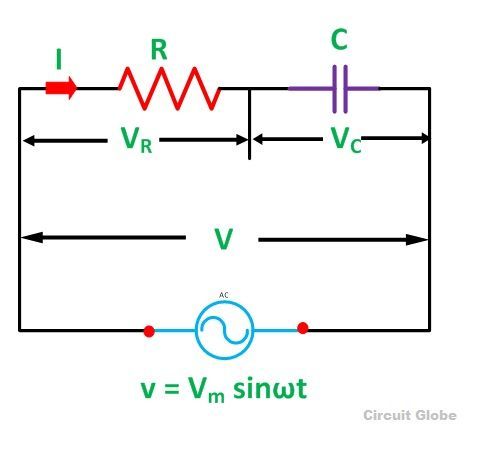
Цепь, которая содержит чистое сопротивление R Ом, соединенное последовательно с чистым конденсатором емкостью C фарад, известна как последовательная цепь RC. Приложено синусоидальное напряжение, и ток I протекает через сопротивление (R) и емкость (C) цепи.
Последовательная цепь RC показана на рисунке ниже:
 Где,
Где,
- В R — напряжение на сопротивлении R
- В C — напряжение на конденсаторе C
- В — полное напряжение в последовательной цепи RC
В комплекте:
Фазорная диаграмма последовательной цепи RC
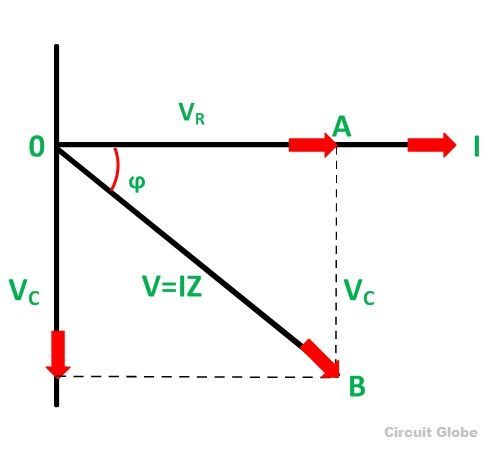
Векторная диаграмма последовательной цепи RC показана ниже:
Шаги построения фазорной диаграммы
Следующие шаги используются для построения векторной диаграммы цепи серии RC
.- Возьмите ток I (г.M.S., значение) в качестве опорного вектора
- Падение напряжения на сопротивлении VR = IR берется синфазно с вектором тока
- Падение напряжения в емкостном реактивном сопротивлении VC = IXC отображается на 90 градусов позади вектора тока, так как ток ведет напряжение на 90 градусов (в чисто емкостной цепи)
- Векторная сумма двух падений напряжения равна приложенному напряжению V (среднеквадратичное значение).
Сейчас,
V R = I R и V C = IX C
Где X C = I / 2πfC
В прямоугольном треугольнике OAB,
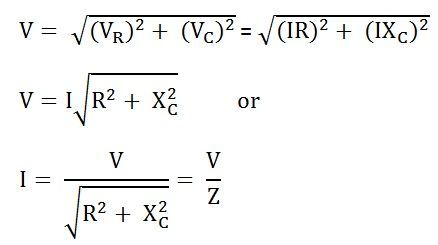
Где,
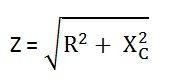
Z представляет собой полное сопротивление протеканию переменного тока последовательной RC цепью и называется импедансом цепи .Измеряется в омах (Ом).
Фазовый угол
Из приведенной выше векторной диаграммы видно, что ток в цепи опережает приложенное напряжение на угол ϕ, и этот угол называется фазовым углом .
Питание в последовательной цепи RC
Если переменное напряжение, приложенное к цепи, определяется уравнением
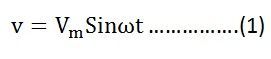
Затем,
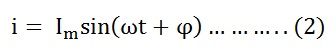
Следовательно, мгновенная мощность определяется как p = vi
Подставляем значения v и i из уравнений (1) и (2) в p = vi
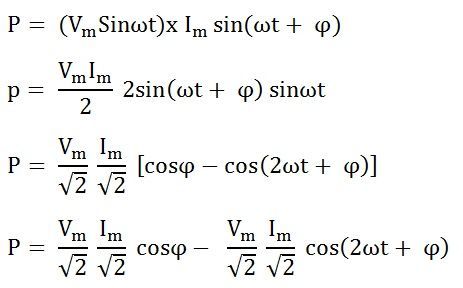
Средняя мощность, потребляемая в цепи за полный цикл, определяется как:
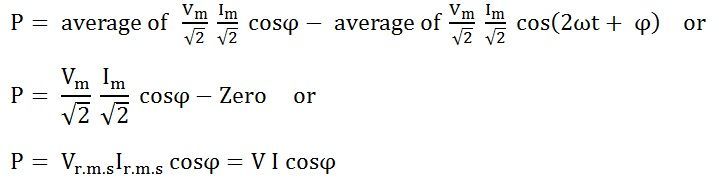
Где cosϕ называется коэффициентом мощности цепи.
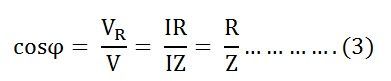
Подставляя значения V и cosϕ из уравнения (3), значение мощности будет
. 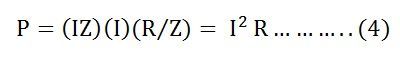
Из уравнения (4) ясно, что мощность фактически потребляется только сопротивлением, а конденсатор не потребляет никакой мощности в цепи.
Форма сигнала и кривая мощности цепи серии RC
Форма волны и кривая мощности RC-цепи показаны ниже:
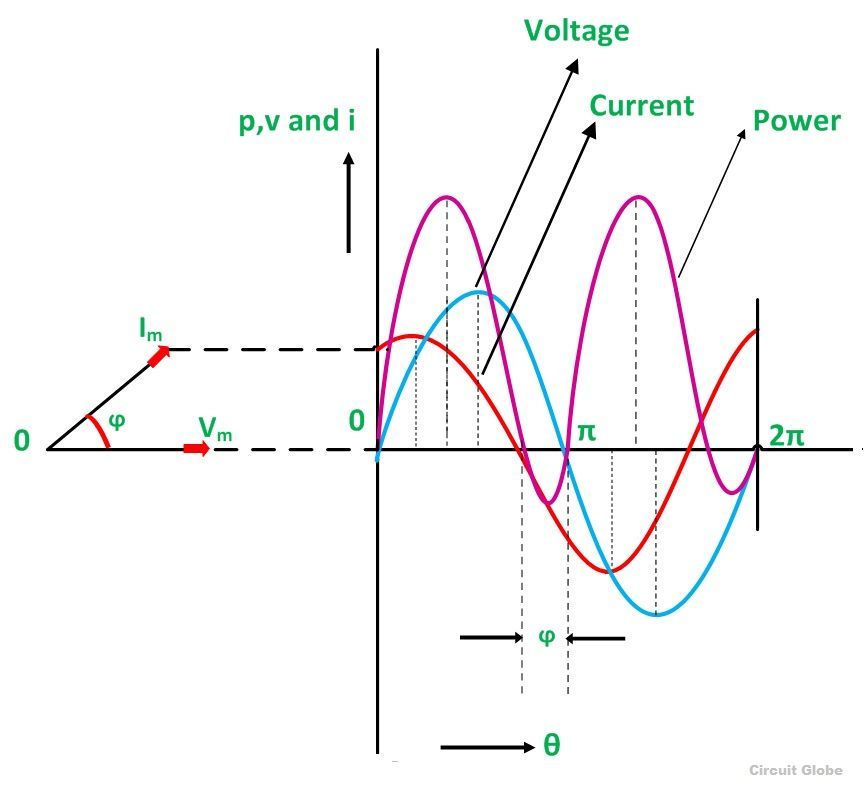 Различные точки на кривой мощности получены из произведения мгновенных значений напряжения и тока.
Различные точки на кривой мощности получены из произведения мгновенных значений напряжения и тока.
Мощность отрицательная между углом (180 ° — ϕ) и 180 ° и между (360 ° -ϕ) и 360 °, а в остальной части цикла мощность положительная. Поскольку площадь под положительными контурами больше, чем под отрицательными контурами, чистая мощность за полный цикл составляет положительных .
,Что такое цепь серии RL? — Диаграмма фазора и кривая мощности
Цепь, которая содержит чистое сопротивление R Ом, соединенное последовательно с катушкой, имеющей чистую индуктивность L (Генри), известна как RL Series Circuit . Когда подается переменное напряжение питания V, в цепи течет ток I.
Итак, I R и I L будут током, протекающим в резисторе и индуктивности соответственно, но величина тока, протекающего через оба элемента, будет одинаковой, поскольку они соединены последовательно друг с другом.Принципиальная схема последовательной цепи RL показана ниже:
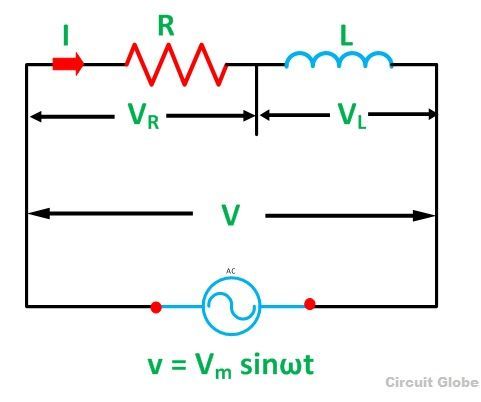 Где,
Где,
- В R — напряжение на резисторе R
- В L — напряжение на индукторе L
- В — Общее напряжение цепи
В комплекте:
Фазорная диаграмма цепи серии RL
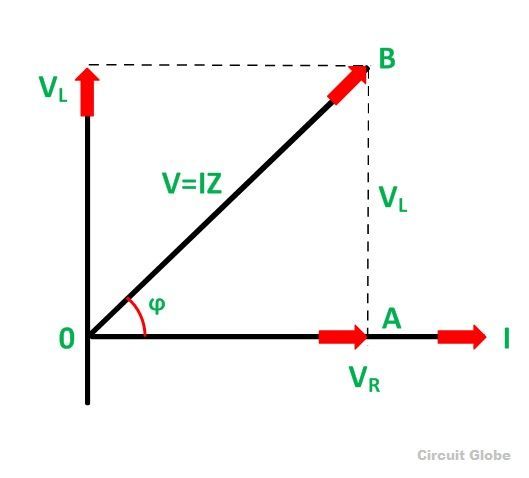
Векторная диаграмма цепи серии RL показана ниже:
Этапы построения фазорной диаграммы цепи серии RL
Ниже приведены следующие шаги, которые необходимо выполнить для пошагового построения векторной диаграммы:
- Ток I взят за эталон.
- Падение напряжения на сопротивлении V R = I R втягивается по фазе с током I.
- Падение напряжения на индуктивном реактивном сопротивлении V L = IX L опережает ток I. Поскольку ток отстает от напряжения на угол 90 градусов в чисто индуктивной цепи.
- Векторная сумма двух падений напряжения V R и V L равна приложенному напряжению V.
Сейчас,
В прямоугольном треугольнике OAB
V R = I R и V L = IX L , где X L = 2πfL
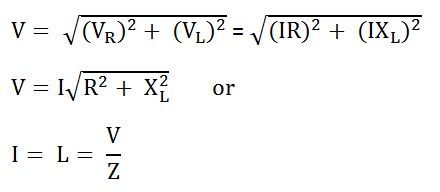
Где,
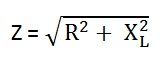
Z — это полное сопротивление протеканию переменного тока цепью серии RL, которое называется импедансом цепи.Измеряется в омах (Ом).
Фазовый угол
В цепи серии RL ток отстает от напряжения на угол 90 градусов, известный как фазовый угол. Это дается уравнением:
Питание в цепи серии R L
Если переменное напряжение, приложенное к цепи, определяется уравнением:
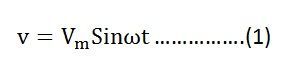
Уравнение тока I имеет вид:
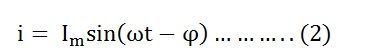
Тогда мгновенная мощность определяется уравнением:

Подставляя значения v и i из уравнений (1) и (2) в уравнение (3), мы получим
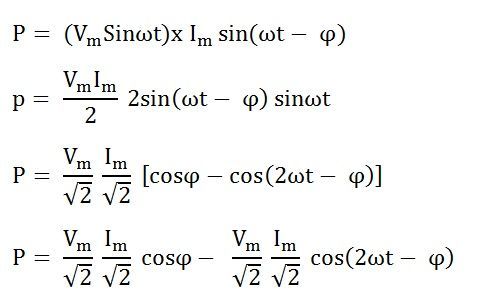
Средняя мощность, потребляемая в цепи за один полный цикл, определяется уравнением, показанным ниже:
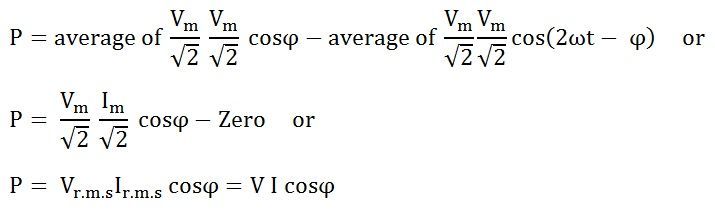
Где cosϕ называется коэффициентом мощности цепи.
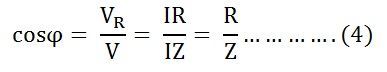
Коэффициент мощности определяется как отношение сопротивления к импедансу цепи переменного тока.
Подставляя значения V и cosϕ из уравнения (4), значение мощности будет:
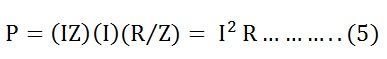
Из уравнения (5) можно сделать вывод, что индуктор не потребляет никакой мощности в цепи.
Форма сигнала и кривая мощности цепи серии RL
Форма сигнала и Кривая мощности последовательной цепи RL показана ниже:
 Различные точки кривой мощности получаются как произведение напряжения и тока.
Различные точки кривой мощности получаются как произведение напряжения и тока.
Если вы внимательно проанализируете кривую, то увидите, что мощность отрицательна между углом 0 и ϕ и между 180 градусами и (180 + ϕ), а в остальной части цикла мощность положительна. Ток отстает от напряжения, и поэтому они не совпадают по фазе друг с другом.
,Трансформатор в состоянии нагрузки — фазовая диаграмма при различной нагрузке
Когда трансформатор находится в нагруженном состоянии, вторичная обмотка трансформатора подключена к нагрузке. Нагрузка может быть резистивной, индуктивной или емкостной. Ток I 2 протекает через вторичную обмотку трансформатора. Величина вторичного тока зависит от напряжения на клеммах V 2 и полного сопротивления нагрузки. Фазовый угол между вторичным током и напряжением зависит от характера нагрузки.
Состав:
Работа трансформатора под нагрузкой
Работа трансформатора под нагрузкой объясняется ниже:
- Когда вторичная обмотка трансформатора остается открытой, она потребляет ток холостого хода из основного источника питания. Ток холостого хода индуцирует магнитодвижущую силу N 0 I 0 , и эта сила устанавливает магнитный поток Φ в сердечнике трансформатора. Схема трансформатора в режиме холостого хода показана на рисунке ниже:

- Разность фаз между V 1 и I 1 дает угол коэффициента мощности ϕ 1 первичной обмотки трансформатора.
- Коэффициент мощности вторичной обмотки зависит от типа нагрузки, подключенной к трансформатору.
- Если нагрузка является индуктивной, как показано на приведенной выше векторной диаграмме, коэффициент мощности будет отстающим, а если нагрузка емкостная, коэффициент мощности будет опережающим. Полный первичный ток I 1 является векторной суммой токов I 0 и I 1 ’. т.е.
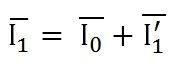
Фазорная диаграмма трансформатора на индуктивной нагрузке
Векторная диаграмма реального трансформатора при индуктивной нагрузке показана ниже:
Фазорная схема трансформатора на индуктивной нагрузке
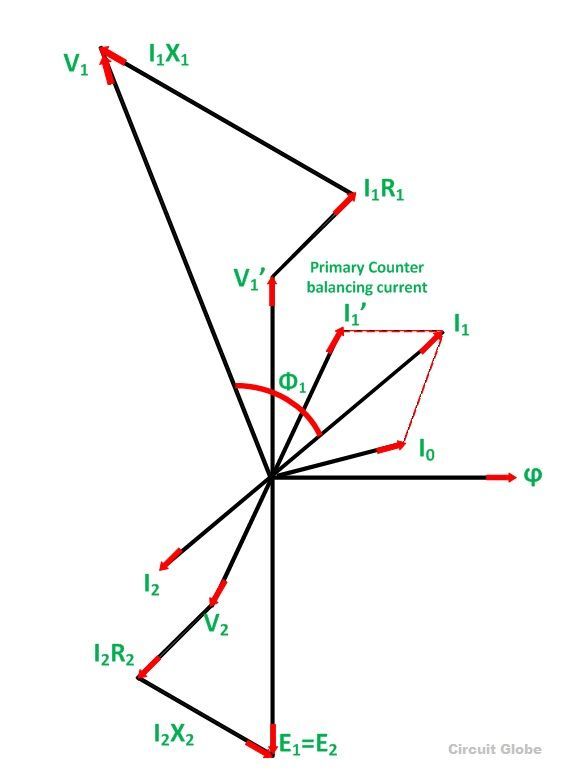
Этапы построения векторной диаграммы
- Взять флюс ϕ, эталон
- Индуцирует ЭДС E 1 и E 2 отстает от потока на 90 градусов.
- Составляющая приложенного напряжения к первичной обмотке, равная наведенной ЭДС в первичной обмотке и противоположная ей. E 1 представлен как V 1 ’.
- Ток I 0 отстает от напряжения V 1 ’на 90 градусов.
- Отстает коэффициент мощности нагрузки. Следовательно, ток I 2 протягивается с отставанием от E 2 на угол ϕ 2 .
- Сопротивление и реактивное сопротивление утечки обмоток приводят к падению напряжения, и, следовательно, напряжение на вторичных клеммах V 2 является разностью фаз E 2 и падением напряжения.
В 2 = E 2 — падение напряжения
I 2 R 2 находится в фазе с I 2 и I 2 X 2 находится в квадратуре с I 2 .
- Полный ток, протекающий в первичной обмотке, равен векторной сумме I 1 ’и I 0 .
- Приложенное первичное напряжение V 1 представляет собой векторную сумму V 1 ’и падения напряжения в первичной обмотке.
- Ток I 1 ’отображается равным и противоположным току I 2
В 1 = В 1 ’+ падение напряжения
I 1 R 1 находится в фазе с I 1 и I 1 X I находится в квадратуре с I 1 .
- Разность векторов между V 1 и I 1 дает угол коэффициента мощности ϕ 1 первичной обмотки трансформатора.
- Коэффициент мощности вторичной обмотки зависит от типа нагрузки, подключенной к трансформатору.
- Если нагрузка является индуктивной, как показано на приведенной выше векторной диаграмме, коэффициент мощности будет отстающим, а если нагрузка емкостная, коэффициент мощности будет опережающим. Где I 1 R 1 — падение сопротивления в первичной обмотке
I 2 X 2 — падение сопротивления во вторичной обмотке
Аналогично
Фазорная диаграмма трансформатора на емкостной нагрузке
Трансформатор на емкостной нагрузке (нагрузка с опережающим коэффициентом мощности) показан ниже на векторной диаграмме.
Фазорная схема трансформатора на емкостной нагрузке
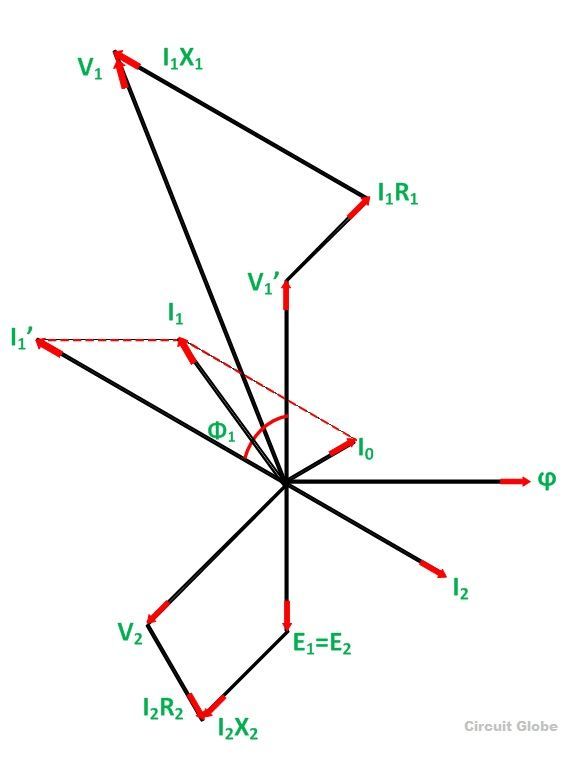
Этапы построения векторной диаграммы при емкостной нагрузке
- Взять флюс ϕ эталон
- Индуцирует ЭДС E 1 и E 2 отстает от потока на 90 градусов.
- Составляющая приложенного напряжения к первичной обмотке, равная наведенной ЭДС в первичной обмотке и противоположная ей. E 1 представлен как V 1 ’.
- Ток I 0 отстает от напряжения V 1 ’на 90 градусов.
- Коэффициент мощности нагрузки является опережающим. Поэтому ток I 2 идет впереди E 2
- Сопротивление и реактивное сопротивление утечки обмоток приводят к падению напряжения, и, следовательно, напряжение на вторичных клеммах V 2 является разностью векторов E 2 и падением напряжения.
В 2 = E 2 — падение напряжения
I 2 R 2 находится в фазе с I 2 и I 2 X 2 находится в квадратуре с I 2 .
- Ток I 1 ’отображается равным и противоположным току I 2
- Полный ток I 1 , протекающий в первичной обмотке, равен векторной сумме I 1 ’и I 0 .
- Приложенное первичное напряжение V 1 представляет собой векторную сумму V 1 ’и падения напряжения в первичной обмотке.
В 1 = В 1 ’+ падение напряжения
I 1 R 1 находится в фазе с I 1 и I 1 X I находится в квадратуре с I 1 .
- Разность векторов между V 1 и I 1 дает угол коэффициента мощности ϕ 1 первичной обмотки трансформатора.
- Коэффициент мощности вторичной обмотки зависит от типа нагрузки, подключенной к трансформатору.
Это все о векторной диаграмме для различных нагрузок.
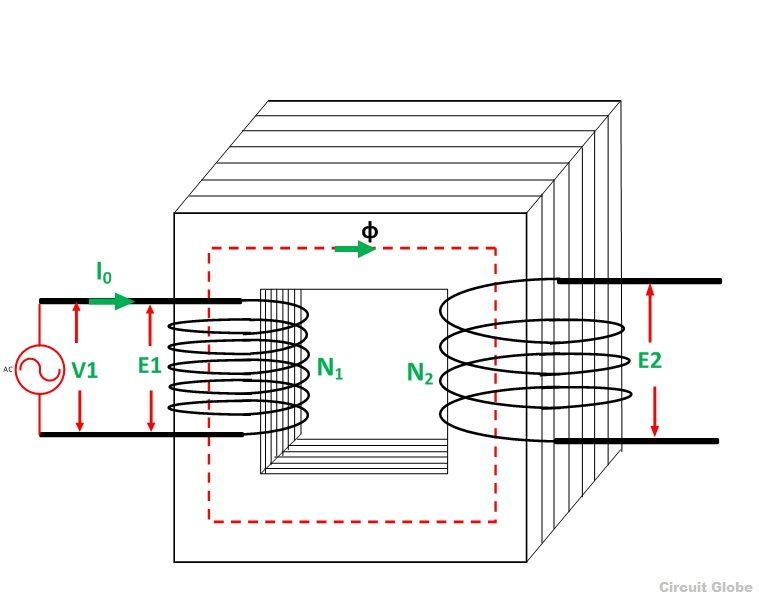
,Трансформаторв режиме холостого хода — его векторная диаграмма
Когда трансформатор работает без нагрузки, вторичная обмотка разомкнута, что означает, что на вторичной стороне трансформатора нет нагрузки и, следовательно, ток во вторичной обмотке будет нулевым. В то время как первичная обмотка несет небольшой ток I 0 , называемый током холостого хода, который составляет от 2 до 10% от номинального тока .
Этот ток обеспечивает потери в стали (гистерезисные и потери на вихревые токи) в сердечнике и очень малую величину потерь в меди в первичной обмотке.Угол запаздывания зависит от потерь в трансформаторе. Коэффициент мощности очень низкий и варьируется от 0,1 до 0,15.
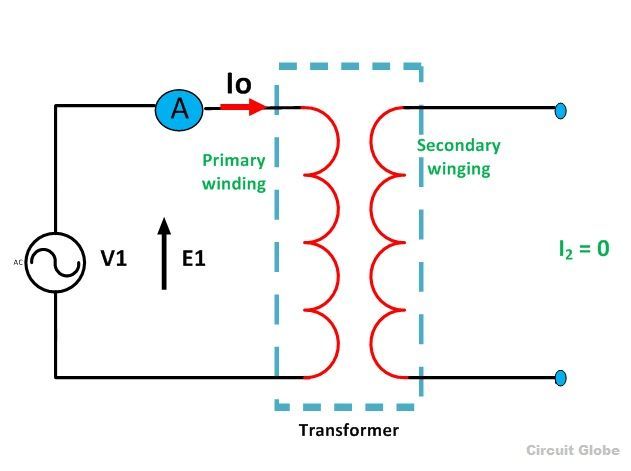 Ток холостого хода состоит из двух составляющих:
Ток холостого хода состоит из двух составляющих:
- Реактивный или намагничивающий компонент I м
(Он находится в квадратуре с приложенным напряжением V 1 . Он создает магнитный поток в сердечнике и не потребляет никакой энергии).
- Активный или силовой компонент I w , также известный как рабочий компонент
(Он находится в фазе с приложенным напряжением V 1 .Он компенсирует потери в стали и небольшие потери в первичной меди).
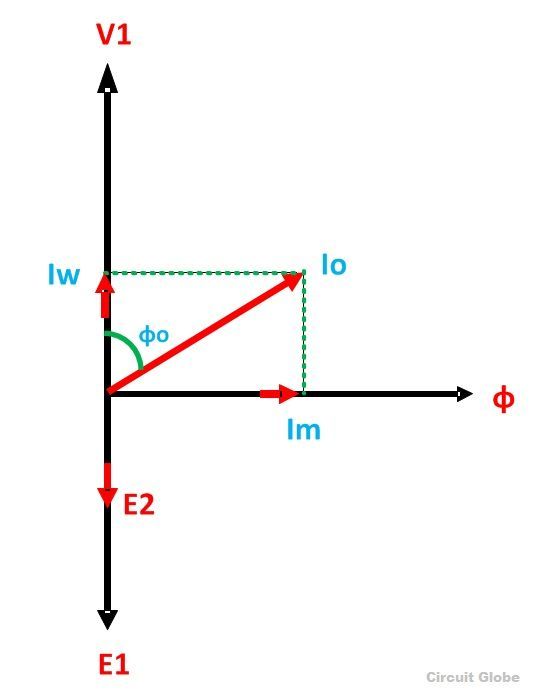
Для построения векторной диаграммы приведены следующие шаги:
- Функция намагничивающего компонента — создавать намагничивающий поток, и, таким образом, он будет находиться в фазе с потоком.
- Наведенная ЭДС в первичной и вторичной обмотках отстает от потока ϕ на 90 градусов.
- Потери в первичной медной цепи не учитываются, а потери вторичного тока равны нулю, так как
I 2 = 0.
Следовательно, ток I 0 отстает от вектора напряжения V 1 на угол ϕ 0 , который называется углом коэффициента мощности без нагрузки и показан на векторной диаграмме выше. - Приложенное напряжение V 1 показано равным и противоположным наведенной ЭДС E 1 , потому что разница между ними без нагрузки незначительна.
- Активный компонент I w включен по фазе с приложенным напряжением V 1 .
- Сумма векторов тока намагничивания I m и рабочего тока I w дает ток холостого хода I 0 .
 Из приведенной выше векторной диаграммы сделаны следующие выводы
Из приведенной выше векторной диаграммы сделаны следующие выводы 
Это все о трансформаторе без нагрузки.
,
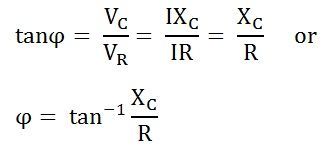
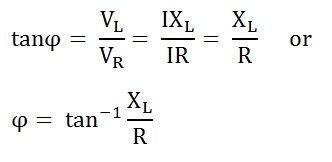
 Из приведенной выше векторной диаграммы сделаны следующие выводы
Из приведенной выше векторной диаграммы сделаны следующие выводы