Что такое индукция магнитного поля и магнитный поток. Физика, 9 класс: уроки, тесты, задания.

1.	Основные формулы и понятия Сложность: лёгкое	1
2.	Зависимость величин Сложность: лёгкое	1
3.	Вычисление магнитного потока Сложность: лёгкое	1
4.	Площадь контура Сложность: среднее	1
5.	Вычисление индукции магнитного поля Сложность: среднее	1
6.	Сила магнитного поля Сложность: среднее	2
7.	Сила тока в проводнике Сложность: среднее	2
8.	Прямоугольная рамка Сложность: среднее	2
9.	Наибольшее и наименьшее значения силы Сложность: среднее	2
10.	Угол между индукцией и током Сложность: среднее	2
11.	Равновесие силы магнитного поля и силы тяжести Сложность: сложное	3
12.	Проводник с током, «парящий» в однородном магнитном поле Сложность: сложное	4

Электромагнитная индукция.

Магнитный поток

На прошлых уроках мы с вами говорили о магнитном поле и его характеристиках. Давайте вспомним, что магнитное поле — это силовое поле, возникающее при движении электрических зарядов независимо от рода проводника или среды, в которой эти заряды движутся.

Силовой характеристикой магнитного поля является вектор магнитной индукции, направление которого в данной точке совпадает с направлением силовой магнитной линии, проходящей через эту точку:

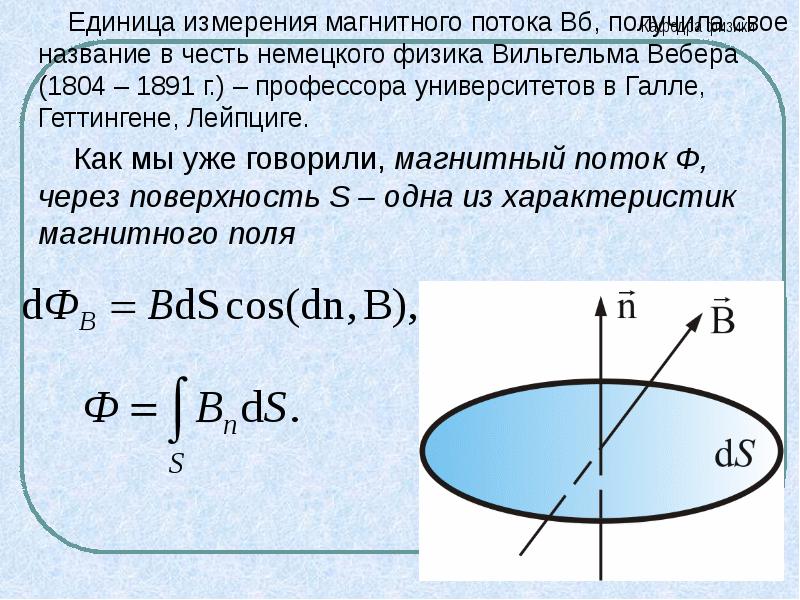
Магнитная индукция характеризует магнитное поле в конкретной точке пространства. А для характеристики магнитного поля во всех точках пространства, ограниченного замкнутым контуром, вводят физическую величину, называемую магнитным потоком (или потоком магнитной индукции).

Что мы понимаем под потоком в обычной жизни? Кто-то подумает о потоках воды в реке, а кто-то о ветре — потоках воздуха.

Аналогично и с магнитным потоком, который можно рассматривать как величину, пропорциональную числу магнитных линий, проходящих через площадь, ограничивающую некоторую поверхность.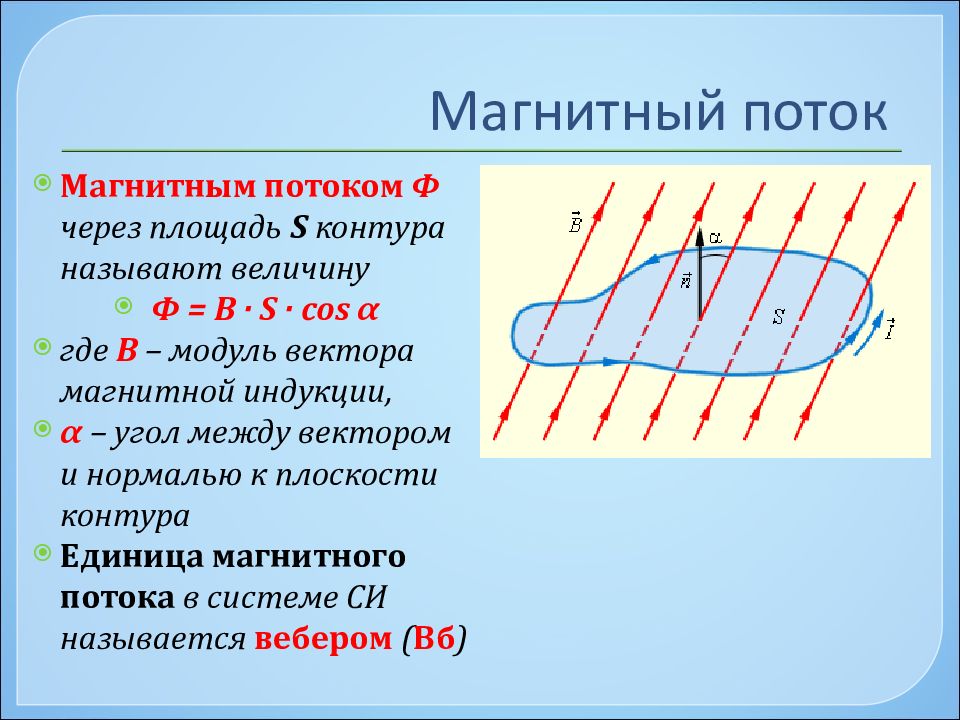

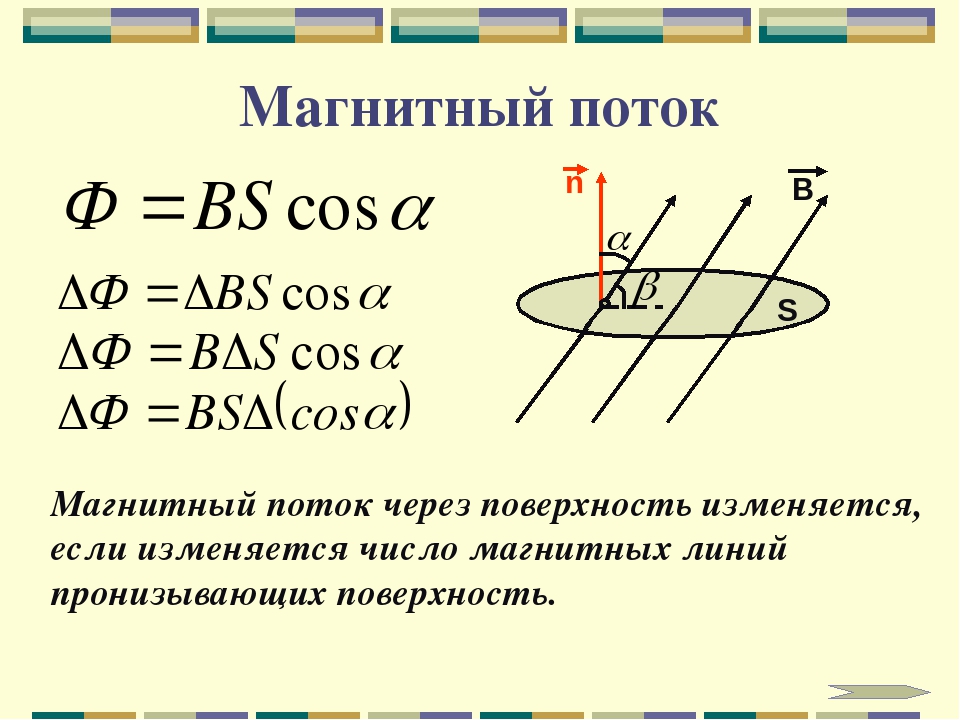
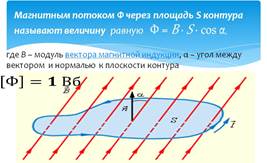
Итак, магнитным потоком через плоскую поверхность, находящуюся в однородном магнитном поле, называют скалярную физическую величину, равную произведению модуля индукции магнитного поля, площади поверхности, ограниченной контуром, и косинуса угла между направлениями нормали к этой поверхности и магнитной индукции:

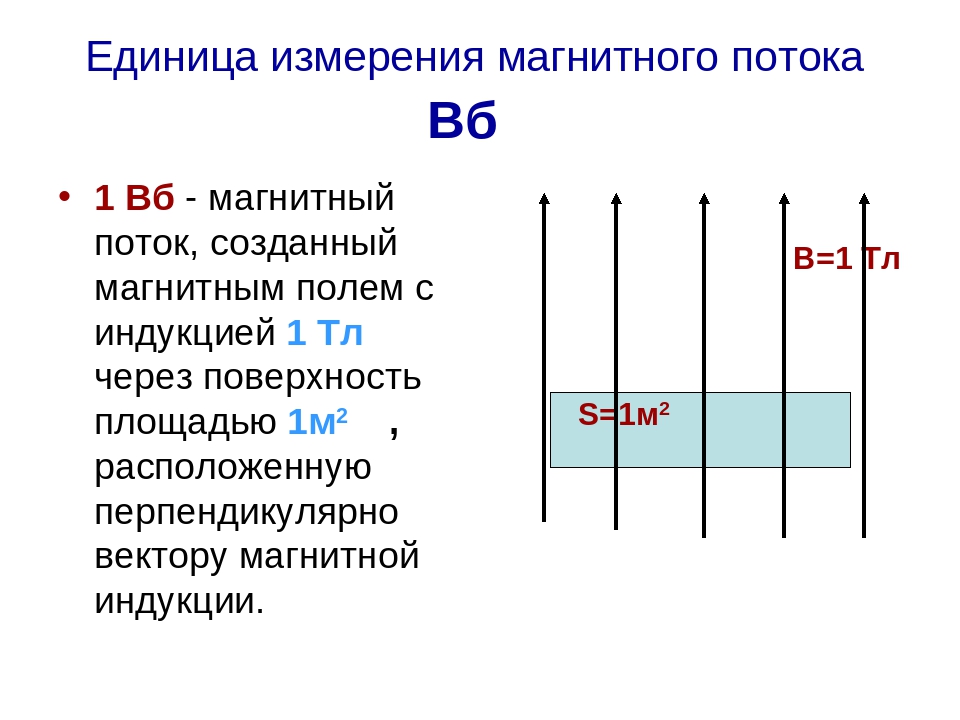
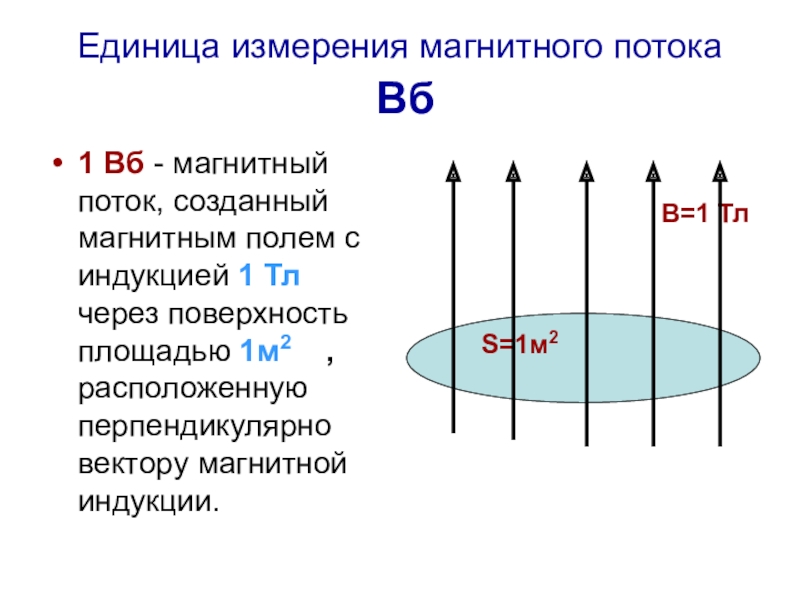
В системе СИ за единицу магнитного потока принят вебер, названный так в честь немецкого учёного Вильгельма Эдуарда Вебера, главные работы которого посвящены изучению магнитных явлений и электричества.

1 Вб — это магнитный поток однородного магнитного поля индукцией 1 Тл через плоскую поверхность площадью 1 м², расположенную перпендикулярно линиям индукции магнитного поля:

Но вернёмся к определению магнитного потока. Его анализ показывает, что изменить магнитный поток через поверхность, ограниченную контуром, можно тремя способами:

изменяя индукцию магнитного поля, в котором находится контур;

размеры этого контура;

а также ориентацию контура в магнитном поле.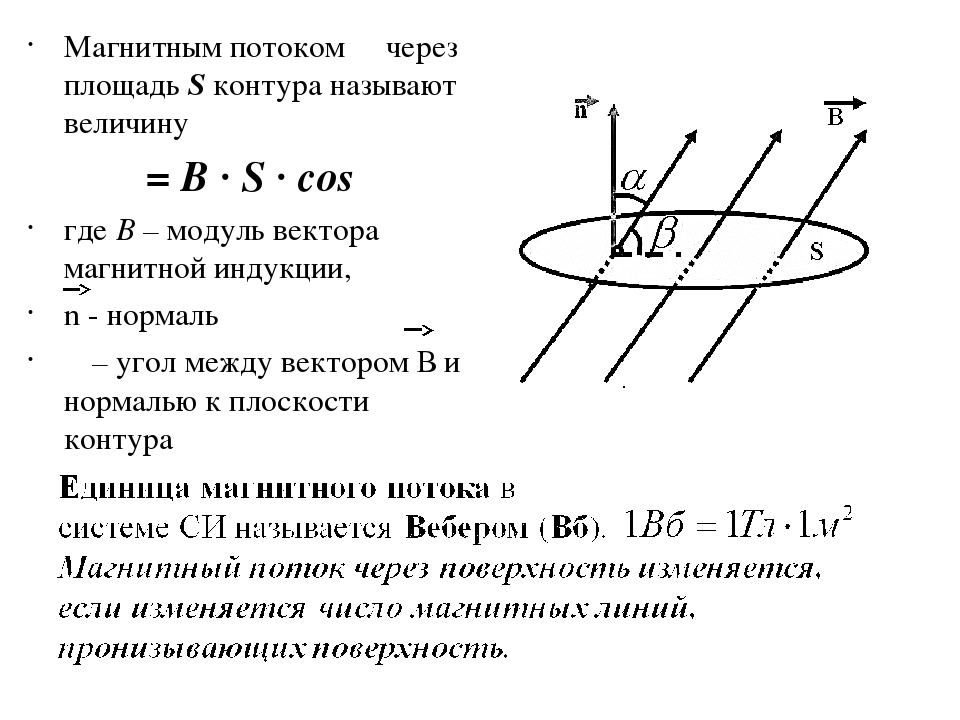 При этом очевидно, что в случаях, когда линии магнитной индукции перпендикулярны плоскости контура, магнитный поток достигает своего максимума. А в случае, когда плоскость контура параллельна линиям индукции, магнитный поток равен нулю.

Теперь, для примера, давайте с вами решим такую задачу. Линии магнитной индукции направлены перпендикулярно к плоскости, в которой с частотой 0,3 Гц вращается прямоугольная рамка с током. Определите время, за которое магнитный поток через рамку уменьшится в два раза?

После опытов Эрстеда и Ампера стало понятно, что электрические и магнитные поля имеют одни и те же источники — движущиеся электрические заряды. Это навело многих учёных на мысль о том, что электрические и магнитные поля должны быть как-то взаимосвязаны друг с другом. Великий английский учёный Майкл Фарадей, в декабре 1821 года в своём дневнике оставил такую запись: «Превратить магнетизм в электричество!»

Учёный рассуждал примерно так: раз электрический ток может намагнитить железный проводник, то не может ли магнит, в свою очередь, вызвать появление электрического тока в проводнике?

Спустя 10 лет, а именно 29 августа 1831 года фундаментальная задача была решена. В течение месяца Майкл Фарадей провёл серию опытов, позволивших ему сделать величайшее открытие того времени. Рассмотрим некоторые из них.

Итак, для начала давайте с вами соберём чувствительную цепь, состоящую из источника тока, двух катушек разного диаметра, гальванометра и ключа.

Одну катушку мы подключим к источнику тока, а концы второй катушки соединим с гальванометром. Вставим одну катушку внутрь второй. Наблюдая за гальванометром, замкнём ключ — стрелка отклоняется на несколько делений, а затем возвращается в исходное положение. Движение стрелки говорит нам о том, что по виткам внутренней катушки прошёл кратковременный электрический ток. А теперь разомкнём цепь — по катушке вновь протекает ток, но уже в обратном направлении.

Повторим опыт, но теперь оставим ключ в замкнутом положении, а катушку, соединённую с гальванометром, будем перемещать относительно первой катушки.

Не трудно заметить, что при движении катушки в цепи протекает ток. Фарадей также заметил, что если перемещать катушку, соединённую с источником тока, оставляя вторую катушку неподвижной, то результат будет тот же.

Эти наблюдаемые Фарадеем мгновенные вторичные токи, которые вызываются влиянием первичных токов, были названы им индукционными токами, то есть наведёнными.

Но учёный не остановился на достигнутом и решил выяснить, не влияет ли на появление индукционных токов источник тока? Для этого Фарадей собрал цепь, состоящую только из катушки и гальванометра. Затем он взял постоянный полосовой магнит и начал вводить его внутрь катушки.

Какого же было удивление учёного, когда он заметил, что во время движения магнита стрелка гальванометра отклонялась, указывая на возникновение индукционного тока в цепи катушки. Это же явление можно наблюдать, если магнит оставить неподвижным, а двигать подключённую к гальванометру катушку. Но вот вращение магнита внутри катушки не вызывало появление индукционного тока.

На основании этого Фарадей пришёл к выводу о том, что «ток возникает лишь при движении магнита относительно провода, а не в силу свойств, присущих ему в покое».

Что бы убедиться в своих выводах, Фарадей проделал ещё несколько опытов. В одном из них он поместил в магнитное поле плоский контур, концы которого были соединены с гальванометром. Когда контур приводился во вращение, стрелка гальванометра отклонялась, то в одну, то в другую сторону, фиксируя появление индукционного тока. Ток возникал и тогда, когда рядом с контуром или внутри него приводился во вращение постоянный магнит.

И несмотря на то, что рассмотренные нами опыты внешне выглядят различно, Фарадей уловил в них нечто общее — то, от чего зависит возникновение индукционного тока. А именно в замкнутом проводящем контуре индукционный ток возникает только тогда, когда изменяется число линий магнитной индукции, пронизывающих поверхность, ограниченную этим контуром.

Чуть ранее мы с вами показали, что число линий индукции, пронизывающих рамку, определяет магнитный поток. Поэтому можно сказать, что при всяком изменении магнитного потока, пронизывающего замкнутый проводящий контур, в этом контуре возникает индукционный ток, существующий в течение всего времени изменения магнитного потока.

В этом состоит суть явления электромагнитной индукции на качественном уровне. О его количественной стороне мы с вами поговорим на одном из следующих занятий.

В дневнике Майкл Фарадей записал дату открытия явления электромагнитной индукции — 29 августа 1831 года. Интересно, но почти одновременно с Фарадеем похожие эксперименты проводил и швейцарский физик Жан-Даниэль Колладон. Его опыты были в целом похожи на опыт Фарадея. Однако, чтобы магнит не оказывал влияния на стрелку гальванометра, выводил концы катушки в соседнюю комнату. Поместив магнит в катушку, Колладон шёл к гальванометру и разочарованно убеждался в отсутствии тока. Интересно, кому бы принадлежало открытие такого замечательного явления, если бы свои опыты Колладон проводил с помощником?

О значимости открытого явления электромагнитной индукции долго спорил научный мир. В архивах даже сохранилась такая запись:

«Однажды после лекции Майкла Фарадея в Королевском обществе, где он демонстрировал свои опыты, к нему подошёл богатый коммерсант, оказывавший обществу материальную поддержку, и надменным голосом спросил:

— Всё, что вы нам здесь показывали, господин Фарадей, действительно красиво. Но теперь скажите мне, для чего годится эта магнитная индукция!?

— А для чего годится только что родившийся ребёнок? — спросил в ответ рассердившийся Фарадей».

В последующие годы на этот вопрос ответили многие учёные и изобретатели. Так Эмилий Христианович Ленц, Борис Семёнович Якоби и Михаил Иосифович Доливо-Добровольский внесли огромный вклад в развитие электротехники.

А французский изобретатель Ипполи́т Пи́кси в 1832)году первую в мире динамо-машину, которая заложила основу для промышленного производства электроэнергии.

В современном мире на явлении электромагнитной индукции работают мобильные телефоны и планшеты, компьютеры и ноутбуки, наушники и микрофоны, модные смарт-часы и фитнес-браслеты. А ведь без явления, которое было открыто Майклом Фарадеем в 1831 году, эти приборы создать было бы невозможно и по сей день.

Тест по физике 10 класс

Тест по физике 10 класс.

Тест по физике для 10-х классов.
Тема: «Электромагнитная индукция».

1. Как обозначается физическая величина, называемая магнитная индукция?
а).     В        б).     L        в).     H        г).     Ф

2. Как обозначается физическая величина, называемая индуктивностью?
а).     В        б).     L        в).     H        г).     Ф

3. Как обозначается физическая величина, называемая магнитным потоком?
а).     В        б).     L        в).     H        г).     Ф

4. Как обозначается физическая величина, называемая индукцией?
а).     В        б).     L        в).     H        г).     Ф

5. Какая сила меняет направление скорости частицы?
а).     FА        б).     FЛ        в).     ЭДС        г).     сила сопротивления

6. Какое поле создается неподвижными зарядами?
а).     магнитное        б).     электрическое
       в).     электростатическое        г).     электродинамическое

7. Какая сила действует на заряженную частицу со стороны магнитного поля?
а).     FА        б).     FЛ        в).     ЭДС        г).     сила притяжения

8. Какая физическая величина равна отношению работы сторонних сил к заряду?
а).     FА        б).     FЛ        в).     ЭДС        г).     Ф

9. Какая физическая величина равна произведению индуктивности на силу тока?
а).     FА        б).     FЛ        в).     ЭДС        г).     Ф

10. В каких единицах измеряется магнитная индукция?
а).     Гн        б).     Вб        в).     В        г).     Тл

11. В каких единицах измеряется магнитный поток?
а).     Гн        б).     Вб        в).     В        г).     Тл

12. В каких единицах измеряется ЭДС индукции?
а).     Гн        б).     Вб        в).     В        г).     Тл

13. В каких единицах измеряется индуктивность?
а).     Гн        б).     Вб        в).     В        г).     Тл

14. Какое поле создается движущимися зарядами?
а).     магнитное        б).     электрическое
       в).     электростатическое        г).     электродинамическое

15. Какая физическая величина равна произведению вектора магнитной индукции на площадь сечения проводника и на синус угла между ними?
а).     FА        б).     FЛ        в).     ЭДС        г).     Ф

Ответы:

1 — а,     2 — б,     3 — г,     4 — в,     5 — б,     6 — б,     7 — б,     8 — в,
9 — г,     10 — г,     11 — б,     12 — в,     13 — а,     14 — а,     15 — г.

Тестирование по физике 10 класс. Механика.                          Олимпиады по физике 10 класс

Магнитные измерения реферат по физике

Министерство образования Украины Запорожский государственный технический университет Кафедра ЕПА Выполнил студент группы Э-219 Шило С.И. Принял Андрияс И.А. 2000 Содержание . Общие сведения о магнитных измерениях . Определение задач магнитных измерений . Магнитные величины и их основные характеристики . Электродинамический логометр . Принцины построения приборов и способы измерения магнитного потока, магнитной индукции и напряженности магнитного поля . Применение баллистического гальванометра . Флюксметр . Пермеаметры . Исследование стали в переменном магнитном поле . Осциллографирование кривой гистерезиса. . Список использованной литературы Напряженность магнитного поля внутри кольцевого соленоида (тороида) может быть подсчитана на основании закона полного тока по формулам: где wi — число витков намагничивающей обмотки; l — значение тока, A; lср — средняя длина силовой магнитной линии в тороиде, отмеченная на рис. 2 пунктиром и легко вычисляемая по геометрическим размерам испытуемого образца. Для определения зависимости B=f(H) в намагничивающей обмотке устанавливают ток, соответствующий заданному значению H и заранее подсчитанный по приведенной формуле, затем быстро изменяют направление тока в обмотке при помощи переключателя 5. При перемене направления тока магнитный поток в сердечнике изменится по некоторому сложному закону от значения +Ф до значения —Ф, т.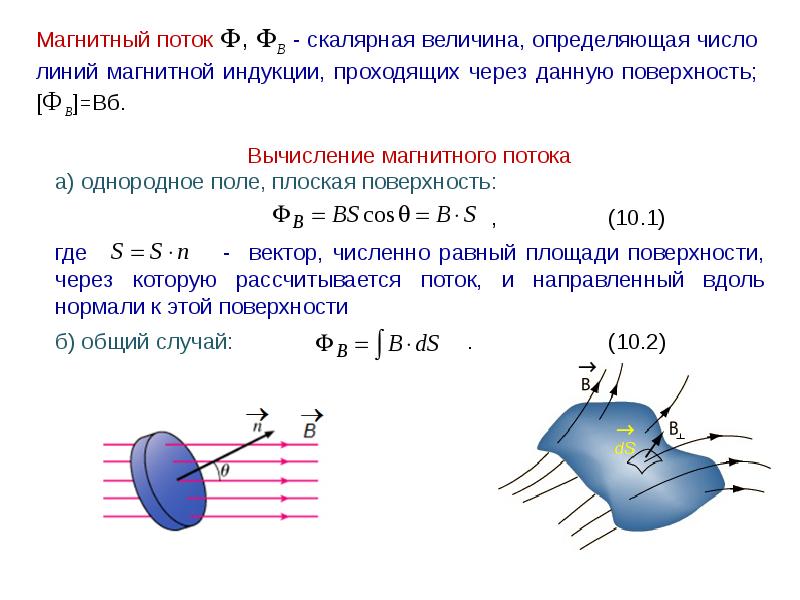 е. изменение потока в измерительной рамке будет равно 2Ф, и с учетом этого подсчитывают поток в сердечнике: Зная поток и поперечное сечение испытуемого образца, находят значение магнитной индукции где s — сечение образца, см2. Найденное значение В и ранее вычисленное значение Н позволяют подсчитать магнитную проницаемость 2. Флюксметр Весьма удобным прибором для измерения постоянного магнитного потока является флюксметр, называемый иногда веберметром или милливеберметром. Флюксметр представляет собой прибор магнитоэлектрической системы, в котором подвод тока к подвижной рамке осуществляется не через пружинки, а через безмоментные спирали, т. е. в его измерительном механизме отсутствует противодействующий момент. Вследствие этого указатель флюксметра при отсутствии тока в обмотке рамки может занимать любое положение относительно шкалы. Флюксметр, как и большинство гальванометров магнитоэлектрической системы, имеет бескаркасную рамку, однако он рассчитывается так, чтобы при внешнем сопротивлении, меньшем 20 ом, подвижная часть оказывалась в режиме переуспокоения. 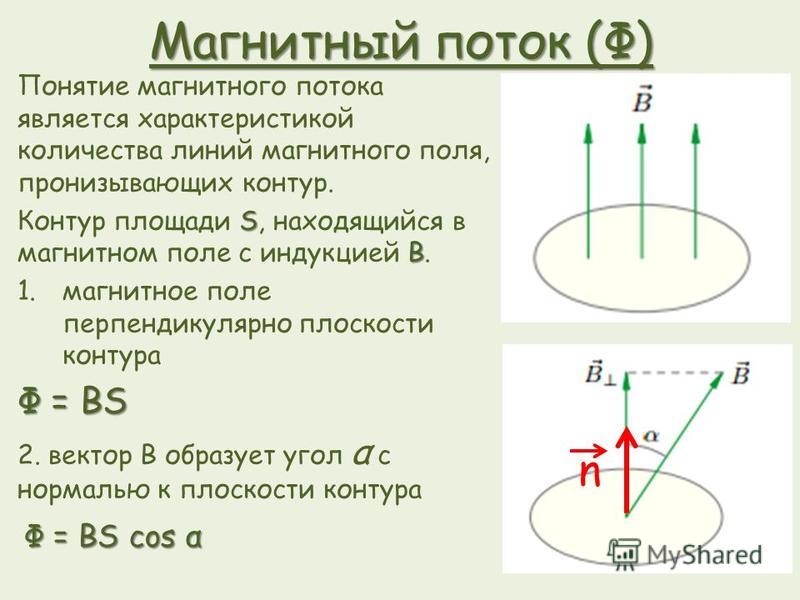Как и у баллистического гальванометра, подвижная часть флюксметра выполняется со сравнительно большим моментом инерции. На рис. 3 приведена схема, поясняющая процесс измерения магнитного потока при помощи флюксметра. Для измерения магнитного потока, например постоянного магнита 1, к зажимам флюксметра присоединяется измерительная рамка 2, состоящая из достаточного количества витков медной проволоки. Если эту рамку надеть на испытуемый магнит так, как это показано на рис. 12.3, то во время перемещения рамки 2 в ней будет наводиться э.д.с., создающая ток в цепи прибора. Под действием этого тока подвижная рамка 3 прибора начнет поворачиваться. После того как измерительная рамка 2 будет приведена в положение, показанное на рис 3, и остановлена, э.д.с., действовавшая в ней, исчезнет, но рамка 3 по инерции будет еще немного продолжать двигаться. Переместившись на некоторый угол a от начального положения, рамка 3 остановится. Теория флюксметра показывает, что движение рамки прекращается после того, как число потокосцеплений витков рамки 3 с потоком магнита 4 изменится на столько же, сколько создалось потокосцеплений измерительной рамки 2 с измеряемым потоком Ф. 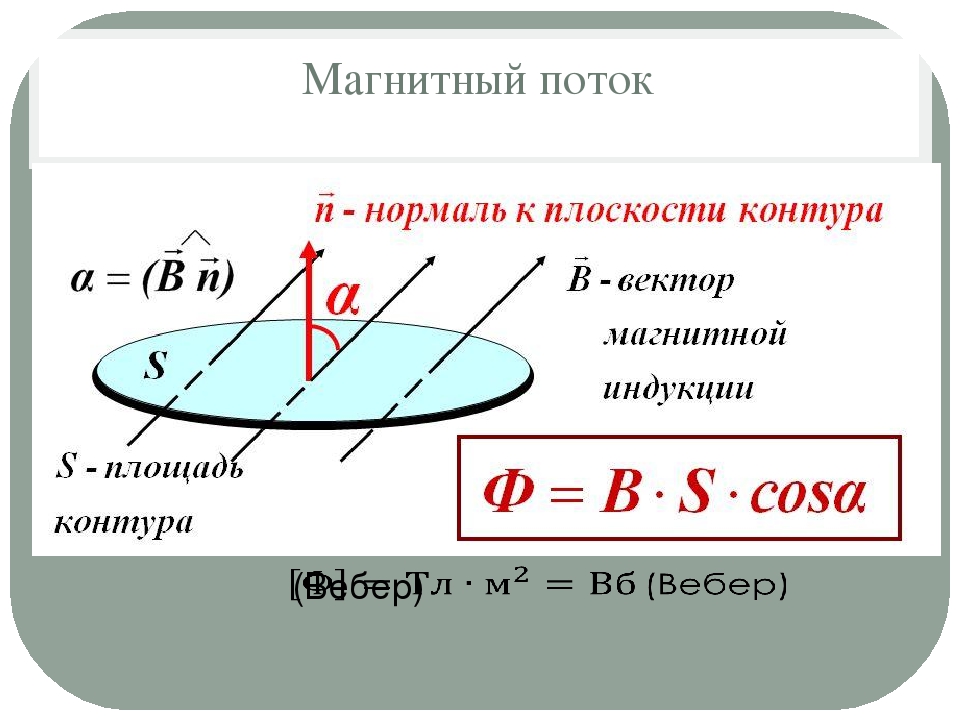Если успокоение прибора достаточно велико, для чего сопротивление цепи рамки не должно превышать некоторый определенный для данной конструкции предел (обычно 8—20 Oм), то между углом поворота стрелки флюксметра и измеряемым магнитным потоком будет иметь место простая зависимость где Ф – измеряемый поток; w — число витков измерительной рамки 2; Сф— постоянная флюксметра в максвелл-витках или вебер-витках на одно деление шкалы. Определение постоянной флюксметра Сф производится таким же способом, как и определение постоянной баллистического гальванометра, с применением образцовых взаимных индуктивностей. При описанном устройстве флюксметра работа с ним затрудняется из-за невозможности установки его подвижной части в нулевое положение, так как при снятии катушки 2 с испытуемого магнита рамка 3 хотя и получит толчок в обратном направлении, но не придет точно в исходное нулевое положение. Это обусловлено неизбежным необратимым рассеиванием энергии в виде тепла, выделяемого током в цепи рамки, а также потерями энергии на трение в опорах подвижной части прибора и трение ее о воздух. В изготовляемых микровеберметрах имеется дополнительное приспособление — электромагнитный корректор, позволяющий устанавливать стрелку прибора в любое положение, в частности и на нулевую отметку. Это приспособление, встроенное в корпус прибора, схематически показано на рис. 12.3 и обведено пунктиром. Устройство его подобно механизму магнитоэлектрического прибора: между полюсами постоянного магнита помещена рамка 5, которую можно поворачивать от руки головкой 6. Для изменения положения указателя флюксметра относительно его шкалы, в частности для установки указателя на нулевую отметку, переключатель 7 переводят в положение, отмеченное буквой К, при котором рамка прибора соединяется с рамкой корректирующего устройства. При этой схеме поворот рамки 5 головкой 6 будет вызывать соответствующее изменение положения указателя флюксметра. Установив указатель флюксметра в желаемое положение, переводят переключатель 7 в рабочее положение, отмеченное на рис. 3 буквой И. Флюксметр является прибором менее чувствительным, чем баллистический гальванометр, и поэтому не может применяться для измерения слабых магнитных полей. При измерении достаточно сильных полей флюксметр имеет ряд преимуществ по сравнению с баллистическим гальванометром. Постоянная флюксметра практически не изменяется при изменении внешнего сопротивления цепи рамки в достаточно широких пределах от нуля до 8—20 Ом Наибольшее допустимое значение этого сопротивления указано на шкале прибора. Показания флюксметра остаются правильными при изменении в широких пределах скорости удаления (или внесения) измерительной рамки из магнитного поля. При работе с баллистическим гальванометром эта операция должна производиться очень быстро (за 0,1—0,2 секунды) Указатель флюксметра, отклонившись на определенный угол, остается в этом положении неподвижным достаточно долго для спокойного отсчета показаний. В противоположность этому, при работе с баллистическим гальванометром для обеспечения правильности отсчета максимального отклонения указателя требуется большое напряжение внимания. 3. Пермеаметры Исследование свойств стали путем снятия кривой намагничивания кольцевой пробы (см рис. 12 2) дает наиболее точные результаты, но практически неудобно из за трудности изготовления образца и из-за сложности наложения на него обмоток. Эти затруднения отпадают при применении пермеаметров — устройств, позволяющих быстро и удобно осуществлять относительно равномерное намагничивание образцов стали, имеющих форму стержней круглого или прямоугольною сечения На рис. 4а, а дан внешний вид одной из конструкций пермеаметра, а на рис 4б приведена схема включения его. где s — сечение магнитопровода. Этой же формулой пользуются и для определения магнитной индукции в каком-либо воздушном зазоре магнитной цепи, если можно пренебречь явлением распора силовых линий. При необходимости измерить индукцию в воздушном зазоре магнитной цепи, когда нельзя пренебречь явлением распора силовых магнитных линий, помещают непосредственно в зазор миниатюрную измерительную рамку с известной площадью sp. В этом случае определяется среднее значение индукции в том месте зазора, где находится рамка, по формуле где sp — площадь рамки, м2. Особым преимуществом описанного способа измерения магнитного потока является отсутствие тока в измерительной рамке. Это позволяет произвести измерение без нарушения нормального режима и распределения магнитных потоков в исследуемом аппарате. Измерение по схеме (рис. 12.7) дает возможность определять не только модуль, но и фазу магнитного потока, и выяснять таким путем полную картину электрических и магнитных процессов в данной конструкции. При помощи потенциометра, в частности, можно снимать основную кривую намагничивания кольцевой пробы на переменном токе и определять потери в образцах стали. Нужно отметить, что при работе с потенциометром переменного тока применяется вибрационный гальванометр, настраиваемый на основную частоту, поэтому измерение магнитного потока с помощью потенциометра дает хорошие результаты только в тех случаях, когда форма кривой измеряемого потока не очень существенно отличается от синусоиды. 5. Осциллографирование кривой гистерезиса. Кривую гистерезисного цикла можно снять по точкам на постоянном токе при помощи баллистического гальванометра, однако она будет несколько отличаться от реальной кривой при работе магнитопровода с переменным магнитным потоком.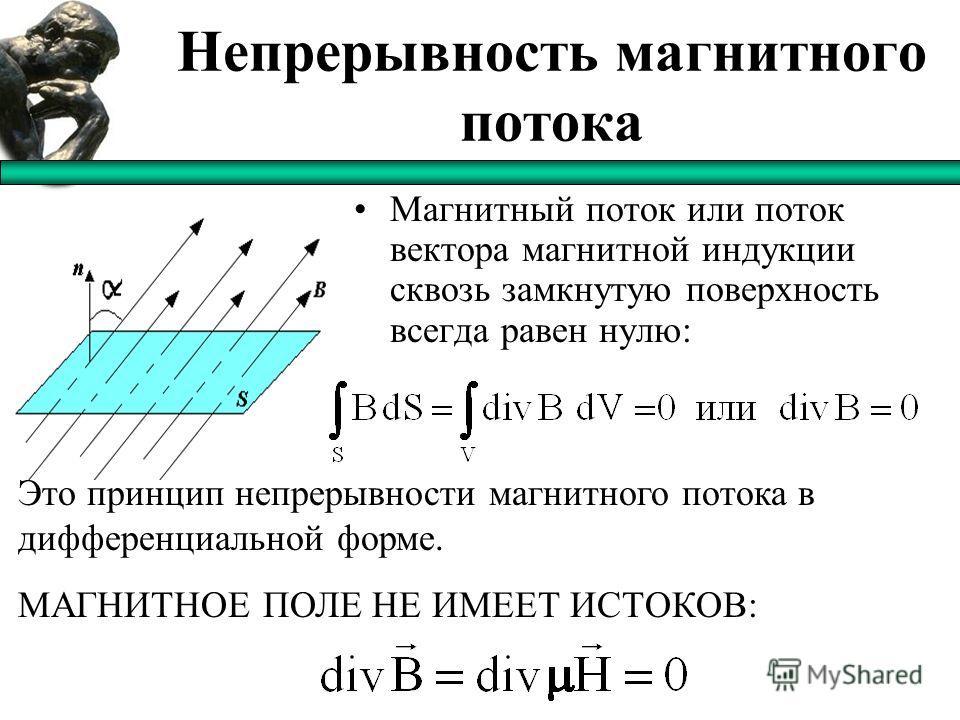 Существует способ, позволяющий визуально наблюдать кривую гистерезисного цикла при намагничивании образца переменным током на экране электронного осциллографа. Применяемая для этого схема приведена на рис.8. Подлежащий исследованию сердечник в форме, например, кольца 1, набранного из листов стали, снабжается намагничивающей 2 и измерительной 3 обмотками. Необходимое значение намагничивающего тока устанавливается по амперметру А. Напряжение с шунта r подается на пластины горизонтального отклонения электронного осциллографа; отклонение луча по горизонтали в каждый данный момент будет пропорционально намагничивающему току и соответственно напряженности поля Н, мгновенное значение падения напряжения на конденсаторе пропорционально мгновенному значению индукции в образце. Это напряжение подается на пластины вертикального отклонения осциллографа, и на экране получается изображение кривой гистерезисного цикла. Кривая гистерезисного цикла, получаемая описанным способом на экране осциллографа, и по форме и по площади отличается от кривой, снятой с данного образца на постоянном токе с помощью баллистического гальванометра. Причина этого заключается в том, что площадь гистерезисной кривой, снимаемой на постоянном токе, определяется только потерями на гистерезис, а на экране осциллографа получается кривая, площадь которой соответствует сумме потерь на гистерезис и на вихревые токи. Литература 2. Таранов С.Г., Феврлёва Н.Е. Магнитные измерения 3. Ю.Н. Маслов Магнитные измерения и приборы 4. Ю.В. Селезнев Методы и устройства магнитных и электрических измерений 1. Применение баллистического гальванометра В лабораторной практике при исследованиях электрических машин, аппаратов, трансформаторов, при испытаниях магнитных материалов, применяемых в производстве на электротехнических заводах, часто возникает необходимость измерения магнитных величин, как то: магнитного потока, магнитной индукции, магнитодвижущей силы, напряженности магнитного поля, магнитной проницаемости, а также потерь на гистерезис и вихревые токи в ферромагнитных материалах. В большинстве случаев магнитные величины измеряют косвенным методом — путем измерения тех или иных электрических величин (тока, э.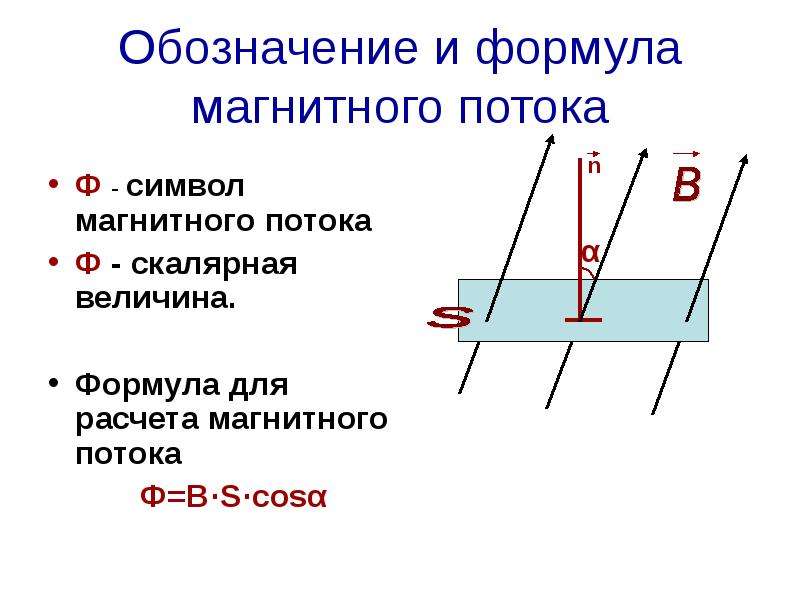 д.с., количества электричества), функционально связанных с измеряемой магнитной величиной. Измерения магнитных величин в настоящее время составляют большой самостоятельный раздел измерительной техники с глубоко развитой теорией. Некоторые методы и аппаратуру для магнитных измерений используют не только в лабораториях, специализированных в области магнитных измерений, но также и в более универсальных лабораториях, занимающихся испытаниями и исследованиями электрических машин и аппаратов. К числу широко распространенных магнитных измерений относятся: а) измерения при помощи баллистического гальванометра; б) измерения с помощью флюксметра; в) определение потерь в стали ваттметровым методом; г) измерения переменных магнитных потоков при помощи потенциометра. На рис.1 приведена схема, поясняющая общий принцип измерения постоянного магнитного потока с помощью баллистического гальванометра. Для измерения магнитного потока к гальванометру необходимо присоединить измерительную рамку с некоторым числом витков w, находящуюся в исследуемом постоянном магнитном поле. 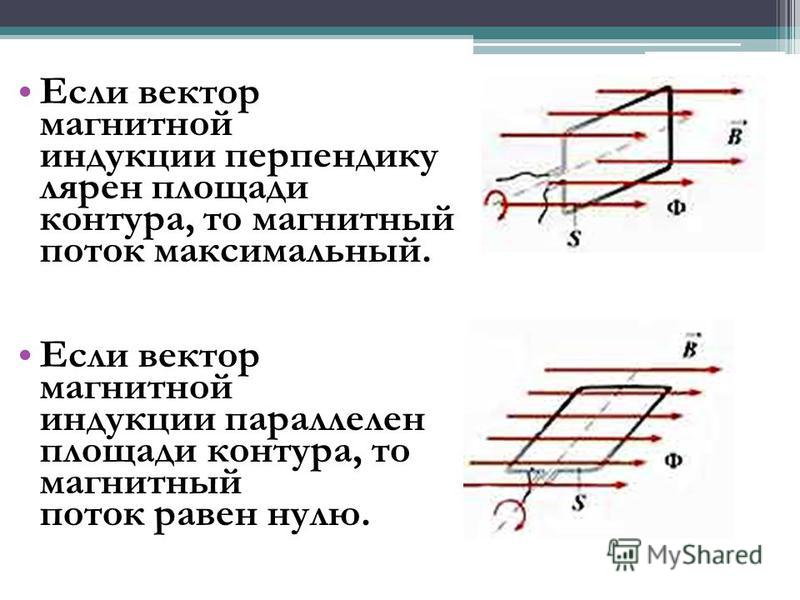Витки рамки будут охватывать некоторый поток Фх. В основу действия данного прибора положен принцип, согласно с которым первый наибольший отброс указателя баллистического гальванометра пропорционален числу

2.5: Плотность магнитного потока — Physics LibreTexts

Плотность магнитного потока — это векторное поле, которое мы идентифицируем с помощью символа \ ({\ bf B} \) и которое имеет единицы СИ в тесла (Т). Прежде чем предложить формальное определение, полезно рассмотреть более широкую концепцию магнитного поля .

Магнитные поля являются неотъемлемым свойством некоторых материалов, особенно постоянных магнитов. Основное явление, вероятно, знакомо и показано на рисунке \ (\ PageIndex {1} \).У стержневого магнита есть «полюса», обозначенные как «N» («север») и «S» («юг»). N-конец одного магнита притягивает S-конец другого магнита, но отталкивает N-конец другого магнита и так далее. Существование векторного поля очевидно, поскольку наблюдаемая сила действует на расстоянии и утверждается в определенном направлении. В случае постоянного магнита магнитное поле возникает из-за механизмов, происходящих в масштабе атомов и электронов, составляющих материал. Эти механизмы требуют некоторого дополнительного объяснения, которое мы пока отложим.

Рисунок \ (\ PageIndex {1} \): свидетельство векторного поля из наблюдений силы, воспринимаемой стержневыми магнитами справа в присутствии стержневых магнитов слева. (CC BY 3.0; Ю. Цинь).

Магнитные поля также появляются при наличии тока. Например, катушка с проводом, по которой проходит ток, влияет на постоянные магниты (и наоборот) так же, как постоянные магниты влияют друг на друга. Это показано на рисунке \ (\ PageIndex {2} \). Из этого мы заключаем, что основной механизм тот же — i.е. векторное поле, создаваемое токонесущей катушкой, представляет собой то же явление, что и векторное поле, связанное с постоянным магнитом. Каким бы ни был источник, теперь мы заинтересованы в количественной оценке его поведения.

Рисунок \ (\ PageIndex {2} \): Доказательство того, что ток также может создавать магнитное поле.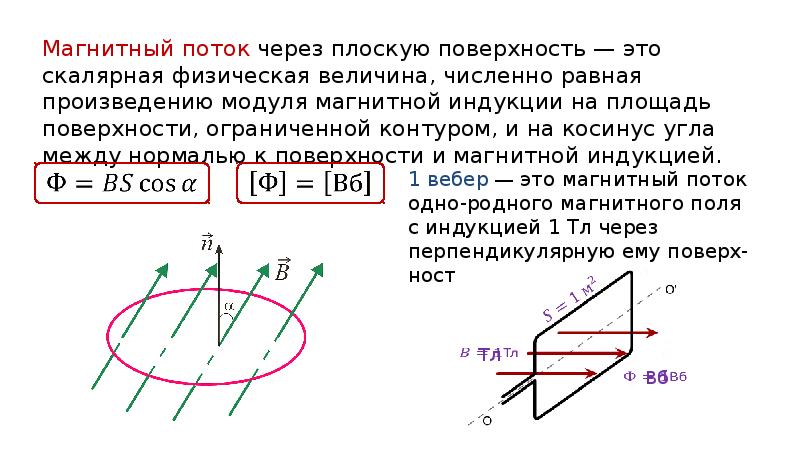 (CC BY 4.0; Ю. Цинь).

Для начала рассмотрим действие магнитного поля на электрически заряженную частицу. Во-первых, представьте себе область свободного пространства без электрических или магнитных полей. Затем представьте, что появляется заряженная частица.Эта частица не будет испытывать силы. Далее появляется магнитное поле; возможно, это связано с постоянным магнитом или током поблизости. Эта ситуация показана на рисунке \ (\ PageIndex {2} \) (вверху). Тем не менее, к частице не приложена сила. Фактически, ничего не происходит, пока частица не придет в движение. На рисунке \ (\ PageIndex {3} \) (внизу) показан пример. Внезапно частица воспринимает силу. Мы скоро перейдем к деталям о направлении и величине, но основная идея теперь очевидна.Магнитное поле — это то, что прилагает силу к движущейся заряженной частице, отличную от силы, связанной с электрическим полем (фактически, в дополнение к ней).

Рисунок \ (\ PageIndex {3} \): сила, воспринимаемая заряженной частицей, которая (вверху) неподвижна и (внизу) движется со скоростью \ (\ mathbf {v} = \ hat {\ mathbf {z}} v \ ), которая перпендикулярна плоскости этого документа и по направлению к читателю (CC BY 4. 0; Y. Qing).

Стоит отметить, что движущаяся одиночная заряженная частица представляет собой простейшую форму тока.Помните также, что для того, чтобы магнитное поле влияло на частицу, необходимо движение. Следовательно, не только ток является источником магнитного поля, магнитное поле также оказывает влияние на ток. Суммируя:

Магнитное поле описывает силу, действующую на постоянные магниты и токи в присутствии других постоянных магнитов и токов.

Итак, как мы можем количественно определить магнитное поле? Ответ из классической физики включает другое экспериментально выведенное уравнение, которое предсказывает силу как функцию заряда, скорости и векторного поля \ ({\ bf B} \), представляющего магнитное поле.Вот оно: сила, приложенная к частице, несущей заряд \ (q \), равна

.

\ [\ mathbf {F} = q \ mathbf {v} \ times \ mathbf {B} \ label {m0005_eFqvB} \]

где \ ({\ bf v} \) — скорость частицы, а «\ (\ times \)» обозначает перекрестное произведение. Перекрестное произведение двух векторов находится в направлении, перпендикулярном каждому из двух векторов, поэтому сила, создаваемая магнитным полем, перпендикулярна как направлению движения, так и направлению, в котором указывает магнитное поле.

Читатель будет вправе задаться вопросом, почему сила, создаваемая магнитным полем, должна быть перпендикулярна к \ ({\ bf B} \). В таком случае, почему сила должна зависеть от \ (\ bf v \)? Это вопросы, на которые классическая физика не дает очевидных ответов. Эффективные ответы на эти вопросы требуют концепций из квантовой механики, где мы находим, что магнитное поле является проявлением фундаментальной и удачно названной электромагнитной силы .Электромагнитная сила также усиливает электрическое поле, и только ограниченная интуиция, основанная на классической физике, заставляет нас воспринимать электрические и магнитные поля как отдельные явления. Для наших настоящих целей — и для наиболее часто встречающихся инженерных приложений — нам не нужны эти концепции. Достаточно принять эту кажущуюся странность как факт и действовать соответственно.

Анализ размеров \ ref {m0005_eFqvB} показывает, что \ ({\ bf B} \) имеет единицы измерения (N \ (\ cdot \) s) / (C \ (\ cdot \) m).В системе СИ эта комбинация единиц известна как тесла (Т).

Мы называем \ ({\ bf B} \) плотностью магнитного потока , и поэтому тесла — это единица плотности магнитного потока. Здесь уместно задать вопрос: что делает это плотностью потока? Короткий ответ заключается в том, что эта терминология несколько произвольна и на самом деле даже не является общепринятой. В инженерной электромагнетике предпочтение называть \ ({\ bf B} \) «плотностью потока» обусловлено тем, что мы часто обнаруживаем, что интегрируем \ ({\ bf B} \) по математической поверхности.2 \)) представляет собой описание магнитного поля, которое можно определить как решение уравнения \ ref {m0005_eFqvB}.

Рисунок \ (\ PageIndex {4} \): Магнитное поле стержневого магнита, иллюстрирующее силовые линии. (CC BY 4.0; Ю. Цин).

При описании магнитных полей мы иногда ссылаемся на концепцию силовой линии , определяемую следующим образом:

Линия магнитного поля — это кривая в пространстве, очерченная в направлении, в котором указывает вектор магнитного поля.

Эта концепция проиллюстрирована на рисунке \ (\ PageIndex {4} \) для постоянного стержневого магнита и на рисунке \ (\ PageIndex {5} \) для токонесущей катушки.

Рисунок \ (\ PageIndex {5} \): Магнитное поле токонесущей катушки, иллюстрирующее силовые линии. (CC BY 4.0; Ю. Цин).

Силовые линии магнитного поля примечательны по следующей причине:

Линия магнитного поля всегда образует замкнутый контур.

В некотором смысле это верно даже для силовых линий, которые кажутся прямыми (например, линии вдоль оси стержневого магнита и катушки на рисунках \ (\ PageIndex {4} \) и \ (\ PageIndex {5) } \), поскольку силовая линия, уходящая в бесконечность в одном направлении, снова возникает из бесконечности в противоположном направлении.

Авторы и авторство

Магнитный поток — Формула, единицы СИ и СГС

Магнитный поток

Поддисциплина физики в области электромагнетизма — это магнитный поток через поверхность, который относится к поверхностному интегралу нормали магнитного поля (B) компонент, проходящий через эту поверхность. Чтобы быть конкретным, магнитный поток определяется как количество силовых линий магнитного поля, проходящих через данную замкнутую поверхность.В этом конкретном сценарии рассматриваемая область может иметь любую ориентацию, соответствующую направлению магнитного поля, и любого размера.

(изображение будет скоро загружено)

Символ и формула магнитного потока

Магнитный поток обозначается греческой буквой Phi и обозначается символом Φ или ΦB.

Для расчета магнитного потока мы можем использовать приведенную ниже формулу:

ΦB = BA = BA cosΦ

Где,

ΦB = Магнитный поток

B = Магнитное поле

A = Площадь

Φ = Угол при котором силовые линии магнитного поля проходят через заданную площадь поверхности

Флюксметр используется для измерения магнитного потока.

(изображения будут загружены в ближайшее время)

SI Единица магнитного потока

Weber (Wb) — единица измерения магнитного потока в системе SI, названная в честь немецкого физика Вильгельма Эдуарда Вебера. Плотность потока, равная одному Веберу на квадратный метр или Вб / м2, равна одной тесла, обозначается буквой T (поясняется в следующем разделе). Довольно часто Вебер выражается во множестве других единиц, как показано ниже:

Wb = кг м2 / с2 A = Vs = HA = T.m2 = J / A = 108Mx

Где, Wb = Weber, T = Тесла, V = вольт, m = метр, J = джоуль, s = секунда, H = Генри, A = ампер и Mx = Максвелл.

Единица магнитного потока CGS

Единица измерения магнитного потока CGS — Максвелл (Mx) или Абвебер (abWb).

Основная единица магнитного потока

Основная единица магнитного потока — вольт-секунды.

Понятие «плотность магнитного потока»

Сила, действующая на единицу длины на провод, расположенный перпендикулярно (под прямым углом) к магнитному полю на единицу тока, является плотностью магнитного потока (B).

• Тесла (Тл) или кг / с A-1 — единица измерения плотности магнитного потока (В) в системе СИ.

• Плотность магнитного потока, обозначенная символом B, является векторной величиной

• Единицей измерения плотности магнитного потока в системе CGS является гаусс, который сокращенно обозначается как G или Gs

Формула для расчета магнитного поля. плотность потока выглядит следующим образом:

B = F / IL

Где,

F = общая сила, действующая на провод

I = ток, протекающий через провод

L = длина провода

Части Weber (Wb)

9

0

0

0 zeptoweber

Значение	Символ SI	Имя
10-1 Wb	7 db	d
10-2 Wb	cWb	сантивейбер
9 0056 10-3 Wb	mWb	milliweber
10-6 Wb	µWb	microweber
nanoweber
10-12 Wb	pWb	picoweber
10-15 Wb	10-15 Wb	10-18 Wb	aWb	attoweber
10-21 Wb	zWb	zeptoweber	yoctoweber

Кратные Weber

daWb

9056 MECO Wb

9056 9056 zettaweber

9056

Значение	Символ СИ	Имя
101 Wb	daWb	hWb	hectoweber
103 Wb	кВтb	киловебер
106 Wb14
106 Wb14	GWb	gigaweber
1012 Wb	TWb	teraweber
1018 Wb	EWb	exaweber
1021 Wb	ZWb	zettaweber	zettaweber

Магнитный поток — обзор

Максвелл исправил недостаток уравнения. 38.14 путем добавления так называемого тока смещения . Ток смещения связан с изменяющимся электрическим полем между пластинами конденсатора. Чтобы установить это соотношение, применим закон Гаусса к замкнутой поверхности, показанной на рис. 38.16. Поверхность содержит чистый заряд q — заряд на одной пластине конденсатора. Этот заряд является источником поля E между пластинами. Заряд q связан с электрическим потоком через поверхность по закону Гаусса (уравнение.38.13):

Рисунок 38.16. Заштрихованная гауссова поверхность содержит заряд q , который создает поле E между пластинами. И q , и E изменяются со временем, когда конденсатор заряжается и разряжается.

q∈o = ∫E · dA = ΦE

Заряд q изменяется со временем, потому что конденсатор заряжается. При изменении q изменяется и поле E . Скорость изменения на составляет

(38. 15) dqdt = εoddt∫E · dA

Здесь dq / dt — скорость, с которой заряд течет на пластину конденсатора; то есть dq / dt равно току в проводе, ведущем к пластине конденсатора.

I = dqdt

Максвелл понял, что величина

(38,16) εoddt∫E · dA≡Idisplacement

, которую он назвал током смещения , эквивалентна току в проводах по обе стороны от пластин конденсатора. .Ток смещения эквивалентен реальному току, потому что он создает такое же поле B . ^* Максвелл модифицировал закон Ампера, уравнение 38.14, добавляя ток смещения к обычному току. То есть в формуле. 38.14 заменил I на I + I _{смещение} . Модифицированная версия закона Ампера:

(38,17) B · ds = μoI + μoεoddt∫E · dA

Линейный интеграл ∮ B · d s оценивается вокруг периферии поверхности, над которой интеграл электрического потока ƒ E · d A (Рисунок 38. 17). В области между пластинами конденсатора нет обычного тока, только ток смещения, и уравнение. 38.17 уменьшается до

Рисунок 38.17.

(38,18) B · ds = μoεoddt∫E · dA

Эта особая форма закона Ампера описывает тот факт, что изменяющийся электрический поток индуцирует поле B . Напомним, что закон Фарадея (уравнение 38.12)

∮E · ds = −ddt∫B · dA = −dΦBdt

описывает, как изменяющийся магнитный поток индуцирует поле E . В совокупности уравнения.38.17 и 38.12 описывают связанный или взаимосвязанный характер изменяющихся во времени полей E — и B . Именно из-за этой связи мы говорим об «электромагнитном поле».

Гений Максвелла позволил ему открыть лежащее в основе единство электрических и магнитных явлений. В честь его вклада набор из четырех основных электромагнитных уравнений теперь называется уравнениями Максвелла :

(38,11) closedsurfaceB · dA = 0

(38,13) ∫closedsurfaceE · dA = qε0 (Гаусс)

(38. 12) ∮E · ds = −ddt∫B · dA (Фарадей)

(38,17) ∮B · ds = μoI + μo∈oddt∫E · dA (Ampère)

Основы магнитных измерений

Как магниты и узлы Прибытие на ваше предприятие от производителей магнитов, инженеры по контролю качества проводят измерения для подтверждения характеристик магнитных характеристик устройства. Тестирование может включать несколько процедур, использующих результаты измерения магнитного поля, в том числе:

• Сортировочные узлы
• Подтверждение зависимости характеристик магнитного поля от приложенного тока
• Отображение формы магнитного поля для компонента или сборки
• Измерение пограничных или остаточных полей
• Диагностика вредного воздействия внешнего поля
• Измерение рассеяния магнитного поля вокруг транспортного контейнера
• Измеритель воздействия магнитных полей на оператора, если применяются местные или федеральные правила

Правильное использование магнитных испытаний на протяжении всего процесса изготовления поможет гарантировать, что конечный собранный продукт или система будет работать так, как задумано.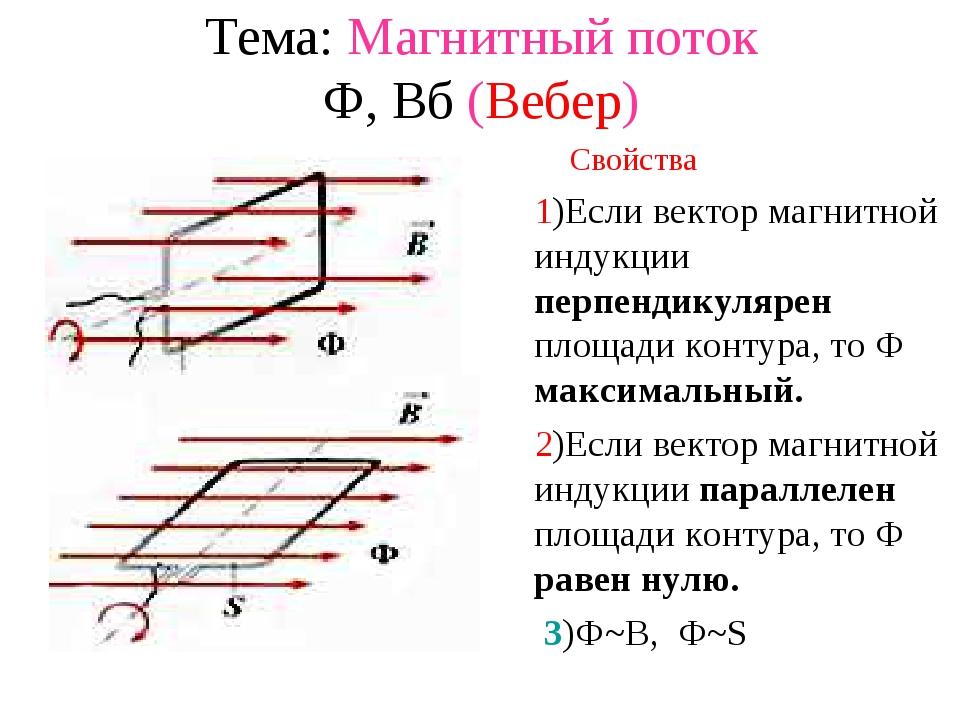

Магнитные единицы измерения

Для измерения магнитов требуется базовое понимание общих единиц измерения и методов определения характеристик магнитных полей. Если вы не привыкли работать с магнитами, такие термины, как тесла , гаусс и эрстед , могут показаться довольно чуждыми. Еще больше сбивает с толку использование в отрасли более одного стандарта измерения — cgs и SI. Хотя многие инженеры в США обычно используют cgs, SI — это система, которую предпочитают ученые и инженеры в мировом сообществе.Пока не будет четкого консенсуса в отношении использования той или иной системы, техническим специалистам и инженерам будет полезно знать, как использовать обе.

Некоторые магнитные блоки используются в промышленных приложениях из-за их удобства или соответствия конкретному применению. Несколько распространенных единиц cgs и SI и преобразований, с которыми столкнутся инженеры по контролю качества, показаны на рисунке 1.

	Кол-во		cgs		SI
	Флюс	Ø	максвелл (Mx)		Вебер (Вт)
	Плотность потока	В	гаусс (Г)		тесла (Т)
	Напряженность магнитного поля	H	эрстед (Oe)		А / м
	Магнитный дипольный момент	м	эму		Wm & Am 2
	Проницаемость	мкм			Г / м
	1 Вебер = 10 8 Максвелл
	1 тесла = 10000 гаусс
	1 эрстед = 79. 6 А / м
	(Вт · см) × (4π × 10 -5 ) = Am 2
	1 миллигаусс = 0,1 микротесла = 100 нанотесла
	1 миллитесла = 0,001 тесла = 10 гаусс
	1 гамма = 0,01 миллигаусс = 1 нанотесла

Рис. 1. Единицы измерения магнетизма

Для тех, кто плохо знаком с магнитными измерениями, полезно сначала рассмотреть магнитный поток, обычно обозначаемый как Ø.Основная составляющая потока, выраженная в единицах Макселла (Mx) или Вебера (W). Величина этого потока на единицу площади или плотности потока обозначается буквой B и выражается в значениях Гаусс (Г) или тесла (Т). Это составляющая поля, измеряемая естественным образом датчиком Холла на основе тесламетра / гауссметра. Плотность потока (B) связана с напряженностью магнитного поля (H), которая естественным образом измеряется с помощью флюксметра.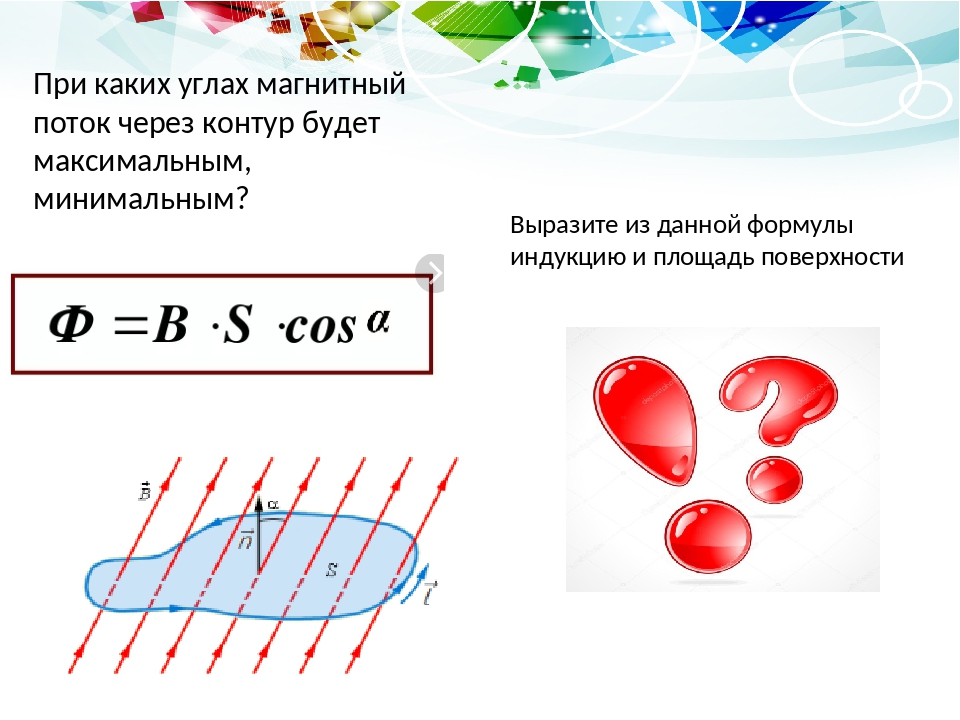

Хотя эти два типа инструментов измеряют несколько разные параметры магнитного поля, между ними возможно преобразование с помощью следующего соотношения:

B = мкГн

Это уравнение служит основой для дополнительного измерения напряженности магнитного поля (H) в воздухе (µ — известная постоянная) с помощью тесламетра на эффекте Холла.Проницаемость (µ) — это мера легкости, с которой магнитное поле течет в среде.

Для измерения магнитных полей требуются специальные датчики и знания физики и электроники. Для измерения магнетизма можно использовать различные инструменты, включая тесламетры, флюксметры и магнитометры.

Независимо от того, какой инструмент вы используете, правильная техника важна для получения точных результатов. Узнайте, как предотвратить ошибки, загрузив технический документ «5 самых распространенных источников ошибок в магнитных измерениях».

Колючие структуры электрического и магнитного поля в экспериментах с флюсовым жгутом

Значение

Явления, исследованные в этой статье, имеют отношение к общей теме границ раздела и перемешивания в контексте многомасштабного переноса в условиях неравновесной плазмы, и эти явления хорошо подходят в тему этого Специального выпуска. Тросы с магнитным потоком состоят из спиральных магнитных полей с переменным шагом, и в многомасштабных процессах, таких как индуцированные магнитные и электрические структуры, встраиваются в веревки с магнитным потоком.Между магнитными жгутами спонтанно возникают структуры во временной области (TDS), которые связаны с магнитным пересоединением. Колючие нелинейные структуры доминируют в электрическом и магнитном поле и не описываются простым степенным законом. Они не предсказываются теорией жидкости и могут быть основным фактором в развитии новых теорий турбулентности.

Abstract

Жгуты магнитного потока — это структуры, которые обычны в короне Солнца и, предположительно, всех звезд. Их можно рассматривать как строительные блоки солнечных структур.Их наблюдали в хвосте магнитосферы Земли, а также около Марса и Венеры. Когда присутствует несколько магнитных жгутов, при их столкновении может происходить пересоединение силовых линий магнитного поля, которое преобразует магнитную энергию в другие формы. Структура нескольких магнитных веревок, взаимодействия между несколькими веревками и их топологические свойства, такие как спиральность и изгиб, изучались теоретически и в лабораторных экспериментах. Здесь мы сообщаем об остроконечном потенциале и магнитных полях, связанных с веревками.Мы показываем, что потенциальные структуры хаотичны для диапазона их временных полуширин, а функция плотности вероятности (PDF) их ширины напоминает статистическое распределение мятой бумаги. Пространственная структура магнитных пиков выявляется методом корреляционного счета. Компьютерное моделирование предполагает, что потенциальные структуры являются нелинейным конечным результатом нестабильности, связанной с относительным дрейфом между ионами и электронами.

Во многих лабораторных экспериментах и ​​наблюдениях на космических аппаратах были зарегистрированы узкие всплески электрического потенциала.Например, лабораторные эксперименты по распространению мощных микроволн в градиентах плотности показали узкие области интенсивного электрического поля, где частота падающей электромагнитной волны соответствует локальной плазменной частоте. Их назвали кавитонами (1), поскольку они сопровождались снижением плотности в этих местах. Эти структуры впоследствии были замечены в ионосфере Земли с помощью наземных антенн в Аресибо, Пуэрто-Рико (2, 3), а также созданы в экспериментах по радиочастотному нагреву на Аляске (4).Другие структуры включают дырки в электронном фазовом пространстве, которые представляют собой всплески размера Дебая, которые появляются в электрическом потенциале. Их видели в нескольких местах в космосе (5⇓ – 7) и наблюдали в лаборатории (8). Возможно, что связанные с ними электрические поля рассеивают электроны и приводят к увеличению удельного электрического сопротивления. Эксперименты по переносу тепла (9) с использованием небольшого эмиттера электронов в фоновой магнитоплазме показывают, что генерируемая турбулентность состоит из возмущений электронной температуры лоренцианской формы, которые приводят к экспоненциальному спектру мощности (10).Структуры временной области (11) (TDS) — название, первоначально данное пакетам электрического поля, обнаруженным космическим аппаратом (12), может быть названием, которое включает в себя все различные вышеупомянутые структуры. Данные зонда Ван Аллена показывают (13), что наблюдаемые ТДС движутся вдоль силовых линий магнитного поля со скоростью, соответствующей скорости электронов от 100 до 200 эВ. Это было близко к тепловой скорости электронов в их условиях и было идентифицировано как электронно-акустические возмущения. TDS, как правило, возникают в большом разнообразии масштабов, начиная от такой малой, как длина Дебая, до глубины электронного скин-слоя и, возможно, большего размера поперек магнитного поля и до альвеновских длин волн вдоль поля.Их много, и они считаются нелинейным конечным состоянием турбулентности. Здесь мы сообщаем о наблюдении как магнитных, так и потенциальных структур, встроенных в магнитопроводы. Они оба демонстрируют узкие, похожие на шипы временные сигнатуры, но, похоже, не связаны друг с другом. Используя статистические методы, мы идентифицируем пространственную структуру, связанную с магнитным TDS (обозначенным TDS _m ), а также показываем, что электрический TDS _e связан с магнитным пересоединением в сталкивающихся веревках.

Жгуты магнитного потока представляют собой структуры со спиральными магнитными полями (и токами), которые, как известно, возникают в космосе и в астрофизической плазме (14, 15). Что отличает их от простых токовых нитей, так это то, что азимутальное магнитное поле, связанное с их током, достаточно велико, чтобы заставить их стать нестабильными изгибами и взаимодействовать с соседними веревками, если они присутствуют. Жгуты потока обычно возникают в пограничном слое магнитопаузы Земли и в хвосте магнитосферы. Поверхность солнца усеяна нитями флюса, которые в УФ или рентгеновском излучении видны как дугообразные нити.Столкновения веревок, происходящие на Солнце, можно имитировать в лаборатории, если потоки веревок пропускают достаточно тока, чтобы изгибы были нестабильными (16). При превышении порога тока кинка каждое столкновение приводит к преобразованию некоторой магнитной энергии в тепло, потоки и волны, что является фундаментальным для процессов пересоединения силовых линий магнитного поля (17).

Экспериментальная установка

Эксперименты с флюсовым жгутом проводились в большом плазменном устройстве (LAPD) (18) в Калифорнийском университете в Лос-Анджелесе (UCLA).В качестве источника плазмы используется катод диаметром 60 см, покрытый оксидом бария (19). Разряд постоянного тока применяется между катодом и анодом, расположенным на расстоянии 50 см, и генерируется импульсами с частотой следования 1 Гц в течение нескольких месяцев с использованием мощного транзисторного ключа (20). LAPD имеет более 450 портов доступа, в которые можно ввести различные датчики с помощью станций вакуумной откачки. Параметры плазмы: ( n _e <3 × 10 ¹² см ⁻³ , T _e = 4–5 эВ, T _i = 1 эВ, δn / n = 3%, L = 18 м, диаметр = 60 см, He).Схема эксперимента представлена ​​на рис. 1 B . Для создания магнитных жгутов второй катод, изготовленный из LaB ₆ с высокой излучательной способностью, был вставлен рядом с концом устройства, противоположным катоду образования плазмы. Второй транзисторный ключ, подключенный к аноду, расположенному на расстоянии 11 м, питал соответствующий разряд веревки. Для создания магнитных жгутов катод LaB ₆ был замаскирован, заставляя эмиссию электронов проходить через отверстия в маске, создавая азимутальные магнитные поля, достаточно большие (5–30 Гс) для генерации магнитных жгутов.

Рис. 1.

( A ) Силовые линии двух магнитных жгутов (синего и оранжевого цвета), исходящие из двух немаскированных областей катода LaB ₆ диаметром 8 см. Справа показаны поверхность и контуры плотности тока троса. Длина в направлении z на этом рисунке составляет 10 м. ( B ) Схема экспериментальной установки, иллюстрирующая производство фоновой плазмы и схему, используемую для включения тросов. Веревки начинаются с z = 0.Движение веревок можно увидеть в фильме S1.

Магнитный ТДС

_м

При исследовании магнитного ТДС _м использовались три экспериментальные геометрии магнитных канатов. В первой конфигурации (случай 1) две веревки диаметром 7,5 см каждая были разделены по вертикали на 1 см (от края до края) в точке их формирования. Общий ток каната составлял 600 А, при напряжении разряда В _канат = 125 В (5,8 А / см ² , 850 Вт / см ² ).Во второй конфигурации (случай 2) две веревки меньшего размера диаметром 3 см каждая, разделенные по горизонтали на 1 см ( I _D = 105 А, В _D = 210 В, 7,8 А / см ² , 500 Вт / см ² ). Третья конфигурация (случай 3) представляла собой одинарный флюсовый жгут с радиусом 2,5 см и током троса и напряжением I _трос = 130 А и В _трос = 100 В (6,6 А / см ² , 662 Вт / см ² ).Объемные данные в десятках тысяч местоположений и временных шагов ( δt = 3,2 × 10 ⁻⁷ с, nt = 24000) были получены для всех трех конфигураций. Производная магнитного поля по времени измерялась с помощью трех трехосных 10-витковых дифференциально намотанных магнитных зондов диаметром 3 мм. В первых двух случаях наблюдался квазисеператрисный слой (21), свидетельствующий о пересоединении силовых линий магнитного поля. В случае 1 данные о магнитном поле были получены в 2810 пространственных точках в каждой из 15 плоскостей (64 см < z <960 см), поперечных фоновому магнитному полю.Трехосный магнитный эталонный зонд помещали на край тросов. Это использовалось для генерации данных, необходимых для усреднения данных с помощью условного триггера (22). Было обнаружено, что веревки с неустойчивым изгибом скручиваются друг вокруг друга и перемещаются по эллиптической схеме с частотой около 5 кГц и периодически повторно соединяются (17).

Рис. 2 A показывает временную кривую одной компоненты магнитного поля, B _x , из одного экспериментального примера случая 1.На рис. 2 B показаны спектры B _x , измеренные отдельным датчиком, зафиксированным в позиции на протяжении всего эксперимента в случае 1. Быстрое преобразование Фурье (БПФ) каждого из 28 050 снимков было получено из Компонента x магнитного поля усредняется, а затем наносится на график в логарифмическом масштабе, как показано на рис. 2 B . Низкочастотные колебания проявляются в виде когерентных пиков, а экспоненциальная область указывает на многочисленные лоренцевы импульсы в данных (23).Используя следующую методику, была определена «средняя» пространственная картина всплесков магнитного поля. Сначала ко всем трем компонентам магнитного поля был применен фильтр верхних частот ( f > 25 кГц) для устранения сигналов перегиба. Затем для каждого кадра в каждой позиции выполнялось БПФ. Затем определяется ширина лоренцевского импульса τ _L путем подгонки прямой линии к наклону экспоненты (рис. 2 B ). В случае 2 для веревок, показанных на рис.3 B (и график времени выборки на рис. 2 C ), τ _L составляет 5 мкс, но отличается от импульса к импульсу. Ширина импульса обычно распределяется с полушириной на полувысоте δt _L = 1 мкс.

Рис. 2.

( A ) B _x ( t ) для одиночного импульса в случае 1. Сигнал датчика B-точки был интегрирован и откалиброван и находится в гауссах. ( B ) Средние спектры Bx в логарифмической шкале, показывающие экспоненциальный хвост при f > 25 кГц.Пики на низкой частоте отражают вращение канатов. ( C ) Однократная трассировка B _x ( t ) для веревок меньшего размера в случае 2, которые имеют вдвое большее напряжение разряда по сравнению со случаем 1 ( A ). «Колючая» природа магнитного поля очевидна.

Рис. 3.

Магнитное поле среднего TDS _m для трех разных случаев, показывающее их структуру в плоскости, поперечной фоновому магнитному полю.( A ) Флюсовые канаты для случая 1 диаметром 7,5 см каждый показаны на рис. 1. В _канат — это напряжение разряда каната, а плотность тока около источника канатов составляет 5 А / см. ² . ( B ) Случай 2: канаты меньшего размера с более высоким разрядным напряжением. В магнитном сигнале намного больше всплесков и структура более четкая, чем в A . ( C ) Случай 3 TDS _{m Морфология} для одинарного флюсового жгута. Во всех случаях δz — это расстояние каждой веревки до исходной точки.

Используя этот метод, строится лоренциан для трех компонентов B (t), каждая с соответствующей шириной, τ _L . Затем лоренцевы коррелируют с отфильтрованными данными, и точки, которые превышают 80% пороговое значение коэффициента корреляции, сохраняются. Их количество и амплитуды усредняются в каждом месте расположения зонда. Если бы пики были полностью случайными, то картина магнитного поля была бы векторами, случайными по величине и ориентации.Это не тот случай. Магнитное поле иглы для трех случаев показано на рис. 3.

Мы предполагаем, что векторные графики, созданные методом подсчета спайков, отражают среднюю мгновенную структуру среднего TDS _m . На Рис. 3 A пространственная структура напоминает структуру вертикально смещенных веревок, наблюдаемых в случае 1 (Рис. 1 A ). Временное магнитное поле, показанное на рис. 2 A , имеет резкие черты, и хорошо видны колебания веревки с частотой 5 кГц.Флюсовые жгуты корпуса 2 также были хаотичными (24), и их соответствующий рисунок показан на рис. 3 B . Он отражает расположение тросов бок о бок, как показано на рис. 1. В случае 3, который представляет собой одиночный флюсовый жгут (25), не было очевидных источников повторного соединения. Однако TDS _м с не наблюдалось. Образцы, показанные на рис. 3, представляют собой снимки топологии среднего TDS _м в трех различных случаях. Нет никакой априорной причины, по которой лоренцевы спайки имеют четко определенную структуру.

Магнитные пики также наблюдались в эксперименте с одиночным флюсовым жгутом (26) в Университете Висконсин-Мэдисон и были приписаны внутреннему пересоединению, а одиночный жгут также наблюдался после инъекции сферомака в линейное устройство (27). Рис. 3 C — диаграмма магнитного поля TDS _м для корпуса с одинарным магнитным канатом. Магнитное поле TDS _m во всех этих случаях составляет порядка 1 мГс, что намного меньше (в 10 ⁻⁴ раз), чем у самих канатов.Канаты могут иметь азимутальные поля величиной до 30 Гс. Было показано, что переход от когерентных к некогерентным магнитным сигналам для одиночного каната (25) зависит от тока каната, а не от входной мощности. Во всех трех случаях, показанных на рис. 3, геометрия существенно различается. Однако плотность тока в случаях 2 и 3 больше, чем в первом случае. На рис. 3 показаны еще тысячи лоренцевых пиков, и их паттерны более четко очерчены.

Электростатические импульсы (TDS

_e )

Данные о высокочастотном потенциале и электрическом поле были получены с помощью трехосных электрических дипольных зондов.Каждый из шести наконечников зонда был внутренним проводником высокочастотного коаксиального кабеля с медным покрытием. Каждый наконечник измерял «плавающий» потенциал, а разность напряжений между каждой парой использовалась в качестве прокси для электрического поля. Потенциал на каждом наконечнике получается путем прекращения сигнала 50 Ом для максимального временного отклика, поэтому, строго говоря, это не плавающий потенциал. Ток зонда был порядка 10 мА. На рис. 4 показан потенциал как функция времени для одного выстрела, измеренный на концах двух зондов.Один датчик фиксируется в ( δx = δy = 0, δz = 767,8 см), а другой перемещается и размещается в том же месте ( y , z ) и разнесен в x на 7,5 мм. Задержка в 4 мкс между сигналами указывает на то, что TDS _e s (рис. 4 B ) движется поперек магнитного поля со скоростью 1,9 × 10 ⁵ см / с. Шипы не воспроизводятся; они возникают в разное время и имеют различную высоту для каждого случая использования флюсовых жгутов.Они никогда не превышают 2 В по величине и в отличие от TDM _m всегда отрицательны. Полуширина потенциального выброса находится в диапазоне от 1 до 50 мкс, в то время как дырки в электронном фазовом пространстве, наблюдаемые в устройстве LAPD (24), имеют время жизни в несколько раз больше обратной плазменной частоты, составляющей 1–10 нс. Два зонда также использовались для корреляции сигналов. Тридцать выстрелов были сохранены в каждом месте для обоих зондов, поскольку подвижный зонд сделал выборку из 2090 точек в плоскостях xz и xy . На обоих датчиках были идентифицированы одиночные иглы, а расстояние между зондами и временная задержка от зонда к зонду показали, что иглы перемещались в плоскости, поперечной фоновому полю, примерно со скоростью ионного звука.Данные использовались для расчета функций плотности вероятности (PDF), пространственных и временных корреляций, средних пространственных местоположений и средних скоростей выбросов. Ширина выступов на трех ортогональных наконечниках в зависимости от амплитуды показана на рис. 5 A . Данные, в которых величина напряжения была меньше 0,1 В, не показаны, поскольку они приближаются к шуму. Видно, что самые большие шипы имеют наименьшую ширину.

Рис. 4.

( A ) Первые 4 мс типичного импульса электрического потенциала как функции времени от одного наконечника на фиксированном датчике (красная кривая) и подвижного датчика (черный).( B ) Расширенный временной ряд, показывающий интервал 320 мкс в A . Один TDS _e , зарегистрированный обоими зондами. Приблизительная временная ширина на полувысоте оценивается в 100 мкс. Каждая последовательность данных была получена для 299000 временных шагов ( δt = 20 нс).

Рис. 5.

( A ) Распределение ширины иглы в зависимости от величины. N указывает количество выступов, используемых на рисунке. Пики с величиной менее 0,1 В не показаны.( B ) PDF амплитуд всплесков для одного компонента фиксированного зонда (Vx) показаны черным цветом. Синяя кривая представляет собой функцию логнормального распределения с наименьшими квадратами с σ = 0,695, µ = -0,879 и x ₀ = 0,058, а красная кривая — это гамма-распределение с x ₀ = 0,1112, β = 1,410 и α = 3,8256. Все параметры подогнаны с точностью до ± 10 ^-4 .

PDF величин спайков показана на рис.5 B , хорошо согласуется с функцией логнормального распределения, но также очень близко к смещенному гамма-распределению. По совпадению, это те же PDF, что и для длин гребней клубка скомканной бумаги (28, 29). Бумагу измельчают в шар и разрезают пополам, после чего определяют длину каждого сгиба и нормируют на их среднюю длину. PDF — это функция логнормального распределения, когда бумага раздавлена ​​с большим средним радиусом кривизны на сгиб (слабое удержание) и гамма-распределением для сильно смятых складок.Аналогом электростатических шипов может быть то, насколько плотно они упакованы в пространстве. Шипы, расположенные рядом друг с другом, будут отталкивать друг друга, поскольку все они отрицательны, что аналогично сопротивлению раздавленной бумаги механическим силам. В этом эксперименте соответствие логарифмической норме немного лучше, но разница, скорее всего, заключается в шуме.

Где находятся потенциальные всплески? Пространственное распределение пиков TDS _e может быть выведено из средней величины всех пиков, подсчитанных в конкретном месте x – y .Это показано на рис. 6 для поперечной плоскости ( x – y ) при δz = 767,8 см. Самые большие всплески видны в области пересоединения между веревками, за ними следуют меньшие всплески градиента тока на краю веревок. Чтобы установить пространственное и временное развитие временных последовательностей TDS _e , как показано на Рис. 4 A , каждая временная последовательность была сегментирована на 21 интервал, а положения TDS _e нанесены на график в виде конусов Гаусса на Рис.7. Показаны три разных момента на одной и той же плоскости. Конструкции TDS _e занимают край двух канатов. Область между веревками с центром ( x , y ) = (0,1 см) является местом пересоединения силовых линий магнитного поля. Между тросами проходит слой квазисеператрисы (30), область, в которой силовые линии магнитного поля пространственно расходятся и указывают на пересоединение. На рис. 7 показано положение наибольших значений TDS _e s в три раза на одной и той же поперечной плоскости.Данные были синтезированы путем суммирования результатов 30 выстрелов в каждой позиции вместе с вкладами от V _{+ x} , V _{+ y} и V _{+ z} on подвижный зонд.

Рис. 6.

Распределение величины пиков потенциала в поперечной плоскости при z = 767,8 см. Есть до 1890 всплесков в каждом из 441 местоположения на плоскости, в которых были получены данные.Цветная полоса показывает среднее абсолютное значение В _y в вольтах.

Рис. 7.

Расположение TDS _e в три разных момента в течение 6-миллисекундного интервала, показанного на рис. 4 A . TDS _e s берут начало в точке «X» между магнитными жгутами, которая находится в центре плоскости, и развиваются во времени, перемещаясь по периферии токовых каналов. Высота маркеров пропорциональна количеству TDS _e s в этом месте.

Данные, представленные на рис. 7, предполагают, что TDS _e s исходит из области пересоединения, которая подробно описана в предыдущих исследованиях (22, 30). Впоследствии они мигрируют к краю веревок, где, как показано на рис. 6, их наиболее вероятно можно найти. Не следует путать гауссовские пики на рис. 7, которые служат инструментом визуализации маркеров местоположения, с реальной формой TDS _e s. Их структуру можно определить с помощью трехмерного корреляционного анализа или подсчета пиков, как это делается с магнитными сигналами.Это потребует сбора большого количества данных (терабайт) и недель машинного времени, и будет предметом будущих исследований.

Что это за структуры и влияют ли они на фоновую плазму и влияют на поведение веревки? Было показано, что сами потоки потока хаотичны, что подтверждается анализом сложности и энтропии Дженсена – Шеннона (31–34). Хаос не проявляется в усредненных данных, как на рис. 1 A . Для визуализации хаотической структуры потребуется 42000 зондов (или примерно такое же количество собранных точек данных), которые регистрируют все три компонента магнитного поля в одном экспериментальном примере.

Первым шагом в вычислении сложности является определение энтропии. Энтропия перестановки Бандта – Помпе временного ряда (31) позволяет вычислить энтропию временного ряда в присутствии шума. Как и в случае с энтропией, связанной с термодинамическими системами, большая энтропия отражает беспорядок. Затем энтропия используется для определения сложности Дженсена – Шеннона (32). Эти величины затем используются для построения диаграммы энтропии сложности на так называемой плоскости C (сложность), H (нормализованная энтропия).Плоскость C – H представляет собой график сложности по ординате и энтропии по абсциссе. Плоскость C – H позволяет отличить детерминированный хаос от случайного шума и используется для изучения множества явлений. Например, Зунино и др. (33) использовали плоскость C – H для изучения аммиачного лазера (хаотический), течения в реке (хаотический), североамериканских колебаний атмосферы (стохастический), динамики цен на сырую нефть и золото (стохастический, а не детерминированный) и человеческий фактор. динамика осанки (шумная и хаотичная). Впервые он был использован для плазмы, насколько нам известно, Мэггсом и Моралесом (34) для классификации флуктуаций электронной температуры в транспортном эксперименте.Затем он был распространен на изучение магнитных флуктуаций в эксперименте с магнитным жгутом, как описано здесь (20). Методика построения плоскости C – H подробно описана в двух предыдущих ссылках (20, 34). Они показаны с данными для потенциальных всплесков (рис. 8), а также сложности и энтропии для нескольких процессов. Например, в левом нижнем углу появляется синусоида с небольшой энтропией и сложностью. Сильно случайные процессы, такие как дробное броуновское движение, имеют большую энтропию, но небольшую сложность, и расположены в правом нижнем углу.Также показаны несколько хаотических процессов, таких как карта Хенона, двойной маятник и т. Д. Эти процессы приводят к хаотическим временным рядам, но описываются итерационными картами или дифференциальными уравнениями. Точки на плоскости C – H окрашены в соответствии с их частотой, определяемой их временной полушириной. Значение, обратное этой частоте, интерпретируется как типичная ширина пика. В центре плоскости C – H находятся высоко хаотические процессы, имеющие большую сложность, но среднюю энтропию. Очень короткоживущие всплески TDS лежат близко к кривой дробного броуновского движения и связаны со случайным шумом.Остальные TDS со временем жизни более 2 мс кажутся хаотическими; наиболее хаотичные ТДС имеют время жизни порядка 1–3 мкс. Наибольшие напряжения TDS _и составляют порядка -2,0 В. Для получения временной сигнатуры электрического поля E → = -∇Vp использовались два расположенных рядом наконечника зонда, расположенных на расстоянии 2 мм, но не быть абсолютно откалиброванным из-за чехлов. Данные предполагают, что оно может достигать 100 В / м, но это только оценка.

Рис. 8.

Плоскость C – H. По оси абсцисс отложена нормализованная энтропия Бандта – Помпа, а по оси ординат — сложность Дженсена Шеннона.Данные, показанные в виде цветных точек, ограничены кривыми минимальной и максимальной сложности. Точки на плоскости C – H эффективно окрашиваются в соответствии с полушириной найденных шипов. Также показано несколько итерационных карт. Случайный шум, который имеет большую энтропию и не является сложным, виден в правом нижнем углу кривой дробного броуновского движения. Датчик расположен в ( x , y , z ) = (0, 0, 767,8 см). Для создания этого графика использовались тридцать временных рядов длительностью 4,2 мс ( δt = 0,66 мкс) Vx.Ионная циклотронная частота 126 кГц.

Обсуждение и выводы

Магнитные и электростатические TDS наблюдались в плазме в сочетании с флюсовыми жгутами. Данные указывают на то, что они не связаны напрямую. TDS _м с наблюдались в двух разных экспериментах, связанных со столкновениями флюсового жгута, а также наблюдались при наличии только одного флюсового жгута. Корреляция магнитных сигналов (отфильтрованных намного выше частот вращения пиков) с лоренцевыми, генерируемыми с использованием экспоненциального спектра в данных, дала морфологию TDS _m .Конструкции похожи на веревки, но недолговечны. Пространственные узоры имеют длину несколько метров и теряются при столкновении флюсовых жгутов. В случае одинарного флюсового жгута рисунки сохраняются на протяжении 10 м. Потенциальные структуры не являются лоренцианами и хаотичны в диапазоне своей полуширины. Их морфология определят будущие корреляционные исследования. Предыдущая работа показала, что магнитные поля, связанные со столкновениями магнитных жгутов, являются хаотическими (24). Отдельный анализ плоскости C – H магнитного TDS _m показывает, что они также хаотичны.

TDS _m s имеет очень малые магнитные поля и вряд ли будет рассеивать частицы или воздействовать на веревки. Их можно рассматривать как «магнитную пену», обломки резкого движения, нагрева и электрических полей веревок. Данные с двумя веревками предполагают, что повторное соединение может играть роль в их образовании.

Пики потенциала, с другой стороны, довольно велики с потенциалами порядка 10% от температуры фоновых электронов. Электронные всплески могут вносить вклад в TDS _e , но маловероятно, что они будут медленно дрейфовать поперек магнитного поля, как показано на рис.4 Б . Колебания температуры могут вносить вклад в колебания (35), но экспериментальное измерение этого затруднено. Электрический потенциал TDS _e s, по-видимому, возникает в области пересоединения, и его величина является наибольшей на краю токовых каналов магнитного жгута. Грубые оценки их электрических полей показывают, что они могут рассеивать частицы. Предыдущее исследование показало, что удельное сопротивление канатов аномально и не может быть описано местным законом Ома (36, 37). TDS _e s может сыграть в этом свою роль.Из рис. 3 мы делаем вывод, что размер TDS _m в поперечном масштабе составляет 3–10 см, а осевая длина — несколько метров. Предварительный корреляционный анализ показывает, что TDS _e s имеет размер шкалы порядка 1 см.

В качестве первого шага в понимании происхождения электростатических импульсов мы рассматриваем модель, управляемую током, в которой предполагается, что относительный дрейф электронов и ионов превышает скорость ионного звука. В эксперименте скорость дрейфа превышает скорость звука в 4–5 раз.Двухмерная имитационная модель частиц в ячейках, которая следует за электронами и ионами и включает электрон-ионные столкновения, используется для моделирования роста и нелинейной эволюции электрического потенциала. Продольный ток инициализируется со скоростью дрейфа, которая в два раза превышает скорость ионного звука, и, как показано на рис.9, A приводит к возникновению управляемой током ионно-акустической неустойчивости, которая нарастает примерно на несколько сотен обратных ионных плазм. периоды. Давно известно, что ионно-акустическая неустойчивость может быть кандидатом в аномальное сопротивление в плазме (38).После насыщения неустойчивости нелинейные электрические потенциальные структуры развиваются и медленно дрейфуют примерно со скоростью ионного звука. Доминирующая длина волны флуктуаций в начале насыщения порядка 0,1 λ _e , где λ _e — длина свободного пробега электрона и иона. Для экспериментальных параметров длина свободного пробега составляет порядка 15 см; поэтому, согласно моделированию, доминирующая длина волны флуктуаций электростатического потенциала составляет примерно 1–1,5 см и на несколько порядков больше, чем масштаб длины Дебая электрона, который будет доминировать в бесстолкновительной ионно-акустической неустойчивости.Этот управляемый током механизм ионно-акустической нестабильности создает отрицательные провалы электростатического потенциала, показанные на рис. 9 B , которые имеют приблизительно величину (приблизительно от -0,2 до 0,4 В) и ширину импульса (∼4-6 мкс) TDS. которые берут начало в области пересоединения в эксперименте, а затем конвектируются в область гало магнитных жгутов. Дальнейшие исследования этого механизма и связи с магнитными пиками изучаются и будут сообщены в другом месте.

Рис. 9.

Частичное моделирование токовой ионно-акустической неустойчивости с начальным относительным электрон-ионным дрейфом V _de = 2 C _s , где C _s — скорость звука иона. Полная энергия электростатического поля ( A ) и электрический потенциал ( B ) в зависимости от времени в фиксированной позиции x в моделировании.

Благодарности

Мы благодарим Джорджа Моралеса за многие полезные обсуждения.Мы также благодарим Золтана Лаки, Марвина Дранделла и Тай Ли за их квалифицированную техническую поддержку. Эксперименты проводились в лаборатории фундаментальных исследований плазмы в Калифорнийском университете в Лос-Анджелесе и финансировались Управлением исследований термоядерной энергии Министерства энергетики и Национальным научным фондом (при финансовой поддержке грантов NSF-PHY-1036140 и DOE-DE-FC02-07ER54918).

Сноски

• Вклад авторов: W.G., S.W.T., T.D., S.V., P.P. и R.S. проведенное исследование; W.G., S.W.T., T.D., S.V. и R.S.проанализированные данные; W.G. написал статью; и С.В. и Р.С. помогли в написании / редактировании.

• Авторы заявляют об отсутствии конфликта интересов.

• Эта статья представляет собой прямое представление PNAS. S.I.A. Приглашенный редактор по приглашению редакционной коллегии.

• Эта статья содержит вспомогательную информацию на сайте www.pnas.org/lookup/suppl/doi:10.1073/pnas.1721343115/-/DCSupplemental.

Магнетизм — Измерение магнитного поля — Called, Measured, Current и Squid

Магнитное поле или магнитный поток Плотность измеряется в метрических единицах гаусс (Г) и соответствующей международной системной единице тесла (Тл).Напряженность магнитного поля измеряется в метрических единицах эрстеда (Э) и международных единицах ампер на метр (А / м). Инструменты, называемые гауссметрами и магнитометрами, используются для измерения величины магнитных полей.

Один из видов гауссметра, который обычно используется в лаборатории, состоит из токонесущего полупроводникового элемента, называемого зондом Холла, который размещается перпендикулярно измеряемому магнитному полю. Как следствие так называемого эффекта Холла перпендикулярное напряжение Компьютерное изображение подковообразного магнита с выровненными вокруг него железными опилками. Фотография Альфреда Пасека. Библиотека научных фотографий, Коллекция Национального общества Одубона / Photo Researchers, Inc. Воспроизведено с разрешения. к полю и к току, генерируемому в зонде. Это индуцированное напряжение пропорционально измеряемому магнитному полю и может быть просто измерено с помощью вольтметра.

Магнитометры — чрезвычайно чувствительные детекторы магнитного поля. В одной из часто используемых форм магнитная сила обнаруживается с помощью чувствительных электронных весов.В этом приборе магнитное вещество помещается на одно плечо весов, которое, в свою очередь, помещается в магнитное поле. Затем магнитная сила, действующая на образец, определяется весом, необходимым для уравновешивания силы, создаваемой магнитным полем. Самый чувствительный магнитометр в современной физической лаборатории использует магнитный чувствительный элемент, называемый СКВИД (что означает сверхпроводящее квантовое интерференционное устройство). СКВИД состоит из чрезвычайно тонкого электрически резистивного перехода (называемого джозефсоновским переходом) между двумя сверхпроводниками.Сверхпроводники — это материалы, которые при низких температурах претерпевают переход в состояние с нулевым электрическим сопротивлением и почти полным исключением магнитных полей. В режиме работы на постоянном токе СКВИД сначала охлаждается до сверхпроводящего состояния, а затем через него пропускается ток, при этом контролируется напряжение на переходе. Когда соединение воспринимает магнитное поле, поток тока изменяется из-за явления интерференции на квантовом уровне между двумя электронными волновыми фронтами через соединение, что приводит к изменению напряжения.Интерференция — это явление, которое обычно возникает из-за смешения двух волновых фронтов; волны складываются в одних регионах и гасятся в других в зависимости от расположения гребня и впадины каждой волны в пространстве. Например, интерференция между звуковыми волнами от двух одновременно воспроизводимых музыкальных инструментов, настроенных на несколько разные частоты, приводит к появлению биений или модуляции интенсивности звука.

Разновидностью СКВИД-магнитометра является СКВИД-градиентометр, который измеряет разницу в магнитных полях в разных положениях.С помощью этого типа прибора можно обнаружить вариации магнитного поля в диапазоне фемтотесла (10 ^-15 тесла). Устройства этого типа использовались для отображения крошечных магнитных сигналов от человеческого мозга .

Электричество — подробное содержание

fast revision: Силовые линии магнитного поля следуют направлению свободно движущегося Северного полюса.

Магнитный поток φ (фи)

По определению, магнитный поток — это мера силы магнитного поля в данной области, перпендикулярной ему.

На приведенной ниже диаграмме показано, как магнитный поток φ на площади A изменяется вокруг полюса магнита.

к началу

Плотность потока B

Мы можем уточнить идею потока, сделав единицу площади (1 м ² ). Это вводит новую концепцию — плотность магнитного потока B .

Для нормального участка (область под прямым углом),

общий магнитный поток = плотность потока x площадь

Шт.

Единицей измерения потока является Weber ( Wb ), а единицей плотности потока — Tesla ( T ).

Плотность потока 1 Тесла равна 1 Веберу на квадратный метр.

1 T = 1 Вт · м ^-2

Для области A под углом θ к магнитному полю нормальная магнитная индукция имеет величину Bcosθ .

Таким образом, полный нормальный поток на площади A под углом θ к полю определяется выражением:

к началу

Магнитные поля вокруг токоведущих проводов

Магнитное поле вокруг токоведущего провода представляет собой серию концентрических силовых линий.Поле не однородное. Линии расположены неравномерно. Поле неравномерное, линии плотно прилегают к проводу и далеко от него отстоят.

Направление силовых линий — по часовой стрелке в направлении текущего направления.

Поле вокруг плоской круглой катушки напоминает поле вокруг короткого стержневого магнита .

Поле вокруг соленоида напоминает поле вокруг стержневого магнита длиной шт.

к началу

Плотность потока для прямого провода

На диаграмме ниже показана плотность потока B в точке P на расстоянии a от провода.

Плотность магнитного потока B описывается уравнением:

, где μ _o — проницаемость свободного пространства.

К сожалению, в настоящее время невозможно дать полный вывод этого уравнения.

к началу

Плотность потока для бесконечно длинного соленоида

Диаграмма показывает плотность потока B в соленоиде с n витками и током катушки I .

Плотность магнитного потока B описывается уравнением:

, где μ _o — проницаемость свободного пространства, а n — количество витков на единицу длины соленоида.

Значение B приблизительно соответствует значению реального соленоида при условии, что длина соленоида не менее x10 его диаметра.

Количество нИ имеет значение. Он равен напряженности магнитного поля H в единицах ампер-виток / метр (Am ^-2 ).
примечание : витка n не имеет единиц

к началу

Однородные магнитные поля — Катушки Гельмгольца

Одноплоскостная катушка с радиусом r , витками N и током I создает плотность магнитного потока B в центре .

, где μ _o — проницаемость свободного пространства.

Катушки Гельмгольца создают область однородного магнитного поля в дискретном объеме. Две одинаковые плоские катушки выровнены вдоль общей оси и расположены на расстоянии r друг от друга, где r — радиус катушки.

Ток I , проходящий через каждую катушку, одинаков и в одном направлении.

Плотность магнитного потока B в объеме однородного поля (заштриховано зеленым) определяется по формуле:

, где μ _o — проницаемость свободного пространства.

Катушки

Гельмгольца особенно полезны для отклонения электронных / ионных пучков. Все заряженные частицы движутся по круговой траектории при попадании в магнитное поле, перпендикулярное их движению. Измеряя радиус пути и независимо от того, идет ли путь по часовой стрелке или против часовой стрелки, можно получить важную информацию о заряде частицы и ее массе.

No related posts.