Скин-эффект — Википедия Переиздание // WIKI 2
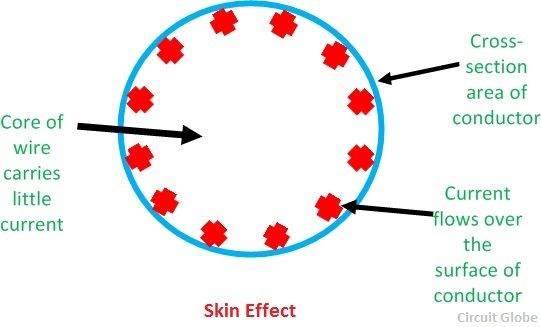
Поверхностный эффект, скин-эффект — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.
Объяснение поверхностного эффекта
Физическая картина возникновения

Физическая картина возникновения скин-эффекта.
Рассмотрим цилиндрический проводник, по которому течёт ток. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на оси проводника. В результате увеличения силы тока возрастает индукция магнитного поля, а форма силовых линий при этом остаётся прежней. Поэтому в каждой точке внутри проводника производная ∂ B ∂ t {\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} направлена по касательной к линии индукции магнитного поля и, следовательно, линии ∂ B ∂ t {\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции
- rot E = − ∂ B ∂ t {\displaystyle \operatorname {rot} \,\mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
создаёт электрическое индукционное поле, силовые линии которого представляют замкнутые кривые вокруг линии индукции магнитного поля. Вектор напряжённости индукционного поля в более близких к оси проводника областях направлен противоположно вектору напряжённости электрического поля, создающего ток, а в более дальних — совпадает с ним. В результате плотность тока уменьшается в приосевых областях и увеличивается вблизи поверхности проводника, то есть возникает скин-эффект.
Уравнение, описывающее скин-эффект
Исходим из уравнения Максвелла,
- rot B = μ j {\displaystyle \operatorname {rot} \mathbf {B} =\mu \mathbf {j} }
и выражения для j {\displaystyle \mathbf {j} } по закону Ома:
- j = γ E {\displaystyle \mathbf {j} =\gamma \mathbf {E} }
Дифференцируя обе части полученного уравнения по времени, находим:
- rot ∂ B ∂ t = μ γ ∂ E ∂ t {\displaystyle \operatorname {rot} {\frac {\partial \mathbf {B} }{\partial t}}=\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}}
- − rot rot E = μ γ ∂ E ∂ t {\displaystyle -\operatorname {rot} \operatorname {rot} \mathbf {E} =\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}} .
Поскольку
- rot rot E = grad div E − ∇ 2 E {\displaystyle \operatorname {rot} \operatorname {rot} \mathbf {E} =\operatorname {grad} \operatorname {div} \mathbf {E} -\nabla ^{2}\mathbf {E} } и div E = 0 {\displaystyle \operatorname {div} \mathbf {E} =0}
окончательно получаем:
- ∇ 2 E = μ γ ∂ E ∂ t {\displaystyle \nabla ^{2}\mathbf {E} =\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}} .

Скин-эффект в бесконечном проводнике с плоской границей.
Для упрощения решения предположим, что ток течёт по однородному бесконечному проводнику, занимающему полупространство y>0 вдоль оси X. Поверхностью проводника является плоскость Y=0. Таким образом,
- j x = j x ( y , t ) , j y = j z = 0 {\displaystyle j_{x}=j_{x}(y,t),\qquad j_{y}=j_{z}=0} ,
- E x = E x ( y , t ) , E y = E z = 0 {\displaystyle E_{x}=E_{x}(y,t),\qquad E_{y}=E_{z}=0} .
Тогда
- ∂ 2 E x ∂ y 2 = μ γ ∂ E x ∂ t {\displaystyle {\frac {\partial ^{2}E_{x}}{\partial y^{2}}}=\mu \gamma {\frac {\partial E_{x}}{\partial t}}} .
В этом уравнении все величины гармонически зависят от t, и можно положить:
- E x ( y , t ) = E 0 ( y ) e i ω t {\displaystyle E_{x}(y,t)=E_{0}(y)e^{i\omega t}} .
Подставим это в наше уравнение и получим уравнение для E 0 ( y ) {\displaystyle E_{0}(y)} :
- ∂ 2 E 0 ∂ y 2 = i γ μ ω E 0 {\displaystyle {\frac {\partial ^{2}E_{0}}{\partial y^{2}}}=i\gamma \mu \omega E_{0}} .
Общее решение этого уравнения таково:
- E 0 = A 1 e − k y + A 2 e k y {\displaystyle E_{0}=A_{1}e^{-ky}+A_{2}e^{ky}} .
Учитывая, что k = i γ μ ω = α ( 1 + i ) {\displaystyle k={\sqrt {i\gamma \mu \omega }}=\alpha (1+i)} , где α = γ μ ω 2 {\displaystyle \alpha ={\sqrt {\frac {\gamma \mu \omega }{2}}}} , находим
- E 0 = A 1 e − α y e − i α y + A 2 e α y e i α y {\displaystyle E_{0}=A_{1}e^{-\alpha y}e^{-i\alpha y}+A_{2}e^{\alpha y}e^{i\alpha y}} .
При удалении от поверхности проводника ( y → ∞ {\displaystyle y\rightarrow \infty } ) второе слагаемое неограниченно возрастает, что является физически недопустимой ситуацией. Следовательно, A 2 = 0 {\displaystyle A_{2}=0} и в качестве физически приемлемого решения остаётся только первое слагаемое. Тогда решение задачи имеет вид:
- E x = A 1 e − α y e i ( ω t − α y ) {\displaystyle E_{x}=A_{1}e^{-\alpha y}e^{i(\omega t-\alpha y)}} .
Взяв действительную часть от этого выражения и перейдя с помощью соотношения j = γ E {\displaystyle \mathbf {j} =\gamma \mathbf {E} } к плотности тока, получим
- j x ( y , t ) = A 1 e − α y cos ( ω t − α y ) {\displaystyle j_{x}(y,t)=A_{1}e^{-\alpha y}\cos {(\omega t-\alpha y)}} .
Принимая во внимание, что j x ( 0 , 0 ) = j 0 {\displaystyle j_{x}(0,0)=j_{0}} — амплитуда плотности тока на поверхности проводника, приходим к следующему распределению объёмной плотности тока в проводнике:
- j x ( y , t ) = j 0 e − α y cos ( ω t − α y ) {\displaystyle j_{x}(y,t)=j_{0}e^{-\alpha y}\cos {(\omega t-\alpha y)}} .
Толщина скин-слоя
Объёмная плотность тока максимальна у поверхности проводника. При удалении от поверхности она убывает экспоненциально и на глубине Δ {\displaystyle \Delta } становится меньше в е раз (примерно на 70%). Эта глубина называется толщиной скин-слоя и на основании полученного выше равна
- Δ = 2 γ μ ω {\displaystyle \Delta ={\sqrt {\frac {2}{\gamma \mu \omega }}}} .
Очевидно, что при достаточно большой частоте ω {\displaystyle \omega } толщина скин-слоя может быть очень малой. Также из экспоненциального убывания плотности тока следует, что практически весь ток сосредоточен в слое толщиной в несколько Δ {\displaystyle \Delta } , так, уменьшение плотности тока в 100 раз происходит на глубине ≈ 4 , 6 Δ {\displaystyle \approx 4,6\Delta } , если общая толщина проводника многократно превышает толщину скин-слоя. В качестве примера приведём зависимость глубины скин-слоя от частоты для медного проводника:
| Частота | Δ {\displaystyle \Delta } | Примечания |
|---|---|---|
| 50 Гц | 9,34 мм | 50 Гц — частота электросети в большинстве стран Евразии и Африки |
| 60 Гц | 8,53 мм | 60 Гц — частота электросети в Северной, Центральной и частично Южной Америке |
| 10 кГц | 0,66 мм | |
| 100 кГц | 0,21 мм | |
| 500 кГц | 0,095 мм | |
| 1 МГц | 0,067 мм | |
| 10 МГц | 0,021 мм |
Если проводник имеет ферромагнитные свойства, то толщина скин-слоя будет во много раз меньше. Например, для стали ( μ {\displaystyle \mu } =1000) Δ {\displaystyle \Delta } =0.74 мм. Это имеет значение, например, при электрификации железных дорог, поскольку там стальные рельсы используются в качестве обратного провода.
Для расчёта толщины скин-слоя в металле (приближённо) можно использовать следующие эмпирические формулы:
- Δ = c 2 ε 0 ω μ m ρ {\displaystyle \Delta =c{\sqrt {2{\frac {\varepsilon _{0}}{\omega \mu _{m}}}\rho }}} .
Здесь ε 0 {\displaystyle \varepsilon _{0}} = 8,85419⋅10−12 Ф/м — электрическая постоянная, ρ {\displaystyle \rho } — удельное сопротивление, c — скорость света, μ m {\displaystyle \mu _{m}} — относительная магнитная проницаемость (близка к единице для пара- и диамагнетиков — меди, серебра, и т. п.), ω = 2 π ⋅ f {\displaystyle \omega =2\pi \cdot f} . Все величины выражены в системе СИ.
- Δ = 503 ρ μ m f {\displaystyle \Delta =503{\sqrt {\frac {\rho }{\mu _{m}f}}}} ,
ρ {\displaystyle \rho } — удельное сопротивление, μ m {\displaystyle \mu _{m}} — относительная магнитная проницаемость, f {\displaystyle f} — частота.
Аномальный скин-эффект
Изложенная теория справедлива лишь при условии, что толщина скин-слоя много больше средней длины свободного пробега электронов, так как мы предполагаем, что при своём движении электрон непрерывно теряет энергию на преодоление омического сопротивления проводника, в результате чего происходит выделение джоулевой теплоты. Такое соотношение справедливо в весьма широких пределах, однако даже при комнатной температуре длина свободного пробега электрона для металлов сопоставима с глубиной скин-слоя — что говорит об аномальном характере эффекта. При очень низкой температуре ситуация только усугубляется[1]: проводимость сильно повышается, а следовательно, увеличивается длина свободного пробега и уменьшается толщина скин-слоя. При этих условиях механизм, приводящий к образованию скин-эффекта, уже не действует. Эффективная толщина слоя, в котором сосредоточен ток, изменяется. Такое явление называется аномальным скин-эффектом.
Применение
На скин-эффекте основано действие взрывомагнитных генераторов (ВМГ), взрывомагнитных генераторов частоты (ВМГЧ) и в частности ударно-волновых излучателей (УВИ).
Благодаря скин-эффекту на высоких частотах теплота выделяется преимущественно в поверхностном слое. Это позволяет раскалить проводник в тонком поверхностном слое без существенного изменения температуры внутренних областей. Данное явление используется в важном, с промышленной точки зрения, методе поверхностной закалки металлов.
Учёт эффекта в технике и борьба с ним
Скин-эффект проявляется всё более явно с увеличением частоты переменного тока, что заставляет учитывать его при конструировании и расчётах электрических схем, работающих с переменным и импульсным током. В связи с тем, что ток высокой частоты течёт по тонкому поверхностному слою проводника, активное сопротивление проводника значительно возрастает, что приводит к быстрому затуханию колебаний высокой частоты. Скин-эффект значительно влияет на характеристики катушек индуктивности и колебательных контуров, такие как добротность, на затухание в линиях передачи, на характеристики фильтров, на расчёты тепловых потерь и КПД, на выбор сечений проводников.
Для уменьшения влияния скин-эффекта применяют проводники различного сечения: плоские (в виде лент), трубчатые (полые внутри), наносят на поверхность проводника слой металла с более низким удельным сопротивлением. Серебро обладает наибольшей удельной проводимостью среди всех металлов, и тонкий его слой, в котором из-за скин-эффекта и протекает бо́льшая часть тока, оказывает заметное влияние (до 10 %) на активное сопротивление проводника. Кроме того, слой сульфида, образующийся на поверхности серебра, не проводит ток и не участвует в скин-эффекте, в отличие от слоя окиси-закиси на поверхности меди, обладающего заметной проводимостью, вдобавок ещё и со свойствами полупроводника, и вносящего дополнительные потери на высоких частотах. Также применяется и покрытие золотом, у которого слой окислов отсутствует вовсе. Напротив, покрытие никелем, оловом или оловянно-свинцовым припоем способно значительно, в несколько раз увеличить сопротивление медных проводников на высоких частотах.
Так, в ВЧ аппаратуре используют катушки индуктивности из посеребрённого провода, серебрят печатные и проволочные проводники, поверхности экранов и обкладки конденсаторов, в высоковольтных линиях электропередач применяют провод в медной либо алюминиевой оболочке со стальным сердечником, в высокомощных генераторах переменного тока обмотка изготавливается из трубок, по которым для охлаждения циркулирует сжиженный водород или дистиллированная вода. Также с целью подавления скин-эффекта используют систему из нескольких переплетённых и изолированных проводов — литцендрат. При передаче больших мощностей на значительные расстояние применяются линии постоянного тока — HVDC, который не подвержен воздействию скин-эффекта.
Покрытие серебром также применяется в сверхвысокочастотном оборудовании, использующем колебательные контуры особой формы: объёмные резонаторы и специфические линии передач — волноводы. Кроме того, на таких частотах особое внимание приходится уделять снижению шероховатости поверхности с целью уменьшения длины пути протекания тока.
Примечания
- ↑ Сивухин Д. В. Общий курс физики. Том 4. Оптика. — 1980. — С. 454.
Литература
- А. Н. Матвеев. Параграф 53 // Электричество и магнетизм. — М.: Высшая школа, 1983. — 463 с.
- A. A. Власов. Глава VI. Параграф 5 // Макроскопическая электродинамика. — 2-е изд.. —
 Эта страница в последний раз была отредактирована 20 февраля 2020 в 16:17.
Эта страница в последний раз была отредактирована 20 февраля 2020 в 16:17.Поверхностный (скин-эффект) в проводнике
Каждый опытный электротехник знает, что распределение плотности тока в проводнике нелинейно. Чем ближе к центральной оси, тем меньше амплитуда сигнала. При высокой частоте для корректного расчета вполне достаточно учитывать прохождение волн через определенный поверхностный слой. Это явление, скин эффект, способно выполнять полезные функции. Для успешного применения на практике, кроме общей теории, нужно изучить методику вычислений.

На основе скин эффекта создают экономичные системы обогрева трубопроводов
Объяснение поверхностного эффекта
Следует подчеркнуть одинаковую плотность тока при подключении проводника к источнику питания с постоянным напряжением. Однако ситуация изменяется при прохождении волнового сигнала.
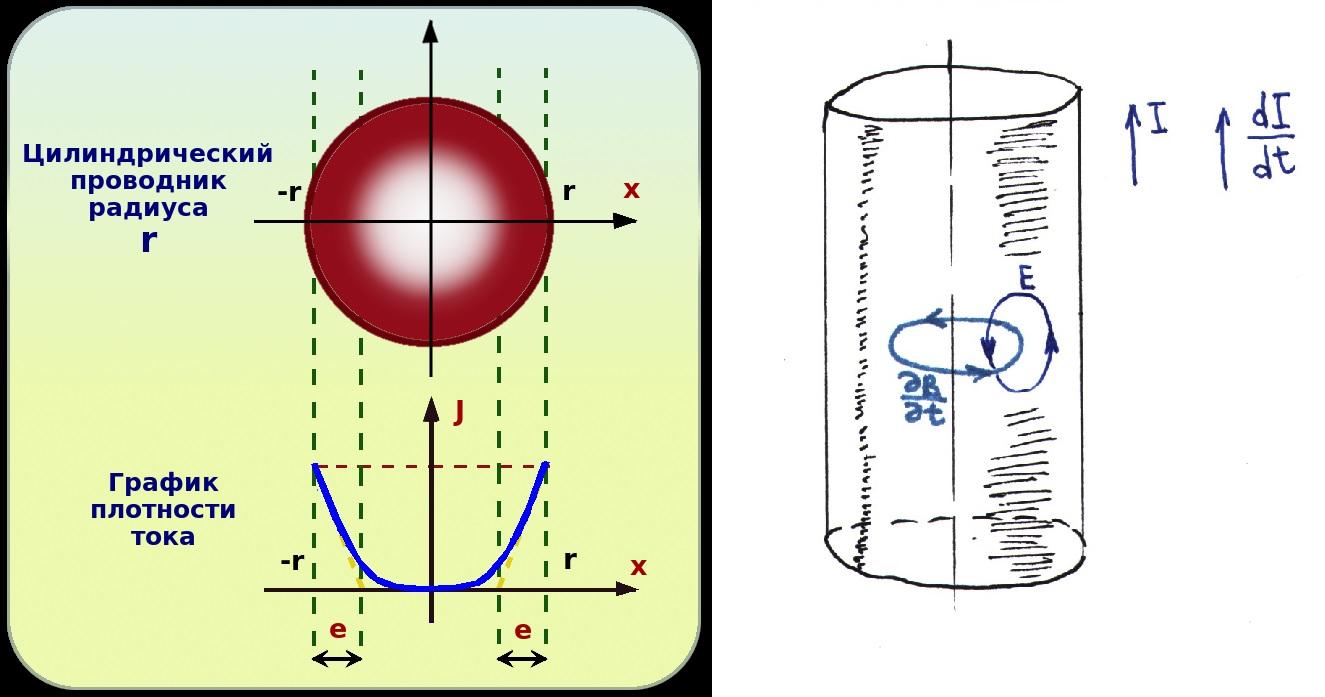
Распределение плотности тока в проводнике
Физическая картина возникновения
Для объяснения причин явления можно использовать вторую часть пояснительной картинки выше. В графической форме показаны силовые воздействия, которые образуются переменным полем. Электрическая составляющая (Е) направлена противоположно току (I), что объясняет возникающее сопротивление и соответствующее уменьшение амплитуды. По мере приближения к поверхности будет проявляться обратный эффект. Он вызван совпадением векторов напряженностей.
Уравнение, описывающее скин-эффект
Для выражения амплитуды через плотность тока берут определяющие соотношения из классических уравнений закона Ома и формул Максвелла. Дифференциалом по заданному временному интервалу можно вычислить значения магнитной и электрической компонент поля. В упрощенном виде рассматривают бесконечный проводящий образец, созданный из однородного материала.
Формула определения частоты среза диаметра проводника
Для практических вычислений отдельными незначительными факторами пренебрегают. Например, чтобы определить частоту среза (Fср), цепь радиотехнического устройства рассчитывают по диаметру (D) соответствующего проводника. В формулу добавляют важнейшую характеристику определенного материала – удельное сопротивление (Rу) или проводимость (Sу). Зависимость отмеченных параметров показывает следующее выражение:
Fср = 4/ (π*μ*Sу*D2),
где μ – постоянная величина (μ = 4* Sу*10-7 Генри на метр).
Глубина проникновения
Аналогичным образом, в упрощенном виде, можно рассчитать критичное расстояние от поверхности. Подразумевается, что в соответствующей области плотность тока уменьшается до минимальной значимой величины (-8,69 дБ, по сравнению с номиналом). Этот параметр (Dпр) называют глубиной проникновения.
Dпр = √( Sу/( π*μ*f)), где f – частота сигнала.
Толщина скин-слоя
Из рассмотренного в предыдущем разделе определения понятна обратная зависимость плотности тока от частоты сигнала. Следующая таблица демонстрирует наглядно «активный» слой медного проводника. При многократном уменьшении энергетического потока в глубине на определенном уровне нецелесообразно применение толстых линий электропередач.
| Параметр | Значения | ||||
|---|---|---|---|---|---|
| Частота сигнала, Гц | 50 | 60 | 10 000 | 100 000 | 1 000 000 |
| Толщина скин слоя, мм | 9,34 | 8,53 | 0,66 | 0,21 | 0,067 |
В первых двух столбцах приведены значения для стандартных сетей переменного тока. Эти данные демонстрируют, что сравнительно незначительное изменение частоты (10 Гц) делает бесполезным 1,62 мм диаметра проводника (медь). Нетрудно вычислить значительную экономию при создании длинной линии после соответствующей оптимизации параметров сигнала. Следует не забывать, что каждый металл отличается глубиной эффективного слоя. Какой выбрать вариант, будет понятно после тщательного изучения целевого назначения конструкции.
Аномальный скин-эффект
Внимательное изучение явления позволяет сделать несколько важных выводов. Как показано на конкретных примерах, скин слой отличается небольшой глубиной. Однако соответствующее расстояние намного меньше средних значений свободного пробега заряженных частиц. Следует не забывать, что на соответствующее перемещение нужно затратить определенную энергию. Преодоление электрического сопротивления материала сопровождается нагревом.
Если снижать температуру, проводимость увеличится. Одновременно станет больше свободный пробег, и уменьшится толщина рассматриваемой части проводника. При определенном уровне стандартный механизм волновых взаимодействий станет ничтожным. Аномальный скин эффект – это изменение размеров слоя, в котором обеспечивается достаточно высокая для практического использования плотность тока.
Применение
Поверхностный эффект позволяет обеспечить локальный нагрев части проводника при пропускании переменного тока. Этот принцип используют, чтобы обогреть трубопровод в зимний период. Правильное применение технологии подразумевает следующие преимущества:
- отсутствие сопроводительных контрольных и функциональных устройств;
- практически неограниченная длина трассы;
- возможность безопасного применения высоких температур.
Частотное распределение плотности токов используют для передачи информационных сигналов по силовым линиям электропередач. При достаточном уменьшении длины волны близость центральной части проводника не будет помехой. Модулированная СВЧ составляющая проходит в поверхностном слое. Для создания пакетов данных и расшифровки применяют специальные кодирующие (декодирующие) устройства.
К сведению. Подобные механизмы используют в нефтяной отрасли для оценки продуктивности скважины. Скин фактор определяет сопротивление перемещению жидкости в близкой технологическому отверстию области пласта. По этому параметру делают оценку реального объема добычи, по сравнению с идеальными условиями.
Учёт эффекта в технике и борьба с ним
Это явление оказывает заметное влияние по мере увеличения частоты сигнала. Следует учитывать скин эффект при проектировании схем с переменными (импульсными) токами. В частности, делают коррекцию расчета катушки фильтра, колебательного контура, трансформатора.
Типовые способы решения обозначенных проблем:
- уменьшение толщины проводника;
- создание полых конструкций;
- образование поверхностного слоя из металла с лучшей проводимостью;
- устранение неровностей;
- плетение из нескольких изолированных жил.
К сведению. Радикальное устранение вредных явлений организуют с помощью передачи электроэнергии постоянным током.
Способы подавления скин эффекта
Перечисленные методики имеют особое значение при работе с высокочастотными радиосигналами. В частности, для улучшения проводимости поверхностный слой создают из серебра, платины, других благородных металлов. Следующие рекомендации применяют на практике при создании качественной аудио аппаратуры:
- для пропускания сигналов используют тонкие (0,25-0,35 мм) жилы;
- плетением кабеля устраняют значительные искажения силовых линий магнитного поля;
- надежной изоляцией предотвращают окисление меди;
- проверяют наличие поблизости других линий, способных оказывать вредное взаимное влияние.

Оптоволоконная линия связи
При переходе в СВЧ диапазон сигналы передают по волноводам. Устраняют возможные негативные проявления с помощью передачи данных сигналами в оптическом диапазоне.
Видео
Скин-эффект — Большая советская энциклопедия
Скин-эффе́кт
(от англ. skin — кожа, оболочка)
поверхностный эффект, затухание электромагнитных волн по мере их проникновения в глубь проводящей среды, в результате которого, например, переменный ток по сечению проводника или переменный магнитный поток по сечению магнитопровода распределяются не равномерно, а преимущественно в поверхностном слое. С.-э. обусловлен тем, что при распространении электромагнитной волны в проводящей среде возникают Вихревые токи, в результате чего часть электромагнитной энергии преобразуется в теплоту. Это и приводит к уменьшению напряжённостей электрического и магнитного полей и плотности тока, т. е. к затуханию волны.
Чем выше частота ν электромагнитного поля и больше магнитная проницаемость μ проводника, тем сильнее (в соответствии с Максвелла уравнениями) вихревое электрическое поле, создаваемое переменным магнитным полем, а чем больше проводимость а проводника, тем больше плотность тока и рассеиваемая в единице объёма мощность (в соответствии с законами Ома и Джоуля — Ленца). Т. о., чем больше ν, μ и σ, тем сильнее затухание, т. е. резче проявляется С.-э.
В случае плоской синусоидальной волны, распространяющейся вдоль оси х в хорошо проводящей, однородной, линейной среде (токами смещения по сравнению с токами проводимости можно пренебречь), амплитуды напряжённостей электрического и магнитного полей затухают по экспоненциальному закону:
 ,
, 
где

— коэффициент затухания, μ0 —Магнитная постоянная. На глубине х = δ = 1/α амплитуда волны уменьшается в е раз. Это расстояние называется глубиной проникновения или толщиной скин-слоя. Например, при частоте 50 гц в меди (σ = 580 ксим/см; μ = 1) σ = 9,4 мм, в стали (α = 100 ксим/см, (μ = 1000) δ = 0,74 мм. При увеличении частоты до 0,5 Мгц δ уменьшится в 100 раз. В идеальный проводник (с бесконечно большой проводимостью) электромагнитная волна вовсе не проникает, она полностью от него отражается. Чем меньше расстояние, которое проходит волна, по сравнению с δ, тем слабее проявляется С.-э.
Для проводников при сильно выраженном С.-э., когда радиус кривизны сечения провода значительно больше δ и поле в проводнике представляет собой плоскую волну, вводят понятие поверхностного сопротивления проводника Zs (поверхностного импеданса). Его определяют как отношение комплексной амплитуды (См. Комплексная амплитуда) падения напряжения на единицу длины проводника к комплексной амплитуде тока, протекающего через поперечное сечение скин-слоя единичной длины. Комплексное сопротивление на единицу длины проводника:

где R0 — активное сопротивление проводника, определяющее мощность потерь в нём, X0 — индуктивное сопротивление, учитывающее индуктивность проводника, обусловленную магнитным потоком внутри проводника, lc — периметр поперечного сечения скин-слоя, ω = 2πν; при этом R0 = X0. При сильно выраженном С.-э. поверхностное сопротивление совпадает с волновым сопротивлением (См. Волновое сопротивление) проводника и, следовательно, равно отношению напряжённости электрического поля к напряжённости магнитного поля на поверхности проводника.
В тех случаях, когда длина свободного пробега l носителей тока становится больше толщины δ скин-слоя (например, в очень чистых металлах при низких температурах), при сравнительно высоких частотах С.-э. приобретает ряд особенностей, благодаря которым он получил название аномального. Поскольку поле на длине свободного пробега электрона неоднородно, ток в данной точке зависит от значения электрического поля не только в этой точке, но и в её окрестности, имеющей размеры порядка l Поэтому при решении уравнений Максвелла вместо закона Ома приходится использовать для вычисления тока кинетическое уравнение Больцмана. Электроны при аномальном С.-э. становятся неравноценными с точки зрения их вклада в электрический ток; при l >> δ основной вклад вносят те из них, которые движутся в скин-слое параллельно поверхности металла или под очень небольшими углами к ней и проводят, т. о., больше времени в области сильного поля (эффективные электроны). Затухание электромагнитной волны в поверхностном слое по-прежнему имеет место, но количественные характеристики у аномального С.-э. несколько иные. Поле в скин-слое затухает не экспоненциально (R0/X0=  ).
).
В инфракрасной области частот электрон за период изменения поля может не успеть пройти расстояние l. При этом поле на пути электрона за период можно считать однородным. Это приводит опять к закону Ома, и С.-э. снова становится нормальным. Т. о., на низких и очень высоких частотах С.-э. всегда нормальный. В радиодиапазоне в зависимости от соотношений между / и δ могут иметь место нормальный и аномальный С.-э. Всё сказанное справедливо, пока частота со меньше плазменной: ω < ω0 —(4πne2/m)1/2 (n — концентрация свободных электронов, е — заряд, m — масса электрона) (относительно более высоких частот см. ст. Металлооптика).
С.-э. часто нежелателен. В проводах переменный ток при сильном С.-э. протекает главным образом по поверхностному слою; при этом сечение провода не используется полностью, сопротивление провода и потери мощности в нём при данном токе возрастают. В ферромагнитных пластинах или лентах магнитопроводов трансформаторов, электрических машин и других устройств переменный магнитный поток при сильном С.-э. проходит главным образом по их поверхностному слою; вследствие этого ухудшается использование сечения магнитопровода, возрастают намагничивающий ток и потери в стали. «Вредное» влияние С.-э. ослабляют уменьшением толщины пластин или ленты, а при достаточно высоких частотах — применением магнитопроводов из магнитодиэлектриков (См. Магнитодиэлектрики).
С др. стороны, С.-э. находит применение в практике. На С.-э. основано действие электромагнитных экранов. Так для защиты внешнего пространства от помех, создаваемых полем силового трансформатора, работающего на частоте 50 гц, применяют экран из сравнительно толстой ферромагнитной стали; для экранирования катушки индуктивности, работающей на высоких частотах, экраны делают из тонкого слоя Al. На С.-э. основана высокочастотная поверхностная закалка стальных изделий (см. Индукционная нагревательная установка).
Лит.: Нетушил А. В., Поливанов К. М., Основы электротехники, т. 3, М., 1956; Поливанов К. М., Теоретические основы электротехники, ч. 3 — Теория электромагнитного поля, М., 1975; Нейман Л. Р., Поверхностный эффект в ферромагнитных телах, Л. — М., 1949. См. также лит. при ст. Металлы.
И. Б. Негневицкий.
Источник: Большая советская энциклопедия на Gufo.me
Значения в других словарях
- скин-эффект — [англ. skin кожа + эффект] – эл. явление, наблюдаемое при протекании по проводнику переменного тока высокой частоты и заключающееся в том, что ток проходит не по всему сечению сплошного проводника, а преимущественно по его поверхностному слою Большой словарь иностранных слов
- СКИН-ЭФФЕКТ — СКИН-ЭФФЕКТ (от англ. skin — кожа, оболочка) — (поверхностный эффект) — неоднородное распределение переменного тока и связанного с ним электромагнитного поля по сечению проводника. Большой энциклопедический словарь
- скин-эффект — сущ., кол-во синонимов: 1 эффект 29 Словарь синонимов русского языка
- скин-эффект — орф. скин-эффект, -а Орфографический словарь Лопатина
- СКИН-ЭФФЕКТ — (от англ. skin — кожа, оболочка) (поверхностный эффект), затухание эл.-магн. волн по мере их проникновения в глубь проводящей среды, в результате к-рого, напр., перем. ток по сечению проводника или перем. магн. Физический энциклопедический словарь

СКИН-ЭФФЕКТ • Большая российская энциклопедия
СКИН-ЭФФЕ́КТ, затухание электромагнитных волн по мере их проникновения в проводящую среду. Переменное электрич. поле и связанное с ним магнитное поле не проникают в глубь проводника, а сосредоточены в осн. в относительно тонком приповерхностном слое толщиной δ, называемой глубиной скин-слоя. С.-э. обусловлен тем, что при распространении электромагнитной волны в проводящей среде возникают вихревые токи (см. Фуко токи), в результате чего часть электромагнитной энергии преобразуется в теплоту. Это приводит к уменьшению напряжённостей электрич. и магнитного полей и плотности тока, т. е. к затуханию волны. Затухание тем сильнее, чем больше частота ω электромагнитного поля, магнитная проницаемость μ и проводимость σ проводника. С.-э. проявляется в металлах, плазме, ионосфере (на коротких волнах), вырожденных полупроводниках и др. средах с достаточно высокой проводимостью.
Глубина скин-слоя зависит от величин σ и ω, а также от состояния поверхности. На малых частотах δ велика, убывает с ростом частоты и для металлов на частотах оптич. диапазона оказывается сравнимой с длиной волны (порядка 10–7 м). Столь малым проникновением электромагнитного поля и почти полным его отражением объясняется металлич. блеск хороших проводников. На частотах, превышающих плазменную частоту ωp, в проводниках оказывается возможным распространение электромагнитных волн.
При нормальном С.-э., когда δ велика по сравнению с эффективной длиной свободного пробега l электронов, распределение поля в проводнике зависит только от дифференциальной проводимости. В пределе низких частот, когда можно не учитывать частотную дисперсию и пренебречь диэлектрич. проницаемостью ионной решётки, глубина скин-слоя δ=c(2πωσ)–1/2 (c – скорость света). С повышением частоты в ИК-области спектра для металлов δ не зависит от частоты: δ=c/ωp.
При l>δ С.-э. приобретает ряд особенностей, благодаря которым он получил назв. аномального. Такой С.-э. наблюдается в СВЧ-диапазоне в чистых металлах при низких темп-pax. Электроны при аномальном С.-э. становятся неравноценными с точки зрения их вклада в электрич. ток. Существенную роль играют электроны с малыми углами скольжения, для которых отражение близко к зеркальному. На аномальный С.-э. влияет постоянное магнитное поле, параллельное поверхности. Закручиваемые им электроны при зеркальном отражении многократно сталкиваются с поверхностью образца и долгое время движутся в пределах скин-слоя. Это приводит к росту проводимости и уменьшению δ. Др. электроны, не сталкивающиеся с поверхностью, возвращаются в скин-слой после каждого оборота в магнитном поле, вследствие чего в металлах наблюдается циклотронный резонанс.
При достаточно высоких значениях напряжённости переменного электромагнитного поля, когда параметры среды (напр., σ) начинают зависеть от величины поля, С.-э. становится нелинейным, т. е. δ также начинает зависеть от интенсивности электромагнитного поля.
В технике С.-э. часто нежелателен. При сильном С.-э. переменный ток протекает гл. обр. по поверхностному слою провода, при этом его сечение используется не полностью, сопротивление провода и потери мощности в нём возрастают. В ферромагнитных пластинах или лентах магнитопроводов трансформаторов, электрич. машин и др. устройств переменный магнитный поток при сильном С.-э. проходит в осн. по их поверхностному слою, вследствие чего возрастают намагничивающий ток и потери в стали. Вредное влияние С.-э. ослабляют уменьшением толщины пластин или ленты, а при достаточно высоких частотах – применением магнитопроводов из магнитных диэлектриков.
На С.-э. основано действие электромагнитных экранов, взрывомагнитных генераторов, взрывомагнитных генераторов частоты, ВЧ поверхностная закалка стальных изделий и др.
Переменный ток сопровождается электромагнитными явлениями, которые приводят к вытеснению электрических зарядов с центра проводника на его периферию. Этот эффект называется — поверхностным эффектом, или скин-эффектом. В результате этого эффекта ток становится неоднородным. На периферии ток оказывается большим по величине, чем в центре. Это происходит из-за различия в плотности свободных носителей зарядов в перпендикулярном сечении проводника относительно направления тока.
Глубина проникновения тока определяется согласно выражению:
Используя приведённую выше формулу для медного проводника получаем, что при частоте тока в 50 Гц глубина проникновения составит приблизительно 9,2 мм. Фактически это означает, что имея проводник с круглым сечением с радиусом более 9,2 мм, ток в центре проводника будет отсутствовать, потому как там не будет свободных носителей зарядов.
Чем выше частота тока, тем меньше глубина проникновения. Увеличение частоты тока в два раза повлечет за собой уменьшение глубины проникновения в корень квадратный из двух. Если частота тока увеличится в 10 раз, то, соответственно, глубина проникновения уменьшится в корень из 10 раз.
График распределения тока.
На графике наглядно показано распределение плотности тока J в проводнике круглого сечения (цилиндрический). За пределами глубины проникновения плотность тока равна нулю или же ничтожно мала, потому как в этих местах проводника отсутствуют свободные электроны. Ток в этих местах отсутствует.
Если из центра такого проводника где отсутствует ток, извлечь проводящий материал, то мы получим полый проводник в виде трубки (трубчатый). Проводящие характеристики от этого не изменятся, потому как тока там и не было, сопротивление такого проводника не изменится, но могут поменяться такие характеристики как индуктивность и емкость проводника.
Сопротивление проводника в цепи переменного тока зависит не только от материала проводника, но также от частоты тока. При высоких частотах, за счет скин-эффекта, весь ток начинает протекать практически по границе проводника, там где он контактирует со внешней, не проводящей средой.
Практическое использование скин-эффекта.
Распределение плотности тока в проводнике в зависимости от частоты тока позволяет по одному проводу передавать электрические сигналы разных частот. Сигналы более высокой частоты проходят по внешнему радиусу (большему) проводника, а сигналы меньшей частоты по меньшему радиусу. Получается нечто вроде слоенного пирога цилиндрической формы, где начинка распределяется сферически. Каждый вид начинки — это как бы отдельная частота тока.
Учитывая глубину проникновения тока для разных частот, если требуется проводник с радиусом большим, чем глубина проникновения, то разумно применять многожильный кабель. Скажем так, для 50 Гц частоты тока, предельный радиус примерно 9 мм, а это значит, что нет смысла эксплуатировать цельный проводник с радиусом больше 9 мм. Это не даст никакого увеличения проводимости, потому как ток в центре проводника будет отсутствовать, что является нерациональным использованием дорогостоящей меди. Вот поэтому при больших сечениях применяют многожильные провода и кабели.
При передачи высокочастотных сигналов, в целях экономии цветного металла, основной несущий провод изготавливают из дешевого стального сплава, который затем покрывают тонким слоем меди. Благодаря скин-эффекту ток протекает практически только по медной оболочке, а в стальном основании он отсутствует. Это позволяет значительно удешевить провода и кабели для высокочастотных средств связи.
Дата: 27.05.2016
© Valentin Grigoryev (Валентин Григорьев)
Скин-эффект — Википедия
Поверхностный эффект, скин-эффект — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.
Объяснение поверхностного эффекта
Физическая картина возникновения
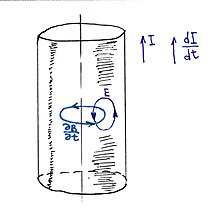 Физическая картина возникновения скин-эффекта.
Физическая картина возникновения скин-эффекта.Рассмотрим цилиндрический проводник, по которому течёт ток. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на оси проводника. В результате увеличения силы тока возрастает индукция магнитного поля, а форма силовых линий при этом остаётся прежней. Поэтому в каждой точке внутри проводника производная ∂ B ∂ t {\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} направлена по касательной к линии индукции магнитного поля и, следовательно, линии ∂ B ∂ t {\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции
- rot E = − ∂ B ∂ t {\displaystyle \operatorname {rot} \,\mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
создаёт электрическое индукционное поле, силовые линии которого представляют замкнутые кривые вокруг линии индукции магнитного поля. Вектор напряжённости индукционного поля в более близких к оси проводника областях направлен противоположно вектору напряжённости электрического поля, создающего ток, а в более дальних — совпадает с ним. В результате плотность тока уменьшается в приосевых областях и увеличивается вблизи поверхности проводника, то есть возникает скин-эффект.
Уравнение, описывающее скин-эффект
Исходим из уравнения Максвелла,
- rot B = μ j {\displaystyle \operatorname {rot} \mathbf {B} =\mu \mathbf {j} }
и выражения для j {\displaystyle \mathbf {j} } по закону Ома:
- j = γ E {\displaystyle \mathbf {j} =\gamma \mathbf {E} }
Дифференцируя обе части полученного уравнения по времени, находим:
- rot ∂ B ∂ t = μ γ ∂ E ∂ t {\displaystyle \operatorname {rot} {\frac {\partial \mathbf {B} }{\partial t}}=\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}}
- − rot rot E = μ γ ∂ E ∂ t {\displaystyle -\operatorname {rot} \operatorname {rot} \mathbf {E} =\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}} .
Поскольку
- rot rot E = grad div E − ∇ 2 E {\displaystyle \operatorname {rot} \operatorname {rot} \mathbf {E} =\operatorname {grad} \operatorname {div} \mathbf {E} -\nabla ^{2}\mathbf {E} } и div E = 0 {\displaystyle \operatorname {div} \mathbf {E} =0}
окончательно получаем:
- ∇ 2 E = μ γ ∂ E ∂ t {\displaystyle \nabla ^{2}\mathbf {E} =\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}} .
 Скин-эффект в бесконечном проводнике с плоской границей.
Скин-эффект в бесконечном проводнике с плоской границей.Для упрощения решения предположим, что ток течёт по однородному бесконечному проводнику, занимающему полупространство y>0 вдоль оси X. Поверхностью проводника является плоскость Y=0. Таким образом,
- j x = j x ( y , t ) , j y = j z = 0 {\displaystyle j_{x}=j_{x}(y,t),\qquad j_{y}=j_{z}=0} ,
- E x = E x ( y , t ) , E y = E z = 0 {\displaystyle E_{x}=E_{x}(y,t),\qquad E_{y}=E_{z}=0} .
Тогда
- ∂ 2 E x ∂ y 2 = μ γ ∂ E x ∂ t {\displaystyle {\frac {\partial ^{2}E_{x}}{\partial y^{2}}}=\mu \gamma {\frac {\partial E_{x}}{\partial t}}} .
В этом уравнении все величины гармонически зависят от t, и можно положить:
- E x ( y , t ) = E 0 ( y ) e i ω t {\displaystyle E_{x}(y,t)=E_{0}(y)e^{i\omega t}} .
Подставим это в наше уравнение и получим уравнение для E 0 ( y ) {\displaystyle E_{0}(y)} :
- ∂ 2 E 0 ∂ y 2 = i γ μ ω E 0 {\displaystyle {\frac {\partial ^{2}E_{0}}{\partial y^{2}}}=i\gamma \mu \omega E_{0}} .
Общее решение этого уравнения таково:
- E x = A 1 e − k y + A 2 e k y {\displaystyle E_{x}=A_{1}e^{-ky}+A_{2}e^{ky}} .
Учитывая, что k = i γ μ ω = α ( 1 + i ) {\displaystyle k={\sqrt {i\gamma \mu \omega }}=\alpha (1+i)} , где α = γ μ ω 2 {\displaystyle \alpha ={\sqrt {\frac {\gamma \mu \omega }{2}}}} , находим
- E 0 = A 1 e − α y e − i α y + A 2 e α y e i α y {\displaystyle E_{0}=A_{1}e^{-\alpha y}e^{-i\alpha y}+A_{2}e^{\alpha y}e^{i\alpha y}} .
При удалении от поверхности проводника ( y → ∞ {\displaystyle y\rightarrow \infty } ) второе слагаемое неограниченно возрастает, что является физически недопустимой ситуацией. Следовательно, A 2 = 0 {\displaystyle A_{2}=0} и в качестве физически приемлемого решения остаётся только первое слагаемое. Тогда решение задачии имеет вид:
- E x = A 1 e − α y e i ( ω t − α y ) {\displaystyle E_{x}=A_{1}e^{-\alpha y}e^{i(\omega t-\alpha y)}} .
Взяв действительную часть от этого выражения и перейдя с помощью соотношения j = γ E {\displaystyle \mathbf {j} =\gamma \mathbf {E} } к плотности тока, получим
- j x ( y , t ) = A 1 e − α y cos ( ω t − α y ) {\displaystyle j_{x}(y,t)=A_{1}e^{-\alpha y}\cos {(\omega t-\alpha y)}} .
Принимая во внимание, что j x ( 0 , 0 ) = j 0 {\displaystyle j_{x}(0,0)=j_{0}} — амплитуда плотности тока на поверхности проводника, приходим к следующему распределению объёмной плотности тока в проводнике:
- j x ( y , t ) = j 0 e − α y cos ( ω t − α y ) {\displaystyle j_{x}(y,t)=j_{0}e^{-\alpha y}\cos {(\omega t-\alpha y)}} .
Толщина скин-слоя
Объёмная плотность тока максимальна у поверхности проводника. При удалении от поверхности она убывает экспоненциально и на глубине Δ {\displaystyle \Delta } становится меньше в е раз. Эта глубина называется толщиной скин-слоя и на основании полученного выше равна
- Δ = 2 γ μ ω {\displaystyle \Delta ={\sqrt {\frac {2}{\gamma \mu \omega }}}} .
Очевидно, что при достаточно большой частоте ω {\displaystyle \omega } толщина скин-слоя может быть очень малой. Также из экспоненциального убывания плотности тока следует, что практически весь ток сосредоточен в слое толщиной в несколько Δ {\displaystyle \Delta } , так, уменьшение плотности тока в 100 раз происходит на глубине ≈ 4 , 6 Δ {\displaystyle \approx 4,6\Delta } , если общая толщина проводника многократно превышает толщину скин-слоя. В качестве примера приведём зависимость глубины скин-слоя от частоты для медного проводника:
| Частота | Δ {\displaystyle \Delta } | Примечания |
|---|---|---|
| 50 Гц | 9,34 мм | 50 Гц — частота электросети в большинстве стран Евразии и Африки |
| 60 Гц | 8,53 мм | 60 Гц — частота электросети в Северной, Центральной и частично Южной Америке |
| 10 кГц | 0,66 мм | |
| 100 кГц | 0,21 мм | |
| 500 кГц | 0,095 мм | |
| 1 МГц | 0,067 мм | |
| 10 МГц | 0,021 мм |
Если проводник имеет ферромагнитные свойства, то толщина скин-слоя будет во много раз меньше. Например, для стали ( μ {\displaystyle \mu } =1000) Δ {\displaystyle \Delta } =0.74 мм. Это имеет значение, например, при электрификации железных дорог, поскольку там стальные рельсы используются в качестве обратного провода.
Для расчёта толщины скин-слоя в металле (приближённо) можно использовать следующие эмпирические формулы:
- Δ = c 2 ε 0 ω μ m ρ {\displaystyle \Delta =c{\sqrt {2{\frac {\varepsilon _{0}}{\omega \mu _{m}}}\rho }}} .
Здесь ε 0 {\displaystyle \varepsilon _{0}} = 8,85419·10−12 Ф/м — электрическая постоянная, ρ {\displaystyle \rho } — удельное сопротивление, c — скорость света, μ m {\displaystyle \mu _{m}} — относительная магнитная проницаемость (близка к единице для пара- и диамагнетиков — меди, серебра, и т. п.), ω = 2 π ⋅ f {\displaystyle \omega =2\pi \cdot f} . Все величины выражены в системе СИ.
- Δ = 503 ρ μ m f {\displaystyle \Delta =503{\sqrt {\frac {\rho }{\mu _{m}f}}}} ,
ρ {\displaystyle \rho } — удельное сопротивление, μ m {\displaystyle \mu _{m}} — относительная магнитная проницаемость, f {\displaystyle f} — частота.
Аномальный скин-эффект
Изложенная теория справедлива лишь при условии, что толщина скин-слоя много больше средней длины свободного пробега электронов, так как мы предполагаем, что при своём движении электрон непрерывно теряет энергию на преодоление омического сопротивления проводника, в результате чего происходит выделение джоулевой теплоты. Такое соотношение справедливо в весьма широких пределах, однако даже при комнатной температуре длина свободного пробега электрона для металлов сопоставима с глубиной скин-слоя — что говорит об аномальном характере эффекта. При очень низкой температуре ситуация только усугубляется[1]: проводимость сильно повышается, а следовательно, увеличивается длина свободного пробега и уменьшается толщина скин-слоя. При этих условиях механизм, приводящий к образованию скин-эффекта, уже не действует. Эффективная толщина слоя, в котором сосредоточен ток, изменяется. Такое явление называется аномальным скин-эффектом.
Применение
На скин-эффекте основано действие взрывомагнитных генераторов (ВМГ), взрывомагнитных генераторов частоты (ВМГЧ) и в частности ударно-волновых излучателей (УВИ).
Благодаря скин-эффекту на высоких частотах теплота выделяется преимущественно в поверхностном слое. Это позволяет раскалить проводник в тонком поверхностном слое без существенного изменения температуры внутренних областей. Данное явление используется в важном, с промышленной точки зрения, методе поверхностной закалки металлов.
Учёт эффекта в технике и борьба с ним
Скин-эффект проявляется всё более явно с увеличением частоты переменного тока, что заставляет учитывать его при конструировании и расчётах электрических схем, работающих с переменным и импульсным током. В связи с тем, что ток высокой частоты течёт по тонкому поверхностному слою проводника, активное сопротивление проводника значительно возрастает, что приводит к быстрому затуханию колебаний высокой частоты. Скин-эффект значительно влияет на характеристики катушек индуктивности и колебательных контуров, такие как добротность, на затухание в линиях передачи, на характеристики фильтров, на расчёты тепловых потерь и КПД, на выбор сечений проводников.
Для уменьшения влияния скин-эффекта применяют проводники различного сечения: плоские (в виде лент), трубчатые (полые внутри), наносят на поверхность проводника слой металла с более низким удельным сопротивлением. Серебро обладает наибольшей удельной проводимостью среди всех металлов, и тонкий его слой, в котором из-за скин-эффекта и протекает бо́льшая часть тока, оказывает заметное влияние (до 10%) на активное сопротивление проводника. Кроме того, слой сульфида, образующийся на поверхности серебра, не проводит ток и не участвует в скин-эффекте, в отличие от слоя окиси-закиси на поверхности меди, обладающего заметной проводимостью, вдобавок ещё и со свойствами полупроводника, и вносящего дополнительные потери на высоких частотах. Также применяется и покрытие золотом, у которого слой окислов отсутствует вовсе. Напротив, покрытие никелем, оловом или оловянно-свинцовым припоем способно значительно, в несколько раз увеличить сопротивление медных проводников на высоких частотах.
Так, в ВЧ аппаратуре используют катушки индуктивности из посеребрённого провода, серебрят печатные и проволочные проводники, поверхности экранов и обкладки конденсаторов, в высоковольтных линиях электропередач применяют провод в медной либо алюминиевой оболочке со стальным сердечником, в высокомощных генераторах переменного тока обмотка изготавливается из трубок, по которым для охлаждения циркулирует водород или дистиллированная вода. Также с целью подавления скин-эффекта используют систему из нескольких переплетённых и изолированных проводов — литцендрат. При передаче больших мощностей на значительные расстояние применяются линии постоянного тока — HVDC, который не подвержен воздействию скин-эффекта.
Покрытие серебром также применяется в сверхвысокочастотном оборудовании, использующем колебательные контуры особой формы: объёмные резонаторы и специфические линии передач — волноводы. Кроме того, на таких частотах особое внимание приходится уделять снижению шероховатости поверхности с целью уменьшения длины пути протекания тока.
Примечания
- ↑ Сивухин Д. В. Общий курс физики. Том 4. Оптика. — 1980. — С. 454.
Литература
- А. Н. Матвеев. Параграф 53 // Электричество и магнетизм. — М.: Высшая школа, 1983. — 463 с.
- A. A. Власов. Глава VI. Параграф 5 // Макроскопическая электродинамика. — 2-е изд.. — М.: Наука, 2005.
Скин-эффект — Википедия
Поверхностный эффект, скин-эффект — эффект уменьшения амплитуды электромагнитных волн по мере их проникновения вглубь проводящей среды. В результате этого эффекта, например, переменный ток высокой частоты при протекании по проводнику распределяется не равномерно по сечению, а преимущественно в поверхностном слое.
Объяснение поверхностного эффекта
Физическая картина возникновения
 Физическая картина возникновения скин-эффекта.
Физическая картина возникновения скин-эффекта.Рассмотрим цилиндрический проводник, по которому течёт ток. Вокруг проводника с током имеется магнитное поле, силовые линии которого являются концентрическими окружностями с центром на оси проводника. В результате увеличения силы тока возрастает индукция магнитного поля, а форма силовых линий при этом остаётся прежней. Поэтому в каждой точке внутри проводника производная ∂ B ∂ t {\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} направлена по касательной к линии индукции магнитного поля и, следовательно, линии ∂ B ∂ t {\displaystyle {\frac {\partial \mathbf {B} }{\partial t}}} также являются окружностями, совпадающими с линиями индукции магнитного поля. Изменяющееся магнитное поле по закону электромагнитной индукции
- rot E = − ∂ B ∂ t {\displaystyle \operatorname {rot} \,\mathbf {E} =-{\frac {\partial \mathbf {B} }{\partial t}}}
создаёт электрическое индукционное поле, силовые линии которого представляют замкнутые кривые вокруг линии индукции магнитного поля. Вектор напряжённости индукционного поля в более близких к оси проводника областях направлен противоположно вектору напряжённости электрического поля, создающего ток, а в более дальних — совпадает с ним. В результате плотность тока уменьшается в приосевых областях и увеличивается вблизи поверхности проводника, то есть возникает скин-эффект.
Уравнение, описывающее скин-эффект
Исходим из уравнения Максвелла,
- rot B = μ j {\displaystyle \operatorname {rot} \mathbf {B} =\mu \mathbf {j} }
и выражения для j {\displaystyle \mathbf {j} } по закону Ома:
- j = γ E {\displaystyle \mathbf {j} =\gamma \mathbf {E} }
Дифференцируя обе части полученного уравнения по времени, находим:
- rot ∂ B ∂ t = μ γ ∂ E ∂ t {\displaystyle \operatorname {rot} {\frac {\partial \mathbf {B} }{\partial t}}=\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}}
- − rot rot E = μ γ ∂ E ∂ t {\displaystyle -\operatorname {rot} \operatorname {rot} \mathbf {E} =\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}} .
Поскольку
- rot rot E = grad div E − ∇ 2 E {\displaystyle \operatorname {rot} \operatorname {rot} \mathbf {E} =\operatorname {grad} \operatorname {div} \mathbf {E} -\nabla ^{2}\mathbf {E} } и div E = 0 {\displaystyle \operatorname {div} \mathbf {E} =0}
окончательно получаем:
- ∇ 2 E = μ γ ∂ E ∂ t {\displaystyle \nabla ^{2}\mathbf {E} =\mu \gamma {\frac {\partial \mathbf {E} }{\partial t}}} .
 Скин-эффект в бесконечном проводнике с плоской границей.
Скин-эффект в бесконечном проводнике с плоской границей.Для упрощения решения предположим, что ток течёт по однородному бесконечному проводнику, занимающему полупространство y>0 вдоль оси X. Поверхностью проводника является плоскость Y=0. Таким образом,
- j x = j x ( y , t ) , j y = j z = 0 {\displaystyle j_{x}=j_{x}(y,t),\qquad j_{y}=j_{z}=0} ,
- E x = E x ( y , t ) , E y = E z = 0 {\displaystyle E_{x}=E_{x}(y,t),\qquad E_{y}=E_{z}=0} .
Тогда
- ∂ 2 E x ∂ y 2 = μ γ ∂ E x ∂ t {\displaystyle {\frac {\partial ^{2}E_{x}}{\partial y^{2}}}=\mu \gamma {\frac {\partial E_{x}}{\partial t}}} .
В этом уравнении все величины гармонически зависят от t, и можно положить:
- E x ( y , t ) = E 0 ( y ) e i ω t {\displaystyle E_{x}(y,t)=E_{0}(y)e^{i\omega t}} .
Подставим это в наше уравнение и получим уравнение для E 0 ( y ) {\displaystyle E_{0}(y)} :
- ∂ 2 E 0 ∂ y 2 = i γ μ ω E 0 {\displaystyle {\frac {\partial ^{2}E_{0}}{\partial y^{2}}}=i\gamma \mu \omega E_{0}} .
Общее решение этого уравнения таково:
- E x = A 1 e − k y + A 2 e k y {\displaystyle E_{x}=A_{1}e^{-ky}+A_{2}e^{ky}} .
Учитывая, что k = i γ μ ω = α ( 1 + i ) {\displaystyle k={\sqrt {i\gamma \mu \omega }}=\alpha (1+i)} , где α = γ μ ω 2 {\displaystyle \alpha ={\sqrt {\frac {\gamma \mu \omega }{2}}}} , находим
- E 0 = A 1 e − α y e − i α y + A 2 e α y e i α y {\displaystyle E_{0}=A_{1}e^{-\alpha y}e^{-i\alpha y}+A_{2}e^{\alpha y}e^{i\alpha y}} .
При удалении от поверхности проводника ( y → ∞ {\displaystyle y\rightarrow \infty } ) второе слагаемое неограниченно возрастает, что является физически недопустимой ситуацией. Следовательно, A 2 = 0 {\displaystyle A_{2}=0} и в качестве физически приемлемого решения остаётся только первое слагаемое. Тогда решение задачии имеет вид:
- E x = A 1 e − α y e i ( ω t − α y ) {\displaystyle E_{x}=A_{1}e^{-\alpha y}e^{i(\omega t-\alpha y)}} .
Взяв действительную часть от этого выражения и перейдя с помощью соотношения j = γ E {\displaystyle \mathbf {j} =\gamma \mathbf {E} } к плотности тока, получим
- j x ( y , t ) = A 1 e − α y cos ( ω t − α y ) {\displaystyle j_{x}(y,t)=A_{1}e^{-\alpha y}\cos {(\omega t-\alpha y)}} .
Принимая во внимание, что j x ( 0 , 0 ) = j 0 {\displaystyle j_{x}(0,0)=j_{0}} — амплитуда плотности тока на поверхности проводника, приходим к следующему распределению объёмной плотности тока в проводнике:
- j x ( y , t ) = j 0 e − α y cos ( ω t − α y ) {\displaystyle j_{x}(y,t)=j_{0}e^{-\alpha y}\cos {(\omega t-\alpha y)}} .
Толщина скин-слоя
Объёмная плотность тока максимальна у поверхности проводника. При удалении от поверхности она убывает экспоненциально и на глубине Δ {\displaystyle \Delta } становится меньше в е раз. Эта глубина называется толщиной скин-слоя и на основании полученного выше равна
- Δ = 2 γ μ ω {\displaystyle \Delta ={\sqrt {\frac {2}{\gamma \mu \omega }}}} .
Очевидно, что при достаточно большой частоте ω {\displaystyle \omega } толщина скин-слоя может быть очень малой. Также из экспоненциального убывания плотности тока следует, что практически весь ток сосредоточен в слое толщиной в несколько Δ {\displaystyle \Delta } , так, уменьшение плотности тока в 100 раз происходит на глубине ≈ 4 , 6 Δ {\displaystyle \approx 4,6\Delta } , если общая толщина проводника многократно превышает толщину скин-слоя. В качестве примера приведём зависимость глубины скин-слоя от частоты для медного проводника:
| Частота | Δ {\displaystyle \Delta } | Примечания |
|---|---|---|
| 50 Гц | 9,34 мм | 50 Гц — частота электросети в большинстве стран Евразии и Африки |
| 60 Гц | 8,53 мм | 60 Гц — частота электросети в Северной, Центральной и частично Южной Америке |
| 10 кГц | 0,66 мм | |
| 100 кГц | 0,21 мм | |
| 500 кГц | 0,095 мм | |
| 1 МГц | 0,067 мм | |
| 10 МГц | 0,021 мм |
Если проводник имеет ферромагнитные свойства, то толщина скин-слоя будет во много раз меньше. Например, для стали ( μ {\displaystyle \mu } =1000) Δ {\displaystyle \Delta } =0.74 мм. Это имеет значение, например, при электрификации железных дорог, поскольку там стальные рельсы используются в качестве обратного провода.
Для расчёта толщины скин-слоя в металле (приближённо) можно использовать следующие эмпирические формулы:
- Δ = c 2 ε 0 ω μ m ρ {\displaystyle \Delta =c{\sqrt {2{\frac {\varepsilon _{0}}{\omega \mu _{m}}}\rho }}} .
Здесь ε 0 {\displaystyle \varepsilon _{0}} = 8,85419·10−12 Ф/м — электрическая постоянная, ρ {\displaystyle \rho } — удельное сопротивление, c — скорость света, μ m {\displaystyle \mu _{m}} — относительная магнитная проницаемость (близка к единице для пара- и диамагнетиков — меди, серебра, и т. п.), ω = 2 π ⋅ f {\displaystyle \omega =2\pi \cdot f} . Все величины выражены в системе СИ.
- Δ = 503 ρ μ m f {\displaystyle \Delta =503{\sqrt {\frac {\rho }{\mu _{m}f}}}} ,
ρ {\displaystyle \rho } — удельное сопротивление, μ m {\displaystyle \mu _{m}} — относительная магнитная проницаемость, f {\displaystyle f} — частота.
Аномальный скин-эффект
Изложенная теория справедлива лишь при условии, что толщина скин-слоя много больше средней длины свободного пробега электронов, так как мы предполагаем, что при своём движении электрон непрерывно теряет энергию на преодоление омического сопротивления проводника, в результате чего происходит выделение джоулевой теплоты. Такое соотношение справедливо в весьма широких пределах, однако даже при комнатной температуре длина свободного пробега электрона для металлов сопоставима с глубиной скин-слоя — что говорит об аномальном характере эффекта. При очень низкой температуре ситуация только усугубляется[1]: проводимость сильно повышается, а следовательно, увеличивается длина свободного пробега и уменьшается толщина скин-слоя. При этих условиях механизм, приводящий к образованию скин-эффекта, уже не действует. Эффективная толщина слоя, в котором сосредоточен ток, изменяется. Такое явление называется аномальным скин-эффектом.
Применение
На скин-эффекте основано действие взрывомагнитных генераторов (ВМГ), взрывомагнитных генераторов частоты (ВМГЧ) и в частности ударно-волновых излучателей (УВИ).
Благодаря скин-эффекту на высоких частотах теплота выделяется преимущественно в поверхностном слое. Это позволяет раскалить проводник в тонком поверхностном слое без существенного изменения температуры внутренних областей. Данное явление используется в важном, с промышленной точки зрения, методе поверхностной закалки металлов.
Учёт эффекта в технике и борьба с ним
Скин-эффект проявляется всё более явно с увеличением частоты переменного тока, что заставляет учитывать его при конструировании и расчётах электрических схем, работающих с переменным и импульсным током. В связи с тем, что ток высокой частоты течёт по тонкому поверхностному слою проводника, активное сопротивление проводника значительно возрастает, что приводит к быстрому затуханию колебаний высокой частоты. Скин-эффект значительно влияет на характеристики катушек индуктивности и колебательных контуров, такие как добротность, на затухание в линиях передачи, на характеристики фильтров, на расчёты тепловых потерь и КПД, на выбор сечений проводников.
Для уменьшения влияния скин-эффекта применяют проводники различного сечения: плоские (в виде лент), трубчатые (полые внутри), наносят на поверхность проводника слой металла с более низким удельным сопротивлением. Серебро обладает наибольшей удельной проводимостью среди всех металлов, и тонкий его слой, в котором из-за скин-эффекта и протекает бо́льшая часть тока, оказывает заметное влияние (до 10%) на активное сопротивление проводника. Кроме того, слой сульфида, образующийся на поверхности серебра, не проводит ток и не участвует в скин-эффекте, в отличие от слоя окиси-закиси на поверхности меди, обладающего заметной проводимостью, вдобавок ещё и со свойствами полупроводника, и вносящего дополнительные потери на высоких частотах. Также применяется и покрытие золотом, у которого слой окислов отсутствует вовсе. Напротив, покрытие никелем, оловом или оловянно-свинцовым припоем способно значительно, в несколько раз увеличить сопротивление медных проводников на высоких частотах.
Так, в ВЧ аппаратуре используют катушки индуктивности из посеребрённого провода, серебрят печатные и проволочные проводники, поверхности экранов и обкладки конденсаторов, в высоковольтных линиях электропередач применяют провод в медной либо алюминиевой оболочке со стальным сердечником, в высокомощных генераторах переменного тока обмотка изготавливается из трубок, по которым для охлаждения циркулирует водород или дистиллированная вода. Также с целью подавления скин-эффекта используют систему из нескольких переплетённых и изолированных проводов — литцендрат. При передаче больших мощностей на значительные расстояние применяются линии постоянного тока — HVDC, который не подвержен воздействию скин-эффекта.
Покрытие серебром также применяется в сверхвысокочастотном оборудовании, использующем колебательные контуры особой формы: объёмные резонаторы и специфические линии передач — волноводы. Кроме того, на таких частотах особое внимание приходится уделять снижению шероховатости поверхности с целью уменьшения длины пути протекания тока.
Примечания
- ↑ Сивухин Д. В. Общий курс физики. Том 4. Оптика. — 1980. — С. 454.
Литература
- А. Н. Матвеев. Параграф 53 // Электричество и магнетизм. — М.: Высшая школа, 1983. — 463 с.
- A. A. Власов. Глава VI. Параграф 5 // Макроскопическая электродинамика. — 2-е изд.. — М.: Наука, 2005.
Неравномерное распределение электрического тока по поверхности или оболочке проводника, несущего a.c, называется скин-эффектом. Другими словами, концентрация заряда ближе к поверхности по сравнению с сердечником проводника. Омическое сопротивление проводника увеличивается из-за концентрации тока на поверхности проводника.
Кожный эффект увеличивается с увеличением частоты.На низкой частоте, такой как 50 Гц, наблюдается небольшое увеличение плотности тока вблизи поверхности проводника; но на высоких частотах, таких как радиочастота, практически все токи протекают по поверхности проводника. Если в проводнике пропускается постоянный ток (частота = 0), ток равномерно распределяется по сечению проводников.
Почему возникает кожный эффект?
Давайте рассмотрим проводник, состоящий из ряда концентрических цилиндров.Когда a.c пропускается в проводнике, магнитный поток индуцируется в нем. Магнитный поток, связывающий цилиндрический элемент рядом с центром, больше, чем магнитный поток, связывающий другой цилиндрический элемент вблизи поверхности проводника. Это связано с тем, что центральный цилиндрический элемент окружен как внутренним, так и внешним потоком, тогда как внешний цилиндрический элемент окружен только внешним потоком.
Самоиндуктивность во внутреннем цилиндрическом элементе больше и, следовательно, будет предлагать большее индуктивное сопротивление, чем внешний цилиндрический элемент.Это различие в индуктивном реактивном сопротивлении дает склонность тока концентрироваться к поверхности или оболочке проводника.
Плотность тока максимальна на поверхности проводника и минимальна в центре проводника. Эффект эквивалентен уменьшению площади поперечного сечения проводника и, следовательно, эффективное сопротивление проводника увеличивается.
Факторы, влияющие на эффект кожи
- Частота — скин-эффект увеличивается с увеличением частоты.
- Диаметр — Увеличивается с увеличением диаметра проводника.
- Форма проводника — скин-эффект больше в сплошном проводнике и меньше в многожильном проводнике, потому что площадь поверхности сплошного проводника больше.
- Тип материала — Повышение скин-эффекта с увеличением проницаемости материала (проницаемость — способность материала поддерживать формирование магнитного поля).
запоминающихся точек
- Эффект Скин незначителен, если частота меньше 50 Гц, а диаметр проводника меньше 1 см.
- В многожильных проводниках, таких как ACSR (усиленная алюминиевая проводниковая сталь), ток протекает в основном во внешнем слое, изготовленном из алюминия, в то время как сталь вблизи центра не несет тока и придает проводнику высокую прочность на разрыв. Концентрация тока вблизи поверхности позволила использовать проводник ACSR.
Skin effect — Википедия переиздано // WIKI 2
«Глубина кожи» перенаправляет сюда. Для глубины (слоев) биологической / органической кожи, смотрите кожу. Распределение тока, протекающего в цилиндрическом проводнике, показано в поперечном сечении. Для переменного тока плотность тока экспоненциально уменьшается от поверхности к внутренней части. Глубина скин-слоя δ определяется как глубина, где плотность тока составляет всего 1 / е (около 37%) от значения на поверхности; это зависит от частоты тока и электрических и магнитных свойств проводника.
Каждый 3-проводной жгут в этой установке для передачи энергии действует как один проводник. Один провод, использующий такое же количество металла на километр, будет иметь большие потери из-за скин-эффекта.
Скин-эффект — это тенденция переменного электрического тока (AC) распределяться внутри проводника, так что плотность тока является наибольшей вблизи поверхности проводника и экспоненциально уменьшается с увеличением глубины в проводнике. Электрический ток протекает в основном по «оболочке» проводника, между наружной поверхностью и уровнем, называемым , с глубиной оболочки .Глубина кожи зависит от частоты переменного тока, причем более высокая частота приводит к меньшей глубине кожи. Кожный эффект уменьшает эффективное сечение проводника и, таким образом, увеличивает его эффективное сопротивление. Скин-эффект обусловлен противодействующими вихревыми токами, вызванными изменяющимся магнитным полем, возникающим в результате переменного тока. При меди 60 Гц глубина обшивки составляет около 8,5 мм. На высоких частотах глубина кожи становится намного меньше.
Повышенное сопротивление переменному току из-за скин-эффекта можно уменьшить с помощью специально сплетенной лицевой проволоки.Поскольку внутренняя часть большого проводника несет так мало тока, трубчатые проводники, такие как труба, могут использоваться для экономии веса и стоимости. Скин-эффект имеет практические последствия при анализе и проектировании радиочастотных и микроволновых цепей, линий передачи (или волноводов) и антенн. Это также важно при частотах сети (50–60 Гц) в системах передачи и распределения электроэнергии переменного тока. Это одна из причин предпочтения постоянного тока высокого напряжения для передачи электроэнергии на большие расстояния.
Эффект был впервые описан в статье Горация Лэмба в 1883 году для случая сферических проводников [1] и был обобщен для проводников любой формы Оливером Хевисайдом в 1885 году.
Причина
 Причина кожного эффекта. Ток I, протекающий через проводник, индуцирует магнитное поле H. Если ток увеличивается, как на этом рисунке, результирующее увеличение H индуцирует циркулирующие вихревые токи I Вт , которые частично отменяют протекание тока в центре и усиливают его вблизи кожа.
Причина кожного эффекта. Ток I, протекающий через проводник, индуцирует магнитное поле H. Если ток увеличивается, как на этом рисунке, результирующее увеличение H индуцирует циркулирующие вихревые токи I Вт , которые частично отменяют протекание тока в центре и усиливают его вблизи кожа.Проводники, обычно в форме проводов, могут использоваться для передачи электрической энергии или сигналов с использованием переменного тока, протекающего через этот проводник. Носители заряда, составляющие этот ток, обычно электроны, приводятся в действие электрическим полем из-за источника электрической энергии. Переменный ток в проводнике создает переменное магнитное поле внутри и вокруг проводника. Когда интенсивность тока в проводнике изменяется, магнитное поле также изменяется. Изменение магнитного поля, в свою очередь, создает электрическое поле, которое противостоит изменению силы тока.Это противоположное электрическое поле называется противоэлектродвижущей силой (обратная ЭДС). Обратный ЭДС является самым сильным в центре проводника, и вынуждает проводящие электроны к внешней стороне проводника, как показано на диаграмме справа. [2] [3]
Независимо от движущей силы плотность тока оказывается наибольшей на поверхности проводника с уменьшенной величиной глубже в проводнике. Это снижение плотности тока известно как скин-эффект , а глубина кожи — это мера глубины, на которой плотность тока падает до 1 / e от ее значения вблизи поверхности.Более 98% тока будет течь в слое, в 4 раза превышающем глубину кожи от поверхности. Это поведение отличается от постоянного тока, который обычно распределяется равномерно по сечению провода.
Переменный ток также может быть индуцированным в проводнике из-за переменного магнитного поля в соответствии с законом индукции. Следовательно, электромагнитная волна, падающая на проводник, обычно создает такой ток; это объясняет отражение электромагнитных волн от металлов.Хотя термин «скин-эффект» чаще всего ассоциируется с приложениями, включающими передачу электрических токов, глубина скин-слоя также описывает экспоненциальное затухание электрического и магнитного полей, а также плотность индуцированных токов внутри объемного материала, когда плоскость волна падает на него при нормальном падении.
Формула
Плотность переменного тока Дж в проводнике экспоненциально уменьшается от его значения на поверхности Дж S в соответствии с глубиной d от поверхности следующим образом: [4] : 362
- J знак равно J S е — ( 1 + J ) d / δ {\ displaystyle J = J _ {\ mathrm {S}} \, e ^ {- {(1 + j) d / \ delta}}}
, где δ называется глубиной скин-слоя .Таким образом, глубина оболочки определяется как глубина под поверхностью проводника, на которой плотность тока упала до 1/
.Кожный эффект | Статья о скин-эффекте от Free Dictionary
(также поверхностный эффект), повышенное затухание электромагнитных волн при проникновении волн в проводящую среду. В результате этого явления переменный ток по поперечному сечению проводника или переменный магнитный поток по поперечному сечению магнитной цепи не распределены равномерно, а расположены главным образом в поверхностном слое. Скин-эффект обусловлен образованием вихревых токов при распространении электромагнитной волны в проводящей среде, в результате чего часть электромагнитной энергии преобразуется в тепло.Это приводит к снижению напряженности электрического и магнитного полей и уменьшению плотности тока, то есть к затуханию волны.
Согласно уравнениям Максвелла, чем выше частота электромагнитной волны v и выше магнитная проницаемость μ проводника, тем сильнее вращательное электрическое поле, вызванное переменным магнитным полем. Согласно закону Ома и закону Джоуля, чем выше проводимость σ проводника, тем больше плотность тока и мощность, рассеиваемая на единицу объема.Таким образом, чем больше , , µ и σ, тем больше затухание, то есть тем более заметен скин-эффект.
В случае плоской синусоидальной волны, распространяющейся вдоль оси x в однородной линейной среде, которая является хорошим проводником (токи смещения незначительны по сравнению с токами проводимости), амплитуды напряженности электрического и магнитного полей равны затухание по экспоненциальному закону:
E = E 0 e — αx и H = H 0 e
где — коэффициент затухания, а μ 0 — магнитная постоянная.На глубине x = δ = 1 / α амплитуда волны уменьшается в и раз. Это расстояние называется глубиной проникновения или глубиной кожи. Например, при частоте 50 герц в меди (σ = 580 килосименс / см и μ = 1), δ = 9,4 мм; в стали (σ = 100 кгс / см и μ = 1000), δ = 0,74 мм. Когда частота увеличивается до 0,5 мегагерц, δ уменьшается в 100 раз. Электромагнитная волна вообще не проникает в идеальный проводник (один с бесконечно большой проводимостью), но полностью отражается от него.Чем короче расстояние, которое проходит волна по сравнению с δ , тем слабее проявление скин-эффекта.
— коэффициент затухания, а μ 0 — магнитная постоянная.На глубине x = δ = 1 / α амплитуда волны уменьшается в и раз. Это расстояние называется глубиной проникновения или глубиной кожи. Например, при частоте 50 герц в меди (σ = 580 килосименс / см и μ = 1), δ = 9,4 мм; в стали (σ = 100 кгс / см и μ = 1000), δ = 0,74 мм. Когда частота увеличивается до 0,5 мегагерц, δ уменьшается в 100 раз. Электромагнитная волна вообще не проникает в идеальный проводник (один с бесконечно большой проводимостью), но полностью отражается от него.Чем короче расстояние, которое проходит волна по сравнению с δ , тем слабее проявление скин-эффекта.Понятие импеданса поверхности (оболочки) Z с вводится для проводников с очень выраженным скин-эффектом, когда радиус кривизны поперечного сечения проводника значительно превышает δ , а поле в проводнике представляет плоская волна. Импеданс оболочки определяется как отношение комплексной амплитуды падения напряжения на единицу длины проводника к комплексной амплитуде тока в поперечном сечении единичной длины оболочки.Комплексное сопротивление проводника на единицу длины составляет
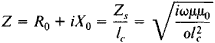
, где R 0 — эффективное сопротивление проводника, определяющее потери мощности, X 0 — индуктивное реактивное сопротивление, которое принимает в учитывать индуктивность проводника, возникающую из-за магнитного потока внутри проводника, l c — периметр поперечного сечения оболочки, а ω = 2 πν ; здесь R 0 = X 0 .Когда скин-эффект выражен, поверхностный импеданс такой же, как характеристический импеданс проводника, и, следовательно, равен отношению напряженности электрического поля к напряженности магнитного поля на поверхности проводника.
В тех случаях, когда длина свободного пробега l для носителей тока становится больше глубины скин-слоя δ — например, в очень чистых металлах при низких температурах — скин-эффект на относительно высоких частотах приобретает ряд характеристик и называется аномальным.Поскольку поле на длине свободного пробега электрона неоднородно, ток в данной точке зависит не только от значения электрического поля для этой точки, но и от значения области вокруг точки, имеющей размер порядка л . Следовательно, при решении уравнений Максвелла необходимо использовать вместо закона Ома кинетическое уравнение Больцмана, чтобы вычислить ток. При аномальном скин-эффекте электроны становятся неравными с точки зрения их вклада в электрический ток.Когда l »δ, основной вклад вносят электроны, которые движутся в коже параллельно поверхности металла или под очень малыми углами к поверхности, тем самым проводя длительное время в области сильного поля. Электромагнитная волна ослабляется в поверхностном слое, как и раньше, но количественные характеристики аномального скин-эффекта несколько отличаются. Поле в скине экспоненциально не затухает 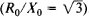 .
.
В инфракрасном диапазоне частот электрон не может пройти расстояние l в течение периода изменения поля.В этом случае поле можно считать однородным по периоду для пути электрона. Это снова приводит к закону Ома, и скин-эффект снова становится нормальным. Таким образом, на низких и очень высоких частотах скин-эффект всегда нормальный. В радиочастотном диапазоне эффект может быть нормальным или аномальным, в зависимости от отношения l к δ . Все вышесказанное действует до тех пор, пока частота ω ниже частоты плазмы: ω <ω 0 ≈ (4 πne 2 / м ) ½ , где n — концентрация свободные электроны, e, — заряд, а m, — масса электрона.( См. METAL OPTICS для более высоких частот.)
Кожный эффект часто нежелателен. В проводниках, имеющих ярко выраженный скин-эффект, переменный ток протекает в основном через поверхностный слой; поперечное сечение проводника не используется в полной мере, а сопротивление и потери мощности в проводнике для данного тока увеличиваются. В ферромагнитных пластинках или полосках для магнитных цепей трансформаторов, электрических машин и других устройств переменный магнитный поток в случае заметного скин-эффекта проходит в основном через поверхностный слой.В результате использование поперечного сечения магнитной цепи становится менее эффективным, ток намагничивания увеличивается, и потери в стали выше. Нежелательное влияние скин-эффекта уменьшается за счет уменьшения толщины пластин или полос и, когда частоты достаточно высоки, за счет использования магнитных цепей из магнитодиэлектриков.
С другой стороны, скин-эффект имеет практическое применение, например, в действии электромагнитных экранов.Чтобы защитить окружающее пространство от помех, создаваемых полем от силового трансформатора, работающего на частоте 50 Гц, используется экран из сравнительно толстой ферромагнитной стали. Чтобы экранировать катушку индуктивности, работающую на высоких частотах, экраны сделаны из тонкого слоя алюминия. Высокочастотное поверхностное упрочнение стальных объектов также основано на скин-эффекте. ( См. ИНДУКЦИОННЫЙ НАГРЕВАТЕЛЬНЫЙ ЗАВОД .)
СПИСОК ЛИТЕРАТУРЫ
Нетушил, А.В. и К. М. Поливанов. Основы электротехники , вып. 3, Москва, 1956., Поливанов К.М. Теоретические основы электротехники , ч.3: Теория электромагнитного поля . М., 1975.
Нейман, Л. Р. Поверхностный эффект в ферромагнитных телах . Ленинград-Москва, 1949.
См. Также ссылки под МЕТАЛЛЫ .
(также о поверхностном эффекте), повышенном затухании электромагнитных волн при проникновении волн в проводящую среду. В результате этого явления переменный ток по поперечному сечению проводника или переменный магнитный поток по поперечному сечению магнитной цепи не распределены равномерно, а расположены главным образом в поверхностном слое. Скин-эффект обусловлен образованием вихревых токов при распространении электромагнитной волны в проводящей среде, в результате чего часть электромагнитной энергии преобразуется в тепло.Это приводит к снижению напряженности электрического и магнитного полей и уменьшению плотности тока, то есть к затуханию волны.
Согласно уравнениям Максвелла, чем выше частота электромагнитной волны v и выше магнитная проницаемость μ проводника, тем сильнее вращательное электрическое поле, вызванное переменным магнитным полем. Согласно закону Ома и закону Джоуля, чем выше проводимость σ проводника, тем больше плотность тока и мощность, рассеиваемая на единицу объема.Таким образом, чем больше , , µ и σ, тем больше затухание, то есть тем более заметен скин-эффект.
В случае плоской синусоидальной волны, распространяющейся вдоль оси x в однородной линейной среде, которая является хорошим проводником (токи смещения незначительны по сравнению с токами проводимости), амплитуды напряженности электрического и магнитного полей равны затухание по экспоненциальному закону:
E = E 0 e — αx и H = H 0 e
где — коэффициент затухания, а μ 0 — магнитная постоянная.На глубине x = δ = 1 / α амплитуда волны уменьшается в и раз. Это расстояние называется глубиной проникновения или глубиной кожи. Например, при частоте 50 герц в меди (σ = 580 килосименс / см и μ = 1), δ = 9,4 мм; в стали (σ = 100 кгс / см и μ = 1000), δ = 0,74 мм. Когда частота увеличивается до 0,5 мегагерц, δ уменьшается в 100 раз. Электромагнитная волна вообще не проникает в идеальный проводник (один с бесконечно большой проводимостью), но полностью отражается от него.Чем короче расстояние, которое проходит волна по сравнению с δ , тем слабее проявление скин-эффекта.
— коэффициент затухания, а μ 0 — магнитная постоянная.На глубине x = δ = 1 / α амплитуда волны уменьшается в и раз. Это расстояние называется глубиной проникновения или глубиной кожи. Например, при частоте 50 герц в меди (σ = 580 килосименс / см и μ = 1), δ = 9,4 мм; в стали (σ = 100 кгс / см и μ = 1000), δ = 0,74 мм. Когда частота увеличивается до 0,5 мегагерц, δ уменьшается в 100 раз. Электромагнитная волна вообще не проникает в идеальный проводник (один с бесконечно большой проводимостью), но полностью отражается от него.Чем короче расстояние, которое проходит волна по сравнению с δ , тем слабее проявление скин-эффекта.Понятие импеданса поверхности (оболочки) Z с вводится для проводников с очень выраженным скин-эффектом, когда радиус кривизны поперечного сечения проводника значительно превышает δ , а поле в проводнике представляет плоская волна. Импеданс оболочки определяется как отношение комплексной амплитуды падения напряжения на единицу длины проводника к комплексной амплитуде тока в поперечном сечении единичной длины оболочки.Комплексное сопротивление проводника на единицу длины составляет
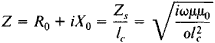
, где R 0 — эффективное сопротивление проводника, определяющее потери мощности, X 0 — индуктивное реактивное сопротивление, которое принимает в учитывать индуктивность проводника, возникающую из-за магнитного потока внутри проводника, l c — периметр поперечного сечения оболочки, а ω = 2 πν ; здесь R 0 = X 0 .Когда скин-эффект выражен, поверхностный импеданс такой же, как характеристический импеданс проводника, и, следовательно, равен отношению напряженности электрического поля к напряженности магнитного поля на поверхности проводника.
В тех случаях, когда длина свободного пробега l для носителей тока становится больше глубины скин-слоя δ — например, в очень чистых металлах при низких температурах — скин-эффект на относительно высоких частотах приобретает ряд характеристик и называется аномальным.Поскольку поле на длине свободного пробега электрона неоднородно, ток в данной точке зависит не только от значения электрического поля для этой точки, но и от значения области вокруг точки, имеющей размер порядка л . Следовательно, при решении уравнений Максвелла необходимо использовать вместо закона Ома кинетическое уравнение Больцмана, чтобы вычислить ток. При аномальном скин-эффекте электроны становятся неравными с точки зрения их вклада в электрический ток.Когда l »δ, основной вклад вносят электроны, которые движутся в коже параллельно поверхности металла или под очень малыми углами к поверхности, тем самым проводя длительное время в области сильного поля. Электромагнитная волна ослабляется в поверхностном слое, как и раньше, но количественные характеристики аномального скин-эффекта несколько отличаются. Поле в скине экспоненциально не затухает 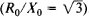 .
.
В инфракрасном диапазоне частот электрон не может пройти расстояние l в течение периода изменения поля.В этом случае поле можно считать однородным по периоду для пути электрона. Это снова приводит к закону Ома, и скин-эффект снова становится нормальным. Таким образом, на низких и очень высоких частотах скин-эффект всегда нормальный. В радиочастотном диапазоне эффект может быть нормальным или аномальным, в зависимости от отношения l к δ . Все вышесказанное действует до тех пор, пока частота ω ниже частоты плазмы: ω <ω 0 ≈ (4 πne 2 / м ) ½ , где n — концентрация свободные электроны, e, — заряд, а m, — масса электрона.( См. METAL OPTICS для более высоких частот.)
Кожный эффект часто нежелателен. В проводниках, имеющих ярко выраженный скин-эффект, переменный ток протекает в основном через поверхностный слой; поперечное сечение проводника не используется в полной мере, а сопротивление и потери мощности в проводнике для данного тока увеличиваются. В ферромагнитных пластинках или полосках для магнитных цепей трансформаторов, электрических машин и других устройств переменный магнитный поток в случае заметного скин-эффекта проходит в основном через поверхностный слой.В результате использование поперечного сечения магнитной цепи становится менее эффективным, ток намагничивания увеличивается, и потери в стали выше. Нежелательное влияние скин-эффекта уменьшается за счет уменьшения толщины пластин или полос и, когда частоты достаточно высоки, за счет использования магнитных цепей из магнитодиэлектриков.
С другой стороны, скин-эффект имеет практическое применение, например, в действии электромагнитных экранов.Чтобы защитить окружающее пространство от помех, создаваемых полем от силового трансформатора, работающего на частоте 50 Гц, используется экран из сравнительно толстой ферромагнитной стали. Чтобы экранировать катушку индуктивности, работающую на высоких частотах, экраны сделаны из тонкого слоя алюминия. Высокочастотное поверхностное упрочнение стальных объектов также основано на скин-эффекте. ( См. ИНДУКЦИОННЫЙ НАГРЕВАТЕЛЬНЫЙ ЗАВОД .)
СПИСОК ЛИТЕРАТУРЫ
Нетушил, А.В. и К. М. Поливанов. Основы электротехники , вып. 3, Москва, 1956., Поливанов К.М. Теоретические основы электротехники , ч.3: Теория электромагнитного поля . М., 1975.
Нейман, Л. Р. Поверхностный эффект в ферромагнитных телах . Ленинград-Москва, 1949.
См. Также ссылки под МЕТАЛЛЫ .