сопротивления через силу тока и напряжение
Электротехника как область науки, занимающаяся использованием электроэнергии, в том числе ее получением, распределением и учетом, оперирует значениями тока, напряжения, мощности и сопротивления. Это основные величины. Кроме этого, имеется множество других характеристик и понятий, но в рамках данной статьи будут рассматриваться именно эти основополагающие понятия.
Многообразие устройств электротехники
Электрический ток
Согласно определению, ток представляет собой упорядоченное движение заряженных частиц в среде. Такими частицами могут быть свободные электроны или ионы, частицы вещества, в которых число протонов в ядре не равно количеству электронов, то есть имеющие определенный заряд, положительный или отрицательный. Электроток может быть постоянный или переменный.
Электрическое напряжение
Электрическое напряжение – это разность потенциалов на противоположных участках цепи. Точное определение понятия подразумевает работу по переносу электрического заряда между участками цепи.
Сопротивление
Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.
Резисторы различных типов
Мощность
Скорость преобразования, передачи и потребления электрической энергии определяется мощностью.
Взаимосвязь параметров электрической цепи
Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.
К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.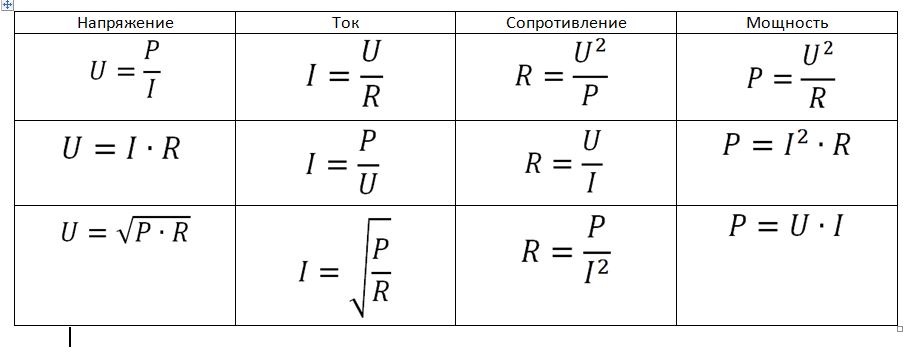
Закон Ома и его основатель
Формула напряжения тока закона Ома выглядит следующим образом:
I=U/R.
Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.
Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:
- I – сила тока;
- U – напряжение;
- R – сопротивление.
Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.
Кроме закона Ома, используется формула расчета мощности:
P=U∙I.
Символом P здесь обозначена мощность тока.
Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.
Единицы измерения в формуле
Невозможно выполнять расчеты или измерения, не зная, какими величинами оперировать. Общепринятые обозначения, согласно международной системе измерения СИ:
Общепринятые обозначения, согласно международной системе измерения СИ:
- Напряжение – Вольт. Обозначается символом В или V в англоязычной литературе;
- Сила тока – Ампер. Обозначается символом А;
- Электрическое сопротивление – Ом. Используется обозначение Ом или Ohm;
- Электрическая мощность – Ватт. Обозначается как Вт или W.
Как работает закон в реальной жизни
Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.
Лампа накаливания
Сила тока формула через мощность:
I=P/U;
Сопротивление:
R=U/I.
Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:
R=U2/P.
Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.
Правило для запоминания расчетов
Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:
P=U2/R.
Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.
Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.
Облегчить расчеты можно, используя онлайн калькулятор.
Пример с обычной водой
Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.
Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.
Зависимость сопротивления воды от содержания солей
Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.
По какой формуле определяется напряжение
Использование той или иной формулы напряжения электрического тока для вычисления зависит от того, какие величины известны:
- Ток и сопротивление – U=I∙R;
- Ток и мощность – U=P/I;
- Мощность и сопротивление – U=√P∙R
Различные используемые величины
Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:
Для обозначений применяют соответствующие приставки:
- Кило – 1000;
- Мега – 1000000;
- Гига – 1000000000;
- Милли – 0.001.
Таким образом, получается:
- Киловольт (кВ) – тысяча вольт;
- Мегаватт (Мвт) – миллион ватт;
- Миллиом (мОм) – одна тысячная Ом;
- Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.
Как найти напряжение
U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.
Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:
U=A/q, где q – величина заряда.
Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.
Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.
Гидравлическая аналогия
Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему.
- Источник питания – насос;
- Проводники – трубы;
- Электроток – движение воды.
Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.
Гидравлическая аналогия
Измерительные приборы
Для измерения параметров электрических цепей служат измерительные приборы:
- Вольтметр;
- Амперметр;
- Омметр.
Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.
Один из самых распространенных авометров
Типичные напряжения
Для стандартизации и возможности использования различного оборудования в быту и технике применяются электрические сети со стандартными значениями:
- Бытовая сеть –220В;
- Бортовая сеть автомобиля – 12 или 24В;
- Батареи и аккумуляторы – 1.5, 3 или 9В.
Потенциал Гальвани
В электрохимии используется понятие потенциала Гальвани, который означает разность потенциала между различными фазами вещества, например, между электродом и электролитом, между электродами из разнородных металлов.
Видео
простое объяснение для чайников с формулой и понятиями
Говорят: «не знаешь закон Ома – сиди дома».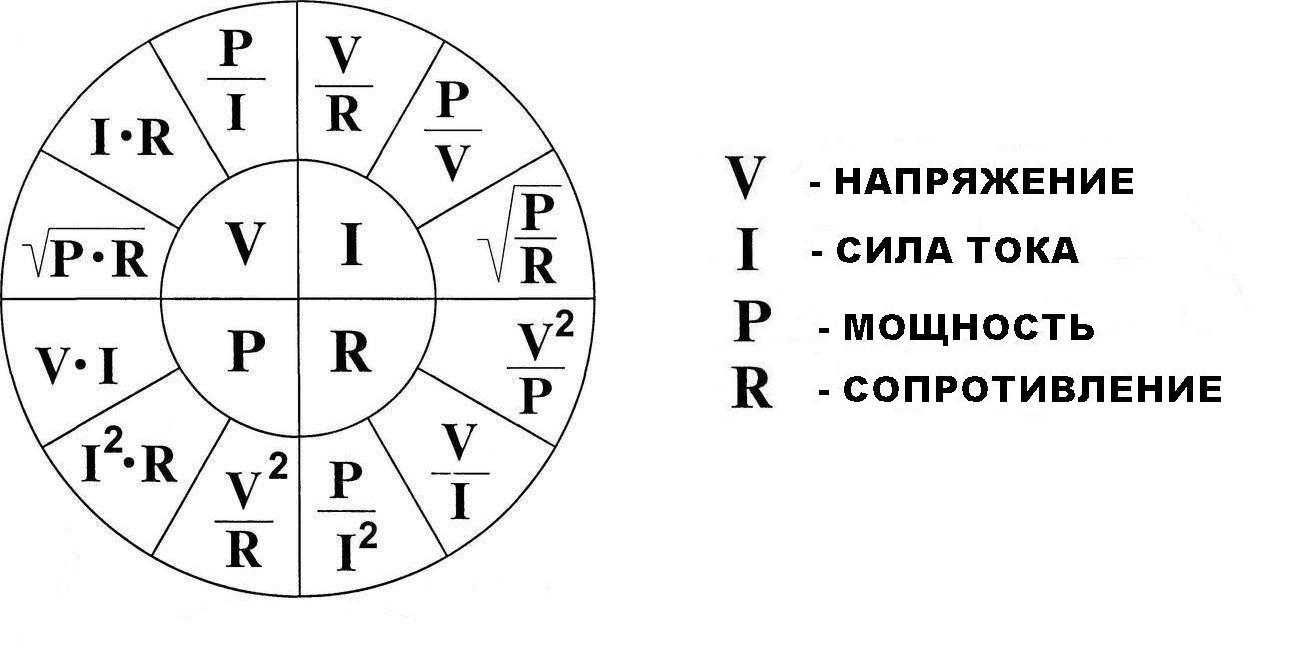 Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.
Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.
Основные понятия закона Ома
Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.
Сила тока I
Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10-19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.
Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах.
Напряжение U, или разность потенциалов
Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.
Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.
Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах. Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль.
Сопротивление R
Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах.
Памятник Георгу Симону Ому
Формулировка и объяснение закона Ома
Закон немецкого учителя Георга Ома очень прост. Он гласит:
Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.
Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря «участок цепи» мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.
Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.
Пусть у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.
Закон запишется в следующем виде:
Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.
Кстати, о том, что такое что такое ЭДС, читайте в нашей отдельной статье.
Как понять закон Ома?
Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.
Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе. Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.
Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.
Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)
Сила тока прямо пропорциональна напряжению.
Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.
Сила тока обратно пропорциональна сопротивлению.
Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.
В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.
В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.
Ток в проводнике
В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.
Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего студенческого сервиса. А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!
формулы и определения / Блог / Справочник :: Бингоскул
Немецкий физик Георг Симон Ом (1787—1854) открыл основной закон электрической цепи.
Закон Ома для участка цепи:
Определение: Cила тока I на участке электрической цепи прямо пропорциональна напряжению U на концах участка и обратно пропорциональна его сопротивлению R.
- I — сила тока (в системе СИ измеряется — Ампер)
- Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.
- Формула: I=\frac{U}{R}
- U — напряжение (в системе СИ измеряется — Вольт)
- Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.
- Формула: U=IR
- R — электрическое сопротивление (в системе СИ измеряется — Ом).
- Электрическое сопротивление R это отношение напряжения на концах проводника к силе тока, текущего по проводнику.
- Формула R=\frac{U}{I}
Определение единицы сопротивления — Ом
1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1 (Вольт) протекает ток 1 (Ампер).
Закон Ома для полной цепи
Определение: Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника
Формула I=\frac{\varepsilon}{R+r}
- \varepsilon — ЭДС источника напряжения, В;
- I — сила тока в цепи, А;
- R — сопротивление всех внешних элементов цепи, Ом;
- r — внутреннее сопротивление источника напряжения, Ом.
Как запомнить формулы закона Ома
Треугольник Ома поможет запомнить закон. Нужно закрыть искомую величину, и два других символа дадут формулу для её вычисления.
.
- U — электрическое напряжение;
- I — сила тока;
- P — электрическая мощность;
- R — электрическое сопротивление
Смотри также:
Для закрепления своих знаний решай задания и варианты ЕГЭ по физике с ответами и пояснениями.
Закон Ома. Формула Закона Ома
Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.
Георг Симон ОмЗакон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.
Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.
Формула закона Ома записывается в следующем виде:
где
I – сила тока в проводнике, единица измерения силы тока — ампер [А];
U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];
R – электрическое сопротивление проводника, единица измерения электрического сопротивления — ом [Ом].
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза
И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.
Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника. В вершине которого находится напряжение, в нижней левой части – сила тока, а в правой – сопротивление.
Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.
Где и когда можно применять закон Ома?
Нужна помощь в написании работы?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.
Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Закон Ома. Для цепей и тока. Формулы и применение
Георг Симон Ом начал свои исследования вдохновляясь знаменитым трудом Жана Батиста Фурье «Аналитическая теория тепла». В этой работе Фурье представлял тепловой поток между двумя точками как разницу температур, а изменение теплового потока связывал с его прохождением через препятствие неправильной формы из теплоизолирующего материала. Аналогично этому Ом обуславливал возникновение электрического тока разностью потенциалов.
История
Исходя из этого Ом стал экспериментировать с разными материалами проводника. Для того, чтобы определить их проводимость он подключал их последовательно и подгонял их длину таким образом, чтобы сила тока была одинаковой во всех случаях.
Важно при таких измерениях было подбирать проводники одного и того же диаметра. Ом, замеряя проводимость серебра и золота, получил результаты, которые по современным данным не отличаются точностью. Так, серебряный проводник у Ома проводил меньше электрического тока, чем золотой. Сам Ом объяснял это тем, что его проводник из серебра был покрыт маслом и из-за этого, по всей видимости, опыт не дал точных результатов.
Однако не только с этим были проблемы у физиков, которые в то время занимались подобными экспериментами с электричеством. Большие трудности с добычей чистых материалов без примесей для опытов, затруднения с калибровкой диаметра проводника искажали результаты тестов. Еще большая загвоздка состояла в том, что сила тока постоянно менялась во время испытаний, поскольку источником тока служили переменные химические элементы. В таких условиях Ом вывел логарифмическую зависимость силы тока от сопротивления провода.
Немногим позже немецкий физик Поггендорф, специализировавшийся на электрохимии, предложил Ому заменить химические элементы на термопару из висмута и меди. Ом начал свои эксперименты заново. В этот раз он пользовался термоэлектрическим устройством, работающем на эффекте Зеебека в качестве батареи. К нему он последовательно подключал 8 проводников из меди одного и того же диаметра, но различной длины. Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.
В результате нового эксперимента Ом пришел к формуле:
Х = a / b + l
Здесь X – интенсивность магнитного поля провода, l – длина провода, a – постоянная величина напряжения источника, b – постоянная сопротивления остальных элементов цепи.
Если обратиться к современным терминам для описания данной формулы, то мы получим, что Х – сила тока, а – ЭДС источника, b + l – общее сопротивление цепи.
Закон Ома для участка цепиЗакон Ома для отдельного участка цепи гласит: сила тока на участке цепи увеличивается при возрастании напряжения и уменьшается при возрастании сопротивления этого участка.
I = U / R
Исходя из этой формулы, мы можем решить, что сопротивление проводника зависит от разности потенциалов. С точки зрения математики, это правильно, но ложно с точки зрения физики. Эта формула применима только для расчета сопротивления на отдельном участке цепи.
Чтобы рассчитать сопротивление проводника, нужно перемножить его длину на удельное сопротивление его материала и разделить на площадь поперечного сечения.
Таким образом формула для расчета сопротивления проводника примет вид:
R = p ⋅ l / s
Закон Ома для полной цепиОтличие закона Ома для полной цепи от закона Ома для участка цепи заключается в том, что теперь мы должны учитывать два вида сопротивления. Это «R» сопротивление всех компонентов системы и «r» внутреннее сопротивление источника электродвижущей силы. Формула таким образом приобретает вид:
I = U / R + r
Закон Ома для переменного токаПеременный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).
Попробуем разобраться, в чем реальная разница между реактивным и активным сопротивлением в цепи с переменным током. Вы уже должны были понять, что значение напряжение и силы тока в такой цепи меняется со временем и имеют, грубо говоря, волновую форму.
Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.
Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.
На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие активного сопротивления от реактивного в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.
Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.
Формула для расчета падения напряжения на индуктивном сопротивлении:
U = I ⋅ ωL
Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).
Формула для расчета падения напряжения на емкостном сопротивлении:
U = I / ω ⋅ С
С – емкость реактивного сопротивления.
Эти две формулы – частные случаи закона Ома для переменных цепей.
Полный же будет выглядеть следующем образом:
I = U / Z
Здесь Z – полное сопротивление переменной цепи известное как импеданс.
Сфера примененияЗакон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:
- Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
- В сверхпроводниках;
- Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
- В вакуумных и газовых радиолампах;
- В диодах и транзисторах.
Похожие темы:
Формула силы натяжения нити — справочник для студентов и школьников
ОПРЕДЕЛЕНИЕ
Сила натяжения нити равна сумме сил, действующих на резьбу, и напротив их в направлении.
Здесь сила растяжения нити является векторной суммой сил, действующих на нить.
Единицей измерения силы является Н (Ньютон).
Эта формула является следствием третьего закона Ньютона применительно к нити. Если некоторый вес подвешен на нитях, которые находятся в состоянии покоя, то модуль натяжения на резьбе будет равен весу этой нагрузки. Обычно в задачи входят невесомые нерастяжимые нити, которые просто тянут власть через себя, но есть задачи, когда нить растягивается под действием силы. Однако он ведет себя как весна, подчиняясь закону Гука:
Где k — жесткость резьбы, — удлинение нити.
Примеры решения проблем на тему «Натяжная сила нити»
ПРИМЕР 1
Корпус весом 5 Н подвешен на невесомой растягивающей нити, жесткость которой . Найдите растягивающуюся нить.
Согласно условию, сила натяжения нити равна массе тела, что означает:
Замените цифры:
(м)
Протяженность нити метров.
ПРИМЕР 2
Два стержня соединены невесомой растягивающей нитью. Сила F действует на первый стержень, приводя оба стержня в направлении, противоположном направлению от первого стержня ко второму. Силы трения, действующие на первый и второй бруски соответственно: и . Жесткость резьбы: k. Найдите удлинение нити.
Обратите внимание, что силы трения действуют на стержни в направлениях, противоположных направлению движения. Нам нужно найти значение сил, растягивающих нить, которая соединена с стержнями. Со стороны первого стержня сила действует на резьбу , поскольку направлена на сжатие нити, а F — при растяжении. Со стороны второго стержня действует сила F. Следовательно:
Так:
Сила тока ?. Формула силы тока. Как обозначается ? единица измерения силы тока?
Автор Даниил Леонидович На чтение 5 мин. Просмотров 5.9k. Опубликовано Обновлено
Электрический ток — это направленный поток отрицательно заряженных частиц. Величину электрического тока определяют по числу электронов, протекающих сквозь проводник с неким поперечным сечением за определенную единицу времени.
Однако в полной мере охарактеризовать ток только движением электронов невозможно. Он также имеет другие параметры. Действительно, объем электричества, равного одному кулону способно проходить через металлический проводник в течение одной секунды или другого промежутка времени.
Если принять во внимание временной промежуток как характеристику, то можно увидеть, что интенсивность потоков в разных случаях будет не одинаковой. Тот объем, который можно пропустить сквозь проводник за секунду именуют силой тока. В качестве обозначения используют Ампер, как международную единицу измерения.
Общее описание силы тока
Сила тока является объемом электрических зарядов, проходящих сквозь поперечные профили проводников в интервале времени, равному одной секунде. Как уже было выше сказано, что за единиц силы тока принимают Ампер, которая и принадлежит к Международной СИ, используемой во всех странах мира.
Один ампер равен силе изменения потока электричества при прохождении по параллельным, парным линейным проводникам бесконечной длины, имеют ничтожно малую площадь кругового сечения. Эти материалы находятся в вакууме друг от друга на расстоянии одного метра. Он вызывает силу взаимного влияние равную 2*10-7. Единица исчисления силы тока Ампер соответствует одному кулону, пройденному за одну секунду через поперечный профиль материала проводника.
В математическом исчислении характеристика выглядит как 1 А = 1 кулон/1 секунда. Величина показателя относительно большая, поэтому для бытовых электроприборов и микросхем применяют дополнительные единицы: 1 мА и 1 мкА, которые равны одной тысячной и одной миллионной части ампера.
Если известна величина электрозаряда, прошедшего сквозь проводник с нужным сечением за требуемый промежуток времени, то параметр можно выразить следующей формулой: l=q/t.
В замкнутой сети без ответвлений за одну секунду времени проходит одинаковое количество электронов в любом участке проводника. Поскольку заряды не могут накапливаться исключительно в одном участке электрической цепи, то его интенсивность не зависит от толщины и сечения кабеля.
Для более сложных цепей с ответвлениями такое утверждение также остается истинным. Но такое определение действует только для отдельных участков схемы, которые следует рассматривать как элементарная сеть.
Способы измерения силы тока
Для того чтобы узнать силу тока на требуемом участке цепи, одних теоретических вычислений не достаточно. Да, можно использовать формулы и узнать величину, но она будет приблизительной. Поскольку приборостроение, электроника и электрика — науки точные и не терпят погрешностей, был изобретен индукционный, а позднее электронный прибор, который способен показывать точные величины.
Амперметр предназначен для измерений силы тока на отдельных участках электрической цепи. Но значения, равные 1 Амперу и более можно увидеть только в силовых установках и сетях. Для снятия показаний с них используют специальные понижающие трансформаторы. Из курсов физики многие знают от чего зависит интенсивность действий электрического тока. Инициатором движения электронов является магнитное поле. От его силы зависит и мощность потока.
Ток подается на основные катушки, в которых создается индукция. С ее помощью во второстепенной катушке генерируется электричество меньшей величины. Показатель зависит от числа витков обмоток. Они прямо пропорциональны. Поэтому даже на крупных предприятиях, где напряжение достигает нескольких тысяч вольт применяют микроамперметры или миллиамперметры. Это связано, прежде всего, с безопасностью обслуживающего персонала.
Довольно часто в обиходе можно услышать термин мультиметр. Его отличие от амперметра заключается в возможности измерять несколько характеристик одновременно, тогда как амперметр является узкоспециализированным прибором.
Включают устройство в разрыв электрической цепи. При таком способе замеров, ток протекает через измеритель к потребителю. Следовательно, соединять прибор нужно до или после элемента нагрузки, так как в простой схеме без ответвлений он будет всегда одинаковым.
Существует ошибочное убеждение, что ток до потребителя и после не одинаковый, так как часть электричества тратится на компонента. Такое утверждение ошибочно, поскольку в ток представляет собой электромагнитный процесс, выполняемый в теле металлического проводника. Результатом становится упорядоченное движение электронов вдоль всей длины проводника. Но саму энергию переносят не электроны, а магнитное поле, которое окружает тело проводника.
Важно!
Через любой поперечный профиль металла простых электрических цепей проходит одинаковое количество электрического заряда. Сколько электронов вышло из положительного полюса источника питания, столько заходит в отрицательный полюс, пройдя через элемент нагрузки. В ходе движения электроны не могут расходоваться, как другие частицы материала. Они составляют единое целое с проводником и их количество всегда одинаковое.
Отличие напряжения от силы тока
Электричество, как и любая другая материя, имеет собственные характеристики, используемые для определения эффективности работы и контроля заданных параметров. В физике существуют такие понятия как «напряжение» и «сила тока». Они описывают одно и тоже явление, но сами по себе как показатели они отличаются друг от друга.
Такие различия заключены в принципе действия электричества. Под силой тока понимают объем потока электронов, способных пройти на расстояние одного метра за установленный интервал времени. Напряжение наоборот выражено в количестве потенциальной энергии. Оба понятия тесно связаны между собой. К внешним факторам влияния на них относят:
- материал, из которого изготовлен проводник;
- температура;
- магнитное поле;
- условия окружающей среды.
Отличия также заключаются в способах получения этих параметров. Когда на заряды проводника воздействует внешнее магнитное поле, формируется напряжение, которое генерирует поток между точками цепи. Так же специалисты выделяют отличия в энергопотреблении, называемым мощностью. Если напряжение характеризует параметры потенциальной энергии, то ток — кинетической.
Заключение
Сила тока является одним из важных параметров, характеризующих электричество. Он показывает, какой объем электрического заряда проходит через поперечный профиль металлического проводника. Данная характеристика широко применяется в электронике и энергетике.
Определение уравнения напряжения — Прочность (механика) материалов
Напряжение — прочность (механика) материалов
Механика материалов
Когда металл подвергается нагрузке (силе), он деформируется или деформируется, независимо от того, насколько прочен металл или легкая нагрузка. Если нагрузка небольшая, искажение, вероятно, исчезнет при снятии нагрузки. Интенсивность или степень искажения известна как деформация .Если деформация исчезает и металл возвращается к своим первоначальным размерам после снятия нагрузки, деформация называется упругой деформацией . Если деформация исчезает, а металл остается деформированным, тип деформации называется , пластическая деформация . Подробнее о штамме мы поговорим в следующей главе. Когда к металлу прилагается нагрузка, сама атомная структура деформируется, сжимается, деформируется или растягивается в процессе. Атомы, составляющие металл, расположены в определенном геометрическом узоре, специфичном для этого конкретного металла или сплава, и поддерживаются в этом узоре за счет межатомных сил.При таком расположении атомы находятся в состоянии минимальной энергии и стремятся оставаться в таком расположении. Над металлом нужно поработать (то есть добавить энергию), чтобы исказить атомный узор. (Работа равна силе, умноженной на расстояние, на которое перемещается сила.)
Напряжение — это внутреннее сопротивление или противодействие материала искажающим эффектам внешней силы или нагрузки. Эти противодействующие силы стремятся вернуть атомы в их нормальное положение.Полное развиваемое сопротивление равно внешней нагрузке. Это сопротивление известно как стресс .
Хотя невозможно измерить интенсивность этого напряжения, можно измерить внешнюю нагрузку и площадь, к которой она приложена. Напряжение (я) можно приравнять к нагрузке на единицу площади или силе (F), приложенной к площади поперечного сечения (A), перпендикулярной силе, как показано в уравнении ниже
Где:
с = напряжение (фунты на кв. Дюйм или фунты силы на дюйм. 2 )
F = приложенная сила (фунты силы)
A = площадь поперечного сечения (дюймы 2 )
Типы стресса
Напряжения возникают в любом материале, который подвергается нагрузке или приложенной силе. Существует много типов напряжений, но все они могут быть классифицированы по одной из шести категорий: остаточные напряжения, структурные напряжения, напряжения давления, напряжения течения, термические напряжения и усталостные напряжения.
Остаточное напряжение
Остаточные напряжения возникают из-за производственных процессов, которые вызывают напряжения в материале. Сварка оставляет в свариваемых металлах остаточные напряжения.
Структурное напряжение
Структурные напряжения — это напряжения, возникающие в элементах конструкции из-за веса, который они поддерживают. Вес обеспечивает нагрузки.Эти напряжения обнаруживаются в фундаментах и каркасах зданий, а также в деталях машин.
Напряжение давления
Напряжения давления — это напряжения, возникающие в сосудах, содержащих материалы под давлением. Нагрузка обеспечивается той же силой, что и давление.
Напряжение течения
Напряжения потока возникают, когда масса текущей жидкости вызывает динамическое давление на стенку трубы.Сила удара жидкости о стену действует как нагрузка. Этот тип напряжения может проявляться неустойчиво при колебаниях расхода. Гидравлический удар является примером переходного напряжения течения.
Термическое напряжение
Термические напряжения возникают всякий раз, когда в материале присутствуют градиенты температуры. Разные температуры вызывают разное расширение и подвергают материалы внутреннему напряжению. Этот тип напряжения особенно заметен в механизмах, работающих при высоких температурах и охлаждаемых холодной жидкостью.
Усталостное напряжение
Усталостные напряжения возникают из-за циклического приложения напряжения. Напряжения могут быть вызваны вибрацией или термоциклированием.
Важность всех напряжений возрастает, когда поддерживающие их материалы имеют дефекты. Дефекты обычно добавляют материалу дополнительную нагрузку. Кроме того, когда нагрузки циклические или нестационарные, напряжения могут сильнее влиять на материал.Дополнительные напряжения, связанные с дефектами и циклическими нагрузками, могут превышать напряжение, необходимое для разрушения материала. Интенсивность напряжения в теле компонента выражается как один из трех основных типов внутренней нагрузки. Они известны как растяжение, сжатие и сдвиг. На рисунке 1 показаны различные типы стресса.
Математически существует только два типа внутренней нагрузки, потому что растягивающее и сжимающее напряжение можно рассматривать как положительную и отрицательную версии одного и того же типа нормальной нагрузки.
Однако в механической конструкции реакция компонентов на эти два условия может быть настолько различной, что лучше и безопаснее рассматривать их как отдельные типы.
Как показано на рисунке 1, плоскость растягивающего или сжимающего напряжения лежит перпендикулярно оси действия силы, от которой оно исходит. Плоскость касательного напряжения лежит в плоскости силовой системы, из которой оно возникает. Очень важно четко понимать эти различия как в уме, так и в способах выражения.
Растягивающее напряжение
Растягивающее напряжение — это такой тип напряжения, при котором две части материала по обе стороны от плоскости напряжения имеют тенденцию разъединяться или удлиняться, как показано на Рисунке 1 (а).
Напряжение сжатия
Напряжение сжатия противоположно напряжению растяжения. Соседние части материала имеют тенденцию давить друг на друга через типичную плоскость напряжения, как показано на рисунке 1 (b).
Напряжение сдвига
Напряжение сдвига возникает, когда две части материала имеют тенденцию скользить друг по другу в любой типичной плоскости сдвига при приложении силы, параллельной этой плоскости, как показано на рисунке 1 (c).
Оценка механических свойств производится по трем основным типам напряжений. Поскольку растягивающие и сжимающие нагрузки создают напряжения, действующие поперек плоскости, в направлении, перпендикулярном (нормальном) к плоскости, растягивающие и сжимающие напряжения называются нормальными напряжениями.
Сокращенные обозначения следующие.
Для растягивающих напряжений: «+ S N » (или «S N ») или «s» (сигма)
Для сжимающих напряжений: «-S N » или «-s» (минус сигма)
Способность материала реагировать на сжимающее напряжение или давление называется сжимаемостью . Например, металлы и жидкости несжимаемы, а газы и пары сжимаемы.Напряжение сдвига равно силе, деленной на площадь поверхности, параллельную направлению действия силы, как показано на Рисунке 1 (c) выше.
Два типа напряжения могут присутствовать одновременно в одной плоскости, при условии, что одно из напряжений является напряжением сдвига. При определенных условиях в материале могут одновременно присутствовать различные комбинации основных типов напряжений. Примером может служить корпус реактора во время работы. Стена испытывает растягивающее напряжение в различных местах из-за температуры и давления жидкости, действующей на стену.Напряжение сжатия прикладывается снаружи к другим участкам стены из-за внешнего давления, температуры и сжатия опор, связанных с резервуаром. В этой ситуации растягивающие и сжимающие напряжения считаются главными напряжениями. Если присутствует, напряжение сдвига будет действовать под углом 45 ° к главному напряжению.
12.3 Напряжение, деформация и модуль упругости — University Physics Volume 1
12.3 Напряжение, деформация и модуль упругости
Цели обучения
К концу этого раздела вы сможете:
- Объясните концепции напряжения и деформации при описании упругих деформаций материалов
- Описать виды упругого деформирования предметов и материалов
Модель твердого тела — идеализированный пример объекта, который не деформируется под действием внешних сил. Это очень полезно при анализе механических систем, а многие физические объекты действительно в значительной степени жесткие.Степень, в которой объект может восприниматься как жесткий, зависит от физических свойств материала, из которого он сделан. Например, мяч для пинг-понга, сделанный из пластика, является хрупким, а теннисный мяч, сделанный из резины, эластичен, когда на него воздействуют сжимающие силы. Однако при других обстоятельствах и мяч для пинг-понга, и теннисный мяч могут хорошо отскакивать как твердые тела. Точно так же тот, кто проектирует протезы конечностей, может приблизиться к механике человеческих конечностей, моделируя их как твердые тела; однако фактическая комбинация костей и тканей представляет собой эластичную среду.
В оставшейся части этой главы мы переходим от рассмотрения сил, влияющих на движение объекта, к тем, которые влияют на форму объекта. Изменение формы из-за приложения силы называется деформацией. Известно, что даже очень небольшие силы вызывают некоторую деформацию. Деформация испытывается объектами или физическими средами под действием внешних сил — например, это может быть сжатие, сжатие, разрыв, скручивание, срезание или растяжение объектов. На языке физики два термина описывают силы, действующие на объекты, подвергающиеся деформации: напряжение и деформация .
Напряжение — это величина, которая описывает величину сил, вызывающих деформацию. Напряжение обычно определяется как сила на единицу площади . Когда силы притягивают объект и вызывают его удлинение, например, при растяжении эластичной ленты, мы называем такое напряжение растягивающим напряжением. Когда силы вызывают сжатие объекта, мы называем это напряжением сжатия. Когда объект сдавливается со всех сторон, как подводная лодка в глубинах океана, мы называем этот вид напряжения объемным напряжением (или объемным напряжением).В других ситуациях действующие силы могут быть ни растягивающими, ни сжимающими, и все же вызывать заметную деформацию. Например, предположим, что вы крепко держите книгу ладонями, затем одной рукой вы нажимаете и тянете переднюю обложку от себя, а другой рукой вы нажимаете и тянете заднюю обложку в направлении ты. В таком случае, когда деформирующие силы действуют по касательной к поверхности объекта, мы называем их «поперечными» силами, а вызываемое ими напряжение — поперечным напряжением.
Единицей измерения напряжения в системе СИ является паскаль (Па). Когда сила в один ньютон воздействует на единицу площади квадратного метра, результирующее напряжение составляет один паскаль:
один паскаль = 1.0Па = 1.0N1.0м2. один паскаль = 1.0Па = 1.0N1.0м2.В имперской системе единиц единицей измерения напряжения является «фунт / кв. Дюйм», что означает «фунт на квадратный дюйм» (фунт / дюйм2) (фунт / дюйм2). Еще одна единица измерения объемного напряжения — атм (атмосфера). Коэффициенты пересчета:
. 1 фунт / кв. Дюйм = 6895 Па и 1 Па = 1,450 × 10−4 фунт / кв. Дюйм · атм = 1.013 × 105 Па = 14,7 фунтов на квадратный дюйм, 1 фунт на квадратный дюйм = 6895 Па и 1 Па = 1,450 × 10-4 фунтов на квадратный дюйм · атм = 1,013 × 105 Па = 14,7 фунтов на квадратный дюйм.Объект или среда под напряжением деформируются. Величина, описывающая эту деформацию, называется деформацией. Деформация задается как частичное изменение длины (при растягивающем напряжении), объема (при объемном напряжении) или геометрии (при напряжении сдвига). Следовательно, деформация — это безразмерное число. Деформация под действием растягивающего напряжения называется деформацией растяжения, деформация под действием объемного напряжения называется объемной деформацией (или объемной деформацией), а деформация, вызванная напряжением сдвига, называется деформацией сдвига.
Чем больше напряжение, тем больше напряжение; однако связь между деформацией и напряжением не обязательно должна быть линейной. Только когда напряжение достаточно низкое, деформация, которую оно вызывает, прямо пропорциональна величине напряжения. Константа пропорциональности в этом отношении называется модулем упругости. В линейном пределе низких значений напряжения общее соотношение между напряжением и деформацией составляет
. напряжение = (модуль упругости) × деформация. напряжение = (модуль упругости) × деформация.12.33
Как видно из анализа размеров этого соотношения, модуль упругости имеет ту же физическую единицу, что и напряжение, поскольку деформация безразмерна.
Из уравнения 12.33 также видно, что, когда объект характеризуется большим значением модуля упругости, влияние напряжения невелико. С другой стороны, небольшой модуль упругости означает, что напряжение вызывает большую деформацию и заметную деформацию. Например, напряжение на резиновой ленте вызывает большую деформацию (деформацию), чем такое же напряжение на стальной ленте тех же размеров, потому что модуль упругости резины на два порядка меньше модуля упругости стали.
Модуль упругости при растяжении называется модулем Юнга; то, что для объемного напряжения называется объемным модулем; а напряжение сдвига называется модулем сдвига. Обратите внимание, что соотношение между напряжением и деформацией — это наблюдаемое соотношение , измеренное в лаборатории. Модули упругости для различных материалов измеряются при различных физических условиях, таких как изменяющаяся температура, и собираются в таблицах технических данных для справки (таблица 12.1). Эти таблицы являются ценными справочными материалами для промышленности и для всех, кто занимается проектированием или строительством.В следующем разделе мы обсудим отношения между деформацией и напряжением за пределами линейного предела, представленного уравнением 12.33, в полном диапазоне значений напряжения до точки разрушения. В оставшейся части этого раздела мы изучаем линейный предел, выражаемый уравнением 12.33.
| Материал | Модуль Юнга × 1010 Па × 1010 Па | Объемный модуль × 1010 Па × 1010 Па | Модуль сдвига × 1010 Па × 1010 Па |
|---|---|---|---|
| Алюминий | 7.0 | 7,5 | 2,5 |
| Кость (растяжение) | 1,6 | 0,8 | 8,0 |
| Кость (компрессия) | 0,9 | ||
| Латунь | 9,0 | 6,0 | 3,5 |
| Кирпич | 1,5 | ||
| Бетон | 2,0 | ||
| Медь | 11.0 | 14,0 | 4,4 |
| Коронное стекло | 6,0 | 5,0 | 2,5 |
| Гранит | 4,5 | 4,5 | 2,0 |
| Волосы (человеческие) | 1,0 | ||
| Твердая древесина | 1,5 | 1,0 | |
| Утюг | 21,0 | 16,0 | 7,7 |
| Свинец | 1.6 | 4,1 | 0,6 |
| Мрамор | 6,0 | 7,0 | 2,0 |
| Никель | 21,0 | 17,0 | 7,8 |
| Полистирол | 3,0 | ||
| Шелк | 6,0 | ||
| Паутинка | 3,0 | ||
| Сталь | 20.0 | 16,0 | 7,5 |
| Ацетон | 0,07 | ||
| Этанол | 0,09 | ||
| Глицерин | 0,45 | ||
| Меркурий | 2,5 | ||
| Вода | 0,22 |
Стол 12.1 Приблизительные модули упругости для выбранных материалов
Напряжение при растяжении или сжатии, деформация и модуль Юнга
Напряжение или сжатие возникает, когда две антипараллельные силы равной величины действуют на объект только вдоль одного из его измерений таким образом, что объект не перемещается. Один из способов представить себе такую ситуацию показан на рисунке 12.18. Сегмент стержня либо растягивается, либо сжимается парой сил, действующих по его длине и перпендикулярно его поперечному сечению.Общий эффект таких сил состоит в том, что стержень изменяет свою длину от исходной длины L0L0, которая была у него до появления сил, на новую длину L , которую он имеет под действием сил. Это изменение длины ΔL = L-L0ΔL = L-L0 может быть либо удлинением (когда L больше исходной длины L0) L0), либо сокращением (когда L меньше исходной длины L0) .L0) . Напряжение растяжения и деформация возникают, когда силы растягивают объект, вызывая его удлинение, и изменение длины ΔLΔL является положительным.Напряжение сжатия и деформация возникают, когда силы сжимают объект, вызывая его сокращение, а изменение длины ΔLΔL отрицательно.
В любой из этих ситуаций мы определяем напряжение как отношение деформирующей силы F⊥F⊥ к площади A поперечного сечения деформируемого объекта. Символ F⊥F⊥, который мы оставляем для деформирующей силы, означает, что эта сила действует перпендикулярно поперечному сечению объекта. Силы, действующие параллельно поперечному сечению, не изменяют длину объекта.Определение растягивающего напряжения —
. растягивающее напряжение = F⊥A. растягивающее напряжение = F⊥A.12,34
Деформация растяжения — это мера деформации объекта при растягивающем напряжении и определяется как частичное изменение длины объекта, когда объект испытывает растягивающее напряжение
деформация растяжения = ΔLL0. деформация растяжения = ΔLL0.12,35
Напряжение сжатия и деформация определяются теми же формулами, уравнением 12.34 и уравнением 12.35, соответственно. Единственное отличие от ситуации с растяжением состоит в том, что для сжимающего напряжения и деформации мы берем абсолютные значения правых частей в уравнении 12.34 и уравнение 12.35.
Фигура 12,18 Когда объект находится в состоянии растяжения или сжатия, результирующая сила, действующая на него, равна нулю, но объект деформируется, изменяя свою исходную длину L0.L0. (a) Натяжение: стержень удлинен на ΔL.ΔL. (b) Сжатие: стержень сжимается на ΔL.ΔL. В обоих случаях деформирующая сила действует по длине стержня и перпендикулярно его поперечному сечению. В линейном диапазоне малых напряжений площадь поперечного сечения стержня не изменяется.Модуль Юнга Y — это модуль упругости, когда деформация вызвана либо растягивающим, либо сжимающим напряжением, и определяется уравнением 12.33. Разделив это уравнение на деформацию растяжения, мы получим выражение для модуля Юнга:
Y = растягивающая деформация растяжения = F⊥ / A∆L / L0 = F⊥AL0∆L.Y = растягивающая деформация растяжения = F⊥ / A∆L / L0 = F⊥AL0∆L.12,36
Пример 12,7
Напряжение сжатия в опоре
Скульптура весом 10 000 Н покоится на горизонтальной поверхности на вершине вертикального столба высотой 6,0 м. Рис. 12.19. Площадь поперечного сечения столба 0,20 м 20,20 м 2, он выполнен из гранита плотностью 2700 кг / м3.2700кг / м3. Найдите сжимающее напряжение в поперечном сечении, расположенном на 3,0 м ниже вершины столба, и значение сжимающей деформации верхнего 3,0-метрового сегмента столба.Фигура 12,19 Колонна Нельсона на Трафальгарской площади, Лондон, Англия. (кредит: модификация работы Кристиана Бортеса)
Стратегия
Сначала мы узнаем вес верхней части столба длиной 3,0 м. Нормальная сила, действующая на поперечное сечение, расположенное на 3,0 м ниже вершины, складывается из веса столба и веса скульптуры.Когда у нас есть нормальная сила, мы используем уравнение 12.34, чтобы найти напряжение. Чтобы найти деформацию сжатия, мы находим значение модуля Юнга для гранита в таблице 12.1 и инвертируем уравнение 12.36.Решение
Объем сегмента колонны высотой h = 3,0мh = 3,0м и площадью поперечного сечения A = 0,20м2A = 0,20м2 составляет V = Ah = (0,20 м 2) (3,0 м) = 0,60 м 3. V = Ah = (0,20 м 2) (3,0 м) = 0,60 м 3.При плотности гранита ρ = 2,7 × 103 кг / м3, ρ = 2,7 × 103 кг / м3 масса сегмента столба составляет
m = ρV = (2,7 × 103 кг / м3) (0.60 м3) = 1,60 × 103 кг.м = ρV = (2,7 × 103 кг / м3) (0,60 м3) = 1,60 × 103 кг.Вес сегмента стойки
wp = mg = (1,60 × 103 кг) (9,80 м / с2) = 1,568 × 104 Н. wp = mg = (1,60 × 103 кг) (9,80 м / с2) = 1,568 × 104 Н.Вес скульптуры равен ws = 1,0 × 104 Н, ws = 1,0 × 104 Н, поэтому нормальная сила на поверхности поперечного сечения, расположенной на 3,0 м ниже скульптуры, составляет
. F⊥ = wp + ws = (1,568 + 1,0) × 104N = 2,568 × 104N. F⊥ = wp + ws = (1,568 + 1,0) × 104N = 2,568 × 104N.Следовательно, напряжение
напряжение = F⊥A = 2,568 × 104N0,20м2 = 1,284 × 105 Па = 128.4 кПа. Напряжение = F⊥A = 2,568 × 104N0,20м2 = 1,284 × 105Па = 128,4 кПа.Модуль Юнга для гранита Y = 4,5 × 1010 Па = 4,5 × 107 кПа. Y = 4,5 × 1010 Па = 4,5 × 107 кПа. Следовательно, деформация сжатия в этом положении равна
. деформация = напряжение Y = 128,4 кПа 4,5 × 107 кПа = 2,85 × 10-6. деформация = напряжение Y = 128,4 кПа 4,5 × 107 кПа = 2,85 × 10-6.Значение
Обратите внимание, что нормальная сила, действующая на площадь поперечного сечения колонны, не является постоянной по всей ее длине, а изменяется от наименьшего значения наверху до наибольшего значения внизу колонны.Таким образом, если опора имеет равномерную площадь поперечного сечения по всей длине, наибольшее напряжение у ее основания.Проверьте свое понимание 12,9
Найдите сжимающее напряжение и деформацию в основании колонны Нельсона.
Пример 12,8
Растяжка стержня
Стальной стержень длиной 2,0 м имеет площадь поперечного сечения 0,30 см2 0,30 см2. Штанга является частью вертикальной опоры, которая удерживает тяжелую 550-килограммовую платформу, которая подвешена к нижнему концу штанги.Пренебрегая весом стержня, каково растягивающее напряжение стержня и удлинение стержня под действием напряжения?Стратегия
Сначала мы вычисляем растягивающее напряжение в стержне под весом платформы в соответствии с уравнением 12.34. Затем мы инвертируем уравнение 12.36, чтобы найти удлинение стержня, используя L0 = 2,0 м. L0 = 2,0 м. Из таблицы 12.1 модуль Юнга для стали равен Y = 2,0 × 1011 Па. Y = 2,0 × 1011 Па.Решение
Подстановка числовых значений в уравнения дает нам F⊥A = (550 кг) (9.8 м / с2) 3,0 × 10–5 м2 = 1,8 × 108 Па ΔL = F⊥AL0Y = (1,8 × 108 Па) 2,0 × 1011 Па = 1,8 × 10–3 м = 1,8 мм. F⊥A = (550 кг) (9,8 м / s2) 3,0 × 10–5 м2 = 1,8 × 108 Па ΔL = F⊥AL0Y = (1,8 × 108 Па) 2,0 м2,0 × 1011 Па = 1,8 × 10–3 м = 1,8 мм.Значение
Как и в примере с колонной, растягивающее напряжение в этом примере неоднородно по длине стержня. Однако, в отличие от предыдущего примера, если принять во внимание вес штанги, напряжение в штанге будет наибольшим в верхней части и наименьшим в нижней части штанги, к которой прикреплено оборудование.Проверьте свое понимание 12.10
Трос длиной 2,0 м растягивается на 1,0 мм под действием нагрузки. Какова деформация растяжения в проволоке?
Объекты часто могут одновременно испытывать и сжимающее, и растягивающее напряжение. Рис. 12.20. Один из примеров — длинная полка, загруженная тяжелыми книгами, которая провисает между концевыми опорами под весом книг. Верхняя поверхность полки испытывает напряжение сжатия, а нижняя поверхность полки — растягивающее напряжение.Точно так же длинные и тяжелые балки провисают под собственным весом. В современном строительстве такие деформации изгиба можно практически исключить с помощью двутавровых балок. Рисунок 12.21.
Фигура 12.20 (a) Объект, изгибающийся вниз, испытывает растягивающее напряжение (растяжение) в верхней части и сжимающее напряжение (сжатие) в нижней части. (б) Элитные тяжелоатлеты часто временно сгибают железные прутья во время подъема, как на Олимпийских играх 2012 года. (кредит б: модификация работы Александра Кочерженко)
Фигура 12.21 год Стальные двутавровые балки используются в строительстве для уменьшения деформаций изгиба. (Источник: модификация работы «Инженерный корпус армии США в Европе» / Flickr)
Объемное напряжение, деформация и модуль
Когда вы ныряете в воду, вы чувствуете силу, давящую на каждую часть вашего тела со всех сторон. Тогда вы испытываете объемный стресс или, другими словами, давление. Объемное напряжение всегда имеет тенденцию к уменьшению объема, заключенного на поверхности погружаемого объекта.Силы этого «сжатия» всегда перпендикулярны погружаемой поверхности. Рис. 12.22. Эффект этих сил заключается в уменьшении объема погруженного объекта на величину ΔVΔV по сравнению с объемом V0V0 объекта при отсутствии объемного напряжения. Этот вид деформации называется объемной деформацией и описывается изменением объема относительно исходного объема:
объемная деформация = ΔVV0. объемная деформация = ΔVV0.12,37
Фигура 12,22 Объект при увеличении объемного напряжения всегда претерпевает уменьшение своего объема.Равные силы, перпендикулярные поверхности, действуют со всех сторон. Эффект этих сил заключается в уменьшении объема на величину ΔVΔV по сравнению с исходным объемом V0.V0.Объемная деформация возникает в результате объемного напряжения, которое представляет собой силу F⊥F⊥, нормальную к поверхности, которая давит на единицу площади A поверхности погруженного объекта. Такая физическая величина или давление p определяется как
давление = p≡F⊥A. давление = p≡F⊥A.12,38
Мы будем изучать давление в жидкостях более подробно в Гидромеханике.Важной характеристикой давления является то, что оно является скалярной величиной и не имеет определенного направления; то есть давление действует одинаково во всех возможных направлениях. Когда вы погружаете руку в воду, вы чувствуете такое же давление, действующее на верхнюю поверхность руки, как на нижнюю, или на боковую, так и на поверхность кожи между пальцами. В этом случае вы ощущаете увеличение давления ΔpΔp по сравнению с тем, что вы привыкли ощущать, когда ваша рука не погружена в воду.Когда ваша рука не погружена в воду, вы чувствуете нормальное давление p0p0 в одну атмосферу, которое служит точкой отсчета. Объемное напряжение — это увеличение давления, или Δp, Δp, по сравнению с нормальным уровнем, p0.p0.
Когда объемное напряжение увеличивается, объемная деформация увеличивается в соответствии с уравнением 12.33. Константа пропорциональности в этом соотношении называется модулем объемного сжатия, B или
. B = объемное напряжение, объемная деформация = −ΔpΔV / V0 = −ΔpV0ΔV. B = объемное напряжение, объемная деформация = −ΔpΔV / V0 = −ΔpV0ΔV.12,39
Знак минус, который появляется в уравнении 12.39, предназначен для согласованности, чтобы гарантировать, что B является положительной величиной. Обратите внимание, что знак минус (-) (-) необходим, потому что увеличение ΔpΔp давления (положительная величина) всегда вызывает уменьшение ΔVΔV в объеме, а уменьшение объема является отрицательной величиной. Величина, обратная модулю объемной упругости, называется сжимаемостью k, k или
. k = 1B = −ΔV / V0Δp.k = 1B = −ΔV / V0Δp.12,40
Термин «сжимаемость» используется в отношении жидкостей (газов и жидкостей).Сжимаемость описывает изменение объема жидкости на единицу увеличения давления. Жидкости, характеризующиеся большой сжимаемостью, относительно легко сжимаются. Например, сжимаемость воды составляет 4,64 × 10–5 / атм. 4,64 × 10–5 / атм, а сжимаемость ацетона составляет 1,45 × 10–4 / атм. 1,45 × 10–4 / атм. Это означает, что при повышении давления на 1,0 атм относительное уменьшение объема для ацетона примерно в три раза больше, чем для воды.
Пример 12.9
Гидравлический пресс
В гидравлическом прессе, рис. 12.23, 250-литровый объем масла подвергается повышению давления на 2300 фунтов на квадратный дюйм. Если сжимаемость масла составляет 2,0 × 10–5 / атм, 2,0 × 10–5 / атм, найдите объемную деформацию и абсолютное уменьшение объема масла при работе пресса.Фигура 12,23 В гидравлическом прессе, когда маленький поршень смещается вниз, давление в масле передается по маслу на большой поршень, заставляя большой поршень двигаться вверх.Небольшая сила, приложенная к маленькому поршню, вызывает большую прижимающую силу, которую большой поршень оказывает на объект, который либо поднимается, либо сжимается. Устройство действует как механический рычаг.
Стратегия
Мы должны обратить уравнение 12.40, чтобы найти объемную деформацию. Во-первых, мы преобразуем увеличение давления из фунтов на квадратный дюйм в атм, Δp = 2300psi = 2300 / 14,7atm≈160atm, Δp = 2300psi = 2300 / 14.7atm≈160atm, и определяем V0 = 250L.V0 = 250L.Решение
Подставляя значения в уравнение, имеем объемная деформация = ΔVV0 = ΔpB = kΔp = (2.0 × 10-5 / атм) (160атм) = 0,0032 ответ: ΔV = 0,0032V0 = 0,0032 (250L) = 0,78L. Объемная деформация = ΔVV0 = ΔpB = kΔp = (2,0 × 10-5 / атм) (160атм) = 0,0032 ответ: ΔV = 0,0032V0 = 0,0032 (250 л) = 0,78 л.Значение
Обратите внимание, что, поскольку сжимаемость воды в 2,32 раза больше, чем у масла, если бы рабочее вещество в гидравлическом прессе этой задачи было заменено на воду, объемная деформация, а также изменение объема были бы в 2,32 раза больше.Проверьте свое понимание 12.11
Если нормальная сила действует на каждую грань кубической 1.Стальной кусок 0-м31,0-м3 заменяют на 1,0 × 107 Н, 1,0 × 107 Н, найдите результирующее изменение объема стального куска.
Напряжение сдвига, деформация и модуль
Понятия напряжения сдвига и деформации относятся только к твердым объектам или материалам. Здания и тектонические плиты являются примерами объектов, которые могут подвергаться сдвиговым напряжениям. В общем, эти концепции не применимы к жидкостям.
Деформация сдвига возникает, когда две антипараллельные силы равной величины прикладываются по касательной к противоположным поверхностям твердого объекта, не вызывая деформации в поперечном направлении к силовой линии, как в типичном примере напряжения сдвига, показанном на рисунке 12.24. Сдвиговая деформация характеризуется постепенным сдвигом ΔxΔx слоев в направлении, касательном к действующим силам. Эта градация ΔxΔx происходит в поперечном направлении на некотором расстоянии L0.L0. Деформация сдвига определяется отношением наибольшего смещения ΔxΔx к поперечному расстоянию L0L0
деформация сдвига = ΔxL0. деформация сдвига = ΔxL0.12,41
Деформация сдвига вызвана напряжением сдвига. Напряжение сдвига возникает из-за сил, действующих на параллельно поверхности. Мы используем символ F∥F∥ для таких сил.Величина F∥F∥ на площадь поверхности A , где применяется сила сдвига, является мерой напряжения сдвига
напряжение сдвига = F∥A. напряжение сдвига = F∥A.12,42
Модуль сдвига — это константа пропорциональности в уравнении 12.33, которая определяется отношением напряжения к деформации. Модуль сдвига обычно обозначается S :
. S = напряжение сдвига деформация сдвига = F∥ / AΔx / L0 = F∥AL0Δx.S = напряжение сдвига деформация сдвига = F∥ / AΔx / L0 = F∥AL0Δx.12,43
Фигура 12.24 Объект под напряжением сдвига: две антипараллельные силы равной величины прикладываются по касательной к противоположным параллельным поверхностям объекта. Контур пунктирной линией показывает результирующую деформацию. Направление, перпендикулярное действующим силам, не изменяется, и поперечная длина L0L0 не изменяется. Сдвиговая деформация характеризуется постепенным сдвигом ΔxΔx слоев в направлении, касательном к силам.Пример 12.10
Старая книжная полка
Уборщик пытается переместить тяжелый старый книжный шкаф по ковровому покрытию, тангенциально толкая поверхность самой верхней полки.Однако единственный заметный эффект от этого усилия аналогичен эффекту, показанному на рисунке 12.24, и он исчезает, когда человек перестает толкать. Книжный шкаф высотой 180,0 см и шириной 90,0 см с четырьмя полками глубиной 30,0 см, частично загруженными книгами. Общий вес книжного шкафа и книг составляет 600,0 Н. Если человек толкает верхнюю полку с силой 50,0 Н, которая смещает верхнюю полку по горизонтали на 15,0 см относительно неподвижной нижней полки, найдите модуль сдвига книжного шкафа.Стратегия
Единственная важная информация — это физические размеры книжного шкафа, величина тангенциальной силы и смещение, вызываемое этой силой.Мы определяем F∥ = 50.0N, Δx = 15.0cm, F∥ = 50.0N, Δx = 15.0cm, L0 = 180.0cm, L0 = 180.0cm и A = (30.0 cm) (90.0 cm) = 2700.0 cm2, A = (30,0 см) (90,0 см) = 2700,0 см2, и мы используем уравнение 12.43 для вычисления модуля сдвига.Решение
Подставляя числа в уравнения, получаем для модуля сдвига S = F∥AL0Δx = 50.0N2700.0cm2180.0cm.15.0cm. = 29Ncm2 = 29 × 104Nm2 = 209 × 103Pa = 2.222 кПа S = F∥AL0Δx = 50.0N2700.0cm2180.0cm.15.0cm. = 29Ncm2 = 29 × 104Нм2 = 209 × 103Па = 2,222 кПа.Мы также можем найти напряжение сдвига и деформацию соответственно:
F∥A = 50.0N2700,0 см2 = 527 кПа = 185,2 Па ΔxL0 = 15,0 см 180,0 см = 112 = 0,083.F∥A = 50,0N2700,0 см2 = 527 кПа = 185,2 Па ΔxL0 = 15,0 см 180,0 см = 112 = 0,083.Значение
Если человек в этом примере толкнет полку здоровым движением, может случиться так, что индуцированный сдвиг превратит ее в груду мусора. Примерно тот же механизм сдвига ответственен за разрушения засыпанных землей дамб и дамб; и в целом по оползням.Проверьте свое понимание 12,12
Объясните, почему концепции модуля Юнга и модуля сдвига неприменимы к жидкостям.
Напряжение, деформация и модуль Юнга
Напряжение
Напряжение — это отношение приложенной силы F к площади поперечного сечения –, определяемой как « силы на единицу площади ».
Напряжение растяжения или сжатия — нормальное напряжение
Напряжение растяжения или сжатия перпендикулярно плоскости обычно обозначается как « нормальное напряжение » или « прямое напряжение » и может быть выражено как
σ = F n / A (1)
где
σ = нормальное напряжение (Па (Н / м 2 ), фунт / кв. дюйм (фунт f / дюйм 2 ))
F n = нормальная сила, действующая перпендикулярно площади (Н, фунт f )
A = площадь (м 2 , дюйм 2 )
- a kip — британская система мер единица силы — равна 1000 фунтов f (фунт-сила)
- 1 кип = 4448.2216 Ньютонов (Н) = 4,4482216 килограммов Ньютонов (кН)
Нормальная сила действует перпендикулярно площади и возникает всякий раз, когда внешние нагрузки имеют тенденцию толкать или тянуть два сегмента тела.
Пример — Растягивающая сила, действующая на стержень
Сила 10 кН действует на круглый стержень диаметром 10 мм . Напряжение в стержне можно рассчитать как
σ = (10 10 3 Н) / (π ((10 10 -3 м) / 2) 2 )
= 127388535 (Н / м 2 )
= 127 (МПа)
Пример — Сила, действующая на квадратную стойку из пихты Дугласа
Сжимающая нагрузка 30000 фунтов действует на короткий квадрат 6 x 6 дюймов пост из пихты Дугласа.Размер опоры в оправе составляет 5,5 x 5,5 дюйма , а напряжение сжатия можно рассчитать как
σ = (30000 фунтов) / ((5,5 дюйма) (5,5 дюйма) )
= 991 (фунт / дюйм 2 , фунт / кв. дюйм)
Напряжение сдвига
Напряжение, параллельное плоскости, обычно обозначается как «напряжение сдвига » и может быть выражено как
τ = F p / A (2)
где
τ = напряжение сдвига (Па (Н / м 2 ), фунт / кв. Дюйм (фунт f / дюйм 2 ))
F p = поперечная сила в плоскости площади (Н, фунт f )
A = площадь (м 2 , в 2 )
Поперечная сила лежит в плоскости области и возникает, когда внешние нагрузки имеют тенденцию вызывать два сегмента тела скользить друг по другу.
Деформация (деформация)
Деформация определяется как «деформация твердого тела под действием напряжения».
- Нормальная деформация — удлинение или сжатие отрезка линии
- Деформация сдвига — изменение угла между двумя отрезками линии, первоначально перпендикулярными
Нормальная деформация, может быть выражена как
ε = dl / l o
= σ / E (3)
, где
dl = изменение длины (м, дюйм)
l o = начальная длина (м, дюйм)
ε = деформация — без единиц
E = Модуль Юнга (модуль упругости) (Па, (Н / м 2 ), фунт / кв. дюйм (фунт f / дюйм 2 ))
- Модуль Юнга
- можно использовать для прогнозирования удлинения или сжатия объекта при воздействии силы.
Обратите внимание, что деформация является безразмерной единицей, поскольку это отношение двух длин.Но также общепринято указывать это как отношение двух единиц длины — например, м / м или дюйм / дюйм .
Пример — напряжение и изменение длины
Стержень в приведенном выше примере имеет длину 2 м и и изготовлен из стали с модулем упругости 200 ГПа (200 10 9 Н / м 2 ) . Изменение длины можно рассчитать, преобразовав (3) в
dl = σ l o / E
= (127 10 6 Па) (2 м) / (200 10 9 Па)
= 0.00127 м
= 1,27 мм
Энергия деформации
Напряжение объекта сохраняет в нем энергию. Для осевой нагрузки запасенная энергия может быть выражена как
U = 1/2 F n дл
где
U = энергия деформации (Дж (Н · м), фут-фунт)
Модуль Юнга — модуль упругости (или модуль упругости) — закон Гука
Большинство металлов деформируются пропорционально приложенной нагрузке в диапазоне нагрузок.Напряжение пропорционально нагрузке, а деформация пропорциональна деформации в соответствии с законом Гука .
E = напряжение / деформация
= σ / ε
= (F n / A) / (дл / л o ) 4)
, где
E = модуль Юнга (Н / м 2 ) (фунт / дюйм 2 , фунт / кв. Дюйм)
Модуль упругости или модуль Юнга обычно используется для металлов и металлических сплавов и выражается в единицах 10 6 фунтов f / дюйм 2 , Н / м 2 или Па .Модуль упругости при растяжении часто используется для пластмасс и выражается в единицах 10 5 фунтов f / дюйм 2 или ГПа .
Модуль упругости при сдвиге — или модуль жесткости
G = напряжение / деформация
= τ / γ
= (F p с) / (F p s / A) / d) (5)
, где
G = модуль упругости при сдвиге — или модуль жесткости (Н / м 2 ) (фунт / дюйм 2 , psi)
τ = напряжение сдвига ((Па) Н / м 2 , psi)
γ = мера деформации сдвига без единицы измерения
F 90 p = сила, параллельная граням, на которые они действуют
A = площадь (м 2 , в 2 )
s = смещение граней (м, дюйм)
d = ди положение между смещенными гранями (м, дюйм)
Объемный модуль упругости
Объемный модуль упругости — или объемный модуль — является мерой сопротивления вещества равномерному сжатию.Объемный модуль упругости — это отношение напряжения к изменению объема материала, подвергающегося осевой нагрузке.
Модули упругости
Модули упругости для некоторых распространенных материалов:
| Материал | Модуль упругости — E — | Модуль упругости — G — | — Объемный модуль 905|
|---|---|---|---|
| (ГПа) (10 6 фунтов на кв. Дюйм) | (ГПа) (10 6 фунтов на кв. Дюйм) | (ГПа) 2 900 ) | |
| Алюминий | 70 | 24 | 70 |
| Латунь | 91 | 36 | |
| 919 11019 9019 9011 | Стекло55 | 23 | 37 |
| Железо | 91 | 70 | 100 | Свинец | 16 | 5.6 | 7,7 |
| Сталь | 200 | 84 | 160 |
- 1 ГПа = 10 9 Па (Н / м 2 ) 9279 905 905
- L = предел пропорциональности, до этого момента действует закон Гука.
- E = предел упругости, за пределами этой точки материал постоянно растягивается и не вернется к своей исходной длине. Упругое поведение — это когда материал возвращается к своей исходной длине, пластическое поведение — это когда растянутый материал не возвращается к своей исходной длине.
- Y = предел текучести, за пределами этой точки небольшое увеличение силы приводит к значительному увеличению длины.
- B = предел прочности / разрывное напряжение, в этой точке материал разрушается.
- E = энергия упругой деформации в джоулях (Дж)
- F = сила в ньютонах (Н)
- DL = изменение длины в метрах (м)
- Определите нормальное напряжение и напряжение сдвига и деформацию и обсудите взаимосвязь между расчетным напряжением, пределом текучести и предельным напряжением
- Расчетные элементы при нагрузках на растяжение, сжатие и сдвиг
- Определение деформации элементов при растяжении и сжатии
- Оценка безопасности конструкции / конструкции
- Дано: величина и распределение нагрузок, свойства материала, форма и размеры элемента
- Найдите: фактическое напряжение и сравните с расчетным напряжением; в качестве альтернативы найдите коэффициент безопасности и решите, является ли он приемлемым в соответствии с применимыми стандартами
- Выбор подходящего материала
- Дано: величина и распределение нагрузок, форма и размеры стержня
- Найдите: какой тип или марка материала обеспечит прочность (предел текучести или предельную) большую, чем требуется, с учетом выбранного или указанного коэффициента безопасности
- Определение формы и размеров поперечного сечения элемента
- Дано: величина и распределение нагрузок, свойства материала
- Найдите: форму и размеры элемента таким образом, чтобы фактическая площадь поперечного сечения была больше требуемого минимума.
- Оценка максимально допустимой нагрузки на компонент
- Дано: тип и распределение нагрузки, свойства материала, форма и размеры элемента
- Найти: максимальная величина нагрузки, которая приводит к приемлемому напряжению
- соотношение, которое описывает распределение силы между двумя материалами
- соотношение, которое коррелирует деформации каждого материала
- Осевое напряжение
(общий случай) - Растягивающее напряжение
(если сила растягивающая) - Напряжение сжатия
(если сила сжимающая) - Будинас-Нисбетт, «Машиностроительный проект Шигли», 8-е издание
- Доулинг, Норман Э., «Механическое поведение материалов: инженерные методы деформации, разрушения и усталости», 3-е издание.
- Гир, Джеймс М., «Механика материалов», 6-е издание
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена на физическую форму», 13-е издание
- Пилки, Уолтер Д. и Пилки, Дебора Ф., «Факторы концентрации стресса Петерсона», 3-е издание.
- «Формулы Рорка для стресса и деформации», 8-е издание
Напряжение
Напряжение, приложенное к материалу, — это сила, приложенная к материалу на единицу площади.Максимальное напряжение, которое может выдержать материал до разрушения, называется разрывным напряжением или пределом прочности при растяжении.
Растяжение означает, что материал находится под напряжением. Действующие на него силы пытаются растянуть материал. Сжатие — это когда силы, действующие на объект, пытаются его раздавить.
Уравнение ниже используется для расчета напряжения.
напряжение = напряжение, измеренное в Нм -2 или паскалях (Па)
F = сила в ньютонах (Н)
A = площадь поперечного сечения в м 2
Штамм
Отношение удлинения к исходной длине называется деформацией. Он не имеет единиц измерения, так как представляет собой отношение двух длин, измеренных в метрах.
деформация = деформация не имеет единиц
DL = удлинение, измеренное в метрах
L = исходная длина, измеренная в метрах
График напряжение-деформация для пластичного материала (например, меди)
График напряжение-деформация для хрупкого материала (например, стекла)
Энергия упругой деформации (энергия, запасенная в растянутой проволоке или пружине)
Энергия, запасенная в растягивающейся проволоке или пружине, — это площадь под графиком «сила-растяжение», как мы можем видеть в приведенном ниже уравнении.
Резина растяжка
Когда резина растягивается и выделяется энергия, теряется в виде тепла, и это называется гистерезисом. Площадь между двумя линиями — это потеря энергии на единицу объема.
Приложение «Напряжение и деформация — сопротивление материалов для энергетики»
напряжение-деформация
Цели обучения
После завершения этой главы вы сможете:
Механическое напряжение
В этом разделе обсуждается влияние механических нагрузок (сил), действующих на элементы.В следующей главе мы рассмотрим влияние тепловых нагрузок (тепловое расширение).
Нормальные, растягивающие и сжимающие напряжения
Растяжение или сжатие в элементе создают нормальные напряжения; они называются «нормальными», потому что поперечное сечение, которое выдерживает нагрузку, перпендикулярно (перпендикулярно) направлению приложенных сил. И растягивающие, и сжимающие напряжения рассчитываются по формуле:
Если элемент имеет переменное поперечное сечение, площадь, которая должна использоваться в расчетах, является минимальной площадью поперечного сечения; это даст вам максимальное напряжение в элементе, что в конечном итоге будет определять дизайн.
При сдвиге площадь поперечного сечения, которая сопротивляется нагрузке, параллельна направлению приложенных сил. В дополнение к этому, при оценке площади сдвига вы должны учитывать, сколько поперечных сечений вносит вклад в общую прочность сборки.
Например, если вы считаете, что штифт дверной петли подвергается действию сдвигающей нагрузки, вы должны подсчитать, сколько поперечных сечений выдерживает эту нагрузку.
Формула для расчета напряжения сдвига та же:
При штамповке область, которая сопротивляется сдвигу, имеет форму цилиндра для круглого отверстия (представьте себе формочку для печенья).Следовательно, площадь сдвига будет найдена путем умножения длины окружности формы на толщину пластины.
Обратите внимание:Глядя на цифры из учебника, вы заметите, что указаны две силы. Это не означает, что сила, которую вы используете в формуле, равна (2 × Сила P), но просто указывает, что одна сила — это сила действия, а вторая — реакция.
Деформация и модуль упругости
Элемент при растяжении или сжатии будет упруго деформироваться пропорционально, помимо других параметров, исходной длине.Деформация, также называемая единичной деформацией, представляет собой безразмерный параметр, выражаемый как:
Если вы решили использовать отрицательное значение для деформации сжатия (уменьшение длины), вы также должны выразить эквивалентное напряжение сжатия как отрицательное значение.
Модуль упругости
Кривая напряжение-деформация построена в результате испытания на растяжение. В упругой области графика деформация прямо пропорциональна нагрузке. Разделив нагрузку на площадь поперечного сечения (константу) и деформацию на исходную длину (константа), можно получить графическое представление зависимости деформации от деформации.Стресс. Постоянное соотношение напряжения и деформации — это модуль Юнга или модуль упругости, свойство каждого материала.
Упругая деформация
Объединение двух вышеуказанных соотношений для деформации и модуля упругости приводит к единой формуле для упругой деформации при растяжении или сжатии.
Это соотношение применимо к элементам с однородным поперечным сечением из однородного материала, подверженным растягивающим или сжимающим нагрузкам, которые приводят к напряжениям ниже пропорционального предела (прямая линия на кривой σ-ε).
Расчетное напряжение и факторы безопасности
Эти темы были охвачены в 1 st year Strength of Materials и представлены здесь в виде краткого обзора.
Стержни, подвергающиеся чрезмерному напряжению, могут выйти из строя из-за разрушения, когда фактическое рабочее напряжение превышает предельное напряжение, или из-за чрезмерной деформации, которая в таком случае становится неработоспособной. Рассмотрим тяжелую линию конденсата, которая прогибается сверх допустимого предела, и, хотя она не ломается, во фланцевых соединениях на концах линий будут возникать утечки из-за углового перемещения.
Расчетное напряжение σ d — это максимальный уровень фактического / рабочего напряжения, который считается приемлемым с точки зрения безопасности. Расчетное напряжение определяется по:
Коэффициент безопасности выбирается проектировщиком на основе опыта, суждений И руководящих принципов / правил соответствующих норм и стандартов, на основе нескольких критериев, таких как риск травм, точность проектных данных, вероятность, отраслевые стандарты и, что не менее важно, стоимость . Стандарты коэффициентов безопасности были установлены инженерами-строителями на основе точных оценок и многолетнего опыта.Стандарты постоянно развиваются, отражая новую и улучшенную философию дизайна. Пример:
Дизайнерские шкафы
При решении задач ученики могут столкнуться с разными сценариями. Хотя теоретические концепции одинаковы, пути к окончательным ответам могут быть разными в зависимости от каждого подхода.
Стержни из двух разных материалов
Бывают случаи, когда элемент при нормальных напряжениях изготавливается из двух (или более) материалов. Одна из целей таких задач — найти напряжение в каждом компоненте.
Например, у вас может быть короткая колонна из стальной трубы, заполненной бетоном, как на рисунке. Учитывая общую нагрузку, свойства материалов и геометрические размеры, мы должны найти индивидуальное напряжение в каждом компоненте.
И стальная труба, и бетонное ядро работают вместе, поддерживая нагрузку, поэтому мы должны найти дополнительные отношения, которые объединят две проблемы в одну. Обычно ищем:
Для этой конкретной задачи мы можем сказать, что:
Уравнение 1: Общая нагрузка P = нагрузка, поддерживаемая сталью P сталь + нагрузка, поддерживаемая бетоном P бетон
, следовательно, P = Напряжение , сталь × Площадь , сталь + Напряжение , бетон × Площадь , бетон
Уравнение 2: деформации обоих материалов одинаковы
поэтому Деформация сталь = Деформация бетон
Учитывая, что модуль упругости = напряжение / деформация, уравнение (2) дает соотношение между напряжением и упругостью обоих материалов
Подстановка этого последнего соотношения в уравнение (1) и решение для Напряжения бетон приводит к следующему соотношению
Далее можно найти Stress , сталь .
Обратите внимание, что в зависимости от проблемы исходные два отношения могут отличаться, поэтому каждый раз может потребоваться полный пошаговый вывод.
Разумные ответыПри решении задач нормального напряжения — деформации, особенно в системе СИ, вы должны суметь судить, являются ли ваши ответы разумными или нет.
Пример: Пруток из углеродистой стали A 36 длиной 1 м и диаметром 20 мм (свойства материалов в приложении B, таблица B2) выдерживает нагрузку 6 тонн.Оцените напряжение и деформацию штанги.
Обратите внимание, что обычно нагрузки выражаются в кН, площади поперечного сечения 10 -3 м 2 и результирующие напряжения в МПа.
Кроме того, поскольку модули упругости выражены в ГПа, деформация (безразмерная) будет в диапазоне 10 -3 . Этот стержень будет растягиваться на 0,9 мм при данной нагрузке.
Назначенные задачиПри решении этих вопросов необходимо использовать приложения учебника.Это ценные справочные материалы по свойствам материалов, геометрическим размерам и т. Д.
Задача 1: Конденсатопровод номинальным диаметром 152 мм, изготовленный из трубы из углеродистой стали сортамента 40, поддерживается подвесами для стержней с резьбой, расположенными на расстоянии 2,5 м от центра к центру. Подвески из углеродистой стали, длиной 50 см, диаметром основания 12 мм. Рассчитайте напряжение и деформацию в подвесках. Для материала подвесов используйте E = 200 ГПа.
Задача 2: Зажимная скоба со штифтом 1/2 дюйма используется в подъемной машине для магазинов.Если штифт изготовлен из стали A36, определите максимальную безопасную нагрузку, используя коэффициент безопасности 2,5, основанный на пределе текучести.
Проблема 3: Котел поддерживается на нескольких коротких стойках, как показано на рисунке, изготовленных из серого чугуна класса 35. Каждая колонна выдерживает нагрузку 50 тонн. Требуемый коэффициент запаса прочности для этой конструкции равен 3. Безопасны ли колонны?
Используйте следующие размеры: A = 30 мм, B = 80 мм, C = 50 мм, D = 140 мм
Задача 4: Натяжной элемент в ферме крыши подвергается нагрузке в 25 тысяч фунтов.Конструкция требует использования уголка L2x2x1 / 4 с поперечным сечением 0,944 дюйма 2 . Для строительных конструкций Американский институт стальных конструкций рекомендует использовать расчетное напряжение 0,60 × S y . Используя таблицу B2 приложения B, укажите подходящий стальной материал.
Задача 5: Гидравлический цилиндр со стяжной тягой, показанный на рисунке, изготовлен из 6-дюймовой трубы из нержавеющей стали Schedule 40 и длиной 15 дюймов. Шесть стяжных шпилек представляют собой шпильки с резьбой 1 / 2-13 UNC с диаметром впадины 0.4822 дюйма и шаг резьбы 13 TPI. При сборке цилиндра требуется усилие зажима, эквивалентное одному полному обороту гайки из положения затяжки вручную.
Определите напряжение в цилиндре и стяжных шпильках. Также рассчитайте деформацию в каждом компоненте, используя модуль упругости E ss = 28 × 10 6 фунтов на квадратный дюйм и стержень E = 30 × 10 6 фунтов на квадратный дюйм.
Задача 6: Предложите одно улучшение для этой главы.
Прочность материалов | Механика материалов
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Сопротивление материалов , также известное как Механика материалов , ориентировано на анализ напряжений и прогибов в материалах под нагрузкой. Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предполагаемые нагрузки.
Напряжение и деформация
Когда к конструктивному элементу прикладывается сила, в этом элементе в результате силы возникают как напряжение, так и деформация. Напряжение — это сила, переносимая элементом на единицу площади, и типичными единицами измерения являются фунт-сила / дюйм 2 (фунт-сила на квадратный дюйм) для обычных единиц США и Н / м 2 (Па) для единиц СИ:
где F — приложенная сила, а A — площадь поперечного сечения, на которую действует сила. Приложенная сила вызовет деформацию конструктивного элемента на некоторую длину, пропорциональную его жесткости.Деформация — это отношение деформации к исходной длине детали:
где L — деформированная длина, L 0 — исходная недеформированная длина, а δ — деформация (разница между ними).
Существуют различные типы нагрузки, которые приводят к различным типам напряжений, как показано в таблице ниже:
| Тип нагрузки | Тип напряжения | Иллюстрация |
|---|---|---|
| Осевая сила | ||
| Сила сдвига | Напряжение поперечного сдвига | |
| Изгибающий момент | Напряжение изгиба | |
| Торсион | Напряжение скручивания |
Осевое напряжение и изгибающее напряжение являются формами нормального напряжения , σ, поскольку направление силы перпендикулярно области, противодействующей силе.Поперечное напряжение сдвига и напряжение скручивания являются формами напряжения сдвига , τ, поскольку направление силы параллельно области, противодействующей силе.
| Нормальное напряжение | |
|---|---|
| Осевое напряжение: | |
| Напряжение изгиба: | |
| Напряжение сдвига | |
|---|---|
| Поперечное напряжение: | |
| Торсионное напряжение: | |
В уравнениях для осевого напряжения и поперечного напряжения сдвига F — это сила, а A — площадь поперечного сечения элемента.В уравнении для изгибающего напряжения M — изгибающий момент, y — расстояние между центральной осью и внешней поверхностью, а I c — центроидный момент инерции поперечного сечения относительно соответствующей оси. В уравнении для напряжения скручивания T — это кручение, r — радиус и J — полярный момент инерции поперечного сечения.
В случае осевого напряжения на прямом участке напряжение распределяется равномерно по всей площади.В случае напряжения сдвига распределение максимально в центре поперечного сечения; однако среднее напряжение определяется как τ = F / A, и это среднее напряжение сдвига обычно используется при расчетах напряжений. Более подробное обсуждение можно найти в разделе о касательных напряжениях в балках. В случае напряжения изгиба и скручивания максимальное напряжение возникает на внешней поверхности. Более подробное обсуждение можно найти в разделе о напряжениях изгиба в балках.
Так же, как основными типами напряжения являются нормальное напряжение и напряжение сдвига, основными типами деформации являются нормальная деформация и деформация сдвига .В случае нормальной деформации деформация перпендикулярна области, на которую действует сила:
В случае деформации поперечного сдвига деформация параллельна области, на которую действует сила:
где γ — деформация сдвига (безразмерная) и & phiv; — деформированный угол в радианах.
В случае деформации кручения элемент поворачивается на угол & phiv; вокруг своей оси.Максимальная деформация сдвига возникает на внешней поверхности. В случае круглого стержня максимальная деформация сдвига определяется как:
где & phiv; — угол закручивания, r — радиус стержня, а L — длина.
Деформации сдвига пропорциональны внутренней части стержня и связаны с максимальной деформацией сдвига на поверхности следующим образом:
где ρ — радиальное расстояние от оси стержня.
Закон Гука
Напряжение пропорционально деформации в упругой области кривой напряжения-деформации материала (ниже предела пропорциональности, когда кривая является линейной).
Нормальное напряжение и деформация связаны между собой:
σ = E & varepsilon;
где E — модуль упругости материала, σ — нормальное напряжение, а & varepsilon; это нормальный штамм.
Напряжение сдвига и деформация связаны между собой:
τ = G γ
где G — модуль сдвига материала, τ — напряжение сдвига, а γ — деформация сдвига.Модуль упругости и модуль сдвига связаны соотношением:
где ν — коэффициент Пуассона.
Закон Гука аналогичен уравнению силы пружины F = k δ. По сути, все можно рассматривать как пружину. Закон Гука можно перестроить, чтобы получить деформацию (удлинение) в материале:
| Осевое удлинение (от нормального напряжения) | ||
| Угол кручения (от напряжения сдвига / скручивания) |
Энергия деформации
Когда к конструктивному элементу прикладывается сила, этот элемент деформируется и накапливает потенциальную энергию, как пружина.Энергия деформации (то есть количество потенциальной энергии, накопленной из-за деформации) равна работе, затраченной на деформацию элемента. Полная энергия деформации соответствует площади под кривой отклонения нагрузки и имеет единицы дюйм-фунт-сила в обычных единицах США и Н-м в единицах СИ. Энергия упругой деформации может быть восстановлена, поэтому, если деформация остается в пределах упругости, то вся энергия деформации может быть восстановлена.
Энергия деформации рассчитывается как:
| Общая форма: | U = Работа = ∫ F dL | (площадь под кривой нагрузки-прогиб) |
| В пределах эластичности: | (площадь под кривой нагрузки-прогиб) | |
| (потенциальная энергия пружины) |
Обратите внимание, что есть два уравнения для энергии деформации в пределах упругости.Первое уравнение основано на площади под кривой прогиба нагрузки. Второе уравнение основано на уравнении для потенциальной энергии, запасенной в пружине. Оба уравнения дают один и тот же результат, просто они выводятся несколько по-разному.
Более подробную информацию об энергии деформации можно найти здесь.
Жесткость
Жесткость, обычно называемая жесткостью пружины, — это сила, необходимая для деформации элемента конструкции на единицу длины.Все конструкции можно рассматривать как совокупность пружин, а силы и деформации в конструкции связаны уравнением пружины:
F = k δ макс
где k — жесткость, F — приложенная сила, а δ max — максимальное отклонение при прогибе в элементе.
Если прогиб известен, то жесткость элемента можно определить, решив k = F / δ max . Однако максимальный прогиб обычно неизвестен, поэтому жесткость необходимо рассчитывать другими способами.Таблицы прогиба балки можно использовать в общих случаях. Два наиболее полезных уравнения жесткости, которые необходимо знать, — это уравнения для балки с приложенной осевой нагрузкой и для консольной балки с концевой нагрузкой. Обратите внимание, что жесткость зависит от модуля упругости материала E, геометрии детали и конфигурации нагрузки.
Торсионный эквивалент уравнения пружины:
Т = к & phiv;
Особый интерес представляет жесткость вала при скручивающей нагрузке:
| Жесткость [дюйм * фунт-сила / рад] | Максимальный прогиб [рад] | Иллюстрация | |
|---|---|---|---|
| Вал с крутильной нагрузкой: |
Конструкция с несколькими путями нагружения
Если в конструкции есть несколько путей загрузки (т.е. в конструкции есть несколько элементов, которые разделяют нагрузку), нагрузка будет выше в более жестких элементах. Чтобы определить нагрузку, которую несет любой отдельный элемент, сначала вычислите эквивалентную жесткость элементов на пути нагружения, рассматривая их как пружины. В зависимости от их конфигурации они будут рассматриваться как некоторая комбинация пружин, включенных последовательно, и пружин, включенных параллельно.
Если элементы на пути нагружения нельзя рассматривать исключительно как пружины, включенные последовательно или как пружины, включенные параллельно, а скорее представляют собой комбинацию пружин, включенных последовательно и параллельно, тогда проблему необходимо будет решать итеративно.Найдите подгруппу элементов, которые находятся либо последовательно, либо параллельно, и используйте приведенные уравнения для расчета эквивалентной жесткости, силы и прогиба в этой подгруппе. Затем подгруппу можно рассматривать как одиночную пружину с рассчитанными жесткостью, силой и прогибом, а затем эту пружину можно рассматривать как часть другой подгруппы пружин. Продолжайте группировать участников и решать, пока не будет достигнут желаемый результат.
Концентрации напряжений
Можно подумать, что силы и напряжения протекают через материал, как показано на рисунке ниже.Когда геометрия материала изменяется, линии потока перемещаются ближе друг к другу или дальше друг от друга, чтобы приспособиться. Если в материале имеется разрыв, такой как отверстие или выемка, напряжение должно течь вокруг неоднородности, и линии потока будут уплотняться вместе вблизи этого разрыва. Это внезапное уплотнение потоковых линий приводит к резкому скачку напряжения — это пиковое напряжение называется концентрацией напряжений . Элемент, вызывающий концентрацию напряжений, называется подъемником напряжений .
Концентрации напряжений учитываются с помощью коэффициентов концентрации напряжений . Чтобы найти фактическое напряжение в вязкости несплошности, рассчитайте номинальное напряжение в этой области и затем увеличьте его с помощью соответствующего коэффициента концентрации напряжений:
σ макс = K σ ном
где σ max — фактическое (масштабированное) напряжение, σ nom — номинальное напряжение, а K — коэффициент концентрации напряжений.При расчете номинального напряжения используйте максимальное значение напряжения в этой области. Например, на рисунке выше должна использоваться наименьшая площадь у основания галтеля.
Многие справочные руководства содержат таблицы и кривые коэффициентов концентрации напряжений для различных геометрических форм. Двумя наиболее полными наборами факторов концентрации напряжения являются факторы концентрации напряжения Петерсона и формулы Рорка для напряжения и деформации. MechaniCalc также предоставляет набор интерактивных графиков для общих факторов концентрации стресса.
По мере того, как мы удаляемся от источника стресса, концентрация стресса рассеивается. Принцип Сен-Венана — это общее практическое правило, гласящее, что расстояние, на котором рассеивается концентрация напряжений, равно наибольшему размеру поперечного сечения, несущего нагрузку.
Расчет концентрации напряжений особенно важен, когда материалы очень хрупкие или когда существует только один путь нагрузки. В пластичных материалах местная податливость позволит перераспределить напряжения и снизит напряжение вокруг стояка.По этой причине коэффициенты концентрации напряжений обычно не применяются к элементам конструкции из пластичных материалов. Коэффициенты концентрации напряжений также обычно не применяются при наличии избыточного пути нагружения, и в этом случае податливость одного элемента позволит перераспределить силы на элементы на других путях нагружения. Примером этого является набор болтов. Если один болт начинает прогибаться, другие болты в шаблоне принимают на себя большую нагрузку.
Комбинированные напряжения
В любой точке нагруженного материала общее состояние напряжения можно описать тремя нормальными напряжениями (по одному в каждом направлении) и шестью напряжениями сдвига (по два в каждом направлении):
Индексы нормальных напряжений σ указывают направление нормальных напряжений.Индексы касательных напряжений τ состоят из двух компонент. Первый указывает направление нормали к поверхности, а второй указывает направление самого напряжения сдвига.
Обычно напряжения в одном направлении равны нулю, так что полное напряжение возникает в одной плоскости, как показано на рисунке ниже. Это называется плоское напряжение . Плоское напряжение возникает в тонких пластинах, но оно также возникает на поверхности любой нагруженной конструкции. Напряжения на поверхности обычно являются наиболее критическими напряжениями, поскольку напряжение изгиба и скручивания максимизируется на поверхности.
На рисунке выше σ x и σ y — нормальные напряжения, а τ — напряжение сдвига. Напряжения уравновешиваются, так что точка находится в статическом равновесии. Поскольку все касательные напряжения равны по величине, для простоты индексы опущены. (Обратите внимание, однако, что знак напряжений на грани x будет противоположен знаку напряжений на грани x ).
Правильные условные обозначения показаны на рисунке.Для нормального напряжения растягивающее напряжение положительное, а сжимающее — отрицательное. Для напряжения сдвига значение по часовой стрелке положительное, а против часовой стрелки — отрицательное.
Если напряжения из рисунка выше известны, можно найти нормальное напряжение и напряжение сдвига в плоскости, повернутой на некоторый угол θ относительно горизонтали, как показано на рисунке ниже. Уравнения преобразования ниже дают значения нормального напряжения и напряжения сдвига на этой повернутой плоскости.
| Нормальное напряжение: | |
| Напряжение сдвига: |
Обратите внимание, что на рисунке выше θ отсчитывается от оси x, а положительное значение θ — против часовой стрелки.
В любой точке материала можно найти углы плоскости, при которых нормальные напряжения и напряжения сдвига максимизируются и минимизируются.Максимальное и минимальное нормальные напряжения называются главных напряжений . Максимальные и минимальные напряжения сдвига называются крайними напряжениями сдвига . Углы главных напряжений и крайних касательных напряжений находятся путем взятия производной каждого уравнения преобразования по θ и нахождения значения θ, при котором производная равна нулю.
| Углы главного напряжения: | |
| Углы предельного напряжения сдвига: |
Указанные выше углы можно подставить обратно в уравнения преобразования, чтобы найти значения главных напряжений и экстремальных касательных напряжений:
| Основные напряжения: | |
| Экстремальные напряжения сдвига: |
Углы, при которых возникают основные напряжения, составляют 90 ° друг от друга.Главные напряжения всегда сопровождаются нулевым напряжением сдвига. Углы возникновения экстремальных касательных напряжений составляют 45 ° от углов главных напряжений. Экстремальные напряжения сдвига сопровождаются двумя равными нормальными напряжениями (σ x & plus; σ y ) / 2.
Вот пара полезных отношений:
| σ 1 и плюс; σ 2 = σ x & плюс; σ y | Сумма нормальных напряжений постоянна. |
| Максимальное напряжение сдвига составляет половину разницы главных напряжений. |
Круг Мора
Круг Мора — это способ визуализировать состояние напряжения в точке нагруженного материала. Это дает интуитивное представление о уравнениях преобразования напряжений и показывает, как напряжения на элементе изменяются в зависимости от угла поворота θ. Из круга Мора также становится ясно, каковы основные напряжения, экстремальные напряжения сдвига и углы, под которыми возникают эти напряжения.Пример круга Мора показан на рисунке ниже:
Чтобы построить круг Мора, сначала найдите центр круга, взяв среднее значение нормальных напряжений:
Поместите точки на окружности, представляющие напряжения на гранях x и y элемента напряжения. Напряжения на грани x будут иметь координаты (σ x , −τ), а напряжения на грани y будут иметь координаты (σ y , τ).Поместите точки на окружности для главных напряжений. Максимальное главное напряжение будет иметь координаты (σ 1 , 0), а минимальное главное напряжение будет иметь координаты (σ 2 , 0). Поместите точки на окружности для экстремальных касательных напряжений. Максимальное экстремальное напряжение сдвига будет иметь координаты (σ c , τ 1 ), а минимальное экстремальное напряжение сдвига будет иметь координаты (σ c , τ 2 ).
Все точки будут лежать по периметру круга.Круг имеет радиус, равный величине предельных касательных напряжений:
Напряженное состояние на гранях x и y элемента напряжения представлено черной линией в круге Мора, соединяющим точки (σ x , −τ) и (σ y , τ). Эта линия в круге Мора соответствует невращающемуся элементу на рисунке ниже. Если эту линию повернуть на некоторый угол, то значения точек на конце повернутой линии дадут значения напряжения на гранях x и y повернутого элемента.Важно отметить, что 360 градусов круга Мора эквивалентны 180 градусам на элементе напряжения. Например, точки для грани x и грани y расположены на 180 градусов друг от друга на круге Мора, но они всего на 90 градусов на элементе напряжения.
Чтобы получить более интуитивное представление о том, как круг Мора связывает напряжения в элементе напряжения и как состояние напряжения изменяется в зависимости от угла поворота, см. Прилагаемый калькулятор круга Мора.
Приложения
Есть много структурных компонентов, которые обычно подвергаются анализу напряжений. Подробности анализа этих компонентов приведены в других разделах:
Расчет допустимого напряжения
Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предполагаемые нагрузки. Всегда желательно, чтобы напряжения в конструкции оставались в пределах прочности конструкции.Предел текучести материала обычно выбирается как предел прочности, с которым сравниваются расчетные напряжения.
Коэффициент запаса прочности , FS, рассчитывается как:
где σ фактическое — это расчетное напряжение в конструкции, а предел — это предел максимального напряжения, обычно прочность материала, например предел текучести (S ty ). Коэффициент запаса прочности показывает, насколько фактическое напряжение ниже предельного напряжения.Значение FS должно быть больше или равно 1, чтобы конструкция не вышла из строя, но инженеры почти всегда проектируют с некоторым требуемым коэффициентом безопасности, превышающим 1. Требуемый коэффициент безопасности будет варьироваться в зависимости от критичности конструкции (т. Е. последствия разрушения конструкции), а также условия нагружения (т. е. какие типы нагрузок применяются, насколько они предсказуемы и т. д.). Высокое значение FS приведет к очень безопасной конструкции, но если значение FS слишком велико, конструкция может стать настолько большой и тяжелой, что больше не сможет успешно выполнять свою функцию.Поэтому при выборе подходящего запаса прочности приходится идти на компромиссы. Типичные значения FS варьируются от 1,15 до 10.
Запас прочности рассчитывается как:
В приведенном выше уравнении любое значение выше нуля указывает на то, что фактическое напряжение ниже предельного напряжения. Хотя запасы прочности обычно указываются в виде десятичных значений, гораздо более интуитивно понятно думать о запасах в процентах. Например, если предельное напряжение конструкции равно 1.В 5 раз превышающее фактическое напряжение, запас прочности составляет 50% (MS = 0,5).
Когда сообщается о факторах безопасности и запасах прочности, иногда требуемый коэффициент безопасности будет «вплетаться» в сообщаемые факторы. Например, инженеры могут потребовать, чтобы конструкция поддерживала коэффициент безопасности не менее 2, так что FS req = 2. Чтобы обеспечить требуемый коэффициент безопасности, сообщаемые FS и MS рассчитываются как:
Обратите внимание, что при включении необходимого коэффициента безопасности, FS req , сообщаемые FS и MS фактически являются запасами по отношению к FS req , а не по напряжению.
PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице о прочности материалов. Этот курс можно использовать для выполнения требований к кредитам PDH для поддержания вашей лицензии PE.
Теперь, когда вы прочитали эту справочную страницу, получите за нее кредит!
Список литературы
Как рассчитать максимальное напряжение
Обновлено 28 декабря 2020 г.
Кевин Бек
«Стресс» в повседневном языке может означать любое количество вещей, но в целом подразумевает некоторую срочность, что-то, что проверяет устойчивость какой-либо поддающейся количественной или, возможно, не поддающейся количественной оценке системе поддержки.В технике и физике напряжение имеет особое значение и относится к количеству силы, которую материал испытывает на единицу площади этого материала.
Расчет максимального напряжения, которое может выдержать данная конструкция или отдельная балка, и согласование его с ожидаемой нагрузкой на конструкцию. это классическая и повседневная проблема, с которой инженеры сталкиваются каждый день. Без математики было бы невозможно построить множество огромных плотин, мостов и небоскребов, которые видели во всем мире.
Силы на Луч
Сумма сил F net , испытываемых объектами на Земле, включает «нормальную» составляющую, направленную прямо вниз и относящуюся к гравитационному полю Земли, которое вызывает ускорение g 9,8 м / с 2 в сочетании с массой m объекта, испытывающего это ускорение. (Из второго закона Ньютона F net = m a. Ускорение — это скорость изменения скорости, которая, в свою очередь, является скоростью изменения смещения.)
Горизонтально ориентированный твердый объект, такой как балка, которая имеет как вертикально, так и горизонтально ориентированные элементы массы, испытывает некоторую степень горизонтальной деформации даже при воздействии вертикальной нагрузки, проявляющейся в изменении длины ΔL. То есть балка заканчивается.
Модуль Юнга Y
Материалы имеют свойство, называемое модулем Юнга или модулем упругости Y , которое является индивидуальным для каждого материала. Более высокие значения означают более высокое сопротивление деформации.Его единицы такие же, как и у давления, в ньютонах на квадратный метр (Н / м 2 ), что также является силой на единицу площади.
Эксперименты показывают, что изменение длины ΔL балки с начальной длиной L 0 , на которую действует сила F на площади поперечного сечения A, определяется уравнением
\ Delta L = \ bigg (\ frac { 1} {Y} \ bigg) \ bigg (\ frac {F} {A} \ bigg) L_0
Напряжение и деформация
Напряжение в данном контексте — это отношение силы к площади F / A , который появляется справа в приведенном выше уравнении изменения длины.Иногда его обозначают σ (греческая буква сигма).
Штамм , с другой стороны, представляет собой отношение изменения длины ΔL к исходной длине L, или ΔL / L. Иногда его обозначают буквой ε (греческая буква эпсилон). Деформация — величина безразмерная, то есть не имеет единиц измерения.
