Резисторы в аналоговой и цифроаналоговой технике
Номинальное значение сопротивления любого резистора всегда соответствует одному из значений стандартного ряда. Эти ряды имеют названия Е3, Е6, Е12, Е24, Е48, Е96 и Е192.
Самым грубым является ряд Е3. Он содержит всего 3 значения. Самым подробным – ряд Е192. Стандартные значения номиналов всех рядов приведены в табл.1 и табл.2.
Таблица 1
|
Е192 |
Е96 |
Е48 |
Е192 |
Е96 |
Е48 |
|
Е96 |
Е48 |
Е192 |
Е96 |
Е48 |
Е192 |
Е96 |
Е48 |
|
|
100 |
100 |
169 |
169 |
169 |
287 |
287 |
287 |
487 |
487 |
|
825 |
825 |
825 |
|
101 |
172 |
291 |
493 |
835 |
||||||||||
|
102 |
102 |
174 |
174 |
294 |
294 |
499 |
499 |
845 |
845 |
|||||
|
104 |
176 |
298 |
505 |
856 |
||||||||||
|
105 |
105 |
105 |
178 |
178 |
178 |
301 |
301 |
301 |
511 |
511 |
511 |
866 |
866 |
866 |
|
106 |
180 |
305 |
517 |
876 |
||||||||||
107 |
107 |
182 |
182 |
309 |
309 |
523 |
523 |
|
887 |
|||||
|
109 |
184 |
312 |
530 |
898 |
||||||||||
|
110 |
110 |
110 |
187 |
187 |
187 |
316 |
316 |
316 |
536 |
536 |
536 |
909 |
909 |
909 |
|
111 |
189 |
|
542 |
920 |
||||||||||
|
113 |
113 |
191 |
191 |
324 |
324 |
549 |
549 |
931 |
931 |
|||||
|
114 |
193 |
328 |
556 |
942 |
||||||||||
|
115 |
115 |
115 |
196 |
196 |
196 |
332 |
332 |
332 |
562 |
562 |
562 |
953 |
953 |
953 |
|
117 |
198 |
336 |
569 |
965 |
||||||||||
|
118 |
118 |
200 |
200 |
340 |
340 |
576 |
576 |
976 |
976 |
|||||
|
120 |
203 |
344 |
583 |
988 |
||||||||||
|
121 |
121 |
121 |
205 |
205 |
205 |
348 |
348 |
348 |
590 |
590 |
590 |
|||
|
123 |
208 |
352 |
597 |
|||||||||||
|
124 |
124 |
210 |
210 |
357 |
357 |
604 |
604 |
|||||||
|
126 |
213 |
361 |
612 |
|||||||||||
|
127 |
127 |
127 |
215 |
215 |
215 |
365 |
365 |
365 |
619 |
619 |
619 |
|||
|
129 |
218 |
370 |
626 |
|||||||||||
|
130 |
130 |
221 |
221 |
374 |
374 |
634 |
634 |
|||||||
|
132 |
223 |
379 |
642 |
|||||||||||
|
133 |
133 |
133 |
226 |
226 |
226 |
383 |
383 |
383 |
649 |
649 |
649 |
|||
|
135 |
229 |
388 |
657 |
|||||||||||
|
137 |
137 |
232 |
232 |
392 |
392 |
665 |
665 |
|||||||
|
138 |
234 |
397 |
673 |
|||||||||||
|
140 |
140 |
140 |
237 |
237 |
237 |
402 |
402 |
402 |
681 |
681 |
681 |
|||
|
142 |
240 |
407 |
690 |
|||||||||||
|
143 |
143 |
243 |
243 |
412 |
412 |
698 |
698 |
|||||||
|
145 |
246 |
417 |
706 |
|||||||||||
|
147 |
147 |
147 |
249 |
249 |
249 |
422 |
422 |
422 |
715 |
715 |
715 |
|||
|
149 |
252 |
427 |
723 |
|||||||||||
|
150 |
150 |
255 |
255 |
432 |
432 |
732 |
732 |
|||||||
|
152 |
258 |
437 |
741 |
|||||||||||
|
154 |
154 |
154 |
261 |
261 |
261 |
442 |
442 |
442 |
750 |
750 |
750 |
|||
|
156 |
264 |
448 |
759 |
|||||||||||
|
158 |
158 |
267 |
267 |
453 |
453 |
768 |
768 |
|||||||
|
Е192 |
Е96 |
Е48 |
Е192 |
Е96 |
Е48 |
Е192 |
Е96 |
Е48 |
Е192 |
Е96 |
Е48 |
Е192 |
Е96 |
Е48 |
|
160 |
271 |
459 |
777 |
|||||||||||
|
162 |
162 |
162 |
274 |
274 |
274 |
464 |
464 |
464 |
787 |
787 |
787 |
|||
|
164 |
277 |
470 |
796 |
|||||||||||
|
165 |
165 |
280 |
280 |
475 |
475 |
806 |
806 |
|||||||
|
167 |
284 |
481 |
816 |
Таблица 2
|
Е24 |
Е12 |
Е6 |
Е3 |
|
10 |
10 |
10 |
10 |
|
11 |
|||
|
12 |
12 |
||
|
13 |
|||
|
15 |
15 |
15 |
|
|
16 |
|||
|
18 |
18 |
||
|
20 |
|||
|
22 |
22 |
22 |
22 |
|
24 |
|||
|
27 |
27 |
||
|
30 |
|||
|
33 |
33 |
33 |
|
|
36 |
|||
|
39 |
39 |
||
|
43 |
|||
|
47 |
47 |
47 |
47 |
|
51 |
|||
|
56 |
56 |
||
|
62 |
|||
|
68 |
68 |
68 |
|
|
75 |
|||
|
82 |
82 |
||
|
91 |
Ряды Е3, Е6, Е12 и Е24 используются для резисторов с допуском на номинальное значение ±5% и более, остальные ряды – для резисторов с меньшим допуском на номинальное значение.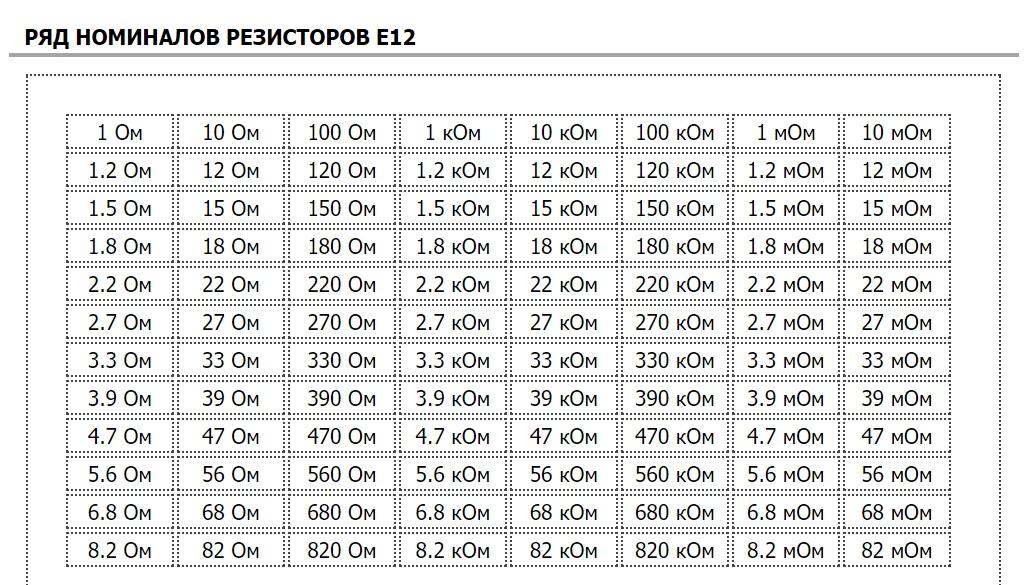
В настоящее время существует несколько систем обозначения номинального сопротивления резисторов. Самой распространенной является система, в которой номинальное значение сопротивления резистора кодируется двумя или тремя десятичными цифрами, последняя из которых представляет собой десятичный порядок, а две или три предыдущие – мантиссу.
Количество цифр зависит от того, к какому стандартному ряду значений относится номинальное значение сопротивления данного резистора.
Для кодирования сопротивлений резисторов, принадлежащих рядам Е3, Е6, Е12 и Е24, используются три десятичные цифры (три для мантиссы и одна для порядка), для принадлежащих другим рядам – четыре (четыре для мантиссы и одна для порядка).
Таким образом, надпись на резисторе 162 означает, что значение номинального сопротивления резистора принадлежит ряду Е24 (в табл.2 значение 16 есть только для этого ряда) и составляет 16*10Е2=1.6 кОм.
Надпись 331 означает, что значение номинального сопротивления резистора принадлежит ряду Е6, Е12 или Е24 (в табл.2 значение 33 есть для всех этих рядов) и составляет 33*10Е1=330 Ом.
Надпись 6654 означает, что значение номинального сопротивления резистора принадлежит ряду Е96 или Е192 (в табл. 1 значение 665 есть обоих рядов) и составляет 665*10Е4=6.65 МОм.
Из описанного выше правила есть два исключения, которые относятся к обозначению номинальных значений сопротивлений менее 1 кОм.
В первом случае в обозначениях номинальных значений сопротивлений таких резисторов может применяться символ R, заменяющий десятичную точку.
Таким образом, например, резистор с номинальным значением сопротивления 0.15 Ом будет иметь обозначение R15, а резистор с номинальным значением 0.013 Ом (13 мОм) – R013.
Использование символа R приводит к тому, что одно и то же значение номинального сопротивления резистора менее 1 кОм может быть обозначено различными способами. Например, обозначения 6260 и 626R эквивалентны и соответствуют 626 Ом.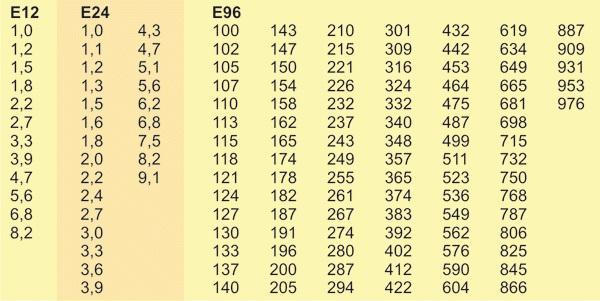
Во втором случае в качестве десятичного порядка используются цифры 7, 8 и 9, смысл которых отличается от описанного ранее.
Так цифра 9 соответствует десятичному порядку 0, цифра 8 – десятичному порядку –1, а цифра 9 – десятичному порядку –2.
Таким образом, надпись на резисторе 438 означает, что значение номинального сопротивления резистора принадлежит ряду Е24 (в табл.2 значение 43 есть только для этого ряда) и составляет 43*10Е-1=4.3 Ом.
Уменьшение размеров SMD резисторов привело к тому, что на многих из них просто нет места для нанесения необходимого количества символов.
Особенно это касается резисторов с номинальными значениями из рядов Е48, Е96 и Е192.
В связи с этим международной электротехнической комиссией (МЭК) предложен новый метод кодировки, позволяющий использовать для обозначения номиналов резисторов из рядов Е48 и Е96 (но не Е192!) только три символа вместо четырех.
В этом методе значение номинального сопротивления резистора кодируется двумя цифрами и одной буквой. Для сокращения количества цифр введена таблица перекодировки (см. табл. 3), а буква в обозначении номинала резистора заменяет десятичный порядок в соответствии с табл. 4.
В соответствии с кодировкой МЭК надпись на резисторе 41Е расшифровывается следующим образом: коду 41 в таблице 3 соответствует значение 261, а букве Е – порядок Е4, следовательно, значение номинального сопротивления резистора составит 261Е4 = 2.61 Мом.
Надпись 90Y будет соответствовать номинальному значению сопротивления 845Е-2 = 8.45 Ом.
Таблица 3
|
Ном. Знач. сопротивления |
код |
Ном. Знач. сопротивления |
код |
Ном. |
код |
Ном. Знач. сопротивления |
Код |
|
100 |
01 |
178 |
25 |
316 |
49 |
562 |
73 |
|
102 |
02 |
182 |
26 |
324 |
50 |
576 |
74 |
|
105 |
03 |
187 |
27 |
332 |
51 |
590 |
75 |
|
107 |
04 |
191 |
28 |
340 |
52 |
604 |
76 |
|
110 |
05 |
196 |
29 |
348 |
53 |
619 |
77 |
|
113 |
06 |
200 |
30 |
357 |
54 |
634 |
78 |
|
115 |
07 |
205 |
31 |
365 |
55 |
649 |
79 |
|
118 |
08 |
210 |
32 |
374 |
56 |
665 |
80 |
|
121 |
09 |
215 |
33 |
384 |
57 |
681 |
81 |
|
124 |
10 |
221 |
34 |
392 |
58 |
698 |
82 |
|
127 |
11 |
226 |
35 |
402 |
59 |
715 |
83 |
|
130 |
12 |
232 |
36 |
412 |
60 |
732 |
84 |
|
133 |
13 |
237 |
37 |
422 |
61 |
750 |
85 |
|
137 |
14 |
243 |
38 |
432 |
62 |
768 |
86 |
|
140 |
15 |
249 |
39 |
442 |
63 |
787 |
87 |
|
143 |
16 |
255 |
40 |
453 |
64 |
806 |
88 |
|
147 |
17 |
261 |
41 |
464 |
65 |
825 |
89 |
|
150 |
18 |
267 |
42 |
475 |
66 |
845 |
90 |
|
154 |
19 |
274 |
43 |
487 |
67 |
866 |
91 |
|
158 |
20 |
280 |
44 |
499 |
68 |
887 |
92 |
|
162 |
21 |
287 |
45 |
511 |
69 |
909 |
93 |
|
165 |
22 |
294 |
46 |
523 |
70 |
931 |
94 |
|
169 |
23 |
301 |
47 |
536 |
71 |
953 |
95 |
|
174 |
24 |
309 |
48 |
549 |
72 |
976 |
96 |
Таблица 4
|
символ |
A |
B |
C |
D |
E |
F |
G |
H |
X |
Y |
Z |
|
Дес. |
E0 |
E1 |
E2 |
E3 |
E4 |
E5 |
E6 |
E7 |
E-1 |
E-2 |
E-3 |
Семенякина О.А.
ЗАО «Реом СПб»
Внимание! Все материалы сайта охраняются законом об авторском праве. Любая перепечатка информации, изложенной в любом разделе допускается только со ссылкой на страницу, откуда взята перепечатанная информация.
Смотрите также: сертификационные испытания ЭКБ
<< Предыдущая Следующая >>★ Ряды номиналов радиодеталей — электронные компоненты .. И
2. Принципы серии.
(The principles of the series) Ряд E24 приблизительно представляет собой геометрическую прогрессию с знаменателем 10 1 / 24. другими словами, в логарифмическом масштабе элементы этого ряда делят отрезок от 1 до 10 на 24 равных частях. для некоторых, видимо, исторических причин, некоторые элементы отличаются от идеальных прогрессии, хотя и никогда не больше, чем на 5 %. номинальные ряды с меньшим количеством элементов получаются методом исключения элементов из диапазона E24 через одного. значения этих рядов образуют приблизительно в геометрической прогрессии с знаменателем 10 1 / 12 E12, 10 1 / 6 E6, 10 1 / 3 E3.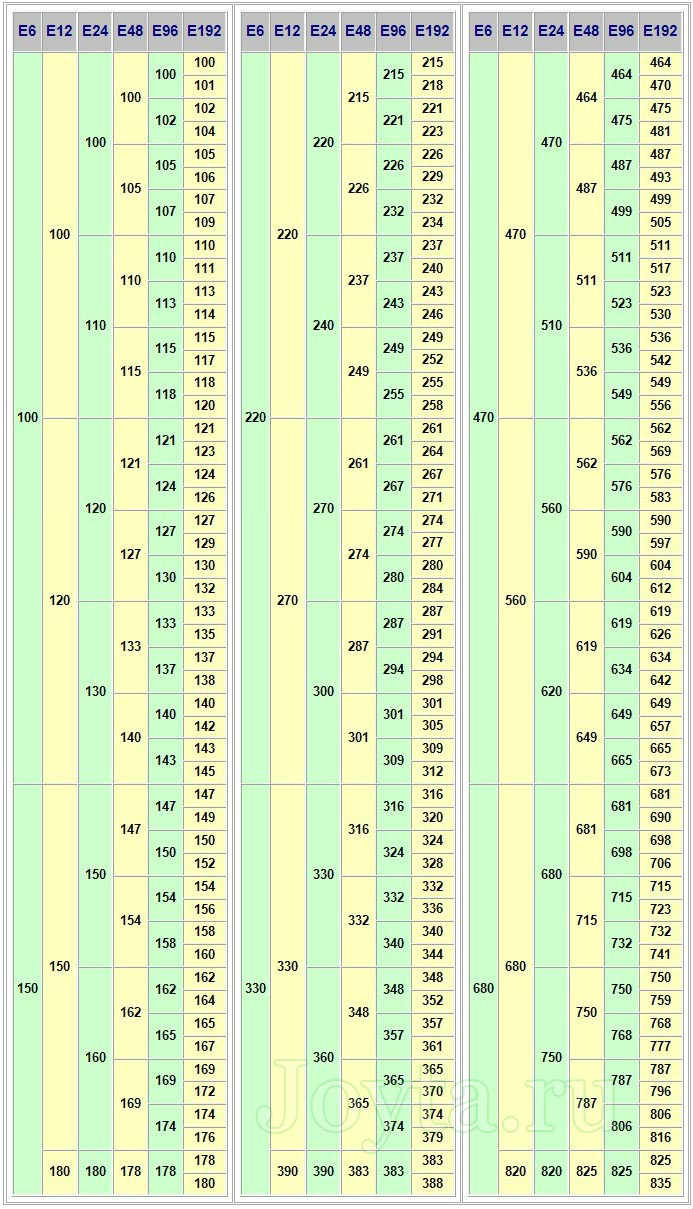 {n / N}=\exp \left{\frac {n}{N}}\cdot \ln 10\right,}
{n / N}=\exp \left{\frac {n}{N}}\cdot \ln 10\right,}
где N {\свойства стиль отображения значение N} — номер ряда 3, 6, 12, 24 и т. д., и n {\свойства стиль отображения значение n} = 0, 1, 2., n порядковый номер номинала в ряду.
Номиналы резисторов ряд номиналов резисторов ряды резисторов таблица номиналов резисторов таблица резис
Номиналы резисторов представлены так именуемыми рядами резисторов (к примеру ряд Е24). Ряды резисторов являются результатом стандартизации номинальных значений резисторов. Для неизменных резисторов существует 6, так именуемых, рядов: Е6, Е12, Е24, Е48, Е96 и Е192, а для переменных резисторов установлен один ряд — Е6. Не считая того существует дополнительный ряд Е3. Цифра после буковкы E обозначает число номинальных значений сопротивлений резисторов в каждом десятичном интервале. Номиналы резисторов соответствуют числам в приведенных ниже таблицах либо числам, приобретенным умножением либо делением этих чисел на 10n (где n — целое положительное либо отрицательное число). К примеру, по ряду Е6 номиналы резисторов в каждой декаде должны соответствовать числам 1- 1,5- 2,2- 3,3- 4,7- 6,8 либо числам, приобретенным умножением либо делением этих чисел на 10n, где n — целое положительное либо отрицательное число. К примеру 10, 100, 15, 150 либо 0.1, 0.01, 0.15, 0.015 и т. д. Принцип построения рядов Е48, Е96 и Е192 аналогичен приведенному с той только различием, что возрастает число промежных значений номиналов.
Номиналы резисторов по ряду Е3, Е6, Е12, Е24 Е3 Е6 Е12 Е24 Е3 Е6 Е12 Е24 Е3 Е6 Е12 Е24 1,0 1,0 1,0 1,0 2,2 2,2 2,2 2,2 4,7 4,7 4,7 4,7 1,1 2,4 5,1 1,2 1,2 2,7 2,7 5,6 5,6 1,3 3,0 6,2 1,5 1,5 1,5 3,3 3,3 3,3 6,8 6,8 6,8 1,6 3,6 7,5 1,8 1,8 3,9 3,9 8,2 8,2 2,0 4,3 9,1
Номиналы резисторов по ряду Е48, Е96, Е192 Е48 Е96 Е192 Е48 Е96 Е192 Е48 Е96 Е192 Е48 Е96 Е192 100 100 100 147 147 147 215 215 215 316 316 316 101 149 218 320 102 102 150 150 221 221 324 324 104 152 223 328 105 105 105 154 154 154 226 226 226 332 332 332 106 156 229 336 107 107 158 158 232 232 340 340 109 160 234 344 110 110 110 162 162 162 237 237 237 348 348 348 111 164 240 352 113 113 165 165 243 243 357 357 114 167 246 361 115 115 115 169 169 169 249 249 249 365 365 365 117 172 252 370 118 118 174 174 255 255 374 374 120 176 258 379 121 121 121 178 178 178 261 261 261 383 383 383 123 180 264 388 124 124 182 182 267 267 392 392 126 184 271 397 127 127 127 187 187 187 274 274 274 402 402 402 129 189 277 407 130 130 191 191 280 280 412 412 132 193 284 417 133 133 133 196 196 196 287 287 287 422 422 422 135 198 291 427 137 200 200 294 294 432 432 138 203 298 437 140 140 140 205 205 205 301 301 301 442 442 442 142 208 305 448 143 143 210 210 309 309 453 453 145 213 312 459 Е48 Е96 Е192 Е48 Е96 Е192 Е48 Е96 Е192 Е48 Е96 Е192 464 464 464 556 665 665 796 470 562 562 562 673 806 806 475 475 569 681 681 681 816 481 576 576 690 825 825 825 487 487 487 583 698 698 835 493 590 590 590 706 845 845 499 499 597 715 715 715 856 505 604 604 723 866 866 866 511 511 511 612 732 732 876 517 619 619 619 741 887 887 523 523 626 750 750 750 898 530 634 634 759 909 909 909 536 536 536 642 768 768 920 542 649 649 649 777 931 931 549 549 657 787 787 787 942 953 953 953 965 976 976 988
После того, как произведен расчет сопротивления того или иного резистора в схеме, необходимо выбрать ближайшее к нему стандартное значение промышленного компонента. Например, значения сопротивлений, образующие серию резисторов Е6, составляют числовой ряд, включающий 6 значений в пределах одного десятичного разряда: 1; 1,5; 2,2; 3,3; 4,7; 6,8. В случае, если необходимо иметь набор резисторов, диапазон изменения величины сопротивлений которых изменяются от 1 Ом до 1 МОм (то есть изменение величины сопротивления достигает 7 порядков), то в результате необходимо будет иметь 43 номинальных значения для резисторов данного ряда (6 значений в каждом из 7 разрядов и значение 10 МОм в качестве первого значения нового разряда). То есть, например, числу 1,5 ряда Е6, будут соответствовать значения стандартных сопротивлений 1,5 Ом, 15 Ом, 150 Ом, 1,5 кОм и т. д. Для формирования полного набора номинальных значений резисторов, образующих серию Е24 (наиболее часто используемую на практике серию), понадобится 169 различных значений сопротивлений. Кроме величины номинального сопротивления, все радиокомпоненты, в том числе резисторы, обладают определенной точностью изготовления, которая для деталей, выпускаемых по нормалям рядов Е, чаще всего напрямую связана с количеством чисел в самой нормали. Так, например, резисторы серии Е6 имеют точность изготовления ±20%. Причина этого заключается в том, что величина сопротивления, соответствующего верхнему полю допуска, будет равно сопротивлению следующего по ряду значению, но имеющего нижнее поле допуска, что не приводит к перекрытиям в ряду. Правда, этот принцип несколько нарушается для резисторов серии Е24, где допуска +5%: (1,3 + 5%) < (1, 5 — 5%). Тепловые параметры резисторов При протекании электрического тока I через резистор R на нем (благодаря закону Ома) всегда падает некоторое напряжение V, а также электрическая энергия преобразуется в тепловую (благодаря закону Джоуля — Ленца), что приводит к рассеиванию на резисторе некоторой мощности Р. Количество энергии, выделяющееся в единицу времени, например в секунду, является той самой мощностью Р, которая, будучи выделенной на резисторе, приводит к увеличению его температуры. Для резистора, установленного в цепи, по которой проходит только слабый сигнал, выделяющаяся мощность окажется незначительной, зато на резисторе анодной нагрузки выделяющаяся мощность может достигать значительных величин и быть опасной для резистора. Ее можно, на первый взгляд, достаточно просто рассчитать, используя соотношение V2/R, и выбрать компонент, удовлетворяющий необходимым требованиям. На практике все обстоит не так просто, как кажется, и существует множество причин, по которым с помощью простой формулы будет получен неправильный результат. Производители обычно указывают мощность, которую способен рассеивать компонент при температуре 70 °С. Если оборудование эксплуатируется при стандартной температуре окружающей среды, составляющей 20 °С, то температура его компонентов должна быть выше, так как любое оборудование (особенно мощное) в процессе работы нагревается, поскольку потребляет электроэнергию, часть которой, выделяется в виде тепла на элементах устройства, так как его КПД меньше 100%. Наиболее вероятной внутри работающего устройства на электронных лампах будет средняя температура, составляющая около 40 °С, хотя отдельные элементы схемы (те же лампы) могут иметь гораздо более высокую температуру. Если учесть, что некоторые люди считают для себя комфортной более высокую температуру окружающей среды, чем 20 °С, то можно принять, что даже температура 35 °С не будет являться чем-то уж очень необычным. По законам физики тепло всегда переходит от более нагретого предмета к более холодному, это позволяет провести некоторые аналогии с электротехникой. Разность температур ΔT(°С) может считаться эквивалентной разности потенциалов. Выделяющаяся тепловая мощность q (Вт) может в первом приближении считаться эквивалентной электрическому току. Тепловое сопротивление R0 (°С/Вт) может считаться эквивалентным электрическому сопротивлению. Используя данные аналогии можно выразить своего рода тепловой «закон Ома» для тепловой цепи: В соответствии с этим законом превышение температуры на тепловом сопротивлении, имеющем определенное значение, над температурой окружающей среды будет тем больше, чем больше будет рассеваемая мощность. В технических паспортах резисторов приводится значение теплового сопротивления R0, однако, следует учитывать, что значения приведены для случая, когда поток воздуха, охлаждающий резистор за счет конвекционных потоков, не имеет никаких препятствий на своем пути перемещения. На практике же резистор практически всегда монтируется на печатной плате, которая в значительной мере препятствует конвекционным потокам, особенно, если плата устанавливается горизонтально. Даже в случае вертикальной установки платы на ней могут находиться крупные детали или компоненты, например, конденсаторы, которые препятствуют свободному обтеканию резистора воздухом. Если учесть всю совокупность аргументов, которые ограничивают протекание воздушных потоков, и возможное увеличение температуры окружающей среды, то общепринятой является рекомендация, чтобы рабочая температура резистор не превышала указанного номинального значения 70 °С, за исключением тех случаев, когда имеется возможность провести полный тепловой расчет схемы. Электрическое сопротивление резистора изменяется с изменением его температуры в соответствии с температурным коэффициентом сопротивления, обычно приводимого в миллионных долях изменения полного сопротивления, приходящегося на изменение температуры в один градус Цельсия. Несмотря на то, что такие изменения кажутся очень незначительными, увеличение температуры на 30 °С может привести к значительному изменению сопротивления резистора. Следовательно, если приходится использовать достаточно дорогие резисторы, имеющие точность изготовления 0,1 %, в наиболее ответственных за качество сигнала цепях схемы, то следует позаботиться о том, чтобы на таких резисторах не происходило значительного тепловыделения, с тем, чтобы значение этого резистора оставалось неизменным при работе схемы. При этом максимальное допустимое рассеяние, часто рекомендуемое разработчиками, и составляющее одну девятую от номинального значения выделяемой мощности, не кажется таким уж очень нереальным требованием. Дополнительно к этому следует всегда убедиться, что такой резистор не будет нагреваться за счет близко расположенных и сильно нагретых соседних элементов. |
Набор 0,25 Вт резисторов (2500 штук) 50 номиналов
Здравствуйте!Сегодня я приветствую всех обзором набора 0,25 Вт резисторов 50 номиналов (от 1 Ома до 10 МОм), по 50 шт каждого номинала, т.е. 2500 шт общего количества.
Выбор номиналов немного странный, т.к. не соответствует ни одному номинальному ряду E3, E6, E12, E24. Ближе всего подходит к ряду Е12.
В наборе резисторы присутствуют как 1%, так и 5%.

В обзоре фото резисторов и 2 лабораторные работы.
Заинтересовавшихся прошу…
Упаковка и комплектация:
В комплекте 50 лент, в каждой из которых по 50 резисторов одинакового номиналаНа каждой ленте присутствует указание номинала, правда прочесть некоторые «оттиски» не всегда у меня получалось.
В наборе присутствуют следующие номиналы:
На резисторы нанесена маркировка в виде цветных колец:Резисторы промаркированы как 4-мя, так и 5-ю кольцами. По этой маркировке можно с помощью специальных таблиц или онлайн калькуляторов вычислить номинал. Но ввиду того, что цвета колец очень тёмные, можно сильно ошибиться, поэтому лучше перепроверить сопротивление с помощью мультиметра:
Лабораторная работа №1
Цель работы: построить график зависимости сопротивления от температуры, вычислить температурный коэффициент сопротивления.Выполнение:
1. Поместим термопару и резистор в термоусадочную трубку
2. Снимем несколько точек с помощью помещения резистора с термопарой в морозильную камеру и электрический чайник.
3. Запишем полученные данные в таблицу и построим график:
4. Вычислим температурный коэффициент сопротивления по формуле:
α=(R2-R1)/(R1*(T2-T1))=(97570-102010)/(102010*(99,9+17)=-0,00037 (1/K)
Лабораторная работа №2
Цель работы: построить гистограмму распределения сопротивлений резисторов в пределах 1 ленты, вычислить максимальное отклонение сопротивления от номинального значения.Выполнение:
1. Измерим сопротивление всех резисторов в ленте:
2. Запишем получившиеся данные в таблицу и по методике взятой отсюда, построим гистограмму распределения
3. Вычислим максимальное отклонение сопротивления от номинального значения по следующей формуле:
x=(Rmax-Rnom)*100/Rnom=(20870-20000)*100/(20000)=4,45%
Итог:
Вполне нормальные резисторы по адекватной цене.Удачи.
Товар предоставлен для написания обзора магазином. Обзор опубликован в соответствии с п.18 Правил сайта.
Обзор опубликован в соответствии с п.18 Правил сайта.
Номинальное сопротивление — резистор — Большая Энциклопедия Нефти и Газа, статья, страница 1
Номинальное сопротивление — резистор
Cтраница 1
Номинальные сопротивления резисторов и емкостей конденсаторов с допустимыми отклонениями менее 5 % определяются более частыми рядами Е48, Е96 и Е192, а переменных резисторов с допустимыми отклонениями 5, 10 и 20 % — более редкими рядами Е6 и ЕЗ. Номинальные емкости электролитических конденсаторов выбирают из ряда. [1]
Номинальные сопротивления резисторов определяются размерами проводящего элемента и свойствами его материала. При допустимых отклонениях 5; 10; 20 % они должны соответствовать числам, приведенным в табл. 21.1, или числам, полученным умножением ряда на 10П, где п — целое положительное или отрицательное число. [2]
Номинальное сопротивление резистора выражает величину его сопротивления в омах или мегомах. Изготовляют резисторы с номинальным сопротивлением от нескольких ом до десятков мегом. Номинальное сопротивление переменного резистора определяет его максимальную величину. [3]
Номинальное сопротивление резистора выражает величину его сопротивления в омах или мегомах. Номинальное сопротивление переменного резистора определяет его максимальную величину. [4]
Номинальные сопротивления резисторов, выпускаемых отечественной промышленностью и зарубежными фирмами, стандартизованы. В СССР установлено шесть рядов ( Е6, Е12, Е24, Е48, Е96, El 92), а по СТ СЭВ 1076 — 78 кроме этих рядов допускается использовать ЕЗ. [5]
Номинальные сопротивления резисторов и емкостей конденсаторов с допустимыми отклонениями менее 5 % определяются более частыми рядами Е48, Е96 и Е192, а переменных резисторов с допустимыми отклонениями — 5, — 10 и 20 % — более редкими рядами Е6 и ЕЗ. [6]
[6]
Номинальные сопротивления резисторов и емкостей конденсаторов с допустимыми отклонениями менее 5 % определяются более частыми рядами Е48, Е96 и Е192, а переменных резисторов с допустимыми отклонениями 5, 10 и 20 % — более редкими рядами Е6 и ЕЗ. Номинальные емкости электролитических конденсаторов выбирают из ряда. [7]
Номинальные сопротивления отечественных резисторов составляют 10 1 — 10-и Ом. Число, стоящее после символа Е, определяет количество номинальных величин в ряду. Каждый ряд задается числовыми коэффициентами, умноженными на 10, где п — целое положительное или отрицательное число. Резисторы изготовляют с номинальными сопротивлениями, соответствующими одному из числовых коэффициентов. Наиболее распространенными являются ряды Е6, Е12, Е24, которые представлены в табл. ПП. [8]
С увеличением номинального сопротивления резистора уменьшается толщина ре-зистивного слоя или концентрация проводящих компонентов в композициях и вследствие этого однородность резистивного элемента ухудшается. Для обычных тонкослойных резисторов этот коэффициент не превышает 1 % и, как правило, его можно не учитывать. Однако в цепях переменного тока в тех случаях, когда требуется высокая степень точности сохранения формы кривой, даже такая малая степень нелинейности может оказаться недопустимой. [10]
В зависимости от номинального сопротивления резистора, его назначения и условий эксплуатации, в качестве резистивного материала применяют металлы и сплавы с высоким удельным сопротивлением, окислы металлов, углерод, кер-меты, композиционные материалы. [11]
В зависимости от номинального сопротивления резистора, его назначений и условий эксплуатации в качестве резистивного материала используют металлы и сплавы с высоким удельным электросопротивлением, оксиды металлов, углерод, керметы, композиционные материалы. Резистивный материал в зависимости от типа резистора может применяться в виде объемного элемента, проволоки различного диаметра или пленки, осаждаемой на диэлектрическую поверхность.
[12]
Резистивный материал в зависимости от типа резистора может применяться в виде объемного элемента, проволоки различного диаметра или пленки, осаждаемой на диэлектрическую поверхность.
[12]
В зависимости от номинального сопротивления резистора, его назначения и условий эксплуатации в качестве резистивного материала применяют металлы и сплавы с высоким удельным сопротивлением, оксиды металлов, углерод, керметы, композиционные материалы. [13]
Достижимые пределы допусков на номинальные сопротивления резисторов необходимо учитывать при проектировании полупроводниковых ИМС. [14]
Страницы: 1 2 3
6.2 Последовательные и параллельные резисторы — Введение в электричество, магнетизм и схемы
ЦЕЛИ ОБУЧЕНИЯ
По окончании раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В книге «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где. В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (рисунок 6.2.1). В последовательной цепи выходной ток первого резистора течет на вход второго резистора; следовательно, ток одинаков в каждом резисторе. В параллельной цепи все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
В параллельной цепи все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
(рисунок 6.2.1)
Рисунок 6.2.1. (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое.Резисторы серии
Считается, что резисторывключены последовательно, когда ток течет через резисторы последовательно. Рассмотрим рисунок 6.2.2, на котором показаны три последовательно включенных резистора с приложенным напряжением, равным.Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
(рисунок 6.2.2)
Рисунок 6.2.2 (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.На рисунке 6.2.2 ток, идущий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор. Согласно закону Ома падение потенциала на резисторе при протекании через него тока рассчитывается по формуле, где — ток в амперах (), а — сопротивление в омах (). Поскольку энергия сохраняется, а напряжение равно потенциальной энергии на заряд, сумма напряжения, приложенного к цепи источником, и падения потенциала на отдельных резисторах вокруг контура должны быть равны нулю:
Это уравнение часто называют петлевым законом Кирхгофа, который мы рассмотрим более подробно позже в этой главе.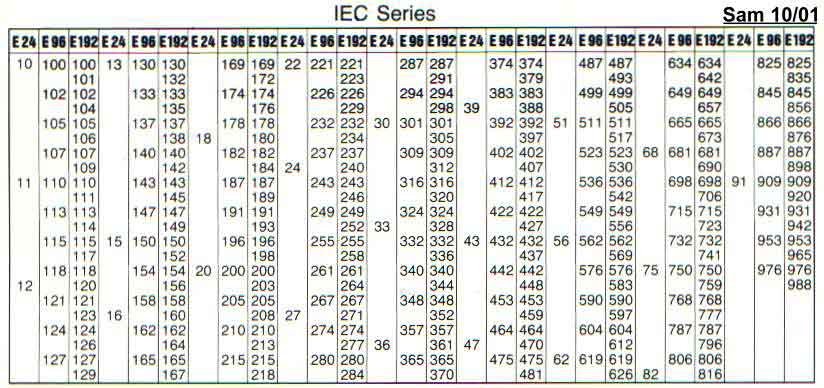 На рисунке 6.2.2 сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
На рисунке 6.2.2 сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:
Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления, которое представляет собой просто сумму сопротивлений отдельных резисторов.
Любое количество резисторов может быть подключено последовательно. Если резисторы соединены последовательно, эквивалентное сопротивление составляет
Ом.(6.2.1)
Одним из результатов включения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
ПРИМЕР 6.2.1
Эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах подключена к цепи, состоящей из четырех и одного последовательно соединенных резисторов (Рисунок 6.2.3). Предположим, что батарея имеет незначительное внутреннее сопротивление. (а) Рассчитайте эквивалентное сопротивление цепи. (б) Рассчитайте ток через каждый резистор. (c) Рассчитайте падение потенциала на каждом резисторе. (d) Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
(рисунок 6.2.3)
Рисунок 6.2.3 Простая последовательная схема с пятью резисторами.Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.Ток в цепи можно найти из закона Ома и равен напряжению, деленному на эквивалентное сопротивление. Падение потенциала на каждом резисторе можно найти с помощью закона Ома. Мощность, рассеиваемая каждым резистором, может быть найдена с помощью, а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемую аккумулятором, можно найти с помощью.
Решение
а. Эквивалентное сопротивление — это алгебраическая сумма сопротивлений:
г.Ток в цепи одинаков для каждого резистора в последовательной цепи и равен приложенному напряжению, деленному на эквивалентное сопротивление:
г. Падение потенциала на каждом резисторе можно найти с помощью закона Ома:
Обратите внимание, что сумма падений потенциала на каждом резисторе равна напряжению, подаваемому батареей.
г. Мощность, рассеиваемая резистором, равна, а мощность, отдаваемая аккумулятором, равна:
Значение
Существует несколько причин, по которым мы использовали бы несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи.Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов. Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
ПРОВЕРЬТЕ ПОНИМАНИЕ 6.2
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи.«Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серию по девять луковиц. Если перегорает слишком много лампочек, в конечном итоге открываются шунты. Что вызывает это?
Давайте кратко резюмируем основные характеристики последовательно соединенных резисторов:
Сопротивления серии- суммируются, чтобы получить эквивалентное сопротивление:
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.
 Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке 6.2.4 показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома, где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
(рисунок 6.2.4)
Рисунок 6.2.4 (a) Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.Ток, протекающий от источника напряжения на рисунке 6.2.4, зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы и. По мере того, как заряды проходят от батареи, некоторые проходят через резистор, а некоторые — через резистор. Сумма токов, протекающих в переходе, должна быть равна сумме токов, текущих из перехода:
Это уравнение называется правилом соединения Кирхгофа и будет подробно рассмотрено в следующем разделе.На рисунке 6.2.4 показано правило соединения. В этой схеме есть две петли, которые приводят к уравнениям и Обратите внимание, что напряжение на резисторах, включенных параллельно, одинаковое (), а ток является аддитивным:
Обобщая для любого количества резисторов, эквивалентное сопротивление параллельного соединения связано с отдельными сопротивлениями с помощью
(6. 2.2)
2.2)
Это соотношение приводит к эквивалентному сопротивлению, которое меньше наименьшего из отдельных сопротивлений.Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
ПРИМЕР 6.2.2
Анализ параллельной цепи
Три резистора, и подключены параллельно. Параллельное соединение подключается к источнику напряжения. а) Какое эквивалентное сопротивление? (б) Найдите ток, подаваемый источником в параллельную цепь. (c) Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.(d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью.
(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив полное сопротивление.
(c) Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение.Полный ток — это сумма отдельных токов:.
(d) Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. Давайте использовать, так как каждый резистор получает полное напряжение.
(e) Полная мощность также может быть рассчитана несколькими способами, используйте.
Решение
а. Общее сопротивление для параллельной комбинации резисторов находится с помощью уравнения 6.2.2.Ввод известных значений дает
Общее сопротивление с правильным количеством значащих цифр составляет. Как и предполагалось, меньше минимального индивидуального сопротивления.
г. Полный ток можно найти из закона Ома, заменив полное сопротивление. Это дает
Полный ток можно найти из закона Ома, заменив полное сопротивление. Это дает
Ток для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример). Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
г. Отдельные токи легко вычислить по закону Ома, поскольку на каждый резистор подается полное напряжение. Таким образом,
Аналогично
и
Общий ток складывается из отдельных токов:
г. Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.Давайте использовать, так как каждый резистор получает полное напряжение. Таким образом,
Аналогично
и
e. Суммарную мощность также можно рассчитать несколькими способами. Выбор и ввод общей текущей доходности
Значение
Суммарная мощность, рассеиваемая резисторами, также составляет:
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
ПРОВЕРЬТЕ ПОНИМАНИЕ 6.3
Рассмотрим одну и ту же разность потенциалов, приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
ПРОВЕРЬТЕ ПОНИМАНИЕ 6.4
Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?
Подведем итог основным характеристикам резисторов параллельно:
- Эквивалентное сопротивление находится из
и меньше любого отдельного сопротивления в комбинации.

- Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это.Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Вы можете вспомнить, что в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. В таблице 6.2.1 приведены уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
(таблица 6.2.1)
| Комбинация серии | Параллельная комбинация | |
|---|---|---|
| Эквивалентная емкость | ||
| Эквивалентное сопротивление |
Таблица 10. 1 Сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях
1 Сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях
Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения.Такие комбинации обычны, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения можно свести к одному эквивалентному сопротивлению, используя методику, показанную на Рисунке 6.2.5. Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден.Здесь мы отмечаем эквивалентное сопротивление как.
(рисунок 6.2.5)
Обратите внимание, что резисторы и включены последовательно. Их можно объединить в одно эквивалентное сопротивление. Один из методов отслеживания процесса — включить резисторы в качестве индексов. Здесь эквивалентное сопротивление и составляет
Схема теперь сокращается до трех резисторов, показанных на Рисунке 6.2.5 (c). Перерисовывая, мы теперь видим, что резисторы и составляют параллельную цепь.Эти два резистора можно уменьшить до эквивалентного сопротивления:
Этот шаг процесса сокращает схему до двух резисторов, показанных на Рисунке 6.2.5 (d). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен. Этот ток проходит через резистор и обозначен как. Падение потенциала можно найти с помощью закона Ома:
Ток, обеспечиваемый источником напряжения, равен. Этот ток проходит через резистор и обозначен как. Падение потенциала можно найти с помощью закона Ома:
Глядя на рис. 6.2.5 (c), остается отбросить параллельную комбинацию и. Проходной ток можно найти с помощью закона Ома:
Резисторы и включены последовательно, поэтому токи и равны
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах.Потенциальные падения равны и. Окончательный анализ — это посмотреть на мощность, подаваемую источником напряжения, и мощность, рассеиваемую резисторами. Мощность, рассеиваемая резисторами
Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, равна. Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
ПРОВЕРЬТЕ ПОНИМАНИЕ 6.5
Рассмотрите электрические цепи в вашем доме. Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если протекает большой ток, провал в проводах также может быть значительным и проявляться в виде тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на Рисунке 6. 2.7. Устройство, представленное значком, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток.Этот увеличенный ток вызывает большее падение в проводах, представленных значком, уменьшая напряжение на лампочке (которая есть), которое затем заметно гаснет.
2.7. Устройство, представленное значком, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток.Этот увеличенный ток вызывает большее падение в проводах, представленных значком, уменьшая напряжение на лампочке (которая есть), которое затем заметно гаснет.
(рисунок 6.2.7)
Рисунок 6.2.7 Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения.Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные.Есть один список для серий, а другой — для параллелей.
- Проверьте, являются ли ответы разумными и последовательными.
ПРИМЕР 6.2.4
Объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно, подключены к двум резисторам, включенным параллельно. Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление.Ток проходит через резистор. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
- Нарисуйте четкую принципиальную схему (рисунок 6.2.8).
(рисунок 6.2.8)
Рисунок 6.2.8 Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи. - Неизвестно напряжение аккумулятора.Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы и включены последовательно, а резисторы и включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов и последовательно с последовательной конфигурацией резисторов и.
- Напряжение, подаваемое батареей, можно найти, умножив ток от батареи на эквивалентное сопротивление цепи.Ток от батареи равен току через и равен. Нам нужно найти эквивалентное сопротивление, уменьшив схему. Чтобы уменьшить схему, сначала рассмотрите два резистора, включенных параллельно. Эквивалентное сопротивление составляет. Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление цепи равно. Таким образом, напряжение, подаваемое батареей, составляет.
- Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами.Мощность, подаваемая аккумулятором, составляет
Поскольку они включены последовательно, сквозной ток равен сквозному току. Т.к. ток через каждый будет. Мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором:
Поскольку мощность, рассеиваемая резисторами, равна мощности, выделяемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений. При поиске параллельного подключения необходимо соблюдать осторожность. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
При поиске параллельного подключения необходимо соблюдать осторожность. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Кандела Цитаты
CC лицензионный контент, конкретная атрибуция
- Загрузите бесплатно по адресу http: // cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution
| Последовательные и параллельные схемы
На этой странице мы изложим три принципа, которые вы должны понимать в отношении последовательных цепей:
- Ток : величина тока одинакова для любого компонента в последовательной цепи.
- Сопротивление : Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
- Напряжение : Напряжение питания в последовательной цепи равно сумме индивидуальных падений напряжения.
Давайте взглянем на несколько примеров последовательных цепей, демонстрирующих эти принципы.
Начнем с последовательной схемы, состоящей из трех резисторов и одной батареи:
Первый принцип, который нужно понять о последовательных цепях, заключается в следующем:
Величина тока в последовательной цепи одинакова для любого компонента в цепи.
Это связано с тем, что в последовательной цепи существует только один путь прохождения тока. Поскольку электрический заряд проходит через проводники, как шарики в трубке, скорость потока (скорость мрамора) в любой точке цепи (трубки) в любой конкретный момент времени должна быть одинаковой.
Использование закона Ома в последовательных цепях
По расположению 9-вольтовой батареи мы можем сказать, что ток в этой цепи будет течь по часовой стрелке от точки 1 к 2, к 3 к 4 и обратно к 1.Однако у нас есть один источник напряжения и три сопротивления. Как мы можем использовать здесь закон Ома?
Важная оговорка к закону Ома заключается в том, что все величины (напряжение, ток, сопротивление и мощность) должны относиться друг к другу с точки зрения одних и тех же двух точек в цепи. Мы можем увидеть эту концепцию в действии на примере схемы с одним резистором ниже.
Использование закона Ома в простой цепи с одним резистором
В схеме с одной батареей и одним резистором мы можем легко вычислить любую величину, потому что все они относятся к одним и тем же двум точкам в цепи:
Поскольку точки 1 и 2 соединены вместе проводом с незначительным сопротивлением, как и точки 3 и 4, мы можем сказать, что точка 1 электрически является общей с точкой 2, а точка 3 электрически общей с точкой 4.Поскольку мы знаем, что у нас есть 9 вольт электродвижущей силы между точками 1 и 4 (непосредственно через аккумулятор), и поскольку точка 2 является общей для точки 1, а точка 3 — общей для точки 4, мы также должны иметь 9 вольт между точками 2 и 3. (прямо через резистор).
Следовательно, мы можем применить закон Ома (I = E / R) к току через резистор, потому что мы знаем напряжение (E) на резисторе и сопротивление (R) этого резистора. Все термины (E, I, R) относятся к одним и тем же двум точкам в цепи, к одному и тому же резистору, поэтому мы можем безоговорочно использовать формулу закона Ома.
Использование закона Ома в схемах с несколькими резисторами
В схемах, содержащих более одного резистора, мы должны соблюдать осторожность при применении закона Ома. В приведенном ниже примере схемы с тремя резисторами мы знаем, что у нас есть 9 вольт между точками 1 и 4, что является величиной электродвижущей силы, управляющей током через последовательную комбинацию R 1 , R 2 и R . 3 . Однако мы не можем взять значение 9 вольт и разделить его на 3 кОм, 10 кОм или 5 кОм, чтобы попытаться найти значение тока, потому что мы не знаем, какое напряжение есть на любом из этих резисторов по отдельности.
3 . Однако мы не можем взять значение 9 вольт и разделить его на 3 кОм, 10 кОм или 5 кОм, чтобы попытаться найти значение тока, потому что мы не знаем, какое напряжение есть на любом из этих резисторов по отдельности.
Цифра 9 вольт — это всего величин для всей цепи, тогда как цифры 3 кОм, 10 кОм и 5 кОм представляют собой отдельных величин для отдельных резисторов. Если бы мы включили цифру для общего напряжения в уравнение закона Ома с цифрой для отдельного сопротивления, результат не будет точно соответствовать какой-либо величине в реальной цепи.
Для R 1 закон Ома будет связывать величину напряжения на R 1 с током через R 1 , учитывая сопротивление R 1 , 3 кОм:
Но, поскольку мы не знаем напряжение на R 1 (только полное напряжение, подаваемое батареей на комбинацию из трех последовательных резисторов), и мы не знаем ток через R 1 , мы можем ‘ t делать какие-либо вычисления с любой формулой.То же самое касается R 2 и R 3 : мы можем применять уравнения закона Ома тогда и только тогда, когда все члены представляют свои соответствующие количества между одними и теми же двумя точками в цепи.
Итак, что мы можем сделать? Нам известно напряжение источника (9 вольт), приложенное к последовательной комбинации R 1 , R 2 и R 3 , и мы знаем сопротивление каждого резистора, но поскольку эти величины не входят в В том же контексте мы не можем использовать закон Ома для определения тока в цепи.Если бы мы только знали, какое общее сопротивление составляет для цепи: тогда мы могли бы вычислить общий ток с нашей цифрой для общего напряжения (I = E / R).
Объединение нескольких резисторов в эквивалентный общий резистор
Это подводит нас ко второму принципу последовательной схемы:
Общее сопротивление любой последовательной цепи равно сумме отдельных сопротивлений.
Это должно иметь интуитивный смысл: чем больше последовательно соединенных резисторов, через которые должен протекать ток, тем труднее будет протекать ток.
В примере задачи у нас были последовательно подключены резисторы 3 кОм, 10 кОм и 5 кОм, что дало нам общее сопротивление 18 кОм:
По сути, мы вычислили эквивалентное сопротивление R 1 , R 2 и R 3 вместе взятых. Зная это, мы могли бы перерисовать схему с одним эквивалентным резистором, представляющим последовательную комбинацию R 1 , R 2 и R 3 :
Расчет тока цепи с использованием закона Ома
Теперь у нас есть вся необходимая информация для расчета тока цепи, потому что у нас есть напряжение между точками 1 и 4 (9 вольт) и сопротивление между точками 1 и 4 (18 кОм):
Расчет напряжений компонентов по закону Ома
Зная, что ток одинаков во всех компонентах последовательной цепи (и мы только что определили ток через батарею), мы можем вернуться к нашей исходной принципиальной схеме и отметить ток через каждый компонент:
Теперь, когда мы знаем величину тока, протекающего через каждый резистор, мы можем использовать закон Ома для определения падения напряжения на каждом из них (применяя закон Ома в его надлежащем контексте):
Обратите внимание на падение напряжения на каждом резисторе и на то, как падает сумма напряжений (1.5 + 5 + 2,5) равно напряжению аккумулятора (питания): 9 вольт.
Это третий принцип последовательной схемы:
Напряжение питания в последовательной цепи равно сумме отдельных падений напряжения.
Анализ простых последовательных цепей с помощью «табличного метода» и закона Ома
Однако метод, который мы только что использовали для анализа этой простой последовательной схемы, можно упростить для лучшего понимания. Используя таблицу для перечисления всех напряжений, токов и сопротивлений в цепи, становится очень легко увидеть, какие из этих величин могут быть правильно связаны в любом уравнении закона Ома:
Используя таблицу для перечисления всех напряжений, токов и сопротивлений в цепи, становится очень легко увидеть, какие из этих величин могут быть правильно связаны в любом уравнении закона Ома:
Правило с такой таблицей — применять закон Ома только к значениям в каждом вертикальном столбце.Например, E R1 только с I R1 и R 1 ; E R2 только с I R2 и R 2 ; и т. д. Вы начинаете свой анализ с заполнения тех элементов таблицы, которые даны вам с самого начала:
Как видно из расположения данных, мы не можем подать 9 вольт ET (полное напряжение) ни на одно из сопротивлений (R 1 , R 2 или R 3 ) ни в каком Формула закона Ома, потому что они находятся в разных столбцах.Напряжение батареи 9 В составляет , а не , приложенное непосредственно к R 1 , R 2 или R 3 . Однако мы можем использовать наши «правила» для последовательных цепей, чтобы заполнить пустые места в горизонтальном ряду. В этом случае мы можем использовать правило ряда сопротивлений для определения общего сопротивления из суммы отдельных сопротивлений:
Теперь, когда значение общего сопротивления вставлено в крайний правый столбец («Всего»), мы можем применить закон Ома I = E / R к общему напряжению и общему сопротивлению, чтобы получить общий ток 500 мкА:
Затем, зная, что ток распределяется поровну между всеми компонентами последовательной цепи (еще одно «правило» последовательной схемы), мы можем заполнить токи для каждого резистора из только что рассчитанного значения тока:
Наконец, мы можем использовать закон Ома для определения падения напряжения на каждом резисторе, по столбцу за раз:
Проверка расчетов с помощью компьютерного анализа (SPICE)
Ради удовольствия, мы можем использовать компьютер для автоматического анализа этой самой схемы. Это будет хороший способ проверить наши расчеты, а также познакомиться с компьютерным анализом. Во-первых, мы должны описать схему компьютеру в формате, распознаваемом программным обеспечением.
Это будет хороший способ проверить наши расчеты, а также познакомиться с компьютерным анализом. Во-первых, мы должны описать схему компьютеру в формате, распознаваемом программным обеспечением.
Программа SPICE, которую мы будем использовать, требует, чтобы все электрически уникальные точки в цепи были пронумерованы, а размещение компонентов понималось по тому, какие из этих пронумерованных точек или «узлов» они разделяют. Для ясности я пронумеровал четыре угла схемы в нашем примере с 1 по 4. SPICE, однако, требует, чтобы где-то в схеме был нулевой узел, поэтому я перерисую схему, немного изменив схему нумерации:
Все, что я здесь сделал, это изменил нумерацию нижнего левого угла цепи на 0 вместо 4.Теперь я могу ввести несколько строк текста в компьютерный файл, описывающий схему в терминах, понятных SPICE, вместе с парой дополнительных строк кода, предписывающих программе отображать данные о напряжении и токе для нашего удовольствия от просмотра. Этот компьютерный файл известен как список соединений в терминологии SPICE:
последовательная цепь v1 1 0 r1 1 2 3к r2 2 3 10к r3 3 0 5k .dc v1 9 9 1 .print dc v (1,2) v (2,3) v (3,0) .конец
Теперь все, что мне нужно сделать, это запустить программу SPICE для обработки списка соединений и вывода результатов:
| v1 | в (1,2) | в (2,3) | в (3) | я (v1) |
|---|---|---|---|---|
| 9.000E + 00 | 1.500E + 00 | 5.000E + 00 | 2.500E + 00 | -5.000E-04 |
Эта распечатка сообщает нам, что напряжение батареи составляет 9 вольт, а падение напряжения на R 1 , R 2 и R 3 составляет 1,5 В, 5 В и 2,5 В соответственно. Падения напряжения на любом компоненте в SPICE обозначаются номерами узлов, между которыми находится компонент, поэтому v (1,2) относится к напряжению между узлами 1 и 2 в цепи, которые являются точками, между которыми находится R 1 .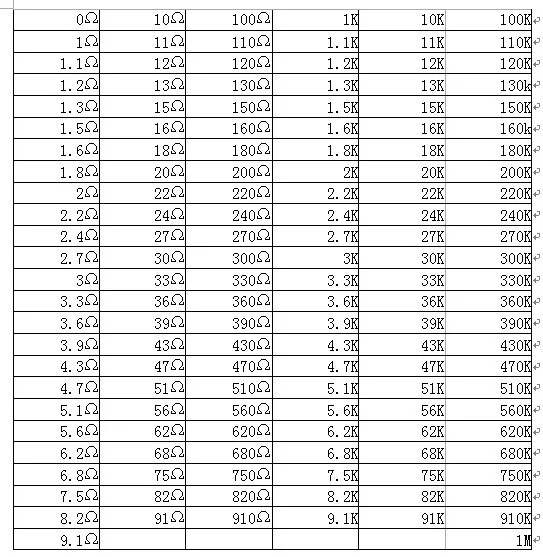 .
.
Порядок номеров узлов важен: когда SPICE выводит число для v (1,2), он учитывает полярность так же, как если бы мы держали вольтметр с красным измерительным проводом на узле 1 и черным измерительным проводом на узел 2. У нас также есть дисплей, показывающий ток (хотя и с отрицательным значением) на уровне 0,5 миллиампер или 500 микроампер. Итак, наш математический анализ был подтвержден компьютером. Эта цифра отображается как отрицательное число в анализе SPICE из-за необычного способа обработки текущих вычислений SPICE.
Таким образом, последовательная цепь определяется как имеющая только один путь, по которому может течь ток. Из этого определения следуют три правила последовательных цепей: все компоненты имеют одинаковый ток; сопротивления складываются, чтобы равняться большему общему сопротивлению; а падение напряжения в сумме равняется большему общему напряжению. Все эти правила находят корень в определении последовательной цепи. Если вы полностью понимаете это определение, то правила — не что иное, как сноски к определению.
ОБЗОР:
- Компоненты в последовательной цепи имеют одинаковый ток: I Всего = I 1 = I 2 =.. . I n
- Общее сопротивление в последовательной цепи равно сумме отдельных сопротивлений: RTotal = R 1 + R 2 +. . . R n
- Общее напряжение в последовательной цепи равно сумме отдельных падений напряжения E Всего = E 1 + E 2 +. . . En
Попробуйте наш Калькулятор закона Ома в разделе Инструменты .
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
10.3: Последовательные и параллельные резисторы
Цели обучения
По окончании раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В книге «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора. По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \). В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)).В последовательной цепи выходной ток первого резистора течет на вход второго резистора; следовательно, ток одинаков в каждом резисторе. В параллельной цепи все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Рисунок \ (\ PageIndex {1} \): (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое. Резисторысерии
Считается, что резисторывключены последовательно, когда ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \).Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения. N R_i.\ label {серия эквивалентных сопротивлений} \]
N R_i.\ label {серия эквивалентных сопротивлений} \]Одним из результатов включения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
- Рассчитайте эквивалентное сопротивление цепи.
- Рассчитайте ток через каждый резистор.
- Рассчитайте падение потенциала на каждом резисторе.
- Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Решение
- Эквивалентное сопротивление — это алгебраическая сумма сопротивлений (уравнение \ ref {серия эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 10 \, \ Омега = 90 \, \ Омега.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W.
 \ nonumber \]
\ nonumber \]
Значение
Существует несколько причин, по которым мы использовали бы несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серию по девять луковиц.Если перегорает слишком много лампочек, в конечном итоге открываются шунты. Что вызывает это?
- Ответ
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление составит 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \). Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к сгоранию шунта.№ Р_и. \]
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке \ (\ PageIndex {4} \) показаны резисторы, включенные параллельно, подключенные к источнику напряжения.
Рисунок \ (\ PageIndex {4} \): Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.Ток, протекающий от источника напряжения на рисунке \ (\ PageIndex {4} \), зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы \ (R_1 \) и \ (R_2 \). По мере того, как заряды идут от аккумулятора, некоторые проходят через резистор \ (R_1 \), а некоторые — через резистор \ (R_2 \).Сумма токов, протекающих в переходе, должна быть равна сумме токов, текущих из перехода:
\ [\ sum I_ {in} = \ sum I_ {out}. \ nonumber \]
Это уравнение называется правилом соединения Кирхгофа и будет подробно обсуждено в следующем разделе. На рисунке \ (\ PageIndex {4} \) правило соединения дает \ (I = I_1 + I_2 \). В этой схеме есть два контура, которые приводят к уравнениям \ (V = I_1R_1 \) и \ (I_1R_1 = I_2R_2 \). Обратите внимание, что напряжение на резисторах, включенных параллельно, одинаковое (\ (V = V_1 = V_2 \)), а ток — аддитивный:
\ [\ begin {align *} I & = I_1 + I_2 \\ [4pt] & = \ frac {V_1} {R_1} + \ frac {V_2} {R_2} \\ [4pt] & = \ frac {V } {R_1} + \ frac {V} {R_2} \\ [4pt] & = V \ left (\ frac {1} {R_1} + \ frac {1} {R_2} \ right) = \ frac {V} {R_ {P}} \ end {align *} \]
Решение для \ (R_ {P} \)
\ [R_ {P} = \ left (\ frac {1} {R_1} + \ frac {1} {R_2} \ right) ^ {- 1}.
 {-1}. \ label {10.3} \]
{-1}. \ label {10.3} \]Это соотношение приводит к эквивалентному сопротивлению \ (R_ {P} \), которое меньше наименьшего из отдельных сопротивлений. Когда резисторы соединены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример \ (\ PageIndex {2} \): Анализ параллельной цепи
Три резистора \ (R_1 = 1,00 \, \ Omega \), \ (R_2 = 2,00 \, \ Omega \) и \ (R_3 = 2,00 \, \ Omega \) подключены параллельно.Параллельное соединение подключается к источнику напряжения \ (V = 3,00 \, V \).
- Какое эквивалентное сопротивление?
- Найдите ток, подаваемый источником в параллельную цепь.
- Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.
- Рассчитайте мощность, рассеиваемую каждым резистором.
- Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью уравнения \ ref {10.3}. (Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив \ (R_ {P} \) на полное сопротивление \ (I = \ frac {V} {R_ {P}} \).
(c) Отдельные токи легко вычислить по закону Ома \ (\ left (I_i = \ frac {V_i} {R_i} \ right) \), поскольку каждый резистор получает полное напряжение.{-1} = 0,50 \, \ Omega. \ Nonumber \] Общее сопротивление с правильным количеством значащих цифр равно \ (R_ {eq} = 0,50 \, \ Omega \). Как и предполагалось, \ (R_ {P} \) меньше наименьшего индивидуального сопротивления.
- Полный ток можно найти из закона Ома, заменив полное сопротивление \ (R_ {P} \). Это дает \ [I = \ frac {V} {R_ {P}} = \ frac {3.00 \, V} {0.50 \, \ Omega} = 6.
 00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.- Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом, \ [I_1 = \ frac {V} {R_1} = \ frac {3.00 \, V} {1.00 \, \ Omega} = 3.00 \, A. \ nonumber \] Аналогично, \ [I_2 = \ frac {V } {R_2} = \ frac {3.00 \, V} {2.00 \, \ Omega} = 1.50 \, A \ nonumber \] и \ [I_3 = \ frac {V} {R_3} = \ frac {3.00 \, V } {2.00 \, \ Omega} = 1.50 \, A. \ nonumber \] Полный ток — это сумма отдельных токов: \ [I_1 + I_2 + I_3 = 6.2} {2.00 \, \ Omega} = 4.50 \, W. \ nonumber \]
- Общую мощность также можно рассчитать несколькими способами. Выбор \ (P = IV \) и ввод общей текущей доходности \ [P = IV = (6.00 \, A) (3.00 \, V) = 18.00 \, W. \ nonumber \]
Значение
Суммарная мощность, рассеиваемая резисторами, также 18,00 Вт:
\ [P_1 + P_2 + P_3 = 9,00 \, W + 4,50 \, W + 4,50 \, W = 18,00 \, W. \ nonumber \]
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
Упражнение \ (\ PageIndex {2A} \)
Рассмотрим ту же разность потенциалов \ ((V = 3,00 \, V) \), приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
- Решение
Эквивалент последовательной схемы будет \ (R_ {eq} = 1.
 00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Упражнение \ (\ PageIndex {2B} \)
Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?
- Решение
Река, текущая горизонтально с постоянной скоростью, разделяется на две части и течет через два водопада. Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение — это потенциальная энергия на каждом резисторе.
При рассмотрении энергии аналогия быстро разрушается.
 В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
Подведем итог основным характеристикам резисторов параллельно:
- Эквивалентное сопротивление находится по формуле \ ref {10.3} и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Как вы помните, в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. Таблица \ (\ PageIndex {1} \) суммирует уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
Таблица \ (\ PageIndex {1} \): Сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях Комбинация серии Параллельная комбинация Эквивалентная емкость \ [\ frac {1} {C_ {S}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +.N R_i \ nonumber \] \ [\ frac {1} {R_ {P}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +. . . \ nonumber \] Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения.
 Такие комбинации обычны, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Такие комбинации обычны, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.Комбинации последовательного и параллельного соединения можно свести к одному эквивалентному сопротивлению, используя технику, показанную на рисунке \ (\ PageIndex {5} \).Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Рисунок \ (\ PageIndex {5} \): (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, и эквивалентное сопротивление равно \ (R_ {34} = 10 \, \ Omega \). (c) Шаг 2: сокращенная схема показывает, что резисторы \ (R_2 \) и \ (R_ {34} \) включены параллельно, с эквивалентным сопротивлением \ (R_ {234} = 5 \, \ Omega \).(d) Шаг 3: сокращенная схема показывает, что \ (R_1 \) и \ (R_ {234} \) включены последовательно с эквивалентным сопротивлением \ (R_ {1234} = 12 \, \ Omega \), которое является эквивалентное сопротивление \ (R_ {eq} \). (e) Уменьшенная схема с источником напряжения \ (V = 24 \, V \) с эквивалентным сопротивлением \ (R_ {eq} = 12 \, \ Omega \). Это приводит к току \ (I = 2 \, A \) от источника напряжения.Обратите внимание, что резисторы \ (R_3 \) и \ (R_4 \) включены последовательно. Их можно объединить в одно эквивалентное сопротивление.Один из методов отслеживания процесса — включить резисторы в качестве индексов. Здесь эквивалентное сопротивление \ (R_3 \) и \ (R_4 \) составляет
\ [R_ {34} = R_3 + R_4 = 6 \, \ Omega + 4 \, \ Omega = 10 \, \ Omega. \ nonumber \]
Схема теперь сокращается до трех резисторов, как показано на рисунке \ (\ PageIndex {5c} \). Перерисовывая, мы теперь видим, что резисторы \ (R_2 \) и \ (R_ {34} \) составляют параллельную цепь.
 {- 1} = 5 \, \ Omega.\ nonumber \]
{- 1} = 5 \, \ Omega.\ nonumber \]Этот шаг процесса сокращает схему до двух резисторов, показанных на рисунке \ (\ PageIndex {5d} \). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
\ [R_ {eq} = R_ {1234} = R_1 + R_ {234} = 7 \, \ Omega + 5 \ Omega = 12 \, \ Omega. \ nonumber \]
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен \ (I = \ frac {V} {R_ {eq}} = \ frac {24 \, V} {12 \, \ Omega} = 2 \, A \). Этот ток проходит через резистор \ (R_1 \) и обозначается как \ (I_1 \). Падение потенциала на \ (R_1 \) можно найти с помощью закона Ома:
\ [V_1 = I_1R_1 = (2 \, A) (7 \, \ Omega) = 14 \, V. \ nonumber \]
Глядя на рисунок \ (\ PageIndex {5c} \), это оставляет \ (24 \, V — 14 \, V = 10 \, V \) отбрасывать через параллельную комбинацию \ (R_2 \) и \ ( R_ {34} \).Ток через \ (R_2 \) можно найти с помощью закона Ома:
\ [I_2 = \ frac {V_2} {R_2} = \ frac {10 \, V} {10 \, \ Omega} = 1 \, A. \ nonumber \]
Резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, поэтому токи \ (I_3 \) и \ (I_4 \) равны
\ [I_3 = I_4 = I — I_2 = 2 \, A — 1 \, A = 1 \, A. \ nonumber \]
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные капли равны \ (V_3 = I_3R_3 = 6 \, V \) и \ (V_4 = I_4R_4 = 4 \, V \).2 (4 \, \ Omega) = 4 \, W, \\ [4pt] P_ {рассеивается} & = P_1 + P_2 + P_3 + P_4 = 48 \, W. \ end {align *} \]
Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет
\ [\ begin {align *} P_s & = IV \\ [4pt] & = (2 \, A) (24 \, V) = 48 \, W \ end {align *} \]
Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.

Пример \ (\ PageIndex {3} \): объединение последовательных и параллельных цепей
На рисунке \ (\ PageIndex {6} \) показаны резисторы, подключенные последовательно и параллельно.Мы можем считать \ (R_1 \) сопротивлением проводов, ведущих к \ (R_2 \) и \ (R_3 \).
- Найдите эквивалентное сопротивление цепи.
- Какое падение потенциала \ (V_1 \) на резисторе \ (R_1 \)?
- Найдите ток \ (I_2 \) через резистор \ (R_2 \).
- Какая мощность рассеивается \ (R_2 \)?
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения \ (R_2 \) и \ (R_3 \). Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с \ (R_1 \).
(b) Ток через \ (R_1 \) можно найти с помощью закона Ома и приложенного напряжения. Ток через \ (R_1 \) равен току от батареи. Падение потенциала \ (V_1 \) на резисторе \ (R_1 \) (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.{-1} = 5.10 \, \ Omega. \ Nonumber \] Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чисто параллельной (\ (20.0 \, \ Omega \) и \ (0.804 \, \ Omega \) ), соответственно).
- Ток через \ (R_1 \) равен току, обеспечиваемому батареей: \ [I_1 = I = \ frac {V} {R_ {eq}} = \ frac {12.0 \, V} {5.10 \, \ Omega} = 2.35 \, A. \ nonumber \] Напряжение на \ (R_1 \) равно \ [V_1 = I_1R_1 = (2.35 \, A) (1 \, \ Omega) = 2.35 \, V. \ nonumber \] Напряжение, приложенное к \ (R_2 \) и \ (R_3 \), меньше напряжения, подаваемого батареей, на величину \ (V_1 \).Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных \ (R_2 \) и \ (R_3 \).

- Чтобы найти ток через \ (R_2 \), мы должны сначала найти приложенное к нему напряжение. Напряжение на двух параллельных резисторах одинаковое: \ [V_2 = V_3 = V — V_1 = 12.0 \, V — 2.35 \, V = 9.65 \, V. \ nonumber \] Теперь мы можем найти ток \ (I_2 \) через сопротивление \ (R_2 \) по закону Ома: \ [I_2 = \ frac {V_2} {R_2} = \ frac {9.65 \, V} {6.00 \, \ Omega} = 1.2 (6.00 \, \ Omega) = 15.5 \, W. \ nonumber \]
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.
Упражнение \ (\ PageIndex {3} \)
Рассмотрите электрические цепи в вашем доме.Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
- Решение
Все цепи верхнего освещения параллельны и подключены к основному питанию, поэтому при перегорании одной лампочки все верхнее освещение не гаснет. У каждого верхнего света будет по крайней мере один переключатель, включенный последовательно с источником света, так что вы можете включать и выключать его.
В холодильнике есть компрессор и лампа, которая загорается при открытии дверцы.Обычно для подключения холодильника к стене используется только один шнур. Цепь, содержащая компрессор, и цепь, содержащая цепь освещения, параллельны, но есть переключатель, включенный последовательно со светом. Термостат управляет переключателем, который включен последовательно с компрессором, чтобы контролировать температуру холодильника.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.
 Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке \ (\ PageIndex {7} \). Устройство, обозначенное символом \ (R_3 \), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, обозначенных \ (R_1 \), уменьшая напряжение на лампочке (которое составляет \ (R_2 \)), которое затем заметно гаснет.
Рисунок \ (\ PageIndex {7} \): Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные.
 Есть один список для серий, а другой — для параллелей.
Есть один список для серий, а другой — для параллелей. - Проверьте, являются ли ответы разумными и последовательными.
Пример \ (\ PageIndex {4} \): объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно \ ((R_1, \, R_2) \), соединены с двумя резисторами, включенными параллельно \ ((R_3, \, R_4) \).Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Через резистор \ (R_1 \) проходит ток 2,00 А. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
Рисунок \ (\ PageIndex {8} \): Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.- Нарисуйте четкую принципиальную схему (Рисунок \ (\ PageIndex {8} \)).
- Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы \ (R_1 \) и \ (R_2 \) включены последовательно, а резисторы \ (R_3 \) и \ (R_4 \) включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов \ (R_3 \) и \ (R_4 \) последовательно с последовательной конфигурацией резисторов \ (R_1 \) и \ (R_2 \).{-1} = 5,00 \, \ Омега. \ nonumber \] Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление схемы равно \ (R_ {eq} = R_1 + R_2 + R_ {34} = (25.00 \, \ Omega \). поэтому напряжение, подаваемое батареей, равно \ (V = IR_ {eq} = 2.00 \, A (25.00 \, \ Omega) = 50.00 \, V \).
- Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами.
 Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]Поскольку мощность, рассеиваемая резисторами, равна мощности, выделяемой батареей, наше решение кажется последовательным.
Значение
Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При нахождении \ (R_ {eq} \) для параллельного соединения необходимо с осторожностью относиться к обратному. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
резисторов серии
Электрические цепи используются в авиакосмической технике, от систем управления полетом до приборов в кабине и двигателей системы управления, чтобы аэродинамическая труба приборостроение и эксплуатация. Самая простая схема состоит из одного резистора . и источник электрического потенциала или напряжения .Электроны проходят через схема, вырабатывающая ток электроэнергии. Сопротивление, напряжение и ток связаны друг с другом соотношением Закон Ома. Обычно в практической схеме используется более одного резистора. При анализе сложной схемы мы часто можем группировать компоненты вместе и разработать схему замещения .
 При анализе схем с
несколько резисторов, мы должны определить, подвержены ли резисторы
какое-то напряжение или такой же ток.Несколько резисторов в
параллельная цепь
подвергаются одинаковому напряжению. Несколько резисторов в последовательная цепь подвергаются одинаковому току. На этой странице мы обсуждаем эквивалентную схему
для резисторов последовательно.
При анализе схем с
несколько резисторов, мы должны определить, подвержены ли резисторы
какое-то напряжение или такой же ток.Несколько резисторов в
параллельная цепь
подвергаются одинаковому напряжению. Несколько резисторов в последовательная цепь подвергаются одинаковому току. На этой странице мы обсуждаем эквивалентную схему
для резисторов последовательно.На рисунке изображена схема, состоящая из источника питания и трех резисторов. соединены последовательно. Если обозначить сопротивление R , ток i и напряжение В , то закон Ома гласит, что для каждого резистора в цепи:
V = i Rя = V / R
Если рассматривать каждый резистор по отдельности, каждый резистор имеет свой ток. ( i1 , i2 и i3 ), сопротивление ( R1 , R2 и R3 ), и напряжение ( V1 , V2 и V3 ).Резисторы подключены друг к другу в узлах . Узлы обозначены маленькие кружочки на фигуре. Для этой схемы есть четыре узла, соединяющие три резистора и источник питания. В каждом узле ток, поступающий в узел должен равняться току, выходящему из узла, согласно закону Фарадея . При таком расположении резисторов есть только один провод, входящий и выходящий. каждый узел. Следовательно, ток через каждый резистор должен быть одинаковым.
я = я1 = я2 = я3Падение напряжения на каждом резисторе определяется законом Ома:
V1 = i R1V2 = я R2
V3 = i R3
Сумма падений напряжения на каждом резисторе должна равняться подаваемому напряжению. по источнику питания:
V = V1 + V2 + V3Теперь мы знаем напряжение, сопротивление и ток в каждой части цепи.
Если бы мы построили эквивалентную схему, как показано в правом нижнем углу, мы бы имеют одинаковое напряжение В , такой же ток от источника питания ie = i , и один эквивалентный резистор Re .
V = i Re Для нашей эквивалентной схемы закон Ома
указывает, что:
Для нашей эквивалентной схемы закон Ома
указывает, что:Мы можем определить значение Re , используя развитые выше соотношения и немного алгебры:
я Re = я R1 + я R2 + я R3Re = R1 + R2 + R3
Мы можем использовать эти знания о цепи последовательного резистора для анализа Мост Уитстона схема, которая используется для контроля температуры в аэродинамической трубе баланс сил используя электронные тензодатчики.
Навигация ..
- Руководство для начинающих Домашняя страница
резисторов последовательно и параллельно
резисторов последовательно и параллельно
следующий: Правила Кирхгофа Up: Электрический ток Предыдущее: ЭДС и внутреннее сопротивление Резисторы, вероятно, встречаются чаще всего. компоненты в электронных схемах. Практические схемы часто содержат очень сложные комбинации резисторов.Поэтому полезно иметь набор правил для поиска эквивалентных сопротивление некоторой общей схемы резисторов. Оказывается, мы можем всегда находите эквивалентное сопротивление повторным применением два простых правил. Эти правила относятся к резисторам, включенным последовательно, и в параллели.Рисунок 18: Два резистора соединены последовательно. Рассмотрим два резистора, соединенных в серию , как показано на рис.18. Понятно, что через оба резистора протекает одинаковый ток. Ибо, если бы это было не так, заряд накапливался бы в одном или другом резисторов, которые не соответствовали бы установившаяся ситуация (таким образом нарушая основное предположение этого раздела). Предположим, что падение потенциала от точки к точке есть. Это падение представляет собой сумму потенциальных падает и на двух резисторах и соответственно.
 Таким образом,
Таким образом, (135)
Согласно закону Ома, эквивалентное сопротивление между и — отношение падения потенциала в этих точках и ток, протекающий между ними.Таким образом,(136)
давая(137)
Здесь мы использовали тот факт, что ток является общим для все три резистора. Следовательно, правилоЭквивалентное сопротивление двух последовательно соединенных резисторов равно сумма отдельных сопротивлений.
Для резисторов, соединенных последовательно, уравнение.(137) обобщает к .Рисунок 19: Два резистора подключены параллельно. Рассмотрим два резистора, соединенных по параллельно , как показано на рис. 19. Это Из рисунка видно, что падение потенциала на двух резисторах равно одно и тоже. В общем, однако, токи и которые протекают через резисторы и соответственно разные. По закону Ома эквивалентное сопротивление между и — отношение падения потенциала через эти точки и текущий которая течет между ними.Этот ток должен равняться сумме токи и протекающие через два резистора, в противном случае заряд будет накапливаться на одном или обоих переходах в цепи. Таким образом,
(138)
Следует, что(139)
давая(140)
Здесь мы использовали тот факт, что падение потенциала является общим для всех трех резисторов. Ясно, что правило
Ясно, что правило Значение, обратное эквивалентному сопротивлению двух сопротивлений. подключенных параллельно — это сумма обратных величин индивидуальные сопротивления.
Для резисторов, соединенных параллельно, уравнение. (140) обобщает на .
следующий: Правила Кирхгофа Up: Электрический ток Предыдущее: ЭДС и внутреннее сопротивление Ричард Фицпатрик 2007-07-1421.1 Последовательные и параллельные резисторы — College Physics: OpenStax
На рисунке 3 показаны резисторы, подключенные параллельно и подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)
Чтобы найти выражение для эквивалентного параллельного сопротивления [латекс] \ boldsymbol {R _ {\ textbf {p}}} [/ latex], давайте рассмотрим протекающие токи и то, как они связаны с сопротивлением. Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, составляют [латекс] \ boldsymbol {I_1 = \ frac {V} {R_1}} [/ latex], [латекс] \ boldsymbol {I_2 = \ frac {V} {R_2}} [/ latex] и [latex] \ boldsymbol {I_3 = \ frac {V} {R_3}} [/ latex].Сохранение заряда подразумевает, что полный ток [латекс] \ boldsymbol {I} [/ latex], производимый источником, является суммой этих токов:
[латекс] \ boldsymbol {I =} [/ latex] [latex] \ boldsymbol {\ frac {V} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_3}} [/ latex] [латекс] \ boldsymbol {= V} [/ latex] [латекс] \ boldsymbol {(\ frac { 1} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [ / latex] [латекс] \ boldsymbol {\ frac {1} {R_3})}.
 [/ latex]
[/ latex][латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_p}} [/ latex] [латекс] \ boldsymbol {= V} [/ латекс ] [latex] \ boldsymbol {(\ frac {1} {R_p})}. [/ latex]
Члены в скобках в последних двух уравнениях должны быть равны. Если обобщить на любое количество резисторов, общее сопротивление [латекс] \ boldsymbol {R_p} [/ latex] параллельного соединения связано с отдельными сопротивлениями соотношением
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_3}} [/ latex] [латекс] \ boldsymbol {+ \ cdots} [/ latex]
Это соотношение приводит к общему сопротивлению [латекс] \ boldsymbol {R_p} [/ latex], которое меньше наименьшего из отдельных сопротивлений.(Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2: Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на Рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: [latex] \ boldsymbol {V = 12.0 \; \ textbf {V}} [/ latex], [latex] \ boldsymbol {R_1 = 1.00 \; \ Omega} [/ latex], [latex] \ boldsymbol {R_2 = 6.00 \; \ Omega} [/ латекс ] и [латекс] \ boldsymbol {R_3 = 13.0 \; \ Omega} [/ latex]. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения. Ввод известных значений дает
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_1}} [/ латекс ] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol { \ frac {1} {R_3}} [/ latex] [latex] \ boldsymbol {=} [/ latex] [latex] \ boldsymbol {\ frac {1} {1.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {6.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {13.0 \; \ Omega}}. [/ latex]
Таким образом,
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1.00} {\ Omega}} [/ латекс] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {0.1667} {\ Omega}} [/ латекс] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {0.07692} {\ Omega}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1.2436} {\ Omega}} [/ латекс]
(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны перевернуть это, чтобы найти полное сопротивление [латекс] \ boldsymbol {R_p} [/ latex]. Это дает
[латекс] \ boldsymbol {R_p =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {1.2436}} [/ latex] [латекс] \ boldsymbol {\ Omega = 0.8041 \; \ Omega}. [ / латекс]
Общее сопротивление с правильным количеством значащих цифр составляет [латекс] \ boldsymbol {R_p = 0.804 \; \ Omega} [/ latex]
Обсуждение для (а)
[latex] \ boldsymbol {R_p} [/ latex], как и предполагалось, меньше минимального индивидуального сопротивления.

Стратегия и решение для (b)
Полный ток можно найти из закона Ома, заменив полное сопротивление [латекс] \ boldsymbol {R_p} [/ latex]. Это дает
[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {0.8041 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 14.92 \; \ textbf {A}} [/ latex]
Обсуждение для (б)
Текущий [latex] \ boldsymbol {I} [/ latex] для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,
[латекс] \ boldsymbol {I_1 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_1}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {1.00 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 12.0 \; \ textbf {A}}. [/ Latex]
Аналогично
[латекс] \ boldsymbol {I_2 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_2}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {6.00 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 2.00 \; \ textbf {A}} [/ latex]
и
[латекс] \ boldsymbol {I_3 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_3}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 0.92 \; \ textbf {A}}. [/ Latex]
Обсуждение для (c)
Общий ток складывается из отдельных токов:
[латекс] \ boldsymbol {I_1 + I_2 + I_3 = 14.92 \; \ textbf {A}}.
 [/ Latex]
[/ Latex]Это соответствует сохранению заряда.
Стратегия и решение для (d)
Мощность, рассеиваемая каждым резистором, может быть найдена с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.2} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 11.1 \; \ textbf {W}}. [/ Latex]
Обсуждение для (d)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общую мощность также можно рассчитать несколькими способами. Выбрав [латекс] \ boldsymbol {P = IV} [/ latex] и введя общий ток, получим
[латекс] \ boldsymbol {P = IV = (14.92 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 179 \; \ textbf {W}}. [/ Latex]
Обсуждение для (e)
Суммарная мощность, рассеиваемая резисторами, также 179 Вт:
[латекс] \ boldsymbol {P_1 + P_2 + P_3 = 144 \; \ textbf {W} + 24.0 \; \ textbf {W} + 11.1 \; \ textbf {W} = 179 \; \ textbf {W}}. [/ латекс]
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
4.1 Последовательные и параллельные резисторы
Последовательные резисторы
Когда резисторы включены последовательно? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током, должен проходить через устройства последовательно. Например, если ток протекает через человека, держащего отвертку, в землю, тогда R1.R1. размер 12 {R rSub {размер 8 {1}}} {} на рис. 4.2 (a) может быть сопротивлением вала отвертки, R2R2 размер 12 {R rSub {размер 8 {2}}} {} сопротивление его ручка, R3R3 размер 12 {R rSub {размер 8 {3}}} {} сопротивление тела человека и R4R4 размер 12 {R rSub {размер 8 {4}}} {} сопротивление ее обуви.

На рисунке 4.3 показаны резисторы, последовательно подключенные к источнику напряжения. Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь на резиновой подошве с высоким сопротивлением. Это могло быть недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением к прибору, который уменьшал бы рабочий ток.
Рисунок 4.3 Три резистора, подключенных последовательно к батарее (слева) и эквивалентному одиночному или последовательному сопротивлению (справа).
Чтобы убедиться, что последовательно включенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения, в каждом резисторе на рис. 4.3.
Согласно закону Ома падение напряжения, V, V, размер 12 {V} {} на резисторе, когда через него протекает ток, рассчитывается по формуле V = IR, V = IR, размер 12 {V = ital «IR»} {}, где размер II 12 {I} {} равен току в амперах (A), а размер RR 12 {R} {} — сопротивление в омах.Ω. размер 12 {слева (% OMEGA справа)} {} Другой способ представить это: VV размером 12 {V} {} — это напряжение, необходимое для протекания тока II размера 12 {I} {} через сопротивление RR размера 12 {R} {}
Итак, падение напряжения на R1R1 размером 12 {R rSub {size 8 {1}}} {} равно V1 = IR1, V1 = IR1, size 12 {V rSub {size 8 {1}} = ital «IR» rSub { размер 8 {1}}} {}, что для R2R2 размер 12 {R rSub {размер 8 {2}}} {} равен V2 = IR2, V2 = IR2, размер 12 {V rSub {size 8 {2}} = ital «IR» rSub {размер 8 {2}}} {}, а для R3R3 размера 12 {R rSub {размер 8 {3}}} {} — V3 = IR3.V3 = IR3. размер 12 {V rSub {size 8 {3}} = ital «IR» rSub {size 8 {3}}} {} Сумма этих напряжений равна выходному напряжению источника; то есть
4,1 В = V1 + V2 + V3. V = V1 + V2 + V3. размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}}} {}
V = V1 + V2 + V3. размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}}} {}Это уравнение основано на сохранении энергии и сохранении обвинять. Электрическая потенциальная энергия может быть описана уравнением PE = qV, PE = qV, size 12 {ital «PE» = ital «qV»} {}, где qq size 12 {q} {} — электрический заряд, а размер VV 12 { V} {} — напряжение.Таким образом, энергия, подаваемая источником, равна qV, qV, размер 12 {ital «qV»} {}, а энергия, рассеиваемая резисторами, равна
. 4.2 qV1 + qV2 + qV3. QV1 + qV2 + qV3. размер 12 {ital «qV» rSub {size 8 {1}} + ital «qV» rSub {size 8 {2}} + ital «qV» rSub {size 8 {3}}} {}Связи: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе.Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, qV = qV1 + qV2 + qV3.qV = qV1 + qV2 + qV3. size 12 {ital «qV» = ital «qV» rSub {size 8 {1}} + ital «qV» rSub {size 8 {2}} + ital «qV» rSub {size 8 {3}}} {} заряд qq размер 12 {q} {} отменяется, давая V = V1 + V2 + V3, V = V1 + V2 + V3, размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2 }} + V rSub {размер 8 {3}}} {}, как указано.(Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
4,3 В = IR1 + IR2 + IR3 = I (R1 + R2 + R3). V = IR1 + IR2 + IR3 = I (R1 + R2 + R3). размер 12 {V = ital «IR» rSub {size 8 {1}} + ital «IR» rSub {size 8 {2}} + ital «IR» rSub {size 8 {3}} = I \ (R rSub { размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}} \)} {}Обратите внимание, что для эквивалентного одиночного последовательного сопротивления Rs, Rs, мы имеем
Это означает что полное или эквивалентное последовательное сопротивление RsRs трех резисторов равно Rs = R1 + R2 + R3.
 Rs = R1 + R2 + R3. размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}}} {}
Rs = R1 + R2 + R3. размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}}} {}Эта логика действительно для любого количества последовательно подключенных резисторов; таким образом, полное сопротивление RsRs последовательного соединения составляет
4,5 Rs = R1 + R2 + R3 + …, Rs = R1 + R2 + R3 + …, размер 12 {R rSub {size 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}} + «.» «.» «.» } {}в соответствии с предложением. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Пример 4.1 Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на Рисунке 4.3 составляет 12,0 В 12,0 В, размер 12 {«12» «.» 0`V} {} и сопротивления: R1 = 1,00 Ом, R1 = 1,00 Ом, размер 12 {R rSub {size 8 {1}} = 1 «.» «00»% OMEGA} {} R2 = 6,00 Ом, R2 = 6,00 Ом, размер 12 {R rSub {размер 8 {2}} = 6 дюймов «. «00»% OMEGA} {} и R3 = 13,0 Ом. R3 = 13,0 Ом. размер 12 {R rSub {размер 8 {3}} = «13» «.» 0% OMEGA} {} (а) Какое полное сопротивление? (б) Найдите ток.(c) Рассчитайте падение напряжения на каждом резисторе и покажите, что в сумме они равны выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление — это просто сумма отдельных сопротивлений, как определено уравнением
4,6 Rs = R1 + R2 + R3 = 1,00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом.Rs = R1 + R2 + R3 = 1,00 Ом + 6,00 Ом + 13,0 Ом = 20,0 Ом.Стратегия и решение для (b)
Ток определяется по закону Ома, V = IR.V = IR. размер 12 {V = ital «IR»} {} Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи.
4,7 I = VRs = 12,0 В 20,0 Ом = 0,600 AI = VRs = 12,0 В 20,0 Ом = 0,600 A, размер 12 {I = {{V} больше {R rSub {size 8 {s}}}} = {{» 12 «». » 0 «V»} больше {«20» «.» «0»% OMEGA}} = 0 «.» «600» «A»} {}
Стратегия и решение для (c)
Падение напряжения — или IRIR размера 12 {ital «IR»} {} — в резисторе определяется законом Ома.Ввод значения тока и значения первого сопротивления дает значение
. 4,8 В1 = IR1 = (0,600 А) (1,0 Ом) = 0,600 В. V1 = IR1 = (0,600 А) (1,0 Ом) = 0,600 В. размер 12 {В rSub {размер 8 {1}} = курсив «IR» rSub {size 8 {1}} = \ (0 «.» «600» «A» \) \ (1 «.» 0% OMEGA \) = 0 «.» «600» «V»} {}Аналогично
4,9 В2 = IR2 = (0,600 А) (6,0 Ом) = 3,60 ВV2 = IR2 = (0,600 А) (6,0 Ом) = 3,60 В, размер 12 {В rSub {размер 8 {2}} = ital «IR» rSub {размер 8 {2}} = \ (0 «.» «600» «A» \) \ (6 «.» 0% OMEGA \) = 3 «.» «60» «V»} {}и
4.10 V3 = IR3 = (0,600 A) (13,0 Ом) = 7,80 В. V3 = IR3 = (0,600 A) (13,0 Ом) = 7,80 В. размер 12 {V rSub {размер 8 {3}} = курсив «IR» rSub {size 8 {3}} = \ (0 «.» «600» «A» \) \ («13» «.» 0% OMEGA \) = 7 «.» «80» «V»} {}Обсуждение для (c)
Три капли IRIR размера 12 {ital «IR»} {} добавляют к 12,0 В, 12,0 В, размер 12 {«12» «». 0`V} {}, как и ожидалось.
4,11 V1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 VV1 + V2 + V3 = (0,600 + 3,60 + 7,80) V = 12,0 В размер 12 {V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}} = \ (0 «.»» 600 «+3». «» 60 «+7». «» 80 «\)» V «=» 12 «». «0» V «} {}Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля, P = IV, P = IV, размер 12 {P = курсив «IV»} {}, где PP размер 12 {P} {} — электроэнергия. В этом случае через каждый резистор протекает одинаковый полный ток. Подставляя закон Ома V = IRV = IR, размер 12 {V = ital «IR»} {} в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как
4. 12 P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт размер 12 {P rSub {размер 8 {1}} = I rSup {размер 8 {2}} R rSub {размер 8 {1}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ (1 «.» «00»% OMEGA \) = 0 «.» «360» «W»} {}
12 P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт размер 12 {P rSub {размер 8 {1}} = I rSup {размер 8 {2}} R rSub {размер 8 {1}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ (1 «.» «00»% OMEGA \) = 0 «.» «360» «W»} {}Аналогично
4,13 P2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 WP2 = I2R2 = (0,600 A) 2 (6,00 Ом) = 2,16 Вт размер 12 {P rSub {размер 8 {2}} = I rSup {размер 8 {2}} R rSub {размер 8 {2}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ (6 «.» «00»% OMEGA \) = 2 «.» «16» «W»} {}и
4.14 P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт. P3 = I2R3 = (0,600 A) 2 (13,0 Ом) = 4,68 Вт. Размер 12 {P rSub {размер 8 {3}} = I rSup {размер 8 {2}} R rSub {размер 8 {3}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ («13» «.» 0% OMEGA \) = 4 «.» «68» «W»} {}Обсуждение для (d)
Мощность также можно рассчитать, используя либо P = IVP = IV, размер 12 {P = ital «IV»} {}, либо P = V2R, P = V2R, размер 12 {P = {{V rSup {size 8 {2}}) } over {R}}} {}, где величина VV 12 {V} {} — это падение напряжения на резисторе (а не полное напряжение источника).Получатся те же значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать P = IV, P = IV, размер 12 {P = ital «IV»} {}, где VV размером 12 {V} {} — это напряжение источника. Это дает
4,15 P = (0,600 A) (12,0 В) = 7,20 WP = (0,600 A) (12,0 В) = 7,20 Вт. Размер 12 {P = \ (0 «.» «600» «A» \) \ («12 «». «0» V «\) = 7″. » «20» «W»} {}Обсуждение для (e)
Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
4,16 P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7,20 W. P1 + P2 + P3 = (0,360 + 2,16 + 4,68) W = 7,20 W. размер 12 {P rSub {размер 8 {1}} + P rSub {размер 8 {2}} + P rSub {размер 8 {3}} = \ (0 «.

 Знач. сопротивления
Знач. сопротивления порядок
порядок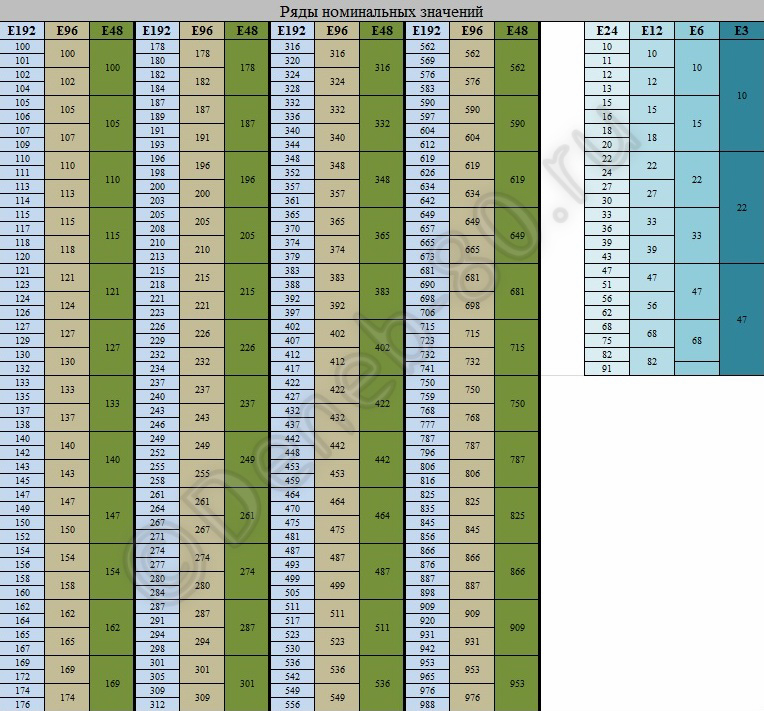 Эти стандартизованные значения сопротивлений образуют последовательности (нормали), которые известны под названием Е-серий или Е-рядов (например, серии Е6, Е12, Е24, Е48 и Е96). Точные значения сопротивлений, образующих каждую из серий номинальных значений резисторов, приведены в разделе Приложения. Каждая из серий характеризуется количеством тех номиналов, которые входят в один десятичный разряд величин сопротивлений.
Эти стандартизованные значения сопротивлений образуют последовательности (нормали), которые известны под названием Е-серий или Е-рядов (например, серии Е6, Е12, Е24, Е48 и Е96). Точные значения сопротивлений, образующих каждую из серий номинальных значений резисторов, приведены в разделе Приложения. Каждая из серий характеризуется количеством тех номиналов, которые входят в один десятичный разряд величин сопротивлений. Но при этих условиях возрастет и температура внутри корпуса аппаратуры.
Но при этих условиях возрастет и температура внутри корпуса аппаратуры.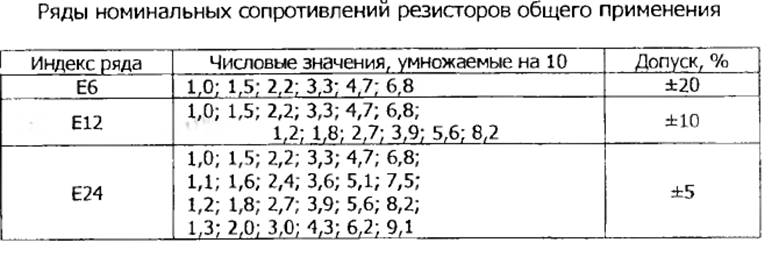 Даже при этой оговорке, резистор, работающий при условии выделения одной трети от номинального значения мощности, будет нагрет значительно сильнее других окружающих его элементов. Поэтому, если изменяется его температура, то следует ожидать изменения его электрических параметров, вплоть до отказа. И они действительно будут наблюдаться.
Даже при этой оговорке, резистор, работающий при условии выделения одной трети от номинального значения мощности, будет нагрет значительно сильнее других окружающих его элементов. Поэтому, если изменяется его температура, то следует ожидать изменения его электрических параметров, вплоть до отказа. И они действительно будут наблюдаться.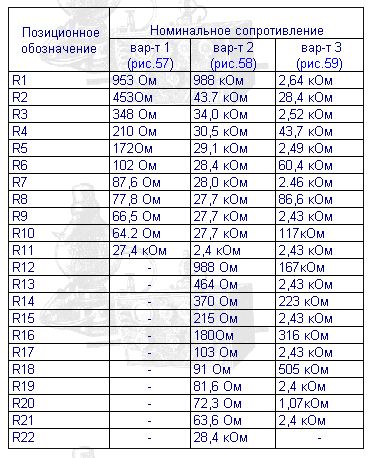 Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
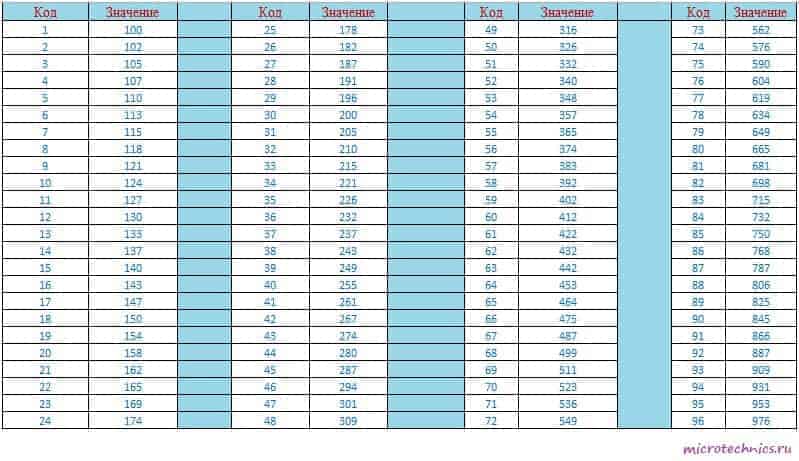 \ nonumber \]
\ nonumber \]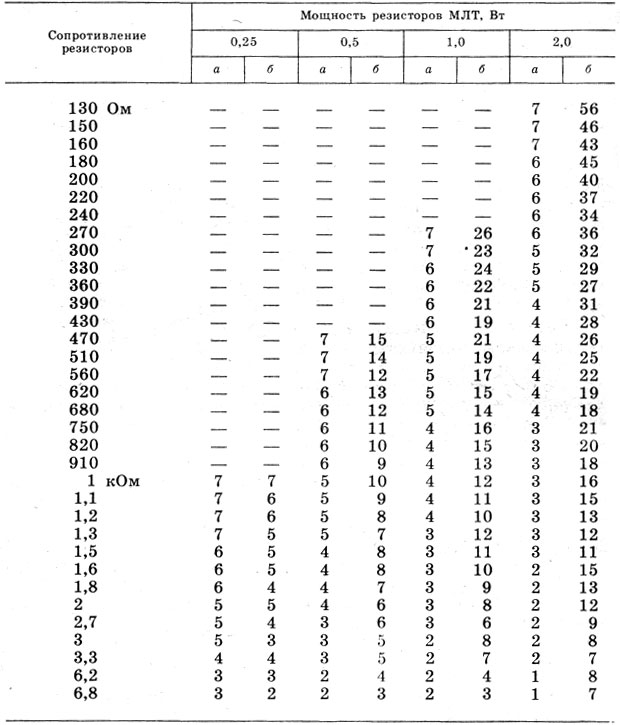 Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании. {-1}. \ label {10.3} \]
{-1}. \ label {10.3} \] 00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно. 00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов, проходящих через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \). В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов. Такие комбинации обычны, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Такие комбинации обычны, особенно если учитывать сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. {- 1} = 5 \, \ Omega.\ nonumber \]
{- 1} = 5 \, \ Omega.\ nonumber \]

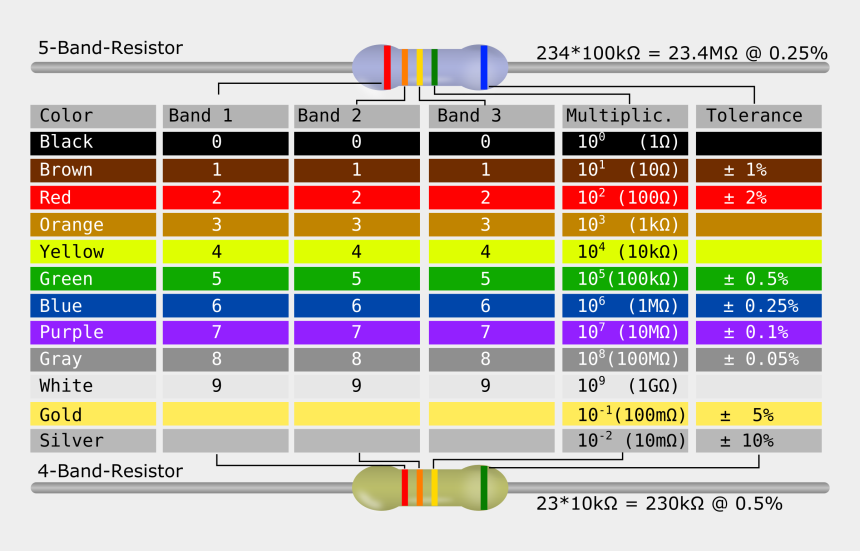 Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре. Есть один список для серий, а другой — для параллелей.
Есть один список для серий, а другой — для параллелей.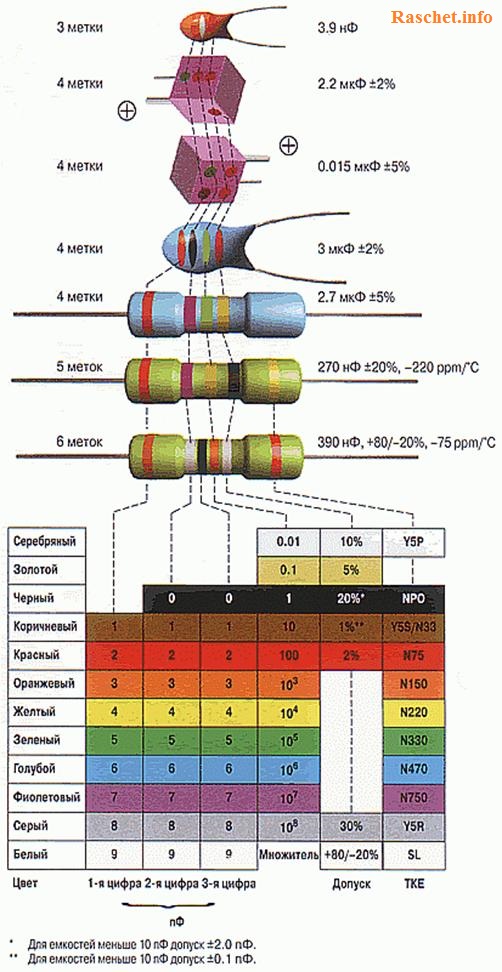 Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \]
Мощность, обеспечиваемая аккумулятором, равна \ (P_ {batt} = IV = 100.2R_4 \\ [4pt] & = 40.00 \, W + 40.00 \, W + 10.00 \, W + 10.00 \, W = 100. \, W. \ end {align *} \] При анализе схем с
несколько резисторов, мы должны определить, подвержены ли резисторы
какое-то напряжение или такой же ток.Несколько резисторов в
параллельная цепь
подвергаются одинаковому напряжению. Несколько резисторов в последовательная цепь подвергаются одинаковому току. На этой странице мы обсуждаем эквивалентную схему
для резисторов последовательно.
При анализе схем с
несколько резисторов, мы должны определить, подвержены ли резисторы
какое-то напряжение или такой же ток.Несколько резисторов в
параллельная цепь
подвергаются одинаковому напряжению. Несколько резисторов в последовательная цепь подвергаются одинаковому току. На этой странице мы обсуждаем эквивалентную схему
для резисторов последовательно. Для нашей эквивалентной схемы закон Ома
указывает, что:
Для нашей эквивалентной схемы закон Ома
указывает, что: Таким образом,
Таким образом,  Ясно, что правило
Ясно, что правило  [/ latex]
[/ latex]
 [/ Latex]
[/ Latex]
 V = V1 + V2 + V3. размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}}} {}
V = V1 + V2 + V3. размер 12 {V = V rSub {размер 8 {1}} + V rSub {размер 8 {2}} + V rSub {размер 8 {3}}} {} Rs = R1 + R2 + R3. размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}}} {}
Rs = R1 + R2 + R3. размер 12 {R rSub {размер 8 {s}} = R rSub {размер 8 {1}} + R rSub {размер 8 {2}} + R rSub {размер 8 {3}}} {}
 12 P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт размер 12 {P rSub {размер 8 {1}} = I rSup {размер 8 {2}} R rSub {размер 8 {1}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ (1 «.» «00»% OMEGA \) = 0 «.» «360» «W»} {}
12 P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт P1 = I2R1 = (0,600 A) 2 (1,00 Ом) = 0,360 Вт размер 12 {P rSub {размер 8 {1}} = I rSup {размер 8 {2}} R rSub {размер 8 {1}} = \ (0 «.» «600» «A» \) rSup {размер 8 {2}} \ (1 «.» «00»% OMEGA \) = 0 «.» «360» «W»} {}