Последовательное и параллельное соединение проводников, резисторов, конденсаторов и катушек индуктивности. Онлайн расчёты.
«- Я тебе как электрику объясняю: Надя спит с мужиками последовательно, а Света параллельно.
Кто из них шмара вавилонская?
— Ну, Света наверное.
— Вот! А мне, как кладовщику, видится немного другое: «поблядушка обыкновенная» — 2 штуки! »
«- А теперь скажи мне отрок, как течёт электричество по проводам электрическим, и цепям рукотворным, последовательным
да параллельным, от плюса к минусу со скоростью света в вакууме?
— С Божьей помощью, батюшка! С Божьей помощью…»
Ну да ладно, достаточно! Шутки — штуками, а пора бы уже дело делать. Так что «Копайте пока здесь! А я тем временем схожу узнаю — где надо…», а заодно набросаю пару-тройку калькуляторов на заданную тему.
Итак.
При последовательном соединении проводников сила тока во всех проводниках одинакова, при этом общее напряжение в цепи
равно сумме напряжений на концах каждого из проводников.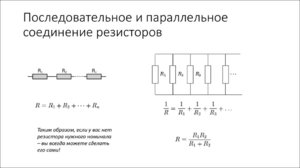
При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов, а сила тока в цепи равна сумме сил токов в отдельных параллельно соединённых проводниках.
Поясним рисунком с распределением напряжений, токов и формулами.
Рис.1
Расчёт проведём для 4 резисторов (проводников), соединённых последовательно или параллельно. Если элементов в цепи меньше, то
оставляем лишние поля в таблице не заполненными.
Заодно, при желании узнать распределение значений токов и напряжений на каждом из элементов при последовательном и параллельном
соединениях, есть возможность ввести величину общего напряжения в цепи U. А есть возможность не вводить…
РАСЧЁТ СОПРОТИВЛЕНИЙ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
проводников
Теперь, что касается последовательных и параллельных соединений конденсаторов и катушек индуктивности.
Схема, приведённая на Рис.1 для проводников и резисторов, остаётся в полной силе и для катушек с конденсаторами, распределение
напряжений и токов тоже никуда не девается, трансформируется лишь осмысление того, что токи эти и напряжения обязаны быть переменными.
А потому, что для постоянных значений этих величин — сопротивление конденсаторов составляет в первом приближении бесконечность, а катушек — ноль, соответственно и токи будут равны либо нулю, либо бесконечности, а для переменных значений иметь ярко выраженную зависимость от частоты.
Поэтому, для желающих рассчитать величины напряжений и токов в последовательных или параллельных цепях, состоящих из конденсаторов и
катушек индуктивности, имеет полный смысл выяснить на странице ссылка на страницу значения
реактивных сопротивлений данных элементов при интересующей Вас частоте и подставить эти значения в таблицу для расчёта проводников
и резисторов.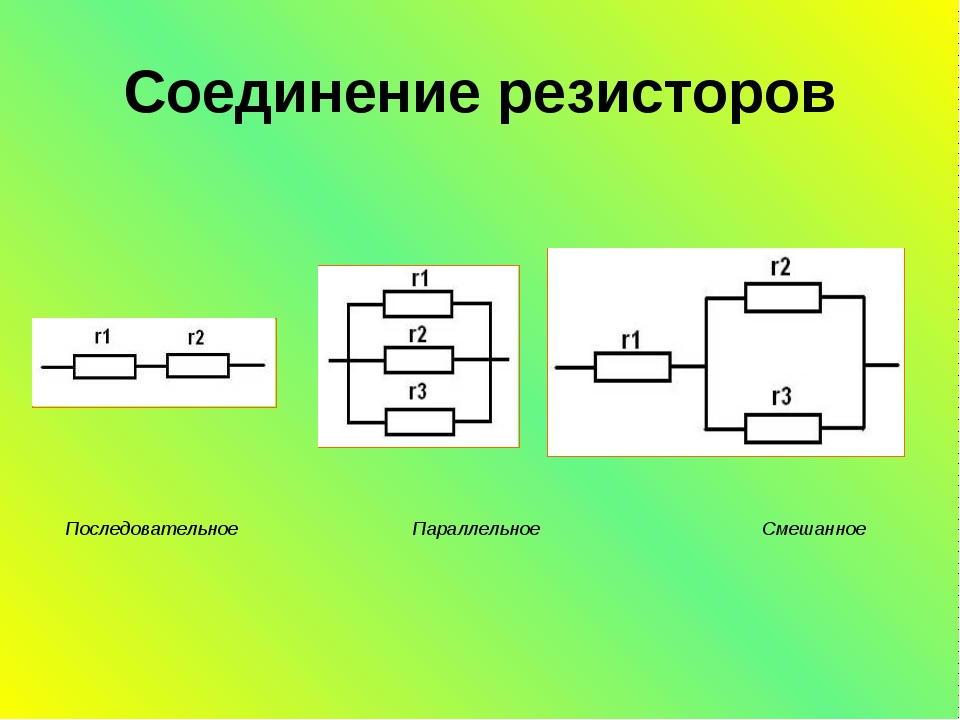
Ну а теперь приведём таблицы для расчёта значений ёмкостей и индуктивностей при условии последовательного и
параллельного соединений конденсаторов и катушек в количестве от 2 до 4 штук.
Расчёт поведём на основании хрестоматийных формул:
С = С1+ С2+….+ Сn и
1/L = 1/L1+ 1/L2 +…+ 1/Ln
для параллельных цепей и
L = L1 + L2 +….+ Ln и
1/С = 1/С1+ 1/С2+…+ 1/Сn для последовательных.
Как и в предыдущей таблице вводные, помеченные * — к заполнению не обязательны.
РАСЧЁТ ЁМКОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
конденсаторов
Ну и в завершении ещё одна таблица.
РАСЧЁТ ИНДУКТИВНОСТИ ПРИ ПАРАЛЛЕЛЬНОМ И ПОСЛЕДОВАТЕЛЬНОМ СОЕДИНЕНИИ
катушек
Тут важно заметить, что приведённые в последней таблице расчёты верны только для индуктивно не связанных катушек, то есть для катушек, намотанных на разных каркасах и расположенных на значительных расстояниях друг от друга, во избежание, пересечения взаимных магнитных полей.
последовательное, параллельное, смешанное соединение. Расчет сопротивления
Резисторы между собой могут быть соединены двумя основными способами: последовательно и параллельно. Смешанное соединение резисторов является их комбинацией.
Сочетания любых соединений резисторов можно привести к одному резистору, расчетом сопротивления которого (R) мы сейчас займемся.
ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Давайте рассчитаем общее сопротивление такой цепи (рисунок 1). Для этого нам понадобится закон Ома — I=U/R и закон Кирхгофа — I=I1+I2+. .In
.In
С учетом этого имеем:
- I=U/R
- I1=U/R1
- I2=U/R2
- In=U/Rn
- U/R=U/R1+U/R2+…U/Rn
- 1/R=1/R1+1/R2+…1/Rn
Последняя формула является основной для расчета сопротивления цепи параллельно соединенных резисторов. Для двух резисторов ее можно записать более удобно:
R=(R
Отсюда следует, что в случае параллельного соединения двух одинаковых по номиналу резисторов (R1=R2) их общее сопротивление будет вдвое меньше любого из них. Это полезно помнить.
ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Используя уже упомянутые законы для цепи последовательно соединенных резисторов (рисунок 2) можем записать:
- U=I*R
- I=I1=I2=…In
- U=U1+U2+…Un
- I*R=I*R1+I*R2+.
 ..I*Rn
..I*Rn - R=R1+R2+…Rn
То есть общее сопротивление резисторов при последовательном соединении равно сумме их сопротивлений.
СМЕШАННОЕ СОЕДИНЕНИЕ РЕЗИСТОРОВ
Такое соединение всегда можно представить как комбинацию последовательного и параллельного соединений (рис.3).
Расчет общего сопротивления цепи при этом производится поэтапно. В приведенном примере рассчитываем:
- последовательное сопротивление резисторов Rпосл=R1+R2
- параллельное соединение R=(Rпосл*R3)/(Rпосл+R3)
Безусловно, могут встретиться более сложные варианты, но методика расчета их сопротивления та же.
Несколько слов про то, когда возникает необходимость соединять резисторы тем или иным способом:
- Отсутствие «под рукой» резистора нужного номинала. При этом следует помнить, что погрешности резисторов будут суммироваться.
Например, для рисунка 3.a, если фактическая погрешность R1 составляет +10%, а R2 имеет +15%, то для Rпосл она будет +25%.

Здесь следует обращать внимание на знак, то есть для -10% и +15% в результате получим +5%.
- Необходимость получить большую мощность.
Здесь надо учесть, что при одинаковых номиналах сопротивлений и мощностей соединяемых резисторов, как при последовательном, так и при параллельном их соединении итоговая мощность будет равна сумме мощностей.
В противном случае следует ее рассчитать, используя закон Ома и формулу для определения рассеиваемой мощности P=I*U.
Про мощность и номиналы резисторов можно почитать здесь.
© 2012-2020 г. Все права защищены.
Представленные на сайте материалы имеют информационный характер и не могут быть использованы в качестве руководящих и нормативных документов
Параллельное соединение резисторов определение — Морской флот
Как правильно соединять резисторы?
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно. Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов.
В жизни последовательное соединение резисторов имеет вид:
Последовательно соединённые резисторы серии МЛТ
Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
Общее номинальное сопротивление составного резистора обозначено как Rобщ.
Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом. Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом. Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов.
Можно соединять резисторы и параллельно:
Два резистора МЛТ-2, соединённых параллельно
Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.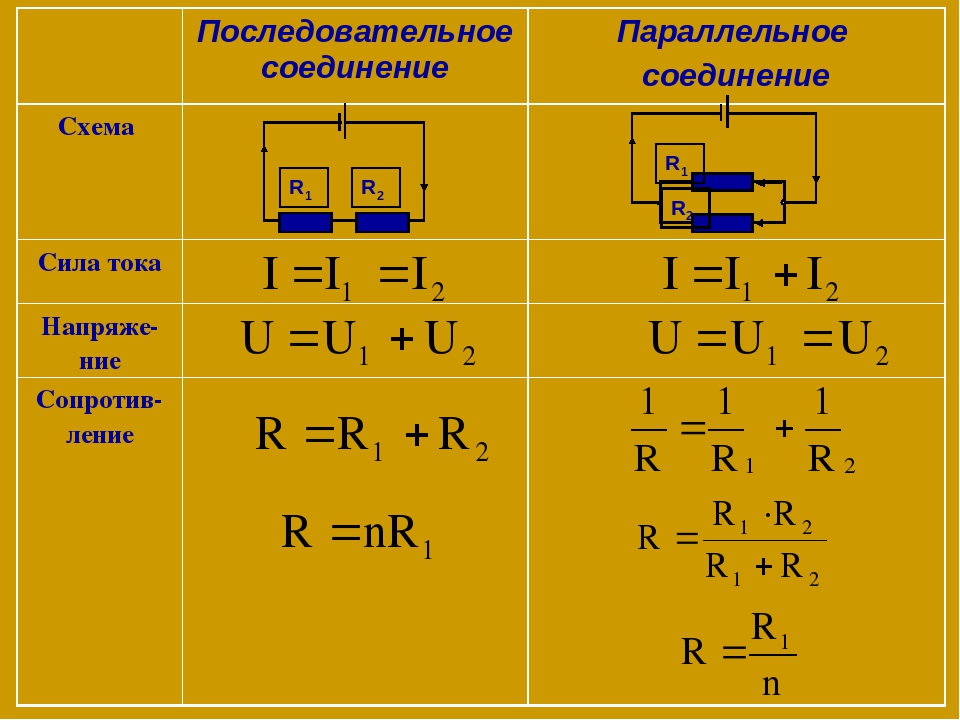
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт.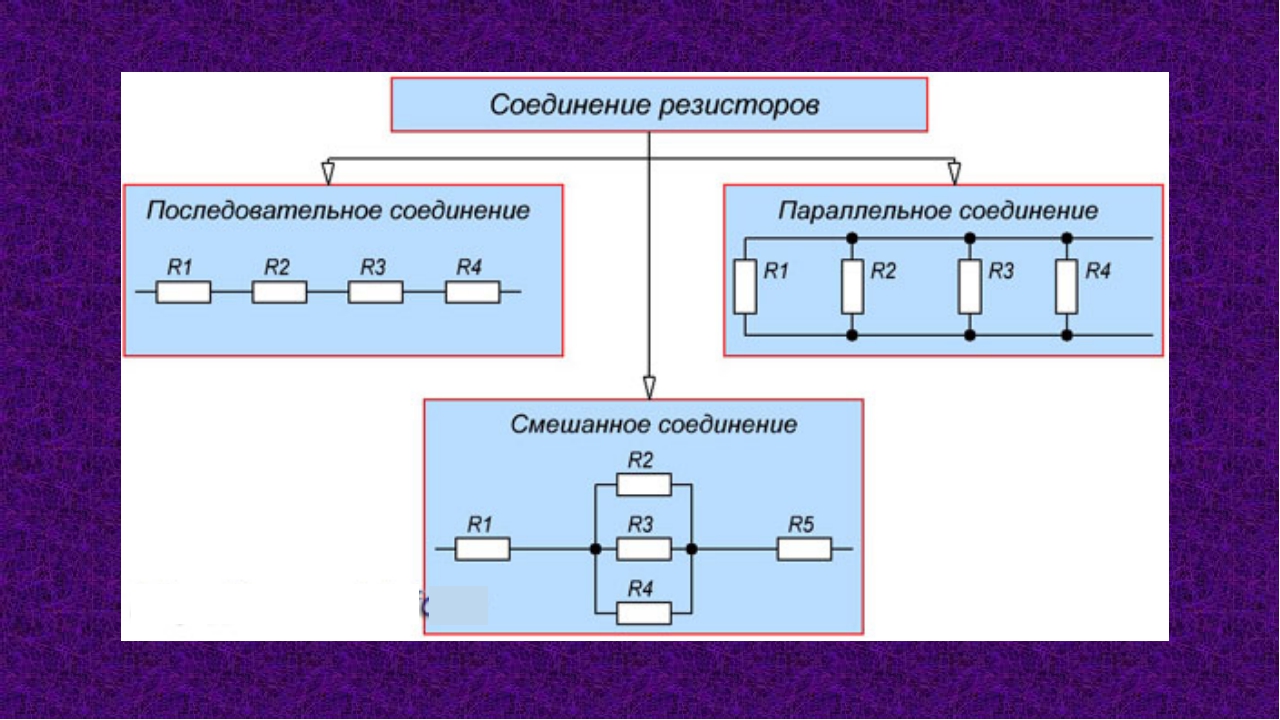 Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора.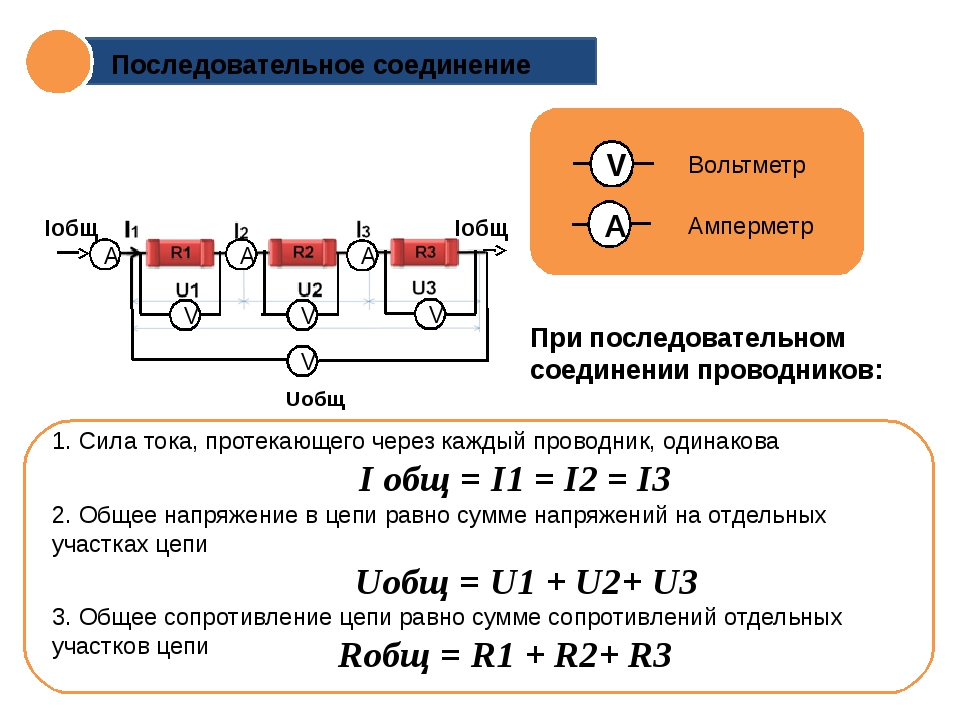 Выполнить расчет просто, и справиться с этой операцией может каждый.
Выполнить расчет просто, и справиться с этой операцией может каждый.
Типы проводников
Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.
Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.
Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:
- Проводники (все металлы, ионизированный газ и электролитические растворы).
- Полупроводники (Si, Ge, GaAs, InP и InSb).
- Непроводники (диэлектрики или изоляторы).
Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.
Зависимость сопротивления
Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:
- Температура окружающей среды и материала.
- Электрические величины.
- Геометрические свойства вещества.
- Тип материала, из которого изготовлен проводник (полупроводник).
К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.
Электрические величины
Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.
Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.
Тип и геометрические параметры
Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.
Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:
- Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
- Визуально определить форму материала.
- Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.
В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.
Температурные показатели
Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.
В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.
Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a Объединение резистивных радиокомпонентов
Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.
Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.
Параллельное соединение
При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.
Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).
При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:
- Номинал резистора в 16 Ом подойдет.
- Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).
В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:
- Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
- Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.
Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).
Последовательное подключение
Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:
- Ток не изменяется на участке цепи.
- Общее напряжение равно сумме падений напряжений на каждом резисторе.
- Rобщ = R1 + R2 + … + Rn.
Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:
- I = I1 = I2 = 0,5 (А).
- Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
- Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).
Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.
Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.
Электрическое сопротивление характеризует свойство проводника препятствовать прохождению через него электрического тока. У каждого материала есть свое удельное сопротивление. Это табличная величина, и условно она считается постоянной.
Условно, потому что во многом эта характеристика зависит от внешних условий, например температуры. Сопротивление же какого-либо конкретного элемента (мы будем говорить о резисторах) складывается из многих факторов, например, из геометрических параметров, а когда речь идет о цепи переменного тока, то в расчеты включают также индуктивное и емкостное сопротивление, но об этом мы расскажем позже. Пока же — немного теории.
Закон Ома
В 1826 году немецкий физик Георг Ом на основе своих опытов вывел закон, согласно которому сила тока на участке цепи прямо пропорциональна напряжению, которое к нему приложено, и обратно пропорциональна сопротивлению участка. Из школьного курса мы знаем этот закон:
I=U/R
Позже он был сформулирован и для полной цепи:
I=ε/(R+r)
Где ε — ЭДС источника, R — сопротивление цепи, а r — сопротивление источника.
Мощность прибора
Электрический заряд при своем перемещении совершает работу. Может быть, это незаметно глазу, но вот пощупать результат этой работы можно: электроприборы у нас греются, а иногда нагрев — это цель, а не побочное явление. Не верите — ну, электроплитки, ТЭНы, утюги как раз это свойство и эксплуатируют. Правда, руками это проверять не советую.
Мощностью у нас называют работу, совершенную за единицу времени. Попробуем вычислить мощность электроприбора, включенного в цепь. Поскольку он обладает сопротивлением, обозначим его R, работу — А, мощность — Р, заряд — Q, а время — Δt. Итак, заряд проходит по цепи под действием напряжения U, которое совершает работу по его перемещению на участке цепи за время Δt:
Р=А/Δt , А=UQ
Р=UQ/Δt
Ну а поскольку Q/Δt — не что иное, как сила тока I, получаем:
Р=UI
Свяжем полученное выражение с законом Ома и получим:
Р=I^2*R, P=U^2/R
Последовательное и параллельное соединение
В реальной жизни мы редко имеем дело с одним проводником и одним источником. Достаточно взглянуть в любую принципиальную электрическую схему, например, такую простенькую:
(это схема микроволновки «Электроника»)
можно увидеть, что элементы в схеме соединены по-разному, но мы покажем вам базовые закономерности, которые работают в цепях.
Правила Кирхгофа
Если взять замкнутую электрическую цепь, по которой течет заряд, то можно определенно сказать: он никуда не денется. Сумма всех зарядов, которые текут в одной цепи, всегда одинакова. Это называется законом сохранения заряда, частным случаем общего закона сохранения (как говорится, если в одном месте что-то убудет, в другом непременно прибудет).
Отсюда мы и выводим тот факт, что в каждом узле цепи сумма токов равна нулю. То есть, если ток «приходит» в точку по ветке и «уходит» по двум — значит, первый равен сумме второго и третьего.
На этой картинке мы видим, что I1+I4=I2+I3
Это называется первым правилом Кирхгофа.
Если наша цепь не будет содержать узлов, значит, ток в ней будет величиной постоянной, а элементы, один за другим поставленные в цепь, будут давать падение напряжения. При этом общее напряжение в цепи останется тем же. Отсюда вытекает второе правило Кирхгофа: сумма напряжений на участках цепи будет равна ЭДС источников тока, входящий в эту цепь. Если у нас источник один, то будет верно равенство:
ε=U1+U2+U3+…+Un
Сумма падений напряжения будет, таким образом, нулевой.
В ситуациях, когда мы имеем дело с переменным током, падение будет наблюдаться на участках с конденсаторами и катушками — в цепях переменного тока у них появляется сопротивление (об этом позже).
Теперь, когда мы познакомились с теоретической частью, можем перейти к более приближенному к суровой реальности вопросу, а именно — расчету последовательного и параллельного соединения резисторов.
Примеры расчетов
Рассчитаем параметры цепей с разным типом соединения.
Как мы видим из рисунка, резисторы соединены один за другим, последовательным способом. Значит, ток в этой цепи — величина постоянная, а напряжение, исходя из второго правила Кирхгофа —
U=U1+U2+U3 /напряжение при последовательном соединении/
Поскольку из закона Ома получается U=IR, то
IR=IR1+IR2+IR3,
следовательно, сопротивление всей цепи
R=R1+R2+R3 /сопротивление при последовательном соединении/
а ее потребляемая мощность
Р=I^2*R
На этой картинке мы видим, что резисторы соединены параллельно друг другу.2/R
Исходя из вышеперечисленных закономерностей, вы сможете рассчитывать самые причудливые соединения резисторов, можете попрактиковаться, взяв в библиотеке задачник.
Типы резисторов
Как уже было сказано ранее, элемент, который ставится в цепь для нагрузки, называется резистором. Ставят его для разных целей, главным образом для того, чтобы изменить тот или иной параметр на участке цепи. Например, понизить напряжение или силу тока, чтобы деталь, стоящая за резистором, не сгорела.
Предприятиями выпускается большой ассортимент таких изделий, и их можно по-разному классифицировать. Номинально резистор имеет то сопротивление, которое указано на нем, а по факту оно может зависеть от напряжения в сети (нелинейность), иметь разброс параметра (иногда до 20% доходит). По применяемой технологии резисторы можно разделить на:
- проволочные;
- композитные;
- металлофольговые;
- угольные;
- интегральные.
Фактическое сопротивление такого элемента может зависеть от температуры окружающей среды и даже от частоты, если мы имеем дело с переменным током. Дело в том, что часть ассортимента резисторов выполнены по проволочной технологии, то есть фактически они представляют собой мини-катушку. При малых частотах (50 Гц) это в расчет не берется, а вот на высоких (мегагерцы) паразитная индуктивность и индуктивное сопротивление может сказаться на работе схемы. Поэтому при выборе резистора для работы с высокочастотными схемами внимательно смотрите. по какой технологии он сделан. Отдайте предпочтение тонкослойным и композиционным изделиям.
Помимо этого, большое распространение получили переменные резисторы, значение сопротивления которых можно регулировать. Делается это чаще всего отверткой. Необходимость в таких изделиях продиктована разбросом параметров у обычных резисторов, а подстроечный вариант позволяет регулировать сопротивление.
Все вышесказанное актуально для цепей постоянного тока и переменного при невысоких частотах, и все это — при нормальных условиях внешней среды. Расчеты цепей при нарушении этих условий нуждаются в дополнительной корректировке: это связано с ограниченностью действия закона Ома. С чем связаны ограничения? Вот несколько примеров:
- при сверхнизких температурах многие проводники проявляют такое интересное явление, как сверхпроводимость;
- также сопротивление может разниться при нагревании;
- неприменим закон Ома для описания электрического тока в газах;
- наконец, обычный резистор можно просто пробить высоким напряжением.
Все это прекрасно работает. Не верите — можете поэкспериментировать у себя дома или провести замеры тестером. Например, изучить елочную гирлянду или показания счетчиков при включенных электроприборах (напомню, что в гирлянде лампочки соединены последовательно, а розетки в доме — параллельно). Удачи!
Формула расчета сопротивления при параллельном соединении резистора
Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.
Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:
Формула параллельного соединения резисторов
Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:
Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:
При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.
Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:
Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:
Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.
Пример расчета №2
Найти общее сопротивление R из трех параллельно соединенных резисторов:
Общее сопротивление R рассчитывается по формуле:
Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.
Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.
Как рассчитать сложные схемы соединения резисторов
Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).
Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:
В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:
Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.
Ток, протекающий в цепи параллельно соединенных резисторах
Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.
Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).
Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .
Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».
- Таким образом, протекающий общий ток в цепи можно определить как:
- I = I1 + I2
- Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:
- Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА
- Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА
- Таким образом, общий ток будет равен:
- I = 0,545 мА + 0,255 мА = 0,8 мА
- Это также можно проверить, используя закон Ома:
- I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)
- где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)
- И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.
Параллельное соединение резисторов — онлайн калькулятор
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.
Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.
Источник: http://www.joyta.ru/7362-parallelnoe-soedinenie-rezistorov/
Последовательное и параллельное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:
После подстановки формулы параллельного соединения вместо «||»:
Источник: http://hightolow.ru/resistor3.php
Параллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
- При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
- Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
2. Делитель токов.
Источник: https://kurstoe.ru/osnovnie-svedeniya/preobrazovanie-tcepej/parallelnoe-soedinenie.html
Последовательное и параллельное соединение резисторов
Последовательное и параллельное соединение резисторов в схемах являются самыми распространенными, также — это база для расчета более сложных схем.
Последовательное подключение
Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше.
Рис. Последовательное подключение.
Обозначение:
Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.
Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам.
В последовательных цепях — складываем, в параллельных — это обратно пропорциональная величина.
Параллельное соединение
Рис. Параллельное подключение.
Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах — //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле. Более наглядно это можно представить в виде формул: 1. Каждый вид соединения находится под одинаковым напряжением: U = U1 = U2; 2. Суммарная сила тока равняется суммарному значению тока каждого участка I = I1 + I2; 3. Сопротивление цепи равно сумме величина обратных сопротивлению участка: 1/R = 1/R1 + 17R2 + . . . + 1/Rn; 4. Сила тока пропорциональна сопротивлению каждого участка I1/I2=R2/R1.
Далее рассмотрим схему как работает не только последовательное параллельное, но и смешанное соединение резисторов.
Смешанное подключение
Рис. Смешанное подключение резисторов
В электрических схемах используются не только типовые схемы, но и смешанное, созданное из критерий определенных требований. Чаще всего в схемах встречается третий вариант, представляющий набор из элементарных типов схем. В смешанных участках учитываются не только элементы, но и направления движения тока. При вычислении мощности резисторов смешанного подключения используются формулы для параллельного и последовательного соединения резисторов, формула также является составной.
Основные законы электротехники, наиболее часто используемые для расчетов
Рассмотрим основные законы электротехники и свойства последовательного и параллельного соединения резисторов для участка цепи
Закон Ома
Напряжение находится по закону Ома по формуле I=U/R — чем больше сопротивление, тем меньше ток. Напряжение можно найти из этой же формулы. U=R*I, ток умножается на сопротивление. Запишем эту формулу для каждого участка U1=R1· I1, Un=Rn · In.
Законы Кирхгофа
Первый закон
Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два.
Рис. иллюстрация к пояснению действия первого закона Кирхгофа.
Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю. Если посмотреть на схему, I1 — это ток, который заходит в узел, I2 и I3 — это электроны, которые вытекают из него. Применяя формулировку первого закона можно записать формулу по-другому:
I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.
Второй закон Кирхгофа
Рис. иллюстрация к пояснению действия второго закона Кирхгофа.
Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре. E1- Е2 = — UR1 — UR2 или E1 = Е2 — UR1 — UR2.
Параллельное и последовательное соединение резисторов, решение задач
Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно.
Рис. Порядок замещения при расчете сложных позиций более простыми.
Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. Рассмотрим схему №1 на рис.
На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1).
Как же правильно определить параллельное и последовательное соединение резисторов?
Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.
Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом. Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше (рис 3).
Теперь образовалась ситуация — включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех.
Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом. Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.
Схема с подключением сопротивлений «треугольником»
Рис. Расчетная схема соединения резисторов в треугольник.
Иногда некоторые затруднения возникают при разборе схемы соединения в треугольник.
Рассмотрим на примере рисунка расчет резисторов по этому подключению. Из схемы видно, что R1 и R2 соединены последовательно Rэ12 будет соединяться R3 последовательно.
Затем Rэ123 соединяется с сопротивлением R4, R5 в последовательную цепь. Затем все это объединяется с Rэ в //.
Проведем несложные вычисления учитывая, что R1, R2, R4, R5 равняется 1 Ом. R3, R7 — 2 Ом.
RЭ1,2 = R1+R2 = 1+1=2 Ом.
Вычисляем параллельное подключение: Rэ 12 с R3. Rэ1,3 = (Rэ12*R3) /(Rэ12+R3) = (2*2) /(2+2) = 1Ом.
Далее мы видим последовательное: RЭ123 + R4 + R5 = 1+1+1 = 3 Ом. И последнее — Rэ123 4 5 с R6 — параллельное.
Общее сопротивление цепи Rц = Rоб = (RЭ1,2,3,4,5 *R6) /(RЭ1,2,3,4,5+R6) = (3 * 2) / (3+2) = 1,2 Ом. Как видно, что расчет подобного варианта также не сложный.
Расчет последовательного и параллельного подключения резисторов онлайн
Подсчитать значение мощность и сопротивлений подставляя их в формулы можно только в учебных целях, или, когда объемы не очень большие.
Наиболее практичный вариант расчета является онлайн калькуляторы, которые расположены на многочисленных интернет ресурсах.
Для расчёта любой сложности нужно правильно определить тип соединения резисторов последовательное или параллельное и внести данные для расчета в поля калькулятора.
Также такая форма расчета подойдет и для проверки результатов решения учебных задач.
Последовательное и параллельное соединение резисторов и конденсаторов
Электрические цепи состоят не только из резисторов, в них применяется большое количество различных деталей, например, конденсатор, которые подключаются в последовательное, // и смешанное соединение.
Рис. Замещения последовательно включенных элементов.
Определение этому элементу можно дать следующее: Конденсатор — это совокупность проводящих тел служащий для накопления электрического заряда. Элементарный конденсатор имеет две пластины, форма этих пластин может быть различной: сферической, круглой, цилиндрической, прямоугольной — по форме пластин разделяется и тип конденсатора.
Важное свойство. Одно из важных свойств конденсатора: если заряжается одна пластина конденсатора, то благодаря явлению электростатической индукции заряжается и вторая половина, но с противоположным знаком.
Устройство конденсатора
Плоский конденсатор состоит из двух плоских пластин отстоящих друг от друга на маленькое расстояние. У конденсатора к двум пластинам припаивается вывод всего их получается два.
Типовые схемы подключения конденсаторов
Рассмотрим различные виды подключения конденсатора.
Последовательное
Первый вид — это последовательное соединение. Предположим, что емкость этих конденсаторов будут равны.
Тогда заряды также будут равны: q1=q2=q3, как и в примере с резисторами, сложный тип позиций с конденсатором можно упростить, заменив несколько элементов одним.
У элементов соединенных друг за другом, общая емкость будет обратно пропорциональная всем имеющимся элементам. То есть: Rэк будет равняться 1/С1 + 1/С2 +…. 1/Сn/
Напряжение складывается, U эк = U1 + U2+ … Un.
Параллельное
Второй тип подключения конденсаторов — это соединение в паралель
Рис. Схема замещения элементов, включенных в параллель.
- Соответственно эти конденсаторов обозначены C1, C2, … Cn заряды: Q1, Q2, … Qn и напряжение: U1, U2, … Un.
- У элементов в // емкость складывается Сэ = C1 + C2 + … C n. Напряжение Un на каждом конденсаторе будет равно напряжению на эквивалентном
- Uэ = U1 = U2 =… = Un — это особенность параллельного подсоединения всех элементов цепи.
- Емкость будет складываться из суммы отдельных элементов Сэ =С1 + С2 + … Сп.
Рис. Расчетные позиции элементов при различном включении.
Простая позиция, которая не требует преобразования №1 — последовательное подключение. По известной формуле для этих поз. запишем 1/Сэ = 1/С1 +1/С2 +1/С3, подставив формулу значения, которые даны в условии задачи, получим 1/Сэ = 1/С1 +1/С2 +1/С3 = 59 мФ.
Не требует преобразования и 2 схема: емкость общего конденсатора будет равняться сумме конденсаторов которые включены в параллельной цепи: Сэ =С1 +С2 +С3 Сэ = 100 + 200 + 500 = 800 мФ.
Рассмотрев рис. №3 видно, что пара конденсаторов включена параллельно и один последовательно. Алгоритм преобразования таких цепей мы уже рассматривали, поэтому: сразу же находим емкость конденсатора Сэ соединения: Сэ = С1+С2 = 200+500 = 700 мФ.
Теперь находим общие эквивалентную емкость элементов с последовательным подключением 1/Сэ = 1/С2,3 +1/ С1 = 89 мф. Практическая задача решена.
Источник: http://themechanic.ru/posledovatelnoe-i-parallelnoe-soedinenie-rezistorov/
Соединение резисторов
Радиоэлектроника для начинающих
О том, как соединять конденсаторы и рассчитывать их общую ёмкость уже рассказывалось на страницах сайта. А как соединять резисторы и посчитать их общее сопротивление? Именно об этом и будет рассказано в этой статье.
Резисторы есть в любой электронной схеме, причём их номинальное сопротивление может отличаться не в 2 – 3 раза, а в десятки и сотни раз. Так в схеме можно найти резистор на 1 Ом, и тут же неподалёку на 1000 Ом (1 кОм)!
Поэтому при сборке схемы либо ремонте электронного прибора может потребоваться резистор с определённым номинальным сопротивлением, а под рукой такого нет. В результате быстро найти подходящий резистор с нужным номиналом не всегда удаётся. Это обстоятельство тормозит процесс сборки схемы или ремонта. Выходом из такой ситуации может быть применение составного резистора.
Для того чтобы собрать составной резистор нужно соединить несколько резисторов параллельно или последовательно и тем самым получить нужное нам номинальное сопротивление. На практике это пригождается постоянно.
Знания о правильном соединении резисторов и расчёте их общего сопротивления выручают и ремонтников, восстанавливающих неисправную электронику, и радиолюбителей, занятых сборкой своего электронного устройства.
Последовательное соединение резисторов
- В жизни последовательное соединение резисторов имеет вид:
- Последовательно соединённые резисторы серии МЛТ
- Принципиальная схема последовательного соединения выглядит так:
На схеме видно, что мы заменяем один резистор на несколько, общее сопротивление которых равно тому, который нам необходим.
Подсчитать общее сопротивление при последовательном соединении очень просто. Нужно сложить все номинальные сопротивления резисторов входящих в эту цепь. Взгляните на формулу.
- Общее номинальное сопротивление составного резистора обозначено как Rобщ.
- Номинальные сопротивления резисторов включённых в цепь обозначаются как R1, R2, R3,…RN.
- Применяя последовательное соединение, стоит помнить одно простое правило:
Из всех резисторов, соединённых последовательно главную роль играет тот, у которого самое большое сопротивление. Именно он в значительной степени влияет на общее сопротивление.
Что это значит?
Так, например, если мы соединяем три резистора, номинал которых равен 1, 10 и 100 Ом, то в результате мы получим составной на 111 Ом.
Если убрать резистор на 100 Ом, то общее сопротивление цепочки резко уменьшиться до 11 Ом! А если убрать, к примеру, резистор на 10 Ом, то сопротивление будет уже 101 Ом.
Как видим, резисторы с малыми сопротивлениями в последовательной цепи практически не влияют на общее сопротивление.
Параллельное соединение резисторов
- Можно соединять резисторы и параллельно:
- Два резистора МЛТ-2, соединённых параллельно
- Принципиальная схема параллельного соединения выглядит следующим образом:
Для того чтобы подсчитать общее сопротивление нескольких параллельно соединённых резисторов понадобиться знание формулы. Выглядит она вот так:
Эту формулу можно существенно упростить, если применять только два резистора. В таком случае формула примет вид:
Есть несколько простых правил, позволяющих без предварительного расчёта узнать, каково должно быть сопротивление двух резисторов, чтобы при их параллельном соединении получить то, которое требуется.
Если параллельно соединены два резистора с одинаковым сопротивлением, то общее сопротивление этих резисторов будет ровно в два раза меньше, чем сопротивление каждого из резисторов, входящих в эту цепочку.
Это правило исходит из простой формулы для расчёта общего сопротивления параллельной цепи, состоящей из резисторов одного номинала. Она очень проста. Нужно разделить номинальное сопротивление одного из резисторов на общее их количество:
Здесь R1 – номинальное сопротивление резистора. N – количество резисторов с одинаковым номинальным сопротивлением.
Ознакомившись с приведёнными формулами, вы скажите, что все они справедливы для расчёта ёмкости параллельно и последовательно соединённых конденсаторов. Да, только в отношении конденсаторов всё действует с точностью до «наоборот”. Узнать подробнее о соединении конденсаторов можно здесь.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
- Замер общего сопротивления при последовательном соединении
- Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
- Измерение сопротивления при параллельном соединении
- Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт. Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А), а сопротивление каждого из них равно 50 Ом, тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт. В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт.
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте тут.
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Главная » Радиоэлектроника для начинающих » Текущая страница
Также Вам будет интересно узнать:
Источник: https://go-radio.ru/connection-of-resistors.html
Параллельное соединение резисторов
Господа, в прошлый раз мы с вами говорили про последовательное сопротивление резисторов. Сегодня я бы хотел вам рассказать про другой возможный вид соединения – параллельное.
Чем различается последовательное и параллельное соединение я уже писал в предыдущей статье. Но все-таки вытащу сюда картинку из той прошлой статьи, я ж знаю, что вам будет лень ходить по ссылкам .
- А) – Последовательное соединение
- В) – Параллельное соединение
- Рисунок 1 – Последовательное и параллельное соединение
- Как мы видим из рисунка 1, параллельное соединение – это такое соединение, при котором одни концы всех резисторов соединены в один узел, а другие концы – в другой узел.
Сейчас наша задача будет разобраться, как ведут себя токи, напряжения, сопротивления и мощности при таком подключении. Для этого прошу вас взглянуть на рисунок 2, где подробно разрисован расклад дел для параллельного соединения. Будем полагать, что мы знаем величины R1, R2 и R3, а также величину приложенного к схеме напряжения U. Про токи же мы ничего не знаем.
Рисунок 2 – Параллельное соединения
Что мы видим на рисунке 2? Ну, в первую очередь – два узла А и B. В узел А сходятся одни концы всех резисторов, а в узел В – другие концы. Пусть узел А имеет потенциал φ1, а узел В – потенциал φ2. Из рисунка 2 видно, что для всех резисторов R1, R2 и R3 у нас одна и та же разность потенциалов U.
Как следует из статьи про потенциалы, это означает, что напряжение на всех резисторах у нас одинаково и равно приложенному напряжению U. Это важный вывод, его следует хорошо запомнить.
С токами дело обстоит по-другому. Проанализируем рисунок 2 слева направо. Пусть у нас в цепи течет ток I. Течет он себе, течет, никого не трогает и тут вдруг натыкается на узел А. Что в этом случае говорит полюбившаяся вам статья про первый закон Кирхгофа? А то, что ток I в узле А разделится на три тока I1, I2, I3. При этом будет выполняться равенство
То есть через резистор R1 будет протекать ток I1, через резистор R2 – ток I2, а через резистор R3 – ток I3.
Итак, у нас в системе уже тихо-мирно текут себе три тока. И все хорошо, пока они не наткнуться на узел В. Тут снова вступает в силу первый закон Кирхгофа. Эти три тока I1, I2, I3 вновь соединятся в один ток I. Причем после узла В ток будет иметь такую же величину I, какой он был до узла А.
То есть если все вышесказанное воплотить в лаконичный язык наскальной живописи, положение дел можно представить себе вот так
Как же найти эти самые токи I1, I2, I3? Господа, полагаю, вы уже догадались, что на помощь нам придет горячо нами всеми любимый закон Ома. Действительно, мы знаем сопротивления резисторов и, кроме того, нам известно, что на всех них падает одно и тоже напряжение U. Поэтому легко находим токи
Отлично, мы разобрались с напряжениями и с токами в такой схеме. А помните в статье про последовательное сопротивление мы ловко преобразовали три резистора в один с эквивалентным им сопротивлением? Нельзя ли и здесь сделать что-то подобное? Оказывается, вполне себе можно. Как мы помним, токи в схеме распределены таким вот образом
- Обзовем эквивалентное сопротивление буковкой R. И подставим в это выражение только что найденные нами токи I1, I2, I3
- Видим, что здесь без проблем можно сократить левую и правую части на U. Получаем
- Господа, важный вывод: при параллельном соединении резисторов обратное эквивалентное сопротивление равно сумме обратных сопротивлений отдельных резисторов.
- То есть для упрощения различных расчетов электрических схем такую вот цепочку параллельно соединенных резисторов можно заменить одним резистором с соответствующим сопротивлением, как показано на рисунке 3.
- Рисунок 3 – Преобразование параллельного соединение
Весьма частый случай на практике, когда соединены параллельно не много резисторов, а всего два. Поэтому полезно знать наизусть итоговое сопротивление такой схемы. Давайте посмотрим, чему оно равно:
То есть, если у вас два сопротивления соединены параллельно, то по этой формуле вы легко высчитаете общее сопротивление. Рассмотрим пример. Пусть у нас параллельно соединены два резистора 10 кОм и 15 кОм. Чему равно их общее сопротивление?
Заметьте, господа, итоговое сопротивление у нас получилось 6 кОм, что меньше 10 кОм и 15 кОм. То есть при параллельном соединении общее сопротивление меньше любого из составляющих.
Это всегда верно для любого количества резисторов, а не только для двух. Итоговое сопротивление всегда уменьшается (в отличии от последовательного сопротивления, где итоговое сопротивление всегда растет).
Этот факт полезно запомнить.
Еще один часто встречающийся на практике случай – когда параллельно соединены несколько резисторов с одинаковым сопротивлением. Допустим, каждый из них обладает сопротивлением R1 и всего их N штук. Тогда по нашей общей формуле для эквивалентного сопротивления
- То есть при параллельном соединении N одинаковых резисторов с сопротивлением R1 итоговое сопротивление будет в N раз меньше этого самого сопротивления R1.
- Так-с, с током разобрались, с напряжением разобрались, с эквивалентным сопротивлением вроде тоже…осталась мощность. Для этого воспользуемся вот этим выражением, которое мы писали чуть выше в статье
- Умножим левую и правую части на напряжение U.
- Как мы помним из статьи про мощность произведение тока на напряжение есть мощность. То есть мы можем записать
- где Р – мощность, выдаваемая источником;
- P1 – мощность, рассеиваемая на резисторе R1;
- P2 – мощность, рассеиваемая на резисторе R2;
- P3 – мощность, рассеиваемая на резисторе R3.
Заметьте, господа, формула в точности такая же, как и для случая последовательного соединения резисторов. И там и там мощность, выдаваемая источником, равна сумме мощностей, рассеиваемых на резисторах цепи.
Итак, господа, мы рассмотрели основные соотношения при параллельном соединении резисторов. Теперь осталось поговорить, где это параллельное соединение можно использовать и для чего.
1) Ну, во-первых, параллельное соединение применяют во всех случаях, когда хотят запитать несколько нагрузок от одного источника напряжения. При этом пользуются тем свойством, что при параллельном соединении напряжения на всех нагрузках одинаково.
То есть, допустим, вы берете источник напряжения, выставляете на нем напряжение 5 В и цепляете к этому источнику сразу несколько своих устройств. Узлами А и В в этом случае будут клеммы источника. На каждое из устройств в этом случае придет напряжение 5 В.
Да и все устройства в вашей квартире (лампочки, компьютеры, телевизоры и все прочее) соединены между собой параллельно.
2) Второе возможное применение встречается не так часто, но, думаю, о нем тоже следует рассказать. Допустим, вы делаете какую-то схему, где необходим очень точный подгон сопротивления. Скажем, надо получить сопротивление 6 кОм. Такое сопротивление найти нелегко, их просто не продают. Зато у вас есть два сопротивления 10 кОм и 15 кОм.
Вы их соединяете параллельно и получаете требуемые 6 кОм. Как показывает практика, 3 параллельных резисторов достаточно для получения итогового результирующего сопротивления требуемого номинала с весьма хорошей точностью. Конечно, таких вещей лучше избегать и, если есть возможность, всегда стараться применять стандартные сопротивления.
Но бывают случаи, когда это невозможно, и тогда приходит на помощь этот метод.
3) Третий пункт будет немного похож на первый. Его суть заключается в следующим. Допустим, нам надо снять с источника питания 10 Вт мощности. А у нас в наличии только резисторы, которые позволяют рассеивать на себе 1 Вт. Что делать? Можно соединить 10 резисторов параллельно и с каждого снимать по 1 Вт. Мы же помним нашу формулу
Конечно, лучше брать не 10 резисторов, а хотя бы 15 и рассеивать на них меньше, чем 1 Вт. Работать на пределе никогда не следует.
Кстати, тут очень вовремя к моменту написания статьи пришли платы с производства! Господа, прошу вас взглянуть на рисунок 4.
Рисунок 4 – Плата нагревателя
На нем изображена плата нагревателя (флешка для масштаба). В чем суть? Имеется весьма сложное устройство, предназначенное для работы в арктических условиях.
Найти же компоненты, которые надежно функционировать при температурах минус 55 градусов и при этом стоят адекватных денег и обладают адекватными размерами бывает непросто. Обычно элементная база в лучшем случае рассчитана на минус 40 градусов.
И было принято решение разработать вот такой вот нагреватель для прогрева чувствительных к холоду аналоговых узлов устройства. Он управляется с микроконтроллера и автоматически включается при температурах меньше минус 40 градусов.
Как вы можете видеть из рисунка 4, этот нагреватель представляет собой 30 параллельно соединенных резисторов с сопротивлениями 150 Ом. Каждый резистор, согласно документации, способен рассеивать до 1 Вт мощности. Используя изученные формулки, мы можем посчитать, что в сумме такая система обладает сопротивлением
- и теоретически может рассеивать мощность
Ну, с сопротивлением вопросов нет, оно действительно равно 5 Ом. Ну, плюс-минус 5 % на допуск резисторов, что в данном случае вообще не критично. А вот с мощностью тут не так все однозначно. Помните про закон Джоуля-Ленца, который мы рассматривали? Резисторы будут греться, причем не слабо.
Как показывает практика, если нагружать резисторы по полной, то есть рассеивать на каждом по 1 Вт, то в течении нескольких секунд их температура улетит за 150 градусов. Такая высокая температура критична для резистора и может привести к его разрушению.
Я был готов к такому развитию событий, поэтому заложил для платы нагревателя максимальное напряжение 9 вольт. Это значит, что на каждом резисторе будет выделяться
- что почти в два раза меньше максимально допустимой мощности в 1 Вт. В сумме на всей плате выделялось, соответственно
Эксперимент показал, что резисторы достигли температуры с комнатных 25 градусов до критичных 120 градусов приблизительно за 10 секунд работы и температура продолжала уверенно расти.
Очевидно, если оставить на длительное время включенным такой нагреватель при комнатной температуре, он неминуемо выйдет из строя.
Возможно, при работе на минус 55 градусах перегрев бы не был столь критичным, однако хотелось исключить вариант спалить плату на столе, поэтому я понизил напряжение, подаваемое на плату на 3 вольта: стал подавать 6 вольт. Теперь на каждом резисторе рассеивалось
- а на всей плате
Теперь температура поднималась до 100-110 градусов примерно за 30-40 секунд работы и оставалась на этом уровне (выходила в точку термодинамического равновесия). Эта температура вполне подходит для нагревателя.
Однако пока это были лишь эксперименты на столе при комнатной температуре, главный эксперимент – в термокамере на минус 55 градусах – впереди. Возможно, по его результатам потребуется чуть увеличить рассеиваемую мощность.
А может все останется как есть и этой мощности будет достаточно для вывода девайса на режим за адекватное время, время покажет .
На сегодня все, господа. Удачи вам и до новых встреч!
Источник: http://myelectronix.ru/postoyannyy-tok/40-parallelnoe-soedinenie-rezistorov
Как отличается параллельное и последовательное соединение резисторов?
Большое разнообразие схем основано на двух видах соединений – последовательное параллельное. Для каждого типа существуют свои собственные законы и принципы. Именно это и позволяет создавать устройства с самыми различными техническими параметрами, в том числе и резисторы. Что же такое резистор?
Резистор – радиодеталь, созданная для контроля напряжения и тока в цепи, увеличивая либо понижая его. Резисторы могут быть двух видов – постоянные и переменные. Так, например, светодиоды требуют для себя совсем небольшого тока. Для этого в электрическую цепочку перед светодиодом устанавливается резистор, который обеспечивает необходимое напряжение для работы последнего.
В статье подробны рассмотрены все аспекты последовательного и параллельного подключения резисторов. Бонусом к статье являются видеоролик и детальная информационная статья на рассматриваемую тему.
Последовательное подключение
Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше. Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим.
Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях — складываем, в параллельных — это обратно пропорциональная величина.
Последовательное соединение характеризуется тем, что элементы идут друг за другом. Конец одного подключается к началу другого. При подключении полученной цепочки к источнику тока получается кольцо.
Теоретическая часть
Последовательное соединение характерно тем, что через все элементы протекает ток одинаковой силы. То есть, если цепочка состоит из двух резисторов R1 и R2 (как на рисунке ниже), то ток протекающий через каждое из них и любую другую часть цепи будет одинаковой (I = I1 = I2).
Суммарное сопротивление всей цепи последовательно соединенных резисторов считается как сумма сопротивлений всех ее элементов. То есть, номиналы складывают. R = R1 + R2 — это и есть формула расчета сопротивления при последовательном соединении резисторов. Если элементов больше двух, будет просто больше слагаемых.
Еще одно свойство последовательного соединения — на каждом элементе напряжение отличается. Ток в цепи одинаковый, а напряжение на резисторе зависит от его номинала.
Последовательное подключение.
Примеры расчета
Давайте рассмотрим пример. Цепь представлена на рисунке выше. Есть источник тока и два сопротивления. Пусть R1=1,2 кОм, R2= 800 Ом, а ток в цепи 2 А. По закону Ома U = I * R. Подставляем наши значения:
- U1 = R1 * I = 1200 Ом * 2 А = 2400 В;
- U2 = R2 * I = 800 Ом * 2А = 1600 В.
Будет интересно➡ SMD резисторы: что это такое и для чего используются?
Общее напряжение цепи считается как сумма напряжений на резисторах: U = U1 + U2 = 2400 В + 1600 В = 4000 В. Полученную цифру можно проверить. Для этого найдем суммарное сопротивление цепи и умножим его на ток. R = R1 + R2 = 1200 Ом + 800 Ом = 2000 Ом.
Если подставить в формулу напряжения при последовательном соединении сопротивлений, получаем: U = R * I = 2000 Ом * 2 А = 4000 В. Получаем, что общее напряжение данной цепи 4000 В.
А теперь посмотрите на схему. На первом вольтметре (возле резистора R1) показания будут 2400 В, на втором — 1600 В. При этом напряжение источника питания — 4000 В. Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Материал по теме: Как проверить варистор мультиметром.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Параллельное подключение резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Если посмотреть на изображение параллельного соединения, заметно, что ко всем элементам прилагается одинаковое напряжение.
То есть, при параллельном соединении резисторов, на каждом из них будет одинаковое напряжение U = U1 = U2 = U3. Получается, что ток разделяется на несколько «ручейков».
То есть, при параллельном соединении резисторов сила тока, протекающего через каждый из элементов, отличается. I = I1+I2+I3. И зависит сила тока (согласно тому же закону Ома) от сопротивления каждого участка цепи.
В случае с параллельным соединением резисторов — от их номинала.
Предлагаем также почитать интересный материал про малоизвестные факты о двигателях постоянного тока в другой нашей статье.
Схема параллельного соединения
Общее сопротивление участка цепи при таком соединении становится ниже. Его высчитывают по формуле: 1/R = 1/R1 + 1/R + 1/R3+. Такая форма хоть и понятна, но неудобна.
Формула расчета сопротивления параллельно подключенных резисторов получается тем сложнее, чем больше элементов соединены параллельно.
Но больше двух-трех редко кто объединяет, так что на практике достаточно знать только две формулы приведенные ниже.
Если подставить значения в эти формулы, то заметим, что результат будет меньше, чем сопротивление резистора с наименьшим номиналом. Это стоит запомнить: результирующее сопротивление включенных параллельно резисторов будет ниже самого маленького номинала. Давайте сначала рассчитаем параллельное соединение двух резисторов разного номинала и посмотрим что получится.
Соединили параллельно 150 Ом и 100 Ом. Считаем результирующее: 150*100 / (150+100) = 15000/250 = 60 Ом. Если соединить 150 Ом и 50 Ом, получим: 150*50 / (150+50) = 7500 / 200 = 37,5 Ом.
Как видим, в обоих случаях результат оказывается меньше чем самый низкий номинал соединенных деталей. Этим и пользуются, если в наличии нет сопротивления небольшого номинала.
Проблема только в том, что подбирать сложновато: надо каждый раз считать используя калькулятор.
Как высчитывать сопротивление составных резисторов
Возможно, вам будет проще, если знать, что соединив два одинаковых резистора параллельно, получим результат в два раза меньше. Например, соединив параллельно два резистора по 100 Ом получим составное сопротивление 50 Ом. Проверим? Считаем: 100*100 / (100+100) = 10000 / 200 = 50 Ом. При соединении параллельно трех резисторов, считать приходится больше, так как формула сложнее.
Если подключить параллельно 150 Ом, 100 Ом и 50 Ом, результирующее будет 27,3 Ом. Попробуем с более низкими номиналами. Если параллельно включены 20 Ом, 15 Ом и 10 Ом. Получим результирующее сопротивление 4,61 Ом. Вот вам подтверждение правила. Суммарное сопротивление параллельно соединенных резисторов меньше чем самый низкий номинал.
Параллельное соединение резисторов
Параллельное соединение резисторов это соединение, в котором начала всех резисторов соединены в одну общую точку (А), а концы в другую общую точку. При этом по каждому резистору течет свой ток. При параллельном соединении при протекании тока из точки А в точку Б, он имеет несколько путей.
Таким образом, увеличение числа параллельно соединенных резисторов ведет к увеличению путей протекания тока, то есть к уменьшению противодействия протеканию тока. А это значит, чем большее количество резисторов соединить параллельно, тем меньше станет значение общего сопротивления такого участка цепи.
Общее сопротивление параллельно соединенных резисторов определяется следующим отношением: 1/Rобщ= 1/R1+1/R2+1/R3+…+1/Rn.
Формулы расчета параллельного и последовательного подключения.
Следует отметить, что здесь действует правило «меньше – меньшего». Это означает, что общее сопротивление всегда будет меньше сопротивления любого параллельно включенного резистора. Общее сопротивление для двух параллельно соединенных резисторов рассчитывается по следующей формуле: Rобщ= R1*R2/R1+R2.
Если имеет место два параллельно соединенных резистора с одинаковыми сопротивлениями, то их общее сопротивление будет равно половине сопротивления одного из них. Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви.
Заменяя лампы резисторами с сопротивлениями R1, R2, R3, При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома: I1=U/R1; I2=U/R2; I3=U/R3.
Источник: https://ElectroInfo.net/radiodetali/rezistory/kak-otlichaetsja-parallelnoe-i-posledovatelnoe-soedinenie-rezistorov.html
Последовательное и параллельное соединение резисторов
Физика > Комбинированные схемы
Последовательное и параллельное соединение резисторов – комбинированные схемы электрической цепи: смешанный тип соединения, схема, законы, решение задач.
Комбинированную схему можно разделить на последовательную или параллельную части.
Задача обучения
- Рассмотреть процесс разделения резисторов в комбинированной схеме.
Основные пункты
- Сложные соединения резисторов демонстрируют использование параллельного и последовательного объединения.
- Разные части комбинированной схемы можно разделить и уменьшить, пока не останется единое сопротивление.
- Сопротивление в проводах сокращает ток и мощность, отправляемые к резистору.
- Если сопротивление высокое в изношенном или слишком длинном шнуре, то потери могут быть ощутимыми.
Термины
- Последовательность – подключение нескольких элементов поочередно.
- Параллельность – элементы расположены так, чтобы ток протекал вдоль двух или более путей.
- Комбинированная схема – электрическая схема с несколькими резисторами, объединенными последовательно и параллельно.
Комбинированные схемы
Иногда сложные соединения резисторов используют сразу последовательное и параллельное подключения. Это частое явление, так как в проводе возникает сопротивление. Такую схему можно разделить на соответствующие части. На рисунке показано, что общее сопротивление вычисляют, связав три резистора параллельно или последовательно. R1 и R2 подключены параллельно, поэтому формула:
В комбинированной схеме резисторы можно разделить на последовательные и параллельные составляющие
R3 соединен последовательно с R1 и R2, поэтому сопротивление будет рассчитываться как:
Комплексные комбинационные схемы
В ситуациях с более сложными схемами части можно идентифицировать как последовательные и параллельные, а потом свести их к эквивалентам и уменьшить к единственному сопротивлению. На нижнем рисунке видно, что комбинацию из 7 резисторов определили как последовательную и параллельную. На начальном этапе два окружных сечения отображают резисторы, расположенные параллельно.
Комбинация из 7 резисторов обладает последовательными и параллельными частями. Каждая определяется и сводится к эквивалентному сопротивлению, пока не достигнуто единственное сопротивление
Уменьшение параллельных резисторов до одного значения позволяет значительно упростить схему. Справа вверху видно, что круглая часть вмещает два последовательных резистора. Можно уменьшить к другому значению, добавив их. Далее видно, что два резистора последовательны. Их также сокращают к одному значению.
Сопротивление в проводах уменьшает количество тока и мощность, поступающие к резистору. Для определения общего сопротивления цепи можно использовать целевую схему. Сопротивление провода – серия резисторов. Если оно слишком велико в длинном или поврежденном проводе, то мы отмечаем значительную потерю тока.
Составной резистор: последовательное, параллельное и смешанное соединение | Энергофиксик
Выполняя сборку какой-либо схемы мы в обязательном порядке используем резисторы и как обычно по всем известному закону получается так, что сопротивления нужного номинала нет под рукой. И выходом из сложившегося положения может стать сборка составного резистора. Вот об этом и пойдет речь в данной статье.
Для сборки составного резистора необходимо соединить несколько резисторов либо параллельным, либо последовательным образом и так можно получить требуемое сопротивление.
На самом деле данные действия на практике применяются очень часто. Любители самоделок и ремонтники со стажем мне не дадут соврать. Так давайте быстро пробежимся по основным правилам последовательного и параллельного соединения.
Последовательное соединение резисторов
На схеме такое соединение выглядит так:
Как видно из схемы мы с вами произвели замену одного резистора на сразу несколько собранных в цепочку. При этом сопротивление обоих вариантов одинаково.
Для того, чтобы высчитать суммарное сопротивление достаточно вспомнить формулу, которая имеет следующий вид:
При этом запомните следующее правило: Главную роль в такой цепочке играют резисторы с наибольшим сопротивлением. То есть если в цепочке у вас стоят сопротивления: 1 000 Ом, 50 Ом и 10 Ом и убрать резистор на 10 Ом, то общее сопротивление особо не изменится, а если убрать резистор на 1 кОм, то общее сопротивление измениться кардинально.
Параллельное соединение
На схеме принципиально параллельное соединение изображается так:
В этом случае для подсчета общего эквивалентного сопротивления необходимо воспользоваться уже другой формулой, которая выглядит следующим образом:
Если в параллель поставлено всего два резистора, то формула имеет упрощенный вид
Также если таким образом соединить резисторы с одинаковым номиналом, то формула расчета общего сопротивления существенно упрощается.
Смешанное соединение
Иногда возникает необходимость получить нестандартное сопротивление и в таком случае используют смешанное соединение.
Для того, чтобы рассчитать общее сопротивление такой цепи ее разбивают на последовательные и параллельные участки и производят расчет.
Небольшой практический опыт
Чтобы наглядно увидеть в действии параллельного и последовательного соединения резисторов давайте проведем простенький эксперимент и возьмем пару резисторов номиналом 100 Ом и 330 Ом и соединим их последовательно.
Как видите, мультиметр показал сумму сопротивлений.
Теперь соединим эти же резисторы параллельно.
Мы получили общее сопротивление 77,8 Ом, что меньше чем сопротивление резистора на 100 Ом.
Важное дополнение при реализации составного резистора
Если вам нужно реализовать составной резистор, то кроме сопротивления вам так же крайне важно учитывать еще один параметр — номинальную мощность рассеивания.
Рассмотрим простой пример. Допустим вам необходимо заменить негодный резистор на 100 Ом рассчитанный на мощность рассеивания 1 Вт. Для этого можно взять 4 резистора по 25 Ом и соединить их последовательным образом.
Так как при последовательном соединении ток через все элементы цепи течет одинаковый, то мощность рассеивания каждого резистора на 25 Ом должно быть не менее 0,25 Вт. В таком случае мы как раз получим составной резистор с общим сопротивлением 100 Ом и мощностью 1 Вт.
Заключение
Это все, что я хотел вам рассказать о составном резисторе, о параллельном, последовательном и смешанном соединении. Если статья оказалась вам полезна или интересна, тогда ставим лайк. Спасибо за ваше внимание!
Лабораторная работа по исследованию свойств параллельного и последовательного соединения резисторов беспаечным способом
В работе исследованы свойства и физические законы соединения резисторов без пайки. При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.
Ключевые слова: резисторы, макетная плата, соединение без пайки, параллельное и последовательное соединение, токи, напряжение и сопротивления при соединения резисторов.
The paper studies the properties and physical laws of connecting resistors without soldering. When building layouts, soldering installation can be completely, abandoned or reduced to a minimum. As experience has shown, the practical use of layout boards can significantly save time and material costs.
Keyword: resistors, layout Board, connection without soldering, parallel and serial connection, currents, voltage and resistance when connecting resistors.
В современном высшем учебном заведении перед каждым преподавателем стоит цель по развитию научно-исследовательских навыков студентов. Один из задач являетсямотивации студента и совершенствование научно-исследовательских навыков в формулировке исследовательского вопроса во время лабораторной работы на уроках физики. В данной работе исследованы свойства и физические законы соединения резисторов без пайки. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты. [1,2].
Цель работы: опытным путем изучить законы протекания тока через последовательно и параллельно соединение резисторовспомощью беспаечное соединение и определить формулы сопротивлений таких участков. Резисторы примениется в электронных приборах и робототехнике. [3].
Последовательным соединением сопротивлений называется такое соединение, при котором конец первого сопротивления соединяется с началом второго, конец второго — с началом третьего и т. д. Рассмотрим физические законы соединения резисторов. Перечень оборудования показаны на рис.1,2,3.
Перечень оборудования
Рис. 1. Резистор и провода
Рис. 2. Мультиметр
Рис. 3. Макетная плата
Последовательно соединенных резисторов
Сопротивление впоследовательной цепи. Общее сопротивление последовательно соединенных резисторов равно сумме их сопротивлений.
Rобщ = R1+R2+R2+ •••+Rn(1)
Если последовательно включено любое количество резисторов одинаковых сопротивлений, то их общее сопротивление можно определить, умножив сопротивление одного резистора на количество резисторов.
Rобщ = nR1 (2)
Пример последовательного соединения двух резисторов показан на рис.4.
Общее сопротивление для двух резисторов.
Rобщ=R1+R2 (3)
Rобщ = 25 Ом+35 Ом=60 Ом (4)
Рис. 4. Последовательное соединение двух резисторов
Величина тока впоследовательной цепи
Так как в данной цепи отсутствует ответвление тока, то очевидно, что количество электричества, протекающее через поперечное сечение проводника за единицу времени в любой точке цепи, будет одинаковым. Следовательно, во всех точках последовательной цепи величина тока одинакова.
Поэтому при последовательном соединении, для измерения тока достаточно включать один амперметр на любом участке цепи.
В качестве примера, можно привести цепь последовательного соединения двух резисторов, который показан на рис.5.
I=I1=I2=0,2A
Рис. 5. Величина тока в последовательнойцепи
Распределение напряжения впоследовательной цепи
Напряжение источника тока, приложенное, к внешнему участку цепи распределяется по участкам цепи прямо пропорционально сопротивлениям этих участков. Напряжение, приложенное, к каждому из этих резисторов определяется по формуле:
U=IR (5)
Так как ток в последовательной цепи везде одинаков, значит, действительно напряжение на ее участках зависит от сопротивления, чем больше сопротивление, тем большее напряжение приложено к данному участку. Сумма напряжений на участках последовательной цепи равна напряжению источника тока.
Uобщ=U1+ U2+ U3+ ••• +Un(6)
Пример, распределение напряжения в последовательной цепи соединения двух резисторов показан на рис.6.
Uобщ=U1+ U2(7)
12В=5В+7В
Параллельное соединение сопротивлений
Параллельным соединением сопротивлений называется такое соединение, при котором к одному зажиму источника подключаются начала сопротивлений, а к другому зажиму — концы.
Рис. 6. Распределение напряжения в последовательной цепи
Сопротивлениев параллельной цепи
Общее сопротивление параллельно включенных сопротивлений определяется по формуле:
(8)
Если параллельно включено любое количество резисторов одинаковых сопротивлений, то их общее сопротивление можно определить, если сопротивление одного резистора разделить на количество резисторов.
Общее сопротивление параллельно включенных сопротивлений всегда меньше наименьшего сопротивления, входящего в данное соединение. Пример, если параллельно включено только два резистора (рис.7), то их общее сопротивление можно определить по формуле:
(10)
Рис. 7. Параллельное соединение двух резисторов
Распределение тока впараллельной цепи
В цепи с параллельным соединением, что электрический ток распределяется по параллельным ветвям обратно пропорционально их сопротивлениям.
Это значит, что чем больше сопротивление, тем меньше по нему пойдет ток.
(11)
Рассматривая точку разветвления А, замечаем, что к ней притекает ток I, а токи I1, I2, утекают из нее. Так как движущиеся электрические заряды не скапливаются в точке, то очевидно, что суммарный заряд, притекающий к точке разветвления, равен суммарному заряду, утекающему от нее:
I=I1+ I2+ I3 +••• +In(12)
Следовательно, величина тока в не разветвленной части цепи равна сумме токов в параллельных ветвях.
Пример, распределение тока в параллельной цепи соединения двух резисторов показан на рис. 8.
I=I1+ I2
Рис. 8. Распределение тока в параллельной цепи
Величина напряжения впараллельных цепях
Так как начала всех сопротивлений сведены в одну общую точку, а концы — в другую, то очевидно, что разность потенциалов на концах любого из параллельно включенных сопротивлений равна разности потенциалов между общими точками.
Итак, при параллельном соединении сопротивлений напряжения на них равны между собой.
U=U1=U2=U3=•••=Un (13)
Содержание хода работы ипоследовательность действий
Техническое задание
1) Собрать электрическую цепь в макетную плату (рис.9.)
2) Снять показания приборов и записать их в таблицу.
3) Произвести расчеты.
4) Ответить на контрольные вопросы.
5) Сделать вывод.
Порядок выполнения работы
1) Собрать схему в макетную плату (Рис. 9.).
2) Установить на схеме величины R1=1 кОм + N, R2=2 кОм + N, R3=3 кОм + N и R4=4 кОм+ N, где N — номер студента по журналу (мощность резисторов более 1 Вт).
3) Включить источник и установить напряжение U=5В, 9В, 12В, 15В.
4) Определите экспериментально с помощью мультиметра (в режиме измерения сопротивлений) сопротивление между точками:
А иВ; Ви С; Аи С; Dи Е.
Запишите эти показания в таблицу 1, 2.
Рис. 9. Схема исследования: а) последовательное соединение, б) параллельное соединение
5) Рассчитайте теоретические значения сопротивлений между указанными точками схемы и сравните их с измеренными.
6) Измерьте с помощью мультиметра (в режиме измерения постоянного тока) токи, текущие через каждое сопротивление. Запишите показания прибора в таблицу 1.
7) Проверьте экспериментально, что в последовательной цепи ток одинаков через все сопротивления, а в параллельной цепи разделяется так, что сумма всех токов через параллельно соединенные элементы, равна полному току через весь участок.
8) Измерьте с помощью мультиметра (в режиме измерения постоянного напряжения) напряжения на каждом сопротивлении. Запишите показания прибора в таблицу 2.
9) Проверьте экспериментально, что в последовательной цепи напряжение на всем участке равно сумме напряжений на каждом элементе, а в параллельной цепи, напряжение одно и то же на каждом элементе.
10) Отключить схему.
Таблица 1
Рассчитанные иизмеренные параметры для последовательного соединения резисторов: Аи В; Ви С; Аи С.
№вар. | Установлено | Рассчитано | Измёренные параметры | ||||||
R1 | R2 | А— В | В— С | А— С | I | U | U1 | U2 | |
кОм | кОм | кОм | кОм | кОм | А | В | В | В | |
Таблица 2
Рассчитанные иизмеренные параметры для параллельного соединения резисторов: Dи Е.
№вар. | Установлено | Рассчитано | Измерённые параметры | ||||||
R3 | R4 | D иЕ | U | I | I1 | I2 | |||
кОм | кОм | кОм | В | А | А | А | |||
Содержание отчета
а) название и цель работы;
б) схемы экспериментов и таблицы полученных экспериментальных данных;
в) результаты расчётов:
г) выводы по работе.
Контрольные вопросы
1) Может ли сопротивление участка двух параллельно соединенных проводников быть больше (меньше) любого из них? Объясните ответ.
2) Как по вольтамперной характеристике определить величину сопротивления цепи?
3) Как по показаниям мультиметра можно определить величину сопротивления участка электрической цепи и потребляемая мощность?
4) Нарисуйте схемы последовательное и параллельное соединение двух резисторов.
5) Объясните физические законы соединения резисторов.
Выводы
В работе исследованы свойства и физические законы параллельного и последовательного соединения резисторов бес применения пайки.
При построении макетов от монтажа пайкой удается полностью отказаться или свести его к минимуму. Как показал, опыт практическое использование макетных плат позволяют, существенно сэкономить временные и материальные затраты.
Литература:
- А. Л. Марченко, Освальд С. В. Лабораторный практикум по электротехнике и электронике в средеMULTISIM. Учебное пособие для вузов.-М.:ДМК Пресс.2010.-448С.
- Л. Г. Белиовская, Белиовский Н. А. Роботизированные лабораторныее работы по физики, Пропедевтетический курс физика. -М.:ДМК Пресс.2016.-164С.
- Википедия [Электронный ресурс]. http://ru.wikipedia.org/wiki/Processing.
Основные термины (генерируются автоматически): общее сопротивление, резистор, сопротивление, последовательная цепь, последовательное соединение, соединение резисторов, величина тока, ком, макетная плата, параллельная цепь, параллельное соединение.
Как рассчитать падение напряжения на резисторе в параллельной цепи
Обновлено 28 декабря 2020 г.
Автор: S. Hussain Ather
••• Syed Hussain Ather
TL; DR (слишком долго; не читал)
На приведенной выше схеме параллельной цепи падение напряжения можно найти, суммируя сопротивления каждого резистора и определив, какое напряжение получается из тока в этой конфигурации. Эти примеры параллельных цепей иллюстрируют концепции тока и напряжения в разных ветвях.
На схеме параллельной цепи, падение напряжения на резисторе в параллельной цепи одинаково для всех резисторов в каждой ветви параллельной цепи. Напряжение, выраженное в вольтах, измеряет электродвижущую силу или разность потенциалов в цепи.
Когда у вас есть цепь с известной величиной тока , потока электрического заряда, вы можете рассчитать падение напряжения в схемах параллельной цепи следующим образом:
- Определите объединенное сопротивление или сопротивление к потоку заряда параллельных резисторов.Суммируйте их как 1 / R всего = 1 / R 1 + 1 / R 2 … для каждого резистора. Для приведенной выше параллельной цепи полное сопротивление можно найти как:
- 1 / R всего = 1/5 Ом + 1/6 Ом + 1/10 Ом
- 1 / R всего = 6/30 Ом + 5/30 Ом + 3/30 Ом
- 1 / R всего = 14/30 Ом
- R всего = 30/14 Ом = 15/7 Ом
- 1 / R всего = 1/5 Ом + 1/6 Ом + 1/10 Ом
- Умножьте ток на общее сопротивление, чтобы получить падение напряжения в соответствии с законом Ома В = IR .Это равно падению напряжения во всей параллельной цепи и на каждом резисторе в параллельной цепи. В этом примере падение напряжения составляет В = 5 А x 15/7 Ом = 75/7 В.
Этот метод решения уравнений работает, потому что ток, входящий в любую точку параллельной цепи, должен быть равен текущий уход. Это происходит из-за текущего закона Кирхгофа, который гласит: «алгебраическая сумма токов в сети проводников, встречающихся в одной точке, равна нулю.»Калькулятор параллельной цепи мог бы использовать этот закон в ветвях параллельной цепи.
Если мы сравним ток, входящий в три ветви параллельной цепи, он должен равняться общему току, выходящему из ветвей. Поскольку падение напряжения остается постоянная на каждом параллельном резисторе, это падение напряжения, вы можете суммировать сопротивление каждого резистора, чтобы получить общее сопротивление и определить напряжение по этому значению. Примеры параллельных цепей показывают это.
Падение напряжения в последовательной цепи
•• • Syed Hussain Ather
В последовательной цепи, с другой стороны, вы можете рассчитать падение напряжения на каждом резисторе, зная, что в последовательной цепи ток постоянен на всем протяжении.Это означает, что падение напряжения на каждом резисторе разное и зависит от сопротивления в соответствии с законом Ома В = IR . В приведенном выше примере падение напряжения на каждом резисторе составляет:
V_1 = R_1I = 3 \ times 3 = 9 \ text {V} \\ V_2 = R_2I = 10 \ times 3 = 30 \ text {V} \\ V_3 = R_3I = 5 \ times 3 = 15 \ text {V}
Сумма каждого падения напряжения должна быть равна напряжению батареи в последовательной цепи. Это означает, что наша батарея имеет напряжение 54 В.
Этот метод решения уравнений работает, потому что падение напряжения на всех резисторах, установленных последовательно, должно в сумме составлять общее напряжение последовательной цепи.Это происходит из-за закона напряжения Кирхгофа, который гласит, что «направленная сумма разностей потенциалов (напряжений) вокруг любого замкнутого контура равна нулю». Это означает, что в любой точке замкнутой последовательной цепи падение напряжения на каждом резисторе должно равняться общему напряжению цепи. Поскольку ток в последовательной цепи постоянный, падение напряжения должно различаться для каждого резистора.
Параллельные и последовательные схемы
В параллельной схеме все компоненты схемы подключаются между одними и теми же точками на схеме.Это дает им их разветвленную структуру, в которой ток разделяется между каждой ветвью, но падение напряжения на каждой ветви остается неизменным. Сумма каждого резистора дает общее сопротивление, обратное каждому сопротивлению ( 1 / R всего = 1 / R 1 + 1 / R 2 … для каждого резистора).
В последовательной цепи, напротив, есть только один путь для прохождения тока. Это означает, что ток остается постоянным на всем протяжении, а падение напряжения на каждом резисторе отличается.Сумма каждого резистора дает общее сопротивление при линейном суммировании ( R всего = R 1 + R 2 … для каждого резистора).
Последовательно-параллельные схемы
Вы можете использовать оба закона Кирхгофа для любой точки или петли в любой цепи и применять их для определения напряжения и тока. Законы Кирхгофа дают вам метод определения тока и напряжения в ситуациях, когда природа цепи как последовательной и параллельной может быть не такой простой.
Как правило, для цепей, в которых есть как последовательные, так и параллельные компоненты, вы можете рассматривать отдельные части схемы как последовательные или параллельные и соответственно комбинировать их.
Эти сложные последовательно-параллельные схемы можно решить несколькими способами. Один из методов — рассматривать их части как параллельные или последовательные. Другой метод — использование законов Кирхгофа для определения обобщенных решений, использующих систему уравнений. Калькулятор последовательно-параллельных цепей учитывает различную природу цепей.
••• Syed Hussain Ather
В приведенном выше примере текущая точка выхода A должна равняться текущей точке выхода A. Это означает, что вы можете написать:
(1). I_1 = I_2 + I_3 \ text {или} I_1-I_2-I_3 = 0
Если рассматривать верхний контур как замкнутую последовательную цепь и рассматривать падение напряжения на каждом резисторе, используя закон Ома с соответствующим сопротивлением, вы можете написать:
(2). V_1-R_1I_1-R_2I_2 = 0
и, проделав то же самое для нижнего контура, вы можете обрабатывать каждое падение напряжения в направлении тока в зависимости от тока и сопротивления, чтобы записать:
(3).V_1 + V_2 + R_3I_3-R_2I_2 = 0
Это дает вам три уравнения, которые можно решить несколькими способами. Вы можете переписать каждое из уравнений (1) — (3) так, чтобы напряжение было с одной стороны, а ток и сопротивление — с другой. Таким образом, вы можете рассматривать три уравнения как зависимые от трех переменных I 1 , I 2 и I 3 с коэффициентами комбинаций R 1 , R 2 и R 3 .
\ begin {align} & (1).I_1-I_2-I_3 = 0 \\ & (2). R_1I_1 + R_2I_2 + 0 \ times I_3 = V_1 \\ & (3). 0 \ times I_1 + R_2I_2-R_3I_3 = V_1 + V_2 \ end {выровнено}
Эти три уравнения демонстрируют, как напряжение в каждой точке цепи каким-то образом зависит от тока и сопротивления. Если вы помните законы Кирхгофа, вы можете создать эти обобщенные решения схемных задач и использовать матричную нотацию для их решения. Таким образом, вы можете подставить значения для двух величин (среди которых напряжение, ток, сопротивление), чтобы найти третью.
Последовательные и параллельные резистивные сети (Revision) | Электрические схемы
Нас просят вычислить три оставшиеся разности потенциалов: \ (V_2 \), \ (V_3 \) и \ (V_4 \). Это показано на схеме ниже:
Мы будем использовать тот же метод для получения трех выражений для \ (V_2 \), \ (V_3 \) и \ (V_4 \), который использовался в Вопросе 3 для \ (V_1 \). Получаем:
\ [V_ {2} = \ frac {V_AR_2} {R_1 + R_2 + R_3 + R_4} ~~~~~ \ text {(10)} \]
\ [V_ {3} = \ frac {V_AR_3} {R_1 + R_2 + R_3 + R_4} ~~~~~ \ text {(11)} \]
\ [V_ {4} = \ frac {V_AR_4} {R_1 + R_2 + R_3 + R_4} ~~~~~ \ text {(12)} \]
Нам предоставлена следующая информация:
- сопротивление \ (R_1 = \ text {7,2} \ text {Ω} \)
- сопротивление \ (R_2 = \ text {4,3} \ text {Ω} \)
- сопротивление \ (R_3 = \ text {7,5} \ text {Ω} \)
- сопротивление \ (R_4 = \ text {4,1} \ text {Ω} \)
- разность потенциалов (напряжение) над батареей \ (V_A = \ text {2,8} \ text {V} \)
Подставляя указанные выше значения в \ (\ text {(10)} \), \ (\ text {(11)} \) и \ (\ text {(12)} \), получаем:
\ begin {align *} V_ {2} & = \ frac {V_AR_2} {R_1 + R_2 + R_3 + R_4} \\ & = \ frac {(\ text {2,8}) (\ text {4,3})} {\ text {7,2} + \ text {4,3} + \ text {7,5} + \ text {4,1}} \\ & = 0,52121 \ ldots ~~~~~ \ text {(вычислено)} \\ & \ приблизительно \ text {0,521} \ text {V} ~~~~~ \ text {(округлено)} \ end {align *}
\ begin {align *} V_ {3} & = \ frac {V_AR_3} {R_1 + R_2 + R_3 + R_4} \\ & = \ frac {(\ text {2,8}) (\ text {7,5})} {\ text {7,2} + \ text {4,3} + \ text {7,5} + \ text {4,1}} \\ & = 0,
\ ldots ~~~~~ \ text {(вычислено)} \\ & \ приблизительно \ text {0,909} \ text {V} ~~~~~ \ text {(округлено)} \ end {align *}
\ begin {align *} V_ {4} & = \ frac {V_AR_4} {R_1 + R_2 + R_3 + R_4} \\ & = \ frac {(\ text {2,8}) (\ text {4,1})} {\ text {7,2} + \ text {4,3} + \ text {7,5} + \ text {4,1}} \\ & = 0,49697 \ ldots ~~~~~ \ text {(вычислено)} \\ & \ приблизительно \ text {0,497} \ text {V} ~~~~~ \ text {(округлено)} \ end {align *}
Следовательно, разность потенциалов (напряжение) на \ (R_2 \) или \ (V_2 \ приблизительно \ text {0,521} \ text {V} \).
Разность потенциалов (напряжение) на \ (R_3 \) или \ (V_3 \ приблизительно \ text {0,909} \ text {V} \).
Разность потенциалов (напряжение) на \ (R_4 \) или \ (V_4 \ приблизительно \ text {0,497} \ text {V} \).
\ (0,521 \) \ (0,909 \) \ (0,497 \) Резисторыв схемах — Практика — Физический гипертекст
Давайте начнем процесс с комбинирования резисторов.В этой схеме четыре последовательных пары.
| R с = 3 Ом + 1 Ом R с = 4 Ом R с = 4 Ом + 2 Ом R с = 6 Ом |
| R с = 2 Ом + 3 Ом R с = 5 Ом R с = 1 Ом + 4 Ом R с = 5 Ом |
Эти пары образуют две параллельные цепи, одну слева и одну справа.
| ||||||||
|
| ||||||||
|
Каждый набор из четырех резисторов включен последовательно с другим.
| R с = 2,4 Ом + 0,6 Ом R с = 3 Ом |
| R с = 2,5 Ом + 0,5 Ом R с = 3 Ом |
Левая и правая половины цепи параллельны друг другу и батарее.
| |||||||||||
|
Теперь, когда у нас есть эффективное сопротивление всей цепи, давайте определим ток от источника питания, используя закон Ома.
| I итого = | В всего | + | 24 В | = 16 А |
| R всего | 1.5 Ом |
Теперь пройдемся по цепи (не буквально, конечно). На каждом соединении ток будет делиться: больше по пути с меньшим сопротивлением и меньше по пути с большим сопротивлением. Поскольку заряд не протекает нигде в полной цепи, ток будет одинаковым для всех элементов, последовательно соединенных друг с другом.
Левая и правая половины схемы идентичны по общему сопротивлению, что означает, что ток будет равномерно делиться между ними.
| 8 A для резистора 0,6 Ом на слева . |
| 8 A для резистора 0,5 Ом на правой стороне . |
С каждой стороны ток снова делится на две параллельные ветви.
| Ветви на слева имеют сопротивления в соотношении… | ||||||||
| ||||||||
| что означает, что токи разделятся в соотношении… | ||||||||
| для резисторов 1 Ом и 3 Ом на слева . | ||||||||
| для резисторов 2 Ом и 4 Ом на слева . |
| Ветви на правом идентичны, поэтому ток разделяется на две равные половины. |
| ☟ |
| ☟ |
| ☟ |
| ☟ |
| ☟ |
| для резисторов 2 Ом и 3 Ом на правой стороне . |
| для резисторов 1 Ом и 4 Ом на справа . |
21.1 Последовательные и параллельные резисторы — Главы физики колледжа 1-17
На рисунке 3 показаны резисторы, подключенные параллельно и подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением.Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен). Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рис. 3 (b).)
Чтобы найти выражение для эквивалентного параллельного сопротивления [латекс] \ boldsymbol {R _ {\ textbf {p}}} [/ latex], давайте рассмотрим протекающие токи и их связаны с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, составляют [латекс] \ boldsymbol {I_1 = \ frac {V} {R_1}} [/ latex], [латекс] \ boldsymbol {I_2 = \ frac {V} {R_2}} [/ latex] и [latex] \ boldsymbol {I_3 = \ frac {V} {R_3}} [/ latex]. Сохранение заряда подразумевает, что общий ток [латекс] \ boldsymbol {I} [/ latex], производимый источником, является суммой этих токов:
[латекс] \ boldsymbol {I =} [/ латекс] [латекс] \ boldsymbol {\ frac {V} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_3}} [/ latex] [латекс] \ boldsymbol {= V} [/ latex] [латекс] \ boldsymbol {(\ frac { 1} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [ / latex] [латекс] \ boldsymbol {\ frac {1} {R_3})}.[/ latex]
[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_p}} [/ latex] [латекс] \ boldsymbol {= V} [/ латекс ] [latex] \ boldsymbol {(\ frac {1} {R_p})}. [/ latex]
Члены в круглых скобках в последних двух уравнениях должны быть равны. Обобщая на любое количество резисторов, общее сопротивление [латекс] \ boldsymbol {R_p} [/ latex] параллельного соединения связано с отдельными сопротивлениями соотношением
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_1}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_3}} [/ latex] [латекс] \ boldsymbol {+ \ cdots} [/ latex]
Это соотношение приводит к общему сопротивлению [латекс] \ boldsymbol {R_p} [/ latex], которое меньше наименьшего из отдельных сопротивлений.(Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2: Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: [латекс] \ boldsymbol {V = 12.0 \; \ textbf {V}} [/ latex], [latex] \ boldsymbol {R_1 = 1.00 \; \ Omega} [/ latex], [latex] \ boldsymbol {R_2 = 6.00 \; \ Omega} [/ латекс ] и [латекс] \ boldsymbol {R_3 = 13.0 \; \ Omega} [/ latex]. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения. Ввод известных значений дает
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1} {R_1}} [/ латекс ] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {1} {R_2}} [/ latex] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol { \ frac {1} {R_3}} [/ latex] [latex] \ boldsymbol {=} [/ latex] [latex] \ boldsymbol {\ frac {1} {1.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [latex] \ boldsymbol {\ frac {1} {6.00 \; \ Omega}} [/ latex] [латекс] \ boldsymbol {+} [/ latex] [латекс] \ boldsymbol {\ frac {1} {13.0 \; \ Omega}}. [/ latex]
Таким образом,
[латекс] \ boldsymbol {\ frac {1} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1.00} {\ Omega}} [/ латекс] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {0.1667} {\ Omega}} [/ латекс] [латекс] \ boldsymbol {+} [/ латекс] [латекс] \ boldsymbol {\ frac {0.07692} {\ Omega}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {1.2436} {\ Omega}} [/ латекс]
(Обратите внимание, что в этих вычислениях каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны перевернуть это, чтобы найти полное сопротивление [латекс] \ boldsymbol {R_p} [/ latex]. Это дает
[латекс] \ boldsymbol {R_p =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {1.2436}} [/ latex] [латекс] \ boldsymbol {\ Omega = 0.8041 \; \ Omega}. [ / латекс]
Общее сопротивление с правильным количеством значащих цифр составляет [латекс] \ boldsymbol {R_p = 0.804 \; \ Omega} [/ latex]
Обсуждение для (а)
[латекс] \ boldsymbol {R_p} [/ latex], как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, заменив полное сопротивление [латекс] \ boldsymbol {R_p} [/ latex]. Это дает
[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_p}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {0.8041 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 14.92 \; \ textbf {A}} [/ latex]
Обсуждение для (б)
Ток [latex] \ boldsymbol {I} [/ latex] для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,
[латекс] \ boldsymbol {I_1 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_1}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {1.00 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 12.0 \; \ textbf {A}}. [/ Latex]
Аналогично
[латекс] \ boldsymbol {I_2 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_2}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {6.00 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 2.00 \; \ textbf {A}} [/ latex]
и
[латекс] \ boldsymbol {I_3 =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {R_3}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {12.0 \; \ textbf {V}} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 0.92 \; \ textbf {A}}. [/ Latex]
Обсуждение для (c)
Общий ток складывается из отдельных токов:
[латекс] \ boldsymbol {I_1 + I_2 + I_3 = 14.92 \; \ textbf {A}}. [/ Latex]
Это соответствует сохранению заряда.
Стратегия и решение для (d)
Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.2} {13.0 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 11.1 \; \ textbf {W}}. [/ Latex]
Обсуждение для (d)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общую мощность также можно рассчитать несколькими способами. Выбирая [латекс] \ boldsymbol {P = IV} [/ latex] и вводя общий ток, получаем
[латекс] \ boldsymbol {P = IV = (14.92 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 179 \; \ textbf {W}}. [/ Latex]
Обсуждение для (e)
Суммарная мощность, рассеиваемая резисторами, также 179 Вт:
[латекс] \ boldsymbol {P_1 + P_2 + P_3 = 144 \; \ textbf {W} + 24.0 \; \ textbf {W} + 11.1 \; \ textbf {W} = 179 \; \ textbf {W}}. [/ латекс]
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
21.1 Последовательные и параллельные резисторы — College Physics
Сводка
- Нарисуйте цепь с резисторами, включенными параллельно и последовательно.
- Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
- Контраст — способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
- Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
- Рассчитайте общее сопротивление цепи, которая содержит смесь резисторов, включенных последовательно и параллельно.
Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи. Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.
Рисунок 1. (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно. Например, если ток течет через человека, держащего отвертку, и попадает в Землю, то $ latex \ boldsymbol {R_1} $ на рисунке 1 (a) может быть сопротивлением вала отвертки, $ latex \ boldsymbol {R_2} $ сопротивление его ручки, $ latex \ boldsymbol {R_3} $ сопротивление тела человека и $ latex \ boldsymbol {R_4} $ сопротивление его обуви.
На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно. (Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с резиновыми подошвами с высоким сопротивлением. прибор, уменьшающий рабочий ток.)
Рисунок 2. Три резистора, подключенных последовательно к батарее (слева) и эквивалентному одиночному или последовательному сопротивлению (справа).Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе на Рисунке 2.
Согласно закону Ома падение напряжения $ latex \ boldsymbol {V} $ на резисторе при протекании через него тока рассчитывается с использованием уравнения $ latex \ boldsymbol {V = IR} $, где $ latex \ boldsymbol {I} $ — ток в амперах (A), а $ latex \ boldsymbol {R} $ — сопротивление в омах $ latex \ boldsymbol {(\ Omega)} $.Другой способ думать об этом: $ latex \ boldsymbol {V} $ — это напряжение, необходимое для протекания тока $ latex \ boldsymbol {I} $ через сопротивление $ latex \ boldsymbol {R} $.
Таким образом, падение напряжения на $ latex \ boldsymbol {R_1} $ составляет $ latex \ boldsymbol {V_1 = IR_1} $, что на $ latex \ boldsymbol {R_2} $ — $ latex \ boldsymbol {V_2 = IR_2} $, и что через $ latex \ boldsymbol {R_3} $ стоит $ latex \ boldsymbol {V_3 = IR_3} $. Сумма этих напряжений равна выходному напряжению источника; то есть
$ латекс \ boldsymbol {V = V_1 + V_2 + V_3}.$
Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия описывается уравнением $ latex \ boldsymbol {PE = qV} $, где $ latex \ boldsymbol {q} $ — электрический заряд, а $ latex \ boldsymbol {V} $ — напряжение. Таким образом, энергия, подводимая источником, равна $ latex \ boldsymbol {qV} $, а энергия, рассеиваемая резисторами, равна
.$ латекс \ boldsymbol {qV_1 + qV_2 + qV_3}. $
Связи: законы сохранения
Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе.Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.
Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии. Таким образом, $ latex \ boldsymbol {qV = qV_1 + qV_2 + qV_3} $. Плата $ latex \ boldsymbol {q} $ отменяется, в результате чего получается $ latex \ boldsymbol {V = V_1 + V_2 + V_3} $, как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.)
Теперь подстановка значений отдельных напряжений дает
$ латекс \ boldsymbol {V = IR_1 + IR_2 + IR_3 = I (R_1 + R_2 + R_3)}. $
Обратите внимание, что для эквивалентного сопротивления одиночной серии $ latex \ boldsymbol {R_s} $ мы имеем
$ латекс \ boldsymbol {V = IR_s}. $
Это означает, что полное или эквивалентное последовательное сопротивление $ latex \ boldsymbol {R_s} $ трех резисторов равно
$ латекс \ boldsymbol {R_s = R_1 + R_2 + R_3} $.
Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление $ latex \ boldsymbol {R_s} $ последовательного соединения равно
$ латекс \ boldsymbol {R_s = R_1 + R_2 + R_3 + \ dots} $
, как предлагается.Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.
Пример 1: Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи
Предположим, что выходное напряжение батареи на рисунке 2 равно $ latex \ boldsymbol {12.0 \; \ textbf {V}} $, а сопротивление равно $ latex \ boldsymbol {R_1 = 1.00 \; \ Omega} $, $ latex \ boldsymbol {R_2 = 6.00 \; \ Omega} $ и $ latex \ boldsymbol {R_3 = 13.0 \; \ Omega} $. а) Каково полное сопротивление? (б) Найдите ток. (c) Вычислите падение напряжения на каждом резисторе и покажите, как полученная сумма равна выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:
$ latex \ begin {array} {r @ {{} = {}} l} \ boldsymbol {R_s} & \ boldsymbol {R_1 + R_2 + R_3} \\ [1em] & \ boldsymbol {1.00 \; \ Omega + 6.00 \; \ Omega + 13.0 \; \ Omega} \\ [1em] & \ boldsymbol {20.0 \; \ Omega}. \ end {array}
долл. СШАСтратегия и решение для (b)
Ток определяется по закону Ома $ latex \ boldsymbol {V = IR} $. Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:
$ latex \ boldsymbol {I =} $ latex \ boldsymbol {=} $ latex \ boldsymbol {= 0.600 \; \ textbf {A}}. $Стратегия и решение для (c)
Напряжение — или падение $ latex \ boldsymbol {IR} $ — в резисторе определяется законом Ома.Ввод значения тока и значения первого сопротивления дает
.$ латекс \ boldsymbol {V_1 = IR_1 = (0.600 \; \ textbf {A}) (1.0 \; \ Omega) = 0.600 \; \ textbf {V}}. $
Аналогично
$ латекс \ boldsymbol {V_2 = IR_2 = (0.600 \; \ textbf {A}) (6.0 \; \ Omega) = 3.60 \; \ textbf {V}} $
и
$ латекс \ boldsymbol {V_3 = IR_3 = (0.600 \; \ textbf {A}) (13.0 \; \ Omega) = 7.80 \; \ textbf {V}}. $
Обсуждение для (c)
Три капли $ latex \ boldsymbol {IR} $ добавляют к $ latex \ boldsymbol {12.0 \; \ textbf {V}} $, прогноз:
$ латекс \ boldsymbol {V_1 + V_2 + V_3 = (0,600 + 3,60 + 7,80) \; \ textbf {V} = 12,0 \; \ textbf {V}}. $
Стратегия и решение для (d)
Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — это использовать закон Джоуля , $ latex \ boldsymbol {P = IV} $, где $ latex \ boldsymbol {P} $ — электрическое мощность. 2 R_1 = (0.2} {R}} $, где $ latex \ boldsymbol {V} $ — это падение напряжения на резисторе (а не полное напряжение источника). Получатся те же значения.
Стратегия и решение для (e)
Самый простой способ рассчитать выходную мощность источника — использовать $ latex \ boldsymbol {P = IV} $, где $ latex \ boldsymbol {V} $ — напряжение источника. Это дает
$ латекс \ boldsymbol {P = (0.600 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 7.20 \; \ textbf {W}}. $
Обсуждение для (e)
Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть
$ латекс \ boldsymbol {P_1 + P_2 + P_3 = (0,360 + 2,16 + 4,68) \; \ textbf {W} = 7.20 \; \ textbf {W}}. $
Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.
Основные характеристики резисторов серии
- Сопротивления серии
- добавляют: $ latex \ boldsymbol {R_s = R_1 + R_2 + R_3 + \ dots} $.
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные резисторы, включенные последовательно, не получают полное напряжение источника, а делят его.
На рис. 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника.
Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)
Рисунок 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (предоставлено Дмитрием Г., Wikimedia Commons)Чтобы найти выражение для эквивалентного параллельного сопротивления $ latex \ boldsymbol {R _ {\ textbf {p}}} $, давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны $ latex \ boldsymbol {I_1 = \ frac {V} {R_1}} $, $ latex \ boldsymbol {I_2 = \ frac {V} { R_2}} $ и $ latex \ boldsymbol {I_3 = \ frac {V} {R_3}} $. Сохранение заряда подразумевает, что полный ток $ latex \ boldsymbol {I} $, производимый источником, является суммой этих токов:
$ латекс \ boldsymbol {I = I_1 + I_2 + I_3}. $
Подстановка выражений для отдельных токов дает
Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает
$ латекс \ boldsymbol {I =} $ латекс \ boldsymbol {= V} $Члены в скобках в последних двух уравнениях должны быть равны.Обобщая для любого количества резисторов, общее сопротивление $ latex \ boldsymbol {R_p} $ параллельного соединения связано с отдельными сопротивлениями на
$ latex \ boldsymbol {=} $ $ latex \ boldsymbol {+} $ $ latex \ boldsymbol {+} $ $ latex \ boldsymbol {+ \ cdots} $Это соотношение приводит к общему сопротивлению $ latex \ boldsymbol {R_p} $, которое меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.
Пример 2: Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи
Пусть выходное напряжение батареи и сопротивления в параллельном соединении на рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: $ latex \ boldsymbol {V = 12.0 \; \ textbf {V}} $, $ latex \ boldsymbol { R_1 = 1.00 \; \ Omega} $, $ latex \ boldsymbol {R_2 = 6.00 \; \ Omega} $ и $ latex \ boldsymbol {R_3 = 13.0 \; \ Omega} $. а) Каково полное сопротивление? (б) Найдите полный ток.(c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия и решение для (а)
Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения. Ввод известных значений дает
Таким образом,
(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
Мы должны перевернуть это, чтобы найти полное сопротивление $ latex \ boldsymbol {R_p} $. Это дает
$ latex \ boldsymbol {R_p =} $ latex \ boldsymbol {\ Omega = 0.8041 \; \ Omega}. $Суммарное сопротивление с правильным количеством значащих цифр равно $ latex \ boldsymbol {R_p = 0.804 \; \ Omega} $
.Обсуждение для (а)
$ latex \ boldsymbol {R_p} $, как и предполагалось, меньше наименьшего индивидуального сопротивления.
Стратегия и решение для (b)
Полный ток можно найти из закона Ома, заменив полное сопротивление $ latex \ boldsymbol {R_p} $.Это дает
$ latex \ boldsymbol {I =} $ latex \ boldsymbol {=} $ latex \ boldsymbol {= 14.92 \; \ textbf {A}} $Обсуждение для (б)
Текущее значение $ latex \ boldsymbol {I} $ для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример). Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
Стратегия и решение для (c)
Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение.Таким образом,
$ latex \ boldsymbol {I_1 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 12.0 \; \ textbf {A}}. $Аналогично
$ latex \ boldsymbol {I_2 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 2.00 \; \ textbf {A}} $и
$ latex \ boldsymbol {I_3 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 0.92 \; \ textbf {A}}. $Обсуждение для (c)
Общий ток складывается из отдельных токов:
$ латекс \ boldsymbol {I_1 + I_2 + I_3 = 14.2} {R}} $, так как каждый резистор получает полное напряжение. Таким образом,
$ latex \ boldsymbol {P_1 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 144 \; \ textbf {W}}. $Аналогично
$ latex \ boldsymbol {P_2 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 24.0 \; \ textbf {W}} $и
$ latex \ boldsymbol {P_3 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 11.1 \; \ textbf {W}}. $Обсуждение для (d)
Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.
Стратегия и решение для (e)
Общую мощность также можно рассчитать несколькими способами. Выбирая $ latex \ boldsymbol {P = IV} $ и вводя полный ток, получаем
$ латекс \ boldsymbol {P = IV = (14.92 \; \ textbf {A}) (12.0 \; \ textbf {V}) = 179 \; \ textbf {W}}. $
Обсуждение для (e)
Суммарная мощность, рассеиваемая резисторами, также 179 Вт:
$ латекс \ boldsymbol {P_1 + P_2 + P_3 = 144 \; \ textbf {W} + 24.0 \; \ textbf {W} + 11.1 \; \ textbf {W} = 179 \; \ textbf {W}}. $
Это соответствует закону сохранения энергии.
Общее обсуждение
Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.
Основные характеристики резисторов, подключенных параллельно
- Параллельное сопротивление определяется из $ latex \ boldsymbol {\ frac {1} {R_p} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} + \ cdots } $, и оно меньше любого отдельного сопротивления в комбинации.
- Каждый резистор, включенный параллельно, имеет то же полное напряжение, что и источник. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одним и тем же напряжением, и для того, чтобы они могли работать независимо.)
- Не каждый параллельный резистор получает полный ток; они делят это.
Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учитывать сопротивление провода.В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения можно свести к одному эквивалентному сопротивлению, используя метод, показанный на рисунке 4. Различные части идентифицируются как последовательные или параллельные, сокращаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс занимает больше времени, чем труден.
Рисунок 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части.Каждый из них идентифицируется и уменьшается до эквивалентного сопротивления, а затем уменьшается до тех пор, пока не будет достигнуто одно эквивалентное сопротивление.Самая простая комбинация последовательного и параллельного сопротивления, показанная на рисунке 5, также является наиболее поучительной, поскольку она используется во многих приложениях. Например, $ latex \ boldsymbol {R_1} $ может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. $ latex \ boldsymbol {R_2} $ и $ latex \ boldsymbol {R_3} $ могут быть стартером и светом салона.Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.
Пример 3: Расчет сопротивления, $ latex \ boldsymbol {IR} $, падения, тока и рассеиваемой мощности: объединение последовательных и параллельных цепей
На рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного подключения. Мы можем рассматривать $ latex \ boldsymbol {R_1} $ как сопротивление проводов, ведущих к $ latex \ boldsymbol {R_2} $ и $ latex \ boldsymbol {R_3} $.(а) Найдите полное сопротивление. (б) Что такое падение $ latex \ boldsymbol {IR} $ в $ latex \ boldsymbol {R_1} $? (c) Найдите текущий $ latex \ boldsymbol {I_2} $ через $ latex \ boldsymbol {R_2} $. (d) Какую мощность рассеивает $ latex \ boldsymbol {R_2} $?
Рисунок 5. Эти три резистора подключены к источнику напряжения, так что R 2 и R 3 параллельны друг другу, и эта комбинация последовательно с R 1 .Стратегия и решение для (а)
Чтобы найти полное сопротивление, отметим, что $ latex \ boldsymbol {R_2} $ и $ latex \ boldsymbol {R_3} $ находятся параллельно, а их комбинация $ latex \ boldsymbol {R_p} $ находится последовательно с $ latex \ boldsymbol { R_1} $. Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет
.$ латекс \ boldsymbol {R _ {\ textbf {tot}} = R_1 + R_p}. $
Сначала мы находим $ latex \ boldsymbol {R_p} $, используя уравнение для параллельных резисторов и вводя известные значения:
Инвертирование дает
$ latex \ boldsymbol {R_p =} $ latex \ boldsymbol {\ Omega = 4.11 \; \ Omega}. $Таким образом, общее сопротивление равно
.$ латекс \ boldsymbol {R _ {\ textbf {tot}} = R_1 + R_p = 1.00 \; \ Omega + 4.11 \; \ Omega = 5.11 \; \ Omega}. $
Обсуждение для (а)
Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чисто параллельной ($ latex \ boldsymbol {20.0 \; \ Omega} $ и $ latex \ boldsymbol {0.804 \; \ Omega} $, соответственно), найденными для тех же резисторы в двух предыдущих примерах.
Стратегия и решение для (b)
Чтобы найти падение $ latex \ boldsymbol {IR} $ в $ latex \ boldsymbol {R_1} $, отметим, что полный текущий $ latex \ boldsymbol {I} $ течет через $ latex \ boldsymbol {R_1} $.Таким образом, его падение $ latex \ boldsymbol {IR} $ равно
.$ латекс \ boldsymbol {V_1 = IR_1}. $
Мы должны найти $ latex \ boldsymbol {I} $, прежде чем сможем вычислить $ latex \ boldsymbol {V_1} $. Полный ток $ latex \ boldsymbol {I} $ находится с помощью закона Ома для схемы. То есть
$ latex \ boldsymbol {I =} $ latex \ boldsymbol {=} $ latex \ boldsymbol {= 2.35 \; \ textbf {A}}. $Вводя это в выражение выше, мы получаем
$ латекс \ boldsymbol {V_1 = IR_1 = (2.35 \; \ textbf {A}) (1.00 \; \ Omega) = 2.35 \; \ textbf {V}}. $
Обсуждение для (б)
Напряжение, приложенное к $ latex \ boldsymbol {R_2} $ и $ latex \ boldsymbol {R_3} $, меньше общего напряжения на величину $ latex \ boldsymbol {V_1} $. Большое сопротивление провода может существенно повлиять на работу устройств, представленных $ latex \ boldsymbol {R_2} $ и $ latex \ boldsymbol {R_3} $.
Стратегия и решение для (c)
Чтобы найти ток через $ latex \ boldsymbol {R_2} $, мы должны сначала найти приложенное к нему напряжение.Мы называем это напряжение $ latex \ boldsymbol {V _ {\ textbf {p}}} $, потому что оно применяется к параллельной комбинации резисторов. Напряжение, приложенное как к $ latex \ boldsymbol {R_2} $, так и к $ latex \ boldsymbol {R_3} $, уменьшается на сумму $ latex \ boldsymbol {V_1} $, и поэтому оно составляет
.$ латекс \ boldsymbol {V_p = V — V_1 = 12.0 \; \ textbf {V} — 2.35 \; \ textbf {V} = 9.65 \; \ textbf {V}}. $
Теперь текущий $ latex \ boldsymbol {I_2} $ через сопротивление $ latex \ boldsymbol {R_2} $ находится по закону Ома:
$ latex \ boldsymbol {I_2 =} $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {= 1.2 (6.00 \; \ Omega) = 15.5 \; \ textbf {W}}. $Обсуждение для (d)
Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если протекает большой ток, падение $ latex \ boldsymbol {IR} $ в проводах также может быть значительным.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, обозначенное $ latex \ boldsymbol {R_3} $, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток.Этот повышенный ток вызывает большее падение $ latex \ boldsymbol {IR} $ в проводах, представленных $ latex \ boldsymbol {R_1} $, что снижает напряжение на лампочке (которое составляет $ latex \ boldsymbol {R_2} $), что потом заметно тускнеет.
Рисунок 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.Проверьте свое понимание
1: Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную комбинации? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.
Стратегии решения проблем для последовательных и параллельных резисторов
- Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных соединений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, уменьшайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при нахождении $ latex \ boldsymbol {R_p} $ необходимо с осторожностью относиться к обратному значению.
- Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и т. Д.
- Полное сопротивление электрической цепи с последовательно включенными резисторами является суммой отдельных сопротивлений: $ latex \ boldsymbol {R_s = R_1 + R_2 + R_3 + \ cdots} $
- Каждый резистор в последовательной цепи имеет одинаковое количество тока, протекающего через него.
- Падение напряжения или рассеиваемая мощность на каждом отдельном резисторе в серии различаются, и их общая сумма складывается с входом источника питания.
- Общее сопротивление электрической цепи с резисторами, подключенными параллельно, меньше наименьшего сопротивления любого из компонентов и может быть определено по формуле: $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {+} $ $ latex \ boldsymbol {+} $ $ latex \ boldsymbol {+ \; \ cdots} $
- Каждый резистор в параллельной цепи имеет одинаковое полное напряжение источника.
- Ток, протекающий через каждый резистор в параллельной цепи, различается в зависимости от сопротивления.
- Если более сложное соединение резисторов представляет собой комбинацию последовательного и параллельного соединения, оно может быть уменьшено до одного эквивалентного сопротивления, идентифицируя его различные части как последовательные или параллельные, уменьшая каждую до своего эквивалента и продолжая до тех пор, пока в конечном итоге не будет достигнуто единое сопротивление. .
Концептуальные вопросы
1: Переключатель имеет переменное сопротивление, близкое к нулю в замкнутом состоянии и чрезвычайно большое в разомкнутом, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рис. 7 на ток в разомкнутом и замкнутом состоянии.
Рисунок 7. Выключатель обычно включен последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)2: Какое напряжение на разомкнутом переключателе на рисунке 7?
3: Напряжение на разомкнутом переключателе, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?
4: Почему мощность, рассеиваемая замкнутым переключателем, как на Рисунке 7, мала?
5: Студент в физической лаборатории по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рис. 8. Объясните, почему лампа горит, когда выключатель разомкнут, и гаснет, когда он замкнут. (Не пытайтесь — батарея сильно разряжается!)
Рис. 8. Ошибка подключения: этот переключатель подключен параллельно устройству, представленному R .(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)6: Зная, что сила удара зависит от величины тока, проходящего через ваше тело, вы бы предпочли быть последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он поражен током? Объяснять.
7: Не потускнели бы ваши фары при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.
8: Некоторые гирлянды праздничных огней подключаются последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкаются накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?
9: Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.
10: Предположим, вы выполняете физическую лабораторию, которая просит вас вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?
11: Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление. Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор.Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.
12: У некоторых лампочек есть три настройки мощности (не включая ноль), полученные от нескольких нитей накала, которые индивидуально переключаются и соединяются параллельно. Какое минимальное количество нитей нити необходимо для трех режимов мощности?
Проблемные упражнения
Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.
1: (a) Каково сопротивление десяти последовательно соединенных резисторов $ latex \ boldsymbol {275 — \; \ Omega} $? (б) Параллельно?
2: (a) Какое сопротивление $ латекс \ boldsymbol {1.2 — \; \ Omega} $ подключены $ latex \ boldsymbol {2.50 — \; \ textbf {k} \ Omega} $ и резистор $ latex \ boldsymbol {4.00 — \; \ textbf {k} \ Omega} $ последовательно? (б) Параллельно?
3: Какие значения наибольшего и наименьшего сопротивления можно получить, подключив $ latex \ boldsymbol {36.0 — \; \ Omega} $, $ latex \ boldsymbol {50.0 — \; \ Omega} $ и $ латексный \ boldsymbol {700 — \; \ Omega} $ резистор вместе?
4: Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?
5: Фара вашего автомобиля мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)
6: (a) Учитывая 48.Аккумулятор 0 В и резисторы $ latex \ boldsymbol {24.0 — \; \ Omega} $ и $ latex \ boldsymbol {96.0 — \; \ Omega} $, найдите для каждого из них ток и мощность при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.
7: Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, вычислите $ latex \ boldsymbol {I_3} $ двумя разными способами: (a) из известных значений $ latex \ boldsymbol {I} $ и $ latex \ boldsymbol {I_2} $; (б) используя закон Ома для $ latex \ boldsymbol {R_3} $.В обеих частях четко показано, как вы выполняете шаги, указанные в Стратегиях решения проблем для последовательных и параллельных резисторов.
8: Ссылаясь на рисунок 5: (a) Вычислите $ latex \ boldsymbol {P_3} $ и обратите внимание на его сравнение с $ latex \ boldsymbol {P_3} $, найденным в первых двух примерах задач в этом модуле. (b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.
9: См. Рис. 6, где обсуждается затемнение света при включении тяжелого прибора.9 — \; \ Omega} $ сопротивление. Рисунок 9. (а) Какое сопротивление относительно земли у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Ясно покажите, как вы выполняете шаги, указанные в Стратегиях решения проблем для последовательных и параллельных резисторов.
Рис. 9. Линия электропередачи высокого напряжения (240 кВ), несущая 5,00 × 10 2 А подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает 1.00 × 10 9 Ом сопротивления каждый.11: Покажите, что если два резистора $ latex \ boldsymbol {R_1} $ и $ latex \ boldsymbol {R_2} $ объединены, и один из них намного больше другого ($ latex \ boldsymbol {R_1 >> R_2} $) : (a) Их последовательное сопротивление почти равно большему сопротивлению $ latex \ boldsymbol {R_1} $. (б) Их параллельное сопротивление почти равно меньшему сопротивлению $ latex \ boldsymbol {R_2} $.
12: Необоснованные результаты
Два резистора, один из которых имеет сопротивление $ latex \ boldsymbol {145 \; \ Omega} $, подключены параллельно, чтобы получить общее сопротивление $ latex \ boldsymbol {150 \; \ Omega} $.а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
13: Необоснованные результаты
Два резистора, один из которых имеет сопротивление $ latex \ boldsymbol {900 \; \ textbf {k} \ Omega} $, соединены последовательно, чтобы обеспечить общее сопротивление $ latex \ boldsymbol {0.500 \; \ textbf {M}. \ Omega} $. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?
Глоссарий
- серии
- последовательность резисторов или других компонентов, включенных в цепь один за другим
- резистор
- компонент, обеспечивающий сопротивление току, протекающему через электрическую цепь
- сопротивление
- вызывает потерю электроэнергии в цепи
- Закон Ома
- взаимосвязь между током, напряжением и сопротивлением в электрической цепи: $ latex \ boldsymbol {V = IR} $
- напряжение
- электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором
- падение напряжения
- потеря электроэнергии при прохождении тока через резистор, провод или другой компонент
- ток
- поток заряда через электрическую цепь мимо заданной точки измерения
- Закон Джоуля
- взаимосвязь между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемая по формуле: $ latex \ boldsymbol {P_e = IV} $
- параллельно
- подключение резисторов или других компонентов в электрической цепи таким образом, что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы
Решения
Проверьте свое понимание
1: Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы.В таких случаях правила Кирхгофа, которые будут представлены в главе 21.3 «Правила Кирхгофа», позволят вам проанализировать схему.
Задачи Упражнения
1: (a) $ latex \ boldsymbol {2.75 \; \ textbf {k} \ Omega} $
(б) $ latex \ boldsymbol {27.5 \; \ Omega} $
3: (a) $ latex \ boldsymbol {786 \; \ Omega} $
(б) $ latex \ boldsymbol {20.3 \; \ Omega} $
5: 29,6 Вт
7: (а) 0.74 А
(б) 0,742 А
9: (а) 60,8 Вт
(б) 3,18 кВт
11: (a) $ latex \ begin {array} {c} \ boldsymbol {R_s = R_1 + R_2} \\ [1em] \ boldsymbol {\ Rightarrow R_s \ приблизительно R_1 (R_1 >> R_2)} \ end {array}
долл. США(b) $ latex \ boldsymbol {=} $ $ latex \ boldsymbol {+} $ $ latex \ boldsymbol {=} $
, так что
$ latex \ boldsymbol {R_p =} $ $ latex \ boldsymbol {\ приблизительно} $ $ latex \ boldsymbol {= R_2 \; (R_1 >> R_2)}.$
13: (a) $ latex \ boldsymbol {-400 \; \ textbf {k} \ Omega} $
(b) Сопротивление не может быть отрицательным.
(c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.
Эпизод 114: Последовательные и параллельные компоненты
Добавление резисторов в схему
Электричество и магнетизм
Эпизод 114: Последовательные и параллельные компоненты
Урок для 16-19
- Время активности 95 минут
- Уровень Продвинутый
Основные цели
Краткое содержание урока
- Демонстрация: последовательное и параллельное соединение ламп (10 минут)
- Обсуждение: Вывод формул (20 минут)
- Рабочий пример: Добавление резисторов (15 минут)
- Студенческий эксперимент: прогнозирование и измерение сопротивления (20 минут)
- Вопросы студентов: практика с формулами (30 минут)
Демонстрация: последовательное и параллельное соединение ламп
Попросите учащихся вспомнить уравнение, определяющее сопротивление.( R = В I где В это pd по компоненту, а I — ток через него.) Подключите 1, 2, а затем 3 лампы последовательно к источнику питания (постоянный pd), показывая им уменьшение тока при том же pd Соотношение В I увеличилось: добавление резисторов увеличивается общее сопротивление. Вы можете каждый раз рассчитывать сопротивление, но имейте в виду, что, поскольку температура ламп будет разной при разных токах, вы вряд ли получите простое соотношение сопротивлений.
Повторите эксперимент, но на этот раз добавьте лампы параллельно. Ток увеличивается, а эффективное (нагрузочное) сопротивление уменьшается. Если вы рассчитываете значения сопротивления, вы должны получить 1: 1/2: 1/3 при добавлении ламп.
Эпизод 114-1: Параллельное и последовательное подключение ламп (Word, 34 КБ)
Обсуждение: Вывод формул
А теперь займемся теорией. Вы пытаетесь найти один резистор R всего , который будет иметь такое же сопротивление, как два или более резистора R 1 , R 2 и т. Д., Включенных последовательно.Выведите уравнения для последовательного и параллельного сочетаний сопротивлений. Отправные точки:
Резисторы серииимеют такой же ток, но добавляются pds, поэтому:
В всего = I × R всего
I R итого = I R 1 & plus; I R 1
разделите на I, чтобы получить:
R итого = R 1 и плюс; р 1
Параллельные резисторы имеют одинаковый pd на всех резисторах, но токи складываются, так что:
I всего = В R всего
I итого = I 1 & plus; Я 2
В R всего = В R 1 & plus; В R 2
затем разделите на V, чтобы получить знакомую формулу.
1 R итого = 1 R 1 & плюс; 1 р 2
Помните, что параллельная формула обычно цитируется как 1 R итого , поэтому им все равно придется брать обратную величину, чтобы получить значение R итого . Это необычно (на уровне A), когда в вопросах задействовано более двух резисторов параллельно, поэтому стоит отметить, что формулу параллельности для двух резисторов можно переставить и получить:
R всего = R 1 R 2 R 1 & plus; р 2
или произведение на сумму
.Это убережет слабонервных от ответных мер!
Также стоит отметить, что когда n резисторов одинакового номинала ( R ) подключены параллельно, в результате получается эффективное сопротивление R n. Свяжите это с n-кратным умножением тока.
Имейте в виду, что даже на этом уровне некоторые студенты будут утверждать, что ток всегда идет по пути наименьшего сопротивления
. (Будьте готовы обсудить, что происходит в крайнем случае, когда компонент закорочен
куском параллельного провода.Обратите внимание на то, что небольшая часть общего тока все еще продолжает протекать через компонент. (Этот случай снова появится позже в потенциальных делителях в
серия 118
Здесь вам может потребоваться указать проводимость. Проводимость G = 1 R и измеряется в сименсах, С. При параллельной комбинации проводимости прибавляются.
Рабочие примеры: Добавление резисторов
Рассмотрите примеры для двух резисторов с подходящими сопротивлениями, например.грамм. 40 Ом и 60 Ом. Это дает 100 Ом последовательно и 24 Ом параллельно. Разрешите учащимся выполнить расчет самостоятельно и помогите учащимся, у которых возникают проблемы с использованием обратной клавиши на своих калькуляторах.
Подчеркните, что для последовательно соединенных резисторов общее всегда больше, чем отдельные сопротивления; параллельно оно меньше любого из отдельных сопротивлений.
Студенческий эксперимент: прогнозирование и измерение сопротивления
Учащиеся могут измерять сопротивление различных комбинаций резисторов с помощью омметра и сравнивать свои ответы с расчетными значениями.
Вы можете проверить использование омметра перед этим упражнением. Диапазон омметра может сбивать с толку. Очевидно, это варьируется от устройства к устройству — убедитесь, что они знакомы с приборами, которые вы собираетесь использовать, и разбираются в них; в противном случае пропадут сведения о последовательной и параллельной цепях.
Эпизод 114-2: Последовательные и параллельные резисторы (Word, 36 КБ)
Вопросы студентов: Практика с формулами
Два набора вопросов с использованием этих формул.
кОм
и мегаом
уловят некоторые, как и мА
.
Эпизод 114-3: Сопротивление цепи (Word, 51 КБ)
Эпизод 114-4: Объединение сопротивлений (Word, 31 КБ)
Что такое последовательные и параллельные схемы?
В различных электрических схемах / гаджетов мы часто используем резисторы в различных комбинациях.
Существует два основных способа соединения резисторов. Это могут быть как последовательные комбинации, так и параллельные комбинации.
Серия Комбинация:Такая комбинация, в которой резисторы соединены последовательно, называется последовательной комбинацией. Положительная клемма одного резистора соединена с отрицательной клеммой другого резистора.
Давайте применим закон Ома к последовательной комбинации, чтобы определить эффективное сопротивление цепи.
V = V 1 + V 2 + V 3
V 1 = IR 1 , V 2 = IR 2 , V = IR 3
Если все три резистора заменяются одним резистором, Req
And I — ток, проходящий через всю цепь,
IR eq = IR 1 + IR 2 + IR 3
Req = R 1 + R 2 + R 3
Та же логика может быть применена к схеме, содержащей более 3 резисторов,
R экв = R 1 + R 2 + R 3 + ———– R n
Таким образом, мы можем заключить, что в последовательной комбинации эффективное сопротивление больше, чем индивидуальное сопротивление.
В схеме, когда резисторы включены параллельно через батарею, мы получаем параллельную схему
В параллельной комбинации было замечено, что полный ток равен сумме отдельных токов через каждую ветвь комбинации.
I = I 1 + I 2
Пусть Rp будет эффективным сопротивлением параллельной комбинации.
Применяя закон Ома,
V / R_p = V / R_1 + V / R_2
1 / R_p = 1 / R_1 + 1 / R_2
Тот же аргумент можно применить и к более чем 2 резисторам,
1 / R_p = 1 / R_1 + 1 / R_2 + 1 / R_3 ± —1 / R_n
Общее или эффективное сопротивление цепи, имеющей параллельную комбинацию, всегда меньше, чем наименьший резистор.
Преимущества параллельной комбинации перед последовательной
В последовательной цепи ток постоянен во всей цепи. Было бы невозможно подключить гаджет (например, гейзер), который требует более высокого значения тока, к гаджету (например, (электрическая лампочка), которая требует меньшего тока последовательно.
Параллельная комбинация работает в приведенном выше случае, поскольку мы можем изменять ток через разные ветви
Еще один серьезный недостаток — если один компонент выходит из строя, выходит из строя вся цепь.
Q.1 общее сопротивление в параллельной комбинации составляет
a) Больше, чем отдельный резистор
b) Меньше, чем отдельный резистор
c) То же, что и каждый резистор
Q.2 Общее сопротивление последовательной комбинации
a) Больше, чем отдельный резистор
b) Меньше, чем отдельный резистор
c) То же, что и каждый резистор
Q.3 Сила тока одинакова на всем протяжении
a) Последовательная схема
b) Параллельная схема
c) Оба вышеперечисленных
d) Ничего из вышеперечисленного
Q.

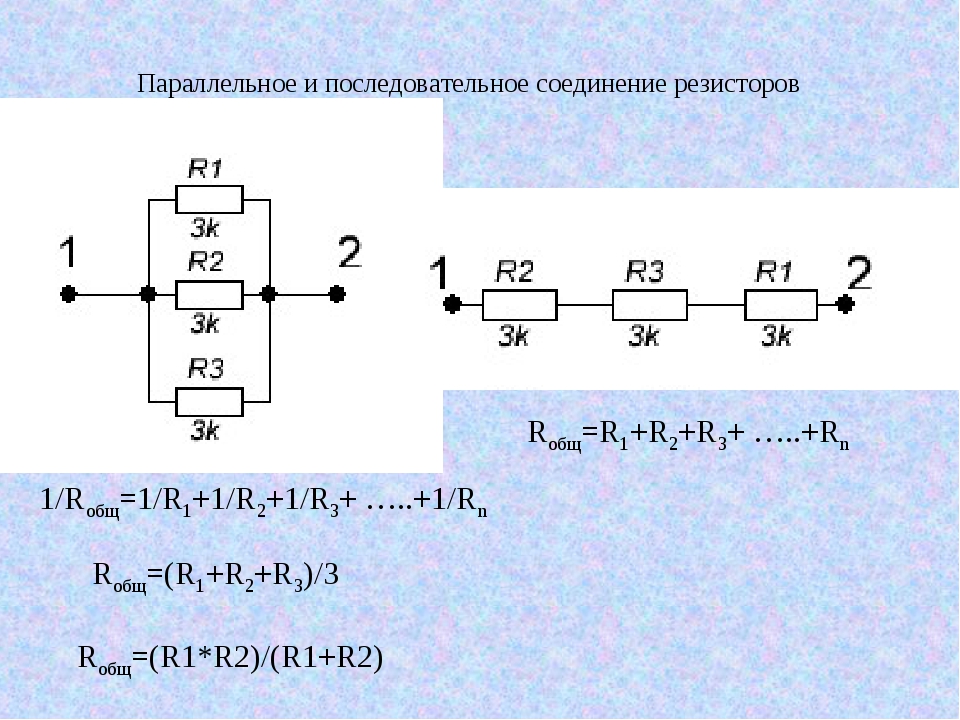 ..I*Rn
..I*Rn