Активное и реактивное сопротивление. Формула ёмкостного сопротивления для цепи переменного тока

В цепи постоянного тока конденсатор представляет собой бесконечно большее сопротивление: постоянный ток не проходит через диэлектрик, разделяющий обкладки конденсатора. Цепи переменного тока конденсатор не разрывает: попеременно заряжаясь и разряжаясь, он обеспечивает движение электрических зарядов, т. е. поддерживает переменный ток во внешней цепи. Исходя из электромагнитной теории Максвелла (см. § 105), можно сказать, что переменный ток проводимости замыкается внутри конденсатора током смещения. Таким образом, для переменного тока конденсатор представляет собой конечное сопротивление, называемое емкостным сопротивлением.

Опыт и теория показывают, что сила переменного тока в проводе существенно зависит от формы, которая придана этому проводу. Сила тока будет, наибольшей в случае прямого провода. Если же провод свернут в виде катушки с большим числом витков, то сила тока в нем значительно уменьшится: особенно резкое снижение тока происходит при введении в эту катушку ферромагнитного сердечника.

Это означает, что для переменного тока проводник помимо омического сопротивления имеет еще дополнительное сопротивление, зависящее от индуктивности проводника и потому называемое индуктивным сопротивлением. Физический смысл индуктивного сопротивления состоит в следующем. Под влиянием изменений тока в проводнике, обладающем индуктивностью, возникает электродвижущая сила самоиндукции, препятствующая этим изменениям, т. е. уменьшающая амплитуду тока а следовательно, и эффективный ток Уменьшение эффективного тока в проводнике равносильно увеличению сопротивления проводника, т. е. равносильно появлению дополнительного (индуктивного) сопротивления.

Получим теперь выражения для емкостного и индуктивного сопротивлений.

1. Емкостное сопротивление. Пусть к конденсатору емкостью С (рис. 258) приложено переменное синусоидальное напряжение

Пренебрегая падением напряжения на малом омическом сопротивлении подводящих проводов, будем считать, что напряжение на обкладках конденсатора равно приложенному напряжению:

В любой момент времени заряд конденсатора равен произведению емкости конденсатора С на напряжение (см. § 83):

Если за малый промежуток времени заряд конденсатора изменяется на величину то это означает, что в подводящих проводах идет ток равный

Так как амплитуда этого тока

то окончательно получим

Запишем формулу (37) в виде

Последнее соотношение выражает закон Ома; величина играющая роль сопротивления, представляет собой сопротивление конденсатора для переменного тока, т. е. емкостное сопротивление

Таким образом, емкостное сопротивление обратно пропорционально круговой частоте тока и величине емкости. Физический смысл этой зависимости нетрудно понять. Чем больше емкость конденсатора и чем чаще изменяется направление тока (т. е. чем больше круговая частота тем больший заряд проходит за единицу времени через поперечное сечение подводящих проводов. Следовательно, ). Но сила тока и сопротивление обратно пропорциональны друг другу.

Следовательно, сопротивление

Рассчитаем емкостное сопротивление конденсатора емкостью включенного в цепь переменного тока частотой Гц:

При частоте Гц емкостное сопротивление того же самого конденсатора снизится приблизительно до 3 Ом.

Из сопоставления формул (36) и (38) видно, что изменения тока и напряжения совершаются в различных фазах: фаза тока на больше фазы напряжения. Это означает, что максимум тока наступает на четверть периода раньше, чем максимум напряжения (рис. 259).

Итак, на емксстном сопротивлении ток опережает напряжение на четверть периода (по времени) или на 90° (по фазе).

Физический смысл этого важного явления можно пояснить следующим образом, В начальный момент времени конденсатор еще не заряжен Поэтому даже очень малое внешнее напряжение легко перемещает заряды к пластинам конденсатора, создавая ток (см. рис. 258). По мере зарядки конденсатора напряжение на его обкладках растет, препятствуя дальнейшему притоку зарядов. В связи с этим ток в цепи уменьшается, несмотря на продолжающееся увеличение внешнего напряжения

Следовательно, в начальный момент времени ток имел максимальное значение ( Когда а вместе с ним и достигнут максимума (что произойдет через четверть периода), конденсатор полностью зарядится и ток в цепи прекратится Итак, в начальный момент времени ток в цепи максимален, а напряжение минимально и только еще начинает нарастать; через четверть периода напряжение достигает максимума, а ток уже успевает уменьшиться до нуля.

Таким образом, действительно ток опережает напряжение на четверть периода.

2. Индуктивное сопротивление. Пусть через катушку самоиндукции с индуктивностью идет переменный синусоидальный ток

обусловленный переменным напряжением приложенным к катушке

Пренебрегая падением напряжения на малом омическом сопротивлении подводящих проводов и самой катушки (что вполне допустимо, если катушка изготовлена, например, из толстой медной проволоки), сбудем считать, что приложенное напряжение уравновешивается электродвижущей силой самоиндукции (равно ей по величине и противоположно по направлению):

Тогда, учитывая формулы (40) и (41), можем написать:

Так как амплитуда приложенного напряжения

то окончательно получим

Запишем формулу (42) в виде

Последнее соотношение выражает закон Ома; величина играющая роль сопротивления, представляет собой индуктивное сопротивление катушки самоиндукции:

Таким образом, индуктивное сопротивление пропорционально круговой частоте тока и величине индуктивности.

Такого рода зависимость объясняется тем, что, как уже отмечалось в предыдущем параграфе, индуктивное сопротивление обусловлено действием электродвижущей силы самоиндукции, уменьшающей эффективный ток и, следовательно, увеличивающей сопротивление.

Величина же этой электродвижущей силы (и, следовательно, сопротивления) пропорциональна индуктивности катушки и скорости изменения тока, т. е. круговой частоте

Рассчитаем индуктивное сопротивление катушки с индуктивностью включенной в цепь переменного тока с частотой Гц:

При частоте Гц индуктивное сопротивление той же самой катушки возрастает до 31 400 Ом.

Подчеркнем, что омическое сопротивление катушки (с железным сердечником), имеющей индуктивность составляет обычно лишь несколько Ом.

Из сопоставления формул (40) и (43) видно, что изменения тока и напряжения совершаются в различных фазах, причем фаза тока на меньше фазы напряжения. Это означает, что максимум тока наступает на четверть периода (774) позже, чем максимум напряжения (рис. 261).

Итак, на индуктивном сопротивлении ток отстает от напряжения на четверть периода (по времени), или на 90° (по фазе). Сдвиг фаз обусловлен тормозящим действием электродвижущей силы самоиндукции: она препятствует как нарастанию, так и убыванию тока в цепи, поэтому максимум тока наступает позднее, чем максимум напряжения.

Если в цепь переменного тока последовательно включены индуктивное и емкостное сопротивления, то напряжение на индуктивном сопротивлении будет, очевидно, опережать напряжение на емкостном сопротивлении на полпериода (по времени), или на 180° (по фазе).

Как уже упоминалось, и емкостное и индуктивное сопротивления носят общее название реактивного сопротивления. На реактивном сопротивлении электроэнергия не расходуется; этим оно существенно отличается от активного сопротивления. Дело в том, что энергия, периодически потребляемая на создание электрического поля в конденсаторе (во время его зарядки), в том же количестве и с той же периодичностью возвращается в цепь при ликвидации этого поля (во время разрядки конденсатора).

Точно так же энергия, периодически потребляемая на создание магнитного поля катушки самоиндукции (во время возрастания тока), в том же количестве и с той же периодичностью возвращается в цепь при ликвидации этого поля (во время убывания тока).

В технике переменного тока вместо реостатов (омического сопротивления), которые всегда нагреваются и бесполезно расходуют энергию, часто применяются дроссели (индуктивное сопротивление). Дроссель представляет собой катушку самоиндукции с железным сердечником. Оказывая значительное сопротивление переменному току, дроссель практически не нагревается и не расходует электроэнергию.

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности.

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.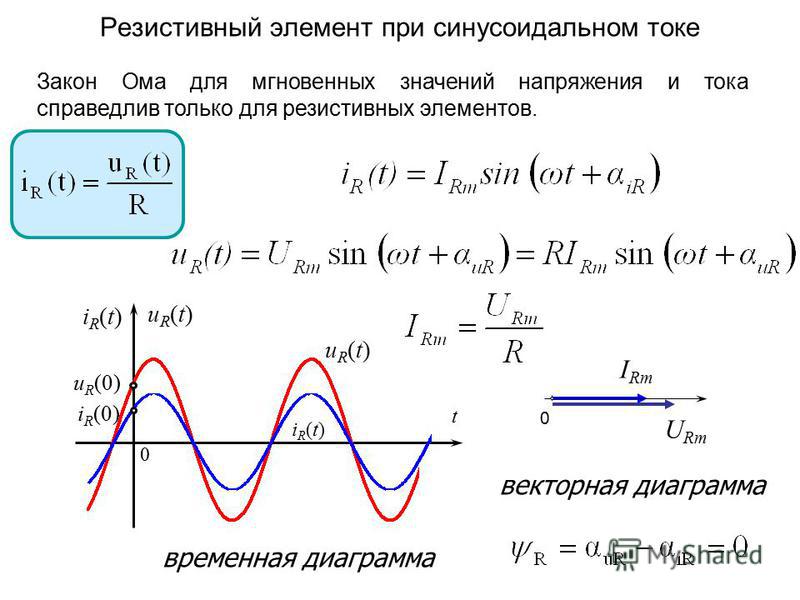
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U , подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение U , ток не может начаться мгновенно по причине противодействия ЭДС, равного -U , поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε ), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt) .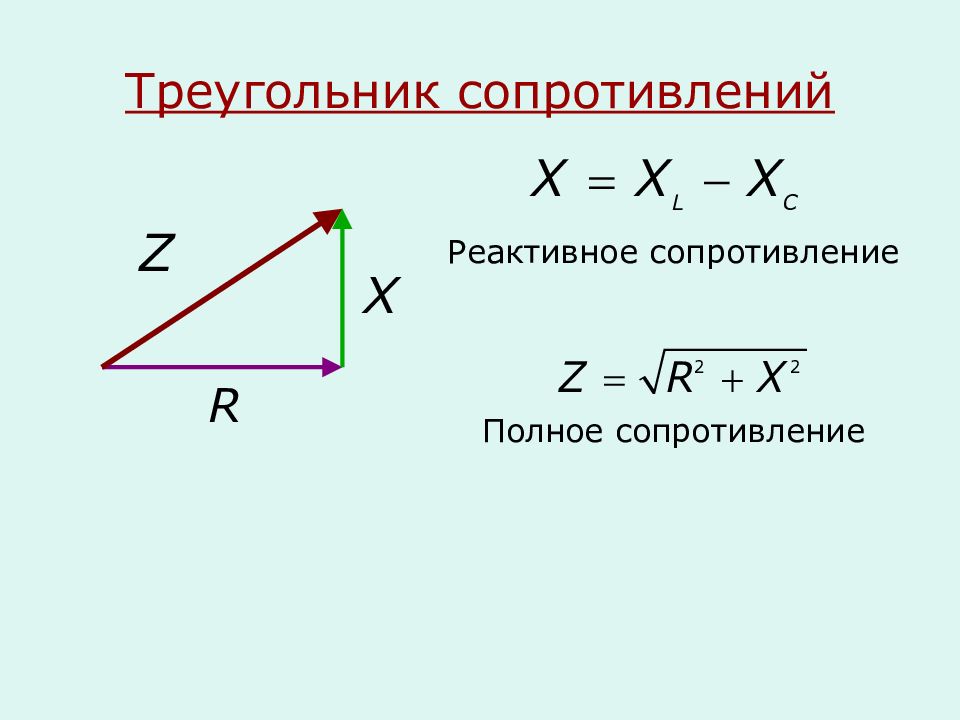
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t) , либо равная ей функция sin(t-π/2) .
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω .
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL , которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора.

Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

Если приложить к конденсатору напряжение U , мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt) .
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2) .
Тогда для синусоидального напряжения u = U amp sin(ωt) запишем выражение мгновенного значения тока следующим образом:

i = U amp ωCsin(ωt+π/2) .

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.

Онлайн-калькулятор расчёта реактивного сопротивления

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Реактивное сопротивление ёмкости X C = 1 /(2πƒC)

ОПРЕДЕЛЕНИЕ

Конденсатор , в простейшем случае состоит из двух металлических проводников (обкладок), которые разделяет слой диэлектрика. Каждая из обкладок конденсатора имеет свой вывод и может быть подключена к электрической цепи.

Конденсатор характеризуют при помощи ряда параметров (емкость, рабочее напряжение и т.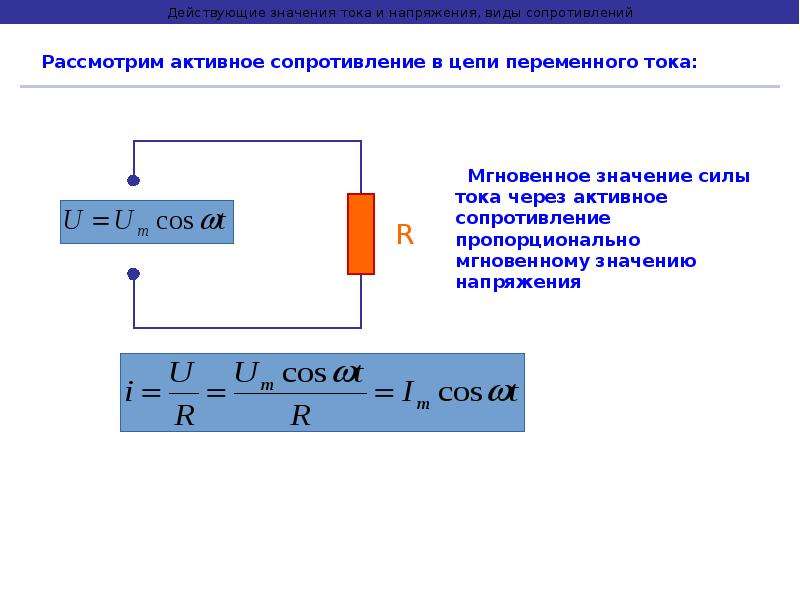 д), одной из таких характеристик является сопротивление. Конденсатор практически не пропускает постоянный электрический ток. То есть сопротивление конденсатора является бесконечно большим для постоянного тока, но это идеальный случай. Через реальный диэлектрик очень малый ток протекать может. Этот ток называют током утечки. Ток утечки является показателем качества диэлектрика, который применяется при изготовлении конденсатора. У современных конденсаторов ток утечки составляет некоторые доли микроампера. Сопротивление конденсатора в таком случае можно вычислить, используя закон Ома для участка цепи, зная величину напряжения, до которой заряжен конденсатор и ток утечки. Но обычно при решении учебных задач сопротивление конденсатора постоянному току считают бесконечно большим.

Сопротивление конденсатора переменному напряжению

При включении конденсатора в цепь с переменным током, ток свободно проходит через конденсатор. Это объясняется очень просто: происходит процесс постоянной зарядки и разрядки конденсатора. При этом говорят, что в цепи присутствует емкостное сопротивление конденсатора, помимо активного сопротивления.

И так, конденсатор, который включен в цепь переменного тока, ведет себя как сопротивление, то есть оказывает влияние на силу тока, текущую в цепи. Величину емкостного сопротивления обозначим как , его величина связана с частотой тока и определена формулой:

где — частота переменного тока; — угловая частота тока; C — емкость конденсатора.

Если конденсатор включен в цепь переменного тока, то в нем не затрачивается мощность, потому что фаза тока сдвинута по отношению к напряжению на . Если рассмотреть один период колебания тока в цепи (T), то происходит следующее: при заряде конденсатора (это составляет ) энергия в поле конденсатора запасается; на следующем отрезке времени () конденсатор разряжается и отдает энергию в цепь. Поэтому ёмкостное сопротивление называют реактивным (безваттным).

Следует заметить, что в каждом реальном конденсаторе реальная мощность (мощность потерь) все же тратится, при течении через него переменного тока. Это вызвано тем, что происходят изменения в состоянии диэлектрика конденсатора. Помимо этого существует некоторая утечка в изоляции обкладок конденсатора, поэтому появляется небольшое активное сопротивление, которое как бы включено параллельно конденсатору.

Примеры решения задач

ПРИМЕР 1

Задание	Колебательный контур имеет сопротивление (R), катушку индуктивности (L) и конденсатор емкости C (рис.1). К нему подключено внешнее напряжение, амплитуда которого равна , а частота составляет . Какова амплитуда силы тока в цепи?
Решение	Сопротивление контура рис.1 складывается из активного сопротивления R, емкостного сопротивления конденсатора и сопротивления катушки индуктивности . Полное сопротивление цепи (Z), которая содержит названные выше элементы, находят как: Закон Ома для нашего участка цепи можно записать как: Выразим искомую амплитуду силы тока из (1.2), подставим вместо Z правую часть формулы (1. 1), имеем:
Ответ

Если в цепь постоянного тока включить конденсатор (идеальный — без потерь), то в течение короткого времени после включения по цепи потечет зарядный ток. После того как конденсатор зарядится до напряжения, соответствующего напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи или бесконечно большое сопротивление.

Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.

При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.

В момент включения напряжение на конденсаторе равно нулю. Если включить конденсатор к переменному напряжению сети, то в течение первой четверти периода, когда напряжение сети будет возрастать (рисунок 1), конденсатор будет заряжаться.

Рисунок 1. Графики и векторная диаграмма для цепи переменного тока, содержащей емкость

По мере накопления зарядов на обкладках конденсатора напряжение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимума, заряд конденсатора прекращается и ток в цепи становится равным нулю.

Ток в цепи конденсатора можно определить по формуле:

где q — количество электричества, протекающее по цепи.

Из электростатики известно:

q = C × u C = C × u ,

где C — емкость конденсатора; u — напряжение сети; u C — напряжение на обкладках конденсатора.

Окончательно для тока имеем:

Из последнего выражения видно, что, когда максимально (положения а , в , д ), i также максимально. Когда (положения б , г на рисунке 1), то i также равно нулю.

Во вторую четверть периода напряжение сети будет уменьшаться, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное. В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд. Из рисунка 1 видно, что ток в цепи с емкостью в своих изменениях опережает по фазе на 90° напряжение на обкладках конденсатора.

Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.

Поскольку мы отметили выше, что скорость изменения тока пропорциональна угловой частоте ω, из формулы

получаем аналогично, что скорость изменения напряжения также пропорциональна угловой частоте ω и для действующего значения тока имеем

I = 2 × π × f × C × U .

Обозначая , где x C называется емкостным сопротивлением , или реактивным сопротивлением емкости . Итак мы получили формулу емкостного сопротивления при включении емкости в цепи переменного тока. Отсюда, на основании выражения закона Ома, мы можем получить ток для цепи переменного тока, содержащей емкость:

Напряжение на обкладках конденсатора

U C = I C × x C .

Та часть напряжения сети, которая имеется на конденсаторе, называется емкостным падением напряжения , или реактивной слагающей напряжения , и обозначается U C .

Емкостное сопротивление x C , так же как индуктивное сопротивление x L , зависит от частоты переменного тока.

Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет уменьшаться.

Пример 1. Определить емкостное реактивное сопротивление конденсатора емкостью 5 мкФ при разных частотах сетевого напряжения. Расчет емкостного сопротивления произведем при частоте 50 и 40 Гц:

при частоте 50 Гц:

при частоте 400 Гц:

Применим формулу средней или активной мощности для рассматриваемой цепи:

P = U × I × cos φ .

Так как в цепи с емкостью ток опережает напряжение на 90°, то

φ = 90°; cos φ = 0 .

Поэтому активная мощность также равна нулю, то есть в такой цепи, как и в цепи с индуктивностью, расхода мощности нет.

На рисунке 2 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.

Рисунок 2. Кривая мгновенной мощности в цепи с емкостью

Энергию, запасаемую конденсатором к моменту прохождения напряжения на нем через максимум, можно определить по формуле:

В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.

За вторую половину периода явление колебаний энергии повторяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без потерь.

Details 08 May 2017

Господа, сегодняшнюю статью можно считать в некотором роде продолжением предыдущей. Сначала я даже хотел поместить весь этот материал в одну статью. Но его получилось довольно много, на горизонте были новые проекты, и я в итоге разделил его на две. Итак, сегодня мы поговорим про . Мы получим выражение, по которому можно будет рассчитать, чему равно сопротивление любого конденсатора, включенного в цепь с переменным током, а в конце статьи рассмотрим несколько примеров такого расчета.

Давайте представим, что у нас есть конденсатор, который включен в цепь с переменным током. В цепи больше нет никаких компонентов, только один конденсатор и все (рисунок 1).

Рисунок 1 — Конденсатор в цепи переменного тока

К его обкладкам приложено некоторое переменное напряжение U(t) , и через него течет некоторый ток I(t) . Зная одно, можно без проблем найти другое. Для этого надо всего лишь вспомнить прошлую статью про конденсатор в цепи переменного тока , там мы про все это довольно подробно говорили. Будем полагать, что ток через конденсатор изменяется по синусоидальному закону вот так

В прошлой статье мы пришли к выводу, что если ток изменятся вот по такому закону, то напряжение на конденсаторе должно меняться следующим образом

Пока что ничего нового мы не записали, это все дословное повторение выкладок из предыдущей статьи. А сейчас самое время их немного преобразовать, придать им чуть другой облик. Если говорить конкретно, то нужно перейти к комплексному представлению сигналов! Помните, на эту тему была отдельная ? В ней я говорил, что она нужна для понимания некоторых моментов в дальнейших статьях. Вот как раз и наступил тот момент, когда пора вспомнить все эти хитрые мнимые единицы. Если говорить конкретно, то сейчас нам потребуется показательная запись комплексного числа. Как мы помним из статьи про комплексные числа в электротехнике, если у нас есть синусоидальный сигнал вида

то его можно представить в показательной форме вот так

Почему это так, откуда взялось, что здесь какая буковка значит — обо всем уже подробно говорили. Для повторения можно перейти по ссылке и еще раз со всем ознакомиться.

Давайте-ка теперь применим это комплексное представление для нашей формулы напряжения на конденсаторе. Получим что-то типа такого

Теперь, господа, я хотел бы вам рассказать еще про один интересный момент, который, наверное, следовало бы описать в статье про комплексные числа в электротехнике. Однако тогда я про него как-то позабыл, поэтому давайте рассмотрим его сейчас. Давайте представим, что t=0 . Это приведет к исключению из расчетов времени и и частоты, и мы переходим к так называемым комплексным амплитудам сигнала. Безусловно, это не значит, что сигнал из переменного становится постоянным. Нет, он все так же продолжает изменяться по синусу с той же самой частотой. Но бывают моменты, когда частота нам не очень важна, и тогда лучше от нее избавиться и работать только с амплитудой сигнала. Сейчас как раз такой момент. Поэтому полагаем t=0 и получаем комплексную амплитуду напряжения

Давайте раскроем скобки в экспоненте и воспользуемся правилами работы с показательными функциями.

Итак, у нас имеется три множителя. Будем разбираться со всеми по порядку. Объединим первые два и запишем выражение следующего вида

Что мы вообще такое записали? Правильно, комплексную амплитуду тока через конденсатор. Теперь выражение для комплексной амплитуды напряжения принимает вид

Результат, к которому мы стремимся, уже близок, но остается еще один не очень приятный множитель с экспонентой. Как с ним быть? А, оказывается, очень просто. И снова нам на помощь придет статья по комплексным числам в электротехнике , не зря ж я ее писал . Давайте преобразуем этот множитель, воспользовавшись формулой Эйлера:

Да, вся эта хитрая экспонента с комплексными числами в показателе превращается всего лишь в мнимую единичку, перед которой стоит знак минус. Согласен, возможно, осознать это не так просто, но тем не менее математика говорит, что это так. Поэтому результирующая формула у нас принимает вид

Давайте выразим из этой формулы ток и приведем выражение к виду, соответствующему закону Ома. Получим

Как мы помним из статьи про закон Ома , у нас ток равнялся напряжению, деленному на сопротивление. Так вот, здесь практически то же самое! Ну, за исключением того, что у нас ток и напряжение — переменные и представлены через комплексные амплитуды. Кроме того, не забываем, что ток течет у нас через конденсатор. Поэтому, выражение, которое стоит в знаменателе, можно рассматривать как емкостное сопротивление конденсатора переменному току :

Да, выражение для сопротивления конденсатора имеет вот такой вот вид. Оно, как вы можете заметить, комплексное . Об этом свидетельствует буковка j в знаменателе дроби. А что значит эта комплексность? На что она влияет и что показывает? А показывает она, господа, исключительно сдвиг фаз в 90 градусов между током и напряжением на конденсаторе. А именно, ток на 90 градусов опережает напряжение. Этот вывод не является для нас новостью, про все это было подробно рассказано в прошлой статье . Чтобы это лучше осознать, надо теперь мысленно пройтись от полученной формулы вверх к тому моменту, где у нас это j возникло. В процессе подъема вы увидите, что мнимая единица j возникло из формулы Эйлера из-за того, что там был компонент . Формула Эйлера у нас возникла из комплексного представления синусоиды. А в исходной синусоиде как раз был заложен сдвиг фазы в 90 градусов тока относительно напряжения. Как-то так. Вроде все логично и ничего лишнего не возникло.

Теперь может возникнуть два совершенно логичных вопроса: как работать с таким представлением и в чем его выгода? Да и вообще, пока лишь какие-то дико абстрактные буковки и нифига не ясно, как взять и оценить сопротивление какого-нибудь конкретно конденсатора, который мы купили в магазине и воткнули в схему. Давайте разбираться постепенно.

Как мы уже говорили, буковка j в знаменателе говорит нам лишь о сдвиге фаз тока и напряжения. Но она не влияет на амплитуды тока и напряжения. Соответственно, если сдвиг фаз нас не интересует , то можно исключить эту буковку из рассмотрения и получить более простое выражение абсолютно без всяких комплексностей:

Что еще мы можем сказать, глядя на эту формулу? Например, то, что чем больше частота сигнала, тем меньше для него сопротивление конденсатора. И чем больше емкость конденсатора, тем меньше его сопротивление переменному току.

По аналогии с резисторами, сопротивление конденсаторов измеряется все так же в Омах . Однако всегда следует помнить, что это немного другое сопротивление, его называют реактивным . И другое оно в первую очередь из-за того самого пресловутого j в знаменателе, то есть из-за сдвига фазы. У «обычных» (которые называют активными ) Омов такого сдвига нет, там напряжение четко совпадает по фазе с током. Давайте построим график зависимости сопротивления конденсатора от частоты. Для определенности емкость конденсатора возьмем фиксированной, скажем, 1 мкФ. График представлен на рисунке 2.

Рисунок 2 (кликабельно) — Зависимость сопротивления конденсатора от частоты

На рисунке 2 мы видим, что сопротивление конденсатора переменному току убывает по закону гиперболы.

При стремлении частоты к нулю (то есть фактически при стремлении переменного току к постоянному) сопротивление конденсатора стремится к бесконечности. Это и логично: мы все помним, что для постоянного тока конденсатор фактически представляет собой разрыв цепи. На практике оно, конечно, не бесконечно, а ограничено сопротивлением утечки конденсатора. Тем не менее, оно все равно очень велико и часто его и считают бесконечно большим.

Есть еще один вопрос, который хотелось бы обговорить, прежде чем начинать рассмотрение примеров. Зачем вообще писать букву j в знаменателе сопротивления? Не достаточно ли просто всегда помнить про сдвиг фаз, а в записи использовать числа без этой мнимой единицы? Оказывается, нет. Представим себе цепь, где одновременно присутствуют резистор и конденсатор. Скажем, они соединены последовательно. И вот тут-то как раз мнимая единичка рядом с емкостью не позволит просто так взять и сложить активное и реактивное сопротивление в одно действительное число. Общее сопротивление такой цепочки будет комплексным, причем состоящим как из действительной части, так и из мнимой. Действительная часть будет обусловлена резистором (активными сопротивлением), а мнимая — емкостью (реактивным сопротивлением). Впрочем, это все тема для другой статьи, сейчас не будем в это углубляться. Давайте лучше перейдем к примерам.

Пусть у нас есть конденсатор емкостью, скажем C=1 мкФ . Требуется определить его сопротивление на частоте f 1 =50 Гц и на частоте f 2 =1 кГц . Кроме того, следует определить амплитуду тока с учетом того, что амплитуда приложенного к конденсатору напряжения равна U m =50 В . Ну и построить графики напряжения и тока.

Собственно, задачка эта элементарная. Подставляем циферки в формулу для сопротивления и получаем для частоты f 1 =50 Гц сопротивление, равное

А для частоты f 2 =1 кГц сопротивление будет

По закону Ома находим величину амплитуды тока для частоты f 1 =50 Гц

Аналогично для второй частоты f 2 =1 кГц

Теперь мы легко можем записать законы изменения тока и напряжения, а также построить графики для этих двух случаев. Полагаем, что напряжение у нас изменяется по закону синуса для первой частоты f 1 =50 Гц следующим образом

А для второй частоты f 2 =1 кГц вот так

и для частоты f 2 =1 кГц

f 1 =50 Гц представлены на рисунке 3

Рисунок 3 (кликабельно) — Напряжение на конденсаторе и ток через конденсаторе, f 1 =50 Гц

Графики тока и напряжения для частоты f 2 =1 кГ ц представлены на рисунке 4

Рисунок 4 (кликабельно) — Напряжение на конденсаторе и ток через конденсаторе, f 2 =1 кГц

Итак, господа, мы сегодня познакомились с таким понятием, как сопротивление конденсатора переменному току, научились его считать и закрепили полученные знания парочкой примеров. На сегодня все. Спасибо что прочитали, всем огромной удачи и пока!

Вступайте в нашу

Простейшие цепи переменного тока — Электротехника — Учебные материалы — Каталог статей

Список всех статей на технические темы

Простая электротехника все статьи

Сначала читаем статью «Переменный ток — краткие сведения»

 

Все электротехнические устройства состоят из сопротивлений индуктивностей и емкостей

 

 

Соотношение индуктивности емкости в цепи переменного тока принципиально определяют свойства цепи переменного тока.

 

Активное сопротивление R — это такой элемент электрической цепи, который оказывает сопротивление току с выделением тепла. Ведет себя одинаково в цепях постоянного и переменного тока, хотя величина сопротивления несколько отличается, это придется учитывать в точных расчетах.

 

 

Индуктивность L –это такой элемент электрической цепи, который состоит из витков провода и при протекании тока создает магнитное поле, это магнитное поле противодействует изменениям тока.

 

 

При протекании постоянного тока индуктивность ведет себя как проволока и не считается сопротивлением. Сопротивлением она является только для переменного тока, чем больше частота переменного тока, тем больше сопротивление индуктивности.

 

Емкость C – это такой элемент электрической цепи, который накапливает заряд, и проводит ток, только пока заряжается, или разряжается, поэтому в цепях постоянного тока, тока не проводит, а в цепях переменного тока все время заряжается – разряжается и, значит, проводит ток. Сопротивление емкости переменному току тем меньше, чем выше частота переменного тока.

 

 

Емкость и индуктивность взаимно противоположные по свойствам элементы, значит, они могут снижать взаимное влияние в цепях переменного тока или совсем отключать друг друга. Емкость и индуктивность оказывают сопротивление переменному току, но не могут выделить тепла, поэтому на них не происходит прямых потерь мощности.

Активное сопротивление R в цепи переменного тока

 

Что нам интересно знать про простейшую электрическую цепь содержащую R ?

 

  

 

Какой ток протекает в ней, какое напряжение на ней действует? и какая мощность может быть получена.

 

    

 

 

 

 

Здесь изображены две синусоиды, которые нельзя сравнивать и говорить какая больше, какая меньше. Они разные для удобства рассмотрения. Красная синусоида изображает переменное напряжение, а синяя синусоида изображает переменный ток

 

Если через активное R сопротивление протекает переменный синусоидальный ток, то на нем действует переменное синусоидальное напряжение. Ток и напряжение имеют одинаковую частоту и совпадают по фазе.

 

Мощность на активном сопротивлении определяется как произведение тока и напряжения. Действующая мощность будет равна произведению действующего значения тока на действующее значение напряжения.

 

 

Черные полуволны показывают, что мощность выделяемая в цепи на активном сопротивление изменяется также по синусоидальному закону,

Только знак остается все время положительным, это значит, что поток мощности однонаправлен. Мощность получается как произведение каждой точки синусоиды тока на каждую точку синусоиды напряжения в один и тот же момент. Плюс напряжения на плюс тока даст нам плюс мощности. Минус напряжения на минус тока даст нам плюс мощности.

Это значит, что при протекании тока через активное сопротивление R, электрическая мощность приводит к выделению тепла.

 

P=UI U = Uа√2 ; I = Iа√2 P = UаIа/2

 

Средняя мощность за период равна постоянной составляющей мощности

Uа Iа/2

 

Физический смысл этого явления состоит в том, что активное сопротивление потребляет энергию от источника, выделяет энергию в виде тепла. Электрическая мощность, которая превращается в тепло, называется активной мощностью и обозначается, как и в цепях постоянного тока, буквой P

 

Активными сопротивлениями в цепях переменного тока являются нагревательные и осветительные приборы, а также резисторы в сигнальных схемах, кроме того, как активные сопротивления проявляют себя все устройства, на которых выделяется полезная мощность в любом виде. Например, электрический мотор, звуковые динамики и т. п.

 

Индуктивное сопротивление в цепи переменного тока

 

X_L = ωL     

 

Чтобы сделать сосредоточенную индуктивность, кусок проволоки сматывают в катушку

Если к цепи с индуктивностью подключить переменное синусоидальное напряжение, то в ней должен протекать переменный синусоидальный ток.

Что же происходит в цепи с индуктивностью при протекании переменного тока.

Оказывается, ток и напряжение действуют не одновременно,

то есть, сдвинуты по фазе

 

На активном сопротивлении R, появление напряжения сразу – в тот же момент,  вызывает появление тока, и они действуют в одной фазе.

На индуктивности так не получается.

Если напряжение от источника начинает нарастать, то ток за ним не успевает.

Почему? В индуктивности изменение тока, приводит к появлению ЭДС самоиндукции, а эта ЭДС направлена на встречу изменения тока. Напряжение растет, и ток хочет расти, но ЭДС самоиндукции препятствует нарастанию тока. Это примерно также, как сила инерции мешает разогнать тележку, когда мы сдвигаем ее с места.

Ток преодолевает сопротивление направленной навстречу ему ЭДС самоиндукции, и начинает нарастать, но это происходит, когда напряжение уже достигло максимального значения. Ток, наконец, достигает максимального значения, но напряжение в этот момент уже снизилось до нуля. Так и повторяется – ток все время отстает от напряжения на 90⁰ то есть на π/2. Значит, фаза тока отрицательна и составляет  — π/2 

 

Откуда берется эта ЭДС самоиндукции, и почему она не мешает в цепи с сопротивлением  R. Это связано с тем, что катушка индуктивности, в отличие от сопротивления R, создает сильное магнитное поле, благодаря большому количеству витков. Магнитное поле не может мгновенно изменяться, оно и рождает внутри провода ЭДС, которая препятствует изменению тока.

 

Более подробно об ЭДС самоиндукции смотри в статье  Начальные представления об электромагнетизме

 

 

Красная синусоида напряжения пресекает ноль каждый раз раньше зеленой синусоиды тока на π/2 

     

 

 

Вывод: В цепи с индуктивностью напряжение впереди тока на 90°.

 

Любое сопротивление ограничивает ток, но бывает активное сопротивление, бывает реактивное..

R — активное сопротивление — на нем выделяется тепло

X — реактивное сопротивление на нем  не выделятся тепло

 

X_L – сопротивление индуктивности

X_L – сопротивление индуктивности L является реактивным, оно равно X_L =ωL, то есть, оно прямо пропорционально частоте ω и индуктивности L, чем больше индуктивность, тем больше реактивное сопротивление и чем выше частота тем больше реактивное сопротивление.

Индуктивность тем сильнее ограничивает ток, чем выше частота тока.

Индуктивность пропускает переменный ток тем лучше, чем меньше индуктивность и чем меньше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток индуктивность пропускает без всякого сопротивления

 

 

Мощность на индуктивности

Мощность определяется как произведение тока на напряжение. Для каждого момента времени точка синусоиды тока умножается на точку синусоиды напряжения и получается точка синусоида мощности. Синусоида мощности получается двунаправленной, положительные полупериоды сменяются отрицательными, значит, мощность пол периода выделяется и пол периода поглощается. Это значит, что индуктивность L полпериода накапливает энергию в магнитном поле, а затем полпериода возвращает ее в источник.

 

 

Частота синусоиды мощности вдвое больше частоты тока и напряжения.

На индуктивности не получается выделение тепла, и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на индуктивности, называется реактивной и обозначается не Р, а другой буквой – Q_L

 

 

 

Емкость в цепи переменного тока

 

X_C =1/ ωc  

 

При включении емкости под переменное напряжение во время t=0, конденсатор полностью разряжен, напряжение на конденсаторе равно 0, и он начинает заряжаться. Поэтому мгновенно появляется ток зарядки. По мере зарядки конденсатора на нем начинает расти напряжение, которое тормозит процесс зарядки, а значит, ток зарядки начинает уменьшаться.

 

 

   

 

 

 

Когда U на конденсаторе достигает максимума, это значит, что оно достигло максимума напряжения источника, зарядка продолжаться не может, поэтому ток становится равным 0.

Синусоида тока (синяя) каждый раз пресекает ноль на π/2 раньше, чем (красная) синусоида напряжения.

То есть, максимальному напряжению на емкости соответствует ток, равный 0, а это значит, что ток на емкости С впереди напряжения на 90° или π/2

 

X_C — сопротивление емкости

X_C — сопротивление емкости является реактивным, оно равно X_C =1/ ωc, то есть оно обратно пропорционально частоте и емкости, чем больше емкость, тем меньше реактивное сопротивление и чем выше частота тем меньше меньше реактивное сопротивление.

Емкость пропускает переменный ток тем лучше, чем больше емкость и чем выше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток емкость вообще не пропускает.

Конденсатор часто ставят в участки цепей, в которых не должен проходить постоянный ток

 

 

Мощность в цепи с емкостью

 

Произведение тока и напряжения для емкости дает синусоиду, которая состоит из положительных и отрицательных полуволн, значит, средняя за период мощность равна 0.

 

 

 

Физический смысл состоит в том, что емкость за пол периода получает энергию, а затем пол периода возвращает ее в источник. Энергия накапливается в электрическом поле емкости, а затем возвращается в источник.  Частота синусоиды мощности вдвое больше частоты тока и напряжения.

Таким образом, на емкости не получается выделение тепла и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на емкости, называется реактивной и обозначается буквой – Qc.

 

Реактивные сопротивления

 

Индуктивность и емкость проявляют себя в электрических цепях как сопротивления.

 

X_C – реактивное сопротивление емкости

X_{L — реактивное сопротивление индуктивности}

Формулы сопротивлений позволяют их использовать для расчета задач по закону Ома для участка цепи.

 

Формула X_C =1/ ωc показывает, что сопротивление емкости зависит от частоты ω. Это означает, что емкость по-разному пропускает ток низкой и высокой частоты.

Емкость пропускает переменный ток тем лучше, чем выше частота.

Емкость вообще не пропускает постоянный ток, и это ее важнейшее свойство. Одно из главных применений емкости (конденсатора) состоит в том, что его ставят в те ветви схем, где запрещено протекание постоянного тока.

 

Формула X_L = ωL _{показывает, что сопротивление индуктивности зависит от частоты. Это означает, что индуктивность по-разному пропускает ток низкой и ток высокой частоты.}

Индуктивность хуже пропускает переменный ток высокой частоты

Чем больше частота. Тем труднее проходит переменный ток. Катушка индуктивности используется для ограничения переменного тока.

Конденсатор и катушка являются противоположностями.

Конденсатор пропускает переменный ток и не пропускает постоянный

Катушка пропускает постоянный ток и не пропускает переменный

 

 

 

Такие цепи содержат сопротивление R, индуктивность L, и ёмкость C.

Реальное сопротивление цепи, содержащей одновременно R, L и C, зависит от величины каждого элемента цепи, и от частоты переменного тока, который протекает в этой цепи.

Расчет цепей переменного тока по аналогии с расчетом цепей постоянного тока невозможен, потому, что необходимо учитывать фазовый сдвиг между током и напряжением.

Можно упростить цепи, если какой-то  элемент: R, L или  C пренебрежительно мал.

 

 

Задачи на переменный ток решаются методом векторных диаграмм.

Ток и напряжение являются векторными величинами.Их изображают как вращающиеся радиус -векторы, в этом смысле они отличаются от векторов сил и скоростей в механике, но правила сложения и вычитания векторов аналогичны.

 

 

Метод векторных диаграмм

 

Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.

 

В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает  изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.

 

Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.

 

Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.

 

Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.

 

 

Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.

Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.

Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.

На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.

 

Векторная диаграмма напряжений представляет собой векторный треугольник напряжений

 

Последовательное соединение L R.

 

Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.

 

 

Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.

Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,

Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.

 

Векторная диаграмма строится так.

 

 

Выберем фазу общего тока равной 0, вектор тока откладывается как горизонтальный вектор слева на право. Далее строим векторную диаграмму напряжений. Сначала откладывается вектор напряжения на сопротивлении R. Этот вектор, пойдет горизонтально, так как его фаза совпадает с фазой тока. Затем строят вектор напряжения на индуктивности L. Его надо откладывать под углом 90

⁰ вверх, это потому, что напряжение на индуктивности впереди на 90⁰.

Второй вектор переносится из центра вращения. Прикладываем его к концу вектора напряжения на активном сопротивлении. Таковы правила сложения векторов.

Теперь остается построить вектор полного напряжения на обоих элементах. Это вектор суммы, он, как известно, строится из начала первого вектора  к концу второго.

Получился прямоугольный треугольник. Любую сторону этого треугольника можно найти по теореме Пифагора.

Острый угол этого треугольника и есть реальный сдвиг фаз в этой цепи между током и общим напряжением. Он обязательно меньше 90 градусов, потому что только на идеально индуктивности он составляет 90 градусов. Активное сопротивление обязательно уменьшает сдвиг фаз.

 

Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление, обозначается Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и X_L

 

Z², = Rа² + X²_L

 

В цепи L R, в отличие от цепи только с L, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.

Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и Q_L

 

S² = Р^{2 +} Q²_L

 

Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников.

 

 

Последовательное соединение RC

Конденсаторы очень часто включают последовательно с сопротивлениями, но если даже специального сопротивления нет, любой конденсатор обладает определённой величиной активного сопротивления, которую необходимо учитывать в точных расчетах. Есть понятие «добротность» конденсатора, которая проявляет  активную составляющую его сопротивления

 

 

При последовательном соединении, через все элементы цепи протекает один ток, который называем – общий.

Сначала откладываем вектор тока, фазу которого принимаем равной нулю. Вектор напряжения на активном сопротивлении, откладываем в том же направлении, так как на активном сопротивлении ток и напряжение совпадают по фазе.

К концу вектора напряжения на активном сопротивлении прикладываем начало вектора напряжения на емкости. Фаза напряжения на емкости отстает от фазы напряжения на активном сопротивлении на 90 градусов, а вектор отстающего напряжения откладывается вниз.

 

Векторная диаграмма напряжений представляет собой прямоугольный треугольник, который позволяет определить все составляющие по теореме Пифагора.

Активное сопротивление R включенное в цепь с катушкой или конденсатором уменьшает угол сдвига фаз.

Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление обозначается буквой Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и X_С

 

Z ² = Rа² + X²_С

 

В цепи L C, в отличие от цепи только с C, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.

 

Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и Q_С

 

S² = Р^{2 +} Q²_С

 

Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников

 

Параллельное соединение RL

 

 

При параллельном соединении RL одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через катушку отстает по фазе от напряжения. на 90⁰. Общий ток отстает от напряжения меньше чем на 90⁰.

Для цепей с параллельным соединением элементов, гораздо удобнее использовать не сопротивления (активные и реактивные) а их обратные величины, которые называются проводимости. Вместо  r используется g, вместо   X_L используется b_L, вместо Xc используется b_c 

 

 

 

 

Параллельное соединение RC

 

При параллельном соединении RС одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через конденсатор опережает по фазе от напряжения. на 90⁰. Общий ток опережает напряжение меньше чем на 90⁰

 

 

 

Значение Cos φ

 

Cos φ в практической электротехнике имеет очень важное значение. Реальные нагрузки, типа электромоторов и трансформаторов, имеют большую индуктивную составляющую сопротивления, то есть, фактически, представляют собой цепи RL. Для таких цепей неизбежно существует сдвиг фаз, который приводит к тому, что полная мощность S значительно превышает активную мощность (P).

 

Из формулы видно, что чем меньше Cos φ (Чем больше угол сдвига фаз), тем меньшую часть активная мощность составляет от полной мощности .

Только активная мощность является полезной, если источник затрачивает полную мощность, а от нагрузки мы можем получить только активную мощность, значит, Cos φ имеет смысл электротехнического КПД или коэффициента мощности.

В идеале источник должен отдавать такую мощность, которую будет потреблять нагрузка. Реальные устройства неизбежно содержат индуктивности (катушки, обмотки, и т.п.), значит, источник вынужден отдавать полную мощность, которая значительно больше, активной.

Проектирование устройств и электрических цепей должно иметь целью получить значение Cos φ как можно ближе к единице, то есть влияние индуктивности надо свести к минимуму. Плохие значения Cos φ приводят к большим неоправданным затратам электроэнергии.

 

Цепи RLC

 

Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.

В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.

 

RLC последовательно

 

 

Как будет выглядеть векторная диаграмма в общем случае?

 

 

 

При последовательном соединении сопротивлений на каждом сопротивлении действует своя часть напряжения. На большем сопротивлении будет большая часть напряжения.

На первой векторной диаграмме видно, что напряжение на конденсаторе U_c больше, чем на катушке U_L тогда суммарный вектор общего напряжения направлен вниз, и видно, xnj угол сдвига фаз отрицательный. На второй диаграмме видно, что напряжение на конденсаторе U_c, значительно меньше, чем U_L , и вектор общего напряжения оказался направленным вверх, угол сдвига фаз стал положительным.

В первом случае цепь имеет емкостный характер, во втором индуктивный.

На определенной частоте наступает равенство Uc = Ul, такое явление называется резонанс напряжений

 

Условие резонанса  X_L = X_C

 

При резонансе напряжений Общее сопротивление цепи становится минимально, а ток становится максимальным, что может быть опасно для источника и требует надежной защиты.

 

 

RLC параллельно

 

 

 

 

 

Векторные диаграммы токов при параллельном соединении

 

 

При параллельно соединении элементов RLC напряжение на всех элементах действует одно и то же, а токи разные, чем меньше сопротивление ветви, тем больше ток. В первом случае ток катушки значительно больше тока конденсатора. Вектор общего тока направлен вниз. Во втором случае ток катушки значительно меньше тока конденсатора и вектор тока направлен вверх.

В первом случае цепь имеет индуктивный характер, во втором емкостный

На определенной частоте наступает равенство токов I_c = I_L  такое явление называется резонанс токов.

При резонансе токов сопротивление цепи становится максимальным и ток уменьшается до величины, которая определяется сопротивлением R, которое остается в цепи.

 

Условия резонанса

Резонанс широко применяется в радиотехнических и различных электронных схемах.

XL = XC

 

 

Устройства для переменного тока и устройства для постоянного тока

Устройства. Которые включаются электрические цепи

Лампочки

Нагреватели

Электромоторы

Электроинструмент

Бытовые приборы

Электроника

И т. п.

 

Лампочки и нагреватели работают одинаково в цепях переменного и постоянного тока. В некоторых случаях разница может быть заметной, так как активное сопротивление в цепи постоянного тока (омическое) может отличаться от сопротивления в цепи переменного тока.

Электромоторы и электроинструмент рассчитанный на переменный ток, при подключении в цепь постоянного тока скорее всего сгорят, так как, у них пропадает индуктивное сопротивление и ток сильно возрастает.

Если моторы, и инструмент рассчитанные на постоянный ток, включены на переменный ток, они сильно потеряют мощность, так как появившееся индуктивное сопротивление и сильно ограничит потребляемый ток.

План-конспект урока по физике. Тема: Реактивное сопротивление в цепи переменного тока ❤️

Цель урока: сформировать у учащихся представление о существовании сопротивления только в цепи переменного тока – это емкостное и индуктивное сопротивления.

Ход урока

Проверка домашнего задания методом выполнения самостоятельной работы

Вариант -1

№1.В колебательном контуре напряжение изменяется по закону: U= 308 QUOTE (B). Определить: а) амплитуду напряжения; б) период, частоту и циклическую

частоту переменного напряжения; в) действующее значение напряжения

№2. В электрическую цепь переменного тока включена электролитическая ванна с раствором медного купороса. Пойдет ли ток через такую цепь? Медь на электродах будет выделяться?

№3. Вращение проволочной рамки в магнитном поле увеличили в 2раза. Во сколько раз поменяется ЭДС индукции и частота переменного тока в рамке?

Вариант -2

№1. В колебательном контуре напряжение меняется по закону: U=60 QUOTE

(B).

Определите: а) амплитуду напряжения; б) период, частоту и циклическую частоту переменного напряжения; в) действующее значение напряжения.

№2. Если электрическая цепь в каком – либо месте рассоединится, то ток сразу прекращается.

Но цепь не разомкнется , если в нее включить конденсатор. Почему?

№3. Рамка площадью 200см2вращается с частотой 10 Гц в однородном магнитном поле индукцией 0,1 Тл. Сколько витков имеет рамка, если амплитудное значение ЭДС равно 53 В?

Изучение нового материала

1. Конденсатор в цепи переменного тока

Постоянный ток не будет идти через цепь, содержащую конденсатор.

Демонстрация опыта; переменный ток в такой цепи существует.

На простых опытах доказываем, что при включении постоянного напряжения лампочка не светится. При включении переменного напряжения лампочка загорается.

Как же переменный ток может идти по цепи , если она разомкнута?

Дело в постоянной перезарядке конденсатора под действием переменного напряжения.

При перезарядке , ток текущий в цепи нагревает нить накала лампочки.

Пренебрегая сопротивлением ,найдем закон изменения силы тока в цепи с емкостью.

U=q/C; QUOTE = Um QUOTE ; Заряд конденсатора меняется по гармоническому закону: q = C Um QUOTE

Производная заряда – сила тока: i = q′= — UmCω QUOTE = UmCω QUOTE QUOTE

Колебания силы тока опережают колебания напряжения на конденсаторе на π/2.

Когда конденсатор начинает заряжаться I=max, а U=0.

В момент когда U=max, I=0. Im= UmCω – амплитуда силы тока

QUOTE = Хс – емкостное сопротивление. I = U/XC – закон Ома для цепи с емкостным сопротивлением справедлив.

Вывод: емкостное сопротивление обратно пропорционально произведению частоты на емкость; колебания напряжения отстают от колебаний силы тока на π/2.

2. Катушка индуктивности в цепи переменного тока.

Демонстрация опыта из которого видно, что индуктивность влияет на силу

переменного тока. Лампа от источника постоянного тока горит ярче, что говорит о том, что действующее значение силы переменного тока меньше силы постоянного тока. Объяснить этос точки зрения самоиндукции (вихревое электрическое поле тормозит движение электронов ).

Сравним напряженности вихревого и кулоновского полей: Е̄I = — Ēk.

Значит, удельная работа вихревого поля равна по величине и противоположна по знаку удельной работе кулоновского поля. ei =- u

Запишем закон по которому меняется сила тока: i= Im QUOTE /

ЭДС самоиндукции: еi= -L i′ = — LωIm QUOTE t. Так как u = — ei, то

u= LωIm QUOTE = LωIm QUOTE = Um QUOTE . Где Um = LωIm – амплитуда напряжения.

Значит, колебания силы тока отстают от колебаний напряжения на π/2.

Амплитуда силы тока в катушке равна : Im= QUOTE

ωL = XL — индуктивное сопротивление I = U/XL — закон Ома справедлив для индуктивного сопротивления в цепи с катушкой.

Вывод: индуктивное сопротивление равно произведению частоты на индуктивность; колебания напряжения опережают колебания силы тока на π/2.

Закрепление изученного материала.

1. Пренебрегая сопротивлением цепи, показать как связаны между собой действующие значени тока и напряжения на конденсаторе и на катушке.

2. Чему равна энергия в цепи, содержащий только катушку или только конденсатор, если пренебречь активным сопротивлением?

3. Выключатель и конденсатор похожи. Почему же выключатель надежно размыкает цепь, а конденсатор служит для других целей?

4. Объяснить почему напряжение и ЭДС самоиндукции имеют противоположные знаки на катушке?

Подведем итоги урока

Домашнее задание: §33, 34, №982.

Реактивное сопротивление катушки индуктивности (XL) и конденсатора (XC)

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора

Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = U_ampsin(ωt) запишем выражение мгновенного значения тока следующим образом:

i = U_ampωCsin(ωt+π/2).

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

Реактивное сопротивление конденсатора называют ёмкостным.

Предлагаем Вам рассмотреть непосредственно связанные с данным материалом статьи:
Что такое коэффициент мощности — Cos(φ)?

2. Последовательные R, L, C цепи | 5. Реактивное сопротивление и импеданс — R, L и C | Часть2

2. Последовательные R, L, C цепи

Последовательные R, L, C цепи

Давайте в качестве примера возьмем следующую схему, и проанализируем её:

 

 

Для начала нам необходимо рассчитать реактивные сопротивления катушки индуктивности и конденсатора.

 

 

Далее, нам нужно выразить все сопротивления (активные и реактивные) в математически общей форме: импедансе. Как вы наверное помните, реактивное сопротивление катушки индуктивности переводится в положительный мнимый импеданс (или импеданс при +90^o), в то время как реактивное сопротивление конденсатора переводится в отрицательный мнимый импеданс (импеданс при -90^o). Сопротивление резистора, конечно же, по-прежнему рассматривается как чисто «реальный» импеданс (полярный угол 0^o):

 

 

 

Теперь, все эти величины сопротивлений переменному току, выраженные в общем формате комплексных чисел (как импедансы, а не как активные или реактивные сопротивления), мы можем обрабатывать по аналогии с простыми сопротивлениями в цепи постоянного тока. Давайте нарисуем уже знакомую нам таблицу, и внесем в неё все известные значения (общее напряжение, а так же импедансы резистора, катушки индуктивности и конденсатора):

 

 

Если не указано иное, то напряжение источника питания будет нашим ориентиром для фазового сдвига. Его угол будет иметь обозначение 0^o. Как вы помните, не существует такого понятия, как «безусловный» угол фазового сдвига для напряжения или тока, поскольку его величина всегда определяется по отношению к какой либо форме волны. Фазовые углы импедансов (резистора, катушки индуктивности и конденсатора) известны точно, поскольку фазовые соотношения между током и напряжением в каждом из компонентов имеют фиксированные значения.

Обратите внимание, мы предполагаем использование идеальных катушки индуктивности и конденсатора, с фазовыми углами импедансов +90 и -90^o соответственно. Несмотря на то, что реальные компоненты не столь совершенны, их значения могут быть довольно близки к идеальным. Для простоты расчетов мы будем использовать именно идеальные компоненты, если не будет указано иное.

Так как в приведенном выше примере используется последовательная цепь, мы знаем, что ее общий импеданс равен сумме импедансов отдельных компонентов:

 

 

Вставим это значение в ячейку общего импеданса нашей таблицы:

 

 

Теперь мы можем применить Закон Ома (I = U/R) к вертикальному столбцу «Общее», чтобы найти общий ток нашей схемы:

 

 

Поскольку в последовательной цепи ток одинаков на всех компонентах, давайте перенесем значение общего тока в соответствующие ячейки резистора, катушки индуктивности и конденсатора:

 

 

И наконец, применим Закон Ома (U = IZ) к каждому из столбцов компонентов, чтобы рассчитать неизвестные напряжения:

 

 

Обратите внимание на одну странность: несмотря на то, что напряжение питания схемы составляет всего 120 вольт, напряжение на конденсаторе равно 137,46 вольт. Как такое могло получиться? Ответ заключается во взаимодействии между индуктивным и емкостным реактивными сопротивлениями. Выразив их как импедансы, мы видим, что катушка индуктивности выступает против тока точно противоположно конденсатору. Выраженный в алгебраической форме импеданс катушки индуктивности имеет положительную мнимую величину, а импеданс конденсатора — отрицательную. Когда эти два противоположных импеданса складываются (последовательно), они, как правило, компенсируют друг друга! Полученная сумма будет меньше значения любого из импедансов (емкостного или индуктивного). Данная ситуация аналогична сложению положительных и отрицательных скалярных чисел: суммарная величина получается меньше любой индивидуальной величины.

Если общий импеданс последовательной цепи (содержащей и индуктивные и емкостные компоненты) меньше любого из импедансов отдельных компонентов, то общий ток в этой цепи должен быть больше, чем ток в цепи, содержащей только индуктивные или только емкостные компоненты. Именно благодаря данному аномально высокому току, проходящему через все компоненты цепи, на отдельных ее компонентах может быть получено напряжение, величина которого превышает величину напряжения источника. Дальнейшие последствия взаимодействия противоположных реактивных сопротивлений катушек индуктивности и конденсаторов мы с вами рассмотрим несколько позже.

После того, как вы освоили технику перевода значений сопротивлений всех компонентов в импедансы (Z), анализ любой цепи переменного тока оказалcя так же прост, как анализ любой цепи постоянного тока (за исключением того, что все операции проводятся с векторными величинами вместо скалярных). В цепях переменного тока используются те же уравнения, что и в цепях постоянного тока, за исключением уравнений, связанных с мощностью (Р). Закон Ома и законы Кирхгофа так же сохраняют свое действие в цепях переменного тока.

Чтобы продемонстрировать действие Второго Закона Кирхгофа в цепи переменного тока, мы можем посмотреть на ответы, полученные для неизвестных значений напряжений на компонентах нашей схемы. Второй Закон Кирхгофа говорит нам, что алгебраическая сумма напряжений на резисторе, катушке индуктивности и конденсаторе должна быть равна напряжению источника питания. Даже при том, что на первый взгляд это не может показаться правдоподобным, сложение комплексных чисел доказывает нам обратное:

 

 

Если не учитывать небольшую ошибку округления, сумма этих напряжений действительно равна 120 вольт. Если бы вы произвели этот расчет на калькуляторе, то ответ был бы ровно 120 + j0 вольт.

Для проверки наших расчетов Мы так же можем воспользоваться программой SPICE:

 

 

ac r-l-c circuit   
v1 1 0 ac 120 sin       
r1 1 2 250      
l1 2 3 650m     
c1 3 0 1.5u     
.ac lin 1 60 60 
.print ac v(1,2) v(2,3) v(3,0) i(v1)    
.print ac vp(1,2) vp(2,3) vp(3,0) ip(v1) 
.end    

freq          v(1,2)      v(2,3)      v(3)        i(v1)       
6.000E+01     1.943E+01   1.905E+01   1.375E+02   7.773E-02
freq          vp(1,2)     vp(2,3)     vp(3)       ip(v1)      
6.000E+01     8.068E+01   1.707E+02  -9.320E+00  -9.932E+01

 

 

Моделирование SPICE показывает, что произведенные нами расчеты верны.

Зависимости реактивного сопротивления, импеданса и мощности

в цепях переменного тока

Зависимости реактивного сопротивления, импеданса и мощности в цепях переменного тока Емкость

была объяснена индивидуально для цепей переменного тока. Остальная часть этой главы будет касаться комбинации индуктивности, емкости и сопротивления в цепях переменного тока. Чтобы объяснить различные свойства, которые существуют в цепях переменного тока, будет использоваться последовательная цепь RLC. Рисунок 4-4 представляет собой принципиальную схему последовательной цепи RLC. Символ, показанный на рисунке 4-4 и помеченный буквой E, является общим символом, используемым для обозначения источника переменного напряжения.»>

Пользовательский поиск

РЕАКТИВНОСТЬ, ИМПЕДАНС И МОЩНОСТЬ В ЦЕПЯХ ПЕРЕМЕННОГО ТОКА До этого момента индуктивность и емкость объяснялись индивидуально в переменном токе. схемы.Остальная часть этой главы будет посвящена комбинации индуктивности, емкость и сопротивление в цепях переменного тока. Для объяснения различных свойств, присущих цепям переменного тока, последовательная цепь RLC будет использоваться. Рисунок 4-4 представляет собой принципиальную схему последовательной цепи RLC. Символ изображенный на рисунке 4-4, который обозначен буквой E, является общим символом, используемым для обозначения переменного напряжения. источник. Рисунок 4 — 4. — Последовательная цепь RLC. РЕАКТИВНОСТЬ Эффект индуктивного реактивного сопротивления заключается в том, что ток отстает от напряжения, в то время как емкостное реактивное сопротивление заставляет ток опережать напряжение.Следовательно, поскольку индуктивное реактивное сопротивление и емкостное реактивное сопротивление совершенно противоположны по своему действию, что будет ли результат, когда они будут объединены? Нетрудно увидеть, что чистый эффект тенденция отменять друг друга, с комбинированным эффектом, равным разнице между их ценностями. Этот результат называется РЕАКТИВНОСТЬЮ; он представлен символом ИКС; и выражается уравнением X = X L — X C или X = X C — х L .Таким образом, если цепь содержит 50 Ом индуктивного сопротивления и 25 Ом емкостное реактивное сопротивление в серии, чистое реактивное сопротивление, или X, составляет 50 Ом — 25 Ом или 25 Ом индуктивного реактивного сопротивления. В качестве практического примера предположим, что у вас есть цепь, содержащая катушку индуктивности 100 мГн последовательно с конденсатором 0,001 мФ и работающую на частоте 4 МГц. Каково значение чистого реактивного сопротивления, или X? Теперь предположим, что у вас есть цепь, содержащая катушку индуктивности 100 — мГн, соединенную последовательно с.0002-мФ, работающий на частота 1 МГц. Каково значение результирующего реактивного сопротивления в этом случае? Вы заметите, что в этом случае индуктивное сопротивление меньше, чем емкостное реактивное сопротивление и поэтому вычитается из емкостного реактивного сопротивления. Эти два примера служат для иллюстрации важного момента: когда емкостный и индуктивные реактивные сопротивления объединяются последовательно, меньшее всегда вычитается из больше, и результирующее реактивное сопротивление всегда принимает характеристики большего. Q.13 Какова формула для определения полного реактивного сопротивления в последовательной цепи, где известны значения X C и X L ? В.14 Каково общее реактивное сопротивление (X) в последовательной цепи, содержащей X L 20 Ом и X C 50 Ом? (Укажите, является ли X емкостным или индуктивная)

Заявление о конфиденциальности
— Информация об авторских правах.- Свяжитесь с нами

Integrated Publishing, Inc. — A (SDVOSB) Малый бизнес, ветеран с отключенными услугами

Индуктивное реактивное сопротивление — Engineer-Educators.com

Переменный ток постоянно изменяется; эффекты магнитных полей представляют собой непрерывно индуцированное противодействие напряжению току в цепи. Это сопротивление называется индуктивным реактивным сопротивлением, обозначаемым XL, и измеряется в омах так же, как измеряется сопротивление.Индуктивность — это свойство цепи противодействовать любому изменению тока и измеряется в генри. Индуктивное реактивное сопротивление — это мера того, насколько противодействующая ЭДС в цепи будет противодействовать изменениям тока.

Индуктивное реактивное сопротивление компонента прямо пропорционально индуктивности компонента и приложенной к цепи частоте. При увеличении индуктивности или приложенной частоты индуктивное реактивное сопротивление также будет увеличиваться и будет оказывать большее сопротивление току в цепи.Это соотношение задается следующим образом:

На рисунке 123 показана последовательная цепь переменного тока, в которой индуктивность составляет 0,146 Генри, а напряжение составляет 110 вольт при частоте 60 циклов в секунду. Индуктивное реактивное сопротивление определяется следующим методом.

Рисунок 123. Цепь переменного тока, содержащая индуктивность.

Чтобы найти ток:

В любой цепи, где есть только сопротивление, выражение для отношения напряжения и тока дается законом Ома: I = E / R.Точно так же, когда есть индуктивность в цепи переменного тока, соотношение между напряжением и током может быть выражено как:

В последовательных цепях переменного тока индуктивные реактивные сопротивления добавляются, как последовательно включенные сопротивления в цепи постоянного тока. [Рисунок 124] Таким образом, полное реактивное сопротивление в показанной цепи равно сумме индивидуальных реактивных сопротивлений.

Рисунок 124. Последовательные индуктивности.

Общее реактивное сопротивление катушек индуктивности, подключенных параллельно, определяется таким же образом, как полное сопротивление в параллельной цепи.[Рисунок 125] Таким образом, полное реактивное сопротивление индуктивностей, соединенных параллельно, как показано, выражается как

Рисунок 125. Параллельно подключенные индуктивности.

6.11 Реактивное сопротивление: индуктивное и емкостное

Конденсаторы и емкостное реактивное сопротивление

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рисунке 6.46. Сопротивление такой схемы можно сделать настолько малым, что оно окажет незначительное влияние по сравнению с конденсатором, и поэтому мы можем предположить, что сопротивление незначительно.Напряжение на конденсаторе и ток показаны на рисунке как функции времени.

Рис. 6.46 (a) Источник переменного напряжения, включенный последовательно с конденсатором C , имеющим незначительное сопротивление. (б) График зависимости тока и напряжения на конденсаторе от времени.

График на рисунке 6.46 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, и ток становится отрицательным по мере разряда конденсатора.В точке a конденсатор полностью разряжен (Q = 0 (Q = 0 размер 12 {Q = 0} {} на нем), и напряжение на нем равно нулю. Ток остается отрицательным между точками a и b, в результате чего напряжение на конденсаторе меняется на противоположное. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд на конденсаторе и доводя напряжение до нуля в точке b. точка c, которая позволяет току достичь максимума.Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. В течение всего цикла напряжение соответствует тому, что делает ток, на одну четверть цикла.

Напряжение переменного тока в конденсаторе

Когда на конденсатор подается синусоидальное напряжение, оно следует за током на одну четверть цикла или на фазовый угол 90º90º.

Конденсатор влияет на ток, имея возможность полностью его остановить, когда он полностью заряжен.Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока II размера 12 {I} {} в цепи, содержащей только конденсатор CC размера 12 {C} {}, определяется другой версией закона Ома. быть

6.57 I = VXC, I = VXC, размер 12 {I = {{V} больше {X rSub {size 8 {C}}}}} {}

, где размер VV 12 {V} {} — среднеквадратичное значение напряжения, а размер XCXC 12 {X rSub {размер 8 {C}}} {} определен (как и для XL, XL, размер 12 {X rSub {размер 8 {L }}} {} это выражение для XCXC размера 12 {X rSub {size 8 {C}}} {}, полученное в результате анализа схемы с использованием правил и расчетов Кирхгофа) должно быть

6.58 XC = 12πfC, XC = 12πfC, размер 12 {X rSub {size 8 {C}} = {{1} больше {2π ital «fC»}}} {}

, где размер XCXC 12 {X rSub {размер 8 {C}}} {} называется емкостным реактивным сопротивлением, поскольку конденсатор препятствует прохождению тока. XCXC размер 12 {X rSub {размер 8 {C}}} {} имеет единицы измерения Ом (проверка оставлена ​​в качестве упражнения для читателя). XCXC размер 12 {X rSub {размер 8 {C}}} {} обратно пропорционален емкости C; C; размер 12 {C} {} чем больше конденсатор, тем больший заряд он может накапливать и тем больше может протекать ток.Она также обратно пропорциональна частоте f; f; размер 12 {f} {} чем выше частота, тем меньше времени требуется для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 6.11 Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора 5,00 мФ при приложении переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток, если приложенное действующее напряжение составляет 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в XC = 12πfC.XC = 12πfC.size 12 {X rSub {size 8 {C}} = {{1} over {2π ital «fC»}}} {} После того, как XCXC был обнаружен на каждой частоте, закон Ома сформулировал как I = V / XCI = V / XC можно использовать для определения тока на каждой частоте.

Решение для (а)

Ввод частоты и емкости в XC = 12πfCXC = 12πfC размер 12 {X rSub {size 8 {C}} = {{1} больше {2π ital «fC»}}} {} дает

6,59 XC = 12πfC = 16,28 (60,0 / с) (5,00 мкФ) = 531 Ом при 60 Гц. XC = 12πfC = 16,28 (60,0 / с) (5,00 мкФ) = 531 Ом при 60 Гц.alignl {stack {size 12 {X rSub {size 8 {C}} = {{1} over {2π ital «fC»}}} {} # «» = {{1} over {6 «).» «28» \ («60» «.» 0 / с \) \ (5 «.» «00» мкФ \)}} = «531»% OMEGA «при 60 Гц» {}}} {}

Аналогично, на 10 кГц,

6,60 XC = 12πfC = 16,28 (1,00 × 104 / с) (5,00 мкФ) = 3,18 Ом при 10 кГц. XC = 12πfC = 16,28 (1,00 × 104 / с) (5,00 мкФ) = 3,18 Ом при 10 кГц. {размер 12 {X rSub {размер 8 {C}} = {{1} больше {2π ital «fC»}} = {{1} больше {6 «.» «28» \ (1 «.» «00» умножить на «10» rSup {размер 8 {4}} / s \) \ (5 «.» «00» мкФ \)}}} {} # «» = 3 «.»» 18 «% OMEGA» на 10 кГц «{}}} {}

Решение для (b)

Среднеквадратичный ток теперь определяется с использованием версии закона Ома в I = V / XC, I = V / XC, размер 12 {I = V / X rSub {size 8 {C}}} {} с учетом приложенного среднеквадратичного напряжения. составляет 120 В. Для первой частоты это дает

6,61 I = VXC = 120 В 531 Ом = 0,226 А при 60 Гц. I = VXC = 120 В 531 Ом = 0,226 А при 60 Гц. размер 12 {I = {{V} больше {X rSub {size 8 {C}}}} = {{«120» «V»} больше {«531″% OMEGA}} = 0 «.» «226» «A»} {}

Аналогично, на 10 кГц,

6.62 I = VXC = 120 В 3,18 Ом = 37,7 А при 10 кГц. I = VXC = 120 В 3,18 Ом = 37,7 А при 10 кГц. размер 12 {I = {{V} больше {X rSub {size 8 {C}}}} = {{«120» «V»} больше {3 «.» «18»% OMEGA}} = «37» «.» 7 «А»} {}

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, а индуктор реагирует прямо противоположным образом. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы одобряют изменения, тогда как индукторы противодействуют изменениям. Конденсаторы больше всего препятствуют низким частотам, так как низкая частота позволяет им успеть зарядиться и остановить ток.Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно с системой воспроизведения звука, избавляет ее от гула 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с напряжением переменного тока, приложенным к конденсатору, присутствует среднеквадратичный ток. Это связано с тем, что напряжение постоянно меняет направление, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), размер XCXC 12 {X rSub {size 8 {C}}} {} стремится к бесконечности, и ток равен нулю после зарядки конденсатора.На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет незначительное реактивное сопротивление и не препятствует току (он действует как простой провод). Конденсаторы имеют противоположное влияние на цепи переменного тока, чем индукторы .

Импеданс

Импеданс

Полное противодействие протеканию тока в цепи переменного тока известно как импеданс и обозначается буквой Z. Комбинированные эффекты сопротивления, индуктивного реактивного сопротивления и емкостного реактивного сопротивления составляют полное сопротивление (полное противодействие к протеканию тока в цепи переменного тока).Чтобы точно рассчитать напряжение и ток в цепях переменного тока, необходимо учитывать влияние индуктивности и емкости наряду с сопротивлением. Импеданс измеряется в омах.

Рисунок 9-22. Применение постоянного и переменного тока в цепи.

Правила и уравнения для цепей постоянного тока применимы к цепям переменного тока только в том случае, если эта цепь содержит только сопротивление, а не индуктивность или емкость. Как в последовательной, так и в параллельной цепях, если цепь переменного тока состоит только из сопротивления, значение импеданса такое же, как и сопротивление, а закон Ома для цепи переменного тока, I = E / Z, точно такой же, как для цепи постоянного тока. схема.На рис. 9-22 показана последовательная схема, содержащая нагревательный элемент с сопротивлением 11 Ом, подключенный к источнику 110 В. Чтобы определить, какой ток протекает при подаче переменного тока 110 В, решается следующий пример:

Рисунок 9-23. Два значения сопротивления, подключенные параллельно к источнику переменного тока. Импеданс равен общему сопротивлению цепи.

Если два значения сопротивления подключены параллельно к источнику переменного тока, как показано на Рисунке 9-23, полное сопротивление равно общему сопротивлению цепи.Опять же, вычисления будут производиться так же, как если бы это была цепь постоянного тока, и применимо следующее:

Поскольку это чисто резистивная цепь R _T = Z (сопротивление = импеданс)

To Определите ток в цепи, используя уравнение:

Импеданс — это полное сопротивление току в цепи переменного тока. Если цепь имеет индуктивность или емкость, необходимо учитывать сопротивление (R), индуктивное реактивное сопротивление (X _L ) и / или емкостное реактивное сопротивление (X _C ) для определения полного сопротивления (Z).В этом случае Z не равно R _T . Сопротивление и реактивное сопротивление (индуктивное или емкостное) нельзя сложить напрямую, но их можно рассматривать как две силы, действующие под прямым углом друг к другу. Таким образом, соотношение между сопротивлением, реактивным сопротивлением и импедансом можно проиллюстрировать прямоугольным треугольником. [Рисунок 9-24] Поскольку эти величины могут быть связаны со сторонами прямоугольного треугольника, формулу для определения импеданса можно найти с помощью теоремы Пифагора. В нем говорится, что квадрат гипотенузы равен сумме квадратов двух других сторон.Таким образом, значение любой стороны прямоугольного треугольника можно найти, если известны две другие стороны.

Рисунок 9-24. Треугольник импеданса Рисунок 9-25. Цепь, содержащая сопротивление и индуктивность.

На практике, если последовательная цепь переменного тока содержит сопротивление и индуктивность, как показано на рисунке 9-25, соотношение между сторонами может быть указано как:

Квадратный корень из обеих частей уравнения дает:

Эту формулу можно использовать для определения импеданса, если известны значения индуктивного реактивного сопротивления и сопротивления.Его можно изменить для определения импеданса в цепях, содержащих емкостное реактивное сопротивление и сопротивление, подставив в формулу X _C вместо X _L . В цепях, содержащих сопротивление с индуктивным и емкостным сопротивлением, реактивные сопротивления можно комбинировать; но поскольку их эффекты в схеме прямо противоположны, они объединяются вычитанием (меньшее число всегда вычитается из большего):

или

Пример 1 показан на рисунке 9-25.Здесь последовательная цепь, содержащая резистор и катушку индуктивности, подключена к источнику 110 вольт при 60 циклах в секунду. Резистивный элемент представляет собой простой измерительный элемент 6 Ом, а индуктивный элемент представляет собой катушку с индуктивностью 0,021 Генри. Какое значение импеданса и тока в цепи?

Решение:

Сначала вычисляется индуктивное реактивное сопротивление катушки:

Затем вычисляется полное сопротивление:

Помните, что при расчетах для Z всегда используйте индуктивное реактивное сопротивление, а не индуктивность, и используйте емкостное реактивное сопротивление. , а не емкость.

После определения полного сопротивления можно рассчитать общий ток.

Поскольку эта цепь является резистивной и индуктивной, существует фазовый сдвиг там, где напряжение ведет к току.

Пример 2 — это проиллюстрированная последовательная схема, в которой конденсатор емкостью 200 мкФ соединен последовательно с резистором 10 Ом. [Рисунок 9-26] Какое значение имеет импеданс, ток и падение напряжения на резисторе?

Рисунок 9-26. Цепь, содержащая сопротивление и емкость.

Решение:

Сначала емкость изменяется с микрофарад на фарады. Так как 1 миллион микрофарад равен 1 фараду, тогда 200 мкФ = 0,000200 фарад

Затем решите емкостное реактивное сопротивление:

Чтобы найти импеданс,

Поскольку эта цепь резистивная и емкостная, существует фазовый сдвиг, при котором ток напряжение проводов:

Чтобы найти ток:

Чтобы найти падение напряжения на резисторе (E _R ):

Чтобы найти падение напряжения на конденсаторе (E _C ):

Сумма этих двух напряжений не равна приложенному напряжению, поскольку ток опережает напряжение.Используйте следующую формулу, чтобы найти приложенное напряжение:

Если в цепи есть сопротивление, индуктивность и емкость, для определения полного сопротивления используется следующее уравнение.

Пример 3: Каково полное сопротивление последовательной цепи, состоящей из конденсатора с емкостным реактивным сопротивлением 7 Ом, катушки индуктивности с индуктивным сопротивлением 10 Ом и резистора с сопротивлением 4 Ом? [Рисунок 9-27] Рисунок 9-27. Цепь, содержащая сопротивление, индуктивность и емкость.

Решение:

Чтобы найти полный ток:

Помните, что индуктивные и емкостные сопротивления могут вызвать сдвиг фаз между напряжением и током. В этом примере индуктивное реактивное сопротивление больше емкостного, поэтому напряжение ведет к току.

Следует отметить, что, поскольку индуктивное реактивное сопротивление, емкостное реактивное сопротивление и сопротивление влияют друг на друга под прямым углом, падения напряжения в любой последовательной цепи переменного тока следует складывать с использованием векторного сложения.На рисунке 9-28 показаны падения напряжения в последовательной цепи переменного тока, описанной в примере 3 выше.

Рисунок 9-28. Падение напряжения.

Чтобы рассчитать отдельные падения напряжения, просто используйте уравнения:

Чтобы определить общее приложенное напряжение для цепи, каждое отдельное падение напряжения должно быть добавлено с использованием векторного сложения.

Параллельные цепи переменного тока

При решении параллельных цепей переменного тока необходимо также использовать производную теоремы Пифагора.Уравнение для определения полного сопротивления в цепи переменного тока выглядит следующим образом:

Чтобы определить полное сопротивление параллельной цепи, показанной на рисунке 9-29, сначала нужно определить емкостное и индуктивное реактивные сопротивления. (Не забудьте перевести микрофарады в фарады.)

Рисунок 9-29. Полный импеданс параллельной цепи.

Затем можно найти полное сопротивление:

Для определения протекания тока в цепи:

Чтобы определить протекание тока через каждый параллельный путь цепи, вычислите I _R , I _L и I _C .

Следует отметить, что общий ток в параллельных цепях определяется с помощью векторного сложения отдельных потоков тока следующим образом:

Мощность в цепях переменного тока

Поскольку напряжение и ток определяют мощность , есть сходства в мощности, потребляемой цепями переменного и постоянного тока. Однако в переменном токе ток зависит как от сопротивления, так и от реактивного сопротивления цепи. Мощность, потребляемая любой цепью переменного тока, является функцией приложенного напряжения, а также сопротивления и реактивного сопротивления цепи.Цепи переменного тока имеют два различных типа мощности: один создается сопротивлением цепи, а другой — реактивным сопротивлением цепи.

Истинная мощность

Истинная мощность любой цепи переменного тока обычно называется рабочей мощностью цепи. Истинная мощность — это мощность, потребляемая участком сопротивления цепи, и измеряется в ваттах (Вт). Истинная мощность обозначается буквой P и указывается любым ваттметром в цепи. Истинная мощность рассчитывается по формуле:

Полная мощность

Полная мощность в цепи переменного тока иногда называется реактивной мощностью цепи.Полная мощность — это мощность, потребляемая всей схемой, включая сопротивление и реактивное сопротивление. Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА). Полная мощность — это произведение эффективного напряжения на эффективный ток. Полная мощность рассчитывается по формуле:

Коэффициент мощности

Как видно на Рисунке 9-30, резистивная мощность и реактивная мощность влияют на схему под прямым углом друг к другу.Коэффициент мощности в цепи переменного тока создается этим эффектом прямого угла.

Рисунок 9-30. Соотношения сил в цепи переменного тока.

Коэффициент мощности можно определить как математическую разницу между истинной мощностью и полной мощностью. Коэффициент мощности (PF) — это коэффициент и всегда измеряется в диапазоне от 0 до 100. Коэффициент мощности напрямую связан с фазовым сдвигом цепи. Чем больше фазовый сдвиг цепи, тем ниже коэффициент мощности. Например, цепь переменного тока, которая является чисто индуктивной (содержит только реактивное сопротивление и не имеет сопротивления), имеет фазовый сдвиг 90 ° и коэффициент мощности 0.0. Цепь переменного тока, которая является чисто резистивной (без реактивного сопротивления), имеет фазовый сдвиг 0 и коэффициент мощности 100. Коэффициент мощности рассчитывается по следующей формуле:

Пример расчета коэффициента мощности: Рисунок 9-31 показывает нагрузку переменного тока, подключенную к источнику питания на 50 В. Потребляемый в цепи ток составляет 5 ампер, а общее сопротивление цепи составляет 8 Ом. Определите истинную мощность, полную мощность и коэффициент мощности для этой цепи.

Рисунок 9-31. Нагрузка переменного тока подключена к источнику питания на 50 В.

Решение:

Коэффициент мощности также может быть представлен в процентах. Используя процентное соотношение для отображения коэффициента мощности, схема в предыдущем примере будет иметь коэффициент мощности 80 процентов.

Следует отметить, что низкий коэффициент мощности нежелателен. Цепи с более низким коэффициентом мощности создают избыточную нагрузку на источник питания и снижают эффективность системы. Генераторы переменного тока для самолетов обычно должны работать с коэффициентом мощности от 90 до 100 процентов.Поэтому очень важно тщательно учитывать коэффициент мощности при проектировании электрической системы самолета.

Бортовой механик рекомендует

Что такое реактивное сопротивление и импеданс в цепи переменного тока?

Реактивное сопротивление определяется как электрическая величина, из-за которой переменному току противодействует индуктор или конденсатор или их комбинация в цепи. Импеданс — это чистый фактор, противодействующий переменному току. Реактивное сопротивление также можно назвать импедансом индуктивности или конденсатора.Реактивное сопротивление обозначено X, а полное сопротивление Z. В этой статье мы подробно обсудим реактивное сопротивление и импеданс.

Что такое реактивность?

Реактивность — это сопротивление протеканию переменного тока. Это противодействие может быть вызвано либо индуктором (L), либо конденсатором (C). Значение реактивного сопротивления индуктора с индуктивностью L равно ωL, тогда как его значение составляет (1 / ωC) для конденсатора с емкостью C.

Объяснение реактивного сопротивления:

Рассмотрим схему для лучшего понимания.В цепи индуктивность с индуктивностью L Генри подключена к источнику переменного тока V = V _м Sinωt. Здесь ω — угловая частота в радианах / сек. ω = 2πf, где f — частота питающей сети в Гц. Сила тока в цепи I.

Ток I, протекающий по цепи, равен [V _m Sin (ωt — π / 2) / (ωL)]. Следовательно, максимальное значение этого тока равно

.

I _м = (V _м / ωL)

= (V _м / X _L )

где X _L = ωL

Внимательно наблюдайте за приведенным выше выражением тока и сравните его с законом Ома (I = V / R).Вы заметите, что здесь X _L выполняет работу R. То есть X _L = ωL противодействует потоку тока, как и сопротивление. Это причина; это называется реактивным сопротивлением. Поскольку он представлен индуктором, он называется индуктивным реактивным сопротивлением и обозначается символом X _L .

Давайте теперь рассмотрим другую схему, состоящую из конденсатора и переменного источника, как показано ниже.

Ток в цепи равен (В _м ωC) Sin (ωt + π / 2).Следовательно, максимальное значение тока будет иметь место, когда Sin (ωt + π / 2) = 1, и это значение указано ниже.

I _м = V _м / (1 / ωC)

= V _м / X _C

При сравнении вышеуказанного значения тока I _m с законом Ома (I = V / R) становится ясно, что X _C противодействует протеканию тока и действует как сопротивление. Это X _C = (1 / ωC) называется емкостным реактивным сопротивлением.

Что такое импеданс?

Импеданс в цепи переменного тока определяется как чистый фактор, противодействующий протеканию тока. Это противодействие может быть связано с сопротивлением и индуктивностью, или сопротивлением и емкостью, или сопротивлением, индуктивностью и емкостью. Обозначается символом Z. Z часто выражается как Z = R + jX, где X — реактивное сопротивление.

Описание импеданса:

Чтобы иметь четкое представление об импедансе, давайте рассмотрим схему, показанную ниже.В этой цепи последовательно соединены чистое сопротивление R и чистая индуктивная катушка с индуктивностью L.

Пусть, V = действующее значение приложенного напряжения

I = действующее значение тока цепи

В _R = Падение напряжения на R

В _L = падение напряжения на катушке

Предположим, что ток цепи является опорным вектором. Падение напряжения на сопротивлении будет синфазным с током I. Однако падение напряжения в индуктивной катушке опережает ток I на 90 °.Эти падения напряжения показаны в треугольнике напряжения OAB.

Вектор OA, AB и OB представляет падение напряжения в сопротивлении (V _R ), индуктивное падение напряжения (V _L ) и напряжение питания (V) соответственно. Напряжение питания (В) — это гипотенуза этого треугольника напряжений. Следовательно, напряжение питания можно рассчитать, как показано ниже.

Величина Z — это полное сопротивление цепи переменного тока. Напряжение питания также можно записать из треугольника напряжения с помощью оператора j.Это показано ниже.

В = (ИК) + j (IX _L )

I = V / (R + jX _L )

= В / З

Таким образом, импеданс Z = R + jX . Таким образом, импеданс — это сложная величина. Угол, который Z образует с опорным вектором, рассчитывается как tanƟ = (X / R).

реактивное сопротивление

Посетите книжную полку VK2TIP. Мой личные рекомендации, спасибо.

ПОСЛЕДНЕЕ ИЗМЕНЕНИЕ:
Пятница, 29-июн-2018 02:34:15 PDT

ВЫ ЗДЕСЬ: ГЛАВНАЯ> ОСНОВЫ> РЕАКТИВНОСТЬ

Автор: Ian C.Purdie VK2TIP

НОВИНКА! ‣ — Пакеты электронных компонентов Amazon. Посетите страницу Amazon Electronic Component Packs.

Что такое реактивное сопротивление?

Реактивное сопротивление — это свойство сопротивляться или препятствовать прохождению переменного тока или переменного напряжения в индукторах и конденсаторах. Обратите внимание, что мы говорим только об переменном токе ac, выражение которого включает audio af и радиочастоты rf.НЕ постоянный ток dc.

Индуктивное реактивное сопротивление

Когда через индуктивность протекает переменный ток, возникает противоэдс или напряжение, противодействующее любому изменению начального тока. Это сопротивление или сопротивление изменению тока измеряется в единицах индуктивного сопротивления.

Индуктивное сопротивление определяется по формуле:

2 * пи * ф * л

где: 2 * пи = 6,2832; f = частота в герцах и L = индуктивность по Генри.

Емкостное реактивное сопротивление

Когда переменное напряжение протекает через емкость, происходит противоположное изменение начального напряжения, это сопротивление или сопротивление изменению напряжения измеряется в единицах емкостного реактивного сопротивления.

Емкостное реактивное сопротивление определяется по формуле:

1 / (2 * пи * f * C)

где: 2 * пи = 6,2832; f = частота в герцах и C = емкость в фарадах.

Некоторые примеры реактивного сопротивления

Какое реактивное сопротивление имеет катушка индуктивности 6,8 мкГн на частоте 7 МГц? Используя формулу выше, мы получаем:

2 * пи * ф * л

где: 2 * пи = 6,2832; f = 7,000,000 Гц и L = 0,0000068 Генри

Ответ: = 299 Ом

Какое реактивное сопротивление у конденсатора 33 пФ на частоте 7 МГц? Используя формулу выше, мы получаем:

1 / (2 * пи * f * C)

где: 2 * пи = 6.2832; f = 7000000 Гц и C = 0,000000000033 фарад

Ответ: = 689 Ом

В реальном мире мы не используем такие большие числа, мы используем экспоненты на нашем карманном калькуляторе, чтобы получить такие числа:

Для индуктивного реактивного сопротивления

где: 2 * пи = 6,2832; f = 7 X 10 ⁺⁶ Гц и L = 6,8 X ^-6 Генри

Ответ: = 299 Ом

Для емкостного реактивного сопротивления

1 / (2 * пи * f * C)

где: 2 * пи = 6.2832; f = 7 X 10 ⁺⁶ Гц и C = 33 X ^-12 Фарад

Ответ: = 689 Ом

Система пользовательского поиска Google

Есть вопросы по этой теме?

Если вы занимаетесь электроникой, подумайте о том, чтобы присоединиться к нашей группе новостей «Электроника Вопросы и ответы», чтобы задать там свой вопрос, а также поделиться своими тернистыми вопросами и ответами. Помогите своим коллегам !.

Абсолютно самый быстрый способ получить ответ на свой вопрос, и да, я DO прочитал большинство сообщений.

Это группа взаимопомощи с очень профессиональной атмосферой. Я ничего не узнал. Это отличный обучающий ресурс как для скрытых, так и для активных участников.

ТЕМЫ, СВЯЗАННЫЕ С РЕАКТИВНОСТЬЮ

емкость

ток

импеданс

индуктивность

напряжение

Ссылка на эту страницу

НОВИНКА! — Как перейти по прямой ссылке на эту страницу

Хотите создать ссылку на мою страницу со своего сайта? Нет ничего проще.Знания HTML не требуются; даже технофобы могут это сделать. Все, что вам нужно сделать, это скопировать и вставить следующий код. Все ссылки приветствуются; Искренне благодарю вас за вашу поддержку.

Скопируйте и вставьте следующий код для текстовой ссылки :

<а href = "https://www.electronics-tutorials.com/basics/reactance.htm" target = "_ top"> посетите страницу Ian Purdie VK2TIP "Reactance"

, и он должен выглядеть так:
посетите страницу Ian Purdie VK2TIP «Reactance»

ВЫ ЗДЕСЬ: ГЛАВНАЯ> ОСНОВЫ> РЕАКТИВНОСТЬ

автор Ян К.Purdie, VK2TIP сайта www.electronics-tutorials.com заявляет о моральном праве на быть идентифицированным как автор этого веб-сайта и всего его содержания. Copyright © 2000, все права защищены. См. Копирование и ссылки. Эти электронные учебные пособия предназначены для индивидуального частного использования, и автор не несет никакой ответственности за применение, использование, неправильное использование любого из этих проектов или учебных пособий по электронике, которое может привести к прямому или косвенному ущербу или убыткам, связанным с этими проектами или учебными пособиями. .Все материалы предоставляются для бесплатного частного и общественного использования.
Коммерческое использование запрещено без предварительного письменного разрешения www.electronics-tutorials.com.

---

Авторские права © 2000, все права защищены. URL — https://www.electronics-tutorials.com/basics/reactance.htm

Обновлено 15 мая 2000 г.

Связаться с ВК2ТИП

23.11 Реактивное сопротивление, индуктивное и емкостное — Физика колледжа: OpenStax

Сводка

• Зависимость напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
• Рассчитайте индуктивное и емкостное сопротивление.
• Рассчитайте ток и / или напряжение в простых индуктивных, емкостных и резистивных цепях.

Многие цепи также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы исследуем, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рисунке 1.Разумно предположить, что сопротивление пренебрежимо мало, поскольку на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на схему. Также показан график зависимости напряжения и тока от времени.

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График зависимости тока и напряжения на катушке индуктивности от времени.

График на Рисунке 2 (b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и повышается до своего пика после напряжения, которое им управляет, точно так же, как это было в случае, когда напряжение постоянного тока было включено в предыдущем разделе. {\ circ}} [/ latex].

Ток отстает от напряжения, поскольку индукторы препятствуют изменению тока. Изменение тока вызывает обратную ЭДС [латекс] \ boldsymbol {V = -L (\ Delta I / \ Delta t)} [/ latex]. Это считается эффективным сопротивлением катушки индуктивности переменному току. Среднеквадратичное значение тока [латекс] \ boldsymbol {I} [/ latex] через катушку индуктивности [латекс] \ boldsymbol {L} [/ latex] определяется версией закона Ома:

[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {X_L}}, [/ latex]

, где [latex] \ boldsymbol {V} [/ latex] — среднеквадратичное значение напряжения на катушке индуктивности, а [latex] \ boldsymbol {X_L} [/ latex] определяется как

[латекс] \ boldsymbol {X_L = 2 \ pi fL}, [/ латекс]

с [latex] \ boldsymbol {f} [/ latex] частотой источника переменного напряжения в герцах (анализ схемы с использованием правила петли Кирхгофа и вычислений фактически дает это выражение).[latex] \ boldsymbol {X_L} [/ latex] называется индуктивным реактивным сопротивлением, потому что катушка индуктивности препятствует прохождению тока. [latex] \ boldsymbol {X_L} [/ latex] имеет единицы измерения в омах ([latex] \ boldsymbol {1 \; \ textbf {H} = 1 \; \ Omega \ cdot \; \ textbf {s}} [/ latex ], так что частота, умноженная на индуктивность, имеет единицы (циклов / с) ([latex] \ boldsymbol {\ Omega \ cdot \; \ textbf {s}} [/ latex]) = [latex] \ boldsymbol {\ Omega} [ / латекс]), что соответствует его роли как эффективного сопротивления. Логично, что [латекс] \ boldsymbol {X_L} [/ latex] пропорционален [латексу] \ boldsymbol {L} [/ latex], поскольку чем больше индукция, тем выше его сопротивление изменениям.Также разумно, чтобы [latex] \ boldsymbol {X_L} [/ latex] пропорционально частоте [latex] \ boldsymbol {f} [/ latex], поскольку более высокая частота означает большее изменение тока. То есть [латекс] \ boldsymbol {\ Delta I / \ Delta t} [/ latex] большой для больших частот (большой [латекс] \ boldsymbol {f} [/ latex] , маленький [латекс] \ boldsymbol { \ Delta t} [/ latex]). Чем больше изменение, тем больше сопротивление катушки индуктивности.

Пример 1: Расчет индуктивного реактивного сопротивления, а затем тока

(a) Рассчитайте индуктивное сопротивление 3.Индуктор 00 мГн при подаче переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток на каждой частоте, если приложенное действующее напряжение составляет 120 В?

Стратегия

Индуктивное реактивное сопротивление находится непосредственно из выражения [latex] \ boldsymbol {X_L = 2 \ pi fL} [/ latex]. Как только [latex] \ boldsymbol {X_L} [/ latex] был обнаружен на каждой частоте, закон Ома, как указано в уравнении [latex] \ boldsymbol {I = V / X_L} [/ latex], может быть использован для определения тока на каждой частоте.

Решение для (а)

Ввод частоты и индуктивности в уравнение [латекс] \ boldsymbol {X_L = 2 \ pi fL} [/ latex] дает

[латекс] \ boldsymbol {X_L = 2 \ pi fL = 6.4 \; \ textbf {/ s}) (3.00 \; \ textbf {mH}) = 188 \; \ Omega \; \ textbf {at} 10 \; \ textbf {kHz}} [/ latex]

Решение для (b)

Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в уравнении [латекс] \ boldsymbol {I = V / X_L} [/ latex], учитывая, что приложенное среднеквадратичное напряжение составляет 120 В. Для первой частоты это дает

[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {X_L}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {120 \; \ textbf {V}} {1.13 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 106 \; \ textbf {A at} \; 60 \; \ textbf {Гц}}.[/ латекс]

Аналогично, на 10 кГц,

[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {X_L}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {120 \; \ textbf {V}} {188 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 0,637 \; \ textbf {A at} \; 10 \; \ textbf {кГц}}. [/ Latex]

Обсуждение

Катушка индуктивности по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток невелик, что соответствует тому, как катушка индуктивности препятствует быстрому изменению.Таким образом, наиболее затруднены высокие частоты. Индукторы могут использоваться для фильтрации высоких частот; например, большую катушку индуктивности можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выводимый из ваших динамиков или высокочастотные всплески мощности на ваш компьютер.

Обратите внимание, что, хотя сопротивлением в рассматриваемой цепи можно пренебречь, переменный ток не очень велик, потому что индуктивное реактивное сопротивление препятствует его протеканию.С переменным током нет времени, чтобы ток стал слишком большим.

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рисунке 2. Сопротивление такой цепи можно сделать настолько малым, что оно окажет незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить, что сопротивление незначительно. Напряжение на конденсаторе и ток показаны на рисунке как функции времени.

Рис. 2. (a) Источник переменного напряжения, включенный последовательно с конденсатором C , имеющим незначительное сопротивление.(б) График зависимости тока и напряжения на конденсаторе от времени.

График на Рисунке 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. {\ circ}} [/ latex].

Конденсатор влияет на ток, имея возможность полностью его остановить, когда он полностью заряжен. Поскольку применяется переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока [латекс] \ boldsymbol {I} [/ latex] в цепи, содержащей только конденсатор [латекс] \ boldsymbol {C} [/ latex] дается другой версией закона Ома равным

[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {X_C}}, [/ latex]

где [latex] \ boldsymbol {V} [/ latex] — среднеквадратичное значение напряжения, а [latex] \ boldsymbol {X_C} [/ latex] определяется (как и в случае [latex] \ boldsymbol {X_L} [/ latex], это выражение для [latex] \ boldsymbol {X_C} [/ latex], полученное в результате анализа схемы с использованием правил и расчетов Кирхгофа) должно быть

[латекс] \ boldsymbol {X_C =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {2 \ pi fC}}, [/ латекс]

, где [latex] \ boldsymbol {X_C} [/ latex] называется емкостным реактивным сопротивлением, поскольку конденсатор препятствует прохождению тока.[latex] \ boldsymbol {X_C} [/ latex] имеет единицы измерения в омах (проверка оставлена ​​в качестве упражнения для читателя). [латекс] \ boldsymbol {X_C} [/ latex] обратно пропорционален емкости [латекс] \ boldsymbol {C} [/ latex]; Чем больше конденсатор, тем больший заряд он может накапливать и тем больше может протекать ток. Он также обратно пропорционален частоте [латекс] \ boldsymbol {f} [/ latex]; чем выше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 2: Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора 5,00 мФ при приложении переменного напряжения 60,0 Гц и 10,0 кГц. (b) Каков среднеквадратичный ток, если приложенное действующее напряжение составляет 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в [latex] \ boldsymbol {X_C = \ frac {1} {2 \ pi fC}} [/ latex]. Как только [latex] \ boldsymbol {X_C} [/ latex] был обнаружен на каждой частоте, закон Ома, сформулированный как [latex] \ boldsymbol {I = V / X_C} [/ latex], можно использовать для определения тока на каждой частоте. .

Решение для (а)

Ввод частоты и емкости в [латекс] \ boldsymbol {X_C = \ frac {1} {2 \ pi fC}} [/ latex] дает

[латекс] \ begin {array} {r @ {{} = {}} l} \ boldsymbol {X_C} & \ boldsymbol {\ frac {1} {2 \ pi fC}} \\ [1em] & \ boldsymbol {\ frac {1} {6.28 (60.0 \; \ textbf {/ s}) (5.00 \; \ mu \ textbf {F})} = 531 \; \ Omega \; \ textbf {at} \; 60 \; \ textbf {Гц.}} \ End {array} [/ latex]

Аналогично, на 10 кГц,

[латекс] \ begin {array} {r @ {{} = {}} l} \ boldsymbol {X_C} & \ boldsymbol {\ frac {1} {2 \ pi fC} = \ frac {1} {6.4 \; \ textbf {/ s}) (5.00 \; \ mu \ textbf {F})}} \\ [1em] & \ boldsymbol {3.18 \; \ Omega \; \ textbf {at} \; 10 \; \ textbf {Гц}}. \ end {array} [/ latex]

Решение для (b)

Среднеквадратичное значение тока теперь определяется с использованием версии закона Ома в [latex] \ boldsymbol {I = V / X_C} [/ latex], учитывая приложенное среднеквадратичное напряжение 120 В. Для первой частоты это дает

[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {X_C}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {120 \; \ textbf {V}} {531 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 0.226 \; \ textbf {А в} \; 60 \; \ textbf {Hz}}. [/ Latex]

Аналогично, на 10 кГц,

[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {X_C}} [/ latex] [латекс] \ boldsymbol {=} [/ latex] [латекс] \ boldsymbol {\ frac {120 \; \ textbf {V}} {3.18 \; \ Omega}} [/ latex] [latex] \ boldsymbol {= 37.7 \; \ textbf {A at} \; 10 \; \ textbf {кГц}}. [/ Latex]

Обсуждение

Конденсатор очень по-разному реагирует на двух разных частотах, а индуктор реагирует прямо противоположным образом.На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы одобряют изменения, тогда как индукторы противодействуют изменениям. Конденсаторы больше всего препятствуют низким частотам, так как низкая частота позволяет им успеть зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно с системой воспроизведения звука, избавляет ее от гула 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с напряжением переменного тока, приложенным к конденсатору, присутствует среднеквадратичный ток.Это связано с тем, что напряжение постоянно меняет направление, заряжая и разряжая конденсатор. Если частота стремится к нулю (DC), [latex] \ boldsymbol {X_C} [/ latex] стремится к бесконечности, и ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет незначительное реактивное сопротивление и не препятствует току (он действует как простой провод). Конденсаторы имеют противоположное влияние на цепи переменного тока, чем индукторы .

В качестве напоминания рассмотрим Рисунок 3, на котором показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. {\ circ}} [/ латекс].{\ circ}} [/ latex] фазовый угол.

Противодействие катушки индуктивности изменению тока выражается как сопротивление переменному току.

Закон Ома для катушки индуктивности

[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {X_L}}, [/ latex]

где [латекс] \ boldsymbol {V} [/ latex] — среднеквадратичное значение напряжения на катушке индуктивности.

[латекс] \ boldsymbol {X_L} [/ latex] определяется как индуктивное реактивное сопротивление, определяемое по формуле

[латекс] \ boldsymbol {X_L = 2 \ pi fL}, [/ латекс]

with [latex] \ boldsymbol {f} [/ latex] частота источника переменного напряжения в герцах.{\ circ}} [/ latex] фазовый угол.

Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора

[латекс] \ boldsymbol {I =} [/ latex] [латекс] \ boldsymbol {\ frac {V} {X_C}}, [/ latex]

где [латекс] \ boldsymbol {V} [/ latex] — среднеквадратичное значение напряжения на конденсаторе.

[латекс] \ boldsymbol {X_C} [/ latex] определяется как емкостное реактивное сопротивление, определяемое по формуле

[латекс] \ boldsymbol {X_C =} [/ latex] [латекс] \ boldsymbol {\ frac {1} {2 \ pi fC}}.[/ латекс]

[latex] \ boldsymbol {X_C} [/ latex] имеет единицы измерения Ом и имеет наибольшее значение на низких частотах.

Концептуальные вопросы

1: Пресбиакузис — это возрастная потеря слуха, которая постепенно влияет на высокие частоты. Усилитель слухового аппарата предназначен для равномерного усиления всех частот. Чтобы отрегулировать его мощность на пресбиакузис, включите ли вы конденсатор последовательно или параллельно динамику слухового аппарата? Объяснять.

2: Используете ли вы большую индуктивность или большую емкость последовательно с системой для фильтрации низких частот, таких как гул 100 Гц в звуковой системе? Объяснять.

3: Высокочастотный шум в сети переменного тока может повредить компьютеры. Использует ли съемный блок, предназначенный для предотвращения этого повреждения, большую индуктивность или большую емкость (последовательно с компьютером) для фильтрации таких высоких частот? Объяснять.

4: Зависит ли индуктивность от тока, частоты или и того, и другого? А как насчет индуктивного сопротивления?

5: Объясните, почему конденсатор на рисунке 4 (a) действует как фильтр низких частот между двумя цепями, тогда как конденсатор на рисунке 4 (b) действует как фильтр высоких частот.

Рисунок 4. Конденсаторы и катушки индуктивности. Конденсатор с высокой и низкой частотой.

6: Если конденсаторы на рис. 4 заменить катушками индуктивности, что будет действовать как фильтр низких частот, а какое как фильтр высоких частот?

Задачи и упражнения

1: На какой частоте индуктор 30,0 мГн будет иметь реактивное сопротивление [латекс] \ boldsymbol {100 \; \ Omega} [/ latex]

2: Какое значение индуктивности следует использовать, если символ [латекс] \ bold {20.0 \; \ textbf {k} \ Omega} [/ latex] реактивное сопротивление нужно при частоте 500 Гц?

3: Какая емкость должна использоваться для создания реактивного сопротивления [латекс] \ boldsymbol {2.00 \; \ textbf {M} \ Omega} [/ latex] при 60,0 Гц?

4: На какой частоте конденсатор 80,0 мФ будет иметь реактивное сопротивление [латекс] \ boldsymbol {0,250 \; \ Omega} [/ latex]?

5: (a) Найдите ток через катушку индуктивности 0,500 H, подключенную к источнику переменного тока 60,0 Гц, 480 В. (б) Каким будет ток на частоте 100 кГц?

6: (а) Какой ток течет при 60.Источник 0 Гц, 480 В переменного тока подключен к конденсатору [latex] \ boldsymbol {0,250 \; \ mu F} [/ latex]? (b) Каким будет ток на частоте 25,0 кГц?

7: Источник 20,0 кГц, 16,0 В, подключенный к катушке индуктивности, вырабатывает ток 2,00 А. Что такое индуктивность?

8: Источник 20,0 Гц, 16,0 В вырабатывает ток 2,00 мА при подключении к конденсатору. Какая емкость?

9: (a) Катушка индуктивности, предназначенная для фильтрации высокочастотного шума от источника питания персонального компьютера, размещается последовательно с компьютером.Какая минимальная индуктивность должна иметь реактивное сопротивление [latex] \ boldsymbol {2.00 \; \ textbf {k} \ Omega} [/ latex] для шума 15,0 кГц? (б) Каково его реактивное сопротивление при 60,0 Гц?

10: Конденсатор на рисунке 4 (а) предназначен для фильтрации низкочастотных сигналов, препятствующих их передаче между цепями. (a) Какая емкость необходима для создания реактивного сопротивления [латекс] \ boldsymbol {100 \; \ textbf {k} \ Omega} [/ latex] на частоте 120 Гц? (б) Каким было бы его реактивное сопротивление на частоте 1,00 МГц? (c) Обсудите значение ваших ответов на (a) и (b).

11: Конденсатор на Рисунке 4 (b) будет фильтровать высокочастотные сигналы, замыкая их на землю / землю. (a) Какая емкость необходима для создания реактивного сопротивления [латекс] \ boldsymbol {10.0 \; \ textbf {m} \ Omega} [/ latex] для сигнала 5,00 кГц? (б) Каким будет его реактивное сопротивление при 3,00 Гц? (c) Обсудите значение ваших ответов на (a) и (b).

12: Необоснованные результаты

При записи напряжений, обусловленных мозговой активностью (ЭЭГ), сигнал 10,0 мВ с 0.К конденсатору прикладывают частоту 500 Гц, создавая ток 100 мА. Сопротивление незначительное. а) Какая емкость? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка ответственны?

13: Создайте свою проблему

Рассмотрим использование индуктора последовательно с компьютером, работающим от электричества 60 Гц. Постройте задачу, в которой вы вычисляете относительное снижение напряжения входящего высокочастотного шума по сравнению с напряжением 60 Гц.Среди вещей, которые следует учитывать, — допустимое последовательное реактивное сопротивление катушки индуктивности для мощности 60 Гц и вероятные частоты шума, проходящего через линии электропередач.

Глоссарий

индуктивное сопротивление

противодействие катушки индуктивности изменению тока; рассчитывается по [latex] \ boldsymbol {X_L = 2 \ pi fL} [/ latex]

емкостное реактивное сопротивление

противодействие конденсатора изменению тока; рассчитывается по [latex] \ boldsymbol {X_C = \ frac {1} {2 \ pi fC}} [/ latex]

Решения

Задачи и упражнения

1: 531 Гц

3: 1.33 нФ

5: (а) 2,55 А

(б) 1,53 мА

7: [латекс] \ boldsymbol {63.7 \; \ mu H} [/ латекс]

9: (а) 21,2 мГн

(b) [латекс] \ boldsymbol {8.00 \; \ Omega} [/ латекс]

11: (а) 3,18 мФ

(b) [латекс] \ boldsymbol {16.7 \; \ Omega} [/ латекс]

.