Реактивное сопротивление равно: Реактивное сопротивление

Содержание

Реактивное сопротивление

Итак, катушки индуктивности и конденсаторы препятствуют протеканию переменного тока. Такое сопротивление по переменному току носит название реактивного сопротивления Х и измеряется в омах. Реактивное сопротивление зависит как от величины индуктивности и емкости, так и от частоты сигнала.

Катушка индуктивности имеет индуктивное реактивное сопротивление VL равное

где f — частота в герцах, a L — индуктивность в генри.
Так как ω = 2πf, то можно записать XL = ωL. Например, реактивное сопротивление катушки с индуктивностью 10 мГн, на которую подается сигнал частотой 1 кГц, равно

XL = 2π*1*103*10 *10-3 = 62,8 Ом.

Реактивное сопротивление катушки индуктивности возрастает с увеличением частоты сигнала (рис. 4.26).
Конденсатор имеет емкостное сопротивление XC равное

где С — емкость в фарадах. Например, реактивное сопротивление конденсатора емкостью 1 мкФ, на который подается сигнал частотой 10 кГц, равно

Рис.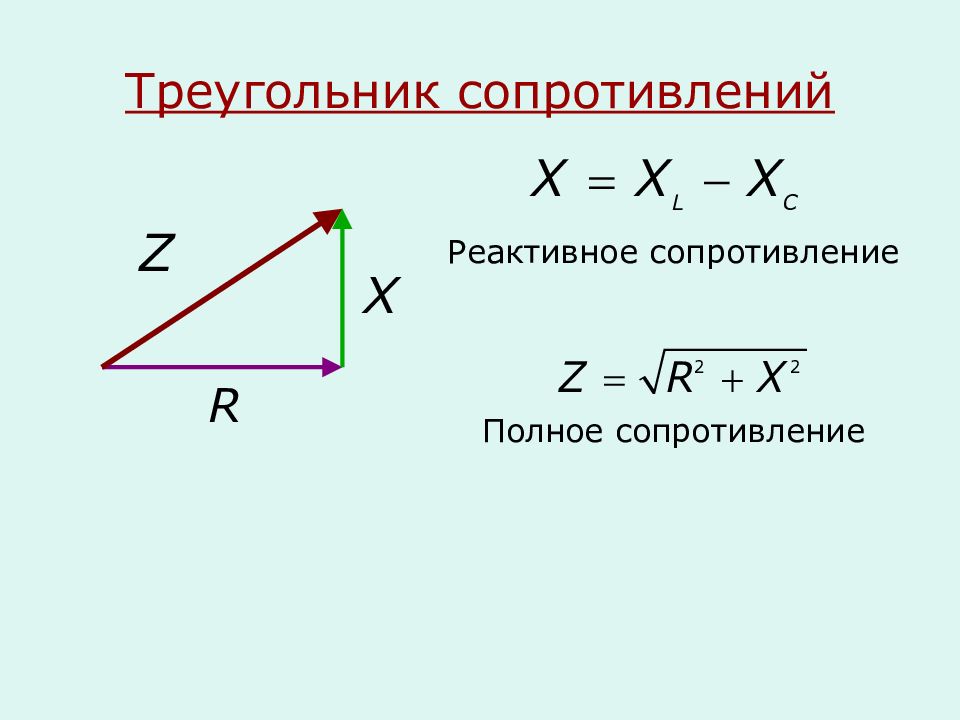 4.26. Зависимость индуктивного Рис. 4.27.
сопротивления от частоты.

Рис. 4.28. Векторная сумма емкостного (XC)

и индуктивного (XL) сопротивлений.

Рис. 4.29.
(а) Катушка индуктивности, соединенная последовательно с резистором R.
(б) Векторное представление R, XL и их векторной суммы Z

Реактивное сопротивление конденсатора уменьшается с увеличением частоты сигнала (рис. 4.27).
Результирующее сопротивление цепи, включающей в себя емкостное сопротивление XC и индуктивное сопротивление XL, равно векторной сумме XC и XL. Векторы XC и XL, как видно из рис. 4.28(б), находятся в противофазе, т. е. разность фаз между ними равна 1800. Поэтому результирующее сопротивление просто равно разности между XC и XL. Например, пусть XL = 100 Ом, а XC = 70 Ом. Тогда результирующее реактивное сопротивление Х = 100 – 70 = 30 Ом и является индуктивным так как XL больше, чем XС.

Импеданс
Результирующее сопротивление цепи, содержащей как активное, так и реактивное (индуктивное либо емкостное) сопротивление, носит название импеданса или полного сопротивления цепи.

Импеданс Z является векторной суммой реактивного сопротивления Х и активного сопротивления R.
Рассмотрим, например, схему, изображенную на рис. 4.29. Она включает в себя индуктивное сопротивление XL соединенное последовательно с резистором R. Как видно из рис. 4.29(б), вектор XL опережает вектор R на 90°. Импеданс равен

Если XL = 400 Ом и R = 300 Ом, то Z = 500 Ом.

Добавить комментарий

Выражение ома для цепи с активным сопротивлением. Активное, реактивное и полное сопротивление цепи

Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток.

Импеданс можно рассчитать при помощи простой формулы.

Формулы

Полное сопротивление Z = R или X L или X C (если присутствует что-то одно)
Полное сопротивление (последовательное соединение) Z = √(R 2 + X 2) (если присутствуют R и один тип X)
Полное сопротивление (последовательное соединение) Z = √(R 2 + (|X L — X C |) 2) (если присутствуют R, X L , X C)
Полное сопротивление (любое соединение) = R + jX (j – мнимое число √(-1))
Сопротивление R = I / ΔV
Индуктивное сопротивление X L = 2πƒL = ωL
Емкостное сопротивление X C = 1 / 2πƒL = 1 / ωL

Шаги

Часть 1

Вычисление активного и реактивного сопротивлений

Импеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:

Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.

Сопротивление – это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R. Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете при помощи мультиметра.

ΔV – это напряжение (разность потенциалов), измеряемое в вольтах (В).
I – сила тока, измеряемая в амперах (А).
R – это сопротивление, измеряемое в омах (Ом).

Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:

Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и измеряется в герцах (Гц). Формула для расчета индуктивного сопротивления:

X L = 2πƒL , где L – индуктивность, измеряемая в генри (Гн).

Вычислите емкостное сопротивление. Это сопротивление обратно пропорционально быстроте изменения направления тока, то есть частоты тока. Формула для вычисления емкостного сопротивления: X C = 1 / 2πƒC . С – это емкость конденсатора, измеряемая в фарадах (Ф).

Вы можете .
Эту формулу можно переписать так: X C = 1 / ωL (объяснения см. выше).

Часть 2

Вычисление полного сопротивления

Если цепь состоит исключительно из резисторов, то импеданс вычисляется следующим образом.
Сначала измерьте сопротивление каждого резистора или посмотрите значения сопротивления на схеме цепи.
- Если резисторы соединены последовательно, то полное сопротивление R = R 1 + R 2 + R 3 . ..
- Если резисторы соединены параллельно, то полное сопротивление R = 1 / R 1 + 1 / R 2 + 1 / R 3 …
Сложите одинаковые реактивные сопротивления. Если в цепи присутствуют исключительно катушки индуктивности или исключительно конденсаторы, то полное сопротивление равно сумме реактивных сопротивлений. Вычислите его следующим образом:

Сопротивление, оказываемое проводником проходящему на нему переменному току, называется активным сопротивлением .

Если какой-либо потребитель не содержит в себе индуктивности и емкости (лампочка накаливания, нагревательный прибор), то он будет являться для переменного тока также активным сопротивлением.

Активное сопротивление зависит от частоты переменного тока, возрастая с ее увеличением.

Однако многие потребители обладают индуктивными и емкостными свойствами при прохождении через них переменного тока. К таким потребителям относятся трансформаторы, дроссели, электромагниты, конденсаторы, различного рода провода и многие другие.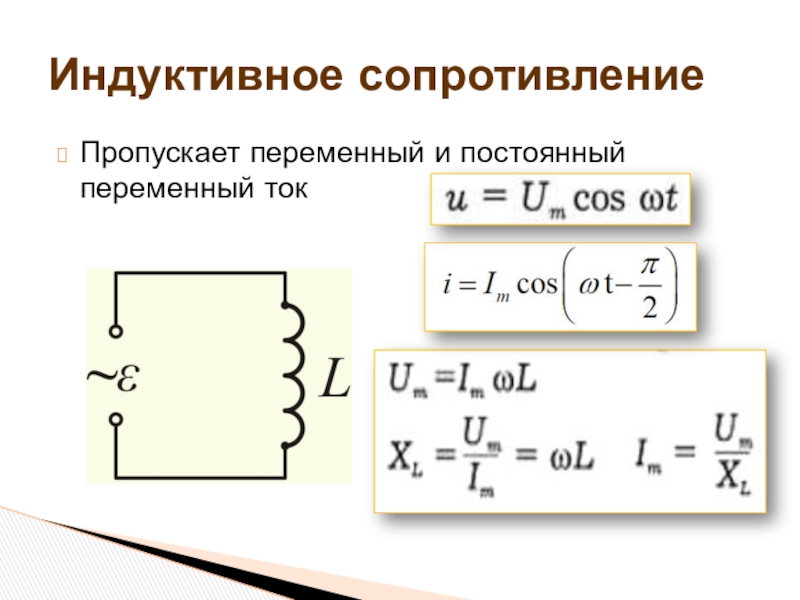

При прохождении через них переменного тока необходимо учитывать не только активное, но и реактивное сопротивление , обусловленное наличием, в потребителе индуктивных и емкостных свойств его.

Активное сопротивление определяет действительную часть импеданса:

Где — импеданс, — величина активного сопротивления, — величина реактивного сопротивления, — мнимая единица.

Активное сопротивление — сопротивление электрической цепи или её участка, обусловленное необратимыми превращениями электрической энергии в другие виды энергии(в тепловую энергию)

Реакти́вное сопротивле́ние — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому или магнитному полю (и обратно).

Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:

Величина полного реактивного сопротивления

Индуктивное сопротивление () обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи.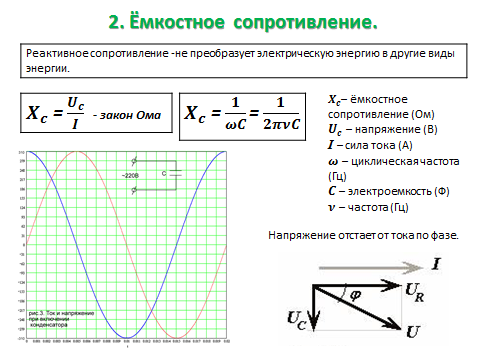

Ёмкостное сопротивление ().

Здесь — циклическая частота

Полное сопротивление цепи при переменном токе:

z =

√

r 2 + x 2

√

r 2 +(x L −x C) 2

Билет №12.

1. 1) Согласование генератора с нагрузкой — обеспечение требуемой величины активного эквивалентного сопротивления нагрузки генераторной лампы, R э, при всех возможных значениях входного сопротивления антенного фидера, которое зависит от его волнового сопротивления и коэффициента бегущей волны (КБВ)

Согласование (в электронике) сводится к правильному выбору сопротивлений генератора (источника), линии передачи и приёмника (нагрузки). Идеального Согласование (в электронике) между линией и нагрузкой можно достичь при равенстве волнового сопротивления линии r полному сопротивлению нагрузки Zh = RH + j ХН, или при RH= r и XH= 0, где RH -активная часть полного сопротивления, XH — его реактивная часть. В этом случае в передающей линии устанавливается режим бегущих волн и характеризующий их коэффициент стоячей волны (КСВ) равен 1. Для линии с пренебрежимо малыми потерями электрической энергии Согласование и, благодаря ему, максимально эффективная передача энергии из генератора в нагрузку достигаются при условии, что полные сопротивления генератора Zr и нагрузки ZH являются комплексно-сопряжёнными, т. е. Zr = Z*H, или Rr = r = R Н =Xr- XH. В этом случае реактивное сопротивление цепи равно нулю, и соблюдаются условия резонанса, способствующие повышению эффективности работы радиотехнических систем (улучшается использование частотных диапазонов, повышается помехозащищенность, снижаются частотные искажения радиосигналов и т.п.). Оценку качества Согласование (в электронике) производят, измеряя коэффициент отражения и КСВ. Практически Согласование (в электронике) считают оптимальным, если в рабочей полосе частот КСВ не превышает 1,2-1,3 (в измерительных приборах 1,05). В отдельных случаях косвенными показателями Согласование (в электронике) могут служить реакции параметров генератора (частоты, мощности, уровня шумов) на изменение нагрузки, наличие электрических пробоев в линии, разогрев отдельных участков линии.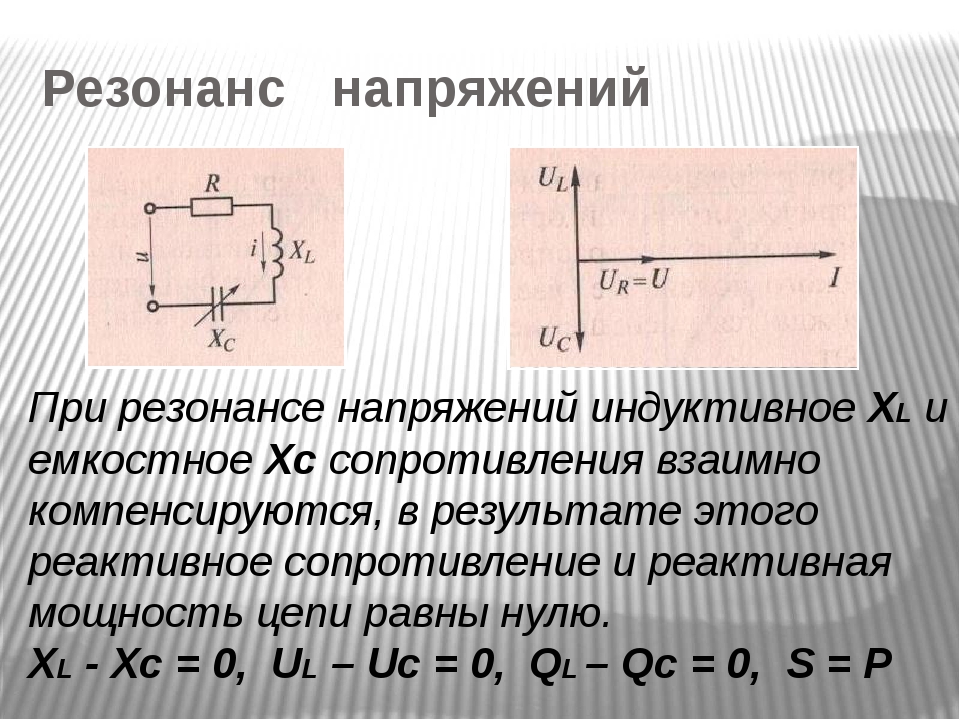

При таком режиме работы в приёмнике выделяется наибольшая мощность, равная половине мощности источника. В этом случае К.П.Д. =0,5. Такой режим используется в измерительных цепях, устройствах средств связи.

При передаче больших мощностей, например по высоковольтным линиям электропередач, работа в согласованном режиме, как правило, недопустима.

Активное сопротивление зависит от материала, сечения и температуры. Активное сопротивление обусловливает тепловые потери проводов и кабелей. Определяется материалом токоведущих проводников и площадью их сечения.

Различают сопротивление проводника постоянному току (омическое) и переменному току (активное). Активное сопротивление больше активного (R а > R ом) из-за поверхностного эффекта. Переменное магнитное поле внутри проводника вызывает противоэлектродвижущую силу, благодаря которой происходит перераспределение тока по сечению проводника. Ток из центральной его части вытесняется к поверхности. Таким образом, ток в центральной части провода меньше, чем у поверхности, то есть сопротивление провода возрастает по сравнению с омическим. Поверхностный эффект резко проявляется при токах высокой частоты, а также в стальных проводах (из-за высокой магнитной проницаемости стали).

Для ЛЭП, выполненных из цветного металла, поверхностный эффект на промышленных частотах незначителен. Следовательно, R а ≈ R ом.

Обычно влиянием колебания температуры на R а проводника в расчётах пренебрегают. Исключение составляют тепловые расчеты проводников. Пересчет величины сопротивления выполняют по формуле:

где R 20 – активное сопротивление при температуре 20 о;

текущее значение температуры.

Активное сопротивление зависит от материала проводника и сечения:

где ρ –удельное сопротивление, Ом мм 2 /км;

l – длина проводника, км;

F – сечение проводника, мм 2 .

Сопротивление одного километра проводника называют погонным сопротивлением:

где удельная проводимость материала проводника, км См/мм 2 .

Для меди γ Cu =53×10 -3 км См/мм2 , для алюминия γ Al =31.7×10 -3 км См/мм2 .

На практике значение r 0 определяют по соответствующим таблицам, где они указаны для t 0 =20 0 С.

Величина активного сопротивления участка сети рассчитывается:

R = r 0 ×l .

Активное сопротивление стальных проводов намного больше омического из-за поверхностного эффекта и наличия дополнительных потерь на гистерезис (перемагничивание) и от вихревых токов в стали:

r 0 = r 0пост + r 0доп,

где r 0пост – омическое сопротивление одного километра провода;

r 0доп – активное сопротивление, которое определяется переменным магнитным полем внутри проводника, r 0доп = r 0поверх.эф + r 0гистер. + r 0вихр.

Изменение активного сопротивления стальных проводников показано на рисунке 4.1.

При малых величинах тока индукция прямо пропорциональна току. Следовательно, r 0 увеличивается. Затем наступает магнитное насыщение: индукция и r 0 практически не изменяются. При дальнейшем увеличении тока r 0 уменьшается из-за снижения магнитной проницаемости стали (m ).

Сопротивление одного и того же проводника для переменного тока будет больше, чем для постоянного.

Это объясняется явлением так называемого поверхностного эффекта, заключающегося в том, что переменный ток вытесняется от центральной части проводника к периферийным слоям. В результате плотность тока во внутренних слоях будет меньше, чем в наружных. Таким образом, при переменном токе сечение проводника используется как бы не полностью. Однако при частоте 50 Гц различие в сопротивлениях постоянному и переменному токам незначительно и практически им можно пренебречь.

Сопротивление проводника постоянному току называют омическим, а переменному току –активным сопротивлением.

Омическое и активное сопротивление зависят от материала (внутренней структуры), геометрических размеров и температуры проводника.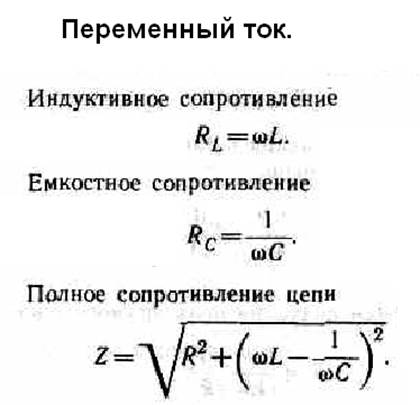 Кроме того, в катушках со стальным сердечником на величину активного сопротивления влияют потери в стали (далее для самоподготовки).

К активным сопротивлениям относят электрические лампы накаливания, электрические печи сопротивления, различные нагревательные приборы, реостаты и провода, где электрическая энергия практически почти целиком превращается в тепловую.

Если цепь переменного тока содержит только резистор R лампа накаливания, электронагревательный прибор и т. д.), к которому приложено переменное синусоидальное напряжение и (рис. 1-5, а):

то ток i в цепи будет определяться значением этого сопротивления:

где — амплитуда тока; при этом ток i и напряжение и совпадают по фазе. Обе эти величины, как видно, можно изобразить на временной (рис. 1-5, б) и векторной (1-5, в) диаграммах. Теперь установим, как изменяется мощность в любой момент времени — мгновенная мощность, характеризующая собой скорость преобразования электрической энергии в другие виды энергии в данный момент времени

где IU — произведение действующих значений тока и напряжения.

Из полученного следует, что мощность в течение периода остается положительной и пульсирует с удвоенной частотой. Графически это можно представить так, как показано на рисунке 1-6. В этом случае электрическая энергия превращается необратимо, например, в теплоту независимо от направления тока в цепи.

Кроме мгновенного значения мощности различают еще среднюю мощность за период:

но так как второй интеграл равен нулю, то окончательно имеем:

Средняя за период мощность переменного тока называется активной мощностью, а соответствующее ей сопротивление — активным.

Средняя мощность и активное сопротивление связаны с безвозвратным преобразованием электрической энергии в другие виды энергии. Активное сопротивление электрической цепи не сводится только к

сопротивлению проводников, в которых электрическая энергия превращается в теплоту. Это понятие значительно шире, так как средняя мощность электрической цепи равна сумме мощностей всех видов энергии, полученной из электрической, на всех участках цепи (теплота, механическая и др. ).

Из полученных соотношений следует, что

которое является математической записью закона Ома для цепи переменного тока с активным сопротивлением.

Сопротивления | Цепи переменного тока

Введем теперь ряд величин, характеризующих цепь синусоидального тока.
Отношение комплексного напряжения к комплексному току называется комплексным сопротивлением:

где — отношение действующего или амплитудного напряжения соответственно к действующему или амплитудному току называется полным сопротивлением. Полное сопротивление равно модулю комплексного сопротивления. Аргумент комплексного сопротивления равен разности фаз напряжения и тока, т. е.
Комплексное сопротивление можно представить в виде

где — действительная часть комплексного сопротивления, называется активным сопротивлением; — значение мнимой части комплексного сопротивления, называется реактивным сопротивлением.
Очевидно, что

Из ( 3. 23а) следует, что для последовательного контура (см. рис. 3.8) комплексное сопротивление

причем реактивное сопротивление

где

называются соответственно индуктивным и емкостным сопротивлениями.
Из ( 3.15) и ( 3.19) видно, что индуктивное сопротивление связывает между собой амплитуды или действующие значения напряжения на индуктивности и тока:

Индуктивное сопротивление прямо пропорционально частоте тока. Это объясняется тем, что напряжение на индуктивном элементе пропорционально скорости изменения тока:
Емкостное сопротивление, как следует из ( 3.16) и ( 3.20), связывает между собой амплитуды или действующие значения напряжения на емкости и тока:

Емкостное сопротивление обратно пропорционально частоте тока. Эту зависимость от частоты легко пояснить, если считать заданным напряжение на емкостном элементе, а искомой величиной ток: . Ток прямо пропорционален скорости изменения напряжения на емкостном элементе, и, следовательно, емкостное сопротивление обратно пропорционально частоте напряжения.
Напряжения на последовательно соединенных индуктивности и емкости противоположны по фазе; поэтому в (3.27) для реактивного сопротивления х сопротивления входят с различными знаками. Напряжения на индуктивности и на емкости сдвинуты по фазе относительно напряжения на сопротивлении соответственно на π/2 и —π/2. Поэтому эти сопротивления входят в Z как .
Следует обратить внимание на то, что индуктивное и емкостное сопротивления являются величинами арифметическими — положительными, а реактивное сопротивление — величина алгебраическая и может быть как больше, так и меньше нуля.
Для ветви, содержащей только индуктивность, реактивное сопротивление х равно индуктивному сопротивлению , а реактивное сопротивление х ветви, содержащей только емкость, равно емкостному сопротивлению, взятому со знаком минус, т. е. .
Заметим также, что для ветвей, каждая из которых содержит только сопротивление r, только индуктивность L или только емкость С, комплексные сопротивления соответственно равны:

Если ветвь содержит несколько последовательно соединенных резистивных, индуктивных и емкостных элементов, то при вычислении сопротивления и тока их можно заменить тремя элементами:

Реактивное сопротивление конденсатора.

Сопротивления в цепи переменного тока

При переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости, через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток).Токи проводимости и поляризацию диэлектрика сопровождают потери энергии.

Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q ) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью Р . Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.

Деление реального конденсатора на два элемента — это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой — реактивной (емкостной) мощностью Q(P = 0).

Схема замещения конденсатора с параллельным соединением элементов

Реальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной G и емкостной B с проводимостей (рис. 13.15), причем активная проводимость определяется мощностью потерь в конденсаторе G = Р/U c 2 , а емкость — конструкцией конденсатора. Предположим, что проводимости G и В с для такой цепи известны, а напряжение имеет уравнение

u = Umsinωt .

Требуется определить токи в цепи и мощность. Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них так же синусоидальны. При параллельном соединении ветвей G и В с, согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:

i = i G + i c , (13.30)

Учитывая, что ток i G совпадает по фазе с напряжением, а ток i c опережает напряжение на четверть периода, уравнение общего тока можно записать в следующем виде:

Векторная диаграмма токов в цепи с конденсатором

Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению

I = I G + I C

Действующие величины составляющих тока:

I G = GU (13. 31)

I C = B C U (13.32)

Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения φ a =0). Вектор I G совпадает по направлению с вектором U, а вектор I C направлен перпендикулярно вектору U с положительным углом. Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ , величина которого больше нуля, но меньше 90º. Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы I G и I C:

При напряжении u = U m sinωt соответствии с векторной диаграммой уравнение тока

i = I m sin(ωt + φ )

Треугольник проводимостей для конденсатора

Стороны треугольников токов, выраженные в единицах тока, разделим на напряжение U. Получим подобный треугольник проводимостей (рис. 13.16, б), катетами которого являются активная G = I G /U и емкостная В с = I с /U проводимости, а гипотенузой — полная проводимость цепи Y = I/U . Из треугольника проводимостей

Связь между действующими величинами напряжения и тока выражается формулами

I = UY

U = I/Y (13.35)

Из треугольников токов и проводимостей определяют величины

cos φ = I G /I = G/Y; sinφ = I c /I = B c /Y; tgφ = I C /I G = B c /G. (13.36)

Мощность цепи с конденсатором

Выражение мгновенной мощности реального конденсатора

p = ui = U m sinωt * I m sin(ωt+φ)

совпадает с выражением мгновенной мощности катушки. Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17. Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки [см. (13.19) — (13.22)]. Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U. В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности; активная

P = UI G = UIcosφ

реактивная

Q = UI C = UIsinφ

полная

Схема замещения конденсатора с последовательным соединением элементов

Реальный конденсатор, так же как и , на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Х с сопротивлениями. На рис. 13.18, а такая схема показана в сравнении со схемой параллельного соединения активной и емкостной проводимостей (рис.13. 18,6). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным. Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью С Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а. Если вам интересно прочитайте которые применяются в промышленности.

Положим теперь, что участок цепи содержит конденсатор емкости C , причем сопротивлением и индуктивностью участка можно пренебречь, и посмотрим, по какому закону будет изменяться напряжение на концах участка в этом случае. Обозначим напряжение между точками а и b через u и будем считать заряд конденсатора q и силу тока i положительными, если они соответствуют рис.4. Тогда

и, следовательно,

Если сила тока в цепи изменяется по закону

то заряд конденсатора равен

Постоянная интегрирования q 0 здесь обозначает произвольный постоянный заряд конденсатора, не связанный с колебаниями тока, и поэтому мы положим .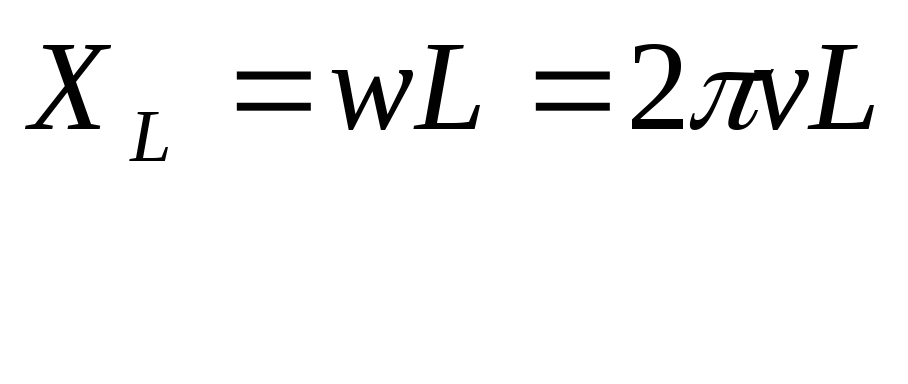 Следовательно,

. (2)

Сравнивая (1) и (2), мы видим, что при синусоидальных колебаниях тока в цепи напряжение на конденсаторе изменяется также по закону косинуса. Однако колебания напряжения на конденсаторе отстают по фазе от колебаний тока на p/2. Изменения тока и напряжения во времени изображены графически на рис.5. Полученный результат имеет простой физический смысл. Напряжение на конденсаторе в какой-либо момент времени определяется существующим зарядом конденсатора. Но этот заряд был образован током, протекавшим предварительно в более ранней стадии колебаний. Поэтому и колебания напряжения запаздывают относительно колебаний тока.

Формула (2) показывает, что амплитуда напряжения на конденсаторе равна

Сравнивая это выражение с законом Ома для участка цепи с постоянным током (), мы видим, что величина

играет роль сопротивления участка цепи, она получила название емкостного сопротивления. Емкостное сопротивление зависит от частоты w, и при высоких частотах даже малые емкости могут представлять совсем небольшое сопротивление для переменного тока. Важно отметить, что емкостное сопротивление определяет связь между амплитудными, а не мгновенными значениями тока и напряжения.

Мгновенная мощность переменного тока

меняется со временем по синусоидальному закону с удвоенной частотой. В течение времени от 0 до T /4 мощность положительна, а в следующую четверть периода ток и напряжение имеют противоположные знаки и мощность становится отрицательной. Поскольку среднее значение за период колебаний величины равно нулю, то средняя мощность переменного тока на конденсаторе .

О заряде конденсатора.

Замкнем цепь. В цепи пойдет ток заряда конденсатора. Это значит что с левой обкладки конденсатора часть электронов уйдет в провод, а из провода на правую обкладку зайдет такое же количество электронов. Обе обкладки будут заряжены разноименными зарядами одинаковой величины.

Между обкладками в диэлектрике будет электрическое поле.

А теперь разомкнем цепь. Конденсатор останется заряженным. Закоротим куском провода его обкладки. Конденсатор мгновенно разрядится. Это значит что с правой обкладки уйдет в провод избыток электронов, а из провода на левую обкладку войдет недостаток электронов. На обоих обкладках электронов будет одинаково, конденсатор разрядится.

До какого напряжения заряжается конденсатор?

Он заряжается до такого напряжения, которое к нему приложено с источника питания.

Сопротивление конденсатора.

Замкнем цепь. Конденсатор начал заряжаться и сразу стал источником тока, напряжения, Э. Д. С.. На рисунке видно что Э. Д. С. конденсатора направлена против заряжающего его источника тока.

Противодействие электродвижущей силы заряжаемого конденсатора заряду этого конденсатора называется емкостным сопротивлением.

Вся энергия затрачиваемая источником тока на преодоление емкостного сопротивления превращается в энергию электрического поля конденсатора. Когда конденсатор будет разряжаться вся энергия электрического поля вернется обратно в цепь в виде энергии электрического тока. Таким образом емкостное сопротивление является реактивным, т.е. не вызывающим безвозвратных потерь энергии.

Почему постоянный ток не проходит через конденсатор, а переменный ток проходит?

Включим цепь постоянного тока. Лампа вспыхнет и погаснет, почему? Потому что в цепи прошел ток заряда конденсатора. Как только конденсатор зарядится до напряжения батареи ток в цепи прекратится.

А теперь замкнем цепь переменного тока. В I четверти периода напряжение на генераторе возрастает от 0 до максимума. В цепи идет ток заряда конденсатора. Во II четверти периода напряжение на генераторе убывает до нуля. Конденсатор разряжается через генератор. После этого конденсатор вновь заряжается и разряжается. Таким образом в цепи идут токи заряда и разряда конденсатора. Лампочка будет гореть постоянно.

В цепи с конденсатором ток проходит во всей замкнутой цепи, в том числе и в диэлектрике конденсатора. В заряжающемся конденсаторе образуется электрическое поле которое поляризует диэлектрик. Поляризация это вращение электронов в атомах на вытянутых орбитах.

Одновременная поляризация огромного количества атомов образует ток, называемый током смещения. Таким образом в проводах идет ток и в диэлектрике причем одинаковой величины.

Емкостное сопротивление конденсатора определяется по формуле

Рассматривая график делаем вывод: ток в цепи с чисто емкостным сопротивлением опережает напряжение на 90 0 .

Возникает вопрос каким образом ток в цепи может опережать напряжение на генераторе? В цепи идет ток от двух источников тока поочередно, от генератора и от конденсатора. Когда напряжение на генераторе равно нулю ток в цепи максимален. Это ток разряда конденсатора.

О реальном конденсаторе

Реальный конденсатор имеет одновременно два сопротивления: активное и емкостное. Их следует считать включенными последовательно.

Напряжение приложенное генератором к активному сопротивлению и ток идущий по активному сопротивлению совпадают по фазе.

Напряжение приложенное генератором к емкостному сопротивлению и ток идущий по емкостному сопротивлению сдвинуты по фазе на 90 0 . Результирующее напряжение приложенное генератором к конденсатору можно определить по правилу параллелограмма.

На активном сопротивлении напряжение U акт и ток I совпадают по фазе. На емкостном сопротивлении напряжение U c отстает от тока I на 90 0 . Результирующее напряжение приложенное генератором к конденсатору определяется по правилу параллелограмма. Это результирующее напряжение отстает от тока I на какой то угол φ всегда меньший 90 0 .

Определение результирующего сопротивления конденсатора

Результирующее сопротивление конденсатора нельзя находить суммируя величины его активного и емкостного сопротивлений. Это делается по формуле

Изменения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вообще говоря, различны. Поэтому если начальную фазу силы тока условно принять за нуль, то начальная фаза напряжения будет иметь некоторое значение φ. При таком условии мгновенные значения силы тока и напряжения и будут выражаться следующими формулами:

i = I m sinωt

u = U m sin(ωt + φ)

a) Активное сопротивление в цепи переменного тока. Сопротивление цепи, которое обусловливает безвозвратные потери электрической энергии на тепловое действие тока, называют активным . Это сопротивление для тока низкой частоты можно считать равным сопротивлению R этого же проводника постоянному току.

В цепи переменного тока, имеющей только активное сопротивление, например, в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. φ = 0. Это означает, что ток и напряжение в такой цепи изменяются в одинаковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.

Будем считать, что напряжение на зажимах цепи меняется по гармоническому закону: и = U т cos ωt.

Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома:

по фазе с колебаниями напряжения.

b) Катушка индуктивности в цепи переменного тока. Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление X L , которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. самоиндукции тем больше, чем больше индуктивность цепи и чем быстрее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω: X L = ωL.

Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь. Для этого предварительно найдем связь между напряжением на катушке и ЭДС самоиндукции в ней. Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой.

Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля E i , порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля Е к, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.

Из равенства E i = -Е к следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции e i) равна по модулю и противоположна по знаку удельной работе кулоновского поля . Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать: e i = -и.

При изменении силы тока по гармоническому закону i = I m sin соsωt, ЭДС самоиндукции равна: е i = -Li» = -LωI m cos ωt. Так как e i = -и, то напряжение на концах катушки оказывается равным

и = LωI m cos ωt = LωI m sin (ωt + π/2) = U m sin (ωt + π/2)

гдеU m = LωI m — амплитуда напряжения.

Следовательно, колебания напряжения на катушке опережают по фазе колебания силы тока на π/2, или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на π/2.

Если ввести обозначение X L = ωL, то получим . Величину X L , равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением. Согласно формуле , значение силы тока связано с значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.

Индуктивное сопротивление зависит от частоты ω. Постоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю. Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока. Следует отметить, что напряжение на индуктивном сопротивлении опережает по фазе ток .

c) Конденсатор в цепи переменного тока. Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.

Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерывно изменяется, поэтому в цепи течет переменный ток. Сила тока будет тем больше, чем больше емкость конденсатора и чем чаще происходит его перезарядка, т. е. чем больше частота переменного тока.

Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивлением Х с . Оно обратно пропорционально емкости С и круговой частоте ω: Х с =1/ωС.

Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь.

Напряжение на конденсаторе u = q/C равно напряжению на концах цепи u = U m cosωt.

Следовательно, q/C = U m cosωt. Заряд конденсатора меняется по гармоническому закону:

q = CU m cosωt.

Сила тока, представляющая собой производную заряда по времени, равна:

i = q» = -U m Cω sin ωt =U m ωC cos(ωt + π/2).

Следовательно, колебания силы тока опережают по фазе колебания напряжения на конденсаторе на π/2.

Величину Х с , обратную произведению ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины аналогична роли активного сопротивления R в законе Ома. Значение силы тока связано с значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока. Это и позволяет рассматривать величину Х с как сопротивление конденсатора переменному току (емкостное сопротивление).

Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Х с. С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты ω.

В заключение отметим, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля. В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.

Из сравнения формул X L = ωL и Х с =1/ωС видно, что катушки индуктивности. представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Индуктивное Х L и емкостное Х C сопротивления называют реактивными.

d) Закон ома для электрической цепи переменного тока.

Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конденсатор емкостью С

Мы видели, что при включении по отдельности в цепь активного сопротивления R, конденсатора емкостью С или катушки с индуктивностью L амплитуда силы тока определяется соответственно формулами:

; ; I m = U m ωC .

Амплитуды же напряжений на активном сопротивлении, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так: U m = I m R; U m = I m ωL;

В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряжение на контуре и напряжения на отдельных элементах цепи, окажется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах. Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.

Действительно, ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлениями. Однако только на активном сопротивлении колебания напряжения и тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колебаний тока на π/2, а на катушке индуктивности колебания напряжения опережают колебания тока на π/2. Если учесть сдвиг фаз между складываемыми напряжениями, то окажется, что

Для получения этого равенства нужно уметь складывать колебания напряжений, сдвинутые по фазе друг относительно друга. Проще всего выполнить сложение нескольких гармонических колебаний с помощью векторных диаграмм. Идея метода основана на двух довольно простых положениях.

Во-первых, проекция вектора с модулем х m вращающегося с постоянной угловой скоростью совершает гармонические колебания: х = х m cosωt

Во-вторых, при сложении двух векторов проекция суммарного вектора равна сумме проекций складываемых векторов.

Векторная диаграмма электрических колебаний в цепи, изображенной на рисунке, позволит нам получить соотношение между амплитудой силы тока в этой цепи и амплитудой напряжения. Так как сила тока одинакова во всех участках цепи, то построение векторной диаграммы удобно начать с вектора силы тока I m . Этот вектор изобразим в виде горизонтальной стрелки. Напряжение на активном сопротивлении совпадает по фазе с силой тока. Поэтому вектор U mR , должен совпадать по направлению с вектором I m . Его модуль равен U mR = I m R

Колебания напряжения на индуктивном сопротивлении опережают колебания силы тока на π/2, и соответствующий вектор U m L должен быть повернут относительно вектора I m на π/2. Его модуль равен U m L = I m ωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор U m L следует повернуть налево. (Можно было бы, конечно, поступить и наоборот.)

Его модуль равен U mC =I m /ωC . Для нахождения вектора суммарного напряжения U m нужно сложить три вектора: 1) U mR 2) U m L 3) U mC

Вначале удобнее сложить два вектора: U m L и U mC

Модуль этой суммы равен , если ωL > 1/ωС. Именно такой случай изображен на рисунке. После этого, сложив вектор (U m L + U mC) с вектором U mR получим вектор U m , изображающий колебания напряжения в сети. По теореме Пифагора:

Из последнего равенства можно легко найти амплитуду силы тока в цепи:

Таким образом, благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи, изображенной на рисунке, выражается так:

От амплитуд силы тока и напряжения можно перейти к действующим значениям этих величин:

Это и есть закон Ома для переменного тока в цепи, изображенной на рисунке 43. Мгновенное значение силы тока меняется со временем гармонически:

i = I m cos (ωt+ φ), где φ — разность фаз между силой тока и напряжением в сети. Она зависит от частоты ω и параметров цепи R, L, С.

e) Резонанс в электрической цепи. При изучении вынужденных механических колебаний мы познакомились с важным явлением — резонансом. Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой внешней силы. При малом трении происходит резкое увеличение амплитуды установившихся вынужденных колебаний. Совпадение законов механических и электромагнитных колебаний сразу же позволяет сделать заключение о возможности резонанса в электрической цепи, если эта цепь представляет, собой колебательный контур, обладающий определенной собственной частотой колебаний.

Амплитуда тока при вынужденных колебаниях в контуре, совершающихся под действием внешнего гармонически изменяющегося напряжения, определяется формулой:

При фиксированном напряжении и заданных значениях R, L и С, сила тока достигает максимума при частоте ω, удовлетворяющей соотношению

Эта амплитуда особенно велика при малом R. Из этого уравнения можно определить значение циклической частоты переменного тока, при которой сила тока максимальна:

Эта частота совпадает с частотой свободных колебаний в контуре с малым активным сопротивлением.

Резкое возрастание амплитуды вынужденных колебаний тока в колебательном контуре с малым активным сопротивлением происходит при совпадении частоты внешнего переменного напряжения с собственной частотой колебательного контура. В этом состоит явление резонанса в электрическом колебательном контуре.

Одновременно с ростом силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности. Эти напряжения становятся одинаковыми и во много раз превосходят внешнее напряжение.

Действительно,

U м, С,рез =

U м, L ,рез =

Внешнее напряжение связано с резонансным током так:

U м = . Если тоU m , C ,рез = U m , L ,рез >> U m

При резонансе сдвиг фаз между током и напряжением становится равным нулю.

Действительно, колебания напряжения на катушке индуктивности и конденсаторе всегда происходят в противофазе. Резонансные амплитуды этих напряжений одинаковы. В результате напряжения на катушке и конденсаторе полностью компенсируют друг друга, и падение напряжения происходит только на активном сопротивлении.

Равенство нулю сдвига фаз между напряжением и током при резонансе обеспечивает оптимальные условия для поступления энергии от источника переменного напряжения в цепь. Здесь полная аналогия с механическими колебаниями: при резонансе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).

Сопротивление реактивное — Справочник химика 21

Гаситель пульсации, как всякое неоднородное включение в трубопроводную систему, оказывает сопротивление движению потока. Полное сопротивление такого включения состоит из активной и реактивной составляющих, причем активная составляющая характеризует потери энергии потока на преодоление сил трения, а реактивная — перераспределение колебательной энергии гармоник в спектре колебаний давления. [c.502]
Реактивные гасители основаны на принципе акустического фильтра, который не пропускает пульсаций на определенной частоте, зависящей от акустической массы и акустической емкости жидкости, заключенной в гасителе. Активное сопротивление реактивных гасителей невелико и не определяет их эффективности. Реактивные гасители имеют строго дискретный спектр гащения. [c.122]

Электрическое сопротивление нефтепродуктов своеобразно изменяется с температурой. На рис. 40 приведены кривые изменения электрического сопротивления реактивного топлива плотностью Р20 =0,789 и содержащего около 0,003% растворенной воды, в диапазоне температур от —25 до 200 °С [1в]. [c.152]

Кроме того, условием, необходимым для работы дуговой печи, через которую с огромной скоростью продувается струя воздуха, является, как уже сказано выше, стабилизация режима горения дуг. С этой целью в электрическую цепь печи вводят необходимые индуктивные сопротивления (реактивные или дроссельные катушки), обеспечивающие, во-первых, понижение напряжения на дуге в момент понижения ее сопротивления для ограничения силы проходящего через дугу тока и, во-вторых, подачу нужного высокого напряжения в момент зажигания дуги, когда сопротивление ее весьма велико. [c.386]

Угол б называется углом диэлектрических потерь из (1.11) видно, что тангенс угла диэлектрических потерь реального конденсатора равен отношению его активного сопротивления в последовательной схеме замеш ения к сопротивлению реактивного участка этой цепи. [c.13]

Для реактивных четырехполюсников сопротивления холостого хода и короткого замыкания представляют собой сопротивления реактивных двухполюсников и, следовательно, можно записать [c.12]

Как видим, при весьма малых а практически можно считать все сопротивление реактивным (ввиду малости 7 по сравнению с У). Поэтому при малых а, принимая во внимание (64) и (70) и вспомнив прежние обозначения, можно полагать [c.768]

Активные гасители (рис. 11.2) работают по принципу поглощения и рассеивания энергии пульсирующего потока в результате преодоления упругих сил вязкого или внутреннего трения. Их реактивное сопротивление незначительно активное сопротивление может быть включено последовательно (а, б) или параллельно (в). Активные гасители наиболее эффективно работают на высоких частотах, так как активное сопротивление пропорционально квадрату скорости, или в данном случае — частоты. [c.503]

Для исследования состояния поверхности металлических образцов и процессов адсорбции на ней, а также свойств окисных и защитных изоляционных пленок на поверхности металла применяют емкостно-омический метод (рис. 358). Емкость и сопротивление исследуемого электрода определяют компенсационным методом — подбором соответствующих величин емкости и сопротивления Из на мостике переменного тока с осциллографом в качестве нуль—инструмента. В электрохимических исследованиях этот метод сочетают с поляризационным методом, измеряя импеданс (полное активное и реактивное сопротивление цепи переменного тока) при различных значениях потенциала исследуемого электрода (см. 166). [c.465]

Реактивные и активные сопротивления короткой сети и печной установки. Расчет параметров х и г) произведен по методу, разработанному ЛенНИИГипрохимом, результаты расчета сведены в табл. 24. [c.141]

Значение реактивных и активных сопротивлений печной установки мощностью 60 МВА [c.141]

Участок Реактивные сопротивления Активные сопротивления [c.141]

Сопротивления повороту, оказываемое последними, вызывает на краях отверстий реактивные моменты, уменьшающие прогибы пластинки и которые можно рассматри,вать. как приложенные [c.452]

Пульсирующая сфера представляет собой поверхность, радиус которой tq колеблется с амплитудой А по гармоническому закону с круговой частотой (о. Полное комплексное сопротивление излучения пульсирующей сферы складывается из активной Rg и реактивной Xg частей [c.51]

Как упоминалось выше, для предотвращения перегрузки трансформаторов, возможной при увеличении проводимости электрического контура внутри электродегидратора, последовательно с первичной обмоткой трансформаторов включают реактивные катушки РОМ-13 6 мощностью 5 ква. При прохождении тока через катушку на ней возникает определенное падение напряжения в результате ее индуктивного сопротивления. Вследствие этого напряжение на первичной обмотке трансформатора снижается. Чем больше сила тока, том больше падает напряжение на реактивной катушке и тем меньше напряжение на трансформаторе. При коротком замыкании в трансформаторе почти все напряжение приходится на долю катушки, и сила тока в цепи ограничивается ее индуктивным сопротивлением. [c.60]

Индуктивность реактивной катушки РОМ-13/6 при включении всех витков составляет 0,1 гн, а ее индуктивное сопротивление при частоте тока 50 пер сек равно 31,4 ом. [c.60]

Для предотвращения аварийных ситуаций пр коротких замыканиях в высоковольтной цепи дегидратора повышающие трансформаторы включают последовательно с ограничителями тока, в качестве которых обычно употребляют катушки реактивной мощности, часто называемые просто реакторами (рис. 2.13). Увеличение силы тока в первичной цепи приводит к возрастанию сопротивления реактора и к увеличению на нем падения напряжения, что в свою очередь обусловливает уменьшение напряжения на первичной обмотке повышающего трансформатора и уменьшение силы тока в первичной цепи. [c.38]

Если Уно — максимальное значение реактивного (емкостного-сопротивления нагрузки, то минимально необходимое индуктивное сопротивление реактора будет определяться равенством [c.42]

Сварочные трансформаторы имеют падающую вольт-ампер-ную характеристику благодаря наличию реактивного индуктивного сопротивления во вторичной цепи, величину которого можно изменять, ограничивая тем самым максимальную величину сварочного тока. У трансформаторов типа СТЭ такое реактивное сопротивление (регулятор) оформлено в виде самостоятельного агрегата, который последовательно включен в цепь вторичной обмотки трансформатора. [c.94]

Под знаком суммы второго члена этого уравнения могут находиться такие внешние силы, как гравитационные, молекулярного притяжения, электростатические, а также силы, возникающие в результате воздействия на каплю несущего потока [13]. Последний член уравнения представляет собой реактивную силу, сообщаемую капле отходящими парами. Для расчетов тепло- и массообмена в вихревом газовом потоке преимущественное значение имеют центробежная сила (Рц) и сила вязкого сопротивления среды (F ), как наиболее важные по интенсивности действия и определяющие характер движения капли. Тогда суммарное воздействие сил, приложенных к капле, с учетом названных сил запишется следующим образом [c.176]

Однако, поскольку в схему моста входит источник переменного тока, балансировка моста осложнена влиянием индуктивностей и емкостей всей цепи. Емкость электролитической ячейки и цепи приводит к тому, что наряду с активной составляющей сопротивления измеряется реактивная составляющая. Выбирая оптимальные значения частоты и плотности тока, кон- [c.106]

Реактивные гасители (рис. 11.3) основаны на принципе акустического фильтра, препятствующего прохождению пульсации определенной частоты, которая зависит от массы и давления газа в ячейках гасителя. Активное сопротивление таких гасителей или гораздо меньше реактивного, или не определяет характера их работы. Реактивные гасители имеют сугубо дискретный спектр гашения. По виду амплитудно-частотной характеристики реактивные гасители можно разделить на широкополосные (а), резонансные (б) и смешанного типа (в). [c.503]

Хп — реактивное сопротивление. Ом/км (для проводов принимается равным 0,6) [c.53]

Применявшаяся нами электрическая измерительная схема неравновесного высокочастотного резонансного моста описана в [1, с. 254]. Эта схема позволяла регистрировать и записывать мгновенные значения изменений реактивного сопротивления датчика (йС, пропорциональные изменения локальной объемной концентрации бог или порозности бе = —бо. По-видимому, более однозначно связанной с объемной концентрацией твердой фазы а и менее зависящей от деталей структуры, является не реактивная составляющая сопротивления измерительного зонда, а тангенс угла диэлектрических потерь в материале зерен слоя [67, с. 291. [c.83]

Текучесть. Как и следовало предполагать, повышение температуры размягчения приводит к снижению текучести или тенденции к проседанию при температурах ниже температуры размягчения. Разработан метод, позволяющий измерять сопротивление текучести, которое сообщает каучук каменноугольным пекам, используемым в покрытиях, стойких к действию реактивного топлива. Этот же метод [c.219]

Простая установка с динамометром показана на рис. П-5. Весь узел привода смонтирован на упорном подшипнике и расположен выше сосуда с перемешиваемой жидкостью. При вращении мешалки создается механическое усилие, которому противодействует жидкость. Сопротивление жидкости передается от вала двигателя к мотору. Этот реактивный крутящий момент вызывает вращение привода на упорном подшипнике в направлении, [c.41]

При переменном токе полное сопротивление системы равно сумме активного и индуктивного (реактивного) сопротивлений [c.209]

Однако изменения сопротивления реактивной катушки можно добиться электрическим путем. С этой целью на сердечник (рис. 1-13,6) наматывается управляющая обмотка Шу, с помощью которой производится подмаг-ничивание сердечника постоянным током. От величины /у будет зависеть индуктивное сопротивление реактивной катушки переменному току. Зависимость такова с увеличением тока подмагничивания уменьшается индуктивное сопротивление и возрастает ток в нагрузочной цепи, и наоборот. Таким образом, магнитный усилитель позво-48 [c.48]

Использование электродных аналогов двойного электрического слоя электрода под током, простейшие из которых представлены на рис. 14.1, позволило разработать методы экспериментального разделения общей поляризационной емкости на ее слагаемые. Методы эти, однако, являются ирибллженными, так как двойнослойная и псевдоемкость взаимосвязаны и изменение одной приводит к изменению другой. Тем не менее они нашли широкое применение и дали возможность получить ценную информацию о поведении границы раздела электрод — электролит в условиях электродной йоляризации. Наиболее часто используются мостовые и другие схемы на переменном токг, которые позволяют находить величину, называемую импедансом 2 и характеризующую полное сопротивление (активное — R и реактивное — С) электрической цепи переменному току. Для цепи, моделирующей электрод, импеданс определяется уравнением [c.289]

Ороситель приводится в движение действием реактивного момента, возникающего при истечении пленочной струи, паправлениой в разные стороны относительгю оси вращения. Момент трения в подвеске оросителя и момент, обусловленный сопротивлением среды, а также гидравлическими потерями, компенсируется встроенной [c.170]

Допускаемые расхождения между параллельными определениями пределов прочности образцов резин после испытания в реактивных топливах не должны превышать 10% среднего арифметического значения. Считают, что топливо прошло испытание, если после контакта с ним образцы резины имеют сопротивление разрьту не менее 8,5 МПа, а относительное удлинение не менее 100%. [c.149]

В связи с зависимостью удельного сопротивления осадка от многих факторов и возникновением уравнения (111,39) сопоставлены величины удельного сопротивления с показателем степени в упомянутом уравнении, который назван кинетическим параметром [151]. Исследовано разделение 15 водных суспензий неорганических реактивных солей при плотности твердых частиц 2,1 — 7,0 г-см и среднем размере их в основном 5—30 мкм. Лабораторные опыты проведены на фильтре с перегородкой из фильтро-миткаля поверхностью 36 см при постоянной разности давлений З-Ю Па. Установлено, что удельное сопротивление осадка меньше для частиц с большей плотностью (хлорид талия), когда наблюдается быстрое оседание частиц и фильтрование происходит при скорости, приближающейся к постоянной это соответствует значениям т, близким к 1. Найдено, что удельное сопротивление осадка больше для тонкодисперсных частиц (сульфат бария), что соответствует значениям т, близким к 0,5. Отмечено, что соответствие между удельным сопротивлением осадка и кинетическим параметром лишь приближенное, причем в некоторых случаях расхождение существенное. Это объяснено влиянием искажающих микрЬ-факторов. [c.141]

Исследована зависимость удельного объемного сопротивления осадков ряда неорганических солей, образующихся при разделении их водных суспензий на фильтре, от концентрации твердых частиц в суспензии [206]. Использованы сульфаты кальция, бария и стронция, карбонат кальция, фторид лития и фосфат магния (МдНР04) реактивной степени чистоты, что сводит влияние примесей на удельное сопротивление осадка до минимума размер [c.188]

Виброгашение. Под виброгашением понимают умепь-ше 1ие уровня вибраций защищаемого объекта при введении в систему дополнительных реактивных сопротивлений. Чаще всего это достигается при установке агрегатов на виброгасящие основания (рис. 9.3). Массу фундамента подбирают таким образом, чтобы амплитуда колебаний подошвы фундамента [c.105]

При турбулентном характере потока образуются зоны вращательного движения газа, появляется дополнительное упругоинерционное воздействие на газовый поток, которое и характеризует реактивную часть полного сопротивления. Гасители, у которых реактивная часть сопротивления мала по сравнению с активной, можно считать чисто активными наоборот, гасители, активная часть сопротивления которых мала по сравнению с реактивной,—чисто реактивными. [c.503]

Вязкости от 0,5 до 3-10 сП могут быть измерены в реометре сопротивления. Этот аппарат в принципе аналогичен прибору Брукфильда. Он состоит из цилиндра (оканчивающегося с обеих сторон, конусами), вращающегося в сосуде с испытуемым материалом. Сопротивление испытуемого материала вращению шпинделя, передаваемое свободно подвешенному мотору, компенсируется градуированной пружиной. С корпусом мотора, испытывающим реактивный вращательный момент, связан указатель, который непр ывнр показывает вязкость на неподвижной шкале. [c.111]

Каменноугольный деготь в дорожных покрытиях. Смеси камен ноугольного дегтя с каучуком используют в дорожных покрытиях, стойких к действию реактивного топлива, и в смесях для герметизации стыков в цементобетоне. Благодаря введению эластомера повышается сопротивление изменению физических свойств от температуры. Деготь в большей степени, чем битум, хрупок при низкой температуре и излишне мягок при высокой температуре. Нит-рильные каучуки в виде крошки или гранул чаш,е всего используют во взлетно-посадочных полосах и площадках для стоянки самолетов, где происходит утечка авиационного топлива. [c.239]

Усилитель постоянного тока и линейные операционные блоки АВМ. Основным элементом большинсгва блоков электронных АВМ является операционный усилитель постоянного тока. Он состоит из трех элементов — собственно усилителя, цепи отрицательной обратной связи и входной цепи. Эти цепи могут содержать как активные, так и реактивные сопротивления. Усилители конструируют так, чтобы они имели очень большой (10″ —10 ) отрицательный коэффициент усиления по напряжению. Это означает, что напряжение, подаваемое с выхода усилителя через цепь обратной связи на ei o вход, уменьшает величину входного напряжения. При выполнении этого условия потенциал на входе усилителя относительно земли очень мал, а входной ток практически отсутствует. Усилитель обладает линейной характеристикой, если выходное напряжение не превышает допустимого значения. В ламповых усилителях это предельное значение составляет 100 В, в полупроводниковых— 10 или 30 В. Входное и выходное-напряжения усилителя имеют разные знаки. [c.327]

Теплогенерация за счет электрической энергии реализуется преодолением активного (омического) сопротивления, поэтому при использовании перемеиного тока нужно стремиться к уменьшению реактивного (индуктивного) сопротивления, являющегося следствием рассеяиия магнитной энергии. В отличие от постоянного тока при переменном токе эффект теплогенерации, кроме общего падения напряжения, зависит еще и от частоты тока. [c.239]

При разработке печей-теплогенератрров с электрическим режимом работы следует стремиться к соэдзегию такой конструкции, когда большая часть общего активного сопротивления сосредоточена в зоне технологического процесса. При этом увеличивается соотношение между активным и реактивным сопротивлениями, повышается os ф и наиболее эффективно используется электрическая энер- [c.241]

Входное и выходное сопротивления газопровода представляют собой эквивалентное сопротивление току, входящему в тело газопровода из земли и выходящему из тела газопровода (рис. 2), и содержат активную и реактивную составляющие. В общем случае не следует определять как входное сопротивление длинной линии с распределенными параметрами. На высоких частотах можно пренебречь активной составляющей входного и выходного сопротивлений и считать их чисто емкостными (Хв и Хвых), равными сопротивлению конденсаторов, образованных участками трубопровода длиной Lb x и землей. [c.105]

РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ

ТЕОРИЯ: ПОНЕМНОГУ — ОБО ВСЕМ

1.6. Реактивное сопротивление.

    Если через обмотку катушки индуктивности с магнитопроводом (сердечником) пропустить переменный ток, изменяющийся по синусоидальному закону simt (см. рис. 3), возникнет, как мы говорили, магнитный поток, намагничивающий магнитопровод. Ток и магнитный поток в магнитопроводе будут также переменными и возбудят в обмотке ЭДС индукции. Она равна напряжению на выводах катушки, и в то же время пропорциональна скорости изменения магнитного потока. В итоге напряжение будет сдвинуто по фазе на -90° относительно тока. Это значит, что ток отстает по фазе на 90° от напряжения.
    Ток, протекающий через катушку, называется реактивным, и в отличие от тока через активное сопротивление, он не приводит к расходованию мощности. Кроме того, напряжение на катушке при фиксированном токе пропорционально частоте, следовательно, сопротивление катушки возрастает с частотой. Напряжение на катушке может быть рассчитано по закону Ома, в который в качестве сопротивления надо подставить индуктивное сопротивление катушки: X_L = jL = j2fL (индуктивное сопротивление). Перед обозначением реактивного сопротивления ставят символ j, в математике обозначающий мнимую величину, равную квадратному корню из -1.
    Посмотрим теперь, что получится, если к пластинам конденсатора приложить переменное напряжение, изменяющееся по синусоидальному закону simt. Через конденсатор потечет переменный ток, вызванный тем, что пластины конденсатора должны будут перезаряжаться столько раз в секунду, сколько раз ток изменяет свое направление. Заряд на пластинах прямо пропорционален приложенному напряжению (q = CU), а ток пропорционален скорости изменения заряда (I = dq/dt).
    Таким образом, ток через конденсатор также реактивный, но опережает напряжение на 90°. Ток пропорционален частоте, следовательно, емкостное сопротивление конденсатора обратно пропорционально частоте: Х_с = 1/jС = -j/С (емкостное сопротивление).
    Зависимости реактивных сопротивлений от частоты показаны на рис. 6,а. В реальных электрических цепях встречаются как реактивные, индуктивные и емкостные, так и активные сопротивления. Вместе они образуют комплексные, или полные сопротивления, обозначаемые буквой Z и математически представляющие собой комплексные числа, содержащие действительную R и мнимую X части: Z = R + jX (полное сопротивление).

Рис. 6

    Как складываются активные сопротивления при последовательном и параллельном соединении, мы уже изучали (рис. 2,г), и теперь нам осталось сказать, что и полные сопротивления складываются точно так же, только не надо забывать про знак реактивного сопротивления и символ j.
    Будет очень полезно, если вы немного потренируетесь и попробуете написать полное сопротивление цепей, содержащих различным образом включенные катушки индуктивности, конденсаторы и резисторы (рис. 6, б-д). Очень скоро вы убедитесь, что одно и то же полное сопротивление на одной, заданной частоте могут иметь цепи, выполненные по-разному, и это открывает возможность их преобразования.
    Например, цепь из последовательно соединенных резистора и конденсатора можно заменить цепью, где те же элементы включены параллельно, но, разумеется, номиналы у них будут другими. Также легко убедиться, что при последовательном соединении двух катушек их индуктивности складываются, а вот емкости складываются при параллельном соединении конденсаторов. Ну а теперь перейдем к обещанному рассказу о трансформаторах.

Радио, 1998

Активное реактивное и полное сопротивление. Треугольники сопротивлений

Активное сопротивление

, где — импеданс, — величина активного сопротивления, — величина реактивного сопротивления, — мнимая единица.

Реактивное сопротивление

Реактивное сопротивление — электрическое сопротивление, обусловленное передачей энергии переменным током электрическому илимагнитному полю (и обратно).

Реактивное сопротивление определяет мнимую часть импеданса:

В зависимости от знака величины какого-либо элемента электрической цепи говорят о трёх случаях:

— элемент проявляет свойства индуктивности.

— элемент имеет чисто активное сопротивление.

— элемент проявляет ёмкостные свойства.

Индуктивное сопротивление ( ) обусловлено возникновением ЭДС самоиндукции в элементе электрической цепи. Изменение тока и, как следствие, изменение его магнитного поля вызывает препятствующее изменению этого тока ЭДС самоиндукции. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока:

Ёмкостное сопротивление ( ). Величина ёмкостного сопротивления зависит от ёмкости элемента и также частоты протекающего тока :

Здесь — циклическая частота, равная .

Прямая и обратная зависимость этих сопротивлений от частоты тока приводит к тому, что с увеличением частоты всё бо?льшую роль начинает играть индуктивное сопротивление и всё меньшую ёмкостное.

Полное сопротивление

Полное сопротивление (z) — это векторная сумма всех сопротивлений: активного, емкостного и индуктивного.

Треугольники сопротивлений

Если стороны треугольника напряжений (155, а) разделить на ток I (.155, б), то углы треугольника от этого не изменятся, и мы получим новый треугольник, подобный первому — треугольник сопротивлений (155, в).

В треугольнике сопротивления, показанном на рис, все стороны обозначают сопротивления, причем гипотенуза его является полным или кажущимся сопротивлением цепи.

Из треугольника сопротивлений видно, что полное или кажущееся сопротивление Z равно геометрической сумме активного R и индуктивного X_l сопротивлений.

Применяя теорему Пифагора к треугольнику сопротивлений, получаем:

Что такое реактивное сопротивление? — Определение из WhatIs.com

Реактивное сопротивление, обозначенное X , является формой сопротивления, которое электронные компоненты демонстрируют прохождению переменного тока (переменного тока) из-за емкости или индуктивности. В некоторых отношениях реактивное сопротивление похоже на переменный аналог постоянного тока , сопротивление . Но эти два явления во многом отличаются друг от друга и могут различаться независимо друг от друга. Сопротивление и реактивное сопротивление вместе образуют импеданс , который определяется в терминах двумерных величин, известных как комплексное число.

Когда переменный ток проходит через компонент, обладающий реактивным сопротивлением, энергия попеременно накапливается и высвобождается из магнитного поля или электрического поля. В случае магнитного поля реактивное сопротивление является индуктивным. В случае электрического поля реактивное сопротивление является емкостным. Индуктивному реактивному сопротивлению присваиваются положительные мнимые числовые значения. Емкостному реактивному сопротивлению присваиваются отрицательные значения мнимого числа.

По мере увеличения индуктивности компонента его индуктивное реактивное сопротивление становится больше в мнимом выражении, если частота остается постоянной.По мере увеличения частоты для данного значения индуктивности индуктивное реактивное сопротивление увеличивается в мнимом выражении. Если L — это индуктивность в генри (Гн), а f — частота в герцах (Гц), то индуктивное реактивное сопротивление + jX _L в мнимых омах определяется по формуле:

+ jX _L = + j (6,2832 fL )

, где 6,2832 примерно равно 2 умноженным на пи, константе, представляющей количество радианов в полном цикле переменного тока, а j представляет собой единичное мнимое число (положительный квадратный корень из -1).Формула также верна для индуктивности в микрогенри (? H) и частоты в МГц (МГц).

В качестве реального примера индуктивного реактивного сопротивления рассмотрим катушку с индуктивностью 10 000 Ом на частоте 2 000 МГц. Используя приведенную выше формулу, можно определить, что + jX _L равно + j 125,66 Ом. Если частоту удвоить до 4.000 МГц, то + jX _L удвоится, до + j 251,33 Ом. Если частота уменьшается вдвое до 1.000 МГц, то + jX _L уменьшается вдвое, до + j 62.832 Ом.

По мере увеличения емкости компонента его емкостное реактивное сопротивление становится меньше (ближе к нулю) в мнимом выражении, если частота остается постоянной. По мере того, как частота увеличивается для данного значения емкости, емкостное реактивное сопротивление становится меньше отрицательно (ближе к нулю) в мнимом выражении. Если C — это емкость в фарадах (F) и f — частота в Гц, то емкостное реактивное сопротивление -jX _C в мнимых числах в омах определяется по формуле:

-jX _C = — j (6.2832 ФК ) ^-1

Эта формула также верна для емкости в микрофарадах (? F) и частоты в мегагерцах (МГц).

В качестве реального примера емкостного реактивного сопротивления рассмотрим конденсатор номиналом 0,0010000 мкФ на частоте 2,0000 МГц. Используя приведенную выше формулу, было найдено, что -jX _C составляет — j 79,577 Ом. Если частота увеличивается вдвое до 4,0000 МГц, то -jX _C уменьшается вдвое, до — j 39.789 Ом. Если частоту уменьшить вдвое до 1,0000 МГц, то -jX _C увеличится вдвое, до — j 159,15 Ом.

Реактивность — обзор | Темы ScienceDirect

8.1.2 Нагрузка сетей с линиями передачи

Схема компенсации реактивного сопротивления также может использоваться для улучшения полосы пропускания СВЧ-транзисторных усилителей, поскольку входные и выходные импедансы транзисторов обычно могут быть представлены последовательными или шунтирующими цепями RLC .Для компенсации реактивной части и преобразования действительной части эквивалентного импеданса выходного транзистора в обычное полное сопротивление нагрузки на основной частоте можно использовать линии передачи на четверть и половину длины волны. Впервые четвертьволновый трансформатор линии передачи был использован для компенсации активного реактивного сопротивления, когда при соединении двух идентичных активных устройств вместе с четвертьволновым трансформатором, инвертированный импеданс одного устройства компенсирует импеданс другого, уменьшая сопротивление. полное реактивное сопротивление цепи [8].

Рассмотрим характеристики ЛЭП как элемента схемы компенсации проводимости, показанной на рис. 8.6. Для параллельной эквивалентной схемы, которая представляет собой выход устройства, входное сопротивление нагрузки сети B _net = Im Y _net можно определить как

Рисунок 8.6. Схема компенсации проводимости проводов.

(8.19) Bnet (ω) = ωLpCp (1 − ω02ω2) + tanθZ0RL2 − Z02RL2 + Z02tan2θ

, где

(8.20) θ = π2ff0k

— электрическая длина линии передачи, Z ₀ — характеристическое сопротивление линии передачи, f ₀ = ω ₀/2 π — передача резонансная частота линии, k = 1, 2,…, ∞.

Применяя условие нулевой проводимости-производной, заданное формулой. (8.4) к формуле. (8.19) позволяет получить параметры цепи компенсации проводимости для различной электрической длины линии передачи в соответствии с

(8.21) 2Cp + π2Z0ω0RL2 − Z02cos2θRL2 − Z02tan2θ (RL2 + Z02tan2θ) 2 = 0.

Для четвертьволновой линии передачи, когда k = 1 и θ = π /2, компенсация проводимости будет выполняться при условии Z ₀ < R _L с характеристический импеданс Z ₀, определяемый квадратным уравнением

(8,22) Z02 + 4QRLπZ0 − RL2 = 0

, где Q = ω ₀ C _p R и R и R Z02 / RL.

В результате требуемое значение характеристического сопротивления Z ₀ получается как

(8,23) Z0 = RL (−2Qπ + (2Qπ) 2 + 1)

или

(8,24) Z0 = R / (- 2Qπ + (2Qπ) 2 + 1).

Используя четверть- и полуволновые трансформаторы, сеть нагрузки с компенсацией реактивного или реактивного сопротивления обычно может быть реализована по-разному для параллельных и последовательных эквивалентных схем выходных транзисторов, как показано в Таблице 8.1 вместе с соответствующими расчетными уравнениями [9,10] .Двумя наиболее важными параметрами устройства в уравнениях являются загруженный коэффициент качества Q и действительная часть R эквивалентного выходного импеданса или проводимости устройства. В зависимости от значений характеристического импеданса линии передачи Z ₁ и Z ₂ каждая цепь обеспечивает компенсацию положительного или отрицательного параллельного резонанса крутизны спада реактивного сопротивления.

Таблица 8.1. Цепи компенсации реактивного сопротивления линии передачи и расчетные уравнения

Тип выходной цепи	Согласованная сеть	Расчетное уравнение
		Z1 = RRLT − 12 (- 2QπL) Z2 = −TRL2 + (TRL2) 2 + RL2
		Z1 = RRLZ2 = πZ1RL2πZ12 − πRL2−4QZ1RL
		Z1 = AZ2Z2 + Rπ (2Qπ) 2+ (1 + A) 2A]
		Z2 = RRLZ1 = (TZ2RL) 21 (RLZ2 − Z2RL) + 4QπT = 2πcosθ2 (θ1 + θ2) θ1 + θ2 = nπ2 → n = 1or3 90

Рисунок 8.7 ( a ) показан пример сети компенсации нагрузки с одинарной проводимостью с последовательной четвертьволновой линией передачи, имеющей характеристический импеданс 61,2 Ом, чтобы соответствовать 50-омной реальной части эквивалентной выходной проводимости устройства на выходе 75-омной нагрузки. и электрическая длина 90 ° при 50 МГц. Комбинация сопротивлений шунтирующей цепи LC (кривая 1) и последовательной четвертьволновой линии передачи (кривая 2) обеспечивает минимальные изменения полного сопротивления Re Z _net, показанного на рис.8.7 ( b ) кривой 3; около 50 Ом в очень широком диапазоне частот. Сопротивление Im Y _net шунтирующего контура, имеющего резонансную частоту 50 МГц, изменяется в зависимости от частоты с положительным наклоном, как показано на рис. 8.7 ( c ) кривой 1. Добавление последовательных четверть- Трансформатор линии передачи с длиной волны между шунтирующей цепью и нагрузкой дает отрицательный наклон, обеспечивающий дополнительную проводимость, как показано на рис. 8.7 ( c ) кривой 2.Выбор надлежащего характеристического импеданса последовательной четвертьволновой линии передачи и сопротивления нагрузки позволяет сделать два значения крутизны идентичными, так что общая крутизна индуктивности вокруг резонанса равна нулю в диапазоне частот от 45 до 65 МГц, как показано. на рис. 8.7 ( c ) кривой 3.

Рисунок 8.7. Схема компенсации подвески с четвертьволновой линией передачи.

Из уравнения. Из (8.23) следует, что максимальное значение характеристического импеданса Z ₀ ограничено сопротивлением нагрузки R _L, и его значение в некоторых случаях, особенно для высокого значения Q , может быть существенно меньше 50 Ом; что вызывает проблемы при практической реализации линии передачи.В этом случае лучше всего применить метод одночастотной эквивалентности, когда четвертьволновую линию передачи можно заменить симметричным участком линии передачи нижних частот типа π с двумя равными шунтирующими емкостями на частоте ω ₀, как показано на рис. 8.8.

Рисунок 8.8. Метод одночастотной эквивалентности линии передачи.

Матрица ABCD для четвертьволновой линии передачи может быть записана как

(8.25) ABCD90 ° = [cos90 ° jZ0sin90 ° jsin90 ° Z0cos90 °] = [0jZ0j1Z00]

, тогда как для участка линии передачи нижних частот типа π мы можем записать

(8,26) ABCDπ = [10jωCT1 ] [cosθTjZTsinθTjsinθTZTcosθT] [10jωCT1] = [cosθT − ωCTZTsinθTjZTsinθTjZT (2ZTωCTcosθT + sinθT − ZT2ω2CT2sinθT) cosθT − ωCTZTsinθT].

Следовательно, приравнивая A и B элементов из каждой матрицы, получаем

(8,27) ZT = Z0sinθT

(8,28) CT = cosθTωZ0.

В результате электрическая длина линии передачи может быть значительно уменьшена за счет увеличения ее характеристического сопротивления.Также такое преобразование очень важно, когда значение выходной емкости устройства превышает требуемое оптимальное значение для оптимальной работы класса E. В этом случае избыточная емкость может использоваться как часть или вся шунтирующая емкость в секции нижних частот типа π , и оптимальные условия переключения класса E будут полностью соблюдены на основной частоте.

1.5: Реактивное сопротивление и импеданс — Engineering LibreTexts

В отличие от резистора, напряжение и ток не будут совпадать по фазе для идеального конденсатора или идеальной катушки индуктивности.Для конденсатора ток опережает напряжение на конденсаторе на 90 градусов. Напомним, что напряжение на конденсаторе не может измениться мгновенно, \ (i = C \, dv / dt \). Для индуктора напряжение опережает ток на 90 градусов. Точно так же ток через катушку индуктивности не может мгновенно измениться из-за \ (v = L \, di / dt \). Хотя идеальные конденсаторы и катушки индуктивности не обладают сопротивлением, напряжение реагирует на ток. Неудивительно, что мы называем это характеристическим реактивным сопротивлением и обозначаем его буквой \ (X \).{\ circ} \), или, что более удобно, мы просто добавляем \ (- j \), как в \ (X_C = −j75 \ Omega \).

Корпус для индуктора аналогичен и оставлен в качестве упражнения. Индуктивное реактивное сопротивление \ (X_L \) можно найти по формуле:

\ [X_L = + j 2 \ pi f L \ label {1.9} \]

Примером может быть \ (X_L = j68 \ Omega \). Как уже говорилось, хотя сопротивление не может быть добавлено непосредственно к реактивному сопротивлению, реактивные сопротивления можно складывать вместе, если мы прислушиваемся к знакам. Например, если у нас есть емкостное реактивное сопротивление \ (- j60 \ Omega \) последовательно с индуктивным реактивным сопротивлением \ (j100 \ Omega \), результатом будет \ (j40 \ Omega \).Это связано с тем, что эти два элемента не совпадают по фазе на 180 градусов друг с другом, поэтому они частично отменяются. Помните, всегда добавляйте или вычитайте одинаковые предметы: реальное (сопротивление) к реальному и мнимое (реактивное сопротивление) к мнимому.

Уравнения \ ref {1.8} и \ ref {1.9} примечательны тем, что реактивное сопротивление является не только функцией емкости или индуктивности, но также функцией частоты. Реактивное сопротивление катушки индуктивности прямо пропорционально частоте, а реактивное сопротивление конденсатора обратно пропорционально частоте.Омические вариации резистора \ (20 \ Omega \), конденсатора 500 \ (\ mu \) F и катушки индуктивности 500 \ (\ mu \) H по частоте показаны на рисунке \ (\ PageIndex {1} \). .

Мы можем видеть, что значение сопротивления не изменяется с частотой, в то время как индуктивное реактивное сопротивление увеличивается с частотой, а емкостное реактивное сопротивление уменьшается.

Рисунок \ (\ PageIndex {1} \): сопротивление и реактивное сопротивление в зависимости от частоты (линейная ось).

Линейная шкала частоты затрудняет отображение изменения конденсатора.Если это построить снова, но с использованием логарифмической шкалы частот, как на рисунке \ (\ PageIndex {2} \), симметрия станет очевидной.

Рисунок \ (\ PageIndex {2} \): Сопротивление и реактивное сопротивление в зависимости от частоты (логарифмическая ось).

Влияние размера и частоты конденсатора показано на рисунке \ (\ PageIndex {3} \) с использованием логарифмической оси частот: чем меньше конденсатор, тем больше емкостное реактивное сопротивление на любой конкретной частоте.

Рисунок \ (\ PageIndex {3} \): изменение емкостного реактивного сопротивления в зависимости от емкости и частоты.

Аналогичным образом влияние размера и частоты катушки индуктивности показано на рисунке \ (\ PageIndex {4} \) с использованием линейной оси частот: чем больше катушка индуктивности, тем больше индуктивное реактивное сопротивление на любой заданной частоте.

Рисунок \ (\ PageIndex {4} \): Изменение индуктивного сопротивления в зависимости от индуктивности и частоты.

Стоит отметить, что графики на рисунках \ (\ PageIndex {3} \) и \ (\ PageIndex {4} \) предназначены для идеальных компонентов. В действительности все компоненты проявляют некоторые резистивные, емкостные и индуктивные эффекты из-за своей конструкции.Например, в конечном итоге индуктивные и резистивные эффекты заставят кривые емкостного реактивного сопротивления на рисунке \ (\ PageIndex {3} \) начать расти на высоких частотах. Точно так же резистивные и емкостные эффекты заставят кривые Рис. \ (\ PageIndex {4} \) сглаживаться на очень низких и очень высоких частотах.

Следует запомнить интересное наблюдение: конденсаторы и катушки индуктивности немного похожи на химеру. То есть в разных источниках они выглядят как разные вещи, смешанные одновременно.Было бы неправильно думать, скажем, о конкретной катушке индуктивности как о «таком большом количестве Ом». Если исходный сигнал состоит из нескольких синусоидальных волн, таких как прямоугольная волна или музыкальная волна, индуктор «выглядит» как разное омическое значение для каждой из различных частотных составляющих одновременно. Это важная концепция, и мы можем воспользоваться ее преимуществами, например, при разработке схем фильтров.

Импеданс

Теперь мы подошли к импедансу. Импеданс представляет собой смесь сопротивления и реактивного сопротивления и обозначается как \ (Z \).{\ circ} \ Omega \), то есть величина 600 Ом, которая включает сопротивление и индуктивное реактивное сопротивление (это должно быть индуктивное реактивное сопротивление, а не емкостное реактивное сопротивление, поскольку знак угла положительный).

Чтобы завершить эту систему, у нас есть прием и прием. Восприимчивость, \ (S \), является обратной величиной реактивного сопротивления. Полная проводимость, \ (Y \), является обратной величиной импеданса. Они аналогичны соотношению между проводимостью и сопротивлением и удобны для комбинаций параллельных цепей.

Пример \ (\ PageIndex {1} \)

Определите реактивные сопротивления катушки индуктивности 1 мГн и конденсатора 2 \ (\ mu \) F на синусоидальную волну 2 кГц. Повторите для частоты 50 кГц.

Используйте уравнения \ ref {1.8} и \ ref {1.9}. Для конденсатора на 2 кГц имеем:

\ [X_C = — j \ frac {1} {2 \ pi f C} \ nonumber \]

\ [X_C = — j \ frac {1} {2 \ pi 1 кГц 2 \ mu F} \ nonumber \]

\ [X_C = — j 79.6 \ Omega \ nonumber \]

Для второго источника 50 кГц в 25 раз больше исходного, а емкостное реактивное сопротивление обратно пропорционально частоте.Следовательно, \ (X_C \) в 25 раз меньше, или \ (- j3.18 \ Omega \).

Для индуктора на 2 кГц,

\ [X_L = + j 2 \ pi f L \ nonumber \]

\ [X_L = + j 2 \ pi 2 кГц 1 мГн \ nonumber \]

\ [X L = + j 12,57 \ Omega \ nonumber \]

Индуктивное реактивное сопротивление прямо пропорционально частоте. Таким образом, увеличение f в 25 раз увеличивает \ (X_L \) в тот же раз, что приводит к \ (j314.2 \ Omega \).

Пример \ (\ PageIndex {2} \)

Определите реактивную сопротивляемость катушки индуктивности \ (j400 \ Omega \). {- 1} \ left (\ frac {400} {1000} \ right) \ nonumber \]

\ [\ theta = 21.{\ circ} \ mu S \).

Реактивное сопротивление и импеданс — Формула

Значение импеданса — Это мера общего сопротивления цепи току, обозначенная Z. Проще говоря, она дает количество цепи, которая препятствует потоку изменений. Импеданс подобен сопротивлению, которое также учитывает влияние индуктивности и емкости. Единица измерения импеданса — ом.

Поскольку импеданс учитывает влияние индуктивности и емкости и изменяется в зависимости от частоты тока, проходящего через цепь, он является более сложным, чем сопротивление.По сравнению с сопротивлением, которое постоянно независимо от частоты, импеданс зависит от частоты.

Когда доходит до определения реактивного сопротивления, это мера противостояния индуктивности и емкости току. Давайте вкратце узнаем об этих двух терминах.

Формула импеданса

Математический символ импеданса — Z, а единица измерения — Ом. Это надмножество сочетания сопротивления и реактивного сопротивления.

В терминах векторов полное сопротивление Z определяется как сумма сопротивления R и реактивного сопротивления X как:

X = R + j X

Где реактивное сопротивление X является суммой индуктивного реактивного сопротивления XL и емкостного Xc

X = XL + Xc

Импеданс, Z = V / I

Сопротивление, R = V / I

V = напряжение в вольтах (В)

I = ток в амперах (A)

Z = полное сопротивление в омах (Ом)

R = сопротивление в омах (Ом)

Импеданс можно разделить на две части:

Переменный ток отстает или опережает напряжение зависит от природы реактивного компонента импеданса (преимущественно индуктивного или емкостного)

Индуктивность и Емкость вызывает фазовый сдвиг между током и напряжением, что означает, что сопротивление и реактивное сопротивление нельзя просто суммировать, чтобы получить полное сопротивление.{2}} \]

Есть четыре электрические величины, которые определяют полное сопротивление (Z) цепи: это сопротивление (R), емкость (C), индуктивность (L) и частота (f).

Что такое реактивность?

Мера противостояния индуктивности и емкости току известна как реактивное сопротивление, обозначаемое X. Оно зависит от частоты электрических сигналов и измеряется в омах.

Реактивное сопротивление бывает двух типов:

Емкостное реактивное сопротивление (Xc) и
Индуктивное реактивное сопротивление (XL).

Формула реактивного сопротивления

Общее реактивное сопротивление (X) равно разнице между двумя:

Полное реактивное сопротивление, X = XL — Xc

a. Емкостное реактивное сопротивление Xc

Реактивное сопротивление, которое велико на низких частотах и мало на высоких частотах, известно как емкостное реактивное сопротивление (Xc). Xc бесконечен для постоянного постоянного тока при нулевой частоте (f = 0 Гц). Это означает, что конденсатор пропускает переменный ток, но блокирует постоянный ток.

Емкостное реактивное сопротивление, Xc = 1 / 2fC

Где,

Xc = реактивное сопротивление в омах (Ом)

f = частота в герцах (Гц)

C = емкость в фарадах (F)

Например, для: 1 мкФ Конденсатор имеет реактивное сопротивление 3.2 кГц для сигнала 50 Гц, но когда частота выше 10 кГц, реактивное сопротивление составляет всего 16.

b. Индуктивное реактивное сопротивление, XL

Реактивное сопротивление, которое мало на низких частотах и велико на высоких частотах, известно как индуктивное реактивное сопротивление. XL равен нулю для постоянного постоянного тока при нулевой частоте (f = 0 Гц). Это означает, что катушка индуктивности пропускает постоянный ток, но блокирует переменный ток.

Формула для расчета индуктивного сопротивления катушки:

Индуктивное реактивное сопротивление, или XL, является произведением двойного p (пи) или 6.28, частота переменного тока в герцах и индуктивность катушки в генри.

XL = 2p x f x L

L = значение индуктивности катушки в генри.

Индуктивное реактивное сопротивление, XL = 2fL

Где,

XL = реактивное сопротивление в омах (Ом)

f = частота в герцах (Гц)

L = индуктивность в генри (H)

Например, индуктор 1 мГн имеет реактивное сопротивление всего 0,3 для сигнала 50 Гц, но когда частота выше 10 кГц, его реактивное сопротивление составляет 63.

Знаете ли вы?

Когда ток и напряжение не синхронизируются, это означает, что имеется фазовый сдвиг. Например, при замене конденсатора напряжение на нем равно нулю. Однако сила тока максимальна. Когда конденсатор заряжен, напряжение будет максимальным, а ток — минимальным. Зарядка и разрядка происходят непрерывно с переменным током, где ток достигает максимума незадолго до того, как напряжение достигает максимума, поэтому это называется текущим опережающим напряжением.

Емкостное реактивное сопротивление

Ваш браузер не поддерживает Java-апплеты.

ЕМКОСТЬ И ИНДУКТИВНАЯ РЕАКТИВНОСТЬ

Отношение напряжения конденсатора к току называется емкостным реактивным сопротивлением. а также сопротивление в омах, обеспечиваемое конденсатором.

Реактивное сопротивление обратно пропорционально частоте и емкость. Для постоянного тока конденсатор открыт. Он блокирует постоянный ток и пропускает переменный ток.

Индуктивное реактивное сопротивление определяется как частотой, так и индуктивностью. В реактивное сопротивление прямо пропорционально этим членам. Из-за индуктивного реактивное сопротивление катушка имеет большую оппозицию к переменному току, чем к постоянный ток.

AC И КОНДЕНСАТОР

В чисто емкостной схеме соотношение фаз 90 градусов. между напряжением и током. Ток начинается с максимума, а напряжение начинается с нуля.Когда напряжение достигает максимума, ток равен нулю.

Ток всегда на 90 градусов опережает напряжение.

Конденсатор вроде пропускает и переменный ток. Поскольку ток течет легко для конденсатора, который находится рядом с разряженным состоянием, увеличивая емкость снижает сопротивление току. Увеличение частоты также уменьшает сопротивление, предлагаемое конденсатором.

Реактивное сопротивление отличается от сопротивления, потому что реактивное сопротивление противоположно что проявляется только при переменном токе.

Сопротивление равно сопротивлению протеканию тока, будь то переменный или постоянный ток.

ЕМКОСТЬ РЕАКТИВНОСТЬ (X _C)

Расчет емкости по XC

C = 1 / (2 пи f X _C)

Расчет частоты по XC

f = 1 / (2 пи C X _C)

СЕРИЯ

— ИЛИ ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ X _C

Поскольку емкостное реактивное сопротивление выражается в омах, последовательно или параллельно подключенные реактивные сопротивления складываются так же, как и резисторы.

XC с последовательным подключением

X _CT = X _C1 + X _C2 + … + X _CN

XC с параллельным подключением

X _CEQ = 1 / (1 / X _C1 + 1 / X _C2 + … + 1 / X _CN)

Формула обратного выражения используется так же, как и для сопротивлений.

AC И ИНДУКТОР

Цепь переменного тока с чистым сопротивлением пропускает через нее переменный ток и напряжение на нем растет и падает вместе.

Сдвиг фазы индуктора на 90

Цепь с чистой индуктивностью имеет разность фаз 90 градусов между напряжение и ток. Поскольку индуктивность противодействует изменениям тока, нет ток течет в течение первого квартала цикла.

Ток начинает течь, когда напряжение достигает максимума. Когда ток достигает максимальное напряжение возвращается к нулю.

ELI ICEman

Конденсаторы и катушки индуктивности действуют как противоположности.

Помощник по запоминанию ELI the ICEman очень полезен.

Напряжение выводит ток в индуктивной (L) цепи.

Напряжение на токоподводах в емкостной (C) цепи.

ИНДУКТИВНАЯ РЕАКТИВНОСТЬ (X _L)

Чем больше индуктивность, тем больше сопротивление переменному току. Также больше частота тем больше оппозиция.

Индуктивное реактивное сопротивление измеряется в омах, обозначается символом XL.

Расчет индуктивности от X _L

L = X _L/2 пи

Расчет частоты от X _L

f = X _L/2 pi L

СЕРИЯ

— ИЛИ ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ X _L

Последовательное соединение X _L

X _LT = X _L1 + X _L2 +… + X _LN

Индуктивные реактивные сопротивления суммируются так же, как и сопротивления.

Подключено параллельно X _L

X _LEQ = 1 / (1 / X _L1 + 1 / X _L2 + … + 1 / X _LN)

Параллельные реактивные сопротивления складываются по обратной формуле, как и в случае сопротивление.

ПОКАЗАТЕЛЬ КАЧЕСТВА, Q

Добротность катушки и показатель способности катушек хранить энергия (а затем высвобождает ее), а не рассеивает ее в виде тепла.

Q = X _L / R _i

Эффективное сопротивление

На низких частотах Ri — это просто сопротивление постоянному току проводника в катушка. На более высоких частотах потери из-за вихревых токов, гистерезиса и др. потери становятся очевидными. Это известно как сопротивление переменному току, чтобы отличить его от Потери в проводниках постоянного тока.

Q = X _L / R _e

Снижение эффективного сопротивления

Воздушные сердечники используются для высокочастотных катушек.Многожильный провод с изолированным пряди можно использовать для уменьшения скин-эффекта.

Разница между сопротивлением и реактивностью (со сравнительной таблицей)

Сопротивление и реактивное сопротивление — два основных термина, которые вместе образуют полное сопротивление электрической цепи. Решающее различие между сопротивлением и реактивным сопротивлением состоит в том, что сопротивление препятствует прохождению электрического тока только через резистор. В отличие от реактивного сопротивления, это сопротивление изменению тока катушкой индуктивности или конденсатора.

В основном, препятствие для прохождения электрического тока в любой цепи определяется как импеданс . Импеданс — это сложный термин, представляющий собой комбинацию реальных и мнимых значений. В этом разделе мы обсудим различные факторы, различающие сопротивление и реактивное сопротивление, используя сравнительную таблицу.

Содержание: сопротивление против реактивного сопротивления

Сравнительная таблица
Определение
Ключевые отличия
Заключение

Сравнительная таблица

Параметр	Сопротивление	Реактивное сопротивление
Basic	Это препятствие, препятствующее прохождению тока резистором.	Это противодействие изменяющемуся току в цепи с помощью катушки индуктивности или конденсатора.
Символическое представление
Обозначается	R	X
Выдается
Тип цепи	Цепи переменного и постоянного тока.	Конкретно цепь переменного тока.
Элемент схемы	Чистый резистор	Идеальный индуктор или конденсатор.
Характер значения	Действительная часть импеданса.	Мнимая часть импеданса.
Зависит от	Размеры, удельное сопротивление и температура проводника.	Частота переменного тока.
Разность фаз между V и I	V и I находятся в одной фазе. Таким образом, разность фаз составляет 0 градусов.	Существует разность фаз в 90 градусов между V и I.
Электроэнергия	Общая мощность рассеивается в виде тепла.	Часть потребляемой мощности сохраняется.

Определение сопротивления

Препятствие на пути тока, протекающего по цепи, называется сопротивлением. Мы знаем, что когда к электрической цепи прикладывается определенный потенциал, через цепь течет ток, пропорциональный приложенному напряжению. Однако на пути протекающего тока также существует определенное препятствие. Это свойство противодействия протекающему току известно как сопротивление .

Сопротивление — это свойство резисторов в электрических цепях. Другими словами, мы можем сказать, что соотношение подаваемого напряжения и протекающего тока в электрической цепи, имеющей резистор в качестве нагрузки, называется сопротивлением. Таким образом, сопротивление цепи определяется как:

Сопротивление любой электрической цепи измеряется в омах и показывает зависимость от удельного сопротивления и размеров соответствующих проводников. Предлагаемое сопротивление указано как:

Здесь следует отметить, что сопротивление проводников одинаково для постоянного или переменного тока.В резистивных цепях потребляемая мощность определяется как:

Поскольку оба термина в продукте являются действительными значениями, потребляемая мощность также будет действительным термином. Тем самым указывается, что подаваемая мощность полностью используется в резистивной цепи.

Определение реактивного сопротивления

Препятствие для прохождения переменного или изменяющегося тока в электрических цепях известно как реактивное сопротивление. Реактивное сопротивление цепи — это противодействие протеканию переменного тока.

Причина, по которой реактивное сопротивление цепи таково, что его значение является фактором наличия конденсатора или индуктора в качестве нагрузки. Таким образом, можно сказать, что отношение приложенного напряжения к изменяющемуся току в электрической цепи с емкостной или индуктивной нагрузкой называется реактивным сопротивлением этой цепи.

Для индуктивной нагрузки реактивное сопротивление определяется как:

В случае емкостной нагрузки реактивное сопротивление определяется как:

Таким образом, в индуктивной цепи реактивное сопротивление прямо пропорционально частоте.Пока он обратно пропорционален емкостной схеме.

Когда переменный ток протекает через цепь с индуктивной или емкостной нагрузкой, изменяющаяся энергия сохраняется либо в электрическом поле, либо в магнитном поле. В случае индуктивной нагрузки возникает изменяющееся магнитное поле. А для емкостной нагрузки есть электрическое поле.

Как мы уже обсуждали, сопротивление и реактивное сопротивление вместе образуют комплексное значение, называемое импедансом, где реактивное сопротивление действует как мнимая часть комплексного значения.Индуктивное реактивное сопротивление обычно является положительным мнимым значением, поэтому с увеличением индуктивной нагрузки реактивное сопротивление также увеличивается.

Ключевые различия между сопротивлением и реактивностью

Сопротивление — это препятствие для прохождения тока в электрической цепи из-за резистора. В то время как реактивное сопротивление — это противодействие зарядному току из-за индуктивности или конденсатора.
— это свойство , связанное с цепью как переменного, так и постоянного тока.Однако реактивное сопротивление собственности связано только с цепями переменного тока.
Чистые резисторы создают сопротивление. В отличие от идеальных катушек индуктивности или конденсаторов возникает реактивное сопротивление в цепи.
Сопротивление связано с действительной частью импеданса. В то время как реактивное сопротивление вносит вклад в мнимую часть значения импеданса.
Разница по фазе между напряжением и током в чисто резистивной цепи равна 0⁰. В то время как разность фаз между напряжением и током в идеальной емкостной или индуктивной цепи составляет 90⁰.В случае индуктивной нагрузки ток отстает от напряжения на 90⁰, а для чисто емкостной нагрузки напряжение отстает от тока на 90⁰.
Сопротивление, обеспечиваемое схемой , зависит от размера, удельного сопротивления и температурных условий проводника. Однако реактивное сопротивление зависит от частотной составляющей переменного тока в цепи. Он показывает пропорциональность с частотой в случае индуктивной нагрузки, тогда как в случае емкостной нагрузки это соотношение является обратным.
В резистивной цепи общая мощность , подаваемая на схему, рассеивается в виде тепла. В то время как в емкостной или индуктивной цепи устройство не полностью потребляет всю подаваемую мощность.

Заключение

Итак, из этого обсуждения можно сделать вывод, что как сопротивление, так и реактивное сопротивление отвечают за противодействие протеканию тока и, таким образом, действуют как импеданс для любой электрической цепи, когда они вместе присутствуют в ней.

Калькулятор индуктивного реактивного сопротивления

Калькулятор индуктивного реактивного сопротивления Omni (калькулятор X _L ) позволяет определить эффективное сопротивление (импеданс), обеспечиваемое катушкой индуктивности . Просто введите индуктивность катушки и частоту сигнала переменного тока, и калькулятор импеданса катушки индуктивности мгновенно выдаст вам реактивное сопротивление катушки (индуктивное сопротивление)!

Продолжайте читать, чтобы узнать , что такое индуктивное реактивное сопротивление и формула для его расчета.Вы также найдете пример того, как рассчитать индуктивное реактивное сопротивление с помощью калькулятора X _L .

Что такое индуктивное реактивное сопротивление? — Определение индуктивного реактивного сопротивления

Индуктивное реактивное сопротивление или индуктивное сопротивление — это эффективное сопротивление , обеспечиваемое индуктором электрическому току, протекающему через него .

Оно похоже на сопротивление резистора в том смысле, что оба сопротивляются потоку электрического заряда.Однако в случае резисторов , противодействие происходит из-за столкновения с электронами , когда они проходят через него. В катушке индуктивности именно самоиндуцированная ЭДС препятствует росту и спаду тока .

Формула индуктивного реактивного сопротивления

Рассмотрим простую схему, состоящую из индуктора, подключенного к источнику переменного напряжения (рисунок 1). Поскольку величина и направление переменного тока непрерывно изменяются , катушка индуктивности будет противодействовать любому изменению тока через нее, индуцируя в себе ЭДС.

Рисунок 1: Цепь переменного тока, состоящая из катушки индуктивности.

Используя закон Фарадея, мы можем выразить эту самоиндуцированную ЭДС ( V ) как:

В = - L * (dI / dt)

где:

L — Самоиндукция индуктора; и
dI / dt — Скорость изменения тока через катушку индуктивности.

Чтобы найти средний ток ( I ) через катушку индуктивности, мы можем использовать версию закона Ома:

I = V / X _L

, где индуктивное сопротивление ( X _L ) зависит от частоты ( ν ) сигнала переменного тока:

X _L = 2 * π * ν * L

Мы также можем рассчитать проводимость ( B _L ), т.е.е., насколько легко схема позволяет току течь через нее, например:

B _L = 1 / X _L

Единица индуктивного сопротивления

Чтобы найти единицу индуктивного реактивного сопротивления, проведем размерный анализ формулы для индуктивного реактивного сопротивления:

X _L = 2 * π * ν * L ⇒ (1 / сек) * Генри = (1 / сек) * [вольт / (ампер / сек)] = вольт / ампер = ом (Ом)

Анализ размеров приведенной выше формулы показывает, что размеры индуктивного реактивного сопротивления такие же, как и размеры сопротивления.Следовательно, индуктивное реактивное сопротивление измеряется в Ом ( Ом, ).

Для измерения проводимости мы используем ту же единицу измерения, что и проводимость, то есть сименс ( S ).

Как пользоваться калькулятором индуктивного сопротивления?

Давайте посмотрим, как использовать калькулятор индуктивного реактивного сопротивления для расчета реактивного сопротивления, предлагаемого катушкой 14 мГн , когда через нее протекает переменный ток 100 Гц .

Введите индуктивность катушки, то есть 14 мГн .
Подключите частоту переменного тока, то есть 100 Гц .
Калькулятор X _L отобразит реактивное сопротивление катушки индуктивности ( X _L ), то есть 8,80 Ом и проводимость ( B _L ), то есть 0.11 S .
Вы также можете использовать этот калькулятор импеданса катушки индуктивности для расчета индуктивности катушки.

Мы также рекомендуем воспользоваться нашим калькулятором емкостного реактивного сопротивления, чтобы узнать, какое эффективное сопротивление конденсатор оказывает протекающему через него току.

Как рассчитать индуктивное реактивное сопротивление?

Для расчета индуктивного сопротивления действуйте следующим образом:

Узнайте частоту сигнала переменного тока.
Умножьте частоту на 2π и индуктивность .
Поздравляю! Вы рассчитали индуктивное сопротивление.

Какое индуктивное сопротивление в цепи постоянного тока?

Ноль . Индуктивное сопротивление прямо пропорционально частоте сигнала. В цепях постоянного тока частота равна нулю . Следовательно, индуктивное реактивное сопротивление в цепях постоянного тока также равно нулю.

В чем разница между индуктивным и емкостным сопротивлением?

Основные различия между индуктивным и емкостным сопротивлением:

Индуктивное реактивное сопротивление — это эффективное сопротивление , обеспечиваемое катушкой индуктивности . Емкостное реактивное сопротивление — это эффективное сопротивление , обеспечиваемое конденсатором .
Индуктивное реактивное сопротивление прямо пропорционально частоте сигнала и индуктивности . Емкостное реактивное сопротивление обратно пропорционально частоте сигнала и емкости .

Как рассчитать индуктивность по реактивному сопротивлению?

Чтобы рассчитать индуктивность по реактивному сопротивлению, следуйте данным инструкциям:

Умножьте на частоту сигнала переменного тока на 2π .
Разделите реактивное сопротивление на значение из шага 1 .
Вы рассчитали индуктивность по реактивному сопротивлению!

Что такое единица измерения индуктивного сопротивления в системе СИ?

Ом . Единица измерения индуктивного реактивного сопротивления в системе СИ такая же, как и у сопротивления, то есть Ом.

.
No related posts.

Разное

Реактивное сопротивление равно: Реактивное сопротивление

Реактивное сопротивление равно: Реактивное сопротивление

Реактивное сопротивление

Добавить комментарий

Выражение ома для цепи с активным сопротивлением. Активное, реактивное и полное сопротивление цепи

Формулы

Шаги

Сопротивления | Цепи переменного тока

Реактивное сопротивление конденсатора.

Схема замещения конденсатора с параллельным соединением элементов

Векторная диаграмма токов в цепи с конденсатором

Треугольник проводимостей для конденсатора

Мощность цепи с конденсатором

Схема замещения конденсатора с последовательным соединением элементов

О заряде конденсатора.

До какого напряжения заряжается конденсатор?

Сопротивление конденсатора.

Почему постоянный ток не проходит через конденсатор, а переменный ток проходит?

О реальном конденсаторе

Определение результирующего сопротивления конденсатора

Сопротивление реактивное — Справочник химика 21

РЕАКТИВНОЕ СОПРОТИВЛЕНИЕ

ТЕОРИЯ: ПОНЕМНОГУ — ОБО ВСЕМ

Активное реактивное и полное сопротивление. Треугольники сопротивлений

Что такое реактивное сопротивление? — Определение из WhatIs.com

Реактивность — обзор | Темы ScienceDirect

8.1.2 Нагрузка сетей с линиями передачи

1.5: Реактивное сопротивление и импеданс — Engineering LibreTexts

Импеданс

Реактивное сопротивление и импеданс — Формула

Формула импеданса

Что такое реактивность?

Формула реактивного сопротивления

Знаете ли вы?

Емкостное реактивное сопротивление

Разница между сопротивлением и реактивностью (со сравнительной таблицей)

Содержание: сопротивление против реактивного сопротивления

Сравнительная таблица

Определение сопротивления

Определение реактивного сопротивления

Ключевые различия между сопротивлением и реактивностью

Заключение

Что такое индуктивное реактивное сопротивление? — Определение индуктивного реактивного сопротивления

Формула индуктивного реактивного сопротивления

Единица индуктивного сопротивления

Как пользоваться калькулятором индуктивного сопротивления?

Как рассчитать индуктивное реактивное сопротивление?

Какое индуктивное сопротивление в цепи постоянного тока?

В чем разница между индуктивным и емкостным сопротивлением?

Как рассчитать индуктивность по реактивному сопротивлению?

Что такое единица измерения индуктивного сопротивления в системе СИ?

Похожие записи

Как правильно промывать нос при насморке: эффективные методы и растворы

Питание кормящей мамы: что можно есть при грудном вскармливании

Лучшая зимняя обувь для детей 2 лет: выбираем комфортные и надежные модели

Детская комната для новорожденного: оформление, дизайн и планировка

Увлажнитель воздуха: польза и вред для здоровья, отзывы специалистов и пользователей

Добавить комментарий Отменить ответ