Урок 27. напряжённость и потенциал электростатического поля. разность потенциалов — Физика — 10 класс

Физика, 10 класс

Урок 27. Напряжённость и потенциал электростатического поля. Разность потенциалов

Перечень вопросов, рассматриваемых на уроке:

1) Теория дальнодействия;

2) Теория близкодействия;

3) Электрическое поле;

4) Скорость электрического поля;

5) Напряжённость электрического поля;

6) Однородное и неоднородное электрическое поле;

7) Принцип суперпозиции полей;

8) Диэлектрическая проницаемость;

9) Электростатическая защита

10) Работа электрического поля;

11) Потенциал и разность потенциалов.

Глоссарий по теме:

Напряжённость — отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду.

Потенциал точки электростатического поля -отношение потенциальной энергии заряда, помещённого в данную точку, к этому заряду.

Напряжение – разность потенциалов.

Потенциальное поле – поле, работа которого по перемещению заряда по замкнутой траектории всегда равна нулю.

Напряжённость направлена в сторону убывания потенциала.

Эквипотенциальные поверхности – поверхности равного потенциала.

Свободные заряды — заряженные частицы, способные свободно перемещаться в проводнике под влиянием электрического поля.

Электростатическая индукция – явление разделения зарядов и их распределение по поверхности проводника во внешнем электрическом поле.

Основная и дополнительная литература

Г. Я. Мякишев, Б. Б. Буховцев, Н. Н. Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 290 – 320.

Рымкевич А.П. Сборник задач по физике. 9 – 11 класс. М. Дрофа, 1999 – С. 93 — 102

Теоретический материал для самостоятельного изучения

Согласно идее Фарадея электрические заряды не действуют друг на друга непосредственно. Каждый из них создаёт в окружающем пространстве электрическое поле.

Электрическое поле — это особый вид материи, посредством которой происходит взаимодействие зарядов. Скорость распространения электрического поля в вакууме равна 300000 км/с.

Напряжённость Е — силовая характеристика электрического поля.

Электрическое поле, напряженность которого одинакова во всех точках, называется однородным. Поле между параллельными пластинами однородно

Главное свойство электрического поля – это действие его на электрические заряды с некоторой силой.

Напряжённость-это отношение силы, действующей на помещаемый в данную точку поля точечный заряд, к этому заряду.

Если в данной точке пространства различные заряженные частицы создают поля, напряжённости которых Е₁, Е₂, то результирующая напряжённость поля в этой точке равна геометрической сумме напряжённостей этих полей. В этом состоит принцип суперпозиции полей.

Заряд, помещенный в электрическое поле обладает потенциальной энергией.

Потенциалом φ точки электростатического поля называют отношение потенциальной энергии Wn заряда, помещённого в данную точку, к этому заряду q.

Напряжение – это работа, совершаемая полем при перемещении заряда 1Кл.

Примеры и разбор решения заданий

1. К каждой позиции первого столбца подберите соответствующую позицию второго

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
Напряженность
Потенциал
Потенциальная энергия заряда в однородном электростатическом поле
Разность потенциалов	qΕd

Решение: вспомнив формулы величин, можем установить:

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ	ФОРМУЛЫ
Напряженность
Потенциал
Потенциальная энергия заряда в однородном электростатическом поле	qΕd
Разность потенциалов

2.

В однородном электрическом поле напряжённостью 1 В/м переместили заряд -25 нКл в направлении силовой линии на 2 см. Найти работу поля, изменение потенциальной энергии заряда и напряжение между начальной и конечной точками перемещения.

Решение.

Работа электрического поля при перемещении заряда вдоль силовой линии:

ΔA = — qΕΔd,

при этом изменение потенциальной энергии равно:

Напряжение между начальной и конечной точками перемещения равно:

Вычисления:

ΔA = -25 · 10^-9 Kл · 10³ B/м · 0,02 м = -0,5 мкДж;

Ответ:

Разность потенциалов | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Определение потенциала, как и потен­циальной энергии, является в подавляющем большинстве случаев промежуточным дей­ствием. Как правило, практическое значе­ние имеет определение работы, которую выполняет электрическое поле. Связанный непосредственно с потенциальной энерги­ей, потенциал может быть определен лишь с точностью до определенной постоянной величины, значение которой зависит от выбора нулевого уровня отсчета.

Значение потенциала опреде­ляется с точностью до неко­торой постоянной величины.

Потенциал точки поля определяется по напряженности электрического поля E

и расстоянию ее от нулевого уровня l.

φ = El.

Работа в электростатическом по­ле определяется однозначно.

Если выбор нулевого уровня произволь­ный, то и значение l может быть произволь­ным. Поэтому часто потенциал записывают в виде

φ = El + C,

С — константа.

Если же определять работу, которая по определению равна изменению потенциаль­ной энергии с противоположным знаком, то получается вполне определенная вели­чина:

A = qEl₁ + C — qEl₂

— C = qEl₁ — qEl₂.

Полученное выражение можно записать в виде

A = q(φ₁ — φ₂) = qΔφ.

Отсюда

Δφ = φ₁ — φ₂ = A / q.

Поскольку работа и электрический заряд измеряются однозначно, то и разность потен­циалов будет иметь вполне определенное значение. Поэтому разность потенциалов

счи­тают отдельной физической величиной.

Физическая величина, характеризующая эне­ргетическое состояние поля и равная отноше­нию работы по перемещению заряженного те­ла из одной точки поля в другую к значению заряда, называется разностью потенциалов.

Разность потенциалов в элект­ростатическом поле определя­ется однозначно.

Для измерения разности потенциалов, как и потенциала, применяется единица 1 вольт и производные от него единицы: 1 мВ, 1 мкВ, 1 кВ, 1 MB. Прибор, которым измеряют

разность потенциалов, называется вольтметром.

Из предыдущего известно, что разность потенциалов в однородном поле связана с напряженностью электрического поля:

φ₁ — φ₂ = E(l₁ — l₂). Материал с сайта http://worldofschool.ru

Отсюда

E = (φ₁ — φ₂) / (l₁ — l₂) = Δφ / Δl.

Последнее выражение использовано для введения единицы напряженности электри­ческого поля. При φ₁ — φ

2= 1 В и l₁ — l₂= 1 м получим Е = 1 В/м.

По разности потенциалов мож­но определить напряженность электростатического поля.

На этой странице материал по темам:

• Каким прибором измеряется разность потенциалов

• Разность потенциалов физика величина

• Htit,ybr yf hfpyjcnm gjntywbfkjd abpbrf

• Презентация измерения разности потенциалов

• Определение разность потенциалов физика

Вопросы по этому материалу:

• Почему неудобно использовать понятие потенциала для ре­шения практических задач?

• Что называется разностью потенциалов?

• Какие единицы измерения разности потенциалов?

• Каким прибором измеряется разность потенциалов?

Электростатика — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Электрический заряд и его свойства

К оглавлению. ..

Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами

q или Q. В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10^–6 Кл), нанокулонами (1 нКл = 10^–9 Кл) и пикокулонами (1 пКл = 10^–12 Кл). Электрический заряд обладает следующими свойствами:

1. Электрический заряд является видом материи.

2. Электрический заряд не зависит от движения частицы и от ее скорости.

3. Заряды могут передаваться (например, при непосредственном контакте) от одного тела к другому. В отличие от массы тела электрический заряд не является неотъемлемой характеристикой данного тела.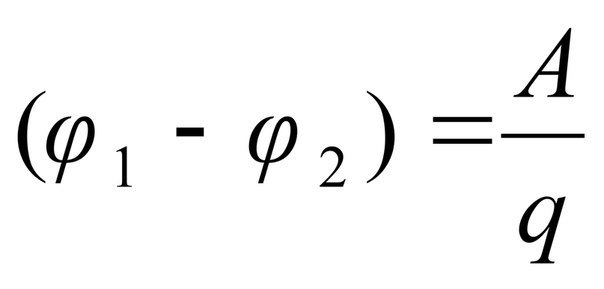 Одно и то же тело в разных условиях может иметь разный заряд.

4. Существует два рода электрических зарядов, условно названных положительными и отрицательными.

5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.

6. Существует минимально возможный (по модулю) электрический заряд, называемый элементарным зарядом. Его значение:

e = 1,602177·10^–19 Кл ≈ 1,6·10^–19 Кл.

Электрический заряд любого тела всегда кратен элементарному заряду:

где: N – целое число. Обратите внимание, невозможно существование заряда, равного 0,5е; 1,7е; 22,7е и так далее. Физические величины, которые могут принимать только дискретный (не непрерывный) ряд значений, называются квантованными. Элементарный заряд e является квантом (наименьшей порцией) электрического заряда.

7. Закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:

Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q₁ и q₂ (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:

С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.

В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов, или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. Обратите внимание, что положительные протоны входят в состав ядра атома, поэтому их число может изменяться только при ядерных реакциях. Очевидно, что при электризации тел ядерных реакций не происходит. Поэтому в любых электрических явлениях число протонов не меняется, изменяется только число электронов. Так, сообщение телу отрицательного заряда означает передачу ему лишних электронов. А сообщение положительного заряда, вопреки частой ошибке, означает не добавление протонов, а отнимание электронов. Заряд может передаваться от одного тела к другому только порциями, содержащими целое число электронов.

Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:

1. Линейная плотность заряда. Используется для описания распределения заряда по нити:

где: L – длина нити. Измеряется в Кл/м.

2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:

где: S – площадь поверхности тела. Измеряется в Кл/м².

3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:

где: V – объем тела. Измеряется в Кл/м³.

Обратите внимание на то, что масса электрона равна:

m_e = 9,11∙10^–31 кг.

 

Закон Кулона

К оглавлению. ..

Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:

Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:

где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:

k = 9∙10⁹ м/Ф.

Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют электростатическим или кулоновским взаимодействием. Раздел электродинамики, изучающий кулоновское взаимодействие, называют электростатикой.

Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:

где: ε₀ = 8,85∙10^–12 Ф/м – электрическая постоянная.

Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.

Запомните также два важных определения:

Проводники – вещества, содержащие свободные носители электрического заряда. Внутри проводника возможно свободное движение электронов – носителей заряда (по проводникам может протекать электрический ток). К проводникам относятся металлы, растворы и расплавы электролитов, ионизированные газы, плазма.

Диэлектрики (изоляторы) – вещества, в которых нет свободных носителей заряда. Свободное движение электронов внутри диэлектриков невозможно (по ним не может протекать электрический ток). Именно диэлектрики обладают некоторой не равной единице диэлектрической проницаемостью ε.

Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):

 

Электрическое поле и его напряженность

К оглавлению…

По современным представлениям, электрические заряды не действуют друг на друга непосредственно. Каждое заряженное тело создает в окружающем пространстве электрическое поле. Это поле оказывает силовое действие на другие заряженные тела. Главное свойство электрического поля – действие на электрические заряды с некоторой силой. Таким образом, взаимодействие заряженных тел осуществляется не непосредственным их воздействием друг на друга, а через электрические поля, окружающие заряженные тела.

Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика — напряженность электрического поля E.

Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:

Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.

Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.

• Силовые линии электростатического поля никогда не пересекаются.
• Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным.
• При изображении электрического поля с помощью силовых линий их густота должна быть пропорциональна модулю вектора напряженности поля.
• Силовые линии начинаются на положительном заряде или бесконечности, а заканчиваются на отрицательном или бесконечности. Густота линий тем больше, чем больше напряжённость.
• В данной точке пространства может проходить только одна силовая линия, т.к. напряжённость электрического поля в данной точке пространства задаётся однозначно.

Электрическое поле называют однородным, если вектор напряжённости одинаков во всех точках поля. Например, однородное поле создаёт плоский конденсатор – две пластины, заряженные равным по величине и противоположным по знаку зарядом, разделённые слоем диэлектрика, причём расстояние между пластинами много меньше размеров пластин.

Во всех точках однородного поля на заряд q, внесённый в однородное поле с напряжённостью E, действует одинаковая по величине и направлению сила, равная F = Eq. Причём, если заряд q положительный, то направление силы совпадает с направлением вектора напряжённости, а если заряд отрицательный, то вектора силы и напряжённости противоположно направлены.

Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:

 

Принцип суперпозиции

К оглавлению. ..

Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:

Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:

Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q < 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.

Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:

Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:

1. Нарисовать рисунок.
2. Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
3. Вычислить каждую из напряжённостей по соответствующей формуле.
4. Сложить вектора напряжённостей геометрически (т.е. векторно).

 

Потенциальная энергия взаимодействия зарядов

К оглавлению…

Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывает потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:

Обратите внимание на отсутствие модулей у зарядов. Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.

Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.

Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью. Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.

 

Потенциал. Разность потенциалов. Напряжение

К оглавлению…

Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.

Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.

Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:

Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал — скалярная величина.

Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:

Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его. Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.

Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.

Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

В этих формулах:

• φ – потенциал электрического поля.
• ∆φ – разность потенциалов.
• W – потенциальная энергия заряда во внешнем электрическом поле.
• A – работа электрического поля по перемещению заряда (зарядов).
• q – заряд, который перемещают во внешнем электрическом поле.
• U – напряжение.
• E – напряженность электрического поля.
• d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.

Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.

Принцип суперпозиции потенциала

Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):

Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.

 

Электрическая емкость. Плоский конденсатор

К оглавлению…

При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:

В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.

Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.

Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:

За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0.  Электроёмкость плоского конденсатора может быть рассчитана по формуле:

Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.

Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:

Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:

Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):

Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.

Энергия электрического поля

Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):

 

Соединения конденсаторов

К оглавлению…

Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:

При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:

Из закона сохранения заряда следует, что заряды на соседних обкладках равны:

Напряжение равно сумме напряжений на отдельных конденсаторах.

Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:

Для N одинаковых последовательно соединённых конденсаторов:

 

Проводящая сфера

К оглавлению…

Напряженность поля внутри заряженного проводника равна нулю. В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.

Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.

На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.

Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю). Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.

Электрическая емкость шара радиуса R:

Если шар окружен диэлектриком, то:

 

Свойства проводника в электрическом поле

К оглавлению…

1. Внутри проводника напряженность поля всегда равна нулю.
2. Потенциал внутри проводника во всех точках одинаков и равен потенциалу поверхности проводника. Когда в задаче говорят, что «проводник заряжен до потенциала … В», то имеют в виду именно потенциал поверхности.
3. Снаружи от проводника вблизи от его поверхности напряженность поля всегда перпендикулярна поверхности.
4. Если проводнику сообщить заряд, то он весь распределится по очень тонкому слою вблизи поверхности проводника (обычно говорят, что весь заряд проводника распределяется на его поверхности). Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся.
5. Снаружи проводника напряженность поля тем больше, чем кривее поверхность проводника. Максимальное значение напряженности достигается вблизи остриев и резких изломов поверхности проводника.

 

Замечания к решению сложных задач

К оглавлению…

1. Заземление чего-либо означает соединение проводником данного объекта с Землей. При этом потенциалы Земли и имеющегося объекта выравниваются, а необходимые для этого заряды перебегают по проводнику с Земли на объект либо наоборот. При этом нужно учитывать несколько факторов, которые следуют из того, что Земля несоизмеримо больше любого объекта находящегося не ней:

• Общий заряд Земли условно равен нолю, поэтому ее потенциал также равен нолю, и он останется равным нолю после соединения объекта с Землей. Одним словом, заземлить – означает обнулить потенциал объекта.
• Для обнуления потенциала (а значит и собственного заряда объекта, который мог быть до этого как положительным так и отрицательным), объекту придется либо принять либо отдать Земле некоторый (возможно даже очень большой) заряд, и Земля всегда сможет обеспечить такую возможность.

2. Еще раз повторимся: расстояние между отталкивающимися телами минимально в тот момент, когда их скорости становятся равны по величине и направлены в одну сторону (относительная скорость зарядов равна нулю). В этот момент потенциальная энергия взаимодействия зарядов максимальна. Расстояние между притягивающимися телами максимально, также в момент равенства скоростей, направленных в одну сторону.

3. Если в задаче имеется система, состоящая из большого количества зарядов, то необходимо рассматривать и расписывать силы, действующие на заряд, который не находится в центре симметрии.

Понятие силы тока, ЭДС и разности потенциалов?

Электрическим током называют упорядоченное движение заряженных частиц (тел). За направление движение электрического тока условно принимают направление движения положительных зарядов. Проходящий через какую-то поверхность электрический ток характеризуется силой тока I. Сила тока является скалярной величиной, численно равная количеству электричества, проходящего через площадь S за единицу времени:

Если за любые равные промежутки времени через любое сечение проводника проходит одинаковое количество электричества с неизменным направлением зарядов, то такой ток называется постоянным:

Сила тока в Международной системе единиц (СИ) является основной и носит название Ампер. Из уравнения (1а) следует определение единицы заряда:

В системе СГС сила тока измеряется в СГС_I, согласно (1а) получим:

Распределение электрического тока по сечению проводника характеризуют плотностью тока, которую можно выразить формулой:

В случае постоянного тока его плотность будет одинакова и равна:

Плотность тока j является векторной величиной, направленной вдоль тока и численно  равная количеству электричества, протекающему через единицу площади, ориентированной перпендикулярно направлению протекания тока, за единицу времени, в системе СИ плотность тока измеряют в А/м².

Важно отметить, что различают несколько видов электрического тока. Предположим, что в пространстве перемещается какое-то заряженное макроскопическое тело (шар, например). Поскольку вместе с этим телом будут перемещаться и заряды, то возникнет направленное движение электрических зарядов – электрический ток. Электрический ток, связанный с движением заряженных макроскопических тел называют конвекционным.

Если огромное количество заряженных частиц упорядоченно перемещаются внутри какого-нибудь тела вследствие того, что в нем создано электрическое поле, то данное явление будет носить название ток проводимости. Для его получения необходимо наличие источника тока и  замкнутой цепи. Вектор напряженности поля Е имеет направление от положительного заряда к отрицательному. Отсюда следует, что находящиеся внутри проводника отрицательные заряженные частицы будут двигаться против поля, а положительные – по полю.

Если электрические заряды движутся под влиянием внешнего поля в вакууме, то данное явление называют электрический ток в вакууме.

Более детально остановимся на отдельных закономерностях, которые больше характерны для тока проводимости.

Представим, что на концах определенного проводника длиной l существует разность потенциалов Δφ = φ₁ – φ₂, которая создает внутри этого проводника электрическое поле Е, направленное в сторону падения потенциала (рисунок ниже):

Согласно формуле:

При этом в проводнике возникнет электрический ток, который будет идти от большего потенциала (φ₁) к меньшему (φ₂).

Движение зарядов от φ₁ к φ₂ приводит к выравниванию потенциалов во всех точках. При этом в проводнике исчезает электрическое поле, и протекание электрического тока прекращается. Отсюда следует, что обязательным условием существования электрического тока является наличие разности потенциалов Δφ = φ₁ – φ₂ ≠ 0, а для его поддержания необходимо специальное устройство, которое будет поддерживать данную разницу потенциалов. Это устройство называют источник тока.

В качестве источников тока могут использовать электрические генераторы, аккумуляторы, термоэлементы и гальванические элементы. Источник тока также выполняет еще одну задачу – замыкает электрическую цепь, по которой и осуществляется непрерывное движение заряженных частиц. Электрический ток протекает по внутренней части – источнику тока, и внешней – проводнику. В источнике тока имеется два полюса – положительный с более высоким потенциалом и отрицательный с более низким потенциалом. При разомкнутой внешней цепи на положительном полюсе источника образуется недостаток электронов, а на отрицательном наоборот – переизбыток. В источнике тока разделение зарядов производят с помощью сторонних сил – направленных против кулоновских сил, действующих на разноименные заряды в проводниках самого источника тока. Сторонние силы могут иметь самое различное происхождение – химическое, биологическое, тепловое, механическое и другое.

Если электрическая цепь замкнута, то по ней протекает электрический ток и при этом совершается работа сторонних сил. Данная работа складывается из работы, совершаемой внутри самого источника тока против сил электрического поля (А_ист), и работы, совершаемой против механических сил сопротивления среды источника (А^/), то есть:

Электродвижущая сила источника тока – это величина, которая равна отношению работы, совершаемой сторонними силами при перемещении положительного точечного заряда вдоль всей электрической цепи, включая и источник тока, к заряду:

По определению работа против сил электрического поля равна:

А^/ = 0 если полюсы источника разомкнуты, и тогда из формулы (5) следует:

Отсюда следует, что электродвижущая сила источника тока при разомкнутой внешней цепи будет равна разности потенциалов на его полюсах.

Работа электрического поля.

Разность потенциалов (напряжение)

1. Работа поля при перемещении заряда

В этой главе мы рассматриваем электрическое поле, созданное покоящимися электрическими зарядами. Такое поле называют электростатическим. (В курсе физики 11-го класса мы рассмотрим также вихревое электрическое поле, которое порождается не электрическими зарядами, а изменяющимся магнитным полем. Для вихревого электрического поля нельзя ввести понятие разности потенциалов, которое рассматривается в этом параграфе.)

На заряд q, находящийся в электростатическом поле, действует сила

= q,

где – напряженность электрического поля в той точке, где находится заряд.

При перемещении заряда эта сила может совершать работу, которую часто называют работой поля. Она может быть положительной, отрицательной, а также равной нулю.

? 1. На рисунке 53.1 изображены линии напряженности однородного электростатического поля. Модуль напряженности поля 100 Н/Кл. Точки А, В, С, D расположены в вершинах квадрата со стороной 10 см. В этом поле перемещают точечный положительный заряд 10 нКл.

Какую работу совершит электрическое поле при перемещении заряда по прямой:
а) из A в B? б) из B в C? в) из C в D? г) из D в A? д) из A в C? е) из B в D?
ж) Как изменится работа поля при любом перемещении заряда, если модуль заряда увеличить в 3 раза?
з) Какую работу совершит электрическое поле при перемещении заряда по замкнутому контуру вдоль всех четырех сторон квадрата? Имеет ли при этом значение, в какой вершине квадрата заряд находился в начальный момент? Имеет ли значение, в каком направлении перемещался заряд – по часовой стрелке или против?

На примере этого задания вы могли заметить, что работа электростатического поля при перемещении заряда из одной точки в другую зависит только от положения начальной и конечной точек и не зависит от траектории движения заряда.

Работа электростатического поля при перемещении заряда по замкнутому контуру равна нулю.

Оказывается, что этими важнейшими свойствами обладает любое электростатическое поле, то есть поле, созданное любыми покоящимися электрическими зарядами.

Например, при перемещении электрического заряда из точки 1 в точку 2 по траекториям а и б (рис. 53.2) электростатическое поле совершает одинаковую работу.

2. Разность потенциалов (напряжение)

Вспомним, что работа силы тяготения и силы упругости по перемещению тела также зависит только от начального и конечного положения тела и не зависит от траектории его движения. Это позволило ввести понятие потенциальной энергии для системы тел, взаимодействующих посредством сил тяготения и упругости.

Поскольку работа электростатического поля по перемещению заряда тоже зависит только от начального и конечного положения заряда, для заряда в электростатическом поле тоже можно ввести понятие потенциальной энергии.

Обозначим потенциальную энергию заряда Wp. Как вы уже знаете, изменение потенциальной энергии равно работе, совершаемой телом или системой тел, взятой со знаком минус. Поэтому если заряд переместился из точки 1 в точку 2, то

W_p2 – W_p1 = –A₁₂,

где A₁₂ – работа, совершенная полем по перемещению заряда из точки 1 в точку 2.

Перепишем эту формулу так:

W_p1 – W_p2 = A₁₂.     (1)

Отсюда видно, что при перемещении заряда из точки 1 в точку 2:
– если поле совершает положительную работу, то потенциальная энергия заряда уменьшается;
– если поле совершает отрицательную работу (например, когда сила направлена противоположно перемещению), то потенциальная энергия заряда увеличивается;
– если работа поля равна нулю (например, сила перпендикулярна перемещению), то потенциальная энергия заряда не изменяется.

? 2. На рисунке 53.3 изображены линии напряженности электростатического поля и отмечено несколько точек. В начальный момент положительный заряд находится в точке А.

При перемещении заряда в какие из отмеченных точек его потенциальная энергия:
а) уменьшается;
б) увеличивается;
в) остается неизменной?
г) Как изменяется потенциальная энергия отрицательного заряда при перемещении его из точки A в точку: B; C; D; E; F; G; H; K?

Работа поля и потенциальная энергия заряда в электростатическом поле пропорциональны величине заряда (так как сила, действующая на заряд, пропорциональна величине заряда). Отсюда следует, что отношение потенциальной энергии заряда в электростатическом поле к величине заряда не зависит от заряда и поэтому характеризует само поле.

Отношение потенциальной энергии заряда в данной точке поля к величине этого заряда называют потенциалом электростатического поля φ в этой точке:

φ = W_p/q. (2)

Из формул (1) и (2) следует, что

разность потенциалов между точками 1 и 2 равна отношению работы поля A₁₂ по перемещению заряда из точки 1 в точку 2 к величине заряда:

φ₁ – φ₂ = A₁₂/q.     (3)

Разность потенциалов между точками 1 и 2 численно равна работе электростатического поля по перемещению единичного положительного заряда из точки 1 в точку 2.

Разность потенциалов называют также напряжением и обозначают U. В дальнейшем мы будем использовать как термин разность потенциалов, так и термин напряжение.

Когда говорят о «потенциале поля в некоторой точке», под этим всегда понимают разность потенциалов между этой точкой и точкой, потенциал поля в которой приняли равным нулю.

Выбор такой точки определяется только соображениями удобства: он не влияет на значение разности потенциалов поля между любыми двумя точками.

Единица разности потенциалов (напряжения). Единицей напряжения является 1 вольт (сокращенно В). Эта единица названа в честь итальянского ученого Алессандро Вольта, который создал первый химический источник постоянного электрического тока.

Если разность потенциалов между двумя точками равна 1 В, то при перемещении положительного заряда в 1 Кл из одной точки в другую электрическое поле совершает работу 1 Дж. Следовательно,

1 В = 1 Дж / 1 Кл.

? 3. Чему равна разность потенциалов между точками 1 и 2, если при перемещении заряда 10 нКл из точки 1 в точку 2 электростатическое поле совершило работу 10^-6 Дж?

? 4. Отрицательный заряд q перемещают из точки с более высоким потенциалом в точку с более низким потенциалом.
а) Какую работу совершает при этом поле: положительную или отрицательную?
б) Чему равна работа поля, если q = -50 нКл, потенциал начальной точки равен 300 В, а конечной точки – равен 100 В?

? 5. Слова напряжение и напряженность очень похожи. Чтобы осознать различия между физическими величинами, которые обозначаются этими словами, ответьте на следующие вопросы и обоснуйте свои ответы.
а) Какая из этих величин – векторная, а какая – скалярная?
б) О какой из этих величин можно говорить применительно только к одной точке пространства, а о какой – применительно только к двум точкам?
в) Какая из этих величин является силовой характеристикой электрического поля, а какая – энергетической?

? 6. Вернемся к заданию 1 (см. рис. 53.1). Чему равна разность потенциалов между точками:
а) А и В; б) В и С; в) С и D; г) D и А; д) А и С; е) В и D?

3. Соотношение между напряжением и напряженностью для однородного поля

Пусть положительный заряд q перемещают в однородном электростатическом поле напряженностью в направлении линий напряженности на расстояние d (рис. 53.4).

На заряд со стороны поля действует сила qe_vec, направление которой совпадает с направлением перемещения. Поэтому при перемещении на расстояние d поле совершает работу A = qEd.

Напряжение связано с работой соотношением U = A/q.

Следовательно,

U = Ed.      (4)

Соотношение между напряженностью однородного поля и напряжением можно записать также в виде

E = U/d     (5)

Из уравнения (5) следует, что единицу напряженности поля можно определить также как 1 вольт на метр (сокращенно В/м). 1 В/м – это напряженность поля, в котором разность потенциалов между точками, расположенными на одной линии напряженности на расстоянии 1 м друг от друга, равна 1 В.

? 7. Объясните, почему

1 В/м = 1 Н/Кл.

? 8. Вблизи поверхности Земли напряженность поля, созданного зарядом Земли, составляет 130 В/м.
а) Чему равно напряжение между точкой, находящейся на уровне головы стоящего человека, и точкой, находящейся на уровне его ног? Рост человека примите равным 170 см.
б) Почему это напряжение безопасно для человека?

4. Эквипотенциальные поверхности

Если работа поля по перемещению заряда из одной точки в другую равна нулю, то равна нулю и разность потенциалов между этими точками. Можно сказать также, что потенциалы этих точек равны.

? 9. На рисунках 53.5 и 53.6 изображены линии напряженности однородного электростатического поля и поля точечного заряда. Объясните, почему потенциалы точек, лежащих на одной н той же пунктирной линии, равны.

Подсказка. Воспользуйтесь тем, что работа силы равна нулю, если сила перпендикулярна перемещению.

Поверхность, все точки которой имеют равный потенциал, называют эквипотенциальной поверхностью. (От латинского слова «эквус» – равный.)

? 10. Объясните, почему поверхность любого проводника в электростатическом поле является эквипотенциальной, если заряды в проводнике находятся в равновесии.

? 11. Объясните, почему все точки проводника (а не только его поверхность!) имеют одинаковый потенциал.

5. Энергия заряженного тела в электростатическом поле

Если на тело действуют только потенциальные силы, то согласно закону сохранения энергии сумма кинетической и потенциальной энергий этого тела остается неизменной. Рассмотрим случай, когда на заряд действует сила со стороны электростатического поля.

? 12. Электрон движется в однородном поле с напряженностью 100 В/м. Как изменились его потенциальная и кинетическая энергия, если он переместился на 0,5 м:
а) в направлении линии напряженности поля?
б) противоположно линии напряженности поля?

Дополнительные вопросы и задания

13. Объясните, почему линии напряженности электростатического поля не могут иметь вид, показанный на рисунке 53.7.

14. Как должна двигаться заряженная частица в однородном электростатическом поле, чтобы ее траектория была прямолинейной? Может ли кинетическая энергия частицы оставаться при этом неизменной?

15. Может ли заряженная частица равномерно двигаться по окружности:
а) в однородном электростатическом поле?
б) в электрическом поле точечного заряда?
(Излучение заряженной частицы при движении с ускорением в этой главе не учитывается.)

16. Заряженная частица массой m, заряд которой равен по модулю q, влетает в однородное электростатическое поле со скоростью v0, направленной перпендикулярно линиям напряженности поля. Модуль напряженности поля E.
а) Какова форма траектории движения частицы?
б) Как изменяется потенциальная энергия частицы: увеличивается, уменьшается или остается постоянной?
в) Как изменяется кинетическая энергия частицы?
г) Чему равна работа поля по перемещению частицы к тому моменту, когда ее кинетическая энергия возрастает в 2 раза по сравнению с начальной кинетической энергией?
д) Чему будет равна в этот момент скорость частицы?
е) На какое расстояние d сместится к этому моменту частица вдоль линий напряженности поля?
ж) Имеет ли значение знак заряда частицы для ответов на предыдущие вопросы?

17. Электрон влетел в однородное электростатическое поле со скоростью 30 км/с, направленной вертикально вверх. Через 2 * 10^-8 с после этого скорость электрона изменила направление на противоположное.
а) Как направлена напряженность поля?
б) Чему равен модуль напряженности поля?

Потенциальная энергия заряженного тела в однородном электростатическом поле.

Разность потенциалов

Как вы знаете, электрическое поле совершает работу по перемещению заряда. Вспомним сначала о том, что такое работа в механике. Работа — это физическая величина, равная произведению модуля силы, модуля перемещения, вызванного этой силой и косинуса угла между направлением силы и направлением перемещения:

Не так давно мы познакомились с силовой характеристикой электрического поля, которая называется напряженностью. Именно с ее помощью можно определить силу, действующую со стороны поля на данный заряд. Давайте поместим пробный заряд в однородное электростатическое поле и найдем работу, которую совершит это поле.

Пробный заряд начнет перемещаться от положительно заряженной пластины к отрицательно заряженной пластине. В этом случае, работа будет равна произведению модуля силы, действующей на заряд и расстояния между пластинами:

Очевидно, что в данном случае, сила и перемещение будут сонаправлены, поэтому, угол альфа равен нулю и, соответственно, косинус альфа равен единице. Сила, как мы уже сказали, будет равна

Если теперь мы рассмотрим случай, когда угол между направлением силы и перемещением отличен от нуля, то убедимся, что работа электрического поля не изменится.

Исходя из нашего чертежа, легко убедится, что произведение модуля перемещения и косинуса угла альфа равно расстоянию между пластинами. Это наталкивает на мысли о том, что работа электрического поля по переносу заряда не зависит от траектории движения заряда.

Рассмотрим произвольную траекторию и используем прием, с которым мы познакомились ранее. Разобьем кривую на множество вертикальных и горизонтальных отрезков.

Работа поля при перемещении заряда в горизонтальном направлении равна нулю, поскольку в этом случае направление силы, действующей на заряд, перпендикулярно направлению перемещения. На вертикальных участках работа будет равна произведению модуля силы и суммы длин всех вертикальных отрезков. Очевидно, что эта сумма равна расстоянию между пластинами.

Итак, мы убедились, что независимо от траектории движения заряда в электрическом поле, работа, совершаемая полем, вычисляется по одной и той же формуле. Таким образом, мы можем сказать, что сила, действующая на заряд, помещенный в электростатическое поле, является консервативной. Следовательно, работа поля равна изменению потенциальной энергии, взятому с противоположным знаком.

Если на отрицательной пластине мы примем потенциальную энергию равной нулю, то получим формулу для потенциальной энергии заряженного тела, находящегося в однородном электростатическом поле:

Обратите внимание, насколько эта формула похожа на формулу, определяющую потенциальную энергию в механике:

В обоих случаях потенциальная энергия зависит только от положения тела, но не от того, каким образом, тело оказалось в том или ином положении.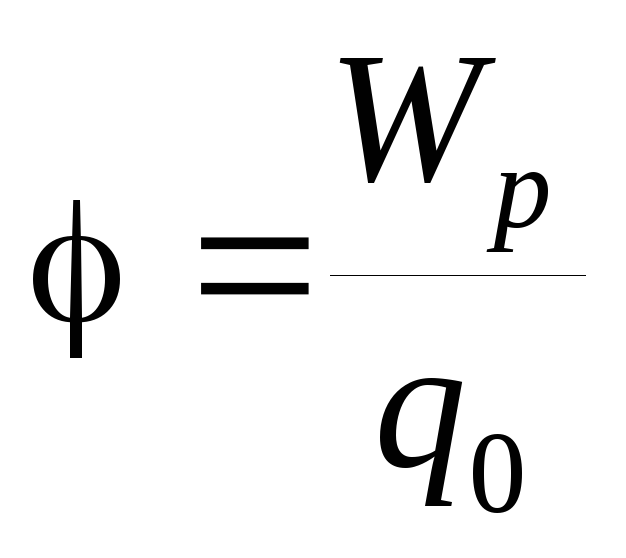 Заряд можно считать за количество электричества, а массу — за количество вещества. Наконец, напряженность — это силовая характеристика электрического поля, а ускорение свободного падения — это силовая характеристика гравитационного поля. Помимо этого сходства, не так давно мы убедились в явном сходстве закона Кулона и закона всемирного тяготения. Эти наблюдения наталкивают на мысли об аналогии электрического поля и гравитационного.

Нетрудно догадаться, что при совершении полем положительной работы, потенциальная энергия тела уменьшается. Исходя из закона сохранения энергии, при этом увеличивается кинетическая энергия заряженного тела. Этот процесс подобен падению тела: поле помогает частице перемещаться, и та набирает скорость. Если же частица будет двигаться в направлении, противоположном направлению вектора напряженности, то поле будет препятствовать движению, совершая отрицательную работу. Этот процесс подобен движению тела вверх. При этом потенциальная энергия увеличивается.

Очевидно, что работа электростатического поля на замкнутой траектории равна нулю. Действительно, если тело вернется в исходную точку, его потенциальная энергия останется прежней, а, значит, изменение потенциальной энергии будет равно нулю.

Итак, мы выяснили, что заряженные частицы в электростатическом поле обладают потенциальной энергией. Поэтому, следует ввести энергетическую характеристику электрического поля, которая называется потенциалом. Потенциал точки электростатического поля — это отношение потенциальной энергии заряда, помещенного в данную точку, к величине этого заряда:

Если мы подставим в эту формулу выражение для потенциальной энергии, то убедимся, что потенциал не зависит от заряда. Именно поэтому, мы можем сказать, что потенциал является характеристикой поля. Исходя из формулы, мы можем определить единицы измерения потенциала — это джоуль на кулон.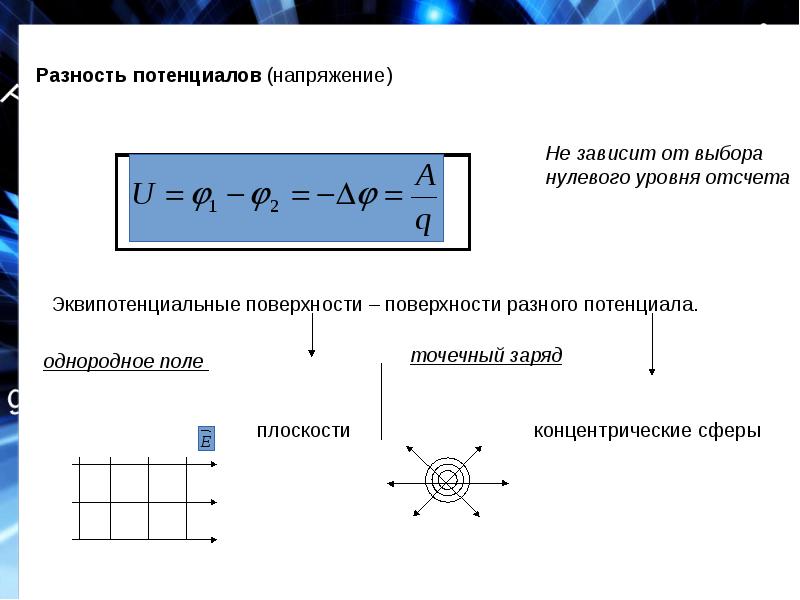 Для данной величины вводится специальная единица измерения, которая называется вольт:

Потенциал, сам по себе, не используется на практике, потому что его величина зависит от выбора нулевого потенциала. Гораздо больший практический интерес представляет разность потенциалов. Рассмотрим формулу, связывающую потенциальную энергию заряженного тела, величину заряда и потенциал. Работа поля по переносу заряда определяется как изменение потенциальной энергии, взятое с противоположным знаком.

Таким образом, работа электрического поля равна произведению заряда и разности потенциалов. Эта разность также называется электрическим напряжением. То есть, разность потенциалов (или напряжение) между двумя точками — это отношение работы электрического поля при перемещении положительного заряда из начальной точки в конечную к величине этого заряда.

Пример решения задачи.

Задача. Пылинка, обладающая зарядом 120 нКл, висит в однородном электростатическом поле между разноименно заряженными пластинами. Если масса пылинки равна 18 мг, то каково напряжение между пластинами? Расстояние между пластинами составляет 6 мм.

Контактная разность потенциалов

Потенциальность электростатического поля

Электрическое поле с напряженностью ​\( \vec{E} \)​ при перемещении заряда ​\( q \)​ совершает работу. Работа ​\( A \)​ электростатического поля вычисляется по формуле:

где ​\( d \)​ – расстояние, на которое перемещается заряд, ​\( \alpha \)​ – угол между векторами напряженности электрического поля и перемещения заряда.

Важно! Эта формула применима для нахождения работы только в однородном электростатическом поле. Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.

Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.

Важно! Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным

Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой ​\( W \)​, так как буквой ​\( E \)​ обозначают напряженность поля:

Потенциальная энергия заряда ​\( q \)​, помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.

Возникновение — контактная разность — потенциал

Возникновение контактной разности потенциалов происходит прежде всего потому, что различные металлы характеризуются разной работой выхода. Электроны легче переходят из металла, для которого работа выхода имеет меньшее значение, в металл, для которого работа имеет большее значение, чем в обратном направлении. Первый металл заряжается положительно, второй отрицательно. При этом на их границе возникает двойной слой разноименных зарядов, внутри которого существует сильное электрическое поле. Легко понять, что это поле будет тормозить дальнейший переход электронов из первого металла во второй и в то же время способствовать их обратному переходу. В результате между этими двумя процессами устанавливается динамическое равновесие, при котором напряженность поля в двойном слое, а следовательно, и разность потенциалов, до которой заряжаются металлы, достигает максимального значения.
 

Возникновение контактной разности потенциалов происходит вследствие двух причин: 1) разная работа выхода электронов, у различных металлов. Металл, имеющий меньшее значение работы выхода электронов, легче их теряет и заряжается положительно, а металл с большей работой выхода накапливает электроны и заряжается отрицательно.
 

Энергетическая диаграмма возникновения внешней контактной разности.| Энергетическая диаграмма возникновения вну.

Возникновение контактной разности потенциалов в случае контакта металл-полупроводник принципиально не отличается от контакта металл-металл, так как она будет определяться разностью работ выхода металла и полупроводника. Однако отличие свойств полупроводника от металла, обусловленное возможностью значительного изменения концентраций носителей заряда в полупроводниках, приводит к возникновению специфических явлений на контакте металл-полупроводник.
 

Возникновение контактной разности потенциалов между соприкасающимися металлическими проводниками было открыто в конце XVI11 в.
 

Схема, поясняющая контактную разность потенциалов в.

Возникновение контактной разности потенциалов определяется следующим процессом. При соприкосновении металлов в месте их контакта происходит взаимное перемещение электронов.
 

Вольт-амперная характеристика полупроводникового диода.

Объясните возникновение контактной разности потенциалов в контакте двух металлов и двух полупроводников.
 

Рассмотрим возникновение контактной разности потенциалов при контакте полупроводника и металла.
 

К объяснению контактной разности потенциалов.

Рассмотрим подробнее возникновение контактной разности потенциалов. Электроны в металле находятся в потенциальной яме. Точки 2 и-3 находятся при одном потенциале, как относящиеся к одному и тому же металлу. Точки 4 и 5 находятся при одном потенциале. Между точками 5 и 6 ( металл В и вакуум) снова будет скачок потенциала, так как электроны в металле В находятся в потенциальной яме. Эта последняя называется внешней контактной разностью потенциалов и она-то обычно и измеряется, поэтому ее часто называют просто контактной разностью потенциалов VAB — Благодаря разности потенциалов между точками / и 6 в зазоре между концами металлов А и В возникает электрическое поле, а на свободных поверхностях металлов А к В — электрические заряды.
 

Характеристики р-ге-перехода.

С другой стороны, возникновение контактной разности потенциалов и электрического поля в переходе приводит к появлению тока проводимости, направленного навстречу диффузионному току. Ток проводимости образуется за счет дрейфа через переход дырок из области с электропроводностью n — титга, где они являются неосновными носителями, в область с электропроводностью р-типа и дрейфа электронов через переход из области с электропроводностью р-типа в область с электропроводностью л-типа. В установившемся режиме при отсутствии внешнего напряжения, поданного на пластину с p — n — переходом, между обоими токами ( проводимости и диффузионным) устанавливается динамическое равновесие. И так как они направлены навстречу друг другу, общий ток через пластину и переход равен нулю. Высота потенциального барьера автоматически устанавливается такой, чтобы было равновесие между двумя токами. \circ\), так как по условию поле поперечное).

Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда), то большой палец, оставленный на 90°, покажет направление силы Лоренца. Пусть мы имеем дело с положительно заряженной частицей, тогда в нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца будет направлена вниз (имеется ввиду направление силы Лоренца в точке 1).

Сила Лоренца \(F_Л\) сообщает частице центростремительное ускорение \(a_ц\), поэтому из второго закона Ньютона следует, что:

\

Центростремительное ускорение \(a_ц\) можно определить через скорость \(\upsilon\) и радиус кривизны траектории \(R\) по формуле:

\

Подставим (4) в (3), тогда:

\

Приравняем правые части (2) и (5):

\

Имеем:

\

Учитывая (1), получим:

\

Возведем в квадрат обе части этого равенства:

\

\

Откуда искомое отношение заряда частицы к массе \(\frac{q}{m}\) равно:

\

Очевидно, что расстояние между точками 1 и 2 равно диаметру окружности, по которой движется заряженная частица в магнитном поле. 8}\;Кл/кг\]

Проводники в электростатическом поле

Размещение проводника в электростатическом поле приводит к тому, что поле начнет действовать на носители заряда внутри проводящего предмета. Носители начинают перемещаться до тех пор, пока электростатическое поле вне поверхности ни обратится в нуль.

Поскольку поле внутри вещества отсутствует, то во всех точках проводящего материала энергия будет постоянной, а поверхность эквипотенциальной. Векторы напряженности поля направлены под прямым углом в любой точке поверхности проводника.

Проводник в электростатическом поле

Под действием поля заряды внутри проводника отсутствуют, поскольку они сосредоточены исключительно на поверхности. Этот факт используется при экранировке – защите тел от влияния внешних электромагнитных и электростатических полей. Для экранирования может использоваться не только сплошной проводящий материал, но и сетка, так называемая «клетка Фарадея».

Клетка Фарадея

Также свойство перемещения заряженных частиц (электронов) используется в электростатических генераторах для получения напряжения в несколько миллионов вольт.

Примеры формул для вычисления напряжения

Измерить напряжение можно, воспользовавшись такой формулой:

U=A/q (U, A и q – величина напряжения, переносящая работа электрополя и заряд, соответственно).

Выразив работу (A=q*U), можно понять, что, чем больше напряженность, тем большую работу потребуется совершить электрополю, чтобы перенести Q

Такие преобразования помогают усвоить, почему важно, чтобы источник питания был мощным. Чем больше потенциальная разница между его клеммами, тем больший объем работы он способен обеспечивать

Чтобы определить напряжение на участке электрической цепи, используется следующее выражение:

U=I*R.

Здесь I – сила протекающего по проводнику электротока, R – сопротивление фрагмента цепи. Для последовательно и параллельно соединенных проводниковых элементов также существуют свои законы, согласно которым рассчитываются напряжение, токовая сила и сопротивление для каждой из веток.

КОНТАКТНАЯ РАЗНОСТЬ ПОТЕНЦИАЛОВ

Если поверхность одного металла (1) привести соприкосновение (контакт) с поверхностью другого металла (2), то происходит переход электронов из одного металла в другой, вследствие чего один из них заряжается положительно, другой — отрицательно. Возникающая при этом разность потенциалов между соприкасающимися телами называется контактной разностью потенциалов.

Появление контактной разности потенциалов обусловлено двумя причинами:

1) различием в работах выхода электрона из металлов, приведенных в соприкосновение. В этом случае силы, действующие на электроны в пограничной области со стороны ионных каркасов обоих Металлов (направленные в противоположные стороны), не уравновешены и поэтому вызывают переход электронов из одного металла в другой;

2) различием в плотностях электронного газа в металлах, вследствие чего возникает диффузный переход электронов из металла, где плотность этого газа большая, в металл, где эта плотность меньше.

Рассмотрим действие каждой из этих причин в отдельности. На электрон, оказавшийся в пограничной области (между ионными решетками обоих металлов), действуют электрические поля созданные поверхностными слоями каждого из металлов (рис. III.35) и направленные в противоположные стороны. Сумма векторов лишь в частном случае может оказаться равной нулю в какой-нибудь точке пограничного слоя. При сложной зависимости этих векторов от расстояния (см. рис. 111.34) их сумма на всем протяжении пограничного слоя будет отлична от нуля и поэтому на электрон, оказавшийся в этой области, действует некоторая результирующая сила, направленная в сторону одного из металлов.

Рис. III.35

На рис. III.35 показаны ионные решетки двух металлов 1 и 2 с различными объемными плотностями ионов. Очевидно, на электроны, оказавшиеся в пограничной области, со стороны металла 1 действуют меньшие силы, чем со стороны металла 2, имеющего более плотную ионную решетку; работа выхода электрона из металла будет Меньше, чем из металла Если то вследствие теплового движения оба металла посылают в пограничный слой (в единицу времени с единицы поверхности) одинаковое число электронов Из этих электронов большая часть Втягивается в металл 2. Таким образом, из пограничного слоя металл 1 получает меньше электронов, чем посылает сам, а металл 2 — больше; первый заряжается положительно, второй — отрицательно. Это вызовет появление в пограничной области внешнего электрического поля направленного от положительно заряженного металла к отрицательно заряженному; оно будет

Потенциал. Разность потенциалов. ЗАДАЧИ с решениями

Формулы, используемые на уроках «Решение задач на тему: Работа перемещения заряда в электрическом поле. Потенциал. Разность потенциалов» для подготовки к ЕГЭ.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.
 Металлический шар диаметром d заряжен с поверхностной плотностью зарядов σ. Найти потенциал φ этого шара, если он окружен заземленной проводящей сферой, имеющей общий с шаром центр. Диаметр сферы D. Среда — воздух.

Задача № 2.
 Потенциал заряженного шара φ₁ = 300 В. Чему равен потенциал φ₂ электрического поля этого шара в точке, отстоящей на расстоянии l = 50 см от его поверхности, если радиус шара R = 25 см?

Задача № 3.
 Определить потенциал φ точки поля, находящейся на расстоянии а =  9 см от поверхности заряженного шара радиусом R = 1 см, если поверхностная плотность зарядов на шаре σ = 1 • 10–11 Кл/см2. Среда — воздух.

Задача № 4.
 В точке 1 поля точечного заряда-источника потенциал φ₁ = 40 В, а в точке 2 φ₂ = 10 В. Найти потенциал φ в точке М, лежащей посередине между точками 1 и 2 (рис. 3-6). 

Задача № 5.
 В трех вершинах квадрата со стороной а = 20 см находятся заряды q₁ = 1 • 10–8 Кл, q₂ = 2 • 10–8 Кл и q₃ = 2 • 10–8 Кл (рис. 3-7). Определить потенциал φ электрического поля, созданного этими зарядами в четвертой вершине. 

Задача № 6.
 Четыре одинаковых точечных заряда q расположены на одной прямой на расстоянии r друг от друга. Какую работу А надо совершить, чтобы переместить эти заряды в вершины тетраэдра со стороной r? Среда — вакуум.

Задача № 7.
Два одинаково заряженных шарика диаметрами d = 0,5 см каждый расположены на расстоянии l = 2 см между их поверхностями (рис. 3-14). До какого потенциала φ они заряжены, если сила их отталкивания друг от друга F = 2 мкН? Среда — воздух. 

Задача № 8.
 В однородном электрическом поле напряженностью Е = 2 кВ/см переместили заряд q = –20 нКл в направлении силовой линии поля на расстояние d = 10 см. Найти работу поля А, изменение потенциальной энергии поля ΔW_п и напряжение (разность потенциалов) U между начальной и конечной точками перемещения.

Задача № 9.
 Между двумя горизонтальными плоскостями, заряженными разноименно и расположенными на расстоянии d = 5 мм друг от друга, находится в равновесии капелька масла массой 20 нг (нанограмм) (рис. 3-10). Найти число избыточных электронов N на этой капельке. Среда — воздух. Разность потенциалов между плоскостями U = 2 кВ. 

Задача № 10.
 На пластине М поддерживается потенциал φ₁ = +80 В, а на пластине N – φ₂ = –80 В (рис. 3-11, а). Расстояние между пластинами d = 10 см. На расстоянии d₁ = 4 см от пластины М помещают заземленную пластину Р (рис. 3-11, б). Найти изменение напряженности ΔЕ₁ поля на участке МР и изменение напряженности поля ΔЕ₂ на участке PN при этом. Построить графики зависимостей напряженностей Е = Е(х) и потенциала φ = φ(х) от расстояния между точками поля и пластинами. 

Это конспект по теме «Потенциал. Разность потенциалов. ЗАДАЧИ с решениями». Выберите дальнейшие действия:

• Вернуться к списку конспектов по Физике.
• Проверить свои знания по Физике.

Понятие потенциала в физике

Что такое потенциал в физике? Это понятие очень часто применяется для описания качеств сил и полей самой разной природы. Скалярная функция, характеризующая некоторую величину, представляющуюся вектором, – вот что это потенциал. Гравитационный потенциал описывает соответствующее поле. В термодинамике это понятие применяется для системной внутренней энергии, в механике – для той или иной приложенной к предмету силы.

Электрика, прежде всего, интересует, что такое потенциал в электричестве. Из общего определения нетрудно вывести, что характеристика электрополя – это электрический потенциал. В своей статической форме электрический потенциал показывает потенциальную энергию одиночного «плюсового» заряда, помещаемого в данное место электрополя, и является одной из разновидностей электромагнитного потенциала. Вторая его форма – векторная (в отличие от скалярной), описывает магнитное поле.

Важно! Характеристика поля, описывающая зависимость работы при передвижении исключительно от исходной точки и места назначения, – это потенциальность поля. Траектория перемещения в этом случае на работу не влияет

Напряжение в цепях трёхфазного тока

В цепях трёхфазного тока различают фазное и линейное напряжения. Под фазным напряжением понимают среднеквадратичное значение напряжения на каждой из фаз нагрузки относительно нейтрали, а под линейным — напряжение между подводящими фазными проводами. При соединении нагрузки в фазное напряжение равно линейному, а при соединении в (при симметричной нагрузке или при глухозаземлённой нейтрали) линейное напряжение в 3{\displaystyle {\sqrt {3}}} раз больше фазного.

На практике напряжение трёхфазной сети обозначают дробью, в числителе которой стоит фазное при соединении в звезду (или, что то же самое, потенциал каждой из линий относительно земли), а в знаменателе — линейное напряжение. Так, в России наиболее распространены сети с напряжением 220/380 В; также иногда используются сети 127/220 В и 380/660 В.

Оцените статью:

Электрическая потенциальная энергия: разница потенциалов

Цели обучения

К концу этого раздела вы сможете:

• Определите электрический потенциал и электрическую потенциальную энергию.
• Опишите взаимосвязь между разностью потенциалов и электрической потенциальной энергией.
• Объясните электрон-вольт и его использование в субмикроскопических процессах.
• Определите электрическую потенциальную энергию по разности потенциалов и количеству заряда.

Рис. 1. Заряд, ускоренный электрическим полем, аналогичен массе, спускающейся с холма. В обоих случаях потенциальная энергия преобразуется в другую форму. Работа совершается силой, но поскольку эта сила консервативна, мы можем записать W = –ΔPE.

Когда свободный положительный заряд q ускоряется электрическим полем, как показано на рисунке 1, ему придается кинетическая энергия. Этот процесс аналогичен ускорению объекта гравитационным полем.Это как если бы заряд спускался по электрическому холму, где его электрическая потенциальная энергия преобразуется в кинетическую. Давайте исследуем работу, совершаемую электрическим полем над зарядом q в этом процессе, чтобы мы могли разработать определение электрической потенциальной энергии.

Электростатическая или кулоновская сила является консервативной, что означает, что работа, проделанная на q , не зависит от пройденного пути. Это в точности аналогично силе гравитации в отсутствие диссипативных сил, таких как трение.Когда сила консервативна, можно определить потенциальную энергию, связанную с силой, и обычно легче иметь дело с потенциальной энергией (потому что она зависит только от положения), чем вычислять работу напрямую.

Мы используем буквы PE для обозначения электрической потенциальной энергии, которая измеряется в джоулях (Дж). Изменение потенциальной энергии ΔPE имеет решающее значение, поскольку работа, совершаемая консервативной силой, является отрицательной по отношению к изменению потенциальной энергии; то есть Вт = –ΔPE. Например, работа W , выполняемая для ускорения положительного заряда из состояния покоя, является положительной и является результатом потери PE или отрицательного ΔPE. Перед ΔPE должен стоять знак минус, чтобы значение W было положительным. PE можно найти в любой точке, взяв одну точку за точку отсчета и вычислив работу, необходимую для перемещения заряда в другую точку.

Потенциальная энергия

W = –ΔPE. Например, работа W , выполняемая для ускорения положительного заряда из состояния покоя, является положительной и является результатом потери PE или отрицательного ΔPE.Перед ΔPE должен стоять знак минус, чтобы значение W было положительным. PE можно найти в любой точке, взяв одну точку за точку отсчета и вычислив работу, необходимую для перемещения заряда в другую точку.

Гравитационная потенциальная энергия и электрическая потенциальная энергия совершенно аналогичны. Потенциальная энергия учитывает работу, выполняемую консервативной силой, и дает дополнительное понимание энергии и преобразования энергии без необходимости иметь дело с силой напрямую. Например, гораздо более распространено использование концепции напряжения (связанного с электрической потенциальной энергией), чем непосредственное рассмотрение кулоновской силы.

Непосредственный расчет работы обычно затруднен, поскольку Вт = Fd cos θ , а направление и величина F ​​ могут быть сложными для нескольких зарядов, для объектов нечетной формы и вдоль произвольных траекторий. Но мы знаем, что, поскольку F ​​ = qE , работа и, следовательно, ΔPE пропорциональны испытательному заряду q. Чтобы получить физическую величину, не зависящую от испытательного заряда, мы определяем электрический потенциал V (или просто потенциал, поскольку подразумевается электрический) как потенциальную энергию на единицу заряда [латекс] V = \ frac {\ text {PE}} {q} \\ [/ латекс].

Электрический потенциал

Это электрическая потенциальная энергия на единицу заряда.

[латекс] \ displaystyle {V} = \ frac {\ text {PE}} {q} \\ [/ latex]

Поскольку PE пропорционален q , зависимость от q отменяется. Таким образом, V не зависит от q . Изменение потенциальной энергии ΔPE имеет решающее значение, поэтому нас беспокоит разница потенциалов или разность потенциалов Δ V между двумя точками, где

[латекс] \ displaystyle \ Delta {V} = V _ {\ text {B}} — V _ {\ text {A}} = \ frac {\ Delta {\ text {PE}}} {q} \\ [/ латекс]

Разность потенциалов между точками A и B, V _B — V _A , таким образом, определяется как изменение потенциальной энергии заряда q , перемещенного от A к B, делится на заряд.Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.

[латекс] 1 \ text {V} = 1 \ frac {\ text {J}} {\ text {C}} \\ [/ latex]

Потенциальная разница

Разность потенциалов между точками A и B, V _B — V _A , определяется как изменение потенциальной энергии заряда q , перемещенного от A к B, деленное на заряд. Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.

[латекс] \ displaystyle {1} \ text {V} = 1 \ frac {\ text {J}} {\ text {C}} \\ [/ latex]

Знакомый термин напряжение — это общее название разности потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, под ним понимается разность потенциалов между двумя точками. Например, каждая батарея имеет две клеммы, и ее напряжение — это разность потенциалов между ними. По сути, точка, которую вы выбираете равным нулю вольт, произвольна. Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный ноль, например, уровень моря или, возможно, пол лекционного зала.

Таким образом, связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется выражением [латекс] \ Delta {V} = \ frac {\ Delta \ text {PE}} {q} \\ [/ latex] и ΔPE = q Δ V .

Разность потенциалов и электрическая потенциальная энергия

Связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется формулой

[латекс] \ Delta {V} = \ frac {\ Delta \ text {PE}} {q} \\ [/ latex] и ΔPE = q Δ V

Второе уравнение эквивалентно первому.

Напряжение — это не то же самое, что энергия. Напряжение — это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между выводами аккумулятора), но один хранит гораздо больше энергии, чем другой, поскольку ΔPE = q Δ V . Автомобильный аккумулятор может заряжать больше, чем аккумулятор мотоцикла, хотя оба аккумулятора — 12 В.

Пример 1. Расчет энергии

Предположим, у вас 12.Батарея мотоцикла 0 В, способная перемещать заряд 5000 C, и автомобильная батарея 12,0 В, способная перемещать заряд 60 000 C. Сколько энергии дает каждый? (Предположим, что числовое значение каждого заряда с точностью до трех значащих цифр.)

Стратегия

Если у нас есть батарея на 12,0 В, это означает, что на ее выводах разность потенциалов составляет 12,0 В. Когда такая батарея перемещает заряд, она пропускает заряд через разность потенциалов 12,0 В, и заряд получает изменение потенциальной энергии, равное ΔPE = q Δ V .

Итак, чтобы найти выходную энергию, мы умножаем перемещенный заряд на разность потенциалов.

Решение

Для аккумулятора мотоцикла: q = 5000 C и Δ V = 12,0 В. Общая энергия, отдаваемая аккумулятором мотоцикла, составляет

[латекс] \ begin {array} {lll} \ Delta \ text {PE} _ {\ text {cycle}} & = & \ left (5000 \ text {C} \ right) \ left (12.0 \ text {V } \ right) \\\ text {} & = & \ left (5000 \ text {C} \ right) \ left (12.0 \ text {J / C} \ right) \\\ text {} & = & 6.5 \ text {J} \ end {array} \\ [/ latex]

Обсуждение

Хотя напряжение и энергия связаны, это не одно и то же. Напряжения батарей идентичны, но энергия, подаваемая каждой из них, совершенно разная. Также обратите внимание, что когда аккумулятор разряжается, часть его энергии используется внутри, а напряжение на его клеммах падает, например, когда фары тускнеют из-за низкого заряда автомобильного аккумулятора. Энергия, подаваемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.

Обратите внимание, что энергии, вычисленные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для аккумулятора отрицательное, так как он теряет энергию. Эти батареи, как и многие другие электрические системы, действительно перемещают отрицательный заряд — в частности, электроны. Батареи отталкивают электроны от своих отрицательных выводов (A) через любую задействованную схему и притягивают их к своим положительным выводам (B), как показано на рисунке 2. Изменение потенциала составляет Δ В = В _B — V _A = +12 В, а заряд q отрицательный, так что ΔPE = q Δ V отрицательный, что означает, что потенциальная энергия батареи уменьшилась, когда q переместились из От А до Б.

Рис. 2. Батарея перемещает отрицательный заряд от отрицательной клеммы через фару к положительной клемме. Соответствующие комбинации химических веществ в батарее разделяют заряды, так что отрицательный вывод имеет избыток отрицательного заряда, который отталкивается им и притягивается к избыточному положительному заряду на другом выводе. Что касается потенциала, положительный вывод находится под более высоким напряжением, чем отрицательный. Внутри батареи движутся как положительные, так и отрицательные заряды.

Пример 2. Сколько электронов проходит через фару каждую секунду?

Когда от автомобильного аккумулятора на 12,0 В работает одна фара мощностью 30,0 Вт, сколько электронов проходит через нее каждую секунду?

Стратегия

Чтобы узнать количество электронов, мы должны сначала найти заряд, который переместился за 1,00 с. Перемещаемый заряд связан с напряжением и энергией уравнением ΔPE = q Δ V . Лампа мощностью 30,0 Вт потребляет 30,0 джоулей в секунду. Поскольку батарея теряет энергию, имеем ΔPE = –30.0 Дж, и, поскольку электроны переходят от отрицательной клеммы к положительной, мы видим, что Δ В = + 12,0 В.

Решение

Чтобы найти перемещенный заряд q , мы решаем уравнение ΔPE = q Δ V : [латекс] q = \ frac {\ Delta \ text {PE}} {\ Delta {V}} \ \[/латекс].

Вводя значения ΔPE и Δ В , получаем

[латекс] q = \ frac {-30.0 \ text {J}} {+ 12.0 \ text {V}} = \ frac {-30.0 \ text {J}} {+ 12.0 \ text {J / C}} — 2.{19} \ text {электроны} \\ [/ latex]

Обсуждение

Это очень большое число. Неудивительно, что мы обычно не наблюдаем отдельных электронов, так много которых присутствует в обычных системах. Фактически, электричество использовалось в течение многих десятилетий, прежде чем было установлено, что движущиеся заряды во многих обстоятельствах были отрицательными. Положительный заряд, движущийся в направлении, противоположном отрицательному, часто производит идентичные эффекты; это затрудняет определение того, что движется или оба движутся.

Электрон вольт

Рис. 3. Типичная электронная пушка ускоряет электроны, используя разность потенциалов между двумя металлическими пластинами. Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов 5000 В производит электроны 5000 эВ.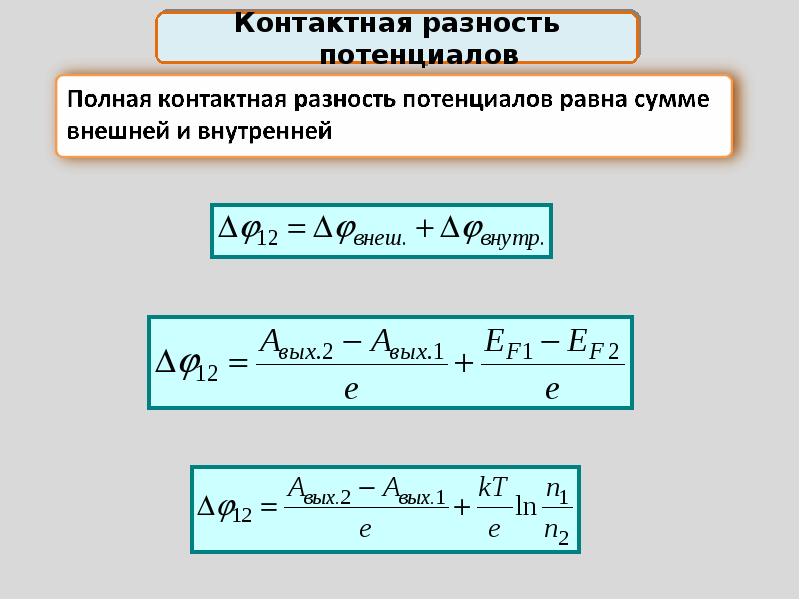

Энергия, приходящаяся на один электрон, очень мала в макроскопических ситуациях, подобных тому, что было в предыдущем примере — крошечная доля джоуля. Но в субмикроскопическом масштабе такая энергия, приходящаяся на частицу (электрон, протон или ион), может иметь большое значение.Например, даже крошечной доли джоуля может быть достаточно, чтобы эти частицы разрушили органические молекулы и повредили живые ткани. Частица может нанести ущерб при прямом столкновении или может создать вредные рентгеновские лучи, которые также могут нанести ущерб. Полезно иметь единицу энергии, относящуюся к субмикроскопическим эффектам. На рисунке 3 показана ситуация, связанная с определением такой единицы энергии. Электрон ускоряется между двумя заряженными металлическими пластинами, как это могло бы быть в телевизионной лампе или осциллографе старой модели.Электрону придается кинетическая энергия, которая позже преобразуется в другую форму — например, в свет в телевизионной трубке. (Обратите внимание, что спуск для электрона означает подъем для положительного заряда. ) Поскольку энергия связана с напряжением соотношением ΔPE = q Δ V , мы можем представить джоуль как кулон-вольт.

В субмикроскопическом масштабе удобнее определить единицу энергии, называемую электрон-вольт, (эВ), которая представляет собой энергию, отдаваемую фундаментальному заряду, ускоренному через разность потенциалов в 1 В.{-19} \ text {J} \ end {array} \\ [/ latex]

Электрону, ускоренному через разность потенциалов 1 В, придается энергия 1 эВ. Отсюда следует, что электрону, ускоренному до 50 В, дается 50 эВ. Разность потенциалов 100000 В (100 кВ) даст электрону энергию 100000 эВ (100 кэВ) и так далее. Аналогичным образом ион с двойным положительным зарядом, ускоренный до 100 В, получит энергию 200 эВ. Эти простые соотношения между ускоряющим напряжением и зарядами частиц делают электрон-вольт простой и удобной единицей энергии в таких обстоятельствах.

Установление соединений: блоки энергии

Электрон-вольт (эВ) — наиболее распространенная единица измерения энергии для субмикроскопических процессов. Особенно это будет заметно в главах, посвященных современной физике. Энергия настолько важна для стольких предметов, что существует тенденция определять специальные единицы энергии для каждой основной темы. Есть, например, калории для пищевой энергии, киловатт-часы для электроэнергии и термы для энергии природного газа.

Электрон-вольт обычно используется в субмикроскопических процессах — химическая валентная энергия, молекулярная и ядерная энергия связи входят в число величин, часто выражаемых в электрон-вольтах.Например, для разрушения некоторых органических молекул требуется около 5 эВ энергии. Если протон ускоряется из состояния покоя через разность потенциалов 30 кВ, ему дается энергия 30 кэВ (30 000 эВ), и он может разрушить до 6000 этих молекул (30 000 эВ ÷ 5 эВ на молекулу = 6000 молекул. ). Энергия ядерного распада составляет порядка 1 МэВ (1000000 эВ) на событие и, таким образом, может нанести значительный биологический ущерб.

Сохранение энергии

Полная энергия системы сохраняется, если нет чистого добавления (или вычитания) работы или теплопередачи. Для консервативных сил, таких как электростатическая сила, закон сохранения энергии утверждает, что механическая энергия постоянна.

Механическая энергия — это сумма кинетической энергии и потенциальной энергии системы; то есть KE + PE = константа. Потеря ПЭ заряженной частицы становится увеличением ее КЭ. Здесь PE — электрическая потенциальная энергия. Сохранение энергии выражается в виде уравнения как KE + PE = постоянная или KE _i + PE _i = KE _f + PE _f , где i и f обозначают начальные и конечные условия.Как мы уже много раз выясняли, учет энергии может дать нам понимание и облегчить решение проблем.

Пример 3. Электрическая потенциальная энергия, преобразованная в кинетическую энергию

Вычислите конечную скорость свободного электрона, ускоренного из состояния покоя через разность потенциалов 100 В. (Предположим, что это числовое значение имеет точность до трех значащих цифр).

Стратегия

У нас есть система только с консервативными силами. Предполагая, что электрон ускоряется в вакууме, и пренебрегая гравитационной силой (мы проверим это предположение позже), вся электрическая потенциальная энергия преобразуется в кинетическую энергию.6 \ text {m / s} \ end {array} \\ [/ latex]

Обсуждение

Обратите внимание, что и заряд, и начальное напряжение отрицательны, как показано на рисунке 3. Из обсуждений в разделе «Электрический заряд и электрическое поле» мы знаем, что электростатические силы, действующие на мелкие частицы, обычно очень велики по сравнению с силой тяжести. Большая конечная скорость подтверждает, что гравитационная сила здесь действительно незначительна. Большая скорость также указывает на то, насколько легко ускорить электроны малым напряжением из-за их очень малой массы.В электронных пушках обычно используются напряжения, намного превышающие 100 В. Эти более высокие напряжения вызывают настолько большие скорости электронов, что необходимо учитывать релятивистские эффекты. Вот почему в этом примере рассматривается (точно) низкое напряжение.

Сводка раздела

• Электрический потенциал — это потенциальная энергия на единицу заряда.
• Разность потенциалов между точками A и B, В _B — В _A , определяемая как изменение потенциальной энергии заряда q , перемещенного от A к B, равна изменению потенциальная энергия, деленная на заряд. Разность потенциалов обычно называется напряжением и обозначается символом Δ В : [латекс] \ Delta V = \ frac {\ Delta \ text {PE}} {q} \\ [/ латекс] и ΔPE = q Δ V .{\ text {-19}} \ text {J.} \ end {array} \\ [/ latex]
• Механическая энергия — это сумма кинетической энергии и потенциальной энергии системы, то есть KE + PE. Эта сумма постоянна.

Концептуальные вопросы

1. Напряжение — это обычное слово для обозначения разности потенциалов. Какой термин более описательный: напряжение или разность потенциалов?
2. Если напряжение между двумя точками равно нулю, можно ли перемещать тестовый заряд между ними при нулевой работе сети? Обязательно ли это делать без применения силы? Объяснять.
3. Какая связь между напряжением и энергией? Точнее, какова связь между разностью потенциалов и электрической потенциальной энергией?
4. Напряжение всегда измеряется между двумя точками. Почему?
5. Как связаны единицы вольт и электронвольт? Чем они отличаются?

Задачи и упражнения

1. Найдите отношение скоростей электрона и отрицательного иона водорода (тот, у которого есть дополнительный электрон), ускоренных одним и тем же напряжением, принимая нерелятивистские конечные скорости.Возьмем массу иона водорода 1,67 × 10 ⁻²⁷ кг.
2. В вакуумной трубке используется ускоряющее напряжение 40 кВ для ускорения электронов, ударов по медной пластине и получения рентгеновских лучей. С нерелятивистской точки зрения, какова максимальная скорость этих электронов?
3. Голое ядро ​​гелия имеет два положительных заряда и массу 6,64 × 10 ⁻²⁷ кг. (а) Вычислите его кинетическую энергию в джоулях при 2,00% скорости света. (б) Что это в электрон-вольтах? (c) Какое напряжение потребуется для получения этой энергии?
4. Интегрированные концепции. Однозарядные ионы газа ускоряются из состояния покоя за счет напряжения 13,0 В. При какой температуре средняя кинетическая энергия молекул газа будет такой же, как у этих ионов?
5. Интегрированные концепции. Считается, что температура около центра Солнца составляет 15 миллионов градусов Цельсия (1,5 × 10 ⁷ ºC). Через какое напряжение должен быть ускорен однозарядный ион, чтобы он имел такую ​​же энергию, как средняя кинетическая энергия ионов при этой температуре?
6. Интегрированные концепции. (a) Какова средняя выходная мощность дефибриллятора сердца, который рассеивает 400 Дж энергии за 10,0 мс? (б) Учитывая высокую выходную мощность, почему дефибриллятор не вызывает серьезных ожогов?
7. Интегрированные концепции. Молния поражает дерево, перемещая 20,0 Кл заряда через разность потенциалов 1,00 × 10 ² МВ. а) Какая энергия была рассеяна? б) Какую массу воды можно было поднять с 15ºC до точки кипения и затем с помощью этой энергии вскипятить? (c) Обсудите ущерб, который может быть нанесен дереву из-за расширения кипящего пара.
8. Интегрированные концепции. Подогреватель бутылочек на 12,0 В нагревает 50,0 г стекла, 2,50 × 10 ² г детской смеси и 2,00 × 10 ² г алюминия с 20,0 ° C до 90,0 ° C. (а) Насколько заряжен аккумулятор? (б) Сколько электронов течет в секунду, если на нагрев формулы требуется 5,00 мин? (Подсказка: предположите, что удельная теплоемкость детской смеси примерно такая же, как удельная теплоемкость воды.)
9. Интегрированные концепции. В автомобиле с батарейным питанием используется 12.Система 0 В. Найдите заряд, который батареи должны быть в состоянии двигаться, чтобы разогнать автомобиль весом 750 кг от состояния покоя до 25,0 м / с, заставить его подняться на холм высотой 2,00 × 10 ² м, а затем заставить его двигаться с постоянной скоростью 25,0 м / с путем приложения силы 5,00 × 10 ² Н в течение часа.
10. Интегрированные концепции. Вероятность слияния значительно увеличивается, когда соответствующие ядра сближаются, но взаимное кулоновское отталкивание должно быть преодолено. Это можно сделать, используя кинетическую энергию ионов высокотемпературного газа или ускоряя ядра друг к другу.(a) Рассчитайте потенциальную энергию двух однозарядных ядер, разделенных расстоянием 1,00 × 10 ⁻¹² м, найдя напряжение одного на таком расстоянии и умножив его на заряд другого. (б) При какой температуре атомы газа будут иметь среднюю кинетическую энергию, равную этой необходимой электрической потенциальной энергии?
11. Необоснованные результаты. (a) Найдите напряжение около металлической сферы диаметром 10,0 см, на которой имеется 8,00 C избыточного положительного заряда. б) Что неразумного в этом результате? (c) Какие допущения ответственны?
12. Создайте свою проблему. Рассмотрим батарею, используемую для питания сотового телефона. Постройте задачу, в которой вы определяете энергию, которая должна быть предоставлена ​​батареей, а затем вычисляете количество заряда, которое она должна иметь возможность перемещать, чтобы обеспечить эту энергию. Среди прочего следует учитывать потребность в энергии и напряжение батареи. Возможно, вам придется заглянуть в будущее, чтобы интерпретировать номинальные характеристики батареи в ампер-часах производителя как энергию в джоулях.

Глоссарий

электрический потенциал: потенциальная энергия на единицу заряда

разность потенциалов (или напряжение): изменение потенциальной энергии заряда, перемещенного из одной точки в другую, деленное на заряд; единицы разности потенциалов — джоули на кулон, известные как

вольт.

электрон-вольт: энергия, отданная фундаментальному заряду, ускоренному через разность потенциалов в один вольт

механическая энергия: сумма кинетической энергии и потенциальной энергии системы; эта сумма является постоянной

Избранные решения проблем и упражнения

1. 42,8

4. 1,00 × 10 ⁵ К

6. (а) 4 × 10 ⁴ Вт; (b) Дефибриллятор не вызывает серьезных ожогов, потому что кожа хорошо проводит электричество при высоких напряжениях, подобных тем, которые используются в дефибрилляторах. Используемый гель способствует передаче энергии телу, а кожа не поглощает энергию, а пропускает ее к сердцу.

8. (а) 7,40 × 10 ³ С; (б) 1,54 × 10 ²⁰ электронов в секунду

9. 3.89 × 10 ⁶ С

11. (а) 1.44 × 10 ¹² В; (б) Это напряжение очень высокое. Сфера диаметром 10,0 см никогда не сможет выдержать такое напряжение; он разрядился бы; (c) Заряд в 8,00 C — это больше заряда, чем можно разумно накопить на сфере такого размера.

Учебное пособие по физике: разность электрических потенциалов

В предыдущем разделе Урока 1 было введено понятие электрического потенциала. Электрический потенциал — это зависящая от местоположения величина, которая выражает количество потенциальной энергии на единицу заряда в определенном месте. Когда кулон заряда (или любое заданное количество заряда) обладает относительно большим количеством потенциальной энергии в данном месте, то это место называется местом с высоким электрическим потенциалом. Точно так же, если кулон заряда (или любое заданное количество заряда) обладает относительно небольшим количеством потенциальной энергии в данном месте, то это место называется местоположением с низким электрическим потенциалом. Когда мы начнем применять наши концепции потенциальной энергии и электрического потенциала к цепям, мы начнем говорить о разнице электрического потенциала между двумя точками.Эта часть Урока 1 будет посвящена пониманию разности электрических потенциалов и ее применению к движению заряда в электрических цепях.

Рассмотрим задачу перемещения положительного испытательного заряда в однородном электрическом поле из точки A в точку B, как показано на схеме справа. При перемещении заряда против электрического поля из точки A в точку B над зарядом должна будет работать внешняя сила. Работа, совершенная над зарядом, изменяет его потенциальную энергию на более высокое значение; а объем проделанной работы равен изменению потенциальной энергии.В результате этого изменения потенциальной энергии также существует разница в электрическом потенциале между точками A и B. Эта разница в электрическом потенциале представлена ​​символом ΔV и формально упоминается как разность электрических потенциалов . По определению, разность электрических потенциалов — это разность электрических потенциалов (В) между конечным и начальным местоположением, когда над зарядом выполняется работа по изменению его потенциальной энергии. В форме уравнения разность электрических потенциалов равна

.

Стандартной метрической единицей измерения разности электрических потенциалов является вольт, сокращенно В, и названный в честь Алессандро Вольта.Один вольт эквивалентен одному джоулю на кулон. Если разность электрических потенциалов между двумя местоположениями составляет 1 вольт, то один кулоновский заряд получит 1 джоуль потенциальной энергии при перемещении между этими двумя местоположениями. Если разность электрических потенциалов между двумя местоположениями составляет 3 вольта, то один кулон заряда получит 3 джоуля потенциальной энергии при перемещении между этими двумя местоположениями. И, наконец, если разность электрических потенциалов между двумя местоположениями составляет 12 вольт, то один кулон заряда получит 12 джоулей потенциальной энергии при перемещении между этими двумя местоположениями.Поскольку разность электрических потенциалов выражается в вольтах, ее иногда называют напряжением .

Разность электрических потенциалов и простые схемы

Электрические цепи, как мы увидим, все связаны с движением заряда между различными местами и соответствующими потерями и увеличением энергии, которые сопровождают это движение. В предыдущей части Урока 1 концепция электрического потенциала была применена к простой электрической цепи с батарейным питанием.В этом обсуждении было объяснено, что необходимо провести работу с положительным тестовым зарядом, чтобы переместить его через ячейки от отрицательного вывода к положительному выводу.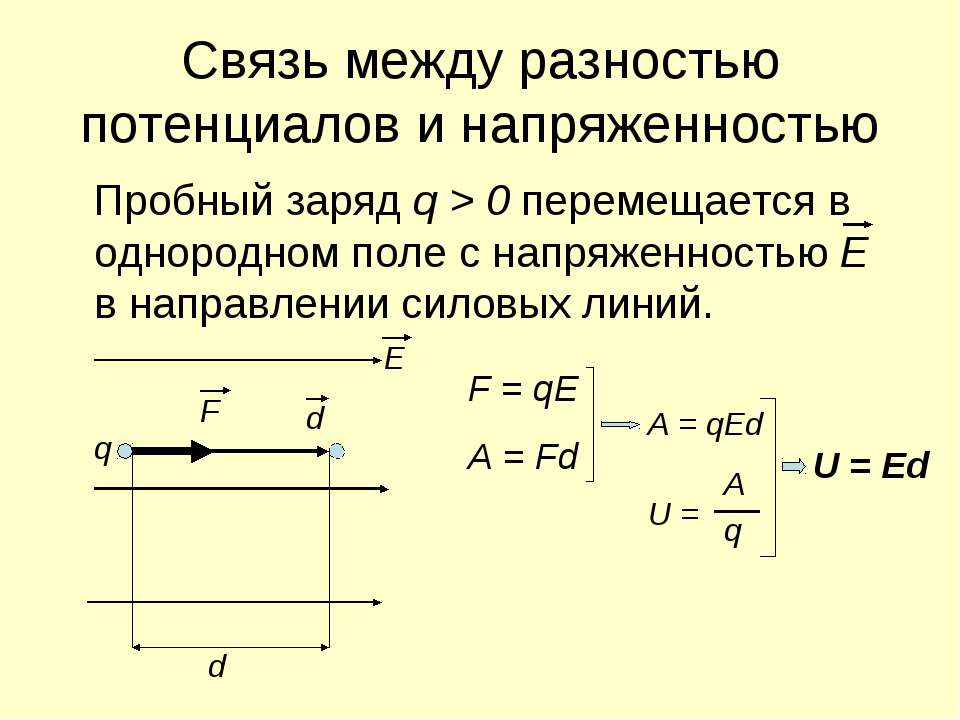 Эта работа увеличит потенциальную энергию заряда и, таким образом, увеличит его электрический потенциал. По мере того, как положительный тестовый заряд перемещается через внешнюю цепь от положительного вывода к отрицательному выводу, он уменьшает свою электрическую потенциальную энергию и, таким образом, имеет низкий потенциал к тому времени, когда он возвращается к отрицательному выводу.Если в цепи используется 12-вольтовая батарея, то каждый кулон заряда получает 12 джоулей потенциальной энергии при прохождении через батарею. Точно так же каждый кулон заряда теряет 12 джоулей электрической потенциальной энергии при прохождении через внешнюю цепь. Потеря этой электрической потенциальной энергии во внешней цепи приводит к увеличению световой энергии, тепловой энергии и других форм неэлектрической энергии.

С четким пониманием разности электрических потенциалов, роли электрохимической ячейки или совокупности ячеек (т.е., аккумулятор) в простой схеме можно правильно понять. Ячейки просто поставляют энергию для работы с зарядом, перемещая его от отрицательного вывода к положительному. Предоставляя энергию для заряда, элемент способен поддерживать разность электрических потенциалов на двух концах внешней цепи. Как только заряд достигнет клеммы с высоким потенциалом, он естественным образом пройдет по проводам к клемме с низким потенциалом. Движение заряда по электрической цепи аналогично движению воды в аквапарке или движению американских горок в парке развлечений.В каждой аналогии необходимо проделать работу на воде или на американских горках, чтобы переместить ее из места с низким гравитационным потенциалом в место с высоким гравитационным потенциалом. Когда вода или американские горки достигают высокого гравитационного потенциала, они естественным образом движутся вниз обратно в место с низким потенциалом. Для водных прогулок или американских горок задача по подъему автомобилей с водой или горками до высокого потенциала требует энергии. Энергия подается водяным насосом с приводом от двигателя или цепью с приводом от двигателя. В электрической цепи с батарейным питанием элементы служат в качестве зарядного насоса для подачи энергии на заряд, чтобы поднять его из положения с низким потенциалом через элемент в положение с высоким потенциалом.

Часто бывает удобно говорить об электрической цепи, такой как простая схема, обсуждаемая здесь, как состоящая из двух частей — внутренней и внешней. Внутренняя цепь — это часть цепи, в которой энергия подается на заряд.Для простой схемы с батарейным питанием, о которой мы говорили, часть схемы, содержащая электрохимические элементы, является внутренней схемой. Внешняя цепь является частью схемы, где заряд движется за пределы ячеек по проводам на своем пути от клеммы с высоким потенциалом к ​​клемме с низким потенциалом. Движение заряда по внутренней цепи требует энергии, поскольку это движение вверх по склону и в направлении, которое составляет против электрического поля .Движение заряда по внешней цепи естественно, так как это движение в направлении электрического поля. Когда на положительном выводе электрохимической ячейки, положительный тестовый заряд находится под высоким электрическим давлением точно так же, как вода в аквапарке находится под высоким давлением после перекачивания на вершину водной горки. Находясь под высоким электрическим давлением, положительный испытательный заряд самопроизвольно и естественным образом перемещается по внешней цепи в место с низким давлением и низким потенциалом.

Когда положительный тестовый заряд проходит через внешнюю цепь, он встречает различные типы элементов схемы. Каждый элемент схемы служит устройством преобразования энергии. Лампочки, двигатели и нагревательные элементы (например, в тостерах и фенах) являются примерами устройств преобразования энергии. В каждом из этих устройств электрическая потенциальная энергия заряда преобразуется в другие полезные (и бесполезные) формы. Например, в лампочке электрическая потенциальная энергия заряда преобразуется в световую энергию (полезная форма) и тепловая энергия (бесполезная форма). Движущийся заряд воздействует на лампочку, производя две разные формы энергии. При этом движущийся заряд теряет свою электрическую потенциальную энергию. При выходе из элемента схемы заряд получает меньшее напряжение. Место непосредственно перед входом в лампочку (или любой элемент схемы) является местом с высоким электрическим потенциалом; и место сразу после выхода из лампочки (или любого элемента схемы) — это место с низким электрическим потенциалом. Ссылаясь на диаграмму выше, местоположения A и B являются местоположениями с высоким потенциалом, а местоположения C и D — местоположениями с низким потенциалом.Потеря электрического потенциала при прохождении через элемент схемы часто упоминается как падение напряжения . К тому времени, когда положительный тестовый заряд возвращается к отрицательному выводу, он находится под 0 вольт и готов к повторному включению, и перекачивается обратно к положительному выводу высокого напряжения.

Диаграммы электрических потенциалов

Диаграмма электрических потенциалов — удобный инструмент для представления разностей электрических потенциалов между различными точками в электрической цепи. Ниже показаны две простые схемы и соответствующие им диаграммы электрических потенциалов.

В цепи A есть D-элемент на 1,5 В и одна лампочка. В цепи B есть батарея на 6 В (четыре D-элемента по 1,5 В) и две лампочки. В каждом случае отрицательный полюс батареи является положением 0 В. Положительный полюс батареи имеет электрический потенциал, равный номинальному напряжению батареи. Аккумуляторная батарея подает заряд на , перекачивает его от клеммы низкого напряжения к клемме высокого напряжения.Таким образом батарея создает разность электрических потенциалов на двух концах внешней цепи. Находясь на под электрическим давлением , заряд теперь будет перемещаться по внешней цепи. Поскольку его электрическая потенциальная энергия преобразуется в световую и тепловую энергию в местах расположения лампочек, заряд снижает свой электрический потенциал. Общее падение напряжения на внешней цепи равно напряжению батареи, когда заряд перемещается от положительного вывода обратно к 0 вольт на отрицательном выводе. В случае контура B во внешней цепи есть два падения напряжения, по одному на каждую лампочку. В то время как величина падения напряжения в отдельной лампочке зависит от различных факторов (которые будут обсуждаться позже), совокупное падение напряжения должно равняться 6 вольт, полученным при прохождении через батарею.

Разность электрических потенциалов на двух вставках бытовой электросети зависит от страны.Используйте виджет Household Voltages ниже, чтобы узнать значения напряжения в домашних условиях для различных стран (например, США, Канады, Японии, Китая, Южной Африки и т. Д.).

Проверьте свое понимание

1. Перемещение электрона в электрическом поле изменило бы ____ электрона.

а. масса офб. сумма заряда нац.потенциальная энергия

2. Если бы электрическая цепь была аналогична водному контуру в аквапарке, то напряжение батареи было бы сопоставимо с _____.

а. скорость, с которой вода течет через контур

г. скорость, с которой вода течет по контуру

г. расстояние, на котором вода протекает через контур

г. давление воды между верхом и низом контура

e.помеха, вызванная препятствиями на пути движущейся воды

3. Если бы электрическая цепь в вашем Walkman была аналогична водной цепи в аквапарке, тогда батарея была бы сопоставима с _____.

а. люди, которые сползают с возвышенности на землю

г. препятствия, стоящие на пути движущейся воды

г. насос, который перекачивает воду с земли на возвышения

г.трубы, по которым течет вода

e. расстояние, на котором вода протекает через контур

4. Что из нижеперечисленного относится к электрической схеме вашего фонарика?

а. Заряд движется по контуру очень быстро — почти со скоростью света.

г. Аккумулятор поставляет заряд (электроны), который движется по проводам.

г.Батарея обеспечивает заряд (протоны), который движется по проводам.

г. Заряд расходуется по мере прохождения через лампочку.

e. Батарея подает энергию, повышающую уровень заряда от низкого до высокого напряжения.

ф. … ерунда! Все это неправда.

5. Если аккумулятор обеспечивает высокое напряжение, он может ____.

а. делать много работы в течение своей жизни

г. много работать над каждым обнаруженным зарядом

г. протолкнуть много заряда через цепь

г. длиться долго

На схеме внизу справа показана лампочка, подключенная проводами к + и — клеммам автомобильного аккумулятора. Используйте диаграмму, чтобы ответить на следующие четыре вопроса.

6. По сравнению с точкой D, точка A имеет _____ электрический потенциал.

а. 12 В выше в

г. 12 В ниже в

г. точно такой же

г. … невозможно сказать

7. Электрическая потенциальная энергия заряда равна нулю в точке _____.

8. Требуется энергия для перемещения положительного тестового заряда ___.

а. через провод из точки А в точку Б

г. через лампочку из точки B в точку C

г. через провод из точки C в точку D

г. через батарею из точки D в точку A

9. Энергия, необходимая для перемещения +2 C заряда между точками D и A, составляет ____ Дж.

а. 0,167b. 2.0c. 6.0d. 12e. 24

10.Следующая схема состоит из D-ячейки и лампочки. Используйте символы>, <и = для сравнения электрического потенциала в точках A и B и между C и D. Укажите, добавляют ли устройства энергию к заряду или удаляют ее.

11. Используйте свое понимание математической взаимосвязи между работой, потенциальной энергией, зарядом и разностью электрических потенциалов, чтобы заполнить следующие утверждения:

а.9-вольтовая батарея увеличит потенциальную энергию заряда в 1 кулон на ____ джоулей.

г. 9-вольтная батарея увеличит потенциальную энергию 2 кулонов заряда на ____ джоулей.

г. 9-вольтовая батарея увеличит потенциальную энергию заряда 0,5 кулонов на ____ джоулей.

г. Аккумулятор ___-вольт увеличит потенциальную энергию 3 кулонов заряда на 18 джоулей.

e. Аккумулятор ___-вольт увеличивает потенциальную энергию 2 кулонов заряда на 3 джоуля.

ф. Батарея на 1,5 В увеличит потенциальную энергию заряда ____ кулонов на 0,75 джоулей.

г. 12-вольтная батарея увеличивает потенциальную энергию ____ кулонов заряда на 6 джоулей.

7.

3: Электрический потенциал и разность потенциалов

Цели обучения

К концу этого раздела вы сможете:

• Определение электрического потенциала, напряжения и разности потенциалов
• Определите электрон-вольт
• Вычислить электрический потенциал и разность потенциалов на основе потенциальной энергии и электрического поля
• Опишите системы, в которых электрон-вольт является полезной единицей
• Применить энергосбережение в электрических системах

Напомним, что ранее мы определили электрическое поле как величину, не зависящую от тестового заряда в данной системе, что, тем не менее, позволяет нам вычислить силу, которая возникнет в результате произвольного тестового заряда.(При отсутствии другой информации предполагается, что пробный заряд положительный.) Мы кратко определили поле для гравитации, но гравитация всегда притягивает, тогда как электрическая сила может быть притягивающей или отталкивающей. Следовательно, хотя потенциальная энергия вполне достаточна в гравитационной системе, удобно определить величину, которая позволяет нам вычислить работу над зарядом независимо от величины заряда. Непосредственный расчет работы может быть затруднен, поскольку \ (W = \ vec {F} \ cdot \ vec {d} \), а направление и величина \ (\ vec {F} \) могут быть сложными для нескольких зарядов, например предметы необычной формы и по произвольным путям.Но мы знаем, что, поскольку \ (\ vec {F} \), работа и, следовательно, \ (\ Delta U \) пропорциональны испытательному заряду \ (q \). Чтобы получить физическую величину, не зависящую от пробного заряда, мы определяем , электрический потенциал \ (В \) (или просто потенциал, поскольку понимается электрический) как потенциальную энергию на единицу заряда:

Электрический потенциал

Потенциальная электрическая энергия на единицу заряда

\ [V = \ dfrac {U} {q}. \ label {eq-1} \]

Поскольку U пропорционален q , зависимость от q отменяется. Таким образом, V не зависит от q . Изменение потенциальной энергии \ (\ Delta U \) имеет решающее значение, поэтому нас беспокоит разница потенциалов или разность потенциалов \ (\ Delta V \) между двумя точками, где

Разница электрических потенциалов

Разность электрических потенциалов между точками A и B , \ (V_B — V_A \) определяется как изменение потенциальной энергии заряда q , перемещенного с A на B , разделенное по заряду.Единицами разности потенциалов являются джоули на кулон, получившие название вольт (В) в честь Алессандро Вольта.

\ [1 \, V = 1 \, J / C \ label {eq0} \]

Знакомый термин напряжение — это общее название разности электрических потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, под ним понимается разность потенциалов между двумя точками.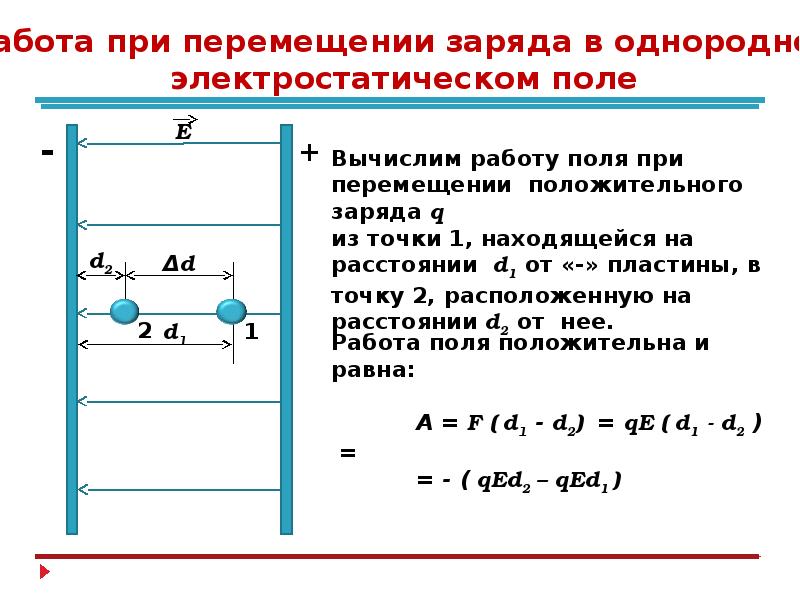 Например, каждая батарея имеет две клеммы, и ее напряжение — это разность потенциалов между ними. По сути, точка, которую вы выбираете равным нулю вольт, произвольна.Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный ноль, например, уровень моря или, возможно, пол лекционного зала. Стоит подчеркнуть различие между разностью потенциалов и электрической потенциальной энергией.

Разность потенциалов и электрическая потенциальная энергия

Связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется формулой

\ [\ Delta V = \ dfrac {\ Delta U} {q} \ label {eq1} \]

или

\ [\ Delta U = q \ Delta V.\ label {eq2} \]

Напряжение — это не то же самое, что энергия. Напряжение — это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между клеммами аккумулятора), но один хранит гораздо больше энергии, чем другой, потому что \ (\ Delta U = q \ Delta V \) .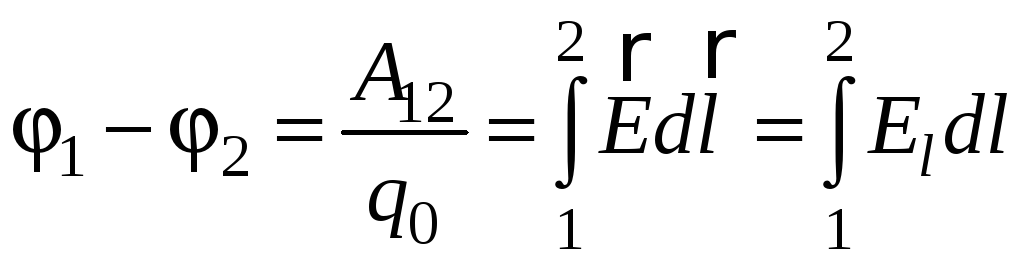 Автомобильный аккумулятор может заряжать больше, чем аккумулятор мотоцикла, хотя оба аккумулятора — 12 В.

Пример \ (\ PageIndex {1} \): расчет энергии

У вас 12.Аккумулятор мотоцикла с напряжением 0 В, который может заряжать 5000 C, и автомобильный аккумулятор на 12 В, который может заряжать 60 000 C. Сколько энергии дает каждый? (Предположим, что числовое значение каждого заряда с точностью до трех значащих цифр.)

Стратегия

Сказать, что у нас батарея на 12,0 В, означает, что на ее выводах разность потенциалов составляет 12,0 В. Когда такая батарея перемещает заряд, она пропускает заряд через разность потенциалов 12,0 В, и заряд получает изменение потенциальной энергии, равное \ (\ Delta U = q \ Delta V \).5 \, J. \ nonumber \]

Значение

Напряжение и энергия связаны, но это не одно и то же. Напряжения батарей идентичны, но энергия, подаваемая каждой из них, совершенно разная. Автомобильный аккумулятор требует запуска гораздо более мощного двигателя, чем мотоцикл. Также обратите внимание, что когда аккумулятор разряжается, часть его энергии используется внутри, а напряжение на его клеммах падает, например, когда фары тускнеют из-за разряда автомобильного аккумулятора. Энергия, подаваемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.

Упражнение \ (\ PageIndex {1} \)

Сколько энергии имеет батарея AAA на 1,5 В, способная нагреться до 100 градусов Цельсия?

Ответ

\ (\ Delta U = q \ Delta V = (100 \, C) (1.5 \, V) = 150 \, J \)

Обратите внимание, что энергии, вычисленные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для аккумулятора отрицательное, так как он теряет энергию. Эти батареи, как и многие другие электрические системы, действительно перемещают отрицательный заряд — в частности, электроны.Батареи отталкивают электроны от своих отрицательных выводов ( A ) через любую задействованную схему и притягивают их к своим положительным выводам ( B ), как показано на рисунке \ (\ PageIndex {1} \). Изменение потенциала равно \ (\ Delta V = V_B — V_A = +12 \, V \), а заряд q отрицательный, так что \ (\ Delta U = q \ Delta V \) отрицательный, что означает потенциальная энергия батареи уменьшилась, когда q переместился с A на B .

Рисунок \ (\ PageIndex {1} \): Аккумулятор перемещает отрицательный заряд от отрицательного вывода через фару к положительному выводу. Соответствующие комбинации химических веществ в батарее разделяют заряды, так что отрицательный вывод имеет избыток отрицательного заряда, который отталкивается им и притягивается к избыточному положительному заряду на другом выводе. С точки зрения потенциала положительный вывод имеет более высокое напряжение, чем отрицательный. Внутри батареи движутся как положительные, так и отрицательные заряды.

Пример \ (\ PageIndex {2} \): Сколько электронов проходит через фару каждую секунду?

Когда автомобильный аккумулятор 12,0 В питает одну фару мощностью 30,0 Вт, сколько электронов проходит через нее каждую секунду?

Стратегия

Чтобы узнать количество электронов, мы должны сначала найти заряд, который перемещается за 1,00 с.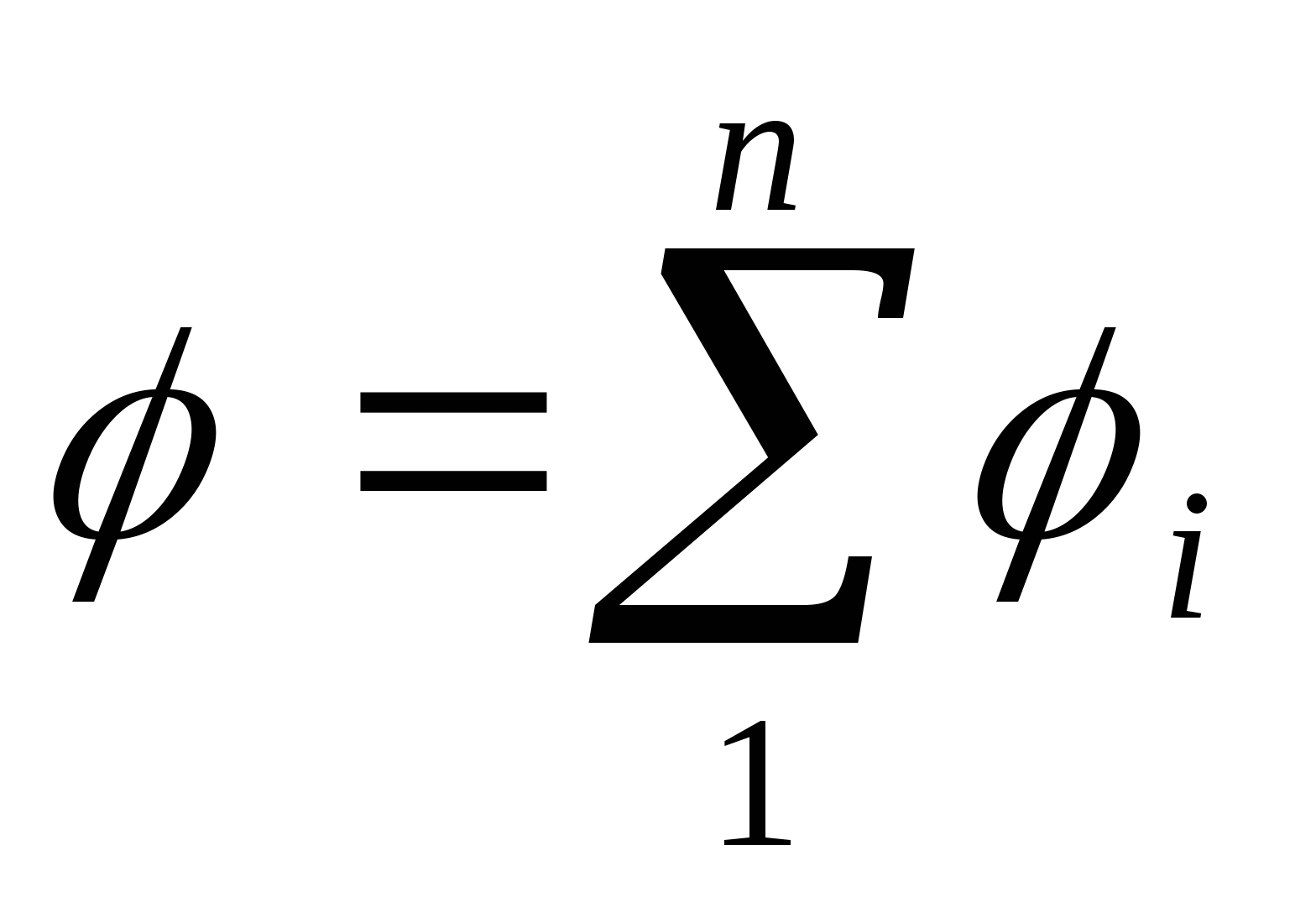 Перемещаемый заряд связан с напряжением и энергией через уравнения \ (\ Delta U = q \ Delta V \). Лампа мощностью 30,0 Вт потребляет 30,0 джоулей в секунду. Поскольку батарея теряет энергию, мы имеем \ (\ Delta U = — 30 \, J \) и, поскольку электроны переходят от отрицательного вывода к положительному, мы видим, что \ (\ Delta V = +12.0 \, V \).

Решение

Чтобы найти заряд q перемещенных, мы решаем уравнение \ (\ Delta U = q \ Delta V \):

\ [q = \ dfrac {\ Delta U} {\ Delta V}. \]

Вводя значения для \ (\ Delta U \) и \ (\ Delta V \), получаем

\ [q = \ dfrac {-30.0 \, J} {+ 12.0 \, V} = \ dfrac {-30.0 \, J} {+ 12.0 \, J / C} = -2,50 \, C. \]

Число электронов \ (n_e \) — это общий заряд, деленный на заряд одного электрона. То есть

\ [n_e = \ dfrac {-2.{19} \, электрон. \]

Значение

Это очень большое число. Неудивительно, что мы обычно не наблюдаем отдельных электронов, так много которых присутствует в обычных системах. Фактически, электричество использовалось в течение многих десятилетий, прежде чем было установлено, что движущиеся заряды во многих обстоятельствах были отрицательными. Положительный заряд, движущийся в направлении, противоположном отрицательному, часто производит идентичные эффекты; это затрудняет определение того, что движется или оба движутся.{19} \, электроны \)

Электрон-вольт

Энергия, приходящаяся на один электрон, очень мала в макроскопических ситуациях, подобных тому, что было в предыдущем примере — крошечная доля джоуля. Но в субмикроскопическом масштабе такая энергия, приходящаяся на частицу (электрон, протон или ион), может иметь большое значение. Например, даже крошечной доли джоуля может быть достаточно, чтобы эти частицы разрушили органические молекулы и повредили живые ткани. Частица может нанести ущерб при прямом столкновении или может создать вредные рентгеновские лучи, которые также могут нанести ущерб.Полезно иметь единицу энергии, относящуюся к субмикроскопическим эффектам.

На рисунке \ (\ PageIndex {2} \) показана ситуация, связанная с определением такой единицы энергии. Электрон ускоряется между двумя заряженными металлическими пластинами, как это могло бы быть в телевизионной лампе или осциллографе старой модели. Электрон приобретает кинетическую энергию, которая позже преобразуется в другую форму — например, в свет в телевизионной трубке. (Обратите внимание, что с точки зрения энергии, «спуск» для электрона означает «подъем» для положительного заряда.) Поскольку энергия связана с напряжением соотношением \ (\ Delta U = q \ Delta V \), мы можем рассматривать джоуль как кулон-вольт.

Рисунок \ (\ PageIndex {2} \): Типичная электронная пушка ускоряет электроны, используя разность потенциалов между двумя разделенными металлическими пластинами. По закону сохранения энергии кинетическая энергия должна равняться изменению потенциальной энергии, так что \ (KE = qV \). Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов 5000 В производит электроны с энергией 5000 эВ.{-19} \, J. \]

Электрону, ускоренному через разность потенциалов 1 В, придается энергия 1 эВ. Отсюда следует, что электрон, ускоренный до 50 В, приобретает 50 эВ. Разность потенциалов 100 000 В (100 кВ) дает электрону энергию 100 000 эВ (100 кэВ) и так далее. Точно так же ион с двойным положительным зарядом, ускоренный до 100 В, получает 200 эВ энергии. Эти простые соотношения между ускоряющим напряжением и зарядами частиц делают электрон-вольт простой и удобной единицей энергии в таких обстоятельствах.

Электрон-вольт обычно используется в субмикроскопических процессах — химическая валентная энергия, молекулярная и ядерная энергия связи входят в число величин, часто выражаемых в электрон-вольтах. Например, для разрушения некоторых органических молекул требуется около 5 эВ энергии. Если протон ускоряется из состояния покоя через разность потенциалов 30 кВ, он приобретает энергию 30 кэВ (30 000 эВ) и может разрушить до 6000 таких молекул \ ((30 000 \, эВ \,: \, 5 \, эВ \, на \, молекула = 6000 \, молекул) \). Энергия ядерного распада составляет порядка 1 МэВ (1000000 эВ) на событие и, таким образом, может нанести значительный биологический ущерб.

Сохранение энергии

Полная энергия системы сохраняется, если нет чистого добавления (или вычитания) из-за работы или теплопередачи. Для консервативных сил, таких как электростатическая сила, закон сохранения энергии утверждает, что механическая энергия постоянна.

Механическая энергия — это сумма кинетической энергии и потенциальной энергии системы; то есть \ (K + U = константа \).Потеря U для заряженной частицы становится увеличением ее K . Сохранение энергии выражается в форме уравнения как

\ [K + U = константа \] или \ [K_i + U_i = K_f + U_f \]

, где i и f обозначают начальные и конечные условия. Как мы уже много раз выясняли, учет энергии может дать нам понимание и облегчить решение проблем.

Пример \ (\ PageIndex {3} \): электрическая потенциальная энергия преобразована в кинетическую энергию

Вычислите конечную скорость свободного электрона, ускоренного из состояния покоя через разность потенциалов 100 В. 6 \, м / с. \]

Значение

Обратите внимание, что и заряд, и начальное напряжение отрицательны, как показано на рисунке \ (\ PageIndex {2} \). Из обсуждения электрического заряда и электрического поля мы знаем, что электростатические силы, действующие на мелкие частицы, обычно очень велики по сравнению с силой тяжести. Большая конечная скорость подтверждает, что гравитационная сила здесь действительно незначительна. Большая скорость также указывает на то, насколько легко ускорить электроны малым напряжением из-за их очень малой массы.В электронных пушках обычно используются напряжения, намного превышающие 100 В. Эти более высокие напряжения вызывают настолько большие скорости электронов, что следует принимать во внимание эффекты специальной теории относительности, которые будут обсуждаться в другом месте. Вот почему в этом примере мы рассматриваем низкое напряжение (точно).

Упражнение \ (\ PageIndex {3} \)

Как этот пример изменится с позитроном? Позитрон идентичен электрону, за исключением того, что заряд положительный. 2 } \ hat {r} \).2} dr = \ dfrac {kq} {r} — \ dfrac {kq} {\ infty} = \ dfrac {kq} {r}. \]

Этот результат,

\ [V_r = \ dfrac {kq} {r} \]

— это стандартная форма потенциала точечного заряда. Это будет подробнее рассмотрено в следующем разделе.

Чтобы изучить другой интересный частный случай, предположим, что однородное электрическое поле \ (\ vec {E} \) создается путем размещения разности потенциалов (или напряжения) \ (\ Delta V \) на двух параллельных металлических пластинах, обозначенных A и B (Рисунок \ (\ PageIndex {3} \)).Изучение этой ситуации покажет нам, какое напряжение необходимо для создания определенного электрического поля. Это также покажет более фундаментальную взаимосвязь между электрическим потенциалом и электрическим полем.

Рисунок \ (\ PageIndex {3} \): соотношение между V и E для параллельных проводящих пластин равно \ (E = V / d \). (Обратите внимание, что по величине \ (\ Delta V = V_ {AB} \). Для заряда, который перемещается от пластины A при более высоком потенциале к пластине B при более низком потенциале, необходимо включить знак минус следующим образом : \ (- \ Delta V = V_A — V_B = V_ {AB} \).)

С точки зрения физика, \ (\ Delta V \) или \ (\ vec {E} \) можно использовать для описания любого взаимодействия между зарядами. Однако \ (\ Delta V \) является скалярной величиной и не имеет направления, тогда как \ (\ vec {E} \) является векторной величиной, имеющей как величину, так и направление. (Обратите внимание, что величина электрического поля, скалярная величина, представлена ​​как E .) Связь между \ (\ Delta V \) и \ (\ vec {E} \) выявляется путем вычисления работы, выполняемой электрическая сила при перемещении заряда из точки A в точку B .Но, как отмечалось ранее, произвольное распределение зарядов требует расчетов. Поэтому мы рассматриваем однородное электрическое поле как интересный частный случай.

Работа, совершаемая электрическим полем на рисунке \ (\ PageIndex {3} \) по перемещению положительного заряда q от A , положительная пластина, более высокий потенциал, к B , отрицательная пластина, более низкий потенциал. , это

\ [W = — \ Delta U = — q \ Delta V. \]

Разница потенциалов между точками A и B составляет

\ [- \ Delta V = — (V_B — V_A) = V_A — V_B = V_ {AB}.\]

Если ввести это в выражение для работы, получится

\ [W = qV_ {AB}. \]

Работа равна \ (W = \ vec {F} \ cdot \ vec {d} = Fd \, cos \, \ theta \): здесь \ (cos \, \ theta = 1 \), поскольку путь параллелен поле. Таким образом, \ (W = Fd \). Поскольку \ (F = qE \), мы видим, что \ (W = qEd \).

Подстановка этого выражения для работы в предыдущее уравнение дает

\ [qEd = qV_ {AB}. \]

Заряд отменяется, поэтому мы получаем для напряжения между точками A и B .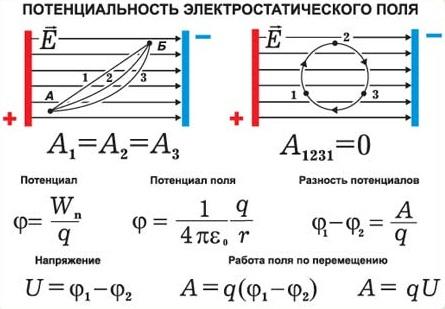

Только в однородном E-поле: \ [V_ {AB} = Ed \] \ [E = \ dfrac {V_ {AB}} {d} \], где d — это расстояние от A до B , или расстояние между пластинами на рисунке \ (\ PageIndex {3} \). Обратите внимание, что это уравнение подразумевает, что единицы измерения электрического поля — вольт на метр. Мы уже знаем, что единицы измерения электрического поля — ньютоны на кулон; таким образом, верно следующее соотношение между единицами:

\ [1 \, N / C = 1 \, В / м. \]

Кроме того, мы можем продолжить это до интегральной формы.B \ vec {E} \ cdot d \ vec {l}. \]

В качестве демонстрации из этого мы можем вычислить разность потенциалов между двумя точками ( A и B ), равноудаленными от точечного заряда q в начале координат, как показано на рисунке \ (\ PageIndex {4} \) .

Рисунок \ (\ PageIndex {4} \): Дуга для вычисления разности потенциалов между двумя точками, которые находятся на одинаковом расстоянии от точечного заряда в начале координат. 2} \ hat {r} \).6 В / м \). Выше этого значения поле создает достаточную ионизацию в воздухе, чтобы сделать воздух проводником. Это допускает разряд или искру, уменьшающие поле. Каково же максимальное напряжение между двумя параллельными проводящими пластинами, разделенными 2,5 см сухого воздуха?

Стратегия

Дано максимальное электрическое поле E между пластинами и расстояние между ними d . Мы можем использовать уравнение \ (V_ {AB} = Ed \) для вычисления максимального напряжения.4 \, V \] или \ [V_ {AB} = 75 \, кВ. \]

(Ответ состоит только из двух цифр, поскольку максимальная напряженность поля является приблизительной.)

Значение

Одно из следствий этого результата состоит в том, что требуется около 75 кВ, чтобы совершить скачок искры через зазор размером 2,5 см (1 дюйм), или 150 кВ для искры 5 см. Это ограничивает напряжения, которые могут существовать между проводниками, возможно, на линии электропередачи. Меньшее напряжение может вызвать искру, если на поверхности есть шипы, поскольку острые точки имеют большую напряженность поля, чем гладкие поверхности.Влажный воздух разрушается при более низкой напряженности поля, а это означает, что меньшее напряжение заставит искру проскочить через влажный воздух. Наибольшие напряжения могут создаваться статическим электричеством в засушливые дни (Рисунок \ (\ PageIndex {5} \)).

Рисунок \ (\ PageIndex {5} \): искровая камера используется для отслеживания траекторий частиц высоких энергий. Ионизация, создаваемая частицами, когда они проходят через газ между пластинами, позволяет искре прыгнуть. Искры расположены перпендикулярно пластинам, следуя силовым линиям электрического поля между ними.Разность потенциалов между соседними пластинами недостаточно высока, чтобы вызвать искры без ионизации, производимой частицами из экспериментов на ускорителях (или космическими лучами). Эта форма детектора сейчас устарела и больше не используется, кроме как в демонстрационных целях. (кредит b: модификация работы Джека Коллинза)

Пример \ (\ PageIndex {1B} \): Поле и сила внутри электронной пушки

Электронная пушка (рисунок \ (\ PageIndex {2} \)) имеет параллельные пластины, разделенные расстоянием 4,00 см, и дает 25 электронов.0 кэВ энергии. а) Какова напряженность электрического поля между пластинами? б) Какую силу это поле окажет на кусок пластика с зарядом \ (0,500- \ мкКл), который проходит между пластинами?

Стратегия

Так как напряжение и расстояние между пластинами указаны, напряженность электрического поля может быть вычислена непосредственно из выражения \ (E = \ frac {V_ {AB}} {d} \). Как только мы знаем напряженность электрического поля, мы можем найти силу, действующую на заряд, используя \ (\ vec {F} = q \ vec {E} \).Поскольку электрическое поле имеет только одно направление, мы можем записать это уравнение в терминах величин, \ (F = qE \).

Решение

а. Выражение для величины электрического поля между двумя однородными металлическими пластинами равно

.

\ [E = \ dfrac {V_ {AB}} {d}. \] Поскольку электрон является однозарядным и ему дается энергия 25,0 кэВ, разность потенциалов должна составлять 25,0 кВ. Вводя это значение для \ (V_ {AB} \) и расстояния между плитами 0,0400 м, получаем \ [E = \ frac {25.5 В / м) = 0,313 \, Н. \]

Значение Обратите внимание, что единицы измерения — ньютоны, поскольку \ (1 \, V / m = 1 \, N / C \). Поскольку электрическое поле между пластинами однородно, сила, действующая на заряд, одинакова независимо от того, где находится заряд между пластинами.

Пример \ (\ PageIndex {4C} \): расчет потенциала точечного заряда

Учитывая точечный заряд \ (q = + 2,0-n C \) в начале координат, вычислите разность потенциалов между точкой \ (P_1 \) на расстоянии \ (a = 4,0 \, см \) от q и \ (P_2 \) расстояние \ (b = 12.2} \ hat {r} \ cdot r \ hat {\ varphi} d \ varphi \), но \ (\ hat {r} \ cdot \ hat {\ varphi} = 0 \) и, следовательно, \ (\ Delta V = 0 \). Складывая две части вместе, получаем 300 В.

Значение

Мы продемонстрировали использование интегральной формы разности потенциалов для получения численного результата. Обратите внимание, что в этой конкретной системе мы могли бы также использовать формулу для потенциала, обусловленного точечным зарядом в двух точках, и просто взять разницу.

Упражнение \ (\ PageIndex {4} \)

Из примеров, как энергия удара молнии зависит от высоты облаков над землей? Считайте систему облако-земля двумя параллельными пластинами.

Ответ

При фиксированной максимальной напряженности электрического поля потенциал, при котором происходит удар, увеличивается с увеличением высоты над землей. Следовательно, каждый электрон будет переносить больше энергии. Определение того, есть ли влияние на общее количество электронов, предстоит определить в будущем.

Прежде чем описывать проблемы, связанные с электростатикой, мы предлагаем стратегию решения проблем, которой следует придерживаться для этой темы.

Стратегия решения проблем: электростатика

1. Изучите ситуацию, чтобы определить, присутствует ли статическое электричество; это может касаться отдельных стационарных зарядов, сил между ними и создаваемых ими электрических полей.
2. Определите интересующую систему. Это включает в себя указание количества, местоположения и типов связанных сборов.
3. Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен. Определите, следует ли учитывать кулоновскую силу напрямую — если да, может быть полезно нарисовать диаграмму свободного тела, используя силовые линии электрического поля.
4. Составьте список того, что дано или может быть выведено из проблемы, как указано (определить известные).Например, важно отличать кулоновскую силу F от электрического поля E .
5. Решите соответствующее уравнение для определяемой величины (неизвестное значение) или проведите линии поля, как требуется.
6. Изучите ответ, чтобы увидеть, разумен ли он: имеет ли он смысл? Правильные ли единицы и разумные ли числа?

Авторы и авторство

• Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами.Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

Определение разницы в электрическом потенциале между двумя точками — видео и стенограмма урока

Равномерное электрическое поле

В однородном электрическом поле уравнение для вычисления разности электрических потенциалов очень просто: В = Ed . В этом уравнении В, — это разность потенциалов в вольтах (или джоулях на кулон), E — напряженность электрического поля в данной области (в ньютонах на кулон), а d — расстояние между двумя пластинами ( в метрах).

Ситуация с параллельными пластинами, о которой я упоминал ранее, является примером однородного электрического поля. Между пластинами силовые линии расположены на равном расстоянии, поэтому поле везде одинаково — оно однородное. Если бы мы хотели вычислить разность потенциалов между пластинами, мы могли бы взять электрическое поле между пластинами, E , и просто умножить его на расстояние между пластинами. Строго говоря, это расстояние, d , всегда должно быть в направлении силовых линий (если вы двигаетесь влево и вправо по этой диаграмме, электрический потенциал вообще не меняется).

Прочность между параллельными пластинами одинакова.

Пример

Пришло время рассмотреть пример. Допустим, вы подключаете конденсатор с параллельными пластинами к батарее 12 В. Когда конденсатор полностью заряжен, между пластинами создается электрическое поле в 10 ньютонов на кулон. Какое должно быть расстояние между пластинами?

Прежде всего, мы должны записать то, что мы знаем. Мы знаем, что напряжение В, составляет 12 вольт.Мы знаем, что электрическое поле E составляет 10 ньютонов на кулон. И нас просят найти d , расстояние между пластинами. Мы знаем это, потому что если вы подключите аккумулятор 12 В к параллельным пластинам, это создаст разность потенциалов в 12 вольт между двумя пластинами.

Итак, все, что нам нужно сделать, это вставить наши числа, переставить их на d и решить. Когда мы это сделаем, мы получим 1,2 метра. Вот и все — вот наш ответ.

Краткое содержание урока

Электрический потенциал в определенной точке пространства — это работа, совершаемая при перемещении положительного заряда из бесконечности в эту точку.Электрический потенциал на бесконечности определяется как ноль. Электрический потенциал связан с электрической потенциальной энергией в том смысле, что электрический потенциал — это электрическая потенциальная энергия на единицу заряда.

В то время как электрическая потенциальная энергия зависит от конкретного заряда, электрический потенциал определяется только положением внутри поля. Разность электрических потенциалов — это разность электрических потенциалов между двумя точками в пространстве. Это действительно все. Он также измеряется в Джоулях на кулон, но обычно сокращается до другой единицы: вольт.

Давайте представим, что у нас есть две параллельные пластины: одна с положительным зарядом, а другая с отрицательным. В электромагнетизме мы используем положительный заряд для определения электрических полей. Если вы высвободите положительный заряд на отрицательной пластине, он никуда не денется, потому что противоположности притягиваются. Но если вы отпустите его на положительной пластине, он будет следовать за линиями поля и «упадет» на отрицательную пластину. Итак, когда мы говорим об электрических полях, мы можем сказать, что силовые линии направлены в сторону уменьшения электрического потенциала.

В однородном электрическом поле уравнение для вычисления разности электрических потенциалов очень просто: В = Ed . В этом уравнении В, — это разность потенциалов в вольтах, E — напряженность электрического поля (в ньютонах на кулон) и d — это расстояние между двумя точками (в метрах).

Результаты обучения

Завершив этот урок, вы должны уметь:

• Описывать электрический потенциал и разность электрических потенциалов
• Вычислить разность электрических потенциалов в однородном поле

3.2 Электрический потенциал и разность потенциалов — Введение в электричество, магнетизм и электрические цепи

ЦЕЛИ ОБУЧЕНИЯ

---

К концу этого раздела вы сможете:

• Определение электрического потенциала, напряжения и разности потенциалов
• Определите электрон-вольт
• Вычислить электрический потенциал и разность потенциалов на основе потенциальной энергии и электрического поля
• Опишите системы, в которых электрон-вольт является полезной единицей
• Применить энергосбережение в электрических системах

Напомним, что ранее мы определили электрическое поле как величину, не зависящую от тестового заряда в данной системе, что, тем не менее, позволяет нам вычислить силу, которая возникнет в результате произвольного тестового заряда.(При отсутствии другой информации предполагается, что пробный заряд положительный.) Мы кратко определили поле для гравитации, но гравитация всегда притягивает, тогда как электрическая сила может быть притягивающей или отталкивающей. Следовательно, хотя потенциальная энергия вполне достаточна в гравитационной системе, удобно определить величину, которая позволяет нам вычислить работу над зарядом независимо от величины заряда. Непосредственный расчет работы может быть затруднен, поскольку направление и величина могут быть сложными для нескольких зарядов, для объектов нечетной формы и вдоль произвольных путей.Но мы знаем это, потому что работа и, следовательно, пропорциональна испытательному заряду. Чтобы получить физическую величину, не зависящую от пробного заряда, мы определяем , электрический потенциал (или просто потенциал, поскольку понимается электрический) как потенциальную энергию на единицу заряда:

ЭЛЕКТРИЧЕСКИЙ ПОТЕНЦИАЛ

---

Потенциальная электрическая энергия на единицу заряда

(3.2.1)

Поскольку U пропорционально q, зависимость от q отменяется.Таким образом, не зависит от. Изменение потенциальной энергии имеет решающее значение, поэтому нас интересует разность потенциалов или разность потенциалов между двумя точками, где

РАЗНИЦА ЭЛЕКТРИЧЕСКИХ ПОТЕНЦИАЛОВ

---

Знакомый термин напряжение — это общее название разности электрических потенциалов. Имейте в виду, что всякий раз, когда указывается напряжение, под ним понимается разность потенциалов между двумя точками. Например, каждая батарея имеет две клеммы, и ее напряжение — это разность потенциалов между ними.По сути, точка, которую вы выбираете равным нулю вольт, произвольна. Это аналогично тому факту, что гравитационная потенциальная энергия имеет произвольный ноль, например, уровень моря или, возможно, пол лекционного зала. Стоит подчеркнуть различие между разностью потенциалов и электрической потенциальной энергией.

ПОТЕНЦИАЛЬНАЯ РАЗНИЦА И ПОТЕНЦИАЛЬНАЯ ЭЛЕКТРИЧЕСКАЯ ЭНЕРГИЯ

---

Связь между разностью потенциалов (или напряжением) и электрической потенциальной энергией определяется формулой

(3.2.2)

Напряжение — это не то же самое, что энергия. Напряжение — это энергия на единицу заряда. Таким образом, аккумулятор мотоцикла и автомобильный аккумулятор могут иметь одинаковое напряжение (точнее, одинаковую разность потенциалов между клеммами аккумулятора), но один хранит гораздо больше энергии, чем другой, потому что. Автомобильный аккумулятор может заряжаться больше, чем аккумулятор мотоцикла, хотя оба являются аккумуляторами.

ПРИМЕР 3.2.1

---

Расчет энергии

У вас есть аккумулятор для мотоцикла, который может заряжаться, и автомобильный аккумулятор, который может двигаться от заряда.Сколько энергии дает каждый? (Предположим, что числовое значение каждого заряда с точностью до трех значащих цифр.)

Стратегия

Сказать, что у нас есть аккумулятор, означает, что на его выводах есть разность потенциалов. Когда такая батарея перемещает заряд, она пропускает заряд через разность потенциалов, и заряд получает изменение потенциальной энергии, равное. Чтобы найти выход энергии, мы умножаем перемещенный заряд на разность потенциалов.

Решение

Для аккумуляторной батареи мотоцикла, и.Полная энергия, отдаваемая аккумулятором мотоцикла, составляет

Аналогично для автомобильного аккумулятора и

Значение

Напряжение и энергия связаны, но это не одно и то же. Напряжения батарей идентичны, но энергия, подаваемая каждой из них, совершенно разная. Автомобильный аккумулятор требует запуска гораздо более мощного двигателя, чем мотоцикл. Также обратите внимание, что когда аккумулятор разряжается, часть его энергии используется внутри, а напряжение на его клеммах падает, например, когда фары тускнеют из-за разряда автомобильного аккумулятора.Энергия, подаваемая батареей, по-прежнему рассчитывается, как в этом примере, но не вся энергия доступна для внешнего использования.

ПРОВЕРЬТЕ ПОНИМАНИЕ 3.4

Сколько энергии у батарейки AAA, которая может двигаться?

Обратите внимание, что энергии, вычисленные в предыдущем примере, являются абсолютными значениями. Изменение потенциальной энергии для аккумулятора отрицательное, так как он теряет энергию. Эти батареи, как и многие другие электрические системы, действительно перемещают отрицательный заряд — в частности, электроны.Батареи отталкивают электроны от своих отрицательных выводов () через любую задействованную схему и притягивают их к своим положительным выводам (), как показано на рисунке 3.2.1. Изменение потенциала равно отрицательному заряду, поэтому он отрицателен, что означает, что потенциальная энергия аккумулятора уменьшилась при переходе от к.

(рисунок 3.2.1)

Рисунок 3.2.1 Аккумулятор перемещает отрицательный заряд от отрицательной клеммы через фару к положительной клемме.Соответствующие комбинации химических веществ в батарее разделяют заряды, так что отрицательный вывод имеет избыток отрицательного заряда, который отталкивается им и притягивается к избыточному положительному заряду на другом выводе. С точки зрения потенциала положительный вывод имеет более высокое напряжение, чем отрицательный. Внутри батареи движутся как положительные, так и отрицательные заряды.

ПРОВЕРЬТЕ ПОНИМАНИЕ 3.5

---

Сколько электронов прошло бы через лампу?

Электрон-вольт

Энергия, приходящаяся на один электрон, очень мала в макроскопических ситуациях, подобных тому, что было в предыдущем примере — крошечная доля джоуля.Но в субмикроскопическом масштабе такая энергия, приходящаяся на частицу (электрон, протон или ион), может иметь большое значение. Например, даже крошечной доли джоуля может быть достаточно, чтобы эти частицы разрушили органические молекулы и повредили живые ткани. Частица может нанести ущерб при прямом столкновении или может создать вредные рентгеновские лучи, которые также могут нанести ущерб. Полезно иметь единицу энергии, относящуюся к субмикроскопическим эффектам.

На рис. 3.2.2 показана ситуация, связанная с определением такой единицы энергии.Электрон ускоряется между двумя заряженными металлическими пластинами, как это могло бы быть в телевизионной лампе или осциллографе старой модели. Электрон приобретает кинетическую энергию, которая позже преобразуется в другую форму — например, в свет в телевизионной трубке. (Обратите внимание, что с точки зрения энергии «спуск» электрона означает «подъем» для положительного заряда.) Поскольку энергия связана с напряжением соотношением, мы можем рассматривать джоуль как кулон-вольт.

(рисунок 3.2.2)

Рис. 3.2.2. Типичная электронная пушка ускоряет электроны, используя разность потенциалов между двумя отдельными металлическими пластинами.По закону сохранения энергии кинетическая энергия должна равняться изменению потенциальной энергии, поэтому. Энергия электрона в электрон-вольтах численно равна напряжению между пластинами. Например, разность потенциалов производит электроны. Концептуальная конструкция, а именно две параллельные пластины с отверстием в одной, показана на (a), а реальная электронная пушка показана на (b).

ЭЛЕКТРОН-ВОЛЬТ

---

В субмикроскопическом масштабе удобнее определить единицу энергии, называемую электрон-вольт (эВ), , которая представляет собой энергию, отдаваемую фундаментальному заряду, ускоренному через разность потенциалов.В форме уравнения:

Электрону, ускоренному через разность потенциалов, придается энергия. Отсюда следует, что электрон ускоряется за счет выигрыша. Разность потенциалов () дает электрону энергию () и так далее. Точно так же ион с двойным положительным зарядом ускоряется за счет увеличения энергии. Эти простые соотношения между ускоряющим напряжением и зарядами частиц делают электрон-вольт простой и удобной единицей энергии в таких обстоятельствах.

Электрон-вольт обычно используется в субмикроскопических процессах — химическая валентная энергия, молекулярная и ядерная энергия связи входят в число величин, часто выражаемых в электрон-вольтах. Например, для разрушения некоторых органических молекул требуется около энергии. Если протон ускоряется из состояния покоя за счет разности потенциалов, равной (), он приобретает энергию () и может разбить любое количество этих молекул (на молекулу молекул). Энергия ядерного распада составляет порядка () на событие и, таким образом, может нанести значительный биологический ущерб.

Сохранение энергии

Полная энергия системы сохраняется, если нет чистого добавления (или вычитания) из-за работы или теплопередачи. Для консервативных сил, таких как электростатическая сила, закон сохранения энергии утверждает, что механическая энергия постоянна.

Механическая энергия — это сумма кинетической энергии и потенциальной энергии системы; то есть, . Потеря для заряженной частицы становится увеличением ее. Сохранение энергии выражается в форме уравнения как

или

, где и обозначают начальные и конечные условия.Как мы уже много раз выясняли, учет энергии может дать нам понимание и облегчить решение проблем.

ПРИМЕР 3.2.3

---

Электрическая потенциальная энергия, преобразованная в кинетическую энергию

Вычислите конечную скорость свободного электрона, ускоряемого из состояния покоя через разность потенциалов. (Предположим, что это числовое значение имеет точность до трех значащих цифр.)

Стратегия

У нас есть система только с консервативными силами. Предполагая, что электрон ускоряется в вакууме, и пренебрегая гравитационной силой (мы проверим это предположение позже), вся электрическая потенциальная энергия преобразуется в кинетическую энергию.Мы можем идентифицировать начальную и конечную формы энергии как,,,.

Решение

Сохранение энергии утверждает, что

Вводя указанные выше формы, получаем

Мы решаем это для:

Ввод значений для, и дает

Значение

Обратите внимание, что и заряд, и начальное напряжение отрицательны, как показано на Рисунке 3.2.2.Из обсуждения электрического заряда и электрического поля мы знаем, что электростатические силы, действующие на мелкие частицы, обычно очень велики по сравнению с силой тяжести. Большая конечная скорость подтверждает, что гравитационная сила здесь действительно незначительна. Большая скорость также указывает на то, насколько легко ускорить электроны малым напряжением из-за их очень малой массы. В электронных пушках обычно используются напряжения намного выше, чем в этой задаче. Эти более высокие напряжения вызывают настолько большие скорости электронов, что необходимо учитывать эффекты специальной теории относительности, и поэтому они выходят за рамки этого учебника.Вот почему в этом примере мы рассматриваем низкое напряжение (точно).

ПРОВЕРЬТЕ ПОНИМАНИЕ 3.6

Как этот пример изменится с позитроном? Позитрон идентичен электрону, за исключением того, что заряд положительный.

Напряжение и электрическое поле

До сих пор мы исследовали взаимосвязь между напряжением и энергией. Теперь мы хотим изучить взаимосвязь между напряжением и электрическим полем. Начнем с общего случая неоднородного поля.Напомним, что наша общая формула для потенциальной энергии пробного заряда в точке относительно реперной точки равна

Когда мы подставляем в определение электрического поля (), это становится

Применяя наше определение потенциала () к этой потенциальной энергии, мы находим, что в общем случае

(3.2.3)

Из нашего предыдущего обсуждения потенциальной энергии заряда в электрическом поле результат не зависит от выбранного пути, и, следовательно, мы можем выбрать наиболее удобный интегральный путь.

Рассмотрим особый случай положительного точечного заряда в начале координат. Чтобы вычислить потенциал, вызванный на расстоянии от начала координат относительно точки отсчета на бесконечности (напомним, что мы сделали то же самое для потенциальной энергии), позвольте и, с помощью и. Когда мы вычисляем интеграл

для этой системы, у нас

, что упрощается до

Этот результат,

— это стандартная форма потенциала точечного заряда.Это будет подробнее рассмотрено в следующем разделе.

Чтобы изучить другой интересный частный случай, предположим, что однородное электрическое поле создается путем размещения разности потенциалов (или напряжения) на двух параллельных металлических пластинах, обозначенных и (рис. 3.2.3). Изучение этой ситуации покажет нам, какое напряжение необходимо для создания определенного электрического поля. Это также покажет более фундаментальную взаимосвязь между электрическим потенциалом и электрическим полем.

(рисунок 3.2.3)

С точки зрения физика, любой или может быть использован для описания любого взаимодействия между зарядами. Однако является скалярной величиной и не имеет направления, тогда как является векторной величиной, имеющей как величину, так и направление. (Обратите внимание, что величина электрического поля, скалярная величина, представлена ​​как.) Связь между и выявляется путем вычисления работы, совершаемой электрической силой при перемещении заряда от точки к точке. Но, как отмечалось ранее, произвольное распределение зарядов требует расчетов.Поэтому мы рассматриваем однородное электрическое поле как интересный частный случай.

Работа, совершаемая электрическим полем на рисунке 3.2.3 по перемещению положительного заряда от положительной пластины с более высоким потенциалом к ​​отрицательной пластине с более низким потенциалом, составляет

Разница потенциалов между точками и равна

Если ввести это в выражение для работы, получится

Работа есть; здесь, так как путь параллелен полю.Таким образом, . Так как мы это видим.

Подстановка этого выражения для работы в предыдущее уравнение дает

Заряд отменяется, поэтому получаем для напряжения между точками и

, где — расстояние от до или расстояние между пластинами на рисунке 3.2.3. Обратите внимание, что это уравнение подразумевает, что единицы измерения электрического поля — вольт на метр. Мы уже знаем, что единицы измерения электрического поля — ньютоны на кулон; таким образом, верно следующее соотношение между единицами:

Кроме того, мы можем продолжить это до интегральной формы.Подставляя уравнение 3.2.2 в наше определение разности потенциалов между точками и, мы получаем

, что упрощается до

В качестве демонстрации из этого мы можем вычислить разность потенциалов между двумя точками (и), равноудаленными от точечного заряда в начале координат, как показано на рисунке 3.2.4.

(рисунок 3.2.4)

Рисунок 3.2.4 Дуга для вычисления разности потенциалов между двумя точками, которые находятся на одинаковом расстоянии от точечного заряда в начале координат.

Для этого мы интегрируем по дуге окружности постоянного радиуса между и, что означает, что мы позволяем при использовании. Таким образом,

(3.2.4)

для этой системы становится

Однако, следовательно,

Этот результат, заключающийся в отсутствии разницы в потенциале вдоль постоянного радиуса от точечного заряда, пригодится при отображении потенциалов.

ПРИМЕР 3.2.6

---

Расчет потенциала точечного заряда

Учитывая точечный заряд в начале координат, вычислите разность потенциалов между точкой на расстоянии от и на расстоянии от, где две точки имеют угол между собой (рисунок 3.2.6).

(рисунок 3.2.6)

Рисунок 3.2.6 Найдите разность потенциалов между и.

Стратегия

Сделайте это в два этапа. Первый шаг — использовать и let и, с и. Затем выполните интеграл. Второй шаг — интегрировать по дуге постоянного радиуса, что означает, что мы позволяем с ограничениями, все еще используем. Затем сложите два результата вместе.

Решение

Для первой части, для этой системы становится, которая вычисляет

Для второго шага становится, но и поэтому.Сложив две части вместе, мы получим.

Значение

Мы продемонстрировали использование интегральной формы разности потенциалов для получения численного результата. Обратите внимание, что в этой конкретной системе мы могли бы также использовать формулу для потенциала, обусловленного точечным зарядом в двух точках, и просто взять разницу.

ПРОВЕРЬТЕ ПОНИМАНИЕ 3.7

Из примеров, как энергия удара молнии зависит от высоты облаков над землей? Считайте систему облако-земля двумя параллельными пластинами.

Прежде чем описывать проблемы, связанные с электростатикой, мы предлагаем стратегию решения проблем, которой следует придерживаться для этой темы.

---

Стратегия решения проблем: электростатика

1. Изучите ситуацию, чтобы определить, присутствует ли статическое электричество; это может касаться отдельных стационарных зарядов, сил между ними и создаваемых ими электрических полей.
2. Определите интересующую систему. Это включает в себя указание количества, местоположения и типов связанных сборов.
3. Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен. Определите, следует ли учитывать кулоновскую силу напрямую — если да, может быть полезно нарисовать диаграмму свободного тела, используя силовые линии электрического поля.
4. Составьте список того, что дано или может быть выведено из проблемы, как указано (определить известные). Например, важно отличать кулоновскую силу от электрического поля.
5. Решите соответствующее уравнение для определяемой величины (неизвестное значение) или проведите линии поля, как требуется.
6. Изучите ответ, чтобы увидеть, разумен ли он: имеет ли он смысл? Правильные ли единицы и разумные ли числа?

Кандела Цитаты

Лицензионный контент CC, особая атрибуция

• Загрузите бесплатно по адресу http://cnx.org/contents/[email protected]. Получено из : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution

Заряд, ток и разница потенциалов

Обозначения схем — вы встречали эти обозначения схем в GCSE Physics.

Обычный ток течет по цепи от положительной (+) стороны ячейки к отрицательной (-). Однако электронов движутся по цепи в противоположном направлении от отрицательной (-) стороны ячейки к положительной (+).

Заряд, ток и разность потенциалов

Заряд (Q) — заряд измеряется в кулонах (Кл).

• Один электрон несет заряд 1,6 x 10 ^-19 Кл.

Ток (I) — измеряется в амперах (А).

• Ток — это скорость потока заряда . Ток в 1 А означает, что 1 кулон заряда проходит через точку в цепи каждую секунду. (1 A = 1 C s ^-1 ) Ток в цепи измеряется с помощью амперметра, который включен последовательно с интересующим компонентом в цепи.

• I = ток в амперах, А
• DQ = заряд в кулонах, К
• Dt = время в секундах, с

Разность потенциалов (В) — измеряется в вольтах (В).

• Потенциальная разница — это работа, выполненная на единицу оплаты . Разность потенциалов 1 В означает, что на один кулон заряда выполняется 1 джоуль работы. (1 В = 1 Дж C ^-1 ) Разность потенциалов в цепи измеряется с помощью вольтметра, который устанавливается параллельно интересующему компоненту в цепи.

• В = разность потенциалов в вольтах, В
• Вт = выполненная работа или переданная энергия в джоулях, Дж
• Q = заряд в кулонах, Кл

Сопротивление (Вт) — это отношение разности потенциалов на компоненте к току, протекающему через него, измеряется в омах (Вт).

• R = сопротивление в Ом, Вт

• В = разность потенциалов в вольтах, В

• I = ток в амперах, А

Примеры;

Q1) Если все электроны несут заряд 1,6 x 10 ^-19 C, сколько электронов потребуется, чтобы получить общий заряд в один кулон?

Q2) Если ток 0.50 ампер протекает через цепь в течение 120 секунд. Сколько заряда будет передано в компонент в цепи?

Q3) Заряд в 4,0 кулонов был перемещен через разность потенциалов 24 вольт, сколько энергии было передано?

Q4) Разность потенциалов на компоненте составляет 12 вольт, а ток через него составляет 0,37 А. Каково сопротивление компонента?

Нахождение потенциальной разницы между двумя точками в цепях с примерами

Поиск потенциальной разницы между двумя точками в цепях

Разница потенциалов между двумя точками в цепи — это энергия, теряемая зарядом при передаче из одной точки в другую.Например, разность потенциалов между A и B находится по следующей формуле;

V _AB = V _B -V _A = ∑ε-∑i.R

Эта формула показывает потерю энергии при перемещении заряда из точки A в точку B.

Сначала мы должны найти направление тока, чтобы определить значения ε и ∑i.R . Если вы принимаете знак батарей, имеющих то же направление тока, что и «+», то вы должны брать противоположно подключенные батареи как «-».

Если направление тока и тока, проходящего через резистор, одинаковы, мы принимаем i.R как «+», если они направлены в противоположные стороны, то мы принимаем i.R как «-».

В схеме, представленной ниже, если направление тока показано, как показано ниже, то разность потенциалов между точками A-B и C-B равна;

V _AB = V _B -V _A = -ε ₂ — (+ i.R ₁ + i.R ₂ )

V _CB = V _B -V _C = -ε ₃ — (- i.R ₃ )

Пример: Найдите разность потенциалов между точками A и B в приведенной ниже схеме.

Ток в цепи соответствует току батареи.

Пример: найти мощность резистора R ₁ .

ε _экв = ε ₂ -ε ₁ = 34V-10V = 24V

Эквивалентное сопротивление цепи составляет;

Экзамены на электрический ток и решения

Электроэнергия и мощность <Предыдущая		Далее> Шпаргалка по электрическому току

.

No related posts.