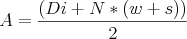Расчет спиральных катушек методом Максвелла
 Как плоская спиральная катушка, так и катушка намотанная тонкой фольгой в программе Coil64 рассчитываются с использованием метода бесконечно тонких круговых нитей Максвелла (далее модель Максвелла). На примере этих двух катушек можно подробнее рассмотреть особенности этого метода. Максвелл знаменит тем, что в своем трактате «Электричество и магнетизм» он теоретически предсказал существование электромагнитных волн и то, что свет тоже является электромагнитной волной. Но в этом же трактате он создал теоретическую базу для расчета индуктивностей, тот самый метод, о котором идет речь. Максвелл вывел формулу взаимоиндукции между двумя бесконечно тонкими замкнутыми соосными круговыми контурами с током:
Как плоская спиральная катушка, так и катушка намотанная тонкой фольгой в программе Coil64 рассчитываются с использованием метода бесконечно тонких круговых нитей Максвелла (далее модель Максвелла). На примере этих двух катушек можно подробнее рассмотреть особенности этого метода. Максвелл знаменит тем, что в своем трактате «Электричество и магнетизм» он теоретически предсказал существование электромагнитных волн и то, что свет тоже является электромагнитной волной. Но в этом же трактате он создал теоретическую базу для расчета индуктивностей, тот самый метод, о котором идет речь. Максвелл вывел формулу взаимоиндукции между двумя бесконечно тонкими замкнутыми соосными круговыми контурами с током:
- M — взаимоиндукция двух замкнутых контуров с одинаковым током;
- r1, r2 — радиусы двух бесконечно тонких круговых нитей с током;
- x — расстояние между центрами кругов, ограниченных этими нитями;
- K(k),E(k) — эллиптические интегралы, соответственно первого и второго рода, расчет которых численными методами не требует больших вычислительных ресурсов;
 При использовании этого метода любую круглую катушку можно представить как набор подобных нитей. Обе наши катушки при этом моделируются в виде набора концентрических колец из таких нитей (x = 0). Число этих колец равно числу витков катушки. Однако при таком преобразовании реального проводника с определенным поперечным сечением в бесконечно тонкую нить нам необходимо определить чему равно расстояние между этими виртуальными нитями. Какое расстояние брать если фигура поперечного сечения провода занимает определенную площадь? Максвелл показал, что это расстояние равно среднему геометрическому расстоянию (GMD — geometric mean distance) между всеми точками поперечного сечения двух проводников [3] и что в случае круглого провода, это расстояние просто равно расстоянию между центрами (осями) провода. Радиус этой нити также считается от оси намотки до оси реального провода. Таким образом преобразование реальной катушки в модель Максвелла в случае провода круглого поперечного сечения получается достаточно простым:
При использовании этого метода любую круглую катушку можно представить как набор подобных нитей. Обе наши катушки при этом моделируются в виде набора концентрических колец из таких нитей (x = 0). Число этих колец равно числу витков катушки. Однако при таком преобразовании реального проводника с определенным поперечным сечением в бесконечно тонкую нить нам необходимо определить чему равно расстояние между этими виртуальными нитями. Какое расстояние брать если фигура поперечного сечения провода занимает определенную площадь? Максвелл показал, что это расстояние равно среднему геометрическому расстоянию (GMD — geometric mean distance) между всеми точками поперечного сечения двух проводников [3] и что в случае круглого провода, это расстояние просто равно расстоянию между центрами (осями) провода. Радиус этой нити также считается от оси намотки до оси реального провода. Таким образом преобразование реальной катушки в модель Максвелла в случае провода круглого поперечного сечения получается достаточно простым:
А как же рассчитать собственную индуктивность отдельного одиночного витка? Максвелл показал, что эта индуктивность равна взаимоиндукции двух виртуальных нитей с одинаковым диаметром окружности, расположенных на определенном расстоянии. Это расстояние также зависит от формы фигуры поперечного сечения провода и было названо средним геометрическим расстоянием этой фигуры «самой от себя». Для круглого провода это расстояние равно:  Где rw — радиус поперечного сечения провода.Таким образом для расчета индуктивности плоской спиральной катушки Тесла методом Максвелла нам известны все аргументы формулы и их связь с реальными размерами катушки. Нам необходимо будет рассчитать собственную индуктивность каждого витка и взаимоиндукцию между каждой парой витков, а затем, поскольку все магнитные потоки суммируются, нам надо просуммировать все эти результаты. Попутно заметим, что так можно рассчитать индуктивность любой круглой катушки, например многослойной.
Где rw — радиус поперечного сечения провода.Таким образом для расчета индуктивности плоской спиральной катушки Тесла методом Максвелла нам известны все аргументы формулы и их связь с реальными размерами катушки. Нам необходимо будет рассчитать собственную индуктивность каждого витка и взаимоиндукцию между каждой парой витков, а затем, поскольку все магнитные потоки суммируются, нам надо просуммировать все эти результаты. Попутно заметим, что так можно рассчитать индуктивность любой круглой катушки, например многослойной.
 Если же поперечное сечение провода не круглое, то GMD уже не равно расстоянию «от центра до центра» провода. Причем оно зависит не только о формы сечения, но и от взаимного расположения таких проводников. Поэтому расчет индуктивности катушки, намотанной фольгой намного сложнее. Добавим еще одно упрощение и представим поперечное сечение фольги в виде бесконечно тонкой линии. В работе [2] было показано, что GMD между двумя такими параллельными линиями определяется следующим выражением:
Если же поперечное сечение провода не круглое, то GMD уже не равно расстоянию «от центра до центра» провода. Причем оно зависит не только о формы сечения, но и от взаимного расположения таких проводников. Поэтому расчет индуктивности катушки, намотанной фольгой намного сложнее. Добавим еще одно упрощение и представим поперечное сечение фольги в виде бесконечно тонкой линии. В работе [2] было показано, что GMD между двумя такими параллельными линиями определяется следующим выражением:
Таким образом расстояние между двумя виртуальными нитями (GMD) не равно расстоянию между центрами реальных витков фольги (g), а имеет сложную зависимость от этого расстояния и от ширины фольги. Более того, учитывая это обстоятельство нам необходимо скорректировать радиусы этих нитей. Они также не равны расстоянию от оси катушки до центра фольги. Для двух разных пар витков фольги преобразования в модель Максвелла не подобны друг другу, поэтому в алгоритме расчета мы вынуждены рассчитывать GMD и радиусы нитей отдельно для каждой такой пары. 
 При расчете собственной индуктивности отдельного витка в качестве радиусов виртуальных нитей мы берем расстояние от оси катушки до центра фольги и GMD бесконечно тонкой линии «самой от себя», которое вычисляется по следующей формуле:
При расчете собственной индуктивности отдельного витка в качестве радиусов виртуальных нитей мы берем расстояние от оси катушки до центра фольги и GMD бесконечно тонкой линии «самой от себя», которое вычисляется по следующей формуле:
В дальнейшем алгоритм расчета суммарной собственной индуктивности катушки намотанной фольгой не отличается от такового для спиральной катушки намотанной круглым проводом.
Особо следует отметить ограничения в расчетах. их несколько:
- Во первых само упрощение реальной геометрии до бесконечно тонких фигур уже вносит некую погрешность. Но она достаточно мала, иначе такое упрощение не имело бы смысла. Есть только два существенных ограничения по геометрии намотки. Во первых, диаметр намотки должен быть больше поперечных размеров провода. Для проволочных катушек это условие чаще всего соблюдается на практике. Трудно представить себе катушку с диаметром намотки сравнимым с диаметром провода. Что касается катушки намотанной фольгой, то ширина фольги может быть и больше диаметра намотки. Если диаметр намотки больше ширины фольги, ошибка расчета не превышает 10%. При более широкой фольге ошибка становится недопустимой. Поэтому данный метод пригоден только для предварительного расчета относительно»узких» катушек. Индуктивность рулона кухонной фольги этим методом рассчитать, к сожалению, не удастся и для расчета подобной катушки придется воспользоваться электромагнитными симуляторами. Например ANSYS MAXWELL 3D с решателем Magnitostatic. Второе ограничение — отношение ширины фольги к ее толщине должно быть не менее 100. В этом случае мы можем считать ее достаточно близкой к бесконечно тонкой линии, как в модели описанной выше.
- Второе ограничение состоит в том, что плотность тока в каждой точке поперечного сечения проводника считается одинаковой. Это справедливо только на постоянном токе. При переменном токе имеет место скин-эффект. Однако на относительно низких частотах погрешность вносимая этим эффектом достаточно мала.
- Третье ограничение состоит в том, что плотность тока по длине проводника также считается одинаковой. Другими словами в каждой замкнутой нити нашей модели течет одинаковый ток. Это также справедливо только на постоянном токе, а на относительно низких частотах отличия от постоянного тока несущественны и не принимаются во внимание.
В заключении обратим ваше внимание на то, что GMD между двумя проводами круглого сечения всегда будет равно расстоянию между их осями, независимо от их взаимного расположения. В случае фольги — это не так. Если два плоских проводника располагаются не друг над другом, а на одной линии, то GMD между ними будет определяться уже по другой формуле и алгоритм расчета снова меняется [1]. Для проводов с другим профилем поперечного сечения нам также заново придется рассчитывать аргументы для формулы Максвелла с учетом формы этого профиля и взаимного расположения проводов.
Ссылки по теме:
- Geometric Mean Distance — Its Derivation and Application in Inductance Calculations — Robert Weaver, Saskatoon, Canada;
- Formulas and Tables for the Calculation of Mutual and Self Induction. E B Rosa & F W Grover, revised 1916 3rd edition, 1948;
- On the Geometrical Mean Distance of two figures in a plane. J C Maxwell, Trans Roy. Soc. Edinburgh, Vol 26, 1872.
Coil32 — Тонкопленочная печатная катушка
Расчет катушек на печатной плате
 Плоские печатные катушки чаще всего применяют в диапазонах метровых и дециметровых волн для уменьшения габаритов устройства. Обычно их выполняют с круглой, квадратной формой витков или в форме меандра, хотя можно и в виде многоугольника. В последнее время с появлением технологии многослойных печатных плат, появились и многослойные катушки на печатной плате. Применение сердечника из магнитного материала малоэффективно, — так как такой сердечник удален от витков катушки и может менять ее индуктивность на 3 — 5 %, что в большинстве случаев недостаточно. Поэтому печатные катушки индуктивности применяются в большинстве случаев тогда, когда не требуется подстройка и величина индуктивности не превышает единиц микрогенри.
Плоские печатные катушки чаще всего применяют в диапазонах метровых и дециметровых волн для уменьшения габаритов устройства. Обычно их выполняют с круглой, квадратной формой витков или в форме меандра, хотя можно и в виде многоугольника. В последнее время с появлением технологии многослойных печатных плат, появились и многослойные катушки на печатной плате. Применение сердечника из магнитного материала малоэффективно, — так как такой сердечник удален от витков катушки и может менять ее индуктивность на 3 — 5 %, что в большинстве случаев недостаточно. Поэтому печатные катушки индуктивности применяются в большинстве случаев тогда, когда не требуется подстройка и величина индуктивности не превышает единиц микрогенри.
Добротность плоских печатных катушек обычно ниже добротности катушек, имеющих обмотку из провода и меньше, чем у цилиндрических катушек с металлизированными дорожками. У катушек на фольгированном стеклотекстолите добротность начинает заметно снижаться уже с частоты 100 Мгц. Собственная емкость печатных катушек индуктивности зависит от ширины спиральных витков, расстояния между ними и материала платы и может достигать 3 — 5 пф, что довольно значительно на таких частотах. Все вышесказанное говорит не в пользу плоских катушек, однако компактность конструкции наряду с применением SMD-компонентов часто играет решающую роль. В тоже время печатные катушки имеют лучшие показатели добротности и меньшую паразитную емкость по сравнению с SMD-катушками.
На нашем сайте можно воспользоваться онлайн калькулятором для расчета катушек на печатной плате
 В программе Coil32, начиная с версии 9.6, плоские печатные катушки с круглой и квадратной формой витков формой витков рассчитываются по общей эмпирической формуле:
В программе Coil32, начиная с версии 9.6, плоские печатные катушки с круглой и квадратной формой витков формой витков рассчитываются по общей эмпирической формуле:



,где
- L— индуктивность (мкГн)
- D — наружный диаметр спирали (мм)
- d — внутренний диаметр спирали (мм)
- N — число витков
- Davg — средний диаметр катушки (мм)
- φ — коэффициент заполнения
Коэффициенты c1 — c4 сведены в таблицу:
| Катушка | C1 | C2 | C3 | C4 |
|---|---|---|---|---|
| Квадратная | 1.27 | 2.07 | 0.18 | 0.13 |
| Круглая | 1.00 | 2.46 | 0.00 | 0.20 |
Шаг намотки на рисунке обозначен как «s«. При неизменном «s«, если увеличивать ширину витка — увеличивается добротность катушки и ее собственная емкость. Обычно для минимизации размеров катушки ширину печатного проводника делают близкой к расстоянию между проводниками, поэтому в формуле влияние «s» на величину индуктивности не учитывается. Оптимальное значение d/D = 0.4 для круглой катушки и его программа выбирает автоматически. Для квадратной катушки оптимальное значение d/D = 0.362 и его программа также выбирает автоматически.
Погрешность расчета индуктивности по этой формуле не превышает 8% при s не более 3w, т.е. если промежуток между полосками не более двойной ширины полоски.
Индуктивный элемент в виде прямого печатного проводника рассчитывается по следующей эмпирической формуле:

 , где:
, где:
- L — индуктивность (мкГн)
- l — длина проводника (мм)
- b — ширина проводника (мм)
Такие индуктивные элементы часто применяют в фильтрах ДМВ диапазона. Поскольку собственная емкость такого индуктивного элемента довольно велика, необходимо иметь в виду, что более корректно представлять его в виде отрезка длинной линии с распределенными параметрами. Однако для приблизительных расчетов принятое здесь упрощение модели вполне приемлемо.
Ссылки:
- Simple Accurate Expressions for Planar Spiral Inductances — Sunderarajan S. Mohan, Maria del Mar Hershenson, Stephen P. Boyd, and Thomas H. Lee, 1999
- Lumped Elements for RF and Microwave Circuits — Inder Bahl, ©2003 ARTECH HOUSE INC.
Назад…
Coil32 — Методы расчета индуктивности катушки.
Методы расчета индуктивностей
 Наиболее полно теоретические основы методов расчета индуктивностей изложены в справочной книге: «Расчет индуктивностей. П.Л.Калантаров Л.А.Цейтлин». Здесь же хотелось бы немного систематизировать подходы к расчету индуктивностей.
Наиболее полно теоретические основы методов расчета индуктивностей изложены в справочной книге: «Расчет индуктивностей. П.Л.Калантаров Л.А.Цейтлин». Здесь же хотелось бы немного систематизировать подходы к расчету индуктивностей.
Прежде всего отметим, что расчет индуктивности можно вести двумя способами:
∙ Численный метод с различной степенью упрощения задачи
∙ Расчет по упрощенным эмпирическим формулам
Эмпирический подход предполагает подбор (подгонку) относительно несложных аппроксимирующих формул по результатам измерений индуктивности реальных катушек. Расчет по упрощенным эмпирическим формулам имеет ограничения в точности и применим только к катушкам с определенной геометрией намотки. Большинство таких формул можно найти здесь. Несмотря на невысокую точность, такой расчет чаще всего вполне достаточен в радиолюбительской практике.
Численные методы основываются на реальных физических моделях катушек индуктивности и их, в свою очередь, можно разбить на две категории:
- Расчет в программах основанных на фундаментальных законах классической электродинамики, так называемых электромагнитных симуляторах. К ним можно отнести COMSOL Multiphysics, FEMM, ANSYS, GAL-ANA и т.п. Эти программы используют специальные численные методы, такие как метод моментов и метод конечных элементов. Расчет в таких программах довольно точен, позволяет учесть множество нюансов, рассчитать катушку произвольной формы, однако требует огромных ресурсов компьютера. Применяется при научном анализе или если катушка работает в режиме, когда ее нельзя представлять как сосредоточенный элемент [пример]
- Численные методы расчета, основанные на фундаментальных формулах физики, применимых к круговым проводникам, выведенных в XIX веке Д.К.Максвеллом. Позволяют провести расчет более точно, чем по эмпирическим формулам, но не требуют запредельных аппаратных ресурсов компьютера. На них следует остановится подробнее, т.к их и использует Coil32…
Расчет индуктивности в программе Coil32 основан на модели Максвелла, в которой катушка представляется как множество соосных бесконечно тонких круговых проводников.
Из Теоремы Гаусса следует, что силовые линии магнитного поля всегда замкнуты. Из этого следует, что магнитный поток порожденный круговым контуром с током весь проходит через поверхность, ограниченную этим контуром. Это обстоятельство отражено в следующей формуле:

Из этой формулы можно вывести определение для собственной индуктивности кругового проводника через двойной контурный интеграл Ф.Е.Неймана для взаимоиндукции [вывод здесь]:

Как показал Д.К.Максвелл, для двух бесконечно тонких круговых соосных проводников этот интеграл имеет однозначное решение, которое выглядит следующим образом:
 |
[1] |
, где:

- M — взаимоиндукция;
- r1, r2 — радиусы двух бесконечно тонких круговых проводников;
- x — расстояние между центрами кругов, ограниченных этими проводниками;
- K,E — эллиптические интегралы, соответственно первого и второго рода;
Численный метод расчета по формуле Максвелла сводится к численным методам решения эллиптических интегралов.
По формуле Максвелла можно рассчитывать как индуктивность многослойных и однослойных катушек, так и взаимную индуктивность двух отдельных катушек. Погрешности модели, связанные с допущением, что провод бесконечно тонкий и представляет собой набор круговых проводников (хотя на самом деле — это спираль), можно уменьшить с помощью соответствующих поправок.
Рассчитывая взаимоиндукцию проводника «самого на себя», т.е. его самоиндукцию (собственную индуктивность), Максвелл использует понятие — «среднее геометрическое расстояние» — GDM (g), для круглого провода:
g = e0.25*rw, где rw — радиус провода.
Очень важен следующий момент. Вся вышеприведенная логика рассуждений и вывода формул, начиная от формулы Неймана, справедлива в случае равномерного распределения плотности тока вдоль катушки. В подавляющем большинстве практических случаев так и есть. Однако если катушка работает вблизи частот собственного резонанса, начинает проявляться неравномерность распределения плотности тока по проводнику! Другими словами, начинает проявляться зависимость индуктивности от частоты, которая в наших расчетах не учитывается. Поэтому индуктивность катушки можно рассчитать корректно только на частотах не превышающих 60-70% от частоты ее собственного резонанса. Таким образом Coil32 не годится для точных расчетов, например, катушек Тесла или спиральных резонаторов. В этом случае и в случае если катушка работает в режиме выше частоты собственного резонанса — ее нужно представлять только в виде модели длинной линии и рассчитывать в программах-электромагнитных симуляторах, либо пользоваться специальными эмпирическими формулами.
Ссылки:
- An introduction to the art of Solenoid Inductance Calculation D W Knight 2013
- Numerical Methods for Inductance Calculation Robert Weaver 2012
- Inductance Calculation Techniques — Part II: Approximations and Handbook Methods Marc T. Thompson 1999
- A new method for inductance calculation M.A.Bueno A K T Assis 1995
Coil32 — О конструкции катушек индуктивности
Для начинающих радиолюбителей хотелось бы немного рассказать об особенностях конструктивного исполнения катушек индуктивности. Основой любой катушки служит каркас, на который наматывается провод в виде спирали. Обычно начинающий радиолюбитель повторяет конструкцию, в описании которой указано, что надо намотать N-витков на каркасе диаметром D. Но очень часто нужного каркаса в наличии нет, а есть другой. Тогда возникают следующие вопросы:
- Сколько витков нужно намотать на другом каркасе?
- Подойдет ли этот каркас и как изменятся характеристики устройства?
Программа Coil32 легко решает первый вопрос. Зная параметры контура, в который входит катушка, или ее конструктивные размеры и число витков из описания устройства, можно вычислить ее индуктивность, а зная индуктивность — рассчитать число витков для нового каркаса, т.е. пересчитать катушку индуктивности.
Во втором вопросе следует разобраться подробнее. Какими параметрами характеризуется катушка индуктивности?
- Прежде всего, это величина индуктивности
- Добротность катушки, характеризующая величину потерь в ней
- Паразитная собственная емкость катушки
- Температурная нестабильность индуктивности
Величина индуктивности обычно прямо пропорциональна диаметру катушки и квадрату числа витков.  Для уменьшения габаритов катушки и числа витков применяют магнитные сердечники – кольцевые, броневые. Разрез броневого сердечника показан на рисунке. Однако они имеют ограничения по частоте и по мощности. Например, в фильтрах для акустики их применение недопустимо, т. к. при большой мощности из-за особенностей магнитного материала, величина индуктивности будет зависеть от амплитуды сигнала и он, соответственно, сильно исказится. В выходных каскадах передатчиков и фильтрах акустики уменьшать габариты катушек нельзя, при этом возрастают потери, а вы же не хотите, что бы мощность усилителя шла на нагрев провода.
Для уменьшения габаритов катушки и числа витков применяют магнитные сердечники – кольцевые, броневые. Разрез броневого сердечника показан на рисунке. Однако они имеют ограничения по частоте и по мощности. Например, в фильтрах для акустики их применение недопустимо, т. к. при большой мощности из-за особенностей магнитного материала, величина индуктивности будет зависеть от амплитуды сигнала и он, соответственно, сильно исказится. В выходных каскадах передатчиков и фильтрах акустики уменьшать габариты катушек нельзя, при этом возрастают потери, а вы же не хотите, что бы мощность усилителя шла на нагрев провода.
Добротность важна для контурных катушек. Она обратно пропорциональна величине сопротивления потерь в ней. Напомню, что программа Coil32 позволяет провести приблизительный расчет добротности однослойных катушек. Однажды, я с удивлением обнаружил, что мой сайт «нагуглили» по запросу — «Единица измерения добротности катушки индуктивности».
Добротность измеряется в относительных единицах и не имеет специальной единицы измерения (типа Ом, Кг). Строго говоря, добротность — это отношение реактивного сопротивления катушки ( 2πƒL ) к ее сопротивлению потерь.
Часто в сети можно встретить online калькуляторы для расчета однослойных катушек, которые еще и вычисляют ее добротность. Однако, они учитывают только омические потери в катушке, что не совсем верно.
Потери складываются из потерь в проводах, диэлектрике, сердечнике и экране, а также потери на излучение.
Потери в проводах вызваны тремя причинами
- Во-первых, провода обмотки обладают омическим сопротивлением, поэтому катушку следует наматывать проводом с наименьшим удельным сопротивлением (медь, серебро)
- Во-вторых, сопротивление провода обмотки переменному току возрастает с ростом частоты, что обусловлено поверхностным эффектом, суть которого состоит в том, что ток протекает не по всему сечению проводника, а по наружной кольцевой части поперечного сечения.

- В третьих, в проводах обмотки, свитой в спираль, проявляется эффект близости, суть которого состоит в вытеснении тока к периферии провода, прилегающей к каркасу, в результате чего сечение, по которому протекает ток, принимает серповидный характер, что ведет к дополнительному возрастанию сопротивления провода. Уменьшить потери обусловленные эффектом близости можно применяя намотку с шагом. Существует оптимальный шаг намотки зависящий от геометрии катушки.
На частотах не превышающих 1,5..2 мегагерц, уменьшить потери в проводах можно применяя провод «литцендрат», состоящий из большего числа жилок, скрученных в жгут. При небольшом диаметре тонких жилок ослабляется поверхностный эффект, а скручивание жилок в жгут ослабляет эффект близости.
На очень высоких частотах проявляется влияние шероховатости провода, т.к. неровности на его поверхности увеличивают его длину для высокочастотного тока и соответственно сопротивление потерь.
Потери в диэлектрике обусловлены тем, что электромагнитная волна, проходя вдоль катушки, теряет энергию при взаимодействии с материалом каркаса.  Эти потери подобны потерям в конденсаторах или коаксиальных кабелях и зависят от качества материала каркаса (tgδ). Уменьшить эти потери можно применяя ребристые каркасы, в результате форма катушки становиться многоугольной, либо полным отказом от каркаса.
Эти потери подобны потерям в конденсаторах или коаксиальных кабелях и зависят от качества материала каркаса (tgδ). Уменьшить эти потери можно применяя ребристые каркасы, в результате форма катушки становиться многоугольной, либо полным отказом от каркаса.
Потери в сердечнике прямо пропорциональны частоте и мощности проходящей через катушку и зависят от материала сердечника. На высоких частотах, для уменьшения потерь применяют немагнитные латунные подстроечные сердечники, либо вовсе их не применяют. Проблеме учета потерь в ферритовых сердечниках посвящена отдельная статья.
Потери в экране обусловлены тем, что ток, протекающий по катушке, индуцирует ток в экране. Для их уменьшения экран должен дальше отстоять от катушки. Диаметр экрана должен превышать диаметр катушки не менее чем в 2,5 — 3 раза. Под влиянием экрана уменьшается индуктивность катушки. Степень этого уменьшения можно оценить с помощью плагина screen
Потери на излучение обусловлены излучением электромагнитного поля катушкой (антенный эффект). Они зависят от формы катушки и также влияют на ее добротность.
Для однослойной катушки — при увеличении ее размеров, сохраняя постоянными величину индуктивности и форму намотки, добротность примерно пропорциональна корню квадратному из диаметра катушки. Кроме того, добротность зависит от отношения длины намотки к ее диаметру и имеет тупой максимум при l/D ≈ 1. Для такой катушки оптимальный шаг намотки практически равен двум диаметрам провода (или другими словами расстояние между витками должно быть равно диаметру провода).
Для ориентировки можно посмотреть таблицу оптимизированных по добротности контурных катушек для радиолюбительских диапазонов.
Собственная емкость является паразитным параметром  катушки индуктивности, ограничивающим возможности ее применения прежде всего по частоте, т.к. эта емкость суммируется с емкостью контура. Кроме того, даже без внешней емкости, эта емкость совместно с индуктивностью катушки образует резонансный контур, резонансная частота которого называется собственной частотой резонанса катушки. Выше этой частоты применение катушки бессмысленно, т.к. она в этом случае уже имеет емкостное сопротивление. Ясно, что нужно по возможности уменьшать эту емкость. Наименьшей собственной емкостью обладают однослойные катушки индуктивности.
катушки индуктивности, ограничивающим возможности ее применения прежде всего по частоте, т.к. эта емкость суммируется с емкостью контура. Кроме того, даже без внешней емкости, эта емкость совместно с индуктивностью катушки образует резонансный контур, резонансная частота которого называется собственной частотой резонанса катушки. Выше этой частоты применение катушки бессмысленно, т.к. она в этом случае уже имеет емкостное сопротивление. Ясно, что нужно по возможности уменьшать эту емкость. Наименьшей собственной емкостью обладают однослойные катушки индуктивности.
У однослойных катушек собственная емкость пропорциональна диаметру катушки, а также зависит от отношения длины намотки к ее диаметру и имеет тупой минимум при l/D ≈ 1. Увеличение шага между витками уменьшает индуктивность такой катушки, при этом собственная емкость практически не меняется.
С физикой явления и методикой расчета собственной емкости однослойных катушек можно ознакомиться здесь.
 Собственная емкость многослойных катушек значительно больше, для ее уменьшения применяют намотку типа «универсаль», либо секционированную намотку. При секционной намотке емкости отдельных секций соединяются последовательно, что уменьшает суммарную емкость. Применение провода в шелковой изоляции также уменьшает эту емкость.
Собственная емкость многослойных катушек значительно больше, для ее уменьшения применяют намотку типа «универсаль», либо секционированную намотку. При секционной намотке емкости отдельных секций соединяются последовательно, что уменьшает суммарную емкость. Применение провода в шелковой изоляции также уменьшает эту емкость.
Каркасы катушек в зависимости от рабочего диапазона частот и назначения могут быть выполнены самыми различными способами и из различных материалов (бумаги, прессшпана, органического стекла, высокочастотной керамики и разнообразных высокочастотных материалов). Материал каркаса влияет на добротность катушки. В отношении электрических характеристик наилучшими, являются не требующие пропитки и влагостойкого покрытия полистироловые каркасы. Затем в порядке ухудшения диэлектрических качеств можно назвать следующие материалы для каркасов: высокочастотная керамика, ультрафарфор, бакелизированные трубки из кабельной бумаги.
Для катушек в задающих генераторах на первое место выходит параметр температурной нестабильности индуктивности и механическая прочность катушки. При этом желательно иметь хорошую добротность. Наивысшими качествами по этим параметрам обладают катушки на сплошном каркасе из высокочастотной керамики с обмоткой нанесенной методом выжигания серебра в каркас.
Плоские печатные катушки применяют на высоких частотах для уменьшения габаритов устройства. До частот 100-150 МГц можно применять фольгированный стеклотекстолит. Заземлять в таких катушках следует внешний вывод. Если печатная плата двусторонняя, то с обратной стороны напротив катушки не должно быть металлизации.
Подводя итоги, можно заметить, что конструкция катушки зависит от особенностей устройства в котором она работает. Однако можно сделать один главный вывод — уменьшение габаритов катушки всегда ведет к ухудшению параметров самой катушки и, соответственно, общих параметров устройства, в состав которого она входит. Например, миниатюризация катушек во входных каскадах приемника ухудшает его избирательность по зеркальному каналу.
Coil32 — О программе
- Информация о материале
- Просмотров: 2227
О программе
 Программа предназначена для расчета индуктивности катушек, на разных каркасах: одно и многослойных, на ферритовых кольцах, в броневом сердечнике, плоских катушек на печатной плате, а также колебательных контуров.
Программа предназначена для расчета индуктивности катушек, на разных каркасах: одно и многослойных, на ферритовых кольцах, в броневом сердечнике, плоских катушек на печатной плате, а также колебательных контуров.
Программа свободна для использования и распространения. Обо всех пожеланиях и замечаниях просьба сообщать разработчику по E-mail: Адрес электронной почты защищен от спам-ботов. Для просмотра адреса в вашем браузере должен быть включен Javascript.
Сайт программы: http://coil32.ru (старая версия сайта: http://coil32.narod.ru).
Когда у радиолюбителя, при конструировании какого-либо устройства, возникает вопрос о реализации катушки индуктивности, то это часто сопряжено с рядом проблем. Во первых, купить готовую катушку с нужными параметрами практически не возможно. Во вторых, даже если Вам и удалось найти готовую катушку, скорее всего по другим параметрам, например добротности, она вам не подойдет. В результате, в большинстве случаев, катушку приходится мотать вручную.
В этом случае очень поможет программа, которая может рассчитать такую катушку. Надеюсь, что Coil32 поможет Вам выполнить эту задачу. В программе учитываются наиболее распространенные варианты каркасов катушек. Можно рассчитать бескаркасною катушку в виде одиночного витка, на каркасах различной формы, на ферритовых кольцах и в броневых сердечниках, а также плоскую печатную катушку с круглой и квадратной формой витков. Для рассчитанной катушки можно рассчитать емкость конденсатора в колебательном контуре. Следует иметь ввиду, что расчетные формулы являются аппроксимирующими и расчет реальной катушки по ним ведется только с определенной степенью точности.
Системные требования:
- ОС — Windows XP Service Pack2 или старше (тестировалась в Windows 7 и 8)
- RAM — 512 Мб
- Разрешение монитора — 1024×768 или выше
Использовалась литература:
- Я.К. Трохименко Ф.Д. Любич «Радиотехнические расчеты на программируемых микрокалькуляторах» Москва «Радио и связь» 1988 г.
- В.П. Дьяконов «Справочник по расчетам на микрокалькуляторах» Москва «Наука» 1985 г.
- «Справочник радиолюбителя конструктора» Москва «Радио и связь» 1983 г.
- “Расчет и проектирование гибридных микросхем” Методическое пособие Воронежского государственного университета, составитель Ю.И.Дикарев Воронеж 2001 г.
- М.В. Немцов «Справочник по расчету параметров катушек индуктивности» Москва «Энергоатомиздат» 1989 г.
- Расчет индуктивностей (справочная книга). П.Л.Калантаров Л.А.Цейтлин 1986г.
- Ю.Ф. Скрипников «Колебательный контур» Москва «Энергия» 1970 г.
- «ПРОЕКТИРОВАНИЕ ПОЛОСКОВЫХ УСТРОЙСТВ СВЧ» Учебное пособие Ульяновского государственного университета. 2001 г.
- «Lumped Elements for RF and Microwave Circuits» Inder Bahl, 2003
- Formulas & tables for the calculation of mutual and self inductance Edward B. Rosa, Frederick W. Grover SPBS-169 USA 1948
- Расчет характеристик элементов цепей РЭА И.Я.Гликман 1976 г.
- Малогабаритн радиоаппаратура Справочник радиолюбителя Р.М.Терещук 1975 г.
Расчет многослойной катушки на печатной плате
 Многослойные катушки на печатной плате понадобятся тем конструкторам, которые хотят создать миниатюрное устройство с применением индуктивности достаточно высокой величины. Ведь однослойная катушка на печатной плате при индуктивности более 10 мкГн уже имеет относительно большие размеры. Решить эту проблему поможет изготовление многослойной печатной катушки. Такие катушки применяются в качестве различных датчиков, элементов радиочастотных фильтров и т.д. Однако следует не забывать, что они имеют относительно низкую добротность, что является естественной платой за минитюаризацию. Но это в сравнении с проволочными катушками. Если же сравнивать с SMD-катушками, многослойные печатные катушки имеют лучшие показатели добротности и меньшую собственную емкость.
Многослойные катушки на печатной плате понадобятся тем конструкторам, которые хотят создать миниатюрное устройство с применением индуктивности достаточно высокой величины. Ведь однослойная катушка на печатной плате при индуктивности более 10 мкГн уже имеет относительно большие размеры. Решить эту проблему поможет изготовление многослойной печатной катушки. Такие катушки применяются в качестве различных датчиков, элементов радиочастотных фильтров и т.д. Однако следует не забывать, что они имеют относительно низкую добротность, что является естественной платой за минитюаризацию. Но это в сравнении с проволочными катушками. Если же сравнивать с SMD-катушками, многослойные печатные катушки имеют лучшие показатели добротности и меньшую собственную емкость.
Расчет многослойной печатной катушки с квадратной формой витков реализован в плагине multi_PCB и основан на исследованиях Jonsenser Zhao – китайского инженера-конструктора. Плагин не входит в основной архив программы Coil32 и доступен для свободного скачивания из менеджера плагинов.
Суммарная индуктивность двух взаимосвязанных катушек определяется по формуле: где:
где:
- Ls — суммарная индуктивность;
- L1, L2 — собственные индуктивности первой и второй катушки;
- M — взаимная индуктивность;
Если катушки в каждом слое идентичны и включены синфазно, тогда формула приобретает следующий вид:
 где:
где:
- L0 — собственная индуктивность одной из катушек;
- Kc — коэффициент связи;
Суммарную индуктивность многослойной печатной катушки мы можем вычислить как сумму индуктивностей каждого слоя плюс взаимоиндукцию каждого слоя со всеми другими слоями. Мы уже применяли эту идею для проволочной многослойной катушки. Только там такой расчет велся для каждого отдельного витка, а в данном случае – для каждого отдельного слоя. Для многослойной печатной катушки с идентичными слоями формула расчета выглядит следующим образом: n — число слоев катушки;
n — число слоев катушки;
Как определить индуктивность одной из спиралей в каждом слое мы с вами знаем. Проблема состоит в определении величины коэффициента связи между отдельными слоями – Kс. Jonsenser Zhao решил эту проблему экспериментальным путем. Был изготовлен ряд многослойных печатных катушек с числом витков от 5-и до 20-и и расстоянием между соседними слоями от 0,75 до 2 мм. По результатам измерений была выведена эмпирическая формула для вычисления коэффициента связи между двумя слоями многослойной печатной катушки:

где:
- Kc — коэффициент связи;
- N — число витков в слое;
- X — расстояние между слоями в мм;
Исследования, в каких пределах формула дает приемлемую точность, не проводились. Однако можно быть уверенным, что для N=5..20 и X=0.75..2 мм — формула работает верно.
 Изготовление такой катушки своими руками не совсем безнадежная затея, как может показаться на первый взгляд. Конечно у нас с вами нет технологии Intel, но такую катушку достаточно несложно изготовить в виде «слоеного пирога» из тонкого одностороннего фольгированного текстолита с применением пустотелых пистонов. При изготовлении важно не перепутать фазировку слоев, в каждом слое витки должны «вращаться» в одну и ту же сторону по ходу движения тока.
Изготовление такой катушки своими руками не совсем безнадежная затея, как может показаться на первый взгляд. Конечно у нас с вами нет технологии Intel, но такую катушку достаточно несложно изготовить в виде «слоеного пирога» из тонкого одностороннего фольгированного текстолита с применением пустотелых пистонов. При изготовлении важно не перепутать фазировку слоев, в каждом слое витки должны «вращаться» в одну и ту же сторону по ходу движения тока.
Ссылки по теме:
- A new calculation for designing multilayer planar spiral inductors — © Jonsenser Zhao, 2010
- Making precision PCB coils by SV3ORA (original idea by SM0VPO)
Соглашение об измерениях и обозначениях
В разных программах (да и в разных версиях этой программы) используются разные способы измерений размеров катушки и разные буквенные обозначения размеров. Во избежании путаницы и ошибок по этому поводу на этой страничке подробно изложены нюансы по этом вопросу.
Прежде всего это касается однослойной катушки. Численные методы расчета индуктивностей основаны на предположении о бесконечно тонком проводе, которым намотана катушка. Реальная толщина провода учитывается в дальнейшем с помощью поправок, однако первоначальное допущение приводит к тому, что все размеры в оригинальных формулах расчета измеряются от центра до центра провода (см. рис1.) 
- D — диаметр намотки
- l — длина намотки
- p — шаг намотки
- d — диаметр провода
- di — диаметр провода в изоляции
В эмпирических формулах это правило сохраняется. Так сложилось исторически. В некоторых популярных программах, например MMANA-GAL, используется размер называемый — «между витками». Это расстояние от края до края провода, т.е. промежуток между витками, причем без учета толщины изоляции, т.е «по меди». В программе Coil32 используется понятие «шаг намотки», «p»-pitch (шаг спирали, резьбы), это расстояние от центра до центра провода соседних витков. Акцентирую на этом внимание, т.к. именно этот момент часто приводит к ошибкам.
Часто в статьях на этом сайте можно встретить понятие форм-фактор катушки. Это отношение длины к диаметру намотки — l/D. Катушки с большим отношением l/D носят название соленоид.
Для упрощения измерений, в программе Coil32 измеряются реальные размеры каркаса и номинальный диаметр провода (без изоляции!) и затем на основании этих измерений вычисляются необходимые размеры «от центра до центра», которые и используются в расчетах. Это касается как однослойной, так и многослойной катушек, а также других видов намотки. Если вы не знаете марку провода и его номинальный диаметр, то измерив диаметр провода с изоляцией, необходимо по справочнику подобрать ближайший номинальный, правда это не гарантирует от ошибок, т.к. у разных марок обмоточного провода толщина изоляции различна. Все размеры и обозначения понятны из рисунков в самой программе. В качестве примера для однослойной катушки смотрите рис2. 
- Dc — диаметр катушки
- lc — длина катушки
- p — шаг намотки
- d — номинальный диаметр провода
- di — диаметр провода в изоляции
- s — расстояние между соседними витками
Таким образом, если речь идет о размерах каркаса на который намотана катушка, мы будем употреблять понятия — диаметр катушки и длина катушки, если же речь идет о бескаркасной катушке, мы будем пользоваться понятиями — диаметр намотки и длина намотки, которые измеряются от центра до центра провода.
Стоит особо отметить, что поскольку толщина изоляции — параметр ненулевой, то даже при намотке «виток к витку», шаг намотки p всегда больше номинального диаметра провода d. Это учитывается в программе.
Подробнее о плоском спиральном воздухе
индукторы с сердечником Что такое индуктор с воздушным сердечником? И недостаток: |
Стили упаковки индуктора
Индукторы — это пассивные устройства, используемые в электронных схемах для накопления энергии в форме магнитного поля. Они представляют собой комплемент конденсаторов, которые накапливают энергию в форме электрического поля. идеальный индуктор является эквивалентом короткого замыкания (0 Ом) для постоянного тока (постоянного тока), и представляет противодействующую силу (реактивное сопротивление) к переменным токам (AC), которая зависит на частоте тока.Реактивное сопротивление (противодействие току) индуктора пропорциональна частоте тока, протекающего через него. Индукторы иногда упоминается как «катушки», потому что большинство индукторов физически построены из спиральных секций провода.
Свойство индуктивности, которое противодействует изменению тока, используется для цель предотвращения прохождения сигналов с более высокой частотой пропуская сигналы низкочастотных компонентов.Вот почему индукторы иногда упоминается как «дроссели», поскольку они эффективно подавляют более высокие частоты. Обычный применение дросселя в цепи смещения радиоусилителя, где коллектор транзистор должен быть снабжен постоянным напряжением, не позволяя радиочастотам (радиочастоте) сигнал от проведения обратно в источник постоянного тока.
При использовании в серия (левый рисунок) или параллельно (правый чертеж) со своей схемой комплимент, конденсатор, комбинация индуктор-конденсатор образует цепь, которая резонирует на определенной частоте, которая зависит от значений каждого компонента.В серии В цепи, полное сопротивление току на резонансной частоте равно нулю с идеальными компонентами. В параллельной цепи (справа) полное сопротивление для протекания тока бесконечно с идеальными компонентами.
Реальные индукторы из физических компонентов проявлять больше, чем просто чистая индуктивность, когда присутствует в цепи переменного тока. Общая схема модель симулятора показана слева. Он включает в себя актуальный идеальный индуктор с параллельным резистивный компонент, который реагирует на переменный ток.DC резистивный компонент последовательно с идеальным индуктором, и конденсатор подключен через весь сборка и представляет емкость, присутствующую из-за близости обмоток катушки. Симуляторы типа SPICE используют эту или даже более сложную модель, чтобы облегчить точные расчеты в широком диапазоне частот.
Связанные страницы по РФ Кафе
— Индукторы и
Расчеты индуктивности
Преобразование индуктивности
Стандартные значения индуктивности
—
Поставщики индукторов
HamWaves.ком на сайте есть очень сложный калькулятор для индуктивности катушки, который позволяет вам диаметр проводника.
Уравнения (формулы) для объединения индукторов последовательно и параллельно приведены ниже. Дополнительные уравнения приведены для индукторов различной конфигурации.
последовательно соединенных индукторов
Общая индуктивность последовательно соединенных индукторов равна сумме отдельных индуктивностей. Держите единицы постоянными.
Тороидальная рана
Прямоугольное сечение
Индуктивность коаксиального кабеля
Прямая проволока индуктивности
Эти уравнения применяются для когда длина проволоки намного больше диаметра проволоки (смотрите диаметр проволоки здесь). Руководство АРРЛ представляет уравнение для единиц дюймов и мкФ:
Для низких частот — до примерно ОВЧ, используйте эту формулу:
Выше ОВЧ-эффекта скин-эффект приводит к тому, что ¾ в верхнем уравнении приближается к единице (1), поэтому используйте это уравнение:
Прямой проводпараллельно плоскости заземления с заземлением на одном конце
ARRL Handbook представляет это уравнение для прямой проволоки, подвешенной над землей плоскость, один конец которой заземлен на плоскость:
a = радиус проволоки, l = длина провода параллельно плоскости заземления
h = высота провода над плоскостью заземления
к нижней части провода
Индуктивность параллельной линии
Многослойная воздушная индуктивность сердечника
Уилера Формула:
параллельно соединенных индукторов
Общая индуктивность параллельно соединенных индукторов равна обратной сумма обратных величин отдельных индуктивностей.Держите единицы постоянными.
Константы и переменные формулы индуктивности
Следующие физические константы и механические размерные переменные применяются к уравнениям на этой странице. Единицы для уравнений указаны в квадратных скобках в конце уравнений; например, означает, что длина в дюймах и индуктивность в Генри. Если единицы не указаны, то могут быть использованы любые до тех пор, пока они едины для всех сущностей; все метры, все мкГн и т. д.
C = Емкость
L = Индуктивность
N = Число витков
Вт = Энергия
ε r = Относительная диэлектрическая проницаемость (безразмерная)
ε 0 = 885 x 10 -12 Ф / м (диэлектрическая проницаемость свободного пространства)
µ r = Относительная проницаемость (безразмерная)
µ 0 = 4π
x 10 -7 H / m (проницаемость свободного пространства)
1 метр = 3,2808 фута <-> 1 фут = 0,3048 метра
1 мм =
0,03937 дюймов <-> 1 дюйм = 25,4 мм
Также точки (не путать с десятичными точками) используются для указания умножения во избежание двусмысленности.
Индуктивное сопротивление
Индуктивное сопротивление (X L , в Ω) пропорционально частоте (ω, в радианах / с или f в Гц) и индуктивности (L в Генри).Чистая индуктивность имеет фазу угол 90 ° (напряжение подводит ток с фазовым углом 90 °).
Энергия, Накапливаемая в Индукторе
Энергия (Вт, в Джоулях), накопленная в индукторе, составляет половину произведения индуктивности (L, у Генри) и ток (у меня, в амперах) через устройство.
Напряжение на Индукторе
Свойство индуктора противодействовать изменению потока тока вызывает встречную ЭДС (напряжение), чтобы сформировать на своих клеммах, противоположных по полярности к приложенному напряжению.
добротность индуктора
Коэффициент качества — это безразмерное отношение реактивного сопротивления к сопротивлению в индуктивности.
Однослойная индуктивность с круглой катушкой
Уилера Формула для D >> A:
В целом для a = радиус провода:
Примечание. Если длины проводов значительны, используйте расчет по прямому проводу, чтобы добавить, что индуктивность.
В поисках эквивалента «R Q »
С «Q» индуктора — отношение реактивного компонента к резистивному компоненту, эквивалентная схема может быть определена резистором параллельно с индуктором. это Уравнение действует только на одной частоте «f» и должно рассчитываться для каждой частоты представляет интерес.
,| Инфо
Это популярная геометрия катушек, используемая в современных беспроводных зарядных устройствах. Формула, используемая в этом расчете, основана на приближениях Гарольда А. Уилера для плоской спиральной катушки индуктивности с воздушным сердечником. 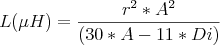 … где:
1 дюйм = 0,0254 м = 2,54 см = 25,4 мм. | Нажмите на изображение, чтобы увеличить  |
Подробнее о плоских спиральных катушках
Плоская спиральная катушка — это тип индуктора с воздушным сердечником
, обычно включаемого в первичную часть генератора Тесла, метки
RFID и бесконтактных детекторов. В той же категории
, что и плоские спиральные катушки, мы имеем плоские спиральные катушки,
плоские квадратные спиральные катушки, плоские прямоугольные спиральные катушки
, плоские шестиугольные спиральные катушки и восьмиугольную спиральную катушку
.Плоские катушки в основном используются в высокочастотных приложениях
и предназначены в качестве дорожек на печатной плате.
Плоская спиральная катушка относится к категории индукторов с воздушным сердечником
«Индуктор с воздушным сердечником» — это индуктор, который не зависит от ферромагнитного материала для достижения заданной индуктивности. Некоторые катушки индуктивности намотаны без катушки и только с воздухом в качестве сердечника. Некоторые другие намотаны на шпульку из бакелита, пластика, керамики и т. Д.
Преимущества катушки с воздушным сердечником:
На его индуктивность не влияет ток, который он несет.
Это контрастирует с ситуацией с катушками, использующими ферромагнитные сердечники, чья индуктивность имеет тенденцию достигать пика при умеренной напряженности поля, а затем падает до нуля при приближении насыщения. Иногда нелинейность в кривой намагничивания может быть допущена; например, при переключении источников питания и в некоторых топологиях переключения это является преимуществом.
В таких цепях, как фильтры с перекрестным звуком в акустических системах Hi-Fi, следует избегать искажений; тогда воздушная катушка — хороший выбор.Большинство радиопередатчиков используют воздушные катушки для предотвращения образования гармоник. Воздушные катушки
также свободны от «потерь в железе», которые связаны с ферромагнитными сердечниками. По мере увеличения частоты это преимущество становится все более важным. Вы получаете лучший добротность, большую эффективность, большую мощность и меньше искажений.
Наконец, воздушные катушки могут быть рассчитаны на работу на частотах до 1 ГГц. Большинство ферромагнитных сердечников, как правило, с потерями выше 100 МГц.
И «минус»:
Без сердечника с высокой проницаемостью для достижения заданного значения индуктивности у вас должно быть больше и / или больше витков.Чем больше витков, тем больше катушки, меньший саморезонанс во время более высокой емкости переплетения и более высокие потери в меди. На более высоких частотах вам обычно не нужна высокая индуктивность, так что тогда это не проблема.
Лучшее поле рассеяния и прием:
При использовании замкнутых магнитных дорожек, используемых в индукторах с сердечником, излучение гораздо менее серьезное. По мере увеличения диаметра в направлении длины волны (лямбда = c / f) потери из-за электромагнитного излучения станут значительными. Вы можете решить эту проблему, заключив катушку в экран или установив ее под прямым углом к другим катушкам, с которыми она может соединяться.
Возможно, вы используете катушку с воздушным сердечником не потому, что вам нужен элемент цепи с определенной индуктивностью как таковой, а потому, что ваша катушка используется в качестве датчика приближения, рамочной антенны, индукционного нагревателя, катушки Тесла, электромагнита, головки магнитометра или отклоняющего ярма. и т.д. Тогда внешнее излучаемое поле может быть тем, что вы хотите.
Пожалуйста, поделитесь этой страницей, если вы считаете ее полезной
Оцените эту статью: [рейтинги]
Coil32 — Как рассчитать индуктивность?
- Подробнее
- Хиты: 7329
Как рассчитать индуктивность? — 5,0 из 5 основанный на 2 отзыва
 Мы можем использовать различные методы для расчета индуктивности, используя численные методы или формулы справочника.Их условно можно разделить на три уровня — высокий, средний и низкий уровень.
Мы можем использовать различные методы для расчета индуктивности, используя численные методы или формулы справочника.Их условно можно разделить на три уровня — высокий, средний и низкий уровень.
Высокий уровень предполагает использование программ, имеющих общее название — электромагнитные тренажеры. Например, Comsol Multisystems с радиочастотным модулем, Ansys HFSS и т. Д. Их работа основана на дифференциальных уравнениях Максвелла для электромагнитного поля, обеспечивающего граничные условия. Преимущества
: точный расчет индуктивности и других параметров катушки с любой геометрией намотки в любом диапазоне частот.
Недостатки: эти программы довольно сложны и требуют предварительного обучения, требуют больших вычислительных ресурсов, расчет занимает много времени. Может использоваться для профессиональной работы, или если индуктор используется на частоте саморезонанса или выше.
Средний уровень основан на упрощенной модели индуктора, представленной J.C.Maxwell. Преимущества
: приемлемая точность расчетов для радиолюбителей, возможность использования в простых программах, низкие требования к вычислительной мощности компьютера.
Недостатки: менее точные расчеты, чем высокий уровень; расчет невозможен для любой геометрии обмотки и может быть только в диапазоне частот, который не превышает 60-70% собственной резонансной частоты (или, скорее, 1-резонанса) катушки.
Низкий уровень основан на простых формулах справочника. Эти формулы основаны на упрощении формул среднего уровня или на основе набора измерений реальных катушек.
Преимущества: простой расчет, нетребовательный к ресурсам компьютера
Недостатки: формулы работают только с ограниченной геометрией обмотки и на частотах, намного меньших частоты саморезонанса.
Подробнее о расчете среднего уровня, который использует Col32 … Великий физик Дж. К. Максвелл показал в конце XIX века в своей знаменитой работе — «Трактат об электричестве и магнетизме». что взаимная индуктивность между двумя бесконечно тонкими круглыми коаксиальными проводниками может быть рассчитана следующим образом: 
Где 

- М — взаимная индуктивность;
- r1, r2 — радиусы двух круговых нитей;
- x — расстояние между центрами окружностей, ограниченных этими нитями;
- K, E — эллиптические интегралы первого и второго рода;
Численный метод расчета формулы Максвелла сводится к численным методам решения эллиптических интегралов.
С помощью уравнения Максвелла можно рассчитать индуктивность однослойной, многослойной или плоской катушки и взаимную индуктивность двух отдельных катушек. Ошибки, связанные с приближением коаксиальных круговых нитей (фактически мы имеем дело с спиралью круглой проволоки), могут быть уменьшены за счет дополнительных исправлений.
,