Калькулятор магнитной индукции соленоида • Магнитостатика, магнетизм и электродинамика • Онлайн-конвертеры единиц измерения
Определения и формулы
Соленоид представляет собой намотанную виток к витку катушку, длина которой значительно больше ее диаметра. Если через катушку соленоида протекает электрический ток, в ней образуется однородное магнитное поле. Соленоиды с ферромагнитными сердечниками часто используются в качестве исполнительных механизмов для преобразования электрической энергии в линейное перемещение сердечника. Самым привычным примером такого соленоида является реле стартера, которое выполняет две функции: подает напряжение на двигатель стартера и вводит шестерню двигателя стартера в зацепление с маховиком коленвала двигателя на время запуска.
Модуль магнитной индукции B длинного соленоида в воздухе без сердечника рассчитывается по формуле
где μ₀=4π × 10⁻⁷ Гн/м — магнитная постоянная, N число витков катушки соленоида, I протекающий через катушку ток и L — длина соленоида.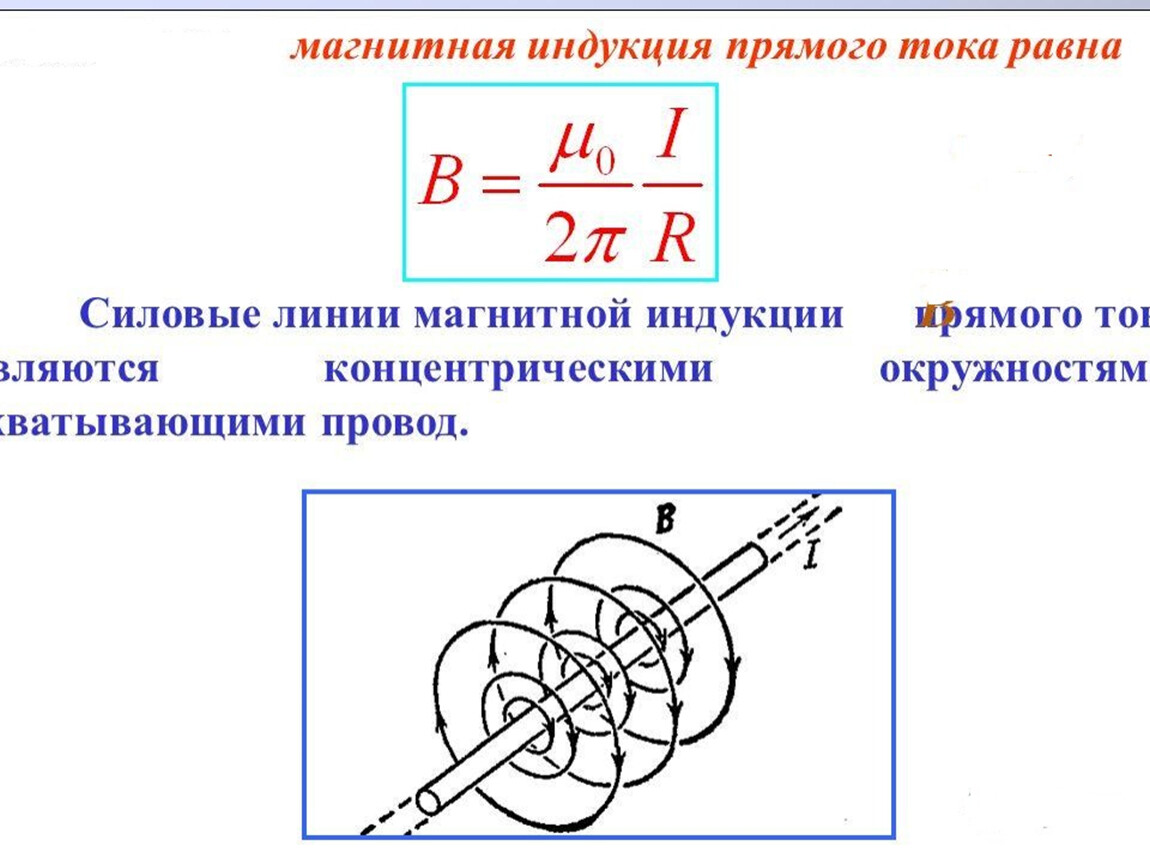
Соленоиды и ферромагнитные жидкости
Соленоидные исполнительные механизмы — довольно шумные устройства, поэтому иногда в зазор между сердечником и каркасом катушки вводят ферромагнитную жидкость. Она уменьшает или даже полностью устраняет шум при срабатывании соленоида, а также увеличивает силу притяжения, что позволяет уменьшить размеры соленоидных исполнительных устройств при сохранении их характеристик. Ферромагнитные жидкости также позволяют уменьшить утечку магнитного поля в магнитопроводе, а также улучшают охлаждение соленоида.
Еще одно применение ферромагнитных жидкостей в соленоидах — в качестве эластичного сердечника. Это позволяет изготовить эластичные соленоиды, которые можно использовать в современных гибких электронных устройствах, например, в носимых компьютерах и устройствах биомедицинского контроля.
Общие сведения
Синий и зеленый лазерные лучи хорошо видны через коллоидную смесь благодаря эффекту Тиндаля
В этой статье поговорим о занимательных и необычных ферромагнитных жидкостях. Если их намагнитить, воздействуя на них магнитным полем, то эти жидкости формируют интересные складки на поверхности. Ферромагнитные жидкости — это коллоидные системы, состоящие из наночастиц размером около 10 нм, распределенных во взвешенном состоянии в воде или в другой жидкости-носителе. Большая часть этих жидкостей-носителей — органические растворители, то есть такие жидкости, в которых можно растворить другое вещество. Коллоидные вещества — это жидкости, представляющие собой смеси жидкости-носителя и частиц другого вещества. Обычно эти частицы не опускаются на дно в виде осадка, и это делает коллоидное вещество довольно однородным. Это свойство особенно относится к ферромагнитным жидкостям. Вдобавок к естественным свойствам частиц оставаться взвешенными в ферромагнитной жидкости, эти частицы покрыты особым веществом, называемым
Если их намагнитить, воздействуя на них магнитным полем, то эти жидкости формируют интересные складки на поверхности. Ферромагнитные жидкости — это коллоидные системы, состоящие из наночастиц размером около 10 нм, распределенных во взвешенном состоянии в воде или в другой жидкости-носителе. Большая часть этих жидкостей-носителей — органические растворители, то есть такие жидкости, в которых можно растворить другое вещество. Коллоидные вещества — это жидкости, представляющие собой смеси жидкости-носителя и частиц другого вещества. Обычно эти частицы не опускаются на дно в виде осадка, и это делает коллоидное вещество довольно однородным. Это свойство особенно относится к ферромагнитным жидкостям. Вдобавок к естественным свойствам частиц оставаться взвешенными в ферромагнитной жидкости, эти частицы покрыты особым веществом, называемым
Пронаблюдать ван-дер-ваальсовы силы в действии можно, когда гекконы, ящерицы анолисы, сцинковые и некоторые насекомые перемещаются по вертикальным поверхностям стен, или даже по потолку
Зеленая ящерица анолис
Молекулы поверхностно-активного вещества присоединяются к наночастицам и окружают каждую частицу, создавая, таким образом, буфер вокруг частицы. Притяжение между наночастицами регулируется
Магнетит
В некоторых случаях поверхностно-активные вещества работают по-другому. Их молекулы присоединяются к наночастице так, что их наружная полярность одинакова по всей наружной поверхности (например, наружная оболочка приобретает положительный заряд). Таким образом, вокруг каждой наночастицы образуется оболочка с определенным зарядом.
Магнетит, как естественный магнит
Мы немного поговорили о жидкостях-носителях. Но из чего же состоят сами наночастицы? Иногда для этого используют частицы магнетита — минерала с магнитными свойствами. Магнетит — минерал, встречающийся в природе, который легко намагнитить. Стоит заметить, что в некоторых особых случаях магнетит имеет свойства постоянного магнита, то есть в обычных условиях его магнитные свойства постоянны и неизменны. Частицы магнетита в ферромагнитных жидкостях не являются постоянным магнитом, то есть их можно намагнитить с помощью магнитного поля, но это намагничивание пропадает, как только магнитное поле перестает на них действовать. Также для изготовления ферромагнитных жидкостей используют высокодисперсные порошки металлов, обладающих магнитными свойствами и некоторые ферримагнитные материалы.
Свойства
Ферромагнитные жидкости под действием магнитного поля — завораживающее зрелище. На поверхности образуются складки похожие на конусы, и при перемещении магнитного поля эти складки движутся за полем. Они располагаются по силовым линиям, и их высота зависит от силы магнитного поля. Сила магнитного поля, в свою очередь, зависит от того, как близко расположен магнит относительно жидкости. Ниже мы обсудим различные применения ферромагнитных жидкостей. Все эти применения основываются на этом свойстве ферромагнитной жидкости двигаться за магнитным полем.
На поверхности образуются складки похожие на конусы, и при перемещении магнитного поля эти складки движутся за полем. Они располагаются по силовым линиям, и их высота зависит от силы магнитного поля. Сила магнитного поля, в свою очередь, зависит от того, как близко расположен магнит относительно жидкости. Ниже мы обсудим различные применения ферромагнитных жидкостей. Все эти применения основываются на этом свойстве ферромагнитной жидкости двигаться за магнитным полем.
Разобранный гидродинамический подшипник накопителя на жестких магнитных дисках
Свойства ферромагнитных жидкостей изменяются с температурой. При очень высоких температурах, известных как температура или точка Кюри, наночастицы теряют магнитные свойства и ферромагнитная жидкость превращается в обычную жидкость. Также, со временем поверхностно-активное вещество теряет отталкивающие свойства, и наночастицы слипаются, так что при этом свойства ферромагнитной жидкости пропадают.
Использование ферромагнитных жидкостей
Ферромагнитные жидкости реагируют на магнит и следуют за ним, поэтому с помощью магнита их можно либо перемещать с места на место, либо удерживать в нужном месте.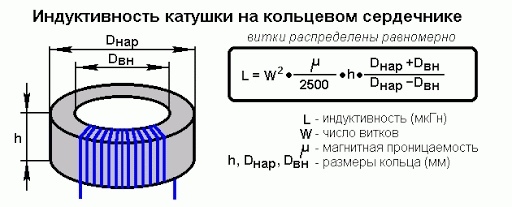 Благодаря этому они нашли широкое применение в науке, технике и медицине.
Благодаря этому они нашли широкое применение в науке, технике и медицине.
Как смазочные вещества
Ферромагнитные жидкости используют как смазки во вращающихся механизмах. Как и традиционные смазки, они помогают уменьшить трение между механическими деталями, но при этом их главное преимущество в том, что с помощью магнита или магнитного поля ферромагнитные жидкости легко удерживать в нужном положении.
Ферромагнитная жидкость под действием сильного магнита
В герметизирующих уплотнениях
В некоторых случаях герметизирующие уплотнения могут быть в виде жидкости — в этой ситуации очень удобно использовать именно ферромагнитные жидкости. Их используют, к примеру, чтобы герметизировать внутреннюю часть накопителя на жестком магнитном диске, в которой находятся электропривод шпинделя, сами жесткие диски и сервопривод блока головок. Магниты удерживают ферромагнитную жидкость в нужном месте, а она, в свою очередь, не пропускает пыль извне в гермозону жесткого диска, и помогает предотвратить повреждение дисков. Некоторые производители ферромагнитных жидкостей продают для этих целей саму жидкость, а некоторые разрабатывают и выпускают полный комплект магнитожидкостных уплотнений, и не продают саму жидкость отдельно, чтобы предотвратить ее неправильное использование.
Некоторые производители ферромагнитных жидкостей продают для этих целей саму жидкость, а некоторые разрабатывают и выпускают полный комплект магнитожидкостных уплотнений, и не продают саму жидкость отдельно, чтобы предотвратить ее неправильное использование.
В искусстве
Некоторые скульпторы и художники используют ферромагнитную жидкость для создания современных произведений искусства. Кроме объемных и подвижных скульптур, которые демонстрируют во всей красе игру складок ферромагнитной жидкости под действием магнита, художники создают также плоские картины из этой жидкости. Ферромагнитные жидкости не смешиваются с водой и красками на водной основе, поэтому такие краски и пигменты (например, люминесцентные) добавляют в ферромагнитную жидкость, а потом двигают ее магнитом для создания красочных форм. На сайте YouTube много интересных примеров картин и скульптур из ферромагнитной жидкости.
Ферромагнитная жидкость под действием сильного магнита
В системах звуковоспроизведения
В электродинамических громкоговорителях систем звуковоспроизведения ферромагнитную жидкость используют для охлаждения звуковой катушки. Из-за низкой энергетической эффективности звуковоспроизводящих систем, во время их работы большая часть электрической энергии преобразуется в тепловую, и это тепло может привести к выводу из строя звуковой катушки, если ее не охладить. Ферромагнитные жидкости отводят это тепло от звуковой катушки, а в зазоре их удерживает магнит, так же как и в других системах, описанных выше.
Из-за низкой энергетической эффективности звуковоспроизводящих систем, во время их работы большая часть электрической энергии преобразуется в тепловую, и это тепло может привести к выводу из строя звуковой катушки, если ее не охладить. Ферромагнитные жидкости отводят это тепло от звуковой катушки, а в зазоре их удерживает магнит, так же как и в других системах, описанных выше.
Ферромагнитные жидкости используют, также, для демпфирования диффузора с катушкой на резонансных частотах. Это сглаживает амплитудно-частотную характеристику динамика. Для этого ферромагнитные жидкости помещают в зазор между звуковой катушкой и магнитом.
При выборе ферромагнитной жидкости руководствуются знаниями о том, в какой среде ее будут использовать. Так, например, выбирая жидкость-носитель или при выборе вязкости ферромагнитной жидкости, учитывают такие факторы как влажность окружающей среды, в которой эта жидкость будет использоваться, или будет ли устройство, в котором используется ферромагнитная жидкость, соприкасаться с водой.
В медицине
В медицине у ферромагнитных жидкостей несколько применений. На данный момент ученые проводят исследования по использованию ферромагнитных жидкостей как носителей лекарств и других необходимых больным препаратов. С помощью магнита эти лекарственные препараты перемещают в определенный участок организма. Обычно в этом случае наночастицы покрывают слоем препарата, после чего ферромагнитную жидкость вводят в организм (чаще всего путем инъекции) и удерживают на месте с помощью магнита, пока препарат не окажет нужное действие. Существует ряд других методов локализированного введения лечебных препаратов, но ученные надеются, что этот метод обеспечит наибольшую точность.
Еще одно интересное применение ферромагнитных жидкостей в медицине — теплотерапия определенных участков тела. Чаще всего она используется для уничтожения раковых клеток. Для этого ферромагнитную жидкость вводят в организм, а после этого заставляют ферромагнитные частицы колебаться с высокой частотой, используя электромагниты. При этом выделяется большое количество тепла, и высокие температуры разрушают ткани на этом участке, убивая раковые клетки.
При этом выделяется большое количество тепла, и высокие температуры разрушают ткани на этом участке, убивая раковые клетки.
В диагностике магнитных носителей
Ферромагнитные жидкости используют для определения структуры магнитных доменов различных магнитных носителей, таких как накопители на магнитной ленте, жесткие диски и кредитные карты. Также с их помощью проверяют дефекты на поверхности материалов, не имеющих отношения к магнитным носителям, например сварочных швов, а также природных минералов и металлов. Это применяется, например, в производстве миниатюрных компонентов. Для этого поверхность материала покрывают ферромагнитной жидкостью, и она распределяется по этой поверхности в соответствии с магнитным полем материала. После того, как жидкость-носитель испарилась, на поверхности остаются ферромагнитные частицы, по которым и определяют структуру магнитного поля поверхности. Обычно для этого нужен микроскоп. Этот метод используют не только для проверки поверхности магнитных носителей и материалов, описанных выше, но и в судебно-медицинской экспертизе. Например, с помощью ферромагнитной жидкости можно определить удаленные в домашних условиях заводские номера на огнестрельном оружии.
Например, с помощью ферромагнитной жидкости можно определить удаленные в домашних условиях заводские номера на огнестрельном оружии.
В теплообменниках
Перегрев — широко распространенная проблема в радиоэлектронике. Чтобы избежать поломки, электронные приборы необходимо охлаждать. Ферромагнитные жидкости иногда используют в этих целях, например в громкоговорителях и некоторых микроэлектронных приборах. В начале этой статьи, когда мы обсуждали свойства ферромагнитных жидкостей, мы уже упоминали, что при высоких температурах (температурах Кюри) ферромагнитные жидкости теряют магнитные свойства. Эту особенность ферромагнитных жидкостей используют в системах охлаждения. Во время охлаждения ферромагнитная жидкость, удерживаемая возле детали, которую охлаждают, теряет свои магнитные свойства после того, как в ней достигнута температуры Кюри. Магнит перестает ее удерживать и ее замещает холодная ферромагнитная жидкость, у которой еще есть магнитные свойства. Новая жидкость нагревается, а нагретая — охлаждается, и процесс периодически повторяется.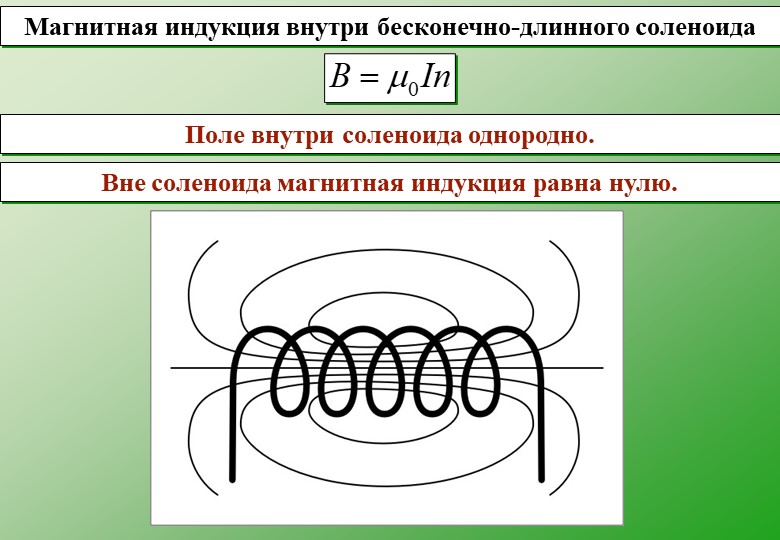 В этом случае магнит выступает в роли насоса, так как он помогает замещать менее намагниченную горячую жидкость более намагниченной холодной.
В этом случае магнит выступает в роли насоса, так как он помогает замещать менее намагниченную горячую жидкость более намагниченной холодной.
В заключение
В этой статье мы поговорили о том, что собой представляют ферромагнитные жидкости и о том, как их использовать. На них очень интересно смотреть, когда они под воздействием магнита, и мы очень советуем вам посмотреть примеры видео ферромагнитных жидкостей в интернете, например на сайте YouTube.
Автор статьи: Kateryna Yuri
Электромагнитный расчет и оптимизация планарных катушек на печатных платах
Планарные катушки используются в самых различных устройствах — от датчиков артериального давления до платежных карт. Они располагаются на печатных платах и хорошо подходят для создания взаимных индуктивных связей, особенно при ограниченном пространстве. При проектировании таких катушек важно точно рассчитать как индуктивность, так и активное сопротивление, так как эти факторы играют ключевую роль в производительности устройства.
Планарные катушки: преимущества и примеры использования
Планарные катушки названы так из-за того, что все их части (витки) находятся практически на одной плоскости (т. е. они почти плоские). Они занимают намного меньше места, чем другие индукторы, и поэтому подходят для любых практических приложений с ограничениями по размерам, что очень актуально, к примеру, в микроэлектромеханических системах (МЭМС) или в имплантированных медицинских устройствах, например, сердечных насосах. Такие катушки могут изготавливаться как на жестких, так и на упругих подложках, и следовательно могут быть интегрированы как на классические печатные платы, так и на элементы для т.н. гибкой электроники. Планарные катушки также могут изготавливаться серийно, что является экономически выгодным.
Благодаря этим качествам, планарные катушки находят применение в различных областях, в основном, в высокочастотных приложениях. Некоторые примеры использования:
Некоторые примеры использования:
- Дистанционный мониторинг состояния здоровья (например, датчики кровяного давления)
- Беспроводная передача энергии (например, носимые/имплантируемые медицинские устройства)
- Радиочастотная идентификация (например, платежные карты)
- Индукционный нагрев (например, индукционные варочные панели)
Планарные катушки могут использоваться на печатных платах в портативных устройствах типа фитнес-трекеров.
В контексте разработки и проектирования планарных катушек наиболее важные характеристики — это индуктивность и сопротивление. Последнее определенно должно быть очень низким (в идеальном случае нулевым), так как любое сопротивление уменьшает эффективность катушки. Индуктивность, напротив, для эффективной связи с другими системами должна быть высокой. Определение сопротивления и индуктивности может являться достаточно сложной задачей, так как необходимо учитывать материал катушки, количество витков, связь между электрическими и магнитными полями.
Инженеры могут получить данные о сопротивлении и индуктивности планарных катушек на печатных платах численно, используя возможности модуля AC/DC для электромагнитных расчетов, являющегося расширением пакета COMSOL Multiphysics. Это модуль содержит в числе прочих физический интерфейс Electric Currents, Layered Shell (Электрические токи в многослойных оболочках), который позволяет эффективно описывать и моделировать в т.ч. конструкции плоских катушек. В качестве примера давайте рассмотрим простую модель планарной катушки.
Представление планарной катушки как многослойной оболочки с помощью модуля AC/DC
Модель представляет собой медную катушку, размещенную на печатной плате. Катушка содержит три витка, два межслойных соединения (перемычки), два контакта-терминала, один из которых служит источником тока, а второй заземлён. Ток с терминала начинает течь по верхнему слою. Затем он переходит по соединительной перемычке (via) на нижний слой, далее – по нему под витками, обратно на верхний слой по второй перемычке (via), и, наконец, проходит по всем виткам к контакту заземления.
Геометрия планарной катушки, цветом на изображении показано распределение электрического потенциала.
Так как медная катушка является очень тонкой (толщина 0.1 мм, длина и ширина 0.5 мм), её предпочтительней моделировать в качестве граничного, а не объёмного компонента. Для того, чтобы описать топологию катушки в плоскости можно воспользоваться функционалом физического интерфейса Electric Currents, Layered Shell, который доступен с версии 5.4 программного обеспечения COMSOL®. К тому же, данный интерфейс можно использовать совместно с физическим интерфейсом
- В рамках физического интерфейса Electric Currents, Layered Shell проводится расчёт как сосредоточенного сопротивления, так и поверхностной плотности тока в области катушки.
 Собственно данный интерфейс и предназначен для решения закона сохранения тока, протекающего по двумерному слою.
Собственно данный интерфейс и предназначен для решения закона сохранения тока, протекающего по двумерному слою.
Не смотря на то, что конкретно этот пример довольно простой, вы можете использовать точно такой же подход для других более сложных геометрий и постановок. Чтобы узнать все детали и настройки выполненные при моделировании, ознакомьтесь с учебным примером Planar PCB Coil. По ссылке вы найдёте pdf-файл с пошаговыми инструкциями по сборке. А если у вас есть действующая лицензия, то сможете скачать и соответствующий MPH-файл модели.
Визуализация результатов электромагнитного расчета
После проведения расчета в результатах автоматически сгенерируются дефолтные графики с наиболее характерными визуализациями и величинами.
Распределение магнитной индукции вокруг катушки (цветом) и плотность тока (стрелки).
В данном примере мы продемонстрировали преимущества использования технологии по заданию многослойных оболочек в модуле AC/DC. С её помощью легко реализовать модель планарной катушки и определить сосредоточенные параметры — сопротивление и индуктивность. Используя расчетные данные, инженеры могут проводить оптимизацию топологий катушек для определенных сфер применения, например, добавляя больше витков для увеличения индуктивности.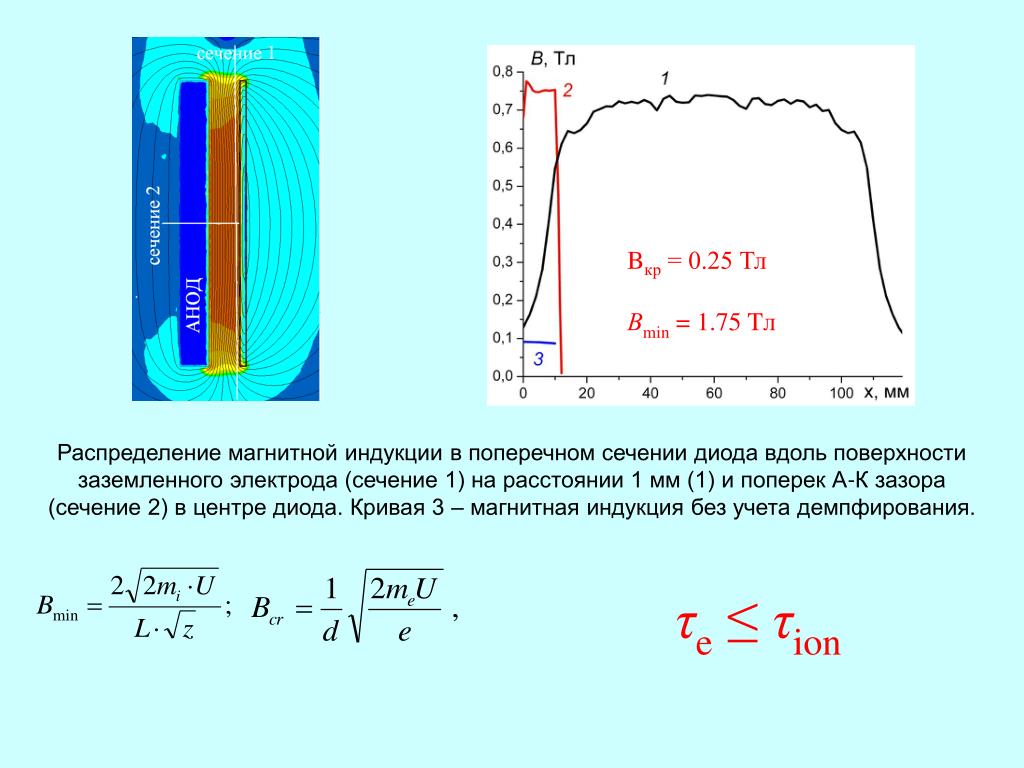 Результаты расчета предсказывают увеличение индуктивности с 0.06 мкГн до 0.11 мкГн при добавлении 4го витка.
Результаты расчета предсказывают увеличение индуктивности с 0.06 мкГн до 0.11 мкГн при добавлении 4го витка.
Сравнение сопротивления и индуктивности для катушек с тремя и четырьмя витками. Визуализация распределения магнитной индукции приведена для случая четырёхвитковой катушки.
Дальнейшие шаги
Поработайте самостоятельно с рассмотренным примером расчета планарной катушки на печатной плате. По нажатию на кнопку вы перейдете в Библиотеку моделей и приложений (Application Gallery,), в которой сможете загрузить MPH-файл и документацию к рассмотренной модели.
Дополнительные материалы
Напряженность магнитного поля, магнитная индукция и магнитный поток
Сила, с которой магнитное поле притягивает железные тела, пропорциональна значению протекающего по проводнику тока. Если провод уложен в виде катушки, то эта сила тем больше, чем больше витков имеет катушка. Произведение силы тока I на число витков w катушки называют ампер-витками. Оно равно магнитодвижущей силе (м. д. с.) катушки, измеряемой в амперах (А). Ампер-витки Iw, приходящиеся на единицу длины L катушки, называют напряженностью магнитного поля H:
Оно равно магнитодвижущей силе (м. д. с.) катушки, измеряемой в амперах (А). Ампер-витки Iw, приходящиеся на единицу длины L катушки, называют напряженностью магнитного поля H:
. Iw
H=——
. l
Единица измерения напряженности магнитного поля
. ампер • виток
1 ———————— = 1 А/м.
. метр
Напряженность, рассчитанная по формуле (4.1), соответствует напряженности внутри цилиндрической катушки. Если катушку замкнуть в виде кольца, то силовые линии замкнутся по кругу без рассеивания, и тогда формула (4.1) будет верна для любой точки такой катушки (тороида).
Магнитная индукция Во, или интенсивность магнитного поля, в катушке без сердечника Во=µо Н, (4.2)
где µо = 4∏10-7 Г/м = 1,256•10-7 Г/м — магнитная постоянная (магнитная проницаемость свободного пространства или вакуума).
Если внутрь катушки ввести железный сердечник, то при тех же витках и силе тока магнитная индукция, или интенсивность магнитного поля, возрастает в значительной мере. Причина этого явления заключается в том, что молекулярные токи в железе под действием магнитного поля ориентируются относительно этого поля. Молекулярные магнитные поля при этом совпадают с внешним магнитным полем и усиливают его. Способность к увеличению интенсивности магнитного поля зависит от свойств материала сердечника, характеризуется относительной магнитной проницаемостью µ:
. Интенсивность магнитного поля в катушке с сердечником В
µ= —————————————————————————————— = — . (4.3)
. Интенсивность магнитного поля в катушке без сердечника Во
Это безразмерная величина. Для воздуха значение µ принимают равным 1.
Произведение µоµ = µа называется абсолютной магнитной проницаемостью. Тогда магнитная идукция В для катушки с сердечником
Тогда магнитная идукция В для катушки с сердечником
В = µаH = µ0µ H, (4.4)
где µ — относительная магнитная проницаемость материала сердечника.
Единица измерения магнитной индукции — тесла (Т):
1 Т = 1 В с/м2.
Пример. Вычислить напряженность магнитного поля внутри сравнительно длинной катушки, если число витков w = 300, длина катушки l= 0,5 м, а ток катушки I=0,6 А. Определить также магнитную индукцию В, если в катушку введен сердечник с µ = 7000.
Решение. Напряженность магнитного поля
. Iw 0,6•300
H=—— = ———— = 360 А/м
. l 0,5
Магнитная индукция в сердечнике В = µоµH = 4∏10-7•7000 • 360 = 3,17 Т.
Магнитным потоком Ф называют произведение магнитной индукции В (Т) на площадь сечения S (м2) сердечника катушки:
Ф = BS.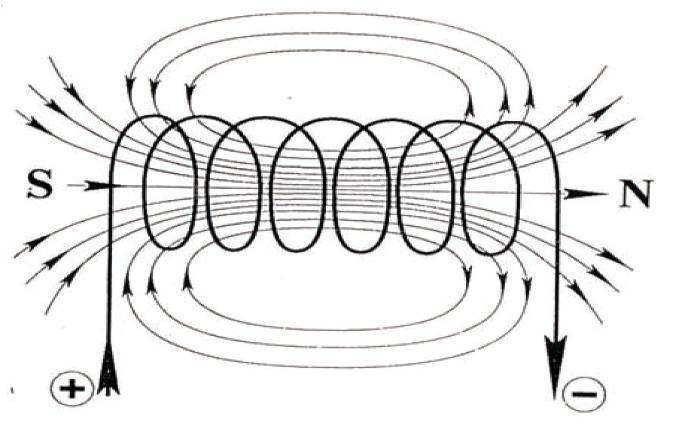 (4.5)
(4.5)
Единица магнитного потока — в е б е р (Вб).
Пример. Найти магнитный поток Ф катушки, длина которой 1 = 0,5 м, число витков w = 300, ток I = 0,6 А, сердечник из электротехнической стали Э42 сечением 10-3 м2.
Решение. Напряженность магнитного поля
. Iw 0,6•300
H=—— = ———— = 360 А/м.
. l 0,5
По кривой намагничивания (рис. 4.5) находим магнитную индукцию при Н = 360 А/м;
B ≈ 1,2 Т.
Магнитный поток Ф = BS= 1,2•10-3 Вб.
| < Предыдущая | Следующая > |
|---|
зависимость индуктивности в катушке от сердечника
Определение и принцип работы
В наших уроках об электромагнетизме мы увидели, что когда электрический ток протекает через проводник, вокруг проводника возникает магнитный поток. Это создает взаимосвязь между направлением магнитного потока, который циркулирует вокруг проводника, и направлением тока, протекающего через тот же проводник, что приводит к хорошо известной взаимосвязи между током и направлением магнитного потока, называемой «Правило правой руки Флеминга».
Это создает взаимосвязь между направлением магнитного потока, который циркулирует вокруг проводника, и направлением тока, протекающего через тот же проводник, что приводит к хорошо известной взаимосвязи между током и направлением магнитного потока, называемой «Правило правой руки Флеминга».
Но есть и другое важное свойство, относящееся к намотанной катушке, которая также существует, а именно то, что вторичное напряжение индуцируется в ту же катушку движением магнитного потока, поскольку оно противостоит любым изменениям электрического тока, протекающего по нему.
Типичный индуктор
В своей основной форме Индуктор — это не что иное, как катушка проволоки, намотанная вокруг центрального сердечника. Для большинства катушек ток I, протекающий через катушку, создает магнитный поток NΦ вокруг нее, который пропорционален этому потоку электрического тока.
Индуктор, называемый также дросселем, является еще одним типом пассивного электрического компонента, который является простой катушкой провода предназначенного, чтобы воспользоваться этой взаимосвязью путем индукции магнитного поля, сам по себе, или в активной зоне в результате тока, проходящем через катушки. Это приводит к гораздо более сильному магнитному полю, чем то, которое создавалось бы простой катушкой из проволоки.
Это приводит к гораздо более сильному магнитному полю, чем то, которое создавалось бы простой катушкой из проволоки.
Индукторы образованы проволокой, плотно обернутой вокруг сплошного центрального сердечника, который может представлять собой либо прямой цилиндрический стержень, либо непрерывную петлю или кольцо для концентрации их магнитного потока.
Схематическое обозначение индуктора — это катушка с проводом, поэтому катушку с проводом можно также назвать индуктором. Индукторы обычно классифицируются в соответствии с типом внутреннего сердечника, вокруг которого они намотаны, например, полый сердечник, твердый железный сердечник или мягкий ферритовый сердечник, причем различные типы сердечников различаются путем добавления непрерывных или пунктирных параллельных линий рядом с проволочная катушкой, как показано ниже.
Как выбрать катушку индуктивности?
Нас часто спрашивают, как выбрать катушку индуктивности для тех или иных задач. Чем отличаются различные катушки индуктивности? Какие технологии применяются? Обо всём этом в данной статье — на примере катушек Mundorf.
Чем отличаются различные катушки индуктивности? Какие технологии применяются? Обо всём этом в данной статье — на примере катушек Mundorf.
Сохранить и прочитать потом —
Выбор проводника катушки
Звуковые характеристики катушки определяются не только сердечником и качеством производства, но также и типом проводника. Чтобы получить соответствующие катушки для каждого типа применения, используются три материала высокой чистоты.
- Беcкислородная медь (OFC)
Катушки, в которых в качестве материала проводника использована беcкислородная медь (чистая медь 99,997%), характеризуются гармоничным и объемным воспроизведением музыки, богатым деталями, а также имеют отличное соотношение цена/качество. - Чистое серебро
Вследствие способности серебра передавать голоса и инструменты с большей динамикой, детальнее, с более широкой сценой и более насыщенными тембрами по сравнению с медью, катушки из чистого (99,99%) серебра высоко ценятся и являются предпочтением для большого числа ценителей хорошего звука.
- Сплав золота с серебром
99% серебра + 1% золота = 100% музыки. Этот сплав не только для конденсаторов самого высокого класса, таких как MCap® SUPREME Classic Silver-Gold.Oil, или аудиокабелей, но и для катушек индуктивности. Чистое золото (99,99%) изменяет кристаллическую структуру серебра и оптимизирует его высокую проводимость. Применение такого сплава позволяет раскрыть всю полноту тембров и характер голосов и инструментов, воспроизвести музыкальное произведение во всех мельчайших деталях без каких либо искажений оригинала. С одной стороны кристально чистое воспроизведение становится в тоже время живым и теплым, отображая ясную, четко локализованную музыкальную картину. Чистота и точность передачи, объединенная с живостью и насыщенностью тембров, отличает этот материал от других.
Провода SolidCore
Воспроизведение музыки с катушками из цельных круглых в сечении проводов (также называемых SolidCore) отличается живостью и точностью, также как и высокой тональной нейтральностью. Еще одним преимуществом круглого проводника являются очень компактные размеры катушки. Как и все катушки MUNDORF, катушки из этих проводов собираются и наматываются вручную в Германии с использованием специальных машин, обеспечивающих наивысшую точность.
Еще одним преимуществом круглого проводника являются очень компактные размеры катушки. Как и все катушки MUNDORF, катушки из этих проводов собираются и наматываются вручную в Германии с использованием специальных машин, обеспечивающих наивысшую точность.
Стандартные OFC
Они являются самыми экономически выгодными проводами для аудиокатушек индуктивности и доступны с диаметрами от 0,5 до 3,9 мм. Однако такие катушки не имеют дополнительной фиксации проводников и поэтому уступают другим типам катушек, производимых MUNDORF. При прохождении переменного сигнала возникает вибрация обмотки катушки. Вследствие микрофонного эффекта (преобразования механической энергии колебаний витков катушки обратно в электрические колебания) дополнительные колебания добавляются к основному сигналу, что приводит к искажениям деталей звукового сигнала. Это отражается как в ухудшении пространственного отображения звука, так и в неестественном воспроизведении тембров. Однако такой нежелательный эффект может быть полностью устранен при использовании запекания в лаке или вакуумной пропитки.
Проводник в спеченном лаке
Эти катушки имеют круглый в сечении проводник из чистой меди OFC, покрытый слоем лака. После намотки катушки она нагревается при помощи электрического импульса, что приводит к плавлению слоя лака. После охлаждения отдельные обмотки оказываются крепко связаны друг с другом спеченным лаком, что препятствует появлению вибраций обмоток и искажению сигнала. К сожалению, такой тип катушек доступен только с диаметром проводника от 0,5 до 1,4 мм. Для больших диаметров используется вакуумная пропитка.
Вакуумная пропитка
Вакуумная пропитка представляет собой процедуру, настолько же эффективную как фиксация проводников при нагреве лака, но используемую для проводников с большим диаметром (от 2 до 3,9 мм). В ходе этой операции катушка пропитывается специальным лаком под действием вакуума вплоть до самых глубоких внутренних витков. Затем пропитанная катушка сушится при 130°С. Таким образом вся катушка превращается практически в монолитное сооружение.
Гепта-проводник
Использование сборки, состоящей из семи отдельных изолированных и связанных друг с другом проводов, позволяет добиться живого и мягкого воспроизведения тембров, в то же время передавая все мельчайшие детали звука. За эти характеристики такие катушки высоко ценятся аудиолюбителями и проектировщиками аудиооборудования, особенно когда требуется сделать звучание акустической системы более детальным и четким без негативного влияния на прозрачность и тональную насыщенность.
Такие характеристики этих катушек обусловлены использованием круглых в сечении проводников в сборке особого типа. Спеченная обмотка и усиленное шасси катушки образуют катушку индуктивности с наивысшей механической стабильностью и равновесием. Таким образом, искажения и изменения окраски звука полностью отсутствуют. Кроме того, большая площадь поверхности семи жил сборки увеличивает эффективную проводимость высокочастотного сигнала (вследствие скин-эффекта). Семижильная сборка 7×0,6 мм соответствует одножильному проводнику диаметром 1,6 мм.
Катушки из фольги
При использовании катушек из цельнометаллической фольги (также известных как ленточные катушки), воспроизведение музыки приобретает невероятную динамику, отличную детальность и объемность, при этом обладая самыми низкими искажениями звука. Даже самые тонкие нюансы звука передаются абсолютно реалистично, полностью раскрывая замысел исполнителя. Вследствие таких характеристик ленточные катушки MUNDORF стали неотъемлемой частью многих аудиокомпонентов высшего класса.
Витки такой катушки намотаны друг на друга, поэтому ленточные катушки гораздо ближе к физически идеальной катушке индуктивности, чем любые другие конструкции катушек. Это, к примеру, отражается на параметрах катушки, которые остаются неизменными вплоть до 100 кГц. Кроме того, эти катушки обладают низкой емкостью, несмотря на сходство конструкции обмотки с конденсатором, что препятствует искажению высоких частот. Большая площадь поверхности фольги увеличивает эффективную проводимость на высоких частотах (как следствие скин-эффекта).
Еще одной заметной особенностью является высокая механическая стабильность этого типа катушек, которые тщательно скрепляются вручную. Вследствие большой площади контакта между витками обмотки и использования пластичной изоляции колебания отдельных витков эффективно гасятся. Таким образом, ленточные катушки имеют самый низкий уровень вибрации из всех типов катушек. Ленточные катушки имеют несколько вариантов ширины фольги, соответствующих использованию круглого в сечении проводника с диаметрами 1,25 мм, 1,60 мм, 2,00 мм и 2,50 мм.
Выбор сердечника катушки
Качество воспроизведения при использовании катушки индуктивности зависит не только от материала проводника и качества изготовления, но также и от типа сердечника. Поскольку каждый материал сердечника имеет свои преимущества и недостатки, катушки имеют четыре различных материала сердечника, тем самым образуя семь различных типов сердечников. Это позволяет подобрать необходимую катушку для каждой отдельной задачи.
Чтобы предотвратить микрофонный эффект, все катушки MUNDORF наматываются на каркас катушки. Это обеспечивает необходимую стабильность катушки, механически развязывает катушку от платы (места установки) и вдобавок упрощает процесс производства.
Воздушные катушки (Air сoils)
Идеальным материалом сердечника для катушки является воздух. Катушки с воздушным сердечником превосходят по характеристикам все катушки с металлическими сердечниками, как по точности передачи импульса, так и по отсутствию искажений звукового сигнала. Они могут быть использованы в любой цепи, и для фильтра пропускающего высокие частоты, как катушку для басового динамика (с большой площадью сечения проводника) или для корректировки компонентов (с малой площадью сечения проводника).
Точность, динамика, тонкие тональные оттенки, высокая детальность и живое воспроизведение звука отличает катушки с воздушным сердечником от других. Таким образом, они являются основой реалистичного и гармоничного звучания акустических систем высокого класса.
Катушки с сердечником
Катушки с сердечником имеют металлический сердечник, который усиливает магнитное поле катушки. По сравнению с воздушными катушками они имеют меньшие размеры, меньшую стоимость, более высокую индуктивность и более низкое активное сопротивление. Однако катушки с металлическим сердечником оказывают негативное влияние на качество звука.
Ферритовый сердечник (Ferrite core)
Такие сердечники получают спеканием метало-пластиковой пудры. Сделанный в Германии материал феррита НР3616, используемый в этих сердечниках, имеет значительно более высокие характеристики, чем материал, произведенный в Азии, часто используемый в других катушках. Для этого материала характерны низкие искажения сигнала и высокая реверсивность магнитного поля (равно и изменение ориентации поля). Музыкальный сигнал имеет сильную задержку, поэтому катушки с ферритовыми сердечниками подходят для использования в цепях коррекции, а также в среднечастотном диапазоне. Однако, только протестированный материал НР3616, удовлетворяющий определенным требованиям по устойчивости и уровню искажений, может быть пригоден для использования в средне-низкочастотном диапазоне и даже в низкочастотной области для усилителей с более низкими характеристиками.
Аронитовый сердечник (Aronit core)
Эти сердечники (также известные как Р-сердечники) состоят из метало-керамической пудры высокой плотности. Сделанные в Германии ферритовые стержни «Wicon» обеспечивают очень низкий уровень искажений, даже при очень высоких нагрузках. Вследствие их компактных размеров, низкого активного сопротивления и отличного соотношения цена/качество они могут быть использованы даже в басовых секциях фильтров акустических систем и сабвуферов.
Фероновый сердечник (Feron core)
Он состоит из железно-кремниевого сплава (также называемый электрическими листами). Высококачественные трансформаторные пластины прокатаны и проштампованы несколько раз в ходе особых операций таким образом, что кристаллы становятся ориентированными в одном направлении, а также кристаллическая решетка становится более однородной. Таким образом, катушки MUNDORF с фероновым сердечником заметно отличаются от обычных катушек того же типа как по результатам измерений, так и по результатам прослушиваний.
Они выделяются вследствие минимальных искажений, минимальных потерь при изменении ориентации магнитного поля и стабильности параметров при высоких нагрузках. Таким образом, они хорошо подходят для различных задач.
Катушки с нулевым сопротивлением (ZOC)
Эти катушки производятся только компанией MUNDORF. Воздушный зазор между двумя наборами фероновых пластин в таких катушках калибруется и точно подстраивается вручную. Этот воздушный зазор определяет индуктивность катушки и требует большого внимания в процессе производства. Высокие затраты на производство этих катушек окупаются максимальной точностью передачи импульса, а также музыкального сигнала. Особая форма феронового сердечника позволяет получить более низкое внутреннее сопротивление по сравнению с другими типами сердечников.
Эту статью прочитали 37 933 раза
Статья входит в разделы:
Как выбрать. Гид покупателя»Сделай сам»
Индуктор на схеме
Ток I, который протекает через катушку индуктивности производит магнитный поток, который пропорционален к нему. Но в отличие от конденсатора, который противодействует изменению напряжения на своих пластинах, индуктор противодействует скорости изменения тока, протекающего через него, из-за накопления самоиндуцированной энергии в его магнитном поле.
Но в отличие от конденсатора, который противодействует изменению напряжения на своих пластинах, индуктор противодействует скорости изменения тока, протекающего через него, из-за накопления самоиндуцированной энергии в его магнитном поле.
Другими словами, катушки индуктивности сопротивляются или противостоят изменениям тока, но легко пропустят постоянный ток. Эта способность индуктора противостоять изменениям тока и которая также связывает ток I с его магнитным потоком NΦ как коэффициент пропорциональности, называется индуктивностью, которому присвоен символ L с единицами измерения Генри ( H ).
Поскольку Генри представляет собой относительно большую единицу индуктивности, для младших индукторов Генри используются для обозначения его значения. Например:
Что такое индуктивность
Этим термином обозначают зависимость, которая устанавливается между силой тока в проводнике (I) и созданным магнитным потоком (Ф):
L = Ф/ I.
С учетом базового определения несложно понять зависимость индуктивности от свойств окружающей среды, оказывающей влияние на распределение силовых линий. Определенное значение имеют размеры и конфигурация проводящего элемента.
Индуктивность подобна механической инерции. Только в данном случае речь идет о действиях с электрическими величинами. Этим коэффициентом характеризуют способность рассматриваемого компонента противодействовать изменению проходящего через него тока.
Префиксы индуктивности
| Префикс | Условное обозначение | мультипликатор | Степень десяти |
| милли | m | 1/1 000 | 10 -3 |
| микро | μ | 1/1000000 | 10 -6 |
| нано | n | 1/1000000000 | 10 -9 |
Таким образом, для отображения подразделов Генри мы будем использовать в качестве примера:
- 1mH = 1 милли-Генри — что равно одной тысячной (1/1000) Генри.

- 100μH = 100 микро-Генри — что равно одной 100-миллионной ( 1/1 000 000) Генри.
Индукторы или катушки очень распространены в электрических цепях, и существует множество факторов, определяющих индуктивность катушки, таких как форма катушки, число витков изолированного провода, число слоев провода, расстояние между витками, проницаемость материала сердечника, размер или площадь поперечного сечения сердечника и т. д.
Катушка индуктивности имеет площадь поперечного сечения сердечника ( A ) с постоянным числом витков провода на единицу длины ( l ). Таким образом, если катушка N витков связана на величину магнитного потока Φ то катушка имеет потокосцепление NΦ и любой ток I, который протекает через катушку будет производить индуцированный магнитный поток в противоположном направлении по отношению к потоку тока. Затем, согласно закону Фарадея, любое изменение в этой связи магнитного потока производит самоиндуцированное напряжение в одной катушке:
Где:
- N — число витков
- А — площадь поперечного сечения в м 2
- Φ — количество потока в Веберах
- μ — проницаемость материала сердечника
- L — длина катушки в метрах
- di / dt — скорость изменения тока в Амперах в секунду
Изменяющееся во времени магнитное поле индуцирует напряжение, которое пропорционально скорости изменения тока, создающего его, с положительным значением, указывающим на увеличение ЭДС, и отрицательным значением, указывающим на уменьшение ЭДС. Уравнение, связывающее это напряжение, ток и индуктивность с самоиндукцией, может быть найдено путем замены μN 2 A / l на L, обозначая постоянную пропорциональности, называемую индуктивностью катушки.
Уравнение, связывающее это напряжение, ток и индуктивность с самоиндукцией, может быть найдено путем замены μN 2 A / l на L, обозначая постоянную пропорциональности, называемую индуктивностью катушки.
Соотношение между потоком в катушке индуктивности и током, протекающим через катушку индуктивности, имеет вид: NΦ = Li . Поскольку катушка индуктивности состоит из катушки с проводящим проводом, это уменьшает приведенное выше уравнение, чтобы получить самоиндуцированную ЭДС, иногда называемую также обратной ЭДС, индуцированной в катушке.
Материал сердечника
Формула ЭДС индукции
Как и в предыдущем примере, для вычисления индукции катушки с сердечником в представленные выше формулы добавляют множитель относительной магнитной проницаемости «m»:
L = m0 * m * N2 * (S/l) = m0 * m * n2 * V.
С помощью этого коэффициента учитывают ферромагнитные свойства определенного материала.
Если для примера взять бесконечный (очень длинный) прямой провод с круглым сечением, то он будет обладать определенной индуктивностью:
L = (m0/2π) * l *(mc * ln(l/r) +1/4m,
где:
- mc – магнитная проницаемость (относительная) среды;
- r – радиус, который намного меньше длины (l) проводника.
Однако простые зависимости действуют только до определенной частоты. С определенного уровня волны малой длины начинают распространяться в поверхностной части проводников (скин-эффект). Дополнительно приходится учитывать влияние вихревых составляющих, экранирующих излучение и меняющих силовые параметры поля.
Современные магнитные материалы
Катушка будет работать в точном соответствии с расчетом, если правильно подобраны все функциональные компоненты конструкции. Как показано выше, существенное значение имеют параметры сердечника. Ниже отмечены важные особенности соответствующих материалов:
- Сталь с низким содержанием примесей стоит недорого.
 Ее рекомендуется применять в цепях постоянного тока, так как при повышении частоты значительно увеличиваются потери.
Ее рекомендуется применять в цепях постоянного тока, так как при повышении частоты значительно увеличиваются потери. - В специальные сорта (трансформаторную сталь) добавляют кремний. Для уменьшения вредного влияния поверхностных эффектов сердечник собирают из пластин. Однако и такие решения не следует использовать при частоте более 1 кГц.
- Сплавы из железа с никелем отличаются увеличенной магнитной проницаемостью. Рабочий диапазон – до 80-120 кГц.
- Порошковые материалы создают со слоем диэлектрика на поверхностях отдельных микроскопических гранул. Они хорошо приспособлены для работы с высокочастотными сигналами, однако не обладают большой магнитной проницаемостью.
- Ферриты – это материалы, созданные на основе керамических компонентов. Они отличаются хорошими техническими характеристиками, малыми потерями. Следует учитывать значительную зависимость от температуры, а также ухудшение рабочих параметров при длительной эксплуатации.
Измерение индуктивности катушки, созданной из медного провода на ферритовом сердечнике
Обратная ЭДС генерируемая индуктором
Где: L — собственная индуктивность, а di / dt — скорость изменения тока.
Таким образом, из этого уравнения мы можем сказать, что «самоиндуцированная ЭДС = индуктивность * скорость изменения тока» и цепь с индуктивностью один Генри будет иметь ЭДС 1 вольт, индуцированную в цепи, когда ток, протекающий через цепь, изменяется со скоростью 1 Ампер в секунду.
Катушка индуктивности
Один важный момент, который нужно отметить относительно приведенного выше уравнения. Он только связывает ЭДС, создаваемую через индуктор, с изменениями тока, потому что, если ток индуктора постоянен и не изменяется, например, в постоянном токе, то индуцированное напряжение ЭДС будет равно нулю, поскольку мгновенная скорость изменения тока равна ноль di / dt = 0.
При постоянном токе, протекающем через индуктор и, следовательно, нулевом индуцированном напряжении на нем, индуктор действует как короткое замыкание, равное куску провода, или, по крайней мере, очень низкое значение сопротивления. Другими словами, противодействие протеканию тока, предлагаемого индуктором, очень различно в цепях переменного и постоянного тока.
Самоиндукция
Индуктивность проводника
Если через замкнутый контур пропускать переменный ток, можно зарегистрировать с помощью простых экспериментов магнитное поле в окружающей среде. Изменение силовых параметров сопровождается появлением в цепи наведенной электродвижущей силы. Данное явление называют самоиндукцией.
Величину ЭДС можно вычислить по формуле:
Е = -L * (Δi/Δt).
Это выражение показывает зависимость напряжения от изменения тока за единицу времени. Поправочный коэффициент (L) обозначает особенности проводника (индукционной катушки). Знак «-» характеризует инерционные свойства явления.
При пропускании синусоидального сигнала следует учитывать отставание напряжения (векторное выражение) от тока на 90 градусов. Амплитуда будет прямо пропорциональна частоте (w):
E = L * I * w.
Постоянная времени индуктора
Теперь мы знаем, что ток не может изменяться мгновенно в индуктивности, потому что для этого ток должен измениться на конечную величину за нулевое время, что приведет к тому, что скорость изменения тока будет бесконечной di / dt = ∞ , делая индуцированную ЭДС бесконечной, а бесконечного напряжения не существует. Однако, если ток, протекающий через индуктор, изменяется очень быстро, например, при работе переключателя, на катушке индуктивности могут возникать высокие напряжения.
Однако, если ток, протекающий через индуктор, изменяется очень быстро, например, при работе переключателя, на катушке индуктивности могут возникать высокие напряжения.
Рассмотрим схему индуктора выше. Когда переключатель ( S1 ) разомкнут, ток через катушку индуктивности не течет. Поскольку через индуктор ток не течет, скорость изменения тока ( di / dt ) в катушке будет равна нулю. Если скорость изменения тока равна нулю, то в катушке индуктивности нет ЭДС самоиндукции ( V L= 0 ).
Если мы теперь закроем переключатель (t = 0), ток будет проходить через цепь и медленно подниматься до своего максимального значения со скоростью, определяемой индуктивностью индуктора. Эта скорость тока, протекающего через катушку индуктивности, умноженная на индуктивность по Генри, приводит к тому, что на катушке образуется некоторая самоиндуцированная ЭДС с фиксированным значением, определенная уравнением Фарадея V L = Ldi / dt.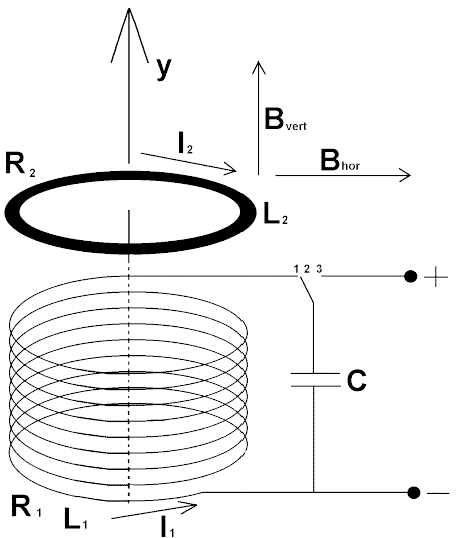
Эта самоиндуцированная ЭДС на катушке индуктивности ( V L ) борется с приложенным напряжением до тех пор, пока ток не достигнет своего максимального значения и не будет достигнуто устойчивое состояние. Ток, который сейчас течет через катушку, определяется только постоянным или «чистым» сопротивлением обмоток катушек, поскольку значение реактивного сопротивления катушки уменьшилось до нуля, поскольку скорость изменения тока (di / dt) равна нулю в устойчивом состоянии. Другими словами, теперь существует только сопротивление катушек постоянного тока, чтобы противостоять потоку тока.
Аналогичным образом, если переключатель ( S1 ) разомкнут, ток, протекающий через катушку, начнет падать, но индуктор снова будет бороться с этим изменением и попытается удержать ток в своем прежнем значении, индуцируя напряжение в другом направлении. Наклон падения будет отрицательным и связан с индуктивностью катушки, как показано ниже.
Терминология
При использовании для подавления помех, сглаживания пульсаций электрического тока, изоляции (развязки) по высокой частоте разных частей схемы и накопления энергии в магнитном поле сердечника часто называют дросселем
, а иногда реактором.
В силовой электротехнике (для ограничения тока при, например, коротком замыкании ЛЭП) называют реактором
.
Цилиндрическую катушку индуктивности, длина которой намного превышает диаметр, называют соленоидом
, магнитное поле внутри длинного соленоида однородно. Кроме того, зачастую
соленоидом
называют устройство, выполняющее механическую работу за счёт магнитного поля при втягивании ферромагнитного сердечника, или
электромагнитом
. В электромагнитных реле называют
обмоткой реле
, реже — электромагнитом.
Нагревательный индуктор
— специальная катушка индуктивности, рабочий орган установок индукционного нагрева.
При использовании для накопления энергии (например, в схеме импульсного стабилизатора напряжения) называют индукционным накопителем
или накопительным дросселем.
Ток и напряжение в индукторе
Сколько индуктивного напряжения будет генерироваться индуктором, зависит от скорости изменения тока. В нашем уроке об электромагнитной индукции закон Ленца гласил: «Направление индуцированной ЭДС таково, что оно всегда будет противостоять изменению, которое его вызывает». Другими словами, индуцированная ЭДС всегда будет противопоставлять движение или изменение, которые изначально вызвали индуцированную ЭДС.
Таким образом, при уменьшении тока полярность напряжения будет действовать как источник, а при увеличении тока полярность напряжения будет действовать как нагрузка. Таким образом, при одинаковой скорости изменения тока через катушку, увеличение или уменьшение величины индуцированной ЭДС будет одинаковым.
Мощность в индукторе
Мы знаем, что индуктор в цепи противостоит потоку тока I через него, потому что поток этого тока индуцирует ЭДС, которая противостоит ему, закон Ленца. Затем необходимо выполнить работу от внешнего источника батареи, чтобы ток протекал против этой индуцированной ЭДС. Мгновенная мощность, используемая для форсирования тока I по отношению к этой самоиндуцированной ЭДС (V L), определяется как:
Мгновенная мощность, используемая для форсирования тока I по отношению к этой самоиндуцированной ЭДС (V L), определяется как:
Мощность в цепи задается как P = V * I, поэтому:
Идеальный индуктор не имеет сопротивления, только индуктивность, поэтому R = 0 Ом, и поэтому мощность в катушке не рассеивается, поэтому можно сказать, что идеальный индуктор имеет нулевую потерю мощности.
Конструкция
Конструктивно выполняется в виде винтовых или винтоспиральных (диаметр намотки изменяется по длине катушки) катушек однослойных или многослойных намоток изолированного одножильного или многожильного (литцендрат) проводника на диэлектрическом каркасе круглого, прямоугольного или квадратного сечения, часто на тороидальном каркасе или, при использовании толстого провода и малом числе витков — без каркаса. Иногда, для снижения распределённой паразитной ёмкости, при использовании в качестве высокочастотного дросселя
однослойные катушки индуктивности наматываются с «прогрессивным» шагом — шаг намотки плавно изменяется по длине катушки.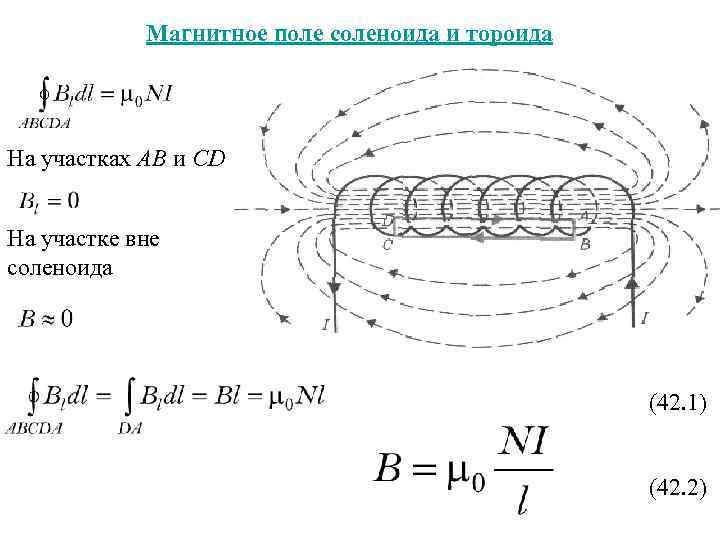 Намотка может быть как
Намотка может быть как
однослойной
(рядовая и с шагом), так и
многослойной
(рядовая, внавал, типа «универсал»). Намотка «универсал» имеет меньшую паразитную ёмкость. Часто, опять же, для снижения паразитной ёмкости, намотку выполняют секционированной, группы витков отделяются пространственно (обычно по длине) друг от друга.
Для увеличения индуктивности катушки часто снабжают замкнутым или разомкнутым ферромагнитным сердечником. Дроссели подавления высокочастотных помех имеют ферродиэлектрические сердечники: ферритовые, флюкстроловые, из карбонильного железа. Дроссели, предназначенные для сглаживания пульсаций промышленной и звуковой частот, имеют сердечники из электротехнических сталей или магнитомягких сплавов (пермаллоев). Также сердечники (в основном ферромагнитные, реже диамагнитные) используют для изменения индуктивности катушек в небольших пределах путём изменения положения сердечника относительно обмотки. На сверхвысоких частотах, когда ферродиэлектрики теряют свою магнитную проницаемость и резко увеличивают потери, применяются металлические (латунные) сердечники.
На печатных платах электронных устройств также иногда делают плоские «катушки» индуктивности: геометрия печатного проводника выполняется в виде круглой или прямоугольной спирали, волнистой линии или в виде меандра. Такие «катушки индуктивности» часто используются в сверхбыстродействующих цифровых устройствах для выравнивания времени распространения группы сигналов по разным печатным проводникам от источника до приемника, например, в шинах данных и адреса[1].
Магнитное поле токоведущего провода
Темы и файлы
E&M Тема
- Электромагнетизм, магнитное поле в катушке
Напильник Capstone
Перечень оборудования
Введение
Цель этого упражнения — измерить магнитное поле, создаваемое токоведущим проводом в форме катушки.Используйте усилитель мощности для создания и измерения тока в катушке и используйте датчик магнитного поля для измерения напряженности магнитного поля в катушке. Используйте Capstone для записи и отображения данных. Рассчитайте проницаемость свободного пространства ( μ 0 ) на основе размера и количества витков в катушке, измеренного тока и измеренного магнитного поля.
Используйте Capstone для записи и отображения данных. Рассчитайте проницаемость свободного пространства ( μ 0 ) на основе размера и количества витков в катушке, измеренного тока и измеренного магнитного поля.Фон
Токоведущий провод испытывает магнитную силу при помещении в магнитное поле, создаваемое внешним источником, например постоянным магнитом.Токоведущий провод также создает собственное магнитное поле. Ганс Кристиан Эрстед (1777–1851) впервые обнаружил этот эффект в 1820 году, когда заметил, что провод с током влияет на ориентацию расположенной рядом стрелки компаса. Стрелка компаса выравнивается с чистым магнитным полем, создаваемым током и землей. Открытие Эрстеда, связавшее движение электрических зарядов с созданием магнитного поля, положило начало важной дисциплине под названием электромагнетизм.Экспериментально обнаружено, что величина B магнитного поля, создаваемого длинным прямым проводом, прямо пропорциональна току I и обратно пропорциональна радиальному расстоянию r от провода, как показано ниже. Константа пропорциональности преобразует выражение в уравнение, которое дает величину магнитного поля вокруг длинного прямого провода. Константа « μ 0 » известна как проницаемость свободного пространства, и ее значение показано ниже.
Константа пропорциональности преобразует выражение в уравнение, которое дает величину магнитного поля вокруг длинного прямого провода. Константа « μ 0 » известна как проницаемость свободного пространства, и ее значение показано ниже.(3)
мкм 0 = 4 π × 10 −7 Тлм / А
Если токопроводящий провод согнут в круговую петлю, силовые линии магнитного поля вокруг петли будут иметь рисунок, подобный тому, что и вокруг стержневого магнита. В центре петли радиусом R магнитное поле перпендикулярно плоскости петли и имеет значение, показанное в уравнении ниже, где I обозначает ток в петле. Часто петля состоит из N и витков провода, намотанных так близко друг к другу, что они образуют плоскую катушку с одной петлей.В этом случае магнитные поля отдельных витков складываются, чтобы получить результирующее поле, которое в Н, в раз больше, чем у одиночной петли.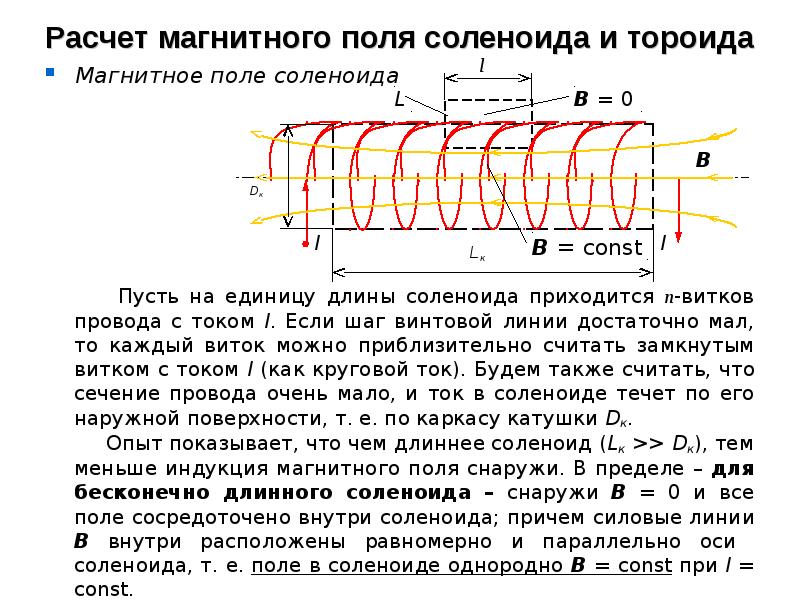 Для такой катушки магнитное поле в центре зависит от количества петель, тока и радиуса петли, как показано в уравнении ниже.
Для такой катушки магнитное поле в центре зависит от количества петель, тока и радиуса петли, как показано в уравнении ниже.Copyright © 2016 Advanced Instructional Systems, Inc. и Физический факультет Университета Центральной Флориды | Кредиты
Магнитная энергия
Магнитная энергияДалее: Цепи переменного тока Up: Магнитная индукция Предыдущий: Взаимная индуктивность Предположим, что к катушке индуктивности, и сопротивления, подключена через клеммы батареи эл.м.ф., Уравнение схемы:
| (932) |
Выходная мощность батареи. [Каждый заряд, который проходит по цепи падает через разность потенциалов. Чтобы вернуть его обратно в пусковой потенциал, чтобы он мог выполнить другую цепь, батарея должна делать Работа .
 Работа, выполненная за единицу времени (, т. Е. , мощность) равна, где —
количество зарядов в единицу времени, проходящих через заданную точку в цепи.Но, значит, выходная мощность такая.] Общая работа, выполняемая аккумулятором в
повышение тока в цепи с нуля на время до
время — это
Работа, выполненная за единицу времени (, т. Е. , мощность) равна, где —
количество зарядов в единицу времени, проходящих через заданную точку в цепи.Но, значит, выходная мощность такая.] Общая работа, выполняемая аккумулятором в
повышение тока в цепи с нуля на время до
время — это | (933) |
Используя уравнение схемы (932), получаем
| (934) |
давая
| (935) |
Второй член в правой части представляет собой необратимое преобразование электрическая энергия в тепловую энергию в резисторе.
 Первый член — это сумма
энергия, запасенная в катушке индуктивности во время. Эта энергия может быть восстановлена после
индуктор отключен от АКБ. Предположим, что аккумулятор отключен
вовремя . Уравнение схемы теперь
Первый член — это сумма
энергия, запасенная в катушке индуктивности во время. Эта энергия может быть восстановлена после
индуктор отключен от АКБ. Предположим, что аккумулятор отключен
вовремя . Уравнение схемы теперь | (936) |
давая
| (937) |
где мы использовали граничное условие. Таким образом, нынешний затухает экспоненциально.Энергия, запасенная в катушке индуктивности, рассеивается как тепло в резисторе. Полная тепловая энергия, возникающая в резисторе после аккумулятор отключен
| (938) |
где использовалась формула.
 (937).
Таким образом, тепловая энергия, возникающая в резисторе, равна
энергия, запасенная в катушке индуктивности. Эта энергия фактически хранится в магнитном
поле, создаваемое вокруг индуктора.
(937).
Таким образом, тепловая энергия, возникающая в резисторе, равна
энергия, запасенная в катушке индуктивности. Эта энергия фактически хранится в магнитном
поле, создаваемое вокруг индуктора. Рассмотрим, опять же, нашу схему с двумя катушками, намотанными одна на другую.Предположим, что
каждая катушка подключена к своей батарее. Таким образом, уравнения схемы выглядят так:
где э.д.с. батареи в первой цепи, и т. д. Работа, выполняемая двумя батареями по увеличению токов в двух цепях, от нуля в момент времени 0 до и в момент времени, соответственно,
Таким образом,
Ясно, что общая магнитная энергия, запасенная в двух катушках, равна
| (942) |
Обратите внимание, что член взаимной индуктивности увеличивает накопленную магнитную энергию, если и одного знака — i.
 е. , если токи в двух катушках текут
в том же направлении, так что они создают магнитные поля, которые усиливают
друг друга. И наоборот, член взаимной индуктивности уменьшает сохраненную
магнитная энергия, если и имеют противоположный знак. Однако общая
накопленная энергия никогда не может быть отрицательной, иначе катушки
будет представлять собой источник энергии (отрицательная накопленная энергия эквивалентна
положительная генерируемая энергия). Таким образом,
е. , если токи в двух катушках текут
в том же направлении, так что они создают магнитные поля, которые усиливают
друг друга. И наоборот, член взаимной индуктивности уменьшает сохраненную
магнитная энергия, если и имеют противоположный знак. Однако общая
накопленная энергия никогда не может быть отрицательной, иначе катушки
будет представлять собой источник энергии (отрицательная накопленная энергия эквивалентна
положительная генерируемая энергия). Таким образом, | (943) |
что можно написать
| (944) |
при условии, что .Следует, что
| (945) |
Знак равенства соответствует ситуации, когда весь поток, создаваемый одной катушкой, проходит через другую.
 Если некоторые из
поток отсутствует, значит знак неравенства соответствующий.
Фактически, приведенная выше формула верна
для любых двух индуктивно связанных цепей.
Если некоторые из
поток отсутствует, значит знак неравенства соответствующий.
Фактически, приведенная выше формула верна
для любых двух индуктивно связанных цепей. Ранее мы предполагали, что энергия, запасенная в катушке индуктивности, на самом деле
хранится в окружающем магнитном поле.Получим теперь
явная формула для энергии, запасенной в магнитном поле. Считайте идеальным
соленоид. Энергия, запасенная в соленоиде, когда через него протекает ток.
является
| (946) |
где — самоиндукция. Мы знаем это
| (947) |
где — количество витков на единицу длины соленоид, радиус и длина.Поле внутри соленоида равно равномерный, с величиной
| (948) |
и равен нулю вне соленоида.
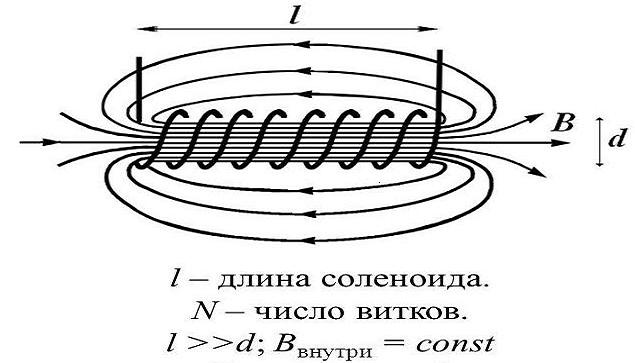 Уравнение (946) можно переписать
Уравнение (946) можно переписать | (949) |
куда объем соленоида. Приведенная выше формула сильно предполагает, что магнитное поле обладает плотностью энергии
| (950) |
Давайте теперь рассмотрим более общее доказательство приведенной выше формулы.Рассмотрим систему
цепей (обозначенных как), по каждой из которых протекает ток.
Магнитный поток через th контур записывается [ ср. ., Уравнение. (900)]
| (951) |
куда , и обозначим a элемент поверхности и линейный элемент этой схемы соответственно.
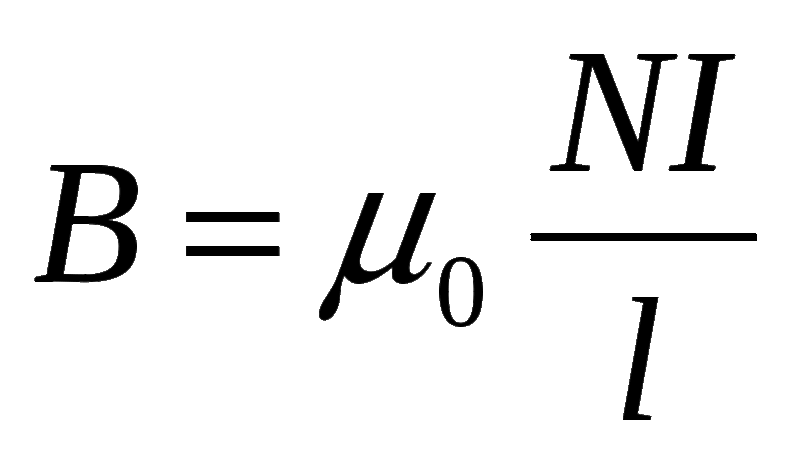 В
назад э.м.ф. индуцированный в -м контуре следует из закона Фарадея:
В
назад э.м.ф. индуцированный в -м контуре следует из закона Фарадея: | (952) |
Скорость работы аккумулятора, поддерживающего ток в ой цепи против этой спины e.м.ф. является
| (953) |
Таким образом, общая необходимая работа поднять токи в цепях с нуля во время 0, чтобы в то время, является
| (954) |
Вышеприведенное выражение для проделанной работы, конечно, эквивалентно общей сумме энергия, хранящаяся в магнитном поле, окружающем различные цепи. Эта энергия не зависит от того, как токи настроены.
 Предположим для простоты, что токи нарастают линейно,
так что
Предположим для простоты, что токи нарастают линейно,
так что | (955) |
Потоки пропорциональны токам, поэтому они также должны линейно нарастать:
| (956) |
Следует, что
| (957) |
давая
| (958) |
Итак, если в цепях, соединяющих мгновенных потоков, то мгновенная накопленная энергия равна
| (959) |
Из уравнений (951) и (959) следует, что
| (960) |
На данном этапе удобно заменить наши линейные токи на Текущий распределения небольшая, но конечная площадь поперечного сечения.
 Уравнение (960)
превращается в
Уравнение (960)
превращается в | (961) |
где — объем, содержащий все схемы. Отметим, что для элемента -й схемы а также , где — площадь поперечного сечения схема. Теперь, (мы пренебрегаем смещением ток в этом расчете), поэтому
| (962) |
Согласно теории векторного поля,
| (963) |
откуда следует, что
| (964) |
Используя теорему Гаусса, и , мы получаем
| (965) |
где — ограничивающая поверхность.
 Возьмем эту поверхность
до бесконечности. Легко показать, что магнитное поле, создаваемое током
петля падает вроде на больших расстояниях. Векторный потенциал
отваливается вроде. Однако площадь поверхности вроде только увеличивается.
Отсюда следует, что поверхностный интеграл пренебрежимо мал в пределе
.
Таким образом, приведенное выше выражение сводится к
Возьмем эту поверхность
до бесконечности. Легко показать, что магнитное поле, создаваемое током
петля падает вроде на больших расстояниях. Векторный потенциал
отваливается вроде. Однако площадь поверхности вроде только увеличивается.
Отсюда следует, что поверхностный интеграл пренебрежимо мал в пределе
.
Таким образом, приведенное выше выражение сводится к | (966) |
Поскольку это выражение справедливо для любого магнитного поля, мы можем с уверенностью заключить, что что плотность энергии общего магнитного поля определяется выражением
| (967) |
Также обратите внимание, что приведенное выше выражение согласуется с выражением (894), которые мы получили при исследовании магнитных СМИ.

Далее: Цепи переменного тока Up: Магнитная индукция Предыдущий: Взаимная индуктивность Ричард Фицпатрик 2006-02-02
Расчет оптимизированной конструкции магнитных экранов со встроенными катушками размагничивания
% PDF-1.4 % 1 0 объект > поток
 N٤o] B / Iiu! 9 + U2m +) [/ s (] [R ~ «ӿ? Wr2,, l {{O; + ЫAdLYl% TK, C_E (P: lHv: 4oxrs5As- ~ Z_y
N٤o] B / Iiu! 9 + U2m +) [/ s (] [R ~ «ӿ? Wr2,, l {{O; + ЫAdLYl% TK, C_E (P: lHv: 4oxrs5As- ~ Z_yАнализ конечных элементов метод электромагнитной индукции в линии связи поездом МАГЛЕВ — Токуда — 2020 — Электроника и связь в Японии
1 ВВЕДЕНИЕ
Когда телекоммуникационные линии прокладываются вблизи высоковольтных линий электропередачи или железных дорог, напряжение, индуцированное электромагнитными полями, представляет собой серьезную проблему для систем связи.В этом контексте IEE Japan учредило Следственный комитет по электромагнитной индукции для выявления механизмов электромагнитной индукции и принятия соответствующих мер по защите телекоммуникационных линий; отчет по этим вопросам был опубликован в 1961 году. 1 После этого комитет был преобразован в Следственный комитет IEEJ / IEICE. 2 Напряжение в линиях связи может создаваться за счет электростатической индукции и электромагнитной индукции; однако при расчетах индукции основным явлением индукции на железных дорогах считается электромагнитная индукция, которая вызывается током, протекающим в цепях питания, состоящих из подстанций, троллейных проводов, вагонов и рельсов. 3, 4
С другой стороны, сверхпроводящие магнитолевые системы, использующие постоянные токи в сверхпроводящих катушках, впервые были рассмотрены Японскими национальными железными дорогами в 1970-х годах, а затем проверены на испытательных треках Миядзаки и Яманаси. 5-16 Затем, в 2014 году министр земли, инфраструктуры, транспорта и туризма утвердил план строительства центральной линии Синкансэн между Синагавой и Нагоя, а компания Central Japan Railway Co. начала строительные работы. 17 В сверхпроводящих линейных поездах движение, левитация и наведение реализуются с использованием сильного магнитного поля, создаваемого сверхпроводящими катушками, что вызывает опасения по поводу высокого напряжения, индуцируемого в соседних телекоммуникационных линиях. Кроме того, механизмы индукции в линиях электросвязи могут отличаться от традиционных железных дорог, поэтому обычные формулы, используемые для оценки наведенного напряжения, могут не быть применимыми.
Что касается исследований явлений электромагнитной индукции в сверхпроводящих линейных системах, в дополнение к расчету токов, индуцируемых в левитации и катушках наведения, есть примеры измерений с использованием катушек обнаружения. 18 Также проводятся исследования по накоплению энергии для бортовых источников питания. 14, 19 Однако нам не известны какие-либо исследования индукционных явлений в телекоммуникационных линиях, проложенных в непосредственной близости от сверхпроводящих линейных систем, кроме исследований, проводимых в нашей лаборатории.
Для решения проблемы электромагнитной индукции, вызванной бегущим магнитным полем, которое сопровождает высокоскоростное движение по железным дорогам маглев, в нашей лаборатории несколько контуров магнитной связи, движущихся относительно друг друга, были представлены изменяющимися во времени матрицами индуктивности и смоделированы с помощью сосредоточенные схемы в попытке выполнить вычисления с MATLAB. 20 Однако эти расчеты предполагают свободное пространство там, где нет земли, таким образом, не отражая реальные магнитолевые системы, расположенные на земле.
С другой стороны, COMSOL multiphysics позволяет проводить расчеты в свободном пространстве на земле; кроме того, можно реалистично моделировать формы сверхпроводящих катушек и других компонентов. Настоящее исследование представляет собой попытку использования COMSOL multiphysics для расчета электромагнитной индукции в телекоммуникационных линиях вблизи центрального линейного синкансена.
2 ЯВЛЕНИЕ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ В ЛИНИЯХ ЭЛЕКТРОСВЯЗИ МАГЛЕВСКИХ ЖЕЛЕЗНЫХ ДОРОГ
Явление электромагнитной индукции, возникающее на местных линиях, линиях Синкансэн и других традиционных электрических железных дорогах, показано на рисунке 1. 3 На электрических железных дорогах электроэнергия для привода поездов подается от подстанций; есть прямой ток, который течет от подстанции к поездам по контактному проводу, и обратный ток, который возвращается на подстанцию от поездов по железной дороге.Когда прямой ток и обратный ток равны по величине, магнитные потоки, проходящие через линию связи, также равны, и в линии не индуцируется ток. Однако обратный ток проходит не только по шине, но и по земле; в результате магнитный поток, проникающий в линию связи, изменяется и становится отличным от магнитного потока между связями прямого тока. Эта разница вызывает индуцированное напряжение в линии.
Явление электромагнитной индукции в обычной электрической железной дороге [Цветной рисунок можно посмотреть на wileyonlinelibrary.com]Принцип движения линейного центрального синкансэн показан на рисунке 2. 21 Тележка автомобиля снабжена четырьмя парами сверхпроводящих катушек; каждая пара создает магнитный поток в обратных направлениях, как показано на рисунке 2. С другой стороны, двигательные катушки расположены вдоль заземляющих направляющих, а их магнитные потоки обратны так же, как в сверхпроводящих катушках. Когда магнитные потоки движущих катушек и сверхпроводящих катушек направлены, как показано на схеме, обе притягиваются друг к другу, и сверхпроводящие катушки перемещаются вместе с магнитным потоком движительных катушек; таким образом, тележка движется вперед.Сверхпроводящая катушка имеет 1167 витков, а приложенный ток — 600 А; то есть создается магнитодвижущая сила 700 кА 22 . С другой стороны, двигательная катушка имеет около 10 витков, в то время как приложенный ток должен быть почти таким же; таким образом, магнитодвижущая сила составляет всего около 6 кА. 23, 24 Следовательно, магнитный поток, создаваемый сверхпроводящими катушками, сильнее примерно на два порядка, и сверхпроводящие катушки рассматриваются ниже как единственный источник магнитного потока, влияющий на соседние телекоммуникационные линии.
Принцип движения в Линейном Центральном Синкансене [Цветной рисунок можно посмотреть на wileyonlinelibrary.com] Электромагнитная индукция, создаваемая сверхпроводящими катушками в линии связи, показана на рисунке 3. Как показано на рисунке 1, линия связи представляет собой кабель, состоящий из нескольких проводов; однако с точки зрения электромагнитной индукции наиболее важным является синфазное напряжение между проводами и землей.Здесь индуцированная линия моделируется синфазным контуром, образованным между опорой, несущей кабель, и землей. Магнитный поток от сверхпроводящей катушки связывается с замкнутой линией связи; по мере движения катушки этот поток изменяется, и в линии индуцируется напряжение в соответствии с законом электромагнитной индукции Фарадея. Следующее соотношение имеет место между магнитным потоком Φ взаимосвязи и наведенным напряжением U. (1) Электромагнитная индукция от сверхпроводящей катушки в линии связи [Цветной рисунок можно посмотреть в wileyonlinelibrary.com]Этот механизм электромагнитной индукции, воздействующей на телекоммуникационные линии в районе Центрального Линейного Синкансена, предполагается ниже.
3 ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ ФАРАДА С ИСПОЛЬЗОВАНИЕМ 2D-МОДЕЛИ
МодульAC / DC в COMSOL multiphysics 25 (далее COMSOL) использовался для расчета напряжения, наведенного в телекоммуникационной линии перемещением сверхпроводящих катушек. COMSOL — это инструмент моделирования на основе МКЭ, который применяется к широкому спектру физики, включая электромагнитные поля, структуры, жидкости, химические реакции и т. Д.; инструмент включает мультифизический анализ для интеграции различных физических явлений на основе сильной связи. Инструмент включает в себя ряд специальных модулей, касающихся электромагнитных и оптических систем, структурных и акустических систем, жидкостных и теплопередающих систем или химических систем; В данном исследовании используется модуль переменного / постоянного тока, предназначенный для области электромагнитного поля и оптики. Модуль AC / DC предназначен для моделирования стационарных или низкочастотных электромагнитных полей.
Со ссылкой на пример расчета напряжения, индуцированного в катушке в форме соленоида магнитом, синусоидально движущимся внутри катушки, была построена модель для расчета напряжения, индуцированного в индукционной петле во время линейного движения сверхпроводящих катушек.Расчетная модель, конфигурация сетки и распределение магнитного поля показаны на рисунке 4; это двухмерная модель, охватывающая полупространство в радиальном направлении от центральной оси.
Расчетная модель для напряжения, индуцированного в индукционной петле движущейся сверхпроводящей катушкой (2D-модель) [цветной рисунок можно увидеть на сайте wileyonlinelibrary.com]Осциллограммы напряжения, индуцированные в контуре движущейся сверхпроводящей катушкой, представлены на рисунке 5. Когда сверхпроводящая катушка входит в контур, магнитный поток увеличивается, и в соответствии с законом Фарадея об электромагнитной индукции генерируется отрицательное импульсное напряжение.С другой стороны, когда катушка выходит из контура, магнитный поток уменьшается и генерируется положительное импульсное напряжение. Наведенное напряжение увеличивается с увеличением скорости движения сверхпроводящей катушки; соотношение между максимальным индуцированным напряжением и скоростью движения показано на рисунке 6. Здесь скорость движения и максимальное индуцированное напряжение нанесены на горизонтальную и вертикальную оси соответственно; обе оси логарифмические. Например, если скорость движения увеличивается в 10 раз, максимальное наведенное напряжение также увеличивается в 10 раз; то есть скорость движения и максимальное индуцированное напряжение находятся в пропорциональной зависимости.
Форма волны напряжения, индуцированная в индукционной петле движущейся сверхпроводящей катушкой [цветной рисунок можно посмотреть на wileyonlinelibrary.com] Взаимосвязь между скоростью движения сверхпроводящей катушки и максимальным наведенным напряжением [Цветной рисунок можно увидеть на сайте wileyonlinelibrary.com]Рассмотрим частотные характеристики форм напряжения, наведенных в контуре. Как видно из рисунка 5, период формы волны индуцированного напряжения составляет около 0.08 с при скорости 2 м / с; при скорости 500 км / ч = 138,89 м / с ≈ 140 м / с период составляет около 1,14 мс. Частота, обратная периоду, составляет 877 Гц, то есть около 1 кГц. Если принять даже десятикратную частоту 10 кГц, длина волны составит 30 км. Таким образом, при длине индукционной петли около 40 м, принятой в данном исследовании, можно предположить систему с сосредоточенными параметрами.
При применении 2D-модели, показанной на рисунке 4, к 3D-модели, интерфейс 3D-магнитного поля не может быть реализован путем перемещения сетки, поскольку векторные элементы в COMSOL не поддерживают прерывность сетки.Таким образом, стремясь к соответствующему способу расчета, ниже информация о местоположении движущихся частей магнитного поля параметризуется, и координаты положения изменяются параметрически вместо временной области; при этом автоматически восстанавливается пространственная сетка.
4 РАСЧЕТ ЭЛЕКТРОМАГНИТНОЙ ИНДУКЦИИ С ПОМОЩЬЮ 3D-МОДЕЛИ С ПОЗИЦИОННОЙ ЗАВИСИМОСТЬЮ, РАССЧИТАННОЙ В ПАРАМЕТРЕ
4.1 Структура 3D-модели
Конструкция сверхпроводящей катушки и тележки, несущей катушки, показана на рисунке 7.Сверхпроводящая катушка, показанная на рисунке 7A, имеет 1167 витков. К катушке прикладывают постоянный ток 600 А, так что магнитодвижущая сила составляет 700 кА. 22
Структура сверхпроводящей катушки и тележки, несущей ее [Цветной рисунок можно посмотреть на сайте wileyonlinelibrary.com]Восемь сверхпроводящих катушек расположены в тележке, как показано на рисунке 7B. 26 Пара сверхпроводящих катушек расположена на расстоянии 2,98 м друг от друга поперек пути Центрального Линейного Синкансена; четыре таких пары расположены 1.На расстоянии 35 м друг от друга по трассе. Магнитные потоки сверхпроводящих катушек в соседних парах направлены противоположно, как показано на рисунке 7B. Тележка вместе со сверхпроводящими катушками движется вправо; первая пара катушек обозначена как № 1, а последняя пара катушек обозначена как № 4.
На рисунке 8 показана модель COMSOL для расчета электромагнитной индукции, вызываемой в телекоммуникационной линии движением сверхпроводящих катушек. Рисунки 8A-C относятся, соответственно, к наклонному виду сверху, поперечному сечению и виду сбоку основной части модели.Центральная часть аналитической области включает сверхпроводящую катушку и телекоммуникационную линию. Чтобы имитировать бесконечное пространство на земле, базовая плоскость модели представляет собой электрическую стену, а боковые плоскости и верхняя плоскость окружены областью бесконечных элементов. На рисунке 8A пространство модели показано в трехмерных координатах; Ось x , y и z относятся к направлению движения тележки, направлению ширины колеи и вертикальному направлению, соответственно.
Модель расчета электромагнитной индукции от COMSOL [Цветной рисунок можно посмотреть в wileyonlinelibrary.com]В Центральном Линейном Синкансене пути часто проходят глубоко под землей, а под ними могут быть проложены линии связи. Кроме того, даже на надземных участках линии связи прокладываются по поверхности земли; однако с помощью COMSOL индукцию в телекоммуникационных линиях можно рассчитать при любом из таких условий. С другой стороны, нет прецедентов применения COMSOL для индукции на линиях связи, проложенных в районе Центрального Линейного Синкансена; поэтому адекватность анализа COMSOL должна быть сначала проверена путем подтверждения основных характеристик на простейшей модели с петлей линии связи, расположенной на металлической поверхности.
Индукция в телекоммуникационной линии включает синфазную цепь; поэтому линия связи моделируется петлей длиной L и высотой H, как показано на рисунке 8C. Поперечное сечение телекоммуникационной линии принято равным 0,1 × 0,1 м 2 , чтобы упростить конфигурацию сетки в расчетах COMSOL. Петля телекоммуникационной линии размещается на базовой плоскости модели в контакте с электрической стенкой. Кроме того, как показано на рисунке 8B, сверхпроводящая катушка на стороне петли линии связи находится на расстоянии D от петли.
4.2 Расчет индуцированного напряжения по позиционной зависимости магнитного потока между связями
Напряжение U, , индуцированное в петле линии связи, и магнитный поток Φ , проникающий в петлю, подчиняются закону электромагнитной индукции Фарадея, как показано в уравнении (1). В 2D COMSOL, описанном в разделе 3, уравнение (1) вычисляется напрямую; с другой стороны, в этом подразделе делается попытка вычисления с координатой положения x , рассматриваемой как параметр: (2)Как показано на рисунке 8A, тележка со сверхпроводящими катушками движется только вдоль оси x ; поэтому используется полная производная, а не частная.В правой части уравнения (2) dΦ / dx представляет собой производную относительно позиционной зависимости магнитного потока взаимосвязи, а dx / dt — скорость тележки. Таким образом, dΦ / dx может быть определено из позиционной зависимости магнитного потока взаимосвязи, а затем умножено на скорость тележки, чтобы получить напряжение U , индуцированное в петле линии связи.
4.3 Позиционная зависимость магнитного потока между связями
На рисунке 9 показано, как магнитный поток, проникающий в телекоммуникационный контур из сверхпроводящей катушки, зависит от положения тележки.Когда расстояние D между сверхпроводящей катушкой и петлей линии связи составляет 0,2 м, петля будет в положении движущей катушки, что является недопустимым состоянием. Тележка со сверхпроводящими катушками, расположенными на ней, как показано на фиг. 7B, движется вправо; поэтому сверхпроводящая катушка № 1, которая сначала проходит рядом с вертикальным проводом на расстоянии 10 м, создает магнитный поток в направлении — y (отрицательное направление). Из-за положительного магнитного потока сверхпроводящей катушки No.2, магнитный поток в том же положении становится положительным. Из-за отрицательного магнитного потока сверхпроводящей катушки № 3 магнитный поток там снова становится отрицательным. Из-за положительного магнитного потока сверхпроводящей катушки № 4 магнитный поток там снова становится положительным; однако с удалением от этого положения положительный и отрицательный магнитные потоки четырех сверхпроводящих катушек компенсируют друг друга, и магнитный поток, проходящий через петлю телекоммуникационной линии, становится нулевым.
Зависимость магнитного потока межсоединения от положения тележки в петле телекоммуникационной линии [Цветной рисунок можно посмотреть в wileyonlinelibrary.com]С другой стороны, когда сверхпроводящая катушка № 1 проходит около 50 м, отрицательный магнитный поток покидает петлю линии связи, и взаимосвязь становится положительной. После этого картина магнитного потока становится противоположной.
Когда расстояние D между сверхпроводящей катушкой и петлей линии связи составляет 2,1 м, линия связи является ближайшей к линейной линии Синкансэн. Другими словами, линию связи нельзя прокладывать ближе, чем на 2.1 мес. При D = 2,1 м магнитный поток между связями уменьшается примерно на порядок по сравнению с D = 0,2, и его изменение становится медленным. При этом общий магнитный поток отрицательный, когда тележка входит в петлю линии связи, и положительный, когда она выходит из петли.
4.4 Позиционная зависимость наведенного напряжения
Зависимость магнитного потока межсоединения от положения тележки в петле телекоммуникационной линии показана на рисунке 9; Затем на рисунке 10 показана производная потока dΦ / dx в зависимости от положения x .Как следует из уравнения (2), напряжение U , индуцированное в контуре телекоммуникационной линии, может быть получено как произведение этих dΦ / dx и dx / dt (то есть скорости тележки). Предполагая, что максимальная скорость на Центральной линии Синкансэн составляет 500 км / ч (138,89 м / с), индуцированное напряжение рассчитывается как dΦ / dx , умноженное на 138,89. Зависимость полученного таким образом напряжения от положения тележки показана на рисунке 11. Пиковое значение индуцированного напряжения достигает примерно ± 35 В при D = 0.2 м, но уменьшается примерно до ± 1,5 В при D = 2,1 м.
Позиционная зависимость дифференциальной формы волны dΦ / d магнитного потока между связями в петле линии связи [Цветной рисунок можно посмотреть на wileyonlinelibrary.com] Напряжение, индуцированное в контуре телекоммуникационной линии при скорости тележки 500 км / ч [Цветной рисунок можно посмотреть на сайте wileyonlinelibrary.com]Из вышеизложенного следует, что напряжение, индуцированное в линии связи сверхпроводящей катушкой, движущейся с произвольной скоростью, может быть рассчитано на основе магнитного потока катушки, проникающего в контур, в частности, путем определения позиционной зависимости магнитного потока между связями и применения закона Фарадея. электромагнитная индукция, как показано в уравнении (2).
5 СРАВНЕНИЕ НАЗЕМНОЙ МОДЕЛИ И ИДЕАЛЬНОЙ МОДЕЛИ СВОБОДНОГО ПРОСТРАНСТВА
Связанный магнитный поток в петле линии связи, создаваемый сверхпроводящей катушкой, был рассчитан COMSOL выше; Чтобы проверить адекватность расчета, мы сравнили модель, сконфигурированную на поверхности земли, как показано на Рисунке 8B, и модель, сконфигурированную в свободном пространстве без земли, как показано на Рисунке 12. На схеме область бесконечных элементов, такая же, как и с боковые плоскости и верхняя плоскость предполагается для базовой плоскости вместо электрической стены на рисунке 8B.В отличие от рисунка 8B, где телекоммуникационный контур контактировал с электрической стенкой (землей), между контуром и областью бесконечного элемента в базовой плоскости предусмотрено пространство 2,5 м.
Расчетная модель электромагнитной индукции в COMSOL в идеальном свободном пространстве [Цветной рисунок можно посмотреть на сайте wileyonlinelibrary.com]Магнитный поток, проходящий через петлю линии связи в наземной модели и в модели совершенного свободного пространства, сравнивается на рисунке 13.Здесь расстояние D между сверхпроводящей катушкой и петлей линии связи рассматривается как параметр. На рисунке 13 значения вычислений MATLAB показаны в дополнение к значениям COMSOL; это будет объяснено ниже.
Сравнение наземной и совершенной моделей свободного пространства для магнитного потока связи в петле линии связи [Цветной рисунок можно посмотреть на wileyonlinelibrary.com]На рисунке 9 магнитный поток между связями в контуре телекоммуникационной линии сначала показывает пик со многими отрицательными составляющими, а затем пик с множеством положительных составляющих.Эти пики одинаковы по форме, отличаются только знаком; таким образом, на фиг. 13 показан только первый из них. Следует отметить, что вертикальная ось представляет собой центробежные значения, поскольку поток взаимосвязей невелик.
Как видно из рисунка 13, магнитный поток между связями при D = 0,2 м лишь немного меньше в модели идеального свободного пространства, чем в модели на земле. Такая же тенденция наблюдается и при D = 2,1 м, но разница несколько больше; разница увеличивается при увеличении D до 5.1 м и 10,1 м.
Чтобы изучить этот вопрос, мы рассмотрим, как магнитный поток, создаваемый сверхпроводящей катушкой, связывается с контуром телекоммуникационной линии, как показано на рисунке 14. На схеме контур телекоммуникационной линии сконфигурирован на земле на различном расстоянии D от сверхпроводящей катушки. , и зеркальное отображение формируется под землей. Без плоскости земли есть только реальное изображение над землей; однако, когда существует заземляющая плоскость, появляется зеркальное изображение, и магнитный поток, проходящий через контур, также удваивается.Когда контур телекоммуникационной линии приближается к сверхпроводящей катушке на расстоянии D = 0,2 м, отрицательный магнитный поток зеркального изображения проходит через реальный контур в дополнение к положительному магнитному потоку реального изображения, так что общий поток межсоединений уменьшается. Точно так же межзависимый поток уменьшается и в зеркальном контуре.
Зеркальное отображение магнитного потока сверхпроводящей катушки, соединенной с петлей телекоммуникационной линии, заземленной на идеальное заземление [Цветной рисунок можно посмотреть в wileyonlinelibrary.com]Как упоминалось выше, магнитный поток наземных межсоединений был почти таким же, как и при идеальном свободном пространстве на D = 2,1 м; это связано с тем, что общая взаимосвязь в реальном изображении составляла примерно половину положительного потока из-за увеличения отрицательного потока, и то же явление произошло в зеркальном отображении. С другой стороны, чем больше D в контуре реального изображения, реальный магнитный поток меньше компенсируется магнитным потоком зеркала; таким образом, при D = 2,1 м магнитный поток наземной связи становится несколько больше, чем при полном свободном пространстве.При дальнейшем увеличении D разница увеличивается, достигая примерно 20% при D = 5,1 м и примерно 50% при D = 10,1 м. То есть результаты, рассчитанные COMSOL для магнитного потока между связями в модели на земле и в модели совершенного свободного пространства, согласуются с качественными тенденциями на рис. 14.
На рис. 15 показано наведенное напряжение, полученное из позиционной зависимости потока межсоединений в петле линии связи на рис. 13. Наведенное напряжение составляет около ± 35 В при D = 0,2 м, где расположены катушки левитации и наведения; однако напряжение падает примерно до ± 1.5 В при D = 2,1 м, ± 0,15 В при D = 5,1 м и ± 0,02 В при D = 10,1 м. В последнем случае уровень наведенного напряжения очень низкий, и результаты COMSOL колеблются из-за ошибок расчетов; эта флуктуация ярко выражена в модели идеального свободного пространства. Однако зависимость индуцированного напряжения от D в обеих моделях совпадает с зависимостью потока межсоединений от D, что очевидно из сравнения рисунков 13 и 15.
Сравнение наземных моделей и моделей в идеальном свободном пространстве для наведенного напряжения в контуре телекоммуникационной линии [Цветной рисунок можно увидеть в wileyonlinelibrary.com]В модели, принятой в этом исследовании, напряжение индуцируется в телекоммуникационной петле, расположенной на металлической поверхности с почти нулевым сопротивлением заземления; то есть рассчитывается наихудший случай. Тем не менее, даже на самом близком расстоянии от линии связи (D = 2,1 м) наведенное напряжение составляет ± 1,5 В, что значительно ниже предельного значения 15 В для нормального наведенного продольного напряжения. С другой стороны, нормальное наведенное шумовое напряжение 0,5 мВ превышено, но это вряд ли проблема, учитывая сопротивление заземления и сопротивление заземления контура телекоммуникационной линии или коэффициент преобразования продольного (синфазного) напряжения в дифференциальное напряжение, и т.п.Кроме того, наведенное напряжение на стандартном расстоянии D = 5,1 м составляет всего около ± 0,15 В, что на порядок меньше по сравнению с D = 2,1 м.
6 СРАВНЕНИЕ С МОДЕЛЬЮ ЦЕПИ С СИСТЕМАМИ С СИГНАЛИЗАЦИЯМИ
В нашей лаборатории расчеты MATLAB проводятся с использованием модели сосредоточенной схемы; при этом несколько контуров магнитной связи, движущихся относительно друг друга, представлены изменяющимися во времени матрицами индуктивности. Мы сравнили эти расчеты с 3D-моделью COMSOL.Модель сосредоточенной схемы для расчета электромагнитной индукции с использованием MATLAB представлена на рисунке 16. В расчетах MATLAB учитываются не только сверхпроводящие катушки, но также комбинированные катушки левитации и наведения. Модель схемы магнитной связи как для сверхпроводящих катушек, так и для левитационных / направляющих катушек также показана на рисунке 16.
Модель расчета электромагнитной индукции с помощью модели сосредоточенной схемы с использованием MATLAB [Цветной рисунок можно просмотреть в wileyonlinelibrary.com] Сверхпроводящие катушки имеют нулевое внутреннее сопротивление, поэтому предполагается, что выводы закорочены; Что касается катушек левитации / наведения, верхняя и нижняя катушки с соответствующим внутренним сопротивлением — соединены в виде восьмерки. Кроме того, для воспроизведения линии нулевого потока подключены две восьмерки. С v , i и Φ , обозначающими, соответственно, напряжение на клеммах, втекающий ток и магнитный поток взаимосвязи каждого контура, получаются следующие уравнения схемы.(3) Кроме того, уравнение (4) может быть получено путем применения матричного представления к уравнению (3) и выражения напряжения и тока через магнитный поток Φ . (4)Здесь K, и R — матрицы коэффициентов для напряжения и тока соответственно, а L — матрица индуктивности; Пожалуйста, обратитесь к литературе 20 для получения этих матриц ( L считается обычным).Уравнение (4) можно рассматривать как одновременные обыкновенные дифференциальные уравнения относительно Φ , но K является сингулярной матрицей и не может быть вычислена как есть. Пожалуйста, обратитесь к литературе 20 для разложения по сингулярным числам K . Используя это разложение по сингулярным значениям, можно найти ток, индуцированный в каждой петле, что делает возможным вычисление магнитного поля в произвольное время и в произвольном месте.
Результаты вышеуказанных вычислений с использованием MATLAB представлены на рисунке 13B-D.Магнитный поток между связями, рассчитанный MATLAB в идеальном свободном пространстве, примерно на 30% выше по сравнению с результатами COMSOL, и это соотношение остается таким же при D = 2,1, 5,1 и 10,1 м. Как бы то ни было, результаты, полученные двумя совершенно разными методами, совпали примерно на 30%, и можно сказать, что адекватность расчетов проверена не только для COMSOL, но и для MATLAB.
Чтобы объяснить разницу в результатах расчетов между COMSOL и MATLAB, вычисления были выполнены с измененной формой сверхпроводящих катушек.В COMSOL форма сверхпроводящих катушек имитирует трехмерную форму реальных катушек, как показано на рисунке 7A; с другой стороны, в MATLAB форма аппроксимируется тонкой линией, проходящей через центр поперечного сечения с шириной и высотой, показанными на фиг. 7A. Когда эта линейная форма использовалась в расчетах COMSOL, магнитный поток между связями был немного меньше при D = 2,1 и 5,1 м, что не могло объяснить разницу. Следовательно, существует еще одна причина, которую еще предстоит изучить.
7 ВЫВОДЫ
Следующее стало очевидным благодаря использованию модуля AC / DC в COMSOL multiphysics для расчета электромагнитной индукции в линиях связи, проложенных в районе Центрального Линейного Синкансена.- (1)
Результаты, рассчитанные на основе закона электромагнитной индукции Фарадея с двумерной подвижной сеткой, показали, что напряжение, индуцированное в контуре телекоммуникационной линии, пропорционально скорости движения сверхпроводящей катушки.
- (2)
При трехмерном анализе зависимость магнитного потока, проходящего через контур телекоммуникационной линии от сверхпроводящей катушки, от положения катушки, чтобы обойтись без движущейся сетки, и наведенное в контуре напряжение рассчитывалось на основе закона электромагнитной индукции Фарадея.
- (3)
С помощью COMSOL магнитный поток, связанный с петлей линии связи, был рассчитан не только для наземной модели, но и для модели совершенного свободного пространства без земли. Таким образом, полученные результаты соответствовали качественно ожидаемым тенденциям; То есть была проверена адекватность расчетов COMSOL.
- (4)
Метод расчета COMSOL с использованием зависимости положения сверхпроводящей катушки был сравнен с методом расчета MATLAB с использованием изменяющихся во времени матриц индуктивности и сосредоточенных схем для представления контуров связи, движущихся относительно друг друга; результаты согласуются в пределах 30%, что подтверждает адекватность обоих методов.
- (5)
В Линейном Центральном Синкансене импульсное напряжение возникает в замкнутой телекоммуникационной линии согласно закону электромагнитной индукции Фарадея, когда сверхпроводящие катушки проходят рядом с вертикальными проводами. Пиковое значение индуцированного таким образом импульсного напряжения зависит от расстояния D между сверхпроводящей катушкой и петлей линии связи и составляет около ± 1,5 В при D = 2,1 м, ± 0,15 В при D = 5,1 м и ± 0,02 В при D = 10,1 м; таким образом, индуцированное напряжение быстро уменьшается с расстоянием.
- (6)
В модели, принятой в этом исследовании, напряжение индуцируется в телекоммуникационной петле, расположенной на металлической поверхности с почти нулевым сопротивлением заземления; то есть рассчитывается наихудший случай. Более того, даже на самом близком расстоянии от линии связи (D = 2,1 м) наведенное напряжение составляет ± 1,5 В, что значительно ниже предельного значения 15 В для нормального наведенного продольного напряжения.
Расчеты в MATLAB дали значения примерно на 30% больше, чем в COMSOL, и причина этого должна быть определена.
Следует рассматривать модель, размещенную на поверхности земли с соответствующей проводимостью, а не на металлической поверхности.
Наведенное напряжение необходимо рассчитать для телекоммуникационных линий, проложенных под железными дорогами в туннеле, что является наиболее частым случаем в Центральном Линейном Синкансене.
ПОДТВЕРЖДЕНИЕ
Мы выражаем глубокую благодарность г-ну Масанори Хасигучи из Keisoku Engineering System Co., Ltd., представителю COMSOL multiphysics в Японии, за его сотрудничество в вычислениях COMSOL с позиционной информацией, рассматриваемой в качестве параметра.
Биографии
Масамицу ТОКУДА — старший член.В 1957 году он окончил университет Хоккайдо, а в 1969 году он закончил магистратуру в университете и был принят на работу в NTT. Он занимался исследованиями в области электромагнитной совместимости волоконно-оптических кабелей, устройств связи и т. Д. В 1996-2001 годах он работал профессором Технологического института Кюсю (электротехника). В 2001-2010 годах он работал профессором Технологического института Мусаси, а в настоящее время работает в Токийском городском университете (англ. Information Network Eng.). В 2010 году он был почетным профессором Токийского городского университета.С 2010 года он был приглашенным исследователем в Токийском университете (Grad. School of Frontier Sci.). С 2017 года он является специальным исследователем в Токийском технологическом институте (факультет электротехники и электроники). Он проводил свои исследования в области электромагнитной индукции, создаваемой в линиях связи системами Маглев. В 2006-2011 гг. Получил степень доктора технических наук. Кроме того, он был председателем IEC / TC 77, а с 2007 года является научным сотрудником IEEE.
Ёсимаса САКАЙ не является членом.В 2017 году он окончил Токийский технологический институт (факультет инженерии, факультет электротехники и электроники) и поступил в магистратуру университета (факультет инженерии, факультет электротехники и электроники). Он провел исследование шума, создаваемого поездами на магнитной подвеске.
Джунки ЯРИТА не является членом. В 2017 году он окончил Токийский технологический институт (школа инженеров, кафедра электротехники и электроники) и поступил в магистратуру института (школа инженеров., Кафедра электротехники и электроники). Он проводил исследования в области тонких световозвращателей.
Атсухиро НИСИКАТА является участником. В 1984 г. окончил Токийский технологический институт (факультет физики). В 1986 году окончил магистратуру института (факультет электротехники и электроники). В 1989 году он получил степень доктора технических наук и работал в исследовательской лаборатории связи Министерства почт и связи.В 1993 году он работает научным сотрудником в Токийском технологическом институте (факультет электроники). В 1995 году работает доцентом в Институте (Центр исследований и разработок образовательных технологий). В 2007 году он работает доцентом, а в 2011 году — адъюнкт-профессором в Grad. Школа Решения Sci. и Тех. (Человеческие системы). В 2016 году работает доцентом в School of Eng. (Электротехника и электроника, англ.). Он проводил свои исследования в области электромагнитной совместимости, электромагнитных волн и акустики.Он является членом IEEE, Общества биоэлектромагнетиков.
ССЫЛКИ
- 1 IEE. IEE Japan, Отчет следственной комиссии по электромагнитной индукции (1963 -9 ). (на японском)
- 2 IEEJ. IEEJ / IEICE, Отчет специальной следственной комиссии по электромагнитной индукции (1993 -11 ).(на японском)
- 3Такеучи К., Ямагути Д. Явления электромагнитной индукции на обочине железной дороги. РУБ . 2106; 73 (8): 8-11. (На японском языке).
- 4 Центр технической помощи и поддержки NTT East. Прогнозный расчет индукции при проектировании оборудования связи. NTT Gijutsu J. 2006; 7: 70-71.(на японском)
- 5Мията С. Концепция исследования и развития системы МАГЛЕВ. Представитель РТРИ . 1994; 8 (10): 1-6. (На японском языке).
- 6Ошаки Х., Такабатаке М., Масада Э. Магнитная градиентная левитация с использованием объемных высокотемпературных сверхпроводников. IEEE Trans Appl Supercond . 1997; 7: 908-911.
- 7Охаси С., Осаки Х., Масада Э.Эквивалентная модель электродинамической подвесной системы боковой стенки. T IEE Япония . 1997; 117-D (6): 758-767. (на японском языке)
- 8Масада Э., Фуджи Дж., Като Дж., Мизума Т. Технология систем MAGLEV. Токио, Япония: ОМ-ша; 1992: 29-108 (на японском языке).
- 9Савада К. Продолжающееся развитие сверхпроводящего маглев. J IEE J . 2000; 120 (4): 204-207. (на японском языке).
- 10Мизума Т. Текущее состояние и перспективы линейных транспортных систем. J IEE J . 2000; 120 (4): 479-481. (на японском языке).
- 11Масада Э. Передовые тенденции систем Maglev. 1. Магнитно-левитирующие железные дороги (Маглев) как транспортная система в 21 веке. J IEE J . 2001; 121 (10): 678-681. (на японском языке).
- 12Косеки Т. Тенденции развития и внедрения зарубежных систем Maglev. J IEE J . 2001; 121 (10): 694-697. (на японском языке).
- 13 Япония IEE. Нелинейные технологии в системах Maglev: к многофункциональности систем Maglev. IEE J Tech Rep .2001 (819): 24-34. (на японском языке).
- 14Kitano J. Система питания сверхпроводящей транспортной системы Маглев. J IEE J . 2004; 124 (8): 520–523. (На японском языке).
- 15Охсаки Х. Сверхпроводящий магнитопровод для сверхскоростной транспортировки. Ойо Бутури . 2011; 80 (5): 403-406. (на японском языке)
- 16Осаки Х.Сверхскоростные / Маглевские железные дороги. Справочник по железнодорожной технике. 1-е изд. Токио, Япония: ОМ-ша; 2102: 9. (на японском языке)
- 17Honda A. III Обзор центрального проекта Синкансэн с использованием сверхпроводящего линейного двигателя. J JSME . 2017; 120 (1179): 16-21. (На японском)
- 18 Фуджимото Т, Айба А, Сузуки Н, Умэки Т, Накамура С.Характеристики электромагнитной силы катушки заземления для левитации и наведения испытательной линии Яманаши Маглева. Представитель РТРИ . 1999; 13 (9): 15-18. (На японском языке).
- 19Касиваги Т., Мураи Т., Ямамото Т., Хасегава Х., Сано Т., Танака Т. Управление выходной мощностью и коэффициентом мощности в преобразователе линейного генератора для системы Маглев. IEEJ Trans IA . 2004; 124 (10): 1029-1035 (на японском языке).
- 20Сакаи Й, Нишиката А, Токуда М.Метод анализа магнитосвязанной петлевой системы с относительным движением для расчета электромагнитной индукции поездом МАГЛЕВ. Технический представитель компании IEICE . 2018; EMCJ2018-2: 7-12. (На японском языке)
- 21Ошима Х. IV Обзор сверхпроводящей линейной технологии. J JSME . 2017; 120 (1179): 22-29. (На японском языке).
- 22Tsuchishima H, Suzuki E, Terai M.Разработка новых сверхпроводящих магнитов для испытательной линии Яманаши. Представитель РТРИ . 1994; 8 (10): 17-22. (На японском языке)
- 23Андо М., Накамичи Ю., Аджики К., Шигида Х., Судзуки М. Имитационная модель распространения помпажа катушек движителя для Maglev. Представитель РТРИ . 2000; 14 (11): 17-22. (На японском языке)
- 24Murai T, Fujimoto T, Fujiwara S.Характеристики линейного синхронного двигателя, сочетающего движение, левитацию и наведение. Представитель РТРИ . 1996; 10 (1): 35-40 (на японском языке).
- 25 Инженерная система Кэйсоку. COMSOL мультифизика. https://kesco.co.jp/service/comsol/multiphysics/, 10 сентября 2019 г.
- 26Azakami M. Разработка системы тележки Maglev на первом составе испытательной линии Яманаси. Представитель РТРИ . 1996; 10 (1): 11-16. (На японском языке)
Уравнение закона Фарадея с простыми решенными примерами
Эксперименты показали, что при изменении магнитного потока через поверхность, ограниченную проводом, в проводе генерируется ЭДС (напряжение), равное скорости изменения магнитного потока.
С простой установкой мы можем продемонстрировать закон Фарадея:
1) Возьмитесь за магнит и переместите его к неподвижному проводящему кольцу из проволоки, подключенному к амперметру.Амперметр показывает прогиб.
2) Теперь отодвиньте магнит от кольца. Опять же, амперметр показывает отклонение, но в обратном направлении.
3) В третьем случае и магнит, и кольцо неподвижны. Амперметр не показывает отклонений.
4) Теперь предположим, что магнит зафиксирован, а петля движется к магниту или от него. Результат: амперметр считывает ток!
Это простое наблюдение показывает, что ток индуцируется в проволочной петле, когда магнит или петля движутся навстречу или от друг друга.
Другими словами, ток индуцируется (создается) в замкнутом проводящем пути, когда существует относительное движение между магнитом и замкнутым контуром. Этот ток создается наведенной ЭДС.
Все вышеперечисленные слова можно резюмировать следующим образом:
Если магнитный поток через петлю изменяется со временем, то вокруг петли индуцируется ЭДС (напряжение). Средняя индуцированная ЭДС равна \ [\ mathcal {E} = — \ frac {\ Delta \ Phi_m} {\ Delta t} \] Это закон индукции Фарадея.
Знак минус в уравнении закона Фарадея связан с направлением наведенной ЭДС.
Основные сведения об уравнении закона Фарадея:
(1) ЭДС индуцируется в замкнутом контуре или любой другой замкнутой проводящей цепи, пока существует изменяющийся магнитный поток.
(2) магнитный поток в приведенном выше уравнении — это полный поток через замкнутый контур. Если катушка имеет $ N $ плотно намотанных петель, то $ \ Phi_m = N \ phi_m $, где $ \ phi_m $ — поток, проходящий через каждую петлю катушки.2} $ располагается перпендикулярно однородному магнитному полю. Без изменения направления магнитного поля его величина уменьшается на $ 0,08 \, {\ rm T} $ в интервале времени $ 0,02 \, {\ rm s} $. Найти среднюю наведенную ЭДС в контуре?
Решение : согласно закону индукции Фарадея, изменяющийся магнитный поток через замкнутую поверхность, ограниченную проводом, создает ЭДС с величиной $ \ mathcal {E} = | \ frac {\ Delta \ Phi_m} { \ Delta t} | $.
Напомним, что поток через поверхность площадью $ A $ определяется как $ \ Phi_m = \ vec {B} \ cdot \ hat {n} A $, где $ \ hat {n} $ — единичный вектор ( вектор, величина которого равна единице), нормальный (перпендикулярный) к этой поверхности.2} $ помещают в однородное магнитное поле с напряженностью $ B = 0,2 \, {\ rm T} $ так, чтобы плоскость петли была перпендикулярна полю. После $ 2 \, {\ rm s} $ магнитное поле меняет свое направление на противоположное. Найдите величину средней ЭДС, наведенной в контуре за это время.
Решение : Согласно закону Фарадея изменяющийся магнитный поток создает ЭДС в замкнутом пути или цепи.
С другой стороны, магнитный поток также является произведением магнитного поля , площади и косинуса угла между $ \ vec {B} $ и единичного вектора, нормального к плоскости.\ circ $ с однородным магнитным полем. Величина магнитного поля изменяется со временем как $ 8 \, {\ rm \ frac {T} {s}} $, пока его направление остается фиксированным. Какова величина наведенной ЭДС в катушке?
Решение : Величина наведенной ЭДС (напряжения) определяется уравнением закона Фарадея как \ [\ mathcal {E} = \ left | \ frac {\ Delta \ Phi_m} {\ Delta t} \ right | \] Здесь из трех факторов, входящих в формулу магнитного потока ($ \ Phi_m = BA \ cos \ theta $), только величина магнитного поля $ B $ изменяется со временем, поэтому, вставив ее в приведенную выше формулу, мы получаем \ begin {align *} \ mathcal {E} & = \ left | \ frac {\ Delta \ Phi_m} {\ Delta t} \ right | \\ \\ & = \ left | \ frac {\ Delta (BA \ cos \ theta)} {\ Delta t} \ right | \\\\ & = \ left | \ left (\ frac {\ Delta B} {\ Delta t} \ right) A \ cos \ theta \ right | \\\\ & = ( 8) (0.\ circ \\ \\ & = 0.64 \ quad {\ rm V} \ end {align *} Это наведенная ЭДС в одном витке катушки с $ N $ витком.
Полная наведенная ЭДС равна количеству витков $ N $, умноженному на ЭДС, индуцированную в каждом витке, как $ \ mathcal {E} _t = N \ mathcal {E} $, таким образом, мы получаем \ [\ mathcal {E} _t = 400 \ times 0,64 = 256 \ quad {\ rm V} \]
Пример (4): Круглая катушка со 100 витками и радиусом $ r = 10 \, {\ rm cm} $ и сопротивлением $ 10 \, {\ rm \ Omega} $ помещена в однородное магнитное поле так, чтобы он перпендикулярен плоскости катушки.{-5} \ quad {\ rm Wb} \ end {align *} Изменение общего потока через катушку составляет \ [\ Delta \ Phi_m = N \ phi_1 = 0,02 \]. Величина наведенной ЭДС получается с использованием закона Фарадея. формулу, как показано ниже \ begin {align *} \ mathcal {E} & = — \ frac {\ Delta \ Phi_m} {\ Delta t} \\ & = — \ frac {0.02} {0.2} \\ & = — 0.1 \ quad {\ rm V} \ end {align *} Минус показывает направление ЭДС, индуцированной в соленоиде.
Чтобы узнать больше о решенных примерах, перейдите по ссылке , здесь .
Дата публикации: 19.02.2021
Автор : Али Немати

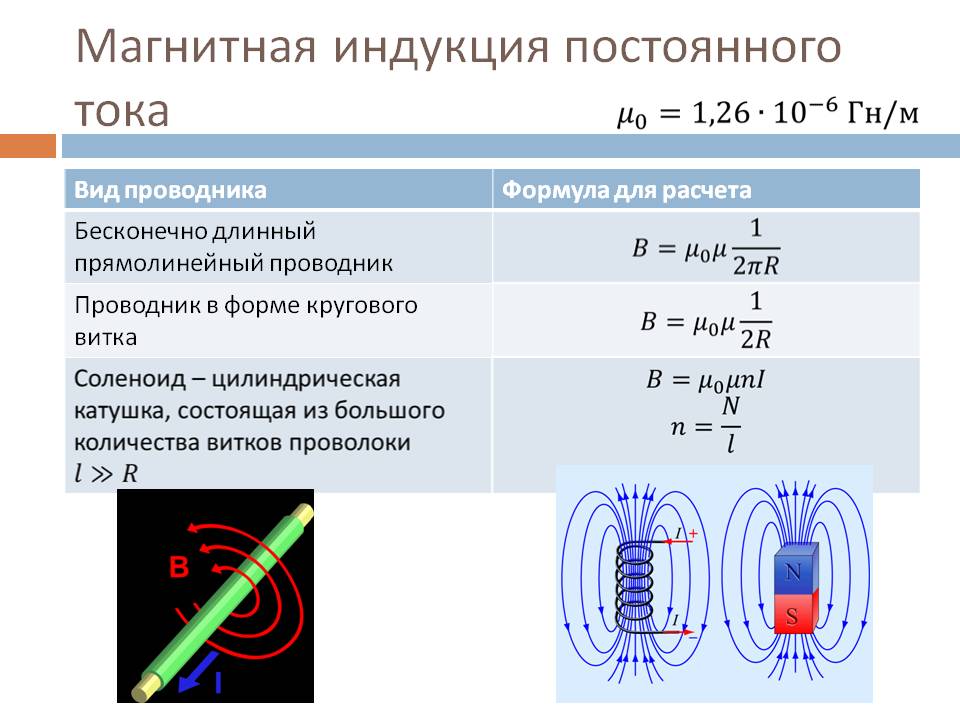 Собственно данный интерфейс и предназначен для решения закона сохранения тока, протекающего по двумерному слою.
Собственно данный интерфейс и предназначен для решения закона сохранения тока, протекающего по двумерному слою.

 Ее рекомендуется применять в цепях постоянного тока, так как при повышении частоты значительно увеличиваются потери.
Ее рекомендуется применять в цепях постоянного тока, так как при повышении частоты значительно увеличиваются потери.