Расчёт делителя напряжения на резисторах онлайн
Р/л технология
Схема такого делителя предназначена для получения заданного выходного напряжения, которое будет ниже, чем входное. Например, источник напряжения 24 Вольта, в нужно получить 6 Вольт. Самым простым способом решить этот вопрос – это применить делитель напряжения, состоящий из двух споротивлний.
Он применяется, как при проектировании схем, так и по прямому назначению. Для его расчета используются формулы, которые основаны на законе Ома. Эти формулы позволяют подобрать нужный номинал сопротивлений. Потребуется лишь знать сопротивление нагрузки, входное и выходное напряжения. От этого сопротивления зависит, насколько точно удастся рассчитать весь делитель и получить точно указанное выходное напряжение. Как правило, сопротивление нагрузки выше, чем сопротивление делителя напряжения.
Если неизвестно выходное напряжение, но известно сопротивление и входное напряжения, то неизвестную величину можно вычислить по указанной формуле.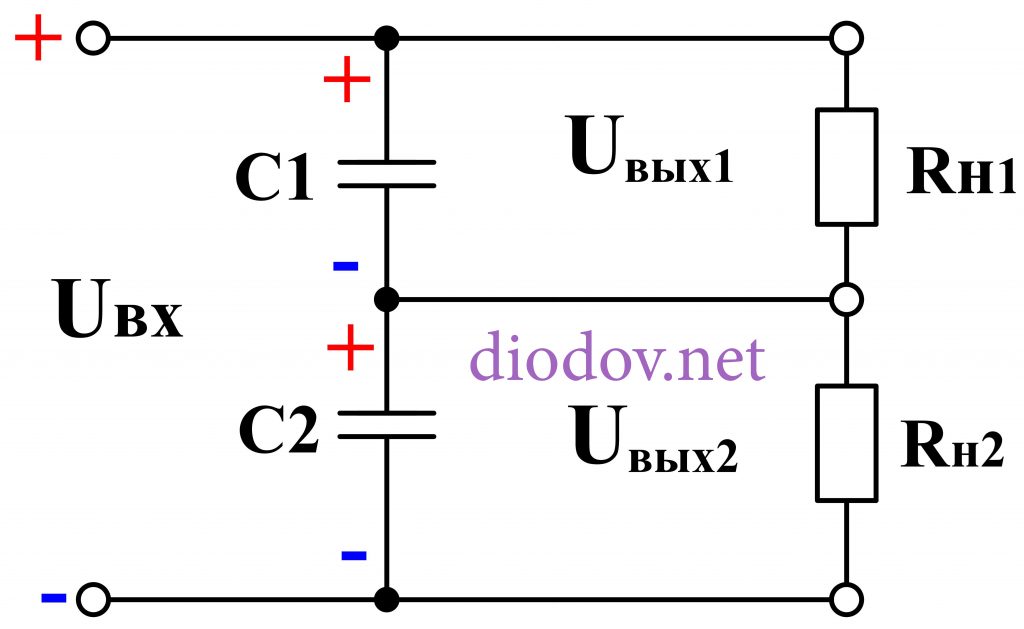
Для того чтобы не считать постоянно по формулам эти величины, были придуманы онлайн-калькуляторы, которые позволяют точно определить значения резисторов или выходного напряжения. Потребуется лишь внести известные величины. Такой расчет можно производить, как на компьютере, с доступом в сеть Интернет, так и при помощи смартфона. Это значительно экономит время и дает стабильную точность расчетов.
Стоит отметить, что современные калькуляторы-онлайн могут рассчитать и мощность, на которую должен быть установлен резистор.
В радиоэлектронике делители напряжения представлены и в готовых конструктивных решениях. Ими служат, к примеру, переменные резисторы и фоторезисторы, которые имеют возможность менять значение сопротивления, при повороте ручки потенциометра или попадании света. В переменном резисторе присутствуют три вывода, с которых можно получить два сопротивления.
Автор: RadioRadar
Мнения читателей
Нет комментариев. Ваш комментарий будет первый.
Ваш комментарий будет первый.
Вы можете оставить свой комментарий, мнение или вопрос по приведенному выше материалу:
Поля, обязательные для заполнения
Добавить
Очистить
Расчёт делителя напряжения
Всем привет, дорогие читатели! Сегодня мы рассмотрим с Вами такую тему как: «Расчёт делителя напряжения».
Перед прочтением статьи, советую ознакомиться со следующим материалом: Что такое ток простыми словами.
Недавно я столкнулся с маленькой проблемой: Надо было завести в контроллер аналоговый сигнал 0-10 Вольт с потенциометра 5кОм, но в шкафу управления у меня было только 24 Вольта. Задача вроде лёгкая, но на мгновение я завис. Сейчас я расскажу, как я легко подобрал сопротивления для делителя напряжения. Дело в том, что с одним потенциометром не получится решить задачу, так как он будет регулировать диапазон от 0 до 24 Вольт, а мне надо от 0 до 10 Вольт.
Давайте сначала поэкспериментируем и изобразим поставленную задачу наглядно. Изобразим схему, на которой мы всё-таки оставили один потенциометр и подали на него 24 Вольта.
Изобразим схему, на которой мы всё-таки оставили один потенциометр и подали на него 24 Вольта.
Воспользуемся законом Ома и определим, какое напряжение будет на верхнем вольтметре. Для начала вычислим ток в цепи:
I = 24 Вольта / 5000 Ом=0,0048 Ампера
А теперь давайте выставим потенциометр так, чтобы сопротивление между средней и верхней точкой было 1 кОм (тогда между средней и нижней точкой сопротивление будет 4 кОм), и найдём падение напряжения на верхнем участке цепи:
U1= I * R= 0,0048 Ампер * 1000 Ом= 4,8 Вольт
Затем вычислим падение напряжения на нижнем участке цепи:
U2= I * R= 0,0048 Ампер * 4000 Ом= 19,2 Вольт
Если вы будете менять сопротивление потенциометра от 0 до 5 кОм, то заметите, что напряжение у Вас будет меняться от 0 до 24 Вольт. А как же нам сделать, чтобы напряжение менялось от 0 до 10 Вольт? Всё просто! Надо добавить в цепь простой резистор.
Расчёт делителя напряжения
Нам надо получить на переменном резисторе 10 Вольт.
Применим второй закон Кирхгофа (ЭДС= сумме падений напряжений на отдельных участках цепи)
24 вольта= 10Вольт+ X
X= 24 Вольта – 10 Вольт = 14 вольт
Значит на другом резисторе у нас должно быть 10 Вольт.
Теперь вычислим ток в нашей цепи согласно закону Ома
I = U / R
I= 10 Вольт/5000 Ом= 0,002 А.
Ток при последовательном соединении резисторов везде одинаковый, значит такой же ток будет и на верхнем резисторе (R1).
Теперь мы можем вычислить номинал верхнего сопротивления по закону Ома.
R = U / I
R= 14 Вольт/ 0,002 А= 7000 Ом.
Вывод: Если мы поставим один резистор номиналом 7000 Ом, то на втором переменном резисторе будет падение напряжения от 0 до 10 Вольт.
Подсказка: Чтобы быстро вычислить номинал резистора воспользуйтесь следующей формулой:
U1 / U2 = R1 / R2
Найдём R1= (14 Вольт * 5000 Ом)/10 Вольт= 7000 Ом.
2.2. Расчет делителя напряжения
Нужно спроектировать делитель напряжения для сигналов a,b,c,d. Уровни логической единицы этих сигналов 10 В.
Для правильной работы микросхем К155ЛА3, использованных в логическом блоке нам надо иметь напряжения U = 2,4 В.
Рис.6
На вход подаётся напряжение Uвх= 10 В, то напряжение на выходе будет сниматься с резистора R19 и будет равно Uвых= 2,4 В;
Возьмём общее сопротивление резисторов равным 500 кОм (R18 + R19 =500 кОм), тогда ток протекающий через все сопротивления при входном напряжении будет равен:
А;
Падение напряжения на резисторе R19 равно U2 = 2,4 В, тогда падение напряжения на резисторе R18 равно U
Исходя из падений напряжений на каждом резисторе, найдём номиналы этих резисторов:
Выберем номинал резистора R18 из ряда Е192, параметры которого:
номинал: 379 кОм;
точность:
±0,25%.
Выберем номинал резистора R32 из ряда Е192, параметры которого:
номинал: 120 кОм;
точность: ±0,25%.
Подобный делитель следует поставить для всех сигналов
2.3. Электронный аналоговый ключ
Электронный аналоговый ключ широко используется в электронике для осуществления передачи аналоговой информации от одного блока к другому. Исходя из параметров разрабатываемого прибора применяем микросхему аналогового ключа КР590КН9, который имеет следующие характеристики: tвкл.=500нс;
U 1вх =0,8…4 В;
U 0вх=0.
UП=15.
На рисунке представлены схемное обозначение и упрощенная физическая модель микросхемы КР590КН9.
Рис.7
Пока на вход Uупр подается сигнал низкого уровня КМОП-транзистор закрыт, сопротивление канала высокое, при подачи на вход напряжение высокого уровня, то транзистор открывается, сопротивление понижается, и ток утечки течет через него.
На входы 4 и 5 подаются входные аналоговые сигналы, которые снимаются с выходов 3 и 6 соответственно. На входы 10 и 15 подаются сигналы управления ключами. К выводам 11 и 13 подводятся напряжения питания ±15 В соответственно. Вывод 14 подключается к общему приводу схемы прибора.
Схема включения ключа:
Рис.8
В
качестве элемента И-НЕ используем один элемент с микросхемы
К155ЛА3.
3. Проектирование цифрового частотомера
Необходимо разработать частотомер, измеряющий частоту в полосе заданных частот (50 … 6000 Гц).
Рис. 9
1. Усилитель ограничитель (на временной диаграмме – F) сигналов (рис.9) предназначен для преобразования аналогового сигнала в цифровой. Построен на триггере Шмитта (К561ТЛ1), ОУ140УД22, стабилитроне Д809 и диоде КД522А. R1 = 2 кОм.
Рис.10
Временные диаграммы формирователя представлены на рис.8, на которых представлены сигналы на входе, после усилителя и после триггера Шмитта.
Рис.11
 9).
9).Рис. 12
В этой схеме включения конденсатор С1 заряжается через резисторы R1 и R2 до напряжения , а разряжается через резистор R1 до напряжения .
Длительность зарядки конденсатора t1=0,69(
 Тогда , R2=145
кОм, R
Тогда , R2=145
кОм, R3. Счетчик состоящий из дешифратора(К176ИЕ4) и индикатора(АЛС324Б)
В частотомере используется 4 таких микросхемы, т.к. разрядность цифрового индикатора частоты равна 4.
4. R–C – цепочка. Предназначена для подачи на вход R кратковременных импульсов для обнуления счетчика и сброса индикатора. Время разряда конденсатора должно быть гораздо меньше по сравнению с величиной
= 1,67-4 с. Зададим = 210-5 с и R = 3 кОм. Так как = RC, тогда С = 6,67 нФ. Из ряда Е192 возьмем С = 6,65 нФ
Временные диаграммы работы частотомера:
Рис. 13
13
схема и расчёт [Амперка / Вики]
Принцип делителя напряжения
Это правило применяют при расчетах электросхем, упрощающих решение. Также оно действительно и для простых схем.
Важно! Основная концепция правила: напряжение делится между двумя резисторами, соединенными последовательно, в прямой зависимости от их сопротивления.
Когда выполняется практический расчет делителя напряжения, составляется электросхема, и выводятся необходимые формулы.
Схема делителя напряжения на резисторах
Схема делителя напряжения включает в себя входной источник напряжения и два резистора. Ниже вы можете увидеть несколько схематических вариантов изображения делителя, но все они несут один и тот же функционал.
Профессиональный цифровой осциллограф
Количество каналов: 1, размер экрана: 2,4 дюйма, разрешен…
Подробнее
Обозначим резистор, который находится ближе к плюсу входного напряжения (Uin) как R1, а резистор находящийся ближе к минусу как R2. Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Падение напряжения (Uout) на резисторе R2 — это пониженное напряжение, полученное в результате применения резисторного делителя напряжения.
Назначение и применение
Для преобразования переменного напряжения применяется трансформатор, благодаря которому можно сохранить достаточно высокое значение тока. Если необходимо в электрическую цепь подключить нагрузку, потребляющую небольшой ток (до сотен мА), то использование трансформаторного преобразователя напряжения (U) не является целесообразным.
В этих случаях можно использовать простейший делитель напряжения (ДН), стоимость которого существенно ниже. После получения необходимой величины U выпрямляется и происходит подача питания на потребитель. При необходимости для увеличения силы тока (I) нужно использовать выходной каскад увеличения мощности. Кроме того, существуют делители и постоянного U, но эти модели применяются реже остальных.
ДН часто применяются для зарядок различных устройств, в которых нужно получить из 220 В более низкие значения U и токов для разного типа аккумуляторов. Кроме того, целесообразно использовать устройства для деления U для создания электроизмерительных приборов, компьютерной техники, а также лабораторных импульсных и обыкновенных блоков питания.
Кроме того, целесообразно использовать устройства для деления U для создания электроизмерительных приборов, компьютерной техники, а также лабораторных импульсных и обыкновенных блоков питания.
В общем случае устройства этого типа выполняют преобразование по формуле Uвых=Uвх*К, где:
- Uвх (вых) – напряжения на входе и выходе, соответственно;
- К – корректирующий множитель, обозначающий передающие способности узла.
Если взять первый пример из рис. выше, для уточнения сути процессов подойдет второй закон Кирхгофа. В соответствии с этим правилом, общее значение напряжений на последовательно соединенных резисторах будет равно сумме ЭДС на каждом элементе. Так как ток не изменяется в замкнутом контуре, для расчета можно использовать закон Ома:
U (напряжение) = I (ток) * R (электрическое сопротивление)
Нижнюю часть схемы (плечо) используют для получения необходимого изменения входного параметра.
Подбор/расчет резисторов для делителя напряжения
Поставим себе задачу собрать определенный делитель напряжения. Нам понадобится рассчитать два резистора для делителя напряжения таким образом, чтобы при входном питающем напряжении Vвх = 5 В, выходное напряжение было равно Vвых=1,9 В.
Итак, с чего начать рассчитывать резисторы делителя напряжения? С закона Ома для участка цепи!
Сила тока, который будет проходить через делитель напряжения при напряжении на входе Vcc=Vвх, равна
Отсюда выходное напряжение Vвых=Vout
Понятно, что чем больше сопротивление резистора R1, тем меньше будет значение выходного напряжения, снимаемого с делителя напряжения на резисторах R1 и R2.
А теперь решим поставленную выше задачу для подбора резисторов делителя напряжения при напряжении на входе делителя = 5В и требуемом выходном напряжении с делителя = 1,9В.
Расчет резисторов делителя напряжения
Итак, собственно, само решение. Подбираем резисторы для делителя напряжения, исходя из вышеупомянутого закона Ома. Отношение выходного напряжения делителя ко входному будет равно 1,9 В / 5 В. Помним, что резистор R2 делителя напряжения подсоединен к земле.
Пример расчета резисторов делителя
Итак. Вход = 5 В. Выход = 1,9 В.
Ответ: R1 = 620 Ом. R2 = 380 Ом.
Конечно же, можно подобрать и другие резисторы, например, 62 Ома и 38 Ом или 295,26 Ом и 481,74 Ом. Главное, чтобы отношение (R2/(R1+R2)) было равно 0,38 (или 1,9/5).
Схема
Вот четыре варианта возможного исполнения:
Схема интегрального делителя напряжения
Можно добиться разных значений, изменяя схему подключения и ориентируясь на задачи. Каждый элемент можно использовать как регулятор для напряжения, необходимо только правильно выстроить цепь, чтобы были отображены именно необходимые данные.
Что такое делитель тока
Делитель тока — это устройство, позволяющее разделить поток тока на две части, чтобы в дальнейшем использовать одну из них. Он нужен, когда устройство не работает с большим током и нужно отделить его меньшее количество, необходимое для использования аппаратуры.
Состоит делитель обычно из двух резисторов, параллельно соединённых, так в каждом из них будет уменьшаться ток.
При последовательном соединении будет уменьшаться напряжение.
Пример 2
Общий ток цепи, содержащей два соединенных параллельно резистора
R1 =70 Ом иR2 =90 Ом, равен 500 мА. Определить токи в каждом из резисторов. Два последовательно соединенных резистора ничто иное, как делитель тока . Определить токи, протекающие через каждый резистор можно с помощью формулы делителя, при этом напряжение в цепи нам не нужно знать, потребуется лишь общий ток и сопротивления резисторов.
Токи в резисторах
В данном случае удобно проверить задачу с помощью первого закона Кирхгофа, согласно которому сумма токов сходящихся, в узле равна нулю.
Если вы не помните формулу делителя тока, то можно решить задачу другим способом. Для этого необходимо найти напряжение в цепи, которое будет общим для обоих резисторов, так как соединение параллельное. Для того чтобы его найти, нужно сначала
Выполняет сразу несколько очень важных задач: служит ограничителем электрического тока в цепи , создает падение напряжения на отдельных ее участках и разделяет пульсирующий ток.
Помимо номинального сопротивления, одним из наиболее важных параметров резистора
является рассеиваемая мощность. Она зависима от напряжения и тока. Мощность — это то тепло, которое выделяется на резисторе, когда под воздействием протекающего тока он нагревается. При пропуске тока, превышающего заданное значение мощности, резистор может сгореть.
Мощность постоянного тока может быть рассчитана по простой формуле P(Вт) = U(В) * I(А)
,
- P(Вт) — мощность,
- U(В) — напряжение,
- I(А) — ток.

Чтобы избежать сгорания резистора тока, необходимо учитывать его мощность. Соответственно, если схема указывает на замену резистора с мощностью 0,5 Ватт — 0,5 Ватт в данном случае — минимум.
Мощность резистора
может зависеть от его размеров. Как правило, чем меньше резистор — тем меньше мощность его рассеивания. Стандартный ряд мощностей резисторов тока состоит из значений:
- 0.125 Вт
- 0.25 Вт
- 0.5 Вт
- Более 2 Вт
Рассмотрим на примере: номинальное сопротивление нашего резистора
тока — 100 Ом. Через него течет ток 0,1 Ампер. Чтобы , на которую рассчитан наш резистор тока, необходимо воспользоваться следующей формулой: P(Вт) = I2(А) * R(Ом),
- P(Вт) — мощность,
- R(Ом) — сопротивление цепи (в данном случае резистора),
- I(А) — ток, протекающий через резистор.
Внимание!
При расчётах следует соблюдать размерность. Например, 1 кА= 1000 А. Это же касается и других величин.
Итак, рассчитаем мощность для нашего резистора тока: P(Вт) = 0,12(А) *100 (Ом)= 1(Вт)
Получилось, что минимальная мощность нашего резистора составляет 1 Ватт. Однако в схему следует установить резистор
с мощностью в 1,5 — 2 раза выше рассчитанной. Соответственно идеальным для нас будет резистор тока мощностью 2 Вт.
Бывает, что ток, протекающий через резистор неизвестен. Для расчёта мощности в таком случае предусмотрена специальная формула:
Соединение цепи может быть последовательным и параллельным. Однако никакого труда не составляет рассчитать мощность резистора тока
как в параллельной, так и в последовательной цепи. Следует учитывать лишь то, что в последовательно цепи через резисторы течет один ток.
Например, нам необходимо произвести замену резистора
тока сопротивлением 100 Ом. Ток, протекающий через него — 0,1 Ампер. Соответственно, его мощность — 1 Ватт. Следует рассчитать мощность двух соединенных последовательно резисторов для его замены. Согласно формуле расчёта мощности, мощность рассеивания резистора на 20 Ом — 0,2 Вт, мощность резистора на 80 Ом — 0,8 Вт. Стандартный ряд мощностей поможет выбрать резисторы тока:
Согласно формуле расчёта мощности, мощность рассеивания резистора на 20 Ом — 0,2 Вт, мощность резистора на 80 Ом — 0,8 Вт. Стандартный ряд мощностей поможет выбрать резисторы тока:
Формула для расчёта делителя напряжения
Как рассчитать резистор для понижения напряжения ?
Для расчёта получаемой в итоге нагрузки, нужно знать следующие данные: U исходное и значение сопротивления в каждом из составных элементов.
Делитель рассчитывается с учётом того, что проходящий через него ток минимум в 10 раз больше, чем на выходе и меньше, чем входящий в сеть.
Можно рассчитать общее сопротивление в резисторах:
R=R1*R2/(R1+R2)
В параллельно соединённых резисторах U1=U2, из это можно сделать вывод, что в сети протекает общий ток: I=I1+I2
Найти общий ток можно, зная закон Ома
Применение делителя напряжения на резисторах
В радиоэлектронике есть много способов применения делителя напряжения. Вот только некоторые примеры где вы можете обнаружить их.
Потенциометры
Потенциометр представляет собой переменный резистор, который может быть использован для создания регулируемого делителя напряжения.
Изнутри потенциометр представляет собой резистор и скользящий контакт, который делит резистор на две части и передвигается между этими двумя частями. С внешней стороны, как правило, у потенциометра имеется три вывода: два контакта подсоединены к выводам резистора, в то время как третий (центральный) подключен к скользящему контакту.
Если контакты резистора подключения к источнику напряжения (один к минусу, другой к плюсу), то центральный вывод потенциометра будет имитировать делитель напряжения.
Переведите движок потенциометра в верхнее положение и напряжение на выходе будет равно входному напряжению. Теперь переведите движок в крайнее нижнее положение и на выходе будет нулевое напряжение. Если же установить ручку потенциометра в среднее положение, то мы получим половину входного напряжения.
Резистивные датчики
Большинство датчиков применяемых в различных устройствах представляют собой резистивные устройства.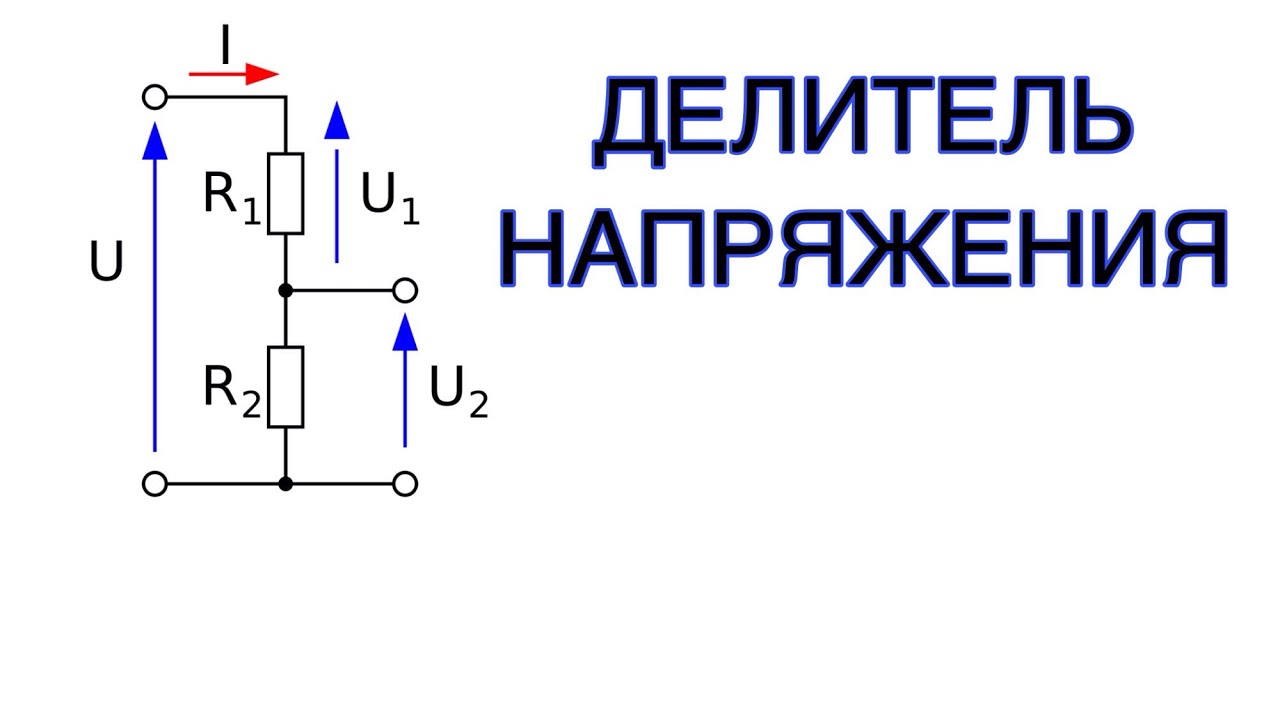 Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.
Фоторезистор представляет собой переменный резистор, который изменяет свое сопротивление, пропорциональное количеству света, падающего на него. Так же есть и другие датчики, такие как датчики давления, ускорения и термисторы и др.
Так же резистивный делитель напряжения помогает измерить напряжение при помощи микроконтроллера (при наличии АЦП).
Пример работы делителя напряжения на фоторезисторе.
Допустим, сопротивление фоторезистора изменяется от 1 кОм (при освещении) и до 10 кОм (при полной темноте). Если мы дополним схему постоянным сопротивлением примерно 5,6 кОм, то мы можем получить широкий диапазон изменения выходного напряжения при изменении освещенности фоторезистора.
Как мы видим, размах выходного напряжения при уровне освещения от яркого до темного получается в районе 2,45 вольт, что является отличным диапазоном для работы большинства АЦП.
Помогите проекту. Поделитесь с друзьями.
Рассмотрим, как рассчитать практически любой делитель напряжения на резисторах. Преимущественное большинство радиоэлектронных элементов и микросхем питаются относительно низким напряжением – 3…5 В. А многие блоки питания выдают U = 9 В, 12 В или 24 В. Поэтому для надежной и стабильной работы различных электронных элементов необходимо снижать величину напряжения до приемлемого уровня. В противном случае может наступить пробой радиоэлектронных элементов. Особенно следует уделять внимание микросхемам – наиболее чувствительным элементам к повышенному напряжению.
Преимущественное большинство радиоэлектронных элементов и микросхем питаются относительно низким напряжением – 3…5 В. А многие блоки питания выдают U = 9 В, 12 В или 24 В. Поэтому для надежной и стабильной работы различных электронных элементов необходимо снижать величину напряжения до приемлемого уровня. В противном случае может наступить пробой радиоэлектронных элементов. Особенно следует уделять внимание микросхемам – наиболее чувствительным элементам к повышенному напряжению.
Существуют много способов, как снизить напряжение. Выбор того или другого способа зависит от конкретной задачи, что в целом определяет эффективность всего устройства. Мы рассмотрим самый простой способ – делитель напряжения на резисторах, который, тем не менее, довольно часто применяется на практике, но исключительно в маломощных цепях, что поясняется далее.
Чтобы сделать и рассчитать простейший делитель напряжения достаточно соединить последовательно два резистора и подключить их источнику питания.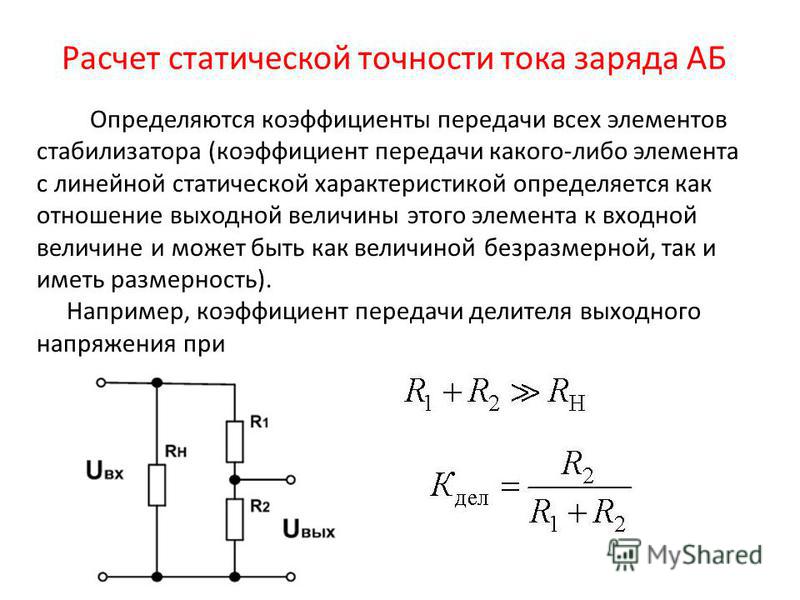 Такая схема очень распространенная и применяется более чем в 90 % случаев.
Такая схема очень распространенная и применяется более чем в 90 % случаев.
Вход схемы имеет два вывода, а выход – три. При одинаковых значения сопротивлений R1 и R2 выходные напряжения Uвых1 и Uвых2 также равны и по величине вдвое меньше входного Uвх. Причем выходное U можно сниматься с любого из резисторов – R1 или R2. Если сопротивления не равны, то выходное U будет на резисторе большего номинала.
Точное соотношение Uвых1 к Uвых2 рассчитаем, обратившись к закону Ома. Резисторы вместе с источником питания образуют последовательную цепь, поэтому величина электрического тока, протекающего через R1 и R2 определяется отношением напряжения источника питания Uвх к сумме сопротивлений:
Следует обратить внимание, чем больше сумма сопротивлений, тем меньший ток I при том же значении Uвх.
Далее, согласно закону Ома, подставив значение тока, находим Uвых1 и Uвых2:
Путем подстановки в две последние формулы значение из самой первой формулы, находим значение выходного U в зависимости от входного и сопротивлений двух резисторов:
Применяя делитель напряжения на резисторах, необходимо понимать и помнить следующее:
- Коэффициент полезного действия такой схемы довольно низкий, поскольку только часть мощности источника питания поступает к нагрузке, а остальная мощность преобразуется в тепло, выделяемое на резисторах.
 Чем больше понижается напряжение, тем меньше мощности от источника питания поступит к нагрузке.
Чем больше понижается напряжение, тем меньше мощности от источника питания поступит к нагрузке. - Так как нагрузка подключается параллельно к одному из резисторов делителя, то есть шунтирует его, то общее сопротивление цепи снижается и происходит перераспределение падений напряжений. Поэтому сопротивление нагрузки должно быть гораздо больше сопротивления резистора делителя. В противном случае схема будет работать нестабильно с отклонением от заданных параметров.
- Распределение U между R1 и R2 определяется исключительно их относительными значениями, а не абсолютными величинами. В данном случае неважно, будут ли R1 и R2 иметь значение 2 кОм и 1 кОм или 200 кОм и 100 кОм. Однако при более низких значениях сопротивлений можно получить большую мощность на нагрузке, но следует помнить, что и больше мощности преобразуется в тепло, то есть израсходуется невозвратно впустую.
Также иногда находят применение и более сложные делители напряжений, состоящие из нескольких последовательно соединенных резисторов.
Делитель напряжения на переменном резисторе
Схему делителя напряжения на переменном резисторе называют схемой потенциометра. Вращая рукоятку громкости музыкального центра или автомагнитолы, вы таким действием плавно изменяете напряжение, подаваемое на усилитель модности звуковой частоты. Принцип работы и сборка простейшего усилителя мощности уже были ранее рассмотрены .
При перемещении (вращении) ручки переменного резистора сверху вниз по чертежу происходит плавное изменение U от значения источника питания до нуля.
В звуковой технике главным образом применяются переменные резисторы с логарифмической зависимостью, поскольку слуховой аппарат человек воспринимает звуки с данной зависимостью. Для регулирования уровня звука одновременно по двум каналам используют сдвоенные переменные резисторы.
В качестве делителя напряжения находят применение переменные резисторы, имеющие следующие зависимости сопротивления от угла поворота ручки: логарифмическую, линейную и экспоненциальную. Конкретный тип зависимости применяется для решения отдельной задачи.
Конкретный тип зависимости применяется для решения отдельной задачи.
Помогите проекту. Поделитесь с друзьями.
Виды и принцип действия
В основе принципа действия устройства, уменьшающего нагрузку сети, лежит первый закон Кирхгофа: сумма сходящихся в узле токов равна нулю.
Принцип работы у всех одинаковый: в них есть U исходное: такое же, как в источнике питания и получаемое на выходе из сети, зависящее от соотношения резисторов в плечах делителя.
Схема, позволяющая понять принцип действия:
Различают разные устройства, в зависимости от элементов в составе:
- резистивный — более популярен из-за простоты устройства.
- ёмкостный;
- индуктивный.
Как работает
На практике использование устройств несколько сложнее, чем просто рассчитать требуемые значения для элементов. Использование схемы замещения для делителей напряжения усложняет реалистичный учет фазовых и амплитудных характеристик. Эта проблема может быть решена исключительно экспериментальным путём. Затруднительно так сделать только если наблюдаются очень высокие частоты.
Эта проблема может быть решена исключительно экспериментальным путём. Затруднительно так сделать только если наблюдаются очень высокие частоты.
Графическое изображение работы
В качестве доступной альтернативы используется экспериментальное определение реакции схемы на прямоугольный импульс. Его суть — наблюдение за состоянием, когда на входе происходит скачкообразное изменение напряжения. При единичном воздействии можно наблюдать особенности работы благодаря переходной функции измерительной схемы.
Реакция определяется двумя способами:
- Первый предполагает, что на вход полностью собранной схемы подают периодически импульсы с амплитудой в 100В (50 или 100 раз в секунду). Фронт их нарастания должен составлять меньше 10-9 с. Получение таких импульсов не является делом сложным. Для этого можно воспользоваться механическими коммутаторами с герконом или ртутным реле. На выходе схемы измеряется реакция посредством осциллографа, на котором присутствует широкополосной усилитель, величина пропускания которого составляет до 109 Гц.

- Второй способ используется для схем, у которых напряжение составляет несколько десятков киловольт. В таком случае делают крутой срез посредством малоиндуктивного искрового промежутка, помещенного в условия сжатого газа. На выходе с помощью обычного осциллографа записывается реакция. Также вместо среза часто обращаются к использованию разряда заряженного кабеля и волнового сопротивления через искровой промежуток.
Описывая работу делителей напряжения, нельзя обойти вниманием постоянную времени. Чтобы правильно измерять показатели быстропротекающих процессов, необходимо добиться различия в 5-10 раз. Постоянная времени делителя должна быть меньше характеристического времени процесса. Если не получить разницу в 5-10 раз, то будут фиксироваться различные искажения. Наиболее вероятные — это затягивание фронта вместе с уменьшением амплитуды сигнала на выходе в сравнении с расчетными показателями.
Важно! При выборе делителя в первую очередь внимание обращают на его возможное влияние, оказываемое на источник напряжения, равно как и искажения основного параметра при измерении. Например, в случае использования обычных ГИН допустимыми считаются резисторные, емкостные и смешанные устройства, но только при соблюдении оговоренных условий. К таковым относятся значения емкости плеча высокого напряжения и сопротивление.
Например, в случае использования обычных ГИН допустимыми считаются резисторные, емкостные и смешанные устройства, но только при соблюдении оговоренных условий. К таковым относятся значения емкости плеча высокого напряжения и сопротивление.
Вам это будет интересно Расцветка шин по фазам
Расчет делителя напряжения на резисторах, конденсаторах и индуктивностях
Делитель на резисторах — отличается своей универсальностью: используют при постоянном и переменном токе, но только при пониженном сопротивлении цепи.
Согласно закону Ома и правилу Кирхгофа через всю цепь будет проходить один и тот же ток.
Тогда на каждом из резисторов: U1= I х R1 и U2 = I х R2 Ток в цепи устройства:
Уменьшение на конденсаторах применяют для цепей с высоким переменным током. В нём минимальная потеря энергии на выходе. Реактивное сопротивление конденсатора зависит от его электроёмкости и частоты напряжения в цепи.
Формула для вычисления сопротивления:
Делитель на индуктивностях используется при переменном низком токе на высоких частотах. Сопротивление катушки переменного тока прямо пропорционально зависит от индуктивности и частоты. У провода катушки имеется активное сопротивление, из-за чего мощность такого прибора больше, чем у аналогов.
Сопротивление катушки переменного тока прямо пропорционально зависит от индуктивности и частоты. У провода катушки имеется активное сопротивление, из-за чего мощность такого прибора больше, чем у аналогов.
Сопротивление катушки находится по формуле:
Делитель напряжения на катушках индуктивностях
Делитель напряжения на индуктивностях применяются в радио устройствах и считаются комплексными сопротивлениями с распределенными параметрами в схемах согласования… В общем если вы не специалист в этой области то вам такое и не надо. Но для общего развития приведу схему с формулой
Замечу, что приведенная формула чисто теоретическая и не учитывает момент включения, насыщение сердечника, межвитковую ёмкость, скин-эффект, механические характеристики.
P.S. Спасибо пользователям “Юра” и “Bagira” с форума Полный писец за помощь в написании статьи.
Практическое применение параллельного и последовательного соединения
Составные элементы прибора соединяют в цепь, чтобы получить из сети нужную для устройства часть энергии.
Пример работы делителя напряжения на фоторезисторе.
Исходное сопротивление меняется от 1кОм в момент полного освещения до 10кОм при отсутствии света, то можно увеличить диапазон сопротивления. При добавлении резисторов с R=5,6кОм, исходящее напряжение меняется следующим образом:
| Освещённость | R1 (кОм) | R2(кОм) | R2/(R1+R2) | U выходное (В) |
| Яркая | 5,6 | 1 | 0,15 | 0,76 |
| Тусклая | 5,6 | 7 | 0,56 | 2,78 |
| Темнота | 5,6 | 10 | 0,67 | 3,21 |
Таким образом, увеличивается диапазон выходного напряжения, и оно становится подходящим для большинства сетей.
Потенциометры
Потенциометры используют в качестве делителя в системе с постоянным током. Их применяют в основном для изменения отдельных параметров в механизме.
Нелинейные делители
Мы упомянули, что к нелинейным делителям относится параметрический стабилизатор. В простейшем виде он состоит из резистора и стабилитрона. У стабилитрона условное обозначение на схеме похоже на обычный полупроводниковый диод. Разница лишь в наличии дополнительной черты на катоде.
Расчет происходит, отталкиваясь от Uстабилизации стабилитрона. Тогда если у нас есть стабилитрон на 3.3 вольта, а Uпитания равно 10 вольт, то ток стабилизации берут из даташита на стабилитрон. Например, пусть он будет равен 20 мА (0.02 А), а ток нагрузки 10 мА (0.01 А).
Тогда:
R=12-3,3/0,02+0,01=8,7/0,03=290 Ом
Разберемся как работает такой стабилизатор. Стабилитрон включается в цепь в обратном включении, то есть если Uвыходное ниже Uстабилизации – ток через него не протекает. Когда Uпитания повышается до Uстабилизации, происходит лавинный или туннельный пробой PN-перехода и через него начинает протекать ток, который называется током стабилизации. Он ограничен резистором R1, на котором гасится разница между Uвходным и Uстабилизации. При превышении максимального тока стабилизации происходит тепловой пробой и стабилитрон сгорает.
Он ограничен резистором R1, на котором гасится разница между Uвходным и Uстабилизации. При превышении максимального тока стабилизации происходит тепловой пробой и стабилитрон сгорает.
Кстати иногда можно реализовать стабилизатор на диодах. Напряжение стабилизации тогда будет равно прямому падению диодов или сумме падений цепи диодов. Ток задаете подходящий под номинал диодов и под нужды вашей схемы. Тем не менее такое решение используется крайне редко. Но такое устройство на диодах лучше назвать ограничителем, а не стабилизатором. И вариант такой же схемы для цепей переменного тока. Так вы ограничите амплитуду переменного сигнала на уровне прямого падения — 0,7В.
Вот мы и разобрались что это такое делитель напряжения и для чего он нужен. Примеров, где применяется любой из вариантов рассмотренных схем можно привести еще больше, даже потенциометр в сущности является делителем с плавной регулировкой коэффициента передачи, и часто используется в паре с постоянным резистором. В любом случае принцип действия, подбора и расчетов элементов остается неизменным.
Напоследок рекомендуем посмотреть видео, на котором более подробно рассматривается, как работает данный элемент и из чего состоит:
Материалы по теме:
- Способы понижения напряжения
- Что такое активная, реактивная и полная мощность
- Как работает реле напряжения
Что такое делитель тока
Какие ассоциации у вас возникают при словосочетании “делитель тока”? У меня сразу возникает ассоциация с делителем потока. Давайте представим себе реку, у которой очень большой поток.
Это поток воды бежит с очень большой скоростью! Он смывает на своем пути камни, землю, деревья. Представьте, что эта река находится рядом с вашим домом. Через год-два ваш дом смоет под чистую! Чтобы этого не произошло, надо ослабить течение реки, чтобы ее поток был слабый. Например как здесь:
Но как это сделать? А почему бы нам не прорыть большой канал, чтобы бОльшая часть воды текла через него. А это хорошая идея не так ли?
Весь смак заключается в том, что в каждой отдельной речке скорость воды будет меньше. В электротехнике и электронике все тоже самое! Река – это провод, сила потока – это сила тока, ширина реки – сопротивление, напряжение – угол наклона реки. Все элементарно и просто!
Схема традиционного резисторного делителя напряжения
Для применения делителя напряжения нам надо уметь рассчитывать три величины: напряжение на выходе делителя, его эквивалентное выходное сопротивление, его входное сопротивление. С напряжением все понятно. Эквивалентное выходное сопротивление скажет нам, насколько изменится напряжение на выходе с изменением тока нагрузки делителя. Если эквивалентное выходное сопротивление равно 100 Ом, то изменение тока нагрузки на 10 мА приведет к изменению напряжения на выходе на 1 В. Входное сопротивление показывает, насколько делитель нагружает источник сигнала или источник питания. Дополнительно посчитаем коэффициент ослабления сигнала. Он может пригодиться при работе с сигналами сложной формы.
( 2 оценки, среднее 4.5 из 5 )
Применимость
Делитель напряжения подходит
для получения необходимого заниженного напряжения в случаях, когда подключенная нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора .
Делитель не подходит
для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.
Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка на сами резисторы. Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое самой нагрузкой.
Если потребление тока нагрузкой неравномерно во времени, V out
также будет неравномерным.
Делитель напряжения применяется, если нужно получить заданное напряжение при условии стабилизированного питания. Сейчас мы поговорим о постоянном токе и резисторных делителях. О делителях с использованием конденсаторов, диодов, стабилитронов, индуктивностей и других элементов будет отдельная статья. Подпишитесь на новости, чтобы ее не пропустить. В конце для примера расскажу, как сделать делитель напряжения для осциллографа, чтобы снимать осциллограммы высокого напряжения.
Резисторные делители также могут применяться для уменьшения в заданное количество раз сигналов сложной формы. На делителях напряжения с регулируемым коэффициентом ослабления строятся, например, регуляторы громкости.
| Вашему вниманию подборка материалов: |
Коэффициент деления по напряжению. Резистивный делитель напряжения. Расчет делителя напряжения на резисторах
Делители напряжения получили широкое распространение в электронике, потому что именно они позволяют оптимальным образом решать задачи регулировки напряжения. Существуют различные схематичные решения: от простейших, например, в некоторых настенных светильниках, до достаточно сложных, как в платах управления переключением обмоток нормализаторов сетевого напряжения.
Что такое делитель напряжения? Формулировка проста — это устройство, которое в зависимости от коэффициента передачи (настраивается отдельно) регулирует значение выходного напряжения относительно входного.
Раньше на прилавках магазинов часто можно было встретить светильник-бра, рассчитанный на две лампы. Его особенностью являлось то, что сами лампы были рассчитаны на работу с напряжением 127 Вольт. При этом вся система подключалась к бытовой электросети с 220 В и вполне успешно работала. Никаких чудес! Все дело в том, что способ соединения проводников формировал не что иное, как делитель напряжения. Вспомним основы электротехники, а именно потребителей. Как известно, при последовательном способе включения равна, а напряжение изменяется (вспоминаем закон Ома). Поэтому в примере со светильником однотипные лампы включены последовательно, что дает уменьшение питающего их напряжения в два раза (110 В). Также делитель напряжения можно встретить в устройстве, распределяющем сигнал с одной антенны на несколько телевизоров. На самом деле примеров много.
Давайте рассмотрим простейший делитель напряжения на основе двух резисторов R1 и R2. Сопротивления включены последовательно, на свободные выводы подается входное напряжение U. Из средней точки проводника, соединяющего резисторы, есть дополнительный вывод. То есть получается три конца: два — это внешние выводы (между ними полное значение напряжения U), а также средний, формирующий U1 и U2.
Выполним расчет делителя напряжения, воспользовавшись законом Ома. Так как I = U / R, то U является произведением тока на сопротивление. Соответственно, на участке с R1 напряжение составит U1, а для R2 составит U2. Ток при этом равен Учитывая закон для полной цепи, получаем, что питающее U является суммой U1+U2.
Чему же равен ток при данных условиях? Обобщая уравнения, получаем:
I = U / (R1+R2).
Отсюда можно определить значение напряжения (U exit) на выходе делителя (это может быть как U1, так и U2):
U exit = U * R2 / (R1+R2).
Для делителей на регулируемых сопротивлениях существует ряд важных особенностей, которые необходимо учитывать как на этапе расчетов, так и при эксплуатации.
Прежде всего, такие решения нельзя использовать для регулировки напряжения мощных потребителей. Например, таким способом невозможно запитать электродвигатель. Одна из причин — это номиналы самих резисторов. Сопротивления на киловатты если и существуют, то представляют собой массивные устройства, рассеивающие внушительную часть энергии в виде тепла.
Значение сопротивления подключенной нагрузки не должно быть меньше, чем схемы самого делителя, в противном случае всю систему потребуется пересчитывать. В идеальном варианте различие R делителя и R нагрузки должно быть максимально большим. Важно точно подобрать значения R1 и R2, так как завышенные номиналы повлекут за собой излишнее а заниженные будут перегреваться, затрачивая энергию на нагрев.
Рассчитывая делитель, обычно подбирают значение его тока в несколько раз (например, в 10) больше, чем ампераж подключаемой нагрузки. Далее, зная ток и напряжение, вычисляют суммарное сопротивление (R1+R2). Далее по таблицам подбирают ближайшие стандартные значения R1 и R2 (учитывая их допустимую мощность, чтобы избежать чрезмерного нагрева).
В составе делителя напряжения для получения фиксированного значения напряжения используют резисторы. В этом случае выходное напряжение U вых связано с входным U вх (без учета возможного сопротивления нагрузки) следующим соотношением:
U вых = U вх х (R2 / R1 + R2)
Рис. 1. Делитель напряжения
Пример. С помощью резисторного делителя нужно получить на нагрузке сопротивлением 100 кОм напряжение 1 В от источника постоянного напряжения 5 В. Требуемый коэффициент деления напряжения 1/5 = 0,2. Используем делитель, схема которого приведена на рис. 1.
Сопротивление резисторов R1 и R2 должно быть значительно меньше 100 кОм. В этом случае при расчете делителя сопротивление нагрузки можно не учитывать.
Следовательно, R2 / (R1 +R2) R2 = 0,2
R2 = 0 ,2R1 + 0,2R2 .
R1 = 4R2
Поэтому можно выбрать R2 = 1 кОм, R1 — 4 кОм. Сопротивление R1 получим путем последовательного соединения стандартных резисторов 1,8 и 2,2 кОм, выполненных на основе металлической пленки с точностью ±1% (мощностью 0,25 Вт).
Следует помнить, что сам делитель потребляет ток от первичного источника (в данном случае 1 мА) и этот ток будет возрастать с уменьшением сопротивлений резисторов делителя.
Для получения заданного значения напряжения следует применять высокоточные резисторы.
Недостатком простого резисторного делителя напряжения является то, что с изменением сопротивления нагрузки выходное напряжение (U вых) делителя изменяется. Ддя уменьшения влияния нагрузки на U выхнеобходимо выбирать соротивление R2 по крайней мере в 10 раз меньше минимального сопротивления нагрузки.
Важно помнить о том, что с уменьшением сопротивлений резисторов R1
и R2 растет ток, потребляемый от источника входного напряжения. Обычно этот ток не должен превышать 1-10 мА.
Резисторы используются также для того, чтобы заданную долю общего тока направить в соответствующее плечо делителя. Например, в схеме на рис. 2 ток I составляет часть общего тока I вх, определяемую сопротивлениями резисторов Rl и R2, т.е. можно записать, что I вых = I вх х (R1 / R2 + R1)
Пример. Стрелка измерительного прибора отклоняется на всю шкалу в том случае, если постоянный ток в подвижной катушке равен 1 мА. Активное сопротивление обмотки катушки составляет 100 Ом. Рассчитайте сопротивление так, чтобы стрелка прибора максимально отклонялась при входном токе 10 мА (см. рис. 3) .
Рис. 2 Делитель тока
Рис. 3.
Коэффициент деления тока определяется соотношением:
I вых / I вх = 1/10 = 0,1 = R1 / R2 + R1 , R2 = 100 Ом.
Отсюда,
0,1R1 + 0,1R2 = R1
0,1R1 + 10 = R1
R1 = 10/0 ,9 = 11,1 Ом
Требуемое сопротивление резистора R1 можно получить путем последовательного соединения двух стандартных резисторов сопротивлением 9,1 и 2 Ом, выполненных на основе толстопленочной технологии с точностью ±2% (0,25 Вт). Заметим еще раз, что на рис. 3 сопротивление R2 — это .
Для обеспечения хорошей точности деления токов следует использовать высокоточные (± 1 %) резисторы.
При проектировании электрических цепей возникают случаи, когда необходимо уменьшить величину напряжения (разделить его на несколько частей) и только часть подавать на нагрузку. Для этих целей используют делители напряжения . Они основаны на втором законе Кирхгофа .
Самая простая схема — резистивный делитель напряжения. Последовательно с подключаются два сопротивления R1 и R2.
При последовательном подключении сопротивлений через них протекает одинаковый ток I.
В результате, согласно закону Ома , напряжения на резисторах делится пропорционально их номиналу.
Подключаем нагрузку параллельно к R1 или к R2. В результате на нагрузке будет напряжение равное U R2 .
Примеры применения делителя напряжения
- Как делитель напряжения. Представьте, что у Вас есть лампочка, которая может работать только от 6 вольт и есть батарейка на 9 вольт. В этом случае при подключении лампочки к батарейке, лампочка сгорит. Для того, чтобы лампочка работала в номинальном режиме, напряжение 9 В необходимо разделить на 6 и 3 вольта. Данную задачу выполняют простейшие делители напряжения на резисторах.
- Датчик параметр — напряжение. Сопротивление резистивных элементов зависит от многих параметров, например температура. Помещаем одно из сопротивлений в среду с изменяющейся температурой. В результате при изменении температуры будет изменяться сопротивление одного из делителей напряжения. Изменяется ток через делитель. Согласно закону Ома входное напряжение перераспределяется между двумя сопротивлениями.
- Усилитель напряжения. Делитель напряжения может использоваться для усиления входного напряжения. Это возможно, если динамическое сопротивление одного из элементов делителя отрицательное, например на участке вольт-амперной характеристики туннельного диода.
Ограничения при использовании резистивных делителей напряжения
- Номинал сопротивлений делителя напряжения на резисторах должен быть в 100 — 1000 раз меньше, чем номинальное сопротивление нагрузки, подключаемой к делителю. В противном случае сопротивление нагрузки уменьшит величину разделенного делителем напряжения.
- Малые значения сопротивлений, являющихся делителем напряжения, приводят к большим потерям активной мощности . Через делитель протекают большие токи. Необходимо подбирать сопротивления, чтобы они не перегорали и могли рассеять такую величину отдаваемой энергии в окружающую среду.
- Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины , нагревательные элементы, индукционные печи.
- Снижение КПД схемы за счет потерь на активных элементах делителя напряжения.
- Для получения точных результатов в делителе напряжения необходимо использовать прецизионные (высокоточные) сопротивления.
). Можно представить как два участка цепи, называемые плечами , сумма напряжений на которых равна входному напряжению. Плечо между нулевым потенциалом и средней точкой называют нижним , а другое — верхним . Различают линейные и нелинейные делители напряжения. В линейных выходное напряжение изменяется по линейному закону в зависимости от входного. Такие делители используются для задания потенциалов и рабочих напряжений в различных точках электронных схем. В нелинейных делителях выходное напряжение зависит от коэффициента нелинейно. Нелинейные делители напряжения применяются в функциональных потенциометрах . Сопротивление может быть как активным , так и реактивным .
Резистивный делитель напряжения
Простейший резистивный делитель напряжения представляет собой два последовательно включённых резистора и , подключённых к источнику напряжения . Поскольку резисторы соединены последовательно, то ток через них будет одинаков в соответствии с Первым правилом Кирхгофа . Падение напряжения на каждом резисторе согласно закону Ома будет пропорционально сопротивлению (ток, как было установлено ранее, одинаков):
Для каждого резистора:
Разделив выражение для на выражение для в итоге получаем:
Таким образом, отношение напряжений и в точности равно отношению сопротивлений и .
Используя равенство
, в котором , а
И, выражая из него соотношение для тока:
Получим формулу, связывающую выходное () и входное () напряжение делителя:
Следует обратить внимание, что сопротивление нагрузки делителя напряжения должно быть много больше собственного сопротивления делителя, так, чтобы в расчетах этим сопротивлением, включенным параллельно можно было бы пренебречь. Для выбора конкретных значений сопротивлений на практике, как правило, достаточно следовать следующему алгоритму . Сначала необходимо определить величину тока делителя, работающего при отключенной нагрузке. Этот ток должен быть значительно больше тока (обычно принимают превышение от 10 раз по величине), потребляемого нагрузкой, но, однако, при этом указанный ток не должен создавать излишнюю нагрузку на источник напряжения . Исходя из величины тока, по закону Ома определяют значение суммарного сопротивления . Остается только взять конкретные значения сопротивлений из стандартного ряда , отношение величин которых близко́ требуемому отношению напряжений, а сумма величин близка расчетной. При расчете реального делителя необходимо учитывать температурный коэффициент сопротивления , допуски на номинальные значения сопротивлений, диапазон изменения входного напряжения и возможные изменения свойств нагрузки делителя, а также максимальную рассеиваемую мощность резисторов — она должна превышать выделяемую на них мощность , где — ток источника при отключенной нагрузке (в этом случае через резисторы течет максимально возможный ток) .
Применение
Делитель напряжения имеет важное значение в схемотехнике. В качестве реактивного делителя напряжения как пример можно привести простейший электрический фильтр , а в качестве нелинейного — параметрический стабилизатор напряжения .
Делители напряжения использовались как электромеханическое запоминающее устройство в АВМ . В таких устройствах запоминаемым величинам соответствуют углы поворота реостатов. Подобные устройства могут неограниченное время хранить информацию.
Усилитель напряжения
Делитель напряжения может использоваться для усиления входного напряжения — это возможно, если , а — отрицательно, например как на участке вольт-амперной характеристики туннельного диода
Ограничения в применении резистивных делителей напряжения
- Номинал сопротивлений делителя должен быть в 100 — 1000 раз меньше, чем номинальное сопротивление нагрузки.
- Малые значения сопротивлений, являющихся делителем напряжения, приводят к возникновению больших токов в делителе. Снижается КПД схемы из-за нагрева сопротивлений.
- Резистивный делитель напряжения нельзя использовать для подключения мощных электрических приборов: электрические машины, нагревательные элементы.
Нормативно-техническая документация
- ГОСТ 11282-93 (МЭК 524-75) — Резистивные делители напряжения постоянного тока
Примечания
Ссылки
Wikimedia Foundation . 2010 .
Смотреть что такое «Делитель напряжения» в других словарях:
делитель напряжения — делитель напряжения Преобразующее устройство, состоящее из плеч высокого и низкого напряжения, таких, что напряжение входа прикладывается ко всему устройству, а напряжение выхода снимается с плеча низкого напряжения. [МЭС… … Справочник технического переводчика
Большой Энциклопедический словарь
Устройство, позволяющее снимать (использовать) только часть имеющегося постоянного или переменного напряжения посредством элементов электрической цепи, состоящей из резисторов, конденсаторов или катушек индуктивности. Используется в радио и… … Энциклопедический словарь
делитель напряжения — įtampos dalytuvas statusas T sritis automatika atitikmenys: angl. potential divider; voltage divider vok. Spannungsteiler, m rus. делитель напряжения, m pranc. diviseur de tension, m … Automatikos terminų žodynas
делитель напряжения — įtampos dalytuvas statusas T sritis Standartizacija ir metrologija apibrėžtis Įtaisas nuolatinei ar kintamajai įtampai dalyti į dvi ar daugiau dalių. atitikmenys: angl. potential divider; voltage divider vok. Spannungsteiler, m rus. делитель… …
делитель напряжения — įtampos dalytuvas statusas T sritis Standartizacija ir metrologija apibrėžtis Įtaisas, sudarytas iš rezistorių, induktyvumo ričių, kondensatorių, transformatorių arba iš šių elementų derinio taip, kad tarp dviejų šio įtaiso taškų susidarytų… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
делитель напряжения — įtampos dalytuvas statusas T sritis chemija apibrėžtis Įtaisas nuolatinei ar kintamajai įtampai dalyti į dvi ar daugiau dalių. atitikmenys: angl. potential divider; voltage divider rus. делитель напряжения … Chemijos terminų aiškinamasis žodynas
делитель напряжения — įtampos dalytuvas statusas T sritis fizika atitikmenys: angl. voltage divider vok. Spannungsteiler, m rus. делитель напряжения, m pranc. diviseur de tension, m … Fizikos terminų žodynas
Электротехническое устройство для деления напряжения постоянного или переменное тока на части. Любой Д. н. состоит из активных или реактивных электрических сопротивлений. Обычно Д. н. применяют для измерения напряжения. При низких… … Большая советская энциклопедия
Электротехническое устройство, позволяющее снимать (использовать) только часть имеющегося постоянного или переменного напряжения посредством элементов электрической цепи, состоящей из резисторов, конденсаторов или катушек индуктивности. При… … Энциклопедия техники
Устройство, в котором входное и выходное напряжение связаны коэффициентом передачи. Делитель можно представить, как два участка цепи, называемые плечами, сумма напряжений на которых равна входному напряжению. Чаще всего делитель напряжения строится из двух резисторов. Такой делитель называют резисторным. Каждый резистор в таком делителе называют плечом. Плечо соединённое с землёй называют нижним, то что соединено с плюсом — верхним. Точка соединения двух резисторов называется средним плечом или средней точкой. Если говорить совсем упрощённо, то можно представить среднее плечо, как бассейн. Делитель напряжения позволяет нам управлять двумя «шлюзами», «сливая» напряжение в землю (уменьшая сопротивление нижнего плеча) или «подливая» напряжения в бассейн (уменьшая сопротивление верхнего плеча). Таким образом, делитель может использоваться для того, чтобы получить из исходного напряжения лишь его часть.
Принципиальная схема делителя напряжения
В рассматриваемом примере на вход (Uвх) подаётся напряжение 9В. Предположим, нам нужно получить на выходе (Uвых) 5В. Каким образом расчитать резисторы для делителя напряжения?
Расчёт делителя напряжения
Многие сталкиваются с тем, что не существует формул для расчёта сопротивлений в делителе. На самом деле, такие формулы легко вывести. Но обо всё по порядку. Для наглядности, начнём расчёт с конца, т.е. расчитаем напряжение на выходе, зная номиналы резисторов.
Ток, протекающий через R1 и R2 одинаков, пока к среднему плечу (Uвых) ничего не подключено. Общее сопротивление резисторов при последовательном соединении равняется сумме их сопротивлений:
Rобщ = R1 + R2 = 400 + 500 = 900 Ом
По закону Ома находим силу тока, протекающего через резисторы:
I = Uвх / Rобщ = 9В / 900 Ом = 0.01 А = 10 мА
Теперь, когда нам известен ток в нижнем плече (ток, проходящий через R2), раcчитаем напряжение в нижнем плече (Опять закон Ома):
Uвых = I * R2 = 0.01А * 500 Ом = 5В
Или упрощая цепочку вычислений:
Uвых = Uвх * (R2 / (R1+R2))
Применив немного математики и прочих знаний, сдобрив всё законом Ома, можно получить следующие формулы:
R1 = (Uвх-Uвых)/Iд+Iн
R2 = Uвых / Iд
Здесь Iд и Iн — ток делителя и ток нагрузки соответственно. В общем случае, не нужно даже знать, что это за токи такие. Можно просто принять их равными Iд = 0.01 А (10 мА), а Iн = 0. То есть рассматривать делитель без нагрузки. Это приемлемо до тех пор, пока мы используем делитель только для измерений напряжения (а во всех примерах в нашей базе знаний он именно так и используется). Тогда формулы упростятся:
R1 = (Uвх-Uвых) * 100
R2 = Uвых * 100
P.S. Это совсем не важно, но обратите внимание: 100 — это не физическая величина. После принятия условия, что Iд у нас всегда равен 0.01 А, это просто коэффициент, получившийся при переносе 0.01 в числитель.
Проверяем:
Входящее напряжение у нас 9 вольт, хотим получить 5 вольт на выходе. Подставляем значения в формулу, получаем:
R1 = (9-5) * 100 = 400 Ом
R2 = 5 * 100 = 500 Ом
Всё сходится!
Применение делителя напряжений
В основном делитель напряжения используется там, где нужно измерить изменяющееся сопротивление. На этом принципе основано считывание значений с фоторезистора: фоторезистор включается в делитель в качестве одного плеча. Второе плечо представляет собой постоянный резистор. Аналогичным образом можно считывать показания терморезистора.
Alex_EXE » Расчёт делителя вольтметра (для 4 и 5 версии)
Ранее на сайте были опубликованы 4 (на PIC16F676) и 5 (для PIC16F688) версии прошивок вольтметра. В эти прошивки были добавлены возможности пользователям самим устанавливать программный делитель вольтметра. Такая возможность позволяет данную конструкцию использовать не только в качестве классического вольтметра, но и так же к нему подключать различные аналоговые датчики с линейной зависимостью, что значительно может расширить сферы его применения.
Вольтметр с 5 версией прошивки
В статье, в общем, и на примере конкретных датчиков будет описан принцип расчёта коэффициентов делителя вольтметра.
У вольтметра на входе 10 разрядное АЦП, на выходе которого можно получить значение от 0 до 1023. Питание вольтметра 5В. Что бы получить какое-нибудь вменяемое значение, а не чистое значение с АЦП, то нужно выполнить какие-нибудь преобразования. Какие, зависит от того, что нужно.
Например: что бы замерить 5В – входное значение домножаем на максимальное замеряемое значение и делим на разрядность АЦП. Что бы измеряемые 5В отобразить, как 5.0В, т.е. сами вольты и десятинные значения. Для начала вспомним, что точка на индикаторе фиксированная, значит на индикатор нужно выводить значение 50, для этого смещаем пятёрку на десяток влево, т.е. ещё домножим на 10.
Для задания настоек преобразования у вольтметра есть 3 целочисленных переменных:
Множитель – M (только положительный, принимает значения от 1 до 31)
Делитель – D (только положительный)
Смещение – O (может быть как положительным, так и отрицательным)
Отмечу, что во время расчёта значений следует учитывать несколько ограничений, об некоторых предупредит калькулятор, о других нет.
Калькулятор предупредит о следующих ограничениях: множитель (M) от 1 до 31, т.к. он домножает входное значение АЦП и знаменатель не должен превышать 32767. И ограничения переменных – для делителя (D) от 0 до 65535 и для смещения (O) от -32768 до 32767.
С остальными ограничениями чуть сложнее, что бы с ними не столкнуться нужно понять, как будут происходить математические преобразования и знать какие программные ограничения установлены.
1. 3-х сегментный дисплей отображает значения только от 0 до 999;
2. Отображаются только положительные значения;
3. Программа производит целочисленное деление, отбрасывая (не округляя) дробную часть.
На самом деле, как видно, в принципе всё просто.
Продолжим расчёт с измерением 5В и отображением 5.0В.
В связи с ограничениями мы вынуждены упростить множитель и делитель, хоть это и приведет к снижению точности:
Для, ставшего уже классическим, вольтметра до 50В с отображением десятичных вольт получаем следующею формулу:
Погрешность до 0,4В.
В программе калькулятора применен более простой алгоритм расчёт, поэтому она предлагает следующею формулу:
Погрешность до 1,2В.
Поэтому для более точных измерений коэффициенты преобразований лучше рассчитывайте самостоятельно.
Рассмотрим пример расчёт для других датчиков.
Датчик MPX4115A
Барометр, подходит для измерения атмосферного давления.
Подключение MPX4115A
Точку не отключал.
Для начала ищём документацию на датчик и из документации берем формулу расчёта его значения.
У нас же наоборот, известно напряжение, а нужно найти давление, т.е. преобразуем:
Но выход датчика в кПа, а нам удобнее воспринимать мм. ртутного столба (задача измерять атмосферное давление), поэтому переведем к более приличному виду, домножим на 7,5
Так же не забываем, что на входе у нас не напряжение, а значение АЦП, т.е. входное значение при 5 В питания от 0 до 1023.
Остаётся только округлить дробные части и проверить: не превышаем ли допусков. Знаменатель должен быть меньше 32767, впрочем, как и остальные части. Проверяем:
1024 – максимальное значение АЦП. Превышает (для множителя максимум 31), значит нужно дробь упростить, даже если придётся числа округлить.
В итоге получаем:
При желании можно сделать более точное округление.
Датчик LM335
Подключение LM335
Датчик температуры: -40 +100грЦ. Берем формулу расчёта из документации к датчику.
Преобразуем
Датчик ACS712ELCTR-30A
Подключение ACS712ELCTR-30A
Датчик постоянного тока +-30А, вольтметр обрабатывает только положительное плечо, т.е. 0..30А. Он, как и все предыдущие, имеет линейную зависимость, 66мВ/А, «0» в 2,5В, исходя из этих данных составляем следующею формулу:
И преобразуем её.
Расчет делителя. Делители напряжения и тока. Применение делителя напряжений
Делители напряжения получили широкое распространение в электронике, потому что именно они позволяют оптимальным образом решать задачи регулировки напряжения. Существуют различные схематичные решения: от простейших, например, в некоторых настенных светильниках, до достаточно сложных, как в платах управления переключением обмоток нормализаторов сетевого напряжения.
Наведите указатель мыши на символ земли, и вы увидите, что ток равен 25 мА. Если мы посмотрим на вторую схему, мы увидим, что теперь верхний резистор опускается вокруг целых 5 В, в то время как два нижних резистора имеют напряжение 99 мВ, потому что соотношение резисторов здесь изменилось.
Поскольку два нижних резистора находятся параллельно, и у нас есть один резистор со значительно большим сопротивлением чем у другого, их комбинированное сопротивление пренебрежимо мало по сравнению с сопротивлением только правого нижнего резистора. Таким образом, теперь выход напряжения значительно отличается от 5 В, который мы получаем в случае отсутствия нагрузки. Теперь давайте посмотрим на противоположную ситуацию: два небольших резистора в делителе напряжения и один большой в качестве нагрузки.
Что такое делитель напряжения? Формулировка проста — это устройство, которое в зависимости от коэффициента передачи (настраивается отдельно) регулирует значение выходного напряжения относительно входного.
Раньше на прилавках магазинов часто можно было встретить светильник-бра, рассчитанный на две лампы. Его особенностью являлось то, что сами лампы были рассчитаны на работу с напряжением 127 Вольт. При этом вся система подключалась к бытовой электросети с 220 В и вполне успешно работала. Никаких чудес! Все дело в том, что способ соединения проводников формировал не что иное, как делитель напряжения. Вспомним основы электротехники, а именно потребителей. Как известно, при последовательном способе включения равна, а напряжение изменяется (вспоминаем закон Ома). Поэтому в примере со светильником однотипные лампы включены последовательно, что дает уменьшение питающего их напряжения в два раза (110 В). Также делитель напряжения можно встретить в устройстве, распределяющем сигнал с одной антенны на несколько телевизоров. На самом деле примеров много.
Опять же, комбинированное сопротивление двух нижних резисторов меньше сопротивления меньшего резистора двух. В этом случае, однако, это не оказывает большого влияния на напряжение, наблюдаемое нагрузкой. Он все еще имеет напряжение 5 В, и до сих пор все в порядке.
С другой стороны, давайте сравним ток, проходящий через делитель в цепи с большими резисторами на делителе и схемой с малыми резисторами на делителе. Дело здесь в том, что ток теряется делителем напряжения, и если это была, например, частью устройства с батарейным питанием, это отрицательно повлияло бы на срок службы батареи. Таким образом, резисторы должны быть как можно большими, чтобы снизить потерянный ток.
Давайте рассмотрим простейший делитель напряжения на основе двух резисторов R1 и R2. Сопротивления включены последовательно, на свободные выводы подается входное напряжение U. Из средней точки проводника, соединяющего резисторы, есть дополнительный вывод. То есть получается три конца: два — это внешние выводы (между ними полное значение напряжения U), а также средний, формирующий U1 и U2.
Это дает нам два противоположных требования о том, чтобы иметь как можно меньше резисторов, чтобы получить лучшее регулирование напряжения на выходе и как можно больше резисторов, чтобы получить как можно меньше потерянного тока. Поэтому, чтобы получить правильное значение, мы должны увидеть, какое напряжение нам нужно на нагрузке, насколько точно оно должно быть, и получить входное сопротивление нагрузки и на основе этого рассчитать размер резисторов, которые нам нужны, чтобы получить нагрузку с допустимым напряжением.
Затем нам нужно поэкспериментировать с значениями резисторов делителя напряжения и посмотреть, как на них повлияет напряжение, и найти точку, в которой мы не можем иметь большее изменение напряжения в зависимости от входного сопротивления. В этот момент у нас есть хороший выбор резисторов делителя напряжения.
Выполним расчет делителя напряжения, воспользовавшись законом Ома. Так как I = U / R, то U является произведением тока на сопротивление. Соответственно, на участке с R1 напряжение составит U1, а для R2 составит U2. Ток при этом равен Учитывая закон для полной цепи, получаем, что питающее U является суммой U1+U2.
Чему же равен ток при данных условиях? Обобщая уравнения, получаем:
Еще один момент, который необходимо учитывать, — это номинальная мощность резисторов. Это касается резисторов с большим сопротивлением, поскольку резисторы с более низким сопротивлением будут рассеивать больше энергии и нагреваться больше. Это означает, что они должны быть больше резисторов с большим сопротивлением.
На практике, как только вы выполняете ряд делителей напряжения, вы увидите несколько популярных значений резисторов делителя напряжения. Многие люди просто выбирают один из них и не слишком сильно задумываются при расчетах, если нет проблемы с выбором.
I = U / (R1+R2).
Отсюда можно определить значение напряжения (U exit) на выходе делителя (это может быть как U1, так и U2):
U exit = U * R2 / (R1+R2).
Для делителей на регулируемых сопротивлениях существует ряд важных особенностей, которые необходимо учитывать как на этапе расчетов, так и при эксплуатации.
Прежде всего, такие решения нельзя использовать для регулировки напряжения мощных потребителей. Например, таким способом невозможно запитать электродвигатель. Одна из причин — это номиналы самих резисторов. Сопротивления на киловатты если и существуют, то представляют собой массивные устройства, рассеивающие внушительную часть энергии в виде тепла.
Рассмотрим задачу перемещения заряда от А к В в однородном электрическом поле. Пусть это движение будет против электрического поля. Некоторая работа будет выполняться внешней силой на этом заряде, и эта работа изменит потенциальную энергию на более высокую ценность. Объем выполненной работы равен изменению потенциальной энергии. Это различие в потенциале называется потенциальной разницей и измеряется в вольтах. Это также называется потенциалом через резистор.
Ток течет в электрической цепи в виде заряда, тогда как потенциал не течет или не перемещается. Потенциальная разница применяется между двумя точками. Вольт определяется как падение потенциала на резисторе 1 Ом с током 1 Ампер тока, протекающего через него. Согласно закону Ома, ток, текущий в линейной цепи, прямо пропорционален разности потенциалов по цепи. Следовательно, если разность потенциалов, приложенная к цепи, больше, то ток, протекающий в цепи, больше.
Значение сопротивления подключенной нагрузки не должно быть меньше, чем схемы самого делителя, в противном случае всю систему потребуется пересчитывать. В идеальном варианте различие R делителя и R нагрузки должно быть максимально большим. Важно точно подобрать значения R1 и R2, так как завышенные номиналы повлекут за собой излишнее а заниженные будут перегреваться, затрачивая энергию на нагрев.
Ток, протекающий в резисторе, равен. Тогда разность потенциалов на резисторе теперь составляет 8 В Ток, протекающий в резисторе в этой ситуации, составляет 8 ампер. Как правило, в электрических цепях нижний потенциал — земля или земля. Следовательно, разность потенциалов равна приложенному напряжению. Земля считается общей точкой в цепи. Эта ссылка земли или земли как общей точки в электрических цепях полезна для легкого понимания схемы.
Потенциальную разницу также называют напряжением. Напряжения, подключенные последовательно, добавляются, чтобы дать общее напряжение в цепи. Это можно наблюдать в резисторах в последовательном соединении. В случае параллельных элементов, напряжение на них равно. Это можно наблюдать в резисторах в параллельном учебнике.
Рассчитывая делитель, обычно подбирают значение его тока в несколько раз (например, в 10) больше, чем ампераж подключаемой нагрузки. Далее, зная ток и напряжение, вычисляют суммарное сопротивление (R1+R2). Далее по таблицам подбирают ближайшие стандартные значения R1 и R2 (учитывая их допустимую мощность, чтобы избежать чрезмерного нагрева).
Рассмотрим резистор сопротивления 10 Ом. Ток, протекающий через резистор, можно рассчитать следующим образом. Два контакта резистора имеют два разных потенциала, то есть 15 В и 5 В соответственно. Тогда ток, протекающий через резистор, может быть рассчитан с использованием закона Ома как.
Резисторы в последовательном соединении используются для создания цепи делителя напряжения. Разделитель напряжения представляет собой линейную схему, выходное напряжение которой является частью входного напряжения. Ниже показана простая схема делителя напряжения с 2 резисторами.
В составе делителя напряжения для получения фиксированного значения напряжения используют резисторы. В этом случае выходное напряжение U вых связано с входным U вх (без учета возможного сопротивления нагрузки) следующим соотношением:
U вых = U вх х (R2 / R1 + R2)
Рис. 1. Делитель напряжения
Пример. С помощью резисторного делителя нужно получить на нагрузке сопротивлением 100 кОм напряжение 1 В от источника постоянного напряжения 5 В. Требуемый коэффициент деления напряжения 1/5 = 0,2. Используем делитель, схема которого приведена на рис. 1.
Потенциал каждого резистора в последовательном соединении зависит от значения сопротивления. Принцип делителя напряжения заключается в создании напряжения, которое является частью входного напряжения. Следующая схема используется для отображения принципа делителя напряжения для нескольких выходных напряжений.
Значение выходного напряжения в типичной цепи делителя напряжения рассчитывается следующим образом. Уравнения для индивидуального падения напряжения на каждом резисторе можно рассчитать по закону Ома. Поэтому из уравнений 1, 2 и 3. В случае цепи делителя напряжения, которая имеет несколько выходов, выходные напряжения могут быть рассчитаны с использованием приведенной ниже формулы.
Сопротивление резисторов R1 и R2 должно быть значительно меньше 100 кОм. В этом случае при расчете делителя сопротивление нагрузки можно не учитывать.
Следовательно, R2 / (R1 +R2) R2 = 0,2
R2 = 0 ,2R1 + 0,2R2 .
R1 = 4R2
Поэтому можно выбрать R2 = 1 кОм, R1 — 4 кОм. Сопротивление R1 получим путем последовательного соединения стандартных резисторов 1,8 и 2,2 кОм, выполненных на основе металлической пленки с точностью ±1% (мощностью 0,25 Вт).
Поэтому возможные выходные напряжения. Рассмотрим следующую цепь делителя напряжения. Он состоит из трех резисторов, соединенных последовательно для создания двух выходных напряжений. Поэтому эквивалентное сопротивление схемы. Теперь два возможных выходных напряжения можно рассчитать следующим образом.
Применение цепей делителя напряжения
Поэтому индивидуальное падение напряжения на каждом резисторе можно рассчитать следующим образом. Резисторы в серии будут формировать цепи делителя напряжения. Принцип делителя напряжения является основой при построении потенциометра, который действует как простой регулятор напряжения.
Следует помнить, что сам делитель потребляет ток от первичного источника (в данном случае 1 мА) и этот ток будет возрастать с уменьшением сопротивлений резисторов делителя.
Для получения заданного значения напряжения следует применять высокоточные резисторы.
Недостатком простого резисторного делителя напряжения является то, что с изменением сопротивления нагрузки выходное напряжение (U вых) делителя изменяется. Ддя уменьшения влияния нагрузки на U выхнеобходимо выбирать соротивление R2 по крайней мере в 10 раз меньше минимального сопротивления нагрузки.
Цепи делителя напряжения используются в цепях датчиков. Наиболее часто используемыми датчиками в виде цепей делителя напряжения являются термисторы и светозависимые резисторы. Разделитель напряжения использует два или более резистивных элемента для вывода более низкого напряжения, чем было введено. Это может иметь много функций, например, обеспечивать связь между устройствами, работающими на разных напряжениях, и действовать как входы для устройств с переменным сопротивлением.
Ниже приведена схема простейшего делителя напряжения. Контрольная точка между двумя резисторами считается выходом для делителя напряжения. Как указано на изображении, измерительное напряжение между контрольной точкой и землей даст 5 вольт. Штырь периферийного устройства будет подключен, когда источник напряжения находится в этой схеме. Вычисление выходного напряжения из этой схемы довольно просто. Давайте рассмотрим уравнение, которое вам нужно использовать.
Важно помнить о том, что с уменьшением сопротивлений резисторов R1
и R2 растет ток, потребляемый от источника входного напряжения. Обычно этот ток не должен превышать 1-10 мА.
Резисторы используются также для того, чтобы заданную долю общего тока направить в соответствующее плечо делителя. Например, в схеме на рис. 2 ток I составляет часть общего тока I вх, определяемую сопротивлениями резисторов Rl и R2, т.е. можно записать, что I вых = I вх х (R1 / R2 + R1)
Вот основное уравнение, определяющее делители напряжения. Реорганизуя уравнение, которое вы можете рассчитать на основе целевого выходного значения, или вычислите выход на основе значений резисторов под рукой. Это уравнение немного менее полезно, если вы хотите использовать переменные резисторы, такие как потенциометр, термистор или фоторезистор. Все это обычные приложения, потому что хорошо настроенная схема делителя напряжения позволит вам измерять выход с помощью аналого-цифрового преобразователя микроконтроллера с отличным разрешением и точностью.
Пример. Стрелка измерительного прибора отклоняется на всю шкалу в том случае, если постоянный ток в подвижной катушке равен 1 мА. Активное сопротивление обмотки катушки составляет 100 Ом. Рассчитайте сопротивление так, чтобы стрелка прибора максимально отклонялась при входном токе 10 мА (см. рис. 3) .
Переменные резисторы в цепях делителя напряжения
Вот схема, использующая фоторезистор как часть делителя. Его можно поместить с обеих сторон, высокая сторона приведет к увеличению выходного напряжения по мере увеличения интенсивности света и наоборот, если он находится на нижней стороне. Для одного резистора с напряжением на нем закон Ома — довольно впечатляющий инструмент. Однако добавьте несколько резисторов вместе, и все становится еще интереснее! Полное сопротивление резисторов в серии — это просто сумма их индивидуальные сопротивления. Объединив эту концепцию с законом Ома, мы можем разработать одну из наиболее часто используемых схем в гитарном усилителе: делитель напряжения.
Рис. 2 Делитель тока
Рис. 3.
Коэффициент деления тока определяется соотношением:
I вых / I вх = 1/10 = 0,1 = R1 / R2 + R1 , R2 = 100 Ом.
Отсюда,
0,1R1 + 0,1R2 = R1
0,1R1 + 10 = R1
R1 = 10/0 ,9 = 11,1 Ом
Требуемое сопротивление резистора R1 можно получить путем последовательного соединения двух стандартных резисторов сопротивлением 9,1 и 2 Ом, выполненных на основе толстопленочной технологии с точностью ±2% (0,25 Вт). Заметим еще раз, что на рис. 3 сопротивление R2 — это .
Он использует два 150-кратных резистора последовательно, чтобы уравнять напряжение на конденсаторах фильтра и действовать в качестве разрядных резисторов, которые медленно разряжают конденсаторы, когда усилитель выключен. Общее напряжение на обоих резисторах составляет 534 вольт.
Каково напряжение на каждом отдельном резисторе? Полное сопротивление на обоих резисторах. Согласно Закону Ома, ток, проходящий через резисторы. Применяя Закон Ома еще раз, мы получаем напряжение на одном резисторе. Просто глядя на два равных резистора, вы можете предположить, что половина напряжения должна быть поперек каждого из них. Но каковы были бы напряжения на двух неравных резисторах?
Для обеспечения хорошей точности деления токов следует использовать высокоточные (± 1 %) резисторы.
Калькулятор делителя напряженияЭто калькулятор делителя напряжения — всеобъемлющий, но простой инструмент, который поможет вам оценить выходной сигнал (то есть напряжение), полученный в одном делителе напряжения. Прочтите, чтобы узнать, что такое делитель напряжения, узнайте основную формулу делителя напряжения и как она распространяется на различные уравнения для разных типов делителей напряжения, а также узнайте, как можно получить некоторую долю входного напряжения, применяя правило делителя напряжения.Кроме того, ознакомьтесь с многочисленными применениями делителя напряжения как в базовых, так и в невероятно сложных системах и убедитесь, что электронные схемы не о чем беспокоиться!
Что такое делитель напряжения?
Простой делитель напряжения — это часть линейной схемы, которая изменяет входное напряжение ( В ₁ ) на выходное напряжение ( В ) , которое представляет собой другое значение. Поскольку схема является пассивной, отношение В₂ / В никогда не превышает 1.Общий делитель напряжения представлен на этой простой схеме:
, где Z₁ и Z₂ — некоторые импедансы. Полные сопротивления могут быть связаны с сопротивлением R , емкостью C или индуктивностью L . Можно выделить несколько основных типов делителей напряжения, к которым применимо правило делителей напряжения:
- Делитель резистивный, RR
- Делитель емкостный, CC
- Индуктивный делитель, LL
- Делители RC и CR (также известные как фильтры RC, CR)
- Делители RL и LR (также известные как фильтры RL, LR)
- Делители CL и LC (также известные как фильтры CL, LC)
Линейка делителя напряжения
Принцип действия делителей напряжения заключается в том, что ток, проходящий через несколько элементов, соединенных последовательно, является постоянным, но напряжение распределяется между ними каким-то образом .Чтобы найти точные значения, мы должны применить к нашей схеме закон Ома. Перед тем как это сделать, необходимо отметить один важный момент:
Состав РР — единственный, применимый к цепям постоянного тока . В этих случаях любой импеданс можно рассматривать как провод с нулевым сопротивлением, а емкости работают как разрыв в цепи, поэтому они имеют бесконечное сопротивление. В остальном все они используются в цепях переменного тока, и правило делителя напряжения применяется для максимального значения разности потенциалов.Также может быть полезно найти фазовый сдвиг для этих напряжений.
Формула делителя напряжения
Общее уравнение (или формула) делителя напряжения для импедансов выглядит следующим образом:
V₂ = Z₂ / (Z₁ + Z₂) * V₁ .
Напоминание: в целом, В₁ и В₂ соответствуют амплитудам сигналов , например синусоидальные.
Если рассматривать только сопротивления, формула делителя напряжения естественным образом меняется на:
V₂ = R₂ / (R₁ + R₂) * V₁ .
Поскольку сопротивление не влияет на фазу сигнала, формула одинакова как для переменного, так и для постоянного тока. Сравниваются значения напряжения в данный момент. Как упоминалось ранее, остальные типы делителей предназначены для цепей переменного тока, поэтому давайте рассмотрим несколько примеров.
Уравнения емкостного и индуктивного делителя напряжения
Для делителя CC нам нужно использовать импедансы конденсаторов: Z = 1 / (j * ω * C) , где j — мнимое число, а ω — угловая частота переменного напряжения. .Подставляя исходное уравнение делителя напряжения этим выражением, получаем:
V₂ = Z₂ / (Z₁ + Z₂) * V₁ = (1 / (jωC₂)) / (1 / (jωC₁) + 1 / (jωC₂)) * V₁ ,
и умножая каждый член на jωC₁C₂ , получаем:
V₂ = C₁ / (C₁ + C₂) * V₁ .
Аналогичная процедура может быть проделана для делителей LL, где Z = j * ω * L . На этот раз выходное напряжение:
V₂ = Z₂ / (Z₁ + Z₂) * V₁ = jωL₂ / (jωL₁ + jωL₂) * V₁ .
Разделив числитель и знаменатель на jω , окончательная формула будет:
V₂ = L₂ / (L₁ + L₂) * V₁ .
В обоих случаях выходное напряжение синфазно относительно входной фазы .
Фильтры RC и CR
Цепи делителя напряжения, состоящие более чем из одного типа элементов, не так просто оценить, как предыдущие примеры. Нам приходится иметь дело с алгеброй комплексных чисел, но, поверьте, это выглядит более пугающим, чем есть на самом деле.
Для RC-делителя формулу делителя напряжения можно расширить до:
V₂ = Z₂ / (Z₁ + Z₂) * V₁ = (1 / (jωC)) / (R + 1 / (jωC)) * V₁ = V₁ / (jωRC + 1) .
Результат — комплексное число, поэтому, чтобы оценить амплитуду выходного напряжения, мы должны найти его модуль:
| V₂ | = | V₁ / (jωRC + 1) | = | V₁ | / √ ((ωRC) ² + 1) .
Если частота увеличивается, выходная амплитуда напряжения уменьшается, поэтому эту схему также называют фильтром нижних частот .Фазовый сдвиг можно вычислить как арктангенс мнимой части, деленной на действительную часть нашего комплексного числа:
Δφ = атан (-ωRC) .
Аналогично можно найти амплитуду и фазовый сдвиг для цепи CR. Первый шаг — вычислить общую формулу для выходного напряжения:
V₂ = Z₂ / (Z₁ + Z₂) * V₁ = R / (R + 1 / (jωC)) * V₁ = jωRC / (jωRC + 1) * V₁ 900 11.
Его амплитуду можно определить как:
| V₂ | = | jωRC / (jωRC + 1) * V₁ | = ωRC / √ ((ωRC) ² + 1) * | V₁ | ,
, а фазовый сдвиг задается как:
Δφ = атан (1 / ωRC) .
На этот раз мы видим, что если частота стремится к 0, то же самое происходит с амплитудой В , а для высоких значений ω она остается такой же, как входное напряжение. Вывод состоит в том, что CR можно рассматривать как фильтр верхних частот .
Фильтры RL и LR
Цепи, содержащие резистивные и индуктивные элементы, мало чем отличаются от RC и CR, когда дело доходит до расчетов, но стоит повторять каждый шаг, чтобы понять все тонкие различия.
В случае фильтра RL мы можем начать, как обычно, с общей формулы делителя напряжения:
V₂ = Z₂ / (Z₁ + Z₂) * V₁ = jωL / (R + jωL) * V₁ .
Чтобы найти амплитуду выходного напряжения, нам нужно оценить модуль этого значения:
| V₂ | = | jωL / (R + jωL) * V₁ | = ωL / √ (R² + (ωL) ²) * | V₁ | ,
и его фазовый сдвиг:
Δφ = атан (R / ωL) .
Для делителя LR мы просто заменяем эти элементы, поэтому уравнение делителя напряжения дает:
V₂ = Z₂ / (Z₁ + Z₂) * V₁ = R / (R + jωL) * V₁ .
Еще раз мы можем определить амплитуду выходного напряжения и фазовый сдвиг:
| V₂ | = | R / (R + jωL) * V₁ | = R / √ (R² + (ωL) ²) * | V₁ | ,
Δφ = атан (-ωL / R) .
Взгляните на результаты; амплитуда В для фильтра RL очень похожа на CR, а амплитуда LR похожа на амплитуду напряжения RC. Как и их фазовые сдвиги. Это очень ценный результат, потому что оказывается, что фильтры RC и RL могут использоваться взаимозаменяемо, если они спроектированы в соответствующей конфигурации, а значения проводимости и индуктивности правильно отрегулированы .Это особенно полезно для схем, размер которых должен быть доведен до нанометрового масштаба, поскольку применение действительно небольших конденсаторов намного проще, чем создание крошечных катушек.
В любом случае, если у вас возникнут проблемы с вычислением свойств выходного сигнала, вы всегда можете вернуться к этим главам или просто попробовать наш калькулятор делителя напряжения! Выберите подходящий вариант, и результат отобразится моментально.
Выше было описано несколько пассивных фильтров, но правило делителя напряжения также может применяться к активным.
CL и LC как резонансные контуры
Мы могли бы выполнить те же вычисления для систем CL и LC, однако некоторые нелепые результаты могут произойти, если мы просто применим правило делителя напряжения. Мы можем заставить амплитуду выходного напряжения уходить в бесконечность! Это вызвано тем, что подключенные LC-элементы иногда называют резонансными контурами . Они используются для генерации и приема радиоволн, что наиболее эффективно на резонансной частоте , задаваемой как:
ω = 1 / √ (L * C) .
В более реалистичной картине мы должны учитывать также некоторое ненулевое сопротивление, поэтому проблема резонатных цепей описана в калькуляторе цепей RLC.
Использование делителя напряжения в более сложных схемах
То, что мы уже сделали, показывает, как делители напряжения работают в простейших возможных системах. Очевидно, вы можете представить, что в реальной жизни они практически нигде не используются, и, как правило, применяются более сложные схемы. Однако все полученные выше результаты могут быть полезны при упрощении более сложных.Например, всякий раз, когда вы можете обнаружить резисторы, включенные последовательно или параллельно, вы можете рассматривать их как единое сопротивление. Точно так же работают конденсаторы и соленоиды. Для смешанных компонентов он оценивается практически так же, но мы должны учитывать импедансы Z вместо R , C или L .
Применение делителя напряжения
Одним из наиболее часто используемых устройств, работающих благодаря концепции делителя напряжения, является потенциометр .Другое слово, описывающее этот элемент, - реостат. Обычно они состоят только из резистивных компонентов. Мы можем различать как аналоговые, так и цифровые, но, в любом случае, сопротивление можно выставить с высокой точностью . Некоторые из самых популярных типов потенциометров - это скользящие горшки, ножницы или подставки для большого пальца, которые различаются по размеру и структуре. Ключевым элементом является скользящий контакт, позволяющий регулировать выходное сопротивление .
Устройства измерения высокого напряжения - Оказывается, что можно измерить высокое напряжение, даже если прямое измерение может быть разрушительным для устройства.В таком случае удобно использовать делитель напряжения, чтобы понизить напряжение до безопасной области . Для исключительно высоких напряжений (скажем, выше 100 кВ) лучше использовать емкостные, а не резистивные.
Поиск неизвестного сопротивления - Можно ли найти какое-либо неизвестное сопротивление, если у вас есть только источник напряжения и другой резистор с известным сопротивлением? Вам повезло, если вы можете прочитать его цветовой код, но что, если его нет? Что ж, вы можете просто создать простую схему с обоими резисторами, расположенными последовательно, установить входное напряжение и измерить напряжение на желаемом резисторе .После этого просто вставьте все эти значения в калькулятор делителя напряжения, и все - тайна раскрыта. Вы всегда можете преобразовать общее уравнение делителя напряжения, чтобы найти
R₂как неизвестный параметр:
R₂ = V₂ / (V₁ - V₂) * R₁.
Плюсы и минусы делителей напряжения
Некоторым из вас может быть интересно, почему люди измеряют неизвестное сопротивление с помощью делителя напряжения, когда они могут просто прочитать значение силы тока, протекающей через резистор при приложении внешнего напряжения - просто закон Ома.Что ж, в общем, для этих методов не должно быть значительной разницы, но мы должны знать, что сопротивление подавляющего большинства материалов зависит от температуры. Хуже того, эти зависимости различны для металлов, полупроводников или изоляторов.
Принимая во внимание металлы, их сопротивление увеличивается с повышением температуры, поэтому для определения сопротивления при некоторой стандартизированной температуре, например T = 25 ° C , мы должны найти тепловой коэффициент (TCR) материала.Это требует точного измерения температуры окружающей среды и выполнения некоторых расчетов, при этом надеясь, что за это время не было допущено никаких ошибок. Однако мы можем сделать это гораздо проще! Как вы уже догадались, можно использовать простой делитель напряжения!
В базовой версии у нас есть два резистора, и если они сделаны из одного материала, это означает, что их температурные зависимости сопротивления примерно такие же . Независимо от того, насколько велика разница температур, эти сопротивления изменяются примерно на один и тот же процент, скажем, на 5% на каждые 20 ° C.Но, , поскольку в общем случае формула делителя напряжения имеет отношение импедансов, любое относительное изменение будет отменено, и выходное напряжение не должно зависеть от температуры (или, по крайней мере, его влияние должно быть значительно уменьшено). Более того, если мы посмотрим на уравнение из предыдущего раздела, мы получим значение сопротивления, такое же, как первое при данной температуре - никаких дополнительных расчетов не требуется!
Во-вторых, делители напряжения удобно использовать при проектировании сложных электрических схем.Вместо использования нескольких различных источников напряжения, каждый из которых создает разный потенциал в системе, мы можем реализовать один источник и применить столько делителей напряжения, сколько нам нужно.
С другой стороны, мы должны осознавать тот факт, что чем длиннее провода в нашей цепи, тем больше вероятность падения напряжения. Что ж, это далеко не так для длинных промышленных кабелей, но все же, если нам нужно провести действительно точные измерения, этот фактор следует принять во внимание и, в идеале, уменьшить как можно больше.
Делитель тока
До сих пор мы были сосредоточены на обработке сигнала - в основном, на изменениях напряжения. Тем не менее, мы можем использовать аналогичную концепцию, которая рассматривает проблему с другой точки зрения - это называется текущим делителем.
Идея почти такая же, но вместо разделения входного напряжения на более мелкие части мы хотим разделить начальную силу тока и получить какое-то конкретное значение на выходе. Отличий всего несколько: во-первых, нам нужен источник тока вместо источника напряжения.Во-вторых, все импедансы (в простом случае, как обычно, два) должны быть расположены параллельно, а не последовательно. Собственно, все это принципиальные отличия. В этой схеме мы снова можем использовать закон Ома. Полученная формула:
Iₓ = Z / (Z + Zₓ) * Iᵢ .
Мы можем заметить интересный и ценный объект. Для делителя напряжения, чем выше выходное сопротивление, тем больше выходное напряжение, в то время как для делителя тока результат ведет себя наоборот .
Точно так же мы можем производить различные типы делителей тока, включая катушки и конденсаторы, и все они применимы для переменного тока, тогда как для постоянного тока работает только состав резисторов. В общих случаях можно оценить как амплитуду, так и фазовый сдвиг протекающего тока. Мы уверены, что после прочтения пошаговых решений этого калькулятора делителя напряжения вам не составит труда выполнить аналогичные вычисления.
Делитель потенциала - онлайн-калькулятор
Делитель потенциала - это простейший способ получения источника с более низким e.м.ф. от источника с более высокой э.д.с.
Выходное напряжение делителя потенциала можно рассчитать как
U out = U in R 2 / (R 1 + R 2 ) (1)
где
U out = выходное напряжение (В)
R = сопротивление (Ом, Ом)
U in = входное напряжение (В)
Пример - потенциальный делитель - Высокое энергопотребление
Выходное напряжение делителя потенциала с двумя резисторами R 1 = 10 Ом и R 2 = 20 Ом и входное напряжение 12 В можно рассчитать как
U выход = (12 В) (20 Ом) / ((10 Ом) + (20 Ом))
= 8 (В)
Ток через делитель потенциала R 1 и 903 рэнд 27 2 (напр.выходной ток) можно рассчитать по закону Ома
I = U / R
= (12 В) / ((10 Ом) + (20 Ом))
= 0,4 А
можно рассчитать потребляемую мощность делителя
P = UI
= (12 В) (0,4 A)
= 4,8 Вт
Пример - Делитель потенциала - меньшее энергопотребление
Выходное напряжение от делителя напряжения с двумя резисторами R 1 = 1000 Ом и R 2 = 2000 Ом и входное напряжение 12 В можно рассчитать как
U out = (12 В) ( 2000 Ом) / ((1000 Ом) + (2000 Ом))
= 8 (В)
Ток через делитель потенциала R 1 и R 2 (пример.выходной ток) можно рассчитать по закону Ома
I = U / R
= (12 В) / ((1000 Ом) + (2000 Ом))
= 0,004 А
можно рассчитать потребляемую мощность делителя
P = UI
= (12 В) (0,004 A)
= 0,048 Вт
Потребляемую мощность в делителе потенциала можно уменьшить за счет увеличения сопротивления .
Делитель потенциала - Калькулятор
входное напряжение U дюйм (вольт)
резистор R 1 (ом)
резистор R 2 (ом)
делитель потенциала Номограмму ниже можно использовать для оценки потенциального делителя.
Загрузите и распечатайте Номограмму делителя потенциала!
Значения по умолчанию на приведенной ниже номограмме для U в = 12 В , R 2 = 47 Ом и U на выходе = 3,3 В . Так как сумма сопротивлений (R 1 + R 2 ) по номограмме составляет примерно 170 Ом - сопротивление R 1 можно рассчитать как
R 1 ≈ ( 170 Ом - 47 Ом)
≈ 123 Ом.
Делитель напряжения Формула
Делитель напряжения - это конфигурация электрической цепи, которая вырабатывает выходное напряжение, составляющее часть входного напряжения, разделяя напряжение источника между одним или несколькими последовательными сопротивлениями.
Предположим, у вас есть источник напряжения (входное напряжение), соединенный последовательно с n импедансами. Чтобы узнать выходное напряжение по общему импедансу, используется закон Ома:
выходное напряжение = (общий импеданс / сумма от первого до n-го импеданса цепи) * входное напряжение.
Уравнение записано
У нас:
В выход = выходное напряжение.
Z i = общий импеданс.
= сумма от первого до n-го импеданса цепи.
В в = входное напряжение.
Формула делителя напряжения Вопросы.
1) У нас есть схема с двумя резисторами, первый 3 Ом и второй 5 Ом, подключенные последовательно, напряжение источника имеет значение 12 В, рассчитайте напряжение деления после первого сопротивления.
Ответ:
Прежде всего следует отметить, что это схема резистивного делителя, поэтому значения импедансов совпадают со значениями сопротивлений. Импеданс Z i принимает значение 3 Ом. Теперь добавим импедансы цепи, чтобы получить делитель напряжения, это
= 3 Ом + 5 Ом = 8 Ом.
Затем мы делим значение второго импеданса на сумму импедансов и умножаем его на значение входного напряжения, чтобы получить делитель напряжения,
В выход = (5 Ом / 8 Ом) * 12 В = 0.625 * 12 В = 7,824 В
В выход = 7,824 В.
2) Рассчитайте делитель напряжения для двух последовательно соединенных конденсаторов, имеющих значения емкости 10 мкФ и 22 мкФ соответственно. Здесь напряжение в цепи составляет 10 В при частоте 40 Гц.
Ответ:
Прежде всего необходимо получить значение импеданса каждого конденсатора.
Z = 1 / (2 * π * f * C)
Z 1 = 1 / (2 * π * 40 Гц * 10 * 10 -6 F) = 400 Ом.
Z 2 = 1 / (2 * π * 40 Гц * 22 * 10 -6 F) = 180 Ом.
Затем,
В выход = = 10 В = 0,31 * 10 В = 3,1 В
В выход = 3,1 В.
Калькулятор делителя напряжения • Информатика и машинное обучение
Делитель напряжения позволяет преобразовывать входное напряжение в более низкое выходное напряжение. Например, вход 5 В можно легко преобразовать в выход 3 В 3. Базовая установка состоит из двух резисторов:
Но правильно выбрать резисторы довольно сложно.Вы можете взять формулу и попробовать некоторые значения, чтобы приблизить значения, или использовать формулу калькулятора:
Возможные значения резистора для входного напряжения 5 В и выходного напряжения 3,3 В, упорядоченные по ошибке:| R1 | R2 | Фактическое значение | Ошибка | Распределение мощности | ||||
|---|---|---|---|---|---|---|---|---|
| 330 Ом | 680 Ом | 3,366 В | 0,066 В | 0,025 Вт | ||||
| 47 Ом | 100 Ом | 401 В0,101 В | 0,170 Вт | |||||
| 47 кОм | 100 кОм | 3,401 В | 0,101 В | 0,000 Вт | ||||
| 4,7 кОм | ||||||||
| 4,7 кОм | 10 кОм | |||||||
| 470 Ом | 1 кОм | 3,401 В | 0,101 В | 0,017 Вт | ||||
| 4,7 Ом | 10 Ом | 3,401 В | 0,106 В 1 70509 | 3.406 В | 0,106 В | 0,036 Вт | ||
| 22 кОм | 47 кОм | 3,406 В | 0,106 В | 0,000 Вт | ||||
| 2,2 кОм | 4,7650 3,42,2 кОм | 4,7650 3,4 W|||||||
| 10 кОм | 22 кОм | 3,438 В | 0,138 В | 0,001 Вт | ||||
| 100 Ом | 220 Ом | 3,438 В | 0,1386 0,09 | 3,438 В | 0,1386 0,092 кОм | 3,438 В | 0,138 В | 0,008 Вт |
| 220 Ом | 330 Ом | 3,000 В | 0,300 В | 0,045 Вт | ||||
| 0,045 Вт | ||||||||
| 2,2 к V | 0,005 Вт |
Обратите внимание: не используйте делитель напряжения для высоких напряжений, так как весь ток должен проходить через резисторы, что сильно повредит им. Альтернатива - регуляторы напряжения! И что еще важнее: В реальных делителях напряжения нельзя использовать резисторы малой стоимости.В столбце «Распределение мощности» указано, сколько энергии преобразуется в тепло, и он должен быть как можно меньше.
Делитель напряжения | Прядильные числа
Очень распространенная и полезная схема резистора носит прозвище делитель напряжения . Мы разберемся, как работает эта схема, и увидим, откуда взялся ник.
Делитель напряжения действительно довольно простой, и вы можете анализировать его с нуля каждый раз, когда встречаетесь с ним. Но это , так что обычно это , поэтому неплохо подготовиться заранее, чтобы вы могли сразу же найти ответ.
Автор Вилли Макаллистер.
Содержание
Куда мы направляемся
«Делитель напряжения» - это комбинация двух последовательно соединенных резисторов, при этом входное напряжение подается на оба конца, а выходное напряжение измеряется на одном из резисторов.
Выходное напряжение является функцией входного напряжения и отношения номиналов резисторов,
$ v_ {out} = v_ {in} \, \ dfrac {\ text R2} {\ text R1 + \ text R2}
$Делитель напряжения выглядит так,
Это простая схема с двумя последовательно включенными резисторами.Одно напряжение подключается к верху и низу, а другое напряжение измеряется на одном из резисторов. Мы думаем о напряжении сверху и снизу как о входном напряжении, а напряжение на единственном резисторе - как о выходном.
Маленькие кружки обозначают порты , делителя напряжения, и они подключены к чему-то, что не показано справа.
Уравнение делителя напряжения
Наша цель - придумать выражение, которое связывает выход $ v_ {out} $ с входом $ v_ {in} $.Ответ будет напоминать этот:
$ v_ {out} = v_ {in} \ times (\ text {something})
$Это очень простая последовательная схема, поэтому для ее понимания не потребуется много усилий.
Прежде чем мы начнем, сделаем очень важное предположение:
Предположим, что ток, вытекающий из делителя из его центрального узла, равен нулю.
Мы предполагаем, что выходной ток делителя напряжения равен $ 0 $.
(в следующей статье мы проверим, что произойдет, если это предположение не соответствует действительности).
Это хорошее место для паузы. Вы понимаете закон Ома и резисторы серии. Посмотрим, сможете ли вы самостоятельно придумать выражение для $ v_ {out} $ через $ v_ {in} $.
Хорошо, отлично. Вы получили выражение для делителя напряжения. Теперь попробую.
Хорошее место для начала - найти ток через $ \ text {R1} $ и $ \ text {R2} $.
Вот один сложный шаг в анализе делителя напряжения: исходя из предположения, мы знаем, что $ \ text {R1} $ и $ \ text {R2} $ имеют одинаковый ток, поэтому мы можем считать, что они подключены последовательно.
$ i _ {\ text {1}} = i _ {\ text {2}} \ qquad $, а пока давайте назовем это просто $ i $.
Давайте напишем уравнение, используя закон Ома, $ v = i \, \ text {R} $, и то, что мы знаем о последовательно соединенных резисторах: резисторы, включенные последовательно, складываются.
$ v_ {in} = i \, (\ text R1 + \ text R2)
$Переставьте уравнение, чтобы найти $ i $,
$ i = v_ {in} \, \ dfrac {1} {\ text R1 + \ text R2}
долларов СШАЭто говорит нам текущий $ i $ в терминах $ v_ {in} $ и обоих резисторов.
Затем мы пишем выражение для $ v_ {out} $, используя закон Ома,
$ v_ {out} = i \, \ text R2 $
$ i = \ dfrac {v_ {out}} {\ text R2}
$Мы заменяем $ i $ в предыдущем уравнении, чтобы получить
$ \ dfrac {v_ {out}} {\ text R2} = v_ {in} \, \ dfrac {1} {\ text R1 + \ text R2}
$и, переместив $ \ text R2 $ вправо, мы получаем уравнение делителя напряжения,
$ v_ {out} = v_ {in} \, \ dfrac {\ text R2} {\ text R1 + \ text R2}
$Коэффициент резистора
Коэффициент соотношения резисторов всегда меньше 1 доллара.Сопротивление - всегда положительное число. Так что это верно для любых значений $ \ text {R1} $ и $ \ text {R2} $. (Найдите секунду, чтобы убедиться в этом.)
Поскольку коэффициент резистора меньше $ 1 $, это означает, что $ v_ {out} $ всегда меньше $ v_ {in} $. Входное напряжение $ v_ {in} $ делится на $ v_ {out} $ фиксированным соотношением, определяемым номиналами резисторов. Отсюда схема получила свое прозвище: делитель напряжения .
Пример
Найдите $ v_ {out} $ для этого делителя напряжения ,
Мы подставляем входное напряжение и значения резистора в уравнение делителя напряжения.Помните, что нижний резистор , $ \ text {R2} $, появляется в числителе.
$ v_ {out} = v_ {in} \, \ dfrac {\ text R2} {\ text R1 + \ text R2}
$$ v_ {out} = 12 \, \ text V \ cdot \ dfrac {3 \, \ text k \ Omega} {1 \, \ text k \ Omega + 3 \, \ text k \ Omega} $
$ v_ {out} = 12 \, \ text V \ cdot \ dfrac {3 \, \ text k \ Omega} {4 \, \ text k \ Omega} $
$ v_ {out} = 12 \, \ text V \ cdot \ dfrac {3} {4} = 9 \, \ text V $
Откройте эту имитационную модель и щелкните DC в меню, чтобы подтвердить рабочую точку постоянного тока.
Заканчиваем двумя дополнительными шагами,
Найдите ток и мощность.
Используйте закон Ома, чтобы найти ток,
$ i = \ dfrac {v_ {in}} {\ text R1 + \ text R2} = \ dfrac {12 \, \ text V} {1 \, \ text k \ Omega + 3 \, \ text k \ Omega } = \ dfrac {12 \, \ text V} {4 \, \ text k \ Omega} = 3 \, \ text {mA} $
Зная ток, мы вычисляем мощность, рассеиваемую нашим делителем напряжения,
$ p = i \, v = 3 \, \ text {mA} \ cdot 12 \, \ text V = 36 \, \ text {mW} $
Резюме: Наш делитель напряжения принимает входное напряжение (в данном случае $ 12 \, \ text V $, но это может быть любое значение) и делит его, чтобы создать выходное напряжение $ v_ {out} $, которое составляет $ 3/4 $. его входное напряжение.Отношение $ 3/4 $ определяется нашим выбором двух номиналов резистора. Ток $ 3 \, \ text {mA} $ протекает через делитель напряжения, заставляя его рассеивать $ 36 \, \ text {mW} $.
Практические проблемы с делителем напряжения
Решайте эти практические задачи двумя способами. Сначала продумайте ответ аналитически с помощью карандаша и бумаги. Затем смоделируйте свой ответ с помощью Circuit Sandbox.
Задача 1
Пусть $ v_ {in} = 6 \, \ text V $, $ \ text R1 = 50 \, \ text k \ Omega $ и $ \ text R2 = 10 \, \ text k \ Omega $.
Найдите $ v_ {out} $
$ v_ {out} = $ _________ $ \, \ text V $
покажи ответ$ v_ {out} = v_ {in} \, \ dfrac {\ text {R2}} {\ text {R1} + \ text {R2}}
$$ v_ {out} = 6 \, \ text V \ cdot \ dfrac {10 \, \ text {k} \ Omega} {10 \, \ text {k} \ Omega + 50 \, \ text {k} \ Омега} $
$ v_ {out} = 6 \, \ text V \ cdot \ dfrac {10 \, \ text {k} \ Omega} {60 \, \ text {k} \ Omega} = 6 \, \ text V \ cdot \ dfrac {1} {6}
долларов США$ v_ {out} = 1 \, \ text V $
Имитационная модель Задачи 1.Щелкните DC в верхнем меню, чтобы найти рабочую точку.
Задача 2
Пусть $ \ text R1 = 90 \, \ text k \ Omega $, $ \ text R2 = 10 \, \ text k \ Omega $ и $ v_ {out} = 1.5 \, \ text V $.
Найдите $ v_ {in} $.
$ v_ {in} = $ _________ $ \ text V $
покажи ответ$ v_ {out} = v_ {in} \, \ dfrac {\ text {R2}} {\ text {R1} + \ text {R2}}
$$ 1.5 \, \ text V = v_ {in} \, \ dfrac {10 \, \ text {k} \ Omega} {10 \, \ text {k} \ Omega + 90 \, \ text {k} \ Omega } $
$ 1.5 \, \ text V = v_ {in} \, \ dfrac {1} {10}
долларов США$ v_ {in} = 10 \ cdot 1.5 \, \ text V $
$ v_ {in} = 15 \, \ text V $
Имитационная модель проблемы 2. Дважды щелкните источник напряжения и введите значение напряжения для $ v_ {in} $, чтобы получить желаемое выходное напряжение. Повторите анализ DC , чтобы подтвердить свой выбор.
Задача 3
Пусть $ v_ {in} = 5 \, \ text V $, $ v_ {out} = 2 \, \ text V $ и $ \ text R1 = 30 \, \ text k \ Omega $.
Найдите $ \ text R2 $.
$ \ text R2 = $ _________ $ \ Omega
$ покажи ответ$ v_ {out} = v_ {in} \, \ dfrac {\ text {R2}} {\ text {R1} + \ text {R2}}
$$ 2 \, \ text V = 5 \, \ text V \ cdot \ dfrac {\ text {R2}} {30 \, \ text k \ Omega + \ text {R2}} $
$ 30 \, \ text k \ Omega + \ text R2 = \ dfrac {5 \, \ text V} {2 \, \ text V} \, \ text R2 $
$ 30 \, \ text k \ Omega = \ left (\ dfrac {5} {2} \, \ text R2 \ right) - \ text R2 = \ dfrac {3} {2} \, \ text R2 $
$ \ text R2 = \ dfrac {2} {3} \, 30 \, \ text k \ Omega $
$ \ text R2 = 20 \, \ text k \ Omega = 20000 \, \ Omega $
Проверьте, вставив $ \ text R2 $ обратно в уравнение делителя напряжения,
$ v_ {out} = 5 \, \ text V \ cdot \ dfrac {20 \, \ text k \ Omega} {30 \, \ text k \ Omega +20 \, \ text k \ Omega} = 5 \ cdot \ dfrac {20} {50} = 2 \, \ text V \ qquad \ checkmark $
Имитационная модель Задачи 3.Дважды щелкните $ \ text R2 $ и введите значение сопротивления, чтобы получить желаемое выходное напряжение. Повторите анализ DC , чтобы подтвердить свой выбор.
Задача 4 - задача проектирования
Пусть $ v_ {in} = 1 \, \ text V $, $ v_ {out} = \ dfrac {v_ {in}} {2} $.
Разработайте делитель напряжения, рассеивающий $ 10 \, \ mu \ text {W} $.
$ \ text R1 = $ _________ $ \ Omega \ qquad $
$ \ text R2 = $ _________ $ \ Omega $
$ v_ {out} = v_ {in} \, \ dfrac {\ text {R2}} {\ text {R1} + \ text {R2}}
$Давайте начнем с выяснения отношения между $ \ text R1 $ и $ \ text R2 $, чтобы получилось $ v_ {out} = v_ {in} / 2 $.
Сделаем это символически,
$ \ dfrac {1} {2} v_ {in} = v_ {in} \, \ dfrac {\ text {R2}} {\ text {R1} + \ text {R2}}
$$ \ dfrac {1} {2} = \ dfrac {\ text {R2}} {\ text {R1} + \ text {R2}}
$$ \ text {R1} + \ text {R2} = 2 \, \ text R2 $
$ \ text R1 = 2 \, \ text R2 - \ text R2 $
$ \ text R1 = \ text R2
$Два резистора имеют одинаковое значение. 5 = 100 \, \ text k \ Omega $
Мы знаем, что резисторы имеют одинаковое значение, и теперь мы знаем их сумму, так что
$ \ text R1 = \ text R2 = 50 \, \ text k \ Omega $
Имитационная модель Задачи 4.Дважды щелкните оба резистора и задайте им значения сопротивления для достижения проектных спецификаций: $ v_ {out} = v_ {in} / 2 $ и $ p = 10 \, \ mu \ text {W} $.
Что в псевдониме?
Мы упомянули, что эта схема называется делителем напряжения . Во многих ситуациях это именно то, что он делает. Однако помните, еще в начале мы сделали предположение, что ток, выходящий из делителя, равен нулю или очень близок к нулю? При определенных условиях (которые мы рассмотрим в следующей статье) фактическое выходное напряжение может быть немного ниже, чем значение, предсказываемое уравнением делителя напряжения.Урок: называйте схему по ее имени, но помните, что это всего лишь псевдоним.
Сводка
Мы даем название «делитель напряжения» шаблону резисторов, который выглядит следующим образом, с входным напряжением, приложенным к обоим концам, и выходным напряжением, измеренным на одном из резисторов.
Выходное напряжение является функцией входного напряжения и отношения номиналов резисторов,
$ v_ {out} = v_ {in} \, \ dfrac {\ text {R2}} {\ text {R1} + \ text {R2}}
$, где $ \ text {R2} $ - резистор внизу делителя.
В следующей статье рассматриваются некоторые тонкости конструкции делителей напряжения, такие как реальные допуски резисторов и ненулевой выходной ток.
Калькулятор делителя напряжения-Apogeeweb
Часто задаваемые вопросы
1. Как рассчитать делитель напряжения?
Формулировка правила проста: Правило деления напряжения: напряжение делится между двумя последовательными резисторами прямо пропорционально их сопротивлению.−v (t) + v1 (t) + v2 (t) = 0 → v (t) = v1 (t) + v2. v (t) = R1i (t) + R2i (t) = (R1 + R2) i (t).
2. Как выбрать резистор делителя напряжения?
Вот очень приблизительное эмпирическое правило: ток, протекающий через два резистора (при условии отсутствия входного тока), должен быть от 10 до 1000 раз больше, чем входной ток. Чем больше тока проходит через эти резисторы, тем меньше влияние входного тока.
3. Параллельно ли включен делитель напряжения?
Параллельную цепь часто называют делителем тока из-за ее способности пропорционально или делить общий ток на дробные части.Еще раз, должно быть очевидно, что ток через каждый резистор связан с его сопротивлением, учитывая, что напряжение на всех резисторах одинаково.
4. Почему используется делитель напряжения?
Резисторные делители напряжения обычно используются для создания опорных напряжений или для уменьшения величины напряжения, чтобы его можно было измерить, а также могут использоваться в качестве аттенюаторов сигналов на низких частотах.
5. Как рассчитать выходное напряжение?
Формула: V = I x R, где V - напряжение, измеренное в вольтах, I - величина тока, измеренная в амперах, а R - сопротивление, измеренное в омах.
6. Как работает делитель напряжения?
Делитель напряжения - это простая схема, которая преобразует большое напряжение в меньшее. Используя всего два последовательных резистора и входное напряжение, мы можем создать выходное напряжение, составляющее часть входного. Делители напряжения - одна из самых фундаментальных схем в электронике.
7. Что такое правило делителя напряжения и тока?
Цепи делителя токаимеют две или несколько параллельных ветвей для протекания токов, но напряжение одинаково для всех компонентов в параллельном блоке.Цепи делителя тока - это параллельные цепи, в которых ток источника или питания делится на несколько параллельных цепей.
8. В чем разница между потенциометром и делителем напряжения?
Делитель потенциала также называется резистивным делителем, напряжение пропорционально делится между цепочкой последовательно соединенных резисторов. Он может быть сформирован из N нескольких отводов и количества (N + 1) постоянных резисторов, но в природе существует гораздо больше его реализаций.
Короче говоря, потенциометр - это компонент, внутри которого используется делитель потенциала.Следовательно, все потенциометры, используемые для получения переменного напряжения, можно назвать делителями напряжения, но все делители напряжения не являются потенциометрами.
9. Как рассчитать делитель потенциала?
Делитель потенциала
Vin = p.d. поставляется ячейкой.
Vout = p.d. через интересующий резистор.
R1 = сопротивление интересующего резистора R1
R2 = сопротивление резистора R2
10. Как работает потенциальный делитель?
Делитель потенциала - это простая схема, в которой используется способ падения напряжения на последовательно соединенных резисторах.Это очень полезная и распространенная схема, которая широко используется в нашем ассортименте электронных комплектов. Идея состоит в том, что, используя два последовательно соединенных резистора, можно разделить напряжение и создать между ними другое напряжение.
11. Зачем использовать делитель напряжения?
Делитель напряжения может использоваться для уменьшения очень высокого напряжения, чтобы его можно было измерить с помощью вольтметра. Высокое напряжение подается на делитель, и выход делителя, который выводит более низкое напряжение, которое находится в пределах входного диапазона измерителя, измеряется измерителем.
12. Как построить делитель напряжения?
13. Что такое схема умножителя напряжения?
Умножитель напряжения - это тип схемы диодного выпрямителя, который может создавать выходное напряжение, во много раз превышающее приложенное входное напряжение. В руководстве по выпрямителям мы увидели, что выходное напряжение постоянного тока, контролируемое выпрямителем, находится на значении ниже входного напряжения сети.
14. Что такое смещение делителя напряжения?
Смещение делителя напряжения, также известное как смещение делителя напряжения, представляет собой метод, используемый для смещения постоянного тока биполярных переходных транзисторов (BJT) в простой схеме усилителя.
15. Почему смещение делителя напряжения называется самосмещением?
Причина его названия «самосмещение» не очень очевидна, за исключением того факта, что резистор, подключенный к эмиттерному выводу транзистора, способствует стабильности смещения.
16. Какое правило делителя напряжения?
Правило делителя напряжения используется для решения схем для упрощения решения. Применение этого правила также может полностью решить простые схемы. Основная концепция этого правила делителя напряжения заключается в том, что «напряжение делится между двумя резисторами, которые соединены последовательно, прямо пропорционально их сопротивлению.
17. Какие бывают типы умножителей напряжения?
Умножители напряжения подразделяются на четыре типа:
Однополупериодный удвоитель напряжения.
Двухполупериодный удвоитель напряжения.
Утроитель напряжения.
Счетверитель напряжения.
18. Как построить в цепи умножитель напряжения?
19. Может ли потенциометр работать как делитель напряжения?
Да. Потенциометр - это переменный резистор, который можно использовать для создания регулируемого делителя напряжения.
20. Почему смещение делителя напряжения более стабильно, чем фиксированное смещение?
Смещение делителя напряжения для транзистора не зависит от бета транзистора, в то время как фиксированное смещение зависит от бета.
Можно показать, что смещение делителя напряжения (тот, который используется в H-образной схеме смещения, обнаруженной вокруг биполярных транзисторов, работающих как почти линейные усилители), создает контур, отображающий свойства отрицательной обратной связи, которые помогают точке смещения быть почти независимой от тока транзистора. усиление, hFE или βF.Это приятное свойство, поскольку в обычных транзисторах этот параметр может иногда варьироваться в диапазоне 1: 3 от устройства к устройству.
Принцип деления напряжения резисторов в серии
В последовательной цепи распределение напряжения пропорционально величине сопротивления, то есть чем больше сопротивление, тем больше распределяется напряжение; Напротив, чем меньше сопротивление, тем меньше распределяется напряжение.
В последовательной цепи напряжение на проводниках пропорционально их сопротивлению.
По I1 = I2,
U1 / R1 = U2 / R2 равно
Объяснение схемы делителя напряжения:
Этот видеоурок по физике дает базовое введение в схемы делителя напряжения. Он предоставляет простую формулу для расчета напряжения на резисторе в последовательной цепи с двумя резисторами, включенными последовательно с батареей.он содержит множество примеров и практических задач. В нем обсуждается влияние на выходное напряжение схемы делителя напряжения, когда нагрузочный резистор включен параллельно R2. В нем обсуждается, как спроектировать схему делителя напряжения в соответствии с определенными требованиями.
Резистор в серии и В делитель напряжения
резисторов включены последовательно, напряжение, получаемое на k-м резисторе:
В заключении:
① В последовательной цепи полное сопротивление равно сумме сопротивлений субрезисторов.
② Напряжение на каждом резисторе соответствует общему напряжению в соответствии с отношением его сопротивления к общему сопротивлению.
Расчет мощности цепи последовательного сопротивления:
Делитель напряжения: что это такое? (Схема и приложения)
Что такое делитель напряжения?
Делитель напряжения - это основная схема в области электроники, которая может генерировать часть входного напряжения в качестве выходного.Он формируется с использованием двух резисторов (или любых пассивных компонентов) и источника напряжения. Резисторы здесь подключены последовательно, и напряжение подается на эти два резистора.
Эту схему также называют делителем потенциала . Входное напряжение распределяется между резисторами (компонентами) схемы делителя напряжения. В результате происходит деление напряжения. Если вам нужна помощь по расчету деления напряжения, воспользуйтесь нашим калькулятором делителя напряжения.
Схема делителя напряжения
Как мы упоминали выше, два последовательных резистора и источник напряжения составляют простой делитель напряжения. Эта схема может быть сформирована несколькими способами, как показано ниже.
На приведенном выше рисунке (A) представляет собой сокращенное обозначение, (B) представляет собой изображение от руки, а (C) и (D) показывают резисторы под разными и одинаковыми углами соответственно.
Но все четыре контура фактически одинаковы. R 1 - резистор, который всегда находится рядом с источником входного напряжения, а R 2 - резистор, который находится рядом с землей.V out - падение напряжения на резисторе, R 2 .
Это фактически напряжение делителя, которое мы получаем от этой схемы в качестве выхода.
Уравнение делителя напряжения в ненагруженном состоянии
Простая схема делителя напряжения относительно земли показана на рисунке ниже. Здесь два электрических импеданса (Z 1 и Z 2 ) или любые пассивные компоненты соединены последовательно. Полные сопротивления могут быть резисторами, катушками индуктивности или конденсаторами.
Выходной сигнал схемы берется через полное сопротивление Z 2 .
В условиях разомкнутой цепи на выходе; то есть на выходе не будет тока, тогда
Теперь мы можем доказать уравнение выходного напряжения (1), используя основной закон, Закон Ома
Подставив уравнение (4) в (3), мы получим
Итак, уравнение доказано.
Передаточная функция приведенного выше уравнения равна
Это уравнение также называется делителем
Цепи емкостного делителя никогда не пропускают вход постоянного тока.Они работают от входа переменного тока.
Для индуктивного делителя с невзаимодействующими катушками индуктивности уравнение принимает следующий вид:
Индуктивный делитель делит вход постоянного тока аналогично схеме резисторного делителя в зависимости от сопротивления и делит вход переменного тока с учетом индуктивности.
Ниже показана базовая схема RC-фильтра нижних частот, которая состоит из резистора и конденсатора.
C → Емкость
R → Сопротивление
X C → Реактивное сопротивление конденсатора
ω → Излучаемая частота
j → Мнимая единица
Здесь отношение напряжений делителя
RC → Постоянная времени цепи, представленной как τ .
Делитель напряжения в состоянии нагрузки
Теперь мы можем увидеть цепь делителя напряжения в нагруженном состоянии. Здесь резисторы (R 1 и R 2 ) взяты для простоты. Резистор (R L ) подключен к выходу. Тогда уравнение принимает следующий вид:
R 2 и R L параллельны друг другу.
Схема в нагруженном состоянии показана ниже.
Применения делителя напряжения
Применения включают смещение логического уровня, измерение датчика, измерение высокого напряжения, регулировку уровня сигнала.
Измерительные приборы, такие как мультиметр и мост Уитстона, состоят из делителя напряжения .



 Чем больше понижается напряжение, тем меньше мощности от источника питания поступит к нагрузке.
Чем больше понижается напряжение, тем меньше мощности от источника питания поступит к нагрузке.