Работа силы
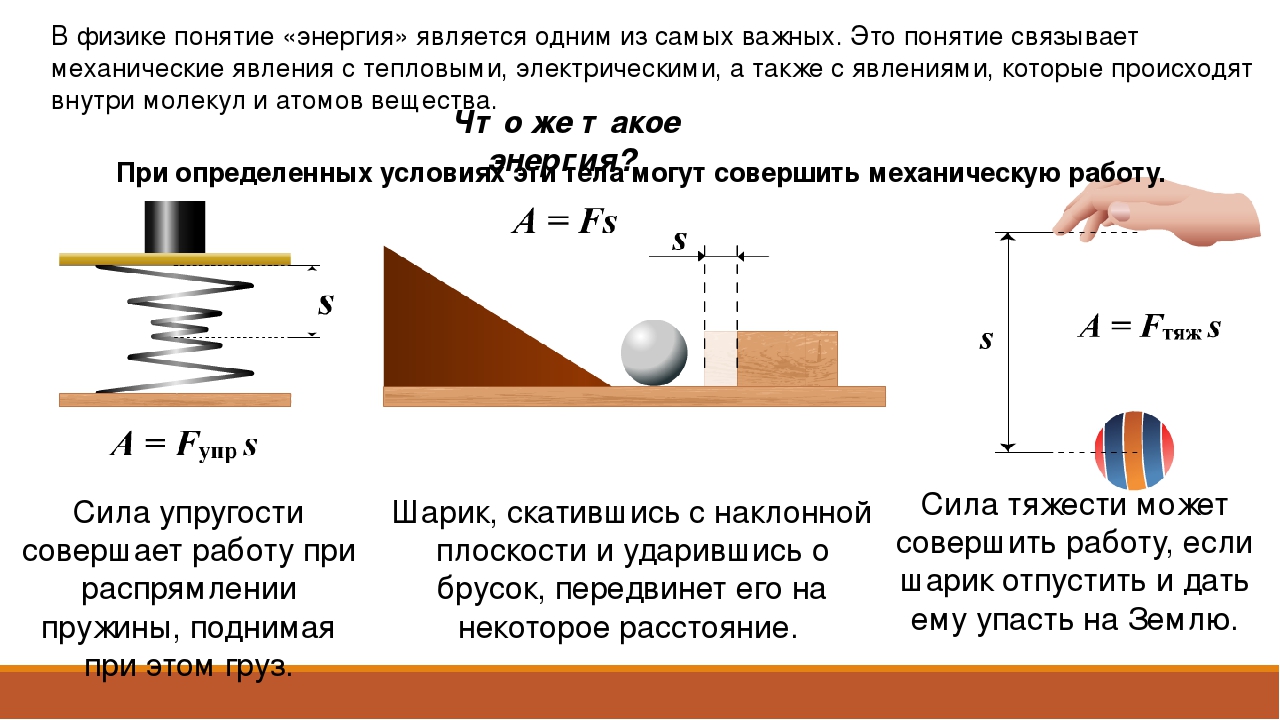
Все мы с детства знаем, что такое физическая работа. Самые элементарные действия, такие как, пододвинуть стол или нести рюкзак — это та или иная работа. И на эту работу, как мы говорим, нужно затратить силы.
Работа силы — это величина, характеризующая воздействие силы, в зависимости как от самой силы, так и от перемещения тела, к которому была приложена сила.
Мы, наверняка скажем, что нести рюкзак целый километр вдвое тяжелее, чем нести этот же рюкзак всего полкилометра. Хотя для того, чтобы удержать рюкзак на спине требуется одна и та же сила, не зависимо от расстояния, которое вы преодолеете.
Таким образом, работа силы в механике равна произведению силы и перемещения тела, к которому была приложена сила:
Напомним, что и сила, и
перемещение являются векторными величинами. Если направление силы, вызвавшей
перемещение, не совпадает с направлением самого перемещения, то работа
определяется как произведение модуля силы, модуля перемещения и косинуса угла
между направлением силы и направлением перемещения.
Поскольку косинус любого угла не может быть больше единицы, и косинус 0о равен единице, можно заключить, что максимальная работа выполняется тогда, когда сила приложения направлена так же, как и перемещение. Это хорошо подтверждается и бытовыми наблюдениями.
Если же, напротив, сила, приложенная к телу, перпендикулярна его перемещению, то работа этой силы равна нулю.
Поскольку косинус принимает отрицательные значения, если аргумент больше, чем 90о, в этом случае, работа будет отрицательной. Ярким примером такой работы является работа силы трения, о которой мы в отдельности поговорим чуть позже. Ведь сила трения препятствует движение, а, значит, совершает отрицательную работу.
Заметим, что работа, сама
по себе, не может быть куда-либо направлена, хотя и определяется с помощью
векторных величин.
Если на тело действуют несколько сил, то сумма работ всех сил равна работе равнодействующей силы.
Единицей измерения работы является джоуль:
1 Дж — это работа, совершаемая силой 1 Н на перемещении 1 м, при условии, что направление этой силы совпадает с направлением перемещения.
Можно привести множество примеров совершения механической работы. Например, если человек двигает шкаф, то он совершает работу. Чем бо́льшую силу он прикладывает, и чем больше перемещает шкаф, тем бо́льшую работу он совершает. Лошадь может тянуть телегу с постоянной скоростью, но чем дальше телега уедет, тем бо́льшую работу совершит лошадь.
Необходимо отметить, что
разделяется два вида работы: полезная работа и работа совершенная.
Рассмотрим простой пример: один мальчик прошел 10 м, а другой — 5 м и вернулся
обратно. Допустим, что оба мальчика затрачивают одинаковую силу на перемещения. При этом оба они прошли 10 м, а, значит, фактически совершили одинаковую
работу. Но, вот полезная работа мальчика, который вернулся в исходную, точку
равна нулю, поскольку его перемещение равно нулю. Мальчик затратил силы, но
добился «нулевого результата»: его положение никак не изменилось.
При этом оба они прошли 10 м, а, значит, фактически совершили одинаковую
работу. Но, вот полезная работа мальчика, который вернулся в исходную, точку
равна нулю, поскольку его перемещение равно нулю. Мальчик затратил силы, но
добился «нулевого результата»: его положение никак не изменилось.
Так вот, в механике, говоря о работе силы, имеют ввиду полезную работу.
Примеры решения задач.
Задача 1. Человек толкнул телегу, приложив силу под углом 45° к горизонту. Модуль этой силы равен 120 Н. Пренебрегая трением, определите работу силы, приложенной человеком, если тележка проехала 3 м в горизонтальном направлении?
Задача 2. При растяжении пружины на 70 см, работа силы упругости составляет . Найдите коэффициент жесткости этой пружины.
И тут у нас возникает
сложность: ведь сила упругости, как мы помним, зависит от того, насколько
сильно растянули пружину, поэтому, мы не можем найти силу упругости, просто
разделив работу на перемещение.
План урока по физике на тему: «Работа силы»
Все мы с детства знаем, что такое физическая работа. Самые элементарные действия, такие как, пододвинуть стол или нести рюкзак — это та или иная работа. И на эту работу, как мы говорим, нужно затратить силы.
Работа силы — это величина, характеризующая воздействие силы, в зависимости как от самой силы, так и от перемещения тела, к которому была приложена сила.
Мы, наверняка скажем, что нести рюкзак целый километр вдвое тяжелее, чем нести этот же рюкзак всего полкилометра. Хотя для того, чтобы удержать рюкзак на спине требуется одна и та же сила, не зависимо от расстояния, которое вы преодолеете.
Таким образом, работа силы в механике равна произведению силы и перемещения тела, к которому была приложена сила:
Напомним, что и сила, и перемещение являются векторными величинами. Если направление силы, вызвавшей перемещение, не совпадает с направлением самого перемещения, то работа определяется как произведение модуля силы, модуля перемещения и косинуса угла между направлением силы и направлением перемещения.
Поскольку косинус любого угла не может быть больше единицы, и косинус 0о равен единице, можно заключить, что максимальная работа выполняется тогда, когда сила приложения направлена так же, как и перемещение. Это хорошо подтверждается и бытовыми наблюдениями.
Если же, напротив, сила, приложенная к телу, перпендикулярна его перемещению, то работа этой силы равна нулю.
Поскольку косинус принимает отрицательные значения, если аргумент больше, чем 90о, в этом случае, работа будет отрицательной. Ярким примером такой работы является работа силы трения, о которой мы в отдельности поговорим чуть позже. Ведь сила трения препятствует движение, а, значит, совершает отрицательную работу.
Заметим, что работа, сама по себе, не может быть куда-либо направлена, хотя и определяется с помощью векторных величин. Поэтому,
Если на тело действуют несколько сил, то сумма работ всех сил равна работе равнодействующей силы.
Единицей измерения работы является джоуль:
1 Дж — это работа, совершаемая силой 1 Н на перемещении 1 м, при условии, что направление этой силы совпадает с направлением перемещения.
Можно привести множество примеров совершения механической работы. Например, если человек двигает шкаф, то он совершает работу. Чем бо́льшую силу он прикладывает, и чем больше перемещает шкаф, тем бо́льшую работу он совершает.
Необходимо отметить, что разделяется два вида работы: полезная работа и работа совершенная. Рассмотрим простой пример: один мальчик прошел 10 м, а другой — 5 м и вернулся обратно. Допустим, что оба мальчика затрачивают одинаковую силу на перемещения. При этом оба они прошли 10 м, а, значит, фактически совершили одинаковую работу. Но, вот полезная работа мальчика, который вернулся в исходную, точку равна нулю, поскольку его перемещение равно нулю. Мальчик затратил силы, но добился «нулевого результата»: его положение никак не изменилось.
Так вот, в механике, говоря о работе силы, имеют ввиду полезную работу.
Примеры решения задач.
Задача 1. Человек толкнул телегу, приложив силу под углом 45° к горизонту. Модуль этой силы равен 120 Н. Пренебрегая трением, определите работу силы, приложенной человеком, если тележка проехала 3 м в горизонтальном направлении?
Задача 2. При растяжении пружины на 70 см, работа силы упругости составляет. Найдите коэффициент жесткости этой пружины.
При растяжении пружины на 70 см, работа силы упругости составляет. Найдите коэффициент жесткости этой пружины.
И тут у нас возникает сложность: ведь сила упругости, как мы помним, зависит от того, насколько сильно растянули пружину, поэтому, мы не можем найти силу упругости, просто разделив работу на перемещение. Тем не менее, зависимость силы упругости от растяжения является линейной, а, следовательно, график зависимости силы упругости от растяжения будет являться прямой линией. Если мы построим такой график, то убедимся, что площадь под ним будет равна работе силы упругости.
В курсе физики 7-го класса мы узнали, что если тело под действием некоторой силы совершает перемещение(см. Рис. 1) в направлении действия силы, то сила совершает работу A, равную произведению модуля силы на модуль перемещения.
Рис. 1. Перемещение тела под действием силы F
Единицей измерения работы в системе СИ является джоуль – работа силы в 1 Н при перемещении точки ее приложения на 1 м:
Данное определение работы ограничено только случаем, когда на тело действует единственная сила, которая с перемещением являются сонаправленными векторами. Поэтому необходимо обобщить данную формулу работы для ситуации, когда перемещение происходит в направлении, не совпадающем с направлением действия силы, и когда на тело действует несколько сил.
Поэтому необходимо обобщить данную формулу работы для ситуации, когда перемещение происходит в направлении, не совпадающем с направлением действия силы, и когда на тело действует несколько сил.
Рис. 2. На тело действует несколько сил
Если на тело действует несколько сил (см. Рис. 2), то в этом случае необходимо в формулу для работы подставлять значение равнодействующей всех сил. Следовательно, работа будет равна сумме всех работ отдельных сил.
Равнодействующая может быть равна нулю, даже если отдельные силы не нулевые. В этом случае работа также должна быть равной нулю, поэтому, в соответствии с формулой , работы отдельных сил должны быть с разными знаками (могут быть отрицательными или положительными). Таким образом, необходимо формулу для вычисления работы привести к такому виду, чтобы можно было получать как положительные, так и отрицательные значения этой величины. Из курса геометрии известно, что операция, позволяющая при умножении векторов получать число (положительное или отрицательное), называется скалярным произведением векторов.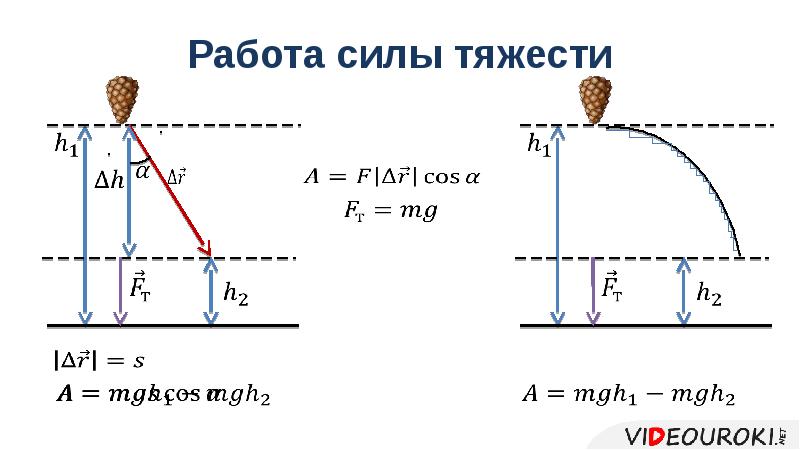
Механической работой называется величина, равная скалярному произведению равнодействующей сил, действующих на тело, на перемещение тела.
Если угол между векторами равнодействующей силы и перемещения острый, то работа положительная (см. Рис. 3).
Рис. 3. Острый угол между векторами равнодействующей силы и перемещения
Если угол между векторами равнодействующей силы и перемещения тупой, то работа отрицательна (см. Рис. 4).
Рис. 4. Тупой угол между векторами равнодействующей силы и перемещения
Для примера: когда человек с помощью верёвки тащит за собой санки, верёвка образует с направлением движения санок острый угол (см. Рис. 5). Следовательно, работа силы, с которой человек тянет санки, имеет положительный знак.
Рис. 5. Работа силы, с которой человек тянет санки
Направление равнодействующей силы может быть перпендикулярно направлению перемещения тела. В этом случае угол между векторами силы и перемещения равен .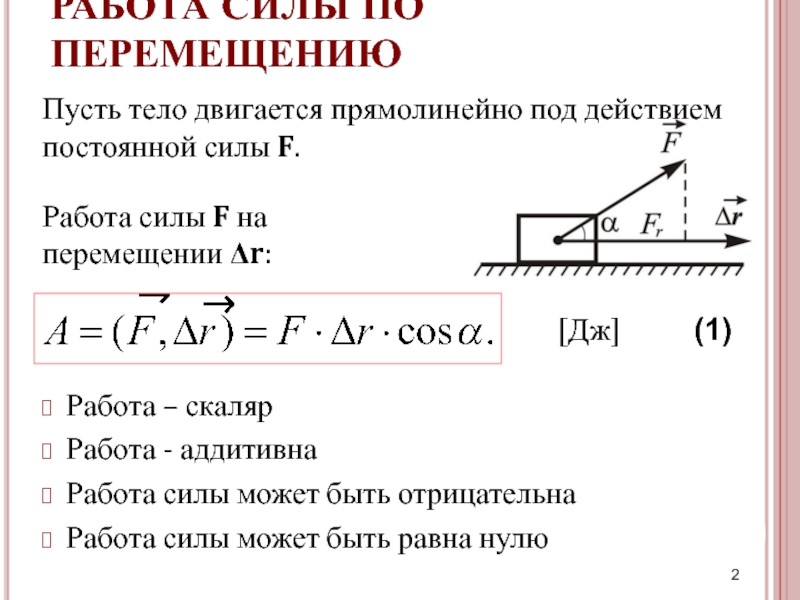 Так как косинус этого угла равен нулю, то работа, совершаемая данной равнодействующей силой над телом, равна нулю.
Так как косинус этого угла равен нулю, то работа, совершаемая данной равнодействующей силой над телом, равна нулю.
Возвращаясь к примеру с санками, можно сказать, что сила тяжести, которая действует на санки, перпендикулярна направлению движения и не совершает работу (см. Рис. 6).
Рис. 6. Сила тяжести не совершает работу
Также не совершает работу при равномерном движении по окружности та сила, которая вынуждает тело двигаться таким образом, так как эта сила в любой точке окружности перпендикулярна направлению скорости тела. Например, не совершает работу сила всемирного тяготения, под действием которой искусственные спутники Земли движутся по круговой орбите.
Мощность
Работа силы. Мощность. | Поурочные планы по физике 7 класс
Работа силы. Мощность.
27.02.2014 5179 0Цель: научить находить
механическую работу силы.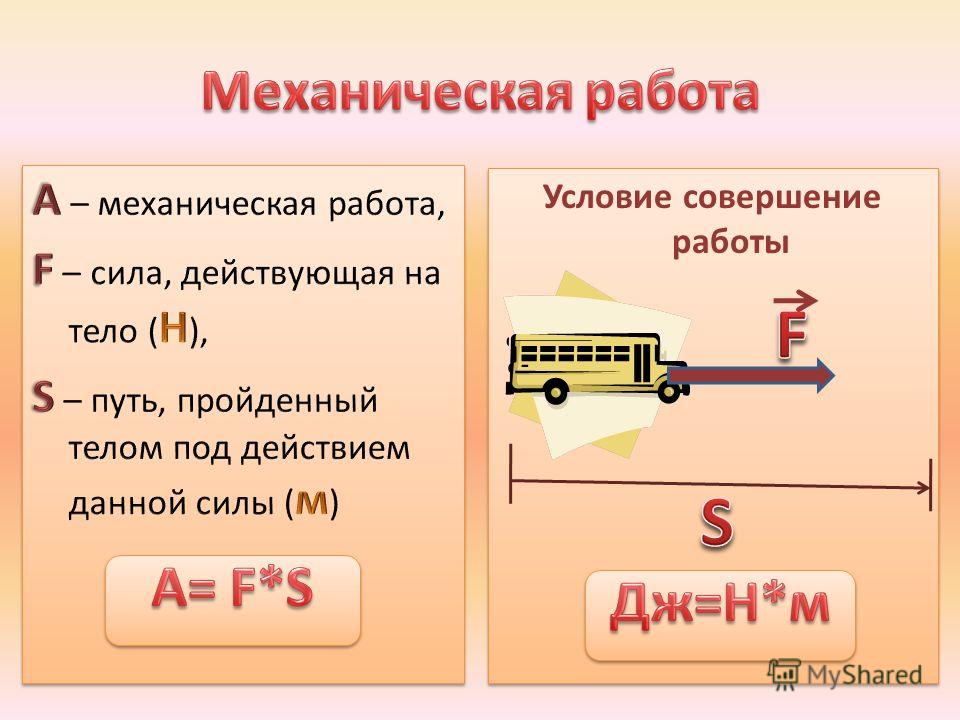 сформировать понятие о мощности. Побуждать учащихся к преодолению трудностей в
процессе умственной деятельности, воспитать интерес к физике.
сформировать понятие о мощности. Побуждать учащихся к преодолению трудностей в
процессе умственной деятельности, воспитать интерес к физике.
Ход урока
I. Организационный момент
II. Проверка домашнего задания
1. Что такое капиллярные явления?
2. Приведите примеры, где используются капиллярные явления?
3. Что такое смачивание?
4. Назовите закон Архимеда?
III. Изучение нового материала
1.По горизонтальной плоскости двигается трактор. Со стороны трактора действует на прицеп постоянная сила тяги. Под действием этой силы прицеп перемещается на 2 км, а затем на 4 км. Между перемещениями имеется отличие. И для характеристики этого отличия понятия силы недостаточно. Введем еще одно понятие — работа: А = Fs => 1 Дж = 1 кгм2/с2
Работа численно равна площади прямоугольника со сторонами , где Fx = F cos a.
Тогда А = F s* cos a.
Работа силы F при перемещении s равна произведению модулей этих векторов на косинус угла между ними.
Работа — скалярная величина.
А > 0, если 0° < а < 90″, cos а > 0
А < 0, если 90° < а = 180″, cos а < 0
А = 0, если а = 90°.
Определить работу не всегда легко. При перемещении по криволинейной траектории угол между силой тяжести и направлением скорости непрерывно меняется. Это осложняет расчет.
Решим задачу. Определить работу силы тяжести Ft = mg при перемещении тела из т. 1 в т. 2. Пусть траектория представляет ступеньку е высоты s0 до высоты s no вертикали, а дальше по горизонтали (
А, = FTs cos 180° = FTs0 — FTs
А2 = FTS cos 90″ = 0 (по горизонтали)
А = А + А2 — FTs — FTs
Пусть ступенек будет две (А = 0)
А, = FTs0 — F от s0 до s
А2 = FTs, — FTs2 от h2 до h2
Суммируя, получим:
А = FT — Fts- Fs.
Уже ясно, сколько бы ступенек не было, результат будет такой же.
A=FTs-mg(s0-s).
Работа силы тяжести по замкнутому контуру (траектории) равна нулю.
2. Очень часто важно знать не только работу, но и время, в течение которого она производится. Поэтому вводят понятие мощности.
Работа может быть совершена как быстро, так и медленно. Временем, в течение которого совершается работа, определяют производительность.
Мощностью называют отношение работы А к интервалу времени t, за который эта работа совершена:
N=A/t
В СИ мощность выражается в ваттах (Вт).
До сих пор иногда применяют старую единицу мощности — лошадиную силу (л.с.):1л.с. = 735Вт.
Мощности, развиваемые двигателями, колеблются в огромном диапазоне: от долей ватта до сотен и тысяч мегаватт (для космических ракет).
Человек может длительное время развивать мощность 70 Вт. Мощность муравья 105Вт.
IV. Повторение. Беседа
Повторение. Беседа
1. Что называют механической работой?
2. Какая формула выражает смысл этого понятия?
3. В каком случае о силе можно сказать, что она совершает работу?
4. В каком случае работа положительна, в каком отрицательна, в каком равна нулю?
5. Единицы работы в системе СИ?
6. Тело брошено вертикально вверх. Укажите, положительную или отрицательную работу совершает сила тяжести?
7.Почему при подъеме автомобиля в гору или при движении по песку шофер включает первую скорость?
8. Как скорость движения автомобиля зависит от мощности двигателя, если силу сопротивления движению считать постоянной?
9. Как скорость движения автомобиля зависит от мощности двигателя, если сила сопротивления при больших скоростях прямо пропорциональна квадрату скорости.
10. Что называют мощностью?
11. Что такое лошадиная сила и каково ее отношение с ваттом?
V. Решение задач
Вагонетку массой 2 т по горизонтальному пути
равномерно перемещает рабочий. Какую работу он совершит на пути 100 м, и какую
работу совершает сила трения, если коэффициент трения равен 0,01.
Какую работу он совершит на пути 100 м, и какую
работу совершает сила трения, если коэффициент трения равен 0,01.
Домашнее задание
§ 63-64 Упражнение 36
Механическая работа. Мощность ❤️ | Физика
1. Определение работы
С механической работой (работой силы) вы уже знакомы из курса физики основной школы. Напомним приведенное там определение механической работы для следующих случаев.
Если сила направлена так же, как перемещение тела, то работа силы
A = Fs (1)
В этом случае работа силы положительна.
Если сила направлена противоположно перемещению тела,
то работа силыA = — Fs (2)
В этом случае работа силы отрицательна.
Если сила f_vec направлена перпендикулярно перемещению s_vec тела, то работа силы равна нулю:
A = 0 (3)
Работа — скалярная величина. Единицу работы называют джоуль (обозначают: Дж) в честь английского ученого Джеймса Джоуля, сыгравшего важную роль в открытии закона сохранения энергии. Из формулы (1) следует:
Из формулы (1) следует:
1 Дж = 1 Н * м.
? 1. Брусок массой 0,5 кг переместили по столу на 2 м, прикладывая к нему силу упругости, равную 4 Н (рис. 28.1). Коэффициент трения между бруском
и столом равен 0,2.Чему равна работа действующей на брусок: а) силы тяжести m? б) силы нормальной реакции ? в) силы упругости ?
г) силы трения скольжения Тр?
Суммарную работу нескольких сил, действующих на тело, можно найти двумя способами: 1. Найти работу каждой силы и сложить эти работы с учетом знаков.
2. Найти равнодействующую всех приложенных к телу сил и вычислить работу равнодействующей.
Оба способа приводят к одному и тому же результату. Чтобы убедиться в этом, вернитесь к предыдущему заданию и ответьте на вопросы задания 2.
? 2. Чему равна: а) сумма работ всех действующих на брусок сил? б) равнодействующая всех действующих на брусок сил? в) работа равнодействующей?
В общем случае (когда сила f_vec направлена под произвольным углом к перемещению s_vec) определение работы силы таково.
Работа A постоянной силы равна произведению модуля силы F на модуль перемещения s и на косинус угла α между направлением силы и направлением перемещения:
A = Fs cos α (4)
? 3. Покажите, что из общего определения работы следуют к выводы, показанные на следующей схеме. Сформулируйте их словесно и запишите в тетрадь.
? 4. К находящемуся на столе бруску приложена сила, модуль которой 10 Н. Чему равен угол между этой силой и перемещением бруска, если при перемещении бруска по столу на 60 см эта сила совершила работу: а) 3 Дж; б) -3 Дж; в) -3 Дж; г) -6 Дж? Сделайте пояснительные чертежи.
2. Работа силы тяжести
Пусть тело массой m движется вертикально от начальной высоты hн до конечной высоты hк.
Если тело движется вниз (hн > hк, рис. 28.2, а), направление перемещения совпадает с направлением силы тяжести, поэтому работа силы тяжести положительна. Если же тело движется вверх (hн < hк, рис. 28.2, б), то работа силы тяжести отрицательна.
В обоих случаях работа силы тяжести
A = mg(hн — hк). (5)
Найдем теперь работу силы тяжести при движении под углом к вертикали.
? 5. Небольшой брусок массой m соскользнул вдоль наклонной плоскости длиной s и высотой h (рис. 28.3). Наклонная плоскость составляет угол α с вертикалью.
а) Чему равен угол между направлением силы тяжести и направлением перемещения бруска? Сделайте пояснительный чертеж. б) Выразите работу силы тяжести через m, g, s, α. в) Выразите s через h и α. г) Выразите работу силы тяжести через m, g, h. д) Чему равна работа силы тяжести при движении бруска вдоль всей этой же плоскости вверх?
Выполнив это задание, вы убедились, что работа силы тяжести выражается формулой (5) и тогда, когда тело движется под углом к вертикали — как вниз, так и вверх.
Но тогда формула (5) для работы силы тяжести справедлива при движении тела по любой траектории, потому что любую траекторию (рис. 28.4, а) можно представить как совокупность малых «наклонных плоскостей» (рис. 28.4, б).
28.4, б).
Таким образом, Работа силы тяжести при движении но любой траектории выражается формулой
Aт = mg(hн — hк),
Где hн — начальная высота тела, hк — его конечная высота. Работа силы тяжести не зависит от формы траектории.
Например, работа силы тяжести при перемещении тела из точки A в точку B (рис. 28.5) по траектории 1, 2 или 3 одинакова. Отсюда, в частности, следует, что рибота силы тяжести при перемещении по замкнутой траектории (когда тело возвращается в исходную точку) равна нулю.
? 6. Шар массой m, висящий на нити длиной l, отклонили на 90º, держа нить натянутой, и отпустили без толчка. а) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия (рис. 28.6)?
б) Чему равна работа силы упругости нити за то же время? в) Чему равна работа равнодействующей сил, приложенных к шару, за то же время?
3. Работа силы упругости
Когда пружина возвращается в недеформированное состояние, сила упругости совершает всегда положительную работу: ее направление совпадает с направлением перемещения (рис. 28.7).
28.7).
Найдем работу силы упругости . Модуль этой силы связан с модулем деформации x соотношением (см. § 15)
F = kx. (6)
Работу такой силы можно найти графически.
Заметим сначала, что работа постоянной силы численно равна площади прямоугольника под графиком зависимости силы от перемещения (рис. 28.8). На рисунке 28.9 изображен график зависимости F(x) для силы упругости. Разобьем мысленно все перемещение тела на столь малые промежутки, чтобы на каждом из них силу можно было считать постоянной.
Тогда работа на каждом из этих промежутков численно равна площади фигуры под соответствующим участком графика. Вся же работа равна сумме работ на этих участках.
Следовательно, и в этом случае работа численно равна площади фигуры под графиком зависимости F(x).
? 7. Используя рисунок 28.10, докажите, что
Работа силы упругости при возвращении пружины в недеформированное состояние выражается формулой
A = (kx2)/2. (7)
? 8. Используя график на рисунке 28. 11, докажите, что при изменении деформации пружины от xн до xк работа силы упругости выражается формулой
11, докажите, что при изменении деформации пружины от xн до xк работа силы упругости выражается формулой
Из формулы (8) мы видим, что работа силы упругости зависит только от начальной и конечной деформации пружины, Поэтому если тело сначала деформируют, а потом оно возвращается в начальное состояние, то работа силы упругости равна нулю. Напомним, что таким же свойством обладает и работа силы тяжести.
? 9. В начальный момент растяжение пружины жесткостью 400 Н/м равно 3 см. Пружину растянули еще на 2 см. а) Чему равна конечная деформация пружины?
б) Чему равна работа силы упругости пружины?
? 10. В начальный момент пружина жесткостью 200 Н/м растянута на 2 см, а в конечный момент она сжата на 1 см. Чему равна работа силы упругости пружины?
4. Работа силы трения
Пусть тело скользит по неподвижной опоре. Действующая на тело сила трения скольжения направлена всегда противоположно перемещению и, следовательно, работа силы трения скольжения отрицательно при любом направлении перемещения (рис. 28.12).
28.12).
Поэтому если сдвинуть брусок вправо, а пегом на такое же расстояние влево, то, хотя он и вернется в начальное положение, суммарная работа силы трения скольжения не будет равна нулю. В этом состоит важнейшее отличие работы силы трения скольжения от работы силы тяжести и силы упругости. Напомним, что работа этих сил при перемещении тела по замкнутой траектории равна нулю.
? 11. Брусок массой 1 кг передвигали по столу так, что его траекторией оказался квадрат со стороной 50 см. а) Вернулся ли брусок в начальную точку?
б) Чему равна суммарная работа действовавшей на брусок силы трения? Коэффициент трения между бруском и столом равен 0,3.
5. Мощность
Часто важна не только совершаемая работа, но и скорость совершения работы. Она характеризуется мощностью.
Мощностью P называют отношение совершенной работы A к промежутку времени t, за который эта работа совершена:
P = A/t. (9)
(Иногда мощность в механике обозначают буквой N, а в электродинамике — буквой P.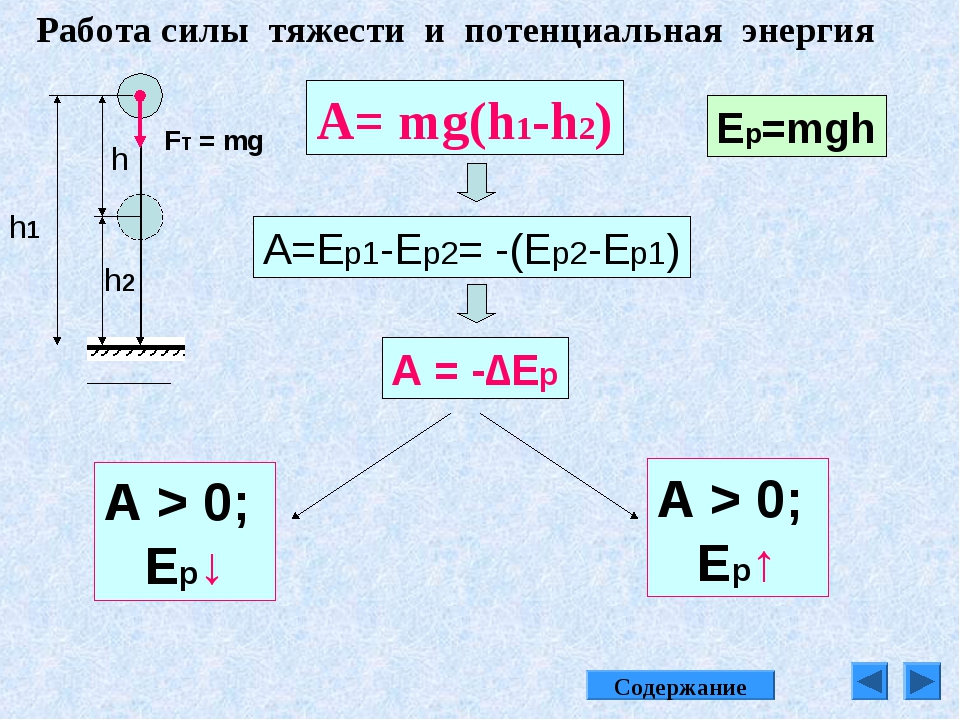 Мы считаем более удобным одинаковое обозначение мощности.)
Мы считаем более удобным одинаковое обозначение мощности.)
Единица мощности — ватт (обозначают: Вт), названная в честь английского изобретателя Джеймса Уатта. Из формулы (9) следует, что
1 Вт = 1 Дж/c.
? 12. Какую мощность развивает человек, равномерно поднимая ведро воды массой 10 кг на высоту 1 м в течение 2 с?
Часто мощность удобно выражать не через работу и время, а через силу и скорость.
Рассмотрим случай, когда сила направлена вдоль перемещения. Тогда работа силы A = Fs. Подставляя это выражение в формулу (9) для мощности, получаем:
P = (Fs)/t = F(s/t) = Fv. (10)
? 13. Автомобиль едет по горизонтальной дороге со скоростью 72 км/ч. При этом его двигатель развивает мощность 20 кВт.
Чему равна сила сопротивления движению автомобиля?
Подсказка. Когда автомобиль движется по горизонтальной дороге с постоянной скоростью, сила тяги равна по модулю силе сопротивления движению автомобиля.
? 14. Сколько времени потребуется для равномерного подъема бетонного блока массой 4 т на высоту 30 м, если мощность двигателя подъемного крана 20 кВт, а КПД электродвигателя подъемного крана равен 75%?
Подсказка. КПД электродвигателя равен отношению работы по подъему груза к работе двигателя.
КПД электродвигателя равен отношению работы по подъему груза к работе двигателя.
Дополнительные вопросы и задания
15. Мяч массой 200 г бросили с балкона высотой 10 и под углом 45º к горизонту. Достигнув в полете максимальной высоты 15 м, мяч упал на землю. а) Чему равна работа силы тяжести при подъеме мяча? б) Чему равна работа силы тяжести при спуске мяча?
в) Чему равна работа силы тяжести за все время полета мяча? г) Есть ли в условии лишние данные?
16. Шар массой 0,5 кг подвешен к пружине жесткостью 250 Н/м и находится в равновесии. Шар поднимают так, чтобы пружина стала недеформированной, и отпускают без толчка. а) На какую высоту подняли шар? б) Чему равна работа силы тяжести за время, в течение которого шар движется к положению равновесия? в) Чему равна работа силы упругости за время, в течение которого шар движется к положению равновесия?
г) Чему равна работа равнодействующей всех приложенных к шару сил за время, в течение которого шар движется к положению равновесия?
17. Санки массой 10 кг съезжают без начальной скорости со снежной горы с углом наклона α = 30º и проезжают некоторое расстояние по горизонтальной поверхности (рис. 28.13). Коэффициент трения между санками и снегом 0,1. Длина основания горы l = 15 м.
Санки массой 10 кг съезжают без начальной скорости со снежной горы с углом наклона α = 30º и проезжают некоторое расстояние по горизонтальной поверхности (рис. 28.13). Коэффициент трения между санками и снегом 0,1. Длина основания горы l = 15 м.
а) Чему равен модуль силы трения при движении санок по горизонтальной поверхности? б) Чему равна работа силы трения при движении санок по горизонтальной поверхности на пути 20 м? в) Чему равен модуль силы трения при движении санок по горе? г) Чему равна работа силы трения при спуске санок? д) Чему равна работа силы тяжести при спуске санок?
е) Чему равна работа равнодействующей сил, действующих на санки, при их спуске с горы?
18. Автомобиль массой 1 т движется со скоростью 50 км/ч. Двигатель развивает мощность 10 кВт. Расход бензина составляет 8 л на 100 км. Плотность бензина 750 кг/м3, а его удельная теплота сгорания 45 МДж/кг. Чему равен КПД двигателя?
Есть ли в условии лишние данные? Подсказка. КПД теплового двигателя равен отношению совершенной двигателем работы к количеству теплоты, которое выделилось при сгорании топлива.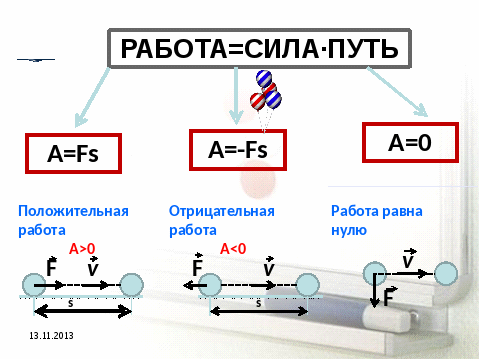
Работа — Физическая энциклопедия
РАБОТА силы — мера действия силы, зависящая от её модуля и направления и от перемещения точки приложения силы. Если сила постоянна по модулю и направлению, а перемещение прямолинейно (рис. 1), то Р. определяется равенством где- угол между направлениями силы и перемещения. Если a < 90°, то А > 0, а если 180°a > 90°, то А < 0; если же a = 90°, т. е. если сила перпендикулярна перемещению, то А = 0. Единицы измерения Р.- джоуль, эрг (1 эрг = 10-7 Дж) и кило-грамм-сила на 1 метр (1 кгс·м9,81 Дж).
Рис. 1.
В общем случае для вычисления Р. силы вводят
понятие элементарной работы
где ds — элементарное перемещение точки приложения силы, a — угол между силой и касательной к траектории её приложения, направленной в
сторону перемещения точки, —
проекция силы на эту касательную (рис. 2). В декартовых координатах х,
y, z — координаты точки её приложения.
2). В декартовых координатах х,
y, z — координаты точки её приложения.
Рис. 2.
где-
проекции силы на координатные оси;
В обобщённых координатах
где qi— обобщённые координаты,
Qi— обобщённые силы. Для сил, действующих на тело, имеющее
неподвижную ось вращениягде Мz — сумма моментов сил относительно оси вращения, f
— угол поворота тела. Для сил давления dA = pdV, где p — давление, V — объём.
Р. силы на конечном перемещении определяется
как предел интегральной суммы соответствующих элементарных работ и при перемещении М0М1 выражается криволинейным интегралом
Для потенциальных сил dA = dU или dA = —dП, где U — силовая ф-ция, П — потенциальная
энергия системы, А = U1 — U0 или А = П0 — П1 где U0,U1,
П0, П1 — значения соответствующих величин в начальном
и конечном положениях системы; в этом случае Р. не зависит от вида траекторий
точек приложения сил. При движении механич. системы сумма работ всех действующих
сил на нек-ром перемещении этой системы равна изменению её кинетической энергии
Т на этом же перемещении, т. е.
не зависит от вида траекторий
точек приложения сил. При движении механич. системы сумма работ всех действующих
сил на нек-ром перемещении этой системы равна изменению её кинетической энергии
Т на этом же перемещении, т. е.
Понятие Р. широко используется в механике и в
др. областях физики, а также в технике. С.
М. Тарг.
Предметный указатель >>
Что такое работа в физике формула. Механическая работа
Вы знаете, что такое работа? Вне всякого сомнения. Что такое работа, знает каждый человек, при условии, что он рожден и живет на планете Земля. А что такое механическая работа?
Это понятие тоже известно большинству людей на планете, хотя некоторые отдельные личности и имеют довольно смутное представление об этом процессе. Но речь сейчас не о них. Еще меньшее число людей имеют представление, что такое механическая работа с точки зрения физики. В физике механическая работа — это не труд человека ради пропитания, это физическая величина, которая может быть совершенно никак не связана ни с человеком, ни с другим каким-нибудь живым существом.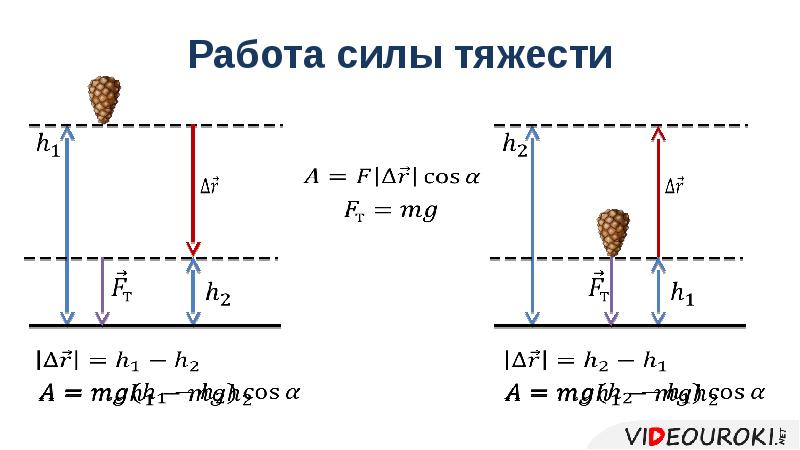 Как так? Сейчас разберемся.
Как так? Сейчас разберемся.
Механическая работа в физике
Приведем два примера. В первом примере воды реки, столкнувшись с пропастью, шумно падают вниз в виде водопада. Второй пример — это человек, который держит на вытянутых руках тяжелый предмет, например, удерживает надломившуюся крышу над крыльцом дачного домика от падения, пока его жена и дети судорожно ищут, чем ее подпереть. В каком случае совершается механическая работа?
Определение механической работы
Практически все, не задумываясь, ответят: во втором. И будут неправы. Дело обстоит как раз наоборот. В физике механическая работа описывается следующими определениями: механическая работа совершается тогда, когда на тело действует сила, и оно движется. Механическая работа прямо пропорциональна приложенной силе и пройденному пути.
Формула механической работы
Определяется механическая работа формулой:
где A — работа,
F — сила,
s — пройденный путь.
Так что, несмотря на весь героизм уставшего держателя крыши, проделанная им работа равна нулю, а вот вода, падая под действием силы тяжести с высокого утеса, совершает самую, что ни на есть, механическую работу. То есть, если мы будем толкать тяжелый шкаф безуспешно, то проделанная нами работа с точки зрения физики будет равна нулю, несмотря на то, что мы прикладываем много сил. А вот если мы сдвинем шкаф на некоторое расстояние, то тогда мы проделаем работу, равную произведению приложенной силы на расстояние, на которое мы передвинули тело.
То есть, если мы будем толкать тяжелый шкаф безуспешно, то проделанная нами работа с точки зрения физики будет равна нулю, несмотря на то, что мы прикладываем много сил. А вот если мы сдвинем шкаф на некоторое расстояние, то тогда мы проделаем работу, равную произведению приложенной силы на расстояние, на которое мы передвинули тело.
Единица работы — 1 Дж. Это работа, совершенная силой в 1 ньютон, по передвижению тела на расстояние в 1 м. Если направление приложенной силы совпадает с направлением движения тела, то данная сила совершает положительную работу. Пример — это когда мы толкаем какое-либо тело, и оно двигается. А в случае, когда сила приложена в противоположную движению тела сторону, например, сила трения , то данная сила совершает отрицательную работу. Если же приложенная сила никак не влияет на движение тела, то сила, совершаемая этой работой, равна нулю.
В повседневной жизни часто приходится встречаться с таким понятием как работа. Что это слово означает в физике и как определить работу силы упругости? Ответы на эти вопросы вы узнаете в статье.
Механическая работа
Работа — это скалярная алгебраическая величина, которая характеризует связь между силой и перемещением. При совпадении направления этих двух переменных она вычисляется по следующей формуле:
- F — модуль вектора силы, которая совершает работу;
- S — модуль вектора перемещения.
Не всегда сила, которая действует на тело, совершает работу. Например, работа силы тяжести равна нулю, если ее направление перпендикулярно перемещению тела.
Если вектор силы образует отличный от нуля угол с вектором перемещения, то для определения работы следует воспользоваться другой формулой:
A=FScosα
α — угол между векторами силы и перемещения.
Значит, механическая работа — это произведение проекции силы на направление перемещения и модуля перемещения, или произведение проекции перемещения на направление силы и модуля этой силы.
Знак механической работы
В зависимости от направления силы относительно перемещения тела работа A может быть:
- положительной (0°≤ α
- отрицательной (90°
- равной нулю (α=90°).

Если A>0, то скорость тела увеличивается. Пример — падение яблока с дерева на землю. При A
Единица измерения работы в СИ (Международной системе единиц) — Джоуль (1Н*1м=Дж). Джоуль — это работа силы, значение которой равно 1 Ньютону, при перемещении тела на 1 метр в направлении действия силы.
Работа силы упругости
Работу силы можно определить и графическим способом. Для этого вычисляется площадь криволинейной фигуры под графиком F s (x).
Так, по графику зависимости силы упругости от удлинения пружины, можно вывести формулу работы силы упругости.
Она равна:
A=kx 2 /2
- k — жесткость;
- x — абсолютное удлинение.
Что мы узнали?
Механическая работа совершается при действии на тело силы, которая приводит к перемещению тела. В зависимости от угла, который возникает между силой и перемещением, работа может быть равна нулю или иметь отрицательный или положительный знак. На примере силы упругости вы узнали о графическом способе определения работы.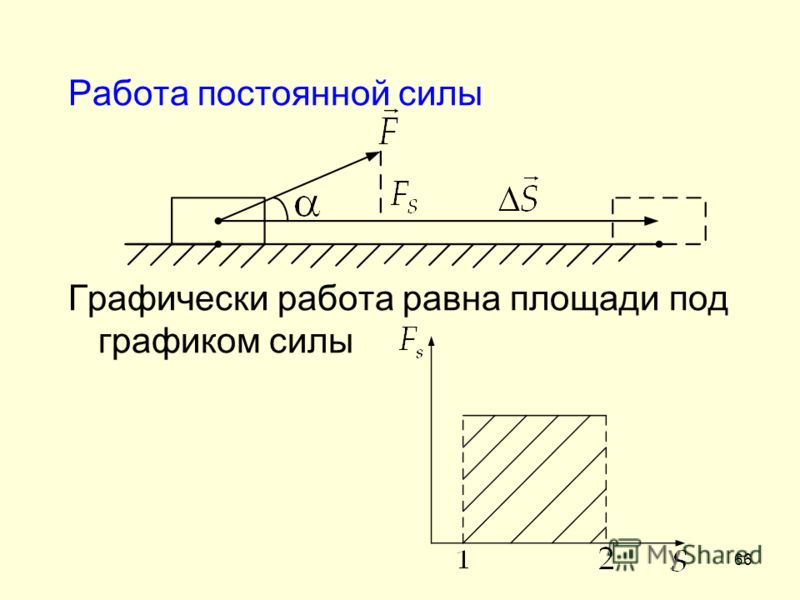
Каждое тело, совершающее движение, можно охарактеризовать работой. Иными словами, она характеризует действие сил.
Работа определяется как:
Произведение модуля силы и пути пройденного телом, умноженное на косинус угла между направлением силы и движения.
Работа измеряется в Джоулях:
1 [Дж] = = [кг* м2/c2]
К примеру, тело A под действием силы в 5 Н, прошло 10 м. Определить работу совершенную телом.
Так как направление движения и действия силы совпадают, то угол между вектором силы и вектором перемещения будет равен 0°. Формула упроститься, потому что косинус угла в 0° равен 1.
Подставляя исходные параметры в формулу, находим:
A= 15 Дж.
Рассмотрим другой пример, тело массой 2 кг, двигаясь с ускорением 6 м/ с2, прошло 10 м. Определить работу проделанную телом, если оно двигалось по наклоненной плоскости вверх под углом 60°.
Для начала, вычислим какую силу нужно приложить, что бы сообщить телу ускорение 6 м/ с2.
F = 2 кг * 6 м/ с2 = 12 H.
Под действием силы 12H, тело прошло 10 м. Работу можно вычислить по уже известной формуле:
Где, а равно 30°. Подставляя исходные данные в формулу получаем:
A= 103, 2 Дж.
Мощность
Множество машин механизмов выполняют одну и ту же работу за различный промежуток времени. Для их сравнения вводится понятие мощности.
Мощность – это величина, показывающая объем работы выполненный за единицу времени.
Мощность измеряется в Ватт, в честь Шотландского инженера Джеймса Ватта.
1 [Ватт] = 1 [Дж/c].
К примеру, большой кран поднял груз весом 10 т на высоту 30 м за 1 мин. Маленький кран на эту же высоту за 1 мин поднял 2 т кирпича. Сравнить мощности кранов.
Определим работу выполняемую кранами. Груз поднимается на 30м, при этом преодолевая силу тяжести, поэтому сила, затрачиваемая на поднятие груза, будет равна силе взаимодействия Земли и груза(F = m * g). А работа – произведению сил на расстояние пройденное грузами, то есть на высоту.
Для большого крана A1 = 10 000 кг * 30 м * 10 м / с2 = 3 000 000 Дж, а для маленького A2 = 2 000 кг * 30 м * 10 м / с2 = 600 000 Дж.
Мощность можно вычислить, разделив работу на время. Оба крана подняли груз за 1 мин (60 сек).
Отсюда:
N1 = 3 000 000 Дж/60 c = 50 000 Вт = 50 кВт.
N2 = 600 000 Дж/ 60 c = 10 000 Вт = 10 к Вт.
Из выше приведенных данных наглядно видно, что первый кран в 5 раз мощнее второго.
Если на тело действует сила, то эта сила совершает работу по перемещению этого тела. Прежде чем дать определение работе при криволинейном движении материальной точки, рассмотрим частные случаи:
В этом случае механическая работа A равна:
A = F s cos =
,
или A = Fcos × s = F S × s ,
где F S – проекция силы на перемещение. В данном случае F s = const ,
и геометрический смысл работы A – это площадь прямоугольника,
построенного в координатах F S , , s .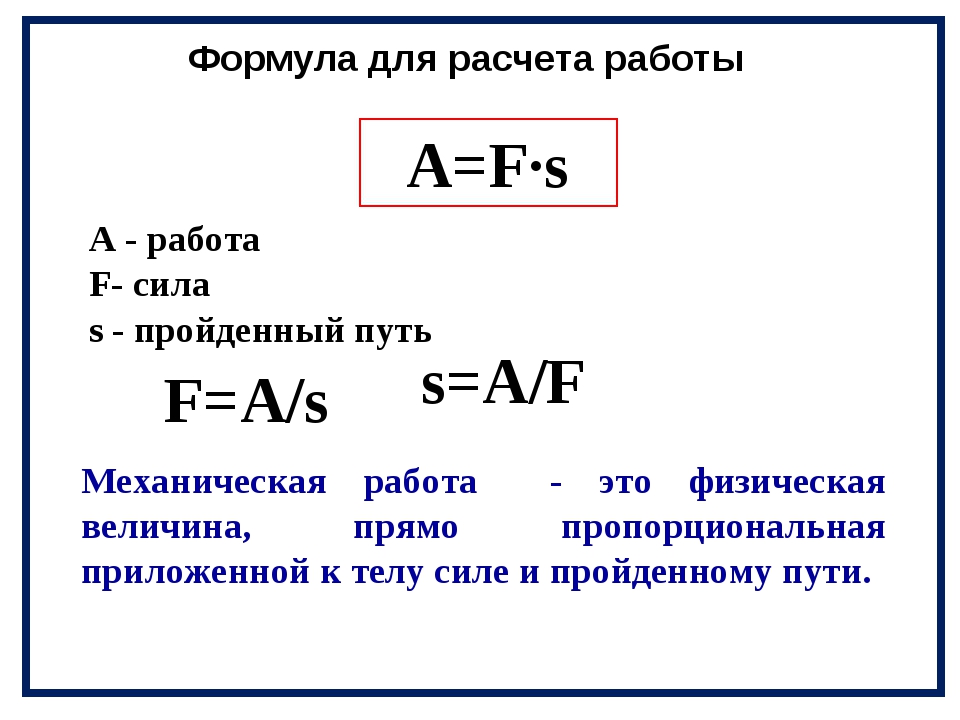
Построим график
проекции силы на направление перемещения F S как функции перемещения s.
Полное перемещение представим как сумму
n
малых перемещений
.
Для малого i -ого
перемещения
работа равна
или площади заштрихованной трапеции
на рисунке.
.
Величина, стоящая
под интегралом будет представлять
элементарную работу по бесконечно
малому перемещению
:
– элементарная работа.
Разбиваем траекторию движения материальной точки на бесконечно малые перемещения и работу силы по перемещению материальной точки из точки 1 в точку 2 определяем как криволинейный интеграл:–работа при криволинейном движении.
Пример 1: Работа
силы тяжести
при криволинейном движении материальной
точки.
.
Далее как постоянную величину можно вынести
за знак интеграла, а интеграл
согласно
рисунку будет представлять полное
перемещение
. .
.
Если обозначить высоту точки 1 от поверхности Земли через , а высоту точки 2 через , то
Мы видим, что в
данном случае работа определяется
положением материальной точки в начальный
и конечный момент времени и не зависит
от формы траектории или пути. Работа
силы тяжести по замкнутому пути равна
нулю:
.
Силы, работа которых на замкнутом пути равна нулю, называется консервативными .
Пример 2 : Работа силы трения.
Это пример неконсервативной силы. Чтобы показать это достаточно рассмотреть элементарную работу силы трения:
,
т.е. работа силы
трения всегда отрицательная величина
и на замкнутом пути не может быть равной
нулю. Работа, совершаемая в единицу
времени, называется мощностью .
Если за время
совершается работа
,
то мощность равна
–механическая мощность .
Взяв
в виде
,
получим для мощности выражение:
.
В СИ единицей
работы является джоуль:
=
1 Дж = 1 Н1
м, а единицей мощности является ватт: 1
Вт = 1 Дж/с.
Механическая энергия.
Энергия является общей количественной мерой движения взаимодействия всех видов материи. Энергия не исчезает и не возникает из нечего: она лишь может переходить из одной формы в другую. Понятие энергии связывает воедино все явления в природе. В соответствии с различными формами движения материи рассматривают разные виды энергии – механическую, внутреннюю, электромагнитную, ядерную и др.
Понятия энергии и работы тесно связаны друг с другом. Известно, что работа совершается за счет запаса энергии и, наоборот, совершая работу, можно увеличить запас энергии в каком-либо устройстве. Другими словами работа – это количественная мера изменения энергии:
.
Энергия также как и работа в СИ измеряется в джоулях: [E ]=1 Дж.
Механическая энергия бывает двух видов – кинетическая и потенциальная.
Кинетическая
энергия (или энергия
движения) определяется массами и
скоростями рассматриваемых тел.
Рассмотрим материальную точку, движущуюся
под действием силы
. Работа этой силы увеличивает кинетическую
энергию материальной точки
Работа этой силы увеличивает кинетическую
энергию материальной точки
.
Вычислим в этом случае малое приращение
(дифференциал) кинетической энергии:
При вычислении
использован
второй закон Ньютона
,
а также
— модуль скорости материальной точки.
Тогда
можно представить в виде:
—
— кинетическая энергия движущейся материальной точки .
Умножив и разделив
это выражение на
,
и учитывая, что
,
получим
—
— связь между импульсом и кинетической энергией движущейся материальной точки .
Потенциальная энергия (или энергия положения тел) определяется действием на тело консервативных сил и зависит только от положения тела.
Мы видели, что
работу силы тяжести
при криволинейном движении материальной
точки
можно представить в виде разности
значений функции
,
взятых в точке 1 и в точке 2 :
.
Оказывается, что
всегда, когда силы консервативны, работу
этих сил на пути 1
2 можно представить в виде:
.
Функция , которая зависит только от положения тела – называется потенциальной энергией .
Тогда для элементарной работы получим
–работа равна убыли потенциальной энергии .
Иначе можно сказать, что работа совершается за счёт запаса потенциальной энергии.
Величину , равную сумме кинетической и потенциальной энергий частицы, называют полной механической энергией тела:
–полная механическая энергия тела .
В заключении
заметим, что используя второй закон
Ньютона
,
дифференциал кинетической энергии
можно представить в виде:
.
Дифференциал
потенциальной энергии
,
как указывали выше, равен:
.
Таким образом, если сила – консервативная сила и отсутствуют другие внешние силы, то , т.е. в этом случае полная механическая энергия тела сохраняется.
Механическая работа. Единицы работы.
В обыденной жизни под понятием «работа» мы понимаем всё.
В физике понятие работа несколько иное. Это определенная физическая величина, а значит, ее можно измерить. В физике изучается прежде всего механическая работа .
Это определенная физическая величина, а значит, ее можно измерить. В физике изучается прежде всего механическая работа .
Рассмотрим примеры механической работы.
Поезд движется под действием силы тяги электровоза, при этом совершается механическая работа. При выстреле из ружья сила давления пороховых газов совершает работу — перемещает пулю вдоль ствола, скорость пули при этом увеличивается.
Из этих примеров видно, что механическая работа совершается, когда тело движется под действием силы. Механическая работа совершается и в том случае, когда сила, действуя на тело (например, сила трения), уменьшает скорость его движения.
Желая передвинуть шкаф, мы с силой на него надавливаем, но если он при этом в движение не приходит, то механической работы мы не совершаем. Можно представить себе случай, когда тело движется без участия сил (по инерции), в этом случае механическая работа также не совершается.
Итак, механическая работа совершается, только когда на тело действует сила, и оно движется .
Нетрудно понять, что чем большая сила действует на тело и чем длиннее путь, который проходит тело под действием этой силы, тем большая совершается работа.
Механическая работа прямо пропорциональна приложенной силе и прямо пропорциональна пройденному пути .
Поэтому, условились измерять механическую работу произведением силы на путь, пройденный по этому направлению этой силы:
работа = сила × путь
где А — работа, F — сила и s — пройденный путь.
За единицу работы принимается работа, совершаемая силой в 1Н, на пути, равном 1 м.
Единица работы — джоуль (Дж ) названа в честь английского ученого Джоуля. Таким образом,
1 Дж = 1Н · м.
Используется также килоджоули (кДж ) .
1 кДж = 1000 Дж.
Формула А = Fs применима в том случае, когда сила F постоянна и совпадает с направлением движения тела.
Если направление силы совпадает с направлением движения тела, то данная сила совершает положительную работу.
Если же движение тела происходит в направлении, противоположном направлению приложенной силы, например, силы трения скольжения, то данная сила совершает отрицательную работу.
Если направление силы, действующей на тело, перпендикулярно направлению движения, то эта сила работы не совершает, работа равна нулю:
В дальнейшем, говоря о механической работе, мы будем кратко называть ее одним словом — работа.
Пример . Вычислите работу, совершаемую при подъеме гранитной плиты объемом 0,5 м3 на высоту 20 м. Плотность гранита 2500 кг/м 3 .
Дано :
ρ = 2500 кг/м 3
Решение :
где F -сила, которую нужно приложить, чтобы равномерно поднимать плиту вверх. Эта сила по модулю равна силе тяж Fтяж, действующей на плиту, т. е. F = Fтяж. А силу тяжести можно определить по массе плиты: Fтяж = gm. Массу плиты вычислим, зная ее объем и плотность гранита: m = ρV; s = h, т. е. путь равен высоте подъема.
Итак, m = 2500 кг/м3 · 0,5 м3 = 1250 кг.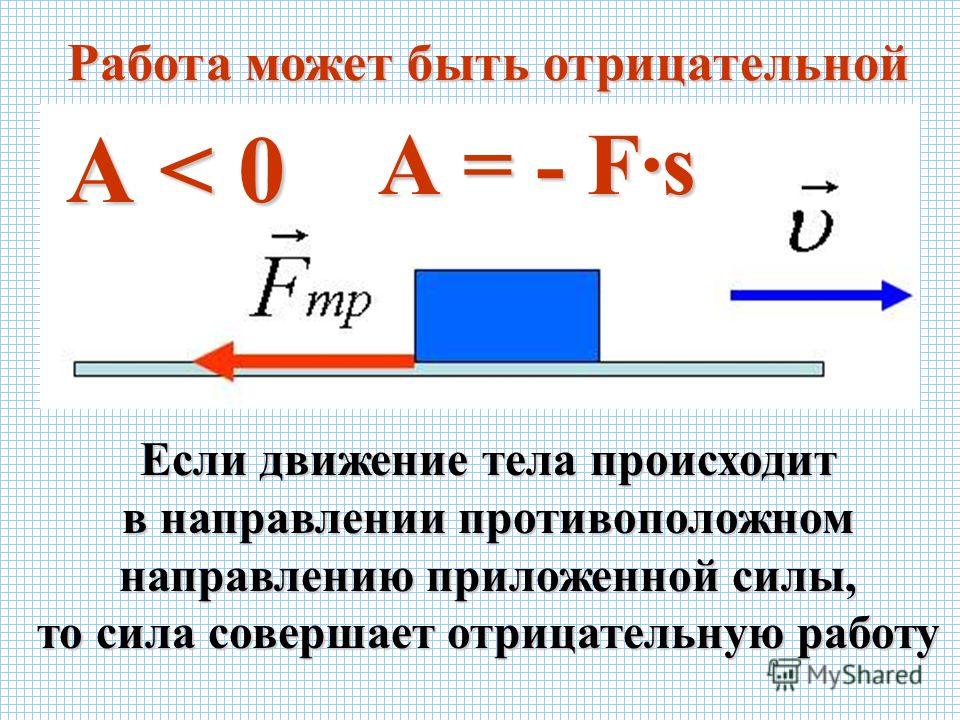
F = 9,8 Н/кг · 1250 кг ≈ 12 250 Н.
A = 12 250 Н · 20 м = 245 000 Дж = 245 кДж.
Ответ : А =245 кДж.
Рычаги.Мощность.Энергия
На совершение одной и той же работы различным двигателям требуется разное время. Например, подъемный кран на стройке за несколько минут поднимает на верхний этаж здания сотни кирпичей. Если бы эти кирпичи перетаскивал рабочий, то ему для этого потребовалось бы несколько часов. Другой пример. Гектар земли лошадь может вспахать за 10-12 ч, трактор же с многолемешным плугом (лемех — часть плуга, подрезающая пласт земли снизу и передающая его на отвал; многолемешный — много лемехов), эту работу выполнит на 40-50 мин.
Ясно, что подъемный кран ту же работу совершает быстрее, чем рабочий, а трактор — быстрее чем лошадь. Быстроту выполнения работы характеризуют особой величиной, называемой мощностью.
Мощность равна отношению работы ко времени, за которое она была совершена.
Чтобы вычислить мощность, надо работу разделить на время, в течение которого совершена эта работа. мощность = работа/время.
мощность = работа/время.
где N — мощность, A — работа, t — время выполненной работы.
Мощность — величина постоянная, когда за каждую секунду совершается одинаковая работа, в других случаях отношение A/t определяет среднюю мощность:
N ср = A/t . За единицу мощности приняли такую мощность, при которой в 1 с совершается работа в Дж.
Эта единица называется ваттом (Вт ) в честь еще одного английского ученого Уатта.
1 ватт = 1 джоуль/ 1 секунда , или 1 Вт = 1 Дж/с.
Ватт (джоуль в секунду) — Вт (1 Дж/с).
В технике широко используется более крупные единицы мощности — киловатт (кВт ), мегаватт (МВт ) .
1 МВт = 1 000 000 Вт
1 кВт = 1000 Вт
1 мВт = 0,001 Вт
1 Вт = 0,000001 МВт
1 Вт = 0,001 кВт
1 Вт = 1000 мВт
Пример . Найти мощность потока воды, протекающей через плотину, если высота падения воды 25 м, а расход ее — 120 м3 в минуту.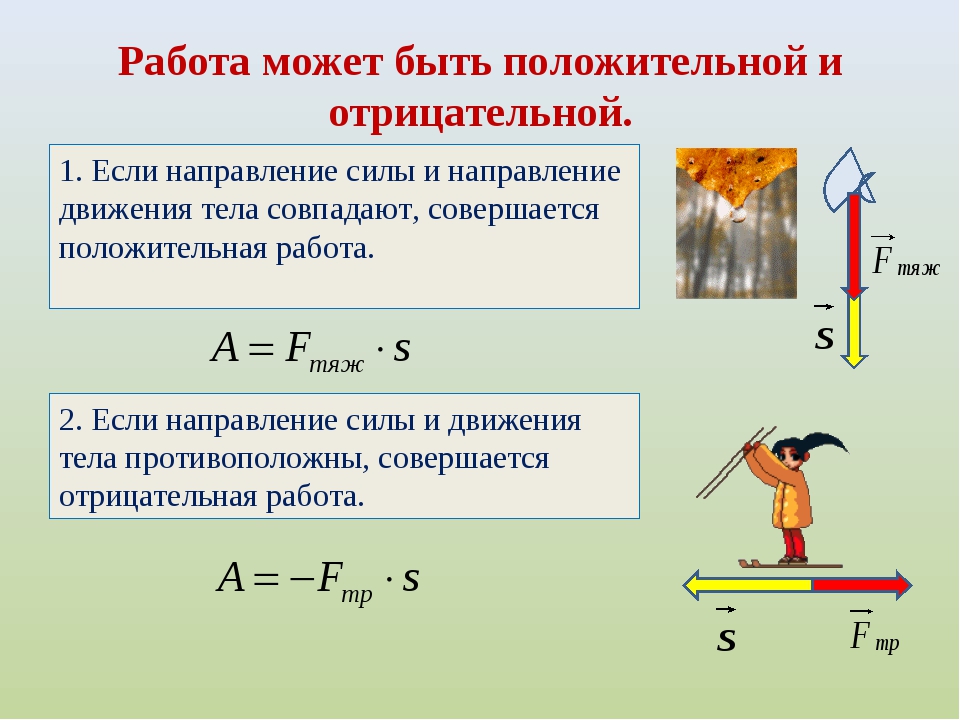
Дано :
ρ = 1000 кг/м3
Решение :
Масса падающей воды: m = ρV ,
m = 1000 кг/м3 · 120 м3 = 120 000 кг (12 · 104 кг).
Сила тяжести, действующая на воду:
F = 9.8 м/с2 · 120 000 кг ≈ 1 200 000 Н (12 · 105 Н)
Работа, совершаемая потоком в минуту:
А — 1 200 000 Н · 25 м = 30 000 000 Дж (3 · 107 Дж).
Мощность потока: N = A/t,
N = 30 000 000 Дж / 60 с = 500 000 Вт = 0,5 МВт.
Ответ : N = 0.5 МВт.
Различные двигатели имеют мощности от сотых и десятых долей киловатта (двигатель электрической бритвы, швейной машины) до сотен тысяч киловатт (водяные и паровые турбины).
Таблица 5.
Мощность некоторых двигателей, кВт.
На каждом двигателе имеется табличка (паспорт двигателя), на которой указаны некоторые данные о двигателе, в том числе и его мощность.
Мощность человека при нормальный условиях работы в среднем равна 70-80 Вт. Совершая прыжки, взбегая по лестнице, человек может развивать мощность до 730 Вт, а в отдельных случаях и еще бóльшую.
Из формулы N = A/t следует, что
Чтобы вычислить работу, необходимо мощность умножить на время, в течение которого совершалась эта работа.
Пример. Двигатель комнатного вентилятора имеет мощность 35 Вт. Какую работу он совершает за 10 мин?
Запишем условие задачи и решим ее.
Дано :
Решение :
A = 35 Вт * 600с = 21 000 Вт* с = 21 000 Дж = 21 кДж.
Ответ A = 21 кДж.
Простые механизмы.
С незапамятных времен человек использует для совершения механической работы различные приспособления.
Каждому известно, что тяжелый предмет (камень, шкаф, станок), который невозможно сдвинуть руками, можно сдвинуть с помощью достаточно длинной палки — рычага.
На данный момент считается, что с помощью рычагов три тысячи лет назад при строительстве пирамид в Древнем Египте передвигали и поднимали на большую высоту тяжелые каменные плиты.
Во многих случаях, вместо того, чтобы поднимать тяжелый груз на некоторую высоту, его можно вкатывать или втаскивать на ту же высоту по наклонной плоскости или поднимать с помощью блоков.
Приспособления, служащие для преобразования силы, называются механизмами .
К простым механизмам относятся: рычаги и его разновидности — блок, ворот; наклонная плоскость и ее разновидности — клин, винт . В большинстве случаев простые механизмы применяют для того, чтобы получить выигрыш в силе, т. е. увеличить силу, действующую на тело, в несколько раз.
Простые механизмы имеются и в бытовых, и во всех сложных заводских и фабричных машинах, которые режут, скручивают и штампуют большие листы стали или вытягивают тончайшие нити, из которых делаются потом ткани. Эти же механизмы можно обнаружить и в современных сложных автоматах, печатных и счетных машинах.
Рычаг. Равновесие сил на рычаге.
Рассмотрим самый простой и распространенный механизм — рычаг.
Рычаг представляет собой твердое тело, которое может вращаться вокруг неподвижной опоры.
На рисунках показано, как рабочий для поднятия груза в качестве рычага, использует лом. В первом случае рабочий с силой F нажимает на конец лома B , во втором — приподнимает конец B .
Рабочему нужно преодолеть вес груза P — силу, направленную вертикально вниз. Он поворачивает для этого лом вокруг оси, проходящей через единственную неподвижную точку лома — точку его опоры О . Сила F , с которой рабочий действует на рычаг, меньше силы P , таким образом, рабочий получает выигрыш в силе . При помощи рычага можно поднять такой тяжелый груз, который своими силами поднять нельзя.
На рисунке изображен рычаг, ось вращения которого О (точка опоры) расположена между точками приложения сил А и В . На другом рисунке показана схема этого рычага. Обе силы F 1 и F 2, действующие на рычаг, направлены в одну сторону.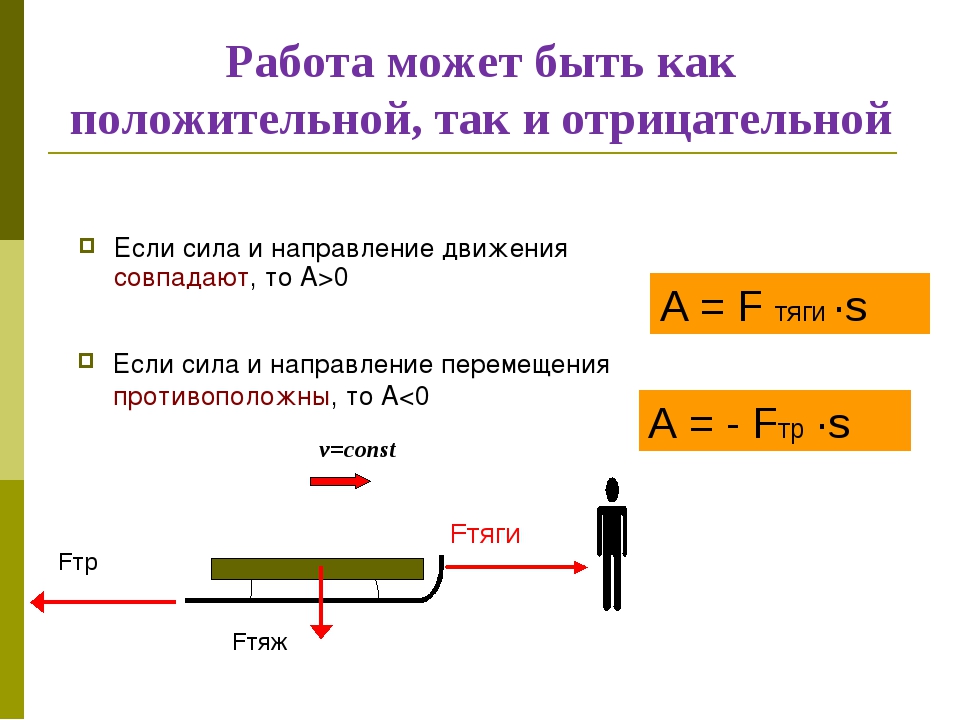
Кратчайшее расстояние между точкой опоры и прямой, вдоль которой действует на рычаг сила, называется плечом силы.
Чтобы найти плечо силы, надо из точки опоры опустить перпендикуляр на линию действия силы.Длина этого перпендикуляра и будет плечом данной силы. На рисунке показано, что ОА — плечо силы F 1; ОВ — плечо силы F 2 . Силы, действующие на рычаг могут повернуть его вокруг оси в двух направлениях: по ходу или против хода часовой стрелки. Так, сила F 1 вращает рычаг по ходу часовой стрелки, а сила F 2 вращает его против часовой стрелки.
Условие, при котором рычаг находится в равновесии под действием приложенных к нему сил, можно установить на опыте. При этом надо помнить, что результат действия силы, зависит не только от ее числового значения (модуля), но и от того, в какой точке она приложена к телу, или как направлена.
К рычагу (см рис.) по обе стороны от точки опоры подвешиваются различные грузы так, что каждый раз рычаг оставался в равновесии.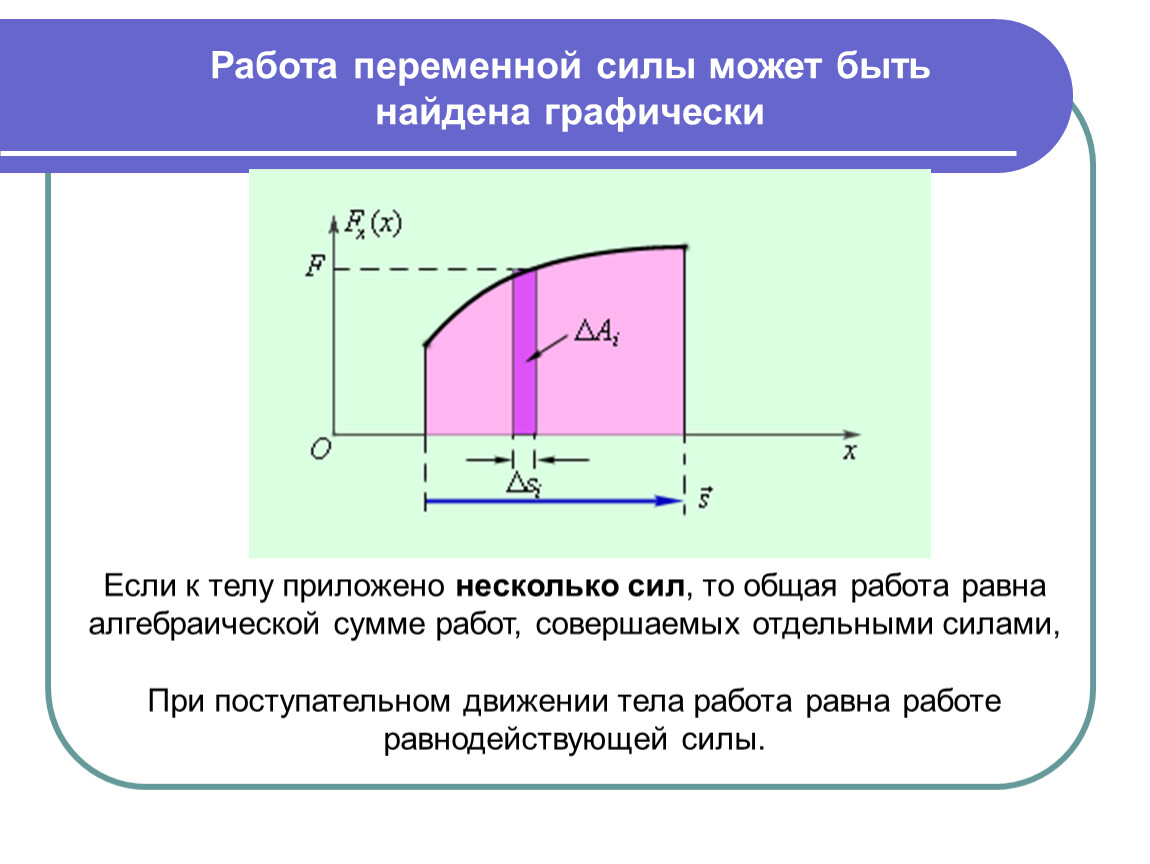 Действующие на рычаг силы, равны весам этих грузов. Для каждого случая измеряются модули сил и их плечи. Из опыта изображенного на рисунке 154, видно, что сила 2 Н уравновешивает силу 4 Н . При этом, как видно из рисунка, плечо меньшей силы в 2 раза больше плеча большей силой.
Действующие на рычаг силы, равны весам этих грузов. Для каждого случая измеряются модули сил и их плечи. Из опыта изображенного на рисунке 154, видно, что сила 2 Н уравновешивает силу 4 Н . При этом, как видно из рисунка, плечо меньшей силы в 2 раза больше плеча большей силой.
На основании таких опытов было установлено условие (правило) равновесия рычага.
Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил.
Это правило можно записать в виде формулы:
F 1/F 2 = l2/ l1 ,
где F 1 и F2 — силы, действующие на рычаг, l 1 и l2 , — плечи этих сил (см. рис.).
Правило равновесия рычага было установлено Архимедом около 287 — 212 гг. до н. э. (но ведь в прошлом параграфе говорилось, что рычаги использовались египтянами? Или тут важную роль играет слово «установлено»?)
Из этого правила следует, что меньшей силой можно уравновесить при помощи рычага бóльшую силу.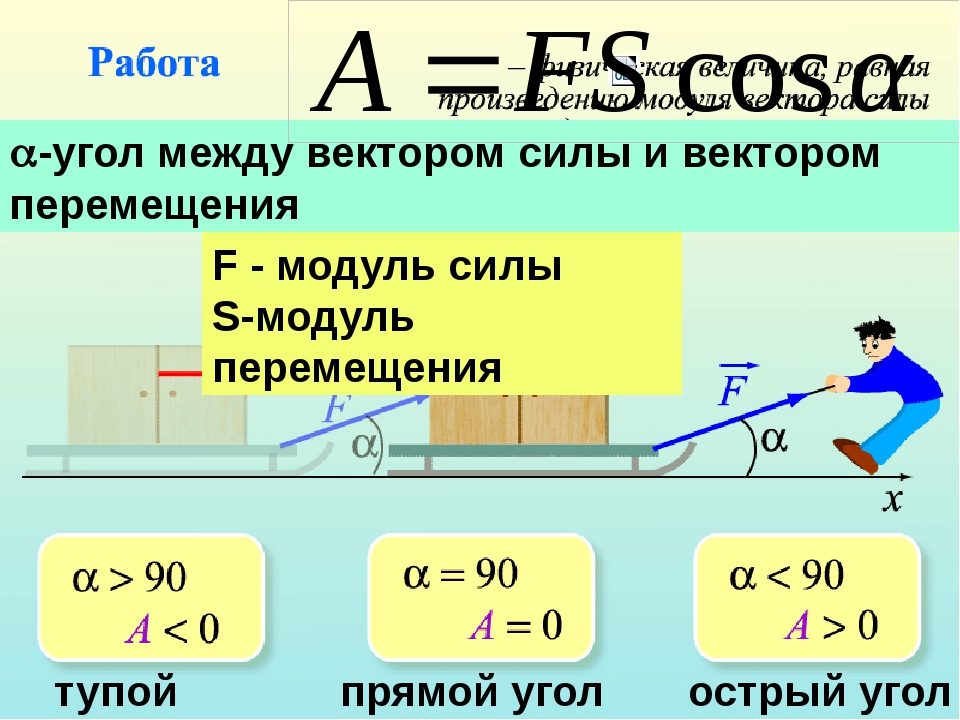 Пусть одно плечо рычага в 3 раза больше другого (см рис.). Тогда, прикладывая в точке В силу, например, в 400 Н, можно поднять камень весом 1200 Н. Что0бы поднять еще более тяжелый груз, нужно увеличить длину плеча рычага, на которое действует рабочий.
Пусть одно плечо рычага в 3 раза больше другого (см рис.). Тогда, прикладывая в точке В силу, например, в 400 Н, можно поднять камень весом 1200 Н. Что0бы поднять еще более тяжелый груз, нужно увеличить длину плеча рычага, на которое действует рабочий.
Пример . С помощью рычага рабочий поднимает плиту массой 240 кг (см рис. 149). Какую силу прикладывает он к большему плечу рычага, равному 2,4 м, если меньшее плечо равно 0,6 м?
Запишем условие задачи, и решим ее.
Дано :
Решение :
По правилу равновесия рычага F1/F2 = l2/l1, откуда F1 = F2 l2/l1, где F2 = Р — вес камня. Вес камня asd = gm, F = 9,8 Н · 240 кг ≈ 2400 Н
Тогда, F1 = 2400 Н · 0,6/2,4 = 600 Н.
Ответ : F1 = 600 Н.
В нашем примере рабочий преодолевает силу 2400 Н, прикладывая к рычагу силу 600 Н. Но при этом плечо, на которое действует рабочий, в 4 раза длиннее того, на которое действует вес камня (l 1 : l2 = 2,4 м: 0,6 м = 4).
Применяя правило рычага, можно меньшей силой уравновесить бóльшую силу. При этом плечо меньшей силы должно быть длиннее плеча большей силы.
При этом плечо меньшей силы должно быть длиннее плеча большей силы.
Момент силы.
Вам уже известно правило равновесия рычага:
F 1 / F2 = l 2 / l1 ,
Пользуясь свойством пропорции (произведение ее крайних членов, равно произведению ее средних членов), запишем его в таком виде:
F 1l 1 = F2 l2 .
В левой части равенства стоит произведение силы F 1 на ее плечо l 1, а в правой — произведение силы F 2 на ее плечо l 2 .
Произведение модуля силы, вращающей тело, на ее плечо называется моментом силы ; он обозначается буквой М. Значит,
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающий его по часовой стрелке, равен моменту силы, вращающей его против часовой стрелки.
Это правило, называемое правилом моментов , можно записать в виде формулы:
М1 = М2
Действительно, в рассмотренном нами опыте, (§ 56) действующие силы были равны 2 Н и 4 Н, их плечи соответственно составляли 4 и 2 давления рычага, т.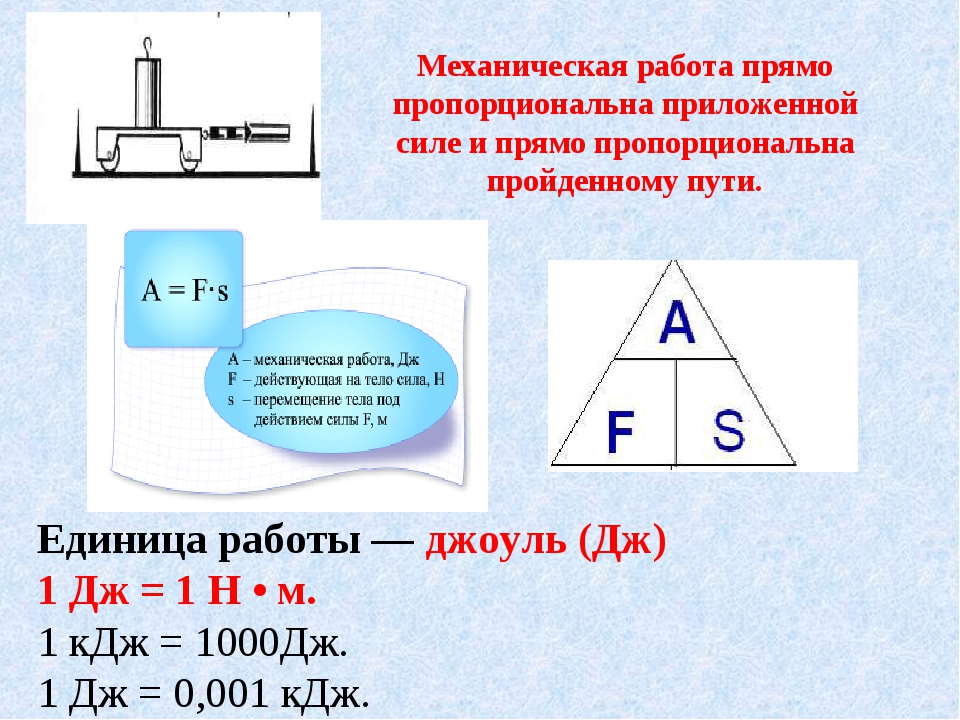 е. моменты этих сил одинаковы при равновесии рычага.
е. моменты этих сил одинаковы при равновесии рычага.
Момент силы, как и всякая физическая величина, может быть измерена. За единицу момента силы принимается момент силы в 1 Н, плечо которой ровно 1 м.
Эта единица называется ньютон-метр (Н · м ).
Момент силы характеризует действие силы, и показывает, что оно зависит одновременно и от модуля силы, и от ее плеча. Действительно, мы уже знаем, например, что действие силы на дверь зависит и от модуля силы, и от того, где приложена сила. Дверь тем легче повернуть, чем дальше от оси вращения приложена действующая на нее сила. Гайку, лучше отвернуть длинным гаечным ключом, чем коротким. Ведро тем легче поднять из колодца, чем длиннее ручка вóрота, и т. д.
Рычаги в технике, быту и природе.
Правило рычага (или правило моментов) лежит в основе действия различного рода инструментов и устройств, применяемых в технике и быту там, где требуется выигрыш в силе или в пути.
Выигрыш в силе мы имеем при работе с ножницами. Ножницы — это рычаг (рис), ось вращения которого, происходит через винт, соединяющий обе половины ножниц. Действующей силой F 1 является мускульная сила руки человека, сжимающего ножницы. Противодействующей силой F 2 — сила сопротивления такого материала, который режут ножницами. В зависимости от назначения ножниц их устройство бывает различным. Конторские ножницы, предназначенные для резки бумаги, имеют длинные лезвия и почти такой же длины ручки. Для резки бумаги не требуется большой силы, а длинным лезвием удобнее резать по прямой линии. Ножницы для резки листового металла (рис.) имеют ручки гораздо длиннее лезвий, так как сила сопротивления металла велика и для ее уравновешивания плечо действующей силы приходится значительно увеличивать. Еще больше разница между длиной ручек и расстоянии режущей части и оси вращения в кусачках (рис.), предназначенных для перекусывания проволоки.
Ножницы — это рычаг (рис), ось вращения которого, происходит через винт, соединяющий обе половины ножниц. Действующей силой F 1 является мускульная сила руки человека, сжимающего ножницы. Противодействующей силой F 2 — сила сопротивления такого материала, который режут ножницами. В зависимости от назначения ножниц их устройство бывает различным. Конторские ножницы, предназначенные для резки бумаги, имеют длинные лезвия и почти такой же длины ручки. Для резки бумаги не требуется большой силы, а длинным лезвием удобнее резать по прямой линии. Ножницы для резки листового металла (рис.) имеют ручки гораздо длиннее лезвий, так как сила сопротивления металла велика и для ее уравновешивания плечо действующей силы приходится значительно увеличивать. Еще больше разница между длиной ручек и расстоянии режущей части и оси вращения в кусачках (рис.), предназначенных для перекусывания проволоки.
Рычаги различного вида имеются у многих машин. Ручка швейной машины, педали или ручной тормоз велосипеда, педали автомобиля и трактора, клавиши пианино — все это примеры рычагов, используемых в данных машинах и инструментах.
Примеры применения рычагов — это рукоятки тисков и верстаков, рычаг сверлильного станка и т. д.
На принципе рычага основано действие и рычажных весов (рис.). Учебные весы, изображенные на рисунке 48 (с. 42), действуют как равноплечий рычаг . В десятичных весах плечо, к которому подвешена чашка с гирями, в 10 раз длиннее плеча, несущего груз. Это значительно упрощает взвешивание больших грузов. Взвешивая груз на десятичных весах, следует умножить массу гирь на 10.
Устройство весов для взвешивания грузовых вагонов автомобилей также основано на правиле рычага.
Рычаги встречаются также в разных частях тела животных и человека. Это, например, руки, ноги, челюсти. Много рычагов можно найти в теле насекомых (прочитав книгу про насекомых и строение их тела), птиц, в строении растений.
Применение закона равновесия рычага к блоку.
Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускается веревка, трос или цепь.
Неподвижным блоком называется такой блок, ось которого закреплена, и при подъеме грузов не поднимается и не опускается (рис).
Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи сил равны радиусу колеса (рис): ОА = ОВ = r . Такой блок не дает выигрыша в силе. (F 1 = F 2), но позволяет менять направление действие силы. Подвижный блок — это блок. ось которого поднимается и опускается вместе с грузом (рис.). На рисунке показан соответствующий ему рычаг: О — точка опоры рычага, ОА — плечо силы Р и ОВ — плечо силы F . Так как плечо ОВ в 2 раза больше плеча ОА , то сила F в 2 раза меньше силы Р :
F = P/2 .
Таким образом, подвижный блок дает выигрыш в силе в 2 раза .
Это можно доказать и пользуясь понятием момента силы. При равновесии блока моменты сил F и Р равны друг другу. Но плечо силы F в 2 раза больше плеча силы Р , а, значит, сама сила F в 2 раза меньше силы Р .
При равновесии блока моменты сил F и Р равны друг другу. Но плечо силы F в 2 раза больше плеча силы Р , а, значит, сама сила F в 2 раза меньше силы Р .
Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис.). Неподвижный блок применяется только для удобства. Он не дает выигрыша в силе, но изменяет направление действия силы. Например, позволяет поднимать груз, стоя на земле. Это пригождается многим людям или рабочим. Тем не менее, он даёт выигрыш в силе в 2 раза больше обычного!
Равенство работ при использовании простых механизмов. «Золотое правило» механики.
Рассмотренные нами простые механизмы применяются при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.
Естественно, возникает вопрос: давая выигрыш в силе или пути, не дают ли простые механизмы выигрыша в работе? Ответ на поставленный вопрос можно получить из опыта.
Уравновесив на рычаге две какие-нибудь разные по модулю силы F 1 и F 2 (рис. ), приводим рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F 2 проходит больший путь s 2 , а точка приложения большей силы F 1 — меньший путь s 1. Измерив эти пути и модули сил, находим, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам:
), приводим рычаг в движение. При этом оказывается, что за одно и то же время точка приложения меньшей силы F 2 проходит больший путь s 2 , а точка приложения большей силы F 1 — меньший путь s 1. Измерив эти пути и модули сил, находим, что пути, пройденные точками приложения сил на рычаге, обратно пропорциональны силам:
s 1 / s 2 = F 2 / F 1.
Таким образом, действуя на длинное плечо рычага, мы выигрываем в силе, но при этом во столько же раз проигрываем в пути.
Произведение силы F на путь s есть работа. Наши опыты показывают, что работы, совершаемые силами, приложенными к рычагу, равны друг другу:
F 1 s 1 = F 2 s 2, т. е. А 1 = А 2.
Итак, при использовании рычага выигрыша в работе не получится.
Пользуясь рычагом, мы можем выиграть или в силе, или в расстоянии. Действуя же силой на короткое плечо рычага, мы выигрываем в расстоянии, но во столько же раз проигрываем в силе.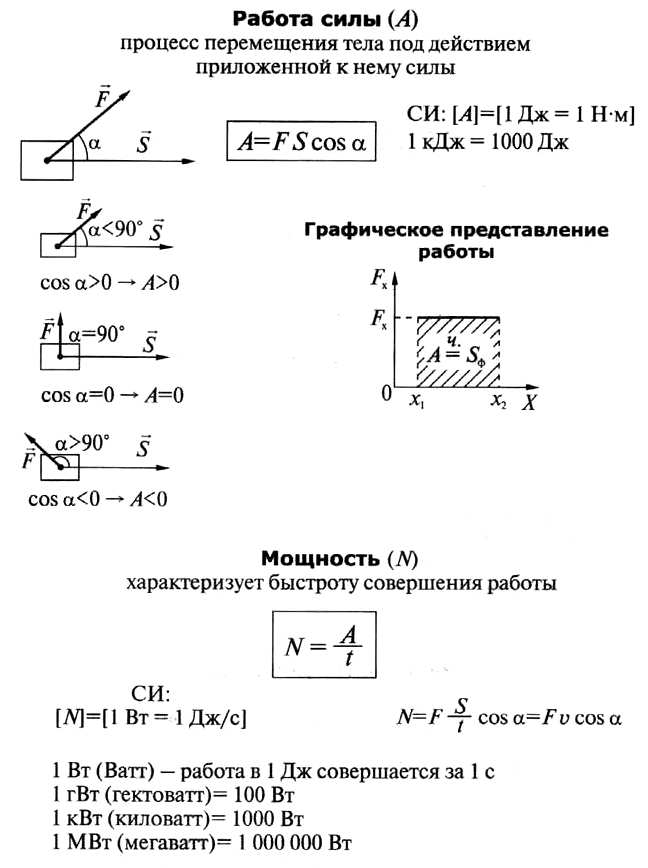
Существует легенда, что Архимед, восхищенный открытием правила рычага, воскликнул: «Дайте мне точку опоры, и я переверну Землю!».
Конечно, Архимед не мог бы справиться с такой задачей, если бы даже ему и дали бы точку опоры (которая должна была бы быть вне Земли) и рычаг нужной длины.
Для подъема земли всего на 1 см длинное плечо рычага должно было бы описать дугу огромной длины. Для перемещения длинного конца рычага по этому пути, например, со скоростью 1 м/с, потребовались бы миллионы лет!
Не дает выигрыша в работе и неподвижный блок, в чем легко убедиться на опыте (см. рис.). Пути, проходимые точками приложения сил F и F , одинаковы, одинаковы и силы, а значит, одинаковы и работы.
Можно измерить и сравнить между собой работы, совершаемые с помощью подвижного блока. Чтобы при помощи подвижного блока поднять груз на высоту h, необходимо конец веревки, к которому прикреплен динамометр, как показывает опыт (рис.), переместить на высоту 2h.
Таким образом, получая выигрыш в силе в 2 раза, проигрывают в 2 раза в пути, следовательно, и подвижный блок, на дает выигрыша в работе.
Многовековая практика показала, что ни один из механизмов не дает выигрыш в работе. Применяют же различные механизмы для того, чтобы в зависимости от условий работы выиграть в силе или в пути.
Уже древним ученым было известно правило, применимое ко всем механизмом: во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии. Это правило назвали «золотым правилом» механики.
Коэффициент полезного действия механизма.
Рассматривая устройство и действие рычага, мы не учитывали трение, а также вес рычага. в этих идеальных условиях работа, совершенная приложенной силой (эту работу мы будем называть полной ), равна полезной работе по подъему грузов или преодоления какого — либо сопротивления.
На практике совершенная с помощью механизма полная работа всегда несколько больше полезной работы.
Часть работы совершается против силы трения в механизме и по перемещению его отдельных частей. Так, применяя подвижный блок, приходится дополнительно совершать работу по подъему самого блока, веревки и по определению силы трения в оси блока.
Какой мы механизм мы не взяли, полезная работа, совершенная с его помощью, всегда составляет лишь часть полной работы. Значит, обозначив полезную работу буквой Ап, полную(затраченную) работу буквой Аз, можно записать:
Ап
Отношение полезной работы к полной работе называется коэффициентом полезного действия механизма.
Сокращенно коэффициент полезного действия обозначается КПД.
КПД = Ап / Аз.
КПД обычно выражается в процентах и обозначается греческой буквой η, читается он как «эта»:
η = Ап / Аз · 100%.
Пример : На коротком плече рычага подвешен груз массой 100 кг. Для его подъема к длинному плечу приложена сила 250 Н. Груз подняли на высоту h2 = 0,08 м, при этом точка приложения движущей силы опустилась на высоту h3 = 0,4 м. Найти КПД рычага.
Найти КПД рычага.
Запишем условие задачи и решим ее.
Дано :
Решение :
η = Ап / Аз · 100%.
Полная (затраченная) работа Аз = Fh3.
Полезная работа Ап = Рh2
Р = 9,8 · 100 кг ≈ 1000 Н.
Ап = 1000 Н · 0,08 = 80 Дж.
Аз = 250 Н · 0,4 м = 100 Дж.
η = 80 Дж/100 Дж · 100% = 80%.
Ответ : η = 80%.
Но «золотое правило» выполняется и в этом случае. Часть полезной работы — 20% ее-расходуется на преодоление трения в оси рычага и сопротивления воздуха, а также на движение самого рычага.
КПД любого механизма всегда меньше 100%. Конструируя механизмы, люди стремятся увеличить их КПД. Для этого уменьшаются трение в осях механизмов и их вес.
Энергия.
На заводах и фабриках, станки и машины приводятся в движения с помощью электродвигателей, которые расходуют при этом электрическую энергию (отсюда и название).
Сжатая пружина (рис), распрямляясь, совершить работу, поднять на высоту груз, или заставить двигаться тележку. Поднятый над землей неподвижный груз не совершает работы, но если этот груз упадет, он может совершить работу (например, может забить в землю сваю). Способностью совершить работу обладает и всякое движущееся тело. Так, скатившийся с наклонной плоскости стальной шарик А (рис), ударившись о деревянный брусок В, передвигает его на некоторое расстояние. При этом совершается работа. Если тело или несколько взаимодействующих между собой тел (система тел) могут совершить работу, говорится, что они обладают энергией. Энергия — физическая величина, показывающая, какую работу может совершить тело (или несколько тел). Энергия выражается в системе СИ в тех же единицах, что и работу, т. е. в джоулях . Чем большую работу может совершить тело, тем большей энергией оно обладает. При совершении работы энергия тел изменяется. Совершенная работа равна изменению энергии. Потенциальная и кинетическая энергия.Потенциальной (от лат. Потенциальной энергией, например, обладает тело, поднятое относительно поверхности Земли, потому что энергия зависит от взаимного положения его и Земли. и их взаимного притяжения. Если считать потенциальную энергию тела, лежащего на Земле, равной нулю, то потенциальная энергия тела, поднятого на некоторую высоту, определится работой, которую совершит сила тяжести при падении тела на Землю. Обозначим потенциальную энергию тела Е п, поскольку Е = А , а работа, как мы знаем, равна произведению силы на путь, то А = Fh , где F — сила тяжести. Значит, и потенциальная энергия Еп равна: Е = Fh, или Е = gmh, где g — ускорение свободного падения, m — масса тела, h — высота, на которую поднято тело. Огромной потенциальной энергией обладает вода в реках, удерживаемая плотинами. Потенциальную энергию молота копра (рис.) используют в строительстве для совершению работы по забиванию свай. Открывая дверь с пружиной, совершается работа по растяжению (или сжатию) пружины. За счет приобретенной энергии пружина, сокращаясь (или распрямляясь), совершает работу, закрывая дверь. Энергию сжатых и раскрученных пружин используют, например, в ручных часах, разнообразных заводных игрушках и пр. Потенциальной энергией обладает всякое упругое деформированное тело. Потенциальную энергию сжатого газа используют в работе тепловых двигателей, в отбойных молотках, которые широко применяют в горной промышленности, при строительстве дорог, выемке твердого грунта и т. д. Энергия, которой обладает тело вследствие своего движения, называется кинетической (от греч. кинема — движение) энергией. Кинетическая энергия тела обозначается буквой Е к. Движущаяся вода, приводя во вращение турбины гидроэлектростанций, расходует свою кинетическую энергию и совершает работу. Кинетической энергией обладает и движущийся воздух — ветер. От чего зависит кинетическая энергия? Обратимся к опыту (см. рис.). Если скатывать шарик А с разных высот, то можно заметить, что чем с большей высоты скатывается шарик, тем больше его скорость и тем дальше он продвигает брусок, т. е. совершает большую работу. Значит, кинетическая энергия тела зависит от его скорости. За счет скорости большой кинетической энергией обладает летящая пуля. Кинетическая энергия тела зависит и от его массы. Еще раз проделаем наш опыт, но будем скатывать с наклонной плоскости другой шарик — большей массы. Брусок В передвинется дальше, т. е. будет совершена бóльшая работа. Значит, и кинетическая энергия второго шарика, больше, чем первого. Чем больше масса тела и скорость, с которой он движется, тем больше его кинетическая энергия. Для того чтобы определить кинетическую энергию тела, применяется формула: Ек = mv^2 /2, где m — масса тела, v — скорость движения тела. Кинетическую энергию тел используют в технике. Удерживаемая плотиной вода обладает, как было уже сказано, большой потенциальной энергией. При падении с плотины вода движется и имеет такую же большую кинетическую энергию. Она приводит в движение турбину, соединенную с генератором электрического тока. За счет кинетической энергии воды вырабатывается электрическая энергия. Энергия движущейся воды имеет большое значение в народном хозяйстве. Эту энергию используют с помощью мощных гидроэлектростанций. Энергия падающей воды является экологически чистым источником энергии в отличие от энергии топлива. Все тела в природе относительно условного нулевого значения обладают либо потенциальной, либо кинетической энергией, а иногда той и другой вместе. Например, летящий самолет обладает относительно Земли и кинетической и потенциальной энергией. Мы познакомились с двумя видами механической энергии. Иные виды энергии (электрическая, внутренняя и др.) будут рассмотрены в других разделах курса физики. Превращение одного вида механической энергии в другой. Явление превращения одного вида механической энергии в другой очень удобно наблюдать на приборе, изображенном на рисунке. Накручивая на ось нить, поднимают диск прибора. Диск, поднятый вверх, обладает некоторой потенциальной энергией. Если его отпустить, то он, вращаясь, начнет падать. По мере падения потенциальная энергия диска уменьшается, но вместе с тем возрастает его кинетическая энергия. В конце падения диск обладает таким запасом кинетической энергии, что может опять подняться почти до прежней высоты. (Часть энергии расходуется на работу против силы трения, поэтому диск не достигает первоначальной высоты.) Поднявшись вверх, диск снова падает, а затем снова поднимается. В этом опыте при движении диска вниз его потенциальная энергия превращается в кинетическую, а при движении вверх кинетическая превращается в потенциальную. Превращение энергии из одного вида в другой происходит также при ударе двух каких-нибудь упругих тел, например резинового мяча о пол или стального шарика о стальную плиту. Если поднять над стальной плитой стальной шарик (рис) и выпустить его из рук, он будет падать. По мере падения шарика его потенциальная энергия убывает, а кинетическая растет, так как увеличивается скорость движения шарика. При ударе шарика о плиту произойдет сжатие как шарика, так и плиты. Кинетическая энергия, которой шарик обладал, превратится в потенциальную энергию сжатой плиты и сжатого шарика. Затем благодаря действию упругих сил плита и шарик, примут свою первоначальную форму. Шарик отскочит от плиты, а их потенциальная энергия вновь превратится в кинетическую энергию шарика: шарик отскочит вверх со скоростью, почти равной скорости, которой обладал в момент удара о плиту. При подъеме вверх скорость шарика, а значит, и его кинетическая энергия уменьшаются, потенциальная энергия увеличивается. отскочив от плиты, шарик поднимается почти до той же высоты, с которой начал падать. В верхней точке подъема вся его кинетическая энергия вновь превратится в потенциальную. Явления природы обычно сопровождается превращением одного вида энергии в другой. Энергия может и передаваться от одного тела к другому. Так, например, при стрельбе из лука потенциальная энергия натянутой тетивы переходит в кинетическую энергию летящей стрелы. |
Главная » Наружная канализация » Что такое работа в физике формула. Механическая работа
Механическая работа
Механическая работа — это скалярная величина, равная произведению модуля силы, действующей на тело, на модуль перемещения и на косинус угла между вектором силы и вектором перемещения (или скорости)
A=F·S·cosa
Если на тело действует сила и тело под действием этой силы перемещается, то говорят, что сила совершает работу.
Работа является скалярной величиной. Она может быть как положительна (0° ≤ α < 90°), так и отрицательна (90° < α ≤ 180°). При α = 90° работа, совершаемая силой, равна нулю.
В системе СИ работа измеряется в джоулях (Дж). Джоуль равен работе, совершаемой силой в 1 Н на перемещении 1 м в направлении действия силы.
1) Если направление силы совпадает с направлением движения тела, т.е.α = 0, cos α = 1 то
A=F·S
2) Если сила направлена перпендикулярно к направлению движения тела, т.е. α = 90º, cos α = 0 то
A = 0
Следовательно, если тело перемещается в направлении, перпендикулярном к направлению действия силы, то сила не производит работы.
3) Если угол между направлением силы и направлением движения тупой, т.е. α > 90º, cos α < 0 то
A=-F·S·cosa
4) Если перемещение происходит в сторону, противоположную направлению вектора силы, т.е. α = 180 º, cos α = -1 то
A=-F·S
значит, работа силы отрицательна (например, работа силы трения).
Графически работа определяется по площади криволинейной фигуры под графиком Fs(x)
Обозначения:
A — Механическая работа
F — Сила, действующая на тело
S — Перемещение, которое тело совершает под действием силы
a — Угол между направлением действия силы и вектором перемещения
Расчет количества работы, выполненной силами
В предыдущей части Урока 1 работа описывалась как имеющая место, когда на объект действует сила, вызывающая смещение. Когда сила действует, заставляя объект смещаться, необходимо знать три величины, чтобы рассчитать работу. Эти три величины — сила, смещение и угол между силой и смещением. Затем работа рассчитывается как сила • смещение • косинус (тета), где тета — угол между векторами силы и смещения.В этой части Урока 1 концепции и математика работы будут применены для анализа различных физических ситуаций.
Проверьте свое понимание
Выразите свое понимание концепции и математики работы, ответив на следующие вопросы. Когда закончите, нажмите кнопку, чтобы просмотреть ответы.
1. Примените уравнение работы, чтобы определить объем работы, выполняемой приложенной силой в каждой из трех ситуаций, описанных ниже.
2. Во многих случаях на объект действует более одной силы. Диаграмма свободного тела — это диаграмма, которая отображает тип и направление всех сил, действующих на объект. Следующие ниже описания и сопровождающие их диаграммы свободного тела показывают силы, действующие на объект. Для каждого случая укажите, какие силы действуют на объект. Затем рассчитайте работу, совершаемую этими силами.
| Свободное тело Схема | Силы, выполняющие работу на Объекте | Объем выполненных работ каждой силой |
| Приложена сила 10 Н, чтобы толкнуть блок по поверхности, свободной от трения, на смещение 5.0 м вправо. | ||
| Сила трения 10 Н замедляет движущийся блок до остановки после смещения на 5,0 м вправо. | ||
| Приложена сила 10 Н, чтобы толкнуть блок по фрикционной поверхности с постоянной скоростью для перемещения 5.0 м вправо. | ||
| Объект весом около 2 кг скользит с постоянной скоростью по поверхности, свободной от трения, на 5 м вправо. | ||
| Объект весом около 2 кг тянется вверх с постоянной скоростью силой 20 Н для вертикального перемещения 5 м. |
3. Перед началом спуска автомобиль с американскими горками всегда поднимается на первый холм на большую начальную высоту. Для достижения этой начальной высоты с автомобилем (обычно с помощью цепи) выполняются работы. Конструктор каботажного судна рассматривает три разных угла наклона, под которыми можно перетащить 2000-килограммовый состав на вершину 60-метрового холма.В каждом случае сила, приложенная к автомобилю, будет прилагаться параллельно холму. Ее критический вопрос: какой угол потребует больше всего работы? Проанализируйте данные, определите проделанную работу в каждом конкретном случае и ответьте на этот важный вопрос.
| Уголок | Сила | Расстояние | Работа (J) | |
а. | 35 град. | 1,12 x 10 4 Н | 105 кв.м. | |
г. | 45 град. | 1,39 x 10 4 Н | 84,9 м | |
г. | 55 град. | 1,61 x 10 4 Н | 73,2 м |
4. Бен Травлун переносит чемодан 200-Н на три лестничных пролета (высота 10,0 м), а затем толкает его с горизонтальной силой 50,0 Н с постоянной скоростью 0,5 м / с на горизонтальное расстояние 35.0 метров. Сколько работы Бен делает со своим чемоданом во время этого движения за все движение ?
5. На блок действует сила 50 Н под углом, показанным на диаграмме. Блок перемещается на 3,0 м по горизонтали. Сколько работы совершает приложенная сила?
6. Сколько работы совершает приложенная сила, чтобы поднять 15-ньютонный блок 3.0 метров по вертикали с постоянной скоростью?
7. Студент массой 80,0 кг преодолевает три лестничных пролета за 12,0 сек. Студент прошел вертикальное расстояние 8,0 м. Определите объем работы, проделанной учеником, чтобы поднять свое тело на эту высоту. Предположим, что его скорость постоянна.
8.Рассчитайте работу, проделанную силой 2,0 Н (направленной под углом 30 ° к вертикали), чтобы переместить 500-граммовый ящик на горизонтальное расстояние 400 см по черновому полу с постоянной скоростью 0,5 м / с. (ПОДСКАЗКА: будьте осторожны с единицами.) |
9. Уставшая белка (масса 1 кг) отжимается, прикладывая силу, поднимающую ее центр масс на 5 см.Оцените количество отжиманий, которое должна сделать уставшая белка, чтобы выполнить примерно 5,0 Джоуля работы.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения It’s All Uphill.Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивное приложение It’s All Uphill Interactive позволяет учащемуся изучить влияние угла наклона на силу и работу, выполняемую при подъеме тележки в гору с постоянной скоростью.Работа
РаботаПара шокеров:
Несомненно, вас учили, что «Работа равна силе, умноженной на расстояние.«Соберитесь. Работайте , иногда силы-раз. расстояние, но не всегда . Работа тоньше, чем это, и чтобы понять энергию, вы должны понимать работу на большую глубину.
Если вы думаете, что «работа равна силе, умноженной на расстояние», то вы вероятно, вы думаете, что вы автоматически выполняете работу каждый раз, когда вы сила. Это тоже неправда!
Почему? Что ж, работа / энергия уравнение говорит, что работа сделана (чистой силой, действующей на объект) равно изменению кинетической энергии объекта.Проще говоря:
Работа = Изменение кинетической энергии
Это означает, что если кинетическая энергия объекта не изменяется, то с объектом не было выполнено никаких работ — независимо от того, была ли применена сила проявил.
На схеме выше зеленый блок движется вправо. В красная сила F1 действительно работает на блок, потому что он имеет компонент по направлению движения.Синий force F2 НЕ работает с блоком, потому что не имеет составляющей в направлении движения. |
- ускорение, в этом случае кинетическая энергия объекта увеличивается ,
- замедление, в этом случае кинетическая энергия объекта убавки ,
- или изменение направления, в этом случае кинетическая энергия не меняет .
Итак, кинетическая энергия объекта изменится, только если сила воздействие на объект изменяет его скорость. Это будет только происходит, если есть составляющая силы в направлении, объект движется.
Следовательно, сила будет работать только , если сила имеет компонент в направлении движения объекта .
Счетная работа может получиться, ну, интересной.К счастью для Физика 1 студент, вам нужно только уметь рассчитывать работу, выполненную сила в четырех показанных простых случаях ниже. Для более зрелых в математическом отношении есть формула, которую вы можете использовать для расчета работы, выполненной постоянная сила. На некоторых из следующих страниц обсуждается расчет работа, выполняемая переменной силой, но это для AP Physics студенты.
Расчет работы, выполняемой константой Сила:
В Physics 1 вам нужно уметь вычислять работу, выполняемую сила в четырех ситуациях:
| Ситуация: | Пример: | Работа, совершаемая силой F: |
Направление силы в том же направлении объект движется. | Сила, толкающая автомобиль по дороге | Сила x расстояние |
Направление силы в направление противоположно направлению движения объекта. | Тормозная сила, с которой автомобиль останавливается | -Сила x расстояние (* см. Примечание) |
Направление силы перпендикулярно направление объект движется. | Гравитационная сила, которую Земля оказывает на Луна | 0 |
Объект не двигаться. | Сила, с которой вы толкаете стену | 0 |
Почему?
Ключ к пониманию:
Уравнение работы / энергии говорит что работа, проделанная с объектом (за счет действующей на него чистой силы), равна его изменение кинетической энергии.Итак, чтобы выяснить, сколько работы проделано над объект, просто рассчитайте изменение его кинетической энергии …
Если сила действует в направлении движения объекта:
Эта сила будет увеличивать скорость объекта. Если увеличивается скорость объекта, затем увеличивается его кинетическая энергия. Если кинетическая энергия увеличивается, изменение кинетической энергии будет положительный. Поскольку уравнение Работа / Энергия гарантирует, что работа выполнено равно изменению кинетической энергии, выполненная работа должна быть положительный.Числовой пример: доступный.
Если сила действует в направлении, противоположном Направление движения объекта:
В этой ситуации сила имеет тенденцию замедлять объект, тем самым уменьшая его кинетическую энергию. Если кинетическая энергия уменьшается, то изменение кинетической энергии отрицательное. Поскольку выполненная работа равна изменению кинетической энергии, работа, выполненная этим сила должна быть отрицательной.
Есть несколько способов справиться с этим:
- Помните, что в данном случае работа = — сила x расстояние.Так что если сила 5 Ньютонов действует на объект на расстоянии 5 метров, и направление силы 5 Ньютонов противоположно направление движения объекта, затем выполненная работа = — сила x расстояние = — (5 Ньютонов) (2 метра) = -10 Джоулей.
- Имейте в виду, что направление имеет значение с силой и расстоянием. Если направление силы противоположно направлению, объект движется, один или другой из них действует в отрицательное направление.Если вы сделаете это, то работа = сила x расстояние в этом случае тоже. В предыдущем примере вы бы сказали, что работает сделано = сила x расстояние = (- 5 Ньютонов) (2 метра) = -10 Джоули.
На самом деле не имеет значения, какой метод вы используете — просто будьте последовательны, и помните, что если направление силы противоположно направлению движения объекта, работа, выполняемая сила отрицательная. Числовой пример имеется.
Если сила перпендикулярна направлению, в котором объект Ходы
В этом случае сила не изменяет скорость объекта — просто его направление.Поскольку скорость объекта не меняется, его кинетическая энергия не меняется. Если изменение кинетической энергии равно 0, работа, проделанная с объектом, тоже равна 0.
Если объект не двигается
Работа — это не всегда сила x расстояние, но работа всегда включает какое-то движение. Нет расстояния — нет работы.
Работа НЕ Сила!
Многие начинающие физики путают «проявление силы» с «действием». работы «. Как показано выше, вы должны изменить кинетическую энергию объект, чтобы поработать с ним — недостаточно просто надавить на него.Даже тот факт, что вы можете устать или даже истощиться, держа тяжелый ящик или толкание о стену, если кинетическая энергия коробки или стена не меняется, ты не работал. «Применение силы» — это НЕ то же самое, что «делать работу»!
Последнее обновление 23 ноября 2007 г., автор: JL Stanbrough
Работа
Сила без движения или сила, перпендикулярная движению, не работает
Эти два примера сил, которые не работают, парадоксальны.Вы определенно можете почувствовать усталость, выполняя любое из этих действий, так как же вы можете сказать, что работа не выполняется?
В случае, показанном слева, независимо от того, насколько сильно и как долго вы толкали ящик, если ящик не двигается, значит, вы не работали с ящиком. Он сидит на том же месте! Почему тогда вы чувствуете усталость (а также разочарование и т. Д.). Решение этой дилеммы приходит в том случае, если учесть, что, когда ваши мышцы используются для приложения силы к чему-либо, отдельные мышечные волокна находятся в непрерывном процессе сокращения и освобождения, чтобы поддерживать общий коллективный результат постоянной силы, воздействующей на внешний объект.Это сокращение и отпускание включает в себя силу и движение и составляет внутреннюю работу в вашем теле. Энергия проявляется в нагревании ваших мышечных тканей, но если ящик не двигается, сетка по-прежнему не работает.
Пример справа — еще один стандартный парадокс в определении работы. Если ящик переносится с постоянной скоростью, то для его движения не требуется никакой чистой силы. Сила, прикладываемая человеком, направлена вверх, равная весу коробки, и эта сила перпендикулярна движению.Если нет движения в направлении силы, то эта сила не совершает никакой работы. Тем не менее, вы определенно чувствуете, что делаете работу, если несете тяжелую коробку. Разрешение парадокса аналогично первому примеру — ваши мышцы должны сохранять дополнительное напряжение, чтобы оставаться в вертикальном положении под нагрузкой. Это требует большего внутреннего сокращения и высвобождения наших мышечных волокон и, следовательно, внутренней работы нашего тела. Но работа, проделанная с коробкой, равна нулю, поскольку при движении по прямой с постоянной скоростью его энергия остается той же самой.
Есть много важных примеров сил, которые не работают, потому что действуют перпендикулярно движению. При круговом движении центростремительная сила всегда действует перпендикулярно движению. Он меняет направление движения, но не воздействует на объект. Это можно применить к любой круговой орбите.
Работа, выполненная силами
Выполненная работа (энергия, передаваемая механической обработкой)
Энергия и теплофизика
Работа, выполняемая силой
Учебное руководство для 14–16
Работа выполняется всякий раз, когда сила перемещает что-либо на расстояние.Вы можете рассчитать переданную энергию или выполненную работу, умножив силу на расстояние, пройденное в направлении силы.
Переданная энергия = выполненная работа = сила x расстояние, пройденное в направлении силы
Когда энергия передается из энергии, химически хранящейся в мышцах, в энергию поднятого груза или в энергию, упруго запасаемую в растянутой пружине, переданная энергия является мерой того, сколько работы было выполнено.
Передаваемая энергия = мгΔч
Это второе уравнение иллюстрируется поднятием килограммов на полки разной высоты.Вы можете показать, что уравнение является хорошим обобщением того, что происходит. Он учитывает массу, высоту и то, поднимается ли килограмм на Земле или на Луне.
Полезная вещь, которую вы получаете от топлива при его сжигании, — это передача энергии, так что груз может быть поднят или объект ускорен.
Однако не вся доступная энергия выполняет полезную работу. Если поднять много кирпичей, можно сильно нагреться. Помимо передачи энергии поднятым кирпичам, часть энергии в ваших мышцах согревает вас.Передача энергии не является 100% эффективной, и не вся переданная энергия представлена величиной м г час . Вы также не знаете, сколько полной энергии хранится гравитационно. Вы можете рассчитать только передаваемую энергию.
Концепции развиваются с паровыми двигателями
Люди сначала приручили животных для выполнения полезной работы, а позже нашли другие способы использования энергии природных источников, таких как падающая вода и ветер. Но абстрактная идея «двигателя» действительно развивалась с помощью паровых двигателей.
К 1820-м годам концепция «работы» как механического воздействия была введена в дискуссии о том, что сейчас называется энергетическими технологиями. Раньше паровые машины в основном использовались для откачки воды из шахт. Такие производители, как Boulton & Watt, убедили владельцев шахт в Корнуолле купить паровой двигатель вместо своих карьерных пони, сравнив объем работы, которую каждый может выполнить.
Ватт пошел еще дальше, разработав концепцию рабочей скорости, или мощности, с его паровыми двигателями, описанными в «лошадиных силах».Паровые двигатели позволили увеличить добычу на многих шахтах Корнуолла в четыре раза.
Аналогия для использования при обучении передаче энергии
Рассмотрим два банковских счета. Если я переведу чек на 1 фунт стерлингов со своей учетной записи на вашу, то моя учетная запись упадет на 1 фунт стерлингов, а ваша — на 1 фунт стерлингов. Но чек — это не наличные деньги. Это указание моему банку перечислить 1 фунт стерлингов на ваш счет. Мы должны платить банкам за выполнение работы за нас, и поэтому, хотя мой счет упадет на 1 фунт стерлингов, ваш вы можете получить только 95 пенсов, потому что вам придется оплатить банковские сборы.В этой транзакции также невозможно узнать, сколько хранится в каждой учетной записи.
Использование этой аналогии до предела помогает показать, что, хотя вы можете хранить реальные деньги в банке (энергия, хранящаяся, например, в топливно-кислородной смеси), чек, который проходит между счетами, — это нечто иное. Чек — это средство передачи денежной стоимости (например, работа, выполняемая при подъёме кирпича). Работа — это передача энергии.
Работа — результат силы Рон Куртус
SfC Home> Физика>
от Рона Куртуса
Когда вы прикладываете достаточно силы к объекту, чтобы преодолеть некоторое сопротивление , так что вы перемещаете этот объект, вы выполняете работу с этим объектом.Другими словами, работа равна приложенной силе, умноженной на пройденное расстояние.
Если вы перемещаете объект, который изначально неподвижен, вы ускоряете объект, а сопротивление движению — это инерция объекта. Таким образом, вы делаете работу против инерции. Поскольку объекты имеют тенденцию продолжать движение после приложения силы, расстояние измеряется только во время приложения силы.
Обычно вы рассматриваете возможность работы против силы сопротивления, такой как трение или гравитация.Приложенная сила должна быть больше, чем сила сопротивления.
Вопросы, которые могут у вас возникнуть:
- Какое отношение имеет работа к силе?
- Что такое работа против инерции?
- Что такое работа против силы сопротивления?
Этот урок ответит на эти вопросы. Полезный инструмент: Конвертация единиц
Работа — это сила, умноженная на расстояние
Определение работы состоит в том, что она равна силе преодоления сопротивления, умноженной на расстояние, пройденное при приложении этой силы.Уравнение:
W = Fd
где:
- W — работа в джоулях (Дж или кг-м² / с²) или фут-фунтах
- F — сила, необходимая для перемещения объекта, в ньютонах (Н или кг-м / с²) или фунтах (фунтах)
- d — расстояние, на которое перемещается объект, в метрах (м) или футах (футах)
- Fd равно F раз d
Примечание : W указывает на работу.Иногда W также указывается как вес. Вы всегда должны обязательно читать определение под уравнением, чтобы убедиться, что вы понимаете, что обозначают буквы.
Когда сопротивление слишком велико
Если к объекту приложена сила и нет движения из-за слишком большого сопротивления, то работы нет. Если вы толкаете тяжелый предмет, но не можете его сдвинуть, вы делаете усилие, но не выполняете никакой работы, согласно научному определению работы.
Работа против инерции
Когда вы прикладываете силу к неподвижному, но свободно движущемуся объекту, вы работаете против его инерции или тенденции оставаться неподвижным. Это также относится к изменению скорости или направления объекта.
Первый закон движения Ньютона часто называют законом инерции . В нем говорится, что:
Материя остается в своем состоянии движения и направления, если на нее не действует сила.
(Дополнительные сведения см. В разделе «Движение и закон инерции» .)
Требуемая сила
Сила, необходимая для перемещения объекта против инерции:
F = ma
где
- м — масса объекта
- a — результирующее ускорение
Таким образом, работа по инерции:
F = mad
(Не сердитесь на это!)
Работа, выполняемая над свободно движущимся объектом, происходит только на расстоянии , когда вы прикладываете силу .Как только вы перестанете прилагать силу, объект будет двигаться свободно, и работа больше не будет выполняться.
Метание мяча
Например, если вы бросаете мяч, проделанная работа состоит из расстояния, на которое вы ускоряли мяч, пока не отпустили его. После того, как вы бросили мяч, он продолжит движение с постоянной скоростью (за вычетом эффекта сопротивления воздуха), и дальнейшая работа не будет выполняться.
Перевозка тяжелого ящика
Если вы держите тяжелую коробку и переносите ее через комнату, то работа, которую вы выполняете против инерции, — это сила, которую вы прикладываете для перемещения коробки ( F = ma ), умноженная на расстояние, на которое вы ее несете.
Обратите внимание на , в некоторых учебниках говорится, что это , а не работа, потому что сила тяжести перпендикулярна вашему движению. К сожалению, им неясно, о какой работе они говорят.
Перемещение ящика по комнате — это работа против инерции ящика, а подъем ящика вверх — работа против силы сопротивления силы тяжести .
Работа против силы сопротивления
Сила сопротивления — это сила, которая заставляет движущийся объект замедляться или препятствует движению неподвижного объекта.Сила сопротивления действует в направлении, противоположном тому, по которому вы хотите переместить объект.
Как и при движении против инерции, расстояние измеряется только при приложении силы, поскольку объект может продолжить движение на короткое расстояние после того, как сила высвободилась, даже если он движется против силы сопротивления.
Работа против силы тяжести
Когда вы поднимаете тяжелый предмет, вы выполняете работу против силы тяжести. Сила, необходимая для жизни объекта, равна его весу
кг.F = мг
где
- F — сила, необходимая для подъема объекта, а также его вес
- м — масса объекта
- g — ускорение под действием силы тяжести (9.8 м / с² или 32 фут / с²)
Объем работы, который вы должны выполнить, равен весу объекта, умноженному на высоту, которую вы его поднимаете. Таким образом, W = mgh , где h — высота, на которую вы его поднимаете. Объем работы, который вы выполняете, чтобы поднять объект массой м на высоту х , представляет собой такой же объем работы, выполняемой под действием силы тяжести, если вы уроните объект с этой высоты.
Другой пример работы против инерции — это работа, совершаемая силой тяжести, когда вы роняете объект с некоторой высоты.Поскольку сила тяжести равна F = mg , где м, — масса объекта, а г, — ускорение свободного падения, работа, выполняемая при падении объекта с высоты h , составляет W = Fd. = mgh .
Обратите внимание на , что уравнение W = mgh такое же, как для потенциальной энергии объекта на некоторой заданной высоте: PE = mgh . ( См. Дополнительную информацию в разделе «Потенциальная энергия». )
Работа против трения
Трение — это сила сопротивления всему, что движется или скользит по поверхности или материалу.Например, если вы толкаете предмет по полу, сила трения оказывает сопротивление движению. Если сдвинуть объект на определенное расстояние по полу, работа будет выполнена
.W = F r d
где:
- W это проделанная работа
- F r — сила сопротивления трения
- d — расстояние, на которое вы сдвинули объект
( См. Дополнительную информацию в разделе «Сила сопротивления трения».)
Если вы толкнули предмет по скользкому полу, он может продолжить скольжение на короткое расстояние после того, как вы перестанете толкать. Ваша работа будет измеряться только на расстоянии, на которое вы толкнули объект.
Сводка
Работа — это результат силы, перемещающей объект на расстояние, измеряемое при приложении этой силы. Уравнение для работы: W = Fd . Работа может быть направлена на преодоление инерции, а также на работу против силы сопротивления. Гравитация может работать против инерции, а вы можете работать против силы тяжести.
Упорно работайте для достижения своих целей
Ресурсы и ссылки
Полномочия Рона Куртуса
Сайты
Физические ресурсы
Книги
(Примечание: Школа чемпионов может получать комиссионные от покупки книг)
Книги по физике труда с самым высоким рейтингом
Поделиться страницей
Нажмите кнопку, чтобы добавить эту страницу в закладки или поделиться ею через Twitter, Facebook, электронную почту или другие службы:
Студенты и исследователи
Веб-адрес этой страницы:
www.school-for-champions.com/science/work.htm
Пожалуйста, включите его в качестве ссылки на свой веб-сайт или в качестве ссылки в своем отчете, документе или диссертации.
Авторские права © Ограничения
Где ты сейчас?
Школа чемпионов
По физике
Работа — результат силы
13.5: Работа, выполняемая непостоянными силами
Рассмотрим тело, движущееся в x-направлении под действием непостоянной силы в x-направлении, \ (\ overrightarrow {\ mathbf {F}} = F_ {x} \ hat {\ mathbf {i}} \).Тело перемещается из исходного положения \ (x_ {i} \) в конечное положение \ (x_ {f} \). Чтобы вычислить работу, совершаемую непостоянной силой, мы разделим смещение точки приложения силы на большое количество N малых смещений \ (\ Delta x_ {j} \), где индекс j отмечает смещение \ (j_ {th} \) и принимает целые значения от 1 до N. Пусть \ (\ left (F_ {x, j} \ right) _ {\ text {ave}} \) обозначает среднее значение x -компоненты силы в интервале смещения \ (\ left [x_ {j- 1}, x_ {j} \ right] \).{x = x_ {f}} F_ {x} (x) d x \]
Это последнее выражение представляет собой определенный интеграл x -компоненты силы по параметру x. На рис. 13.5 мы графически изображаем x-составляющую силы как функцию параметра x. Рабочий интеграл — это площадь под этой кривой между \ (x = x_ {i} \) и \ (x = x_ {f} \).
Рисунок 13.5 График x -компоненты силы образца \ (F_ {x} (x) \) как функции от x.Пример \ (\ PageIndex {1} \): работа, выполненная Spring Force
Подсоедините один конец нерастянутой пружины длиной \ (l_ {0} \) с жесткостью пружины k к объекту, лежащему на гладком столе без трения, и прикрепите другой конец пружины к стене.Выберите начало координат, как показано на рисунке. Растяните пружину на величину \ (x_ {i} \) и отпустите объект. Сколько работы пружина выполняет с объектом, когда пружина растягивается на величину \ (x_ {f} \)?
Рисунок 13.6 Равновесие, начальное и конечное состояния пружиныРаствор
Сначала мы начинаем с выбора системы координат, в которой начало координат находится в положении объекта, когда пружина не растянута (или не сжата). Мы выбираем единичный вектор \ (\ hat {\ mathbf {i}} \), чтобы указывать направление движения объекта при растяжении пружины.Мы выбираем координатную функцию x для обозначения положения объекта относительно начала координат. Мы показываем координатную функцию и диаграмму силы свободного тела на рисунке ниже.
Рисунок 13.6a Сила пружиныСила пружины на объекте определяется выражением (Рисунок 13.6a)
\ [\ overrightarrow {\ mathbf {F}} = F_ {x} \ hat {\ mathbf {i}} = — k x \ hat {\ mathbf {i}} \]
На рисунке 13.7 показан график x -компоненты силы пружины \ (F_ {x} (x) \) как функции от x
. Рисунок 13.{2} \ right) \]Этот результат не зависит от знака \ (x_ {i} \) и \ (x_ {f} \), потому что обе величины отображаются в виде квадратов. Если пружина в конечном состоянии растянута или сжимается меньше, чем в исходном состоянии, то абсолютное значение \ (\ left | x_ {f} \ right | <\ left | x_ {i} \ right | \) и работа, выполняемая силой пружины, положительна. Сила пружины оказывает положительное воздействие на тело, когда пружина переходит из состояния «большего напряжения» в состояние «меньшего напряжения».
Расчетная работа — Высшая школа физики
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
.
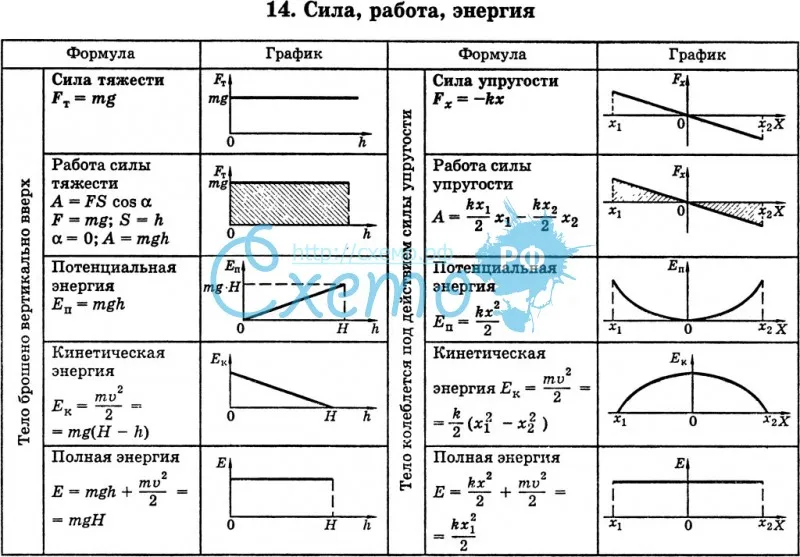
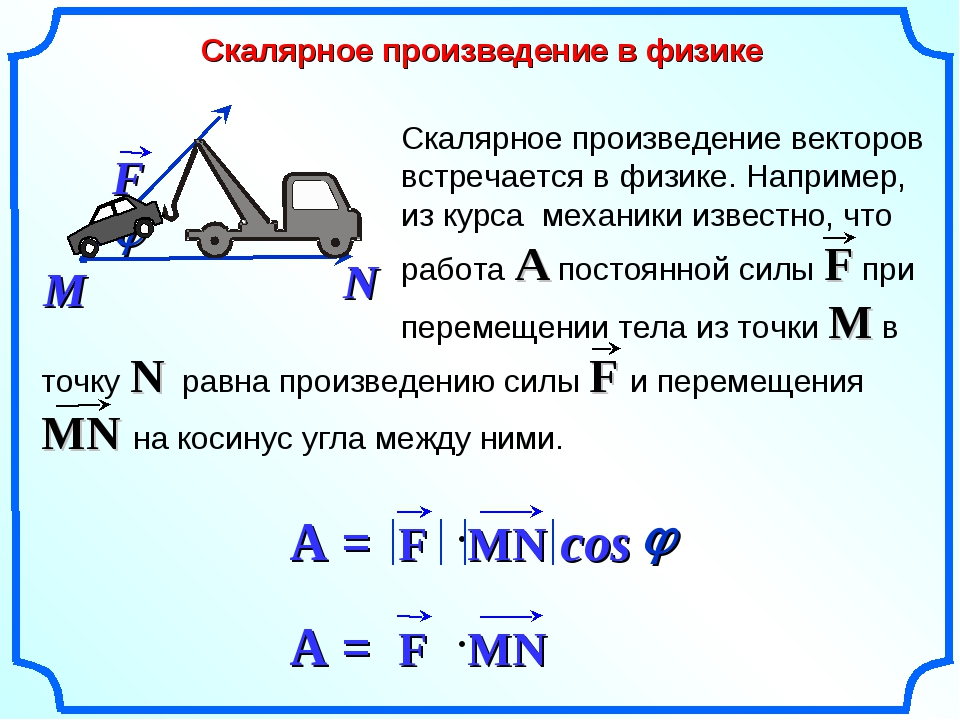
 потенция — возможность) энергией называется энергия, которая определяется взаимным положением взаимодействующих тел и частей одного и того же тела.
потенция — возможность) энергией называется энергия, которая определяется взаимным положением взаимодействующих тел и частей одного и того же тела.  Падая вниз, вода совершает работу, приводя в движение мощные турбины электростанций.
Падая вниз, вода совершает работу, приводя в движение мощные турбины электростанций.