Работа электрического поля при перемещении заряда.

 ??? Вопросы

1. Формула работы электрического поля по перемещению заряда?

2. Единица измерения работы электрического поля?

3. В каких случаях работа электрического поля А=0, А>0, A<0?

4. Зависит ли работа электрического поля по перемещению заряда от формы траектории?

5. Какое электрическое поле называют однородным? Приведите пример?

Рассмотрим ситуацию: заряд q₀ попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q₀ со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.

Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным .

Потенциал

Система «заряд — электростатическое поле» или «заряд — заряд» обладает потенциальной энергией, подобно тому, как система «гравитационное поле — тело» обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал — это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.

Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело — наоборот.
Потенциальная энергия поля — это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.

Разность потенциалов

Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов

Эту формулу можно представить в ином виде
Эквипотенциальная поверхность (линия) — поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.

Напряжение

Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
От величины напряжения зависит ток в цепи и энергия заряженной частицы.

Принцип суперпозиции

Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности

Работа электрического поля при перемещении заряда

Чем на самом деле является напряжение? Это способ описания и измерения напряженности электрического поля. Само по себе напряжение не может существовать без электронного поля вокруг положительных и отрицательных зарядов. Так же, как магнитное поле окружает Северный и Южный полюса.

По современным понятиям, электроны не оказывают взаимного влияния. Электрическое поле – это нечто, что исходит от одного заряда и его присутствие может ощущаться другим.

О понятии напряженности можно сказать то же самое! Просто это помогает нам представить, как электрическое поле может выглядеть. Честно говоря, оно не обладает ни формой, ни размером, ничем подобным. Но поле функционирует с определённой силой на электроны.

Силы и их действие на заряженную частицу

На заряженный электрон, воздействует сила с некоторым ускорением, заставляя его перемещаться все быстрее и быстрее. Этой силой совершается работа по передвижению электрона.

Силовые линии – это воображаемые очертания, которые возникают вокруг зарядов (определяется электрическим полем), и если мы поместим какой-либо заряд в эту область, он испытает силу.

Свойства силовых линий:

• путешествуют с севера на юг;
• не имеют взаимных пересечений.

Почему у двух силовых линий не возникает пересечений? Потому что не бывает этого в реальной жизни. То, о чём говорится, является физической моделью и не более. Физики изобрели её для описания поведения и характеристик электрического поля. Модель очень хороша при этом. Но помня, что это всего лишь модель, мы должны знать о том, для чего такие линии нужны.

Силовые линии демонстрируют:

• направления электрических полей;
• напряженность. Чем ближе линии, тем больше сила поля и наоборот.

Если нарисованные силовые линии нашей модели пересекутся, расстояние меж ними станет бесконечно малыми. Из-за силы поля, как формы энергии, и из-за фундаментальных законов физики это невозможно.

Что такое потенциал?

Потенциалом называется энергия, которая затрачивается на передвижение заряженной частицы из первой точки, имеющей нулевой потенциал во вторую точку.

Разность потенциалов меж пунктами А и Б – это работа, производимая силами для передвижения некоего положительного электрона по произвольной траектории из А в Б.

Чем больший потенциал у электрона, чем больше плотность потока на единицу площади. Такое явление подобно гравитации. Чем больше масса, тем больше потенциал, тем интенсивнее и плотнее гравитационное поле на единицу площади.

Небольшой заряд с низким потенциалом, с прореженной плотностью потока показан на следующем рисунке.

А ниже показан заряд с большим потенциалом и плотностью потока.

Например: во время грозы электроны истощаются в одной точке и собираются в другой, образуя электрическое поле. Когда сила станет достаточной, чтобы сломать диэлектрическую проницаемость, получается удар молнии (состоящий из электронов). При выравнивании разности потенциалов электрическое поле разрушается.

Электростатическое поле

Это разновидность электрического поля, неизменного повремени, образуемого зарядами, которые не двигаются. Работа передвижения электрона определяется соотношениями,

где r1 и r2 – расстояния заряда q до начальной и конечной точки траектории движения. По полученной формуле видно, что работа при перемещении заряда из точки в точку не зависит от траектории, а зависит лишь от начала и конца перемещения.

На всякий электрон действует сила, и поэтому при перемещении электрона в поле выполняется определенная работа.

В электростатическом поле работа зависит лишь от конечных пунктов следования, а не от траектории. Поэтому, когда движение происходит по замкнутому контуру, заряд приходит в исходное положение, и величина работы становится равной нулю. Это происходит потому, что падение потенциала нулевое (поскольку электрон возвращается в ту же самую точку). Так как разность потенциалов нулевая, чистая работа будет также нулевой, ведь потенциал падения равен работе, деленной на значение заряда, выраженное в кулонах.

Об однородном электрическом поле

Однородным называется электрическое поле меж двух противоположно заряженных плоских металлических пластин, где линии напряженности параллельны между собой.

Почему сила действия на заряд в таком поле всегда одинаковая? Благодаря симметрии. Когда система симметрична и есть только одна вариация измерения, всякая зависимость исчезает. Есть много других фундаментальных причин для ответа, но фактор симметрии – самый простой.

Работа по передвижению положительного заряда

Электрическое поле – это поток электронов от «+» до «-», приводящий к высокой напряженности области.

Поток – это количество линий электрического поля, проходящих через него. В каком направлении будут положительные электроны двигаться? Ответ: по направлению электрического поля от положительного (высокого потенциала) к отрицательному (низкому потенциалу). Поэтому положительно заряженная частица будет двигаться именно в этом направлении.

Интенсивность поля во всякой точке определяется как сила, воздействующая на положительный заряд, помещенный в эту точку.

Работа заключается в переносе электронных частиц по проводнику. По закону Ома, можно определить работу разными вариациями формул, чтобы провести расчет.

Из закона сохранения энергии следует, что работа – это изменение энергии на отдельном отрезке цепи. Перемещение положительного заряда против электрического поля требует совершения работы и в результате получается выигрыш в потенциальной энергии.

Заключение

Из школьной программы мы помним, что электрическое поле образуется вокруг заряженных частиц. На любой заряд в электрическом поле воздействует сила, и вследствие этого при движении заряда выполняется некоторая работа. Большим зарядом создается больший потенциал, который производит более интенсивное или сильное электрическое поле. Это означает, что возникает больший поток и плотность на единицу площади.

Важный момент заключается в том, что должна быть выполнена определенной силой работа по перемещению заряда от высокого потенциала к низкому. Тем самым уменьшается разница заряда между полюсами. Перемещение электронов от токи до точки требует энергии.

Пишите комментарии, дополнения к статье, может я что-то пропустил. Загляните на карту сайта, буду рад если вы найдете на моем сайте еще что-нибудь полезное.

Похожее

1.5 Работа сил электростатического поля

Работа перемещения заряда. На положительный точечный заряд q в электрическом поле с напряжённостью E действует сила
F = q E. При перемещении заряда на отрезке dl силами поля совершается работа

dA = F dl = q E dl cos (E, dl).

При перемещении заряда q силами электрического поля на произвольном конечном отрезке из точки 1 в точку 2 эта работа равна

.

Рассмотрим перемещение точечного заряда q в поле точечного заряда Q, напряженность поля которого 

.

Проекция отрезка dl на направление вектора E (рис. 1.5) есть dr = dl cos (E, dl).

Работа, совершаемая электрическим полем при перемещении заряда q из точки 1 в точку 2, определяется следующим образом:

Отсюда следует, что работа сил электрического поля не зависит от формы пути, а определяется только начальным и конечным положениями заряда q. Если оба заряда, q и Q, положительны, то работа сил поля положительна при удалении зарядов и отрицательна при их взаимном сближении.

Для электрического поля, созданного системой зарядов Q₁, Q₂,¼, Q_n, работа перемещения заряда q равна алгебраической сумме работ составляющих сил:

.

Таким же образом, как и каждая из составляющих работ, суммарная работа зависит только от начального и конечного положений заряда q.

Циркуляция вектора напряженности электрического поля. Работа, совершаемая силами электрического поля при перемещении единичного положительного заряда по замкнутому контуру длиной l, определяется как циркуляция вектора напряженности электрического поля:

Так как для замкнутого пути положения начальной и конечной точек перемещения заряда совпадают, то работа сил электрического поля на замкнутом пути равна нулю, а значит, равна нулю и циркуляция вектора напряженности, т. е.

.

Равенство нулю означает, что силы электрического поля являются силами консервативными, а само поле — потенциальным.

---

Вопросы

1)   Как доказать, что электростатическое поле является потенциальным.

2)   Напишите выражение для работы, совершаемой силами однородного поля напряженностью Е над зарядом q при его перемещении из точки 1 заданной радиус вектором r₁ в точку 2 с радиус вектором r₂ по произвольной траектории

наверх

Работа э/стат поля. Потенциал | От урока до экзамена

Электростатическое поле — это электрическое поле неподвижного заряда. Сила F эл, которая действует на заряд, перемещает его, совершая работу. В однородном электрическом поле F_эл = q E — постоянная величина. Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным полем.где ​d​ – расстояние, на которое перемещается заряд. Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой ​W​, так как буквой ​E​ обозначают напряженность поля: Потенциальная энергия заряда ​q​, помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Если поле совершает положительную работу ( вдоль силовых линий ), то потенциальная энергия заряженного тела уменьшается (но согласно закону сохранения энергии увеличивается кинетическая энергия ) и наоборот. Потенциал э/статического поля – это энергетическая характеристика электрического поля. Обозначается – φ (фи), единица измерения в СИ – вольт (В). Потенциал равен отношению потенциальной энергии заряда в поле к этому заряду:  Потенциал — скалярная физическая величина, определяющая потенциальную энергию заряда в любой точке электрического поля. Величина потенциала считается относительно выбранного нулевого уровня.  Разность потенциалов (или иначе напряжение) — это разность потенциалов в начальной и конечной точках траектории заряда Δφ = φ₁−φ₂, а не изменение потенциала Δφ = φ₂−φ₁. Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:         1 В = 1 Дж/ 1Кл Связь между напряженностью поля и разностью потенциалов:, или  Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля.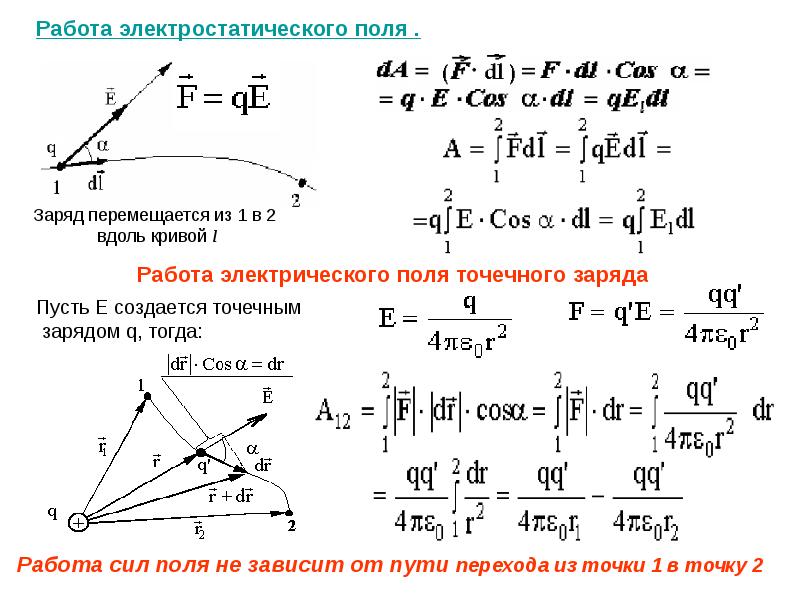 Напряженность электрического поля направлена в сторону уменьшения потенциала. Эквипотенциальные поверхности (ЭПП)  — это поверхности, все точки которых имеют одинаковый потенциал  для однородного поля — это плоскость, а для поля точечного заряда — это концентрические сферы Эквипотенциальная поверхность имеется у любого проводника в электростатическом поле, т.к. силовые линии перпендикулярны поверхности проводника. Все точки внутри проводника имеют одинаковый потенциал ( φ=0). Напряженность внутри проводника = 0, значит и разность потенциалов внутри = 0.

Найти работу сил поля по перемещению заряда. Работа в электрическом поле

Если в электростатическом поле точечного заряда q из точки 1 в точку 2 вдоль произвольной траектории перемещается другой точечный заряд q 0 , то сила, приложенная к заряду, совершает работу. Работа силы на элементарном перемещении dl равна

Работа при перемещении заряда q 0 из точки 1 в точку 2

Работа A 12 не зависит от траектории перемещения, а определяется только положениями начальной и конечной точек . Следовательно, электростатическое поле точечного заряда является потенциальным , а электростатические силы — консервативными .

Таким образом, работа перемещения заряда в электростатическом поле по любому замкнутому контуру L равна нулю

Интеграл называется циркуляцией вектора напряженности. Из обращения ее в нуль следует, что линии напряженности электростатического поля никогда не могут быть замкнуты сами на себя. Они начинаются и кончаются на зарядах, либо уходят в бесконечность. Это свидетельствует о наличии в природе двух родов электрических зарядов. Формула справедлива только для электростатического поля.

При перемещении зарядов изменяется их взаимное расположение, поэтому работа, совершаемая электрическими силами, в этом случае равна изменению потенциальной энергии перемещаемого заряда:

Потенциальная энергия заряда q 0 , находящегося в поле заряда q на расстоянии r от него равна

Считая, что при удалении заряда на бесконечность, потенциальная энергия обращается в нуль, получаем: const = 0.

Для одноименных зарядов потенциальная энергия их взаимодействия (отталкивания) положительна , для разноименных зарядов потенциальная энергия из взаимодействия (притяжения) отрицательна .

В любой точке поля потенциальная энергия W заряда численно равна работе, которую необходимо совершить для перемещения заряда из бесконечности в эту точку.

Отношение зависит только от q и r . Эту величину называют потенциалом:

Единица электрического потенциала – вольт (В).

Она характеризует потенциальную энергию, которой обладал бы по­ложительный единичный заряд, помещенный в данную точку поля.Для поля точечного заряда: . Потенциал данной точки поля равен работе перемещения единичного положительного заряда из данной точки в бесконечность.

Потенциал поля, создаваемого системой точечных зарядов, равен алгебраической сумме потенциалов всех этих зарядов : .

Работа сил поля при перемещении заряда q’ из точки 1 в точку 2 может быть записана в виде:

Величину называют разностью потенциалов (напряжением) электрического поля.

Чем на самом деле является напряжение? Это способ описания и измерения напряженности электрического поля. Само по себе напряжение не может существовать без электронного поля вокруг положительных и отрицательных зарядов. Так же, как магнитное поле окружает Северный и Южный полюса.

По современным понятиям, электроны не оказывают взаимного влияния. Электрическое поле – это нечто, что исходит от одного заряда и его присутствие может ощущаться другим.

О понятии напряженности можно сказать то же самое! Просто это помогает нам представить, как электрическое поле может выглядеть. Честно говоря, оно не обладает ни формой, ни размером, ничем подобным. Но поле функционирует с определённой силой на электроны.

Силы и их действие на заряженную частицу

На заряженный электрон, воздействует сила с некоторым ускорением, заставляя его перемещаться все быстрее и быстрее. Этой силой совершается работа по передвижению электрона.

Силовые линии – это воображаемые очертания, которые возникают вокруг зарядов (определяется электрическим полем), и если мы поместим какой-либо заряд в эту область, он испытает силу.

Свойства силовых линий:

• путешествуют с севера на юг;
• не имеют взаимных пересечений.

Почему у двух силовых линий не возникает пересечений? Потому что не бывает этого в реальной жизни. То, о чём говорится, является физической моделью и не более. Физики изобрели её для описания поведения и характеристик электрического поля. Модель очень хороша при этом. Но помня, что это всего лишь модель, мы должны знать о том, для чего такие линии нужны.

Силовые линии демонстрируют:

• направления электрических полей;
• напряженность. Чем ближе линии, тем больше сила поля и наоборот.

Если нарисованные силовые линии нашей модели пересекутся, расстояние меж ними станет бесконечно малыми. Из-за силы поля, как формы энергии, и из-за фундаментальных законов физики это невозможно.

Что такое потенциал?

Потенциалом называется энергия, которая затрачивается на передвижение заряженной частицы из первой точки, имеющей нулевой потенциал во вторую точку.

Разность потенциалов меж пунктами А и Б – это работа, производимая силами для передвижения некоего положительного электрона по произвольной траектории из А в Б.

Чем больший потенциал у электрона, чем больше плотность потока на единицу площади. Такое явление подобно гравитации. Чем больше масса, тем больше потенциал, тем интенсивнее и плотнее гравитационное поле на единицу площади.

Небольшой заряд с низким потенциалом, с прореженной плотностью потока показан на следующем рисунке.

А ниже показан заряд с большим потенциалом и плотностью потока.

Например: во время грозы электроны истощаются в одной точке и собираются в другой, образуя электрическое поле. Когда сила станет достаточной, чтобы сломать диэлектрическую проницаемость, получается удар молнии (состоящий из электронов). При выравнивании разности потенциалов электрическое поле разрушается.

Электростатическое поле

Это разновидность электрического поля, неизменного повремени, образуемого зарядами, которые не двигаются. Работа передвижения электрона определяется соотношениями,

где r1 и r2 – расстояния заряда q до начальной и конечной точки траектории движения. По полученной формуле видно, что работа при перемещении заряда из точки в точку не зависит от траектории, а зависит лишь от начала и конца перемещения.

На всякий электрон действует сила, и поэтому при перемещении электрона в поле выполняется определенная работа.

В электростатическом поле работа зависит лишь от конечных пунктов следования, а не от траектории. Поэтому, когда движение происходит по замкнутому контуру, заряд приходит в исходное положение, и величина работы становится равной нулю. Это происходит потому, что падение потенциала нулевое (поскольку электрон возвращается в ту же самую точку). Так как разность потенциалов нулевая, чистая работа будет также нулевой, ведь потенциал падения равен работе, деленной на значение заряда, выраженное в кулонах.

Об однородном электрическом поле

Однородным называется электрическое поле меж двух противоположно заряженных плоских металлических пластин, где линии напряженности параллельны между собой.

Почему сила действия на заряд в таком поле всегда одинаковая? Благодаря симметрии. Когда система симметрична и есть только одна вариация измерения, всякая зависимость исчезает. Есть много других фундаментальных причин для ответа, но фактор симметрии – самый простой.

Работа по передвижению положительного заряда

Электрическое поле – это поток электронов от «+» до «-», приводящий к высокой напряженности области.

Поток – это количество линий электрического поля, проходящих через него. В каком направлении будут положительные электроны двигаться? Ответ: по направлению электрического поля от положительного (высокого потенциала) к отрицательному (низкому потенциалу). Поэтому положительно заряженная частица будет двигаться именно в этом направлении.

Интенсивность поля во всякой точке определяется как сила, воздействующая на положительный заряд, помещенный в эту точку.

Работа заключается в переносе электронных частиц по проводнику. По закону Ома, можно определить работу разными вариациями формул, чтобы провести расчет.

Из закона сохранения энергии следует, что работа – это изменение энергии на отдельном отрезке цепи. Перемещение положительного заряда против электрического поля требует совершения работы и в результате получается выигрыш в потенциальной энергии.

Заключение

Из школьной программы мы помним, что электрическое поле образуется вокруг заряженных частиц. На любой заряд в электрическом поле воздействует сила, и вследствие этого при движении заряда выполняется некоторая работа. Большим зарядом создается больший потенциал, который производит более интенсивное или сильное электрическое поле. Это означает, что возникает больший поток и плотность на единицу площади.

Важный момент заключается в том, что должна быть выполнена определенной силой работа по перемещению заряда от высокого потенциала к низкому. Тем самым уменьшается разница заряда между полюсами. Перемещение электронов от токи до точки требует энергии.

Пишите комментарии, дополнения к статье, может я что-то пропустил. Загляните на , буду рад если вы найдете на моем еще что-нибудь полезное.

ЭЛЕКТРИЧЕСКИЙ ЗАРЯД. ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ.

Электрический заряд q — физическая величина, определяющая интенсивность электромагнитного взаимодействия.

[q] = l Кл (Кулон).

Атомы состоят из ядер и электронов. В состав ядра входят положительно заряженные протоны и не имеющие заряда нейтроны. Электроны несут отрицательный заряд. Количество электронов в атоме равно числу протонов в ядре, поэтому в целом атом нейтрален.

Заряд любого тела: q = ±Ne , где е = 1,6*10 -19 Кл — элементарный или минимально возможный заряд (заряд электрона), N — число избыточных или недостающих электронов.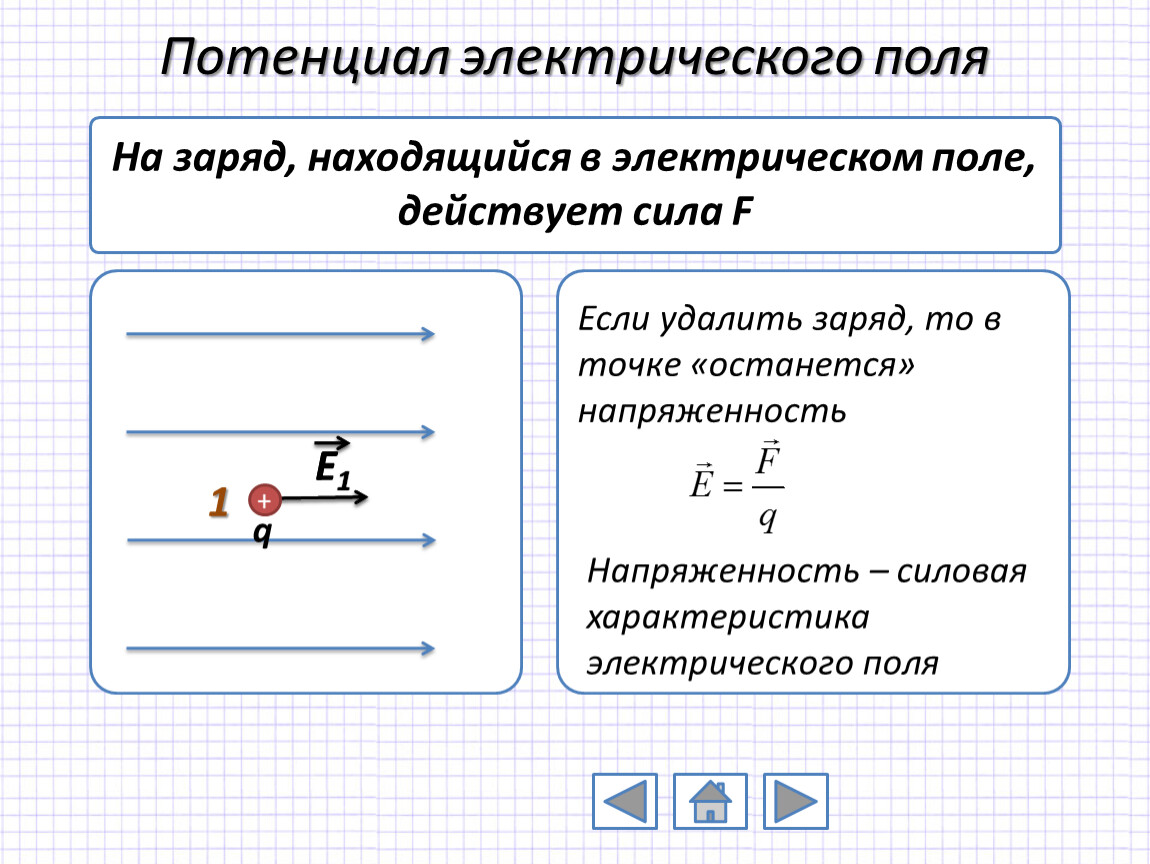 В замкнутой системе алгебраическая сумма зарядов остается постоянной:

q 1 + q 2 + … + q n = const.

Точечный электрический заряд — заряженное тело, размеры которого во много раз меньше расстояния до другого наэлектризованного тела, взаимодействующего с ним.

Закон Кулона

Два неподвижных точечных электрических заряда в вакууме взаимодействуют с силами, направленными по прямой, соединяющей эти заряды; модули этих сил прямо пропорциональны произведению зарядов и обратно пропорциональны квадрату расстояния между ними:

Коэффициент пропорциональности

где — электрическая постоянная.

где 12 — сила, действующая со стороны второго заряда на первый, а 21 — со стороны первого на второй.

ЭЛЕКТРИЧЕСКОЕ ПОЛЕ. НАПРЯЖЕННОСТЬ

Факт взаимодействия электрических зарядов на расстоянии можно объяснить наличием вокруг них электрического поля — материального объекта, непрерывного в пространстве и способного действовать на другие заряды.

Поле неподвижных электрических зарядов называют электростатическим.

Характеристикой поля является его напряженность.

Напряженность электрического поля в данной точке — это вектор, модуль которого равен отношению силы, действующей на точечный положительный заряд, к величине этого заряда, а направление совпадает с направлением силы.

Напряженность поля точечного заряда Q на расстоянии r от него равна

Принцип суперпозиции полей

Напряженность поля системы зарядов равна векторной сумме напряженностей полей каждого из зарядов системы:

Диэлектрическая проницаемость среды равна отношению напряженностей поля в вакууме и в веществе:

Она показывает во сколько раз вещество ослабляет поле. Закон Кулона для двух точечных зарядов q и Q , расположенных на расстоянии r в среде c диэлектрической проницаемостью:

Напряженность поля на расстоянии r от заряда Q равна

ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ЗАРЯЖЕННОГО ТЕЛА В ОДНОРОДНОМ ЭЛЕКТРО-СТАТИЧЕСКОМ ПОЛЕ

Между двумя большими пластинами, заряженными противоположными знаками и расположенными параллельно, поместим точечный заряд q .

Так как электрическое поле между пластинами с напряженностью однородное, то на заряд во всех точках действует сила F = qE , которая при перемещении заряда на расстояние вдоль совершает работу

Эта работа не зависит от формы траектории, то есть при перемещении заряда q вдоль произвольной линии L работа будет такой же.

Работа электростатического поля по перемещению заряда не зависит от формы траектории, а определяется исключительно начальным и конечным состояниями системы. Она, как и в случае с полем сил тяжести, равна изменению потенциальной энергии, взятому с противоположным знаком:

Из сравнения с предыдущей формулой видно, что потенциальная энергия заряда в однородном электростатическом поле равна:

Потенциальная энергия зависит от выбора нулевого уровня и поэтому сама по себе не имеет глубокого смысла.

ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ И НАПРЯЖЕНИЕ

Потенциальным называется поле, работа которого при переходе из одной точки поля в другую не зависит от формы траектории. Потенциальными являются поле силы тяжести и электростатическое поле.

Работа, совершаемая потенциальным полем, равна изменению потенциальной энергии системы, взятой с противоположным знаком:

Потенциал — отношение потенциальной энергии заряда в поле к величине этого заряда:

Потенциал однородного поля равен

где d — расстояние, отсчитываемое от некоторого нулевого уровня.

Потенциальная энергия взаимодействия заряда q с полем равна .

Поэтому работа поля по перемещению заряда из точки с потенциалом φ 1 в точку с потенциалом φ 2 составляет:

Величина называется разностью потенциалов или напряжением.

Напряжение или разность потенциалов между двумя точками — это отношение работы электрического поля по перемещению заряда из начальной точки в конечную к величине этого заряда:

[U]=1Дж/Кл=1В

НАПРЯЖЕННОСТЬ ПОЛЯ И РАЗНОСТЬ ПОТЕНЦИАЛОВ

При перемещении заряда q вдоль силовой линии электрического поля напряженностью на расстояние Δ d поле совершает работу

Так как по определению, то получаем:

Отсюда и напряженность электрического поля равна

Итак, напряженность электрического поля равна изменению потенциала при перемещении вдоль силовой линии на единицу длины.

Если положительный заряд перемещается в направлении силовой линии, то направление действия силы совпадает с направлением перемещения, и работа поля положительна:

Тогда , то есть напряженность направлена в сторону убывания потенциала.

Напряженность измеряют в вольтах на метр:

[E]=1 B/м

Напряженность поля равна 1 В/м, если напряжение между двумя точками силовой линии, расположенными на расстоянии 1 м, равна 1 В.

ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ

Если независимым образом измерять заряд Q , сообщаемый телу, и его потенциал φ, то можно обнаружить, что они прямо пропорциональны друг другу:

Величина С характеризует способность проводника накапливать электрический заряд и называется электрической емкостью. Электроемкость проводника зависит от его размеров, формы, а также электрических свойств среды.

Электроёмкостъ двух проводников — отношение заряда одного из них к разности потенциалов между ними:

Емкость тела равно 1 Ф , если при сообщении ему заряда 1 Кл оно приобретает потенциал 1 В.

КОНДЕНСАТОРЫ

Конденсатор — два проводника, разделенные диэлектриком, служащие для накопления электрического заряда. Под зарядом конденсатора понимают модуль заряда одной из его пластин или обкладок.

Способность конденсатора накапливать заряд характеризуется электроемкостью, которая равна отношению заряда конденсатора к напряжению:

Емкость конденсатора равна 1 Ф, если при напряжении 1 В его заряд равен 1 Кл.

Емкость плоского конденсатора прямо пропорциональна площади пластин S , диэлектрической проницаемости среды, и обратно пропорциональна расстоянию между пластинами d :

ЭНЕРГИЯ ЗАРЯЖЕННОГО КОНДЕНСАТОРА.

Точные эксперименты показывают, что W=CU 2 /2

Так как q = CU , то

Плотность энергии электрического поля

где V = Sd — объем, занимаемый полем внутри конденсатора. Учитывая, что емкость плоского конденсатора

а напряжение на его обкладках U=Ed

получаем:

Пример.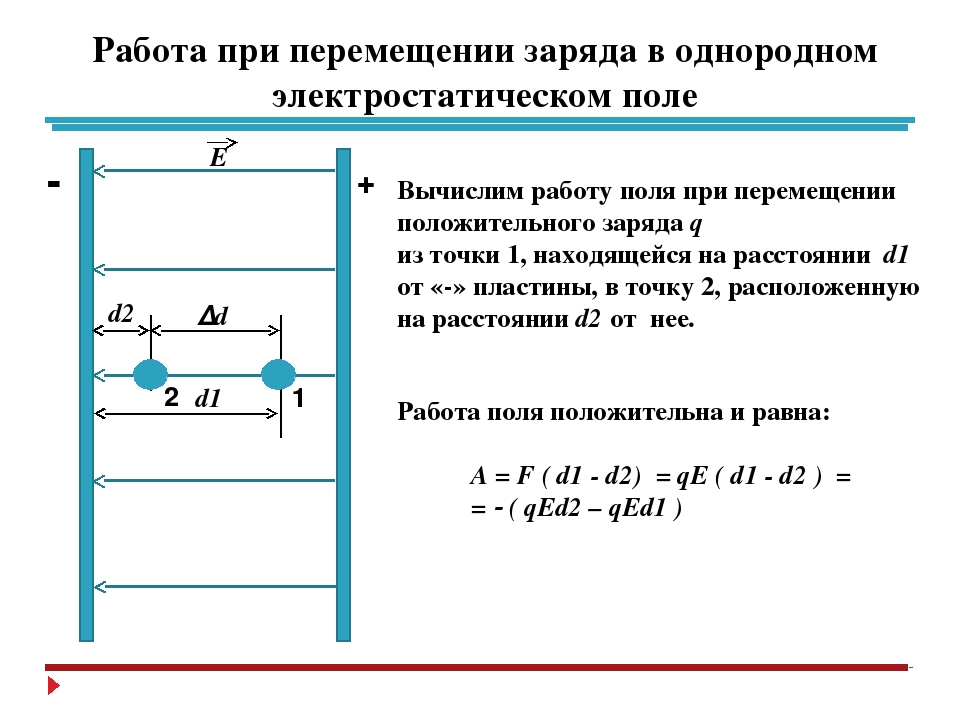 Электрон, двигаясь в электрическом поле из точки 1 через точку 2, увеличил свою скорость от 1000 до 3000 км/с. Определите разность потенциалов между точками 1 и 2.

Одним из основных понятий в электричестве является электростатическое поле. Его важным свойством считается работа по перемещению заряда в электрическом поле, которое создается распределенным зарядом, не изменяющимся во времени.

Условия выполнения работы

Сила, находящиеся в электростатическом поле, перемещает заряд из одного места в другое. На нее совершенно не влияет форма траектории. Определение силы зависит только от положения точек в начале и конце, а также, от общей величины заряда.

Исходя из этого, можно сделать следующий вывод: Если траектория при перемещении электрозаряда является замкнутой, то вся работа сил в электростатическом поле имеет нулевое значение. При этом, форма траектории не имеет значения, поскольку кулоновские силы производят одинаковую работу. Когда направление, в котором перемещается электрозаряд, изменяется на противоположное, то сама сила также изменяет свой знак.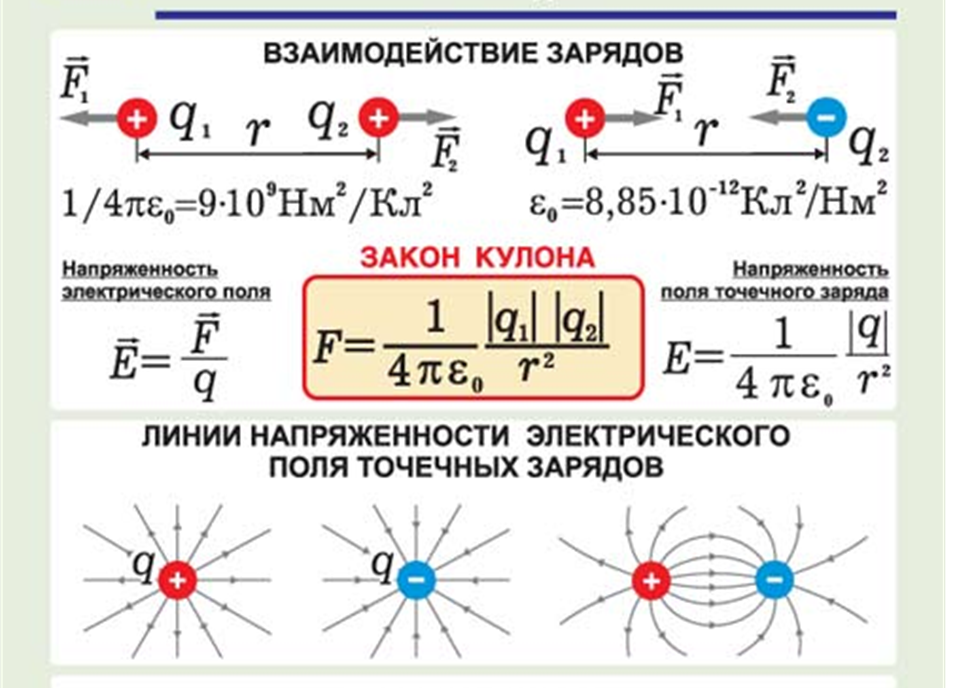 Поэтому, замкнутая траектория, независимо от своей формы, определяет всю работу, производимую кулоновскими силами, равной нулю.

Если в создании электростатического поля принимает участие сразу несколько точечных зарядов, то их общая работа будет складываться из суммы работ, производимых кулоновскими полями этих зарядов. Общая работа, независимо от формы траектории, определяется исключительно местом расположения начальных и конечных точек.

Понятие потенциальной энергии заряда

Свойственная электростатическому полю, позволяет определять потенциальную энергию какого-либо заряда. Кроме того, с ее помощью более точно устанавливается работа по перемещению заряда в электрическом поле. Чтобы получить это значение, в пространстве необходимо выбрать определенную точку и потенциальную энергию заряда, размещаемого в данной точке.

Заряд, помещаемый в любую точку, имеет потенциальную энергию, равной работе, совершаемой электростатическим полем, во время перемещения заряда из одной точки в другую.

В физическом смысле, потенциальная энергия представляет собой значение для каждой из двух разных точек пространства. При этом, работа по перемещению заряда находится вне зависимости от путей его перемещения и выбранной точки. Потенциал электростатического поля в данной пространственной точке, равняется работе, совершаемой электрическими силами, когда единичный положительный заряд удаляется из этой точки в бесконечное пространство.

Работа электрического поля

На любой заряд, который находится в электрическом поле, воздействует сила. В связи с этим при передвижении заряда в поле происходит определенная работа электрического поля. Как же произвести расчет этой работы?

Работа электрического поля состоит в переносе электрозарядов вдоль проводника. Она будет равняться произведению напряжения, и времени, потраченного на работу.

Применив формулу закона Ома, мы можем получить несколько различных вариантов формулы для проведения подсчета работы тока:

A = U˖I˖t = I²R˖t = (U²/R)˖t.

В соответствии с законом сохранения энергии работа электрического поля равняется изменению энергии отдельно взятого участка цепи, в связи с чем энергия, выделяемая проводником, будет равняться работе тока.

Выразим в системе СИ:

[А] = В˖А˖с = Вт˖с = Дж

1 кВт˖час = 3600000 Дж.

Проведем опыт. Рассмотрим передвижение заряда в одноименном поле, которое образовано двумя параллельно расположенными пластинами А и В и заряженными разноименными зарядами. В таком поле силовые линии на всем своем протяжении перпендикулярны этим пластинам, и когда пластина А будет заряжена положительно, тогда Е будет направлена от А к В.

Предположим, что позитивный заряд q передвинулся из точки a в точку b по произвольному пути ab = s.

Так как сила, которая действует на заряд, который находится в поле, будет равняться F = qE, то работа, совершенная при передвижении заряда в поле согласно заданному пути, определится по равенству:

A = Fs cos α, или A = qFs cos α.

Но s cos α = d, где d — дистанция между пластинами.

Отсюда следует: A = qEd.

Допустим, теперь заряд q переместится из a и b по сути acb. Работа электрического поля, совершенная на этом пути, равняется сумме работ, совершенных на отдельных участках его: ac = s₁, cb = s₂, т.е.

A = qEs₁ cos α₁ + qEs₂ cos α₂,

A = qE(s₁ cos α₁ + s₂ cos α₂,).

Но s₁ cos α₁ + s₂ cos α₂ = d, а значит, и в данном случае A = qEd.

Кроме того, предположим, что заряд q передвигается из a в b по произвольной кривой линии. Чтобы подсчитать работу, совершенную на данном криволинейном пути, необходимо расслоить поле между пластинами А и В некоторым количеством которые будут настолько близки одна к другой, что отдельные участки пути s между данными плоскостями можно будет считать прямыми.

В таком случае работа электрического поля, произведенная на каждом из данных отрезков пути, будет равняться A₁ = qEd₁, где d₁ — дистанция между двумя сопредельными плоскостями. А полная работа на всем пути d будет равняться произведению qE и суммы расстояний d₁, равной d.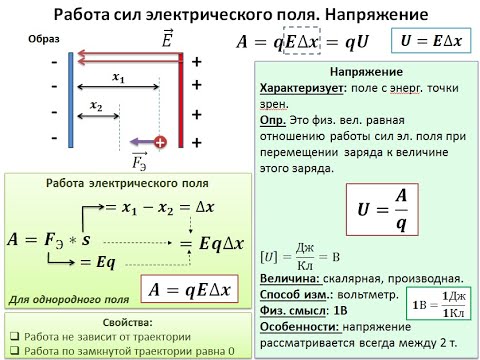 Таким образом, и в результате криволинейного пути совершенная работа будет равняться A = qEd.

Примеры, рассмотренные нами, показывают, что работа электрического поля по перемещению заряда из какой-либо точки в другую не зависит от формы пути передвижения, а зависит исключительно от положения данных точек в поле.

Кроме того, мы знаем, что работа, которая совершается силой тяжести при передвижении тела по наклонной плоскости, имеющей длину l, будет равняться работе, которую совершает тело при падении с высоты h, и высоте наклонной плоскости. Значит, работа или, в частности, работа при передвижении тела в поле тяжести, тоже не зависит от формы пути, а зависит только от разности высот первой и последней точек пути.

Так можно доказать, что таким важным свойством может обладать не только однородное, а и всякое электрическое поле. Похожим свойством обладает и сила тяжести.

Работа электростатического поля по перемещению точечного заряда из одной точки в другую определяется линейным интегралом:

A₁₂ = ∫ L₁₂q (Edl),

где L₁₂ — траектория движения заряда, dl — бесконечно малое перемещение вдоль траектории.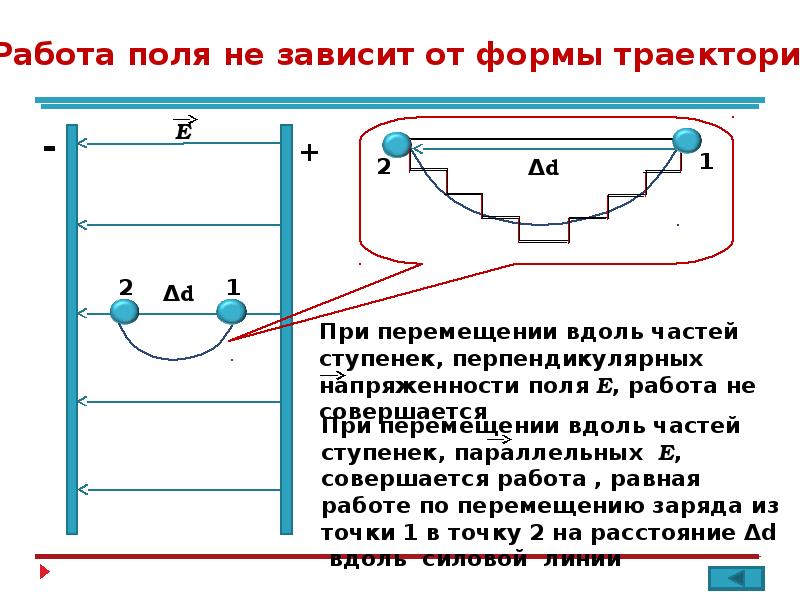 Если контур замкнутый, то для интеграла используется символ ∫; в этом случае предполагается, что выбрано направление обхода контура.

Работа электростатических сил не зависит от формы пути, а только лишь от координат первой и последней точек перемещения. Следовательно, силы поля консервативны, а само поле — потенциально. Стоит отметить, что работа любой по замкнутому пути будет равняться нулю.

Работа электростатического поля. Потенциальное поле | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко

Легкий металлический шарик подвесим на тонкой шелковой нити и разместим меж­ду металлическими пластинами, соединен­ными с источником высокого напряжения (рис. 4.52). Подведем шарик к одной из пластин и после касания отпустим его. Ша­рик начнет осуществлять колебательное дви­жение, касаясь то одной, то другой пласти­ны. Такое движение шарик будет совершать до тех пор, пока пластины будут заряжены и между ними будет электрическое поле.

Рассмотренный опыт показывает, что электрическое поле может выполнять ра­боту.

В механике работа рассчитывается по формуле

A = F • s • cos α,

где F — сила, действующая на тело; s — модуль перемещения; α — угол между си­лой и перемещением.

Применим знания из механики к вы­числению работы электростатического поля.

Рис. 4.52. Движение металлического ша­рика в электрическом поле

Рассмотрим точечное тело, имеющее по­ложительный электрический заряд и на­ходящееся в однородном электрическом по­ле между двумя параллельными пластинами, которые имеют разноименные заряды и размеры, намного больше, чем расстояния между ними (рис. 4.53).

На тело, находящееся в точке A, дейст­вует электрическая сила

F̅_э = qE̅,

которая имеет постоянное значение и на­правление. Тело удалено от левой пласти­ны на расстояние l₁.

Пусть тело движется из точки A в точку B вследствие действия электрической силы F̅_э. Эта сила будет выполнять работу

A = F_э • s • cos α.

В точке B тело будет находиться на рас­стоянии l₂ от левой пластины.

Модуль перемещения s = AB.

Рис. 4.53. Передвижение заряженного те­ла в электрическом поле

Рис. 4.54. Передвижение заряженного те­ла в электрическом поле

Построим проекцию перемещения на на­правление действия силы. На рис. 4.54 она изображена отрезком AC.

Из правил построения проекций в на­шем случае можно сделать вывод, что най­денная точка C, как и точка B, находится на расстоянии l₂ от левой пластины.

Учитывая последнее, можно записать, что s • cos α = l₁ — l₂.

Таким образом,

A = F_э(l₁ — l₂) = q₀E(l₁ — l₂).

Такая же работа будет выполнена и при перемещении заряженного тела из точки A в точку D или точку E, поскольку для этих перемещений также

s • cos α = l₁ — l₂.

Рис. 4.55. Передвижение не зависит от формы траектории

Такой же результат получим и в том случае, если заряженное тело будет переме­щаться в точку C из разных точек, отдален­ных от левой пластины на расстояние l₁.

Работа по перемещению заряженного тела в электростатическом поле не зависит от пути, а зависит от положения начальной и конечной точек движения.

Подобный вывод можно сделать и для движения тела по произвольной траектории. Если при движении тело будет описывать кривые, начинающиеся в точке A и закан­чивающиеся в точке B (рис.4.55), то модуль перемещения s̅ будет одним и тем же.

Работа по перемеще­нию заряженного тела в электростатическом по­ле не зависит от формы траектории дви­жения.

Если в процессе движения в электри­ческом поле заряженное тело описывает замкнутую траекторию, то есть возвращает­ся в начальную точку, то работа электростати­ческого поля равна нулю. Ведь если l₂ = l₁, то Материал с сайта http://worldofschool.ru

A = q₀E(l₁ — l₂) = q₀E(l₁ — l­₁) = 0.

При перемещении заряженно­го тела в электростатическом поле по замкнутой траектории работа равна нулю.

Сделанные выводы подобны выводам от­носительно работы силы тяжести, которая рассматривалась в механике. В частности,

A = mg(h₁ — h₂),

а при h₁ = h₂

A = mg(h₁ — h₁) = 0.

Поля, в которых работа не зависит от формы траектории и определяется только положениями тела в начальный и конечный моменты движения, называются потенциаль­ными.

Таким образом, заряженное тело в элект­ростатическом поле имеет потенциальную энергию так же, как и тело определенной массы в поле тяжести.

Электрически заряженное тело в электрическом поле имеет потенциальную энергию.

На этой странице материал по темам:

• Конспект работа и потенциал электростатического поля. 10 класс

• Потенциальное поле физика

• Конспект работа и потенциал электрического поля

• Знак и величину заряда иона обозначают правым верхним индексом.

Вопросы по этому материалу:

• При каких условиях в электрическом поле выполняется работа?

• От чего зависит работа в однородном электрическом поле?

• Как доказать, что работа в электростатическом поле не зависит от пути?

• Почему работа при движении по замкнутой траектории в элект­ростатическом поле равна нулю?

• Почему электростатическое поле потенциальное?

Потенциальная энергия заряженного тела. Потенциал и разность потенциалов.

Электростатическое поле — электрическое поле неподвижного заряда. Электрическая сила, действующая на заряд, перемещает его, совершая работу. В однородном электрическом поле Fэл = qE — постоянная величина

А₁₂ = Fs ^.Cos (F,s) = qEΔd

А₂₃ = 0, т.к.  Cos 90^о = 0

А₃₄ = — qEΔd,  т.к.  Cos 180^о = -1

А₄₁ = 0, т.к.  Cos 270^о = 0

А₁₂₃₄₁ = А₁₂  + А₂₃  + А₃₄  + А₄₁ = 0

Работа электрического поля не зависит от формы траектории и на замкнутой траектории равна нулю. Поля, обладающие таким свойством, называют потенциальными. Потенциальный характер, в частности, имеет электростатическое поле точечного заряда.

Электростатическая энергия — потенциальная энергия системы заряженных тел (т.к. они взаимодействуют и способны совершить работу).

А = qEΔd = qE(d₁ – d₂) = — (qEd₂ – qEd₁)

Работу потенциального поля можно выразить через изменение потенциальной энергии. Так как работа поля не зависит от формы траектории, то  A = — ΔW_п = — (W_п2 — W_п1) справедлива для любого электростатического поля. Но только в случае однородного поля потенциальная энергия выражается формулой W_п = qEd. Если поле совершает положительную работу (вдоль силовых линий), то потенциальная энергия заряженного тела уменьшается (но согласно закону сохранения энергии увеличивается кинетическая энергия) и наоборот.

ПОТЕНЦИАЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯ

— энергетическая характеристика электростатического поля.

— равен отношению потенциальной энергии заряда в поле к этому заряду.

— скалярная величина, определяющая потенциальную энергию заряда в любой точке эл. поля.

φ = W / q = const     [φ] = Дж / Кл = 1В

φ – скаляр; φ > 0, если +q,  φ < 0, если –q.

φ = ± φ₁ ± φ₂ ± φ₃     принцип суперпозиции.

Величина потенциала считается относительно выбранного нулевого уровня.

 

РАЗНОСТЬ ПОТЕНЦИАЛОВ (или иначе НАПРЯЖЕНИЕ)

— это разность потенциалов в начальной и конечной точках траектории заряда.

А = -(W_п2 — W_п1) = -(q φ₂  — qφ₁) = q(φ₁  — φ₂)

φ₁  — φ₂ = U = A / q;  [U] = Дж / Кл = В

Напряжение U между двумя точками равно разности потенциалов этих точек и равно работе поля по перемещению единичного заряда.

 

СВЯЗЬ МЕЖДУ НАПРЯЖЕННОСТЬЮ ПОЛЯ И РАЗНОСТЬЮ ПОТЕНЦИАЛОВ

 

A = q E Δd; A = qU => E = U / Δd.     [E] = B / м   

Чем меньше меняется потенциал на отрезке пути, тем меньше напряженность поля. Напряженность электростатического поля направлена в сторону уменьшения потенциала.

 

ЭКВИПОТЕНЦИАЛЬНЫЕ ПОВЕРХНОСТИ

 

— поверхности, все точки которых имеют одинаковый потенциал

  

для однородного поля — это плоскость                                               для поля точечного заряда — это концентрические

                                                                                                                                                                                        сферы.

Эквипотенциальные поверхности перпендикулярны силовым линиям и  φ₁ = φ₂ = φ_{3  = …}  

Эквипотенциальная поверхность имеется у любого проводника в электростатическом поле, т.к. силовые линии перпендикулярны поверхности проводника. Все точки внутри проводника имеют одинаковый потенциал. Напряженность внутри проводника равна 0, значит и разность потенциалов внутри равна 0.

Электрическая потенциальная энергия (U) и Электрический потенциал (V): (Примечания из C

Электрическая потенциальная энергия (U) и электрический потенциал (V): ( Записи лекций К. Эркалса PHYS 221 )

Рассмотрим конденсатор с параллельными пластинами, который производит однородную электрическое поле между его большими пластинами. Это достигается путем подключения каждой пластины к одному из выводов источник питания (например, аккумулятор).

Рисунок 1: Электрическое поле создается заряженными пластинами. разделенные расстоянием l. Обвинения на пластинах стоят + Q и Q.

Рисунок 2: Электрический заряд q перемещается из точки A в сторону точка B с внешней силой T против электрической силы qE.

Рис. 3, 4: Когда он перемещается на расстояние d, его потенциальная энергия в точке B равна qEd относительно точки A.

Рисунок 5: При отпускании из B (T = 0) он будет ускоряться к нижней пластине. Как он движется по направлению к нижней пластине его потенциальная энергия уменьшается, а кинетическая энергия увеличивается. Когда он достигает нижнего пластина (где мы можем выбрать потенциальную энергию равной нулю), ее потенциал энергия в точке A полностью преобразуется в кинетическую энергию в точке B:

Обратите внимание, что qEd — это работа, выполняемая полем в качестве заряда движется под действием силы qE от B к A.Здесь m — масса заряда q, а v — его скорость при достижении точка А. Здесь мы предположили, что электрическая поле однородное! Выполнено работ по E field:

Давайте вспомним теорему о кинетической энергии-работе (Work Energy принцип):

, где мы ввели понятие потенциальной энергии и консервативная сила (сила, под которой можно определить потенциальную энергию так что проделанная работа зависит только от разницы потенциальной энергии функция оценивается в конечных точках).

Практическое правило определения того, является ли EPE увеличение:

Если заряд движется в том направлении, при нормальном движении его электрическая потенциальная энергия уменьшается. Если заряд движется в направлении, противоположном к тому, что он обычно двигался бы, его электрическая потенциальная энергия увеличивается. Эта ситуация похожа на ситуацию постоянное гравитационное поле (g = 9,8 м / с ² ). Когда вы поднимаете предмет, вы увеличивая его гравитационную потенциальную энергию.Точно так же, когда вы опускаете объект, его гравитационная энергия равна уменьшается.

Общая формула потенциальной разницы:

Работа, выполняемая полем E, когда оно действует на заряд q для перемещения. он от точки A до точки B определяется как разность электрических потенциалов между точки A и B:

Ясно, что потенциальную функцию V можно сопоставить каждому точка в пространстве, окружающем распределение заряда (например, параллельное тарелки).Приведенная выше формула обеспечивает простой рецепт для расчета работы, проделанной при перемещении заряда между двумя точками где мы знаем значение разности потенциалов. Приведенные выше утверждения и формула действительны независимо от путь, по которому перемещается заряд. Особый интерес представляет потенциал точечного заряда Q. Его можно найти, просто выполнив интегрирование по простому пути (например, по прямой) из точки A расстояние от Q которого равно r до бесконечности.Путь выбирается по радиальной линии, так что становится просто Edr. Поскольку электрическое поле Q равно kQ / r ² ,

Этот процесс определяет электрический потенциал точечного плата. Обратите внимание, что потенциальная функция скалярная величина в отличие от электрического поля, являющегося векторной величиной. Теперь мы можем определить электрический потенциал энергия системы зарядов или зарядовых распределений.Предположим, мы вычисляем проделанную работу относительно электрические силы при перемещении заряда q из бесконечности в точку на расстоянии r от заряд Q. Работу выдал:

Обратите внимание, что если q отрицательное, его знак должен использоваться в уравнение! Следовательно, система состоящий из отрицательного и положительного точечного заряда, имеет отрицательный потенциальная энергия.

Отрицательная потенциальная энергия означает, что работа должна быть выполнена против электрического поля при раздвижении зарядов!

Теперь рассмотрим более общий случай, связанный с потенциал в окрестности ряда зарядов, как показано на рисунке ниже:

Пусть r ₁ , r ₂ , r ₃ будет расстояния зарядов до точки поля А, и r ₁₂ , r ₁₃ , r ₂₃ представляют собой расстояние между зарядами.Электрический потенциал в точке A:

Пример:

Если мы принесем заряд Q из бесконечности и поместим его в точку A проделанная работа будет:

Суммарная электрическая потенциальная энергия этой системы обвинения, а именно, работа, необходимая для того, чтобы довести их до их нынешних должностей, может быть рассчитывается следующим образом: сначала приведите q1 (нулевая работа, так как нет заряда еще), затем в поле q1 вывести q2, затем в поля q1 и q2 принести q3.Добавьте всю работу, необходимую для вычислить общую работу. Результат будет:

Обнаружение электрического поля по электрическому потенциалу:

Компонент E в любом направлении является отрицательным скорость изменения потенциала с расстоянием в этом направлении:

Символ называется Градиент. Электрическое поле — это градиент электрического потенциала.Линии электрического поля всегда перпендикулярно эквипотенциальным поверхностям.

Поверхности равных хвостов:

Это воображаемые поверхности, окружающие заряд. распределение. В частности, если распределение заряда сферическое (точечный заряд или однородно заряженная сфера), поверхности сферические, концентрические с центром заряда распределение. Силовые линии электрического поля всегда перпендикулярно эквипотенциальным поверхностям.Уравнение подразумевает, что из-за отрицательный знак, направление E противоположно направлению, в котором V увеличивается; E направлен с более высоких уровней V на более низкие (с более высоких потенциал для снижения потенциала). Другой словами, градиент скаляра (в данном случае E-поля) нормален к поверхности постоянного значения (эквипотенциальная поверхность) скаляра и в направлении максимальная скорость изменения постоянного скаляра. Запомните это утверждение, когда мы проводим эксперимент.

Электрический потенциал и электрическое поле

Электрический потенциал и электрическое поле
следующий: Электрический потенциал Up: Электрический потенциал Предыдущее: Электрический потенциал

Электрический потенциал и электрическое поле Мы видели, что разница в электрическом потенциале двух произвольные точки в пространстве — это функция электрического поля, пронизывающего пространство, но не зависит от испытательного заряда, используемого для измерения этой разницы.Давайте исследуем связь между электрическим потенциалом и электрическим поле.

Рассмотрим заряд, который медленно перемещается на бесконечно малое расстояние. по оси. Предположим, что разность электрических потенциалов между конечным и начальным положениями заряда есть. По определению изменение в электрической потенциальной энергии заряда дан кем-то

(84)

Из уравнения.(76) работа, которую мы совершаем при перемещении заряда, равна

(85)

где — местная напряженность электрического поля, а — угол наклона между направлением поля и осью. По определению, , где — -компонента локального электрического поля. Энергосбережение требует, чтобы (, то есть , увеличение энергии заряда соответствует работа выполнена за заряд), или

(86)

что сводится к

(87)

Величину мы называем градиентом градиента электрический потенциал в -направлении.Он в основном измеряет, насколько быстро потенциал меняется при изменении координаты (но координаты и остаются постоянными). Таким образом, приведенная выше формула говорит что -компонента электрического поля в данной точке пространства равна до минус локальный градиент электрического потенциала в -направление.

Согласно формуле. (87) напряженность электрического поля имеет размеры разности потенциалов по длине. Отсюда следует, что единицами измерения электрического поля являются вольты. на метр ( .Конечно, эти новые агрегаты полностью эквивалентны ньютонов на кулон: , т.е. ,

(88)

Рассмотрим частный случай однородно направленного электрического поля. генерируется двумя равномерно заряженными параллельными плоскостями, перпендикулярными оси -оси. это ясно, из уравнения. (87), что если между пластинами должно быть постоянным тогда должно изменяться линейно с в этом регионе. На самом деле это легко показать, что

(89)

где — произвольная постоянная.Согласно формуле. (89) электрический потенциал уменьшается непрерывно, пока мы двигаемся по направлению электрического поля. Поскольку положительный заряд ускоренных в этом направлении, мы заключаем, что положительные заряды ускоренный вниз градиента электрического потенциала, почти таким же образом когда массы падают вниз по градиентам гравитационного потенциала (что, конечно, пропорционально высоте). Таким же образом ускоряются отрицательные заряды с до . градиенты электрического потенциала.

Согласно формуле. (87) -компонента электрического поля равна к минусу градиента электрического потенциала в -направлении. Поскольку в -направлении нет ничего особенного, аналогичные правила должны существовать для — и -компонентов поля. Эти три правила можно объединить, чтобы получить

(90)

Здесь производная берется постоянной и, и т. Д. Вышеприведенное выражение показывает, как электрическое поле , которое является векторным полем, связано с электрическим потенциал, который является скалярным полем.

Мы видели, что электрические поля суперпозиционны. То есть электрический поле, создаваемое набором зарядов, распределенных в пространстве, равно просто векторная сумма электрических полей, генерируемых каждым зарядом взяты отдельно. Что ж, если электрические поля наложены друг на друга, отсюда следует из уравнения. (90) что электрические потенциалы также должны быть наложены друг на друга. Таким образом, электрический потенциал, создаваемый набором зарядов, распределенных в пространстве представляет собой всего лишь скалярную сумму потенциалов, генерируемых каждым зарядом, взятым по отдельности.Ясно, что гораздо проще определить потенциал, генерируемый множеством зарядов, чем для определения электрического поля, так как мы можем суммировать потенциалы генерируется отдельными зарядами алгебраически, и вам не нужно беспокоиться о их направления (так как у них нет направлений).

Уравнение (90) выглядит довольно устрашающе. К счастью, однако, это возможно. переписать это уравнение в более привлекательной форме. Рассмотрим два соседних точки и. Предположим, что — векторное смещение точки относительно точки.Пусть будет разность электрического потенциала между этими двумя точками. Предположим, что мы путешествуем из в, сначала пройдя расстояние по оси, затем двигаясь по оси, и, наконец, двигаясь по оси. Чистый прирост в электрическом потенциале, когда мы переходим от к представляет собой просто сумму увеличения по мере движения по оси -оси, по мере движения по оси -ax и по оси-оси:

(91)

Но, согласно формуле.(90), , и др. Итак, получаем

(92)

что эквивалентно

(93)

где — угол между вектором и местное электрическое поле. Обратите внимание, что достигает его наиболее отрицательное значение, когда. Другими словами, направление электрическое поле в точке соответствует направлению, в котором электрическое поле потенциал снижается наиболее быстро.Положительный заряд помещен в точку ускоряется в этом направлении. Точно так же отрицательный заряд, помещенный в ускоряется в том направлении, в котором потенциал увеличивается наиболее быстро (, т.е. , ). Предположим, что мы переходим от точки к соседней точке в направлении, перпендикулярном направлению местного электрического поле ( т.е. , ). В этом случае из уравнения (93) что точки и лежат при одном и том же электрическом потенциале (, т.е. ,). Геометрическое место всех точек в окрестности точки, лежащих в тот же потенциал, что и плоскость, перпендикулярная направлению местный электрический поле.В более общем смысле, поверхности постоянного электрического потенциала, так называемые эквипотенциальные поверхности , существуют как набор не взаимоблокирующихся поверхностей, которые везде перпендикулярно направлению электрического поля. На рисунке 14 показан эквипотенциальные поверхности (пунктирные линии) и силовые линии электрического поля (сплошные линии) генерируется положительным точечным зарядом. В этом случае эквипотенциальные поверхности имеют вид сферы с центром в заряде.

Рисунок 14: Эквипотенциальные поверхности (пунктирные линии) и электрические силовые линии (сплошные линии) точечного положительного заряда.

в разд. 4.3, мы обнаружили, что электрическое поле непосредственно над поверхностью проводник направлен перпендикулярно этой поверхности. Таким образом, ясно, что поверхность проводника должна соответствовать эквипотенциальной поверхности. Фактически, поскольку там нет электрического поля внутри проводника (и, следовательно, нет градиента в электрическом поле). потенциал), следует, что весь проводник (, т.е. , как поверхность, так и внутренняя часть) находится при таком же электрическом потенциале.

---

следующий: Электрический потенциал Up: Электрический потенциал Предыдущее: Электрический потенциал

Ричард Фицпатрик 2007-07-14

Electric Potential — The Physics Hypertextbook

Обсуждение

введение

Вспомните историю развития электростатики.

1. Начисления существуют.
2. Заряды действуют друг на друга.
3. Эта сила действует на расстояния любого размера.

У нас с вами нет проблем с этой последней идеей, но в свое время она называлась «действие на расстоянии» — довольно вежливое оскорбление. Чтобы избежать концептуальных проблем, связанных с взаимодействием с бестелесной силой, Майкл Фарадей изобрел электрическое поле, и мир остался доволен.

Ну, какое-то время доволен. Затем кто-то указал, что электрическое поле является векторной величиной, и они вспомнили, что векторы громоздки и с ними трудно работать. Концептуальный комфорт был получен, но практическая реализация осталась неизменной.Будь прокляты эти ученые. Всегда ищу лучшее из всех возможных миров. Они хотели чего-то и концептуально удовлетворительного, и математически простого. Какая безрассудность!

Вы не поверите, но проблема уже была решена физиками и математиками, работающими над темами, не имеющими ничего общего с электричеством. Вода, ветер, тепло и растворенные вещества текут. Некоторые концептуальные и математические приемы, используемые для понимания этих предметов, также могут быть использованы для понимания электричества, а затем магнетизма и гравитации.

Что такое силовые линии, если не какая-то схема течения? Линии электрического поля «перетекают» от положительных зарядов к отрицательным. Положительный заряд — это как открытый кран, а отрицательный — как открытый сток. Любой, у кого есть работающая раковина, может сделать грубую модель электрического диполя на кухне или в ванной одним движением руки. Аналогичные аналогии существуют для ветра, тепла и растворенных веществ. (Технически тепло и растворенные вещества диффундируют, а не текут, поэтому здесь аналогии немного слабее.)

Подумайте на мгновение о других вещах, которые текут, и подумайте о том, что заставляет их течь. Это будет ответ на нашу следующую концептуальную проблему. Составим таблицу, в которой сравниваются похожие явления. Во всех случаях будет что-то, что течет, и что-то, что вызывает поток.

поток…	вызвано разницей в…
река (жидкая вода)	высота
ветер (атмосферные газы)	атмосферное давление
тепло (внутренняя энергия)	температура
растворенные вещества (растворенные вещества)	концентрация

В каждом случае то, что течет, может быть описано векторным полем (величина, которая имеет величину и направление в любом месте), а то, что вызывает поток, может быть описано разницей в скалярном поле ( количество, имеющее величину только в любом месте).

поток…	вызвано разницей в…
векторное поле	скалярное поле

Если мы сможем идентифицировать электрическое скалярное поле, которое вызывает электрическое векторное поле, мы упростили все электричество математически, поскольку скаляры математически проще векторов. «Определить», вероятно, не подходящее слово. «Define» больше нравится. Мы собираемся определить величину, которая играет ту же роль, что высота для рек, давление — для ветра, температура — для тепла, а концентрация — для растворенных веществ.

«Поток» электрического поля «вызван» разностью электрических потенциалов .

поток…	вызвано разницей в…
электрическое поле (пробные заряды)	электрический потенциал

Теперь вы должны спросить себя, что такое «электрический потенциал».

Во-первых, вторая половина термина «потенциал» не подразумевает, что у него есть возможность произойти или что-то, что может привести к полезности в будущем.Электрический потенциал места в космосе буквально не «может стать электрическим». Это неверное представление основано на другом значении слова «потенциал».

Настоящее значение слова «потенциал» в этом контексте сейчас неясно и, таким образом, является источником потенциальной путаницы. В контексте этого обсуждения потенциал означает нечто более близкое к тому, что дает силу, мощь, мощь или способность. Для физика существительное «потенциал» более тесно связано с прилагательными «мощный» или «потенция».В наши дни слово «потенциал» кажется скорее бессильным, чем мощным. «У меня есть power » — фраза, которая вдохновляет. «У меня есть потенциал , » — это фраза в поисках вдохновения.

Во-вторых, когда я писал термин «электрический потенциал», я не отрезал две трети пути от записи электрической потенциальной энергии. Это две отдельные (но взаимосвязанные) концепции. Посмотрите, сможете ли вы проследить эту цепочку рассуждений. Обратите внимание, как я сказал «рассуждение», а не «логику». Это не доказательство.Математика покажет, как все взаимосвязано.

Разница в электрическом потенциале порождает электрическое поле. (Это концепция, которую я представляю вам в этой главе, которую вы читаете прямо сейчас.) Электрическое поле — это сила, приходящаяся на заряд, действующая на воображаемый пробный заряд в любом месте в космосе. (Эта концепция была представлена ​​в главе перед этой.) Работа, проделанная путем помещения действительного заряда в электрическое поле, дает заряду электрическую потенциальную энергию. (Эта концепция называется теоремой работы-энергии и была представлена ​​очень давно, в одной далекой-далекой главе.) По переходному свойству (я полагаю) электрический потенциал порождает электрическую потенциальную энергию; и согласно рефлексивному свойству (другое предположение), электрический потенциал — это энергия на заряд, которую воображаемый пробный заряд имеет в любом месте в космосе.

Это слова. Нам нужна математика. Мы можем сделать это трудным путем (без исчисления) или простым способом (с исчислением). Твой выбор.

В любом случае, вот правила для символов, специфичные для этой темы…

• Электрическое поле выделено жирным прописным шрифтом E .Полужирно, потому что это векторная величина. Это прописные буквы из-за произвольного выбора. Это буква E, потому что это имеет смысл. Если вы видите выделенный курсивом символ с полосой в верхней части, например, E , это означает, что вы используете только среднее значение величины. Иногда этого достаточно.
• Обозначение электрической потенциальной энергии курсивом, прописными буквами U . Оно выделено курсивом, потому что это скалярная величина. Это прописные буквы, потому что… никто не знает. Это U, потому что вам нужно использовать какую-то букву.Думаю, теперь очередь за вами. Поскольку мы имеем дело с электрической потенциальной энергией, мы должны добавить нижний индекс в верхнем регистре E. Это дает нам U _E . Если я забыл добавить подпись E, это потому, что вы должны знать из контекста, что это электрическая потенциальная энергия, а не что-то еще.
• Обозначение электрического потенциала выделено курсивом прописными буквами V . Оно выделено курсивом, потому что это скалярная величина. Это заглавные буквы, чтобы соответствовать электрической потенциальной энергии (возможно).Это V, потому что V следует за U в алфавите… я думаю. Возможно, это также связано с названием единицы измерения электрического потенциала — вольт. Вы можете подумать, что я должен добавить к этому символу прописную букву E с нижним индексом, например V _E , но я этого не сделаю. Никто не делает. Так редко обсуждают неэлектрические формы скалярного потенциала, что добавление нижнего индекса делается только для исключений — например, для гравитационного потенциала, В _g .

без исчисления

Начнем с теоремы об энергии работы.Когда работа закончена ( W ), энергия изменяется (∆ E ).

Вт = ∆ E

Более конкретно, когда работа выполняется против электрической силы ( F _E ), электрическая потенциальная энергия изменяется (∆ U _E ). Напомним, что работа — это сила, умноженная на смещение ( d ). Над символом силы есть полоса, указывающая, что мы будем использовать среднее значение. Это одно из ограничений выводов без исчисления.

F _E d = ∆ U _E

Разделите обе стороны по заряду ( q ).

Немного переставить.

Отношение силы к заряду слева называется электрическим полем ( E ). Это старая идея, которая обсуждалась ранее в этой книге. Единственное, что изменилось, это то, что сейчас мы имеем дело со средними значениями. Отношение энергии к заряду справа называется , электрический потенциал ( В, ).Это новая идея, которая сейчас обсуждается в этой книге.

Электрическое поле — это сила, действующая на пробный заряд, деленная на его заряд для каждого места в космосе. Поскольку оно происходит от силы, это векторное поле. Электрический потенциал — это электрическая потенциальная энергия пробного заряда, деленная на его заряд для каждого места в космосе. Поскольку оно получено из энергии, это скалярное поле. Эти два поля связаны.

Электрическое поле и электрический потенциал связаны смещением.Временное смещение поля потенциальное…

Ed = ∆ V

или поле является потенциально избыточным смещением, если хотите.

На языке причудливого математического анализа поле — это градиент потенциала, потому что реальный мир причудлив, я имею в виду трехмерный. Градиент — это трехмерный эквивалент наклона. Обычный уклон одномерный, потому что линия одномерная (даже если она не прямая). При движении по кривой нужно принимать только одно решение.Мне идти вперед или вернуться? В обычном евклидовом пространстве у нас есть три варианта. Вверх или вниз? Влево или вправо? Вперед или назад?

исчисление

Начнем с теоремы об энергии работы. Когда работа закончена ( W ), энергия изменяется (∆ E ).

Вт = ∆ E

Более конкретно, когда работа выполняется против электрической силы ( F _E ), электрическая потенциальная энергия изменяется (∆ U _E ).Напомним, что работа — это интеграл сила-перемещение.

–

⌠ ⌡

F E · d r = ∆ U E

Разделите обе стороны по заряду ( q ).

–	1	⌠ ⌡	F E · d r =	1	∆ U E
	q			q

Немного переставить.

–	⌠ ⌡	Ф E	· d r =	∆ U E
		q		q

Отношение силы к заряду слева называется электрическим полем ( E ). Это старая идея, которая обсуждалась ранее в этой книге. Отношение энергии к заряду справа называется , электрический потенциал ( В, ).Это новая идея, которая сейчас обсуждается в этой книге.

Электрическое поле — это сила, действующая на пробный заряд, деленная на его заряд для каждого места в космосе. Поскольку оно происходит от силы, это векторное поле. Электрический потенциал — это электрическая потенциальная энергия пробного заряда, деленная на его заряд для каждого места в космосе. Поскольку оно получено из энергии, это скалярное поле. Эти два поля связаны.

Электрическое поле и электрический потенциал связаны интегралом по путям, который работает для всех видов ситуаций.Мой совет при работе с интегралом по путям — всегда выбирать самый простой путь для работы. Электричество — это консервативная сила, поэтому выполняемая им работа не зависит от выбранного пути. Это уравнение говорит о более поразительном. Интеграл слева настолько независим от пути, что его значение зависит только от электрического потенциала в начале и в конце пути. Если вам удастся найти эти два числа и вычесть их, вы сделали интеграл целиком. Если бы таким образом работало больше интегралов, студенты не зацикливались бы на исчислении.

–

⌠ ⌡

E · d r = ∆ V

Электрическое поле и электрический потенциал также связаны производной, которая работает только для одномерных ситуаций — ситуаций со сферической, цилиндрической или плоской симметрией.

E = —	д	В r̂
	др

В терминах изящных вычислений поле — это градиент потенциала, потому что реальный мир более интересен, чем одномерная задача.Градиент является эквивалентом производной в более высоких измерениях (в этой книге — двух и трех измерениях). Это соотношение работает для всех видов симметрии и несимметрии.

E = −∇ В

Греческая буква , дельта выглядит как треугольник, направленный вверх (∆). Перевернутая дельта называется дель (∇). Символы дельта и дель являются примерами математических устройств, называемых операторами , — символами, указывающими на необходимость выполнения операции над переменной.Дельта-оператор неоднократно обсуждался в этой книге. Оператор del немного реже.

Оператор дельты используется всякий раз, когда требуется изменение или разность количества. Вернемся немного назад к уравнению, которое связывает электрическое поле с электрическим потенциалом через интеграл по путям.

—

⌠ ⌡

E · d r = ∆ V

Здесь ∆ V означает разность электрического потенциала между двумя точками — обычно начальным или начальным положением (обозначено в этой книге с нижним индексом ноль) и конечным или конечным положением (указанным в этой книге без подстрочного индекса). .

	r
–	⌠ ⌡	E · d r = V — V 0
	r 0

В декартовых координатах оператор del представляет собой сумму частных производных в трех направлениях единичного вектора. (В некартовых координатах del немного сложнее).

∇ = î	∂	+ ĵ	∂	+ кО	∂
	∂ x		∂ y		∂ z

Когда оператор del применяется к скалярному полю, результирующая операция известна как градиент . Вернитесь немного назад. Уравнение, которое говорит, что электрическое поле — это градиент электрического потенциала…

E = −∇ В

выглядит так при раскрытии оператора del…

E = — î	∂	В — ĵ	∂	V — k̂	∂	В
	∂ x		∂ y		∂ z

и тому подобное, когда термины переставлены так, что скаляры предшествуют векторам…

E = —	∂	В –—	∂	В ĵ —	∂	V k̂
	∂ x		∂ y		∂ z

Может быть, теперь вы понимаете, почему был изобретен символ дель.В компактном уравнении 5 символов (не считая пробелов). В расширенном уравнении 23 (с учетом «шляп», но без учета пробелов).

Подождите. В чем дело со всеми этими знаками минус? Позвольте мне объяснить… позже.

шт.

электрический потенциал

Что нового в этой главе этой книги? Все понятие электрического потенциала. Я представил электрический потенциал как способ решить проблемы векторной природы электрического поля, но электрический потенциал — это концепция, которая имеет право на существование сама по себе.Электрический потенциал — это электрическая потенциальная энергия тестового заряда, деленная на заряд этого тестового заряда.

Старые вещи. SI — это сокращение от le Système international d’unités на французском языке или International System of Units на английском языке. Единица измерения энергии в системе СИ — джоуль, названная в честь Джеймса Джоуля, английского пивовара, ставшего физиком, который определил, что тепло и электричество являются формами энергии, эквивалентными другим формам механической энергии, таким как гравитационная потенциальная энергия и кинетическая энергия.Единицей заряда в системе СИ является кулон, названный в честь Шарля-Огюстена Кулона, французского дворянина и солдата, ставшего физиком, открывшего правило обратных квадратов электростатической силы. Единица смещения (или расстояния) в системе СИ — это метр — слово, названное в честь никого и в конечном итоге образованное от греческого слова «мера» (μετρον, metron ).

Новинка. Единицей измерения электрического потенциала в системе СИ является вольт, названный в честь итальянского дворянина, ставшего физиком Алессандро Вольта, полное имя которого — удивительно длинный граф Алессандро Джузеппе Антонио Анастасио Вольта.Сегодняшняя шутка состоит в том, что полное имя Вольты было настолько длинным, что, когда они сократили его до названия подразделения, они зашли слишком далеко и отрезали последнюю букву «а». Единицей электрического потенциала по праву следует называть вольта, а не вольт (шутка, которую ценят только педантичные из нас). Граф Вольта известен прежде всего как изобретатель электрохимической ячейки — того, что мы теперь ошибочно называем батареей (еще одно отличие, которое ценится только педантиками — батарея — это совокупность электрохимических ячеек).Для тех, кто заботится о важных вещах, вольт — это джоуль на кулон.

[V = J / C]

Разность электрических потенциалов между двумя точками равна одному вольт, если для перемещения одного кулона заряда из одного места в другое требуется один джоуль работы.

электрическое поле

Электрический потенциал — это способ объяснить «сложное» векторное поле в терминах «легкого» скалярного поля. По определению электрическое поле — это сила, приходящаяся на заряд воображаемого пробного заряда.

Посредством длинного объяснения, электрическое поле — это также градиент электрического потенциала (скорость изменения электрического потенциала со смещением).

Установите две величины равными…

, а затем установите их единицы равными.

[N / C = В / м]

Ньютон на кулон и вольт на метр являются эквивалентными единицами измерения электрического поля. Вольт на метр чаще используют те, кто действительно измеряет вещи, потому что вольт (который можно измерить с помощью вольтметра) и измеритель (который можно измерить линейкой любого размера, включая метрическую палочку с соответствующим названием) намного больше. легче измерить, чем силу (которую, я полагаю, можно измерить с помощью пружинной шкалы или тензодатчика, прикрепленного к заряженному объекту) и заряд (который можно измерить с помощью какого-либо известного мне устройства).

электрическая потенциальная энергия

Если вольт — это джоуль на кулон, то джоуль — это кулон-вольт. Когда один кулон заряда перемещается через разность электрических потенциалов в один вольт, его энергия изменяется на один джоуль.

[J = CV]

Для некоторых приложений джоуль слишком велик, в основном потому, что кулон слишком велик. Обычная малая единица заряда — элементарный заряд [е]. Это самый маленький заряд, который когда-либо наблюдался. Некоторые частицы, такие как протон, имеют этот заряд со знаком плюс ( q _протон = +1 e), а некоторые, как электрон, имеют его со знаком минус ( q _{электрон} = −1 e ).Когда один элементарный заряд перемещается через разность электрических потенциалов в один вольт, его энергия изменяется на один электронвольт [эВ] — плюс или минус один электронвольт в зависимости от знака заряда и знака разности потенциалов. Электронвольт используется для некоторых приложений в электромагнетизме; твердое тело, атомная физика, ядерная физика и физика элементарных частиц; и смежные науки, такие как биофизика, химия и астрономия. Это хороший маленький блок для небольших физических систем, таких как атомы и молекулы.На самом деле это слишком мало для ядерной физики и физики элементарных частиц, но следующей по величине единицей СИ является джоуль, который на 19 порядков больше.

кв	=	кв
1 электронвольт	=	(1 элементарный заряд) (1 вольт)
1 электронвольт	=	(1,6 × 10 −19 кулонов) (1 вольт)
1 электронвольт	=	1.6 × 10 −19 джоулей
1 эВ	=	1,6 × 10 −19 Дж

Электронвольт на самом деле не является единицей СИ, поскольку элементарный заряд не определяется как единица измерения. Заряд электрона, протона или чего-либо еще с элементарным зарядом должен быть получен экспериментально и, следовательно, не определен. Электронвольт был «принят для использования» с SI CIPM ( le Comité international des poids et mesures или Международный комитет мер и весов).

эксперимент милликена

Роберт Милликен (1865–1953) США

аппарат

вывода

ЭЛЕКТРОСТАТИЧЕСКИЙ ПОТЕНЦИАЛ

ЭЛЕКТРОСТАТИЧЕСКИЙ ПОТЕНЦИАЛ

---

Электростатическая сила — это консервативная сила. Это означает, что работа от частицы зависит только от начального и конечного положения частица, а не на пройденном пути.С каждой консервативной силой потенциальная энергия может быть связана. Введение потенциальной энергии полезен, так как позволяет нам применять сохранение механической энергии, которая упрощает решение большого количества задач.

Потенциальная энергия U, связанная с консервативной силой F, определяется в следующим образом

(25,1)

где U (P ₀ ) — потенциальная энергия в исходной позиции. P ₀ (обычно U (P ₀ ) = 0), а интеграл по траектории определяется по любому удобный путь, соединяющий P ₀ и P ₁ .Поскольку сила F является консервативным, интеграл в уравнении (25.1) не будет зависеть от выбранного пути. Если работа W положительна (сила и перемещение указывают на одно и то же направлении) потенциальная энергия при P ₁ будет меньше, чем потенциальная энергия при P ₀ . Если энергия сохраняется, уменьшение потенциальная энергия приведет к увеличению кинетической энергии. Если работа W отрицателен (сила и смещение направлены в противоположные стороны), потенциальная энергия при P ₁ будет больше, чем потенциальная энергия при П ₀ .Если энергия сохраняется, увеличение потенциальной энергии приведет к уменьшению кинетической энергии. Если в электростатических проблемах контрольную точку P ₀ обычно выбирают так, чтобы она соответствовала бесконечное расстояние, и потенциальная энергия в этой точке отсчета принимается равной быть равным нулю. Тогда уравнение (25.1) можно переписать как:

(25,2)

Чтобы описать потенциальную энергию, связанную с распределением заряда, представлена ​​концепция электростатического потенциала V .В электростатический потенциал V в данном положении определяется как потенциал энергия пробной частицы, деленная на заряд q этого объекта:

(25,3)

На последнем шаге уравнения (25.3) мы предположили, что реперная точка P ₀ берется на бесконечности, и что электростатический потенциал на эта точка равна 0. Поскольку сила, приходящаяся на единицу заряда, является электрическим поле (см. главу 23), ур. (25.3) можно переписать как

(25.4)

Единица электростатического потенциала — вольт (В), а 1 В = 1 Дж / К = 1 Нм / Кл. Уравнение (25.4) показывает, что в качестве единицы электрического поля мы также можем использовать В / м.

Обычно используемая единица измерения энергии частицы — электрон-вольт (эВ). который определяется как изменение кинетической энергии электрона, который движется над разностью потенциалов 1 В. Электрон-вольт можно связать с Джоуля через уравнение (25.3). Уравнение (25.3) показывает, что изменение энергии электрон, когда он пересекает разность потенциалов 1 В, равна 1,6 ^. 10 ^-19 Дж и, таким образом, заключаем, что 1 эВ = 1,6 ^. 10 ^-19 Дж

Заряд q перемещается из P ₀ в P ₁ в непосредственной близости от заряд q ‘(см. рисунок 25.1). Электростатический потенциал при P ₁ может определяться с использованием ур. (25.4) и вычисляя интеграл по показанной траектории на рисунке 25.1. Вдоль круговой части пути электрическое поле и смещения перпендикулярны, а изменение электростатического потенциала будет ноль. Таким образом, уравнение (25.4) можно переписать как

(25,5)

Если заряд q ‘положительный, потенциал увеличивается с уменьшением расстояние r. Электрическое поле направлено в сторону от положительного заряда, и мы пришли к выводу, что электрическое поле направлено из областей с высоким электростатическим потенциал в сторону областей с низким электростатическим потенциалом.

Рисунок 25.1. Путь, по которому следует заряд q между P ₀ и П ₁ . Из определения электростатического потенциала в терминах потенциальной энергии (уравнение (25.3)) ясно, что потенциальная энергия заряд q под действием электрического поля, создаваемого зарядом q ‘, равен предоставлено

(25,6)

Пример: Задача 25.21

Суммарный заряд Q равномерно распределен по прямому стержню длина L.Найдите потенциал в точке P на расстоянии h от середины стержень (см. рисунок 25.2).

Потенциал в точке P из-за небольшого сегмента стержня длиной dx и заряд dQ, расположенный в позиции, указанной на рисунке 25.3, равен

(25,7)

Заряд dQ сегмента связан с общим зарядом Q и длиной L

. (25,8)

Комбинируя уравнения (25.7) и (25.8) получаем следующее выражение для dV:

(25.9)

Рисунок 25.2. Проблема 25.21. Рисунок 25.3. Решение проблемы 25.21. Полный потенциал в точке P может быть получен суммированием по всем небольшие сегменты. Это эквивалентно интегрированию уравнения (25.9) между x = — L / 2 и х = L / 2.

(25.10)

Пример: задача 25.15

Альфа-частица с кинетической энергией 1.7 x 10 ^-12 Дж составляет выстрелил прямо в ядро ​​платины с очень большого расстояния. Что будет быть расстоянием ближайшего приближения? Электрический заряд альфы частица — 2e, а ядра платины — 78e. Лечить альфу частицы и ядра как сферические зарядовые распределения и пренебречь движение ядра.

Начальная механическая энергия равна кинетической энергии альфа частица

(25.11)

Из-за электрического отталкивания между альфа-частицей и платиной ядра, альфа-частица замедлится. На расстоянии ближайшего приближаются к нулю скорость альфа-частицы, и, следовательно, ее кинетическая энергия равна нулю. Полная механическая энергия в этой точке равна потенциальная энергия системы

(25.12)

где q ₁ — заряд альфа-частицы, q ₂ — заряд ядра платины, d — расстояние наибольшего сближения.Применяя закон сохранения механической энергии, получаем

(25,13)

Расстояние ближайшего сближения может быть получено из уравнения (25.13)

(25,14)

Электрическое поле является консервативным полем, поскольку электрическая сила — это консервативная сила. Отсюда следует, что интеграл по путям

(25,15)

между точкой P ₀ и точкой P ₁ не зависит от пути между этими двумя точками.В этом случае интеграл по путям для любого замкнутого пути будет нулем:

(25,16)

Уравнение (25.16) можно использовать для доказательства интересной теоремы:

«внутри закрытой пустой полости внутри однородного проводника электрическая поле точно равно нулю ».

Рисунок 25.4. Поперечное сечение полости внутри сферической формы. дирижер. На рис. 25.4 показано поперечное сечение возможной полости внутри. сферический проводник. Предположим, что внутри проводника есть поле и один линий поля показано на рисунке 25.4. Рассмотрим интеграл по путям от уравнение (25.16) по пути, указанному на рисунке 25.4. В главе 24 было показано что электрическое поле внутри проводника равно нулю. Таким образом, вклад путь внутри проводника до интеграла по путям равен нулю. Поскольку оставшаяся часть пути выбирается вдоль силовой линии, направление движения поле параллельно направлению пути, поэтому интеграл по пути будет ненулевым. Это, очевидно, нарушает уравнение (25.16), и мы должны заключить, что поле внутри полости равно нулю (в этом случае интеграл по путям равен конечно равно нулю).

Электростатический потенциал V связан с электростатическим полем E. Если электрическое поле E известно, электростатический потенциал V можно получить, используя уравнение (25.4), и наоборот. В этом разделе мы обсудим, как электрические поле E можно получить, если известен электростатический потенциал.

Рисунок 25.5. Расчет электрического поля E. Рассмотрим две точки, показанные на рисунке 25.5. Эти двое почти идентичные позиции разделены бесконечно малым расстоянием dL.В изменение электростатического потенциала между P ₁ и P ₂ дается

(25,17)

где угол [тета] — это угол между направлением электрического поле и направление смещения (см. рисунок 25.5). Уравнение (25.17) можно переписать как

(25.18)

где E _L обозначает составляющую электрического поля вдоль Ось L.Если выбрать направление смещения, совпадающее с По оси абсцисс уравнение (25.18) принимает вид

(25,19)

Для смещений по оси y и оси z получаем

(25.20)

(25.21)

Полное электрическое поле E можно получить из электростатического потенциала V комбинируя уравнения (25.19), (25.20) и (25.21):

(25.22)

Уравнение (25.22) обычно записывается в следующем виде:

(25,23)

где —V — градиент потенциала V.

Во многих электростатических задачах электрическое поле определенного заряда распространение должно быть оценено. Расчет электрического поля может быть осуществляется двумя разными методами:

1. электрическое поле можно рассчитать, применяя закон Кулона и вектор сложение вкладов от всех начислений распределения заряда.

2. полный электростатический потенциал V может быть получен из алгебраической суммы потенциала из-за всех зарядов, составляющих распределение зарядов, и затем используя уравнение (25.23) для расчета электрического поля E.

Во многих случаях метод 2 проще, поскольку расчет электростатической потенциал включает алгебраическую сумму, в то время как метод 1 полагается на векторную сумму.

Пример: задача 25.32

В некоторой области космоса электростатический потенциал имеет следующий вид: функция x, y и z:

(25.24)

где потенциал измеряется в вольтах, а расстояние — в метрах. Найди электрическое поле в точках x = 2 м, y = 2 м.

Компоненты x, y и z электрического поля E могут быть получены из градиент потенциала V (уравнение (25.23)):

(25,25)

(25,26)

(25,27)

Оценка уравнений (25.25), (25.26) и (25.27) при x = 2 м и y = 2 м дает

(25.28)

(25.29)

(25.30)

Таким образом,

(25,31)

Пример: задача 25.36

Кольцо (диск с отверстием) из бумаги имеет внешний радиус R и внутренний радиус R / 2 (см. рисунок 25.6). Величина электрического заряда Q равна равномерно распределяется по бумаге.

а) Найдите потенциал как функцию расстояния на оси кольцевое пространство.

б) Найдите электрическое поле на оси кольцевого пространства.

Определим ось x так, чтобы она совпадала с осью кольцевого пространства (см. Рис. 25,7). Первый шаг в вычислении полного электростатического потенциала в точке P из-за кольцевого пространства необходимо вычислить электростатический потенциал в точке P из-за небольшого участка затрубного пространства. Рассмотрим кольцо радиуса r и ширины dr, как показано на рисунке 25.7. Электростатический потенциал dV при P, создаваемый это кольцо выдается

(25.32)

где dQ — заряд кольца. Плотность заряда [rho] кольцевого пространства равна равно

(25.33)

Рисунок 25.6. Проблема 25.36. (25.33) заряд кольца dQ можно вычислить

(25,34)

Подставляя уравнение (25.34) в уравнение (25.32), получаем

(25,35)

Полный электростатический потенциал может быть получен путем интегрирования уравнения (25.35) по всему затрубному пространству:

(25.36)

Рисунок 25.7. Расчет электростатического потенциала в Задаче 25,36. Из-за симметрии задачи электрическое поле будет направлен по оси абсцисс. Напряженность поля можно получить, применив от уравнения (25.23) до уравнения (25.36):

(25,37)

Поскольку электростатическое поле и электростатический потенциал связаны, мы может заменить силовые линии так называемыми эквипотенциальными поверхностями . Эквипотенциальные поверхности определяются как поверхности, на которых каждая точка имеет одинаковые электростатический потенциал.Компонента электрического поля, параллельная этому поверхность должна быть равна нулю, так как изменение потенциала между всеми точками на эта поверхность равна нулю. Это означает, что направление электрического поле перпендикулярно эквипотенциальным поверхностям.

На рисунке 25.8 показан электрический диполь, расположенный вдоль оси z. Это состоит из два заряда + Q и — Q, разделенные расстоянием L. потенциал в точке P можно найти, суммируя потенциалы, генерируемые каждым из двух зарядов:

(25.38)

Рисунок 25.8. Электрический диполь. Если точка P находится далеко от диполя (r >> L), мы можно сделать приближение, что r ₁ и r ₂ параллельны. В данном случае

(25,39)

и

(25,40)

Теперь электростатический потенциал в точке P можно переписать как

. (25,41)

где p — дипольный момент распределения заряда.Электрическое поле диполь можно получить из уравнения (25.41), взяв градиент (см. уравнение (25.23)).

---

Отправляйте комментарии, вопросы и / или предложения по электронной почте на адрес [email protected] и / или посетите домашнюю страницу Фрэнка Вольфса.

Электростатическое поле — обзор

27.4 Форма капли

Влияние электростатического поля на форму капли — хорошо известное явление, растягивающее каплю в направлении поля, как показано на рисунке 27.6. В 1882 году лорд Рэлей первым начал исследование взаимодействия зарядов и электрических полей на каплях жидкости. Он теоретически вывел критическое количество зарядов, необходимое для дестабилизации изолированной сферической капли с поверхностным зарядом. Его работа вдохновила начало электрогидродинамики (Melcher and Taylor, 1969).

За последние три десятилетия форма и устойчивость сидячих капель под действием электрических полей анализировались во многих работах. Розенкильде (1969) исследовал равновесие и устойчивость несжимаемой диэлектрической капли, находящейся в однородном электрическом поле.Предполагая, что капля эллипсоидальная, он предложил связь между равновесной деформацией, напряженностью электрического поля, размерами капли и поверхностным натяжением. Также была указана причина нестабильности высоких диэлектрических проницаемостей жидкости (Rosenkilde, 1969).

Миксис (1981) предложил численную модель для расчета формы осесимметричной капли под действием постоянного электрического поля, что дает хорошее согласие с экспериментами. Его результаты показывают критическое значение диэлектрической проницаемости, при котором капли удлиняются и сохраняют свою первоначальную сфероидальную форму.Выше этого критического значения капля приобрела коническую форму.

В своих численных работах Basaran и Wohlhuter (Wohlhuter and Basaran, 1992; Basaran and Wohlhuter, 1992) рассчитали форму и устойчивость осесимметричного кулона и сидячих капель или пузырьков с учетом того, что линия контакта фиксирована или задана. Их первые расчеты основывались на предположении, что проводящие капли являются линейно поляризуемыми материалами (Wohlhuter and Basaran, 1992). Равновесная форма и устойчивость капель определяются одновременным решением уравнений Лапласа и Юнга – Лапласа.Исследование, учитывающее нелинейную поляризацию капель, было выполнено путем замены уравнения Максвелла уравнением Лапласа (Basaran and Wohlhuter, 1992). Их расчеты показали важность изменения расстояния между пластинами конденсатора, которое влияет на напряженность электрического поля и размер капли.

Резник и др. (2004) выделили три сценария эволюции формы капли в сильных электрических полях, определяемых значениями электрического числа Бонда и основанных на численном решении уравнений Стокса.В слабом электрическом поле капли подвергаются максвелловским напряжениям и имеют стационарную форму. В сильных электрических полях и при малых статических углах смачивания капли приобретают коническую форму и струйка начинается с кончика капли. Окончательный сценарий соответствует отрыву почти всей капли (то есть явлению капания) в результате сильного электрического поля и краевого угла смачивания, превышающего критическое значение. Численная модель хорошо согласуется с экспериментальными результатами для капель полимера (Резник и др., 2004).

Bateni et al. (2004; 2005a, b) основывали свою методологию ADSA-EF на предположении об осесимметричной форме капли. ADSA-EF можно использовать для измерения поверхностного натяжения капли в электрическом поле с гравитационным эффектом и без него. Из уравнения Юнга – Лапласа, описываемого формулой. В уравнении (27.2) они считали электрическое давление Δ P _e , которое зависит от диэлектрической проницаемости жидкостей, силы и направления электрического поля, следующим образом:

(27.11) ΔPe = 12 [ε0En (g) 2 − ε0 (εr − 1) Et2]

, где E _t и E _n — тангенциальная и нормальная составляющие электрического поля соответственно. на поверхности капли, а верхние индексы l и g относятся к капельной жидкости и окружающей среде, рассматриваемой как воздух, соответственно. Когда капля является проводящей жидкостью, внутри капли нет электрического поля, и уравнение Юнга – Лапласа упрощается как

(27.12) γ (1R1−1R2) = ΔP0 + (Δρ) gz + 12ε0En (g) 2

Из уравнения. (27.12) и модуль электростатического поля, они численно предсказали форму капли с итерационной схемой, как показано на рисунке 27.5.

Рисунок 27.5. Прогнозирование формы капли с помощью итерационных расчетов (Bateni et al., 2004).

Di Marco et al. (2013) оценили электрическую силу, действующую на поверхность раздела сидячей капли этанола, и сравнили экспериментальные результаты с теоретической моделью, основанной на равновесном действии сидящей капли с учетом электрического поля и силы тяжести.Экспериментальная установка состоит из плоской алюминиевой пластины, снабженной отверстием для впрыска капель. Пластина электрически заземлена и покрыта слоем тефлона. Электрод из нержавеющей стали в форме шайбы размером 4 мм × 15 мм укладывают параллельно пластине на расстоянии 6 мм и подключают к положительному полюсу источника высокого напряжения, который может обеспечивать до 8 кВ постоянного тока. Результирующее электрическое поле в резонаторе имеет среднюю напряженность 13,3 · 10 ³ В · см ⁻¹ . Форма полученных капель показана на рисунке 27.6. Капли, подвергнутые воздействию электрического поля, вытянуты в направлении электрического поля из-за изменения кривизны границы раздела под локальным электрическим напряжением, как сообщалось ранее. Краевой угол и кривизна на вершине капли увеличиваются с увеличением напряженности электрического поля.

Рисунок 27.6. Форма капли этанола для разной напряженности электрического поля (Di Marco et al., 2013).

Профиль капель и их геометрические параметры (угол смачивания, размеры капли и объем) обрабатываются специальным программным обеспечением для обработки изображений, которое может идентифицировать и интерполировать профиль капли.Эти измерения позволяют оценить результирующие силы, действующие на каплю из-за веса, адгезии и внутреннего давления. В отсутствие электрического поля экспериментальные значения силы, действующей на каплю, хорошо согласуются с теоретическими предсказаниями, и это подтвердило метод. Следовательно, в присутствии электрического поля результирующую электрическую силу, действующую на каплю, можно оценить по разнице и сравнить с теоретическими моделями.

Уравнение электромагнитного поля Максвелла No.1

Уравнение электромагнитного поля Максвелла № 1

Максвеллс Электромагнитный Полевое уравнение № 1

Автор Джордж Дж. Спикс

1.0 Формулировка уравнения

Следующее электростатическое поле уравнения будут разработаны в этом разделе:

Составная форма	Дифференциальные формы

Первое уравнение Максвелла основано на Гауссе закон электростатики, опубликованный в 1832 году, в котором Гаусс установил взаимосвязь между статическими электрическими зарядами и их сопутствующими статические поля.

Приведенное выше интегральное уравнение утверждает, что электрический поток через закрытая поверхность равна общему приложенному заряду.

Дифференциальная форма уравнения утверждает, что дивергенция или исходящий поток электрического потока из точки равен объемному заряду плотность в этой точке.

1.1. Уравнение Максвелла № 1; Площадь Интеграл

Выведем интеграл уравнение, рассматривая сумму плотности электрического потока на площадь поверхности, а затем как сумма объемов, содержащих электрические плата.Показано, что два интеграла равны, если они основаны на такое же обвинение. Два примера с использованием уравнений: показано.

1.1.1 Закон Гаусса

Закон электростатики Гаусса гласит, что линии электрического поток,

f _E , исходит от положительного заряда, q , и прекращаются, если они прекращаются, на отрицательном заряде. Пространство внутри на которое оказывают свое влияние заряды, называется электростатическим полем.

Схема на рис. 1.1 представляет заряды и три размерное поле. Поле визуализируется как состоящее из линий поток. Для изолированного заряда линии потока не оканчиваются и имеют вид считается продолжающимся до бесконечности.

Чтобы получить уравнение, связывающее электрическую заряда q и его потока

f _E , предположим, что заряд центрирован в сфере радиус r метров. Плотность электрического потока, D , тогда равна электрический поток, исходящий от заряда, q , деленный на площадь сфера.

кулонов на квадратный метр; где площадь перпендикулярно линиям потока. (Один кулон равен величина заряда 6,25

X 10 ¹⁸ электронов.) Тогда заряд, заключенный в сфере, равен электрическому потоку плотность на его поверхности, умноженная на площадь, вмещающую заряд.

q (кулоны включены) =

D x 4 r ² .

Линии потока, вносящие вклад в плотности потока те, которые оставляют сферу перпендикулярно поверхности сферы.Это приводит к интегральной формулировке этой части Закон Гаусса;

Знак интеграла указывает на суммирование бесконечно малые площади, d

a , чтобы получить всю площадь поверхности.

Кружок на знаке интеграла означает, что интеграл или Суммирование площадей ведется по замкнутой сплошной поверхности.

Полужирные буквы обозначают, что буква представляет вектор, т. Е. эта величина имеет величину и направление.Расстояние, скорость, ускорение и сила — общие примеры векторов.

Д

— вектор плотности электрического потока в кулонах на квадратный метр.

(указанная точка) следующий Д показывает, что при умножении двух векторы, D и d a .

Скалярное произведение (обсуждается ниже) указывает, что величины два вектора умножаются вместе, а затем этот продукт умножается косинусом угла между двумя векторами.Точечный продукт здесь позволяет определить эффективные линии потока, протекающего через поверхность.

1.1.2 Векторное произведение точек

Приложение векторного скалярного произведения может быть проиллюстрировано вычислением работать над следующей проблемой физики.

Напомним, что работа = сила, умноженная на расстояние. Работа равна продукту силы, то есть в направлении движения силы, умноженное на расстояние, на которое движется сила.

В следующем примере предположим, что человек толкает швабру по пол с ручкой швабры под углом 60 градусов к полу, как в Рисунок 1.2. На этих диаграммах стрелки используются для обозначения векторов.

Через ручка швабры. Как показано на диаграмме, только эта составляющая силы в направление параллельно полу используется при расчете работ. Мы видим, что сила параллельна полу;

20 фунтов x косинус 60 ⁰ = 10 фунтов.

Какая работа выполняется при проталкивании швабры на 8 футов по полу?

10 фунтов x 8 футов = 80 футов.фунты.

Используя скалярное произведение, можно получить уравнение работы:

Работа = F orce d istance.

Скалярное произведение означает, что работа равна величине силы. умножить на величину пройденного расстояния, умножить на косинус угла между двумя векторами.

Или, работа = сила на ручке швабры, умноженная на расстояние, на которое сила перемещается, умноженное на косинус угла между силой и полом.

Работа = 20 фунтов умножить на 8 футов умножить на 1/2 = 80 фут-фунтов.

Только та составляющая полной силы в направлении, параллельном пол, полученный с помощью скалярного произведения, используется в расчет работы.

Это показывает, что скалярное произведение определяется как метод вектора умножение, в котором векторные величины умножаются вместе и затем этот продукт умножается на косинус включенных векторов угол.Всегда должен быть вектор на каждую сторону точки в скалярном произведении.

Следовательно, когда скалярное произведение используется в законе Гаусса, только то, что составляющая потока, параллельная вектору, представляющему площадь, будет вносят свой вклад в общую вложенную плату.

1.2 Закон Гаусса; Интегральная площадь Примеры

Метод определения начисления с помощью скалярного произведения аналогично нахождению Работы как скалярного произведения между приложенной Силой и Расстояние.С помощью этого метода только те компоненты векторных линий потока в том же направлении, что и вектор, представляющий площадь, будет суммируется в расчете начисления. Или, иначе говоря: только эти силовые линии, перпендикулярные поверхности, включены в результат скалярного произведения для получения прилагаемого заряда.

Скалярное значение всегда является результатом скалярного произведения. В этом случае, результат — количество кулонов. Примеры других скалярных величин температура, масса и мощность.Скалярная величина, в отличие от вектор, не имеет направления.

Дифференциальный элемент площади равен

d a . Вектор Представляющая область указывается перпендикулярно этой области. Использование скалярного произведения между вектором, представляющим площадь d a и плотность потока D , приводит к получению эффективного потока через площадь. Суммирование всей площади в квадратные метры.

Предварительное уравнение (закон Гаусса) в нашей процедуре для получения Первое уравнение Максвелла теперь;

Это интегральное уравнение утверждает, что величина плотности электрического потока, нормального к поверхности, вызвана удельное количество заряда, q , заключенное в поверхность.

Рассмотрим следующие примеры определения плотности электрического потока на сферической поверхности и на цилиндрической поверхности.

1.2.1 Определение плотности потока на сфере

Предположим, что заряд в один кулон центрирован в сфере радиуса r. метров как на рисунке 1.3. Рассчитайте плотность электрического потока

D по поверхность на сфере. Интеграл или сумма площадей сфера 4 p r ² квадратных метров.

Вектор, представляющий область, направлен нормально к этой области. Вектор, представляющий небольшую область,

d a , тогда находится прямо на одной линии с линия электрического потока, выходящая из сферы. D представляет плотность линий электрического потока, выходящих из сфера. Угол между плотностью смещения, D , и стрелкой представляющий бесконечно малую область — ноль градусов. Косинус нуля градусов один.

Переформулируя интегральное уравнение площадей закона Гаусса:

q (кулоны включены) =

один кулон = D x 4 p r ² .

кулонов на квадратный метр на поверхности сфера.

1.2.2 Определение плотности потока на цилиндре

Предположим, что длинная линия стационарных зарядов составляет q кулонов на метр, как показано на рисунке 1.4. Имеется цилиндр длиной «L» и радиусом «r» с центром на зарядах. Какая плотность электрического потока на поверхность цилиндра?

Уравнение Гаусса:

Q _T , полный прилагаемый заряд = q кулонов на метр x L метров.

= Q _T = D x 2pr x L.

D

в кулонах на квадратный метр =

1,3 Уравнение Максвелла № 1; Объемный интеграл

Закон электростатики Гаусса также записано как интеграл объема:

Это уравнение утверждает, что заряд заключенный в объем, равен объемной плотности заряда,

r , (rho) суммированы для весь том.

q — заряд, заключенный в томе.

r

— объемная плотность заряда в кулонах на кубический метр.

— бесконечно малый элемент объема.

Весь объем в кубических метрах.

Суммарный заряд, заключенный в объем, — это объем в кубических метрах. умноженное на плотность заряда в кулонах на кубический метр. Средняя громкость Плотность заряда, просуммированная для всего объема, является вложенным зарядом.А обсуждение r можно найти в разделе 1.5.3.

1,4 Уравнение Максвелла № 1; Полная форма заполнена

Для получения интегральной формы Уравнение Максвелла № 1, предположим, что эксперимент настроен так, что одинаковый заряд q кулонов содержится в каждом из уравнений закона Гаусса. Тогда интегралы от одного заряда должны быть равны.

Затем,

Таким образом, мы получили интегральный вид Уравнение Максвелла No.1. Это уравнение утверждает, что эффективная электрическая поле через поверхность, ограничивающую объем, равно полному заряду в объеме. Уравнение показывает что область, заключенная в левом интеграле, должна охватывать объем правого интеграла. Это похоже на утверждение, что площадь поверхности шара или коробки включает в себя объем мяча или коробки. Площадь и объем, указанный в уравнениях потребность не наблюдаемые физические поверхности, часто они будут математическими пределы.

Чтобы запомнить интегральную форму уравнения Максвелла № 1, рассмотрим что заряд q , заключенный в объем, должен быть равен объему плотность заряда,

r, умноженная на объем. Кроме того, тот же заряд q вызовет поток определенной площади. плотность, D , раз больше определенной площади. Площадь должна охватывать объем. В интегралы (суммы) должны быть равны, поскольку одинаковые количество кулонов должно быть получено с каждой стороны от знака равенства.

1,5 уравнение Максвелла № 1; Дифференциальная форма

Дифференциальная форма Уравнение Максвелла № 1:

это дифференциальный оператор читается как «del» (обсуждается ниже).

читается как «расхождение».

Д

— плотность электрического потока в кулонах на квадратный метр.

р

(rho) — объемная плотность заряда в кулонов на кубический метр.

1.5.1 Обсуждение (del)

— математическое расширение обычного одномерного измерения. производная исчисления в трех измерениях.

Мы начнем обсуждение с обзора обычных производных.

В качестве примера для обозначения скорости используется производная. Скорость (v) — это увеличение расстояния, с , для увеличения время, т .

Скорость (v) =.

Поскольку изменение во времени очень мало, дифференциальное исчисление символ используется для скорости.

Теперь рассмотрим обычное одномерное измерение. производная для ускорения.

Вспомните уравнение для определения скорости объекта, когда он упал с высоты. Скорость, которой достигает объект, определяется;

Скорость, v, = ускорение свободного падения, g, умноженное на время в течение который объект падает.

Скорость = v = g t. Или

В интегральной форме закона Гаусса мы просуммировали бесконечно малые значения площади и объема, да и дв.Здесь мы используем дифференциала, ds, dv и dt, чтобы найти мгновенные скорости изменения расстояние и скорость относительно времени.

Существует правило дифференциального исчисления, на которое мы укажем здесь. так как мы будем использовать правило ниже.

Обратите внимание, что скорость равна ускорению (g), умноженному на время (t). Итак, мы можно взять производную от скорости следующим образом:

Правило исчисления состоит в том, что производная от умноженная на константу переменная — это константа.

Теперь мы расширим эту концепцию обычных производных до частичных производные, что позволит нам получить скорость изменения объема в трех измерениях, что, в свою очередь, приводит к определению

Ñ (дел). Чтобы проиллюстрировать скорость изменения трех измерений, предположим, что коробка находится в начале прямоугольного систему координат, как показано на рисунке 1.5.

Объем коробки, V, = длина x ширина x высота; знак равно Д x Ш x В.

Какова скорость изменения объема, когда только длина увеличивается на небольшое количество, но ширина и высота остаются неизменными?

Здесь используется символ частной производной. В символ для частных производных немного отличается от символа для обыкновенные (одномерные) производные. Символ указывает, что только один независимых переменных меняется на данный момент на рассмотрении. Зависимая переменная, объем,

v изменений, определяемых изменениями независимых переменных; L, W и H.Когда меняется только длина;

Символ частной производной показывает, что изменение объема только из-за изменения длины. Ширина и высота удерживаются постоянный. Мы также видим, что производная переменной, умноженная на константу — постоянная, W умноженная на H. Из симметрии следует, что скорость изменение объема в зависимости от ширины или высоты выражается как частная производная.

Когда изменение объема происходит из-за одновременного изменения длины, ширины и высоты, изменения будут происходить в направлениях x, y и z и частные производные складываются, чтобы найти результирующую скорость изменения объем.Это достигается в векторной форме путем умножения каждого частичного производная по единичным векторам, указывающим в направлениях x, y и z. Ед. изм векторы указаны здесь и обсуждаются далее в разделе 1.5.2. С использованием единичные векторы и одновременные изменения в трех измерениях, общая изменение объема обозначено:

Для более общего случая тома

В изменение в направления x , y и z ;

Это обсуждение обычных и частичных производных была направлена ​​на получение группы трех частных производных термины в скобках выше.

означает градиент. В этой статье мы не будем использовать градиент.

Нам понадобится Ñ (del dot, обсуждается ниже) и Ñ 5 (дель-крест, обсуждается в Раздел 3).

1.5.2 Обсуждение компонентов вектора по отношению к

Прежде чем продолжить части дифференциальной формы уравнения Максвелла № 1, мы должны рассмотрим компоненты x, y и z вектора в прямоугольные координаты.

В разделе 1.1.2 скалярное произведение двух векторов, силы и расстояния, использовался для расчета работы. Здесь мы рассчитаем ту же работу, используя компоненты вектора силы и расстояния и используют скалярное произведение.

Обратите внимание, что компоненты вектора силы в прямоугольном координаты размещаются либо на нуле, либо на 90 градусах к расстоянию движение. Косинус нуля градусов равен единице, а косинус 90 градусов. равно нулю.

Из рисунка 1.3;

Компоненты вектора силы = 17,3 фунта. y + 10 фунтов. х .

Компоненты вектора расстояния = 0 футов y + 8 футов x .

Теперь процедура умножения векторов (точек) заключается в умножении величины компонент вектора и косинус угла между ними, посрочно.

Нулевое расстояние y, умноженное на две составляющие силы, равно нулю.

8 футов x расстояние, умноженное на 17.8 фунтов силы в направлении y раз косинус 90 градусов равен нулю. Направленное расстояние 8 футов x, умноженное на Сила 10 фунтов в направлении x, умноженная на косинус нуля градусов, составляет те же 80 фут-фунтов, которые мы нашли в предыдущем примере.

Следуют этой процедуре умножения компонент вектора x, y и z. при выполнении продукта ниже. Умножение компонентов вектора, которые всегда равны нулю или 90 градусов друг от друга, значительно упрощает векторную математику.

Мы определили компоненты в разделе 1.5.1. Выше мы обсуждали умножение скалярного произведения векторов, используя их компоненты. Эти две концепции сейчас используются для рассчитать

1.5.3 Вычислить

Компоненты вектора D являются его проекциями на x, y и z ось. Векторные направления D компонентов обозначены единичные векторы x, y и z .На рисунке 1.6 вектор D начинается в начале координат, указывает вверх и вправо и является обозначен как выходящий из бумаги. Величины проекций Д по осям D _x , Dy, и D _z . На рисунке 1.7 показаны единичные векторы в направлениях x, y и z, которые дают компоненты D их векторные отношения. Одинаковый единичные векторы обозначены в

Уравнение для вектора

D в проекции на три оси координат, D = D _x x + D _y y + D _z z. Теперь займемся указано скалярное произведение.

Скалярное произведение означает, что мы должны умножить скобки, член по члену, умноженному на косинус включенного угла между каждой парой термины. Эта серия умножений может дать девять членов, но обратите внимание, что единичный вектор, разделенный точками на один и тот же единичный вектор:

Остальные шесть комбинаций единичного вектора Умножение скалярного произведения содержит косинус 90 градусов и следовательно, ноль.

Окончательный результат операция — это скаляр из трех членов:

Это уравнение указывает сумму изменения по плотности электрического потока,

D , в каждом из трех ортогональных направлений. В изменение происходит из-за небольшого, (приближающегося ноль), расстояние изменяется в тех же ортогональных направлениях.

Изменение расстояния в трех ортогональных направлениях представляет собой объем измените, как показано в разделе 1.5.1. Следовательно, электрическая плотность ( D ) изменение в трех направлениях, которое мы получили с использованием скалярного произведения с единичными векторами в del, на самом деле изменение объема блока. Поскольку заряд измеряется в кулонах, сумма заряд в кулонах. Результат сложения трех электрических плотностей изменения — кулоны на кубический метр. Это определяет

r , объемная плотность заряда, , как указано в разделе 1.3.

1,6 Уравнение № 1, дифференциальное Форма заполнена

Выполняя указанные операция, которую мы получили

r , объемная плотность заряда. Это разница формулировка уравнения Максвелла №1.

Уравнение утверждает, что дивергенция плотность электрического потока в точке равна заряду на единицу объем в этот момент. Скалярное произведение, как всегда, дает скаляр результат.В этом случае результат —

р, количество кулонов расход за кубометр.

1.7 Теорема о расходимости

Здесь поучительно продолжить использование только что разработанных интегральных и дифференциальных уравнений для уравнения Максвелла № 1, чтобы проиллюстрировать векторную идентичность называется «Теорема о расходимости Гаусса». Этот тождество приравнивает векторный интеграл по поверхности к векторному интегралу по объему, и потребуется позже в Разделе 2.5.

Из раздела 1.4,

из раздела 1.5;

Путем замены на

r в интегральном уравнении получаем;

Это типичная иллюстрация Гаусса. Теорема расходимости на примере вектора

D . В Дело в том, что каждый раз, когда у нас есть векторный поверхностный интеграл этого типа мы можем заменить интеграл объема. Если у нас есть векторный объем интеграл указанного выше типа можно заменить поверхностным интегралом.В интеграл расходимости вектора, просуммированный по объему, равен равный интегралу произведения вектора на его эффективную площадь просуммирована по площади. Это аналогично заявлению о том, что объем шара содержится в пределах его площади поверхности. Круг на знак интеграла означает, что интеграл берется по непрерывной площадь.

Если бы мы просто использовали теорему о расходимости Гаусса из списка учебников векторных тождеств, мы могли бы сразу записать дифференциальная форма уравнения Максвелла No.1 из интегральной формы. Этот более подробный способ получения личности будет полезно в более поздних выводах.

1,8 Связь

D , E и e

Пространство, в котором электрическая заряды, оказывающие свое влияние, называют полем электрического заряда. Электрический заряд q окружает электрическое поле поля прочность

E . Напряженность электрического поля, E , вызывает величина плотности потока, D , в зависимости от диэлектрической проницаемости, е окружающая среда.

D

находится в кулонов на квадратный метр.

E

в ньютонах на кулон или в вольтах на метр.

и

в кулонах ² на ньютон-метр ² .

E

— это напряжение в пространстве, которое вызывает проявление D . В связи к этому уравнению и по причинам, обсуждаемым в разделе 3.7, D есть часто обозначается как плотность смещения электрического потока в дополнение к плотность электрического потока.Кроме того, в разделе 4 будет показано, что магнитно-индуцированное электрическое поле также обозначен E , с размером вольт на метр. Это индуцированное электрическое поле то же поле, что и напряженность статического поля, обсуждаемая здесь, но это генерируется изменяющимся магнитным полем.

Диэлектрическая проницаемость

e — это степень, в которой окружающая среда позволяют плотности электрического потока, D , происходить из-за с учетом напряженности электрического поля, E .В воздухе или в свободном пространстве,

и

= 8,85×10 ^-12 кулон ² на ньютон-метр ² .

Эти понятия и определения будут использоваться в разделах 6 и 7.

1.9 Закон Кулона

В разделе 1.2.1 мы обнаружили, что плотность электрического потока D за счет заряда q, находящегося внутри сфера:

Затем, используя E и e, как определено в разделе 1.8;

При следующем заряде q ₂ , размещены на расстоянии r метров от q ₁ , сила испытывает q ₂ . Сила составляет

E раз q ₂ Ньютонов. Или,

, где q ₁ и q ₂ обозначают физическое лицо обвинения. Это уравнение является законом Кулона. Напомним, что сила одного Ньютон разгонит массу в один килограмм на один метр в секунду ² .

Закон Кулона гласит, что сила между двумя зарядами пропорционально произведению двух зарядов на расстояние между двумя зарядами в квадрате. Уравнение — это основа для экспериментального определения силы между двумя зарядами и диэлектрическая проницаемость различных сред. Этот важный электрический закон не включен в список Максвелла, поскольку считается производным от Гаусса закон, и не используется в этих уравнениях поля.

На этом обсуждение уравнения Максвелла завершено. Нет.1.

19.2 Электрический потенциал в однородном электрическом поле — Физика колледжа, главы 1-17

Цели обучения

• Опишите взаимосвязь между напряжением и электрическим полем.
• Выведите выражение для электрического потенциала и электрического поля.
• Рассчитайте напряженность электрического поля с учетом расстояния и напряжения.

В предыдущем разделе мы исследовали взаимосвязь между напряжением и энергией. В этом разделе мы исследуем взаимосвязь между напряжением и электрическим полем.Например, однородное электрическое поле [латекс] \ textbf {E} [/ latex] создается путем размещения разности потенциалов (или напряжения) [латекс] \ boldsymbol {\ Delta V} [/ latex] на двух параллельных металлических пластинах, помечены буквами A и B. (См. рис. 1.) Изучив это, мы узнаем, какое напряжение необходимо для создания определенной напряженности электрического поля; это также покажет более фундаментальную взаимосвязь между электрическим потенциалом и электрическим полем. С точки зрения физика, для описания любого распределения заряда можно использовать [latex] \ boldsymbol {\ Delta V} [/ latex] или [latex] \ textbf {E} [/ latex].[latex] \ boldsymbol {\ Delta V} [/ latex] наиболее тесно связан с энергией, тогда как [latex] \ textbf {E} [/ latex] наиболее тесно связан с силой. [latex] \ boldsymbol {\ Delta V} [/ latex] — это скалярная величина и не имеет направления, тогда как [latex] \ textbf {E} [/ latex] представляет собой векторную величину , имеющую как величину, так и направление . (Обратите внимание, что величина напряженности электрического поля, скалярная величина, представлена ​​ниже как [latex] \ textbf {E} [/ latex].) Связь между [latex] \ boldsymbol {\ Delta V} [/ latex] и [latex] \ textbf {E} [/ latex] раскрывается путем вычисления работы, совершаемой силой при перемещении заряда из точки A в точку B.Но, как отмечалось в главе 19.1 «Электрическая потенциальная энергия: разность потенциалов», это сложно для произвольных распределений заряда, требующих расчетов. Поэтому мы рассматриваем однородное электрическое поле как интересный частный случай.

Рис. 1. Соотношение между V и E для параллельных проводящих пластин составляет E = V / d . (Обратите внимание, что Δ В = В _AB по величине. Для заряда, который перемещается от пластины A с более высоким потенциалом к ​​пластине B с более низким потенциалом, необходимо включить знак минус следующим образом: –Δ V = V _A — V _B = V _AB .Подробности см. В тексте.)

Работа, совершаемая электрическим полем на Рисунке 1 по перемещению положительного заряда [латекс] \ boldsymbol {q} [/ latex] от A, положительной пластины, более высокий потенциал, к B, отрицательной. пластина, нижний потенциал, составляет

[латекс] \ boldsymbol {W = — \ Delta \ textbf {PE} = -q \ Delta V.} [/ Latex]

Разница потенциалов между точками A и B составляет

[латекс] \ boldsymbol {- \ Delta V = — (V _ {\ textbf {B}} — V _ {\ textbf {A}}) = V _ {\ textbf {A} — V _ {\ textbf {B}}} = V _ {\ textbf {AB}}} [/ латекс].

Если ввести это в выражение для работы, получаем

[латекс] \ boldsymbol {W = qV _ {\ textbf {AB}}} [/ латекс].

Работа [латекс] \ boldsymbol {W = Fd \; \ textbf {cos} \ theta} [/ latex], так как путь параллелен полю, поэтому [латекс] \ boldsymbol {W = Fd} [/ латекс]. Поскольку [latex] \ boldsymbol {F = qE} [/ latex], мы видим, что [latex] \ boldsymbol {W = qEd} [/ latex]. Подстановка этого выражения для работы в предыдущее уравнение дает

[латекс] \ boldsymbol {qEd = qV _ {\ textbf {AB}}} [/ латекс].

Заряд прекращается, и поэтому напряжение между точками A и B составляет

[латекс] \ begin {array} {l} \ boldsymbol {V _ {\ textbf {AB}} = Ed} \\ \ boldsymbol {E = \ frac {V _ {\ textbf {AB}}} {d}} \ end {array} [/ latex] [latex] \} [/ latex] [latex] \ boldsymbol {\ textbf {(uniform} \; E \; \ textbf {- только поле)}}, [/ latex]

где [latex] \ boldsymbol {d} [/ latex] — это расстояние от A до B, или расстояние между пластинами на рисунке 1. Обратите внимание, что приведенное выше уравнение подразумевает, что единицы измерения электрического поля — вольт на метр.Мы уже знаем, что единицы измерения электрического поля — ньютоны на кулон; таким образом, верно следующее соотношение между единицами:

[латекс] \ boldsymbol {1 \; \ textbf {N} / \ textbf {C} = 1 \; \ textbf {V} / \ textbf {m}}. [/ Latex]

Напряжение между точками A и B

[латекс] \ begin {array} {l} \ boldsymbol {V _ {\ textbf {AB}} = Ed} \\ \ boldsymbol {E = \ frac {V _ {\ textbf {AB}}} {d}} \ end {array} [/ latex] [latex] \} [/ latex] [latex] \ boldsymbol {\ textbf {(uniform} \; E \; \ textbf {- только поле)}}, [/ latex]

где [latex] \ boldsymbol {d} [/ latex] — это расстояние от A до B, или расстояние между пластинами.6 \; \ textbf {V} / \ textbf {m}} [/ latex]. Выше этого значения поле создает достаточную ионизацию в воздухе, чтобы сделать воздух проводником. Это допускает разряд или искру, которые уменьшают поле. Каково же максимальное напряжение между двумя параллельными проводящими пластинами, разделенными 2,5 см сухого воздуха?

Стратегия

Нам дано максимальное электрическое поле [латекс] \ boldsymbol {E} [/ latex] между пластинами и расстояние [латекс] \ boldsymbol {d} [/ latex] между ними. Таким образом, уравнение [латекс] \ boldsymbol {V _ {\ textbf {AB}} = Ed} [/ latex] может использоваться для расчета максимального напряжения.4 \; \ textbf {V}} [/ латекс]

или

[латекс] \ boldsymbol {V _ {\ textbf {AB}} = 75 \; \ textbf {kV}}. [/ Latex]

(Ответ состоит только из двух цифр, поскольку максимальная напряженность поля является приблизительной.)

Обсуждение

Одним из следствий этого результата является то, что требуется около 75 кВ, чтобы совершить скачок искры через зазор 2,5 см (1 дюйм), или 150 кВ для искры 5 см. Это ограничивает напряжения, которые могут существовать между проводниками, возможно, на линии электропередачи.Меньшее напряжение вызовет искру, если на поверхности есть точки, поскольку точки создают большие поля, чем гладкие поверхности. Влажный воздух разрушается при более низкой напряженности поля, а это означает, что меньшее напряжение заставит искру проскочить через влажный воздух. Самые большие напряжения могут создаваться, например, статическим электричеством в засушливые дни.

Рис. 2. Искровая камера используется для отслеживания траектории частиц высоких энергий. Ионизация, создаваемая частицами при прохождении через газ между пластинами, позволяет искре прыгнуть.Искры расположены перпендикулярно пластинам, следуя силовым линиям электрического поля между ними. Разность потенциалов между соседними пластинами недостаточно высока, чтобы вызвать искры без ионизации, создаваемой частицами из экспериментов на ускорителях (или космическими лучами). (Источник: Дадро, Wikimedia Commons)

Пример 2: Поле и сила внутри электронной пушки

(a) Электронная пушка имеет параллельные пластины, разделенные расстоянием 4,00 см, и дает электронам энергию 25,0 кэВ. Какая напряженность электрического поля между пластинами? (б) Какую силу это поле окажет на кусок пластика с [латексным] \ boldsymbol {0.500 \; \ mu \ textbf {C}} [/ latex] заряд, который попадает между пластинами?

Стратегия

Поскольку указаны напряжение и расстояние между пластинами, напряженность электрического поля можно рассчитать непосредственно из выражения [latex] \ boldsymbol {E = \ frac {V _ {\ textbf {AB}}} {d}} [/ latex]. Как только напряженность электрического поля известна, сила, действующая на заряд, определяется с помощью [latex] \ boldsymbol {\ textbf {F} = q \ textbf {E}} [/ latex]. Поскольку электрическое поле имеет только одно направление, мы можем записать это уравнение в терминах величин, [латекс] \ boldsymbol {F = q \; E} [/ латекс].

Решение для (а)

Выражение для величины электрического поля между двумя однородными металлическими пластинами равно

[латекс] \ boldsymbol {E =} [/ latex] [латекс] \ boldsymbol {\ frac {V _ {\ textbf {AB}}} {d}} [/ латекс].

Поскольку электрон является однозарядным, и ему дается энергия 25,0 кэВ, разность потенциалов должна составлять 25,0 кВ. Вводя это значение для [latex] \ boldsymbol {V _ {\ textbf {AB}}} [/ latex] и расстояния между пластинами 0,0400 м, получаем

[латекс] \ boldsymbol {E =} [/ latex] [латекс] \ boldsymbol {\ frac {25.5 \; \ textbf {V} / \ textbf {m}) = 0,313 \; \ textbf {N}}. [/ Latex]

Обсуждение

Обратите внимание, что единицы измерения — ньютоны, поскольку [latex] \ boldsymbol {1 \; \ textbf {V} / \ textbf {m} = 1 \; \ textbf {N} / \ textbf {C}} [/ latex]. Сила, действующая на заряд, одинакова независимо от того, где находится заряд между пластинами. Это потому, что электрическое поле между пластинами однородно.

В более общих ситуациях, независимо от того, однородно ли электрическое поле, оно указывает в направлении уменьшения потенциала, потому что сила, действующая на положительный заряд, направлена ​​в направлении [латекс] \ textbf {E} [/ латекс], а также в направлении более низкого потенциала [латекс] \ boldsymbol {V} [/ латекс].Кроме того, величина [latex] \ textbf {E} [/ latex] равна скорости уменьшения [latex] \ boldsymbol {V} [/ latex] с расстоянием. Чем быстрее [латекс] \ boldsymbol {V} [/ latex] уменьшается с расстоянием, тем сильнее электрическое поле. В форме уравнения общая связь между напряжением и электрическим полем равна

[латекс] \ boldsymbol {E =} [/ latex] [латекс] \ boldsymbol {- \ frac {\ Delta V} {\ Delta s}}, [/ латекс]

где [latex] \ boldsymbol {\ Delta s} [/ latex] — это расстояние, на котором происходит изменение потенциала, [latex] \ boldsymbol {\ Delta V} [/ latex].Знак минус говорит нам, что [latex] \ textbf {E} [/ latex] указывает в направлении уменьшения потенциала. Электрическое поле называется градиентом (по степени или наклону) электрического потенциала.

Связь между напряжением и электрическим полем

В форме уравнения общая связь между напряжением и электрическим полем равна

[латекс] \ boldsymbol {E =} [/ latex] [латекс] \ boldsymbol {- \ frac {\ Delta V} {\ Delta s}}, [/ латекс]

где [latex] \ boldsymbol {\ Delta s} [/ latex] — это расстояние, на котором происходит изменение потенциала, [latex] \ boldsymbol {\ Delta V} [/ latex].Знак минус говорит нам, что [latex] \ textbf {E} [/ latex] указывает в направлении уменьшения потенциала. Электрическое поле называется градиентом (по степени или наклону) электрического потенциала.

Для непрерывно меняющихся потенциалов [latex] \ boldsymbol {\ Delta V} [/ latex] и [latex] \ boldsymbol {\ Delta s} [/ latex] становятся бесконечно малыми, и для определения электрического поля необходимо использовать дифференциальное исчисление.

• Напряжение между точками A и B равно

  [латекс] \ begin {array} {l} \ boldsymbol {V _ {\ textbf {AB}} = Ed} \\ \ boldsymbol {E = \ frac {V _ {\ textbf {AB}}} {d}} \ end {array} [/ latex] [latex] \} [/ latex] [latex] \ boldsymbol {\ textbf {(uniform} \; E \; \ textbf {- только поле)}}, [/ latex]

  где [latex] \ boldsymbol {d} [/ latex] — это расстояние от A до B, или расстояние между пластинами.

• В форме уравнения общая связь между напряжением и электрическим полем выглядит следующим образом:

  [латекс] \ boldsymbol {E =} [/ latex] [латекс] \ boldsymbol {- \ frac {\ Delta V} {\ Delta s}}, [/ латекс]

  где [latex] \ boldsymbol {\ Delta s} [/ latex] — это расстояние, на котором происходит изменение потенциала, [latex] \ boldsymbol {\ Delta V} [/ latex]. Знак минус говорит нам, что [латекс] \ textbf {E} [/ latex] указывает в направлении уменьшения потенциала.) Электрическое поле называется градиентом (по степени или наклону) электрического поля. потенциал.

Концептуальные вопросы

1: Обсудите, как связаны разность потенциалов и напряженность электрического поля. Приведите пример.

2: Какова напряженность электрического поля в области, где электрический потенциал постоянен?

3: Будет ли отрицательный заряд, первоначально находящийся в состоянии покоя, двигаться к более высокому или более низкому потенциалу? Объяснить, почему.

Задачи и упражнения

1: Покажите, что единицы измерения напряженности электрического поля В / м и Н / К действительно эквивалентны.3 \; \ textbf {V}} [/ latex] прилагается? (б) Насколько близко друг к другу могут быть пластины при приложенном напряжении?

6: Напряжение на мембране, образующей клеточную стенку, составляет 80,0 мВ, а толщина мембраны составляет 9,00 нм. Какая напряженность электрического поля? (Значение на удивление велико, но верно. Мембраны обсуждаются в главе 19.5 «Конденсаторы и диэлектрики» и главе 20.7 «Нервная проводимость — электрокардиограммы».) Вы можете предположить однородное электрическое поле.

7: Стенки мембран живых клеток имеют удивительно большие электрические поля из-за разделения ионов.(Мембраны более подробно обсуждаются в главе 20.7 Нервная проводимость — Электрокардиограммы.) Каково напряжение на мембране толщиной 8,00 нм, если напряженность электрического поля на ней составляет 5,50 МВ / м? Вы можете предположить однородное электрическое поле.

8: Две параллельные проводящие пластины разделены расстоянием 10,0 см, и предполагается, что одна из них имеет нулевое напряжение. (а) Какова напряженность электрического поля между ними, если потенциал 8,00 см от нулевой пластины (и 2,00 см от другой) составляет 450 В? б) Какое напряжение между пластинами?

9: Найдите максимальную разность потенциалов между двумя параллельными проводящими пластинами, разделенными на 0.6 \; \ textbf {V} / \ textbf {m}} [/ latex]. (а) Какая энергия в кэВ передается электрону, если он ускоряется на 0,400 м? (б) На какое расстояние его нужно будет ускорить, чтобы увеличить его энергию на 50,0 ГэВ?

Глоссарий

скаляр

физическая величина с величиной, но без направления

вектор

физическая величина с величиной и направлением

Решения

Задачи и упражнения

3: (а) 3.6 \; \ textbf {V} / \ textbf {m})} [/ latex].

(б) 1,7 мм

7: 44,0 мВ

9: 15 кВ

11: (а) 800 кэВ

б 25.0 км

.

No related posts.