Оптика и волны
Может случиться так, что осциллятор принимает участие в двух одинаково направленных колебаниях с разными амплитудами, частотами и начальными фазами. Рассмотрим сложение таких колебаний.
Сложение колебаний с одинаковыми частотами
Для простоты рассмотрим сначала случай, когда частоты складываемых колебаний одинаковы. Общие решения складываемых гармонических колебаний имеют вид:
|
|
(1.34) |
где x1, x2— переменные, описывающие колебания, A1, A2— их амплитуды, а , — начальные фазы. Результирующее колебание
удобно найти с помощью векторной диаграммы. Этот метод использует аналогию между вращением и колебательным процессом.
Этот метод использует аналогию между вращением и колебательным процессом.
Возьмем общее решение (1.23) для гармонического колебания. Выберем ось 0x. Из точки 0 отложим вектор длиной A, образующий с осью 0x угол . Если привести этот вектор во вращение с угловой скоростью , то проекция конца этого вектора будет перемещаться по оси 0x от +A до –A, причем величина проекции будет изменяться по закону
|
|
(1.35) |
Таким образом, проекция конца вектора на ось 0x будет совершать гармонические колебания с амплитудой, равной длине вектора, с круговой частотой, равной угловой скорости вращения вектора, и с начальной фазой, равной углу, образуемому вектором с осью в начальный момент времени (рис. 1.12).
1.12).
Рис. 1.12. Векторная диаграмма для общего решения (1.23)
Применим теперь эту технику к сложению колебаний (1.34). Представим оба колебания с помощью векторов А1 и А2 Возьмем их векторную сумму (рис. 1.13)
Рис. 1.13. Векторная диаграмма для сложения одинаково направленных колебаний одинаковой частоты
Проекция вектора А1 на ось 0x равна сумме проекций соответствующих векторов
Таким образом, вектор А представляет собой результирующее колебание. Этот вектор вращается с той же угловой скоростью , так что результирующее движение будет гармоническим колебанием с частотой , амплитудой A и начальной фазой a. Согласно теореме косинусов:
Согласно теореме косинусов:
|
|
(1.36) |
В частности, если фазы складываемых колебаний равны или отличаются на величину, кратную (то есть ), то амплитуда результирующего колебания равна сумме амплитуд
Если же складываемые колебания находятся в противофазе (то есть ), то
Биения
В этом разделе мы рассмотрим случай сложения одинаково направленных гармонических колебаний с разными частотами. На практике особый интерес представляет случай, когда складываемые колебания мало отличаются по частоте. Как мы увидим, в результате сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой, называемые 
|
Биения — это периодическое изменение амплитуды колебаний, возникающее при сложении двух гармонических колебаний с близкими частотами. |
Для простоты рассмотрим случай, когда амплитуды складываемых колебаний равны A, а начальные фазы обоих колебаний равны нулю. Частоты складываемых колебаний равны, соответственно, и . Итак,
|
|
(1.37) |
Складываем эти выражения и учитываем известную формулу тригонометрии:
|
|
(1. |
Если то в аргументе второго косинуса мы можем пренебречь сдвигом частоты:
|
|
(1.39) |
Кроме того, множитель в скобках меняется медленно по сравнению с . Поэтому результирующее колебание x можно рассматривать как модулированное гармоническое колебание с частотой
|
|
(1. |
Подчеркнем, что в строгом смысле такое колебание не является гармоническим, и еще раз напомним, что, согласно определению, колебание гармоническое, если оно происходит по закону , причем все три его параметра: строго постоянны во времени.
Рис. 1.14. Биения при сложении колебаний с близкими частотами
Частота пульсаций амплитуды (ее называют частотой биений) равна разности частот складываемых колебаний. Период биений равен
|
|
(1.41) |
Видео 1.12 Биения на экране осциллографа
Видео 1. 13 Биения: осциллограф и динамик
13 Биения: осциллограф и динамик
Видео 1.14 «Двойной» маятник: запись песком картины биений
Колебания двух связанных осцилляторов
Приведем поучительный пример системы, в которой возникают биения. Рассмотрим два груза массой m, которые могут колебаться под действием двух одинаковых пружин с коэффициентами жесткости k. Пусть грузы соединены также мягкой пружиной с коэффициентом жесткости K<<k. Будем полагать длины всех пружин в нерастянутом состоянии одинаковыми и равными 2L (рис. 1.15).
Рис. 1.15. Пример связанных осцилляторов.
Колебания происходят вдоль оси 0х, сила тяжести не учитывается
Тогда в положении равновесия координаты грузов равны
При колебаниях координаты равны, соответственно, x1(t), x2(t). Удлинения пружин записываются как
Мы имеем дело с системой с двумя степенями свободы. Составим уравнения движения. На первый груз действуют сила со стороны пружины k, равная
Составим уравнения движения. На первый груз действуют сила со стороны пружины k, равная
и сила со стороны пружины K, равная
На второй груз действуют аналогичные силы
и
Соответственно, уравнения движения имеют вид
|
|
(1.42) |
Эти уравнения не слишком похожи на первый взгляд на уравнения гармонических колебаний, потому что на колебания x1оказывают влияния колебания x2и наоборот. Поэтому преобразуем уравнения к новым переменным, уравнения для которых были бы независимыми (такие переменные называют нормальными координатами, а соответствующие им колебания — нормальными колебаниями (модами)).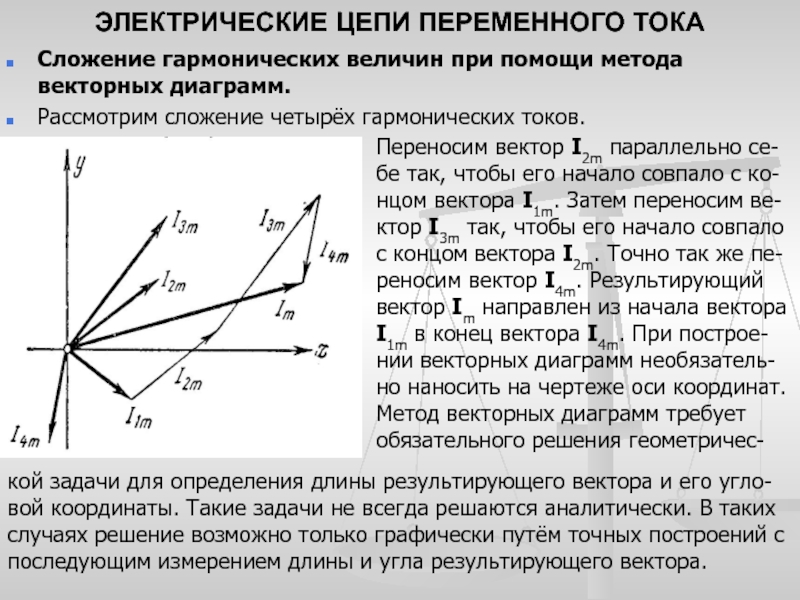 Именно, введем новые переменные x1 и x2:
Именно, введем новые переменные x1 и x2:
|
|
(1.43) |
Как легко убедиться, положениям равновесия соответствуют нулевые значения этих координат
В этих переменных уравнения (1.42) принимают вид:
|
|
(1.44) |
Складывая и вычитая эти уравнения, приходим к паре независимых уравнений для введенных нормальных координат:
|
|
(1. |
Первое уравнение описывает гармонические колебания с частотой
совпадающей с частотой колебаний пружинных маятников в отсутствие соединительной пружины К. Второе уравнение описывает колебания со сдвинутой частотой
Так как K<<k, имеем
|
|
(1.46) |
Соответственно, мы получаем общее решение системы уравнений:
|
|
(1. |
Общее решение для координат х1 и х2 колеблющихся точек следуют из (1.47) и (1.43):
|
|
(1.48) |
Для примера рассмотрим случай, когда первая масса смещается на расстояние от положения равновесия и отпускается с нулевой начальной скоростью, а вторая масса остается в положении равновесия:
|
|
(1. |
Этому соответствуют следующие начальные значения нормальных координат:
|
|
(1.50) |
Такие начальные условия уже рассматривались выше. Соответствующие им решения имеют вид
|
|
(1.51) |
Подставляя найденные амплитуды и начальные фазы в (1.48), получаем решения, описывающие колебания рассматриваемых масс около их положений равновесия:
|
|
(1. |
Графики функций x1(t), x2(t) показаны на рис. 1.16. Видна характерная картина биений.
Рис. 1.16. Биения в системе двух связанных осцилляторов
В начальный момент времени колеблется лишь первый груз. Затем начинает колебаться второй, а амплитуда колебаний первого уменьшается. Через время первый груз останавливается, а второй колеблется с максимально возможной амплитудой. Произошла «перекачка» энергии от первого маятника ко второму. Затем процесс «перекачки» энергии идет в обратном направлении и к моменту первый маятник колеблется с максимальной амплитудой, а второй покоится.
На рис. 1.17 демонстрируются биения в системе двух связанных математических маятников.
Рис. 1.17. Биения в системе связанных маятников
Выясним теперь физический смысл нормальных мод, соответствующих чисто гармоническим колебаниям системы. Если возбуждены колебания только первой из них (x1), то A2 = 0 и, как следует из общего решения (1.48),
Если возбуждены колебания только первой из них (x1), то A2 = 0 и, как следует из общего решения (1.48),
|
|
(1.53) |
Из (1.53) видно, что первая нормальная мода соответствует такому колебанию, когда оба груза смещаются на одинаковые расстояния от их положений равновесия, но в противоположные стороны, другими словами — они колеблются в противофазе. Скорости движения грузов также равны по величине и противоположны по направлению, так что центр масс грузов остается неподвижным. Колебания происходят под действием пружин с жесткостью k, к которым добавляется соединительная пружина с жесткостью К. Как следствие, частота таких колебаний больше частоты колебаний несвязанных осцилляторов
Возбуждение только второй (x2) нормальной моды означает, что A1 = 0:
|
|
(1. |
В этом случае грузы смещаются из положения равновесия в одну сторону на одинаковые расстояния, другими словами – они колеблются синфазно. Скорости их также одинаковы по величине и направлению. Соединительная пружина колеблется вместе с грузами, но остается не растянутой и потому не оказывает влияния, так что частота колебаний совпадает с частотой колебаний несвязанных маятников.
В разобранном случае мы познакомились с нормальными модами и выяснили, что их частоты сдвигаются по сравнению с частотами колебаний несвязанных маятников. Любое другое колебательное движение системы можно представить как суперпозицию нормальных мод. Аналогичным образом можно рассмотреть цепочку из множества связанных друг с другом осцилляторов и изучить их нормальные колебания. Такая система представляет собой модель кристаллической решетки.
Дополнительная информация
http://allphysics.ru/feynman/bieniya — Фейнмановские лекции по физике. {i \delta}$ — комплексная амплитуда колебания. Комплексный характер амплитуды $А$ обозначает, что колебание имеет начальную фазу неравную нулю.
{i \delta}$ — комплексная амплитуда колебания. Комплексный характер амплитуды $А$ обозначает, что колебание имеет начальную фазу неравную нулю.
Для того чтобы раскрыть физический смысл выражения типа (6), предположим, что частота колебаний (${\omega }_0$) имеет вещественную и мнимую части, и ее можно представить как:
Тогда выражение (6) можно записать как:
В том случае, если ${\omega }2>0,$ то выражение (8) описывает затухающие гармонические колебания с круговой частотой $\omega1$ и показателем затухания ${\omega }_2$. Если ${\omega }_2
Замечание
Над комплексными величинами можно проводить многие математические операции так, как будто величины являются вещественными. Операции возможны, если они сами линейны и вещественны (такими являются сложение, умножение, дифференцирование по вещественной переменной и другие, но не все). Надо помнить, что комплексные величины сами по себе не соответствуют никаким физическим величинам.
Метод векторных диаграмм
Пусть точка $A$ равномерно вращается по окружности радиуса $r$ (рис. 1), скорость ее вращения ${\omega }_0$.
1), скорость ее вращения ${\omega }_0$.
Рисунок 1.
Положение точки $А$ на окружности можно задать с помощью угла $\varphi $. Этот угол равен:
где $\delta =\varphi (t=0)$ величина угла поворота радиус-вектора $\overrightarrow{r}$ в начальный момент времени. Если точка $М$ вращается, то ее проекция на $ось X$ движется по диаметру окружности, совершая гармонические колебания между точками $М$ $N$. Абсциссу точки $А$ можно записать как:
Подобным способом можно представлять колебания любых величин.
Необходимо только принять изображение величины, которая совершает колебания абсциссой точки $А$, которая равномерно вращается по окружности. Можно, конечно использовать и ординату:
Замечание 1
Для того чтобы представлять затухающие колебания, надо брать не окружность, а логарифмическую спираль, которая приближается к фокусу. Если скорость приближения движущейся по спирали точки постоянна и очка движется к фокусу, то проекция этой точки на $ось X$ даст формулы затухающих колебаний.
Замечание 2
Вместо точки можно использовать радиус-вектор, который будет равномерно вращаться вокруг начала координат. Тогда величина, которая совершает гармонические колебания, будет изображаться как проекция этого вектора на $ось X$. При этом математические операции над величиной $x$ заменяют операциями над вектором.
Так операцию суммирования двух величин:
удобнее заменить суммированием двух векторов (используя правило параллелограмма). Векторы выбрать так, что их проекции на избранную $ось X$ являются выражениями $x_1\ и\ x_2$. Тогда результат операции суммирования векторов в проекции на ось абсцисс будет равен $x_1+\ x_2$.
Пример 1
Продемонстрируем применение метода векторных диаграмм.
Итак, представим комплексные числа векторами на комплексной плоскости. Величина, изменяющаяся по гармоническому закону, изображена вектором, который вращается с частотой ${\omega }0$ вокруг своего начала против часовой стрелки. Длина вектора равна амплитуде колебаний. 0$ против часовой стрелки, а умножение на ($-i$) на тот же угол по часовой стрелке. Из рис.2 ледует, что:
0$ против часовой стрелки, а умножение на ($-i$) на тот же угол по часовой стрелке. Из рис.2 ледует, что:
где $-\frac{\pi }{2}\le \varphi \le \frac{\pi }{2}.$ Изменение угла $\varphi $ зависит от соотношения между импедансами элементов цепи и частотами. Внешнее напряжение может изменяться по фазе, от совпадающего с напряжением на индуктивности, до совпадающего с напряжением на емкости. Выражается это обычно в виде отношения между фазами напряжений на элементах цепи и фазой внешнего напряжения:
Фаза напряжения на индуктивности ${(U}L=i\omega LI)$ всегда опережает фазу внешнего напряжения на угол от $0$ до $\pi .$
Фаза напряжения на емкости ${(U}C=-\frac{iI}{\omega C}$) всегда отстает от фазы внешнего напряжения на угол между $0$ и —$\ \pi .$
При этом фаза на сопротивлении может как опережать, так и отставать от фазы внешнего напряжения на угол между- $\frac{\pi }{2}$ и $\frac{\pi }{2}$.
 2.\]
2.\]Причина ошибки в том, что операция возведения в квадрат не является линейной.
Векторные диаграммы. Построение векторных диаграмм
При расчете электрических цепей переменного тока пользуются весьма простым и наглядным способом графического изображения синусоидальных величин при помощи вращающихся векторов.
Обоснование векторной диаграммы
Предположим, что ток задан уравнением
i = Imsin(ωt +Ψ)
Проведем две взаимно перпендикулярные оси и из точки пересечения осей проведем вектор Im, длина которого в определённом масштабе Mi выражает амплитуду тока Im:
Im = Im/Mi
Направление вектора выберем так, чтобы с положительным направлением горизонтальной оси вектор составлял угол, равный начальной фазе Ψ (рис.
 12.10).
12.10).Проекция этого вектора на вертикальную ось определяет мгновенный ток в начальный момент времени: i0 = ImsinΨ.
Представим себе, что вектор Im вращается против движения часовой стрелки с угловой скоростью, равной угловой частоте ω. Его положение в любой момент времени определяется углом ωt +Ψ ,
Тогда мгновенный ток для произвольного момента времени t можно определить проекцией вектора Im на вертикальную ось в этот момент времени.
Следующая статья сложение и вычитания векторов векторной диаграммы.
Например, для t = t1
i1 = Imsin(ωt1 +Ψ)
в общем случае
i = Imsin(ωt +Ψ)
Получили такое же уравнение, каким был задан переменный ток, что свидетельствует о возможности изображения тока вращающимся вектором при нанесении его на чертеж в начальном положении.

Построение векторной диаграммы
Вращая вектор Im‘ против движения часовой стрелки, в прямоугольной системе координат построим график изменения проекции его на вертикальную ось в пределах одного оборота (одного периода). Получим известный уже график синусоидальной функции, соответствующий заданному уравнению.
При построении векторов положительные углы отсчитывают от положительного направления горизонтальной оси против вращения часовой стрелки, а отрицательные — по ее движению.
В процессе расчета электрической цепи определяется ряд синусоидальных величин. Все их можно изобразить на одном чертеже при помощи вращающихся векторов, привязав к одной паре взаимно перпендикулярных осей.
Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты в начальный момент времени, называется векторной диаграммой.
Например, напряжение и ток в электрической цепи выражаются уравнениями:
u = 125 sin(ωt + 30°)
i = 12 sin(ωt — 20°).

Векторная диаграмма такой цепи изображена на рис. 12.11. Если выбрать масштабы напряжения и тока
Mu = 50 В/см; Mi = 4 А/см;
то
Um = Um/Mu = 125/50 = 2,5 см; Im = Im = im/Mi = 12/4 = 3 см.
Векторная диаграмма содержит векторы синусоидальных величин одинаковой частоты, поэтому они вращаются с одинаковой частотой и их взаимное расположение не меняется.
Начало отсчета времени выбирают произвольно, поэтому один из векторов диаграммы можно направить произвольно; остальные же нужно располагать с учетом сдвига фаз по отношению к первому или предыдущему вектору.
Сложение и вычитание векторов
Главным достоинством векторных — это возможность простого сложения и вычитания двух величин.
 Например: требуется сложить, два тока, заданных уравнениями
Например: требуется сложить, два тока, заданных уравнениямиСложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:
Im = Im1 + Im2
Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель
но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.Вектор Im, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).
Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис.
 12.13):
12.13):При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.
Векторная диаграмма токов и напряжений: график, обозначения, виды
Использование векторных диаграмм при анализе, расчете цепей переменного тока делает возможным рассмотреть более доступно и наглядно происходящие процессы, а также в некоторых случаях значительно упростить выполняемые расчеты.
Векторной диаграммой принято называть геометрическое представление изменяющихся по синусоидальному (либо косинусоидальному) закону направленных отрезков — векторов, отображающих параметры и величины действующих синусоидальных токов, напряжений либо их амплитудных величин.
Широкое применение векторные диаграммы нашли в электротехнике, теории колебаний, акустике, оптике и т.д.
Различают 2-х вида векторных диаграмм:
- точные;
- качественные.

Интересное видео о векторных диаграммах смотрите ниже:
Точные изображаются по результатам численных расчетов при условии соответствия масштабов действующих значений. При их построении можно геометрически определить фазы и амплитудные значения искомых величин.
Васильев Дмитрий Петрович
Профессор электротехники СПбГПУ
Качественные диаграммы изображаются с учетом взаимных соотношений между электрическими величинами, без указания численных характеристик.
Они являются одним из основных средств анализа электрических цепей, позволяя наглядно иллюстрировать и качественно контролировать ход решения задачи и легко установить квадрант, в котором располагается искомый вектор.
Для удобства при построении диаграмм анализируют неподвижные векторы для определенного момента времени, который выбирается таким образом, чтобы диаграмма имела удобный для понимания вид.
 Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.Векторы, изображаемые на такой диаграмме, характеризуются равновеликой угловой частотой ω. В виду чего при вращении их взаимное расположение не изменяется.
Ещё одно полезное видео о векторных диаграммах:
Поэтому при изображении векторных диаграмм один вектор можно направить произвольным образом (например, по оси ОХ).
А остальные — изображать по отношению к исходному под различными углами, соответственно равными углам сдвига фаз.
Таким образом, векторная диаграмма дает отчетливое представление об опережении либо отставании различных электрических величин.

Допустим у нас есть ток, величина которого изменяется по некоторому закону:i = Im sin (ω t + φ).
С начала координат 0 под углом φ проведем вектор Im, величина которого соответствует Im. Его направление выбирается так, чтобы с положительным направлением оси OX вектор составлял угол — соответствующий фазе φ.
Абрамян Евгений Павлович
Доцент кафедры электротехники СПбГПУ
Проекция вектора на вертикальную ось и определяет значение мгновенного тока в начальный момент времени.
В основном векторные диаграммы изображают для действующих значений, а не амплитудных. Векторы действующих значений количественно отличаются от амплитудных значений — масштабом, поскольку:
I = Im /√2.
Основным преимуществом векторных диаграмм называют возможность простого и быстрого сложения и вычитания 2-х параметров при расчете электроцепей.Векторная диаграмма — Энциклопедия по машиностроению XXL
Отверстие перенесено в нейтральную зону (расположение отверстия должно быть согласовано с векторной диаграммой нагрузок) [c. 325]
325]Если в некотором сечении бруса, где действуют изгибающие моменты и Му (рис. 322, а), нужно найти положение нейтральной линии, то удобно для наглядности сначала показать положение силовой линии р—р. Наиболее просто выполнить это, построив векторную диаграмму моментов (рис, 322, б), которая показывает направление результирующего вектора-момента М и, следовательно, определяет угол а наклона его плоскости действия (силовой линии р—р) [c.333]
Из уравнений (4.7) видно, что Ёф является функцией 1а, а следовательно, /ф, т. е. ЭДС источника определяется режимом работы. цепи. В частном случае неявнополюсной синхронной машины, когда xa=xq, Ёф определяется только ЭДС возбуждения и не зависит от тока цепи. Если учесть также влияние магнитного насыщения, то в общем случае не только ЭДС, но и параметры схемы замещения будут иметь нелинейные характеристики в зависимости от тока цепи. Тем не менее переход к схемам замещения и векторным диаграммам позволяет использовать для решения хорошо известные методы расчета линейных и нелинейных электрических цепей постоянного и переменного тока.
[c.88]
Тем не менее переход к схемам замещения и векторным диаграммам позволяет использовать для решения хорошо известные методы расчета линейных и нелинейных электрических цепей постоянного и переменного тока.
[c.88]Расчетные зависимости, включаемые в расчетные блоки и модели ЭМП первого класса, выбираются в основном исходя из известных геометрических и тригонометрических закономерностей, связывающих конструктивные данные, и методов теории цепей для установившихся режимов (схемы замещения, векторные диаграммы и т. п.), рассмотренных в 4.1. Эти методы используются для расчета большинства электромагнитных, механических и тепловых характеристик ЭМП в установившихся режимах и приводят в общем случае к совокупности нелинейных алгебраических уравнений, решаемых в определенной последовательности. Если указанные методы оказываются не применимыми к расчету тех или иных характеристик, то для получения аналогичных выражений используются статистические и кибернетические методы ( 4.
 3, 4.4).
[c.124]
3, 4.4).
[c.124]Анализ структурного графа на рис. 5.4 вскрывает последовательный, многоэтапный характер электромагнитного расчета, основанного на методологии, изложенной в [8]. В данном случае можно выделить три основных этапа. На первом этапе вводятся НД, ОД, геометрические размеры воздушного зазора и паза якоря, что дает возможность определить векторную диаграмму и ненасыщенные параметры, расчетные коэффициенты магнитной цепи и магнитные характеристики воздушного зазора (поток, индукция, МДС). На втором этапе вводятся дополнительно высота спинки якоря и характеристики стали якоря, в результате чего определяются магнитные характеристики якоря вместе с коэффициентом насыщения и насыщенные значения параметров. На третьем этапе определяется необходимая МДС возбуждения, для чего требуется дополнительный ввод геометрических размеров и характеристик стали индуктора. [c.126]
Векторное уравнение (3.5) можно изобразить в виде векторной диаграммы, которая называется планом ускорений и показана на рис. 3.5, б. Для этого из произвольной точки -л, называемой полюсом плана ускорений, отложим вектор т.а, который в масштабе изображает вектор ускорения полюса ал. Масштабный коэффициент = ол/(т а) показывает, сколько единиц ускорения содержится в одном миллиметре вектора на плане.
[c.32]
3.5, б. Для этого из произвольной точки -л, называемой полюсом плана ускорений, отложим вектор т.а, который в масштабе изображает вектор ускорения полюса ал. Масштабный коэффициент = ол/(т а) показывает, сколько единиц ускорения содержится в одном миллиметре вектора на плане.
[c.32]Следовательно, при сложении двух гармонических колебаний одинакового периода, происходящих вдоль одной прямой, возникает результирующее гармоническое колебание той же частоты вдоль той же прямой, амплитуда и начальная фаза которого определяются из векторной диаграммы (рис. 4.1) [c.69]
Построим теперь так называемую векторную диаграмму импульсов. Сначала изобразим вектор р1 отрезком АВ (рис. 4.13), затем векторы р/ и р2, каждый из которых представляет собой, согласно (4.65), сумму двух векторов. [c.118]
Таким образом, для построения векторной диаграммы импульсов, соответствующей упругому столкновению двух частиц (одна из которых первоначально покоилась) необходимо [c.
 118]
118]И наконец, из той же векторной диаграммы импульсов можно найти связь между углами i и . [c.119]
Следует, однако, обратить внимание на одно принципиальное обстоятельство. Векторная диаграмма импульсов, в основе которой лежат законы сохранения импульса и энергии, давая нам полную картину всех возможных случаев разлета частиц после столкновения — результат сам по себе весьма существенный, — совершенно не говорит о том, какой из этих возможных случаев реализуется конкретно. Для установления этого необходимо обратиться к более детальному рассмотрению процесса столкновения с помощью уравнений движения. При этом выясняется, например, что угол рассеяния di налетающей частицы зависит от характера взаимодействия сталкивающихся частиц и от так называемого прицельного п ар а м етр а , неоднозначность же решения в случае т >т2 объясняется тем, что один и тот же угол рассеяния i9 i может реализоваться при двух значениях прицельного параметра, причем независимо от закона взаимодействия частиц.
 [c.120]
[c.120]Теперь рассмотрим тот же вопрос в /(-системе отсчета, где частица массы mi с импульсом pi испытывает столкновение с покоЯ L с щейся частицей массы Шг. Для определения возможных случаев разлета частиц после столкновения здесь также полезно воспользоваться векторной диаграммой импульсов. Ее построение аналогично тому, как это было сделано для упругого столкновения. Им-пульс налетающей частицы pt= [c.121]
Если же tni m.2, то физический смысл имеют оба знака перед корнем — ответ в этом случае неоднозначен под углом импульс рассеянной частицы может иметь одно из двух значений (это зависит от относительного расположения частиц в момент соударения). Последний случай соответствует векторной диаграмме, показанной на рис. 4.14, в. [c.130]
Воспользуемся векторной диаграммой импульсов, соответствующей предельному углу di пр (рис. 4.21). Из прямоугольного треугольника АСО следует, что [c.131]
Распад частицы.
 Частица с импульсом ро (в К-системе) распалась на лету на две частицы с массами mi и т . При этом выделилась энергия Q — энергия распада (она перешла в кинетическую энергию). Построить векторную диаграмму импульсов для этого процесса и найти с помощью нее возможные импульсы pi и р2 возникших частиц.
[c.131]
Частица с импульсом ро (в К-системе) распалась на лету на две частицы с массами mi и т . При этом выделилась энергия Q — энергия распада (она перешла в кинетическую энергию). Построить векторную диаграмму импульсов для этого процесса и найти с помощью нее возможные импульсы pi и р2 возникших частиц.
[c.131]С помощью этих формул построим векторную диаграмму импульсов (рис. 4.22). Изобразим сначала отрезок АВ, равный импульсу ро. Затем радиусом р проведем окружность с центром в точке О, которая делит отрезок АВ на две части в отношении mi отг- Эта окружность и есть геометрическое место точек всех возможных положений вершины С треугольника импульсов AB . [c.132]
Векторная диаграмма для определения амплитуды колебаний [c.264]
В чем заключается метод векторных диаграмм в применении к задачам дифракции Разберите таким способом дифракцию света на круглом отверстии и крае экрана. [c.458]
Рис.  8.7. Векторная диаграмма суммирования действия отдельных участков зоны.
8.7. Векторная диаграмма суммирования действия отдельных участков зоны.
Для того чтобы учесть действие второй зоны, надо продолжить нашу векторную диаграмму. Тогда мы получим рис. 8.9, причем хорда дуги несколько меньше, чем у дуги ОМ , вследствие [c.159]Рис. 8.8. Векторная диаграмма действия центральной (первой) зоны. Рис. 8.9. Векторная диаграмма действия первой и второй зон.
Подобно тому как мы построили векторную диаграмму для учета действия различных кольцевых зон (см.Рис. 8.10. Векторная диаграмма действия всей волны.  35), можно построить графически диаграмму действия различных лунок. Очевидно, получится также кривая в форме спирали, однако вследствие
[c.166]
35), можно построить графически диаграмму действия различных лунок. Очевидно, получится также кривая в форме спирали, однако вследствие
[c.166]Графически результат сложения амплитуд для любой точки экрана можно представить векторными диаграммами рис. 9.1. [c.174]
Кроме того, наличие фазового сдвига, равного я/2, указывает на сдвиг фазы между колебаниями в реальной световой волне и во вторичных волнах Френеля. Поэтому в соответствии с выводом, полученным в 38 с помощью рассмотрения векторной диаграммы, источникам вторичных волн следует приписывать фазу, увеличенную на /2Я по сравнению с фазой световых колебаний, т. е. ввести член /гя в аргумент косинуса в выражении (43.1). [c.190]
Для определения величины и направления равнодействующей будем последовательно складывать силы по правилу силового треугольника. Чтобы не загромождать рисунка, проделаем это в стороне, построив векторную диаграмму — силовой многоугольник.
 [c.22]
[c.22]На практике, как правило, определяют не сами потери, а тангенс угла диэлектрических потерь. Эту величину вводят следующим образом. Построим векторную диаграмму токов для конденсатора, заполненного диэлектриком с потерями. Как известно, потери в электротехнике обычно описываются углом ф между векторами напряжения и тока (рис. 8.15). [c.303]
Чтобы отобрать тройки состояний, которые дают вклад в (5.7) при фиксированном к, можно задать к, тогда к» определится уравнением (5.3). (Это эквивалентно выбору точки А на векторной диаграмме фиг. 4.) Однако резонансный множитель [1 — os (поверхности вращения вокруг оси к (или к-[-2-к Ь), причем поверхность задается уравнением [c.233]Рис. 8.15. Векторная диаграмма токов Чтобы сосчитать число процессов, дающих существенный вклад в (7.
 8), рассмотрим замкнутую векторную диаграмму, как на фиг. 4. При данном к, любая вершина А соответствует решению уравнения (5.3а), но существенными являются лишь те решения, которым соответствуют вершины, лежащие на поверхности вращения, задаваемой уравнением (5.8). Таким образом, число решений с к в интервале от к до k +dk примерно пропорционально k dk.
[c.240]
8), рассмотрим замкнутую векторную диаграмму, как на фиг. 4. При данном к, любая вершина А соответствует решению уравнения (5.3а), но существенными являются лишь те решения, которым соответствуют вершины, лежащие на поверхности вращения, задаваемой уравнением (5.8). Таким образом, число решений с к в интервале от к до k +dk примерно пропорционально k dk.
[c.240]Для изучения случаев, когда тело одновременно участвует в нескольких гармонических колебаниях, удобно пользоваться графическим способом изображения колебаний — с помощью так называемой векторной диаграммы. [c.176]
Результирующее смещение тела в данный момент определяется суммой независимых смещений, приобретаемых телом в каждом из складываемых колебаний x = Xi+X2. Это результирующее смещение можно найти с помощью векторной диаграммы. Построим для этого по правилу сложения векторов вектор амплитуды результирующего колебания а (рис. 139). Очевидно, проекция его на ось ОХ равна сумме проекций Xi и Хг векторов амп.литуды И] и аг на эту же ось и изменяется со временем по закону [c.177]
Пользуясь векторной диаграммой, можно складывать не только два, но и любое число колебаний с разными амплитудами и начальными фазами, но с одинаковой частотой. Причем если не требуется слишком большая точность, то амплитуда и начальная фаза результирующего колебания могут быть измерены по векторной диаграмме. [c.178]
Векторная диаграмма 176 Вес тела 36, 94 Водоизмещение 134 Волна 199 [c.254]
Такие процессы называются нормальными, или Ы-про-цессами. Из векторной диаграммы согласно (1.45) следует, что Ы-процессы не меняют направление передачи энергии и поэтому не влияют на тепловое сопротивление. [c.45]
Если из точки О в каждый данный момент времени отложить соответствующий ему вектор мгновенной скорости и провести через концы таких векторов поверхность, можно получить векторную диаграмму скорости — так называемый годограф скорости. [c.126]
При помощи основных уравнений учитываются особенности каждого лопастного колеса и связываются параметры потока с геометрическими размерами гидротрансформатора методом векторных диаграмм скоростей. [c.308]
Рис, 13,44. К определению положения корректирующей массы при уравновешивании ротора а) положение г.ектора центробежной силы при первом испытании б) векторная диаграмма дейстаующнх сил после установки корректирующей массы в) векторная дна-грамгла действующих сил при третьем испытании о корректирующей массой [c.298]Тогда переменгение, скорость и ускорение точки, совершающей гармонические колебания, может быть представлена простой векторной диаграммой (рис. 5.5), где проекция скорости движения представляется 12 [c.355]
Если каждую зону Френеля разбить на бесконечное большое число элементарных зон, то ломаные линии превратятся в дугу и каждой зоне Френеля будет соответствовать одна полуокружность. В результате при учете влияния всех зон получится спираль с фокусом в точке N (рис. 6.6, б). Угол, которь ш составляет результирующий вектор сданным направлением, соответствует фазе результирующего колебания в точке наблюдения. Построенная таким образом векторная диаграмма позволяет определить амплитуду и фазу результирующего колебания для произвольного числа действующих зон Френеля. Например, если открыта половина первой зоны, то результирующая амплитуда будет изображаться вектором ОК- Аналогично, ONi, ОN2, ON3, ONi, ON , ON будут соответствовать [c.129]
Для иостроения векторной диаграммы проведем ось ОХ (рис. 138). Из точки О под углом а к оси ОХ, равным начальной фазе колебаний, отложим отрезок прямой, длина которого в выбранном масштабе равна амплитуде колебаний. Этот отрезок принято называть вектором амплитуды. [c.176]
На этой же векторной диаграмме можно изобразить скорость и ускорение колеблющегося тела. Скорость может быть представлена как проекция вектора длины асоо, вращающегося с той же угловой скоростью соо, что и вектор амплитуды, но повернутого относительно него на я/2. Аналогично, ускорение можно представить как проекцию вектора длины асоо , вращающегося также с угловой скоростью соо, но уже повернутого относительно вектора амплитуды на угол я (рис. 138). [c.177]
Векторные диаграммы. построение векторных диаграмм
Обоснование векторной диаграммы
Предположим, что ток задан уравнением
i = Imsin(ωt +Ψ)
Проведем две взаимно перпендикулярные оси и из точки пересечения осей проведем вектор Im, длина которого в определённом масштабе Mi выражает амплитуду тока Im:
Im = Im/Mi
Направление вектора выберем так, чтобы с положительным направлением горизонтальной оси вектор составлял угол, равный начальной фазе Ψ (рис. 12.10).
Проекция этого вектора на вертикальную ось определяет мгновенный ток в начальный момент времени: i = ImsinΨ.
Представим себе, что вектор Im вращается против движения часовой стрелки с угловой скоростью, равной угловой частоте ω. Его положение в любой момент времени определяется углом ωt +Ψ ,
Тогда мгновенный ток для произвольного момента времени t можно определить проекцией вектора Im на вертикальную ось в этот момент времени.
Следующая статья сложение и вычитания векторов векторной диаграммы.
Например, для t = t1
i1 = Imsin(ωt1 +Ψ)
в общем случае
i = Imsin(ωt +Ψ)
Получили такое же уравнение, каким был задан переменный ток, что свидетельствует о возможности изображения тока вращающимся вектором при нанесении его на чертеж в начальном положении.
Сложение и вычитание векторов
Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями
Сложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:
Im = Im1 + Im2
Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель
но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.Вектор Im, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).
Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):
При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.
Примеры применения
В следующих разделах приведены описания задач, которые решают с помощью представленной методики. Следует подчеркнуть, что применение комплексных чисел пригодно для сложных расчетов с высокой точностью. Однако на практике достаточно часто сравнительно простой векторной графики с наглядным отображением исходной информации на одном рисунке.
Механика, гармонический осциллятор
Таким термином обозначают устройство, которое можно вывести из равновесного состояния. После этого система возвращается в сторону исходного положения, причем сила (F) соответствующего воздействия зависит от дальности первичного перемещения (d) прямо пропорционально. Величину ее можно уточнить с помощью постоянного корректирующего коэффициента (k). Отмеченные определения связаны формулой F=-d*k
Формулы для расчета основных параметров гармонического осциллятора
К сведению. Аналогичные процессы происходят в системах иной природы. Пример – создание аналога на основе электротехнического колебательного контура (последовательного или параллельного). Формулы остаются теми же с заменой соответствующих параметров.
Свободные гармонические колебания без затухания
Продолжая изучение темы на примерах механических процессов, можно отметить возможность построения двухмерной схемы. Скорость в этом случае на оси Х отображается так же, как и в одномерном варианте. Однако здесь можно учесть дополнительно фактор ускорения, которое направляют под углом 90° к предыдущему вектору.
Гармонический осциллятор с затуханием и внешней вынуждающей силой
В этом случае также можно воспользоваться для изучения взаимного влияния дополнительных факторов векторной графикой. Как и в предыдущем примере, скорость и другие величины представляют в двухмерном виде. Чтобы правильно моделировать процесс, проверяют суммарное воздействие внешних сил. Его направляют к центру системы (точке равновесия). С применением геометрических формул вычисляют амплитуду механических колебаний после начального воздействия с учетом коэффициента затухания и других значимых факторов.
Расчет электрических цепей
Векторную графику применяют для сравнительно несложных цепей, которые созданы из набора элементов линейной категории: конденсаторы, резисторы, катушки индуктивности. Для более сложных схем пользуются методикой расчета «Комплексных амплитуд», в которой реактивные компоненты определяют с помощью импедансов.
Векторная диаграмма для схемы соединений без нейтрального провода – звезда
Векторная диаграмма в данном случае выполняет функцию вспомогательного чертежа, который упрощает решение геометрических задач. Для катушек и конденсаторов, чтобы не пользоваться комплексным исчислением, вводят специальный термин – реактивное сопротивление. При синусоидальном токе изменение напряжения на индуктивном элементе описывается формулой U=-L*w*I0sin(w*t+f0).
Несложно увидеть подобие с классическим законом Ома. Однако в данном примере изменяется фаза. По этому параметру на конденсаторе напряжение отстает от тока на 90°. В индуктивности – обратное распределение. Эти особенности учитывают при размещении векторов на рисунке. В формуле учитывается частота, которая оказывает влияние на величину этого элемента.
Схемы и векторные диаграммы для идеального элемента и диэлектрика с потерями
Преобразование Фурье
Векторные технологии применяют для анализа спектров радиосигналов в определенном диапазоне. Несмотря на простоту методики, она вполне подходит для получения достаточно точных результатов.
Сложение двух синусоидальных колебаний
В ходе изучения таких источников сигналов рекомендуется работать со сравнительно небольшой разницей частот. Это поможет создать график в удобном для пользователя масштабе.
Фурье-образ прямоугольного сигнала
В этом примере оперируют суммой синусоидальных сигналов. Последовательное сложение векторов образует многоугольник, вращающийся вокруг единой точки. Для правильных расчетов следует учитывать отличия непрерывного и дискретного распределения спектра.
Для этого случая пользуются тем же отображением отдельных синусоид в виде векторов, как и в предыдущем примере. Суммарное значение также вписывается в окружность.
Топографическая векторная диаграмма
Топографическая векторная диаграмма рис. 12.7, а, в которой векторы фазных напряжений сходятся в одной точке, соответствующей нулевой точке приемника, обычно заменяется диаграммой рис. 12.7, б, где эти векторы выходят из этой же точки; так как при этом все векторы фазных и линейных напряжений изменяют свои направления на обратные, приведенные выше соотношения между напряжениями сохраняются.
Преимущество топографической векторной диаграммы заключается в том, что она может быть построена без изменения топографии цепи и потому является потенциальной диаграммой.
По топографической векторной диаграмме легко определить вектор напряжения между двумя произвольными точками цепи.
Схема ( а и топографическая векторная диаграмма ( б цепи, состоящей из двух параллельных ветвей.
По топографической векторной диаграмме легко определяется вектор напряжения между двумя произвольными точками цепи. Этот вектор обычно обозначают индексом, первой буквой которого является точка более высокого потенциала. К ней направлен вектор на диаграмме.
При построении топографической векторной диаграммы схемы рис. 5.10, а вектор тока направляем горизонтально и обход цепи против направления тока начинаем с точки а, потенциал которой принимаем за исходный.
При построении топографической векторной диаграммы схемы рис. 7.10, а на рис. 7.10, б вектор тока направлен горизонтально. Предположим, что обход цепи против тока начат с точки а, потенциал которой примем за исходный. Потенциал точки с будет выше потенциала точки Ь на величину, падения напряжения на втором участке, вектор которого с / 2 r2 / — jxj имеет активную и емкостную составляющие. Векторы этих падений напряжений отложены на диаграмме в той же последовательности, в какой совершается обход цепи. Аналогично построены векторы напряжений и других участков цепи.
Z при помощи топографической векторной диаграммы и аналитически.
Топографическая векторная диаграмма для схемы 9 — 5.
Полученные соотношения позволяют построить топографическую векторную диаграмму, представленную на рис. 9 — 8, которая дает возможность найти непосредственно графическим путем напряжение между любыми двумя пунктами схемы.
Векторная диаграмма трехфазного трансформатора в режиме холостого хода.
На рис. 13.26 6 построены топографические векторные диаграммы, поясняющие это положение. Заметим, что одноименными называют напряжения, векторы которых имеют одинаковый буквенный индекс. При построении этих диаграмм учитывалось совпадение по направлению векторов одноименных фазных напряжений первичной и вторичной обмоток, так как они создаются общими фазными потоками в стержнях магнитопровода.
В этом легко убедиться непосредственно из топографической векторной диаграммы или аналитического вывода. На рис. 9 — 3, в показаны векторы и соответствующие мгновенные значения междуфазных напряжений.
Для цепи с несколькими участками обычно строят топографическую векторную диаграмму напряжений, каждая точка которой соответствует определенной точке электрической цепи. Чтобы осуществить соответствие точек диаграммы и цепи, построение векторов топографической векторной диаграммы ведут в той же последовательности, в какой обходят электрическую цепь. Обычно направление обхода выбирают противоположным положительному направлению тока в цепи.
На рис. 5 — 31, б построена топографическая векторная диаграмма: отложен вектор U, от него — под углом cpj в сторону отст.
Разновидности векторных диаграмм
Для корректного отображения переменных величин, которые определяют функциональность радиотехнических устройств, хорошо подходит векторная графика. Подразумевается соответствующее изменение основных параметров сигнала по стандартной синусоидальной (косинусоидальной) кривой. Для наглядного представления процесса гармоническое колебание представляют, как проекцию вектора на координатную ось.
С применением типовых формул несложно рассчитать длину, которая получится равной амплитуде в определенный момент времени. Угол наклона будет показывать фазу. Суммарные влияния и соответствующие изменения векторов подчиняются обычным правилам геометрии.
Различают качественные и точные диаграммы. Первые применяют для учета взаимных связей. Они помогают сделать предварительную оценку либо используются для полноценной замены вычислений. Другие создают с учетом полученных результатов, которые определяют размеры и направленность отдельных векторов.
Круговая диаграмма
Допустим, что надо изучить изменение параметров тока в цепи при разных значениях сопротивления резистора в диапазоне от нуля до бесконечности. В этой схеме напряжение на выходе (U) будет равно сумме значений (UR и UL) на каждом из элементов. Индуктивный характер второй величины подразумевает перпендикулярное взаимное расположение, что хорошо видно на части рисунка б). Образованные треугольники отлично вписываются в сегмент окружности 180 градусов. Эта кривая соответствует всем возможным точкам, через которые проходит конец вектора UR при соответствующем изменении электрического сопротивления. Вторая диаграмма в) демонстрирует отставание тока по фазе на угол 90°.
Линейная диаграмма
Здесь изображен двухполюсный элемент с активной и реактивной составляющими проводимости (G и jB, соответственно). Аналогичными параметрами обладает классический колебательный контур, созданный с применением параллельной схемы. Отмеченные выше параметры можно изобразить векторами, которые расположены постоянно под углом 90°. Изменение реактивной компоненты сопровождается перемещением вектора тока (I1…I3). Образованная линия располагается перпендикулярно U и на расстоянии Ia от нулевой точки оси координат.
Оцените статью:1
Первый слайд презентации: Сложение колебаний
Сложение однонаправленных колебаний, происходящих с одинаковой частотой. Метод векторных диаграмм.
Изображение слайда
2
Слайд 2
Сложение однонаправленных колебаний. Пусть материальная точка участвует одновременно в двух гармонических колебаниях, причем движение совершается вдоль одного направления. Тогда её смещение из положения равновесия складывается из двух смещений: Если частоты колебаний различны, то картина движения точки будет достаточно сложной. Если же частоты одинаковы, результирующее движение также будет гармоническим колебанием. Электромагнитные колебания (например, колебания силы тока в цепях переменного тока) также подчиняются гармоническому закону. Если в цепи происходят одновременно два гармонических колебания, то результирующий ток можно записать так:
Изображение слайда
3
Слайд 3
Для колебаний с одинаковыми частотами имеем: Сложение однонаправленных колебаний. Уравнения, описывающие как механические, так и электромагнитные колебания, одинаковы, следовательно метод сложения колебаний будет одним и тем же, а результаты сходными.
Изображение слайда
4
Слайд 4
Метод векторных диаграмм. Идея метода основана на двух простых положениях. Проекция вектора с модулем R на любую из координатных осей, вращающегося с постоянной угловой скоростью, совершает гармонические колебания. При сложении двух векторов проекция суммарного вектора равна сумме проекций складываемых векторов.
Изображение слайда
5
Слайд 5
Метод векторных диаграмм. , Проекции вектора на оси: Если вектор вращается с постоянной угловой скоростью ω, то = t + 0. С течением времени величины проекций вращающегося вектора изменяются так:
Изображение слайда
6
Слайд 6
Метод векторных диаграмм. Видно, что каждая из величин проекций вектора изменяется по гармоническому закону, так же, как и любые величины, совершающие гармонические колебания. В дальнейшем будем рассматривать только проекции векторов на ось OX.
Изображение слайда
7
Слайд 7
Метод векторных диаграмм. Пусть теперь в плоскости XY вокруг оси, проходящей через начало координат вращаются два вектора. Если векторы вращаются с одинаковой угловой скоростью , то При этом угол между векторами
Изображение слайда
8
Слайд 8
Метод векторных диаграмм. Углы 01 и 02 можно отождествить с начальными фазами гармонических колебаний, модули векторов – с амплитудами гармонических колебаний, а величину угловой скорости вращения векторов – с циклической частотой гармонических колебаний. В таком случае величина 0 является разностью фаз двух гармонических колебаний.
Изображение слайда
9
Слайд 9
Метод векторных диаграмм. Сумма проекций векторов на ось OX Таким образом, сумма проекций векторов равна сумме двух гармонических функций с одинаковой циклической частотой и разными фазами. Геометрически сумма проекций двух векторов на ось OX равна проекции на ось OX вектора
Изображение слайда
10
Слайд 10
Метод векторных диаграмм. При этом, так как угол между векторами не зависит от времени, вектор будет вращаться в плоскости XY с той же угловой скоростью , что и векторы и.
Изображение слайда
11
Слайд 11
Метод векторных диаграмм. Алгоритм применения графического способа сложения гармонических колебаний с одинаковой частотой, называемого методом векторных диаграмм. 1. Выбрать оси координат и построить векторные диаграммы складываемых колебаний. Длина вектора должна быть равна амплитуде колебаний, а угол наклона к оси – начальной фазе колебаний. 2. Построить, пользуясь правилом параллелограмма, вектор, равный сумме двух складываемых векторов. 3. Длина (модуль) суммарного вектора равна амплитуде суммарного колебания, угол наклона суммарного вектора к оси – его начальной фазе.
Изображение слайда
12
Слайд 12
Метод векторных диаграмм. Модуль суммарного вектора можно определить с помощью теоремы косинусов cos ( — ) = — cos ( )
Изображение слайда
13
Слайд 13
Метод векторных диаграмм. Начальную фазу суммарного колебания можно определить так. Из треугольника OPN
Изображение слайда
14
Слайд 14
Метод векторных диаграмм.
Изображение слайда
15
Слайд 15
Метод векторных диаграмм.
Изображение слайда
16
Слайд 16
Метод векторных диаграмм.
Изображение слайда
17
Последний слайд презентации: Сложение колебаний
Метод векторных диаграмм.
Изображение слайда
Фазоры и фазовая алгебра
«Фазор» определяется как «Комплексное число в полярной форме, с помощью которого мы можем анализировать схему». Это векторная величина. В этом векторном представлении мы используем декартову плоскость.
Ось Y представляет величину и фазовый угол формы волны в виде мнимых величин, а ось X представляет реальные величины, такие как период времени формы волны. Величина формы волны обычно измеряется как среднеквадратичное значение напряжения. Итак, векторами мы представляем среднеквадратичное значение напряжения.
Всегда вектор вращается против часовой стрелки вместе с фазой сигнала. В векторном представлении комплексное число включает величину и фазовый угол любой формы волны.
Комплексное число состоит из действительного и мнимого числа. Давайте разберемся с этим ясно.
- Действительное число: Действительное число в векторном комплексном числе представляет величину или амплитуду сигнала. Его также можно назвать длиной вектора.
- Мнимое число: Мнимое число представляет фазовый угол сигнала.Вектор вращается в комплексной плоскости в пределах диапазона переменного синусоидального сигнала, то есть от 0 до 2. Вектор вращается в координатах X и Y, когда амплитуда и фазовые углы изменились. Если мы представим взаимозаменяемые значения вместо действительной и мнимой частей, мы можем получить неверное значение, и это повлияет на общий анализ системы.
В начало
Определение фазора
Каждая переменная волна имеет положительный полупериод и отрицательный полупериод в своем полном цикле вращения вместе с осью координат.Конечно, вектор также представляет волновые свойства только в координатной плоскости. Фаза сигнала на один полный оборот составляет 2π или 360 0 . В векторе мы представляем мгновенное напряжение (или амплитуду) движущимся вектором, как показано на рисунке ниже.
На приведенном выше рисунке линия A представляет максимальную амплитуду формы волны, а линия «I» — величину в точке P векторного представления вектора. Вектор представляет значения от 0 0 до 360 0 на оси в различные моменты времени.
Вектор представляет величину и фазу сигнала. Величина отображается по вертикальной оси, а фаза формы волны отображается по горизонтальной оси. Фаза сигнала может быть представлена в градусах или радианах.
Разность фаз
Когда мы анализируем две формы волны или две характеристики одной формы волны, мы сравниваем эти две формы волны в одной координатной плоскости. Затем нам нужно проанализировать каждую форму волны в каждой позиции.Например, сравнивая напряжение и ток формы волны, мы представляем их на одной оси, как показано ниже.
Для нашего анализа предположим, что есть цепь с напряжением и током. Здесь волна «I» представляет характеристики тока, а волна «v» представляет характеристики напряжения волны. Разность фаз двух сигналов отображается как «θ». Волна тока опережает волну напряжения с разностью фаз θ. Уравнения для математического выражения напряжения и тока приведены ниже.
В t = V м sin (ωt)
I t = I м sin (ωt — Φ)
Где Vm — максимальное напряжение, а Φ — фазовый угол.
В начало
Фазорная диаграмма синусоидальной формы волны
Чтобы нарисовать векторную диаграмму, мы должны следовать некоторым правилам, согласно которым вектор векторного вектора всегда вращается по часовой стрелке, а нулевая фаза сигнала отображается на положительной оси X.
Векторная диаграмма соответствует фазе и величине формы волны.Мы представляем период времени или фазовый угол по оси X и величину по оси Y. Длина вектора вектора пропорциональна значениям напряжения или тока в любой момент времени.
Как мы уже знаем, в случае резисторов нет разности фаз между волной напряжения и волной тока. Но в случае катушек индуктивности вектор тока отстает от вектора напряжения на фазовый угол Φ, и эти два вектора вращаются против часовой стрелки.
Это потому, что напряжение отстает в направлении отрицательных координат.Таким образом, фазовый угол также измеряется против часовой стрелки.
Если мы остановим векторы напряжения и тока под углом 30 0 , то векторы векторов будут выглядеть, как показано на рисунке ниже
Поскольку две формы сигнала имеют одинаковую частоту, они будут поддерживать одинаковую разность фаз на всем протяжении время. Таким образом, даже под углом 300 мы можем наблюдать, что вектор тока отстает от вектора напряжения. Другими словами, вектор напряжения опережает вектор тока.
Но, чтобы сказать, что один вектор опережает, а другой вектор или отстает от другого вектора; Сначала мы должны сделать один из двух векторов векторов эталоном.Исходя из этого, мы можем сказать ведущие или запаздывающие векторы векторов.
В начало
Phasor Algebra
Каждый вектор имеет величину и угловое смещение или разность фаз вдоль их оси X и оси Y. Если мы хотим выполнить математические операции, такие как сложение или вычитание, умножение или деление, над этими векторами, сначала нам нужно разделить векторы на его компоненты вектора, такие как компонент X: VA cos ϕ и компонент Y: VAsin ϕ, используя основы тригонометрии.
Добавление фазора
Чтобы проанализировать две или более волн, нам нужно добавить или вычесть векторы сигналов. Если мы анализируем цепи переменного тока, синфазные волны не имеют разности фаз, а разность фаз несинфазированных волн измеряется в градусах или радианах.
Пример: Если две формы волны напряжения 25 В и 32 В с одинаковой частотой и предположим, что они синфазны. Мы можем сложить два напряжения, чтобы найти сумму напряжений, мы получаем 57 вольт.
Если два напряжения имеют разные фазы, что означает, что формы волны не совпадают по фазе, мы не можем добавить их напрямую, чтобы найти общее напряжение. Это потому, что две формы волны имеют разные направления.
В этом случае мы можем найти полное напряжение цепи переменного тока, сложив две формы волны векторным методом. Это называется «Векторная сумма» или «Результирующий вектор» с использованием тригонометрического закона, называемого «законом параллелограмма».
Сложение двух фазоров
Давайте посмотрим на примере, чтобы понять, что такое сложение фазоров.
Предположим, что цепь переменного тока имеет две формы волны напряжения, например 20 вольт и 30 вольт, скажем, V1 и V2 соответственно. Если волна напряжения V1 опережает V2 на фазу 60 0 . Давайте найдем полное напряжение цепи переменного тока методом сложения векторов или векторов.
Сначала мы должны нарисовать векторную диаграмму вектора с двумя векторами напряжения, параллелограмм. Как показано ниже.
После этого найдите сумму напряжений обычным методом сложения, например V1 + V2, а затем найдите длину диагонали.Это называется «результирующий вектор» или «вектор r». Этот результирующий вектор представлен как «VT». Он проводится от начала координат (нуля) до poi (точки пересечения) двух векторов напряжения, скажем, OA.
Хотя графический метод сложения векторов дает нам точные результаты о схеме, очень много времени уходит на то, чтобы нарисовать и масштабировать все векторы напряжения в масштабе. Если эти векторы нарисованы неточно, мы можем получить ошибочный отчет о цепи переменного тока. Затем следует следовать аналитическому методу.
В методе сложения векторов мы должны складывать векторы напряжения с учетом их вертикального и горизонтального направлений. Метод использования компонентов синуса и косинуса называется «Метод прямоугольной формы».
В этом методе комплексное число векторов Z = a ± by делится на две части: одна — мнимая, а другая — действительная.
Определение сложной синусоиды
Величина напряжения в аналитическом методе задается как
Vm = cos (Φ) + j Vm (sin Φ)
Суммирование векторов приведено ниже.
Если первый вектор — это V1 = a + jb, а второй вектор — это V2 = x + jy; тогда результирующая векторная сумма дается как
Vr = V1 + V2 = (a + x) + j (b + y)
Сложение векторов с использованием прямоугольной формы
Напряжение второго вектора составляет 30 вольт в горизонтальном направлении и 0 в вертикальном направлении. Таким образом, его действительная и мнимая части могут быть объяснены как
Горизонтальная составляющая = 30 cos 0 0 = 30 вольт
Вертикальная составляющая = 30 sin0 0 = 0 вольт
Таким образом, напряжение V2 в сложной форме равно V2 = 30 + j0
Аналогично, напряжение второго вектора составляет 20 вольт в горизонтальном направлении и, поскольку он опережает напряжение на 600 в вертикальном направлении.Таким образом, его действительная и мнимая части могут быть объяснены как
Горизонтальная составляющая = 20 cos 60 0 = 20 x 0,5 = 10 вольт
Вертикальная составляющая = 20 sin 60 0 = 20 x 0,866 = 17,32 вольт
Итак Напряжение V1 в сложной форме равно V1 = 10 + j17.32
Результирующее напряжение VT может быть вычислено путем сложения горизонтальной и вертикальной составляющих. То есть
VHorizontal = сумма реальных частей V1 и V2 = 30 + 10 = 40 вольт
VVertical = сумма мнимых частей V1 и V2 = 0 + 17.32 = 17,32 В
Теперь величину результирующего вектора VT можно вычислить с помощью теоремы Пифагора для треугольника.
Результирующий вектор VT показан на приведенном ниже рисунке.
В начало
Вычитание фазора
Как мы говорили ранее, мы можем выполнять все математические операции, такие как сложение, вычитание и умножение, деление и т. Д. Мы узнали, как складывать два вектора и находить результирующий вектор. Теперь давайте посмотрим на вычитание двух векторов.
Вычитание векторов или векторов очень похоже на сложение векторов. При векторном вычитании разность двух векторов V1 и V2 равна диагонали параллелограмма. Это показано на рисунке.
Вычитание вектора приведено ниже.
Если первый вектор — это V1 = a + jb, а второй вектор — это V2 = x + jy; тогда результирующая разность векторов дается как
Vr = V1 + V2 = (a + x) — j (b + y)
Вернуться к началу
Представление трехфазного фазора
Мы узнали об однофазной катушке переменного тока генерируемые синусоидальные волны, т.е.е. однофазные синусоидальные волны. Теперь есть еще одна фаза, которую мы чаще всего используем при передаче энергии в электронике. Это «Три фазы». Обычно мы часто встречаем это слово в повседневной жизни. Теперь давайте посмотрим, что на самом деле означает 3 фазы?
- В однофазном режиме только одна катушка или провод будет вращаться в магнитном поле, но в трехфазном будет три вала, вращающихся в магнитном поле под углом 120 0 друг к другу и подключенных к одному и тому же вал.
- Эти 3 катушки будут иметь одинаковое количество витков coli.Таким образом, мы можем сказать, что ток, генерируемый тремя катушками, подключенными к одному (одному) ротору, разделенным углом 120 0 , называется «трехфазным током».
- Трехфазный источник питания будет иметь 3 отдельных синусоидальных напряжения с одинаковой частотой и величиной (амплитудой) с разными фазами. Чтобы легко понять и идентифицировать концепцию трех фаз, мы представляем три фазы разными цветами.
- В качестве однофазных векторов три фазовых вектора также вращаются против часовой стрелки с угловой скоростью ω радиан / сек.
Трехфазный симметричный вектор при соединении треугольником показан ниже.
Требования к 3-фазной сбалансированной системе
Чтобы сбалансировать 3-фазную систему, мы должны установить 3 синусоидальные волны в соответствии с условиями, перечисленными ниже.
I. Все 3 переменные должны иметь одинаковую амплитуду.
II. Все 3 переменные должны иметь одинаковую амплитуду.
III. Все 3 переменные должны быть разделены в фазе 120 0 .
Представление трехфазной синусоидальной волны показано на рисунке ниже.
Из приведенного выше рисунка мы можем сказать, что форма волны с фазой «а» (синего цвета) не в фазе с формой волны фазы «b» (фиолетового цвета), и эта форма волны не в фазе с третьим сигналом фазы «c» (зеленым цветом).
Разность фаз между этими тремя сигналами составляет 120 0 . Эти формы волны могут представлять ток или напряжение в цепи переменного тока.
3-фазные уравнения напряжения
Напряжения трех форм волны представлены как
Va = √2Vm cos (ωt + Φ)
Vb = √2Vm cos (ωt + Φ — 120 0 )
Vc = √2Vm cos (ωt + Φ- 240 0 ) = √2Vm cos (ωt + Φ +120 0 )
Проще говоря, мы можем сказать, что фаза «b» следует за 120 0 после «a », А фаза« c »следует за фазой« b »120 0 .
В начало
Резюме
Давайте резюмируем концепцию, векторные диаграммы и векторную алгебру.
- Комплексное число в полярной форме — это фазор. Величина отображается по оси Y действительным числом; период времени или фаза отображается на оси X с мнимым числом.
- Векторы всегда вращаются против часовой стрелки.
- Векторы могут представлять две или более синусоидальных величин в любой момент времени, как по величине, так и за период времени в направлении их вращения.
- Длина вектора вектора представляет среднеквадратичную скорость формы волны.
- Мы используем векторы для представления фазы напряжения, формы волны тока и анализа схемы.
- Фазор — это векторные величины, которые подходят только для синусоидальных волн.
- На любой векторной диаграмме представленные формы волн должны иметь одинаковую частоту и одинаковую амплитуду.
- Если разность фаз между формами волны равна нулю, то формы волны называют «синфазными».
- Если формы волны имеют разность фаз между собой, как Φ; говорят, что они «не в фазе».
- Мы можем выполнять все типы математических операций с векторными векторами, найдя результирующий вектор данных векторов.
- Вектор, полученный путем сложения или вычитания двух векторов, называется «Результирующий вектор». Он обозначен буквой «Vr».
- В дополнение к векторному сложению результирующий вектор задается как Vr = V1 + V2 = (a + x) + j (b + y)
- При векторном вычитании результирующий вектор задается как Vr = V1 + V2 = (a + x) — j (b + y)
- Трехфазное векторное представление будет иметь 3 вектора, представляющие 3 вращающиеся катушки одного и того же проводника.
- В трехфазной системе три вектора (формы волны) будут разделены друг от друга фазой 120 0 .
Вернуться к началу
Взаимодействие со звуковыми волнами | Безграничная физика
Наложение
Суперпозиция происходит, когда две волны занимают одну и ту же точку (волна в этой точке находится путем сложения двух амплитуд волн).
Цели обучения
Определить условия, необходимые для наложения двух волн
Основные выводы
Ключевые моменты
- Когда две волны занимают одну и ту же точку, происходит наложение.Суперпозиция приводит к сложению двух волн вместе.
- Конструктивная интерференция — это когда две волны накладываются друг на друга, и результирующая волна имеет более высокую амплитуду, чем предыдущие волны.
- Деструктивная интерференция — это когда две волны накладываются и нейтрализуют друг друга, что приводит к снижению амплитуды.
- Большинство волновых суперпозиций включают смесь конструктивной и деструктивной интерференции, поскольку волны не полностью идентичны.
Ключевые термины
- наложение : для размещения объекта поверх другого объекта.
Волны чаще всего описываются вариациями некоторых параметров в пространстве и времени — высоты в водной волне, давления в звуковой волне или электромагнитного поля в световой волне. Значение этого параметра называется амплитудой волны; сама волна представляет собой функцию, определяющую амплитуду в каждой точке.
Когда две или более волны достигают одной и той же точки, они накладываются друг на друга. В частности, возмущения волн накладываются друг на друга, когда они собираются вместе (явление, называемое суперпозицией).Каждому возмущению соответствует сила или амплитуда (и силы складываются). Если возмущения расположены на одной линии, результирующая волна представляет собой простое сложение возмущений отдельных волн. То есть их амплитуды складываются.
Суперпозиция : Суперпозиция — это когда две волны складываются. На этом рисунке две волны складываются и уравновешиваются, не оставляя волн. Это деструктивное вмешательство.
Наложение волн приводит к так называемой интерференции, которая проявляется двух типов: конструктивная и деструктивная.Конструктивная интерференция возникает, когда две волны складываются вместе в суперпозиции, создавая волну с кумулятивно более высокой амплитудой, как показано на. При деструктивной интерференции две волны складываются, но взаимно компенсируются (например, добавление положительного и отрицательного числа). Деструктивная помеха показана на.
.Хотя чисто конструктивная и чисто деструктивная интерференции действительно возникают, они требуют точно совмещенных идентичных волн. Наложение большинства волн создает комбинацию конструктивной и деструктивной интерференции и может меняться от места к месту и время от времени.Например, звук из стереосистемы может быть громким в одном месте, но тихим в другом. Различная громкость означает, что звуковые волны частично конструктивно и частично деструктивно складываются в разных местах. В стереосистеме есть как минимум два динамика, создающие звуковые волны, которые могут отражаться от стен. Все эти волны накладываются друг на друга. Примером звуков, которые со временем меняются от конструктивных до разрушительных, является комбинированный вой самолетов, слышимый неподвижным пассажиром. Комбинированный звук может колебаться вверх и вниз по громкости, поскольку звук от двух двигателей изменяется во времени от конструктивного до разрушительного.
Эти примеры волн похожи. показывает, что при наложении неодинаковых волн результат представляет собой смесь конструктивного и деструктивного вмешательства.
Суперпозиция неидентичных волн : Суперпозиция неидентичных волн обнаруживает как конструктивную, так и деструктивную интерференцию.
Помехи
Интерференция возникает, когда несколько волн взаимодействуют друг с другом, и представляет собой изменение амплитуды, вызванное встречей нескольких волн.
Цели обучения
Контрастная конструктивная и деструктивная интерференция
Основные выводы
Ключевые моменты
- Интерференция — это явление взаимодействия волн. Когда две волны встречаются в одной точке, они мешают друг другу.
- Есть два типа вмешательства: конструктивное и деструктивное.
- При конструктивной интерференции амплитуды двух волн складываются, в результате чего получается более высокая волна в точке их встречи.
- При деструктивной интерференции две волны нейтрализуются, что приводит к снижению амплитуды в точке, где они встречаются.
Ключевые термины
- смещение : векторная величина, которая обозначает расстояние с направленным компонентом.
- амплитуда : Максимальное абсолютное значение некоторой переменной величины.
- когерентный : Из волн, имеющих то же направление, длину и фазу, что и свет в лазере.
В отличие от твердых объектов, две волны могут иметь общую точку в пространстве.В физике интерференция — это явление, при котором две волны (проходящие через одну и ту же точку) накладываются друг на друга, образуя результирующую волну большей или меньшей амплитуды. Интерференция обычно относится к взаимодействию волн, которые коррелированы или когерентны друг с другом (т. Е. «Мешают» друг другу), либо потому, что они исходят из одного источника, либо потому, что они имеют одинаковую или почти одинаковую частоту.
Эффекты интерференции можно наблюдать со всеми типами волн, например, световыми, радио, акустическими и поверхностными водными волнами.Идея о том, что интерференция вызвана суперпозицией, означает, что когда две волны встречаются, их две амплитуды (их максимальное абсолютное значение) объединяются.
Интерференция : Две перекрывающиеся волны обнаруживают интерференцию.
Вмешательство может быть конструктивным или деструктивным. При конструктивной интерференции две амплитуды волн складываются и приводят к большему смещению, чем было бы, если бы была только одна волна. Пример конструктивного вмешательства можно увидеть в.
Конструктивная интерференция : Чистая конструктивная интерференция двух идентичных волн дает одну с удвоенной амплитудой, но той же длины волны.
Деструктивная интерференция — это когда две волны складываются вместе и в результате получается меньшее смещение, чем могло бы быть. Пример деструктивной интерференции можно увидеть на рисунке. Когда волны имеют противоположные амплитуды в точке, где они встречаются, они могут деструктивно интерферировать, в результате чего амплитуда в этой точке отсутствует.Например, так работают наушники с шумоподавлением. При воспроизведении звука с амплитудой, противоположной входящему звуку, две звуковые волны деструктивно интерферируют, и это нейтрализует друг друга.
ударов
Наложение двух волн одинаковых, но не идентичных частот дает пульсацию, известную как биение.
Цели обучения
Определите условия наложения, которые приводят к биению
Основные выводы
Ключевые моменты
- Когда две волны одинаковой частоты интерферируют, получается частота биений.
- Частота биений — это пульсирующий звук, громкость которого повышается и понижается.
- По мере того, как две волны входят и выходят из фазы, изменяющаяся конструктивная и деструктивная интерференция заставляет волну расти и уменьшаться по амплитуде. Для звуковых волн это производит звук биения.
Ключевые термины
- частота : Частное количество раз, когда периодическое явление происходит за время [latex] \ text {t} [/ latex], в котором оно происходит: [latex] \ text {f} = \ text {n } / \ text {t} [/ латекс].
- мешают : (волн) Для корреляции друг с другом при наложении или наложении.
- суперпозиция : Суммирование двух или более вкладов полей, занимающих одно и то же пространство.
При ударе по двум соседним клавишам пианино возникает комбинация трелей (обычно считается неприятной для уха). Виной всему наложение двух волн схожих, но не одинаковых частот. Когда две волны одинаковой частоты достигают одной и той же точки и накладываются друг на друга, они попеременно конструктивно и деструктивно интерферируют.Это чередование известно как биение, потому что оно производит неприятный пульсирующий звук.
Другой пример часто можно увидеть на рулении реактивного самолета (особенно двухмоторного). Громкость комбинированного звука двигателей увеличивается и уменьшается. Эта переменная громкость возникает из-за того, что звуковые волны имеют похожие, но не идентичные частоты. Несогласованные трели фортепиано и колеблющаяся громкость шума реактивного двигателя происходят из-за попеременного конструктивного и деструктивного взаимодействия, когда две волны входят в фазу и выходят из нее.иллюстрирует это явление графически.
Частота биений : Биения образуются наложением двух волн немного разных частот, но одинаковых амплитуд. Волны чередуются во времени между конструктивной интерференцией и деструктивной интерференцией, давая результирующей волне изменяющуюся во времени амплитуду.
Волна, возникающая в результате наложения двух волн одинаковой частоты, имеет среднюю частоту. Эта волна колеблется по амплитуде или биениям с частотой, называемой частотой биений.Мы можем определить частоту биений математически, сложив две волны вместе.
Также можно напрямую измерить частоту биений. Когда вы слышите ритм, исходящий из двух несогласованных звуков (скажем, двух нот на фортепиано), вы можете посчитать количество ударов в секунду. Число ударов в секунду или частота ударов показывает разницу в частоте между двумя нотами. Музыканты часто используют этот феномен, чтобы убедиться, что две ноты настроены (если они настроены, то ударов нет).
Ухо
Ухо — это орган чувств, который улавливает звуковые волны из воздуха и превращает их в нервные импульсы, которые можно посылать в мозг.
Цели обучения
Опишите, как звуковые волны собираются и преобразуются в нервные импульсы
Основные выводы
Ключевые моменты
- Задача уха состоит в том, чтобы преобразовывать сигналы в волнах отскакивающих молекул воздуха в электрические нервные сигналы, сохраняя при этом как можно больше информации в сигналах.
- Звук собирается во внешней части уха; звуковое давление усиливается через среднюю часть уха и передается из воздушной среды в жидкую.
- Это звуковое давление усиливается через среднюю часть уха и передается из воздушной среды в жидкую.
- Звуковые волны, проходящие через жидкость во внутреннем ухе, стимулируют волосковые клетки, заставляя их выделять химические нейротрансмиттеры. Таким образом звуковые волны преобразуются в нервные импульсы.
Ключевые термины
- эпителий : мембранная ткань, состоящая из одного или нескольких слоев клеток, которые образуют покрытие большинства внутренних и внешних поверхностей тела и его органов (внутри — выстилка сосудов и других небольших полостей; снаружи — кожа).
- нервный импульс : сигнал, передаваемый по нервному волокну либо в ответ на раздражитель (например, прикосновение, боль или тепло), либо в качестве инструкции (например, заставляя мышцу сокращаться)
- нейромедиатор : любое вещество, такое как ацетилхолин или дофамин, отвечающее за передачу нервных сигналов через синапс между двумя нейронами
Звуковые волны — это колебания в воздухе.Ухо — это орган чувств, который улавливает звуковые волны из окружающего воздуха и превращает их в нервные импульсы, которые затем отправляются в мозг. Звуковые волны несут в себе много информации — язык, музыку и шум — и все это смешано вместе. Задача уха — превратить сигналы в этих волнах отскакивающих молекул воздуха в электрические нервные сигналы, сохраняя при этом как можно больше информации в сигнале. (Задача мозга — затем сортировать сигналы и разбираться в них.) Нелегко превратить один вид сигнала в другой без потери информации, но ухо хорошо приспособлено для этой задачи.
Анатомия человеческого уха : Анатомия человеческого уха; длина слухового прохода увеличена для просмотра
Воздух окружает голову и заполняет слуховой проход и среднее ухо. Следовательно, когда внешняя часть уха собирает звук, а среднее ухо усиливает это звуковое давление, эти процессы происходят в среде воздуха. Однако полые каналы внутреннего уха (которое встроено в височную кость, самую плотную кость тела) заполнены жидкостью.Итак, когда звук попадает во внутреннее ухо, он переходит из воздушной среды в жидкую. Эти каналы внутреннего уха содержат сенсорный эпителий, усыпанный волосковыми клетками. Микроскопические «волоски» — это структурные белковые нити, которые выступают в жидкость. При стимуляции волосковые клетки выделяют химический нейромедиатор. Звуковые волны, движущиеся в жидкости, толкают волокна; если волокна достаточно изгибаются, волосковые клетки излучают химические сигналы. Таким образом звуковые волны преобразуются в нервные импульсы.Нервные импульсы проходят от левого и правого ушей через восьмой черепной нерв к обеим сторонам ствола головного мозга и до той части коры головного мозга, которая отвечает за звук (слуховая кора, расположенная в височной доле).
Приложения: ультразвук, сонар и медицинская визуализация
Звуковые волны по-разному отражаются от разных материалов (когда отражения собираются, они могут предоставлять информацию и изображения).
Цели обучения
Обсудить применение звуковых волн в медицине и навигации
Основные выводы
Ключевые моменты
- Когда волны сталкиваются с границей между двумя материалами, часть волны отражается, а часть передается.
- Используя высокочастотные звуковые волны, врачи могут создавать изображения частей тела, которые обычно не видны.
- Путем передачи звуковых волн и измерения времени между передачей и приемом отражения корабли могут использовать звуковые волны для навигации. Это называется сонар.
Ключевые термины
- частота : Частное количество раз, когда периодическое явление происходит за время [latex] \ text {t} [/ latex], в котором оно происходит: [latex] \ text {f} = \ text {n } / \ text {t} [/ латекс].
Управляемое использование звуковых волн имеет множество применений в науке. Контролируемое отражение таких волн позволяет получать изображения.
УЗИ
Ультразвук — это звук с частотой выше 20 кГц. Это выше человеческого слуха. Чаще всего ультразвук используется для создания изображений в промышленности и медицине. Использование ультразвука для создания изображений основано на отражении и пропускании волны на границе. Когда ультразвуковая волна распространяется внутри объекта, состоящего из разных материалов (например, человеческого тела), каждый раз, когда он встречается с границей (например,g., между костью и мышцей или мышцей и жиром) часть волны отражается, а часть передается. Отраженные лучи обнаруживаются и используются для построения изображения объекта.
Эхолот
показывает, как корабль в океане использует отражающие свойства звуковых волн для определения глубины океана. Звуковая волна передается и отражается от морского дна. Поскольку скорость звука известна и можно измерить промежуток времени между отправкой и получением звука, можно определить расстояние от корабля до дна океана.Этот метод называется сонар (первоначально аббревиатура от SOund Navigation And Ranging).
Sonar : Корабли в океане используют отражающие свойства звуковых волн для определения глубины океана. Звуковая волна передается и отражается от морского дна. Поскольку скорость звука известна и можно измерить промежуток времени между отправкой и получением звука, можно определить расстояние от корабля до дна океана.
Так же, как корабли в океане, некоторые животные, такие как дельфины и летучие мыши, используют звуковые волны (сонар) для навигации или поиска пути.Ультразвуковые волны излучаются, а затем отражаются от предметов вокруг животного. Затем летучие мыши или дельфины используют отраженные звуки для формирования «картины» своего окружения (это называется эхолокацией).
Сложение и вычитание векторов: графические методы
Используйте графическую технику для добавления векторов, чтобы найти полное смещение человека, который идет следующими тремя путями (смещениями) на плоском поле. Сначала она проходит 25,0 м в направлении 49,0º к северу от востока.Затем она проходит 23,0 м в направлении 15,0º к северу от востока. Наконец, она поворачивается и проходит 32,0 м в направлении 68,0 ° к югу от востока.
СтратегияИзобразите каждый вектор смещения графически стрелкой, обозначив первый A , второй B и третий C , сделав длины пропорциональными расстоянию и направлениям, указанным относительно линии восток-запад. Описанный выше метод «голова к хвосту» позволит определить величину и направление результирующего смещения, обозначенное как R .
Решение(1) Нарисуйте три вектора смещения.
(2) Поместите векторы голова к хвосту, сохраняя их начальную величину и направление.
(3) Нарисуйте результирующий вектор, R .
(4) Используйте линейку, чтобы измерить звездную величину R , и транспортир, чтобы измерить направление R . Хотя направление вектора можно указать разными способами, самый простой способ — измерить угол между вектором и ближайшей горизонтальной или вертикальной осью.Поскольку результирующий вектор находится к югу от оси, направленной на восток, мы переворачиваем транспортир вверх дном и измеряем угол между осью, направленной на восток, и вектором.
Рисунок 11
В этом случае видно, что полное смещение R имеет величину 50,0 м и лежит в направлении 7,0 ° к югу от востока. Используя его величину и направление, этот вектор можно выразить как R = 50,0 м и θ = 7,0 ° к югу от востока.
ОбсуждениеГрафический метод сложения векторов «голова к хвосту» работает для любого количества векторов.Также важно отметить, что результат не зависит от порядка добавления векторов. Следовательно, мы можем складывать векторы в любом порядке, как показано на рисунке 12, и мы все равно получим то же самое решение.
Здесь мы видим, что когда одни и те же векторы добавляются в другом порядке, результат тот же. Эта характеристика верна во всех случаях и является важной характеристикой векторов. Сложение вектора — , коммутативное . Векторы можно добавлять в любом порядке.
A + B = B + A.
(Это также верно и для сложения обычных чисел — вы получите тот же результат, если сложите, например, 2 + 3 или 3 + 2 ).
Суперпозиция волн
Суперпозиция волнДэниел А. Рассел , аспирантура по акустике, Государственный университет Пенсильвании
Эта работа Дэна Рассела находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 Международная лицензия.
На основе работы по адресу http://www.acs.psu.edu/drussell/demos.html. Дополнительная информация об использовании этого содержимого доступна по адресу http://www.acs.psu.edu/drussell/Demos/copyright.html.Содержание этой страницы было первоначально опубликовано 25 июля 1996 г. . HTML-код был изменен для соответствия HTML5 27 января 2014 г.
Принцип суперпозиции может применяться к волнам, когда две (или более) волны проходят через одну и ту же среду одновременно.Волны проходят сквозь друг друга, не беспокоясь. Чистое смещение среды в любой точке пространства или времени — это просто сумма смещений отдельных волн. Это верно для волн конечной длины (волновые импульсы) или непрерывных синусоидальных волн.
Наложение двух волновых импульсов противоположного направления
Анимация слева показывает, что два гауссовых волновых импульса распространяются в одной и той же среде, но в противоположных направлениях. Две волны проходят друг через друга без помех, и чистое смещение является суммой двух отдельных смещений.
Следует также отметить, что эта среда является недисперсной (все частоты распространяются с одинаковой скоростью), поскольку импульсы гауссовой волны не меняют свою форму при распространении. Если бы среда была дисперсной, то волны меняли бы свою форму.
Солитоны — это примеры нелинейных волн, которые не подчиняются принципу суперпозиции при взаимодействии друг с другом.
Конструктивное и деструктивное вмешательство
Две волны (с одинаковой амплитудой, частотой и длиной волны) распространяются в одном направлении.Используя принцип суперпозиции, результирующее волновое смещение можно записать как:
$$ y (x, t) = y_m \ sin (kx — \ omega t) + y_m \ sin (kx — \ omega t + \ phi) = 2 y_m \ cos (\ phi / 2) \ sin (kx — \ омега t + \ phi / 2) $$— бегущая волна, амплитуда которой зависит от фазы \ (\ phi \). Когда две волны синфазны, (\ (\ phi = 0 \)), они интерферируют конструктивно, , и в результате амплитуда в два раза превышает амплитуду отдельных волн. o \)), они интерферируют деструктивно и нейтрализуют друг друга.
Анимация слева показывает, как две синусоидальные волны с одинаковой амплитудой и частотой могут складываться либо деструктивно, либо конструктивно в зависимости от их относительной фазы. (ПРИМЕЧАНИЕ: эта анимация не изображает распространение реальных волн в среде — она служит только для иллюстрации эффекта изменения фазового сдвига между двумя волнами и результирующей конструктивной или деструктивной интерференции). Разность фаз между двумя волнами увеличивается со временем, так что можно увидеть эффекты как конструктивной, так и деструктивной интерференции.Когда две отдельные волны точно совпадают по фазе, в результате получается большая амплитуда. Когда две серые волны становятся точно в противофазе, суммарная волна равна нулю.
Две синусоидальные волны, распространяющиеся в противоположных направлениях, создают стоячую волну
Бегущая волна перемещается из одного места в другое, тогда как стоячая волна , кажется, стоит на месте, вибрируя на месте. В этой анимации две волны (с одинаковой амплитудой, частотой и длиной волны) движутся в противоположных направлениях.Используя принцип суперпозиции, результирующую амплитуду волны можно записать как:
$$ y (x, t) = y_m \ sin (kx — \ omega t) + y_m \ sin (kx + \ omega t) = 2 y_m \ cos (\ omega t) \ sin (kx) $$Эта волна больше не является бегущей волной, потому что зависимости положения и времени были разделены. Амплитуда волны как функция положения равна \ (2y_m \ sin (kx) \). Эта амплитуда не перемещается, а остается неподвижной и колеблется вверх и вниз согласно \ (\ cos (\ omega t) \). Для стоячих волн характерны места с максимальным смещением ( пучностей, ) и места с нулевым смещением ( узлов, ).
Фильм слева показывает, как стоячая волна может быть создана из двух бегущих волн. Если две синусоидальные волны, имеющие одинаковую частоту (и длину волны) и одинаковую амплитуду, распространяются в противоположных направлениях в одной и той же среде, то при использовании суперпозиции чистое смещение среды является суммой двух волн. Как показано в фильме, когда две волны не совпадают по фазе на 180 ° друг с другом, они нейтрализуются, а когда они точно синфазны друг с другом, они складываются.Когда две волны проходят друг через друга, конечный результат меняется от нуля до некоторой максимальной амплитуды. Однако этот паттерн просто колеблется; она не движется ни вправо, ни влево, поэтому ее называют «стоячей волной ».
Я поставил на веревке две точки: одну в пучности, а другую в узле. Что есть что?
Посмотрите мою связанную анимацию, чтобы увидеть, как в среде могут возникать стоячие волны из-за отражения волны от границы.
Две синусоидальные волны с разными частотами: удары
Две волны одинаковой амплитуды движутся в одном направлении. Две волны имеют разные частоты и длины волн, но обе движутся с одинаковой скоростью. Используя принцип суперпозиции, результирующее смещение частицы можно записать как:
$$ y (x, t) = y_m \ sin (k_1 x — \ omega_1 t) + y_m \ sin (k_2 x + \ omega_2 t) = 2y_m \ cos \ bigg [\ frac {k_1-k_2} {2} x — \ гидроразрыв {\ omega_1- \ omega_2} {2} t \ bigg] \ sin \ bigg [\ frac {k_1 + k_2} {2} x — \ frac {\ omega_1 + \ omega_2} {2} t \ bigg] $$Это результирующее движение частицы является продуктом двух бегущих волн .Одна часть представляет собой синусоидальную волну, которая колеблется со средней частотой f = ½ ( f 1 + f 2 ). Это частота, которую воспринимает слушатель. Другая часть представляет собой косинусоидальную волну, которая колеблется с разностной частотой f = ½ ( f 1 — f 2 ). Этот термин контролирует амплитуду «огибающей» волны и вызывает восприятие «биений». Частота биений на самом деле в два раза больше разностной частоты, f биений = ( f 1 — f 2 ).
На анимации слева направо движутся две волны с немного разными частотами. Поскольку две волны движутся в одной среде, они движутся с одинаковой скоростью. Результирующая суммарная волна суперпозиции распространяется в том же направлении и с той же скоростью, что и две составляющие волны, но ее локальная амплитуда зависит от того, имеют ли две отдельные волны одинаковую или противоположную фазу. Волна «биений» колеблется со средней частотой, и ее амплитудная огибающая изменяется в соответствии с разностной частотой.
16.6 Стоячие волны и резонанс — University Physics Volume 1
На протяжении этой главы мы изучали бегущие волны или волны, переносящие энергию из одного места в другое. При определенных условиях волны могут отскакивать назад и вперед через определенную область, фактически становясь стационарными. Они называются стоячими волнами .
Другой связанный эффект известен как резонанс. В книге «Колебания» мы определили резонанс как явление, при котором движущая сила малой амплитуды может вызвать движение большой амплитуды.Представьте ребенка на качелях, которые можно смоделировать как физический маятник. Толчки со стороны родителя относительно небольшой амплитуды могут вызывать колебания большой амплитуды. Иногда этот резонанс хорош — например, при создании музыки на струнном инструменте. В других случаях последствия могут быть разрушительными, например, обрушение здания во время землетрясения. В случае стоячих волн стоячие волны с относительно большой амплитудой создаются наложением составляющих волн с меньшей амплитудой.
Стоячие волны
Иногда кажется, что волны не двигаются; скорее, они просто вибрируют на месте. Например, вы можете увидеть неподвижные волны на поверхности стакана с молоком в холодильнике. Вибрация двигателя холодильника создает волны на молоке, которые колеблются вверх и вниз, но не движутся по поверхности. (Рисунок) показывает эксперимент, который вы можете попробовать дома. Возьмите миску с молоком и поставьте ее на обычный вентилятор. Вибрация вентилятора вызывает в молоке стоячие круглые волны.Волны на фото видны благодаря отражению от лампы. Эти волны образуются наложением двух или более бегущих волн, как показано на (Рисунок) для двух идентичных волн, движущихся в противоположных направлениях. Волны движутся друг через друга, и их возмущения добавляются по мере прохождения. Если две волны имеют одинаковую амплитуду и длину волны, то они чередуются между конструктивной и деструктивной интерференцией. Результирующая волна выглядит как стоячая волна и, следовательно, называется стоячей волной.
Рис. 16.25 Стоячие волны образуются на поверхности миски с молоком, установленной на ящичном веере. Вибрация вентилятора заставляет поверхность молока колебаться. Волны видны из-за отражения света от лампы. рисунок 16.26 Временные снимки двух синусоидальных волн. Красная волна движется в направлении -x, а синяя волна движется в направлении + x. Результирующая волна показана черным цветом. Рассмотрим результирующую волну в точкахи обратите внимание, что результирующая волна всегда равна нулю в этих точках, независимо от времени.Эти точки называются фиксированными точками (узлами). Между каждыми двумя узлами находится пучность, место, где среда колеблется с амплитудой, равной сумме амплитуд отдельных волн.
Рассмотрим две одинаковые волны, движущиеся в противоположных направлениях. Первая волна имеет волновую функцию
., а вторая волна имеет волновую функцию
. Волны интерферируют и образуют результирующую волну
Это можно упростить с помощью тригонометрического идентификатора
где
и
, что дает нам
, что упрощается до
Обратите внимание, что результирующая волна является синусоидальной волной, которая является функцией только положения, умноженной на функцию косинуса, которая является функцией только времени.Графики зависимости x ( x , t ) от x для различных времен показаны на (Рисунок). Красная волна движется в отрицательном направлении x , синяя волна движется в положительном направлении x , а черная волна является суммой двух волн. По мере того, как красная и синяя волны движутся друг через друга, они входят и выходят из-за конструктивной интерференции и деструктивной интерференции.
Первоначально, в момент времени
две волны находятся в фазе, и в результате получается волна, которая в два раза превышает амплитуду отдельных волн.Волны также находятся в фазе в момент
.Фактически, волны находятся в фазе в любом целом кратном половине периода:
В остальное время две волны равны
не в фазе, и результирующая волна равна нулю. Это происходит по адресу
Обратите внимание, что некоторые положения результирующей волны x всегда равны нулю, независимо от фазового соотношения. Эти позиции называются узлами .Где возникают узлы? Рассмотрим решение суммы двух волн
Нахождение позиций, в которых функция синуса равна нулю, обеспечивает положение узлов.
Есть также позиции, где y колеблется между
. Это пучности . Мы можем найти их, посчитав, какие значения x дают
.
В результате получается стоячая волна, как показано на (Рисунок), где показаны снимки результирующей волны двух идентичных волн, движущихся в противоположных направлениях.Результирующая волна выглядит как синусоидальная волна с узлами в целых кратных полуволнах. Пучности колеблются между
.из-за члена косинуса,
, который колеблется между
.
Результирующая волна кажется неподвижной, без видимого движения в направлении x , хотя она состоит из одной волновой функции, движущейся в положительном направлении, тогда как вторая волна движется в отрицательном направлении x .(Рисунок) показывает различные снимки результирующей волны. Узлы отмечены красными точками, а пучности отмечены синими точками.
Рисунок 16.27 Когда две идентичные волны движутся в противоположных направлениях, результирующая волна является стоячей волной. Узлы появляются в целых числах, кратных половине длины волны. Пучности появляются с нечетными числами, кратными четверти длины волны, где они колеблются междуУзлы отмечены красными точками, а пучности отмечены синими точками.
Типичным примером стоячих волн являются волны, создаваемые струнными музыкальными инструментами. Когда струна защипывается, импульсы проходят по струне в противоположных направлениях. Концы струн фиксируются на месте, поэтому на концах струн появляются узлы — граничные условия системы, регулирующие резонансные частоты в струнах. Резонанс, создаваемый струнным инструментом, можно смоделировать в физической лаборатории с помощью устройства, показанного на (Рисунок).
Рисунок 16.28 Лабораторная установка для создания стоячих волн на струне. У струны есть узел на каждом конце и постоянная линейная плотность. Длина между фиксированными граничными условиями равна L. Подвешенная масса обеспечивает натяжение струны, а скорость волн на струне пропорциональна квадратному корню из натяжения, деленному на линейную плотность массы.Лабораторная установка показывает струну, прикрепленную к струнному вибратору, который колеблет струну с регулируемой частотой f .Другой конец струны проходит над шкивом без трения и привязан к подвешенной массе. Величина натяжения тетивы равна весу подвешенной массы. Струна имеет постоянную линейную плотность (масса на длину)
, а скорость, с которой волна распространяется по струне, равна
.(рисунок). Симметричные граничные условия (узел на каждом конце) определяют возможные частоты, которые могут возбуждать стоячие волны.Начиная с нулевой частоты и медленно увеличивая частоту, первая мода
выглядит так, как показано на (Рисунок). Первая мода, также называемая основной модой или первой гармоникой, показывает, что сформировалась половина длины волны, поэтому длина волны равна удвоенной длине между узлами
. Основная частота , или частота первой гармоники, которая управляет этим режимом, равна
., где скорость волны
Сохранение постоянного напряжения и увеличение частоты приводит ко второй гармонике или
режим.Этот режим — полная длина волны
, а частота в два раза больше основной частоты:
Рисунок 16.29 Стоячие волны, созданные на цепочке длиной L. Узлы возникают на каждом конце цепочки. Узлы — это граничные условия, которые ограничивают возможные частоты, возбуждающие стоячие волны. (Обратите внимание, что амплитуды колебаний оставались постоянными для визуализации. Возможные модели стоячих волн на струне известны как нормальные моды.Проведение этого эксперимента в лаборатории приведет к уменьшению амплитуды при увеличении частоты.)Следующие две моды или третья и четвертая гармоники имеют длины волн
.и
работает на частотах
и
Все частоты выше частоты
известны как обертона . Уравнения для длины волны и частоты можно резюмировать как:
Модели стоячей волны, которые возможны для струны, первые четыре из которых показаны на (Рисунок), известны как нормальные моды с частотами, известными как нормальные частоты.Таким образом, первая частота, вызывающая нормальный режим, называется основной частотой (или первой гармоникой). Любые частоты выше основной частоты являются обертонами. Вторая частота
нормальный режим струны — это первый обертон (или вторая гармоника). Частота
нормальный режим — это второй обертон (или третья гармоника) и так далее.
Решения, показанные как (Уравнение) и (Уравнение), предназначены для строки с граничным условием узла на каждом конце.Когда граничные условия с обеих сторон одинаковы, говорят, что система имеет симметричные граничные условия. (Уравнение) и (Уравнение) подходят для любых симметричных граничных условий, то есть узлов на обоих концах или пучностей на обоих концах.
Пример
Стоячие волны на струне
Рассмотрим строку
, прикрепленный к струнному вибратору с регулируемой частотой, как показано на (Рисунок). Волны, создаваемые вибратором, распространяются по струне и отражаются фиксированным граничным условием на шкиве.Струна, имеющая линейную массовую плотность
проходит через шкив без трения с незначительной массой, а натяжение обеспечивается подвешенной массой 2,00 кг. а) Какова скорость волн на струне? (b) Нарисуйте эскиз первых трех нормальных мод стоячих волн, которые могут возникать на струне, и пометьте каждой длиной волны. (c) Перечислите частоты, на которые струнный вибратор должен быть настроен, чтобы произвести первые три нормальные моды стоячих волн.
Рисунок 16.30 Струна, прикрепленная к струнному вибратору с регулируемой частотой.Стратегия
- Скорость волны можно найти с помощью
Натяжение обеспечивается весом подвешенной массы.
- Стоячие волны будут зависеть от граничных условий. На каждом конце должен быть узел. Первая мода будет составлять половину волны. Вторую можно найти, добавив половину длины волны. Это самая короткая длина, которая приведет к образованию узла на границах.Например, добавление одной четверти длины волны приведет к образованию пучности на границе и не является режимом, который удовлетворял бы граничным условиям. Это показано на (Рисунок).
- Поскольку скорость волны равна длине волны, умноженной на частоту, частота равна скорости волны, деленной на длину волны. Рисунок 16.31 (a) На рисунке представлен второй режим строки, который удовлетворяет граничным условиям узла на каждом конце строки. (b) Этот рисунок не может быть нормальным режимом для струны, потому что он не удовлетворяет граничным условиям.На одном конце есть узел, а на другом — пучность.
Решение
- Начните со скорости волны на струне. Натяжение равно весу подвешенной массы. Даны линейная массовая плотность и масса подвешенной массы:
- Первая нормальная мода, имеющая узел на каждом конце, составляет половину длины волны. Следующие две моды находятся путем добавления половины длины волны.
- Частоты первых трех мод находятся с помощью
Значение
Три режима стоя в этом примере были созданы путем поддержания натяжения струны и регулировки частоты возбуждения.Сохранение постоянного натяжения струны приводит к постоянной скорости. Те же самые режимы можно было бы получить, сохранив постоянную частоту и регулируя скорость волны в струне (изменяя висящую массу).
Проверьте свое понимание
Уравнения для длин волн и частот мод волны, создаваемой на струне:
были получены путем рассмотрения волны на струне, где были симметричные граничные условия узла на каждом конце.Эти режимы являются результатом двух синусоидальных волн с идентичными характеристиками, за исключением того, что они движутся в противоположных направлениях, ограниченных областью L с узлами, необходимыми на обоих концах. Будут ли работать те же уравнения при наличии симметричных граничных условий с пучностями на каждом конце? Как бы выглядели нормальные режимы для среды, которая могла бы свободно колебаться на каждом конце? Не беспокойтесь, если вы не можете представить себе такую среду, просто рассмотрите две синусоидальные волновые функции в области длиной L с пучностями на каждом конце.
Да, уравнения будут одинаково хорошо работать для симметричных граничных условий среды, свободно колеблющейся на каждом конце, где на каждом конце есть пучности. Ниже показаны нормальные режимы первых трех режимов. Пунктирная линия показывает положение равновесия среды.
Обратите внимание, что первая мода составляет две четверти или половину длины волны. Вторая мода — это четверть длины волны, за которой следует половина длины волны, за которой следует четверть длины волны, или одна полная длина волны.Третья мода — полторы длины волны. Это тот же результат, что и у строки с узлами на каждом конце. Уравнения для симметричных граничных условий одинаково хорошо работают как для фиксированных граничных условий, так и для свободных граничных условий. К этим результатам мы вернемся в следующей главе, когда будем обсуждать звуковую волну в открытой трубке.
Свободные граничные условия, показанные в последней проверке понимания, могут показаться трудными для визуализации. Как может быть система, которая может свободно колебаться на каждом конце? На (Рисунок) показаны две возможные конфигурации металлических стержней (показаны красным), прикрепленных к двум опорам (показаны синим).В части (а) стержень поддерживается на концах, и на обоих концах имеются фиксированные граничные условия. При соответствующей частоте стержень может быть приведен в резонанс с длиной волны, равной длине стержня, с узлами на каждом конце. В части (b) стержень поддерживается в положениях, составляющих одну четверть длины от каждого конца стержня, и на обоих концах имеются свободные граничные условия. При правильной частоте этот стержень также можно привести в резонанс с длиной волны, равной длине стержня, но на каждом конце есть пучности.Если у вас возникли проблемы с визуализацией длины волны на этом рисунке, помните, что длину волны можно измерить между любыми двумя ближайшими идентичными точками, и примите во внимание (рисунок).
Рисунок 16.32 (a) Металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на каждом конце. При движении на соответствующей частоте стержень может резонировать с длиной волны, равной длине стержня с узлом на каждом конце. (b) Тот же металлический стержень длиной L (красный), поддерживаемый двумя опорами (синий) на расстоянии четверти длины стержня с каждого конца.При движении на соответствующей частоте стержень может резонировать с длиной волны, равной длине стержня с пучностями на каждом конце. Рисунок 16.33 Длину волны можно измерить между двумя ближайшими повторяющимися точками. На волне на веревке это означает одинаковую высоту и наклон. (а) Длина волны измеряется между двумя ближайшими точками, где высота равна нулю, а наклон является максимальным и положительным. (b) Длина волны измеряется между двумя идентичными точками, где высота максимальна, а наклон равен нулю.Обратите внимание, что изучение стоячих волн может стать довольно сложным. На (Рисунок) (а) модель
Показана мода стоячей волны, которая дает длину волны, равную L . В этой конфигурации
Режимтакже был бы возможен с стоячей волной, равной 2 L . Можно ли получить
для конфигурации, показанной в части (b)? Ответ — нет. В этой конфигурации помимо граничных условий устанавливаются дополнительные условия.Поскольку стержень установлен в точке, составляющей четверть длины с каждой стороны, там должен существовать узел, и это ограничивает возможные режимы стоячих волн, которые могут быть созданы. Мы оставляем читателю в качестве упражнения подумать, возможны ли другие режимы стоячих волн. Следует отметить, что когда система приводится в действие на частоте, которая не вызывает резонанс системы, вибрации все еще могут возникать, но амплитуда колебаний будет намного меньше, чем амплитуда при резонансе.
Область машиностроения использует звук, производимый вибрирующими частями сложных механических систем, для устранения проблем с системами. Предположим, часть автомобиля резонирует с частотой двигателя автомобиля, вызывая нежелательные вибрации в автомобиле. Это может привести к преждевременной поломке двигателя. Инженеры используют микрофоны для записи звука, производимого двигателем, затем используют метод, называемый анализом Фурье, чтобы найти частоты звука, производимого с большими амплитудами, а затем просматривают список деталей автомобиля, чтобы найти деталь, которая будет резонировать на этой частоте.Решение может быть таким простым, как изменение состава используемого материала или изменение длины рассматриваемой детали.
Есть и другие многочисленные примеры резонанса стоячих волн в физическом мире. Воздух в трубке, например, в музыкальном инструменте, таком как флейта, может вызвать резонанс и произвести приятный звук, как мы обсуждаем в разделе «Звук».
В других случаях резонанс может вызвать серьезные проблемы. Более пристальный взгляд на землетрясения дает доказательства наличия условий, подходящих для резонанса, стоячих волн, а также конструктивных и деструктивных помех.Здание может вибрировать в течение нескольких секунд с частотой возбуждения, соответствующей частоте собственной вибрации здания, что вызывает резонанс, в результате которого одно здание рушится, а соседние — нет. Часто здания определенной высоты разрушаются, в то время как другие более высокие здания остаются нетронутыми. Высота здания соответствует условию создания стоячей волны для данной высоты. Также важен пролет крыши. Часто можно увидеть, что спортзалы, супермаркеты и церкви страдают от повреждений, в то время как отдельным домам наносится гораздо меньший ущерб.Крыши с большой площадью поверхности, поддерживаемые только краями, резонируют с частотами землетрясений, вызывая их обрушение. Поскольку волны землетрясения распространяются по поверхности Земли и отражаются от более плотных горных пород, в определенных точках возникает конструктивная интерференция. Часто участки, расположенные ближе к эпицентру, не повреждаются, а участки дальше — повреждены.
Добавление фазора. Из Physclips
Здесь мы обсуждаем сложение фазора: простой способ сложения двух или более простых гармонических колебаний.Это фоновая страница к мультимедийной главе «Помехи». Весенняя месса: знакомство с фазорами
В главе о простом гармоническом движении мы показали, как его можно представить как проекцию равномерного кругового движения. Теперь давайте будем откровенны:На этом кадре из анимации выше, график справа показывает смещение y простого гармонического движения с амплитудой A, угловой частотой ω и нулевой начальной фазой:
Если равномерное круговое движение имеет радиус A, угловую частоту ω и нулевую начальную фазу, то угол между радиусом (длиной A) и осью x равен ωt, как показано.Вращающийся рычаг здесь называется вектором , который представляет собой комбинацию вектора и фазы, потому что направление вектора (угол, который он составляет с осью x) дает фазу.Два вектора с фиксированной фазой
Давайте посмотрим, насколько полезно это представление вектора, когда мы добавляем простые гармонические движения, имеющие одинаковую частоту, но разные фазы.
Вот коричневый вектор с величиной A и начальной фазой 0
и зеленый с величиной A и начальной фазой φ:- y 2 = B sin (ωt + φ).
Из сложения векторов мы видим, что красный вектор является суммой коричневого и зеленого. Затем амплитуду и фазу красного фазора можно получить с помощью тригонометрии или геометрии.
Смешивание двух звуков
Этот видеоролик из главы Интерференция показывает пример сложения двух синусоидальных волн с различной амплитудой и фазой.Оба динамика приводятся в действие одним и тем же генератором, и, если предположить, что динамики похожи, каждый из них выдает одну и ту же звуковую волну. Тот, что ближе к камере и микрофону, будет громче (с большей амплитудой) и впереди по фазе. Добавление таких сигналов становится немного сложнее.
Конструктивное и структурное вмешательство
Когда добавляются два простых гармонических движения с одинаковой частотой и разной фазой, результирующая амплитуда зависит от их относительной фазы, от угла между двумя векторами.В этой анимации мы изменяем относительную фазу, чтобы показать эффект.Здесь векторная диаграмма показывает, что максимальная амплитуда возникает, когда они находятся в фазе: это называется конструктивной интерференцией . Минимальная сумма возникает, когда они сдвинуты по фазе на 180 °, что называется деструктивной интерференцией .
Что делать, если частоты разные?
Если одно простое гармоническое колебание имеет угловую частоту ω 1 , а другое — угловую частоту ω 2 , можно сказать, что второе опережает первое на переменный угол φ, где dφ / dt = ω 2 — ω 1 .В общем, такое представление обычно не приводит к существенному упрощению. Однако возникает интересный феномен, когда- f 2 / f 1 = ω 2 / ω 1 = m / n, где m и n — небольшие целые числа.
На этой анимации показано, как можно продемонстрировать созвучие с помощью фигур Лиссажу, в которых одно гармоническое колебание отображается как координата y, а другое — как координата x.У нас есть отдельная страница, посвященная фигурам Лиссажу.
Приложения
Фазорные суммы используются для анализа интерференции и консонанса в звуке, интерференции и дифракции волн в целом и электричества переменного тока.
16.10 Наложение и интерференция | Texas Gateway
Задачи обучения
К концу этого раздела вы сможете делать следующее:
- Определить результирующую форму волны, когда две волны действуют в суперпозиции друг относительно друга
- Объясните стоячие волны
- Опишите математическое представление обертонов и частоты ударов
Рисунок 16.35 Эти волны возникают в результате наложения нескольких волн от разных источников, образующих сложную картину. (Источник: Waterborough, Wikimedia Commons)
Большинство волн не выглядят очень простыми. Они больше похожи на волны на рис. 16.35, чем на простую водную волну, рассматриваемую в «Волнах». Простые волны могут создаваться простым гармоническим колебанием и, таким образом, иметь синусоидальную форму. Сложные волны интереснее, даже красивее, но выглядят грозно. Большинство волн кажутся сложными, потому что они возникают в результате сложения нескольких простых волн.К счастью, правила добавления волн довольно просты.
Когда две или более волны прибывают в одну и ту же точку, они накладываются друг на друга. В частности, возмущения волн накладываются друг на друга, когда они собираются вместе — явление, называемое суперпозицией. Каждому возмущению соответствует сила, а силы складываются. Если возмущения расположены вдоль одной и той же линии, то результирующая волна представляет собой простое сложение возмущений отдельных волн, то есть их амплитуды складываются.Рисунки 16.36 и 16.37 иллюстрируют суперпозицию в двух частных случаях, оба из которых дают простые результаты.
Рисунок 16.36 показывает две идентичные волны, которые приходят в одну и ту же точку точно по фазе. Гребни двух волн точно выровнены, как и впадины. Эта суперпозиция производит чистую конструктивную интерференцию. Поскольку помехи складываются, чистая конструктивная интерференция создает волну, которая имеет двойную амплитуду, чем отдельные волны, но имеет ту же длину волны.
На рисунке 16.37 показаны две идентичные волны, которые приходят точно в противофазе, то есть точно выровнены от гребня к впадине, что создает чистую деструктивную интерференцию. Поскольку для этой суперпозиции возмущения имеют противоположное направление, результирующая амплитуда равна нулю для чистой деструктивной интерференции — волны полностью гасятся.
Рис. 16.36 Чистая конструктивная интерференция двух идентичных волн дает одну с удвоенной амплитудой, но той же длины волны.
Рисунок 16.37 Чистая деструктивная интерференция двух идентичных волн дает нулевую амплитуду или полное подавление.
Хотя чисто конструктивная и чисто деструктивная интерференции действительно возникают, они требуют точно совмещенных идентичных волн. Наложение большинства волн создает комбинацию конструктивной и деструктивной интерференции и может меняться от места к месту и время от времени. Например, звук из стереосистемы может быть громким в одном месте и тихим в другом.Различная громкость означает, что звуковые волны частично конструктивно и частично деструктивно складываются в разных местах. В стереосистеме есть как минимум два динамика, создающие звуковые волны, которые могут отражаться от стен. Все эти волны накладываются друг на друга. Примером звуков, которые со временем меняются от конструктивных до разрушительных, является комбинированный вой самолетов, слышимый неподвижным пассажиром. Комбинированный звук может колебаться вверх и вниз по громкости, поскольку звук от двух двигателей изменяется во времени от конструктивного до разрушительного.


 40)
40) 45)
45) 47)
47) 49)
49) 52)
52) 54)
54) 2.\]
2.\] 12.10).
12.10).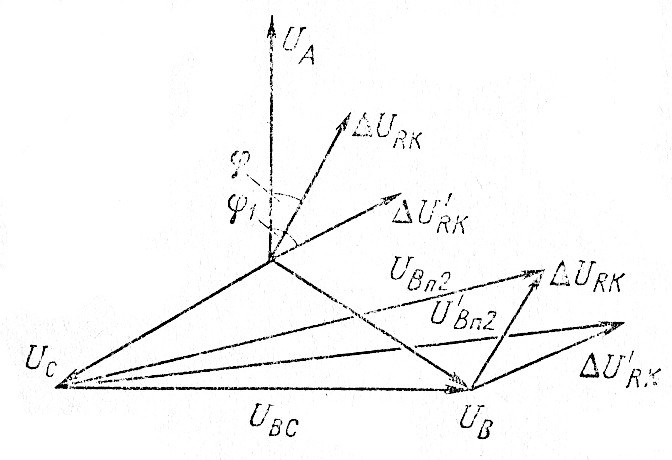

 Например: требуется сложить, два тока, заданных уравнениями
Например: требуется сложить, два тока, заданных уравнениями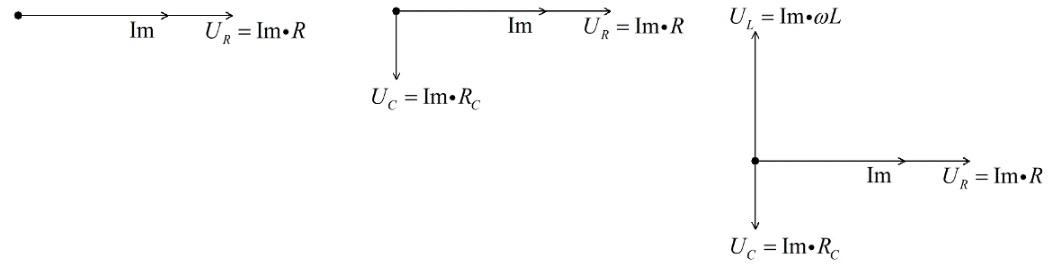 12.13):
12.13):
 Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
Ось OХ соответствует величинам действительных чисел, ось OY — оси мнимых чисел (мнимая единица). Синусоида отображает движение конца проекции на ось OY. Каждому напряжению и току соответствует собственный вектор на плоскости в полярных координатах. Его длина отображает амплитудное значение величины тока, при этом угол равен фазе.
 325]
325] Тем не менее переход к схемам замещения и векторным диаграммам позволяет использовать для решения хорошо известные методы расчета линейных и нелинейных электрических цепей постоянного и переменного тока.
[c.88]
Тем не менее переход к схемам замещения и векторным диаграммам позволяет использовать для решения хорошо известные методы расчета линейных и нелинейных электрических цепей постоянного и переменного тока.
[c.88] 3, 4.4).
[c.124]
3, 4.4).
[c.124]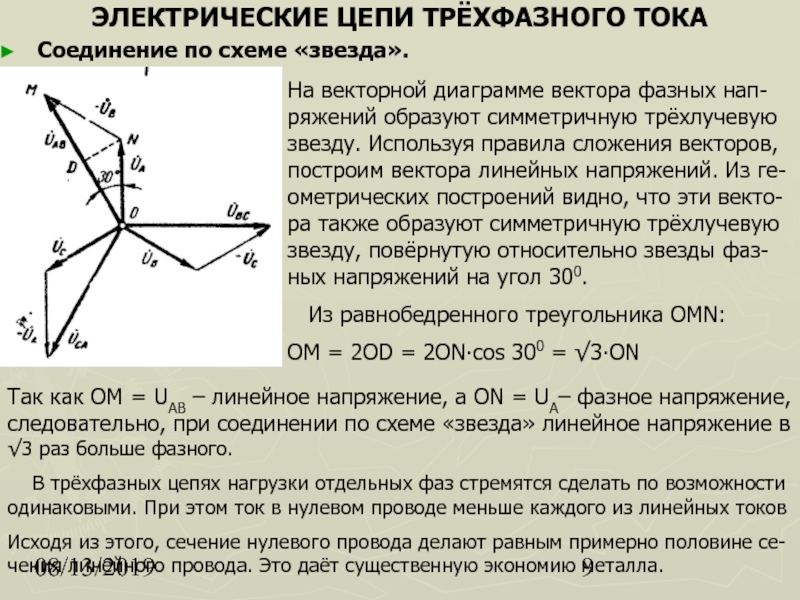 3.5, б. Для этого из произвольной точки -л, называемой полюсом плана ускорений, отложим вектор т.а, который в масштабе изображает вектор ускорения полюса ал. Масштабный коэффициент = ол/(т а) показывает, сколько единиц ускорения содержится в одном миллиметре вектора на плане.
[c.32]
3.5, б. Для этого из произвольной точки -л, называемой полюсом плана ускорений, отложим вектор т.а, который в масштабе изображает вектор ускорения полюса ал. Масштабный коэффициент = ол/(т а) показывает, сколько единиц ускорения содержится в одном миллиметре вектора на плане.
[c.32] 118]
118] [c.120]
[c.120]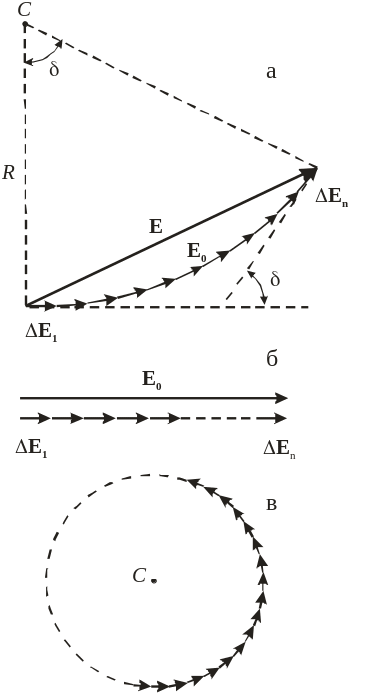 Частица с импульсом ро (в К-системе) распалась на лету на две частицы с массами mi и т . При этом выделилась энергия Q — энергия распада (она перешла в кинетическую энергию). Построить векторную диаграмму импульсов для этого процесса и найти с помощью нее возможные импульсы pi и р2 возникших частиц.
[c.131]
Частица с импульсом ро (в К-системе) распалась на лету на две частицы с массами mi и т . При этом выделилась энергия Q — энергия распада (она перешла в кинетическую энергию). Построить векторную диаграмму импульсов для этого процесса и найти с помощью нее возможные импульсы pi и р2 возникших частиц.
[c.131] 8.7. Векторная диаграмма суммирования действия отдельных участков зоны.
8.7. Векторная диаграмма суммирования действия отдельных участков зоны.
 35), можно построить графически диаграмму действия различных лунок. Очевидно, получится также кривая в форме спирали, однако вследствие
[c.166]
35), можно построить графически диаграмму действия различных лунок. Очевидно, получится также кривая в форме спирали, однако вследствие
[c.166] [c.22]
[c.22] 8), рассмотрим замкнутую векторную диаграмму, как на фиг. 4. При данном к, любая вершина А соответствует решению уравнения (5.3а), но существенными являются лишь те решения, которым соответствуют вершины, лежащие на поверхности вращения, задаваемой уравнением (5.8). Таким образом, число решений с к в интервале от к до k +dk примерно пропорционально k dk.
[c.240]
8), рассмотрим замкнутую векторную диаграмму, как на фиг. 4. При данном к, любая вершина А соответствует решению уравнения (5.3а), но существенными являются лишь те решения, которым соответствуют вершины, лежащие на поверхности вращения, задаваемой уравнением (5.8). Таким образом, число решений с к в интервале от к до k +dk примерно пропорционально k dk.
[c.240]