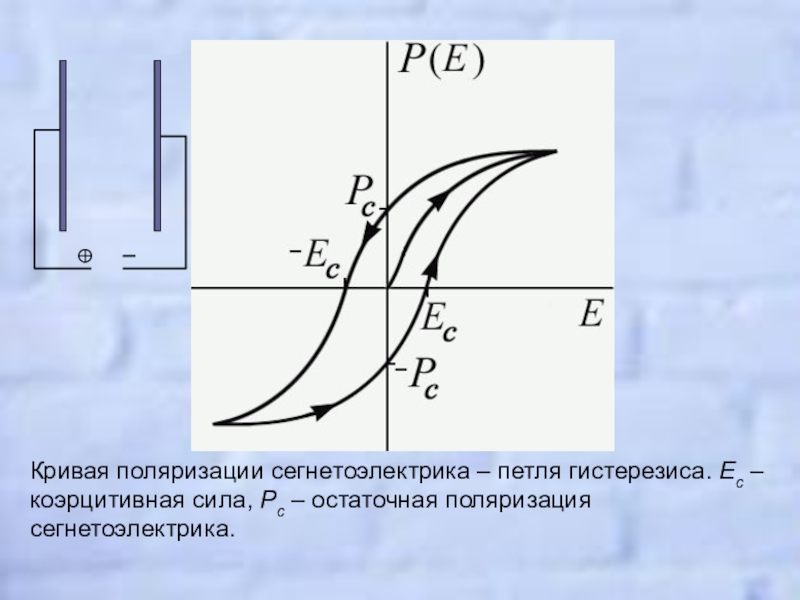
Гистерезиз и его магнитная петля
Явление остаточного магнетизма достаточно изучено и понятно. Любой металлический сердечник после определённого времени нахождения в электромагнитном поле сохраняет однонаправленные магнитные свойства. Для того чтобы его перемагнитить, требуется его помещение в магнитное поле обратной направленности. Тут возникает достаточно интересное явление – магнитная индукция не успевает изменяться в момент изменения магнитного потока, для этого требуется некоторый период времени. Именно это явление получило название гистерезиса. Для объяснения этого понятия и термина «петля гистерезиса» придётся уточнить некоторые базисные понятия, связанные с магнитными свойствами.
Графическое отображение петли гистерезиса
Вещества и их магнитные свойства
Вещества, обладающие естественными магнитными свойствами, называют ферромагнетиками. Обычно они используются как постоянные магниты, по составу обычно это металлы, но встречаются и ферримагнитные составы, состоящие из неметаллических элементов. Нужно отметить, что естественная намагниченность существует только при определённом диапазоне температур. По достижении температуры, так называемой точки Кюри, все магнитные свойства элемента теряются. Точка Кюри для разных минералов и веществ отличается.
Нужно отметить, что естественная намагниченность существует только при определённом диапазоне температур. По достижении температуры, так называемой точки Кюри, все магнитные свойства элемента теряются. Точка Кюри для разных минералов и веществ отличается.
Природный магнетизм этих веществ изучен и с древних времён поставлен на службу человечеству. Например, всем известен магнитный компас или неодимовые магниты. Основной характеризующий признак этих элементов – это способность создавать собственное магнитное поле, без влияния любого рода извне. Присутствие в составе атомов этих минералов и их смесей некомпенсированных спиновых магнитных моментов служит основной причиной возникновения такого явления, как ферромагнетизм. Обмен при взаимодействии электронов элемента при строго определённом отношении диаметра орбиты атома и его оболочки, при положительной величине интеграла энергии приводит к параллельной ориентации спинов. Ориентация спинов такого рода обеспечивает значение минимальной суммы энергии обменно-магнитного взаимодействия. Нужно отметить что вещества, обладающие обратными характеристиками, обычно называют антиферромагнетиками – это такие металлы, как марганец и хром.
Нужно отметить что вещества, обладающие обратными характеристиками, обычно называют антиферромагнетиками – это такие металлы, как марганец и хром.
При таком распределении возникают однонаправленные области естественной намагниченности – домены, при включении их в замкнутую сеть достигается наибольшая эффективность действия общего магнитного поля. Но при различной направленности в рядом расположенных доменах между ними появляются пограничные слои, в которых вектор намагниченности постепенно поворачивается в сторону направления вектора следующего домена.
В качестве наиболее простого примера можно взять железо. Кристалл этого металла наиболее легко намагничивается в направлении рёбер, грани обладают средним коэффициентом намагниченности, в то время как точкой наиболее сложной поддающейся намагничиванию является пересечение диагоналей кристалла. В отсутствии магнитного поля кристалл железа размагничен, но при воздействии на него внешнего поля он генерирует собственное. При этом на рост доменов влияет как направление поля, так и сама структура кристалла. Преодоление дефектов структуры и вызывает скачкообразный прирост собственного магнитного поля. В результате такого нарастания появляются импульсы напряжения, вектора которых при увеличении силы внешнего поля поворачиваются в его сторону, до полного совпадения по направлению с ним.
Преодоление дефектов структуры и вызывает скачкообразный прирост собственного магнитного поля. В результате такого нарастания появляются импульсы напряжения, вектора которых при увеличении силы внешнего поля поворачиваются в его сторону, до полного совпадения по направлению с ним.
Магнитные вещества по своим характеристикам делятся на:
- магнитомягкие;
- магнитотвердые.
Магнитомягкие вещества обладают значительной коэрцитивной силой, за счёт чего их насыщение производится сравнительно быстро и при малых затратах энергии. Твёрдые вещества обладают малыми магнетическими способностями, но в то же время успешно работают при больших потерях энергии.
Магнитное поле железа
Гистерезис и его петля
Это идеальная область полного насыщения ферромагнетика, при спаде поля в ферромагнетике останется остаточное намагничивание. Сам магнитный гистерезис – это отставание намагниченности элемента в зоне действия магнитного поля от воздействия внешнего источника поля. Фактически домены элемента, включаясь в замкнутую магнитную сеть, уменьшают рассеивание, точнее объем занимаемый его полем, и урезают собственную свободную энергию системы.
Фактически домены элемента, включаясь в замкнутую магнитную сеть, уменьшают рассеивание, точнее объем занимаемый его полем, и урезают собственную свободную энергию системы.
Гистерезис определяется как разность величины насыщения поля элемента-ферромагнетика и намагниченности замыкающих участков цепи-доменов. Для размагничивания используется отрицательное поле – коэрцитивная сила, при её приложении и достижении ферромагнетиком полного технического насыщения происходит процесс его полного размагничивания. Тут появляется такое понятие, как петля гистерезиса.
Если выводить этот процесс в виде графика, то видно, что кривая намагниченности замыкается, образуя остроугольную замкнутую петлю, – это и есть предельная петля. По её объёму можно узнать затраты энергии на размагничивание, так как она пропорциональна им. Площадь петли гистерезиса – знаковый объект, он используется для определения параметров магнитного поля и самой системы в целом.
Бортовой самописец
Использование явления гистерезиса
Одним из основных направлений использования ферромагнитных элементов является создание записывающих устройств.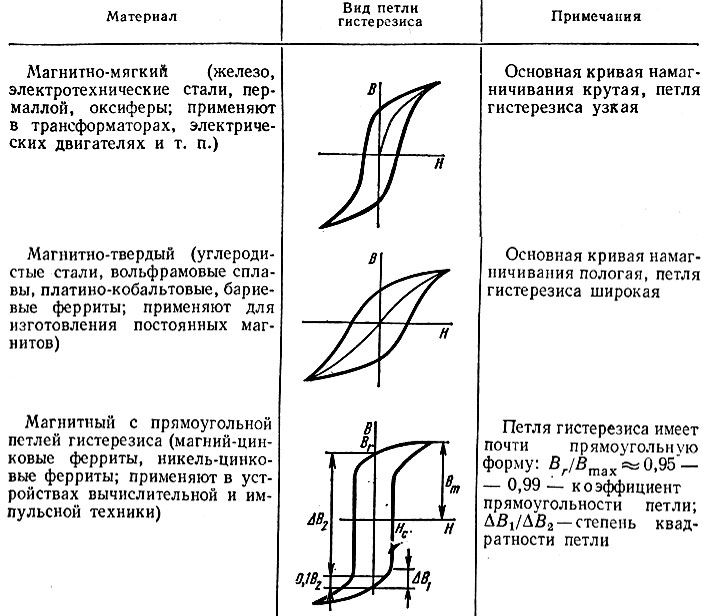 Для примера можно привести металлическую проволоку в бортовых самописцах водного и воздушного транспорта, ферритовые кольца оперативной памяти и триггеры Шмидта, а также другие магнитные носители.
Для примера можно привести металлическую проволоку в бортовых самописцах водного и воздушного транспорта, ферритовые кольца оперативной памяти и триггеры Шмидта, а также другие магнитные носители.
На этой основе работают электромоторы, устройства шумо-, и помехоподавления, в том числе предназначенные для коммутации логических схем.
Магнитный гистерезис, точнее его действие, активно используется в научных исследованиях, в том числе для управления некоторым оборудованием. Использование графического изображения петель гистерезиса в основе своей применятся для упрощения расчётов характеристик магнитных полей и параметров систем.
Триггер Шмидта
Видео
Оцените статью:ГИСТЕРЕЗИС • Большая российская энциклопедия
В книжной версии
Том 7.
 Москва, 2007, стр. 186-187
Москва, 2007, стр. 186-187Скопировать библиографическую ссылку:
Авторы: Б. Н. Филиппов, Б. А. Струков, В. Н. Кузнецов
ГИСТЕРЕ́ЗИС (от греч. ὑστέρησις – отставание, запаздывание), запаздывание изменения физич. величины, характеризующей состояние вещества, от изменения др. физич. величины, определяющей внешние условия. Г. имеет место в тех случаях, когда состояние тела в данный момент времени определяется внешними условиями не только в тот же, но и в предшествующие моменты времени. В результате для циклич. процесса (рост и уменьшение внешнего воздействия) получается петлеобразная (неоднозначная) диаграмма, которая называется петлёй гистерезиса.
Магнитный Г. – неоднозначная зависимость намагниченности $\boldsymbol M$ магнитоупорядоченного вещества (магнетика, напр., ферро- или ферримагнетика) от внешнего магнитного поля $\boldsymbol H$ при его циклич. изменении (увеличении и уменьшении). Причиной существования магнитного Г. является наличие в определённом интервале изменения $\boldsymbol H$ среди состояний магнетика, отвечающих минимуму термодинамич. потенциала, метастабильных состояний (наряду со стабильными) и необратимых переходов между ними. Магнитный Г. можно также рассматривать как проявление магнитных ориентационных фазовых переходов 1-го рода, для которых прямой и обратный переходы между фазами в зависимости от $\boldsymbol H$ происходят, в силу указанной метастабильности состояний, при разл.
Рис. 1. Петли магнитного гистерезиса:1 – максимальная, 2 – частная; а – кривая намагничивания, б и в – кривые перемагничивания; МR – остаточная намагниченность, Нс – коэрцитивная сила, Ms – намагничен…
На рис. 1 схематически показана типичная зависимость $M$ от $H$ в ферромагнетике; из состояния $M=0$ при $H=0$ с увеличением $H$ значение $M$ растёт (осн. кривая намагничивания, $\it а$) и в достаточно сильном поле $H⩾H_{\text m}$ $M$ становится практически постоянной и равной намагниченности насыщения $M_{\text s}$. При уменьшении $H$ от значения $H_{\text m}$ намагниченность изменяется вдоль ветви $\it б$ и при $H=0$ принимает значение $M=M_{\text R}$ (остаточная намагниченность). Для размагничивания вещества ($M=0$) необходимо приложить обратное поле $H= –H_{\text c}$, называемое коэрцитивной силой.
Описанные петли Г. характерны для достаточно медленных (квазистатических) процессов перемагничивания. Отставание $M$ от $H$ при намагничивании и размагничивании приводит к тому, что энергия, приобретаемая магнетиком при намагничивании, не полностью отдаётся при paзмагничивании. Теряемая за один цикл энергия определяется площадью петли Г. Эти потери энергии называются гистерезисными. При динамич. перемагничивании образца переменным магнитным полем $\boldsymbol H_{\sim}$ петля Г. оказывается шире статической вследствие того, что к квазиравновесным гистерезисным потерям добавляются динамические, которые могут быть связаны с вихревыми токами (в проводниках) и релаксационными явлениями.
Теряемая за один цикл энергия определяется площадью петли Г. Эти потери энергии называются гистерезисными. При динамич. перемагничивании образца переменным магнитным полем $\boldsymbol H_{\sim}$ петля Г. оказывается шире статической вследствие того, что к квазиравновесным гистерезисным потерям добавляются динамические, которые могут быть связаны с вихревыми токами (в проводниках) и релаксационными явлениями.
Форма петли Г. и наиболее важные характеристики магнитного Г. (гистерезисные потери, $H_с$, $M_{\text R}$ и др.) зависят от химич. состава вещества, его структурного состояния и темп-ры, от характера и распределения дефектов в образце, а следовательно, от технологии его пригoтовления и последующих физич. обработок (тепловой, механич., термомагнитной и др.). С магнитным Г. связано гистерезисное поведение целого ряда др.
Сегнетоэлектрический Г. – неоднозначная зависимость величины вектора электрич. поляризации $\boldsymbol P$ сегнетоэлектриков от напряжённости $\boldsymbol E$ внешнего электрич. поля при циклич. изменении последнего. Сегнетоэлектрики обладают в определённом температурном интервале спонтанной (т. е. самопроизвольной, возникающей в отсутствие внешнего поля) поляризацией $\boldsymbol P_{сп}$. Направление поляризации может быть изменено электрич. полем, при этом значение $\boldsymbol P$ при данном $\boldsymbol E$ зависит от предыстории, т. е. от того, каким было электрич. поле в предшествующие моменты времени. Сегнетоэлектрич. Г. имеет вид характерной петли (петля Г.), осн. параметрами которой являются остаточная поляризация $\boldsymbol P_{ост}$ при $\boldsymbol E=0$ и коэрцитивное поле $\boldsymbol E_к$, при котором происходит изменение направления (переключение) вектора $\boldsymbol P_{сп}$.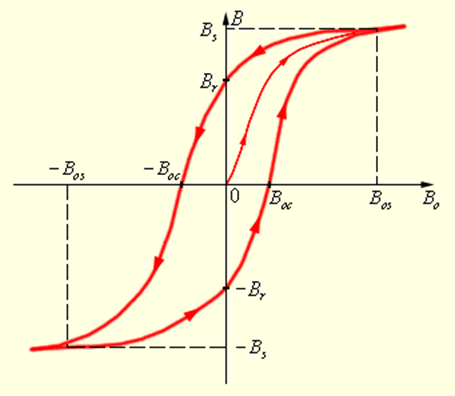
Существование сегнетоэлектрич. Г. следует из феноменологич. теории сегнетоэлектрич. явлений, в соответствии с которой равновесным значениям $\boldsymbol P_{сп}$ при любой темп-ре ниже темп-ры сегнетоэлектрич. фазового перехода отвечают два симметричных минимума термодинамич. потенциала, разделённые потенциальным барьером. При $E=±E_к$ один из минимумов исчезает, и кристалл оказывается в состоянии с определённым направлением вектора $\boldsymbol P_{сп}$. При циклич. переключении спонтанной поляризации площадь петли Г. определяет гистерезисные потери – количество энергии электрич. поля, переходящей в теплоту.
Рис. 2. Петля упругого гистерезиса.
Появление упругого Г. в металлах связано с тем, что в некоторых зёрнах поликристалла микронапряжения существенно превышают ср.
Упругий Г. как проявление отличия реального упругого тела от идеально упругого наблюдается у всех твёрдых тел, даже при весьма низких темп-рах. Упругий Г. является причиной затухания свободных колебаний упругих тел, затухания в них звука, уменьшения коэф. восстановления при неупругом ударе и др. В общем случае отклонение упругости от идеальной включается в понятие внутреннего трения.
Что такое петля гистерезиса
Гистерезис – это свойство биологических, физических и прочих систем, в которых мгновенный отклик на воздействия зависит от их текущего состояния, а на интервале времени поведение системы определяется ее предысторией. Петлей гистерезиса называется график, демонстрирующий это свойство.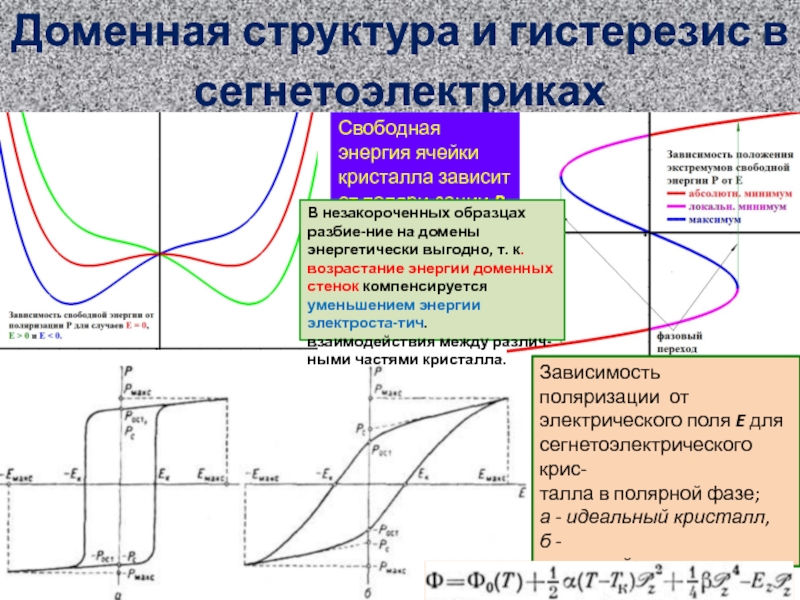 Наличие остроугольной петли на графике обусловливается неодинаковостью траекторий между соседними расстояниями, а также эффектом «насыщения». Гистерезис часто путают с инерционностью, однако это не одно и то же. Инерционность – это такая модель поведения, которая обозначает постоянное, однородное и монотонное сопротивление системы изменениям ее состояния.
Наличие остроугольной петли на графике обусловливается неодинаковостью траекторий между соседними расстояниями, а также эффектом «насыщения». Гистерезис часто путают с инерционностью, однако это не одно и то же. Инерционность – это такая модель поведения, которая обозначает постоянное, однородное и монотонное сопротивление системы изменениям ее состояния.Гистерезис в физике
В физике это свойство систем представлено тремя основными разновидностями: магнитным, сегнетоэлектрическим и упругим гистерезисом.
Магнитный гистерезис – явление, которое отражает зависимость вектора напряженности магнитного поля и вектора намагничивания в веществе. Причем как от приложенного внешнего поля, так и от предыстории конкретного образца. Существование постоянных магнитов обуславливается именно этим явлением.
Модель петли представляет собой определенный цикл, который некоторые свойства отправляет на повторную проверку и согласование, а некоторые использует дальше. Избирательный характер зависит от свойств конкретной системы.
Сегнетоэлектрический гистерезис – изменяющаяся зависимость поляризации сегнетоэлектриков от циклического изменения внешнего электрического поля.
Упругий гистерезис – поведение упругих материалов, способных сохранять и утрачивать деформацию под воздействием больших давлений. Это явление обуславливает анизотропию механических характеристик и высокие механические качества кованных изделий.
Гистерезис в электронике
В электротехнике и электронике свойством гистерезиса пользуются устройства, которые используют различные магнитные взаимодействия. Например, магнитные носители информации или триггер Шмитта.
Это свойство необходимо знать, чтобы использовать его для подавления шумов в момент переключения определенных логических сигналов (дребезга контактов, быстрых колебаний).
Упругий гистерезис бывает двух видов: динамический и статический. В первом случае график будет изображать постоянно изменяющуюся петлю, во втором – равномерную.
Во всех приборах электронного типа наблюдается тепловой гистерезис. После того как прибор был нагрет, а затем охлажден, его характеристики не принимают прежнего значения.
Это происходит из-за того, что неодинаковое тепловое расширение корпусов микросхем, кристаллодержателей, печатных плат и кристаллов полупроводников вызывает механическое напряжение, сохраняющееся и после охлаждения.
Наиболее заметно это явление в прецизионных источниках опорного напряжения, которые используются в измерительных преобразователях.
Петля Гистерезиса
Петля
гистерезиса. При циклическом изменении
напряженности постоянного магнитного
поля от 0 до +Н, от +Н до –Н и снова от –Н
до +Н кривая изменения индукции (кривая
перемагничивания) имеет форму замкнутой
кривой – петли гистерезиса. Для слабых
полей петля имеет вид эллипса. При
увеличении значения напряженности
магнитного поля Н получают серию
заключенных одна в другую петель
гистерезиса. Когда все векторы
намагниченности доменов сориентируются
вдоль направления поля, процесс
намагничивания закончится состоянием
технического насыщения намагниченности
материала. Петлю гистерезиса, полученную
при условии насыщения намагничивания,
называют предельной петлей гистерезиса.
Она характеризуется максимально
достигнутым значением индукции Bs,
называется индукцией насыщения. При
уменьшении напряженности магнитного
поля от +Н до 0 магнитная индукция
сохраняет остаточную индукцию Вс. Чтобы
получить остаточную магнитную индукцию,
равную 0, необходимо приложить
противоположно направленное
размагничивающее поле определенной
напряженности -Нс. Отрицательная
напряженность магнитного поля -Нс
называется коэрцитивной силой материала.
При достижении напряженности магнитного
поля значения –Н, а затем 0 вновь возникает
остаточная индукция –Вс. Если повысить
напряженность магнитного поля до +Нс,
то остаточная магнитная индукция Вс
будет равна 0.
При
увеличении значения напряженности
магнитного поля Н получают серию
заключенных одна в другую петель
гистерезиса. Когда все векторы
намагниченности доменов сориентируются
вдоль направления поля, процесс
намагничивания закончится состоянием
технического насыщения намагниченности
материала. Петлю гистерезиса, полученную
при условии насыщения намагничивания,
называют предельной петлей гистерезиса.
Она характеризуется максимально
достигнутым значением индукции Bs,
называется индукцией насыщения. При
уменьшении напряженности магнитного
поля от +Н до 0 магнитная индукция
сохраняет остаточную индукцию Вс. Чтобы
получить остаточную магнитную индукцию,
равную 0, необходимо приложить
противоположно направленное
размагничивающее поле определенной
напряженности -Нс. Отрицательная
напряженность магнитного поля -Нс
называется коэрцитивной силой материала.
При достижении напряженности магнитного
поля значения –Н, а затем 0 вновь возникает
остаточная индукция –Вс. Если повысить
напряженность магнитного поля до +Нс,
то остаточная магнитная индукция Вс
будет равна 0. Площадь гистерезисных
петель в промежуточных и предельных
состояниях характеризует рассеивание
электрической энергии в процессе
перемагничивания материала, т.е. потери
на гистерезис. Площадь гистерезисной
петли зависит от свойств материала, его
геометрических размеров и частоты
перемагничивания.
По предельной петле
гистерезиса определяют такие характеристики
магнитных материалов, как индукцию
насыщения Bs, остаточную индукцию Вс,
коэрцитивную силу Нс.
Площадь гистерезисных
петель в промежуточных и предельных
состояниях характеризует рассеивание
электрической энергии в процессе
перемагничивания материала, т.е. потери
на гистерезис. Площадь гистерезисной
петли зависит от свойств материала, его
геометрических размеров и частоты
перемагничивания.
По предельной петле
гистерезиса определяют такие характеристики
магнитных материалов, как индукцию
насыщения Bs, остаточную индукцию Вс,
коэрцитивную силу Нс.
Кривая намагничивания
Кривая намагничивания. Это важнейшая характеристика магнитных материалов, она показывает зависимость намагниченности или магнитной индукции материала от напряженности внешнего поля Н. Магнитная индукция материала Bi измеряется в теслах (Тл) и связана с намагниченностью . Основная (коммутационная) кривая намагничивания представляет собой геометрическое место вершин петель гистерезиса, полученных при циклическом перемагничивании и отражает изменение магнитной индукции В в зависимости от напряженности магнитного поля Н, которое создается в материале при намагничивании. Напряженность магнитного поля в образце в виде тороида, когда магнитная цепь замкнута, равна напряженности внешнего поля Нв. В разомкнутой магнитной цепи на концах образца появляются магнитные полюса, создающие размагничивающее поле Нр. Разница между магнитными напряженностями внешнего и размагничивающего полей определяют внутреннюю магнитную напряженность Hi материала. Основная кривая намагничивания имеет ряд характерных участков, которые можно условно выделить при намагничивании монокристалла ферромагнетика. Первый участок кривой намагничивания соответствует процессу смещения границ менее благоприятно ориентированных доменов. На втором участке происходит поворот векторов намагниченности доменов в направлении внешнего магнитного поля. Третий участок соответствует парапроцессу, т.е. завершающему этапу процесса намагничивания, когда сильное магнитное поле поворачивает в направлении своего действия не сориентированные магнитные моменты доменов ферромагнетика.
Петля упругого гистерезиса — Энциклопедия по машиностроению XXL
При высоких температурах петля упругого гистерезиса не меняется и =0, при умеренных температурах >,>0 п принимают равным единице или двум. [c.115]В экспериментах ряд конструкционных материалов переходил в состояние, когда петля гистерезиса уменьшалась до величины, сопоставимой с величиной петли упругого гистерезиса. [c.71]
Площадь, заключенная на диаграмме а = ст (е) внутри петли гистерезиса, численно равна необратимой удельной энергии (работе), превращающейся при выполнении каждого цикла деформации в тепловую энергию. Отставание деформаций от напряжений и порождаемая им петля упругого гистерезиса связаны с так называемым внутренним трением материала. В главе XVH при рассмотрении упругих колебаний систем показано, что наличие петли гистерезиса, порожденной внутренним трением, является причиной затухания свободных колебаний и стабилизации величин амплитуд вынужденных колебаний в районе резонанса. При каждом цикле колебания происходит поглощение удельной работы, равной площади, заключенной внутри петли гистерезиса. С этой точки зрения, [c.153]
Если напряжение, изменяясь периодически, все время остается одного знака, но в течение цикла уменьшается до нуля, то петля упругого гистерезиса имеет вид, показанный ка рис. 2.53, в. Наконец, если периодически изменяющиеся напряжения имеют максимальное значение, превышающее предел текучести, но остаются одного знака, доходя до нуля, то петля гистерезиса получается такой, как это изображено на рис. 2.53, г. [c.155]
Петля упругого гистерезиса 163, 154, 155, [c.826]
| Фиг. 2. I. Параметры петли упругого гистерезиса. |
| Рис. I. Петля упругого гистерезиса при одностороннем нагружении |
| Рис. 5.15. Петля упругого гистерезиса |
При большом числе циклов диаграмма деформирования упрочняющихся материалов стягивается в достаточно узкую петлю, ширина которой сопоставима с петлей упругого гистерезиса, и можно считать, что в предельном случае диаграмма деформирования может быть выражена прямой, сдвинутой на величину предельной остаточной деформации [c.93]
Иная картина наблюдается при перекатывании катка под действием некоторой силы или момента пары сил, когда известным образом проявляются силы внутреннего трения между частицами деформируемых материалов обоих тел и в результате теряется работа внешних сил. Для несовершенно упругих тел эта работа может быть определена по площади петли упругого гистерезиса в координатной системе сила —деформация. Процесс нагружения и разгружения в зоне площадки сжатия этих тел всегда протекает в условиях, благоприятных для проявления гистерезиса. [c.218]
Если, после того как стержень из таких материалов растянут, снять нагрузку, то кривая разгрузки ЛВС не пройдет через точку О (рис. 277) участок ОС носит название остаточной деформации. Последующее приложение нагрузки даст деформацию, которая будет проходить по кривой СОЕ, образующей с кривой разгрузки петлю упругого гистерезиса (гистерезис — отставание). Диаграмму напряжение— деформация, типичную для материалов, обладающих пла- [c.460]
Внутреннее трение — свойство твердого тела при циклическом нагружении обращать часть упругой энергии механических колебаний в тепловую. Внутреннее трение проявляется в затухании свободных колебаний твердого тела, а также в наличии петли упругого гистерезиса. Имеются материалы с высоким внутренним трением (высокой способностью к рассеиванию колебаний или, иначе, высокой демпфирующей способностью) и низким внутренним трением. [c.25]
| Рис. 4. Петля упругого гистерезиса по оси абсцисс — деформация, по оси ординат — напряжение. |
Амплитуду пластической деформации ширины петли упруго-пластического гистерезиса ip или как раз- [c.237]
Определение зависимости между напряжением и деформацией в пластической области имеет большое теоретическое и практическое значение при проектировании конструкций, работаюш,их при знакопеременном нагружении. К настоящему времени в литературе известны в основном два подхода к решению этой задачи. Один из них базируется на феноменологических представлениях с использованием классической теории упругости и пластичности, например [1—4], другой — на статистической теории дислокаций [5, 6]. На основании статистической теории дислокаций были получены зависимости между деформацией и напряжением начальной кривой деформации, нисходящей и восходящей ветвей симметричной петли механического гистерезиса. Эти зависимости представлены в виде бесконечных степенных рядов по величине приложенного напряжения, для которого можно считать плотность дислокаций постоянной. При достаточно больших напряжениях (деформациях) экспериментальные данные показывают, что плотность дислокаций изменяется, петли механического гистерезиса несимметричны и разомкнуты. [c.159]
При нагружении металла в пределах, не превышающих упругой деформации, линия нагружения не совпадает с линией разгружения (рис. 14). Это несовпадение, называемое упругим гистерезисом, показывает, что работа деформации, затрачиваемая при нагружении образца, больше работы деформации, возвращающейся при его разгружении. Поэтому считают, что упругий гистерезис обусловливается некоторым запаздыванием деформации в первые периоды нагружения и разгружения (рис. 15). Для пластического гистерезиса характерно отставание напряжения от деформации (см. рис. 15). Ширина пет- Рис. И. Петли гистерезиса характеризует циклическую вяз- [c.51] Исходя из предположения, что каждая компонента тензора деформаций может рассматриваться как сумма двух компонент — упругой и неупругой, для сложного напряженного состояния с пропорциональным изменением его компонент нами установлена связь [1] между рассеянной энергией в окрестности точки и площадью петли деформационного гистерезиса находящейся в плоскости двух [c.21]
Другое направление учитывает роль пластических деформаций в механизме демпфирования энергии при колебаниях. Отметим здесь две гипотезы. Это прежде всего гипотеза упругого гистерезиса, предложенная Н. Н. Давиденковым зависимость напряжения от деформации при повторном нагружении является степенной функцией, определяемой амплитудой деформации, а не скоростью. Гипотеза Н, Н. Давиденкова нашла многих сторонников, она получила подтверждение опытными данными для многих конструкционных материалов. Упомянем также комплексное представление Е. С. Сорокина для связи между напряжением и деформацией при циклическом нагружении, когда неупругая циклическая деформация отстает по фазе от упругой на 90°. Для петли гистерезиса гипотеза Е. С. Сорокина дает эллиптическую зависимость, что удобно при расчетах. [c.6]
Диаграмма циклического деформирования строится на основании формул (5.6)—(5.8) в виде ломаной, состоящей из трех линейных участков (рис. 5.10) (мгновенно-упругая деформация е(1) = ( >, не влияющая на петли пластического гистерезиса, на этом рисунке не показана). Эта аппроксимирующая ломаная вписывается в реальную диаграмму деформирования, причем может быть любой коэффициент асимметрии R. Величины Са, и С, отвечают переломам аппроксимирующей линии, причем j может рассматриваться как технический предел текучести при циклическом деформировании. Коэффициент жесткости Ез представляет собой тангенс угла наклона первого линейного участка теоретической кривой деформирования, а два других коэффициента жесткости 4 и определяются по фактической диаграмме циклического деформирования с учетом формул (5.7) и (5.8) как [c.174]
Концепция поверхности текучести приводит к противоречию и при интерпретации опытов на циклическое деформирование. Известно, что при уменьшении амплитуды напряжений ширина петли пластического гистерезиса не становится равной нулю, а лишь, постепенно уменьшается поскольку касательный модуль в этом случае близок к модулю упругости, она имеет заостренную форму. Понятие упругого гистерезиса как некоторого несовершенства упругих свойств не спасает положения, поскольку усталостное разрушение обоснованно связывают с возникновением пластических, сдвигов в микрообъемах материала. [c.123]
Наконец, в случае циклически стабильных материалов (например, среднеуглеродистые и аустенитные стали) ширина петли упруго-пластического гистерезиса практически не зависит от числа циклов деформирования. При различной ширине петель в четных и нечетных полуциклах происходит одностороннее накопление деформации. Для таких материалов, стабилизируюш,ихся при определенном числе полуциклов к = k, ширина петли определяется по формуле (21.29) при k = k. [c.621]
Долговечность в обласчи малоцикловой усталости при нагружении с постоянной общей амплитудой деформации за цикл зависит от упругой и пластической составляющих, которые определяются из параметров петли механического гистерезиса (рис. 5) [c.11]
Известно, что оно невелико и не превышает 10% [62]. Модуль разгрузки во всех полуциклах принимался равным модулю разгрузки в первом полуцикле. Точками на рис. 2.6.1, а обозначены условные границы раздела упругого и упругопластического участков диаграммы, установленные по допуску 0,05%. По такой диаграмме можно определить значения функции С (X) в начале каждого полуцикла (Сх, ) Соответствующие значения параметра X (Ях, Яз,.. . ) находятся по ширине петли йластического гистерезиса, что дает возможность построить график функции (Я). [c.127]
Для получения расчетных характеристик, соответствующих экспериментально установленной области существования нерас-пространяющихся усталостных трещин, были использованы опытные данные Н. Фроста (см. рис. 5). Характеристики исследуемого материала модуль упругости = 2-10 МПа, предел текучести От = 300 МПа, коэффициент упрочнения 1,2-10 МПа. Для упрощения построения петли циклического гистерезиса были приняты одинаковые характеристики материала при растяжении и сжатии. Были выбраны три уровня амплитуд внешнего нагружения, соответствующие трем характерным областям гЬ5,7 кН — для области, где усталостная трещина развивается по полного разрушения образца 3,5 кН — для области, где было обнаружено существование нераспространяющихся усталостных трещин, и 2,1 кН —для области, где вообще не наблюдали возникновения усталостных трещин. [c.67]
Рассмотрим особенности развития микропластических деформаций при циклических нагрузках. Наличие резко выраженной неоднородности деформации по локальньпг областям поликристаллического сплава создает предпосылки для постепенного входа в пластическое деформирование слабых микрообъемов по мере уве.личения числа циклов. Кроме того, в каждом цикле нагрузка — разгрузка и с изменением напряжения при обходе по восходящей и нисходящей ветвям петли механического гистерезиса будет непрерывно изменяться доля неупруго-деформирующихся микрообъемов. Такие локальные пластические деформации, проходящие иа фоне общей упругой деформации матрицы [5], еще не приводят к выделению остаточной де- [c.124]
На рис. 1.7 показана кривая циклического деформирования некоторого материала, обладающего свойством так называемой циклической стабильности . Напряженное состояние является линейным, и линия ОА представляет собой кривую первичного нагружения. Рассмотрим два деформационных процесса. В первом случае происходит разгрузка из состояния А до В, затем нагрузка сжимающим напряжением до состояния С по закону упругости, снова разгрузка до Б, нагрузка растягивающим напряжением до Л и т.д. Так как начальная пластическая деформация ОВ в ходе дальнейшего деформирования не изменяется, то в данном случае имеет место приспособление. Во втором случае (приспособление отсутствует) материал проходит начальное нагружение до того же состояния А, затем разгрузку АВ и нагрузку сжимающим напряжением по кривой BDE, далее разгрузку по линии EF и снова нагрузку по кривой FGA. При периодическом повторении такого цикла нагружения путь пластического деформирования FB совершается каждый раз дважды от исходного состояния О к В п от В к О, затем от О к F и от F снова к О. Площадь петли пластического гистерезиса FGADE численно равна необратимой работе деформирования в каждом цикле. Основная часть этой работы переходит в тепло и рассеивается путем теплообмена, а некоторая, относительно очень малая доля, расходуется на развитие повреждений малоцикловой усталости. При наличии же приспособления может иметь место лишь многоцикловая усталость, связанная не со знакопеременным пластическим деформированием макроскопических объемов материала, а с развитием локальных пластических деформаций в отдельных кристаллических зернах. [c.15]
При нагружении металла в пределах, не превышающих упругой деформации, линия нагружения не совпадает с линией разгружения (рис. 1). Это несовпадение называется упругим гистерезисом и показывает, что работа деформации, затрачиваемая при нагружении образца, больше работы деформации, возвращающейся при его разгружении. Поэтому считают, что упругий гистерезис обусловливается некоторым запаздыванием деформации в первые периоды нагружения и разгружения (рис. 2,а). Для пластического гистерезиса характерно отставание напряжения от деформации (рис. 2,6). Ширина петли гистеризиса характеризует циклическую вязкость, т. е. способность металла поглощать зне,ргию IB -необратимой форме при действии ци1кл1ическ1и повторяющихся односторонних или знакопеременных напряжений. [c.9]
Циклические ползучесть и релаксация. При выводе уравнений состояния (7.38)—(7.40) игнорировалось различие диаграмм деформирования реономных и склерономных стержней. Получаемая ошибка, малозаметная в каждом этапе нагружения, в определенных условиях может накапливаться. Например, циклическое несимметричное нагружение в соответствии с указанными уравнениями дает замкнутую (неподвижную) петлю пластического гистерезиса фактически часто наблюдается постепенное сползание петли вследствие реономности материала — в зависимости от условий возникают эффекты, называемые циклической ползучестью (задаются напряжения) или циклической релаксацией (задаются деформации). При непосредственном расчете кинетики деформаций в стержнях модели (без использования допущений, принятых при выводе указанных уравнений состояния) эти эффекты находят отражение. Однако можно воспользоваться уже рассмотренными методами анализа (исследование эпюр распределения упругих деформаций) для получения асимптотических решений в общей форме, т. е. определения границ сползания петель гистерезиса, если они существуют, и определения условий, в которых циклическая ползучесть происходит неограниченно (вплоть до ква-зистатического разрушения). [c.210]
При первом нагружении напряжения и соответствующие деформации связаны уравнением (рис. 1, б) а = Ф (8). Если образец после нагружения до точки А (а > а ) разгружается и нагружается вторично, то кривая разгрузки будет AB с остаточной деформацией ОС. Вторичное нагружение будет изображаться кривой DAE. То же самое будем наблюдать, если образец нагрузим до точки Е, а потом разгрузим. При циклических нагружениях с изменением напряжения а = 0 о ,ах будем наблюдать протекание процесса примерно по кривой D А В. Образующаяся петля гистерезиса весьма незначительная, т. е. того же порядка, что и петля упругого деформирования. [c.102]
Следует подчеркнуть, что к области малоцикловой усталости отнесены разрушения при числе нагружений до 5-10 — Ю циклов. Это соответствует нижней по числу циклов границе, от которой традиционно начинаются испытания в области многоцикловой усталости. диапазоне чисел циклов до 5-10 — 10 пластичные материалы средней прочности, какими являются широко распро- страненные конструкционные стали и сплавы, деформируются в ус- ловиях циклического нагружения за пределами упругости при на-i личии петли упругопластического гистерезиса. [c.5]
Matplotlib: петля гистерезиса с использованием зеркальной или разделенной оси x
Когда у вас есть время, вы можете использовать его для значений оси x и просто изменить метки X-тиков:
import numpy as np
import matplotlib.pyplot as plt
# Time, Distance, Pressure
data = [[0, 0, 0],
[1, 2, 10],
[2, 4, 30],
[3, 6, 60],
[4, 4, 35],
[5, 2, 15],
[6, 0, 0]]
# convert to array to allow indexing like [i, j]
data = np.array(data)
fig = plt.figure()
ax = fig.add_subplot(111)
max_ticks = 10
skip = (data.shape[0] / max_ticks) + 1
ax.plot(data[:, 0], data[:, 2]) # Pressure(time)
ax.set_xticks(data[::skip, 0])
ax.set_xticklabels(data[::skip, 1]) # Pressure(Distance(time)) ?
ax.set_ylabel('Pressure [Pa?]')
ax.set_xlabel('Distance [m?]')
fig.show()
skip — это просто так, чтобы у вас не было слишком много тиков на графике, меняйтесь, как вам нравится.
Как было сказано в комментарии, вышесказанное справедливо только для равномерных изменений расстояния как функции времени. Для неоднородных изменений вам придется использовать что-то вроде:
data = [[0, 0, 0],
[1, 2, 10],
[2, 4, 30],
[3, 6, 60],
[3.5, 5.4, 40],
[4, 4, 35],
[5, 2, 15],
[6, 0, 0]]
# convert to array to allow indexing like [i, j]
data = np.array(data)
def find_max_pos(data, column=0):
return np.argmax(data[:, column])
def reverse_unload(data, unload_start):
# prepare new_data with new column:
new_shape = np.array(data.shape)
new_shape[1] += 1
new_data = np.empty(new_shape)
# copy all correct data
new_data[:, 0] = data[:, 0]
new_data[:, 1] = data[:, 1]
new_data[:, 2] = data[:, 2]
new_data[:unload_start+1, 3] = data[:unload_start+1, 1]
# use gradient to fill the rest
gradient = -np.gradient(data[:, 1])
for i in range(unload_start + 1, data.shape[0]):
new_data[i, 3] = new_data[i-1, 3] + gradient[i]
return new_data
data = reverse_unload(data, find_max_pos(data, 1))
fig = plt.figure()
ax = fig.add_subplot(111)
max_ticks = 10
skip = (data.shape[0] / max_ticks) + 1
ax.plot(data[:, 3], data[:, 2]) # Pressure("Distance")
ax.set_xticks(data[::skip, 3])
ax.set_xticklabels(data[::skip, 1])
ax.grid() # added for clarity
ax.set_ylabel('Pressure [Pa?]')
ax.set_xlabel('Distance [m?]')
fig.show()
Что касается того факта, что использование измеренных значений в качестве тиков приводит к тому, что они не являются круглыми хорошими числами, я обнаружил, что просто легче сопоставить автоматические тики от matplotlib до правильных значений:
import numpy as np
import matplotlib.pyplot as plt
data = [[0, 0, 0],
[1, 2, 10],
[2, 4, 30],
[3, 6, 60],
[3.5, 5.4, 40],
[4, 4, 35],
[5, 2, 15],
[6, 0, 0]]
# convert to array to allow indexing like [i, j]
data = np.array(data)
def find_max_pos(data, column=0):
return np.argmax(data[:, column])
def reverse_unload(data):
unload_start = find_max_pos(data, 1)
# prepare new_data with new column:
new_shape = np.array(data.shape)
new_shape[1] += 1
new_data = np.empty(new_shape)
# copy all correct data
new_data[:, 0] = data[:, 0]
new_data[:, 1] = data[:, 1]
new_data[:, 2] = data[:, 2]
new_data[:unload_start+1, 3] = data[:unload_start+1, 1]
# use gradient to fill the rest
gradient = data[unload_start:-1, 1]-data[unload_start+1:, 1]
for i, j in enumerate(range(unload_start + 1, data.shape[0])):
new_data[j, 3] = new_data[j-1, 3] + gradient[i]
return new_data
def create_map_function(data):
"""
Return function that maps values of distance
folded over the maximum pressure applied.
"""
max_index = find_max_pos(data, 1)
x0, y0 = data[max_index, 1], data[max_index, 1]
x1, y1 = 2*data[max_index, 1], 0
m = (y1 - y0) / (x1 - x0)
b = y0 - m*x0
def map_function(x):
if x < x0:
return x
else:
return m*x+b
return map_function
def process_data(data):
data = reverse_unload(data)
map_function = create_map_function(data)
fig, ax = plt.subplots()
ax.plot(data[:, 3], data[:, 2])
ax.set_xticklabels([map_function(x) for x in ax.get_xticks()])
ax.grid()
ax.set_ylabel('Pressure [Pa?]')
ax.set_xlabel('Distance [m?]')
fig.show()
if __name__ == '__main__':
process_data(data)
Моделирование в электроэнергетике — Общие сведения о моделировании петли гистерезиса
Общие сведения о моделировании петли гистерезиса
Совершенствование электромагнитной модели силового трансформатора или измерительного трансформатора напряжения (в том числе шунтирующих и токоограничивающих реакторов) требует адекватного описания процессов, происходящих в его магнитной системе. Для этого должны быть воспроизведены гистерезисные свойства ферромагнитного материала и его поведение при произвольном законе изменения индукции (учет частотной зависимости). Ферромагнитный материал обладает способностью проводить магнитный поток (Ф), поэтому данный материал используют для создания магнитопроводов для силовых или измерительных трансформаторов. При возбуждении переменного магнитного потока в магнитопроводе электротехнических устройств происходит непрерывное циклическое перемагничивание ферромагнитного материала. Изменение намагничивания сердечника (магнитной индукции) всегда отстает от изменения величины магнитного потока (напряженности магнитного поля), создаваемого внешней обмоткой. Это отставание магнитной индукции от напряженности магнитного поля носит название гистерезиса.
Моделирование явления гистерезиса представляет сложную задачу при создании расчетных алгоритмов, направленных на исследование процессов происходящих в электромагнитных устройствах, в конструкции которых присутствуют ферромагнитные элементы. Описание процессов в листовой холоднокатаной стали выполняется с использованием известного принципа разделения общих потерь в ферромагнетике на составляющие, обусловленные гистерезисом, макро- и микроскопическими вихревыми токами. При условии равномерности распределения магнитного потока по сечению листа (отсутствие выраженного поверхностного эффекта) упомянутое разделение потерь эквивалентно разделению магнитного поля на поверхности листа на три слагаемые, называемые гистерезисным полем , классическим полем и дополнительными полем . Таким образом, напряженность магнитного поля в ферромагнетике определяется по следующему выражению (см. рис. 1):
Рис. 1. Гистерезисная петля намагничивания
Условные обозначения:
1-статическая петля гистерезиса
2-статическая петля гистерезиса + потери на вихревые токи
3-полная модель гистерезиса, которая учитывает статическую петлю гистерезиса, потери на вихревые токи и магнитную вязкость материала.
Первое слагаемое в представленном выражении рассчитывается с использованием статической модели гистерезиса. Данный вид обусловлен процессами перемагничивания, происходящими в ферромагнитном материале, такими как смещение границ доменов ферромагнетика и вращение магнитных моментов доменов при действии внешнего магнитного поля и т.д.
Второе слагаемое в представленном выражении называется классическим полем и зависит от вихревых потерь в стали, поэтому в литературе данное явление называют «вихревой» составляющей гистерезиса. Данное явление выражено тем резче, чем выше частота магнитного потока, и зависит от толщины листа и удельного сопротивления материала .
При учете только двух составляющих гистерезиса ( и ), потери активной мощности в трансформаторе меньше по сравнению с экспериментально измеренными потерями. Для устранения «дефицита» потерь вводят третье слагаемое , в технической литературе данное явление получило название «вязкостный эффект». При этом удается воспроизвести так называемые аномальные или добавочные потери и добиться совпадения результатов моделирования и эксперимента в широком диапазоне частот и индукций магнитного поля.
Следует заметить, что статический гистерезис не зависит от производной частоты (см. рис.2), в силу своей природы возникновения. Динамический гистерезис («вихревая» и «вязкостная» составляющая гистерезиса), напротив, зависит от производной частоты. Таким образом, на высоких частотах увеличиваются потери в расчетной схеме (см. рис.2).
Рис. 2. Зависимость петли гистерезиса от изменения частоты
Представленная концепция позволяет моделировать магнитный гистерезис в стали магнитопровода трансформатора/реактора и исследовать процессы, которые возникают при работе силового оборудования в нормальных и аварийных режимах работы. Несмотря на то, что модели гистерезиса такого типа являются, строго говоря, не физическими, а феноменологическими, их приемлемость для сложных законов изменения магнитной индукции подтверждается рядом численных и натурных экспериментов.
Правильный учет петли гистерезиса позволяет уточнить гармонический состав тока холостого хода и броска тока намагничивания, исследовать сложные режимы включения и отключения силового трансформаторного оборудования, а также проводить качественный анализ случаев повреждения трансформаторного оборудования связанный с возникновением остаточной намагниченности или феррорезонансными явлениями.
Для того, чтобы добавить Ваш комментарий к статье, пожалуйста, зарегистрируйтесь на сайте.
Петля гистерезиса | Кривая намагничивания
Определение петли гистерезисаКривая или петля, построенная в координатах B-H, показывающая, как намагниченность ферромагнитного материала изменяется при воздействии периодически изменяющегося магнитного поля, известна как петля гистерезиса.
Определение гистерезиса
Гистерезис — это отставание намагниченности ферромагнитного материала от силы намагничивания H.
Используя график с координатами B-H, мы можем построить гистерезисные характеристики данного ферромагнитного материала.Такая кривая изображена на следующем рисунке и называется петлей гистерезиса. Периодически меняя намагничивающую силу, мы можем построить график изменения значений B в материале.
Фактически, петля гистерезиса представляет собой кривую B-H под действием силы намагничивания переменного тока. Значения плотности потока B показаны по вертикальной оси в теслах. Сила намагничивания H отложена по горизонтальной оси.
На рисунке выше предполагается, что образец не увеличен, а ток начинается с нуля в центре графика.Когда H положительно увеличивается, B следует по красной пунктирной кривой от начала до точки насыщения a, обозначенной B max .
Когда H уменьшается до нуля, поток следует кривой ab и падает до B r , что указывает на удерживающуюся или остаточную индукцию. Эта точка представляет количество магнитного потока, остающегося в сердечнике после снятия намагничивающей силы.
Когда H начинается в отрицательном направлении, сердечник теряет свой магнетизм, как показано на кривой от точки b до c.Величина намагничивающей силы, необходимая для полного размагничивания сердечника, называется коэрцитивной силой и обозначена на рисунке как –H c .
По мере приближения к пику отрицательного цикла поток следует за участком кривой, обозначенным cd. Точка –B max представляет насыщение в противоположном направлении от B max . От точки d значение — H уменьшается до точки e, которая соответствует нулевой намагничивающей силе.Flux –B r все еще остается в активной зоне.
Коэрцитивная сила + H c требуется для уменьшения намагниченности сердечника до нуля. Поскольку магнитная сила продолжает увеличиваться в положительном направлении, часть петли от точки f до точки a завершается. Периодическое изменение силы намагничивания заставляет магнитный поток в сердечнике неоднократно отслеживать петлю гистерезиса.
Размагничивание или размагничиваниеПроцесс, с помощью которого намагниченность в ферромагнитных материалах уменьшается до нуля, подвергаясь воздействию сильного переменного магнитного поля, которое постепенно уменьшается до нуля.
Чтобы размагнитить любой магнитный материал, мы должны уменьшить его остаточный магнетизм B r до нуля. Это можно сделать, подключив подходящую катушку к источнику переменного тока и поместив ее близко к объекту, подлежащему размагничиванию. Медленное перемещение катушки и объекта друг от друга приводит к постепенному уменьшению петли гистерезиса. Наконец, достигается точка, в которой контур уменьшается до нуля и остаточный магнетизм не остается.
Из петли гистерезиса мы можем сделать вывод о различных магнитных свойствах материала, таких как:
Сопротивление — Противодействие, которое магнитная цепь представляет прохождению через нее магнитных линий.
Сохраняемость — Способность ферромагнитного материала сохранять остаточный магнетизм называется его удерживающей способностью.
Остаточный магнетизм — Магнетизм, остающийся после удаления внешней силы намагничивания.
Коэрцитивная сила — Напряженность магнитного поля, необходимая для уменьшения остаточного магнетизма до нуля, называется коэрцитивной силой.
Проницаемость — Проницаемость — это мера легкости, с которой магнитные силовые линии проходят через данный материал.
Петля гистерезиса — обзор
3.1 Определения и измерения
Намагниченность M : магнитный момент на единицу объема, векторная величина величиной M .
Петля гистерезиса : график зависимости намагниченности M от магнитного поля H (рис. 5). Это многозначная функция, зависящая от последовательности, в которой применяется изменяющееся во времени поле. На рисунке предполагается, что измерение производится, начиная с очень большого поля в любом направлении.
Рис. 5. Схема петли гистерезиса (по Хогленду и Монсону, 1991 г.).
Намагниченность насыщения M s : строго, намагниченность однородно намагниченной области (домена) в однородной магнитной среде. Это внутреннее свойство, функция температуры и слабо зависящее от магнитного поля и напряжения. На практике M s также используется для намагничивания M любого (не обязательно однородного) магнитного материала в большом приложенном поле.
Остаточная намагниченность (или остаточная намагниченность) M r : намагничивание магнитного объекта, которое остается после намагничивания в большом приложенном поле, которое впоследствии удаляется. Реманентность — это внешняя величина, которая зависит от микроструктуры, формы и фазы луны (этот последний фактор предназначен для обозначения разочарования экспериментатора иногда кажущимися случайными колебаниями в результатах очень тщательно контролируемых измерений).Связанная величина, наиболее значимая для магнитной записи, особенно с тонкими носителями, — это произведение остаточной намагниченности и толщины M r t . Эта величина определяет магнитный момент, связанный с битовой ячейкой заданного размера, и, следовательно, способность ее обнаруживать. M r t образца известной площади можно точно измерить в VSM, даже если M r и t определены плохо.
Кривая остаточной намагниченности M r ( H ): график последовательности конечных значений M , достигнутых при циклировании образца следующим образом: насыщение большим приложенным полем; применение реверсивного поля H , которое затем обнуляется; повторное насыщение; и повторение с другим реверсивным полем. На этой кривой остаточная намагниченность, как определено выше, составляет M r (0).
Кривая остаточной намагниченности образца может быть измерена непосредственно, например, в VSM, следуя этой процедуре, которая требует много времени.Достаточное приближение может быть построено из петли гистерезиса путем рисования линий с наклоном петли на остаточной силе от петли с несколькими значениями реверсивного поля до оси M и привязки к каждому значению поля значения M на пересечении с осью.
Кривая остаточной намагниченности носителя записи также может быть измерена неразрушающим методом на спиннинге путем измерения выходного напряжения ненасыщающих переходов.
Коэрцитивная сила H c : значение обратного приложенного магнитного поля, необходимого для уменьшения намагниченности с остаточной намагниченности до нуля в присутствии реверсивного поля.
Остаточная коэрцитивная сила H cr : значение обратного приложенного магнитного поля, необходимого для уменьшения намагниченности с остаточной намагниченности до нуля после выключения реверсивного поля.
Прямоугольность : мера степени, в которой форма петли гистерезиса аппроксимируется прямоугольником. Обычно используются две меры прямоугольности: остаточная прямоугольность S = M r / M s , которая измеряет, насколько близки верхняя и нижняя дорожки петли к горизонтали; и коэрцитивная прямоугольность S * (см. рис.5), который измеряет, насколько близка касательная к петле в точке H c к вертикали.
Энергия анизотропии : энергия, связанная с направлением вектора намагниченности M относительно заданного набора осей. Энергия связана с формой магнита и его кристаллической структурой. В эллипсоидном теле энергия анизотропии формы (внешняя) минимальна, когда M лежит вдоль самой длинной главной оси, и выше, когда она лежит вдоль любого другого направления (например, намагниченность магнитной иглы имеет тенденцию выравниваться вдоль иглы, не поперёк).Энергия магнитокристаллической анизотропии (собственная) K a — это энергия на единицу объема, связанная с направлением M относительно осей кристалла. Например, в одноосном кристалле, таком как кобальт, K a = K sin 2 ϕ, где K — константа анизотропии, а ϕ — угол относительно оси c.
Поле анизотропии H k : магнитное поле, которое представляет собой магнитокристаллическую анизотропию в форме K a = −M · H k .В одноосном кристалле величина H k равна (2 K / M s ) sin 2ϕ.
Магнитострикция : деформация магнитного образца при изменении его намагниченности M и, наоборот, влияние деформации на M . Обменная энергия и энергия дипольного взаимодействия атомных магнитов на кристаллической решетке зависит от их ориентации, а также от длин связей и валентных углов. Эта энергия может быть представлена как магнитоупругая постоянная, внутреннее свойство материала, умноженное на произведение тензора деформации и направляющих косинусов M .Равновесная ориентация и деформация минимизируют сумму магнитоупругой энергии, которая является линейной, и упругой энергии, которая квадратична по деформации (см. Также Магнитоупругие явления ).
Магнитная вязкость S : мера термически активированной скорости затухания намагниченности M . Экспериментально установлено, что намагниченность намагниченного тела логарифмически спадает в широком диапазоне времени: M ( t ) = M (0) — S log t .Такое поведение считается суммой экспоненциальных распадов типа Аррениуса в типичном диапазоне энергетических барьеров. Вязкость S — это свойство магнитного материала, которое является функцией температуры и приложенного реверсивного поля, и обычно она максимальна, когда реверсивное поле равно коэрцитивной силе (см. Магнитная вязкость ).
Размер зерен и распределение по размерам : наиболее широко используемые носители для записи на жестких дисках — это поликристаллические пленки, достаточно тонкие, чтобы состоять из одного слоя зерен.Отдельные зерна этих пленок слишком малы, чтобы поддерживать магнитные доменные стенки, и поэтому намагничены приблизительно однородно. Для измерения размера зерна можно использовать просвечивающую или сканирующую электронную микроскопию. Распределение размеров зерен может влиять на распределение поля переключения и термическую стабильность.
Межгранулярные взаимодействия, графики Хенкеля и δ M : размер зерна устанавливает окончательный предел для коммутационного блока и, следовательно, плотности хранения.Однако межгранулярные взаимодействия могут влиять на переключение соседних зерен и вносить вклад в средний шум. Межгранулярное обменное взаимодействие может приводить к образованию кластеров зерен; диполярные взаимодействия могут способствовать параллельности (в продольных средах) и антипараллельности (в перпендикулярных средах) соседних зерен.
Измерение межкристаллитного взаимодействия может быть получено с помощью графика Хенкеля или эквивалентной кривой δ M . График Хенкеля создается путем получения кривой, названной изотермической остаточной намагниченностью M ri ( H ).Эта кривая измеряется той же процедурой, что и M r ( H ), описанной выше (в этом контексте иногда обозначается M rd ( H )), за исключением того, что теперь начальной точкой каждого цикла является ac размагничивания, при M ri (0) = 0. Легко видеть, что теперь, поскольку изначально половина коммутационных блоков уже находится в направлении, предпочтительном для реверсивного поля, только половина из них будет реверсировать с каждым шагом поля. Таким образом, можно ожидать, что M rd ( H ) = M ri (∞) –2 M ri ( H ).Это соотношение, однако, справедливо только для невзаимодействующих коммутационных блоков, а отклонения указывают на наличие межкристаллитной связи. Традиционная форма представления отклонений — график Хенкеля, M rd ( H ) / M ri (∞) = 1-2 M ri ( H ) / M ri (∞) + δ M ( H ), с δ M положительно для взаимодействий, благоприятствующих параллелизму, отрицательно для антипараллельности.
Измерение может быть выполнено на образце среды в VSM или неразрушающим методом на спиновой стойке путем измерения выходных напряжений от переходов, записанных на среде в насыщенном и переменном токе. размагниченные состояния.
Распределение коммутационного поля (SFD) : доля средней намагниченности, измененная на приращение диапазона реверсивного поля δ M / δ H . Это функция от H с максимумом на H c или около него.SFD также иногда определяют как диапазон реверсивного поля, необходимый для уменьшения намагниченности изначально насыщенной среды с M r /2 до — M r /2. SFD можно определить по кривой остаточной намагниченности. Это также было измерено путем сравнения изображений MFM и подсчета событий переключения.
Временная зависимость измерений : результат измерения может зависеть от шкалы времени, в которой выполняется измерение. Петля гистерезиса образца обычно измеряется с помощью VSM по шкале времени в минутах или часах или с помощью измерителя петли B — H во временной шкале, обычно составляющей десятки миллисекунд.Перемагничивание при записи записывающих переходов происходит за наносекунды. Как упоминалось ранее, реакция среды на магнитное поле не мгновенная. В частности, коэрцитивная сила среды зависит от шкалы времени измерения, что приводит к концепции динамической коэрцитивной силы, которая увеличивается с увеличением скорости приложения поля. Была разработана феноменологическая теория, которая довольно успешно объясняет такие эффекты (Sharrock and Flanders 1990).
Коэффициент ориентации : желательно, чтобы в некоторых средах магнитные свойства вдоль дорожки отличались от магнитных свойств вдоль дорожки.Для ленты коэрцитивная сила вдоль ленты может быть больше, чем у нее, а для дисков круговая (направление записи) коэрцитивная сила может быть больше, чем радиальная коэрцитивность на десятки процентов. Это явление заложено в материале во время производства и может контролироваться условиями осаждения, особенно углом падения и приложенными магнитными полями, или анизотропией в подложке, особенно микроцарапанием. Традиционной мерой этого является отношение макроскопически измеренной записи к коэрцитивности кросс-трека.
Магнитный гистерезис — Engineering LibreTexts
Магнитный гистерезис , иначе известный как петля гистерезиса , представляет собой представление силы намагничивания (H) в зависимости от плотности магнитного потока (B) ферромагнитного материала. Кривизна гистерезиса характерна для типа наблюдаемого материала и может различаться по размеру и форме (то есть узкая или широкая). Петля может быть создана с помощью датчика Холла для измерения величины магнитного поля в различных точках — в присутствии магнитного поля, когда оно удаляется из магнитного поля и когда прикладывается сила, приводящая к магнитному полю. поток обратно к нулю.Эти петли важны для емкости памяти устройств для аудиозаписи или магнитного хранения данных на дисках компьютера.
Рисунок \ (\ PageIndex {1} \): б). Эти дипольные моменты настолько упорядочены, что при удалении от магнитного поля остается некоторая остаточная намагниченность. Чтобы уменьшить магнитный поток обратно до нуля, необходимо применить коэрцитивную силу, при которой дипольные моменты компенсируют друг друга. Таким образом, эта петля гистерезиса суммирует путь, который проходит ферромагнитный материал от добавления и удаления намагничивающей силы.Структура петли гистерезиса
Петли гистерезиса начинаются в начальной точке (H = 0), в которой ее магнитные дипольные моменты дезориентированы, а материал изображает парамагнетизм. Когда к материалу добавляется намагничивающая сила (H), он следует по пути до точки насыщения (+ Hs). В этот момент все магнитные дипольные моменты выровнены в направлении силы намагничивания, и магнитный поток больше не увеличивается. Когда H уменьшается до нуля, остается некоторая остаточная намагниченность; эта точка известна как точка удержания (+ Br).Чтобы удалить эту остаточную намагниченность, коэрцитивная сила намагничивания применяется в обратном направлении. Точка, в которой больше нет магнитного потока (B = 0) из-за компенсации дипольных моментов, действующих в противоположных направлениях, называется точкой коэрцитивности (-Hc). Когда сила намагничивания увеличивается в отрицательном направлении, происходит такое же насыщение, как и раньше, но в противоположном направлении (-Hs). Цикл продолжается с равной, но противоположной точкой удерживания (-Br) и точкой коэрцитивности (+ Hc) до исходной точки насыщения (+ Hs).На рисунке 2 изображена петля гистерезиса полного цикла, в которой точки a и d представляют собой +/- Hs, точки b и e представляют собой +/- Br, а точки c и f представляют собой +/- Hc. Спины магнитного диполя в этих соответствующих точках можно увидеть на рисунке 3, где спины сначала дезориентируются, затем выравниваются с магнитным полем и, наконец, не выравниваются до тех пор, пока моменты не уравняются друг с другом, чтобы не создавать результирующий магнитный момент. Также обратите внимание, что кривая никогда не возвращается в начало координат (B и H = 0). Чтобы вернуться к этому моменту, материал необходимо размагнитить (т.е.е. вернуться к парамагнитному поведению), ударяя материалом о поверхность, изменяя направление намагничивающего поля на обратное или нагревая его до превышения температуры Нееля. При этой температуре ферромагнитный материал становится парамагнитным из-за тепловых флуктуаций магнитных дипольных моментов, которые дезориентируют спины.
Варианты петель гистерезиса
| Металл | Hs [А / м] |
|---|---|
| Fe | 1.75 х 10 6 |
| Со | 1,45 x 10 6 |
| Ni | 0,51 х 10 6 |
Важность петель гистерезиса
Петли гистерезиса важны при создании нескольких электрических устройств, которые подвержены быстрому изменению магнетизма или требуют хранения в памяти. Магнитомягкие материалы (т.е.те, которые имеют меньшие и более узкие области гистерезиса) и их быстрое изменение магнетизма полезны в электрическом оборудовании, которое требует минимального рассеивания энергии. Трансформаторы и сердечники, используемые в электродвигателях, получают выгоду от использования этих материалов, поскольку они теряют меньше энергии в виде тепла. Твердые магнитные материалы (т. Е. Петли с большей площадью) имеют гораздо более высокую удерживающую способность и коэрцитивную силу. Это приводит к более высокой остаточной намагниченности, полезной в постоянных магнитах, где размагничивание трудно достичь.Жесткие магнитные материалы также используются в устройствах памяти, таких как аудиозаписи, дисководы компьютеров и кредитные карты. Высокая коэрцитивная сила этих материалов не позволяет легко стереть память.
Вопросы
1. Обозначьте следующую петлю гистерезиса.
2. Какими 3 способами размагнитить ферромагнитный материал?
3. Какой из этих элементов (Fe, Co, Cr, Ni) не будет создавать петлю гистерезиса? Почему?
ответы
1.а) Точка насыщения — HS
б) Точка удержания —
руб.c) Точка коэрцитивности — Hc
2. Ударьте ферромагнитным материалом о поверхность, чтобы дезориентировать магнитные дипольные моменты, изменить направление петли гистерезиса, нагреть материал выше его критической температуры.
3. Cr не создает петли гистерезиса, потому что он антиферромагнитен. Fe, Co и Ni являются ферромагнитными и поэтому создают петлю гистерезиса.
Список литературы
- Хаммель, Рольф Э. Электронные свойства материалов: введение для инженеров. Берлин: Springer-Verlag, 1985. Печать.
- Чиказуми, Сошин и К.Д. Грэм. Физика ферромагнетизма. Oxford: Claredon, 1997. Печать.
- Раллс, Кеннет М., Томас Х. Кортни и Джон Вульф. Введение в материаловедение и инженерию. Нью-Йорк: Wiley, 1976. Печать.
- Бертотти, Джорджо. Гистерезис в магнетизме: для физиков, материаловедов и инженеров. Сан-Диего: Академический, 1998. Печать.
Авторы и авторство
- Саманта Дрис (бакалавр материаловедения и инженерии, Калифорнийский университет в Дэвисе | июнь 2016 г.)
Петля гистерезиса или кривая B-H и потеря гистерезиса
Что такое петля гистерезиса или кривая B-H? Петля гистерезиса дает информацию о магнитных свойствах материала. Изучая петлю гистерезиса, можно легко отследить всю информацию, относящуюся к магнитным свойствам материала.
Другими словами, мы можем определить петлю гистерезиса следующим образом: «Когда ферромагнитный материал намагничен в одном направлении, он не вернется к нулевой намагниченности при снятии приложенного намагничивающего поля. Он должен быть доведен до нуля под действием намагничивающего поля в обратном или обратном направлении. Если к материалу приложить переменное магнитное поле, его намагничивание будет образовывать петлю (в виде кривой графика), называемую петлей гистерезиса.
Отсутствие возможности повторного отслеживания кривой намагничивания (H) — это свойство, называемое гистерезисом, и оно связано с наличием магнитных доменов в материале.
Петля гистерезиса показывает взаимосвязь между наведенной плотностью магнитного потока (B) и силой намагничивания (H). По этой причине ее также называют кривой B-H. На рисунке ниже показан пример петли гистерезиса;
| Петля гистерезиса или кривая B-H |
Пункты ниже объясняют петлю гистерезиса или кривую B-H;
- Петля создается путем измерения магнитного потока (B) ферромагнитного материала при изменении приложенной силы намагничивания (H).
- Ферромагнитный материал, который никогда ранее не подвергался намагничиванию или размагничиванию, будет перемещаться по пунктирной линии (см. Рисунок) при увеличении силы намагничивания (H).
- Пунктирная линия показывает, что чем больше величина приложенного тока (H +), тем сильнее магнитное поле в компоненте (B +).
- В точке «а» почти все магнитные домены выровнены, и дополнительное увеличение силы намагничивания приведет к очень небольшому увеличению магнитного потока.
- Достигнута точка магнитного насыщения материала.
- Когда сила намагничивания (H) уменьшается до нуля, кривая переместится или изменится от точки «a» к точке «b».
- В этот момент мы можем заметить, что некоторые остатки магнитного потока в материале, даже если сила намагничивания (H) равна нулю. Это называется точкой удержания на графике и показывает остаточный магнетизм или уровень остаточного магнетизма в материале. Некоторые магнитные домены остаются выровненными, но некоторые магнитные домены теряют выравнивание.
- При приложении силы намагничивания в обратном направлении кривая переместится в точку «c», где магнитный поток уменьшился до нуля. Эта точка называется точкой коэрцитивности на кривой или петле. Обращенная сила намагничивания перевернула множество доменов, так что оставшийся поток внутри материала равен нулю.
- Чтобы удалить остаточный магнетизм с материала, необходимо приложить силу, эта требуемая сила называется коэрцитивной силой или коэрцитивной силой материала.
- В отрицательном направлении, когда сила намагничивания увеличивается, материал снова становится магнитонасыщенным, или материал не переходит в насыщение, но в противоположном или обратном направлении, то есть к точке «d».
- Уменьшение силы намагничивания (H) до нуля приводит кривую к точке «e». Доступный уровень остаточного магнетизма равен уровню, достигнутому в другом направлении.
- Увеличение силы намагничивания (H) в положительном направлении вернет или вернет магнитный поток (B) к нулю.
- Мы можем заметить, что кривая не вернулась к началу или исходной точке графика, потому что для удаления оставшегося или остаточного магнетизма требуется некоторая сила намагничивания.
- Теперь кривая на графике будет идти по разному или другому пути от точки «f» обратно до точки насыщения, здесь, в этой точке, она завершает цикл.
| Измерение кривой B-H на осциллографе |
- Процесс намагничивания ферромагнитного сердечника.
- Часть кривой, на которую намагничивается ферромагнитный сердечник, определяет плотность потока, потому что это зависит от предыдущей истории схемы, которая придает сердечнику форму «памяти».
- Ферромагнетики обладают памятью, потому что они остаются намагниченными после снятия внешнего магнитного поля.
- Реле, соленоиды и трансформаторы можно легко намагнитить и размагнитить, потому что они сделаны из мягких ферромагнитных материалов, таких как кремнистая сталь или железо, которые имеют очень узкие петли магнитного гистерезиса, что приводит к очень небольшому остаточному магнетизму.
- Остаточный магнетизм можно преодолеть с помощью коэрцитивной силы; Используемая энергия рассеивается в магнитном материале в виде тепла. Это тепло известно как гистерезисные потери, величина коэрцитивной силы материала определяет величину потерь.
- Очень небольшая коэрцитивная сила может быть получена с очень узкой петлей гистерезиса путем добавления добавок к металлическому железу, например кремнию. Намагничивание и размагничивание магнитомягких материалов с узкими петлями гистерезиса очень просто.
| Петля гистерезиса для мягких и твердых материалов |
Из-за присутствия магнитных доменов в материале кривая намагничивания не отслеживается повторно (это называется гистерезисом). После переориентации магнитных доменов потребуется некоторое намагничивающее поле или энергия, чтобы повернуть их обратно.Эта характеристика ферромагнитных материалов полезна как магнитная «память». Некоторые конфигурации ферромагнитных материалов будут поддерживать принудительное намагничивание вечно и могут использоваться в качестве «постоянных магнитов». Свойства магнитной памяти из оксидов хрома и железа полезны при записи аудиокассет, а также для магнитного хранения данных на жестких дисках компьютеров.
Мягкие магниты с низкой коэрцитивной силой, например оксид железа, используются для ферритовых сердечников в электромагнитах. Низкая коэрцитивная сила снижает потери энергии, связанные с гистерезисом.Эти низкие потери энергии во время петли гистерезиса являются основной причиной использования мягкого железа для электродвигателей и сердечников трансформаторов.
Потеря гистерезиса Поскольку ток течет в прямом и обратном направлениях, происходит намагничивание и размагничивание сердечника, что приводит к потере гистерезиса.Когда мы прикладываем внешнюю намагничивающую силу к материалу и увеличиваем намагничивающую силу (ток), магнитный поток также увеличивается, но когда намагничивающая сила (ток) уменьшается, магнитный поток уменьшается постепенно, а не с той же скоростью.Таким образом, когда сила намагничивания достигает нуля, плотность потока не достигает нуля и все еще имеет положительное значение. Теперь намагничивающая сила должна быть приложена в отрицательном направлении, чтобы плотность потока достигла нуля.
Связь между силой намагничивания (H) и плотностью магнитного потока (B) показана на петле или кривой гистерезиса. Энергия, необходимая для завершения полного цикла намагничивания и размагничивания, показана площадью петли гистерезиса. Также эта область контура характеризует потерю энергии во время этого процесса намагничивания.
Ниже приведено уравнение потерь на гистерезис;
η = коэффициент гистерезиса Штейнмеца, в зависимости от материала (Дж / м³)
Bmax = максимальная плотность потока (Вт / м²)
n = показатель степени Штейнмеца, варьируется от 1,5 до 2,5, в зависимости от материала
f = частота перемагничивания в секунду (Гц)
V = объем магнитного материала (м³)
Гистерезисные потери приводят к потере энергии, которая пропорциональна площади петли магнитного гистерезиса.
В трансформаторах переменного тока гистерезисные потери всегда являются проблемой, когда ток постоянно меняет направление потока, в результате чего магнитные полюса постоянно протекают в обратном направлении и вызывают потери в сердечнике.
Заключение Петля гистерезиса предоставляет информацию о магнитных свойствах материала. Важно, чтобы петля гистерезиса B-H была как можно меньше, чтобы потери были меньше, потому что форма кривой B-H определяет потери. Чем больше площадь, тем больше потери, и наоборот.Форма петли гистерезиса зависит от природы используемого материала, т. Е. Железа или стали. Более подробную информацию о феррите вы можете найти в моем предыдущем блоге;Магнитная индукция против намагничивания (сходства, различия и точки на графике) — Материаловедение и инженерия
Давайте посмотрим правде в глаза: если вы не защищаете докторскую степень в области магнитных материалов или физики конденсированного состояния, вы действительно понимаете магнетизм? (Для справки, моя докторская степень — , а не по поводу магнетизма, поэтому я отношу себя к неофитам.)
Конечно, если вы посещали колледж или курс физики AP, вы, вероятно, сможете нарисовать кривую магнетизма B и H (или M против H?). На самом деле, оказывается, даже ваш класс в колледже мог вас неправильно учить! Недавно я наткнулся на статью Сунга и Рудовича, в которой высмеивали ошибки, сделанные примерно в 300 учебниках физики для студентов.
Вы можете найти эту статью здесь, если хотите прочитать ее напрямую, но если у вас нет подписки и / или вы хотите получить объяснение, для понимания которого не требуется докторская степень, продолжайте читать.
Разница между магнитной индукцией (B) и намагниченностью (M) является вопросом удобства. Магнитная индукция — это напряженность магнитного поля внутри образца, а намагниченность — это магнитный момент на единицу объема. B и M можно записать в терминах друг друга, а графики B-H и M-H выглядят очень похоже, но есть несколько ключевых причин, чтобы выбрать один граф вместо другого.
Определения M, B и H
Начнем с М. M — это общая намагниченность , или магнитный момент на единицу объема.
Общая намагниченность (М)
Каждый атом вносит в ваш материал определенный магнитный момент . Магнитные моменты исходят из квантовой механики и структуры атома. Атомы организованы в кристаллические структуры (особенно с разными атомами), которые могут объединяться, создавая более сильный или более слабый магнитный момент. Эти элементарные ячейки могут составлять магнитных доменов или кристаллических зерен, которые все могут влиять на общей намагниченности или собственного магнитного поля, M , материала.
Вот что такое M, просто добавление всех этих магнитных эффектов, нормированных по объему. В формальном уравнении это выглядит так:
Где — общая намагниченность, m — индивидуальный магнитный момент, а — общий объем. Теперь у вас есть значение намагниченности, которое будет постоянным для любого материала, независимо от его размера.
Прикладное магнитное поле (H)
Намагничивание может зависеть от многих факторов, но одним из наиболее важных факторов является приложенное магнитное поле , H .H — некоторое магнитное поле, добавленное к материалу извне.
Например, если я возьму магнит из холодильника и прилеплю его к железу, намагниченность утюга изменится. H — это поле магнита моего холодильника, а M — намагниченность моего железа. Мы можем назвать H «приложенным полем», а M — «индуцированным полем» или внутренней намагниченностью.
В общем, мое железо начнется с нулевой чистой М. Хотя у железа есть много магнитных доменов, которые вносят свой собственный магнитный момент, в целом эти домены указывают в случайных направлениях, поэтому железо не создает собственного магнитного поля.
Однако, как только я добавляю внешнее магнитное поле от магнита холодильника, домены в железе выстраиваются в одном направлении, и материал генерирует собственное магнитное поле, представленное M.
Как вы можете видеть на графике, в зависимости от силы магнита моего холодильника намагниченность моего утюга будет меняться. В какой-то момент железо достигло максимальной намагниченности, когда все домены выровнены (это называется точкой насыщения, но об этом позже).
Как материаловед, я бы предпочел увидеть график зависимости M от H, чтобы понять поведение намагничивания моего материала. Я думаю, что это самый простой вариант, и он прямо говорит мне о том, как ведет себя мой материал.
Однако другим инженерам обычно необходимо понимать, как ведет себя вся система. Другими словами, они хотят знать общее магнитное поле внутри моего утюга. Сюда входят , — собственная намагниченность железа, и — приложенное магнитное поле.
Магнитная индукция (B)
Этот термин для общего магнитного поля, проходящего через материал, называется магнитной индукцией или плотностью магнитного потока (B) . Если вы когда-либо посещали уроки физики по электромагнетизму, это то, что вы использовали для большинства своих уравнений.
Магнитная индукция — это собственное и приложенное магнитные поля, умноженные на проницаемость свободного пространства. В форме уравнения:
где — проницаемость свободного пространства (вакуума),
Как видите, если вы знаете два из B, M и H, вы можете вычислить другое.Кроме того, поскольку M часто намного больше H, графики M-H и B-H во многих случаях могут выглядеть очень похожими. Это может вызвать большую путаницу, когда M равно , а не , так как намного больше, чем H.
Наиболее очевидное различие состоит в том, что при бесконечно большом H B также стремится к бесконечности, но M остается на постоянном значении.
Значения на кривых намагничиванияЕсли вы не умеете читать кривую магнитного гистерезиса,
- Я впечатлен тем, что вы нашли эту страницу без ссылки из одной из моих более простых статей,
- Я написал целую статью, посвященную пониманию кривой магнитного гистерезиса, если вы хотите узнать больше, и
- я предоставлю краткий обзор прямо сейчас, в виде сворачиваемого текста
До сих пор я показывал вам только небольшую часть графика. Я также не упомянул, что эти графики относятся к ферромагнитным или ферримагнитным материалам. Парамагнитные, диамагнитные и антиферромагнитные материалы не проявляют такого поведения.
Реальные графики M и H (для ферромагнитного материала) выглядят так:
Эта петля называется гистерезисом петлей , и это результат зависимости моего ферромагнетика от истории.
Помните, как я говорил о выравнивании всех магнитных доменов, что привело к общей намагниченности в железе? Что ж, как только приложенное магнитное поле уходит, эти выровненные домены создают свое собственное магнитное поле, и остаются выровненными на . Вот почему на графике есть точка, обозначенная Mr, где H равно нулю, но все еще присутствует собственная намагниченность самого железа.
На самом деле вам нужно приложить магнитное поле в направлении , противоположном направлению (так что H отрицательно), прежде чем вы сможете заставить магнитные домены железа переключаться.Если вы довели приложенное магнитное поле до нуля, теперь есть отрицательный.
Циклическое переключение между положительным и отрицательным полюсами создает эту петлю гистерезиса, которая имеет множество применений и значений для магнитов в технике. Если вы хотите увидеть полную статью о петлях гистерезиса, которую я написал, перейдите по этой ссылке.
На самом деле вам не нужно знать применение кривой гистерезиса, чтобы понять эту статью, но я полагаю, что это будет довольно скучно, если вы не поймете значения таких пунктов, как и.
Теперь давайте обсудим, чем отличаются кривые M-H и B-H. Следуя терминологии Сунга и Рудовича, я назову кривую M-H «внутренней» кривой гистерезиса, поэтому B-H будет просто «нормальной» кривой гистерезиса.
На этом графике отображается H по оси x и M или B по оси y. Помните об этом, так что эти графики показывают реакцию того же материала на приложенное магнитное поле.
Магнитная проницаемость и восприимчивость
Когда вы читаете журналы по материаловедению, обычно указывается свойство материала , магнитная восприимчивость , символизируемая причудливым греческим языком.
Восприимчивость — это наклон кривой M-H, так же как проницаемость — это наклон кривой B-H.
Другими словами:
и
Согласно определению,
и могут быть записаны относительно друг друга так:
Если положительный, материал парамагнитный. Если отрицательный, материал диамагнитен. Если переменная (и очень большая), материал ферромагнитный или ферримагнитный.
Итак, даны ли вам график B-H или M-H, восприимчивость или проницаемость, преобразование между ними относительно тривиально.
Чтобы наглядно продемонстрировать этот момент, позвольте мне показать вам еще два примера. Вы уже видели, как выглядят кривые ферромагнитного гистерезиса на графиках B-H и M-H, но как насчет парамагнитных и диамагнитных материалов? С ними еще проще!
Теперь давайте посмотрим на некоторые конкретные значения ферромагнитных кривых M-H и B-H и обсудим, чем эти значения различаются и когда они могут быть приблизительно одинаковыми.
Заблуждение 1: Коэрцитивность
Коэрцитивная сила или коэрцитивная сила — это сила приложенного магнитного поля, необходимая для приведения магнитной индукции к нулю. Другими словами, это точки пересечения по оси Y на кривой B-H.
В частности, отрицательная точка пересечения по оси Y равна, а положительная точка пересечения по оси Y -. Эта же точка на кривой M-H равна внутренней коэрцитивности .
Многие думают, но это неправда. Например, вы можете подумать, что внутренняя намагниченность материала равна нулю при.Нет, это происходит в.
Для мягких магнитов M намного больше, чем H, так и поэтому.
Однако для жестких магнитов разница между Hc и Hci может быть очень значительной.
Для справки, вот значения Hc и Hci, собранные Сунгом и Рудовичем.Заблуждение 2: Индукция не насыщает
Это заблуждение кажется мне очевидным, если вы понимаете разницу между индукцией (B) и намагничиванием (M), но я не изучал 300 учебников, так что молчу.
Термин «насыщенность» предполагает наличие верхнего предела. В намагничивании есть верхний предел. Независимо от того, насколько сильно приложенное магнитное поле (H), в какой-то момент M останется постоянным и больше не будет увеличиваться. Это значение M и есть магнетизм насыщения.
Однако B представляет собой комбинацию M и H. Это происходит в той же точке, что и, когда вклад от M больше не увеличивается с H. Однако H все еще увеличивается, поэтому B всегда будет увеличиваться с H.
будет точкой закрытия петли гистерезиса, а после кривой будет прямая линия с наклоном =.
Заблуждение 3: Симметрия
Эти кривые B-H или M-H всегда рисуются симметрично, но в этом нет необходимости. Во многих случаях его «легче» или «труднее» достичь в зависимости от кристаллографического направления.
Однако значение всегда одно и то же, независимо от того, является ли направление «легким» или «сложным». Для этого может потребоваться более сильное приложенное поле, но в конечном итоге будет достигнуто то же значение.Например, на приведенном выше графике показано различие между легким и сложным направлениями.
В этом случае фактически не достигается в трудном направлении. Если вы расширите график до более высоких значений H, жесткое направление в конечном итоге сойдется с легким направлением.
Заблуждение 4: Масштаб
Ага, я распространял это заблуждение даже на этом сайте! Когда мы обсуждаем твердые и мягкие магниты, мы часто используем эту иллюстрацию:
Однако на самом деле это должно выглядеть так:
Да, это трудно понять, поэтому вы можете понять, почему возникает заблуждение.Если вы посмотрите на фактические значения, вы обнаружите, что твердые магниты обычно имеют значения в 1000–10 000 раз больше, чем значения мягких магнитов.
Последние мысли
Вот и все! Различия между намагниченностью (M) и индукцией (B).
Вы узнали, как преобразовать из M в B, каковы эквивалентные точки на кривых M-H и B-H, а также типичные ошибки, которые люди допускают при использовании M вместо B.
В качестве бонуса мы рассказали о некоторых других ошибках, которые иногда допускают учебники при рисовании кривых M-H и B-H.
Ссылки и дополнительная литература
Журнальная статья, которая вдохновила на создание этой публикации
Щелкните здесь, чтобы узнать больше о магнитной восприимчивости и проницаемости.
Здесь вы найдете дополнительную информацию о классах магнитных материалов.
Петля гистерезиса — Все производители — eTesters.com
Отображение недавних результатов 1 — 15 из 19 найденных продуктов.
Устройство для отслеживания петли гистерезиса
MESA — Shb Instruments
MESA — единственный на рынке измеритель петли гистерезиса, который может выполнять измерения в частотном диапазоне 10 Гц и ниже.Конкурирующие устройства работают с более легко генерируемыми полями возбуждения 60 Гц и могут иметь ошибки до 30% в измерениях коэрцитивной силы (Hc).
Тестер мягкого железа
WP2 — MAGMESS Magnet-Messtechnik
Компьютерный измерительный комплект для автоматического измерения петли гистерезиса магнитомягких материалов. Позволяет измерять детали различной длины и поперечного сечения.
Тестер магнитов
MP — MAGMESS Magnet-Messtechnik
Компьютерный измерительный стол для автоматического измерения петли гистерезиса магнитотвердых материалов. Используйте полюсные наконечники со встроенными измерительными катушками или окружающие катушки с J-компенсацией.
Гистерезисграф постоянного тока
MATS-2010SD — Hunan Linkjoin Technology Co., ООО
Автоматическое измерение основной кривой намагничивания и петли магнитного гистерезиса в статическом состоянии магнитомягкого материала, точное измерение параметров статических магнитных характеристик, таких как начальная проницаемость µi, максимальная проницаемость µm, магнитная индукция насыщения Bs, остаточная намагниченность Br, коэрцитивная Hc и гистерезисные потери Pu
График гистерезиса постоянного тока
DX-2012SD — Dexing Magnet Tech.Co., Ltd
Автоматическое измерение основной кривой намагничивания и петли магнитного гистерезиса в статическом состоянии магнитомягкого материала, точное измерение параметров статических магнитных характеристик, таких как начальная проницаемость µi, максимальная проницаемость µm, магнитная индукция насыщения Bs, остаточная намагниченность Br, коэрцитивная Hc и гистерезисные потери Pu .
Испытание магнитов — редкоземельные элементы — AlNiCo — ферритовые магниты
Ферриты Индия
Испытания магнитов AlniCo, феррита, NdFeB, SmCo5, Sm2Co17 и построены их контуры B-H и MH с использованием индикаторов петель гистерезиса серии H-21 производства Ferrites India.Полная система состоит из намагничивающего устройства для намагничивания испытуемого образца, электромагнита и лупплоттера BH. Также могут быть проверены магниты с коэрсивностью 13 кЭ и более.
Автоматическая система проверки графика гистерезиса
DX-4DMT — Dexing Magnet Tech. Co., Ltd
Система автоматического гистерезисаX-4DMT соответствует стандартной испытательной системе постоянного магнита GB3217-92, используемой для измерения основных и второстепенных петель гистерезиса, кривых размагничивания, петель гистерезиса отдачи и кривых начального намагничивания при различных температурах феррита, AlNiCo, SmCo, NdFeB и закаленный материал, и дает магнитные параметры, Br, Hcb, Hcj, (BH) max, Hk и т. Д., И может соответствовать различным требованиям к функциям испытаний, точности, мощности, надежности, эффективности, цене, местной среде от лаборатория к производственной линии предприятия.
Гистерезисграф переменного тока
ATS-300M — Hunan Linkjoin Technology Co., Ltd.
ATS-300M Железный сердечник Магнитные параметры Тестер применяется для измерения сердечника статора двигателя (кремнистая сталь), железного сердечника трансформатора промышленной частоты, готового трансформатора, сердечника из аморфного, ультракристаллитного и пермаллойного железа (образец с замкнутым контуром) при частоте 50 Гц и динамическая петля гистерезиса 60 Гц, кривая намагничивания и кривая потерь мощности
Гистерезисграф постоянного тока
MATS-2010H — Hunan Linkjoin Technology Co., ООО
Автоматическое измерение петли гистерезиса и кривой размагничивания материала постоянного магнита, точное измерение параметров магнитных характеристик, таких как остаточная намагниченность Br, коэрцитивная сила HcB, собственная коэрцитивная сила HcJ и максимальное произведение магнитной энергии (BH) макс.
Комплекты для испытаний CT PT
Компания Chongqing Gold Mechanical & Electric Equipment Co., Ltd
Испытания трансформатора тока: 1) Кривая возбуждения и проверка параметров 2) Проверка коэффициента трансформации 3) Проверка соотношения и фазовой погрешности 4) Проверка полярности 5) Измерение сопротивления катушки 6) Измерение нагрузки вторичного контура 7) Проверка кривой линии ошибки для защиты CT8) Проверка переходных параметров трансформатора тока 9) Предположение на паспортной табличке трансформатора тока 10) Измерение кривой гистерезиса насыщения
Гистерезисграф переменного тока
MATS-2010SA — Hunan Linkjoin Technology Co., ООО
Автоматическое измерение петли гистерезиса магнитомягкого материала в динамических условиях (AC), точное измерение параметров динамических магнитных характеристик, таких как амплитудная проницаемость µa, угол потерь d, потери в железе Pc, остаточная намагниченность Br и коэрцитивная сила Hc.
Магнитный анализатор
МА — Специальная научная инженерия. ООО
Он измеряет как минимум шесть параметров петли гистерезиса: коэрцитивную силу, остаточную индукцию, магнитную проводимость, площадь петли и параметры релаксации.Он автоматически преобразует эти параметры в физические характеристики в соответствии с заданными уравнениями. Работой прибора управляет персональный компьютер, что обеспечивает полную автоматизацию измерений, сбора и обработки данных. Математический аппарат отличается необычайной гибкостью и способностью подстраиваться под любые задачи при производстве.
Гистерезисграф переменного тока
MATS-2010M — Hunan Linkjoin Technology Co., ООО
Автоматическое измерение динамической петли гистерезиса магнитомягкого материала (кремнистая сталь) при частотах 50 Гц, 60 Гц, 400 Гц и 1 кГц, точное измерение параметров динамических магнитных характеристик, таких как амплитуда магнитной проницаемости µa, угол потерь d, общие потери Ps, остаточная намагниченность Br и коэрцитивная сила Hc
Магнитометр с вибрационным образцом
VSM — Dexing Magnet Tech. Co., Ltd
VSM (также называемый M-H CURVE Hysteresis Graph TEST SYSTEM) может использоваться для измерения основных магнитных свойств магнитных материалов.Такие как петли гистерезиса материалов, кривая намагничивания, кривая нагревания, кривая нагревания / охлаждения, кривая охлаждения и изменения температуры с течением времени, тогда мы получим некоторые магнитные параметры, такие как насыщенная сила намагничивания, левая сила намагничивания, коэрцитивная сила, максимальное произведение магнитной энергии, температура Кюри и магнитная проводимость (начальная магнитная проводимость включена). Он также может измерять магнитные материалы, такие как порошок, частицы, пленки, жидкость и массив.
Кривая гистерезиса — Все производители — eTesters.com
Отображение последних результатов 1 — 11 из 11 найденных продуктов.
Универсальный прибор для отслеживания кривых B-H
UBHCT-001 — Mittal Enterprises
Исследование кривых гистерезиса штамповок трансформаторов, ферритов и других магнитных материалов различной формы и определение их потерь энергии. Изучение кривой гистерезиса как функции магнитного поля.Определение насыщения, намагниченности, остаточной силы и коэрцитивной силы магнитных материалов. Определение насыщения, намагниченности, остаточной силы и коэрцитивной силы магнитных материалов
Магнитометр с вибрационным образцом
VSM — Dexing Magnet Tech. Co., Ltd
VSM (также называемый M-H CURVE Hysteresis Graph TEST SYSTEM) может использоваться для измерения основных магнитных свойств магнитных материалов.Такие как петли гистерезиса материалов, кривая намагничивания, кривая нагревания, кривая нагревания / охлаждения, кривая охлаждения и изменения температуры с течением времени, тогда мы получим некоторые магнитные параметры, такие как насыщенная сила намагничивания, левая сила намагничивания, коэрцитивная сила, максимальное произведение магнитной энергии, температура Кюри и магнитная проводимость (начальная магнитная проводимость включена). Он также может измерять магнитные материалы, такие как порошок, частицы, пленки, жидкость и массив.
Тестер магнитных свойств HyMAC
Metis Instruments & Equipment NV
Тестер магнитных свойств HyMAC — это универсальный прибор для определения магнитных свойств при переменном токе магнитомягких стальных листов и ферритовых сердечников. Основные функции прибора — это график гистерезиса: измерение кривых гистерезиса B-H.
Гистерезисграф постоянного тока
MATS-2010SD — Hunan Linkjoin Technology Co., ООО
Автоматическое измерение основной кривой намагничивания и петли магнитного гистерезиса в статическом состоянии магнитомягкого материала, точное измерение параметров статических магнитных характеристик, таких как начальная проницаемость µi, максимальная проницаемость µm, магнитная индукция насыщения Bs, остаточная намагниченность Br, коэрцитивная Hc и гистерезисные потери Pu
График гистерезиса постоянного тока
DX-2012SD — Dexing Magnet Tech.Co., Ltd
Автоматическое измерение основной кривой намагничивания и петли магнитного гистерезиса в статическом состоянии магнитомягкого материала, точное измерение параметров статических магнитных характеристик, таких как начальная проницаемость µi, максимальная проницаемость µm, магнитная индукция насыщения Bs, остаточная намагниченность Br, коэрцитивная Hc и гистерезисные потери Pu .
Комплекты для испытаний CT PT
Компания Chongqing Gold Mechanical & Electrical Equipment Co., ООО
Испытания трансформатора тока: 1) Кривая возбуждения и проверка параметров 2) Проверка коэффициента трансформации 3) Проверка соотношения и фазовой погрешности 4) Проверка полярности 5) Измерение сопротивления катушки 6) Измерение нагрузки вторичного контура 7) Проверка кривой линии ошибки для защиты CT8) Проверка переходных параметров трансформатора тока 9) Предположение на паспортной табличке трансформатора тока 10) Измерение кривой гистерезиса насыщения
Автоматическая система проверки графика гистерезиса
DX-4DMT — Dexing Magnet Tech.Co., Ltd
Система автоматического гистерезисаX-4DMT соответствует стандартной испытательной системе постоянного магнита GB3217-92, используемой для измерения основных и второстепенных петель гистерезиса, кривых размагничивания, петель гистерезиса отдачи и кривых начального намагничивания при различных температурах феррита, AlNiCo, SmCo, NdFeB и закаленный материал, и дает магнитные параметры, Br, Hcb, Hcj, (BH) max, Hk и т. Д., И может соответствовать различным требованиям к функциям испытаний, точности, мощности, надежности, эффективности, цене, местной среде от лаборатория к производственной линии предприятия.
Гистерезисграф переменного тока
ATS-300M — Hunan Linkjoin Technology Co., Ltd.
ATS-300M Железный сердечник Магнитные параметры Тестер применяется для измерения сердечника статора двигателя (кремнистая сталь), железного сердечника трансформатора промышленной частоты, готового трансформатора, сердечника из аморфного, ультракристаллитного и пермаллойного железа (образец с замкнутым контуром) при частоте 50 Гц и динамическая петля гистерезиса 60 Гц, кривая намагничивания и кривая потерь мощности
Гистерезисграф постоянного тока
MATS-2010H — Hunan Linkjoin Technology Co., ООО
Автоматическое измерение петли гистерезиса и кривой размагничивания материала постоянного магнита, точное измерение параметров магнитных характеристик, таких как остаточная намагниченность Br, коэрцитивная сила HcB, собственная коэрцитивная сила HcJ и максимальное произведение магнитной энергии (BH) макс.
Весоизмерительное устройство для ВЫСОКОЭФФЕКТИВНЫХ ячеек
PSL HE — Berger Lichttechnik GmbH & Co.КГ
PSL HE оптимизирован для полностью автоматизированных производственных линий. Он записывает четыре полные кривые IV при 1000 Вт / м2, 500 Вт / м2, темном обратном направлении и темном прямом направлении за один цикл измерения. В сочетании с PSS 10 HE и программным пакетом HE устраняются эффекты гистерезиса во время измерений высокоэффективных ячеек.

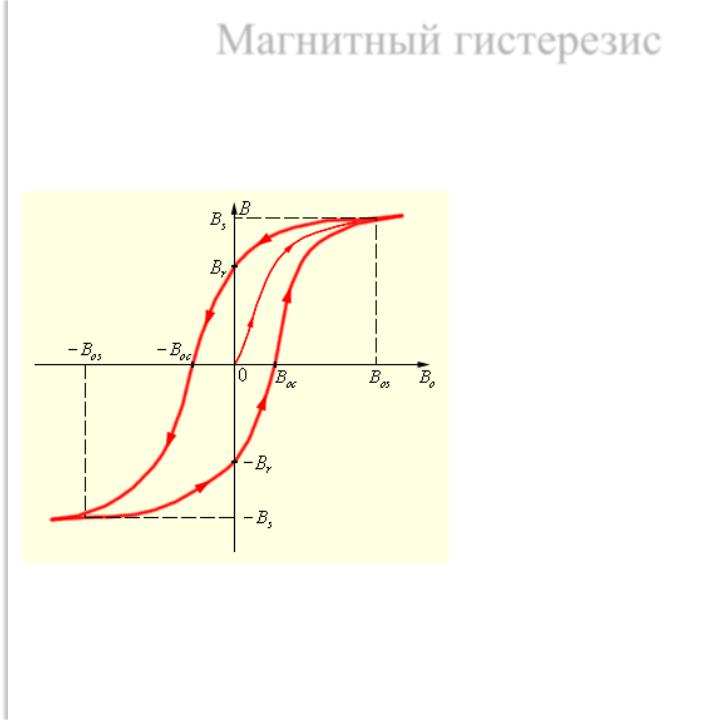 Москва, 2007, стр. 186-187
Москва, 2007, стр. 186-187