Переменный электрический ток.

Лекция №5

Переменным называется ток, изменение которого по величине и направлению повторяется периодически через равные промежутки времени Т.

В области производства, передачи и распределения электрической энергии переменный ток имеет по сравнению с постоянным, два основных преимущества:

1) возможность (при помощи трансформаторов) просто и экономично повышать и понижать напряжение, это имеет решающее значение для передачи энергии на большие расстояния.

2) большую простоту устройств электродвигателей, а следовательно, и их меньшую стоимость.

Значение переменной величины (тока, напряжения, ЭДС) в любой момент времени t называется мгновенным значением и обозначается строчными буквами (ток i, напряжение u, ЭДС – е).

Наибольшее из мгновенных значений периодически изменяющихся токов, напряжений или ЭДС, называются максимальными или амплитудными значениями и обозначаются прописными буквами с индексом «м» (I_м, U_м).

Наименьший промежуток времени, по прошествии которого мгновенные значения переменной величины (ток, напряжение, ЭДС) повторяется в той же последовательности, называется периодом Т, а совокупность изменений, происходящих в течение периода, — циклом.

Величина обратная периоду называется частотой и обозначается буквой f.

, т.е. частота – число периодов за 1 секунду.

Единица частоты 1/сек – называется герц (Гц). Более крупные единицы частоты – килогерц (кГц) и мегагерц (МГц).

Стандартная (техническая)	50 Гц
Частота для промышленных установок Европе, Японии и Америки	60 Гц

Получение переменного синусоидального тока.

Переменные токи и напряжения в технике стремятся получить по простейшему периодическому закону – синусоидальному. Т. к. синусоида – единственная периодическая функция, имеющая подобную себе производную, в результате чего во всех звеньях электрической цепи форма кривых напряжений и токов получается одинаковой, чем значительно упрощаются расчеты.

Для получения токов промышленной частоты служат генераторы переменного тока в основе работы которых лежит закон электромагнитной индукции, согласно которому при движении замкнутого контура в магнитном поле в нем возникает ток.

Схема простейшего генератора переменного тока

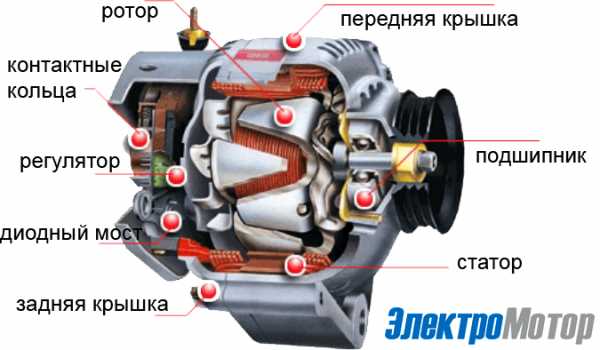
Генераторы переменного тока большой мощности, рассчитанные на напряжения 3 – 15 кв, выполняются с неподвижной обмоткой на статоре машины и вращающимся электромагнитом-ротором. При такой конструкции легче надежно изолировать провода неподвижной обмотки и проще отвести ток во внешнюю цепь.

Одному обороту ротора двухполюсного генератора соответствует один период переменной ЭДС, наведенной на его обмотке.

Если ротор делает n оборотов в минуту, то частота индуктированной ЭДС

.

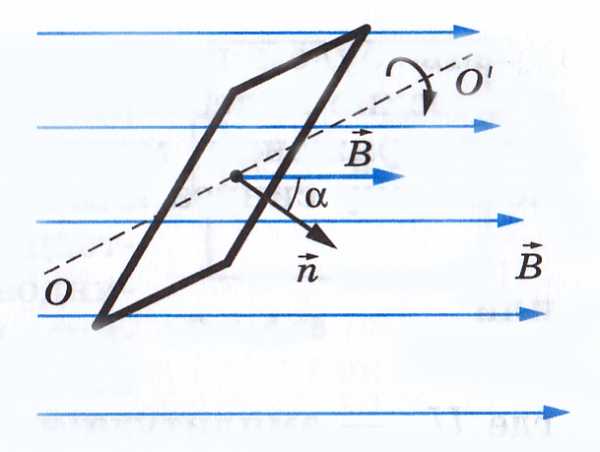Т.к. при этом угловая скорость генератора , то между ней и частотой, наведенной ЭДС существует соотношение

.

Фаза. Сдвиг фаз.

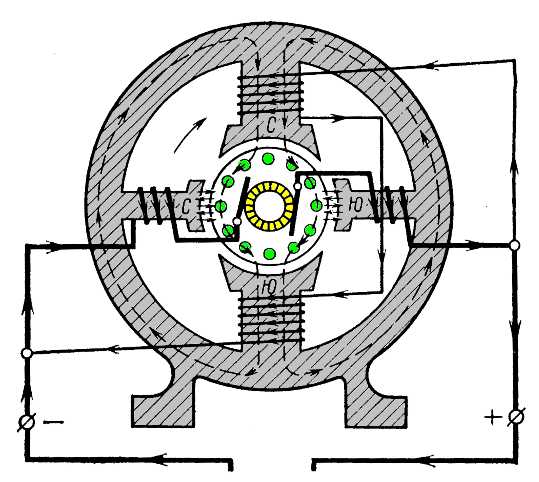
Предположим, что генератор имеет на якоре два одинаковых витка, сдвинутых в пространстве. При вращении якоря в витках наводятся ЭДС одинаковой частоты и с одинаковыми амплитудами, т.к. витки вращаются с одинаковой скоростью в одном и том же магнитном поле. Но вследствие сдвига витков в пространстве ЭДС достигают амплитудных знамений неодновременно.

Если в момент начала отсчета времени (t=0) виток 1 расположен относительно нейтральной плоскости под углом

, а виток 2 под углом. То наведенная в первом витке ЭДС:,

а во втором:

В момент отсчета времени:

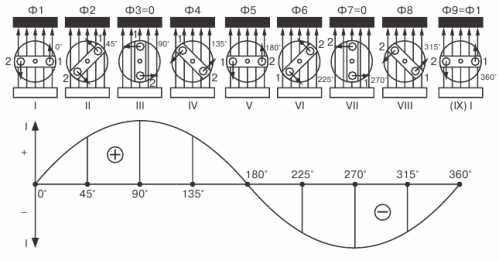Электрические углы иопределяющие значения ЭДС в начальный момент времени, называетсяначальными фазами.

Разность начальных фаз двух синусоидальных величин одной частоты называется

углом сдвига фаз.

Та величина, у которой нулевые значения (после которых она принимает положительные значения), или положительные амплитудные значения достигаются раньше, чем у другой, считается опережающей по фазе, а та у которой те же значения достигаются позже – отстающей по фазе.

Если две синусоидальные величины одновременно достигают своих амплитудных и нулевых значений, то говорят, что величины совпадают по фазе . Если угол сдвига фаз синусоидальных величин равен 180⁰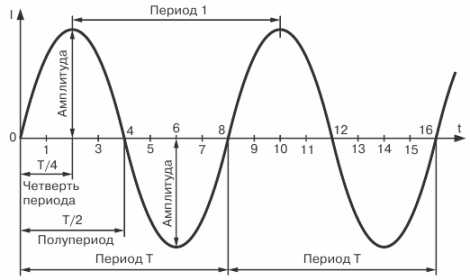

, то говорят, что они изменяются впротивофазе.

studfiles.net

Referat. Переменный ток — PhysBook

Переменный ток

Как известно, сила тока в любой момент времени пропорциональна ЭДС источника тока (закон Ома для полной цепи). Если ЭДС источника не изменяется со временем и остаются неизменными параметры цепи, то через некоторое время после замыкания цепи изменения силы тока прекращаются, в цепи течет постоянный ток.

Однако в современной технике широко применяются не только источники постоянного тока, но и различные генераторы электрического тока, в которых ЭДС периодически изменяется. При подключении в электрическую цепь генератора переменной ЭДС в цепи возникают вынужденные электромагнитные колебания или переменный ток.

Переменный ток – это периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника

или

Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.

Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:

\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,

где u – мгновенное значение напряжения, U_m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае

\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,

где φ_c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.

Резистор в цепи переменного тока

Пусть цепь состоит из проводников с малой индуктивностью и большим сопротивлением R (из резисторов). Например, такой цепью может быть нить накаливания электрической лампы и подводящие провода. Величину R, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением. В цепи переменного тока могут быть и другие сопротивления, зависящие от индуктивности цепи и ее емкости. Сопротивление

R называется активным потому, что, только на нем выделяется энергия, т.е.

Сопротивление элемента электрической цепи (резистора), в котором происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением.

Итак, в цепи имеется резистор, активное сопротивление которого R, а катушка индуктивности и конденсатор отсутствуют (рис. 1).

Рис. 1

Пусть напряжение на концах цепи меняется по гармоническому закону

\(~u = U_m \cdot \sin \omega t\) .

Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому можно считать, что мгновенное значение силы тока определяется законом Ома:

\(~i = \frac{U}{R} = \frac{U_m \cdot \sin \omega t}{R} = I_m \cdot \sin \omega t\) .

Следовательно, в проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения (рис. 2), а амплитуда силы тока равна амплитуде напряжения, деленной на сопротивление:

Рис. 2

При небольших значениях частоты переменного тока активное сопротивление проводника не зависит от частоты и практически совпадает с его электрическим сопротивлением в цепи постоянного тока.

Катушка в цепи переменного тока

Индуктивность влияет на силу переменного тока в цепи. Это можно обнаружить с помощью простого опыта. Составим цепь из катушки большой индуктивности и лампы накаливания (рис. 3). С помощью переключателя можно присоединять эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть одинаковы. Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы тока в рассматриваемой цепи меньше силы постоянного тока.

Рис. 3

Объясняется это самоиндукцией. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов. Лишь по прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех установившихся значений, которые она приобрела бы с течением времени при постоянном напряжении, равном максимальному значению переменного напряжения. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью L цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.

Докажем это математически. Пусть в цепь переменного тока включена идеальная катушка с электрическим сопротивлением провода, равным нулю (рис. 4). При изменениях силы тока по гармоническому закону

\(~i = I_m \cdot \cos \omega t\) .

в катушке возникает ЭДС самоиндукции

\(~e = -L \cdot i’ = I_m \cdot L \cdot \omega \cdot \sin \omega t\) ,

где L – индуктивность катушки, ω – циклическая частота переменного тока.

Рис. 4

Так как электрическое сопротивление катушки равно нулю, то ЭДС самоиндукции в ней в любой момент времени равна по модулю и противоположна по знаку напряжению на концах катушки, созданному внешним генератором:

\(~u = -e = -I_m \cdot L \cdot \omega \cdot \sin \omega t\) .

Следовательно, при изменении силы тока в катушке по гармоническому закону напряжение на ее концах изменяется тоже по гармоническому закону, но со сдвигом фазы:

\(~u = I_m \cdot L \cdot \omega \cdot \cos (\omega t + \frac{\pi}{2})\) .

Следовательно, колебания напряжения на катушке индуктивности опережают колебания силы тока на π/2, или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на π/2.

В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю (рис. 5). В момент, когда напряжение становится равным нулю, сила тока максимальна по модулю.

Рис. 5

Произведение \(I_m \cdot L \cdot \omega\) является амплитудой колебаний напряжения на катушке:

\(~U_m = I_m \cdot L \cdot \omega\) .

Отношение амплитуды колебаний напряжения на катушке к амплитуде колебаний силы тока в ней называется индуктивным сопротивлением (обозначается X_L):

\(~X_L = \frac{U_m}{I_m} = L \cdot \omega\) .

Связь амплитуды колебаний напряжения на концах катушки с амплитудой колебаний силы тока в ней совпадает по форме с выражением закона Ома для участка цепи постоянного тока:

\(~I_m = \frac{U_m}{X_L}\) .

В отличие от электрического сопротивления проводника в цепи посто-янного тока, индуктивное сопротивление не является постоянной величиной, характеризующей данную катушку. Оно прямо пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в катушке при постоянном значении амплитуды колебаний напряжения должна убывать обратно пропорционально частоте. Постоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю (X_L = 0).

Зависимость амплитуды колебаний силы тока в катушке от частоты приложенного напряжения можно наблюдать в опыте с генератором пере-менного напряжения, частоту которого можно изменять. Опыт показывает, что увеличение в два раза частоты переменного напряжения приводит к уменьшению в два раза амплитуды колебаний силы тока через катушку.

Конденсатор в цепи переменного тока

Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. Если подключить конденсатор к источнику постоянного тока, то в цепи возникнет кратковременный импульс тока, который зарядит конденсатор до напряжения источника, а затем ток прекратится. Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы.

При включении конденсатора в цепь переменного тока процесс его зарядки длится четверть периода. После достижения амплитудного значения напряжение между обкладками конденсатора уменьшается и конденсатор в течение четверти периода разряжается. В следующую четверть периода конденсатор вновь заряжается, но полярность напряжения на его обкладках изменяется на противоположную и т.д. Процессы зарядки и разрядки конденсатора чередуются с периодом, равным периоду колебаний приложенного переменного напряжения.

Как и в цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды не проходят. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора по проводам, соединенным с его выводами, течет переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока (рис. 6), кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы.

Рис. 6

Установим связь между амплитудой колебаний напряжения на обкладках конденсатора и амплитудой колебаний силы тока. При изменениях напряжения на обкладках конденсатора по гармоническому закону

\(~u = U_m \cdot \cos \omega t\) ,

заряд на его обкладках изменяется по закону:

\(~q = C \cdot u = U_m \cdot C \cdot \cos \omega t\) .

Электрический ток в цепи возникает в результате изменения заряда конденсатора: i = q’. Поэтому колебания силы тока в цепи происходят по закону:

\(~i = -U_m \cdot \omega \cdot C \cdot \sin \omega t = U_m \cdot \omega \cdot C \cdot \cos (\omega t + \frac{\pi}{2})\) .

Следовательно, колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на π/2 или колебания силы тока опережают по фазе колебания напряжения на π/2 (рис. 7). Это означает, что в момент, когда конденсатор начинает заряжаться, сила тока максимальна, а напряжение равно нулю. После того как напряжение достигает максимума, сила тока становится равной нулю и т.д.

Рис. 7

Произведение \(U_m \cdot \omega \cdot C\) является амплитудой колебаний силы тока:

\(~I_m = U_m \cdot \omega \cdot C\) .

Отношение амплитуды колебаний напряжения на конденсаторе к амплитуде колебаний силы тока называют емкостным сопротивлением конденсатора (обозначается Х_C):

\(~X_C = \frac{U_m}{I_m} = \frac{1}{\omega \cdot C}\) .

Связь между амплитудным значением силы тока и амплитудным значением напряжения по форме совпадает с выражением закона Ома для участка цепи постоянного тока, в котором вместо электрического сопротивления фигурирует емкостное сопротивление конденсатора:

\(~I_m = \frac{U_m}{X_C}\) .

Емкостное сопротивление конденсатора, как и индуктивное сопротивление катушки, не является постоянной величиной. Оно обратно пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте.

Закон Ома для электрической цепи переменного тока

Рассмотрим электрическую цепь, состоящую из последовательно соединенных резистора, конденсатора и катушки (рис. 8). Если к выводам этой электрической цепи приложить электрическое напряжение, изменяющееся по гармоническому закону с частотой ω и амплитудой U_m, то в цепи возникнут вынужденные колебания силы тока с той же частотой и некоторой амплитудой I_m. Установим связь между амплитудами колебаний силы тока и напряжения.

Рис. 8

В любой момент времени сумма мгновенных значений напряжений на последовательно включенных элементах цепи равна мгновенному значению приложенного напряжения:

\(~u = u_R + u_L + u_C\) . (1)

Во всех последовательно включенных элементах цепи изменения силы тока происходят практически одновременно, так как электромагнитные взаимодействия распространяются со скоростью света. Поэтому можно считать, что колебания силы тока во всех элементах последовательной цепи происходят по закону:

\(~i = I_m \cdot \cos \omega t\) . (2)

Колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, а колебания напряжения на катушке опережают по фазе колебания силы тока на π/2. Поэтому уравнение (1) можно записать так:

\(~u = U_{Rm} \cdot \cos \omega t + U_{Lm} \cdot \cos (\omega t + \frac{\pi}{2}) + U_{Cm} \cdot \cos (\omega t — \frac{\pi}{2})\) , (3)

где U_Rm, U_Cm и U_Lm – амплитуды колебаний напряжения на резисторе, конденсаторе и катушке.

Амплитуду колебаний напряжения в цепи переменного тока можно выразить через амплитудные значения напряжения на отдельных ее элементах, воспользовавшись методом векторных диаграмм.

При построении векторной диаграммы необходимо учитывать, что колебания напряжения на резисторе совпадают по фазе с колебаниями силы тока, поэтому вектор, изображающий амплитуду напряжения U_Rm, совпадает по направлению с вектором, изображающим амплитуду силы тока I_m. Колебания напряжения на конденсаторе отстают по фазе на π/2 от колебаний силы тока, поэтому вектор \(~\vec U_{Cm}\) отстает от вектора \(~\vec I_{m}\) на угол 90°. Колебания напряжения на катушке опережают колебания силы тока по фазе на π/2, поэтому вектор \(~\vec U_{Lm}\) опережает вектор \(~\vec I_{m}\) на угол 90° (рис. 9).

Рис. 9

На векторной диаграмме мгновенные значения напряжения на резисторе, конденсаторе и катушке определяются проекциями на горизонтальную ось векторов \(~\vec U_{Rm}\) , \(~\vec U_{Cm}\) и \(~\vec U_{Lm}\) , вращающихся с одинаковой угловой скоростью ω против часовой стрелки. Мгновенное значение напряжения во всей цепи равно сумме мгновенных напряжений u_R, u_C и u_L на отдельных элементах цепи, т. е. сумме проекций векторов \(~\vec U_{Rm}\) , \(~\vec U_{Cm}\) и \(~\vec U_{Lm}\) на горизонтальную ось. Так как сумма проекций векторов на произвольную ось равна проекции суммы этих векторов на ту же ось, то амплитуду полного напряжения можно найти как модуль суммы векторов:

\(~\vec U_m = \vec U_{Rm} + \vec U_{Cm} + \vec U_{Lm}\) .

Из рисунка 9 видно, что амплитуда напряжений на всей цепи равна

\(~U_m = \sqrt{U^2_{Rm} + (U_{Lm} — U_{Cm})^2}\) , (4)

или

\(~U_{m} = \sqrt{(I_m R)^2 + (I_m X_L — I_m X_C)^2} = I_m \cdot \sqrt{R^2 + (X_L — X_C)^2} = I_m \cdot \sqrt{R^2 + (L \omega — \frac{1}{C \omega})^2}\) .

Отсюда

\(~I_m = \frac{U_m}{\sqrt{R^2 + (L \omega — \frac{1}{C \omega})^2}}\) . (5)

Введя обозначение для полного сопротивления цепи переменного тока

\(~Z = \sqrt{R^2 + (L \omega — \frac{1}{C \omega})^2}\) , (6)

выразим связь между амплитудными значениями силы тока и напряжения в цепи переменного тока следующим образом:

\(~I_m = \frac{U_m}{Z}\) . (7)

Это выражение называют законом Ома для цепи переменного тока.

Из векторной диаграммы, приведенной на рисунке 9, видно, что фаза колебаний полного напряжения равна ω∙t + φ. Поэтому мгновенное значение полного напряжения определяется формулой:

\(~u = U_m \cdot \cos (\omega t + \varphi)\) . (8)

Начальную фазу φ можно найти из векторной диаграммы:

\(~\cos \varphi = \frac{U_{Rm}}{U_m} = \frac{I_m \cdot R}{I_m \cdot \sqrt{R^2 + (L \omega — \frac{1}{C \omega})^2}} = \frac{R}{Z}\) . (9)

Величина cos φ играет важную роль при вычислении мощности в электрической цепи переменного тока.

Мощность в цепи переменного тока

Мощность в цепи постоянного тока определяется произведением напряжения на силу тока:

\(~P = U \cdot I\) .

Физический смысл этой формулы прост: так как напряжение U численно равно работе электрического поля по перемещению единичного заряда, то произведение U∙I характеризует работу по перемещению заряда за единицу времени, протекающего через поперечное сечение проводника, т.е. является мощностью. Мощность электрического тока на данном участке цепи положительна, если энергия поступает к этому участку из остальной сети, и отрицательна, если энергия с этого участка возвращается в сеть. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока определяется такой же формулой:

\(~p = u \cdot i\) .

Пусть напряжение на концах цепи меняется по гармоническому закону

\(~u = U_m \cdot \cos \omega t\)

(с тем же успехом, разумеется, вместо \(~u = U_m \cdot \cos \omega t\) можно было бы записать \(~u = U_m \cdot \sin \omega t\)), то и сила тока будет меняться со временем гармонически с той же частотой, но в общем случае будет сдвинута по фазе относительно напряжения:

\(~i = I_m \cdot \cos (\omega t + \varphi_c)\) ,

где φ_c – сдвиг фаз между силой тока и напряжением. Поэтому для мгновенной мощности можно записать:

\(~p = u \cdot i = U_m \cdot I_m \cdot \cos \omega t \cdot \cos (\omega t + \varphi_c)\) .

При этом мощность меняется со временем как по модулю, так и по знаку. В течение одной части периода энергия поступает к данному участку цепи (р > 0), но в течение другой части периода некоторая доля энергии вновь возвращается в сеть (р < 0). Как правило, во всех случаях нам надо знать среднюю мощность на участке цепи за достаточно большой промежуток времени, включающий много периодов. Для этого достаточно определить среднюю мощность за один период.

Чтобы найти среднюю мощность за период, преобразуем полученную формулу таким образом, чтобы выделить в ней член, не зависящий от времени. С этой целью воспользуемся известной формулой для произведения двух косинусов:

\(~\cos \alpha \cdot \cos \beta = \frac{\cos (\alpha — \beta) + \cos (\alpha + \beta)}{2}\) .

В рассматриваемом случае α = ω∙t и β = ω∙t + φ_c. Поэтому

\(~p = \frac{U_m \cdot I_m}{2} [\cos \varphi_c + \cos (2 \omega t + \varphi_c)] = \frac{U_m \cdot I_m}{2} \cos \varphi_c + \frac{U_m \cdot I_m}{2} \cos (2 \omega t + \varphi_c)\) .

Выражение для мгновенное мощности состоит из двух слагаемых. Первое не зависит от времени, а второе дважды за каждый период изменения напряжения изменяет знак: в течение какой-то части периода энергия поступает в цепь от источника переменного напряжения, а в течении другой части возвращается обратно. Поэтому среднее значение второго слагаемого за период равно нулю. Следовательно, средняя мощность Р за период равна первому члену, не зависящему от времени:

\(~P = \frac{U_m \cdot I_m}{2} \cos \varphi_c\) . (10)

При совпадении фазы колебаний силы тока и напряжения (для активного сопротивления R) среднее значение мощности равно:

\(~P = \frac{U_m \cdot I_m}{2} = \frac{I^2_m \cdot R}{2}\) .

Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = I∙U = I²∙R), вводятся понятия действующих значений силы тока и напряжения. Из равенства мощностей получим

\(~P = \frac{I^2_m \cdot R}{2} =I^2 \cdot R\) или \(~\frac{I^2_m}{2} =I^2\) .

Действующим значением силы тока называют величину, в \(~\sqrt{2}\) раз меньшую ее амплитудного значения:

\(~I = \frac{I_m}{\sqrt{2}}\) .

Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока.

Аналогично можно доказать, что

действующее значение переменного напряжения в \(~\sqrt{2}\) раз меньше его амплитудного значения:

\(~U = \frac{U_m}{\sqrt{2}}\) .

Заметим, что обычно электрическая аппаратура в цепях переменного тока показывает действующие значения измеряемых величин. Переходя к действующим значениям силы тока и напряжения, уравнение (10) можно переписать:

\(~P = \frac{U_m}{\sqrt{2}} \cdot \frac{I_m}{\sqrt{2}} \cos \varphi_c = U \cdot I \cos \varphi_c\) . (10)

Таким образом, мощность переменного тока на участке цепи определяется именно действующими значениями силы тока и напряжения. Она зависит также от сдвига фаз φ_c между напряжением и током. Множитель cos φ_c в формуле называется коэффициентом мощности.

В случае, когда φ_c = ± π/2 , энергия, поступающая к участку цепи за период, равна нулю, хотя в цепи и существует ток. Так будет, в частности, если цепь содержит только катушку индуктивности или только конденсатор. Как же средняя мощность может оказаться равной нулю при наличии тока в цепи? Это поясняют приведенные на рисунке 10 графики изменения со временем мгновенных значений напряжения, силы тока и мощности при φ_c = — π/2 (чисто индуктивное сопротивление участка цепи). График зависимости мгновенной мощности от времени можно получить, перемножая значения силы тока и напряжения в каждый момент времени. Из этого графика видно, что в течение одной четверти периода мощность положительна и энергия поступает к данному участку цепи; но в течение следующей четверти периода мощность отрицательна, и данный участок отдает без потерь обратно в сеть полученную ранее энергию. Поступающая в течение четверти периода энергия запасается в магнитном поле тока, а затем без потерь возвращается в сеть.

Рис. 10

Лишь при наличии проводника с активным сопротивлением в цепи, не содержащей движущихся проводников, электромагнитная энергия превращается во внутреннюю энергию проводника, который нагревается. Обратного превращения внутренней энергии в электромагнитную на участке с активным сопротивлением уже не происходит.

При проектировании цепей переменного тока нужно добиваться, чтобы cos φ_c не был мал. Иначе значительная часть энергии будет циркулировать по проводам от генератора к потребителям и обратно. Так как провода обладают активным сопротивлением, то при этом энергия расходуется на нагревание проводов.

Неблагоприятные условия для потребления энергии возникают при включении в сеть электродвигателей, так как их обмотка имеет малое активное сопротивление и большую индуктивность. Для увеличения cos φ_c в сетях питания предприятий с большим числом электродвигателей включают специальные компенсирующие конденсаторы. Нужно также следить, чтобы электродвигатели не работали вхолостую или с недогрузкой. Это уменьшает коэффициент мощности всей цепи. Повышение cos φ_c является важной народнохозяйственной задачей, так как позволяет с максимальной отдачей использовать генераторы электростанций и снизить потери энергии. Это достигается правильным проектированием электрических цепей. Запрещается использовать устройства с cos φ_c < 0,85.

Литература

1. Мякишев Г.Я., Синяков А.З. Физика: Колебания и волны. 11 кл.: Учеб. для углубленного изучения физики. – М.: Дрофа, 2002. – 288 с.
2. Физика: Учеб. пособие для 11 кл. шк. и классов с углубл. изуч. физики / А.Т. Глазунов, О.Ф. Кабардин, А.Н. Малинин и др.; Под ред. А.А. Пинского. – М.: Просвещение, 1995.– 432 с.

www.physbook.ru

Переменный ток: получение и применение

Переменный ток – род тока, направление протекания которого непрерывно меняется. Становится возможным, благодаря наличию разницы потенциалов, подчиняющейся закону. В повседневном понимании форма переменного тока напоминает синусоиду. Постоянный способен изменяться по амплитуде, направление прежнее. В противном случае получаем переменный ток. Трактовка радиотехников противоположна школьной. Ученикам говорят — постоянный ток одной амплитуды.

Создание переменного тока

Как образуется переменный ток

Начало переменному току положил Майкл Фарадей, читатели подробнее узнают ниже по тексту. Показано: электрическое и магнитное поля связаны. Ток становится следствием взаимодействия. Современные генераторы работают за счет изменения величины магнитного потока через площадь, охватываемую контуром медной проволоки. Проводник может быть любым. Медь выбрана из критериев максимальной пригодности при минимальной стоимости.

Статический заряд преимущественно образуется трением (не единственный путь), переменный ток возникает в результате незаметных глазу процессов. Величина пропорциональна скорости изменения магнитного потока через площадь, охваченную контуром.

История открытия переменного тока

Впервые переменным токам стали уделять внимание ввиду коммерческой ценности после появления на свет изобретений, созданных Николой Тесла. Материальный конфликт с Эдисоном отметил сильным отпечатком судьбы обоих. Когда американский предприниматель забрал назад обещания перед Николой Тесла, потерял немалую выгоду. Выдающемуся ученому не понравилось вольное обращение, серб выдумал двигатель переменного тока промышленного типа (изобретение сделал намного раньше). Предприятия пользовались исключительно постоянным. Эдисон продвигал указанный вид.

Тесла впервые показал: переменным напряжением можно достичь гораздо больших результатов. В особенности, когда энергию приходится передавать на большие расстояния. Использование трансформаторов без труда позволяет повысить напряжение, резко снижая потери на активном сопротивлении. Приемная сторона параметры вновь возвращает к исходным. Неплохо сэкономите на толщине проводов.

Сегодня показано: передача постоянного тока экономически выгоднее. Тесла изменил ход истории. Придумай ученый преобразователи постоянного тока, мир выглядел бы иначе.

Начало активному использованию переменного тока положил Никола Тесла, создав двухфазный двигатель. Опыты передачи энергии на значительные расстояния расставили факты по своим местам: неудобно переносить производство в район Ниагарского водопада, гораздо проще проложить линию до места назначения.

Школьный вариант трактовки переменного и постоянного тока

Переменный ток демонстрирует ряд свойств, отличающих явление от постоянного. Вначале обратимся к истории открытия явления. Родоначальником переменного тока в обиходе человечества считают Отто фон Герике. Первым заметил: заряды природные двух знаков. Ток способен протекать в разном направлении. Касательно Тесла, инженер больше интересовался практической частью, авторские лекции упоминают двух экспериментаторов британского происхождения:

1. Вильям Споттисвуд лишен странички русскоязычной Википедии, национальная часть — замалчивает работы с переменным током. Подобно Георгу Ому, ученый — талантливый математик, остается сожалеть, что с трудом можно узнать, чем именно занимался муж науки.
2. Джеймс Эдвард Генри Гордон намного ближе практической части вопроса применения электричества. Много экспериментировал с генераторами, разработал прибор собственной конструкции мощностью 350 кВт. Много внимания уделял освещению, снабжению энергией заводов, фабрик.

Считается, первые генераторы переменного тока созданы в 30-е годы XIX века. Майкл Фарадей экспериментально исследовал магнитные поля. Опыты вызывали ревность сэра Хемфри Дэви, критиковавшего ученика за плагиат. Сложно потомкам выяснить правоту, факт остается фактом: переменный ток полвека просуществовал невостребованным. В первой половине XIX-го века выдуман электрический двигатель (авторство Майкла Фарадея). Работал, питаемый постоянным током.

Никола Тесла впервые догадался реализовать теорию Араго о вращающемся магнитном поле. Понадобились две фазы переменного тока (сдвиг 90 градусов). Попутно Тесла отметил: возможны более сложные конфигурации (текст патента). Позднее изобретатель трехфазного двигателя, Доливо-Добровольский, тщетно силился запатентовать детище плодотворного ума.

Продолжительное время переменный ток оставался невостребованным. Эдисон противился внедрению явления в обиход. Промышленник боялся крупных финансовых потерь.

Никола Тесла изучал электрические машины

Почему переменный ток используется чаще постоянного

Ученые доказали недавно: передавать постоянный ток выгоднее. Снижаются потери излучения линии. Никола Тесла перевернул ход развития истории, правда восторжествовала.

Никола Тесла: вопросы безопасности и эффективности

Никола Тесла посетил конкурирующую с эдисоновской компанию, продвигая новое явление. Увлекся, часто ставил эксперименты на себе. В противовес сэру Хемфри Дэви, который укоротил жизнь, вдыхая различные газы, Тесла добился немалого успеха: покорил рубеж 86 лет. Ученый обнаружил: изменение направления течения тока со скоростью выше 700 раз в секунду делает процесс безопасным для человека.

Во время лекций Тесла брал руками лампочку с платиновой нитью накала, демонстрировал свечение прибора, пропуская через собственное тело токи высокой частоты. Утверждал: явление безвредно, даже приносит пользу здоровью. Ток, протекая по поверхности кожи, одновременно очищает. Тесла говорил, экспериментаторы прежних дней (смотрите выше) пропускали удивительные явления по указанным причинам:

• Несовершенные генераторы механического типа. Вращающееся поле использовалось в прямом смысле: при помощи двигателя раскручивался ротор. Подобный принцип бессилен выдать токи высокой частоты. Сегодня проблематично, невзирая на нынешний уровень развития технологии.
• В простейшем случае применялись ручные размыкатели. Вовсе нечего говорить о высоких частотах.

Сам Тесла использовал явление заряда и разряда конденсатора. Подразумеваем RC-цепочку. Будучи заряжен до определённого уровня, конденсатор начинает разряжаться через сопротивление. Параметров элементов определяют скорость процесса, протекающего согласно экспоненциальному закону. Тесла лишен возможности использовать методы управления контуров полупроводниковыми ключами. Термионные диоды были известны. Рискнем предположить, Тесла мог использовать изделия, имитируя стабилитроны, оперируя с обратимым пробоем.

Однако вопросы безопасности лишены почетного первого места. Частоту 60 Гц (общепринятая США) предложил Никола Тесла, как оптимальную для функционирования двигателей собственной конструкции. Сильно отличается от безопасного диапазона. Проще сконструировать генератор. Переменный ток в обоих смыслах выигрывает у постоянного.

Через эфир

Поныне безуспешно ведутся споры, касаемо первооткрывателя радио. Прохождение волны через эфир обнаружил Герц, описав законы движения, показав, сродство оптическим. Сегодня известно: переменное поле бороздит пространстве. Явление Попов (1895 год) использовал, передавая первое Земное сообщение «Генрих Герц».

Видим, ученые мужи дружны между собой. Сколько уважения демонстрирует первое сообщение. Дата остается спорной, каждое государство первенство хочет присвоить безраздельно. Переменный ток создает поле, распространяющееся через эфир.

Сегодня общеизвестны диапазоны вещания, окна, стены атмосферы, различных сред (вода, газы). Важное место отводится частоте. Установлено, каждый сигнал можно представить суммой элементарных колебаний-синусоид (согласно теоремам Фурье). Спектральный анализ оперирует простейшими гармониками. Суммарный эффект рассматривается, как равнодействующая элементарных составляющих. Произвольный сигнал раскладывается преобразованием Фурье.

Окна атмосферы определяются аналогичным образом. Увидим частоты, проходящие сквозь толщу хорошо и плохо. Не всегда последнее оказывается негативным эффектом. Микроволновые печи используют частоты 2,4 ГГц, ударно поглощаемые парами воды. Для связи волны бесполезны, зато хороши кулинарными способностями!

Новичков тревожит вопрос распространения волны через эфир. Обсудим подробнее неразрешенную поныне учеными загадку.

Диполь антенна Герца

Вибратор Герца, эфир, электромагнитная волна

Взаимосвязь электрического, магнитного полей впервые продемонстрировал в 1821 году Майкл Фарадей. Чуть позднее показали: конденсатор пригоден для создания колебаний. Нельзя сказать, чтобы связь двух событий немедленно осознали. Феликс Савари разряжал лейденскую банку через дроссель, сердечником которому служила стальная игла.

Неизвестно доподлинно, чего добивался астроном, результат оказался любопытным. Иногда игла оказывалась намагниченной в одном направлении, иногда — противоположном. Ток генератора одного знака. Ученый правильно сделал вывод: затухающий колебательный процесс. Толком не зная индуктивных, емкостных реактивных сопротивлений.

Теорию процесс подвели позже. Опыты повторены Джозефом Генри, Вильямом Томпсоном, определившим резонансную частоту: где процесс продолжался максимальный период времени. Явление позволило количественно описать зависимости характеристик цепи от элементов составляющих (индуктивность и емкость). В 1861 году Максвелл вывел знаменитые уравнения, одно следствие особенно важно: «Переменное электрическое поле порождает магнитное и наоборот».

Возникает волна, векторы индукции взаимно перпендикулярны. Пространственно повторяют форму породившего процесса. Волна бороздит эфир. Явление использовал Генрих Герц, развернув обкладки конденсатора в пространстве, плоскости стали излучателями. Попов догадался закладывать информацию в электромагнитную волну (модулировать), что используется сегодня повсеместно. Причем в эфире и внутри полупроводниковой техники.

Где используется переменный ток

Переменный ток лежит в основе принципа действия большинства известных сегодня приборов. Проще сказать, где применяется постоянный, читатели сделают выводы:

1. Постоянный ток применяется в аккумуляторах. Переменный порождает движение – не может храниться современными устройствами. Потом в приборе электричество преобразуется в нужную форму.
2. КПД коллекторных двигателей постоянного тока выше. По этой причине выгодно применять указанные разновидности.
3. При помощи постоянного тока действуют магниты. К примеру, домофонов.
4. Постоянное напряжение применяется электроникой. Потребляемый ток варьируется в некоторых пределах. В промышленности носит название постоянного.
5. Постоянное напряжение применяется кинескопами для создания потенциала, увеличения эмиссии катода. Случаи назовем аналогами блоков питания полупроводниковой техники, хотя иногда различие значительно.

В остальных случаях переменный ток выказывает весомое преимущество. Трансформаторы — неотъемлемая составляющая техники. Даже в сварке далеко не всегда господствует постоянный ток, но в любом современном оборудовании этого типа имеется инвертор. Так гораздо проще и удобнее получить достойные технические характеристики.

Хотя исторически первыми получены были статические заряды. Вспомним шерсть и янтарь, с которыми работал Фалес Милетский.

vashtehnik.ru

14 Переменный Электрический Ток

Вынужденные Электромагнитные Колебания

Вынужденными электромагнитными колебаниями называют периодические изменения силы тока и напряжения в электрической цепи, происходящие под действием переменной ЭДС от внешнего источника. Внешним источником ЭДС в электрических цепях являются генераторы переменного тока, работающие на электростанциях.

Принцип действия генератора переменного тока легко показать при рассмотрении вращающейся рамки провода в магнитном поле.

В однородное магнитное поле с индукцией В помещаем прямоугольную рамку, образованную проводниками (abсd).

Пусть плоскость рамки перпендикулярна индукции магнитного поля В и ее площадь равна S.

Магнитный поток в момент времени t₀ = 0 будет равен Ф = В*8.

При равномерном вращении рамки вокруг оси OO₁ с угловой скоростью w магнитный поток, пронизывающий рамку, будет изменяться с течением времени по закону:

Изменение магнитного потока возбуждает в рамке ЭДС индукцию, равную

где Е₀= ВSw — амплитуда ЭДС.

Если с помощью контактных колец и скользящих по ним щеток соединить концы рамки с электрической цепью, то под действием ЭДС индукции, изменяющейся со временем по гармоническому закону, в электрической цепи возникнут вынужденные гармонические колебания силы тока — переменный ток.

На практике синусоидальная ЭДС возбуждается не путем вращения рамки в магнитном поле, а путем вращения магнита или электромагнита (ротора) внутри статора — неподвижных обмоток, навитых на сердечники из магнитомягкого материала. В этих обмотках находится переменная ЭДС, что позволяет избежать снятия напряжения с помощью контактных колец. 

Переменный Ток

Рассмотрим процессы, происходящие в проводнике, включенном в цепь переменного тока.

Если индуктивность проводника настолько мала, что при включении его в цепь переменного тока индукционными полями можно пренебречь по сравнению с внешним электрическим полем, то движение электрических зарядов в проводнике определяется действием только внешнего электрического поля, напряженность которого пропорциональна напряжению на концах проводника.

При изменении напряжения по гармоническому закону U = U_m cos wt напряженность электрического поля в проводнике изменяется по такому же закону.

Под действием переменного электрического поля в проводнике возникает переменный электрический ток, частота и фаза колебаний которого совпадает с частотой и фазой колебаний напряжения:

где i — мгновенное значение силы тока, I_m— амплитудное значение силы тока.

Колебания силы тока в цепи являются вынужденными электрическими колебаниями, возникающими под действием приложенного переменного напряжения.

Амплитуда силы тока равна: 

При совпадении фаз колебаний силы тока и напряжения мгновенная мощность переменного тока равна:

Среднее значение квадрата косинуса за период равно 0,5. В результате средняя мощность за период

Для того чтобы формула для расчета мощности переменного тока совпадала по форме с аналогичной формулой для постоянного тока (Р = PR), вводится понятие действующих значений силы тока и напряжения. Из равенства мощностей получим

Действующим значением силы тока называют величину, в корень из 2 раз меньшую ее амплитудного значения:

Действующее значение силы тока равно силе такого постоянного тока, при котором средняя мощность, выделяющаяся в проводнике в цепи переменного тока, равна мощности, выделяющейся в том же проводнике в цепи постоянного тока.

Действующее значение переменного напряжения в корень из 2 раз меньше его амплитудного значения:

Средняя мощность переменного тока при совпадении фаз колебаний силы тока и напряжения равна произведению действующих значений силы тока и напряжения:

Сопротивление элемента электрической цепи, в которой происходит превращение электрической энергии во внутреннюю энергию, называют активным сопротивлением. Активное сопротивление участка цепи можно определить как частное от деления средней мощности на квадрат действующего значения силы тока:

Активным сопротивлением R называется физическая величина, равная отношению мощности к квадрату силы тока , что получается из выражения для мощности . При небольших частотах практически не зависит от частоты и совпадает с электрическим сопротивлением проводника.

Пусть в цепь переменного тока включена катушка. Тогда при изменении силы тока по закону в катушке возникает ЭДС самоиндукции . Т.к. электрическое сопротивление катушки равно нулю, то ЭДС равна минус напряжению на концах катушки, созданному внешним генератором (??? Каким еще генератором???) . Следовательно, изменение силы тока вызывает изменение напряжения, но со сдвигом по фазе . Произведение является амплитудой колебаний напряжение, т.е. . Отношение амплитуды колебаний напряжения на катушке к амплитуде колебаний тока называется индуктивным сопротивлением .

Пусть в цепи находится конденсатор. При его включение он четверть периода заряжается, потом столько же разряжается, потом то же самое, но со сменой полярности. При изменении напряжения на конденсаторе по гармоническому закону заряд на его обкладках равен . Ток в цепи возникает при изменении заряда: , аналогично случаю с катушкой амплитуда колебаний силы тока равна . Величина, равная отношению амплитуды к силе тока, называется емкостным сопротивлением .

АКТИВНОЕ СОПРОТИВЛЕНИЕ.  ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.

Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.   Сопротивление R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от  генератора. Эта энергия превращается во внутреннюю энергию проводников — они  нагреваются.   Будем  считать, что напряжение на зажимах цепи меняется по гармоническому закону: u = U_m cos t. Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома:   В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой P = I²R.       (4.18) На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.  Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой P = i²R.                                              (4.19) Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение  График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем  .  Зато на протяжении следующей восьмой части периода, когда cos 2t < 0, мощность в любой момент времени меньше    чем  . Среднее за период значение cos 2t равно нулю, а значит равно нулю второе слагаемое в уравнении (4.20). Средняя мощность  равна, таким образом, первому члену в формуле (4.20): Действующие значения силы тока и напряжения. Из формулы (4.21) видно, что величина   есть среднее за период значение квадрата силы тока:     Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I: Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока: Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем Это закон Ома для участка цепи переменного тока с резистором.

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры ивольтметры переменного тока.

Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока: P = I²R = UI. Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

Переменный ток оценивается его действием, эквивалентной действия постоянного тока. Активным сопротивлением называют такое сопротивление проводника, в котором электрическая энергия необратимо превращается во внутреннюю. Пусть напряжение в цепи переменного тока изменяется по гармоничным законом. Под действием переменного электрического поля в проводнике возникает переменный ток, частота и фаза колебаний которого совпадает с частотой и фазой колебания напряжения. Амплитудное значение силы тока равна отношению амплитудного значения напряжения к сопротивлению проводника. Мощность тока равна произведению силы тока и напряжения. Тогда активное сопротивление можно определить как отношение мощности переменного тока на участке цепи к квадрату действующей силы тока. Действующим значением силы тока называется сила постоянного тока, благодаря которой в проводнике выделяется за одинаковое время такое же количество теплоты, что и переменным током. Найти действующее значение силы тока можно как отношение амплитудного значения силы тока до квадратного корня из двух. Действующее значение напряжения также в корень из двух меньше его амплитудного значения.

При изучении вынужденных механических колебаний мы ознакомились с явлением резонанса. Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой изменения внешней силы. Если трение мало, то амплитуда установившихся вынужденных колебаний при резонансе резко увеличивается. Совпадение вида уравнений для описания механических и электромагнитных колебаний (позволяет сделать заключение о возможности резонанса также и в электрической цепи, если эта цепь представляет собой колебательный контур, обладающий определенной собственной частотой колебаний.

При механических колебаниях резонанс выражен отчетливо при малых значениях коэфициента трения . В электрической цепи роль коэффициента трения выполняет ее активное сопротивление R. Ведь именно наличие этого сопротивления в цепи приводит к превращению энергии тока но внутреннюю энергию проводника (проводник нагревается). Поэтому резонанс в электрическом колебательном кон-lype должен быть выражен отчетливо при малом активном сопротивлении R.

Мы с вами уже знаем, что если активное сопротивление мало, то собственная циклическая частота колебаний в контуре определяется формулой Сила тока при вынужденных колебаниях должна достигать максимальных значений, когда частота переменного напряжения, приложенного к контуру, равна собственной частоте колебательного контура: Резонансом в электрическом колебательном контуре называется явление резкого возрастания амплитуды вынужденных колебаний силы тока при совпадении частоты внегннего переменного напряжения с собственной частотой колебательного контура.

Амплитуда силы тока при резонансе. Как и в случае механического резонанса, при резонансе в колебательном контуре создаются оптимальные условия для поступления энергии от внешнего источника в контур. Мощность в контуре максимальна в том случае, когда сила тока совпадает по фазе с напряжением. Здесь наблюдается полная аналогия с механическими колебаниями: при резонансе в механической колебательной системе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).

Не сразу после включения внешнего переменного напряжения в цепи устанавливается резонансное значение силы тока. Амплитуда колебаний силы тока нарастает постепенно — до тех пор, пока энергия, выделяющаяся за период на резисторе, не сравняется с энергией, поступающей в контур за это же время:  Отсюда амплитуда установившихся колебаний силы тока при резонансе определяется уравнением    При R  0 резонансное значение силы тока неограниченно возрастает: (I_m)_рез  . Наоборот, с увеличением R максимальное значение силы тока уменьшается, и при больших R говорить о резонансе уже не имеет смысла. Зависимость амплитуды силы тока от частоты при различных сопротивлениях (R₁ < R₂ < R₃) показана на рисунке 4.19. 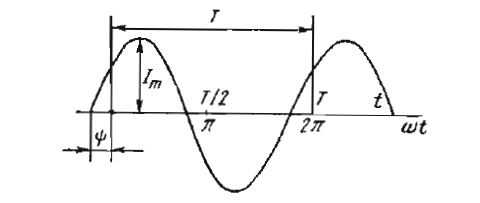Одновременно с увеличением силы тока при резонансе резко возрастают напряжения на конденсаторе и катушке индуктивности. Эти напряжения при ма.пом активном сопротивлении во много раз превышают внешнее напряжение.

Использование резонанса в радиосвязи. Явление электрического резонанса широко используется при осуществлении радиосвязи. Радиоволны от различных передающих станций возбуждают в антенне радиоприемника переменные токи различных частот, так как каждая передающая радиостанция работает на своей частоте. С антенной индуктивно связан колебательный контур (рис. 4.20). Вследствие электромагнитной индукции в контурной катушке возникают переменные ЭДС соответствующих частот и вынужденные колебания силы тока тех же частот. Но только при резонансе колебания силы тока в контуре и напряжения в нем будут значительными, т. е. из колебаний различных частот, возбуждаемых в антенне, контур выделяет только те, частота которых равна его собственной частоте. Настройка контура на нужную частоту  обычно осуществляется путем изменения емкости конденсатора. В этом обычно состоит настройка радиоприемника на определенную радиостанцию. Необходимость учета возможности резонанса в электрической цепи. В некоторых случаях резонанс в электрической цепи может принести большой вред. Если цепь не рассчитана на работу в условиях резонанса, то его возникновеие может привести к аварии.

Чрезмерно большие токи могут перегреть провода. Большие напряжения приводят к пробою изоляции.

Такого рода аварии нередко случались еще сравнительно недавно, когда плохо представляли себе законы электрических колебаний и не умели правильно рассчитывать электрические цепи.

При вынужденных электромагнитных колебаниях возможен резонанс — резкое возрастание амплитуды колебаний силы тока и напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний. На явлении резонанса основана вся радиосвязь.

Изучение цепей переменного тока с активным, емкостным и индуктивным сопротивлениями происходит в следующей логической последовательности: сначала дается понятие о том или ином виде сопротивлений в цепи переменного тока (сравнение с его поведением в цепи постоянного тока), затем фазовые соотношения, формула соответствующего сопротивления, преобразования энергии в цепи, содержащей только активное, емкостное или индуктивное сопротивление. Последовательность изучения сопротивлений в цепи переменного тока может быть и несколько иной.  Понятие действующего значения силы тока и напряжения можно ввести так: вначале выводят выражение для расчета мгновенных значений мощности на активном сопротивлении, отсюда находят среднее значение мощности за период и выясняют, что 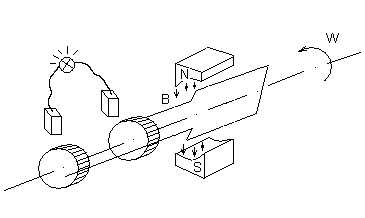 есть среднее значение квадрата силы тока за период. Вводят определение: корень квадратный из этой величины называют действующим значением переменного тока. Название связано с тем, что при прохождении такого тока по участку с активным сопротивлением выделяется мощность 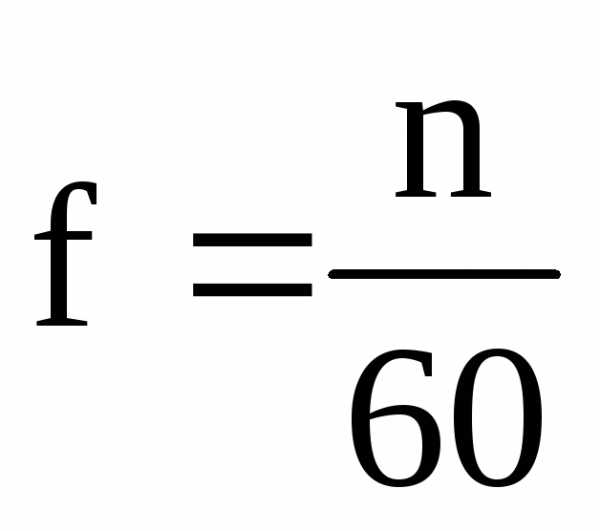Такая же мощность выделяется в цепи постоянного тока, величина которого равна действующему значению переменного тока. Итак, действующим значением переменного тока является такое значение постоянного тока, которое в резисторе R выделяет такое же количество теплоты, что и переменный ток. Очень важно отметить, что шкалы электроизмерительных приборов, для измерения переменных с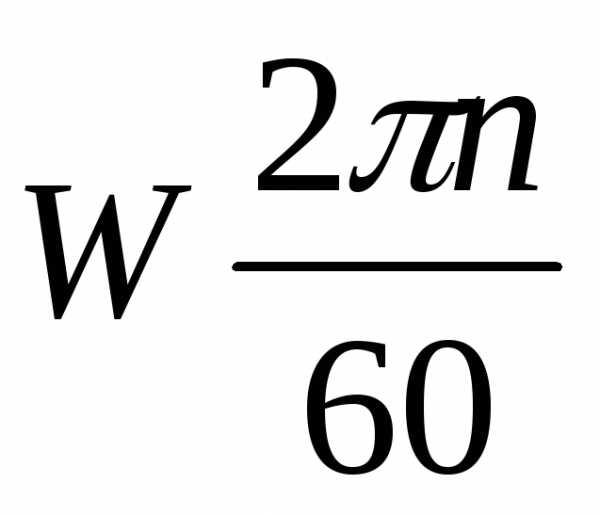илы тока и напряжения градуируют именно в действующих значениях этих величин. Рассмотрение цепи переменного тока со смешанным сопротивлением начинают с эксперимента — измеряют напряжение на каждом из последовательно включенных элементов цепи (лампе, катушке и батарее конденсаторов), подключенных к источнику переменного напряжения. Обращают внимание на следующие опытные факты: 1. Общее напряжение не равно сумме напряжений на отдельных участках, как это имело место для цепей постоянного тока. 2. Напряжение на участке, включающем в себя катушку и конденсатор, равно не сумме, а разности напряжений на каждом из них в отдельности. Объяснить этот результат можно предложить самим учащимся; им известно, что на индуктивности напряжение опережает ток на π/2, а на электроемкости отстает от него на ту же величину. Так как мгновенное значение силы тока в цепи всюду одно и то же, то ясно, что колебания напряжения на индуктивности и электроемкости происходят со сдвигом фаз, равным π, т. е. их фазы противоположны. 3. Полное сопротивление цепи меньше суммы всех включенных в нее сопротивлений (активного, индуктивного и емкостного). Учащихся нужно убедить, что чем меньше сдвиг фаз между током и напряжением, тем большую часть мощности, подводимой к цепи, используют полезно, необратимо превращая в другие виды энергии. Далее рассматривают устройство и работу трансформатора. На примере однофазного трансформатора показывают его действие (повышение и понижение напряжения) и устройство. Вначале рассматривают режим холостого хода, а затем нагруженного трансформатора. В качестве нагрузки целесообразно использовать реостат, так как им проще изменять нагрузку. Показывают, что при увеличении нагрузки возрастает с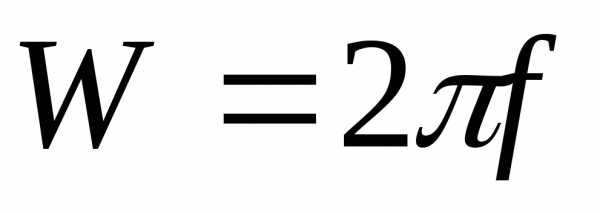ила тока как во вторичной, так и в первичной обмотке трансформатора. Учащимся предлагают самим с энергетических позиций объяснить возрастание силы тока в первичной цепи (увеличение потребления энергии на нагрузке естественно должно сопровождаться увеличением потребления энергии первичной обмоткой от генератора). Для изучения электромагнитных колебаний широко используется школьный прибор- звуковой генератор школьный ГЗШ. Он перекрывает диапазон генерируемых частот синусоидальных колебаний от 20 до 20000 Гц с диапазонами: «X1» (от 20 до 200 Гц), «X10» (от 200 до 2000 Гц), «X100» ( от 2000 до 20000 Гц), питается от сети переменного тока напряжением 220 В. На лицевую панель генератора выведены тумблёр включения генератора в сеть, сигнальная лампочка, переключатель поддиапазонов на три фиксированных положения, отмеченных «X1», «X10», «X100», диск с неравномерной шкалой деления (от 20 до 200) ручка переменного резистора, позволяющая менять амплитуду выходного сигнала, выходные зажимы, рассчитанные на подключение цепей с разным сопротивлением (5, 600, 5000 Ом). Если для опытов необходимы частоты 20 – 200 Гц, то переключатель устанавливают в положение «X1» если 200 – 2000 Гц – в положение «X10», а для частот 2000 – 20000 Гц используют положение «X100». Плавную регулировку частоты осуществляют поворотом диска.  Так же широко используются выпрямители ВУП-1 и ВУП-2 ВУП-2 предназначен для обеспечения питанием демонстрационных установок в опытах по электричеству. Технические данные: Прибор позволяет получить на выходных зажимах: выпрямленное напряжение 350В при максимальной силе тока 220мА; постоянное отфильтрованное напряжение 250В при максимальной нагрузке 50мА; регулируемое напряжение от 0 до 250В постоянного тока до 50мА; регулируемое напряжение от 0 до +100В и от 0 до-100В постоянного тока до 10мА; напряжение 6.3В переменного тока до 3А. Еще один источник питания без которого практически невозможно осуществлять многие опыты по электричеству РНШ. Регулятор напряжения школьный предназначен для плавного регулирования напряжения однофазного переменного тока с частотой 50 Гц, при проведении лабораторных и демонстрационных опытов в физических кабинетах школ. Прибор присоединяется к сети выводным шнуром. Прибор можно включить в сеть напряжением 127 и 220В. Рабочее напряжение снимается с зажимов, обозначенных «Выходное напряжение». В целях правильной эксплуатации регулятора напряжения в паспорте прибора приведена таблица допустимых значений электрической мощности нагрузки регулятора при разных напряжениях, подаваемых на нагрузку, и при сетевых напряжениях 127 и 220В. 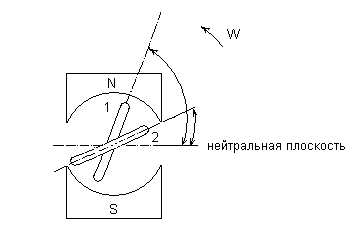Установленный в регуляторе напряжения вольтметр имеет неравномерную шкалу. Достоверный отсчет можно вести только при 50В. В случае необходимости снимать с регулятора более низкие напряжения нужно параллельно выходным зажимам подключать дополнительный вольтметр с соответствующим пределом измерения. Регулятор напряжения может быть использован как для повышения, так и для понижения напряжений переменного тока, при разных демонстрационных и лабораторных опытах Для наглядного отображения электромагнитных колебаний применяют школьные осциллографы ОДШ-2 и ОЭШ-70.  Наиболее широко при­меняют осциллографы для исследования периодических процессов, а также для изучения вольтамперных характеристик диода и трио­да, петли гистерезиса и др. В простейшем случае осциллограф состоит из четырех блоков: блока электронно-лучевой трубки ЭЛТ, генератора развертки ГР, усилителя исследуемого сигнала УС и блока питания БП . Основным элементом первого блока является электронно-лучевая трубка, на экране которой формируется картина исследуемого сиг­нала (осциллограмма). Нить накала НН подогревает ка­тод К, с поверхности которого вылетают элект­роны. Электроны, пролетев через отверстия уп­равляющего электрода, фокусирующего ци­линдра ФЦ и анода А, а также между пласти­нами XX и УУ, попадают на экран и вызывают его свечение. Изменением разности потенциалов между катодом и управляющим электродом мож­но менять число электронов в пучке, а это по­зволяет регулировать яркость изображения на экране. Чем больше по модулю отрицательный потенциал на управляющем электроде относи­тельно катода, тем меньше электронов пройдет через управляющий электрод и достигнет анода. Осциллограф снабжен ручкой «яркость» для уп­равления потоком электронов в пучке. Электрическое поле между фокусирующим цилиндром и анодом способно фокусировать рас­ходящийся электронный пучок. Обычно на передней стенке смонтированы выключатель сети, сигнальная лампочка, за­жимы «Вход У», «Вход X» и делитель входного сигнала. На боко­вую панель выведены ручки управления электронным пучком, «Синхронизация», «Внутр. — от сети — внешн.», «Уси­ление», ручки развертки, «Диапазоны 0, 30, 150, 500 Гц, 2, 8, 16 кГц», «Частота плавно», а также ручки усиления сигнала «Уси­ление У», «Усиление X». Осциллограф ОДШ-2 отличается от ОЭШ-70 конструктивно и внешним оформлением. На переднюю панель выведен не только экран электронно-лучевой трубки, но и основные ручки уп­равления. Верхний ряд ручек предназначен для управления элек­тронным пучком: «Яркость», «Фокус», «Вверх-вниз», «Влево-вправо». Во втором ряду сверху смонтированы ручки управления уси­лителем «Усиление У» и делитель напряжения 1:1, 1:10, 1:30, 1:1OO, 1:1000, а также выключатель сети с сигнальной лампоч­кой. В третьем ряду сверху расположены ручки и кнопки генера­тора развертки: «Частота плавно», «Вкл. 1, 2, 3, 4», «Усиление X». Кнопочный переключатель позволяет менять пилообразное напря­жение частотой от 20 Гц до 20 кГц. Генератор развертки рабо­тает только при нажатой кнопке «Вкл». В нижнем ряду располо­жены зажимы «Вход У», «Вход X», «Внешн. синхр», кнопки син­хронизации «Внешн.», «Внутр.» и ручка синхронизации. На боковую панель осциллографа ОДШ-2 выведены ручки уп­равления двухканальным коммутатором с двумя входами. Комму­татор позволяет наблюдать на экране осциллографа одновремен­но сигналы от двух источников переменного тока. Если частоты источников одинаковы, то по полученным осциллограммам мож­но судить о сдвиге фаз поданных сигналов. Например, на один вход можно подать сигнал, пропорциональный напряжению на конденсаторе, а на другой — пропорциональный силе тока, текущего через конденсатор. Тогда на экране осциллографа можно наблю­дать две синусоиды, сдвинутые по фазе на 90°. Применяя комму­татор, можно сравнивать частоту исследуемого сигнала со стан­дартной частотой, если эти сигналы отличаются по частоте. На задней стенке осциллографов ОДШ-2 и ОЭШ-70 смонтиро­ваны гнезда, позволяющие подавать исследуемый сигнал непосред­ственно на пластины электронно-лучевой трубки. Возможность подавать исследуемый сигнал непосредственно на пластины позво­ляет применить осциллограф и для цепей постоянного тока. По­давая сигнал постоянного напряжения на пластины XX (или УУ) при отключенной развертке, можно наблюдать смещение светя­щейся точки по горизонтали (или вертикали), причем отклонение этой точки пропорционально приложенному напряжению. Следо­вательно, осциллограф можно применить как вольтметр с боль­шим внутренним сопротивлением. Для усиления электромагнитных колебаний применяют усилители низкой частоты. Усилитель низкой частоты – электронный прибор. Предназначенный для усиления электрических колебаний звуковой частоты от 20 Гц до 20 кГц. Обычно усилитель состоит из нескольких блоков: предварительного усилителя напряжения, усилителя мощности, согласующего выходного трансформатора и блока питания. Для школ выпускаются усилители разной конструкции и отличающиеся по внешнему виду. Усилитель УНЧ-3 на лицевой панели имеет ручку регулятора громкости и сигнальную лампочку. Ручкой регулятора громкости производят также включение и выключение сети. В крайнем левом положении ручки при повороте против часовой стрелки прибор отключен. Включение осуществляют поворотом ручки по часовой стрелке после щелчка. Так как усилитель собран на электронных лампах, то он начинает работать после их прогрева.  На боковой стенке смонтированы три входных гнезда: для подключения М – микрофона, АД – адаптера, Л – линии. Нижние гнёзда соединены с корпусом прибора. На задней стенке имеются две пары гнёзд: Гр – для подключения громкоговорителя (низкоомный выход) и Л – высокоомный выход. Здесь же имеются вывод сетевого шнура с вилкой и октальная панель, в которую вставлена специальная вилка с предохранителем (на 0,5 А) для сети с напряжением 220 В. Вилку можно устанавливать в двух положениях: «220 В» и «127 В». Усилитель УНЧ-5 собран на транзисторах. На лицевой панели усилителя смонтирован выключатель сети с индикаторной лампочкой, гнезда выхода, гнезда входа для микрофона и звукоснимателя, разъем для подключения микрофона, ручки регулировки тембра по низкой и высокой частоте, ручка регулировки уровня сигнала, индикатор перегрузки. На задней стенке имеются вывод сетевого шнура с вилкой и предохранитель (на 0,5 А). На вход усилителя могут подаваться сигналы не только с микрофона и звукоснимателя, но и от других датчиков электрических колебаний напряжением от нескольких милливольт до вольт (сигналы с элементов цепи переменного тока, звукового генератора и т.д.). К выходу усилителя можно подключить не только громкоговоритель, но и другие приборы: осциллограф, измерительные приборы переменного тока, головные телефоны и пр. Потребляемая усилителем мощность не более 40 Вт, выходная – около 5 Вт. Запрещается при эксплуатации усилителя менять предохранитель, разбирать и ремонтировать прибор, включенный в сеть. Усилитель на вертикальной панели входит в комплект демонстрационных приборов по радиотехнике. Слева смонтированы универсальные зажимы входа усилителя. Первая лампа работает в режиме усиления напряжения, вторая – как усилитель мощности. В анодную цепь второй лампы включен согласующий трансформатор, вторичная обмотка которого соединена с зажимами низкого и высокого выходного напряжения. Три нижних зажима служат для подключения питания от ВУП –2, на два нижних зажима подаётся напряжение переменного тока 6,3 В для питания накала ламп, а на средний и третий снизу – напряжение постоянного тока 250 В для анодной цепи ламп, причём на третий снизу зажим подаётся положительный потенциал. Подключение блока питания и сборку установок с усилителем на панели запрещается выполнять при включённом в сеть выпрямителе ВУП-2. В демонстрационных установках предпочтение следует отдавать усилителю УНЧ-5.

studfiles.net

Электрические цепи переменного тока

Электрическая энергия почти во всех случаях производится, распределяется и потребляется в виде энергии переменного тока.

Широкое применение переменного тока в различных областях техники объясняется легкостью его получения и преобразования, а также простотой устройства генераторов и двигателей переменного тока, надежностью их работы и удобством эксплуатации.

Переменный ток, меняет свое значение и направление, определенное число раз в секунду. При переменном токе электроны движутся вдоль провода сначала в одном направлении, затем на мгновение останавливаются, далее движутся в обратную сторону, опять останавливаются и снова повторяют движение вперед и назад. То есть электроны совершают в проводе колебательное движение. Вследствие своей малой скорости движения (V_эл= 10^-4м/с = 0,1 мм/с) электроныпри таких колебаниях успевают сделать лишь небольшие перемещения вдоль провода.

Наиболее часто встречается, так называемый синусоидальный переменный ток. Изменение электрических величин (силы тока, напряжения, ЭДС) со временем показывает плавная кривая линия, называемая синусоидой).

Электрические цепи, в которых значения и направления ЭДС, напряжения и тока периодически изменяются со временем по синусоидальному закону, называются цепями синусоидального тока. Иногда их называют просто цепями переменного тока.

Для переменного тока была выбрана синусоидальная форма, так как она обеспечивает более экономичные производство, передачу, распределение и использование электрической энергии.

Кроме того, именно синусоидальная форма электрических величин остается неизменной во всех участках сколь угодно сложной электрической цепи, то есть индуктивные и емкостные элементы, входящие в состав электрических цепей не изменяют синусоидальной формы тока и напряжения.

Электрические цепи переменного тока по сравнению с цепями постоянного тока имеют ряд особенностей. Эти особенности определяются:

• во-первых, тем, что в состав цепей переменного тока входят новые элементы: трансформаторы, конденсаторы, катушки индуктивности;

• во-вторых, тем, что переменные токи и напряжения в этих элементах порождают переменные электрические и магнитные поля, которые в свою очередь приводят к возникновению явления самоиндукции, взаимной индукции и токов смещения.

Все это оказывает существенное влияние на протекающие электрической цепи процессы. Анализ процессов в цепях усложняется.

Для цепи переменного синусоидального тока большое значение имеет частота f. От частоты зависит влияние емкостей и индуктивностей на процессы в цепи.

Особенности цепей синусоидального тока обуславливают ряд новых, специфических для этих цепей явлений: сдвиг фаз, явление резонанса, появление реактивных мощностей.

Коэффициент мощности.

На современных промышленных предприятиях большинство потребителей электрической энергии переменного тока представляют собой активно-индуктивную нагрузку в виде асинхронных электродвигателей, силовых трансформаторов, сварочных трансформаторов, преобразователей и так далее. В такой нагрузке в результате протекания переменного тока индуктируются ЭДСсамоиндукции, обуславливающие сдвиг по фазе между током и напряжением. Этот сдвиг по фазе обычно увеличивается, аcos уменьшается при малой нагрузке. Например, еслиcos двигателей переменного тока при полной нагрузке составляет 0,75 — 0,8, то при малой нагрузке он уменьшается до 0,2 — 0,4.

Если мощность, потребляемая всеми приемниками в данных цепях, является вполне определенной, то при неизменном напряжении на зажимах приемника их ток: I = P / (Ucos )

С уменьшением cos ток нагрузки электростанций и подстанций будет увеличиваться при одной и той же отдаваемой мощности.

Вместе с тем электрические генераторы, трансформаторы и линии электропередачи рассчитываются на определенное напряжение и ток. Увеличение тока потребителя при снижении cosне должно превышать определенных пределов, так как питающие их генераторы рассчитываются на определенную номинальную мощностьS_ном = U_ном I_ном, вследствие чего они не должны оказаться перегруженными. Для того чтобы ток генератора не превышал номинального значения при сниженииcos потребителя, необходимо снижать его активную мощность. Таким образом, понижениеcos потребителей вызывает неполное использование мощности синхронных генераторов, трансформаторов и линий электропередачи. Они бесполезно загружаются за счет индуктивного реактивного тока.

cos, характеризующий использование установленной мощности, часто называют коэффициентом мощности.

Коэффициентом мощности определяют как отношение активной мощности к полной:

cos  = P/S.

(2.71)

2.25 Коэффициент мощности (Адрес Блок 4) Коэффициентом мощности определяют как отношение активной мощности к полной:cos  = P/S. Коэффициент мощности показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии и, в частности, используется на выполнение полезной работы.

Коэффициент мощности (2.25)показывает, какая часть электрической энергии необратимо преобразуется в другие виды энергии и, в частности, используется на выполнение полезной работы. Нормальным считаетсяcos 0,85 — 0,9. При низком коэффициенте мощности на предприятия, потребляющие электроэнергию, накладывается штраф, при высоком — предприятия премируются.

Для улучшения коэффициента мощности проводится ряд мероприятий:

2.заменяются двигатели переменного тока, нагруженные относительно мало, двигателями меньшей мощности;

2.включаются параллельно приемникам конденсаторы.

studfiles.net

Однофазные электрические цепи переменного тока

Основные понятия и определения

Широкое применение в электрических цепях находят периодические ЭДС, напряжения и токи.

Периодические величины изменяются во времени по значению и направлению, причем эти изменения повторяются через некоторые промежутки времени Т, называемые периодом.

На практике подавляющее большинство промышленных источников переменного тока (генераторы электростанций) создают ЭДС, изменяющуюся по синусоидальному закону.

Преимущества такого закона:

а) простота получения;

б) напряжение легко трансформируется;

в) синусоидальная функция является единственной, которая в процессе интегрирования и дифференцирования не меняет своей формы и в процессе передачи и преобразования (в процессе трансформации) напряжения временная зависимость остается неизменной, т.е. синусоидальной.

Любая периодическая величина, изменяющаяся по синусоидальному закону, имеет ряд характерных параметров:

1. период — Т [c];

2) частота — f [Гц] .

Величина обратная периоду называется частотой:

.

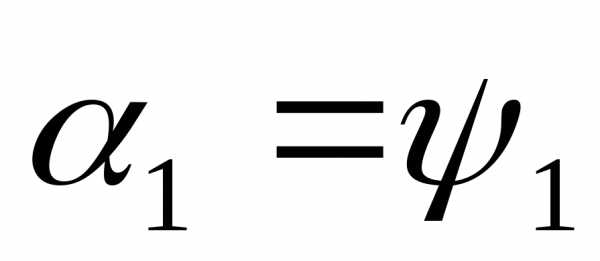Частота для всех электроустановок строго нормируется:

— для наземных систем — 50 (60)Гц;

— в авиации — 400Гц;

— космические летательные аппараты — 1000Гц.

Увеличение частоты позволяет уменьшить габариты электроустановок.

3) Циклическая частота — ω=2πf.

Для частоты 50Гц циклическая частота ω=2*3,14*50=314рад/с или 1/с.

4) Мгновенное значение — значение периодически изменяющейся величины в рассматриваемый момент времени.

Мгновенные значения обозначают — e, i, u.

5) Амплитудное значение

Максимальное значение или амплитуду ЭДС, напряжения и тока обозначают — E_m, U_m, I_m.

6) Действующее значение

Действующее значение ЭДС, напряжения и тока обозначают — E, U, I.

Для количественной оценки синусоидального тока, который в течение времени непрерывно, периодически изменяется, используют значение постоянного тока, эквивалентное значению переменного тока по совершаемой работе. Такое значение будет действующим для синусоидального тока.

Действующим (или эффективным)значением синусоидального тока называют такое значение постоянного тока, при протекании которого в одном и том же резисторе с сопротивлением R за время одного периода Т выделятся столько же тепла, сколько при прохождении синусоидальнего тока.

При синусоидальном токе:

i=I_msinωt

количество теплоты, выделяемое в резисторе R за время Т равно:

,

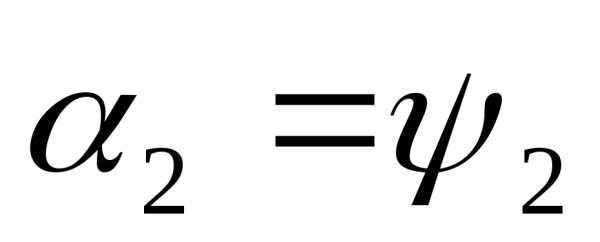а при постоянном токе

.

Согласно определению Q_≈=Q_— , тогда

, .

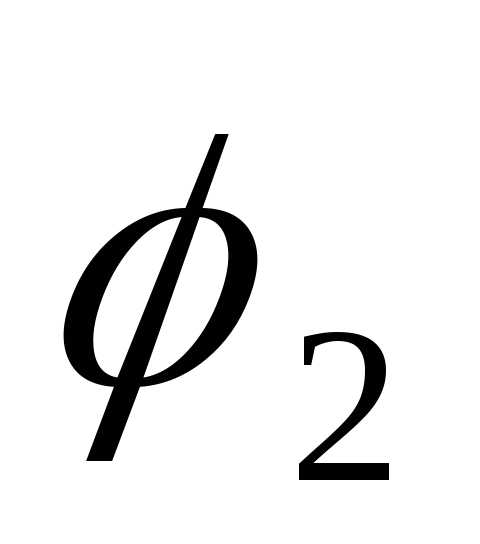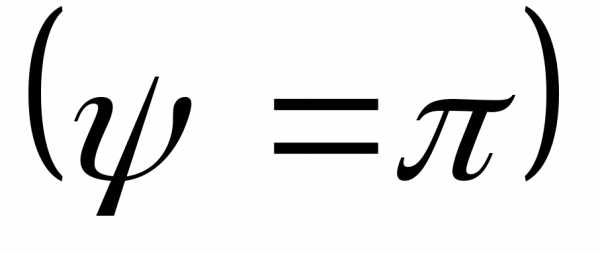Таким образом действующее значение синусоидального тока I является его среднеквадратичным значением за период Т

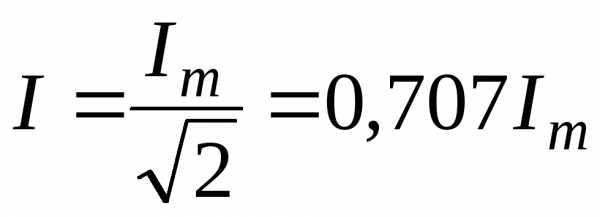
Действующее значение переменного тока обозначается как постоянный ток и в 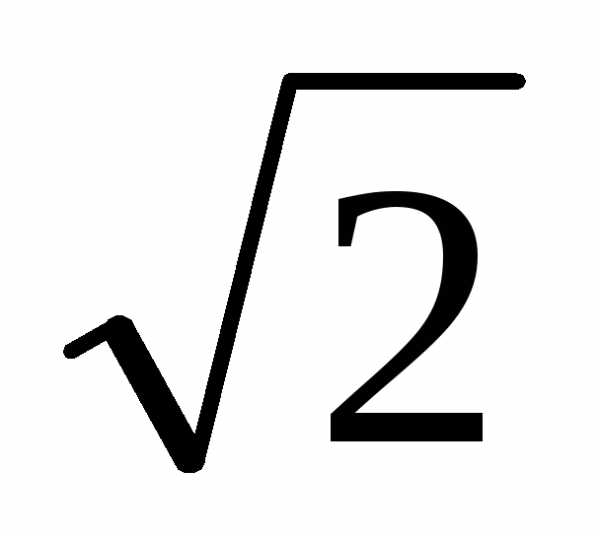раз меньше чем его амплитуда.

Аналогично

.

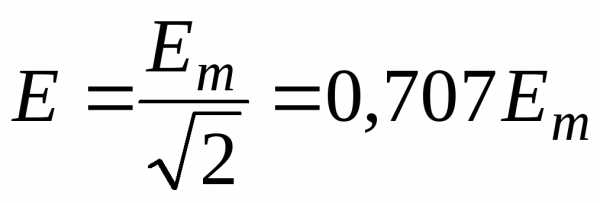
Большинство электроизмерительных приборов работают на тепловом или электродинамическом эффекте, поэтому они всегда показывают действующее значение. Основные расчеты электроцепей синусоидального тока проводятся по действующим значениям. Для несинусоидальных величин эти соотношения будут другими.

7) Среднее значение

Среднее значение синусоидальной величины это ее среднеарифметическое значение. Однако, если определять среднее значение синусоидальной величины за период Т, то оно будет равно нулю, так как положительная и отрицательная полуволны синусоидальной кривой совпадают по форме. Поэтому среднее значение определяют за полпериода.

За среднее значение синусоидального тока принимают такое значение постоянного тока, при котором за полпериода переносится такой же электрический заряд, что и при синусоидальном токе:

,

,

/

Таким образом, среднее значение меньше действующего.

Изображение синусоидальных величин в прямоугольных координатах

В общем случае синусоидальные величины (рис.1), могут быть записаны:

e=E_msin(ωt+ψ_e)

u=U_msin(ωt+ψ_u),

i=I_msin(ωt+ψ_i),

где e,u,i — мгновенные значения ЭДС, напряжения и тока;

E_m,U_m,I_m — амплитуды ЭДС, напряжения и тока.

(ωt+ψ_e) — фазовый угол;

ψ_e, ψ_u, ψ_i — начальные фазы ЭДС, тока и напряжения.

На практике чаще имеют место случаи, когда электрические величины не совпадают по фазе.

Из рис. 1 видно, что напряжение опережает ток на угол ψ_u-ψ_i . Разность фазовых углов называется разностью или сдвигом фаз.

φ=ψ_u-ψ_i — разность фаз между напряжением и током.

При этом пользуются правилом: начальные фазы расположенные по левую сторону от начала координат имеют положительные значения, а по правую отрицательные.

Если угол φ >0, то ток отстает от напряжения по фазе. Если φ<0, то ток опережает напряжение по фазе.

При сложении двух синусоидальных величин (одинаковой частоты), изображенных в прямоугольных координатах, необходимо сложить ординаты для ряда значений угла ωt и по точкам построить суммарную синусоиду. Получается новая амплитуда, новый фазовый сдвиг, причем:

I_m ≠ I_m1 + I_m2;

φ_i≠ φ_i1+ φ_i2.

Такой расчет является трудоемким и имеет недостаточную точность.

Векторное изображение синусоидальных величин

Рис.2

Наиболее просто складывать синусоидальные величины, представив их вращающимися векторами (рис.3).

Рис.3

В плоскости с осями ОX и ОY рассмотрим вращающийся с постоянной скоростью, равной угловой частоте ω, вектор ОА, длина которого равна амплитуде синусоидальной ЭДС, т.е. .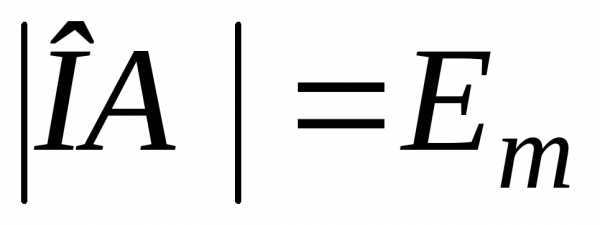

Мгновенное значение ЭДС описывается известным соотношением:

e=E_msin(ωt+ψ_e).

За положительное направление вращения принимают направление против часовой стрелки, а угол поворота отсчитывают от оси ОX. В начальном положении (при t=0) вектор ОА повернут по отношению к оси OX на угол ψ_e

Построим проекцию вектора ОА на ось OY, которые изменяются по мере поворота вектора на угол ωt по отношению к начальному положению. В начальном положении (при t=0) проекция ОА₀= E_msinψ_e=e₀, т.е. равна мгновенному значению ЭДС при t=0.

Через некоторое время (t=t₁) вектор ОА будет повернут на угол ωt₁ и составлять с осью ОX угол (ωt₁+ψ_e). Проекция его на ось OY :

ОА₁= E_msin(ωt₁+ψ_e)=e₁, т.е. равна мгновенному значению ЭДС при t=t₁.

При t=t₂ вектор ОА совпадает с осью OY и его проекция ОА₂= E_m= e₂. При дальнейшем вращении вектора АО его проекции на ось YO начнут уменьшаться, затем станут отрицательными и т.д.

Таким образом, проекции на ось OY вектора, вращающегося с постоянной скоростью ω и имеющего длину, равную амплитуде ЭДС, изменяются по синусоидальному закону, т.е. представляют собой мгновенные значения синусоидальной ЭДС. Следовательно, справедливо и обратное: если имеем синусоидальную величину. то ее можно представить вращающимся вектором.

Правила построения векторных диаграмм

1. Любую синусоидально изменяющуюся во времени величину (ЭДС, напряжение, ток) можно представить в виде вращающегося вектора, длина которого равна амплитуде, а угловая скорость угловой частоте этой синусоидальной величины.

2. Начальное положение вращающегося вектора определяется углом, равным начальной фазе синусоидальной величины и откладываем от положительного направления оси O в сторону, противоположную вращению часовой стрелки.

3. В одних и тех же осях можно представить векторы всех ЭДС, действующих в данной цепи, напряжений на всех участках данной цепи и токов во всех ее ветвях (в заданных масштабах).

4. Так как синусоидальные величины имеют одинаковую частоту, то изображающие их векторы вращаются с одинаковой скоростью. Их взаимное положение на плоскости, относительно друг друга, остается неизменным. Поэтому на практике векторы не вращают, а строят их, соблюдая углы между векторами (углы сдвига фаз).

5. Отказавшись от вращения вектора можно строить векторы не только максимальных, но и действующих значений.

6. Вектора можно складывать, по правилу параллелограмма, получив при этом суммарный вектор (рис. 4).

Рис.4

7. В связи с отсутствием необходимости вращения нас интересует только взаимное расположение векторов, один из которых можно строить по направления оси OX, остальные вектора направляются относительно этого вектора (рис.5).

Например, если к элементам электрической цепи подается переменное напряжение u=U_msin(ωt+ψ_u), то возникнет переменный ток i=I_msin(ωt-ψ_i). В этом случае ток отстает от напряжения по фазе на угол φ=ψ_u-ψ_i. Начальные фазы ψ_u и ψ_i на векторной диаграмме не изображают, так как взаимное положение векторов определяется полностью разностью фаз — φ. Принимаем начальную фазу тока равную нолю (ψ_i=0), тогда начальная фаза напряжения ψ_u равна сдвигу фаз — φ.

Рис.5

Графический метод расчета является грубым неточным. На практике переходят к точным математическим методам расчета на основе теории комплексных чисел.

Понятия о комплексных числах

Комплексная плоскость — прямоугольная системе координат, на которой по одной оси откладываются вещественные числа +1, на другой (перпедикулярной) — мнимые числа +j.

Здесь j=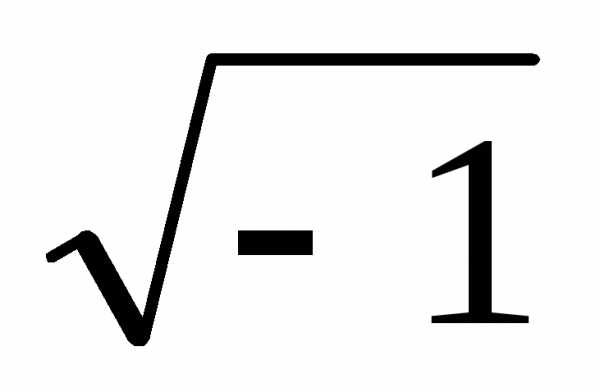 — мнимая единица.

Действия с мнимой единицей:

1) j²=-1; 2)

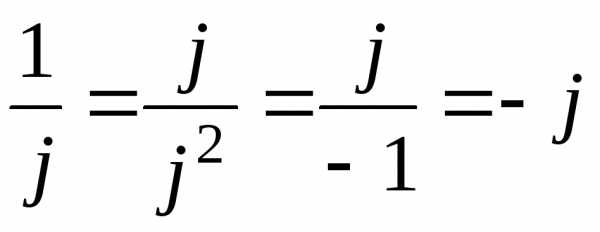
Любую точку на комплексной плоскости можно охарактеризовать комплексным числом. Известно, что комплексное число С имеет вещественную Re и мнимую Im составляющие.

Алгебраическая форма записи комплексного числа:

С=а+jв,

где а= Аcosα – реальная часть комплексного числа,

в= Аsinα – мнимая часть, γ=arctg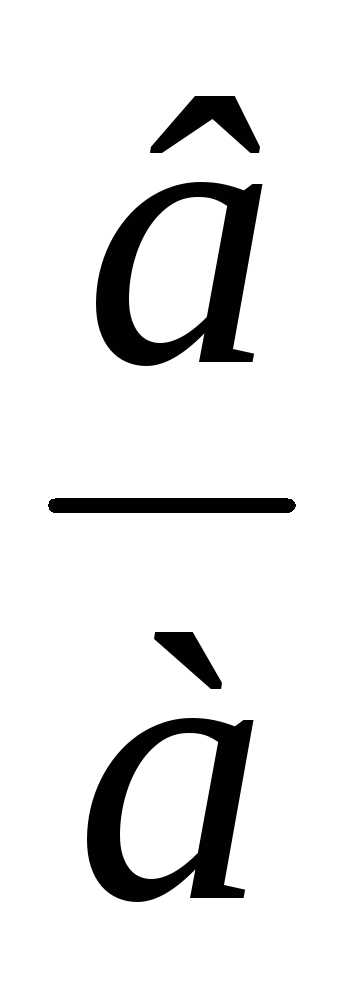 — фаза,

с=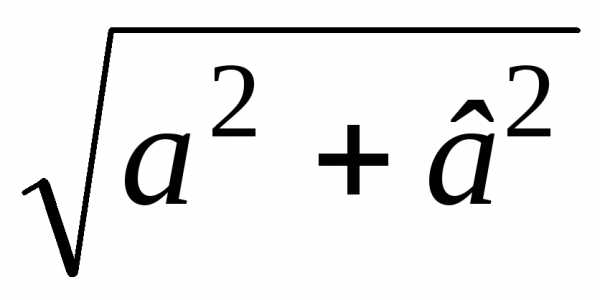 — модуль комплексного числа.

Тригонометрическая форма записи комплексного числа:

С=с(cosγ+jsinγ).

Показательная форма записи комплексного числа:

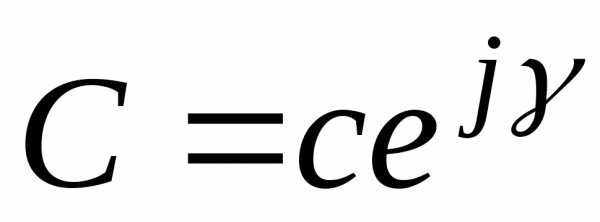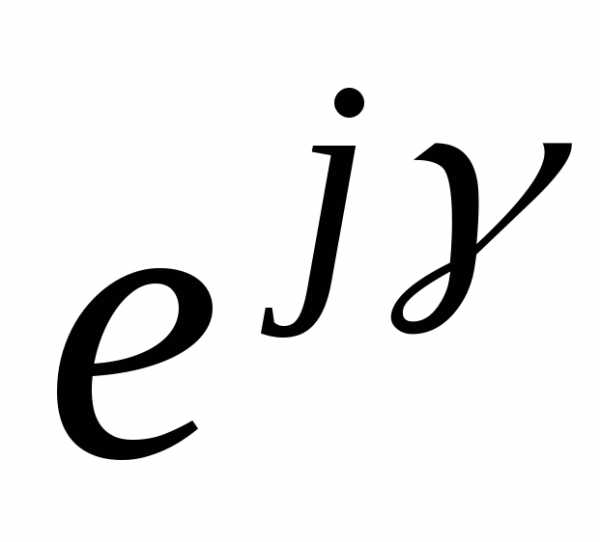, где — оператор поворота (поворотный множитель).

cosγ + jsinγ = 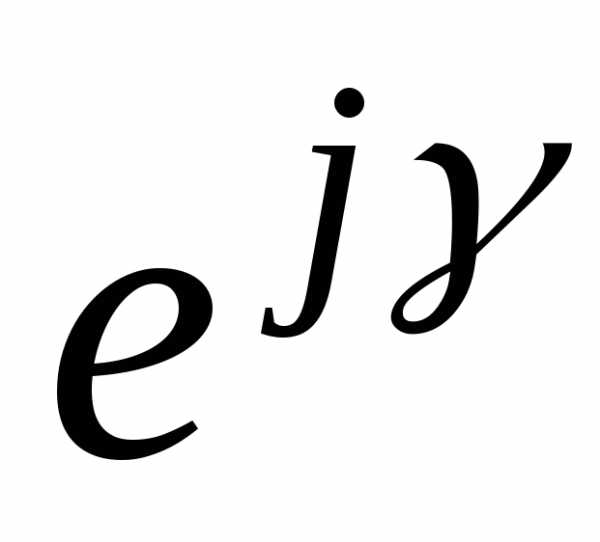— формула Эйлера.

Частные случаи:

Для γ= π/2 ;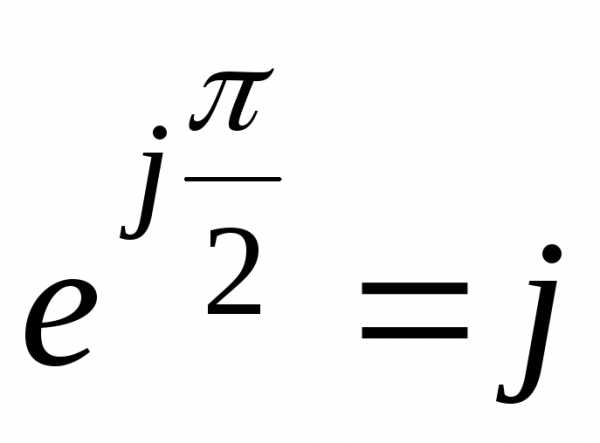

γ= -π/2 ;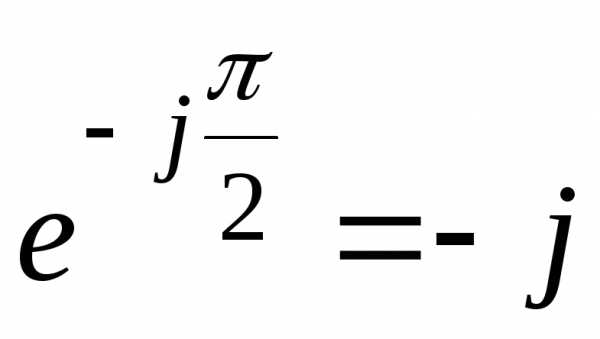

γ= π .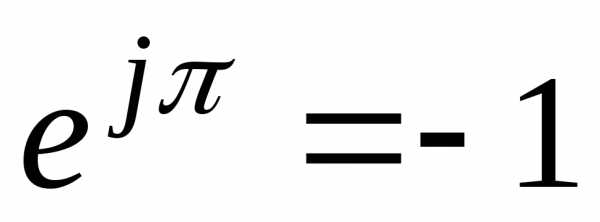

Тригонометрическая форма записи служит для перехода из алгебраической формы в показательную и наоборот.

studfiles.net

11. Электрические цепи однофазного переменного тока. Основные определения

     Переменным называется электрический ток, величина и направление которого изменяются во времени.      Область применения переменного тока  намного шире,  чем  постоянного. Это объясняется тем, что напряжение переменного тока можно легко понижать или повышать с помощью трансформатора, практически в любых пределах. Переменный ток легче транспортировать на большие расстояния. Но физические процессы, происходящие в цепях переменного тока, сложнее, чем в цепях постоянного тока из-за наличия переменных магнитных и электрических полей.         Значение переменного тока в рассматриваемый момент времени называют мгновенным значением и обозначают строчной буквой i.       Мгновенный ток называется периодическим, если значения его повторяются через одинаковые промежутки времени

Наименьший промежуток времени, через который значения переменного тока повторяются, называется периодом.      Период T измеряется в секундах. Периодические токи, изменяющиеся по синусоидальному закону, называются синусоидальными.          Мгновенное значение синусоидального тока определяется по формуле

          где I_m — максимальное, или амплитудное, значение тока.          Аргумент синусоидальной функции называют фазой; величину φ, равную фазе в момент времени t = 0, называют начальной фазой. Фаза измеряется в радианах или градусах. Величину, обратную периоду, называют частотой. Частота f измеряется в герцах.- частотой50 Гц.        Величину называют круговой, или угловой, частотой. Угловая частота измеряется в рад/c.          Если у синусоидальных токов начальные фазы при одинаковых частотах одинаковы, говорят, что эти токи совпадают по фазе. Если неодинаковы по фазе, говорят, что токи сдвинуты по фазе. Сдвиг фаз двух синусоидальных токов измеряется разностью начальных фазДействующим значением переменного тока называется среднеквадратичное значение тока за период. Действующее значение тока (для синусоиды)

.

        Аналогично определяются действующие значения ЭДС и напряжений

.

        Действующие значения переменного тока, напряжения, ЭДС меньше максимальных в √2 раз.        Законы Ома и Кирхгофа справедливы для мгновенных значений токов и напряжений.        Закон Ома для мгновенных значений: .                Законы Кирхгофа для мгновенных значений:.       6.2)

.    

12. Изображения синусоидальных функций времени в векторной форме

       При расчете электрических цепей часто приходится складывать или вычитать величины токов или напряжений, являющиеся синусоидальными функциями времени. Графические построения или тригонометрические преобразования в этом случае могут оказаться слишком громоздкими.      Задача  упрощается, если  представить наши синусоидальные функции в векторной форме. Имеем синусоидальную функцию . Известно, что проекция отрезка, вращающегося вокруг оси с постоянной угловой скоростью, на любую линию, проведенную в плоскости вращения, изменяется по синусоидальному закону.      Пусть отрезок прямой длиной I_m начинает вращаться вокруг оси 0 из положения, когда он образует с горизонтальной осью угол φ, и вращается против часовой стрелки с постоянной угловой скоростью ω. Проекция отрезка на вертикальную ось в начальный момент времени . Когда отрезок повернется на угол α₁, проекция его . Откладывая углы α₁, α₂, … на горизонтальной оси, а проекции отрезка прямой — на вертикальной оси, получим ряд точек синусоиды (рис. 6.1).

       Пусть даны два синусоидальных тока: и

                         .       Нужно сложить эти токи и получить результирующий ток: Представим синусоидальные токи i₁ и i₂ в виде двух радиус — векторов, длина которых равна в соответствующем масштабе I_1m и I_2m. Эти векторы расположены в начальный момент времени под углами φ₁ и φ₂ относительно горизонтальной оси. Сложим геометрически отрезки I_1m и I_2m. Получим отрезок, длина которого равна амплитудному значению результирующего тока I_3m. Отрезок расположен под углом φ₃ относительно горизонтальной оси. Все три отрезка вращаются вокруг оси 0 с постоянной угловой скоростью ω. Проекции отрезков на вертикальную ось изменяются по синусоидальному закону. Будучи остановленными для рассмотрения, данные отрезки образуют векторную диаграмму (рис. 6.2).       Векторная диаграмма — это совокупность векторов, изображающих синусоидальные напряжения, токи и ЭДС одинаковой частоты.

     Необходимо отметить, что напряжение, ток и ЭДС — это скалярные, а не векторные величины.       Мы представляем их на векторной диаграмме в виде не пространственных, а временных радиус — векторов, вращающихся с одинаковой угловой скоростью.      Изображать на векторной диаграмме два вектора, вращающихся с различной угловой скоростью, бессмысленно.

                 Рис. 6.2        Положительным считается направление вращения векторов против часовой стрелки.       Векторные  диаграммы  используются  для  качественного анализа электрических цепей, а также при решении некоторых электротехнических задач.

       При расчетах цепей синусоидального тока используют символический метод расчета или метод комплексных амплитуд. В этом методе сложение двух синусоидальных токов заменяют сложением двух комплексных чисел, соответствующих этим токам. Комплексное число может быть представлено в виде радиус — вектора в комплексной плоскости. Вектор длиной, равной модулю c, расположен в начальный момент времени под углом φ относительно вещественной оси (рис.6.3).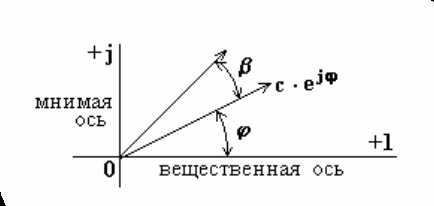

     Умножим комплексное число на множитель .- комплексную функцию времени для напряжения.- комплексная амплитуда напряжения (исходное положение вектора в комплексной плоскости). Определим, чему равна мнимая часть комплексной функции времени для напряжения.

    Мгновенное синусоидальное напряжение (ток, ЭДС) является мнимой частью соответствующей комплексной функции времени.

13.Сопротивление в цепи синусоидального тока

      Если напряжение подключить к сопротивлению R, то через него протекает токАнализ выражения (6.7) показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе.         Формула (6.7) в комплексной форме записи имеет видгдеи- комплексные  амплитуды  тока и напряжения.           Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению.      Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току — активным сопротивлением.                                Рис.6.4      Активное сопротивление больше омического из-за явления поверхностного эффекта. Поверхностный эффект заключается в том, что ток вытесняется из центральных частей к периферии сечения проводника.

studfiles.net