Параллельные сопротивления: Формула расчета сопротивления при параллельном соединении резистора

Параллельная схема: характеристики, преимущества и недостатки

В статье узнаете что такое параллельная схема соединения, как ее сделать, характеристики, сила тока в параллельной цепи, его сопротивление и мощность. А также преимущества и недостатки параллельной схемы.

Поведение схемы полностью зависит от конфигурации ее компонентов. В соответствии с конфигурацией их подключения эти цепи подразделяются на параллельные и последовательные. Этот пост раскрывает значение параллельной цепи, как создать параллельную схему, ее различные характеристики, области применения, преимущества и недостатки.

Содержание

Что такое параллельная цепь

Схема называется параллельной, когда два или более компонентов подключены к одному узлу, а обе стороны компонентов подключены непосредственно к батарее или любому другому источнику. Ток в параллельной цепи имеет два или более пути прохождения через него.

Наиболее распространенным примером параллельной цепи является проводка автомобильных фар. Если бы фары были включены последовательно, то когда одна фара выходила из строя, другая также бы выключалась

Пример автомобильных фар, подключенных по параллельной цепи

Как сделать параллельную цепь

Два или более компонентов схемы соединены через общий источник напряжения для формирования параллельной цепи. На рисунке ниже показан типичный параллельный контур, в котором резисторы (R1, R2, R3, R4) соединены параллельно. Обе стороны резисторов подключены непосредственно к источнику напряжения. Параллельный путь называется ветвью, и напряжение на всех ветвях одинаково, но ток может быть разным.

Принципиальная схема параллельной цепи

Характеристики параллельной цепи

Основные характеристики параллельной цепи перечислены ниже:

Сила тока в параллельной цепи

Согласно закону Ома, I = U / R. Это подразумевает, что каждый резистор в этой цепи будет потреблять ток от источника. Следовательно, общий ток, потребляемый от источника, равен сумме токов ветвления, и ток, протекающий в каждом тракте, зависит от сопротивления ветви. Тем не менее, напряжение остается неизменным и создает разность потенциалов на его клеммах.

Общий ток (I_t) может быть рассчитан с использованием уравнения,

I_t = I₁ + I₂ + I₃ +…. In

Где ( I₁ + I₂ + I₃ +… I_n ) — токи ветвления

Давайте рассмотрим, что параллельная цепь построена с двумя резисторами (R1 и R2) с разными значениями (10 Ом и 5 Ом) соответственно. Напряжение 10V подается через резисторы , в результате тока 1А , проведенной от батареи через R1 и R2, который получен из уравнения I = U / R.

Следовательно, два тока ветвления в цепи составляют 1А и 2А, которые суммируют до 3А.

I_t = 1 + 2 = 3А

Сопротивления в параллельной цепи

Общее сопротивление любого количества резисторов рассчитывается по уравнению,

Взаимное значение R1 = 1/R1 = 1/10 = 0,1

Взаимное от R2 = 1/R2 = 1/5 = 0,2

Сумма обратных выше = 0,3

R _t = 1 / 0,3 = 3,33 Ом

Мощность в параллельной цепи

Как только общий ток и приложенные значения напряжения известны, мощность может быть рассчитана с использованием уравнения P = UI . В приведенном выше примере, приложенное напряжение U = 10В и I = 3A, P = 10×3 = 30 Вт

Применение параллельной цепи

Приложения параллельных цепей включают в себя:

Электропроводка к точкам питания в каждом доме выполнена в форме параллельных цепей.
Источник питания постоянного тока в автомобильной промышленности использует параллельные цепи.
Аппаратное обеспечение компьютера разработано с использованием параллельных цепей.

Преимущества параллельной цепи

Преимущества параллельных цепей включают в себя:

Равное напряжение распределяется на каждый компонент в цепи.
На ток не влияет даже то, что в цепь добавлено или удалено больше компонентов (резисторов).

Недостатки параллельной цепи

Недостатки параллельных цепей перечислены ниже:

Дорого строить
Короткое замыкание может произойти случайно в параллельной проводке и может начаться пожар
Даже если один из компонентов неисправен, ток все равно может проходить через цепь.

Последовательное и параллельное соединение резисторов

Последовательное и параллельное соединение резисторов в схемах являются самыми распространенными, также – это база для расчета более сложных схем.

Последовательное подключение

Начнем с последовательного соединения. По этой схеме каждый резистор подключается с другим только в одной точке, их может быть в цепи 2, 3 и больше.

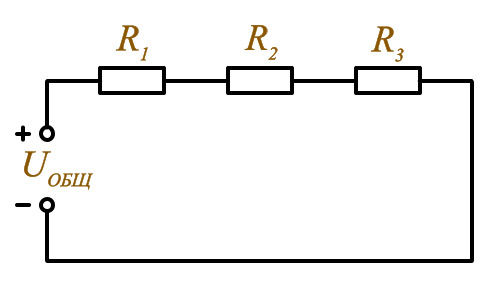
Последовательное и параллельное соединение резисторов

Рис. Последовательное подключение.

Обозначение:

Обозначим сопротивления: R1, R2, R3 и напряжение источника в цепи Uц. При подключении источника питания в ней начнет протекать ток Iц. В цепи с последовательным соединением ток протекает по всем резисторам один за другим. Поскольку ток течет через все резисторы их сопротивления и ток суммируется, Iц = I1+I2+I3, Rц = R1 +R2 + R3, чем больше отдельно взятое сопротивление, тем тяжелее электронам преодолевать участок цепи. Мощность резисторов при последовательном и параллельном соединении рассчитывается по разным формулам. В последовательных цепях – складываем, в параллельных – это обратно пропорциональная величина.

Параллельное соединение

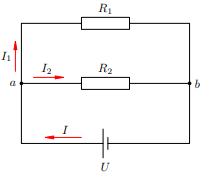
Рис. Параллельное подключение.

Данный вид подключения характерен тем, что все элементы цепи соединяется выводами в одной точке друг другу, т.е. точка входа и выхода всех нагрузок сходятся в одну точку (или еще одно обозначение на схемах – //). Электроток, двигаясь по проводнику, дойдя до общего соединения делится на количество имеющихся веток. Если представить движение воды в трубе, то можно сказать, что вода двигающиеся по одной трубе, равномерно перетекает в несколько отводов, подсоединенных к ней. В нашем случае заряженные электроны, двигающиеся по проводнику, также растекаются на количества предложенных веток в узле.
Более наглядно это можно представить в виде формул:
1. Каждый вид соединения находится под одинаковым напряжением:
U = U1 = U2;
2. Суммарная сила тока равняется суммарному значению тока каждого участка
I = I1 + I2;
3. Сопротивление цепи равно сумме величина обратных сопротивлению участка:
1/R = 1/R1 + 17R2 + . . . + 1/Rn;
4. Сила тока пропорциональна сопротивлению каждого участка
I1/I2=R2/R1.
Далее рассмотрим схему как работает не только последовательное параллельное, но и смешанное соединение резисторов.

Смешанное подключение

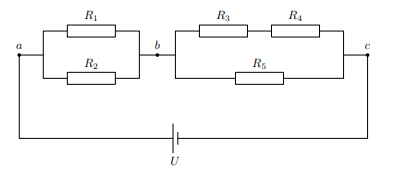
Рис. Смешанное подключение резисторов

В электрических схемах используются не только типовые схемы, но и смешанное, созданное из критерий определенных требований. Чаще всего в схемах встречается третий вариант, представляющий набор из элементарных типов схем. В смешанных участках учитываются не только элементы, но и направления движения тока.
При вычислении мощности резисторов смешанного подключения используются формулы для параллельного и последовательного соединения резисторов, формула также является составной.

Основные законы электротехники, наиболее часто используемые для расчетов

Рассмотрим основные законы электротехники и свойства последовательного и параллельного соединения резисторов для участка цепи

Закон Ома

Напряжение находится по закону Ома по формуле I=U/R – чем больше сопротивление, тем меньше ток. Напряжение можно найти из этой же формулы. U=R*I, ток умножается на сопротивление. Запишем эту формулу для каждого участка U1=R1· I1, Un=Rn · In.

Законы Кирхгофа

Первый закон

Ещё один очень важный закон — это закон Кирхгофа. Для участка цепи постоянного тока их два.

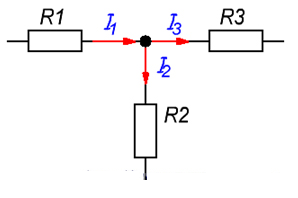
Рис. иллюстрация к пояснению действия первого закона Кирхгофа.

Первый закон имеет формулировку: Сумма всех токов, входящих в узел и выходящих из него равна нулю.
Если посмотреть на схему, I1 – это ток, который заходит в узел, I2 и I3 – это электроны, которые вытекают из него.
Применяя формулировку первого закона можно записать формулу по-другому:
I1-I2+I3=0. В этой формуле знаки плюс имеют значения, которые прибывают в узел, минус, который отходит от него.

Второй закон Кирхгофа.

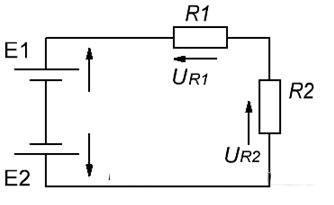
Рис. иллюстрация к пояснению действия второго закона Кирхгофа.

Если к цепи с включенными сопротивлениями подключен один источник ЭДС (батарея питания) тогда всё понятно, можно обойтись законом Ома. А, если, источников несколько и схема с различным схемным расположением элементов, тогда вступает в силу второй закон, который гласит: сумма токов всех источников питания для замкнутого контура, равна сумме падений напряжения на всех сопротивлениях участка в этом контуре.
E1- Е2 = – UR1 – UR2 или E1 = Е2 – UR1 – UR2.

Параллельное и последовательное соединение резисторов, решение задач

Алгоритм расчёта смешанных подключений находится в тех же правилах, что и в элементарных схемах расчета последовательного и параллельного соединения резисторов. Ничего нового нет: нужно правильно разбить предложенную схему на пригодные для расчета участки. Участки, с элементами, подключены поочередно либо параллельно.

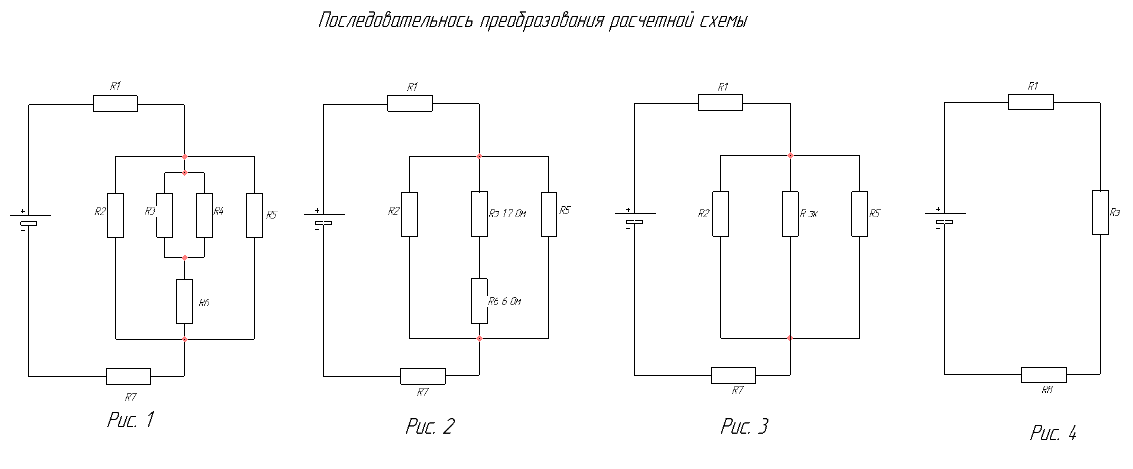
Рис. Порядок замещения при расчете сложных позиций более простыми.

Для решения задачи на последовательное и параллельное соединение резисторов необходимо правильно оценить цепи элементов. Рассмотрим схему №1 на рис.
На схеме присутствует параллельная и последовательная часть соединения элементов. Для расчета очень важно аккуратно, шаг за шагом упрощать цепи и не брать сразу всю схему (рис.1). Как же правильно определить параллельное и последовательное соединение резисторов?

Для примера расчета возьмем резисторы R3, R4, которые подключены параллельно. Эквивалентный резистор этих элементов, будет равенRэ. = 1/R34 =1/R3 + 1/R4, после преобразования формулы и приведения к одному знаменателю получим R34 = R3 · R4 / (R3 + R4). Э. = 1/3+1/4 /(3+4) =1,7 Ом.

Далее видно, что приведённая эквивалентное R эк и R6 соединены последовательно, чтобы узнать сопротивление их необходимо сложить, тогда общее сопротивление будет равно R346 = R34 + R6, тогда Rэк346 = 1,7 + 6 = 7, 7 Ом.
Заменяем на схеме одним общим элементом, теперь, позиция упрощается еще больше (рис 3).

Теперь образовалась ситуация – включение трех элементов в //. Как вычисляется такое соединение нам уже известно, 1/ R23465 = 1/ R2 +1/R346 + 1/R5 после вычисления правой части получаем 0,82 Ом. После окончательного вычисления получаем R23465 = 2,1 Ом. Здесь следует обратить внимание, что общее сопротивление получилось меньше самого меньшего из трех.

Заменяем эти сопротивление одним эквивалентным R23465. В конечном итоге все выглядит уже намного проще. Rц = Rэк + R1+ R2. R об. = R ц = 1,21 +7+1 =9,21 Ом.
Из приведенного алгоритма расчёта видно, как из сложной схемы путем простого математического вычисления и применения правил сокращения резисторов участок становится простой и понятной.

Схема с подключением сопротивлений «треугольником»

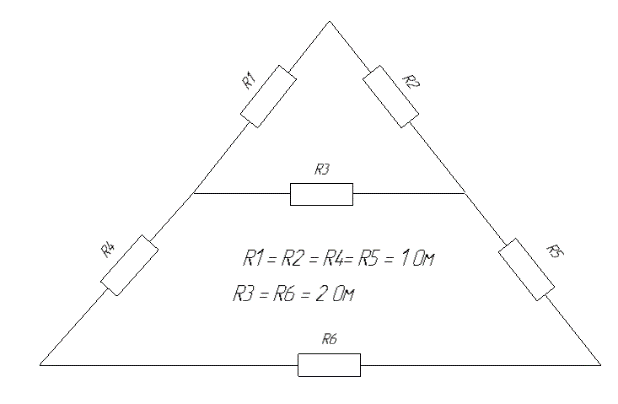
Рис. Расчетная схема соединения резисторов в треугольник.

Иногда некоторые затруднения возникают при разборе схемы соединения в треугольник.

Рассмотрим на примере рисунка расчет резисторов по этому подключению.
Из схемы видно, что R1 и R2 соединены последовательно Rэ12 будет соединяться R3 последовательно.

Затем Rэ123 соединяется с сопротивлением R4, R5 в последовательную цепь. Затем все это объединяется с Rэ в //.

Проведем несложные вычисления учитывая, что
R1, R2, R4, R5 равняется 1 Ом. R3, R7 – 2 Ом.
RЭ1,2 = R1+R2 = 1+1=2 Ом.

Вычисляем параллельное подключение: Rэ 12 с R3. Rэ1,3 = (Rэ12*R3) /(Rэ12+R3) = (2*2) /(2+2) = 1Ом.

Далее мы видим последовательное: RЭ123 + R4 + R5 = 1+1+1 = 3 Ом.
И последнее – Rэ123 4 5 с R6 – параллельное.

Общее сопротивление цепи Rц = Rоб = (RЭ1,2,3,4,5 *R6) /(RЭ1,2,3,4,5+R6) = (3 * 2) / (3+2) = 1,2 Ом. Как видно, что расчет подобного варианта также не сложный.

Расчет последовательного и параллельного подключения резисторов онлайн

Подсчитать значение мощность и сопротивлений подставляя их в формулы можно только в учебных целях, или, когда объемы не очень большие. Наиболее практичный вариант расчета является онлайн калькуляторы, которые расположены на многочисленных интернет ресурсах. Для расчёта любой сложности нужно правильно определить тип соединения резисторов последовательное или параллельное и внести данные для расчета в поля калькулятора.

Также такая форма расчета подойдет и для проверки результатов решения учебных задач.

Последовательное и параллельное соединение резисторов и конденсаторов

Электрические цепи состоят не только из резисторов, в них применяется большое количество различных деталей, например, конденсатор, которые подключаются в последовательное, // и смешанное соединение.

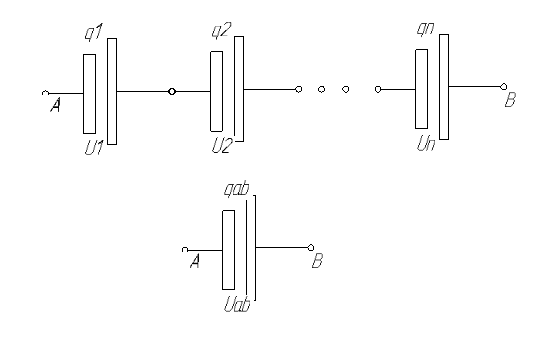
Рис. Замещения последовательно включенных элементов.

Определение этому элементу можно дать следующее: Конденсатор – это совокупность проводящих тел служащий для накопления электрического заряда.
Элементарный конденсатор имеет две пластины, форма этих пластин может быть различной: сферической, круглой, цилиндрической, прямоугольной – по форме пластин разделяется и тип конденсатора.

Важное свойство. Одно из важных свойств конденсатора: если заряжается одна пластина конденсатора, то благодаря явлению электростатической индукции заряжается и вторая половина, но с противоположным знаком.

Устройство конденсатора

Плоский конденсатор состоит из двух плоских пластин отстоящих друг от друга на маленькое расстояние. У конденсатора к двум пластинам припаивается вывод всего их получается два.

Типовые схемы подключения конденсаторов

Рассмотрим различные виды подключения конденсатора.

Последовательное

Первый вид — это последовательное соединение.
Предположим, что емкость этих конденсаторов будут равны. Тогда заряды также будут равны: q1=q2=q3, как и в примере с резисторами, сложный тип позиций с конденсатором можно упростить, заменив несколько элементов одним. У элементов соединенных друг за другом, общая емкость будет обратно пропорциональная всем имеющимся элементам. То есть: Rэк будет равняться 1/С1 + 1/С2 +…. 1/Сn/
Напряжение складывается, U эк = U1 + U2+ … Un.

Параллельное

Второй тип подключения конденсаторов – это соединение в паралель

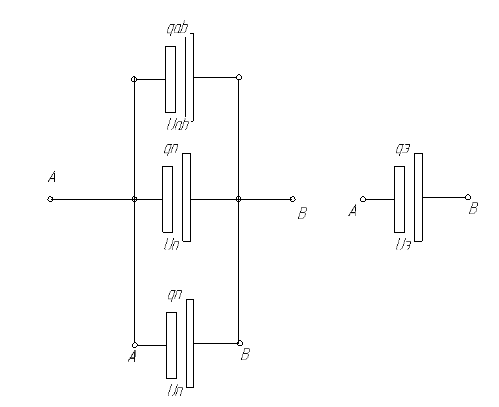
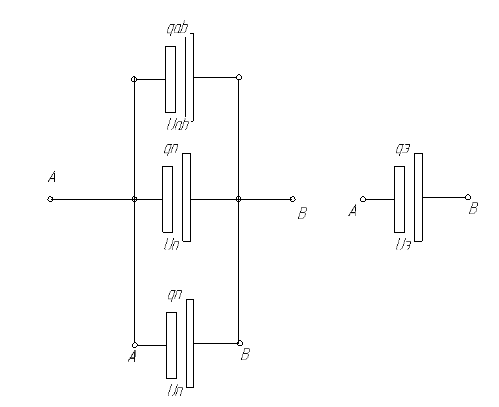Рис. Схема замещения элементов, включенных в параллель.

Соответственно эти конденсаторов обозначены C1, C2, … Cn заряды: Q1, Q2, … Qn и напряжение: U1, U2, … Un.

У элементов в // емкость складывается Сэ = C1 + C2 + … C n.
Напряжение Un на каждом конденсаторе будет равно напряжению на эквивалентном
Uэ = U1 = U2 =… = Un – это особенность параллельного подсоединения всех элементов цепи.

Емкость будет складываться из суммы отдельных элементов Сэ =С1 + С2 + … Сп.

Рис. Расчетные позиции элементов при различном включении.

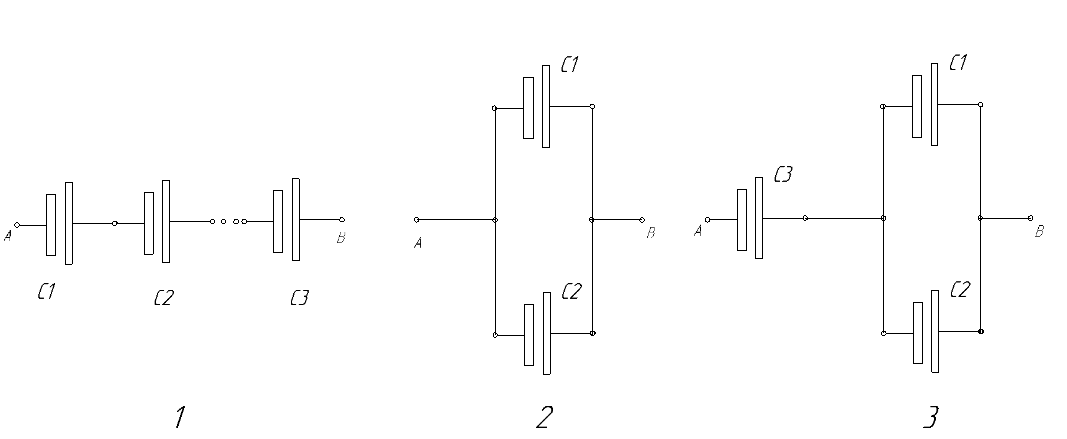
Простая позиция, которая не требует преобразования №1 – последовательное подключение. По известной формуле для этих поз. запишем 1/Сэ = 1/С1 +1/С2 +1/С3, подставив формулу значения, которые даны в условии задачи, получим 1/Сэ = 1/С1 +1/С2 +1/С3 = 59 мФ.

Не требует преобразования и 2 схема: емкость общего конденсатора будет равняться сумме конденсаторов которые включены в параллельной цепи: Сэ =С1 +С2 +С3
Сэ = 100 + 200 + 500 = 800 мФ.

Рассмотрев рис. №3 видно, что пара конденсаторов включена параллельно и один последовательно. Алгоритм преобразования таких цепей мы уже рассматривали, поэтому: сразу же находим емкость конденсатора Сэ соединения: Сэ = С1+С2 = 200+500 = 700 мФ.

Теперь находим общие эквивалентную емкость элементов с последовательным подключением 1/Сэ = 1/С2,3 +1/ С1 = 89 мф.
Практическая задача решена.

Facebook

Twitter

Вконтакте

Google+

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:

+7(499)403 39 91

Доставка подшипников по РФ и зарубежью.

Каталог подшипников на сайте themechanic.ru

Внимание покупателей подшипников

Уважаемые покупатели, отправляйте ваши вопросы и заявки по приобретению подшипников и комплектующих на почту или звоните сейчас:
tel:+7 (495) 646 00 12
[email protected]
Доставка подшипников по РФ и зарубежью.
Каталог подшипников на сайте

Внимание покупателей подшипников

Соединения проводников — материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: параллельное и последовательное соединение проводников, смешанное соединение проводников.

Есть два основных способа соединения проводников друг с другом — это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.

Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.

Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1):

Slider

Рис. 1. Резистор

Напряжение на резисторе — это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.

Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.

Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2):

Рис. 2.

Стационарное поле совершает при этом положительную работу .

Так как и , то и , т. е. .

Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .

Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3):

$U = \varphi_a = \varphi_b$

Рис. 3.

Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным. В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.

Последовательное соединение

При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.

Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.

Рис. 4. Последовательное соединение

Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.

1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.

2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике.

Действительно, напряжение на участке — это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке — это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:

Можно и более формально, без всяких словесных объяснений:

3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.

Пусть — сопротивление участка . По закону Ома имеем:

что и требовалось.

Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .

Сопротивления проводников равны:

Эти два проводника образуют единый проводник длиной и сопротивлением

Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае — если различны также вещества проводников и их поперечные сечения.

Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.

Параллельное соединение

При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы — к другой точке.

Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5).

$R=\rho \frac{\displaystyle l_1 + l_2}{\displaystyle S \vphantom{1^a}}=\rho \frac{\displaystyle l_1}{\displaystyle S \vphantom{1^a}}+\rho \frac{\displaystyle l_2}{\displaystyle S \vphantom{1^a}}=R_1 + R_2.$

Рис. 5. Параллельное соединение

Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями; участок от к (по направлению тока) называется неразветвлённой частью цепи.

Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.

1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:

Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.

2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору — заряд .

Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:

что и требовалось.

3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть — сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:

Сокращая на , получим:

(1)

что и требовалось.

Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:

Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.

Из соотношения (1) можно найти :

(2)

К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением

(3)

Тем не менее, один полезный вывод из формулы (3) сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:

$\frac{\displaystyle 1}{\displaystyle R \vphantom{1^a}}=\frac{\displaystyle 1}{\displaystyle R_1 \vphantom{1^a}}+\frac{\displaystyle 1}{\displaystyle R_1 \vphantom{1^a}}+ \ldots + \frac{\displaystyle 1}{\displaystyle R_1 \vphantom{1^a}} = \frac{\displaystyle n}{\displaystyle R_1 \vphantom{1^a}}$

откуда

Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.

Смешанное соединение

Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.

Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.

Рассмотрим пример смешанного соединения проводников (рис. 6).

Рис. 6. Смешанное соединение

Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.

Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :

Ом.

Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:

Ом.

Сопротивление цепи:

Ом.

Теперь находим силу тока в цепи:

Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:

(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)

Оба резистора и находятся под напряжением , поэтому:

(В сумме имеем А, как и должно быть при параллельном соединении.)

Сила тока в резисторах и одинакова, так как они соединены последовательно:

А.

Стало быть, через резистор течёт ток A.

формула расчета сопротивления при параллельном соединении резистора

Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.

Общий вид

Особенности включения

Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.

Для такого включения типичны следующие особенности:

Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.

В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.

Расчёт

Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).

Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:

I= U/R (одного из резисторов).

После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.

Типичные подключения

Пример №1

Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление. При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).

Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.

Из неё следует:

16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.

Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.

Пример №2

В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.

Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.

Пример

В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:

1/R = 1/200+1/220+1/470 = 0,0117;

R=1/0,0117 = 85,67Ом.

В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.

Важно! Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.

Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.

Расчёт комбинированных схем

Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.

Смешанная схема

В приведённом выше примере требуется посчитать суммарное значение номиналов цепи, состоящей из трех резисторов.

Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.

Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.

Для элементов из группы 2 значение общего сопротивления находится как сумма R2 и R3:

R (2+3) = R2 + R3.

Для получения окончательного результата приводим схему к виду, получаемому при параллельном соединении двух сопротивлений. После этого суммарное значение для всей схемы в целом вычисляется согласно уже рассмотренной ранее формуле.

В заключение отметим, что для проведения расчётных операций, относящихся к категории сложных соединений, можно воспользоваться теми же методиками. В их основу заложены всё те же закон Ома и правила Кирхгофа, известные ещё со школьной скамьи. Главное – это грамотно распорядиться всеми описанными выше формулами.

Видео

Оцените статью:

параллельного резисторного калькулятора R1 + R2 = эквивалентный резистор R сопротивление цепи в эквиваленте суммарный резистор искатель легко сделать контрейлер = параллельный Параллельный резисторный калькулятор R1 + R2 = эквивалентный резистор R сопротивление цепи в эквиваленте суммарный резистор искатель легко сделать контрейлер = параллель — sengpielaudio Sengpiel Berlin

R _всего

Формула:
R _всего = R1 × R2 / (R1 + R2)

Пожалуйста, введите два значения резистора , будет рассчитано третье значение параллельной цепи.
Вы даже можете ввести общее сопротивление R _всего и одно известное сопротивление R ₁ или R ₂.

Формула (уравнение) для расчета двух сопротивлений R ₁ и R ₂, соединенных параллельно:

Расчет необходимого параллельного резистора R ₂, когда R ₁ и полное сопротивление R _всего дается:

Решение по формуле R _итого = ( R ₁ × R ₂) / ( R ₁ + R ₂) для R ₁:
Первый шаг — очистить все дроби, умножив на самое низкое значение
. общий знаменатель, то есть R _т × R ₁ × R ₂… так мы получаем:
1/ R _всего = 1/ R ₁ + 1/ R ₂
R _всего × R ₁ × R ₂ [1/ R _всего = 1/ R ₁ + 1/ R ₂]
R ₁ × R ₂ = R _всего × R ₂ + R _всего × R ₁, затем соберите члены с R ₁ и решить
R ₁ × R ₂ — R _всего × R ₁ = R _всего × R ₂
R ₁ ( R ₂ — R _всего) = R ₂ × R _всего
Последний шаг:
R ₁ = R ₂ × R _всего / ( R ₂ — R _всего)
или:
R ₂ = R ₁ × R _всего / ( R ₁ — R _всего)

Примечание: Этот калькулятор также может решать другие математические задачи.Расчет резисторов параллельно составляет
точно так же, как расчеты, необходимые для параллельных индукторов или последовательно соединенных конденсаторов.

Два резистора параллельно и полученное суммарное сопротивление: два одинаковых значения,
также покажите уравнение, что результаты всегда наполовину. Это облегчает, когда
проектирование схем или прототипирование. С заглавными буквами он всегда двойной, потом опять заглавные буквы просто
просто сложить параллельно.

• Поисковые сопротивления R ₁ и R ₂, когда известно целевое сопротивление (эквивалентное сопротивление) •

Расчет: резисторные пары — обратный инженерный калькулятор
Поиск R ₁ и R ₂ с известным сопротивлением цели

● Рассчитать много резисторов параллельно ●

Этот калькулятор определяет сопротивление от до 10 резисторов параллельно .
Введите сопротивления в поля ниже и, когда все значения были введены,
нажмите на кнопку «Рассчитать», и результат появится в поле под этой кнопкой.
В качестве теста, если мы введем сопротивления 4, 6 и 12 Ом, ответ должен быть 2 Ом.
Примечание: очистка полей вручную не сбрасывает сохраненные значения. Используйте «сброс».

закон Ома — калькулятор и формулы

Два резистора параллельно и полученное суммарное сопротивление
Сопротивление в диапазоне от 1 Ом до 100 Ом

R2	R1
R2	1	1.5	2,2	3,3	4,7	6,8	10	15	22	33	47	68
1	0,5	0,6	0.69	0,77	0,83	0,87	0,91	0,93	0,95	0,97	0,98	0,99
1,5	0,6	0,75	0,89	1,03	1,14	1,22	1,30	1,36	1,40	1.43	1,45	1,46
2,2	0,69	0,89	1,1	1,32	1,50	1,66	1,82	1,92	2,0	2,06	2,10	2,13
3,3	0,77	1.03	1,32	1,65	1,94	2,22	2,48	2,70	2,87	3,00	3,08	3,14
4,7	0,83	1,14	1,50	1,94	2,35	2,78	3,20	3,58	3.87	4,12	4,27	4,39
6,8	0,87	1,22	1,66	2,22	2,78	3,40	4,05	4,68	5,19	5,64	5,94	6,18
10	0.91	1,30	1,82	2,48	3,20	4,05	5,0	6,0	6,9	7,7	8,3	8,7
15	0,93	1,36	1,92	2,70	3,58	4,68	6,0	7.50	8,9	10,3	11,4	12,2
22	0,95	1,40	2,00	2,87	3,87	5,19	6,9	8,9	11,0	13,2	15.0	16,6
33	0.97	1,43	2,06	3,0	4,12	5,64	7,7	10,3	13,2	16,5	19,4	22,2
47	0,98	1,45	2,1	3,08	4,27	5,94	8,3	11.4	15,0	19,4	23,5	27,8
68	0,99	1,46	2,13	3,14	4,39	6,18	8,7	12,2	16,6	22,2	27,8	34,0

Мощность, рассеиваемая в резисторе: P = В × I , P = В ²/ R , P = I ² × R .

Примечание: Для последовательно включенных резисторов ток для каждого резистора равен ,
и для параллельных резисторов напряжение одинаково для каждого резистора.

,Серия

и параллельные резисторы

Изучив этот раздел, вы сможете:
Рассчитать значения полного сопротивления в последовательных сетях сопротивления.
Используйте соответствующие формулы для расчета сопротивления в параллельных сетях сопротивления.
• Взаимный от суммы взаимных.
• Товар сверх суммы.

Рассчитать значения полного сопротивления в последовательных / параллельных сетях.

Расчеты в последовательных и параллельных резисторных сетях

Компоненты, включая резисторы в цепи, могут быть соединены вместе двумя способами:

В СЕРИИ, так что через все компоненты протекает один и тот же ток, но для каждого из них может существовать разная разность потенциалов (напряжение).

В ПАРАЛЛЕЛЬНОМ, так что одинаковая разность потенциалов (напряжение) существует во всех компонентах, но каждый компонент может нести различный ток.

Рис. 4.2.1 Резисторы в серии

Рис. 4.2.2 Параллельные резисторы

В любом случае (для резисторов) общее сопротивление этой части цепи, содержащей резисторы, можно рассчитать, используя методы, описанные ниже.

Способность рассчитать комбинированное (общее) значение резисторов таким способом позволяет легко вычислять неизвестные значения сопротивления, тока и напряжения для довольно сложных цепей, используя относительно простые методы.Это очень полезно для поиска неисправностей.

ПЕРЕД ПОЛУЧЕНИЕМ ДАЛЕЕ, ПРАКТИКА С ИСПОЛЬЗОВАНИЕМ ФОРМУЛ ДЛЯ РАСЧЕТА ВСЕГО ЗНАЧЕНИЯ СЕРИИ И ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ.

Для резисторов в серии:

Полное сопротивление двух или более резисторов, соединенных последовательно , дается простым сложением отдельных значений резисторов, чтобы найти общую сумму (R _TOT):

Для резисторов параллельно:

Для расчета полного сопротивления цепи с параллельными резисторами можно использовать следующую формулу.

Обратите внимание, однако, что эта формула НЕ дает вам полное сопротивление R _TOT. Это дает вам Взаимное R _TOT или:

Это совсем другое значение — и НЕ является полным сопротивлением. Это 1 делится на R _TOT. Чтобы получить правильное значение для R _TOT (которое будет равно 1 / R _TOT, то есть R _TOT/1, просто нажмите ответную клавишу на вашем калькуляторе (отмечено 1 / x или x-1) ,

Еще один способ расчета параллельных цепей.

Общее сопротивление двух резисторов в параллельном соединении , которое не связано с взаимными ответами, определяется как:

Эта формула часто упоминается как «Продукт над суммой».

Он рассчитывает только два резистора параллельно? Ну да, но это не большая проблема. Если имеется более двух параллельных резисторов, просто выберите два из них и определите общее сопротивление для этих двух — затем используйте это общее значение, как если бы это был один резистор, и создайте другую пару с третьим резистором.Отрабатывайте новый итог и так далее, пока не включите все параллельные резисторы в эту конкретную сеть.

О, еще одна вещь, которую нужно помнить о продукте над суммой, см. Скобки вокруг суммы (нижняя часть) формулы? Это означает, что вы должны решить это, прежде чем использовать его, чтобы разделить продукт (верхняя часть) на. Если вы этого не сделаете, ваш ответ будет неверным.

Звучит сложно? Не совсем, это просто вопрос повторения, и на практике вы не часто сталкиваетесь со многими параллельными сетями с более чем двумя резисторами.Тем не менее, какая формула вы выбираете, зависит от вас, взаимных или переоценки продукта.

Советы

по взаимному методу

Если вы используете Взаимный метод для параллельных цепей, НЕ ЗАБУДЬТЕ, когда вы добавили ответные сигналы отдельных резисторов — Вы должны снова найти ответные сигналы.1 / R1 + 1 / R2 + 1 / R3 = 1 / R _TOT и чтобы найти R _TOT вы должны найти обратную величину 1 / R _TOT.

Упрощающие схемы

Для комбинированных последовательных и параллельных цепей сначала определите участок цепи (последовательный или параллельный).Затем заново нарисуйте схему, заменив участок, сопротивление которого вы нашли, одним резистором. Теперь у вас есть упрощенная схема, в которой можно найти R _TOT.

Вы можете использовать формулу «продукт сверх суммы»:

Для цепей с более чем двумя параллельными резисторами, просто отработайте два параллельных резистора одновременно, используя формулу произведения по сумме, а затем заново проведите схему, заменив два резистора одним резистором, значение которого представляет собой объединенное сопротивление двух ,

Теперь вы можете использовать ваше первое объединенное значение как один резистор со следующим параллельным резистором и так далее. Таким образом, можно рассчитать большое количество параллельных резисторов, используя произведение на сумму.

Когда все параллельные резисторы имеют одинаковое значение.

Если подключено несколько идентичных параллельных резисторов, общее сопротивление будет значением резистора, умноженным на величину, обратную количеству резисторов.

, т. Е. Два параллельных резистора 12 кОм имеют суммарное сопротивление

12K x 1/2 = 6K

Три параллельных резистора 12K имеют суммарное сопротивление

12K x 1/3 = 4K и т. Д.

Проверка вашего ответа

Суммарное значение любого количества параллельных резисторов всегда будет МЕНЬШЕ, чем значение наименьшего отдельного резистора в сети. Используйте этот факт, чтобы проверить свои ответы.

серии и параллельные комбинированные

Попробуйте несколько расчетов на основе последовательных и параллельных резисторных сетей. Для этого вам просто нужно использовать информацию на этой странице и страницу «Советы по расчету резисторов». Вас просят определить общее сопротивление для каждой цепи.Вы можете выбрать, какую формулу использовать

Вы также можете найти помощь по математике, загрузив нашу бесплатную брошюру Maths Tips.

Прежде чем начать, подумайте об этих нескольких советах. Они облегчат проблемы, если вы будете внимательно следить за ними.

1. Отработайте ответы, используя карандаш и бумагу; перерисовать схему, над которой вы работаете.

2. Конечно, ответ — это не просто число, это будет определенное количество Ом, не забудьте указать правильную единицу измерения (например,грамм. Ω, KΩ или MΩ) или ваш ответ не имеет смысла.

3. Когда вы вводите значения в свой калькулятор, преобразуйте все значения KΩ или MΩ в Ом, используя клавишу EXP. Если вы проскользнете сюда, это даст действительно глупые ответы, тысячи раз слишком большие или слишком маленькие.

Итак, теперь вы прочитали эти инструкции, вы готовы начать. Вот способ решить типичную проблему на бумаге, чтобы (с практикой) вы не запутались.

Серия

и пример параллельной цепи.

Хорошо, хорошо, что стоит вспомнить, так почему бы не попробовать некоторые практические вопросы в модуле 4.5 резисторов по нахождению полного сопротивления некоторых резисторных сетей?

Электрическое сопротивление в последовательных и параллельных сетях

Последовательное соединение

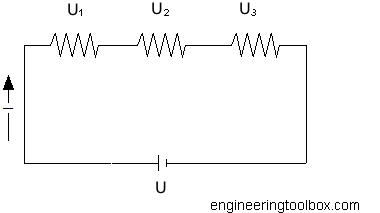
Общее сопротивление для последовательно включенных резисторов можно рассчитать как

R = R ₁ + R ₂ + …. + R _n (1)

где

R = сопротивление (Ом, Ом)

Резисторы — Стандартные значения

Пример — резисторы в серии

Три резистора 33 Ом , 33 ом и 47 ом подключены последовательно.Общее сопротивление можно рассчитать как

R = ( 33 Ом) + ( 33 Ом) + ( 47 Ом)

= 113 Ом

Резисторы — цветовые коды Калькулятор

Параллельное соединение

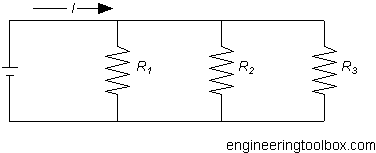
Общее сопротивление для параллельно включенных резисторов можно рассчитать как

1 / R = 1 / R ₁ + 1 / R ₂ +…. + 1 / R _n (2)

Эквивалентное сопротивление двух параллельно включенных резисторов можно выразить как

R = R ₁ R ₂ / (R ₁ + R ₂) ₍₃₎

Пример — Параллельные резисторы

Три резистора 33 Ом , 33 Ом и 47 Ом соединены параллельно. Общее сопротивление можно рассчитать как

1 / R = 1 / ( 33 Ом ) + 1 / ( 33 Ом ) + 1 / (47 Ом )

= 0.082 (1 / Ом)

R = 1 / (0,082 Ом)

= 12,2 Ом

Если напряжение аккумулятора составляет 12 В — ток через цепь можно рассчитать с помощью омов закон

I = U / R

= (12 В) / (12,2 Ом)

= 0,98 Ампер

Ток через каждый резистор можно рассчитать

I ₁ = U / R ₁ = (12 В) / (33 Ом) = 0.36 ампер

I ₂ = U / R ₂ = (12 В) / (33 Ом) = 0,36 ампер

I ₃ = U / R ₃ = (12 V) / (47 Ом) = 0,26 ампер

Параллельно подключенные резисторы — Калькулятор

Добавьте сопротивления до пяти параллельно подключенных резисторов и (дополнительно) напряжение цепи.

Общее сопротивление и ток — и отдельные токи во всех резисторах — будут рассчитаны:

R ₁ (Ом) I ₁ (ампер)

R ₂ (Ом) I ₂ (ампер)

R ₃ (Ом) I ₃ (ампер)

R ₄ (Ом ) I ₄ (ампер)

R ₅ (Ом) I ₅ (ампер)

Напряжение (В)

R (Ом) I (ампер)

Сопротивление R и C параллельно Калькулятор

Цель использования: Сравнить результаты с пользовательской конструкцией анализатора импеданса ,

Цель использования: Убедитесь, что я правильно рассчитываю полное сопротивление для параллельная цепь переменного тока для класса электроники.

Назначение: Определить значения R, C для желаемого гистерезиса, используемого с операционным усилителем (Horowitz & Hill стр. 134-5)

Назначение: bangin ur mom

Цель использования: проверить свою интуицию по задаче домашнего задания

Цель использования: Проверка прибора Fluke RCL, чтобы убедиться, что он все еще функционирует ОК
действительно оценил вашу прекрасную программу

Назначение Используйте: Регулятор вентилятора
Комментарий / Запрос: Дайте мне принципиальную схему с номинальным компонентом конденсаторной базы регулятора вентилятора

Цель использования: расчет устойчивости плода
Комментарий / запрос: Я считаю, что плод может быть представлен RC-цепью, и я хотел бы провести измерение с известной частотой.Я могу измерить «Z» и фазовый сдвиг в градусах.
Я хотел бы извлечь » R » и » C ».
Уточнение: Наличие: » F », » Z », » Phase », необходимо извлечь: » R » и » C ».

Назначение: Очень удобно для быстрого выполнения расчетов по широкому кругу предметов. Спасибо, что сделали его доступным.

Назначение: Разработка контуров обратной связи в регулируемых источниках питания
Комментарий / запрос: Отрицательный знак для фазы правильный, так как определение «задержка тока от напряжения».Поскольку ток опережает напряжение в этой цепи, «задержка» является отрицательной.

Разное