Последовательное и параллельное соединение

В данной статье речь пойдет о последовательном и параллельном соединении проводников. На примерах будут рассмотрены данные соединения и как при таких соединениях будут изменяться такие величины как:

• ток;
• напряжение;
• сопротивление.

В таблице 1.8 [Л2, с.24] приведены схемы и формулы по определению сопротивлений, токов и напряжений при параллельном и последовательном соединении.

Последовательное соединение

Последовательным соединением называются те участки цепи, по которым всегда проходят одинаковые токи.

При последовательном соединении:

• сила тока во всех проводниках одинакова;
• напряжение на всём соединении равно сумме напряжений на отдельных проводниках;
• сопротивление всего соединения равно сумме сопротивлений отдельных проводников.

Пример 1

Последовательно подключены две лампы накаливания одинаковой мощности Рл1=Рл2=100 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляет Rл1=Rл2=122 Ом. Номинальное напряжение для ламп равно 220 B. На рис.1 показано последовательное включение ламп.

Решение

Составляем схему замещения, выражая каждую из входящих элементов цепи (в данном случае лампы накаливания) в виде сопротивлений.

1. Определяем ток протекающей по участкам цепи:

Iн = Uн/Rл1+ Rл2 = 220/122+122 = 0,9 A

2. Определяем напряжение на каждой из ламп накаливания, так как мощность ламп у нас одинаковая, то и напряжение для каждой из ламп будет одинаково:

Uл1=Uл2 = Iн*R = 0,9*122 = 110 B

Как мы видим напряжение источника (в данном примере 220 В) разделиться поровну, между обоими последовательно включенными лампами. При этом лампы будут ели светит, их накал будет неполным.

Для того чтобы лампы горели с полным накалом, нужно увеличить напряжение источника с 220В до 440В, при этом на каждой из ламп установиться номинальное (рабочее) напряжение равное 220В.

Пример 2

Последовательно подключены две лампы накаливания мощность Рл1 = 100 Вт и Рл2 = 75 Вт к сети с напряжением Uн=220В. Сопротивление нити в лампах составляют Rл1= 122 Ом для стоваттной лампы и Rл2= 153 Ом для семидесяти пяти ватной лампы.

Решение

1. Определяем ток протекающей по участкам цепи:

Iн = Uн/Rл1+ Rл2 = 220/100+75 = 0,8 A

2. Определяем напряжение на каждой из ламп накаливания:

Uл1= Iн*Rл1 = 0,8*122 = 98 B
Uл2= Iн*Rл2 = 0,8*153 = 122 B

Исходя из результатов расчетов, более мощная лампа 100 Вт получает при этом меньшее напряжение. Но ток в двух последовательно включенных даже разных лампах остается одинаковым. Например, если одна из ламп перегорит (порвется ее нить накаливания), погаснут обе лампы.

Данное соединение лампочек, например, используется в трамвайном вагоне для освещения салона.

Параллельное соединение

Параллельное соединение – это соединение, при котором начала всех проводников присоединяются к одной точке цепи, а их концы к другой.

Точки цепи, к которым сходится несколько проводов, называют узлами. Участки цепи, соединяющие между собой узлы, называют ветвями.

При параллельном соединении:

• напряжение на всех проводниках одинаково;
• сила тока в месте соединения проводников равна сумме токов в отдельных проводниках;
• величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.

Пример 3

Определить токи и напряжения всех участков цепи (рис.5), если известно:

• Номинальное напряжение сети Uн = 220В;
• Сопротивление нити в лампах HL1 и HL2 составляют Rл1 = Rл2 = 122 Ом.
• Сопротивление нити в лампе HL3 составляют Rл3 = 153 Ом.

Решение

Составляем схему замещения для схемы, представленной на рис.5.

1. Определяем проводимость всей цепи [Л1, с.47] и согласно таблицы 1.8:

2. Определяем сопротивление всей цепи [Л1, с.47]:

3. Определяем силу тока цепи по закону Ома:

4. Определяем токи для каждой цепи [Л1, с.47]:

5. Выполним проверку, согласно которой, сила тока в месте соединения проводников равна сумме токов в отдельных проводниках:

Iл1+ Iл2+ Iл3=Iобщ.=1,8+1,8+1,44=5,04=5,04 (условие выполняется)

Смешанное соединение

Смешанным соединением – называется последовательно-параллельное соединение сопротивлений или участков цепи.

Пример 4

Определить токи и напряжения всех участков цепи (рис.7), если известно:

• Номинальное напряжение сети Uн = 220В;
• Сопротивление нити в лампах HL1, HL2, HL3 составляют Rл1 = Rл2 = Rл3 = 122 Ом.
• Сопротивление нити в лампе HL4 составляют Rл4 = 153 Ом.
• Результаты расчетов для участка цепи ВС (параллельное соединение проводников) применим из примера 3:
  Сопротивление цепи ВС составляет Rвс = 43,668 Ом.

Решение

Составляем схему замещения для схемы, представленной на рис.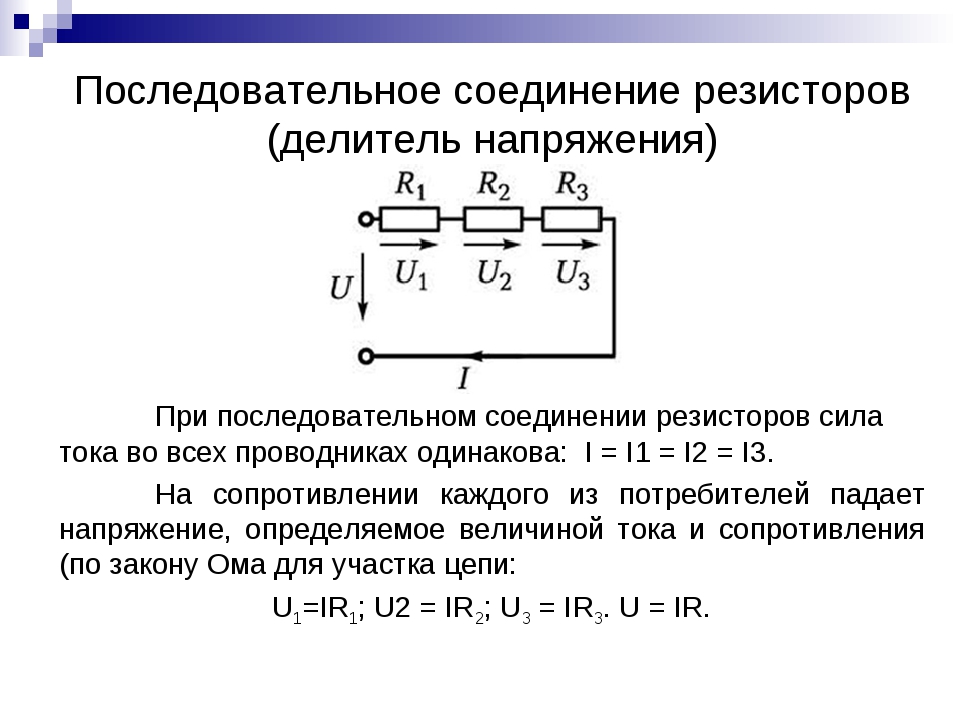 7.

1. Определяем сопротивление всей цепи:

Rобщ = Rав+Rвс = Rл1+Rвс = 122+43,688 = 165,688 Ом

2. Определяем силу тока цепи, согласно закона Ома:

3. Определяем напряжение на первом сопротивлении:

Uав=Uл1= Iобщ*Rл1 = 1,33*122 = 162 B

4. Определяем напряжение на участке ВС:

Uвс= Iобщ*Rвс = 1,33*43,688 = 58,1 B

5. Определяем токи для каждой цепи участка ВС:

6. Выполним проверку для участка цепи ВС:

Iл2+ Iл3+ Iл4= Iобщ.=0,48+0,48+0,38=1,33=1,33 (условие выполняется)

Литература:

1. Общая электротехника с основами электроники, В.С. Попов, 1972 г.
2. Справочная книга электрика. В.И. Григорьева. 2004 г.

Всего наилучшего! До новых встреч на сайте Raschet.info.

Последовательное и параллельное соединение проводников

Последовательное и параллельное соединение очень широко используется в электронике и электротехнике и порой даже необходимо для правильной работы того или иного узла электроники.

И начнем, пожалуй, с самых простых компонентов радиоэлектронных цепей – проводников.

Для начала давайте вспомним, что такое проводник? Проводник – это вещество или какой-либо материал, который отлично проводит электрический ток. Если какой-либо проводник отлично проводит электрический ток, то он в любом случае обладает каким-либо сопротивлением. Сопротивление проводника мы находим по формуле:

формула сопротивление проводника

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м²

l – длина проводника, м

Более подробно об этом я писал здесь.

Следовательно, любой проводник представляет из себя резистор с каким-либо сопротивлением. Значит, любой проводник можно нарисовать так.

обозначение резистора на схемах

Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

Пример

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

Решение

R_общее =R₁ + R₂ + R₃ = 3+5+2=10 Ом.

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор R_AB .

показать на реальном примере с помощью мультиметра
Видео где подробно расписывается про эти соединения:

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.

Получается, если через резистор R_AB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R₁ , R₂ , R₃ , то получится, что через них течет та же самая сила тока, которая текла через резистор R

AB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R₁ течет такая же сила тока, как и через резистор R₂ и такая же сила тока течет через резистор R₃ .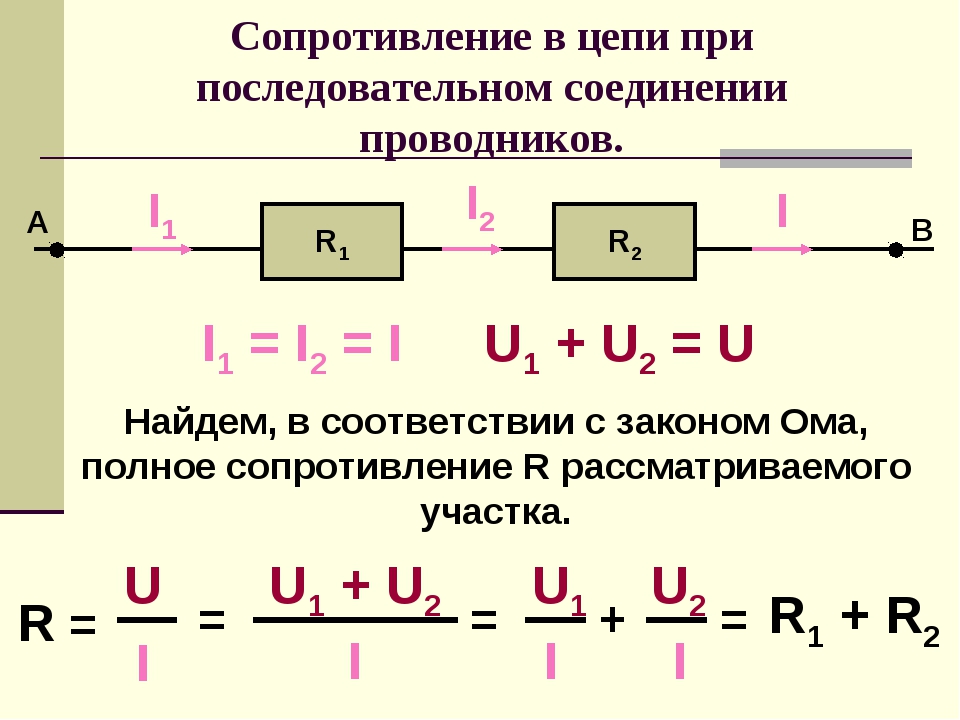

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на  любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае R_AB =R₁ + R₂ + R₃ = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения U_R1 , U_R2 , U_R3 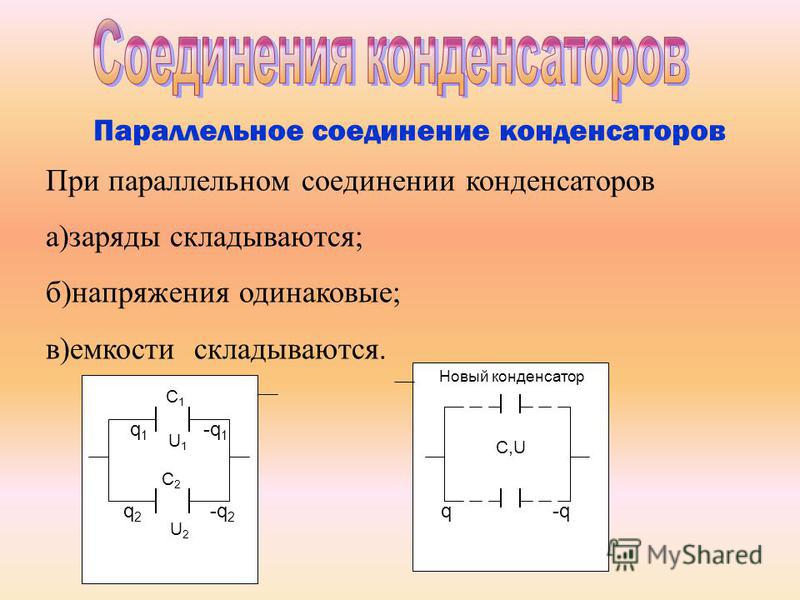 . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Следовательно,

U_R1 = IR₁ =1×2=2 Вольта

U_R2 = IR₂ = 1×3=3 Вольта

U_R3 = IR₃ =1×5=5 Вольт

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Получается

U=U_R1+U_R2+U_R3

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

 

Параллельное соединение проводников

Параллельное соединение проводников выглядит вот так.

параллельное соединение резисторов

Ну что, думаю, начнем с сопротивления.

Сопротивление при параллельном соединении проводников

Давайте пометим клеммы как А и В

В этом случае общее сопротивление R_AB будет находиться по формуле

 

Если же мы имеем только два параллельно соединенных проводника

То в этом случае можно упростить длинную неудобную формулу и она примет вид такой вид.

Напряжение при параллельном соединении проводников

Здесь, думаю ничего гадать не надо. Так как все проводники соединяются параллельно, то и напряжение у всех будет одинаково.

Получается, что напряжение на R1 будет такое же как и на R2, как и на R3, так и на Rn

Сила тока при параллельном соединении проводников

Если с напряжением все понятно, то с силой тока могут быть небольшие затруднения. Как вы помните, при последовательном соединении сила тока через каждый проводник была одинакова. Здесь же совсем наоборот. Через каждый проводник будет течь своя сила тока. Как же ее вычислить? Придется опять прибегать к Закону Ома.

Чтобы опять же было нам проще, давайте рассмотрим все это дело на реальном примере. На рисунке ниже видим параллельное соединение трех резисторов, подключенных к источнику питания U.

Как мы уже знаем, на каждом резисторе одно и то же напряжение U. Но будет ли сила тока такая же, как и во всей цепи? Нет. Поэтому для каждого резистора мы должны вычислить свою силу тока по закону Ома I=U/R. В результате получаем, что

I₁ = U/R₁

I₂ = U/R₂

I₃ = U/R₃

Если бы у нас еще были резисторы, соединенные параллельно, то для них

I_n = U/R_n

В этом случае, сила тока в цепи будет равна:

Задача

Вычислить силу тока через каждый резистор и силу тока в цепи, если известно напряжение источника питания и номиналы резисторов.

Решение

Воспользуемся формулами, которые приводили выше.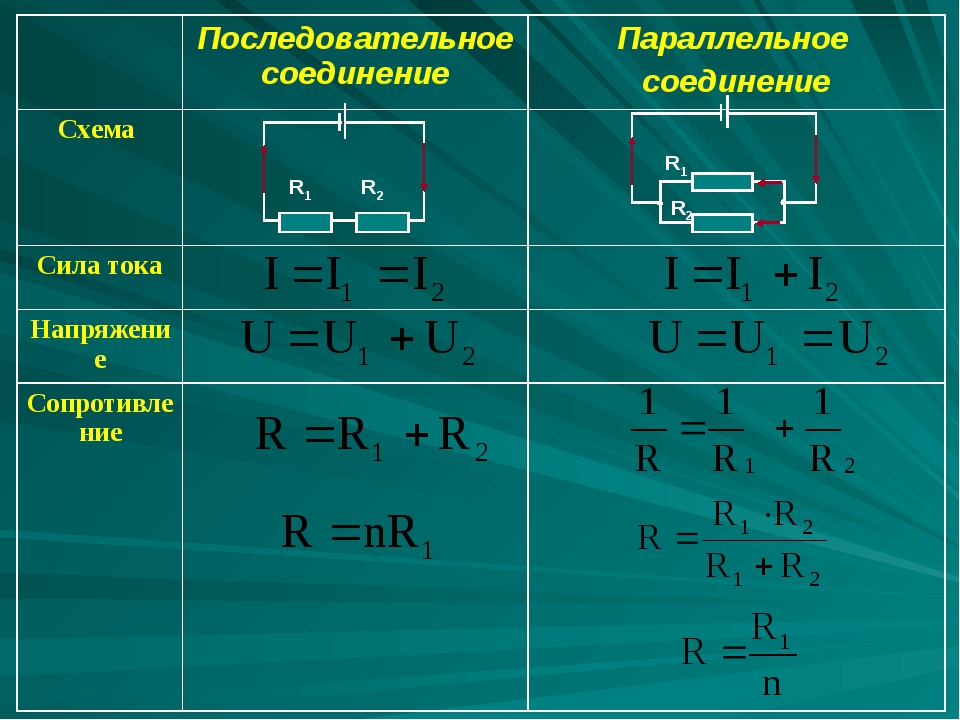

I₁ = U/R₁

I₂ = U/R₂

I₃ = U/R₃

Если бы у нас еще были резисторы, соединенные параллельно, то для них

I_n = U/R_n

Следовательно,

I₁ = U/R₁ = 10/2=5 Ампер

I₂ = U/R₂ = 10/5=2 Ампера

I₃ = U/R₃ = 10/10=1 Ампер

Далее, воспользуемся формулой

чтобы найти силу тока, которая течет в цепи

I=I₁ + I₂ + I₃ = 5+2+1=8 Ампер

2-ой способ найти I

I=U/R_общее

Чтобы найти R_общее мы должны воспользоваться формулой

Чтобы не париться с вычислениями, есть онлайн калькуляторы. Вот один из них. Я за вас уже все вычислил. Параллельное соединение 3-ех резисторов номиналом в 2, 5, и 10 Ом равняется 1,25 Ом, то есть R_общее = 1,25 Ом.

I=U/R_общее = 10/1,25=8 Ампер.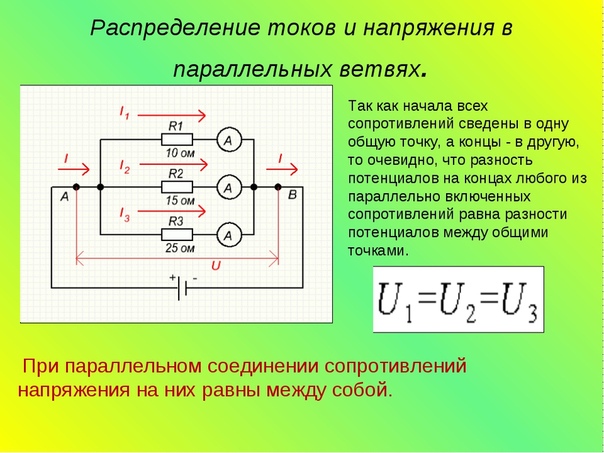

Параллельное соединение резисторов в электронике также называется делителем тока, так как резисторы делят ток между собой.

Ну а вот вам бонусом объяснение, что такое последовательное и параллельное соединение проводников от лучшего преподавателя России.

Подробное объяснение на видео:

Похожие статьи по теме “последовательное и параллельное соединение”

Закон Ома

Проводник (электрический проводник)

Что такое резистор

Делитель напряжения

Делитель тока

Что такое напряжение

Что такое сила тока

Параллельное соединение проводников: напряжение соединения, формулы

Существует множество схем с различным видом подключения. Для каждого электроприбора существует свой тип подключения проводника. В этой статье представлены формулы последовательного и параллельного соединения в проводниках.

Определение параллельного соединения

При таком виде, все проводники устанавливаются параллельно друг с другом. Они соединены в одну общую точку и все концы также скрепляются вместе. Если рассматривать энное количество одинаковых проводников, соединенных по данному принципу, то он будет называться разветвленным.

Какие виды подключений бывают

В каждом отсеке располагается один проводник. Поток электронов в виде тока, доходит до отметки ветвления, переходит на каждый проводник, и будет равен суммарным токам на всех сопротивлениях. Напряжение при таком подключении также будет равное.

Все проводники можно сменить одним общим резистором. Если применить правило Ома, то можно получить параметры сопротивления. При параллельном сопротивлении складываются показатели обратные их значениям.

Формулы для разных последовательностей

Сила тока при параллельном подключении

Если было использовано последовательное подключение в цепи, то сила не изменится ни на одном участке ветви. Найти напряжение можно, применяя стандартное правило — нужно суммировать все показатели, которые присутствуют на концах каждого из резисторов, в итоге получится результат. Но при параллельном соединения намного сложней найти силу тока.

Даже при малой нагрузке в цепи будет формироваться определенное сопротивление. И тогда оно будет мешать продвижению электрического тока и будут потери. В общем, ток перемещается постепенно, от источника по подключенным заранее резисторам к нагруженным деталям.

Классическая формула Ома

Чтобы выполнить доступное прохождение тока по резисторам, нужно, чтобы он мог быстро и просто отдавать электроны, проще говоря иметь проводимость.

В современное время в основном применяются медные проводники, а важным элементом будут приемники электрической энергии. Такой элемент вызывает небольшую нагрузку и имеет свое сопротивление. Ниже описаны формулы для последовательного и параллельного соединения сопротивлений.

Также при подключении необходимо использовать катушку индуктивности. Она способна подавлять помехи в электроцепи.

Как выглядит формула Георга Ома

Примером такого типа подключения резисторов может быть соединение цепи потребителей электроэнергии в многоквартирном доме. Так, светодиоды, отопительный радиатор, микроволновка и другие приборы установлены в цепи параллельно.

Вольтметр, который подключают в цепь, будет показывать напряжение на всех резисторах. Тогда оно везде будет равным и формулу можно записать как:

U1 = U2 = U.

Схема параллельного соединения

Когда образуются ветви при подключении, то часть общего напряжения проходит через первый резистор, а часть — через второй и так далее. Поэтому при таком виде соединения резисторов Fтока в неразветвлённой точке будет равняться суммарной Fтока в отдельных резисторах и записывается как:

I = I1 + I2.

Расчет силы тока при помощи закона Ома записывается как:

I = U/R;

I1 = U1/R1;

I2 = U2/R2.

Из формулы следует:

U/R = U1/R1 + U2/R2;

U = U1 = U2;

1/R = 1/R1 + 1/R2.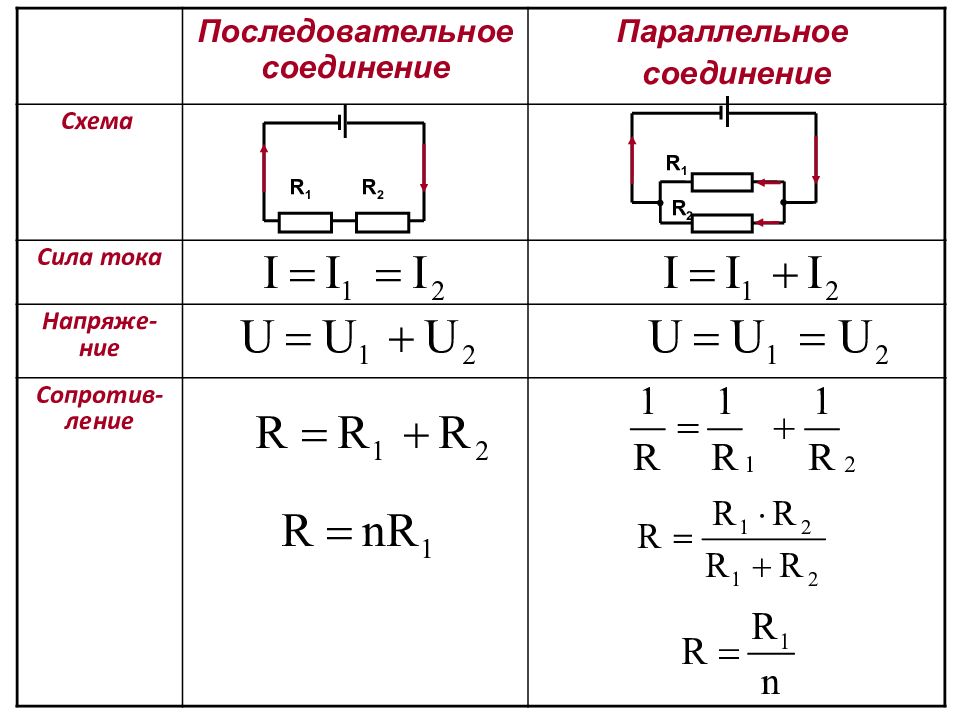

Дословно правило звучит так: число, обратное общему сопротивлению при параллельном подключении, будет суммарно равно числу обратного сопротивления.

Отличия между двумя видами подключений

Схема последовательного подключения говорит о том, что проводники установлены в особом расположении друг за другом. Поэтому сила тока у них одинаковая. Эти элементы создают в цепи Uобщее.

 

Пример подключения с предохранителем

Заряды не собираются в узлах электрической цепи, иначе было бы видно, как напряжение меняется. Минусом этой схемы будет то, что если любой элемент сломается, то вся цепь разорвется и перестанет работать. Например, если взять новогоднюю гирлянду. Если одна лампочка перестала работать, то другие тоже не загораются. Это и будет главным различием между последовательным и параллельным соединением. Ниже описана характеристика резисторов при параллельном объединении.

Свойства резисторов при параллельном подключении

При данном виде соединении скачки напряжения будут одинаковы на всех участках цепи.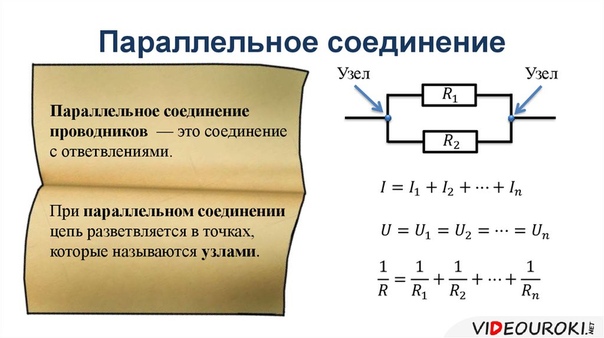 При этом показатель, обратный суммарному сопротивлению цепи, равен общей величине резисторов.

Обратите внимание! F тока в неразветвленной точке цепи равняется суммарной силе тока на отдельных участках проводника.

Стандартная формула напряжения

Формула для вычисления напряжения

При данном виде соединения все линии будут находиться в двух точках. Потому напряжение для всех резисторов будет равным.

При подсоединении двух и более приборов друг с другом, напряжение на выводах такой схемы — это показатель на каждом резисторе.

Напряжения условно обозначаются как U. По закону Ома, зная, что I = U/R, можно рассчитать по формуле:

U = U1 = U2 = … = Uобщ.

Обратите внимание! Помимо вычисления напряжения, рекомендуется знать мощность проводников. Они не должны сильно отличаться друг от друга. Параллельное соединение также можно встретить в лампочках, кабелях сигнализации автомобиля, фарах и прочем.

Также иногда можно встретить смешанный вид подключения. Это когда в цепи применяется два типа подключения, и параллельное, и последовательное. Оно чаще всего используется в контурных обогревателях.

Желательно изучить каждый вид подключения и схемы к ним. Профессиональные электрики рекомендует не выполнять подключений самостоятельно, если у человека совсем нет опыта в этой сфере. Так как в цепи может случиться короткое замыкание или возгорание, в лучшем случае выход из строя прибора.

Определение мощности на примере ламп

В заключении необходимо отметить, каждому человеку желательно знать свойства последовательного и параллельного соединения проводников. Чтобы в будущем не путаться при выполнении простых работ в электрике своего дома.

Последовательное и параллельное соединение. Применение и схемы

В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.

Последовательное соединение

При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.

Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.

Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.

Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.

Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.

Применение

Последовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.

Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.

Параллельное соединение

В этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.

Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.

Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.

Применение

Если рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.

Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга.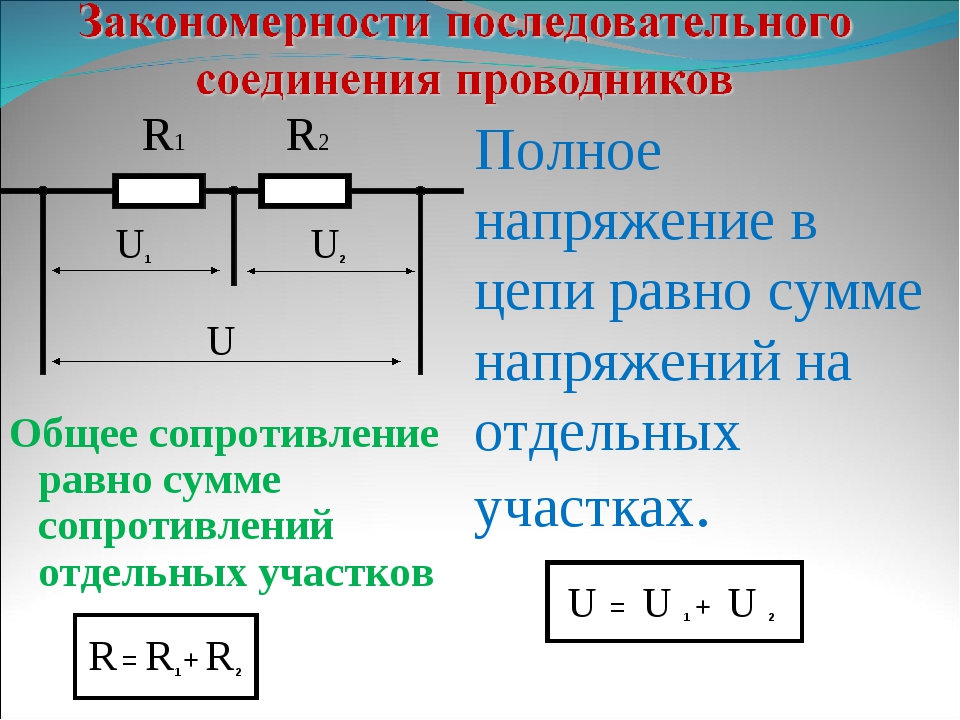 Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.

Работа тока

Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:

А = I х U х t, где А – работа тока, t – время течения по проводнику.

Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:

А=I х (U1 + U2) х t

Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.

Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:

А = А1+А2

Мощность тока

При рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:

Р=U х I

После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:

Р=Р1 + Р2

Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.

Влияние схемы соединения на новогоднюю гирлянду

После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.

При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.

Последовательное и параллельное соединение для конденсаторов

При последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:

q_общ= q1 = q2 = q3

Для определения напряжения на любом конденсаторе, необходима формула:

U= q/С

Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:

С= q/(U1 + U2 + U3)

Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:

1/С= 1/С1 + 1/С2 + 1/C3

Немного иначе рассчитывается параллельное соединение конденсаторов.

Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:

С= (q1 + q2 + q3)/U

Это значение рассчитывается как сумма каждого прибора в схеме:

С=С1 + С2 + С3

Смешанное соединение проводников

В электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.

Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.

Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.

Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.

Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.

Теперь используем формулу расчета сопротивления:

• Первая формула для последовательного вида соединения.
• Далее, для параллельной схемы.
• И окончательно для последовательной схемы.

Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.

Похожие темы:

Соединение элементов питания и батарей

Источники напряжения обычно называют источниками питания. Для увеличения тока или напряжения, а может и того и другого источники питания (элементы, батареи) могут соединяться вместе. Существует три типа соединения элементов питания:
1. Последовательное соединение элементов.
2. Параллельное соединение элементов.
3. Последовательно-параллельное (смешанное) соединение элементов.

Последовательное соединение элементов.

При последовательном соединении элементов питания выделяются две схемы: последовательно-дополняющая и последовательно-препятствующая.
В последовательно-дополняющей схеме положительный вывод первого элемента питания соединяется с отрицательным выводом второго элемента питания; положительный вывод второго элемента питания соединяется с отрицательным выводом третьего элемента питания и т.д. (рисунок 3.11.)

Рисунок 3.11.Последовательное соединение элементов питания.

При таком соединении источников питания через все элементы будет течь одинаковый ток:

Iобщ=I1=I2=I3

Индексы в обозначениях токов указывают на номера отдельных источников питания (элементов или батарей питания)
А полное напряжение при последовательном соединении равно сумме напряжений (ЭДС) отдельных элементов:

Еобщ = Е1 + Е2 + Е3.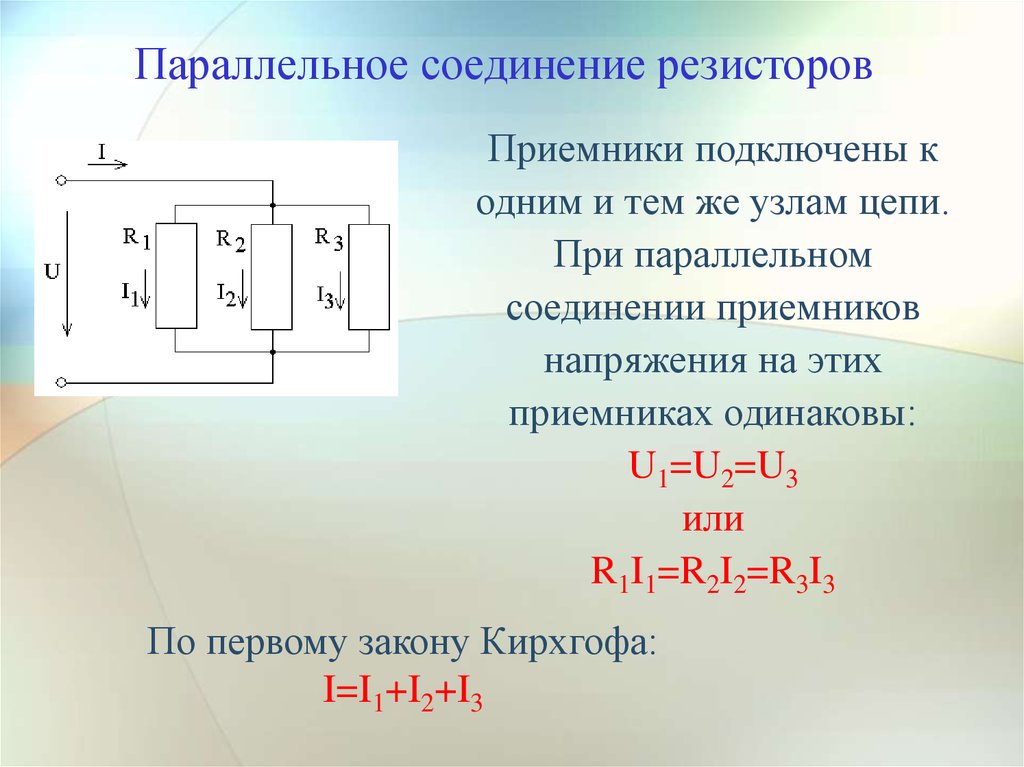

При последовательно-препятствующем включении источников питания, они соединяются друг с другом одноименными выводами. Но на практике такая схема не применяется или применяется, но очень редко.

Параллельное соединение элементов.

При параллельном соединении элементов питания, их одноименные выводы соединяются вместе, то есть плюс к плюсу, минус к минусу (рис 3.12).

Рисунок 3.11.Параллельное соединение элементов питания.

В этом случае общий ток будет равен сумме токов каждого элемента:

Iобщ=I1+I2+I3

Общее напряжение при параллельном включении источников питания будет равно напряжению каждого отдельного источника.

Еобщ = Е1 = Е2 = Е3.

Последовательно-параллельное соединение элементов напряжения.

Источники питания включают по последовательно-параллельной схеме для увеличения, как тока, так и напряжения. При этом основываются на том, что параллельное включение увеличивает силу тока, а последовательное увеличивает общее напряжение. На рисунке 3.13 показаны примеры последовательно-параллельных схем включения элементов питания.

Рисунок 3.11.Последовательно-параллельное соединение элементов питания.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Параллельное соединение проводников | Физика

При параллельном соединении все проводники (резисторы, лампы и т.д.) подключаются к одной и той же паре точек A и B (рис. 43). Связь между общими значениями силы тока, напряжения и сопротивления с их значениями на отдельных участках цепи при этом отличается от той, что была при последовательном соединении. Теперь соответствующие формулы имеют вид

I = I₁ + I₂, (17.1)     U = U₁ = U₂, (17.2)      R = (R₁R₂) / (R₁ + R₂). (17.3)

Чтобы убедиться в справедливости этих соотношений, следует собрать цепь и с помощью амперметра и вольтметра произвести необходимые измерения.

Итак, при параллельном соединении проводников напряжение на всех участках цепи одно и то же, общая сила тока равна сумме сил токов на отдельных проводниках, а общее сопротивление двух проводников находится как отношение произведения их сопротивлений к их сумме.

Первые две из этих закономерностей справедливы для любого числа параллельно соединенных проводников, последняя — только для двух.

Если R₁ = R₂, то

R = (R₁R₂) / (R₁ + R₂) = R₁²/2R₁ = R₁/2      (17.4)

Мы видим, что общее сопротивление двух одинаковых проводников в 2 раза меньше сопротивления одного проводника. Эта закономерность допускает обобщение: если параллельно соединено n одинаковых потребителей электроэнергии (резисторов, ламп и т.д.), то их общее сопротивление в n раз меньше сопротивления каждого из них:

R = R₁/n      (17.5)

Отсюда следует, что с увеличением числа проводников общее сопротивление будет становиться все меньше и меньше. Это может показаться странным. На самом деле ничего удивительного в этом нет: ведь при параллельном соединении проводников происходит как бы увеличение общей площади их поперечного сечения, а с увеличением площади сечения проводника, как известно, его сопротивление уменьшается.

Отличительной особенностью параллельного соединения нескольких потребителей является то, что при выключении одного из них остальные продолжают работать. Так, например, вывернув одну лампу в цепи, изображенной на рисунке 44, мы увидим, что другая будет по-прежнему гореть.

Большинство потребителей электроэнергии — электронагревательные приборы, холодильники, швейные машины, магнитофоны, телевизоры и т. д. — рассчитаны на напряжение сети 220 В. Поэтому все они должны включаться в сеть параллельно, ибо только в этом случае они окажутся под одним и тем же напряжением (220 В) и будут продолжать работать при выключении одного из них.

На рисунке 45 приведена упрощенная схема квартирной электропроводки. Провода сети, между которыми существует напряжение 220 В, обозначены буквами Ф и О. Первый из них называют фазным, второй — нулевым. Нулевой провод соединен с землей. Именно с ним соединяют все потребители. И наоборот, все выключатели соединяют с фазным проводом. Такой порядок подключения потребителей и выключателей обеспечивает наибольшую безопасность человека.

??? 1. Какое соединение называют параллельным? 2. Начертите схему цепи, изображенной на рисунке 44. 3. Какие три закономерности справедливы для параллельного соединения проводников? 4. Как находится общее сопротивление параллельно соединенных проводников, когда они одинаковые? 5. Перечислите все элементы электрической цепи, изображенной на рисунке 45. 6. Предположим, что при замене лампы человек случайно коснулся металлического контакта в патроне лампы и одновременно с этим какой-либо заземленной части здания (например, батареи отопления). Под каким напряжением он окажется? Рассмотрите ситуацию, когда лампа и выключатель подсоединены к проводам сети так, как это показано на рисунке 45. Что произойдет, если лампу и выключатель поменять местами? 7. Почему у вольтметров делают большое внутреннее сопротивление, а у амперметров — малое?

Последовательное и параллельное соединение конденсаторов

Соединение конденсаторов в электрической цепи может быть последовательным, параллельным и последовательно-пареллельным (смешанным).

Если провести аналогию между соединением конденсаторов и соединением резисторов , то стоит отметить, что формулы расчета общей емкости и общего сопротивления идентичны, только между разными типами соединений:

Формула C_общ при параллельном соединении конденсаторов = формула R_общ при последовательном соединении резисторов.

Формула C_общ при последовательном соединении конденсаторов = формула R_общ при параллельном соединении резисторов.

• C_общ — общая емкость
• R_общ — общее сопротивление

Параллельное соединение конденсаторов

Параллельное соединение конденсаторов — это соединение при котором конденсаторы соединяются собой обоими контактами. В результате к одной точке может быть присоединено несколько конденсаторов.

При параллельном соединении формируется один большой конденсатор с площадью обкладок, равной сумме площадей обкладок всех отдельных компонентов. Поскольку емкость конденсаторов прямо пропорциональна площади обкладок, общая емкость С_общ при параллельном соединении равняется сумме емкостей всех конденсаторов в цепи.

Параллельное соединение конденсаторов

Напряжение при параллельном соединении

На все параллельно соединенные конденсаторы падает одинаковое напряжение. Так происходит, потому что существует всего лишь две точки, между которыми может быть разность потенциалов (напряжение). Другими словами, можно сказать что при параллельном соединении все конденсаторы подключены к одному источнику напряжения.

Падение напряжения при параллельном соединении

Ток при параллельном соединении

Ток конденсатора во время переходного периода зависит от его емкости и изменения напряжения:

• i_c — ток конденсатора
• C — Емкость конденсатора
• ΔV_C/Δt – Скорость изменения напряжения

При параллельном соединении через каждый конденсатор потечет одельный ток, в зависимости от емкости конденсатора:

Ток при параллельном соединении

Последовательное соединение конденсаторов

Последовательное соединение конденсаторов – это соединение двух или более конденсаторов в форме цепи, в которой каждый отдельный конденсатор соединяется с другим отдельным конденсатором только в одной точке.

Последовательное соединение конденсаторов

Ток при последовательном соединении

Ток (i_C), заряжающий последовательную цепь конденсаторов, будет одинаковым для всех конденсаторов, поскольку у него есть только один возможный путь прохождения:

Вследствие того что через все последовательно соединенные конденсаторы течет одинаковый ток, количество накопленого электрического заряда для каждого конденсатора будет одинаковым, независимо от его емкости. Так происходит, потому что электрический заряд, накапливаемый на обкладке любого конденсатора, должен прийти с обкладки примыкающего конденсатора.

Таким образом, последовательно соединенные конденсаторы имеют одинаковый электрический заряд:

Посмотрим на последовательную цепь из трех конденсаторов на рисунке выше. Правая обкладка первого конденсатора С1 соединяется с левой второго конденсатора С2, у которого правая обкладка соединяется с левой третьего конденсатора С3.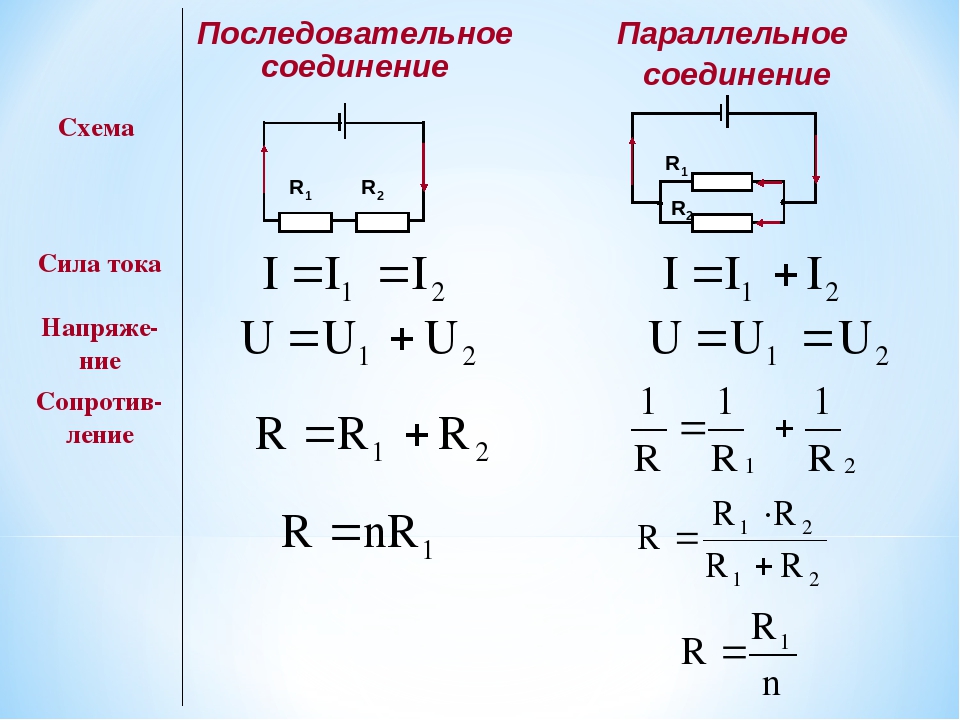 Это означает, что в режиме постоянного тока конденсатор С2 электрически изолирован от общей цепи.

В итогое эффективная площадь обкладок уменьшается до площади обкладок самого маленького конденсатора. Это объясняется тем, что как только обкладки наименшей площади заполнятся электрическим зарядом, данный конденсатор перестанет пропускать ток. В результате ток прекратиться во всей цепи, и процесс зарядки остальных конденсаторов также прекратится.

При последовательном соединении общее расстояние между обкладками увеличивается до суммы расстояний между обкладками всех конденсаторов.

Таким образом, последовательная цепь формирует один большой конденсатор с площадью обкладок элемента с наименьшей емкостью, и расстоянием между обкладками, равному сумме всех расстояний в цепи.

Площадь и расстояние между обкладками при последовательном соединении

Падение напряжения и общая емкость при последовательном соединении

На каждый отдельный конденсатор в последовательной цепи падает разное напряжение. Поскольку емкость обратно пропрциональна напряжению (С = Q/V), то чем меньше емкость конденсатора, тем большее напряжение на него упадет.

Применим закон Кирхгофа для напряжения в последовательной цепи из трех конденсаторов:

Падение напряжения при последовательном соединении

Емкость конденсатора прямо пропорциональна его заряду и обратно пропорциональна его напряжению — C = Q/V. Как уже упоминалось выше, последовательно соединенные конденсаторы имеют одинаковый электрический заряд — Qобщ = Q1 = Q2 = Q3.

Следовательно:

Разделив все выражение на Qобщ мы получим уравнение для общей емкости при последовательном соединении:

Из данного уравнения можно легко вывести формулу общей емкости для любого частного случая последовательного соединения.

Например, общая емкость для трех конденсаторов:

Общая емкость для двух конденсаторов:

Смешанное соединение конденсаторов

Если в цепи есть и последовательное и параллельное соединение, то такую цепь называют смешанной или последовательно-параллельной. Тем не менее, смешанное соединение может иметь как последовательный, так и параллельный характер.

Смешанное соединение конденсаторов

Общая емкость смешанного соединения конденсаторов

Чтобы посчитать общую емкость смешанного соединения конденсаторов, следуют такому же алгоритму, как и при расчете общего сопротивления смешанного соединения резисторов.

• Цепь разбивают на участки с только пареллельным или только последовательным соединением
• Вычисляют общую емкость для каждого отдельного участка.
• Вычисляют общую емкость для всей цепи смешанного соединения.

Так это будет выглядеть для схемы 2:

Преобразование смешанного соединения в параллельное

Зачем все это нужно?

Вполне справедливым может оказаться вопрос, для чего надо соединять конденсаторы последовательно, если общая емкость будет меньше? Скорее всего, первым что приходит в голову — это чтобы получить новый эквивалентный конденсатор с меньшей емкостью. Но в производстве микросхем вряд ли будут делать подобное, поскольку, во -первых, обычно нужно экономить место на печатной плате, а во-вторых, нет смысла тратить деньги на два компонента или больше, если можно купить один с требуемой емкостью.

Но если в параллельном или последовательном соединении конденсаторов еще есть хоть какая-то логика, то кому вообще нужно смешанное?

Дело в том, что емкостью, то есть способностью накапливать электрический заряд, обладает любое тело в природе, даже человеческое. Если мы говорим о электрической цепи, то все ее элементы на практике обладают емкостью, и их можно представить как конденсаторы. Часто такую емкость еще называют паразитической, потому как она создает разного рода помехи.

Например, у нас есть какая-то электронная цепь с множеством различных компонентов, которая принимает сигнал, обрабатывает его определенным образом и выдает на выход результат. Известно, что время задержки сигнала, в основном, зависит от паразитической емкости электронных компонентов схемы. Поскольку должно пройти время зарядки паразитической емкости, прежде чем она начнет пропускать сигнал. Если мы хотим узнать время задержки, нужно посчитать общую емкость всех компонентов, конвертировав их в цепь из конденсаторов.

Учебное пособие по физике: Параллельные схемы

Как упоминалось в предыдущем разделе Урока 4, два или более электрических устройства в цепи могут быть соединены последовательным или параллельным соединением. Когда все устройства соединены с использованием параллельных соединений, схема называется параллельной схемой . В параллельной схеме каждое устройство помещается в свою отдельную ветвь . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить через внешнюю цепь.Каждый заряд, проходящий через контур внешней цепи, будет проходить через единственный резистор, присутствующий в одной ветви. По прибытии в место разветвления или узел плата выбирает , через какую ветвь пройти на обратном пути к терминалу с низким потенциалом.

Краткое сравнение и контраст между последовательными и параллельными цепями было сделано в предыдущем разделе Урока 4. В этом разделе было подчеркнуто, что добавление большего количества резисторов в параллельную цепь приводит к довольно неожиданному результату — уменьшению общего сопротивления. .Поскольку существует несколько путей, по которым может протекать заряд, добавление еще одного резистора в отдельную ветвь обеспечивает еще один путь, по которому заряд может проходить через основную область сопротивления в цепи. Это уменьшенное сопротивление в результате увеличения количества ветвей будет иметь эффект увеличения скорости, с которой течет заряд (также известной как ток). Чтобы сделать этот довольно неожиданный результат более разумным, была введена аналогия с платными дорогами. Плата за проезд — это основное место сопротивления автомобильному потоку на платной дороге.Добавление дополнительных пунктов взимания платы за проезд в пределах их собственного отделения на платной дороге обеспечит больше путей для автомобилей, проезжающих через станцию ​​взимания платы. Эти дополнительные пункты пропуска снизят общее сопротивление потоку автомобилей и увеличат скорость их движения.

Текущая

Скорость, с которой заряд проходит через цепь, называется током. Заряд НЕ накапливается и не начинает накапливаться в любом заданном месте, так что ток в одном месте больше, чем в других местах.Заряд НЕ расходуется резисторами таким образом, что в одном месте ток меньше, чем в другом. В параллельной схеме заряд делит на отдельные ветви, так что в одной ветви может быть больше тока, чем в другой. Тем не менее, если брать в целом, общая сумма тока во всех ветвях при сложении равна величине тока в местах за пределами ветвей. Правило, что ток везде одинаковый все еще работает, только с закруткой.Сила тока вне ветвей равна сумме токов в отдельных ветвях. Это все еще та же величина тока, только разделенная на несколько путей.

В форме уравнения этот принцип можно записать как

I _всего = I ₁ + I ₂ + I ₃ + …

, где I _всего — это общая сумма тока вне ветвей (и в батарее), а I ₁ , I ₂ и I ₃ представляют ток в отдельных ветвях цепи.

В этом блоке широко использовалась аналогия между расходом заряда и расходом воды. Еще раз вернемся к аналогии, чтобы проиллюстрировать, как сумма текущих значений в ветвях равна сумме вне ветвей. Поток заряда в проводах аналогичен потоку воды в трубах. Рассмотрим приведенные ниже схемы, на которых поток воды в трубах делится на отдельные ответвления. В каждом узле (место разветвления) вода проходит двумя или более отдельными путями.Скорость, с которой вода поступает в узел (измеряется в галлонах в минуту), будет равна сумме расходов в отдельных ветвях за пределами узла. Точно так же, когда две или более ветви подаются в узел, скорость, с которой вода вытекает из узла, будет равна сумме расходов в отдельных ветвях, которые подаются в узел.

Тот же принцип разделения потока применяется к электрическим цепям. Скорость, с которой заряд поступает в узел, равна сумме расходов в отдельных ветвях за пределами узла.Это проиллюстрировано в приведенных ниже примерах. В примерах вводится новый символ схемы — буква A, заключенная в круг. Это символ амперметра — устройства, используемого для измерения силы тока в определенной точке. Амперметр способен измерять ток, оказывая при этом незначительное сопротивление потоку заряда.

Диаграмма A показывает два резистора, подключенных параллельно с узлами в точках A и B. Заряд течет в точку A со скоростью 6 ампер и делится на два пути — один через резистор 1, а другой — через резистор 2.Ток в ветви с резистором 1 составляет 2 ампера, а ток в ветви с резистором 2 — 4 ампера. После того, как эти две ветви снова встретятся в точке B, чтобы сформировать единую линию, ток снова станет равным 6 ампер. Таким образом, мы видим, что принцип, согласно которому ток вне ветвей равен сумме тока в отдельных ветвях, верен.

I _итого = I ₁ + I ₂

6 ампер = 2 ампера + 4 ампера

Схема B выше может быть немного сложнее, если три резистора расположены параллельно.На схеме обозначены четыре узла, обозначенные буквами A, B, C и D. Заряд течет в точку A со скоростью 12 ампер и делится на два пути: один проходит через резистор 1, а другой направляется к точке B (и резисторам 2). и 3). 12 ампер тока делятся на 2-амперную (через резистор 1) и 10-амперную (в направлении точки B). В точке B происходит дальнейшее разделение потока на два пути — один через резистор 2, а другой через резистор 3. Ток 10 ампер, приближающийся к точке B, делится на 6-амперный путь (через резистор 2) и 4-канальный. -амперный тракт (через резистор 3).Таким образом, видно, что значения тока в трех ветвях составляют 2 ампера, 6 ампер и 4 ампера, и что сумма значений тока в отдельных ветвях равна току вне ветвей.

I _итого = I ₁ + I ₂ + I ₃

12 ампер = 2 ампер + 6 ампер + 4 ампер

Также может быть проведен анализ потока в точках C и D, и будет замечено, что сумма расходов потока в этих точках равна скорости потока, находящейся непосредственно за этими точками.

Эквивалентное сопротивление

Фактическая величина тока всегда изменяется обратно пропорционально величине общего сопротивления. Существует четкая взаимосвязь между сопротивлением отдельных резисторов и общим сопротивлением набора резисторов. Чтобы исследовать эту взаимосвязь, давайте начнем с простейшего случая, когда два резистора помещены в параллельные ветви, каждый из которых имеет одинаковое значение сопротивления 4 Ом.Поскольку схема предлагает два равных путей для потока заряда, только половина заряда выберет для прохождения через данную ветвь. В то время как каждая отдельная ветвь предлагает сопротивление 4 Ом любому заряду, который проходит через нее, только половина всего заряда, протекающего по цепи, будет встречать сопротивление 4 Ом этой отдельной ветви. Таким образом, что касается батареи, которая накачивает заряд, наличие двух параллельно подключенных резисторов 4 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи.Таким же образом, наличие двух параллельно подключенных резисторов сопротивлением 6 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом. А наличие двух параллельных резисторов 12 Ом было бы эквивалентно наличию в цепи одного резистора 6 Ом.

Теперь давайте рассмотрим другой простой случай, когда параллельно соединены три резистора, каждый из которых имеет одинаковое сопротивление 6 Ом. При трех равных путях прохождения заряда через внешний контур только одна треть заряда будет проходить через данную ветвь.Каждая отдельная ветвь обеспечивает сопротивление 6 Ом проходящему через нее заряду. Однако тот факт, что только одна треть заряда проходит через определенную ветвь, означает, что общее сопротивление цепи составляет 2 Ом. Что касается батареи, которая накачивает заряд, наличие трех параллельных резисторов 6 Ом было бы эквивалентно наличию одного резистора 2 Ом в цепи. Таким же образом, наличие трех параллельно подключенных резисторов сопротивлением 9 Ом было бы эквивалентно наличию в цепи одного резистора сопротивлением 3 Ом.А наличие трех параллельных резисторов 12 Ом было бы эквивалентно наличию одного резистора 4 Ом в цепи.

Это концепция эквивалентного сопротивления. Эквивалентное сопротивление цепи — это величина сопротивления, которая потребуется одному резистору, чтобы сравняться с общим эффектом от набора резисторов, присутствующих в цепи. Для параллельных цепей математическая формула для вычисления эквивалентного сопротивления ( _{R eq} ) составляет

. 1/ _экв. = 1/ ₁ + 1/ ₂ + 1/ ₃ +…

, где R ₁ , R ₂ и R ₃ — значения сопротивления отдельных резисторов, подключенных параллельно. Приведенные выше примеры можно рассматривать как простые случаи, в которых все пути обладают одинаковым сопротивлением отдельному заряду, который проходит через них. Приведенные выше простые случаи были выполнены без использования уравнения. Тем не менее, это уравнение подходит как для простых случаев, когда резисторы ответвления имеют одинаковые значения сопротивления, так и для более сложных случаев, когда резисторы ответвления имеют разные значения сопротивления.Например, рассмотрим применение уравнения к одному простому и одному сложному случаю ниже.

Случай 1 : три резистора 12 Ом включены параллельно	1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (12 Ом) + 1 / (12 Ом) + 1 / (12 Ом) Использование калькулятора … 1 / R экв. = 0,25 Ом -1 R экв = 1 / (0,25 Ом -1 ) R экв = 4,0 Ом
Случай 2 : резисторы 5,0 Ом, 7,0 Ом и 12 Ом включены параллельно	1 / R экв = 1 / R 1 + 1 / R 2 + 1 / R 3 1 / R экв = 1 / (5.0 Ом) + 1 / (7,0 Ом) + 1 / (12 Ом) Использование калькулятора … 1 / R экв = 0,42619 Ом-1 R экв = 1 / (0,42619 Ом -1 ) R экв. = 2,3 Ом

Ваша очередь попробовать

Нужно больше практики? Используйте два параллельных резистора виджет ниже, чтобы попробовать некоторые дополнительные проблемы.Введите любые два желаемых значения сопротивления. Воспользуйтесь калькулятором, чтобы определить значения _{рэндов экв.} . Затем нажмите кнопку Отправить , чтобы проверить свои ответы. Попробуйте столько раз, сколько хотите, с разными значениями сопротивления.

Падения напряжения для параллельных ветвей

В разделе «Схемы» учебного пособия «Физический класс» подчеркивалось, что любое повышение напряжения, полученное за счет заряда батареи, теряется из-за заряда, когда он проходит через резисторы внешней цепи.Общее падение напряжения во внешней цепи равно увеличению напряжения при прохождении заряда через внутреннюю цепь. В параллельной схеме заряд не проходит через каждый резистор; скорее, он проходит через единственный резистор. Таким образом, полное падение напряжения на этом резисторе должно соответствовать напряжению батареи. Не имеет значения, проходит ли заряд через резистор 1, резистор 2 или резистор 3, падение напряжения на резисторе, которое выбирает для прохождения , должно равняться напряжению батареи.В форме уравнения этот принцип можно было бы выразить как

В _{аккумулятор} = В ₁ = В ₂ = В ₃ = …

Если три резистора размещены в параллельных ветвях и питаются от 12-вольтовой батареи, то падение напряжения на каждом из трех резисторов составляет 12 вольт. Заряд, протекающий по цепи, встретит только один из этих трех резисторов и, таким образом, столкнется с одним падением напряжения на 12 вольт.

Диаграммы электрических потенциалов были представлены в Уроке 1 этого устройства и впоследствии использовались для иллюстрации последовательных падений напряжения, происходящих в последовательных цепях.Диаграмма электрического потенциала — это концептуальный инструмент для представления разности электрических потенциалов между несколькими точками электрической цепи. Рассмотрим приведенную ниже принципиальную схему и соответствующую диаграмму электрических потенциалов.

Как показано на диаграмме электрического потенциала, все позиции A, B, C, E и G имеют высокий электрический потенциал. Один заряд выбирает только один из трех возможных путей; таким образом, в позиции B один заряд будет двигаться к точкам C, E или G, а затем пройдет через резистор, находящийся в этой ветви.Заряд не теряет свой высокий потенциал до тех пор, пока не пройдет через резистор, либо от C к D, от E к F или от G к H. После того, как он пройдет через резистор, заряд вернется почти до 0 вольт и вернется к отрицательному значению. клемму аккумуляторной батареи для повышения ее напряжения. В отличие от последовательных цепей, заряд в параллельной цепи встречает единственное падение напряжения на своем пути через внешнюю цепь.

Ток через заданную ветвь можно предсказать, используя уравнение закона Ома, падение напряжения на резисторе и сопротивление резистора.Поскольку падение напряжения на каждом резисторе одинаково, фактором, определяющим, что резистор имеет наибольший ток, является сопротивление. Резистор с наибольшим сопротивлением испытывает наименьший ток, а резистор с наименьшим сопротивлением — наибольший ток. В этом смысле можно сказать, что заряд (как и люди) выбирает путь наименьшего сопротивления. В форме уравнения это может быть указано как

I 1 = Δ V 1 / R 1

I 2 = Δ V 2 / R 2

I 3 = Δ V 3 / R 3

Этот принцип иллюстрируется схемой, показанной ниже.Произведение I • R одинаково для каждого резистора (и равно напряжению батареи). Но в каждом резисторе ток разный. Ток наибольший там, где сопротивление наименьшее, и ток наименьший, где сопротивление наибольшее.

Математический анализ параллельных цепей

Приведенные выше принципы и формулы могут использоваться для анализа параллельной цепи и определения значений тока и разности электрических потенциалов на каждом из резисторов в параллельной цепи.Их использование будет продемонстрировано математическим анализом схемы, показанной ниже. Цель состоит в том, чтобы использовать формулы для определения эквивалентного сопротивления цепи (R _eq ), тока через батарею (I _до ), а также падений напряжения и тока для каждого из трех резисторов.

Анализ начинается с использования значений сопротивления отдельных резисторов для определения эквивалентного сопротивления цепи.

1 / R _экв = 1 / R ₁ + 1 / R ₂ + 1 / R ₃ = (1/17 Ω) + (1/12 Ω) + (1/11 Ω)

1 / R _экв = 0.23306 Ом ^-1

R _экв = 1 / (0,23306 Ом ^-1 )

R _экв = 4,29 Ом

(округлено от 4,29063 Ом)

Теперь, когда известно эквивалентное сопротивление, ток в батарее можно определить с помощью уравнения закона Ома. При использовании уравнения закона Ома (ΔV = I • R) для определения тока в батарее важно использовать напряжение батареи для ΔV и эквивалентное сопротивление для R.Расчет показан здесь:

I _до = ΔV _{аккумулятор} / R _eq = (60 В) / (4,29063 Ом)

I _до = 14,0 А

(округлено от 13,98396 А)

Напряжение батареи 60 В представляет собой усиление электрического потенциала за счет заряда, проходящего через батарею. Заряд теряет такое же количество электрического потенциала при любом прохождении через внешнюю цепь.То есть падение напряжения на каждом из трех резисторов такое же, как и напряжение, полученное в батарее:

ΔV _{аккумулятор} = ΔV ₁ = ΔV ₂ = ΔV ₃ = 60 В

Осталось определить три значения — ток каждого отдельного резистора. Закон Ома снова используется для определения значений тока для каждого резистора — это просто падение напряжения на каждом резисторе (60 В), деленное на сопротивление каждого резистора (указанное в формулировке задачи).Расчеты показаны ниже.

I 1 = ΔV 1 / R 1 I 1 = (60 В) / (17 Ом) I 1 = 3,53 А

I 2 = ΔV 2 / R 2 I 2 = (60 В) / (12 Ом) I 2 = 5,00 А

I 3 = ΔV 3 / R 3 I 3 = (60 В) / (11 Ом) Я 3 = 5.45 ампер

В качестве проверки точности выполненных математических расчетов целесообразно проверить, удовлетворяют ли вычисленные значения принципу, согласно которому сумма значений тока для каждого отдельного резистора равна общему току в цепи (или в батарее). . Другими словами, I _to = I ₁ + I ₂ + I ₃ ?

Является ли I _tot = I ₁ + I ₂ + I ₃ ?

Из 14.0 ампер = 3,53 ампер + 5,00 ампер + 5,45 ампер?

14,0 А = 13,98 А?

Да !!

(Разница в 0,02 ампера — это просто результат предыдущего округления значения I _до от 13,98.)

Математический анализ этой параллельной цепи включал смесь концепций и уравнений. Как это часто бывает в физике, отделение понятий от уравнений при принятии решения физической проблемы является опасным актом.Здесь необходимо учитывать концепции, согласно которым падение напряжения на каждом из трех резисторов равно напряжению батареи и что сумма тока в каждом резисторе равна общему току. Эти представления необходимы для завершения математического анализа. В следующей части Урока 4 будут исследованы комбинированные или составные схемы, в которых одни устройства включены параллельно, а другие — последовательно.

Создавайте, решайте и проверяйте свои собственные проблемы с помощью виджета Equivalent Resistance ниже.Создайте себе проблему с любым количеством резисторов и любыми номиналами. Решать проблему; затем нажмите кнопку «Отправить», чтобы проверить свой ответ.

Мы хотели бы предложить … Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействовать — это именно то, что вы делаете, когда используете одно из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключить их так, как захотите. Вольтметры и амперметры позволяют измерять падение тока и напряжения. Нажатие на резистор или источник напряжения позволяет изменять сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванне).

Проверьте свое понимание

1. По мере того, как в цепь добавляется все больше и больше резисторов, эквивалентное сопротивление цепи ____________ (увеличивается, уменьшается) и общий ток цепи ____________ (увеличивается, уменьшается).

2.Три одинаковых лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают местоположения вдоль цепи. Какое из следующих утверждений верно?

а. Ток в точке Y больше, чем ток в точке Q.

г. Ток на Y больше, чем на P.

.

г. Ток в точке Y больше, чем ток в точке Z.

г. Ток в точке P больше, чем ток в точке Q.

.

e.Ток на Q больше, чем на P.

.

ф. Сила тока одинакова во всех местах.

3. Три одинаковые лампочки подключены к D-ячейке, как показано ниже. P, Q, X, Y и Z обозначают местоположения вдоль цепи. В каком (а) месте (ах), если таковые имеются, будет ток …

а. … так же, как у X?

г…. такой же, как у Q?

г. … так же, как у Y?

г. … меньше, чем у Q?

e. … меньше, чем у P?

ф. … вдвое больше, чем у Z?

г. … в три раза больше, чем в Y?

4. Какие настройки можно внести в схему ниже, чтобы уменьшить ток в ячейке? Перечислите все подходящие варианты.

а. Увеличьте сопротивление лампы X.

г. Уменьшите сопротивление лампы X.

г. Увеличьте сопротивление лампы Z.

г. Уменьшите сопротивление лампы Z.

.

e. Увеличьте напряжение ячейки (как-нибудь).

ф. Уменьшите напряжение ячейки (как-нибудь).

г. Снять лампу Y.

.

5.Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключаются, как показано на рисунке. Ток в резисторе 12 Ом равен ____ току в резисторе 4 Ом.

а. 1/3	г. 1/2	г. 2/3
г. то же, что		e.1,5 раза
ф. дважды		г. трижды
ч. четыре раза

6. Аккумулятор на 12 В, резистор на 12 Ом и резистор на 4 Ом подключаются, как показано.Падение напряжения на резисторе 12 Ом равно ____ падению напряжения на резисторе 4 Ом.

а. 1/3	г. 1/2	г. 2/3
г. то же, что		e. 1,5 раза
ф.дважды		г. трижды
ч. четыре раза

7. Аккумулятор на 12 В и резистор на 12 Ом подключаются, как показано на схеме. Резистор на 6 Ом добавлен к резистору на 12 Ом, чтобы создать цепь Y, как показано.Падение напряжения на резисторе 6 Ом в цепи Y равно ____ падению напряжения на резисторе в цепи X.

а. больше, чем

г. меньше

г. то же, что

8. Используйте свое понимание эквивалентного сопротивления, чтобы заполнить следующие утверждения:

а. Два резистора сопротивлением 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.

г. Три резистора 6 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное одному резистору _____ Ом.

г. Три резистора сопротивлением 8 Ом, помещенные параллельно, обеспечат сопротивление, эквивалентное сопротивлению одного резистора _____ Ом.

г. Три резистора с сопротивлением 2 Ом, 4 Ом и 6 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

e. Три резистора с сопротивлением 5 Ом, 6 Ом и 7 Ом размещены параллельно.Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

ф. Три резистора с сопротивлением 12 Ом, 6 Ом и 21 Ом размещены параллельно. Они обеспечили бы сопротивление, эквивалентное одному резистору _____ Ом.

9. На основании ваших ответов на вышеуказанный вопрос заполните следующую формулировку:

Общее или эквивалентное сопротивление трех параллельно включенных резисторов будет _____.

а. больше, чем сопротивление самого большого значения R.

г. меньше, чем сопротивление наименьшего значения R из трех.

г. где-то между наименьшим значением R и наибольшим значением R.

г. … бред какой то! Такого обобщения сделать нельзя. Результаты меняются.

10. Три резистора включены параллельно.При размещении в цепи с источником питания 12 В. Определите эквивалентное сопротивление, полный ток цепи, падение напряжения и ток в каждом резисторе.

Серия

и параллельные схемы — learn.sparkfun.com

Добавлено в избранное Любимый 53 Серия

и параллельные схемы

Простые схемы (состоящие всего из нескольких компонентов) обычно довольно просты для понимания новичками.Но, когда на вечеринку приходят другие компоненты, все может запутаться. Куда идет ток? Что делает напряжение? Можно ли это упростить для облегчения понимания? Не бойся, бесстрашный читатель. Ценная информация приводится ниже.

В этом руководстве мы сначала обсудим разницу между последовательными и параллельными схемами, используя схемы, содержащие самые основные компоненты — резисторы и батареи, — чтобы показать разницу между двумя конфигурациями. Затем мы рассмотрим, что происходит в последовательных и параллельных цепях, когда вы комбинируете компоненты разных типов, например конденсаторы и катушки индуктивности.

Рассматривается в этом учебном пособии

• Как выглядят конфигурации последовательной и параллельной цепей
• Как пассивные компоненты действуют в этих конфигурациях
• Как источник напряжения будет воздействовать на пассивные компоненты в этих конфигурациях

Рекомендуемая литература

Вы можете посетить эти учебные пособия по основным компонентам, прежде чем углубляться в построение схем в этом учебном пособии.

Видео

Цепи серии

Узлы и текущий поток

Прежде чем мы углубимся в это, мы должны упомянуть, что такое узел .Ничего особенного, просто представление электрического соединения между двумя или более компонентами. Когда схема моделируется на схеме, эти узлы представляют собой провода между компонентами.

Пример схемы с четырьмя узлами уникального цвета.

Это полдела на пути к пониманию разницы между последовательным и параллельным. Нам также нужно понять , как ток течет по цепи. Ток течет от высокого напряжения к более низкому напряжению в цепи.Некоторое количество тока будет проходить по каждому пути, который может пройти, чтобы добраться до точки с наименьшим напряжением (обычно называемой землей). Используя приведенную выше схему в качестве примера, вот как будет течь ток, когда он проходит от положительной клеммы аккумулятора к отрицательной:

Ток (обозначенный синей, оранжевой и розовой линиями), протекающий по той же примерной схеме, что и выше. Разные токи обозначены разными цветами.

Обратите внимание, что в некоторых узлах (например, между R ₁ и R ₂ ) ток на входе такой же, как на выходе.В других узлах (в частности, трехходовой переход между R ₂ , R ₃ и R ₄ ) основной (синий) ток разделяется на два разных. Это ключевое различие между последовательным и параллельным подключением!

Определение цепей серии

Два компонента соединены последовательно, если они имеют общий узел и если через них протекает один и тот же ток . Вот пример схемы с тремя последовательными резисторами:

В вышеуказанной цепи есть только один способ протекания тока.Начиная с положительного полюса аккумуляторной батареи, ток сначала достигает ₁ рандов. Оттуда ток пойдет прямо на ₂ рандов, затем на ₃ рандов и, наконец, обратно на отрицательную клемму аккумулятора. Обратите внимание, что у текущего есть только один путь. Эти компоненты включены последовательно.

Параллельные схемы

Определение параллельных цепей

Если компоненты совместно используют два общих узла , они работают параллельно.Вот пример схемы трех резисторов, подключенных параллельно к батарее:

От положительного полюса аккумуляторной батареи ток течет на ₁ … и ₂ рандов, а также на ₃ рандов. Узел, который соединяет аккумулятор с R ₁ , также подключен к другим резисторам. Другие концы этих резисторов аналогично связываются вместе, а затем снова подключаются к отрицательной клемме батареи. Существует три различных пути, по которым ток может пройти, прежде чем вернуться в батарею, и соответствующие резисторы считаются параллельными.

Если все последовательные компоненты имеют одинаковые токи, протекающие через них, все параллельные компоненты имеют одинаковое падение напряжения на них — series: current :: parallel: Voltage.

Совместная работа параллельных цепей и серии

Оттуда мы можем смешивать и сочетать. На следующем снимке мы снова видим три резистора и батарею. С положительной клеммы аккумуляторной батареи ток сначала достигает ₁ рандов. Но на другой стороне R ₁ узел разделяется, и ток может идти как на R ₂ , так и на R ₃ .Затем токопроводящие дорожки через R ₂ и R ₃ снова связываются вместе, и ток возвращается к отрицательной клемме батареи.

В этом примере R ₂ и R ₃ параллельны друг другу, а R ₁ идут последовательно с параллельной комбинацией R ₂ и R ₃ .

Расчет эквивалентных сопротивлений в последовательных цепях

Вот некоторая информация, которая может оказаться для вас более полезной.Когда мы соединяем резисторы таким образом, последовательно и параллельно, мы меняем способ протекания тока через них. Например, если у нас есть питание 10 В через 10 кОм; резистора, закон Ома гласит, что у нас протекает ток 1 мА.

Если потом поставить еще 10к & ом; резистор, включенный последовательно с первым и оставив питание без изменений, мы сократили ток вдвое, потому что сопротивление увеличилось вдвое.

Другими словами, по-прежнему существует только один путь для прохождения тока, и мы только усложнили прохождение тока.Насколько сложнее? 10к & Ом; + 10к & Ом; = 20 кОм ;. Вот как мы рассчитываем последовательно подключенные резисторы — всего суммируют их значения .

Если выразить это уравнение в более общем виде: полное сопротивление Н — произвольное количество резисторов — это их общая сумма.

Расчет эквивалентных сопротивлений в параллельных цепях

А как насчет параллельных резисторов? Это немного сложнее, но ненамного.Рассмотрим последний пример, в котором мы начали с источника питания 10 В и 10 кОм; резистор, но на этот раз мы добавляем еще 10кОм; параллельно, а не последовательно. Теперь у тока есть два пути. Поскольку напряжение питания не изменилось, закон Ома гласит, что первый резистор по-прежнему будет потреблять 1 мА. Но то же самое и со вторым резистором, и теперь у нас есть в общей сложности 2 мА, поступающие от источника питания, что вдвое превышает первоначальный 1 мА. Это означает, что мы уменьшили общее сопротивление вдвое.

Пока можно сказать, что 10к & ом; || 10к & Ом; = 5 кОм; («||» примерно переводится как «параллельно»), у нас не всегда будет 2 одинаковых резистора.Что тогда?

Уравнение для добавления произвольного количества резисторов параллельно:

Если обратные значения вам не подходят, мы также можем использовать метод, называемый «произведение на сумму», когда у нас есть два параллельных резистора:

Однако этот метод подходит только для двух резисторов в одном вычислении. Мы можем объединить более двух резисторов этим методом, взяв результат R1 || R2 и вычисление этого значения параллельно с третьим резистором (снова как произведение на сумму), но обратный метод может быть меньше работы.

Время эксперимента — Часть 1

Что вам понадобится:

Давайте проведем простой эксперимент, чтобы доказать, что все работает именно так, как мы говорим.

Во-первых, мы собираемся подключить 10 кОм; последовательно подключите резисторы и наблюдайте, как они складываются самым необычным образом. Используя макетную плату, поместите один 10 кОм; резистор, как показано на рисунке, и измерьте его мультиметром. Да, мы уже знаем, что на нем будет указано 10 кОм, но это то, что мы в бизнесе называем «проверкой работоспособности».Убедившись, что мир существенно не изменился с тех пор, как мы в последний раз смотрели на него, поместите еще один аналогично, но с выводами каждого резистора, электрически подключенными через макетную плату, и снова произведите измерения. Теперь измеритель должен показывать что-то близкое к 20 кОм.

Вы можете заметить, что сопротивление, которое вы измеряете, может быть не совсем таким, каким должно быть резистор. Резисторы имеют определенный допуск , что означает, что они могут быть отключены на определенный процент в любом направлении.Таким образом, вы можете прочитать 9.99k & ohm; или 10.01кОм. Пока оно близко к правильному значению, все должно работать нормально.

Читателю следует продолжать это упражнение до тех пор, пока он не убедится, что знает, что будет в результате, прежде чем делать это снова, или у него закончатся резисторы, которые можно вставить в макет, в зависимости от того, что наступит раньше.

Время эксперимента — Часть 2

Теперь давайте попробуем это с резисторами в параллельной конфигурации .Поместите один 10 кОм; резистор в макетной плате, как и раньше (мы полагаем, что читатель уже считает, что один резистор 10 кОм будет измерять на мультиметре что-то близкое к 10 кОм). Теперь поместите второй 10k & ohm; резистор рядом с первым, следя за тем, чтобы выводы каждого резистора находились в электрически соединенных рядах. Но перед тем, как измерить комбинацию, вычислите, используя метод «произведение над суммой» или обратный метод, каким должно быть новое значение (подсказка: оно будет 5 кОм;).Затем измерьте. Это что-то близкое к 5к & ом ;? Если это не так, дважды проверьте отверстия, в которые вставлены резисторы.

Повторите упражнение с резисторами 3, 4 и 5. Расчетные / измеренные значения должны быть 3,33 кОм, 2,5 кОм; и 2кОм соответственно. Все ли получилось по плану? Если нет, вернитесь и проверьте свои соединения. Если это так, EXCELSIOR! Прежде чем продолжить, выпейте молочный коктейль. Ты заслужил это.

Практические правила для последовательных и параллельных резисторов

Есть несколько ситуаций, которые могут потребовать творческих комбинаций резисторов.Например, если мы пытаемся установить очень конкретное опорное напряжение, вам почти всегда потребуется очень конкретное соотношение резисторов, значения которых вряд ли будут «стандартными» значениями. И хотя мы можем получить очень высокую степень точности значений резисторов, мы можем не захотеть ждать X дней, необходимых для доставки чего-либо, или платить цену за нестандартные значения, отсутствующие на складе. Так что в крайнем случае мы всегда можем создать собственные номиналы резисторов.

Совет №1: Равнопараллельные резисторы

Добавление N резисторов с одинаковым номиналом R , включенных параллельно, дает нам R / N Ом.Допустим, нам нужен 2,5 кОм; резистор, но все, что у нас есть, это ящик, полный 10 кОм. Объединение четырех из них параллельно дает нам 10 кОм / 4 = 2,5 кОм.

Совет № 2: Допуск

Знайте, какую терпимость вы можете терпеть. Например, если вам нужен 3.2k & ohm; резистор, можно было поставить 3 10кОм; резисторы параллельно. Это даст вам 3,3 кОм, что составляет около 4% отклонения от необходимого значения. Но если схема, которую вы строите, должна иметь допуск ближе, чем 4%, мы можем измерить наш запас в 10 кОм, чтобы увидеть, какие из них являются самыми низкими значениями, потому что они также имеют допуск.По идее, если заначка 10к & ом; резисторы имеют допуск 1%, мы можем получить только 3,3 кОм. Но производители запчастей, как известно, допускают именно такого рода ошибки, поэтому стоит немного покопаться.

Совет № 3: Номинальная мощность при последовательном / параллельном подключении

Такая комбинация резисторов последовательно и параллельно работает и с номинальной мощностью. Допустим, нам нужен 100 & Ом; резистор рассчитан на 2 Вт (Вт), но все, что у нас есть, это связка 1 кОм; резисторы на четверть ватта (Вт) (а сейчас 3 часа ночи, вся Mountain Dew исчезла, а кофе остыл).Вы можете объединить 10 из 1 кОм, чтобы получить 100 Ом; (1 кОм / 10 = 100 Ом), а номинальная мощность будет 10×0,25 Вт или 2,5 Вт. Не очень красиво, но это поможет нам завершить финальный проект и даже может принести нам дополнительные баллы за способность думать на ногах.

Нам нужно быть немного более осторожными, когда мы объединяем резисторы разных номиналов параллельно, когда речь идет об общем эквивалентном сопротивлении и номинальной мощности. Для читателя это должно быть совершенно очевидно, но …

Совет № 4: Разные резисторы параллельно

Суммарное сопротивление двух резисторов разного номинала всегда меньше, чем резистор наименьшего номинала.Читатель будет поражен тем, сколько раз кто-то объединяет значения в своей голове и приходит к значению, которое находится посередине между двумя резисторами (1 кОм || 10 кОм; НЕ равняется чему-либо около 5 кОм ;!). Общее параллельное сопротивление всегда будет приближаться к резистору с наименьшим значением. Сделайте себе одолжение и прочитайте совет №4 10 раз.

Совет № 5: Параллельное рассеяние мощности

Мощность, рассеиваемая при параллельной комбинации резисторов разных номиналов, не распределяется между резисторами равномерно, поскольку токи не равны.Используя предыдущий пример (1k & ohm; || 10k & ohm;), мы видим, что 1k & ohm; будет потреблять в 10 раз больше тока 10 кОм. Поскольку закон Ома гласит, что мощность = напряжение x ток, отсюда следует, что 1 кОм; резистор рассеивает в 10 раз мощность, превышающую 10 кОм.

В конечном счете, уроки советов 4 и 5 заключаются в том, что мы должны уделять больше внимания тому, что мы делаем при параллельном соединении резисторов разного номинала. Но советы 1 и 3 предлагают несколько удобных ярлыков, когда значения совпадают.

Конденсаторы серии

и параллельные

Объединение конденсаторов аналогично объединению резисторов … только наоборот. Как бы странно это ни звучало, это абсолютная правда. Почему это могло быть?

Конденсатор — это две пластины, расположенные очень близко друг к другу, и его основная функция — удерживать целую группу электронов. Чем больше значение емкости, тем больше электронов она может удерживать. Если размер пластин увеличивается, емкость увеличивается, потому что физически больше места для электронов.И если пластины раздвинуть дальше друг от друга, емкость падает, потому что напряженность электрического поля между ними уменьшается с увеличением расстояния.

Теперь предположим, что у нас есть два конденсатора по 10 мкФ, соединенных последовательно, и предположим, что они оба заряжены и готовы к разряду в друга, сидящего рядом с вами.

Помните, что в последовательной цепи есть только один путь для прохождения тока. Отсюда следует, что количество электронов, выходящих из колпачка внизу, будет таким же, как и количество электронов, выходящих из колпачка наверху.Значит, емкость не увеличилась?

На самом деле все еще хуже. Разместив конденсаторы последовательно, мы эффективно раздвинули пластины дальше друг от друга, потому что расстояние между пластинами двух конденсаторов складывается. Так что у нас нет 20 мкФ или даже 10 мкФ. У нас 5 мкФ. Результатом этого является то, что мы добавляем значения последовательного конденсатора так же, как мы добавляем значения параллельного резистора. И метод «произведение над суммой», и метод взаимности действительны для последовательного добавления конденсаторов.

Может показаться, что нет смысла добавлять конденсаторы последовательно. Но следует отметить, что мы получили вдвое большее напряжение (или номинальное напряжение). Как и в случае с батареями, когда мы соединяем конденсаторы последовательно, напряжения складываются.

Добавление конденсаторов параллельно похоже на последовательное добавление резисторов: значения просто складываются, никаких уловок. Почему это? Их параллельное расположение эффективно увеличивает размер пластин без увеличения расстояния между ними.Чем больше площадь, тем больше емкость. Простой.

Время эксперимента — часть 3

Что вам понадобится:

Давайте посмотрим, как работают последовательно и параллельно соединенные конденсаторы. Это будет немного сложнее, чем примеры резисторов, потому что измерить емкость напрямую мультиметром труднее.

Давайте сначала поговорим о том, что происходит, когда конденсатор заряжается с нуля вольт. Когда ток начинает идти в один из выводов, равное количество тока выходит из другого.А если последовательно с конденсатором нет сопротивления, может быть довольно большой ток. В любом случае ток течет до тех пор, пока конденсатор не начнет заряжаться до значения приложенного напряжения, и медленнее будет стекать, пока напряжения не станут равными, когда ток полностью прекратится.

Как указано выше, потребляемый ток может быть довольно большим, если нет сопротивления последовательно с конденсатором, а время зарядки может быть очень коротким (например, миллисекунды или меньше). Для этого эксперимента мы хотим иметь возможность наблюдать за зарядом конденсатора, поэтому мы собираемся использовать 10 кОм; резистор, включенный последовательно, чтобы замедлить действие до точки, где мы его легко увидим.Но сначала нам нужно поговорить о том, что такое постоянная времени RC.

В приведенном выше уравнении говорится, что одна постоянная времени в секундах (называемая тау) равна сопротивлению в омах, умноженному на емкость в фарадах. Простой? Нет? Продемонстрируем на следующей странице.

Время эксперимента — часть 3, продолжение …

В первой части этого эксперимента мы будем использовать один резистор 10 кОм и один резистор 100 мкФ (что равно 0,0001 фарад). Эти две части создают постоянную времени в 1 секунду:

При зарядке нашего конденсатора 100 мкФ через 10 кОм; резистора, мы можем ожидать, что напряжение на цоколе вырастет примерно до 63% от напряжения питания за 1 постоянную времени, которая составляет 1 секунду.После 5 постоянных времени (в данном случае 5 секунд) конденсатор заряжается примерно на 99% до напряжения питания, и он будет следовать кривой заряда, похожей на график ниже.

Теперь, когда мы это знаем, мы собираемся подключить схему, показанную на схеме (убедитесь, что полярность на этом конденсаторе правильная!).

С помощью нашего мультиметра, установленного для измерения вольт, проверьте выходное напряжение батареи при включенном переключателе. Это наше напряжение питания, и оно должно быть около 4.5В (будет немного больше, если батарейки новые). Теперь подключите схему, убедившись, что переключатель на батарейном блоке находится в положении «ВЫКЛ», прежде чем вставлять его в макетную плату. Также позаботьтесь о том, чтобы красный и черный провода были в нужных местах. Если это более удобно, вы можете использовать зажимы типа «крокодил», чтобы прикрепить измерительные щупы к ножкам конденсатора для измерения (вы также можете немного раздвинуть эти ножки, чтобы было легче).

Когда мы убедимся, что схема выглядит правильно, а наш счетчик включен и настроен на считывание вольт, переведите переключатель на батарейном блоке в положение «ВКЛ».Примерно через 5 секунд показания счетчика должны быть довольно близкими к напряжению аккумуляторной батареи, что демонстрирует, что уравнение верное, и мы знаем, что делаем. Теперь выключите выключатель. Он все еще довольно хорошо держит это напряжение, не так ли? Это потому, что у тока нет пути для разряда конденсатора; у нас разомкнутая цепь. Для разряда конденсатора можно использовать еще один резистор на 10 кОм параллельно. Примерно через 5 секунд он вернется к почти нулевому значению.

Experiment Time — Часть 3, и даже больше…

Теперь мы переходим к интересным моментам, начиная с подключения двух конденсаторов последовательно. Помните, что мы сказали, что результат будет аналогичен параллельному соединению двух резисторов. Если это правда, мы можем ожидать (используя произведение над суммой)

Что это будет делать с нашей постоянной времени?

Имея это в виду, подключите другой конденсатор последовательно с первым, убедитесь, что измеритель показывает ноль вольт (или около того), и переведите переключатель в положение «ON».Зарядка до напряжения аккумуляторной батареи занимала примерно половину времени? Это потому, что емкость вдвое меньше. Электронный бензобак стал меньше, поэтому на его зарядку уходит меньше времени. Для этого эксперимента предлагается третий конденсатор, просто чтобы доказать это, но мы держим пари, что читатель сможет увидеть надпись на стене.

Теперь мы попробуем подключить конденсаторы параллельно, помня, что мы говорили ранее, что это будет похоже на последовательное добавление резисторов. Если это правда, то мы можем ожидать 200 мкФ, верно? Тогда наша постоянная времени станет

.

Это означает, что теперь потребуется около 10 секунд, чтобы увидеть, как параллельные конденсаторы заряжаются до напряжения питания 4.5В.

Для доказательства начнем с нашей исходной схемы из одного 10 кОм; последовательно подключены резистор и один конденсатор емкостью 100 мкФ, как показано на первой схеме этого эксперимента. Мы уже знаем, что конденсатор заряжается примерно за 5 секунд. Теперь подключите второй конденсатор параллельно. Убедитесь, что показания измерителя близки к нулю (разрядите через резистор, если он не показывает нулевое значение), и переведите переключатель на батарейном блоке в положение «ON». Нужно много времени, не правда ли? Разумеется, мы увеличили размер электронного бензобака, и теперь на его заполнение уходит больше времени.Чтобы убедиться в этом, попробуйте добавить третий конденсатор емкостью 100 мкФ и понаблюдайте, как он заряжается в течение долгого времени.

Катушки индуктивности серии

и параллельные

Катушки индуктивности серии

и параллельные

Случаи, когда индукторы необходимо добавлять последовательно или параллельно, довольно редки, но не редкость. В любом случае, давайте рассмотрим их для полноты картины.

Вкратце, они складываются так же, как и резисторы, то есть они складываются со знаком плюс, когда соединены последовательно, и с превышением произведения при параллельном соединении.Сложность возникает, когда они размещаются близко друг к другу, чтобы иметь взаимодействующие магнитные поля, намеренно или нет. По этой причине предпочтительнее иметь один компонент, чем два или более, хотя большинство индукторов экранированы для предотвращения взаимодействия магнитных полей.

В любом случае достаточно сказать, что они добавляют, как резисторы. Дополнительная информация о катушках индуктивности выходит далеко за рамки этого руководства.

Ресурсы и дальнейшее развитие

Теперь, когда вы знакомы с основами последовательных и параллельных цепей, почему бы не ознакомиться с некоторыми из этих руководств?

• Делители напряжения — Одна из самых простых и повторяющихся схем — это делитель напряжения.Это схема, которая действительно основана на концепциях, рассмотренных в этом руководстве.
• Что такое Ардуино? — Теперь, когда у вас есть основы схемотехники, вы можете перейти непосредственно к изучению микроконтроллеров с одной из самых популярных платформ: Arduino.
Основы переключателя
• — В этом руководстве мы говорили о некоторых наиболее основных элементах схемы, но это не был один из них. Переключатели являются важным компонентом практически в каждом электронном проекте.Узнайте все о переключателях в этом руководстве
• Шитье проводящей нитью — схемы не обязательно должны состоять из макетов и проводов. Электронный текстиль использует токопроводящую нить для вшивания светильников и другой электроники в одежду или другую ткань.

резисторов последовательно и параллельно

Цели обучения

К концу этого раздела вы сможете:

• Нарисуйте цепь с резисторами, включенными параллельно и последовательно.
• Рассчитайте падение напряжения тока на резисторе, используя закон Ома.
• Контраст — способ расчета общего сопротивления для резисторов, включенных последовательно и параллельно.
• Объясните, почему полное сопротивление параллельной цепи меньше наименьшего сопротивления любого из резисторов в этой цепи.
• Рассчитайте общее сопротивление цепи, которая содержит смесь резисторов, соединенных последовательно и параллельно.

Большинство схем имеет более одного компонента, называемого резистором , который ограничивает поток заряда в цепи.Мера этого предела расхода заряда называется сопротивлением . Простейшие комбинации резисторов — это последовательное и параллельное соединение, показанное на рисунке 1. Общее сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения.

Рис. 1. (a) Последовательное соединение резисторов. (б) Параллельное соединение резисторов.

Когда резисторы в серии ? Резисторы включены последовательно всякий раз, когда поток заряда, называемый током , должен проходить через устройства последовательно.Например, если ток течет через человека, держащего отвертку, и попадает в Землю, тогда R ₁ на Рисунке 1 (a) может быть сопротивлением вала отвертки, R ₂ сопротивлением ее ручки , R ₃ сопротивления тела человека и R ₄ сопротивления его обуви. На рисунке 2 показаны резисторы, последовательно подключенные к источнику напряжения . Кажется разумным, что полное сопротивление является суммой отдельных сопротивлений, учитывая, что ток должен проходить через каждый резистор последовательно.(Этот факт был бы преимуществом для человека, желающего избежать поражения электрическим током, который мог бы уменьшить ток, надев обувь с высоким сопротивлением на резиновой подошве. Это могло бы стать недостатком, если бы одно из сопротивлений было неисправным шнуром с высоким сопротивлением. прибор, уменьшающий рабочий ток.) ​​

Рис. 2. Три резистора, подключенных последовательно к батарее (слева), и эквивалентное одиночное или последовательное сопротивление (справа).

Чтобы убедиться, что последовательно соединенные сопротивления действительно складываются, давайте рассмотрим потерю электроэнергии, называемую падением напряжения , в каждом резисторе на Рисунке 2.Согласно закону Ома падение напряжения В на резисторе при протекании через него тока рассчитывается по формуле В = IR , где I равно току в амперах (A) и R — сопротивление в Ом (Ом). Другой способ представить это: В — это напряжение, необходимое для протекания тока I через сопротивление R . Таким образом, падение напряжения на R ₁ составляет В ₁ = IR ₁ , что на R ₂ составляет В ₂ = IR ₂ и что через R ₃ равно V ₃ = IR ₃ .Сумма этих напряжений равна выходному напряжению источника; то есть

В = В ₁ + В ₂ + В ₃ .

Это уравнение основано на сохранении энергии и сохранении заряда. Электрическая потенциальная энергия может быть описана уравнением PE = qV , где q — электрический заряд, а V — напряжение. Таким образом, энергия, поставляемая источником, составляет кв , а энергия, рассеиваемая резисторами, составляет

.

qV ₁ + qV ₂ + qV ₃ .

Установление связей: законы сохранения

Вывод выражений для последовательного и параллельного сопротивления основан на законах сохранения энергии и сохранения заряда, которые утверждают, что общий заряд и полная энергия постоянны в любом процессе. Эти два закона непосредственно участвуют во всех электрических явлениях и будут многократно использоваться для объяснения как конкретных эффектов, так и общего поведения электричества.

Эти энергии должны быть равны, потому что в цепи нет другого источника и другого назначения для энергии.Таким образом, qV = qV ₁ + qV ₂ + qV ₃ . Сбор q отменяется, давая V = V ₁ + V ₂ + V ₃ , как указано. (Обратите внимание, что одинаковое количество заряда проходит через батарею и каждый резистор за заданный промежуток времени, поскольку нет емкости для хранения заряда, нет места для утечки заряда и заряд сохраняется.) Теперь подстановка значений для отдельных напряжений дает

В = IR ₁ + IR ₂ + IR ₃ = I ( R ₁ + R ₂ + R ₃ ).

Обратите внимание, что для эквивалентного сопротивления одиночной серии R _с , мы имеем

В = ИК _с .

Это означает, что полное или эквивалентное последовательное сопротивление R _с трех резисторов составляет R _с = R ₁ + R ₂ + R ₃ .Эта логика действительна в общем для любого количества резисторов, включенных последовательно; таким образом, полное сопротивление R _с последовательного соединения равно

R _с = R ₁ + R ₂ + R ₃ +…,

, как предлагается. Поскольку весь ток должен проходить через каждый резистор, он испытывает сопротивление каждого, а последовательно соединенные сопротивления просто складываются.

Пример 1. Расчет сопротивления, тока, падения напряжения и рассеиваемой мощности: анализ последовательной цепи

Предположим, что выходное напряжение батареи на рисунке 2 равно 12.0 В, а сопротивления равны R ₁ = 1,00 Ом, R ₂ = 6,00 Ом и R ₃ = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите ток. (c) Вычислите падение напряжения на каждом резисторе и покажите, как полученная сумма равна выходному напряжению источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)

Общее сопротивление — это просто сумма отдельных сопротивлений, определяемая следующим уравнением:

[латекс] \ begin {array} {lll} {R} _ {\ text {s}} & = & {R} _ {1} + {R} _ {2} + {R} _ {3} \ \ & = & 1.00 \ text {} \ Omega + 6.00 \ text {} \ Omega + 13.0 \ text {} \ Omega \\ & = & 20.0 \ text {} \ Omega \ end {array} \\ [/ latex].

Стратегия и решение для (b)

Ток определяется по закону Ома, В = IR . Ввод значения приложенного напряжения и общего сопротивления дает ток для цепи:

[латекс] I = \ frac {V} {{R} _ {\ text {s}}} = \ frac {12.0 \ text {V}} {20.0 \ text {} \ Omega} = 0.60 \ text {A }\\[/латекс].

Стратегия и решение для (c)

Напряжение — или падение IR — на резисторе определяется законом Ома.Ввод значения тока и значения первого сопротивления дает

.

В ₁ = ИК ₁ = (0,600 A) (1,0 Ом) = 0,600 В.

Аналогично

В ₂ = ИК ₂ = (0,600 A) (6,0 Ом) = 3,60 В

и

V3 = IR ₃ = (0,600 A) (13,0 Ом) = 7,80 В.

Обсуждение для (c)

Три капли IR в сумме дают 12.0 В, прогноз:

В ₁ + В ₂ + В ₃ = (0,600 + 3,60 + 7,80) В = 12,0 В.

Стратегия и решение для (d)

Самый простой способ рассчитать мощность в ваттах (Вт), рассеиваемую резистором в цепи постоянного тока, — использовать закон Джоуля , P = IV , где P — электрическая мощность. В этом случае через каждый резистор протекает одинаковый полный ток.Подставляя закон Ома В = IR в закон Джоуля, мы получаем мощность, рассеиваемую первым резистором, как

P ₁ = I ² R ₁ = (0,600 A) ² (1,00 Ом) = 0,360 Вт

Аналогично

P ₂ = I ² R ₂ = (0,600 A) ² (6,00 Ом) = 2,16 Вт

и

P ₃ = I ² R ₃ = (0.{2}} {R} \\ [/ latex], где В — это падение напряжения на резисторе (а не полное напряжение источника). Будут получены те же значения.

Стратегия и решение для (e)

Самый простой способ рассчитать выходную мощность источника — использовать P = IV , где В, — напряжение источника. Это дает

P = (0,600 A) (12,0 В) = 7,20 Вт.

Обсуждение для (e)

Обратите внимание, что по совпадению общая мощность, рассеиваемая резисторами, также равна 7.20 Вт, столько же, сколько мощность, выдаваемая источником. То есть

P ₁ + P ₂ + P ₃ = (0,360 + 2,16 + 4,68) W = 7,20 Вт

Мощность — это энергия в единицу времени (ватт), поэтому для сохранения энергии требуется, чтобы выходная мощность источника была равна общей мощности, рассеиваемой резисторами.

Основные характеристики резисторов серии

1. Последовательные сопротивления добавить: R _с = R ₁ + R ₂ + R ₃ +….
2. Одинаковый ток протекает последовательно через каждый резистор.
3. Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.

На рисунке 3 показаны резисторы параллельно , подключенные к источнику напряжения. Резисторы включены параллельно, когда каждый резистор подключен непосредственно к источнику напряжения с помощью соединительных проводов с незначительным сопротивлением. Таким образом, к каждому резистору приложено полное напряжение источника. Каждый резистор потребляет такой же ток, как если бы он один был подключен к источнику напряжения (при условии, что источник напряжения не перегружен).Например, автомобильные фары, радио и т. Д. Подключены параллельно, так что они используют полное напряжение источника и могут работать полностью независимо. То же самое и в вашем доме, или в любом другом здании. (См. Рисунок 3 (b).)

Рис. 3. (a) Три резистора, подключенных параллельно батарее, и эквивалентное одиночное или параллельное сопротивление. (б) Электроснабжение в доме. (Источник: Dmitry G, Wikimedia Commons)

Чтобы найти выражение для эквивалентного параллельного сопротивления R _p , давайте рассмотрим протекающие токи и их связь с сопротивлением.Поскольку каждый резистор в цепи имеет полное напряжение, токи, протекающие через отдельные резисторы, равны [латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} \\ [/ latex] , [латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} \\ [/ latex] и [латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} \\ [/ латекс]. Сохранение заряда подразумевает, что полный ток I , производимый источником, является суммой этих токов:

I = I ₁ + I ₂ + I ₃ .

Подстановка выражений для отдельных токов дает

[латекс] I = \ frac {V} {{R} _ {1}} + \ frac {V} {{R} _ {2}} + \ frac {V} {{R} _ {3}} = V \ left (\ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} \ справа) \\ [/ латекс].

Обратите внимание, что закон Ома для эквивалентного одиночного сопротивления дает

[латекс] I = \ frac {V} {{R} _ {p}} = V \ left (\ frac {1} {{R} _ {p}} \ right) \\ [/ latex].

Члены в скобках в последних двух уравнениях должны быть равны. Обобщая для любого количества резисторов, общее сопротивление R _p параллельного соединения связано с отдельными сопротивлениями на

[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ гидроразрыв {1} {{R} _ {\ text {.} 3}} + \ text {.} \ Text {…} \\ [/ latex]

Это соотношение приводит к общему сопротивлению R _p , которое меньше наименьшего из отдельных сопротивлений. (Это видно в следующем примере.) При параллельном подключении резисторов от источника течет больше тока, чем протекает по любому из них по отдельности, поэтому общее сопротивление ниже.

Пример 2. Расчет сопротивления, тока, рассеиваемой мощности и выходной мощности: анализ параллельной цепи

Пусть выходное напряжение батареи и сопротивления в параллельном соединении на Рисунке 3 будут такими же, как и в ранее рассмотренном последовательном соединении: В = 12.0 В, R ₁ = 1,00 Ом, R ₂ = 6,00 Ом и R ₃ = 13,0 Ом. а) Каково полное сопротивление? (б) Найдите полный ток. (c) Рассчитайте токи в каждом резисторе и покажите, как они складываются, чтобы равняться общему выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия и решение для (а)

Общее сопротивление для параллельной комбинации резисторов находится с помощью следующего уравнения.Ввод известных значений дает

[латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3}} = \ frac {1} {1 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {6 \ text {. } \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} \\ [/ latex].

Таким образом,

[латекс] \ frac {1} {{R} _ {p}} = \ frac {1.00} {\ text {} \ Omega} + \ frac {0 \ text {.} \ Text {1667}} {\ текст {} \ Omega} + \ frac {0 \ text {.} \ text {07692}} {\ text {} \ Omega} = \ frac {1 \ text {.} \ text {2436}} {\ text { } \ Omega} \\ [/ латекс].

(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.) Мы должны перевернуть это, чтобы найти полное сопротивление R _p . Это дает

[латекс] {R} _ {\ text {p}} = \ frac {1} {1 \ text {.} \ Text {2436}} \ text {} \ Omega = 0 \ text {.} \ Text { 8041} \ text {} \ Omega \\ [/ latex].

Суммарное сопротивление с правильным количеством значащих цифр составляет R _p = 0,804 Ом

Обсуждение для (а)

R _p , как и предполагалось, меньше наименьшего индивидуального сопротивления.

Стратегия и решение для (b)

Полный ток можно найти из закона Ома, заменив полное сопротивление R _p . Это дает

[латекс] I = \ frac {V} {{R} _ {\ text {p}}} = \ frac {\ text {12.0 V}} {0.8041 \ text {} \ Omega} = \ text {14} \ text {.} \ text {92 A} \\ [/ latex].

Обсуждение для (б)

Ток I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.

Стратегия и решение для (c)

Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом,

[латекс] {I} _ {1} = \ frac {V} {{R} _ {1}} = \ frac {12.0 \ text {V}} {1.00 \ text {} \ Omega} = 12.0 \ text {A} \\ [/ латекс].

Аналогично

[латекс] {I} _ {2} = \ frac {V} {{R} _ {2}} = \ frac {12.0 \ text {V}} {6.00 \ text {} \ Omega} = 2 \ text {.} \ text {00} \ text {A} \\ [/ latex]

и

[латекс] {I} _ {3} = \ frac {V} {{R} _ {3}} = \ frac {\ text {12} \ text {.} 0 \ text {V}} {\ text {13} \ text {.} \ Text {0} \ text {} \ Omega} = 0 \ text {.} \ Text {92} \ text {A} \\ [/ latex].

Обсуждение для (c)

Общий ток складывается из отдельных токов:

I ₁ + I ₂ + I ₃ = 14,92 A.

Это соответствует сохранению заряда.{2}} {13.0 \ text {} \ Omega} = 11.1 \ text {W} \\ [/ latex].

Обсуждение для (d)

Мощность, рассеиваемая каждым резистором при параллельном подключении, значительно выше, чем при последовательном подключении к тому же источнику напряжения.

Стратегия и решение для (e)

Общую мощность также можно рассчитать несколькими способами. Выбрав P = IV и введя полный ток, получим

.

P = IV = (14,92 A) (12,0 В) = 179 Вт.

Обсуждение для (e)

Суммарная мощность, рассеиваемая резисторами, также 179 Вт:

P ₁ + P ₂ + P ₃ = 144 Вт + 24,0 Вт + 11,1 Вт = 179 Вт

Это соответствует закону сохранения энергии.

Общее обсуждение

Обратите внимание, что как токи, так и мощность при параллельном подключении больше, чем для тех же устройств, подключенных последовательно.

Основные характеристики параллельных резисторов

1. Параллельное сопротивление определяется из [latex] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {1}} + \ frac {1} { {R} _ {2}} + \ frac {1} {{R} _ {3}} + \ text {…} \\ [/ latex], и оно меньше любого отдельного сопротивления в комбинации.
2. На каждый параллельно включенный резистор подается такое же полное напряжение источника. (В системах распределения электроэнергии чаще всего используются параллельные соединения для питания бесчисленных устройств, обслуживаемых одинаковым напряжением, и для того, чтобы они могли работать независимо.)
3. Параллельные резисторы не получают суммарный ток каждый; они делят это.

Сочетания последовательного и параллельного

Более сложные соединения резисторов иногда представляют собой просто комбинации последовательного и параллельного. Они часто встречаются, особенно если учесть сопротивление провода. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно. Комбинации последовательного и параллельного подключения можно свести к одному эквивалентному сопротивлению, используя методику, показанную на рисунке 4.Различные части идентифицируются как последовательные или параллельные, уменьшаются до их эквивалентов и далее уменьшаются до тех пор, пока не останется единственное сопротивление. Процесс более трудоемкий, чем трудный.

Рис. 4. Эта комбинация из семи резисторов имеет как последовательные, так и параллельные части. Каждый из них идентифицируется и уменьшается до эквивалентного сопротивления, а затем уменьшается до тех пор, пока не будет достигнуто одно эквивалентное сопротивление.

Самая простая комбинация последовательного и параллельного сопротивления, показанная на рисунке 4, также является наиболее поучительной, поскольку она используется во многих приложениях.Например, R ₁ может быть сопротивлением проводов от автомобильного аккумулятора к его электрическим устройствам, которые подключены параллельно. R ₂ и R ₃ могли быть стартером и светом салона. Ранее мы предполагали, что сопротивление провода незначительно, но, когда это не так, оно имеет важные последствия, как показывает следующий пример.

Пример 3. Расчет сопротивления,

IR Падение, ток и рассеиваемая мощность: объединение последовательных и параллельных цепей

На рис. 5 показаны резисторы из двух предыдущих примеров, подключенные другим способом — комбинацией последовательного и параллельного подключения.Мы можем считать R ₁ сопротивлением проводов, ведущих к R ₂ и R ₃ . (а) Найдите полное сопротивление. (b) Каково падение IR в R ₁ ? (c) Найдите текущие I ₂ через R ₂ . (d) Какую мощность рассеивает R ₂ ?

Рисунок 5. Эти три резистора подключены к источнику напряжения, так что R ₂ и R ₃ параллельны друг другу, и эта комбинация последовательно с R ₁ .

Стратегия и решение для (а)

Чтобы найти полное сопротивление, отметим, что R ₂ и R ₃ находятся параллельно, а их комбинация R _p находится последовательно с R ₁ . Таким образом, полное (эквивалентное) сопротивление этой комбинации составляет

.

R _итого = R ₁ + R _p .

Сначала мы находим R _p , используя уравнение для параллельных резисторов и вводя известные значения:

[латекс] \ frac {1} {{R} _ {\ text {p}}} = \ frac {1} {{R} _ {2}} + \ frac {1} {{R} _ {3 }} = \ frac {1} {6 \ text {.} \ text {00} \ text {} \ Omega} + \ frac {1} {\ text {13} \ text {.} 0 \ text {} \ Omega} = \ frac {0.2436} {\ text {} \ Омега} \\ [/ латекс].

Инвертирование дает

[латекс] {R} _ {\ text {p}} = \ frac {1} {0,2436} \ text {} \ Omega = 4.11 \ text {} \ Omega \\ [/ latex].

Таким образом, общее сопротивление равно

.

R _общ = R ₁ + R _p = 1,00 Ом + 4,11 Ом = 5,11 Ом.

Обсуждение для (а)

Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чистой параллели (20.0 Ом и 0,804 Ом соответственно), найденные для тех же резисторов в двух предыдущих примерах.

Стратегия и решение для (b)

Чтобы найти падение IR в R ₁ , отметим, что полный ток I протекает через R ₁ . Таким образом, его падение с IR равно

.

В ₁ = ИК ₁

Мы должны найти I , прежде чем сможем вычислить V ₁ .Полный ток I находится с помощью закона Ома для схемы. То есть

[латекс] I = \ frac {V} {{R} _ {\ text {tot}}} = \ frac {\ text {12.0} \ text {V}} {5.11 \ text {} \ Omega} = 2.35 \ text {A} \\ [/ latex].

Вводя это в выражение выше, мы получаем

В ₁ = ИК ₁ = (2,35 А) (1,00 Ом) = 2,35 В.

Обсуждение для (б)

Напряжение, приложенное к R ₂ и R ₃ , меньше полного напряжения на В ₁ .Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных R ₂ и R ₃ .

Стратегия и решение для (c)

Чтобы найти ток через R ₂ , мы должны сначала найти приложенное к нему напряжение. Мы называем это напряжение В _p , потому что оно приложено к параллельной комбинации резисторов. Напряжение, приложенное как к R ₂ , так и к R ₃ , уменьшается на величину В ₁ , и поэтому оно составляет

.

В _p = В — В ₁ = 12.0 В — 2,35 В = 9,65 В.

Теперь ток I ₂ через сопротивление R ₂ находится по закону Ома:

[латекс] {I} _ {2} = \ frac {{V} _ {\ text {p}}} {{R} _ {2}} = \ frac {9.65 \ text {V}} {6.00 \ текст {} \ Omega} = 1,61 \ text {A} \\ [/ latex].

Обсуждение для (c)

Ток меньше, чем 2,00 А, которые протекали через R ₂ , когда он был подключен параллельно к батарее в предыдущем примере параллельной цепи.

Стратегия и решение для (d)

Мощность, рассеиваемая R ₂ определяется

P ₂ = ( I ₂ ) ² R ₂ = (1,61 A) ² (6,00 Ом) = 15,5 Вт

Обсуждение для (d)

Мощность меньше 24,0 Вт, рассеиваемых этим резистором при параллельном подключении к источнику 12,0 В.

Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным.

Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).

То, что происходит в этих сильноточных ситуациях, показано на рисунке 6. Устройство, обозначенное как R ₃ , имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот повышенный ток вызывает большее падение IR в проводах, представленных R ₁ , уменьшая напряжение на лампе (которое составляет R ₂ ), которое затем заметно гаснет.

Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.

Проверьте свое понимание

Можно ли любую произвольную комбинацию резисторов разбить на последовательную и параллельную? Посмотрите, сможете ли вы нарисовать принципиальную схему резисторов, которые нельзя разбить на комбинации последовательно и параллельно.

Решение Нет, есть много способов подключения резисторов, которые не являются комбинациями последовательного и параллельного, включая петли и переходы. В таких случаях правила Кирхгофа, которые будут включены в Правила Кирхгофа, позволят вам проанализировать схему.

Стратегии решения проблем для последовательных и параллельных резисторов

1. Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает список известных проблем, поскольку они отмечены на вашей принципиальной схеме.
2. Точно определите, что необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
3. Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
4. Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей. Если ваша проблема представляет собой комбинацию последовательного и параллельного соединения, уменьшайте ее поэтапно, рассматривая отдельные группы последовательных или параллельных соединений, как это сделано в этом модуле и примерах. Особое примечание: при нахождении R необходимо соблюдать осторожность.
5. Проверьте, являются ли ответы разумными и последовательными. Единицы и числовые результаты должны быть разумными. Общее последовательное сопротивление должно быть больше, а общее параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и так далее.

Сводка раздела

Концептуальные вопросы

1. Переключатель имеет переменное сопротивление, которое почти равно нулю в замкнутом состоянии и очень велико в разомкнутом состоянии, и он включен последовательно с устройством, которым он управляет.Объясните влияние переключателя на рис. 7 на ток в разомкнутом и замкнутом состоянии.

Рис. 7. Выключатель обычно включается последовательно с источником сопротивления и напряжения. В идеале переключатель имеет почти нулевое сопротивление в замкнутом состоянии, но имеет чрезвычайно большое сопротивление в разомкнутом состоянии. (Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)

2. Какое напряжение на разомкнутом переключателе на Рисунке 7?

3. На разомкнутом переключателе есть напряжение, как на Рисунке 7.Почему же тогда мощность, рассеиваемая разомкнутым переключателем, мала?

4. Почему мощность, рассеиваемая замкнутым переключателем, как на Рисунке 7, мала?

5. Студент в физической лаборатории по ошибке подключил электрическую лампочку, батарею и выключатель, как показано на рисунке 8. Объясните, почему лампочка горит, когда выключатель разомкнут, и гаснет, когда он замкнут. (Не пытайтесь — батарея сильно разряжается!)

Рис. 8. Ошибка подключения. Включите этот переключатель параллельно устройству, обозначенному [латекс] R [/ латекс].(Обратите внимание, что на этой диаграмме скрипт E представляет напряжение (или электродвижущую силу) батареи.)

6. Зная, что сила удара зависит от величины тока, протекающего через ваше тело, вы бы предпочли, чтобы он был включен последовательно или параллельно с сопротивлением, таким как нагревательный элемент тостера, если он потрясен им? Объяснять.

7. Были бы ваши фары тусклыми при запуске двигателя автомобиля, если бы провода в вашем автомобиле были сверхпроводниками? (Не пренебрегайте внутренним сопротивлением батареи.) Объяснять.

8. Некоторые гирлянды праздничных огней соединены последовательно для экономии затрат на проводку. В старой версии использовались лампочки, которые при перегорании прерывали электрическое соединение, как открытый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и имеет 40 одинаковых лампочек, каково нормальное рабочее напряжение каждой? В более новых версиях используются лампы, которые при перегорании замыкаются накоротко, как замкнутый выключатель. Если одна такая лампочка перегорит, что случится с остальными? Если такая цепочка работает от 120 В и в ней осталось 39 идентичных лампочек, каково тогда рабочее напряжение каждой?

9.Если две бытовые лампочки мощностью 60 и 100 Вт подключить последовательно к бытовой электросети, какая из них будет ярче? Объяснять.

10. Предположим, вы проводите физическую лабораторию, в которой вас просят вставить резистор в цепь, но все прилагаемые резисторы имеют большее сопротивление, чем запрошенное значение. Как бы вы соединили доступные сопротивления, чтобы попытаться получить меньшее запрошенное значение?

11. Перед Второй мировой войной некоторые радиостанции получали питание через «шнур сопротивления», который имел значительное сопротивление.Такой резистивный шнур снижает напряжение до желаемого уровня для ламп радиоприемника и т.п., и это экономит расходы на трансформатор. Объясните, почему шнуры сопротивления нагреваются и тратят энергию при включенном радио.

12. У некоторых лампочек есть три уровня мощности (не включая ноль), получаемые от нескольких нитей накала, которые индивидуально переключаются и соединяются параллельно. Какое минимальное количество нитей нити необходимо для трех режимов мощности?

Задачи и упражнения

Примечание. Можно считать, что данные, взятые из цифр, имеют точность до трех значащих цифр.

1. (а) Каково сопротивление десяти последовательно соединенных резисторов сопротивлением 275 Ом? (б) Параллельно?

2. (a) Каково сопротивление последовательно соединенных резисторов 1,00 × 10 ² Ом, 2,50 кОм и 4,00 кОм? (б) Параллельно?

3. Какое наибольшее и наименьшее сопротивление можно получить, соединив резисторы на 36,0 Ом, 50,0 Ом и 700 Ом?

4. Тостер на 1800 Вт, электрическая сковорода на 1400 Вт и лампа на 75 Вт подключены к одной розетке в цепи 15 А, 120 В.(Три устройства работают параллельно, если подключены к одной розетке.) а) Какой ток потребляет каждое устройство? (b) Перегорит ли эта комбинация предохранитель на 15 А?

5. Фара мощностью 30,0 Вт и стартер мощностью 2,40 кВт обычно подключаются параллельно в систему на 12,0 В. Какую мощность потребляли бы одна фара и стартер при последовательном подключении к батарее 12,0 В? (Не обращайте внимания на любое другое сопротивление в цепи и любое изменение сопротивления в двух устройствах.)

6.(a) Учитывая батарею 48,0 В и резисторы 24,0 Ом и 96,0 Ом, найдите для каждого из них ток и мощность при последовательном соединении. (b) Повторите, когда сопротивления включены параллельно.

7. Ссылаясь на пример комбинирования последовательных и параллельных цепей и рисунок 5, вычислите I ₃ двумя следующими способами: (a) по известным значениям I и I ₂ ; (б) используя закон Ома для R ₃ . В обеих частях явно показано, как вы следуете шагам, описанным в Стратегии решения проблем для последовательных и параллельных резисторов выше.

Рисунок 5. Эти три резистора подключены к источнику напряжения, так что R ₂ и R ₃ параллельны друг другу, и эта комбинация последовательно с R ₁ .

8. Ссылаясь на рисунок 5: (a) Вычислите P ₃ и обратите внимание на его сравнение с P ₃ , найденным в первых двух примерах задач в этом модуле. (b) Найдите полную мощность, отдаваемую источником, и сравните ее с суммой мощностей, рассеиваемых резисторами.

9. См. Рисунок 6 и обсуждение затемнения света при включении тяжелого прибора. (a) Учитывая, что источник напряжения составляет 120 В, сопротивление провода составляет 0,400 Ом, а номинальная мощность лампы составляет 75,0 Вт, какая мощность будет рассеиваться лампой, если при включении двигателя через провода пройдет в общей сложности 15,0 А? Предположите незначительное изменение сопротивления лампы. б) Какая мощность потребляет двигатель?

Рис. 6. Почему гаснет свет при включении большого прибора? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.

10. Линия электропередачи 240 кВ с 5,00 × 10 ² подвешена к заземленным металлическим опорам с помощью керамических изоляторов, каждый из которых имеет сопротивление 1,00 × 10 ⁹ Ом (рис. 9 (а)). Какое сопротивление на землю у 100 изоляторов? (b) Рассчитайте мощность, рассеиваемую 100 из них. (c) Какая доля мощности, переносимой линией, составляет это? Ясно покажите, как вы следуете шагам, описанным в Стратегии решения проблем для последовательных и параллельных резисторов выше.

Рис. 9. Высоковольтная (240 кВ) линия электропередачи 5,00 × 10 ² подвешена к заземленной металлической опоре электропередачи. Ряд керамических изоляторов обеспечивает сопротивление 1,00 × 10 ⁹ Ом каждый.

11. Покажите, что если два резистора R ₁ и R ₂ объединены, и один из них намного больше другого ( R ₁ >> ​​ R ₂ ): (a ) Их последовательное сопротивление почти равно большему сопротивлению R ₁ .(б) Их параллельное сопротивление почти равно меньшему сопротивлению R ₂ .

12. Необоснованные результаты Два резистора, один из которых имеет сопротивление 145 Ом, подключены параллельно, чтобы получить общее сопротивление 150 Ом. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

13. Необоснованные результаты Два резистора, один из которых имеет сопротивление 900 кОм, соединены последовательно, чтобы получить общее сопротивление 0.500 МОм. а) Каково значение второго сопротивления? б) Что неразумного в этом результате? (c) Какие предположения необоснованны или непоследовательны?

Глоссарий

серия:

последовательность резисторов или других компонентов, включенных в цепь один за другим

резистор:

компонент, обеспечивающий сопротивление току, протекающему через электрическую цепь

сопротивление:

вызывает потерю электроэнергии в цепи

Закон Ома:

соотношение между током, напряжением и сопротивлением в электрической цепи: В = IR

напряжение:

электрическая потенциальная энергия на единицу заряда; электрическое давление, создаваемое источником питания, например аккумулятором

падение напряжения:

потеря электроэнергии при прохождении тока через резистор, провод или другой компонент

текущий:

поток заряда через электрическую цепь мимо заданной точки измерения

Закон Джоуля:

соотношение между потенциальной электрической мощностью, напряжением и сопротивлением в электрической цепи, определяемое следующим образом: [latex] {P} _ {e} = \ text {IV} [/ latex]

параллельно:

разводку резисторов или других компонентов в электрической цепи, так что каждый компонент получает одинаковое напряжение от источника питания; часто изображается на диаграмме в виде лестницы, где каждый компонент находится на ступеньке лестницы

Избранные решения проблем и упражнения

1.(а) 2,75 кОм (б) 27,5 Ом

3. (а) 786 Ом (б) 20,3 Ом

5. 29,6 Вт

7. (а) 0,74 А (б) 0,742 А

9. (а) 60,8 Вт (б) 3,18 кВт

11. (a) [латекс] \ begin {array} {} {R} _ {\ text {s}} = {R} _ {1} + {R} _ {2} \\ \ Rightarrow {R} _ {\ text {s}} \ приблизительно {R} _ {1} \ left ({R} _ {1} \ text {>>} {R} _ {2} \ right) \ end {array} \\ [/ латекс]

(b) [латекс] \ frac {1} {{R} _ {p}} = \ frac {1} {{R} _ {1}} + \ frac {1} {{R} _ {2} } = \ frac {{R} _ {1} + {R} _ {2}} {{R} _ {1} {R} _ {2}} \\ [/ latex],

, так что

[латекс] \ begin {array} {} {R} _ {p} = \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1} + {R} _ {2}} \ приблизительно \ frac {{R} _ {1} {R} _ {2}} {{R} _ {1}} = {R} _ {2} \ left ({R} _ {1 } \ text {>>} {R} _ {2} \ right) \ text {.} \ end {array} \\ [/ latex]

13. (a) –400 кОм (b) Сопротивление не может быть отрицательным. (c) Считается, что последовательное сопротивление меньше, чем у одного из резисторов, но должно быть больше, чем у любого из резисторов.

6.2 Последовательные и параллельные резисторы — Введение в электричество, магнетизм и схемы

ЦЕЛИ ОБУЧЕНИЯ

---

По окончании раздела вы сможете:

• Определите термин эквивалентное сопротивление
• Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
• Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно

В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора.По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где

. В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.

Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (рисунок 6.2.1). В схеме серии выходной ток первого резистора течет на вход второго резистора; следовательно, ток в каждом резисторе одинаков. В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора.Сумма отдельных токов равна току, протекающему по параллельным соединениям.

(рисунок 6.2.1)

Рисунок 6.2.1 (a) При последовательном соединении резисторов ток одинаков в каждом резисторе. (b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое.

Резисторы серии

Считается, что резисторы

включены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок 6.2.2, на котором показаны три последовательно включенных резистора с приложенным напряжением, равным

.Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.

(рисунок 6.2.2)

Рисунок 6.2.2 (a) Три резистора, последовательно подключенных к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.

На рисунке 6.2.2 ток, идущий от источника напряжения, протекает через каждый резистор, поэтому ток через каждый резистор одинаков.Ток в цепи зависит от напряжения, подаваемого источником напряжения, и сопротивления резисторов. Для каждого резистора происходит падение потенциала, равное потере электрической потенциальной энергии при прохождении тока через каждый резистор. Согласно закону Ома падение потенциала

на резисторе при протекании через него тока рассчитывается по формуле, где — ток в амперах (), а — сопротивление в омах (). Поскольку энергия сохраняется, а напряжение равно потенциальной энергии на заряд, сумма напряжения, приложенного к цепи источником, и падения потенциала на отдельных резисторах вокруг контура должны быть равны нулю:

Это уравнение часто называют законом петли Кирхгофа, который мы рассмотрим более подробно позже в этой главе.На рисунке 6.2.2 сумма падения потенциала каждого резистора и напряжения, подаваемого источником напряжения, должна равняться нулю:

Поскольку ток через каждый компонент одинаков, равенство можно упростить до эквивалентного сопротивления, которое представляет собой просто сумму сопротивлений отдельных резисторов.

Любое количество резисторов может быть подключено последовательно. Если резисторы

соединены последовательно, эквивалентное сопротивление равно

.

(6.2.1)

Одним из результатов включения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.

ПРИМЕР 6.2.1

---

Эквивалентное сопротивление, ток и мощность в последовательной цепи

Батарея с напряжением на клеммах

подключена к цепи, состоящей из четырех и одного последовательно соединенных резисторов (рисунок 6.2.3). Предположим, что батарея имеет незначительное внутреннее сопротивление. (а) Рассчитайте эквивалентное сопротивление цепи. (б) Рассчитайте ток через каждый резистор. (c) Рассчитайте падение потенциала на каждом резисторе. (d) Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.

(рисунок 6.2.3)

Рисунок 6.2.3 Простая последовательная схема с пятью резисторами.

Стратегия

В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.Ток в цепи можно найти из закона Ома и равен напряжению, деленному на эквивалентное сопротивление. Падение потенциала на каждом резисторе можно найти с помощью закона Ома. Мощность, рассеиваемая каждым резистором, может быть найдена с помощью

, а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, обеспечиваемую аккумулятором, можно найти с помощью.

Решение

а. Эквивалентное сопротивление — это алгебраическая сумма сопротивлений:

.

г.Ток в цепи одинаков для каждого резистора в последовательной цепи и равен приложенному напряжению, деленному на эквивалентное сопротивление:

г. Падение потенциала на каждом резисторе можно найти с помощью закона Ома:

Обратите внимание, что сумма падений потенциала на каждом резисторе равна напряжению, подаваемому батареей.

г. Мощность, рассеиваемая резистором, равна

, а мощность, отдаваемая батареей, равна:

Значение

Есть несколько причин, по которым мы могли бы использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи.Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов. Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.2

Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи.«Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серию по девять луковиц. Если перегорает слишком много лампочек, в конечном итоге открываются шунты. Что вызывает это?

Кратко обозначим основные характеристики последовательно соединенных резисторов:

Сопротивления серии
1. суммируются, чтобы получить эквивалентное сопротивление:

2. Одинаковый ток протекает последовательно через каждый резистор.
3. Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его.Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.

Параллельные резисторы

На рисунке 6.2.4 показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома

, где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в ​​вашем доме или любом здании.

(рисунок 6.2.4)

Рисунок 6.2.4 (a) Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.

Ток, протекающий от источника напряжения на рисунке 6.2.4, зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы

,

и. По мере того, как заряды проходят от батареи, некоторые проходят через резистор, а некоторые — через резистор.Сумма токов, текущих в переход, должна быть равна сумме токов, текущих из перехода:

Это уравнение называется правилом соединения Кирхгофа и будет подробно обсуждено в следующем разделе. На рисунке 6.2.4 правило соединения дает

. В этой схеме есть две петли, что приводит к уравнениям и Обратите внимание, что напряжение на резисторах, включенных параллельно, одинаковое (), а ток является аддитивным:

Если обобщить на любое количество резисторов

, эквивалентное сопротивление параллельного соединения связано с отдельными сопротивлениями на

(6.2.2)

Это соотношение приводит к эквивалентному сопротивлению

, которое меньше наименьшего из отдельных сопротивлений. Когда резисторы подключены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.

ПРИМЕР 6.2.2

---

Анализ параллельной цепи

Три резистора

,, и включены параллельно. Параллельное соединение подключается к источнику напряжения.а) Какое эквивалентное сопротивление? (б) Найдите ток, подаваемый источником в параллельную цепь. (c) Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника. (d) Рассчитайте мощность, рассеиваемую каждым резистором. (e) Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.

Стратегия

(a) Общее сопротивление для параллельной комбинации резисторов находится с использованием

.

(Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)

(b) Ток, подаваемый источником, можно найти по закону Ома, заменив полное сопротивление

.

(c) Отдельные токи легко вычислить по закону Ома

, поскольку каждый резистор получает полное напряжение. Полный ток — это сумма отдельных токов:.

(d) Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны.Давайте использовать

, так как каждый резистор получает полное напряжение.

(e) Полная мощность также может быть рассчитана несколькими способами, используйте

.

Решение

а. Общее сопротивление для параллельной комбинации резисторов находится с помощью уравнения 6.2.2. Ввод известных значений дает

Суммарное сопротивление с правильным количеством значащих цифр составляет

. Как и предполагалось, меньше минимального индивидуального сопротивления.

г. Полный ток можно найти из закона Ома, заменив полное сопротивление

. Это дает

Current

для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. Предыдущий пример). Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.

г. Отдельные токи легко вычислить по закону Ома, поскольку на каждый резистор подается полное напряжение.Таким образом,

Аналогично

и

Общий ток складывается из отдельных токов:

г. Мощность, рассеиваемую каждым резистором, можно найти с помощью любого из уравнений, связывающих мощность с током, напряжением и сопротивлением, поскольку все три известны. Давайте использовать

, так как каждый резистор получает полное напряжение. Таким образом,

Аналогично

и

e.Суммарную мощность также можно рассчитать несколькими способами. Выбрав

и введя общую текущую доходность

Значение

Общая мощность, рассеиваемая резисторами, также равна

:

Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.3

---

Рассмотрим одинаковую разность потенциалов

, приложенную к одним и тем же трем последовательно включенным резисторам.Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.4

---

Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?

Суммируем основные характеристики резисторов параллельно:

1. Эквивалентное сопротивление находится из

   и меньше любого отдельного сопротивления в комбинации.

2. Падение потенциала на каждом параллельном резисторе одинаковое.
3. Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.

В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Вы можете вспомнить, что в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно.Цепи часто содержат как конденсаторы, так и резисторы. В таблице 6.2.1 приведены уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательного и параллельного соединения.

(таблица 6.2.1)

	Комбинация серий	Параллельная комбинация
Эквивалентная емкость
Эквивалентное сопротивление

Таблица 10.1 Сводка по эквивалентному сопротивлению и емкости в последовательном и параллельном соединениях

Сочетания последовательного и параллельного

Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учесть сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.

Последовательные и параллельные комбинации можно уменьшить до одного эквивалентного сопротивления, используя методику, показанную на Рисунке 6.2.5. Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс более трудоемкий, чем трудный. Здесь мы отмечаем эквивалентное сопротивление как

.

(рисунок 6.2.5)

Обратите внимание, что резисторы

и

включены последовательно. Их можно объединить в одно эквивалентное сопротивление. Один из методов отслеживания процесса — включить резисторы в качестве индексов.Здесь эквивалентное сопротивление и равно

.

Теперь схема сокращается до трех резисторов, показанных на Рисунке 6.2.5 (c). Перерисовывая, теперь мы видим, что резисторы

и

составляют параллельную цепь. Эти два резистора можно уменьшить до эквивалентного сопротивления:

Этот шаг процесса сокращает схему до двух резисторов, показанных на Рисунке 6.2.5 (d). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно.Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:

Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.

Теперь мы можем проанализировать схему. Сила тока, обеспечиваемая источником напряжения, составляет

. Этот ток проходит через резистор и обозначен как. Падение потенциала можно найти с помощью закона Ома:

Глядя на рисунок 6.2.5 (c), остается отбрасывать

через параллельную комбинацию и. Проходной ток можно найти с помощью закона Ома:

Резисторы

и

включены последовательно, поэтому токи и равны

.

Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные падения —

и. Окончательный анализ заключается в рассмотрении мощности, подаваемой источником напряжения, и мощности, рассеиваемой резисторами.Мощность, рассеиваемая резисторами

Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет

. Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.

ПРОВЕРЬТЕ ПОНИМАНИЕ 6.5

---

Рассмотрите электрические цепи в вашем доме. Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.

Практическое применение

Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор. Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение

в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.

Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет.Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).

Что происходит в этих сильноточных ситуациях, показано на Рисунке 6.2.7. Устройство, представленное

, имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение в проводах, представленных значком, уменьшая напряжение на лампочке (которая есть), которое затем заметно гаснет.

(рисунок 6.2.7)

Рисунок 6.2.7 Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение напряжения в проводах и снижает напряжение на свету.

Стратегия решения проблем: последовательные и параллельные резисторы

---

1. Нарисуйте четкую принципиальную схему, обозначив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
2. Точно определите, что необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
3. Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно. Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
4. Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой — для параллелей.
5. Проверьте, являются ли ответы разумными и последовательными.

ПРИМЕР 6.2.4

---

Объединение последовательных и параллельных цепей

Два резистора, подключенных последовательно.

подключаются к двум резисторам, включенным параллельно. Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Ток проходит через резистор.Какое напряжение подается от источника напряжения?

Стратегия

Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.

Решение

1. Нарисуйте четкую принципиальную схему (рисунок 6.2.8).
   

   (рисунок 6.2.8)

   Рисунок 6.2.8 Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.
2. Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
3. В этой схеме мы уже знаем, что резисторы и включены последовательно, а резисторы и включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов и последовательно с последовательной конфигурацией резисторов и.
4. Напряжение, подаваемое батареей, можно найти, умножив ток от батареи на эквивалентное сопротивление цепи. Ток от аккумулятора равен току через него и равен.Нам нужно найти эквивалентное сопротивление, уменьшив схему. Чтобы уменьшить схему, сначала рассмотрите два резистора, включенных параллельно. Эквивалентное сопротивление составляет. Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление цепи равно. Таким образом, напряжение, подаваемое батареей, составляет.
5. Один из способов проверить соответствие ваших результатов — это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами. Мощность, подаваемая аккумулятором, составляет

   Так как они включены последовательно, ток через

   равен сквозному току.Т.к. ток через каждый будет. Мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором:
   

   
   Поскольку мощность, рассеиваемая резисторами, равна мощности, выделяемой батареей, наше решение кажется последовательным.

Значение

Если проблема имеет комбинацию последовательного и параллельного соединения, как в этом примере, ее можно уменьшить поэтапно, используя предыдущую стратегию решения проблемы и рассматривая отдельные группы последовательных или параллельных соединений.При поиске

для параллельного подключения необходимо соблюдать осторожность. Кроме того, единицы и числовые результаты должны быть разумными. Эквивалентное последовательное сопротивление должно быть больше, а эквивалентное параллельное сопротивление, например, должно быть меньше. Мощность должна быть больше для одних и тех же устройств, подключенных параллельно, по сравнению с последовательными и так далее.

Кандела Цитаты

Лицензионный контент CC, конкретная атрибуция

• Загрузите бесплатно по адресу http: // cnx.org/contents/[email protected]. Получено с : http://cnx.org/contents/[email protected]. Лицензия : CC BY: Attribution

электричество — Почему напряжение остается неизменным в параллельной цепи

Это заблуждение можно устранить с помощью самого определения.

Напряжение — это энергия, приходящаяся на один свободный электрон (которая способствует протеканию тока в проводнике), тогда как ток — это скорость потока свободных электронов через площадь поперечного сечения проводника.Другими словами, ток — это количество материала, который проходит через поперечное сечение в течение заданного периода времени, а напряжение — это то, что движет материалом.

Начисление — это сохраняемая величина. То, что вы воспринимаете как тепло, — это энергия частиц ¹ , движущихся со скоростью дрейфа (около нескольких миллиметров в секунду). Это просто напряжение, которое преобразуется в тепло. Свободные электроны не могут учуять и делиться соответственно в зависимости от сопротивления на каждом пути цепи. Это просто случайный поток.Они просто ходят по кругу, и когда встречается разделение пути, некоторые проходят одним путем, а некоторые — другим.

Чтобы копнуть глубже, давайте рассмотрим параллельную сеть, подобную этой (ABCDEFA). Батарея (DC) поддерживает разность потенциалов (насколько сейчас не имеет значения), которой достаточно для того, чтобы заряды ² начали течь. Эти заряды встречаются по пути на перекрестке B. Как уже говорилось ранее, нет никаких особых условий, которые перенаправляют платежи в какое-либо предпочтительное направление.Это просто случайно. Следовательно, некоторые идут по пути BE, а остальные идут через CD, чтобы добраться до батареи.

Скажите сопротивление $ R_2> R_1 $. Что случилось бы? Время, затрачиваемое зарядами на прохождение через $ R_2 $, больше, чем через $ R_1 $. Таким образом, в течение определенного периода времени из $ R_1 $ может быть снято много сборов, тогда как в случае $ R_2 $ их количество будет меньше. И это происходит в течение нескольких секунд после установления разности потенциалов, и поэтому мы понимаем, что ток через $ R_2 $ меньше, чем через $ R_1 $ (что является причиной того, что «ток делит в параллельных цепях). .

Когда заряды выходят из резисторов, электрического поля батареи достаточно, чтобы свести их с ума (поскольку провод имеет относительно более низкое сопротивление). И заряды снова получают свою энергию. По этой причине мы говорим, что напряжение в параллельных цепях одинаковое ³ .

---

^{1: Я упомянул «частицы» просто потому, что свободные электроны не обязательно движутся со скоростью дрейфа (что может привести к другому заблуждению). Они всегда на релятивистской скорости.Скорость дрейфа — это просто представление их вклада в текущий поток в макромасштабе …}

^{2: Грубо говоря, я просто использовал «заряды», потому что обычный ток течет от положительного к отрицательному, тогда как поток электронов — наоборот (что мне довольно сложно выразить). Под зарядами я имел в виду заряженные частицы.}

^{3: Также обратите внимание, что напряжение и ток остаются одинаковыми для резисторов с одинаковым сопротивлением независимо от того, подключены они параллельно или последовательно…}

Распределение тока и напряжения параллельно и последовательно

Вот краткое объяснение, чтобы знать о распределении тока и напряжения при последовательном и параллельном подключении.

Распределение тока при параллельном соединении: Когда все устройства соединены с использованием параллельного соединения, схема называется параллельной схемой. В параллельной схеме каждое устройство помещается в свою отдельную ветвь . Наличие ответвлений означает, что существует несколько путей, по которым заряд может проходить через внешнюю цепь.

Когда резисторы соединены параллельно, разность потенциалов на них равна, а ток делится обратно пропорционально их сопротивлению. Поскольку i = V / R, где i — ток, V — напряжение, а R — сопротивление, а для параллельной цепи V остается неизменным, поэтому i α V / R

Например: i₁: i₂: i₃ = ½: ⅓: ¼ = 6: 4: 3

так \ ({{i} _ {1}} = \ frac {6i} {6 + 4 + 3} = \ frac {6i} {13}; \, {{i} _ {2}} = \ frac {4i} {6 + 4 + 3} = \ frac {4i} {13}; \, {{i} _ {3}} = \ frac {3i} {6 + 4 + 3} = \ frac {3i} {13} \).

Распределение потенциала в последовательной цепи: когда резисторы соединены последовательно, сквозной ток одинаков, а потенциал распределяется в соотношении их сопротивлений, потому что V = iRAnd для тех же i, i α V / R

Например, V₁: V₂: V₃ = 2: 3: 4

Итак, \ ({{V} _ {1}} = \ left (\ frac {2} {2 + 3 + 4} \ right) V = \ frac {2V} {9} \).

\ ({{V} _ {2}} = \ left (\ frac {3} {2 + 3 + 4} \ right) V = \ frac {3V} {9}; \, {{V} _ { 3}} = \ left (\ frac {4} {2 + 3 + 4} \ right) V = \ frac {4V} {9} \).

Определение эквивалентной ЭДС более чем одной разнородной ячейки, соединенной параллельно : Предположим, что n элементов с ЭДС E₁, E₂… E _n и их внутренним сопротивлением r₁, r₂… r _n соединены параллельно, как показано.{-1}} \).

Для двух параллельных ячеек \ ({{E} _ {eq}} = \ frac {{{E} _ {1}} {{r} _ {2}} + {{E} _ {2}} { {r} _ {1}}} {{{r} _ {1}} + {{r} _ {2}}} \).

или \ ({{r} _ {eq}} = \ frac {{{r} _ {1}} {{r} _ {2}}} {{{r} _ {1}} + {{r } _ {2}}} \).

Обратите внимание, что положительные выводы всех ячеек находятся в одной точке, а отрицательные выводы — в другой общей точке. Если некоторые из ячеек имеют противоположное соединение, то \ ({{E} _ {eq}} = \ frac {\ frac {{{E} _ {1}}} {{{r} _ {1}}} — \ frac {{{E} _ {2}}} {{{r} _ {2}}} +… + \ frac {{{E} _ {n}}} {{{r} _ {n}} }} {\ frac {1} {{{r} _ {1}}} + \ frac {1} {{r} _ {2}}} +… + \ frac {1} {{{r} _ {n}}}} \).

\ (\ frac {1} {{{r} _ {eq}}} = \ frac {1} {{{r} _ {1}}} + \ frac {1} {{{r} _ {2 }}} +… \ Frac {1} {{{r} _ {n}}} \).

Подключение параллельной цепи

| CE

Параллельное подключение электрических элементов означает, что у каждого из них будет свой отдельный контур. Следовательно, есть несколько путей, по которым может течь ток.

Где
R ₁ и R ₂ : Резисторы
В: Источник напряжения
I ₁ , I ₂ и I ₃ : Значения тока

Напряжение в параллельной проводке

---

На схеме ниже каждый резистор подключается напрямую и независимо к источнику напряжения.Если бы какой-либо резистор был удален, создав разомкнутую цепь в одном из контуров, ток все равно мог бы течь через другой резистор. Общее падение напряжения в каждом контуре должно быть равно напряжению, подаваемому на контур. Следовательно, в схеме, подобной показанной ниже, где один источник напряжения подает напряжение на несколько нагрузок, подключенных параллельно, падение напряжения на каждой будет одинаковым.

Где
В: Источник напряжения
R ₁ и R ₂ : Резисторы
В ₁ и V ₂ : Падение напряжения на каждом резисторе

В = V ₁ = V ₂

Когда два источника напряжения подключены параллельно, положительный вывод одного источника подключается к положительному выводу другого.Таким образом, напряжения, обеспечиваемые каждым источником, не складываются друг с другом — напряжение, подаваемое в цепь, равно напряжению отдельных источников. Следовательно, источники напряжения, соединенные параллельно, должны иметь одинаковое напряжение.

Если два источника напряжения, подключенные параллельно выше, представляют собой 3-вольтовые фотоэлектрические модули, общее напряжение на резисторе составит 3 вольта. В этой конфигурации положительный (красный) вывод первого модуля подключен к положительному выводу следующего модуля, а отрицательный (черный) вывод первого — к отрицательному выводу следующего.Обратите внимание, что на схеме есть связь между положительной стороной двух источников и между отрицательной стороной. Независимо от того, сколько 3-вольтовых фотоэлектрических модулей соединено вместе в этой конфигурации, напряжение, подаваемое на резистор, всегда будет 3-вольтовым.

В _всего = V ₁ = V ₂ = V ₃ = … = V _n

Ток в параллельной проводке

---

In В параллельной цепи есть несколько путей, по которым может течь ток, и он будет делиться в соответствии с сопротивлением в каждой ветви.

No related posts.