Расчет полной мощности — Help for engineer
Расчет полной мощности
Полная мощность (S) образуется из двух составляющих:
— активная мощность (P) – выполняет полезную работу (полезная мощность), превращается в другие виды энергии (тепловая энергия: водонагреватель, утюг и т.д. являются активной нагрузкой)
— реактивная мощность (Q) – бывает индуктивная и емкостная, в зависимости от нагрузки в сети. Чаще всего дома мы используем индуктивную мощность, любой электрический прибор, где есть катушка, обмотки, является реактивной нагрузкой (электродрель, миксер, холодильник). Энергия не рассеивается на реактивных элементах, она на них за один полупериод накапливается и отдается обратно в сеть. Хотя без реактивной составляющей была бы невозможна работа многих электрических приборов, ее присутствие вызывает появление ряда негативных факторов:
| — нагрев проводников; | ||
| — влияние на сеть – добавление в нее реактивной составляющей, которая плохо сказывается в дальнейшем на потребителях. |
Конечно же между выше упомянутыми параметрами существуют зависимости. Расчет полной мощности осуществляется по следующей формуле:
 |
где U и I – действующие значения напряжения и тока соответственно.
Активная и реактивная мощности находятся в прямой зависимости с коэффициентом мощности (cosφ):
  |
Полная мощность дает потребителям все необходимые составляющие и рассчитывается:
 |
На рисунке ниже (треугольник мощностей) изображена зависимость полной мощности и ее составляющих от угла cosφ, который является углом сдвига между напряжением и током.

Единицы измерений приняты немного разные, хотя смысл их остается один и тот же, полная мощность измеряется в ВА (Вольт Ампер), активная мощность в Вт (Ватт), а реактивная в ВАр (Вольт Ампер реактивный).
Недостаточно прав для комментирования
h4e.ru
Полная мощность | Все формулы
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Полная мощность — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на её зажимах
Реактивная мощность связана с полной мощностью и активной :
Полная мощность — есть ничто иное как вся мощность. Она необходима для определения коэффициента мощности (отношение активной мощности к полной мощности)
Так же есть :
Реактивная мощность
Активная мощность тока
В формуле мы использовали :
— Полная мощность
— Напряжение цепи
— Сила тока
— Реактивная мощность
— Активная мощность
— Угол сдвига фаз
xn--b1agsdjmeuf9e.xn--p1ai
полная мощность — это… Что такое полная мощность?
- полная мощность
- по́лная мо́щность
(кажущаяся мощность) (эл.–техн.), величина, равная произведению действующих значений периодического электрического тока
* * *
ПОЛНАЯ МОЩНОСТЬПО́ЛНАЯ МО́ЩНОСТЬ (кажущаяся мощность), в электротехнике — величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на ее зажимах. Для синусоидального тока равна
,
где P и Q — активная и реактивная мощности. Единица измерения — В.А.
Энциклопедический словарь. 2009.
- полная вода
- полное внутреннее отражение
Смотреть что такое «полная мощность» в других словарях:
Полная мощность — Длительная эффективная мощность двигателя, назначаемая и гарантируемая изготовителем при заданной частоте вращения двигателя, заданных окружающих условиях, полной комплектности и рабочих условиях, для которых предназначен дизель, устанавливаемая… … Словарь-справочник терминов нормативно-технической документации
полная мощность — Величина, равная произведению действующих значений электрического напряжения и электрического тока на входе двухполюсника. [ГОСТ Р 52002 2003] полная мощность Произведение действующих значений напряжения и тока, относящихся к одному и тому же… … Справочник технического переводчика
ПОЛНАЯ МОЩНОСТЬ — (кажущаяся мощность) в электротехнике величина, равная произведению действующих значений периодического электрического тока I в цепи и напряжения U на ее зажимах. Для синусоидального тока равна,где P и Q активная и реактивная мощности. Единица… … Большой Энциклопедический словарь
полная мощность — суммарная мощность Словарь русских синонимов … Словарь синонимов
полная мощность — pilnutinė galia statusas T sritis fizika atitikmenys: angl. total power vok. Gesamtleistung, f; Totalleistung, f rus. общая мощность, f; полная мощность, f; суммарная мощность, f pranc. puissance totale, f … Fizikos terminų žodynas
полная мощность — pilnutinė galia statusas T sritis automatika atitikmenys: angl. apparent power; total power vok. Gesamtleistung, f; Scheinleistung, f; Totalleistung, f rus. кажущаяся мощность, f; полная мощность, f pranc. puissance apparente, f; puissance totale … Automatikos terminų žodynas
полная мощность — pilnutinė galia statusas T sritis Standartizacija ir metrologija apibrėžtis Dydis, išreiškiamas efektinės įtampos ir efektinio srovės stiprio sandauga: S = U · I; čia U – efektinė įtampa, I – efektinis srovės stipris, S – pilnutinė galia.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
полная мощность — pilnutinė galia statusas T sritis Standartizacija ir metrologija apibrėžtis Kompleksinės galios modulis. Matavimo vienetas – voltamperas (V · A). atitikmenys: angl. apparent power; total power vok. Gesamtleistung, f; Scheinleistung, f;… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
Полная мощность — кажущаяся мощность, величина, равная произведению действующих значений периодического электрического тока в цепи I и напряжения U на её зажимах: S=U․I; для синусоидального тока (в комплексной форме) комплексное действующее значение… … Большая советская энциклопедия
ПОЛНАЯ МОЩНОСТЬ — см. в ст. Мощность электрическая … Большой энциклопедический политехнический словарь
dic.academic.ru
Мощность переменного тока ⚡ определение, формула, виды, обозначение и единицы измерения, баланс мощностей в цепи переменного тока, примеры вычислений

Общее понятие
Электрическое напряжение определяется как отношение работы поля по переброске пробного заряда из одной заданной точки в другую к размеру потенциала. При дислокации единичного резерва выполняется работа, которая равняется напряжению на искомом участке. Общая мощность получают умножением работы электрического поля для единичного заряда на число потенциалов за определенную единицу времени.
В переменной электрической цепи выделяется 3 вида мощности:
- активный P;
- реактивный Q;
- полного типа S.
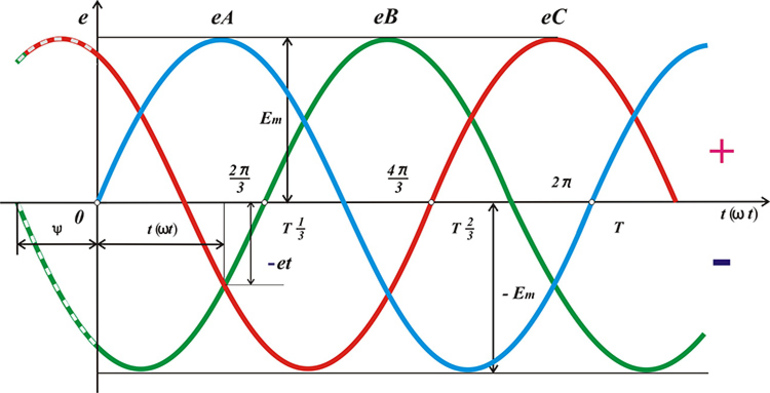
В цепи переменного электричества формула для расчета постоянного тока применяется только для вычисления мгновенной мощности. Этот показатель претерпевает изменения во времени и почти не имеет практического смысла для всех остальных расчетов. Среднезначимый показатель мощности требует временной интеграции. Мгновенная мощность объединяется в течение определенного промежутка для расчета величины в магистрали с периодическим изменением силы переменного потока и синусоидального напряжения.
Применяется концепция комплексных чисел для связывания всех трех видов мощности. Это понятие обозначает, что в переменной цепи нагрузка выражается подобным числом так, что активная разновидность представляется действительной составляющей. Реактивный показатель выступает мнимым показателем, а полная мощность показывается в форме модуля. В этих расчетах принимает участие угол сдвига фаз φ, который является аргументом баланса мощностей в цепи переменного тока.
Активная мощность
Активная скорость преобразования выражается также через взаимное отношение силы потока, напряжения к значению активной составляющей сопротивления. В магистрали синусоидального и несинусоидального движения электронов активная нагрузка приравнивается к сумме аналогичных значений на отдельных участках.
Для определения среднего периодического размера используется активная мощность переменного тока, формула расчета P = U . I . cos φ (косинус), где:
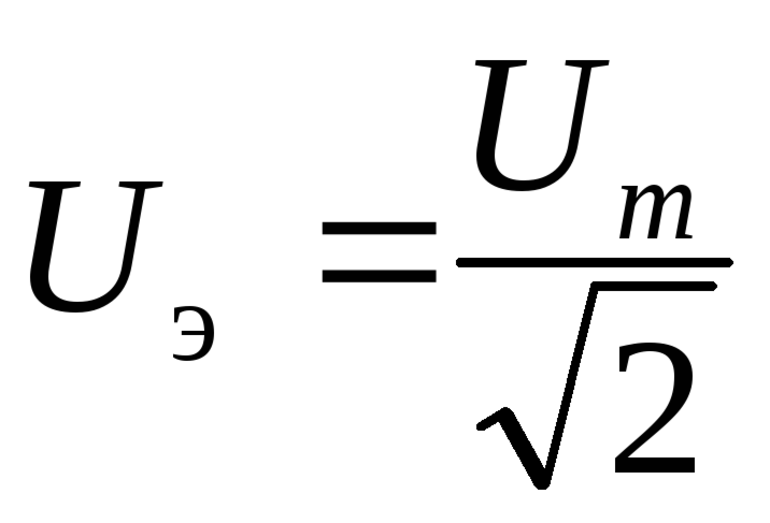
- U — мощность.
- I — сила потока.
- φ — угол смещения фаз.
Средний показатель мгновенной скорости преобразования в однофазной цепи берется в виде среднеквадратичного значения тока и напряжения с определенным углом сдвига. В цепях несинусоидального электричества мощность приравнивается к сумме соответствующих показателей отдельных перемещений. С помощью активной мощности характеризуется интенсивность необратимого видоизменения электроэнергии в другие разновидности, например, электромагнитную или тепловую.
Проходящая мощность используется в качестве активной в концепции длинных магистралей для анализа электромагнитных течений, протяженность которых сопоставляется с размерностью волны. Искомое значение рассчитывается как разница между понижающейся и отражающейся мощностями. От свойств коэффициента углового смещения зависят полученные показатели отрицательной или положительной нагрузки активного типа.
Реактивная характеристика
Для обозначения применяется дополнительно единица вольт-ампер реактивный (вар). В русских аналогах используется вар, а международные специалисты применяют var. В РФ единица допускается для электротехнических расчетов в форме внесистемного значения.
Нахождение производится по формуле P = U . I . sin φ (синус), где:
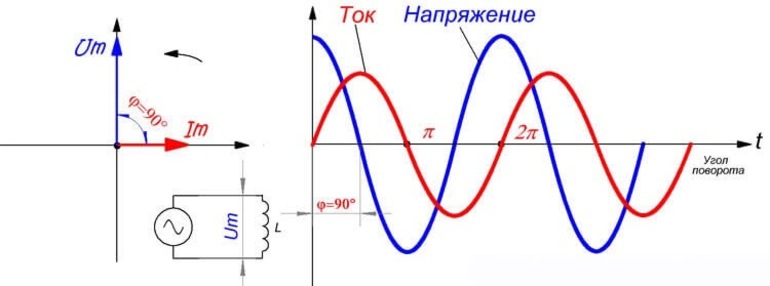
- U — среднеквадратичная мощность.
- I — среднеквадратичная сила потока.
- φ — угол фазного смещения, значения синуса, определяются по таблицам.
При диапазоне показателя от 0 до 90º (ток отстает от напряжения, а нагрузка носит активно-индуктивный вид) синус φ будет иметь положительное значение. При угловом сдвиге от 0 до -90º (поток электронов опережает нагрузку, мощность отличается активно-емкостным свойством) константа всегда показывает отрицательный знак. Реактивная мощность характеризует напряженность, которая возникает в электромеханических приборах и цепях при изменении энергетических волн поля в магистрали переменного синусоидального потока.
В физическом смысле реактивная нагрузка показывает энергию, которая перекачивается от источника тока на конденсаторы, индукторы, двигательные обмотки, а впоследствии возвращается к источнику за один колебательный период. Реактивная мощность не принимает участия в работе электротока. В случае положительной характеристики устройство потребляет, а нагрузка с отрицательным знаком говорит о производстве энергии.

Это обстоятельство рассматривается в условном контексте, т. к. почти все энергопотребляющие приборы, например, двигатели асинхронной работы, а также полезная нагрузка, подаваемая через трансформатор, относятся к активно-индуктивным видам. Синхронные двигатели электростанций одновременно производят и потребляют энергию в зависимости от максимальной величины электротока возбуждения в роторных обмотках. Эта особенность применяется для координации уровня нагрузки в магистрали в электротехнике.
С помощью современных преобразователей производится компенсация реактивной нагрузки во избежание перегрузок и для увеличения коэффициента мощности электроустановок. Приборы более точно оценивают размер энергии, которая поступает в обратном направлении от индуктора к источнику переменного тока.
Полная нагрузка
Показатель используется в физике для описания потребляемой мощности, которая прилагается к подводящим агрегатам электросети с использованием резисторов. Суммируются параметры ЭДС распределительных щитков, кабелей, проводов, ЛЭП, трансформаторов.
Полную нагрузку можно рассчитать по формуле S = U . I, где:
- S — параметр полной нагрузки (В/а).
- U — расчетная нагрузка в генераторе.
- I — комплексный показатель силы тока в сочетании с обмоточным значением.
Параметр темпа преобразований зависит от характеристик применяемого тока, а не от свойств фактически использованной нагрузки. По этой причине полная мощность распределительных электрощитов и трансформаторных агрегатов измеряется в вольт-амперах, а значение ватт к ней не применяется.
Работа в различных условиях
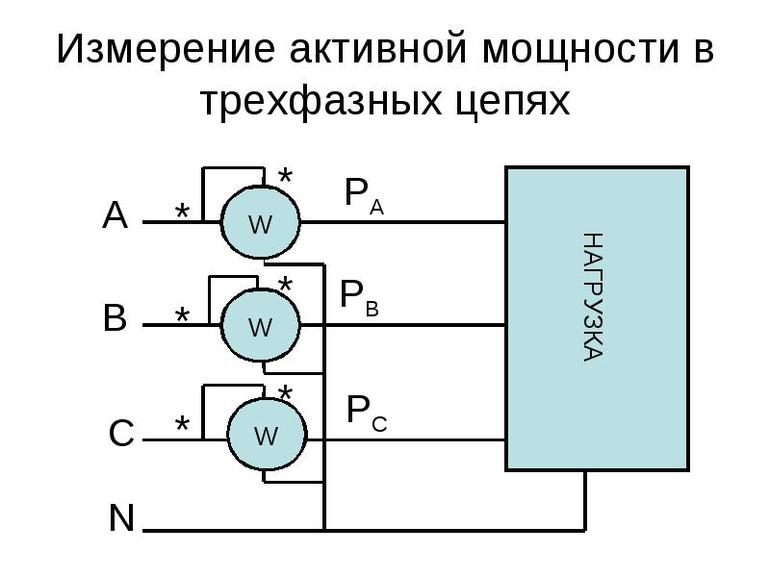
Модуль комплексного показателя интенсивности передвижения равняется показателю полной нагрузки. Действительная составляющая часть приравнивается к активной силе, а мнимая считается реактивным видом. Имеет место положительный или отрицательный знак, что зависит от интенсивности загруженности цепи. Комплексная мощность должна соответствовать сопряженному электрическому сопротивлению. Положительная нагрузка характеризуется соотношением Р > 0, а знак минус проявляется в случае Р < 0.
Измерение мощностных характеристик переменного потока электронов проводится при пропускании равного по значению тока по фазным проводникам. Показатели силы течения заряженных частиц с применением нулевого проводника имеют ничтожную размерность. Равномерная или симметричная фазовая нагрузка в трехфазной магистрали зависит от величины протекающих токов. Неравномерная или несимметричная нагрузка зависит от прохождения потока по нейтральным или нулевым кабелям. Общий мощностной уровень находится суммированием.
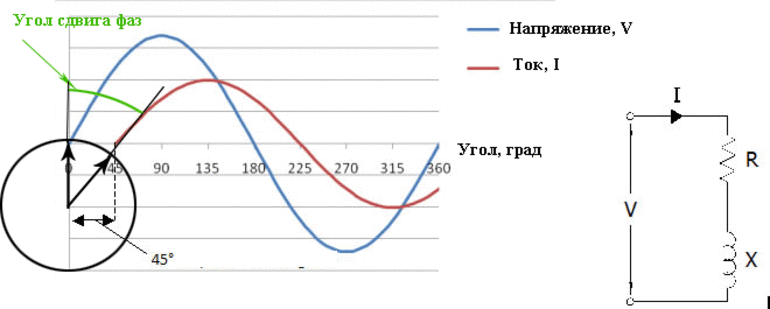
Если присутствует фазовый сдвиг между напряжением и силой тока, то он совпадает с углом смещения между векторными радиусами показателей электротока. В условиях переменного напряжения совпадение векторных радиусов тока и вольтажа отмечается только при отсутствии в цепи конденсаторов и катушек индукции. Установка индукторов не мешает совпадению фазных значений. При этом происходит векторное вращение равной интенсивности. График смещения внутреннего угла остается постоянным.
Если в магистрали происходит сдвиг напряжения и переменного тока, то мощностные показатели представляются значением с отрицательным знаком, так как калькулятор перемножает положительные и отрицательные величины. Продолжительность периодов зависит от уровня смещения фаз. При этом длительность отрицательных нагрузок определяет характеристики сдвига. При расчетах используются показатели сопротивления, которые знакомы из физического закона Ома.
Коэффициент скорости преобразования

Мощностной коэффициент является показателем потребления тока при присутствии реактивного компонента и искажающей нагрузки. Значение коэффициента отличается от понятия косинуса сдвигаемого угла. Второе понятие характеризуется смещением протекающего переменного тока, напряжения и используется только при синусоидальном токе и силе равного значения.
Коэффициент равняется отношению расходуемой нагрузки к ее полному значению. При этом работа совершается за счет активного вида преобразования. При синусоидальном токе и вольтаже полная нагрузка находится в виде суммы реактивной и активной форм. Активная нагрузка приравнивается к усредненному произведению силы тока и напряжения и не может быть выше произведения аналогичных среднеквадратических размерностей. Мощностной коэффициент показывается в диапазоне от 0 до 1 или ставится в процентах от 0 до 100.
При математическом расчете числовой множитель интерпретируется в качестве косинуса угла между токовыми векторами и направлением приложения вольтажа. Поэтому при синусоидальных характеристиках размерность коэффициента может совпадать с косинусом угла. Если применяется только синусоидальный вольтаж, а ток используется несинусоидальный с нагрузкой без реактивного компонента, то числовой переходник равняется части нагрузки при первых искажениях потребительского тока.
Если реактивный элемент присутствует в нагрузке, то, помимо мощностного коэффициента, указывается характер работы (емкостно-активный или индуктивно-активный). Коэффициент в этих случаях отличается и является отстающим или опережающим значением.
Практическое применение и коррекция
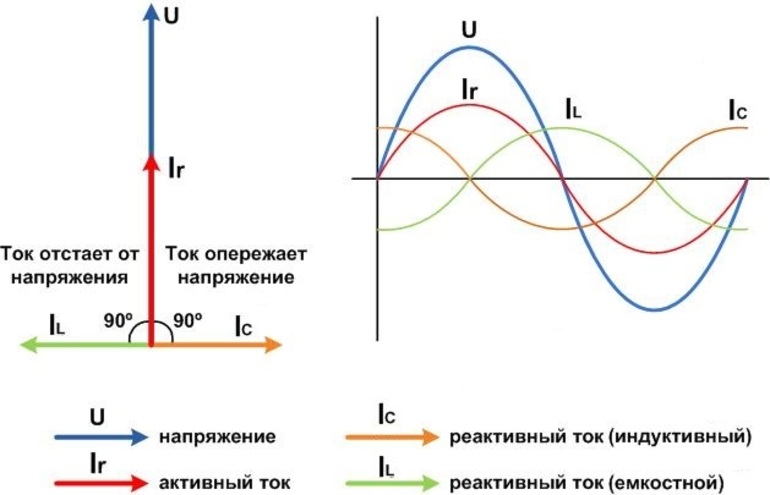
Если к розетке с синусоидальным напряжением 50 Гц и 230 В подсоединить нагрузку с опережением или отставанием тока от напряжения на какую-то угловую величину, то на активной внутренней катушке будет создаваться увеличенная мощность. Это значит, что при работе в таких условиях выделяется много тепла, и электростанция отводит его в увеличенном количестве, по сравнению с применением активной нагрузки.
Коэффициенты полезного действия и мощности отличаются друг от друга. Мощностной показатель не влияет на потребление приемника, подключенного к сети, но изменяет энергетические потери в подводных проводах и местах выработки энергии или ее преобразования. В доме электросчетчик не реагирует на проявление мощности, так как оплачивается только та энергия, за счет которой работают приборы.
КПД влияет на потребляемую активную нагрузку. Например, энергосберегающая лампа потребляет в полтора раза больше электричества, чем аналогичный прибор накаливания. Это говорит о высоком коэффициенте полезного действия у первой лампы. Но показатель нагрузки может быть низким и высоким в обоих вариантах.
Коррекция заключается в приведении потребления прибора с низким мощностным коэффициентом к стандартным показателям при питании от силовой цепи переменного тока. Технически это осуществляется применением действенной схемы на входном устройстве, которая помогает равномерно использовать фазную мощность и исключает перегрузку нулевого провода. При этом снижаются всплески потребительского тока на верхушке синусоиды питающего вольтажа.
Реактивная нагрузка корректируется при включении в магистраль элемента с обратным действием. Например, в двигателе переменного тока для компенсации действия ставится конденсатор параллельно питающей линии. Применяется система активного или пассивного корректора при изменении используемого тока во время колебательного периода подпитывающего напряжения для преобразования коэффициента. Простым примером является последовательное подключение дросселя. При этом конечные приборы потребляют ток непропорционально гармоничным искажениям. Катушка сглаживает волновые импульсы.
nauka.club
Репетитор-онлайн — подготовка к ЦТ
Пример 15. При замыкании на сопротивление 5,0 Ом батарея элементов дает ток силой 2,0 А. Ток короткого замыкания батареи равен 12 А. Рассчитать наибольшую полезную мощность батареи.
Решение. Проанализируем условие задачи.
1. При подключении батареи к сопротивлению R 1 = 5,0 Ом в цепи течет ток силой I 1 = 2,0 А, как показано на рис. а, определяемый законом Ома для полной цепи:
I1=ℰR1+r,
где ℰ — ЭДС источника тока; r — внутреннее сопротивление источника тока.
2. При замыкании батареи накоротко в цепи течет ток короткого замыкания, как показано на рис. б. Сила тока короткого замыкания определяется формулой
i=ℰr,
где i — сила тока короткого замыкания, i = 12 А.
3. При подключении батареи к сопротивлению R 2 = r в цепи течет ток силой I 2, как показано на рис. в, определяемый законом Ома для полной цепи:
I2=ℰR2+r=ℰ2r;
в этом случае в цепи выделяется максимальная полезная мощность:
Pполезнmax=I22R2=I22r.
Таким образом, для расчета максимальной полезной мощности необходимо определить внутреннее сопротивление источника тока r и силу тока I 2.
Для того чтобы найти силу тока I 2, запишем систему уравнений:
i=ℰr,I2=ℰ2r}
и выполним деление уравнений:
iI2=2.
Отсюда следует:
I2=i2=122=6,0 А.
Для того чтобы найти внутреннее сопротивление источника r, запишем систему уравнений:
I1=ℰR1+r,i=ℰr}
и выполним деление уравнений:
I1i=rR1+r.
Отсюда следует:
r=I1R1i−I1=2,0⋅5,012−2,0=1,0 Ом.
Рассчитаем максимальную полезную мощность:
Pполезнmax=I22r=6,02⋅1,0=36 Вт.
Таким образом, максимальная полезная мощность батареи составляет 36 Вт.
vedy.by
2.4. Активная, реактивная и полная мощности. Баланс мощностей
Мгновенной мощностью называют произведение мгновенного напряжения на входе цепи на мгновенный ток. Пусть напряжение и ток являются синусоидальными функциями времени:
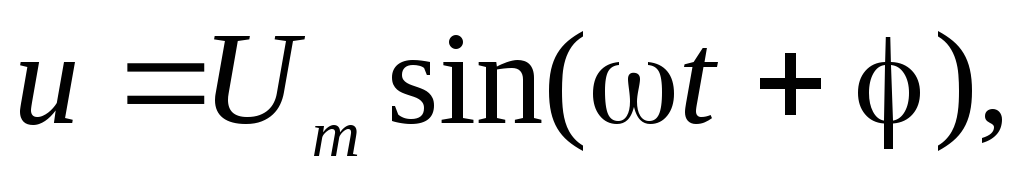
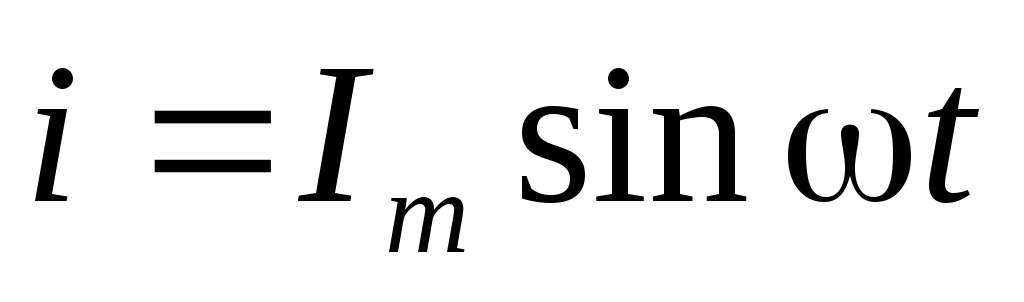 .
.
Получим
выражение для мгновенной мощности: 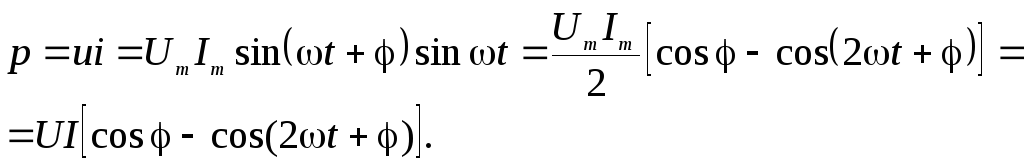 (2.29)
(2.29)
Из
(2.29) следует, мгновенная мощность
изменяется с частотой 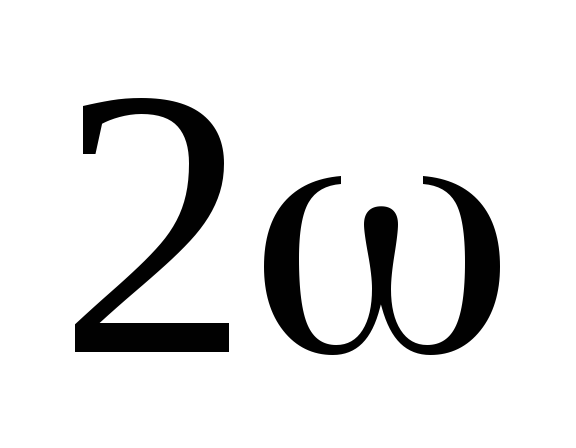 ,
в два раза превышающей частоту тока и
напряжения.
,
в два раза превышающей частоту тока и
напряжения.
Среднее значение мгновенной мощности за период T называют активной мощностью и обозначают буквой P:
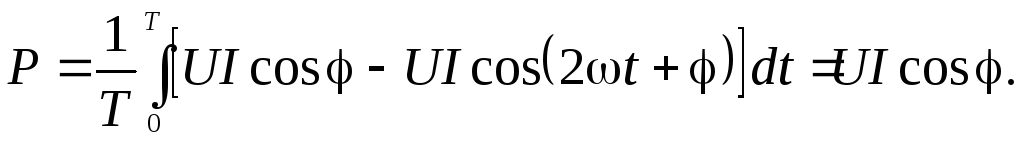 (2.30)
(2.30)
При
выводе (2.30) учтено равенство 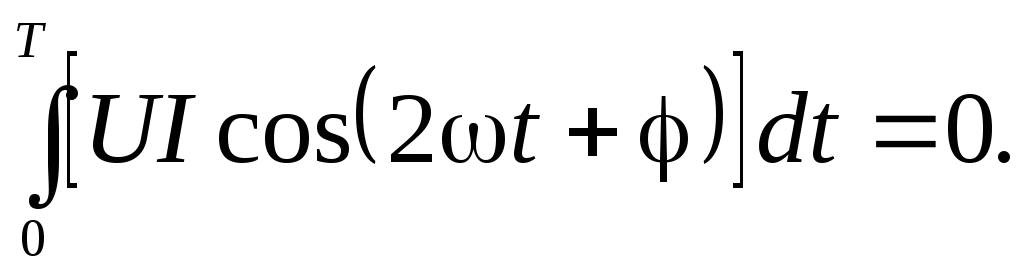
Учитывая
из треугольника сопротивлений (рис.2.15)
соотношение 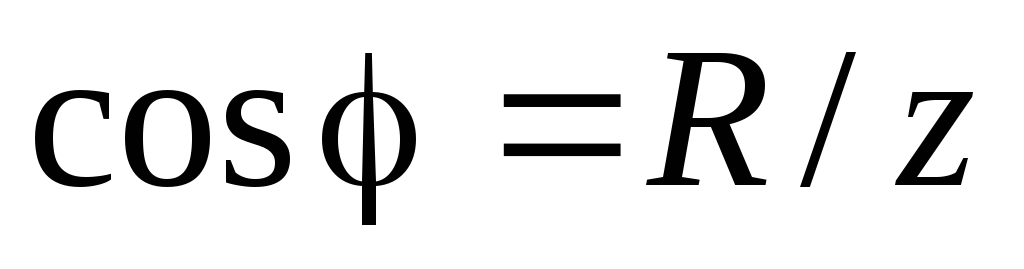 и из треугольника проводимостей
(рис.2.16)
и из треугольника проводимостей
(рис.2.16)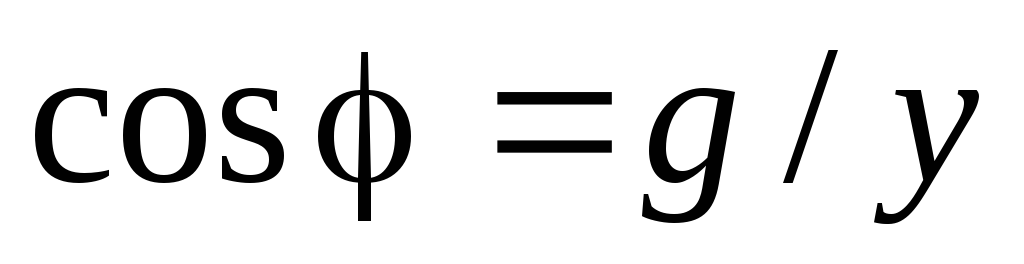 ,
получаем из (2.30) следующие выражения
для активной мощности:
,
получаем из (2.30) следующие выражения
для активной мощности:
 (2.31)
(2.31)
Активная мощность измеряется в ваттах (Вт) и характеризует необратимое преобразование электрической энергии, которая выделяется в виде теплоты на участках цепи в активных сопротивлениях. В электрических двигателях потребляемая из сети активная мощность преобразуется в механическую мощность (за вычетом потерь в процессе преобразования) и является их основной характеристикой.
Множитель 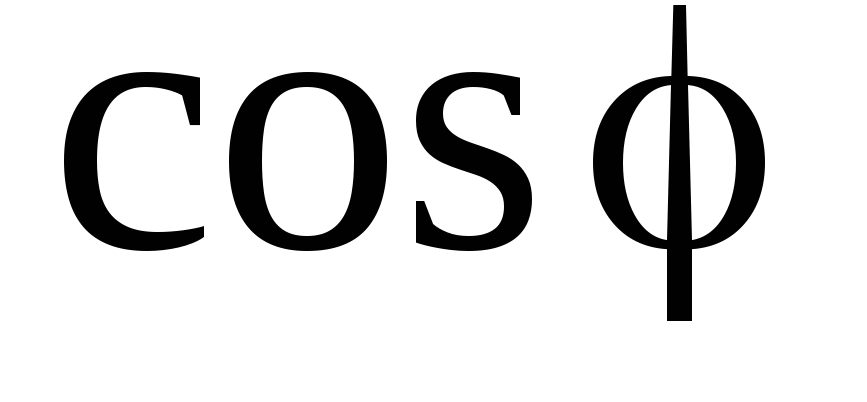 называется коэффициентом мощности.
Коэффициент мощности является
одной из важнейших характеристик
электротехнических устройств, и повышение
его до предельного значения
называется коэффициентом мощности.
Коэффициент мощности является
одной из важнейших характеристик
электротехнических устройств, и повышение
его до предельного значения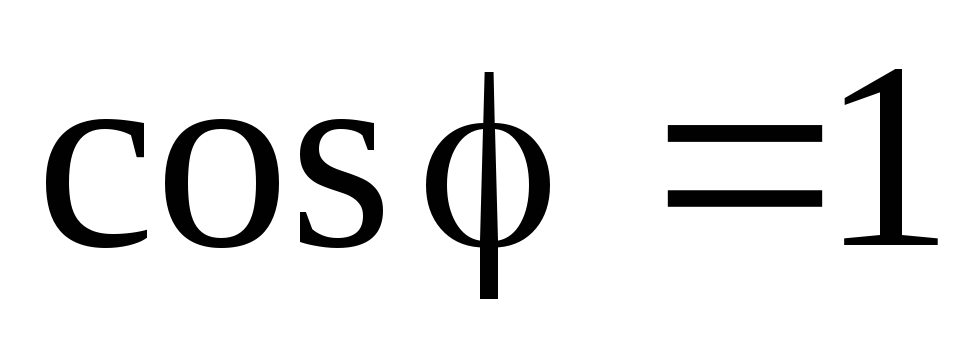 остается одной из основных задач
энергосбережения.
остается одной из основных задач
энергосбережения.
Рассмотрим
идеальные реактивные элементы
(индуктивность и емкость). Активная
мощность в этих элементах равна нулю,
так как напряжение и ток в индуктивности
или емкости различаются по фазе на 90o и 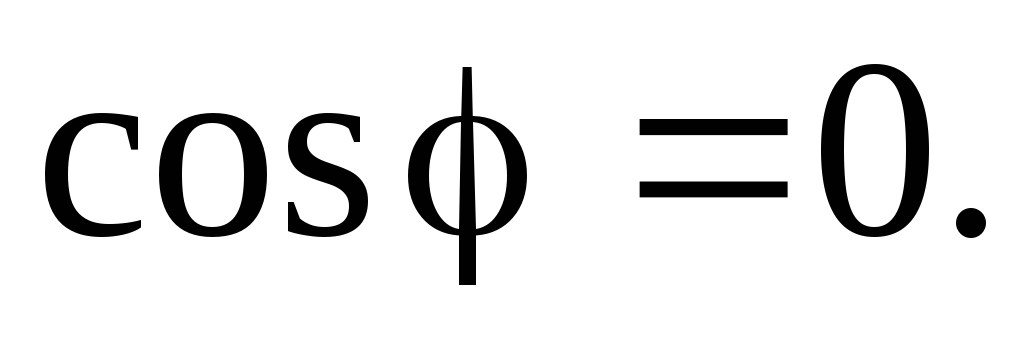
В реактивных элементах отсутствуют необратимые потери электрической энергии, не происходит нагрева элементов. Происходит обратимый процесс в виде обмена электрической энергией между источником и приемником. Для качественной оценки интенсивности обмена энергией вводится понятие реактивной мощности Q.
Преобразуем выражение (2.29) для мгновенной мощности:
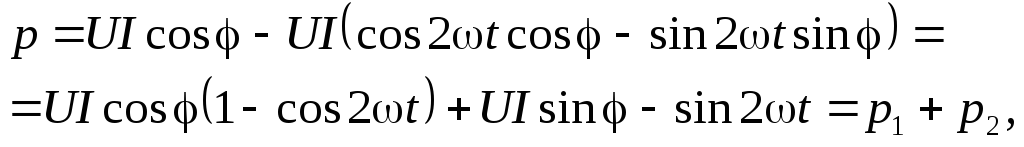
где 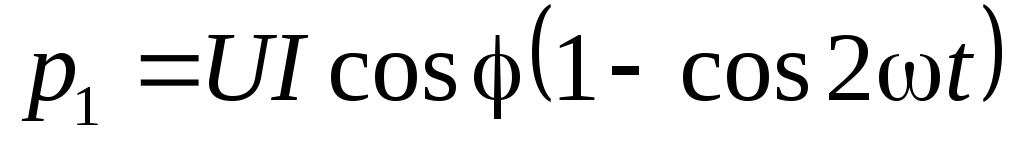 —
мгновенная мощность в активном
сопротивлении;
—
мгновенная мощность в активном
сопротивлении;
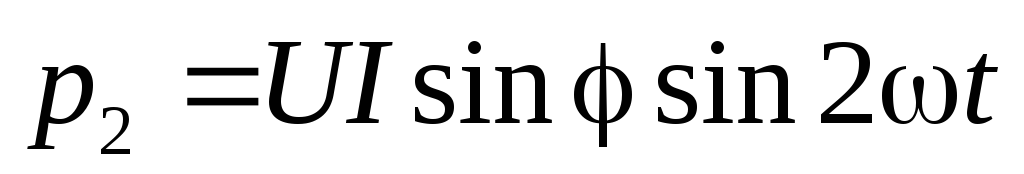 —
мгновенная мощность в реактивном
элементе (в индуктивности или в емкости).
—
мгновенная мощность в реактивном
элементе (в индуктивности или в емкости).
Максимальное или амплитудное значение мощности p2 называется реактивной мощностью:
Q =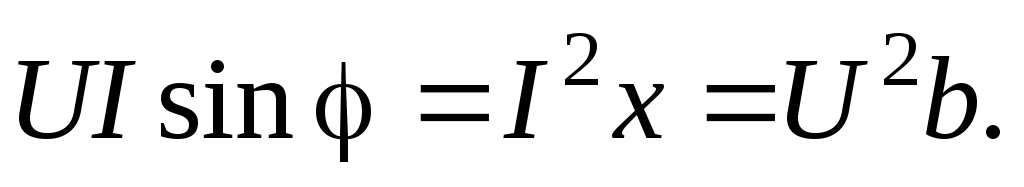
 (2.32)
(2.32)
где x, b – соответственно реактивные сопротивление и проводимость. Реактивная мощность измеряется в вольт-амперах реактивных (ВАр) и расходуется на создание магнитного поля в индуктивности или электрического поля в емкости. Энергия, накопленная в емкости или в индуктивности, периодически возвращается источнику питания.
Амплитудное значение суммарной мощности p = p1 + p2 называется полной мощностью. Полная мощность, измеряемая в вольт-амперах (ВА), равна произведению действующих значений напряжения и тока:
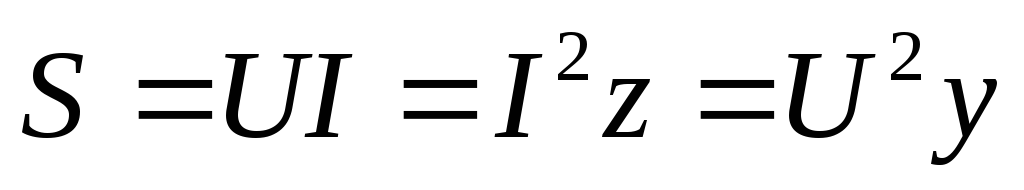 .
(2.33)
.
(2.33)
Возьмем треугольник сопротивлений (рис.2.15) и умножим его стороны на квадрат тока в цепи. Получим подобный треугольник мощностей (рис. 2.17).
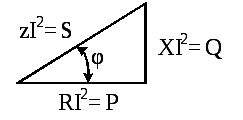
Рис. 2.17
Из треугольника мощностей получим соотношения между мощностями P, Q, S:
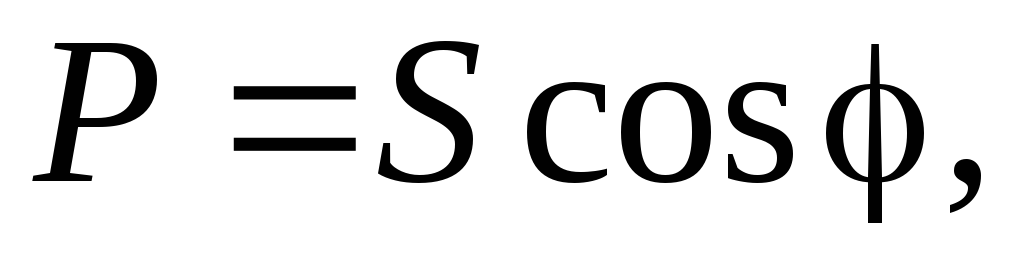 Q
=
Q
=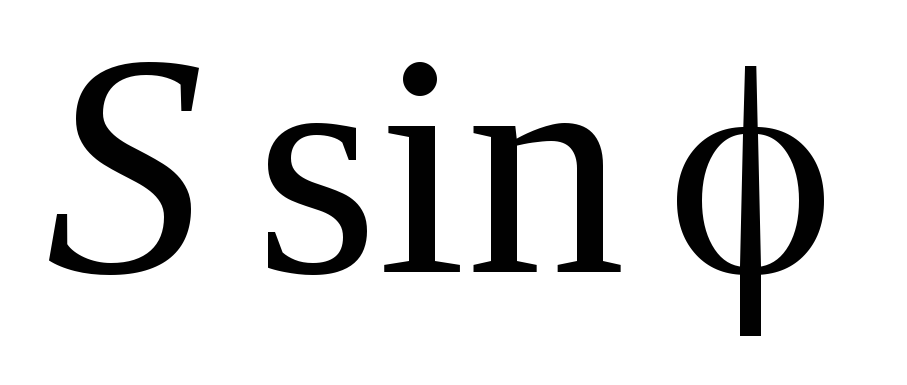 ,
, 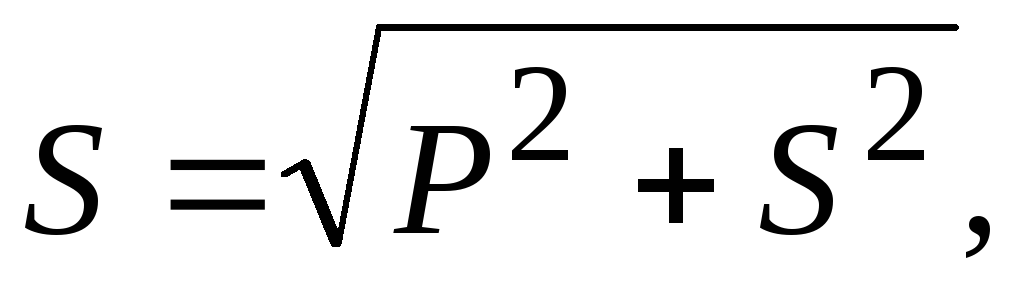
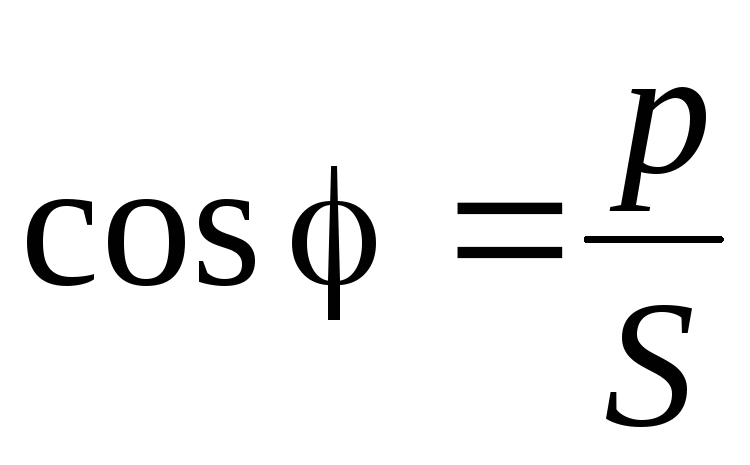 .
(2.34)
.
(2.34)
При
расчете электрических цепей комплексным
методом используют выражение комплексной
мощности, равное произведению комплексного
напряжения на сопряженный комплекс
тока. Для цепи, имеющей
активно-индуктивный характер, ток по
фазе отстает от напряжения на угол 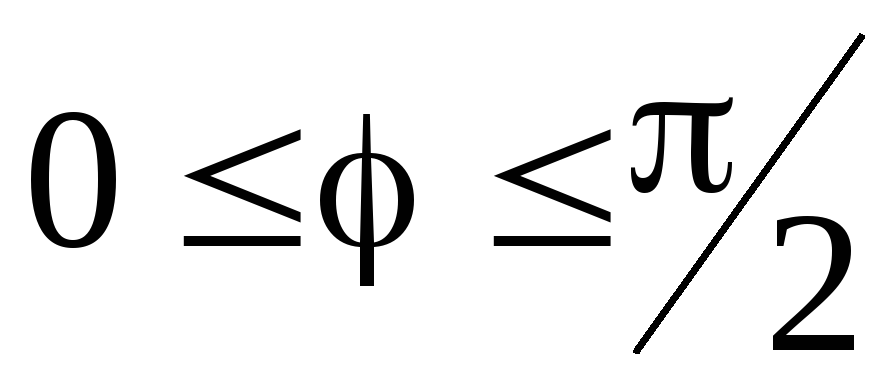
 ,
,
где
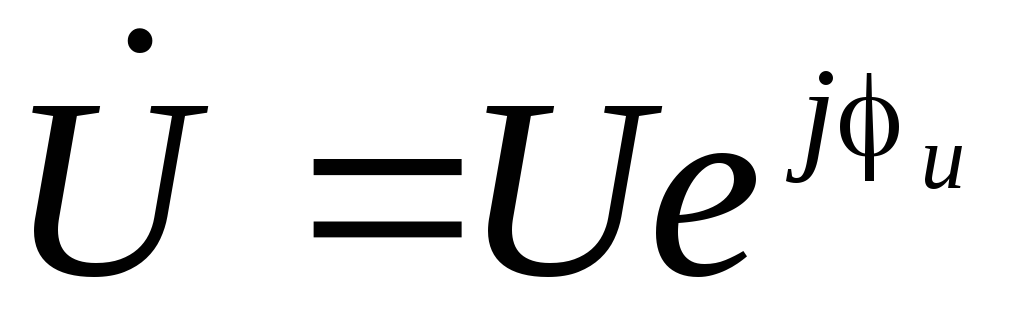 —
комплекс напряжения;
—
комплекс напряжения;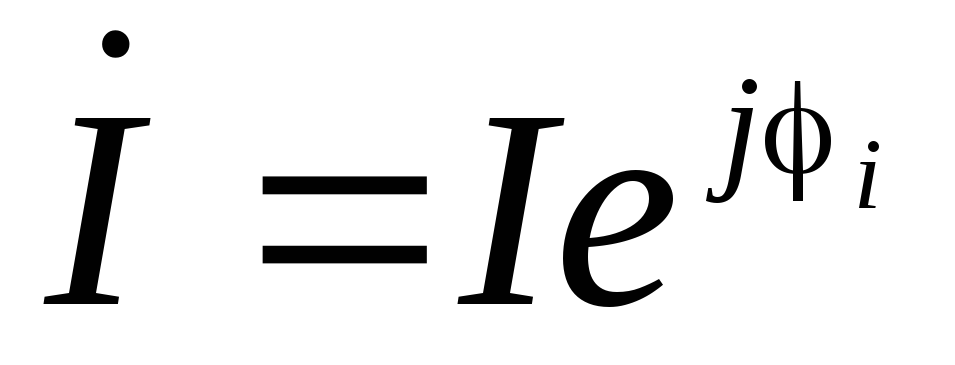 — комплекс тока;
— комплекс тока;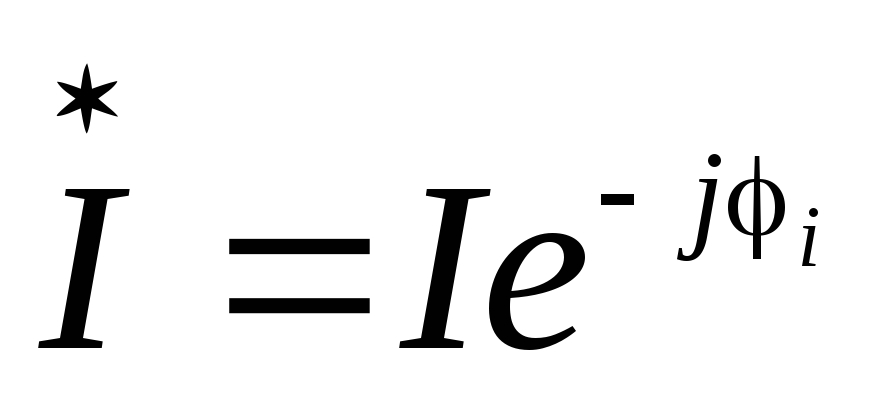 — сопряженный комплекс тока;
— сопряженный комплекс тока;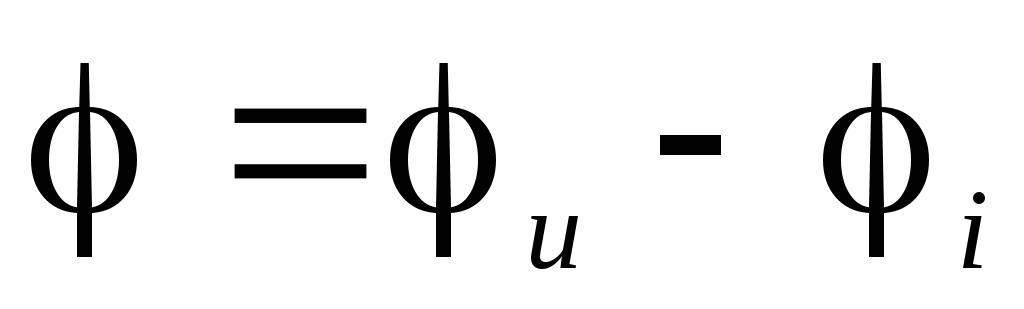 — сдвиг по фазе между напряжением и
током.
Вещественной
частью полной комплексной мощности
является активная мощность, мнимой
частью комплексной мощности — реактивная
мощность:
— сдвиг по фазе между напряжением и
током.
Вещественной
частью полной комплексной мощности
является активная мощность, мнимой
частью комплексной мощности — реактивная
мощность:
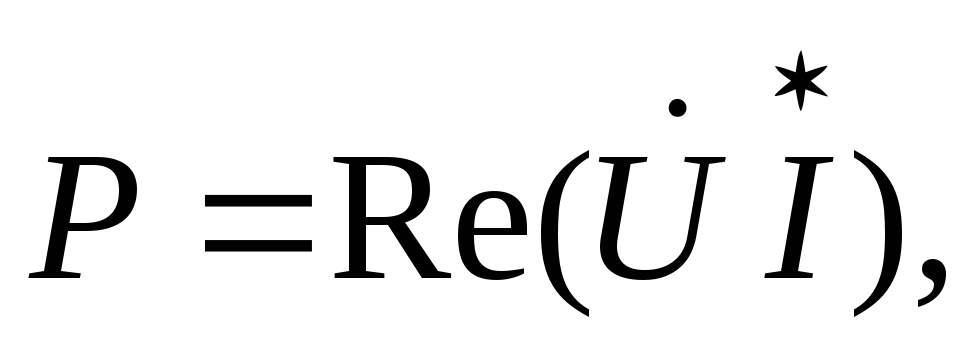 Q =
Q = 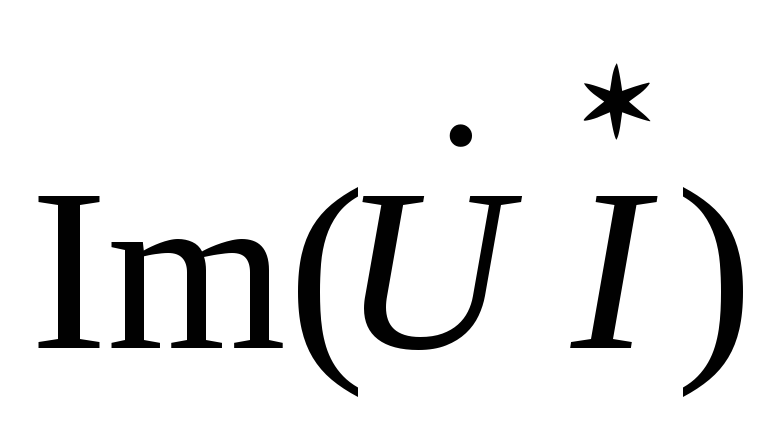 . (2.35)
. (2.35)
Для
цепи, имеющей активно-емкостной характер,
ток по фазе опережает напряжение 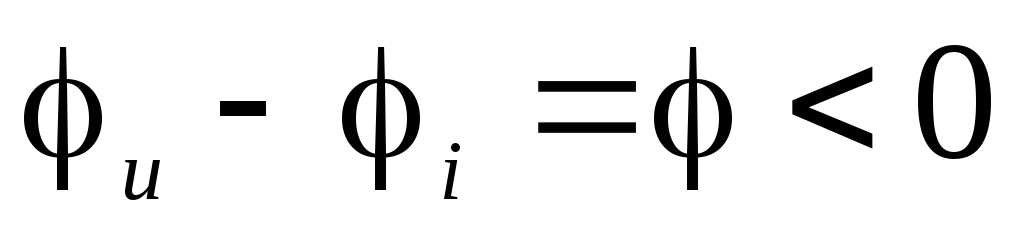 .
.
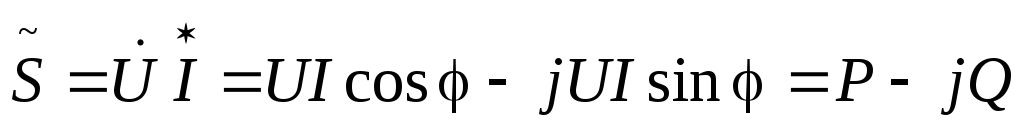
Активная мощность всегда положительна. Реактивная мощность в цепи, имеющей индуктивный характер, — положительна, а в цепи с емкостным характером — отрицательна.
При выводе полученных соотношений предполагалось, что на зажимах цепи действует напряжение U. Если к зажимам цепи присоединен идеальный источник синусоидальной ЭДС с действующим значением E, то выражения (2.31)-(2.33), (2.35) для источника имеют следующий вид:
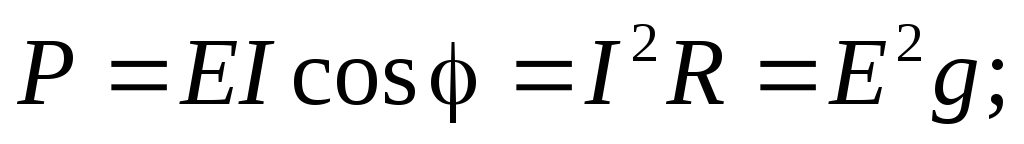 Q=
Q=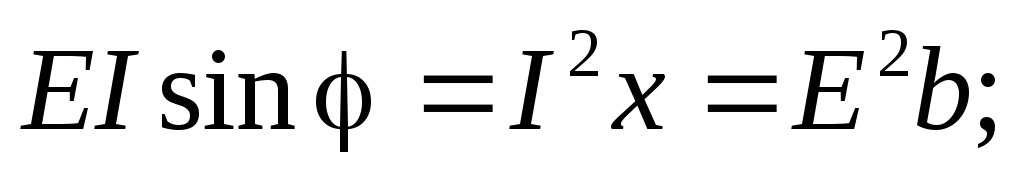
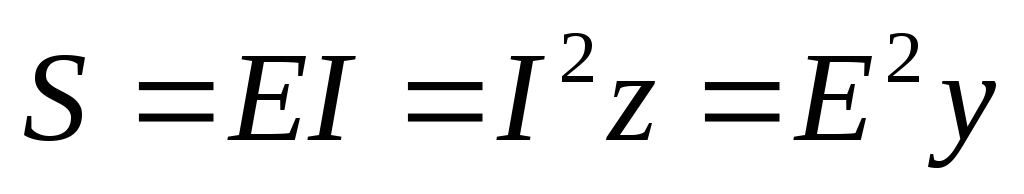 ;
; 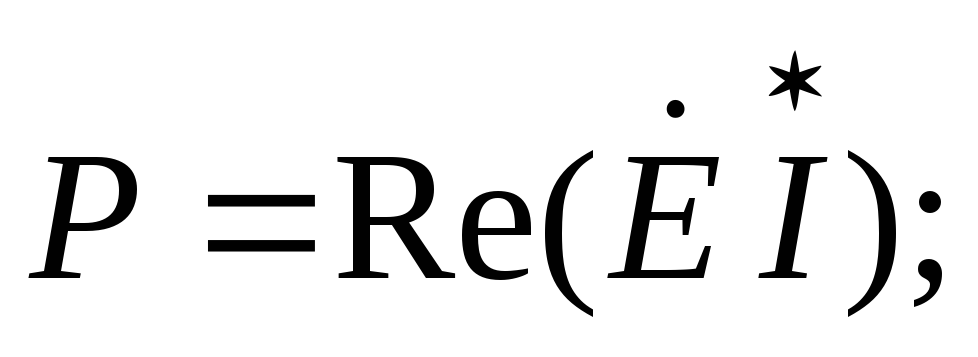 Q =
Q = 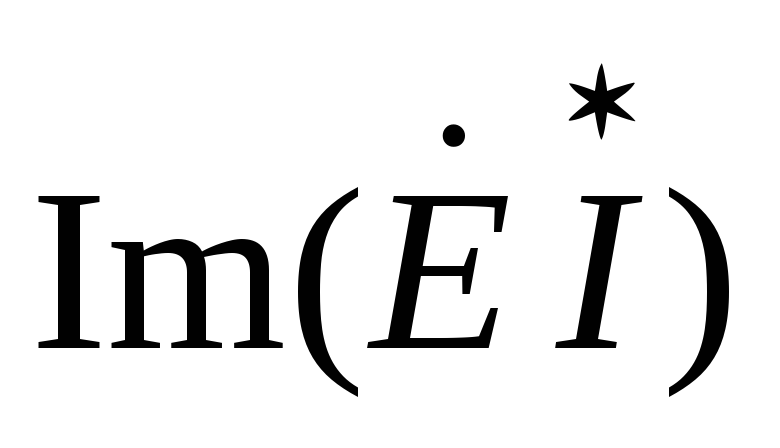 .
(2.36)
.
(2.36)
Из закона сохранения энергии следует, что для электрической цепи соблюдается закон баланса активных мощностей: активная мощность, генерируемая источниками, равна активной мощности, потребляемой всеми приемниками.
Покажем, что соблюдается баланс и для комплексных, и, следовательно, для реактивных мощностей. Определим комплексные мощности для схемы (рис.2.7), содержащей идеальный источник синусоидальной ЭДС, последовательно соединенные активные и реактивные сопротивления приемника.
Запишем уравнение по второму закону Кирхгофа, умножим левую и правую части уравнения на сопряженный комплекс тока и учтем свойства произведения комплексно сопряженных чисел:
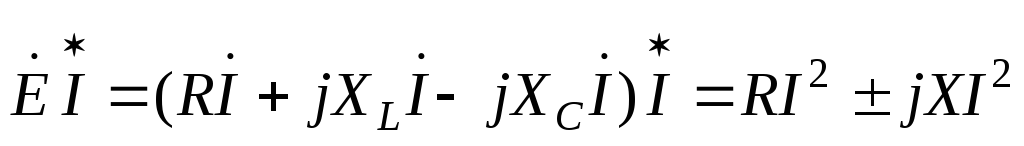 ,
, 
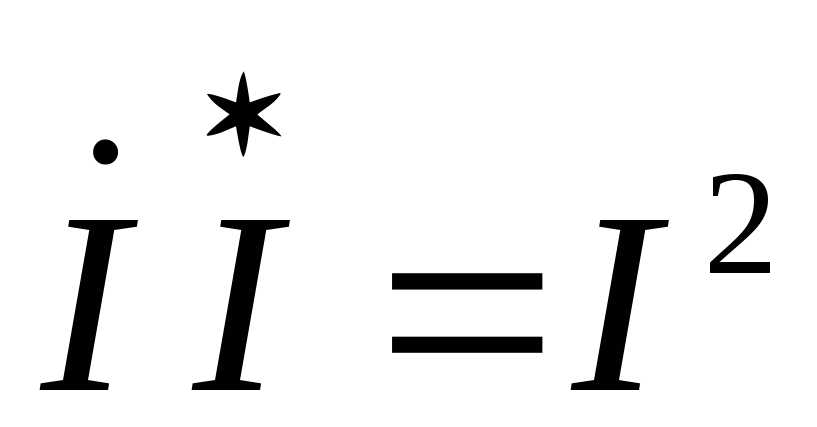 ,
,
где
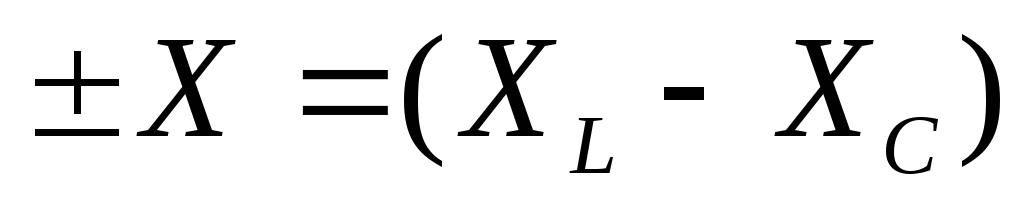 — результирующее реактивное сопротивление.
— результирующее реактивное сопротивление.
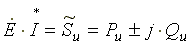 ,
,
где
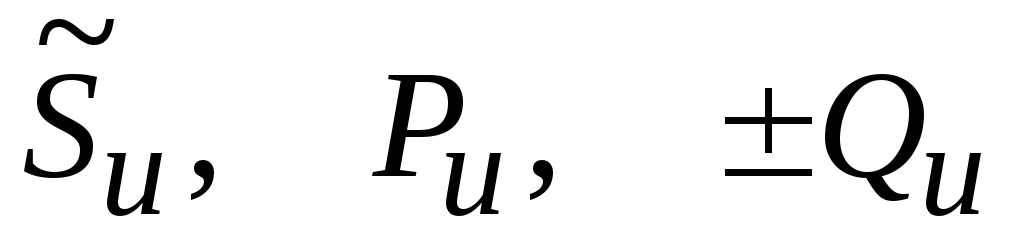 —
полная комплексная, активная и реактивная
мощности источника питания.
—
полная комплексная, активная и реактивная
мощности источника питания.
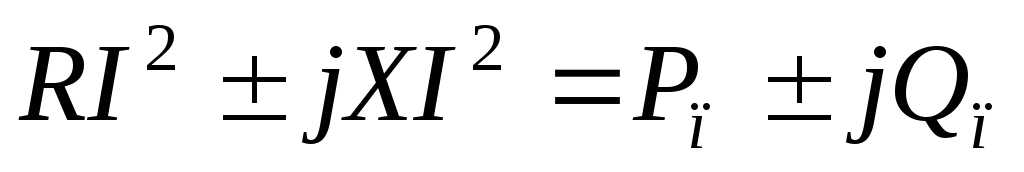 ,
,
где 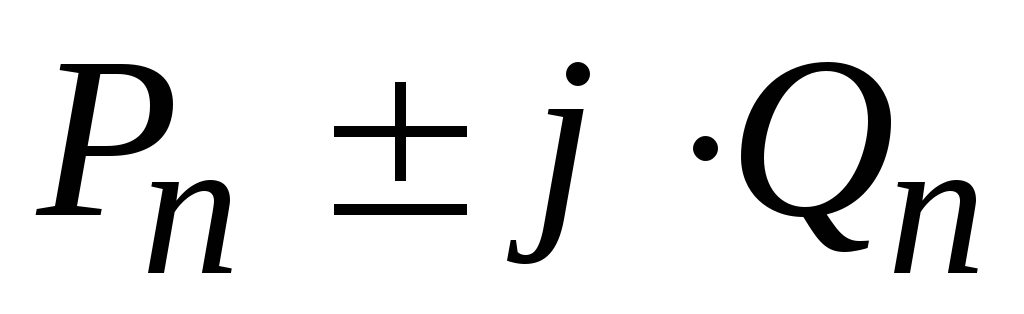 активная
и реактивная мощности, потребляемые
элементами схемы.
активная
и реактивная мощности, потребляемые
элементами схемы.
Получим уравнение для комплексных мощностей источника и приемника:
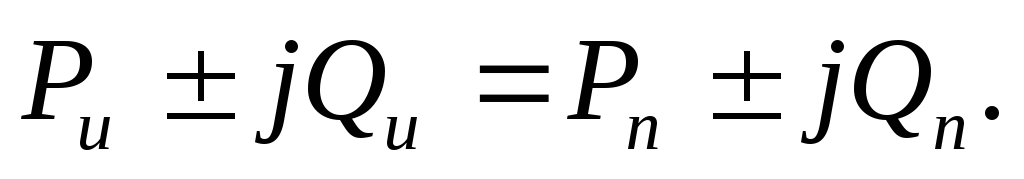 (2.37)
(2.37)
Равенство (2.37) выражает баланс комплексных мощностей источника и приемника. При равенстве комплексных чисел равны по отдельности их вещественные и мнимые части, следовательно, уравнение (2.37) можно записать в следующей форме:
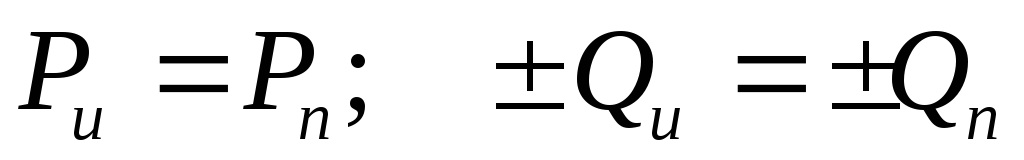 .
(2.38)
.
(2.38)
Из следует (2.38), что для электрической цепи соблюдается закон баланса реактивных мощностей: реактивная мощность, отдаваемая источниками, равна реактивной мощности, потребляемой всеми приемниками.
Рассмотрим условие передачи источником максимальной мощности при заданном коэффициенте мощности приемника.
В
схеме на рис. 2.18 обозначены : 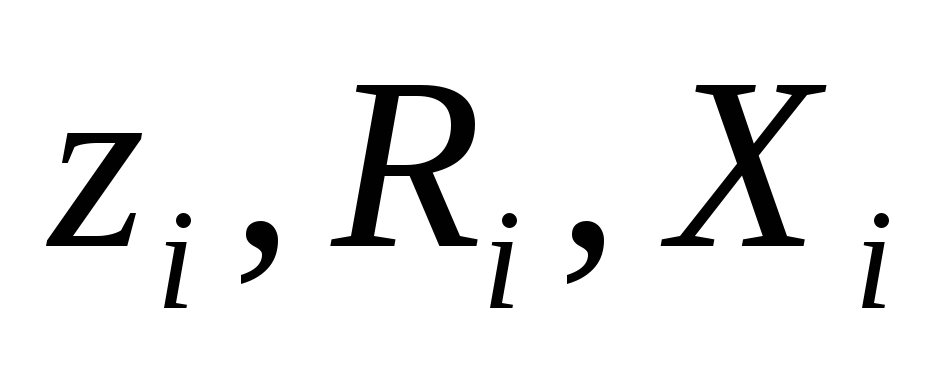 — полное, активное и реактивное
сопротивления источника ЭДС,
— полное, активное и реактивное
сопротивления источника ЭДС,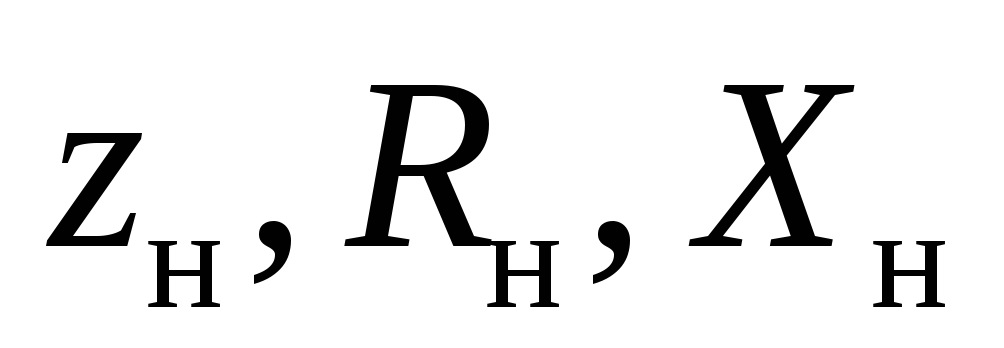 — полное, активное и реактивное
сопротивления нагрузки.
— полное, активное и реактивное
сопротивления нагрузки.
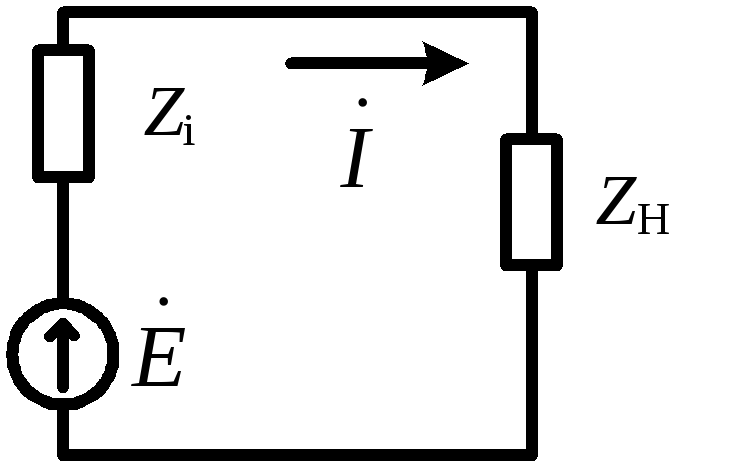
Рис. 2.18
Активная мощность может выделяться только в активных сопротивлениях цепи переменного тока. Активная мощность, выделяемая в нагрузке,
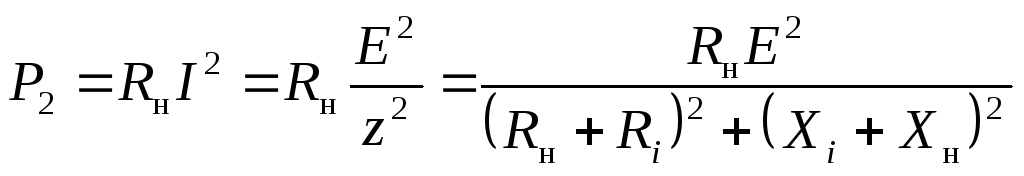 .
(2.39)
.
(2.39)
Активная
мощность, развиваемая генератором 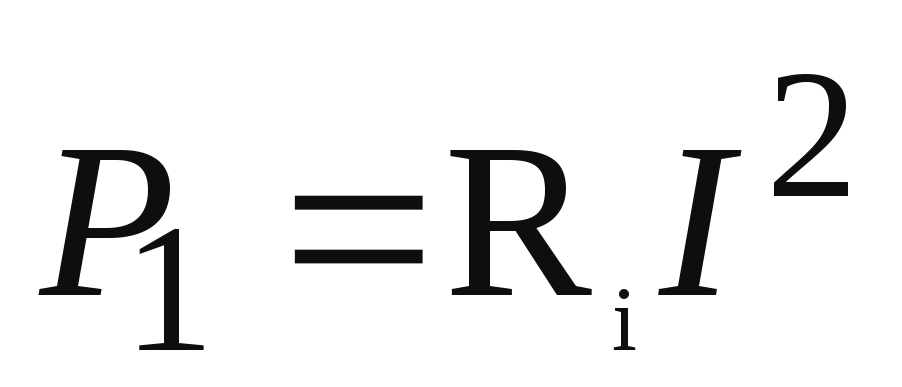 .
Коэффициент
полезного действия (КПД) для данной
схемы:
.
Коэффициент
полезного действия (КПД) для данной
схемы:
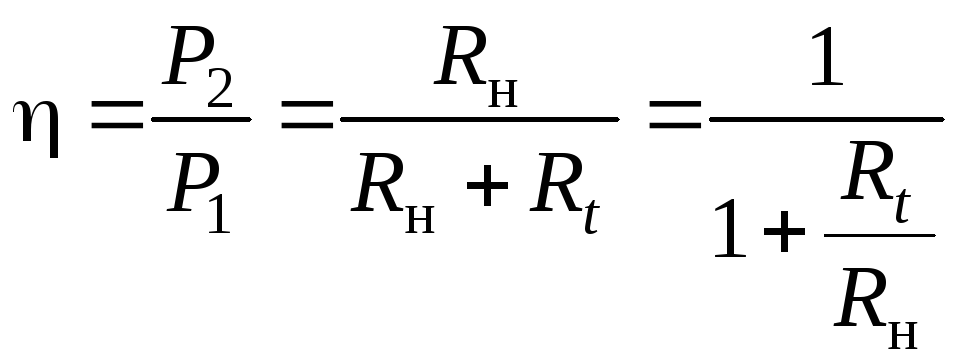 .
.
Из
(2.39) видно, что выделяемая в нагрузке
мощность будет максимальной, когда
знаменатель минимален. Последнее имеет
место при 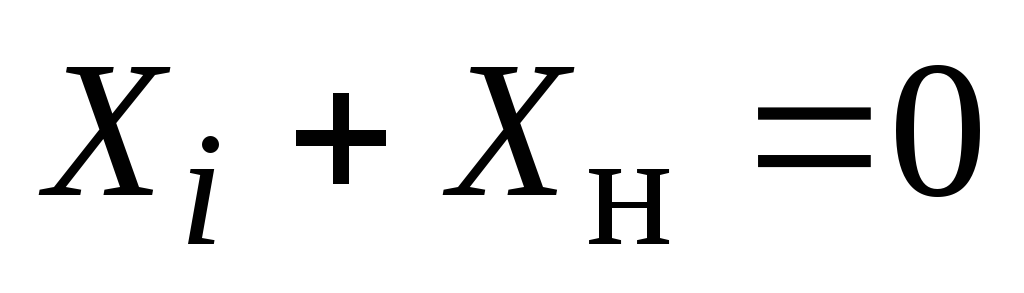 ,
т.е. при
,
т.е. при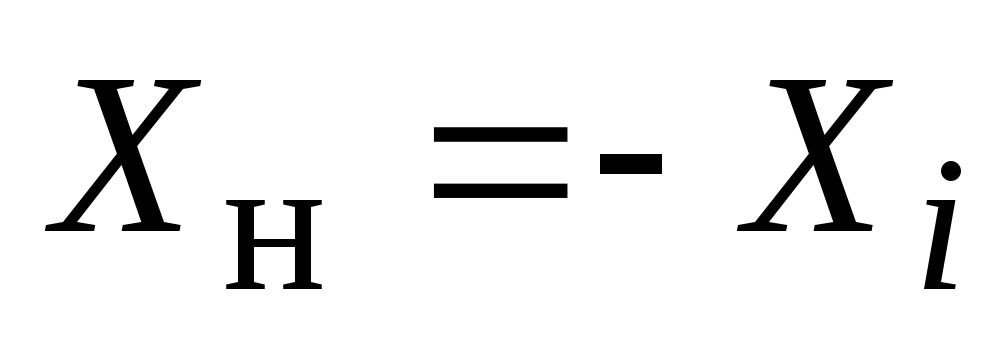 .
Это означает, что реактивные сопротивления
источника и нагрузки должны быть
одинаковы по модулю и иметь разнородный
характер. При индуктивном характере
реактивного сопротивления источника
реактивное сопротивление нагрузки
должно быть емкостным, и наоборот:
.
Это означает, что реактивные сопротивления
источника и нагрузки должны быть
одинаковы по модулю и иметь разнородный
характер. При индуктивном характере
реактивного сопротивления источника
реактивное сопротивление нагрузки
должно быть емкостным, и наоборот:
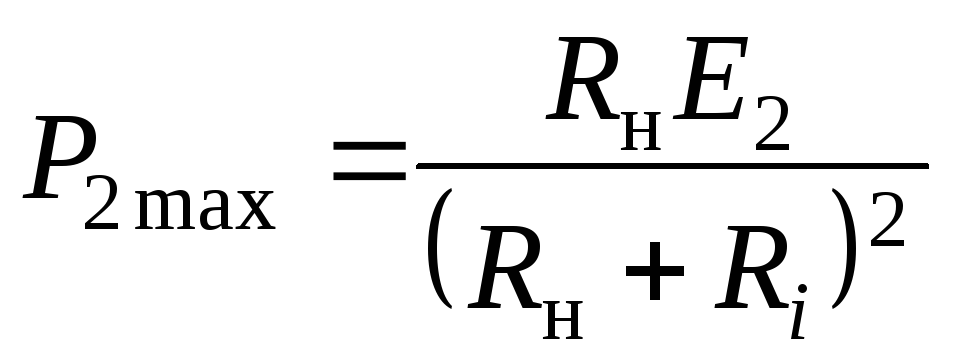 .
(2.40)
.
(2.40)
Установим условие, при котором от источника к нагрузке будет передаваться наибольшая мощность:
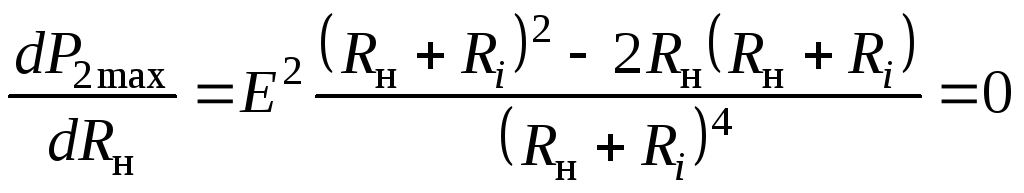 .
.
отсюда 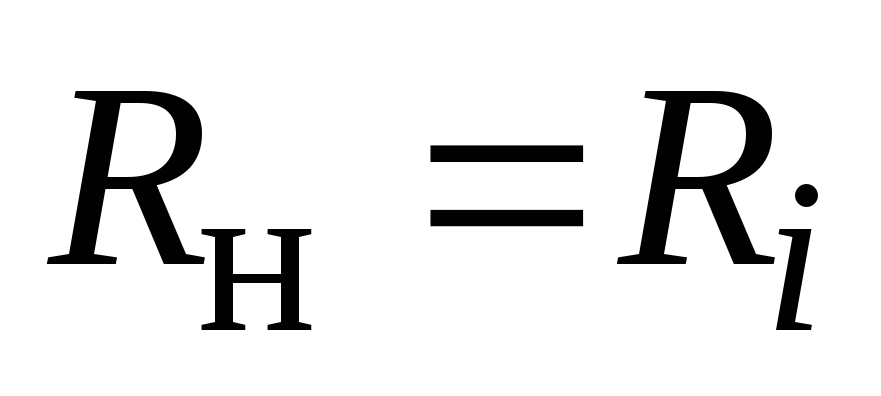 .
.
От источника к нагрузке передается наибольшая мощность, когда
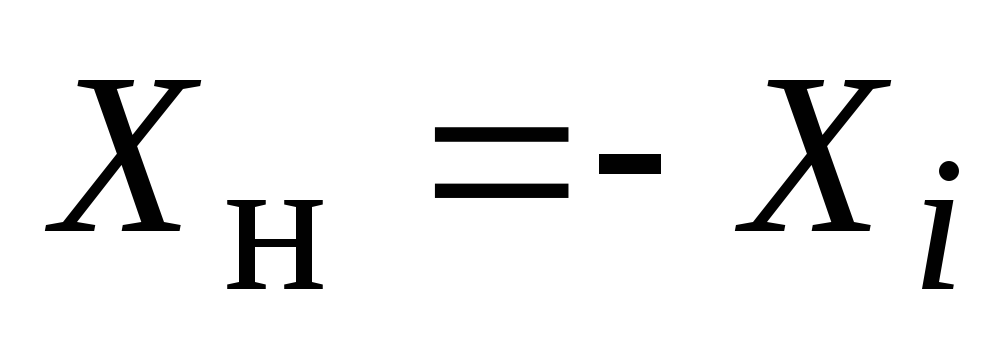 ;
;
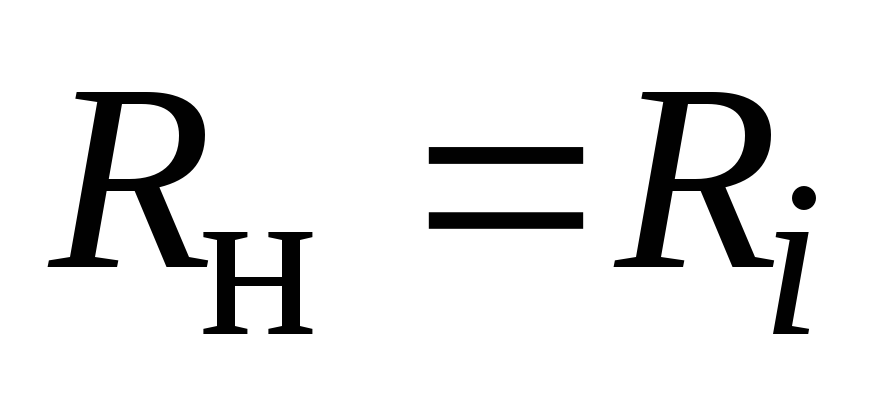 .
(2.41)
.
(2.41)
Величина наибольшей мощности
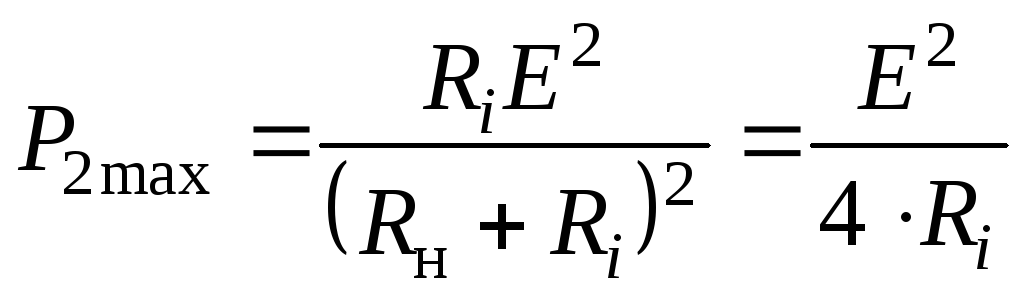 . (2.42)
. (2.42)
Режим передачи наибольшей мощности от источника к нагрузке называется согласованным режимом, а подбор сопротивлений согласно равенствам (2.41) — согласованием нагрузки с источником.
В согласованном режиме величина КПД составляет:
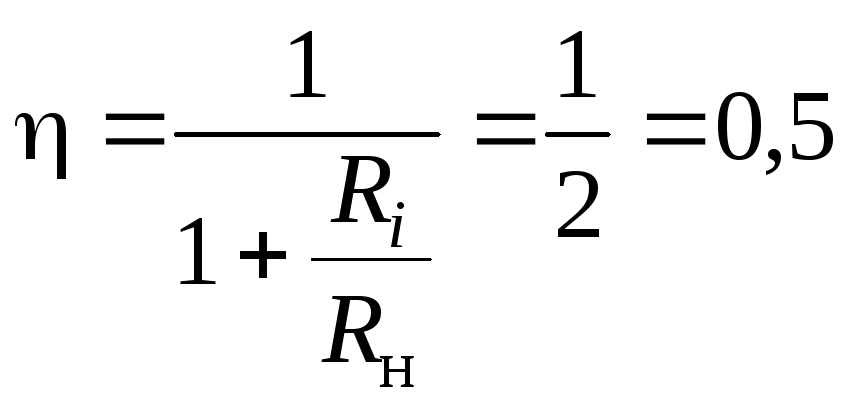 .
.
Половина мощности теряется внутри источника. Поэтому согласованный режим не используется в силовых энергетических цепях. Этот режим используют в информационных цепях, где мощности могут быть малыми, и решающими являются не соображения экономичности передачи сигнала, а максимальная мощность сигнала в нагрузке.
studfile.net
Дайте определение полной, активной и реактивной мощности — КиберПедия
Активная мощность (P) Другими словами активную мощность можно назвать: фактическая, настоящая, полезная, реальная мощность. В цепи постоянного тока мощность, питающая нагрузку постоянного тока, определяется как простое произведение напряжения на нагрузке и протекающего тока, то есть
P = U I
потому что в цепи постоянного тока нет понятия фазового угла между током и напряжением. Другими словами, в цепи постоянного тока нет никакого коэффициента мощности.
Но при синусоидальных сигналах, то есть в цепях переменного тока, ситуация сложнее из-за наличия разности фаз между током и напряжением. Поэтому среднее значение мощности (активная мощность), которая в действительности питает нагрузку, определяется как:
P = U I Cosθ
В цепи переменного тока, если она чисто активная (резистивная), формула для мощности та же самая, что и для постоянного тока: P = U I.
Формулы для активной мощности
P = U I — в цепях постоянного тока
P = U I cosθ — в однофазных цепях переменного тока
P = √3 UL IL cosθ — в трёхфазных цепях переменного тока
Активная мощность = √ (Полная мощность2 – Реактивная мощность2
Реактивная мощность (Q) Также её мощно было бы назвать бесполезной или безваттной мощностью.
Мощность, которая постоянно перетекает туда и обратно между источником и нагрузкой, известна как реактивная (Q).
Реактивной называется мощность, которая потребляется и затем возвращается нагрузкой из-за её реактивных свойств. Единицей измерения активной мощности является ватт, 1 Вт = 1 В х 1 А. Энергия реактивной мощности сначала накапливается, а затем высвобождается в виде магнитного поля или электрического поля в случае, соответственно, индуктивности или конденсатора.
Реактивная мощность определяется, как
Q = U I sinθ
и может быть положительной (+Ue) для индуктивной нагрузки и отрицательной (-Ue) для емкостной нагрузки.
Единицей измерения реактивной мощности является вольт-ампер реактивный (вар): 1 вар = 1 В х 1 А. Проще говоря, единица реактивной мощности определяет величину магнитного или электрического поля, произведённого 1 В х 1 А.
Формулы для реактивной мощности
Q = U I sinθ
Реактивная мощность = √ (Полная мощность2 – Активная мощность2)
Полная мощность (S)
Полная мощность – это произведение напряжения и тока при игнорировании фазового угла между ними. Вся мощность в сети переменного тока (рассеиваемая и поглощаемая/возвращаемая) является полной.
Комбинация реактивной и активной мощностей называется полной мощностью. Произведение действующего значения напряжения на действующее значение тока в цепи переменного тока называется полной мощностью.
Она является произведением значений напряжения и тока без учёта фазового угла. Единицей измерения полной мощности (S) является ВА, 1 ВА = 1 В х 1 А. Если цепь чисто активная, полная мощность равна активной мощности, а в индуктивной или ёмкостной схеме (при наличии реактивного сопротивления) полная мощность больше активной мощности.
Формула для полной мощности
S = U I
Полная мощность = √ (Активная мощность2 + Реактивная мощность2)
Следует заметить, что:
— резистор потребляет активную мощность и отдаёт её в форме тепла и света.
— индуктивность потребляет реактивную мощность и отдаёт её в форме магнитного поля.
— конденсатор потребляет реактивную мощность и отдаёт её в форме электрического поля.
Все эти величины тригонометрически соотносятся друг с другом, как показано на рисунке:
Осциллятор
Осцилля́тор (лат. oscillo — качаюсь) — система, совершающая колебания, то есть показатели которой периодически повторяются во времени.
Гармони́ческий осцилля́тор (в классической механике) — система, которая при выведении её из положения равновесия испытывает действие возвращающей силы F, пропорциональной смещению x:
F=-kx
где k — постоянный коэффициент.
Если F — единственная сила, действующая на систему, то систему называют простым или консервативным гармоническим осциллятором. Свободные колебания такой системы представляют собой периодическое движение около положения равновесия (гармонические колебания). Частота и амплитуда при этом постоянны, причём частота не зависит от амплитуды.
Если имеется ещё и сила трения (затухание), пропорциональная скорости движения (вязкое трение), то такую систему называют затухающим или диссипативным осциллятором. Если трение не слишком велико, то система совершает почти периодическое движение — синусоидальные колебания с постоянной частотой и экспоненциально убывающей амплитудой. Частота свободных колебаний затухающего осциллятора оказывается несколько ниже, чем у аналогичного осциллятора без трения.
Если осциллятор предоставлен сам себе, то говорят, что он совершает свободные колебания. Если же присутствует внешняя сила (зависящая от времени), то говорят, что осциллятор испытывает вынужденные колебания.
Механическими примерами гармонического осциллятора являются математический маятник (с малыми углами отклонения), груз на пружине, торсионный маятник и акустические системы. Среди немеханических аналогов гармонического осциллятора можно выделить электрический гармонический осциллятор (см. LC-цепь).
Любая система, в которой происходит простое гармоническое движение, обладает двумя ключевыми свойствами:
• когда система выведена из состояния равновесия, должна существовать возвращающая сила, стремящаяся вернуть систему в равновесие;
• возвращающая сила должна в точности или приближённо быть пропорциональна перемещению.
• Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы . F=kx;
• Потенциальная энергия частицы
• Гармонический осциллятор в квантовой механике описывается уравнением Шредингера:
Полная энергия осциллятора.
где n=0,1,2….
cyberpedia.su
