Формула активного сопротивления переменного тока. Как найти полное сопротивление
Активное сопротивление зависит от материала, сечения и температуры. Активное сопротивление обусловливает тепловые потери проводов и кабелей. Определяется материалом токоведущих проводников и площадью их сечения.
Различают сопротивление проводника постоянному току (омическое) и переменному току (активное). Активное сопротивление больше активного (R а > R ом) из-за поверхностного эффекта. Переменное магнитное поле внутри проводника вызывает противоэлектродвижущую силу, благодаря которой происходит перераспределение тока по сечению проводника. Ток из центральной его части вытесняется к поверхности. Таким образом, ток в центральной части провода меньше, чем у поверхности, то есть сопротивление провода возрастает по сравнению с омическим. Поверхностный эффект резко проявляется при токах высокой частоты, а также в стальных проводах (из-за высокой магнитной проницаемости стали).
Для ЛЭП, выполненных из цветного металла, поверхностный эффект на промышленных частотах незначителен. Следовательно,
Обычно влиянием колебания температуры на R а проводника в расчётах пренебрегают. Исключение составляют тепловые расчеты проводников. Пересчет величины сопротивления выполняют по формуле:
где R 20 – активное сопротивление при температуре 20 о;
текущее значение температуры.
Активное сопротивление зависит от материала проводника и сечения:
где ρ –удельное сопротивление, Ом мм 2 /км;
l – длина проводника, км;
F – сечение проводника, мм 2 .
Сопротивление одного километра проводника называют погонным сопротивлением:
где удельная проводимость материала проводника, км См/мм 2 .
Для меди γ Cu =53×10 -3 км См/мм2 , для алюминия γ Al =31.7×10 -3 км См/мм2 .
На практике значение r 0 определяют по соответствующим таблицам, где они указаны для t 0 =20 0 С.
Величина активного сопротивления участка сети рассчитывается:
R = r 0 ×l .
Активное сопротивление стальных проводов намного больше омического из-за поверхностного эффекта и наличия дополнительных потерь на гистерезис (перемагничивание) и от вихревых токов в стали:
r 0 = r 0пост + r 0доп,
где r 0пост – омическое сопротивление одного километра провода;
r 0доп – активное сопротивление, которое определяется переменным магнитным полем внутри проводника,
Изменение активного сопротивления стальных проводников показано на рисунке 4.1.
При малых величинах тока индукция прямо пропорциональна току. Следовательно, r 0 увеличивается. Затем наступает магнитное насыщение: индукция и r 0 практически не изменяются. При дальнейшем увеличении тока r 0 уменьшается из-за снижения магнитной проницаемости стали (m ).
Полное сопротивление, или импеданс, характеризует сопротивление цепи переменному электрическому току. Данная величина измеряется в омах. Для вычисления полного сопротивления цепи необходимо знать значения всех активных сопротивлений (резисторов) и импеданс всех катушек индуктивности и конденсаторов, входящих в данную цепь, причем их величины меняются в зависимости от того, как меняется проходящий через цепь ток. Импеданс можно рассчитать при помощи простой формулы.
Формулы
- Полное сопротивление Z = R или X L или X C (если присутствует что-то одно)
- Полное сопротивление (последовательное соединение) Z = √(R 2 + X 2) (если присутствуют R и один тип X)
- Полное сопротивление (последовательное соединение) Z = √(R 2 + (|X L — X C |) 2) (если присутствуют R, X L , X C)
- Полное сопротивление (любое соединение) = R + jX (j – мнимое число √(-1))
- Сопротивление R = I / ΔV
- Индуктивное сопротивление X L = 2πƒL = ωL
- Емкостное сопротивление X C = 1 / 2πƒL = 1 / ωL
Шаги
Часть 1
Вычисление активного и реактивного сопротивленийИмпеданс обозначается символом Z и измеряется в омах (Ом). Вы можете измерить импеданс электрической цепи или отдельного элемента. Импеданс характеризует сопротивление цепи переменному электрическому току. Есть два типа сопротивления, которые вносят вклад в импеданс:
- Активное сопротивление (R) зависит от материала и формы элемента. Наибольшим активным сопротивлением обладают резисторы, но и другие элементы цепи обладают небольшим активным сопротивлением.
- Реактивное сопротивление (X) зависит от величины электромагнитного поля. Наибольшим реактивным сопротивлением обладают катушки индуктивности и конденсаторы.
Сопротивление – это фундаментальная физическая величина, описываемая законом Ома: ΔV = I * R. Эта формула позволит вам вычислить любую из трех величин, если вы знаете две другие. Например, чтобы вычислить сопротивление, перепишите формулу так: R = I / ΔV. Вы также можете при помощи мультиметра.
- ΔV – это напряжение (разность потенциалов), измеряемое в вольтах (В).
- I – сила тока, измеряемая в амперах (А).
- R – это сопротивление, измеряемое в омах (Ом).
Реактивное сопротивление имеет место только в цепях переменного тока. Как и активное сопротивление, реактивное сопротивление измеряется в омах (Ом). Есть два типа реактивного сопротивления:
Вычислите индуктивное сопротивление. Это сопротивление прямо пропорционально быстроте изменения направления тока, то есть частоты тока. Эта частота обозначается символом ƒ и
skupaem-auto.ru
Активное сопротивление в цепи переменного тока
Электрические лампы накаливания, печи сопротивления, бытовые нагревательные приборы, реостаты и другие приемники, где электрическая энергия преобразуется в тепловую, на схемах замещения обычно представлены только сопротивлением R.
Для схемы, изображенной на рис. 13.1, а, заданы сопротивление R и напряжение, изменяющееся по закону
u = Umsinωt
Найдём ток и мощность в цепи.
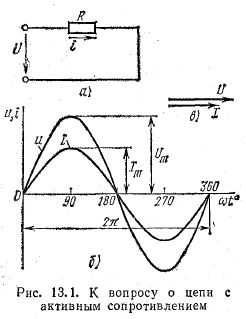
Ток в цепи переменного тока с активным сопротивлением.
По закону Ома найдем выражение для мгновенного тока:
где Im = Um/R — амплитуда тока
Из уравнений напряжения и тока видно, что начальные фазы обеих кривых одинаковы, т. е. напряжение и ток в цепи с сопротивлением R совпадают по фазе. Это показано на графиках и векторной диаграмме (рис. 13.1, б, б).
Действующий ток найдем, разделив амплитуду на √ 2:
Формулы (13.1) выражают закон Ома для цепи переменного тока с сопротивлением R. Внешне они ничем не отличаются от формулы для цепи постоянного тока, если переменные напряжение и ток выражены действующими величинами.
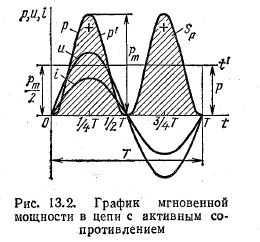
Мгновенная мощность в цепи переменного тока с активным сопротивлением.
При переменных величинах напряжения и тока скорость преобразования электрической энергии в приемнике, т. е. его мощность, тоже изменяется. Мгновенная мощность равна произведению мгновенных величин напряжения и тока: p = Umsinωt * Imsinωt = UmImsin2ωt
Из тригонометрии найдём
Более наглядное представление о характере изменения мощности в цепи дает график в прямоугольной системе координат, который строится после умножения ординат кривых напряжения и тока, соответствующих ряду значений их общего аргумента — времени t. Зависимость мощности от времени — периодическая кривая (рис. 13.2). Если ось времени t поднять по чертежу на величину р = Pm√2 = UmIm√2, то относительно новой оси t’ график мощности является синусоидой с двойной частотой и начальной фазой 90°:
Таким образом, в первоначальной системе координат мгновенная, мощность равна сумме постоянной величины Р = UmIm√2 и перемен- ной р’:
р = Р + р’
Анализируя график мгновенной мощности, нетрудно заметить, что мощность в течение периода остается положительной, хотя ток и напряжение меняют свой знак. Это получается благодаря совпадению по фазе напряжения и тока.
Постоянство знака мощности говорит о том, что направление потока электрической энергии остается в течение периода неизменным, в данном случае от сети (от источника энергии) в приемник с сопротивлением R, где электрическая энергия необратимо преобразуется в другой вид энергии. В этом случае электрическая энергия называется активной.
Если R — сопротивление проводника, то в соответствии с законом Ленца — Джоуля электрическая энергия в нем преобразуется в тепло.
Активная мощность для цепи переменного тока с активным сопротивлением
Скорость преобразования электрической энергии в другой вид энергии за конечный промежуток времени, значительно больший периода изменения тока, характеризуется средней мощностью. Она равна средней мощности за период, которую называют активной.
Активная мощность — среднее арифметическое мгновенной мощности за период.
Для рассматриваемой цепи активную мощность Р нетрудно определить из графика рис. 13.2. Средняя величина мощности равна высоте прямоугольника с основанием Т, равновеликого площади, ограниченной кривой р(t) и осью абсцисс (на рисунке заштриховано).
Равенство площадей РТ = Sp выполняется, если высоту прямоугольника взять равной половине наибольшей мгновенной мощности Pm.
В этом случае часть площади Sp , находящаяся выше прямоугольника, точно укладывается в оставшуюся незаштрихованной его часть:
P = UI
Активная мощность для данной цепи равна произведению действующих величин тока и напряжения:
P = UI = I2R = U2R
С математической точки зрения активная мощность является постоянной составляющей в уравнении мгновенной мощности p(t) [см. выражение (13.2)].
Среднюю мощность за период можно найти интегрированием уравнения (13.2) в пределах периода:
Сопротивление R, определяемое из формулы (13.3) отношением активной мощности цепи к квадрату действующего тока, называется активным электрическим сопротивлением.
electrikam.com
1.3. Закон Ома для участка цепи. Омическое сопротивление проводника.
Закон Ома устанавливает зависимость между силой тока в проводнике и разностью потенциалов (напряжением) между двумя точками (сечениями) этого проводника. В 1826 г. немецким физиком Георгом Омом (1787-1854) экспериментально было обнаружено, что отношение разности потенциалов (напряжения) на концах металлического проводника к силе тока есть величина постоянная:
U/I=R=const
Эта величина, зависящая от геометрических и электрических свойств проводника и от температуры, называется омическим (активным) сопротивлением, или просто сопротивлением.
Согласно закону Ома для участка цепи
Сила тока прямо пропорциональна разности потенциалов (напряжению) на концах участка цепи и обратно пропорциональна сопротивлению этого участка:
I=U/R,
где U — напряжение на данном участке цепи, R, — сопротивление данного участка цепи. Произведение силы тока на сопротивление называется иногда падением напряжения:
U=I*R
Сопротивление проводника является его основной электрической характеристикой, определяющей упорядоченное перемещение носителей тока в этом проводнике (или на участке цепи).
Единица омического сопротивления в СИ — ом (Ом). Проводник имеет сопротивление 1 Ом, если при силе тока в нем 1 А разность потенциалов (напряжения) на его концах равна 1 В, т.е. 1 Ом — 1 В/1 А.
Сопротивление К зависит от свойств проводника и от его геометрических размеров:
R=p*l/S,
Где p — удельное сопротивление вещества, I — длина проводника, S — площадь поперечного сечения. Единицей удельного сопротивления в СИ является 1 Ом • м (или 1 Ом • м/м2).
Удельное сопротивление вещества численно равно сопротивлению однородного цилиндрического проводника, изготовленного из данного материала и имеющего длину 1 м и площадь поперечного сечения 1 м , или численно равно сопротивлению проводника в форме куба с ребром 1 м, если направление тока совпадает с направлением нормали к двум противоположным граням куба.
В зависимости от удельного сопротивления все вещества делятся на проводники (удельное сопротивление мало), диэлектрики (очень большое удельное сопротивление) и полупроводники с промежуточным значением удельного сопротивления.
1.4. Зависимость удельного сопротивления от температуры.
Сверхпроводимость.
С изменением температуры удельное сопротивление изменяется:
р=p0*(1+at),
гдер 0 — удельное сопротивление проводника при 0°С, ( температура по шкале Цельсия) — удельное сопротивление при температуре ^, а —. температурный коэффициент сопротивления. Этот коэффициент характеризует зависимость сопротивления вещества от температуры.
Температурный коэффициент сопротивления равен относительному изменению сопротивления проводника при нагревании на 1°К. Его можно определить из условия:
R-R0/R=at,
если До — сопротивление проводника при 0°С, К — сопротивление проводника при температуре {.
Сопротивление проводника меняется за счет изменения удельного сопротивления, так как при нагревании геометрические размеры проводника меняются незначительно.
Для всех металлов к > 1 и мало меняется при изменении температуры проводника.
Удельное сопротивление проводника линейно зависит от температуры (рис. 61). У чистых металлов, а =1/273*K-1, для растворов электролитов, а < 0 и с увеличением температуры сопротивление уменьшается. ,
столкновении с ионами электроны теряют скорость направленного движения. Это и приводит
Возрастание удельного сопротивления можно объяснить тем, что с ростом температуры амплитуда колебаний ионов кристаллической решетки металлов увеличивается и возрастает вероятность их столкновения с электронами. Это и приводит к возрастанию удельного сопротивления. Столкновении с ионами электроны теряют скорость направленного движения.
Рис.2 Зависимость удельного сопротивления от температуры.
Рис.3 Зависимость удельного сопротивления от температуры для ртути.
Зависимость сопротивления металлов от температуры используется, например, в термометрах сопротивления.
Многие проводники обладают свойством сверхпроводимости, состоящей в том, что их сопротивление скачком падает до нуля при охлаждении ниже определенной критической температуры Т^, характерной для данного материала. Такие вещества получили название сверхпроводники.
Впервые это явление наблюдал в 1911 г. нидерландский физик Гейке Камерлинг-Оннес (1853-1926). Он обнаружил, что ртуть при Т = 4,15°К переходит в новое состояние, названное сверхпроводящим (рис. 62). Позже им было установлено, что электрическое сопротивление ртути восстанавливается при T < Tk в достаточно сильном магнитном поле. Прохождение тока в сверхпроводниках происходит без потерь энергии, поэтому их используют в электромагнитах со сверхпроводящей обмоткой. На основе явления сверхпроводимости иногда работают элементы памяти счетно-вычислительных устройств. Устройство переключающих элементов электронных вычислительных машин иногда основано на принципе разрушения сверхпроводящего состояния магнитным полем.
Ведутся исследования по созданию сверхпроводящих линий электропередачи, но главная трудность здесь в необходимости глубокого охлаждения всей линии для перехода в сверхпроводящее состояние до температуры ниже 20°К.
studfiles.net
Активное и индуктивное сопротивление кабелей и проводов. Емкостная проводимость линий электропередач
Для того, чтобы произвести расчет электрической сети на потерю напряжения необходимо знать параметры линий, а именно их сопротивления и проводимости. Если производятся расчеты цепей постоянного тока, то вполне достаточно знать только омическое сопротивление линии. А вот при расчете линии переменного тока одного омического сопротивления бывает недостаточно, и помимо активных сопротивлений, необходимо знать еще индуктивные сопротивления и емкостные проводимости проводов и кабелей.
Активное сопротивление проводов и кабелей
Из электротехники известно, что полное сопротивление при равных условиях переменному и постоянному току будут отличаться. Касается это также проводов и кабелей. Это вызвано тем, что переменный ток распределяется по сечению неравномерно (поверхностный эффект). Однако для проводов из цветных металлов и с частотой переменного напряжения 50 Гц этот эффект не оказывает слишком большого влияния и им можно пренебречь. Таким образом, при расчете проводников из цветных металлов, их сопротивления переменному и постоянному току принимаются равными.
На практике активное сопротивление медных и алюминиевых проводников рассчитывают по формуле:
Где: l – длина в км, γ – удельная проводимость материала провода м/ом∙мм2, r0 – активное сопротивление 1 км провода на фазу Ом/км, s – площадь поперечного сечения, мм2.
Величина r0, как правило, берется из таблиц справочников.
На активное сопротивление провода влияет и температура окружающей среды. Величину r0 при температуре Θ можно определить по формуле:
Где: α – температурный коэффициент сопротивления; r20 – активное сопротивление при температуре 20 0С, γ20 – удельная проводимость при температуре в 20 0С.
Стальные провода обладают значительно большими активными сопротивлениями, чем аналогичные провода из цветных металлов. Его увеличение обусловлено значительно меньшей величиной удельной проводимости и поверхностным эффектом, который у стальных проводов выражен гораздо более ярко, чем у алюминиевых или медных. Более того, в стальных проводах присутствуют потери активной энергии на вихревые токи и перемагничивание, что в схемах замещения линий учитывают дополнительной составляющей активного сопротивления.
Активное сопротивление стальных проводов (в отличии от проводов из цветных металлов) сильно зависит от величины протекаемого тока, поэтому использовать постоянное значение удельной проводимости при расчетах нельзя.
Активное сопротивление стальных проводов в зависимости от протекающего тока аналитически выразить весьма трудно, поэтому для его определения используют специальные таблицы.
Индуктивное сопротивление проводов и кабелей
Для определения индуктивного сопротивления (обозначается Х) кабельной или воздушной линии определенной протяженности в километрах удобно пользоваться выражением:
Где: Х0 – индуктивное сопротивление одного километра провода или кабеля на фазу, Ом/км.
Х одного километра воздушной или кабельной линии можно определить по формуле:
Где: Dср – расстояние среднее между проводами или центрами жил кабелей, мм; d – диаметр токоведущей жилы кабеля или диаметр провода, мм; μт – относительная магнитная проницаемость материала провода;
Первый член правой части уравнения обусловлен внешним магнитным полем и называется внешним индуктивным сопротивлением Х0/. Из этого выражения видно, что Х0/ зависит только от расстояния между проводами и их диаметра, а так как расстояние между проводами выбирается исходя из номинального напряжения линии, соответственно Х0/ будет расти с ростом номинального напряжения линии. Х0/ воздушных линий больше, чем кабельных. Это связано с тем, что токоведущие жилы кабеля располагаются друг к другу значительно ближе, чем провода воздушных линий.
Для одной фазы:
Где: D1:2 расстояние между проводами.
Для одинарной трехфазной линии при расположении проводов по треугольнику:
При горизонтальном или вертикальном расположении проводов трехфазной линии в одной плоскости:
Увеличение сечения проводов линии ведет к незначительному уменьшению Х0/.
Второй член уравнения для определения X0 обусловлен магнитным полем внутри проводника. Он выражает внутреннее индуктивное сопротивление Х0//.
Таким образом выражение для Х0 можно представить в виде:
Для линий из немагнитными материалов μ = 1 внутреннее индуктивное сопротивление Х0// по сравнению с внешним Х0/ составляет ничтожную величину, поэтому им очень часто пренебрегают.
В таком случае формула для определения Х0 примет вид:
Для практических расчетов индуктивные сопротивления кабелей и проводов определяют по соответствующим таблицам.
В случае приближенных расчетов можно считать для воздушных линий напряжением 6-10 кВ Х0 = 0,3 – 0,4 Ом/км, а для кабельных Х0 = 0,08 Ом/км.
Внутренне индуктивное сопротивление стальных проводов сильно отличается от Х0// проводов из цветных металлов. Это вызвано тем, что Х0// пропорционально магнитной проницаемости μr, которая сильно зависит от величины тока в проводе. Если для проводов из цветных металлов μr = 1, то для стальных проводов μr может достигать величины в 103 и даже выше.
Х0// для линий прокладываемых стальными проводами пренебрегать нельзя. Как правило, данную величину берут из таблиц, составленных на основе экспериментальных данных.
Сопротивления r0 и Х0// при некоторых значениях тока могут достигать максимальных значений, а затем с увеличением тока уменьшатся. Это явление объясняется магнитным насыщением стали.
Емкостная проводимость линий
Электрические линии, кроме активного и индуктивного сопротивлений, характеризуются и емкостной проводимостью, которая обусловлена емкостью между проводами и между проводам и землей.
Величину рабочей емкости в трехфазной воздушной линии приближенно можно определить по формуле:
Из данной формулы видно, что рабочая емкость будет увеличиваться с увеличением сечения проводов и уменьшением расстояния между ними. Поэтому при равных сечениях токоведущих частей линии низкого напряжения имеют большую рабочую емкость, чем линии высокого напряжения. В следствии небольших расстояний между токоведущими жилами кабеля и большей диэлектрической проницаемости изоляции по сравнению с воздухом рабочая емкость кабельной линии значительно больше, чем емкость воздушной линии.
Емкостная проводимость одноцепной воздушной линии определяется по формуле:
Определение рабочей емкости кабельной линии по формулам, в которые входят диэлектрическая проницаемость изоляции кабеля, геометрические размеры и другие конструктивные особенности, задача не из легких, поэтому значения рабочей емкости определяют по специальным таблицам, составленным заводом изготовителем для различных марок кабелей, в зависимости от их номинального напряжения.
Емкостной ток вначале линии при холостом ходе (при отключенных электроприемниках) можно определить из формулы:
Где: U – линейное напряжение сети, В; l – длина линии, км;
Емкостные токи имеют серьезное значение в воздушных линиях с рабочим напряжением 110 кВ и выше и в кабельных линиях с напряжением выше 10 кВ. При расчете электрических сетей с напряжениями ниже, чем выше перечисленные, емкость линии могут не учитывать. Емкость токопроводящих частей линии по отношению к земле имеет значение при расчете заземляющих устройств и защиты.
В сети с изолированной нейтралью величину емкостного тока однофазного замыкания на землю приближенно можно определить по формулам:
- Для воздушной линии:
- Для кабельной линии:
elenergi.ru
Активное и реактивное сопротивление в цепи переменного тока
В электрической цепи переменного тока существует два вида сопротивлений: активное и реактивное. Это является существенным отличием от цепей постоянного тока.
Активное сопротивление
При прохождении тока через элементы, имеющие активное сопротивление, потери выделяющейся мощности необратимы. Примером может служить резистор, выделяющееся на нем тепло, обратно в электрическую энергию не превращается. Кроме резистора активным сопротивлением может обладать линии электропередач, соединительные провода, обмотки трансформатора или электродвигателя.
Отличительной чертой элементов имеющих чисто активное сопротивление – это совпадение по фазе тока и напряжения, поэтому вычислить его можно по формуле
Активное сопротивление зависит от физических параметров проводника, таких как материал, площадь сечения, длина, температура.
Реактивное сопротивление
При прохождении переменного тока через реактивные элементы возникает реактивное сопротивление. Оно обусловлено в первую очередь ёмкостями и индуктивностями.
Индуктивностью в цепи переменного тока обладает катушка индуктивности, причём в идеальном случае, активным сопротивлением её обмотки пренебрегают. Реактивное сопротивление катушки переменному току создаётся благодаря её ЭДС самоиндукции. Причем с ростом частоты тока, сопротивление также растёт.
Реактивное сопротивление катушки зависит от частоты тока и индуктивности катушки
Конденсатор обладает реактивным сопротивлением благодаря своей ёмкости. Его сопротивление с увеличением частоты тока уменьшается, что позволяет его активно использовать в электронике в качестве шунта переменной составляющей тока.
Сопротивление конденсатора можно рассчитать по формуле
Треугольник сопротивлений
Цепи переменного тока обладают полным сопротивлением. Полное сопротивление цепи определяется как сумма квадратов активного и реактивного сопротивлений
Графическим изображением этого выражения служит треугольник сопротивлений, который можно получить в результате расчёта последовательной RLC-цепи. Выглядит он следующим образом:
На треугольнике видно, что катетами являются активное и реактивное сопротивление, а полной сопротивление гипотенуза.
Формула активного сопротивления в цепи переменного тока
В электротехнике активное сопротивление в цепи переменного тока, так же как и реактивная нагрузка, относится к разряду труднодоступных для понимания тем. Только немногие специалисты могут понятно объяснить, какие процессы происходят на участке электрической схемы. Для начала понимания нужно обратиться к словарю и узнать, что означает слово «активный». Это деятельный, инициативный и энергичный элемент или объект. В электротехнике под сопротивлением с активным свойством понимают элемент, способный потреблять электроэнергию и превращать ее в иной вид энергии (свет, тепло или химические реакции). Специалисты его называют еще ваттным сопротивлением. К активным элементам в электрической схеме тока с переменной характеристикой относят различные накаливаемые элементы и, конечно же, лампы с нитью накаливания. Графически активное сопротивление рисуют в виде резистора.
Графическое обозначение элемента с активным свойством в электротехнике
Сопротивление с активным свойством в цепи с переменной характеристикой
Если в цепь с переменной характеристикой тока подключить активную нагрузку, то по проводнику начнет протекать электрический ток по синусоидальной траектории. Это происходит за счет видоизменения напряжения по синусоиде:
u = Um sin ωt.
Отсюда и силу тока можно выразить формулой:
i = Im sin ωt,
где максимальная амплитуда силы тока считается по формуле:
Im =Um/R.
Важно знать! Сила тока в цепи с переменной характеристикой переменяется по тому закону, что и напряжение. То есть прохождение нулевой отметки у них происходит синхронно, так же как и достижение пиковой вершины.
Графика видоизменения силы тока и напряжения
Из графика видно, что за счет идеального активного в цепи сопротивления ток и напряжение совмещаются по фазе. Если в формуле:
i = Im sin ωt
каждую сторону поделить на √2, то получим формулу, выражающую закон Ома:
I=U/R.
Отсюда следует вывод, что для электрической схемы с переменной характеристикой, имеющей активное сопротивление, основополагающим законом является закон Ома.
Характеристики потерь
Причиной потерь с активной нагрузкой в схеме с переменной характеристикой тока являются:
- Омическое сопротивление самого материала проводника;
- Кроме этого, нельзя не обращать внимания на другие причины, как, например, наличие конденсатора (в электротехнике под ним можно подразумевать, например, кабель в изоляции).В такой схеме энергия теряется за счет постоянно изменяющего поляризацию диэлектрика такой изоляции. Это происходит за счет систематического «переворачивания» парных зарядов молекул, в свою очередь, приводящее к нагреву диэлектрического слоя. Такие потери в электротехнике называют диэлектрическими утечками;
- Кроме диэлектрических потерь в конденсаторном элементе, в схеме переменного тока присутствует потеря утечки. Она возникает за счет несовершенства материала изоляции;
- Также нельзя исключать потери на гистерезис, за счет постоянного присутствия переменного магнитного поля. Это приводит к нагреванию металлических частей схемы, так как наличествует систематическое переворачивание в такт с частотой переменного тока магнитиков;
- Токи Фуко также порождают высокие утраты в электрической цепи с переменной характеристикой. Они представляют собой индуктивные круговые токи и подвергают нагреванию все элементы схемы.
Присутствие всех перечисленных потерь значительно увеличивает активное сопротивление в схеме с переменным током.
Мощность в схеме с активной нагрузкой
Когда схема функционирует на переменном напряжении и токе, то напряженность преобразования электрической энергии в иной вид энергии изменяется. Отсюда получается, что такое изменение меняет мощность. Из формулы:
p = Umsinωt * Imsinωt = UmImsin2ωt
следует, что мгновенная мощность равноправна произведению мгновенного напряжения на мгновенную составляющую силы тока.
Генерация активной составляющей мощности
После тригонометрических переустройств видим, что мгновенная мощность одинакова по сумме с мгновенной и постоянной составляющими:
р = Р + р’, где Р = UmIm√2.
Важно знать! Под понятием активная мощность следует понимать, что она представляет собой среднее арифметическое мгновенных составляющих за определенный период времени.
На простом языке активная мощность – это положительная характеристика электрической схемы с переменным током. Она относится к разряду основных свойств в ходе выбора электрических нагрузок и учета потребления электрической энергии.
Взгляд на эффект с поверхностным влиянием
Активное сопротивление электрической цепи, функционирующей от переменного напряжения, постоянно больше от сопротивления с активной функцией в цепи постоянного напряжения. Основанием этому является то, что переменный ток по равноправному уровню разделяется по всей поперечной плоскости проводника. От этого полезная плоскость значительно убавляется, а сопротивление растет. Этот физический процесс называется эффектом поверхностного действия.
При поверхностном эффекте заряженные частицы в основном двигаются по внешней оболочке проводника, так как поверхность проводника становится полезным сечением. С увеличением частоты электроны двигаются, максимально приближаясь к внешним границам. Для понижения данного явления изготавливают провода специального устройства. Их делают с трубчатыми жилами или покрывают жилы металлами, имеющими идеальную проводимость. Схемы с серебряными выводами очень хорошо знакомы многим специалистам.
Понижение поверхностного эффекта
На практике для повышения активной мощности в электрических схемах применяют специальные устройства и технологии, позволяющие снизить потери и уменьшить реактивную характеристику мощности. Самыми распространенными являются компенсирующие конденсаторные установки, а в быту – это индивидуальные блоки питания. Также перед созданием электрической сети в проекты закладываются проводники с наибольшей проводимостью и требуемым от нагрузок сечением. Кроме этого, в сложных схемах немаловажным является равномерное распределение активных нагрузок потребителей.
Видео
Оцените статью:elquanta.ru
Емкостное сопротивление | Формулы и расчеты онлайн
Конденсатор емкостью C имеет в цепи постоянного тока бесконечно большое сопротивление. Если же приложить к конденсатору переменное напряжение, то он будет периодически перезаряжаться, и в цепи потечет ток. Напряжение на конденсаторе достигает максимального значения в те моменты, когда ток равен нулю.
Если R = 0, то напряжение на конденсаторе совпадает с приложенным напряжением и u = q/C. Мгновенное значение тока определяется выражением:
\[ i = \frac{dq}{dt} = C \frac{du}{dt} = C \frac{d}{dt}(U_{m} \sin(ωt)) \]
Отсюда следует
\[ i = ωCU_{m} \cos(ωt) = ωCU_{m} \sin(ωt + \frac{π}{2}) \]
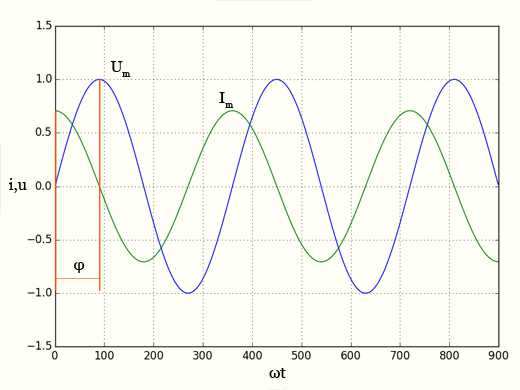
Емкостное сопротивление — график тока и напряжения
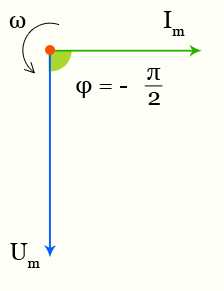
Между напряжением и током имеется разность фаз —π/2.
В чисто емкостной цепи переменного тока ток опережает напряжение на π/2 (или Т/4).
В соответствии с приведенным выше уравнением амплитуда тока Im = ωCUm. Сравнение с законом Ома U = RI показывает, что величина 1/ωС играет роль сопротивления.
Цепь переменного тока, содержащая емкость C, обладает сопротивлением переменному току; оно называется емкостным сопротивлением ХC.
Единица СИ емкостного сопротивления: [XC] = Ом.
Если
| ХC | емкостное сопротивление цепи переменного тока, | Ом |
|---|---|---|
| ω = 2πf | круговая частота переменного тока, | радиан/Секунда |
| C | емкость, | Фарад |
то
\[ X_{C} = \frac{1}{ωC} \]
$ $Ток в цепи, обладающей только емкостным сопротивлением, определяется выражением
\[ I = UωC \]
Вычислить, найти емкостное сопротивление
В помощь студенту
Емкостное сопротивление |
стр. 687 |
|---|
www.fxyz.ru
