Окружная скорость формула через число оборотов: Вращательное движение

Содержание

Вращательное движение

Вращательное движение является периодическим движением.

Период обозначается буквой T.

Чтобы найти период обращения, надо время вращения разделить на число оборотов:

Физическая величина, равная отношению числа полных оборотов тела ко времени, в течение которого эти обороты совершены, называется частотой вращения.

Частота вращения обозначается буквой n.

Чтобы найти частоту вращения, надо число оборотов разделить на время, в течение которого эти обороты совершены:

Частота вращения и период обращения связаны друг с другом как взаимообратные величины: Период измеряется в секундах: [T] = 1 с.

Единица частоты – секунда в минус первой степени: [n] = 1 с^–1.

Эта единица имеет собственное название – 1 герц (1 Гц).

Проведем аналогию между вращательным и поступательным движениями.

Поступательно движущееся тело изменяет свое положение в пространстве относительно других тел.

Тела, совершающие вращательное движение поворачиваются на некоторый угол.

Если за любые равные промежутки времени поступательно движущееся тело совершает равные перемещения, движение называется равномерным.

Если за любые равные промежутки времени вращающееся тело поворачивается на один и тот же угол, то такое вращение называется равномерным. Характеристикой равномерного поступательного движения служит скорость Соответствующей характеристикой вращательного движения служит угловая скорость:

Угловая скорость – это физическая величина, равная отношению угла поворота тела ко времени, в течение которого этот поворот совершен.

Угловая скорость показывает, на какой угол поворачивается тело за единицу времени.

Чтобы получить единицу угловой скорости, нужно в ее определяющую формулу подставить единицу – 1 радиан, и времени – 1 с. Получаем: [ω] = 1

Аналогично можно ввести характеристику неравномерного вращения. Если видом неравномерного поступательного движения является равнопеременное движение, то для вращательного движения можно ввести понятие равнопеременного вращения.

Характеристикой равнопеременного поступательного движения является ускорение:

Соответственно, для вращательного движения можно ввести величину, определяемую отношением изменения угловой скорости ко времени, в течение которого это изменение происходит – угловое ускорение: Угловое ускорение показывает, на сколько изменилась угловая скорость за единицу времени.

Чтобы получить единицу углового ускорения, нужно в его определяющую формулу подставить единицы угловой скорости 1 рад/с и времени – 1 с. Получаем:

Продолжая аналогию дальше, запишем уравнение для перемещения при прямолинейном равноускоренном движении

Так как при вращении перемещению тела соответствует угол вращения, линейной скорости – угловая скорость, линейному ускорению – угловое ускорение, то аналогичное уравнение для вращательного движения будет иметь вид:

Другому уравнению для поступательного движения будет соответствовать уравнение для вращательного движения:

Метод, который использовался в данном случае, называется методом аналогий.

Точки тела, совершающего вращательное движение, поворачиваются относительно оси вращения на некоторые углы и движутся по дугам окружностей, проходя определенные пути.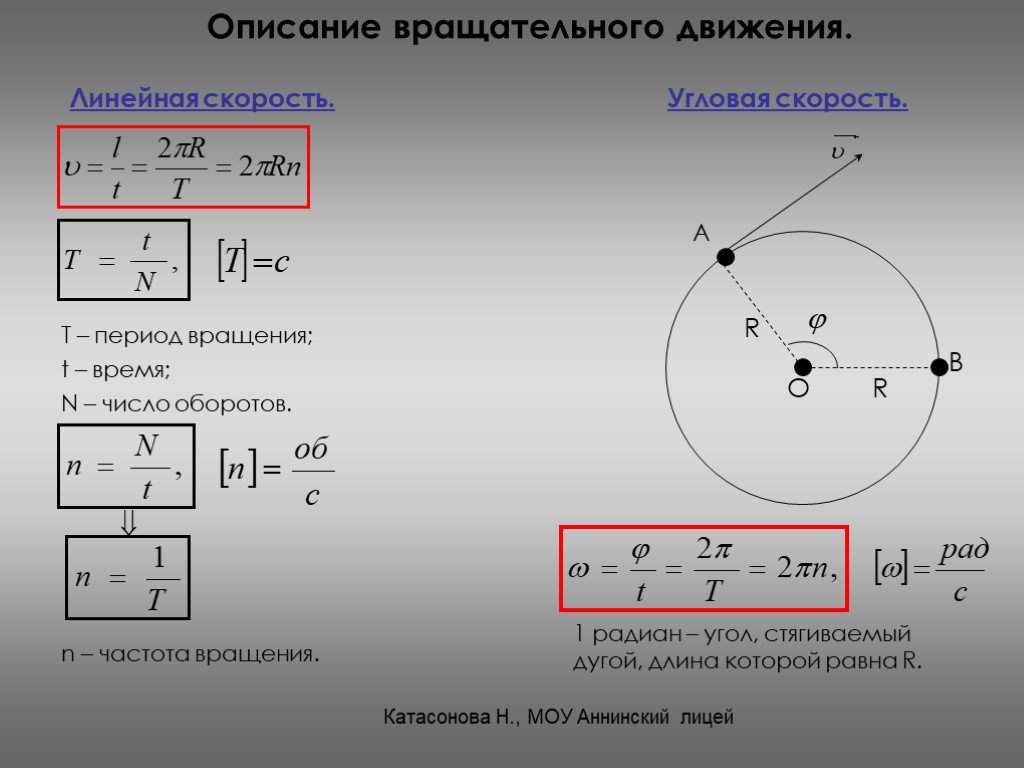

Таким образом, характеристиками вращательного движения являются и угловая, и линейная скорости.

Линейная скорость точки направлена по касательной к окружности, по которой она движется.

Об этом свидетельствует слетающая с колес автомобиля грязь или искры, летящие от металлического предмета, прижатого к наждачному кругу.

Чем дальше от оси вращения находится точка, тем больше ее линейная скорость. Угловая же скорость точек, лежащих на одном радиусе, одинакова. Следовательно, линейная скорость точки прямо пропорциональна радиусу окружности, по которой она вращается.

За время, равное периоду, точка проходит путь, равный длине окружности. Её линейная скорость при этом равна Отношение же угла поворота ко времени поворота на этот угол равно угловой скорости

Таким образом, линейная скорость вращающейся точки связана с ее угловой скоростью соотношением:

При равномерном вращении скорость меняется по направлению, но не изменяется по величине.

Поскольку всякое изменение скорости характеризуется понятием ускорения, то для равномерного вращения следует ввести еще одно ускорение, изменяющееся не по величине, а по направлению. Это ускорение называют центростремительным.

Пусть вращающееся тело в начальный момент времени находится в точке A и скорость его направлена по касательной. В следующий момент времени тело находится в точке B. При этом скорость его изменилось только по направлению и направлена по касательной к окружности.

Найдем вектор разности скоростей, воспользовавшись правилом действия с векторами. Из чертежа видно, что вектор разности направлен в сторону близкую к центру окружности. Чем меньше угол поворота, тем ближе направлен вектор скорости к направлению на центр вращения.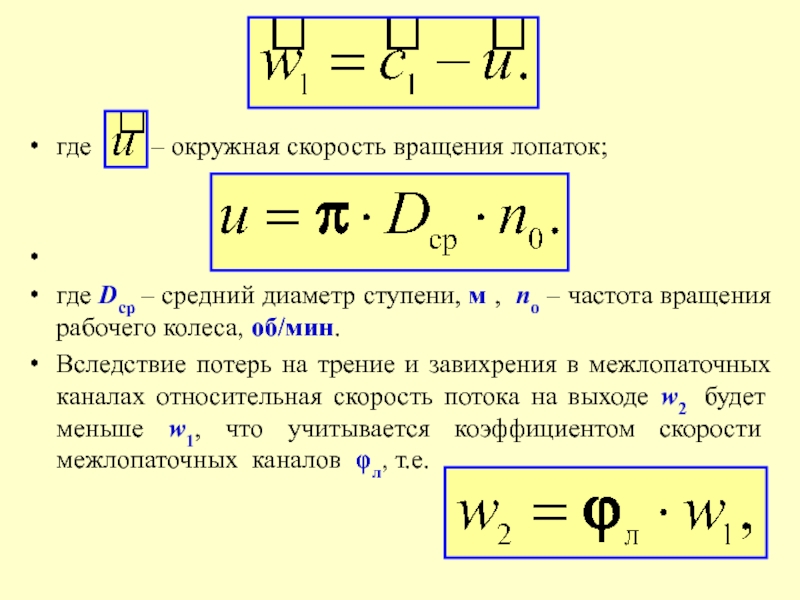

При малом времени движения изменение положения тела незначительно. Поэтому можно считать, что вектор скорости характеризующий изменение скорости по направлению, направлен на центр. Отсюда и происходит название центростремительного ускорения.

Угловое же ускорение, характеризующее изменение скорости по величине, называют еще касательным или тангенциальным ускорением (при неравномерном вращении).

Получим выражение для центростремительного ускорения. Будем считать, что угол поворота очень мал. Соединим точки A и B. Угол MAN = φ по построению.

Мы имеем два равнобедренных треугольника. Треугольник OAB, ребра которого R и AB, и треугольник MAN, ребра которого и

Так как треугольники подобны (по двум сторонам и углу между ними), то можно записать:

Дуга окружности и хорда практически равны из-за малости угла поворота. Поэтому дуга Следовательно, Получим

Разделив правую и левую части последнего уравнения на t, получим:

Отсюда Таким образом,

Полученная формула является формулой для расчета центростремительного ускорения.

Центростремительное ускорение, при движении тела по окружности, равно отношению квадрата скорости к радиусу окружности, по которой движется тело:

1.9.2 Угловая и линейная скорости вращения

Вращательное движение вокруг неподвижной оси — еще один частный случай движения твердого тела.

Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения (рис.2.4).
В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолетов.
Угловая скорость. Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и различные точки проходят за время разные пути.

Так, , поэтому модуль скорости точки А больше, чем у точки В (рис.2.5). Но радиусы окружностей поворачиваются за время на один и тот же угол . Угол — угол между осью ОХ и радиус-вектором , определяющим положение точки А (см. рис.2.5).
Пусть тело вращается равномерно, т. е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол , а другое — на угол , то мы говорим, что первое тело вращается быстрее второго в 2 раза.
Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела к промежутку времени , за который этот поворот произошел.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению
Угловая скорость выражается в радианах в секунду (рад/с).

Например, угловая скорость вращения Земли вокруг оси равна 0,0000727 рад/с, а точильного диска — около 140 рад/с¹.
Угловую скорость можно выразить через частоту вращения, т. е. число полных оборотов за 1с. Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде:
Полному обороту тела соответствует угол . Поэтому согласно формуле (2.1)
Если при равномерном вращении угловая скорость известна и в начальный момент времени угол поворота , то угол поворота тела за время t согласно уравнению (2.1) равен:
Если , то , или .
Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательные, когда он уменьшается.
Тем самым мы можем описать положение точек вращающегося тела в любой момент времени.

Связь между линейной и угловой скоростями. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости.
Мы уже отмечали, что при вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.
Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так:
Так как , то
Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Для точек земного экватора , а для точек на широте Санкт-Петербурга . На полюсах Земли .
Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:
Следовательно,
Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет.

Итак, мы научились полностью описывать движение абсолютно твердого тела, вращающегося равномерно вокруг неподвижной оси, так как, пользуясь формулами , можем находить положение, модули скорости и ускорения любой точки тела в произвольный момент времени. Знаем мы и направления и , a также форму траекторий точек.

Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями

Подробности: Просмотров: 637

«Физика — 10 класс»

Угловая скорость.

Каждая точка тела, вращающегося вокруг неподвижной оси, проходящей через точку О, движется по окружности, и различные точки проходят за время Δt разные пути. Так, АА₁ > ВВ₁ (рис. 1.62), поэтому модуль скорости точки А больше, чем модуль скорости точки В. Но радиус-векторы, определяющие положение точек А и В, поворачиваются за время Δt на один и тот же угол Δφ.

Угол φ — угол между осью ОХ и радиус-вектором определяющим положение точки А (см. рис. 1.62).

Пусть тело вращается равномерно, т. е. за любые равные промежутки времени радиус-векторы поворачиваются на одинаковые углы.

Чем больше угол поворота радиус-вектора, определяющего положение какой-то точки твёрдого тела, за определённый промежуток времени, тем быстрее вращается тело и тем больше его угловая скорость.

Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела υφ к промежутку времени υt, за который этот поворот произошёл.

Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению

Угловая скорость в СИ выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси 0,0000727 рад/с, а точильного диска — около 140 рад/с.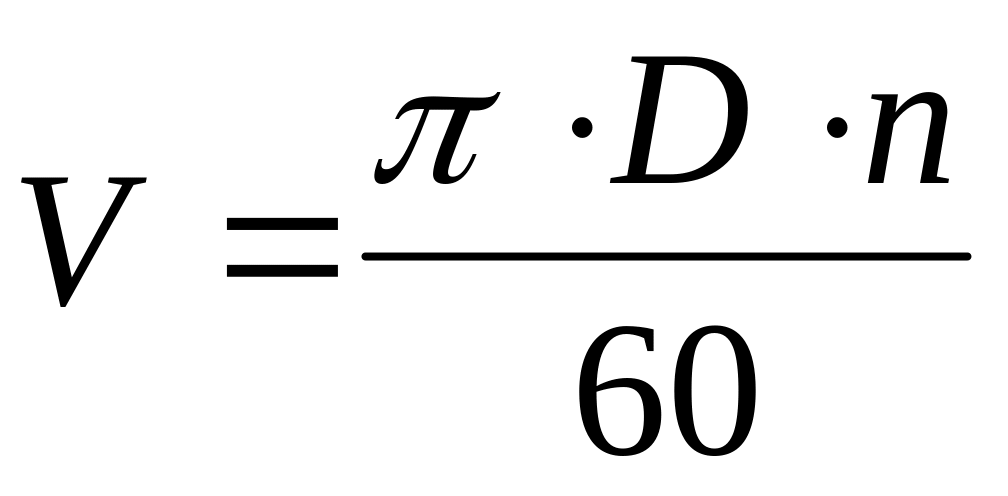

Угловую скорость можно связать с частотой вращения.

Частота вращения — число полных оборотов за единицу времени (в СИ за 1 с).

Если тело совершает ν (греческая буква «ню») оборотов за 1 с, то время одного оборота равно 1/ν секунд.

Время, за которое тело совершает один полный оборот, называют периодом вращения и обозначают буквой Т.

Таким образом, связь между частотой и периодом вращения можно представить в виде

Полному обороту тела соответствует угол Δφ = 2π. Поэтому согласно формуле (1.26)

Если при равномерном вращении угловая скорость известна и в начальный момент времени t₀ = 0 угол φ₀ = 0, то угол поворота радиус-вектора за время t согласно уравнению (1.26)

φ = ωt.

Если φ₀ ≠ 0, то φ — φ₀ = ωt, или φ = φ₀ ± ωt.

Радиан равен центральному углу, опирающемуся на дугу, длина которой равна радиусу окружности, 1 рад = 57°17’48». В радианной мере угол равен отношению длины дуги окружности к её радиусу: φ = l/R.

Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твёрдого тела, и осью ОХ увеличивается (рис. 1.63, а), и отрицательные, когда он уменьшается (рис. 1.63, б).

Тем самым мы можем найти положение точек вращающегося тела в любой момент времени.

Связь между линейной и угловой скоростями.

Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть её отличие от угловой скорости.

Мы уже отмечали, что при вращении абсолютно твёрдого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова.

Установим связь между линейной скоростью любой точки вращающегося тела и его угловой скоростью. Точка, лежащая на окружности радиусом R, за один оборот пройдёт путь 2πR. Поскольку время одного оборота тела есть период Т, то модуль линейной скорости точки можно найти так:

Так как ω = 2πν, то

Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше её линейная скорость. Для точек земного экватора υ = 463 м/с, а для точек на широте Санкт-Петербурга υ = 233 м/с. На полюсах Земли υ = 0.

Модуль центростремительного ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности:

Следовательно,

а_цс = ω²R.

Запишем все возможные расчётные формулы для центростремительного ускорения:

Мы рассмотрели два простейших движения абсолютно твёрдого тела — поступательное и вращательное. Однако любое сложное движение абсолютно твёрдого тела можно представить как сумму двух независимых движений: поступательного и вращательного.

На основании закона независимости движений можно описать сложное движение абсолютно твёрдого тела.

Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский

Кинематика — Физика, учебник для 10 класса — Класс!ная физика

Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»

Скорость тела, окружная — Энциклопедия по машиностроению XXL

Вращательную скорость точек, лежащих на поверхности цилиндра (шкива, барабана, махового колеса, вала и т.

п.), вращающегося вокруг своей оси, называют окружной скоростью тела. Окружная скорость равна произведению ш [c.173]

Для снижения центробежных сил, которые в многооборотных подшипниках могут значительно превышать рабочие. нагрузки, а также для уменьшения тепловыделения, пропорционального четвертой степени окружной скорости тел качения, уменьшают диаметр шариков и средний диаметр подшипников. [c.538]

Скорость V в отличие от угловой скорости тела называют иногда еще линейной или окружной скоростью точки М. [c.123]

Таким образом, в зависимости от модуля начальной скорости возможны следующие случаи движения тела в поле земного тяготения (рис. 174) при Оо=7,9 км/с траектория тела — окружность при 7,9 км/с С Оо 11,2 км/с —гипербола. [c.208]

Установим зависимость между скоростью произвольной точки вращающегося тела и его угловой скоростью (применительно к вращающемуся телу вместо скорость точки часто I говорят линейная скорость или окружная [c. 115]

Чтобы подчеркнуть отличие угловой скорости тела от скорости какой-либо его точки, последнюю называют часто линейной скоростью, а иногда окружной скоростью. [c.216]

Скорости и ускорения точек тела, вращающегося вокруг неподвижной оси. Рассмотрим какую-нибудь точку М вращающегося тела, находящуюся на расстоянии h от оси вращения z (рис. 187, 188). При вращении тела точка УИ будет описывать окружность радиуса h, плоскость которой перпендикулярна к оси вращения, а центр Oj лежит на самой оси. Так как угловая скорость тела не зависит от выбора подвижной плоскости Q, то мы всегда можем выбрать эту плоскость так, чтобы она проходила через рассматриваемую точку УИ (рис. 187). Будем определять положение точки М на ее траектории дуговой координатой s, отсчитываемой от взятой на плоскости Р неподвижной точки А, причем за положительное направление отсчета дуги s примем положительное направление отсчета угла поворота 9 (рис. 187, 188). [c. 296]

Таким образом, линейная скорость какой-либо точки вращающегося твердого тела равняется произведению угловой скорости тела на расстояние от этой точки до оси вращения. Вектор линейной скорости V точки М направлен по касательной к окружности, которую описывает точка М, и, следовательно, перпендикулярен к плоскости, проходящей через ось вращения и точку М. [c.297]

Существует ряд полуэмпирических формул для определения мощности, затрачиваемой на трение и вентиляцию. Они основаны на том, что эти потери зависят от плотности рабочего тела, окружной скорости, диаметра, длины лопатки, степени парциальности, зазоров, режима течения в них, направления вращения и т. п. Ниже приведена формула Стодолы [341, в которой кВт, [c.136]

Мы положим OA = OQ = b, GQ = а, так что а обозначает радиус катящегося тела. Если угол AOQ обозначить через в, то скорость точки G будет Ь — а) Й, так как эта точка описывает с угловой скоростью в окружность радиуса Ь — а.

Но, с другой стороны, если обозначить через о> угловую скорость вращения подвижного цилиндра, то мы найдем, что та же скорость равна и, так как точка Q представляет мгновенный центр вращения. Следовательно, [c.161]

Параметры и результаты закалки. Основными параметрами поверхностной закалки при контактном электронагреве являются а) сила тока во вторичной цепи или плотность тока на 1 пог. им ширины ролика б) скорость обработки (окружная скорость для тел вращения и линейная для плоскостей) в) давление [c.181]

Краевые условия (задаются для скоростей, давлений и температур) окружные скорости тел V , V -, скорость скольжения — Fj [c.167]

На тело массой т=1 кг действует постоянная по модулю сила, направленная перпендикулярно к вектору скорости тела (рис. 81). Начальная скорость тела 0=2 м/с, сила F=2 Н. Определите форму траектории и закон движения. (Окружность S=2t.) [c.326]

Так как в формуле А5 = гАф приращение угла Аф должно быть обязательно выражено в радианах, то и угловая скорость (О в формуле (88) должна обязательно выражаться в рад/с, рад/мин и т. д., но не в об/с или в об/мин. Только в этом случае будет получаться правильная размерность скорости и. На практике часто приходится находить скорость точек, лежащих на боковой поверхности вращающегося цилиндрического тела (вала, шкива и т. п.), которая называется иногда в этих случаях окружной скоростью. Если при этом угловая скорость тела будет выражена в об/мин, то окружная скорость [c.208]

Скорость точки в каждый момент времени прямо пропорциональна ее расстоянию от оси вращения, следовательно, график скоростей точек, например диаметра В В , будет представлять собой два треугольника (см. рис. 10.3). Очевидно, что вектор скорости точки вращающегося тела направлен перпендикулярно к радиусу, соединяющему эту точку с осью вращения. Если точка лежит на поверхности вращающегося тела, то ее скорость называют окружной. [c.112]

Линейная скорость V направлена по касательной к окружности, которую описывает точка М, и, следовательно, перпендикулярна к плоскости, проходящей через эту точку и ось вращения тела (рис. 196 и 197). Итак, модуль линейной скорости точки вращающегося твердого тела равен произведению абсолютного (значения угловой скорости тела на расстояние этой точки от оси вращения. [c.282]

Формула (54) выраллинейную скорость его точки) в зависимости от диаметра и числа оборотов в минуту. Если заданы диаметр и окружная скорость, а требуется определить число оборотов, то та же формула примет такой вид [c.129]

Во фрикционных вариаторах разность окружных скоростей тел качения по длине площадки касания должна быть минимальной Это достигается подбором схемы передачи и выбором формы тел качения, обеспечивающей малую длину площадки контакта. [c.437]

В тех случаях, когда источник перемещается с постоянной скоростью по окружности в теле вращения, температурное поле является периодическим [19]. [c.125]

Во фрикционных передачах трущиеся тела (цилиндры, конусы, плоские диски) при вращении обкатывают одно другое по определенной окружности. Аналогично этому при вращении находящихся в зацеплении зубчатых колес (шестерен) можно себе представить геометрические фигуры, катящиеся одна по другой с одинаковыми окружными скоростями и окружными усилиями. Эти воображаемые, реально не существующие фигуры называют начальными телами зубчатого зацепления. При равномерной передаче они должны быть телами вращения (цилиндрами, конусами, гиперболоидами), оси которых совпадают с осями зубчатых колес. Если начальные тела перекатываются без скольжения, то передачи называются передачами качения. В противоположность им в винтовых передачах имеется одновременно дополнительное движение скольжения вдоль общей образующей, являющейся линией соприкосновения перекатывающихся тел. По расположению осей вращения различают несколько основных форм зацепления (табл. Г). [c.307]

Пример 1. Пусть Р — точка, жестко связанная с телом и движущаяся вместе с ним, выбрана так, что живая сила тела равна сумме живой силы, обусловленной поступательным перемещением тела вместе с точкой Р, и живой силы в движении относительно точки Р.

Доказать, что точка Р лежит на окружности, опирающейся на отрезок G/ как на диаметр, где / — мгновенный центр вращения, а G — центр тяжести. Для доказательства этого заметим, что если ш — угловая скорость тела относительно точки /, а Q — положение произвольной частицы массой m, то по условию [c.126]

Задачи такого рода часто можно очень легко решать при помощи непосредственного применения принципа Даламбера. В только что рассматривавшейся задаче каждая частица тела описывает с постоянной угловой скоростью горизонтальную окружность, центр которой лежит на вертикальной оси. Если г — радиус этой окружности, то эффективная сила для частицы, направленная вдоль радиуса, равна тсй т Таким образом, можно считать, что тело находится в состоянии равновесия под действием его веса и системы сил, направленных перпендикулярно к оси и изменяющихся пропорционально расстоянию от оси. Найденное выше уравнение можно получить, если брать моменты сил относительно оси Ог. [c. 236]

Скорость в апогее или в афелии Скорость в перигее или перигелии Суммарная скорость Скорость небесных тел Окружная скорость небесного тела Скорость небесного тела в афелии Скорость небесного тела в перигелии Средняя скорость небесного тела [c.14]

Точка падения ракеты даже при строго вертикальном пуске всегда будет удалена на некоторое расстояние от места пуска. Это происходит главным образом вследствие влияния ветра, но при достаточно большой высоте подъема может сказаться и влияние вращения Земли, так как окружная скорость тела, находящегося на вертикали на некотором расстоянии от Земли, [c.89]

Для уходящих в бесконечность траекторий годограф скорости находится выше полярной оси. Это показано на рис.6. Особый интерес представляет точка В касания прямой, проведенной из начала координат, с окружностью годографа скорости. Отрезок ОВ представляет вектор скорости.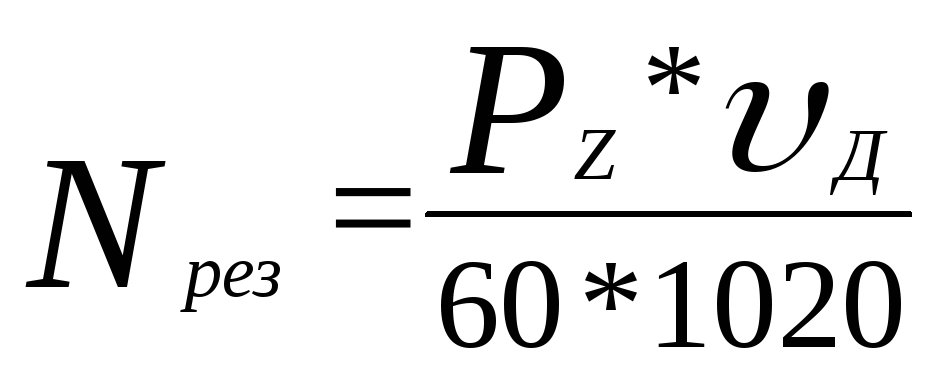

Определим направление радиуса-вектора положения тела г для этого момента. Из (12) следует, что г перпендикулярен к радиусу окружности годографа скорости, проведенному в точку наблюдения. В нашем случае это значит, что г перпендикулярен к радиусу СВ, т.е. по направлению совпадает с касательной ОВ. Оказывается, в точке В скорость тела направлена вдоль прямой, соединяющей его с силовым центром, т.е. траектория улетающего в бесконечность тела выходит на прямую и дальнейшее движение происходит вдоль этой прямой, В этом как раз и проявился отмеченный ранее выход траектории распадающейся системы тел на прямолинейную асимптоту в бесконечности. Понятно, что точке В на годографе скорости отвечает бесконечно удаленная точка траектории. [c.111]

На рис. I показаны траектории тел, вылетевших из точки А, лежащей вблизи поверхности Земли, с различными скоростями ). Во всех случаях скорость направлена горизонтально. Траекторией тела является окружность, если скорость тела V [c. 17]

Удельная работа лопаточной машины, выраженная в джоулях на килограмм, не зависит от рода рабочего тела, так как его физические параметры не входят в уравнение Эйлера. Эта работа зависит только от окружных составляющих абсолютных скоростей и окружных скоростей вращения колеса. [c.50]

Следует сказать о ньютоновой аппроксимации безударного движения шара по окружности движением по вписанному в окружность правильному многоугольнику У Ньютона есть несколько вариантов этого перехода к пределу. Наиболее убедительным для него является, видимо, тот, который использован в Prin ipia . Ход рассуждений там таков. Изменение количества движения шара при ударе в каждой верпшне очевидным образом пропорционально скорости тела. С другой стороны, в течение определенного промежутка времени оно пропорционально числу ударов, т. е. числу сторон многоугольника, по которым прокатится шар за это время. Это число сторон меняется пропорционально скорости движения шара и обратно пропорционально радиусу окружности.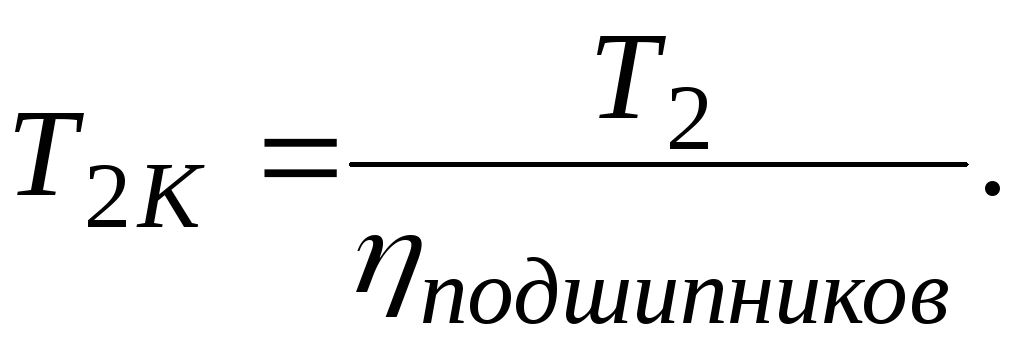 Остается допустить законность перехода к пределу (когда число сторон вписанного многоугольника неограниченно растет и он сколь угодно мало отличается от окружности) и мы получим для движения по окружности то, что доказано для многоугольника центростремительная сила пропорциональна квадрату скорости шара и обратно про- [c.115]

Попытка теоретического объяснения этих весьма сложных явлений в пограничных слоях на вращающихся телах вращения, обтекаемых в направлении оси вращения, сделана в работах Г. Шлихтинга э. Труккенбродта д 0 Парра [ ]. Во всех этих работах для исследования был использован приближенный метод, изложенный в начале этого параграфа. Хотя при обтекании вращающегося тела вращения в направлении оси вращения осевая симметрия пограничного слоя сохраняется, однако наряду с составляющей скорости в меридианном направлении появляется, вследствие вращения, также составляющая скорости в окружном направлении. По этой причине при применении для расчета пограничного слоя теоремы импульсов необходимо составить уравнение импульсов дважды один раз для меридианного направления х и другой раз для окружного направления 2. Для тела вращения, имеющего угловую скорость со и обтекаемого в направлении [c.237]

Теперь предположи.ч, что тело к.меет ось симметрии ОС, и прямая 01 движется вокруг этой оси по полодип, представляющей собой окружность малого радиуса. Следовательно, оси 01 и 0L почти совпадают с осью ОС. Пусть тело находится под действием произвольной пары сил с моменто.м Q. Разложим этот момент на два один (Q ) направим по прямой 0L, другой (Q») — — по перпендикуляру к 0L. Тогда действие пары сил с моментом Q не изменяет полодию. Так как моментQ» почти перпендикулярен к прямой 01, он мало изменяет полодию. Если же угловая скорость тела так велика, что величина Q. мала по сравнению с величиной G, [c.176]

Элементарное определение стационарного датгния. Поскольку часто требуется определить стационарное движение тара но шероховатой поверхности вращения, полезно исс 1едопать это движение отделыю. Центр тяжести G описывает с постоянной скоростью горизонтальную окружность, радиус которой GN перпендикулярен к оси теля вращения (рис. 40). Следовательно, трение [c.206]

В предложении VI используется понятие угловой скорости тела и показывается (в современных обозначениях), что нри горизонтальном враш,епни точки но окружности радиуса К = д (радиус равен численной величине ускорения свободного падения) с угловой скоростью о = 1 па нее будет действовать центробежная сила, равная весу. Следующие девять теорем посвящены силам инерции, возникающим нри движении точки но конической поверхности. П последние две теоремы устанавливают величину силы натяжения нити маятника в его пнжпем положении В в случае начала движения с уровня точки подвеса С и из верхней точки О траектории (вертикальной окружности, рис. 2.9.1). [c.89]

В результате описанных действий нам удалось найти из уравнений движения зависимость скорости от углового положения тела на траектории. Если зависимость г(полярное уравнение траектории тела на координатной плоскости х, у , то аналогичная зависимость для скорости у(полярное уравнение так называемого годографа скорости на плоскости и , иу . Немного поразмышляв, нетрудно сообразить, что геометрически формула (12) представляет собой окружность радиусом Но е/2 с центром на вертикальной оси в точке еуио(1-е/2) (рис.1). При движении тела по траектории радиус-вектор его положения поворачивается из начальной точки на угол тела, поворачивается при этом из начального положения на вертикальной оси в положение ОУ и представляет собой векторную сумму постоянного вектора ОС, направленного вдоль вертикальной оси, и вектора СУ, направленного вдоль радиуса из центра окружности С. Самое важное в том, что это второе слагаемое в векторе скорости поворачивается вместе с радиусом-вектором положения тела и всегда ему перпендикулярно, опережая радиус-вектор на п12. [c.108]

Движение, аналогичное рассматриваемому, можно наблюдать при обтекании вращающихся тел реальной жидкостью, так как вращающиеся тела увлекают -вязкую жидкость в циркуляционное движение (величина циркуляции скорости определяется окружной скоростью поверхности тела).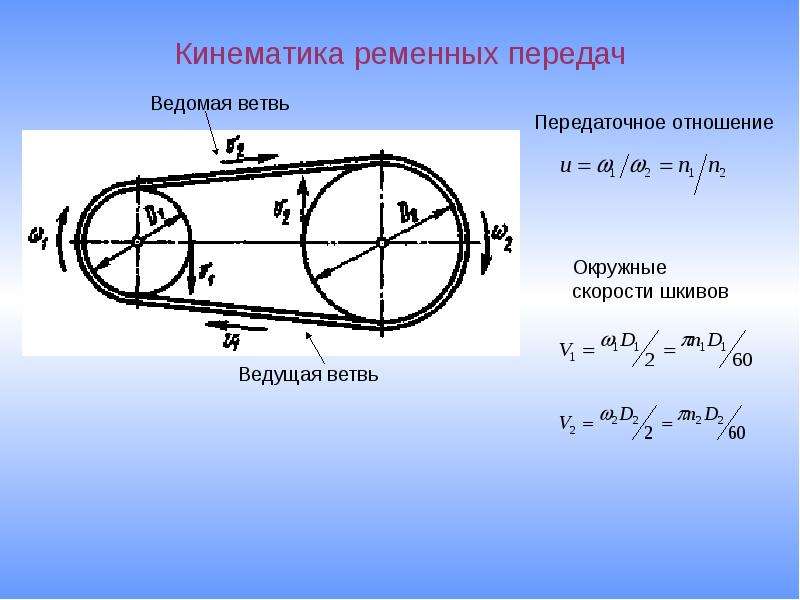 В этом случае возникновение силы, поперечной к вектору скорости невозмущенного потока, называется эффектом Магнуса. Эффект Магнуса использовался при создании ротора Флетнера — вертикальной, вращаемой башни, устанавливаемой на палубе корабля и создающей при ветре силу тяги, перпендикулярную к направлению етра. Аналогично теннисные и волейбольные мячи, в за-висимости от направления и интенсивности закрутки, меняют направление полета самым неожиданным образом . [c.89]

Упругое скольжение связано с упругими деформациями в зоне контакта. Элементарно это можно объяснить на примере цилиндрической передачи (см. рис. U.1). Если бы катки были абсолютно жесткими, то пс рвоначальный контакт по линии оставался бы таким и под нагрузкой. При этом окружные скорости по всей линии контакта равны и 1 кольжения не происходит. При упругих телах первоначальный контакт по линии переходит под нагрузкой в контакт по некоторой пло-П1,адке. Равенство окружных скоростей соблюдается только в точках, расположенных ira одной из линий этой площадки. Во всех других точках образуется скольжение. [c.216]

Движение по окружности | fizmatuski.narod.ru

Движение по окружности

Движение по окружности – частный случай криволинейного движения.
При движении по окружности движение может быть:
С постоянной по величине скоростью V=const
С одинаково изменяющейся по величине скоростью   Δ V= const
С неодинаково изменяющейся по величине скоростью, ΔV разное, изменяется не одинаково.
!!! Но при этом во всех 3-х случаях V изменяется по направлению (всегда). Движение по окружности – это периодически повторяющееся движение.
Основными характеристиками такого движения являются:
— период – это время 1 полного оборота (t – все время, N – число оборотов за время t)
— частота – число оборотов за 1с. (Гц)
l = 2πR – путь за 1 поворот (длина окружности) (м)
L = 2πRN – путь за N оборотов (м).
1.Рассмотрим движение с постоянной по величине скоростью. По определению, скорость это путь, пройденнфй телом за единицу времени:
  —   это путевая скорость движения тела по окружности. Зная значения величин, входящих в эту формулу, получим формулы скорости, которые выражают зависимость от основных характеристик движения по окружности:

ω = 2πn – циклическая частота или угловая скорость (число оборотов за 2π секунды), измеряется в (Гц = рад/с).
(Гц)
Аналогия: тело со V тело проходит путь L, со скоростью ω проходит угловой путь φ (поворачивается на угол).
Угловое расстояние:   φ = ωt или      φ = 2πN
— ускорение, которое показываем изменение направления скорости ( но не величины) т.к. всегда перпендикулярна и направлена к центру окружности, то это ускорение называется центростремительным:
— формула, определяющая центростремительное ускорение. Подставляя вместо скорости её формулы, получим расчётные формулы для центростремительного ускорения:
— формулы для вычисления центростремительного ускорения через основные характеристики.
Рассмотрим частные случаи движения тел по окружности:
1. Движение по одному кругу, но по окружностям разного радиуса:

Если т.А и т.В двигаются синхронно то они вместе совершают 1 оборот, значит Т₁ = Т₂ (периоды их оборотов одинаковы), а из этого   следует
=> n₁ = n₂ => ω₁ = ω₂,      Зная связь   между линейной и угловой скоростями, между ускорением   и угловой скоростью, получим выражения:

2. Рассмотрим случай, когда   два тела совершают круговые движения, но связаны   ременной или зубчатой передачей
             ременная связь                           или                              зубчатая связь
В этом случае скорости движения двух тел равны (нет провисания ремня ): V₁ = V₂
Зная формулы, связывающие линейную скорость с периодом вращения и   с ускорением,   получим:
2. Более сложный случай, когда скорость изменяется по величине.
  —   это средняя   путевая скорость движения тела по окружности, где её изменение по величине характеризуется тангенциальным ускорением: а_т , изменение скорости по направлению характеризуется центростремительным ускорением а_ц, которое в каждой точке разное, так как разной будет скорость движения по величине: . Эти два ускорения взаимно перпендикулярны т.к.    а_цнаправлено к центру окружности, а а_т — по касательной ( если разгон, то по направлению скорости, если торможение, то в противоположную сторону).
Так как тангенциальное ускорение не изменяется, а центростремительное изменяется, то будет    изменяться   и общее ускорение
Изменение скорости приведёт к изменению связанных с ним характеристик: периода, частоты и угловой скорости вращения.

Вернуться к конспектам урока

9 класс

13.11.2021

Задание на неделю с 15.11 до 19.11

Задание 1.

Тема. Искусственные спутники Земли

Просмотр видеоролика

https://www.youtube.com/watch?v=U2pPJhwOMq8

Тема. Вес тела. Невесомость

Просмотр видеоролика

https://www.youtube.com/watch?v=lvbmcoriU0Y

Задание 2.

В понедельник я сниму видео, в котором подтробно покажу и расскажу, как решать и оформлять задачи на законы Ньютона. Вы посмотрите и запишите задачи в тетрадь для решения задач. Фото пришлете мне.

Ссылку сброшу. Затем я запишу Вам задачи, а Вы их решите по алгоритму.

08.11.2021 (задание на 3 урока)

Тема. Контрольная работа по разделу «Основы кинематики»

Вариант 1

1.Поезд подходит к станции со скоростью 36 км/ч и останавливается через минуту после начала торможения. С каким ускорением двигался поезд?

2.Определите, какую скорость развивает мотоциклист за 15 с, двигаясь из состояния покоя с ускорением 1,3 м/с2.

3.Какой должна быть длина взлётной полосы, если известно, что самолет для взлета должен приобрести скорость 240 км/ч, а время разгона самолета равно примерно 30 с?

4.Спортсмен съехал на лыжах с горы длиной 40 м за 5 с. Определите ускорение движения и скорость спортсмена у подножия горы.

5.Тормоз легкового автомобиля считается исправен, если при скорости движения 8 м/с его тормозной путь равен 7,2 м. Каково время торможения и ускорение автомобиля

Выслать до 10.11 на двойном листике. Если зрешение задач будут списаны из Интернета, а значит оформлены не по алгоритму, будет оценка 3. Алгоритм: СИ, рисунок, формулы, проверка единиц измерения, вычисления, ответ.

Тема. Силы в природе

1. Просмотреть презентацию и оформить в тетради в виде таблицы:

https://docs.google.com/presentation/d/1iExtwvNVKhW5KgHX96exW1CfFvZr0yPk/edit?usp=sharing&ouid=106548949822356979545&rtpof=true&sd=true

2. Повторить по тетрадям 7 класса и определениям по Крапивкиной эту тему.

3. Просмотреть видеоролики по решению задач, но не записывать их в тетрадь

https://www.youtube.com/watch?v=CYSPC3bhGT0

Домашнее задание: решить задачи и выслать до 12.11

1. Масса автомобиль900 кг. Чему равна сила тяжести?

2. Конькобежец движется по льду. Определите силу трения скольже¬ния, если коэффициент трения 0,02, а сила давления равна 800 Н.

3.Стальная проволока удлинилась на 0,002 м. С какой силой действо¬вали на проволоку, если ее жесткость 100 000 Н/м.

31/10/2021

Памятка для учащихся

на период дистанционного обучения

Дорогие ребята! Обращаем ваше внимание, что дистанционное обучение – это не каникулы, образовательный процесс сохраняется, вы учитесь согласно расписанию. Ознакомьтесь с подробной инструкцией, чтобы вы не испытывать трудности с этим процессом.

1. Помнить, что учащиеся будут обучаться дома, получая информацию и выполняя задания средствами Интернет-технологий.

2. Выясните учебные платформы для дистанционного обучения, используемые учителями.

3. Проверьте Вашу регистрацию на данной платформе.

4. Разместите расписание занятий и режим обучения на видном месте. Начало занятий в 8.00; продолжительность занятий – 30 минут; перерыв между занятиями – 15 — 20 минут.

5. Необходимо изучить обучающие ресурсы к занятию. Прочитать тему урока в текстовом формате, прослушать тему урока в аудио формате, изучить Интернет-ресурсы, просмотреть презентации и видео-файлы.

6. После изучения обучающих ресурсов к занятию (в соответствии с расписанием) необходимо выполнить задания.

8. Задания отправляются преподавателю.

7. Выполненное задание можно отправить в формате:

• текстового документа,

• графического файла – фото или скан листа, написанного от руки,

• архива файлов.

9. Отсутствие выполненного задания автоматически приравнивается к пропуску занятия.

10. При необходимости любому обучающемуся может быть оказана учебно-методическая помощь, в том числе в форме индивидуальных консультаций, оказываемых дистанционно с использованием информационных и телекоммуникационных технологий.

11. Старайтесь во время отдыха не напрягать зрение, а выполнять упражнения для глаз и короткие физические упражнения для тела.

Помните, дистанционное обучение — не каникулы, а продолжение обучения в другом формате. Успешность результатов обучения полностью зависит от взаимодействия всех участников образовательных отношений!

ЗАДАНИЕ НА НЕДЕЛЮ! фОТО С ВЫПОЛНЕННЫМ ДОМАШНИМ ЗАДАНИЕМ НЕОБХОДИМО ВЫПОЛНИТЬ ДО 08.11.2021. И ВЫСЛАТЬ НА ПОЧТУ

[email protected]

Тема. Инерциальная система отсчета. Первый, второй и третий законы Ньютона.

1. Посмотреть видеоролик по теории

https://www.youtube.com/watch?v=gLxCiIRWtuE&t=1613s

https://www.youtube.com/watch?v=XAsji3sgMg4

https://www.youtube.com/watch?v=OijNRhnYokY

2. Посмотреть видеоролик по решению задач и записать их в тетрадь для решения задач:

3. Прочитать параграф 10 — 12 по учебнику автора Перышкин и выписать в тетрадь формулировки: инерциальной системы отсчета, 1, 2 и 3 законы Ньютона. Ссылка на учебник

https://drive.google.com/file/d/1lt8kWal2kGK9wuXgx9GIaCOv8a0pZ8w0/view?usp=sharing

Домашнее задание: прислать фото по теории заполненной и записанных из видео задач. Больше пока ничего не задаю из-за большой нагрузки. Законы выучить на память!

20/10/2021

Тема. Решение задач на применение на применения свободного падения.

1. Посмотреть видеоролик

https://www.youtube.com/watch?v=d6eqXfoAD78

Тема. Равномерное движение по окружности. Период и частота обращения.

1. Посмотреть видеоролик по теории

2. Посмотреть видеоролик по решению задач

https://www.youtube.com/watch?v=X3hqk-0a4yw

3. распечатать ОК и вклеить в тетрадь

1. Период.
Период – время, в течении которого тело совершает один полный оборот, называют периодом обращения. , где t – время всех оборотов, N – число оборотов.
Период обозначается буквой Т. Формула для нахождения периода, где – время всех оборотов, – количество оборотов. Единицей измерения периода в СИ является секунда.
2. Частота.
Частота – число оборотов за единицу времени (секунду). , (в честь учёного Генриха Герца).
Частота и период обращения связаны между собой. , а .
Коленчатые валы двигателей трактора имеют частоту вращения от 60 до 100 оборотов в секунду. Ротор газовой турбины вращается с частотой от 200 до 300 об/с. Пуля, вылетающая из автомата Калашникова, вращается с частотой 3000 об/с.
3. Связь модуля скорости с периодом обращения и частотой.
Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности и период или частоту обращения. Один полный оборот тело совершает за время, равное периоду обращения. Путь, пройденный телом равен длине окружности: , поэтому .
С учётом этого можно найти центростремительное ускорение:

4. По желанию, проверить свои знания
1.Тело движется равноускоренно прямолинейно, если скорость и ускорение направлены
1)сонаправленно вдоль оси координат; 2)вдоль оси координат; 3) под прямым углом друг к другу; 4)вдоль оси координат в противоположных направлениях
2.Выбери верное утверждение: 1)чем больше радиус окружности, тем меньше линейная скорость движения точки; 2) чем больше радиус окружности, тем больше центростремительное ускорение; 3) период вращения и линейная скорость находятся в прямой зависимости; 4) угловая и линейная скорости прямо пропорциональны друг другу
3. Тело совершает за 4с 8 оборотов. Период его вращения равен 1) 32с; 2) 2с; 3)0,5 с
4.Частота вращения 600об/мин показывает, что тело совершает 1)за 1 секунду 600 оборотов; 2) за 600с один оборот; 3) за 1 секунду 10 оборотов
5.Линейная скорость увеличилась в 2 раза. Угловая скорость при этом 1) уменьшилась в 2 раза; 2) увеличилась в 2 раза; 3) не изменилась; 4) увеличилась в 4 раза; 5) уменьшилась в 4 раза
6. Линейная скорость уменьшилась в 2 раза .Центростремительное ускорение при этом 1) уменьшилось в 2 раза; 2) увеличилось в 2 раза; 3) не изменилось; 4) увеличилось в 4 раза; 5) уменьшилось в 4 раза
7.Движется ли кузов автомобиля поступательно ,когда машина движется на повороте? 1)да; 2) нет
8. Величина, которая показывает число оборотов за единицу времени, называется 1)угловой скоростью; 2)периодом вращения; 3) линейной скоростью; 4) частотой вращения
9.Период вращения равен 2с. Частота вращения тела равна 1) 2 об/с ; 2) 0,5 об/мин; 3) 2 об/мин; 4)0,5 об/с
10.Выбери неверное утверждение: 1)чем меньше частота вращения тела, тем линейная скорость меньше; 2) чем больше период вращения, тем угловая скорость меньше; 3) чем дальше точка от оси вращения, тем больше ее линейная скорость; 4)чем меньше радиус окружности, тем меньше центростремительное ускорение тела
11.Угловая скорость равна 2 рад/с, а линейная скорость 0,5 м/с.Центростремительное ускорение равно
1) 1 м/с ; 2) 4 м/с² ; 3) 0,25 м/с² ; 4) 1 м/с²
12.При движении по окружности вектор линейной скорости направлен 1)по касательной к траектории в данной точке; 2) к центру окружности
13.Тело начало двигаться по окружности радиусом в 4 раза меньшим, но с той же скоростью. Центростремительное ускорение тела1) уменьшилось в 2 раза; 2) увеличилось в 2 раза; 3) не изменилось; 4) увеличилось в 4 раза; 5) уменьшилось в 4 раза
Тема. Инерциальная система отсчета. Первый закон Ньютона и инерция
1. Посмотреть видеоролик по теории
2. Посмотреть видеоролик по решению задач
https://www.youtube.com/watch?v=X3hqk-0a4yw
3. распечатать ОК и вклеить в тетрадь

Как узнать, сколько раз вращается колесо? — MVOrganizing
Как узнать, сколько раз вращается колесо?
Итак, если мы хотим знать, сколько оборотов должны сделать наши колеса, мы делим 200 сантиметров на 24,92 сантиметра на оборот (помните, что окружность — это расстояние, на которое колесо проходит за один оборот). Число оборотов равно: 200 см / 24,92 (см / оборот) = 8,03 оборота.
Сколько раз колесо автомобиля поворачивается за 1 милю?
Например, если шина имеет диаметр 20 дюймов, умножьте 20 на 3.1416, чтобы получить 62,83 дюйма. Наконец, разделите 63 360 дюймов на милю на окружность шины, чтобы найти количество оборотов на милю. Завершая пример, вы должны разделить 63 360 на 62,83, чтобы получить 1008,44 оборотов на милю.
Сколько раз шина автомобиля проворачивается, прежде чем потребуется замена?
Он рекомендует менять шины примерно каждые 3000-5000 миль или, по крайней мере, каждый раз, когда вы идете на замену масла. Если в руководстве по эксплуатации указано, что вашему автомобилю не нужно менять масло так часто, то планируйте замену шин не реже одного раза в шесть месяцев.
Сколько полных оборотов делает автомобильная шина диаметром 25 дюймов, когда автомобиль проезжает одну милю?
Ответ: Автомобильная шина делает 807 полных оборотов, когда проходит 1 милю.
Как найти оборот с учетом диаметра и расстояния?
Каждый оборот велосипед проходит расстояние, равное длине окружности шины (если только вы не заносите!) Шины велосипеда обычно измеряются по диаметру. Чтобы вычислить длину окружности, вы можете просто умножить диаметр на π, что примерно равно 3.142. Это дает вам расстояние для каждого оборота.
Сколько оборотов в миле для шины 37?
116,2 560
Какой размер у шины 37?
Таблица эквивалентных размеров шин для шин 33 ″, 35 ″, 37 ″ или 40 ″:
Шины 33 ″ (общий диаметр +/- 0,50 ″)
35X12.50-15 315 / 75-16 325 / 45-24
Шины 37 ″ (общий диаметр +/- 0,50 ″)
15 ″ 16 ″ 24 ″
37X14.50-17 385 / 70-16 315 / 50-24
Сколько оборотов 35-дюймовая шина делает за милю?
ДИАМЕТР, РАЗВЕРТЫВАНИЕ (ОКРУЖЕНИЕ) И ОБОРОТЫ НА МИЛИ ТАБЛИЦА
Диаметр Внедрение Об / миль *
35 110,0 593
35,5 111,5 585
36 113.1 576
36,5 114,7 568
Что такое обороты шины на милю?
оборотов на милю указывает, сколько раз шина вращается, когда она преодолевает расстояние в одну милю. В зависимости от производителя шин количество оборотов на милю может быть измерено в лаборатории или получено из расчетов, основанных на их предыдущем опыте испытаний.
Шины 285 — это то же самое, что и 33?
ДА, 285 широкие шины — это то же самое, что и 33-дюймовые шины, хотя 285 — это ширина протектора в миллиметрах, а 33 ″ — диаметр шины.285/75/16 — обычно принятый метрический эквивалент размера 33. 16,831 ″ + 16 ″ колесо = приблизительный диаметр шины 32,831 ″.
Больше или меньше оборотов на милю лучше?
Чем меньше оборотов делает шина, тем меньше оборотов делает двигатель, что должно означать меньшее потребление топлива. И шина с большим диаметром / окружностью вращается меньше на милю, чем меньшая.
Какова высота 17-дюймовой шины?
ШИНЫ 17 ДЮЙМОВ ВЫСОТА ШИНЫ
225 35 17 23.20
245 35 17 23,75
315 35 17 25,68
335 35 17 26,23
Какая шина самая большая для обода 17 дюймов?
Размеры шин по диаметру колес
17 ″ Опции
215 / 40-17 245 / 35-17 275 / 55-17
215 / 45-17 245 / 40-17 275 / 60-17
215 / 50-17 245 / 45-17 275 / 65-17
215 / 55-17 245 / 50-17 275 / 70-17
Какая шина 17 дюймов самая широкая?
335/35/17 — самые широкие шины для 17-дюймовых колес.
Можно ли поставить 35-дюймовые шины на 17-дюймовые диски?
33-дюймовые шины хорошо работают с ободами шириной 15 или 16 дюймов, а 35-дюймовые шины следует использовать только с ободами шириной не менее 17 дюймов. Для более крупных шин требуются более широкие диски, чтобы максимально улучшить профиль шины и улучшить маневренность вашего Jeep.
Можно ли поставить шину любого размера на обод 17 дюймов?
Что касается диаметра, вы должны быть уверены, что ваши шины и колеса точно соответствуют друг другу, например Шина 215 / 65R17 подходит только для колеса диаметром 17 дюймов.Для спортивных автомобилей общее практическое правило — подбирать ширину колеса и ширину протектора в дюймах. Например, шина размером 285 / 35-19 имеет ширину протектора 9,9 дюйма.
Какая шина 18 дюймов самая широкая?
A 295 — самая широкая шина с ободом 7,5. Ни один шинный магазин не установит 12,5 на стандартный обод шириной. 275 / 70р18 подойдет.
Шину какого размера можно установить на обод 18 дюймов?
Размеры шин по диаметру колес
18 ″ Опции
155 / 90-18 245 / 35-18 315 / 35-18
165 / 70-18 245 / 40-18 315 / 40-18
165 / 90-18 245 / 45-18 325 / 45-18
175 / 90-18 245 / 50-18 325 / 60-18
Могут ли 35-дюймовые шины поместиться на 18-дюймовые диски?
И да, вы можете установить 35-дюймовые шины на 18-дюймовые диски.Вам понадобятся либо плоские расширители крыльев, либо подъемник и колесные проставки, пока вы не купите послепродажные колеса с лучшим зазором.
Шины какого размера подходят для колес 18 × 9?
225/40 или 235/40 — стандартная комплектация для B5 S4 18s. Я бы использовал это. Лучше всего 245 / 35-18, но в зависимости от колеса может потребоваться валик крыльев. У нас нет ничего шире, чем 18 × 8.
Как узнать размер шин?
Что означает размер моей шины?
Двухзначное число после косой черты — это соотношение сторон, которое измеряет поперечное сечение шины к ее ширине.
Если размер шины 255/60 R16, 60 означает, что высота составляет 60% от ширины шины. Чем больше соотношение сторон, тем больше будет боковина шины.
Могу ли я поставить 17-дюймовые шины на 18-дюймовые диски?
Шины
могут «растягиваться» вбок, но не наружу… иначе, шина 17 дюймов НЕ будет работать на колесе 18 дюймов…
Подходят ли все 18-дюймовые шины к 18-дюймовым колесам?
Нет, шины рассчитаны на определенный диапазон ширины колес. Re: подойдет ли любая 18-дюймовая шина к любому 18-дюймовому ободу? Нет, шины рассчитаны на определенный диапазон ширины колес.
Как рассчитать количество оборотов?
Поскольку 1 оборот = 2π рад, мы можем найти количество оборотов, найдя θ в радианах. Нам даны α и t, и мы знаем, что ω0 равно нулю, поэтому θ можно получить, используя θ = ω0t + 12αt2 θ = ω 0 t + 1 2 α t 2.
Какова формула революции?
Для этого используйте формулу: оборотов в минуту = скорость в метрах в минуту / окружность в метрах. Следуя примеру, количество оборотов в минуту равно: 1,877 / 1.89 = 993 об / мин.
Как рассчитать количество оборотов в час?
Процесс расчета конверсионной стоимости
1 оборот в минуту = (точно) (160) (13600) (1 60) (1 3600) = 60 оборотов в час.
1 оборот в час = (точно) (13600) (160) (1 3600) (1 60) = 0,016666666666667 оборотов в минуту.
Обороты — это скорость?
Оборотов в минуту (сокращенно об / мин, об / мин, об / мин, или с обозначением мин-1) — это количество оборотов за одну минуту.Это единица измерения скорости вращения или частоты вращения вокруг фиксированной оси.
Сколько метров в радианах?
Радиан
Система единиц Производная единица СИ
Единица из Уголок
Обозначение рад, c или r
В единицах Безразмерный с длиной дуги, равной радиусу, т.е. 1 мм
Как вы измеряете скорость вала?
Скорость вала, как и вы, часто указывается в об / мин.Его также можно указывать в радианах в секунду или, скажем, в дюймах в секунду для поверхностной скорости. В радианах в минуту это 58,2 x 2 пи = 365,7 радиан в минуту. В радианах в секунду это 58,2 x 2 x пи / 60 = 6,09 радиан в секунду.
Какое соотношение скорости?
Некоторыми примерами переменных, использующих шкалу соотношений, могут быть расстояние, скорость, вес, температура (Кельвин) и т. Д. Физика определяет скорость как «пройденное расстояние, разделенное на время в пути».
Как рассчитать частоту вращения вала трансмиссии?
Расчет выходной скорости с использованием диаметра шкива и входной скорости
Выходные обороты / входные обороты = коэффициент умножения.Для вентилятора с ременным приводом требуются две основные скорости — это частота вращения двигателя и частота вращения вентилятора.
Формула. Входные обороты / Выходные обороты = Выходной диаметр / Внутренний диаметр.
Формула. Входные обороты / Выходные обороты = Выходной диаметр / Внутренний диаметр.
оборотов в минуту на выходе = 1 002,13.
Как передаточное число влияет на скорость?
Более низкое (более высокое) передаточное число обеспечивает более высокую максимальную скорость, а более высокое (более короткое) передаточное число обеспечивает более быстрое ускорение. . Помимо шестерен в трансмиссии, есть еще шестерня в заднем дифференциале.
Что такое передаточное число главной передачи?
Передаточное число главной передачи — это обычно передаточное число для дифференциала или конечное место, где передаточное число изменяется перед передачей на колеса. Повышение передаточного числа главной передачи также означает, что вы будете на более высоких оборотах на высшей передаче, что приведет к увеличению оборотов двигателя на шоссе.
Что лучше — 3,42 или 3,73?
3,73 на 9% выше 3,42. Это означает, что ваши обороты на любой заданной скорости будут на 9% выше. Вы должны иметь возможность ускоряться примерно на 9% быстрее, по крайней мере, на более низких передачах.Ваша максимальная скорость на каждой передаче снизится на 9%.
Какое передаточное число лучше всего подходит для скорости?
4,10: 1
Влияет ли передаточное число на мощность в лошадиных силах?
Вот что означают числа, как они связаны и как влияют на производительность: крутящий момент — это мера силы вращения, приложенной к коленчатому валу двигателя и, в конечном итоге, к ведущим колесам. Более высокое числовое передаточное число (4,11: 1) позволяет двигателю работать в более высоком диапазоне мощности, тем самым улучшая характеристики.
Какой самый дешевый способ увеличить мощность?
Больше топлива / воздуха — больше лошадиных сил. Воздухозаборники также (как следует из названия) забирают более холодный воздух из-за пределов моторного отсека автомобиля. Более холодный воздух более плотный, что опять же приводит к увеличению количества топлива компьютером, помогая двигателю увеличить мощность.
3,08 — хорошее передаточное число?
Да, вы совершенно правы, буксировка с 6 скоростями с 3,08 все же лучше, чем буксировка с 4 скоростями и 3.73с. Если это тяжелый прицеп, вы, вероятно, никогда не будете использовать 5-ю и 6-ю передачи, но кого это волнует? кривошипа поворачивает, чтобы повернуть задние колеса, когда это считается.
Какое передаточное число лучше для крутящего момента?
Численно более высокое передаточное число обеспечивает механическое преимущество, заключающееся в передаче большего количества доступного крутящего момента двигателя на задние шины (и передние шины в полноприводном автомобиле), но вы платите за это на топливном насосе. Таким образом, грузовик с дополнительными передачами 3,73 буксирует более тяжелый прицеп, чем прицеп с 3 передачами.55 или 3,21.
Означает ли более высокое передаточное число больший крутящий момент?
Как правило, более низкое передаточное число главной передачи приводит к меньшему крутящему моменту на колесах, но более высокой максимальной скорости. Между тем, более высокое передаточное число приведет к противоположному, то есть к большему крутящему моменту на колесах, но к более низкой максимальной скорости.
Что лучше: 3,73 или 4,10?
Передаточное число задней оси 4,10 идеально подходит для буксировки более крупных прицепов 5-го колеса или прицепа Gooseneck. ФАКТ: Передаточное число 3,73 идеально подходит для буксировки тяжелых грузов по ровной местности и обеспечивает повышенную экономию топлива при устойчивом движении по шоссе на большие расстояния.
Какое передаточное число лучше всего для экономии топлива?
Например, 3:31 дает лучшую экономию топлива, чем 3:73. С другой стороны, 3:73 или, возможно, 4:10 будет буксировать намного больше, в то время как экономия топлива значительно снизится. Самым популярным передаточным числом в задней части грузовиков сегодня является 3:55, что соответствует среднему значению тягового усилия и экономии топлива.
6.1 Угол поворота и угловая скорость
Угловая скорость
Насколько быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости.Рассмотрим сначала угловую скорость (ω) (ω) — это скорость, с которой изменяется угол поворота. В форме уравнения угловая скорость равна
6.2 ω = ΔθΔt, ω = ΔθΔt,
, что означает, что угловое вращение (Δθ) (Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота в данный момент времени, он имеет большую угловую скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Теперь давайте рассмотрим направление угловой скорости, а это значит, что теперь мы должны называть ее угловой скоростью.Направление угловой скорости — вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость указывает от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.
Угловая скорость (ω) — это угловая версия линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим углубление на вращающемся компакт-диске.Эта яма перемещается по длине дуги (Δs) (Δs) за короткий промежуток времени (Δt) (Δt) (Δt) (Δt), поэтому его тангенциальная скорость равна
Из определения угла поворота, Δθ = ΔsrΔθ = Δsr, мы видим, что Δs = rΔθΔs = rΔθ. Подставляя это в выражение для v , получаем
v = rΔθΔt = rω. v = rΔθΔt = rω.
Уравнение v = rωv = rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем крае CD (с большим r ), чем для точки ближе к центру CD (с меньшим r ).Это имеет смысл, потому что точка, находящаяся дальше от центра, должна покрывать большую длину дуги за то же время, что и точка ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. Рисунок 6.4.
Рис. 6.4 Точки 1 и 2 вращаются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги (Δs2Δs2), поскольку она дальше от центра вращения.
Теперь рассмотрим другой пример: шина движущегося автомобиля (см. Рисунок 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое v , потому что v = rωv = rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет создавать большую линейную (тангенциальную) скорость, v, для автомобиля. Это связано с тем, что больший радиус означает, что большая длина дуги должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.
Рисунок 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω.Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят домкратом и колеса вращались, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад по отношению к оси с тангенциальной скоростью v = rωv = rω, где r — радиус шины. Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Чем больше угловая скорость шины, тем больше линейная скорость автомобиля.
Однако есть случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда автомобиль вращает свои колеса по льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля на льду длина дуги, по которой движутся протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль. Это похоже на бег на беговой дорожке или на велотренажере; вы буквально никуда не денетесь.
Советы для успеха
Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны включить величину и направление.Направление угловой скорости — вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как вверх, вниз, влево, вправо, север, юг, восток или запад, как показано на рисунке 6.6.
Рис. 6.6. Поскольку муха на краю старинной виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена по касательной к кругу.Направление угловой скорости в данном случае указано на странице.
Watch Physics
Взаимосвязь между угловой скоростью и скоростью
В этом видео рассматриваются определение и единицы угловой скорости и их связь с линейной скоростью. Здесь также показано, как преобразовать число оборотов в радианы.
Проверка захвата
Для объекта, движущегося по круговой траектории с постоянной скоростью, изменится ли линейная скорость объекта при увеличении радиуса пути?
Да, потому что тангенциальная скорость не зависит от радиуса.
Да, потому что тангенциальная скорость зависит от радиуса.
Нет, поскольку тангенциальная скорость не зависит от радиуса.
Нет, потому что тангенциальная скорость зависит от радиуса.
Вращение
Чтобы описать движение вращающихся или вращающихся объектов, нам нужен более естественный набор переменных, чем x, v и a, которые мы использовали до сих пор. Например, каждая точка вращающегося объекта имеет разную скорость, но мы можем определить угловую скорость, одинаковую для всех точек.v пропорционально r, поэтому все, что нам действительно нужно сделать, это разделить r.
Угловые переменные
Угловое смещение (угол): θ = s / r
Угловая скорость: ω = v / r
Угловое ускорение: α = a _t / r
Обратите внимание, что угловое ускорение связано с тангенциальным ускорением, а не с центростремительным ускорением. Угловое ускорение возникает только при изменении скорости вращения.
Если угловая скорость постоянна, то скорость точки на вращающемся объекте равна:
v = 2πr / Тл
где T — период, время, которое нужно обойти один раз.
Угловая скорость ω = v / r = 2π / T
Эти угловые переменные являются векторами, как и их собратья по прямолинейному движению. В какую сторону они указывают? Возьмите пальцы правой руки и согните их, как вращается предмет. Вытяните большой палец, и вы получите направление угловой скорости. Угловое ускорение будет в том же направлении, если объект ускоряет свое вращение, и в противоположном направлении, если он замедляется.
Мы часто будем использовать по часовой стрелке и против часовой стрелки, чтобы указать направление.Как и в случае прямолинейного движения, мы можем определить положительное направление в зависимости от того, что удобно в конкретном случае.
Соединение с прямолинейным движением
Мы сосредоточимся на вращении вокруг одной оси вращения, которое аналогично одномерному прямолинейному движению. По сути, если вы понимаете одномерное движение, вы можете выполнять вращение — вращательное движение — это просто прямолинейное движение, свернутое в круг.
Смещение, скорость и ускорение имеют эквиваленты вращения.Существуют также вращательные эквиваленты массы, силы, законов Ньютона, кинетической энергии, импульса и т. Д. Любое уравнение, которое мы использовали для прямолинейного движения, имеет вращательную форму, которую можно найти, подставив эквивалентные вращательные переменные.
Например, как связаны углы, угловые скорости и угловые ускорения? Таким же образом линейные переменные:
Угловая скорость — это скорость изменения угла
Мгновенная угловая скорость: ω = d θ / dt
Средняя угловая скорость = ω _ср. = Δ θ / Δt
Δ θ = ∫ ω dt
Угловое ускорение — это скорость изменения угловой скорости
Мгновенное угловое ускорение: α = d ω / dt
Среднее угловое ускорение = α _ср. = Δ ω / Δt
Δ ω = ∫ α dt
Уравнения постоянного ускорения
Эти уравнения связывают смещение, скорость, ускорение и время и применяются при следующих условиях:
ускорение постоянное
движение отсчитывается от t = 0
тот факт, что несколько переменных являются векторами, учитывается соответствующими знаками плюс и минус
Прямолинейное движение Вращательное движение
v = v _o + at ω = ω _o + α t
x — x _o = v _o t + ½ при ² θ — θ _o = ω _o t + ½ α t ²
x — x _o = ½ (v + v _o) t θ — θ _o = ½ (ω + ω _o) t
v ² = v _o ² + 2 a (x — x _o) ω ² = ω _o ² + 2 α (θ — θ _o)
Пример задачи
Вы находитесь на колесе обозрения, которое вращается со скоростью 1 оборот каждые 8 секунд.Оператор колеса обозрения решает остановить его и включает тормоз. Тормоз производит постоянное ускорение -0,11 радиан / с ².
(a) Если ваше сиденье на колесе обозрения находится на расстоянии 4,2 м от центра колеса, какова ваша скорость, когда колесо вращается с постоянной скоростью до того, как будет применен тормоз?
(b) Сколько времени нужно, чтобы колесо обозрения остановилось?
(c) Сколько оборотов делает колесо, когда оно останавливается?
(d) Как далеко вы проедете при замедлении колеса?
θ _o = 0
θ =?
ω _o = 0.785 рад / с
ω = 0
α = -0,11 рад / с ²
Решение
(a) Колесо вращается со скоростью 1 оборот каждые 8 секунд, или 0,125 об / с. Это начальная угловая скорость. Часто удобнее всего работать с угловой скоростью в радианах / с; выполнение преобразования дает:
ω = 0,125 об / с * 2π рад / об = 0,785 рад / с
Ваша скорость — это просто угловая скорость, умноженная на расстояние от центра колеса:
v = r ω = 4.2 * 0,785 = 3,30 м / с
(b) Мы вычислили начальную угловую скорость, конечная угловая скорость равна нулю, а угловое ускорение составляет -0,11 рад / с ². Это позволяет определить время остановки:
ω = ω _o + α t
t = (ω — ω _o) / α
t = (0 — 0,785) / (- 0,11) = 7,14 с
(c) Один из способов определить количество оборотов, которое совершает колесо при замедлении до остановки, — это определить угол, на который оно движется:
θ — θ _o = ω _o t + ½ α t ²
θ = (0.785 * 7,14) + ½ (-0,11) * (7,14) ² = 2,80 радиан
Это может быть преобразовано в обороты:
2,80 рад / (2π рад / об) = 0,446 оборота.
(d) Чтобы определить расстояние, которое вы прошли во время замедления колеса, угловое смещение (в радианах) можно преобразовать в смещение, умножив его на r:
s = rθ = 4,2 * 2,80 = 11,8 м
Ремни — диаметр шкива в зависимости от скорости
Шкив — диаметр в зависимости от скоростиКалькулятор скорости
Одинарная ременная передача — один ведущий шкив и один ведомый шкив
Для системы с двумя валами и двумя шкивами — как показано со шкивами 1 и 2 на рисунке выше:
d ₁ n ₁ = d ₂ n ₂ (1)
где
d ₁ = диаметр ведущего шкива (дюйм, мм)
07 907 = обороты ведущего шкива (об / мин — оборотов в минуту)
d ₂ = диаметр ведомого шкива (дюйм, мм)
n ₂ = оборотов ведомого шкива (об / мин — оборотов в минуту)
Уравнение (1) можно преобразовать, чтобы выразить
Обороты ведомого шкива
n _{2 90 819} = d ₁ n ₁ / d ₂ (2)
Обороты ведущего шкива
n = d ₂ n ₂ / d ₁ (3)
Диаметр ведомого шкива
d 9018 d 9018 ₁ n ₁ / n ₂ (4)
Диаметр ведущего шкива
d _{908 d508 1} n ₂ / n ₁ (5)
Системы с несколькими ремнями передачи
Для системы a с тремя валами и четырьмя шкивами — как показано на рисунке выше:
n ₂ = n ₃ (6)
n ₄ = n ₁ (d ₁ d ₃) / (d ₂ d ₄) (7)
Пример — система с несколькими ремнями передачи
Число оборотов вала 4 в многоременной передаче, как показано на рисунке выше, где
n ₁ = 1000 об / мин
d ₁ = 100 мм
d ₂ = 50 мм
d ₃ = 110 мм
d ₄ = 60 мм
можно рассчитать как
n ₄ = (1000 об / мин) (100 м м) (110 мм) / ((50 мм) (60 мм))

= 3667 об / мин
1.НАЗНАЧЕНИЕ:
Чтобы проверить уравнение для центростремительной силы, в частности, подтверждая функционал зависимость центростремительной силы от массы, радиуса и частоты.
2. АППАРАТ:
Ротационный аппарат Сарджента-Велча. Гири с прорезями. Подбор пружин; скрепки. Наручные часы или секундомер.
3. ТЕОРИЯ:
См. Любой учебник, в котором выводится уравнение ускорения тела, движущегося с постоянная скорость по круговой траектории:

v ² Центростремительное ускорение , a _c = —— = Rω ² = 4π ² Rf ², р

Определение: Центростремительный сила — это радиальная составляющая чистой силы, действующей на тело.
где мы используем:
v для скорости тела,
R — радиус его пути,
f для частоты (об / сек),
ω = 2πf для угловой частоты (в радианах),
Τ ≡ 1 / ф.
Вектор ускорения направлен радиально внутрь к центру окружности. В вектор ускорения, следовательно, направлен перпендикулярно мгновенной скорости тело во все времена.Следовательно, ускорение не меняет размер скорости, он только меняет направление скорости.
Тело, движущееся по круговой траектории, требует радиальной силы для создания этой радиальной ускорение. Согласно закону Ньютона, F = Ma, эта радиальная сила называется центростремительной силой. это:

Mv ² Центростремительное ускорение , a _c = ——— = MRω ² = 4π ² MRf ², р

где M = масса тела.F _c — реальная сила, действующая на тело, направленная в сторону центр круга. Центростремительная сила по определению является радиальной составляющей чистая сила, действующая на тело. Вы будете непосредственно измерять эту силу на движущемся теле и проверить уравнение. (2).
4. КОНКРЕТНЫЕ ЗАДАЧИ
В качестве одной из целей эксперимента мы хотим проверить отношения, описанные формула центростремительной силы. Эта формула (уравнение 2) зависит от массы, радиуса и частоты, поэтому необходимо экспериментально проверить зависимость центростремительной силы от эти количества из ваших экспериментальных данных.Вы должны:
1. Покажите, что центростремительная сила прямо пропорциональна массе.
2. Покажите, что центростремительная сила пропорциональна квадрату частота.
3. Если у вас есть время собрать достаточно данных, вы можете показать, что центростремительная сила прямо пропорциональна радиусу кругового движения.
Полезная стандартная процедура, называемая «изоляцией переменных», сохраняет все переменные постоянными. кроме двух, взяв данные по всему диапазону этих переменных.Затем сделайте то же самое для двоих разные переменные и так далее, пока вы не соберете данные о связи между каждой парой переменных
Растянутая пружина обеспечивает центростремительную силу, величина которой зависит от количество его растяжения. Вы будете измерять силу этой пружины на каждом радиусе, путем прямого статического измерения.
5А. ИСПОЛЬЗОВАНИЕ АППАРАТА PASCO:
Рис.2А. Аппарат PASCO, настроенный для
статическое измерение силы пружины.
Аппарат (рис. 1) имеет вращающийся вал (G) с высококачественным шарикоподшипником (B). Поверните вал, поворачивая рифленую часть вал (чуть выше подшипника) вручную. Горизонтальный поперечный рычаг в верхней части этого вала имеет Т-образный стержень на конце (F). На нем висит боб массой M, стабилизированный бифилярная подвеска. Регулируемый противовес (C) уравновешивает вес боба.Низ боба (M) есть указатель. Когда боб вращается, этот указатель проходит рядом с фиксированным указателем ссылки (A). Пружина (H) обеспечивает центростремительную силу на боб.
Статическое измерение силы пружины. В в аппарате также есть шкив (P), который используется только тогда, когда вы измеряете силу пружины в статике условия (с покоящимся бобом). Сделать это, прикрепите веревку к бобу и проденьте ее поверх шкив к подвеске груза.Добавьте веса (Вт) к вешалке, пока указатель боба не совместится непосредственно над указателем ссылки. В этом случае вы можете определить усилие пружины когда боб вращается на любой радиус (измеренный от центра вала).
Вы можете выбрать другие радиусы, изменив положение основания указателя ссылки (в A). Это может варьироваться в пределах нескольких сантиметров.
Снимайте данные на трех разных радиусах движения, один на минимальном радиусе, другой на максимальный радиус и еще один между этими крайностями.Мы предлагаем вам сделать каждый измерение статической силы непосредственно перед выполнением динамических измерений на этом радиусе. потом вам не придется воспроизводить точные настройки указателя (что может привести к ошибке).
Рис. 3A. Динамическое измерение.
Динамические измерения. Вращайте вал и увеличивайте его скорость, пока стрелка боба проходит прямо над ссылкой указатель.
Затем поддерживайте скорость постоянной, пока хронометраж n оборотов. Подсчитайте большой количество оборотов (не менее n = 40) при измерении общего времени с помощью наручные часы или секундомер. Выберите n больших достаточно, чтобы дать желаемую точность для период и частота.
Вы можете изменить массу боба на добавление грузов с прорезями в верхнюю часть боб (массой до 100 грамм).Позиция их так, чтобы их прорези были направлены наружу, и надежно закрепите их рифленой орех, чтобы не слетали.
Каждый раз, когда вы меняете радиус или массу боба, вы должны повторно сбалансировать вращающийся узел. Для этого ослабьте установочный винт в точке D и переместите противовес. (C) до тех пор, пока плечо не уравновесится. Затем снова затяните установочный винт перед вращением вал.
Вы можете изменять натяжение пружины, заменяя другие пружины, более сильные или более слабые.В качестве альтернативы вы можете подсоединить шнурок, проволоку или звено скрепки к одному концу (E) пружина, чтобы уменьшить натяжение пружины.
5Б. ИСПОЛЬЗОВАНИЕ УСТРОЙСТВА CENCO:
Рис. 2B. Аппарат CENCO.
Устройство CENCO, показанное на рис. 2B, имеет массу (M) и прочную пружину (Z) в прочной клетке (Y), которая приводится в движение двигателем с регулируемой скоростью. Это устройство не позволяет регулировать радиус движения массы, но позволяет изменять скорость и натяжение пружины.
Регулируемый винт (S) регулирует длину пружины и, следовательно, ее натяжение. Имеет индекс и микрометрическую шкалу. Скорость регулируется фрикционным приводом. Колесо с резиновым покрытием (D) прижимается к диску с плоским покрытием (W), который приводится в движение двигателем. Регулировочный винт 8 позволяет устанавливать фрикционный ролик на разные радиусы, но эту регулировку следует производить только при работающем устройстве.
Старые модели могут не иметь защиты ремня, поэтому держите руки подальше от ремня и шкивов.Даже в новых моделях присутствует фрикционный привод, который также может быть опасным. Перед запуском двигателя убедитесь, что блок центростремительной силы надежно прикреплен к вертикальному валу. Попросите инструктора проверить прибор. Держите выключатель двигателя в руке и будьте готовы быстро выключить двигатель, если что-то пойдет не так.
Частота вращения определяется путем подсчета количества оборотов за данный момент времени. Некоторые модели могут иметь счетчик оборотов.
Рис. 3B. Динамическое измерение. Рис. 4В. Индекс скорости.
Рис. 5B. Статическое измерение
силы пружины.
На рисунке 4B указатель индекса скорости (P) указывает на контрольный индекс (I) на оси вращения, и это можно легко увидеть, даже когда устройство вращается. Когда пружина растягивается, груз (m) нажимает на рычаг указателя (Q), поворачиваясь вокруг своей оси (O) и перемещая указатель (P).
Динамические измерения: при заданном натяжении пружины отрегулируйте скорость вращения до тех пор, пока указатель не окажется на отметке. Запишите скорость (оборотов в секунду) и значение натяжения пружины (S). Сделайте это для полного диапазона натяжения пружины.
В этом аппарате нет возможности изменять массу.
Рис. 3B также показывает индексную линию (M), начерченную на массе в ее центре масс, и микрометровую шкалу на рамке (Y), которую можно использовать для определения фактического радиуса движения массы, когда указатель указатель (P на рис.4B) находится на индексной метке (I на рис. 4B).
Калибровка силы пружины: Вся клетка в сборе может быть снята с приводного вала. Он может быть подвешен вертикально с подвесом для груза, прикрепленным к грузу. Для каждого положения винта натяжения пружины запишите его настройку (на микрометрической шкале (S), а также величину веса, необходимого для позиционирования указателя (P) на индексной метке (I). Таким образом вы можете откалибруйте индикатор натяжения пружины (S).
Одним из преимуществ этого устройства является то, что центр масс пружины находится очень близко к оси вращения. Следовательно, динамическое натяжение пружины почти такое же, как статическое натяжение, которое вы измеряете при подвешивании пружины вертикально. Это интересная проблема инженерного проектирования, и вы можете проанализировать ее самостоятельно, чтобы увидеть, достигает ли проект своей предполагаемой цели.
6. НАБЛЮДЕНИЯ:
Вот удобный способ расположить столбцы таблицы данных:
Полковник: 1 2 3 4 5 6 ИСПЫТАТЕЛЬНЫЙ РАДИУС ИЗМЕРЕННОЙ МАССЫ КОЛИЧЕСТВО ОБЩИХ ОБОРОТОВ / ВЫЧИСЛЕННЫЙ% СКОРОСТИ НЕТ. ВРЕМЯ ПРУЖИНЫ СЕК. ЦЕНТРИПЕТАЛЬНАЯ ЖЕСТКОСТЬ R FORCE M n t f FORCE между (Статический) (Динамический) Колонки 2 и 5
Получите как можно более широкий диапазон значений всех переменных, насколько позволяет аппарат.В «измеренная центростремительная сила» обозначает значения, полученные прямым статическим измерением усилие, необходимое для растяжения пружины до этого радиуса. «Расчетная центростремительная сила» значения берутся из расчета на основе данных в столбцах с 1 по 3 с использованием уравнения (2).
Вам нужно будет распланировать свое время. Если вы использовали четыре разных значения радиуса и для для каждого из них вы взяли данные о четырех различных значениях массы боба, у вас будет 16 случаев измерять.Тогда, если вы измените натяжение пружины четыре раза, у вас будет всего 64 случаи!
В качестве практического компромисса мы предлагаем вам выбрать три различных значения радиусов, и три различных значения массы для каждого радиуса. Затем сделайте такое же количество дел со значительно меньшим натяжением пружины (за счет использования более слабой пружины или добавления звеньев) до конца весны). Эти 18 случаев представляют собой минимум данных для достижения цель этого эксперимента.Постарайтесь получить большой диапазон разных частот вращение.
7. АНАЛИЗ:
Для справки мы пронумеровали важные столбцы предлагаемой таблицы данных. В другие столбцы содержат промежуточные расчетные значения, в данном случае не требуемые. обсуждение.
Мы хотим показать, существуют ли отношения между центростремительной силой, массой, радиусом и частоты согласуются с предсказаниями теории (ур.2). Это отношение говорит нам, что центростремительная сила пропорциональна массе и радиусу и пропорциональна квадрат частоты.
Поскольку для каждого R есть только одно значение Fc (для данной пружины), мы переставляем уравнение:
Рис. 6. График зависимости центростремительной силы / радиуса от
квадрат частоты с массой в качестве параметра.
Графический анализ предоставляет очень значимый и профессиональный способ сделать это.участок F _c / R по сравнению с f ² для каждого из четырех значений масса. Если уравнение 4 верно, этот график должен чтобы выглядеть примерно так, как на рис. 3. Если точки для каждого значения массы попадают прямые линии, вы продемонстрировали, что F _c пропорциональна к f ², для каждого из значений масс.
Если этот участок состоит из прямых линий проходя через начало координат, то у вас есть продемонстрировал, что уравнение. 4 не имеет дополнительных срок с правой стороны.
Показывает ли сюжет ожидаемые отношения? Комментарий.
Уклон каждой из четырех линий должен иметь значение 4π ² м. [m представляет собой массу, соответствующую каждой строке, a различное значение для каждой строки.] Рассчитайте экспериментальное расхождение.
Вы можете проверить значение константы пропорциональности 4π2 многими другими способами. Вот еще один. Сравните два последних столбцы таблицы данных (Cols.2 и 5). Поскольку при вычислении столбца 5 вы использовали коэффициент 4π2, соответствие между столбцы 2 и 5 подтверждают этот фактор, а процентное расхождение между столбцами 2 и 5 измеряет, насколько хорошо вы экспериментально подтвердили уравнение. 3.
Другой способ проверить зависимость центростремительной силы от массы: построить другой график. построение графика зависимости F _c от M с использованием всех данных.
Для проверки зависимости центростремительной силы от радиуса потребуется изготовить новый график, построение F _c vs.R, используя все данные.
8. УРАВНЕНИЕ ОШИБКИ:
Вы можете легко получить уравнение максимальной ошибки, соответствующее уравнению (2), с помощью правила распространения ошибок для умножения и деления:

ΔF ΔM ΔR Δf —— = —— + —— + 2 ——. F M R f

Символ ΔF означает «погрешность в F». [Вывести это уравнение для детерминированных ошибок. Верно ли это и для неопределенных ошибок?]
Используйте здравый смысл и свой собственный опыт (проведя этот эксперимент), чтобы оценить размер каждого термина справа.Выразите их в процентах. Что вносит наибольший вклад в общую экспериментальная ошибка? Какая наименьшая? Рассчитайте предполагаемую максимальную ошибку в процентах (в центростремительная сила), которую вы бы предсказали для этого эксперимента. Наблюдали ли вы несоответствие лежит в пределах этой оценки?
Это уравнение ошибки может помочь вам в разработке экспериментальной процедуры. Он может ответить такие вопросы, как: «Сколько оборотов нужно рассчитать, чтобы частота иметь погрешность не хуже, чем у других измеряемых величин? »
Число оборотов n, полученное в результате простого подсчета, считается ошибочным. бесплатно.Измерение времени для n отсчетов может иметь инструментальную ошибку из-за часы (вероятно, незначительные) и время реакции при запуске и остановке часов. В уравнение f = n / t имеет уравнение ошибки Δf / f = Δn / n — Δt / t, что сводится примерно к Δf / f ≅ -Δt / t. Знак минус просто означает, что для определенного ошибок, ошибка, которая делает t слишком большим, сделает f слишком маленьким. Для неопределенного ошибки убираем знак, так как предполагаем, что неопределенные ошибки не имеют смещения относительно знака.
Уравнение. 5 дают оценку ошибки почти того же размера, что и ваш экспериментальный несоответствие (Кол. 6)?
9. ВОПРОСЫ (Аппарат PASCO):
Помеченные (*) вопросы требуют больше размышлений и понимания, чем другие.
(1) Выведите формулу работы, совершаемой центростремительной силой над массой за один революция.
(2) Очевидно, вы действительно работали, когда вращали вал, сохраняя постоянную скорость.Однако кинетическая энергия системы оставалась постоянной. Куда делась эта работа?
(3) Предположим, что подвешенная масса движется по горизонтальному кругу с постоянно уменьшающейся скоростью. Является ли результирующая сила, действующая на этот объект, радиальной? Почему или почему нет? Объяснять.
(4) Предположим, что M = 500 г, R = 15 см и статическое измерение силы пружины было 500 гм. Вы оцениваете погрешность измерения времени Δt = 1 секунда. Как долго вы должны считать обороты, чтобы измерение времени внесло не более 1% в ошибку центростремительной силы?
(5) Предположим, что M = 500 г, R = 15 см и статическое измерение силы пружины было 500 г (эквивалент).Вы оцениваете неопределенность измерения времени как Δt = 1 секунда. Как долго вы должны считать обороты, чтобы измерение времени внесло не более 1% в ошибку центростремительной силы?
(6 *) Предположим, что бифилярная подвеска не была вертикальной, скажем, на 5 ° от вертикали, и экспериментатор этого не заметил. Никаких других грубых ошибок в процедуре или измерении не было. В том же духе, что и вопрос 6, рассчитайте какую определенную ошибку может вызвать эта ошибка между действительной центростремительной силой и измеренное значение центростремительной силы.
(7 *) Предположим, что бифилярная подвеска была слишком короткой, и экспериментатор этого не заметил. Других промахов не было. Более конкретно, предположим, что подвеска была настолько короткой, что пружина составляла угол 5 ° с горизонтом. Предполагая процедура, как в этом эксперименте, M = 500 г, R = 15 см, и сила пружины, статические измерения составили 500 гр. Четко сформулируйте любые другие предположения, которые вы делаете и рассчитываете определенная ошибка, которую может вызвать эта грубая ошибка, между действительной центростремительной силой и измеренное значение центростремительной силы.
10. ВОПРОСЫ (Аппарат CENCO):
Помеченные (*) вопросы требуют больше размышлений и понимания, чем другие.
(1) Выведите формулу работы, совершаемой центростремительной силой над массой за один революция.
(2) Очевидно, двигатель работал, когда вращал вал, поддерживая постоянную скорость. Однако кинетическая энергия системы оставалась постоянной. Куда делась эта работа?
(3) Предположим, что вращающаяся масса движется по горизонтальному кругу с постоянно уменьшающейся скоростью.Является ли результирующая сила, действующая на этот объект, радиальной? Почему или почему нет? Объяснять.
(4) Предположим, что M = 500 г, R = 15 см и статическое измерение силы пружины было 500 г (эквивалент). Вы оцениваете погрешность измерения времени Δt = 1 секунда. Как долго вы должны считать обороты, чтобы измерение времени внесло не более 1% в ошибку центростремительной силы?
(5) Предположим, что M = 500 гм, R = 15 см и статическое измерение силы пружины было 500 гм.Вы оцениваете погрешность измерения времени как Δt = 1 секунда. Как долго вы должны считать обороты, чтобы измерение времени внесло не более 1% в ошибку центростремительной силы?
(6 *) Предположим, что вращающийся вал был не совсем вертикальным, скажем, на 5 ° от вертикали, и экспериментатор этого не заметил. Никаких других грубых ошибок в процедуре или измерении не было. В том же духе, что и в вопросе 6, вычислите, какую определенную ошибку может вызвать эта грубая ошибка между фактической центростремительной силой и измеренным значением центростремительной силы.
Текст и штриховые рисунки © 1997, 2004 Дональд Э. Симанек.
Понимание уравнений резки | Производство режущего инструмента
Площадь в футах в минуту, нагрузка стружки, недеформированная толщина стружки и утонение стружки — это привычные рабочие термины. Однако за последние несколько недель несколько происшествий в нашем цехе заставили меня понять, что многие профессионалы в области металлообработки не понимают этих терминов и связанных с ними расчетов. Независимо от того, работаете ли вы в небольшой мастерской или у крупного контрактного производителя, важно понимать расчеты режущего инструмента и то, как их использовать, чтобы добиться значительного повышения эффективности.
Расчеты скорости резания могут быть самыми важными. Они просты в использовании и, после небольшого объяснения, их легко понять. Скорость резания инструмента выражается в поверхностных футах в минуту (sfm) или поверхностных метрах в минуту (м / мин). Подобно миль в час для автомобиля, sfm — это линейное расстояние, которое режущий инструмент проходит за минуту. Чтобы лучше понять масштаб, например, 300 SFM преобразуется в 3,4 мили в час.
Инструментальщики рекомендуют скорость резания для различных типов обрабатываемых материалов.Когда производитель инструмента предлагает 100 футов в минуту, это означает, что внешняя поверхность вращающегося инструмента должна двигаться со скоростью, равной 100 погонным футам в минуту. Если инструмент имеет окружность (диаметр × π) 12 дюймов, ему потребуется вращаться со скоростью 100 об / мин для достижения 100 футов в минуту.
Все изображения любезно предоставлены C. Tate
Представьте себе режущий инструмент как катящееся кольцо или цилиндр. Расстояние, пройденное за один оборот, умноженное на об / мин, и есть его поверхностная скорость. Если круг выше имел диаметр 3.82 дюйма, окружность будет 12 дюймов. В результате каждый оборот будет производить линейное расстояние в 1 фут, а скорость шпинделя 100 об / мин будет скоростью резания 100 sfm.
Для расчета скорости шпинделя используется следующее уравнение: об / мин = sfm ÷ диаметр × 3,82, где диаметр — это диаметр режущего инструмента или диаметр детали на токарном станке в дюймах, а 3,82 — константа, полученная в результате алгебраического упрощения более сложная формула: rpm = (sfm × 12) ÷ (диаметр × π).
Поскольку диаметр инструмента измеряется в дюймах, «футы» в SFM необходимо преобразовать в дюймы, а поскольку в футе 12 дюймов, умножьте SFM на 12.Кроме того, длина окружности инструмента определяется путем умножения диаметра инструмента на π или 3,14 для упрощения. Результат: об / мин = (sfm × 12) ÷ (диаметр × π) = (sfm ÷ диаметр) × (12 ÷ π) = (sfm ÷ диаметр) × 3,82.
Обратите внимание на вертикальные линии, называемые метками инструмента, на внешней стороне обрабатываемой детали. По мере увеличения скорости подачи расстояние между линиями также увеличивается. Толщина стружки примерно равна подаче.
Скорости резания публикуются в SFM, потому что идеальная скорость резания для определенного семейства инструментов теоретически будет одинаковой независимо от размера инструмента.Ожидается, что инженер, программист или машинист рассчитает число оборотов в минуту, необходимое для обеспечения правильной скорости резания для каждого выбранного инструмента.
Так о чем это нам говорит? Допустим, инструмент диаметром 1 дюйм должен работать со скоростью 100 футов в минуту. Согласно уравнению, этот инструмент должен вращаться со скоростью 382 об / мин, чтобы достичь 100 футов в минуту: 100 ÷ 1 × 3,82 = 382.
Другой способ рассмотреть эту концепцию — это подумать о расстоянии, которое бы прошел 1-дюймовый инструмент, если бы он совершил 382 оборота по цеху. В этом сценарии он прошел бы 100 футов; сделайте это за 60 секунд, и он будет путешествовать 100 SFM.
Токарные станки, конечно, разные, потому что вместо фрезы вращается заготовка. Поскольку формула для скорости резания зависит от диаметра, по мере уменьшения диаметра заготовки число оборотов в минуту должно увеличиваться, чтобы поддерживать постоянную скорость резания. После каждого кругового резания на токарном станке OD детали уменьшается или ID увеличивается, и необходимо увеличивать частоту вращения детали для поддержания желаемой скорости резания. В результате производители ЧПУ разработали функцию постоянной площади поверхности для управления токарным станком.Эта функция позволяет программисту вводить желаемую скорость резания в sfm или м / мин. и система управления вычисляет правильные обороты для изменяющегося диаметра.
Пока инструмент или деталь вращаются, станок должен знать, с какой скоростью двигаться, когда фреза входит в заготовку. Подача — это термин, который описывает скорость перемещения при резании.
Скорость подачи при фрезеровании обычно выражается в дюймах в минуту (ipm) и рассчитывается по формуле: ipm = об / мин × количество. канавок × загрузка стружки.
Что такое загрузка микросхемы? При фрезеровании это количество материала, которое режущая кромка удаляет каждый раз при вращении. При токарной обработке это расстояние, на которое деталь перемещается за один оборот, когда она находится в контакте с инструментом. Иногда это называют толщиной стружки, что в некотором роде верно. Толщина стружки может измениться при изменении других параметров, таких как радиальный DOC или угол подъема инструмента.
Инструментальные мастера публикуют рекомендации по нагрузке на стружку вместе с рекомендациями по скорости резания и выражают их в тысячных долях дюйма (миллиметры для метрических единиц).Для фрезерных и сверлильных операций нагрузка стружки выражается в тысячных долях дюйма на канавку. Канавки, зубья и режущие кромки описывают одно и то же, и должен быть по крайней мере один, но теоретически нет ограничений на количество, которое может иметь инструмент.
Рекомендации по загрузке стружки для токарных операций чаще всего даются в тысячных долях дюйма на оборот или подаче на оборот. Это расстояние, на которое инструмент продвигается каждый раз, когда деталь выполняет один оборот.
Какие обороты и скорость подачи должны быть запрограммированы для концевой фрезы с 4 канавками, 1 дюйм, работающей с рекомендованной скоростью резания 350 sfm и рекомендуемой стружкой 0.005 дюймов на зуб (IPT)? Используя уравнение, об / мин = sfm ÷ диаметр × 3,82 = 350 ÷ 1,0 × 3,82 = 1,337, скорость подачи = об / мин × количество. канавок × нагрузка на стружку = 1337 × 4 × 0,005 = 26,74 дюймов в минуту.
Здесь все становится интересно, потому что при изменении значений в формуле взаимосвязь различных переменных становится очевидной. Попробуйте применить 2-дюймовый инструмент вместо 1-дюймового. Что происходит? Скорость вращения и скорость подачи уменьшаются вдвое.
Понимание этих взаимоотношений и творческое мышление могут значительно повысить эффективность.Я расскажу, как использовать эти отношения в своей следующей колонке. CTE
Об авторе: Кристофер Тейт (Christopher Tate) — старший технический специалист по передовым технологиям в Milwaukee Electric Tool Corp., Брукфилд, Висконсин. Он работает на производственном предприятии компании в Джексоне, штат Миссисипи. Он имеет 19-летний опыт работы в металлообрабатывающей промышленности и имеет ученую степень. Магистр и бакалавр наук Государственного университета Миссисипи. Электронная почта: [email protected].
Угловая скорость: определение, формула и примеры — видео и стенограмма урока
Радианы
Перед тем, как перейти к угловой скорости, нам нужно рассмотреть еще одну вещь, а именно радианы.Когда мы имеем дело с угловой скоростью, мы используем радианную меру угла, поэтому важно, чтобы мы были знакомы с радианной мерой. Техническое определение радиан. Измерение — это длина дуги, образуемой углом, деленная на радиус окружности, частью которой является угол, где протяженность означает, что она противоположна углу и проходит от одной точки на круг к другому, оба отмечены углом. Это говорит нам, что угол theta = s / r радиан, где s = длина дуги, соответствующей тета, и r = радиус круга, частью которого является тета.
Радианная мера угла
Так как большинство из нас привыкли к градусному измерению углов, удобно, что мы можем легко преобразовать градус в радиан, умножив градус на пи / 180. Например, угол в 45 градусов имеет радиан. мера 45 (пи / 180), что равно пи / 4 радиана.
Угловая скорость
Угловая скорость встречается реже, чем линейная скорость, поскольку она применяется только к объектам, движущимся по круговой траектории.Например, гоночная машина на круговой трассе, шар рулетки на колесе рулетки или колесо обозрения — все они имеют угловую скорость.
Примеры угловой скорости
Угловая скорость объекта — это угловое смещение объекта относительно времени. Когда объект движется по круговой траектории, центральный угол, соответствующий положению объекта на круге, изменяется. Угловая скорость, представленная как w , представляет собой скорость изменения этого угла во времени.
Угловая скорость
Например, колесо обозрения может вращать пи / 6 радиан каждую минуту. Следовательно, угловая скорость колеса обозрения будет равна пи / 6 радиан в минуту.
Формулы угловой скорости
Существует трех формул , которые мы можем использовать для определения угловой скорости.
Вариант 1
Первое вытекает прямо из определения.Угловая скорость — это скорость изменения позиционного угла объекта во времени, поэтому w = theta / t , где w = угловая скорость, theta = позиционный угол и t = время.
Например, если гоночный автомобиль движется по круговой трассе и проезжает 1 круг или 2pi радиана за 4 минуты, то мы можем найти угловую скорость автомобиля, подставив theta = 2pi радиан и t = 4 минуты в наша формула, чтобы получить w = 2pi / 4 = pi / 2 радиан в минуту.Угловая скорость автомобиля составляет пи / 2 радиана в минуту.
Вариант 2
Чтобы получить нашу вторую формулу для угловой скорости, мы понимаем, что тета дается в радианах, а определение радианной меры дает theta = с / r . Таким образом, мы можем подставить theta = с / r в нашу первую формулу угловой скорости. Это дает w = ( s / r ) / t . Упрощение дает w = с / ( r t ), где с = длина дуги, r = радиус и t = время.
Например, если колесо рулетки имеет радиус 10 дюймов, а шарик проходит 7 дюймов по круговой траектории за 2 секунды, то мы можем определить угловую скорость шара, вставив s = 7 дюймов, r = 10 дюймов, и t = 2 секунды на w = s / ( r t ), чтобы получить w = 7 / (10 * 2) = 0,35 радиан в секунду. Угловая скорость мяча составляет 0,35 радиана в секунду.
Вариант 3
Последняя формула исходит из признания того, что мы можем переписать нашу вторую формулу угловой скорости как w = с / ( r t ) = ( s / t ) (1/ r ).Напомним, что с / t — наша линейная скорость, поэтому мы можем переписать эту формулу как w = v (1/ r ) = v / r , где v = линейный скорость и r = радиус круга.
Например, если гоночный автомобиль движется по круговой трассе со скоростью 110 миль в час, а радиус гоночной трассы составляет 0,2 мили, то мы можем найти угловую скорость автомобиля, подключив v = 110 миль в час и r = 0.2 мили в нашу формулу, чтобы получить w = 110 / 0,2 = 550 радиан в час.
Резюме урока
Мы рассмотрели линейную скорость, , скорость изменения положения объекта, движущегося по прямой линии, относительно времени и радиан, мера угла (тета = с / r , где s = длина дуги и r = радиус). Мы видели, что оба они играют важную роль в угловой скорости. Угловая скорость — это угловое смещение во времени объекта или частицы, которые движутся по круговой траектории.
No related posts.

Шины 33 ″ (общий диаметр +/- 0,50 ″)
35X12.50-15	315 / 75-16	325 / 45-24
Шины 37 ″ (общий диаметр +/- 0,50 ″)
15 ″	16 ″	24 ″
37X14.50-17	385 / 70-16	315 / 50-24

Диаметр	Внедрение	Об / миль *
35	110,0	593
35,5	111,5	585
36	113.1	576
36,5	114,7	568

ШИНЫ 17 ДЮЙМОВ	ВЫСОТА ШИНЫ
225 35 17	23.20
245 35 17	23,75
315 35 17	25,68
335 35 17	26,23

17 ″ Опции
215 / 40-17	245 / 35-17	275 / 55-17
215 / 45-17	245 / 40-17	275 / 60-17
215 / 50-17	245 / 45-17	275 / 65-17
215 / 55-17	245 / 50-17	275 / 70-17

18 ″ Опции
155 / 90-18	245 / 35-18	315 / 35-18
165 / 70-18	245 / 40-18	315 / 40-18
165 / 90-18	245 / 45-18	325 / 45-18
175 / 90-18	245 / 50-18	325 / 60-18

Радиан
Система единиц	Производная единица СИ
Единица из	Уголок
Обозначение	рад, c или r
В единицах	Безразмерный с длиной дуги, равной радиусу, т.е. 1 мм

Прямолинейное движение	Вращательное движение
v = v _o + at	ω = ω _o + α t
x — x _o = v _o t + ½ при ²	θ — θ _o = ω _o t + ½ α t ²
x — x _o = ½ (v + v _o) t	θ — θ _o = ½ (ω + ω _o) t
v ² = v _o ² + 2 a (x — x _o)	ω ² = ω _o ² + 2 α (θ — θ _o)


Рис.2А. Аппарат PASCO, настроенный для статическое измерение силы пружины.


Рис. 3A. Динамическое измерение.


Рис. 2B. Аппарат CENCO.


Рис. 3B. Динамическое измерение.	Рис. 4В. Индекс скорости.


Рис. 5B. Статическое измерение силы пружины.


Рис. 6. График зависимости центростремительной силы / радиуса от квадрат частоты с массой в качестве параметра.

Разное