Формула магнитной индукции, B
Формулы определяющие величину вектора магнитной индукции получают, используя выражение для силы Ампера, силы Лоренца и применяя понятие вращающего момента.
Формула величины вектора магнитной индукции
Формулой, которая определяет величину вектора магнитной индукции в конкретной точке магнитного поля можно считать следующее выражение:
где – максимальный вращающий момент, действующий на рамку, которая обладает магнитным моментом , равным единице, если нормаль к рамке перпендикулярна направлению поля.
При помощи силы Ампера величина вектора магнитной индукции задана как:
где модуль равен пределу отношения величины силы (), с которой магнитное поле действует на бесконечно малый проводник с током, к силе тока (I) умноженной на длину этого проводника (), если длина проводника стремится к нулю. Как известно кроме величины вектор магнитной индукции имеет направление. В данном случае перпендикулярен к направлению силы и перпендикулярен направлению элемента проводника.
Используя силу Лоренца, получают формулу для магнитной индукции в виде:
где – модуль силы Лоренца; q – заряд частицы, движущейся со скоростью v в магнитном поле; – это угол между векторами и . Направления , векторов и связаны между собой правилом левой руки.
Закон Био-Савара-Лапласа
Данный закон предоставляет нам возможность вычислить вектор магнитной индукции () в любой точке магнитного поля, которое создается в вакууме элементарным проводником с током:
где I – сила тока; – вектор элементарный проводник по модулю он равен длине проводника, при этом его направление совпадает с направлением течения тока; – радиус-вектор, который проводят от элементарного проводника к точке, в которой находят поле; – магнитная постоянная. Вектор является перпендикулярным к плоскости, в которой расположены и , конкретное направление вектора магнитной индукции определяют при помощи правила буравчика (правого винта).
Для однородного и изотропного магнетика, заполняющего пространство, вектор магнитной индукции в вакууме( и в веществе (), при одинаковых условиях, связывает формула:
где – относительная магнитная проницаемость вещества.
Частные случаи формул для вычисления величины вектора магнитной индукции
Формула для вычисления модуля вектора индукции в центре кругового витка с током (I):
где R – радиус витка.
Модуль вектора магнитной индукции поля, которое создает бесконечно длинный прямой проводник с током:
где r – расстояние от оси проводника до точки, в которой рассматривается поле.
В средней части соленоида магнитная индукция поля вычисляется при помощи формулы:
где n – количество витков соленоида на единицу длины; I – сила тока в витке.
Принцип суперпозиции
Магнитная индукция поля (), которое является наложением нескольких полей, находится как векторная сумма магнитных индукций отдельных полей ():
Примеры решения задач по теме «Магнитная индукция»
формула, от чего зависит, линии индукции
Все мы знаем, что есть магниты более сильные и менее сильные. Маленький магнитик сможет притянуть пару гвоздей и все, а гораздо более мощный электромагнит домофона удерживает дверь в подъезд так, что несколько взрослых мужчин не смогут открыть ее силой.
Маленький магнитик сможет притянуть пару гвоздей и все, а гораздо более мощный электромагнит домофона удерживает дверь в подъезд так, что несколько взрослых мужчин не смогут открыть ее силой.
Величина, характеризующая величину силы магнита
То есть, мы можем говорить о некой величине, характеризующей величину силы магнитов, а точнее, магнитного поля, создаваемого ими. Магнитное поле характеризуется векторной величиной, которая носит название индукции магнитного поля или магнитной индукции. (см. подробнее электромагнитная индукция)
Обозначается индукция буквой B. Магнитная индукция это не сила, действующая на проводники, это величина, которая находится через данную силу по следующей формуле:
B=F / (I*l)
Или в виде определения:
Модуль вектора магнитной индукции B равен отношению модуля силы F, с которой магнитное поле действует на расположенный перпендикулярно магнитным линиям проводник с током, к силе тока в проводнике I и длине проводника l.
От чего зависит магнитная индукция
Магнитная индукция не зависит ни от силы тока, ни от длины проводника, она зависит только от магнитного поля. То есть, если мы, например, уменьшим силу тока в проводнике, не меняя больше ничего, то уменьшится не индукция, с которой сила тока связана прямо пропорционально, а сила воздействия магнитного поля на проводник. Величина же индукции останется постоянной. В связи с этим индукцию можно считать количественной характеристикой магнитного поля.
Измеряется магнитная индукция в теслах (1 Тл). При этом 1 Тл=1 Н/(А*м) .
Линии индукции магнитного поля
Магнитная индукция имеет направление. Графически ее можно зарисовывать в виде линий. Линии индукции магнитного поля это и есть то, что мы до сих пор в более ранних темах называли магнитными линиями или линиями магнитного поля. Так как мы выше вывели определение магнитной индукции, то мы можем дать определение и
Линии магнитной индукции это линии, касательные к которым в каждой точке поля совпадают с направлением вектора магнитной индукции.
В однородном магнитном поле линии магнитной индукции параллельны, и вектор магнитной индукции будет направлен так же во всех точках.
В случае неоднородного магнитного поля, например, поля вокруг проводника с током, вектор магнитной индукции будет меняться в каждой точке пространства вокруг проводника, а касательные к этому вектору создадут концентрические окружности вокруг проводника. Так и будут выглядеть линии индукции магнитного поля расширяющиеся окружности вокруг проводника.
Нужна помощь в учебе?
Предыдущая тема: Обнаружение магнитного поля по его действию на электрический ток
Следующая тема:   Магнитный поток: определение, направление и количество + пример
Магнитная индукция формула единица измерения
Единица измерения магнитной индукции
Тесла — единица измерения магнитной индукции в системе СИ
Единица магнитной индукции ($overline$) в международной системе единиц (СИ) называется тесла (Тл), по имени сербского ученого Н. Тесла, который успешно работал в области радиотехники и электроники.
Тесла, который успешно работал в области радиотехники и электроники.
Единицу измерения магнитной индукции определим исходя из закона Ампера. Рассмотрим прямолинейный проводник, длиной $l$ по которому течет ток $I$. Пусть этот проводник находится в однородном магнитном поле $overline$, причем вектор индукции поля перпендикулярен проводнику. В таком случае модуль силы Ампера ($>_A$), воздействующей на проводник равен:
Выразим магнитную индукцию из формулы (1), получим:
Из выражения (2) мы видим, что тесла (единица измерения магнитной индукции) — это величина, соответствующая магнитной индукции однородного магнитного поля, действующего на каждый метр прямого проводника, находящегося в магнитном поле перпендикулярно направлению $overline$, с силой в один ньютон, при силе тока в проводнике в один ампер:
Единица измерения магнитной индукции (тесла) является производной в системе Международных единиц (СИ). Через основные единицы СИ Тл, как единицу измерения магнитной индукции выражают, учитывая, что:
Стандартные приставки системы СИ можно использовать с Тл при обозначении десятичных кратных и дольных единиц. 3Тл$. Магнитное поле Земли может существенно отличаться в зависимости от местоположения на планете, оно составляет порядка $approx $10 мкТл.
3Тл$. Магнитное поле Земли может существенно отличаться в зависимости от местоположения на планете, оно составляет порядка $approx $10 мкТл.
Гаусс — единица измерения магнитной индукции в системе единиц СГС
В системе единиц СГС (сантиметр, грамм, секунда) единицей измерения магнитной индукций служит гаусс (Гс). Соотношение между гауссом и тесла:
Данная единица измерения именована в честь немецкого ученого К.Ф. Гаусса.
Используя основные единицы системы СГС, единица измерения магнитной индукции выражается как:
Примеры задач с решением
Задание. Получите единицу измерения магнитной индукции в Международной системе единиц, используя формулу, связывающую ее с магнитным потоком ($Ф$).
Решение. По условию задачи в качестве основы для ее решения используем выражение:
где$ Ф$- поток вектора магнитной индукции через площадку S;$ S$ — величина площади площадки; $alpha $ — угол между направлением нормали к площади S и направлением вектора магнитной индукции. Выразим модуль вектора магнитной индукции из формулы (1.1), имеем:
Выразим модуль вектора магнитной индукции из формулы (1.1), имеем:
Учитывая, что в системе СИ $$ — величина безразмерная, поток вектора магнитной индукции измеряется в веберах (Вб):
а единицы измерения площади:
Ответ. Мы получили, что тесла — единица измерения магнитной индукции, и ее можно выразить как: $Тл=frac$
Задание. Определите размерность индукции магнитного поля, используя формулу для модуля $overline$ кругового витка с током.
Решение. Найдем величину вектора магнитной индукции в центре кругового вика с током (рис.1).
Получим формулу для вычисления модуля вектора магнитной индукции в центре витка с током $I$, будем считать, что радиус витка равен R, виток находится в вакууме. Выделим элементарный участок кругового тока ($dl$) (см. рис.1). Величина индукции в очке О от избранного элемента $dl$ равна (из закона Био-Савара — Лапласа):
Для нашего случая все элементы $dl$ перпендикулярны соответствующим радиус-векторам, соединяющим их с точкой, где мы ищем поле, значит $=1. $ Кроме того для всех участков витка $r=R.$ Выражение (2.1) преобразуется к виду:
$ Кроме того для всех участков витка $r=R.$ Выражение (2.1) преобразуется к виду:
Все элементы кругового тока будут образовывать вектор, направленный по оси X (рис.1). Для нахождения полного поля перейдем к интегралу:
[B=ointlimits_L_0 >Рассмотрим единицы измерения правой части выражения (2.3), имеем:
Ответ. Мы получили, что тесла можно выразить как: $Тл=frac$
Магнитная индукция
Магнитное поле, так же как и электрическое поле, является одной из сторон электромагнитного поля и представляет собой один из видов материи. Оно возникает, например, при движении электрических зарядов и, в частности, вокруг проводов с током. Магнитное поле обладает энергией называемой энергией магнитного поля, которая проявляет себя различным образом, например в действии одного провода с током на другой провод с током, находящийся в магнитном поле первого, или в действии магнитного поля проводника с током на магнитную стрелку.Направление, которое указывается северным кон цом магнитной стрелки, установившейся под дей ствием сил магнитного поля, принимается за направление магнитного поля.
Рис. 3-1. Правило буравчика.
Магнитное поле изображается магнитными линиями (линиями магнитной индукции), Они проводятся так, чтобы направление касательной в каждой точке линии совпадало с направлением поля.
Направление магнитного поля связано с направлением тока. Эта связь устанавливается правилом буравчика: если поступательное движение буравчика совпадает с направлением тот (рис 3-1), то направление вращения рукоятки буравчика укажет направление магнитных линий. Иногда лучше пользоваться другой формулировкой этого правила: если направление вращения рукоятки буравчика совпадает с направлением тока в контуре (рис. 3-2), то поступательное движение его укажет направление магнитных линий, пронизывающих поверхность, ограниченную контуром.
Поместим в магнитное поле перпендикулярно его направлению участок прямолинейного провода длиной l, по которому проходит ток I (рис. 3-3).
Из опыта можно убедиться, что на участок провода будет действовать сила F, по величине пропорциональная току, длине участка проводника и интенсивности магнитного поля, которая характеризуется величиной магнитной индукции В.
Таким образом, сила
Рис. 3-2. Правило буравчика для коль цевого тока.
Из написанного следует, что
т. е. магнитная индукция измеряется отношением механической силы, действующей на участок провода, по которому проходит ток, к произведению тока и длины участка про вода, причем провод должен быть расположен перпендикулярно направлению поля.
В международной системе единиц (СИ) сила измеряется в ньютонах, ток — в амперах, длина — в метрах, поэтому единица измерения магнитной индукции
Единица вольт-секунда называется в е б е р (вб), а вебер, деленный на квадратный метр, — тесла (тл),
Кроме единицы тесла, иногда применяется гаусс (гс) — единица магнитной индукции, не принадлежащая к системе
1 гс — 10 -4 тл, или 1 тл = 10 4 гс.
Рис. 3-3. Провод с током в магнитном поле.
Магнитная индукция — векторная величина. Направление вектора магнитной индукции совпадает с направлением поля в данной точке.
Магнитное поле, во всех точках которого векторы магнитной индукции одинаковы по величине и параллельны друг другу, называется однородным.
Магнитные линии можно использовать не только для указания направления поля, но и для характеристики его интенсивности. Для этого условно через единичную площадку, перпендикулярную к направлению поля, проводят число линий, равное или пропорциональное величине магнитной индукции в данном месте поля.
Произведение магнитной индукции В на площадь S, перпендикулярную к вектору магнитной индукции, называется магнитным потоком, т. е.
Так как магнитная индукция измеряется в теслах (тл), а площадь — в квадратных метрах, и учитывая, что 1 тл = 1вб : 1м2 получим, что магнитный поток измеряется в веберах:
Более мелкой единицей магнитного потока, не относящейся к системе СИ, является максвелл
1 мкс = 10 -8 вб = 1 гс•см 2 .
Так как магнитная индукция характеризуется числом магнитных линий, проходящих через единицу площади поверхности, перпендикулярной направлению поля, то магнитный поток будет характеризоваться числом линий, проходящих через площадь S.
Статья на тему Магнитная индукция
Что такое магнитная индукция
В этой статье мы постараемся разобраться в том, что такое магнитная индукция, как она связана с магнитным полем, какое отношение имеет магнитная индукция к току, и как действует на ток. Вспомним основные правила, определяющие направление индукционных линий, а также отметим некоторые формулы, которые помогут в решении задач магнитостатики.Силовой характеристикой магнитного поля в выбранной точке пространства является магнитная индукция В. Эта векторная величина определяет силу, с которой магнитное поле действует на движущуюся в нем заряженную частицу. Если заряд частицы равен q, ее скорость равна v, а индукция магнитного поля в данной точке пространства равна В, то на частицу в данной точке со стороны магнитного поля действует сила, равная:
Таким образом, В — это вектор, величина и направление которого таковы, что сила Лоренца, действующая на движущийся заряд со стороны магнитного поля равна:
Здесь альфа — это угол между вектором скорости и вектором магнитной индукции. Вектор силы Лоренца F перпендикулярен вектору скорости и вектору магнитной индукции. Его направление для случая движения положительно заряженной частицы в однородном магнитном поле определяется правилом левой руки:
Вектор силы Лоренца F перпендикулярен вектору скорости и вектору магнитной индукции. Его направление для случая движения положительно заряженной частицы в однородном магнитном поле определяется правилом левой руки:
«Если левую руку расположить так, чтобы вектор магнитной индукции входил в ладонь, а четыре вытянутых пальца были направлены по направлению движения положительно заряженной частицы, то отогнутый на 90 градусов большой палец покажет направление силы Лоренца».
Поскольку ток в проводнике является движением заряженных частиц, то магнитную индукцию можно определить и как отношение максимального механического момента, действующего со стороны однородного магнитного поля на рамку с током, к произведению силы тока в рамке на площадь рамки:
Магнитная индукция — фундаментальная характеристика магнитного поля, как напряженность для электрического поля . В системе СИ магнитная индукция измеряется в тесла (Тл), в системе СГС — в гауссах (Гс). 1 тесла = 10000 гаусс. 1 Тл — это индукция такого однородного магнитного поля, в котором на рамку площадью 1 м2, по которой течет ток в 1 А, действует максимальный вращающий механический момент сил, равный 1 Н • м.
Кстати, индукция магнитного поля Земли на широте 50° в среднем составляет 0,00005 Тл, а на экваторе — 0,000031 Тл. Вектор магнитной индукции всегда направлен по касательной к магнитной силовой линии.
Контур, помещенный в однородное магнитное поле, пронизывается магнитным потоком Ф, — потоком вектора магнитной индукции. Величина магнитного потока Ф зависит от направления вектора магнитной индукции относительно контура, от его величины, и от площади контура, пронизываемого линиями магнитной индукции. Если вектор В будет перпендикулярен площади контура, то магнитный поток Ф, пронизывающий контур, будет максимальным.
Сам термин индукция происходит от латинского «индукцио», что означает «наведение» (например, навести на мысль – то есть вызвать мысль). Синонимы: наведение, возникновение, образование. Не путать с явлением электромагнитной индукции.
Проводник с током имеет вокруг себя магнитное поле. Открыл магнитное поле электрического тока в 1820 году датский физик Ханс Кристиан Эрстед. Для определения направления силовых линий индукции магнитного поля В электрического тока I, текущего по прямолинейному проводнику, пользуются правилом правого винта или буравчика:
Для определения направления силовых линий индукции магнитного поля В электрического тока I, текущего по прямолинейному проводнику, пользуются правилом правого винта или буравчика:
«Направление вращения рукоятки буравчика показывает направление линий магнитной индукции В, а поступательное движение буравчика тогда соответствует направлению тока в проводнике.»
При этом величина магнитной индукции B на расстоянии R от проводника с током I может быть найдена про формуле:
где магнитная постоянная:
Если линии напряженности электростатического поля Е начинаясь на положительных зарядах, заканчиваются на отрицательных, то линии магнитной индукции B замкнуты всегда. В отличие от электрических зарядов, магнитных зарядов, которые бы создавали полюса подобно электрическим зарядам, в природе не обнаружено.
Теперь несколько слов о постоянных магнитах. Еще в начале 19 века, французский исследователь и физик-естествоиспытатель Андре-Мари Ампер выдвинул гипотезу о молекулярных токах. Согласно Амперу, движения электронов вокруг атомных ядер порождают элементарные токи, которые в свою очередь создают вокруг себя элементарные магнитные поля. И если кусок ферромагнетика поместить во внешнее магнитное поле, то эти микроскопические магнитики сориентируются во внешнем поле, и кусок ферромагнетика станет магнитом.
Согласно Амперу, движения электронов вокруг атомных ядер порождают элементарные токи, которые в свою очередь создают вокруг себя элементарные магнитные поля. И если кусок ферромагнетика поместить во внешнее магнитное поле, то эти микроскопические магнитики сориентируются во внешнем поле, и кусок ферромагнетика станет магнитом.
Вещества с большим значением остаточной намагниченности, такие как сплав неодим-железо-бор, позволяют сегодня получать мощные постоянные магниты. Неодимовые магниты теряют не более 1-2 % своей намагниченности за 10 лет. Но их можно легко размагнитить, нагрев до температуры +70°C и более.
Надеемся, что данная статья помогла Вам получить общее представление о том, что такое магнитная индукция и откуда на возникает.
Вектор магнитной индукции
Вектор магнитной индукции (В) — это основная силовая характеристика магнитного поля (обозначается В). Пробный контур, помещенный в магнитное поле, испытывает со стороны магнитного поля действие вращающего момента сил М.
Бесконечно длинный ток величины I создает на расстоянии r от себя магнитное поле:
где Мо — магнитная постоянная, R — расстояние, I — сила тока в проводнике.Магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой в данной точке магнитного поля.
Единица магнитной индукции — тесла (Тл).
Магнитная индукция
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .В вакууме B = μH.
Более конкретно,
— это такой вектор, что сила Лоренца , действующая со стороны магнитного поля на заряд , движущийся со скоростью , равнагде косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора
перпендикулярно им обоим и направлено по правилу буравчика).
Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции.
Опытным путем было установлено, что для одной и той же точки магнитного поля максимальный вращающий момент М (момент сил) пропорционален произведению силы тока I в контуре на его площадь S. Величину IS называют магнитным моментом контура Pm.
| Рисунок– Электрический ток (I), проходя по проводнику, создаёт магнитное поле (B) вокруг проводника. | Рисунок – Правило буравчика |
Правило буравчика (винта): Если направление поступательного движения буравчика (винта) совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением вектора магнитной индукции поля, создаваемого этим током.
На практике удобно пользоваться следующим правилом: Если обхватить соленоид (катушку) правой рукой так, что бы четыре пальца были направлены по току, то отогнутый большой палец покажет направление магнитного поля внутри соленоида.
Рисунок 3.2 – А) Образование магнитного потока в соленоиде
Б) Схема полей в соленоиде при протекании по обмотке переменного тока
Единица измерения В в СИ — тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9656 —
| 7533 — или читать все.188.64.174.65 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Электромагнитная индукция
Явление электромагнитной индукции
Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции было открыто М. Фарадеем.
- На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
- Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
- Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.
Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.
Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.
Объяснения возникновения индукционного тока
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.
Свойства вихревого электрического поля:
- источник – переменное магнитное поле;
- обнаруживается по действию на заряд;
- не является потенциальным;
- линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.
Магнитный поток
Магнитным потоком через площадь ( S ) контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ( B ) , площади поверхности ( S ) , пронизываемой данным потоком, и косинуса угла ( alpha ) между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):
Обозначение – ( Phi ) , единица измерения в СИ – вебер (Вб).
Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м 2 , расположенную перпендикулярно вектору магнитной индукции:
Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.
В зависимости от угла ( alpha ) магнитный поток может быть положительным ( ( alpha ) ( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.
Если ( alpha ) = 90°, то магнитный поток равен 0.
Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).
В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.
Закон электромагнитной индукции Фарадея
Закон электромагнитной индукции (закон Фарадея):
ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:
Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.
Если контур состоит из ( N ) витков, то ЭДС индукции:
Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ( R ) :
При движении проводника длиной ( l ) со скоростью ( v ) в постоянном однородном магнитном поле с индукцией ( vec ) ЭДС электромагнитной индукции равна:
где ( alpha ) – угол между векторами ( vec ) и ( vec ) .
Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.
Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.
Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:
- магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
- вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.
 В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:
- в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
- в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.
Правило Ленца
Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.
Алгоритм решения задач с использованием правила Ленца:
- определить направление линий магнитной индукции внешнего магнитного поля;
- выяснить, как изменяется магнитный поток;
- определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
- по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.
Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.
Самоиндукция
Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.
При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.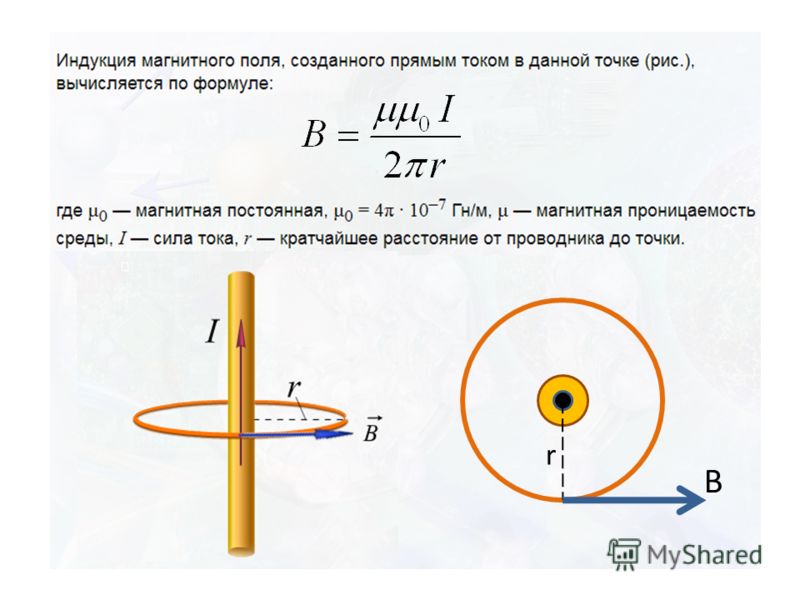
В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.
Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.
При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.
Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.
Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.
При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.
ЭДС самоиндукции ( varepsilon_ ) , возникающая в катушке с индуктивностью ( L ) , по закону электромагнитной индукции равна:
ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.
Индуктивность
Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ( Phi ) через контур из этого проводника пропорционален модулю индукции ( vec ) магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.
Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:
Индуктивность – коэффициент пропорциональности ( L ) между силой тока ( I ) в контуре и магнитным потоком ( Phi ) , создаваемым этим током:
Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.
Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:
Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.
Энергия магнитного поля
При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.
Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.
Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:
Основные формулы раздела «Электромагнитная индукция»
Алгоритм решения задач по теме «Электромагнитная индукция»:
1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.
2. Записать формулу:
- закона электромагнитной индукции;
- ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.
3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.
4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).
5. Решить полученную систему уравнений относительно искомой величины.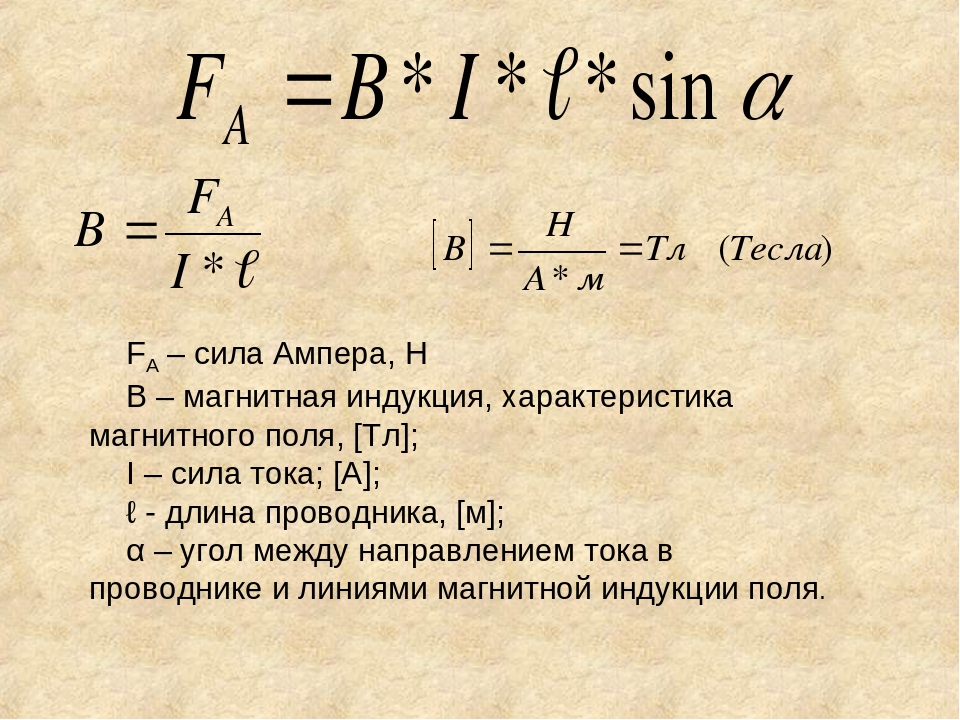
Что такое магнитная индукция
Магнитная индукция – что это такое простым языком
Магнитная индукция – одна из основных характеристик магнитного поля. Представляет собой векторную величину и характеризует силу магнитного действия поля на перемещающиеся внутри него заряженные частицы.
Физический смысл
С научной точки зрения данное явление можно объяснить таким образом. В основе любого металла лежит кристаллическая решётка. В этой кристаллической решётке содержатся отрицательно заряженные частицы – электроны. В ситуации, когда на проводник не оказывается никакого внешнего магнитного воздействия, заряженные частицы находятся в состоянии полного покоя.
Но в ситуации, когда проводник подпадает под воздействие магнитного поля переменной направленности, эти частицы приходят в движение. Прибор для создания магнитного поля и наблюдения явления индукции в лабораторных условиях состоит из металлической катушки, и перемещающегося в ней постоянного магнита. В результате перемещения внутри металла образуется электроток. Сила возникающего в катушке электротока зависит от нескольких факторов:
В результате перемещения внутри металла образуется электроток. Сила возникающего в катушке электротока зависит от нескольких факторов:
- Свойств металла, из которого сделана катушка.
- Свойств магнита, перемещающегося внутри катушки.
- Скорости движения катушки и магнита относительно друг друга.
В результате воздействия силового поля магнита на кристаллическую решётку катушки, электроны, содержащиеся в ней, разворачиваются на определённый угол, выстраиваясь вдоль направления силовых линий поля.
И чем сильнее магнитное воздействие, тем большее число электронов внутри металла поворачиваются, однороднее становится их положение в кристаллической решётке. При этом магнитные поля отдельных частиц не нейтрализуют друг друга, а наоборот, усиливают и формируют единое магнитное поле.
Формула и обозначения
Обозначается магнитная индукция латинским символом «В», и определяет силу внешнего влияния, оказываемого магнитным полем на заряженные частицы – в нашем случае электроны, обозначаемые «q», – в некоторой точке. Скорость движения заряженных частиц обозначается буквой «U».
Скорость движения заряженных частиц обозначается буквой «U».
Сама физическая формула магнитной индукции выглядит следующим образом:
- Fмач– наибольшая сила, воздействующая на проводник.
- L – его длина.
- I – сила тока заряженных частиц в металле.
Единицей индукции в международной системе СИ является «тесла», сокращённо в русском варианте «Тл», в международном – «Т». Это название дано в честь сербского учёного Н. Теслы. В старой метрической системе СГС единица индукции обозначалась в честь германского физика «гаусс»: Гс – среди русскоязычных учёных, и G – в интернациональном варианте.
Магнитное поле
Под данным термином в физике подразумевается некое силовое поле, оказывающее определённое влияние на перемещающиеся заряженные частицы, и на прочие тела, имеющие определённый магнитный момент. Воздействие оказывается не зависимо от того, находятся ли эти частицы в состоянии покоя, либо же в движении. Кроме вектора магнитной индукции, дополнительной характеристикой поля выступает векторный потенциал. Он носит альтернативный характер, но при этом, в физическом смысле, неразрывно связан с магнитной индукцией.
Кроме вектора магнитной индукции, дополнительной характеристикой поля выступает векторный потенциал. Он носит альтернативный характер, но при этом, в физическом смысле, неразрывно связан с магнитной индукцией.
Для поля, действующего в абсолютном вакууме, главной характеристикой обычно выбирается не индукция, а его напряжённость, обозначаемая Н. Однако, подобная замена в сфере действия земного магнитного поля уже не имеет особого смысла, в связи с чем, в практических опытных измерениях и наблюдениях за основную характеристику магнитного поля всё же принимается вектор магнитной индукции.
Фактически, магнитное поле допустимо определить, как особую материю, с помощью которой происходит взаимодействие меж некими заряженными элементарными частицами, передвигающимися с определённой скоростью.
При этом не стоит путать магнитную и электромагнитную индукцию. Под электромагнитной индукцией понимается закономерность, установленная англичанином М. Фарадеем. Суть закономерности состоит в возникновении электромагнитного силового поля под действием переменного электротока, протекающего в замкнутом проводниковом контуре. В контуре возникает определённая движущая сила, в свою очередь, порождающая индукционный ток. Магнитное поле, наряду с электрическим полем, выступает как одна из двух частей электромагнитного поля.
Фарадеем. Суть закономерности состоит в возникновении электромагнитного силового поля под действием переменного электротока, протекающего в замкнутом проводниковом контуре. В контуре возникает определённая движущая сила, в свою очередь, порождающая индукционный ток. Магнитное поле, наряду с электрическим полем, выступает как одна из двух частей электромагнитного поля.
Теория о постоянных магнитах, своим воздействием вызывающих возникновение индукции, была разработана французским физиком А-М. Ампером, в честь него позднее была названа единица мощности электротока. Он впервые установил, что движения электронов вокруг центра атома в итоге порождают микроскопические, или элементарные магнитные поля. Также им был открыто свойство металлических проводников сохранять магнитные свойства некоторое время после прекращения воздействия на них магнитным полем.
Магнетизм — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Сила Ампера
К оглавлению. ..
..
Заряженные тела способны создавать кроме электрического еще один вид поля. Если заряды движутся, то в пространстве вокруг них создается особый вид материи, называемый
Для описания магнитного поля необходимо ввести силовую характеристику поля, аналогичную вектору напряженности E электрического поля. Такой характеристикой является вектор B
где: В – индукция магнитного поля, I – сила тока в проводнике, l – его длина. Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику.
Сила Ампера направлена перпендикулярно вектору магнитной индукции и направлению тока, текущего по проводнику.
Для определения направления силы Ампера обычно используют
Если угол α между направлениями вектора магнитной индукции и тока в проводнике отличен от 90°, то для определения направления силы Ампера надо взять составляющую магнитного поля, которая перпендикулярна направлению тока. Решать задачи этой темы нужно так же как и в динамике или статике, т.е. расписав силы по осям координат или складывая силы по правилам сложения векторов.
Момент сил, действующих на рамку с током
Пусть рамка с током находится в магнитном поле, причём плоскость рамки перпендикулярна полю. Силы Ампера будут сжимать рамку, а их равнодействующая будет равна нулю.
где: S — площадь рамки, α — угол между нормалью к рамке и вектором магнитной индукции (нормаль — вектор, перпендикулярный плоскости рамки), N – количество витков, B
Сила Лоренца
К оглавлению…
Сила Ампера, действующая на отрезок проводника длиной Δl с силой тока I, находящийся в магнитном поле B может быть выражена через силы, действующие на отдельные носители заряда. Эти силы называют силами Лоренца. Сила Лоренца, действующая на частицу с зарядом q в магнитном поле B, двигающуюся со скоростью v, вычисляется по следующей формуле:
Угол α в этом выражении равен углу между скоростью и вектором магнитной индукции. Направление силы Лоренца, действующей на
Направление силы Лоренца, действующей на
Сила Лоренца направлена перпендикулярно векторам скорости и индукции магнитного поля. При движении заряженной частицы в магнитном поле сила Лоренца работы не совершает
Сила Лоренца в этом случае играет роль центростремительной силы.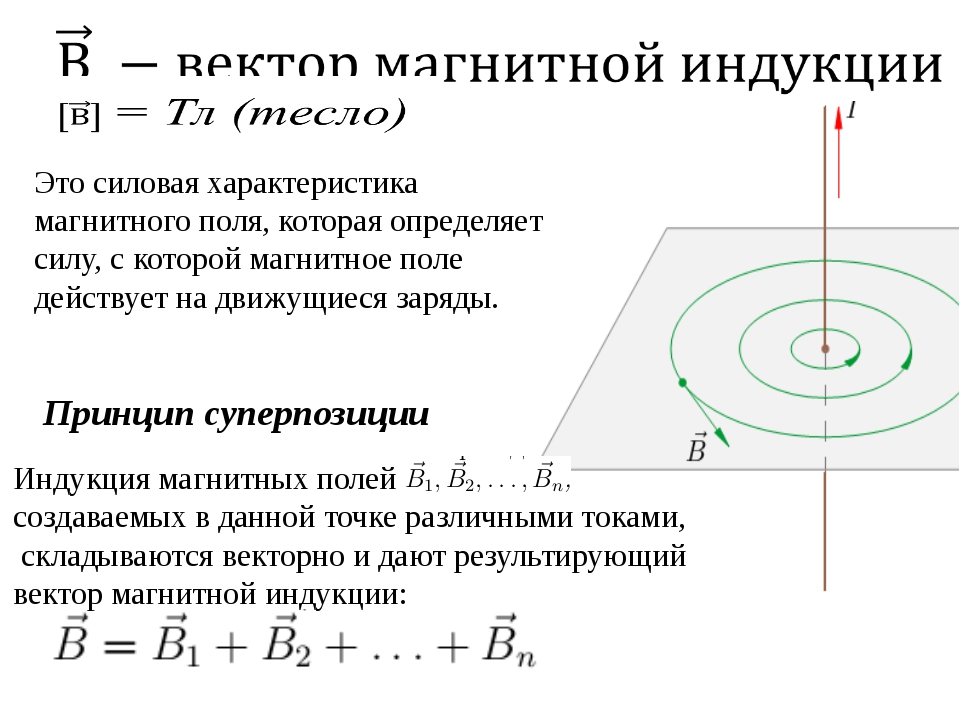 Период обращения частицы в однородном магнитном поле равен:
Период обращения частицы в однородном магнитном поле равен:
Последнее выражение показывает, что для заряженных частиц заданной массы m период обращения (а значит и частота, и угловая скорость) не зависит от скорости (следовательно, и от кинетической энергии) и радиуса траектории R.
Теория о магнитном поле
К оглавлению…
Магнитное взаимодействие токов
Если по двум параллельным проводам идёт ток в одном направлении, то они притягиваются; если в противоположных направлениях, то отталкиваются. Закономерности этого явления были экспериментально установлены Ампером. Взаимодействие токов вызывается их магнитными полями: магнитное поле одного тока действует силой Ампера на другой ток и наоборот. Опыты показали, что модуль силы, действующей на отрезок длиной Δl каждого из проводников, прямо пропорционален силам тока I1 и I2 в проводниках, длине отрезка Δl и обратно пропорционален расстоянию R между ними:
где: μ0 – постоянная величина, которую называют магнитной постоянной. Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:
Введение магнитной постоянной в СИ упрощает запись ряда формул. Ее численное значение равно:
μ0 = 4π·10–7 H/A2 ≈ 1,26·10–6 H/A2.
Сравнивая приведенное только что выражение для силы взаимодействия двух проводников с током и выражение для силы Ампера нетрудно получить выражение для индукции магнитного поля создаваемого каждым из прямолинейных проводников с током на расстоянии R от него:
где: μ – магнитная проницаемость вещества (об этом чуть ниже). Если ток протекает по круговому витку, то в центре витка индукция магнитного поля определяется по формуле:
Силовыми линиями магнитного поля называют линии, по касательным к которым располагаются магнитные стрелки. Магнитной стрелкой называют длинный и тонкий магнит, его полюса точечны. Подвешенная на нити магнитная стрелка всегда поворачивается в одну сторону. При этом один её конец направлен в сторону севера, второй — на юг. Отсюда название полюсов: северный (N) и южный (S). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N) и южный (красным цветом или буквой S). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом. Даже если магнит разломать, то у каждой части будет по два разных полюса.
При этом один её конец направлен в сторону севера, второй — на юг. Отсюда название полюсов: северный (N) и южный (S). Магниты всегда имеют два полюса: северный (обозначается синим цветом или буквой N) и южный (красным цветом или буквой S). Магниты взаимодействуют так же, как и заряды: одноименные полюса отталкиваются, а разноименные – притягиваются. Невозможно получить магнит с одним полюсом. Даже если магнит разломать, то у каждой части будет по два разных полюса.
Вектор магнитной индукции
Вектор магнитной индукции — векторная физическая величина, являющаяся характеристикой магнитного поля, численно равная силе, действующей на элемент тока в 1 А и длиной 1 м, если направление силовой линии перпендикулярно проводнику. Обозначается В, единица измерения — 1 Тесла. 1 Тл — очень большая величина, поэтому в реальных магнитных полях магнитную индукцию измеряют в мТл.
Вектор магнитной индукции направлен по касательной к силовым линиям, т. е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.
е. совпадает с направлением северного полюса магнитной стрелки, помещённой в данное магнитное поле. Направление вектора магнитной индукции не совпадает с направлением силы, действующей на проводник, поэтому силовые линии магнитного поля, строго говоря, силовыми не являются.
Силовая линия магнитного поля постоянных магнитов направлена по отношению к самим магнитам так, как показано на рисунке:
В случае магнитного поля электрического тока для определения направления силовых линий используют правило «Правой руки»: если взять проводник в правую руку так, чтобы большой палец был направлен по току, то четыре пальца, обхватывающие проводник, показывают направление силовых линий вокруг проводника:
В случае прямого тока линии магнитной индукции — окружности, плоскости которых перпендикулярны току. Вектора магнитной индукции направлены по касательной к окружности.
Соленоид — намотанный на цилиндрическую поверхность проводник, по которому течёт электрический ток I. Магнитное поле соленоида подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):
Магнитное поле соленоида подобно полю прямого постоянного магнита. Внутри соленоида длиной l и количеством витков N создается однородное магнитное поле с индукцией (его направление также определяется правилом правой руки):
Линии магнитного поля имеют вид замкнутых линий — это общее свойство всех магнитных линий. Такое поле называют вихревым. В случае постоянных магнитов линии не оканчиваются на поверхности, а проникают внутрь магнита и замыкаются внутри. Это различие электрического и магнитного полей объясняется тем, что, в отличие от электрических, магнитных зарядов не существует.
Магнитные свойства вещества
Все вещества обладают магнитными свойствами. Магнитные свойства вещества характеризуются относительной магнитной проницаемостью μ, для которой верно следующее:
Данная формула выражает соответствие вектора магнитной индукции поля в вакууме и в данной среде. В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики — кислород, платина, магний — несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков — железо, никель, кобальт — μ >> 1. Например, у железа μ ≈ 25000.
В отличие от электрического, при магнитном взаимодействии в среде можно наблюдать и усиление, и ослабление взаимодействия по сравнению с вакуумом, у которого магнитная проницаемость μ = 1. У диамагнетиков магнитная проницаемость μ немного меньше единицы. Примеры: вода, азот, серебро, медь, золото. Эти вещества несколько ослабляют магнитное поле. Парамагнетики — кислород, платина, магний — несколько усиливают поле, имея μ немного больше единицы. У ферромагнетиков — железо, никель, кобальт — μ >> 1. Например, у железа μ ≈ 25000.
Магнитный поток. Электромагнитная индукция
К оглавлению…
Явление электромагнитной индукции было открыто выдающимся английским физиком М.Фарадеем в 1831 году. Оно заключается в возникновении электрического тока в замкнутом проводящем контуре при изменении во времени магнитного потока, пронизывающего контур. Магнитным потоком Φ через площадь S контура называют величину:
где: B – модуль вектора магнитной индукции, α – угол между вектором магнитной индукции B и нормалью (перпендикуляром) к плоскости контура, S – площадь контура, N – количество витком в контуре.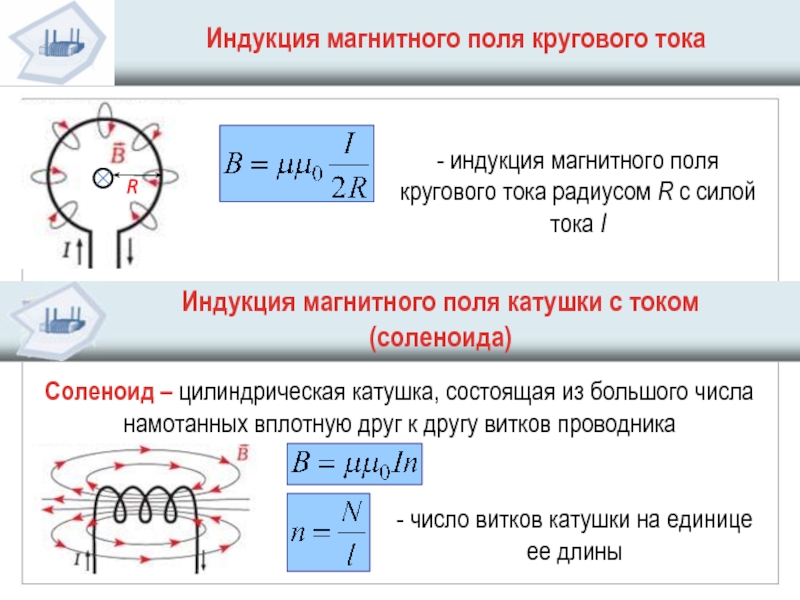 Единица магнитного потока в системе СИ называется Вебером (Вб).
Единица магнитного потока в системе СИ называется Вебером (Вб).
Фарадей экспериментально установил, что при изменении магнитного потока в проводящем контуре возникает ЭДС индукции εинд, равная скорости изменения магнитного потока через поверхность, ограниченную контуром, взятой со знаком минус:
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум возможным причинам.
- Магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле. Возникновение ЭДС индукции объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.
- Вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре.
При решении задач важно сразу определить за счет чего меняется магнитный поток. Возможно три варианта:
Возможно три варианта:
- Меняется магнитное поле.
- Меняется площадь контура.
- Меняется ориентация рамки относительно поля.
При этом при решении задач обычно считают ЭДС по модулю. Обратим внимание также внимание на один частный случай, в котором происходит явление электромагнитной индукции. Итак, максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:
Движение проводника в магнитном поле
К оглавлению…
При движении проводника длиной l в магнитном поле B со скоростью v на его концах возникает разность потенциалов, вызванная действием силы Лоренца на свободные электроны в проводнике. Эту разность потенциалов (строго говоря, ЭДС) находят по формуле:
где: α — угол, который измеряется между направлением скорости и вектора магнитной индукции. В неподвижных частях контура ЭДС не возникает.
В неподвижных частях контура ЭДС не возникает.
Если стержень длиной L вращается в магнитном поле В вокруг одного из своих концов с угловой скоростью ω, то на его концах возникнет разность потенциалов (ЭДС), которую можно рассчитать по формуле:
Индуктивность. Самоиндукция. Энергия магнитного поля
К оглавлению…
Самоиндукция является важным частным случаем электромагнитной индукции, когда изменяющийся магнитный поток, вызывающий ЭДС индукции, создается током в самом контуре. Если ток в рассматриваемом контуре по каким-то причинам изменяется, то изменяется и магнитное поле этого тока, а, следовательно, и собственный магнитный поток, пронизывающий контур. В контуре возникает ЭДС самоиндукции, которая согласно правилу Ленца препятствует изменению тока в контуре. Собственный магнитный поток Φ, пронизывающий контур или катушку с током, пропорционален силе тока I:
Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции или индуктивностью катушки. Единица индуктивности в СИ называется Генри (Гн).
Единица индуктивности в СИ называется Генри (Гн).
Запомните: индуктивность контура не зависит ни от магнитного потока, ни от силы тока в нем, а определяется только формой и размерами контура, а также свойствами окружающей среды. Поэтому при изменении силы тока в контуре индуктивность остается неизменной. Индуктивность катушки можно рассчитать по формуле:
где: n — концентрация витков на единицу длины катушки:
ЭДС самоиндукции, возникающая в катушке с постоянным значением индуктивности, согласно формуле Фарадея равна:
Итак ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в ней.
Магнитное поле обладает энергией. Подобно тому, как в заряженном конденсаторе имеется запас электрической энергии, в катушке, по виткам которой протекает ток, имеется запас магнитной энергии. Энергия Wм магнитного поля катушки с индуктивностью L, создаваемого током I, может быть рассчитана по одной из формул (они следуют друг из друга с учётом формулы Φ = LI):
Соотнеся формулу для энергии магнитного поля катушки с её геометрическими размерами можно получить формулу для объемной плотности энергии магнитного поля (или энергии единицы объёма):
Правило Ленца
К оглавлению. ..
..
Инерция – явление, происходящее и в механике (при разгоне автомобиля мы отклоняемся назад, противодействуя увеличению скорости, а при торможении отклоняемся вперёд, противодействуя уменьшению скорости), и в молекулярной физике (при нагревании жидкости увеличивается скорость испарения, самые быстрые молекулы покидают жидкость, уменьшая скорость нагревания) и так далее. В электромагнетизме инерция проявляется в противодействии изменению магнитного потока, пронизывающего контур. Если магнитный поток нарастает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать нарастанию магнитного потока, а если магнитный поток убывает, то возникающий в контуре индукционный ток направлен так, чтобы препятствовать убыванию магнитного потока.
Правило Ленца для определения направления индукционного тока: возникающий в контуре индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует изменению магнитного потока, которое вызывало этот ток.
Глава 23. Закон электромагнитной индукции
Если в магнитном поле находится замкнутый проводящий контур, не содержащий источников тока, то при изменении магнитного поля в контуре возникает электрический ток. Это явление называется электромагнитной индукцией. Появление тока свидетельствует о возникновении в контуре электрического поля, которое может обеспечить замкнутое движение электрических зарядов или, другими словами, о возникновении ЭДС. Электрическое поле, которое возникает при изменении поля магнитного и работа которого при перемещении зарядов по замкнутому контуру не равна нулю, имеет замкнутые силовые линии и называется вихревым.
Для количественного описания электромагнитной индукции вводится понятие магнитного потока (или потока вектора магнитной индукции) через замкнутый контур. Для плоского контура, расположенного в однородном магнитном поле (а только такие ситуации и могут встретиться школьникам на едином государственном экзамене), магнитный поток определяется как
(23. |
где — индукция поля, — площадь контура, — угол между вектором индукции и нормалью (перпендикуляром) к плоскости контура (см. рисунок; перпендикуляр к плоскости контура показан пунктиром). Единицей магнитного потока в международной системе единиц измерений СИ является Вебер (Вб), который определяется как магнитный поток через контур площади 1 м2 однородного магнитного поля с индукцией 1 Тл, перпендикулярной плоскости контура.
Величина ЭДС индукции , возникающая в контуре при изменении магнитного потока через этот контур, равна скорости изменения магнитного потока
(23.2) |
Здесь — изменение магнитного потока через контур за малый интервал времени . Важным свойством закона электромагнитной индукции (23.2) является его универсальность по отношению к причинам изменения магнитного потока: магнитный поток через контур может меняться из-за изменения индукции магнитного поля, изменения площади контура или изменения угла между вектором индукции и нормалью, что происходит при вращении контура в поле.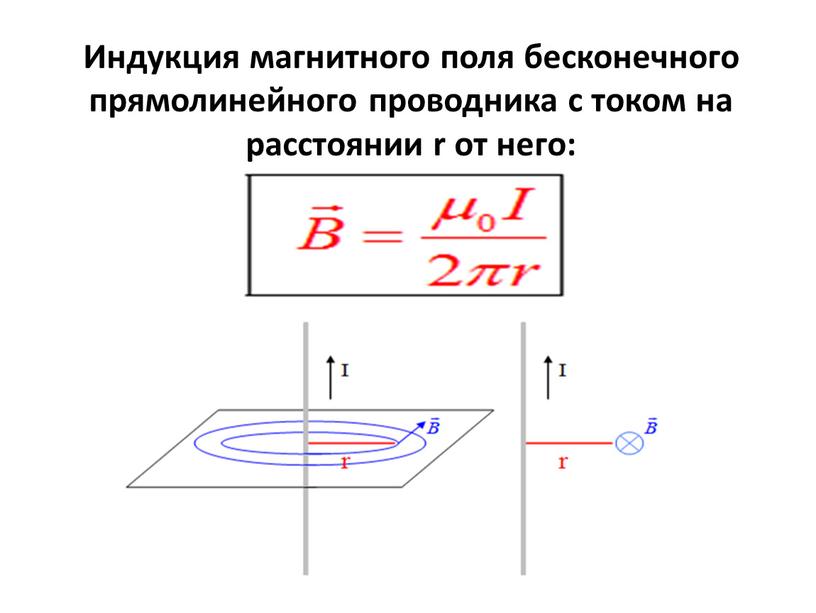 Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.
Во всех этих случаях по закону (23.2) в контуре будет возникать ЭДС индукции и индукционный ток.
Знак минус в формуле (23.2) «отвечает» за направление тока, возникающего в результате электромагнитной индукции (правило Ленца). Однако понять на языке закона (23.2), к какому направлению индукционного тока приведет этот знак при том или ином изменении магнитного потока через контур, не так-то просто. Но достаточно легко запомнить результат: индукционный ток будет направлен таким образом, что созданное им магнитное поле будет «стремиться» компенсировать то изменение внешнего магнитного поля, которое этот ток и породило. Например, при увеличении потока внешнего магнитного поля через контур в нем возникнет индукционный ток, магнитное поле которого будет направлено противоположно внешнему магнитному полю так, чтобы уменьшить внешнее поле и сохранить, таким образом, первоначальную величину магнитного поля. При уменьшении потока поля через контур поле индукционного тока будет направлено так же, как и внешнее магнитное поле.
Если в контуре с током ток в силу каких-то причин изменяется, то изменяется и магнитный поток через контур того магнитного поля, которое создано самим этим током. Тогда по закону (23.2) в контуре должна возникать ЭДС индукции. Явление возникновения ЭДС индукции в некоторой электрической цепи в результате изменения тока в самой этой цепи называется самоиндукцией. Для нахождения ЭДС самоиндукции в некоторой электрической цепи необходимо вычислить поток магнитного поля, создаваемого этой цепью через нее саму. Такое вычисление представляет собой сложную проблему из-за неоднородности магнитного поля. Однако одно свойство этого потока является очевидным. Поскольку магнитное поле, создаваемого током в цепи, пропорционально величине тока, то и магнитный поток собственного поля через цепь пропорционален току в этой цепи
(23.3) |
где — сила тока в цепи, — коэффициент пропорциональности, который характеризует «геометрию» цепи, но не зависит от тока в ней и называется индуктивностью этой цепи. Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции
Единицей индуктивности в международной системе единиц СИ является Генри (Гн). 1 Гн определяется как индуктивность такого контура, поток индукции собственного магнитного поля через который равен 1 Вб при силе тока в нем 1 А. С учетом определения индуктивности (23.3) из закона электромагнитной индукции (23.2) получаем для ЭДС самоиндукции
(23.4) |
Благодаря явлению самоиндукции ток в любой электрической цепи обладает определенной «инерционностью» и, следовательно, энергией. Действительно, для создания тока в контуре необходимо совершить работу по преодолению ЭДС самоиндукции. Энергия контура с током и равна этой работе. Необходимо запомнить формулу для энергии контура с током
(23.5) |
где — индуктивность контура, — сила тока в нем.
Явление электромагнитной индукции широко применяется в технике. На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.
На нем основано создание электрического тока в электрических генераторах и электростанциях. Благодаря закону электромагнитной индукции происходит преобразование механических колебаний в электрические в микрофонах. На основе закона электромагнитной индукции работает, в частности, электрическая цепь, которая называется колебательным контуром (см. следующую главу), и которая является основой любой радиопередающей или радиопринимающей техники.
Рассмотрим теперь задачи.
Из перечисленных в задаче 23.1.1 явлений только одно есть следствие закона электромагнитной индукции — появление тока в кольце при проведении сквозь него постоянного магнита (ответ 3). Все остальное — результат магнитного взаимодействия токов.
Как указывалось во введении к настоящей главе, явление электромагнитной индукции лежит в основе работы генератора переменного тока (задача 23.1.2), т.е. прибора, создающего переменный ток, заданной частоты (ответ 2).
Индукция магнитного поля, создаваемого постоянным магнитом, уменьшается с увеличением расстояния до него. Поэтому при приближении магнита к кольцу (задача 23.1.3) поток индукции магнитного поля магнита через кольцо изменяется, и в кольце возникает индукционный ток. Очевидно, это будет происходить при приближении магнита к кольцу и северным, и южным полюсом. А вот направление индукционного тока в этих случаях будет различным. Это связано с тем, что при приближении магнита к кольцу разными полюсами, поле в плоскости кольца в одном случае будет направлено противоположно полю в другом. Поэтому для компенсации этих изменений внешнего поля магнитное поле индукционного тока должно быть в этих случаях направлено по-разному. Поэтому и направления индукционных токов в кольце будут противоположными (ответ 4).
Для возникновения ЭДС индукции в кольце необходимо, чтобы менялся магнитный поток через кольцо. А поскольку магнитная индукция поля магнита зависит от расстояния до него, то в рассматриваемом в задаче 23. 1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1).
1.4 случае поток через кольцо будет меняться, в кольце возникнет индукционный ток (ответ 1).
При вращении рамки 1 (задача 23.1.5) угол между линиями магнитной индукции (а, значит, и вектором индукции) и плоскостью рамки в любой момент времени равен нулю. Следовательно, магнитный поток через рамку 1 не изменяется (см. формулу (23.1)), и индукционный ток в ней не возникает. В рамке 2 индукционный ток возникнет: в положении показанном на рисунке, магнитный поток через нее равен нулю, когда рамка повернется на четверть оборота — будет равен , где — индукция, — площадь рамки. Еще через четверть оборота поток снова будет равен нулю и т.д. Поэтому поток магнитной индукции через рамку 2 изменяется в процессе ее вращения, следовательно, в ней возникает индукционный ток (ответ 2).
В задаче 23.1.6 индукционный ток возникает только в случае 2 (ответ 2). Действительно, в случае 1 рамка при движении остается на одном и том же расстоянии от проводника, и, следовательно, магнитное поле, созданное этим проводником в плоскости рамки, не изменяется.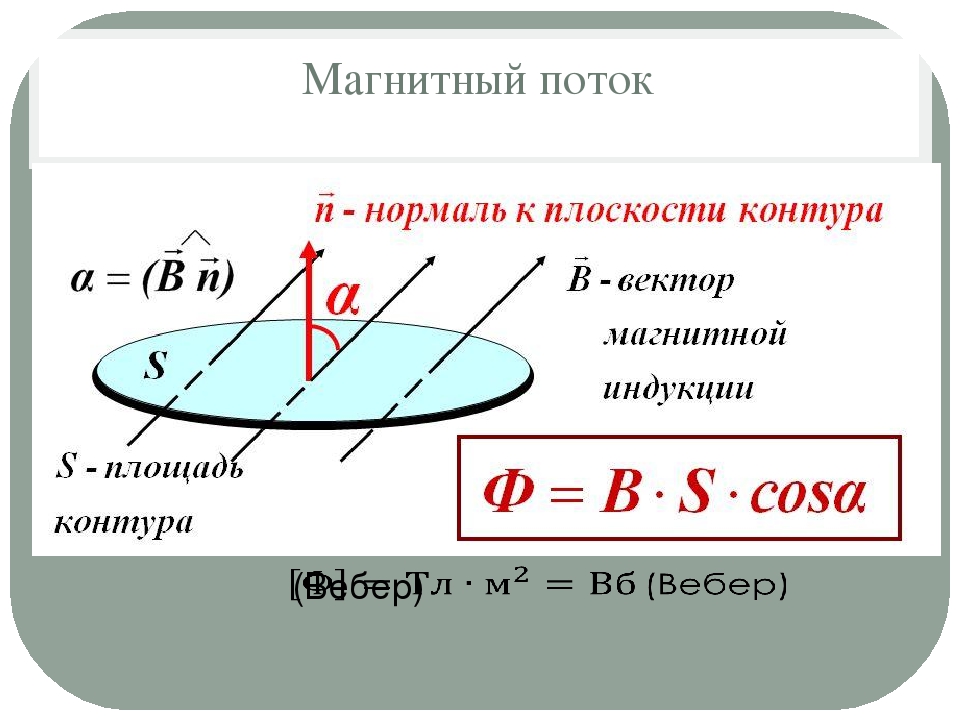 При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток
При удалении рамки от проводника магнитная индукция поля проводника в области рамки изменяется, меняется магнитный поток через рамку, и возникает индукционный ток
В законе электромагнитной индукции утверждается, что индукционный ток в кольце будет течь в такие моменты времени, когда изменяется магнитный поток через это кольцо. Поэтому пока магнит покоится около кольца (задача 23.1.7) индукционный ток в кольце течь не будет. Поэтому правильный ответ в этой задаче — 2.
Согласно закону электромагнитной индукции (23.2) ЭДС индукции в рамке определяется скоростью изменения магнитного потока через нее. А поскольку по условию задачи 23.1.8 индукция магнитного поля в области рамки изменяется равномерно, скорость ее изменения постоянна, величина ЭДС индукции не изменяется в процессе проведения опыта (ответ 3).
В задаче 23.1.9 ЭДС индукции, возникающая в рамке во втором случае, вчетверо больше ЭДС индукции, возникающей в первом (ответ 4).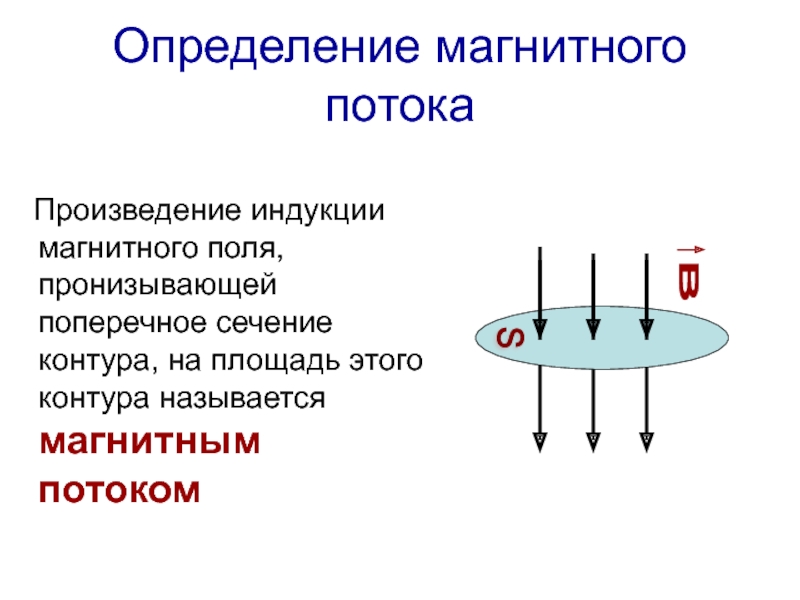 Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.
Это связано с четырехкратным увеличением площади рамки и, соответственно, магнитного потока через нее во втором случае.
В задаче 23.1.10 во втором случае в два раза увеличивается скорость изменения магнитного потока (индукция поля меняется на ту же величину, но за вдвое меньшее время). Поэтому ЭДС электромагнитной индукции, возникающая в рамке во втором случае, в два раза больше, чем в первом (ответ 1).
При увеличении тока в замкнутом проводнике в два раза (задача 23.2.1), величина индукции магнитного поля возрастет в каждой точке пространства в два раза, не изменившись по направлению. Поэтому ровно в два раза изменится магнитный поток через любую малую площадку и, соответственно, и весь проводник (ответ 1). А вот отношение магнитного потока через проводник к току в этом проводнике, которое и представляет собой индуктивность проводника , при этом не изменится (задача 23.2.2 — ответ 3).
Используя формулу (23.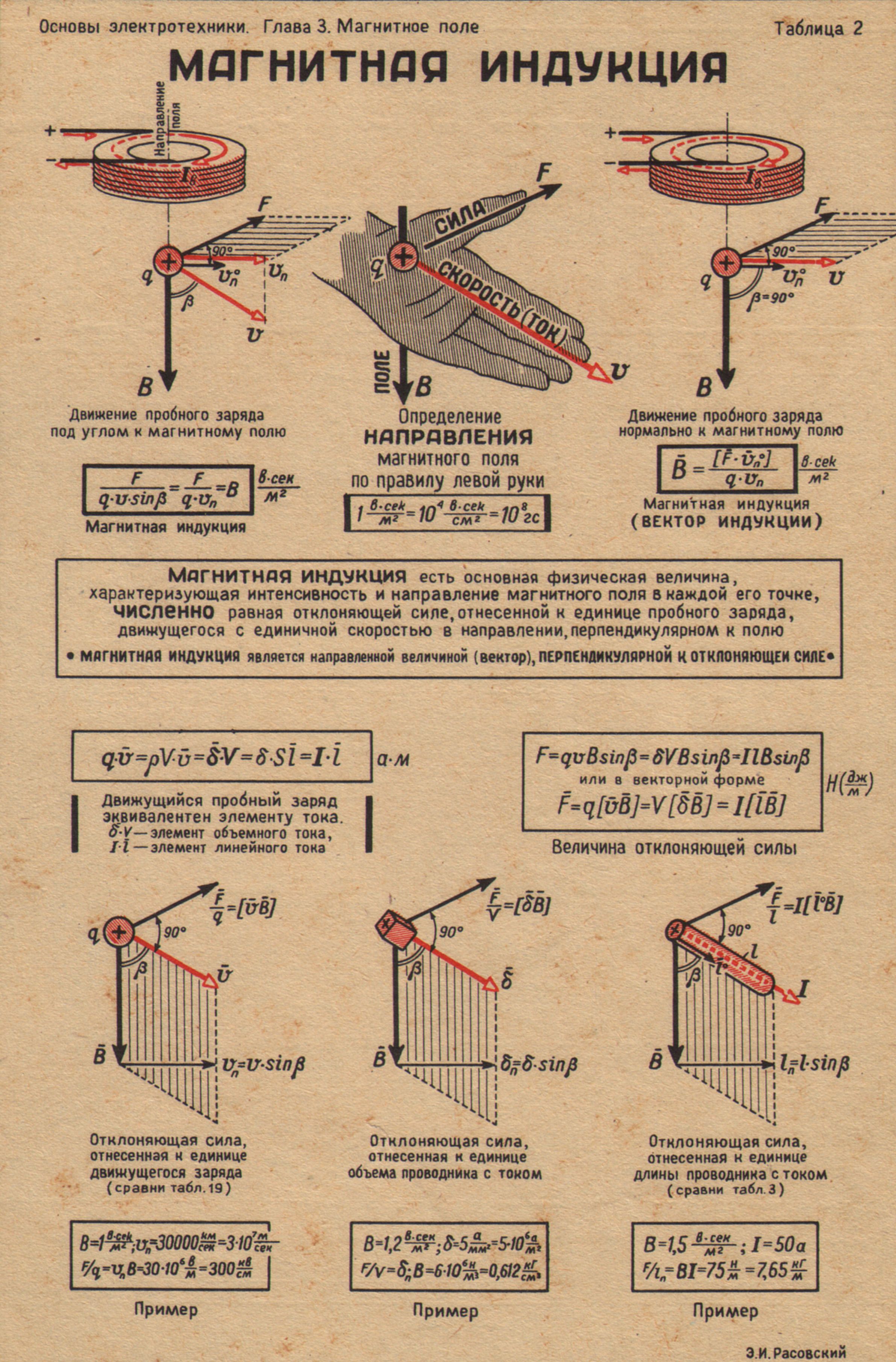 3) находим в задаче 32.2.3 Гн (ответ 4).
3) находим в задаче 32.2.3 Гн (ответ 4).
Связь между единицами измерений магнитного потока, магнитной индукции и индуктивности (задача 23.2.4) следует из определения индуктивности (23.3): единица магнитного потока (Вб) равна произведению единицы тока (А) на единицу индуктивности (Гн) — ответ 3.
Согласно формуле (23.5) при двукратном увеличении индуктивности катушки и двукратном уменьшении тока в ней (задача 23.2.5) энергия магнитного поля катушки уменьшится в 2 раза (ответ 2).
Когда рамка вращается в однородном магнитном поле, магнитный поток через рамку меняется из-за изменения угла между перпендикуляром к плоскости рамки и вектором индукции магнитного поля. А поскольку и в первом и втором случае в задаче 23.2.6 этот угол меняется по одному и тому же закону (по условию частота вращения рамок одинакова), то ЭДС индукции меняются по одному и тому же закону, и, следовательно, отношение амплитудных значений ЭДС индукции в рамках равно единице (ответ 2).
Магнитное поле, создаваемое проводником с током в области рамки (задача 23.2.7), направлено «от нас» (см. решение задач главы 22). Величина индукции поля провода в области рамки при ее удалении от провода будет уменьшаться. Поэтому индукционный ток в рамке должен создать магнитное поле, направленное внутри рамки «от нас». Используя теперь правило буравчика для нахождения направления магнитной индукции, заключаем, что индукционный ток в рамке будет направлен по часовой стрелке (ответ 1).
При увеличении тока в проводе будет возрастать созданное им магнитное поле и в рамке возникнет индукционный ток (задача 23.2.8). В результате возникнет взаимодействие индукционного тока в рамке и тока в проводнике. Чтобы найти направление этого взаимодействия (притяжение или отталкивание) можно найти направление индукционного тока, а затем по формуле Ампера силу взаимодействия рамки с проводом. Но можно поступить и по-другому, используя правило Ленца. Все индукционные явления должны иметь такое направление, чтобы компенсировать вызывающую их причину. А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.
А поскольку причина — увеличение тока в рамке, сила взаимодействия индукционного тока и провода должна стремиться уменьшить магнитный поток поля провода через рамку. А поскольку магнитная индукция поля провода убывает с увеличением расстояния до него, то эта сила будет отталкивать рамку от провода (ответ 2). Если бы ток в проводе убывал, то рамка притягивалась бы к проводу.
Задача 23.2.9 также связана с направлением индукционных явлений и правилом Ленца. При приближении магнита к проводящему кольцу в нем возникнет индукционный ток, причем направление его будет таким, чтобы компенсировать вызывающую его причину. А поскольку эта причина — приближение магнита, кольцо будет отталкиваться от него (ответ 2). Если магнит отодвигать от кольца, то по тем же причинам возникло бы притяжение кольца к магниту.
Задача 23.2.10 — единственная вычислительная задача в этой главе. Для нахождения ЭДС индукции нужно найти изменение магнитного потока через контур .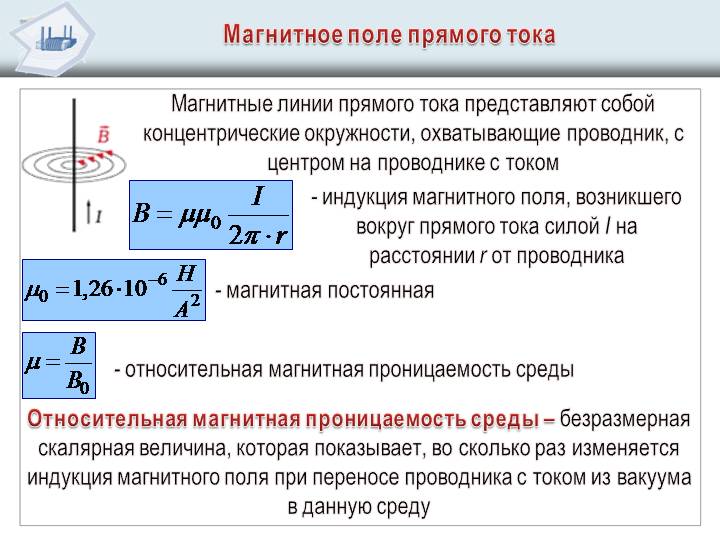 Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).
Это можно сделать так. Пусть в некоторый момент времени перемычка находилась в положении, показанном на рисунке, и пусть прошел малый интервал времени . За этот интервал времени перемычка переместится на величину . Это приведет к увеличению площади контура на величину . Поэтому изменение магнитного потока через контур будет равно , а величина ЭДС индукции (ответ 4).
Электродинамическое взаимодействие, образованное токами электрического смещения поля
| ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ |
«Всякое возмущение в пространстве распространяется со
скоростью не выше скорости света. В частности, электрическое поле при
смещении точечного заряда не просто переместится вместе с зарядом, как в
случае бесконечно большой скорости распространения поля, а меняется более
сложным образом. Возникают эффекты, связанные с запаздыванием появления поля
на больших расстояниях от заряда, которые могут быть описаны введением
индукции магнитного поля.»
Возникают эффекты, связанные с запаздыванием появления поля
на больших расстояниях от заряда, которые могут быть описаны введением
индукции магнитного поля.»
Основы физики. Л.А.Грибов, Н.И.Прокофьев. 1995.
С.300.
Магнитное поле (поток) можно рассматривать как
релятивистский эффект (эффект движения), связанный с запаздыванием
распространения электрического смещения поля. Согласно формуле преобразования
полей B = μ0[vD],
магнитная индукция возникает при движении электрического потока. Магнитную
энергию можно трактовать как кинетическую энергию движущихся электрических потоков
Wм = Mэv2 sin2a,
где Mэ — масса электрического потока, v — скорость
движения, a — угол между направлением движения и вектором D.
« B = [vE]/c2 »
Электромагнетизм. И. Е.Иродов. 1991. С.135.
Е.Иродов. 1991. С.135.
«В результате магнитное поле можно рассматривать как неизбежный
релятивистский результат движения электрических зарядов (тока) и
нестационарности создаваемого ими электрического поля (тока смещения).»
Физическая энциклопедия. ЭЛЕКТРОДИНАМИКА.
Магнитное поле возникает как результат движения
электрических зарядов (потоков), но еще недостаточно рассмотрен сам механизм
его возникновения. Постараюсь проанализировать и описать электродинамические
процессы, протекающие при движении электрических зарядов.
Возмущения поля не распространяются мгновенно, для возникновения возмущения
требуется определенное время. При движении заряда возмущение поля, возникая в
том месте, куда переместился заряд, и одновременно исчезая в том месте,
откуда он переместился, образует в пространстве токи электрического
смещения, которые имеют обратное направление. Примеры расчетов обратных токов
смещения приведены в учебниках.
«Пример. Точечный заряд q движется равномерно и прямолинейно с
нерелятивистской скоростью v. Найти вектор плотности тока смещения в
точке P, находящейся на расстоянии r от заряда на прямой,
перпендикулярной его траектории и проходящей через заряд. Решение:
jсм = -qv/4πr3.»
Электромагнетизм. И.Е.Иродов. 2000. С.302.
Отсюда, за пределами радиуса r от движущегося
точечного заряда течет обратный ток смещения:
Iсм = -qv/2r.
Получается, если заряд в 1 Кл движется со скоростью
2 м/с, то за пределами радиуса в 1 м течет обратный ток смещения
силой в 1 А, плотность же обратного тока смещения на расстоянии 1 м
равна 0.16 А/м2. Т.е., если движется заряженный шар радиусом
в 1 м, с зарядом в 1 Кл и со скоростью 2 м/с, то полный
обратный ток смещения, который он создает, равен 1 А. Отсюда следует,
что ток смещения не влияет на величину магнитной индукции, так как независимо
от величины тока смещения (размера шара) магнитная индукция вокруг шара
всегда равна B = μ0q[vr]/4πr3.
То, что ток электрического смещения не создает магнитную индукцию, входит
в противоречие с постулатом, утверждающим, что ток смещения создает такое же
магнитное поле, как и ток проводимости. Причина возникновения такого
противоречия в том, что на ток смещения, без экспериментальной проверки, были
перенесены магнитные свойства тока проводимости. Т.е. был упущен тот факт,
что магнитное поле, согласно электродинамике, представляет движущийся
электрический поток B = μ0[vD], а не ток, так как в формуле D — это
плотность электрического потока. Соответственно, для определения магнитной
индукции необходимо рассматривать не то, как течет ток проводимости или
смещения, а как движется электрический поток.
Отсюда следует,
что ток смещения не влияет на величину магнитной индукции, так как независимо
от величины тока смещения (размера шара) магнитная индукция вокруг шара
всегда равна B = μ0q[vr]/4πr3.
То, что ток электрического смещения не создает магнитную индукцию, входит
в противоречие с постулатом, утверждающим, что ток смещения создает такое же
магнитное поле, как и ток проводимости. Причина возникновения такого
противоречия в том, что на ток смещения, без экспериментальной проверки, были
перенесены магнитные свойства тока проводимости. Т.е. был упущен тот факт,
что магнитное поле, согласно электродинамике, представляет движущийся
электрический поток B = μ0[vD], а не ток, так как в формуле D — это
плотность электрического потока. Соответственно, для определения магнитной
индукции необходимо рассматривать не то, как течет ток проводимости или
смещения, а как движется электрический поток. Данная формула, представляя
закон магнитной индукции, лежит в основе всех остальных формул. Например,
вместе с движущимся зарядом движется его электрический поток. Зная плотность
связанного с зарядом движущегося электрического потока
D = qr/4πr3,
можно, согласно B = μ0[vD], вычислить плотность магнитного потока
вокруг заряда B = μ0q[vr]/4πr3.
Аналогичным образом, зная, что с каждым движущимся зарядом связан движущийся
электрический поток, выводятся и другие формулы для расчета магнитной
индукции. Например, плотность движущегося электрического потока вокруг
прямого бесконечного провода с током
D = P/2πr = q/2πrL,
где P — плотность движущихся зарядов в проводе
(P = q/L), r — расстояние от провода. Согласно
B = μ0[vD],
получим B = μ0qv/2πrL = μ0I/2πr, где I — сила тока
(I = Pv = qv/L).
Данная формула, представляя
закон магнитной индукции, лежит в основе всех остальных формул. Например,
вместе с движущимся зарядом движется его электрический поток. Зная плотность
связанного с зарядом движущегося электрического потока
D = qr/4πr3,
можно, согласно B = μ0[vD], вычислить плотность магнитного потока
вокруг заряда B = μ0q[vr]/4πr3.
Аналогичным образом, зная, что с каждым движущимся зарядом связан движущийся
электрический поток, выводятся и другие формулы для расчета магнитной
индукции. Например, плотность движущегося электрического потока вокруг
прямого бесконечного провода с током
D = P/2πr = q/2πrL,
где P — плотность движущихся зарядов в проводе
(P = q/L), r — расстояние от провода. Согласно
B = μ0[vD],
получим B = μ0qv/2πrL = μ0I/2πr, где I — сила тока
(I = Pv = qv/L). Все это относится
как к току проводимости, так и к току смещения, т.е. сначала надо рассмотреть
движение электрических потоков, а потом, согласно
B = μ0[vD],
определить магнитную индукцию.
Все это относится
как к току проводимости, так и к току смещения, т.е. сначала надо рассмотреть
движение электрических потоков, а потом, согласно
B = μ0[vD],
определить магнитную индукцию.
«… поле B точечного заряда q, движущегося с постоянной нерелятивистской скоростью v. … B = μ0q[vr]/4πr3 …»
Электромагнетизм. И.Е.Иродов. 2000. С.155.
«… магнитная индукция поля прямого тока B = μ0I/2πr.»
Курс физики. Т.И.Трофимова. 1998. С.208.
Знак минус в формуле Iсм = -qv/2r означает, что ток смещения течет в обратном направлении. При этом ток смещения возникает независимо от того, движется ли заряд самостоятельно или, например, по проводнику, где ток смещения распространяется в пространстве за пределами проводника и, если рядом находится другой проводник, то в нем обратный ток смещения будет переходить в ток проводимости.
 Т.е. ток смещения будет
замыкаться током проводимости — это явление называется электромагнитной
индукцией.
Т.е. ток смещения будет
замыкаться током проводимости — это явление называется электромагнитной
индукцией.«Для магнитного поля, так же как для электрического, справедлив принцип суперпозиции; …»
Справочник по физике. Б.М.Яворский, А.А.Детлаф. 1996. С.236.
«… ток смещения по своей сути — это изменяющееся со временем электрическое поле.»
Курс физики. Т.И.Трофимова. 1998. С.250.
Для тока смещения, как и для поля, действует принцип суперпозиции (для любого тока действует принцип суперпозиции), т.е., если движутся несколько зарядов, то их обратные токи смещения складываются в пространстве согласно принципу суперпозиции. Например, плотность обратного постоянного тока смещения вокруг тонкого прямого провода бесконечной длины:
jсм = -I/2πr2,
где r — расстояние от оси провода, I -
постоянный ток в проводе.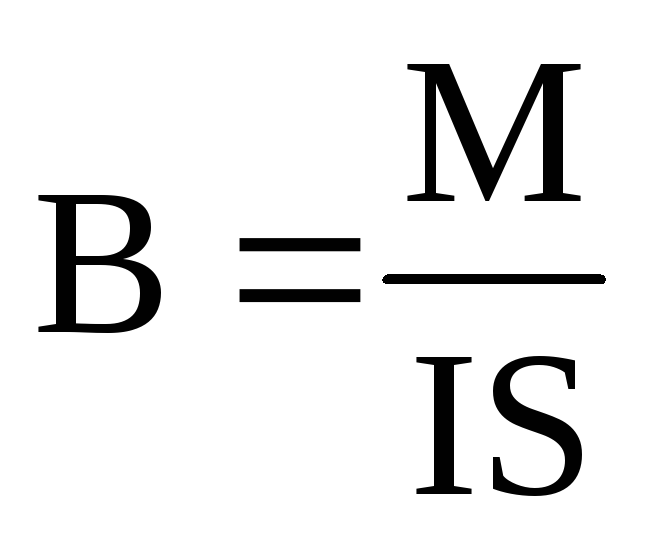 Т.е. не только вокруг движущегося заряда, но и
вокруг проводника с током течет обратный ток смещения.
Т.е. не только вокруг движущегося заряда, но и
вокруг проводника с током течет обратный ток смещения.
«… каждый заряд возбуждает поле, совершенно не зависящее от наличия других зарядов.»
Общий курс физики. Электричество. Д.В.Сивухин. 1996. Т.3. Ч.2. С.204.
Независимо от того движется заряд самостоятельно или, например, в проводнике, всегда в окружающем пространстве вместе с ним движется электрический поток. Там, где происходит движение электрических потоков, всегда течет ток смещения, даже если не изменяется электрическое поле (электрическая напряженность). Например, если движется заряд, то вокруг него возникает электрический ток смещения, когда же по проводнику движется множество зарядов, представляя постоянный ток проводимости, то электрическое поле в пространстве не изменяется, но суперпозиция токов смещения от всех движущихся зарядов представляет постоянный ток смещения, который течет в обратном направлении.

«Ток смещения входит в Максвелла уравнения на равных правах с током, обусловленным движением зарядов.»
Физический энциклопедический словарь. ЭЛЕКТРИЧЕСКИЙ ТОК.
«Ток смещения, в отличие от тока проводимости, не сопровождается выделением теплоты.»
Справочник по физике. Б.М.Яворский, А.А.Детлаф. 1996. С.290.
Электрический ток смещения поля течет без сопротивления, а раз нет сопротивления, то нет и напряженности (закон Ома). Электрическая напряженность поля возникает только при изменении тока смещения как вихревое электрическое поле. Например, возникновение вихревого электрического поля при включении и выключении электромагнита говорит о том, что ток смещения поля при включении возрастает, а при выключении уменьшается. В период, когда магнитное поле не изменяется, плотность тока смещения также не изменяется и, соответственно, нет вихревого электрического поля, поэтому постоянное магнитное поле не действует на покоящиеся электрические заряды.
 Линиями тока
смещения поля можно наглядно представить электродинамику полевых процессов,
так как любые изменения поля всегда связаны с токами смещения. В книгах по
электродинамике хотя и говорится, что при движении зарядов в окружающем
пространстве текут токи смещения, но, к сожалению, ни одного рисунка,
наглядно изображающего этот процесс, так и не удалось найти.
Линиями тока
смещения поля можно наглядно представить электродинамику полевых процессов,
так как любые изменения поля всегда связаны с токами смещения. В книгах по
электродинамике хотя и говорится, что при движении зарядов в окружающем
пространстве текут токи смещения, но, к сожалению, ни одного рисунка,
наглядно изображающего этот процесс, так и не удалось найти.Рассмотрим токи смещения, возникающие при движении электрических зарядов.
На рисунке знаком (+) обозначена
область, куда переместился положительный заряд и где возникает возмущение
(электрическое смещение поля), т.е. распространяется положительное
электрическое возмущение поля. Знаком (-) обозначена
область, где раньше был заряд и где исчезает возмущение, т.е.
распространяется отрицательное возмущение. Линиями изображен обратный ток
смещения поля, стрелками — направление тока. Надо заметить, что ток смещения
«стекает» в (-)-область, хотя возмущение распространяется из (-)-области
(аналогия с током проводимости, где отрицательно заряженные электроны
движутся в одну сторону, но принято считать, что ток течет в обратном
направлении). Распространение возмущения из (+)-области
совпадает с направлением тока смещения. Когда движутся несколько зарядов, надо
отдельно рассматривать каждый движущийся заряд, а потом суммировать все токи
смещения, которые их сопровождают, на основе принципа суперпозиции. При
движении цепочки зарядов поперечные токи смещения, имеющие встречное
направление, взаимонейтрализуются и образуется постоянный обратный ток смещения.
Надо заметить, что ток смещения
«стекает» в (-)-область, хотя возмущение распространяется из (-)-области
(аналогия с током проводимости, где отрицательно заряженные электроны
движутся в одну сторону, но принято считать, что ток течет в обратном
направлении). Распространение возмущения из (+)-области
совпадает с направлением тока смещения. Когда движутся несколько зарядов, надо
отдельно рассматривать каждый движущийся заряд, а потом суммировать все токи
смещения, которые их сопровождают, на основе принципа суперпозиции. При
движении цепочки зарядов поперечные токи смещения, имеющие встречное
направление, взаимонейтрализуются и образуется постоянный обратный ток смещения.
Ток проводимости представляет движение
зарядов, поэтому в окружающем пространстве возникает обратный ток смещения.
Когда ток течет по витку, то в окружающем пространстве возникает круговой ток
смещения, имеющий обратное направление. При изменении тока смещения
образуется вихревое электрическое поле. Если рядом с витком тока расположить,
например, сверхпроводящий контур, то в нем за счет обратного тока
электрического смещения синхронно, но в обратном направлении возникает
индукционный ток. Ток смещения как бы замыкается через сверхпроводящий проводник.
При изменении тока смещения
образуется вихревое электрическое поле. Если рядом с витком тока расположить,
например, сверхпроводящий контур, то в нем за счет обратного тока
электрического смещения синхронно, но в обратном направлении возникает
индукционный ток. Ток смещения как бы замыкается через сверхпроводящий проводник.
«… вихревое поле без каких бы то ни было добавочных сил может вызвать
непрерывное течение электричества по замкнутым проводам. Это течение и
наблюдается в виде индукционных токов.»
Общий курс физики. Электричество. Д.В.Сивухин.
1996. Т.3. Ч.1. С.252.
Также самоиндукция связана с обратными токами смещения,
с запаздыванием распространения возмущений. При остановке зарядов обратные
токи смещения, еще некоторое время продолжая течь (как возмущения поля),
воздействуют на заряды.
«Максвелл приписал току смещения лишь одно — способность создавать в
окружающем пространстве магнитное поле. »
»
Курс физики. Т.И.Трофимова. 1998. С.250.
Точнее, ток смещения сам представляет магнитное поле.
Магнитная сила притяжения возникает между двумя проводниками с током,
когда обратные токи смещения полевой среды текут в одном направлении, — токи
стремятся слиться. Отталкивание же возникает, когда обратные токи смещения
полевой среды текут навстречу друг другу, — токи стремятся разойтись. Таким
образом, магнитная сила — это обычная гидродинамическая сила, возникающая
между текущими потоками среды. Например, если два диска вращаются в одном
направлении, то между ними возникает сила притяжения. Если же они вращаются в
противоположных направлениях, то, наоборот, возникает сила отталкивания. Это
происходит потому, что своим вращением диски увлекают воздух, потоки которого
создают гидродинамическую силу притяжения или отталкивания. На покоящийся
заряд магнитное поле не действует, так как вокруг него не текут токи
электрического смещения поля.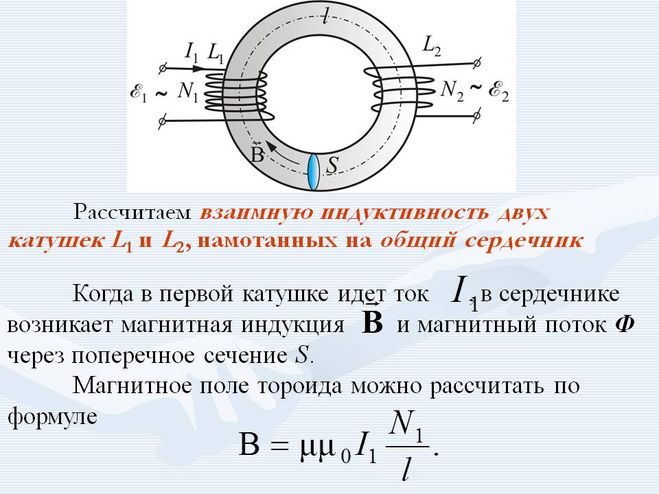 На практике же не рассматривают
распространяющиеся смещения поля, представляющие движущиеся электрические
потоки, а пользуются линиями магнитной индукции, рассматривая взаимодействие
с ними электрических токов. Линии магнитной индукции не являются силовыми
линиями (линиями действия силы), например, направление вектора магнитной
силы, возникающей между параллельными проводниками с постоянным током, не
совпадает с направлением линий магнитной индукции. Т.е. индукционные линии
магнитных полей силовыми не являются, так как не показывают направление силы,
действующей на элементарный ток. Также в данном примере видно, что магнитное
поле не является вихревым, так как у вихревых полей работа сил при движении
по замкнутой линии может быть отлична от нуля, что является признаком
вихревого поля. Вихревые поля могут возбуждать вихревые электрические токи.
Таким образом, постоянное магнитное поле является соленоидальным, но не вихревым.
На практике же не рассматривают
распространяющиеся смещения поля, представляющие движущиеся электрические
потоки, а пользуются линиями магнитной индукции, рассматривая взаимодействие
с ними электрических токов. Линии магнитной индукции не являются силовыми
линиями (линиями действия силы), например, направление вектора магнитной
силы, возникающей между параллельными проводниками с постоянным током, не
совпадает с направлением линий магнитной индукции. Т.е. индукционные линии
магнитных полей силовыми не являются, так как не показывают направление силы,
действующей на элементарный ток. Также в данном примере видно, что магнитное
поле не является вихревым, так как у вихревых полей работа сил при движении
по замкнутой линии может быть отлична от нуля, что является признаком
вихревого поля. Вихревые поля могут возбуждать вихревые электрические токи.
Таким образом, постоянное магнитное поле является соленоидальным, но не вихревым.
«Прямая, вдоль которой направлена сила, называется линией действия силы. »
»
Физическая энциклопедия. СИЛА.
«Работа сил вихревого электрического поля при движении электрического
заряда по замкнутой линии может быть отлична от нуля.»
Физика. О.Ф.Кабардин. 1991. С.189.
Работа сил вихревого электрического поля или вихревого
магнитного поля при движении электрического заряда или магнита по замкнутой
линии может быть отлична от нуля. Например, в электромагнитных волнах
электрические и магнитные потоки являются вихревыми.
«… магнитное же поле — соленоидальное.»
Электромагнетизм. И.Е.Иродов. 2000. С.170.
«… ускоритель, использующий вихревое магнитное поле.»
Физическая энциклопедия. БЕТАТРОН.
Магнитное поле, хотя соленоидально, но не всегда
является вихревым. Надо заметить, что некоторые авторы книг по
электродинамике путают соленоидальные поля с вихревыми, индукционные линии с
силовыми. У электрического поля, действительно, индукционные линии совпадают
с силовыми, но это никак не относится к магнитному полю, где индукционные
линии не всегда совпадают с силовыми линиями действия поля.
Также по линиям магнитной индукции, например, невозможно определить
направление силы, действующей на покоящийся электрический заряд в момент
включения электромагнита в случае, когда магнит и заряд находятся в покое,
т.е. по линиям магнитной индукции невозможно определить направление силы,
действующей на покоящийся заряд в переменном магнитном поле. Представляя
магнитное поле линиями токов смещения, таких проблем не возникает. По
силе, действующей на покоящийся электрический заряд в момент включения
электромагнита, можно определить направление тока смещения в конкретной
точке магнитного поля. Изменение любого электрического тока всегда связано
с электрической напряженностью.
«Магнитное поле, непостоянное во
Магнитная индукция | Физика. Закон, формула, лекция, шпаргалка, шпора, доклад, ГДЗ, решебник, конспект, кратко
Тема: Магнетизм
Наблюдения за магнитными явлениями в природе, в лаборатории, на производстве показывают, что действие магнитного поля на различные объекты может быть различным.
Если магнитное поле лабораторного электромагнита может удерживать груз массой 1—2 кг, то в промышленных электромагнитах эта масса составляет несколько тонн.
Магнитное поле Земли слабо действует на магнитную стрелку компаса, поэтому ее приходится устанавливать на специальных подшипниках. Если же к компасу поднести электромагнит, в обмотках которого проходит электрический ток, то действие на стрелку будет значительно сильнее.
Интенсивность магнитного взаимодействия может быть различной.
По-разному взаимодействуют и параллельные проводники с током. Сила взаимодействия этих проводников будет изменяться, если изменять силу тока в них, расстояние между ними, среду, в которой они находятся.
Во всех таких и подобных случаях говорят о поле «слабом» или «сильном». Если для характеристики силового действия электрического поля на электрически заряженное тело используется напряженность, то для магнитного поля — магнитная индукция. Поскольку магнитная индукция характеризует силовое действие магнитного поля, она является векторной величиной. Для определения направления магнитной индукции сначала воспользуемся магнитной стрелкой, насаженной на тонкое острие, для уменьшения силы трения. Материал с сайта http://worldofschool.ru
Поскольку магнитная индукция характеризует силовое действие магнитного поля, она является векторной величиной. Для определения направления магнитной индукции сначала воспользуемся магнитной стрелкой, насаженной на тонкое острие, для уменьшения силы трения. Материал с сайта http://worldofschool.ru
| Рис. 6.4. Продольная ось магнитной стрелки, которая находится в центре витка с током, перпендикулярна его плоскости |
Исследуем с помощью такого устройства магнитное поле проволочного витка, по которому проходит ток. Поднося стрелку к витку с различных сторон, заметим, что она все время изменяет свою ориентацию в пространстве, поворачиваясь к витку одним из своих концов. Самым сильным действие магнитного поля витка будет тогда, когда стрелка будет находиться в его центре (рис. 6.4). В этом случае продольная ось магнитной стрелки будет перпендикулярной плоскости витка.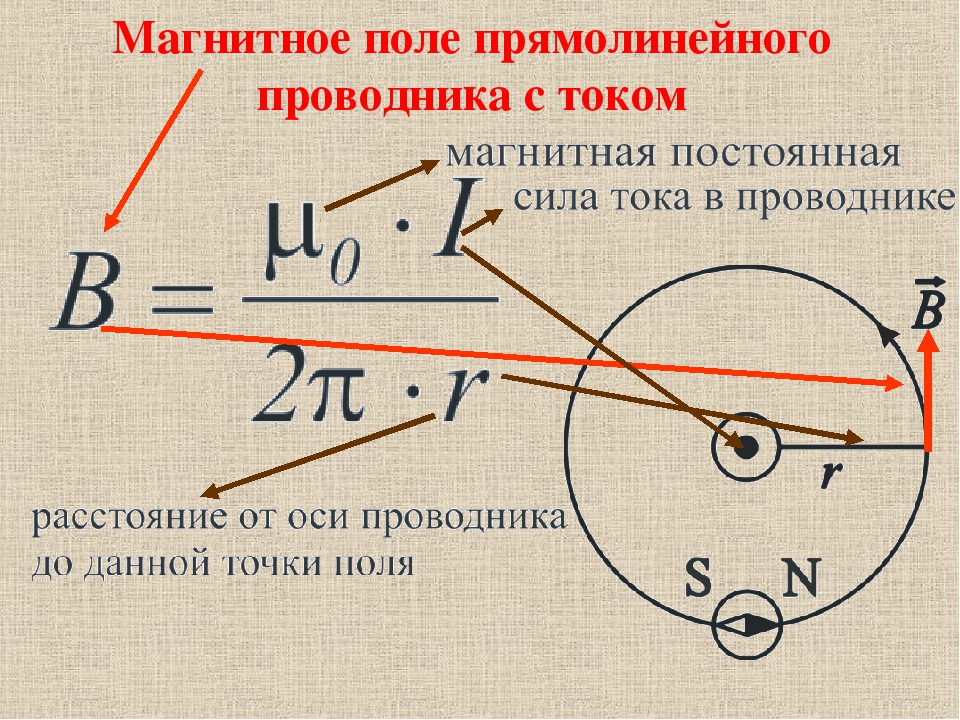 Направление, которое указывает магнитная стрелка своим северным полюсом, считается направлением магнитной индукции поля. Таким образом, магнитная индукция витка или прямоугольной рамки с током имеет максимальное значение в центре витка или рамки.
Направление, которое указывает магнитная стрелка своим северным полюсом, считается направлением магнитной индукции поля. Таким образом, магнитная индукция витка или прямоугольной рамки с током имеет максимальное значение в центре витка или рамки.
Как физическая величина магнитная индукция обозначается буквой B̅.
Магнитная индукция — это силовая характеристика магнитного поля.
На этой странице материал по темам:Доклад индукция магнитного поля
Магнитная индукция доклад
Почему магнитная индукция считается силовой характеристикой магнитного поля?
Что общего и отличного между напряженностью электрического поля и магнитной индукцией магнитного поля?
Электромагнитная индукция — Energy Education
Рис. 1. Одно из первых устройств Майкла Фарадея для демонстрации индукции. [1]
1. Одно из первых устройств Майкла Фарадея для демонстрации индукции. [1] Электромагнитная индукция — это производство электродвижущей силы (ЭДС), возникающей в результате относительного движения между магнитным полем и проводником. Он был открыт в 1831 году Майклом Фарадеем, [2] и закладывает основу для выработки электроэнергии на электростанциях, электродвигателях и схемах переменного тока, которые питают электросети, трансформаторы и многие другие явления.
Уравнение, математически описывающее электромагнитную индукцию, — это закон Фарадея , который гласит, что любое изменение магнитной среды витого провода вызывает индуцирование напряжения (ЭДС). [3] Фарадей нашел много способов для этого, например, изменение напряженности магнитного поля, перемещение магнита через катушку с проволокой и перемещение катушки через магнитное поле, и это лишь некоторые из них. Напряжение (ЭДС), генерируемое в катушке с проволокой, можно описать следующим уравнением: [3]
[математика] EMF = -N \ frac {\ Delta (BA)} {\ Delta t} [/ math]где
- [math] N [/ math] — количество витков провода.

- [math] \ Delta (BA) [/ math] — изменение магнитного потока.
- [math] \ Delta t [/ math] — это изменение во времени.
Способы, которые Фарадей нашел для изменения этого потока, как указано выше, могут быть представлены в этом уравнении.Причина, по которой это уравнение является отрицательным, заключается в законе Ленца, который требует, чтобы любое изменение магнитного потока воспроизводилось проводом с одинаковой силой, но в противоположном направлении.
Закон Фарадея важен для многих электромагнитных приложений в мире, включая автомобили. Система зажигания в двигателе внутреннего сгорания автомобиля потребляет от аккумулятора всего 12 вольт и увеличивает его до 40000 вольт! Посетите Hyperphysics, чтобы узнать, как это сделать.
PhET Моделирование индукции
PhET любезно позволил нам использовать их модели, а приведенное ниже демонстрирует закон электромагнитной индукции Фарадея.Видно, что напряжение изменяется по мере изменения магнитного потока через него.
Для дальнейшего чтения
Для получения дополнительной информации см. Соответствующие страницы ниже:
Список литературы
Что такое электрическая индукция? | Универсальный класс
Что такое электрическая индукция?
Электричество. Определения
Термин электричество , как мы узнали из изучения различных разделов физики, трудно определить с помощью одного всеобъемлющего определения.Ученые и ученые часто расходятся во мнениях относительно истинного значения этого термина. Чтобы проиллюстрировать диапазон существующих определений, мы включили несколько различных.
1. Определение ученых. Электричество относится исключительно к электронам и протонам; по сути, электрический заряд объекта.
2. Повседневное определение. Электричество — это энергия электромагнитного поля, передаваемая батареями и генераторами.
3. Начальная школа Определение. Электричество — это текущее движение, создаваемое электрическим зарядом.
Начальная школа Определение. Электричество — это текущее движение, создаваемое электрическим зарядом.
4. Рабочее определение. Электричество — это величина дисбаланса между количеством электронов и протонов.
И некоторые дополнительные, менее часто используемые определения, включают:
5. Текущее движение электрической энергии.
6. Электрический потенциал (электронное поле).
7. Просто область науки.
Основываясь на таком широком выборе определений, трудно понять истинное значение термина электрический , что усложняет процесс формирования определения для электрической индукции .
Индукция. Определение
Это подводит нас к определению индукции . Согласно Мерриам-Вебстеру, индукция — это «процесс, посредством которого электрический проводник становится электрифицированным, когда он находится рядом с заряженным телом, посредством которого намагничиваемое тело становится намагниченным, когда оно находится в магнитном поле или в магнитном потоке, создаваемом магнитодвижущей силой или что электродвижущая сила создается в цепи путем изменения магнитного поля, связанного с цепью.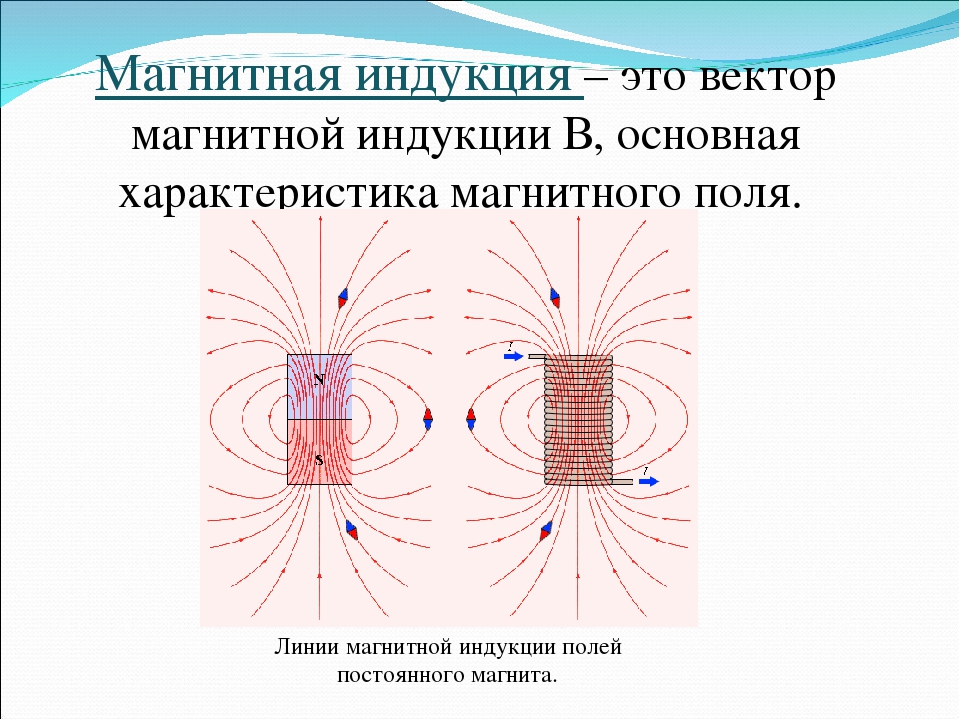 «
«
Комбинируя определения «электрический» и «индукционный», мы можем получить следующие определения: Изменяющееся магнитное поле приводит к разности потенциалов (обычно известной как напряжение) в проводнике.
В то время как стационарное магнитное поле не будет влиять на провод или токовую петлю, движущееся или изменяющееся магнитное поле будет генерировать электрический ток с низким током или напряжение, распространяющееся по концам токовой петли. Ток или напряжение, в основном известные как электромагнитная индукция, называют индуцированным током или индуцированным напряжением.
Электрическая индукция. Принцип действия
Электромагнитная индукция — это основной принцип, который используется для объяснения того, как работают электрические генераторы (также называемые генераторами переменного тока), микрофоны, электрогитары и трансформаторы.
Ток, содержащийся в проводнике, называется альтернативой , потому что его ток течет вперед и назад в результате того, что проводник сначала поднимается, а затем опускается в магнитном поле. Короче говоря, токи помогают создавать магнитные поля.
Короче говоря, токи помогают создавать магнитные поля.
Движущееся или изменяющееся магнитное поле действительно создает ток в токовой петле или напряжение на концах токовой петли. Это называется электромагнитной индукцией, а ток или напряжение — индуцированным током или индуцированным напряжением.
Электрическая индукция. История
Одно из самых важных достижений в области науки, открытие электромагнитной индукции, было описано Майклом Фарадеем в 1831 году. Официально он был первым ученым и математиком, который задокументировал свои открытия после проведения серии испытаний катушки, которую он сделал. обмотка бумажного цилиндра проволокой.
Когда он подключил катушку к гальванометру, а затем перемещал магнит вперед и назад внутри цилиндра, Фарадей сообщил, что величина напряжения, создаваемого в проводнике, была пропорциональна скорости изменения магнитного потока (чередование уровней электрического токи).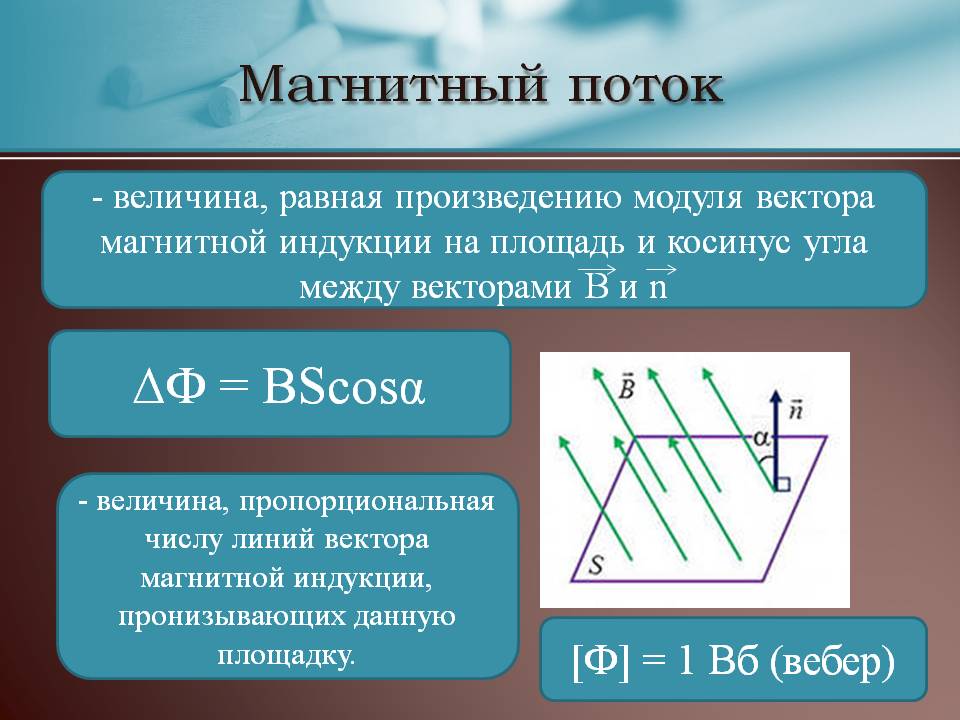
Более того, Фарадей обнаружил, что это утверждение истинно и применимо независимо от того, изменяется ли сила самого потока или проводник перемещается через магнитное поле. Как указывалось ранее, электромагнитная индукция является основным принципом, который объясняет работу генераторов и асинхронных двигателей, а также большинства других электрических машин.
Закон электромагнитной индукции Фарадея гласит, что где — электродвижущая сила (ЭДС) в вольтах, N, — количество витков провода, а Wb — магнитный поток по Веберсу. Далее немецкий ученый H.F.E. Ленц, используя «Закон Ленца», дает направление наведенной ЭДС, таким образом:ЭДС, индуцированная в электрической цепи, всегда действует в таком направлении, что ток, который она протекает по цепи, противодействует изменению магнитного потока, которое создает ЭДС.
Электрическая индукция. Резюме основных принципов
Следовательно, мы можем различить, что магнитный поток — это сила магнитного поля, которое проходит через определенную область. С точки зрения формулы, это произведение магнитного поля (B) на площадь (A), которая проходит через угол (a) между линией, идущей под углом 90 градусов к области, и линиями магнитного поля.
С точки зрения формулы, это произведение магнитного поля (B) на площадь (A), которая проходит через угол (a) между линией, идущей под углом 90 градусов к области, и линиями магнитного поля.
Магнитный поток представлен символом F. По этой причине физики часто формулируют следующую формулу как данность: F = B * A * cos (a), и результирующая единица измерения будет Tm 2 , где T (обычно как тета, θ) — единица измерения магнитного поля, м 2 — единица измерения площади.
Или, говоря упрощенно, вы можете думать о потоке как о «воздушном потоке», продувающем воздух через окно. Размер окна (A), скорость воздуха (B) и направление (тета) определяют, сколько воздуха проходит через окно.
Переменный магнитный поток создает электродвижущую силу (ЭДС). В свою очередь, эта сила оказывает давление на свободные электроны определенным образом, вызывая ток.
Электромагнитная индукция. Современные приложения
После того, как была установлена взаимная связь между электричеством и магнетизмом, практическое применение стало практически безграничным.
Генератор, например, открыл путь к широкому спектру инновационных промышленных концепций. Преобразуя механическую энергию в электрическую, генератор опирался на основной принцип электромагнитной индукции — прохождение электрического проводника через магнитное поле.
Как объяснялось ранее, когда одна сторона катушки проходит через магнитное поле, сначала в одном направлении, а затем в другом направлении, конечным результатом является переменный ток (магнитный поток).Этот тип генератора переменного тока аналогичен тому, который используется в транспортных средствах для выработки постоянного потока энергии.
Кроме того, трансформаторы могут передавать переменные токи из одной электрической цепи в другую посредством индукции электромагнита. В каждом районе есть трансформатор, расположенный на централизованной опоре питания; это канал для передачи электричества во все отдельные дома.
По большей части, эти типы силовых трансформаторов передают мощность с постоянной частотой. Радиочастотные (ВЧ) трансформаторы работают на более высоких частотах, что позволяет использовать ВЧ-генераторы во многих отраслях промышленности.
Радиочастотные (ВЧ) трансформаторы работают на более высоких частотах, что позволяет использовать ВЧ-генераторы во многих отраслях промышленности.
20.2 Электромагнитная индукция | Texas Gateway
Индуцированная электродвижущая сила
Если в катушке индуцируется ток, Фарадей рассуждал, что должно быть то, что он назвал электродвижущей силой , проталкивающей заряды через катушку.Эта интерпретация оказалась неверной; вместо этого внешний источник, выполняющий работу по перемещению магнита, добавляет энергию зарядам в катушке. Энергия, добавляемая на единицу заряда, измеряется в вольтах, поэтому электродвижущая сила на самом деле является потенциалом. К сожалению, название «электродвижущая сила» прижилось, а вместе с ним и возможность спутать его с реальной силой. По этой причине мы избегаем термина электродвижущая сила и просто используем сокращение эдс , которое имеет математический символ ε.ε. ЭДС может быть определена как скорость, с которой энергия отбирается от источника на единицу тока, протекающего по цепи. Таким образом, ЭДС — это энергия на единицу заряда , добавленная источником, которая контрастирует с напряжением, которое представляет собой энергию на единицу заряда , высвобождаемую , когда заряды протекают по цепи.
К сожалению, название «электродвижущая сила» прижилось, а вместе с ним и возможность спутать его с реальной силой. По этой причине мы избегаем термина электродвижущая сила и просто используем сокращение эдс , которое имеет математический символ ε.ε. ЭДС может быть определена как скорость, с которой энергия отбирается от источника на единицу тока, протекающего по цепи. Таким образом, ЭДС — это энергия на единицу заряда , добавленная источником, которая контрастирует с напряжением, которое представляет собой энергию на единицу заряда , высвобождаемую , когда заряды протекают по цепи.
Чтобы понять, почему ЭДС создается в катушке из-за движущегося магнита, рассмотрим рисунок 20.27, на котором показан стержневой магнит, движущийся вниз относительно проволочной петли.Первоначально через петлю проходят семь силовых линий магнитного поля (см. Изображение слева). Поскольку магнит удаляется от катушки, только пять силовых линий магнитного поля проходят через петлю за короткое время ΔtΔt (см. Изображение справа). Таким образом, когда происходит изменение количества силовых линий магнитного поля, проходящих через область, определяемую проволочной петлей, в проволочной петле индуцируется ЭДС. Подобные эксперименты показывают, что наведенная ЭДС пропорциональна скорости изменения магнитного поля.Математически мы выражаем это как
Поскольку магнит удаляется от катушки, только пять силовых линий магнитного поля проходят через петлю за короткое время ΔtΔt (см. Изображение справа). Таким образом, когда происходит изменение количества силовых линий магнитного поля, проходящих через область, определяемую проволочной петлей, в проволочной петле индуцируется ЭДС. Подобные эксперименты показывают, что наведенная ЭДС пропорциональна скорости изменения магнитного поля.Математически мы выражаем это как
, где ΔBΔB — изменение величины магнитного поля за время ΔtΔt, а A — площадь петли.
Рис. 20.27 Стержневой магнит перемещается вниз относительно проволочной петли, так что количество силовых линий магнитного поля, проходящих через петлю, со временем уменьшается. Это вызывает индукцию ЭДС в контуре, создающую электрический ток.
Обратите внимание, что силовые линии магнитного поля, лежащие в плоскости проволочной петли, на самом деле не проходят через петлю, как показано крайней левой петлей на рисунке 20. 28. На этом рисунке стрелка, выходящая из петли, представляет собой вектор, величина которого равна площади петли, а направление перпендикулярно плоскости петли. На рисунке 20.28 петля повернута от θ = 90 ° θ = 90 °.
до θ = 0 °, θ = 0 ° вклад силовых линий магнитного поля в ЭДС увеличивается. Таким образом, для создания ЭДС в проволочной петле важна составляющая магнитного поля, которая находится на перпендикулярно плоскости петли, то есть Bcosθ.Bcosθ.
28. На этом рисунке стрелка, выходящая из петли, представляет собой вектор, величина которого равна площади петли, а направление перпендикулярно плоскости петли. На рисунке 20.28 петля повернута от θ = 90 ° θ = 90 °.
до θ = 0 °, θ = 0 ° вклад силовых линий магнитного поля в ЭДС увеличивается. Таким образом, для создания ЭДС в проволочной петле важна составляющая магнитного поля, которая находится на перпендикулярно плоскости петли, то есть Bcosθ.Bcosθ.
Это аналог паруса на ветру.Представьте, что проводящая петля — это парус, а магнитное поле — как ветер. Чтобы максимизировать силу ветра на парусе, парус ориентируют так, чтобы вектор его поверхности указывал в том же направлении, что и ветер, как в самой правой петле на рис. 20.28. Когда парус выровнен так, что его вектор поверхности перпендикулярен ветру, как в крайней левой петле на рис. 20.28, тогда ветер не оказывает силы на парус.
Таким образом, с учетом угла наклона магнитного поля по отношению к площади пропорциональность E∝ΔB / ΔtE∝ΔB / Δt становится равной
20. 11E∝ΔBcosθΔt.E∝ΔBcosθΔt. Рис. 20.28 Магнитное поле лежит в плоскости самой левой петли, поэтому в этом случае оно не может генерировать ЭДС. Когда петля поворачивается так, что угол магнитного поля с вектором, перпендикулярным области петли, увеличивается до 90 ° 90 ° (см. Крайнюю правую петлю), магнитное поле вносит максимальный вклад в ЭДС в петле. Точки показывают, где силовые линии магнитного поля пересекают плоскость, определяемую петлей.
11E∝ΔBcosθΔt.E∝ΔBcosθΔt. Рис. 20.28 Магнитное поле лежит в плоскости самой левой петли, поэтому в этом случае оно не может генерировать ЭДС. Когда петля поворачивается так, что угол магнитного поля с вектором, перпендикулярным области петли, увеличивается до 90 ° 90 ° (см. Крайнюю правую петлю), магнитное поле вносит максимальный вклад в ЭДС в петле. Точки показывают, где силовые линии магнитного поля пересекают плоскость, определяемую петлей.Другой способ уменьшить количество силовых линий магнитного поля, проходящих через проводящую петлю на Рисунке 20.28 не для перемещения магнита, а для уменьшения размера петли. Эксперименты показывают, что изменение площади проводящей петли в стабильном магнитном поле вызывает в петле ЭДС. Таким образом, ЭДС, создаваемая в проводящей петле, пропорциональна скорости изменения произведения перпендикулярного магнитного поля и площади петли
. 20.12ε∝Δ [(Bcosθ) A] Δt, ε∝Δ [(Bcosθ) A] Δt,, где BcosθBcosθ — перпендикулярное магнитное поле, а A — площадь контура. Продукт BAcosθBAcosθ очень важен.Оно пропорционально количеству силовых линий магнитного поля, которые проходят перпендикулярно через поверхность площадью A . Возвращаясь к нашей аналогии с парусом, он будет пропорционален силе ветра на парусе. Он называется магнитным потоком и обозначается как ΦΦ.
Продукт BAcosθBAcosθ очень важен.Оно пропорционально количеству силовых линий магнитного поля, которые проходят перпендикулярно через поверхность площадью A . Возвращаясь к нашей аналогии с парусом, он будет пропорционален силе ветра на парусе. Он называется магнитным потоком и обозначается как ΦΦ.
Единицей измерения магнитного потока является Вебер (Вб), который представляет собой магнитное поле на единицу площади, или Т / м 2 . Вебер — это также вольт-секунда (Vs).
Индуцированная ЭДС фактически пропорциональна скорости изменения магнитного потока через проводящую петлю.
20,14ε∝ΔΦΔtε∝ΔΦΔtНаконец, для катушки, изготовленной из петель N , ЭДС в N раз сильнее, чем для одиночной петли. Таким образом, наведенная изменяющимся магнитным полем ЭДС в катушке из петель N составляет
ε∝NΔBcosθΔtA. ε∝NΔBcosθΔtA.
ε∝NΔBcosθΔtA. Последний вопрос, на который нужно ответить, прежде чем мы сможем преобразовать пропорциональность в уравнение: «В каком направлении течет ток?» Русский ученый Генрих Ленц (1804–1865) объяснил, что ток течет в направлении, которое создает магнитное поле, которое пытается сохранить постоянный поток в контуре.Например, снова рассмотрим рисунок 20.27. Движение стержневого магнита вызывает уменьшение количества направленных вверх силовых линий магнитного поля, которые проходят через петлю. Следовательно, в контуре генерируется ЭДС, которая направляет ток в направлении, которое создает больше направленных вверх линий магнитного поля. Используя правило правой руки, мы видим, что этот ток должен течь в направлении, показанном на рисунке. Чтобы выразить тот факт, что индуцированная ЭДС действует, чтобы противодействовать изменению магнитного потока через проволочную петлю, знак минус вводится в пропорциональность ε∝ΔΦ / Δtε∝ΔΦ / Δt, которая дает закон индукции Фарадея.) внутри катушки, направленной влево. Это будет противодействовать увеличению магнитного потока, направленного вправо. Чтобы увидеть, в каком направлении должен течь ток, направьте большой палец правой руки в желаемом направлении магнитного поля B → катушка, B → катушка, и ток будет течь в направлении, указанном сгибанием ваших пальцев правой руки. Это показано изображением правой руки в верхнем ряду рисунка 20.29. Таким образом, ток должен течь в направлении, показанном на рисунке 4 (а).
Это будет противодействовать увеличению магнитного потока, направленного вправо. Чтобы увидеть, в каком направлении должен течь ток, направьте большой палец правой руки в желаемом направлении магнитного поля B → катушка, B → катушка, и ток будет течь в направлении, указанном сгибанием ваших пальцев правой руки. Это показано изображением правой руки в верхнем ряду рисунка 20.29. Таким образом, ток должен течь в направлении, показанном на рисунке 4 (а).
На Рисунке 4 (b) направление, в котором движется магнит, обратное.В катушке направленное вправо магнитное поле B → magB → mag из-за движущегося магнита уменьшается. Закон Ленца гласит, что, чтобы противостоять этому уменьшению, ЭДС возбуждает ток, который создает дополнительное направленное вправо магнитное поле B → катушка B → катушка в катушке. Опять же, направьте большой палец правой руки в желаемом направлении магнитного поля, и ток будет течь в направлении, указанном сгибанием ваших пальцев правой руки (Рисунок 4 (b)).
Наконец, на Рисунке 4 (c) магнит перевернут, так что южный полюс находится ближе всего к катушке. Теперь магнитное поле B → magB → mag направлено на магнит, а не на катушку. По мере приближения магнита к катушке увеличивается магнитное поле, направленное влево. Закон Ленца гласит, что ЭДС, индуцированная в катушке, будет управлять током в направлении, которое создает магнитное поле, направленное вправо. Это будет противодействовать увеличению магнитного потока, направленного влево из-за магнита. Повторное использование правила правой руки, как показано на рисунке, показывает, что ток должен течь в направлении, показанном на рисунке 4 (c).
Теперь магнитное поле B → magB → mag направлено на магнит, а не на катушку. По мере приближения магнита к катушке увеличивается магнитное поле, направленное влево. Закон Ленца гласит, что ЭДС, индуцированная в катушке, будет управлять током в направлении, которое создает магнитное поле, направленное вправо. Это будет противодействовать увеличению магнитного потока, направленного влево из-за магнита. Повторное использование правила правой руки, как показано на рисунке, показывает, что ток должен течь в направлении, показанном на рисунке 4 (c).
Рис. 20.29 Закон Ленца говорит нам, что ЭДС, индуцированная магнитным полем, будет управлять током, который сопротивляется изменению магнитного потока в цепи. Это показано на панелях (а) — (с) для различных ориентаций и скоростей магнита. Правые руки справа показывают, как применить правило правой руки, чтобы найти, в каком направлении наведенный ток течет вокруг катушки.
Виртуальная физика
Электромагнитная лаборатория Фарадея
Это моделирование предлагает несколько действий.А пока щелкните вкладку Pickup Coil, на которой представлен стержневой магнит, который можно перемещать через катушку. Когда вы это сделаете, вы увидите, как электроны движутся в катушке, и загорится лампочка, или вольтметр покажет напряжение на резисторе. Обратите внимание, что вольтметр позволяет вам видеть знак напряжения при перемещении магнита. Вы также можете оставить стержневой магнит в покое и переместить катушку, хотя наблюдать за результатами сложнее.
Проверка захвата
Сориентируйте стержневой магнит так, чтобы северный полюс был направлен вправо, и поместите приемную катушку справа от стержневого магнита.Теперь переместите стержневой магнит к катушке и посмотрите, в каком направлении движутся электроны. Это такая же ситуация, как показано ниже. Протекает ли ток в симуляции в том же направлении, что и показано ниже? Объясните, почему да или почему нет.- Да, ток в моделировании течет в том же направлении, потому что направление тока противоположно направлению потока электронов.
- Нет, ток в моделировании течет в противоположном направлении, потому что направление тока совпадает с направлением потока электронов.
Watch Physics
Наведенный ток в проводе
В этом видео объясняется, как можно индуцировать ток в прямом проводе, перемещая его через магнитное поле. Лектор использует перекрестное произведение , которое является типом векторного умножения. Не волнуйтесь, если вы не знакомы с этим, он в основном объединяет правило правой руки для определения силы, действующей на заряды в проводе, с уравнением F = qvBsinθ.F = qvBsinθ.
Проверка захвата
Какая ЭДС создается на прямом проводе 0.через однородное магнитное поле (0,30 Тл) ẑ ? Проволока проходит в направлении ŷ . Кроме того, какой конец провода находится под более высоким потенциалом — пусть нижний конец провода находится на y = 0, а верхний конец на y = 0,5 м)?
- 0,15 В и нижний конец провода будет иметь более высокий потенциал
- 0,15 В и на верхнем конце провода будет более высокий потенциал
- 0,075 В и нижний конец провода будет иметь более высокий потенциал
- 0.075 В и на верхнем конце провода будет более высокий потенциал
Рабочий пример
ЭДС, индуцированная в проводящей катушке движущимся магнитом
Представьте, что магнитное поле проходит через катушку в направлении, указанном на рисунке 20.31. Диаметр катушки 2,0 см. Если магнитное поле изменится с 0,020 до 0,010 Тл за 34 с, каковы направление и величина индуцированного тока? Предположим, что катушка имеет сопротивление 0,1 Ом.
Рисунок 20.31 Катушка, через которую проходит магнитное поле B .
СТРАТЕГИЯ
Используйте уравнение ε = −NΔΦ / Δtε = −NΔΦ / Δt, чтобы найти наведенную ЭДС в катушке, где Δt = 34 sΔt = 34 с. Подсчитав количество петель в соленоиде, находим, что у него 16 петель, поэтому N = 16.N = 16. Используйте уравнение Φ = BAcosθΦ = BAcosθ для расчета магнитного потока
20,16Φ = BAcosθ = Bπ (d2) 2, Φ = BAcosθ = Bπ (d2) 2,, где d — диаметр соленоида, и мы использовали cos0 ° = 1. cos0 ° = 1. Поскольку площадь соленоида не меняется, изменение магнитного потока через соленоид составляет
20.17ΔΦ = ΔBπ (d2) 2.ΔΦ = ΔBπ (d2) 2.Найдя ЭДС, мы можем использовать закон Ома, ε = IR, ε = IR, чтобы найти ток.
Наконец, закон Ленца гласит, что ток должен создавать магнитное поле, которое препятствует уменьшению приложенного магнитного поля. Таким образом, ток должен создавать магнитное поле справа.
Решение
Объединение уравнений ε = −NΔΦ / Δtε = −NΔΦ / Δt и Φ = BAcosθΦ = BAcosθ дает
20,18ε = −NΔΦΔt = −NΔBπd24Δt.ε = −NΔΦΔt = −NΔBπd24Δt.Решив закон Ома для тока и используя этот результат, получаем
20.19I = εR = −NΔBπd24RΔt = −16 (−0,010 Тл) π (0,020 м) 24 (0,10 Ом) (34 с) = 15 мкА.I = εR = −NΔBπd24RΔt = −16 (−0,010 Тл) π (0,020 м ) 24 (0,10 Ом) (34 с) = 15 мкА.Закон Ленца гласит, что ток должен создавать магнитное поле вправо. Таким образом, мы направляем большой палец правой руки вправо и сжимаем пальцы правой руки вокруг соленоида. Ток должен течь в том направлении, в котором указывают наши пальцы, поэтому он входит в левый конец соленоида и выходит на правом конце.
Обсуждение
Давайте посмотрим, имеет ли смысл знак минус в законе индукции Фарадея.Определите направление магнитного поля как положительное. Это означает, что изменение магнитного поля отрицательное, как мы обнаружили выше. Знак минус в законе индукции Фарадея отрицает отрицательное изменение магнитного поля, оставляя нам положительный ток. Следовательно, ток должен течь в направлении магнитного поля, что мы и обнаружили.
Теперь попробуйте определить положительное направление как направление, противоположное направлению магнитного поля, то есть положительное направление находится слева на рисунке 20.31. В этом случае вы обнаружите отрицательный ток. Но поскольку положительное направление находится влево, отрицательный ток должен течь вправо, что снова согласуется с тем, что мы обнаружили с помощью закона Ленца.
Рабочий пример
Магнитная индукция из-за изменения размера цепи
Схема, показанная на рисунке 20.32, состоит из U-образного провода с резистором, концы которого соединены скользящим токопроводящим стержнем. Магнитное поле, заполняющее область, ограниченную контуром, имеет постоянное значение 0.01 T. Если стержень тянется вправо со скоростью v = 0,50 м / с, v = 0,50 м / с, какой ток индуцируется в цепи и в каком направлении он течет?
Рисунок 20.32 Схема ползунка. Магнитное поле постоянное, и шток тянется вправо со скоростью v . Изменяющаяся область, заключенная в цепи, вызывает в цепи ЭДС.
СТРАТЕГИЯ
Мы снова используем закон индукции Фарадея, E = −NΔΦΔt, E = −NΔΦΔt, хотя на этот раз магнитное поле остается постоянным и площадь, ограниченная контуром, изменяется.Схема состоит из одного контура, поэтому N = 1.N = 1. Скорость изменения площади ΔAΔt = vℓ.ΔAΔt = vℓ. Таким образом, скорость изменения магнитного потока составляет
20,20ΔΦΔt = Δ (BAcosθ) Δt = BΔAΔt = Bvℓ, ΔΦΔt = Δ (BAcosθ) Δt = BΔAΔt = Bvℓ,, где мы использовали тот факт, что угол θθ между вектором площади и магнитным полем равен 0 °. Зная ЭДС, мы можем найти ток, используя закон Ома. Чтобы найти направление тока, мы применяем закон Ленца.
Решение
Закон индукции Фарадея дает
20.21E = −NΔΦΔt = −Bvℓ.E = −NΔΦΔt = −Bvℓ.Решение закона Ома для тока и использование предыдущего результата для ЭДС дает
20,22I = ER = −BvℓR = — (0,010 Тл) (0,50 м / с) (0,10 м) 20 Ом = 25 мкА.I = ER = −BvℓR = — (0,010 Тл) (0,50 м / с) (0,10 м ) 20 Ом = 25 мкА.Когда стержень скользит вправо, магнитный поток, проходящий через контур, увеличивается. Закон Ленца говорит нам, что индуцированный ток создаст магнитное поле, которое будет противодействовать этому увеличению. Таким образом, магнитное поле, создаваемое индуцированным током, должно попадать на страницу.Сгибание петли пальцами правой руки по часовой стрелке заставляет большой палец правой руки указывать на страницу, что является желаемым направлением магнитного поля. Таким образом, ток должен течь по цепи по часовой стрелке.
Обсуждение
Сохраняется ли энергия в этой цепи? Внешний агент должен тянуть стержень с достаточной силой, чтобы просто уравновесить силу на проводе с током в магнитном поле — вспомните, что F = IℓBsinθ.F = IℓBsinθ. Скорость, с которой эта сила действует на стержень, должна уравновешиваться скоростью, с которой схема рассеивает мощность.Используя F = IℓBsinθ, F = IℓBsinθ, сила, необходимая для протягивания проволоки с постоянной скоростью v , равна
20.23Fpull = IℓBsinθ = IℓB, Fpull = IℓBsinθ = IℓB,, где мы использовали тот факт, что угол θθ между током и магнитным полем составляет 90 ° .90 °. Подставляя приведенное выше выражение для тока в это уравнение, получаем
20.24Fpull = IℓB = −BvℓR (ℓB) = — B2vℓ2R.Fpull = IℓB = −BvℓR (ℓB) = — B2vℓ2R.Сила, создаваемая агентом, тянущим стержень, равна Fpullv, или Fpullv, или
. 20.25Ppull = Fpullv = −B2v2ℓ2R.Потяните = Fpullv = −B2v2ℓ2R.Мощность, рассеиваемая цепью
. 20,26Pdissipated = I2R = (- BvℓR) 2R = B2v2ℓ2R.Pdissipated = I2R = (- BvℓR) 2R = B2v2ℓ2R.Таким образом, мы видим, что Ppull + Pdissipated = 0, Ppull + Pdissipated = 0, что означает, что мощность сохраняется в системе, состоящей из цепи и агента, который тянет стержень. Таким образом, в этой системе сохраняется энергия.
магнитных терминов, используемых в магнитных цепях. Определение и формулы
Магнит и магнетизм Важные термины, определения и формулы
Магнитное поле или магнитная индукция (B)Магнит или электромагнит создает магнитное поле.Поле, в котором магнит притягивает или отталкивает магнитные материалы, такие как железо, сталь и т. Д., Может быть определено как сила, действующая на движущийся заряд,
F = qxvx B
Где
- F = Сила,
- V = скорость частиц,
- B = величина поля.
Полезно знать:
Это векторная величина, а единица магнитного поля в системе СИ — Тесла, где 1 Тесла = (Ньютон x секунда) / (кулон x метр) 10000 Гаусс.Формула для магнитного поля в СИ: B = µ ○ (H + M), а в CGS — B = H + 4π M.
Провод, по которому проходит постоянный ток или постоянный магнит, создает магнитостатическое (стационарное) поле и его величина и направление остаются прежними. При переменном токе или пульсирующем постоянном токе проводник создает переменное магнитное поле, которое непрерывно меняет свое направление и величину.
Также прочтите
Напряженность магнитного поля (H)Величина намагничивающей силы (сколько силы она имеет для намагничивания магнитных материалов, таких как железо, сталь и т. Д.) Называется силой магнитного поля, которая обозначается ( ЧАС).Он обратно пропорционален длине провода и прямо пропорционален току, проходящему по нему. В системе СИ единица измерения напряженности магнитного поля — Ампер / метр (А / м), это векторная величина, а формула СИ для напряженности магнитного поля:
H = NI / 1c
, где 1c = магнитный путь в метрах.
Магнитный поток (Φ)Простыми словами, Магнитное поле x площадь, перпендикулярная магнитному полю (B), называется Магнитным потоком, который обозначается Φ или Φ м или Φ B .Или это величина магнитного поля или магнитных силовых линий, проходящих через поверхность, такую как проводящая область, пространство, воздух и т. Д. Единица измерения магнитного потока в системе СИ — Wb (Вебер). Формула для нахождения магнитного потока в системе СИ:
Φ = BAc
Где
Ac = площадь в м 2
И единица измерения CGS и формула для магнитного потока — Максвелл (M) и Φ = BAc Ac = площадь в см 2 соответственно.
Намагничивание (M)Состояние намагничиваемого материала или процесс намагничивания магнитных материалов.Это плотность дипольных моментов постоянного магнита или электромагнита в магнитных материалах. Или магнитный момент (м) на единицу объема (v) магнитным полем называется намагниченностью. Единица намагничивания в системе СИ — ампер / метр (А / м), также это векторная величина. Формула СИ для намагничивания:
M = m / V
, где
- m = общий магнитный момент
- и V = объем в м 3 .
Единица CGS и формула намагничивания: Emu / cm 3 и M = m / V соответственно, где m = общий магнитный момент, V = объем в см 3 и EMU = электромагнитные единицы.Это также может быть определено как M = (N / V) x m → M = nm ……. (N / V) = п. Где «m» — это магнитный момент, а «n» — это плотность магнитных моментов.
Магнитная проницаемость вакуума (µ ○ )Говоря забавными словами, Пермь = Разрешение и способность — это особенность или умение что-то делать. Т.е. проницаемость (µ) — это способность материала, при помощи которого он легко намагничивается?
Магнитная проницаемость вакуумаЭто величина сопротивления магнитному полю при формовании в вакууме.
Единица измерения проницаемости в системе СИ — (H · m −1 ) или Ньютон на квадратный ампер (N · A −2 ). Единица СИ и формулы магнитной проницаемости вакуума: Ньютон / Ампер 2 и µ ○ = 4πx10 -7 ≈ 1,2566370614 Гн · м −1 соответственно. Единица измерения магнитной проницаемости вакуума CGS — 1.
Полезно знать: Противоположность магнитной проницаемости — это магнитная относительность.
Полезно знать: известное магнитное соотношение: B = µH, где µ — проницаемость, которая является скалярной величиной, B — магнитное поле, а H — сила намагничивания или напряженность магнитного поля.
Индуктивность (L)Индуктивность — это свойство проводника, катушки или проволоки, которое препятствует изменению тока, протекающего через них. Изменение тока, протекающего по проводнику, создает напряжение, называемое обратной ЭДС или электродвижущей силой.
Даже Изменение тока, протекающего через проводник или катушку, создает напряжение через них, которое называется самоиндуцированной ЭДС, и в любых соседних катушках или проводниках, которое называется взаимной индуктивностью. В системе СИ единица индуктивности (L) — это Генри «H», а формула:
L = µ ○ µN 2 Ac / 1c
Где
- N = Обороты
- Ac = Площадь в м 2
- 1c = магнитный путь в счетчике
Единица CGS и формула индуктивности — Генри «H» (Джозеф Генри) и L = 0.4π µN 2 Ac / 1c x10 -8 соответственно
где;
- L = Индуктивность
- N = Обороты
- Ac = Площадь в см 2
- 1c = магнитный путь в см.
Полезно знать : 1 H = 1 Вт / А (один Генри = 1 Вебер на ампер)
Формула самоиндукции
L = µ ○ (N 2 xA) / л
Где:
- L = в Генри
- μ ο = проницаемость свободного пространства (4.π.10 -7 )
- N = Число витков
- A = Площадь внутреннего сердечника (π.r 2 ) в м 2
- l = длина спирали в метрах
Формула взаимной индуктивности
M = μ ο μ r N 1 N 2 A / l
Где:
- µ o = проницаемость свободного пространства (4 .π.10 -7 )
- µ r = относительная проницаемость сердечника из мягкого железа
- N = количество витков катушки
- A = площадь поперечного сечения в м 2
- l = длина катушек в метрах
Связанные сообщения:
Voltage или E.М.Ф. (В)Разница электрических потенциалов между двумя точками называется напряжением. Или работа, совершаемая на единицу заряда в статическом электрическом поле для перемещения заряда между двумя точками, поэтому уравнение принимает вид
В = Вт / q или E / q.
Где;
- В = напряжение
- E = энергия в джоулях
- q = заряд в кулонах
Или электрическая потенциальная энергия на единицу заряда называется напряжением.
По закону Ома напряжение = V = I x R, где I = ток в амперах и R = сопротивление в омах (Ом)
Единицей измерения напряжения в системе СИ является вольт (В) или джоуль на кулон.Где 1 В = 1 Джоуль / 1 Кулон
Формула СИ для напряжения:
В = -N dΦ / dt
Где;
- N = количество витков катушки
- dΦ = скорость изменения магнитного потока
- t = время
Полезно знать: Другие родственные слова, используемые для напряжений и ЭДС: Разница электрических потенциалов , Электрическое напряжение , Электрическое давление, разность потенциалов, Pd, ЭДС, электродвижущая сила и это скалярная величина, и это тип электрической энергии.
В следующей таблице показаны все вышеперечисленные основные термины, используемые в магнитных цепях с единицами измерения SI и CGS и формулами.
| Количество | Символ | Единица СИ | Уравнение СИ | Единица CGS | Уравнение CGS | 6 906 906 9069 Коэффициент преобразования 906 | B | Тесла (T) | B = µ ○ (H + M) | Gauss (G) | B = H + 4π M | 1T = 10 4 G |
| Магнитное поле Прочность | H | Ампер / метр (А / м) | H = NI / 1c 1c = магнитный путь в м | Эрстед Oe | H = 0.4πNI / 1c 1c = магнитный путь в см | 1A / м = 4πx10 -3 Oe | ||||||
| Магнитный поток | Φ | Weber (Wb) | c4 Φ = BA000 м 2 | Maxwell M | Φ = BAc Ac = площадь в см 2 | 1Wb = 10 8 M | ||||||
| A намагничивание | 906 M намагниченность 906 / м) M = m / V m = Общий магнитный момент, V = объем в м 3 | Emu / cm 3 Где EMU = Электромагнитные блоки | M = m / V м = общий магнитный момент, V = объем в см 3 | 1A / м = 10- 3 emu / cm 3 | ||||||||
| Магнитная проницаемость вакуума | µ ○ | Ньютон / Ампер 2 | µ ○ 90 374 = 4πx10 -7 ≈ 1.2566370614 H · м −1 | 1 | — | 4πx10 -7 | ||||||
| Индуктивность | L | Генри | L = µ ○ N 9000/4 Ac Оборотов Ac = Площадь в м 2 1c = Магнитный путь в м | Генри | L = 0,4π мкН 2 Ac / 1c x10 -8 N = Оборотов Ac = Площадь в см 2 1c = магнитный путь в см | 1 | ||||||
| Напряжение или ЭДС | В | Вольт | В = — NdΦ / dt N = Оборотов | В = -10 -8 xNxdΦ / dt N = Обороты | 1 |
Ниже приводится таблица в формате изображения для справки.
Похожие сообщения:
Электромагнитная индукция — Физика A-Level
Изучив этот раздел, вы должны уметь:
- рассчитать потокосцепление через катушку с проводом в магнитном поле
- объяснить, как возникает электромагнитная индукция из-за изменений в потокосцеплении
- применять закон Фарадея и закон Ленца
В этом разделе рассматриваются следующие темы
Флюсовая и флюсовая передача
Почти все, что мы делаем, кроме сна в темноте, основано на электромагнитной индукции .Индукция используется для выработки электроэнергии на электростанциях и для преобразования ее напряжения при прохождении через распределительную систему.
Эффекты индукции объясняются с помощью концепции потока . Хотя существование потока давно дискредитировано, понимание его значения полезно для понимания законов индукции, изложенных Фарадеем и Ленцем.
Flux представляет собой полезную модель для объяснения эффектов магнитных полей.
Магнитные поля действуют на расстоянии, как гравитационное и электрическое поля.Картины магнитного поля используются, чтобы показать силы, действующие вокруг магнита или электрического тока. Эти силы действуют без какой-либо физической связи между магнитом или током, который вызывает поле, и магнитным материалом или током, помещенным в поле. Во времена Фарадея и Ленца их приписывали эффектам потока.
В настоящее время считается, что эти силы могут быть приписаны «обмену частицами».
При рисовании диаграмм магнитного поля:
- относительная напряженность в различных точках поля показана разделением силовых линий
- чем ближе линии вместе, тем сильнее поле
- эти силовые линии представляют магнитный поток , который, как представляется, занимает пространство вокруг магнита и отвечает за эффект магнитного поля.
Чтобы интегрировать модель потока с сегодняшним объяснением магнитных эффектов с точки зрения напряженности магнитного поля, это можно представить в терминах плотности потока, представленной концентрацией силовых линий магнитного поля. Плотность потока — это поток на единицу площади, поэтому поток теперь определяется в терминах напряженности магнитного поля и площади, через которую поле проникает.
КЛЮЧЕВОЙ МОМЕНТ — Магнитный поток Φ, проходящий через область A, определяется как произведение напряженности магнитного поля и площади, перпендикулярной полю.
Φ = B × A
Магнитный поток измеряется в сетках (Wb), где 1 Wb — поток через площадь 1 м 2 , нормальный к однородному полю с напряженностью 1 T.
Это определение связывает эквивалентность современной концепции напряженности магнитного поля и более старой концепции «магнитной индукции».
На схеме показан поток через прямоугольную катушку в однородном магнитном поле.
Когда катушка вращается, она «прорезает» магнитный поток или силовые линии и эл.м.ф. индуцируется.
Размер или величина наведенной ЭДС. зависит от:
- количество потока через катушку
- скорость вращения
- количество витков на катушке.
Каждый оборот катушки имеет потокосцепление, которое изменяется при вращении катушки. Потоковая связь катушки с Н и витками составляет НФ , где Ф — это поток через катушку.
Движение катушки параллельно полю не вызывает эл.m.f., поскольку никакие силовые линии не «срезаются». Индуцированная э.д.с. имеет наибольшее значение, когда движение катушки перпендикулярно полю.
Закон Фарадея
Электромагнитная индукция возникает всякий раз, когда магнитное поле через проводник изменяется. Это может быть из-за того, что проводник движется через магнитное поле, или проводник находится в фиксированном положении в изменяющемся магнитном поле, например, из-за переменного тока.Оба они приводят к ЭДС. индуцируется в проводнике.
Примеры электромагнитной индукции:
- перемещение магнита внутри проволочной катушки
- генерирует высокое напряжение, необходимое для ионизации пара в люминесцентной лампе и вызывает искру, необходимую для воспламенения взрывоопасной смеси в бензиновом двигателе
- изменение напряжения переменного тока с помощью трансформатора.
На электростанции электричество вырабатывается электромагнитом, вращающимся внутри медных катушек.
На приведенной ниже диаграмме показана разница в размере ЭДС. когда магнит движется в катушке с разной скоростью.
Закон Фарадея связывает величину наведенной ЭДС. к изменению потокосцепления.
КЛЮЧ. Закон Фарадея гласит, что величина наведенной ЭДС. пропорциональна скорости изменения потокосцепления. Поскольку константа пропорциональности равна 1, для равномерной скорости изменения потокосцепления это можно записать как:
величина наведенной e.м.ф. N = ΔΦ / Δt, где ΔΦ — изменение потока во времени Δt.
Чтобы создать высокое напряжение, необходимое для возникновения искры, магнитный поток должен быстро измениться. Это происходит при отключении тока в электромагните.
В каком направлении?
Закон Фарадея можно использовать для определения величины наведенной ЭДС. например, через концы крыла самолета, летящего в магнитном поле Земли. В Великобритании поле Земли составляет угол 20 ° с вертикалью, см. Следующий рисунок.
В отличие от стержневого магнита, магнитное поле Земли направлено с юга на север. Можно считать, что он состоит из двух компонентов: вертикального и горизонтального.
Самолет, летящий в направлении север-юг, пересекает только вертикальную составляющую, в то время как полет с востока на запад включает в себя дополнительно пересечение горизонтальной составляющей.
Индуцированная э.д.с. возникает как следствие действия силы на свободные электроны в металле корпуса самолета.Когда самолет движется по воздуху, движение этих электронов формирует ток, противоположный направлению полета. Правило левой руки Флеминга можно использовать для определения направления силы, действующей на электроны, и, следовательно, направления индуцированной ЭДС.
Все заряженные частицы испытывают силу из-за своего движения через магнитное поле, но эта сила слишком мала, чтобы воздействовать на что-либо, кроме свободных электронов.
В случае полета самолета с севера на юг:
- текущее — юг – север
- «разрезаемое» магнитное поле направлено вертикально вниз
- сила, действующая на свободные электроны, направлена на восток.
Это приводит к дисбалансу заряда и возникновению напряжения на законцовках крыла. Направление э.д.с. индуцируется в самолете и когда магнит движется в катушку с проволокой, можно вычислить, используя закон Ленца .
КЛЮЧЕВЫЙ МОМЕНТ — Закон Ленца гласит, что направление индуцированной ЭДС. всегда противостоит изменению, которое его вызывает.
Если наведенная э.д.с. в самолете заставлял электроны течь с запада на восток, это создавало силу в северном направлении — противоположном движению самолета.Этого не происходит, потому что нет полной схемы.
На диаграмме ниже показано, что когда северный полюс магнита перемещается в один конец катушки, индуцированная ЭДС. вызывает индуцированный ток в направлении против часовой стрелки. Когда ток проходит в катушке, магнитное поле похоже на магнитное поле стержневого магнита, причем северный полюс является концом, по которому ток проходит против часовой стрелки.
Направление индуцированного тока меняется на противоположное путем изменения направления магнита или его движения.
Если бы индуцированный ток был в противоположном направлении, он притягивал бы магнит в катушку и генерировал электричество без подвода энергии.
Закон Ленца — это переформулировка принципа сохранения энергии; индуцированный ток противодействует движению магнита, поэтому необходимо выполнить работу по перемещению магнита против индуцированного магнитного поля. Эта работа представляет собой передачу энергии в цепь, необходимую для возникновения тока.
Объединение законов Фарадея и Ленца дает уравнение для индуцированной e.м.ф .:
КЛЮЧ — где ε — наведенная ЭДС. Отрицательный знак показывает, что наведенная э.д.с. противостоит вызывающему его изменению потока.
Трансформатор
Трансформаторы используют изменяющиеся магнитные поля для изменения величины переменного напряжения. Переменный ток, протекающий в одной катушке (первичной обмотке), вызывает э.д.с. в соседней катушке (вторичной).
На схеме ниже показан поток, когда две катушки намотаны на железный сердечник.
Э.д.с. индуцируется независимо от наличия вторичной цепи. Если есть замкнутая цепь, есть также индуцированный ток.
В трансформаторе:
- переменный ток в первичной обмотке создает переменное магнитное поле
- это усилено железным сердечником с высокой проницаемостью
- флюс концентрируется в чугуне
- Э.д.с. индуцируется во вторичной обмотке из-за изменения магнитной связи.
Железо легко намагничивается; его магнитные домены вносят свой вклад в силу магнитного поля.
Из последнего пункта следует, что индуцированная ЭДС. пропорционально количеству витков вторичной катушки.
КЛЮЧЕВЫЙ МОМЕНТ — соотношение между напряжениями и количеством витков для идеального трансформатора:
Трансформатор, построенный из катушек с низким сопротивлением на многослойном железном сердечнике, близок к идеалу.
Это означает, что напряжения находятся в том же соотношении, что и количество витков. В идеальном трансформаторе нет потерь энергии в проводах или сердечнике, поэтому выходная мощность вторичной обмотки равна мощности, потребляемой первичной обмоткой, а токи обратно пропорциональны напряжению.
ПРОВЕРКА ПРОГРЕССА
Устройство магнитной индукции
— важные примечания по электромагнитной индукции
Магнитная индукция — одна из самых важных тем физики при подготовке к экзамену по электросети JEE.Одной из важных тем, относящихся к теме электромагнитной индукции, является устройство магнитной индукции. Данная статья наиболее эффективно обобщает тему магнитоиндукционного блока. Сначала мы кратко обсудим магнитный поток и магнитную индукцию, а затем рассмотрим блок магнитной индукции.
Магнитный потокКоличество силовых линий магнитного поля, которые обычно пересекают любую поверхность, называется магнитным потоком.
Обозначается Ø.
Ø = B. A
Ø = BA Cos
Здесь B — магнитное поле
A — площадь, через которую проходят силовые линии магнитного поля
And — угол между вектором площади и линиями магнитного поля.
В системе СИ единица измерения магнитного потока — Вебер.
Магнитная индукцияКогда заряженная частица движется, она испытывает силу, которая обычно определяется как магнитное поле, или магнитная индукция, или интенсивность магнитного потока.Обозначается символом «B». На заряд q в электрическом поле E действует сила F = qE. Кроме того, эксперименты показали, что заряженная частица испытывает силу, пропорциональную ее относительной скорости, по отношению к проводу с током. Часть, которая зависит от скорости, может быть отделена так, чтобы сила, действующая на частицу, удовлетворяла закону силы Лоренца,
F = q (E + v B)
Здесь B — магнитное поле или магнитная индукция.
B также определяется как количество магнитных линий, проходящих на единицу площади, которое называется плотностью магнитного потока.
В системе СИ единицей магнитной индукции (В) является тесла.
Одна тесла равна одному Веберу на квадратный метр.
Устройство магнитной индукцииСогласно силе Лоренца, частица, несущая заряд в 1 кулон и движущаяся перпендикулярно через магнитное поле в 1 тесла, двигаясь со скоростью 1 метр в секунду, испытывает силу, равную 1 ньютон.
Единица индукции магнитного поля
Тесла также может быть выражена как-
На рисунке выше показаны единицы индукции магнитного поля или единицы магнитной индукции.
Часто задаваемые вопросы по устройству магнитной индукции
Q.1 Магнитный поток учитывает силовые линии магнитного поля, которые пересекают поверхность вертикально, тангенциально или перпендикулярно?
Ans.1Магнитный поток учитывает силовые линии магнитного поля, которые пересекают поверхность перпендикулярно, а не вертикально или тангенциально.
Q.2 Приведите формулу силы, действующей на заряженную частицу в электрическом поле.
Ans.2На заряд q в электрическом поле E действует сила F = qE.
Q.3 Определить 1 тесла
Ans.3Согласно силе Лоренца, частица, несущая заряд в 1 кулон и движущаяся перпендикулярно через магнитное поле в 1 тесла, движется со скоростью 1 метр в секунду, испытать силу, равную 1 ньютону.
Q.4 Магнитная индукция и магнитный поток прямо пропорциональны друг другу?
Отв.4На заряд q в электрическом поле E действует сила F = qE.
Эта тема является критической с учетом программы вступительных экзаменов по инженерным наукам. Форма JEE Mains Application закрыта. Желаем всего наилучшего зарегистрированным кандидатам.
Создайте бесплатную учетную запись, чтобы продолжить чтение
Получите мгновенные оповещения о вакансиях бесплатно!
Получите ежедневный GK и текущие новости Капсула и PDF-файлы
Получите 100+ бесплатных пробных тестов и викторин
Зарегистрироваться бесплатно Создать бесплатный аккаунт? Войти
Next Post
Магнитная индукция — статья энциклопедии
В физике и, в частности, в теории электромагнетизма, магнитная индукция (также известная как плотность магнитного потока ) описывает магнитное поле (вектор) в каждой точке пространства.Магнитная индукция обычно обозначается как B ( r , t ) и является векторным полем, то есть зависит от положения r и времени t . В нерелятивистской физике пространство, в котором определяется B , является трехмерным евклидовым пространством — бесконечным миром, в котором мы живем. Поле B тесно связано с магнитным полем H , часто называемым напряженность магнитного поля , а иногда просто H -поле.Фактически, некоторые авторы называют B магнитным полем, а H — вспомогательным полем.
Физический источник поля B может быть
или комбинации этих трех. Вблизи этих источников существует магнитное поле. В общем, сила магнитного поля уменьшается как малая мощность 1/ R , обратная расстоянию R до источника.
Магнитная сила может воздействовать на
- постоянный магнит (который представляет собой магнитный диполь или, примерно, два магнитных монополя),
- намагничивающийся (ферромагнитный) материал, такой как железо,
- движущиеся электрические заряды (за счет силы Лоренца)
- элементарных частиц из-за их собственного спина, который связан с их собственными магнитными свойствами через их гиромагнитные отношения.
Термин плотность магнитного потока относится к тому факту, что B — это магнитный поток. на единицу поверхности. Это соотношение основано на законе магнитной индукции Фарадея.
Единицей измерения прочности B является Т (тесла = Вебер / м 2 ), а единицей Гаусса B является G (гаусс = максвелл / см 2 ). Одна тесла равна 10 000 гаусс.
Для обозначения величин: магнитное поле (или лучше: магнитная индукция) Земли составляет около 0.5 Г (50 мкТл). Магнит подковы составляет около 100 Гс. Медицинский диагностический аппарат МРТ обычно поддерживает поле до 2 Тл (20 кГ). В настоящее время самые сильные магниты в лабораториях имеют мощность около 30 Т (300 кГс).
Примечание к номенклатуре
В большинстве учебников по электричеству и магнетизму различают магнитное поле H и магнитную индукцию B . Тем не менее, на практике физики и химики почти всегда называют B магнитным полем , потому что термин «индукция» предполагает индуцированный магнитный момент.Поскольку индуцированный момент обычно не проявляется, термин индукция может сбивать с толку. Среди ученых распространены такие фразы, как: «Этот спектр ЭПР был измерен при магнитном поле 3400 гаусс» и «Наш магнит может создавать магнитные поля величиной до 20 тесла». То есть большинство ученых используют термин «поле» в единицах тесла или гаусса, в то время как, строго говоря, гаусс и тесла — это единицы B . Некоторые авторы идут еще дальше и резервируют название «магнитное поле» для B и называют H «вспомогательным магнитным полем».
Связь между
B и HВ вакууме (также известном как микроскопический случай, см. Уравнения Максвелла), в отсутствие намагничивающейся среды поля B и H связаны следующим образом:
где μ 0 — магнитная постоянная (равная 4π⋅10 −7 N / A 2 ). Обратите внимание, что в гауссовых единицах размеры H (Oer) и B (G = гаусс) равны, 1 Oer = 1 G, хотя единицы имеют другое определение (Oer основано на поле соленоида , G — магнитный поток на поверхность).При отсутствии намагничивающейся среды нет необходимости вводить как B , так и H , потому что они отличаются точным и постоянным коэффициентом (единица для гауссовых единиц и μ 0 для единиц СИ).
На микроскопическом уровне магнитный поток B и электрическое поле E определяют поведение зарядов. Например, один движущийся заряд подчиняется закону силы Лоренца, который в единицах СИ равен:
Однако рассматривать все заряды в системе на микроскопическом уровне нецелесообразно, поэтому вводятся приближения.Некоторые части системы рассматриваются под микроскопом, а некоторые рассматриваются как «материалы», в частности, диэлектрики и магнитные материалы. Отклик магнитного материала на магнитный поток вводится через намагниченность материала, другое векторное поле M ( r , t ).
В присутствии намагничивающейся среды соотношение между B и H включает намагниченность M среды,
Чтобы фактически определить поведение системы, намагниченность M должна быть определена в терминах B или H , чтобы реакция системы зависела только от одной переменной поля.Это определение M может быть очень сложным. Например, это может включать введение квантовой механики и статистической механики, изучаемой в области физики конденсированного состояния. Однако во многих неферромагнитных средах намагниченность M линейна в H ,
Для магнитно-изотропной среды тензор магнитной восприимчивости χ представляет собой постоянную, умноженную на единичную матрицу 3 × 3, χ = χ м 1 .Для изотропной среды соотношение между B и H выражается в единицах СИ и гауссовых единицах соответственно,
Константа материала μ, которая выражает «легкость» намагничивания среды, представляет собой магнитную проницаемость среды. В большинстве неферромагнитных материалов χ m << 1 и, следовательно, B ≈ μ 0 H (SI) или B ≈ H (гауссовский). Для ферромагнитных материалов магнитная проницаемость μ может быть значительной (χ м >> 1).В этом случае намагничивание среды сильно увеличивает магнитное поле.
Два макроскопических уравнения Максвелла, которые содержат заряды и токи, являются уравнениями для H и электрического смещения D . Это является следствием того, что плотности тока Дж и электрические поля E (за счет зарядов) модифицируются намагниченностью M и поляризацией P среды. В единицах СИ уравнение Максвелла для магнитного поля имеет следующий вид:
Микроскопическая (без среды) форма этого уравнения получается путем исключения D и H через D = ε 0 E и H = B / μ 0 ( P = 0 и M = 0).
Два уравнения Максвелла, которые не содержат токов и зарядов, дают отношения между основными полями E и B , а не между вспомогательными полями H и D . Например, закон индукции Фарадея в единицах СИ:
Это уравнение справедливо как микроскопически (вакуум), так и макроскопически (в присутствии среды). Но, конечно, в микроскопическом случае появляются подробные микроскопические токи и заряды, обусловленные элементарными источниками, тогда как в макроскопическом случае некоторые из этих микроскопических токов и зарядов учитываются в свойствах материала, например, в различных диэлектрических и магнитных проницаемости.Таким образом, поля E и B в этих двух ситуациях различаются, причем макроскопические поля усредняются для удаления некоторых микроскопических деталей.
.
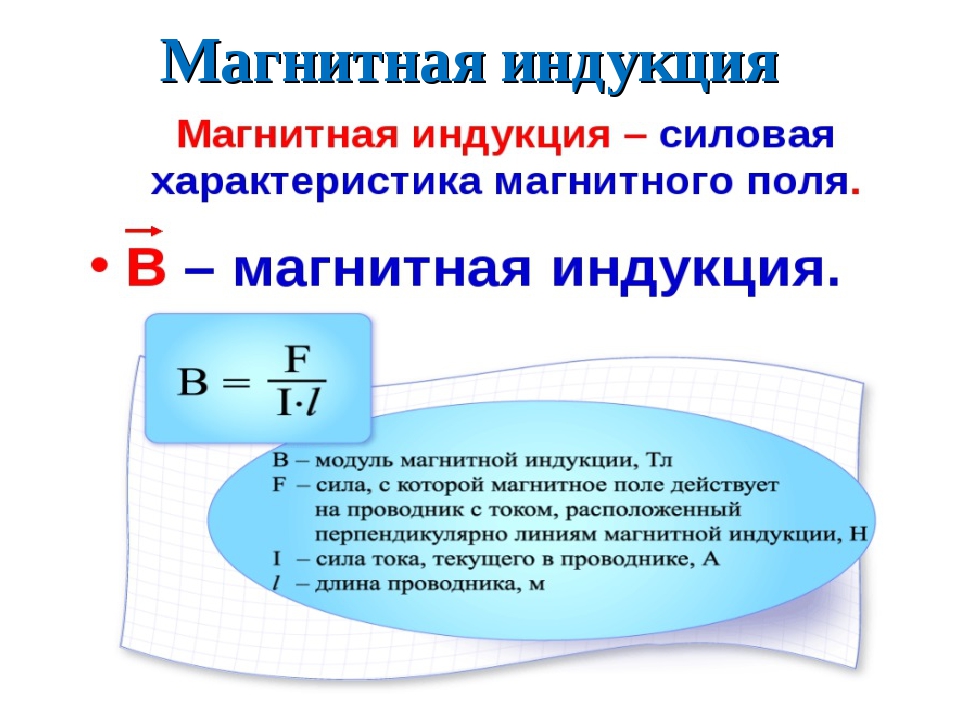
 В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.
В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.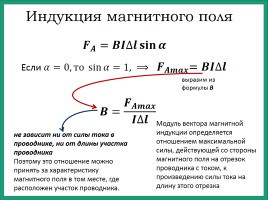 1)
1)