Глава 7. Вращательное движение. Кинематика и динамика
Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел
(7.1) |
В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7.
(7.2) |
Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.
Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим
(7.3) |
Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.
Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна
(7.4) |
Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах
(7.5) |
Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине
(7.6) |
Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.
Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.
Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»).
Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем
(правильный ответ – 2).
Применяя определение угловой скорости к колесу (задача 7.1.3), получаем
(правильный ответ 1).
Из формулы (7.2) имеем
(задача 7.1.4 – правильный ответ 4).
Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска
А теперь по формуле (7. 5) для второй точки получаем
5) для второй точки получаем
(ответ 2).
Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ –
Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно
(ответ 4).
Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи –
 Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).
Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).
Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с2, получим для равнодействующей =2 Н (ответ 2).
Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из
(ответ 1).
Для сравнения центростремительных ускорений материальных точек в задаче 7. 2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем
(ответ 3).
Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим
(7.5) |
Поэтому
(ответ 1).
Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)
где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем
Учитывая, что , получаем
(ответ 2).
Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения
Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства
(ответ 4).
В задаче 7. 2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем
(ответ 3).
В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает
(1) |
На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем
Подставляя в эту формулу силу из формулы (1), находим (ответ 2).
В задаче 7. 2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем
где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим
(ответ 3).
Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):
где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно
(задача 7. 2.9 – ответ 1).
2.9 – ответ 1).
Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).
Урок 5. поступательное движение. вращательное движение твердого тела — Физика — 10 класс
Физика, 10 класс
Урок 05. Поступательное движение. Вращательное движение твёрдого тела
Перечень вопросов, рассматриваемых на уроке:
- Поступательное и вращательное движение абсолютно твердого тела.
- Характеристики вращательного движения абсолютно твердого тела.
Глоссарий по теме
1. Абсолютно твердое тело – это тело, расстояние между любыми двумя точками которого остается постоянным при его движении.
2. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе. Одинаковыми остаются при поступательном движении перемещение, траектория, путь, скорость, ускорение.
Одинаковыми остаются при поступательном движении перемещение, траектория, путь, скорость, ускорение.
3. Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой перпендикулярной плоскостям этих окружностей. Сама эта прямая есть ось вращения.
4. Угол поворота – угол, на который поворачивается радиус-вектор, соединяющий центр окружности с точкой вращающегося тела.
5. Угловая скорость — отношение угла поворота φ к промежутку времени, в течение которого совершен этот поворот при равномерном движении.
6. Линейная скорость – отношение длины дуги окружности пройденной точкой тела к промежутку времени, в течение которого этот поворот совершен.
7. Период — промежуток времени, за который тело делает один полный оборот.
8. Частота обращения тела – число оборотов за единицу времени
Основная и дополнительная литература по теме урока:
Мякишев Г. Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. – С. 57-61
Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. – С. 57-61
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Вы знаете, что в физике для упрощения исследования реальных ситуаций часто используются модели. Одной из механических моделей, используемых при описании движения и взаимодействия тел, является абсолютно твёрдое тело- тело, расстояние между любыми двумя точками которого остаётся постоянным при его движении.
2. Поступательным называется такое движение абсолютно твёрдого тела, при котором любой отрезок, соединяющий любые две точки тела, остаётся параллельным самому себе. Примером поступательного движения может служить свободное падение тел, движение лифта, поезда на прямолинейном участке дороги. При поступательном движении все точки тела описывают одинаковые траектории, совершают одинаковые перемещения, проходят одинаковые пути, в каждый момент времени имеют равные скорости и ускорения.
При поступательном движении все точки тела описывают одинаковые траектории, совершают одинаковые перемещения, проходят одинаковые пути, в каждый момент времени имеют равные скорости и ускорения.
Для описания поступательного движения абсолютно твёрдого тела достаточно написать уравнение движения одной из его точек.
3. Вращательным движением абсолютно твёрдого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения. При этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения.
Вращательное движение позволяет осуществить непрерывный процесс работы с использованием больших скоростей. Вращающиеся механизмы более компактны и более экономичны, так как потери энергии на преодоление сил трения качения меньше, чем на преодоление сил трения скольжения. Поэтому в современной технике вращательное движение рабочих частей машин всё более вытесняет возвратно-поступательное. Например, вместо ножовочной пилы в технике используют вращающуюся дисковую пилу, поршневые насосы в большинстве случаев вытесняются центробежными.
Например, вместо ножовочной пилы в технике используют вращающуюся дисковую пилу, поршневые насосы в большинстве случаев вытесняются центробежными.
4. Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела ∆φ к промежутку времени ∆t, за которое этот поворот произошёл.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению запишем формулу угловой скорости;
При равномерном вращательном движении угловая скорость у всех точек вращающегося тела одинаковая. Поэтому угловая скорость, так же как и угол поворота, является характеристикой движения всего вращающегося тела, а не только отдельных его частей.
Примером вращательного движения, близкого к равномерному, может служить вращение Земли вокруг своей оси.
Угловая скорость в СИ выражается в радианах в секунду (рад/с).
Один радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
Угловая скорость положительна, если угол между радиусом вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательным, когда он уменьшается
5.Число полных оборотов за единицу времени называют частотой обращения.
Частоту обозначают греческой буквой «ню». Единица измерения частоты является секунда в минус первой степени
Время, за которое тело совершает один полный оборот, называют периодом обращения и обозначают буквой Т.
7. Связь между линейной и угловой скоростями:
8. Связь между ускорением и угловой скоростью:
Итак, мы рассмотрели два простейших движения абсолютно твердого тела – поступательное и вращательное. В жизни мы чаще встречаем сложное движение абсолютно твердого тела, однако, в этом случае любое сложное движение можно представить как сумму двух независимых движений: поступательного и вращательного.
Примеры и разбор типового тренировочного задания
- Ротор мощной паровой турбины делает 100 оборотов за 2 с.
 Определите угловую скорость.
Определите угловую скорость.
Дано:
N=100 об.
t = 2 c
Найти: ω.
Решение:
2. Два шкива, соединенные друг с другом ремнем, вращаются вокруг неподвижных осей (см.рис). Больший шкив радиусом 20см делает 50 оборотов за 10 секунд, а частота вращения меньшего шкива 2400 оборотов в минуту. Чему равен радиус меньшего шкива? Шкивы вращаются без проскальзывания.
Дано:
Найти —
Решение:
Из условия задачи ученик видит что, шкивы соединены ремнем, следовательно, линейные скорости их равны:
но частота вращения разная.
Сокращает на 2π обе части.
Отсюда имеем:
и так, как в условии известно , то можем записать:
Отсюда находим радиус второго шкива:
Вторая неизвестная величина
Запишем формулу периода обращения для большего шкива:
так как по условию задачи нам известно число оборотов за 10 секунд.
Подставим в формулу (1) и получим конечную формулу:
Т. Движение по окружности — PhysBook
Движение тела по окружности с постоянной по модулю скоростью
Движение тела по окружности с постоянной по модулю скоростью — это движение, при котором тело за любые равные промежутки времени описывает одинаковые дуги.
Положение тела на окружности определяется радиусом-вектором \(~\vec r\), проведенным из центра окружности. Модуль радиуса-вектора равен радиусу окружности R (рис. 1).
Рис. 1
За время Δt тело, двигаясь из точки А в точку В, совершает перемещение \(~\Delta \vec r\), равное хорде АВ, и проходит путь, равный длине дуги l.
Радиус-вектор поворачивается на угол Δφ. Угол выражают в радианах.
Скорость \(~\vec \upsilon\) движения тела по траектории (окружности) направлена по касательной к траектории. Она называется линейной скоростью. Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt за который эта дуга пройдена:
Модуль линейной скорости равен отношению длины дуги окружности l к промежутку времени Δt за который эта дуга пройдена:
Скалярная физическая величина, численно равная отношению угла поворота радиуса-вектора к промежутку времени, за который этот поворот произошел, называется угловой скоростью:
\(~\omega = \frac{\Delta \varphi}{\Delta t}.\)В СИ единицей угловой скорости является радиан в секунду (рад/с).
При равномерном движении по окружности угловая скорость и модуль линейной скорости — величины постоянные: ω = const; υ = const.
Положение тела можно определить, если известен модуль радиуса-вектора \(~\vec r\) и угол φ, который он составляет с осью Ox (угловая координата). Если в начальный момент времени t0 = 0 угловая координата равна φ0, а в момент времени t она равна φ, то угол поворота Δφ радиуса-вектора за время \(~\Delta t = t — t_0 = t\) равен \(~\Delta \varphi = \varphi — \varphi_0\). Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности:
Тогда из последней формулы можно получить кинематическое уравнение движения материальной точки по окружности:
Оно позволяет определить положение тела в любой момент времени t. Учитывая, что \(~\Delta \varphi = \frac{l}{R}\), получаем\[~\omega = \frac{l}{R \Delta t} = \frac{\upsilon}{R} \Rightarrow\]
\(~\upsilon = \omega R\) — формула связи между линейной и угловой скоростью.Промежуток времени Τ, в течение которого тело совершает один полный оборот, называется периодом вращения:
\(~T = \frac{\Delta t}{N},\)где N — число оборотов, совершенных телом за время Δt.
За время Δt = Τ тело проходит путь \(~l = 2 \pi R\). Следовательно,
\(~\upsilon = \frac{2 \pi R}{T}; \ \omega = \frac{2 \pi}{T} .\)Величина ν, обратная периоду, показывающая, сколько оборотов совершает тело за единицу времени, называется частотой вращения:
\(~\nu = \frac{1}{T} = \frac{N}{\Delta t}. \)
\)Следовательно,
\(~\upsilon = 2 \pi \nu R; \ \omega = 2 \pi \nu .\)Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 18-19.
Равномерное движение тела по окружности – FIZI4KA
1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.
При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности.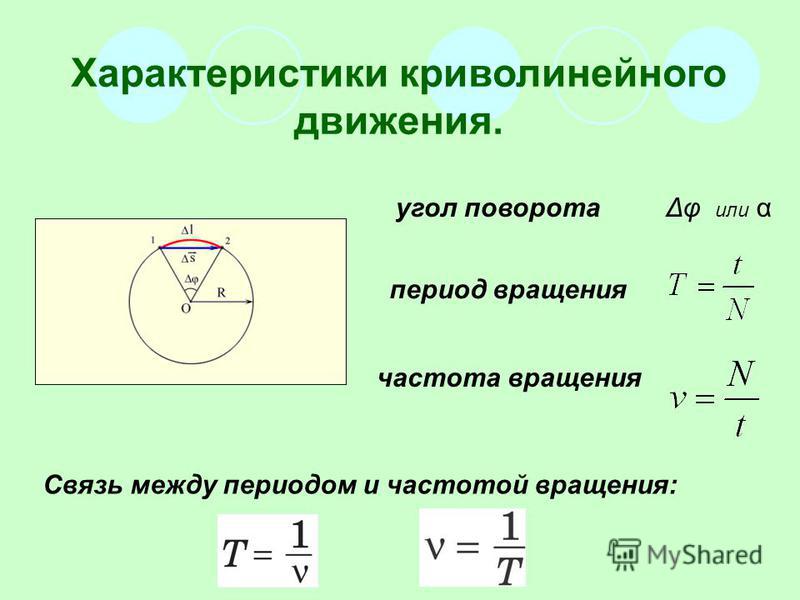 Под телом в данном случае имеют в виду материальную точку.
Под телом в данном случае имеют в виду материальную точку.
2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности \( T \) — время, в течение которого тело совершает один полный оборот. Единица периода — \( [\,T\,] \) = 1 с.
Частота обращения \( (n) \) — число полных оборотов тела за одну секунду: \( n=N/t \). Единица частоты обращения — \( [\,n\,] \) = 1 с-1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и периодом обращения выражается формулой: \( n=1/T \).
Пусть некоторое тело, движущееся по окружности, за время \( t \) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол \( \varphi \).
Быстроту обращения тела характеризуют угловая и линейная скорости.
Угловая скорость \( \omega \) — физическая величина, равная отношению угла поворота \( \varphi \) радиуса-вектора к промежутку времени, за которое этот поворот произошел: \( \omega=\varphi/t \). Единица угловой скорости — радиан в секунду, т.е. \( [\,\omega\,] \) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен \( 2\pi \). Поэтому \( \omega=2\pi/T \).
Линейная скорость тела \( v \) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.
Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: \( \vec{v}=l/t \). За один оборот точка проходит путь, равный длине окружности. Поэтому \( \vec{v}=2\pi\!R/T \).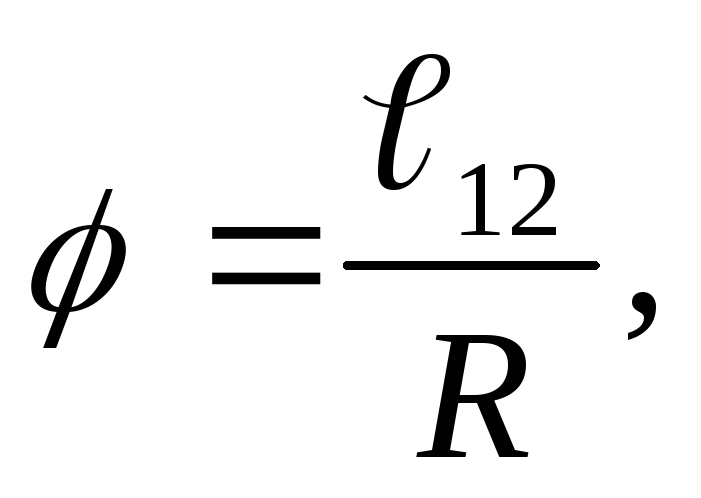 2R \).
2R \).
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. При равномерном движении тела по окружности
1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости
2. Линейная скорость точки 1, находящейся на расстоянии \( R_1 \) от центра вращающегося колеса, равна \( v_1 \). Чему равна скорость \( v_2 \) точки 2, находящейся от центра на расстоянии \( R_2=4R_1 \)?
1) \( v_2=v_1 \)
2) \( v_2=2v_1 \)
3) \( v_2=0,25v_1 \)
4) \( v_2=4v_1 \)
3. Период обращения точки по окружности можно вычислить по формуле:
1) \( T=2\pi\!Rv \)
2) \( T=2\pi\!R/v \)
3) \( T=2\pi v \)
4) \( T=2\pi/v \)
4. 2 \)
2 \)
3) \( \omega=vR \)
4) \( \omega=v/R \)
5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?
1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась
6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза
7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза
8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?
1) 200 000 с
2) 3300 с
3) 3·10-4 с
4) 5·10-6 с
9. 2/R \)
2/R \)
3) \( v/R \)
4) \( \omega R \)
5) \( 1/n \)
12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась
Часть 2
13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?
Ответы
Равномерное движение тела по окружности
3. 2 (63.33%) 12 votes
2 (63.33%) 12 votes| Криволинейное движение. | |
| При криволинейном движении вектор скорости всегда направлен по касательной к траектории движения. Любое криволинейное движение можно представить в виде суммы прямолинейных движений и движений по окружностям разных радиусов.Скорость изменяется как по величине, так и по направлению. Вектор ускорения направлен под углом к вектору скорости. | |
| РАВНОМЕРНОЕ ДВИЖЕНИЕ ТОЧКИ ПО ОКРУЖНОСТИ. | |
Равномерное движение точки по окружности — движение точки с постоянной по модулю скоростью (v=const) по траектории, представляющей собой окружность. Но, т.к. скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. В этом случае скорость точки называется линейной скоростью (ℓ–длина дуги). Вектор линейной скорости направлен по касательной к окружности в данной точке. | |
Можно характеризовать изменение положения тела с помощью углового перемещения (угла поворота) φ. Возьмем несколько концентрических окружностей и построим для всех центральный угол φ так, чтобы радиусы этих окружностей, образующие угол, накладывались друг на друга. Из рисунка видно, что одному и тому же углу φ соответствуют у одной окружности дуга ℓ и радиус r, а у другой – дуга L и радиус R. За меру угла можно принять отношение длины дуги к радиусу:. Единица измерения угла в этом случае наз. радианом(сокращение – рад). | |
Центральный угол равен одному радиану, если длина дуги равна радиусу окружности. Если точка совершила полный оборот, то длина дуги равна длине окружности. Следовательно: — полный оборот точки соответствует 2π радиан. Для перевода единиц составим пропорцию: . Следовательно: | |
Равномерное движение точки по окружности – это движение, при котором точка за любые равные промежутки времени совершает одинаковые угловые перемещения (поворачивается на одинаковые углы). Если характеризовать движение углом поворота, то удобно ввести угловую скорость: — угловая скорость показывает, на какой угол поворачивается точка при равномерном движении по окружности за единицу времени. Единица измерения в СИ — рад/с. | |
Можно сказать, что равномерным движением по окружности наз. движение с постоянной угловой скоростью. Линейная и угловая скорости связаны между собой: , т.е. . движение с постоянной угловой скоростью. Линейная и угловая скорости связаны между собой: , т.е. . | |
К важным характеристикам вращательного движения относятся частота и период. Период— физическая величина, показывающая, чему равно время, за которое точка совершает один полный оборот. Если обозначить N – число оборотов, а Т – период, то: . Единица измерения в СИ – с. Т.к. за период точка поворачивается на угол 2π, то . Частота – количество оборотов, которое совершила точка за единицу времени: .
Единица измерения в СИ – Гц (герц). Частота равна одному герцу, если за 1 секунду точка совершает один полный оборот (1Гц=1с-1). Частота и период – взаимно обратные величины: . Следовательно: . |
|
ФИЗИКА: Задачи на Движение тела по окружности
Задачи на Движение тела по окружности с решениямиФормулы, используемые на уроках «Задачи на Движение тела по окружности».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Какова линейная скорость тела, движущегося по окружности радиусом 40 м с ускорением 2,5 м/с2 ?
Задача № 2. С какой наибольшей скоростью может двигаться автомобиль массой 1 т на повороте радиусом 100 м, чтобы его не «занесло», если максимальная сила трения 4 кН?
Задача № 3. Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.
Задача № 4. Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Задача № 5. Велосипедист ехал со скоростью 25,2 км/ч. Сколько оборотов совершило колесо диаметром 70 см за 10 мин?
Задача № 6.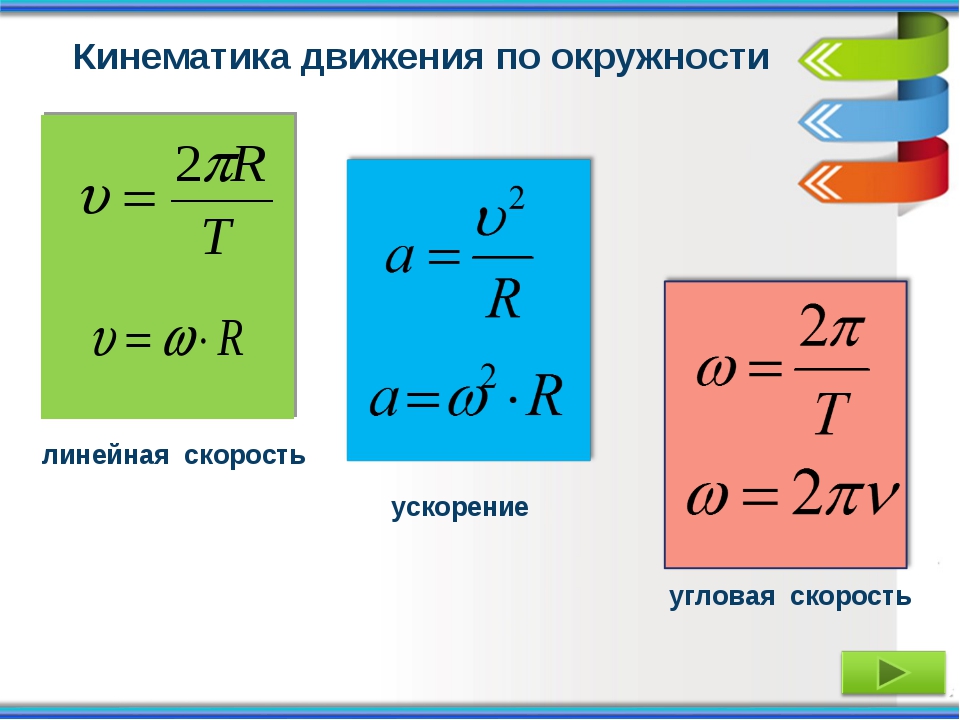 Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.
Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.
Задача № 7. Автомобиль движется по закруглению дороги, радиус которой равен 20 м. Определите скорость автомобиля, если центростремительное ускорение равно 5 м/с2.
Задача № 8. Шкив радиусом 30 см имеет частоту вращения 120 об/мин. Определите частоту, период обращения, угловую скорость шкива и центростремительное ускорение точек шкива, наиболее удаленных от оси вращения.
Задача № 9. Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли. Радиус Земли считайте равным 6370 км.
Задача № 10. ОГЭ Точка движется равномерно по окружности. Как изменится её центростремительное ускорение, если скорость возрастёт вдвое, а радиус окружности вдвое уменьшится?
Задача № 11. ЕГЭ
Линейная скорость точек обода вращающегося диска v1 = 3 м/с, а точек, находящихся на l = 10 см ближе к оси вращения, v2 = 2 м/с. Найти частоту вращения диска.
ЕГЭ
Линейная скорость точек обода вращающегося диска v1 = 3 м/с, а точек, находящихся на l = 10 см ближе к оси вращения, v2 = 2 м/с. Найти частоту вращения диска.
Краткая теория для решения Задачи на Движение тела по окружности.
Это конспект по теме «ЗАДАЧИ на Движение тела по окружности». Выберите дальнейшие действия:
Основные определения и формулы
Скорость резания V (м/мин) – это окружная скорость перемещения режущих кромок фрезы. Эта величина определяет эффективность обработки и лежит в рекомендованных для каждого инструментального материала пределах. За один оборот фрезы точка режущей кромки, находящаяся на окружности фрезы диаметра D (мм), сможет пройти путь, равный длине окружности, то есть πD. Для того чтобы определить длину пути, пройденного точкой за одну минуту, нужно умножить длину пути за один оборот на частоту вращения фрезы, то есть πDN (мм/мин). Таким образом, формула для определения скорости резания будет следующей:
Для того чтобы определить длину пути, пройденного точкой за одну минуту, нужно умножить длину пути за один оборот на частоту вращения фрезы, то есть πDN (мм/мин). Таким образом, формула для определения скорости резания будет следующей:
V = πDN/1000 (мм/мин).
Частота вращения шпинделя N (об/мин) равняется числу оборотов фрезы в минуту. Вычисляется в соответствии с рекомендованной для данного типа обработки скоростью резания:
N = 1000V/nD (об/мин).
При фрезеровании различают минутную подачу, подачу на зуб и подачу наоборот фрезы.
Подача на зуб Fz (мм/зуб) – величина перемещения фрезы или рабочего стола с заготовкой за время поворота фрезы на один зуб.
Подача на оборот Fo (мм/об) – величина перемещения фрезы или рабочего стола с заготовкой за один оборот фрезы. Подача на оборот равняется произведению подачи на зуб на число зубьев фрезы Z:
Fo = FzZ (мм/об).
Минутной подачей Fm (мм/мин) называется величина относительного перемещения фрезы или рабочего стола с заготовкой за одну минуту.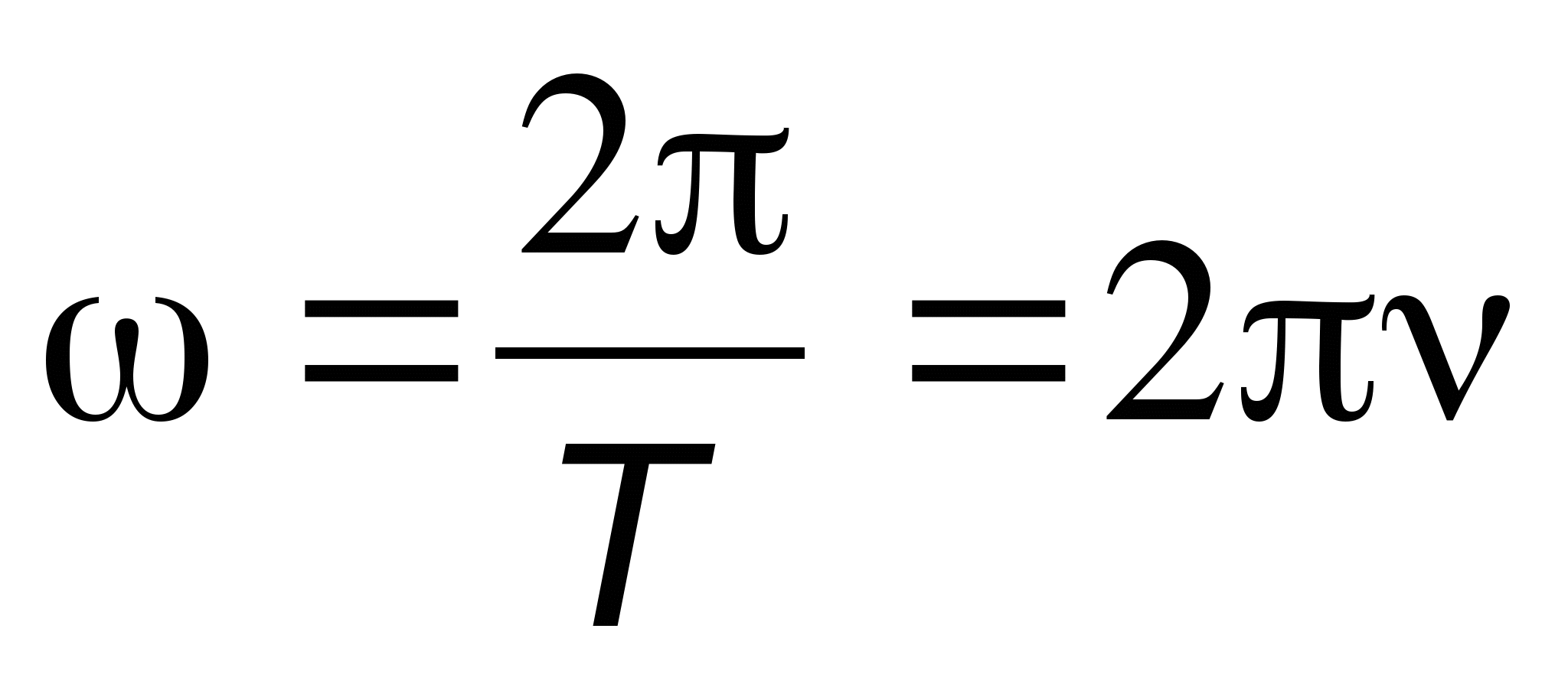 Минутная подача равняется произведению подачи на оборот на частоту вращения фрезы:
Минутная подача равняется произведению подачи на оборот на частоту вращения фрезы:
Fm = FoN = FzZN (мм/мин).
Глубиной фрезерования h (мм) называется расстояние между обработанной и необработанной поверхностями, измеряемое вдоль оси фрезы.
Шириной фрезерования b (мм) называется величина срезаемого припуска, измеренная в радиальном направлении, или ширина контакта заготовки и инструмента.
Производительность снятия материала Q (см3) – это объем удаляемого материала в единицу времени, определяемый глубиной, шириной обработки и величиной подачи.
Q = (h × b × Fm)/1000.
Формула линейной скорости (вращающийся объект)
Линейная скорость точки на вращающемся объекте зависит от ее расстояния от центра вращения. Угловая скорость — это угол, под которым объект движется за определенный промежуток времени. Угловая скорость измеряется в радианах в секунду (рад / с). В полном круге 2π радиана. На расстоянии r от центра вращения точка на объекте имеет линейную скорость, равную угловой скорости, умноженной на расстояние r. Единицами линейной скорости являются метры в секунду, м / с.
В полном круге 2π радиана. На расстоянии r от центра вращения точка на объекте имеет линейную скорость, равную угловой скорости, умноженной на расстояние r. Единицами линейной скорости являются метры в секунду, м / с.
линейная скорость = угловая скорость x радиус вращения
v = ωr
v = линейная скорость (м / с)
ω = угловая скорость (радиан / с)
r = радиус вращения (м)
Формула линейной скорости (вращающийся объект) Вопросы:
1) Электродрель включена и вращается со скоростью 10,0 оборотов в секунду (об / с). Диаметр сверла 4,00 мм. Какова линейная скорость точки на поверхности сверла в метрах в секунду?
Ответ: Первый шаг — найти угловую скорость сверла.Число оборотов в секунду необходимо перевести в радианы в секунду. В полном круге 2π радиана.
ω = 10,0 об / с
Расстояние между центром вращения и точкой на поверхности сверла равно радиусу. Диаметр сверла указан в миллиметрах. Радиус в метрах:
Радиус в метрах:
∴r = 0,002 м
Используя формулу v = ωr, линейная скорость точки на поверхности бурового долота равна
v = ωr
∴v = (62.8 радиан / с) (0,002 м)
Линейная скорость точки на поверхности сверла составляет приблизительно 0,126 м / с. Радианы — это единица «заполнителя», поэтому они не включаются при записи решенного значения для линейной скорости.
2) Еще вопрос.
Датчик, подключенный к автомобильному колесу, измеряет линейную скорость. Датчик находится на 0,080 м от центра вращения. В этом положении датчик показывает, что линейная скорость колеса равна 8.00 м / с. Если радиус колеса 0,220 м, какова линейная скорость на внешней кромке колеса?
Ответ: Линейная скорость различается на разных расстояниях от центра вращения, но угловая скорость одинакова во всех частях колеса. Чтобы решить эту проблему, сначала найдите угловую скорость, используя линейную скорость в положении датчика 0,080 м. Формулу v = ωr можно переформулировать, чтобы найти угловую скорость ω:
Формулу v = ωr можно переформулировать, чтобы найти угловую скорость ω:
Это также угловая скорость на внешней кромке колеса, где радиус r = 0.220 м. Формулу v = ωr можно снова использовать для определения линейной скорости на этом радиусе:
v = ωr
v = (100 рад / с) (0,220 м)
∴v = 22,0 м / с
Линейная скорость автомобильного колеса по внешнему краю 22,0 м / с.
Угловая и линейная скорость и
об / минPurplemath
По некоторым причинам учебники часто обращаются к вопросам угловой скорости, линейной скорости и числа оборотов в минуту (об / мин) вскоре после объяснения секторов круга, их площадей и длины дуги.
Длина дуги — это расстояние до части окружности; и линейное расстояние, которое преодолевает, скажем, велосипед, связано с радиусом его шин. Если вы отметите одну точку на передней шине велосипеда (скажем, точку напротив клапана шины) и посчитаете количество оборотов колеса, вы сможете найти количество окружностей окружности, на которые переместилась отмеченная точка.
Если вы отметите одну точку на передней шине велосипеда (скажем, точку напротив клапана шины) и посчитаете количество оборотов колеса, вы сможете найти количество окружностей окружности, на которые переместилась отмеченная точка.
MathHelp.com
Если вы «раскрутите» эти окружности, чтобы получить прямую линию, то вы найдете расстояние, которое проехал велосипед. Я думаю, что именно из-за такого рода взаимосвязи между различными показателями эта тема часто возникает на данном этапе исследования.
Во-первых, нам нужна техническая терминология и определения.
«Угловая скорость» — это показатель поворота в единицу времени. Он сообщает вам размер угла, под которым что-то вращается за определенный промежуток времени. Например, если колесо вращается шестьдесят раз за одну минуту, то его угловая скорость составляет 120π радиан в минуту. Затем угловая скорость измеряется в радианах в секунду, греческая строчная омега (ω) часто используется в качестве названия.
«Линейная скорость» — это мера расстояния в единицу времени. Например, если колесо в предыдущем примере имеет радиус 47 сантиметров, то каждый проход по окружности составляет 94π см, или около 295 см. Поскольку колесо совершает шестьдесят таких оборотов за одну минуту, общая пройденная длина составляет 60 × 94 & pi = 5 640π см, или около 177 метров, за одну минуту. (Это примерно 10,6 км / ч или около 6,7 миль / ч)
«Число оборотов в минуту», обычно сокращенно обозначаемое как «об / мин», является мерой вращения за единицу времени, но единица времени — всегда одна минута. И вместо того, чтобы указывать угол поворота, он просто дает количество оборотов. Когда вы смотрите на тахометр на приборной панели автомобиля, вы смотрите на текущие обороты двигателя автомобиля. В приведенном выше примере частота вращения будет просто «60».
И вместо того, чтобы указывать угол поворота, он просто дает количество оборотов. Когда вы смотрите на тахометр на приборной панели автомобиля, вы смотрите на текущие обороты двигателя автомобиля. В приведенном выше примере частота вращения будет просто «60».
«Частота» f — это мера вращения (или вибрации) за единицу времени, но единицей времени всегда является одна секунда. Единицей измерения частот является «герц», который обозначается как Гц.
Соотношение между частотой f (в Гц), об / мин и угловой скоростью ω (в радианах) показано ниже (все элементы в любой строке эквивалентны):
Однако вы можете обнаружить, что «угловая скорость» используется как синонимы (но только неофициально, не учеными) с оборотами в минуту или частотой.Кроме того, некоторые (например, физики) считают, что «угловая скорость» — это векторная величина, а ω — скалярная величина, называемая «угловой частотой».
Пожалуйста, не запоминайте эти потенциальные слияния и не беспокойтесь о том, какими могут быть «векторы» или «скаляры». Я говорю вам об этом, чтобы предупредить вас, что вы должны уделять очень пристальное внимание тому, как ваш конкретный учебник и ваш конкретный преподаватель определяют различные термины для этого конкретного класса.И знайте, что на следующем уроке термины и определения могут быть другими.
Колесо имеет диаметр 100 сантиметров. Если колесо поддерживает тележку, движущуюся со скоростью 45 километров в час, то какова частота вращения колеса с точностью до целого числа оборотов в минуту?
«Об / мин» — это количество оборотов колеса в минуту.Чтобы выяснить, сколько раз это колесо вращается за одну минуту, мне нужно найти (линейное или прямое) расстояние, пройденное (за минуту) при движении со скоростью 45 км / ч. Затем мне нужно найти длину окружности колеса и разделить общее поминутное (линейное) расстояние на это расстояние «один раз вокруг». Количество окружностей, которые умещаются внутри общего расстояния, — это количество оборотов колеса за этот период времени.
Затем мне нужно найти длину окружности колеса и разделить общее поминутное (линейное) расстояние на это расстояние «один раз вокруг». Количество окружностей, которые умещаются внутри общего расстояния, — это количество оборотов колеса за этот период времени.
Во-первых, я переведу (линейную) скорость тележки из км / ч в «сантиметры в минуту», используя то, что я узнал о преобразовании единиц.(Почему «сантиметры в минуту»? Потому что я ищу «обороты в минуту», поэтому минуты — лучшая единица времени, чем часы. Кроме того, диаметр указывается в сантиметрах, так что это лучшая единица длины, чем километры. )
Итак, расстояние, пройденное за одну минуту, составляет 75 000 сантиметров. Диаметр колеса — 100 см, поэтому радиус — 50 см, а длина окружности — 100π см. Сколько из этих окружностей (или оборотов колеса) умещается внутри 75 000 см? Другими словами, если бы я снял протектор этого колеса с тележки и разложил его ровно, то получилось бы расстояние 100π см. Сколько из этих длин укладывается на все расстояние, пройденное за одну минуту? Чтобы узнать, сколько из (этого) вписывается в такое количество (этого), я должен разделить (это) на (это), поэтому:
Сколько из этих длин укладывается на все расстояние, пройденное за одну минуту? Чтобы узнать, сколько из (этого) вписывается в такое количество (этого), я должен разделить (это) на (это), поэтому:
Затем, округляя до ближайшего целого числа оборотов (то есть округляя ответ до целого числа), мой ответ:
Примечание. Эта скорость не такая высокая, как может показаться: она чуть меньше четырех оборотов в секунду. Вы можете сделать это на своем велосипеде, не беспокоясь.Вот еще одно примечание: источник, из которого я получил свою схему для вышеупомянутого упражнения, использовал «угловую скорость» и «ω» для «числа оборотов в минуту». Да, в учебнике алгебры использовались неправильные единицы измерения.
Предыдущее упражнение давало информацию о скорости автомобиля и колесе. Отсюда мы нашли количество оборотов в минуту. Мы можем пойти и другим путем; мы можем начать с числа оборотов в минуту (плюс информацию о колесе) и найти скорость транспортного средства.
Велосипедное колесо имеет диаметр 78 см. Если колесо вращается со скоростью 120 оборотов в минуту, какова линейная скорость велосипеда в километрах в час? Округлите ответ до одного десятичного знака.
Линейная скорость — это расстояние по прямой, которое велосипед проходит за определенный период времени.Они дали мне количество оборотов колеса в минуту. Фиксированная точка на шине (скажем, камешек на протекторе шины) перемещает длину окружности за каждый оборот. Раскручивая это расстояние по земле, велосипед будет перемещаться по земле на одинаковое расстояние, по одной окружности за раз, за каждый оборот. Итак, этот вопрос просит меня найти длину окружности, а затем использовать ее, чтобы найти общее расстояние, пройденное за минуту.
Поскольку диаметр равен 78 см, то окружность равна C = 78π см. Разматывая путь шины по прямой линии на земле, это означает, что велосипед перемещается на 78π см вперед за каждый оборот шины. Таких оборотов в минуту 120, итого:
Разматывая путь шины по прямой линии на земле, это означает, что велосипед перемещается на 78π см вперед за каждый оборот шины. Таких оборотов в минуту 120, итого:
(78π см / об) × (120 об / мин) = 9,360π см / мин
Теперь мне нужно преобразовать это из сантиметров в минуту в километры в час:
Велосипед движется со скоростью около 17,6 км / ч.
… или около одиннадцати миль в час.
Предположим, что орбита Земли круглая с радиусом 93 000 000 миль, и пусть «один год» равен 365,25 дням. В этих условиях найдите линейную скорость Земли в милях в секунду. Округлите ответ до одного десятичного знака.
Скорость — это (линейное или эквивалентное прямолинейное) расстояние, пройденное за одну секунду, деленное на одну секунду. Они дали мне информацию за год, так что я начну с этого. Окружность круга с r = 93 000 000 миль будет линейным расстоянием, которое Земля преодолеет за один год.
Они дали мне информацию за год, так что я начну с этого. Окружность круга с r = 93 000 000 миль будет линейным расстоянием, которое Земля преодолеет за один год.
C = 2π (93000000 миль) / год = 186000000π миль / год
Это количество миль, пройденных за один год, но мне нужно количество миль, пройденных за одну секунду. В сутках двадцать четыре часа, в часе шестьдесят минут и в минуте шестьдесят секунд, поэтому общее количество секунд в этом году составляет:
Тогда линейная скорость, представляющая собой общее линейное расстояние, деленное на общее время и выраженное в единицах скорости, равна:
Тогда, округленная до одного десятичного знака, линейная скорость Земли равна:
«Эй!» Я слышу, как ты плачешь. «Когда мы собираемся использовать угловые меры для чего-нибудь?» Хотя многие («большинство»?) Упражнений в вашей книге, вероятно, будут похожи на вышеприведенные, иногда вы можете столкнуться с фактическими радианами и градусами.
«Когда мы собираемся использовать угловые меры для чего-нибудь?» Хотя многие («большинство»?) Упражнений в вашей книге, вероятно, будут похожи на вышеприведенные, иногда вы можете столкнуться с фактическими радианами и градусами.
Поезд движется со скоростью 10 миль в час по кривой радиусом 3000 футов. На какой угол повернется поезд за одну минуту? Округлить до ближайшего целого числа градусов.
«Кривая радиусом 3000 футов» означает, что, если бы я попытался плотно подогнать круг внутри кривой, наилучшим образом подошел бы круг с радиусом r = 3000 футов.Другими словами, я могу использовать факты круга, чтобы ответить на этот вопрос.
Поскольку радиус кривой измеряется в футах и мне нужно найти угол, пройденный за одну минуту, я начну с преобразования скорости миль в час в футы в секунду:
(10 миль / час) (5280 фут / миль) (1 час / 60 мин) = 880 фут / мин
Длина изогнутого пути, который проходит поезд, также является частью окружности круга. Итак, эти 880 футов и есть длина дуги, и теперь мне нужно найти поднятый угол (подразумеваемого) сектора круга:
Итак, эти 880 футов и есть длина дуги, и теперь мне нужно найти поднятый угол (подразумеваемого) сектора круга:
Но это значение в радианах (потому что это то, что использует формула длины дуги), и мне нужно, чтобы мой ответ был в градусах, поэтому мне нужно преобразовать:
Поезд поворачивает на угол примерно:
Представьте, что вы стоите в центре этого воображаемого круга (то есть на расстоянии трех тысяч футов от поворота, более чем в полумиле) и наблюдаете, как поезд движется по повороту.Если вы протянете руку на расстоянии вытянутой руки, сожмете кулак и, крепко удерживая средние пальцы вниз большим пальцем, поднимите мизинец и указательный пальцы, расстояние между ними будет примерно пятнадцать градусов. Поезд вряд ли продвинется дальше. Если бы вы держали кулак на расстоянии вытянутой руки и вытянули мизинец и большой палец, расстояние было бы около двадцати пяти градусов. Поезд не выйдет из ваших пальцев в отведенное время.
Поезд не выйдет из ваших пальцев в отведенное время.
(Иногда я узнаю самые крутые вещи, когда исследую проблемы со словами.Опять же, мое определение «крутой» может быть немного грустным ….)
URL: https://www.purplemath.com/modules/sectors3.htm
1.4: Скорость и угловая скорость
Длина дуги на окружности
В разделе 1.3 мы узнали, что величина угла в радианах равна длине дуги единичной окружности, связанной с этим углом.Таким образом, дуга длины 1 на единичной окружности образует угол в 1 радиан. Бывают моменты, когда также будет полезно знать длину дуг на других кругах, которые образуют тот же угол.
Рисунок \ (\ PageIndex {1} \): Дуги, заключенные под углом в 1 радиан.
На рисунке \ (\ PageIndex {1} \) внутренний круг имеет радиус 1, внешний круг имеет радиус \ (r \), а показанный угол имеет меру \ (\ theta \) радиан. . Таким образом, длина дуги на единичной окружности, образуемой углом, равна \ (\ theta \), и мы использовали s для обозначения длины дуги на окружности радиуса \ (r \), образуемой этим углом.
. Таким образом, длина дуги на единичной окружности, образуемой углом, равна \ (\ theta \), и мы использовали s для обозначения длины дуги на окружности радиуса \ (r \), образуемой этим углом.
Напомним, что длина окружности радиуса \ (r \) равна \ (2 \ pi r \), а окружность круга радиуса 1 равна \ (2 \ pi \). Следовательно, отношение длины дуги \ (s \) на окружности радиуса \ (r \), которая образует угол в \ (\ theta \) радиан к соответствующей дуге единичной окружности, равно \ (\ dfrac {2 \ pi r} {2 \ pi} = r \). Отсюда следует, что
\ [\ dfrac {s} {\ theta} = \ dfrac {2 \ pi r} {\ pi} \]
\ [s = r \ theta \]
Определение
На окружности радиуса \ (r \) длина s дуги, пересекаемая центральным углом с радианами, равна
.\ [s = r \ theta \]
Примечание
Важно помнить, что для расчета длины дуги необходимо измерить центральный угол в радианах.
(Непонятно, почему буква \ (s \) обычно используется для обозначения длины дуги.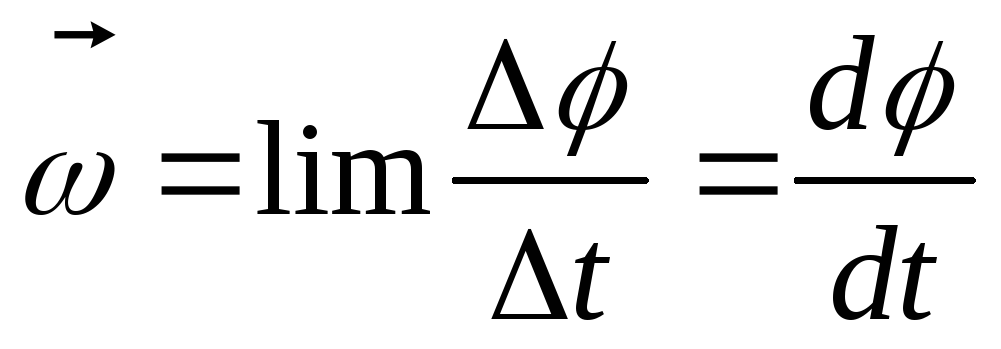 Одно из объяснений состоит в том, что дуга «расширяет» угол.)
Одно из объяснений состоит в том, что дуга «расширяет» угол.)
Упражнение \ (\ PageIndex {1} \)
Использование кружков в начале действия для этого раздела:
- Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 10 футов, которая образует центральный угол в \ (\ dfrac {\ pi} {2} \) радиан. Результат равен одной четверти длины окружности?
- Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 20 футов, которая образует центральный угол в \ (\ dfrac {\ pi} {2} \) радиан.\ circ}) = \ dfrac {11 \ pi} {90} \) и \ [s = r \ theta = (3ft) \ dfrac {11 \ pi} {90} \] \ [s = \ dfrac {11 \ pi} {30} \] Длина дуги составляет \ (\ dfrac {11 \ pi} {30} \) футов или около \ (1.1519 \) футов.
Почему радианы?
Градус знаком и удобен, так зачем вводить единицу радиан? Это хороший вопрос, но на него есть тонкий ответ. Как мы только что видели, длина \ (s \) дуги на окружности радиуса \ (r \), образуемой углом в \ (\ theta \) радиан, равна \ (s = r \ theta \), поэтому \ (\ theta = \ dfrac {s} {r} \). В результате радиан — это отношение двух длин (отношение длины дуги к радиусу окружности), что делает радиан безразмерной величиной. Таким образом, измерение в радианах можно рассматривать как действительное число. Это удобно для работы с длиной дуги (и угловой скоростью, как мы скоро увидим), а также будет полезно при изучении периодических явлений в главе 2. По этой причине радианная мера повсеместно используется в математике, физике и технике как в отличие от степеней, потому что, когда мы используем градусную меру, мы всегда должны учитывать градусное измерение в вычислениях.Это означает, что радианы на самом деле более естественны с математической точки зрения, чем градусы.
В результате радиан — это отношение двух длин (отношение длины дуги к радиусу окружности), что делает радиан безразмерной величиной. Таким образом, измерение в радианах можно рассматривать как действительное число. Это удобно для работы с длиной дуги (и угловой скоростью, как мы скоро увидим), а также будет полезно при изучении периодических явлений в главе 2. По этой причине радианная мера повсеместно используется в математике, физике и технике как в отличие от степеней, потому что, когда мы используем градусную меру, мы всегда должны учитывать градусное измерение в вычислениях.Это означает, что радианы на самом деле более естественны с математической точки зрения, чем градусы.
Линейная и угловая скорость
Связь между дугой на окружности и углом, который она образует, измеряемым в радианах, позволяет нам определять величины, связанные с движением по окружности. Объекты, движущиеся по круговой траектории, обладают двумя типами скорости: линейной и угловой скоростью .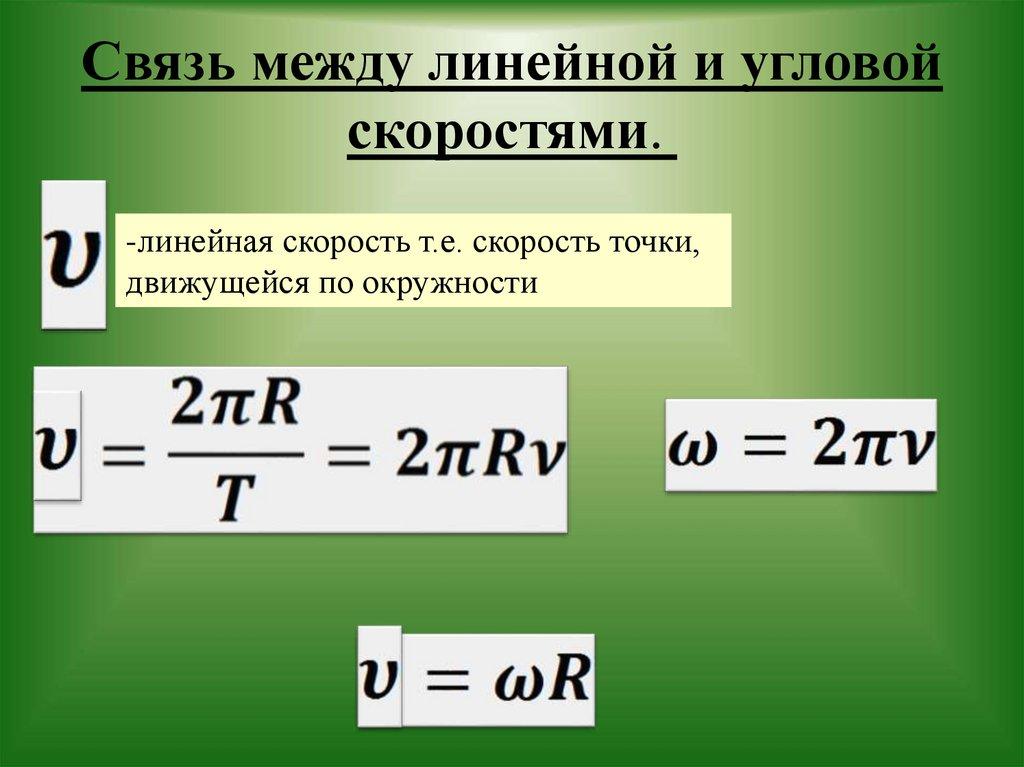 Подумайте о вращении на карусели. Если вы уроните камешек с края движущейся карусели, он не упадет прямо вниз.Вместо этого он продолжит двигаться вперед со скоростью, которую имела карусель в тот момент, когда камешек был выпущен. Это линейная скорость гальки. Линейная скорость измеряет, как длина дуги изменяется во времени.
Подумайте о вращении на карусели. Если вы уроните камешек с края движущейся карусели, он не упадет прямо вниз.Вместо этого он продолжит двигаться вперед со скоростью, которую имела карусель в тот момент, когда камешек был выпущен. Это линейная скорость гальки. Линейная скорость измеряет, как длина дуги изменяется во времени.
Рассмотрим точку \ (P \), движущуюся с постоянной скоростью по окружности радиуса \ (r \). Это называется равномерным круговым движением . Предположим, что P перемещается на расстояние s единиц за время \ (t \). Линейная скорость v точки \ (P \) — это расстояние, которое она преодолела, деленное на прошедшее время.То есть \ (v = \ dfrac {s} {t} \). Расстояние s — это длина дуги, и мы знаем, что \ (s = r \ theta \).
Определение: линейная скорость
Рассмотрим точку \ (P \), движущуюся с постоянной скоростью по окружности радиуса \ (r \). Линейная скорость \ (v \) точки \ (P \) определяется как
\ [v = \ dfrac {s} {t} = \ dfrac {r \ theta} {t} \]
где \ (\ theta \), измеренный в радианах, — это центральный угол, образованный дугой длиной \ (s \).
Другой способ измерить, насколько быстро объект движется с постоянной скоростью по круговой траектории, называется угловой скоростью. В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени.
Определение: угловая скорость
Рассмотрим точку P, движущуюся с постоянной скоростью по окружности радиуса r по дуге, соответствующей центральному углу измерения \ (\ theta \) (в радианах).Угловая скорость точки \ (\ omega \) — это радианная мера угла \ (\ theta \), деленная на время t, необходимое для того, чтобы охватить этот угол. То есть
\ [\ omega = \ dfrac {\ theta} {t}. \]
Примечание
Символ \ (\ omega \) — это строчная греческая буква «омега». Также обратите внимание, что угловая скорость не зависит от радиуса r.
Это несколько специализированное определение угловой скорости, которое немного отличается от обычного термина, используемого для описания скорости вращения точки по окружности. Этот срок составляет оборотов в минуту или оборотов в минуту . Иногда используется единица измерения оборотов в секунду . Лучший способ представить количество оборотов в минуту — использовать «дробную часть» \ (\ dfrac {rev} {min} \). Поскольку 1 оборот равен \ (2 \ pi \) радианам, мы видим, что если объект min движется со скоростью x оборотов в минуту, то
Этот срок составляет оборотов в минуту или оборотов в минуту . Иногда используется единица измерения оборотов в секунду . Лучший способ представить количество оборотов в минуту — использовать «дробную часть» \ (\ dfrac {rev} {min} \). Поскольку 1 оборот равен \ (2 \ pi \) радианам, мы видим, что если объект min движется со скоростью x оборотов в минуту, то
\ [\ omega = x \ dfrac {rev} {min} \ cdot \ dfrac {2 \ pi rad} {rev} = x (2 \ pi) \ dfrac {rad} {min}. \]
Упражнение \ (\ PageIndex {2} \)
Предположим, круглый диск вращается со скоростью 40 оборотов в минуту.Мы хотим определить линейную скорость v (в футах в секунду) точки, находящейся на расстоянии 3 футов от центра диска.
- Определите угловую скорость \ (\ omega \) точки в радианах в минуту. Подсказка : Используйте формулу \ [\ omega = x \ dfrac {rev} {min} \ cdot \ dfrac {2 \ pi rad} {rev}. \]
- Теперь мы знаем \ (\ omega = \ dfrac {\ theta} {t} \).
 Поэтому используйте формулу \ (v = \ dfrac {r \ theta} {t} \), чтобы определить \ (v \) в футах в минуту.
Поэтому используйте формулу \ (v = \ dfrac {r \ theta} {t} \), чтобы определить \ (v \) в футах в минуту. - Наконец, преобразуйте линейную скорость v из футов в минуту в футы в секунду.
- Ответ
1. Мы видим, что
\ [\ omega = 40 \ dfrac {rev} {min} \ times \ dfrac {2 \ pi \ space rad} {rev} \]
\ [\ omega = 80 \ pi \ dfrac {rad} {min} \ ]2. Результат части (а) дает
\ [v = r (\ dfrac {\ theta} {r}) = r \ omega \]
\ [v = (3ft) \ times 80 \ pi \ dfrac {rad} {min} \]
\ [v = 240 \ pi \ dfrac {ft} {min} \]3. Теперь мы переводим футы в минуту в футы в секунду.
\ [v = 240 \ pi \ dfrac {ft} {min} \ times \ dfrac {1 \ space min} {60 \ space sec} \]
\ [v = 4 \ pi \ dfrac {ft} {sec} \ около 12.566 \ dfrac {ft} {sec} \]
Обратите внимание, что в упражнении 1.18 после определения угловой скорости мы смогли определить линейную скорость. То, что мы сделали в этом конкретном случае, мы можем сделать в целом. Существует простая формула, которая напрямую связывает линейную скорость с угловой скоростью. Наша формула для линейной скорости: \ (v = \ dfrac {s} {t} \ dfrac {r \ theta} {t} \). Обратите внимание, что мы можем записать это как \ (v = r \ dfrac {\ theta} {t} \). То есть \ (v = r \ omega \)
То, что мы сделали в этом конкретном случае, мы можем сделать в целом. Существует простая формула, которая напрямую связывает линейную скорость с угловой скоростью. Наша формула для линейной скорости: \ (v = \ dfrac {s} {t} \ dfrac {r \ theta} {t} \). Обратите внимание, что мы можем записать это как \ (v = r \ dfrac {\ theta} {t} \). То есть \ (v = r \ omega \)
Примечание
Рассмотрим точку \ (P \), движущуюся с постоянной (линейной) скоростью \ (v \) по окружности радиуса \ (r \).Если угловая скорость равна \ (\ omega \), то
\ [v = r \ omega \]
Итак, в упражнении 1.18, когда мы определили, что \ (\ omega = 80 \ pi \ dfrac {rad} {min} \), мы могли бы определить v следующим образом:
\ [v = r \ omega = (3 \ space ft) (80 \ pi \ dfrac {rad} {min} = 240 \ pi \ dfrac {ft} {min}). \]
Обратите внимание, что, поскольку радианы «без единиц измерения», мы можем отбросить их при работе с уравнениями, такими как предыдущее.
Пример \ (\ PageIndex {1} \): линейная и угловая скорость
LP (долгоиграющая) или виниловая пластинка со скоростью 331 об / мин является аналоговым носителем для хранения звука и долгое время использовалась для прослушивания музыки. LP обычно имеет диаметр 12 или 10 дюймов. Чтобы работать с нашими формулами для линейной и угловой скорости, нам нужно знать угловую скорость в радианах в единицу времени. Для этого мы конвертируем \ (33 \ dfrac {1} {3} \) оборотов в минуту в радианы в минуту. Мы будем использовать тот факт, что \ (33 \ dfrac {1} {3} = \ dfrac {100} {3} \)
LP обычно имеет диаметр 12 или 10 дюймов. Чтобы работать с нашими формулами для линейной и угловой скорости, нам нужно знать угловую скорость в радианах в единицу времени. Для этого мы конвертируем \ (33 \ dfrac {1} {3} \) оборотов в минуту в радианы в минуту. Мы будем использовать тот факт, что \ (33 \ dfrac {1} {3} = \ dfrac {100} {3} \)
\ [\ omega = \ dfrac {100} {3} \ dfrac {rev} {min} \ times \ dfrac {2 \ pi \ space rad} {1 \ space rev} = \ dfrac {200 \ pi} {3 } \ dfrac {rad} {min} \]
Теперь мы можем использовать формулу v D r! для определения линейной скорости точки на краю 12-дюймовой пластинки.Радиус 6 дюймов и так
\ [v = r \ omega = (6 \ пробел дюймов) (\ dfrac {200 \ pi} {3} \ dfrac {rad} {min}) = 400 \ pi \ dfrac {дюймы} {min} \]
Было бы удобнее выразить это как десятичное значение в дюймах в секунду. Получаем
\ [v = 400 \ pi \ dfrac {дюймы} {мин} \ times \ dfrac {1 \ space min} {60 \ space sec} \ приблизительно 20. 944 \ dfrac {дюймы} {sec} \]
Линейная скорость составляет приблизительно 20,944 дюйма в секунду.
Упражнение \ (\ PageIndex {3} \)
Для этих задач мы предположим, что Земля представляет собой сферу с радиусом 3959 миль.Когда Земля вращается вокруг своей оси, человек, стоящий на Земле, будет путешествовать по кругу, перпендикулярному оси.
- Земля вращается вокруг своей оси каждые \ (24 \) часа. Определите угловую скорость Земли в радианах в час. (Оставьте свой ответ в виде числа �� \ (\ pi \).)
- Когда Земля вращается, человек, стоящий на экваторе, будет путешествовать по кругу с радиусом 3959 миль. Определите линейную скорость этого человека в милях в час.\ circ \) север будет двигаться по кругу радиусом 2800 миль. Определите линейную скорость этого человека в милях в час и футах в секунду.
- Ответ
- Один оборот соответствует \ (2 \ pi \) радианам. Итак, \ [\ omega = \ dfrac {2 \ pi \ space rad} {24 \ space hr} = \ dfrac {\ pi \ space rad} {12 \ space hr}. \]
- Для определения линейной скорости используем формулу \ (v = r \ omega \) \ [v = r \ omega = (3959mi) (\ dfrac {\ pi} {12} \ dfrac {rad} {hr}) = \ dfrac {3959 \ pi} {12} \ dfrac {mi} {hr} \] Линейная скорость приблизительно равна 1036.
 5 миль в час.
5 миль в час. - Для определения линейной скорости используем формулу \ (v = r \ omega \) \ [v = r \ omega = (2800mi) (\ dfrac {\ pi} {12} \ dfrac {rad} {hr}) = \ dfrac {2800 \ pi} {12} \ dfrac {mi} {hr} \] Линейная скорость составляет примерно 733,04 мили в час. Чтобы преобразовать это в футы в секунду, мы используем тот факт, что в одной миле 5280 футов, в часе 60 минут и в минуте 60 секунд. Итак
\ [v = (\ dfrac {2800 \ pi} {12} \ dfrac {mi} {hr}) (\ dfrac {5280 \ space ft} {1 \ space mi}) (\ dfrac {1 \ space hr } {60 \ space min}) (\ dfrac {1 \ space min} {60 \ space sec}) = \ dfrac {(2800 \ pi) (5280)} {12 \ cdot 60 \ cdot 60} \ dfrac {ft } {сек} \]
Таким образом, линейная скорость приблизительно равна \ (1075.1 \) футов в секунду.
Сводка
В этом разделе мы изучили следующие важные концепции и идеи:
- На окружности радиуса \ (r \) длина дуги \ (s \), пересеченная центральным углом с радианной мерой, равна \ [s = r \ theta \]
- Равномерное круговое движение — это когда точка движется с постоянной скоростью по окружности круга.
 Линейная скорость — это длина дуги, пройденная точкой, деленная на истекшее время.В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки — это радианная мера угла, деленная на время, необходимое для того, чтобы подметать этот угол.
Линейная скорость — это длина дуги, пройденная точкой, деленная на истекшее время.В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки — это радианная мера угла, деленная на время, необходимое для того, чтобы подметать этот угол. - Для точки \ (P \), движущейся с постоянной (линейной) скоростью v по окружности радиуса \ (r \), имеем \ [v = r \ omega \], где \ (\ omega \) — угловая скорость точки.
Кинематика вращательного движения | Физика
Цели обучения
К концу этого раздела вы сможете:
- Соблюдайте кинематику вращательного движения.
- Составьте уравнения кинематики вращения.
- Оцените стратегии решения проблем для вращательной кинематики.
Просто используя нашу интуицию, мы можем начать видеть, как вращательные величины, такие как θ , ω и α , связаны друг с другом.Например, если колесо мотоцикла имеет большое угловое ускорение в течение довольно длительного времени, оно быстро вращается и совершает много оборотов. С технической точки зрения, если угловое ускорение α колеса велико в течение длительного периода времени t , то конечная угловая скорость ω и угол поворота θ будут большими. Вращательное движение колеса в точности аналогично тому, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим.
Кинематика — это описание движения. Кинематика вращательного движения описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем. Начнем с нахождения уравнения, связывающего ω , α и t . Чтобы определить это уравнение, вспомним известное кинематическое уравнение поступательного или прямолинейного движения:
[латекс] v = {v} _ {0} + {at} \\ [/ latex] (константа a )
Обратите внимание, что во вращательном движении a = a t , и с этого момента мы будем использовать символ a для тангенциального или линейного ускорения.Как и в линейной кинематике, мы предполагаем, что a является постоянным, что означает, что угловое ускорение α также является постоянным, потому что a = rα . Теперь давайте подставим v = rω и a = rα в приведенное выше линейное уравнение:
rω = rω 0 + крыс.
Радиус r сокращается в уравнении, давая
ω = ω 0 + ат. (постоянная a )
, где ω 0 — начальная угловая скорость. Это последнее уравнение представляет собой кинематическое соотношение между ω , α и t , то есть оно описывает их соотношение без ссылки на силы или массы, которые могут влиять на вращение. По форме он аналогичен своему переводному аналогу.
Выполнение подключений Кинематика вращательного движения полностью аналогична поступательной кинематике, впервые представленной в «Одномерной кинематике».Кинематика занимается описанием движения без учета силы или массы. Мы обнаружим, что поступательные кинематические величины, такие как смещение, скорость и ускорение, имеют прямые аналоги во вращательном движении.Исходя из четырех кинематических уравнений, которые мы разработали в Одномерной кинематике, мы можем вывести следующие четыре кинематических уравнения вращения (представленные вместе с их аналогами для поступательного движения):
| Вращающийся | Трансляционный | |
|---|---|---|
| [латекс] \ theta = \ bar {\ omega} t \\ [/ latex] | [латекс] x = \ bar {v} t \\ [/ latex] | |
| ω = ω 0 + αt | v = v o + при | (постоянная α , a ) |
| [латекс] \ theta = {\ omega} _ {0} t + \ frac {1} {2} {\ alpha t} ^ {2} \\ [/ latex] | [латекс] x = {v} _ {0} t + \ frac {1} {2} {\ text {at}} ^ {2} \\ [/ latex] | (постоянная α , a ) |
| ω 2 = ω 0 2 + 2 α θ | v 2 = v o 2 + 2ax | (постоянная α , a ) |
В этих уравнениях индекс 0 обозначает начальные значения ( θ 0 , x 0 и t 0 — начальные значения) и среднюю угловую скорость [латекс] \ bar {\ omega} \\ [/ latex] и средняя скорость [latex] \ bar {v} \\ [/ latex] определяются следующим образом:
[латекс] \ bar {\ omega} = \ frac {{\ omega} _ {0} + \ omega} {2} \ text {и} \ overline {v} = \ frac {{v} _ {0} + v} {2} \\ [/ латекс].
Уравнения, приведенные выше в таблице 1, могут использоваться для решения любой задачи вращательной или поступательной кинематики, в которой a и α постоянны.
Стратегия решения проблем для вращательной кинематики- Изучите ситуацию, чтобы определить, задействована ли кинематика вращения (вращательное движение) . Должно быть задействовано вращение, но без учета сил или масс, влияющих на движение.
- Определите, что именно необходимо определить в проблеме (определите неизвестные) .Набросок ситуации полезен.
- Составьте список того, что дано или может быть выведено из проблемы, как указано (определить известные) .
- Решите соответствующее уравнение или уравнения для величины, которую необходимо определить (неизвестное) . Может быть полезно подумать о переводном аналоге, потому что теперь вы знакомы с таким движением.
- Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численные решения вместе с единицами измерения .Обязательно используйте радианы для углов.
- Проверьте свой ответ, чтобы узнать, разумен ли он: Имеет ли смысл ваш ответ ?
Пример 1. Расчет ускорения рыболовной катушки
Глубоководный рыбак ловит большую рыбу, которая отплывает от лодки, стягивая леску со своей рыболовной катушки. Вся система изначально находится в состоянии покоя, и леска разматывается с катушки на радиусе 4,50 см от оси вращения. Катушке дается угловое ускорение 110 рад / с 2 для 2.00 с, как показано на рисунке 1. (a) Какова конечная угловая скорость барабана? (b) С какой скоростью леска покидает катушку по истечении 2,00 с? (c) Сколько оборотов делает катушка? (d) Сколько метров лески сошло с катушки за это время?
СтратегияВ каждой части этого примера стратегия такая же, как и для решения задач линейной кинематики. В частности, идентифицируются известные значения, и затем ищется взаимосвязь, которая может использоваться для решения неизвестного.
Решение для (a)Здесь даны α и t , и необходимо определить ω . Наиболее простое уравнение для использования: ω = ω 0 + αt , потому что неизвестное уже находится на одной стороне, а все остальные члены известны. Это уравнение утверждает, что
ω = ω 0 + αt .
Нам также дано, что ω 0 = 0 (начинается с состояния покоя), так что
ω = 0 + (110 рад / с 2 ) (2.00 с) = 220 рад / с
Решение для (b)
Теперь, когда ω известно, скорость v проще всего найти, используя соотношение
v = rω ,
, где радиус r катушки задан равным 4,50 см; таким образом,
v = (0,0450 м) (220 рад / с) = 9,90 м / с.
Еще раз обратите внимание, что радианы всегда должны использоваться в любых вычислениях, касающихся линейных и угловых величин.{2} = \ text {220 рад}. \ End {array} \\ [/ latex]
Преобразование радианов в обороты дает
[латекс] \ theta = (220 \ text {rad}) \ frac {1 \ text {rev}} {2 \ pi \ text {rad}} = 35.0 \ text {rev} \\ [/ latex]
Решение для (d)Количество метров лески x , которое может быть получено через ее соотношение с θ:
x = rθ = (0,0450 м) (220 рад) = 9,90 м.
ОбсуждениеЭтот пример показывает, что отношения между вращательными величинами очень похожи на отношения между линейными величинами.Мы также видим в этом примере, как связаны линейные и вращательные величины. Ответы на вопросы реалистичны. После разматывания в течение двух секунд катушка вращается со скоростью 220 рад / с, что составляет 2100 об / мин. (Неудивительно, что барабаны иногда издают высокие звуки.) Длина разыгранной лески составляет 9,90 м, что примерно соответствует ситуации, когда клюет большая рыба.
Рис. 1. Леска, сходящая с вращающейся катушки, движется линейно. В примерах 10.3 и 10.4 рассматриваются отношения между вращательными и линейными величинами, связанными с рыболовной катушкой.
Пример 2. Расчет продолжительности, когда рыболовная катушка замедляется и останавливается
Теперь давайте посмотрим, что произойдет, если рыбак затормозит вращающуюся катушку, получив угловое ускорение -300 рад / с 2 . Сколько времени нужно, чтобы барабан остановился?
СтратегияНас просят найти время t , за которое барабан остановится. Начальные и конечные условия отличаются от условий в предыдущей задаче, в которой использовалась та же рыболовная катушка.Теперь мы видим, что начальная угловая скорость равна ω 0 = 220 рад / с, а конечная угловая скорость ω равна нулю. Угловое ускорение составляет α = -300 рад / с 2 . Изучая доступные уравнения, мы видим, что все величины, кроме t , известны в ω = ω 0 + αt , что упрощает использование этого уравнения.
РастворУравнение утверждает
ω = ω 0 + αt .{2}} = 0 \ text {.} \ Text {733 s} \\ [/ latex].
ОбсуждениеОбратите внимание, что следует проявлять осторожность со знаками, указывающими направление различных величин. Также обратите внимание, что время остановки барабана довольно мало, потому что ускорение довольно большое. Леска иногда ломается из-за участвующих в ней ускорений, и рыбаки часто позволяют рыбе плавать некоторое время, прежде чем затормозить катушку. Уставшая рыба будет медленнее, требуя меньшего ускорения.
Пример 3. Расчет медленного ускорения поездов и их колес
Большие грузовые поезда очень медленно ускоряются. Предположим, что один такой поезд ускоряется из состояния покоя, придавая своим колесам радиусом 0,350 м угловое ускорение 0,250 рад / с 2 . После того, как колеса совершат 200 оборотов (предполагая отсутствие пробуксовки): (а) Как далеко поезд продвинулся по рельсам? б) Какова конечная угловая скорость колес и линейная скорость поезда?
СтратегияВ части (а) нас просят найти x , а в (b) нас просят найти ω и v .Нам даны число оборотов θ , радиус колес r и угловое ускорение α .
Решение для (a)Расстояние x очень легко найти из отношения между расстоянием и углом поворота:
[латекс] \ theta = \ frac {x} {r} \\ [/ latex].
Решение этого уравнения для x дает
x = rθ.
Перед использованием этого уравнения мы должны преобразовать количество оборотов в радианы, потому что мы имеем дело с соотношением между линейными и вращательными величинами:
[латекс] \ theta = \ left (\ text {200} \ text {rev} \ right) \ frac {2 \ pi \ text {rad}} {\ text {1 rev}} = \ text {1257} \ текст {рад} \\ [/ латекс].{1/2} \\ & = & \ text {25,1 рад / с.} \ End {array} \\ [/ latex]
Мы можем найти линейную скорость поезда, v , через ее отношение к ω :
v = rω = (0,350 м) (25,1 рад / с) = 8,77 м / с.
ОбсуждениеПройденное расстояние довольно велико, а конечная скорость довольно мала (чуть менее 32 км / ч).
Существует поступательное движение даже для чего-то, вращающегося на месте, как показано в следующем примере.На рис. 2 изображена муха на краю вращающейся пластины микроволновой печи. В приведенном ниже примере вычисляется общее пройденное расстояние.
Рис. 2. На изображении представлена микроволновая пластина. Муха совершает обороты, пока еда разогревается (вместе с мухой).
Пример 4. Расчет расстояния, пройденного мухой на краю плиты микроволновой печи
Человек решает использовать микроволновую печь, чтобы разогреть обед. При этом муха случайно влетает в микроволновку, приземляется на внешний край вращающейся пластины и остается там.Если тарелка имеет радиус 0,15 м и вращается со скоростью 6,0 об / мин, рассчитайте общее расстояние, пройденное мухой за 2,0-минутный период приготовления. (Игнорируйте время запуска и замедления.)
СтратегияСначала найдите общее количество оборотов θ , а затем пройденное линейное расстояние x . [Latex] \ theta = \ bar {\ omega} t \\ [/ latex] можно использовать, чтобы найти θ потому что [latex] \ bar {\ omega} \\ [/ latex] задано равным 6,0 об / мин.
РастворВвод известных значений в [latex] \ theta = \ bar {\ omega} t \\ [/ latex] дает
[латекс] \ theta = \ bar {\ omega} t = \ left (\ text {6.0 об / мин} \ right) \ left (\ text {2.0 min} \ right) = \ text {12 rev} \\ [/ latex].
Как всегда, необходимо преобразовать обороты в радианы перед вычислением линейной величины, такой как x , из угловой величины, такой как θ :
[латекс] \ theta = \ left (\ text {12 rev} \ right) \ left (\ frac {2 \ pi \ text {rad}} {\ text {1 rev}} \ right) = 75,4 \ text { рад} \\ [/ латекс].
Теперь, используя соотношение между x и θ , мы можем определить пройденное расстояние:
x = rθ = (0.15 м) (75,4 рад) = 11 м.
ОбсуждениеНеплохая поездка (если выживет)! Обратите внимание, что это расстояние — это общее расстояние, пройденное мухой. Смещение фактически равно нулю для полных оборотов, потому что они возвращают муху в исходное положение. Различие между общим пройденным расстоянием и перемещением было впервые отмечено в «Одномерной кинематике».
Проверьте свое понимание
Кинематика вращения имеет множество полезных взаимосвязей, часто выражаемых в форме уравнений.Являются ли эти отношения законами физики или они просто описательны? (Подсказка: тот же вопрос относится к линейной кинематике.)
РастворВращательная кинематика (как и линейная кинематика) носит описательный характер и не отражает законы природы. С помощью кинематики мы можем описать многие вещи с большой точностью, но кинематика не учитывает причины. Например, большое угловое ускорение описывает очень быстрое изменение угловой скорости без учета его причины.
Сводка раздела
Задачи и упражнения
1. С помощью струны гироскоп из состояния покоя разгоняется до 32 рад / с за 0,40 с. а) Каково его угловое ускорение в рад / с 2 ? б) Сколько революций происходит в процессе?
2. Допустим, на компакт-диске оказался кусок пыли. Если скорость вращения компакт-диска составляет 500 об / мин, а пылинка находится на расстоянии 4,3 см от центра, каково общее расстояние, пройденное пылью за 3 минуты? (Игнорируйте ускорения из-за вращения компакт-диска.)
3. Гироскоп замедляется от начальной скорости 32,0 рад / с до 0,700 рад / с 2 . а) Сколько времени нужно, чтобы успокоиться? б) Сколько оборотов он делает перед остановкой?
4. При очень быстрой остановке автомобиль замедляется со скоростью 700 м / с 2 .
(a) Каково угловое ускорение его шин радиусом 0,280 м, если предположить, что они не скользят по тротуару?
(b) Сколько оборотов делают шины перед остановкой, если их начальная угловая скорость равна 95.0 рад / с?
(c) Сколько времени нужно автомобилю, чтобы полностью остановиться?
(d) Какое расстояние машина проезжает за это время?
(e) Какова была начальная скорость автомобиля?
(f) Кажутся ли полученные значения разумными, учитывая, что эта остановка происходит очень быстро?
Рис. 3. Йо-йо — это забавные игрушки, которые демонстрируют значительную физику и созданы для повышения производительности на основе физических законов. (Источник: Beyond Neon, Flickr)
5. Повседневное применение: Предположим, у йо-йо есть центральный вал с цифрой 0.Радиусом 250 см и натягивается его струна.
(a) Если струна неподвижна и йо-йо ускоряется от нее со скоростью 1,50 м / с 2 , каково угловое ускорение йо-йо?
(b) Какова угловая скорость через 0,750 с, если она начинается из состояния покоя?
(c) Внешний радиус йо-йо составляет 3,50 см. Каково тангенциальное ускорение точки на краю?
Глоссарий
- кинематика вращательного движения:
- описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем
Избранные решения проблем и упражнения
1.{2} \\ [/ latex] (b) 1.0 rev
3. (а) 45,7 с (б) 116 изм.
5. (а) 600 рад / с 2 (б) 450 рад / с (в) 21,0 м / с
Движение по кругу — Математика A-Level, редакция
Эта страница описывает движение по кругу.
Угловая скорость
Представьте, что объект движется по круговой траектории.
Угловая скорость — это скорость изменения угла (который я пометил «а»).Таким образом, он измеряет, насколько быстро объект движется по кругу.
Угловая скорость обычно измеряется в радиан, в секунду (рад с -1 ), то есть на сколько радиан проходит частица за секунду. Кроме того, его можно измерить в оборотах в секунду, т.е. сколько полных кругов объект проходит за секунду.
Существует формула, соединяющая «нормальную» скорость (обычно называемую «линейной скоростью») и угловую скорость:
где v — линейная скорость, r — радиус окружности, а w — угловая скорость.
Пример
Частица движется по окружности радиусом 10 см. Угловая скорость — 2 рад с -1 . Найдите (линейную) скорость.
Нам нужен радиус в метрах, то есть 0,1 м. Используя формулу выше, получаем:
v = 0,1 × 2 = 0,2
Значит скорость 0,2 мс -1 .
Обратите внимание, что если вам дана угловая скорость в оборотах в секунду, вам сначала нужно будет преобразовать ее в радианы в секунду.Для этого помните, что 1 оборот в секунду равен 2p радианам в секунду, потому что в круге 2p радиан.
Радиальное ускорение
Если тело движется по окружности, даже если оно движется с постоянной скоростью, оно ускоряется. Это потому, что он меняет направление (не движется по прямой).
Направление этого ускорения — к центру круга, а его величина определяется выражением:
где v — скорость, а r — радиус круга.
Используя нашу формулу выше, это также можно записать как:
Какой из них вы будете использовать, будет зависеть от того, имеете ли вы дело со скоростью или угловой скоростью.
Ускорение происходит из-за действующей силы:
Представьте, что вы едете в машине, которая быстро свернет за поворот налево. Вы почувствуете силу, тянущую вас в сторону (левую сторону). Это сила, вызывающая ускорение. Сила действует по направлению к центру круга.
Конический маятник
Конический маятник выглядит примерно так:
P — частица.AP — это строка. P движется по синему кругу с угловой скоростью w.
Пример
Предположим, что у нас есть конический маятник, как указано выше, где частица имеет массу 2 кг, радиус круга, по которому движется частица, составляет 0,5 м, а угол при A равен 45 градусам. Найдите угловую скорость P.
Вес 2 г (W = мг), где g — ускорение свободного падения.
Вертикальное разрешение: Tcos45 = 2g
Следовательно (√2T) / 2 = 2g, поэтому T = 2√2 g (1)
Теперь используйте 2-й закон Ньютона, чтобы найти уравнение движения в радиальном направлении:
(«F = m r w 2 »)
Tsin45 = 2 × 5 × w 2
Используйте (1), чтобы исключить T:
2√2 g × (√2) / 2 = 10w 2
g / 5 = w 2
Таким образом, w = √ (g / 5)
Принимая g = 9.8, получаем, что угловая скорость составляет 1,4 рад с -1
Движение на береговой поверхности
Теперь рассмотрим движение частицы по «наклонной поверхности». Под этим я имею в виду, например, кольцевую гоночную трассу, которая наклонена вверх от центра, чтобы помочь автомобилям / мотоциклам оставаться на трассе на высоких скоростях.
Так вот, если машина едет очень быстро, она будет скользить по склону, двигаясь по кругу. Если он будет двигаться медленно, он поскользнется.
Если автомобиль не имеет тенденции к скольжению, силы и ускорение на теле будут такими, как на этой диаграмме (сила трения отсутствует):
Однако, если бы машина двигалась быстрее, она бы соскользнула по склону при движении по трассе. Поэтому сила трения будет действовать, пытаясь предотвратить это:
Вращение
Чтобы описать движение вращающихся или вращающихся объектов, нам нужен более естественный набор переменных, чем x, v и a, которые мы использовали до сих пор.Например, каждая точка вращающегося объекта имеет разную скорость, но мы можем определить угловую скорость, одинаковую для всех точек. v пропорционально r, поэтому все, что нам действительно нужно сделать, это разделить r.
Угловые переменные
Угловое смещение (угол): θ = s / r
Угловая скорость: ω = v / r
Угловое ускорение: α = a t / r
Обратите внимание, что угловое ускорение связано с тангенциальным ускорением, а не с центростремительным ускорением.Угловое ускорение возникает только при изменении скорости вращения.
Если угловая скорость постоянна, то скорость точки на вращающемся объекте равна:
v = 2πr / T
где T — период, время, которое нужно пройти один раз.
Угловая скорость ω = v / r = 2π / T
Эти угловые переменные являются векторами, как и их собратья по прямолинейному движению. В какую сторону они указывают? Возьмите пальцы правой руки и согните их, как вращается предмет.Высуньте большой палец наружу, и вы получите направление угловой скорости. Угловое ускорение находится в том же направлении, если объект ускоряет свое вращение, и в противоположном направлении, если он замедляется.
Мы часто будем использовать по часовой стрелке и против часовой стрелки, чтобы указать направление. Как и в случае прямолинейного движения, мы можем определить положительное направление в зависимости от того, что удобно в конкретном случае.
Соединение с прямолинейным движением
Мы сосредоточимся на вращении вокруг единственной оси вращения, которое аналогично одномерному прямолинейному движению.В принципе, если вы понимаете одномерное движение, вы можете выполнять вращение — вращательное движение — это просто прямолинейное движение, свернутое в круг.
Смещение, скорость и ускорение имеют эквиваленты вращения. Существуют также вращательные эквиваленты массы, силы, законов Ньютона, кинетической энергии, импульса и т. Д. Любое уравнение, которое мы использовали для прямолинейного движения, имеет вращательную форму, которую можно найти, подставив эквивалентные вращательные переменные.
Например, как связаны углы, угловые скорости и угловые ускорения? Таким же образом линейные переменные:
Угловая скорость — это скорость изменения угла
Мгновенная угловая скорость: ω = d θ / dt
Средняя угловая скорость = ω ср. = Δ θ / Δt
Δ θ = ∫ ω dt
Угловое ускорение — это скорость изменения угловой скорости
Мгновенное угловое ускорение: α = d ω / dt
Среднее угловое ускорение = α ср. = Δ ω / Δt
Δ ω = ∫ α dt
Уравнения постоянного ускорения
Эти уравнения связывают смещение, скорость, ускорение и время и применимы при следующих условиях:
- ускорение постоянное
- движение отсчитывается от t = 0
- тот факт, что несколько переменных являются векторами, учитывается соответствующими знаками плюс и минус
| Прямолинейное движение | Вращательное движение |
|---|---|
| v = v o + at | ω = ω o + α t |
| x — x o = v o t + ½ при 2 | θ — θ o = ω o t + ½ α t 2 |
| x o = ½ (v + v o ) t | θ — θ o = ½ (ω + ω o ) t |
| v 2 = v o 2 + 2 a (x — x o ) | ω 2 = ω o 2 + 2 α (θ — θ o ) |
Пример задачи
Вы находитесь на колесе обозрения, которое вращается со скоростью 1 оборот каждые 8 секунд.Оператор колеса обозрения решает остановить его и включает тормоз. Тормоз производит постоянное ускорение -0,11 радиан / с 2 .
(a) Если ваше сиденье на колесе обозрения находится на расстоянии 4,2 м от центра колеса, какова ваша скорость, когда колесо вращается с постоянной скоростью до того, как будет применен тормоз?
(b) Сколько времени нужно, чтобы колесо обозрения остановилось?
(c) Сколько оборотов делает колесо, когда оно останавливается?
(d) Как далеко вы проедете, когда колесо замедлится?
θ o = 0 θ =? ω o = 0.785 рад / с ω = 0 α = -0,11 рад / с 2 |
Решение
(a) Колесо вращается со скоростью 1 оборот каждые 8 секунд, или 0,125 об / с. Это начальная угловая скорость. Часто удобнее всего работать с угловой скоростью в радианах / с; выполнение преобразования дает:
ω = 0,125 об / с * 2π рад / об = 0,785 рад / с
Ваша скорость — это просто угловая скорость, умноженная на ваше расстояние от центра колеса:
v = r ω = 4.2 * 0,785 = 3,30 м / с
(b) Мы рассчитали начальную угловую скорость, конечная угловая скорость равна нулю, а угловое ускорение равно -0,11 рад / с 2 . Это позволяет определить время остановки:
ω = ω o + α t
t = (ω — ω o ) / α
t = (0 — 0,785) / (- 0,11) = 7,14 с
(c) Один из способов определить количество оборотов, которое совершает колесо при замедлении до остановки, — это определить угол, на который оно движется:
θ — θ o = ω o t + ½ α t 2
θ = (0.785 * 7,14) + ½ (-0,11) * (7,14) 2 = 2,80 радиан
Это может быть преобразовано в обороты:
2,80 рад / (2π рад / об) = 0,446 оборота.
(d) Чтобы определить расстояние, которое вы прошли, пока колесо замедлялось, угловое смещение (в радианах) можно преобразовать в смещение, умножив его на r:
s = rθ = 4,2 * 2,80 = 11,8 м
Калькулятор угловой скорости
Как найти угловую скорость Земли?
Как насчет того, чтобы использовать наш калькулятор угловой скорости? Оценим угловую скорость Земли! Во-первых, мы рассматриваем скорость вращения.Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за 23 ч 56 мин 4 с , что составляет примерно 23,934 ч . Полное вращение составляет угол 2π рад , поэтому результирующая угловая скорость равна:
ω₁ = 2π рад / 23,934 h = 0,2625 рад / час = 0,00007292 рад / с ,
или 7,292 * 10⁻⁵ рад / с (в экспоненциальном представлении).
Теперь, когда мы знаем угловую скорость вращения Земли, мы можем оценить ее линейную скорость на экваторе.Для этого нам нужен радиус Земли, который составляет примерно 6,371 км . Единственное, что нам нужно сделать, это вставить значения во вторую формулу угловой скорости:
v₁ = r₁ * ω₁ = 6,371 км * 7,292 * 10⁻⁵ рад / с = 0,4646 км / с = 464,6 м / с .
Чтобы вычислить линейную скорость относительно центра Земли, все, что вам нужно сделать, это умножить полученный результат на косинус широты вашего города. Кстати, вы когда-нибудь задумывались, почему ракеты обычно запускаются с космодрома, расположенного вблизи экватора, а не с полюсов? Ну, почти 500 м / с ускорение в начале — это значительная часть его конечной скорости.Таким образом, перемещение стартовой точки как можно ближе к экватору уменьшает количество топлива, необходимого для разгона ракеты.
После этого мы можем еще раз спросить, как найти угловую скорость Земли, но на этот раз орбитальную. Все вычисления аналогичны, но нам нужно изменить время с 23,943 ч на один год, что составляет примерно 365,25 дней.

 Определите угловую скорость.
Определите угловую скорость. Значит равномерное движение по окружности – ускоренное движение! Точка совершает перемещение с постоянной по модулю скоростью, следовательно:.
Значит равномерное движение по окружности – ускоренное движение! Точка совершает перемещение с постоянной по модулю скоростью, следовательно:.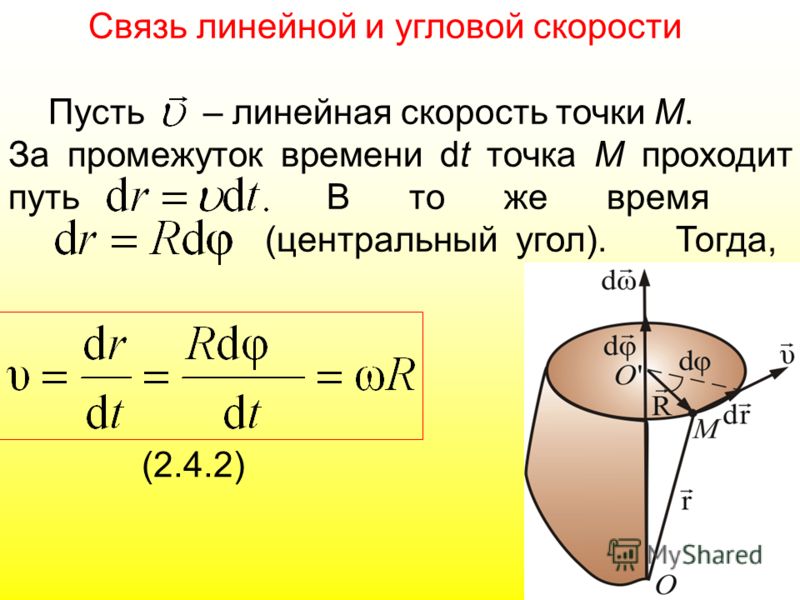
 Поэтому используйте формулу \ (v = \ dfrac {r \ theta} {t} \), чтобы определить \ (v \) в футах в минуту.
Поэтому используйте формулу \ (v = \ dfrac {r \ theta} {t} \), чтобы определить \ (v \) в футах в минуту. 5 миль в час.
5 миль в час. Линейная скорость — это длина дуги, пройденная точкой, деленная на истекшее время.В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки — это радианная мера угла, деленная на время, необходимое для того, чтобы подметать этот угол.
Линейная скорость — это длина дуги, пройденная точкой, деленная на истекшее время.В то время как линейная скорость измеряет, как длина дуги изменяется во времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол во времени. Угловая скорость точки — это радианная мера угла, деленная на время, необходимое для того, чтобы подметать этот угол.